典范相关分析
典范相关分析.

设x变数的线性组合为: ξ=a’x =a1x1+a2x2+…+apxp; y变数的线性组合为: η=b’y=b1y1+b2y2+…+bqyq a’=(a1, a2, …, ap), b’=(b1, b2, …,bq), 能否有a, b,使ξ与η之间有一个最大的 相关?即,ρξη=max
在求 a, b时,须满足的条件有: E(ξ)=E(η)=0, V(ξ)=V(η)=1
Matlab中的命令: [a,b,r,u,v,stats]=canoncorr(x,y)
help canoncorr
CANONCORR Canonical correlation analysis. [A,B] = CANONCORR(X,Y) computes the sample canonical coefficients for the N-by-P1 and N-by-P2 data matrices X and Y. X and Y must have the same number of observations (rows) but can have different numbers of variables (cols). A and B are P1-by-D and P2-by-D matrices, where D = min(rank(X),rank(Y)). The jth columns of A and B contain the canonical coefficients, i.e. the linear combination of variables making up the jth canonical variable for X and Y, respectively. Columns of A and B are scaled to make COV(U) and COV(V) (see below) the identity matrix. If X or Y are less than full rank, CANONCORR gives a warning and returns zeros in the rows of A or B corresponding to dependent columns of X or Y. [A,B,R] = CANONCORR(X,Y) returns the 1-by-D vector R containing the sample canonical correlations. The jth element of R is the correlation between the jth columns of U and V (see below). [A,B,R,U,V] = CANONCORR(X,Y) returns the canonical variables, also known as scores, in the N-by-D matrices U and V. U and V are computed as U = (X - repmat(mean(X),N,1))*A and V = (Y - repmat(mean(Y),N,1))*B.
23种常用的资料分析方式汇总

23种常⽤的资料分析⽅式汇总社会科学的研究步骤在每⼀个环节都需要理论的指导。
其中,在检验研究假设结束之后,需要与现有的⽂献对话,再次发现新问题,开始新⼀轮的研究过程。
在这个环节之中,资料分析作为重要⼀环,对于社会科学的研究极为重要。
资料分析的⽅式分类教育研究包含多样化的研究⽅法及分类。
⼀般情况下,按照认识论基础,研究⽅法可以分为定量研究、定性研究和混合研究。
也有部分学者按照研究⽬的、⼿段等对研究⽅法进⾏分类。
⽐如别敦荣和彭阳红将研究⽅法分为:理论思辨、经验总结、历史研究、调查研究、⽐较研究、数学分析、质的研究和个案研究;在国内,根据刘良华对研究⽅法的分类⼤体上有三个基本类型:实证研究(量化的、质化的)、思辨研究(⼜称理论研究)、实践研究(常以教育对策、教育反思、教育改⾰形式显现)。
实证研究是基于“事实”的⽅式进⾏论证并有规范的研究设计和研究报告。
陈向明指出,“研究⽅法”⼀般包含三个层⾯:第⼀,⽅法论,即指导研究的思想体系,其中包括基本的理论假定、原则、研究逻辑和思路等;第⼆,研究⽅法或⽅式,即贯穿于研究全过程的程序与操作⽅式;第三,具体的技术和技巧,即在研究的某⼀阶段使⽤的具体⼯具、⼿段和技巧等。
⽂中所采取的分类是按照陈向明定义中的第三个层⾯为标准进⾏的分类。
在实际的研究过程中⼤多数时候是以⼀种研究⽅法为主,其他为辅,交叉使⽤的。
以下内容是介绍每⼀种具体的⽅式。
那么资料搜集上来了?该如何分析呢?具体的资料分析⽅式- 01 -思辨分析1、历史研究⽅法历史研究法是运⽤历史资料,按照历史发展的顺序对过去事件进⾏研究的⽅法。
亦称纵向研究法,是⽐较研究法的⼀种形式。
在政治学领域中,它着重对以往的政治制度、政治思想、政治⽂化等的研究。
历史研究的⽬的在于解决政治制度的现状及其演变趋向。
但不是断章取义地分析政治制度的现状,⽽是系统地研究它们以往的发展及其变迁的原因。
历史研究法主要是研究政治制度的发展历史,从各种事件的关系中找到因果线索,演绎出造成制度现状的原因,推测该制度未来的变化。
cca算法具体计算过程

cca算法具体计算过程
CCA(Canonical Correlation Analysis,典范相关分析)是一种多变量统计分析方法,用于探索两组变量之间的相关性。
它的计算过程可以分为以下几个步骤:
1. 数据准备,首先,我们需要准备两组变量的数据,通常分别表示为X和Y。
每组变量可以包含多个变量,但是它们的观测值需要是成对的。
2. 数据标准化,为了消除量纲的影响,通常会对X和Y进行标准化处理,使它们的均值为0,标准差为1。
3. 计算相关系数矩阵,接下来,我们计算X和Y的相关系数矩阵。
这可以通过计算X和Y的协方差矩阵,然后将其标准化得到相关系数矩阵。
4. 计算特征值和特征向量,对相关系数矩阵进行特征值分解,得到特征值和对应的特征向量。
5. 选择特征向量,根据特征值的大小,我们选择与较大特征值
对应的特征向量。
通常,我们选择与前k个最大特征值对应的特征
向量,其中k是我们希望保留的维度数量。
6. 计算典范变量,将所选的特征向量与原始数据进行线性变换,得到典范变量。
这些典范变量是X和Y的线性组合,使它们之间的
相关性最大化。
7. 计算典范相关系数,最后,我们计算典范变量之间的相关系数,这些相关系数被称为典范相关系数,它们衡量了X和Y之间的
相关性。
总的来说,CCA的计算过程涉及数据准备、数据标准化、相关
系数矩阵的计算、特征值分解、特征向量的选择和典范变量的计算。
通过这些步骤,我们可以找到X和Y之间最大化相关性的线性组合,从而探索它们之间的关系。
如何分析事例

如何分析事例第一篇:如何分析事例如何分析事例1、导入:人的成功往往不是一蹴而就的,而是经过一次又一次的失败,一次又一次的打击后不断勇往直前而获得的。
瞧!古今中外哪个成功者不是这样的。
越王勾践亡国后,决心奋力图强,他朝必定复国。
他放下自尊去当吴王的奴隶。
卧薪尝胆,经历千辛万苦,最终三千越甲吞吴。
林肯——美国历史上最受人民尊敬的总统之一。
但是,谁也没想到他在当选为美国总统之前,受到了多少打击。
九次竞选九次失败,再加上失妻之痛,生活贫困几乎让他陷入绝望的深渊。
但是,他却没有因此而绝望,并决心去竞选美国总统。
无论受到他的对手——美国贵族道格拉斯这种又那种的鄙视,他依然没有放弃。
最终,当选为美国总统。
你有没有吃过肯德基?那你认不认识桑德斯上校?他是谁?他就是肯德基的创始人。
他一生坎坷。
在受到妻子的离异、失业等挫折后,他已经是个六十多岁的老人了。
他还能做什么?当他接到那一点点救济金时,他还有他的炸鸡秘方,而是他找遍了全美国的饭店,看看是否有人愿意购买他的秘方。
终于,肯德基也成为全球著名的连锁店。
同学们常犯的错误是:只叙述事例,不进行分析。
譬如要写提倡创新精神,则马上就“A有创新精神,B有创新精神,C有创新精神,所以我们要有创新精神”。
这是千万要不得的,这样文章不伦不类。
我说好像没什么说服力,我们看看高考作文评审组的评价:高考通常有这一类考生,他们写议论文的时候只会提观点和举例子,通篇没有自己的意见和看法,这类考生往往缺乏对事物的认知和辨析能力,这类作文只能给中能或以下档次。
正常议论文应该摆事实讲道理双管齐下。
这种“不讲道理”的议论文,论点无论怎样正确,也不足以服人;论据无论怎样充足,也不过是一堆零碎的材料。
也就是形成“论据+论据=作文失败”的错误形式,其实应用事实论据写作文好比用砖垒墙,事例是砖,而分析议论则是砖与砖之间的泥,离开这“泥”墙就不牢固。
所以我们写议论文时要有既典型又生动的论据,事例叙述完后要对所叙述的事例进行分析,使事例与论点水乳交融。
典范相关分析

讲稿下面我们将一边分析文章,一边为大家讲解如何利用典型相关分析的原理分析两组变量之间的关系。
典型相关分析的研究焦点是,研究一组变量的线性组合和另一组变量的线性组合之间的相关关系。
想法是这样的:首先求一对线性组合,它有最大相关系数,下一步则从最初挑选的这对线性组合不相关的线性组合配对中,选出有最大相关性的一对,如此继续下去,这些选出的线性组合配对成为典型变量,它们的相关系数称为典型相关系数。
而本文所研究的职业流动(Occupational mobility),是指劳动者在不同职业之间的变动,是劳动者放弃又获得劳动角色的过程。
职业流动是社会流动形式之一。
将典型相关分析应用到对职业流动的研究中是因为。
Part1在以往对代际间和代际内的职业流动的研究中,在为流动表中职业类别分配分数或权重的问题上,社会科学家在为流动表中职业类别分配分数或权重的问题的两大困难:(这里流动表中的职业类别指的是父亲的职业类别和儿子的职业类别):1父亲的职业和他们的儿子的职业之间的相关性会有所不同,这取决于分配给职业的分布上个月。
2反映当前儿子职业中某些基础维度差异的分数可能不同于反映父亲在同一维度上的职业差异的分数。
换句话说,尽管两代人的职业分类是相同的,但人们可能希望给父亲的职业分配不同的权重。
解决职业评分问题两个主要方向:1职业声望(occupational prestige scores):要求人们对特定职业的“社会地位”进行排名或评分。
但这种方法只能获得少数职业的声望得分,而无法得知所有职业或所有社会成员的声望位置,这不能满足社会学家进行社会声望分层的需要。
2职业的社会经济指数(a socioeconomic index of occupations):邓肯:基于职业声望测量所获得的各类职业的声望得分,以及相应职业的平均收入和教育水平,建立一个回归方程,求出收入和教育对职业声望的回归系数(即权数),然后应用这一回归方程,求出所有职业的声望得分。
典范对应分析

GIS即地理信息系统(Geographic Information System),地理信息系统是以地理空间数据库为基础,在计算机软硬件的支持下,运用系统工程和信息科学的理论,科学管理和综合分析具有空间内涵的地理数据,以提供管理、决策等所需信息的技术系统。
简单的说,GIS是综合处理和分析地理空间数据的一种技术系统,是以测绘测量为基础,以数据库作为数据储存和使用的数据源,以计算机编程为平台的全球空间分析即时技术。
地理信息系统作为获取、存储、分析和管理地理空间数据的重要工具、技术和学科,近年来得到了广泛关注和迅猛发展。
对应分析(Correspondence analysis)也称关联分析、R-Q型因子分析,是近年新发展起来的一种多元相依变量统计分析技术,通过分析由定性变量构成的交互汇总表来揭示变量间的联系。
可以揭示同一变量的各个类别之间的差异,以及不同变量各个类别之间的对应关系。
主要应用在市场细分、产品定位、地质研究以及计算机工程等领域中。
原因在于,它是一种视觉化的数据分析方法,它能够将几组看不出任何联系的数据,通过视觉上可以接受的定位图展现出来。
对应分析的基本思想是将一个联列表的行和列中各元素的比例结构以点的形式在较低维的空间中表示出来。
它最大特点是能把众多的样品和众多的变量同时作到同一张图解上,将样品的大类及其属性在图上直观而又明了地表示出来,具有直观性。
另外,它还省去了因子选择和因子轴旋转等复杂的数学运算及中间过程,可以从因子载荷图上对样品进行直观的分类,而且能够指示分类的主要参数(主因子)以及分类的依据,是一种直观、简单、方便的多元统计方法。
对应分析法整个处理过程由两部分组成:表格和关联图。
对应分析法中的表格是一个二维的表格,由行和列组成。
每一行代表事物的一个属性,依次排开。
列则代表不同的事物本身,它由样本集合构成,排列顺序并没有特别的要求。
在关联图上,各个样本都浓缩为一个点集合,而样本的属性变量在图上同样也是以点集合的形式显示出来。
典范对应分析课件

16
关键问题:
(1)RDA或CCA的选择问题:RDA是基于线性模型,CCA是 基于单峰模型。一般我们会选择CCA来做直接梯度分析。 但是如果CCA排序的效果不太好,就可以考虑是不是用 RDA分析。RDA或CCA选择原则:先用species-sample资料 做DCA分析,看结果中Lengths of gradient 的第一轴的大小, 如果大于4.0就应该选CCA, 如果在3.0-4.0之间, 选RDA和 CCA均可,如果小于3.0, RDA的结果要好于CCA.
第九步:计算环境因子的排序坐标: 先求得以上得到的两个样方排序轴与环境因子间的相关系数 akm的下表:(相关系数akm可以在EXCEL中求得)
典范对应分析
13
环境因子 1 2
第一排序轴 0.630 -0.720
第二排序轴 0.383 0.125
再计算环境因子的的坐标:
fkm m(1m)akm
fkm代表第k个环境因子在第m排序轴上的坐标值,λm为第一排 序轴的特征值,akm为第k个环境因子与第m个排序轴间的系数。 比如:
第五步:计算样方新值 Z=Ub
比如:z1=2.2.5+0.225*(-0.03)+0.655*(-0.14)=2.15 同法可得:
Z=(2.15,2.38,2.32,2.11,2.19,2.32,2.28)
第六步:对Z值进行标准化: a计算样方坐标值的形心V
N
N
V CjZj / Cj
j1
j1
典范对应分析
典范对应分析 CCA DCCA
典范对应分析
引言
• CCA方法简介 • CCA方法优缺点 • CCA排序的基本步骤 • DCCA排序
典范对应分析
CANOCO学习笔记

生态学统计分析方法的选择如果我们要数量统计方法描述一个或多个响应变量(群落学通常是物种的数据),如何选择合适的统计模型要依赖所研究的响应变量是一个还是多个,是否有解释变量(环境因子)。
其实无非就四种情况:1如果只有一个响应变量数据,而没解释变量,我们仅仅需要、也只能归纳这个变量的分布特征(如通过直方图、中值,标准差、四分位极差等)。
2如果有多个响应变量,依然没有解释变量,我们可以用排序(间接梯度分析)来分析数据,例如可以用主成分分析(PCA)、对应分析(CA)、去趋势对应分析(DCA、)和非度量多维尺度分析NMDS),当然也可以用等级分类,如聚类的方法将样方分为有区别的几类。
如果是比较多组数据是否显著差异,可以用方差分析、T检验(仅用两组数据)、相关分析(仅用两组数据)、典范相关分析等等。
3如果我们有一个或多个的解释变量,要分析一个响应变量,可以用广义的回归模型,包括传统的回归模型和方差分析、协方差分析。
这类分析统称为一般线性模型(general linear model),最近在一般线性模型基础,发展了广义线性模型(generalized linear models, GLM)和广义可加模型(generalized additive models, GAM)。
4如果有多个响应变量需要分析,解释变量一个或多个,我们可以通过直接梯度排序来分析解释变量与多个响应变量之间的关系。
常用的有冗余分析(RDA)和典范对应分析(CCA)等排序技术。
当我们同时有环境数据和物种组成数据的时候,我们可以首先做非约束排序分析,看看物种数据整体的情况,然后再作约束排序(将环境因子加上到排序图上),当然可以直接进行约束排序。
这两种途径是互补的,但两种方法必须都用。
首先做非约束排序分析,我们才不会丢失物种组成变化量的大部分信息,如果直接做约束排序,很多不是由所测的环境因子的引起变化量就丢掉了。
通过计算约束排序,我们不会丢掉与所测环境因子相关的大部分变量信息,但会丢掉与未测的环境因子相关的物种变量信息。
典范英语课堂教学设计与策略研究

典范英语课堂教学设计与策略研究1. 引言英语是世界上使用最广泛的语言之一,也是全球最重要的国际交流语言之一。
在中国,学习英语已经成为很多学生的必修课程。
如何设计和运用有效的教学策略,提高学生的英语水平,成为了英语教学中的重要课题。
本文将围绕典范英语课堂教学设计与策略展开深入研究。
2. 典范英语课堂教学设计典范英语课堂教学设计是指基于英语教学的相关理论和实践经验,结合学生的实际情况、学习需求和特点,设计出一套科学、合理的课程内容、教学方法和评价体系。
一个成功的英语课堂教学设计不仅能够激发学生的学习兴趣,提高他们的学习动机,还能够使学生获得更多的语言技能和知识。
在典范英语课堂教学设计中,教师需要合理安排教学内容。
根据教学大纲和学生的学习需求,将课程内容进行分类和整合,确定每个学习单元的重点和难点,并设计相应的教学活动,以便学生能够更好地理解和掌握知识。
在课堂教学设计中,教师需要注重教学方法和手段的选择。
传统的英语教学方法已经不能满足学生的需要,教师需要结合现代教学技术和方法,如多媒体教学、互动教学等,提高教学效果。
教师还可以引入任务型教学、合作学习等新的教学方法,使学生更加主动地参与到学习中去。
典范英语课堂教学设计也需要注重评价体系的建立。
教师应该设计多样化的评价方式,如考试、作业、口语表达、小组讨论等,以便全面、客观地评价学生的英语水平和能力。
评价结果不仅能够反馈学生的学习情况,还能够帮助教师及时调整教学策略,提高教学质量。
3. 典范英语课堂教学策略教学策略是指在教学过程中,教师根据教育理论和实践经验,灵活运用各种教学手段和方法,引导学生进行有效学习的一种方法。
在英语教学中,教师需要灵活运用多种教学策略,以便提高学生的语言能力和综合素质。
多元化的教学策略可以提高学生的学习兴趣。
教师可以采用游戏教学、音乐教学、演讲比赛等多种方式,激发学生的学习兴趣,提高他们的学习动机。
在教学过程中,教师还可以通过引入寓教于乐的教学内容,让学生在轻松愉快的氛围中获得知识。
小麦网络性状间的典范相关分析

小麦网络性状间的典范相关分析摘要:为探讨茎叶及穗粒重网络性状间的关系,本文利用20个小麦基因型的相关研究资料,对小麦茎叶性状与穗粒重网络性状间进行了典范相关分析。
结果表明,株高組成、株高构成指数、各节茎粗、各节茎秆干物重和各节单位茎长干物重与穗粒数的典范相关系数分别为0.8302、0.6633、0.8552、0.9687和0.6275,相关显著;株高組成与穗粒重的典范相关系数为0.66330,达到显著相关;在叶性状中叶鞘长性状与穗粒数典范相关系数为0.9687,显著相关。
关键词:小麦茎叶穗粒重网络性状典范相关茎叶是小麦重要的光合器官,承担着支撑植株、有机物的生产和运输,是产量形成的物质基础。
由于小麦茎叶及穗粒重性状组成部分较多、系统复杂,形成了各部分之间错综复杂的网络关系。
过去人们在研究植株性状与穗粒重或产量的时候,大多从某单一性状与产量性状进行分析,其结果是片面的、不完全合理的。
随着小麦产量水平的不断提高,系统研究茎叶性状与产量及其构成因素的关系,已成为选育超高产小麦品种的客观需要。
利用典范相关分析可以研究两组变量间的总相关,也可以研究某一组性状对另一组性状中某一性状的多元相关,这对于探讨茎叶结构特性与产量性状的内在本质联系,提高超高产小麦新品种选育效率具有重要意义[1-3]。
本文以20个超高产小麦基因型为试验材料,小麦茎叶性状与穗粒重性状间的关系进行了典范相关分析。
1 试验材料与方法试验在淮北师范大学试验田进行。
选用产量潜力在9000 kg/hm 以上的超高产基因型鲁麦23号、兰考906、莱州2458、鲁麦14号、莱州137、鲁淄92-1、92(4)402、鲁麦21号、济宁13号、H92—112、冀麦38号、8017—2、济南17号、95(6)161、93(5)031、泰山021、烟辐188、淄麦12号、滨州98-1和滨州98—11,共计参试品种(系)20个。
田间试验为随机区组排列,重复3次,小区长6.0 m、宽2.0 m,行距为25 cm。
典范相关分析

典范变数的几点特征:
1)ξi 与ξj 是相互独立的,ηi 与ηj 也是独
立的,这可从特征值、特征向量(亦
即主成分)的特性可知;
2)ξi与ηj是相互独立的,它们间的相关系数为0;
由于
到此,似乎解决了所有的问题,但 中的 怎么算?对于
若有特征值θi与特征向量li,则: 该式称为矩阵Σ 的谱分解 (spectrum decomposition)
由于两组多维变数的关系退化成两个 1维变数之间的关系,这种关系可用图 形的形式表示出来,使这种关系一目 了然,便于对结果的分析与解释。
3、典范相关系数的测验
Bartlett(1941)提出了一个测验方法,对于第1典范相 关系数λ1:
对于第2典范相关系数λ2:
对于第j个典范相关系数λj:
4、一些例子
实用多变数分析 5、因子分析
Factor Analysis
1、导言
20世纪初,Karl Pearson & Charles Spearman 就开始用此方 法分析一些问题,后者曾对一些学生的考试成绩进行分析。 根据这些变数(成绩)及其它们之间的相互关系,用少量但 本质的成分如:理解力、逻辑思维能力、记忆力等来说明学 生的考试成绩。一开始由于涉及智力和精神分析方面的解释, 带有一点神秘感,另加上计算繁琐的阻滞,此法一经提出, 未见有多大进展。计算机的出现和广泛使用,因子分析计算 量大的问题基本得到解决,再加上软件的普遍使用,因子分 析的应用有所抬头,经常看到有关因子分析的文献。因子分 析的基本目的在于通过变数之间的相互关系,可能的话,用 少量不可观察的(unobservable)、但起根本性作用(underlying) 的因子(factors)来描述。
2、因子分析模式 设x是一个p维变数,具有平均数μ和方差Σ ,x变数可由一些未知的、不可观察的、具 有本质作用的m个公共因子(F1, F2, ..., Fm, m<p)再加上p个特殊因子的线性可加模型所 表示:
典范对应分析

zj =
∑x
i =1 p i =1
p
ij
yj
Zj为样方排序值
7
∑x
ij
得到一组样方排序值,并用下式调试,使得Zj的最大值为 100,最小值为0,这是为了阻止排序坐标值在迭代过程 中逐步变小
zj
(a)
= 100 ×
z j − min z j max z j − min z j
第三步:再用加权平均法求样方新值,得: (2.09,2.57,2.24,2.2.5,2.17,2.30,2.11)
典范对应分析 CCA DCCA
引言
◆CCA方法简介 ◆CCA方法优缺点 ◆CCA排序的基本步骤 ◆DCCA排序
2
一、CCA方法简介 CCA方法简介
◆ 典范对应分析(canonical correspondence analysis, CCA), 典范对应分析( CCA), 是基于对应分析发展而来的一种排序方法, 是基于对应分析发展而来的一种排序方法,将对应分析与多元 回归分析相结合,每一步计算均与环境因子进行回归, 回归分析相结合,每一步计算均与环境因子进行回归,又称多 元直接梯度分析。其基本思路是在对应分析的迭代过程中, 元直接梯度分析。其基本思路是在对应分析的迭代过程中,每 次得到的样方排序坐标值均与环境因子进行多元线性回归。 次得到的样方排序坐标值均与环境因子进行多元线性回归。 CCA要求两个数据矩阵 一个是植被数据矩阵, 要求两个数据矩阵, CCA要求两个数据矩阵,一个是植被数据矩阵,一个是环境数 据矩阵。首先计算出一组样方排序值和种类排序值( 据矩阵。首先计算出一组样方排序值和种类排序值(同对应分 ),然后将样方排序值与环境因子用回归分析方法结合起来 然后将样方排序值与环境因子用回归分析方法结合起来, 析),然后将样方排序值与环境因子用回归分析方法结合起来, 这样得到的样方排序值即反映了样方种类组成及生态重要值对 群落的作用,同时也反映了环境因子的影响, 群落的作用,同时也反映了环境因子的影响,再用样方排序值 加权平均求种类排序值, 加权平均求种类排序值,使种类排序坐标值值也间接地与环境 因子相联系。其算法可由Canoco软件快速实现。 Canoco软件快速实现 因子相联系。其算法可由Canoco软件快速实现。
【国家自然科学基金】_蒸腾系数_基金支持热词逐年推荐_【万方软件创新助手】_20140803
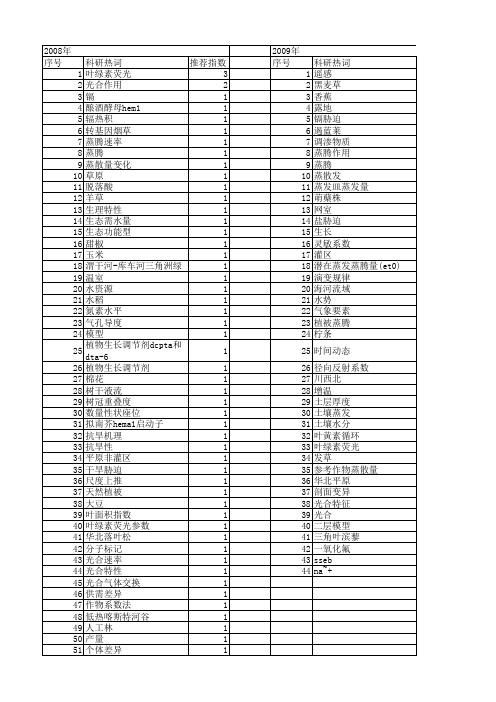
科研热词 光合特性 冬小麦 胡杨 胁迫 羊草群落 浑善达克沙地 水分胁迫 水分利用效率 无性系 叶绿素荧光 双作物系数法 光合作用 黑河下游 黄土高原 鱼藤 高温胁迫 高分辨率影像 雷公藤 锰胁迫 超微结构 蒸腾速率 蒸腾 臭氧 耗水量 耗水特性 耐性 红树林 相关性分析 盐度 生长 生育期需水量 生理生态因子 生理特性 甜菜 甜瓜属 灰胡杨 灌溉试验 潜热水分通量 液流通量密度 涝灾 涝渍连续抑制天数 洼地 水分通量 水分生产力 水分利用率
53 54 55 56 57
dta-6 dcpta c4作物 c3作物 ala
1 1 1 1 1
推荐指数 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2010年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52
53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106
107 3种引种杨树 108 3种乡土杨树
1 1
2011年 科研热词 光合特性 光合作用 蒸腾速率 叶绿素荧光 豌豆 综合评判 灰关联 气孔导度 气体交换参数 干旱胁迫 叶绿素荧光参数 华北落叶松 髯毛箬竹 高温耐性 除草剂 降雨 铝胁迫 铁过量 采后果实 遥感 通径分析 边材液流 计算机模拟 蓼科植物 蒸腾系数 蒸腾作用 蒸腾 蒸散发 蒸散 蒸发蒸腾 葡萄 荧光参数 膜流动性 脂肪酸 缺铁胁迫 纳米tio2 碳水耦合模型 碳循环 盐胁迫 生长 生态系统边界层 生态地区 珙桐 环境影响因子 环境因子 热空气处理 灌溉农田 灌溉 渗漏 液流 汇水区域 水稻灌区 推荐指数 4 4 3 3 2 2 2 2 2 2 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
关于经典大学生创业案例分析

关于经典大学生创业案例分析为缓解就业压力,从根本上解决大学生就业的难题,党中央、地方政府和高校都鼓励大学生创业,以创业带动就业。
那么下面是店铺整理的关于经典大学生创业案例分析相关内容,欢迎参阅。
关于经典大学生创业案例分析篇一一、问题的提出高校扩招,为国家和社会输送了大量具有专业素质的大学毕业生的同时,也增加了涌向劳动力市场的大学生数量,致使这一层面劳动力市场的供求关系发生变化,大学生就业形势日趋严峻。
经济周期性变化带来的不确定因素的增加,使大学生的就业境况更加不容乐观。
此外,我国大学生就业中存在的结构性矛盾,更是充分就业难以实现的梗阻性因素。
在这种现实情况下,党的十七大提出了“以创业带动就业”的口号,中央及各地方政府出台了一系列促进大学毕业生创业的政策措施。
在宽松的外部环境下,越来越多的大学毕业生选择了自主创业。
但是怎样选择目标行业?如何获得各种资源?如何避免创业失败?通过对大学生自主创业案例的介绍,对比分析大学生创业的优、劣势,以期对有志于创业的大学生有所启发。
二、大学生创业的可行性和必要性(一)大学生创业的可行性创业是劳动者以个人、社会的发展需要为基础,有效整合个人资源,发现、创造机遇并选择、开拓能够产生经济价值和社会效益的活动过程。
它需要创业者具备良好的身体素质、心理素质、知识储备、创新能力、团队管理能力等各方面的条件。
大学生作为新兴的创业群体,有着来自自身、外界的优势。
1.专业素质。
大学生与其他创业群体相比,具备较全面的理论知识,有着较高层次的技术优势,具备独特的知识资本。
2.政策支持。
国家为了鼓励大学生、研究生和科技人员兴办科技民营企业,出台了一系列政策和措施予以大力支持,包括简化登记注册程序、减免各类费用、优先贷款支持、适当信用贷款、税务减免优惠等多项扶持政策。
各省市也制订了一系列政策措施,设立大学生创业孵化基地,支持和鼓励大学毕业生自主创业。
3.时代背景。
21世纪是知识经济时代,知识成为一种新的社会生产的资源。
白洋淀浮游植物群落及其与环境因子的典范对应分析

Ca o ia O r s 0 d n e a ay i o h t pa ko o n nc l re p n e c n lss fp yo ln t n c mm u i n s e vr n e t c nt a d i n i m na y t o
f c o s i h a e B ia g i n a t r te L k ay n da n
白洋淀浮游植物群落及其与环境 因子的典范对应分析
沈会 涛 ,刘存歧 ”
( : 东师范 大学环 境科学 系,上海 2 0 6 ) I华 0 0 2
(: 北大学 生命科 学学 院, 定 0 10) 2河 保 70 2
摘
要: 为掌 握 白洋淀浮 游植物 的群落 特征,于 20 年 4月至 1 06 O月间 对其进行 了 5 次采 样调查 , 经显 微镜 检,共鉴定 出浮游植
C o i l ors o d n ea a s ( C W p l dt x l et e t nhpb t e h t l ko p c sad e v o me t n a nc r p n e c n l i C A) a a pi e po erl i si e ac e ys s e o rh ao wen p yo a t se i n n i n na pn n e r l
L k c. 泊 科 学)2 0 , 01: 37 9 aeSi湖 ( ,0 82 () 7 -7 7 ht: w j ks r. — ij k s ils c n t / w.ae. g Ema :l e@nga. . p/ w l o l a ac  ̄2 0 y o ra o L k Sine 0 8b J un lf a e cecs
5 . 1 cl / 7 48 1 e s. T e h t l ko o u i Sd mi t y C a o h t C y tp y n h rp y . 5  ̄ 0 e s t 1 0 . 0cl / . h yo a t nc m nt Wa o n e b y n p ya rpo h t a d C l o h t 5 1 lL o x lI , p pn y ad , a o a
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
讲稿下面我们将一边分析文章,一边为大家讲解如何利用典型相关分析的原理分析两组变量之间的关系。
典型相关分析的研究焦点是,研究一组变量的线性组合和另一组变量的线性组合之间的相关关系。
想法是这样的:首先求一对线性组合,它有最大相关系数,下一步则从最初挑选的这对线性组合不相关的线性组合配对中,选出有最大相关性的一对,如此继续下去,这些选出的线性组合配对成为典型变量,它们的相关系数称为典型相关系数。
而本文所研究的职业流动(Occupational mobility),是指劳动者在不同职业之间的变动,是劳动者放弃又获得劳动角色的过程。
职业流动是社会流动形式之一。
将典型相关分析应用到对职业流动的研究中是因为。
Part1在以往对代际间和代际内的职业流动的研究中,在为流动表中职业类别分配分数或权重的问题上,社会科学家在为流动表中职业类别分配分数或权重的问题的两大困难:(这里流动表中的职业类别指的是父亲的职业类别和儿子的职业类别):1父亲的职业和他们的儿子的职业之间的相关性会有所不同,这取决于分配给职业的分布上个月。
2反映当前儿子职业中某些基础维度差异的分数可能不同于反映父亲在同一维度上的职业差异的分数。
换句话说,尽管两代人的职业分类是相同的,但人们可能希望给父亲的职业分配不同的权重。
解决职业评分问题两个主要方向:1职业声望(occupational prestige scores):要求人们对特定职业的“社会地位”进行排名或评分。
但这种方法只能获得少数职业的声望得分,而无法得知所有职业或所有社会成员的声望位置,这不能满足社会学家进行社会声望分层的需要。
2职业的社会经济指数(a socioeconomic index of occupations):邓肯:基于职业声望测量所获得的各类职业的声望得分,以及相应职业的平均收入和教育水平,建立一个回归方程,求出收入和教育对职业声望的回归系数(即权数),然后应用这一回归方程,求出所有职业的声望得分。
彼特·布劳和邓肯后来在对美国职业结构的研究中,进一步发展了这一方法,他们用45种职业声望调查取得的收入和教育权数,估计出446种职业的社会经济地位指数,并根据各个职业的社会经济地位指数的高低,把这些职业归为17个社会地位等级群体。
本文在职业流动研究中使用Duncan社会经济指数,并认为社会经济地位(SES)是决定职业流动的最主要因素。
正如Blau和Duncan所做的那样,在职业流动研究中使用Duncan社会经济指数(后来称为Duncan SES指数),这就意味着社会经济地位(SES)是决定职业流动的最主要因素。
在本文中,我们提出两个假设:1.职业之间的社会经济距离决定了流动表中两组职业之间的相关性。
2.职业的相对地位依然存在。
Part2这些假设将通过为职业分配权重或者分数的标准来检验,这些职业的社会经济地位在分析上是独立的(但不一定在经验上独立)。
这里的权重指的是,将两组职业各自分配到一个表格中,使得两组变量的线性组合之间产生最大相关系数时的权重。
通过这一程序获得的权重与职业类别的收入和教育等SES衡量因素相关联,以检验SES是否是代际内以及代际间职业流动的最重要变量(即变量产生了表格的最大相关性)。
此外,通过检验父亲和儿子的职业之间的最大相关性是否是通过对两组职业分配相似的权重而得到的,验证职业的相对地位随着时间的推移保持不变(就他们之间的流动的可预测性而言)。
用于从职业类别的交叉分类中获得受访者之间的最大相关性的方法是典型相关性的方法,并且为了最大化相关性而分配给类别的权重或分数是典型相关系数。
与典型相关的通常用法不同,目前情况下的变量是“虚拟”或二元变量,其值代表每个职业类别中个体存在或者不存在,然后在交叉分类表中表示的两组虚拟变量之间获得典型相关性(例如,一组用于父亲职业类别和一个儿子职业类别)。
该技术在数学上等同于由Guttman和Hayashi独立开发并由Alker 描述的属性定量缩放技术。
Part3在讨论我们的数据和应用典型相关技术的结果之前,我们应该提及两个关于典型相关性的具体使用的技术要点。
其中之一是,为父亲的职业和儿子的职业设置的虚拟变量均包含线性依赖性(a linear dependency)。
为了消除这种依赖性,我们在每个集合中消除了一个类别(即农场劳动者)。
所有系数(coefficients)都表示为与省略的类别的偏差(deviations),得到的权重为零。
第二点是系数全部以非标准化的形式呈现。
由于原始变量是虚拟变量或二元变量,每个原始变量的方差取决于属于该类别的案例的比例;因此,我们不会表达与其变异性相关的系数(通过标准化)。
要做到这一点,就要让系数在很大程度上由边际频率决定。
下面的结果是基于对Blau和Duncan提出的三个基本频率表的分析。
这些表格是:1、儿子1962年的职业和父亲的职业交叉分类2、儿子的第一份工作和父亲的职业交叉分类3、儿子1962年的职业和儿子的第一份工作交叉分类这些数据代表了美国人口普查局调查的20至64岁男性的全国样本,以研究“一代人的职业变化”。
Blau和Duncan提出的三个移动表的最大相关系数如下:以下各项之间的最大相关性(第一个典型相关性)父亲的职业和儿子的1962年职业= 0.447父亲的职业和儿子的第一份工作= 0.577儿子的第一份工作和儿子的1962年职业= .574这些相关性与Blau和Duncan使用Duncan的SES指数[3,pp.117-281。
Blau和Duncan 在他们对上述变量的测量之间得到了.405,417和.541的相关性。
他们与父亲的职业和儿子的第一份工作的相关性与我们的相关性之间存在着最大的差异。
由邓肯的SES指数分配给职业的分数产生了父亲的职业和儿子的第一份工作之间的相关性,这大大低于可以使用不同分数获得的最大相关性,这表明:1.最大相关性的一部分是由于职业SES以外的其他因素,以及(通过暗示),2.最大化这种相关性的分数是由一个变量产生的,它与最大化前面列出的其他两个相关性的变量略有不同表1中给出了三种移动性表中每一种的非标准化典范系数或第一个典型变量。
在每一组中,系数除以一个常数,因此最大系数等于1.0。
没有必要仔细检查分数。
除了少数几个例外情况外,当人们从专业人员到农场劳动力职位的任何一栏中都可以看到稳定的单调下降趋势。
如表2所示,当这些系数与中位收入,中位数教育和邓肯的相关职业类别的SES指数相关时,我们发现所有情况下的潜在变量似乎主要是社会经济地位。
任何一组系数与任何SES变量之间的最低相关系数为0.646,最高为0.952。
然而,相关性的模式总体上支持推论:SES(由这些变量衡量)在确定儿子第一份工作的系数时不足以从父亲的职业中预测,反之亦然,因为它是其他系数的系数。
与其他相关性相比,涉及这些系数组的相关性相当弱。
但是,它们足够强大,足以表明任何可能更充分地代表基础因素的变量都必须与SES高度相关(比赛,也许?)。
总而言之,我们可以说,我们的研究结果提供了经验证据,即对于决定他们之间流动性的职业的一个最重要的维度是他们在社会经济地位上的差异。
在典范系数的基础上,我们也可以回答这个问题:决定职业间距离的因素在多大程度上(在距离由最大化父亲和儿子的职业地位之间的相关性的分数决定的范围内)随时间推移保持不变?权重集合之间的差异表明,父亲职业分数的基础因素不同于儿子职业基础分数的基础因素,即职业地位模式在世代之间发生了变化。
如下面的相关性所示,情况并非如此。
典范系数(第一典型变量)之间的关系为:父亲的职业预测从儿子的1962年职业和儿子的1962年职业预测父亲的职业= .982 父亲的职业从儿子的第一份工作和儿子的第一份工作预测的父亲的职业预测= .988儿子的第一份工作预计从儿子的1962年的职业和儿子的1962年的职业预测从儿子的第一份工作= .995当然,相关性是对称的,所以预测的方向可以颠倒。
这些相关性的大小显着地表明,职业地位的基础连续统一体的位置在代际间或代际内都没有改变。
作为父亲职业得分基础的变量实际上与儿子1962年职业得分的基础相同,因此通过另一种方法证实了Hodge,Siege1和Rossi [9]的结论,即职业声望结构随时间保持显着不变。
将典型相关方法获得的权重与另一种方法分配的分数进行比较也是有益的,该方法也不使用预先分配的职业分数。
Blau和Duncan进行了Guttman-Lingoes最小空间分析-I关于职业目的地相对于起源的距离,反之亦然,用相异指数衡量(任意两类职业起源之间的正百分比差异的总和关于职业目的地,以及任何两类目的地之间的原产地)。
在Guttman-Lingoes技术中,解决方案的标准是最小化一组点之间的距离,在这种情况下的点是职业之间成对距离的三角矩阵,用不相似度的指数来度量。
解决方案可以是obt。
根据期望的多个维度排列,取决于解与原始数据矩阵之间所需的拟合优度。
然而,Blau 和Duncan决定采用二维解(在因子分析中使用前两个因子或前两组典型变量)。
他们通过检查结果得出结论,第一维表现为SES。
邓肯慷慨地为我们提供了在本文讨论的三个表格上计算的二维解决方案中职业得分或价值观的差异指数。
表3显示了第一维和我们的第一个典型变量之间的相关性。
如表3所示,在二维Guttman-Lingoes最小空间分析解中得到的第一维与我们的第一组典型变量非常相似,证实了再次相似的研究结果是以非常不同的方法得出的。
Part 4除第一典型变量以外,我们还没有分析其他典型变量。
然而,这并不意味着这些并不重要。
因为特定移动性表格中的每个权重组在与个人相关时,与该表格的其他正交。
考虑到本研究中三个流动表的第二个典型相关系数,从父亲职业所预测的儿子1962年职业为0.80,从父亲职业所预测的儿子第一份职业为0.343,而儿子的第一份工作预测的儿子1962年职业为0.413。
从父亲职业所预测的儿子1962年职业为0.80为最大相关系数。
接下来若要继续研究,第二组典型变量可以用与第一组相似的方式进行分析,以查看哪些其他因素决定了职业系统中流动性的可预测性。
从权重本身来看,这些因素可能是不明显的。
Part 5本研究的重要性在于它提供了对这个假设的独立验证,即职业之间的距离是由最大化父亲与儿子职业地位之间相关性的因素所定义的一个连续体(事实证明,是沿着社会经济连续体的距离)对于两代人以及在一代人中的初始和后期职业阶段是相同的。
前面的分析还表明,与父亲的职业和儿子的第一份工作之间的关系相比,社会经济因素包括中位数收入,中等教育和邓肯SES指数更准确地反映了父亲职业与儿子目前职业之间以及儿子第一份工作与儿子目前职业之间关系的变量。
