Matlab简单实例学习

合集下载

MATLAB程序设计及应用实例

程序如下： price=input('请输入商品价格'); switch fix(price/100) case {0,1} rate=0; case {2,3,4} rate=3/100; case num2cell(5:9) rate=5/100; case num2cell(10:24) rate=8/100; case num2cell(25:49) rate=10/100; otherwise rate=14/100; end price=price*(1-rate)
c=input('请输入一个字符','s'); if c>='A' & c<='Z'
disp(setstr(abs(c)+1)); elseif c>='a'& c<='z'
disp(setstr(abs(c)-1)); elseif c>='0'& c<='9'
disp(abs(c)-abs('0')); else
disp(c); end
5.1.4 选择结构- switch语句
switch语句
其语句格式为： switch 表达式 case 值1 语句组1 case 值2 语句组2 …… case 值m 语句组m otherwise 语句组m+1 end
5.1.4 选择结构- switch语句
例某商场对顾客所购买的商品实行打折销售，已知打折标准，求所售商品的实际销售价格
例矩阵乘法运算要求两矩阵的维数相容，否则会出错。先求两矩阵的乘积，若出错，则自动转去求两矩阵的点乘

MATLAB程序设计及应用实例

MATLAB程序设计及应用实例MATLAB（Matrix Laboratory）是一种用于算法开发、数据分析、可视化和数值计算的高级技术计算语言和环境。

它的强大功能和灵活性使其成为各个领域研究和工程实践中广泛使用的工具。

下面将介绍几个MATLAB程序设计及应用的实例。

1.信号处理：MATLAB是信号处理的强大工具，它可以用于滤波、频谱分析、小波变换、分析和合成音频信号等。

例如，可以利用MATLAB进行语音信号的去噪处理，通过设计特定的滤波器来去除信号中的噪声成分，从而提取出清晰的语音信号。

2.图像处理：MATLAB可以进行图像的加载、处理和分析。

它提供了丰富的图像处理函数和工具箱，可以实现图像的滤波、二值化、边缘检测、图像增强等操作。

例如，可以使用MATLAB对医学图像进行分割，将感兴趣的区域提取出来，辅助医生进行病灶诊断。

3.控制系统设计：MATLAB是控制系统设计的有效工具。

它提供了丰富的控制系统分析和设计函数，可以进行系统建模、模拟和优化。

例如，可以使用MATLAB进行PID控制器的参数调整，通过对系统建模和后续仿真，优化PID控制器的参数，提高控制系统的性能和稳定性。

4.机器学习：MATLAB提供了强大的机器学习和深度学习工具箱，可以进行数据预处理、特征提取、模型训练和评估等操作。

例如，可以利用MATLAB进行图像分类，通过构建深度卷积神经网络模型，将输入的图像进行分类和识别。

5.数值计算：MATLAB对线性代数、数值优化和统计分析等有着强大的支持。

它提供的优化和求解函数可以解决复杂的线性和非线性优化问题，例如最小二乘拟合和参数估计等。

此外，MATLAB还拥有强大的统计分析工具，可以进行假设检验、数据拟合、方差分析等统计分析操作。

6.仿真模拟：MATLAB可以进行动态系统的建模和仿真，通过搭建系统方程和初始条件，可以对系统的动态响应进行模拟。

例如，在电力系统中，可以使用MATLAB进行电力系统稳定性分析，对电力系统的动态响应进行跟踪和分析。

遗传算法的MATLAB程序实例讲解学习

遗传算法的M A T L A B程序实例遗传算法的程序实例如求下列函数的最大值f(x)=10*sin(5x)+7*cos(4x) x∈[0,10]一、初始化(编码)initpop.m函数的功能是实现群体的初始化，popsize表示群体的大小，chromlength表示染色体的长度(二值数的长度)，长度大小取决于变量的二进制编码的长度(在本例中取10位)。

代码:%Name: initpop.m%初始化function pop=initpop(popsize,chromlength)pop=round(rand(popsize,chromlength));% rand随机产生每个单元为 {0,1} 行数为popsize，列数为chromlength的矩阵，% roud对矩阵的每个单元进行圆整。

这样产生的初始种群。

二、计算目标函数值1、将二进制数转化为十进制数(1)代码:%Name: decodebinary.m%产生 [2^n 2^(n-1) ... 1] 的行向量，然后求和，将二进制转化为十进制function pop2=decodebinary(pop)[px,py]=size(pop); %求pop行和例数for i=1:pypop1(:,i)=2.^(py-1).*pop(:,i);py=py-1;endpop2=sum(pop1,2); %求pop1的每行之和2、将二进制编码转化为十进制数(2)decodechrom.m函数的功能是将染色体(或二进制编码)转换为十进制，参数spoint表示待解码的二进制串的起始位置。

(对于多个变量而言，如有两个变量，采用20为表示，每个变量10为，则第一个变量从1开始，另一个变量从11开始。

本例为1)，参数1ength表示所截取的长度（本例为10）。

代码:%Name: decodechrom.m%将二进制编码转换成十进制function pop2=decodechrom(pop,spoint,length)pop1=pop(:,spoint:spoint+length-1);pop2=decodebinary(pop1);3、计算目标函数值calobjvalue.m函数的功能是实现目标函数的计算，其公式采用本文示例仿真，可根据不同优化问题予以修改。

matlab_简明实例教程__目录索引整理

南京航空航天大学王正盛 4
在 MATLAB 工作内存中表称为永久变量 Predefined variables
还驻留几个由系统本身在启动时定义的变量如下 Permanent variables 或称为预定义变量
系统预定义的变量 eps 计算机的最小正数在 pc 机上它等于 2 −52 pi 圆周率 π 的近似值 3.14159265358979 inf 或 Inf 无穷大 NaN 不定量 i,j 虚数单位定义 i = j = − 1 flops 浮点运算次数用于统计计算量说明 1 它们是在 MATLAB 启动时自定义的 2 它们不会被清除内存变量指令 clear 所清除 3 他们可以重新定义为其他值但用 clear 可清除重定义值恢复预定义值 [例1] 无穷大 s=1/0 Warning: Divide by zero. s = Inf 无穷大 a=Inf/inf a = NaN 2.5 数与表达式 MATLAB 的数值采用习惯的十进制表示可以带小数点或负号如下是合法的 3 -99 0.0013 9.2445154 1.2434e-6 4.673e33 在采用 IEEE 浮点算法的计算机上数值的相对精度是 eps 即大约保持 16 位有效数字数值范围大致为 1 × 10 −308 ~ 1 × 10 308 表达式由下列算符构成并按习惯的优先次序进行运算 + 加法减法 * 乘法 / 右除 \ 左除 ^ 乘方注意设置两种除法是为了方便矩阵的运算对标量而言两者作用相同 [例 1] x=2*pi/3+2^3/5-0.3e-3 x = 3.6941 2.6 复数和复矩阵 MATLAB 认识复数并定义 i 和 j 作为虚数单位变量和由它们组成的表达式

matlab_简明实例教程

matlab_简明实例教程MATLAB是一种强大的科学计算工具，广泛应用于科学研究、数据分析和工程计算等领域。

它具有简单易用的语法和丰富的函数库，可以快速实现复杂的计算任务。

本教程将为你提供一些简单实例，帮助你入门MATLAB。

1.计算圆的面积和周长```matlabradius = input('请输入圆的半径：');area = pi * radius^2;circumference = 2 * pi * radius;disp(['圆的面积为：', num2str(area)]);disp(['圆的周长为：', num2str(circumference)]);```2.计算两个向量的点积```matlabv1 = input('请输入向量1（用逗号分隔元素）：');v2 = input('请输入向量2（用逗号分隔元素）：');dot_product = dot(v1, v2);disp(['两个向量的点积为：', num2str(dot_product)]);```3.绘制正弦曲线```matlabx = 0:0.1:2*pi;y = sin(x);plot(x, y);xlabel('x');ylabel('sin(x)');title('正弦曲线');```4.求解方程```matlabsyms x;eqn = x^2 - 4 == 0;sol = solve(eqn, x);disp(['方程的解为：', char(sol)]); ```5.读取和写入文件```matlabfilename = 'data.txt';data = importdata(filename);disp('文件中的数据：');disp(data);output = [1 2 3; 4 5 6; 7 8 9];dlmwrite('result.txt', output, 'delimiter', '\t', 'precision', 4);disp('结果已保存到result.txt文件中。

matlab龙格库塔法程序,给出实例

一、介绍龙格库塔法龙格库塔法（Runge-Kutta method）是一种数值计算方法，用于求解常微分方程的数值解。

它通过多步迭代的方式逼近微分方程的解，并且具有较高的精度和稳定性。

二、龙格库塔法的原理龙格库塔法采用迭代的方式来逼近微分方程的解。

在每一步迭代中，计算出当前时刻的斜率，然后根据这个斜率来求解下一个时刻的值。

通过多步迭代，可以得到微分方程的数值解。

三、龙格库塔法的公式龙格库塔法可以表示为以下形式：k1 = f(tn, yn)k2 = f(tn + h/2, yn + h/2 * k1)k3 = f(tn + h/2, yn + h/2 * k2)k4 = f(tn + h, yn + h * k3)yn+1 = yn + h/6 * (k1 + 2k2 + 2k3 + k4)其中，k1、k2、k3、k4为斜率，h为步长，tn为当前时刻，yn为当前时刻的解，yn+1为下一个时刻的解。

四、使用matlab实现龙格库塔法在MATLAB中，可以通过编写函数来实现龙格库塔法。

下面是一个用MATLAB实现龙格库塔法的简单例子：```matlabfunction [t, y] = runge_kutta(f, tspan, y0, h)t0 = tspan(1);tf = tspan(2);t = t0:h:tf;n = length(t);y = zeros(1, n);y(1) = y0;for i = 1:n-1k1 = f(t(i), y(i));k2 = f(t(i) + h/2, y(i) + h/2 * k1);k3 = f(t(i) + h/2, y(i) + h/2 * k2);k4 = f(t(i) + h, y(i) + h * k3);y(i+1) = y(i) + h/6 * (k1 + 2*k2 + 2*k3 + k4);endend```以上就是一个简单的MATLAB函数，可以利用该函数求解给定的微分方程。

(整理)matlab实例教程-比较实用.

实验一特殊函数与图形一、问题背景与实验目的二、相关函数（命令）及简介三、实验内容四、自己动手一、问题背景与实验目的著名的Riemann函数大家都很熟悉了，但是关于它的图像你是否清楚呢除了最上面那几点，其他都很难画吧你想不想看看下面那些“挤在一起”的点是怎样分布的呢还有几何中的马鞍面、单叶双曲面等是怎样由直线生成的，是不是也想目睹一下呢这些，都离不开绘图．实际上绘图一直是数学中的一种重要手段，借助图形，往往可以化繁为简，使抽象的对象得到明白直观的体现．比如函数的基本性质，一个图形常可以使之一目了然，非常有效．它虽不能代替严格的分析与证明，但在问题的研究过程中，可以帮助研究人员节约相当一部分精力．此外，它还可以使计算、证明、建模等的结果得到更明白易懂的表现，有时，这比科学论证更有说服力．同时，数学的教学与学习过程也离不开绘图．借助直观的图形，常可以使初学者更容易接受新知识．如数学分析中有不少函数，其解析式着实让人望而生畏，即使对其性质作了详尽的分析，还是感到难明就里；但如果能看到它的图形，再配合理论分析，则问题可以迎刃而解．又如在几何的学习中，会遇到大量的曲线与曲面，也离不开图形的配合．传统的手工作图，往往费力耗时，效果也不尽理想．计算机恰恰弥补了这个不足，使你可以方便地指定各种视角、比例、明暗，从各个角度进行观察．本实验通过对函数的图形表示和几个曲面（线）图形的介绍，一方面展示它们的特点，另一方面，也将就Matlab软件的作图功能作一个简单介绍．大家将会看到，Matlab 的作图功能非常强大．二、相关函数（命令）及简介1．平面作图函数：plot，其基本调用形式：plot(x,y,s)以x作为横坐标，y作为纵坐标．s是图形显示属性的设置选项．例如：x=-pi:pi/10:pi;y=sin(x);plot(x,y,'--rh','linewidth',2,'markeredgecolor','b','markerfacecolor','g')图1在使用函数plot时，应当注意到当两个输入量同为向量时，向量x与y必须维数相同，而且必须同是行向量或者同是列向量．绘图时，可以制定标记的颜色和大小，也可以用图形属性制定其他线条特征，这些属性包括：linewidth 指定线条的粗细．markeredgecolor 指定标记的边缘色markerfacecolor 指定标记表面的颜色．markersize 指定标记的大小．若在一个坐标系中画几个函数，则plot的调用格式如下：plot(x1,y1,s1,x2,y2,s2,……)2．空间曲线作图函数：plot3，它与plot相比，只是多了一个维数而已．其调用格式如下：plot3(x,y,z,s)．例如：x=0:pi/30:20*pi;y=sin(x);z=cos(x);plot3(x,y,z)得到三维螺旋线：图23．空间曲面作图函数：（1）mesh函数．绘制彩色网格面图形．调用格式：mesh(z)，mesh(x,y,z)和mesh(x,y,z,c)．其中，mesh(x,y,z,c)画出颜色由c指定的三维网格图．若x、y均为向量，则length(x)=n，length(y)=m，[m,n]=size(z)．（2）surf在矩形区域内显示三维带阴影曲面图．调用格式与mesh类似．（3）ezmesh用符号函数作三维曲面网格图．调用格式：ezmesh(x,y,z)其中x = x(s,t), y = y(s,t),z = z(s,t)．画图区域默认为： -2*pi < s < 2*pi 且-2*pi < t < 2*pi.或者用格式：ezmesh(x,y,z,[smin,smax,tmin,tmax])（4）ezsurf用符号函数作三维曲面图．调用格式与ezmesh类似．（5）sphere画球体命令．4．meshgrid，调用格式：[x,y]=meshgrid(m,n)，这里的m，n为给定的向量，可以定义网格划分区域和划分方法．矩阵x和矩阵y是网格划分后的数据矩阵．5．图像的修饰与其他函数：（1）axis equal 控制各个坐标轴的分度，使其相等；（2）colormap设置绘图颜色．调用格式：colormap([r g b])其中r,g,b都是0-1之间的数．或者用格式：colormap(s)s颜色映像相应的颜色系颜色映像相应的颜色系autumn红黄色系hsv色调饱和色系gray线性灰色系hot黑红黄白色系cool青和洋红色系pink柔和色系（3（4）find找出符合条件的元素在数组中的位置．调用格式：y=find(条件)例如：输入：a=[4 5 78 121 4 665 225 4 1];b=find(a>7)输出： b =3 4 6 7三、实验内容数学分析中，特别是积分部分，我们接触了不少有趣的函数，由于其中有的不是一一对应的，用上面的方法无法画出它们的图像，这时就只能用参数了．此外还有些图形只能用参数来画，比如空间曲线，在计算机上不接受“两个曲面的交线”这种表示，所以也只能用参数来实现．用参数方式作图的关键在于找出合适的参数表示，尤其是不能有奇点，最好也不要用到开方．所以要找的参数最好是有几何意义的．当然这也不可一概而论，需要多积累经验．1．利用函数plot在一个坐标系中画以下几个函数图像，要求采用不同颜色、不同线形、不同的符号标记．函数为：．程序如下：t=0:pi/20:2*pi;x=sin(t);y=cos(t);z=sin(2*t);plot(t, x, '--k*', t, y, '-rs', t, z, ':bo')图像如下：图32．绘制类似田螺线的一条三维螺线(方程自己设计)．程序如下：t=0:.1:30;x=2*(cos(t)+t.*sin(t));y=2*(sin(t)-t.*cos(t));z=*t;plot3(x,y,-z) %取–z 主要是为了画图看起来更清楚axis equal图像如下：图43．利用函数，绘制一个墨西哥帽子的图形．程序如下：[a,b]=meshgrid(-8:.5:8); %先生成一个网格c=sqrt(a.^2+b.^2)+eps;z=sin(c)./c;mesh(a,b,z)axis square图像如下：图5思考：这里的 eps 是什么其作用是什么4．利用surf绘制马鞍面图形（函数为：）．程序如下：[x,y]=meshgrid(-25:1:25,-25:1:25);z=x.^2/9-y.^2/4;surf(x,y,z)title('马鞍面')grid off图像如下：图65．分别用ezmesh和ezsurf各绘制一个圆环面，尝试将两个圆环面放在一个图形界面内，观察它们有什么不同之处．提示：圆环面的方程为：，而圆环面的参数方程为：程序参见附录1．图像如下：图76．绘制黎曼函数图形，加深对黎曼函数的理解．说明：黎曼函数的定义为程序参见附录2．图像如下：图8四、自己动手1．作出下图所示的三维图形：图9提示：图形为圆环面和球面的组合.2．作出下图所示的墨西哥帽子及其剪裁图形：图103．画出球面、椭球面、双叶双曲面、单叶双曲面．4．若要求田螺线的一条轴截面的曲边是一条抛物线：时．试重新设计田螺线的参数方程，并画出该田螺线．5．作出下图所示的马鞍面（颜色为灰色，并有一个标题：“马鞍面”）：图116．绘制图8所示的黎曼函数图形，要求分母的最大值的数值由键盘输入（提示：使用input语句）．回目录下一页实验二定积分的近似计算一、问题背景与实验目的二、相关函数（命令）及简介三、实验内容1．矩形法2．梯形法3．抛物线法4. 直接应用Matlab命令计算结果四、自己动手一、问题背景与实验目的利用牛顿—莱布尼兹公式虽然可以精确地计算定积分的值，但它仅适用于被积函数的原函数能用初等函数表达出来的情形．如果这点办不到或者不容易办到，这就有必要考虑近似计算的方法．在定积分的很多应用问题中，被积函数甚至没有解析表达式，可能只是一条实验记录曲线，或者是一组离散的采样值，这时只能应用近似方法去计算相应的定积分．本实验将主要研究定积分的三种近似计算算法：矩形法、梯形法、抛物线法．对于定积分的近似数值计算，Matlab有专门函数可用．二、相关函数（命令）及简介1．sum(a)：求数组a的和．2．format long：长格式，即屏幕显示15位有效数字．（注：由于本实验要比较近似解法和精确求解间的误差，需要更高的精度）．3．double()：若输入的是字符则转化为相应的ASCII码；若输入的是整型数值则转化为相应的实型数值．4．quad()：抛物线法求数值积分．格式： quad(fun,a,b) ，注意此处的fun是函数，并且为数值形式的，所以使用*、/、^等运算时要在其前加上小数点，即 .*、./、.^等．例：Q = quad('1./(x.^3-2*x-5)',0,2);5．trapz()：梯形法求数值积分．格式：trapz(x,y)其中x为带有步长的积分区间；y为数值形式的运算（相当于上面介绍的函数fun）例：计算x=0:pi/100:pi;y=sin(x);trapz(x,y)6．dblquad()：抛物线法求二重数值积分．格式：dblquad(fun,xmin,xmax,ymin,ymax)，fun可以用inline定义，也可以通过某个函数文件的句柄传递．例1：Q1 = dblquad(inline('y*sin(x)'), pi, 2*pi, 0, pi)顺便计算下面的Q2，通过计算，比较Q1 与Q2结果（或加上手工验算），找出积分变量x、y的上下限的函数代入方法．Q2 = dblquad(inline('y*sin(x)'), 0, pi, pi, 2*pi)例2：Q3 = dblquad(@integrnd, pi, 2*pi, 0, pi)这时必须存在一个函数文件：function z = integrnd(x, y)z = y*sin(x);7．fprintf（文件地址，格式，写入的变量）：把数据写入指定文件．例：x = 0:.1:1;y = [x; exp(x)];fid = fopen('','w'); %打开文件fprintf(fid,'% %\n',y); %写入fclose(fid) %关闭文件8．syms 变量1 变量2 …：定义变量为符号．9．sym('表达式')：将表达式定义为符号．解释：Matlab中的符号运算事实上是借用了Maple的软件包，所以当在Matlab中要对符号进行运算时，必须先把要用到的变量定义为符号．10．int(f,v,a,b)：求f关于v积分，积分区间由a到b．11．subs(f，'x'，a)：将 a 的值赋给符号表达式 f 中的 x，并计算出值．若简单地使用subs(f)，则将f的所有符号变量用可能的数值代入，并计算出值．三、实验内容1．矩形法根据定积分的定义，每一个积分和都可以看作是定积分的一个近似值，即在几何意义上，这是用一系列小矩形面积近似小曲边梯形的结果，所以把这个近似计算方法称为矩形法．不过，只有当积分区间被分割得很细时，矩形法才有一定的精确度．针对不同的取法，计算结果会有不同，我们以为例（取），（1）左点法：对等分区间，在区间上取左端点，即取，，理论值，此时计算的相对误差（2）右点法：同（1）中划分区间，在区间上取右端点，即取，，理论值，此时计算的相对误差（3）中点法：同（1）中划分区间，在区间上取中点，即取，，理论值，此时计算的相对误差如果在分割的每个小区间上采用一次或二次多项式来近似代替被积函数，那么可以期望得到比矩形法效果好得多的近似计算公式．下面介绍的梯形法和抛物线法就是这一指导思想的产物．2．梯形法等分区间，相应函数值为（）．曲线上相应的点为（）将曲线的每一段弧用过点，的弦（线性函数）来代替，这使得每个上的曲边梯形成为真正的梯形，其面积为，．于是各个小梯形面积之和就是曲边梯形面积的近似值，，即，称此式为梯形公式．仍用的近似计算为例，取，，理论值，此时计算的相对误差很显然，这个误差要比简单的矩形左点法和右点法的计算误差小得多．3．抛物线法由梯形法求近似值，当为凹曲线时，它就偏小；当为凸曲线时，它就偏大．若每段改用与它凸性相接近的抛物线来近似时，就可减少上述缺点，这就是抛物线法．将积分区间作等分，分点依次为，，对应函数值为（），曲线上相应点为（）．现把区间上的曲线段用通过三点，，的抛物线来近似代替，然后求函数从到的定积分：由于，代入上式整理后得同样也有……将这个积分相加即得原来所要计算的定积分的近似值：，即这就是抛物线法公式，也称为辛卜生（Simpson）公式．仍用的近似计算为例，取，=，理论值，此时计算的相对误差4. 直接应用Matlab命令计算结果（1）数值计算方法1：int('1/(1+x^2)','x',0,1) (符号求积分)方法2：quad('1./(1+x.^2)',0,1) （抛物线法求数值积分）方法3：x=0::1;y=1./(1+x.^2);trapz(x,y) （梯形法求数值积分）（2）数值计算方法1：int(int('x+y^2','y',-1,1),'x',0,2) （符号求积分）方法2：dblquad(inline('x+y^2'),0,2,-1,1) （抛物线法二重数值积分）四、自己动手1．实现实验内容中的例子，即分别采用矩形法、梯形法、抛物线法计算，取，并比较三种方法的精确程度．2．分别用梯形法与抛物线法，计算，取．并尝试直接使用函数trapz()、quad()进行计算求解，比较结果的差异．3．试计算定积分．（注意：可以运用trapz()、quad()或附录程序求解吗为什么）4．将的近似计算结果与Matlab中各命令的计算结果相比较，试猜测Matlab中的数值积分命令最可能采用了哪一种近似计算方法并找出其他例子支持你的观点．5．通过整个实验内容及练习，你能否作出一些理论上的小结，即针对什么类型的函数（具有某种单调特性或凹凸特性），用某种近似计算方法所得结果更接近于实际值6．学习的程序设计方法，尝试用函数 sum 改写附录1和附录3的程序，避免for 循环．上一页回目录下一页实验三求代数方程的近似根（解）一、问题背景和实验目的二、相关函数（命令）及简介三、实验内容四、自己动手一、问题背景和实验目的求代数方程的根是最常见的数学问题之一（这里称为代数方程，主要是想和后面的微分方程区别开．为简明起见，在本实验的以下叙述中，把代数方程简称为方程），当是一次多项式时，称为线性方程，否则称之为非线性方程．当是非线性方程时，由于的多样性，尚无一般的解析解法可使用，但如果对任意的精度要求，能求出方程的近似根，则可以认为求根的计算问题已经解决，至少能满足实际要求．本实验介绍一些求方程实根的近似值的有效方法，要求在使用这些方法前先确定求根区间，或给出某根的近似值．在实际问题抽象出的数学模型中，可以根据物理背景确定；也可根据的草图等方法确定，还可用对分法、迭代法以及牛顿切线法大致确定根的分布情况．通过本实验希望你能：1. 了解对分法、迭代法、牛顿切线法求方程近似根的基本过程；2. 求代数方程（组）的解．二、相关函数（命令）及简介1．abs( )：求绝对值函数．2．diff(f)：对独立变量求微分，f 为符号表达式．diff(f, 'a')：对变量a求微分，f 为符号表达式．diff(f, 'a', n)：对变量 a 求 n 次微分，f 为符号表达式．例如：syms x tdiff(sin(x^2)*t^6, 't', 6)ans=720*sin(x^2)3．roots([c(1), c(2), …, c(n+1)])：求解多项式的所有根．例如：求解：．p = [1 -6 -72 -27];r = roots(p)r =4．solve('表达式')：求表达式的解．solve('2*sin(x)=1')ans =1/6*pi5．linsolve(A, b)：求线性方程组 A*x=b 的解．例如：A= [9 0; -1 8]; b=[1; 2];linsolve(A, b)ans=[ 1/9][19/72]6．fzero(fun, x0)：在x0附近求fun 的解．其中fun为一个定义的函数，用“@函数名”方式进行调用．例如：fzero(@sin, 3)ans=7．subs(f, 'x ', a)：将 a 的值赋给符号表达式 f 中的 x，并计算出值．例如：subs('x^2 ', 'x ', 2)ans = 4三、实验内容首先，我们介绍几种与求根有关的方法：1．对分法对分法思想：将区域不断对分，判断根在某个分段内，再对该段对分，依此类推，直到满足精度为止．对分法适用于求有根区间内的单实根或奇重实根．设在上连续，，即，或，．则根据连续函数的介值定理，在内至少存在一点，使．下面的方法可以求出该根：(1)令，计算；(2)若，则是的根，停止计算，输出结果．若，则令，，若，则令，；．……，有、以及相应的．(3) 若 (为预先给定的精度要求)，退出计算，输出结果；反之，返回(1)，重复(1)，(2)，(3)．以上方法可得到每次缩小一半的区间序列，在中含有方程的根．当区间长很小时，取其中点为根的近似值，显然有以上公式可用于估计对分次数．分析以上过程不难知道，对分法的收敛速度与公比为的等比级数相同．由于，可知大约对分10次，近似根的精度可提高三位小数．对分法的收敛速度较慢，它常用来试探实根的分布区间，或求根的近似值．2. 迭代法1)迭代法的基本思想：由方程构造一个等价方程从某个近似根出发，令，可得序列，这种方法称为迭代法．若收敛，即，只要连续，有即可知，的极限是的根，也就是的根．当然，若发散，迭代法就失败．以下给出迭代过程收敛的一些判别方法：定义：如果根的某个邻域中，使对任意的，迭代过程，收敛，则称迭代过程在附近局部收敛．定理1：设，在的某个邻域内连续，并且，，则对任何，由迭代决定的序列收敛于．定理2：条件同定理 1，则定理3：已知方程，且(1) 对任意的，有．(2) 对任意的，有，则对任意的，迭代生成的序列收敛于的根，且．以上给出的收敛定理中的条件要严格验证都较困难，实用时常用以下不严格的标准：当根区间较小，且对某一，明显小于1时，则迭代收敛(参见附录3)．2) 迭代法的加速：a) 松弛法：若与同是的近似值，则是两个近似值的加权平均，其中称为权重，现通过确定看能否得到加速．迭代方程是：其中，令，试确定：当时，有，即当，时，可望获得较好的加速效果，于是有松弛法：，松弛法的加速效果是明显的 (见附录4)，甚至不收敛的迭代函数经加速后也能获得收敛．b) Altken方法：松弛法要先计算，在使用中有时不方便，为此发展出以下的 Altken 公式：，是它的根，是其近似根．设，，因为，用差商近似代替，有，解出，得由此得出公式；；，这就是Altken 公式，它的加速效果也是十分明显的，它同样可使不收敛的迭代格式获得收敛(见附录5)．3. 牛顿(Newton)法（牛顿切线法）1) 牛顿法的基本思想：是非线性方程，一般较难解决，多采用线性化方法．记：是一次多项式，用作为的近似方程．的解为记为，一般地，记即为牛顿法公式.2) 牛顿法的收敛速度：对牛顿法，迭代形式为：注意分子上的，所以当时，，牛顿法至少是二阶收敛的，而在重根附近，牛顿法是线性收敛的．牛顿法的缺点是：(1)对重根收敛很慢；(2)对初值要求较严，要求相当接近真值．因此，常用其他方法确定初值，再用牛顿法提高精度．4. 求方程根(解)的其它方法(1) solve('x^3-3*x+1=0')(2) roots([1 0 -3 1])(3) fzero('x^3-3*x+1', -2)(4) fzero('x^3-3*x+1',(5) fzero('x^3-3*x+1',(6) linsolve([1, 2, 3; 4, 5, 6; 7, 8, 0], [1, 2, 3]')体会一下，(2)(5) 用了上述 1 3 中的哪一种方法以下是本实验中的几个具体的实验，详细的程序清单参见附录．具体实验1：对分法先作图观察方程：的实根的分布区间，再利用对分法在这些区间上分别求出根的近似值．输入以下命令，可得的图象：f='x^3-3*x+1';g='0';ezplot(f, [-4, 4]);hold on;ezplot(g, [-4, 4]); %目的是画出直线 y=0，即 x 轴grid on;axis([-4 4 -5 5]);hold off请填写下表：实根的分布区间该区间上根的近似值在某区间上求根的近似值的对分法程序参见附录1．具体实验2：普通迭代法采用迭代过程：求方程在附近的根，精确到第 4 位小数．构造等价方程：用迭代公式：，用 Matlab 编写的程序参见附录2．请利用上述程序填写下表：分析：将附录2第4行中的分别改为以及，问运行的结果是什么你能分析得到其中的原因吗看看下面的“具体实验3”是想向你表达一个什么意思．用 Matlab 编写的程序参见附录3．具体实验3：收敛/发散判断设方程的三个根近似地取，和，这些近似值可以用上面的对分法求得．迭代形式一：收敛 (很可能收敛，下同)不收敛 (很可能不收敛，下同)不收敛迭代形式二：收敛不收敛不收敛迭代形式三：不收敛收敛收敛具体实验4：迭代法的加速1——松弛迭代法，，迭代公式为程序参见附录4．具体实验5：迭代法的加速2——Altken迭代法迭代公式为：，，程序参见附录5．具体实验6：牛顿法用牛顿法计算方程在-2到2之间的三个根．提示：，迭代公式：程序参见附录6 （牛顿法程序）．具体实验7：其他方法求下列代数方程（组）的解：（1）命令：solve('x^5-x+1=0')（2）命令：[x, y]=solve('2*x+3*y=0', '4*x^2+3*y=1')(3) 求线性方程组的解，已知，命令：for i=1:5for j=1:5m(i, j)=i+j-1;endendm(5, 5)=0;b=[1:5]'linsolve(m, b)思考：若，或是类似的但阶数更大的稀疏方阵，则应如何得到四、自己动手1．对分法可以用来求偶重根附近的近似解吗为什么2．对照具体实验2、4、5，你可以得出什么结论3．选择适当的迭代过程，分别使用：（1）普通迭代法；（2）与之相应的松弛迭代法和 Altken 迭代法．求解方程在附近的根，精确到4位小数，请注意迭代次数的变化．4．分别用对分法、普通迭代法、松弛迭代法、Altken 迭代法、牛顿切法线等5种方法，求方程的正的近似根，．(建议取．时间许可的话，可进一步考虑的情况．)上一页回目录下一页。

matlab简单实例

matlab简单实例
当谈到MATLAB的简单实例时，有很多可以选择的示例。

以下是一个关于计算圆的面积和周长的简单实例：
matlab.
% 输入圆的半径。

radius = input('请输入圆的半径，');
% 计算圆的面积。

area = pi radius^2;
% 计算圆的周长。

circumference = 2 pi radius;
% 显示结果。

fprintf('圆的面积为，%.2f\n', area);
fprintf('圆的周长为，%.2f\n', circumference);
在这个实例中，我们首先通过`input`函数从用户获取圆的半径。

然后，我们使用半径计算圆的面积和周长，分别存储在`area`和
`circumference`变量中。

最后，我们使用`fprintf`函数将结果显
示出来。

这个实例展示了MATLAB的基本语法和数学计算功能。

你可以根
据需要修改和扩展这个实例，以适应更复杂的计算或问题。

除了计算圆的面积和周长，MATLAB还可以用于数据分析、图像
处理、信号处理、控制系统设计等各种应用领域。

你可以根据自己
的兴趣和需求，选择适合的实例进行学习和实践。

希望这个简单的实例能够帮助你了解MATLAB的基本用法和潜力。

如果你有其他关于MATLAB的问题，请随时提问。

matlab gui界面设计实例

matlab gui界面设计实例
以下是一个简单的MATLAB GUI界面设计实例：
1. 打开MATLAB软件并创建一个新的GUI文件，首先需要添加一个静态文本标签来说明该程序的用途。

2. 在接下来的步骤中，我们将添加一个单选按钮和一组复选框，允许用户选择他们的喜好和选项。

3. 其他元素可添加日期选择器，文本框和按钮等等。

4. 最后，我们需要添加一个事件处理程序，以便处理用户点击“提交”按钮时的操作。

通过这样一个简单的实例，我们可以学习到MATLAB GUI界面的基本设计原则和步骤，以及如何处理用户交互事件并使用MATLAB功能实现功能。

matlab编程实例100例(精编文档).doc

【最新整理，下载后即可编辑】1-32是：图形应用篇33-66是：界面设计篇67-84是：图形处理篇85-100是：数值分析篇实例1：三角函数曲线（1）function shili01h0=figure('toolbar','none',...'position',[198****0300],...'name','实例01');h1=axes('parent',h0,...'visible','off');x=-pi:0.05:pi;y=sin(x);plot(x,y);xlabel('自变量X');ylabel('函数值Y');title('SIN( )函数曲线');grid on实例2：三角函数曲线（2）function shili02h0=figure('toolbar','none',...'position',[200 150 450 350],...'name','实例02');x=-pi:0.05:pi;y=sin(x)+cos(x);plot(x,y,'-*r','linewidth',1);grid onxlabel('自变量X');ylabel('函数值Y');title('三角函数');实例3：图形的叠加function shili03h0=figure('toolbar','none',...'position',[200 150 450 350],...'name','实例03');x=-pi:0.05:pi;y1=sin(x);y2=cos(x);plot(x,y1,...'-*r',...x,y2,...'--og');grid onxlabel('自变量X');ylabel('函数值Y');title('三角函数');实例4：双y轴图形的绘制function shili04h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例04');x=0:900;a=1000;b=0.005;y1=2*x;y2=cos(b*x);[haxes,hline1,hline2]=plotyy(x,y1,x,y2,'semilogy','plot'); axes(haxes(1))ylabel('semilog plot');axes(haxes(2))ylabel('linear plot');实例5：单个轴窗口显示多个图形function shili05h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例05');t=0:pi/10:2*pi;[x,y]=meshgrid(t);subplot(2,2,1)plot(sin(t),cos(t))axis equalsubplot(2,2,2)z=sin(x)-cos(y);plot(t,z)axis([0 2*pi -2 2])subplot(2,2,3)h=sin(x)+cos(y);plot(t,h)axis([0 2*pi -2 2])subplot(2,2,4)g=(sin(x).^2)-(cos(y).^2);plot(t,g)axis([0 2*pi -1 1])实例6：图形标注function shili06h0=figure('toolbar','none',...'position',[200 150 450 400],...'name','实例06');t=0:pi/10:2*pi;h=plot(t,sin(t));xlabel('t=0到2\pi','fontsize',16);ylabel('sin(t)','fontsize',16);title('\it{从0to2\pi 的正弦曲线}','fontsize',16) x=get(h,'xdata');y=get(h,'ydata');imin=find(min(y)==y);imax=find(max(y)==y);text(x(imin),y(imin),...['\leftarrow最小值=',num2str(y(imin))],...'fontsize',16)text(x(imax),y(imax),...['\leftarrow最大值=',num2str(y(imax))],...'fontsize',16)实例7：条形图形function shili07h0=figure('toolbar','none',...'position',[200 150 450 350],...'name','实例07');tiao1=[562 548 224 545 41 445 745 512];tiao2=[47 48 57 58 54 52 65 48];t=0:7;bar(t,tiao1)xlabel('X轴');ylabel('TIAO1值');h1=gca;h2=axes('position',get(h1,'position'));plot(t,tiao2,'linewidth',3)set(h2,'yaxislocation','right','color','none','xticklabel',[]) 实例8：区域图形function shili08h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例08');x=91:95;profits1=[88 75 84 93 77];profits2=[51 64 54 56 68];profits3=[42 54 34 25 24];profits4=[26 38 18 15 4];area(x,profits1,'facecolor',[0.5 0.9 0.6],...'edgecolor','b',...'linewidth',3)hold onarea(x,profits2,'facecolor',[0.9 0.85 0.7],...'edgecolor','y',...'linewidth',3)hold onarea(x,profits3,'facecolor',[0.3 0.6 0.7],...'edgecolor','r',...'linewidth',3)hold onarea(x,profits4,'facecolor',[0.6 0.5 0.9],...'edgecolor','m',...'linewidth',3)hold offset(gca,'xtick',[91:95])set(gca,'layer','top')gtext('\leftarrow第一季度销量') gtext('\leftarrow第二季度销量') gtext('\leftarrow第三季度销量') gtext('\leftarrow第四季度销量') xlabel('年','fontsize',16);ylabel('销售量','fontsize',16);实例9：饼图的绘制function shili09h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例09');t=[54 21 35;68 54 35;45 25 12;48 68 45;68 54 69];x=sum(t);h=pie(x);textobjs=findobj(h,'type','text');str1=get(textobjs,{'string'});val1=get(textobjs,{'extent'});oldext=cat(1,val1{:});names={'商品一：';'商品二：';'商品三：'};str2=strcat(names,str1);set(textobjs,{'string'},str2)val2=get(textobjs,{'extent'});newext=cat(1,val2{:});offset=sign(oldext(:,1)).*(newext(:,3)-oldext(:,3))/2; pos=get(textobjs,{'position'});textpos=cat(1,pos{:});textpos(:,1)=textpos(:,1)+offset;set(textobjs,{'position'},num2cell(textpos,[3,2]))实例10：阶梯图function shili10h0=figure('toolbar','none',...'position',[200 150 450 400],...'name','实例10');a=0.01;b=0.5;t=0:10;f=exp(-a*t).*sin(b*t);stairs(t,f)hold onplot(t,f,':*')hold offglabel='函数e^{-(\alpha*t)}sin\beta*t的阶梯图'; gtext(glabel,'fontsize',16)xlabel('t=0:10','fontsize',16)axis([0 10 -1.2 1.2])实例11：枝干图function shili11h0=figure('toolbar','none',...'position',[200 150 450 350],...'name','实例11');x=0:pi/20:2*pi;y1=sin(x);y2=cos(x);h1=stem(x,y1+y2);hold onh2=plot(x,y1,'^r',x,y2,'*g');hold offh3=[h1(1);h2];legend(h3,'y1+y2','y1=sin(x)','y2=cos(x)') xlabel('自变量X');ylabel('函数值Y');title('正弦函数与余弦函数的线性组合'); 实例12：罗盘图function shili12h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例12');winddirection=[54 24 65 84256 12 235 62125 324 34 254];windpower=[2 5 5 36 8 12 76 14 10 8];rdirection=winddirection*pi/180;[x,y]=pol2cart(rdirection,windpower); compass(x,y);desc={'风向和风力','北京气象台','10月1日0：00到','10月1日12：00'};gtext(desc)实例13：轮廓图function shili13h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例13');[th,r]=meshgrid((0:10:360)*pi/180,0:0.05:1); [x,y]=pol2cart(th,r);z=x+i*y;f=(z.^4-1).^(0.25);contour(x,y,abs(f),20)axis equalxlabel('实部','fontsize',16);ylabel('虚部','fontsize',16);h=polar([0 2*pi],[0 1]);delete(h)hold oncontour(x,y,abs(f),20)实例14：交互式图形function shili14h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例14');axis([0 10 0 10]);hold onx=[];y=[];n=0;disp('单击鼠标左键点取需要的点'); disp('单击鼠标右键点取最后一个点'); but=1;while but==1[xi,yi,but]=ginput(1);plot(xi,yi,'bo')n=n+1;disp('单击鼠标左键点取下一个点');x(n,1)=xi;y(n,1)=yi;endt=1:n;ts=1:0.1:n;xs=spline(t,x,ts);ys=spline(t,y,ts);plot(xs,ys,'r-');hold off实例14：交互式图形function shili14h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例14');axis([0 10 0 10]);hold onx=[];y=[];n=0;disp('单击鼠标左键点取需要的点'); disp('单击鼠标右键点取最后一个点'); but=1;while but==1[xi,yi,but]=ginput(1);plot(xi,yi,'bo')n=n+1;disp('单击鼠标左键点取下一个点');x(n,1)=xi;y(n,1)=yi;endt=1:n;ts=1:0.1:n;xs=spline(t,x,ts);ys=spline(t,y,ts);plot(xs,ys,'r-');hold off实例15：变换的傅立叶函数曲线function shili15h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例15');axis equalm=moviein(20,gcf);set(gca,'nextplot','replacechildren')h=uicontrol('style','slider','position',...[100 10 500 20],'min',1,'max',20)for j=1:20plot(fft(eye(j+16)))set(h,'value',j)m(:,j)=getframe(gcf);endclf;axes('position',[0 0 1 1]);movie(m,30)实例16：劳伦兹非线形方程的无序活动function shili15h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例15');axis equalm=moviein(20,gcf);set(gca,'nextplot','replacechildren')h=uicontrol('style','slider','position',...[100 10 500 20],'min',1,'max',20)for j=1:20plot(fft(eye(j+16)))set(h,'value',j)m(:,j)=getframe(gcf);endclf;axes('position',[0 0 1 1]);movie(m,30)实例17：填充图function shili17h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例17');t=(1:2:15)*pi/8;x=sin(t);y=cos(t);fill(x,y,'r')axis square offtext(0,0,'STOP',...'color',[1 1 1],...'fontsize',50,...'horizontalalignment','center') 例18：条形图和阶梯形图function shili18h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例18');subplot(2,2,1)x=-3:0.2:3;y=exp(-x.*x);bar(x,y)title('2-D Bar Chart')subplot(2,2,2)x=-3:0.2:3;y=exp(-x.*x);bar3(x,y,'r')title('3-D Bar Chart')subplot(2,2,3)x=-3:0.2:3;y=exp(-x.*x);stairs(x,y)title('Stair Chart')subplot(2,2,4)x=-3:0.2:3;y=exp(-x.*x);barh(x,y)title('Horizontal Bar Chart')实例19：三维曲线图function shili19h0=figure('toolbar','none',...'position',[200 150 450 400],...'name','实例19');subplot(2,1,1)x=linspace(0,2*pi);y1=sin(x);y2=cos(x);y3=sin(x)+cos(x);z1=zeros(size(x));z2=0.5*z1;z3=z1;plot3(x,y1,z1,x,y2,z2,x,y3,z3)grid onxlabel('X轴');ylabel('Y轴');zlabel('Z轴');title('Figure1:3-D Plot')subplot(2,1,2)x=linspace(0,2*pi);y1=sin(x);y2=cos(x);y3=sin(x)+cos(x);z1=zeros(size(x));z2=0.5*z1;z3=z1;plot3(x,z1,y1,x,z2,y2,x,z3,y3)grid onxlabel('X轴');ylabel('Y轴');zlabel('Z轴');title('Figure2:3-D Plot')实例20：图形的隐藏属性function shili20h0=figure('toolbar','none',...'position',[200 150 450 300],...'name','实例20');subplot(1,2,1)[x,y,z]=sphere(10);mesh(x,y,z)axis offtitle('Figure1:Opaque')hidden onsubplot(1,2,2)[x,y,z]=sphere(10);mesh(x,y,z)axis offtitle('Figure2:Transparent') hidden off实例21PEAKS函数曲线function shili21h0=figure('toolbar','none',...'position',[200 100 450 450],...'name','实例21');[x,y,z]=peaks(30);subplot(2,1,1)x=x(1,:);y=y(:,1);i=find(y>0.8&y<1.2);j=find(x>-0.6&x<0.5);z(i,j)=nan*z(i,j);surfc(x,y,z)xlabel('X轴');ylabel('Y轴');zlabel('Z轴');title('Figure1:surfc函数形成的曲面') subplot(2,1,2)x=x(1,:);y=y(:,1);i=find(y>0.8&y<1.2);j=find(x>-0.6&x<0.5);z(i,j)=nan*z(i,j);surfl(x,y,z)xlabel('X轴');ylabel('Y轴');zlabel('Z轴');title('Figure2:surfl函数形成的曲面') 实例22：片状图function shili22h0=figure('toolbar','none',...'position',[200 150 550 350],...'name','实例22');subplot(1,2,1)x=rand(1,20);y=rand(1,20);z=peaks(x,y*pi);t=delaunay(x,y);trimesh(t,x,y,z)hidden offtitle('Figure1:Triangular Surface Plot'); subplot(1,2,2)x=rand(1,20);y=rand(1,20);z=peaks(x,y*pi);t=delaunay(x,y);trisurf(t,x,y,z)title('Figure1:Triangular Surface Plot'); 实例23：视角的调整function shili23h0=figure('toolbar','none',...'position',[200 150 450 350],...'name','实例23');x=-5:0.5:5;[x,y]=meshgrid(x);r=sqrt(x.^2+y.^2)+eps;z=sin(r)./r;subplot(2,2,1)surf(x,y,z)xlabel('X-axis')ylabel('Y-axis')zlabel('Z-axis')title('Figure1')view(-37.5,30)subplot(2,2,2)surf(x,y,z)xlabel('X-axis')ylabel('Y-axis')zlabel('Z-axis')title('Figure2')view(-37.5+90,30) subplot(2,2,3)surf(x,y,z)xlabel('X-axis')ylabel('Y-axis')zlabel('Z-axis')title('Figure3')view(-37.5,60)subplot(2,2,4)surf(x,y,z)xlabel('X-axis')ylabel('Y-axis')zlabel('Z-axis')title('Figure4')view(180,0)实例24：向量场的绘制function shili24h0=figure('toolbar','none',...'position',[200 150 450 350],...'name','实例24');subplot(2,2,1)z=peaks;ribbon(z)title('Figure1')subplot(2,2,2)[x,y,z]=peaks(15);[dx,dy]=gradient(z,0.5,0.5); contour(x,y,z,10)hold onquiver(x,y,dx,dy)hold offtitle('Figure2')subplot(2,2,3)[x,y,z]=peaks(15);[nx,ny,nz]=surfnorm(x,y,z);surf(x,y,z)hold onquiver3(x,y,z,nx,ny,nz)hold offtitle('Figure3')subplot(2,2,4)x=rand(3,5);y=rand(3,5);z=rand(3,5);c=rand(3,5);fill3(x,y,z,c)grid ontitle('Figure4')实例25：灯光定位function shili25h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例25');vert=[1 1 1;1 2 1;2 2 1;2 1 1;1 1 2;12 2;2 2 2;2 1 2];fac=[1 2 3 4;2 6 7 3;4 3 7 8;15 8 4;1 2 6 5;5 6 7 8];grid offsphere(36)h=findobj('type','surface');set(h,'facelighting','phong',...'facecolor',...'interp',...'edgecolor',[0.4 0.4 0.4],...'backfacelighting',...'lit')hold onpatch('faces',fac,'vertices',vert,...'facecolor','y');light('position',[1 3 2]);light('position',[-3 -1 3]);material shinyaxis vis3d offhold off实例26：柱状图function shili26h0=figure('toolbar','none',...'position',[200 50 450 450],...'name','实例26'); subplot(2,1,1)x=[5 2 18 7 39 8 65 5 54 3 2];bar(x)xlabel('X轴');ylabel('Y轴');title('第一子图');subplot(2,1,2)y=[5 2 18 7 39 8 65 5 54 3 2];barh(y)xlabel('X轴');ylabel('Y轴');title('第二子图');实例27：设置照明方式function shili27h0=figure('toolbar','none',...'position',[200 150 450 350],...'name','实例27');subplot(2,2,1)sphereshading flatcamlight leftcamlight rightlighting flatcolorbaraxis offtitle('Figure1')subplot(2,2,2)sphereshading flatcamlight leftcamlight rightlighting gouraudcolorbaraxis offtitle('Figure2')subplot(2,2,3)sphereshading interpcamlight rightcamlight leftlighting phongaxis offtitle('Figure3')subplot(2,2,4)sphereshading flatcamlight leftcamlight rightlighting nonecolorbaraxis offtitle('Figure4')实例28：羽状图function shili28h0=figure('toolbar','none',...'position',[200 150 450 350],...'name','实例28');subplot(2,1,1)alpha=90:-10:0;r=ones(size(alpha));m=alpha*pi/180;n=r*10;[u,v]=pol2cart(m,n);feather(u,v)title('羽状图')axis([0 20 0 10])subplot(2,1,2)t=0:0.5:10;y=exp(-x*t);feather(y)title('复数矩阵的羽状图')实例29：立体透视（1）function shili29h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例29');[x,y,z]=meshgrid(-2:0.1:2,...-2:0.1:2,...-2:0.1:2);v=x.*exp(-x.^2-y.^2-z.^2);grid onfor i=-2:0.5:2;h1=surf(linspace(-2,2,20),...linspace(-2,2,20),...zeros(20)+i);rotate(h1,[1 -1 1],30)dx=get(h1,'xdata');dy=get(h1,'ydata');dz=get(h1,'zdata');delete(h1)slice(x,y,z,v,[-2 2],2,-2)hold onslice(x,y,z,v,dx,dy,dz)hold offaxis tightview(-5,10)drawnowend实例30：立体透视（2）function shili30h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例30');[x,y,z]=meshgrid(-2:0.1:2,...-2:0.1:2,...-2:0.1:2);v=x.*exp(-x.^2-y.^2-z.^2); [dx,dy,dz]=cylinder;slice(x,y,z,v,[-2 2],2,-2)for i=-2:0.2:2h=surface(dx+i,dy,dz);rotate(h,[1 0 0],90)xp=get(h,'xdata');yp=get(h,'ydata');zp=get(h,'zdata');delete(h)hold onhs=slice(x,y,z,v,xp,yp,zp);axis tightxlim([-3 3])view(-10,35)drawnowdelete(hs)hold offend实例31：表面图形function shili31h0=figure('toolbar','none',...'position',[200 150 550 250],...'name','实例31');subplot(1,2,1)x=rand(100,1)*16-8;y=rand(100,1)*16-8;r=sqrt(x.^2+y.^2)+eps;z=sin(r)./r;xlin=linspace(min(x),max(x),33); ylin=linspace(min(y),max(y),33); [X,Y]=meshgrid(xlin,ylin);Z=griddata(x,y,z,X,Y,'cubic'); mesh(X,Y,Z)axis tighthold onplot3(x,y,z,'.','Markersize',20) subplot(1,2,2)k=5;n=2^k-1;theta=pi*(-n:2:n)/n;phi=(pi/2)*(-n:2:n)'/n;X=cos(phi)*cos(theta);Y=cos(phi)*sin(theta);Z=sin(phi)*ones(size(theta)); colormap([0 0 0;1 1 1])C=hadamard(2^k);surf(X,Y,Z,C)axis square实例32：沿曲线移动的小球h0=figure('toolbar','none',...'position',[198****8468],...'name','实例32');h1=axes('parent',h0,...'position',[0.15 0.45 0.7 0.5],...'visible','on');t=0:pi/24:4*pi;y=sin(t);plot(t,y,'b')n=length(t);h=line('color',[0 0.5 0.5],...'linestyle','.',...'markersize',25,...'erasemode','xor');k1=uicontrol('parent',h0,...'style','pushbutton',...'position',[80 100 50 30],...'string','开始',...'callback',[...'i=1;',...'k=1;,',...'m=0;,',...'while 1,',...'if k==0,',...'break,',...'end,',...'if k~=0,',...'set(h,''xdata'',t(i),''ydata'',y(i)),',...'drawnow;,',...'i=i+1;,',...'if i>n,',...'m=m+1;,',...'i=1;,',...'end,',...'end,',...'end']);k2=uicontrol('parent',h0,...'style','pushbutton',...'position',[180 100 50 30],...'string','停止',...'callback',[...'k=0;,',...'set(e1,''string'',m),',...'p=get(h,''xdata'');,',...'q=get(h,''ydata'');,',...'set(e2,''string'',p);,',...'set(e3,''string'',q)']); k3=uicontrol('parent',h0,...'style','pushbutton',...'position',[280 100 50 30],...'string','关闭',...'callback','close');e1=uicontrol('parent',h0,...'style','edit',...'position',[60 30 60 20]);t1=uicontrol('parent',h0,...'style','text',...'string','循环次数',...'position',[60 50 60 20]);e2=uicontrol('parent',h0,...'style','edit',...'position',[180 30 50 20]);t2=uicontrol('parent',h0,...'style','text',...'string','终点的X坐标值',...'position',[155 50 100 20]);e3=uicontrol('parent',h0,...'style','edit',...'position',[300 30 50 20]);t3=uicontrol('parent',h0,...'style','text',...'string','终点的Y坐标值',...'position',[275 50 100 20]);实例33：曲线转换按钮h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例33');x=0:0.5:2*pi;y=sin(x);h=plot(x,y);grid onhuidiao=[...'if i==1,',...'i=0;,',...'y=cos(x);,',...'delete(h),',...'set(hm,''string'',''正弦函数''),',...'h=plot(x,y);,',...'grid on,',...'else if i==0,',...'i=1;,',...'y=sin(x);,',...'set(hm,''string'',''余弦函数''),',...'delete(h),',...'h=plot(x,y);,',...'grid on,',...'end,',...'end'];hm=uicontrol(gcf,'style','pushbutton',...'string','余弦函数',...'callback',huidiao);i=1;set(hm,'position',[250 20 60 20]);set(gca,'position',[0.2 0.2 0.6 0.6])title('按钮的使用')hold on实例34：栅格控制按钮h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例34');x=0:0.5:2*pi;y=sin(x);plot(x,y)huidiao1=[...'set(h_toggle2,''value'',0),',...'grid on,',...];huidiao2=[...'set(h_toggle1,''value'',0),',...'grid off,',...];h_toggle1=uicontrol(gcf,'style','togglebutton',...'string','grid on',...'value',0,...'position',[20 45 50 20],...'callback',huidiao1);h_toggle2=uicontrol(gcf,'style','togglebutton',...'string','grid off',...'value',0,...'position',[20 20 50 20],...'callback',huidiao2);set(gca,'position',[0.2 0.2 0.6 0.6])title('开关按钮的使用')实例35：编辑框的使用h0=figure('toolbar','none',...'position',[200 150 350 250],...'name','实例35');f='Please input the letter';huidiao1=[...'g=upper(f);,',...'set(h2_edit,''string'',g),',...];huidiao2=[...'g=lower(f);,',...'set(h2_edit,''string'',g),',...];h1_edit=uicontrol(gcf,'style','edit',...'position',[100 200 100 50],...'HorizontalAlignment','left',...'string','Please input the letter',...'callback','f=get(h1_edit,''string'');',...'background','w',...'max',5,...'min',1);h2_edit=uicontrol(gcf,'style','edit',...'HorizontalAlignment','left',...'position',[100 100 100 50],...'background','w',...'max',5,...'min',1);h1_button=uicontrol(gcf,'style','pushbutton',...'string','小写变大写',...'position',[100 45 100 20],...'callback',huidiao1);h2_button=uicontrol(gcf,'style','pushbutton',...'string','大写变小写',...'position',[100 20 100 20],...'callback',huidiao2);实例36：弹出式菜单h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例36');x=0:0.5:2*pi;y=sin(x);h=plot(x,y);grid onhm=uicontrol(gcf,'style','popupmenu',...'string',...'sin(x)|cos(x)|sin(x)+cos(x)|exp(-sin(x))',...'position',[250 20 50 20]);set(hm,'value',1)huidiao=[...'v=get(hm,''value'');,',...'switch v,',...'case 1,',...'delete(h),',...'y=sin(x);,',...'h=plot(x,y);,',...'grid on,',...'case 2,',...'delete(h),',...'y=cos(x);,',...'h=plot(x,y);,',...'grid on,',...'case 3,',...'delete(h),',...'y=sin(x)+cos(x);,',...'h=plot(x,y);,',...'grid on,',...'case 4,',...'delete(h),',...'y=exp(-sin(x));,',...'h=plot(x,y);,',...'grid on,',...'end'];set(hm,'callback',huidiao)set(gca,'position',[0.2 0.2 0.6 0.6]) title('弹出式菜单的使用')实例37：滑标的使用h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例37');[x,y]=meshgrid(-8:0.5:8);r=sqrt(x.^2+y.^2)+eps;z=sin(r)./r;h0=mesh(x,y,z);h1=axes('position',...[0.2 0.2 0.5 0.5],...'visible','off');htext=uicontrol(gcf,...'units','points',...'position',[20 30 45 15],...'string','brightness',...'style','text');hslider=uicontrol(gcf,...'units','points',...'position',[10 10 300 15],...'min',-1,...'max',1,...'style','slider',...'callback',...'brighten(get(hslider,''value''))'); 实例38：多选菜单h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例38');[x,y]=meshgrid(-8:0.5:8);r=sqrt(x.^2+y.^2)+eps;z=sin(r)./r;h0=mesh(x,y,z);hlist=uicontrol(gcf,'style','listbox',...'string','default|spring|summer|autumn|winter',...'max',5,...'min',1,...'position',[20 20 80 100],...'callback',[...'k=get(hlist,''value'');,',...'switch k,',...'case 1,',...'colormap default,',...'case 2,',...'colormap spring,',...'case 3,',...'colormap summer,',...'case 4,',...'colormap autumn,',...'case 5,',...'colormap winter,',...'end']);实例39：菜单控制的使用h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例39');x=0:0.5:2*pi;y=cos(x);h=plot(x,y);grid onset(gcf,'toolbar','none')hm=uimenu('label','example');huidiao1=[...'set(hm_gridon,''checked'',''on''),',...'set(hm_gridoff,''checked'',''off''),',...'grid on'];huidiao2=[...'set(hm_gridoff,''checked'',''on''),',...'set(hm_gridon,''checked'',''off''),',...'grid off'];hm_gridon=uimenu(hm,'label','grid on',...'checked','on',...'callback',huidiao1);hm_gridoff=uimenu(hm,'label','grid off',...'checked','off',...'callback',huidiao2);实例40：UIMENU菜单的应用h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例40');h1=uimenu(gcf,'label','函数');h11=uimenu(h1,'label','轮廓图',...'callback',[...'set(h31,''checked'',''on''),',...'set(h32,''checked'',''off''),',...'[x,y,z]=peaks;,',...'contour3(x,y,z,30)']);h12=uimenu(h1,'label','高斯分布',...'callback',[...'set(h31,''checked'',''on''),',...'set(h32,''checked'',''off''),',...'mesh(peaks);,',...'axis tight']);。

MATLAB的功能快速入门案例

第2讲MATLAB数学建模快速入门作者：卓金武, MathWorks 中国MATLAB功能很强大，但MATLAB上手却很容易，尤其是2013a以后的版本，使用起来更容易。

现在使用MATLAB的一个理念就是像Word一样去使用MATLAB。

本讲将通过一个实例介绍如何像Word一样去使用MATLAB，真正将MATLAB当工具来使用，即使对于从来没有用过MATLAB的模友来说，也可以轻松使用MATLAB。

2.1 MATLAB的功能如果想用MATLAB就要首先了解MATLAB具有哪些功能，图2-1是MATLAB家族产品的结构，包含了众多工具箱，所以其应用领域非常广泛。

在各行业和学术机构中，工程师和科学家使用MATLAB大大提高了他们的工作效率。

了解MATLAB具有哪些功能，就知道在什么情况下可以使用MATLAB, 纵观这幅图就可以知道，无论从事哪个行业，只要用到科学计算或工程设计，都可以使用MATLAB。

图2-1 MATLAB家族产品结构图2.2 快速入门案例MATLAB虽然也是一款程序开发工具，但依然是工具，所以它可以像其他工具（如Word）一样易用。

而传统的学习MATLAB方式一般是从学习MATLAB知识开始，比如MATLAB矩阵操作、绘图、数据类型、程序结构、数值计算等内容。

学这些知识的目地是能够将MATLAB 用起来，可是即便学完了，很多人还是不自信自己能独立、自如地使用MATLAB。

这是因为在我们学习这些知识的时候，目标是虚无的，不是具体的目标，具体的目标应该是要解决某一问题。

数模哥虽然已使用多年的MATLAB，但记住的MATLAB命令不超过20个，每次都靠几个常用的命令一步一步地实现各种项目。

所以说想使用MATLAB并需要那么多知识的积累，只要掌握住MATLAB的几个小技巧就可以了。

下面将通过一个小项目，带着大家如何一步一步用MATLAB解决一个实际问题，并假设我们都是MATLAB的门外汉（还不到菜鸟的水平）。

matlab简单函数实例

matlab简单函数实例Matlab是一种功能强大的数学软件，它提供了许多简单函数，方便用户进行各种数学计算和数据处理。

本文将以几个简单函数实例为主题，介绍Matlab中的一些常用函数的使用方法和实际应用。

一、rand函数rand函数是一个常用的随机数生成函数，它可以生成0到1之间的均匀分布的随机数。

我们可以使用rand函数来模拟抛硬币的实验，例如模拟投掷10次硬币，统计正面出现的次数。

首先，我们可以使用rand函数生成一个1x10的随机数矩阵，然后使用条件判断来统计正面出现的次数。

最后，我们可以将结果打印出来，以便查看统计结果。

二、max函数max函数是一个常用的求最大值的函数，它可以返回一组数据中的最大值。

我们可以使用max函数来求解一个数组中的最大值，并将结果打印出来。

例如，我们可以定义一个包含10个随机数的数组，然后使用max函数求解最大值。

三、min函数min函数是一个常用的求最小值的函数，它可以返回一组数据中的最小值。

我们可以使用min函数来求解一个数组中的最小值，并将结果打印出来。

例如，我们可以定义一个包含10个随机数的数组，然后使用min函数求解最小值。

四、sum函数sum函数是一个常用的求和函数，它可以返回一组数据的和。

我们可以使用sum函数来求解一个数组中所有元素的和，并将结果打印出来。

例如，我们可以定义一个包含10个随机数的数组，然后使用sum函数求解和。

五、mean函数mean函数是一个常用的求平均值函数，它可以返回一组数据的平均值。

我们可以使用mean函数来求解一个数组中所有元素的平均值，并将结果打印出来。

例如，我们可以定义一个包含10个随机数的数组，然后使用mean函数求解平均值。

六、std函数std函数是一个常用的求标准差函数，它可以返回一组数据的标准差。

标准差是描述一组数据的离散程度的指标，它越大表示数据的离散程度越大，越小表示数据的离散程度越小。

我们可以使用std 函数来求解一个数组中所有元素的标准差，并将结果打印出来。

matlab实例讲解欧拉法求解微分方程

欧拉法是数值分析中常用的一种方法，用于求解常微分方程的数值解。

在MATLAB中，可以通过编写相应的代码来实现欧拉法求解微分方程。

下面我们将通过具体的实例来讲解MATLAB中如何使用欧拉法求解微分方程。

我们要了解欧拉法的基本原理。

欧拉法是一种通过迭代逼近微分方程解的方法，它基于微分方程的定义，通过离散化的方法逼近微分方程的解。

其基本思想是利用微分方程的导数定义，将微分方程以差分形式进行逼近。

具体而言，欧拉法通过将微分方程转化为差分方程的形式，然后通过迭代逼近得到微分方程的数值解。

接下来，我们通过一个具体的实例来讲解MATLAB中如何使用欧拉法求解微分方程。

假设我们要求解以下的一阶常微分方程：(1) dy/dx = x + y(2) y(0) = 1现在我们来编写MATLAB代码来实现欧拉法求解这个微分方程。

我们需要确定微分方程的迭代步长和迭代范围。

假设我们将x的范围取为0到10，步长为0.1。

接下来，我们可以编写MATLAB代码如下：```matlab欧拉法求解微分方程 dy/dx = x + y定义迭代步长和范围h = 0.1;x = 0:h:10;初始化y值y = zeros(1,length(x));y(1) = 1;使用欧拉法迭代求解for i = 1:(length(x)-1)y(i+1) = y(i) + h * (x(i) + y(i));end绘制图像plot(x,y,'-o');xlabel('x');ylabel('y');title('欧拉法求解微分方程 dy/dx = x + y');```在这段MATLAB代码中，我们首先定义了迭代的步长和范围，并初始化了微分方程的初始值y(0) = 1。

然后通过for循环使用欧拉法进行迭代求解微分方程，最后绘制出了微分方程的数值解的图像。

通过以上的实例讲解，我们可以看到，在MATLAB中使用欧拉法求解微分方程是非常简单而直观的。

简单Matlab_GUI实例

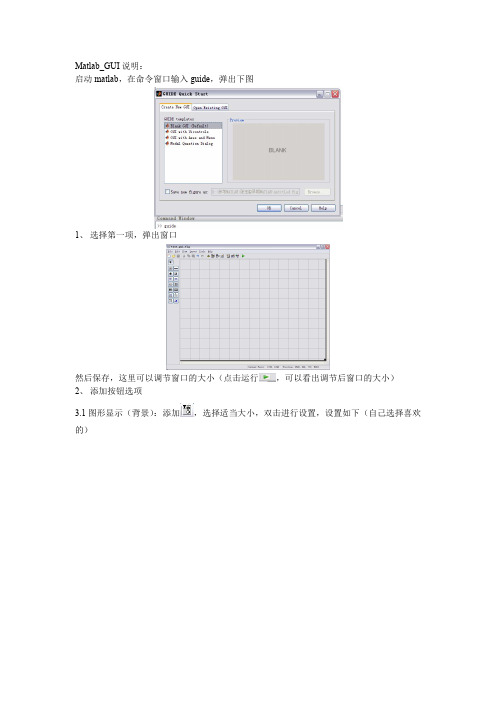
Matlab_GUI说明：
启动matlab，在命令窗口输入guide，弹出下图
1、选择第一项，弹出窗口
然后保存，这里可以调节窗口的大小（点击运行，可以看出调节后窗口的大小）
2、添加按钮选项
3.1图形显示（背景）：添加，选择适当大小，双击进行设置，设置如下（自己选择喜欢的）
3.2在背景中加入axis（），如下图（自己调节大小）
3.3加入按钮（所需）
本程序比较简单，所以按钮比较少
产生一线性调频信号：所需带宽B，脉宽tao，采样率fs等等静态按钮（）（带宽、脉宽………）
输入参数：
B的设置
Fs设置
以下都是一样的设置，这里特别注意Tag标签的使用，在以后加载程序时，Tag标签会让自己很明白这个代表什么物理量。

然后加入画图按钮：
这里添加一些附件功能
1）使得运行后窗口具有放大功能（tools-gui options）
选择
就Ok啦
2）添加图形放大、打印、等等按钮
选择tools-toolbar-edite，需要什么添加即可
完成后保存运行，附加功能出现
然后添加程序，这里找到那个m文件
我们从画图按钮开始（最后点画图，程序就开始执行）
这里从时域、频域开始
从tplot_callback,时画时域图
注意：在不同的按钮间相互调用，必须在程序间加global变量，这样下个按钮会认识到前个按钮所用变量。

如在fft_plot中用到tplot_callback中的t，我们在两个按钮间全加global t global t
详细看test.m
So easy吧！呵呵。

matlab程序设计实例解析

matlab程序设计实例解析MATLAB程序设计实例解析1.引言在本文档中，我们将详细分析几个MATLAB程序设计的实例，以帮助读者理解并掌握MATLAB的基本概念和应用。

每个实例都将包括程序代码、运行结果和解析过程。

2.实例一：________计算圆的面积2.1 实例描述本实例将演示如何使用MATLAB计算圆的面积。

给定圆的半径，程序将计算并输出圆的面积。

2.2 程序代码```% 计算圆的面积radius = input('请输入圆的半径：________'）area = pi radius^2。

disp('圆的面积为：________', num2str(area)）```2.3 运行结果及解析输入圆的半径为3，运行程序后，输出结果为：________```圆的面积为：________28.2743```程序中使用了`input`函数获取用户输入的半径值，并将其存储在变量`radius`中。

接着，通过`pi radius^2`计算圆的面积，并以字符串形式输出。

3.实例二：________矩阵相加3.1 实例描述本实例将演示如何使用MATLAB进行矩阵相加的运算。

给定两个矩阵，程序将计算并输出它们的和。

3.2 程序代码```% 矩阵相加matrix1 = 1, 2, 3。

4, 5, 6。

7, 8, 9。

matrix2 = 9, 8, 7。

6, 5, 4。

3, 2, 1。

sum_matrix = matrix1 + matrix2。

disp('两个矩阵的和为：________'）disp(sum_matrix）```3.3 运行结果及解析运行程序后，输出结果为：________```两个矩阵的和为：________10 10 1010 10 1010 10 10```程序中，我们事先定义了两个矩阵`matrix1`和`matrix2`。

通过`matrix1 + matrix2`进行矩阵相加运算，并将结果存储在变量`sum_matrix`中。

matlab 类的使用实例

Matlab是一种高级的技术计算语言和交互式环境，它可以进行各种科学计算、数据分析和可视化操作。

Matlab类的使用是Matlab开发中的重要组成部分，它可以帮助我们更好地组织和管理程序代码，提高代码的复用性和可维护性。

在本文中，我们将介绍Matlab类的基本概念和使用方法，并通过实例演示其在实际开发中的应用。

一、Matlab类的基本概念1.1 类和对象在面向对象的程序设计中，类是一种抽象的数据类型，它定义了一组属性和方法，用来描述某一类对象的共性特征。

对象则是类的实例，它包含了类定义的属性和方法，并可以进行相应的操作。

1.2 类的定义在Matlab中，可以使用关键字class来定义一个类，然后在类定义中添加属性和方法。

类的定义通常保存在以类名命名的.m文件中，类文件的文件名必须与类名一致。

1.3 类的继承Matlab支持类的继承机制，子类可以继承父类的属性和方法，并可以在此基础上进行扩展和重写。

继承可以帮助我们更好地组织和管理类，提高代码的复用性和可维护性。

1.4 类的实例化在Matlab中，可以使用构造函数来创建类的实例。

构造函数是一种特殊的方法，用来初始化类的实例，并可以接受参数进行定制化的初始化操作。

二、Matlab类的使用方法2.1 类的定义和属性定义一个简单的Matlab类，用来描述一个图形的基本属性和方法。

创建一个名为Shape的类，然后在类定义中添加属性和方法。

属性可以用来描述图形的颜色、形状等特征，方法可以用来计算图形的面积、周长等操作。

```matlabclassdef Shapepropertiescolorareaperimeterendmethodsfunction obj = Shape(color)obj.color = color;endfunction calculateArea(obj)计算图形的面积...endfunction calculatePerimeter(obj)计算图形的周长...endendend```2.2 类的继承和重写在上面的例子中，我们创建了一个基本的图形类Shape，现在我们需要创建一个具体的图形类，比如圆形类Circle。

关于matlab符号计算的综合实例

关于matlab符号计算的综合实例在科学计算领域，matlab是一种非常常用的软件工具，它具有强大的符号计算功能，可以对符号表达式进行求导、积分、解方程等操作，为科学研究和工程设计提供了便利。

本文将通过一些实例，介绍matlab符号计算功能的应用和操作技巧。

一、符号变量的定义和基本运算我们需要明白matlab中符号计算需要先定义符号变量。

在matlab中，可以使用syms命令定义符号变量，比如：syms x y这样就定义了两个符号变量x和y。

接下来，我们就可以进行基本的符号运算，比如加法、减法、乘法和除法，示例代码如下：1. 加法：z = x + y2. 减法：w = x - y3. 乘法：4. 除法：v = x / y通过这些简单的示例，我们可以看到，matlab对于符号变量的基本运算操作和数学运算规则是一致的，只是使用符号变量进行运算，可以得到符号表达式作为结果。

二、符号函数的求导和积分在科学计算中，求导和积分是非常常见的操作，matlab可以对符号函数进行求导和积分操作，示例代码如下：1. 求导：f = x^2 + 3*x + 2df = diff(f, x)2. 积分：F = int(f, x)通过这些示例，我们可以看到，matlab可以对符号函数进行求导和积分操作，并得到相应的结果。

这对于解决一些数学问题和工程问题非三、符号方程的求解在科学研究和工程设计中，经常会遇到需要求解符号方程的情况，matlab提供了符号求解方程的功能，示例代码如下：1. 求解一元方程：syms xeqn = x^2 - 4*x + 3 == 0;sol = solve(eqn, x)2. 求解多元方程：syms x yeqn1 = x + y == 3;eqn2 = x - y == 1;sol = solve([eqn1,eqn2],[x,y])通过这些示例，我们可以看到，matlab可以对符号方程进行求解，并得到相应的结果。

模糊控制在matlab中的实例

模糊控制在matlab中的实例以下是一个模糊控制在MATLAB中的简单实例：假设我们要设计一个模糊控制器来控制一个水箱中水位的高低。

我们可以先建立一个模糊推理系统，其中包含输入和输出变量以及规则。

1. 输入变量：水箱中的水位（假设范围为0到100）。

2. 输出变量：水泵的流量（假设范围为0到10）。

我们需要定义一组模糊规则，例如：如果水箱中的水位为低，则水泵的流量为低。

如果水箱中的水位为中等，则水泵的流量为中等。

如果水箱中的水位为高，则水泵的流量为高。

将这些规则转换成模糊集合，如下所示：输入变量：- 低：[0, 30]- 中等：[20, 50]- 高：[40, 100]输出变量：- 低：[0, 3]- 中等：[2, 6]- 高：[4, 10]接下来，我们可以使用MATLAB的Fuzzy Logic Toolbox来建立模糊推理系统。

以下是一个简单的MATLAB脚本：```% 定义输入变量water_level = fisvar("input", "Water Level", [0 100]); water_level.addmf("input", "low", "trapmf", [0 0 30 40]); water_level.addmf("input", "medium", "trimf", [20 50 80]);water_level.addmf("input", "high", "trapmf", [60 70 100 100]);% 定义输出变量pump_flow = fisvar("output", "Pump Flow", [0 10]);pump_flow.addmf("output", "low", "trapmf", [0 0 3 4]); pump_flow.addmf("output", "medium", "trimf", [2 6 8]); pump_flow.addmf("output", "high", "trapmf", [7 8 10 10]); % 建立模糊推理系统rule1 = "If Water Level is low then Pump Flow is low"; rule2 = "If Water Level is medium then Pump Flow is medium"; rule3 = "If Water Level is high then Pump Flow is high"; rules = char(rule1, rule2, rule3);fis = newfis("Water Tank Fuzzy Controller");fis = addvar(fis, water_level);fis = addvar(fis, pump_flow);fis = addrule(fis, rules);% 模糊控制器输入water_level_value = 70;% 运行模糊推理系统pump_flow_value = evalfis([water_level_value], fis);disp(["Water level: " num2str(water_level_value) "%"]); disp(["Pump flow: " num2str(pump_flow_value)]);```在这个简单的例子中，我们使用了Fuzzy Logic Toolbox来定义输入和输出变量以及规则，并运行模糊推理系统来计算输出值。

MATLAB游戏编程实例(拼图)

MATLAB游戏编程实例（拼图）这是一个简单的游戏，只要把数字按顺序排好就可以了。

游戏方法是用鼠标点中数字，如果该数字相邻的格子为空，则自动移到到该空格。

本程序是由realghost编写，如果有问题可以与联系。

附图如下：function pintu1()A = gen()G = [1 2 3;4 5 6;7 8 0];drawmap(A);while 1[xpos,ypos] = ginput(1);col = ceil(xpos);row = 3-ceil(ypos)+1;num = A(row,col);if row>1&A(row-1,col)==0A(row-1,col) = num;A(row,col) = 0;endif row<3&A(row+1,col)==0A(row+1,col) = num;A(row,col) = 0;endif col>1&A(row,col-1)==0A(row,col-1) = num;A(row,col) = 0;endif col<3&A(row,col+1)==0A(row,col+1) = num;A(row,col) = 0;enddrawmap(A)zt = abs(A-G);if sum(zt(:))==0msgbox('??ò??-3é1|?′o?í?￡?')breakendendfunction drawmap(A)clf;hold online([0 3],[0 0],'linewidth',4);line([3 3],[0 3],'linewidth',4);line([0 3],[3 3],'linewidth',4);line([0 0],[0 3],'linewidth',4);for i = 1:3for j = 1:3drawrect([j-1 3-i],[j 3-i],[j 3-i+1],[j-1 3-i+1],'y',A(i,j));endendaxis equalaxis offfunction drawrect(x1,x2,x3,x4,color,num)x = [x1(1) x2(1) x3(1) x4(1)];y = [x1(2) x2(2) x3(2) x4(2)];fill(x,y,color)if num==0text*(x1(1)+x2(1)),*(x1(2)+x4(2)),' ','fontsize',24)elsetext*(x1(1)+x2(1)),*(x1(2)+x4(2)),num2str(num),'fontsize',24)endfunction y = gen()y = inf*ones(1,9);for i = 1:9while 1a = randint(1,1,9);if isempty(find(y==a)) y(i) = a;breakendendendy = reshape(y,3,3);。

MATLAB综合应用实例分享与解析

MATLAB综合应用实例分享与解析近年来，作为一种功能强大且易于使用的科学计算软件，MATLAB在各个领域都有着广泛的应用。

它不仅可以进行数值计算、数据可视化和矩阵操作，还可以进行图像处理、机器学习、信号处理等复杂的科学研究。

本文将介绍几个MATLAB的综合应用实例，并对其实现原理进行解析，希望能够帮助读者更好地了解和使用MATLAB。

一、图像处理在图像处理领域，MATLAB具有强大的功能和丰富的工具箱。

下面以图像去噪和图像分割为例，介绍MATLAB在图像处理方面的应用。

1. 图像去噪图像去噪是图像处理的一项重要任务，可以提高图像的质量和清晰度。

MATLAB提供了一系列的去噪函数，其中最常用的是基于小波变换的方法。

首先，将图像进行小波分解得到各个频率分量，然后通过阈值处理将一些较小的分量置零，最后对处理后的分量进行小波逆变换得到去噪后的图像。

2. 图像分割图像分割是将图像划分为不同的区域或对象的过程，是图像分析和计算机视觉中的重要步骤。

MATLAB利用图像的灰度值、颜色信息或纹理特征等进行图像分割。

其中，最常用的方法是基于阈值的分割和基于区域的分割。

基于阈值的分割通过选择适当的阈值将图像转化为二值图像，而基于区域的分割则使用聚类分析或图割算法将图像划分为多个区域。

二、数值计算除了图像处理，MATLAB在数值计算方面也具有强大的功能。

下面以微分方程求解和曲线拟合为例，介绍MATLAB在数值计算方面的应用。

1. 微分方程求解微分方程是描述自然界中变化规律的重要数学工具，MATLAB提供了多种求解微分方程的函数。

对于常微分方程，可以使用ode45函数进行数值求解。

该函数通过自适应步长方法，将微分方程转化为差分方程，并使用龙格-库塔方法进行积分。

对于偏微分方程，可以使用pdepe函数进行求解。

该函数基于有限差分或有限元等方法，将偏微分方程转化为代数方程组，并通过迭代求解得到结果。

2. 曲线拟合曲线拟合是通过已知数据点来估计未知函数的方法，MATLAB提供了polyfit和lsqcurvefit等函数来进行曲线拟合。

Matlab简单实例学习

MATLAB程序设计及应用实例

MATLAB程序设计及应用实例

遗传算法的MATLAB程序实例讲解学习

matlab_简明实例教程__目录索引整理

matlab_简明实例教程

matlab龙格库塔法程序,给出实例

(整理)matlab实例教程-比较实用.

matlab简单实例

matlab gui界面设计实例

matlab编程实例100例(精编文档).doc

MATLAB的功能快速入门案例

matlab简单函数实例

matlab实例讲解欧拉法求解微分方程

简单Matlab_GUI实例

matlab程序设计实例解析

matlab 类的使用 实例

关于matlab符号计算的综合实例

模糊控制在matlab中的实例

MATLAB游戏编程实例(拼图)

MATLAB综合应用实例分享与解析

matlab 类的使用实例