三角函数求值的方法与技巧
(完整版)三角函数化简求值证明技巧
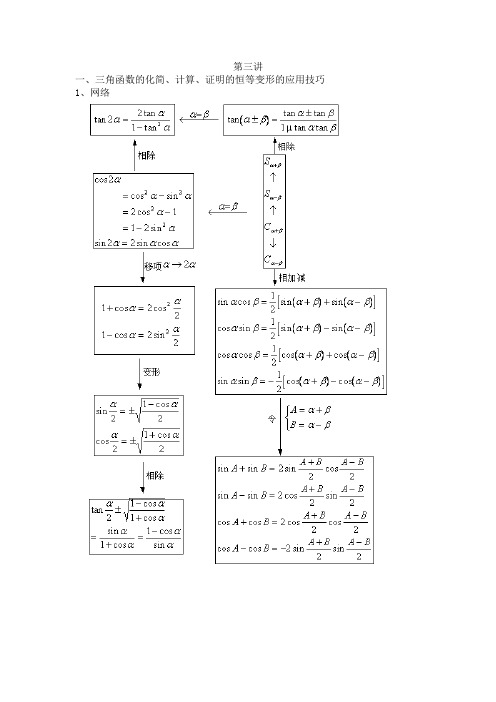
第三讲一、三角函数的化简、计算、证明的恒等变形的应用技巧1、网络2、三角函数变换的方法总结(1)变换函数名对于含同角的三角函数式,通常利用同角三角函数间的基本关系式及诱导公式,通过“切割化弦”,“切割互化”,“正余互化”等途径来减少或统一所需变换的式子中函数的种类,这就是变换函数名法.它实质上是“归一”思想,通过同一和化归以有利于问题的解决或发现解题途径。
【例1】已知θ同时满足和,且a、b 均不为0,求a、b的关系。
练习:已知sin(α+β)=,cos(α-β)=,求的值。
2)变换角的形式对于含不同角的三角函数式,通常利用各种角之间的数值关系,将它们互相表示,改变原角的形式,从而运用有关的公式进行变形,这种方法主要是角的拆变.它应用广泛,方式灵活,如α可变为(α+β)-β;2α可变为(α+β)+(α-β);2α-β可变为(α-β)+α;α/2可看作α/4的倍角;(45°+α)可看成(90°+2α)的半角等等。
【例2】求sin(θ+75°)+cos(θ+45°)-cos(θ+15°)的值。
练习已知,求的值【例3】已知sinα=Asin(α+β)(其中cosβ≠A),试证明:tan(α+β)=提示:sin[(α+β)-β]=Asin (α+β)(3)以式代值利用特殊角的三角函数值以及含有1的三角公式,将原式中的1或其他特殊值用式子代换,往往有助于问题得到简便地解决。
这其中以“1”的变换为最常见且最灵活。
“1”可以看作是sin2x+cos2x, sec2x-tan2x, csc2x -cot2x,tanxcotx, secxcosx, tan45°等,根据解题的需要,适时地将“1”作某种变形,常能获得较理想的解题方法。
【例4】化简:(4)和积互化积与和差的互化往往可以使问题得到解决,升幂和降次实际上就是和积互化的特殊情形。
这往往用到倍、半角公式。
三角函数化简求值的技巧

三角函数化简求值的技巧
一、三角函数的重要性质:
1、正弦函数sin x、余弦函数cos x、正切函数tanx和其逆函数的
关系:
sin x=1/cos x,cos x=1/sin x,tan x=1/cot x,cot x=1/tan x,cos x=1/csc x,csc x=1/cos x。
2、三角函数的基本性质:
sin2x+cos2x=1,sin2x=2sin(x/2)cos(x/2),cos2x=cos2(x/2)
-sin2(x/2),2sin xcos x=sin2x+cos2x=2sin2(x/2)=2cos2(x/2)。
3、三角函数的对称性:
sin(-x)=-sin x,cos(-x)=cos x,tan(-x)=-tan x,cot(-x)=-cot x,csc(-x)=-csc x。
二、用三角函数化简求值的常用方法:
1、用公式和定义:
用三角函数的基本公式来把表达式中的各个项拆分开明确每个项的意义,然后把各个项的值累加求值。
2、用对称性:
对变量进行绝对值化,然后利用三角函数的对称性变换变量或表达式,从而达到化简的目的。
3、用反函数求值:
把表达式中的三角函数换成其对应的反函数,然后利用反函数的性质进行化简,获得原函数的表达式。
四、利用三角函数化简求值的实例:
例1:求Sin(60°)
解:
1、用公式求值:
可以用公式sin 2x=2sin xcos x来求值。
三角函数化简求值的技巧

三角函数化简与求值常用技巧
三角函数在高考中通常以中低档题型出现,难度不大,但由 于三角公式的特殊性,解题中往往也涉及一些小的变换技 巧,如果处理得当,往往可以事半功倍,快速而准确地得到 正确结论.通常情况下,三角变换应从“角度、函数、常数、 次数、结构”等几方面着手解决.
一、三角变换,角为先锋 三角函数作为一种特殊函数,其“角”的特殊性不容忽视,因此我们在三角函数恒等变换 中,应该首先注意角的形式,从统一角的角度出发,往往能够达到事半功倍的效果.
【例 1】已 知α、 β为 锐角,cos α=
3 5
,tan (α−β)=−
1 3
,则
tan β=(
)
A、
1 3
B、 3
【变式演练】已知 sin
x-π
4
=3,则
sin
2x 的值为(
)
5
A.- 7 25
B. 7 25
C. 9 25
D.16 25
【解析】法一、sin 2x=cos(2x- π )=1-2sin2(x- π )=1-2×(3)2= 7 ,选 B.
2
4
5 25
法二、依题意得 2(sin x-cos x)=3,1(sin x-cos x)2= 9 ,1-sin 2x=18,sin 2x= 7 ,选
C、
9 13
D、
13 9
【例
1】已 知α、 β为 锐角,cos α=
3 5
,tan (α−β)=−
1 3
,则
tan β=(
)
A、
1 3
B、 3
C、
9 13
D、
13 9
【分析】依题意,可求得 tan α=
三角函数化简求值常用技巧

三角函数化简求值常用技巧三角函数式的化简和求值是高考考查的重点内容之一。
掌握化简和求值问题的解题规律和一些常用技巧,以优化我们的解题效果,做到事半功倍。
这也是解决三解函数问题的前提和出发点。
一、切割化弦例1、已知 )2(cot tan22≥=+m m x x ,求xx 4cos 14cos 3-+的值。
解: 24cos 14cos 34cos 1)4cos 3(24cos 12cos 444cos 1)2cos 1(484cos 12sin 48)4cos 1(812sin 2112sin 412sin 2112sin 41cos sin 2)cos (sin cos sin cos sin sin cos cos sin 2cot tan 2222222222222244222222m x x m x x x x x x x x x x x x x x x x x x x x x x x x x x x =-+∴=-+=-+=---=--=--=-=-+=+=+∴=+Θ 点评:由已知式与待求式的差异知,若选择“从已知到未知”,必定要“切切割化弦”;利用降幂公式实现已知与未知的统一。
二、统一配凑例2、已知2π<β<α<43π,cos(α-β)=1312,sin(α+β)=-53,求sin2α的值. 解:注意到2α= (α-β)+(α+β),于是可用配凑法求解。
∵2π<β<α<43π,∴0<α-β<4π.π<α+β<43π, ∴sin(α-β)=.54)(sin 1)cos(,135)(cos 122-=+--=+=--βαβαβα ∴sin2α=sin [(α-β)+(α+β)]=sin(α-β)cos(α+β)+cos(α-β)sin(α+β).6556)53(1312)54(135-=-⨯+-⨯=点评:本题以凑角的形式来实现未知与已知的统一,这是三角函数化简求值的常用技巧之一。
三、异角化同例3、已知cos(4π+x )=53,(1217π<x <47π),求x x x tan 1sin 22sin 2-+的值. 752853)54(257)4cos()4sin(2sin sin cos cos )cos (sin sin 2cos sin 1sin 2cos sin 2tan 1sin 22sin 54)4sin(,2435,471217.257)4(2cos 2sin ,53)4cos(:22=-⨯=++=-+=-+=-+-=+∴<+<∴<<=+-=∴=+x x x x x x x x x x x x x x x x x x x x x x x ππππππππππ又解Θ 点评:本题求解关键是将如何将已知条件中的角与目标关系式中的角统一起来。
三角函数求值的几种方法

三角函数求值的几种方法三角函数是数学中重要的一部分,它与圆的关系密切。
三角函数的求值是在给定一个角度时,计算其正弦、余弦、正切等函数值的过程。
本文将介绍三角函数求值的几种常见方法。
一、定义法三角函数的定义法是最基本的方法,它直接使用三角函数的定义公式进行计算。
例如,正弦函数的定义为sin(x) = b/c,其中b和c分别为角x所对应直角三角形的对边和斜边的长度。
通过观察角度对应的三角形特点,可以求出函数值。
二、图表法三角函数图表法是通过查阅三角函数表格,根据给定的角度,在表格中查找对应的函数值。
例如,可以查阅三角函数表格得到30°的正弦函数值为0.5三、计算器法计算器法是利用现代科技设备来进行三角函数求值的方法。
几乎所有的计算器都内置了三角函数求值功能,只需输入角度值,即可得到相应的函数值。
四、迭代法迭代法是一种数值计算方法,通过连续迭代计算来逼近精确解。
使用迭代法计算三角函数值时,可以使用泰勒级数展开式或欧拉公式来逼近函数值。
例如,sin(x)可以展开为无穷级数:sin(x) = x - x^3/3! +x^5/5! - x^7/7! + ...,通过截取有限项和进行计算,可以得到近似的函数值。
五、差值法差值法是一种数值逼近方法,通过已知点的函数值来估计其它点的函数值。
三角函数的差值法是利用已知的函数值,通过插值公式逼近所求函数值。
例如,当已知sin(30°) = 0.5,sin(45°) = 0.7071时,可以使用线性插值的方法来估计sin(40°)的值。
六、三角恒等式法三角函数有很多恒等式,可以用于简化三角函数的计算。
例如,利用和差角公式sin(x + y) = sin(x)cos(y) + cos(x)sin(y),可以将复杂角度的三角函数值转化为已知角度的三角函数值来计算。
总结:本文介绍了三角函数求值的几种常见方法,包括定义法、图表法、计算器法、迭代法、差值法和三角恒等式法。
三角函数解题技巧最实用的解题方法推荐

三角函数解题技巧最实用的解题方法推荐下面给大家介绍一下三角函数解题技巧,希望能够帮助到大家哦!三角函数解题技巧一、见“给角求值”问题,运用“新兴”诱导公式一步到位转换到区间(-90o,90o)的公式.1.sin(kπ α)=(-1)ksinα(k∈Z);2. cos(kπ α)=(-1)kcosα(k∈Z);3. tan(kπ α)=(-1)ktanα(k∈Z);4. cot(kπ α)=(-1)kcotα(k∈Z).二、见“sinα±cosα”问题,运用三角“八卦图”1.sinα cosα>0(或<0)óα的终边在直线y x=0的上方(或下方);2. sinα-cosα>0(或<0)óα的终边在直线y-x=0的上方(或下方);3.|sinα|>|cosα|óα的终边在Ⅱ、Ⅲ的区域内;4.|sinα|<|cosα|óα的终边在Ⅰ、Ⅳ区域内.三、见“知1求5”问题,造Rt△,用勾股定理:熟记常用勾股数(3,4,5),(5,12,13),(7,24,25),仍然注意“符号看象限”。
四、见“切割”问题,转换成“弦”的问题。
五、“见齐思弦”=>“化弦为一”已知tanα,求sinα与cosα的齐次式,有些整式情形还可以视其分母为1,转化为sin2α cos2α.六、见“正弦值或角的平方差”形式,启用“平方差”公式:1.sin(α β)sin(α-β)= sin2α-sin2β;2. cos(α β)cos(α-β)= cos2α-sin2β.七、见“sinα±cosα与sinαcosα”问题,用平方法则:(sinα±cosα)2=1±2sinαcosα=1±sin2α,故1.若sinα cosα=t,(且t2≤2),则2sinαcosα=t2-1=sin2α;2.若sinα-cosα=t,(且t2≤2),则2sinαcosα=1-t2=sin2α.八、见“tanα tanβ与tanαtanβ”问题,启用变形公式:tanα tanβ=tan(α β)(1-tanαtanβ).思考:tanα-tanβ=九、见三角函数“对称”问题,启用图象特征代数关系:(A≠0)1.函数y=Asin(wx φ)和函数y=Acos(wx φ)的图象,关于过最值点且平行于y轴的直线分别成轴对称;2.函数y=Asin(wx φ)和函数y=Acos(wx φ)的图象,关于其中间零点分别成中心对称;3.同样,利用图象也可以得到函数y=Atan(wx φ)和函数y=Acot(wx φ)的对称性质。
三角函数求值的八种常用方法

ʏ摆扬虎三角函数求值的常用方法有:巧用三角函数的定义,弦切互化,和积转换, 1 的变换,巧用三角公式,以及利用三角函数的图像等㊂下面举例分析,供同学们学习与参考㊂方法一:巧用三角函数的定义例1 已知角α的终边经过点(3,-4),则s i n α+1c o s α=㊂因为角α的终边经过点(3,-4),所以r =5㊂由三角函数的定义得s i n α=-45,c o s α=35,所以s i n α+1c o s α=-45+53=1315㊂评注:已知角α终边上一点P (x ,y ),且P (x ,y )不是单位圆上的点,可先求r =x 2+y 2,再求s i n α=y r ,c o s α=x r的值㊂方法二:巧用弦切互化例2 若s i n θ+2c o s θs i n θ-c o s θ=2,则s i n θ㊃c os θ=㊂由s i n θ+2c o s θs i n θ-c o s θ=2,整理可得t a n θ=4,所以s i n θc o s θ=s i n θc o s θs i n 2θ+c o s 2θ=t a n θ1+t a n 2θ=417㊂评注:解答本题的关键是利用公式t a n α=s i n αc o s α进行弦切互化㊂方法三:巧用和积转换例3 如果s i n x +c o s x =15,且0<x <π,那么ta n x 的值是㊂由已知等式两边平方得s i n x c o s x =-1225㊂因为0<x <π,所以s i n x >0,c o s x <0㊂结合s i n 2x +c o s 2x =1解得s i n x =45,c o s x =-35,所以t a n x =-43㊂评注:解答本题的关键是利用(s i n x ʃc o s x )2=1ʃ2s i n x c o s x 和s i n 2x +c o s 2x =1的关系进行变形和转化㊂方法四:巧用 1 的变换例4 化简s i n 2α+c o s 4α+s i n 2αc o s 2α的结果是㊂原式=s i n 2α+c o s 2α(c o s 2α+s i n 2α)=s i n 2α+c o s 2α=1㊂评注:解题时要灵活应用 1的变换,常见的 1 的变换有1=s i n 2θ+c o s 2θ=c o s 2θ㊃(1+t a n 2θ)=t a nπ4等㊂方法五:巧用诱导公式例5c o s (-585ʎ)s i n 495ʎ+s i n (-570)ʎ的值等于;s i n 585ʎc o s 1290ʎ+c o s (-30ʎ)s i n 210ʎ+t a n 135ʎ的值等于㊂结合诱导公式求值㊂原式=c o s (360ʎ+225ʎ)s i n (360ʎ+135ʎ)-s i n (360ʎ+210ʎ)=c o s (180ʎ+45ʎ)s i n (180ʎ-45ʎ)-s i n (180ʎ+30ʎ)=-c o s 45ʎs i n 45ʎ-(-s i n 30ʎ)=-2222+12=2-2㊂原式=s i n585ʎc o s1290ʎ+c o s30ʎ㊃s i n 210ʎ+t a n 135ʎ=s i n (360ʎ+225ʎ)c o s (3ˑ360ʎ+210ʎ)+c o s 30ʎs i n210ʎ+t a n (180ʎ-45ʎ)=s i n225ʎc o s 210ʎ+c o s 30ʎs i n210ʎ-t a n 45ʎ=s i n (180ʎ+45ʎ)c o s (180ʎ+30ʎ)+c o s 30ʎs i n (180ʎ+30ʎ)-t a n45ʎ=s i n45ʎ㊃c o s 30ʎ-c o s 30ʎs i n 30ʎ-t a n 45ʎ=22ˑ32-32ˑ12-1=6-3-44㊂评注:利用诱导公式求任意角的三角函数值的四个步骤: 负化正 ,即用三角公式转31知识结构与拓展高一数学 2022年12月Copyright ©博看网. All Rights Reserved.化; 大化小 ,即用三角公式将角化为0ʎ到360ʎ间的角; 小化锐 ,即用三角公式将大于90ʎ的角转化为锐角; 锐求值 ,即得到锐角三角函数后求值㊂方法六:巧用和差公式例6 若s i n 2α=55,s i n (β-α)=1010,且αɪπ4,π,βɪπ,3π2,则α+β的值是㊂因为αɪπ4,π,所以2αɪπ2,2π ㊂因为si n2α=55>0,所以2αɪπ2,π ,所以αɪπ4,π2 ,且c o s2α=-255㊂又因为s i n (β-α)=1010,βɪπ,3π2,所以β-αɪπ2,5π4,c o s (β-α)=-31010㊂故c o s (α+β)=c o s [(β-α)+2α]=c o s (β-α)c o s2α-s i n (β-α)s i n2α=-31010ˑ-255-1010ˑ55=22㊂又α+βɪ5π4,2π,所以α+β=7π4㊂评注:三角函数常见的角变换有:α=(α-β)+β,α=α+β2+α-β2,2α=(α+β)+(α-β),2β=(α+β)-(α-β)等㊂方法七:巧用倍角公式例7 已知函数f (x )=s i n2x -c o s 2x -23s i n x c o s x (x ɪR ),则f 2π3的值为㊂因为f (x )=s i n 2x -c o s 2x-23s i n x c o s x =-c o s 2x -3s i n 2x =-2s i n 2x +π6 ,所以f 2π3=-2s i n4π3+π6=-2s i n 3π2=2㊂评注:三角函数的角变换的常见公式有:1ʃs i n2α=s i n 2α+c o s 2αʃ2s i n αc o s α=(s i n αʃc o s α)2,1+c o s2α=2c o s 2α,1-c o s 2α=2s i n 2α,c o s 2α=1+c o s 2α2,s i n 2α=1-c o s 2α2等㊂方法八:巧用三角函数的图像例8 图1是函数f (x )=A s i n (ωx +φ)A >0,ω>0,|φ|<π2的图像的一部分,对任意的x 1,x 2ɪ[a ,b ],且x 1ʂx 2,若f (x 1)=f (x 2),都有f (x1+x 2)=1,则φ的值为( )㊂图1A .π12B .π6C .π4D .π3由图得A =2㊂由题意知x 1,x 2关于函数f (x )图像的对称轴对称,直线x =x 1+x 22是函数f (x )图像的一条对称轴,且fx 1+x 22=2,所以2s i n ω㊃x 1+x 22+φ =2,所以ωx 1+x22 +φ=π2+2k π(k ɪZ )㊂因为f (x 1+x 2)=1,所以2s i n [ω(x 1+x 2)+φ]=1,所以ω(x 1+x 2)+φ=π6+2k π(k ɪZ )或ω(x 1+x 2)+φ=5π6+2k π(k ɪZ )㊂令k =0,据上消去ω(x 1+x 2),可得φ=π6或φ=5π6㊂又因为|φ|<π2,所以φ=π6㊂应选B ㊂评注:解答本题的关键是熟练掌握正弦函数和余弦函数的图像与性质㊂作者单位:甘肃省临夏州积石山县积石中学(责任编辑 郭正华)41 知识结构与拓展 高一数学 2022年12月Copyright ©博看网. All Rights Reserved.。
高中数学:三角函数求值的方法

高中数学:三角函数求值的方法
1. 角的拼凑
适当地变化角的表达式,可以给三角函数求值带来便利。
如单角α可以看成角α+β与角β的差,也可以
看成角α-β与角β的和,既可以看成是的二倍,也可以看成是2α的一半。
角的分拆与配凑也是变角的常用策略。
如2α=(α+β)+(α-β),α-β=2α-(α+β)等。
当条件所给角都是非特殊角时,要仔细观察非特殊角与特殊角之间的联系,可通过三角公式转化为特殊角,并且消除非特殊角的三角函数值而得解。
例1. 已知,
,求cos(α+β)的值。
分析:所求余弦中的角与已知正、余弦中的角,其运算结构不同,所以要做角的拆拼,注意到。
解:因为,
所以,
于是
所以
从而
例2. 求的值。
分析:此题给出的是非特殊角,要设法把非特殊角化为特殊角,相互低消、约分求出值。
解:
2. 化弦(切)法
当已知的式子中切、割、弦混合时,从函数名称的角度去考虑,切割化弦是三角函数求值的常用方法。
例3. 求的值。
解:原式
3. 公式变形
对三角公式不仅要正用,还要注意逆用和变用,要熟悉公式的变形,只有这样才能全面掌握公式。
如
可变化为
特别地,若,有
可变形为;
例4. 化简
解:原式
例5. 化简
解:利用结论:若,得
原式
例6. 计算
解:原式
▍ ▍ ▍。
三角函数求值及角度方法(高考必考)

三角函数求值及求角的方法(高考必考)必背公式(一)、和角与差角公式:(1)、sin()sin cos cos sin αβαβαβ±=±;(2)、cos()cos cos sin sin αβαβαβ±= (3)tan (α±β)=tanα±tanβ1∓tanα∙tanβ(二)二倍角公式sin 22sin cos ααα=;22cos2cos sin ααα=-.=22cos1α- =212sin α- 22tan tan 21tan ααα=- (三)、诱导公式:(有分母且分母为2的,变函数名,符号看象限) 公式一:sin(2k π+α)=sin α,cos(2k π+α)=cosα 公式二:sin(-α)=−sinα,cos(-α)=cosα 公式三:sin(π+α)=−sinα,cos(π+α)=−cosα 公式四:sin(π-α)=sinα,cos(π-α)=−cosα. 公式五:sin(π2−α)=cosα,cos(π2−α)=sin α.公式六:sin (π2+α)=cosα,cos(π2+α)=-sin α.sin (3π2+α)=−cosα,cos(3π2+α)=sin α.公式同样适用正切:tan(π+α)=tanα,tan(π-α)=−tanα一、三角函数定义求:设点(),A x y 为角α终边上任意一点:sin yrα=,cos x r α=,tan y x α=(r =)1.(2015·福建)若sin α=-513,且α为第四象限角,则tan α的值等于( )A.125 B .-125 C.512 D .-5122、(2017.全国1,15)已知α∈(0,π2),tanα=2,则cos (α−π4)=___________3、 (2011·江西,14,易)已知角θ的顶点为坐标原点,始边为x 轴的正半轴. 若P (4,y )是角θ终边上一点,且sin θ=-255,则y =________.二、平方关系:1cos sin 22=+αα.2、 商数关系:αααcos sin tan = 例题:已知,计算: (1); (2)三、角度关系1、已知θ是第一象限角,且536cos =⎪⎭⎫ ⎝⎛+πθ,则θsin =2、(2018.全国2,15)已知tan(α−5π4)=15,则tan α=_________3tan =αααααsin 3cos 5cos 2sin 4+-2)cos (sin αα+3、已知sin(α+π12)=13,则cos(α+7π12)=________.4.设α为锐角,若cos(α+π6)=45,则sin(2α+π3)的值为()A. 1225B. 2425C. −2425D. −1225四、凑角1、设都是锐角,且55cos =α,()54cos -=+βα,则=βcos ( ) A 、2552 B 、552 C 、2552和552 D 、255和552、已知tan (α+β)=25,tanβ=13,则tan (α+π4)的值为___________五、倍角公式求值1、(2013·课标Ⅱ,6,易)已知sin 2α=23,则cos 2⎝⎛⎭⎪⎫α+π4=( ) A.16 B.13 C.12 D.232、(2017.全国三,4)已知sinα−cosα=43,则sin2α=___________六、求角:5、已知α,β都是锐角,若sinα=√55,sin β=√1010,则α+β等于=()A.π4B.3π4C.π4或3π4D.−π4或−3π46、(2012·全国卷)已知a ,b ,c 分别为△ABC 三个内角A ,B ,C 的对边, c =3a sin C -c cos A . 则A 等于 ___________练习:1.已知cos(α-π)=-513,且α是第四象限角,则sin α=( ) A .-1213 B.1213 C.512 D .±12132.已知sin(π+θ)=-3cos(2π-θ),|θ|<π2,则θ等于( )A .-π6 B.-π3 C.π6 D .π33、已知sin2α=13,则cos 2(α−π4)=A.-13B. 13C. 23D. −234.若cos(π8−α)=16,则cos(3π4+2α)的值为( ) A.1718B. −1718C.1819D. −18195.已知cos(23π−2θ)=−79,则sin(π6+θ)的值等于( ) A. 13B. ±13C. −19D. 197.(2016·全国2)△ABC 的内角A ,B ,C 的对边分别为a ,b ,c , 已知2cos C (a cos B +b cos A )=c .则C 等于_________8、(2014·天津)在△ABC 中,内角A ,B ,C 所对的边分别为a ,b ,c ,已知 a -c =66b ,sin B =6sin C .则cos A 的值为__________。
三角函数的条件求值

三角函数的条件求值
方案一:从角度之间的关系寻求突破。
三角函数求值题往往从角度之间的关系入手,可以从给定角度的特殊关系中找到突破口。
然后可以用三角函数的归纳法公式和变换公式求解,三角函数值已知的“角”和三角函数公式中的“角”往往通过“变角”和“拼角”的方式转换成同一个角。
方案二:从功能关系上寻求突破。
在三角函数中,两个基本类别是“截”和“串”。
解题时注意“串”“切”思路的运用。
方案三:从结构特征上寻求突破。
观察问题条件和待解公式的结构特征,或者角点的结构特征,从这些特征中寻求突破,进行三角恒等式变换,然后进行求值。
三角函数求值要注意以下几点:
1.利用同角三角函数关系和归纳法公式进行简化和求值。
证明时要仔细观察题目的特点,注意培养观察问题、分析问题的能力,注意解题后的总结,如“切弦”、“巧代1”、sinxcosx、sinx-cosx、sinx cosx三个公式之间的关系等。
2.在遇到问题时注意对角度、函数名及其整体结构的分析,注意公式选择的恰当性,有利于缩短运算程序,提高解题效率。
3.已知一个角度的三角函数值,计算该角度的其他三角函数值时,要注意中间角度的范围,针对不同的象限计算相应的值。
4.注意公式的变形和使用,弦切交替,三角代换和消去,这些都是三角变换的重要方法。
要尽量减少平方根运算,谨慎确定符号。
5.注意变换,体现了化未知为已知的思想方法,是解决三角形中角度变换问题的常用数学方法之一。
1。
三角函数给角求值

三⾓函数给⾓求值前⾔三⾓函数中的给⾓求值类问题,⼤多给定的是分式形式,或者可以化为分式形式的,⽐如含有弦和切,当切化弦后就变成了分式;并且这类题⽬往往需要将⾮特殊⾓拆分,然后最后⼀步约掉含有⾮特殊⾓的代数式,就得到了最终的值。
注意⾼频变形:分式约分,和加减抵消;相关变形切化弦[整式变分式],1的代换,分式通分约分,根式升幂;配⽅展开,提取公因式,公式的逆⽤,变⽤,常⽤的互余、互补代换:sin70^{\circ}=cos20^{\circ},cos40^{\circ}=sin50^{\circ};sin140^{\circ}=sin40^{\circ},cos110^{\circ}=-sin70^{\circ}=-cos20^{\circ};常见的⾓的拆分:47^{\circ}=17^{\circ}+30^{\circ};8^{\circ}=15^{\circ}-7^{\circ};1+sin\theta+cos\theta=(1+cos\theta)+sin\theta=2cos^2\cfrac{\theta}{2}+2sin\cfrac{\theta}{2}cos\cfrac{\theta}{2}1+sin\theta-cos\theta=(1-cos\theta)+sin\theta=2sin^2\cfrac{\theta}{2}+2sin\cfrac{\theta}{2}cos\cfrac{\theta}{2}常见的互余,倍⾓等(\cfrac{\pi}{4}+\theta)+(\cfrac{\pi}{4}-\theta)=\cfrac{\pi}{2};(\cfrac{\pi}{3}+\theta)+(\cfrac{\pi}{6}-\theta)=\cfrac{\pi}{2};2x\pm\cfrac{\pi}{2}=2(x\pm\cfrac{\pi}{4});2\alpha\pm\cfrac{\pi}{3}=2(\alpha\pm\cfrac{\pi}{6});常见的配⾓技巧:2\alpha=(\alpha+\beta)+(\alpha-\beta);2\beta=(\alpha+\beta)-(\alpha-\beta);3\alpha-\beta=2(\alpha-\beta)+(\alpha-\beta);3\alpha+\beta=2(\alpha+\beta)+(\alpha-\beta);\alpha=(\alpha+\beta)-\beta;\beta=\alpha-(\alpha-\beta);\alpha=\cfrac{\alpha+\beta}{2}+\cfrac{\alpha-\beta}{2};\beta=\cfrac{\alpha+\beta}{2}-\cfrac{\alpha-\beta}{2};\alpha=(\alpha+\beta)-\beta;(\cfrac{\pi}{6}-\alpha)+(\cfrac{\pi}{3}+\alpha)=\cfrac{\pi}{2};(\cfrac{\pi}{4}-\alpha)+(\cfrac{\pi}{4}+\alpha)=\cfrac{\pi}{2};(\cfrac{\pi}{3}-\alpha)+(\cfrac{2\pi}{3}+\alpha)=\pi;(\cfrac{\pi}{4}-\alpha)+(\cfrac{3\pi}{4}+\alpha)=\pi;难点变形常涉及“切化弦”,“分式通分”,“辅助⾓公式”等⾼频变形;\tan\theta-\sqrt{3}=\cfrac{\sin\theta}{\cos\theta}-\cfrac{\sqrt{3}\cos\theta}{\cos\theta}=\cfrac{2(\sin\theta\cdot \cfrac{1}{2}-\cos\theta\cdot\cfrac{\sqrt{3}}{2})}{\ cos\theta}1+\sqrt{3}\tan\theta=\cfrac{\cos\theta}{\cos\theta}+\cfrac{\sqrt{3}\sin\theta}{\cos\theta}=\cfrac{\cos\theta+\sqrt{3}\sin\theta}{\cos\theta}=\cfrac{2(\cos\theta\cd ot \cfrac{1}{2}+\sin\theta\cdot\cfrac{\sqrt{3}}{2})}{\cos\theta}注:在具体题⽬中,⾓\theta可以是具体的值,⽐如\tan12^{\circ}-\sqrt{3},或1+\sqrt{3}\tan21^{\circ}典例剖析№1求值:\cfrac{cos85^{\circ}+sin25^{\circ}cos30^{\circ}}{cos25^{\circ}}分析:这类题⽬往往需要将⾮特殊⾓拆分,然后约掉含有⾮特殊⾓的代数式,就得到了最终的值。
三角函数解题技巧

三角函数是中考必不可少的的考点,也是初中数学学习的重难点。
下面小编整理了三角函数解题技巧,赶快收藏吧!数学三角函数解题方法1.直接法顾名思义,就是直接进行正确的运算和公式变形,结合已知条件,得到正确的答案。
三角函数中大量的题型都是根据该方法求值解答的,它要求我们对三角函数的基本公式要牢牢掌握。
2.换元法换元法就是用一个量替代另一个量,发现题设中(隐含)条件,进行带式替换,从而将三角函数求值转变成代数式求值。
3.比例法对三角等式变形,找出与之有关的函数值,利用比例性质,对三角函数值进行计算。
三角函数解题思路求三角函数值的问题,可依循三种途径:1、先化简再求值,将式子化成能够利用题设已知条件的最简形式;2、从已知条件出发,选择合适的三角公式进行变换,推出要求式的值;3、将已知条件与求值式同时化简再求值。
三角函数公式特殊三角度数的特殊值sin30°=1/2sin45°=√2/2sin60°=√3/2cos30°=√3/2cos45°=√2/2cos60°=1/2tan30°=√3/3tan45°=1tan60°=√3cot30°=√3cot45°=1cot60°=√3/3两角和公式sin(A+B)=sinAcosB+cosAsinBsin(A-B)=sinAcosB-sinBcosAcos(A+B)=cosAcosB-sinAsinBcos(A-B)=cosAcosB+sinAsinBtan(A+B)=(tanA+tanB)/(1-tanAtanB)tan(A-B)=(tanA-tanB)/(1+tanAtanB)ctg(A+B)=(ctgActgB-1)/(ctgB+ctgA)ctg(A-B)=(ctgActgB+1)/(ctgB-ctgA)半角公式sin(A/2)=√((1-cosA)/2)sin(A/2)=-√((1-cosA)/2) cos(A/2)=√((1+cosA)/2)cos(A/2)=-√((1+cosA)/2 tan(A/2)=√((1-cosA)/((1+cosA))tan(A/2)=-√((1-cosA)/((1+cosA))ctg(A/2)=√((1+cosA)/((1-cosA))ctg(A/2)=-√((1+cosA)/((1-cosA))和差化积公式2sinAcosB=sin(A+B)+sin(A-B)2cosAsinB=sin(A+B)-sin(A-B)2cosAcosB=cos(A+B)-sin(A-B)-2sinAsinB=cos(A+B)-cos(A-B)sinA+sinB=2sin((A+B)/2)cos((A-B)/2 cosA+cosB=2cos((A+B)/2)sin((A-B)/2) tanA+tanB=sin(A+B)/cosAcosBtanA-tanB=sin(A-B)/cosAcosB锐角三角函数公式sinα=∠α的对边/斜边cosα=∠α的邻边/斜边tanα=∠α的对边/∠α的邻边cotα=∠α的邻边/∠α的对边倍角公式Sin2A=2SinA.CosACos2A=CosA^2-SinA^2=1-2SinA^2=2CosA^2-1 tan2A=(2tanA)/(1-tanA^2)(注:SinA^2是sinA的平方sin2(A))。
三角函数解题技巧和公式(已整理)

浅论关于三角函数的几种解题技巧本人在十多年的职中数学教学实践中.面对三角函数内容的相关教学时.积累了一些解题方面的处理技巧以及心得、体会。
下面尝试进行探讨一下:一、关于)2sin (cos sin cos sin ααααα或与±的关系的推广应用:1、由于ααααααααcos sin 21cos sin 2cos sin )cos (sin 222±=±+=±故知道)cos (sin αα±.必可推出)2sin (cos sin ααα或.例如: 例1 已知θθθθ33cos sin ,33cos sin -=-求。
分析:由于)cos cos sin )(sin cos (sin cos sin 2233θθθθθθθθ++-=-]cos sin 3)cos )[(sin cos (sin 2θθθθθθ+--=其中.θθcos sin -已知.只要求出θθcos sin 即可.此题是典型的知sin θ-cos θ.求sin θcos θ的题型。
解:∵θθθθcos sin 21)cos (sin 2-=-故:31cos sin 31)33(cos sin 212=⇒==-θθθθ ]cos sin 3)cos )[(sin cos (sin cos sin 233θθθθθθθθ+--=- 3943133]313)33[(332=⨯=⨯+=2、关于tg θ+ctg θ与sin θ±cos θ.sin θcos θ的关系应用:由于tg θ+ctg θ=θθθθθθθθθθcos sin 1cos sin cos sin sin cos cos sin 22=+=+ 故:tg θ+ctg θ.θθcos sin ±.sin θcos θ三者中知其一可推出其余式子的值。
例2 若sin θ+cos θ=m 2.且tg θ+ctg θ=n.则m 2 n 的关系为( )。
三角函数求值怎么计算公式

三角函数求值怎么计算公式三角函数是数学中重要的一部分,它在数学和物理学中都有着广泛的应用。
三角函数包括正弦函数、余弦函数、正切函数等,它们可以用来描述角度和长度之间的关系,解决各种问题。
在实际应用中,我们经常需要用三角函数来求值,下面将介绍三角函数求值的计算公式。
1. 正弦函数的求值公式。
正弦函数的求值公式为,sin(θ) = 对边/斜边。
其中,θ为角度,对边指的是角度对应的直角三角形中与该角度相对的边的长度,斜边指的是直角三角形的斜边长度。
举个例子,如果要求sin(30°)的值,可以先构造一个30°的直角三角形,然后根据公式sin(30°) = 对边/斜边,计算出对边和斜边的比值,从而求得sin(30°)的值。
2. 余弦函数的求值公式。
余弦函数的求值公式为,cos(θ) = 邻边/斜边。
其中,θ为角度,邻边指的是角度对应的直角三角形中与该角度相邻的边的长度,斜边指的是直角三角形的斜边长度。
举个例子,如果要求cos(45°)的值,可以先构造一个45°的直角三角形,然后根据公式cos(45°) = 邻边/斜边,计算出邻边和斜边的比值,从而求得cos(45°)的值。
3. 正切函数的求值公式。
正切函数的求值公式为,tan(θ) = 对边/邻边。
其中,θ为角度,对边指的是角度对应的直角三角形中与该角度相对的边的长度,邻边指的是角度对应的直角三角形中与该角度相邻的边的长度。
举个例子,如果要求tan(60°)的值,可以先构造一个60°的直角三角形,然后根据公式tan(60°) = 对边/邻边,计算出对边和邻边的比值,从而求得tan(60°)的值。
除了以上三种常见的三角函数,还有其它一些三角函数,如余切函数、正割函数和余割函数等,它们的求值公式也可以类似地通过构造直角三角形来求得。
在实际应用中,三角函数的求值可以帮助我们解决各种问题,比如在工程中用来计算力的方向和大小、在天文学中用来计算星体的位置和运动轨迹等。
高中数学:三角函数中的参数求值或求范围问题

高中数学:三角函数中的参数求值或求范围问题
1、等式恒成立型
这一类型包括奇偶性概率、周期性概念、存在性问题三种,解决方法有一般定义法或先用特值求解再进行证明两个思路。
例1、若是奇函数,求θ的值。
若是偶函数呢?
解法1 定义法:因为是奇函数,所以对恒成立,即恒成立,所以为所求。
解法2 特值法:因为是奇函数,所以f(0)=0,得,故,此时,而,故为所求。
解法3:因为是奇函数,所以对恒成立,即恒成立,进而恒成立,所以,即为所求。
2、不等式恒成立型
这类问题的理论依据是:若将含参数t的关于x的不等式分离,通过求g(x)的最值,再求t的取值范围。
(1);
(2)。
例2、已知函数恒成立,求实数a的范围。
解析:,
由,由对。
3、函数最值型
此类问题主要是分离变量转换为求函数值域或者转换为二次函数分类讨论求最值。
例3:若函数的最小值是-6,求实数a的值。
解析:令。
(1)上递增,所以,得a=-7。
(2)当时,g(t)在[-1,1]上递减,所以,得a=7;
(3)当时,g(t)在递增。
所以,舍去;综上所述,得。
热文推荐:
下酒菜排名,第一名实至名归,不流口水就服你!最好看的青春校园小说小故事,噗的笑出来
矮个子女生穿衣搭配宝典,穿出大长腿!
矮个子女生显瘦重要,还是显高更重要?
男生学生党穿衣服搭配青春显活力
十二星座谁爱吃飞醋
汽车保养周期表,强烈建议收藏!
你孤单吗?
英语作文万能模板!轻松获取高分秘籍!
成熟不是年龄,而是一种境界。
