2020年高职自主招生考试数学试卷A套
2020年贵州省高职(专科)分类招生中职生文化综合考试试卷—数学解析

2020年贵州省高职(专科)分类招生中职生文化综合考试 (数学真题解析、另有视频讲解,解析原创作者:范玉柏)一、单项选择题(本题共有20小题,每小题3分,共60分)51.设集合A={1,3,4,5},B={2,3,4,5},则A ∪B =( ).A.{1}B.{2}C.{3,4,5}D.{1,2,3,4,5} 解析:本题考核内容是集合的基本运算——并集。
A ∪B 表示并集,就是“取集合A 和集合B 的所有元素,重复的元素只取一次”,正确答案为D.[扩展]如果是A ∩B=( ),求交集,则“取A 、B 共有元素”,结果为{3,4,5}; 如果U={1,2,3,4,5},则C U A=( ) ,求补集,表示“U 中所有不属于A 的元素组成的集合”,即集合U 中去掉集合A 中所有元素后的剩余元素,则为{2}.52.若f(x)=1-2x ,则f(-1) =( ).A.3B.-3C.1D.-1解析:本题考核内容是函数解析式的理解与应用。
给出函数解析式,将自变量x 的值代入,就可求出函数值. 题中“f(-1)”表示当x=-1时,求函数值. 把x=-1代入解析式求出函数值,即:f(-1)=1-2 (-1)=1+2 = 3,正确答案为A.53.函数y=-x+3的图像不经过...( ). A.第一象限 B.第二象限 C.第三象限 D.第四象限解析:本题考核内容是一次函数图像。
一次函数斜率k 决定函数图像方向,斜率k 与y 轴上的截距b 共同决定函数图像要经过的象限。
当k>0函数图像过一、三象限(如b>0过一二三象限,如b<0过一三四象限);当k<0函数图像过二、四象限(如b>0过一二四象限,如b<0过二三四象限)。
本题k=-1,b=3,即k<0且b>0图像过一二四象限,不过第三象限,故正确答案为C. 54.等差数列3,8,13,18,……的第10项是( ).A.38B.48C.58D.68解析:本题考核内容是等差数列通项公式。
2020年云南省高等职业技术教育招生考试数学试题

2020年云南省高等职业技术教育招生考试试题数 学本试题纸共3页,满分100分。
考试时间120分钟注意事项1.答卷前,考生务必用黑色碳素笔将自己的姓名、准考证号、考场号、座位号填写在答题卡上,并认真核准条形码上的准考证号、姓名、考场号、座位号及科目,在规定的位置贴好条形码。
2.作答时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交一、单项选择题(本大题共20小题,每小题2分,满分40分。
在每小题给出的四个选项中选出一项符合题目要求的)1、若实数a ,b 在数轴上的位置如右图所示,则化简=--2a b a 。
A. b -B. b a -2C. bD. b a +22、已知两数的和为6,这两个数的差的绝对值为8,那么以这两个数为根的一元二次方程是 。
A. 0862=+-x xB. 0762=--x xC. 0862=-+x xD. 0762=++x x3、已知命题甲:”“3>x ,命题乙”“3>x ,那么命题甲是乙的 。
A. 充分不必要条件 B. 必要不充分条件C. 充分必要条件D. 既不充分也不必要条件4、若5654-->a a ,则a 的取值范围是 。
A. 10<<aB.0>aC.1>aD.1<a5、函数43)1ln(2+--+=x x x y 的定义域为 。
A. )(1,4--B. ]1,4-(C. )(1,1-D.]1,1-( 6、已知213)12(+=-x x f ,则=)32(f 。
A. 5 B. 3 C. 1 D.21 7、设集合},10{R x x x M ∈<<=,},2{R x x x N ∈<=则下面选项中,正确的是 。
A. M N M =B. N N M =C. M N M =D. R N M =8、一钟(表)的时针经过40分钟所转过的角度是 。
A. 34πB. 34π-C. 9πD. 9π-9、已知ABC ∆中,125tan -=A ,则=A cos 。
2020年浙江省新高考改革单独考试招生文化考试数学试题(含参考答案)

A.0
B.√2
C.2
6.直线 x = √3的倾斜角为( )
D. 2√2
A.0°
B.30°
C. 60°
7.角 α 的终边上有一点 P(12,-5)则 sinα =( )
D. 90°
A.- 5
12
5 B.
12
5 C.
13
8.双曲线 x2 − y2 = 1 与直线 x - y = 1 交点的个数为( )
D. - 5
A.-2
B.-1Βιβλιοθήκη C.1D.220.设直线 y = x + m 与曲线 x2 + y2 = 1(x≥0)有公共点,则实数 m 的取值范围是 ( )
A.[-√2 , √2]
B.[ -1 , 1]
C.[-1 , √2]
D.[-√2 , 1]
二、填空题(本大题共 7 个小题,每小题 4 分,共 28 分) x2 + 1,x<2
B.第二象限
C.第三象限
D.第四象限
13.已知点 A(3,-4),B(7,6),则线段 AB 的中点坐标为( )
A.(5,1) B.(2,5)
C.(10,2)
D.(4,10)
14.若函数 y = x2 + kx +1 的图像与 x 轴没有交点,则 k 的取值范围是。( )
A.(2,+∞)
B. (-∞,-2)
1
25. 函数( 2x2 - ) 6 展开式中第 2 项的系数为
x
26. 如右图图所示,某几何体由正四棱锥和正方体构成,正四棱锥
侧棱长为√3,正方体棱长为 1,则 PB = 2
27.
已知双曲线
x2 a2
-
2020年贵州省高职(专科)分类招生中职生文化综合考试试卷—数学解析

2020年贵州省高职(专科)分类招生中职生文化综合考试 (数学真题解析、另有视频讲解,解析原创作者:范玉柏)一、单项选择题(本题共有20小题,每小题3分,共60分)51.设集合A={1,3,4,5},B={2,3,4,5},则A ∪B =( ).A.{1}B.{2}C.{3,4,5}D.{1,2,3,4,5} 解析:本题考核内容是集合的基本运算——并集。
A ∪B 表示并集,就是“取集合A 和集合B 的所有元素,重复的元素只取一次”,正确答案为D.[扩展]如果是A ∩B=( ),求交集,则“取A 、B 共有元素”,结果为{3,4,5}; 如果U={1,2,3,4,5},则C U A=( ) ,求补集,表示“U 中所有不属于A 的元素组成的集合”,即集合U 中去掉集合A 中所有元素后的剩余元素,则为{2}.52.若f(x)=1-2x ,则f(-1) =( ).A.3B.-3C.1D.-1解析:本题考核内容是函数解析式的理解与应用。
给出函数解析式,将自变量x 的值代入,就可求出函数值. 题中“f(-1)”表示当x=-1时,求函数值. 把x=-1代入解析式求出函数值,即:f(-1)=1-2 (-1)=1+2 = 3,正确答案为A.53.函数y=-x+3的图像不经过...( ). A.第一象限 B.第二象限 C.第三象限 D.第四象限解析:本题考核内容是一次函数图像。
一次函数斜率k 决定函数图像方向,斜率k 与y 轴上的截距b 共同决定函数图像要经过的象限。
当k>0函数图像过一、三象限(如b>0过一二三象限,如b<0过一三四象限);当k<0函数图像过二、四象限(如b>0过一二四象限,如b<0过二三四象限)。
本题k=-1,b=3,即k<0且b>0图像过一二四象限,不过第三象限,故正确答案为C. 54.等差数列3,8,13,18,……的第10项是( ).A.38B.48C.58D.68解析:本题考核内容是等差数列通项公式。
2020年浙江省“三位一体”自主招生数学测试试卷(72)(有答案解析)
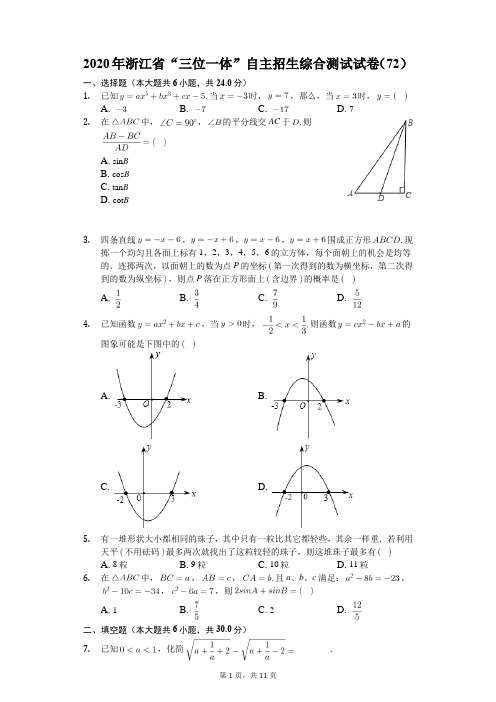
2020年浙江省“三位一体”自主招生综合测试试卷(72)一、选择题(本大题共6小题,共24.0分)1.已知当时,,那么,当时,A. B. C. D. 72.在中,,的平分线交AC于则A. sin BB. cos BC. tan BD. cot B3.四条直线,,,围成正方形现掷一个均匀且各面上标有1,2,3,4,5,6的立方体,每个面朝上的机会是均等的.连掷两次,以面朝上的数为点P的坐标第一次得到的数为横坐标,第二次得到的数为纵坐标,则点P落在正方形面上含边界的概率是A. B. C. D.4.已知函数,当时,则函数的图象可能是下图中的A. B.C. D.5.有一堆形状大小都相同的珠子,其中只有一粒比其它都轻些,其余一样重.若利用天平不用砝码最多两次就找出了这粒较轻的珠子,则这堆珠子最多有A. 8粒B. 9粒C. 10粒D. 11粒6.在中,,,且a、b、c满足:,,,则A. 1B.C. 2D.二、填空题(本大题共6小题,共30.0分)7.已知,化简______ .8.若关于x的方程有四个不同的解,则k的取值范围是______ .9.对于大于或等于2的自然数m的n次幂进行如下方式的“分裂”:仿上,的“分裂”中最大的数是______,若的“分裂”中最小数是21,则______.10.已知,则______.11.如图,在中,,为AB上一点,以O为圆心,OB为半径的圆交BC于D,且与AC相切.则D到AC的距离为______ .12.在十进制的十位数中,被9整除并且各位数字都是0或5的数有______个.三、计算题(本大题共1小题,共11.0分)13.甲,乙两辆汽车同时从同一地点A出发,沿同一方向直线行驶,每辆车最多只能带240L汽油,途中不能再加油,每升油可使一辆车前进12km,两车都必须沿原路返回出发点,但是两车相互可借用对方的油.请你设计一种方案,使其中一辆车尽可能地远离出发地点A,并求出这辆车一共行驶了多少千米?四、解答题(本大题共5小题,共55.0分)14.用1,2,3三个数字组成六位数,若每个数字用两次,相邻位不允许用相同的数字.试写出四个符合上述条件的六位数;请你计算出符合上述条件的六位数共有多少个?15.已知关于x的方程:有一个增根为b,另一根为二次函数与x轴交于P和Q两点.在此二次函数的图象上求一点M,使得面积最大.16.如图,已知锐角的外心为O,线段OA和BC的中点分别为点M,若,求的大小.17.已知实数a,b,c满足:,又,为方程的两个实根,试求的值.18.如图,已知菱形ABCD,,内一点M满足,若直线BA与CM交于点P,直线BC与AM交于点Q,求证:P,D,Q三点共线.答案和解析1.【答案】C【解析】解:把,代入得:,即把代入得:故选C.把代入解得,把当成一个整体代入后面式子即可解答.能够根据指数的意义发现代数式之间的关系,然后整体代值计算.2.【答案】A【解析】【分析】此题主要考查角平分线的性质和三角函数的定义.根据角平分线上的任意一点到角的两边距离相等计算.【解答】解:过点D作于E.则.可证≌,.,又,,,.故选A.3.【答案】D【解析】解:连掷两次,以面朝上的数为点P的坐标第一次得到的数为横坐标,第二次得到的数为纵坐标,共种;符合题意的有:共15个,概率是.故选:D.首先确定点P的坐标,根据这个坐标可求出点P落在正方形面上含边界的概率.本题将概率的求解设置于点P的坐标中,考查学生对简单几何概型的掌握情况,既避免了单纯依靠公式机械计算的做法,又体现了数学知识在现实生活、甚至娱乐中的运用,体现了数学学科的基础性.用到的知识点为:概率所求情况数与总情况数之比.4.【答案】A【解析】解:因为函数,当时,所以可判断,可知,所以可知,,则,不妨设则函数为函数即则可判断与x轴的交点坐标是,,故选A.当时,,所以可判断,可知,,所以可知,,则,不妨设进而得出解析式,找出符合要求的答案.要考查了从图象上把握有用的条件,准确选择数量关系解得a,b,c的值.从条件可判断出,可知,;所以可知,,,从而可判断后一个函数图象.5.【答案】B【解析】解:这堆珠子最多有9个.将这堆珠子平均分成3组,将其中的两组放在天平的两边进行第一次测量;若天平平衡,那么较轻的珠子在没称的那堆珠子里;若天平不平衡,那么较轻的珠子就在较轻的那堆珠子里;然后将较轻的那堆珠子进行第二次测量,同第一次测量一样,将其中两个放在天平的两端;若天平平衡,那么没称的珠子就是所找的珠子;若天平不平衡,那么较轻的珠子就是所找的珠子.因此最多用两次即可找出较轻的珠子.故选B.已知最多两次就找出这粒较轻的珠子,那么第二次所测的珠子的个数最多为3个;即将其中的两个放在天平的两边,若天平平衡,那么不在天平中的珠子就是最轻的珠子,如果天平不平衡,很较轻的珠子就是所找的珠子.同理,在第一次测量中,最多可测出三组珠子,因此这堆珠子最多有9个.本题的解答关键是找出每次能测量出的珠子堆的最多的个堆数.6.【答案】C【解析】解:,,,,,,,,,这个三角形的形状是直角三角形,,故选:C.利用完全平方公式把这个式子写成平方几个非负数的和的形式,求得a,b,c的值,进而判断出三角形的形状即可.再运用三角函数定义求解即可.本题考查完全平方公式和勾股定理的逆定理在实际中的运用,注意运用几个非负数的和为0,那么这几个数均为0这个知识点是解题关键.7.【答案】【解析】解:,,原式.因为,,又,所以,即.注意当时,.8.【答案】【解析】解:关于x的方程有四个不同的解,,即,解得或,而时,的值不可能等于0,所以.故填空答案:.因为关于x的方程有四个不同的解,所以,即,解得或;又因为方程中一次项中未知数带着绝对值符号,一次项的系数不能为正数,否则等式不成立.所以当时,不符合题意,故取.本题考查了一元二次方程根的判别式的应用,也涉及了绝对值方程的应用,同时注意通过根与系数的关系求出的k值一定要代入到原方程检验,把不符合题意的值舍去.本题最后舍去是最容易出错的地方,要求具有严谨的数学思维.9.【答案】9 5【解析】解:中,最大数是;若的“分裂”中最小数是21,则,或负数舍去.根据所给的数据,不难发现:在中所分解的最大的数是;在中,所分解的最小数是根据发现的规律,则中,最大数是;若的“分裂”中最小数是21,则,或负数舍去.此题首先要根据所提供的数据具体发现规律,然后根据发现的规律求解.规律为:在中所分解的最大的数是;在中,所分解的最小数是.10.【答案】0【解析】解:,,即,整理得,.本题不应考虑直接求出与的值,而应根据已知等式的特点,用配方法进行求解.本题考查了完全平方公式,根据式子特点,等式两边都减去,转化为完全平方式是解题的关键.11.【答案】15【解析】解:连接OD、OE,则;,;,,;;因此OE即为所求的D到AC的距离.,,解得:.故D到AC的距离为15.设AC与的切点为E,连接OE、OD;在等腰和等腰中,可求得,由此可证得;由于AC与相切,所以,那么OE即为所求的D到AC的距离.在中,已知了斜边OA的长和的正弦值,即可求出OE的长.本题考查了切线的性质、等腰三角形的性质、平行线的判定、正弦的概念等知识的综合应用能力.12.【答案】9【解析】解:只能出现0或5,因此必须有9个5,0不能出现在首位,因此共有9个.故答案为9.被9整除的数,数字和一定是9的倍数.只能出现0或5,因此必须有9个5,0不能出现在首位,因此共有9个.解决本题的关键是得到被9整除的十位数的特点.13.【答案】解:设尽可能远离A地的甲汽车共走了x千米,乙汽车共走了y千米,则,且所以x最大为4320千米.设从A到尽可能的离A的距离是m千米,其中借给对方油的那辆车走了n千米后停下,那么千米那么需要用油升,那么就是走这个最远距离一次单趟需要120升油,那么可得出的方案是:甲,乙共同走720千米,乙停下等甲,并且给甲60升汽油,甲再走1440千米后回头与乙会合,乙再给甲60升汽油后,两车同时回到A地.也可画图表示为:如右图.【解析】本题中由于两车相互借对方的油,那么他们所走的距离和,他们所走的距离差由此可得出自变量的取值范围.如果要让一辆车尽可能的远离A地并同时返回,那么就必须让一辆车行驶一段后,把油给对方要刚好留下回A地的油,让对方走掉加的这些油后开始向A地返回,两者碰头后一起回A地.那么这个离A地最远的距离就应该是车行驶一段的距离停下后给对方的油量可行驶的距离要留下回A地的油根据此关系可求出走这个最远距离所需的油量,然后进行分配即可.本题考查一元一次不等式的应用,将现实生活中的事件与数学思想联系起来,读懂题列出不等式关系式即可求解.14.【答案】解:以1开头的数有等10个数;,131232,123123,123132,121323,121332,132123,132132,123213,132312,213123,213132,312123,312132,212313,213213,312312,313212,213231,312321,231213,231312,321213,321312,231231,231321,321231,321321,232131,323121则共30个符合条件的六位数.【解析】为了让相邻位不允许用相同的数字,可以依次对1、2、3进行排列.如123123,132132等;根据要求,先确定1的位置,再依次确定2,3的位置,从而求解.解决问题的关键是读懂题意,要特别注意:相邻位不允许用相同的数字.15.【答案】解:由题意可得,代入方程得.二次函数为与x轴的交点为,,当点M的横坐标为或或时,的面积可能取最大,经比较可得时,的面积取最大,此时即点,.【解析】方程可化简为方程只有时才有增根,可推出;将代入方程得即,再根据a的值求出c并确定解析式,再根据顶点坐标公式和x的取值范围确定面积最大时M点的坐标.学会巧妙地利用分式方程的性质来解决问题,同时要明确增根问题可按如下步骤进行:确定增根;化分式方程为整式方程;把增根代入整式方程即可求得相关字母的值.16.【答案】解:设,则,;,,,为等腰三角形,;,,.【解析】设,则,根据三角形的外心到三角形三个顶点的距离相等,得根据等腰三角形的三线合一和等边对等角的性质和三角形的内角和定理,分别表示出和,进一步计算出发现等腰三角形则ON是OB的一半,根据直角三角形的性质可以求得度.再求得的大小.综合运用了等腰三角形和直角三角形的性质.要熟练掌握三角形和圆的有关性质才能灵活解题.17.【答案】解:,,,2ab为方程的二根,,由得,或把两组值代入原方程得到的方程相同.即,.【解析】把,2ab分别看作一个整体,利用一元二次方程根与系数的关系解答则可.本题考查了一元二次方程根与系数的关系,将根与系数的关系与代数式变形相结合解题是一种经常使用的解题方法.18.【答案】证明:连接PD,DQ,由已知,,∽,∽.,.,又.,又,∽,.,,D,Q三点共线.【解析】求证:P,D,Q 三点共线就是证明平角的问题,可以求证,根据∽,∽,可以得出;进而证明∽,得出,则结论可证.本题是证明三点共线的问题,这类题目可以转化为求证平角的问题.并且本题利用相似三角形的性质,对应角相等.第11页,共11页。
2020年四川数学单招真题-答案

四川省2020年普通高等学校高职教育单独招生文化考试(中职类)㊃数学参考答案及评分标准一㊁单项选择题:本大题共10小题,每小题5分,共50分.1.B2.C3.C4.D5.C6.D7.A8.B9.A 10.D二㊁填空题:本大题共3小题,每小题4分,共12分.11.81 12.30 13.2三㊁解答题:本大题共3小题,第14小题12分,第15㊁16小题各13分,共38分.14.(Ⅰ)a +2b =(2,-3)+(6,4)=(8,1),(3分) b -a =(3,2)-(2,-3)=(1,5).(6分) (Ⅱ)因为a ㊃b =2ˑ3+(-3)ˑ2=0,(9分) 所以a ʅb .(12分) 15.(Ⅰ)已知在әP A C 中,P A =P C ,O 为A C 的中点,所以P O ʅA C .(2分) 又因为平面P A C ʅ底面A B C D ,A C 为平面P A C 和底面A B C D 的交线,所以P O ʅ底面A B C D .(5分) (Ⅱ)已知底面A B C D 是正方形,所以A B ʅB C ,A B =B C .在等腰直角әA B C 中,A C =A B 2+B C 2=2,所以A B =B C =1,正方形A B C D 的面积S A B C D =1.(8分)已知O 为A C 的中点,所以A O =12A C =22,在直角әP A O 中,P O =P A 2-A O 2=62.(11分) 由(Ⅰ)可知P O ʅ底面A B C D ,所以四梭锥P A B C D 的体积V P A B C D =13㊃P O ㊃S A B C D =66.(13分) 16.(Ⅰ)由双曲线C 的一个顶点为(4,0),可知a =4.又由渐近线方程为y =ʃ34x ,可知b a =34,b =3.(4分) 所以双曲线C 的标准方程为x 216-y 29=1.(6分)(Ⅱ)由点A (8,m )在双曲线C 上,可知8216-m 29=1,解之得m 2=27.(8分)双曲线C 的半焦距c =a 2+b 2=42+32=5,所以右焦点的坐标为(5,0).(10分)点A 到双曲线C 右焦点的距离为(8-5)2+(m -0)2=32+m 2=6.(13分)。
四川省2020年普通高等学校高职单独招生文化考试(中职类)数学真题及参考答案

高职草招文化考试(中职类)•数学 第1页共4页机老★启用前□ □□□□□□□□□^w iH r 四川省2020年普通高等学校高职教育单独招生文化考试(中职类) 7.设-b 均为大于0且不等于1的常救.ISttBS 数几rr”与gW 二/銅一宜介坐标系 中的大蚀象如图所示.则下册论lEtttfjft 注意事项: 1.2. 3. 文化考试时间150分珞 满分300分(语文、数学、英语各100分〉. 文化考试包括语文、数学、英语三个部分,每部分分为第I 卷和第(1卷.第I 卷为选择SL 第II 卷为非选择题•选择题部分,考生必须使用2B 铅笔,在答題卡上填涂,答在试卷、草稿址上无效, 4・非选择题部分,考生必须使用蓝色或黑色字巡的钢笔或签字笔,在指定位置作答;答在指 定位置以外的地方无效,数学第I 卷(共50分) 一、单项选择锤本大題共10小題,每小题5分,共50分.在每小题歹魅的四个备送项中,只有 —T 是符合題目更求的,请将其选岀.错迄 多这或未选均无分. 1.函数©X 丄的定义域足x-3 A. {x|x 芒2} B. {x\x^3} C ・{x|x>2} D ・{x\x>3} 2.已知集合* = {1,0}, 3={-ba},且40 W 则2A. -2B. 0C. 1 D ・23・已知log 』= 3, 9Ab =A. 2B. 6 C ・ 8 D. 9 4.不等式|“1|>2的解集为A. [-3J] C. (-3.1) 在寻杀数列{%}中,4=1, a 厂5,则心= A. 5B. 7 C ・ 9 D. 11 为了得到函数j = 2sinx 的图象.只需把函数尸5iru 的图象上所有点的 横坐标缩短到原来的*倍,纵坐标不变横坐标伸阍原来的2傢纵坐标不变纵坐标缩•短到原来的+借,横坐标不变 D. 纵坐标伸K 到原来的2倍.横坐标不变B.+D ・(Y,二 3)U (l ,+ 8) 5. 6. A. B. C. B. 7 A ・ a">l B. h>a>] C. l>d>6>0 D. l>fr>a>0 8•从4名女同学和2名男同学中任选2人多!B 志愿者活动・即庭中的2人部是女同学的擬率 为 A •+ B.彳 C ・ g D.- 5 5 5 5 9・已知〉=/("是定义在R 上的奇函敢.U 当*>0时.则/(T )二 人7 B.・2 C ・: D. 4 10・MC 的内角A. B. C 的对边分划为<J , b ・c.巳知血4丄cosB = —. “2・ 2 2 A ¥ B.呼 a Z D.M 第II 卷(共50分) 总分 题号 第II 卷 二 三 核分人 @分 12 W 复ffA 得分 得分 评卷人 复音人 二、淇颈:本大孰共3小題,再小题4分,共12分.请在毎 小题的空格中滇上正确答灵・钳填、不填均无分. 在茅比数列他}中.a 严1.冷=3,則比・__. 12臬中学高一年级学生人数为700.高二年级学生人数为他 高三年级学生人数为600.现 学校决定采用分层抽样的方法.从这三个年级抽取100名学生进行学习储汎调玄.则应从 盲三年级枫的学生人数为_. 13.已知直线"血・3 = 0与岡(才-1卄八2相交于八点.膛眼肿的眩为 矗醍单招文化考试(屮职类)•数学第2页共4贞三、Mfix本大题共3小题,第14小题12分,第15、16得分评坯人复査人小誣各13分,共38分.解答应葛岀文字说明、证明过程或演算步毀・14. 已知向ftd = (2.-3). 6=(3.2).(I)求向fta + 2*和向t»-a的坐标;(D)判断liJttd与D是否垂直・15. 如图,在四校锥P-MCD屮■底面肋CD为正方影.平IftiPACL JU而朋CD.PA = PC = AC^, 0为“的中点.(I)证明:P0丄底面ABCD;(U)求四艇tPTBCD的体积・高职单招文化考试(中职类)•数学笫3页共4页16. 已知双曲线C:^--^ = l(a>0,6>0)的T頂点为(4,0),渐近线方程为y=±-x. (C b 4⑴求双曲线C的标准方程;(D)设点d(8,m)为双曲线C上的T•点.求点到双曲技C右集点的距离.高职单招文化考试(中取类)•数学第4页共4页★居用前 ttffi ★ E 用后5年四川笞2020年普通高等学校高职教用单独招生 文化考试(中职类)・数学参考答案及评分标准 iMH 如亂'本無件恰出广忡解比•供总与.如泉步供的解汝与本解芥不词•斫根常试憊的卞熒质 柯懈比贰用分标准購幼世的漳分细対1 mm.当牲的解答伍某甘H 诚体巩时.m 頫催協分的解林改变该总的内 和帰度.可乂瞬的颐蚯册郁加胎分,但不刃fiu 跖盼册解粉劇数的•性 如航财分的解料较产細顽・则不im3,解存右启所壮分股.衣尿勺生正确畑这亠步应诩的JK 加分St< HfftKft 分arrJKftim 空思不恰中何分一・型顶选HHK :本大JS 共m 小1L 15小廉5分.共50分.I. I)2. C3. C 4 D 5. C 6 I) 7. A 8. li 9. A 10. D本大题共3小18.聖14小題12分.第15、16小12ft 13分・共38分. (3分)b a -(3t2)-(2t-3)*(h5). .......................... ••“(6 分) (Il )闵为・ 6• 2x3+(-3)x2* 0 ・……luu,M, (9分) 所LL 丄从 • (12 分) |,・(J)已知屮.PA^PC. O^JAC 的屮点,所以HUM. 乂因为申而MC1底面ABCD. JC 为甲面PAC^^ABCDtfi 交线. 所以 PO1JH taABCD ・— ................... (II )已知庇而価加£正方形・ 衍以APLBC ・AB ・BC AC =応TH 』. 听以 (2分) (8分) 1E 方比MCD 的面枳S*R C 知。
2020年高职自主招生考试数学试卷A套

职业学院2020年自主招生数学试卷(第一套)单项选择题(每题2分,共20题,共计40分。
下列备选答案中,只有一个正确答案,请将答案写在下表中)1. 1-14 的倒数为( ). A. 54 B. 45 C. 45- D. 43-2. 把多项式分解因式,结果正确的是( ).A .B .C .D .3. 点(0,2)A -与点(6,0)B 之间的距离为( ).A. 4B. 6C. 8D.4. 下列结论正确的是( ).A. 一个数的相反数一定是负数B. 一个数的绝对值一定不是负数2288x x -+()224x -()224x -()222x -()222x +C. 一个数的绝对值一定是正数D. 一个数的相反数一定是正数5. 直线35y x =+的斜率为( ).A .2B .3C .5D .86. 一个正方形的边长增加了cm 2,面积相应增加了232cm ,则这个正方形的边长为( ).A. 6cmB. 5cmC. 8cmD. 7cm7. 设集合{0},{1},A x x B x x A B =>=≤=I 则交集( ).A. {01}x x ≤<B. {01}x x <≤C. {0}x x <D. {1}x x >8. 下列表格列出了一项实验的统计数据,表示皮球从高度d 落下时,弹跳高度b 与下落高度d 的关系,试问下面的哪个式子能表示这种关系(单位cm )( ).A. 2d b =B. d b 2=C. 25+=d bD. 2d b = 9. 若分式12x x -+的值为零,则x 的值是( ).A .0B .1C .D .10. 把弯曲的河道改直,能够缩短船舶航行的路程,这样做的道理是( ). A. 垂线段最短 B. 两点确定一条直线 C. 两点之间,直线最短 D. 两点之间,线段最短11. 在函数1y x =-中,自变量x 的取值范围是( ). A. 3x > B. 31x x <≠且 C. 3x ≥ D. 31x x ≤≠且12. 小明每秒钟跑6米,小彬每秒钟跑5米,小彬站在小明前10米处,两人同时起跑,小明多少秒钟追上小彬( ).A. 5秒B. 6秒C. 8秒D. 10秒13. 现有两根木棒,它们的长分别是40cm 和50cm ,若要钉成一个三角形木架,则在下列四根木棒中应选取( ) .A .10cm 的木棒B .40cm 的木棒C .90cm 的木棒D .100cm 的木棒14. 已知函数2()1f x x =+,那么(1)f a +的值为( ).A. 22a a ++B. 21a +C. 222a a ++D. 221a a ++15. 与b a 2是同类项的是 ( ).A. a b 2B. bc a 2C. 522ba - D. 2)(ab16. 下列图形中,既是中心对称图形又是轴对称图形的是( ).A. 平行四边形B. 等边三角形 C. 等腰梯形 D. 圆17. 已知2253x y xy x y +=-=+=,,则( ).A. 25B. 25-C. 19D. 19-18. 若,a b 均为正数,,c d 均为负数,则下列式子中值最大的是( ).A . ()a b c d -+-B . ()a c b d --+C . ()a b c d --+D . ()a b c d +-+ 19. 下列各组数中,值相等的是( ).A. 32与23B. 32-与3)2(-C. 2)3(-与)3(2-D. 2×32与(2×3)220. 如图所示,直线AB 、CD 相交于O ,OD 平分∠BOE ,∠AOC=42°, 则∠AOE 的度数为( ).A. 126°B. 96°C. 102°D. 138°OEDCBA。
自主招生考试数学试卷及参考答案

自主招生考试数学试卷及参考答案(总9页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--22第2自主招生考试 数学试题卷亲爱的同学:欢迎你参加考试!考试中请注意以下几点:1.全卷共三大题,满分120分,考试时间为100分钟。
2.全卷由试题卷和答题卷两部分组成。
试题的答案必须做在答题卷的相应位置上。
做在试题卷上无效。
3.请用钢笔或圆珠笔在答题卷密封区上填写学校、姓名、试场号和准考证号,请勿遗漏。
4.答题过程不准使用计算器。
祝你成功!一、选择题(本题共6小题,每小题5分,共30分.在每小题的四个选项中,只有一个符合题目要求)1.如果一直角三角形的三边为a 、b 、c ,∠B=90°,那么关于x 的方程a(x 2-1)-2cx+b(x 2+1)=0的根的情况为A 有两个相等的实数根B 有两个不相等的实数根C 没有实数根D 无法确定根的情况2.如图,P P P 123、、是双曲线上的三点,过这三点分别作y 轴的垂线,得三个三角形P A O P A O P A O 112233、、,设它们的面积分别是S S S 123、、,则 A S S S 123<< B S S S 213<< C S S S 132<<D S S S 123==3.如图,以BC 为直径,在半径为2圆心角为900的扇形内作半圆,交弦AB 于点D ,连接CD ,则阴影部分的面积是33第5A π-1B π-2C 121-πD 221-π4.由325x y a x y a x y a m-=+⎧⎪+=⎪⎨>⎪⎪>⎩得a>-3,则m 的取值范围是A m>-3B m ≥-3C m ≤-3D m<-3 5.如图,矩形ABCG (AB <BC )与矩形CDEF 全等,点B 、C 、D 在同一条直线上,APE ∠的顶点P 在线段BD 上移动,使APE ∠为直角的点P 的个数是 A 0 B 1 C 2 D 36.已知抛物线y=ax 2+2ax+4(0<a<3),A (x 1,y 1)B(x 2,y 2)是抛物线上两点,若x 1<x 2,且x 1+x 2=1-a,则A y 1< y 2B y 1= y 2C y 1> y 2D y 1与y 2的大小不能确定二、填空题(本题共6小题,每小题5分,共30分.把答案填写在题中横线上)7. 二次函数y =ax 2+(a -b )x —b 的图象如图所示,44那么化简222||a ab b b -+-的结果是______▲________.8. 如图所示,在正方形 ABCD 中,AO ⊥BD 、OE 、FG 、HI 都垂直于 AD ,EF 、GH 、IJ 都垂直于AO ,若已知 S ΔA JI =1, 则S 正方形ABCD = ▲9.将一个棱长为8、各个面上均涂有颜色的正方体,锯成64个同样大小的小正方体,其中所有恰有2面涂有颜色的小正方体表面积之和为 ▲ 10.用黑白两种颜色正方形的纸片按黑色纸片数逐渐加l 的规律拼成一列图案:(1)第4个图案中有白色纸片 ▲ 张 (2)第n 个图案中有白色纸片 ▲ 张(3)从第1个图案到第100个图案,总共有白色纸片 ▲ 张第10题 第7题第8题5511.如图所示,线段AB 与CD 都是⊙O 中的弦,其中108,,36,O O AB AB a CD CD b ====,则⊙O 的半径R= ▲12.阅读下列证明过程: 已知,如图四边形ABCD 中,AB =DC ,AC =BD ,AD ≠BC ,求证:四边形ABCD 是等腰梯形.读后完成下列各小题.(1)证明过程是否有错误?如有,错在第几步上,答: ▲ . (2)作DE ∥AB 的目的是: ▲ .(3) 判断四边形ABED 为平行四边形的依据是: ▲ . (4)判断四边形ABCD 是等腰梯形的依据是 ▲ .(5)若题设中没有AD ≠BC ,那么四边形ABCD 一定是等腰梯形吗为什么 答 ▲ .自主招生考试第11题第12题66数学标准答案一、选择题(本题共6小题,每小题5分,共30分.在每小题的四个选项中,只有一个符合题目要求)二、填空题(本题共6小题,每小题5分,共30分.把答案填写在题中横线上)7. ______-1__________ 8. 256 9. 57610.(1) 13 (2) 3n+1 (3) 15250 11. a b12.(1)没有错误 (2)为了证明AD ∥BC(3) 一组对边平行且相等的四边形是平行四边形(4)梯形及等腰梯形的定义 (5) 不一定,因为当AD =BC 时,四边形ABCD 是矩形 三、解答题(本题共5小题,共60分.解答应写出必要的计算过程、推演步骤或文字说明)13.(本小题10分)某公园门票每张10元,只供一次使用,考虑到人们的不同需求,也为了吸引更多游客,该公园除保留原有的售票方法外,还推出一种“购个人年票”的售票方法(个人年票从购买之日起,可供持票者使用一年)。
2020年自主招生数学试题及解答

2020年自主招生数学试题及解答1.(仅文科做)02απ<<,求证:sin tan ααα<<. 【解析】 不妨设()sin f x x x =-,则(0)0f =,且当02x π<<时,()1cos 0f x x '=->.于是()f x 在02x π<<上单调增.∴()(0)0f x f >=.即有sin x x >. 同理可证()tan 0g x x x =->.(0)0g =,当02x π<<时,21()10cos g x x '=->.于是()g x 在02x π<<上单调增。
∴在02x π<<上有()(0)0g x g >=。
即tan x x >。
注记:也可用三角函数线的方法求解.2.AB 为边长为1的正五边形边上的点.证明:AB(25分) 【解析】 以正五边形一条边上的中点为原点,此边所在的直线为x 轴,建立如图所示的平面直角坐标系.⑴当,A B 中有一点位于P 点时,知另一点位于1R 或者2R 时有最大值为1PR ;当有一点位于O 点时,1max AB OP PR =<;⑵当,A B 均不在y 轴上时,知,A B 必在y 轴的异侧方可能取到最大值(否则取A 点关于y 轴的对称点A ',有AB A B '<).不妨设A 位于线段2OR 上(由正五边形的中心对称性,知这样的假设是合理的),则使AB 最大的B 点必位于线段PQ 上.且当B 从P 向Q 移动时,AB 先减小后增大,于是max AB AP AQ =或;对于线段PQ 上任意一点B ,都有2BR BA ≥.于是22max AB R P R Q == 由⑴,⑵知2max AB R P =.不妨设为x .下面研究正五边形对角线的长.IHG F E 1111x x-1如右图.做EFG ∠的角平分线FH 交EG 于H . 易知5EFH HFG GFI IGF FGH π∠=∠=∠=∠=∠=. 于是四边形HGIF 为平行四边形.∴1HG =. 由角平分线定理知111EFEH x FG x HG ===-.解得x =3.AB 为21y x =-上在y 轴两侧的点,求过AB 的切线与x 轴围成面积的最小值.(25分)【解析】 不妨设过A 点的切线交x 轴于点C ,过B 点的切线交x 轴于点D ,直线AC 与直线BD 相交于点E .如图.设1122(,),(,)B x y A x y ,且有222211121,1,0y x y x x x =-=->>.由于2y x '=-,于是AC 的方程为2222x x y y =--;① BD 的方程为1122x x y y =--. ②联立,AC BD 的方程,解得121221(,1)2()y y E x x x x ---. 对于①,令0y =,得222(,0)2y C x -;对于②,令0y =,得112(,0)2y D x -. 于是221212121222112222y y x x CD x x x x --++=-=-. 121(1)2ECD S CD x x ∆=-.不妨设10x a =>,20x b -=>,则 2222111111()(1)(22)44ECD a b S ab a b a b ab a b a b∆++=++=+++++1111()(2)(2)44a b ab ab ab ab=+++⋅++≥ ③0s >,则有331111111(2)(.....)223399ECD S s s s s s s s s ∆=++=++++++ 6个 9个1243691616111116)]8()29s s s ⋅⋅[⋅(⋅()=⋅≥3218)3=⋅( ④又由当12x a x b s ==-=∴min ()ECD S ∆=注记:不妨设311()(2)2g s s s s=++,事实上,其最小值也可用导函数的方法求解. 由2211()(32)2g s s s '=+-知当2103s <<时()0g s '<;当213s <时()0g s '>.则()g s 在(0,上单调减,在)+∞上单调增.于是当s =时()g s 取得最小值. 4.向量OA 与OB 已知夹角,1OA =,2OB =,(1)OP t OA =-,OQ tOB =,01t ≤≤.PQ在0t 时取得最小值,问当0105t <<时,夹角的取值范围.(25分) 【解析】 不妨设OA ,OB 夹角为α,则1,2OP t OQ t =-=,令 222()(1)42(1)2cos g t PQ t t t t α==-+-⋅-⋅2(54cos )(24cos )1t t αα=++--+. 其对称轴为12cos 54cos t αα+=+.而12()54x f x x +=+在5(,)4-+∞上单调增,故12cos 1154cos 3αα+-+≤≤. 当12cos 1054cos 3αα++≤≤时,012cos 1(0,)54cos 5t αα+=∈+,解得223αππ<<. 当12cos 1054cos αα+-<+≤时,()g t 在[0,1]上单调增,于是00t =.不合题意. 于是夹角的范围为2[,]23ππ.5.(仅理科做)存不存在02x π<<,使得sin ,cos ,tan ,cot x x x x 为等差数列.(25分) 【解析】 不存在;否则有(cos sin )(cos sin )cos sin cot tan sin cos x x x x x x x x x x-+-=-=, 则cos sin 0x x -=或者cos sin 1sin cos x x x x+=.若cos sin 0x x -=,有4x π=.而此时1,122不成等差数列;若cos sin 1sin cos x x x x+=,有2(sin cos )12sin cos x x x x =+.解得有sin cos 1x x =. 而11sin cos sin 2(0,]22x x x =∈,矛盾!2020年自主招生数学试题及解答2020年自主招生数学试题及解答。
2020年数学高职考试卷

2020年数学高职考试卷(总分100分)姓名: 班级:一、选择题(共10小题,每小题6分,共60分,在每个小题给出的四个备选项中,只有一项是符合题目要求的.)1.设集合A={0,1},B={-1,0,1},则AUB=( )(A){-1} (B)(0,1) (C){-1,1} (D){-1,0,1) 2.若log a 8=3,则实数a =( )(A)12(B)2 (C)3 (D)4 3.不等式|2x+1|<3的解集为( )(A)(-2,1) (B)(-∞,-2)U(1,+∞) (C)(-2,2) (D)(-∞,-2)U(2,+∞) 4.sin(-π3)的值等于( ) (A)- 32 (B)- 12 (C)12 (D)3225.函数f (x )=x 2−x +2的增区间为( )(A)(-∞,-12) (B) [-12,+∞)(C)(-∞,12] (D)[12,+∞)6.在∆ABC 中,内角A,B,C 所对的边分别为a ,b ,c ,若a =3,b =5,c=2,则B=( ) (A)π6 (B )π4 (C )π3 (D )3π47.若实数a 、b 满足a <b ,则下列结论一定成立的是( ) (A )-a >-b (B )-a <-b (C )a 2<b 2 (D ) a 2>b 28.某学习小组有男生5人,女生3人,现从男生中任选2人,从女生中任选1人参加测试,则不同的选法有( )(A )15种 (B )20种 (C)30种 (D)40种 9.设函数f (x )、g (x )的定义域均为R ,且f (x )为奇函数,g (x )为偶函数,则下列说法正确的是( )(A )f (x )+g (x )必为奇函数 (B )f (x )+g (x )必为偶函数 (C )f (x )g (x )必为奇函数 (D)f (x )g (x )必为偶函数10.已知桐圆C 的中心在原点,右焦点坐标为(5,0),半长轴与半短轴的长度之和为5,则C 的标准方程为( ) (A)x 25+y 29=1 (B)x 24+y 29=1 (C)x 29+y 25=1 (D)x 29+y 24=1二、解答题(共3小题,共40分)11.(本小题满分14分,(1)小问7分,(Ⅱ)小问7分) 在等比数列{a n }中,a 2=8,公比q =12,(I )求a 8的值;(Ⅱ)若{a n }的前k 项和为31,求k 的值.12.(本小题满分13分,(I)小问6分,(Ⅱ)小问7分) 设直线4x-3y+12=0与x 轴、y 轴的交点分别为A 、B . (I )求|AB|;(II)求过点A 、B 和原点的圆的方程。
2020年陕西省西安市部分学校自主招生数学试卷

2020年陕西省西安市部分学校自主招生数学试卷一、选择题(共6小题,每小题3分,计18分,每小题只有一-个选项是符合题意的)1.(3分)已知等腰三角形一个外角是110°,则它的底角的度数为()A.110°B.70°C.55°D.70°或55°2.(3分)下列不等式变形中,一定正确的是()A.若ac>bc,则a>bB.若a>b,则ac2>bc2C.若ac2>bc2,则a>bD.若a>0,b>0,且,则a>b3.(3分)若关于x的方程kx2﹣3x﹣=0有实数根,则实数k的取值范围是()A.k=0B.k≥﹣1且k≠0C.k≥﹣1D.k>﹣14.(3分)把函数y=﹣2x+3的图象向右平移3个单位长度,再向下平移2个单位长度,可得到的图象的函数解析式是()A.y=﹣2x﹣5B.y=﹣2x+7C.y=﹣2x﹣7D.y=﹣2x+11 5.(3分)如图,在边长为8的等边△ABC中,D,E分别为AB,AC的中点,EF⊥AC于F,G为EF的中点,连接DG,则DG的长为()A.4B.C.D.6.(3分)抛物线y=ax2+bx+c的图象如图,则下列结论:①abc>0;②a+b+c=2;③a>;④b<1.其中正确的结论是()A.①②B.②③C.②④D.③④二、填空题(共3小题,每小题3分,计9分)7.(3分)如图:已知∠BAD=∠DAC=9°,AD⊥AE,且AB+AC=BE.则∠B=.8.(3分)如图,已知反比例函数y=(x>0)的图象经过点A(3,4),在该图象上面找一点P,使∠POA=45°,则点P的坐标为.9.(3分)在如图的正方形方格纸中,每个小的四边形都是相同的正方形,A,B,C,D都在格点处,AB与CD相交于O,则tan∠BOD的值等于.三、解答题(共7小题,计53分.解答题应写出过程)10.(4分)计算:﹣12018﹣6tan30°+()﹣2+|1﹣|.11.(5分)化简并计算:•﹣,其中x=2.12.(7分)如图,河流的两岸PQ、MN互相平行,河岸PQ上有一排小树,已知相邻两树之间的距离CD=50米,某人在河岸MN的A处测的∠DAN=35°,然后沿河岸走了130米到达B处,测的∠CBN=60°,求河流的宽度CE(结果保留整数).(参考数据:sin35°≈0.6,cos35°≈0.8,tan35°≈0.7,≈1.7)13.(7分)如图,在矩形ABCD中,AB=6,AD=6,E、F分别为AB、CD边上两动点,EF⊥AC,求DE+BF的最小值.14.(8分)小亮家今年种植的“翠香”猕猴桃喜获丰收,采摘上市20天全部销售完,小亮对销售情况进行跟踪记录,并将记录情况绘成图象,日销售量y(单位:千克)与上市时间x(单位:天)的函数关系如图1所示,猕猴桃价格z(单位:元/千克)与上市时间x (单位:天)的函数关系式如图2所示.(1)求小亮家猕猴桃的日销售量y与上市时间x的函数解析式;(2)试比较第10天与第12天的销售金额哪天多?请直接写出答案.15.(10分)已知二次函数y=mx2+nx+2图象的顶点横坐标是,与x轴交于A(x1,0)、B (x2,0),x1<0<x2,与y轴交于点C,且△ABC为直角三角形,∠ACB=90°.(1)求这个抛物线的解析式;(2)作垂直x轴的直线x=t,在第一象限交直线BC于N,交这个抛物线于M,求当t 取何值时,MN有最大值?最大值是多少?(3)在(2)的情况下,以C、M、N、D为顶点作平行四边形,求第四个顶点D的坐标.16.(12分)旋转是一种重要的图形变换,当图形中有一组邻边相等时,往往可以通过旋转解决问题.如图1,四边形ABCD中,AD=CD,∠ABC=120°,∠ADC=60°,AB=4,BC=2,连接BD,请利用旋转变换求出四边形ABCD的面积;如图2,四边形ABCD中,AD=CD,∠ABC=75°,∠ADC=60°,AB=4,BC=2,求出四边形ABCD的面积;如图3,四边形ABCD中,AD=CD,∠ADC=90°,AB=4,BD=4,若B、C两点落在直线AD的同侧,求BC的最小值.。
2020年广东省普通高等学校招收中等职业学校毕业生统一考试数学试题

2020年广东省普通高等学校招收中等职业学校毕业生统一考试数学试卷一、选择题1.已知集合M={x|1<x<5},N={x|−2<x<2},则N∩M=A.{x|−2<x<5}B.{x|1<x<2}C.{x|1<x<5}D.{x|−2<x<2}2.函数y=lg(3x−2)的定义域是)A.(−∞,23]B.(−∞,23,+∞)C.(23,+∞)D.[233.函数y=2x−1的反函数为g(x),则g(−3)=A.−1B.9C.1D.−94.不等式x2−x−6<0的解集是A.(−∞,−2)∪(3,+∞)B.(−∞,−3)∪(2,+∞)C.(−2,3)D.(−3,2)5.点(3,2)到直线x−2y+2=0的距离是A.2√55B.√5C.5D.√556.某射击运动员的第一次打靶成绩为8,8,9,8,7,第二次打靶成绩为7,8,9,9,7,则该运动员哪次打靶成绩稳定A.一样稳定B.第一次稳定C.第二次稳定D.无法确定7.等差数列{a n}中,a1,a2,a4成等比,则数列{a n}的公差为A.2B.1C.4D.−28.双曲线x 217−y28=1的右焦点坐标为A.(0,5)B.(0,−5)C.(5,0)D.(−5,0)9.抛物线y2=4x的准线方程为A.y=−1B.x=1C.x=−1D.y=110.已知角α的顶点与原点重合,始边与x轴正半轴重合,终边经过(3,4),则sinα=A.45B.35C.−35D.−4511.−2<x<1是2x<2的A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件12.已知向量a⃗=(1,x),b⃗⃗=(2,4),若a⃗∥b⃗⃗,则x=A.12B.−12C.−2D.213.若tanα=3,则sinα−cosαsinα+cosα=A.35B.34C.23D.1214.扔两个质地均匀的骰子,则朝上的点数之和为5的概率是A.16B.19C.112D.11815.偶函数f (x )在(0,+∞)上单调递减,若f (x −1)>f (3),则x 的取值范围A.(−∞,−12)∪(14,+∞)B.(−4,2)C.(−∞,14)∪(12,+∞) D.(−2,4)二、填空题16.已知向量a ⃗=(1,−2),b ⃗⃗=(x,−4),且a ⃗⊥b⃗⃗,则x = 17.从3本语文书,4本数学书中任意拿2本,恰好能拿到1本数学书的拿法有_______种18.已知数列{a n }为等差数列,且a 2+a 8=1,则2a 32a 7=19.函数f (x )=√3sin x +cos x 的最大值为20.直线x +y −3=0被圆(x −2)2+(y +1)2=4所截的弦长为三、解答题21.函数f (x )=(sin x +cos x )2−1(1)求函数的最小正周期(2)若α∈(0,π2),且f (π4−α)=12,求cos α 22.已知点A =(4,0),∠AOC =π4(1)若|OC |=2,求C 点的坐标(2)设|OC |=2m ,点P 为线段OC 的中点,OC 的中垂线交x 轴于点D ,记三角形ODP 的面积为S 1,平行四边形的面积为S 2,若S 2=4S 1,则求m 的值23.已知等差数列{a n }中,a 1=−2,a 12=20(1)求{a n }的通项公式(2)令b n =a 1+a 2+⋯+a n n,求数列{3b n }的前n 项和T n 24.已知椭圆x 2a z +y 2b 2=1(a >b >0),左右焦点分别为F 1,F 2,且|F 1F 2|=2√5,离心率ⅇ=√53 (1)求椭圆方程(2)点P (x 0,y 0)为椭圆上一点,当∠F 1PF 2为锐角时,求x 0的取值范围。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
职业学院
2020年自主招生数学试卷(第一套)
单项选择题(每题2分,共20题,共计40分。
下列备选答案中,只有一个正确答案,
请将答案写在下表中)
1. 1
-1
4 的倒数为( ). A. 54 B. 4
5 C. 45- D. 43
-
2. 把多项式2288x x -+分解因式,结果正确的是( ).
A .()2
24x - B .()2
24x -
C .()2
22x -
D .()2
22x +
3. 点(0,2)A -与点(6,0)B 之间的距离为( ).
A. 4
B. 6
C. 8
D.
4. 下列结论正确的是( ).
A. 一个数的相反数一定是负数
B. 一个数的绝对值一定不是负数
C. 一个数的绝对值一定是正数
D. 一个数的相反数一定是正数
5. 直线35y x =+的斜率为( ).
A .2
B .3
C .5
D .8
6. 一个正方形的边长增加了cm 2,面积相应增加了232cm ,则这个正方形的边长为( ).
A. 6cm
B. 5cm
C. 8cm
D. 7cm
7. 设集合{0},{1},A x x B x x A B =>=≤=I 则交集( ).
A. {01}x x ≤<
B. {01}x x <≤
C. {0}x x <
D. {1}x x >
8. 下列表格列出了一项实验的统计数据,表示皮球从高度d 落下时,弹跳高度b 与下落高度d 的关系,
试问下面的哪个式子能表示这种关系(单位cm )( ).
A. 2d b =
B. d b 2=
C. 25+=d b
D. 2
d b = 9. 若分式
1
2
x x -+的值为零,则x 的值是( ).
A .0
B .1
C .
D .
10. 把弯曲的河道改直,能够缩短船舶航行的路程,这样做的道理是( ). A. 垂线段最短 B. 两点确定一条直线 C. 两点之间,直线最短 D. 两点之间,线段最短
11. 在函数y =
中,自变量x 的取值范围是( ). A. 3x > B. 31x x <≠且 C. 3x ≥ D. 31x x ≤≠且
12. 小明每秒钟跑6米,小彬每秒钟跑5米,小彬站在小明前10米处,两人同时起跑,小明多少秒钟追上小彬( ).
A. 5秒
B. 6秒
C. 8秒
D. 10秒
13. 现有两根木棒,它们的长分别是40cm 和50cm ,若要钉成一个三角形木架,则在下列四根木棒中应选取( ) .
A .10cm 的木棒
B .40cm 的木棒
C .90cm 的木棒
D .100cm 的木棒
14. 已知函数2()1f x x =+,那么(1)f a +的值为( ).
A. 22a a ++
B. 21a +
C. 222a a ++
D. 221a a ++
15. 与b a 2是同类项的是 ( ).
A. a b 2
B. bc a 2
C. 5
22
ba - D. 2)(ab
16. 下列图形中,既是中心对称图形又是轴对称图形的是( ).
A. 平行四边形
B. 等边三角形 C. 等腰梯形 D. 圆
17. 已知2253x y xy x y +=-=+=,,则( ).
A. 25
B. 25-
C. 19
D. 19-
18. 若,a b 均为正数,,c d 均为负数,则下列式子中值最大的是( ).
A . ()a b c d -+-
B . ()a c b d --+
C . ()a b c d --+
D . ()a b c d +-+ 19. 下列各组数中,值相等的是( ).
A. 32与23
B. 32-与3)2(-
C. 2)3(-与)3(2-
D. 2×32与(2×3)2
20. 如图所示,直线AB 、CD 相交于O ,OD 平分∠BOE ,∠AOC=42°, 则∠AOE 的度数为( ).
A. 126°
B. 96°
C. 102°
D. 138°
O
E
D
C
B
A。
