数值分析实验报告Matlab仿真
数值分析matlab实验报告

数值分析matlab实验报告数值分析MATLAB实验报告引言:数值分析是一门研究利用计算机进行数值计算和解决数学问题的学科。
它在科学计算、工程技术、金融等领域中有着广泛的应用。
本实验旨在通过使用MATLAB软件,探索数值分析的基本概念和方法,并通过实际案例来验证其有效性。
一、插值与拟合插值和拟合是数值分析中常用的处理数据的方法。
插值是通过已知数据点之间的函数关系,来估计未知数据点的值。
拟合则是通过一个函数来逼近一组数据点的分布。
在MATLAB中,我们可以使用interp1函数进行插值计算。
例如,给定一组离散的数据点,我们可以使用线性插值、多项式插值或样条插值等方法,来估计在两个数据点之间的未知数据点的值。
拟合则可以使用polyfit函数来实现。
例如,给定一组数据点,我们可以通过最小二乘法拟合出一个多项式函数,来逼近这组数据的分布。
二、数值积分数值积分是数值分析中用于计算函数定积分的方法。
在实际问题中,往往无法通过解析的方式求得一个函数的积分。
这时,我们可以使用数值积分的方法来近似计算。
在MATLAB中,我们可以使用quad函数进行数值积分。
例如,给定一个函数和积分区间,我们可以使用quad函数来计算出该函数在给定区间上的定积分值。
quad函数使用自适应的方法,可以在给定的误差限下,自动调整步长,以保证积分结果的精度。
三、常微分方程数值解常微分方程数值解是数值分析中研究微分方程数值解法的一部分。
在科学和工程中,我们经常遇到各种各样的微分方程问题。
而解析求解微分方程往往是困难的,甚至是不可能的。
因此,我们需要使用数值方法来近似求解微分方程。
在MATLAB中,我们可以使用ode45函数进行常微分方程数值解。
例如,给定一个微分方程和初始条件,我们可以使用ode45函数来计算出在给定时间范围内的解。
ode45函数使用龙格-库塔方法,可以在给定的误差限下,自动调整步长,以保证数值解的精度。
结论:本实验通过使用MATLAB软件,探索了数值分析的基本概念和方法,并通过实际案例验证了其有效性。
数值分析matlab完整版实验报告范文

数值分析matlab完整版实验报告范文运用matlab软件实现,数值分析中求解非线性方程的根,实验数据完整,格式完整《数值分析》报告运用Matlab求解非线性方程的根学院:专业:班级:姓名:学号:运用matlab软件实现,数值分析中求解非线性方程的根,实验数据完整,格式完整1.目的掌握非线性方程求根的方法,并选取实例运用MATLAB软件进行算法的实现,分别用牛顿法、弦截法和抛物线法求非线性方程的根。
2.报告选题报告选取《数值分析(第四版)》290页习题7作为研究对象,即求f(某)某33某10在某02附近的根。
根的准确值某某1.87938524...,要求结果准确到四位有效数字。
(1)用牛顿法;(2)用弦截法,取某02,某11.9;(3)用抛物线法,取某01,某13,某22。
3.理论基础(1)牛顿迭代法牛顿迭代法是一种特殊的不动点迭代法,其计算公式为f(某k),k0,1,2,...f'(某k)f(某)f'(某)其迭代函数为(某)某牛顿迭代法的收敛速度,当f(某某)0,f'(某某)0,f''(某某)0时,容易证明,f'(某某)0,''(某某)f''(某某)0f'(某某),牛顿迭代法是平方收敛的,且limek1f''(某某)ke22f'(某某)。
k(2)弦截法将牛顿迭代法中的f'(某k)用f(某)在某k1,某k处的一阶差商来代替,即可得弦截法f(某k)(某k某k1)f(某k)f(某k1)(3)抛物线法运用matlab软件实现,数值分析中求解非线性方程的根,实验数据完整,格式完整弦截法可以理解为用过(某k1,f(某k1)),(某kf(某k))两点的直线方程的根近似替f(某)0的根。
若已知f(某)0的三个近似根某k,某k1,某k2用过(某k,f(某某(f,k某)k)某,某的抛物线方程的根近似代替())f(某)0的k)),k11(2,(fk2根,所得的迭代法称为抛物线法,也称密勒(Muller)法。
matlab仿真实验报告

matlab仿真实验报告Matlab仿真实验报告引言:Matlab是一种广泛应用于科学和工程领域的数值计算软件,它提供了强大的数学和图形处理功能,可用于解决各种实际问题。
本文将通过一个具体的Matlab 仿真实验来展示其在工程领域中的应用。
实验背景:本次实验的目标是通过Matlab仿真分析一个电路的性能。
该电路是一个简单的放大器电路,由一个输入电阻、一个输出电阻和一个放大倍数组成。
我们将通过Matlab对该电路进行仿真,以了解其放大性能。
实验步骤:1. 定义电路参数:首先,我们需要定义电路的各个参数,包括输入电阻、输出电阻和放大倍数。
这些参数将作为Matlab仿真的输入。
2. 构建电路模型:接下来,我们需要在Matlab中构建电路模型。
可以使用电路元件的模型来表示电路的行为,并使用Matlab的电路分析工具进行仿真。
3. 仿真分析:在电路模型构建完成后,我们可以通过Matlab进行仿真分析。
可以通过输入不同的信号波形,观察电路的输出响应,并计算放大倍数。
4. 结果可视化:为了更直观地观察仿真结果,我们可以使用Matlab的图形处理功能将仿真结果可视化。
可以绘制输入信号波形、输出信号波形和放大倍数的变化曲线图。
实验结果:通过仿真分析,我们得到了以下实验结果:1. 输入信号波形与输出信号波形的对比图:通过绘制输入信号波形和输出信号波形的变化曲线,我们可以观察到电路的放大效果。
可以看到输出信号的幅度大于输入信号,说明电路具有放大功能。
2. 放大倍数的计算结果:通过对输出信号和输入信号的幅度进行计算,我们可以得到电路的放大倍数。
通过比较不同输入信号幅度下的输出信号幅度,可以得到放大倍数的变化情况。
讨论与分析:通过对实验结果的讨论和分析,我们可以得出以下结论:1. 电路的放大性能:根据实验结果,我们可以评估电路的放大性能。
通过观察输出信号的幅度和输入信号的幅度之间的比值,可以判断电路的放大效果是否符合设计要求。
数值分析实验报告Matlab仿真资料

数值分析实验报告学院:电气工程与自动化学院专业:控制理论与控制工程姓名:李亚学号:61201401622014 年 12 月24日实验一 函数插值方法一、目的和意义1、 学会常用的插值方法,求函数的近似表达式,以解决其它实际问题;2、 明确插值多项式和分段插值多项式各自的优缺点;3、 熟悉插值方法的程序编制;4、 如果绘出插值函数的曲线,观察其光滑性。
二、实验原理1、 Lagrange 插值公式00,()n ni n k k i i k k i x x L x y x x ==≠⎛⎫-= ⎪-⎝⎭∑∏编写出插值多项式程序;2、 给出插值多项式或分段三次插值多项式的表达式;三、实验要求对于给定的一元函数)(x f y =的n+1个节点值(),0,1,,j j y f x j n ==。
试用Lagrange 公式求其插值多项式或分段二次Lagrange 插值多项式。
数据如下:(1求五次Lagrange 多项式5L ()x ,计算(0.596)f ,(0.99)f 的值。
(提示:结果为(0.596)0.625732f ≈, (0.99) 1.05423f ≈)试构造Lagrange 多项式6,和分段三次插值多项式,计算的(1.8)f ,(6.15)f 值。
(提示:结果为(1.8)0.164762f ≈, (6.15)0.001266f ≈)四、实验过程1.进入matlab开发环境;2.根据实验内容和要求编写程序,程序如下所示,程序通过运用function 函数编写,生成.m文件。
调用时只需要在命令窗口调用y=Lagrange(A,input)就可以实现任意次数拉格朗日插值法求解。
function y=Lagrange(A,input)[a,b]=size(A);x=input;y=0;for j=1:aMj=1;Nj=1;for k=1:aif(k==j)continue;endMj=Mj*(x-A(k,1));Nj=Nj*(A(j,1)-A(k,1));endy=y+A(j,2)*Mj/Nj;end3.调试程序并运行程序;调用拉格朗日脚本文件对以上两个表格数据求解,表格一对应MATLAB向量A;表格二对应向量I。
数值分析matlab实验报告

数值分析matlab实验报告《数值分析MATLAB实验报告》摘要:本实验报告基于MATLAB软件进行了数值分析实验,通过对不同数学问题的数值计算和分析,验证了数值分析方法的有效性和准确性。
实验结果表明,MATLAB在数值分析领域具有较高的应用价值和实用性。
一、引言数值分析是一门研究利用计算机进行数值计算和分析的学科,其应用范围涵盖了数学、物理、工程等多个领域。
MATLAB是一种常用的数值计算软件,具有强大的数值分析功能,能够进行高效、准确的数值计算和分析,因此在科学研究和工程实践中得到了广泛的应用。
二、实验目的本实验旨在通过MATLAB软件对数值分析方法进行实验验证,探究其在不同数学问题上的应用效果和准确性,为数值分析方法的实际应用提供参考和指导。
三、实验内容1. 利用MATLAB进行方程求解实验在该实验中,利用MATLAB对给定的方程进行求解,比较数值解和解析解的差异,验证数值解的准确性和可靠性。
2. 利用MATLAB进行数值积分实验通过MATLAB对给定函数进行数值积分,比较数值积分结果和解析积分结果,验证数值积分的精度和稳定性。
3. 利用MATLAB进行常微分方程数值解实验通过MATLAB对给定的常微分方程进行数值解,比较数值解和解析解的差异,验证数值解的准确性和可靠性。
四、实验结果与分析通过对以上实验内容的实际操作和分析,得出以下结论:1. 在方程求解实验中,MATLAB给出的数值解与解析解基本吻合,验证了MATLAB在方程求解方面的高准确性和可靠性。
2. 在数值积分实验中,MATLAB给出的数值积分结果与解析积分结果基本吻合,验证了MATLAB在数值积分方面的高精度和稳定性。
3. 在常微分方程数值解实验中,MATLAB给出的数值解与解析解基本吻合,验证了MATLAB在常微分方程数值解方面的高准确性和可靠性。
五、结论与展望本实验通过MATLAB软件对数值分析方法进行了实验验证,得出了数值分析方法在不同数学问题上的高准确性和可靠性。
基于MATLAB数值分析实验报告

基于MATLAB数值分析实验报告班级:072115姓名:李凯学号:20111003943实验二:矩阵与向量运算实验目的:在MATLAB里,会对矩阵与向量进行加、减、数乘、求逆及矩阵特征值运算,以及矩阵的LU分解。
设A是一个n×n方阵,X是一个n维向量,乘积Y=AX可以看作是n维空间变换。
如果能够找到一个标量λ,使得存在一个非零向量X,满足:AX=λX (3.1)则可以认为线性变换T(X)=AX将X映射为λX,此时,称X 是对应于特征值λ的特征向量。
改写式(3.1)可以得到线性方程组的标准形式:(A-λI)X=0 (3.2)式(3.2)表示矩阵(A-λI)和非零向量X的乘积是零向量,式(3.2)有非零解的充分必要条件是矩阵(A-λI)是奇异的,即:det(A-λI)=0该行列式可以表示为如下形式:a11–λa12 (1)a21 a22 –λ…a2n =0 (3.3)…………A n1 a n2 …a nn将式(3.3)中的行列式展开后,可以得到一个n阶多项式,称为特征多项式:f(λ)=det(A-λI)=(-1)n(λn+c1λn-1+c2λn-2+…+c n-1λ+c n) (3.4) n阶多项式一共有n个根(可以有重根),将每个根λ带入式(3.2),可以得到一个非零解向量。
习题:求下列矩阵的特征多项式的系数和特征值λj:3 -1 0A= -1 2 -10-1 3解:在MATLAB中输入命令:A=【3 -1 0;-1 2 -1;0 -1 3】;c=poly(A)roots(c)得到:实验四:Lagrange插值多项式实验目的:理解Lagrange插值多项式的基本概念,熟悉Lagrange插值多项式的公式源代码,并能根据所给条件求出Lagrange插值多项式,理解龙格现象。
%功能:对一组数据做Lagrange插值%调用格式:yi=Lagran_(x,y,xi)%x,y:数组形式的数据表%xi:待计算y值的横坐标数组%yi:用Lagrange还擦之算出y值数组function fi=Lagran_(x,f,xi)fi=zeros(size(xi));np1=length(f);for i=1:np1z=ones(size(xi));for j=i:np1if i~=j,z=z.*(xi-x(j))/(x(i)-x(j));endendfi=fi+z*f(i);endreturn习题:已知4对数据(1.6,3.3),(2.7,1.22),(3.9,5.61),(5.6,2.94)。
数值分析实验报告matlab

数值分析实验报告matlab数值分析实验报告引言:数值分析是一门研究利用计算机数值方法解决数学问题的学科,它在科学计算、工程设计、金融分析等领域具有重要的应用价值。
本实验报告旨在通过使用MATLAB软件,探索数值分析的基本原理和方法,并通过实际案例加深对数值分析的理解。
一、误差分析在数值计算中,误差是无法避免的。
误差分析是数值分析中的重要一环,它帮助我们了解数值计算的准确性和稳定性。
在实验中,我们通过计算机模拟了一个简单的数学问题,并分别计算了绝对误差和相对误差。
通过比较不同算法的误差大小,我们可以选择最适合的算法来解决实际问题。
二、插值与拟合插值和拟合是数值分析中常用的方法,它们可以通过已知的数据点来推导出未知数据点的近似值。
在本实验中,我们通过MATLAB的插值函数和拟合函数,分别进行了插值和拟合的实验。
通过比较不同插值和拟合方法的结果,我们可以选择最适合的方法来处理实际问题。
三、数值积分数值积分是数值分析中的重要内容,它可以用来计算曲线下的面积或函数的积分值。
在实验中,我们通过MATLAB的数值积分函数,对一些简单的函数进行了积分计算。
通过比较数值积分和解析积分的结果,我们可以评估数值积分的准确性和稳定性,并选择最适合的积分方法来解决实际问题。
四、常微分方程的数值解法常微分方程是数值分析中的重要内容,它可以用来描述许多自然现象和工程问题。
在实验中,我们通过MATLAB的常微分方程求解函数,对一些简单的微分方程进行了数值解法的计算。
通过比较数值解和解析解的结果,我们可以评估数值解法的准确性和稳定性,并选择最适合的数值解法来解决实际问题。
五、线性方程组的数值解法线性方程组是数值分析中的经典问题,它在科学计算和工程设计中广泛应用。
在实验中,我们通过MATLAB的线性方程组求解函数,对一些简单的线性方程组进行了数值解法的计算。
通过比较数值解和解析解的结果,我们可以评估数值解法的准确性和稳定性,并选择最适合的数值解法来解决实际问题。
数值分析实验报告(Matlab实现)(同名6593)

学生实验报告实验课程名称数值分析开课实验室数学与统计学院实验室学院2010 年级数学与应用数学专业班01班学生姓名学号开课时间2012 至2013 学年第一学期end y=x;format short ;% 设置为默认格式显示,显示5位(2) 建立MATLAB 界面利用MA TLAB 的GUI 建立如下界面求解线性方程组:详见程序。
五、 计算实例、数据、结果、分析下面我们对以上的结果进行测试,求解:⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡------725101391444321131243301024321x x x x 输入数据后点击和,得到如下结果:更改以上数据进行测试,求解如下方程组:123443211343212343112341x x x x ⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦得到如下结果:六、 实验中遇到的问题及解决办法在本实验中,遇到的问题主要有两个:(1) 如何将上述的Gauss 消元法的算法在MA TLAB 中实现针对此问题我借鉴了网上以及 课本上的算法的MATLAB 实现的程序;(2) 如何将建立界面使得可以随意输入想要求解的相关矩阵后就可以直接求解针对此问题,我通过网上的一些关于MA TLAB 的GUI 设计的相关资料,总结经验完成了此项任务。
七、 实验结论通过以上的测试,我们发现以上算法和程序能够求出线性方程组的比较精确解。
八、 参考文献[1]杨大地,王开荣 .2006.数值分析.北京:科学出版社[2]何光辉.2008. 数值分析实验. 重庆大学数理学院数学实验教学中心 [3]百度文库,百度知道教师签名年 月 日详见程序。
五、计算实例、数据、结果、分析下面我们对以上的问题进行测试:输入数据:计算结果如下:当x=2.101时,x=4.234时,同理可以测试(4)中的5的值。
六、实验中遇到的问题及解决办法在本实验中,遇到的问题主要有两个:(3)如何将上述的插值的算法在MA TLAB中实现针对此问题我借鉴了网上以及课本上的算法的MATLAB实现的程序;(4)如何将建立界面使得可以随意输入想要求解的相关矩阵后就可以直接求解针对此问题,我通过网上的一些关于MA TLAB的GUI设计的相关资料,总结经验完成了此项任务。
matlab实验报告

matlab实验报告实验报告:Matlab实验分析1. 实验目的本实验旨在通过Matlab软件完成一系列数值计算和数据分析的任务,包括绘制曲线、解方程、矩阵运算等,以加深对Matlab软件的理解和掌握。
2. 实验内容2.1 绘制函数曲线首先,我们通过在Matlab中输入函数的表达式来绘制函数曲线。
例如,我们可以输入y = sin(x)来绘制正弦函数的曲线。
另外,我们还可以设置曲线的颜色、线型和坐标轴范围等。
2.2 解方程接下来,我们使用Matlab来解方程。
对于一元方程,我们可以使用solve函数来求出方程的解。
例如,我们输入syms x; solve(x^2 - 2*x - 8)来解方程x^2 - 2x - 8 = 0。
而对于多元方程组,我们可以使用solve函数的向量输入形式来求解。
例如,我们输入syms x y; solve(x^2 + y^2 - 1, x - y - 1)来求解方程组x^2 + y^2 - 1 = 0和x - y - 1 = 0的解。
2.3 矩阵运算Matlab也可以进行矩阵运算。
我们可以使用矩阵相乘、相加和取逆等运算。
例如,我们可以输入A = [1 2; 3 4]和B = [5 6;7 8]来定义两个矩阵,然后使用A * B来计算它们的乘积。
3. 实验结果与分析在本实验中,我们成功完成了绘制函数曲线、解方程和矩阵运算等任务。
通过Matlab软件,我们可以快速、准确地进行数值计算和数据分析。
使用Matlab的高级函数和工具箱,我们可以更方便地处理复杂的数值计算和数据分析问题。
4. 实验总结通过本次实验,我们进一步加深了对Matlab软件的理解和掌握。
Matlab提供了丰富的函数库和工具箱,适用于各种不同的数值计算和数据分析任务。
在日常科研和工程实践中,Matlab是一个非常强大和方便的工具,可以帮助我们更高效地完成任务。
MATLAB系统仿真实验报告一

MATLAB系统仿真实验报告(一实验一、MATLAB语言环境与基本运算一、实验目的及要求1.学习了解MATLAB语言环境2.练习MATLAB命令的基本操作3.练习MATLAB数值运算相关内容4.练习MATLAB符号运算相关内容5.撰写实验报告二、实验内容1.熟悉Matlab语言环境1).学习了解MATLAB语言环境MATLAB语言操作界面(主界面的各个窗口)主界面:工具栏:状态栏:命令窗口:文件窗口:工作空间窗口:历史命令窗口:变量查询命令who, whosWho:列出当前存储器中的所有变量Whos:列出当前工作空间中的所有变量,包括与他们的维数、字节、类型有关的变量目录与目录结构目录,文件夹,文件搜索路径联机帮助2).MATLAB基本操作命令demos,clc,clf,clear,contro-c(^c),diary Demos:Clc:命令窗口清屏。
Clf:清楚当前图形。
清楚工作空间。
Control+c:复制选定区域到粘贴板。
Diary:用于记录MATLAB窗口的输入的命令和响应输出,diary off关闭记录,diary on打开记录。
2.Matlab数值运算与符号运算1).MATLAB数值运算相关内容MATLAB变量及变量赋值变量名以字母开头,后接字母、数字或下划线的字符序列,最多63个字符。
变量名区分大小写,不可使用保留字。
变量赋值:变量名=表达式。
初等矩阵函数ones, zeros, eye, rand, randn, sizeOnes:生成常熟1构成的数组。
Zeros:零数组。
Eye:生成单位矩阵。
Rand:生成随机数和矩阵。
产生标准正态分布的随机数或矩阵的函数。
Size:求矩阵的维数。
矩阵的基本运算+ 加- 减* 乘^ 乘方‘共轭转置/或\ 矩阵相除./或.\ 数组相除矩阵的特征运算det, eig, rank, svdDet:求行列式。
Eig:求特征值和特征向量。
Rank:计算矩阵的秩。
实验四 MATLAB简单仿真实验(已完成)
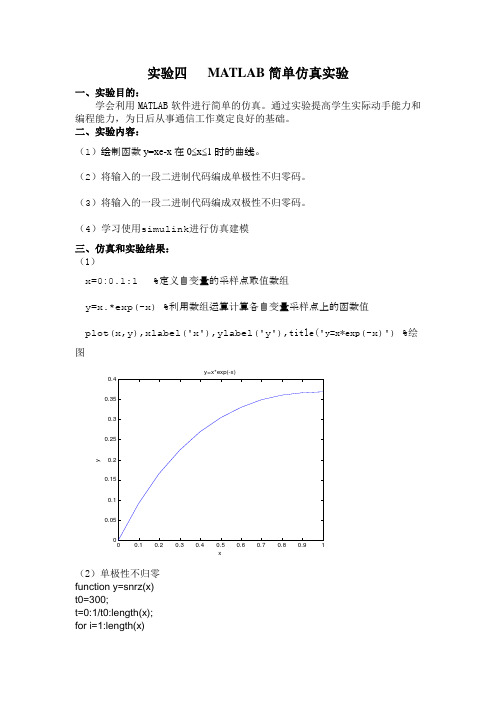
实验四 MATLAB 简单仿真实验一、实验目的:学会利用MATLAB 软件进行简单的仿真。
通过实验提高学生实际动手能力和编程能力,为日后从事通信工作奠定良好的基础。
二、实验内容:(1)绘制函数y=xe-x 在0≤x ≤1时的曲线。
(2)将输入的一段二进制代码编成单极性不归零码。
(3)将输入的一段二进制代码编成双极性不归零码。
(4)学习使用simulink 进行仿真建模三、仿真和实验结果:(1)x=0:0.1:1 %定义自变量的采样点取值数组y=x.*exp(-x) %利用数组运算计算各自变量采样点上的函数值plot(x,y),xlabel('x'),ylabel('y'),title('y=x*exp (-x)') %绘图00.10.20.30.40.50.60.70.80.91x y y=x*exp(-x)(2)单极性不归零function y=snrz(x)t0=300;t=0:1/t0:length(x);for i=1:length(x)if(x(i)==1)for j=1:t0y((i-1)*t0+j)=1;endelsefor j=1:t0y((i-1)*t0+j)=0;endendendy=[y,x(i)];M=max(y);m=min(y);subplot(2,1,1)plot(t,y);grid on;axis([0,i,m-0.1,M+0.1]);title('1 0 0 1 1 0 0 0 0 1 0 1');>>x=[1 0 0 1 1 0 0 0 0 1 0 1];y=snrz(x)(3)双极性不归零function y=dnrz(x)t0=300;t=0:1/t0:length(x);for i=1:length(x)if(x(i)==1)for j=1:t0y((i-1)*t0+j)=1;endelsefor j=1:t0y((i-1)*t0+j)=-1;endendendy=[y,x(i)];M=max(y);m=min(y);subplot(2,1,1)plot(t,y);grid on;axis([0,i,m-0.1,M+0.1]);title('1 0 0 1 1 0 0 0 0 1 0 1');>>x=[1 0 0 1 1 0 0 0 0 1 0 1];y=dnrz(x)(4)a)在MATLAB的命令窗运行指令simulink,或点击命令窗中的图标,便打开SIMULINK模型库浏览器(simulink Library Browser)。
数值分析matlab实验报告

数值分析matlab实验报告数值分析 Matlab 实验报告一、实验目的数值分析是研究各种数学问题数值解法的学科,Matlab 则是一款功能强大的科学计算软件。
本次实验旨在通过使用 Matlab 解决一系列数值分析问题,加深对数值分析方法的理解和应用能力,掌握数值计算中的误差分析、数值逼近、数值积分与数值微分等基本概念和方法,并培养运用计算机解决实际数学问题的能力。
二、实验内容(一)误差分析在数值计算中,误差是不可避免的。
通过对给定函数进行计算,分析截断误差和舍入误差的影响。
例如,计算函数$f(x) =\sin(x)$在$x = 05$ 附近的值,比较不同精度下的结果差异。
(二)数值逼近1、多项式插值使用拉格朗日插值法和牛顿插值法对给定的数据点进行插值,得到拟合多项式,并分析其误差。
2、曲线拟合采用最小二乘法对给定的数据进行线性和非线性曲线拟合,如多项式曲线拟合和指数曲线拟合。
(三)数值积分1、牛顿柯特斯公式实现梯形公式、辛普森公式和柯特斯公式,计算给定函数在特定区间上的积分值,并分析误差。
2、高斯求积公式使用高斯勒让德求积公式计算积分,比较其精度与牛顿柯特斯公式的差异。
(四)数值微分利用差商公式计算函数的数值导数,分析步长对结果的影响,探讨如何选择合适的步长以提高精度。
三、实验步骤(一)误差分析1、定义函数`compute_sin_error` 来计算不同精度下的正弦函数值和误差。
```matlabfunction value, error = compute_sin_error(x, precision)true_value = sin(x);computed_value = vpa(sin(x), precision);error = abs(true_value computed_value);end```2、在主程序中调用该函数,分别设置不同的精度进行计算和分析。
(二)数值逼近1、拉格朗日插值法```matlabfunction L = lagrange_interpolation(x, y, xi)n = length(x);L = 0;for i = 1:nli = 1;for j = 1:nif j ~= ili = li (xi x(j))/(x(i) x(j));endendL = L + y(i) li;endend```2、牛顿插值法```matlabfunction N = newton_interpolation(x, y, xi)n = length(x);%计算差商表D = zeros(n, n);D(:, 1) = y';for j = 2:nfor i = j:nD(i, j) =(D(i, j 1) D(i 1, j 1))/(x(i) x(i j + 1));endend%计算插值结果N = D(1, 1);term = 1;for i = 2:nterm = term (xi x(i 1));N = N + D(i, i) term;endend```3、曲线拟合```matlab%线性最小二乘拟合p = polyfit(x, y, 1);y_fit_linear = polyval(p, x);%多项式曲线拟合p = polyfit(x, y, n);% n 为多项式的次数y_fit_poly = polyval(p, x);%指数曲线拟合p = fit(x, y, 'exp1');y_fit_exp = p(x);```(三)数值积分1、梯形公式```matlabfunction T = trapezoidal_rule(f, a, b, n)h =(b a) / n;x = a:h:b;y = f(x);T = h ((y(1) + y(end))/ 2 + sum(y(2:end 1)));end```2、辛普森公式```matlabfunction S = simpson_rule(f, a, b, n)if mod(n, 2) ~= 0error('n 必须为偶数');endh =(b a) / n;x = a:h:b;y = f(x);S = h / 3 (y(1) + 4 sum(y(2:2:end 1))+ 2 sum(y(3:2:end 2))+ y(end));end```3、柯特斯公式```matlabfunction C = cotes_rule(f, a, b, n)h =(b a) / n;x = a:h:b;y = f(x);w = 7, 32, 12, 32, 7 / 90;C = h sum(w y);end```4、高斯勒让德求积公式```matlabfunction G = gauss_legendre_integration(f, a, b)x, w = gauss_legendre(5);%选择适当的节点数t =(b a) / 2 x +(a + b) / 2;G =(b a) / 2 sum(w f(t));end```(四)数值微分```matlabfunction dydx = numerical_derivative(f, x, h)dydx =(f(x + h) f(x h))/(2 h);end```四、实验结果与分析(一)误差分析通过不同精度的计算,发现随着精度的提高,误差逐渐减小,但计算时间也相应增加。
数值分析第二章MATLAB计算实验报告

数值分析MATLAB 计算实验报告姓名 班级 学号一、实验名称根据给定数据利用MATLAB 编程做出4次牛顿插值与三次样条插值的插值函数与被插值函数图形 二、实验目的1.理解牛顿插值的定义并且编写出与其算法对应的MATLAB 程序代码;2.了解三次样条插值的构造方法并且编写出与其算法对应的MATLAB 程序代码; 3.体会利用MATLAB 软件进行数值计算 。
三、实验内容已知函数在下列各点的值为:x i 0.2 0.4 0.6 0.8 1 .0 f(x i )0.980.920.810.640.38试用4次牛顿插值多项式P 4(x)及三样条函数S(x)(自然边界条件)对数据进行插值。
使用Matlab 软件用图给出{(x i ,y i ),x i =0.2+0.08i, i=0,1,11,10},P 4(x)及S(x) 四、算法描述 1.牛顿插值公式:P n (x)=f(x 0)+f[x 0,x 1](x-x 0)+f[x 0,x 1,x 2](x-x 0)(x-x 1)+… +f[x 0,x 1,…,x n ](x-x 0)…(x-x n-1),当n=4时,将插值点x i 及插值点对应的函数值f(x i )带入上式可得4次牛顿插值多项式。
2.三次样条插值:使用三弯矩法,令n i x s M i i ,,2,1,0),( =''=, 首先,以(x i ,M i ),(x i-1,M i-1)为结点作线性插值:i ii i i i M h x x M h x x x s 11)(---+--='',其中h i =x i -x i-1紧接着,连续积分两次:213131)(6)(6)(c x c x x h M x x h M x s i ii i i i ++-+-=--再利用插值条件11)(,)(--==i i i i y x s y x s)()6()()6()(6)(6)(1113131-------+--+-+-=i i ii i i i i i i i i i i i i x x h M h y x x h Mh y x x h M x x h M x sn i x x x i i ,,2,1,1 =≤≤-然后利用s '(x)在内结点连续的条件求M i ,s '(x i -0)=s '(x i +0))6()6()(2)(2)(112121i i i i i i i i i i i i i i h Mh y h M h y x x h M x x h M x s -+---+--='----ii ii i i i i i i i i h y y M M h x x h M x x h M 112121)(6)(2)(2-----+---+--=ii x x x ≤≤-11111211211)(6)(2)(2)(++++++++-+---+--='i ii i i i i i i i i i h y y M M h x x h M x x h M x s1+≤≤i i x x xii i i i i i i h y y M h M h x s 1163)0(---++=-'1111163)0(+++++-+--=+'i ii i i i i i h y y M h M h x s得i i i i i i i h y y M h M h 1163---++1111163+++++-+--=i ii i i i i h y y M h M hii i i i i i i i i i i i h y y h y y M h M h h M h 11111116)33(6-+++++----=+++)(62111111111ii i i i i i i i i i i i i i i i h y y h y y h h M h h h M M h h h -++++++-+---+=++++1,,2,1,211-==+++-n i M M M i i i i i i βαγ最后,根据三条边界条件,求出的值。
matlab实验一实验报告

matlab实验一实验报告实验一:Matlab实验报告引言:Matlab是一种强大的数学软件工具,广泛应用于科学计算、数据分析和工程设计等领域。
本实验旨在通过使用Matlab解决实际问题,探索其功能和应用。
一、实验目的本次实验的主要目的是熟悉Matlab的基本操作和常用函数,了解其在科学计算中的应用。
二、实验内容1. 数值计算在Matlab中,我们可以进行各种数值计算,包括基本的加减乘除运算,以及更复杂的矩阵运算和方程求解。
通过编写相应的代码,我们可以实现这些功能。
例如,我们可以使用Matlab计算两个矩阵的乘积,并输出结果。
代码如下:```matlabA = [1 2; 3 4];B = [5 6; 7 8];C = A * B;disp(C);```2. 数据可视化Matlab还提供了强大的数据可视化功能,可以将数据以图表的形式展示出来,更直观地观察数据的规律和趋势。
例如,我们可以使用Matlab绘制一个简单的折线图,来展示某个物体在不同时间下的位置变化。
代码如下:```matlabt = 0:0.1:10;x = sin(t);plot(t, x);xlabel('Time');ylabel('Position');title('Position vs. Time');```3. 图像处理Matlab还可以进行图像处理,包括图像的读取、处理和保存等操作。
我们可以通过Matlab对图像进行增强、滤波、分割等处理,以及进行图像的压缩和重建。
例如,我们可以使用Matlab读取一张图片,并对其进行灰度化处理。
代码如下:```matlabimg = imread('image.jpg');gray_img = rgb2gray(img);imshow(gray_img);```三、实验结果与分析在本次实验中,我们成功完成了数值计算、数据可视化和图像处理等任务。
matlab实验报告

matlab实验报告实验名称:MATLAB数值分析实验报告摘要:本实验通过使用MATLAB软件,实现了一些数值分析中重要的算法,包括线性方程组求解、非线性方程求根、数值积分与微分以及常微分方程求解。
在算法实现的过程中,通过观察输出结果验证了算法的正确性和可靠性,并探讨了一些算法实现中需要注意的问题。
1.线性方程组求解线性方程组求解是数值分析中的重要算法之一,是很多数学问题的基础。
本实验中使用了三种求解线性方程组的算法:高斯消元法、LU分解法和共轭梯度法。
在实验中,我们需要注意选取矩阵的条件数,使用一些特殊矩阵,如对角矩阵、三对角矩阵和希尔伯特矩阵等来验证算法的正确性。
2.非线性方程求根非线性方程求根是MATLAB中一个非常实用的函数,能够快速解决大量的非线性方程。
本实验中,我们更深入地探讨了二分法、牛顿法和割线法等算法,通过实现代码,实现了对非线性方程的求解。
同时,对不同的算法进行比较,从而选择合适的算法。
3.数值积分与微分数值积分与微分是宏观物理中需要用到的重要数学问题之一。
本实验中,我们使用了梯形法、辛普森法和龙贝格法等多种数值积分算法实现了函数的数值积分。
同时,也对数值微分的误差和稳定性进行了研究和探讨。
4.常微分方程求解常微分方程求解是MATLAB中最常用的功能之一。
本实验中,我们实现了欧拉法、龙格-库塔法等常微分方程求解算法。
并不断尝试对算法进行改进,提高其效率和精度。
实验结果表明,使用MATLAB实现数值分析算法是非常可靠和高效的。
同时,也需要注意在算法实现中注意问题和选择合适的算法。
matlab数值分析实验报告

matlab数值分析实验报告Matlab数值分析实验报告引言数值分析是一门研究利用计算机进行数值计算和模拟的学科,它在科学计算、工程技术和金融等领域有着广泛的应用。
本次实验报告将介绍在Matlab环境下进行的数值分析实验,包括数值微分、数值积分和线性方程组求解等内容。
一、数值微分数值微分是通过数值方法计算函数的导数,常用的数值微分方法有前向差分、后向差分和中心差分。
在Matlab中,可以使用diff函数来计算函数的导数。
例如,对于函数f(x)=x^2,在Matlab中可以使用如下代码进行数值微分的计算:```matlabsyms x;f = x^2;df = diff(f, x);```二、数值积分数值积分是通过数值方法计算函数的定积分,常用的数值积分方法有梯形法则、辛普森法则和龙贝格积分法。
在Matlab中,可以使用trapz、quad和integral等函数来进行数值积分的计算。
例如,对于函数f(x)=sin(x),可以使用如下代码进行数值积分的计算:```matlabx = linspace(0, pi, 100);y = sin(x);integral_value = trapz(x, y);```三、线性方程组求解线性方程组求解是数值分析中的重要问题,常用的求解方法有高斯消元法和LU 分解法。
在Matlab中,可以使用\操作符来求解线性方程组。
例如,对于线性方程组Ax=b,可以使用如下代码进行求解:```matlabA = [1, 2; 3, 4];b = [5; 6];x = A\b;```四、实验结果与分析在本次实验中,我们分别使用Matlab进行了数值微分、数值积分和线性方程组求解的计算。
通过实验结果可以发现,Matlab提供了丰富的数值计算函数和工具,能够方便地进行数值分析的计算和求解。
数值微分的计算结果与解析解相比较,可以发现数值微分的误差随着步长的减小而减小,但是当步长过小时,数值微分的误差会受到舍入误差的影响。
数值分析matlab上机实验报告

数值分析matlab上机实验报告matlab软件实验报告数学上机课实验报告matlab实验报告总结数值分析试卷篇一:《MATLAB与数值分析》第一次上机实验报告标准实验报告(实验)课程名称学生姓名:李培睿学号:2013020904026指导教师:程建一、实验名称《MATLAB与数值分析》第一次上机实验二、实验目的1. 熟练掌握矩阵的生成、加、减、乘、除、转置、行列式、逆、范数等运算操作。
(用.m文件和Matlab函数编写一个对给定矩阵进行运算操作的程序)2. 熟练掌握算术符号操作和基本运算操作,包括矩阵合并、向量合并、符号转换、展开符号表达式、符号因式分解、符号表达式的化简、代数方程的符号解析解、特征多项式、函数的反函数、函数计算器、微积分、常微分方程的符号解、符号函数的画图等。
(用.m 文件编写进行符号因式分解和函数求反的程序)3. 掌握Matlab函数的编写规范。
4、掌握Matlab常用的绘图处理操作,包括:基本平面图、图形注释命令、三维曲线和面的填充、三维等高线等。
(用.m 文件编写在一个图形窗口上绘制正弦和余弦函数的图形,并给出充分的图形注释)5. 熟练操作MATLAB软件平台,能利用M文件完成MATLAB的程序设计。
三、实验内容1. 编程实现以下数列的图像,用户能输入不同的初始值以及系数。
并以x,y为坐标显示图像x(n+1) = a*x(n)-b*(y(n)-x(n) ); y(n+1) = b*x(n)+a*(y(n)-x(n) )2. 编程实现奥运5环图,允许用户输入环的直径。
3. 实现对输入任意长度向量元素的冒泡排序的升序排列。
不允许使用sort函数。
四、实验数据及结果分析题目一:①在Editor窗口编写函数代码如下:并将编写的函数文件用“draw.m”储存在指定地址;②在Command窗口输入如下命令:③得到图形结果如下:题目二:①在Editor窗口编写函数代码如下:并将编写的函数文件用“circle.m”储存在指定地址;②再次在Editor窗口编写代码:并将编写的函数文件用“Olympic.m”储存在指定地址;③在Command窗口输入如下指令(半径可任意输入):④按回车执行,将在图形窗口获得五环旗:题目三:①在Editor窗口编写函数代码如下:并用.将编写的函数文件用“qipaofa.m”储存在指定地址;②在Command窗口输入一组乱序数值,则可以得到升序排序结果如下:五、总结及心得体会1. 要熟悉MATLAB编译软件的使用方法,明白有关语法,语句的基本用法,才可以在编写程序的时候游刃有余,不至于寸步难行。
数值分析MATLAB实验报告

实验 2.1 多项式插值的震荡现象问题提出:考虑在一个固定的区间上用插值逼近一个函数。
显然Lagrange 插值中使用的节点越多,插值多项式的次数越高,我们自然关心插值多项式的次数增加时,)(x L n 是否也更加靠近被逼近的函数。
Runge 给出的一个例子是极著名并富有启发性的。
设区间[-1,1]上函数.2511)(2xx f +=实验内容:考虑空间[-1,1]的一个等距划分,分点为 nix i 21+-=, =i 0,1,2 ...,n , 则拉格朗日插值多项式为)(2511)(02x l xx L ini n ∑=+=. 其中,n i x l i ,...,2,1,0),(=是n 次Lagrange 插值基函数。
实验要求:(1)选择不断增大的分点数目,...,3,2=n 画出原函数)(x f 及插值多项式函数)(x L n 在[-1,1]上的图像,比较并分析实验结果。
(2)选择其他的函数,例如定义在区间[-5,5]上的函数 ,1)(4xxx h +=)arctan()(x x g =, 重复上述的实验看其结果如何。
首先编写拉格朗日插值函数的Matlab 实现: Matlab 程序为:function y=lagrange(x0,y0,x) %Lagrange 插值 n=length(x0); m=length(x); for i=1:m z=x(i); s=0.0; for k=1:n p=1.0; for j=1:n if(j~=k)p=p*(z-x0(j))/(x0(k)-x0(j)); end ends=s+p*y0(k); endy(i)=s; end(1)当函数为.2511)(2xx f +=时, Matlab 程序为:x=linspace(-1,1,100); y=1./(1+25*x.^2); plot(x,y) hold on; for i=2:2:10x0=linspace(-1,1,i+1); y0=1./(1+25*x0.^2); y=laglanri(x0,y0,x); plot(x,y,'r--') hold on end运行结果:结果分析:从图上看到在区间[-1,1]的两端点附近,随着插值点数的增加,插值函数)(x L n 与)(x f 偏离的越远,而且出现了振荡现象。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数值分析实验报告学院:电气工程与自动化学院专业:控制理论与控制工程姓名:***学号:**********2014 年 12 月24日实验一 函数插值方法一、目的和意义1、 学会常用的插值方法,求函数的近似表达式,以解决其它实际问题;2、 明确插值多项式和分段插值多项式各自的优缺点;3、 熟悉插值方法的程序编制;4、 如果绘出插值函数的曲线,观察其光滑性。
二、实验原理1、 Lagrange 插值公式00,()n ni n k k i i k k i x x L x y x x ==≠⎛⎫-= ⎪-⎝⎭∑∏编写出插值多项式程序;2、 给出插值多项式或分段三次插值多项式的表达式;三、实验要求对于给定的一元函数)(x f y =的n+1个节点值(),0,1,,j j y f x j n ==。
试用Lagrange 公式求其插值多项式或分段二次Lagrange 插值多项式。
数据如下:(1求五次Lagrange 多项式5L ()x ,计算(0.596)f ,(0.99)f 的值。
(提示:结果为(0.596)0.625732f ≈, (0.99) 1.05423f ≈)试构造Lagrange 多项式6,和分段三次插值多项式,计算的(1.8)f ,(6.15)f 值。
(提示:结果为(1.8)0.164762f ≈, (6.15)0.001266f ≈)四、实验过程1.进入matlab开发环境;2.根据实验内容和要求编写程序,程序如下所示,程序通过运用function 函数编写,生成.m文件。
调用时只需要在命令窗口调用y=Lagrange(A,input)就可以实现任意次数拉格朗日插值法求解。
function y=Lagrange(A,input)[a,b]=size(A);x=input;y=0;for j=1:aMj=1;Nj=1;for k=1:aif(k==j)continue;endMj=Mj*(x-A(k,1));Nj=Nj*(A(j,1)-A(k,1));endy=y+A(j,2)*Mj/Nj;end3.调试程序并运行程序;调用拉格朗日脚本文件对以上两个表格数据求解,表格一对应MATLAB向量A;表格二对应向量I。
在命令窗口调用y=Lagrange(A,input),求解如下面截图。
图1 表一数据的解图2 表二数据的解4.实验总结通过对插值法算法编程,加深了对插值方法的理解,熟悉了MATLAB编写脚本函数。
通过计算机求解,能更加方便快捷求解。
实验二 函数逼近与曲线拟合一、目的和意义1、掌握曲线拟合的最小二乘法;2、最小二乘法亦可用于解超定线代数方程组;3、探索拟合函数的选择与拟合精度间的关系。
二、实验原理对于给定的测量数据(x i ,f i )(i=1,2,…,n ),设函数分布为∑==mj j j x a x y 0)()(ϕ特别的,取)(x j ϕ为多项式j j x x =)(ϕ (j=0, 1,…,m )则根据最小二乘法原理,可以构造泛函∑∑==-=ni mj i j j i m x a f a a a H 110))((),,,(ϕ令0=∂∂ka H(k=0, 1,…,m ) 则可以得到法方程⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡),(),(),(),(),(),(),(),(),(),(),(),(1010101111000100m m m m m m m m f f f a a a ϕϕϕϕϕϕϕϕϕϕϕϕϕϕϕϕϕϕϕϕϕ 求该解方程组,则可以得到解m a a a ,,,10 ,因此可得到数据的最小二乘解∑=≈mj j j x a x f 0)()(ϕ三、实验要求1、用最小二乘法进行曲线拟合;2、近似解析表达式为23123()t a t a t a t ϕ=++;3、打印出拟合函数()t ϕ,并打印出()j t ϕ与()j y t 的误差,1,2,,12j =;4、另外选取一个近似表达式,尝试拟合效果的比较;5、绘制出曲线拟合图。
四、实验步骤:1.进入matlab 开发环境;2.根据实验内容和要求编写程序如下;代码一公式S(x)=a1*t+a2*t^2+a3*t^3;代码二公式S(x)=a2*t^2+a3*t^3+a4*t^4.代码一:function error=mintwomultiply(A) %S(x)=a1*t+a2*t^2+a3*t^3 [a,b]=size(A); M=zeros(3); N=zeros(3,1); error=0; for i=1:aM(1,1)=M(1,1)+A(i,1)*A(i,1); M(1,2)=M(1,2)+A(i,1)*A(i,1)^2; M(2,1)=M(1,2);M(1,3)=M(1,3)+A(i,1)*A(i,1)^3; M(3,1)=M(1,3);M(2,2)=M(2,2)+A(i,1)^2*A(i,1)^2; M(2,3)=M(2,3)+A(i,1)^2*A(i,1)^3; M(3,2)=M(2,3);M(3,3)=M(3,3)+A(i,1)^3*A(i,1)^3; N(1,1)=N(1,1)+A(i,1)*A(i,2); N(2,1)=N(2,1)+A(i,1)^2*A(i,2); N(3,1)=N(3,1)+A(i,1)^3*A(i,2); end%[a1,a2,a3]=solve(M,N)I=M\N;for i=1:aA(i,3)=I(1,1)*A(i,1)+I(2,1)*A(i,1)^2+I(3,1)*A(i,1)^3;error=error+(A(i,3)-A(i,2))^2;endhold on;plot(A(:,1),A(:,3),'r','LineWidth',2);plot(A(:,1),A(:,2),'b','LineWidth',2);legend('原始图像',拟合图像',2);hold off;代码二:function error=mintwomultiply2(A)%S(x)=a2*t^2+a3*t^3+a4*t^4[a,b]=size(A);M=zeros(3);N=zeros(3,1);error=0;for i=1:aM(1,1)=M(1,1)+A(i,1)^2*A(i,1)^2;M(1,2)=M(1,2)+A(i,1)^2*A(i,1)^3;M(2,1)=M(1,2);M(1,3)=M(1,3)+A(i,1)^2*A(i,1)^4;M(3,1)=M(1,3);M(2,2)=M(2,2)+A(i,1)^3*A(i,1)^3;M(2,3)=M(2,3)+A(i,1)^3*A(i,1)^4;M(3,2)=M(2,3);M(3,3)=M(3,3)+A(i,1)^4*A(i,1)^4;N(1,1)=N(1,1)+A(i,1)^2*A(i,2);N(2,1)=N(2,1)+A(i,1)^3*A(i,2);N(3,1)=N(3,1)+A(i,1)^4*A(i,2);end%[a1,a2,a3]=solve(M,N)I=M\N;for i=1:aA(i,3)=I(1,1)*A(i,1)^2+I(2,1)*A(i,1)^3+I(3,1)*A(i,1)^4 error=error+(A(i,3)-A(i,2))^2;endhold on;plot(A(:,1),A(:,3),'r','LineWidth',2);plot(A(:,1),A(:,2),'b','LineWidth',2);legend('原始图像',拟合图像',2);hold off;3.调试程序并运行程序;在某冶炼过程中,根据统计数据的含碳量与时间关系,试求含碳量与时间t 的拟合曲线。
根据以上数据调用代码一和代码二,结果如下图,返回的结果为error为误差,拟合图像蓝的为原始图像,红的为拟合图像,具体图像见下图:图1 公式一误差图2 公式一拟合图图3 公式二误差图4 公式二拟合图4.实验总结从不同公式产生的误差来看,公式一明显误差小;从产生的拟合图像来看公式一更稳定,更平稳。
由此可得,公式的选取对结果的影响很大。
实验三 线方程组的直接解法一、目的和意义1、通过该课题的实验,体会模块化结构程序设计方法的优点;2、运用所学的计算方法,解决各类线性方程组的直接算法;3、提高分析和解决问题的能力,做到学以致用;4、学习Gauss 消去法的原理;5、了解列主元的意义;6、确定什么时候系数阵要选主元。
二 实验数学原理:由于一般线性方程在使用Gauss 消去法求解时,从求解的过程中可以看到,若)1(-k kk a =0,则必须进行行交换,才能使消去过程进行下去。
有的时候即使≠-)1(k kk a 0,但是其绝对值非常小,由于机器舍入误差的影响,消去过程也会出现不稳定得现象,导致结果不正确。
因此有必要进行列主元技术,以最大可能的消除这种现象。
这一技术要寻找行r ,使得)1()1(max ||->-=k ik ki k rk a a并将第r 行和第k 行的元素进行交换,以使得当前的)1(-k kk a 的数值比0要大的多。
这种列主元的消去法的主要步骤如下: 1. 消元过程对k =1,2,…,n -1,进行如下步骤。
1) 选主元,记ik ki rk a a >=max ||若||rk a 很小,这说明方程的系数矩阵严重病态,给出警告,提示结果可能不对。
2) 交换增广阵A 的r ,k 两行的元素。
kj rj a a ↔ (j=k,…,n +1)3) 计算消元kk kj ik ij ij a a a a a /-= (i=k+1,…,n ; j =k +1,……,n +1)2. 回代过程对k= n, n-1,…,1,进行如下计算)/(11,∑-=+-=nk j kk j kjn k k a x aa x至此,完成了整个方程组的求解。
三、实验要求1、对下述方程组分别利用Gauss 顺序消去法与Gauss 列主元消去法;2、应用结构程序设计编出通用程序;3、比较计算结果,分析数值解误差的原因;4、设线性方程组如下123456789104231210000865365010042213210310215131194426167332386857172635021342530116101191734212246271392012400183248631x x x x x x x x x x --⎡⎡⎤⎢⎢⎥--⎢⎢⎥⎢⎢⎥---⎢⎢⎥---⎢⎢⎥⎢⎢⎥---⎢⎢⎥--⎢⎢⎥⎢⎢⎥--⎢⎢⎥---⎢⎥⎢⎥-⎢⎥⎢⎥-----⎣⎦⎣5123234613381921⎤⎡⎤⎥⎢⎥⎥⎢⎥⎥⎢⎥⎥⎢⎥⎥⎢⎥⎥⎢⎥=⎥⎢⎥⎥⎢⎥⎥⎢⎥⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎦方程的解:(1,1,0,1,2,0,3,1,1,2)Tx *=--四、实验要求1.进入matlab 开发环境;2.根据实验内容和要求编写程序;代码分为两个,Gauss 顺序消去法与Gauss 列主元消去法;代码一:Gauss 顺序消去法function x=orderGauss(A,B) [m,n]=size(A); k=rank(A); if m==n&&m==k for i=1:n-1for j=i+1:nB(j,:)=B(j,1)-A(j,i)*B(i,1)/A(i,i);A(j,:)=A(j,:)-A(j,i)*A(i,:)/A(i,i);endendx(n,1)=B(n,1)/A(n,n);for i=n-1:-1:1sum=0;for j=i+1:nsum=sum+A(i,j)*x(j,1);endx(i,1)=(B(i,1)-sum)/A(i,i);endend代码二:Gauss列主元消去法此代码分为两部分,即两个功能函数。
