八年级数学上册 第十一章三角形小结与复习课件2_11-13
合集下载
八年级数学上册 11 三角形小结复习课件 (新版)新人教版

八年级 上册
第十一章 小结与复习
K12课件
1
学习说明
• 学习目标: 1.复习本章内容,整理本章知识,形成知识体系, 体会研究几何问题的思路和方法. 2.进一步发展推理能力,能够有条理地思考、解决 问题.
• 学习重点: 复习本章内容并运用它们进行有关的计算与证明, 构建本章知识结构.
K12课件
2
梳理知识
K12课件
13
ቤተ መጻሕፍቲ ባይዱ
典型例题
例2 如图,在△ABC 中,∠ ABC ,∠ ACB 的平
分线BD,CE 交于点O.
若∠ABC =40°,∠ACB =60°,则:
∠BOC = 130° .
A
E
O
D
B
K12课件
C
14
典型例题
例2 如图,在△ABC 中,∠ ABC ,∠ ACB 的平
分线BD,CE 交于点O.
三边,所以不能围成腰长5 cm的等腰三角形.
K12课件
12
典型例题
变式2 小明用一条长20 cm的细绳围成了一个等腰 三角形,他想使这个三角形的一边长是另一边长的2倍, 那么这个三角形的各边的长分别是多少?
解:若较长的边为腰,则 x + 2x + 2x =20. 解得 x =4. 所以,这个三角形的三边分别为: 4 cm, 8 cm, 8 cm.
C
K12课件
18
课堂小结
(1)本章的核心知识有哪些?这些知识间有什么样 的联系?
(2)通过本节课的复习,你能说说三角形内角和定 理的由来及作用吗?
K12课件
19
2.如图:
A
(1)若AD ⊥BC,垂足
为D,则:
第十一章 小结与复习
K12课件
1
学习说明
• 学习目标: 1.复习本章内容,整理本章知识,形成知识体系, 体会研究几何问题的思路和方法. 2.进一步发展推理能力,能够有条理地思考、解决 问题.
• 学习重点: 复习本章内容并运用它们进行有关的计算与证明, 构建本章知识结构.
K12课件
2
梳理知识
K12课件
13
ቤተ መጻሕፍቲ ባይዱ
典型例题
例2 如图,在△ABC 中,∠ ABC ,∠ ACB 的平
分线BD,CE 交于点O.
若∠ABC =40°,∠ACB =60°,则:
∠BOC = 130° .
A
E
O
D
B
K12课件
C
14
典型例题
例2 如图,在△ABC 中,∠ ABC ,∠ ACB 的平
分线BD,CE 交于点O.
三边,所以不能围成腰长5 cm的等腰三角形.
K12课件
12
典型例题
变式2 小明用一条长20 cm的细绳围成了一个等腰 三角形,他想使这个三角形的一边长是另一边长的2倍, 那么这个三角形的各边的长分别是多少?
解:若较长的边为腰,则 x + 2x + 2x =20. 解得 x =4. 所以,这个三角形的三边分别为: 4 cm, 8 cm, 8 cm.
C
K12课件
18
课堂小结
(1)本章的核心知识有哪些?这些知识间有什么样 的联系?
(2)通过本节课的复习,你能说说三角形内角和定 理的由来及作用吗?
K12课件
19
2.如图:
A
(1)若AD ⊥BC,垂足
为D,则:
人教版八年级数学上册第11章三角形全等小结复习ppt

八年级数学第十一章 全等三角形 复习
定义 性质
全 全 等 等 三 形 角 形
判定
应用
全等三角形对应边相等 全等三角形对应角相等 全等三角形的面积相等 SSS SAS (一般三角形) ASA AAS HL (直角三角形) 解决问题
角的平分线的性质: 角平分线上的一点到角的两边距离相等 角的平分线的判定: 到角的两边的距离相等的点在角平分线上
A
∵AB=AC,BD=CD,AD=AD ∴△ABD≌△ACD(SSS); 在△ABH和△ACH中
∵BD=CD,BH=CH,DH=DH ∴△DBH≌△DCH(SSS)
D B
H
C
例3、如图,在△ABC中,已知AB=AC=12cm,BC=8cm, 点M是AB的中点,如果点P在线段BC上以2cm/s的速度 由点B向C运动,同时点Q在线段AC上以同样的速度由 点C向A运动,当P到达点C或点Q到达A时运动停止。 (1)经过1s后△BPM与以点C、P、Q为顶点组成的三 角形是否全等?为什么? (2)如果点Q的运动速度与点P的不相等,在运动过程 中,能否出现△BPM与以点C、P、Q为顶点组成的 A 三角形全等?若能,请你求出此时点Q的运 动速度和运动时间分别是多少? M 若不能,请说明理由。 Q P B C
例8.已知:∠ACB=∠ADB=900,AC=AD,P是AB 上任意一点,求证:CP=DP
C A
P
D
B
∴∠1=∠2 在△APC和△APD中
AC=AD ∠1=∠2 AP=AP
∴∆APC≌∆APD(SAS) ∴CP=DP
证明:在Rt∆ABC和Rt∆ABD中
AC AD AB AB
∴Rt∆ABC≌Rt∆ABD
例7. 如图,已知CE ⊥AB,DF ⊥ AB, AC=BD,AF=BE,则CE=DF。请说明理由。
定义 性质
全 全 等 等 三 形 角 形
判定
应用
全等三角形对应边相等 全等三角形对应角相等 全等三角形的面积相等 SSS SAS (一般三角形) ASA AAS HL (直角三角形) 解决问题
角的平分线的性质: 角平分线上的一点到角的两边距离相等 角的平分线的判定: 到角的两边的距离相等的点在角平分线上
A
∵AB=AC,BD=CD,AD=AD ∴△ABD≌△ACD(SSS); 在△ABH和△ACH中
∵BD=CD,BH=CH,DH=DH ∴△DBH≌△DCH(SSS)
D B
H
C
例3、如图,在△ABC中,已知AB=AC=12cm,BC=8cm, 点M是AB的中点,如果点P在线段BC上以2cm/s的速度 由点B向C运动,同时点Q在线段AC上以同样的速度由 点C向A运动,当P到达点C或点Q到达A时运动停止。 (1)经过1s后△BPM与以点C、P、Q为顶点组成的三 角形是否全等?为什么? (2)如果点Q的运动速度与点P的不相等,在运动过程 中,能否出现△BPM与以点C、P、Q为顶点组成的 A 三角形全等?若能,请你求出此时点Q的运 动速度和运动时间分别是多少? M 若不能,请说明理由。 Q P B C
例8.已知:∠ACB=∠ADB=900,AC=AD,P是AB 上任意一点,求证:CP=DP
C A
P
D
B
∴∠1=∠2 在△APC和△APD中
AC=AD ∠1=∠2 AP=AP
∴∆APC≌∆APD(SAS) ∴CP=DP
证明:在Rt∆ABC和Rt∆ABD中
AC AD AB AB
∴Rt∆ABC≌Rt∆ABD
例7. 如图,已知CE ⊥AB,DF ⊥ AB, AC=BD,AF=BE,则CE=DF。请说明理由。
第十一章 三角形(复习与小结)(课件)八年级数学上册(人教版)

且△ABC的面积为32,求△BEF的面积.
A
E F
B
D
C
探究新知
8.如图,已知:点D为△ABC内一点,求证:AB+AC>DB+DC.
证明:延长BD交AC于点E
∵在△ABE中,AB+AE>BE=BD+DE,①
D
∵在△DEC中,DE+EC>DC,②
∴由①+②得AB+AE+ DE+EC> BD+DE+DC
三角形的边:三边关系定理
与三角形有 关的线段
高线 中线:把三角形面积平分
角平分线
三角形内角和:180°
与三角形有 关的角
三角形的分类
定义
对角线
多边形的内外角和
三角形外角和:360°
内角与外角关系
多边形转化为三角形和 四边形的重要辅助线
内角和:(n-2) ×180 ° 外角和:360 °
正多边形
内角=(n 2)180 n
考点聚焦
4.如图,AD平分∠BAC,∠EAD=∠EDA. (1)求证:∠EAC=∠B;(2)若∠B=50°,∠CAD∶∠E=1∶3,求∠E的度 数.
(2)由(1)可知∠EAC=∠B=50°. 设∠CAD=x, 则∠E=3x,∠EAD=∠ADE=x+50°, ∴50°+x+50°+x+3x=180°. ∴x=16°. ∴∠E=3x=48°.
∴AB+AC>DB+DC.
B
A E C
知识梳理
知识点二与三角形有关的角
1、三角形的内角和定理 三角形三个内角的和等于180°.
2、直角三角形的性质 直角三角形的两个锐角互余.
人教版数学八上第十一章三角形复习课件共34张PPT

2
。
(3,3,1;2,2,3)
1、如图,求△ABC各内角的度数。 A
解:3x + 2x + x = 180
35xx
6x=180
X=30
23xx
B
xx C
∴三角形各内角的度数分别为:30°,60°,90°
2、已知三角形三个内角的度数比为1:3:5, 求解这:三设个三内个角内的角度分数别。为x,3x,5x
B A
小莉的设计方案:先在池塘旁取一个能
直接到达A和B处的点C,连结AC并延长至
D点,使AC=DC,连结BC并延长至E点,
使BC=EC,连结CD,用米尺测出DE的长,
这个长度就等于A,B两点的距离。请你说
明理由。
解: AC=DC
∠ACB=∠DCE
A
B
BC=EC
C
△ACB≌△DCE(SAS)
E
D
AB=DE
则x + 3x + 5x = 180 x=20
∴三角形三个内角分别为:20°,60°,100°
题型考查
1.符合条件∠A+∠B=62°的三角形是( C )
A、锐角三角形 C、钝角三角形
B、直角三角形 D、不能确定
2.在下列长度的四根木棒中,能与4㎝,9㎝ 两根木棒围成三角形的是( C )
A、4㎝ B、5㎝ C、9㎝ D、14㎝ 3.如图,在△ABC中,∠A=70° A
点,∠1=∠2,AE=DE,
试求AB=DC。
AD
12
BEC
简解:∵E是BC的中点, ∴BE=EC。又∴ ∠1=∠2,AE=DE, △ABE≌△DCE(SAS),∴AB=DC 。
3.如图,已知BE⊥AD, CF⊥AD,且BE=CF,请你 判断AD是△ABC的中线还是
人教版八年级上册11三角形单元复习课件(共41张)

;由三角形的外角性质,∠4+∠5=∠2成立,故B选项正确;由
三角形的内角和定理与对顶角相等,∠1+∠3+∠6=180°,
∠1+∠5+∠4=180°成立,故C、D选项正确.
正解:A.
过关训练
3.如图Z11-1-4,在△ABC中,E是AB上的一点,D是BC延长线上的
一点,DE交AC于点F.
(1)如果∠D>∠A,比较∠AEF与∠A的大小,并说明理由;
∴∠BDC=65°,则△BDC不满足“准直角三角形”的条件.
综上所述,△ABD是“准直角三角形”.
7.(几何直观、推理能力、模型观念)已知在△ABC中,AE平分
∠BAC(∠C>∠B),F为直线AE上一点,且FD⊥BC于D.
(1)如图Z11-5-7①,若∠B=40°,∠C=60°,点F在线段AE上
,求∠EFD的度数;
解:(1)设底边长为x cm,则腰长为2x cm.
由题意,得x+2x+2x=24.解得x=4.8.
∴底边长为4.8
cm.
(2)能.理由如下:
①当底边长为6
cm时,腰长为(24-6)÷2=9(cm),因为9+
9>6,所以此时能围成三角形;
②当腰长为6
cm时,底边长为24-6×2=12(cm),因为6+6=
所对的角_______________;
相等或互补
(3)模型应用:在钝角三角形ABC中,∠A=45°,高BD和CE所在
的直线交于点H,则∠BHC的度数为______.
45°
解:(1)∠BHC+∠A=180°或∠BHC=∠A.
当∠ACB<90°时,△ABC为锐角三角形,如答图Z11-1-2①.
三角形的内角和定理与对顶角相等,∠1+∠3+∠6=180°,
∠1+∠5+∠4=180°成立,故C、D选项正确.
正解:A.
过关训练
3.如图Z11-1-4,在△ABC中,E是AB上的一点,D是BC延长线上的
一点,DE交AC于点F.
(1)如果∠D>∠A,比较∠AEF与∠A的大小,并说明理由;
∴∠BDC=65°,则△BDC不满足“准直角三角形”的条件.
综上所述,△ABD是“准直角三角形”.
7.(几何直观、推理能力、模型观念)已知在△ABC中,AE平分
∠BAC(∠C>∠B),F为直线AE上一点,且FD⊥BC于D.
(1)如图Z11-5-7①,若∠B=40°,∠C=60°,点F在线段AE上
,求∠EFD的度数;
解:(1)设底边长为x cm,则腰长为2x cm.
由题意,得x+2x+2x=24.解得x=4.8.
∴底边长为4.8
cm.
(2)能.理由如下:
①当底边长为6
cm时,腰长为(24-6)÷2=9(cm),因为9+
9>6,所以此时能围成三角形;
②当腰长为6
cm时,底边长为24-6×2=12(cm),因为6+6=
所对的角_______________;
相等或互补
(3)模型应用:在钝角三角形ABC中,∠A=45°,高BD和CE所在
的直线交于点H,则∠BHC的度数为______.
45°
解:(1)∠BHC+∠A=180°或∠BHC=∠A.
当∠ACB<90°时,△ABC为锐角三角形,如答图Z11-1-2①.
人教版八年级数学上册第十一章三角形章末复习课件(共70张)

稳定性
概念
三角形
章末复习
与三角形 有关的角
与三角形 有关的角
三角形 的外角
三角形三个内角 的和等于180°
三角形的外角 和等于360°
三角形的外角等于与它不相 邻的两个内角的和
直角三 角形
三角形
性质 直角三角形的两个锐角互余 判定 有两个角互余的三角形是直角三角形
章末复习
三条高(或三条高所在
的直线)相交于一点
章末复习
当a=6时,2+3<6,不能组成三角形,故舍去; 当a=2时,2+2>3,能组成三角形, ∴a=2,b=2,c=3. ∵2+2+3=7, ∴△ABC的周长为7.
章末复习
专题四 复杂图形中角度的计算
【要点指导】求复杂图形中的角度时, 常利用转化的思想将分 散的角转化到一个多边形中, 再利用多边形的内角和与外角和 来解答.
章末复习
分析
AM⊥BC, AD⊥BE, ∠BAC=90°
∠2+∠ADB=90°, ∠3+∠ADB=90°
等量 代换
∠2 =∠3
∠1+∠AEB=90°, ∠4+∠AEB=90°
等量 代换
∠1 =∠4
∠1 =∠2
章末复习
解 在Rt△BDF与Rt△ADM中, ∵∠2+∠ADB=90°, ∠3+∠ADB=90°, ∴∠2=∠3. 在Rt△ABE与Rt△AEF中, ∵∠1+∠AEB=90°, ∠4+∠AEB=90°, ∴∠1=∠4. 又∵∠1=∠2, ∴∠2=∠3=∠4.
章末复习
例3 设a, b, c是△ABC的三边长, 化简:|a-b-c|+|b-c-a|+|c+a-b|.
概念
三角形
章末复习
与三角形 有关的角
与三角形 有关的角
三角形 的外角
三角形三个内角 的和等于180°
三角形的外角 和等于360°
三角形的外角等于与它不相 邻的两个内角的和
直角三 角形
三角形
性质 直角三角形的两个锐角互余 判定 有两个角互余的三角形是直角三角形
章末复习
三条高(或三条高所在
的直线)相交于一点
章末复习
当a=6时,2+3<6,不能组成三角形,故舍去; 当a=2时,2+2>3,能组成三角形, ∴a=2,b=2,c=3. ∵2+2+3=7, ∴△ABC的周长为7.
章末复习
专题四 复杂图形中角度的计算
【要点指导】求复杂图形中的角度时, 常利用转化的思想将分 散的角转化到一个多边形中, 再利用多边形的内角和与外角和 来解答.
章末复习
分析
AM⊥BC, AD⊥BE, ∠BAC=90°
∠2+∠ADB=90°, ∠3+∠ADB=90°
等量 代换
∠2 =∠3
∠1+∠AEB=90°, ∠4+∠AEB=90°
等量 代换
∠1 =∠4
∠1 =∠2
章末复习
解 在Rt△BDF与Rt△ADM中, ∵∠2+∠ADB=90°, ∠3+∠ADB=90°, ∴∠2=∠3. 在Rt△ABE与Rt△AEF中, ∵∠1+∠AEB=90°, ∠4+∠AEB=90°, ∴∠1=∠4. 又∵∠1=∠2, ∴∠2=∠3=∠4.
章末复习
例3 设a, b, c是△ABC的三边长, 化简:|a-b-c|+|b-c-a|+|c+a-b|.
八年级数学上册 第十一章 三角形小结与复习课件 (新版)新人教版

解:若较长的边为腰,则 x + 2x + 2x =20. 解得 x =4. 所以,这个三角形的三边分别为: 4 cm, 8 cm, 8 cm.
已知a、b、c是三角形的三边长,试化简:
bca acb abc cba
知识点2
与三角形有关的线段: 高、中线、角平分线
2.如图:
3.若三角形的两边分别为3 和5 ,第三边长为整数,
这样的三角形的周长的最小值是 11
,
最大值是 15
。
3、下列条件中能组成三角形的是( C )
A、 5cm, 13cm, 7cm B、 3cm, 5cm, 9cm C、 14cm, 9cm, 6cm D、 5cm, 6cm, 11cm
典型例题
1、已知等腰三角形的两边长分别为10 和 6 ,则 三角形的周长是 22或26 。
F
角平分线,则:
O
∠AEC = 100°;
(3)若BF 是△ABC 的
B
高,与角平分线
E
C
AE 相交于点O,则∠EOF = 130° .
熟练运用三角形的内角和定理:
1、在△ABC中,∠A=400, ∠B=∠C,
则∠C等于( C )
A、400 B、600 C、700
D、800
2、已知△ABC中,∠B是∠A的2倍 ,∠C比∠A
则两个锐角的度数分别为
。
直角三角形的两个锐角互余; 有两个角互余的三角形是直角三角形。
2、在△ABC中,AD⊥BC于点D,∠1=∠B,试说明: △ABC是直角三角形。 A
BD
C
典型例题
例2 如图,在△ABC 中,∠ ABC ,∠ ACB 的平
分线BD,CE 交于点O.
已知a、b、c是三角形的三边长,试化简:
bca acb abc cba
知识点2
与三角形有关的线段: 高、中线、角平分线
2.如图:
3.若三角形的两边分别为3 和5 ,第三边长为整数,
这样的三角形的周长的最小值是 11
,
最大值是 15
。
3、下列条件中能组成三角形的是( C )
A、 5cm, 13cm, 7cm B、 3cm, 5cm, 9cm C、 14cm, 9cm, 6cm D、 5cm, 6cm, 11cm
典型例题
1、已知等腰三角形的两边长分别为10 和 6 ,则 三角形的周长是 22或26 。
F
角平分线,则:
O
∠AEC = 100°;
(3)若BF 是△ABC 的
B
高,与角平分线
E
C
AE 相交于点O,则∠EOF = 130° .
熟练运用三角形的内角和定理:
1、在△ABC中,∠A=400, ∠B=∠C,
则∠C等于( C )
A、400 B、600 C、700
D、800
2、已知△ABC中,∠B是∠A的2倍 ,∠C比∠A
则两个锐角的度数分别为
。
直角三角形的两个锐角互余; 有两个角互余的三角形是直角三角形。
2、在△ABC中,AD⊥BC于点D,∠1=∠B,试说明: △ABC是直角三角形。 A
BD
C
典型例题
例2 如图,在△ABC 中,∠ ABC ,∠ ACB 的平
分线BD,CE 交于点O.
第11章《三角形小结》PPT课件人教版数学八年级上册

是( C ) 从三角形的一个顶点向它所对的边所在直线画垂线,顶点与垂足之间的线段叫做三角形的这条边上的高.
∴ ∠ACD=∠A+∠B=110°.
9cm
B.
各个角都相等,各个边都相等的多边形叫做正多边形.
A.4 三角形三个内角的和等于180°.
此时5+5<13,不能构成三角形.
B.5
C.6
D.7
周长为5+5+2=12(cm).
重难剖析 下列具有稳定性的是( )
解:∵△ABC是等边三角形,
(3) 若AF是△ABC的角平分线,则(
)= (
).
则2∵a∠+51B2+=bx2+.x(一=2∠3A,C+个.∠解C得)多x,=9. 边形的内角和是720°,则这个多边形的边数
连接三角形的一个顶点和它所对的边的中点,所得线段叫做三角形这条边上的中线.
解析:∵正多边形的一个内角等于120°, ∴正多边形的一个外角等于60°, ∴边数为360°÷60°=6.
三角形的外角等于与它不相邻的两个内角的和. ∴a+b>c,c-a<b,即a+b-c>0,c-a-b<0.
∴∠ABD=∠A+∠ACB, 一个多边形的内角和是720°,则这个多边形的边数是( )
∴∠ABD=∠A+∠ACB,
5
C.
4.三角形外角和的性质 三角形三个内角的和等于180°.
4
B.
解:∵AB⊥BC,
则(
)=(
)=90°;
三角形的外角和等于360°.
解得n=6. 1cm,1cm,2cm
D.
则5+x+x=23,解得x=9.
初中数学人教八年级上册第十一章 三角形 三角形复习PPT
AA
D
?1
┌
BB
D
D
CC
A
D
E
B
C
考点二 三角形的内角和
例2:如图,CD是∠ACB的平分线,DE∥BC,
∠A=50°,∠B=70°,求∠EDC,∠BDC 的度数。
知识点梳理:
A
7.三角形外角
(1)外角的定义:
1
B
C
∠1=∠A+∠B ∠1+∠ACB=180°
(2)三角形的一个外角等于 与它不相邻 的两个
2
BC=2BD=2CD
三角形的角平分线
A
︶1 2
B
●
D
C
1
∠1=∠2= 2 ∠BAC
∠BAC=2∠1=2∠2
考点二:三角形的高、中线、角平分线
例2:如图,若AD是△ABC的中线,已知
△ABD的周长为25cm,AB比AC长6cm,
则:△ACD的周长为( A)
BB
A. 19cm B. 22cm C. 25cm D. 31cm
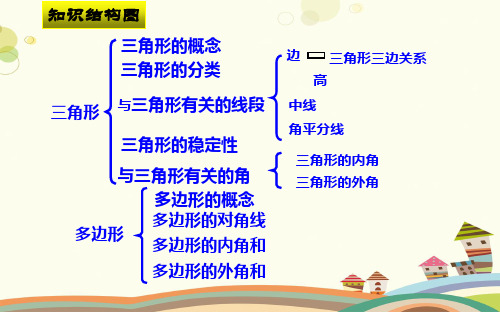
知识结构图
三角形的概念 三角形的分类
三角形 与三角形有关的线段
三角形的稳定性
与三角形有关的角
多边形
多边形的概念 多边形的对角线
多边形的内角和
多边形的外角和
边 三角形三边关系 高
中线 角平分线
三角形的内角 三角形的外角
知识点梳理:
由不在同一条直线上的三线 1.三角形的定义: 段 首尾顺次相接 所组成的图形叫做
例1:(2014 ∙西宁)以下列各组线段长为边,能 组成三角形的是( D )
A. 2, 2, 4 B. 2, 6, 3 C. 12, 5, 6 D. 7, 3, 6
人教版数学八年级上册 第十一章 小结 课件(共33张PPT)

B 1 2 A X
34
C
解 :
A 1 2 3 4 180
又 A 100 , 1 2, 3 4
100 22 24 180
2(2 4) 80
2 4 40
又 2 4 X 180
X 180 40 140
5.如图,△ABC中,∠A=∠ABD, ∠C=∠BDC=∠ABC,求∠DBC的度数。
2.三角形外角和定理 三角形的外角和等于360°。
3.三角形的外角与内角的关系 三角形的一个外角等于与它不相邻的两个内角的和。
三角形的一个外角大于与它不相邻的任何一个内角。
三角形木架的形状不会改变,而四边形 木架的形状会改变。
这就是说,三角形具有稳定性,而四边 形没有稳定性。
多边形的定义
三角形 长方形 四边形 六边形
C.三角形的外角中必有两个角是钝角;
D.锐角三角形中两锐角的和必然小于60°。
二、填空题
1. 一 个 三 角 形 的 三 边 长 是 整 数 , 周 长 为 5 , 则 最 小 边 为 1;
2.木工师傅做完门框后,为防止变形,通常在角上钉一 斜条,根据是 三角形具有稳定性 ;
3.小明绕五边形各边走一圈,他共转了 360 度;
A
解:设A X
A ABD,ABD X
BDC A ABD 2X
D
又 C ABC BDC
C ABC 2X
DBC ABC ABD
B
C
2X X X
又 C DBC BDC 180
2X X 2X 180
5X 180
X 36 ,即DBC 36
6.求∠A+∠B+∠C+∠D+∠E+∠F+∠G的度数。 G
AB//CD。
D
人教版八年级数学上册课件 第十一章 三角形 复习小结 (共25张PPT)

B
E
D
C
图9
广东省怀集县凤岗镇初级中学
黎方和
二. 强化训练 解: B 20,C 80
BAC 80 又 AE 平分ABC 和BAC BAE 40
AEC 60 (三角形的外角) 又 AD BC ADE 90 EAD 180 90 60 30
A
A、3 C、9
B、6
E
D、12
B
C D
广东省怀集县凤岗镇初级中学
黎方和
一、基础知识 3、如图2,在△ABC中,∠A = 40°,∠B = 72°,CE平分∠ACB,CD⊥AB于D,DF⊥CE, 则∠CDF = 74 度。
4、造房子时,屋顶常用三角形结构,从数 学角度来看,是应用了 三角形的稳定性 , 而活动挂架则用了四边形的 不稳定性 .
广东省怀集县凤岗镇初级中学 黎方和
一、基础知识 练一练:
1、以下列各组线段为边,能组成三角形的是( B ). A.2 cm,3 cm,5 cm
B.5 cm,6 cm,10 cm
C.1 cm,1 cm,3 cm
D.3 cm,4 cm,9 cm
广东省怀集县凤岗镇初级中学
黎方和
一、基础知识 2、如图1,在△ABC中,AD是BC上的中线,BE 是△ABD中AD边上的中线,若△ABC的面积是 24,则ABE的面积是( B )
“引导学生读懂数学书” 课题研究成果配套课件
宝剑锋从磨砺出,梅花香自苦寒来。 ----朱熹
“引导学生读懂数学书” 课题研究成果配套课件
第十一章 三角形 复习小结
凤岗中学 黎方和
一、基础知识 知识点一 与三角形有关的线段
1、三角形两边的和 大于 第三边;三 角形两边的差 小于 第三边. 2、从三角形的一个顶点向它所对的边所在 三角形顶点 和 垂足 之间 直线作垂线, 的 线段 ,叫做三角形的高.
人教版八年级上册数学第十一章三角形课件PPT

1 2
∠ABC
F
OE
∵CF是△ABC的角平分线
∴∠ACB=2___∠_A__C=F2____∠BCF B
D
C
三角形的角平分线与角的平分 线有什么区别?
思
三角形的角平分线是一条
考
线段 , 角的平分线是一条
射线
练一练
如图,在△ABC中, ∠1=∠2,G为AD中点,延长BG 交AC于E,F为AB上一点,CF⊥AD于H,判断下列 说法那些是正确的,哪些是错误的?
腰与底不等的等腰三角形
等腰三角形 等边三角形
直角三角形
三角形
锐角三角形
斜三角形
钝角三角形
下面图形中一共有多少个三角形?锐角 三角形、直角三角形、钝角三角形各有多少个?Leabharlann AB DE
C
13
下面图形中一共有多少个三角形?锐角 三角形、直角三角形、钝角三角形各有多少个?
A
B D
E
C
14
下面图形中一共有多少个三角形?锐角 三角形、直角三角形、钝角三角形各有多少个?
A
3
2
B D
E
C
1
这个图形中一共有6个三角形。
21
下面图形中一共有多少个三角形?锐角 三角形、直角三角形、钝角三角形各有多少个?
A
3
2
B D
E
C
1
这个图形中一共有6个三角形。
锐角三角形有2个;
22
下面图形中一共有多少个三角形?锐角 三角形、直角三角形、钝角三角形各有多少个?
A
3
2
B D
E
C
1
这个图形中一共有6个三角形。
C
人教版八年级上册数学第十一章《三角形》复习课件

;
C
EDF
B
(2)∠BAD=
=
;
(3)∠AFB=
=90°;
(4)SΔABC=
.
知识点三:三角形中的线段
变式练习:
1.在ΔABC中,CD是中线,已知BC-AC=5cm, ΔDBC的周长为25cm,求ΔADC的周长.
A
D
B
C
知识点三:三角形中的线段
变式练习:
1.在ΔABC中,CD是中线,已知BC-AC=5cm,
知识点一:三角形的三边关系
变式练习: 1.若三角形三边长为2,4,m,则m的值不可以是(D) A.3 B.4 C.5 D.6 2.若等腰三角形的两边长是3cm和5cm,则它的周长是( C ) A.11cm B.13cm C.11cm或13cm D.无法确定 3.若等腰三角形的两边长是3cm和6cm,则它的周长是( B ) A.12cm B.15cm C.12cm或15cm D.无法确定 4.若三角形的两边长是3cm和6cm,若第三边为奇数,则它的周长 可能是( C ) A.12cm B.13cm C. 14cm D.15cm
如图1,∠BAD=∠CAD,则线段AD是△ABC的一条角 平分线.
在三角形中,连接一个顶点与它的对边中点的线段叫作 三角形的中线.
如图2,BE=EC,则线段AE是△ABC的BC边上的中线.
知识点三:三角形中的线段
例1.如图,在ΔABC中,AE是中线,AD是角
A
平分线,AF是高。填空:
(1)BE=
=
《三角形》复习用课件
知识点一:三角形的三边关系
三角形的任意两边之和大于第三边; 三角形的任意两边之差小于第三边;
知识点一:三角形的三边关系
人教版八年级数学上册第十一章三角形小结与复习课件

例11 如图,∠A=51°,∠B=20°, ∠C=30°,求∠BDC的度数.
A
51 °
20 ° D B
C
解:连接AD并延长于点E.
A
在△ABD中,∠1+∠ABD=∠3,
在△ACD中,∠2+∠ACD=∠4.
D
20 °
因为∠BDC=∠3+∠4,
B
∠BAC=∠1+∠2,
E
所以∠BDC=∠BAC+∠ABD+∠ACD
(2)设∠A=2x,∠B=3x,∠C=4x , 则2x + 3x + 4x = 180° ,解得 x=20°, ∴∠A=40°,∠B=60°,∠C=80°.
例9 如图,CD是∠ACB的平分线,DE∥BC,∠A= 50°,∠B=70°,求∠EDC,∠BDC的度数.
解:∵∠A=50°,∠B=70°, ∴∠ACB=180°-∠A-∠B=60°. ∵CD是∠ACB的平分线, ∴∠BCD= 1∠ACB=30°.
n边形的外角和等于360°.
正多边形的每个内角的度数是 (n 2)180 , n
正多边形的每个外角的度数是 360 .
n
考点讲练
考点一 三角形的三边关系
例1 有两根长度分别为5cm和8cm的木棒,用长度 为2cm的木棒与它们能摆成三角形吗?为什么?长 度为13cm的木棒呢?
解:取长度为2cm的木棒时,由于2+5=7<8,出 现了两边之和小于第三边的情况,所以它们不能 摆成三角形.取长度为13cm的木棒时,由于 5+8=13,出现了两边之和等于第三边的情况,所 以它们也不能摆成三角形.
⊥AC, △BDE是等边三角形,求∠C的度数.
解:设∠C=x °,则∠ABC=x°,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
◆化归思想 如图,△AOC与△BOD是有一组对顶角的三角形,其形状像数字
“8”,我们不难发现有一重要结论: ∠A+∠C=∠B+∠D.这一图形
也是常见的基本图形模型,我们称它为“8字
例11 如图,求∠A+∠B+∠C+∠D+∠E+∠F+∠G的度
数.
解析:所求问题不是常见的求多边形的内角和
A
问题,我们发现,只要连接CD便转化为求五
边形的内角和问题.
BG
E F
C
D
解:连接CD,由“8字型”模型图可知 ∠FCD+∠GDC=∠F+∠G,所
以∠A+∠B+∠C+∠D+∠E+∠F+∠G=(5-2) ×180 °=540
°.
图库 https://
◆分类讨论思想 例10 已知等腰三角形的两边长分别为10 和6 ,则 三角形的周长是 26或22 .
【解析】 由于没有指明等腰三角形的腰和底,所以要分两种情况讨论: 第一种10为腰,则6为底,此时周长为26;第二种10为底,则6为腰,此时 周长为22.
【易错提示】别忘了用三边关系检验能否组成三角形这一重要解题环节.
