高中精品-数学:三角形五心定理
三角形的五心

三角形的五心
(1)重心和三顶点的连线所构成的三个三角形面积相等;
(2)外心扫三顶点的距离相等;
(3)垂心与三顶点这四点中,任一点是其余三点构成的三角形的垂心;
(4)内心、旁心到三边距离相等;
(5)垂心是三垂足构成的三角形的内心,或者说,三角形的内心是它旁心三角形的垂心;
(6)外心是中点三角形的垂心;
(7)中心也是中点三角形的重心;
(8)三角形的中点三角形的外心也是其垂足三角形的外心.
三角形的五心
一定理
重心定理:三角形的三条中线交于一点,这点到顶点的
离是它到对边中点距离的2倍.该点叫做三角形的重心.
外心定理:三角形的三边的垂直平分线交于一点.该点叫做三角形的外心.
垂心定理:三角形的三条高交于一点.该点叫做三角形的垂心.
内心定理:三角形的三内角平分线交于一点.该点叫做三角形的内心.
旁心定理:三角形一内角平分线和另外两顶点处的外角平分线交于一点.该点叫做三角形的旁心.三角形有三个旁心.
三角形的重心、外心、垂心、内心、旁心称为三角形的五心.它们都是三角形的重要相关点.。
三角形五心定律—搜狗百科
三角形五心定律—搜狗百科
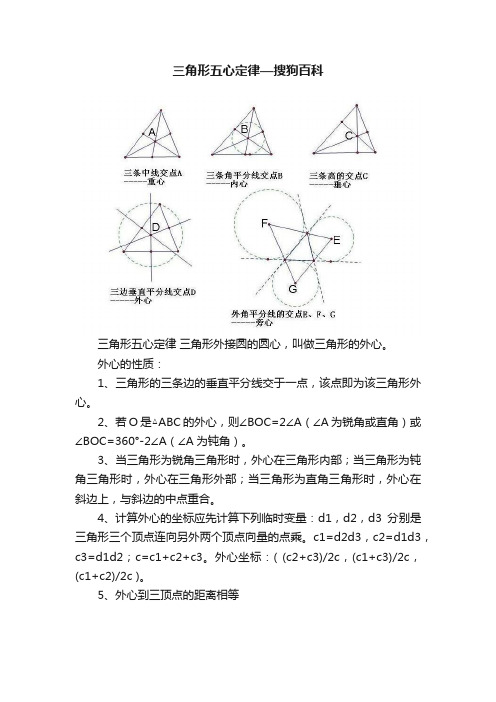
三角形五心定律三角形外接圆的圆心,叫做三角形的外心。
外心的性质:
1、三角形的三条边的垂直平分线交于一点,该点即为该三角形外心。
2、若O是△ABC的外心,则∠BOC=2∠A(∠A为锐角或直角)或∠BOC=360°-2∠A(∠A为钝角)。
3、当三角形为锐角三角形时,外心在三角形内部;当三角形为钝角三角形时,外心在三角形外部;当三角形为直角三角形时,外心在斜边上,与斜边的中点重合。
4、计算外心的坐标应先计算下列临时变量:d1,d2,d3分别是三角形三个顶点连向另外两个顶点向量的点乘。
c1=d2d3,c2=d1d3,c3=d1d2;c=c1+c2+c3。
外心坐标:( (c2+c3)/2c,(c1+c3)/2c,(c1+c2)/2c )。
5、外心到三顶点的距离相等。
三角形的、外心、内心、重心、垂心、和旁心(五心定理)

三角形的外心、内心、重心、垂心、旁心(五心定理)
4
三
角
形的
垂心
三角形的三条高交于一点,这点称
为三角形的垂心 1,三角形任一顶点到垂心的距离,等于外
心到对边的距离的2倍;锐角三角形的垂
心到三顶点的距离之和等于其内切圆与外接圆半径之和的2倍;
2,锐角三角形的垂心在三角形内;直角三角形的垂心在直角顶点上;钝角三角形的
垂心在三角形外 ;
5
三角形的旁心
三角形的一条内角平分线与另两
个外角平分线交
于一点,称为三角形的旁心(旁切圆圆心)
1, 每个三角形都有三个旁心;
2, 旁心到三边的距离相等
附:三角形的中心:只有正三角形才有中心,这时重心,内心,外心,垂心,四心合一。
A
B
C
D
E F
I a
A B
C D
E
F O。
三角形五心定律

三角形五心定律重心定理三角形的三条边的中线交于一点。
该点叫做三角形的重心。
三中线交于一点可用证明,十分简单。
(重心原是一个物理概念,关于等厚度的质量均匀的三角形薄片,其重心恰为此三角形三条中线的交点,重心因此得名)重心的性质:一、重心到极点的距离与重心到对边中点的距离之比为2︰1。
二、重心和三角形任意两个极点组成的3个三角形面积相等。
即重心到三条边的距离与三条边的长成反比。
3、重心到三角形3个极点距离的平方和最小。
4、在中,重心的坐标是极点坐标的算术平均数,即其重心坐标为((X1+X2+X3)/3,(Y1+Y2+Y3)/3)。
5. 以重心为起点,以三角形三极点为终点的三条向量之和等于零向量。
外心定理三角形的圆心,叫做三角形的外心。
外心的性质:一、三角形的三条边的交于一点,该点即为该。
二、假设O是△ABC的外心,那么∠BOC=2∠A(∠A为锐角或)或∠BOC=360°-2∠A(∠A为钝角)。
3、当三角形为时,外心在三角形内部;当三角形为钝角三角形时,外心在三角形外部;当三角形为时,外心在斜边上,与斜边的中点重合。
4、计算外心的坐标应先计算以下临时变量:d1,d2,d3别离是三角形三个极点连向另外两个极点的点乘。
c1=d2d3,c2=d1d3,c3=d1d2;c=c1+c2+c3。
外心坐标:( (c2+c3)/2c,(c1+c3)/2c,(c1+c2)/2c )。
五、外心到三极点的距离相等垂心定理三角形的三条高(所在直线)交于一点,该点叫做三角形的垂心。
的性质:一、三角形三个极点,三个,这7个点能够取得6个四点圆。
二、O、重心G和H,且OG︰GH=1︰2。
(此直线称为三角形的(Euler line))3、到三角形一极点距离为此到此极点距离的2倍。
4、分每条高线的两部份乘积相等。
已知:ΔABC中,AD、BE是两条高,AD、BE相交于点O,连接CO并延长交AB于点F ,求证:CF⊥AB证明:连接DE ∵∠ADB=∠AEB=90度∴A、B、D、E ∴∠ADE=∠ABE∵∠EAO=∠DAC ∠AEO=∠ADC ∴ΔAEO∽ΔADC∴AE/AO=AD/AC ∴ΔEAD∽ΔOAC ∴∠ACF=∠ADE=∠ABE又∵∠ABE+∠BAC=90度∴∠ACF+∠BAC=90度∴CF⊥AB因此,垂心定理成立!内心定理三角形内切圆的圆心,叫做三角形的内心。
三角形的重心、外心、垂心、内心和旁心(五心定理).doc

三角形五心定理(三角形的重心,外心,垂心,内心和旁心称Z为三角形的五心)三角形五心定理是指三角形重心定理,外心定理,垂心定理,内心定理, 旁心定理的总称。
、三角形重心定理三角形的三条边的中线交于一点。
该点叫做三角形的重心。
三中线交于一点可用燕尾定理证明,十分简单。
(重心原是一个物理概念,对于等厚度的质量均匀的三角形薄片,其重心恰为此三角形三条中线的交点, 重心因而得名)重心的性质:1、重心到顶点的距离与重心到对边中点的距离Z比为2 : 1o2、重心和三角形3个顶点组成的3个三角形面积相等。
即重心到三条边的距离与三条边的长成反比。
3、重心到三角形3个顶点距离的平方和最小。
4、在平面直角坐标系中,重心的坐标是顶点坐标的算术平均,即其重心坐标为((X1 +X2+X3)/3, (Y1 +Y2+Y3)/3o二、三角形外心定理三角形外接圆的圆心,叫做三角形的外心。
外心的性质:仁三角形的三条边的垂直平分线交于一点,该点即为该三角形外心。
2、若0是ZXABC的外心,则ZB0C=2ZA ( ZA为锐角或宜角)或Z BOC=360°-2ZA (ZA 为钝角)。
3、当三角形为锐角三角形时,外心在三角形内部;当三角形为钝角三角形时, 外心在三角形外部;当三角形为直角三角形时,外心在斜边上,与斜边的中点重合。
4、计算外心的坐标应先计算下列临时变量:d1, d2, d3分别是三角形三个顶点连向另外两个顶点向量的点乘od=d2d3, c2=d1d3, c3=d1d2; c=c1+c2+c3o 重心坐标:((c2+c3)/2c, (c1+c3)/2c, (c1+c2)/2c )o5、外心到三顶点的距离相等三、三角形垂心定理三角形的三条高(所在直线)交于一点,该点叫做三角形的垂心。
垂心的性质:1>三角形三个顶点,三个垂足,垂心这7个点可以得到6个四点圆。
2、三角形外心O、重心G和垂心H三点共线,且0G : GH=1 : 2。
三角形五心(外心内心重心旁心)相关结论与应用汇总(精品)
(h
a)
b
(h
b)
a
h
(b
a)
0.
(h b) a 0
AH BC.
垂心
又∵点D在AH的延长线上,∴AD、BE、CF相交于一点.
例2.已知O为⊿ABC所在平面内一点,且满足:
证明外心定理
证明: 设AB、BC的中垂线交于点O,
则有OA=OB=OC,
A
故O也在AC的中垂线上, 因为O到三顶点的距离相等,
A
故点O是ΔABC外接圆的圆心.
O
因而称为外心.
O
B
C
B
C
若 O 为 ABC内一点,OA OB OC
则 O 是 ABC 的( B )
A.内心 B.外心 C.垂心 D.重心
可以大显神通了.
思考练习 3. AB 为半圆 O 的直径,其弦 AF、BE 相交于 Q, 过 E、F 分别作半圆的切线得交点 P,求证:PQ⊥AB.
3答案
思考练习 3. AB 为半圆 O 的直径,其弦 AF、BE 相交于 Q, 过 E、F 分别作半圆的切线得交点 P,求证:PQ⊥AB. 分析:延长 EP 到 K,使 PK=PE,连 KF、AE、EF、BF, 直线 PQ 交 AB 于 H.因∠EQF=∠AQB =( 90 -∠1)+( 90 +∠2) =∠ABF+∠BAE=∠QFP+∠QEP, 又由 PK=PE=PF 知∠K=∠PFK, ∴∠EQF+∠K=∠QFK+∠QEK= 180 , 从而 E、Q、F、K 四点共圆. 由 PK=PF=PE 知,P 为△EFK 的外心,显然 PQ=PE=PF.于 是∠1+∠AQH=∠1+PQF=∠1+∠PFQ=∠1+∠AFP=∠1+∠ ABF=90º .由此知 QH⊥AH,即 PQ⊥AB.
三角形的重心、外心、垂心、内心和旁心(五心定理)(优选.)

最新文件---------------- 仅供参考--------------------已改成-----------word文本 --------------------- 方便更改三角形五心定理(三角形的重心,外心,垂心,内心和旁心称之为三角形的五心)三角形五心定理是指三角形重心定理,外心定理,垂心定理,内心定理,旁心定理的总称。
一、三角形重心定理三角形的三条边的中线交于一点。
该点叫做三角形的重心。
三中线交于一点可用燕尾定理证明,十分简单。
(重心原是一个物理概念,对于等厚度的质量均匀的三角形薄片,其重心恰为此三角形三条中线的交点,重心因而得名)重心的性质:1、重心到顶点的距离与重心到对边中点的距离之比为2∶1。
2、重心和三角形3个顶点组成的3个三角形面积相等。
即重心到三条边的距离与三条边的长成反比。
3、重心到三角形3个顶点距离的平方和最小。
4、在平面直角坐标系中,重心的坐标是顶点坐标的算术平均,即其重心坐标为((X1+X2+X3)/3,(Y1+Y2+Y3)/3。
二、三角形外心定理三角形外接圆的圆心,叫做三角形的外心。
外心的性质:1、三角形的三条边的垂直平分线交于一点,该点即为该三角形外心。
2、若O是△ABC的外心,则∠BOC=2∠A(∠A为锐角或直角)或∠BOC=360°-2∠A(∠A为钝角)。
3、当三角形为锐角三角形时,外心在三角形内部;当三角形为钝角三角形时,外心在三角形外部;当三角形为直角三角形时,外心在斜边上,与斜边的中点重合。
4、计算外心的坐标应先计算下列临时变量:d1,d2,d3分别是三角形三个顶点连向另外两个顶点向量的点乘。
c1=d2d3,c2=d1d3,c3=d1d2;c=c1+c2+c3。
重心坐标:( (c2+c3)/2c,(c1+c3)/2c,(c1+c2)/2c )。
5、外心到三顶点的距离相等三、三角形垂心定理三角形的三条高(所在直线)交于一点,该点叫做三角形的垂心。
五心记忆口诀

五心记忆口诀
三角形五心记忆口诀如下:
三角形有五颗心,重外垂内和旁心,五心性质很重要,认真掌握莫记混。
1.重心定理:三角形的三条中线交于一点,这点到顶点的距离是它到对边中点距离的2倍。
该点叫做三角形
的重心。
2.外心定理:三角形的三边的垂直平分线交于一点。
该点叫作三角形的外心。
3.垂心定理:三角形的三条高交于一点。
该点叫作三角形的垂心。
4.内心定理:三角形的三内角平分线交于一点。
该点叫作三角形的内心。
5.旁心定理:三角形一内角平分线和另外两顶点处的外角平分线交于一点。
该点叫作三角形的旁心。
三角形
有三个旁心。
这个口诀是用来记忆三角形五心的,包括重心、外心、垂心、内心和旁心。
通过这个口诀,可以更好地理解和记忆三角形的五心性质和定理,从而更好地应用它们解决实际问题。
三角形的、外心、内心、重心、垂心、和旁心(五心定理)
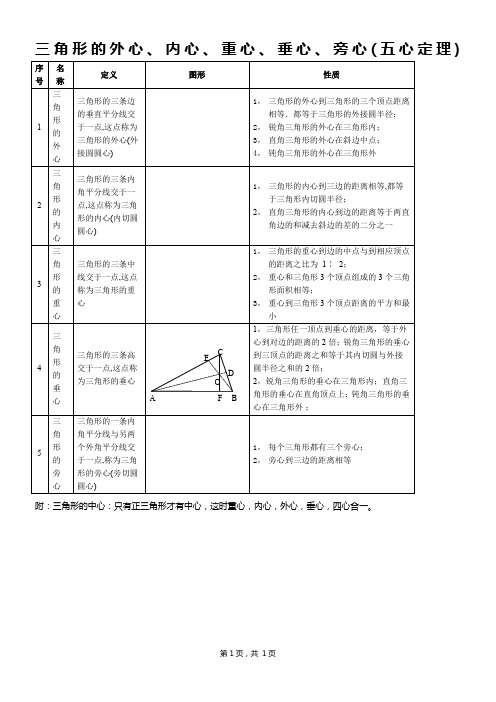
三角形的内心
三角形的三条内角平分线交于一点,这点称为三角形的内心(内切圆圆心)
1,三角形的内心到三边的距离相等,都等于三角形内切圆半径;
2,直角三角Байду номын сангаас的内心到边的距离等于两直角边的和减去斜边的差的二分之一
3
三角形的重心
三角形的三条中线交于一点,这点称为三角形的重心
1,三角形的重心到边的中点与到相应顶点的距离之比为1∶2;
2,重心和三角形3个顶点组成的3个三角形面积相等;
3,重心到三角形3个顶点距离的平方和最小
4
三角形的垂心
三角形的三条高交于一点,这点称为三角形的垂心
1,三角形任一顶点到垂心的距离,等于外心到对边的距离的2倍;锐角三角形的垂心到三顶点的距离之和等于其内切圆与外接圆半径之和的2倍;
2,锐角三角形的垂心在三角形内;直角三角形的垂心在直角顶点上;钝角三角形的垂心在三角形外;
三角形的外心、内心、重心、垂心、旁心(五心定理)
序号
名称
定义
图形
性质
1
三角形的外心
三角形的三条边的垂直平分线交于一点,这点称为三角形的外心(外接圆圆心)
1,三角形的外心到三角形的三个顶点距离相等.都等于三角形的外接圆半径;
2,锐角三角形的外心在三角形内;
3,直角三角形的外心在斜边中点;
4,钝角三角形的外心在三角形外
5
三角形的旁心
三角形的一条内角平分线与另两个外角平分线交于一点,称为三角形的旁心(旁切圆圆心)
1,每个三角形都有三个旁心;
2,旁心到三边的距离相等
附:三角形的中心:只有正三角形才有中心,这时重心,内心,外心,垂心,四心合一。
三角形五心定理

三角形五心定理
三角形五心定理是关于三角形的重要性质,分别对应重心定理、外心定理、内心定理、旁心定理和重内心定理等。
重心定理:三角形的三条中线交于一点,这点到三边的距离相等;外心定理:三角形三条边的垂直平分线交于一点,这点到三个顶点的距离相等;
内心定理:三角形的三条内角平分线交于一点,这点到三边的距离相等;
旁心定理:三角形一内角平分线和另外两顶点处的外角平分线交于一点,这点到三边的距离相等。
旁心又叫作外心,可利用重内心定理证明;
重内心定理:三角形的重心是三边上的力的三等分交点,内心是三个顶点对它的张力的中心。
三角形五心

三角形五心三角形五心是指三角形的重心、外心、内心、垂心、旁心。
三条中线的交点是重心,三边垂直平分线的交点是外心,三条内角平分线的交点为内心,三角形三条高线的交点为垂心。
重心、外心、内心、垂心只有一个,但旁心有三个。
与三角形的一边及其他两边的延长线都相切的圆叫做三角形的旁切圆,旁切圆的圆心叫做三角形旁心。
重心定理:设三角形重心为O,BC边中点为D,则有AO = 2 OD。
重心坐标为三顶点坐标平均值(在平面直角坐标系中,重心的坐标是顶点坐标的算术平均数,即其坐标为[(X1+X2+X3)/3,(Y1+Y2+Y3)/3])。
三条中线相交的点叫做重心。
外心三角形三边的垂直平分线的交点,称为三角形外心。
外心到三顶点距离相等。
过三角形各顶点的圆叫做三角形的外接圆,外接圆的圆心即三角形外心,这个三角形叫做这个圆的内接三角形。
三角形有且只有一个外接圆。
内心三角形内心为三角形三条内角平分线的交点。
与三角形各边都相切的圆叫做三角形的内切圆,内切圆的圆心即是三角形内心,内心到三角形三边距离相等。
这个三角形叫做圆的外切三角形。
三角形有且只有一个内切圆。
垂心三角形三边上的三条高或其延长线交于一点,称为三角形垂心。
锐角三角形的垂心在三角形内;直角三角形的垂心在直角的顶点;钝角三角形的垂心在三角形外。
旁心与三角形的一边及其他两边的延长线都相切的圆叫做三角形的旁切圆,旁切圆的圆心叫做三角形旁心。
三角形的一条内角平分线与其他两个角的外角平分线交于一点,即三角形的旁心。
旁心到三角形一边及其他两边延长线的距离相等。
三角形有三个旁切圆,三个旁心。
这三个旁心到三角形三条边的延长线的距离相等。
五心的性质三角形的五心有许多重要性质,它们之间也有很密切的联系,如:(1)三角形的重心与三顶点的连线所构成的三个三角形面积相等;(2)三角形的外心到三顶点的距离相等;(3)三角形的垂心与三顶点这四点中,任一点是其余三点所构成的三角形的垂心;(4)三角形的内心、旁心到三边距离相等;(5)三角形的垂心是它垂足三角形的内心;或者说,三角形的内心是它旁心三角形的垂心;(6)三角形的外心是它的中点三角形的垂心;(7)三角形的重心也是它的中点三角形的重心;(8)三角形的中点三角形的外心也是其垂足三角形的外心.(9)三角形的任一顶点到垂心的距离,等于外心到对边的距离的二倍.下面是更为详细的性质:垂心性质三角形三边上的高的交点称为三角形的垂心。
三角形中心、外心、内心、重心

三角形中心、外心、内心、重心三角形五心定理目录三角形五心定理一、三角形重心定理二、三角形外心定理三、三角形垂心定理四、三角形内心定理五、三角形旁心定理有关三角形五心的诗歌三角形五心定理三角形的重心,外心,垂心,内心和旁心称之为三角形的五心。
三角形五心定理是指三角形重心定理,外心定理,垂心定理,内心定理,旁心定理的总称。
一、三角形重心定理三角形的三条边的中线交于一点。
该点叫做三角形的重心。
三中线交于一点可用燕尾定理证明,十分简单。
(重心原是一个物理概念,对于等厚度的质量均匀的三角形薄片,其重心恰为此三角形三条中线的交点,重心因而得名) 重心的性质:1、重心到顶点的距离与重心到对边中点的距离之比为2:1。
2、重心和三角形3个顶点组成的3个三角形面积相等。
即重心到三条边的距离与三条边的长成反比。
3、重心到三角形3个顶点距离的平方和最小。
4、在平面直角坐标系中,重心的坐标是顶点坐标的算术平均,即其重心坐标为((X1+X2+X3)/3,(Y1+Y2+Y3)/3。
二、三角形外心定理三角形外接圆的圆心,叫做三角形的外心。
外心的性质:1、三角形的三条边的垂直平分线交于一点,该点即为该三角形外心。
2、若O是?ABC的外心,则?BOC=2?A(?A为锐角或直角)或?BOC=360?-2?A(?A为钝角)。
3、当三角形为锐角三角形时,外心在三角形内部;当三角形为钝角三角形时,外心在三角形外部;当三角形为直角三角形时,外心在斜边上,与斜边的中点重合。
4、计算外心的坐标应先计算下列临时变量:d1,d2,d3分别是三角形三个顶点连向另外两个顶点向量的点乘。
c1=d2d3,c2=d1d3,c3=d1d2;c=c1+c2+c3。
重心坐标:( (c2+c3)/2c,(c1+c3)/2c,(c1+c2)/2c )。
5、外心到三顶点的距离相等三、三角形垂心定理三角形的三条高(所在直线)交于一点,该点叫做三角形的垂心。
垂心的性质:1、三角形三个顶点,三个垂足,垂心这7个点可以得到6个四点圆。
三角形的五心

三角形的中心,重心,垂心,内心,外心。
五心的定义和性质是什么如果你知道了三角形的重心,垂心,内心,外心,那么对以等边三角形,这四心是合一的,也叫中心,中心具有所有四心的性质。
需要补充的是三角形还有一个旁心,通常把三角形的重心,外心,垂心,内心和旁心称之为三角形的五心。
一、三角形重心定理三角形的三条边的中线交于一点。
该点叫做三角形的重心。
重心位置:于三角形内部三中线交于一点可用燕尾定理证明,十分简单。
(重心原是一个物理概念,对于等厚度的质量均匀的三角形薄片,其重心恰为此三角形三条中线的交点,重心因而得名)重心的性质:1、重心到顶点的距离与重心到对边中点的距离之比为2︰1。
2、重心和三角形任意两个顶点组成的3个三角形面积相等。
即重心到三条边的距离与三条边的长成反比。
3、重心到三角形3个顶点距离的平方和最小。
4、在平面直角坐标系中,重心的坐标是顶点坐标的算术平均数,即其重心坐标为((X1+X2+X3)/3,(Y1+Y2+Y3)/3。
二、三角形垂心定理三角形的三条高(所在直线)交于一点,该点叫做三角形的垂心。
垂心的位置:于锐角三角形内部,直角三角形的两只角边交点,钝角三角形的外部。
垂心的性质:1、三角形三个顶点,三个垂足,垂心这7个点可以得到6个四点圆。
2、三角形外心O、重心G和垂心H三点共线,且OG︰GH=1︰2。
(此直线称为三角形的欧拉线(Euler line))3、垂心到三角形一顶点距离为此三角形外心到此顶点对边距离的2倍。
4、垂心分每条高线的两部分乘积相等。
定理证明已知:ΔABC中,AD、BE是两条高,AD、BE交于点O,连接CO并延长交AB于点F ,求证:CF ⊥AB证明:连接DE ∵∠ADB=∠AEB=90度∴A、B、D、E四点共圆∴∠ADE=∠ABE∵∠EAO=∠DAC ∠AEO=∠ADC∴ΔAEO∽ΔADC∴AE/AO=AD/AC ∴ΔEAD∽ΔOAC ∴∠ACF=∠ADE=∠ABE又∵∠ABE+∠BAC=90度∴∠ACF+∠BAC=90度∴CF⊥AB因此,垂心定理成立!三、三角形内心定理三角形内切圆的圆心,叫做三角形的内心。
三角形的五心

三角形的五心
一定理
重心定理:三角形的三条中线交于一点,这点到顶点的
离是它到对边中点距离的2倍。
该点叫做三角形的重心。
外心定理:三角形的三边的垂直平分线交于一点。
该点叫做三角形的外心。
垂心定理:三角形的三条高交于一点。
该点叫做三角形的垂心。
内心定理:三角形的三内角平分线交于一点。
该点叫做三角形的内心。
旁心定理:三角形一内角平分线和另外两顶点处的外角平分线交于一点。
该点叫做三角形的旁心。
三角形有三个旁心。
外心:垂直平分线交点,到各顶点距离相等,所以是外接圆圆心,简称外心;内心:角平分线交点,到各边距离相等,所以是内切圆圆心,简称内心;
垂心:各边高(垂线)交点,所以叫垂心:
重心:各边中线的交点,
.三角形共有六心内心:三条角平分线的交点,也是三角形内切圆的圆心。
性质:到三边距离相等。
外心:三条中垂线的交点,也是三角形外接圆的圆心。
性质:到三个顶点距离相等。
重心:三条中线的交点。
性质:三条中线的三等分点,到顶点距离为到对边中点距离的2倍。
垂心:三条高所在直线的交点。
性质:此点分每条高线的两部分乘积
旁心:三角形任意两角的外角平分线和第三个角的内角平分线的交点
性质:到三边的距离相等。
界心:经过三角形一顶点的把三角形周长分成1:1的直线与三角形一边的交点。
性质:三角形共有3个界心,三个界心分别与其对应的三角形顶点相连而成的三条直线交于一点。
欧拉线:三角形的外心、重心、九点圆圆心、垂心,依次位于同一直线上,这条直线就叫三角形的欧拉线。
【高中】三角形的五心【强烈推荐】[1]
![【高中】三角形的五心【强烈推荐】[1]](https://img.taocdn.com/s3/m/ea1d3f2b482fb4daa58d4b4a.png)
三角形的五心三角形中有许多重要的特殊点,特别是三角形的“五心”,在解题时有很多应用,在本节中将分别给予介绍. 三角形的“五心”指的是三角形的外心,内心,重心,垂心和旁心. 1、三角形的外心三角形的三条边的垂直平分线交于一点,这点称为三角形的外心(外接圆圆心). 三角形的外心到三角形的三个顶点距离相等. 都等于三角形的外接圆半径. 锐角三角形的外心在三角形内; 直角三角形的外心在斜边中点; 钝角三角形的外心在三角形外. 2、三角形的内心三角形的三条内角平分线交于一点,这点称为三角形的内心(内切圆圆心). 三角形的内心到三边的距离相等,都等于三角形内切圆半径. 内切圆半径r 的计算:设三角形面积为S ,并记p =12(a +b +c ),则r =S p .特别的,在直角三角形中,有 r =12(a +b -c ).3、三角形的重心三角形的三条中线交于一点,这点称为三角形的重心.上面的证明中,我们也得到了以下结论:三角形的重心到边的中点与到相应顶点的距离之比为 1∶ 2. 4、三角形的垂心三角形的三条高交于一点,这点称为三角形的垂心.斜三角形的三个顶点与垂心这四个点中,任何三个为顶点的三角形的垂心就是第四个点.所以把这样的四个点称为一个“垂心组”.5、三角形的旁心三角形的一条内角平分线与另两个外角平分线交于一点,称为三角形的旁心(旁切圆圆心).每个三角形都有三个旁切圆. A 类例题例1 证明重心定理。
证法1 如图,D 、E 、F 为三边中点,设BE 、CF 交于G ,连接EF ,显然EF ∥=12BC ,由三角形相似可得GB =2GE ,GC =2GF . 又设AD 、BE 交于G ',同理可证G 'B =2G 'E ,G 'A =2G 'D ,即G 、G '都是BE 上从B 到E 的三分之二处的点,故G '、G 重合.即三条中线AD 、BE 、CF 相交于一点G .ABCOABCD EFGAB CDEFI aIK HEFD ABCMABCDEFG证法2 设BE 、CF 交于G ,BG 、CG 中点为H 、I .连EF 、FH 、HI 、IE ,因为EF ∥=12BC ,HI ∥=12BC , 所以 EFHI 为平行四边形.所以 HG =GE 、IG=GF ,GB =2GE ,GC =2GF .同证法1可知AG =2GD ,AD 、BE 、CF 共点. 即定理证毕.C情景再现1.设G 为△ABC 的重心,M 、N 分别为AB 、CA 的中点,求证:四边形GMAN 和△GBC 的面积相等.2.三角形的任一顶点到垂心的距离,等于外心到对边的距离的二倍.B 类例题例3 过等腰△ABC 底边BC 上一点P 引PM ∥CA 交AB 于M ;引PN ∥BA 交AC 于N . 作点P 关于MN 的对称点P '.试证:P '点在△ABC 外接圆上.(杭州大学《中学数学竞赛习题》)分析 分析点M 和N 的性质,即能得到解题思路。
三角形的五心定理

三角形的五心定理重心定理三角形的三条中线交于一点,这点到顶点的距离是它到对边中点距离的2倍.上述交点叫做三角形的重心.外心定理三角形的三边的垂直平分线交于一点.这点叫做三角形的外心.垂心定理三角形的三条高交于一点.这点叫做三角形的垂心.内心定理三角形的三内角平分线交于一点.这点叫做三角形的内心.旁心定理三角形一内角平分线和另外两顶点处的外角平分线交于一点.这点叫做三角形的旁心.三角形有三个旁心.三角形的重心、外心、垂心、内心、旁心称为三角形的五心.它们都是三角形的重要相关点.上述的几个结论早在欧几里得时代均已被人发现,欧几里得除垂心定理外,均把它们作为重要定理收集在自己的《几何原本》里,但后来关于三角形这些特殊相关点的诸多研究及由此得出的许多著名结论表明,遗漏垂心定理不能不算是《几何原本》作者的一个疏忽.二引伸与推广1.重要性质及其相互间的联系三角形的五心有许多重要性质,它们之间也有很密切的联系,如:(1)三角形的重心与三顶点的连线所构成的三个三角形面积相等;(2)三角形的外心到三顶点的距离相等;(3)三角形的垂心与三顶点这四点中,任一点是其余三点所构成的三角形的垂心;(4)三角形的内心、旁心到三边距离相等;(5)三角形的垂心是它垂足三角形的内心;或者说,三角形的内心是它旁心三角形的垂心;(6)三角形的外心是它的中点三角形的垂心;(7)三角形的重心也是它的中点三角形的重心;(8)三角形的中点三角形的外心也是其垂足三角形的外心.上述性质读者可自行证明,下面我们给出几个推广.2.重心定理的推广证明如图7,直线CKF截ΔABD,由梅涅劳斯定理,有虽然当n=2时,有S△GHK=0,G、H、K重合于重心.如果我们称n(≥3)边形某顶点同除该点以外的n-1个顶点所决定的n-1边形的重心的连线,为n边形的中线,(当n-1=2时,n-1边形退化成一线段,此时重心即为线段的中心)那么重心定理可推广如下:定理2n边形的各条中线(若有重合,只算一条)相交于一点,各中线被该点分为:(n-1)∶1的两条线段,这点叫n边形的重心.证明当n=3时为重心定理,结论成立,假设n=k-1,(k≥4)时,命题成立,则当n=k 时,在k边形A1A2…Ak中,如图8,若S是k-2边形A1A2…Ak-2的重心,则Ak-1S、AkS 分别是k-1边形A1A2…Ak-2Ak-1和A1A2…Ak-2Ak的中线.设Ok-1和O′k-1分别是k-1边形A1A2…Ak-2Ak-1和A1A2…Ak-2Ak的重心,则根据假设有连接AkOk-1、Ak-1O′k-1,则它们是k边形的两条中线,且交于一点,设交点为O,连接Ok-1O′k-1,则有Ok-1O′k-1∥Ak-1Ak,所以ΔOOk-1O′k-1∽ΔOAk-1Ak.因此,k边形A1A2…Ak的相邻两条中线Ak-1O′k-1,AkOk-1交于O点,且被O点内分为(k-1)∶1.同理可证k边形A1A2…Ak的任意相邻两条中线的交点内分每条中线为(k-1)∶1,由此推得,k边形的所有中线过一点,且被这点内分为(k-1)∶1.综上所述,定理得证.3.外心定理的推广定理3过ΔABC三边中点D、E、F分别作与三边倾斜角均为α的斜线且顺序一致,三斜线相交得ΔGHK,则SΔGHK=cos2α·SΔABC.证明如图9,首先我们证ΔKGH∽ΔABC,因为∠KFA=α=∠KEA,因为A、K、F、E四点共圆,所以∠GKH=∠BAC.同理可证∠G=∠B,∠H=∠C,故ΔKGH∽ΔABC.又由正弦定理,有同理,B、G、D、F共圆,有①+②得显然,当α=90°,即S△KGH=0时正是外心定理.对外心定理,还有下面的推广证明略.4.垂心定理的推广定理5从ΔABC三顶点分别作对边的斜线,与对边的交角为α,且顺序一致,三斜线相交成ΔGHK.则SΔGHK=4cos2α·SΔABC.证明如图10,过A、B、C分别作对边的平行线交得ΔA′B′C′,则A、B、C分别为ΔA′B′C′三边的中点,由定理3有SΔGHK=cos2α·SΔA′B′C′=4cos2α·SΔABC.显然,α=90°时为垂心定理.垂心定理还可理解为三角形一顶点与另两条高交点的连线垂直于对边,那么对五边形,我们有定理6在一五边形中,若有四个顶点向对边所作的高交于一点,则第五个顶点与其交点的边线也垂直于对边.证明如图11,设在五边形ABCDE中,AF⊥CD、BG⊥DE、CH⊥AE,DI⊥AB;且AF、BG、CH、DI交于O点,连接EO并延长交BC于K,连HG,则四边形AHFC、AIFD、BIGD、OHEG各内接于圆.所以OA·OF=OH·OC,OA·OF=OI·OD.OI·OD=OB·OG,∠1=∠2.所以OH·OC=OB·OG,故C、B、H、G内接于圆.所以∠2=∠3,则∠1=∠3.所以四边形BEGK内接于圆.而BG⊥DE,故EK⊥BC,命题得证.此结论可推广到2n+1边形.三.定理的应用例1设G为△ABC的重心,M、N分别为BC、CA的中点,求证:四边形GMCN和△GAB的面积相等.证明如图12,连GC,则例2三角形的任一顶点到垂心的距离,等于外心到对边的距离的二倍.证明如图13,O为ΔABC的外心,H为垂心,连CO交ΔABC外接圆于D,连DA、DB,则DA⊥AC,BD⊥BC,又AH⊥BC,BH⊥AC.又DB=2OM,所以AH=2OM.同理可证BH=2ON,CH=2OK.证毕.例3AD是ΔABC的一条高;以AB、AC为边向外作正方形ABEF和ACGH,连BG、EC,求证:AD、BG、CE相交于一点.证明如图14,延长DA至K,使AK=BC,连FK、KH;则ΔKAH≌ΔBCA,ΔKAF≌ΔCBA,连KC、KB,则可得ΔKAC≌ΔBCG,ΔKAB≌ΔCBE.于是∠ACK=∠CGB,∠KBA=∠BEC,且它们分别为∠KCG及∠KBE的余角.所以BG⊥KC,CE⊥KB,从而AD、BG、CE为ΔKBC的三条高线,故它们相交于一点.例4在ΔABC中,AB=AC,圆O内切ΔABC的外接圆于D,且与边AB、AC分别相切于P、Q,证明:线段PQ的中点是ΔABC的内心.证明如图15,连接AD、PD、QD,易知AD平分∠PDQ及∠A,因为PQ∥BC,所以∠APQ=∠ABC①又AB切⊙O于P,则∠APQ=∠PDQ=2∠PDM②再连BD、BM,由于∠PBD=∠PMD=90°,故P、B、D、M四点共圆.所以∠PBM=∠PDM.③由①、②、③可得:∠PBM=∠MBC.即BM是∠ABC的平分线,而AM是∠A的平分线,所以交点M是ΔABC的内心.这是第20届国际数学奥林匹克竞赛试题,其实当AB≠AC时,结论也成立,这个问题留给有兴趣的读者进一步探究.练习与思考1.证明本章“引伸与推广部分命题(1)—(8).2.G为ΔABC的重心,∠A=90°,求证:GB2+GC2=5GA2.3.ΔABC的外心和垂心分别为O、H,∠A=60°,求证:AO=AH.4.ΔABC中,BC=14cm,BC边上的高AD=12cm,内接圆半径r=4cm,求AB、AC之长.。
三角形五心性质[]
![三角形五心性质[]](https://img.taocdn.com/s3/m/ec7ec82adaef5ef7bb0d3c43.png)
三角形的五心定理一、三角形五心定义内心是二角形的二内角平分线交点.也是二角形内切圆的圆心.重心是三角形的三条中线的交点.(重心原是一个物理概念,对于等厚度的质量均匀的 三角形薄片,其重心恰为此三角形三条中线的交点,重心因而得名)文档来自于网络搜索 外心是三角形的三边的垂直平分线的交点.三角形外接圆的圆心. 垂心是三角形的三条高的交点旁心是三角形一内角平分线和另外两顶点处的外角平分线的交点.三角形的旁切圆 (与三角形的一边和其他两边的延长线相切的圆)的圆心 文档来自于网络搜索二、三角形五心性质 内心:1、直角三角形的内心到边的距离等于两直角边的和减去斜边的差的二分之一2、P 为AABC 所在平面上任意一点,点 0是A ABC 内心的充要条件是:向量— (ax PA + bx PB +c x PC)a +b +c3、O 为三角形的内心, A 、B 、C 分别为三角形的三个顶点,延长AO 交BC 边于 N ,则有 AO : ON = AB : BN =AC :CN =(AB + AC): BC . 重心:1、重心到顶点的距离与重心到对边中点的距离之比为 2、重心和三角形3个顶点组成的3个三角形面积相等.即重心到三条边的距离与三 条边的长成反比.3、重心到三角形3个顶点距离的平方和最小4、在平面直角坐标系中,重心的坐标是顶点坐标的算术平均数,即其重心坐标为 (X 1 + X 2 + X 3 y 1 + y 2 + y 3)3 3外心:1、当三角形为锐角三角形时,外心在三角形内部;当三角形为钝角三角形时,外心 在三角形外部;当三角形为直角三角形时,外心在斜边上,与斜边的中点重合 档来自于网络搜索2、若0是 MBC 的外心,则N BOC=2NA (N A 为锐角或直角)或N BOC =360°-2N A (N A 为钝角).向另外两个顶点向量的点乘。
c^ d 2d 3, c^d 1d 3, c^ = d 1d 2 ;c = ci +c 2+c 3. 重心坐标:(°十°3 c '十c3 G + c2).文档来自于网络搜索2c ' 2c ' 2c2 : 1.3、计算外心的坐标应先计算下列临时变量:d i , d 2 , d 3分别是三角形三个顶点连4、外心到三顶点的距离相等垂心:1、三角形三个顶点,三个垂足,垂心这7个点可以得到6个四点圆.2、三角形外心0、重心G和垂心H三点共线,且OG:GH =1:2.(此直线称为三角形的欧拉线(Eulerline ))3、垂心到三角形一顶点距离为此三角形外心到此顶点对边距离的4、垂心分每条高线的两部分乘积相等.OA OB =OB OC =OC OA旁心:1、每个三角形都有三个旁心2、旁心到三边的距离相等注:三角形的中心:只有正三角形才有中心,这时重心,内心,外心,垂心,四心合一。
三角形的五心定理

1三角形的五心0.1外心定理定理0.1(外心定理)三角形三边的垂直平分线交于一点,这点是三角形外接圆的圆心,称为外心。
如图,已知△ABC的三边a,b,c,以及三边的垂直平分线分别为l a,l b,l c,求证l a,l b,l c交于一点。
AOB C证明0.1BC边的垂直平分线为l a,AC边的垂直平分线为l b,设这两直线相交于点O.因为O在BC的垂直平分线上,所以OB=OC;因为O在AC的垂直平分线上,所以OA=OC.所以OA=OB,故O在AB的垂直平分线上.即AB的垂直平分线过点O.所以三边的垂直平分线交于一点O.O到三个顶点的距离相等,O是外接圆的圆心.0.2内心定理定理0.2(内心定理)三角形三个内角的平分线交于一点,这点是三角形内切圆的圆心,称为内心.如图,在△ABC中,AD,BE,CF是三个内角的平分线,求证,这三线交于一点。
2 ABCEDI证明0.2设AD与BE交于一点I.设I到三边的距离为d a,d b,d c,因为I在A的平分线上,所以d b=d c,因为I在B的平分线上,所以d a=d c,所以d a=d b,故有I在C的平分线上,即CF经过点I.所以,三条角平分线交于一点I.I到三边的距离相等,因此,以I为圆心,该距离为半径,可作三角形的内切圆。
0.3旁心定理定理0.3(旁心定理)三角形一个内角的平分线与另外两个外角平分线交于一点,这点是三角形旁切圆的圆心,称作旁心.ABCO′旁心到三角形三边的距离也相等,证明方法与内心一样,证明略.3 0.4垂心定理定理0.4(垂心定理)三角形的三条高交于一点,这点叫做三角形的垂心.如图,三角形ABC中,AD,BE,CF是三边的高,求证这三线交于一点.ABCDEFA′B′C′证明0.3如图,过△ABC的三个顶点作对边的平行线,如图标记交点为A′,B′,C′.BC//B′C′,AC//A′C′,四边形AC′BC为平行四边形,AC′=BC,BC//B′C′,AB//A′B′,四边形ABCB′为平行四边形,AB′=BC,所以AC′=AB′,点A是线段B′C′的中点.BC//B′C′,AD垂直于BC,故DA垂直于B′C′.所以DA是B′C′的垂直平分线.同理,F C是A′B′的垂直平分线,EB是A′C′的垂直平分线.在△A′B′C′中,由外心定理,可知这三线交于一点.即△ABC的三条高交于一点,这点是△ABC的垂心.0.5重心定理定理0.5(重心定理)三角形的三条中线交于一点,这点是三角形的重心.如图,三角形ABC的三中线为AD,BE,CF,求证,这三线交于一点.4DAB CEF GD ′K证明0.4设中线BE 与CF 交点为G ,直线AG 交BC 于点D ′.延长GE 到点K ,使得EK =GE ,连接AK ,CK ,则四边形AGCK 的对角线互相平分,四边形AGCK 为平行四变形.故GC //AK ,即F G //AK .F B =F A ,所以GB =GK .又AG //KC ,即GD ′//KC ,故D ′B =D ′C .所以D ′与BC 的中点D 重合.因此,三边上的中线交于一点G.由以上证明过程可知BG :GE =2:1,即重心到顶点与到对边中点的距离之比为2:1.外心、重心、垂心共线,见欧拉线.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三角形五心定理
目录
三角形五心定理
一、三角形重心定理
二、三角形外心定理
三、三角形垂心定理
四、三角形内心定理
五、三角形旁心定理
有关三角形五心的诗歌
三角形五心定理
三角形的重心,外心,垂心,内心和旁心称之为三角形的五心。
三角形五心定理是指三角形重心定理,外心定理,垂心定理,内心定理,旁心定理的总称。
一、三角形重心定理
三角形的三条边的中线交于一点。
该点叫做三角形的重心。
三中线交于一点可用燕尾定理证明,十分简单。
(重心原是一个物理概念,对于等厚度的质量均匀的三角形薄片,其重心恰为此三角形三条中线的交点,重心因而得名)
重心的性质:
1、重心到顶点的距离与重心到对边中点的距离之比为2︰1。
2、重心和三角形3个顶点组成的3个三角形面积相等。
即重心到三条边的距离与三条边的长成反比。
3、重心到三角形3个顶点距离的平方和最小。
4、在平面直角坐标系中,重心的坐标是顶点坐标的算术平均,即其重心坐标为((X1+X2+X3)/3,(Y1+Y2+Y3)/3。
二、三角形外心定理
三角形外接圆的圆心,叫做三角形的外心。
外心的性质:
1、三角形的三条边的垂直平分线交于一点,该点即为该三角形外心。
2、若O是△ABC的外心,则∠BOC=2∠A(∠A为锐角或直角)或∠BOC=360°-2∠A(∠A为钝角)。
3、当三角形为锐角三角形时,外心在三角形内部;当三角形为钝角三角形时,外心在三角形外部;当三角形为直角三角形时,外心在斜边上,与斜边的中点重合。
4、计算外心的坐标应先计算下列临时变量:d1,d2,d3分别是三角形三个顶点连向另外两个顶点向量的点乘。
c1=d2d3,c2=d1d3,c3=d1d2;c=c1+c2+c3。
重心坐标:( (c2+c3)/2c,(c1+c3)/2c,(c1+c2)/2c )。
5、外心到三顶点的距离相等
三、三角形垂心定理
三角形的三条高(所在直线)交于一点,该点叫做三角形的垂心。
垂心的性质:
1、三角形三个顶点,三个垂足,垂心这7个点可以得到6个四点圆。
2、三角形外心O、重心G和垂心H三点共线,且OG︰GH=1︰2。
(此直线称为三角形的欧拉线(Euler line))
3、垂心到三角形一顶点距离为此三角形外心到此顶点对边距离的2倍。
4、垂心分每条高线的两部分乘积相等。
定理证明
已知:ΔABC中,AD、BE是两条高,AD、BE交于点O,连接CO并延长交A B于点F ,求证:CF⊥AB
证明:
连接DE ∵∠ADB=∠AEB=90度∴A、B、D、E四点共圆∴∠ADE=∠ABE ∵∠EAO=∠DAC ∠AEO=∠ADC∴ΔAEO∽ΔADC
∴AE/AO=AD/AC ∴ΔEAD∽ΔOAC ∴∠ACF=∠ADE=∠ABE
又∵∠ABE+∠BAC=90度∴∠ACF+∠BAC=90度∴CF⊥AB
因此,垂心定理成立!
四、三角形内心定理
三角形内切圆的圆心,叫做三角形的内心。
内心的性质:
1、三角形的三条内角平分线交于一点。
该点即为三角形的内心。
2、直角三角形的内心到边的距离等于两直角边的和减去斜边的差的二分之一。
3、P为ΔABC所在平面上任意一点,点I是ΔABC内心的充要条件是:向量PI =(a×向量PA+b×向量PB+c×向量PC)/(a+b+c).
4、O为三角形的内心,A、B、C分别为三角形的三个顶点,延长AO交BC边于N,则有AO:ON=AB:BN=AC:CN=(AB+AC):BC
五、三角形旁心定理
三角形的旁切圆(与三角形的一边和其他两边的延长线相切的圆)的圆心,叫做三角形的旁心。
旁心的性质:
1、三角形一内角平分线和另外两顶点处的外角平分线交于一点,该点即为三角形的旁心。
2、每个三角形都有三个旁心。
3、旁心到三边的距离相等。
如图,点M就是△ABC的一个旁心。
三角形任意两角的外角平分线和第三个角的内角平分线的交点。
一个三角形有三个旁心,而且一定在三角形外。
附:三角形的中心:只有正三角形才有中心,这时重心,内心,外心,垂心,四心合一。
有关三角形五心的诗歌
三角形五心歌(重外垂内旁)
三角形有五颗心,重外垂内和旁心,五心性质很重要,认真掌握莫记混.
重心
三条中线定相交,交点位置真奇巧,交点命名为“重心”,重心性质要明了,重心分割中线段,数段之比听分晓;长短之比二比一,灵活运用掌握好.
外心
三角形有六元素,三个内角有三边.作三边的中垂线,三线相交共一点.
此点定义为外心,用它可作外接圆.内心外心莫记混,内切外接是关键.
垂心
三角形上作三高,三高必于垂心交.高线分割三角形,出现直角三对整,
直角三角形有十二,构成六对相似形,四点共圆图中有,细心分析可找清.
内心
三角对应三顶点,角角都有平分线,三线相交定共点,叫做“内心”有根源;
点至三边均等距,可作三角形内切圆,此圆圆心称“内心”,如此定义理当然.本文由52求学网论坛微光整理。
