高一数学必修一幂函数及基本初等函数综合
高中数学人教A版必修1第二章 基本初等函数——幂函数(共14张PPT)

f(x 1 )f(x2 )x 1x2(x 1x x 2 1 )+ (x x 2 1+x2)
x1 x2 x1 + x2
方法技巧:分子有理化
因 x 1 x 2 , x 为 1 , x 2 [ 0 , + ) 所 ,x 1 x 2 以 0 ,x 1 + x 2 0 ,
所 f(x 以 1 )f(x2 )即 , 幂 f(x) 函 x在 [0 数 ,+)上 的 .
课堂小结
(1) 幂函数的定义; (2)五个基本幂函数的图像画法及特征; (3) 幂函数的性质。
作业:P79习题2.3: 1,2,3。
谢谢指导
不知道自己缺点的人,一辈子都不会想要改善。成功的花,人们只惊慕她现时的明艳!然而当初她的芽儿,浸透了奋斗的泪泉,洒遍了牺牲的血雨。成功的条件在于勇气和 信乃是由健全的思想和健康的体魄而来。成功了自己笑一辈子,不成功被人笑一辈子。成功只有一个理由,失败却有一千种理由。从胜利学得少,从失败学得多。你生而有 前进,形如蝼蚁。你一天的爱心可能带来别人一生的感谢。逆风的方向,更适合飞翔。只有承担起旅途风雨,才能最终守得住彩虹满天只有创造,才是真正的享受,只有拚 活。知识玩转财富。志不立,天下无可成之事。竹笋虽然柔嫩,但它不怕重压,敢于奋斗、敢于冒尖。阻止你前行的,不是人生道路上的一百块石头,而是你鞋子里的那一 爱,不必呼天抢地,只是相顾无言。最值得欣赏的风景,是自己奋斗的足迹。爱的力量大到可以使人忘记一切,却又小到连一粒嫉妒的沙石也不能容纳。生活不可能像你想 不会像你想的那么糟。时间告诉你什么叫衰老,回忆告诉你什么叫幼稚。不要总在过去的回忆里缠绵,昨天的太阳,晒不干今天的衣裳。实现梦想往往是一个艰苦的坚持的 到位,立竿见影。那些成就卓越的人,几乎都在追求梦想的过程中表现出一种顽强的毅力。世界上唯一不变的字就是“变”字。事实胜于雄辩,百闻不如一见。思路决定出 细节决定成败,性格决定命运虽然你的思维相对于宇宙智慧来说只不过是汪洋中的一滴水,但这滴水却凝聚着海洋的全部财富;是质量上的一而非数量上的一;你的思维拥 所有过不去的都会过去,要对时间有耐心。人总会遇到挫折,总会有低潮,会有不被人理解的时候。如果你希望成功,以恒心为良友,以经验为参谋,以小心为兄弟,以希 个人不知道他要驶向哪个码头,那么任何风都不会是顺风。沙漠里的脚印很快就消逝了。一支支奋进歌却在跋涉者的心中长久激荡。上天完全是为了坚强你的意志,才在道 碍。拥有资源不能成功,善用资源才能成功。小成功靠自己,大成功靠团队。炫耀什么,缺少什么;掩饰什么,自卑什么。所谓正常人,只是自我防御比较好的人。真正的 防而又不受害。学习必须如蜜蜂一样,采过许多花,这才能酿出蜜来态度决定高度。外在压力增加时,就应增强内在的动力。我不是富二代,不能拼爹,但为了成功,我可 站在万人中央成为别人的光。人一辈子不长不短,走着走着,就进了坟墓,你是要轰轰烈烈地风光下葬,还是一把骨灰撒向河流山川。严于自律:不能成为自己本身之主人 他周围任何事物的主人。自律是完全拥有自己的内心并将其导向他所希望的目标的惟一正确的途径。生活对于智者永远是一首昂扬的歌,它的主旋律永远是奋斗。眼泪的存 伤不是一场幻觉。要不断提高自身的能力,才能益己及他。有能力办实事才不会毕竟空谈何益。故事的结束总是满载而归,就是金榜题名。一个人失败的最大原因,是对自 的信心,甚至以为自己必将失败无疑。一个人炫耀什么,说明内心缺少什么。一个人只有在全力以赴的时候才能发挥最大的潜能。我们的能力是有限的,有很多东西飘然于 之外。过去再优美,我们不能住进去;现在再艰险,我们也要走过去!即使行动导致错误,却也带来了学习与成长;不行动则是停滞与萎缩。你的所有不甘和怨气来源于你 你可以平凡,但不能平庸。懦弱的人只会裹足不前,莽撞的人只能引为烧身,只有真正勇敢的人才能所向披靡。平凡的脚步也可以走完伟大的行程。平静的湖面锻炼不出精 生活打造不出生活的强者。人的生命似洪水在奔流,不遇着岛屿、暗礁,难以激起美丽的浪花人生不怕重来,就怕没有将来。人生的成败往往就在于一念之差。人生就像一 为你在看别人耍猴的时候,却不知自己也是猴子中的一员!人生如天气,可预料,但往往出乎意料。人生最大的改变就是去做自己害怕的事情。如果不想被打倒,只有增加 你向神求助,说明你相信神的能力;如果神没有帮助你,说明神相信你的能力。善待自己,不被别人左右,也不去左右别人,自信优雅。活是欺骗不了的,一个人要生活得 象这杯浓酒,不经三番五次的提炼呵,就不会这样一来可口!生命不止需要长度,更需要宽度。时间就像一张网,你撒在哪里,你的收获就在哪里。世上最累人的事,莫过于 你感到痛苦时,就去学习点什么吧,学习可以使我们减缓痛苦。当世界都在说放弃的时候,轻轻的告诉自己:再试一次。过错是暂时的遗憾,而错过则是永远的遗憾!很多 结果,但是不努力却什么改变也没有。后悔是一种耗费精神的情绪后悔是比损失更大的损失,比错误更大的错误所以不要后悔。环境不会改变,解决之道在于改变自己。积 成功者的最基本要素。激情,这是鼓满船帆的风。风有时会把船帆吹断;但没有风,帆船就不能航行。即使道路坎坷不平,车轮也要前进;即使江河波涛汹涌,船只也航行 粹取出来的。浪费时间等于浪费生命。老要靠别人的鼓励才去奋斗的人不算强者;有别人的鼓励还不去奋斗的人简直就是懦夫。不要问别人为你做了什么,而要问你为别人 遥远的梦想和最朴素的生活,即使明天天寒地冻,金钱没有高贵,低贱之分。金钱在高尚人的手中,就会变得高尚;金钱在庸俗人手中,就会变得低级庸俗。涓涓细流一旦 大海也就终止了��
高中数学必修1基本初等函数常考题型幂函数
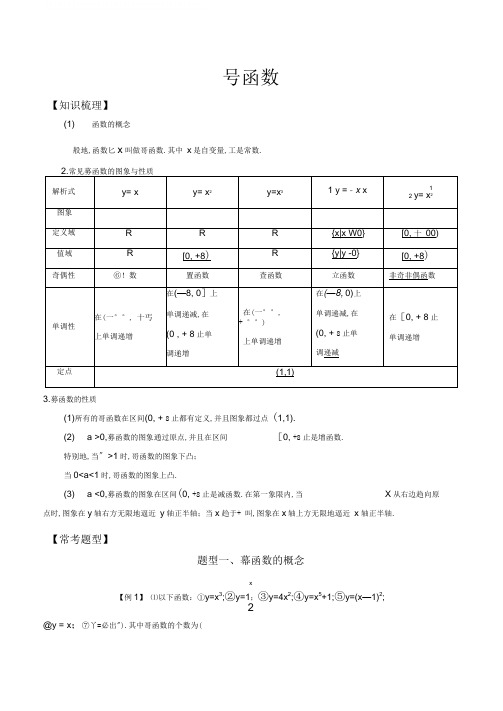
号函数【知识梳理】(1) 函数的概念般地,函数匕x叫做哥函数.其中x是自变量,工是常数.解析式y= x y= x2y=x3 1 y = - x x12 y= x2图象定义域R R R{x|x W0}[0, 十00)值域R[0, +8) R{y|y -0}[0, +8) 奇偶性⑥!数置函数查函数立函数非奇非偶函数单调性在(一°°, 十丐上单调递增在(—8, 0]上单调递减,在(0 , + 8止单调递增在(一°°,+ °°)上单调递增在(—8, 0)上单调递减,在(0, + 8止单调递减在[0, + 8止单调递增定点(1,1)3.募函数的性质(1)所有的哥函数在区间(0, + 8止都有定义,并且图象都过点(1,1).(2) a >0,募函数的图象通过原点,并且在区间[0, +8止是增函数.特别地,当〞>1时,哥函数的图象下凸;当0<a<1时,哥函数的图象上凸.(3) a <0,募函数的图象在区间(0, +8止是减函数.在第一象限内,当X从右边趋向原点时,图象在y轴右方无限地逼近y轴正半轴;当x趋于+ 叫,图象在x轴上方无限地逼近x 轴正半轴.【常考题型】题型一、幕函数的概念x【例1】⑴以下函数:①y=x3;②y=1;③y=4x2;④y=x5+1;⑤y=(x—1)2;2@y = x;⑦丫=必出").其中哥函数的个数为(D. 4C. 32(2)哥函数y= m2m 1 x m 2m 3,求此募函数的解析式,并指出定义域.(1)[解析]②⑦为指数函数,③中系数不是1,④中解析式为多项式,⑤中底数不是自变量本身,所以只有①⑥是哥函数,应选B.[答案]B2(2)[解]-. y= m m 1 x m m为募函数,m2— m — 1 = 1,解得m = 2 或m = — 1.当m = 2 时,m2—2m — 3=— 3,那么y = x 3,且有xw&当m = —1 时,m2— 2m— 3=0,那么y = x0,且有xw0.故所求募函数的解析式为y = x 3, {x|x w哦y=x0, {x|x W0.}【类题通法】判断一个函数是否为募函数的方法判断一个函数是否为备函数的依据是该函数是否为y= x (“为常数)的形式,即函数的解析式为一个哥的形式,且需满足:(1)指数为常数;(2)底数为自变量;(3)系数为1.反之,假设一个函数为募函数,那么该函数应具备这一形式,这是我们解决某些问题的隐含条件.【对点练习】2函数f(x)= m m 1 x 是哥函数,且当xe(0, +8时,f(x)是增函数,求f(x)的解析式.解:根据哥函数的定义得2—m — 1 = 1.解得m = 2 或m= — 1.m当m = 2时,f(x) =x3在(0, + °°)上是增函数;当m = —1时,f(x) = x 3在(0, + 8止是减函数,不符合要求.故f(x) = x3.题型二、幕函数的图象【例2】(1)如图,图中曲线是募函数y= x在第一象限的大致图1 1象,a取一2, —2, : 2四个值,那么相应于曲线C1,C2, C3, C4的a的值依次为()2'本文档如对你有帮助,请帮助下载支持!11 1八1C.— 2,—2,2,2D. 2, 2,-2, 22(2)如图是募函数v= x m与y= x n在第一象限内的图象,那么(A. — 1<n<0<m<1B. n< —1,0<m<1C. — 1<n<0 , m>1D. n< — 1, m>1[解析](1)令x = 2,贝U 22>22>2-1>2 2,1 1故相应于曲线C1,C2, C3, C4的“值依次为2, 2,一了一2.应选B.(2)此类题有一简捷的解决方法,在(0,1)内取xo,作直线x=x.,与各图象有交点,那么熏低指数大如图,0<m<1 , n<—1.[答案](1)B (2)B【类题通法】解决哥函数图象问题应把握的两个原那么(1)依据图象上下判断哥指数大小,相关结论为:在(0,1)上,指数越大,哥函数图象越靠近x轴(简记为指大图低);在(1, + 8止,指数越大,哥函数图象越远离x轴(简记为指大图高).(2)依据图象确定哥指数a与0,1的大小关系,即根据哥函数在第一象限内的图象(类似于y1=x-1或y = x2或y= x3)来判断.【对点练习】函数y=x a, y=x b, y=x c的图象如下图,那么a, b, c的大小关系为()A. c<b<aB. a<b<cC. b<c<aD. c<a<b解析:选A 由募函数的图象特征知, c<0, a>0, b>0.由哥函数的性质知,当x>1 ,哥指数大的募函数的函数值就大, 那么a>b.综上所述,可知c<b<a.题型三、利用幕函数的性质比拟大小【例3】比拟以下各组数中两个数的大小.0.50.52(2)3[解](1),.,哥函数X0.5在(0, +8止是单调递增的,2 又5冶0.5 0.51> —3(2厂•哥函数0)上是单调递减的, 又一2<一 |,(3)二,函数y1 = 为R上的减函数,又3 24>3,又「函数y2=2X3在(0, + 8止是增函数,l 3 2且4>323石—>4【类题通法】比拟骞值大小的方法(1)假设指数相同,底数不同, 那么考虑骞函数;(2)假设指数不同,底数相同, 那么考虑指数函数;(3)假设指数与底数都不同, 那么考虑插入中间数,使这个数的底数与所比拟数的一个底数相同, 指数与另一个数的指数相同,那么这个数就介于所比拟的两数之间,进而比拟大小.【对点练习】比拟以下各题中两个骞的值的大小:(1) 2.34, 2.44;_ 3 _ (2) V2 2, V33 2;6 6(3) 0.31 5, 0.355.3解:〔1〕,「y=x〞为[0, + 8止的增函数,且2.3<2.4,3 32.34 < 2.4".3〔2〕-「y= x 2为〔0, 止的减函数,且在〈布,_ 3 _ 3,\5 2> ,3 2.6 6 6〔3〕:y= x5为R上的偶函数,0.31 M = 0.31.6又函数y=x5为[0, + 8止的增函数,且0.31<0.35,6 6 6 6••• 0.315 < 0.355 ,即0.31 5 <0.355.【练习反应】1 .以下函数是募函数的是〔〕A. y=2xB. y=2x 1C. y=〔x+1〕2D. y= V x2解析:选D 由哥函数的概念可知D正确.2 .以下命题:①哥函数的图象都经过点〔1,1〕和点〔0,0〕;②哥函数的图象不可能在第四象限;③n=0,函数y= xn的图象是一条直线;④哥函数y= x n当n>0时,是增函数;⑤哥函数y=x n当n<0时,在第一象限内函数值随x值的增大而减小.正确的命题为〔〕A.①④B.④⑤C.②③D.②⑤解析:选D y=x 1不过〔0,0〕点,,①错误,排除A;当n = 0时,y=x n的图象为两条射线,③错误,排除C; y=x2不是增函数,④错误,排除B;因此答案选D.13 .哥函数f(x)的图象过点(4,2),那么f 8 =1斛析:设 f(x) = X ,那么 4"= 2, 1. a= 2,11 即 f(x) = X2 , f -8答案:2m 2m 1 x m是哥函数,且在xe (o, +8时是减函数,那么实数解析:由 m 2—m+1=1,得 m=0 或 m=1,再把m = 0和m=1分别代入 m 2+2m —3<0检验,得 m = 0. 答案:05.比拟以下各题中两个哥的值的大小:11113⑴1.12, 0.92; (2)1.1 土,0.9 5 ;(3)3 4 ,1解:(1)=y= x_2为[0, + 00止的增函数,又 1.1>0.9,111.12>0.92.1(2) .■ y = x 2 为(0, + 00止的减函数,又 1.1>0.9, 11- - 1.1 2 <0.9 23- 3 4<4.函数 f(x)=3-(3) •- 3 4 =31 4 …一,函数33y = x 4为[0, + 8让的增函数,且1 1 3<2'。
高中数学必修1课件 第二章基本初等函数之二次函数和幂函数

2.二次函数y=f(x)与y=g(x)的图像开口大 小相同, 开口方向也相同,已知函数g(x)=x2+1, f(x)图像 的顶点为(3,2),则f(x)的表达式为Y=(x-3) 2+2
发展性训练 1.由y=3(x+2)2+4的图像经过怎样的平移 变换, 可以得到y=3x2的图像. 右移2单位,下移4单位 2.把函数y=x2-2x的图像向右平移2个单 位, 再向下平移3个单位所得图像对应的函 数 2 -2(x-2)-3=x 2 -6x+5= (x-3) 2 -4 Y=(x-2) 解析式为
2、(2002河南两广高考)已知 a>0,f(x)=ax-bx2. (1)b>0时,若对任意x ∈ R都有 f(x)≤ 1,证明a≤ 2 . b (2)b>1时,证明 对任意 x ∈[ 0,1 ], │ f(x) │≤1的充要条件是 b-1 ≤ a ≤ 2 b
(3)0<b ≤ 1时, 求 对任意 x∈[ 0, 1 ], │ f(x) │≤ 1的充要条件。
求下列函数的定义域和值域:
x 3 x 4 (1) y= 2 x 3 x 4
2
(2) y= 1 2x x (3) y= 1 x x 3
作函数的图象的常用方法
1. 描点作图法; 2. 变换作图法.
基础练习
画出下列函数的图象, 并 说明它们的关系:
(1) (2)
(3)
变换作图法
平移变换
对称变换
作 业
画出下列函数的图象:
(1) (2) y=x2+2 x +1 y= x 2 x
2
② y=-x2-2x+3, x∈[-5, 0] ③ y= x 1 x
数学必修一基本初等函数知识点

数学必修一基本初等函数知识点
1. 线性函数:y = kx + b(k和b为常数),其中k称为斜率,b称为截距。
2. 幂函数:y = x^n(n为常数),其中n可以是正整数、零、负整数。
3. 指数函数:y = a^x(a为正实数且a≠1)。
4. 对数函数:y = loga(x)(a为正实数且a≠1),其中x为正实数。
5. 三角函数(正弦函数、余弦函数、正切函数、余切函数等):y = sinx,y = cosx,y = tanx,y = cotx等。
6. 反三角函数(反正弦函数、反余弦函数、反正切函数、反余切函数等):y = arcsinx,y = arccosx,y = arctanx,y = arccotx等。
7. 绝对值函数:y = |x|。
8. 双曲函数(双曲正弦函数、双曲余弦函数、双曲正切函数等):y = sinh(x),y = cosh(x),y = tanh(x)等。
9. 分段函数:根据不同条件定义函数的不同表达式,例如:y = f(x) =
{ x+1, (x≤0)
{ x^2, (0<x≤1)
{ 2x-1, (x>1)
10. 复合函数:将一个函数的输出作为另一个函数的输入进行运算,例如:f(g(x))。
以上是数学必修一中较为基本的初等函数知识点,只覆盖了一部分内容。
学习初等函数的重点是掌握其基本性质、图像和应用。
2019_2020学年高中数学第二章基本初等函数(Ⅰ)2.3幂函数课件新人教A版必修1

(A)2
(B)1
(C) 1 2
(D)0
解析:(1)因为函数 f(x)=ax2a+1+b+1 是幂函数,
所以
a b
1, 1
0,
即
a b
1, 1,
所以 a+b=0,故选 D.
(2)(2018·福建龙岩期中)若函数f(x)=(m2-m-1)xm是幂函数,且图象与坐
标轴无交点,则f(x)( )
.
24
解析:(2)因为幂函数 f(x)=xa 的图象过点( 1 , 1 ), 24
所以( 1 )a= 1 ,解得 a=2, 24
所以 loga8=log28=3. 答案:(2)3
题型二 幂函数的图象 [例 2] (1)与下列幂函数对应的图象序号正确的一组是( )
a.y=x5;b.y=
x
4 3
;c.y=
(A)是偶函数
(B)是奇函数
(C)是单调递减函数 (D)在定义域内有最小值
解析:(2)幂函数f(x)=(m2-m-1)xm的图象与坐标轴无交点,可得m2-m1=1,且m≤0,解得m=-1,则函数f(x)=x-1,所以函数是奇函数,在定义 域上不是减函数,且无最值,故选B.
易错警示
(1)幂函数解析式的结构特征:①解析式是单项式;②幂指数为常数, 底数为自变量,系数为1. (2)幂函数y=xα的图象与坐标轴无交点,则α≤0,而不是α<0.
3
2
(4)4. 15
,3.
8
2 3
和(-1.9)
3 5
.
2
2
解:(4)因为幂函数 y= x 5 在(0,+∞)上为增函数,且 4.1>1,所以 4.15 >1,
高一数学必修一第二章知识总结

高一数学必修一第二章知识总结高一数学必修一第二章知识总结高一数学必修一第二章知识总结一、指数函数(一)指数与指数幂的运算1.根式的概念:一般地,如果xna,那么x叫做a的n次方根,其中n>1,且n∈N*.负数没有偶次方根;0的任何次方根都是0,记作n00。
当n是奇数时,anna,当n是偶数时,ann(a0)a|a|a(a0)2.分数指数幂正数的分数指数幂的意义,规定:maanmnna(a0,m,nN,n1)1mnm*,*1na0的正分数指数幂等于0,0的负分数指数幂没有意义3.实数指数幂的运算性质am(a0,m,nN,n1)(1)a〃aa(a0,r,sR);(2)(3)(a)arrsrsrrrs(a0,r,sR);(ab)aars(a0,r,sR).(二)指数函数及其性质1、指数函数的概念:一般地,函数yax(a0,且a1)叫做指数函数,其中x是自变量,函数的定义域为R.注意:指数函数的底数的取值范围,底数不能是负数、零和1.2、指数函数的图象和性质a>10(2)若x0,则f(x)1;f(x)取遍所有正数当且仅当xR;(3)对于指数函数f(x)ax(a0且a1),总有f(1)a;二、对数函数(一)对数1.对数的概念:一般地,如果axN(a0,a1),那么数x叫做以.a为底..N的对数,记作:xlog数,logxaN(a底数,N真aN对数式)说明:○1注意底数的限制a0,且a1;2aNlogNx;○3注意对数的书写格式.○alogaN两个重要对数:1常用对数:以10为底的对数lgN;○2自然对数:以无理数e2.71828为底的对数的对数lnN○指数式与对数式的互化幂值真数a=NlogaN=bb.底数指数对数(二)对数的运算性质如果a0,且a1,M0,N0,那么:1loga(M〃N)logaM+logaN;○2log○3log○MaNMnlogaM-logaaN;anlogM(nR).注意:换底公式logcblogab(a0,且a1;c0,且c1;b0).logca利用换底公式推导下面的结论(1)logambnnmloga(2)logb;ab1logba.(二)对数函数1、对数函数的概念:函数ylogax(a0,且a1)叫做对数函数,其中x是自变量,函数的定义域是(0,+∞).注意:○1对数函数的定义与指数函数类似,都是形式定义,注意辨别。
高一数学 基本初等函数(对、指、幂函数)高考考纲及典型例题高考真题解析

.
2
a 3 3a
【法二】 8 x 8 x 2 x
2
3 2
x 3
2 2 2 x 2 x 2 x 2 x 2 x 2 x
1
2 3
3
37 48
5 9 37 100 3 100 . 3 16 48
4
(4)原式 0.4 1 1 2 2 3 0.1
5 1 1 1 143 . 1 2 16 8 10 80
4.函数 f x a 2 7a 7 a x 是指数函数,求实数 a 的值. 【解析】∵函数 f x a 2 7a 7 a x 是指数函数,
1
0 a2 a1 1 a4 a3 . 1 又由题知: 0 10 1 3 10 ,∴ A 项正确. 3
1 x
a1 a2
O
x 1 x
b 7.已知二次函数 y ax 2 bx 与指数函数 y 的图象只能是下列图形中的 a y
1 1
1 2
1 1 , y x 2 的图像,了解它们的变化情况. x
二、重点知识总结
1.指数与指数幂运算 (1)①
a
n n n
n
a. a , 当n是奇数时 . a , 当n是偶数时
② a
(2)分数指数幂 ①a ②a
m n
n a m ( a 0 , m, n N * ,且 n 1 )
x y
2
是非负数,故④对.
7 (3) 2 9
【成才之路】高中数学 第二章 基本初等函数(Ⅰ) 幂函数 幂函数课件 新人教版必修1

A.1,3
B.-1,1
()
C.-1,3
D.-1,1,3
[答案] A [解析] α=-1 时,y=1x,定义域不为 R. α=1 时,y=x,满足题意. α=12时,y=x21,定义域为{x|x≥0}. α=3 时,y=x3,满足题意.
二、解答题
7.比较下列各组中三个值的大小,并说明理由:
1
1
1
(1)1.12,1.42,1.13;
答:平均每年需增长11.9%.
[例4] 幂函数y=(m2-m-1)xm2-2m-3当x∈(0,+∞) 时为减函数,求实数m的值.
[解析] ∵y=(m2-m-1)xm2-2m-3为幂函数, ∴m2-m-1=1, 即(m-2)(m+1)=0, ∴m=2,或m=-1. 当m=-1时,m2-2m-3=0不满足题意,舍去. 当m=2时,m2-2m-3=-3满足题设条件, ∴m=2.
R
{y|y≥ 抛物 ∞)增, 0} 线 (-∞,
偶
0]减
y=x3 R
R 拐线 增
奇
函数
定义域
值域
图象 形状
单调性
奇偶 性
图象
(-∞,
y=x-1
{x∈R|x ≠0}
{y∈R| y≠0}
双曲 线
0)减, (0,+
奇
∞)减
(-∞,
y=x-2
{x∈R|x ≠0}
{y∈R| y>0}
双曲 线型
0)增, (0,+
∵
2
=2
1 2
=(23)
1 6
=8
1 6
,
3
1
11
1
3 =3 3 =(32) 6 =9 6 而8<9.∴8 6
高一数学必修一函数知识点总结

二、函数的有关概念1.函数的概念:设A、B是非空的数集,如果按照某个确定的对应关系f,使对于集合A中的任意一个数x,在集合B中都有唯一确定的数f(x)和它对应,那么就称f:A→B为从集合A到集合B的一个函数.记作: y=f(x),x∈A.其中,x叫做自变量,x的取值范围A叫做函数的定义域;与x的值相对应的y值叫做函数值,函数值的集合{f(x)| x∈A }叫做函数的值域.注意:1.定义域:能使函数式有意义的实数x的集合称为函数的定义域。
求函数的定义域时列不等式组的主要依据是:(1)分式的分母不等于零;(2)偶次方根的被开方数不小于零;(3)对数式的真数必须大于零;(4)指数、对数式的底必须大于零且不等于1.(5)如果函数是由一些基本函数通过四则运算结合而成的.那么,它的定义域是使各部分都有意义的x的值组成的集合.(6)指数为零底不可以等于零,(7)实际问题中的函数的定义域还要保证实际问题有意义.相同函数的判断方法:①表达式相同(与表示自变量和函数值的字母无关);②定义域一致 (两点必须同时具备)(见课本21页相关例2)2.值域 : 先考虑其定义域(1)观察法(2)配方法(3)代换法3. 函数图象知识归纳(1)定义:在平面直角坐标系中,以函数y=f(x) , (x∈A)中的x为横坐标,函数值y为纵坐标的点P(x,y)的集合C,叫做函数y=f(x),(x ∈A)的图象.C上每一点的坐标(x,y)均满足函数关系y=f(x),反过来,以满足y=f(x)的每一组有序实数对x、y为坐标的点(x,y),均在C上 .(2) 画法A、描点法:B、图象变换法常用变换方法有三种1)平移变换2)伸缩变换3)对称变换4.区间的概念(1)区间的分类:开区间、闭区间、半开半闭区间(2)无穷区间(3)区间的数轴表示.5.映射一般地,设A、B是两个非空的集合,如果按某一个确定的对应法则f,使对于集合A中的任意一个元素x,在集合B中都有唯一确定的元素y与之对应,那么就称对应f:A→B为从集合A到集合B的一个映射。
高中数学人教版必修一基本初等函数

必修1 第二章基本初等函数2.1 指数函数 2.1.1 指数与指数幂的运算:①我们已经知道了指数幂的运算关系为,422=、823=、4121222-==、aa-21a 2=为正整数)(等; ②根式:如果a x 2=,那么x 叫做a 的平方根,例如±2就是4的平方根;如果3x =a ,那么x 叫做a 的立方根,例如2就是8的立方根; ③类似地,由于(±2)4=16,那么就把±2叫做16的四次方根;25=32,就把2叫做32的五次方根;④如果x n =a ,那么x 就叫做a 的n 次方根,其中n>1,且n ∈N*(正整数); 当n 为奇数时,正数的n 次方根为一个正数,负数的n 次方根为一个负数,此时a 的n 次方根用n a 表示,如2(325=(奇数)正数),2-(32-5=(奇数)负数);当n 为偶数时,正数的n 次方根有2个,一正一负对称,而负数的无意义(因为没有一个数的偶次方结果还是负数);例如16的4次方根为±2164±=.(0的任何次方都是0)⑤式子n a 叫做根式,这里的n 叫做根指数,a 叫做被开方数。
所以a a nn =)(,例如5522=)(,3-3-55=)( ⑥分数指数幂:如下例子2552510a a a ==)(、5335315a a a ==)(,通过以上例子我们在数学中推算出nmn ma a =(a>0,m ,n ∈N*,且n>1)此式为分子的指数幂关系。
所以如上面表示2133=。
❀❀❀❀❀❀❀❀❀❀❀❀❀❀❀❀❀❀❀❀❀❀❀❀❀❀❀❀❀The stupid speak of the past, the wise of the present, and fools of the future!!⑦0的正分数指数幂等于0,0的负分数指数幂没有意义;理解一下定理:⎪⎩⎪⎨⎧∈>>=∈>=∈>=⨯+),0,0()(3)),,0())(2(),,0()1(Q r b a b a ab Q s r a a a Q s r a a a a rr r rs s r s r s r (;(结合例题自己去验算)如:252212a aa a ==⨯+,352131021342342a a a a a a==⨯=)()(无理数指数幂的解法:一般的,无理数指数幂n a (a>0,a 是无理数)是一个确定的实数,有理数指数幂的运算性质同样适用于无理数指数幂。
高一数学必修1第二章基本初等函数知识点总结归纳

必修1第二章基本初等函数(Ⅰ)知识点整理〖2.1〗指数函数2.1.1指数与指数幂的运算(1)根式的概念 ①如果,,,1nxa a R x R n =∈∈>,且n N +∈,那么x 叫做a 的n 次方根.当n 是奇数时,a 的n当n 是偶数时,正数a 的正的nn次方根用符号表示;0的n 次方根是0;负数a 没有n 次方根.(2(3(4〖2.2〗对数函数【2.2.1】对数与对数运算(1)对数的定义①若(0,1)xaN a a =>≠且,则x 叫做以a 为底N 的对数,记作log a xN =,其中a 叫做底数,N叫做真数.②负数和零没有对数.③对数式与指数式的互化:log (0,1,0)x a x N a N a a N =⇔=>≠>.(2)几个重要的对数恒等式:l o g 10a =,log 1a a =,log b a a b =.(3)常用对数与自然对数:常用对数:lg N ,即10log N ;自然对数:ln N ,即log e N (其中 2.71828e =…).(4【(5(6)反函数的概念设函数()y f x =的定义域为A ,值域为C ,从式子()y f x =中解出x ,得式子()x y ϕ=.如果对于y 在C 中的任何一个值,通过式子()xy ϕ=,x 在A 中都有唯一确定的值和它对应,那么式子()x y ϕ=表示x 是y 的函数,函数()x y ϕ=叫做函数y =(7③将x=(8①原函数y ②函数y =③若(,P a (1一般地,函数(2(3①三象限,时,图象分布在第一、二象限(图象关于y轴对称);是奇函数时,图象分布在第一、三象限(图象关于原点对称);是非奇非偶函数时,图象只分布在第一象限. 幂函数在(0,)+∞都有②过定点:所有的通过点(1,1).定义,并且图象都0α>,则幂函数的图③单调性:如果象过原点,并且在[0,)+∞上为增函数.如果0α<,则幂函数的图象在(0,)+∞上为减函数,在第一象限内,图象无限接近x 轴与y 轴.④奇偶性:当α为奇数时,幂函数为奇函数,当α为偶数时,幂函数为偶函数.当q pα=(其中,p q 互质,p 和q Z ∈),若p 为奇数q 为奇数时,则q py x =是奇函数,若p 为奇数q 为偶数时,则q py x =是偶函数,若p 为偶数q 为奇数时,则qpy x =是非奇非偶函数. ⑤图象特征:幂函数,(0,)y x x α=∈+∞,当1α>时,若01x <<,其图象在直线y x =下方,若1x >,其图象在直线y x=上方,当α(1①一般式:f ③两根式:f (2(3①二次函数f ②当0a >当0a <.③二次函数11221212(,0),(,0),||||||M x M x M M x x a =-=. (4)一元二次方程20(0)axbx c a ++=≠根的分布一元二次方程根的分布是二次函数中的重要内容,这部分知识在初中代数中虽有所涉及,但尚不够系统和完整,且解决的方法偏重于二次方程根的判别式和根与系数关系定理(韦达定理)的运用,下面结合二次函数图象的性质,系统地来分析一元二次方程实根的分布.设一元二次方程20(0)axbx c a ++=≠的两实根为12,x x ,且12x x ≤.令2()f x ax bx c =++,从以下四个方面来分析此类问题:①开口方向:a ②对称轴位置:2bx a=-③判别式:∆④端点函数值符号. ①k <x 1≤x 2⇔ ②x 1≤x 2<k ⇔ ③x 1<k <x 2⇔af (k )<0 ④k 1<x 1≤x 2<k 2⇔⑤有且仅有一个根x 1(或x 2)满足k 1<x 1(或x 2)<k 2⇔f (k 1)f (k 2)<0,并同时考虑f (k 1)=0或f (k 2)=0这两种情况是否也符合⑥k 1<x 1<k 2≤p 1<x 2<p 2⇔ 此结论可直接由⑤推出. (5)二次函数2设f (p) )2b a -f x0x (q) 0x x ??0x xx。
人教A版数学必修一第2章《基本初等函数》(1)(幂函数)备课资料

人教A版数学必修一第2章《基本初等函数》(1)(幂函数)备课资料中学高中数学必修1第2章基本初等函数(1)-4.备课资料(幂函(数字)历史上数学计算方面的三大发明你知道数学计算的三大发明吗?这些是阿拉伯数字、十进制和对数研究自然数遇到的第一个问题是计数法和进位制的问题,我们采用的十进制是中国人的一大发明.在商代中期的甲骨文中已有十进制,其中最大的数是3万,印度最早到六世纪末才有十进制.但是,目前使用的计数法和阿拉伯数字1,2,3,4,5,6,7,8,9,0是印度人最早开始使用,后来传到阿拉伯,由阿拉伯人传到欧洲,并被欧洲人所接受.小数点计数法的诞生是自然数发展史上的一次飞跃。
同一个数因其位置不同而具有不同的值。
无限自然数可以由有限个符号控制,所有自然数都可以轻松清晰地表达出来16世纪前半叶,由于实际的需要,对计算技术的改进提出了前所未有的要求.这一时期计算技术最大的改进是对数的发明和应用,它的产生主要是由于天文和航海计算的迫切需要.为了简化天文航海方面所遇到的繁杂数值计算,自然希望将乘除法归结为简单的加减法.苏格兰数学家纳皮尔(napier,j.1550~1617)在球面天文学的三角学研究中,首先发明了对数方法.1614年他在题为《奇妙的对数定理说明书》一书中,阐述了他的对数方法,对数的使用价值为纳皮尔的朋友――英国数学家布里格斯(birggs,h.1561~1630)所认识,他与纳皮尔合作,并于1624年出版了《对数算术》一书,公布了以10为底的14位对数表,并称以10为底的对数为常用对数.常用对数曾经在简化计算上为人们做过重大贡献,而自然对数以及以e为底的指数函数成了研究科学、了解自然的必不可少的工具.恩格斯曾把对数的发明与解析几何的创始,微积分学的建立并称为17世纪数学的三大成就.法国著名的数学家、天文学家拉普拉斯曾说:“对数的发明以其节省劳力而延长了天文学家的寿命.”直到一8世纪,瑞士数学家欧拉(l.1707~1783)才发现指数和对数之间的关系。
人教A版(老课标)数学必修1- 第二章 基本初等函数-2.3 幂函数

栏目 导引
第二章 基本初等函数(Ⅰ)
幂函数 y=x
y=x2
y=x3
y=x12
y=x-1
奇偶性 _奇___
__偶__
_奇___
_非__奇___ _非__偶___
_奇___
单调性
_增___
x∈[0,+∞), _增___ x∈(-∞,0], _减___
_增___
x∈(0,+ _增___ ∞),_减___
性质,并会应用
第二章 基本初等函数(Ⅰ)
问题导学 预习课本 P77-79,思考以下问题: (1)幂函数的定义是什么? (2)幂函数的解析式有什么特点? (3)幂函数的图象有什么特点? (4)幂函数的性质有哪些?
栏目 导引
第二章 基本初等函数(Ⅰ)
1.幂函数的概念 函数 y=__x_α_叫做幂函数,其中__x__是自变量,__α__是常数.
栏目 导引
第二章 基本初等函数(Ⅰ)
若幂函数 f(x)=xα 的图象经过点2,14,则 f13=________. 解析:因为幂函数 f(x)=xα 的图象经过点2,14,所以 2α=14, 则 α=-2,所以 f(x)=x-2,所以 f13=13-2=9. 答案:9
+1;⑤y=(x-1)2;⑥y=x;⑦y=ax(a>1).其中幂函数的个数
为( )
A.1
B.2
C.3
D.4
栏目 导引
第二章 基本初等函数(Ⅰ)
(2)若函数 y=(m2+2m-2)xm 为幂函数且在第一象限为增函数,
则 m 的值为( )
A.1
B.-3
C.-1
D.3
栏目 导引
第二章 基本初等函数(Ⅰ)
栏目 导引
苏教版高一数学必修一基本初等函数与函数的性质综合复习

高一数学基本初等函数模块一 函数的性质一. 知识梳理1. 函数的单调性单调性定义,当12x x <时1221()D ()()()D ()()f x f x f x f x f x f x ⇔<⎧⎪⎨⇔<⎪⎩在区间上是增函数在区间上是增函数复合函数单调性的求解法则:同增异减单调性常见已知形式:1212()()0f x f x x x ->-2. 函数的奇偶性)(x f 是偶函数()()()()()01()f x f x f x f x f x f x -⇔-=⇔--=⇔= )(x f 是奇函数⇔()()()()()01()f x f x f x f x f x f x --=-⇔-+=⇔=-二.例题解析根据奇偶性求函数解析式【例1】已知()f x 是R 上的奇函数,当x >0时,2()1f x x x =++, 则()f x 的解析式为 .函数单调区间与单调性的应用【例2】 函数2()lg(23)f x x x =--的单调增区间是 .年级 高一科目数学上课时间课题 函数的性质、指对数函数复习【例3】已知函数2()3f x x x =+, 满足对于在区间(21,)m -+∞内的任意两个不同的12,x x 都有1212()()1f x f x x x ->-,实数m 的取值范围是 .函数的性质综合运用【例4】已知()f x 是定义在实数集R 上的偶函数,且在区间(],0-∞上单调递增,若实数x 满足(34)(2)f x f -≤,则x 的取值范围是 .【例5】已知函数()()211log 1aa x x f x x x --≤⎧⎪=⎨>⎪⎩,,.若在()-∞+∞,上单调递增,则实数的取值范围为()A .()12,B .()23,C .(]23,D .()2+∞,【例6】已知函数5()1,(3,2)51x xaf x x b b =-∈-+是奇函数. (1)求,a b 的值(2)证明:()f x 是区间(3,2)b b -上的减函数;(3)若2(32)(2)0f t f t -+≥,求实数t 的取值范围.三. 巩固训练1.函数()()32log 221+--=x x x f 的单调增区间是 .2.已知函数()x x f y +=是偶函数,且()12=f ,则()2-f = .3.已知函数1()33xxf x x ⎛⎫=-⎪⎝⎭,若()14log 20f a f ⎛⎫--≥ ⎪⎝⎭,则实数a 的取值范围是 .4.已知函数,0()(3)4,0x a x f x a x a x ⎧≤=⎨-+≥⎩,满足12x x ≠对任意1212()()0f x f x x x -<-成立,则a 的取值范围是 .5.若函数4()41x x mf x +=-为奇函数,则:(1) 求m 的值; (2) 求()f x 的值域; (3) 解关于t 的不等式:3317()3115f t ≤<.模块二 指对数函数幂函数一.知识梳理1.有理数指数幂的运算:a r a s =a r +s ;(a r )s =a rs ;(ab )r =a r b r2.对数的运算法则与重要公式:(0,0,01M N a a >>>≠且); (1)积的对数:log log log a a a MN M N =+log a y x =(2)商的对数:log ()log log a a a MM N N=- (3)幂的对数:log log m na a nb b m= (4)换底公式:abb c c a log log log =,1log log b a a b=.3.函数图像的变换:左加右减,上加下减;绝对值图像的变换。
人教版数学必修第一册综合复习:基本初等函数、函数与方程课件

B.(1,2)
C.(-2,-1)
3 −1 , > 0
作出函数f(x)= ൝ 2
的图象,如图.
− − 2 + 1, ≤ 0
关于x的方程[f(x)]2+(a-1)f(x)-a=0有7个不等的实数根,
即[f(x)+a][f(x)-1]=0有7个不等的实数根,易知f(x)=1有3
个不相等的实数根,则f(x)=-a必须有4个不相等的实数
因为x,y,z为正数,所以t>1,
因为 2 =
6
因为 2 =
10
6
23 =
5
25
所以 5 < 2 <
=
3
x
8,
10
3
3=
32,
5
6
32 =
5=
10
6
9,所以 2 <
25,所以 2 >
5
3.
3
x
5
x
分别作出y=( 2) ,y=( 3) ,y=( 5) 的图象,如图.
则3y<2x<5z.
3
3;
5,
)
[例3] (课标全国Ⅱ,14,5分)已知f(x)是奇函数, 且当x<0时, f(x)=-eax.
B.[0,+∞)
)
C.[-1,+∞)
D.[1,+∞)
, ≤ 0
[例6] (课标全国Ⅰ,9,5分)已知函数f(x)= ቊ
,g(x)=f(x)+x+a.若g(x)
ln, > 0
存在2个零点,则a的取值范围是( C )
A.[-1,0)
B.[0,+∞)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
幂函数及基本初等函数综合教学目标1、掌握幂函数的概念及图形特征;2、熟悉函数图象与性质的应用。
知识梳理1、幂函数的概念一般地,我们把形如a xy=的函数称为幂函数,其中x是自变量,a是常数。
注意:(1)幂函数a xaay x且中,底数是y=的底数是自变量,指数是常数与指数函数)1=a,0(≠>常数,指数是自变量。
(2)只有形如a xy a+=(a是不为y=的函数才是幂函数,否则不是。
例如:axy=,aaxy=0,1的常数)。
a xy=中的a是任意实数。
(3)幂函数a xy=的定义域由a决定。
(4)幂函数a x2、幂函数的图像3、幂函数作图技巧y=在第一象限内的图像;(1)作出幂函数a xy=的定义域,左边是否有图像;(2)判断幂函数a x(3)若左边有图像,判断奇偶性,作出左边图像。
4、基本初等函数的综合应用知识点1:幂函数的概念【例1】下列函数中不是幂函数的是【 】x y = B.3x y = C.x y 22= D.1-=x y【例2】函数112)22(--+=m xm m y 是幂函数,则m =________。
【随堂练习】1、下面的函数中是幂函数的是___________。
① 22+=x y ; ②21x y = ; ③32x y =; ④43xy =; ⑤131+=x y .2、已知)32().22(1122-+-+=-n x m m y m 是幂函数,求m 、n 的值。
知识点2:幂函数的解析式【例1】已知幂函数)(x f y =的图象过点)22,2(,则=)(x f ________。
【例2】如果幂函数()f x x α=的图象经过点2(2,)2,则(4)f 的值等于【 】 A. 16 B. 2 C. 116 D. 12【例3】已知幂函数αkx x f =)(),(R R k ∈∈α的图像过点1,22⎛⎫⎪⎝⎭,则k α+=【 】 A .12 B .1 C .32D .2【随堂练习】1、若幂函数)(x f 的图像经过点)22,2(,则=)9(f ______。
2、已知幂函数)(x f 的图象过点)21,4(,则()8f 的值为【 】A .42B .64C .22D .641知识点3:幂函数的图像【例1】函数()1,2ny xn N n =∈>的图象只可能是【 】A. B .C .D .【例2】若幂函数αx y =在第一象限内的图象如图所示,则α的取值可能为【 】 A .-1 B .2 C .3 D. 12【例3】幂函数m y x =与n y x =在第一象限内的图象如图所示,则【 】A .101n m -<<<<B .1,01n m <-<<C .10,1n m -<<>D .1,1n m <->【随堂练习】1、如图的曲线是幂函数nx y =在第一象限内的图象.已知n 分别取2±,12±四个值,与曲线1c 、2c 、3c 、4c 相应的n 依次为【 】A .112,,,222--B .112,,2,22--C .11,2,2,22--D .112,,,222--2、、请把相应的幂函数图象代号填入表格.① 23y x =; ② 2y x -=;③ 12y x =; ④ 1y x -=;⑤13y x=;⑥43yx=;⑦12y x-=;⑧53y x=.3、若幂函数222)33(--+-=mmxmmy的图像不过原点,则实数m的取值范围为【】A.21≤≤-m B.2=m或1=m C.2=m D.1=m【例4】函数31,0()1(),03xx xf xx⎧+<⎪=⎨≥⎪⎩的图象大致为【】【随堂练习】1、分别在四个坐标系中画出幂函数123233,,,y x y x y x y x-====的草图。
知识点4:幂函数的单调性【例1】若幂函数1()mf x x-=在()0,+∞上是增函数,则【】A.1m> B.1m< C.1m= D.不能确定函数代号①②③④⑤⑥⑦⑧图象代号【例2】幂函数2223()(1)m m f x m m x --=--在(0,)+∞上是减函数,则实数m 的值为【 】A 、2B 、3C 、4D 、5【例3】设⎭⎬⎫⎩⎨⎧--∈3,2,1,21,1,2α,使幂函数a y x =为奇函数且在(0,)+∞上单调递增的a 值的个数为【 】A .0B .1C .2D .3 【随堂练习】1、已知幂函数()y f x =的图像经过点)41,2(,则它的单调增区间为【 】 A .),0(+∞ B .[)+∞,0 C .)0,(-∞ D .),(+∞-∞2、若幂函数()()21m f x m m x =--在()0,+∞上为增函数,则实数m =【 】 A.2 B.1- C.3 D.1- 或23、已知幂函数)(x f y =图像过点2,2(),则该幂函数的值域是_____________.4、若幂函数αx y =在 ),0(+∞上是增函数,则α一定【 】A .0>αB .0<αC .1>αD .不确定知识点5:幂函数综合应用【例1】若3132)(--=x x x f ,则满足0)(>x f 的x 的取值范围 .【例2】已知函数3222)1()(----=m m x m m x f 是幂函数,且当)0,(-∞∈x 时为减函数。
(1)求实数m 的值;(2)判断函数)(x f 奇偶性并说明理由。
【例3】已知幂函数2242()(1)m m f x m x -+=-在(0,)+∞上单调递增,函数()2xg x k =-(1)求m 的值;(2)当[1,2]x ∈时,记()f x ,()g x 的值域分别为集合,A B ,若A B A = ,求实数k 的取值范围。
【例4】已知幂函数21()(22)m f x m m x +=-++为偶函数。
(1)求()f x 的解析式;(2)若函数()2(1)1y f x a x =--+在区间(2,3)上为单调函数,求实数a 的取值范围。
知识点6:基本初等函数综合【例1】函数xy a -=和函数log ()a y x =-(a>0,且a ≠0)的图象画在同一个坐标系中,得到的图象只可能是下面四个图象中的【 】【随堂练习】1、已知0,0a b >>,且1ab =,则函数()xf x a =与函数()log b g x x =-的图像可能是【 】2、若函数()log 0,1a y x a a =>≠且的图象如图所示,则下列函数图象正确的是【 】【例2】已知31.2lg =a ,31.1lg =b ,则ab=【 】 A .1001 B .101 C .10 D .100【例3】三个数 3.3320.99,log ,log 0.8π的大小关系为【 】A . 3.332log 0.99log 0.8π<<B . 3.323log 0.8log 0.99π<<C . 3.3230.99log 0.8l og π<< D . 3.323log 0.80.99log π<<【随堂练习】1、已知2log 3a =,12log 3b =,123c -=,则【 】A .c b a >>B .c a b >>C .a b c >>D .a c b >>【例4】设函数f (x )=122,11log ,1x x x x -⎧≤⎨->⎩,则满足()2≤x f 的x 的取值范围是【 】A .[-1,2]B .[0,2]C .[1,+∞)D .[0,+∞)【随堂练习】1、设函数()⎪⎩⎪⎨⎧≥<=-1,1,311x x x e x f x 则使得()2≤x f 成立的x 的取值范围是【 】A .(]1,∞-B .(]2ln 1,+∞-C .(]8,∞-D .[)8,1【例5】函数()12221+-⎪⎭⎫ ⎝⎛=x x x f 的单调增区间为______________。
【随堂练习】1、函数22log (56)y x x 单调递减区间是______________。
2、函数212log (6)=+-y x x 的单调增.区间是【 】 A .1(,]2-∞ B .1(2,]2- C .1[,)2+∞ D .1[,3)2【例6】函数2212x xy -+⎛⎫= ⎪⎝⎭的值域是【 】A .RB .1,2⎡⎫+∞⎪⎢⎣⎭C .(2,+∞)D .(0,+∞) 【随堂练习】1、函数()2lg 45y x x =--的值域为【 】 A .(),-∞+∞B .()1,5-C .()5,+∞D .(),1-∞-【例7】已知关于x 的不等式222(log )2log 30x x --≤的解集为M .(1)求集合M ;(2)若M x ∈,求函数22()[log (2)](log )32xf x x =⋅的最值.。
