随机信号分析实验
实验四 随机信号分析

实验四随机信号分析生物医学工程系罗融编一、实验目的:1.理解随机信号的各种数字特征及相关函数。
2.学习用MATLAB语言编写数字特征及相关函数计算程序。
3.观察脑电信号的数字特征及相关函数。
二、实验内容:1.产生1千点的白噪声信号,并计算它的均值、均方值、均方根值、方差。
(产生白噪声可用语句n=10^3;x=randn(1,n))2.计算一白噪声加10Hz正弦信号构成的随机信号并作图显示该随机信号与它的自相关函数。
(白噪声加10Hz正弦信号可用语句x2=x+sin(2*pi*10*[0:999]/250);其中抽样率fs=250Hz)3.计算白噪声的自相关函数并作图显示白噪声与它的自相关函数。
4.计算脑电信号的均值、均方值、均方根值、方差,计算脑电信号的自相关函数并作图显示脑电信号与它的自相关函数。
5.计算含有噪声的心电信号的自相关函数并作图显示含有噪声的心电信号与它的自相关函数。
含有噪声的心电信号与脑电信号由数据文件shiyansi.mat提供,用load shiyansi命令后,shiyansi数据文件中的变量zshecg与eeg即在matlab工作空间中,可用plot(zshecg)语句观察该含有噪声的心电信号,用plot(eeg)语句观察脑电信号。
三、报告要求:报告格式要求同实验一。
报告内容应包含实验名称,实验目的,实验内容,实验程序代码及结果,实验结果分析与讨论等附录:1)均值:3)均方:4)相关函数:2.MATLAB语言说明:1)mean函数:2)var函数:(2)option为’biased’时,计算有偏互相关估计(3)option为’unbiased’时,计算无偏互相关估计。
随机信号分析实验报告

随机信号分析实验报告引言:随机信号是指信号在时间或空间上的其中一种特性是不确定的,不能准确地预测其未来行为的一类信号。
随机信号是一种具有随机性的信号,其值在一段时间内可能是不确定的,但是可以通过概率论和统计学的方法来描述和分析。
实验目的:通过实验,学习了解随机信号的基本概念和特性,学习了解和掌握常见的随机信号分析方法。
实验原理:随机信号可以分为离散随机信号和连续随机信号。
离散随机信号是信号在离散时间点上,在该时间点上具有一定的随机性;而连续随机信号是信号在连续时间上具有随机性。
常见的随机信号分析方法包括概率密度函数、功率谱密度函数等。
实验器材:计算机、MATLAB软件、随机信号产生器、示波器、电缆、电阻等。
实验步骤:1.配置实验仪器:将随机信号产生器和示波器与计算机连接。
2.生成随机信号:调节随机信号产生器的参数,产生所需的随机信号。
3.采集数据:使用示波器采集随机信号的样本数据,并将数据导入MATLAB软件。
4.绘制直方图:使用MATLAB软件绘制样本数据的直方图,并计算概率密度函数。
5.计算统计特性:计算随机信号的均值、方差等统计特性。
6.绘制功率谱密度函数:使用MATLAB软件绘制随机信号的功率谱密度函数。
实验结果和讨论:我们采集了一段长度为N的随机信号样本数据,并进行了相应的分析。
通过绘制直方图和计算概率密度函数,我们可以看出随机信号的概率分布情况。
通过计算统计特性,我们可以得到随机信号的均值、方差等重要参数。
通过绘制功率谱密度函数,我们可以分析随机信号的频谱特性。
结论:本实验通过对随机信号的分析,加深了对随机信号的理解。
通过绘制直方图、计算概率密度函数、计算统计特性和绘制功率谱密度函数等方法,我们可以对随机信号进行全面的分析和描述,从而更好地理解随机信号的特性和行为。
2.王五,赵六.随机信号分析方法.物理学报,2024,30(2):120-130.。
随机信号分析实验报告

实验一 随机噪声的产生与性能测试一、实验内容1.产生满足均匀分布、高斯分布、指数分布、瑞利分布的随机数,长度为N=1024,并计算这些数的均值、方差、自相关函数、概率密度函数、概率分布函数、功率谱密度,画出时域、频域特性曲线; 2.编程分别确定当五个均匀分布过程和5个指数分布分别叠加时,结果是否是高斯分布; 3.采用幅度为2, 频率为25Hz 的正弦信号为原信号,在其中加入均值为2 , 方差为0.04 的高斯噪声得到混合随机信号()X t ,编程求 0()()tY t X d ττ=⎰的均值、相关函数、协方差函数和方差,并与计算结果进行比较分析。
二、实验步骤 1.程序N=1024; fs=1000; n=0:N —1;signal=chi2rnd (2,1,N); %rand(1,N)均匀分布 ,randn(1,N )高斯分布,exprnd(2,1,N )指数分布,raylrnd (2,1,N)瑞利分布,chi2rnd(2,1,N )卡方分布 signal_mean=mean(signal ); signal_var=var (signal );signal_corr=xcorr(signal,signal ,'unbiased ’); signal_density=unifpdf(signal ,0,1); signal_power=fft(signal_corr); %[s,w]=periodogram (signal); [k1,n1]=ksdensity(signal);[k2,n2]=ksdensity (signal,’function ’,'cdf ’); figure ;hist(signal);title (’频数直方图’); figure ;plot (signal);title(’均匀分布随机信号曲线’); f=n *fs/N ; %频率序列 figure;plot(abs (signal_power)); title('功率幅频’); figure;plot(angle (signal_power)); title ('功率相频'); figure;plot (1:2047,signal_corr); title ('自相关函数’); figure;plot(n1,k1);title('概率密度’);figure;plot(n2,k2);title('分布函数’);结果(1)均匀分布(2)高斯分布(3)指数分布(4)瑞利分布(5)卡方分布2.程序N=1024;signal_1=rand(1,N);signal_2=rand(1,N);signal_3=rand(1,N);signal_4=rand(1,N);signal_5=rand(1,N);signal=signal_1+signal_2+signal_3+signal_4+signal_5; [k1,n1]=ksdensity(signal);figure(1)subplot(1,2,1);hist(signal);title('叠加均匀分布随机数直方图');subplot(1,2,2);plot(n1,k1);title(’叠加均匀分布的概率密度');结果指数分布叠加均匀分布叠加结果:五个均匀分布过程和五个指数分布分别叠加时,结果是高斯分布。
随机信号分析实验
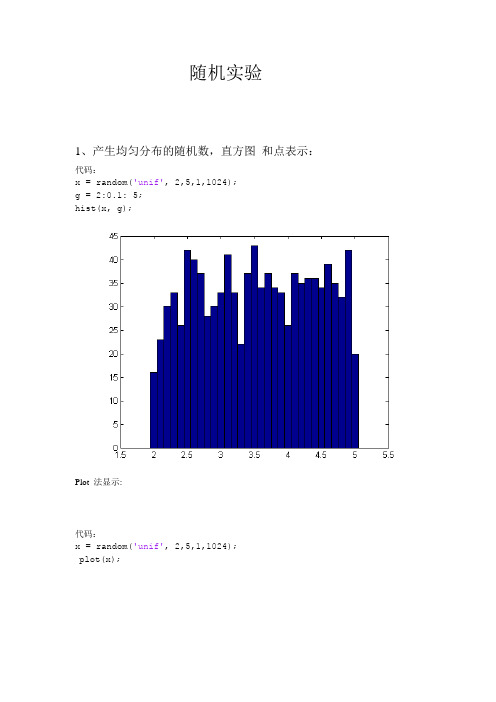
随机实验1、产生均匀分布的随机数,直方图和点表示:代码:x = random('unif', 2,5,1,1024);g = 2:0.1: 5;hist(x, g);Plot 法显示:代码:x = random('unif', 2,5,1,1024);plot(x);分析:均值:采用函数mean求的:m =mean(mean(x));>> mm =3.4940大约是3.5 和理论值差不多方差:var(x)ans =0.7223和理论值0.75 也差不多,说明点还是取的不够多的2、高斯随机数分布直方图均值为1,方差为0代码:N = 200000;g = -5:0.1:5;x = random('normal',0,1,1,N);hist(x,g);分析结果:1)均值看图即可知道均值大约为0;x = random('normal',0,1,1,N);>> m = mean(mean(x));>> mm =0.0025大概N的取值再大一些,这样均值会更接近0 的2)方差var(x)ans =0.9976方差和1 是比较接近的3、相互独立的随机数作和1)J均匀分布随机数作和0 ~ 2区间代码:N = 200000;g = 0:0.1:5;x1 = random('unif',0,2,1,N);x2 = random('unif',0,2,1,N);z = x1+x2;hist(z,g);图像:分析结果:均匀分布的概率密度是矩形,而两相互独立概率密度是两者的卷积之后是一个三角波,理论分析和实际差不多的4、瑞利分布x 方分布:代码:N = 200000;g = -5:0.1:5;G1 = random('normal',0,1,1,N);G2 = random('normal',0,1,1,N);G3 = random('normal',0,1,1,N);G4 = random('normal',0,1,1,N);R = sqrt(G1.*G1 + G2.*G2);X2 = G1.*G1 + G2.*G2+ G3.*G3 + G4.*G4; subplot(311); hist(G1,g);subplot(312); hist(R,0:0.05:5);subplot(313); hist(X2,0:0.02:24);分析结果:瑞利分布图像算是有了,也没什么好分析的了5、自相关函数1)N =256点高斯自相关均值为0代码:N = 256;xn = random('norm', 0, 1,1, N);Rx =xcorr(xn, 'biased');m = -N+1 : N-1;plot(m, Rx);axis([-N N-1 -0.5 1.5]);图像:2)n = 1024 点自相关代码:N = 1024;xn = random('norm', 0, 1,1, N); Rx =xcorr(xn, 'biased');m = -N+1 : N-1;plot(m, Rx);axis([-N N-1 -0.5 1.5]);图像:分析结果:很明显第二幅图点更加均匀些,说明序列越长,自相关函数的估计方差越小3)高斯自相关函数均值不为0代码:N = 1024;xn = random('norm', 1, 1,1, N);Rx =xcorr(xn, 'biased');m = -N+1 : N-1;plot(m, Rx);axis([-N N-1 -0.5 1.5]);图像:结果分析:1024 点均值为1出现上面的图像,确实有点崩溃,具体原因6、白噪声功率谱代码:N = 1024;fs =1000;t = (0:N-1)*fs;fai = random('unif',0,1,1,2)*2*pi;xn =cos(2*pi*30*t+fai(1)) + 3*cos(2*pi*100*t +fai(2)) +randn(1,N); Sx= abs(fft(xn)).^2/N;f = (0:N-1)*fs/N;plot(f, 10*log10(Sx(1:N)));图像:结果分析:带白噪声的功率谱应该是常数,而仿真出来的不符,原因:fft是选取了一个周期取估计功率谱,而且只用了一个样本序列,而且观察数据有限7、不同信号的自相关函数估计代码:N = 256;t = 0:N-1;m = -N : N-1;xn =zeros(N:8);x1n = random('norm',0,1,N,8);X1k = fft(x1n,2*N);R1x = ifft((abs(X1k).^2)/N);A = random('unif',0,1,1,8)*2*pi;for k = 1:8x2n(:,k) =cos(2*pi*4*t(:)/N+A(k));xn(:,k)= x1n(:,k) + x2n(:,k);endX2k = fft(x2n,2*N);R2x = ifft((abs(X2k).^2)/N);Xk = fft(xn,2*N);Rx = ifft((abs(Xk).^2)/N);subplot(311); plot(m,fftshift(R1x)); axis([-N N-1 -0.5 1.5] );subplot(312); plot(m,fftshift(R2x)); axis([-N N-1 -0.5 1.5] );subplot(313); plot(m,fftshift(Rx)); axis([-N N-1 -0.5 1.5] );图像:。
随机信号分析实验报告(基于MATLAB语言)

随机信号分析实验报告——基于MATLAB语言姓名:_班级:_学号:专业:目录实验一随机序列的产生及数字特征估计 (2)实验目的 (2)实验原理 (2)实验内容及实验结果 (3)实验小结 (6)实验二随机过程的模拟与数字特征 (7)实验目的 (7)实验原理 (7)实验内容及实验结果 (8)实验小结 (11)实验三随机过程通过线性系统的分析 (12)实验目的 (12)实验原理 (12)实验内容及实验结果 (13)实验小结 (17)实验四窄带随机过程的产生及其性能测试 (18)实验目的 (18)实验原理 (18)实验内容及实验结果 (18)实验小结 (23)实验总结 (23)实验一随机序列的产生及数字特征估计实验目的1.学习和掌握随机数的产生方法。
2.实现随机序列的数字特征估计。
实验原理1.随机数的产生随机数指的是各种不同分布随机变量的抽样序列(样本值序列)。
进行随机信号仿真分析时,需要模拟产生各种分布的随机数。
在计算机仿真时,通常利用数学方法产生随机数,这种随机数称为伪随机数。
伪随机数是按照一定的计算公式产生的,这个公式称为随机数发生器。
伪随机数本质上不是随机的,而且存在周期性,但是如果计算公式选择适当,所产生的数据看似随机的,与真正的随机数具有相近的统计特性,可以作为随机数使用。
(0,1)均匀分布随机数是最最基本、最简单的随机数。
(0,1)均匀分布指的是在[0,1]区间上的均匀分布, U(0,1)。
即实际应用中有许多现成的随机数发生器可以用于产生(0,1)均匀分布随机数,通常采用的方法为线性同余法,公式如下:,序列为产生的(0,1)均匀分布随机数。
定理1.1若随机变量X 具有连续分布函数,而R 为(0,1)均匀分布随机变量,则有2.MATLAB中产生随机序列的函数(1)(0,1)均匀分布的随机序列函数:rand用法:x = rand(m,n)功能:产生m×n 的均匀分布随机数矩阵。
(2)正态分布的随机序列函数:randn用法:x = randn(m,n)功能:产生m×n 的标准正态分布随机数矩阵。
随机信号分析实验报告

一、实验名称微弱信号的检测提取及分析方法二、实验目的1.了解随机信号分析理论如何在实践中应用2.了解随机信号自身的特性,包括均值、方差、相关函数、频谱及功率谱密度等3.掌握随机信号的检测及分析方法三、实验原理1.随机信号的分析方法在信号与系统中,我们把信号分为确知信号和随机信号。
其中随机信号无确定的变化规律,需要用统计特新进行分析。
这里我们引入随机过程的概念,所谓随机过程就是随机变量的集合,每个随机变量都是随机过程的一个取样序列。
随机过程的统计特性一般采用随机过程的分布函数和概率密度来描述,他们能够对随机过程作完整的描述。
但由于在实践中难以求得,在工程技术中,一般采用描述随机过程的主要平均统计特性的几个函数,包括均值、方差、相关函数、频谱及功率谱密度等来描述它们。
本实验中算法都是一种估算法,条件是N要足够大。
2.微弱随机信号的检测及提取方法因为噪声总会影响信号检测的结果,所以信号检测是信号处理的重要内容之一,低信噪比下的信号检测是目前检测领域的热点,而强噪声背景下的微弱信号提取又是信号检测的难点。
噪声主要来自于检测系统本身的电子电路和系统外空间高频电磁场干扰等,通常从以下两种不同途径来解决①降低系统的噪声,使被测信号功率大于噪声功率。
②采用相关接受技术,可以保证在信号功率小于噪声功率的情况下,人能检测出信号。
对微弱信号的检测与提取有很多方法,常用的方法有:自相关检测法、多重自相法、双谱估计理论及算法、时域方法、小波算法等。
对微弱信号检测与提取有很多方法,本实验采用多重自相关法。
多重自相关法是在传统自相关检测法的基础上,对信号的自相关函数再多次做自相关。
即令:式中,是和的叠加;是和的叠加。
对比两式,尽管两者信号的幅度和相位不同,但频率却没有变化。
信号经过相关运算后增加了信噪比,但其改变程度是有限的,因而限制了检测微弱信号的能力。
多重相关法将当作x(t),重复自相关函数检测方法步骤,自相关的次数越多,信噪比提高的越多,因此可检测出强噪声中的微弱信号。
随机信号分析实验报告

随机信号分析实验报告实验一:平稳随机过程的数字特征实验二:平稳随机过程的谱分析实验三:随机信号通过线性系统的分析实验四:平稳时间序列模型预测班级:姓名:学号:一、实验目的1、加深理解平稳随机过程数字特征的概念2、掌握平稳随机序列期望、自相关序列的求解3、分析平稳随机过程数字特征的特点二、实验原理平稳随机过程数字特征求解的相关原理三、实验过程function y = experimentnumber = 49; %学号49I = 8; %幅值为8u = 1/number;Ex = I*0.5 + (-I)*0.5;N = 64;C0 = 1; %计数p(1) = exp(-u);for m = 2:Nk = 1:m/2;p(m) = exp(-u*m) + sum((u*m).^(2*k)./factorial(2*k)*exp(-u*m));2222()[()()]{()()}{()()}X R m E X n X n m I P X n X n m I I P X n X n m I =+=+=-+=-E[X(n)]= I P{X(n)=+I}+(-I)P{X(n)=-I}=0⨯⨯0m >当时,/2220(){()()}(2)!m k m k m P X n X n m I e P k λλ⎢⎥⎣⎦-=+===∑222()(1)(21)X R m I P I P I P =--=-2()()X X X C m R m m =-me I m n X n X E m R λ22)]()([)(-=+=end;pp = [fliplr(p) C0 p];Rx = (2*pp - 1)*I^2;m = -N:N;Kx = Rx - Ex*Ex;rx = Kx/25;subplot(211), plot(m,Rx); axis([-N N 0 I*I]); title('自相关序列');subplot(212), plot(m,rx); axis([-N N 0 1]); title('自相关序数');四、实验结果及分析自相关序列的特点分析:m>0时Rx(m)随着m的增大而减小,m<0时Rx(m)随着m的增大而增大。
随机信号分析教学实验

方差
方差也有直接计算法和递推计算法两种: 直接计算法
和 递推计算法(适合于实时计算)
2
2
2 n
1 N ( xn m)2 N n1
1 N xn m2 N n1
n 1 2 1 ( xn mn1 )2 n 1 n n
例:
r=raylrnd(1) r= 1.7648 r=raylrnd(1,1,5) r= 0.9466 1.4313 1.7903
2018/10/22
1.6072
1.4110
随机变量的数字特征
数学期望
数学期望又为均值,对于随机数序列有两种计算 方法:直接计算法和递推计算法。
直接计算法
高斯分布(正态分布) (参 例 r=normrnd(0,1) 见《随机信号分析》25 r= 页)
r = normrnd(μ, σ) r = normrnd(μ, σ, m, n) μ:为高斯随机变量的均
值; σ:为高斯随机变量的标 准差。
-0.4326 r=normrnd(0,1,3,3) r= -1.6656 -1.1465 0.0376 0.1253 1.1909 0.3273 0.2877 1.1892 0.1746
r = binornd(n, p)
2018/10/22
例:
r=binornd(1000,0.5) r=
491 r=binornd(1000,0.5,2,3) r= 512 503 489
491 466 512
2018/10/22
泊松分布
泊松分布(参见《随 例: 机信号分析》24页): r=poissrnd(10)
随机信号分析实验报告

随机信号分析实验报告目录随机信号分析 (1)实验报告 (1)理想白噪声和带限白噪声的产生与测试 (2)一、摘要 (2)二、实验的背景与目的 (2)背景: (2)实验目的: (2)三、实验原理 (3)四、实验的设计与结果 (4)实验设计: (4)实验结果: (5)五、实验结论 (12)六、参考文献 (13)七、附件 (13)1理想白噪声和带限白噪声的产生与测试一、摘要本文通过利用MATLAB软件仿真来对理想白噪声和带限白噪声进行研究。
理想白噪声通过低通滤波器和带通滤波器分别得到低通带限白噪声和帯通带限白噪声。
在仿真的过程中我们利用MATLAB工具箱中自带的一些函数来对理想白噪声和带限白噪声的均值、均方值、方差、功率谱密度、自相关函数、频谱以及概率密度进行研究,对对它们进行比较分析并讨论其物理意义。
关键词:理想白噪声带限白噪声均值均方值方差功率谱密度自相关函数、频谱以及概率密度二、实验的背景与目的背景:在词典中噪声有两种定义:定义1:干扰人们休息、学习和工作的声音,引起人的心理和生理变化。
定义2:不同频率、不同强度无规则地组合在一起的声音。
如电噪声、机械噪声,可引伸为任何不希望有的干扰。
第一种定义是人们在日常生活中可以感知的,从感性上很容易理解。
而第二种定义则相对抽象一些,大部分应用于机械工程当中。
在这一学期的好几门课程中我们都从不同的方面接触到噪声,如何的利用噪声,把噪声的危害减到最小是一个很热门的话题。
为了加深对噪声的认识与了解,为后面的学习与工作做准备,我们对噪声进行了一些研究与测试。
实验目的:了解理想白噪声和带限白噪声的基本概念并能够区分它们,掌握用MATLAB 或c/c++软件仿真和分析理想白噪声和带限白噪声的方法,掌握理想白噪声和带限白噪声的性质。
三、实验原理所谓白噪声是指它的概率统计特性服从某种分布而它的功率谱密度又是均匀的。
确切的说,白噪声只是一种理想化的模型,因为实际的噪声功率谱密度不可能具有无限宽的带宽,否则它的平均功率将是无限大,是物理上不可实现的。
随机信号分析实验

随机信号分析实验实验⼀随机序列得产⽣及数字特征估计⼀、实验⽬得1、学习与掌握随机数得产⽣⽅法;2、实现随机序列得数字特征估计。
⼆、实验原理1、随机数得产⽣随机数指得就是各种不同分布随机变量得抽样序列(样本值序列).进⾏随机信号仿真分析时,需要模拟产⽣各种分布得随机数。
在计算机仿真时,通常利⽤数学⽅法产⽣随机数,这种随机数称为伪随机数.伪随机数就是按照⼀定得计算公式产⽣得,这个公式称为随机数发⽣器。
伪随机数本质上不就是随机得,⽽且存在周期性,但就是如果计算公式选择适当,所产⽣得数据瞧似随机得,与真正得随机数具有相近得统计特性,可以作为随机数使⽤。
(0,1)均匀分布随机数就是最最基本、最简单得随机数.(0,1)均匀分布指得就是在[0,1]区间上得均匀分布,即U(0,1)。
实际应⽤中有许多现成得随机数发⽣器可以⽤于产⽣(0,1)均匀分布随机数,通常采⽤得⽅法为线性同余法,公式如下:(1、1)序列为产⽣得(0,1)均匀分布随机数。
下⾯给出了上式得3组常⽤参数:(1) ;(2)(IBM随机数发⽣器);(3)(ran0);由均匀分布随机数,可以利⽤反函数构造出任意分布得随机数。
定理1、1若随机变量X具有连续分布函数F(x),⽽R为(0,1)均X匀分布随机变量,则有(1、2)由这⼀定理可知,分布函数为F X(x)得随机数可以由(0,1)均匀分布随机数按上式进⾏变换得到。
2、MATLAB 中产⽣随机序列得函数(1)(0,1)均匀分布得随机序列函数:rand⽤法:x=rand(m,n)功能:产⽣m×n得均匀分布随机数矩阵。
(2)正态分布得随机序列函数:randn⽤法:x = randn(m,n)功能:产⽣m×n 得标准正态分布随机数矩阵。
如果要产⽣服从分布得随机序列,则可以由标准正态随机序列产⽣。
(3) 其她分布得随机序列MATLAB上还提供了其她多种分布得随机数得产⽣函数,下表列出了部分函数。
北理工随机信号分析实验报告
本科实验报告实验名称:随机信号分析实验实验一 随机序列的产生及数字特征估计一、实验目的1、学习和掌握随机数的产生方法。
2、实现随机序列的数字特征估计。
二、实验原理1、随机数的产生随机数指的是各种不同分布随机变量的抽样序列(样本值序列)。
进行随机信号仿真分析时,需要模拟产生各种分布的随机数。
在计算机仿真时,通常利用数学方法产生随机数,这种随机数称为伪随机数。
伪随机数是按照一定的计算公式产生的,这个公式称为随机数发生器。
伪随机数本质上不是随机的,而且存在周期性,但是如果计算公式选择适当,所产生的数据看似随机的,与真正的随机数具有相近的统计特性,可以作为随机数使用。
(0,1)均匀分布随机数是最最基本、最简单的随机数。
(0,1)均匀分布指的是在[0,1]区间上的均匀分布,即 U(0,1)。
实际应用中有许多现成的随机数发生器可以用于产生(0,1)均匀分布随机数,通常采用的方法为线性同余法,公式如下:)(m od ,110N ky y y n n -=N y x n n /=序列{}n x 为产生的(0,1)均匀分布随机数。
下面给出了上式的3组常用参数: 1、10N 10,k 7==,周期7510≈⨯;2、(IBM 随机数发生器)3116N 2,k 23,==+周期8510≈⨯; 3、(ran0)315N 21,k 7,=-=周期9210≈⨯;由均匀分布随机数,可以利用反函数构造出任意分布的随机数。
定理 1.1 若随机变量 X 具有连续分布函数F X (x),而R 为(0,1)均匀分布随机变量,则有)(1R F X x -=由这一定理可知,分布函数为F X (x)的随机数可以由(0,1)均匀分布随机数按上式进行变换得到。
2、MATLAB 中产生随机序列的函数(1)(0,1)均匀分布的随机序列 函数:rand 用法:x = rand(m,n)功能:产生m ×n 的均匀分布随机数矩阵。
(2)正态分布的随机序列 函数:randn 用法:x = randn(m,n)功能:产生m ×n 的标准正态分布随机数矩阵。
随机信号分析上机实验

《随机信号分析》上机实验实验一1、熟悉并练习使用下列Matlab的函数,给出各个函数的功能说明和内部参数的意义,并给出至少一个使用例子和运行结果:1)rand()2)randn()3)normrnd()4)mean()5)var()6)xcorr()7)periodogram()8)fft()9)normpdf()10)normcdf()11)unifpdf()12)unifcdf()13)raylpdf()14)raylcdf()15)exppdf()16)expcdf()17)chol()18)ksdensity()19)hist()20)int()2、产生高斯随机变量(1) 产生数学期望为0,方差为1的高斯随机变量;(2) 产生数学期望为5,方差为10的高斯随机变量;(3) 利用计算机求上述随机变量的100个样本的数学期望和方差,并与理论值比较;χ分布的随机变量3、产生2χ分布的随机变量;(1) 产生自由度为2,数学期望为2,方差为4的具有中心2χ分布的随机变量;(2) 产生自由度为2,数学期望为4,方差为12的具有非中心2(3) 利用计算机求上述随机变量的100个样本的数学期望和方差,并与理论值比较;4、利用Matlab现有pdf和cdf函数,画出均值为零、方差为4的高斯随机变量的概率密度曲线和概率分布曲线。
5、产生长度为1000数学期望为5,方差为10的高斯随机序列,并根据该序列值画出其概率密度曲线。
(不使用pdf函数)6、利用Matlab求随机变量的统计特性1)参照上述例题,求:2)参照上述例题,求:2Y X =的数学期望和方差。
实验二1、产生一组(0,1)均匀分布的白噪声序列,画出其自相关函数和功率谱密度;2、产生一组服从()~2,5N 的正态白噪声序列,画出其自相关函数和功率谱密度;3、估计随机过程()()()()cos 600cos 640X t t t N t ππ=++的自相关函数和功率谱,其中()N t 服从()~0,1N 的高斯分布。
随机信号分析实验百度

《随机信号分析》试验报告班级班学号_______________姓名_________________实验一1、熟悉并练习使用下列 Matlab 的函数,给出各个函数的功能说明和内部参数 的意义,并给出至少一个使用例子和运行结果:1)randn()产生随机数数组或矩阵,其元素服从均值为 0,方差为 1 的正态分布1) Y = randn产生一个伪随机数 2) Y = randn(n) 产生 n x n 的矩阵, 的正态分布其元素服从均值为0,方差为 13)Y = randn(m,n)产生 m x n 的矩阵, 的正态分布其元素服从均值为0,方差为 14) Y= randn([m n]) 产生 m x n 的矩阵, 的正态分布其元素服从均值为0,方差为 1选择( 2)作为例子,运行结果如下: >> Y = randn(3)1.3005 0.0342 0.97920.2691 0.9913 -0.8863 -0.1551 -1.3618 -0.3562生成n 々随机矩阵,其元素在(0, 1)内 生成mxn 随机矩阵 生成m x n 随机矩阵生成mxn 和x …随机矩阵或数组 生成m x n 和x …随机矩阵或数组 生成与矩阵 A 相同大小的随机矩阵 选择( 3)作为例子,运行结果如下:>> Y = rand([3 4])Y =0.05790.0099 0.1987 0.19883)normrnd()产生服从均值为mu 标准差为sigma 的随机数, mu 和sigma 可以为向量、矩阵、或多维数组。
(2)R = normrnd (mu,sigma,v ) 产生服从均值为 mu 标准差为 sigma 的随机数,v 是一个行向量。
如果v 是一个1 X 2的向量, 则R 为一个1行2列的矩阵。
如果v 是1X n 的, 那么R 是一个n 维数组(3)R = normrnd (mu,sigma,m,n ) 产生服从均值为 mu 标准差为 sigma 的随机数,2)rand()(1)Y = rand(n) (2)Y = rand(m,n) (3)Y = rand([m n])(4) Y = rand(m,n,p,…) (5) Y = rand([m n p …]) (6) Y = rand(size(A)) 0.3529 0.81320.1389 0.2028 0.6038 0.2722 0.0153 0.7468产生服从正态分布的随机数(1)R= normrnd(mu,sigma)标量m和n是R的行数和列数。
随机信号分析实验报告范文

随机信号分析实验报告范文HaarrbbiinnIInnttiittuutteeooffTTeecchhnnoollooggyy实验报告告课程名称:院系:电子与信息工程学院班级:姓名:学号:指导教师:实验时间:实验一、各种分布随机数得产生(一)实验原理1、、均匀分布随机数得产生原理产生伪随机数得一种实用方法就是同余法,它利用同余运算递推产生伪随机数序列.最简单得方法就是加同余法为了保证产生得伪随机数能在[0,1]内均匀分布,需要M为正整数,此外常数c与初值y0亦为正整数。
加同余法虽然简单,但产生得伪随机数效果不好。
另一种同余法为乘同余法,它需要两次乘法才能产生一个[0,1]上均匀分布得随机数ﻩﻩﻩ式中,a为正整数。
用加法与乘法完成递推运算得称为混合同余法,即ﻩﻩﻩ用混合同余法产生得伪随机数具有较好得特性,一些程序库中都有成熟得程序供选择。
常用得计算语言如Baic、C与Matlab都有产生均匀分布随机数得函数可以调用,只就是用各种编程语言对应得函数产生得均匀分布随机数得范围不同,有得函数可能还需要提供种子或初始化。
Matlab提供得函数rand()可以产生一个在[0,1]区间分布得随机数,rand(2,4)则可以产生一个在[0,1]区间分布得随机数矩阵,矩阵为2行4列。
Matlab提供得另一个产生随机数得函数就是random(’unif’,a,b,N,M),unif表示均匀分布,a与b就是均匀分布区间得上下界,N与M分别就是矩阵得行与列。
2、、随机变量得仿真根据随机变量函数变换得原理,如果能将两个分布之间得函数关系用显式表达,那么就可以利用一种分布得随机变量通过变换得到另一种分布得随机变量。
若X就是分布函数为F(某)得随机变量,且分布函数F(某)为严格单调升函数,令Y=F(某),则Y必为在[0,1]上均匀分布得随机变量.反之,若Y就是在[0,1]上均匀分布得随机变量,那么即就是分布函数为F某(某)得随机变量。
随机信号分析报告实验:随机过程通过线性系统地分析报告

实验三 随机过程通过线性系统的分析实验目的1. 理解和分析白噪声通过线性系统后输出的特性。
2. 学习和掌握随机过程通过线性系统后的特性,验证随机过程的正态化问题。
实验原理1.白噪声通过线性系统设连续线性系统的传递函数为)(ωH 或)(s H ,输入白噪声的功率谱密度为2)(0N S X =ω,那么系统输出的功率谱密度为2)()(02N H S Y ⋅=ωω (3.1) 输出自相关函数为⎰∞∞-=ωωπτωτd e H N R j Y 20)(4)( (3.2)输出相关系数为)0()()(Y Y Y R R ττγ=(3.3) 输出相关时间为⎰∞=00)(ττγτd Y (3.4)输出平均功率为[]⎰∞=202)(2)(ωωπd H N t Y E (3.5)上述式子表明,若输入端是具有均匀谱的白噪声,则输出端随机信号的功率谱主要由系统的幅频特性)(ωH 决定,不再是常数。
2.等效噪声带宽在实际中,常常用一个理想系统等效代替实际系统的)(ωH ,因此引入了等效噪声带宽的概念,他被定义为理想系统的带宽。
等效的原则是,理想系统与实际系统在同一白噪声的激励下,两个系统的输出平均功率相等,理想系统的增益等于实际系统的最大增益。
实际系统的等效噪声带宽为⎰∞=∆022max)()(1ωωωωd H H e (3.6)或⎰∞∞--=∆j j e ds s H s H H j )()()(212maxωω (3.7)3.线性系统输出端随机过程的概率分布 (1)正态随机过程通过线性系统若线性系统输入为正态过程,则该系统输出仍为正态过程。
(2)随机过程的正态化随机过程的正态化指的是,非正态随机过程通过线性系统后变换为正态过程。
任意分布的白噪声通过线性系统后输出是服从正态分布的;宽带噪声通过窄带系统,输出近似服从正态分布。
实验内容设白噪声通过图3.1所示的RC 电路,分析输出的统计特性。
图3.1 RC 电路(1)试推导系统输出的功率谱密度、相关函数、相关时间和系统的等效噪声带宽。
随机信号分析与处理实验报告

随机信号分析与处理实验题目:对音频信号的随机处理班级:0312412姓名:肖文洲学号:031241217指导老师:钱楷时间:2014年11月25日实验目的:1、学会利用MATLAB模拟产生各类随机序列。
2、熟悉和掌握随机信号数字特征估计的基本方法。
3、熟悉掌握MATLAB的函数及函数调用、使用方法。
4、学会在MATLAB中创建GUI文件。
实验内容:1、选用任意一个音频信号作为实验对象,进行各种操作并画出信号和波形。
2、操作类型:(1)、概率密度;(2)、希尔伯特变换;(3)、误差函数;(4)、randn;(5)、原始信号频谱;(6)、axis;(7)、原始信号;(8)、normpdf;(9)、unifpdf;(10)、unifcdf;(11)、raylpdf;(12)、raylcdf;(13)、exppdf;(14)、截取声音信号的频谱;(15)、expcdf;(16)、periodogram;(17)、weibrnd;(18)、rand;(19)、自相关函数;(20)、截取信号的均方值。
实验步骤:1、打开MATLAB软件,然后输入guide创建一个GUI文件。
2、在已经创建好的GUI文件里面穿件所需要的.fig面板(以学号姓名格式命名)。
入下图所示:图为已经创建好的.fig面板3、右击“概率密度”,查看回调,然后点击“callback”.在相应的位置输入程序。
然后点击运行,出现下图:4、依次对后续操作方式进行类似的操作。
5、当完成所有按键的“callback”后,出现的均为上图。
实验程序:function varargout = xiaowenzhou(varargin)% XIAOWENZHOU M-file for xiaowenzhou.fig% XIAOWENZHOU, by itself, creates a new XIAOWENZHOU or raises the existing% singleton*.%% H = XIAOWENZHOU returns the handle to a new XIAOWENZHOU or the handle to% the existing singleton*.%% XIAOWENZHOU('CALLBACK',hObject,eventData,handles,...) calls the local% function named CALLBACK in XIAOWENZHOU.M with the given input arguments.%% XIAOWENZHOU('Property','Value',...) creates a new XIAOWENZHOU or raises the% existing singleton*. Starting from the left, property value pairs are% applied to the GUI before xiaowenzhou_OpeningFunction gets called. An% unrecognized property name or invalid value makes property application% stop. All inputs are passed to xiaowenzhou_OpeningFcn via varargin.%% *See GUI Options on GUIDE's Tools menu. Choose "GUI allows only one% instance to run (singleton)".%% See also: GUIDE, GUIDATA, GUIHANDLES% Edit the above text to modify the response to help xiaowenzhou% Last Modified by GUIDE v2.5 02-Dec-2014 23:14:41% Begin initialization code - DO NOT EDITgui_Singleton = 1;gui_State = struct('gui_Name', mfilename, ...'gui_Singleton', gui_Singleton, ...'gui_OpeningFcn', @xiaowenzhou_OpeningFcn, ...'gui_OutputFcn', @xiaowenzhou_OutputFcn, ...'gui_LayoutFcn', [] , ...'gui_Callback', []);if nargin && ischar(varargin{1})gui_State.gui_Callback = str2func(varargin{1});endif nargout[varargout{1:nargout}] = gui_mainfcn(gui_State, varargin{:});elsegui_mainfcn(gui_State, varargin{:});end% End initialization code - DO NOT EDIT% --- Executes just before xiaowenzhou is made visible.function xiaowenzhou_OpeningFcn(hObject, eventdata, handles, varargin)% This function has no output args, see OutputFcn.% hObject handle to figure% eventdata reserved - to be defined in a future version of MATLAB% handles structure with handles and user data (see GUIDATA)% varargin command line arguments to xiaowenzhou (see VARARGIN)% Choose default command line output for xiaowenzhouhandles.output = hObject;% Update handles structureguidata(hObject, handles);% UIWAIT makes xiaowenzhou wait for user response (see UIRESUME)% uiwait(handles.figure1);% --- Outputs from this function are returned to the command line. function varargout = xiaowenzhou_OutputFcn(hObject, eventdata, handles) % varargout cell array for returning output args (see VARARGOUT);% hObject handle to figure% eventdata reserved - to be defined in a future version of MATLAB% handles structure with handles and user data (see GUIDATA)% Get default command line output from handles structurevarargout{1} = handles.output;% --- Executes on button press in pushbutton1.function pushbutton1_Callback(hObject, eventdata, handles)[y,Fs,bits]=wavread('Íõ·Æ.wav');y=y(1:5000);N=length(y);i=1:N;[f,i]=ksdensity(y);plot(i,f);grid;xlabel('x');ylabel('f(x)');axis();title('¸ÅÂÊÃܶÈ');% hObject handle to pushbutton1 (see GCBO)% eventdata reserved - to be defined in a future version of MATLAB% handles structure with handles and user data (see GUIDATA)% --- Executes on button press in pushbutton2.function pushbutton2_Callback(hObject, eventdata, handles)x=wavread('Íõ·Æ.wav');x=x(20000:40000);y=hilbert(x);y=real(y);plot(x);% hObject handle to pushbutton2 (see GCBO)% eventdata reserved - to be defined in a future version of MATLAB % handles structure with handles and user data (see GUIDATA)% --- Executes on button press in pushbutton3.function pushbutton3_Callback(hObject, eventdata, handles)x=wavread('Íõ·Æ.wav');x=randn(500,1);plot(x);% hObject handle to pushbutton3 (see GCBO)% eventdata reserved - to be defined in a future version of MATLAB % handles structure with handles and user data (see GUIDATA)% --- Executes on button press in pushbutton4.function pushbutton4_Callback(hObject, eventdata, handles)x=wavread('Íõ·Æ.wav');y=erf(x);plot(y);% hObject handle to pushbutton4 (see GCBO)% eventdata reserved - to be defined in a future version of MATLAB % handles structure with handles and user data (see GUIDATA)% --- Executes on button press in pushbutton5.function pushbutton5_Callback(hObject, eventdata, handles)x=wavread('Íõ·Æ.wav');plot(x);axis([0 5000 -0.01 0.01]);% hObject handle to pushbutton5 (see GCBO)% eventdata reserved - to be defined in a future version of MATLAB % handles structure with handles and user data (see GUIDATA)% --- Executes on button press in pushbutton6.x=wavread('Íõ·Æ.wav');x=x(20000:40000);plot(x);% hObject handle to pushbutton6 (see GCBO)% eventdata reserved - to be defined in a future version of MATLAB % handles structure with handles and user data (see GUIDATA)% --- Executes on button press in pushbutton7.function pushbutton7_Callback(hObject, eventdata, handles)x=wavread('Íõ·Æ.wav');x=-6:0.01:7;y=normpdf(x,1,2);plot(y);% hObject handle to pushbutton7 (see GCBO)% eventdata reserved - to be defined in a future version of MATLAB % handles structure with handles and user data (see GUIDATA)% --- Executes on button press in pushbutton8.function pushbutton8_Callback(hObject, eventdata, handles)x=wavread('Íõ·Æ.wav');x=0:0.1:5;y=unifpdf(x,1,30);plot(y);% hObject handle to pushbutton8 (see GCBO)% eventdata reserved - to be defined in a future version of MATLAB % handles structure with handles and user data (see GUIDATA)% --- Executes on button press in pushbutton9.function pushbutton9_Callback(hObject, eventdata, handles)x=wavread('Íõ·Æ.wav');x=0:0.1:5;y=unifcdf(x,1,5);plot(y);% hObject handle to pushbutton9 (see GCBO)% eventdata reserved - to be defined in a future version of MATLAB % handles structure with handles and user data (see GUIDATA)% --- Executes on button press in pushbutton10.x=wavread('Íõ·Æ.wav');x=0:0.1:3;y=raylpdf(x,2);plot(y);% hObject handle to pushbutton10 (see GCBO)% eventdata reserved - to be defined in a future version of MATLAB % handles structure with handles and user data (see GUIDATA)% --- Executes on button press in pushbutton11.function pushbutton11_Callback(hObject, eventdata, handles)x=wavread('Íõ·Æ.wav');x=0:0.1:3;y=raylcdf(x,10);plot(y);% hObject handle to pushbutton11 (see GCBO)% eventdata reserved - to be defined in a future version of MATLAB % handles structure with handles and user data (see GUIDATA)% --- Executes on button press in pushbutton12.function pushbutton12_Callback(hObject, eventdata, handles)x=wavread('Íõ·Æ.wav');x=0:0.01:5;y=exppdf(x,1);plot(y);% hObject handle to pushbutton12 (see GCBO)% eventdata reserved - to be defined in a future version of MATLAB % handles structure with handles and user data (see GUIDATA)% --- Executes on button press in pushbutton13.function pushbutton13_Callback(hObject, eventdata, handles)x=wavread('Íõ·Æ.wav');x=0:0.01:5;y=expcdf(x,1);plot(y);% hObject handle to pushbutton13 (see GCBO)% eventdata reserved - to be defined in a future version of MATLAB % handles structure with handles and user data (see GUIDATA)% --- Executes on button press in pushbutton14.[y,Fs,bits]=wavread('Íõ·Æ.wav');y1=y(1:1000);t=0:1/Fs:1;y1=periodogram(y1,[],1000,Fs);plot(y1);% hObject handle to pushbutton14 (see GCBO)% eventdata reserved - to be defined in a future version of MATLAB % handles structure with handles and user data (see GUIDATA)% --- Executes on button press in pushbutton15.function pushbutton15_Callback(hObject, eventdata, handles)x=wavread('Íõ·Æ.wav');x=0:0.01:5;x=weibrnd(1,1.5,100,1);plot(x);% hObject handle to pushbutton15 (see GCBO)% eventdata reserved - to be defined in a future version of MATLAB % handles structure with handles and user data (see GUIDATA)% --- Executes on button press in pushbutton16.function pushbutton16_Callback(hObject, eventdata, handles)x=wavread('Íõ·Æ.wav');x=rand(200,1);plot(x);% hObject handle to pushbutton16 (see GCBO)% eventdata reserved - to be defined in a future version of MATLAB % handles structure with handles and user data (see GUIDATA)% --- Executes on button press in pushbutton17.function pushbutton17_Callback(hObject, eventdata, handles)[x,Fs,bits]=wavread ('Íõ·Æ.wav');x=x (:,1);X=fft (x,4096);magX=abs (X);angX=angle (X);plot (X); title ('Ô-ʼÐźÅƵÆ×');% hObject handle to pushbutton17 (see GCBO)% eventdata reserved - to be defined in a future version of MATLAB % handles structure with handles and user data (see GUIDATA)% --- Executes on button press in pushbutton18.function pushbutton18_Callback(hObject, eventdata, handles)[y,Fs,bits]=wavread('Íõ·Æ.wav');y=y(500:1000);h=[ones(1,20) zeros(1,20)];y2=conv(h,y);stem(y2,'.');grid;title('½ØÈ¡ÉùÒôÐźŵľí»ý');% hObject handle to pushbutton18 (see GCBO)% eventdata reserved - to be defined in a future version of MATLAB % handles structure with handles and user data (see GUIDATA)% --- Executes on button press in pushbutton19.function pushbutton19_Callback(hObject, eventdata, handles)[y,Fs,bits]=wavread('Íõ·Æ.wav');y=y(1:5000);R=xcorr(y);plot(R);grid;title('×ÔÏà¹Øº¯Êý');% hObject handle to pushbutton19 (see GCBO)% eventdata reserved - to be defined in a future version of MATLAB % handles structure with handles and user data (see GUIDATA)% --- Executes on button press in pushbutton20.function pushbutton20_Callback(hObject, eventdata, handles)[y,Fs,bits]=wavread('Íõ·Æ.wav');y=y(1:1000);n=length(y);x=randn(50,n);square=zeros(1,50);for i=1:50for j=1:1000square(i)=square(i)+x(i,j).^2;endsquare(i)=square(i)/1000;endRMS=sum(square)/30;plot(square);grid;title('½ØÈ¡ÉùÒôÐźŵľù·½Öµ');% hObject handle to pushbutton20 (see GCBO)% eventdata reserved - to be defined in a future version of MATLAB% handles structure with handles and user data (see GUIDATA)% --- Executes during object creation, after setting all properties. function pushbutton1_CreateFcn(hObject, eventdata, handles)% hObject handle to pushbutton1 (see GCBO)% eventdata reserved - to be defined in a future version of MATLAB% handles empty - handles not created until after all CreateFcns called 实验结果:(1)概率密度(2)希尔伯特变换(3)randn(4)误差函数(5)axis(6)原始信号(7)normpdfd(8)unifpdf(9)unifcdf(10)raylpdf(11)raylcdf(12)exppdf(13)截取声音信号的卷积(14)expcdf(15)periodogram(16)weibrnd(17)rand(18)原始信号频谱(19)自相关函数(20)截取信号的均方值实验总结:随机信号分析与处理是研究随机信号的特点及其处理方法的专业基础课,是目标检测、估计、滤波等信号处理理论的基础。
随机信号分析实验

4 概率密度估计 概率密度的估计有两个函数:ksdensity(),hist()
ksdensity()函数直接估计随机序列概率密度的估计,
它的用法是: [f,xi] = ksdensity(x) 它的功能是估计用矢量x表示的随机序列在xi处的概率 密度f。也可以指定xi,估计对应点的概率密度值,用
x=rand(100,1)
2、任意分布随机数的产生
反函数法
变换法
(1)反函数法
定理:如果随机变量X具有连续分 布函数FX(x),而r=是(0,1)上均匀 分布的随机变量,则X=Fx-1(r)
ri FX ( x)
xi
f X ( x)dx
由此等式,根据(0,1)随机 序列可以产生服从分布 fX(x)的随机序列xi
% 产生瑞利分布随机数 N=500; sigma=1; r=rand(N,1); x=sigma*sqrt(-2*log(r)); subplot(2,1,1); plot(x); y=ksdensity(x) subplot(2,1,2); plot(y);
韦泊分布
1 x f X ( x)
x(n),矢量Y表示序列y(n)。xcorr(x)计算X的自相关。
option选项是:
'biased'
1 ˆ Rx (m) N
N m 1
n 0
xnm xn
'unbiased'
ˆ (m) R x
1 Nm
N m 1
n 0
xnm xn
'coeff'
Normalizes the sequence so the autocorrelations at zero lag are identically 1.0 to use the raw, unscaled cross-correlations (default)
哈尔滨工业大学(威海)随机信号分析实验一报告

《随机信号分析》实验报告班级: 1302502学号:姓名:《随机信号分析》实验报告实验一一、实验目的:熟悉并练习使用随机信号Matlab的函数二、实验内容:1、熟悉并练习使用下列Matlab 的函数,给出各个函数的功能说明和内部参数的意义,并给出至少一个使用例子和运行结果:1)rand() 11)unifpdf()2)randn() 12)unifcdf()3)normrnd() 13)raylpdf()4)mean() 14)raylcdf()5)var() 15)exppdf()6)xcorr() 16)expcdf()7)periodogram() 17)chol()8)fft()18)ksdensity()9)normpdf() 19)hist()10)normcdf() 20)int()用法、功能、程序如下:1)randn(m,n)功能:返回一个从标准正态分布中得到的伪随机标量。
>> r = randn(5) %由标准正态分布随机数组成的5×5 矩阵。
r =-1.0689 -0.7549 0.3192 0.6277 -1.2141-0.8095 1.3703 0.3129 1.0933 -1.1135-2.9443 -1.7115 -0.8649 1.1093 -0.00681.4384 -0.1022 -0.0301 -0.8637 1.53260.3252 -0.2414 -0.1649 0.0774 -0.76972)rand(m,n)功能:返回一个从开区间(0,1) 上的标准均匀分布得到的伪随机标量。
r = rand(5) %生成一个由介于0 和1 之间的均匀分布的随机数组成的5×5 矩阵>>r =0.5469 0.9572 0.9157 0.8491 0.39220.9575 0.4854 0.7922 0.9340 0.65550.9649 0.8003 0.9595 0.6787 0.17120.1576 0.1419 0.6557 0.7577 0.70600.9706 0.4218 0.0357 0.7431 0.03183)normrnd(mu,sigma,m,n)功能:以均值μ和标准差σ为参数的正态分布随机数mxn>> normrnd(0,1,3,4) %生成均值μ=0,σ=1的3x4正态分布随机数ans =0.2761 0.3919 -0.7411 0.0125-0.2612 -1.2507 -0.5078 -3.02920.4434 -0.9480 -0.3206 -0.45704)mean(A,dim)功能:数组的平均值mean(A,dim) dim=1,返回列平均数,默认为1dim=2,返回列平均数dim>2,返回AA = [0 1 1; 2 3 2; 1 3 2; 4 2 2] %M = mean(A) 沿A 的大小不等于1 的第一个数组维度返回均值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验一 随机序列的产生及数字特征估计一、实验目的1、学习和掌握随机数的产生方法;2、实现随机序列的数字特征估计。
二、实验原理1. 随机数的产生随机数指的是各种不同分布随机变量的抽样序列(样本值序列)。
进行随机信号仿真分析时,需要模拟产生各种分布的随机数。
在计算机仿真时,通常利用数学方法产生随机数,这种随机数称为伪随机数。
伪随机数是按照一定的计算公式产生的,这个公式称为随机数发生器。
伪随机数本质上不是随机的,而且存在周期性,但是如果计算公式选择适当,所产生的数据看似随机的,与真正的随机数具有相近的统计特性,可以作为随机数使用。
(0,1)均匀分布随机数是最最基本、最简单的随机数。
(0,1)均匀分布指的是在[0,1]区间上的均匀分布,即U(0,1)。
实际应用中有许多现成的随机数发生器可以用于产生(0,1)均匀分布随机数,通常采用的方法为线性同余法,公式如下:Ny x N ky Mod y y n n n n /))((110===-, (1.1)序列{}n x 为产生的(0,1)均匀分布随机数。
下面给出了上式的3组常用参数: (1) 7101057k 10⨯≈==,周期,N ;(2) (IBM 随机数发生器)8163110532k 2⨯≈+==,周期,N ; (3) (ran0)95311027k 12⨯≈=-=,周期,N ;由均匀分布随机数,可以利用反函数构造出任意分布的随机数。
定理1.1 若随机变量X 具有连续分布函数F X (x),而R 为(0,1)均匀分布随机变量,则有)(1R F X x -= (1.2)由这一定理可知,分布函数为F X (x)的随机数可以由(0,1)均匀分布随机数按上式进行变换得到。
2. MATLAB 中产生随机序列的函数(1) (0,1)均匀分布的随机序列 函数:rand用法:x = rand(m,n)功能:产生m ×n 的均匀分布随机数矩阵。
(2) 正态分布的随机序列 函数:randn用法:x = randn(m,n)功能:产生m ×n 的标准正态分布随机数矩阵。
如果要产生服从2N(,)μσ分布的随机序列,则可以由标准正态随机序列产生。
(3) 其他分布的随机序列MATLAB 上还提供了其他多种分布的随机数的产生函数,下表列出了部分函数。
MATLAB 中产生随机数的一些函数表1.1 MATLAB 中产生随机数的一些函数3、随机序列的数字特征估计对于遍历过程,可以通过随机序列的一条样本函数来获得该过程的统计特性。
这里我们假定随机序列X (n)为遍历过程,样本函数为x(n),其中n=0,1,2,…,N-1。
那么,X (n)的均值、方差和自相关函数的估计为利用MATLAB 的统计分析函数可以分析随机序列的数字特征。
(1) 均值函数函数:mean用法:m = mean(x)功能:返回按上面第一式估计X (n)的均值,其中x为样本序列x(n)。
(2) 方差函数函数:var用法:sigma2 = var(x)功能:返回按上面第二式估计X (n)的方差,其中x为样本序列x(n),这一估计为无偏估计。
(3) 互相关函数函数:xcorr用法:c = xcorr(x,y)c = xcorr(x)c = xcorr(x,y,'opition')c = xcorr(x,'opition')功能:xcorr(x,y)计算X (n)与Y(n)的互相关,xcorr(x)计算X (n)的自相关。
option 选项可以设定为:'biased' 有偏估计,即(1.6)'unbiased' 无偏估计,即按(1.5)式估计。
'coeff' m = 0 时的相关函数值归一化为1。
'none' 不做归一化处理。
三、实验内容1.采用线性同余法产生均匀分布随机数1000个,计算该序列均值和方差与理论值之间的误差大小。
改变样本个数重新计算。
实验代码:num=input('Num=');N=2^31;k=2^16+3;Y=zeros(1,num);X=zeros(1,num);Y(1)=1;for i=2:numY(i)=mod(k*Y(i-1),N);endX=Y/N;a=0;b=1;m0=(a+b)/2;sigma0=(b-a)^2/12;m=mean(X);sigma=var(X);delta_m=abs(m-m0);delta_sigma=abs(sigma-sigma0);plot(X,'k');xlabel('n');ylabel('X(n)');实验结果:(1) Num=1000时:delta_m=0.0110,delta_sigma=0.0011(2) Num=5000时:delta_m =2.6620e-04,delta_sigma =0.0020实验结果分析:样本越大,误差越小,实际值越接近理论值。
2. 参数为的指数分布的分布函数为x x e F λ--=1利用反函数法产生参数为0.5 的指数分布随机数1000 个,测试其方差和相关函数。
实验代码: R=rand(1,1000); lambda=0.5; X=-log(1-R)/lambda; DX=var(X); [Rm,m]=xcorr(X); subplot(211);plot(X,'k');xlabel('n');ylabel('X(n)'); subplot(212);plot(m,Rm,'k');xlabel('m');ylabel('R(m)');实验结果:实验结果分析:方差的实际值为4.1201,理论值为1/(0.5^2)=4,基本一致。
3.产生一组N(1,4)分布的高斯随机数(1 000个样本),估计该序列的均值、方差和相关函数。
实验代码:X=normrnd(1,2,[1,1000]);Mx=mean(X);Dx=var(X);[Rm,m]=xcorr(X);subplot(211);plot(X,'k');xlabel('n');ylabel('X(n)');subplot(212);plot(m,Rm,'k');xlabel('m');ylabel('R(m)');实验结果:实验结果分析:实验中的均值为0.9937,方差为3.8938。
理论上均值为1,基本一致。
四、实验心得体会通过这次实验,我学习和掌握了随机数的产生方法、实现随机序列的数字特征估计,并用MATLAB产生相应的图形,更直观的了解了相关的知识。
本次实验的难点在于用线性同余法产生随机序列,多次试验后终于攻克了难关。
实验二 随机过程的模拟与数字特征一、实验目的1、学习利用MATLAB 模拟产生随机过程的方法;2、熟悉和掌握特征估计的基本方法及其MATLAB 实现。
二、实验原理1. 正态分布白噪声序列的产生MATLAB 提供了许多产生各种分布白噪声序列的函数,其中产生正态分布白噪声序列的函数为randn 。
函数:randn用法:x = randn(m,n)功能:产生m ×n 的标准正态分布随机数矩阵。
如果要产生服从),(2συN 分布的随机序列,则可以由标准正态随机序列产生。
如果X~N(0,1),则2X ~N(,)μ+σμσ。
2. 相关函数估计MATLAB 提供了函数xcorr 用于自相关函数的估计。
函数:xcorr 用法:c = xcorr(x,y) c = xcorr(x)c = xcorr(x,y,'opition') c = xcorr(x,'opition')功能:xcorr(x,y)计算X (n)与Y(n)的互相关,xcorr(x)计算X (n)的自相关。
option 选项可以设定为: 'biased' 有偏估计。
'unbiased' 无偏估计。
'coeff' m=0时的相关函数值归一化为1。
'none' 不做归一化处理。
3. 功率谱估计对于平稳随机序列X(n),如果它的相关函数满足∞<∑+∞-∞=m xm R )( (2.1)那么它的功率谱定义为自相关函数R x (m)的傅里叶变换:∑+∞-∞=-=m jm xX em R S ωω)()( (2.2)功率谱表示随机信号频域的统计特性,有着重要的物理意义。
我们实际所能得到的随机信号总是有限的,用有限长度的信号所得的功率谱只是真实功率谱的估计,称为谱估计或谱分析。
(1) 自相关法先求自相关函数的估计,然后对自相关函数做傅里叶变换∑---=-=1)1(^^)()(N N m jm xX em R S ωω (2.3)其中N 表示用于估计样本序列的样本个数。
(2) 周期图法先对样本序列x(n)做傅里叶变换∑-=-=10)()(N n jm e n x X ωω (2.4)其中10-≤≤N n ,则功率谱估计为2^)(1)(ωωX N S = (2.5)MATLAB 函数periodogram 实现了周期图法的功率谱估计。
函数:periodogram用法:[Pxx,w] = periodogram(x)[Pxx,w] = periodogram(x,window) [Pxx,w] = periodogram(x,window,nfft) [Pxx,f] = periodogram(x,window,nfft,fs) periodogram(...)功能:实现周期图法的功率谱估计。
其中: Pxx 为输出的功率谱估计值;f为频率向量;w为归一化的频率向量;window代表窗函数,这种用法对数据进行了加窗,对数据加窗是为了减少功率谱估计中因为数据截断产生的截断误差,表2.1列出了产生常用窗函数的MATLAB函数。
nfft设定FFT算法的长度;fs表示采样频率;如果不指定输出参量(最后一种用法),则直接会出功率谱估计的波形。
三、实验内容1.按如下模型产生一组随机序列=-+ωx(n)0.8x(n1)(n)其中(n)ω是均值为1,方差为4的正态分布白噪声序列。
估计过程的自相关函数和功率谱。
实验代码:y0=randn(1,500); %产生一长度为500的随机序列y=1+2*y0;x(1)=y(1);n=500;for i=2:1:nx(i)=0.8*x(i-1)+y(i); %按题目要求产生随机序列x(n)endsubplot(311);plot(x);title('x(n)');subplot(312);c=xcorr(x); %用xcorr函数求x(n)的自相关函数plot(c);title('R(n)');p=periodogram(x); %用periodogram函数求功率谱密度subplot(313);plot(p);title('S(w)');实验结果:其中x(n)为样本序列,长度为500;R(n)为x(n)的自相关函数,S(w)为x(n)的功率谱。
