北理工随机信号分析实验报告
北京理工大学信号与系统实验实验报告

北京理工大学信号与系统实验实验报告信号与系统实验报告姓名:肖枫学号:1120111431班号:05611102专业:信息对抗技术学院:信息与电子学院12实验1 信号的时域描述与运算一、实验目的1. 掌握信号的MATLAB表示及其可视化方法。
2. 掌握信号基本时域运算的MATLAB实现方法。
3. 利用MATLAB分析常用信号,加深对信号时域特性的理解。
二、实验原理与方法1. 连续时间信号的MATLAB表示连续时间信号指的是在连续时间范围内有定义的信号,即除了若干个不连续点外,在任何时刻信号都有定义。
在MATLAB中连续时间信号可以用两种方法来表示,即向量表示法和符号对象表示法。
从严格意义上来说,MATLAB并不能处理连续时间信号,在MATLAB中连续时间信号是用等时间间隔采样后的采样值来近似表示的,当采样间隔足够小时,这些采样值就可以很好地近似表示出连续时间信号,这种表示方法称为向量表示法。
表示一个连续时间信号需要使用两个向量,其中一个向量用于表示信号的时间范围,另一个向量表示连续时间信号在该时间范围内的采样值。
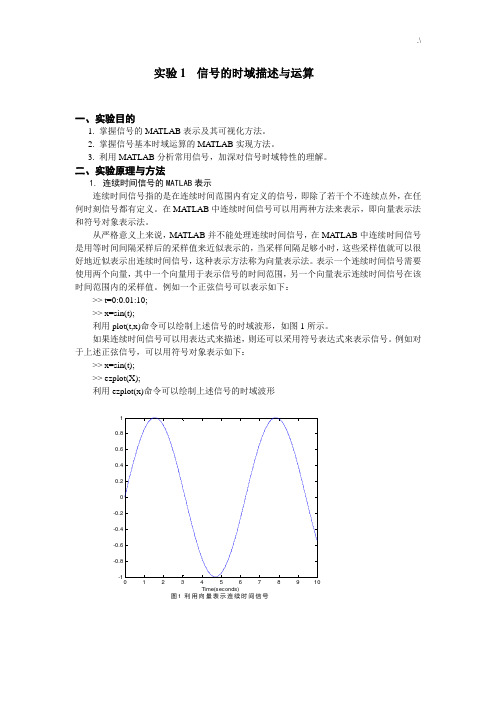
例如一个正弦信号可以表示如下:>> t=0:0.01:10;>> x=sin(t);利用plot(t,x)命令可以绘制上述信号的时域波形,如图1所示。
如果连续时间信号可以用表达式来描述,则还可以采用符号表达式來表示信号。
例如对于上述正弦信号,可以用符号对象表示如下:>> x=sin(t);>> ezplot(X);利用ezplot(x)命令可以绘制上述信号的时域波形10.80.60.40.2-0.2-0.4-0.6-0.8-1012345678910Time(seconds)图1 利用向量表示连续时间信号3sin(t)10.5-0.5-1-6-4-20246t图 2 利用符号对象表示连续时间信号常用的信号产生函数函数名功能函数名功能 heaviside 单位阶跃函数 rectpuls 门函数 sin 正弦函数 tripuls 三角脉冲函数 cos 余弦函数 square 周期方波 sinc sinc函数 sawtooth 周期锯齿波或三角波 exp 指数函数2.连续时间信号的时域运算对连续时间信号的运算包括两信号相加、相乘、微分、积分,以及位移、反转、尺度变换(尺度伸缩)等。
北京理工大学信号与系统实验实验报告
实验1 信号的时域描述与运算一、实验目的1. 掌握信号的MATLAB表示及其可视化方法。
2. 掌握信号基本时域运算的MA TLAB实现方法。
3. 利用MA TLAB分析常用信号,加深对信号时域特性的理解。
二、实验原理与方法1. 连续时间信号的MATLAB表示连续时间信号指的是在连续时间范围内有定义的信号,即除了若干个不连续点外,在任何时刻信号都有定义。
在MATLAB中连续时间信号可以用两种方法来表示,即向量表示法和符号对象表示法。
从严格意义上来说,MATLAB并不能处理连续时间信号,在MATLAB中连续时间信号是用等时间间隔采样后的采样值来近似表示的,当采样间隔足够小时,这些采样值就可以很好地近似表示出连续时间信号,这种表示方法称为向量表示法。
表示一个连续时间信号需要使用两个向量,其中一个向量用于表示信号的时间范围,另一个向量表示连续时间信号在该时间范围内的采样值。
例如一个正弦信号可以表示如下:>> t=0:0.01:10;>> x=sin(t);利用plot(t,x)命令可以绘制上述信号的时域波形,如图1所示。
如果连续时间信号可以用表达式来描述,则还可以采用符号表达式來表示信号。
例如对于上述正弦信号,可以用符号对象表示如下:>> x=sin(t);>> ezplot(X);利用ezplot(x)命令可以绘制上述信号的时域波形Time(seconds)图1 利用向量表示连续时间信号t图 2 利用符号对象表示连续时间信号sin(t)2.连续时间信号的时域运算对连续时间信号的运算包括两信号相加、相乘、微分、积分,以及位移、反转、尺度变换(尺度伸缩)等。
1)相加和相乘信号相加和相乘指两信号对应时刻的值相加和相乘,对于两个采用向量表示的可以直接使用算术运算的运算符“+”和“*”来计算,此时要求表示两信号的向量时间范围和采样间隔相同。
采用符号对象表示的两个信号,可以直接根据符号对象的运算规则运算。
随机信号分析实验报告

实验一 随机噪声的产生与性能测试一、实验内容1.产生满足均匀分布、高斯分布、指数分布、瑞利分布的随机数,长度为N=1024,并计算这些数的均值、方差、自相关函数、概率密度函数、概率分布函数、功率谱密度,画出时域、频域特性曲线; 2.编程分别确定当五个均匀分布过程和5个指数分布分别叠加时,结果是否是高斯分布; 3.采用幅度为2, 频率为25Hz 的正弦信号为原信号,在其中加入均值为2 , 方差为0.04 的高斯噪声得到混合随机信号()X t ,编程求 0()()tY t X d ττ=⎰的均值、相关函数、协方差函数和方差,并与计算结果进行比较分析。
二、实验步骤 1.程序N=1024; fs=1000; n=0:N —1;signal=chi2rnd (2,1,N); %rand(1,N)均匀分布 ,randn(1,N )高斯分布,exprnd(2,1,N )指数分布,raylrnd (2,1,N)瑞利分布,chi2rnd(2,1,N )卡方分布 signal_mean=mean(signal ); signal_var=var (signal );signal_corr=xcorr(signal,signal ,'unbiased ’); signal_density=unifpdf(signal ,0,1); signal_power=fft(signal_corr); %[s,w]=periodogram (signal); [k1,n1]=ksdensity(signal);[k2,n2]=ksdensity (signal,’function ’,'cdf ’); figure ;hist(signal);title (’频数直方图’); figure ;plot (signal);title(’均匀分布随机信号曲线’); f=n *fs/N ; %频率序列 figure;plot(abs (signal_power)); title('功率幅频’); figure;plot(angle (signal_power)); title ('功率相频'); figure;plot (1:2047,signal_corr); title ('自相关函数’); figure;plot(n1,k1);title('概率密度’);figure;plot(n2,k2);title('分布函数’);结果(1)均匀分布(2)高斯分布(3)指数分布(4)瑞利分布(5)卡方分布2.程序N=1024;signal_1=rand(1,N);signal_2=rand(1,N);signal_3=rand(1,N);signal_4=rand(1,N);signal_5=rand(1,N);signal=signal_1+signal_2+signal_3+signal_4+signal_5; [k1,n1]=ksdensity(signal);figure(1)subplot(1,2,1);hist(signal);title('叠加均匀分布随机数直方图');subplot(1,2,2);plot(n1,k1);title(’叠加均匀分布的概率密度');结果指数分布叠加均匀分布叠加结果:五个均匀分布过程和五个指数分布分别叠加时,结果是高斯分布。
北京理工大学数信实验报告

实验1 利用DFT 分析信号频谱一、实验目的1、加深对DFT 原理的理解。
2、应用DFT 分析信号的频谱。
3、深刻理解利用DFT 分析信号频谱的原理,分析实现过程中出现的现象及解决方法。
二、实验设备与环境计算机、MATLAB 软件环境。
三、实验基础理论1.DFT 与DTFT 的关系:有限长序列的离散时间傅里叶变换(e )j X ω 在频率区间(02)ωπ≤≤ 的N 个等间隔分布的点2(0k N 1)kk N πω=≤≤-上的N 个取样值可以有下式表示:2120(e )|(n)e(k)(0k N 1)N jkn j Nkk NX x X πωπω--====≤≤-∑由上式可知,序列(n)x 的N 点DFT (k)X ,实际上就是(n)x 序列的DTFT 在N 个等间隔频率点2(0k N 1)kk N πω=≤≤-上样本(k)X 。
2.利用DFT 求DTFT方法1:由(k)X 恢复出(e )j X ω的方法如下:由流程知:11(e )(n)e[(k)W]e N j j nkn j nNn n k X x X Nωωω∞∞----=-∞=-∞===∑∑∑继续整理可得到:12()(k)()Ni k kx e X N ωπφω==-∑其中(x)φ为内插函数:sin()2()sin()2N N ωφωω=方法2:实际在MATLAB 计算中,上述插值运算不见得是最好的办法。
由于DFT 是DTFT 的取样值,其相邻两个频率样本点的间距为2N π,所以如果我们增加数据的长度N ,使得到的DFT 谱线就更加精细,其包络就越接近DTFT 的结果,这样就可以利用DFT 计算DTFT 。
如果没有更多的数据,可以通过补零来增加数据长度。
3.利用DFT 分析连续信号的频谱采用计算机分析连续时间信号的频谱,第一步就是把连续信号离散化,这里需要进行两个操作:一是采样,二是截断。
对于连续时间非周期信号(t)a x ,按采样间隔T 进行采样,阶段长度M ,那么:1(j )(t)e(nT)e M j tj nTa a a n X x dt T x -∞-Ω-Ω-∞=Ω==∑⎰对(j )a X Ω 进行N 点频域采样,得到:2120(j )|(nT)e(k)M jkn Na a M kn NTX T x TX ππ--Ω==Ω==∑采用上述方法计算信号(t)a x 的频谱需要注意如下三个问题:(1)频谱混叠;(2)栅栏效应和频谱分辨率; (3)频谱泄露。
随机信号分析实验报告

H a r b i n I n s t i t u t e o f T e c h n o l o g y实验报告课程名称:随机信号分析院系:电子与信息工程学院班级:姓名:学号:指导教师:实验时间:实验一、各种分布随机数的产生(一)实验原理1.均匀分布随机数的产生原理产生伪随机数的一种实用方法是同余法,它利用同余运算递推产生伪随机数序列。
最简单的方法是加同余法)(mod 1M c y y n n +=+My x n n 11++= 为了保证产生的伪随机数能在[0,1]内均匀分布,需要M 为正整数,此外常数c 和初值y0亦为正整数。
加同余法虽然简单,但产生的伪随机数效果不好。
另一种同余法为乘同余法,它需要两次乘法才能产生一个[0,1]上均匀分布的随机数)(mod 1M ay y n n =+ My x n n 11++= 式中,a 为正整数。
用加法和乘法完成递推运算的称为混合同余法,即)(mod 1M c ay y n n +=+ My x n n 11++= 用混合同余法产生的伪随机数具有较好的特性,一些程序库中都有成熟的程序供选择。
常用的计算语言如Basic 、C 和Matlab 都有产生均匀分布随机数的函数可以调用,只是用各种编程语言对应的函数产生的均匀分布随机数的范围不同,有的函数可能还需要提供种子或初始化。
Matlab 提供的函数rand()可以产生一个在[0,1]区间分布的随机数,rand(2,4)则可以产生一个在[0,1]区间分布的随机数矩阵,矩阵为2行4列。
Matlab 提供的另一个产生随机数的函数是random('unif',a,b,N,M),unif 表示均匀分布,a 和b 是均匀分布区间的上下界,N 和M 分别是矩阵的行和列。
2.随机变量的仿真根据随机变量函数变换的原理,如果能将两个分布之间的函数关系用显式表达,那么就可以利用一种分布的随机变量通过变换得到另一种分布的随机变量。
随机信号分析实验百度

《随机信号分析》试验报告班级班学号姓名实验一1、熟悉并练习使用下列Matlab 的函数,给出各个函数的功能说明和内部参数的意义,并给出至少一个使用例子和运行结果:1)randn()产生随机数数组或矩阵,其元素服从均值为0,方差为1的正态分布(1)Y = randn 产生一个伪随机数(2)Y = randn(n) 产生n×n的矩阵,其元素服从均值为0,方差为1的正态分布(3)Y = randn(m,n) 产生m×n的矩阵,其元素服从均值为0,方差为1的正态分布(4)Y= randn([m n]) 产生m×n的矩阵,其元素服从均值为0,方差为1的正态分布选择(2)作为例子,运行结果如下:>> Y = randn(3)Y =1.3005 0.0342 0.97920.2691 0.9913 -0.8863-0.1551 -1.3618 -0.35622)rand()(1)Y = rand(n) 生成n×n 随机矩阵,其元素在(0,1)内(2)Y = rand(m,n) 生成m×n 随机矩阵(3)Y = rand([m n]) 生成m×n 随机矩阵(4)Y = rand(m,n,p,…) 生成m×n×p×…随机矩阵或数组(5)Y = rand([m n p…]) 生成m×n×p×…随机矩阵或数组(6)Y = rand(size(A)) 生成与矩阵A 相同大小的随机矩阵选择(3)作为例子,运行结果如下:>> Y = rand([3 4])Y =0.0579 0.0099 0.1987 0.19880.3529 0.1389 0.6038 0.01530.8132 0.2028 0.2722 0.74683)normrnd()产生服从正态分布的随机数(1)R = normrnd(mu,sigma) 产生服从均值为mu,标准差为sigma的随机数,mu和sigma可以为向量、矩阵、或多维数组。
北京理工大学信号与系统实验报告

北京理工大学信号与系统实验报告本科实验报告实验名称:信号与系统实验实验1 信号的时域描述与运算(基础型实验)一、实验目的1.掌握信号的MATLAB表示及其可视化方法。
2.掌握信号基本时域运算的MATLAB实现方法。
3.利用MATLAB分析常用信号,加深对信号时域特性的理解。
二、实验原理及方法1.连续时间信号的MATLAB表示连续时间信号在连续时间范围内除若干不连续点外在任何时刻都有定义,在MATLAB中的表示法包括向量表示法和符号对象表示法。
1)向量表示法MATLAB从严格意义上来说并不能处理连续时间信号,但可以通过等时间间隔采样后的采样值来近似表示,如果采样间隔足够小,则采样值就可以很好地近似表示出连续时间信号。
这种方法称为向量表示法。
表示一个连续时间信号需要用到两个向量,一个表示时间范围,另一个表示连续时间信号在相对应时间范围内的采样值。
2)符号对象表示法如果连续时间信号可以用表达式来描述,则可以采用符号对象表达法。
例:对于余弦信号,采用两种方式来表示:>> t=0:0.01:10;>> x=sin(t);>> subplot(121)>> plot(t,x)>> title('向量表示法')>> clear>> syms t>> x=sin(t);>> subplot(122)>> ezplot(x)>> title('符号对象表示法')符号对象表示法向量表示法t常用信号产生函数2.连续时间信号的时域运算连续时间信号的运算包括两信号相加、相乘、微分、积分,以及移位、反转、尺度变换等。
1) 相加和相乘信号的相加和相乘指两信号对应时刻值相加或相乘。
两个采用向量表示法的信号可以直接使用‘+’和‘*’进行运算,此时要求二者的向量时间范围以及采样间隔相同。
随机信号分析实验报告

随机信号分析实验报告实验一:平稳随机过程的数字特征实验二:平稳随机过程的谱分析实验三:随机信号通过线性系统的分析实验四:平稳时间序列模型预测班级:姓名:学号:一、实验目的1、加深理解平稳随机过程数字特征的概念2、掌握平稳随机序列期望、自相关序列的求解3、分析平稳随机过程数字特征的特点二、实验原理平稳随机过程数字特征求解的相关原理三、实验过程function y = experimentnumber = 49; %学号49I = 8; %幅值为8u = 1/number;Ex = I*0.5 + (-I)*0.5;N = 64;C0 = 1; %计数p(1) = exp(-u);for m = 2:Nk = 1:m/2;p(m) = exp(-u*m) + sum((u*m).^(2*k)./factorial(2*k)*exp(-u*m));2222()[()()]{()()}{()()}X R m E X n X n m I P X n X n m I I P X n X n m I =+=+=-+=-E[X(n)]= I P{X(n)=+I}+(-I)P{X(n)=-I}=0⨯⨯0m >当时,/2220(){()()}(2)!m k m k m P X n X n m I e P k λλ⎢⎥⎣⎦-=+===∑222()(1)(21)X R m I P I P I P =--=-2()()X X X C m R m m =-me I m n X n X E m R λ22)]()([)(-=+=end;pp = [fliplr(p) C0 p];Rx = (2*pp - 1)*I^2;m = -N:N;Kx = Rx - Ex*Ex;rx = Kx/25;subplot(211), plot(m,Rx); axis([-N N 0 I*I]); title('自相关序列');subplot(212), plot(m,rx); axis([-N N 0 1]); title('自相关序数');四、实验结果及分析自相关序列的特点分析:m>0时Rx(m)随着m的增大而减小,m<0时Rx(m)随着m的增大而增大。
数字信号实验报告二,北京理工大学,实验报告

实验三利用FFT计算线性卷积一、实验目的1.掌握利用FFT计算线性卷积的原理及具体实现方法。
2.加深理解重叠相加法和重叠保留法。
3.考察利用FFT计算线性卷积各种方法的适用范围。
二、实验设备与环境计算机、MATLAB软件环境三、实验基础理论1.线性卷积与圆周卷积设为L点序列,为M点序列,和的线性卷积为的长度为L+M-1。
和的N点圆周卷积为圆周卷积与线性卷积相等而不产生交叠的必要条件为圆周卷积定理:根据DFT的性质,和的N点圆周卷积的DFT等于它们DFT的乘积2.快速卷积快速卷积算法用圆周卷积实现线性卷积,根据圆周卷积定理利用FFT算法实现圆周卷积。
可以将快速卷积的步骤归纳如下:(1)为了使线性卷积可以利用圆周卷积来计算,必须选择;同时为了能使用基2-FFT 完成卷积运算,要求N =。
采用补零的办法是和的长度均为N 。
(2)计算和的N 点FFTFFT −−−→(3)组成卷积(4)利用IFFT 计算IDFT ,得到线性卷积(k)()IFFT Y y n −−−→3.分段卷积我们考察单位取样响应为的线性系统,输入为,输出为,则当输入序列时再开始进行卷积,会使输出相对输入有较大的延时,再者如果序列太长,需要大量的存储单元。
为此,我们把,分别求出每段的卷积,合在一起其到最后的总输出。
这种方法称为分段卷积。
分段卷积可细分为重叠相加法和重叠保留法。
重叠保留法:设的长度为,的长度为M 。
我们把序列分成多段N 点序列,每段与前一段重叠M-1个样本。
由于第一段没有前一段保留信号,为了修正,我们在第一个输入段前面填充M-1个零。
计算每一段的圆周卷积,则其每段卷积结果的前M-1个样本不等于线性卷积值,不是正确的样本值。
所以我们将每段卷积结果的前M-1个样本舍去,只保留后面的N-M+1个正确输出样本,把这些输出样本合起来得到总的输出。
利用FFT 实现重叠保留法的步骤如下:(1)在前面填充M-1个零,扩大以后的序列为1ˆ(){0,0,0,()}M x n x n -=个(2)将分为若干N 点子段,设L=N-M+1为每一段的有效数据长度,则第i 段〖ˆ(m)x1,0,01iL m iL N i n N ≤≤+-≥≤≤- (3)计算每一段与的N 点圆周卷积,利用FFT 计算圆周卷积:FFT−−−→(k)()IFFT i i Y y n −−−→(4)舍去每一段卷积结果的前M-1个样本,连接剩下样本,得到卷积结果。
随机信号分析实验报告

随机信号分析实验报告目录随机信号分析 (1)实验报告 (1)理想白噪声和带限白噪声的产生与测试 (2)一、摘要 (2)二、实验的背景与目的 (2)背景: (2)实验目的: (2)三、实验原理 (3)四、实验的设计与结果 (4)实验设计: (4)实验结果: (5)五、实验结论 (12)六、参考文献 (13)七、附件 (13)1理想白噪声和带限白噪声的产生与测试一、摘要本文通过利用MATLAB软件仿真来对理想白噪声和带限白噪声进行研究。
理想白噪声通过低通滤波器和带通滤波器分别得到低通带限白噪声和帯通带限白噪声。
在仿真的过程中我们利用MATLAB工具箱中自带的一些函数来对理想白噪声和带限白噪声的均值、均方值、方差、功率谱密度、自相关函数、频谱以及概率密度进行研究,对对它们进行比较分析并讨论其物理意义。
关键词:理想白噪声带限白噪声均值均方值方差功率谱密度自相关函数、频谱以及概率密度二、实验的背景与目的背景:在词典中噪声有两种定义:定义1:干扰人们休息、学习和工作的声音,引起人的心理和生理变化。
定义2:不同频率、不同强度无规则地组合在一起的声音。
如电噪声、机械噪声,可引伸为任何不希望有的干扰。
第一种定义是人们在日常生活中可以感知的,从感性上很容易理解。
而第二种定义则相对抽象一些,大部分应用于机械工程当中。
在这一学期的好几门课程中我们都从不同的方面接触到噪声,如何的利用噪声,把噪声的危害减到最小是一个很热门的话题。
为了加深对噪声的认识与了解,为后面的学习与工作做准备,我们对噪声进行了一些研究与测试。
实验目的:了解理想白噪声和带限白噪声的基本概念并能够区分它们,掌握用MATLAB 或c/c++软件仿真和分析理想白噪声和带限白噪声的方法,掌握理想白噪声和带限白噪声的性质。
三、实验原理所谓白噪声是指它的概率统计特性服从某种分布而它的功率谱密度又是均匀的。
确切的说,白噪声只是一种理想化的模型,因为实际的噪声功率谱密度不可能具有无限宽的带宽,否则它的平均功率将是无限大,是物理上不可实现的。
北京理工大学随机信号分析实验报告

北京理工大学随机信号分析实验报告本科实验报告实验名称:随机信号分析实验实验一随机序列的产生及数字特征估计一、实验目的1、学习和掌握随机数的产生方法。
2、实现随机序列的数字特征估计。
二、实验原理1、随机数的产生随机数指的是各种不同分布随机变量的抽样序列(样本值序列)。
进行随机信号仿真分析时,需要模拟产生各种分布的随机数。
在计算机仿真时,通常利用数学方法产生随机数,这种随机数称为伪随机数。
伪随机数是按照一定的计算公式产生的,这个公式称为随机数发生器。
伪随机数本质上不是随机的,而且存在周期性,但是如果计算公式选择适当,所产生的数据看似随机的,与真正的随机数具有相近的统计特性,可以作为随机数使用。
(0,1)均匀分布随机数是最最基本、最简单的随机数。
(0,1)均匀分布指的是在[0,1]区间上的均匀分布,即 U(0,1)。
实际应用中有许多现成的随机数发生器可以用于产生(0,1)均匀分布随机数,通常采用的方法为线性同余法,公式如下:)(m od ,110N ky y y n n -=Ny x n n /=序列{}nx 为产生的(0,1)均匀分布随机数。
下面给出了上式的3组常用参数: 1、10N 10,k 7==,周期7510≈⨯;2、(IBM 随机数发生器)3116N 2,k 23,==+周期8510≈⨯;3、(ran0)315N 21,k 7,=-=周期9210≈⨯;由均匀分布随机数,可以利用反函数构造出任意分布的随机数。
定理 1.1 若随机变量 X 具有连续分布函数F X (x),而R 为(0,1)均匀分布随机变量,则有)(1R F X x -=由这一定理可知,分布函数为F X (x)的随机数可以由(0,1)均匀分布随机数按上式进行变换得到。
2、MATLAB 中产生随机序列的函数(1)(0,1)均匀分布的随机序列函数:rand用法:x = rand(m,n)功能:产生m×n 的均匀分布随机数矩阵。
北京理工大学信号与系统实验实验报告

北京理工大学信号与系统实验实验报告信号与系统实验报告姓名:肖枫学号:1120111431班号:05611102专业:信息对抗技术学院:信息与电子学院12实验1 信号的时域描述与运算一、实验目的1. 掌握信号的MATLAB表示及其可视化方法。
2. 掌握信号基本时域运算的MATLAB实现方法。
3. 利用MATLAB分析常用信号,加深对信号时域特性的理解。
二、实验原理与方法1. 连续时间信号的MATLAB表示连续时间信号指的是在连续时间范围内有定义的信号,即除了若干个不连续点外,在任何时刻信号都有定义。
在MATLAB中连续时间信号可以用两种方法来表示,即向量表示法和符号对象表示法。
从严格意义上来说,MATLAB并不能处理连续时间信号,在MATLAB中连续时间信号是用等时间间隔采样后的采样值来近似表示的,当采样间隔足够小时,这些采样值就可以很好地近似表示出连续时间信号,这种表示方法称为向量表示法。
表示一个连续时间信号需要使用两个向量,其中一个向量用于表示信号的时间范围,另一个向量表示连续时间信号在该时间范围内的采样值。
例如一个正弦信号可以表示如下:>> t=0:0.01:10;>> x=sin(t);利用plot(t,x)命令可以绘制上述信号的时域波形,如图1所示。
如果连续时间信号可以用表达式来描述,则还可以采用符号表达式來表示信号。
例如对于上述正弦信号,可以用符号对象表示如下:>> x=sin(t);>> ezplot(X);利用ezplot(x)命令可以绘制上述信号的时域波形10.80.60.40.2-0.2-0.4-0.6-0.8-1012345678910Time(seconds)图1 利用向量表示连续时间信号3sin(t)10.5-0.5-1-6-4-20246t图 2 利用符号对象表示连续时间信号常用的信号产生函数函数名功能函数名功能 heaviside 单位阶跃函数 rectpuls 门函数 sin 正弦函数 tripuls 三角脉冲函数 cos 余弦函数 square 周期方波 sinc sinc函数 sawtooth 周期锯齿波或三角波 exp 指数函数2.连续时间信号的时域运算对连续时间信号的运算包括两信号相加、相乘、微分、积分,以及位移、反转、尺度变换(尺度伸缩)等。
北京理工大学信号与系统实验报告3 信号的频域分析

实验3 信号的频域分析(综合型实验)一、实验目的1)深入理解信号频谱的概念,掌握信号的频域分析方法。
2)观察典型周期信号和非周期信号的频谱,掌握其频谱特性。
二、实验原理与方法1.连续周期信号的频谱分析如果周期信号满足Dirichlet 条件,就可展开为傅里叶级数的形式,即0(t)jk tkk x c eω+∞=-∞=∑(1)0001(t)e jk tk T c x dt T ω-=⎰(2) 其中0T 表示基波周期,002/T ωπ=为基波频率,0(...)T ⎰表示任一个基波周期内的积分。
上面两式为周期信号复指数形式的傅里叶级数,系数k c 成为x(t)的傅里叶系数。
周期信号的傅里叶级数还可由三角函数的线性组合来表示,即00011(t)cos sin k k k k x a a k t b k t ωω+∞+∞===++∑∑(3)其中000000000122(t),(t)cosk ,(t)sink k k T T T a x dt a x tdt b x tdt T T T ωω===⎰⎰⎰(4) (3)式中同频率的正弦、余弦项合并可以得到三角函数形式的傅里叶级数,即001(t)cos(k t )k k k x A A ωθ+∞==++∑ (5)其中00,arctankk k kb A a A a θ===- (6) 任何满足Dirichlet 条件的周期信号都可以表示成一组谐波关系的复指数函数或三角函数的叠加。
周期信号表示为傅里叶级数时需要无限多项才能完全逼近原信号,但在实际应用中常采用有限项级数代替,所选级数项越多就越接近原信号。
2.连续非周期信号的频谱分析对于非周期连续时间信号,信号的傅里叶变换和傅里叶逆变换定义为()(t)ej tX x dt ωω+∞--∞=⎰(7)1(t)()e 2j t x X d ωωωπ+∞-∞=⎰(8)以上两式把信号的时频特性联系起来,确立了非周期信号(t)x 和频谱()X ω之间的关系。
北理工大学数字信号处理实验报告

实验1利用DFT分析信号频谱一、实验目的1.加深对DFT原理的理解。
2.应用DFT分析信号的频谱。
3.深刻理解利用DFT分析信号频谱的原理,分析实现过程中出现的现象与解决方法。
二、实验设备与环境计算机、MATLAB软件环境。
三、实验原理1. DFT与 DTFT的关系有限长序列的离散时间傅里叶变换在频率区间的N个等间隔分布的点上的N个取样值可以由下式表示:由上式可知,序列x(n)的N 点DFT X(k),实际上就是x(n)序列的DTFT在N 个等间隔频率点上样本X(k)。
2. 利用DFT 求DTFT法一:由X (k)恢复出的方法:法二:然而在实际 MATLAB计算中,上述插值运算不见得是最好的办法。
由于DFT是 DTFT 的取样值,其相邻两个频率样本点的间距为2/N,所以如果我们增加数据的长度N,使得到的DFT谱线就更加精细,其包络就越接近DTFT的结果,这样就可以利用DFT来近似计算DTFT。
如果没有更多的数据,可以通过补零来增加数据长度。
3.利用DFT分析连续时间信号的频谱采用计算机分析连续时间信号的频谱,第一步就是把连续时间信号离散化,这里需要进行两个操作:一是采样,二是截断。
将利用DFT分析连续非周期信号频谱的步骤归纳如下:(1)确定时域采样间隔T,得到离散序列x(n);(2)确定截取长度M,得到M点离散序列,这里为窗函数。
(3)确定频域采样点数N,要求。
(4)利用FFT计算离散序列的N点DFT,得到。
(5)根据式(2-6)由计算采样点的近似值。
采用上述方法计算的频谱,需要注意如下三个问题:(1)频谱混叠。
如果不满足采样定理的条件,频谱会出现混叠误差。
对于频谱无限宽的信号,应考虑覆盖大部分主要频率分量的围。
(2)栅栏效应和频谱分辨率。
使用DFT计算频谱,得到的结果只是N个频谱本值,样本值之间的频谱是未知的,像通过一个栅栏观察频谱,称为“栅栏效应”。
频谱分辨率与记录长度成反比,要提高频谱分表率,就要增加记录时间。
北理工随机信号分析实验报告
本科实验报告实验名称:随机信号分析实验实验一 随机序列的产生及数字特征估计一、实验目的1、学习和掌握随机数的产生方法。
2、实现随机序列的数字特征估计。
二、实验原理1、随机数的产生随机数指的是各种不同分布随机变量的抽样序列(样本值序列)。
进行随机信号仿真分析时,需要模拟产生各种分布的随机数。
在计算机仿真时,通常利用数学方法产生随机数,这种随机数称为伪随机数。
伪随机数是按照一定的计算公式产生的,这个公式称为随机数发生器。
伪随机数本质上不是随机的,而且存在周期性,但是如果计算公式选择适当,所产生的数据看似随机的,与真正的随机数具有相近的统计特性,可以作为随机数使用。
(0,1)均匀分布随机数是最最基本、最简单的随机数。
(0,1)均匀分布指的是在[0,1]区间上的均匀分布,即 U(0,1)。
实际应用中有许多现成的随机数发生器可以用于产生(0,1)均匀分布随机数,通常采用的方法为线性同余法,公式如下:)(m od ,110N ky y y n n -=N y x n n /=序列{}n x 为产生的(0,1)均匀分布随机数。
下面给出了上式的3组常用参数: 1、10N 10,k 7==,周期7510≈⨯;2、(IBM 随机数发生器)3116N 2,k 23,==+周期8510≈⨯; 3、(ran0)315N 21,k 7,=-=周期9210≈⨯;由均匀分布随机数,可以利用反函数构造出任意分布的随机数。
定理 1.1 若随机变量 X 具有连续分布函数F X (x),而R 为(0,1)均匀分布随机变量,则有)(1R F X x -=由这一定理可知,分布函数为F X (x)的随机数可以由(0,1)均匀分布随机数按上式进行变换得到。
2、MATLAB 中产生随机序列的函数(1)(0,1)均匀分布的随机序列 函数:rand 用法:x = rand(m,n)功能:产生m ×n 的均匀分布随机数矩阵。
(2)正态分布的随机序列 函数:randn 用法:x = randn(m,n)功能:产生m ×n 的标准正态分布随机数矩阵。
北京理工大学 数字信号处理 实验报告 程序

数字信号处理实验报告1.深入掌握应用DFT分析信号的频谱的理论方法,针对该问题进行一次全面综合练习,完成一个完整的信号分析软件实现方法和流程,这种全面完整的综合练习可以帮助学生深入理解和消化基本理论,锻炼学生独立解决问题的能力,培养学生的创新意识,为今后的科研和工作打下良好的实践基础。
2.综合利用数字信号处理的理论知识完成数字滤波器的设计与实现,完成一个完整的数字滤波器设计软件的实现方法和流程。
这种全面完整的综合练习可以帮助学生深入理解和消化基本理论,锻炼学生独立解决问题的能力,培养学生的创新意识,为今后的科研和工作打下良好的实践基础。
二、实验设备与环境计算机、MATLAB软件环境三、实验内容1.基于Matlab GUI的离散傅里叶变换分析2.基于Matlab GUI的数字滤波器分析设计1.基于Matlab GUI的离散傅里叶变换分析信号: t=1:100;x=2*sin(t/25*2*pi)+5*sin(t/5*2*pi);说明:输入信号从Matlab Command Windows中生成,通过变量名导入本软件,并可输出DFT变换后的结果,默认名为DFT_输入变量名。
2.基于Matlab GUI的数字滤波器分析设计IIR 低通:(巴特沃兹)IIR高通:(切比雪夫I)IIR带通:(切比雪夫II)IIR带阻:(椭圆滤波器)FIR低通:(矩形窗)FIR高通:(汉宁窗)FIR带通:(布莱克曼窗)FIR带阻:(凯瑟窗)五、程序界面设计及程序源代码1.基于Matlab GUI的离散傅里叶变换分析界面设计:程序代码:function varargout =SignalDFTSoftware(varargin)% SIGNALDFTSOFTWARE MATLAB code for SignalDFTSoftware.fig% SIGNALDFTSOFTWARE, by itself, creates a new SIGNALDFTSOFTWARE or raises the existing% singleton*.%% H = SIGNALDFTSOFTWARE returns the handle to a new SIGNALDFTSOFTWARE or the handle to% the existing singleton*.%%SIGNALDFTSOFTWARE('CALLBACK',hObject,even tData,handles,...) calls the local% function named CALLBACK in SIGNALDFTSOFTWARE.M with the given input arguments.%%SIGNALDFTSOFTWARE('Property','Value',...) creates a new SIGNALDFTSOFTWARE or raises the% existing singleton*. Starting from the left, property value pairs are% applied to the GUI before SignalDFTSoftware_OpeningFcn gets called.An% unrecognized property name or invalid value makes property application% stop. All inputs are passed to SignalDFTSoftware_OpeningFcn via varargin. %% *See GUI Options on GUIDE's Tools menu. Choose "GUI allows only one% instance to run (singleton)".%% See also: GUIDE, GUIDATA, GUIHANDLES% Edit the above text to modify the response to help SignalDFTSoftware% Last Modified by GUIDE v2.5 26-Nov-2011 12:55:11% Begin initialization code - DO NOT EDITgui_Singleton = 1;gui_State = struct('gui_Name',mfilename, ...'gui_Singleton', gui_Singleton, ...'gui_OpeningFcn',@SignalDFTSoftware_OpeningFcn, ...'gui_OutputFcn',@SignalDFTSoftware_OutputFcn, ...'gui_LayoutFcn', [] , ...'gui_Callback', []);if nargin&&ischar(varargin{1})gui_State.gui_Callback = str2func(varargin{1}); endif nargout[varargout{1:nargout}] =gui_mainfcn(gui_State, varargin{:});elsegui_mainfcn(gui_State, varargin{:});end% End initialization code - DO NOT EDIT% --- Executes just before SignalDFTSoftware is made visible.function SignalDFTSoftware_OpeningFcn(hObjec t, eventdata, handles, varargin)% This function has no output args, see OutputFcn.% hObject handle to figure% eventdata reserved - to be defined in a future version of MATLAB% varargin command line arguments to SignalDFTSoftware (see VARARGIN)% Choose default command line output for SignalDFTSoftwarehandles.output = hObject;% Update handles structure guidata(hObject, handles);% UIWAIT makes SignalDFTSoftware wait for user response (see UIRESUME)% uiwait(handles.figure1);% --- Outputs from this function are returned to the command line.function varargout =SignalDFTSoftware_OutputFcn(hObject, eventdata, handles)% varargout cell array for returning output args (see VARARGOUT);% hObject handle to figure% eventdata reserved - to be defined in a future version of MATLAB% Get default command line output from handles structurevarargout{1} = handles.output;% --- If Enable == 'on', executes on mouse press in 5 pixel border.% --- Otherwise, executes on mouse press in 5 pixel border or over random.function random_ButtonDownFcn(hObject, eventdata, handles)% hObject handle to random (see GCBO)% eventdata reserved - to be defined in a future version of MATLAB% --- Executes on button press in random. function random_Callback(hObject, eventdata, handles)% hObject handle to random (see GCBO)% eventdata reserved - to be defined in a future version of MATLABglobal x;global x_flag;x=rand(1,50)*20-10;x_flag=1;if(x_flag)plot(handles.TD,0:(length(x)-1),x);end% --- Executes on button press in Delete.function Delete_Callback(hObject, eventdata, handles)% hObject handle to Delete (see GCBO)% eventdata reserved - to be defined in a future version of MATLABglobal x;global X;global x_flag;global X_flag;x=0;X=0;x_flag=0;X_flag=0;plot(handles.TD,0,0);plot(handles.FD,0,0);% --- If Enable == 'on', executes on mouse press in 5 pixel border.% --- Otherwise, executes on mouse press in 5 pixel border or over Delete.function Delete_ButtonDownFcn(hObject, eventdata, handles)% hObject handle to Delete (see GCBO)% eventdata reserved - to be defined in a future version of MATLAB% --- If Enable == 'on', executes on mouse press in 5 pixel border.% --- Otherwise, executes on mouse press in 5 pixel border or over Analyse.function Analyse_ButtonDownFcn(hObject, eventdata, handles)% hObject handle to Analyse (see GCBO)% eventdata reserved - to be defined in a future version of MATLAB% --- Executes on button press in Analyse. function Analyse_Callback(hObject, eventdata, handles)% hObject handle to Analyse (see GCBO)% eventdata reserved - to be defined in a future version of MATLAB global x;global X;global x_flag;global X_flag;if(x_flag)X=fft(x);X_flag=1;endif(X_flag)stem(handles.FD,linspace(0,2*pi,length(X)),abs( X));xlim(handles.FD,[0,2*pi])end% --- Executes on button press in Export. function Export_Callback(hObject, eventdata, handles)% hObject handle to Export (see GCBO)% eventdata reserved - to be defined in a future version of MATLABglobal X;global X_flag;if(X_flag)assignin('base',get(handles.edit4,'String'),X); end% --- Executes during object creation, after setting all properties.function text1_CreateFcn(hObject, eventdata, handles)% hObject handle to text1 (see GCBO)% eventdata reserved - to be defined in a future version of MATLAB% handles empty - handles not created until after all CreateFcns calledglobal x_flag;global X_flag;global x;global X;x_flag=0;X_flag=0;x=0;X=0;function name_Callback(hObject, eventdata, handles)% hObject handle to name (see GCBO)% eventdata reserved - to be defined in a future version of MATLAB% Hints: get(hObject,'String') returns contents of name as text% str2double(get(hObject,'String')) returns contents of name as a double% --- Executes during object creation, after setting all properties.function name_CreateFcn(hObject, eventdata, handles)if ispc&&isequal(get(hObject,'BackgroundColor'), get(0,'defaultUicontrolBackgroundColor')) set(hObject,'BackgroundColor','white'); end% --- Executes on button press in import. function import_Callback(hObject, eventdata, handles)global x;global x_flag;global signal_name;signal_name=get(,'String');x='empty';set(,'String','Notexist,Retry!');x=evalin('base',signal_name);set(,'String','Succeed');x_flag=1;if(x_flag)plot(handles.TD,0:(length(x)-1),x);endset(handles.edit4,'String',strcat('DFT_',signal_na me));function edit4_Callback(hObject, eventdata, handles)function edit4_CreateFcn(hObject, eventdata, handles)if ispc&&isequal(get(hObject,'BackgroundColor'), get(0,'defaultUicontrolBackgroundColor')) set(hObject,'BackgroundColor','white'); endglobal signal_name;2.基于Matlab GUI的数字滤波器分析设计界面设计:程序设计:function varargout = filter(varargin)%EDIT By Yu Yizhe%V1.0%2011/11/20%all right reserve% Begin initialization code - DO NOT EDITgui_Singleton = 1;gui_State = struct('gui_Name', mfilename, ...'gui_Singleton', gui_Singleton, ...'gui_OpeningFcn', @filter_OpeningFcn, ...'gui_OutputFcn', @filter_OutputFcn, ...'gui_LayoutFcn', [], ...'gui_Callback', []);if nargin&&ischar(varargin{1})gui_State.gui_Callback = str2func(varargin{1}); endif nargout[varargout{1:nargout}] =gui_mainfcn(gui_State, varargin{:});elsegui_mainfcn(gui_State, varargin{:});end% End initialization code - DO NOT EDIT% --- Executes just before filter is made visible. function filter_OpeningFcn(hObject, eventdata, handles, varargin)% This function has no output args, see OutputFcn.% hObject handle to figure% eventdata reserved - to be defined in a future version of MATLAB% varargin unrecognizedPropertyName/PropertyValue pairs from the% command line (see VARARGIN)% Choose default command line output for filter handles.output = hObject;% Update handles structureguidata(hObject, handles);% UIWAIT makes filter wait for user response (see UIRESUME)% uiwait(handles.figure1);% --- Outputs from this function are returned tothe command line.function varargout = filter_OutputFcn(hObject, eventdata, handles)% varargout cell array for returning output args (see VARARGOUT);% hObject handle to figure% eventdata reserved - to be defined in a future version of MATLAB% Get default command line output from handles structurevarargout{1} = handles.output;function text1_CreateFcn(hObject, eventdata, handles)global ch1;global ch2;global ch31;global ch32;ch1=1;ch2=1;ch31=1;ch32=1;function IIRtype_Callback(hObject, eventdata, handles)global ch1;global ch2;global ch31;global ch32;ch31=get(hObject,'Value');function IIRtype_CreateFcn(hObject, eventdata, handles)if ispc&&isequal(get(hObject,'BackgroundColor'), get(0,'defaultUicontrolBackgroundColor'))set(hObject,'BackgroundColor','white');endfunction e11_Callback(hObject, eventdata, handles)function e11_CreateFcn(hObject, eventdata, handles)if ispc&&isequal(get(hObject,'BackgroundColor'), get(0,'defaultUicontrolBackgroundColor')) set(hObject,'BackgroundColor','white'); endfunction e12_Callback(hObject, eventdata, handles)function e12_CreateFcn(hObject, eventdata, handles)if ispc&&isequal(get(hObject,'BackgroundColor'), get(0,'defaultUicontrolBackgroundColor')) set(hObject,'BackgroundColor','white'); endfunction e21_Callback(hObject, eventdata, handles)function e21_CreateFcn(hObject, eventdata, handles)if ispc&&isequal(get(hObject,'BackgroundColor'), get(0,'defaultUicontrolBackgroundColor')) set(hObject,'BackgroundColor','white'); endfunction e22_Callback(hObject, eventdata, handles)function e22_CreateFcn(hObject, eventdata, handles)if ispc&&isequal(get(hObject,'BackgroundColor'), get(0,'defaultUicontrolBackgroundColor')) set(hObject,'BackgroundColor','white'); endfunction e31_Callback(hObject, eventdata, handles)function e31_CreateFcn(hObject, eventdata, handles)if ispc&&isequal(get(hObject,'BackgroundColor'), get(0,'defaultUicontrolBackgroundColor')) set(hObject,'BackgroundColor','white'); endfunction e32_Callback(hObject, eventdata, handles)function e32_CreateFcn(hObject, eventdata, handles)if ispc&&isequal(get(hObject,'BackgroundColor'), get(0,'defaultUicontrolBackgroundColor')) set(hObject,'BackgroundColor','white'); endfunction e41_Callback(hObject, eventdata, handles)function e41_CreateFcn(hObject, eventdata, handles)if ispc&&isequal(get(hObject,'BackgroundColor'), get(0,'defaultUicontrolBackgroundColor')) set(hObject,'BackgroundColor','white'); endfunction e42_Callback(hObject, eventdata, handles)function e42_CreateFcn(hObject, eventdata, handles)if ispc&&isequal(get(hObject,'BackgroundColor'), get(0,'defaultUicontrolBackgroundColor')) set(hObject,'BackgroundColor','white'); endfunction generate_Callback(hObject, eventdata, handles)global ch1;global ch2;global ch31;global ch32;global typech;global w1p;global w1s;global w2p;global w2s;global rp;global rs;if ch1==1typech=ch1*100+ch2*10+ch31;elseif ch2==2typech=ch1*100+ch2*10+ch32;endw1p=str2num(get(handles.e11,'String'));w1s=str2num(get(handles.e12,'String'));w2p=str2num(get(handles.e21,'String'));w2s=str2num(get(handles.e22,'String'));rp=str2num(get(handles.e41,'String'));rs=str2num(get(handles.e42,'String')); Generate(handles);function FIRtype_Callback(hObject, eventdata, handles)global ch1;global ch2;global ch31;global ch32;ch32=get(hObject,'Value');function FIRtype_CreateFcn(hObject, eventdata, handles)if ispc&&isequal(get(hObject,'BackgroundColor'), get(0,'defaultUicontrolBackgroundColor')) set(hObject,'BackgroundColor','white'); endfunction poptype_Callback(hObject, eventdata, handles)global ch1;global ch2;global ch31;global ch32;ch2=get(hObject,'Value');reprint(handles);function poptype_CreateFcn(hObject, eventdata, handles)if ispc&&isequal(get(hObject,'BackgroundColor'), get(0,'defaultUicontrolBackgroundColor')) set(hObject,'BackgroundColor','white'); endfunction iirchoose_ButtonDownFcn(hObject, eventdata, handles)function firchoose_Callback(hObject, eventdata, handles)global ch1;global ch2;global ch31;global ch32;if(get(handles.firchoose,'Value')==0)set(handles.iirchoose,'Value',1);set(handles.FIRtype,'Visible','off');set(handles.IIRtype,'Visible','on');ch1=1;endif(get(handles.firchoose,'Value')==1)set(handles.iirchoose,'Value',0);set(handles.FIRtype,'Visible','on');set(handles.IIRtype,'Visible','off');ch1=2;endreprint(handles);function firchoose_ButtonDownFcn(hObject, eventdata, handles)function iirchoose_Callback(hObject, eventdata, handles)global ch1;global ch2;global ch31;global ch32;if(get(handles.iirchoose,'Value')==0)set(handles.firchoose,'Value',1);set(handles.FIRtype,'Visible','on');set(handles.IIRtype,'Visible','off');ch1=2;endif(get(handles.iirchoose,'Value')==1)set(handles.firchoose,'Value',0);set(handles.FIRtype,'Visible','off');set(handles.IIRtype,'Visible','on');ch1=1;endreprint(handles);function reprint(handles)global ch1;global ch2;global ch31;global ch32;temp=ch1*10+ch2;tempswitch tempcase {11,12}set(handles.add1,'Visible','off');set(handles.add2,'Visible','off');set(handles.e21,'Visible','off');set(handles.e22,'Visible','off');set(handles.pr,'Visible','on'); case{13,14}set(handles.add1,'Visible','on');set(handles.add2,'Visible','on');set(handles.e21,'Visible','on');set(handles.e22,'Visible','on');set(handles.pr,'Visible','on'); case{21,22},set(handles.add1,'Visible','off');set(handles.add2,'Visible','off');set(handles.e21,'Visible','off');set(handles.e22,'Visible','off');case{23,24},set(handles.add1,'Visible','on');set(handles.add2,'Visible','on');set(handles.e21,'Visible','on');set(handles.e22,'Visible','on');otherwisefprintf('switch error\n');endfunction Generate(handles)global ch1;global ch2;global ch31;global ch32;global typech;global w1p;global w1s;global w2p;global w2s;global rp;global rs;N=0;Wn=0;Wp=0;Wst=0;Rp=0;As=0;ftype='a';b=0;a=0;switch ch2case 1,ftype='low';case 2,ftype='high';case 3,ftype='bandpass';case 4,ftype='stop';endswitch ch2case {1,2}Wp=w1p;Wst=w1s;Rp=rp;As=rs;case {3,4}Wp=[w2p w1p];Wst=[w2s w1s];Rp=rp;As=rs;endswitch ch1 %IIR case 1,switch ch31case 1,[N,Wn]=buttord(Wp,Wst,Rp,As);[b,a]=butter(N,Wn,ftype); case 2,[N,Wn]=cheb1ord(Wp,Wst,Rp,As);[b,a]=cheby1(N,Rp,Wn,ftype);case 3,[N,Wn]=cheb2ord(Wp,Wst,Rp,As);[b,a]=cheby2(N,As,Wn,ftype); case 4,[N,Wn]=ellipord(Wp,Wst,Rp,As);[b,a]=ellip(N,Rp,As,Wn,ftype);endprint4(a,b,handles);case 2 %FIR tranbw=0;N=0;hw=0;Wn=(Wp+Wst)/2;switch ch32case 1, %Rectangular tranbw=1.8;N=ceil(tranbw/abs(w1s-w1p))+1;hw=boxcar(N);case 2, %Hanning tranbw=6.2;N=ceil(tranbw/abs(w1s-w1p))+1;hw=hanning(N);case 3, %Hamming tranbw=6.6;N=ceil(tranbw/abs(w1s-w1p))+1;hw=hamming(N);case 4, %Blackman tranbw=11;N=ceil(tranbw/abs(w1s-w1p))+1;hw=blackman(N);case 5, %KaiserN=(rs-7.95)/2.285/abs(w1s-w1p)+1;N=ceil(N);if (rs>=50)BTA=0.1102*(rs-8.7); elseif(rs>21)BTA=0.5842*(rs-21)^0.4+0.07886*(rs-21);elseBTA=0.5;endhw=kaiser(N,BTA);endh=fir1(N-1,Wn,ftype,hw');print4(h,N,handles);endfunction print4(a,b,handles)global ch1;if(ch1==1) %IIRw=[0:500]*pi/500;axes(handles.axes1);H=freqz(b,a,w);plot(handles.axes1,w/pi,abs(H)); xlabel('\Omega(\pi)');ylabel('|H(j\Omega)|');%axis ([0,0.5,0,1]);axes(handles.axes2);plot(handles.axes2,w/pi,20*log10((abs(H))/max(a bs(H))));xlabel('\Omega(\pi)');ylabel('|H(j\Omega)|,dB');% axis([0,0.5,-30,0]);axes(handles.axes3);plot(handles.axes3,w/pi,angle(H)/pi); xlabel('\Omega(\pi)');ylabel('Phase of H(j\Omega)(\pi)');%axis([0,0.5,-1,1]);t=0:30;axes(handles.axes4);h=impulse(b,a,t);stem(handles.axes4,t,h);xlabel('n');ylabel('Impulse Response');elseif(ch1==2) %FI RN=b;h=a;[H,w]=freqz(h,1);axes(handles.axes1);plot(handles.axes1,w/pi,abs(H)); xlabel('\Omega(\pi)');ylabel('|H(j\Omega)|');%axis ([0,0.5,0,1]);axes(handles.axes2);plot(handles.axes2,w/pi,20*log10((abs(H))/max(a bs(H))));xlabel('\Omega(\pi)');ylabel('|H(j\Omega)|,dB');% axis([0,0.5,-30,0]);axes(handles.axes3);plot(handles.axes3,w/pi,angle(H)/pi); xlabel('\Omega(\pi)');ylabel('Phase ofH(j\Omega)(\pi)');%axis([0,0.5,-1,1]);t=0:N-1;axes(handles.axes4);stem(handles.axes4,t,h);xlabel('n');ylabel('Impulse Response');end六、实验总结这次的数字信号处理实验非常有意义,让我学会了用计算机进行数字信号处理,计算各种参数,绘制出信号的波形,频谱。
随机信号分析实验报告

.随机信号分析实验报告实验一 各种分布随机数的产生一、 实验目的在很多系统仿真的过程中,需要产生不同分布的随机变量。
利用计算机可以很方便地产生不同分布的随机变量,各种分布的随机变量的基础是均匀分布的随机变量。
有了均匀分布的随机变量,就可以用函数变换等方法得到其他分布的随机变量。
二、 实验内容产生均匀分布的随机数、高斯分布的随机数和其它分布的随机数。
三、 实验原理1. 均匀分布随机数的产生原理产生伪随机数的一种实用方法是同余法,它利用同余运算递推产生伪随机数序列。
最简单的方法是加同余法)(mod 1M c y y n n +=+M y x n n 11++=为了保证产生的伪随机数能在[0,1]内均匀分布,需要M 为正整数,此外常数c 和初值y0亦为正整数。
加同余法虽然简单,但产生的伪随机数效果不好。
另一种同余法为乘同余法,它需要两次乘法才能产生一个[0,1]上均匀分布的随机数)(mod 1M ay y n n =+ M y x n n 11++=式中,a 为正整数。
用加法和乘法完成递推运算的称为混合同余法,即)(mod 1M c ay y n n +=+ M y x n n 11++=用混合同余法产生的伪随机数具有较好的特性,一些程序库中都有成熟的程序供选择。
常用的计算语言如Basic 、C 和Matlab 都有产生均匀分布随机数的函数可以调用,只是用各种编程语言对应的函数产生的均匀分布随机数的范围不同,有的函数可能还需要提供种子或初始化。
Matlab 提供的函数rand()可以产生一个在[0,1]区间分布的随机数,rand(2,4)则可以产生一个在[0,1]区间分布的随机数矩阵,矩阵为2行4列。
Matlab 提供的另一个产生随机数的函数是random('unif',a,b,N,M),unif 表示均匀分布,a 和b 是均匀分布区间的上下界,N 和M 分别是矩阵的行和列。
2. 随机变量的仿真根据随机变量函数变换的原理,如果能将两个分布之间的函数关系用显式表达,那么就可以利用一种分布的随机变量通过变换得到另一种分布的随机变量。
北理工信号与系统实验报告

������������ ������ ������������ ������ 0 ������
������������ =
1 ������0
������(������)������ −������������ ������ 0 ������ ������������
������0
上述两式定义为周期信号复指数形式的傅里叶级数,系数 Ck 称为 x(t)的傅 里叶级数。周期信号的傅里叶级数还可以由三角函数的线性组合来表示,即
xlabel('n') title('y[n]') 程序运行结果如下:
x[n] 1 0.5 0 -0.5 -1 1 0.5 0 -0.5 -1 y[n] 4 h[n]
0
5
10 n
15
20
0
5
10 n
15
20
2
0
-2
0
5
10
15
20 n
25
30
35
40
7.已知两个连续时间信号,求两个信号的卷积。 程序如下: w1=2; w2=4; dt=0.01; t1=-2:dt:2; t2=-4:dt:4; x1=2*rectpuls(t1,w1) x2=rectpuls(t2,w2) x=conv(x1,x2); x=x*dt; t0=t1(1)+t2(1); t3=length(x1)+length(x2)-2; t=t0:dt:(t3*dt+t0); plot(t,x); axis([-4 4 -2 6]); xlabel('t'); title('x(t)'); 程序运行结果如下:
an y (n) (t ) an1 y (n1) (t ) a1 y ' (t ) a0 y(t ) bm x (m) (t ) bm1 x (m1) (t ) b1 x ' (t ) b0 x(t )
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
本科实验报告实验名称:随机信号分析实验实验一 随机序列的产生及数字特征估计一、实验目的1、学习和掌握随机数的产生方法。
2、实现随机序列的数字特征估计。
二、实验原理1、随机数的产生随机数指的是各种不同分布随机变量的抽样序列(样本值序列)。
进行随机信号仿真分析时,需要模拟产生各种分布的随机数。
在计算机仿真时,通常利用数学方法产生随机数,这种随机数称为伪随机数。
伪随机数是按照一定的计算公式产生的,这个公式称为随机数发生器。
伪随机数本质上不是随机的,而且存在周期性,但是如果计算公式选择适当,所产生的数据看似随机的,与真正的随机数具有相近的统计特性,可以作为随机数使用。
(0,1)均匀分布随机数是最最基本、最简单的随机数。
(0,1)均匀分布指的是在[0,1]区间上的均匀分布,即 U(0,1)。
实际应用中有许多现成的随机数发生器可以用于产生(0,1)均匀分布随机数,通常采用的方法为线性同余法,公式如下:)(m od ,110N ky y y n n -=N y x n n /=序列{}n x 为产生的(0,1)均匀分布随机数。
下面给出了上式的3组常用参数:1、10N 10,k 7==,周期7510≈⨯;2、(IBM 随机数发生器)3116N 2,k 23,==+周期8510≈⨯; 3、(ran0)315N 21,k 7,=-=周期9210≈⨯;由均匀分布随机数,可以利用反函数构造出任意分布的随机数。
定理 1.1 若随机变量 X 具有连续分布函数F X (x),而R 为(0,1)均匀分布随机变量,则有)(1R F X x -=由这一定理可知,分布函数为F X (x)的随机数可以由(0,1)均匀分布随机数按上式进行变换得到。
2、MATLAB 中产生随机序列的函数(1)(0,1)均匀分布的随机序列 函数:rand 用法:x = rand(m,n)功能:产生m ×n 的均匀分布随机数矩阵。
(2)正态分布的随机序列 函数:randn 用法:x = randn(m,n)功能:产生m ×n 的标准正态分布随机数矩阵。
如果要产生服从2N(,)μσ分布的随机序列,则可以由标准正态随机序列产生。
(3)其他分布的随机序列MATLAB 上还提供了其他多种分布的随机数的产生函数,下表列出了部分函数。
MATLAB 中产生随机数的一些函数3、随机序列的数字特征估计对于遍历过程,可以通过随机序列的一条样本函数来获得该过程的统计特性。
这里我们假定随机序列 X (n)为遍历过程,样本函数为x(n),其中n=0,1,2,…,N -1。
那么,X (n)的均值、方差和自相关函数的估计为利用MATLAB 的统计分析函数可以分析随机序列的数字特征。
(1)均值函数函数:mean用法:m = mean(x)功能:返回按上面第一式估计X (n)的均值,其中x 为样本序列x(n)。
(2)方差函数函数:var用法:sigma2 = var(x)功能:返回按上面第二式估计X (n)的方差,其中x 为样本序列x(n),这一估计为无偏估计。
(3)互相关函数函数:xcorr用法:c = xcorr(x,y)c = xcorr(x)c = xcorr(x,y,'opition')c = xcorr(x,'opition')功能:xcorr(x,y)计算X (n)与Y(n)的互相关,xcorr(x)计算X (n)的自相关。
option 选项可以设定为:'biased' 有偏估计,即'unbiased' 无偏估计,即按上面第三式估计。
'coeff' m = 0 时的相关函数值归一化为1。
'none' 不做归一化处理。
三、实验内容1、采用线性同余法产生均匀分布随机数1000 个,计算该序列均值和方差与理论值之间的误差大小。
改变样本个数重新计算。
num=input('num=');n=2^31;k=2^16+3;y=zeros(1,num);x=zeros(1,num);y(1)=1;for i=2:numy(i)=mod(k*y(i-1),num);endx=y/num;m=mean(x);si=var(x);plot(x,'k');xlabel('n');ylabel('x(n)');axis tight;已知理论值均值为0.5方差为0.0833Num=1000m =0.4900 >> sisi =0.0834 NUM=5000mm =0.4950 >> sisi =0.0834Num=3000mm =0.4833>> sisi =0.0832Num=5000mm =0.4980>> sisi =0.08332、参数为λ的指数分布的分布函数为x x e F λ--=1利用反函数法产生参数为0.5 的指数分布随机数1000 个,测试其方差和相关函数。
R=rand(1,1000); lambda=0.5;x=-log(1-R)/lambda; Dx=var(x); [Rm,m]=xcorr(x); subplot(211);plot(x,'k');xlabel('n');ylabel('x(n)');axis tight ;subplot(212);plot(m,Rm,'k');xlabel('m');ylabel('R(m)');axis tight ;Dx Dx =4.0781理论上方差的值为1/(0.5^2)=4,实际值为4.1201,因为取样个数有限,导致存在一定偏差。
但大体相近。
3、产生一组N(1,4)分布的高斯随机数(1000个样本),估计该序列的均值、方差和相关函数。
x=normrnd(1,2,[1,1000]);Mx=mean(x);Dx=var(x);[Rm,m]=xcorr(x);subplot(211);plot(x,'k');xlabel('n');ylabel('x(n)');axis tight;subplot(212);plot(m,Rm,'k');xlabel('m');ylabel('R(m)');axis tight;MxMx =1.0934>> DxDx =4.1071理论上的均值为1,方差为4。
而在实验中得到的均值为1.0934,方差为4.1071。
考虑到取样点有限,误差可以接受,理论值和实验值基本相同。
四、实验体会本次实验内容是随机序列的产生及数字特征估计,通过实验我学习和掌握随机数的产生方法,比如线性同余法,生成已知分布函数的随机数,rand 函数等,也实现了对随机序列数字特征的估计,初步达到了实验的预期目的。
实验二 随机过程的模拟与数字特征一、实验目的1、学习利用MATLAB 模拟产生随机过程的方法。
2、熟悉和掌握特征估计的基本方法及其MATLAB 实现。
二、实验原理1、正态分布白噪声序列的产生MATLAB 提供了许多产生各种分布白噪声序列的函数,其中产生正态分布白噪声序列的函数为randn 。
函数:randn用法:x = randn(m,n)功能:产生m ×n 的标准正态分布随机数矩阵。
如果要产生服从),(2συN 分布的随机序列,则可以由标准正态随机序列产生。
如果N(0,1),则2X ~N(,)μ+σμσ。
2、相关函数估计MATLAB 提供了函数xcorr 用于自相关函数的估计。
函数:xcorr用法:c = xcorr(x,y) c = xcorr(x)c = xcorr(x,y,'opition') c = xcorr(x,'opition')功能:xcorr(x,y)计算X (n)与Y(n)的互相关,xcorr(x)计算X (n)的自相关。
option 选项可以设定为: 'biased' 有偏估计。
'unbiased' 无偏估计。
'coeff' m=0 时的相关函数值归一化为1。
'none' 不做归一化处理。
3、功率谱估计MATLAB 函数periodogram 实现了周期图法的功率谱估计。
函数:periodogram用法:[Pxx,w] = periodogram(x) [Pxx,w] = periodogram(x,window) [Pxx,w] = periodogram(x,window,nfft) [Pxx,f] = periodogram(x,window,nfft,fs) periodogram(...)功能:实现周期图法的功率谱估计。
其中:Pxx 为输出的功率谱估计值;f 为频率向量;w 为归一化的频率向量;window 代表窗函数,这种用法对数据进行了加窗,对数据加窗是为了减少功率谱估计中因为数据截断产生的截断误差,下图列出了产生常用窗函数的MATLAB函数。
nfft设定FFT算法的长度;fs表示采样频率;三、实验内容1、按如下模型产生一组随机序列=-+ωx(n)0.8x(n1)(n)其中(n)ω是均值为1,方差为 4的正态分布白噪声序列。
估计过程的自相关函数和功率谱。
y=1+2*randn(1,2000); %产生均值为1,方差为4的正态分布白噪声序列x(1)=y(1);n=2000;for i=2:1:nx(i)=0.8*x(i-1)+y(i); %按题目要求产生随机序列x(n)=0.8x(n-1)+w(n)endplot(x); %画出随机序列x的图形title('x(n)');y=1+2*randn(1,2000); %产生均值为1,方差为4的正态分布白噪声序列x(1)=y(1);n=2000;for i=2:1:nx(i)=0.8*x(i-1)+y(i); %按题目要求产生随机序列x(n)=0.8x(n-1)+w(n) endsubplot(211);c=xcorr(x); %画出x的自相关函数plot(c);title('R(n)');p=periodogram(x);subplot(212);plot(p);%画出x的功率谱title('S(w)');2、设信号为其中 12.0,05.021==f f ,)(n w 为正态分布白噪声序列,试在N =256和N=1024点时,分别产生随机序列x(n),画出x(n)的波形并估计x(n)的相关函数和功率谱。
