电力系统不对称故障的分析
5(C-8)不对称故障分析 - 电力系统 湖南大学

(b) 短路电压:短路两相V相等,为非短路相的1/2 且相位相反。 特别:
Zff(2) =Zff(1) then Vfa =Vf[0] & Vfb =Vfc = 1 Vf[0] 2
9
8-1 简单不对称短路的分析
三、两相接地短路: (1) 边界条件:
Vfa Vfb
Vfb Vfc I fa=0 Ifb I fc
I fa (1) I fa (2) I fa (0) 1 I fa 3
I fa(2)
I fa(0)
Zff(1) + V f [0 ]
V f a (1 )
Zff(2)
V fa (2 )
Zff(0)
Vfa(0)
-
I fa(1) I fa(2) I fa(0)
= Zff(1) + (Zff(2) + Zff(0) ) Zff(1) + Z(1) Δ 4
3 Vf[0]
3 Vf[0]
8-1 简单不对称短路的分析
一、单相接地短路: (5) 故障(短路)口的各相电压
Vfb = a 2Vfa(1) + aVfa(2) + Vfa(0) = -j 23 2Z ff(2) + Z ff(0) - j 3Z ff(0) I fa(1) 2 3 Vfc = aVfa(1) + a Vfa(2) + Vfa(0) = -j 2 - 2Z ff(2) + Z ff(0) - j 3Z ff(0) I fa(1) Vfa = 0
Ifc = aIfa(1) + a 2Ifa(2) + Ifa(0) = a Zff(2) + a 2Zff(0)
电力系统不对称故障分析与计算及其程序设计

电力系统不对称故障分析与计算及其程序设计电力系统是现代社会不可或缺的组成部分。
在电力系统中,不对称故障是一种严重的故障,其影响可以导致电力系统的瘫痪。
因此,不对称故障分析与计算非常重要,是电力系统维护的基础工作之一。
本文将重点讨论电力系统不对称故障分析与计算及其程序设计。
1. 不对称故障的概念不对称故障是指在电力系统中,一侧电源与另一侧负载不对称导致的故障。
不对称故障通常包括短路故障和开路故障两种情况。
短路故障是指两个相之间或者相与地之间的短路,导致电路异常加热、设备损坏、电压降低等问题。
开路故障是指电路中出现的缺失和断路,导致电流无法正常流动,使电力系统无法正常运行。
2. 不对称故障分析与计算在出现不对称故障时,需要进行分析和计算。
基本的不对称故障分析和计算包括以下内容:(1)不对称故障电流的计算。
不对称故障电流是指出现不对称故障时电路中的电流。
不同类型的故障电流计算方法不同,需要根据具体情况进行计算。
不对称故障电流的计算非常关键,可以为后续的故障处理提供依据。
(2)故障影响分析。
不对称故障会对电力系统产生不同程度的影响,包括电压降低、设备故障、负荷损失等。
需要进行故障影响分析,为后续处理提供依据。
(3)电力系统稳态分析。
在不对称故障发生时,需要进行电力系统的稳态分析,分析电力系统受故障干扰后的运行情况,为后续处理提供可靠的指导。
3. 不对称故障计算程序设计对于电力系统不对称故障计算,可以设计相应的计算程序,以提高计算效率和准确性。
根据不同的故障情况和计算需求,可以设计不同的计算程序。
一般而言,不对称故障计算程序应包括以下部分:(1)输入信息。
输入信息主要包括电路图、电力系统参数、故障类型等。
输入信息的准确性对计算结果具有重要的影响。
(2)故障电流计算。
根据输入的电路图和电力系统参数,计算不对称故障电流。
不对称故障电流是不对称故障计算的基础。
(3)故障影响分析。
根据不对称故障电流,计算电力系统电压降低、设备故障等影响,预测故障对电力系统的影响程度。
电力系统不对称故障的分析计算

电力系统不对称故障的分析计算1. 引言电力系统是现代社会中不可或缺的根底设施之一。
然而,由于各种原因,电力系统可能会发生不对称故障,导致电力系统的正常运行受到严重影响甚至导致短路事故。
因此,对电力系统不对称故障进行分析和计算是非常重要的。
本文将分析电力系统不对称故障的原因、特点以及进行相应计算的方法,并使用Markdown文本格式进行输出。
2. 不对称故障的原因和特点不对称故障是指电力系统中出现相序不对称的故障。
其主要原因包括:单相接地故障、双相接地故障以及两相短路故障等。
不对称故障的特点如下:1.电流和电压的相位不同:在不对称故障中,电流和电压的相位不同,通常表现为电流和电压波形的不对称。
2.非对称系统功率:由于不对称故障,电力系统中的功率将变得非对称。
正常情况下,三相电流和电压的功率应该平衡,但在不对称故障中,这种平衡被破坏。
3.对称分量的存在:在不对称故障中,由于相序的不同,电流和电压中会存在对称正序分量、对称负序分量和零序分量。
3. 不对称故障的分析计算方法对于不对称故障的分析计算,一般可以采用以下步骤:3.1 系统参数获取首先,需要获取电力系统的各项参数,包括发电机、变压器、线路和负载的参数等。
这些参数将用于后续的计算。
3.2 故障状态建模根据故障的类型和位置,对故障状态进行建模。
常见的故障状态包括单相接地故障、双相接地故障和两相短路故障等。
3.3 网络方程建立基于故障状态的建模,可以建立电力系统的节点方程或潮流方程。
通过求解节点方程或潮流方程,可以得到电流和电压的分布情况。
3.4 不对称故障计算根据网络方程的求解结果,可以计算不对称故障中电流、电压和功率的各项指标,包括正序分量电流、负序分量电流、零序电流等。
3.5 故障保护和控制根据不对称故障的计算结果,可以对故障保护和控制系统进行设计和优化。
通过故障保护和控制系统的响应,可以及时检测和隔离故障,保证电力系统的平安运行。
4. 结论电力系统不对称故障的分析计算是确保电力系统平安运行的重要步骤。
电力系统分析第章电力系统简单不对称故障的

电力系统分析第章电力系统简单不对称故障的处理电力系统是现代社会中不可或缺的一部分,其稳定运行对于保障人们的生活质量,维持经济的发展和社会的稳定至关重要。
在电力系统的运行过程中,经常会出现各种各样的故障,随着电力系统的不断发展和提高,各种故障也越来越多样化和复杂化。
其中,不对称故障是一种非常重要的故障类型,本文将对电力系统中简单的不对称故障进行详细的分析和处理。
不对称故障的定义不对称故障是指电力系统中发生的一种故障,其导致各相之间电路参数不一致,从而导致电流的不均衡。
不对称故障主要有以下几种形式:•单相短路故障(短路故障发生在一条支路上);•两相短路故障(短路故障发生在两条支路上);•相间短路故障(短路故障发生在两个相之间);•单相接地故障(故障相接地);•两相接地故障(两个相接地);•相间接地故障(两个相接地)。
不对称故障的分析不对称故障的分析过程主要分为两个步骤,分别是故障检测和故障定位。
故障检测的主要目的是确定发生故障的支路或电气设备,以便进行故障隔离和修复。
常用的故障检测方法有以下几种:•变压器过热检测法;•相序保护法;•电流差动保护法;•波形比较法;•同步检测法。
故障定位故障定位的主要目的是确定故障的位置,以便快速修复。
常用的故障定位方法有以下几种:•距离保护法;•相位比较法;•反演法;•差动保护法不对称故障的处理不对称故障的处理主要分为两个步骤,分别是故障隔离和故障恢复。
故障隔离的主要目的是将故障部分与正常工作部分切断联系,以免故障扩大影响,损坏更多的设备甚至引起电力系统的崩溃。
常用的故障隔离方法有以下几种:•手动隔离法;•自动隔离法;•线路转换法。
故障恢复故障恢复的主要目的是修复故障,恢复电力系统的正常运行。
故障恢复的步骤主要分为以下几个阶段:•修复故障部分;•恢复与故障部分切断的联系;•逐步恢复电力系统的正常运行。
结论不对称故障是电力系统中常见的故障类型之一,其在电力系统的运行过程中有着重要的意义。
不对称短路故障分析与计算(电力系统课程设计)

不对称短路故障分析
02
不对称短路故障类型
单相接地短路
其中一相电流通过接地电阻,其余两 相保持正常。
两相短路
两相接地短路
两相电流通过接地电阻,另一相保持 正常。
两相之间没有通过任何元件直接短路。
不对称短路故障产生的原因
01
02
03
设备故障
设备老化、绝缘损坏等原 因导致短路。
外部因素
如雷击、鸟类或其他异物 接触线路导致短路。
操作错误
如误操作或维护不当导致 短路。
不对称短路故障的危害
设备损坏
短路可能导致设备过热、烧毁或损坏。
安全隐患
短路可能引发火灾、爆炸等安全事故。
停电
短路可能导致电力系统的局部或全面停电。
经济损失
停电和设备损坏可能导致重大的经济损失。
不对称短路故障计算
03
方法
短路电流的计算
短路电流的计算是电力系统故障分析中的重要步骤,它涉及到电力系统的 运行状态和设备参数。
不对称短路故障分析与 计算(电力系统课程设计)
contents
目录
• 引言 • 不对称短路故障分析 • 不对称短路故障计算方法 • 不对称短路故障的预防与处理 • 电力系统不对称短路故障案例分析 • 结论与展望
引言
01
课程设计的目的和意义
掌握电力系统不对称短路故障的基本原理和计算 方法
培养解决实际问题的能力,提高电力系统安全稳 定运行的水平
故障描述
某高校电力系统在宿舍用电高峰期发生不对称短路故障,导致部 分宿舍楼停电。
故障原因
经调查发现,故障原因为学生私拉乱接电线,导致插座短路。
解决方案
加强学生用电安全教育,规范用电行为;加强宿舍用电管理,定 期检查和维护电路。
电力系统不对称故障穿越能力分析

电力系统不对称故障穿越能力分析1. 引言电力系统是现代社会不可或缺的重要基础设施,其稳定运行对保障国家经济发展和人民生活水平至关重要。
然而,由于各种因素的影响,电力系统中可能出现各种故障,其中不对称故障是一种常见情况。
本文将对电力系统不对称故障穿越能力进行分析,以探讨系统在面对不对称故障时的可靠性和稳定性。
2. 不对称故障的定义与分类不对称故障是指系统中的故障电流在幅值和相位上不与正常运行时的电流一致的故障形态。
根据故障发生时电流的不对称度,不对称故障可以分为正序故障、负序故障和零序故障。
正序故障是指故障电流各相之间幅值相等且相位相同的故障,负序故障是指故障电流各相之间幅值相等但相位相差120度的故障,零序故障是指故障电流各相之间的幅值相等但相位相同的故障。
3. 不对称故障对电力系统的影响不对称故障会对电力系统的稳定性和可靠性产生重要影响。
首先,不对称故障会导致电力系统中的不对称电磁力和不对称阻尼,进而引起设备的振动和过大的压力,给系统带来附加的应力,可能导致设备的损坏和系统的故障。
其次,不对称故障会导致电网内电压降低、频率波动和短期不平衡,从而影响用户的用电质量和系统的可靠供电。
4. 不对称故障穿越能力的评估方法为了评估电力系统在面对不对称故障时的穿越能力,可以运用以下方法进行分析。
首先,可以通过模拟电力系统的稳定运行来获取故障穿越能力的统计数据,以此评估系统的可靠性。
其次,可以利用电力系统辅助计算软件进行数值模拟和仿真,观察系统在不同故障情况下的响应和稳定性。
此外,还可以采用试验验证的方法,通过对实际系统进行故障注入和监测,获得系统的穿越能力数据。
5. 提高电力系统不对称故障穿越能力的措施为了提高电力系统在不对称故障下的可靠性和稳定性,可以采取一系列相应的措施。
首先,可以加强对系统的监测和预警,及时发现和处理潜在的不对称故障。
其次,可以优化系统的保护和自动化控制策略,提高系统对不对称故障的检测和处理能力。
电力系统发生不对称短路故障分析

摘要电力系统发生不对称短路故障的可能性是最大的,本课题要求通过对电力系统分析不对称短路故障进行分析与计算,为电力系统的规划设计、安全运行、设备选择和继电保护等提供重要的依据。
关键字:标么值;等值电路;不对称故障目录一、基础资料 (3)二、设计内容 (3)1.选择110kV为电压基本级,画出用标幺值表示的各序等值电路。
并求出各序元件的参数。
(3)2.化简各序等值电路并求出各序总等值电抗。
(6)3.K处发生单相直接接地短路,列出边界条件并画出复合相序图。
求出短路电流。
(7)4.设在K处发生两相直接接地短路,列出边界条件并画出复合相序图。
求出短路电流。
(9)5.讨论正序定则及其应用。
并用正序定则直接求在K处发生两相直接短路时的短路电流。
(11)三、设计小结 (12)四、参考文献 (12)附录 (12)一、基础资料1. 电力系统简单结构图如图1所示。
图1 电力系统结构图在K 点发生不对称短路,系统各元件标幺值参数如下:(为简洁,不加下标*) 发电机G1和G2:S n =120MV A ,U n =10.5kV ,次暂态电动势标幺值1.67,次暂态电抗标幺值0.9,负序电抗标幺值0.45;变压器T1:S n =60MV A ,U K %=10.5 变压器T2:S n =60MV A ,U K %=10.5线路L=105km ,单位长度电抗x 1= 0.4Ω/km ,x 0=3 x 1, 负荷L1:S n =60MV A ,X 1=1.2,X 2=0.35 负荷L2:S n =40MV A ,X 1=1.2,X 2=0.35 取S B =120MV A 和U B 为所在级平均额定电压。
二、设计内容1.选择110kV 为电压基本级,画出用标幺值表示的各序等值电路。
并求出各序元件的参数(要求列出基本公式,并加说明)在产品样本中,电力系统中各电器设备如发电机、变压器、电抗器等所给出的都是标么值,即以本身额定值为基准的标么值或百分值。
电力系统不对称故障的分析计算

电力系统不对称故障的分析计算电力系统不对称故障是指系统中发生了一相接地、两相短路或者两相间接地短路等故障情况。
这些故障会引起系统中电流、电压的不对称变化,给电力设备和系统带来了严重的影响和损坏。
因此,对于电力系统不对称故障的分析计算具有重要的理论和实际意义。
首先,在进行不对称故障分析计算之前,需要了解电力系统的基本参数和特性。
电力系统由发电机、变电站、输电线路和用户负载等组成,其中电力设备的参数包括电阻、电抗和电导等。
在进行计算时,需要收集和记录各个电力设备的参数。
然后,可以进行电力系统的不对称故障计算。
根据不同类型的故障情况,可以采用不同的计算方法和理论模型。
一般来说,对于发生了一相接地故障的情况,可以采用等值法来计算。
即将一相接地作为一个等效阻抗连接到系统中,然后进行系统的节点分析和电流计算。
对于发生了两相短路或者两相间接地短路的情况,可以采用对称分量法进行计算。
即将系统中的电流、电压分解为正序、负序和零序三个部分,然后分别计算其大小和方向,并根据这些结果来判断系统中的故障情况和对电力设备的影响程度。
不对称故障分析计算的输出结果主要包括故障电流、故障电压和故障功率等。
这些结果可以用来评估系统中电力设备的可靠性和安全性,并为对故障设备的维修和更换提供参考依据。
此外,还可以利用这些结果进行系统的保护和自动化控制设计,以提高电力系统的性能和可操作性。
总之,电力系统不对称故障的分析计算是电力系统研究和运行中的重要内容。
通过对故障情况的分析和计算,可以更好地了解和解决系统中的故障问题,提高系统的可靠性和稳定性,保障电力供应的安全和稳定。
电力系统不对称故障的分析计算

第八章 电力系统不对称故障的分析计算主要内容提示:电力系统中发生的故障分为两类:短路和断路故障。
短路故障包括:单相接地短路、两相短路、三相短路和两相接地短路;断路故障包括:一相断线和两相断线。
除三相短路外,均属于不对称故障,系统中发生不对称故障时,网络中将出现三相不对称的电压和电流,三相电路变成不对称电路。
直接解这种不对称电路相当复杂,这里引用120对称分量法,把不对称的三相电路转换成对称的电路,使解决电力系统中各种不对称故障的计算问题较为方便。
本章主要内容包括:对称分量法,电力系统中主要元件的各序参数及各种不对称故障的分析与计算。
§8—1 对称分量法及其应用利用120对称分量法可将一组不对称的三相量分解为三组对称的三序分量(正序分量、负序分量、零序分量)之和。
设c b a F F F ∙∙∙为三相系统中任意一组不对称的三相量、可分解为三组对称的三序分量如下:()()()()()()()()()021021021c c c c b b b b a a a a F F F F F F F F F F F F ∙∙∙∙∙∙∙∙∙∙∙∙++=++=++= 三组序分量如图8-1所示。
正序分量: ()1a F ∙、()1b F ∙、()1c F ∙三相的正序分量大小相等,彼此相位互差120°,与系统正常对称运行方式下的相序相同,达到最大值的顺序a →b →c ,在电机内部产生正转磁场,这就是正序分量。
此正序分量为一平衡的三相系统,因此有:()()()111c b a F F F ∙∙∙++=0。
负序分量:()2a F ∙、()2b F ∙、()2c F ∙三相的负序分量大小相等,彼此相位互差120°,与系图 8-1 三序分量Fc(0) ·零序F b(0) ·F a(0) ·120°120° 120° 正序F b(1)·F a(1)·F c(1) ·ω120°120°120°负序 F a(2)·F c(2)·F b(2)·ω统正常对称运行方式下的相序相反,达到最大值的顺序a →c →b ,在电机内部产生反转磁场,这就是负序分量。
电力系统不对称故障的分析计算

电力系统不对称故障的分析计算6.3 不对称短路时故障处的短路电流和电压字体大小:小中大简单不对称短路包括:利用对称分量法可以求解简单不对称短路,但需要根据不对称短路的边界条件再列出三个方程。
(6-3)➢单相接地短路边界条件:➢两相短路边界条件:复合序网:➢两相接地短路边界条件:复合序网:6.3.1 单相接地短路边界条件:由式6-1直接可以得到(略去了a相的下标a):由式6-2可以得到:所以(略去了a相的下标a):(6-4)将式6-3和式6-4联立求解,则(6-5)根据式6-4可以得到单相接地短路的复合序网。
复合序网—根据边界条件所确定的短路点各序量之间的关系,将各序网络连接起来所形成的网络。
显然,由复合序网也可以直接得到式6-5。
此外:再利用式6-1,可以得到短路点的故障相电流:短路点的非故障相电压:一般X1∑≈X2∑,因此,如果X0∑<X1∑,则单相短路电流大于同一地点的三相短路电流;反之,则单相短路电流小于三相短路电流。
[例6-2] 在图示电力系统中,变压器T2高压侧发生a相接地短路,不计负荷作用,试计算短路瞬间故障点的短路电流。
解:取功率基准值SB=120MVA ,各级电压基准值U B =U av =115、37、10.5kV 。
计算各元件的电抗标幺值,并做出正序、负序和零序等值电路。
X G1=X G2=0.14X L1=105×0.4×120/1152=0.381=X L2 X L0=3×0.381=1.143X T1_1=10.5/100×120/120=0.105=X T1_2=X T1_0 X T2_1=10.5/100×120/60=0.21=X T2_2=X T2_0化简正序、负序和零序等值电路,并做出单相接地短路的复合序网。
X 1∑=X G1+X T1_1+X L1=0.626=X 2∑短路点的故障相电流:短路电流有效值:6.3.2 两相短路边界条件:复合序网:由复合序网可以得到:再利用式6-1可以得到短路点的故障相电流:如果,则:短路点的各相对地电压:6.3.3 两相接地短路边界条件:复合序网:由复合序网可以得到:再利用式6-1可以得到短路点的故障相电流:短路点的非故障相电压:6.3.4 正序等效定则及其应用三种不对称短路时,正序电流分别为:单相接地短路两相短路两相接地短路因此,三种不对称短路时,正序电流可以归纳为:正序等效定则—简单不对称短路故障的短路点正序电流分量,与在短路点每一相中加入附加电抗后发生的三相短路时的电流相等。
电力系统不对称故障分析

一、基础资料1. 电力系统简单结构图如图1所示。
图1 电力系统结构图在K 点发生不对称短路,系统各元件标幺值参数如下:(为简洁,不加下标*)发电机G1和G2:S n =120MV A ,U n =10.5kV ,次暂态电动势标幺值1.67,次暂态电抗标幺值0.9,负序电抗标幺值0.45;变压器T1:S n =60MV A ,U K %=10.5 变压器T2:S n =60MV A ,U K %=10.5线路L=105km ,单位长度电抗x 1= 0.4Ω/km ,x 0=3 x 1, 负荷L1:S n =60MV A ,X 1=1.2,X 2=0.35 负荷L2:S n =40MV A ,X 1=1.2,X 2=0.35取S B =120MV A 和U B 为所在级平均额定电压。
二、设计任务1、各元件参数标么值的计算,画出电力系统短路时的等值电路 (1)、进行电力系统计算时,采用没有单位的阻抗、导纳、电压、电流、功率等的相对值进行运算,成为标么值。
标么值的定义为:标么值=有名值/相应的基准值(2)、在作整个电力系统的等值网络图时,必须将其不同电压级的各元件参数阻抗、导纳以及相应的电压、电流归算至同一电压等级——基本级。
而基本级一般电力低通中取最高电压级。
有名值归算时按下式计算(3)、电力元件参数标么值计算,取B S =120MV A ,KV U U AVB 115==(4)变压器T1电抗标么值: ,,变压器中主要是指电抗,因其电抗T T R X =,即T R 忽略,由变压器电抗有名值推出其标为:式中K U %---变压器阻抗电压百分数B S ---基准容量,MVNTNT US ,---变压器铭牌参数给定额定容量,MV 、额定电压KV;B U ----基准电压B U 取平均电压av U ,KV(5)发电机1G 电抗标么值N N B d G S S X X ϕ1``11*=式中``d X ---发电机铭牌参数给定电抗; B S ---基准容量。
电力系统不对称故障的分析-PPT

a1
.
Uc
.
.
aU a1 a 2 U a2
.
U a1
jX 2
. I a1
短路点得电流、电压相量图
Ua
IC
Ia2 Ia1 0
Ub Uc Ua
电压向量图
Ib
电流向量图
三、两相短路接地
Ua Ub Uc
a b c
Ia
Ib
Ic
jX f
➢短路点得边界条件为
U
b U c
Ia 0 j(Ib
.
Ib
.
I a0 a2
.
I a1 a
.
I a2
(a2
X 2 aX 0 X2 X0
)
.
I
a1
.
Ic.Leabharlann I a0.a I a1
a2
.
I a2
(a
X 2
a2 X0
. ) I a1
X2 X0
.
.
.
.
.
U a U a0 U a1 U a2 3U a1 j3
X 2 X 0
.
I a1
X 2 X 0
X 0 X1
E1
1.5
X 0 X1
2
X 0 X1
j
3 2
E1
Uc
j [(a
a2 ) X1
(a 1) X 0 ]
E12 j (2 X1
X0 )
(a
a2) 2
(a 1)
X 0 X1
X 0 X1
E1
1.5
X 0 X1
2 X0 X1
j
3 2
E1
➢非故障相电压得绝对值为
电力系统不对称故障的分析和计算
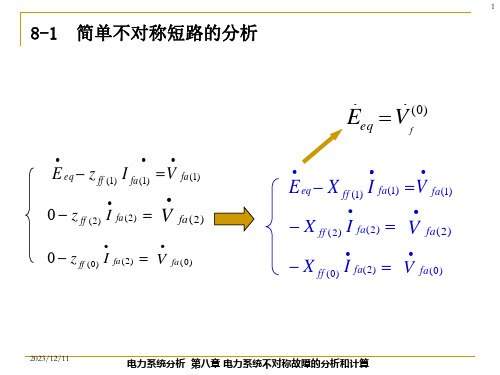
•
•
•
aV fa(1) a2 V fa(2) V fa(0) 0
2023/12/11
电力系统分析 第八章 电力系统不对称故障的分析和计算
16
化简整理后,得
•
•
•
I fa(1) I fa(2) I fa(0) 0
•
•
•
V fa(1) V fa(2) V fa(0)
2023/12/11
I
fb
2
•
I
•
fa(1) I
•
I fa(2)
fa ( 0)
( 2
X ff (2)
X
ff
(0)
)
•
I
fa (1)
X ff (2) X ) ff (0)
•
I
fc
•
I
•
fa(1) 2 I
•
I fa(2) fa(0)
(
X ff (2)
2
X
ff
(0)
)
•
I
fa (1)
X ff (2) X ff (0) )
9
Vfa(1)
Vfc(2) Vfc(2) Vfc(1)
Vfb(2)
Vfb(1)
V Vfc(0) Vfc Vfa(2) Vfa(0)
fb
Vfb(0)
2023/12/11
电力系统分析 第八章 电力系统不对称故障的分析和计算
10
短路点故障相电流为
• (1) •
•
•
•
•
I f I fa I fa(1) I fa(2) I fa(0) 3 I fa(1)
•
V
fa (1)
电力系统不对称故障分析与计算及其程序设计

电力系统不对称故障分析与计算及其程序设计电力系统不对称故障是指系统中至少有一个相数不相等的故障,其中至少一个相与其他相之间的短路发生。
此类故障会产生较大的电流和较高的瞬态电压,对电力设备带来严重的损坏,并可能引发系统崩溃。
因此,对电力系统不对称故障进行准确的分析与计算,并进行相应的程序设计具有重要意义。
首先,对于电力系统的不对称故障分析,需要进行故障类型及位置的识别。
常见的不对称故障类型包括对地短路故障、对线短路故障和对相短路故障。
针对不同类型的故障,需要使用不同的分析方法和计算模型来进行准确的故障分析和计算。
对于不对称故障的计算,主要包括短路电流计算和瞬态电压计算两个方面。
短路电流计算是为了确定故障点附近电力设备的额定电流和相对短路电流,以便评估系统的稳定性,并为保护装置的选择提供参考。
瞬态电压计算是为了确定故障点附近的电力设备所受到的瞬态电压,以评估设备的耐受能力和选择适当的绝缘等级。
针对电力系统不对称故障的分析与计算,可以采用数值计算方法和仿真软件进行。
数值计算方法包括传统的对称分量法、复数隔离法和序列分解法等。
这些方法可以通过求解线性方程组和迭代计算等手段,得到故障前后系统的电压、电流等参数。
而仿真软件,如PSCAD、EMTP-RV等,能够通过建立系统拓扑模型和设备参数,模拟不对称故障并进行动态仿真分析,实现系统参数的精确计算和分析。
为了更好地进行电力系统不对称故障的分析与计算,需要进行相应的程序设计。
程序设计的关键是实现数值计算方法和仿真软件的算法流程,并配以友好的用户界面和可视化展示。
常用的程序设计语言包括C++、MATLAB等,通过编写相关的算法和模块,实现故障分析与计算的自动化和高效化。
程序设计的目标是提高计算速度和精度,减少人工操作的难度和错误。
总之,电力系统不对称故障的分析与计算是保障电力系统安全稳定运行的关键环节。
通过准确的分析与计算,可以评估系统的稳定性和设备的耐受能力,为保护装置的选择和系统运行的优化提供参考。
电力系统不对称故障的分析

电力系统不对称故障的分析电力系统不对称故障是指在三相电力系统中,其中一相发生了损坏或故障,导致系统中三相电压、电流、功率等参数不再保持对称。
不对称故障会导致电力系统运行不稳定,甚至造成设备损坏和系统瘫痪。
因此,对电力系统不对称故障的分析非常重要。
首先,对电力系统不对称故障进行分析需要进行故障现象的测量和记录。
可以通过测量故障相电压和电流、功率因素等参数来了解故障的具体情况。
同时,还可以记录故障发生时的系统状态和操作情况,为后续的故障分析提供依据。
其次,根据故障现象的测量和记录,初步判断故障的类型。
电力系统不对称故障可以分为单相短路故障、单相接地故障和线路不平衡故障等。
通过分析故障相电压和电流的变化规律,可以初步判断故障的类型。
然后,根据故障类型,进行故障点的定位。
故障点的定位可以通过测量故障传播速度和故障电流的方向来实现。
根据故障点位置的确定,可以进行局部化抢修和恢复供电,减少故障对系统的影响。
最后,进行故障原因分析。
故障原因分析是解决电力系统不对称故障的关键步骤,可以通过多种方法来实现。
例如,可以通过现场勘查、设备检测和故障模拟等方法来找出故障的具体原因。
同时,还可以利用故障记录仪、故障模拟软件等辅助工具,对故障进行仿真和分析。
在进行故障原因分析时,还需要考虑故障的影响范围、时间和条件等因素。
通过对故障原因的准确分析,可以采取相应的措施来防止和排除类似故障的再次发生。
综上所述,电力系统不对称故障的分析是一个复杂而重要的过程,需要对故障现象进行测量和记录,初步判断故障类型,进行故障点的定位,并最终进行故障原因分析。
通过准确的故障分析,可以及时恢复系统运行,确保电力系统的稳定和安全。
电力系统简单不对称故障的分析计算

Ia1 Va1
Ia2 Va2
Ia0 Va0
0
E
jX 1 Ia1 jX 2 Ia2
Va1 Va
2
jX 0 Ia0
Va
0
两相短路接地故障相电流
Ib
a 2 Ia1
aIa2
Ia0
a 2
X 2 aX 0 X 2 X 0
Ia1
3X
2 j 3(X 2 2( X 2 X 0 )
3Ia1
I
(2) f
Ib
Ic
3I a1
Ia1
E j( X 1 X 2 )
Ia2 Va1
Ia1 Va2 jX 2 Ia2
jX
2
Ia1
两相短路的电压
Va Vb
Va1 Va2 Va0 2Va1 j2 X 2 Ia1
a 2Va1
aVa2
Va0
Va1
1 2
Va
Vc
Vb
开关位置 1
绕组端点与外电路的连接 与外电路断开
2
与外电路接通
3
与外电路断开,但与励磁支路并联
变压器零序等值电路与外电路的联接
4.自耦变压器的零序阻抗及其等值电路
• 中性点直接接地的自耦变压器
中性点经电抗接地的自耦变压器
X X
I II
X I 3X n X II 3X
(1 n k12
k12 ) (k12
X2
1 2
( X d
X q)
无阻尼绕组 X 2 X d X q
• 发电机负序电抗近似估算值
有阻尼绕组 X 2 1.22 X d 无阻尼绕组 X2 1.45Xd
• 无确切数值,可取典型值
电机类型 电抗
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(四)向量图(假定阻抗为纯电抗 ):
参考相量: U ka1
U ka 0 I ka 0 Z 0 U ka 2 I ka 2 Z 2
I ka1
Z1 Z 2 Z 0
(1) Z1 Z
(3)短路点故障相电压等于零。 (4)若 Z0 Z 2 两非故障相电压的幅值总相 Z 等,相位差 u的大小决定于 0 Z2 Z0 0 60 180 如果 有 u Z2
(三)故障点电流电压向量关系(向量图):
先确定参考相量:
U fa1
可以直观的了 解三相电流、 电压的相对大 小和它们之间 的相位关系。
三、两相接地短路(bc相接地) (一)故障边界条件:
I fa 0,U fb U fc 0
转换为对称分量(a为基准相)
I fa (1) I fa (2) I fa (0) 0 U fa (1) U fa (2) U fa (0)
(四)向量图:
Ifc(2) Ifb(1) Ifc(1) Ifb(2)
Ufc(0) Ufc Ufc(2) Ifa(1) Ifa(2) Ifa
Ufa(0)
Ufa(1)
Ufb(1) Ufb Ufb(0) Ufb(2)
电流相量图
电压相量图
(五)基本特点:
(1)短路点各序电流大小相等,方向相同。 (2)短路点正序电流大小与短路点原正序网络上 (1) Z 2 Z0 而发生三相短路 增加一个附加阻抗 Z 时的电流相等: E a1 E a1
3
1 k 0
3
k
0
0
I
kb
I kc 3 I k
k0 1
I kb
I kc
I
3
k
k
0
3 3 I kb I kc 2 I k
U
U
U
ka1
j x 1 I ka 0 ka1 U ka1 U ka 0
U ka2 U ka0
二. 两相短路
(一)故障边界条件:
0, I I , I fa fb fc U U fb fc
转换为对称分量(a为基准相):
I fa (1) I fa ( 2) 0 U fa (1) U fa ( 2)
I fa (0) 0
I ka1
E a1 E a1 (2) Z1 Z 2 Z1 Z
(5)短路点两故障相电压总是相等,数值上为非故障相电压的一 半,相位上总是与非故障相电压方向相反。
令
x 0 k0
x
2
I kb I kc 3
1 k 1 k
0 0
2
1 2 k 0 I k
I fa1
U
(0) fa
j ( X ff (1) X ff (2) X ff (0) )
I fa 2 I fa 0
(二)复合序网
I fa (1)
(三)短路点电气量
jX ff (1)
+ -
I fa (1)
V fa (1)
(0) U f j ( X ff (1) X ff (2) X ff (0) )
2
I fa (1)
3U U fa fa (1) j
3 X ff (2) X ff (0) X ff (2) X ff (0)
I fa (1)
(四)向量图(假定阻抗为纯电抗):
参考相量: U fa (1)
X ff (0) X ff (2)
(四)两相经阻抗短路
1.方法一:
(二)复合序网
I fa (1)
(三)短路点电气量
jX ff (1)
+ -
I fa (1)
V fa (1)
(0) U f j ( X ff (1) X ff (2) )
(0) V f
I fa (2) I fa (1)
I fa (2)
U fa (1) U fa (2) jX ff (2) I fa (2) jX ff (2) I fa (1)
(一)故障边界条件:
U fa 0, I fb I fc 0
转换为对称分量(a为基准相),如下:
U fa U fa1 U fa 2 U fa 0 0
2 I fb I fa 0 a I fa1 a I fa 2 2 I I a I a I fa 2 fc fa 0 fa 1
I fa (1)
+
+
E eq
Z ff (2)
I fa (2)
U fa (1)
-
+
U fa (2)
-
Z ff (0)
I fa (0)
根据边界条件写出另外三个方 程式。
+
U fa (0)
-
系统各序等值电路
一、单相接地短路(a相)
a b c
I
fa
f (1)
I
fb
I
fc
(0) V f
I fa (2) I fa (0)
I fa (2)
U fa (0) jX ff (0) I fa (0) jX ff (0) I fa (1) U fa (2) jX ff (2) I fa (2) jX ff (2) I fa (1) U fa (1) U
E a1 Z1 Z 2 Z f
U ka 2 I ka 2 Z 2 I ka1 Z 2 U ka1 U ka 2 I ka1 Z f I ka1 ( Z 2 Z f )
2. 方法二:
K’故障边界条件为:
I ka 0, I kb I kc U k 'b I k ' c
2 2 I j a a X a 1 X ff (2) ff (0) fa (1) 2 aU U a U fa (2) U fc fa (1) fa (0) 2 j a a X a 1 X I ff (2) ff (0) fa (1)
I fa 0,U fb U fc 0
转换为对称分量(a为基准相)
I fa (1) I fa (2) I fa (0) 0 U fa (1) U fa (2) U fa (0)
1 U fa 3
I ka1 I ka 2
jX I E U eq ff (1) fa (1) fa (1) 0 jX ff (2) I fa (2) U fa (2) 0 jX ff (0) I fa (0) U fa (0)
3个方程式,6个未知量。?
Z ff (1)
I fb I fc I
(1,1) f
2 X ff (2) aX ff (0) a I fa (1) X ff (2) X ff (0) X ff (2) a 2 X ff (0) a I fa (1) X ff (2) X ff (0) I fb 3 1 X ff (2) X ff (0) ( X ff (2) X ff (0) )
I ka 0 0, I ka1 I ka 2 U k 'a1 I k 'a 2
在K点发生的两相短路可等 值的看成是在K’点发生的 两相金属性短路。
(五) 两相短路的基本特点:
(1)短路电压电流中不存在零序分量; (2)两故障相中的短路电流的绝对值相等,方向相反, 数值上为正序电流的 3 倍; (3)当在远离发电机的地方发生两相短路时,可通过对序网 进行三相短路计算来近似求两相短路的电流; (4)两相短路时的正序电流在数值上与在短路点加一个附加阻 (2) Z 抗 构成一个增广正序网而发生三相短路时的电流相等。即
3U fa1
ka
fa 0
x x x x x x
2 1 1 2
0
0
x 2 x 0
3U fa
1 2 k 0
k
0
k0 0
k
0
1
0 U U U
ka
ka 0
3 ka U ka 0 U k0 2 3 非故障相电压升高 2 倍,比单相接地小。
故障点边界条件:
I ka 0, I kb I kc U kb U kc I kb Z f
转换为对称分量:
I ka 0 0, I ka1 I ka 2 U ka1 U ka 2 I ka1 Z f
三、两相接地短路(bc相接地) (一)故障边界条件:
2 2 (a a) I fa1 (a a ) I fa 2 2 0 I fa 0 (a a) I fa1
1 I fa1 I fa 2 I fa 0 3 I fa U fa1 U fa 2 U fa 0 0
第八章 电力系统不对称故障的 分析和计算
内容
8-1 简单不对称短路的分析
概述:
简单不对称故障: 仅在一处发生短路或断线的故障。可分为二类: (1)横向不对称故障:两相短路、单相接地短路、 两相接地短路;其特点为由系统网络中的某一点( 节点)和公共参考点(接地点)构成故障端口。 (2)纵向不对称故障:一相断线、二相断线;其特 点为由电力网络中的两个高电位点之间构成故障端 口。 分析方法: (1)解析法:联立求解三序网络方程和故障边界条 件方程; (2)借助于复合序网进行求解。
