九年级相似三角形综合练习题附答案】
初三相似三角形练习题及答案

初三相似三角形练习题及答案相似三角形是初中数学中一个重要的概念,它在几何形状比较相似的情况下,能够帮助我们快速推导出一些性质和结果。
为了帮助同学们更好地掌握相似三角形的相关知识,下面给出一些练习题及其详细答案,希望能够对大家的学习有所帮助。
1. 如图,已知△ABC与△ADE相似,其中∠B=∠D=90°,AB=10cm,BC=15cm,DE=6cm,求AD和AC的长度。
解析:由于∠B=∠D=90°,所以△ABC与△ADE是直角三角形。
根据直角三角形的性质,我们知道在两个直角三角形中,如果一个角相等,那么它们就是相似三角形。
因此,△ABC与△ADE相似。
根据相似三角形的定义,我们知道相似三角形的对应边的比例相等。
所以我们可以列出比例方程:AB/AD = BC/DE代入已知的数值,得到:10/AD = 15/6进一步计算,可以得到:AD = (10 * 6) / 15 = 4cm同理,我们可以使用相似三角形的对应边比例相等的性质,求解出AC的长度。
列出比例方程:AB/AC = BC/AE10/AC = 15/AD代入AD = 4cm,可以得到:10/AC = 15/4进一步计算,得到:AC = (10 * 4) / 15 = 8/3 cm所以,AD的长度为4cm,AC的长度为8/3 cm。
2. 如图,已知△PQR与△XYZ相似,PR = 12cm,YZ = 6cm,PQ = 9cm,求XZ的长度。
解析:根据相似三角形的性质,我们可以列出比例方程:PQ/PX = QR/XZ代入已知数值,得到:9/PX = 12/XZ进一步计算,得到:PX * XZ = 9 * 12PX * XZ = 108根据已知条件,我们可以得到两个三角形的一对边已知,它们分别是PR和YZ,由于两个三角形相似,我们可以列出另一个比例方程:PR/YZ = PQ/XZ12/6 = 9/XZ进一步计算,得到:2 = 9/XZ解方程,可以得到:XZ = 9/2 = 4.5cm所以,XZ的长度为4.5cm。
(完整word版)九年级数学相似三角形综合练习题及答案

九年级数学相似三角形综合练习题及答案1填空(本题14 分)(1 )若a=8cm , b=6cm , c=4cm ,贝U a 、b 、c 的第四比例项 d= ; a 、c 的比例中项 x=_。
(2) (2 x):x x:(1 x)。
贝U x= _______________ 。
(3) _______________________________________________________________ 在比例尺为1: 10000的地图上,距离为 3cm 的两地实际距离为 _________________________________ 公里。
(4) _______________________________ 圆的周长与其直径的比为 。
a 5 a b(5 )右,贝V= 。
b 3 b(6) 若 a :b : c=1 : 2: 3, 且 a bc 6,贝U a= ________ , b= ______ , c= _______ 。
ABACBC3CE(7) 如图 1, -- —— --- -,则(1)——(2)若 BD=10cm ,则 AD= cm 。
ADAE DE 2BC ,AB16cm ,则△ ABC 的周长为 (8)若点AEABc是线段AB的黄金分割点,且AC CB ,竺AC2•选择题 (1) 根据 A . 0 B .(2) 若线段bA.- d d C.—c(本题 9分)ab=cd ,共可写出以a 为第四比例项的比例式的个数是(1 C .2 D . 3a 、b 、c 、d 成比例,则下列各式中一定能成立的是(d b bC . DB AB ADEC AC AEBC DB ECECAB ACa3•已知:即3。
求(1)严3;;(2)愛。
(本题10分)4.若x: y:z=2: 7:5, x 2y 3z 6,求的值。
(本题6 分)za c e 25.已知:& d f 3,且2b d 5f 18。
九年级数学相似三角形练习题及答案

相似三角形练习题1、如图,当四边形PABN 的周长最小时,a =.2、如图,等腰三角形 ABC 的边AB 长为2 ,DE 是它的中位线,那么下面四个结论: 〔1〕DE=1,〔2〕CDE ∆~CAB ∆,(3)CDE ∆的面积与CAB ∆面积之比为1:4,其中正确的有〔 〕A 、0个B 、1个C 、2个D 、3个 3、如图〔3〕,等腰ABC ∆中,底边BC=a ,A ∠=036,ABC ∠的平分线交AC 于D ,BCD ∠的512k -=,那么DE=( ) A 、2K a B 、3K a C 、2akD 、3a k4、:ABC ∆与DFE ∆相似且面积比为4:25,那么ABC ∆与DFE ∆的相似比为。
5、〔2021年滨州〕如下图,给出以下条件: ①B ACD ∠=∠;②ADC ACB ∠=∠;③AC AB CD BC=;④2AC AD AB =. 其中单独能够判定ABC ACD △∽△的个数为〔 〕 A .1B .2C .3D .4〔5题图〕〔6题图〕6、2021年XX 市)如图,AB CD EF ∥∥,那么以下结论正确的选项是〔 〕 A .AD BCDF CE=B .BC DFCE AD=C .CD BCEF BE=D .CD ADEF AF=7、(2021XX)△ABC ∽△DEF ,且AB :DE=1:2,那么△ABC 的面积与△DEF 的面积之比为 (A)1:2 (B)1:4 (C)2:1 (D)4:18、〔2021XX 綦江〕假设△ABC ∽△DEF, △ABC 与△DEF 的相似比为1∶2,那么△ABC 与△DEF 的周长比为〔 〕 A .1∶4B .1∶2C .2∶1D 2y P (a ,0) N (a +2,A (1,-3)〔1题图〕 B (4,-1)O9、〔2021年XX 市〕如果一个直角三角形的两条边长分别是6和8,另一个与它相似的直角三角形边长分别是3和4及x ,那么x 的值〔 〕 A .只有1个 B .可以有2个 C .有2个以上但有限 D .有无数个10、(2021年XX 市〕如图,菱形ABCD 中,对角线AC 、BD 相交于点O ,M 、N 分别是边AB 、AD 的中点,连接OM 、ON 、MN ,那么以下表达正确的选项是〔 〕A .△AOM 和△AON 都是等边三角形B .四边形MBON 和四边形MODN 都是菱形C .四边形AMON 与四边形ABCD 是位似图形 D .四边形MBCO 和四边形NDCO 都是等腰梯形11、〔2021年XX 省〕如图,在55 方格纸中,将图①中的三角形甲平移到图② 中所示的位置,与三角形乙拼成一个矩形,那么,下面的平 移方法中,正确的选项是〔 〕 A .先向下平移3格,再向右平移1格 B .先向下平移2格,再向右平移1格 C .先向下平移2格,再向右平移2格 D .先向下平移3格,再向右平移2格(11题图)〔13题图〕12、(2021年义乌)在中华经典美文阅读中,小明同学发现自己的一本书的宽与长之比为黄金比。
九年级相似三角形综合练习题附答案】

相似三角形综合练习题一、填空题:1. 已知a ba b+-=2295,则a b:=__________2. 若三角形三边之比为3:5:7,与它相似的三角形的最长边是21cm,则其余两边之和是__________cm3. 如图,△ABC中,D、E分别是AB、AC的中点,BC=6,则DE=__________;△ADE与△ABC的面积之比为:__________。
4. 已知线段a=4cm,b=9cm,则线段a、b的比例中项c为__________cm。
5. 在△ABC中,点D、E分别在边AB、AC上,DE∥BC,如果AD=8,DB=6,EC=9,那么AE=__________6. 已知三个数1,2,3,请你添上一个数,使它能构成一个比例式,则这个数是__________7. 如图,在梯形ABCD中,AD∥BC,EF∥BC,若AD=12cm,BC=18cm,AE:EB=2:3,则EF=__________8. 如图,在梯形ABCD中,AD∥BC,∠A=90°,BD⊥CD,AD=6,BC=10,则梯形的面积为:__________二、选择题:1. 如果两个相似三角形对应边的比是3:4,那么它们的对应高的比是__________A. 9:16B. 3:2C. 3:4D. 3:72. 在比例尺为1:m的某市地图上,规划出长a厘米,宽b厘米的矩形工业园区,该园区的实际面积是__________米2A. 104mabB.1042mabC.abm104D.abm24103. 已知,如图,DE∥BC,EF∥AB,则下列结论:①AEECBEFC=②ADBFABBC=③EFABDEBC=④CECFEABF=其中正确的比例式的个数是__________A. 4个B. 3个C. 2个D. 1个4. 如图,在△ABC中,AB=24,AC=18,D是AC上一点,AD=12,在AB上取一点E,使A、D、E三点为顶点组成的三角形与△ABC相似,则AE的长是__________A. 16B. 14C. 16或14D. 16或95. 如图,在Rt△ABC中,∠BAC=90°,D是BC的中点,AE⊥AD,交CB的延长线于点E,则下列结论正确的是__________A. △AED∽△ACBB. △AEB∽△ACDC. △BAE∽△ACED. △AEC∽△DAC三、解答题:1. 如图,AD∥EG∥BC,AD=6,BC=9,AE:AB=2:3,求GF的长。
2023年中考九年级数学高频考点拔高训练--相似三角形的综合题

2023年中考九年级数学高频考点拔高训练--相似三角形的综合题1.如图1,直线y=﹣43x+8,与x轴、y轴分别交于点A、C,以AC为对角线作矩形OABC,点P、Q分别为射线OC、射线AC上的动点,且有AQ=2CP,连结PQ,设点P的坐标为P(0,t).(1)求点B的坐标.(2)若t=1时,连接BQ,求△ABQ的面积.(3)如图2,以PQ为直径作△I,记△I与射线AC的另一个交点为E.①若PEPQ=35,求此时t的值.②若圆心I在△ABC内部(不包含边上),则此时t的取值范围为是多少?2.如图,在Rt△ABC中,△ACB=90°,AC=8cm,BC=6cm,点P沿AB边从点A开始以2cm/s的速度向点B运动,点Q沿CB边从点C开始以1cm/s的速度向点B运动,P、Q同时出发,用t (s)表示运动的时间(0≤t≤5).(1)当t为何值时,以P、Q、B为顶点的三角形与△ABC相似.(2)分别过点A,B作直线CP的垂线,垂足为D,E,设AD+BE=y,求y与t的函数关系式;并求当t为何值时,y有最大值.(3)直接写出PQ中点移动的路径长度.3.如图,在矩形ABCD中,以AB的中点O为圆心,以OA为半径作半圆,连接OD交半圆于点E,在BE⌢上取点F,使EF⌢=AE⌢,连接BF,DF.(1)求证:DF与半圆相切;(2)如果AB=10,BF=6,求矩形ABCD的面积.4.如图,已知MN//BC,A是MN上一点,AM=AN,MC交AB于D,NB交AC于E,连接DE.(1)求证:DE//BC;(2)设MC与BN的交点为点G,如果DE=1,BC=4,求C△MGNC△CGB的值.5.已知:如图,在四边形ABCD中,AD△BC,△C=90°,AB=AD=50,BC=64,连结BD,AE△BD 垂足为E,(1)求证:△ABE△△DCB;(2)求线段DC的长.6.在▱ABCD中,E是DC的中点,连接AE并延长,交BC的延长线于点F.(1)求证:BC=CF;(2)点G是CF上一点,连接AG交CD于点H,且∠DAF=∠GAF.若CG=2,GF=5,求AН的长.7.已知直线m△n,点C是直线m上一点,点D是直线n上一点,CD与直线m、n不垂直,点P 为线段CD的中点.(1)操作发现:直线l△m,l△n,垂足分别为A、B,当点A与点C重合时(如图①所示),连接PB,请直接写出线段PA与PB的数量关系:;(2)猜想证明:在图①的情况下,把直线l向上平移到如图②的位置,试问(1)中的PA与PB的关系式是否仍然成立?若成立,请证明;若不成立,请说明理由;(3)延伸探究:在图②的情况下,把直线l绕点A旋转,使得△APB=90°(如图③所示),若两平行线m、n之间的距离为2k.求证:PA•PB=k•AB.8.如图,在平面直角坐标系中,直线y=kx+3与x轴、y轴分别交于A,B两点. 抛物线y=−14x2+32x经过点A,且交线段AB于点C,BC=√5.(1)求k的值.(2)求点c的坐标.(3)向左平移抛物线,使得抛物线再次经过点C,求平移后抛物线的函数解析式.9.如图,在△ABCD中,点G是对角线AC上一点,DE垂直平分CG,交GC于点O,交BC于点E,作GF△AD交DE于点F,连接FC.(1)求证:四边形GFCE是菱形;(2)点H为线段AO上一点,连接HD,HF,当△1=△2时,若AD=6,CF=2,求AH•CH的值.10.如图,已知直线y=12x+1与y轴交于点A,与x轴交于点D,抛物线y=ax2+bx+c与直线交于A,E两点,与x轴交于B(1,0),C(2,0)两点.(1)求该抛物线的解析式;(2)动点P在x轴上移动,当△PAE是直角三角形时,请通过计算写出一个满足条件点P的坐标.11.Rt△ABC在直角坐标系内的位置如图所示,反比例函数y=k x(k≠0)在第一象限内的图象与BC边交于点D(4,m),与AB交于点E(2,n)(1)求m与n的数量关系.(2)当tan∠BAC=12时,记△BDE面积为S,用含有k的式子表示S.(3)若△BDE的面积为2.设P是线段AB边上的点,在(2)的条件下,是否存在点P,以B,C,P为顶点的三角形与△EDB相似?若存在,求出此时点P的坐标;若不存在,请说明理由. 12.将抛物线C:y=(x﹣1)2向下平移4个单位长度得到抛物线C1,再将抛物线C1向左平移1个单位长度得到抛物线C2.(1)直接写出抛物线C1,C2的解析式;(2)如图(1),抛物线C1 与x轴交于A,B两点,与y轴交于C点,且D为第四象限抛物线上一点,连接AD,BC交于点E,连接BD,记△BDE的面积为S1,△ABE的面积为S2,求S1 S2的最大值;(3)如图(2),直线y=kx(k≠0,k为常数)与抛物线C2交于E,F两点,M为线段EF的中点;直线y=−4k x与抛物线C2交于G,H两点,N为线段GH的中点.求证:直线MN经过一个定点.13.如图,点E是矩形ABCD的边BC的中点,连接DE交AC于点F。
初三数学相似三角形测试题及答案

初三数学相似三角形测试题及答案1、若b m m a 2,3==,则_____:=b a 。
2、已知653z y x ==,且623+=z y ,则__________,==y x 。
3、在等腰Rt △ABC 中,斜边长为c ,斜边上的中线长为m ,则______:=c m . 4、反向延长线段AB 至C ,使2AC =AB ,那么BC :AB = 。
5、△ABC ∽△A ′B ′C ′,相似比为3:2,它们周长的差为40厘米,则△A ′B ′C ′的周长为 厘米。
7、如图,△ABC 中,∠ACB =90°,CD ⊥AB 于D ,若∠A =30°,则BD :BC = 。
若BC =6,AB =10,则BD = ,CD = 。
8、如图,梯形ABCD 中,DC ∥AB ,DC =2cm ,AB =3。
5cm,且MN ∥PQ ∥AB , DM =MP =PA,则MN = ,PQ = 。
9、如图,四边形ADEF 为菱形,且AB =14,BC =12,AC =10,那BE = 。
10、梯形的上底长1.2厘米,下底长1.8厘米,高1厘米,延长两腰后与下底所成的三角形的高为 厘米。
11、下面四组线段中,不能成比例的是( )A 、4,2,6,3====d c b aB 、3,6,2,1====d c b aC 、10,5,6,4====d c b aD 、32,15,5,2====d c b a12、等边三角形的中线与中位线长的比值是( )A 、1:3B 、2:3C 、23:21 D 、1:3CB DAD C NPN QAB14、已知直角三角形三边分别为b a b a a 2,,++,()0,0>>b a ,则=b a :( ) A 、1:3 B 、1:4 C 、2:1 D 、3:115、△ABC 中,AB =12,BC =18,CA =24,另一个和它相似的三角形最长的一边是36,则最短的一边是( ) A 、27 B 、12 C 、18 D 、20 16、已知c b a ,,是△ABC 的三条边,对应高分别为cb a h h h ,,,且6:5:4::=c b a ,那么cb a h h h ::等于( )A 、4:5:6 B 、6:5:4 C 、15:12:10 D 、10:12:1517、一个三角形三边长之比为4:5:6,三边中点连线组成的三角形的周长为30cm ,则原三角形最大边长为( ) A 、44厘米 B 、40厘米 C 、36厘米 D 、24厘米 18、下列判断正确的是( )A 、不全等的三角形一定不是相似三角形B 、不相似的三角形一定不是全等三角形C 、相似三角形一定不是全等三角形D 、全等三角形不一定是相似三角形19、如图,△ABC 中,AB =AC ,AD 是高,EF ∥BC ,则图中与△ADC 相似的三角形共有( ) A 、1个 B 、2个 C 、3个 D 、多于3个20、如图,在平行四边形ABCD 中,E 为BC 边上的点,若BE :EC =4:5,AE 交BD 于F ,则BF :FD 等于( ) A 、4:5 B 、3:5 C 、4:9 D 、3:821、已知()3:2:=-y y x ,求y x yx 2352-+的值。
人教九下数学 第27章 相似三角形的判定及有关性质综合测试(含答案)

人教九下数学 第27章 相似三角形的判定及有关性质综合测试(含答案)一、选择题(每小题6分,共48分)1.在△ABC 中,D 、F 是AB 上的点,E 、H 是AC 上的点,直线DE//FH//BC ,且DE 、FH 将△ABC 分成面积相等的三部分,若线段FH=65,则BC 的长为( ) A .15 B .10 C.6215 D .15322.在△ABC 中,DE//BC ,DE 交AB 于D ,交AC 于E ,且S △ADE :S 四边形DBCE=1:2,则梯形的高与三角形的边BC 上的高的比为( )A .1:2B .1:)12(-C .1:)13(-D .)13(-:33.在Rt △ABC 中,∠C=90°,CD 是斜边AB 上的高,AC=5,BC=8,则S △ACD :S △CBD 为( ) A .85B .6425 C .3925 D .8925 4.如图1—5—1,D 、E 、F 是△ABC 的三边中点,设△DEF 的面积为4,△ABC 的周长为9,则△DEF 的周长与△ABC 的面积分别是( )A.29,16 B. 9,4 C. 29,8 D. 49,165.如图1—5—2,在△ABC 中,AD ⊥BC 于D ,下列条件:(1)∠B+∠DAC=90°;(2)∠B=∠DAC ; (3)ABAC AD CD =;(4)AB 2=BD ·BC 。
其中一定能够判定△ABC 是直角三角形的共有( ) A .3个B .2个C .1个D .0个6.如图1—5—3,在正三角形ABC 中,D ,E 分别在AC ,AB 上,且31AC AD =,AE=BE ,则有( )A. △AED ∽△BED B .△AED ∽△CBD C. △AED ∽△ABD D .△BAD ∽△BCD7.如图1—5—4,PQ//RS//AC ,RS=6,PQ=9,SC 31QC =,则AB 等于( ) A. 415B. 436C. 217D. 58.如图1—5—5,平行四边形ABCD 中,O 1、O 2、O 3是BD 的四等分点,连接AO 1,并延长交BC 于E ,连接EO 2,并延长交AD 于F ,则FDAD等于( )A .3:1B .3:1C .3:2 D. 7:39.如果一个三角形的一条高分这个三角形为两个相似三角形,那么这个三角形必是( ) A .等腰三角形 B. 任意三角形C .直角三角形D .直角三角形或等腰三角形10.在△ABC 和△A'B'C'中,AB : AC=A'B':A'C',∠B=∠B',则这两个三角形( ) A .相似,但不全等 B .全等C .一定相似D .无法判断是否相似11.如图1—6—1,正方形ABCD 中,E 是AB 上的任一点,作EF ⊥BD 于F ,则BEEF为( )A .22B .21C .36D .2图1—6—112.如图1—6—2,把△ABC 沿边AB 平移到△A'B'C'的位置,它们的重叠部分(图中阴影部分)的面积是△ABC 的面积的一半,若2AB =,则此三角形移动的距离AA'是( )A .12-B .22C .1D .21 图1—6—213.如图1—6—3,在四边形ABCD 中,∠A=135°,∠B=∠D=90°,BC=32,AD=2,则四边形ABCD 的面积是( )A .24B .34C .4D .6 图1—6—314.如图1—6—4,平行四边形ABCD 中,G 是BC 延长线上一点,AG 与BD 交于点E ,与DC 交于点F ,则图中相似三角形共有( )A .3对B .4对C .5对D .6对15.在直角三角形中,斜边上的高为6cm ,且把斜边分成3:2两段,则斜边上的中线的长为( )A.265cm B .64cm C .65cmD .325cm16.AD 为Rt △ABC 斜边BC 上的高,作DE ⊥AC 于E ,45AC AB =,则EACE=( ) A .2516 B .54C .45D .162517.如图1—6—5,△ABC 中,AB=AC ,∠A=36°,BD 平分∠ABC ,已知AB=m ,BC=n ,求CD 的长。
浙教版数学九年级上册 第四章 相似三角形 单元练习(含答案)

浙教版数学九年级上册第四章相似三角形一、选择题1.如果2a =5b ,那么下列比例式中正确的是( )A .a b =25B .a 5=2b C .a 2=b 5D .a 5=b 22.如图,直线l 1∥l 2∥l 3,AC =6,DE =3,EF =2,则AB 的长为( )A .3B .125C .165D .1853.如图,点P 是线段AB 的黄金分割点,且PA >PB ,若AB =2,则PA 的长度是( )A .5−1B .3−5C .25−4D .14.如图, 在▱ABCD 中, E 是边AB 上一点, 连结AC ,DE 相交于点F . 若AE EB =23,则 AF CF 等于( )A .13B .23C .25D .355.如图,小正方形的边长均为1,则图中三角形(阴影部分)与△ABC 相似的是( )A .B .C.D.6.△ABC和△DEF是两个等边三角形,AB=2,DE=4,则△ABC与△DEF的面积比是( ) A.1:2B.1:4C.1:8D.1:27.如图,在△ABC中,BC=6,AC=8,∠C=90°,以B为圆心,BC长为半径画弧,与AB交于点D,再分别以点A,D为圆心,大于12AD的长为半径画弧,两弧交于点M,N,作直线MN,分别交AC,AB于点E,F,则AE的长度为( )A.52B.103C.3D.228.如图,△ABC和△A1B1C1是以点O为位似中心的位似图形,点A在线段O A1上,若OA:A A1=1:2,则△ABC和△A1B1C1的周长之比为( )A.1:2B.2:1C.1:3D.3:19.如图,在△ABC中,D为线段AC上一点,点E在AC的延长线上,过点D作DF∥AB交BC于点F,连结BE,EF,若A C2+D E2=A E2,则△BEF与△DCF的面积比为( )A.1:2B.1:3C.2:3D.2:510.如图,矩形ABCD中,AB=4,AD=2,E为边AD上一个动点,连接BE,取BE的中点G,点G绕点E逆时针旋转90°得到点F,连接CF,则△CEF面积的最小值是( )A .4B .154C .3D .114二、填空题11.如图,AC 、BD 交于点O ,连接AB 、CD ,若要使△AOB ∽△COD ,可以添加条件 .(只需写出一个条件即可)12.已知△ABC ∽△DEF ,且AB:DE =1:3,△ABC 与△DEF 的周长比是 .13.如图,在这架小提琴中,点C 是线段AB 的黄金分割点(BC >AC ).若AB =60cm ,则BC = cm .14.如图,在Rt △ABC 中,∠ABC =90°,AB =4,AC =5,AE 平分∠BAC ,点D 是AC 的中点,AE 与BD交于点O ,则的值AOOE .15.如图,矩形ABCD 中,AB =3 6 ,BC =12,E 为AD 中点,F 为AB 上一点,将△AEF 沿EF 折叠后,点A 恰好落到CF 上的点G 处,则折痕EF 的长是 .16.如图,正方形ABCD 中,BF =FG =CG ,BE =2AE ,CE 交DF 、DG 于M 、N 两点,有下列结论:①DF ⊥EC ;②S △MFC =59S 四边形MFBE ;③DM :MF =2:1;④MN NC =913.其中,正确的有 .三、解答题17.(1)已知线段a =2,b =6,求线段a ,b 的比例中项线段c 的长.(2)已知x :y =3:2,求2x−yx的值.18.如图,已知D 、E 分别是△ABC 的边AB 、AC 上的点,DE ∥BC ,AD BD =32,求DE BC 的值.19.如图,AD 、BC 相交于点P ,连接AC 、BD ,且∠1=∠2,AC =6,CP =4,DP =2,求BD 的长.20. 如图,在平行四边形ABCD 中,E 为DC 边上一点,∠EAB =∠EBC .(1)求证:△ABE∽△BEC ;(2)若AB=4,DE=3,求BE的长.21.如图,在四边形ABCD中,OA=OC,OB=OD,AB=BC,AC=12,BD=16.(1)求证:四边形ABCD时菱形;(2)延长BC至点M,连接OM交CD于点N,若∠M=12∠BAC,求MNOM.22.如图,AB∥CD,且AB=2CD,E是AB的中点,F是边BC上的动点(F不与B,C重合),EF与BD相交于点M.(1)求证:△FDM∽△FBM;(2)若F是BC的中点,BD=18,求BM的长;(3)若AD=BC,BD平分∠ABC,点P是线段BD上的动点,是否存在点P使DP⋅BP=BF⋅CD,若存在,求出∠CPF的度数;若不存在,请说明理由.23.如图,在平面直角坐标系中,已知抛物线y=12x2+bx+c与x轴交于A、B两点,与y轴交于C点,且OB=OC=4.(1)求抛物线的解析式;(2)在抛物线上是否存在点M,使∠ABC=∠BCM,如果存在,求M点的坐标,如果不存在,说明理由;(3)若D是抛物线第二象限上一动点,过点D作DF⊥x轴于点F,过点A、B、D的圆与DF交于E点,求△ABE的面积.答案解析部分1.【答案】D2.【答案】D3.【答案】A4.【答案】C5.【答案】B6.【答案】B7.【答案】A8.【答案】C9.【答案】A10.【答案】B11.【答案】∠A=∠C(答案不唯一)12.【答案】1:313.【答案】(305−30)14.【答案】9415.【答案】21516.【答案】①④17.【答案】(1)解:∵线段a=2,b=6,线段c是线段a、b的比例中项,∴c2=ab=12,∴c=23(负值舍去);(2)解:∵x:y=3:2,∴可设x=3k,y=2k(k≠0),∴2x−yx=6k−2k3k=43.18.【答案】3519.【答案】BD=320.【答案】(1)证明:∵平行四边形ABCD,∴AB//CD,∴∠EBA=∠BEC,又∵∠EAB=∠EBC,∴△ABE∽△BEC.(2)解:∵四边形ABCD 平行四边形,∴AB =DC =4,∵DE =3,∴CE =1,∵△ABE∽△BEC ,∴AB EB =EBEC,∴AB ⋅CE =B E 2=4×1=4,∴BE =2.21.【答案】(1)证明:∵ 在四边形ABCD 中,OA=OC ,OB=OD∴ 四边形ABCD 是平行四边形 ∵ AB=BC∴ 平行四边形ABCD 是菱形。
完整版)九年级数学相似三角形综合练习题及答案

完整版)九年级数学相似三角形综合练习题及答案1.填空题:1) 若$a=8$cm,$b=6$cm,$c=4$cm,则$a$、$b$、$c$的第四比例项$d=\underline{12}$;$a$、$c$的比例中项$x=\underline{5}$。
2) $(2-x):x=x:(1-x)$。
则$x=\underline{1}$。
3) 在比例尺为1:的地图上,距离为3cm的两地实际距离为\underline{30}公里。
4) 圆的周长与其直径的比为\underline{$\pi$}。
5) $\frac{a^5-ab}{b^3}=\frac{a^4}{b^2}$,则$\frac{a}{b}=\underline{a^2}$。
6) 若$a:b:c=1:2:3$,且$a-b+c=6$,则$a=\underline{2}$,$b=\underline{1}$,$c=\underline{3}$。
7) 如图1,则$\frac{AB}{AC}=\frac{BC}{CE}=\underline{\frac{3}{2}}$;若$BD=10$cm,则$AD=\underline{6}$cm;若$\triangle ADE$的周长为16cm,则$\triangle ABC$的周长为\underline{24}cm。
8) 若点$c$是线段$AB$的黄金分割点,且$AC>CB$,则$\frac{AC}{AB}=\underline{\frac{1+\sqrt{5}}{2}}$,$\frac{CB}{AB}=\underline{\frac{\sqrt{5}-1}{2}}$。
2.选择题:1) 根据$ab=cd$,共可写出以$a$为第四比例项的比例式的个数是()A.$1$,B.$2$,C.$3$,D.$4$。
答案:B。
2) 若线段$a$、$b$、$c$、$d$成比例,则下列各式中一定能成立的是()A.$abcd=1$,B.$a+b=c+d$,C.$\frac{a}{b}=\frac{c}{d}$,D.$a^2+b^2=c^2+d^2$。
初三数学相似三角形典例及练习题含答案

初三数学相似三角形典例及练习题含答案典例典例1已知三角形ABC中,∠B=90°,AC=6cm,BD垂直AC于D点,BD=3cm,求BC的长度。
解析:根据勾股定理可得:BC^2 = AB^2 + AC^2 = BD^2 + AD^2 + AC^2因为∆ABC与∆ABD相似,所以可以得到:\frac{AD}{AB}=\frac{AB}{AC}即:AD = \frac{AB^2}{AC}将公式代入原式中,得到:BC^2 = BD^2 + \frac{AB^4}{AC^2} + AC^2因为AC=6,BD=3,所以代入可得:BC^2 = 3^2 + \frac{AB^4}{6^2} + 6^2化简得:BC^2 = AB^4 \cdot \frac{1}{36} + 45AB^4 = 36(BC^2 - 45)因此,我们可以得到:AB = \sqrt[4]{36(BC^2 - 45)}典例2已知两个三角形ABC和DEF,且它们相似,已知AC=20cm,EF=12cm,AB=15cm,计算DE的长度。
解析:由于两个三角形相似,所以可以得到:\frac{AB}{DE}=\frac{AC}{EF}将已知条件带入即可得到:\frac{15}{DE}=\frac{20}{12}解得:DE = \frac{36}{4} = 9因此,DE的长度为9cm。
典例3已知三角形ABC和DEF相似,且AB=5cm,DE=2.5cm,BC=6cm,计算EF的长度。
解析:由于两个三角形相似,所以可以得到:\frac{AB}{DE}=\frac{BC}{EF}将已知条件带入即可得到:\frac{5}{2.5}=\frac{6}{EF}解得:EF = 12因此,EF的长度为12cm。
练习题练习题1已知三角形ABC中,∠B=90°,AB=3cm,AC=4cm,D、E、F分别是BC、AC、AB上的点,且∆DEF与∆ABC相似。
初三数学相似三角形经典题(含答案)

相似三角形经典习题例1 从下面这些三角形中,选出相似的三角形.例2 已知:如图,ABCD 中,2:1:=EB AE ,求AEF ∆与CDF ∆的周长的比,若是2cm 6=∆AEF S ,求CDF S ∆.例3 如图,已知ABD ∆∽ACE ∆,求证:ABC ∆∽ADE ∆.例4 以下命题中哪些是正确的,哪些是错误的?(1)所有的直角三角形都相似. (2)所有的等腰三角形都相似.(3)所有的等腰直角三角形都相似. (4)所有的等边三角形都相似.例5 如图,D 点是ABC ∆的边AC 上的一点,过D 点画线段DE ,使点E 在ABC ∆的边上,而且点D 、点E 和ABC ∆的一个极点组成的小三角形与ABC ∆相似.尽可能多地画出知足条件的图形,并说明线段DE 的画法.例6 如图,一人拿着一支刻有厘米分画的小尺,站在距电线杆约30米的地址,把手臂向前伸直,小尺竖直,看到尺上约12个分画恰好遮住电线杆,已知手臂长约60厘米,求电线杆的高.例7 如图,小明为了测量一高楼MN 的高,在离N 点20m 的A 处放了一个平面镜,小明沿NA 后退到C 点,正好从镜中看到楼顶M 点,假设5.1=AC m ,小明的眼睛离地面的高度为,请你帮忙小明计算一下楼房的高度(精准到).例8 格点图中的两个三角形是不是是相似三角形,说明理由.例9 依照以下各组条件,判定ABC ∆和C B A '''∆是不是相似,并说明理由:(1),cm 4,cm 5.2,cm 5.3===CA BC AB cm 28,cm 5.17,cm 5.24=''=''=''A C C B B A .(2)︒='∠︒='∠︒=∠︒=∠35,44,104,35A C B A .(3)︒='∠=''=''︒=∠==48,3.1,5.1,48,6.2,3B C B B A B BC AB .例10 如图,以下每一个图形中,存不存在相似的三角形,若是存在,把它们用字母表示出来,并简要说明识别的依照.例11 已知:如图,在ABC ∆中,BD A AC AB ,36,︒=∠=是角平分线,试利用三角形相似的关系说明AC DC AD ⋅=2.例12 已知ABC ∆的三边长别离为五、1二、13,与其相似的C B A '''∆的最大边长为26,求C B A '''∆的面积S .例13 在一次数学活动课上,教师让同窗们到操场上测量旗杆的高度,然后回来交流各自的测量方式.小芳的测量方式是:拿一根高米的竹竿直立在离旗杆27米的C 处(如图),然后沿BC 方向走到D 处,这时目测旗杆顶部A 与竹竿顶部E 恰好在同一直线上,又测得C 、D 两点的距离为3米,小芳的目高为米,如此即可明白旗杆的高.你以为这种测量方式是不是可行?请说明理由.例14.如图,为了估算河的宽度,咱们能够在河对岸选定一个目标作为点A ,再在河的这一边选点B 和C ,使BC AB ⊥,然后再选点E ,使BC EC ⊥,确信BC 与AE 的交点为D ,测得120=BD 米,60=DC 米,50=EC 米,你能求出两岸之间AB 的大致距离吗?例15.如图,为了求出海岛上的山峰AB 的高度,在D 和F 处树立标杆DC 和FE ,标杆的高都是3丈,相隔1000步(1步等于5尺),而且AB 、CD 和EF 在同一平面内,从标杆DC 退后123步的G 处,可看到山峰A 和标杆顶端C 在一直线上,从标杆FE 退后127步的H 处,可看到山峰A 和标杆顶端E 在一直线上.求山峰的高度AB 及它和标杆CD 的水平距离BD 各是多少?(古代问题)例16 如图,已知△ABC 的边AB =32,AC =2,BC 边上的高AD =3.(1)求BC 的长;(2)若是有一个正方形的边在AB 上,另外两个极点别离在AC ,BC 上,求那个正方形的面积.。
九年数学经典相似三角形练习题(附参考答案)

(3)若李华在点A朝着影子(如图箭头)的方向以v1匀速行走,试求他影子的顶端在地面上移动的速度v2.
27.如图①,分别以直角三角形ABC三边为直径向外作三个半圆,其面积分别用S1,S2,S3表示,则不难证明S1=S2+S3.
解答:
证明:∵FD∥AB,FE∥AC,
∴∠B=∠FDE,∠C=∠FED,
∴△ABC∽△FDE.
点评:
本题很简单,考查的是相似三角形的判定定理:
(1)如果两个三角形的两个角对应相等,那么这两个三角形相似;
(2)如果一个三角形的两条边和另一个三角形的两条边对应成比例,并且夹角相等,那么这两个三角形相似;
初中数学经典相似三角形练习题(附参考答案)
一.解答题(共30小题)
1.如图,在△ABC中,DE∥BC,EF∥AB,求证:△ADE∽△EFC.
2.如图,梯形ABCD中,AB∥CD,点F在BC上,连DF与AB的延长线交于点G.
(1)求证:△CDF∽△BGF;(2)当点F是BC的中点时,过F作EF∥CD交AD于点Байду номын сангаас,若AB=6cm,EF=4cm,求CD的长.
16.如图,∠ACB=∠ADC=90°,AC= ,AD=2.问当AB的长为多少时,这两个直角三角形相似.
17.已知,如图,在边长为a的正方形ABCD中,M是AD的中点,能否在边AB上找一点N(不含A、B),使得△CDM与△MAN相似?若能,请给出证明,若不能,请说明理由.
18.如图在△ABC中,∠C=90°,BC=8cm,AC=6cm,点Q从B出发,沿BC方向以2cm/s的速度移动,点P从C出发,沿CA方向以1cm/s的速度移动.若Q、P分别同时从B、C出发,试探究经过多少秒后,以点C、P、Q为顶点的三角形与△CBA相似?
27.2相似三角形综合训练练习人教版2024—2025学年九年级下册

27.2相似三角形综合训练练习人教版2024—2025学年九年级下册一、填空1.已知==,且a +b ﹣2c=6,则a 的值为2.如图,E 为▱ABCD 的边AB 延长线上的一点,且BE :AB=2:3,连接DE 交BC于点F ,则CF :AD= .3.如图,已知AB ∥CD ,AD 与BC 相交于点O .若=,AD=10,则AO= .4.如图,△ABC 中,点D 、E 分别在边AB 、BC 上,DE ∥AC .若BD=4,DA=2,BE=3,则EC= .5.如图,DE ∥AB ,AC=3AD ,S △ABC =5,则△CED 的面积是 .6.如图,∠B=∠ACD=90°,BC ∥AD ,若AC=6,AD=10,则AB= .7.两个相似三角形的最短边分别是5cm 和3cm ,它们的周长之差是12cm ,那么小三角形的周长为 .8.如图,在△ABC 中,点D 是边AB 上的一点,∠ADC=∠ACB ,AD=2,BD=6,则边AC 的长为9.如图,在平行四边形ABCD 中,点E 在边DC 上,DE :EC=3:1,连接AE 交BD 于点F ,则△DEF 的面积与△BAF 的面积之比为10.如图,AB ∥GH ∥CD ,点H 在BC 上,AC 与BD 交于点G ,AB=2,CD=3,则GH 的长为 .11.如图,梯形ABCD 中,AB ∥CD ,∠B=∠C=90°,点F 在BC 边上,AB=8,CD=2,BC=10,若△ABF 与△FCD 相似,则CF 的长为 .第2题第5题 第6题第8题第10题 第9题 第11题12.如图,△ABC 是等边三角形,被一平行于BC 的矩形所截,AB 被截成三等分,则图中阴影部分的面积是△ABC 的面积的 .13.如图所示,正方形ABCD 边长是2,BE=CE ,MN=1,线段MN 的端点M 、N 分别在CD 、AD 上滑动,当DM= 时,△ABE 与以D 、M 、N 为顶点的三角形相似.14.如图,在边长为10cm 的正方形ABCD 中,P 为AB 边上任意一点(P 不与A 、B 两点重合),连结DP ,过点P 作PE ⊥DP ,垂足为P ,交BC 于点E ,则BE 的最大长度为 cm .15.一块直角三角板ABC 按如图放置,顶点A 的坐标为(0,1),直角顶点C 的坐标为(﹣3,0),∠B=30°,则点B 的坐标为 .二、解答题1.如图,平行四边形ABCD ,AE ⊥BC 交点E ,连接DE ,F 为DE 上一点,且∠AFE=∠B=60°.(1)求证:△ADF ∽△DEC ;(2)若AE=3,AD=4,求EF 的长.第14题第13题 第12题2.如图,四边形ABCD是菱形,对角线AC,BD相交于点O,过点D作DH⊥AB于H,交AO于G,连接OH.(1)求证:AG•GO=HG•GD;(2)若AC=8,BD=6,求DG的长.3.如图,在平面直角坐标系中,二次函数y=(x﹣a)(x﹣3)(0<a<3)的图象与x轴交于点A、B(点A在点B的左侧),与y轴交于点D,过其顶点C作直线CP⊥x轴,垂足为点P,连接AD、BC.(1)求点A、B、D的坐标;(2)若△AOD与△BPC相似,求a的值;(3)点D、O、C、B能否在同一个圆上?若能,求出a的值;若不能,请说明理由.4.在平面直角坐标系中,二次函数y=ax2+x+c的图象经过点C(0,2)和点D(4,﹣2).点E是直线y=﹣x+2与二次函数图象在第一象限内的交点.(1)求二次函数的解析式及点E的坐标.(2)如图①,若点M是二次函数图象上的点,且在直线CE的上方,连接MC,OE,ME.求四边形COEM面积的最大值及此时点M的坐标.(3)如图②,经过A、B、C三点的圆交y轴于点F,求点F的坐标.5.如图,平面直角坐标系中,矩形OABC的顶点A、C分别在x轴和y轴的正半轴上,反比例函数y=在第一象限的图象分别交矩形OABC的边AB、BC边点于E、F,已知BE=2AE,四边形的OEBF的面积等于12.(1)求k的值;(2)若射线OE对应的函数关系式是y=,求线段EF的长;(3)在(2)的条件下,连结AC,试证明:EF∥AC.6.如图,正方形ABCD的边长为10,点E、F分别在边BC、CD上,且∠EAF=45°,AH⊥EF于点H,AH=10,连接BD,分别交AE、AH、AF于点P、G、Q.(1)求△CEF的周长;(2)若E是BC的中点,求证:CF=2DF;(3)连接QE,求证:AQ=EQ.。
部编数学九年级下册专项33相似三角形一线三等角模型综合应用(解析版)含答案
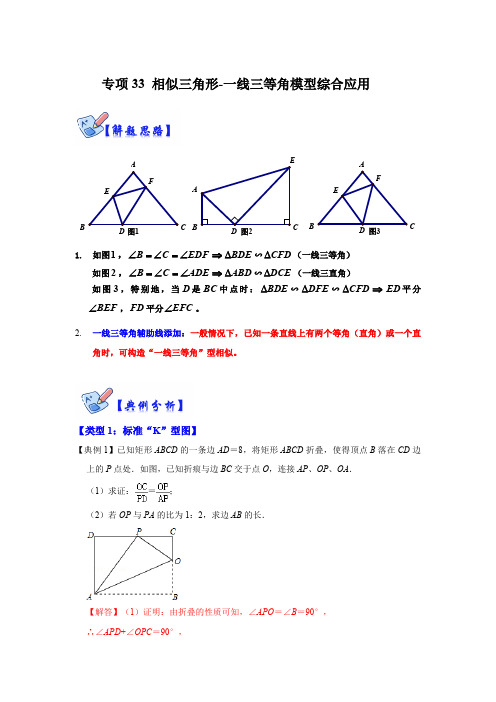
专项33 相似三角形-一线三等角模型综合应用1.如图1,BDE EDF C B ∆⇒∠=∠=∠∽CFD ∆(一线三等角)如图2,ABD ADE C B ∆⇒∠=∠=∠∽DCE ∆(一线三直角)如图3,特别地,当D 是BC 中点时:BDE ∆∽DFE ∆∽CFD ∆⇒ED 平分BEF ∠,FD 平分EFC ∠。
2.一线三等角辅助线添加:一般情况下,已知一条直线上有两个等角(直角)或一个直角时,可构造“一线三等角”型相似。
【类型1:标准“K ”型图】【典例1】已知矩形ABCD 的一条边AD =8,将矩形ABCD 折叠,使得顶点B 落在CD 边上的P 点处.如图,已知折痕与边BC 交于点O ,连接AP 、OP 、OA .(1)求证:=;(2)若OP 与PA 的比为1:2,求边AB 的长.【解答】(1)证明:由折叠的性质可知,∠APO =∠B =90°,∴∠APD +∠OPC =90°,CB BC A A∵四边形ABCD为矩形,∴∠D=∠C=90°,∴∠POC+∠OPC=90°,∴∠APD=∠POC,∴△OCP∽△PDA,∴=;(2)解:∵△OCP∽△PDA,∴,∵OP与PA的比为1:2,AD=8,∴,∴PC=4,设AB=x,则DC=x,AP=x,DP=x﹣4,在Rt△APD中,AP2=AD2+PD2,∴x2=82+(x﹣4)2,解得:x=10,∴AB=10.【变式1-1】如图,正方形ABCD中,点E在BC边上,且AE⊥EF,若BE=2,CF=,求正方形ABCD的边长.【解答】解:∵∠AEB+∠CEF=90°,∠BAE+∠AEB=90°,∴∠BAE=∠CEF,又∵∠B=∠C=90°,∴△BAE∽△CEF,∴=,∵AB=BC,∴,∴,∴CE=4,∴BC=CE+BE=4+2=6,∴正方形ABCD的边长为6.【变式1-2】如图,在正方形ABCD中,M为BC上一点,ME⊥AM,ME交CD于F,交AD的延长线于点E.(1)求证:△ABM∽△MCF;(2)若AB=4,BM=2,求△DEF的面积.【解答】(1)证明:∵四边形ABCD是正方形,∴AB=BC=CD,∠B=∠C=90°,BC∥AD,∴∠BAM+∠AMB=90°,∵ME⊥AM,∴∠AME=90°,∴∠AMB+∠FMC=90°,∴∠BAM=∠FMC,∴△ABM∽△MCF;(2)解:∵AB=4,∴AB=BC=CD=4,∵BM=2,∴MC=BC﹣BM=4﹣2=2,由(1)得:△ABM∽△MCF,∴=,∴=,∴CF=1,∴DF=CD﹣CF=4﹣1=3,∵BC∥AD,∴∠EDF=∠MCF,∠E=∠EMC,∴△DEF∽△CMF,∴=,∴=,∴DE=6,∴△DEF的面积=DE•DF=×6×3=9,答:△DEF的面积为9【类型2:做辅助线构造“K”型图】【典例2】已知:在△EFG中,∠EFG=90°,EF=FG,且点E,F分别在矩形ABCD的边AB,AD上.(1)如图1,填空:当点G在CD上,且DG=1,AE=2,则EG= ;(2)如图2,若F是AD的中点,FG与CD相交于点N,连接EN,求证:∠AEF=∠FEN;(3)如图3,若AE=AD,EG,FG分别交CD于点M,N,求证:MG2=MN•MD.【解答】(1)解:∵∠EFG=90°,∴∠AFE+∠DFG=90°,∵∠AEF+∠AFE=90°,∴∠AEF=∠DFG,又∵∠A=∠D=90°,EF=FG,∴△AEF≌△DFG(AAS),∴AE=FD=2,∴FG=,∴EG=FG=,故答案为:;(2)证明:延长EA、NF交于点M,∵点F为AD的中点,∴AF=DF,∵AM∥CD,∴∠M=∠DNF,∠MAD=∠D,∴△MAF≌△NDF(AAS),∴MF=FN,∵EF⊥MG,∴ME=GE,∴∠MEF=∠FEN;(3)证明:如图,过点G作GP⊥AD交AD的延长线于P,∴∠P=90°,同(1)同理得,△AEF≌△PFG(AAS),∴AF=PG,PF=AE,∵AE=AD,∴PF=AD,∴AF=PD,∴PG=PD,∵∠P=90°,∴∠PDG=45°,∴∠MDG=45°,在Rt△EFG中,EF=FG,∴∠FGE=45°,∴∠FGE=∠GDM,∵∠GMN=∠DMG,∴△MGN∽△MDG,∴,∴MG2=MN•MD.【变式2-1】(2021春•永川区期末)如图,在边长为6的正方形ABCD中,E为BC上一点,CE=2BE,将△ABE沿AE折叠得到△AFE,连接DF,则线段DF的长为 .【解答】解:过点F作FN⊥BC,垂足为N,延长NF交AD于点M,∵四边形ABCD是正方形,∴AB=BC=AD=6,∠B=90°,AD∥BC,∴FM⊥AD,∴∠AMF=∠FNE=∠DMF=90°,∴四边形ABNM是矩形,∴AM=BN,∵CE=2BE,∴BE=BC=2,由折叠得:BE=FE=2,AB=AF=6,∠B=∠AFE=90°,∴∠AFM+∠EFN=90°,∵∠FEN+∠EFN=90°,∴∠FEN=∠AFM,∴△ENF∽△FMA,∴===,设EN=x,则FM=3x,∴AM=BN=BE+EN=2+x,在Rt△AFM中,AM2+FM2=AF2,∴(2+x)2+(3x)2=36,∴x=或x=﹣2(舍去),∴AM=2+x=,FM=3x=,∴DM=AD﹣AM=,在Rt△DMF中,DF===,故答案为:.【变式2-2】(2022秋•皇姑区校级月考)已知,如图,矩形ABCD中,AB=5,AD=3,点E是射线BC上一动点,将矩形ABCD沿直线AE翻折,点B落在点F处.(1)若点F恰好落在CD边上,如图1,求线段BE的长;(2)若BE=1,如图2,直接写出点F到BC边的距离;(3)若△CEF为直角三角形,直接写出CE所有值.【解答】解:(1)∵四边形ABCD是矩形,∴CD=AB=5,BC=AD=3,∠B=∠C=∠D=90°,由折叠的性质得:BE=FE,AF=AB=5,∴DF===4,∴CF=CD﹣DF=5﹣4=1,设BE=FE=x,则CE=BC﹣BE=3﹣x,在Rt△CEF中,由勾股定理得:CF2+CE2=FE2,即12+(3﹣x)2=x2,解得:x=,即线段BE的长为;(2)如图2,过F作FG⊥BC于G,延长GF交AD于H,则∠FGE=90°,四边形ABGH是矩形,∴HG=AB=5,BG=AH,∠AHF=90°=∠FGE,由折叠的性质得:AF=AB=5,∠AFE=∠B=90°,FE=BE=1,∴∠AFH+∠EFG=90°,∵∠AFH+∠FAH=90°,∴∠EFG=∠FAH,∴△EFG∽△FAH,∴==,∴AH=5FG,设FG=x,则BG=AH=5x,∴EG=BG﹣BE=5x﹣1,在Rt△EFG中,由勾股定理得:x2+(5x﹣1)2=12,解得:x=或x=0(不符合题意舍去),∴FG=,即点F到BC边的距离为;(3)分三种情况:①∠CFE=90°时,如图3,∵∠AFE=90°,∴∠AFE+∠CFE=180°,∴A、F、C三点共线,∵四边形ABCD是矩形,∴CD=AB=5,∠B=∠D=90°,AD∥BC,∴∠ECF=∠CAD,AC===,由折叠的性质得:AF=AB=5,FE=BE,∠AFE=∠B=90°,∴∠CFE=90°=∠D,CF=AC﹣AF=﹣5,∴△CEF∽△ACD,∴=,即=,解得:CE=;②点F在CD上,∠ECF=90°时,如图4,由(1)可知,BE=,∴CE=BC﹣BE=3﹣=;③∠CEF=90°时,如图5,由折叠的性质得:∠AEB=∠AEF=45°,∴△ABE是等腰直角三角形,∴BE=AB=5,∴CE=BE﹣BC=5﹣3=2;④点F在CD延长线上,∠ECF=90°时,如图6,由折叠的性质得:AF=AB=5,∠AFE=∠B=90°,∵∠ADF=180°﹣∠ADC=90°,∴DF===4,∴CF=CD+DF=5+4=9,∵∠CFE+∠CEF=90°,∠CFE+∠DFA=90°,∴∠CEF=∠DFA,∵∠ECF=∠ADF=90°,∴△CEF∽△DFA,∴===3,∴CE=3DF=12;综上所述,若△CEF为直角三角形,则CE的值为或或2或12.【类型2:特殊“K”型图】【典例3】(2021秋•通许县期中)感知:(1)数学课上,老师给出了一个模型:如图1,∠BAD=∠ACB=∠AED=90°,由∠1+∠2+∠BAD=180°,∠2+∠D+∠AED=180°,可得∠1=∠D;又因为∠ACB=∠AED =90°,可得△ABC∽△DAE,进而得到= .我们把这个数学模型称为“一线三等角”模型.应用:(2)实战组受此模型的启发,将三等角变为非直角,如图2,在△ABC中,点D在边BC上,并且DA=DE,∠B=∠ADE=∠C.若BC=a,AB=b,求CE的长度(用含a,b的代数式表示).拓展:(3)创新组突发奇想,将此模型迁移到平行四边形中,如图3,在▱ABCD中,E为边BC上的一点,F为边AB上的一点.若∠DEF=∠B.求证:AB•FE=BE•DE.【解答】(1)解:∵△ABC∽△DAE,∴,故答案为:;(2)解:∵∠B=∠ADE=∠C,∠ADC=∠B+∠BAD,∠ADC=∠ADE+∠EDC,∴∠EDC=∠BAD,∵DA=DE,在△ADB与△DEC中,,∴△ADB≌△DEC(AAS),∴EC=BD,AB=DC=b,∴BD=BC﹣DC=a﹣b,即CE=a﹣b;(3)解:∵∠DEF=∠B,∴∠BFE+∠BEF=∠BEF+∠DEC,∴∠BFE=∠DEC,作CG∥FE交DE于点G,如图:∴∠DEF=∠EGC,∴∠B=∠EGC,∴△FBE∽△EGC,∴,∵四边形ABCD是平行四边形,∴∠B+∠BCD=180°,∵∠EGC+∠DGC=180°,∵∠B=∠EGC,∴∠DGC=∠BCD,∵∠EDC=∠CDG,∴△DGC∽△DCE,∴,∴,∴DC•FE=BE•DE,∵四边形ABCD是平行四边形,∴AB=DC,∴AB•FE=•BE•DE.解法二:延长BC到M,使得DC=DM.∵DC=DM,∵DC∥AB,∴∠DCM=∠B,∴∠B=∠M,∵∠BFE=∠DEM,∴△BFE∽△MED.∴=,∵AB=CD=DM,∴AB•FE=•BE•DE.【变式3-1】如图,AB=9,AC=8,P为AB上一点,∠A=∠CPD=∠B,连接CD.(1)若AP=3,求BD的长;(2)若CP平分∠ACD,求证:PD2=CD•BD.【解答】(1)解:∵AB=9,AC=3,∴BP=AB﹣AP=9﹣3=6,∵∠A=∠CPD,∠ACP+∠APC=180°﹣∠A,∠APC+∠BPD=180°﹣∠CPD,∴∠ACP=∠BPD,∵∠A=∠B,∴△ACP∽△BPD,∴=,∴=,∴BD=,∴BD的长为;(2)证明:∵CP平分∠ACD,∴∠PCD=∠ACP,∴∠PCD=∠DPB,∵∠CPD=∠B,∴△CPD∽△PBD,∴=,∴PD2=CD•BD.【变式3-2】(2022春•定海区校级月考)【基础巩固】(1)如图1,在△ABC中,∠ACB=90°,直线l过点C,分别过A、B两点作AE⊥l,BD⊥l,垂足分别为E、D.求证:△BDC∽△CEA.【尝试应用】(2)如图2,在△ABC中,∠ACB=90°,D是BC上一点,过D作AD的垂线交AB 于点E.若BE=DE,,AC=20,求BD的长.【拓展提高】(3)如图3,在平行四边形ABCD中,在BC上取点E,使得∠AED=90°,若AE=AB,,CD=,求平行四边形ABCD的面积.【解答】(1)证明:∵∠ACB=90°,∴∠BCD+∠ACE=90°,∵AE⊥CE,∴∠AEC=90°,∴ACE+∠CAE=90°.∴∠BCD=∠CAE.∵BD⊥DE,∴∠BDC=90°,∴∠BDC=∠AEC.∴△BDC∽△CEA.(2)解:过点E作EF⊥BC于点F.由(1)得△EDF∽△DAC.∴.∵AD⊥DE,,AC=20,∴,∴DF=16.∵BE=DE,∴BF=DF.∴BD=2DF=32.(3)解:过点A作AM⊥BC于点M,过点D作DN⊥BC的延长线于点N.∴∠AMB=∠DNC=90°.∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD.∴∠B=∠DCN.∴△ABM≌△DCN(AAS).∴BM=CN,AM=DN.∵AB=AE,AM⊥BC,∴BM=ME,∵,设AM=b,BE=4a,EC=3a.∴BM=ME=CN=2a,EN=5a.∵∠AED=90°,由(1)得△AEM∽△EDN.∴,∴,∴,∵,∴(2a)2+b2=14,∴a=1,.∴平行四边形ABCD的面积=.1.(2021秋•南京期末)如图,在矩形ABCD中,E,F,G分别在AB,BC,CD上,DE ⊥EF,EF⊥FG,BE=3,BF=2,FC=6,则DG的长是( )A.4B.C.D.5【答案】B【解答】解:∵EF⊥FG,∴∠EFB+∠GFC=90°,∵四边形ABCD为矩形,∴∠A=∠B=∠C=90°,AB=CD,∴∠GFC+∠FGC=90°,∴∠EFB=∠FGC,∴△EFB∽△FGC,∴,∵BE=3,BF=2,FC=6,∴,∴CG=4,同理可得△DAE∽△EBF,∴,∴,∴AE=,∴BA=AE+BE=+3=,∴DG=CD﹣CG=﹣4=.故选:B.2.(2022秋•二道区月考)如图,在△ABC中,AB=AC=9,BC=12,D,E分别是BC,AB上的动点(点D与B,C不重合),且2∠ADE+∠BAC=180°,若BE=4,则CD 的长为 .【答案】6【解答】解:∵AB=AC,∴∠C=∠B,∴∠C+∠B+∠BAC=2∠C+∠BAC=180°,又∵2∠ADE+∠BAC=180°,∴∠C=∠ADE,又∵∠BDE+∠ADC=180°﹣∠ADE,∠CAD+∠ADC=180°﹣∠C,∴∠BDE=∠CAD,∴△BDE∽△CAD,∴=,即=,解得CD=6.故答案为:6.3.(2022•杭州模拟)如图,点E是矩形ABCD边BC上一点,沿AE折叠,点B恰好落在CD边上的点F处.设=x(x>1),(1)若点F恰为CD边的中点,则x= .(2)设=y,则y关于x的函数表达式是 .【解答】解:(1)∵点F为CD边的中点,∴DC=2DF,∵四边形ABCD是矩形,∴AB=DC,∠B=∠C=∠D=90°,∴∠FEC+∠EFC=90°,由折叠得:BE=EF,AB=AF,∠B=∠AFE=90°,∴AB=AF=DC=2DF,∵∠EFC+∠AFD=90°,∴∠AFD=∠FEC,∴△AFD∽△FEC,∴==2,∴=2,∴x=2,故答案为:2;(2)由(1)可得AB=AF=DC=DF+CF,∵△AFD∽△FEC,∴=,∴=,∴x=,∴x=1+,∴x=1+,∴y=,故答案为:y=.4.(2021•海州区校级二模)如图,△DEF的三个顶点分别在等边△ABC的三条边上,BC =4,∠EDF=90°,=,则DF长度的最小值是 .【答案】【解答】解:过点F作FH⊥BC,垂足为H,∵∠EDF=90°,tan∠EFD==,∴∠EFD=60°,∴∠AFE+∠DFC=120°,∵△ABC是等边三角形,∴∠C=∠A=60°,AC=BC=4,∴∠AFE+∠AEF=120°,∴∠AEF=∠DFC,∴△AEF∽△CFD,∴=,∵∠EDF=90°,∠EFD=60°,∴cos∠EFD==,∴=2,∴设CD=a,则AF=2a,∴CF=AC﹣AF=4﹣2a,在Rt△CFH中,∠C=60°,∴CH=CF=2﹣a,∴FH=CH=2﹣a,∴DH=CD﹣CH=a﹣(2﹣a)=2a﹣2,在Rt△DFH中,DF2=DH2+FH2=(2a﹣2)2+(2﹣a)2=7a2﹣20a+16=7(a﹣)2+,∴DF2的最小值为,∴DF的最小值为:.5.如图,在等边三角形ABC中,点E,D分别在BC,AB上,且∠AED=60°,求证:△AEC∽△EDB.【解答】证明:∵△ABC是等边三角形,∴∠B=∠C=60°,∴∠EDB+∠BED=120°,∠CAE+∠AEC=120°∵∠AED=60°,∴∠BED+∠AEC=180°﹣60°=120°,∴∠BED=∠CAE,∴△AEC∽△EDB.6.如图,在等腰直角△ABC中,∠BAC=90°,AB=AC,点D、E分别在边BC、AC上,连接AD、DE,有∠ADE=45°.(1)证明:△BDA∽△CED.(2)若BC=6,当AE=ED时,求BD的长.【解答】(1)证明:∵∠AED=∠C+∠EDC=45°+∠EDC,而∠ADC=∠ADE+∠EDC.∵∠ADE=45°,∴∠ADC=45°+∠EDC,∴∠AED=∠ADC.∴∠DEC=∠ADB(等角的补角相等).而∠B=∠C=45°,∴△ABD∽△DCE.故△ABD∽△DCE得证.(2)解:当AE=DE时,∴∠ADE=∠DAE,∵∠ADE=45°,∴∠ADE=∠DAE=45°,∵∠BAC=90°,∠BAD=∠EAD=45°,∴AD平分BAC,∴AD垂直平分BC,∴BD=3.7.(2022•安徽三模)如图,在四边形ABCD中,∠A=∠D=90°,AD=AB,以BC为直径的半⊙O与边AD相切于点E.(1)求证:∠BCE=∠DCE;(2)若,求DE的长.【解答】(1)证明:连接OE,∵半⊙O与边AD相切于点E,∴∠OEA=90°,∵∠D=90°,∴∠D=∠OEA=90°,∴OE∥CD,∴∠ECD=∠OEC,∵OE=OC,∴∠OEC=∠OCE,∴∠BCE=∠DCE;(2)解:连接BE,∵BA⊥AD,OE⊥AD,CD⊥AD,∴AB∥CD∥OE,∵OB=OC,∴AE=DE,设DE=AE=x,则AD=AB=2x,∵BC为⊙O的直径,∴∠BEC=90°,∴∠DEC+∠AEB=180°﹣∠BEC=90°,∵∠A=∠D=90°,∴∠ABE+∠AEB=90°,∴∠ABE=∠DEC,∴△ABE∽△DEC,∴,∴,解得:,∴DE的长为.8.(2022•钦州一模)已知下列各图中,△ABC是直角三角形,∠ABC=90°.【基本模型感知】如图1,分别过A,C两点作经过点B的直线的垂线,垂足分别为M、N.求证:△ABM∽△BCN;【基本模型应用】如图2,点P是边BC上一点,∠BAP=∠C,,求tan C的值;【灵活运用】如图3,点D是边CA延长线上一点,AE=AB,∠DEB=90°,,,请直接写出tan∠BEC的值.【解答】(1)证明:∵AM⊥MN,CN⊥MN,∴∠AMB=∠BNC=90°.∴∠BAM+∠ABM=90°.∵∠ABC=90°,∴∠ABM+∠CBN=90°.∴∠BAM=∠CBN.又∵∠AMB=∠CNB,∴△ABM∽△BCN.(2)解:如图2,过点P作PF⊥AP交AC于点F,过点F作FQ⊥BC交BC于点Q,在Rt△AFP中,tan∠PAC===,与(1)同理得,△ABP∽△PQF.∴===.设AB=a,PQ=2a(a>0),∵∠BAP=∠C=∠FPQ,∴PF=CF,且FQ⊥BC.∴PQ=CQ=2a.∴BC=BP+PQ+CQ=BP+2a+2a=4a+BP.∵∠BAP=∠C,∠B=∠B=90°,∴△ABP∽△CBA.∴=.∴BP⋅BC=AB2,即BP⋅(4a+BP)=.∴BP=a,BC=5a,在Rt△ABC中,tan C==.(3)解:在Rt△ABC中,sin∠BAC==,如图3,过点A作AG⊥BE于点G,过点C作CH⊥BE交EB的延长线于点H,∵∠DEB =90°,∴CH ∥AG ∥DE .∴==.与(1)同理得,△ABG ∽△BCH∴===.设BG =4m ,CH =3m ,AG =4n ,BH =3n ,∵AB =AE ,AG ⊥BE ,∴EG =BG =4m .∴GH =BG +BH =4m +3n .∴=.∴n =2m .∴EH =EG +GH =4m +4m +3n =8m +3n =8m +6m =14m .在Rt △CEH 中,tan ∠BEC ==.9.(2021•坪山区一模)如图,抛物线y =x 2+bx +c 与x 轴交于点A (﹣3,0)、B ,与y 轴交于点C (0,﹣3).(1)求抛物线的解析式;(2)在抛物线上求点P ,使S △BCP =2S △BCO ,求点P 的坐标;(3)如图2,直线y =x +3交抛物线于第一象限的点M ,若N 是抛物线y =x 2+bx +c 上一点,且∠MAN =∠OCB ,求点N 的坐标.【解答】解:(1)将C (0,﹣3)代入到抛物线解析式中得,c =﹣3,将B (﹣3,0)代入到抛物线解析式中得,9﹣3b ﹣3=0,∴b =2,∴抛物线解析式为:y =x 2+2x ﹣3;(2)令y =0,则x 2+2x ﹣3=0,解得x 1=﹣3,x 2=1,∴B (1,0),∴,∵S △BCP =2S △BCO ,∴S △BCP =3,如图1,过P 作PM ∥BC 交x 轴于M ,连接MC ,则S △MBC =S △BCP =3,∴,∴MB =2,∴M (﹣1,0),设直线BC 为y =k 1x ﹣3,代入点B (1,0)得,k 1=3,∴直线BC 为:y =3x ﹣3,则直线PM 设为:y =3x +b ,代入点M (﹣1,0)得,b =3,∴直线PM 为:y =3x +3,联立,解得,,∴P(3,12)或(﹣2,﹣3);(3)∵直线y=x+3交抛物线于第一象限的点M,∴联立,解得,,∴A(﹣3,0),M(2,5),在Rt△OBC中,tan∠OCB=,∴,①如图2,当N在AM下方时,过A作y轴平行线,过M作x轴平行线,两线交于点G过M作MQ⊥AM交AN于Q,过Q作y轴平行线交GM于H,∴∠AGM=∠MHQ=90°,∴∠AMG+∠GAM=90°,又AM⊥MQ,∴∠AMQ=90°,∴∠AMG+∠HMQ=90°,∴∠GAM=∠HMQ,又∠AGM=∠MHQ=90°,∴△AGM∽△MHQ,∴=,∵A(﹣3,0),M(2,5),∴AG=5,GM=5,∴MH=HQ=,∴Q(),设直线AQ为:y=k2(x+3),代入点Q,得,∴直线AQ为,联立,化简得,2x2+3x﹣9=0,解得x=或﹣3,当x=时,y=,∴N(),②当N在AM上方时,同理可得,N(3,12),∴N()或(3,12).。
相似三角形测试题及答案

相似三角形测试题及答案一、选择题1. 若三角形ABC与三角形DEF相似,且AB:DE = 2:3,则BC:EF的比值为:A. 2:3B. 3:2C. 4:6D. 3:4答案:B2. 在相似三角形中,对应角相等,对应边成比例。
以下哪项不是相似三角形的性质?A. 对应角相等B. 对应边成比例C. 周长比等于相似比D. 面积比等于相似比的平方答案:D二、填空题3. 若三角形ABC与三角形DEF相似,相似比为2:3,则三角形ABC的周长是三角形DEF周长的____。
答案:2/34. 若三角形ABC与三角形DEF相似,且AB = 6cm,DE = 9cm,则BC 与EF的比值为______。
答案:2:3三、解答题5. 已知三角形ABC与三角形DEF相似,且AB = 8cm,DE = 12cm,求三角形ABC的周长,已知三角形DEF的周长为36cm。
答案:三角形ABC的周长 = (8/12) * 36cm = 24cm6. 已知三角形ABC与三角形DEF相似,且∠A = ∠D = 50°,∠B =∠E = 60°,求∠C和∠F的度数。
答案:∠C = ∠F = 70°四、证明题7. 已知三角形ABC与三角形DEF相似,且AB = 4cm,DE = 6cm,BC = 5cm,EF = 7.5cm,证明AC = 6.25cm。
答案:由于三角形ABC与三角形DEF相似,根据相似三角形的性质,对应边成比例,所以AC/DF = AB/DE = 4/6 = 2/3。
已知EF = 7.5cm,所以AC = (2/3) * EF = (2/3) * 7.5cm = 5cm。
因此,AC = 6.25cm。
8. 已知三角形ABC与三角形DEF相似,且∠A = ∠D,∠B = ∠E,求证:∠C = ∠F。
答案:由于三角形ABC与三角形DEF相似,根据相似三角形的性质,对应角相等。
已知∠A = ∠D,∠B = ∠E,所以∠C = 180° - (∠A+ ∠B) = 180° - (∠D + ∠E) = ∠F。
浙教版数学九年级上册 第四章 相似三角形 综合测试卷(原卷+答案)

第四章综合测试卷 相似三角形班级 学号 得分 姓名一、选择题(本大题有10小题,每小题3分,共30分)1.己知 ab =25,则a +b b的值为( )A 25B 35C 75D 232.如图,已知△ABC∽△DEF,AB:DE=1:2,则下列等式一定成立的是( )A.BC DF=12 B.∠A 的度数∠D 的度数=12C.△ABC的面积△def 的面积= 12 D. △ABC 的周长△def 的周长= 123.如图,在直角坐标系中,△OAB 的顶点为O(0,0),A(4,3),B(3,0).以点O 为位似中心,在第三象限内作与△OAB 的位似比 13的位似图形△OCD,则点C 坐标为( )A. (-1,-1)B.(−43,−1)C.(−1,−43) D. (-2,-1)4. 如图,四边形ABCD 是正方形,E 是CD 的中点,P 是BC 边上的一点,下列条件中,不能推出 △ABP 与△ECP 相似的是( )A.∠APB=∠EPCB. ∠APE=90°C. 点 P 是BC 的中点D. BP: BC=2:35.如图,在△ABC 中,点D 在BC 边上,连结AD,点E 在AC 边上,过点E 作EF∥BC,交 AD 于点F,过点E 作EG∥AB,交BC 于点G,则下列式子一定正确的是( ) A.AE EC=EF CDB.EF CD=EG ABC.AFFD=BG GCD.CG BC=AF AD6. 如图,小明为了测量一凉亭的高度AB(顶端A 到水平地面BD 的距离),在凉亭的旁边放置一个与凉亭台阶BC 等高的台阶DE(DE=BC=0.5m ,A ,B ,C 三点共线),把一面镜子水平放置在平台上的点 G 处,测得CG=15m ,然后沿直线CG 后退到点E 处,这时恰好在镜子里看到凉亭的顶端A ,测得 EG=3m ,小明身高EF=1.6m,则凉亭的高度AB 约为( )A. 8.5mB. 9mC. 9.5mD. 10m7. 在如图所示的象棋盘(各个小正方形的边长均相等)中,根据“马走日”的规则,“马”落在下列哪个位置处,能使“马”、“车”、“炮”所在位置的格点构成的三角形与“帅”、“相”、“兵”所在位置的格点构成的三角形相似( )A. ①处B. ②处C. ③处D. ④处8. 如图,在△ABC 中,AD 平分∠BAC,按如下步骤作图:第一步,分别以点A ,D 为圆心,以大 12AD 的长为半径在AD 两侧作弧,交于两点M ,N第二步,连结MN 分别交AB,AC 于点E,F;第三步,连结DE,DF.若BD=6,AF=4,CD=3,则BE 的长是( )A. 2B. 4C. 6D. 89. 如图,在△ABC 中,点 D 为BC 边上的一点,且AD=AB=2,AD⊥AB,过点 D 作DE⊥AD,DE 交AC 于点E,若DE=1,则△ABC 的面积为( )A. 2B. 4C.25D. 810. 在四边形 ABCD 中,∠B=90°,AC=4,AB∥CD,DH 垂直平分 AC,点 H 为垂足.设AB=x ,AD=y ,则y 关于x 的函数关系用图象大致可以表示为( )二、填空题(本大题有6小题,每小题4分,共24分)11. 如图所示,点 E 是平行四边形ABCD 的边BC 延长线上一点,连结AE ,交 CD 于点F ,连结BF.写出图中任意一对相似三角形: .12. 已知 a6=b5=c4,且a+b-2c=6,则a 的值为 .13. 如图,在平行四边形ABCD 中,AB=10,AD=6,点E 是AD 的中点,在AB 上取一点F,使△CBF∽△CDE,则 BF 的长是 .14. 如图,在一块斜边长为30cm 的直角三角形木板(Rt△ACB)上截取一个正方形CDEF ,点D 在边BC 上,点E 在斜边AB 上,点F 在边AC 上,若AF :AC=1:3,则这块木板截取正方形 CDEF 后,剩余部分的面积为 .15.如图①,长、宽均为3,高为8的长方体容器,放置在水平桌面上,里面盛有水,水面高为6,绕底面一棱进行旋转倾斜后,水面恰好触到容器口边缘,图②是此时的示意图,则图②中水面高度为16. 如图所示,在直角坐标系中有两点A(4,0),B(0,2).如果点C 在x 轴上,且点 C 与点O 及点A 不重合,当点 C 的坐标为 时,使得由点B ,O ,C 构成的三角形与△AOB 相似(至少找出两个符合条件的点).三、解答题(本大题有8小题,共66分)17.(6分)如图,在△ABC中,DE‖BC,EF‖AB,求证:△ADEO△EFC.18. (6分)如图,一块材料的形状是锐角三角形 ABC,边BC=120mm,高AD=80mm,把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB,AC上,这个正方形零件的边长是多少?19.(6分)如图,点 P 是⊙O的直径AB 延长线上一点,且AB=4,点 M为A AB上一个动点(不与A,B重合),射线 PM与⊙O交于点 N(不与M重合).(1)当M在什么位置时,△MAB的面积最大? 并求出这个最大值;(2)求证:△PAN∽△PMB.20. (8 分)如图,在△ABC中,AB=8,BC=4,CA=6,CD∥AB,BD是∠ABC的平分线,BD交AC于点E,求AE的长.21. (8分)如图,在△ABC中,点 D,E分别在边AB,AC上,且∠ABE=∠ACD,BE,CD交于点G,连结DE.(1)求证:△AEDO△ABC;(2)如果BE平分∠ABC,求证:DE=CE.22.(10分)如图,在 △ABC 中,点D,E,F 分别在AB,BC,AC 边上, DE‖AC,EF‖AB.(1)求证: △BDEO △EFC.(2)设AF FC=12,①若. BC =12,,求线段BE 的长;②若△EFC 的面积是20,求△ABC 的面积.23.(10分)在矩形ABCD 中,AE⊥BD 于点E,点 P 是边AD 上一点.(1)若BP 平分∠ABD,交 AE 于点G,PF⊥BD 于点F,如图①,证明四边形 AGFP 是菱形;(2)如图②,若PE⊥EC,求证:AE·AB=DE·AP;(3)在(2)的条件下,若AB=1,BC=2,求AP 的长.24.(12分)如图,已知 △ABC 是边长为6cm 的等边三角形,动点P ,Q 同时从A ,B 两点出发,分别沿AB,BC 匀速运动,其中点 P 运动的速度是 1cm/s,点 Q 运动的速度是2cm/s,当点 Q 到达点C 时,P ,Q 两点都停止运动.设运动时间为t(s),解答下列问题:(1) 当 t =2时,判断 △BPQ 的形状,并说明理由;(2)设 △BPQ 的面积为 S (cm²),求S 与t 的函数表达式;(3)如图,作 QR//BA 交AC 于点R,连结PR,当t 为何值时,△APR∽△PRQ?第四章综合测试卷 相似三角形1. C2. D3. B4. C5. C6. A7. B8. D9. B 10. D 11. △ADF∽△ECF(答案不唯一)12. 12 13. 1.8 14. 100cm² 15.24516. (-1,0)或(1,0)或(-4,0)(答案不唯一)17. 证明:∵DE∥BC,∴△ADE∽△ABC,∵EF∥AB,∴△EFC∽△ABC,∴△ADE∽△EFC.18. 解:设这个正方形零件的边长为 xmm ,则△AEF 的边EF 上的高AK=(80-x) mm.∵四边形EF-HG是正方形,∴EF∥GH,即 EF∥BC.∴△AEF CABC.∴EF BC=AK AD,即 x 120=80−x 80⋅∴x =48.∴这个正方形零件的边长是48mm.19. (1)解:当点 M 在 AB 的中点处时,△MAB 的面积最大,此时( OM⟂AB,∵OM =12AB =12×4=2,∴S ABM =12AB ⋅OM =12×4×2=4. (2)证明:∵∠PMB=∠PAN,∠P=∠P,∴△PAN∽△PMB.20. 解: ∵BD 为∠ABC 的平分线,∴∠ABD =∠CBD,∵AB∥CD,∴∠D=∠ABD,∴∠D=∠CBD,∴BC=CD.∵BC=4,∴CD=4.∵AB∥ CD,∴ABECDE,∴AB CD=AE CE,∴84=AE CE,∴AE=2CE,∵AC=6=AE+CE,∴AE=4.21. 证明:(1)∵∠ABE=∠ACD,且∠A 是公共角, ∴ABEACD.∴AE AD=AB AC,即AEAB =ADAC ,又∵∠A 是公共角,∴△AED∽△ABC. (2)∵∠ABE=∠ACD,∠BGD=∠CGE,∴△BGD∽ CGE.:DG EG=BG CG,即DG BG=EG CG.又∵∠DGE=∠BGC,∴△DGE∽△BGC.∴∠GBC=∠GDE,∵BE 平分∠ABC,∴∠GBC=∠ABE,∵∠ABE=∠ACD,∴∠GDE=∠ACD.∴DE=CE.22. (1)证明:∵DE∥AC,∴∠BED=∠C.∵EF∥AB,∴∠B=∠FEC,∴△BDE∽△EFC.(2)解:①∵EF//AB,∴BE EC=AF FC=12.∵BC = 12,∴BE12−BE =12,∴BE =4.②∵EF∥AB,∴△EFC∽△BAC,∴S△BC= (EC BC)2⋅∴BE EC=12,∴EC BC=23.又∵△EFC 的面积是20, ∴20SABC=(23)2,∴SABC=45,即△ABC 的面积是45.23. (1)证明:∵四边形 ABCD 是矩形,∴∠BAD=90°,∵AE⊥BD,∴∠AED=90°,∴∠BAE+∠EAD=90°,∠EAD+∠ADE=90°,∴∠BAE=∠ADE,∵BP 平分∠ABD,∴∠ABG=∠PBD.∵∠AGP=∠BAG+∠ABG,∠APB =∠ADE+∠PBD,∠ABG=∠PBD,∴∠AGP=∠APG,∴AP=AG,∵PA⊥AB,PF⊥BD,BP 平分∠ABD,∴PA=PF,∴PF=AG,∵AE⊥BD,PF⊥BD,∴PF∥AG,∴四边形AGFP 是平行四边形,∵PA=PF,∴四边形AGFP 是菱形.(2)证明:∵AE⊥BD,PE⊥EC,∴∠AED=∠PEC=90°,∴∠AEP=∠DEC,∵∠EAD+∠ADE=90°,∠ADE+∠CDE=90°,∴∠EAP=∠EDC,∴△AEP∽△DEC,∴DE·AP.(3)解:∵四边形 ABCD 是矩形,∴AD=BC=2,∠BAD=90°,∴BD=√AB²+AD² =5,∵AE ⊥BD,∴S ABD =12⋅BD ⋅AE = 12⋅AB ⋅AD,∴AE =255,∴DE =AD 2−AE 2=455,∵AE ⋅AB =DE ⋅AP,∴ AP =255×1455=12.24. 解:(1)△BPQ 是等边三角形.当t=2时,AP=21 =2( cm),BQ=2×2=4( cm),∴BP=AB-AP=6-2=4( cm),∴BQ=BP,又∵∠B = 60°,∴△BPQ 是等边三角形.(2)如图,过点 Q 作QE⊥AB,垂足为 E,由 QB=2tcm,∠B=60°,∠BEQ=90°,得 QE =3tcm,由AP= tcm,得 PB =(6−t )cm,∴S =12BP ⋅QE = 12×(6−t )×3t =−32t 2+33t.(3)∵QR‖BA,∴∠QRC=∠A=60°,∠RQC=∠B=60°,∴△QRC是等边三角形,∴QR=RC=QC=(6-2t)cm⋅:BE=12BQ=12×2t=t(cm),∴EP=AB−AP−BE=6−t−t=6−2t(cm),∵EP‖QR,EP=QR,∴四边形 EPRQ是平行四边形,∴PR=EQ3tcm.又∵∠PEQ=90°,∴∠APR∠PRQ=90°,∴△APR∽△PRQ,∴∠QPR=∠A=60∘,QRPR=6−2t3t=3,解得t=65.∴当t=65时,△APR∽△PRQ.。
初三相似三角形练习题含答案

初三相似三角形练习题含答案1. 某个角的度数是60°。
它的补角和它的和是多少?解答:补角是90°减去该角的度数,即90°- 60° = 30°。
和角是该角的度数加上补角的度数,即60° + 30° = 90°。
2. 给出三角形ABC,其中∠ABC = 90°, AB = 6cm,AC = 8cm。
根据比例的性质,我们可以得出DE = ? (ADE与ABC相似,DE = x cm)解答:由三角形相似的性质可知,AB/DE = AC/AD。
代入已知条件可得6/DE = 8/AD。
交叉相乘得到8DE = 6AD,进一步可以得到4DE = 3AD。
根据题意可知AD = AE + DE,即8 = AE + x。
将此代入前面的等式中,可以得到4x = 3(8-x)。
解这个方程可以得到x = 6。
所以DE = 6cm。
3. 已知两个三角形ABC和DEF相似。
已知BC = 12cm,EF = 8cm,且BC/EF = 3/2。
求AB的长度。
解答:根据相似三角形的性质,AB/DE = BC/EF。
代入已知条件得到AB/8 = 12/8。
交叉相乘可得到8AB = 12 × 8,即AB = 12 × 8 ÷ 8 =12cm。
所以AB的长度为12cm。
4. 两个三角形相似,已知小三角形的面积为25cm²,大三角形的面积是多少?解答:根据相似三角形的性质,如果两个三角形相似,它们对应边的比例的平方等于对应高的比例的平方。
假设小三角形的面积为S,大三角形的面积为T,对应边的比例为k,对应高的比例为h,那么我们可以得到:T/S = (k² × h²)/(k² × h²) = (k² × h²)/(1) = k² × h²根据题意,已知小三角形的面积为25cm²,所以S = 25。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
相似三角形综合练习题一、填空题:
1. 已知a b
a b
+
-
=
2
2
9
5
,则a b
:=__________
2. 若三角形三边之比为3:5:7,与它相似的三角形的最长边是21cm,则其余两边之和是__________cm
3. 如图,△ABC中,D、E分别是AB、AC的中点,BC=6,则DE=__________;△ADE与△ABC的面积之比为:__________。
4. 已知线段a=4cm,b=9cm,则线段a、b的比例中项c为__________cm。
5. 在△ABC中,点D、E分别在边AB、AC上,DE∥BC,如果AD=8,DB=6,EC=9,那么AE=__________
6. 已知三个数1,2,3,请你添上一个数,使它能构成一个比例式,则这个数是
__________
7. 如图,在梯形ABCD中,AD∥BC,EF∥BC,若AD=12cm,BC=18cm,AE:EB=2:3,则EF=__________
8. 如图,在梯形ABCD中,AD∥BC,∠A=90°,BD⊥CD,AD=6,BC=10,则梯形的面积为:__________
二、选择题:
1. 如果两个相似三角形对应边的比是3:4,那么它们的对应高的比是__________
A. 9:16
B. 3:2
C. 3:4
D. 3:7
2. 在比例尺为1:m的某市地图上,规划出长a厘米,宽b厘米的矩形工业园区,该园区的实际面积是__________米2
A. 104m
ab
B.
1042m
ab
C.
abm
104
D.
abm2
4
10
3. 已知,如图,DE∥BC,EF∥AB,则下列结论:
①AE
EC
BE
FC
=②
AD
BF
AB
BC
=③
EF
AB
DE
BC
=④
CE
CF
EA
BF
=
其中正确的比例式的个数是__________
A. 4个
B. 3个
C. 2个
D. 1个
4. 如图,在△ABC中,AB=24,AC=18,D是AC上一点,AD=12,在AB上取一点E,使A、
D、E三点为顶点组成的三角形与△ABC相似,则AE的长是__________
A. 16
B. 14
C. 16或14
D. 16或9
5. 如图,在Rt△ABC中,∠BAC=90°,D是BC的中点,AE⊥AD,交CB的延长线于点E,则下列结论正确的是__________
A. △AED∽△ACB
B. △AEB∽△ACD
C. △BAE∽△ACE
D. △AEC∽△DAC
三、解答题:
1. 如图,AD∥EG∥BC,AD=6,BC=9,AE:AB=2:3,求GF的长。
2. 如图,△ABC中,D是AB上一点,且AB=3AD,∠B=75°,∠CDB=60°,求证:△ABC ∽△CBD。
3. 如图,BE为△ABC的外接圆O的直径,CD为△ABC的高,求证:AC·BC=BE·CD。
4. 如图,Rt△ABC中,∠ACB=90°,AD平分∠CAB交BC于点D,过点C作CE⊥AD于E,
CE的延长线交AB于点F,过点E作EG∥BC交AB于点G,AE·AD=16,AB 45。
(1)求证:CE=EF。
(2)求EG的长。
[参考答案]
一、填空题: 1. 19:13 2. 24 3. 3;1:4
4. 6
5. 12
6. 只要是使得其中两个数的比值等于另外两个数的比值即可,如:222
2
、
等。
7. 14.4
8. 166
二、选择题:
1. C
2. D
3. B
4. D
5. C
三、解答题:
1. 解:∵AD ∥EG ∥BC ∴在△ABC 中,有
EG BC AE
AB =
在△ABD 中,有EF AD BE
AB
=
∵AE :AB=2:3 ∴BE :AB=1:3 ∴EG BC EF AD =
=231
3
, ∵BC=9,AD=6
∴EG=6,EF=2 ∴GF=EG -EF=4
2. 解:过点B 作BE ⊥CD 于点E , ∵∠CDB=60°,∠CBD=75° ∴∠DBE=30°,
∠CBE=∠CBD -∠DBE=75°-30°=45° ∴△CBE 是等腰直角三角形。
∵AB=3AD ,设AD=k ,则AB=3k ,BD=2k ∴DE=k ,BE =3k
∴BC k =
6
∴
BD BC k
k ==262
3,
BC AB k
k
==6323
∴
BD BC BC
AB
= ∴△ABC ∽△CBD
3. 连结EC ,
∵BC BC ⋂=⋂
∴∠E=∠A
又∵BE 是⊙O 的直径 ∴∠BCE=90° 又∵CD ⊥AB ∴∠ADC=90° ∴△ADC ∽△ECB ∴
AC EB CD
BC
=
即AC ·BC=BE ·CD 4. (1)∵AD 平分∠CAB ∴∠CAE=∠FAE 又∵AE ⊥CF
∴∠CEA=∠FEA=90° 又∵AE=AE
∴△ACE ≌△AFE (ASA ) ∴CE=EF
(2)∵∠ACB=90°,CE ⊥AD ,∠CAE=∠DAC ∴△CAE ∽△DAC ∴
AC AD AE
AC
=
∴AC AE AD 2
16==· 在Rt △ACB 中
BC AB AC 2
2
2
2
451664=-=-=() ∴BC =8
又∵CE=EF ,EG ∥BC ∴FG=GB
∴EG 是△FBC 的中位线 ∴EG BC ==1
2
4。
