材料力学(金忠谋)第六版答案第10章
材料力学(金忠谋)第六版课后习题及答案

解
(1) ∆l1
=
1 3
Ρxl1
Ε 1Α1
∆l1 = ∆l2 x = 0.6m
∆l 2
=
1 3
Ρ (3 − x)l2
Ε 2Α2
(2) Ρ ≤ 3Ε1Α1 = 3× 200 × 2 ×10−1 = 200ΚΝ
xl1
0.6× 2
2-11 铰接的正方形结构如图所示,各杆材料皆为铸铁,许用拉应力[σ +]=400kg/cm2, 许用压应力[σ − ]=600kg/cm2,各杆的截面积均等于25cm2。试求结构的许用载荷P。
习题
2-1 一木柱受力如图示,柱的横截面为边长20cm的正方形,材料服从虎克定律,其
弹性模量 E = 0.10 ×105 MPa.如不计柱自重,试求:
(1) (2) (3) (4)
作轴力图; 各段柱横截面上的应力; 各段柱的纵向线应变; 柱的总变形.
解:
(1) 轴力图
(2) AC 段应力
σ
=
−100 ×103 0.2 2
= −2.5×106 Ρa = −2.5ΜΡa
CB 段应力
σ
=
− 260 ×103 0.2 2
= −6.5×106 Ρa = −6.5ΜΡa
(3) AC 段线应变
ε = σ = −2.5 = −2.5×10−4 Ε 0.1×105 CB 段线应变
ε
=σ Ε
=
−6.5 0.1×10 5
解:
AC、CB、BD、DA 杆受拉力,大小为 Τ1 =
Ρ 2
DC 杆受压力,大小为 Τ2 = Ρ
[σ
+
]≥
Τ1 Α
得 Ρ1 ≤ 2 × 400 × 25 = 14142kg
材料力学(金忠谋)第六版答案第15章

习 题14-1 195-2c 型柴油机连杆大头螺栓如图示,工作时所受最大拉力P max =9.58 kN ,P min=8.71 kN ,螺栓最小直径d =8.5mm 。
试求其应力幅a σ,平均应力m σ和循环特征r ,并作出t -σ曲线。
解:()()MPaA P P A P a a67.7105.814.3412/1071.858.92//623min max =⨯⨯⨯⨯⨯-=-==-σ ()()MPaA P P A P m m161105.814.3412/1071.858.92//623min max =⨯⨯⨯⨯⨯+=+==-σ91.0maxmin ==σσr14-2 某阀门弹簧如图所示,当阀门关闭时,最小工作载荷P min =200N , 当阀门顶开时最大工作载荷P max =500N 。
设簧丝的直径d =5mm ,弹簧外径mm D 361=,试求平均应力m τ,应力振幅a τ,循环特性r ,并作出t -τ曲线。
解:4.14/==d D C∴()()09.134/24=-+=C C K∴MPadD P Km m 28010514.31023625002001609.12/169333=⨯⨯⨯⨯+⨯⨯==--πτMPadD P Ka a 12010514.31023622005001609.12/169333=⨯⨯⨯⨯-⨯⨯==--πτ4.0/max min ==P P r14-3 阶梯轴如图所示。
材料为铬镍合金钢,MPa b 920=σ,MPa 4201=-σ,MPa 2501=-τ。
轴的尺寸d =40mm ,D =50mm ,r =5mm 。
试计算弯曲和 扭转时的有效应力集中系数和尺寸系数。
解: 由已知条件25.1=d D ,125.0=dr查图表14-12(c )可得57.1=σK 由图表14-16,当d=40mm 时对MPa b 500=σ的钢材,84.0=σε 对MPa b 1200=σ的钢材,73.0=σε 对MPa b 920=σ的钢材, ()774.073.084.05001200920120073.0=-⨯--+=σε14-4 图示为一货车车轴,轴上的载荷P =110kN ,轴的材料为碳钢,MPa b 550=σ,MPa 2401=-σ,mm a 118=,mm l 1435=,mm d 133=,mm D 146=,mm r 20=,轴表面经磨削加工,规定安全系数8.1=n 。
材料力学(金忠谋)第六版答案第10章
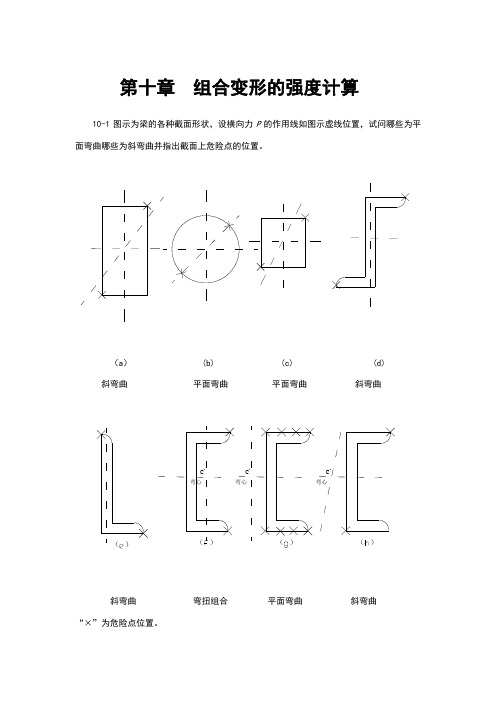
第十章 组合变形的强度计算10-1图示为梁的各种截面形状,设横向力P 的作用线如图示虚线位置,试问哪些为平面弯曲哪些为斜弯曲并指出截面上危险点的位置。
(a ) (b) (c) (d) 斜弯曲 平面弯曲 平面弯曲 斜弯曲弯心()()弯心弯心()()斜弯曲 弯扭组合 平面弯曲 斜弯曲“×”为危险点位置。
10-2矩形截面木制简支梁AB ,在跨度中点C 承受一与垂直方向成ϕ=15°的集中力P =10 kN 作用如图示,已知木材的弹性模量MPa 100.14⨯=E 。
试确定①截面上中性轴的位置;②危险截面上的最大正应力;③C 点的总挠度的大小和方向。
解:66.915cos 10cos =⨯==οϕP P y KN59.215sin 10sin =⨯==οϕP P z KN4310122015=⨯=z J 4cm 3310cm W z =335625121520cm J y =⨯=3750cm W y =25.74366.94max =⨯==l P M y z KN-M 94.14359.24m ax =⨯==l P M z y KN-MMPaW M W M yy z z 84.9107501094.110101025.763633maxmax max=⨯⨯+⨯⨯=+=--σ 中性轴:οο47.2515tan 562510tan tan tan 411=⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫⎝⎛-=--ϕαy z J J 2849333105434.0101010104831066.948--⨯=⨯⨯⨯⨯⨯⨯==z y y EJ l P f m28933310259.010562510104831059.248--⨯=⨯⨯⨯⨯⨯⨯==y z z EJ l P f m 602.0259.05434.022=+=f cm方向⊥中性轴:ο47.25=α10-3 矩形截面木材悬臂梁受力如图示,P 1=800 N ,P 2=1600 N 。
材料力学(金忠谋编)第六版答案第13章

第十二章超静定系统12-1 试问下列结构(梁或刚架)中那些是静定的?哪些是超静定的?若是超静定的,试说明它的次数。
答:a , 静定b , f , 一次超静定d ,e , 二次超静定g , h , 三次超静定c , 几何可变12-2 试求下列各超静定梁的支反力,设各梁均为等截面梁,其抗弯刚度为EI。
a)解:图a 可分解如下图0=+BR BP f f ---------(1) EIL R f EIPL L L EIPlf B BR BP 3485)23(2432=-=--=代入(1)式得 163;)(1611;)(165PL MR P R AA B =↑=↑=( )b)解:设支承B 反力为B R由P 和B R 共同作用下B 点的总挠度要求为零,即有 ()()↓=↑==+-⨯-=+P R P EI L R L L EIPLf f C B BR BP 43;47R 03)5.13(60B 32PL MC41=(⌫)c)解:设支承B 反力为B R ,则必定有0=+BR BP f f ---------(1)EIlR EIl R f EIb l Pb f B B BR BP 648)2(48]4)2(3[3322==--=代入(1)式 得 3222)3(lb l Pb R B -=d)解:0M MA-= ( ))(23)(2323;23,3)(,2002032↓=↑+==-=--=-==+lM R P l M R lM P R EIl M l EIP R l EIP R f EI Mlf f f A B B B B BRP BM BRP BMe)解:e 图可由下图e ’和e ”叠加而成因为BB RB qp RB qp R EIlEIl R f qlEIl l EIl ql l EIqlEI qlf f f 383)2(4895)236(6))((68)1(033422334==-=--⋅--=-----=+代入(1)式得 )(12895↑=q l R B ; )(256`161↑=q l R A ;26433q l MA-= ( )f)解:A , B 端转角为零,则有:0,0=+BAMAMAq θθ ----------(1) 0,0=+BAMBMBq θθ ----------(2)式中,EIlq Aq 3608300-=θ ; EIlq Bq 3607300=θEI lMEI lMBAMAMBA63,⋅+⋅=θEIlMEIlMABMBMBA63,⋅-⋅-=θ将以上θ表达式代入(1),(2)联立求解得:20201l q MA=; 20301l q MB=; l q R A 0207= ; l q R B 0203=12-3 梁AB 的一端固定,另端由拉杆拉住,梁与杆系用同一材料两成,其弹性模量为E ,梁截面惯矩为I ,拉杆的截面积为A ,梁上承受均布载荷q ,试求拉杆BC 的内力。
材料力学答案第十章

衿解:在材料相同、截面相同的情况下,螆相当长度最小的压杆的临界力最大。
For personal use only in studyand research; not for commercial use薄第十章压杆稳定羃第十章答案蚈10.1图示为支撑情况不同的圆截面细长杆 ,各杆直径和材料相同,哪个杆的临界力最大。
蚁(a ) U =2 l =2l '' '■'艿(b ) J l =1 1.3l =1.3l羈(c ) T =0.7 1.7l =1.19l腿(d ) J l =0.5 2l =l ,临界力最大。
莃10.2图示为支撑情况不同的两个细长杆,两个杆的长度和材料相同,为使两个压杆的临 界力相等,b 2与b 1之比应为多少: 1 )膈蕿解:芈 F cr 「(1) 二2EI 2(2I)2 (2)蚂令(1) = (2): I 2 12莈解: -2EI2 = Feos J (2lJ 2(1) (2)b 2 = 2b 薂10.3铰接结构ABC 由截面和材料相同的细长杆组成, 若由于杆件在 ABC 平面内失稳而引起破坏,试确定荷载F 为最大时(两个杆同时失稳时)的0 (0v 0< TI /2)角。
(带arctan (1/3)=18.44 ° )-2EI(2®薄10.4图示压杆,型号为 20a 工字钢,在xoz 平面内为两端固定,在 xoy 平面内为一端固 定,一端自由,材料的弹性模量 E = 200GPa ,比例极限 萨200MPa ,试求此压杆的临 界力。
(F c r = 402.2kN )膂解:(1)柔度计算 查表知:例极限OP = 200MPa ,屈服极限 数n st =2.5,试校核结构是否安全。
OS= 240MPa ,强度安全系数n=2,规定的稳定安全系 (P cr =45.2kN,压杆安全,拉(y= 67.52MPa,安全) 袅解:(1)受力分析: AN 杆受拉力F N1=1.414F=21.21Kn肃BC 杆受压力F N2=F=15Kn聿(2)强度计算:[刁= 120MPa -2 F N1 3 4 21.1 10■: 2023 4 15 10 JI 202= 67.5MPa :::[刁,强度够;= 47.7MPa 十] 上=81.5mm,y 21.1mm ,A = 3558mm螇(2)xoz 平面内失稳: * = 竺 =2000二94.78i y 21.1蒄为中柔度杆,二⑴=a —b \ =197.8MPa, F cr = ;: cr A = 704kN (2)膂(2)xoy 平面内失稳: Z =,2~ = 8000 =98.16i Z 81.5葿为中柔度杆, 二r =a-b z =194.1MPa, F cr 二二cr A = 690kN袇10.5结构如图,二杆的直径均为 d=20mm ,材料相同,材料的弹性模量 E = 210GPa ,比= 100, 0a -;「S 2E (1)=60肇(3)稳定性分析:1 ,3 巾732F,F N2 2、3F 13 螁(2)稳定性分析:膀取[F ]=F2=47.6kNI = 1m , d = 40mm ,材料的 q = 240MPa ,直线经验公, q r =,一端自由, 圆形截面杆长为 0.8I ,试确 入圆=3.2( d /d),矩形截面杆临界应力小,| F 羅解:对细长杆, cr 蒃矩形: i r 荿圆形: 二2E (1.2d) d V 121.2d二 2EI (7) 「— 3.46』 r i r d叫0.81)4'薁满足稳定性条件 肂10.6图示二圆截面压杆的长度、直径和材料均相同,已知 弹性模量E = 200GPa ,比例极限q p = 200MPa ,屈服极限 304-1.12入(MPa),试求二压杆的临界力。
材料力学(金忠谋)第六版完整版问题详解

第一章 绪论1-1 求图示杆在各截面(I )、(II )、(III )上的力,并说明它的性质.解:(a )I-I 截面: N = 20KN (拉)II-II 截面: N = -10KN (压)III-III 截面: N = -50KN (压)(b )I-I 截面: N = 40KN (拉)II-II 截面: N = 10KN (拉)III-III 截面: N = 20KN (拉)1-2 已知P 、M 0、l 、a ,分别求山下列图示各杆指定截面(I )、(II)上的力解:(a ):(I )截面:力为零。
(II )截面:M = Pa (弯矩)Q = -P (剪力)(b ):(I )截面:θsin 31P Q =θsin 61PL M = (II )截面:θsin 32P Q = θsin 92PL M =(c ):(I )截面:L M Q 0-= 021M M = (II )截面:L M Q 0-= 031M M =1-3 图示AB 梁之左端固定在墙,试求(1)支座反力,(2)1-1、2-2、3-3各横截面上的力(1-1,2-2是无限接近集中力偶作用点.)解:10110=⨯=A Y (KN )1055.110-=+⨯-=A M (KN-M )(1-1) 截面:10110=⨯=Q (KN )521110-=⨯⨯-=M (KN-M ) (2-2)截面:10=Q (KN )055=-=M (KN-M )(2-3)截面:10=Q (KN )551110-=+⨯⨯-=M (KN-M )1-4 求图示挂钩AB 在截面 1-1、2-2上的力.解:(1-1)截面:P N 32=a P M ⋅=43 (2-2)截面:P Q 32=a P M ⋅=321-5 水平横梁AB 在A 端为固定铰支座,B 端用拉杆约束住,求拉杆的力和在梁1-1截面上的力.解:(1)拉杆力T :1230sin 0⨯=⨯⋅=∑P T M A ο 10030sin 2100=⨯=οT (KN )(拉) (2)(1-1)截面力:Q 、N 、M :5030sin -=-=οT Q (KN )6.8630cos -=-=οT N (KN )(压)()2550.030sin =⨯=οT M (KN-M )1-6 一重物 P =10 kN 由均质杆 AB 及绳索 CD 支持如图示,杆的自重不计。
材料力学(金忠谋)第六版完整编辑版规范标准答案

解:(a):(I)截面:内力为零。
(II)截面:M = Pa(弯矩)
Q = -P(剪力)
(b):(I)截面:
(II)截面:
(c):(I)截面:
(II)截面:
1-3图示AB梁之左端固定在墙内,试求(1)支座反力,(2)1-1、2-2、3-3各横截面上的内力(1-1,2-2是无限接近集中力偶作用点.)
解:
(1)
(2)
即
解得
各杆的长度为
2-37图示三杆结构中,杆(1)是铸铁的,E1=120Gpa, =80MPa;杆(2)是铜的,EA=100GPa, =60Gpa;杆(3)是钢的,EA=200GPa, =120Mpa。载荷P=160kN,设A1:A2:A3=2:2:1,试确定各杆的截面积。
解:
各杆的应力关系为
解
(1)
(2)
2-11铰接的正方形结构如图所示,各杆材料皆为铸铁,许用拉应力[ +]=400kg/cm2,许用压应力[ ]=600kg/cm2,各杆的截面积均等于25cm2。试求结构的许用载荷P。
解:
AC、CB、BD、DA杆受拉力,大小为
DC杆受压力,大小为
得
得
故
2-12图示拉杆沿斜截面m-n由两部分胶合而成,设在胶合面上许用拉应力[ ]=100MPa,许用剪应力 =50MPa,胶合面的强度控制杆件的拉力,试求:为使杆件承受最大拉力P, 角的值应为多少?若横截面面积为4cm2,并规定 ,试确定许可载荷P。
解:
只计P时,有
只计2P时,有
且有
联立,解得
(方向水平向左) (方向水平向右)
(b)
材料力学(金忠谋)第六版答案第08章之欧阳学创编
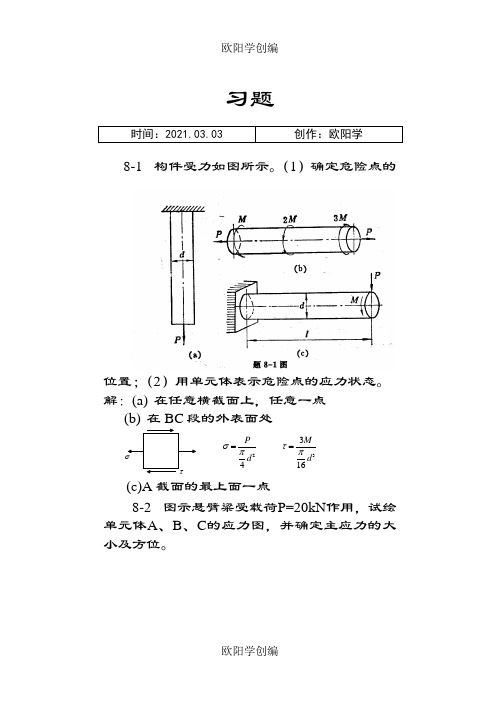
习题时间:2021.03.03 创作:欧阳学8-1 构件受力如图所示。
(1)确定危险点的位置;(2)用单元体表示危险点的应力状态。
解:(a) 在任意横截面上,任意一点24P d σπ=3316M dτπ= τσ (c)A 截面的最上面一点8-2 图示悬臂粱受载荷P=20kN 作用,试绘单元体A 、B 、C 的应力图,并确定主应力的大小及方位。
解:8-3主应力单元体各面上的应力如图所示,试用解析法或图解法计算指定斜截面上的正应力ασ和剪应力ατ,并找出最大剪应力值及方位(应力单位:MPa )。
解:(a) ()()1212205205cos 2cos 6013.752222MPaασσσσσα+---+-=+=+= 45α= (与120σ=方向夹角)(b)()()()121220102010cos 2cos 135 5.6062222M ασσσσσα+---+-=+=+-=-()()122010sin 2sin 13510.60622MPa ασστα---==-=- 45α= (与1σ方向夹角)或135(与水平方向交角)(c)45α= (与140σ=方向夹角)(d)8-4单元体各面的应力如图示(应力单位为MPa ),试用解析法和图解法计算主应力的大小及所在截面的方位,并在单元体内注明。
解:(a)(b)(c)(d)8-5作出图示单元体的三向应力图,并求出主应力和最大剪应力,画出主单元体。
解:(a) (b) (c ) (d)(e)8-6 已知矩形截面梁某截面上的弯矩和剪力分别为M =10kN·m ,FS =120kN ,试绘出截面上1、2、3、4各点单元体的应力状态,并求其主应力。
解:8-7在棱柱形单元体的AB 面上以及与ABC 面平行的前后面上(与纸平面平行的面),均无应力作用。
在AC 面和BC 面上的正应力均为-15MPa ,试求AC 和BC 面上的剪应力与此单元体主应力的大小和方向。
材料力学(金忠谋)第六版答案第02章

习 题2-1 一木柱受力如图示,柱的横截面为边长20cm 的正方形,材料服从虎克定律,其弹性模量51010.0⨯=E MPa .如不计柱自重,试求:(1)作轴力图; (2)各段柱横截面上的应力; (3)各段柱的纵向线应变; (4) 柱的总变形.解:(1) 轴力图(2) AC 段应力a a MP P σ5.2105.22.010100623-=⨯-=⨯-= CB 段应力 a a MP P σ5.6105.62.010260623-=⨯-=⨯-=(3) AC 段线应变 45105.2101.05.2-⨯-=⨯-==E σε N-图CB 段线应变45105.6101.05.6-⨯-=⨯-==E σε (4) 总变形 m 3441035.15.1105.65.1105.2---⨯=⨯⨯-⨯⨯-=AB ∆2-2 图(a)所示铆接件,板件的受力情况如图(b)所示.已知:P =7 kN ,t =0.15cm ,b 1=0.4cm ,b 2=0.5cm ,b 3=0.6cml 。
试绘板件的轴力图,并计算板内的最大拉应力。
解:(1)轴力图(2)a MP σ4.194101024.015.0767311=⨯⨯⨯⨯⨯=-a MP σ1.311101025.015.0767322=⨯⨯⨯⨯⨯=- a MP σ9.388101026.015.07673=⨯⨯⨯⨯=- 最大拉应力a MP σσ9.3883max == 2-3 直径为1cm 的圆杆,在拉力P =10 kN 的作用下,试求杆内最大剪应力,以及与横截面夹角为α=30o 的斜截面上的正应力与剪应力。
解:(1) 最大剪应力a d MP ππP στ66.6310101102212672241max =⨯⨯⨯⨯===- (2) ︒=30α界面上的应力()a MP ασσα49.952366.632cos 12=⨯=+= a MP αστα13.5530sin 66.632sin 2=⨯=⨯=︒2-4 图示结构中ABC 与CD 均为刚性梁,C 与D 均为铰接,铅垂力P =20kN 作用在C 铰,若(1)杆的直径d 1=1cm ,(2)杆的直径d 2=2cm ,两杆的材料相同,E =200Gpa ,其他尺寸如图示,试求(1)两杆的应力;(2)C 点的位移。
[工学]材料力学金忠谋第六版答案第12章
![[工学]材料力学金忠谋第六版答案第12章](https://img.taocdn.com/s3/m/9ba43daf7fd5360cba1adbe1.png)
第十一章 变形能法11-1求图示两等直杆的变形能。
已知两杆的抗拉刚度EA 相同。
解:(a )EAdxN dU 22=lP q =2EIDAlllAll⎰⎰=====llEAlP dx EAl x P dU U x tP qx N 0222262(b)EAl P dx EA l x P U lx P N l 6721)1(2022=⎪⎭⎫⎝⎛+=+=⎰11-2两根圆截面直杆的材料相同,尺寸如图所示,其中一根为等截面杆,另一根为变截面杆,试比较两根杆的变形能。
(各杆自重不计)解:杆(a )2222242Ed l P dE lP U a ππ=⨯= 杆(b )22222287424)2(4283EdlP d E l P d E lP U b πππ=⨯⨯+⨯⨯= 故716=b a U U11-3图示桁架各杆材料相同,截面面积相等,试求在P 力作用下,桁架的变形能。
解:支反力2P R R P R B AyAx ===各杆的轴力和变形能如表所示故珩架的变形能为EA lP EA l P Ui U i 2251957.04122=+==∑=11-4 试计算图示各杆的变形能。
(a) 轴材料的剪切弹性模量为G ,1223d d =; (b) 梁的抗弯刚度EI ,略去剪切变形的影响。
解:(a )m M mM n n ==211421P GJ l m U =2422P GJ lm U = 41321d J P π=41423206.5322d d J P ππ==412216.9d G lm U U U π=+= (b) 支反力 lM R R B A == 111x l M x R M A -=-= (301l x ≤≤) 222x l M x R M B == (3202l x ≤≤)⎰⎰=⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛-=+=3202222130211822l l BCAC EJl M dx EJ x l M dx FJ x l M U U U11-5 试求图示悬臂梁的弹性变形能,梁的抗弯刚度为EI ,并求自由端的挠度。
《材料力学》第十章课后习题答案

在解题前要认真审题,明确题目要求和解题方向 ,避免出现理解偏差或误解题意的情况。同时, 在解题过程中要细心计算,注意检查计算过程和 结果是否正确。
05 知识点拓展与延伸
相关概念深入理解
材料的力学性能
材料在受到外力作用时,其变形、 破坏以及抵抗变形的能力,包括
弹性、塑性、强度、韧性等。
应力与应变
错误原因剖析
学习态度不认真
部分学生平时学习态度不认真,对课 堂知识掌握不扎实,导致在解题时无 法正确运用所学知识。
缺乏练习
部分学生平时缺乏练习,对解题方法 和技巧不熟悉,导致在考试时无法熟 练应对各种问题。
思维能力不足
部分学生思维能力较弱,无法灵活运 用所学知识解决实际问题。
粗心大意
部分学生在解题过程中粗心大意,忽 略了一些关键信息或步骤,导致解题 错误。
《材料力学》第十章课后习题答案
contents
目录
• 第十章课后习题概览 • 习题解答方法与技巧 • 典型习题详解 • 易错习题剖析及避免方法 • 知识点拓展与延伸 • 自我检测与提高建议
01 第十章课后习题概览
习题类型与数量
选择题
共10道,涵盖基本概念和理论 应用。
填空题
共5道,考查对知识点的理解和 记忆。
典型选择题解析
题目:下列关于剪切应力的说法中, 错误的是?
B. 剪切应力与材料的剪切模量成正比。
A. 剪切应力是相邻两部分材料发生相 对错动时的阻力。
典型选择题解析
C. 剪切应力只存在于受扭转的 杆件中。
D. 剪切应力的方向与材料错动 的方向垂直。
解析:正确答案是C。剪切应力 不仅存在于受扭转的杆件中,还 存在于受剪切的梁、板等构件中。
理论力学 第六版部分习题答案 第十章

上式代入式(4)得
FN = 4mB g − mB
10-6 如图 11-10a 所示,质量为 m 的滑块 A,可以在水平光滑槽中运动,具有刚性系 数为 k 的弹簧 1 端与滑块相连接,另 1 端固定。杆 AB 长度为 l,质量忽略不计,A 端与滑 块 A 铰接,B 端装有质量 m1,在铅直平面内可绕点 A 旋转。设在力偶 M 作用下转动角速度 ω 为常数。求滑块 A 的运动微分方程。
F = 1 068 N = 1.068 kN 10-3* 如图 11-3a 所示浮动起重机举起质量 m1=2 000 kg 的重物。设起重机质量 m2=20 000 kg,杆长 OA=8 m;开始时杆与铅直位置成 60°角,水的阻力和杆重均略去不计。当起 重杆 OA 转到与铅直位置成 30°角时,求起重机的位移。
vC = 2vC1 = lω
代入式(1),得
149
p=
lω (5m1 + 4m2 ) (方向如图 11-7b 所示) 2
A
p
vC
C
vC1
ω
O
ωt
C1
B
(a) 图 11-7
(b)
10-5
质量为 m1 的平台 AB,放于水平面上,平台与水平面间的动滑动摩擦因数为 f。
质量为 m2 的小车 D,由绞车拖动,相对于平台的运动规律为 s = 不计绞车的质量,求平台的加速度。
棱柱 B 接触水平面时系统质心坐标
a b ⎤ ⎡ m A (l − ) + m B ⎢l − (a − )⎥ 3 3 ⎦ 3(m A + m B )l − a(m A + 3m B ) + m B b ⎣ ′ = = xC m A + mB 3(m A + m B )
材料力学第六版答案第06章

材料力学(金忠谋)第六版答案第06章(总27页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--2弯曲应力6-1 求图示各梁在m -m 截面上A 点的正应力和危险截面上最大正应力。
题 6-1图解:(a )m KN M m m ⋅=-5.2 m KN M ⋅=75.3max 48844108.49064101064m d J x --⨯=⨯⨯==ππMPa A 37.20108.490104105.2823=⨯⨯⨯⨯=--σ (压)3 MPa 2.38108.4901051075.3823max =⨯⨯⨯⨯=--σ (b )m KN M m m ⋅=-60 m KN M ⋅=5.67max488331058321210181212m bh J x --⨯=⨯⨯== MPa A 73.611058321061060823=⨯⨯⨯⨯=--σ (压) MPa 2.104105832109105.67823max =⨯⨯⨯⨯=--σ (c )m KN M m m ⋅=-1 m KN M ⋅=1max48106.25m J x -⨯=36108.7m W x -⨯=cm y A 99.053.052.1=-=MPa A 67.38106.251099.0101823=⨯⨯⨯⨯=--σ (压) MPa 2.128106.2510183max =⨯⨯=-σ 6-2 图示为直径D =6 cm 的圆轴,其外伸段为空心,内径d =4cm ,求轴内最大正应力。
4解:)1(32431απ-=D W x⎪⎭⎫ ⎝⎛-⨯⨯⨯=-463)64(110326π 361002.17m -⨯=3463321021.213210632m D W x --⨯=⨯⨯==ππMPa 88.521002.17109.0631=⨯⨯=-σ MPa 26.551021.2110172.1631=⨯⨯=-σ MPa 26.55max =σ6-3 T 字形截面铸铁梁的尺寸与所受载荷如图示。
材料力学第十章课后习题答案

第10章 疲劳强度的概念思考题10-1 什么是交变应力?举例说明。
答 随时间作周期性变化的应力称交变应力。
如下图所示的圆轴以角速度ω匀速转动,轴上一点A 的位置随时间变化,从A 到A ′,再到A ′′,再到A ′′′,又到A 处,如此循环往复。
轴上该点的正应力A σ也从0到,再到0,再到,又到0,产生拉压应力循环。
该点的应力即为交变应力。
+max σ−max σ10-2 疲劳失效有何特点?疲劳失效与静载失效有什么区别?疲劳失效时其断口分成几个区域?是如何形成的?答 (1)疲劳失效时的应力σ远低于危险应力u σ(静载荷下的强度指标);需要经过一定的应力循环次数;构件(即使是塑性很好的材料)破坏前和破坏时无显著的塑性变形,呈现脆性断裂破坏特征。
(2)疲劳失效的最大工作应力σ远低于危险应力u σ;静载失效的最大工作应力σ为危险应力u σ。
(3)疲劳失效时其断口分成2个区域:光滑区域和颗粒状粗糙区域。
(4)构件在微观上,其内部组织是不均匀的。
在足够大的交变应力下,金属中受力较大或强度较弱的晶粒与晶界上将出现滑移带。
随着应力变化次数的增加,滑移加剧,滑移带开裂形成微观裂纹,简称“微裂纹”。
另外,构件内部初始缺陷或表面刻痕以及应力集中处,都可能最先产生微裂纹。
这些微裂纹便是疲劳失效的起源,简称“疲劳源”。
微裂纹随着应力交变次数的继续增加而不断扩展,形成了裸眼可见的宏观裂纹。
在裂纹的扩展过程中,由于应力交替变化,裂纹两表面的材料时而互相挤压、时而分离,这样就形成了断口表面的光滑区。
宏观裂纹继续扩展,致使构件的承载截面不断被削弱,类似在构件上形成尖锐的“切口”。
这种切口造成的应力集中,使局部区域内的应力达到很大数值。
最终在较低的应力水平下,由于累积损伤,致使构件在某一次载荷作用时突然断裂。
断口表面的颗粒状区域就是这种突然断裂造成的,所以疲劳失效的过程可以理解为裂纹产生、扩展直至构件断裂的一个过程。
10-3 什么是对称循环?什么是脉冲循环? 答 对称循环是指最大应力与最小应力大小相等,正负号相反的应力循环。
材力习题册(第六版)参考答案(1-3章)

D
)
2.轴向拉伸细长杆件如图 2 所示,其中 1-1 面靠近集中力作用的左端面,则正确的说法 A.1-1、2-2 面上应力皆均匀分布 B.1-1、2-2 面上应力皆非均匀分布 C.1-1 面上应力非均匀分布, 2-2 面上应力均匀分布 D.1-1 面上应力均匀分布, 2-2 面上应力非均匀分布
(图 B 端 D 任意点 A ) B 都是横截面 D 都是 45 斜截面
0 0
14. 轴向拉伸杆,正应力最大的截面和剪应力最大的截面 (
15. 设轴向拉伸杆横截面上的正应力为 σ ,则 45 斜截面上的正应力和剪应力 ( D )。 B 均为 σ D 均为 σ /2 C δ 和ψ D σ s、 δ 和 ψ
17. 由拉压变形公式 l A C A C
F l FN l 即 E N 可知,弹性模量 ( A )。 A l EA
B 与载荷成正比 D 与横截面面积成正比
与载荷、杆长、横截面面积无关 与杆长成正比 A )是正确的。 内力随外力增大而增大 内力随外力增大而减小 C B D
18. 在下列说法,(
B 内力与外力无关 D 内力沿杆轴不变 ) 。 σ >300MPa σ <200MPa B ) 。 B. 剪切面面积为 bh,挤压面面积为 bc; D. 剪切面面积为 bh,挤压面面积为 ch。 C ) ,计算挤压面积
19. 一拉伸钢杆,弹性模量 E=200GPa,比例极限为 200MPa,今测得其轴向应变 ε = 0.0015,则横截面上的正应力 ( A C σ =Eε =300MPa 200MPa<σ <300Mpa
= -2(arctan
)=2.5×
rad
2.试求图示结构 m m 和 n n 两截面的内
-2-
材料力学课后答案

材料力学课后答案第一章材料单向静拉伸载荷下的力学性能一、解释下列名词滞弹性:在外加载荷作用下,应变落后于应力现象。
静力韧度:材料在静拉伸时单位体积材科从变形到断裂所消耗的功。
弹性极限:试样加载后再卸裁,以不出现残留的永久变形为标准,材料能够完全弹性恢复的最高应力。
比例极限:应力—应变曲线上符合线性关系的最高应力。
包申格效应:指原先经过少量塑性变形,卸载后同向加载,弹性极限(σP)或屈服强度(σS)增加;反向加载时弹性极限(σP)或屈服强度(σS)降低的现象。
解理断裂:沿一定的晶体学平面产生的快速穿晶断裂。
晶体学平面--解理面,一般是低指数,表面能低的晶面。
解理面:在解理断裂中具有低指数,表面能低的晶体学平面。
韧脆转变:材料力学性能从韧性状态转变到脆性状态的现象(冲击吸收功明显下降,断裂机理由微孔聚集型转变微穿晶断裂,断口特征由纤维状转变为结晶状)。
静力韧度:材料在静拉伸时单位体积材料从变形到断裂所消耗的功叫做静力韧度。
是一个强度与塑性的综合指标,是表示静载下材料强度与塑性的最佳配合。
二、金属的弹性模量主要取决于什么?为什么说它是一个对结构不敏感的力学姓能?答案:金属的弹性模量主要取决于金属键的本性和原子间的结合力,而材料的成分和组织对它的影响不大,所以说它是一个对组织不敏感的性能指标,这是弹性模量在性能上的主要特点。
改变材料的成分和组织会对材料的强度(如屈服强度、抗拉强度)有显著影响,但对材料的刚度影响不大。
三、什么是包辛格效应,如何解释,它有什么实际意义?答案:包辛格效应就是指原先经过变形,然后在反向加载时弹性极限或屈服强度降低的现象。
特别是弹性极限在反向加载时几乎下降到零,这说明在反向加载时塑性变形立即开始了。
包辛格效应可以用位错理论解释。
第一,在原先加载变形时,位错源在滑移面上产生的位错遇到障碍,塞积后便产生了背应力,这背应力反作用于位错源,当背应力(取决于塞积时产生的应力集中)足够大时,可使位错源停止开动。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
材料力学(金忠谋)第六版答案第10章第十章组合变形的强度计算10-1图示为梁的各种截面形状,设横向力P 的作用线如图示虚线位置,试问哪些为平面弯曲?哪些为斜弯曲?并指出截面上危险点的位置。
(a)(b) (c) (d)斜弯曲平面弯曲平面弯曲斜弯曲弯心()()弯心弯心()()斜弯曲 弯扭组合平面弯曲 斜弯曲 “×”为危险点位置。
10-2矩形截面木制简支梁AB ,在跨度中点C 承受一与垂直方向成ϕ=15°的集中力P =10 kN 作用如图示,已知木材的弹性模量MPa100.14⨯=E 。
试确定①截面上中性轴的位置;②危险截面上的最大正应力;③C 点的总挠度的大小和方向。
解:66.915cos 10cos =⨯== ϕP P y KN 59.215sin 10sin =⨯== ϕP P z KN4310122015=⨯=z J4cm3310cm Wz=335625121520cm J y =⨯=3750cm W y =25.74366.94max =⨯==l P M y z KN-M 94.14359.24m ax =⨯==l P M z y KN-MMPaW M W M yy z z 84.9107501094.110101025.763633maxmax max =⨯⨯+⨯⨯=+=--σ中性轴:47.2515tan 562510tan tan tan 411=⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫⎝⎛-=--ϕαy z J J2849333105434.0101010104831066.948--⨯=⨯⨯⨯⨯⨯⨯==z y y EJ l P f m 28933310259.010562510104831059.248--⨯=⨯⨯⨯⨯⨯⨯==y z z EJ l P f m602.0259.05434.022=+=f cm方向⊥中性轴:47.25=α10-3 矩形截面木材悬臂梁受力如图示,P 1=800 N ,P 2=1600 N 。
材料许用应力[σ]=10MPa ,弹性模量E =10GPa ,设梁截面的宽度b 与高度h 之比为1:2。
①试选择梁的截面尺寸;②求自由端总挠度的大小和方向。
解:(I )6.112m ax=⨯=P Mz KN 6.120max =⨯=P M y KN 322326)2(6bb b bh W z ===33231626bb bh W y ===hbP 220cm15cm[]633133323m ax m ax m ax1010106.1106.1⨯=≤⨯+⨯=+=σσb b W M W M Y y z zb = 9 cm , h = 18 cm (II)cm m EJ P EJ P EJ P f zz y 97.11097.11213132223232231=⨯⎪⎪⎭⎫⎝⎛⨯⨯+⨯+⎪⎪⎭⎫ ⎝⎛⨯=-1.81,305.095.1tan ===ααy z f f10-4简支梁的受力及横截面尺寸如图示。
钢材的许用应力[σ]=160 MPa ,试确定梁危险截面中性轴的方向与校核此梁的强度。
解:43434748.909126410321232cm bh d J z =⨯-⨯=-=ππ43434748.949124610321232cm bh d J y =⨯-⨯=-=ππ中性轴:77.4345tan 748.949748.909tan tan tan 11-=⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛-=--ϕαy z J J危险点: cmz 918.677.43sin 10=⋅=*cmy 221.777.43cos 10=⋅=*14114max =⨯=M KN m ⋅9.945sin 9.945cos max max =⋅==⋅=M M M M z y[]σσ≤=⨯⨯⨯⨯+⨯⨯⨯⨯=----MPa 69.15010748.90910221.7109.910748.94910918.6109.9823823max10-5 图示简支梁的截面为200⨯200⨯20(mm )的等边角钢,若 P =25kN ,试求最大弯矩截面上A 、B 和C 点的弯曲正应力。
401180.04y J cm = ,404554.55z J cm =30322.06z W cm = , 3146.55y Wcm =解:MPaz J M y J M mKN M M M m KN plM A y yA z z A z y o O 2.1461004.11801095.601068.171055.45541042.1411068.1768.1745cos 254433833max -=⨯⨯⨯⨯-⨯⨯⨯⨯-=⋅-⋅-=⋅=⋅==⋅==----σ42.36-=⋅-⋅=A y y A z zCz J M y J M oO σ MPaMPaz J M B y y B O56.1201047.801004.11801068.17383=⨯⨯⨯⨯=⋅=--σ10-6 旋臂式吊车梁为16号工字钢,尺寸如图所示,允许吊重 P =10kN ,材料的[σ]=160MPa 。
试校核吊车梁的强度。
解: B 点:()KNH H N KNP H 76.3757.158.094.18.094.157.1594.194.108.1=⨯===+⨯=No16 工字钢:21.26cm A = ,41130cm Jz= ,3141cmW z()[]σσ<=⨯⨯⨯+⨯⨯=+=--压MPa W M A N 1.91101411008.110101.261076.376343max10-7图示等截面构件的许用应力[σ]=120MPa ,矩形截面尺寸 2.5⨯10cm 2,试确定许用载荷[P ],并作危险截面上的应力分布图,指出最大应力发生在哪一点?60cm解:N = P2m ax 1060-⨯=P M , 32667.416105.2cm W =⨯=225105.2cm A =⨯=[]σ≤+WM A NKNN P 108.8810810667.41106010251101206246==⎪⎪⎭⎫ ⎝⎛⨯⨯+⨯⨯=---最大应力点:10-8悬重构架如图所示,立柱AB 系用No25a 的工字钢制成。
许用应力[σ]=160 MPa ,在构架C 点承受载荷P =20kN 。
①绘立柱 AB 的内力图;②找出危险截面,校核立柱强度;③列式表示顶点B 的水平位移。
解:(i )图图 (II )[]σσ<=⨯=⨯⨯+⨯⨯=+=--MPa Pa W M A N 42.1531042.15310883.4011060105.48102066343m ax(III)()()→=-⨯⨯-⨯=EJP EJ P EJ P f B 11769366392310-9图示起重结构,A 及B 处可作铰链支承CB60c ms看待,C 、D 与E 均用销钉连结。
AB 柱的截面为20cm ⨯30cm 的矩形。
试求其危险截面上的最大正应力。
解:KNR A 6667.166.3/4.225=⨯=N = 25 KNmKN M ⋅=⨯⨯-⨯⨯=20104.2667.164.2102533m ax206.03.02.0M A =⨯= 22003.063.02.0M W =⨯=PaM W M A N 083.7003.0102006.0102533=⨯+⨯=+=σ10-10有一等直实心圆杆,其B 端为铰支承,A 端靠在光滑的竖直墙面上(摩擦力可略去)如图示。
杆长L ,杆截面直径d ,已知杆的总重P 及倾角α。
试确定自A 点至由于杆自重产生最大压应力的横截面之距离S 。
解:设杆的自重为q (N/M ) 轴向分量:αsin ⋅q 横向分量:αcos ⋅q0=∑B Mαααcot 21sin 2cos ql l q R A =⋅⋅=在S 截面:()S q ql S q RN A ⨯⋅+⋅⋅=⋅⋅+⋅=αααααsin cos cot 21sin cos22cos 21sin cot 21)cos (21)sin ()(S q S ql S q S R s M A ⋅-⋅=⋅⋅-⋅⋅=ααααα0=+=dsd WMA N σσ,()02sin cos sin cos 21sin cot 211sin 1=⎪⎭⎫⎝⎛⨯⨯⨯-⋅⋅⋅+⋅s q l q W q A ααααααα00tan 82cot 82αα⋅+=+=dl d l S10-11某厂房柱子,受到吊车梁的铅垂轮压P =220 kN ,屋架传给柱顶的水平力Q =8 kN ,及风载荷q =1kN/m 的作用。
P 力作用线离柱的轴线距离 e =0.4m ,柱子底部截面为矩形,尺寸为lm ⨯0.3m ,试计算柱子底部危险点的应力。
解:KNP N 220==mKN M ⋅=⨯-⨯+⨯=129.575.984.022025.912maxMPa W M A N 876.141.013.0610129.573.0110220233-=⨯⨯⨯±⨯⨯-=±-=σ10-12简单夹钳如图示。
如夹紧力 P =6kN ,材料的许用应力[σ]=140MPa 。
试校核其强度。
解:[]σσ<=⨯=⨯⨯⨯⨯⨯⨯+⨯⨯⨯=+=---MPa Pa bh Peb A P 130101301032106106610321066622343210-13轮船上救生艇的吊杆尺寸及受力情况如图示,图中载荷W 系包括救生艇自重及被救人员重量在内。
试求其固定端A -A 截面上的最大应力。
解:KNN 18=mKN M ⋅=⨯=275.118MPaW M A N 75.1601032121027104121018623423=⨯⨯⨯+⨯⨯⨯=+=--ππσ10-14正方形截面拉杆受拉力 P =90kN 作用,a =5cm ,如在杆的根部挖去1/4如图示。
试求杆内最大拉应力之值。
解: 形心位置:cma a a e 179.132222=⨯⎪⎪⎭⎫⎝⎛⨯=42242246.3642212122cm e a a a e a a J z =⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛-++⎪⎪⎭⎫ ⎝⎛⨯+=8223423m ax 106.36410)179.1252)(10179.11090(10531090)22(----⨯⨯+⨯⨯⨯⨯+⨯⨯⨯=++=z J e Pe AP σMPaPa 72.251072.256=⨯=10-15承受偏心拉伸的矩形截面杆如图示,今用电测法测得该杆上、下两侧面的纵向应变1ε和2ε。
试证明偏心距 e 在与应变1ε,2ε在弹性范围内满足下列关系式h解:⎪⎭⎫ ⎝⎛+==21161bh Pe bh P E E σε ⎪⎭⎫ ⎝⎛-==221261bh Pe bh P E Eσεbh P E 2121⋅=+∴εεbhPeE 12121⋅=-εε 故e h bhP bh Pe ⨯==+-621222121εεεε62121he ⨯+-=∴εεεε10-16图示正方形截面折杆:外力 P 通过A 和B 截面的形心。
