理论力学之动力学习题答案
理论力学动力学部分试题及答案

1物体自地球表面以速度眄铅直上抛.试求该物体返回地面时的速度巧・假定空气阻力R=mkv2,其中k是比例常量,搜数值它等于单位质量在单位速度时所受的阻力。
m是物体质V 是物体速度,重力加速度认为不变.答:叮解:阻力方向在上升与下降阶段不同(其方向与速度y相反),故分段考虑(1)上升阶段:tn— - -tng一dt通过坐标变换有加V字二-刃护-加£ ,积分得axvdv(2)下落阶段:(1)g2.静止中心0以引力F=k2mr吸弓I质量是m的质点M,其中k是比例常量,r=OM是点M的矢径.运动开始时OMo=b,初速度时呵并与阪成夹角求质点M的运动方程。
x = b cos 处 + —cosasin ktky = —sinasin^k解:取坐标如图,质点M在任意位貳将fna = F 沿x、y轴投彫,得mx = 一F cos<p= -k2fnrcos (p= -Qmxfny = 一Fsin cp= -k2fnr sin (p= -k^my艮卩x+k2x = 0 , y+^2y = 0徽分方程得通解为:x = s coskt+c2 sin kt求导得x = -kc x sin kt + kc2 coskt , y = -kc3 sin kt + kc^ cos kt (2)已知初始条件f=0 z 妒b z /o=0,x0 = v0 sin a ,代入方程(1),(2)得点M的运动方程为v =—cosax = 2?cos Ar/ +—kcos ar sin kt -I sin asin kt y =c3 cos kt + c^ sin kt (1)九=v0 sin a3单摆M 的悬线长/,摆重G 支点B 具有水平向左的均加速度a.如将摆在&=0处静止 释啟,试确定悬线的张力T (表示成&的函数).解:质点的相对徴分方程为 ma r = mg+f +©投影到法线方向由式(2)得T = Gsin3 + —acos0 + — v 2g 0T = G 3 sin + 3 — cos — 2 —\ g S )答・ T - G(3sin3-cos^- 2-) g g投影到切线方向= T-Gsin^-0e cosB g !(2)由式(1)得 妙=gcos^-usin 0分离变量并积分|*V Xiv = \ f geos^10- [ asm Odd v 2 = 2"gsin &+ocos&-a 1(3)将式(3)代入上式代入式(2)得dt dt积分得4.水平面内弯成任意形状的细管以匀角速度G 绕点0转动.光滑小球M 在管內可自由 运动.设初瞬时小球在吆处,OMo=©相对初速^v o =0,求小球相对速度大小冬与极径r的关系。
动力学基本定律习题答案

动力学基本定律习题答案动力学基本定律习题答案动力学是物理学中研究物体运动的学科,它描述了物体如何受力而运动的规律。
动力学基本定律是研究物体运动的基础,通过习题的形式来理解和应用这些定律是学习动力学的重要环节。
下面将给出一些动力学基本定律习题的答案,并对其中的一些关键点进行解析。
一、牛顿第一定律习题答案1. 问题描述:一个小球在光滑水平面上以匀速运动,它受到的合外力为零吗?答案:是的,根据牛顿第一定律,一个物体如果受到的合外力为零,它将保持静止或匀速直线运动。
二、牛顿第二定律习题答案1. 问题描述:一个质量为2kg的物体受到一个3N的力,求物体的加速度。
答案:根据牛顿第二定律,力等于物体的质量乘以加速度,即F = ma。
代入已知数据,可得3N = 2kg * a,解得a = 1.5 m/s²。
三、牛顿第三定律习题答案1. 问题描述:一个物体受到一个力,它对施力物体的作用力是多大?答案:根据牛顿第三定律,作用力和反作用力大小相等,方向相反。
因此,该物体对施力物体的作用力大小与所受力的大小相等。
四、摩擦力习题答案1. 问题描述:一个物体在水平地面上受到一个10N的水平拉力,摩擦系数为0.2,求物体的摩擦力大小。
答案:摩擦力的大小可以通过乘以摩擦系数和物体的法向力得到。
由于物体受到的水平拉力和摩擦力平衡,所以摩擦力的大小等于10N * 0.2 = 2N。
五、重力习题答案1. 问题描述:一个质量为5kg的物体在重力加速度为10m/s²的情况下,求它所受到的重力大小。
答案:重力的大小可以通过物体的质量乘以重力加速度得到。
所以重力的大小等于5kg * 10m/s² = 50N。
六、弹力习题答案1. 问题描述:一个弹簧的弹性系数为100N/m,它被拉伸2m,求所产生的弹力大小。
答案:弹力的大小可以通过弹性系数乘以弹簧的伸长量得到。
所以弹力的大小等于100N/m * 2m = 200N。
理论力学课后答案-谢传峰、王琪-动力学第九章、第十章

1 2
2l m dx(
x sin )2 0 2l
2 ml 2
2 sin2 3
O C
系统的动能 T T1 T2 。 取 900 为势能零点,则系统的势能为:
V mgl cos
则拉格朗日函数:
L T V 2 ml2 (2
2 sin2 ) mgl cos 3
x
楔块 B 的速度 vB ,以及 B 相对于 A 的相对速度
满足如下的矢量关系(方向如图所示):
vB vA vBr
系统的动能为:
vBr vA
T
1 2
m
Av
A
2
1 2
mBvB 2
P1 2g
x 2
P2 2g
[(x
s cos)2
(ssin)2 ]
1 2g
(P1
P2 )x 2
度
转动。物体的质心 G 在垂直于 O1O2 的直线上,O3G l 。设 O1O2 和 O3G 是物体过 O3
点的惯量主轴,转动惯量为 J1 和 J 2 ,物体对另一过 O3 点的惯量主轴的转动惯量为 J 3 ,试
求物体的动能表达式并建立物体的运动微分方程。 解:
以该物体为研究对象,有一个自由度,取 O3G 和 OC 的夹角 为广义坐标。若以框架 O1O2OC 为动系,则物体的相对运动是以角速度 绕轴 O1O2 的定轴转动,牵连运动是以角 速度
垂直于 O1O2 的平面
z’
O3
θ G
y’
坐标系 O3 x y z 的三个坐标轴为过 O3 点的三个惯量主轴,则系统的动能为:
T
《理论力学》动力学典型习题+答案
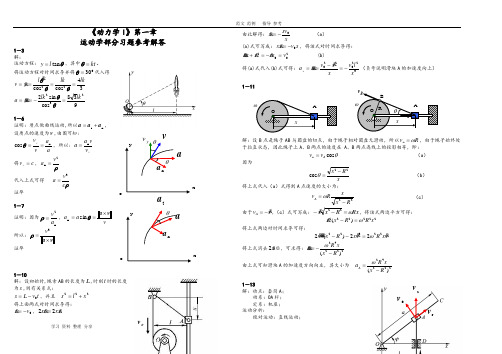
学习 资料 整理 分享《动力学I 》第一章 运动学部分习题参考解答1-3 解:运动方程:θtan l y =,其中kt =θ。
将运动方程对时间求导并将030=θ代入得34cos cos 22lklk l y v ====θθθ 938cos sin 2232lk lk y a =-==θθ1-6证明:质点做曲线运动,所以n t a a a +=, 设质点的速度为v ,由图可知:a a v v yn cos ==θ,所以: yv va a n =将c v y =,ρ2n v a =代入上式可得 ρc v a 3=证毕 1-7证明:因为n2a v =ρ,v a a v a ⨯==θsin n所以:va ⨯=3v ρ证毕1-10解:设初始时,绳索AB 的长度为L ,时刻t 时的长度 为s ,则有关系式:t v L s 0-=,并且 222x l s +=将上面两式对时间求导得: 0v s-= ,x x s s 22= 由此解得:xsv x-= (a ) (a)式可写成:s v x x 0-= ,将该式对时间求导得: 2002v v s x x x =-=+ (b)将(a)式代入(b)式可得:3220220xlv x x v x a x -=-==(负号说明滑块A 的加速度向上)1-11解:设B 点是绳子AB 与圆盘的切点,由于绳子相对圆盘无滑动,所以R v B ω=,由于绳子始终处于拉直状态,因此绳子上A 、B 两点的速度在 A 、B 两点连线上的投影相等,即: θcos A B v v = (a ) 因为xR x 22cos -=θ (b ) 将上式代入(a )式得到A 点速度的大小为: 22Rx x Rv A -=ω (c )由于x v A -=,(c )式可写成:Rx R x xω=--22 ,将该式两边平方可得: 222222)(x R R x xω=- 将上式两边对时间求导可得:x x R x x R x xx 2232222)(2ω=-- 将上式消去x2后,可求得:22242)(R x xR x --=ω由上式可知滑块A 的加速度方向向左,其大小为 22242)(R xxR a A -=ω1-13解:动点:套筒A ;动系:OA 杆; 定系:机座; 运动分析:绝对运动:直线运动;o vo va ve vr vxovxot学习 资料 整理 分享 相对运动:直线运动; 牵连运动:定轴转动。
理论力学习题及解答1
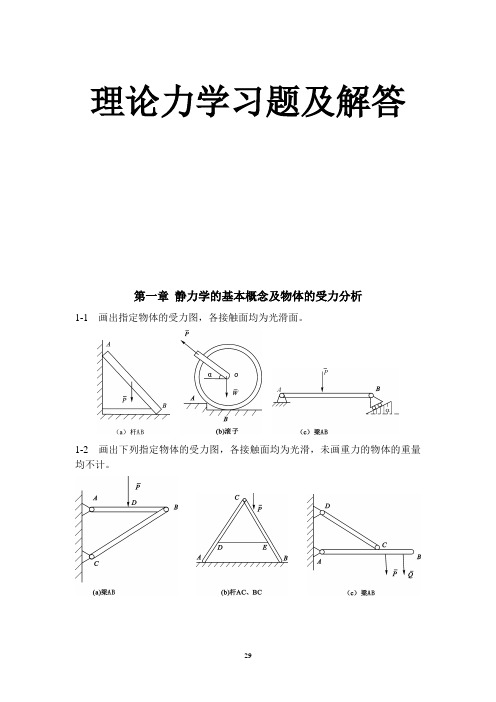
理论力学习题及解答第一章静力学的基本概念及物体的受力分析1-1 画出指定物体的受力图,各接触面均为光滑面。
1-2 画出下列指定物体的受力图,各接触面均为光滑,未画重力的物体的重量均不计。
1-3 画出下列各物体以及整体受力图,除注明者外,各物体自重不计,所有接触处均为光滑。
(a) (b)(c) (d)(e) (f)第二章平面一般力系2-1 物体重P=20kN,用绳子挂在支架的滑轮B上,绳子的另一端接在铰车D 上,如图所示。
转动铰车,物体便能升起,设滑轮的大小及滑轮转轴处的摩擦忽略不计,A、B、C三处均为铰链连接。
当物体处于平衡状态时,试求拉杆AB和支杆CB所受的力。
2-2 用一组绳悬挂重P=1kN的物体,求各绳的拉力。
2-3 某桥墩顶部受到两边桥梁传来的铅直力P1=1940kN,P2=800kN及制动力T=193kN,桥墩自重W=5280kN,风力Q=140kN。
各力作用线位置如图所示,求将这些力向基底截面中心O简化的结果,如能简化为一合力,试求出合力作用线的位置。
2-4 水平梁的支承和载荷如图所示,试求出图中A、B处的约束反力。
2-5 在图示结构计算简图中,已知q=15kN/m,求A、B、C处的约束力。
2-6 图示平面结构,自重不计,由AB、BD、DFE三杆铰接组成,已知:P=50kN,M=40kN·m,q=20kN/m,L=2m,试求固定端A的反力。
图2-6 图2-72-7 求图示多跨静定梁的支座反力。
2-8 图示结构中各杆自重不计,D、E处为铰链,B、C为链杆约束,A为固定端,已知:q G=1kN/m,q=1kN/m,M=2kN·m,L1=3m,L2=2m,试求A、B、C 处约束反力。
图2-8 图2-92-9 支架由两杆AO、CE和滑轮等组成,O、B处为铰链,A、E是固定铰支座,尺寸如图,已知:r=20cm,在滑轮上吊有重Q=1000N的物体,杆及轮重均不计,试求支座A和E以及AO杆上的O处约束反力。
922144-理论力学之动力学-第二章d大纲习题

1.质点系的动量
n
p mivi
i 1
2.微分形式
dp
dt
n
Fi (e)
i 1
FR(e)
3.积分形式
pt2
pt1
n
I
(e) i
i 1
t2 t1
FR(e)dt
动量守恒
当:FRe 0
n
当: Fxei 0
i 1
则: p p0
则: px p0x
9
小结
一、动量定理
质点系相对定点与相对运动点动量矩的关系
Lo rA mvC rAC mvA LrA
Lo rC mvC LrC
质点系相对于动点的动量矩定理
dLrA
dt
n i1
M A(Fi(e) ) rAC
(maA)
质点系相对于质心的动量矩定理
dLrC
dt
n i1
MC (Fi(e) )
12
小结
三、动能定理
绳索AM的拉力与未剪断绳索 BM时相比,是增大了还是减
小了? =?绳索AM的拉力
不变。
剪断前: F mg
2 cos 剪断后: F mg cos
2
物块A、B放在半径为R处于静
止的水平圆盘的边缘,两者间的静
滑动摩擦因数为f,物块的质量分别
为mA > mB,将物块视为质点。圆盘
以角速度ω=αt 绕铅垂轴转动。
i1
Lo rC mv
Lz J z
2.相对于惯性参考系中定点的动量矩定理
dLo
dt
n
Mo (Fi(e))
i1 n
守恒情况: Mo (Fi(e)) 0 则:Lo (t) Lo (t0 )
理论力学--动力学习题+答案

A
B
2g 5r
aC
4 5
g
(2)选圆柱A为研究对象
1 2
P g
r 2 A
M
Tr
(1)
选圆柱B为研究对象
1 2
P g
r
2
B
T
'r
(2)
P g
aC
T 'P
(3)
运动学关系:
aC ae ar r A r B (4)
由(1)~(4)式得:
B
4gM 2g 5 Pr2
mv1x
py 0
mv2x mv3x
5 2
ml1()
所以
p
px
5 2
ml1
A
方向水平向左
B
O
例9-5在静止的小船中间站着两个人,其中甲m1=50kg,面向船首方向走动1.5m。 乙m2=60kg,面向船尾方向走动0.5m。若船重M=150kg,求船的位移。水的阻力不计。
【解受】力有三个重力和一个水的浮力,因无水平力,水平方向质心运动守恒,
0 3.67rad/s
如图所示,均质杆AB质量为m,长为l,由图示位置( )无初速度地倒下4,5求0 该瞬
时A端所受到地面的约束反力。
B
C C
A
例10-13 如图所示均质细长杆,质量为M,长为l,放置在光滑水平面上。若在A 端 作用一垂直于杆的水平力F,系统初始静止,试求B端的加速度。
Pr
A
6gM 5
2g Pr2
Pr
aC
E420-理论力学-动力学第三章部分习题解答

动力学第三章部分习题解答3-3 取套筒B 为动点,OA 杆为动系 根据点的复合运动速度合成定理r e a v v v +=可得:l v v ω==e 0a 30cos ,l v v v BC B ω332a === 研究AD 杆,应用速度投影定理有:030cos D A v v =,l v D ω334=再取套筒D 为动点,BC 杆为动系,根据点的复合运动速度合成定理r D BC D v v v +=将上式在x 轴上投影有:r D BC D v v v +-=-,l v v v BC D D ω332r =+-=3-4 AB 构件(灰色物体)作平面运动, 已知A 点的速度s A O v A /0cm 4510==ωAB 的速度瞬心位于C ,应用速度瞬心法有:rad/s 23==AC v A AB ω BC v AB B ω=,设OB 杆的角速度为ω,则有rad/s 415==OB v B ω 设P 点是AB 构件上与齿轮I 的接触点, 该点的速度:CP v AB P ω=齿轮I 的角速度为:rad/s 61==r v PI ω a v e vr vA vDv rD v A vB P v CAB ωI ω3-6 AB 杆作平面运动,取A 为基点 根据基点法公式有:BA A B v v v +=将上式在AB 连线上投影,可得0,01==B O B v ω因此,041ωω==AB v A AB因为B 点作圆周运动,此时速度为零,因此只有切向加速度(方向如图)。
根据加速度基点法公式n t BA BAA B aaa a ++=将上式在AB 连线上投影,可得n060cos BA A B a a a +=-,r a B 205.2ω-=201231ωα-==B O a B B O (瞬时针)3-7 齿轮II 作平面运动,取A 为基点有nt BA BA A B a a a a ++= n t 1BA BA a a a a ++=将上式在x 投影有:n 1cos BA a a a -=-β由此求得:212n 2cos 2r a a r a BAII βω+==再将基点法公式在y 轴上投影有:2t2sin r a a II BA αβ==,由此求得22sin r a II βα=再研究齿轮II 上的圆心,取A 为基点n t n t2222A O AO A O O aaa aa++=+将上式在y 轴上投影有2sin 2t t 22βαa r a a II AO O ===, B vBAv A vAa Ba t BA an BA atBA anBA axyt2A Oa n 2AO a xyn 2O a t 2Oa由此解得:)(2sin 2121t 221r r a r r a OO O +=+=βα再将基点法公式在x 轴上投影有:n1n22A O O a a a -=- 由此解得:2cos 1n2a a a O -=β,又因为221n 212)(O O O r r a ω+= 由此可得:)(2cos 21121r r a a O O +-±=βω3-9 卷筒作平面运动,C 为速度瞬心, 其上D 点的速度为v ,卷筒的角速度为r R vDC v -==ω 角加速度为rR ar R v -=-== ωα 卷筒O 点的速度为:rR vRR v O -==ω O 点作直线运动,其加速度为 rR aRr R R v va O O -=-==研究卷筒,取O 为基点,求B 点的加速度。
《理论力学》第九章_质点动力学_习题解

AC
g l AC
( cos )
F
n
TAC W cos man W an g
W an g
TAC W cos TAC W cos
W W 2 a n W cos l AC AC g g
初瞬时, AC 0 ,故: TAC W cos (2)求小球 A 运动到铅垂位置时,AC 绳中的拉力 小球运动到铅垂位置时,由上一步骤可知:
dx 9 cos(2t )d (2t ) dt
2
dx 9 sin(2t ) C1 dt
x 9 sin(2t ) C1
x |t 0 x0 9 sin(2 0) C1 C1 0
dx 9 sin(2t ) dt 9 x sin(2t )d (2t ) 2 9 x cos(2t ) C 2 2 9 9 x |t 0 x0 cos(2 0) C 2 C 2 4.5(m) C 2 (m) 0.04(m) 2 2
y
v0
30 0
1m
地面
v x v0 cos 30 0 dx 13 3 dt 2 x 13 3 t C1 2
13 3 (m / s ) 2
mg
O
x
x |t 0
13 3 0 C1 C1 0 2
x
13 3 t 2
v y v0 sin 30 0 gt 6.5 9.8t
x
y
5
[习题 9-4] 通过光滑圆环 C 的绳索将物体 A 与 B 相连,已知 m A 7.5kg , mB 6.0kg , 物体 A 与水平面的摩擦因素 f 0.6 , 在图示瞬时, 物体 B 具有朝右上方的速度 v B 2m / s 。 若在此时突然剪断墙与物体间的绳子,求该瞬时物体 A 的加速度 a A 解: (1)求 AB 间绳子的拉力 以 B 为研究对象,其受力如图所示。
清华大学版理论力学课后习题答案大全第13章 动力学普遍方程习题解
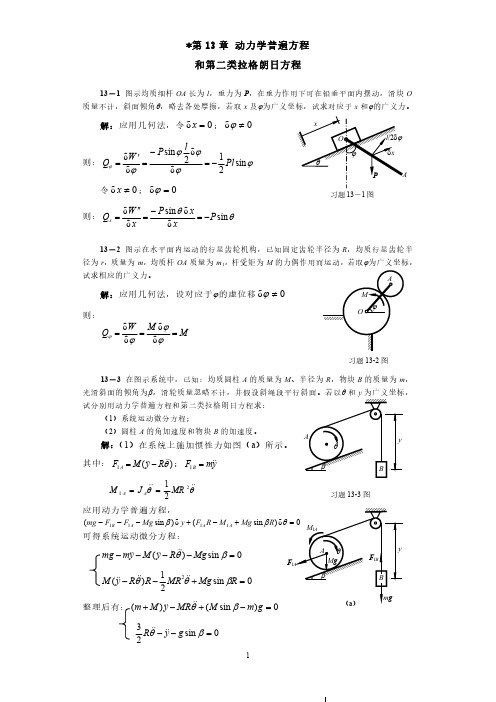
习题13-1图*第13章动力学普遍方程和第二类拉格朗日方程13-1图示均质细杆OA 长为l ,重力为P ,在重力作用下可在铅垂平面内摆动,滑块O 质量不计,斜面倾角θ,略去各处摩擦,若取x 及ϕ为广义坐标,试求对应于x 和ϕ的广义力。
解:应用几何法,令0δ=x ;0δ≠ϕ则:ϕϕϕϕϕϕsin 21δδ2sin δδPl lP W Q -=-='=令0δ≠x ;0δ=ϕ则:θθsin δδsin δδP xxP x W Q x -=-=''=13-2图示在水平面内运动的行星齿轮机构,已知固定齿轮半径为R ,均质行星齿轮半径为r ,质量为m ,均质杆OA 质量为m 1,杆受矩为M 的力偶作用而运动,若取ϕ为广义坐标,试求相应的广义力。
解:应用几何法,设对应于ϕ的虚位移0δ≠ϕ则:M M W Q ===ϕϕϕϕδδδδ13-3在图示系统中,已知:均质圆柱A 的质量为M 、半径为R ,物块B 的质量为m ,光滑斜面的倾角为β,滑轮质量忽略不计,并假设斜绳段平行斜面。
若以θ 和y 为广义坐标,试分别用动力学普遍方程和第二类拉格朗日方程求:(1)系统运动微分方程;(2)圆柱A 的角加速度和物块B 的加速度。
解:(1)在系统上施加惯性力如图(a )所示。
其中:)(I θ R y M F A -=;y m F B=I θθ2I 21MR J M A A ==应用动力学普遍方程,δ)sin (δ)sin (I I I I +-+---θββR Mg M R F y Mg F F mg A A A B 可得系统运动微分方程:0sin )(=----βθMg R y M y m mg 0sin 21)(2=+--R Mg MR R R yM βθθ 整理后有:0)sin ()(=-+-+g m M MR yM m βθ 0sin 23=--βθg yR习题13-2图习题13-3图F应用第二类拉格朗日方程:2222)(21212121θθ R y M MR y m T -+⋅+=;)(sin θβR y Mg mgy V -+-==-=V T L 2222)(21212121θθ R y M MR y m -+⋅+)(sin θβR y Mg mgy --+)(d d θ R yM y m y L t -+=∂∂;βsin Mg mg y L -=∂∂0d d =∂∂-∂∂y L y L t ;0)sin ()(=-+-+g m M MR y M m βθ (a ))(21d d 2θθθ R y RM MR L t --=∂∂;R Mg L βθsin =∂∂0d d =∂∂-∂∂θθL L t;0sin 23=--βθg y R (b )(2)求圆柱A 的角加速度和物块B 的加速度。
理论力学习题答案
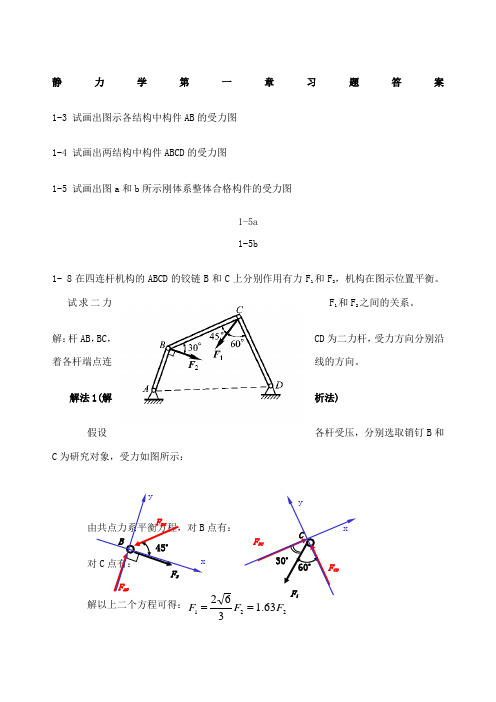
静力学第一章习题答案1-3 试画出图示各结构中构件AB 的受力图1-4 试画出两结构中构件ABCD 的受力图1-5 试画出图a 和b 所示刚体系整体合格构件的受力图1-5a 1-5b1- 8在四连杆机构的ABCD 的铰链B 和C 上分别作用有力F 1和F 2,机构在图示位置平衡。
试求二力F 1和F 2之间的关系。
解:杆AB ,BC ,CD 为二力杆,受力方向分别沿着各杆端点连线的方向。
解法1(解析法)假设各杆受压,分别选取销钉B 和C 为研究对象,受力如图所示:由共点力系平衡方程,对B 点有:对C 点有:解以上二个方程可得:22163.1362F F F ==F 2F BC F ABB45oyxF BCF CDC 60oF 130oxy解法2(几何法)分别选取销钉B 和C 为研究对象,根据汇交力系平衡条件,作用在B 和C 点上的力对B 2BC F F =对C 点由几何关系可知: 0130cos F F BC =解以上两式可得:2163.1F F =静力学第二章习题答案2-3 在图示结构中,二曲杆重不计,曲杆AB 上作用有主动力偶M 。
试求A 和C 点处的约束力。
解:BC 为二力杆(受力如图所示),故曲杆AB 在B 点处受到约束力的方向沿BC 两点连线的方向。
曲杆AB 受到主动力偶M 的作用,A 点和B 点处的约束力必须构成一个力偶才能使曲杆AB 保持平衡。
AB 受力如图所示,由力偶系作用下刚体的平衡方程有(设力偶逆时针为正):其中:31tan =θ。
对BC 杆有:aM F F F A B C 354.0=== A ,C 两点约束力的方向如图所示。
2-4解:机构中AB 杆为二力杆,点A,B 出的约束力方向即可确定。
由力偶系作用下刚体的平衡条件,点O,C 处的约束力方向也可确定,各杆的受力如图所示。
对BC 杆有: 0=∑MF CD F AB030sin 20=-⋅⋅M C B F B对AB 杆有: A B F F = 对OA 杆有: 0=∑M01=⋅-A O F M A求解以上三式可得:m N M ⋅=31, N F F F C O AB 5===,方向如图所示。
理论力学 第7章质点动力学习题解答

1第七章 质点动力学 习题解答7-1 质量为40 g 的小球M 以初速度v =8 j (m/s)从点A (0, 0, 0.3m)抛出后,受到沿i 方向恒定的电磁力作用,其大小F = 0.8 kN ,如图所示。
求小球M 到达xy 平面点B 时,点B 的坐标和小球的速度。
解:取小球M 为研究对象,小球所受到的主动力为 k i F mg F R -=由质点运动微分方程R F m =r ,写出投影式F x m = ,0=ym ,mg z m -= 初始条件为000====t t y x ,3.00==t z ;000====t t z x,v y t ==0 解得质点的速度方程为t mFx= ,v y = ,gt z -= 质点的运动方程为 22t m F x =,vt y =,3.022+-=t gz 当0=z 时,小球到达xy 平面,由03.022=+-=t g z 解得s 247.01=t ,于是小球到达xy 平面时的各速度分量为m/s 7.494811===t mFxt t ,m/s 81===v y t t ,m/s 425.211-=-==gt z t t . 各坐标为m 2.6122211===t m F x t t ,m 979.111===vt y t t ,m 137.23.02211-=+-==t gz tt .7-2 图示A ,B 两物体的质量分别为m A 和m B ,二者用一细绳连接,此绳跨过一定滑轮,滑轮半径为r 。
运动开始时,两物体的高度差为h ,且m A > m B ,不计滑轮质量。
求由静止释放后,两物体达到相同高度时所需的时间。
解:分别取A 和B 物体为研究对象,受力图如图示,列出动力学方程TA A A A F W x m -= , TB B B B F W x m -= , 式中g m W A A =,g m W B B =,根据题意,有TB TA F F =,B A x x -=,B A xx -= 初始条件00==t A x ,h x t B ==0,00==t A x,00==t B x . 解以上初值问题,得题7-2图题7-2受力图2g m m m m xBA B A A +-= , ()22gt m m m m x B A BA A +-=g m m m m x B A B A B +--= , ()h gt m m m m x B A BA B ++--=22令B A x x =,即()()h gt m m m m gt m m m m B A BA B A B A ++--=+-2222解得当两物体达到相同高度时 ()()gm m h m m t B A B A -+=...7-3 质量为m 的质点M 受到引力F = -k 2m r 的作用,其中k 为常量,运动开始时,质点M在轴x 上,OM 0 = b ,初速度v 0与轴x 的夹角为β,如图所示。
理论力学习题答案

静力学第一章习题答案1-3 试画出图示各结构中构件AB 的受力图 1-4 试画出两结构中构件ABCD 的受力图1-5 试画出图a 和b 所示刚体系整体合格构件的受力图1-5a 1-5b1- 8在四连杆机构的ABCD 的铰链B 和C 上分别作用有力F 1和F 2,机构在图示位置平衡。
试求二力F 1和F 2之间的关系。
解:杆AB ,BC ,CD 为二力杆,受力方向分别沿着各杆端点连线的方向。
解法1(解析法)假设各杆受压,分别选取销钉B 和C 为研究对象,受力如图所示:由共点力系平衡方程,对B 点有: 对C 点有:解以上二个方程可得:2163.1362F F F ==解法2(几何法)分别选取销钉B 和C 为研究对象,根据汇交力系平衡条件,作用在B 和C 点上的力构成封闭的力多边形,如图所示。
对B 点由几何关系可知:0245cos BC F F = 对C 点由几何关系可知: 0130cos F F BC =解以上两式可得:2163.1F F =静力学第二章习题答案2-3 在图示结构中,二曲杆重不计,曲杆AB 上作用有主动力偶M 。
试求A 和C 点处的约束力。
解:BC 为二力杆(受力如图所示),故曲杆AB 在B 点处受到约束力的方向沿BC 两点连线的方向。
曲杆AB 受到主动力偶M 的作用,A 点和B 点处的约束力必须构成一个力偶才能F 2F BCF AB B 45oyx F BCF CDC60oF 130o xyF BC F CD 60oF 130o F 2F BC F AB 45o使曲杆AB 保持平衡。
AB 受力如图所示,由力偶系作用下刚体的平衡方程有(设力偶逆时针为正): 其中:31tan =θ。
对BC 杆有:aM F F F A B C 354.0=== A ,C 两点约束力的方向如图所示。
2-4解:机构中AB 杆为二力杆,点A,B 出的约束力方向即可确定。
由力偶系作用下刚体的平衡条件,点O,C 处的约束力方向也可确定,各杆的受力如图所示。
《理论力学》动力学典型习题 答案_图文.

《动力学 I 》第一章运动学部分习题参考解答1-3 解:运动方程:θtan l y =,其中kt =θ。
将运动方程对时间求导并将 030=θ代入得34cos cos 22lk lk l y v ====θθθ98cos sin 2232lk lk y a =-==θθ1-6证明:质点做曲线运动 , 所以 n t a a a +=, 设质点的速度为 v , 由图可知 : a a vv y n cos ==θ,所以 : yv va a n = 将c v y =, ρ2n va =代入上式可得ρc v a 3=证毕 1-7证明:因为 n2a v=ρ, va a v a ⨯==θsin n所以:va ⨯=3v ρ证毕1-10解:设初始时 , 绳索 AB 的长度为 L , 时刻 t 时的长度为 s , 则有关系式: t v L s 0-=,并且 222x l s +=将上面两式对时间求导得:0v s-= , x x s s 22= 由此解得:xsv x-= (a (a式可写成:s v x x 0-= ,将该式对时间求导得: 2002v v s x x x=-=+ (b 将 (a式代入 (b式可得:3220220xlv x x v x a x -=-==(负号说明滑块 A 的加速度向上1-11解:设 B 点是绳子 AB 与圆盘的切点,由于绳子相对圆盘无滑动,所以R v B ω=,由于绳子始终处于拉直状态,因此绳子上 A 、 B 两点的速度在 A、 B 两点连线上的投影相等,即: θcos A B v v = (a 因为xR x 22cos -=θ (b 将上式代入(a 式得到 A 点速度的大小为: 22Rx x Rv A -=ω (c由于 x v A -=, (c 式可写成:Rx R x xω=--22 ,将该式两边平方可得: 222222 (x R R x x ω=- 将上式两边对时间求导可得:x x R x x R x xx 2232222 (2ω=-- 将上式消去 x 2后,可求得:22242(R x xR x--=ω由上式可知滑块 A 的加速度方向向左,其大小为 2 2242(R x xR a A -=ω1-13解:动点:套筒 A ;动系:OA 杆; 定系:机座; 运动分析:绝对运动:直线运动; 相对运动:直线运动; 牵连运动:定轴转动。
理论力学第8章习题解答

理论力学第8章习题解答第八章质点系动力学:矢量方法习题解答8-1 一个质量为5 kg 弹头M 以水平速度v = 60 m/s 飞行,在D 处爆炸成位于同一水平面内如图示速度方向的两块碎片A 和B 。
已知碎片A 的速度大小v A = 90 m/s 。
试求:(1) 碎片A 的质量m A ;(2) 碎片B 的速度大小v B 。
解:取弹头M 为研究对象,弹头爆炸前后动量守恒 () 30cos B A v m M Mv -= () 30sin 0B A A A v m M v m --=解得M v vm A A 33=,AA B v v vv v 32--=,代入数据得:kg 92.1=A m ,m/s 64.112=B v .8-2 一个质量为m 1的人手里拿着质量为m 2的物体,以仰角θ,速度v 0向前跳起。
当他到达最高点时将物体以相对速度u 水平地向后抛出。
如果不计空气阻力,问由于物体的抛出,跳远距离增加了多少?解:取m 1和m 2物体系统为研究对象,人跳至最高点时只有水平速度 ?c o s 01v v =,所费时间 gv t ?sin 0=。
抛物前后系统水平动量守恒,即 ()()u v m v m v m m -+=+1211021c o s ?,式中1v 为抛物后人的速度。
解得21201c o s m m um v v ++=?,可见,人的速度增量为2121Δm m um v +=,从而跳远距离增加()gm m uv m v t s 21021sin ΔΔ+==?.8-3质量为m 1的平台AB 放在水平面上,平台与水平面间的滑动摩擦因数为f 。
质量为m 2的小车D 由绞车拖动,相对平台的运动规律为221bt s =,其中b 为已知常数。
不计绞车质量,求平台的加速度。
解:1)设平台与水平面间的滑动摩擦因数比较小,当小车D 相对平台运动时,平台AB 的有速度1v (向左),小车D 的相对速度bt sv == r ,(向右),小车D 的绝对速度bt v v v v +-=+-=1r e a ,(向右),滑动摩擦力为 N fF F = 题8-3图题8-3受力图题8-1图由动量定理,()[]F v bt m v m t=-+-1211d d()021=++-N F g m m解得()212121m m g m m f b m a ++-=, ()g m m bm f 212+≤.当()gm m bm f 212+>时,01=a .8-4 质量为m 1的矩形板可在如图所示的光滑水平面上运动。
高中动力学试题及答案

高中动力学试题及答案一、选择题(每题3分,共30分)1. 质量为m的物体在水平面上受到一个水平方向的恒定力F作用,物体的加速度大小为a,若物体的质量增加到2m,而力F不变,则物体的加速度大小变为:A. a/2B. 2aC. 2a/3D. a2. 根据牛顿第二定律,作用在物体上的合力等于物体质量与加速度的乘积。
若物体的质量为m,加速度为a,则合力F的大小为:A. F = maB. F = m/aC. F = a/mD. F = a^2/m3. 一个物体从静止开始做匀加速直线运动,加速度为a,经过时间t 后,其速度v和位移s的关系为:A. v = atB. s = 1/2at^2C. v = 2s/tD. s = vt - 1/2at^24. 牛顿第三定律指出,作用力和反作用力大小相等、方向相反。
如果一个物体对地面施加了100N的力,地面对这个物体的反作用力大小为:A. 100NB. 50NC. 200ND. 0N5. 一个物体在水平面上做匀速直线运动,其受到的摩擦力为f,若物体速度增加,则摩擦力:A. 增加B. 减少C. 不变D. 无法确定6. 根据动能定理,一个物体的动能变化等于作用在物体上的合外力做的功。
如果一个物体的动能从E1增加到E2,则合外力做的功W为:A. W = E1 - E2B. W = E2 - E1C. W = (E1 + E2)/2D. W = E1 * E27. 一个物体从高度h处自由下落,忽略空气阻力,其下落过程中重力做的功W与物体的质量m和高度h的关系为:A. W = mgB. W = mghC. W = h/mD. W = g/mh8. 一个物体在斜面上做匀速直线运动,斜面的倾角为θ,物体的重力为G,摩擦力为f,则物体所受的合力为:A. G*sinθ - fB. G*cosθ - fC. G*sinθ + fD. G*cosθ + f9. 一个物体在水平面上做匀加速直线运动,其加速度为a,若物体的质量为m,作用力为F,则物体所受的合力为:A. F - maB. F + maC. maD. F10. 一个物体在竖直方向上做自由落体运动,其加速度大小为g,则物体的位移s与时间t的关系为:A. s = 1/2gt^2B. s = gt^2C. s = 2gtD. s = gt二、填空题(每题3分,共30分)1. 一个物体的质量为2kg,受到的力为10N,根据牛顿第二定律,其加速度大小为______ m/s^2。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
由运动分析可知点的绝对速度、相对速度和牵连速度的方向如图所示,
其中:
根据速度合成定理:
可以得到:
,
加速度如图所示,其中:
,
根据加速度合成定理:
将上式在 轴上投影,可得: ,由此求得:
1-21
解:求汽车B相对汽车A的速度是指以汽车A为参考系观察汽车B的速度。
取:动点:汽车B;
动系:汽车A(Ox’y’);
定系:路面。
运动分析
绝对运动:圆周运动;
相对运动:圆周运动;
牵连运动:定轴转动(汽车A绕O做定轴转动)
求相对速度,根据速度合成定理
将上式沿绝对速度方向投影可得:
因此
其中: ,
由此可得:
求相对加速度,由于相对运动为圆周运动,
相对速度的大小为常值,因此有:
1-23质量为 销钉M由水平槽带动,使其在半径为 的固定圆槽内运动。设水平槽以匀速 向上运动,不计摩擦。求图示瞬时,圆槽作用在销钉M上的约束力。
将 和式(b)代入式(c),并利用 ,可得:
再由方程(a)中的第一式可得
2-1解:当摩擦系数 足够大时,平台AB
相对地面无滑动,此时摩擦力
取整体为研究对象,受力如图,
系统的动量:
将其在 轴上投影可得:
根据动量定理有:
(a)
因为
(b)
将上式代入(a)式得到A点速度的大小为:
(c)
由于 ,(c)式可写成: ,将该式两边平方可得:
将上式两边对时间求导可得:
将上式消去 后,可求得:
(d)
由上式可知滑块A的加速度方向向左,其大小为
取套筒A为研究对象,受力如图所示,
根据质点矢量形式的运动微分方程有:
将该式在 轴上投影可得直角坐标形式的
运动微分方程:
其中:
,
将其代入直角坐标形式的运动微分方程可得
1-13
解:动点:套筒A;
动系:OC杆;
定系:机座;
运动分析:
绝对运动:直线运动;
相对运动:直线运动;
牵连运动:定轴转动。
根据速度合成定理
有: ,因为AB杆平动,所以 ,
由此可得: ,OC杆的角速度为 , ,所以
当 时,OC杆上C点速度的大小为:
取:动点:滑块M;
动系:OC摇杆;
定系:机座;
运动分析:
绝对运动:圆周运动;
相对运动:直线运动;
牵连运动:定轴转动。
根据速度合成定理
可求得:
, ,
根据加速度合成定理
将上式沿 方向投影可得:
由于 , , ,根据上式可得:
,
1-20
解:取小环M为动点,OAB杆为动系
运动分析
绝对运动:直线运动;
相对运动:直线运动;
1-15
解:动点:销子M
动系1:圆盘
动系2:OA杆
定系:机座;
运动分析:
绝对运动:曲线运动
相对运动:直线运动
牵连运动:定轴转动
根据速度合成定理有
,
由于动点M的绝对速度与动系的选取无关,即 ,由上两式可得:
(a)
将(a)式在向在x轴投影,可得:
由此解得:
1-17
解:动点:圆盘上的C点;
动系:O1A杆;
解:销钉M上作用有水平槽的约束力 和圆槽的约束力 (如图所示)。由于销钉M的运动是给定的,所以先求销钉的加速度,在利用质点运动微分方程求约束力。取销钉为动点,水平槽为动系。由运动分析可知销钉的速度图如图所示。
根据速度合成定理有
由此可求出: 。再根据加速度合成定理有:
由于绝对运动是圆周运动,牵连运动是匀速直线平移,所以 ,并且上式可写成:
因为 ,所以根据上式可求出: 。
根据矢量形式的质点运动微分方程有:
将该式分别在水平轴上投影:
由此求出:
1-24图示所示吊车下挂一重物M,绳索长为 ,初始时吊车与重物静止。若吊车从静止以均加速度 沿水平滑道平移。试求重物M相对吊车的速度与摆角 的关系式。
解:由于要求重物相对吊车的速度,所以取吊车为动系,重物M为动点。根据质点相对运动微分方程有
,
由此解得: (a)
(a)式可写成: ,将该式对时间求导得:
(b)
将(a)式代入(b)式可得: (负号说明滑块A的加速度向上)
取套筒A为研究对象,受力如图所示,根据质点矢量形式的运动微分方程有:
将该式在 轴上投影可得直角坐标形式的运动微分方程:
其中:
将其代入直角坐标形式的运动微分方程可得:
1-11
解:设B点是绳子AB与圆盘的切点,由于绳子相对圆盘无滑动,所以 ,由于绳子始终处于拉直状态,因此绳子上A、B两点的速度在 A、B两点连线上的投影相等,即:
解:取小环为动点,金属丝为动系,根据题意,相对平衡位置为 ,因为金属丝为曲线,所以 ,因此在本题中相对平衡位置就是相对静止位置。小环受力如图所示。其中 分别为约束力、牵连惯性力和小环的重力。根据质点相对运动微分方程有:
其中: ,将上式分别在 轴上投影有
(a)
以为 , , ,因此
(b)
由(a)式可得
(c)
解:取小球为动点,板为动系,小球在水平面的受力如图所示(铅垂方向的力未画出)。根据质点相对运动微分方程有:
将上式在 上投影有
因为 , , ,所以上式可写成
整理该式可得:
将该式积分有:
初始时 , ,由此确定积分常数 ,因此得到相对速度为
1-27重为P的小环M套在弯成 形状的金属丝上,该金属丝绕铅垂轴 以匀角速度 转动,如图所示。试求小环M的相对平衡位置以及金属丝作用在小环上的约束力。
将上式在切向量方向投影有
因为 ,所以上式可写成
整理上式可得
将上式积分:
其中 为积分常数(由初始条件确定),因为相对速度 ,上式可写成
初始时 ,系统静止, ,根据速度合成定理可知 ,由此确定 。重物相对速度与摆角的关系式为:
1-26水平板以匀角速度 绕铅垂轴O转动,小球M可在板内一光滑槽中运动(如图7-8),初始时小球相对静止且到转轴O的距离为 ,求小球到转轴的距离为 时的相对速度。
动力学
1-3
解:
运动方程: ,其中 。
将运动方程对时间求导并将 代入得
1-6
证明:质点做曲线运动,
所以质点的加速度为: ,
设质点的速度为 ,由图可知:
,所以:
将 ,
代入上式可得
证毕
1-7
证明:因为 ,
所以:
证毕
1-10
解:设初始时,绳索AB的长度为 ,时刻 时的长度
为 ,则有关系式:
,并且
将上面两式对时间求导得:
定系:机座;
运动分析:绝对运动:圆周运动;
相对运动:直线运动(平行于O1A杆);
牵连运动:定轴转动。
根据速度合成定理有
(a)
将(a)式在垂直于O1A杆的轴上投影以及在O1C轴上投影得:
,
, ,
根据加速度合成定理有
(b)
将(b)式在垂直于O1A杆的轴上投影得
其中: , ABM弯杆平移,所以有
