小学奥数图形找规律题库学生版
五年级奥数专题 图形找规律(学生版)

图形找规律学生姓名授课日期教师姓名授课时长知识定位学会通过观察图形找到规律进而得到某一位置未知的图形。
掌握平移、旋转、合并等常见规律。
知识梳理1、主要变化规律:图形变化边数、方向变化、数量变化、位置变化、填充样式或颜色变化、其他变化2、主要位置变化方式:平移:一般根据图形每行或者每列与相邻列之间变化情况来判断平移的方向,之后来判断未知图形。
旋转:根据相邻图像判断旋转方向。
合并:根据相邻图像判断合并规则。
交换:图形的位置或者颜色、填充样式间进行某种规则的交换。
注意:图形规律题不一定只在同一方向上有规律,或者不止一种规律,需要根据题目情况进行判断,全面考虑,得出符合全部规律的图形。
例题精讲:(★★★)【试题来源】【题目】按规律填出空白图形。
(★★★)【试题来源】【题目】聪明的小朋友们,请你仔细观察下面的图片,然后将空白的部分补充完整。
(★★★)【试题来源】【题目】下面各种各样的娃娃头好看吗?认真观察你能找到它们排列的规律吗?根据规律把最后一个画出来。
(★★★★)【试题来源】【题目】根据下面图形排列的规律,问号的地方应该画什么图形?聪明的孩子们,动手画一画吧!(★★★★★)【试题来源】【题目】观察给出图形的变化规律,“?”处应该画什么图形。
(★★★★★)【试题来源】【题目】根据下列图形的规律,空白的地方应该填什么?请选择。
总结:课后练习【试题来源】【题目】1.★★★按照下面的规律,画一画。
第二排第三个是( ),第三排第二个是( )。
A.●B.▲●C.●D.●▲【试题来源】【题目】2.★★★观察下列各组图的变化规律,并在空白处画出相关的图形。
正确的选项是( ) A.B.C.D.【试题来源】【题目】3.★★★根据规律画出后面的图形。
正确的选项是( )A.B.C.D.【试题来源】【题目】4.★★★★根据规律接着画。
下面选项正确的是( )A.B.C.D.以上答案都不对【试题来源】【题目】5.★★★★★找出下图的变化规律,下一个应该画出什么图形?正确的选项是( )A.B.C.D.【试题来源】【题目】6.★★★★★先找一找方框里八个图形每行排列的规律,再从右面挑选一个合适的图形,把这个图形的号码填入空格内。
一年级奥数图形找规律
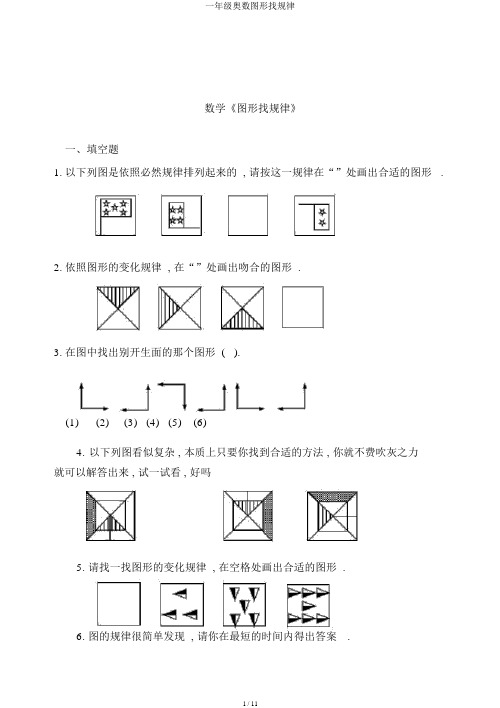
数学《图形找规律》一、填空题1.以下列图是依照必然规律排列起来的 , 请按这一规律在“”处画出合适的图形 .2.依照图形的变化规律 , 在“”处画出吻合的图形 .3.在图中找出别开生面的那个图形 ( ).(1)(2) (3) (4) (5) (6)4.以下列图看似复杂 , 本质上只要你找到合适的方法 , 你就不费吹灰之力就可以解答出来 , 试一试看 , 好吗5.请找一找图形的变化规律 , 在空格处画出合适的图形 .6. 图的规律很简单发现 , 请你在最短的时间内得出答案.ΟΟΟΟΟΟΟ△ΟΟ△△Ο△ △7.找一下规律 , 从 a, b, c, d, e 中选入一幅图填入空格内 .a b c d e8.依照以下列图形的变化规律 , 空白处应是什么样的图形 .9.按规律填图 .若是变成那么应变成10.下面一组图形的阴影变化是有规律的 , 请依照这个规律把第四幅图的阴影部分画出来 .二、解答题11.图中 , 哪个图形别开生面(1)(2)(3)(4)(5)12.有一个立方体 , 每个面上分别写上数字 1、2、3、4、5、6、, 有 3 个人从不同样的角度观察的结果以以下列图所示 , 这个立方体的每一个数字的对面各是什么数字62141313.下面是由几何图形组成的帆船图形 , 请依照必然的规律 , 在标序号处画出吻合规律的小帆船 .①③②———————————————答案——————————————————————1.这一组图形我们应该从两方面来看 : 一是旌旗的方向 , 二是旌旗上星星的颗数 .第一我们看一下旌旗的方向. 第 1 面旌旗向右 , 第 2 面向上 , 第 4 面向下 ,能够发现 , 旌旗的方向是按逆时针旋转的, 并依次旋转 90 , 因此第 3 面旌旗应是第 2 面逆时针旋转 90 得来的 , 旌旗应向下倒立 .其次我们看旗上星星的颗数. 第 1 面是 5 颗, 第 2 面是 4 颗, 第 4 面是 2 颗,可见颗数是依次减少 1 颗, 因此第 3 面旗上应是 3 颗星星 . 因此“”处的图形应为 :2.这组图形的变化只在于正方形中阴影部分的地址 . 经过观察 , 我们能够发现阴影部分是依照逆时针方向依次旋转 90 获取的 . 因此“”处的图形应为:3.选(4). 因为变化规律是从左到右依次逆时针旋转 90 .4.在这组图形中 , 不变的有以下几点 : 大小正方形不变 , 两条对角线不变. 因此“”处也应有大小两个正方形和两条对角线 . 发生变化的有 : 一、阴影部分和黑色部分的地址 . 经过观察 , 我们能够看出这两部分都是按逆时针方向依次旋转 90 获取的 , 因此“”处的阴影部分应是小正方形的右边 , 黑色部分应在大正方形的下部 . 二、小竖线的地址 . 小竖线是从图形中心到相应的边所作的一条垂线 . 它的变化规律是按逆时针方向依次旋转 90 , 这样 , 整个图形我们就解析完了 , 下面看一看你画出的图形和书上的同样吗若是同样 , 就做对了 .5.因为要填的是第 1 幅图 , 我们能够从后往前看 . 第一三角形的个数是发生变化的 , 依次是 7、5、3. 能够发现是从后向前依次减少 2 个的 . 因此第 1 幅图中应有 1 个三角形 . 其次三角形的方向也是有变化的 , 从后边观察 , 三角形是按逆时针方向依次旋转 90 , 因此第 1 幅图中的三角形应向上 , 阴影部分在右边 . 以以下列图所示 :6.横行观察 , 圆的个数逐次减少 1 个, 因此到第 4 行, 圆的个数应为 1,因此“”处应是“△”.也许从三角形考虑 , 三角形的个数为0、1、2, 是逐次增加 1, 因此第 4 行中三角形的个数应为3, 因此“”处应为“△”因此最后的图形为 :7.选 a. 依照对角图形规律 , 可知右下角图形是 a 图.8.解析 : 先看不变的部分 . 在整个变化过程中 , 图形中大、小两个圆圈没有变化 , 因此能够必然空白处的图形必然也有大、 小两个圆圈 , 地址一里一外 .变化的部分可为两部分 : ①图形中的直线部分 , 其变化规律是每次顺时针旋转 90 ; ②图形中的阴影部分 , 其变化规律是每次逆时针旋转90 , 黑色部分交替出现 .解 : 依照上面的解析 , 可画出空白处的图形以下列图 .9. 先应找出变化的规律, 尔后再依此规律 , 在空白处填画出所缺的图形.从第一行能够看到 , 当左边的图形变成右边的图形时 , 下部图形移到上面 , 里面的图形移到下面 , 上面的外面图形移到里面 , 各部分的颜色都没有变 . 依照这一规律 , 我们能够把下面图形变成 :10.先看第 1 行, 阴影部分所在的地址是 1、2、3. 是逐次向后一个 , 因此第四幅图中第 1 行的阴影部分应在第 4 格. 同样 , 第 2 行是 2、 3、再向后应是 5 了, 但没有第 5 个格 , 因此折回到第 1 个格 . 同理可推出第3 行的阴影部分在 第 2格,第4 行的阴影部分在第 3 格.还可以够这样想占去了第 1、2、3: 在同一行中 , 阴影部分都不在同一地址 , 因此第 1 行已经被格 , 因此第四幅图的第一行阴影部分必然是第 4 格 , 同理推出第 2、 3、 4 行中阴影部分的地址 . 最后的答案以以下列图所示.11.解析: 这五辆汽车车窗一致, 车轮一致 , 车底一致, 差异就只幸亏车头、车身部分去搜寻 . 从车身看 ,(3) 别开生面 , 只用一笔画成 , 可是它的车头与(1)同; 从车头看 :(2) 别开生面 ,( 因车头 (1) 与 (3) 同 ,(4) 与 (5) 同 ), 可是 (2) 的车身与 (1) 、(4) 、(5) 近似 . 因此从车头、车身这些特色比较出来的图形, 原由不足以说服人 . 我们把目光转移到笔画多少上 , 就可以找到与众不一的车辆了.解 : 别开生面的汽车是 (1). 其他四车均是由一个矩形、两个圆以及四条直线段、一段弧线画成 , 而(1) 多一条直线段 .12.这个题目其实不难 . 可是 , 推理方法不正确的话 , 也很难看出答案 . 直接考虑数字 1 的对面是什么数 , 想不出来 . 不如换一种思想方式 , 想一想 1 的对面不是什么数 . 从第 1 个图看出 1 的对面不是 4 和 6; 从第 2 个图看出 1 的对面不是 2 和 3, 因此 1 的对面只能是 5. 同样的方法能够获取 ,4 的对面是 2;3 的对面是 6.13.因为正锥体的每个极点连接三个面 . 当正锥体在雪花格纸上按顺时针方向旋转时 , 只有写有 1、2、4 三面所围出的极点素来在雪花格的中心 , 因此只有 1、2、4 贴纸面旋转 , 雪花格有 6 个小格 , 正好能够转两圈 , 因此回到原地各面数字仍是原样分布 .14.每一只小帆船都由三部分组成 : 船体、帆和小旗 . 这三部分都是变化的,别的船体的颜色也是变化的. 下面我们逐一来解析 .①船体的形状 : 帆船的船体都是由半圆、梯形、三角形组成, 并且每一横行 ( 或竖行 ) 都没有重复 . 依照这一规律 , 我们能够确定船体的形状 . 因为①所在的地址横行、竖行都只有1 个图形, 因此不能够确定, 能够先确定②或③ . 看②所在的横行 , 船体形状只有和 , 缺 , 因此②的船体形状应为梯形 . 看①所在的竖行 , 有和,缺,因此①的船体形状为.看③所在的竖行, 有和,缺,因此③的船体形状为.②船体的颜色 . 每一横行 ( 或竖行 ) 都由阴影、黑色、白色三色组成 , 并且在同一行中没有重复颜色, 依照这一规律, 确定出①号船体为白色, ②号船体为黑色 , ③号船体为黑色 .③帆船的形状 .确定方法和前面同样 .④小旗的形状 .最后的答案为 :①②③一年级奥数图形找规律11 / 11。
三年级b版找规律的奥数题及答案

三年级b版找规律的奥数题及答案在三年级奥数题中,找规律是一个常见的题型,它旨在培养学生的观察力、分析力和推理能力。
以下是一些典型的三年级奥数找规律题目及答案:题目1:数字规律1, 3, 5, 7, 9, __, 13, ...答案1:观察数字序列可以发现,这是一个等差数列,公差为2。
所以下一个数字应该是9+2=11。
题目2:图形规律下面的图形序列中,下一个图形是什么?○△△□○△△□__...答案2:观察图形序列,可以发现这是一个周期性的重复模式,每四个图形为一个周期:○△△□。
所以下一个图形应该是□。
题目3:数列规律2, 5, 10, 17, 26, __, 50, ...答案3:观察数列,可以发现每一项与前一项的差分别是3, 5, 7, 9,这是一个等差数列,公差为2。
所以下一个数字与26的差应该是9+2=11,因此下一个数字是26+11=37。
题目4:图形与数字结合规律图形序列:○○□□○○□□○○__...数字序列:1, 2, 3, 4, 5, __, 7, ...答案4:图形序列中,每两个图形为一组,重复出现。
数字序列中,每一项比前一项多1。
所以图形序列的下一个应该是□,数字序列的下一个应该是6。
题目5:组合规律A, B, C, A, B, C, __, A, B, C, ...答案5:观察序列,可以发现这是一个由三个字母A、B、C组成的周期性重复模式。
所以下一个字母组合应该是C。
通过这些题目,学生可以学习到如何观察数字或图形的排列规律,并运用这些规律来解决问题。
在解决这类题目时,重要的是要仔细观察,找出规律,并合理推断出缺失的部分。
小学奥数教程之-图形找规律 (35) (含答案)

【考点】图形找规律 【难度】2 星 【题型】填空 【解析】 (方法一)横着看,每行三角形的个数依次减少,而正方形的个数依次增加,但每行图形的总个数
不变.因为三角形的个数是按 4、3、?、1 的顺序变化的,显然“?”处应填一个三角形△. (方法二)竖着看,三角形由左而右依次减少,而正方形由左而右依次增加,三角形按照 4、?、2、1 的顺序变化,也可以看出 “?”处应是三角形△. 【答案】△
D
【答都是由 A、B、C、D(线段或圆)中的两个组合而成,记为 A★B、C★D、A★D.请 你画出表示 A★C 的图形.
A★B
C★D
A★D
【考点】图形找规律 【难度】2 星 【题型】填空 【解析】观察上图,第一个图形和第三个图形的共同之处是都有一条竖向线段,而它们共有的字母是 A,因
的个数是按 4、3、?、1 的顺序变化的,显然“?”处应填一个圆形。 【答案】圆形
【巩固】 观察图形的变化,想一想,按图形的变化规律,在带“?”的空格处应画什么样的图形?
【考点】图形找规律 【难度】2 星 【题型】填空 【解析】 (方法一)横着看,每行圆形的个数一次减少,而三角形的个数依次增加,但每行图形的总个数不
按照这个规律,第 5 个点群(即方框中的点群)包含的点数是:5×5=25(个).
(2)按发现的规律推出,第十个点群的点数是:10×10=100(个).
(3)前十个点群,所有的点数是:
【答案】(1) 25 ,(2)100 ,(3) 385
【例 8】 观察下面由点组成的图形(点群),请回答:
(1)方框内的点群包含
如:甲图中,A 在左方;而乙图中,A 在上方,……我们把这样一种位置的变化称为图形的旋转, 乙图可以看作是甲图沿顺时针方向旋转 90°得到的,甲图也可以看成是乙图沿逆时针旋转 90°而得到
小学奥数 图形找规律 精选例题练习习题(含知识点拨)
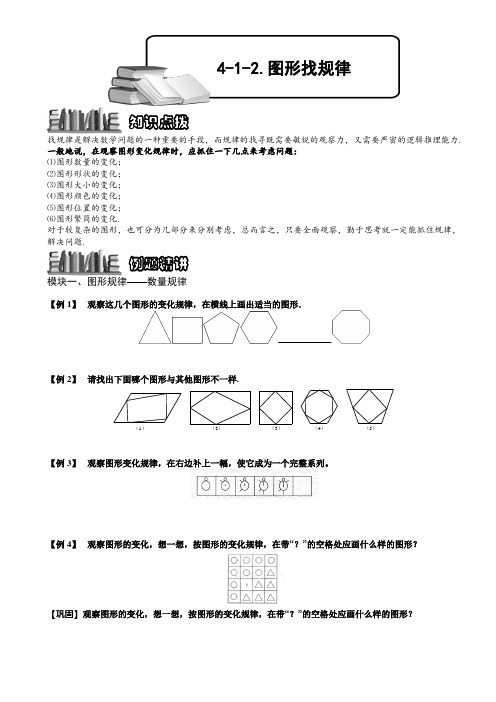
找规律是解决数学问题的一种重要的手段,而规律的找寻既需要敏锐的观察力,又需要严密的逻辑推理能力.一般地说,在观察图形变化规律时,应抓住一下几点来考虑问题: ⑴图形数量的变化; ⑵图形形状的变化; ⑶图形大小的变化; ⑷图形颜色的变化; ⑸图形位置的变化; ⑹图形繁简的变化.对于较复杂的图形,也可分为几部分来分别考虑,总而言之,只要全面观察,勤于思考就一定能抓住规律,解决问题.模块一、图形规律——数量规律【例 1】 观察这几个图形的变化规律,在横线上画出适当的图形.【例 2】 请找出下面哪个图形与其他图形不一样.(1)(2)(3)(4)(5)【例 3】 观察图形变化规律,在右边补上一幅,使它成为一个完整系列。
【例 4】 观察图形的变化,想一想,按图形的变化规律,在带“?”的空格处应画什么样的图形?【巩固】 观察图形的变化,想一想,按图形的变化规律,在带“?”的空格处应画什么样的图形?例题精讲知识点拨4-1-2.图形找规律【巩固】观察图形的变化,想一想,按图形的变化规律,在带“?”的空格处应画什么样的图形??【例5】观察下面的图形,按规律在“?”处填上适当的图形.(4)?【例6】观察图形变化规律,在右边再补上一幅,使它们成为一个完整的系列.【例7】观察下图中的点群,请回答:(1)方框内的点群包含个点;(2)推测第10个点群中包含个点;(3)前10个点群中,所有点的总数是。
【例8】观察下面由点组成的图形(点群),请回答:(1)方框内的点群包含个点;(2)第(10)个点群中包含个点;(3)前十个点群中,所有点的总数是。
【例9】下图表示“宝塔”,它们的层数不同,但都是由一样大的小三角形摆成的.仔细观察后,请回答:(1)五层的“宝塔”的最下层包含多少个小三角形?(2)整个五层“宝塔”一共包含多少个小三角形?【例 10】 在纸上画5条直线,最多可有 个交点。
模块二、图形规律—— 旋转、轮换型规律【例 11】 相传古时候一位老人留在人间很多宝盒,里面装着世界上最宝贵的财富,但是并不是拥有宝盒都可以得到这笔财富,在宝盒的上面设置了密码,只有写出密码的人才会真正拥有这笔财富,聪明的你你能找出密码吗? ○ □ ☆ △ ○ □ ☆ △ △ ○ □ ☆ △ ○ □ ☆ ☆ △ ○ □ ☆ △ ○ □ ()()()()()()()()【例 12】 下面的图形是按一定规律排列的,请仔细观察,并在“?”处填上适当的图形.(1)(2)(3)【例 13】 观察下图的变化规律,画出丙图.甲DA乙BC丙【例 14】 图中的三个图形都是由A 、B 、C 、D (线段或圆)中的两个组合而成,记为A ★B 、C ★D 、A ★D .请你画出表示A ★C 的图形.A★B C★D A★D【例15】(希望杯五年级一试第7题,6分)下列四个图形是由四个简单图形A、B、C、D(线段和正方形)组合(记为*)而成。
奥数-01找规律填图形+答案

练习一
找规律画图。
1、
2、
3、
【例 2】 找规律填图。
解析:相邻图形之间是空心与实心的变化,从形状看,以三角形、五角星、正 方形和圆 4 个图形为一组,所以填 和●。 练习二
找规律在框内填图。 1、
2、
3、A 和 B 重叠后得到右边的四个图形,根据变化规律,画出第 4 个图。
5
【例 3】 找规律填图。 解析:先看台灯底座的颜色,每一
【例 6】 根据前面几幅图的规律,接着画。 解析:前两幅图重叠后得到第三幅图。
练习六
根据前面几幅图的规律,接着画图。
1、
2、
3、
4、
5、
6、
4
【例 1】 要使下面的图形按一定的规律排列,那么应在三个空白处填上怎样的图 形?请你画一画。
解析:这里既有形状的变化,又有大 小的变化,每行都有大、小正方形、圆和 三角形,根据这一规律,画上所缺的图形。
二、方向的变化
观察下图,在空白处填出适当的图形。
三、形状变化
在下图中寻找变化规律,在图 的空白处填上合适的图形。
四、位置变化
仔细观察下图,并按照它的变 化规律,在空白处填上适当的图。
五、循环变化
黑棋子和白棋子排成一行,如图所示,问:第 99 个棋子是什么颜色?这 99 个棋 子中,有多少个白棋子?
1
观察右图,按照变 化规律在“?”处画图。
【例 4】 观察下图,并按照变化规律在右边空白处填上合适的图形
解析:既有位置的变化,又有方向的变化。 练习四
观察图,按照变化规律在空白处填上合适的图形。 1、
3
2、
【例 5】 按照下图的排列规律,第 23 个图形是什么小动物?
小学奥数专题-图形找规律

4-1-2.图形找规律知识点拨找规律是解决数学问题的一种重要的手段,而规律的找寻既需要敏锐的观察力,又需要严密的逻辑推理能力.一般地说,在观察图形变化规律时,应抓住一下几点来考虑问题:⑴图形数量的变化;⑵图形形状的变化;⑶图形大小的变化;⑷图形颜色的变化;⑸图形位置的变化;⑹图形繁简的变化.对于较复杂的图形,也可分为几部分来分别考虑,总而言之,只要全面观察,勤于思考就一定能抓住规律,解决问题.例题精讲模块一、图形规律——数量规律【例 1】观察这几个图形的变化规律,在横线上画出适当的图形.【考点】图形找规律【难度】1星【题型】填空【解析】几个图形的边数依次增加,因此横线上应为一个七边形.【答案】七边形【例 2】请找出下面哪个图形与其他图形不一样.(1)(2)(3)(4)(5)【考点】图形找规律【难度】1星【题型】填空【解析】这组图形的共同特征是,连接各边上一点,组成一个复合图形.所不同的是,第四个图形是一个六边形,而其它几个都是四边形,这样,只有(4)与其它不一样【答案】(4)【例 3】观察图形变化规律,在右边补上一幅,使它成为一个完整系列。
【考点】图形找规律【难度】2星【题型】填空【解析】观察发现,乌龟的顺序是:头、身→一只脚、背上一个点→两只脚、背上两个点→两只脚、一条尾、背上三个点→三只脚、一条尾、背上四个点,根据这个规律,最后一幅图应该是:→四只脚、一条尾、背上五个点.即:【答案】【例 4】 观察图形的变化,想一想,按图形的变化规律,在带“?”的空格处应画什么样的图形?【考点】图形找规律 【难度】2星 【题型】填空 【解析】 横着看,每行圆形的个数一次减少,而三角形的个数依次增加,但每行图形的总个数不变.因为圆形的个数是按4、3、?、1的顺序变化的,显然“?”处应填一个圆形。
【答案】圆形【巩固】 观察图形的变化,想一想,按图形的变化规律,在带“?”的空格处应画什么样的图形?【考点】图形找规律 【难度】2星 【题型】填空 【解析】 (方法一)横着看,每行圆形的个数一次减少,而三角形的个数依次增加,但每行图形的总个数不变.因为圆形的个数是按5、4、3、?、1的顺序变化的,显然“?”处应填一个圆形.(方法二)竖着看,圆形由左而右依次减少,而三角形由左而右依次增加,圆形按照5、4、?、2、1的顺序变化,也可以看出 “?”处应是圆形.【答案】圆形【巩固】 观察图形的变化,想一想,按图形的变化规律,在带“?”的空格处应画什么样的图形??【考点】图形找规律 【难度】2星 【题型】填空 【解析】 (方法一)横着看,每行三角形的个数依次减少,而正方形的个数依次增加,但每行图形的总个数不变.因为三角形的个数是按4、3、?、1的顺序变化的,显然“?”处应填一个三角形△.(方法二)竖着看,三角形由左而右依次减少,而正方形由左而右依次增加,三角形按照4、?、2、1的顺序变化,也可以看出 “?”处应是三角形△.【答案】△【例 5】 观察下面的图形,按规律在“?”处填上适当的图形.(5)(4)(3)(2)(1)?【考点】图形找规律 【难度】2星 【题型】填空 【解析】 本题中,几何图形的变化表现在数量关系上,图中黑三角形的个数从左到右依次增多,从(2)起,每一个格比前面一个格多两个黑三角形,所以,第(4)个方框中应填七个黑三角形.【答案】七个黑三角形【例 6】 观察图形变化规律,在右边再补上一幅,使它们成为一个完整的系列.【考点】图形找规律 【难度】2星 【题型】填空 【解析】 第一格有8个圆圈,第二格有4个圆圈,第三格有2个圆圈,第四格有1个圆圈,第五格有半个圆圈.由此发现,前一格中的图减少一般,正好是后一格的图.所以第六格的图应该是第五格图的一半,即:【答案】【例 7】观察下图中的点群,请回答:(1)方框内的点群包含个点;(2)推测第10个点群中包含个点;(3)前10个点群中,所有点的总数是。
六年级找规律奥数题

例5用3个三角形最多可以把平面分成几部分?10个三角形呢?
1.求十五边形的内角和。
2.6条直线与2个圆最多形成多少个交点?
3.两个四边形最多把平面分成几部分?
例2四边形内有10个点以四边形的4个顶点和这10个点为三角形的顶点最多能剪出多少个小三角形
六年级找规律奥数题
找规律四边形的4个顶点和这10个点为三角形的顶点,最多能剪出多少个小三角形?
例3n棱柱有多少条棱?如果将不相交的两条棱称为一对,那么n棱柱共有多少对不相交的棱?
小学奥数:图形找规律.专项练习及答案解析

找规律是解决数学问题的一种重要的手段,而规律的找寻既需要敏锐的观察力,又需要严密的逻辑推理能力.一般地说,在观察图形变化规律时,应抓住一下几点来考虑问题:⑴图形数量的变化;⑵图形形状的变化;⑶图形大小的变化;⑷图形颜色的变化;⑸图形位置的变化;⑹图形繁简的变化.对于较复杂的图形,也可分为几部分来分别考虑,总而言之,只要全面观察,勤于思考就一定能抓住规律,解决问题.模块一、图形规律——数量规律【例 1】观察这几个图形的变化规律,在横线上画出适当的图形.【考点】图形找规律【难度】1星【题型】填空【解析】几个图形的边数依次增加,因此横线上应为一个七边形.【答案】七边形【例 2】请找出下面哪个图形与其他图形不一样.(1)(2)(3)(4)(5)【考点】图形找规律【难度】1星【题型】填空【解析】这组图形的共同特征是,连接各边上一点,组成一个复合图形.所不同的是,第四个图形是一个六边形,而其它几个都是四边形,这样,只有(4)与其它不一样【答案】(4)【例 3】观察图形变化规律,在右边补上一幅,使它成为一个完整系列。
【考点】图形找规律【难度】2星【题型】填空【解析】观察发现,乌龟的顺序是:头、身→一只脚、背上一个点→两只脚、背上两个点→两只脚、一条尾、背上三个点→三只脚、一条尾、背上四个点,根据这个规律,最后一幅图应该是:→四只脚、一条尾、背上五个点.即:例题精讲知识点拨4-1-2.图形找规律【答案】【例 4】观察图形的变化,想一想,按图形的变化规律,在带“?”的空格处应画什么样的图形?【考点】图形找规律【难度】2星【题型】填空【解析】横着看,每行圆形的个数一次减少,而三角形的个数依次增加,但每行图形的总个数不变.因为圆形的个数是按4、3、?、1的顺序变化的,显然“?”处应填一个圆形。
【答案】圆形【巩固】观察图形的变化,想一想,按图形的变化规律,在带“?”的空格处应画什么样的图形?【考点】图形找规律【难度】2星【题型】填空【解析】(方法一)横着看,每行圆形的个数一次减少,而三角形的个数依次增加,但每行图形的总个数不变.因为圆形的个数是按5、4、3、?、1的顺序变化的,显然“?”处应填一个圆形.(方法二)竖着看,圆形由左而右依次减少,而三角形由左而右依次增加,圆形按照5、4、?、2、1的顺序变化,也可以看出“?”处应是圆形.【答案】圆形【巩固】观察图形的变化,想一想,按图形的变化规律,在带“?”的空格处应画什么样的图形??【考点】图形找规律【难度】2星【题型】填空【解析】(方法一)横着看,每行三角形的个数依次减少,而正方形的个数依次增加,但每行图形的总个数不变.因为三角形的个数是按4、3、?、1的顺序变化的,显然“?”处应填一个三角形△.(方法二)竖着看,三角形由左而右依次减少,而正方形由左而右依次增加,三角形按照4、?、2、1的顺序变化,也可以看出“?”处应是三角形△.【答案】△【例 5】观察下面的图形,按规律在“?”处填上适当的图形.(5)(4)(3)(2)(1)?【考点】图形找规律【难度】2星【题型】填空【解析】本题中,几何图形的变化表现在数量关系上,图中黑三角形的个数从左到右依次增多,从(2)起,每一个格比前面一个格多两个黑三角形,所以,第(4)个方框中应填七个黑三角形.【答案】七个黑三角形【例 6】观察图形变化规律,在右边再补上一幅,使它们成为一个完整的系列.【考点】图形找规律【难度】2星【题型】填空【解析】第一格有8个圆圈,第二格有4个圆圈,第三格有2个圆圈,第四格有1个圆圈,第五格有半个圆圈.由此发现,前一格中的图减少一般,正好是后一格的图.所以第六格的图应该是第五格图的一半,即:【答案】【例 7】观察下图中的点群,请回答:(1)方框内的点群包含个点;(2)推测第10个点群中包含个点;(3)前10个点群中,所有点的总数是。
一年级数学10道奥数练习题立体图形找规律计算解决问题附答案

一年级数学10道奥数练习题立体图形找规律计算解决问题附
答案
一直觉得奥数属于兴趣特长类的学习,比较适合数学方面有天赋和爱好的孩子。
如果孩子乐于钻研,奥数其实是很有趣的,而且特别锻炼孩子的思维。
答案解析——
2.用一个平底锅烙饼,每次最多只能烙2个,烙熟一个需要2分钟(正面反面各需用时1分钟),若烙熟3个至少需要用时几分钟?
答案解析——
3.图形认知——
答案解析——
4.立体图形——
答案解析——
5、立体图形认知——
答案解析——
6.一共多少人在一起玩游戏。
答案解析——
7.计算——
答案解析——
8.计算——
9.计算——
答案解析——
10.卡片组成数——
答案解析——
奥数题算是兴趣训练,如果孩子对数学感兴趣,并在这方面有特长,可以每天做一道奥数题活动活动脑子。
图形找规律专项练习60题(有答案)(可编辑修改word版)

图形找规律专项练习 60 题(有答案)1.按如下方式摆放餐桌和椅子:填表中缺少可坐人数;.2.观察表中三角形个数的变化规律:图形横截线条数0 1 2 …n三角形个数6 ??…?(用含n 的代数式表示).3.如图,在线段 AB 上,画 1 个点,可得 3 条线段;画 2 个不同点,可得 6 条线段;画 3 个不同点,可得 10 条线段;…照此规律,画10 个不同点,可得线段条.4.如图是由数字组成的三角形,除最顶端的 1 以外,以下出现的数字都按一定的规律排列.根据它的规律,则最下排数字中x 的值是,y 的值是.5.下列图形都是由相同大小的单位正方形构成,依照图中规律,第六个图形中有个单位正方形.6.如图,用相同的火柴棒拼三角形,依此拼图规律,第7 个图形中共有根火柴棒.7.图1 是一个正方形,分别连接这个正方形的对边中点,得到图 2;分别连接图 2 中右下角的小正方形对边中点,得到图 3;再分别连接图 3 中右下角的小正方形对边中点,得到图 4;按此方法继续下去,第 n 个图的所有正方形个数是个.8.观察下列图案:它们是按照一定规律排列的,依照此规律,第6 个图案中共有个三角形.9.如图,依次连接一个边长为 1 的正方形各边的中点,得到第二个正方形,再依次连接第二个正方形各边的中点,得到第三个正方形,按此方法继续下去,则第二个正方形的面积是.;第六个正方形的面积是10.下列各图形中的小正方形是按照一定规律排列的,根据图形所揭示的规律我们可以发现:第 1 个图形有 1 个小正方形,第 2 个图形有 3 个小正方形,第 3 个图形有 6 个小正方形,第 4 个图形有 10 个小正方形…,按照这样的规律,则第10 个图形有个小正方形.11.如图,用围棋子按下面的规律摆图形,则摆第n 个图形需要围棋子的枚数为.12.为庆祝“六一”儿童节,幼儿园举行用火柴棒摆“金鱼”比赛,如图所示,则摆 n 条“金鱼”需用火柴棒的根数为.13.如图,两条直线相交只有 1 个交点,三条直线相交最多有 3 个交点,四条直线相交最多有 6 个交点,五条直线相交最多有10 个交点,六条直线相交最多有个交点,二十条直线相交最多有个交点.14.用火柴棒按如图所示的方式搭图形,按照这样的规律搭下去,填写下表:图形编号(1)(2)(3)…n火柴根数.15.图(1)是一个黑色的正三角形,顺次连接三边中点,得到如图(2)所示的第 2 个图形(它的中间为一个白色的正三角形);在图(2)的每个黑色的正三角形中分别重复上述的作法,得到如图(3)所示的第 3 个图形.如此继续作下去,则在得到的第5 个图形中,白色的正三角形的个数是.16.如图,一块圆形烙饼切一刀可以切成 2 块,若切两刀最多可以切成 4 块,切三刀最多可以切成 7 块…通过观察、计算填下表(其中S 表示切n 刀最多可以切成的块数)后,可探究一圆形烙饼切n 刀最多能切成块(结n 0 1 2 3 4 5 …nS 1 2 4 717.如图,是用相同的等腰梯形拼成的等腰梯形图案.第(1)个图案只有 1 个等腰梯形,其两腰之和为 4,上下底之和为 3,周长为 7;第(2)个图案由 3 个等腰梯形拼成,其周长为 13;…第(n)个图案由(2n﹣1)个等腰梯形拼成,其周长为.(用正整数 n 表示)(用含 n 18.下列各图均是用有一定规律的点组成的图案,用S 表示第n 个图案中点的总数,则S=的式子表示).19.如图,由若干盆花摆成图案,每个点表示一盆花,几何图形的每条边上(包括两个顶点)都摆有 n(n≥3)盆花,每个图案中花盆总数为S,按照图中的规律可以推断S 与n(n≥3)的关系是.20.用火柴棍象如图这样搭图形,搭第n 个图形需要根火柴棍.21.现有黑色三角形“”和白色三角形“”共有2011 个,按照一定的规律排列如下:则黑色三角形有个.22.假设有足够多的黑白围棋子,按照一定的规律排成一行:○●●○○●○●●○○●○●●○○●○●●○○●…请问第2011 个棋子是黑的还是白的?答:.梯形的个数 1 2 3 4 5 …图形的周长 5 8 11 14 17 …24.如图,下面是一些小正方形组成的图案,第4 个图案有个小正方形组成;第n 个图案有个小正方形组成.25.如图所示是由火柴棒按一定规律拼出的一系列图形:依照此规律,第7 个图形中火柴棒的根数是.26.图中的每个图形都是由若干个棋子围成的正方形图案,图案的每条边(包括两个顶点)上都有 n(n≥2)个棋子,每个图案的棋子总数为s,按图的排列规律推断,s 与n 之间的关系可用式子表示.27.观察下列图形,它是按一定规律排列的,那么第个图形中,十字星与五角星的个数和为 27 个.28.2 条直线最多只有 1 个交点;3 条直线最多只有 3 个交点;4 条直线最多只有 6 个交点;2000 条直线最多只有个交点.29.以下各图分别由一些边长为 1 的小正方形组成,请填写图 2、图 3 中的周长,并以此推断出图 10 的周长为.30.如图所示,第 1 个图案是由黑白两种颜色的正六边形地面砖组成,第 2 个,第 3 个图案可以看作是第 1 个图案经过平移而得,那么设第n 个图案中有白色地面砖m 块,则m 与n 的函数关系式是.31.用同样大小的黑色棋子按如图所示的规律摆放:(1)分别写出第 6、7 两个图形各有多少颗黑色棋子?(2)写出第 n 个图形黑色棋子的颗数?(3)是否存在某个图形有 2012 颗黑色棋子?若存在,求出是第几个图形;若不存在,请说明理由.32.如图,给出四个点阵,s 表示每个点阵中点的个数,按照图形中的点的个数变化规律,(1)猜想第n 个点阵中的点的个数s= .(2)若已知点阵中点的个数为 37,问这个点阵是第几个?33.用棋子摆出下列一组图形:(1)图形编号 1 2 3 4 5 6图中棋子数 5 8 11 14 17 20(2)(3)其中某一图形可能共有 2011 枚棋子吗?若不可能,请说明理由;若可能,请你求出是第几个图形.34.观察图中四个顶点的数字规律:(1)数字“30”在个正方形的;(2)请你用含有 n(n≥1的整数)的式子表示正方形四个顶点的数字规律;(3)数字“2011”应标在什么位置.35. 如图,各图表示若干盆花组成的形如三角形的图案,每条边(包括两个顶点)有 n (n >1)盆花,每个图案中花盆的总数为 S .问:①当每条边有 2 盆花时,花盆的总数 S 是多少? ②当每条边有 3 盆花时,花盆的总数 S 是多少? ③当每条边有 4 盆花时,花盆的总数 S 是多少? ④当每条边有 10 盆花时,花盆的总数 S 是多少?⑤按此规律推断,当每条边有 n 盆花时,花盆的总数 S 是多少?36. 如下图是用棋子摆成的“上”字:如果按照以上规律继续摆下去,那么通过观察,可以发现: (1) 第④、第⑤个“上”字分别需用 和 枚棋子;(2) 第 n 个“上”字需用 枚棋子; (3) 七(3)班有 50 名同学,把每一位同学当做一枚棋子,能否让这 50 枚“棋子”按照以上规律恰好站成一个“上” 字?若能,请计算最下一“横”的学生数;若不能,请说明理由.线段上点的个数线段的总条数11+2=31+2+3=6……(1) (2) 若在同一线段上有 10 个点,则线段的总条数为 条线段(用含 n 的式子表示) ;若在同一线段上有 n 个点,则有 (3) 若你所在的班级有 60 名学生,20 年后参加同学聚会,见面时每两个同学之间握一次手,共握手次.38.如图是用棋子摆成的“H”字.(1)摆成第一个“H”字需要;个棋子;摆第 x 个“H”字需要的棋子数可用含 x 的代数式表示为(2)问第几个“H”字棋子数量正好是 2012 个棋子?39.我们知道,两条直线相交只有一个交点.请你探究:(1)三条直线两两相交,最多有(2)四条直线两两相交,最多有(3)n 条直线两两相交,最多有个交点;个交点;个交点(n 为正整数,且n≥2).40.如图所示,小王玩游戏:一张纸片,第一次将其撕成四小片,手中共有 4 张纸片,以后每次都将其中一片撕成更小的四片.如此进行下去,当小王撕到第 n 次时,手张共有 S 张纸片.根据上述情况:(1)用含 n 的代数式表示 S;(2)当小王撕到第几次时,他手中共有 70 张小纸片?41.如图①是一张长方形餐桌,四周可坐 6 人,2 张这样的桌子按图②方式拼接,四周可坐 10 人.现将若干张这样的餐桌按图③方式拼接起来:(1)三张餐桌按题中的拼接方式,四周可坐(2)n 张餐桌按上面的方式拼接,四周可坐人;人(用含 n 的代数式表示).若用餐人数为 26 人,则这样的餐桌需要张.42.用棋子摆出下列一组图形:(1)图形编号12 3 4 5 6图形中的棋子(2)(3)如果某一图形共有 99 枚棋子,你知道它是第几个图形吗?43.如图①,图②,图③,图④,…,是用围棋棋子按照某种规律摆成的一行“广”字,按照这种规律,(1)第5 个“广”字中的棋子个数是.(2)第n 个“广”字需要多少枚棋子?44.如图,用同样规格黑白两色的正方形瓷砖铺设矩形地面,请观察图形并解答有关问题:(1)在第n 个图中共有块黑瓷砖,块白瓷砖;(2)是否存在黑瓷砖与白瓷砖块数相等的情形?你能通过计算说明吗?45.用火柴棒按如图的方式搭三角形.照这样搭下去:(1)搭4 个这样的三角形要用(2)搭n 个这样的三角形要用根火柴棒;13 根火柴棒可以搭根火柴棒(用含 n 的代数式表示).个这样的三角形;46. 观察图中的棋子:(1) 按照这样的规律摆下去,第 4 个图形中的棋子个数是多少? (2) 用含 n 的代数式表示第 n 个图形的棋子个数; (3) 求第 20 个图形需棋子多少个?47. 如图,用正方体石墩垒石梯,下图分别表示垒到一、二、三阶梯时的情况.那么照这样垒下去,请你观察规律, 并完成下列问题.(1)阶梯级数 一级 二级 三级 四级石墩块数 3 9(2) n=100 时,共用正方体石墩多少块?48. 有一张厚度为 0.05 毫米的纸,将它对折 1 次后,厚度为 2×0.05 毫米. (1) 对折 3 次后,厚度为多少毫米? (2) 对折 n 次后,厚度为多少毫米? (3) 对折 n 次后,可以得到多少条折痕?49. 如图所示,用同样规格正方形瓷砖铺设矩形地面,请观察下图:按此规律,第 n 个图形,每一横行有示)块瓷砖,每一竖列有 块瓷砖(用含 n 的代数式表按此规律,铺设了一矩形地面,共用瓷砖 506 块,请问这一矩形的每一横行有多少块瓷砖,每一竖列有多少瓷砖?50.找规律:观察下面的星阵图和相应的等式,探究其中的规律.(1)在④、⑤和⑥后面的横线上分别写出相应的等式:①1=12②1+3=22③1+3+5=32④;⑤;⑥;(2)通过猜想,写出第 n 个星阵图相对应的等式.51.将一张正方形纸片剪成四个大小一样的小正方形,然后将其中的一个正方形再剪成四个小正方形,如此循环下去,如图所示:(1)所剪次数 n 1 2 3 4 5正方形个数 Sn 4(2)剪n 次共有S n 个正方形,请用含n 的代数式表示S n= ;(3)若原正方形的边长为1,则第n 次所剪得的正方形边长是(用含 n 的代数式表示).52.如图是用五角星摆成的三角形图案,每条边上有 n(n>1)个点(即五角星),每个图案的总点数(即五角星总数)用S 表示.(1)观察图案,当n=6 时,S= ;(2)分析上面的一些特例,你能得出怎样的规律?(用n 表示S)(3)当 n=2008 时,求 S.53.用水平线和竖直线将平面分成若干个边长为 1 的小正方形格子,小正方形的顶点,叫格点.观察图中每一个正方形(实线)四条边上的格点的个数,请回答下列问题:(1)由里向外第1 个正方形(实线)四条边上的格点个数共有个;由里向外第 2 个正方形(实线)个;由里向外第3 个正方形(实线)四条边上的格点个数共有四条边上的格点个数共有个;(2)由里向外第10 个正方形(实线)四条边上的格点个数共有个;(3)由里向外第n 个正方形(实线)四条边上的格点个数共有个.54.下列各图是由若干花盆组成的形如正方形的图案,每条边(包括两个顶点)有n(n>1)个花盆,每个图案花盆总数是 S.n 2 3 4 5 …S 4 8 12 ….(3)写出S 与n 的关系式:S= .(4)用42 个花盆能摆出类似的图案吗?55.如图,用同样规格的黑白两色正方形瓷砖铺设矩形地面,请观察下列图形,探究并解答下列问题.(1)在第1 个图中,共有白色瓷砖块.(2)在第2 个图中,共有白色瓷砖块.(3)在第3 个图中,共有白色瓷砖块.(4)在第10 个图中,共有白色瓷砖块.(5)在第n 个图中,共有白色瓷砖块.56. 淮北市为创建文明城市,各种颜色的菊花摆成如下三角形的图案,每条边(包括两个顶点)上有 n (n >1)盆花,每个图案花盆的总数为 S ,当 n=2 时,S=3;n=3 时,S=6;n=4 时,S=10.(1)当 n=6 时,S=;n=100 时,S=.(2)你能得出怎样的规律?用 n 表示 S .57. 下面是按照一定规律画出的一系列“树枝”经观察,图(2)比图(1)多出 2 个“树枝”,图(3)比图(2)多出 4 个“树枝”,图(4)比图(3)多出 8 个“树枝”,按此规律:图(5)比图(4)多出 图(6)比图(5)多出 图(8)比图(7)多出 …个树枝; 个树枝; 个树枝; 图(n+1)比图(n )多出个树枝.58. 如图是用棋子成的“T”字图案.从图案中可以出,第一个“T”字图案需要 5 枚棋子,第二个“T”字图案需要 8 枚棋子,第三个“T”图案需要 11 枚棋子.(1) 照此规律,摆成第八个图案需要几枚棋子? (2) 摆成第 n 个图案需要几枚棋子? (3) 摆成第 2010 个图案需要几枚棋子?59.用黑白两种颜色的正六边形地砖按如下所示的规律拼成若干图案:(1)当黑砖n=1 时,白砖有块.(2)第n 个图案中,白色地砖共块,当黑砖n=2 时,白砖有块.块,当黑砖 n=3 时,白砖有60.下列图案是晋商大院窗格的一部分.其中,“o”代表窗纸上所贴的剪纸.探索并回答下列问题:(1)第6 个图案中所贴剪纸“o”的个数是;(2)第n 个图案中所贴剪纸“o”的个数是;(3)是否存在一个图案,其上所贴剪纸“o”的个数为 2012 个?若存在,指出是第几个;若不存在,请说明理由.图形找规律 60 题参考答案:1.结合图形和表格,不难发现:1 张桌子座 6 人,多一张桌子多 2 人.4 张桌子可以座 10+2=12.即n 张桌子时,共座 6+2(n﹣1)=2n+4.2.当横截线有 n 条时,在 6 个的基础上多了 n 个6,即三角形的个数共有 6+6n=6(n+1)个.故应填 6(n+1)或6n+63.∵画1 个点,可得 3 条线段,2+1=3;画2 个点,可得 6 条线段,3+2+1=6;画 3 个点,可得 10 条线段,4+3+2+1=10;…;画n 个点,则可得(1+2+3+…+n+n+1)=条线段.所以画10 个点,可得=66 条线段;4.根据图形可以发现,第七排的第一个数和第二数与第八排的第二个数相等,而第八排的第二个数就是 x,所以 x=61.另外,由图形可知,x 右边的数是2×61=122,y 左边的数是2×61+56=178,所以 y=178+46=2245.根据题意分析可得:第 1 个图案中正方形的个数 2 个,第2 个图案中正方形的个数比第 1 个图案中正方形的个数多4 个,第3 个图案中正方形的个数比第 2 个图案中正方形的个数多 6 个…,依照图中规律,第六个图形中有2+4+6+8+10+12=42 个单位正方形6.图形从上到下可以分成几行,第 n 行中,斜放的火柴有 2n 根,下面横放的有 n 根,因而图形中有 n 排三角形时,火柴的根数是:斜放的是2+4+…+2n=2(1+2+…+n)横放的是:1+2+3+…+n,则每排放 n 根时总计有火柴数是:3 (1+2+…+n)= 3n(n 1) 把n=7 代入就可以求出.2故第7 个图形中共有=84 根火柴棒7.图1 中,是 1 个正方形;图 2 中,是 1+4=5 个正方形;图 3 中,是1+4×2=9 个正方形;依此类推,第n 个图的所有正方形个数是1+4(n﹣1)=4n ﹣3.8.∵第1 个图案中有2×2+2×1=6个三角形;第2 个图案中有2×3+2×2=10个三角形;第3 个图案中有2×4+2×3=14个三角形;…∴第 6 个图案中有2×7+2×6=26 个三角形.故答案为 269.∵正方形的边长是 1,所以它的斜边长是:=,所以第二个正方形的面积是:×=,第三个正方形的面积为=()2,以此类推,第n 个正方形的面积为()n﹣1,所以第六个正方形的面积是()6﹣1= ;故答案为:,.10.∵第一个有 1 个小正方形,第二个有 1+2 个,第三个有1+2+3 个,第四个有1+2+3+4,第五个有1+2+3+4+5,∴则第 10 个图形有 1+2+3+4+5+6+7+8+9+10=55 个.故答案为:5511.依题意得:(1)摆第 1 个“小屋子”需要 5 个点;摆第 2 个“小屋子”需要 11 个点;摆第 3 个“小屋子”需要 17 个点.当n=n 时,需要的点数为(6n﹣1)个.故答案为 6n﹣112.由图形可知:第一个金鱼需用火柴棒的根数为:2+6=8;第二个金鱼需用火柴棒的根数为:2+2×6=14;第三个金鱼需用火柴棒的根数为:2+3×6=20;…;第n 个金鱼需用火柴棒的根数为:2+n×6=2+6n.故答案为 2+6n13.6 条直线两两相交,最多有n(n﹣1)=×6×5=15,20 条直线两两相交,最多有n(n﹣1)=×20×19=190.故答案为:15,190.图形编号(1)(2)(3)…n火柴根数7 12 17 …5n+215.设白三角形 x 个,黑三角形 y 个,则:n=1 时,x=0,y=1;n=2 时,x=0+1=1,y=3;n=3 时,x=3+1=4,y=9;n=4 时,x=4+9=13,y=27;当 n=5 时,x=13+27=40,所以白的正三角形个数为:40,故答案为:4016.n=1 时,S=1+1=2,n=2 时,S=1+1+2=4,n=3 时,S=1+1+2+3=7,n=4 时,S=1+1+2+3+4=11,…所以当切n 刀时,S=1+1+2+3+4+…+n=1+n(n+1)=n2+ n+1.故答案为n2+ n+117.根据题意得:第(1)个图案只有 1 个等腰梯形,周长为3×1+4=7;第(2)个图案由 3 个等腰梯形拼成,其周长为3×3+4=13;第(3)个图案由 5 个等腰梯形拼成,其周长为3×5+4=19;…第(n)个图案由(2n﹣1)个等腰梯形拼成,其周长为3(2n ﹣1)+4=6n+1;故答案为:6n+118.观察发现:第 1 个图形有S=9×1+1=10个点,第 2 个图形有S=9×2+1=19个点,第3 个图形有S=9×3+1=28个点,…第n 个图形有 S=9n+1 个点.故答案为:9n+119.n=3 时,S=6=3×3﹣3=3,n=4 时,S=12=4×4﹣4,n=5 时,S=20=5×5﹣5,…,依此类推,边数为 n 数,S=n•n﹣n=n(n﹣1).故答案为:n(n﹣1).20.结合图形,发现:搭第 n 个三角形,需要 3+2(n﹣1)=2n+1(根).故答案为 2n+121.因为2011÷6=335…1.余下的 1 个根据顺序应是黑色三角形,所以共有1+335×3=1006.故答案为:1006 22.从所给的图中可以看出,每六个棋子为一个循环,∵2011÷6=335…1,∴第 2011 个棋子是白的.故答案为:白23.依题意可求出梯形个数与图形周长的关系为 3n+2= 周长,当梯形个数为 2007 个时,这时图形的周长为3×2007+2=6023.故答案为:6023.24.观察图形知:第一个图形有 1=12个小正方形;第二个图形有 1+3=4=22个小正方形;第三个图形有 1+3+5=9=32个小正方形;…第 n 个图形共有1+2+3+…+(2n﹣1)=n2个小正方形,当n=4 时,有 n2=42=16 个小正方形.故答案为:16,n225.根据已知图形可以发现:第2 个图形中,火柴棒的根数是 7;第3 个图形中,火柴棒的根数是 10;第4 个图形中,火柴棒的根数是 13;∵每增加一个正方形火柴棒数增加 3,∴第 n 个图形中应有的火柴棒数为:4+3(n﹣1)=3n+1.当n=7 时,4+3(n﹣1)=4+3×6=22,故答案为:2226.观察图形发现:当 n=2 时,s=4,当n=3 时,s=9,当n=4 时,s=16,当n=5 时,s=25,…当n=n 时,s=n2,故答案为:s=n227.∵第 1 个图形中,十字星与五角星的个数和为3×2=6,第2 个图形中,十字星与五角星的个数和为3×3=9,第3 个图形中,十字星与五角星的个数和为3×4=12,…而27=3×9,∴第 8 个图形中,十字星与五角星的个数和=3×9=27.故答案为:828.2 条直线最多的交点个数为 1,3 条直线最多的交点个数为 1+2=3,4条直线最多的交点个数为 1+2+3=6,5条直线最多的交点个数为 1+2+3+4=10,…所以 2000 条直线最多的交点个数为1+2+3+4+ (1999)=1999000.故答案为 199900029.∵小正方形的边长是 1,∴图 1 的周长是:1×4=4,图 2 的周长是:2×4=8,图3 的周长是3×4=12,…第 n 个图的周长是 4n,∴图 10 的周长是10×4=40;故答案为:8,12,4030.首先发现:第一个图案中,有白色的是 6 个,后边是依次多 4 个.所以第 n 个图案中,是 6+4(n﹣1)=4n+2.∴m与n 的函数关系式是m=4n+2.故答案为:4n+2. 31.第一个图需棋子 6,第二个图需棋子 9,第三个图需棋子 12,第四个图需棋子 15,第五个图需棋子 18,…第 n 个图需棋子 3(n+1)枚.(1)当n=6 时,3×(6+1)=21;当n=7 时,3×(7+1)=24;(2)第n 个图需棋子 3(n+1)枚.(3)设第 n 个图形有 2012 颗黑色棋子,根据(1)得3(n+1)=2012解得n=,所以不存在某个图形有 2012 颗黑色棋子32.(1)由点阵图形可得它们的点的个数分别为:1,5,9,13,…,并得出以下规律:第一个点数:1=1+4×(1﹣1)第二个点数:5=1+4×(2﹣1)第三个点数:9=1+4×(3﹣1)第四个点数:13=1+4×(4﹣1)…因此可得:第n 个点数:1+4×(n﹣1)=4n﹣3.故答案为:4n﹣3;(2)设这个点阵是 x 个,根据(1)得:1+4×(x﹣1)=37解得:x=10.答:这个点阵是 10 个33.(1)观察图形,得出枚数分别是,5,8,11,…,每个比前一个多 3 个,所以图形编号为 5,6 的棋字子数分别为 17,20.故答案为:17 和 20.(2)由(1)得,图中棋子数是首项为 5,公差为 3 的等差数列,所以摆第 n 个图形所需棋子的枚数为:5+3(n﹣1)=3n+2.(3)不可能由3n+2=2010,解得:n=669,∵n 为整数,∴n=669 不合题意故其中某一图形不可能共有 2011 枚棋子34.(1)由图可知,每个正方形标 4 个数字,∵30÷4=7…2,∴数字 30 在第8 个正方形的第 2 个位置,即右上角;故答案为:8,右上角;(2)左下角是 4 的倍数,按照逆时针顺序依次减 1,即正方形左下角顶点数字:4n,正方形左上角顶点数字:4n﹣1,正方形右上角顶点数字:4n﹣2,正方形右下角顶点数字:4n﹣3;(3)2011÷4=502…3,所以,数字“2011”应标第 503 个正方形的左上角顶点处35.依题意得:①n=2,S=3=3×2﹣3.②n=3,S=6=3×3﹣3.③n=4,S=9=3×4﹣3④n=10,S=27=3×10﹣3.…⑤按此规律推断,当每条边有 n 盆花时,S=3n﹣3 36.(1)第①个图形中有 6 个棋子;第②个图形中有 6+4=10 个棋子;第③个图形中有6+2×4=14 个棋子;∴第⑤个图形中有6+3×4=18个棋子;第⑥个图形中有6+4×4=22个棋子.故答案为 18、22;(3 分)(2)第 n 个图形中有 6+(n﹣1)×4=4n+2.故答案为 4n+2.(3 分)(3)4n+2=50,解得 n=12.最下一横人数为 2n+1=25.(4 分)37.(1)5 个点时,线段的条数:1+2+3+4=10,6 个点时,线段的条数:1+2+3+4+5=15;(2)10 个点时,线段的条数:1+2+3+4+5+6+7+8+9=45,n 个点时,线段的条数:1+2+3+…+(n﹣1)=;(3)60 人握手次数==1770.故答案为:(2)45,;(3)1770. 38.(1)摆成第一个“H”字需要 7 个棋子,第二个“H”字需要棋子 12 个;第三个“H”字需要棋子 17 个;…第 x 个图中,有 7+5(x﹣1)=5x+2(个).(2)当 5x+2=2012 时,解得:x=402,故第 402 个“H”字棋子数量正好是 2012 个棋子39.(1)如图(1),可得三条直线两两相交,最多有 3 个交点;(2)如图(2),可得三条直线两两相交,最多有 6 个交点;(3)由(1)得,=3,由(2)得,=6;∴可得,n 条直线两两相交,最多有个交点(n 为正整数,且 n≥2). 故答案为 3;6;.40.(1)由题目中的“每次都将其中﹣片撕成更小的四片”,可知:小王每撕一次,比上一次多增加 3 张小纸片. ∴s=4+3(n ﹣1)=3n+1;(2)当 s=70 时,有 3n+1=70,n=23.即小王撕纸 23 次41.(1)结合图形,发现:每个图中,两端都是坐 2 人, 剩下的两边则是每一张桌子是 4 人.则三张餐桌按题中的拼接方式,四周可坐 3×4+2=14 (人);(2)n 张餐桌按上面的方式拼接,四周可坐(4n+2)人; 若用餐人数为 26 人,则 4n+2=26, 解得 n=6.故答案为:14;(4n+2),642.(1)如图所示: 图形 编号 1 2 3456图形 中的棋子6 912 15 18 216+3(n ﹣1)=6+3n ﹣3=3n+3;(3) 由上题可知此时 3n+3=99,∴n=32.答:第 32 个图形共有 99 枚棋子13.由题目得:第 1 个“广”字中的棋子个数是 7; 第 2 个“广”字中的棋子个数是 7+(2﹣1)×2=9; 第 3 个“广”字中的棋子个数是 7+(3﹣1)×2=11; 第 4 个“广”字中的棋子个数是 7+(4﹣1)×2=13; 发现第 5 个“广”字中的棋子个数是 7+(5﹣1)× 2=15…进一步发现规律:第n 个“广”字中的棋子个数是7+(n ﹣ 1)×2=2n+5. 故答案为:1544.(1)在第 n 个图形中,需用黑瓷砖 4n+6 块,白瓷砖 n (n+1)块;(2)根据题意得 n (n+1)=4n+6,n 2﹣3n ﹣6=0, 此时没有整数解, 所以不存在.故 答 案 为 :4n+6;n (n+1) 45.(1)结合图形,发现:后边每多一个三角形,则需要多 2 根火柴.则搭 4 个这样的三角形要用 3+2×3=9 根火柴棒;13 根火柴棒可以搭(13﹣3)÷2+1=6 个这样的三角形; (2)根据(1)中的规律,得搭 n 个这样的三角形要用 3+2(n ﹣1)=2n+1 根火柴棒. 故答案为 9;6;2n+146.(1)第 4 个图形中的棋子个数是 13; (2)第 n 个图形的棋子个数是 3n+1; (3)当 n=20 时,3n+1=3×20+1=61∴第 20 个图形需棋子 61 个47.(1)第一级台阶中正方体石墩的块数为:=3;第一级台阶中正方体石墩的块数为:=9; 第一级台阶中正方体石墩的块数为:;…依此类推,可以发现:第几级台阶中正方体石墩的块数为:3 与几的乘积乘以几加 1,然后除以 2. 阶梯级数 一级 二级 三级 四级 石墩块数 3 9 18 30级阶梯时,共用正方体石墩块;当 n=100 时,∴当 n=100 时,共用正方体石墩 15150 块. 答:当垒到第 n 级阶梯时,共用正方体石墩块;当 n=100 时,共用正方体石墩 15150 块48.由题意可知:第一次对折后,纸的厚度为 2×0.05;可以得到折痕为 1条;第二次对折后,纸的厚度为 2×2×0.05=22×0.05;可以得到折痕为 3=22﹣1 条;第三次对折后,纸的厚度为 2×2×2×0.05=23×0.05; 可以得到折痕为 7=23﹣1 条; …;第n 次对折后,纸的厚度为2×2×2×2× (2)0.05=2n×0.05.可以得到折痕为 2n﹣1 条.故:(1)对折 3 次后,厚度为 0.4 毫米;(2)对折 n 次后,厚度为 2n×0.05毫米;(3)对折 n 次后,可以得到 2n﹣1 条折痕49.由图形我们不难看出横行砖数量为 n+3,竖行砖数量为n+2,总数量为 n2+5n+6;若用瓷砖 506 块,可以求n2+5n+6=506;所以答案为:(1)n+3,n+2;(2)每一行有 23 块,每一列有 22 块50.等号左边是从 1 开始,连续奇数相加,等号右边是奇数个数也就是 n 的平方.(1)①1+3+5+7=42;②1+3+5+7+9=52;③1+3+5+7+9+11=62.(2)1+3+5+…+(2n﹣1)=n2(n≥1 的正整数)(2)可知剪 n 次时,S n=3n+1.(3)n=1 时,边长=;n=2 时,边长= ;n=3 时,边长= ;…;剪n 次时,边长= .52.(1)S=15(2)∵n=2 时,S=3×(2﹣1)=3;n=3 时,S=3×(3﹣1)=6;n=4 时,S=3×(4﹣1)=9;…∴S=3×(n﹣1)=3n﹣3.(3)当 n=2008 时,S=3×2008﹣3=6021.53.第1 个正方形四条边上的格点共有 4 个第2 个正方形四条边上的格点个数共有(4+4×1)个第3 个正方形四条边上的格点个数共有(4+4×2)个…第10 个正方形四条边上的格点个数共有(4+4×9)=40 个第n 个正方形四条边上的格点个数共有[4+4×(n﹣1)]=4n 个54.由图可知,每个图形为边长是 n 的正方形,因此四条边的花盆数为 4n,再减去重复的四个角的花盆数,即S=4n﹣4;(1)将n=5 代入S=4n﹣4,得S=16;(2)将 n=10 入 S=4n﹣4,得 S=36;(3)S=4n﹣4;(4)将S=42 代入S=4n﹣4 得, 4n﹣4=42解得 n=11.5所以用 42 个花盆不能摆出类似的图案55.(1)在第 1 个图中,共有白色瓷砖1×(1+1)=2 块,(2)在第 2 个图中,共有白色瓷砖2×(2+1)=6 块,(3)在第 3 个图中,共有白色瓷砖3×(3+1)=12 块,(4)在第 10 个图中,共有白色瓷砖10×(10+1)=110 块,(5)在第 n 个图中,共有白色瓷砖 n(n+1)块56.(1)由分析得:当 n=6 时,s=1+2+3+4+5+6=21;当n=100 时,s=1+2+3+…+99+100=5050;(2)用 n 表示 S 得:S= 57.(1)图(5)比图(4)多出 25﹣1=16 个;(2)图(6)比图(5)多出 26﹣1=32 个;(3)图(8)比图(7)多出 28﹣1=128 个;(4)图(n+1)比图(n)多出 2n 个.58.(1)首先观察图形,得到前面三个图形的具体个数,不难发现:在 5 的基础上依次多 3 枚.即第 n 个图案需要 5+3(n﹣1)=3n+2.那么当 n=8 时,则有 26 枚;故摆成第八个图案需要 26 枚棋子.(2)因为第①个图案有 5 枚棋子,第②个图案有(5+3×1)枚棋子,第③个图案有(5+3×2)枚棋子,依此规律可得第 n 个图案需5+3×(n﹣1)=5+3n﹣3= (3n+2)枚棋子.(3)3×2010+2=6032(枚)即第 2010 个图案需 6032 枚棋子59.(1)观察图形得:当黑砖 n=1 时,白砖有 6 块,当黑砖 n=2 时,白砖有 10 块,当黑砖 n=3 时,白砖有 14 块;(2)根据题意得:∵每个图形都比其前一个图形多 4 个白色地砖,∴可得规律为:第 n 个图形中有白色地砖 6+4(n﹣1)=4n+2 块.故答案为 6,10,14,4n+260.第一个图案为 3+2=5 个窗花;第二个图案为2×3+2=8个窗花;第三个图案为3×3+2=11个窗花;…从而可以探究:第 n 个图案所贴窗花数为(3n+2)个.(1)20所剪次数 n 1 2 3 4 5 正方形个数 Sn 4 7 10 13 16。
奥数一年级练习题找规律

奥数一年级练习题找规律一、数字规律1. 观察下列数字序列,找出下一个数字:2, 4, 6, 8, ____2. 找出规律,填写缺失的数字:5, 10, 15, ____, 25, ____3. 完成下列数字序列:1, 3, 5, 7, 9, ____2, 4, 8, 16, ____5. 找出规律,填写缺失的数字:3, 6, 9, 12, ____, 18二、图形规律1. 观察下列图形,找出下一个图形:○○ ● ● ○○ ● ● ____2. 找出规律,画出缺失的图形:△▲ △▲ △▲ ____3. 完成下列图形序列:□■□■□■□ ____○○○ ●●● ____5. 找出规律,画出缺失的图形:▲▼▲▼▲ ____三、字母规律1. 观察下列字母序列,找出下一个字母:A, C, E, G, ____2. 找出规律,填写缺失的字母:B, D, F, ____, H3. 完成下列字母序列:X, V, T, ____, PZ, Y, X, ____5. 找出规律,填写缺失的字母:L, M, N, O, ____四、混合规律1. 观察下列序列,找出下一个元素:1, A, 2, B, 3, ____2. 找出规律,填写缺失的元素:○, A, ●, B, ____, C3. 完成下列序列:△, B, □, C, ____, D4, D, 5, E, ____5. 找出规律,填写缺失的元素:●, F, ▲, G, ____, H五、时间规律1. 观察下列时间序列,找出下一个时间: 8:00, 8:15, 8:30, 8:45, ____2. 找出规律,填写缺失的时间:9:00, 9:10, 9:20, ____, 9:403. 完成下列时间序列:10:00, 10:20, 10:40, ____, 11:20 12:00, 12:05, 12:10, ____5. 找出规律,填写缺失的时间:1:00, 1:15, 1:30, ____, 1:55六、颜色规律1. 观察下列颜色序列,找出下一个颜色:红色,黄色,蓝色,绿色, ____2. 找出规律,填写缺失的颜色:白色,黑色,灰色, ____, 深灰色3. 完成下列颜色序列:橙色,紫色,粉色, ____, 棕色蓝色,浅蓝色,深蓝色, ____5. 找出规律,填写缺失的颜色:红色,粉红色,橙色, ____, 黄色七、动物规律1. 观察下列动物序列,找出下一个动物:猫,狗,猪,牛, ____2. 找出规律,填写缺失的动物:鸟,鱼,青蛙, ____, 蛇3. 完成下列动物序列:老虎,狮子,豹子, ____, 狼蜜蜂,蝴蝶,蜻蜓, ____5. 找出规律,填写缺失的动物:马儿,羊羔,猴子, ____, 鸽子八、物品规律1. 观察下列物品序列,找出下一个物品:铅笔,尺子,橡皮,书本, ____2. 找出规律,填写缺失的物品:椅子,桌子,床, ____, 柜子3. 完成下列物品序列:手机,电脑,电视, ____, 空调杯子,碗,筷子, ____5. 找出规律,填写缺失的物品:袜子,鞋子,裤子, ____, 外套答案一、数字规律1. 102. 20, 303. 114. 325. 15, 21二、图形规律1. ○○2. △3. ■4. ○○○5. ▲三、字母规律2. G3. S4. W5. O四、混合规律1. C2. ○, C3. □, D4. 6, F5. ▲, H五、时间规律1. 9:002. 9:253. 11:004. 12:155. 1:45六、颜色规律1. 紫色2. 浅灰色3. 红色4. 天蓝色5. 橙色七、动物规律2. 老鼠3. 猎豹4. 蜜蜂5. 猴子八、物品规律1. 笔记本2. 沙发3. 洗衣机4. 盘子5. 衬衫。
找规律小学奥数题100道及答案(完整版)

找规律小学奥数题100道及答案(完整版)题目1:1,3,5,7,9,()答案:11(相邻两个数的差为2,依次递增)题目2:2,4,6,8,10,()答案:12(相邻两个数的差为2,依次递增)题目3:5,10,15,20,25,()答案:30(相邻两个数的差为5,依次递增)题目4:1,4,9,16,25,()答案:36(分别是1、2、3、4、5 的平方,下一个是 6 的平方)题目5:3,6,9,12,15,()答案:18(相邻两个数的差为3,依次递增)题目6:1,2,4,8,16,()答案:32(后一个数是前一个数的2 倍)题目7:2,6,12,20,30,()答案:42(相邻两个数的差依次为4、6、8、10、12)题目8:1,1,2,3,5,8,()答案:13(前两个数相加等于后一个数)题目9:3,4,7,11,18,()答案:29(前两个数相加等于后一个数)题目10:1,3,7,13,21,()答案:31(相邻两个数的差依次为2、4、6、8、10)题目11:2,5,10,17,26,()答案:37(相邻两个数的差依次为3、5、7、9、11)题目12:9,16,25,36,()答案:49(分别是3、4、5、6 的平方,下一个是7 的平方)题目13:1,8,27,64,()答案:125(分别是1、2、3、4 的立方,下一个是5 的立方)题目14:5,12,19,26,33,()答案:40(相邻两个数的差为7,依次递增)题目15:3,8,15,24,()答案:35(相邻两个数的差依次为5、7、9、11)题目16:2,3,5,8,13,()答案:21(前两个数相加等于后一个数)题目17:1,4,10,22,46,()答案:94(相邻两个数的差依次为3、6、12、24、48)题目18:1,5,14,30,55,()答案:91(相邻两个数的差依次为4、9、16、25、36)题目19:2,6,18,54,()答案:162(后一个数是前一个数的3 倍)题目20:7,14,28,56,()答案:112(后一个数是前一个数的2 倍)题目21:1,2,6,24,120,()答案:720(后一个数依次是前一个数乘2、3、4、5、6)题目22:3,5,9,17,33,()答案:65(相邻两个数的差依次为2、4、8、16、32)题目23:1,3,8,19,42,()答案:89(相邻两个数的差依次为2、5、11、23、47,这些差依次增加3、6、12、24)题目24:2,4,10,28,82,()答案:244(相邻两个数的差依次为2、6、18、54、162,后一个差是前一个差的 3 倍)题目25:5,9,17,33,65,()答案:129(相邻两个数的差依次为4、8、16、32、64)题目26:1,4,27,256,()答案:3125(分别是1、2、3、4 的1、2、3、4 次方,下一个是5 的 5 次方)题目27:1,6,21,66,201,()答案:606(相邻两个数的差依次为5、15、45、135、405,后一个差是前一个差的3 倍)题目28:3,8,15,24,35,()答案:48(相邻两个数的差依次为5、7、9、11、13)题目29:2,3,7,18,47,()答案:123(7 = 3×2 + 1,18 = 7×2 + 4,47 = 18×2 + 11,下一个数应为47×2 + 16 = 123)题目30:1,2,5,14,41,()答案:122(相邻两个数的差依次为1、3、9、27、81,后一个差是前一个差的3 倍)题目31:2,5,11,23,47,()答案:95(相邻两个数的差依次为3、6、12、24、48)题目32:4,9,16,25,36,()答案:49(分别是2、3、4、5、6 的平方,下一个是7 的平方)题目33:6,12,20,30,42,()答案:56(相邻两个数的差依次为6、8、10、12、14)题目34:1,3,7,15,31,()答案:63(相邻两个数的差依次为2、4、8、16、32)题目35:3,9,27,81,()答案:243(后一个数是前一个数的3 倍)题目36:5,13,25,41,()答案:61(相邻两个数的差依次为8、12、16、20)题目37:2,8,32,128,()答案:512(后一个数是前一个数的4 倍)题目38:7,16,29,46,()答案:67(相邻两个数的差依次为9、13、17、21)题目39:1,5,13,25,()答案:41(相邻两个数的差依次为4、8、12、16)题目40:6,18,54,162,()答案:486(后一个数是前一个数的3 倍)题目41:8,18,32,50,()答案:72(相邻两个数的差依次为10、14、18、22)题目42:1,4,13,40,()答案:121(相邻两个数的差依次为3、9、27、81)题目43:3,10,21,36,()答案:55(相邻两个数的差依次为7、11、15、19)题目44:5,15,45,135,()答案:405(后一个数是前一个数的3 倍)题目45:2,6,14,30,()答案:62(相邻两个数的差依次为4、8、16、32)题目46:9,25,49,81,()答案:121(分别是3、5、7、9 的平方,下一个是11 的平方)题目47:7,19,37,61,()答案:91(相邻两个数的差依次为12、18、24、30)题目48:4,12,36,108,()答案:324(后一个数是前一个数的3 倍)题目49:1,6,15,28,()答案:45(相邻两个数的差依次为5、9、13、17)题目50:8,20,36,56,()答案:80(相邻两个数的差依次为12、16、20、24)题目51:3,11,23,39,()答案:59(相邻两个数的差依次为8、12、16、20)题目52:6,15,35,77,()答案:143(相邻两个数的差依次为9、20、42、66,差依次增加11、22、24)题目53:2,9,28,65,()答案:126(分别是1、2、3、4 的立方加1,下一个是5 的立方加1)题目54:1,7,19,37,()答案:61(相邻两个数的差依次为6、12、18、24)题目55:5,16,29,46,()答案:67(相邻两个数的差依次为11、13、17、21)题目56:3,12,27,48,()答案:75(相邻两个数的差依次为9、15、21、27)题目57:7,18,33,52,()答案:77(相邻两个数的差依次为11、15、19、25)题目58:2,10,30,68,()答案:130(相邻两个数的差依次为8、20、38、62,差依次增加12、18、24)题目59:4,15,32,55,()答案:84(相邻两个数的差依次为11、17、23、29)题目60:6,21,42,72,()答案:106(相邻两个数的差依次为15、21、30、34)题目61:1,9,25,49,()答案:81(分别是1、3、5、7 的平方,下一个是9 的平方)题目62:8,24,48,80,()答案:120(相邻两个数的差依次为16、24、32、40)题目63:3,13,31,57,()答案:91(相邻两个数的差依次为10、18、26、34)题目64:5,19,41,71,()答案:105(相邻两个数的差依次为14、22、30、34)题目65:2,11,26,47,()答案:76(相邻两个数的差依次为9、15、21、29)题目66:9,27,51,81,()答案:117(相邻两个数的差依次为18、24、30、36)题目67:7,17,33,55,()答案:83(相邻两个数的差依次为10、16、22、28)题目68:4,14,30,52,()答案:78(相邻两个数的差依次为10、16、22、26)题目69:6,18,36,60,()答案:90(相邻两个数的差依次为12、18、24、30)题目70:1,11,27,51,()答案:81(相邻两个数的差依次为10、16、24、30)题目71:5,17,33,53,()答案:77(相邻两个数的差依次为12、16、20、24)题目72:3,14,31,58,()答案:91(相邻两个数的差依次为11、17、27、33)题目73:8,22,42,70,()答案:106(相邻两个数的差依次为14、20、28、36)题目74:2,13,30,53,()答案:84(相邻两个数的差依次为11、17、23、31)题目75:9,29,55,91,()答案:133(相邻两个数的差依次为20、26、36、42)题目76:7,20,39,64,()答案:95(相邻两个数的差依次为13、19、25、31)题目77:4,16,36,64,()答案:100(分别是2、4、6、8 的平方,下一个是10 的平方)题目78:3,15,33,57,()答案:87(相邻两个数的差依次为12、18、24、30)题目79:6,22,44,74,()答案:110(相邻两个数的差依次为16、22、30、36)题目80:1,13,29,53,()答案:89(相邻两个数的差依次为12、16、24、36)题目81:5,21,41,67,()答案:99(相邻两个数的差依次为16、20、26、32)题目82:8,26,50,82,()答案:118(相邻两个数的差依次为18、24、32、36)题目83:3,17,37,67,()答案:107(相邻两个数的差依次为14、20、30、40)题目84:7,23,45,73,()答案:107(相邻两个数的差依次为16、22、28、34)题目85:2,14,32,56,()答案:88(相邻两个数的差依次为12、18、24、32)题目86:9,31,59,95,()答案:139(相邻两个数的差依次为22、28、36、44)题目87:6,24,48,84,()答案:126(相邻两个数的差依次为18、24、36、42)题目88:1,15,33,57,()答案:87(相邻两个数的差依次为14、18、24、30)题目89:5,23,47,77,()答案:113(相邻两个数的差依次为18、24、30、36)题目90:8,28,52,82,()答案:118(相邻两个数的差依次为20、24、30、36)题目91:3,19,41,69,()答案:105(相邻两个数的差依次为16、22、28、36)题目92:7,27,51,81,()答案:117(相邻两个数的差依次为20、24、30、36)题目93:4,18,38,66,()答案:100(相邻两个数的差依次为14、20、28、34)题目94:6,26,50,80,()答案:116(相邻两个数的差依次为20、24、30、36)题目95:2,16,36,60,()答案:90(相邻两个数的差依次为14、20、24、30)题目96:9,33,63,99,()答案:141(相邻两个数的差依次为24、30、36、42)题目97:8,28,56,92,()答案:136(相邻两个数的差依次为20、28、36、44)题目98:5,21,43,71,()答案:105(相邻两个数的差依次为16、22、28、34)题目99:3,17,37,67,()答案:107(相邻两个数的差依次为14、20、30、40)题目100:7,25,49,79,()答案:115(相邻两个数的差依次为18、24、30、36)。
图形找规律专项练习60题(有答案)
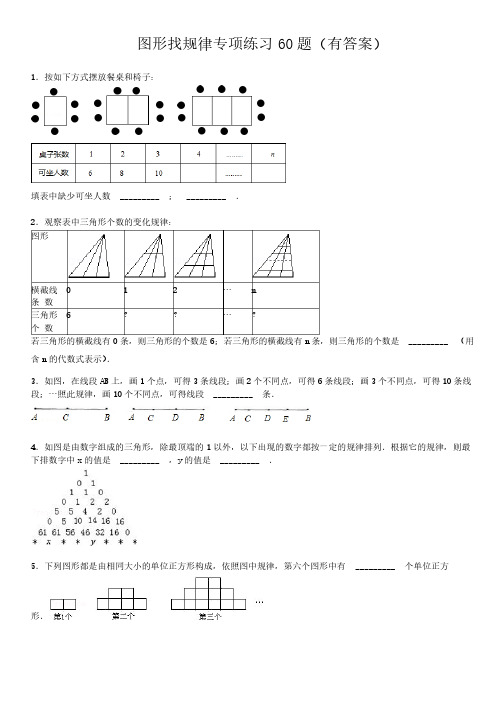
图形找规律专项练习60题(有答案)题(有答案)1.按如下方式摆放餐桌和椅子:.按如下方式摆放餐桌和椅子:填表中缺少可坐人数填表中缺少可坐人数 _________ _________ ;;_________ _________ ..2.观察表中三角形个数的变化规律:.观察表中三角形个数的变化规律: 图形图形横截线横截线 条 数 0 1 2 … n 三角形三角形 个 数6 ? ? … ? 若三角形的横截线有0条,则三角形的个数是6;若三角形的横截线有n 条,则三角形的个数是条,则三角形的个数是 _________ _________ (用(用含n 的代数式表示).3.如图,在线段AB 上,画1个点,可得3条线段;画2个不同点,可得6条线段;画3个不同点,可得10条线段;…照此规律,画10个不同点,可得线段个不同点,可得线段 _________ _________ 条.条.条.4.如图是由数字组成的三角形,除最顶端的1以外,以下出现的数字都按一定的规律排列.根据它的规律,则最下排数字中x 的值是的值是 _________ _________ ,,y 的值是的值是 _________ _________ ..5.下列图形都是由相同大小的单位正方形构成,依照图中规律,第六个图形中有 _________ _________ 个单位正方个单位正方形.6.如图,用相同的火柴棒拼三角形,依此拼图规律,第7个图形中共有个图形中共有 _________ _________ 根火柴根火柴棒.7.图1是一个正方形,分别连接这个正方形的对边中点,得到图2;分别连接图2中右下角的小正方形对边中点,得到图3;再分别连接图3中右下角的小正方形对边中点,得到图4;按此方法继续下去,第n 个图的所有正方形个数是个数是 _________ _________ 个.个.个.8.观察下列图案:.观察下列图案:它们是按照一定规律排列的,依照此规律,第6个图案中共有个图案中共有 _________ _________ 个三角形.个三角形.个三角形.9.如图,依次连接一个边长为1的正方形各边的中点,得到第二个正方形,再依次连接第二个正方形各边的中点,得到第三个正方形,按此方法继续下去,则第二个正方形的面积是得到第三个正方形,按此方法继续下去,则第二个正方形的面积是 _________ _________ ;第六个正方形的面积是;第六个正方形的面积是;第六个正方形的面积是 _________ _________ ..1010.下列各图形中的小正方形是按照一定规律排列的,根据图形所揭示的规律我们可以发现:第.下列各图形中的小正方形是按照一定规律排列的,根据图形所揭示的规律我们可以发现:第1个图形有1个小正方形,第2个图形有3个小正方形,第3个图形有6个小正方形,第4个图形有10个小正方形…,按照这样的规律,则第10个图形有个图形有 _________ _________ 个小正方形.个小正方形.个小正方形.1111.如图,用围棋子按下面的规律摆图形,则摆第.如图,用围棋子按下面的规律摆图形,则摆第n 个图形需要围棋子的枚数为个图形需要围棋子的枚数为 _________ _________ ..1212.为庆祝“六一”儿童节,幼儿园举行用火柴棒摆“金鱼”比赛,如图所示,则摆.为庆祝“六一”儿童节,幼儿园举行用火柴棒摆“金鱼”比赛,如图所示,则摆n 条“金鱼”需用火柴棒的根数为数为 _________ _________ ..1313.如图,两条直线相交只有.如图,两条直线相交只有1个交点,三条直线相交最多有3个交点,四条直线相交最多有6个交点,五条直线相交最多有10个交点,六条直线相交最多有个交点,六条直线相交最多有 _________ _________ 个交点,二十条直线相交最多有个交点,二十条直线相交最多有个交点,二十条直线相交最多有 _________ _________ 个交点.个交点.1414.用火柴棒按如图所示的方式搭图形,按照这样的规律搭下去,填写下表:.用火柴棒按如图所示的方式搭图形,按照这样的规律搭下去,填写下表:.用火柴棒按如图所示的方式搭图形,按照这样的规律搭下去,填写下表:图形编号图形编号 (1) (2) (3) … n 火柴根数火柴根数 从左到右依次为从左到右依次为 _________ _________ _________ _________ _________ _________ _________ _________ .. 1515.图(.图(.图(11)是一个黑色的正三角形,顺次连接三边中点,得到如图()是一个黑色的正三角形,顺次连接三边中点,得到如图(22)所示的第2个图形(它的中间为一个白色的正三角形);在图(;在图(22)的每个黑色的正三角形中分别重复上述的作法,得到如图()的每个黑色的正三角形中分别重复上述的作法,得到如图(33)所示的第3个图形.如此继续作下去,则在得到的第5个图形中,白色的正三角形的个数是个图形中,白色的正三角形的个数是 _________ _________ ..1616..如图,一块圆形烙饼切一刀可以切成2块,若切两刀最多可以切成4块,切三刀最多可以切成7块…通过观察、计算填下表(其中S 表示切n 刀最多可以切成的块数)后,可探究一圆形烙饼切n 刀最多能切成刀最多能切成 _________ _________ 块块(结果用n 的代数式表示).1717.如图,是用相同的等腰梯形拼成的等腰梯形图案.第(.如图,是用相同的等腰梯形拼成的等腰梯形图案.第(.如图,是用相同的等腰梯形拼成的等腰梯形图案.第(11)个图案只有1个等腰梯形,其两腰之和为4,上下底之和为3,周长为7;第(;第(22)个图案由3个等腰梯形拼成,其周长为1313;…第(;…第(;…第(n n )个图案由()个图案由(2n 2n 2n﹣﹣1)个等腰梯形拼成,其周长为拼成,其周长为 _________ _________ ..(用正整数n 表示)表示)1818.下列各图均是用有一定规律的点组成的图案,用.下列各图均是用有一定规律的点组成的图案,用S 表示第n 个图案中点的总数,则S= S= _________ _________ _________ (用含(用含n 的式子表示).1919.如图,由若干盆花摆成图案,每个点表示一盆花,几何图形的每条边上(包括两个顶点)都摆有.如图,由若干盆花摆成图案,每个点表示一盆花,几何图形的每条边上(包括两个顶点)都摆有n (n ≥3)盆花,每个图案中花盆总数为S ,按照图中的规律可以推断S 与n (n ≥3)的关系是)的关系是 _________ _________ ..2020.用火柴棍象如图这样搭图形,搭第.用火柴棍象如图这样搭图形,搭第n 个图形需要个图形需要 _________ _________ 根火柴棍.根火柴棍.根火柴棍.2121.现有黑色三角形“.现有黑色三角形“”和白色三角形“”共有2019个,按照一定的规律排列如下:则黑色三角形有则黑色三角形有 _________ _________ 个.个.个.2222.假设有足够多的黑白围棋子,按照一定的规律排成一行:.假设有足够多的黑白围棋子,按照一定的规律排成一行:.假设有足够多的黑白围棋子,按照一定的规律排成一行: ○●●○○●○●●○○●○●●○○●○●●○○●…○●●○○●○●●○○●○●●○○●○●●○○●… 请问第2019个棋子是黑的还是白的?答:个棋子是黑的还是白的?答: _________ _________ ..2323.观察下列由等腰梯形组成的图形和所给表中数据的规律后填空:.观察下列由等腰梯形组成的图形和所给表中数据的规律后填空:.观察下列由等腰梯形组成的图形和所给表中数据的规律后填空: 梯形的个数梯形的个数 1 2 3 4 5 … 图形的周长图形的周长 58 11 14 17 … 当梯形个数为2019个时,这时图形的周长为个时,这时图形的周长为 _________ _________2424..如图,下面是一些小正方形组成的图案,第4个图案有个图案有 _________ _________ 个小正方形组成;个小正方形组成;第n 个图案有个图案有 _________个小正方形组成.2525.如图所示是由火柴棒按一定规律拼出的一系列图形:.如图所示是由火柴棒按一定规律拼出的一系列图形:.如图所示是由火柴棒按一定规律拼出的一系列图形:依照此规律,第7个图形中火柴棒的根数是个图形中火柴棒的根数是 _________ _________ ..2626.图中的每个图形都是由若干个棋子围成的正方形图案,图案的每条边(包括两个顶点)上都有.图中的每个图形都是由若干个棋子围成的正方形图案,图案的每条边(包括两个顶点)上都有n (n ≥2)个棋子,每个图案的棋子总数为s ,按图的排列规律推断,,按图的排列规律推断,s s 与n 之间的关系可用式子之间的关系可用式子 _________ _________ 表示.表示.表示.2727.观察下列图形,它是按一定规律排列的,那么第.观察下列图形,它是按一定规律排列的,那么第.观察下列图形,它是按一定规律排列的,那么第 _________ _________ 个图形中,十字星与五角星的个数和为个图形中,十字星与五角星的个数和为27个.2828..2条直线最多只有1个交点;个交点;33条直线最多只有3个交点;个交点;44条直线最多只有6个交点;个交点;20192019条直线最多只有条直线最多只有 _________ _________ 个交点.个交点.个交点.2929.以下各图分别由一些边长为.以下各图分别由一些边长为1的小正方形组成,请填写图2、图3中的周长,并以此推断出图10的周长为的周长为_________ _________ ..3030.如图所示,第.如图所示,第1个图案是由黑白两种颜色的正六边形地面砖组成,第2个,第3个图案可以看作是第1个图案经过平移而得,那么设第n 个图案中有白色地面砖m 块,则m 与n 的函数关系式是的函数关系式是 _________ _________ ..3131.用同样大小的黑色棋子按如图所示的规律摆放:.用同样大小的黑色棋子按如图所示的规律摆放:.用同样大小的黑色棋子按如图所示的规律摆放:(1)分别写出第6、7两个图形各有多少颗黑色棋子?两个图形各有多少颗黑色棋子? (2)写出第n 个图形黑色棋子的颗数?个图形黑色棋子的颗数?(3)是否存在某个图形有2019颗黑色棋子?若存在,求出是第几个图形;若不存在,请说明理由.颗黑色棋子?若存在,求出是第几个图形;若不存在,请说明理由.3232.如图,给出四个点阵,.如图,给出四个点阵,.如图,给出四个点阵,s s 表示每个点阵中点的个数,按照图形中的点的个数变化规律,表示每个点阵中点的个数,按照图形中的点的个数变化规律,(1)猜想第n 个点阵中的点的个数s= s= _________ _________ _________ .. (2)若已知点阵中点的个数为3737,问这个点阵是第几个?,问这个点阵是第几个?,问这个点阵是第几个?3333.用棋子摆出下列一组图形:.用棋子摆出下列一组图形:.用棋子摆出下列一组图形:(1)填写下表:)填写下表: 图形编号图形编号 1 2 3 4 5 6 图中棋子数图中棋子数 58 11 14 17 20 (2)照这样的方式摆下去,写出摆第n 个图形所需棋子的枚数;个图形所需棋子的枚数;(3)其中某一图形可能共有2019枚棋子吗?若不可能,请说明理由;若可能,请你求出是第几个图形.枚棋子吗?若不可能,请说明理由;若可能,请你求出是第几个图形.3434.观察图中四个顶点的数字规律:.观察图中四个顶点的数字规律:.观察图中四个顶点的数字规律: (1)数字“)数字“303030”在”在”在 _________ _________ 个正方形的个正方形的个正方形的 _________ _________ ;;(2)请你用含有n (n ≥1的整数)的式子表示正方形四个顶点的数字规律;的整数)的式子表示正方形四个顶点的数字规律; (3)数字“)数字“201920192019”应标在什么位置.”应标在什么位置.”应标在什么位置.3535.如图,各图表示若干盆花组成的形如三角形的图案,每条边(包括两个顶点)有.如图,各图表示若干盆花组成的形如三角形的图案,每条边(包括两个顶点)有n (n >1)盆花,每个图案中花盆的总数为S .问:①当每条边有2盆花时,花盆的总数S 是多少?是多少? ②当每条边有3盆花时,花盆的总数S 是多少?是多少? ③当每条边有4盆花时,花盆的总数S 是多少?是多少? ④当每条边有10盆花时,花盆的总数S 是多少?是多少?⑤按此规律推断,当每条边有n 盆花时,花盆的总数S 是多少?是多少?3636.如下图是用棋子摆成的“上”字:.如下图是用棋子摆成的“上”字:.如下图是用棋子摆成的“上”字:如果按照以上规律继续摆下去,那么通过观察,可以发现:如果按照以上规律继续摆下去,那么通过观察,可以发现: (1)第④、第⑤个“上”字分别需用)第④、第⑤个“上”字分别需用 _________ _________ 和和 _________ _________ 枚棋子;枚棋子;枚棋子;(2)第n 个“上”字需用个“上”字需用 _________ _________ 枚棋子;枚棋子;枚棋子; (3)七(3)班有50名同学,把每一位同学当做一枚棋子,能否让这50枚“棋子”按照以上规律恰好站成一个“上”字?若能,请计算最下一“横”的学生数;若不能,请说明理由.字?若能,请计算最下一“横”的学生数;若不能,请说明理由.3737.下列表格是一张对同一线段上的个数变化及线段总条数的探究统计..下列表格是一张对同一线段上的个数变化及线段总条数的探究统计..下列表格是一张对同一线段上的个数变化及线段总条数的探究统计. 线段上点的个数线段上点的个数 线段的总条数线段的总条数1 1+2=3 1+2+3=6… …(1)请你完成探究,并把探究结果填在相应的表格里;)请你完成探究,并把探究结果填在相应的表格里; (2)若在同一线段上有10个点,则线段的总条数为个点,则线段的总条数为 _________ _________ ;若在同一线段上有;若在同一线段上有n 个点,则有个点,则有 _________ 条线段(用含n 的式子表示)的式子表示)(3)若你所在的班级有60名学生,名学生,2020年后参加同学聚会,见面时每两个同学之间握一次手,共握手年后参加同学聚会,见面时每两个同学之间握一次手,共握手 _________ 次.次.3838.如图是用棋子摆成的“.如图是用棋子摆成的“.如图是用棋子摆成的“H H ”字.”字. (1)摆成第一个“)摆成第一个“H H ”字需要”字需要 _________ _________ 个棋子;摆第个棋子;摆第x 个“个“H H ”字需要的棋子数可用含x 的代数式表示为的代数式表示为 _________ _________ ;; (2)问第几个“)问第几个“H H ”字棋子数量正好是2019个棋子?个棋子?3939.我们知道,两条直线相交只有一个交点.请你探究:.我们知道,两条直线相交只有一个交点.请你探究:.我们知道,两条直线相交只有一个交点.请你探究: (1)三条直线两两相交,最多有)三条直线两两相交,最多有 _________ _________ 个交点;个交点;个交点; (2)四条直线两两相交,最多有)四条直线两两相交,最多有 _________ _________ 个交点;个交点;个交点; (3)n 条直线两两相交,最多有条直线两两相交,最多有 _________ _________ 个交点(个交点(个交点(n n 为正整数,且n ≥2).4040.如图所示,小王玩游戏:一张纸片,第一次将其撕成四小片,手中共有.如图所示,小王玩游戏:一张纸片,第一次将其撕成四小片,手中共有4张纸片,以后每次都将其中一片撕成更小的四片.如此进行下去,当小王撕到第n 次时,手张共有S 张纸片.根据上述情况:张纸片.根据上述情况:(1)用含n 的代数式表示S ;(2)当小王撕到第几次时,他手中共有70张小纸片?张小纸片?4141.如图①是一张长方形餐桌,四周可坐.如图①是一张长方形餐桌,四周可坐6人,人,22张这样的桌子按图②方式拼接,四周可坐10人.现将若干张这样的餐桌按图③方式拼接起来:的餐桌按图③方式拼接起来:(1)三张餐桌按题中的拼接方式,四周可坐)三张餐桌按题中的拼接方式,四周可坐 _________ _________ 人;人;人; (2)n 张餐桌按上面的方式拼接,四周可坐张餐桌按上面的方式拼接,四周可坐 _________ _________ 人(用含人(用含n 的代数式表示).若用餐人数为26人,则这样的餐桌需要样的餐桌需要 _________ _________ 张.张.张.4242.用棋子摆出下列一组图形:.用棋子摆出下列一组图形:.用棋子摆出下列一组图形:(1)填写下表:)填写下表: 图形编号图形编号 1 23 4 5 6 图形中的棋子图形中的棋子(2)照这样的方式摆下去,写出摆第n 个图形棋子的枚数;(用含n 的代数式表示)的代数式表示) (3)如果某一图形共有99枚棋子,你知道它是第几个图形吗?枚棋子,你知道它是第几个图形吗?4343.如图①,图②,图③,图④,…,是用围棋棋子按照某种规律摆成的一行“广”字,按照这种规律,.如图①,图②,图③,图④,…,是用围棋棋子按照某种规律摆成的一行“广”字,按照这种规律, (1)第5个“广”字中的棋子个数是个“广”字中的棋子个数是 _________ _________ .. (2)第n 个“广”字需要多少枚棋子?个“广”字需要多少枚棋子?4444.如图,用同样规格黑白两色的正方形瓷砖铺设矩形地面,请观察图形并解答有关问题:.如图,用同样规格黑白两色的正方形瓷砖铺设矩形地面,请观察图形并解答有关问题: (1)在第n 个图中共有个图中共有 _________ _________ 块黑瓷砖,块黑瓷砖,块黑瓷砖, _________ _________ 块白瓷砖;块白瓷砖;块白瓷砖; (2)是否存在黑瓷砖与白瓷砖块数相等的情形?你能通过计算说明吗?)是否存在黑瓷砖与白瓷砖块数相等的情形?你能通过计算说明吗?4545.用火柴棒按如图的方式搭三角形..用火柴棒按如图的方式搭三角形..用火柴棒按如图的方式搭三角形.照这样搭下去:照这样搭下去:4646.观察图中的棋子:.观察图中的棋子:.观察图中的棋子:(1)按照这样的规律摆下去,第4个图形中的棋子个数是多少?个图形中的棋子个数是多少? (2)用含n 的代数式表示第n 个图形的棋子个数;个图形的棋子个数; (3)求第20个图形需棋子多少个?个图形需棋子多少个?4747.如图,用正方体石墩垒石梯,下图分别表示垒到一、二、三阶梯时的情况.那么照这样垒下去,请你观察规律,.如图,用正方体石墩垒石梯,下图分别表示垒到一、二、三阶梯时的情况.那么照这样垒下去,请你观察规律,并完成下列问题.并完成下列问题.(1)填出下表中未填的两个空格:)填出下表中未填的两个空格: 阶梯级数阶梯级数 一级一级 二级二级 三级三级 四级四级 石墩块数石墩块数3 9 (2)当垒到第n 级阶梯时,共用正方体石墩多少块(用含n 的代数式表示)?并求当n=100时,共用正方体石墩多少块?多少块?4848.有一张厚度为.有一张厚度为0.05毫米的纸,将它对折1次后,厚度为2×0.05毫米.毫米. (1)对折3次后,厚度为多少毫米?次后,厚度为多少毫米? (2)对折n 次后,厚度为多少毫米?次后,厚度为多少毫米? (3)对折n 次后,可以得到多少条折痕?次后,可以得到多少条折痕?4949.如图所示,用同样规格正方形瓷砖铺设矩形地面,请观察下图:.如图所示,用同样规格正方形瓷砖铺设矩形地面,请观察下图:.如图所示,用同样规格正方形瓷砖铺设矩形地面,请观察下图:按此规律,铺设了一矩形地面,共用瓷砖506块,请问这一矩形的每一横行有多少块瓷砖,每一竖列有多少瓷砖?块,请问这一矩形的每一横行有多少块瓷砖,每一竖列有多少瓷砖?5050.找规律:观察下面的星阵图和相应的等式,探究其中的规律..找规律:观察下面的星阵图和相应的等式,探究其中的规律..找规律:观察下面的星阵图和相应的等式,探究其中的规律.(1)在④、⑤和⑥后面的横线上分别写出相应的等式:)在④、⑤和⑥后面的横线上分别写出相应的等式: ①1=12②1+3=22③1+3+5=32④ _________ _________ ;; ⑤ _________ _________ ;; ⑥ _________ _________ ;;(2)通过猜想,写出第n 个星阵图相对应的等式.个星阵图相对应的等式.5151.将一张正方形纸片剪成四个大小一样的小正方形,然后将其中的一个正方形再剪成四个小正方形,如此循环下.将一张正方形纸片剪成四个大小一样的小正方形,然后将其中的一个正方形再剪成四个小正方形,如此循环下去,如图所示:去,如图所示:(1)完成下表:)完成下表: 所剪次数n 1 2 3 4 5 正方形个数Sn 4(2)剪n 次共有S n 个正方形,请用含n 的代数式表示S n = = _________ _________ _________ ;; (3)若原正方形的边长为1,则第n 次所剪得的正方形边长是次所剪得的正方形边长是 _________ _________ (用含(用含n 的代数式表示).5252.如图是用五角星摆成的三角形图案,每条边上有.如图是用五角星摆成的三角形图案,每条边上有n (n >1)个点(即五角星),每个图案的总点数(即五角星总数)用S 表示.表示.(1)观察图案,当n=6时,时,S= S= S= _________ _________ _________ ;;(2)分析上面的一些特例,你能得出怎样的规律?(用n 表示S ) (3)当n=2019时,求S .5353.用水平线和竖直线将平面分成若干个边长为.用水平线和竖直线将平面分成若干个边长为1的小正方形格子,小正方形的顶点,叫格点.观察图中每一个正方形(实线)四条边上的格点的个数,请回答下列问题:方形(实线)四条边上的格点的个数,请回答下列问题:(1)由里向外第1个正方形(实线)四条边上的格点个数共有个正方形(实线)四条边上的格点个数共有 _________ _________ 个;由里向外第个;由里向外第2个正方形(实线)四条边上的格点个数共有四条边上的格点个数共有 _________ _________ 个;由里向外第个;由里向外第3个正方形(实线)四条边上的格点个数共有个正方形(实线)四条边上的格点个数共有 _________ 个;个;(2)由里向外第10个正方形(实线)四条边上的格点个数共有个正方形(实线)四条边上的格点个数共有 _________ _________ 个;个;个; (3)由里向外第n 个正方形(实线)四条边上的格点个数共有个正方形(实线)四条边上的格点个数共有 _________ _________ 个.个.个.5454.下列各图是由若干花盆组成的形如正方形的图案,每条边(包括两个顶点)有.下列各图是由若干花盆组成的形如正方形的图案,每条边(包括两个顶点)有n (n >1)个花盆,每个图案花盆总数是S .(1)按要求填表:)按要求填表: n 2 3 4 5 … S 4 8 12…(2)写出当n=10时,时,S= S= S= _________ _________ _________ .. (3)写出S 与n 的关系式:的关系式:S= S= S= _________ _________ _________ .. (4)用42个花盆能摆出类似的图案吗?个花盆能摆出类似的图案吗?5555.如图,用同样规格的黑白两色正方形瓷砖铺设矩形地面,请观察下列图形,探究并解答下列问题..如图,用同样规格的黑白两色正方形瓷砖铺设矩形地面,请观察下列图形,探究并解答下列问题.(1)在第1个图中,共有白色瓷砖个图中,共有白色瓷砖 _________ _________ 块.块.块. (2)在第2个图中,共有白色瓷砖个图中,共有白色瓷砖 _________ _________ 块.块.块. (3)在第3个图中,共有白色瓷砖个图中,共有白色瓷砖 _________ _________ 块.块.块. (4)在第10个图中,共有白色瓷砖个图中,共有白色瓷砖 _________ _________ 块.块.块. (5)在第n 个图中,共有白色瓷砖个图中,共有白色瓷砖 _________ _________ 块.块.块.5656.淮北市为创建文明城市,各种颜色的菊花摆成如下三角形的图案,每条边(包括两个顶点)上有.淮北市为创建文明城市,各种颜色的菊花摆成如下三角形的图案,每条边(包括两个顶点)上有n (n >1)盆花,每个图案花盆的总数为S ,当n=2时,时,S=3S=3S=3;;n=3时,时,S=6S=6S=6;;n=4时,时,S=10S=10S=10..(1)当n=6时,时,S= S= S= _________ _________ _________ ;;n=100时,时,S= S= S= _________ _________ _________ .. (2)你能得出怎样的规律?用n 表示S .5757.下面是按照一定规律画出的一系列“树枝”经观察,图(.下面是按照一定规律画出的一系列“树枝”经观察,图(.下面是按照一定规律画出的一系列“树枝”经观察,图(22)比图()比图(11)多出2个“树枝”, 图(图(33)比图()比图(22)多出4个“树枝”,图(,图(44)比图()比图(33)多出8个“树枝”,按此规律:,按此规律: 图(图(55)比图()比图(44)多出)多出 _________ _________ 个树枝;个树枝;个树枝; 图(图(66)比图()比图(55)多出)多出 _________ _________ 个树枝;个树枝;个树枝; 图(图(88)比图()比图(77)多出)多出 _________ _________ 个树枝;个树枝;个树枝; … 图(图(n+1n+1n+1)比图()比图()比图(n n )多出)多出 _________ _________ 个树枝.个树枝.个树枝.5858.如图是用棋子成的“.如图是用棋子成的“.如图是用棋子成的“T T ”字图案.从图案中可以出,第一个“”字图案.从图案中可以出,第一个“T T ”字图案需要5枚棋子,第二个“枚棋子,第二个“T T ”字图案需要8枚棋子,第三个“枚棋子,第三个“T T ”图案需要11枚棋子.枚棋子.(1)照此规律,摆成第八个图案需要几枚棋子?)照此规律,摆成第八个图案需要几枚棋子? (2)摆成第n 个图案需要几枚棋子?个图案需要几枚棋子? (3)摆成第2019个图案需要几枚棋子?个图案需要几枚棋子?5959.用黑白两种颜色的正六边形地砖按如下所示的规律拼成若干图案:.用黑白两种颜色的正六边形地砖按如下所示的规律拼成若干图案:.用黑白两种颜色的正六边形地砖按如下所示的规律拼成若干图案:(1)当黑砖n=1时,白砖有时,白砖有 _________ _________ 块,当黑砖块,当黑砖n=2时,白砖有时,白砖有 _________ _________ 块,当黑砖块,当黑砖n=3时,白砖有时,白砖有 _________ _________ 块.块.块.(2)第n 个图案中,白色地砖共个图案中,白色地砖共 _________ _________ 块.块.块.6060.下列图案是晋商大院窗格的一部分.其中,.下列图案是晋商大院窗格的一部分.其中,“o ”代表窗纸上所贴的剪纸.”代表窗纸上所贴的剪纸.探索并回答下列问题:探索并回答下列问题:(1)第6个图案中所贴剪纸“个图案中所贴剪纸“o o ”的个数是”的个数是 _________ _________ ;; (2)第n 个图案中所贴剪纸“个图案中所贴剪纸“o o ”的个数是”的个数是 _________ _________ ;;(3)是否存在一个图案,其上所贴剪纸“)是否存在一个图案,其上所贴剪纸“o o ”的个数为2019个?若存在,指出是第几个;若不存在,请说明理由.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
找规律是解决数学问题的一种重要的手段,而规律的找寻既需要敏锐的观察力,又需要严密的逻辑推理能力.一般地说,在观察图形变化规律时,应抓住一下几点来考虑问题:
⑴图形数量的变化;⑵图形形状的变化;⑶图形大小的变化;
⑷图形颜色的变化;⑸图形位置的变化;⑹图形繁简的变化.
对于较复杂的图形,也可分为几部分来分别考虑,总而言之,只要全面观察,勤于思考就一定能抓住规律,解决问题.
板块一数量规律
【例 1】请找出下面哪个图形与其他图形不一样.
【例 2】观察图形的变化,想一想,按图形的变化规律,在带“?”的空格处应画什么样的图形?
【巩固】观察图形的变化,想一想,按图形的变化规律,在带“?”的空格处应画什么样的图形?
?
【巩固】观察图形的变化,想一想,按图形的变化规律,在带“?”的空格处应画什么样的图形?
【例 3】观察下面的图形,按规律在“?”处填上适当的图形.
(5)
(4)
(3)
(2)
(1)
?
【例 4】观察图形变化规律,在右边补上一幅,使它成为一个完整系列。
图形找规律
【例 5】观察图形变化规律,在右边再补上一幅,使它们成为一个完整的系列.
【例 6】观察下图中的点群,请回答:
(1)方框内的点群包含多少个点?
(2)推测第10个点群中包含多少个点?
(3)前10个点群中,所有点的总数是多少?
【例 7】观察下面由点组成的图形(点群),请回答:
(1)方框内的点群包含多少个点?
(2)第(10)个点群中包含多少个点?
(3)前十个点群中,所有点的总数是多少?
【例 8】下图表示“宝塔”,它们的层数不同,但都是由一样大的小三角形摆成的.仔细观察后,请回答:(1)五层的“宝塔”的最下层包含多少个小三角形?
(2)整个五层“宝塔”一共包含多少个小三角形?
板块二旋转、轮换型规律
【例 9】相传古时候一位老人留在人间很多宝盒,里面装着世界上最宝贵的财富,但是并不是拥有宝盒都可以得到这笔财富,在宝盒的上面设置了密码,只有写出密码的人才会真正拥有这笔财富,聪明的你你能找出密码吗?
○□☆△○□☆△
△○□☆△○□☆
☆△○□☆△○□
()()()()()()()()
【例 10】下面的图形是按一定规律排列的,请仔细观察,并在“?”处填上适当的图形.
(1)
?
(2)
?
第3组
第1组
(3)
★
★
★★★
?
第3组
第1组
【例 11】 观察下图的变化规律,画出丙图.
D
B
A
丙
乙甲
C
B A
【例 12】 有六种不同图案的瓷砖,每种各6块.将它们砌在如下图那样的地面上,使每一横行和每一竖行
都没有相同图案的瓷砖.你会怎样设计?
【例 13】 下面各种各样的娃娃头好看吗?认真观察你能找到它们排列的规律吗?根据规律把最后一个画
出来.
【例 14】 观察图中所给出图形的变化规律,然后在空白处填画上所缺的图形. 【例 15】 琪琪特别喜欢蝴蝶,她用直尺和圆规在纸上画了9幅蝴蝶图,并用剪刀将它们一一剪下来.她将
这9只纸蝴蝶摆在桌上,见下图1,她发现这些纸蝴蝶排列挺有规律,突然一阵风来,吹走了3只纸蝴蝶,见下图2.你能找出蝴蝶的排列规律,将图2的3只蝴蝶放入图1的空缺处吗?
图1
9
87
6
54
3
2
1图2
B C
A
【例 16】 请观察下图中已有的几个图形,并按规律填出空白处的图形
.
【例 17】 观察下列各组图的变化规律,并在“?”处画出相关的图形.
(1)
?
(2)
丁
丙
乙甲
?
【例 18】
如图,根据图中已知3个方格表中阴影的规律,在空白的方格表中也填上相应的阴影
.
【巩固】根据前三个方格表中阴影部分的变化规律,填上第(10)个方格表中阴影部分的小正方形内的几个
数之和。
698754
321
......
(10)
【例 19】
按照下列图形的变化规律,空白处应是什么样的图形?
?【巩固】按照下列图形的变化规律,空白处应是什么样的图形?
?
【例 20】请你认真仔细观察,按照下面图形的变化规律,在“?”处画出合适的图形。
【例 21】观察下图的变化规律,在“?”处填入适当的图形.
【例 22】下图中的图形是按一定规律排列的,请仔细观察,并在“?”处填上适当的图形.
?
?
?
i
h
g
f
e
d
c
b
a
【巩固】下面的图形是按一定规律排列的,请仔细观察,并在“?”处填上适当的图形。
【例 23】按照变化规律在“?”处填上合适的图形.
(1)
(2)
(d )
(c )
(b )
(a )
【例 24】
观察下列各组图的变化规律,并在“?”处画出相关的图形.
【例 25】 仔细观察下列图形的变化,请先回答:
(1)在方框(4)中应画出怎样的图形?
(2)再按(1)、(2)、(3)……的顺序数下去,第(10)个方框是怎样的图形?
【巩固】仔细观察下列图形的变化,请先回答:
(1) 在方框(4)中应画出怎样的图形?
(2) 再按(1)、(2)、(3)、……的顺序数下去,第(10)个方框是怎样的图形?
【例 26】 顺序观察下面图形,并按其变化规律在“?”处填上合适的图形.
(1)
(2)
(3)
(4)
板块三 其他
【例 27】
请找出下面哪个图形与其他图形不一样。
【例 28】选择合适的图形,填入虚线框内。
(1)
(2)
【例 29】根据左边图形的关系,画出右边图形的另一半.
(1)
(2)
(3)
【例 30】在下面图形中找出一个与众不同的.
【例 31】顺序观察给出图形的变化,按照这种变化规律,在空格中填上应有的图形.
【巩固】顺序观察给出图形的变化,按照这种变化规律,在空格中填上应有的图形.
【例 32】观察下图,看看右图中哪一个图形可以代替“?”
【例 33】仔细观察下图中图形的变化规律,并在“?”处填入合适的图形.
c
b
a
?
?
【巩固】根据下图,画出第三幅图。
【例 34】下图是由9个小人排列的方阵,但有一个小人没有到位,请你从下面图10—2中的6个小人中,选一位小人放到问号的位置,你认为最合适的人选是几号?
【例 35】将“猫”“狗”“兔”“鸡”“猴”“虎”六个动物名称分别写在六个正方体的六个面上,从下面三种不同摆法中,判断这个正方体上哪些动物名名称分别写在相对面上.
【例 36】将A、B、C、D、E、F六个字母分别写在正方体的六个面上,从下面三种不同摆法中判断这个正方体中,哪些字母分别写在相对的面上.
【例 37】四个小动物排座位,一开始,小鼠坐在第1号位子上,小猴坐在第2号,小兔坐在第3号,小猫坐在第4号.以后它们不停地交换位子,第一次上下两排交换.第二次是在第一次交换后左右两列
交换,第三次再上下两排交换,第四次再左右两列交换…这样一直换下去.问:第五次交换位子后,小兔坐在第几号位子上?
【巩固】四个小动物排座位,一开始,小鼠坐在第1号位子上,小猴坐在第2号,小兔坐在第3号,小猫坐在第4号.以后它们不停地交换位子,第一次上下两排交换.第二次是在第一次交换后左右两列交换,第三次再上下两排交换,第四次再左右两列交换…这样一直换下去.问:第十次交换位子后,小兔坐在第几号位子上?。
