spss之统计挖掘第6章 方差分析
《统计分析与SPSS的应用(第五版)》课后练习答案(第6章)

《统计分析与SPSS的应用(第五版)》(薛薇)课后练习答案第6章SPSS的方差分析1、入户推销有五种方法。
某大公司想比较这五种方法有无显著的效果差异,设计了一项实验。
从应聘人员中尚无推销经验的人员中随机挑选一部分人,并随机地将他们分为五个组,每组用一种推销方法培训。
一段时期后得到他们在一个月内的推销额,如下表所示:第一组20.016.817.921.223.926.822.4第二组24.921.322.630.229.922.520.7第三组16.020.117.320.922.026.820.8第四组17.518.220.217.719.118.416.5第五组25.226.226.929.330.429.728.21)请利用单因素方差分析方法分析这五种推销方式是否存在显著差异。
2)绘制各组的均值对比图,并利用LSD方法进行多重比较检验。
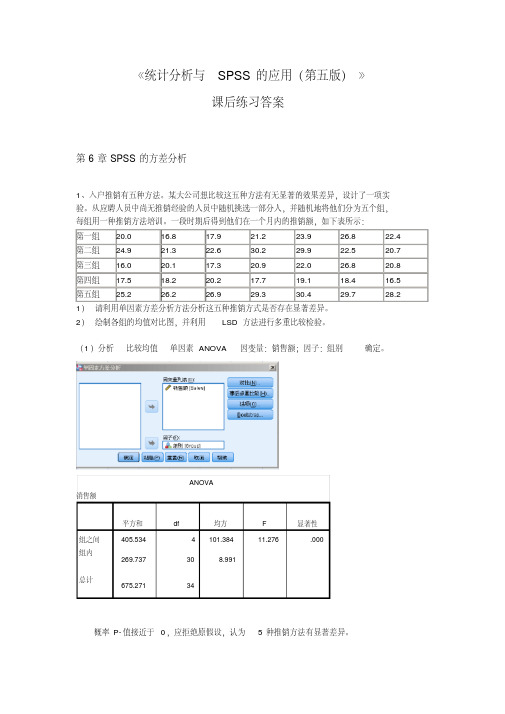
(1)分析比较均值单因素ANOVA因变量:销售额;因子:组别确定。
ANOVA销售额平方和df均方F显著性组之间405.5344101.38411.276.000组内269.737308.991总计675.27134概率P-值接近于0,应拒绝原假设,认为5种推销方法有显著差异。
(2)均值图:在上面步骤基础上,点选项均值图;事后多重比较LSD多重比较因变量:销售额LSD(L)95%置信区间平均差(I)组别(J)组别(I-J)标准错误显著性下限值上限第一组第二组-3.30000 *1.60279.048-6.5733-.0267第三组.728571.60279.653-2.54484.0019第四组3.057141.60279.066-.21626.3305第五组-6.70000 *1.60279.000-9.9733-3.4267*1.60279.048.02676.5733第二组第一组3.30000第三组4.02857 *1.60279.018.75527.3019*1.60279.0003.08389.6305第四组6.35714*第五组-3.400001.60279.042-6.6733-.1267第三组第一组-.728571.60279.653-4.00192.5448第二组-4.02857 *1.60279.018-7.3019-.7552第四组2.328571.60279.157-.94485.6019第五组-7.42857 *1.60279.000-10.7019-4.1552第四组第一组-3.057141.60279.066-6.3305.2162第二组-6.35714 *1.60279.000-9.6305-3.0838第三组-2.328571.60279.157-5.6019.9448第五组-9.75714 *1.60279.000-13.0305-6.4838*1.60279.0003.42679.9733第五组第一组6.70000*1.60279.042.12676.6733第二组3.40000*1.60279.0004.155210.7019第三组7.42857*1.60279.0006.483813.0305第四组9.75714*.均值差的显著性水平为0.05。
方差分析_spss_操作_讲解

上一张 下一张 主 页 退 出
(6-4)、(6-6)两式告诉我们:
每 个 观 测 值 都包含处理效应(μi-μ 或 xi. x.. ),与误差( xij i 或 ),故 xij xi. kn个观测值的总变异可分解为处理间的变异 和处理内的变异两部分。
二、平方和与自由度的剖分
在方差分析中是用样本方差即均方(mean squares)来度量资料的变异程度的。
指标也不相同。在畜禽 、水产试验中常用的试
验指标有 :日增重 、产仔数 、产奶量 、产蛋
率、瘦肉率、某些生理生化和体型指标(如血糖
含量、体高、体重)等。
上一张 下一张 主 页 退 出
2、试验因素(experimental factor) 试验中所研究的影响试验指标的因素叫试验 因素。如研究如何提高猪的日增重时,饲料的配 方、猪的品种、饲养方式、环境温湿度等都对日 增重有影响,均可作为试验因素来考虑。 当试验中考察的因素只有一个时,称为单因 素试验; 若同时研究两个或两个以上的因素对试验指 标的影响时,则称为两因素或多因素试验。试验
上一张 下一张 主 页 退 出
(一)总平方和的剖分
在表6-1中,反映 全部观测值总变异的
总平方和是各观测值xij与总平均数的离均差 平方和,记为SST。即
kn
SST
(xij x..)2
i1 j1
上一张 下一张 主 页 退 出
SPSS_方差分析

第6章方差分析6.1实验目的在现实生活中,影响具体某个事物的因素往往很多,我们常常需要正确确定哪些因素的影响是显著的,方差分析(简称为ANOV A)就是解决这一问题的有效方法。
由于方差分析在统计分析工作中,是不可或缺的关键性的一个环节,因此掌握方差分析的原理及方法使非常必要的。
本实验的目的在于利用方差分析(简称为ANOV A)来进行相关的假设检验和统计决策。
具体有以下三个方面:1.帮助学生深入了解理解方差及方差分析的基本概念,掌握方差分析的基本思想和原理。
理解总离差(SST)、组间平方和(SSR)、组内平方和或残差平方和(SSE)、组间均方差(MSR)、组内均方差(MSE)、自由度、F统计量等基本概念及其相互关系。
2.掌握方差分析的过程:One-Way过程:单因素简单方差分析过程。
在Compare Means菜单项中,可以进行单因素方差分析、均值多重比较和相对比较;General Linear Model(简称GLM)过程:GLM过程由Analyze菜单直接调用。
这些过程可以完成简单的多因素方差分析和协方差分析,不但可以分析各因素的主效应,还可以分析各因素间的交互效应。
3.增强学生的实践能力,使学生能够利用SPSS统计软件,熟练进行单因素方差分析、两因素方差分析、协方差分析等操作,初步了解多元方差分析、重复测量的方差分析等操作,激发学生学习兴趣,增强自我学习和研究的能力。
6.2实验原理6.2.1统计原理方差分析是一种通过分析样本资料各项差异的来源以检验三个或三个以上总体平均数是否相等或者是否具有显著性差异的方法。
该方法在现实统计分析中应用非常广泛。
方差分析的方法是否正确,直接影响到统计分析的正确性和决策的科学性。
统计上存在两类误差:随机误差和系统误差。
随机误差是指在因素的同一水平(同一个总体)下,样本的各观察值之间的差异。
比如,同一种颜色的饮料在不同超市上的销售量是不同的;不同超市销售量的差异可以看成是随机因素的影响,或者说是由于抽样的随机性所造成的,这类差异称为随机误差。
方差分析SPSS操作流程PPT课件

ANOVA
WEIGHT
Sum of Squares Betwee2n05G3r8o.u7p0s Within G6r5o2u.p1s59 Total 21190.86
dfMean Square F 36846.231357.467
15 43.477 18
Sig. .000
• 第一栏:方差来源
• 第二栏:离均差平方和
.;
22
• Homogeneity of variance复选项,要求进行方差齐次性检验 ,并输出检验结果。
• Brown-Forsythe:检验各组均数相等,当不能确定方差齐性 检验时,该统计量优于F统计量。
• Welch:检验各组均数相等,当不能确定方差齐性检验时,该 统计量优于F统计量。
• Mean plot复选项,即均数分布图,横轴为分类变量,纵轴为 反应变量的均数线图;
重比较对每个水平的均值逐对进行比较,以判断具体是哪些水
平间存在显著差异。
• 常用方法备选:
– LSD法:t检验的变形,在变异和自由度的计算上利用了整个样本信息
。
– Duncan 新复极差测验法
– Tukey 固定极差测验法
– Dunnett最小显著差数测验法 等
• 实现手段:
– 方差分析菜单中的“Post ho. c test…”按钮
• One-Way ANOVA过程要求:
因(分析)变量属于正态分布总体,若因(分析 )变量的分布明显的是非正态,应该用非参数分 析过程。
对被观测对象的实验不是随机分组的,而是进行 的重复测量形成几个彼此不独立的变量,应该用 Repeated Measure菜. 单项,进行重复测量方差8
• analyze→compare means→one-way ANVOA
《统计分析与SPSS的应用(第五版)》课后练习答案(第6章)
(2 )分析 一般线性模型 单变量 因变量:得分;因子:性别、是否使用手机
确定。
主体间因子
性别
1
2
是否使用手机
1
2
值标签 男 女 使用 不使用
数字 12 12 12 12
因变量 : Score 源 校正的模型 截距 Sex UsePhone Sex * UsePhone 错误
总计
校正后的总变异
主体间效应的检验
在剔除加盟时间的影响下,因 果有显著差异。
P- 值为 0.034 ,小于 0.05 ,应拒绝原假设,两种培训方式效
第三组
(J) 组别 第二组 第三组 第四组 第五组 第一组 第三组 第四组 第五组 第一组 第二组 第四组 第五组
平均差 (I-J) 标准 错误 -3.30000 * 1.60279
.72857
1.60279
3.05714 -6.70000 * 3.30000 * 4.02857 * 6.35714 * -3.40000 *
scoreadd ID
Method month
scoreadd
1
1
1.5
9
10
2
2
12
2
1
2.5
10.5
11
2
4.5
14
3
1
5.5
13
12
2
7
16
4
1
1
8
13
2
0.5
9
5
1
4
11
14
2
4.5
12
6
1
5
9.5
15
2
4.5
10
第6章SPSS的方差分析课件

方差分析的三种变异
方差分析的三种变异
三种变异之间的关系
方差分析的基本思想
• 明确观测变量和控制变量 • 剖析观测变量的方差 • 比较观测变量总离差平方和各部分的比例
方差分析的应用条件
各样本是相互独立的随机样本; 各样本来自正态总体; 各处理组总体方差相等,即方差齐性或齐同。
二、单因素方差分析
练习
• 完成上例,并利用得到的数据进行分 析
方差分析
提纲
1 方差分析概述 2 单因素方差分析 3 多因素方差分析
协方差分析
4
一、方差分析概述
在实际中常常要了解各种因素对产品的性能、产量等的 影响.例如在化工生产中,有原料成分、催化剂、反应温度、 压力、溶液浓度、反应时间等因素(factor). 有些因素是可以控制的,可控因素所处的不同状态称为 因素的水平(level)。 方差分析正是从观测变量的方差入手,研究诸多控制变 量中哪些变量是对观测变量有显著影响的变量。对观测 变量有显著影响的各个控制变量其不同水平以及各水平 的交互搭配是如何影响观测变量的。
步骤
• 1)分析→比较均值→单因素AVONA • 2因子”框
进一步:方差齐性检验
目的:对控制变量不同水平下各观测变量总体的 方差是否相等进行分析。 实现方法:同两独立样本t检验中的方差检验
进一步:多重比较检验
目的:进一步确定控制变量的不同水平对观测变 量的影响程度如何,其中哪个水平的作用明显区 别于其他水平,哪个水平的作用是不显著的,等 等。 原假设:相应两水平下观测变量总体的均值不存 在显著差异。
目的:用来研究一个控制变量的不同水平是否对 观测变量产生了显著影响。
应用举例
某企业在制定某商品的广告策略时,对不同 广告形式在不同地区的广告效果进行了评估 。 以商品销售额为观测变量,广告形式和地区 为控制变量,利用单因素方差分析分别对广 告形式、地区对销售额的影响进行分析。
SPSS第6单元多因素方差分析

SPSS应用
SPSS应用
SPSS应用
以上F统计量服从F分布。SPSS将自动计算 F值,并根据F分布表给出相应的相伴概率值。
SPSS应用
SPSS应用
6.2 SPSS中实现过程
表6-1
研究问题
三组不同性别学生的数学成绩
人 名 hxh yaju yu shizg hah s watet jess wish 2_new1 2_new2 2_new3 2_new4 2_new5 2_new6 2_new7 2_new8 2_new9 数 学 99.00 88.00 99.00 89.00 94.00 90.00 79.00 56.00 89.00 99.00 70.00 89.00 55.00 50.00 67.00 67.00 56.00 56.00 组 别 0 0 0 0 0 0 2 2 2 2 2 2 1 1 1 1 1 1 性 别 male female male male female male male female male male female male female male female male female male
SPSS应用
图5-11 “Univariate:Model”对话框
SPSS应用
图5-12 “Univariate:Profile Plots”对话框
SPSS应用
图5-13 “Univariate:Contrasts”对话框
SPSS应用
5.3.3 结果和讨论
(1)SPSS输出结果文件中的第一部分如 下两表所示。
SPSS应用
Байду номын сангаас
第一因素的主效应:在平衡第二因素各水平之间效应的前提 下,因变量在第一因素各水平上的均值是否存在显著差异。
SPSS的方差分析PPT课件

SST SSA SSE
(xij x)2
i1 j1
组间偏差平方和
k
SSA ni (xi x)2 i 1
自由度=k-1
组内偏差平方和
k ni
SSE
(xij xi )2
i1 j1
自由度=n-k
组间均方和组内均方: MSA SSA , k 1
MSE SSE nk
量的不同水平。
3
单因素方差分析
4
单因素方差分析的基本思想
研究一个控制变量的不同水平是否对观测 变量产生了显著影响。由于仅研究单个因 素对观测变量的影响,因此称为单因素方 差分析。
明确观测变量和控制变量 剖析观测变量的方差 比较观测变量总离差平方和和各部分的比例
5
有关公式
总偏差平方和
k ni
不同品牌的彩电在5个地区的销售量数据
地区因素
地区1 地区2 地区3 地区4
365
350
343
340
345
368
363
330
358
323
353
343
288
280
298
260
地区5 323 333 308 298
13
2020/1/11
14
数据结构
15
分析步骤
(提出假设)
提出假设
对行因素提出的假设为
16
分析步骤
(构造检验的统计量)
计算平方和(SS)
总误差平方和
行因素误差平方和
k r
SST
xij x 2
i1 j1
kr
SSR xi. x 2 i1 j 1
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
5.“两两比较”
6.“保存”
▪ 单击“保存”按钮,弹出图6-18所示的“单变 量:保存”对话框
7.“选项”
▪ 单击“选项”按钮,弹出图6-19所示的“单变 量:选项”对话框。
析因设计方差分析
▪ 例6.3 A、B两种药物联合应用对红细胞增加数 的影响,数据见表6-8。数据库见6-3.sav。
▪ 1.操作步骤
▪ (4)单击“选项”按钮,将“因子与因子交互 ”列表中的“组别”移入右侧“显示均值”框 ,同时勾选“比较主效应”复选框;“输出” 列表中选择“描述统计”和“方差齐性检验” ,单击“继续”按钮,返回主对话框,单击“ 确定”按钮运行。
▪ 2.主要结果解读
▪ 图6-33所示给出两组的例数、均值和标准差; 图6-34所示为两组治疗后血压的Levene方差齐 性检验,本例F=0.049,P=0.826>0.05,因此 方差齐性,符合方差分析条件要求;图6-35所 示为协方差分析结果,可见组别因素F=0.820, P=0.373,组别因素(即两种药物)对降压效果 没有差别;而治疗前血压因素的F=6.463, P=0.017,说明治疗前血压确实对治疗后血压有 影响。
▪ (1)单击“分析”|“一般线性模型”|“单变 量”命令。
▪ (2)将“治疗后血压”放入“因变量”框;将 分组变量“组别”放入“固定因子”框;将“ 治疗前血压”放入“协变量”框。
▪ (3)单击“模型”按钮,在弹出框中将“因子 与协变量”列表中的“组别”和“治疗前血压 ”放入右侧“模型”列表。“构建项”中类型 选择“主效应”。其他默认,单击继续返回。
▪ 实例详解
▪ 例6.1:比较三个不同电池生产企业生产电池的 寿命,见例6-1.sav。此例企业为因素,不同厂 家为水平,本例为单因素3水平设计。
▪ 1.操作步骤
▪ (1)选择“分析”|“比较均值”|“单因素ANOVA” 命令,如图6-6所示;
▪ (2)将因变量“寿命”放入“因变量列表”框;将因 素“企业”放入“因子”框;
▪ (5)图6-11所示为均值图,对不同电池生产企 业电池寿命的均值进行作图,可形象展示各组 间均值的差异,图中可见企业2与企业1、3均值 相差较大,结果与LSD法相同。
随机区组设计方差分析
▪ 例6.2 某研究机构研究了3种动物饲料对4种品系 小鼠体重增加的影响,数据见表6-5,数据库文 件见6-2.sav。
▪ 3.“两两比较”按钮
▪ 单击“两两比较”按钮,弹出图6-3所示的“ 两两比较”对话框。
▪ 4.“选项按钮”
▪ (1)统计量栏包含如下5项:
▪ 描述性:选中该项,则结果中输出每个因变量的个案数、均 值、标准差、均值的标准误、最小值、最大值和均值的95% 可信区间。
▪ 固定和随机效果:表示显示固定效应模型的标准差、标准误 和95%置信区间以及显示随机效应模型的标准误、95%置信 区间、方差成分间的估计值。
▪ (5)“WLS权重”:为权重变量框,在该框中给出 加权二乘分析的权重变量。权重变量必须是数值型 变量,如果权重是零、负数或者缺失,则该变量将 不计入模型。另外如果一个变量已经放入上面某个 对话框,就不能在作为权重变量。
2.“模型”
▪ “模型”对话框中含有两种设定类型,其一为 “全因子”模型,其二为“设定”模型。
▪ 模块解读
▪ 1.调用单变量程序
▪ 单击“分析”|“一般线性模型”|“单变量”命 令,弹出图6-12所示的“单变量”对话框。
▪ (1)“因变量”:为本次所要研究的结果变量。下 面几个变量框均为影响结果变量的原因变量,按照变 量性质分为几种。
▪ (2)“固定因子”:指的是该因素在样本中所有可 能的水平都出现了,一般为该变量自身属性为分类变 量,如血型、不同治疗方案、不同宣传方法等。
▪ (1)“因子”列表:其 中显示主对话框中选择 的因素。每个因素后面 括号内显示其对比的方 法。
▪ (2)“更改对比”框: 选中“因子”列表中某 因素,单击“对比”下 拉列表,选择对比方法 ,单击更改,即可完成 设置。
▪ 4.“绘制”
▪ 单击“绘制”按钮,弹出图6-16所示的对话框。此对话框可以绘 制一个或多个因素变量作用后的因变量的均值分布图。“因子” 列表中显示出此次参与分析的因素列表,“水平轴”是指横坐标 轴,放入该框的变量作为均值图的横坐标,“单图”为均值线分 割依据,放入该框变量的每一水平将会产生独立一条均值线。“ 多图”框,放入变量含义为,以此变量水平分类,做出多个统计 图。“单图”框中变量为同一统计图中分成的多条线。
IBM-SPSS
第6章 方差分析
▪ 方差分析的应用条件如下:
▪ (1)独立,各组数据相互独立,互不相关;( 2)正态:即各组数据符合正态分布;(3)方 差齐性:即各组方差相等。
▪ 统计学上的因素是指研究者所关心的实验条件 ,而水平是指因素的具体表现形式。如温度( 30、60、90)℃、药物种类(A、B、C)药, 产地(山东、安徽、江苏)。此处的温度、药 物种类和产地就是因素,而每个因素里具体的 不同形式就称为水平。
▪ 1.操作步骤
▪ (1)单击“分析”|“一般线性模型”|“单变 量”命令,弹出单变量对话框,将凝血酶原时 间(tt)移入“因变量”列表,将阶段(stage )和药物类型(drug)放入“固定因子”框, 将(subject)放入“随机因子”框。
▪ (2)单击“模型”按钮,弹出模型对话框,选 中“设定”,将stage、drug和subject移入右侧 模型框中,并将“构建项”框中“类型”改为 主效应模型,单击“继续”返回,单击“确定 ”运行。
嵌套设计方差分析
▪ 嵌套设计被称为巢式设计(nested design)有些教科书上称 这类资料为组内又分亚组的分类资料。根据因素数的不同, 套设计可分为二因素(二级)、三因素(三级)等设计。 将 全部k个因素按主次排列,依次称为1级,2级 … k级因素, 再将总离差平和及自由度进行分解,其基本思想与一般方差 分析相同。所不同的是分解法有明显的区别,它侧重于主要 因素,并且,第i级因素的显著与否,是分别用第i级与第i+1 级因素的均方为分子和分母来构造F统计量,并以F测验为其 理论根据的。
▪ (3)图6-9所示为单因素方差分析的结果,并 且进行了趋势检验,结果显示不同企业间方差 分析统计量F=38.771,P值=0.000<0.01,因此 认为不同企业间生产电池的寿命不同。
▪ (4)图6-10所示为两两比较的结果,分别为 LSD法和Tamhane法,显著性小于0.05表示有 差异。本例应该看LSD的结果,因为前面 Levene方差齐性检验显示方差齐。
单因素设计方差分析
▪ 例6.1 比较三个不同电池 生产企业生产电池的寿 命,见例6-1.sav。此例 企业为因素,不同厂家 为水平,本例为单因素3 水平设计。
▪ 2.“对比”按钮
▪ 单击“对比”按钮,弹 出图6-2所示的“对比 ”对话框,此对话框是 用于对组间平方和进行 分解并确定均值的多项 式比较。
▪ (1)单击“分析”|“一般线性模型”|“单变 量”命令。
▪ (2)将红细胞增加数“X”变量放入“因变量 ”框,将药物“A”、“B”放入“固定因子” 框。
▪ (3)单击“模型”按钮,选择系统默认的“全 因子模型”,单击“继续”返回主对话框。
▪ (4)单击“选项”按钮,选择输出栏的“描述 统计”复选框,单击“继续”返回主对话框, 单击“确定”运行。本例为2因素,每因素2个 水平,因此不必进行“两两比较”。
▪ 2.主要结果解读
▪ 主要结果如图6-28所示,本例不同药物drug间 比较,F=0.580,P=0.456,不能拒绝H0,两种 药物间凝血酶原时间差异无显著性意义;不同 阶段stage间比较,F=1.470,P=0.241,不能拒 绝H0,两阶段间凝血酶原时间差异无显著性意 义;不同个体subject间比较,F=3.108, P=0.010,拒绝H0,接收H1,可以认为不同个体 间凝血酶原时间差异有显著性意义。
▪ (3)单击“对比”按钮,弹出图6-2所示的对话框,选 中“多项式”复选框,并在“度”下拉菜单中选择“线 性”选型,单击“继续”按钮,返回主对话框。
▪ (4)单击“两两比较”按钮,弹出图6-3所示的对话框 ,本例选择LSD法和Tamhane’s T2法进行讲解。
▪ (5)单击“选项”按钮,弹出图6-4所示的对 话框,选择“描述性”、“方差同质性检验” 和“均值图”。
▪ (1)“全因子”模型:此项为系统默认,一旦 选择此项,系统将分析所有因素变量、协变量 主效应以及因素与因素间的交互作用,但不包 括协变量的交互作用,如图6-13所示。
▪ (2)“设定”模型:即自定义模型,如图6-14 所示。选择该项后,“因子与协变量”、“模 型”与“构建项”被激活。
▪ 3.“对比”
▪ (3)“缺失值”栏:选择处理缺失值的方式, “按分析顺序排除个案”表示在分析时,检验 变量中含有缺失值的将不被计算;“按列表排 除个案”表示任何一个变量中含有缺失值的个 案都不被计算。
▪ 5.“Bootstrap”按钮
▪ (1)“Bootstrap”(自助法)按钮主要功能为让 计算机对研究样本进行反复抽样,根据多次抽样的 结果对总体均数的置信区间进行估计。单击“自助 法”按钮,弹出图6-5所示的对话框,如选中“执行 Bootstrap”复选框,图6-5所示中其他复选框被激 活。建议样本数不低于1000,“设置Mersenne Twister种子”数,是为了让分析结果能够复制,即 再运行时,设置同样的种子数,会得到相同的结果 。
▪ (6)单击“继续”返回主菜单,单击“确定” 按钮运行,输出结果。
▪ 2.结果解读
▪ (1)图6-7所示为描述性统计量的结果,分别 列出了3个不同电池企业的样本量、均数、标准 差、标准误、均数的95%置信区间以及最大和 最小值。
▪ (2)图6-8所示为Levene方差齐性检验的结果 ,本例Levene统计量为0.390。显著性P值为 0.680>0.05,故3组数据方差齐性。
