常用反三角函数公式
常用反三角函数公式表(完整资料).doc

常⽤反三⾓函数公式表(完整资料).doc 此⽂档下载后即可编辑
反三⾓函数公式
arc sin x + arc sin y = arc sin x – arc sin y = arc cos x + arc cos y = arc cos x – arc cos y = arc tan x + arc tan y = arc tan x – arc tan y = 2 arc sin x = 2 arc cos x =
2 arc tanx = cos (n arc cos x) =
反三⾓函数图像与特征
反正弦曲线图像与特征反余弦曲线图像与特征
拐点(同曲线对称中⼼):,该点切线斜率为1
拐点(同曲线对称中⼼):
,该点切线斜率为-1 反正切曲线图像与特征反余切曲线图像与特征拐点(同曲线对称中⼼):,该点切线斜率为1 拐点:
,该点切线斜率为-1
渐近线:
渐近线:
名称反正割曲线反余割曲线
⽅程
图像
顶点
渐近线
反三⾓函数的定义域与主值范围
函数主值记号定义域主值范围
反正弦若,则
反余弦若,则
反正切若,则
反余切若,则
反正割若,则
反余割若,则
式中n为任意整数.。
常用反关于三角函数公式表--实用

反三角函数公式arc sin x + arc sin y =arc sin x–arc sin y = arc cos x + arc cos y =arc cos x–arc cos y = arc tan x + arc tan y =arc tan x–arc tan y = 2 arc sin x = 2 arc cos x =2 arc tanx =cos (n arc cos x) =反三角函数图像与特点反正弦曲线图像与特点反余弦曲线图像与特点拐点 ( 同曲线对称中心 ) :拐点 ( 同曲线对称中心 ) :,该点切线斜率为 1,该点切线斜率为- 1 反正切曲线图像与特点反余切曲线图像与特点拐点:拐点 ( 同曲线对称中心 ) :,该点切线斜率为 1,该点切线斜率为- 1渐近线:渐近线:名称反正割曲线反余割曲线方程图像极点渐近线反三角函数的定义域与主值范围函数主值记号定义域主值范围反正弦若,则反余弦若,则反正切若,则反余切若,则反正割若,则反余割若,则一般反三角函数与主值的关系为式中 n 为随意整数 .反三角函数的互相关系arc sin x =arc cos x =arc tan x =arc cot x =sin x = x-x3/3!+ x5/5!-...(-1)k-1* x2k-1/(2k-1)!+... (- ∞<x<∞)cos x = 1- x2/2!+ x4/4!-...(-1)k* x2k/(2k)!+... (- ∞<x<∞)arcsin x = x + 1/2* x3/3 + 1*3/(2*4)*x5/5 + ... (| x|<1)arccos x = π- ( x + 1/2* x3/3 + 1*3/(2*4)* x5/5 + ... ) (| x|<1)arctan x = x - x^3/3 + x^5/5 - ... ( x≤1)ArcSin(x)函数功能:返回一个指定数的反正弦值,以弧度表示,返回种类为Double。
反三角函数公式大全

反三角函数公式大全反三角函数,顾名思义就是与三角函数相反的函数,它们是一组用来求解三角形的边长和角度的函数。
在数学中,反三角函数有着非常重要的作用,它们是三角函数的逆运算,可以帮助我们解决很多与三角函数相关的问题。
本文将为大家详细介绍反三角函数的公式,希望能够帮助大家更好地理解和运用这些重要的数学工具。
一、反三角函数的定义。
反三角函数是指正弦、余弦、正切三角函数的反函数,分别记作sin-1(x)、cos-1(x)、tan-1(x),其中x是一个实数。
反三角函数的定义域是[-1,1],值域是[-π/2,π/2],它们的图像是关于y=x对称的。
二、反三角函数的公式。
1. 反正弦函数的公式。
反正弦函数的公式可以表示为,y=sin-1(x),其中x∈[-1,1],y∈[-π/2,π/2]。
反正弦函数的图像是一条在[-1,1]区间上的曲线,它是一条增函数,且在x=0处有一个拐点。
2. 反余弦函数的公式。
反余弦函数的公式可以表示为,y=cos-1(x),其中x∈[-1,1],y∈[0,π]。
反余弦函数的图像是一条在[-1,1]区间上的曲线,它是一条减函数,且在x=0处有一个拐点。
3. 反正切函数的公式。
反正切函数的公式可以表示为,y=tan-1(x),其中x∈R,y∈(-π/2,π/2)。
反正切函数的图像是一条在整个实数轴上的曲线,它是一个奇函数,且在x=0处有一个渐近线。
三、反三角函数的性质。
1. 反三角函数的定义域和值域。
反正弦函数的定义域是[-1,1],值域是[-π/2,π/2];反余弦函数的定义域是[-1,1],值域是[0,π];反正切函数的定义域是整个实数轴,值域是(-π/2,π/2)。
2. 反三角函数的导数。
反正弦函数的导数是1/√(1-x^2),反余弦函数的导数是-1/√(1-x^2),反正切函数的导数是1/(1+x^2)。
3. 反三角函数的反函数关系。
正弦函数与反正弦函数、余弦函数与反余弦函数、正切函数与反正切函数之间存在着反函数的关系,它们互为反函数。
常用反三角函数公式表

常用反三角函数公式表在数学的广袤领域中,反三角函数是一个重要的概念,它们在解决各种数学问题和实际应用中都发挥着关键作用。
反三角函数包括反正弦函数(arcsin)、反余弦函数(arccos)、反正切函数(arctan)等。
为了更好地理解和运用这些函数,我们需要熟悉一些常用的反三角函数公式。
一、反正弦函数(arcsin)公式1、 arcsin(x) = arcsinx这个公式表明,反正弦函数是一个奇函数,即其函数值的正负与自变量的正负相反。
2、 sin(arcsinx) = x ,其中-1 ≤x ≤ 1这是反正弦函数的定义式,意味着对一个在-1, 1范围内的数 x ,其反正弦函数的正弦值就是 x 本身。
3、 arcsinx + arcsin(x) = 0 ,其中-1 ≤ x ≤ 1这个公式进一步说明了反正弦函数的奇偶性。
二、反余弦函数(arccos)公式1、 arccos(x) =π arccosx反余弦函数不是奇函数,而是满足上述关系。
2、 cos(arccosx) = x ,其中-1 ≤ x ≤ 1与反正弦函数类似,这是反余弦函数的定义式。
3、 arccosx + arccos(x) =π ,其中-1 ≤ x ≤ 1体现了反余弦函数的特殊性质。
三、反正切函数(arctan)公式1、 arctan(x) = arctanx反正切函数是奇函数。
2、 tan(arctanx) = x ,x 为实数这是反正切函数的定义式。
3、 arctanx + arctan(1/x) =π/2 ,其中 x > 0这个公式在一些计算和证明中经常用到。
四、反三角函数的和差公式1、 arcsinx + arcsiny=arcsin(x√(1 y²) +y√(1 x²)),其中-1 ≤ x ≤ 1 ,-1 ≤ y ≤ 1 2、 arcsinx arcsiny=arcsin(x√(1 y²) y√(1 x²)),其中-1 ≤ x ≤ 1 ,-1 ≤ y ≤ 1 3、 arccosx + arccosy=arccos(xy √(1 x²)√(1 y²)),其中-1 ≤ x ≤ 1 ,-1 ≤ y ≤ 14、 arccosx arccosy= arccos(xy +√(1 x²)√(1 y²)),其中-1 ≤ x≤ 1 ,-1 ≤ y ≤ 15、 arctanx + arctany= arctan((x + y)/(1 xy)),其中xy ≠ 16、 arctanx arctany= arctan((x y)/(1 + xy)),其中xy ≠ -1五、反三角函数的倍角公式1、arcsin(2x√(1 x²))= 2arcsinx ,其中-1/√2 ≤ x ≤ 1/√22、 arccos(2x² 1) = 2arccosx ,其中0 ≤ x ≤ 13、 arctan(2x/(1 x²))= 2arctanx ,其中-1 < x < 1六、反三角函数的半角公式1、arcsin(√((1 x)/2))=(1/2)arcsinx ,其中0 ≤ x ≤ 12、arccos(√((1 + x)/2))=(1/2)arccosx ,其中-1 ≤ x ≤ 13、arctan(√((1 x)/(1 + x)))=(1/2)arctanx ,其中-1 <x < 1七、反三角函数的万能公式1、 arcsin(2tan(x/2)/(1 + tan²(x/2)))= x ,其中π/2 ≤ x ≤ π/22、 arccos((1 tan²(x/2))/(1 + tan²(x/2)))= x ,其中0 ≤ x ≤ π3、 arctan(2tan(x/2)/(1 tan²(x/2)))= x ,其中π/2 < x <π/2掌握这些常用的反三角函数公式,对于解决涉及三角函数和反三角函数的问题非常有帮助。
常用反三角函数公式
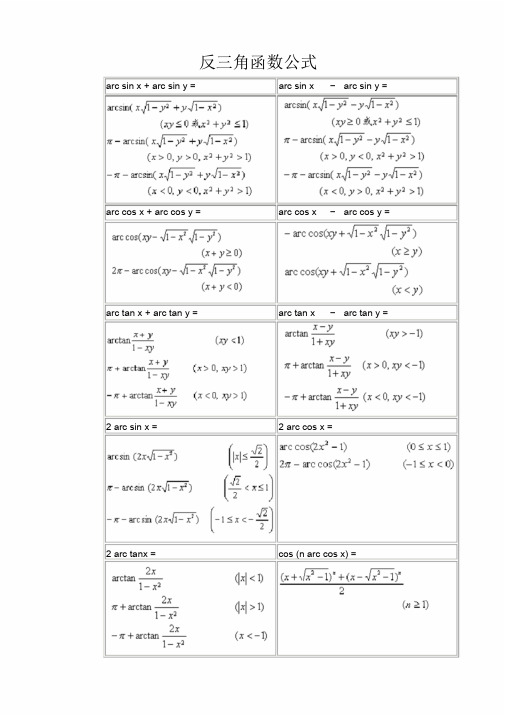
WORD格式专业分享反三角函数公式arc sin x + arc sin y = arc sin x –arc sin y = arc cos x + arc cos y = arc cos x –arc cos y = arc tan x + arc tan y = arc tan x –arc tan y = 2 arc sin x = 2 arc cos x =2 arc tanx = cos (n arc cos x) =WORD格式专业分享反三角函数图像与特征反正弦曲线图像与特征反余弦曲线图像与特征拐点( 同曲线对称中心) :拐点( 同曲线对称中心) :,该点切线斜率为 1,该点切线斜率为- 1 反正切曲线图像与特征反余切曲线图像与特征拐点:拐点( 同曲线对称中心) :,该点切线斜率为1,该点切线斜率为- 1渐近线:渐近线:WORD格式名称反正割曲线反余割曲线方程图像顶点渐近线反三角函数的定义域与主值范围函数主值记号定义域主值范围反正弦若,则反余弦若,则反正切若,则反余切若,则反正割若,则反余割若,则一般反三角函数与主值的关系为式中n为任意整数.专业分享反三角函数的相互关系arc sin x = arc cos x = arc tan x = arc cot x =sin x= x-x3/3!+x5/5!-...(-1)k-1* x2k-1/(2k-1)!+... (- ∞<x<∞)cos x= 1- x2/2!+ x4/4!-...(-1)k* x2k/(2k)!+... (- ∞<x<∞)arcsin x= x+ 1/2* x3/3 + 1*3/(2*4)* x5/5 + ... (|x|<1)arccos x= π- ( x+ 1/2* x3/3 + 1*3/(2*4)* x5/5 + ... ) (|x|<1)arctan x= x- x^3/3 + x^5/5 - ... (x≤ 1)ArcSin(x) 函数为Double。
常用反三角函数公式表

百度文库・让每个人平等地提升白我女三角曲数公式女三角晶数画像与特征2次三角曲数的定义域S至位范凰Arc sin 工二打产十(一1)° arcsin AArccos n = 2 %± arccos xArc tan. x = tz 死 +arc tan 汗3式中n为任意整数. 4及三角晶数的巡及关系sin x = x-x3/3!+x5/5!-...(-l)k-l*x2k-l/(2k-l)!+... (-co<x<oo) cosx= 1 -x2/2!+x4/4!-...(-1 )k*x2k/(2k)!+... (-oo<x<oo) arcsinx = x+ l/2*x3/3 + 1 *3/(2*4)*x5/5 + ... (Ixl<l)arccos x =兀-(x + l/2*x3/3 + l*3/(2*4)*x5/5 +...) (Ixkl) arctan x = x - xA3/3 + x A5/5 -... (x<l)ArcSin (x)函数功能:返回一个指定数的反正弦值,以弧度表示,返回类型为Double。
语法:ArcSin (x)。
说明:其中,x的取值范围为[-1, 1], x的数据类型为Double。
程序代码:Function ArcSin(x As Double) As DoubleIf x >= -1 And x < -0. 5 Then ArcSin = -Atn(Sqr(1 - x*x)/x) - 2* Atn(l) 4If x >= -0. 5 And x <= 0. 5 Then ArcSin = Atn(x / Sqr (1 - x * x))If x > 0. 5 And x <= 1 Then ArcSin = -Atn(Sqr(1 - x*x)/x)+2* Atn(l)End FunctionArcCos (x)函数功能:返回一个指定数的反余弦值,以弧度表示,返回类型为Double。
常用反三角函数公式表

反三角函数公式arc sin x + arc sin y = arc sin x – arc sin y = arc cos x + arc cos y = arc cos x – arc cos y = arc tan x + arc tan y = arc tan x – arc tan y = 2 arc sin x = 2 arc cos x =2 arc tanx = cos (n arc cos x) =反三角函数图像与特征反正弦曲线图像与特征反余弦曲线图像与特征拐点(同曲线对称中心):,该点切线斜率为1拐点(同曲线对称中心):,该点切线斜率为-1 反正切曲线图像与特征反余切曲线图像与特征拐点(同曲线对称中心):,该点切线斜率为1 拐点:,该点切线斜率为-1:渐近线:名称反正割曲线反余割曲线方程图像顶点渐近线反三角函数的定义域与主值范围函数主值记号定义域主值范围反正弦若,则反余弦若,则反正切若,则反余切若,则反正割若,则反余割若,则一般反三角函数与主值的关系为式中n为任意整数.反三角函数的相互关系arc sin x = arc cos x = arc tan x = arc cot x =sin x = x-x3/3!+x5/5!-...(-1)k-1*x2k-1/(2k-1)!+... (-∞<x<∞)cos x = 1-x2/2!+x4/4!-...(-1)k*x2k/(2k)!+... (-∞<x<∞)arcsin x = x + 1/2*x3/3 + 1*3/(2*4)*x5/5 + ... (|x|<1)arccos x = π - ( x + 1/2*x3/3 + 1*3/(2*4)*x5/5 + ... ) (|x|<1)arctan x = x - x^3/3 + x^5/5 - ... (x≤1)ArcSin(x) 函数功能:返回一个指定数的反正弦值,以弧度表示,返回类型为Double。
常用反三角函数公式表

反三角函数公式arc sin x + arc sin y = arc sin x – arc sin y = arc cos x + arc cos y = arc cos x – arc cos y = arc tan x + arc tan y = arc tan x – arc tan y = 2 arc sin x = 2 arc cos x =2 arc tanx = cos (n arc cos x) =反三角函数图像与特征反正弦曲线图像与特征反余弦曲线图像与特征拐点(同曲线对称中心):,该点切线斜率为1拐点(同曲线对称中心):,该点切线斜率为-1 反正切曲线图像与特征反余切曲线图像与特征拐点(同曲线对称中心):,该点切线斜率为1 拐点:,该点切线斜率为-1渐近线:渐近线:名称反正割曲线反余割曲线方程图像顶点渐近线反三角函数的定义域与主值范围函数主值记号定义域主值范围反正弦若,则反余弦若,则反正切若,则反余切若,则反正割若,则反余割若,则一般反三角函数与主值的关系为式中n为任意整数.反三角函数的相互关系arc sin x = arc cos x = arc tan x = arc cot x =sin x = x-x3/3!+x5/5!-...(-1)k-1*x2k-1/(2k-1)!+... (-∞<x<∞)cos x = 1-x2/2!+x4/4!-...(-1)k*x2k/(2k)!+... (-∞<x<∞)arcsin x = x + 1/2*x3/3 + 1*3/(2*4)*x5/5 + ... (|x|<1)arccos x = π - ( x + 1/2*x3/3 + 1*3/(2*4)*x5/5 + ... ) (|x|<1)arctan x = x - x^3/3 + x^5/5 - ... (x≤1)ArcSin(x) 函数功能:返回一个指定数的反正弦值,以弧度表示,返回类型为Double。
常用反三角函数公式

常用反三角函数公式-CAL-FENGHAI.-(YICAI)-Company One1反三角函数公式arc sin x + arc sin y = arc sin x – arc sin y = arc cos x + arc cos y = arc cos x – arc cos y = arc tan x + arc tan y = arc tan x – arc tan y = 2 arc sin x = 2 arc cos x =2 arc tanx = cos (n arc cos x) =反三角函数图像与特征反正弦曲线图像与特征反余弦曲线图像与特征拐点(同曲线对称中心):,该点切线斜率为1拐点(同曲线对称中心):,该点切线斜率为-1 ?反正切曲线图像与特征反余切曲线图像与特征拐点(同曲线对称中心):,该点切线斜率为1拐点:,该点切线斜率为-1渐近线:渐近线:?名称反正割曲线反余割曲线方程图像顶点渐近线反三角函数的定义域与主值范围函数主值记号定义域主值范围反正弦若,则反余弦若,则反正切若,则反余切若,则反正割若,则反余割若,则式中n为任意整数.反三角函数的相互关系arc sin x = arc cos x = arc tan x = arc cot x =sin x = x-x3/3!+x5/5!-...(-1)k-1*x2k-1/(2k-1)!+... (-∞<x<∞)cos x = 1-x2/2!+x4/4!-...(-1)k*x2k/(2k)!+... (-∞<x<∞)arcsin x = x + 1/2*x3/3 + 1*3/(2*4)*x5/5 + ... (|x|<1)arccos x= π - ( x + 1/2*x3/3 + 1*3/(2*4)*x5/5 + ... ) (|x|<1)arctan x = x - x^3/3 + x^5/5 - ... (x≤1)ArcSin(x) 函数功能:返回一个指定数的反正弦值,以弧度表示,返回类型为Double。
反三角函数公式

反三角函数公式: arcsin(-x)=-arcsinx arccos(-x)=∏-arccosx arctan(-x)=-arctanx arccot(-x)=∏-arccotx arcsinx+arccosx=∏/2=arctanx+arccotx sin(arcsinx)=x=cos(arccosx)=tan(arctanx)=cot(arccotx) 当x∈〔—∏/2,∏/2〕时,有arcsin(sinx)=x 当x∈〔0,∏〕,arccos(cosx)=x x∈(—∏/2,∏/2),arctan(tanx)=x x∈(0,∏),arccot(cotx)=x x〉0,arctanx=arctan1/x,arccotx类似 若(arctanx+arctany)∈(—∏/2,∏/2),则arctanx+arctany=arctan(x+y/1-xy) 同角三角函数的基本关系式 倒数关系: 商的关系:平方关系: tanα ·cotα=1 sinα ·cscα=1 cosα ·secα=1 sinα/cosα=tanα=secα/cscα cosα/sinα=cotα=cscα/secα sin2α+cos2α=1 1+tan2α=sec2α 1+cot2α=csc2α 诱导公式 sin(-α)=-sinα cos(-α)=cosα tan(-α)=-tanα cot(-α)=-cotα sin(π/2-α)=cosα cos(π/2-α)=sinα tan(π/2-α)=cotα cot(π/2-α)=tanα sin(π/2+α)=cosα cos(π/2+α)=-sinα tan(π/2+α)=-cotα cot(π/2+α)=-tanα sin(π-α)=sinα cos(π-α)=-cosα tan(π-α)=-tanα cot(π-α)=-cotα sin(π+α)=-sinα cos(π+α)=-cosα tan(π+α)=tanα cot(π+α)=cotα sin(3π/2-α)=-cosα cos(3π/2-α)=-sinα tan(3π/2-α)=cotα cot (3π/2-α)=tanα sin(3π/2+α)=-cosα cos(3π/2+α)=sinα tan(3π/2+α)=-cotα cot(3π/2+α)=-tanα sin(2π-α)=-sinα cos(2π-α)=cosα tan(2π-α)=-tanα cot(2π-α)=-cotα sin(2kπ+α)=sinα cos(2kπ+α)=cosα tan (2kπ+α)=tanα cot(2kπ+α)=cotα (其中k∈Z) 两角和与差的三角函数公式万能公式 sin(α+β)=sinαcosβ+cosαsinβ sin(α-β)=sinαcosβ-cosαsinβ cos(α+β)=cosαcosβ-sinαsinβ cos(α-β)=cosαcosβ+sinαsinβ tanα+tanβ tan(α+β)=—————— 1-tanα ·tanβ tanα-tanβ tan(α-β)=—————— 1+tanα ·tanβ 2tan(α/2) sinα=—————— 1+tan2(α/2) 1-tan2(α/2) cosα=—————— 1+tan2(α/2) 2tan(α/2) tanα=—————— 1-tan2(α/2) 半角的正弦、余弦和正切公式三角函数的降幂公式 二倍角的正弦、余弦和正切公式三倍角的正弦、余弦和正切公式 sin2α=2sinαcosα cos2α=cos2α-sin2α=2cos2α-1=1-2sin2α 2tanα tan2α=————— 1-tan2α sin3α=3sinα-4sin3α cos3α=4cos3α-3cosα 3tanα-tan3α tan3α=—————— 1-3tan2α 三角函数的和差化积公式三角函数的积化和差公式 α+β α-β sinα+sinβ=2sin—--·cos—-— 2 2 α+β α-β sinα-sinβ=2cos—--·sin—-— 2 2 α+β α-β cosα+cosβ=2cos—--·cos—-— 2 2 α+β α-β cosα-cosβ=-2sin—--·sin—-— 2 2 1 sinα ·cosβ=-[sin(α+β)+sin(α-β)] 2 1 cosα ·sinβ=-[sin(α+β)-sin(α-β)] 2 1 cosα ·cosβ=-[cos (α+β)+cos(α-β)] 2 1 sinα ·sinβ=--[cos(α+β)-cos(α-β)] 2首先∵-1≤x≤1,∴-1≤-x≤1,-x属于arccosx的定义域,arccos(-x)有意义。
常用反三角函数公式表

常用反三角函数公式表在数学的世界里,反三角函数是一类重要的函数。
它们在解决各种数学问题,特别是涉及三角形和几何图形的问题时,发挥着关键作用。
接下来,让我们详细了解一下常用的反三角函数公式。
首先,我们来认识一下反三角函数的定义。
反三角函数是三角函数的反函数。
常见的反三角函数包括反正弦函数(arcsin x)、反余弦函数(arccos x)、反正切函数(arctan x)等。
反正弦函数(arcsin x)的公式:若 y = arcsin x,则 x = sin y ,且-1 ≤ x ≤ 1 ,π/2 ≤ y ≤ π/2 。
反正弦函数的一些重要性质和公式:1、 arcsin(x) = arcsin x ,这表明反正弦函数是一个奇函数。
2、 sin(arcsin x) = x ,对于-1 ≤ x ≤ 1 。
反余弦函数(arccos x)的公式:若 y = arccos x,则 x = cos y ,且-1 ≤ x ≤ 1 ,0 ≤ y ≤ π 。
反余弦函数的一些性质和公式:1、 arccos(x) =π arccos x ,反余弦函数不是奇函数也不是偶函数。
2、 cos(arccos x) = x ,对于-1 ≤ x ≤ 1 。
反正切函数(arctan x)的公式:若 y = arctan x,则 x = tan y ,且 x 为实数,π/2 < y <π/2 。
反正切函数的一些重要性质和公式:1、 arctan(x) = arctan x ,反正切函数是奇函数。
2、 tan(arctan x) = x ,对于 x 为实数。
反三角函数的和差公式也是非常有用的。
arcsin x + arcsin y =arcsin(x√(1 y²) +y√(1 x²)),但要注意-1 ≤ x,y ≤ 1 且 x²+y² ≤ 1 。
arcsin x arcsin y =arcsin(x√(1 y²) y√(1 x²)),同样需要满足相应条件。
常用反三角函数公式表

反三角函数公式反三角函数图像与特征渐近线: 渐近线:反三角函数的定义域与主值范围般反三角函数与主值的关系为式中n为任意整数.反三角函数的相互关系sin x = x-x3/3!+ x5/5!-...(-1)k-1* x2k-1/(2k-1)!+... (- m<x<^)cos x = 1- x2/2!+ x4/4!-...(-1)k* |x2k/(2k)!+... (- m<x<^)arcsin x = x + 1/2* x3/3 + 1*3/(2*4)* x5/5 + ... (| x|<1) arccos x = n - ( x + 1/2* x3/3 + 1*3/(2*4)* x5/5 + ... ) (| |x|<1)arctan x = x - x A3/3 + x A5/5 - ... ( x < 1)ArcSi n(x)函数功能:返回一个指定数的反正弦值,以弧度表示,返回类型为Double语法:ArcSin (x)。
说明:其中,x的取值范围为[-1,1],x的数据类型为Double。
程序代码:Function ArcSin (x As Double) As DoubleIf x >= -1 And x < Then ArcSin = -Atn(Sqr(1 - x * x) / x) - 2 * Atn⑴If x >= And x <= Then ArcSin = Atn( x / Sqr(1 - |x * x))If x > And x <= 1 Then ArcSin = -Atn(Sqr(1 - |x * |x) / |x) + 2 * Atn(1) End Fun cti onArcCos(x)函数功能:返回一个指定数的反余弦值,以弧度表示,返回类型为Double语法:ArcCos(x)。
说明:其中,x的取值范围为[-1,1],x的数据类型为Double 程序代码:Function ArcCos( x As Double) As DoubleIf x >= -1 And x < Then ArcCos = Atn(Sqr(1 - x * |x) / |x) + 4 * Atn(1)If x >= And x <= Then ArcCos = -Atn( x / Sqr(1 - x * x)) + 2 * Atn(1)If x > And x <= 1 Then ArcCos = Atn(Sqr(1 - x * x) / x)End Fun cti on。
常用反三角函数公式表

反三角函数公式arc sin x + arc sin y = arc sin x – arc sin y = arc cos x + arc cos y = arc cos x – arc cos y = arc tan x + arc tan y = arc tan x – arc tan y = 2 arc sin x = 2 arc cos x =2 arc tanx = cos (n arc cos x) =反三角函数图像与特征反正弦曲线图像与特征反余弦曲线图像与特征拐点(同曲线对称中心):,该点切线斜率为1拐点(同曲线对称中心):,该点切线斜率为-1 反正切曲线图像与特征反余切曲线图像与特征拐点(同曲线对称中心):,该点切线斜率为1 拐点:,该点切线斜率为-1渐近线:渐近线:名称反正割曲线反余割曲线方程图像顶点渐近线反三角函数的定义域与主值范围函数主值记号定义域主值范围反正弦若,则反余弦若,则反正切若,则反余切若,则反正割若,则反余割若,则一般反三角函数与主值的关系为式中n为任意整数.反三角函数的相互关系arc sin x = arc cos x = arc tan x = arc cot x =sin x = x-x3/3!+x5/5!-...(-1)k-1*x2k-1/(2k-1)!+... (-∞<x<∞)cos x = 1-x2/2!+x4/4!-...(-1)k*x2k/(2k)!+... (-∞<x<∞)arcsin x = x + 1/2*x3/3 + 1*3/(2*4)*x5/5 + ... (|x|<1)arccos x = π - ( x + 1/2*x3/3 + 1*3/(2*4)*x5/5 + ... ) (|x|<1)arctan x = x - x^3/3 + x^5/5 - ... (x≤1)ArcSin(x) 函数功能:返回一个指定数的反正弦值,以弧度表示,返回类型为Double。
反三角函数基本公式

反三角函数基本公式
反三角函数是数学中一类特殊的函数,它们是由正弦、余弦、正切以及其它三角函数反求而来的。
这类函数描述了一个角度和其对应三角函数值之间的关系。
反三角函数有两个特点:一是它们的定义域是实数,即对任意实数都有定义;二是它们的值域也是实数,即它们的输出也是实数。
因此,反三角函数可以用来求解三角函数的结果,从而实现从角度到三角函数值的变换,以及从三角函数值到角度的变换。
反三角函数的基本公式可以表示为:y = f(x) = sin^-1(x)、cos^-1(x)、tan^-1(x)等,其中sin^-1(x)表示正弦函数的反函数,cos^-1(x)表示余弦函数的反函数,tan^-1(x)表示正切函数的反函数。
反三角函数还有两个附加公式:cot^-1(x)和sec^-1(x),其中cot^-1(x)表示余切函数的反函数,sec^-1(x)表示正割函数的反函数。
反三角函数的应用非常广泛,它们可以用来解决各种复杂的数学问题,比如求解复平面几何问题、求解空间几何问题、求解概率统计问题等。
另外,它们还可以用来求解物理方程,甚至可以用来解决微积分问题。
反三角函数是数学中一类重要的函数,其基本公式描述了角度和三角函数值之间的关系,它们的应用非常广泛,可以用来解决各种复
杂的数学问题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
精品文档
.
反三角函数公式
arc sin x + arc sin y =
arc sin x – arc sin y =
arc cos x + arc cos y =
arc cos x – arc cos y =
arc tan x + arc tan y =
arc tan x – arc tan y =
2 arc sin x =
2 arc cos x =
2 arc tanx =
cos (n arc cos x) =
精品文档
.
反三角函数图像与特征
反正弦曲线图像与特征
反余弦曲线图像与特征
拐点(同曲线对称中心):,该点切线斜率为1
拐点(同曲线对称中心):
,该点切线斜率为-1
反正切曲线图像与特征
反余切曲线图像与特征
拐点(同曲线对称中心):,该点切线斜率
为1
拐点:
,该点切线斜率为-1
渐近线:
渐近线:
精品文档
. 名称
反正割曲线反余割曲线
方程
图像
顶点
渐近线
反三角函数的定义域与主值范围
函数主值记号定义域主值范围
反正弦若,则
反余弦若,则
反正切若,则
反余切若,则
反正割若,则
反余割若,则
式中n为任意整数.
精品文档
.
反三角函数的相互关系
arc sin x = arc cos x = arc tan x = arc cot x =
sin x = x -x 3/3!+x 5/5!-...(-1)k-1*x 2k-1/(2k-1)!+... (-∞<x <∞) cos x = 1-x 2/2!+x 4/4!-...(-1)k*x 2k/(2k)!+... (-∞<x <∞) arcsin x = x + 1/2*x 3/3 + 1*3/(2*4)*x 5/5 + ... (|x |<1) arccos x = π - ( x + 1/2*x 3/3 + 1*3/(2*4)*x 5/5 + ... ) (|x |<1)
arctan x = x - x ^3/3 + x ^5/5 - ... (x ≤1)
ArcSin(x) 函数
功能:返回一个指定数的反正弦值,以弧度表示,返回类型为Double 。
语法:ArcSin (x )。
说明:其中,x 的取值范围为[-1,1],x 的数据类型为Double 。
程序代码:
Function ArcSin (x As Double) As Double
If x >= -1 And x < -0.5 Then ArcSin = -Atn(Sqr(1 - x * x ) / x ) - 2 * Atn(1) If x >= -0.5 And x <= 0.5 Then ArcSin = Atn(x / Sqr(1 - x * x ))
If x > 0.5 And x <= 1 Then ArcSin = -Atn(Sqr(1 - x * x ) / x ) + 2 * Atn(1) End Function
精品文档ArcCos(x) 函数
功能:返回一个指定数的反余弦值,以弧度表示,返回类型为Double。
语法:ArcCos(x)。
说明:其中,x的取值范围为[-1,1],x的数据类型为Double。
程序代码:
Function ArcCos(x As Double) As Double
If x >= -1 And x < -0.5 Then ArcCos = Atn(Sqr(1 - x * x) / x) + 4 * Atn(1) If x >= -0.5 And x <= 0.5 Then ArcCos = -Atn(x / Sqr(1 - x * x)) + 2 * Atn(1) If x > 0.5 And x <= 1 Then ArcCos = Atn(Sqr(1 - x * x) / x)
End Function
.。
