2020桂林市中考数学试题及答案
桂林市2020年中考数学试卷(I)卷

桂林市2020年中考数学试卷(I)卷姓名:________ 班级:________ 成绩:________一、选择题(下列备选答案中,只有一个是正确的,共8小题,每小题3 (共8题;共16分)1. (2分)(2016·庐江模拟) 下列各数中,最小的数是()A . 0B . 1C . ﹣1D . ﹣2. (2分)(2017·呼兰模拟) 由四个相同的小正方体堆成的物体如图所示,它的俯视图是()A .B .C .D .3. (2分)地球的表面积约为510000000km2 ,将510000000用科学记数法表示为()A . 0.51×109B . 5.1×109C . 5.1×108D . 0.51×1074. (2分)(2020·合肥模拟) 以下运算正确的是()A .B .C .D .5. (2分)(2019·莲湖模拟) 在平面直角坐标系中,点A的坐标是(– 1,2),作点A关于y轴的对称点,得到点A',再将点A'向下平移4个单位,得到点A″,则点A″的坐标是()A . (– 1,– 2)B . (1,2)C . (1,– 2)D . (–2,1)6. (2分) (2019八下·淮安月考) 以下说法合理的是:()A . “打开电视,正在播放新闻节日”是必然事件B . “抛一枚硬币,正面朝上的概率为”表示每抛两次就有一次正面朝上C . “抛掷一枚均匀的骰子,出现点数6的概率是”表示随着抛掷次数的增加“出现点数6”这一事件发生的频率稳定在附近D . 为了解某品牌火腿的质量,选择全面检测7. (2分)已知:一次函数y=(a-1)x+b的图象如图所示,那么a的取值范围是()A . a>1B . a<1C . a>0D . a<08. (2分)(2020·北京模拟) 如图,经过直线AB外一点C作这条直线的垂线,作法如下:⑴任意取一点K,使点K和点C在AB的两旁.⑵以点C为圆心,CK长为半径作弧,交AB于点D和E.⑶分别以点D和点E为圆心,大于的长为半径作弧,两弧相交于点F.⑷作直线CF.则直线CF就是所求作的垂线.根据以上尺规作图过程,若将这些点作为三角形的顶点,其中不一定是等腰三角形的为()A . △CDFB . △CDKC . △CDED . △DEF二、填空题(共8小题,每小题4分,满分32分) (共8题;共8分)9. (1分)(2019·零陵模拟) 分解因式: =________.10. (1分)数据4,7,7,8,9的众数是________.11. (1分) (2020八上·襄城期末) 如图,五边形ABCDE的内角都相等,且∠BAC=∠BCA,∠EAD=∠EDA,则∠CAD度数为________.12. (1分)若 >0, <0,则ac________0.13. (1分) (2018九上·青浦期末) 如果两个相似三角形周长的比是,那么它们面积的比是________.14. (1分) (2020八下·吴兴期末) 如图,在平面直角坐标系中,点O为坐标原点,等边△ABO的边OB和菱形CDEO的边EO均在x轴上,点C在AO上,,反比例函数的图像经过A点,则k的值为________.15. (1分) (2017七上·闵行期末) 如果关于x的多项式x2﹣kx+9是一个完全平方式,那么k=________.16. (1分)如图,在菱形中,对角线、交于点,若,,则菱形的面积为________.三、解答题(共3小题,17、18各8分,19题10分,共26分) (共3题;共25分)17. (5分)(2019·南宁模拟) 计算: .18. (10分)(2017·无棣模拟) 为了解外来务工子女就学情况,某校对七年级各班级外来务工子女的人数情况进行了统计,发现各班级中外来务工子女的人数有1名、2名、3名、4名、5名、6名共六种情况,并制成如下两幅统计图:(1)求该校七年级平均每个班级有多少名外来务工子女?并将该条形统计图补充完整;(2)学校决定从只有2名外来务工子女的这些班级中,任选两名进行生活资助,请用列表法或画树状图的方法,求出所选两名外来务工子女来自同一个班级的概率.19. (10分) (2017八上·腾冲期中) 如图,已知△ABC为等边三角形,点D、E分别在BC、AC边上,且AE=CD,AD与BE相交于点F。
广西桂林市2020版中考数学试卷(II)卷

广西桂林市2020版中考数学试卷(II)卷姓名:________ 班级:________ 成绩:________一、选择题: (共10题;共20分)1. (2分)如图,四个有理数在数轴上的对应点分别为M,P,N,Q,若原点在点N与点P之间,则绝对值最大的数表示的点是()A . 点MB . 点PC . 点QD . 点N2. (2分)下列事件中,属于随机事件的是()A . 掷一枚质地均匀的正方体骰子,向上的一面点数小于7B . 某射击运动员射击一次,命中靶心C . 在只装了红球的袋子中摸到白球D . 在三张分别标又数字2、4、6的卡片中摸两张,数字和是偶数3. (2分)(2017·淮安模拟) 用5个完全相同的小正方体组合成如图所示的立体图形,它的主视图为()A .B .C .D .4. (2分)在元旦游园晚会上有一个闯关活动:将5张分别画有等腰梯形、平行四边形、等腰三角形、圆、菱形的卡片任意摆放,将有图形的一面朝下,从中任意翻开一张,如果翻开的图形是中心对称图形,就可以过关,那么一次过关的概率是()A .B .C .D .5. (2分)下列计算错误的是()A .B .C . 3 =3D .6. (2分)下列数据是某班六位同学定点投篮(每人投10个)的情况,投进篮筐的个数为6,9,8,4,0,3,这组数据的平均数、中位数和极差分别是()A . 6,6,9B . 6,5,9C . 5,6,6D . 5,5,97. (2分)(2018·通辽) 小刚从家去学校,先匀速步行到车站,等了几分钟后坐上了公交车,公交车匀速行驶一段时后到达学校,小刚从家到学校行驶路程s(单位:m)与时间r(单位:min)之间函数关系的大致图象是()A .B .C .D .8. (2分) (2019七下·梁子湖期中) 下列四个命题:①如果两个数的绝对值相等,那么这两个数的平方相等;②内错角相等;③在同一平面内,垂直于同一条直线的两条直线平行;④两个无理数的和一定是无理数. 其中真命题的个数是()A . 4个B . 3个C . 1个D . 2个9. (2分) (2016九上·上城期中) 已知二次函数y=x2﹣x+a(a>0),当自变量x取m时,其相应的函数值y<0,那么下列结论中正确的是()A . m﹣1的函数值小于0B . m﹣1的函数值大于0C . m﹣1的函数值等于0D . m﹣1的函数值与0的大小关系不确定10. (2分)将一张长方形纸片按如图所示的方式折叠,BC,BD为折痕,则∠CBD的度数为()A . 60°B . 75°C . 90°D . 95°二、填空题 (共6题;共7分)11. (1分) (2017七上·鄞州月考) 尽管受到国际金融危机的影响,但义乌市经济依然保持了平稳增长.据统计,截止到今年4月底,该市金融机构存款余额约为1193亿元,用科学记数法应记为________元。
2020年广西桂林中考数学试题及参考答案(word解析版)

2020年桂林市初中学业水平考试试卷数学(全卷满分120分,考试用时120分钟)一、选择题(本大题共12小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.有理数2,1,﹣1,0中,最小的数是()A.2 B.1 C.﹣1 D.02.如图,直线a,b被直线c所截,a∥b,∠1=50°,则∠2的度数是()A.40° B.50° C.60° D.70°3.下列调查中,最适宜采用全面调查(普查)的是()A.调查一批灯泡的使用寿命 B.调查漓江流域水质情况C.调查桂林电视台某栏目的收视率 D.调查全班同学的身高4.下面四个几何体中,左视图为圆的是()A. B. C. D.5.若=0,则x的值是()A.﹣1 B.0 C.1 D.26.因式分解a2﹣4的结果是()A.(a+2)(a﹣2) B.(a﹣2)2 C.(a+2)2 D.a(a﹣2)7.下列计算正确的是()A.x•x=2x B.x+x=2x C.(x3)3=x6 D.(2x)2=2x28.直线y=kx+2过点(﹣1,4),则k的值是()A.﹣2 B.﹣1 C.1 D.29.不等式组的整数解共有()A.1个 B.2个 C.3个 D.4个10.如图,AB是⊙O的弦,AC与⊙O相切于点A,连接OA,OB,若∠O=130°,则∠BAC的度数是()A.60° B.65° C.70° D.75°11.参加足球联赛的每两支球队之间都要进行两场比赛,共要比赛110场,设参加比赛的球队有x 支,根据题意,下面列出的方程正确的是()A.x(x+1)=110 B.x(x﹣1)=110 C.x(x+1)=110 D.x(x﹣1)=11012.如图,已知的半径为5,所对的弦AB长为8,点P是的中点,将绕点A逆时针旋转90°后得到,则在该旋转过程中,点P的运动路径长是()A.π B.π C.2π D.2π二、填空题(本大题共6小题,每小题3分,共18分)13.2020的相反数是.14.计算:ab•(a+1)=.15.如图,在Rt△ABC中,∠C=90°,AB=13,AC=5,则cosA的值是.16.一个正方体的平面展开图如图所示,任选该正方体的一面出现“我”字的概率是.17.反比例函数y=(x<0)的图象如图所示,下列关于该函数图象的四个结论:①k>0;②当x<0时,y随x的增大而增大;③该函数图象关于直线y=﹣x对称;④若点(﹣2,3)在该反比例函数图象上,则点(﹣1,6)也在该函数的图象上.其中正确结论的个数有个.18.如图,在Rt△ABC中,AB=AC=4,点E,F分别是AB,AC的中点,点P是扇形AEF的上任意一点,连接BP,CP,则BP+CP的最小值是.三、解答题(本大题共8小题,共66分.解答应写出必要的文字说明、证明过程或演算步骤)19.(6分)计算:(π+)0+(﹣2)2+|﹣|﹣sin30°.20.(6分)解二元一次方程组:.21.(8分)如图,在平面直角坐标系中,△ABC的三个顶点分别是A(1,3),B(4,4),C(2,1).(1)把△ABC向左平移4个单位后得到对应的△A1B1C1,请画出平移后的△A1B1C1;(2)把△ABC绕原点O旋转180°后得到对应的△A2B2C2,请画出旋转后的△A2B2C2;(3)观察图形可知,△A1B1C1与△A2B2C2关于点(,)中心对称.22.(8分)阅读下列材料,完成解答:材料1:国家统计局2月28日发布了2019年国民经济和社会发展统计公报,该公报中的如图发布的是全国“2015﹣2019年快递业务量及其增长速度”统计图(如图1).材料2:6月28日,国家邮政局发布的数据显示:受新冠疫情影响,快递业务量快速增长,5月份快递业务量同比增长41%(如图2).某快递业务部门负责人据此估计,2020年全国快递业务量将比2019年增长50%.(1)2018年,全国快递业务量是亿件,比2017年增长了%;(2)2015﹣2019年,全国快递业务量增长速度的中位数是%;(3)统计公报发布后,有人认为,图1中表示2016﹣2019年增长速度的折线逐年下降,说明2016﹣2019年全国快递业务量增长速度逐年放缓,所以快递业务量也逐年减少.你赞同这种说法吗为什么(4)若2020年全国快递业务量比2019年增长50%,请列式计算2020年的快递业务量.23.(8分)如图,在菱形ABCD中,点E,F分别是边AD,AB的中点.(1)求证:△ABE≌△ADF;(2)若BE=,∠C=60°,求菱形ABCD的面积.24.(8分)某学校为丰富同学们的课余生活,购买了一批数量相等的象棋和围棋供兴趣小组使用,其中购买象棋用了420元,购买围棋用了756元,已知每副围棋比每副象棋贵8元.(1)求每副围棋和象棋各是多少元(2)若该校决定再次购买同种围棋和象棋共40副,且再次购买的费用不超过600元,则该校最多可再购买多少副围棋25.(10分)如图,将一副斜边相等的直角三角板按斜边重合摆放在同一平面内,其中∠CAB=30°,∠DAB=45°,点O为斜边AB的中点,连接CD交AB于点E.(1)求证:A,B,C,D四个点在以点O为圆心的同一个圆上;(2)求证:CD平分∠ACB;(3)过点D作DF∥BC交AB于点F,求证:BO2+OF2=EF•BF.26.(12分)如图,已知抛物线y=a(x+6)(x﹣2)过点C(0,2),交x轴于点A和点B(点A在点B的左侧),抛物线的顶点为D,对称轴DE交x轴于点E,连接EC.(1)直接写出a的值,点A的坐标和抛物线对称轴的表达式;(2)若点M是抛物线对称轴DE上的点,当△MCE是等腰三角形时,求点M的坐标;(3)点P是抛物线上的动点,连接PC,PE,将△PCE沿CE所在的直线对折,点P落在坐标平面内的点P′处.求当点P′恰好落在直线AD上时点P的横坐标.答案与解析一、选择题(本大题共12小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.有理数2,1,﹣1,0中,最小的数是()A.2 B.1 C.﹣1 D.0【知识考点】有理数大小比较.【思路分析】有理数大小比较的法则:①正数都大于0;②负数都小于0;③正数大于一切负数;④两个负数,绝对值大的其值反而小,据此判断即可.【解题过程】解:根据有理数比较大小的方法,可得﹣1<0<1<2,∴在2,1,﹣1,0这四个数中,最小的数是﹣1.故选:C.【总结归纳】此题主要考查了有理数大小比较的方法,要熟练掌握,解答此题的关键是要明确:①正数都大于0;②负数都小于0;③正数大于一切负数;④两个负数,绝对值大的其值反而小.2.如图,直线a,b被直线c所截,a∥b,∠1=50°,则∠2的度数是()A.40° B.50° C.60° D.70°【知识考点】平行线的性质.【思路分析】根据平行线的性质和∠1的度数,可以得到∠2的度数,本题得以解决.【解题过程】解:∵a∥b,∴∠1=∠2,∵∠1=50°,∴∠2=50°,故选:B.【总结归纳】本题考查平行线的性质,解答本题的关键是明确题意,利用数形结合的思想解答.3.下列调查中,最适宜采用全面调查(普查)的是()A.调查一批灯泡的使用寿命 B.调查漓江流域水质情况C.调查桂林电视台某栏目的收视率 D.调查全班同学的身高【知识考点】全面调查与抽样调查.【思路分析】由普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似.【解题过程】解:A、调查一批灯泡的使用寿命,由于具有破坏性,应当使用抽样调查,故本选项不合题意;B、调查漓江流域水质情况,应当采用抽样调查的方式,故本选项不合题意;C、调查桂林电视台某栏目的收视率,人数多,耗时长,应当采用抽样调查的方式,故本选项不合题意.D、调查全班同学的身高,应当采用全面调查,故本选项符合题意.故选:D.【总结归纳】本题考查了抽样调查和全面调查的区别,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大时,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.4.下面四个几何体中,左视图为圆的是()A. B. C. D.【知识考点】简单几何体的三视图.【思路分析】根据四个几何体的左视图进行判断即可.【解题过程】解:下面四个几何体中,A的左视图为矩形;B的左视图为三角形;C的左视图为矩形;D的左视图为圆.故选:D.【总结归纳】本题考查了简单几何体的三视图,解决本题的关键是掌握几何体的三视图.5.若=0,则x的值是()A.﹣1 B.0 C.1 D.2【知识考点】算术平方根.【思路分析】利用算术平方根性质确定出x的值即可.【解题过程】解:∵=0,∴x﹣1=0,解得:x=1,则x的值是1.故选:C.【总结归纳】此题考查了算术平方根,熟练掌握算术平方根的性质是解本题的关键.6.因式分解a2﹣4的结果是()A.(a+2)(a﹣2) B.(a﹣2)2 C.(a+2)2 D.a(a﹣2)【知识考点】因式分解﹣运用公式法.【思路分析】利用平方差公式进行分解即可.【解题过程】解:原式=(a+2)(a﹣2),故选:A.【总结归纳】此题主要考查了公式法分解因式,关键是掌握平方差公式a2﹣b2=(a+b)(a﹣b).7.下列计算正确的是()A.x•x=2x B.x+x=2x C.(x3)3=x6 D.(2x)2=2x2【知识考点】合并同类项;幂的乘方与积的乘方.【思路分析】分别根据同底数幂的乘法法则,合并同类项法则,幂的乘方运算法则以及积的乘方运算法则逐一判断即可.【解题过程】解:A.x•x=x2,故本选项不合题意;B.x+x=2x,故本选项符合题意;C.(x3)3=x9,故本选项不合题意;D.(2x)2=4x2,故本选项不合题意.故选:B.【总结归纳】本题主要考查了同底数幂的乘法,合并同类项以及幂的乘方与积的乘方,熟记相关运算法则是解答本题的关键.8.直线y=kx+2过点(﹣1,4),则k的值是()A.﹣2 B.﹣1 C.1 D.2【知识考点】一次函数图象上点的坐标特征.【思路分析】由直线y=kx+2过点(﹣1,4),利用一次函数图象上点的坐标特征可得出关于k 的一元一次方程,解之即可得出k值.【解题过程】解:∵直线y=kx+2过点(﹣1,4),∴4=﹣k+2,∴k=﹣2.故选:A.【总结归纳】本题考查了一次函数图象上点的坐标特征,牢记直线上任意一点的坐标都满足函数关系式y=kx+b是解题的关键.9.不等式组的整数解共有()A.1个 B.2个 C.3个 D.4个【知识考点】一元一次不等式组的整数解.【思路分析】分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集,从而得出答案.【解题过程】解:解不等式x﹣1>0,得:x>1,解不等式5﹣x≥1,得:x≤4,则不等式组的解集为1<x≤4,所以不等式组的整数解有2、3、4这3个,故选:C.【总结归纳】本题考查的是一元一次不等式组的整数解,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.10.如图,AB是⊙O的弦,AC与⊙O相切于点A,连接OA,OB,若∠O=130°,则∠BAC的度数是()A.60° B.65° C.70° D.75°【知识考点】切线的性质.【思路分析】由“AC与⊙O相切于点A“得出AC⊥OA,根据等边对等角得出∠OAB=∠OBA.求出∠OAC及∠OAB即可解决问题.【解题过程】解:∵AC与⊙O相切于点A,∴AC⊥OA,∴∠OAC=90°,∵OA=OB,∴∠OAB=∠OBA.∵∠O=130°,∴∠OAB==25°,∴∠BAC=∠OAC﹣∠OAB=90°﹣25°=65°.故选:B.【总结归纳】本题考查切线的性质,等腰三角形的性质等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.11.参加足球联赛的每两支球队之间都要进行两场比赛,共要比赛110场,设参加比赛的球队有x 支,根据题意,下面列出的方程正确的是()A.x(x+1)=110 B.x(x﹣1)=110 C.x(x+1)=110 D.x(x﹣1)=110【知识考点】由实际问题抽象出一元二次方程.【思路分析】设有x个队参赛,根据参加一次足球联赛的每两队之间都进行两场比赛,共要比赛110场,可列出方程.【解题过程】解:设有x个队参赛,则x(x﹣1)=110.故选:D.【总结归纳】本题考查由实际问题抽象出一元二次方程,关键是根据总比赛场数做为等量关系列方程求解.12.如图,已知的半径为5,所对的弦AB长为8,点P是的中点,将绕点A逆时针旋转90°后得到,则在该旋转过程中,点P的运动路径长是()A.π B.π C.2π D.2π【知识考点】勾股定理;垂径定理;圆心角、弧、弦的关系;轨迹;旋转的性质.【思路分析】根据已知的半径为5,所对的弦AB长为8,点P是的中点,利用垂径定理可得AC=4,PO⊥AB,再根据勾股定理可得AP的长,利用弧长公式即可求出点P的运动路径长.【解题过程】解:如图,设的圆心为O,连接OP,OA,AP',AP,AB'∵圆O半径为5,所对的弦AB长为8,点P是的中点,根据垂径定理,得AC=AB=4,PO⊥AB,OC==3,∴PC=OP﹣OC=5﹣3=2,∴AP==2,∵将绕点A逆时针旋转90°后得到,∴∠PAP′=∠BAB′=90°,∴L PP′==π.则在该旋转过程中,点P的运动路径长是π.故选:B.【总结归纳】本题考查了轨迹、垂径定理、勾股定理、圆心角、弧、弦的关系、弧长计算、旋转的性质,解决本题的关键是综合运用以上知识.二、填空题(本大题共6小题,每小题3分,共18分.请把答案填在题中的横线上)13.2020的相反数是.【知识考点】相反数.【思路分析】直接利用相反数的定义得出答案.【解题过程】解:2020的相反数是:﹣2020.故答案为:﹣2020.【总结归纳】本题考查相反数.熟练掌握相反数的求法是解题的关键.14.计算:ab•(a+1)=.【知识考点】单项式乘多项式.【思路分析】根据整式的运算法则即可求出答案.【解题过程】解:原式=a2b+ab,故答案为:a2b+ab.【总结归纳】本题考查整式的运算,解题的关键是熟练运用整式的运算法则,本题属于基础题型.15.如图,在Rt△ABC中,∠C=90°,AB=13,AC=5,则cosA的值是.【知识考点】勾股定理;锐角三角函数的定义.【思路分析】根据余弦的定义解答即可.【解题过程】解:在Rt△ABC中,cosA==,故答案为:.【总结归纳】本题考查的是锐角三角函数的定义,掌握锐角A的邻边b与斜边c的比叫做∠A的余弦是解题的关键.16.一个正方体的平面展开图如图所示,任选该正方体的一面出现“我”字的概率是.【知识考点】几何体的展开图;概率公式.【思路分析】根据概率公式解答就可求出任选该正方体的一面出现“我”字的概率.【解题过程】解:∵共有六个字,“我”字有2个,∴P(“我”)==.故答案为:.【总结归纳】此题考查了概率公式的应用.注意概率=所求情况数与总情况数之比.17.反比例函数y=(x<0)的图象如图所示,下列关于该函数图象的四个结论:①k>0;②当x <0时,y随x的增大而增大;③该函数图象关于直线y=﹣x对称;④若点(﹣2,3)在该反比例函数图象上,则点(﹣1,6)也在该函数的图象上.其中正确结论的个数有个.【知识考点】正比例函数的性质;反比例函数的图象;反比例函数的性质;反比例函数图象上点的坐标特征;轴对称的性质.【思路分析】观察反比例函数y=(x<0)的图象可得,图象过第二象限,然后根据反比例函数的图象和性质即可进行判断.【解题过程】解:观察反比例函数y=(x<0)的图象可知:图象过第二象限,∴k<0,所以①错误;因为当x<0时,y随x的增大而增大;所以②正确;因为该函数图象关于直线y=﹣x对称;所以③正确;因为点(﹣2,3)在该反比例函数图象上,所以k=﹣6,则点(﹣1,6)也在该函数的图象上.所以④正确.所以其中正确结论的个数为3个.故答案为3.【总结归纳】本题考查了反比例函数图象上点的坐标特征、反比例函数的性质、轴对称的性质,解决本题的关键是掌握反比例函数的性质.18.如图,在Rt△ABC中,AB=AC=4,点E,F分别是AB,AC的中点,点P是扇形AEF的上任意一点,连接BP,CP,则BP+CP的最小值是.【知识考点】等腰直角三角形;相似三角形的判定与性质.【思路分析】在AB上取一点T,使得AT=1,连接PT,PA,CT.证明△PAT∽△BAP,推出==,推出PT=PB,推出PB+CP=CP+PT,根据PC+PT≥TC,求出CT即可解决问题.【解题过程】解:在AB上取一点T,使得AT=1,连接PT,PA,CT.∵PA=2.AT=1,AB=4,∴PA2=AT•AB,∴=,∵∠PAT=∠PAB,∴△PAT∽△BAP,∴==,∴PT=PB,∴PB+CP=CP+PT,∵PC+PT≥TC,在Rt△ACT中,∵∠CAT=90°,AT=1,AC=4,∴CT==,∴PB+PC≥,∴PB+PC的最小值为.故答案为.【总结归纳】本题考查等腰直角三角形的性质,相似三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造相似三角形解决问题,属于中考常考题型.三、解答题(本大题共8小题,共66分.解答应写出必要的文字说明、证明过程或演算步骤)19.(6分)计算:(π+)0+(﹣2)2+|﹣|﹣sin30°.【知识考点】实数的运算;零指数幂;特殊角的三角函数值.【思路分析】原式利用零指数幂、乘方运算法则,绝对值的代数意义,以及特殊角的三角函数值计算即可求出值.【解题过程】解:原式=1+4+﹣=5.【总结归纳】此题考查了实数的运算,零指数幂,以及特殊角的三角函数值,熟练掌握运算法则是解本题的关键.20.(6分)解二元一次方程组:.【知识考点】解二元一次方程组.【思路分析】方程组利用加减消元法求出解即可.【解题过程】解:①+②得:6x=6,解得:x=1,把x=1代入①得:y=﹣1,则方程组的解为.【总结归纳】此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.21.(8分)如图,在平面直角坐标系中,△ABC的三个顶点分别是A(1,3),B(4,4),C(2,1).(1)把△ABC向左平移4个单位后得到对应的△A1B1C1,请画出平移后的△A1B1C1;(2)把△ABC绕原点O旋转180°后得到对应的△A2B2C2,请画出旋转后的△A2B2C2;(3)观察图形可知,△A1B1C1与△A2B2C2关于点(,)中心对称.【知识考点】作图﹣平移变换;作图﹣旋转变换.【思路分析】(1)依据平移的方向和距离,即可得到平移后的△A1B1C1;(2)依据△ABC绕原点O旋转180°,即可画出旋转后的△A2B2C2;(3)依据对称点连线的中点的位置,即可得到对称中心的坐标.【解题过程】解:(1)如图所示,△A1B1C1即为所求;(2)如图所示,△A2B2C2即为所求;(3)由图可得,△A1B1C1与△A2B2C2关于点(﹣2,0)中心对称.故答案为:﹣2,0.【总结归纳】此题主要考查了平移变换和旋转变换,正确根据题意得出对应点位置是解题关键.22.(8分)阅读下列材料,完成解答:材料1:国家统计局2月28日发布了2019年国民经济和社会发展统计公报,该公报中的如图发布的是全国“2015﹣2019年快递业务量及其增长速度”统计图(如图1).材料2:6月28日,国家邮政局发布的数据显示:受新冠疫情影响,快递业务量快速增长,5月份快递业务量同比增长41%(如图2).某快递业务部门负责人据此估计,2020年全国快递业务量将比2019年增长50%.(1)2018年,全国快递业务量是亿件,比2017年增长了%;(2)2015﹣2019年,全国快递业务量增长速度的中位数是%;(3)统计公报发布后,有人认为,图1中表示2016﹣2019年增长速度的折线逐年下降,说明2016﹣2019年全国快递业务量增长速度逐年放缓,所以快递业务量也逐年减少.你赞同这种说法吗为什么(4)若2020年全国快递业务量比2019年增长50%,请列式计算2020年的快递业务量.【知识考点】用样本估计总体;条形统计图;中位数.【思路分析】(1)由材料1中的统计图中的信息即可得到结论;(2)由材料1中的统计图的信息即可得到结论;(3)根据统计图中的信息即可得到结论;(4)根据题意列式计算即可.【解题过程】解:(1)由材料1中的统计图可得:2018年,全国快递业务量是亿件,比2017年增长了%;(2)由材料1中的统计图可得:2015﹣2019年,全国快递业务量增长速度的中位数是%;(3)不赞同,理由:由图1中的信息可得,2016﹣2019年全国快递业务量增长速度逐年放缓,但是快递业务量却逐年增加;(4)×(1+50%)=(亿件),答:2020年的快递业务量为亿件.故答案为:,,.【总结归纳】本题考查了条形统计图,中位数的定义,正确的理解题意是解题的关键.23.(8分)如图,在菱形ABCD中,点E,F分别是边AD,AB的中点.(1)求证:△ABE≌△ADF;(2)若BE=,∠C=60°,求菱形ABCD的面积.【知识考点】全等三角形的判定与性质;等边三角形的判定与性质;菱形的性质.【思路分析】(1)由SAS证明△ABE≌△ADF即可;(2)证△ABD是等边三角形,得出BE⊥AD,求出AD即可.【解题过程】(1)证明:∵四边形ABCD是菱形,∴AB=AD,∵点E,F分别是边AD,AB的中点,∴AF=AE,在△ABE和△ADF中,,∴△ABE≌△ADF(SAS);(2)解:连接BD,如图:∵四边形ABCD是菱形,∴AB=AD,∠A=∠C=60°,∴△ABD是等边三角形,∵点E是边AD的中点,∴BE⊥AD,∴∠ABE=30°,∴AE=BE=1,AB=2AE=2,∴AD=AB=2,∴菱形ABCD的面积=AD×BE=2×=2.【总结归纳】本题考查了菱形的性质、全等三角形的判定与性质、等边三角形的判定与性质、直角三角形的性质等知识;熟练掌握菱形的性质是解题的关键.24.(8分)某学校为丰富同学们的课余生活,购买了一批数量相等的象棋和围棋供兴趣小组使用,其中购买象棋用了420元,购买围棋用了756元,已知每副围棋比每副象棋贵8元.(1)求每副围棋和象棋各是多少元(2)若该校决定再次购买同种围棋和象棋共40副,且再次购买的费用不超过600元,则该校最多可再购买多少副围棋【知识考点】分式方程的应用;一元一次不等式的应用.【思路分析】(1)设每副围棋x元,则每副象棋(x﹣8)元,根据420元购买象棋数量=756元购买围棋数量列出方程并解答;(2)设购买围棋m副,则购买象棋(40﹣m)副,根据题意列出不等式并解答.【解题过程】解:(1)设每副围棋x元,则每副象棋(x﹣8)元,根据题意,得=.解得x=18.经检验x=18是所列方程的根.所以x﹣8=10.答:每副围棋18元,则每副象棋10元;(2)设购买围棋m副,则购买象棋(40﹣m)副,根据题意,得18m+10(40﹣m)≤600.解得m≤25.故m最大值是25.答:该校最多可再购买25副围棋.【总结归纳】本题考查了分式方程的应用和一元一次不等式的应用,分析题意,找到关键描述语,找到合适的数量关系是解决问题的关键.25.(10分)如图,将一副斜边相等的直角三角板按斜边重合摆放在同一平面内,其中∠CAB=30°,∠DAB=45°,点O为斜边AB的中点,连接CD交AB于点E.(1)求证:A,B,C,D四个点在以点O为圆心的同一个圆上;(2)求证:CD平分∠ACB;(3)过点D作DF∥BC交AB于点F,求证:BO2+OF2=EF•BF.【知识考点】圆的综合题.【思路分析】(1)利用直角三角形斜边的中线等于斜边的一半,判断出OA=OB=OC=OD,即可得出结论;(2)利用等弧所对的圆周角相等,即可得出结论;(3)先判断出△DEF∽△BDF,得出DF2=BF•EF,再利用勾股定理得出OD2+OF2=DF2,即可得出结论.【解题过程】证明:(1)如图,连接OD,OC,在Rt△ABC中,∠ACB=90°,点O是AB的中点,∴OC=OA=OB,在Rt△ABD中,∠ADB=90°,点O是AB的中点,∴OD=OA=OB,∴OA=OB=OC=OD,∴A,B,C,D四个点在以点O为圆心的同一个圆上;(2)由(1)知,A,B,C,D四个点在以点O为圆心的同一个圆上,且AD=BD,∴,∴CD平分∠ACB;(3)由(2)知,∠BCD=45°,∵∠ABC=60°,∴∠BEC=75°,∴∠AED=75°,∵DF∥BC,∴∠BFD=∠ABC=60°,∵∠ABD=45°,∴∠BDF=180°﹣∠BFD﹣∠ABD=75°=∠AED,∵∠DFE=∠BFD,∴△DEF∽△BDF,∴,∴DF2=BF•EF,连接OD,则∠BOD=90°,OB=OD,在Rt△DOF中,根据勾股定理得,OD2+OF2=DF2,∴OB2+OF2=BF•EF,即BO2+OF2=EF•BF.【总结归纳】此题是圆的综合题,主要考查了四点共圆的判断方法,相似三角形的判定和性质,直角三角形斜边的中线等于斜边的一半的性质,等腰三角形的判定和性质,勾股定理,三角形内角和定理,判断出∠BDF=∠AED是解本题的关键.26.(12分)如图,已知抛物线y=a(x+6)(x﹣2)过点C(0,2),交x轴于点A和点B(点A在点B的左侧),抛物线的顶点为D,对称轴DE交x轴于点E,连接EC.(1)直接写出a的值,点A的坐标和抛物线对称轴的表达式;(2)若点M是抛物线对称轴DE上的点,当△MCE是等腰三角形时,求点M的坐标;(3)点P是抛物线上的动点,连接PC,PE,将△PCE沿CE所在的直线对折,点P落在坐标平面内的点P′处.求当点P′恰好落在直线AD上时点P的横坐标.【知识考点】二次函数综合题.【思路分析】(1)将点C坐标代入抛物线解析式中,即可得出结论;(2)分三种情况:直接利用等腰三角形的性质,即可得出结论;(3)先判断出△PQE≌△P'Q'E(AAS),得出PQ=P'Q',EQ=EQ',进而得出P'Q'=n,EQ'=QE =m+2,确定出点P'(n﹣2,2+m),将点P'的坐标代入直线AD的解析式中,和点P代入抛物线解析式中,联立方程组,求解即可得出结论.【解题过程】解:(1)∵抛物线y=a(x+6)(x﹣2)过点C(0,2),∴2=a(0+6)(0﹣2),∴a=﹣,∴抛物线的解析式为y=﹣(x+6)(x﹣2)=﹣(x+2)2+,∴抛物线的对称轴为直线x=﹣2;针对于抛物线的解析式为y=﹣(x+6)(x﹣2),令y=0,则﹣(x+6)(x﹣2)=0,∴x=2或x=﹣6,∴A(﹣6,0);(2)如图1,由(1)知,抛物线的对称轴为x=﹣2,∴E(﹣2,0),∵C(0,2),∴OC=OE=2,∴CE=OC=2,∠CED=45°,∵△CME是等腰三角形,∴①当ME=MC时,∴∠ECM=∠CED=45°,∴∠CME=90°,∴M(﹣2,2),②当CE=CM时,∴MM1=CM=2,∴EM1=4,∴M1(﹣2,4),③当EM=CE时,∴EM2=EM3=2,∴M2(﹣2,﹣2),M3(﹣2,2),即满足条件的点M的坐标为(﹣2,2)或(﹣2,4)或(﹣2,2)或(﹣2,﹣2);(3)如图2,由(1)知,抛物线的解析式为y=﹣(x+6)(x﹣2)=﹣(x+2)2+,∴D(﹣2,),令y=0,则(x+6)(x﹣2)=0,∴x=﹣6或x=2,∴点A(﹣6,0),∴直线AD的解析式为y=x+4,过点P作PQ⊥x轴于Q,过点P'作P'Q'⊥DE于Q',∴∠EQ'P'=∠EQP=90°,由(2)知,∠CED=∠CEB=45°,由折叠知,EP'=EP,∠CEP'=∠CEP,∴△PQE≌△P'Q'E(AAS),∴PQ=P'Q',EQ=EQ',设点P(m,n),∴OQ=m,PQ=n,∴P'Q'=n,EQ'=QE=m+2,∴点P'(n﹣2,2+m),∵点P'在直线AD上,∴2+m=(n﹣2)+4①,∵点P在抛物线上,∴n=﹣(m+6)(m﹣2)②,联立①②解得,m=或m=,即点P的横坐标为或.【总结归纳】此题是二次函数综合题,主要考查了待定系数法,等腰三角形的性质,全等三角形的判定和性质,用分类讨论的思想解决问题是解本题的关键.。
2020桂林市中考数学试题及答案

2020年桂林市初中毕业升学考试试卷数学 (考试用时:120分钟满分:120分) 注意事项: 1 .试卷分为试题卷和答题卡两部分,在本试 题卷上作答无效。
2. 答题前,请认真阅读答题.卡上的注意事项。
3. 考试结束后,将本试卷和答题 卡一并交回。
(共12小题,每小题3分,共36分•在每小题给出的四个选项中只有一项是符 用2B 铅笔把答题 卡上对应题目的答案标号涂黑 ).4•下列图形分别是桂林、 湖南、甘肃、佛山电视台的台徽,其中为中心对称图形的是 ().6. 如图,已知 Rt A ABC 中,/ C =90°, BC=3, 则sinA 的值为( ).A . 3B . 4 43 3 4C . -D .- 5 5一、选择题 合要求的, 1 . 2011的倒数是A .—— 2011 2. 在实数2、 A . 2 3. 下面四个图形中,B . 2011C . 2011D .1、 2 中, 最小的实数是( ).B . 0C . 1D .21-/2 疋成立的疋( ). 1 2011 2li5.下列运算正确的是( c 2 c 2 2A. 3x 2x x(2a)2 2a 2 C . (a b)2 a 2 b 2). C)• D1 2a7. 如图,图1是一个底面为正方形的直棱柱;现将图 1切割成图2的几何体,则图2的 俯视图是().12.如图,将边长为 a 的正六边形 A 1 A 2 A s A A s A 6在直线l 上由图1的位置按顺时针方 向向右作无滑动滚动,当A 1第一次滚动到图2位置时,顶点 A 1所经过的路径的 长为(). 、填空题(共6小题,每小题3分,共18分,请将答案填在答题 卡上).13 .因式分解: a 2 2a _______________14 .我市在临桂新区正在建设的广西桂林图书馆、 桂林博物馆、桂林大剧院及文化广场,建成后总面积达163500平方米,将成为我市“文化立市”和文化产业大发展的新标志,把163500平方米用科学记数法可表示为 _______________ 平方米./ ZS一/ / 图丨 圈2 第極图&直线y kx 1 一定经过点(A . (1, 0)B . (1, k )C . (0,k ) 9. 下面调查中,适合采用全面调查的事件是(). A •对全国中学生心理健康现状的调查.B. 对我市食品合格情况的调查.C. 对桂林电视台《桂林板路》收视率的调查. D . (0, - 1) 10. 若点P ( a , a — 2)在U a B . 0v a v 2C . a >2 11.在平面直角坐标系中,将抛物线y x 2 2x 抛物线的解析式是(). A . y (x 1)2 2 B . y C .y 2 (x 1) 2 D . y 3绕着它与y 轴的交点旋转180 °,所得 (x 1)2 42 (x 1) 4 4 23 A. a C. J a D.A学生&镇长对初中生騎 家反对初中生騎电动车上学的态度统il 图215•当x 2时,代数式—的值是x 116.如图,等腰梯形 ABCD 中,AB // DC, BE // AD,梯形ABCD的周长为26 , DE=4,则厶BEC 的周长为 _________ .417•双曲线y i 、y 在第一象限的图像如图, y iX过y 1上的任意一点 A ,作x 轴的平行线交 y 于B ,1 * 1 * 1 18.右玄1 1 , a ? 1 , a 3 1 ,… •:则a 2011的值为.(用含m的代数式表示)一”假期,随机抽查了本校若干名学生和部分家长对“初中生骑电动车上学”现象的 看法,统计整理制作了如下的统计图,请回答下列问题:(1) 这次抽查的家长总人数为 ________ ;(2) 请补全条形统计图和扇形统计图;(3) 从这次接受调查的学生中,随机抽查一个学生恰好抽到持“无所谓”态度的概率交y 轴于C ,若S AOB 1,则y 的解析式是解答题(本大题共 8题,共 66分, 请将答案写在答题卡上).19. (本题满分 6分) 计算:(、2 1)0 2 1 . 2tan45 | 晝220. (本题满分 6分) 解二元一次方程组:x 3y 5 3y 8 2x 21. 22. (本题满分 已知:求证: 证明:(本题满8 分) 8 分) 求证:角平分线上的点到这个角的两边距离相等 “初中生骑电动车上学”的现象越来越受到社会的关注, 卫1慮関 » 11某校利用“五3.(本题满分8分)某市为争创全国文明卫生城,2020年市政府对市区绿化工程投入的资金是2020万元,2020年投入的资金是2420万元,且从2020年到2020年,两年间每年投入资金的年平均增长率相同•(1 )求该市对市区绿化工程投入资金的年平均增长率;(2)若投入资金的年平均增长率不变,那么该市在2020年需投入多少万元?24. (本题满分8分)某校志愿者团队在重阳节购买了一批牛奶到“夕阳红”敬老院慰问孤寡老人,如果给每个老人分5盒,则剩下38盒,如果给每个老人分6盒,则最后一个老人不足5盒,但至少分得一盒.(1)设敬老院有x名老人,则这批牛奶共有多少盒?(用含x的代数式表示).(2 )该敬老院至少有多少名老人?最多有多少名老人?1 25. (本题满分10分)如图,在锐角厶ABC中,AC是最短边;以AC中点O为圆心,—AC2 长为半径作O O,交BC于E,过O作OD // BC交O O于D,连结AE、AD、DC .(1)求证:D是AE的中点;(2)求证:/ DAO =/B +/BAD ;S 1(3)若一,且AC=4,求CF的长.S2OCD1 2326. (本题满分12分)已知二次函数y —x X的图象如图.4 2(1 )求它的对称轴与X轴交点D的坐标;(2)将该抛物线沿它的对称轴向上平移,设平移后的抛物线与x轴,y轴的交点分别为A、B、C三点,若/ ACB=90 °,求此时抛物线的解析式;(3)设(2)中平移后的抛物线的顶点为M,以AB为直径,D为圆心作O D,试判断直线CM与O D的位置关系,并说明理由.解:(1) 100 ; 2分2020年桂林市初中毕业升学考试数学参考答案及评分标准 、选择题:题号 12 3 4 5 6 7 8 9 10 11 12 答案 AD B C A C C D D B B A 二、:填空题: 13. a(a 2)14. 1.635 105 15.4 3 16. 18 6 18. 1 1 17. y 2 —x m三、 解答题:19.(本题满分 6分)解:原式 =1 i 1 .... 4分 (求出一个值给1分) 1 •… 6 分20. (本题满分6分)解:x 3y 5①3y 8 2x ②把①代入②得:3y 8 2(3y 5)21. (本题满分8分)已知:如图,OC 是/ AOB 的平分线,P 是OC 上任意一点,PE 丄OA , PF 丄OB , 垂足分别为E 、F ................ 2分22. (本题满分8分)y 把y 2代入①可得:x x 所以此二元一次方程组的解为2 ........................... 3分 3 2 5 ......... ................. 4分1........ 5分 x 1 ............... 6分 y 2求证:PE=PF ...................... ..................... 3分证明:••• OC 是/ AOB 的平分线•••/ POE = Z POF ••… .................... 4分 •/ PE 丄 OA , PF 丄 OB•••/ PEO = Z PFO ...............5分 又••• OP=OP .................. •• 6分•••△ POEPOF …… 7分 • PE=PF .................... ……8分1x4 4 (2) 条形统计图:70, ................... 4分扇形统计图:赞成:10%,反对:70%; .......... 6分2(3) . .................... 8 分523. (本题满分8分)解:(1 )设该市对市区绿化工程投入资金的年平均增长率为x , .................... 1分 根据题意得,2000(1 x)2 2420............... 3分 得 x 1 10% , x 2 2.1 (舍去) ...... 5 分答:该市对市区绿化工程投入资金的年平均增长率为10% . ....... 6分 (2) 2020 年需投入资金:2420 (1 10%)2 2928.2 (万元) .................. 7 分 答:2020年需投入资金 2928.2万元. ......... 8分24. (本题满分8分)解:(1)牛奶盒数:(5x 38)盒 ....... 1分5x 38 6(x 1) 5 八 (2)根据题意得:'7 ....... 4分 5x 38 6(x 1) 1•••不等式组的解集为:39v x < 43 6分 ••• x 为整数 • x 40, 41, 42, 43 答:该敬老院至少有 40名老人,最多有43名老人. 8分25. (本题满分10分)证明:(1)v AC 是O O 的直径• AE 丄 BC ............. 1 分•/ OD // BC• AE 丄 OD ............... 2 分•- D 是AE 的中点 ............ 3分(2)方法一:如图,延长OD 交AB 于G ,则OG // BC …4分• / AGD=Z B•••/ ADO=Z BAD + Z AGD .................. 5 分又••• OA=OD• Z DAO=Z ADO• Z DAO=Z B +Z BAD ................... 6 分方法二:如图,延长AD 交BC 于H …4分则 Z ADO=Z AHCvZ AHC=Z B +Z BAD .......................... 5 分• Z ADO = Z B +Z BAD又 v OA=OD• Z DAO=Z B +Z BAD ....................... 6 分vZ ACD=Z FCE •△ ACD FCE1 (3) v AO=OC 'S OCD 匚 S ACD 2..S CEF 1 S CEF 1 ••…7分S OCD 2 S ACD 4Z ADC=Z FEC=90°....................... 8分1x 44• S CEFS ACD • CF=2 CF 、2 刚 1 CF 2 ()即:—() AC 4 4 ............. 10分 26.(本题满分 解:(1)由y ••• D 12分)1 2 X 4 (3,0) |x 得 x 2a 3 .......... 2分 (2)方法一: 如图1,设平移后的抛物线的解析式为 12 3. y x x k4 2 则 C (0, k)OC=k 1 :_x 4 得X 1 • A (3 • AB 2 AC 2 3 、4k 9 4r-9,0), (.4k 9 3 3 x k 2 x 2 3 4k B (3 ,4F~9,0) 3 ,4k 9)2 2 k 2 BC 2 k 2 (3 .4k 9) 2 2k 8k 2 2 2 ••• AC BC AB 即:2k 8k 36 得 k ) 4 36 •抛物线的解析式为 方法 设抛物线向上平移 •••平移后的抛物线 16k k 2 36 0(舍去) 1 2 X 4 3x 4 2 4分 16k 36 ............ 5分 (3 4k 9)2 ...... 6分 •••顶点坐标 h 个单位,则得到C 9 0,h ,顶点坐标M 3, 4 h 0, 4 B (3 • △ AOC COB • A (3 4h 9,0) •••/ ACB=90° • OC 2 OA • OB h 2 -4h 9 3 ■ 4h 91•平移后的抛物线:y 1 4h 9,0) x 1 3 ,4^9 X i 得hi 4,h 2 0舍去 3 4h 9(3)方法1 2 3 如图2,由抛物线的解析式 y x 2 x 4可得4 225A(-2 , 0) , B(8 , 0) , C( 4, 0) , M (3,) 4 过C 、M 作直线,连结CD ,过M 作MH 垂直则MH 32 25 2625 二 DM 2 ( )2 4 162 2 2 2 25 2 225 CM MH CH3 ( 4)4 16在 Rt A COD 中,CD= , 32 42 5=AD •••点C 在O D 上 ........... 10分2 25 2 625••• DM 2 ( )2 4 16CD 2 CM 252 225 洱)2 竺 16 416 2 2 2 • DM CM CD• △ CDM 是直角三角形,• CD 丄CM •直线CM 与O D 相切 ........ 12分 方法二:如图3,由抛物线的解析式可得A(-2 ,0) , B(8, 0) , C( 4, CM,过D 作DE 丄CM 25 ,由勾股定理得CM 4 •/ DM // OC • / MCH= / EMD • Rt A CMH • _DE "MH 作直线 DM s Rt A DME .............. MD 得DE 5 CM 心25、 0) , M (3,) 4 于E,过M 作 15 10分 由⑵知AB 10 「.O D 的半径为5 •直线CM 与O D 相切 .......... 12分MH 垂直y 轴于H,则MH 3, 11分 y 轴于H,1x 44。
2020年广西桂林中考数学试题(解析版)

2020年广西桂林中考数学试卷一、选择题(本大题共12小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.(3分)有理数2,1,﹣1,0中,最小的数是()A.2B.1C.﹣1D.02.(3分)如图,直线a,b被直线c所截,a∥b,∠1=50°,则∠2的度数是()A.40°B.50°C.60°D.70°3.(3分)下列调查中,最适宜采用全面调查(普查)的是()A.调查一批灯泡的使用寿命B.调查漓江流域水质情况C.调查桂林电视台某栏目的收视率D.调查全班同学的身高4.(3分)下面四个几何体中,左视图为圆的是()A.B.C.D.5.(3分)若=0,则x的值是()A.﹣1B.0C.1D.26.(3分)因式分解a2﹣4的结果是()A.(a+2)(a﹣2)B.(a﹣2)2C.(a+2)2D.a(a﹣2)7.(3分)下列计算正确的是()A.x•x=2x B.x+x=2x C.(x3)3=x6D.(2x)2=2x2 8.(3分)直线y=kx+2过点(﹣1,4),则k的值是()A.﹣2B.﹣1C.1D.29.(3分)不等式组的整数解共有()A.1个B.2个C.3个D.4个10.(3分)如图,AB是⊙O的弦,AC与⊙O相切于点A,连接OA,OB,若∠O=130°,则∠BAC的度数是()A.60°B.65°C.70°D.75°11.(3分)参加足球联赛的每两支球队之间都要进行两场比赛,共要比赛110场,设参加比赛的球队有x支,根据题意,下面列出的方程正确的是()A.x(x+1)=110B.x(x﹣1)=110C.x(x+1)=110D.x(x﹣1)=11012.(3分)如图,已知的半径为5,所对的弦AB长为8,点P是的中点,将绕点A逆时针旋转90°后得到,则在该旋转过程中,点P的运动路径长是()A.πB.πC.2πD.2π二、填空题(本大题共6小题,每小题3分,共18分.请把答案填在题中的横线上)13.(3分)2020的相反数是.14.(3分)计算:ab•(a+1)=.15.(3分)如图,在Rt△ABC中,∠C=90°,AB=13,AC=5,则cos A的值是.16.(3分)一个正方体的平面展开图如图所示,任选该正方体的一面出现“我”字的概率是.17.(3分)反比例函数y=(x<0)的图象如图所示,下列关于该函数图象的四个结论:①k>0;②当x<0时,y随x的增大而增大;③该函数图象关于直线y=﹣x对称;④若点(﹣2,3)在该反比例函数图象上,则点(﹣1,6)也在该函数的图象上.其中正确结论的个数有个.18.(3分)如图,在Rt△ABC中,AB=AC=4,点E,F分别是AB,AC的中点,点P是扇形AEF的上任意一点,连接BP,CP,则BP+CP的最小值是.三、解答题(本大题共8小题,共66分.解答应写出必要的文字说明、证明过程或演算步骤)19.(6分)计算:(π+)0+(﹣2)2+|﹣|﹣sin30°.20.(6分)解二元一次方程组:.21.(8分)如图,在平面直角坐标系中,△ABC的三个顶点分别是A(1,3),B(4,4),C(2,1).(1)把△ABC向左平移4个单位后得到对应的△A1B1C1,请画出平移后的△A1B1C1;(2)把△ABC绕原点O旋转180°后得到对应的△A2B2C2,请画出旋转后的△A2B2C2;(3)观察图形可知,△A1B1C1与△A2B2C2关于点(,)中心对称.22.(8分)阅读下列材料,完成解答:材料1:国家统计局2月28日发布了2019年国民经济和社会发展统计公报,该公报中的如图发布的是全国“2015﹣2019年快递业务量及其增长速度”统计图(如图1).材料2:6月28日,国家邮政局发布的数据显示:受新冠疫情影响,快递业务量快速增长,5月份快递业务量同比增长41%(如图2).某快递业务部门负责人据此估计,2020年全国快递业务量将比2019年增长50%.(1)2018年,全国快递业务量是亿件,比2017年增长了%;(2)2015﹣2019年,全国快递业务量增长速度的中位数是%;(3)统计公报发布后,有人认为,图1中表示2016﹣2019年增长速度的折线逐年下降,说明2016﹣2019年全国快递业务量增长速度逐年放缓,所以快递业务量也逐年减少.你赞同这种说法吗?为什么?(4)若2020年全国快递业务量比2019年增长50%,请列式计算2020年的快递业务量.23.(8分)如图,在菱形ABCD中,点E,F分别是边AD,AB的中点.(1)求证:△ABE≌△ADF;(2)若BE=,∠C=60°,求菱形ABCD的面积.24.(8分)某学校为丰富同学们的课余生活,购买了一批数量相等的象棋和围棋供兴趣小组使用,其中购买象棋用了420元,购买围棋用了756元,已知每副围棋比每副象棋贵8元.(1)求每副围棋和象棋各是多少元?(2)若该校决定再次购买同种围棋和象棋共40副,且再次购买的费用不超过600元,则该校最多可再购买多少副围棋?25.(10分)如图,将一副斜边相等的直角三角板按斜边重合摆放在同一平面内,其中∠CAB =30°,∠DAB=45°,点O为斜边AB的中点,连接CD交AB于点E.(1)求证:A,B,C,D四个点在以点O为圆心的同一个圆上;(2)求证:CD平分∠ACB;(3)过点D作DF∥BC交AB于点F,求证:BO2+OF2=EF•BF.26.(12分)如图,已知抛物线y=a(x+6)(x﹣2)过点C(0,2),交x轴于点A和点B (点A在点B的左侧),抛物线的顶点为D,对称轴DE交x轴于点E,连接EC.(1)直接写出a的值,点A的坐标和抛物线对称轴的表达式;(2)若点M是抛物线对称轴DE上的点,当△MCE是等腰三角形时,求点M的坐标;(3)点P是抛物线上的动点,连接PC,PE,将△PCE沿CE所在的直线对折,点P落在坐标平面内的点P′处.求当点P′恰好落在直线AD上时点P的横坐标.2020年广西桂林中考数学试卷参考答案与试题解析一、选择题(本大题共12小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.(3分)有理数2,1,﹣1,0中,最小的数是()A.2B.1C.﹣1D.0【分析】有理数大小比较的法则:①正数都大于0;②负数都小于0;③正数大于一切负数;④两个负数,绝对值大的其值反而小,据此判断即可.【解答】解:根据有理数比较大小的方法,可得﹣1<0<1<2,∴在2,1,﹣1,0这四个数中,最小的数是﹣1.故选:C.2.(3分)如图,直线a,b被直线c所截,a∥b,∠1=50°,则∠2的度数是()A.40°B.50°C.60°D.70°【分析】根据平行线的性质和∠1的度数,可以得到∠2的度数,本题得以解决.【解答】解:∵a∥b,∴∠1=∠2,∵∠1=50°,∴∠2=50°,故选:B.3.(3分)下列调查中,最适宜采用全面调查(普查)的是()A.调查一批灯泡的使用寿命B.调查漓江流域水质情况C.调查桂林电视台某栏目的收视率D.调查全班同学的身高【分析】由普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似.【解答】解:A、调查一批灯泡的使用寿命,由于具有破坏性,应当使用抽样调查,故本选项不合题意;B、调查漓江流域水质情况,应当采用抽样调查的方式,故本选项不合题意;C、调查桂林电视台某栏目的收视率,人数多,耗时长,应当采用抽样调查的方式,故本选项不合题意.D、调查全班同学的身高,应当采用全面调查,故本选项符合题意.故选:D.4.(3分)下面四个几何体中,左视图为圆的是()A.B.C.D.【分析】根据四个几何体的左视图进行判断即可.【解答】解:下面四个几何体中,A的左视图为矩形;B的左视图为三角形;C的左视图为矩形;D的左视图为圆.故选:D.5.(3分)若=0,则x的值是()A.﹣1B.0C.1D.2【分析】利用算术平方根性质确定出x的值即可.【解答】解:∵=0,∴x﹣1=0,解得:x=1,则x的值是1.故选:C.6.(3分)因式分解a2﹣4的结果是()A.(a+2)(a﹣2)B.(a﹣2)2C.(a+2)2D.a(a﹣2)【分析】利用平方差公式进行分解即可.【解答】解:原式=(a+2)(a﹣2),故选:A.7.(3分)下列计算正确的是()A.x•x=2x B.x+x=2x C.(x3)3=x6D.(2x)2=2x2【分析】分别根据同底数幂的乘法法则,合并同类项法则,幂的乘方运算法则以及积的乘方运算法则逐一判断即可.【解答】解:A.x•x=x2,故本选项不合题意;B.x+x=2x,故本选项符合题意;C.(x3)3=x9,故本选项不合题意;D.(2x)2=4x2,故本选项不合题意.故选:B.8.(3分)直线y=kx+2过点(﹣1,4),则k的值是()A.﹣2B.﹣1C.1D.2【分析】由直线y=kx+2过点(﹣1,4),利用一次函数图象上点的坐标特征可得出关于k的一元一次方程,解之即可得出k值.【解答】解:∵直线y=kx+2过点(﹣1,4),∴4=﹣k+2,∴k=﹣2.故选:A.9.(3分)不等式组的整数解共有()A.1个B.2个C.3个D.4个【分析】分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集,从而得出答案.【解答】解:解不等式x﹣1>0,得:x>1,解不等式5﹣x≥1,得:x≤4,则不等式组的解集为1<x≤4,所以不等式组的整数解有2、3、4这3个,故选:C.10.(3分)如图,AB是⊙O的弦,AC与⊙O相切于点A,连接OA,OB,若∠O=130°,则∠BAC的度数是()A.60°B.65°C.70°D.75°【分析】利用切线的性质及等腰三角形的性质求出∠OAC及∠OAB即可解决问题.【解答】解:∵AC与⊙O相切于点A,∴AC⊥OA,∴∠OAC=90°,∵OA=OB,∴∠OAB=∠OBA.∵∠O=130°,∴∠OAB==25°,∴∠BAC=∠OAC﹣∠OAB=90°﹣25°=65°.故选:B.11.(3分)参加足球联赛的每两支球队之间都要进行两场比赛,共要比赛110场,设参加比赛的球队有x支,根据题意,下面列出的方程正确的是()A.x(x+1)=110B.x(x﹣1)=110C.x(x+1)=110D.x(x﹣1)=110【分析】设有x个队参赛,根据参加一次足球联赛的每两队之间都进行两场比赛,共要比赛110场,可列出方程.【解答】解:设有x个队参赛,则x(x﹣1)=110.故选:D.12.(3分)如图,已知的半径为5,所对的弦AB长为8,点P是的中点,将绕点A逆时针旋转90°后得到,则在该旋转过程中,点P的运动路径长是()A.πB.πC.2πD.2π【分析】根据已知的半径为5,所对的弦AB长为8,点P是的中点,利用垂径定理可得AC=4,PO⊥AB,再根据勾股定理可得AP的长,利用弧长公式即可求出点P的运动路径长.【解答】解:如图,设的圆心为O,∵圆O半径为5,所对的弦AB长为8,点P是的中点,根据垂径定理,得AC=AB=4,PO⊥AB,OC==3,∴PC=OP﹣OC=5﹣3=2,∴AP==2,∵将绕点A逆时针旋转90°后得到,∴∠P AP′=∠BAB′=90°,∴L PP′==π.则在该旋转过程中,点P的运动路径长是π.故选:B.二、填空题(本大题共6小题,每小题3分,共18分.请把答案填在题中的横线上)13.(3分)2020的相反数是﹣2020.【分析】直接利用相反数的定义得出答案.【解答】解:2020的相反数是:﹣2020.故答案为:﹣2020.14.(3分)计算:ab•(a+1)=a2b+ab.【分析】根据整式的运算法则即可求出答案.【解答】解:原式=a2b+ab,故答案为:a2b+ab.15.(3分)如图,在Rt△ABC中,∠C=90°,AB=13,AC=5,则cos A的值是.【分析】根据余弦的定义解答即可.【解答】解:在Rt△ABC中,cos A==,故答案为:.16.(3分)一个正方体的平面展开图如图所示,任选该正方体的一面出现“我”字的概率是.【分析】根据概率公式解答就可求出任选该正方体的一面出现“我”字的概率.【解答】解:∵共有六个字,“我”字有2个,∴P(“我”)==.故答案为:.17.(3分)反比例函数y=(x<0)的图象如图所示,下列关于该函数图象的四个结论:①k>0;②当x<0时,y随x的增大而增大;③该函数图象关于直线y=﹣x对称;④若点(﹣2,3)在该反比例函数图象上,则点(﹣1,6)也在该函数的图象上.其中正确结论的个数有3个.【分析】观察反比例函数y=(x<0)的图象可得,图象过第二象限,然后根据反比例函数的图象和性质即可进行判断.【解答】解:观察反比例函数y=(x<0)的图象可知:图象过第二象限,∴k<0,所以①错误;因为当x<0时,y随x的增大而增大;所以②正确;因为该函数图象关于直线y=﹣x对称;所以③正确;因为点(﹣2,3)在该反比例函数图象上,所以k=﹣6,则点(﹣1,6)也在该函数的图象上.所以④正确.所以其中正确结论的个数为3个.故答案为3.18.(3分)如图,在Rt△ABC中,AB=AC=4,点E,F分别是AB,AC的中点,点P是扇形AEF的上任意一点,连接BP,CP,则BP+CP的最小值是.【分析】在AB上取一点T,使得AT=1,连接PT,P A,CT.证明△P AT∽△BAP,推出==,推出PT=PB,推出PB+CP=CP+PT,根据PC+PT≥TC,求出CT 即可解决问题.【解答】解:在AB上取一点T,使得AT=1,连接PT,P A,CT.∵P A=2.AT=1,AB=4,∴P A2=AT•AB,∴=,∵∠P AT=∠P AB,∴△P AT∽△BAP,∴==,∴PT=PB,∴PB+CP=CP+PT,∵PC+PT≥TC,在Rt△ACT中,∵∠CAT=90°,AT=1,AC=4,∴CT==,∴PB+PC≥,∴PB+PC的最小值为.故答案为.三、解答题(本大题共8小题,共66分.解答应写出必要的文字说明、证明过程或演算步骤)19.(6分)计算:(π+)0+(﹣2)2+|﹣|﹣sin30°.【分析】原式利用零指数幂、乘方运算法则,绝对值的代数意义,以及特殊角的三角函数值计算即可求出值.【解答】解:原式=1+4+﹣=5.20.(6分)解二元一次方程组:.【分析】方程组利用加减消元法求出解即可.【解答】解:①+②得:6x=6,解得:x=1,把x=1代入①得:y=﹣1,则方程组的解为.21.(8分)如图,在平面直角坐标系中,△ABC的三个顶点分别是A(1,3),B(4,4),C(2,1).(1)把△ABC向左平移4个单位后得到对应的△A1B1C1,请画出平移后的△A1B1C1;(2)把△ABC绕原点O旋转180°后得到对应的△A2B2C2,请画出旋转后的△A2B2C2;(3)观察图形可知,△A1B1C1与△A2B2C2关于点(﹣2,0)中心对称.【分析】(1)依据平移的方向和距离,即可得到平移后的△A1B1C1;(2)依据△ABC绕原点O旋转180°,即可画出旋转后的△A2B2C2;(3)依据对称点连线的中点的位置,即可得到对称中心的坐标.【解答】解:(1)如图所示,△A1B1C1即为所求;(2)如图所示,△A2B2C2即为所求;(3)由图可得,△A1B1C1与△A2B2C2关于点(﹣2,0)中心对称.故答案为:﹣2,0.22.(8分)阅读下列材料,完成解答:材料1:国家统计局2月28日发布了2019年国民经济和社会发展统计公报,该公报中的如图发布的是全国“2015﹣2019年快递业务量及其增长速度”统计图(如图1).材料2:6月28日,国家邮政局发布的数据显示:受新冠疫情影响,快递业务量快速增长,5月份快递业务量同比增长41%(如图2).某快递业务部门负责人据此估计,2020年全国快递业务量将比2019年增长50%.(1)2018年,全国快递业务量是507.1亿件,比2017年增长了26.6%;(2)2015﹣2019年,全国快递业务量增长速度的中位数是28%;(3)统计公报发布后,有人认为,图1中表示2016﹣2019年增长速度的折线逐年下降,说明2016﹣2019年全国快递业务量增长速度逐年放缓,所以快递业务量也逐年减少.你赞同这种说法吗?为什么?(4)若2020年全国快递业务量比2019年增长50%,请列式计算2020年的快递业务量.【分析】(1)由材料1中的统计图中的信息即可得到结论;(2)由材料1中的统计图的信息即可得到结论;(3)根据统计图中的信息即可得到结论;(4)根据题意列式计算即可.【解答】解:(1)由材料1中的统计图可得:2018年,全国快递业务量是507.1亿件,比2017年增长了26.6%;(2)由材料1中的统计图可得:2015﹣2019年,全国快递业务量增长速度的中位数是28%;(3)不赞同,理由:由图1中的信息可得,2016﹣2019年全国快递业务量增长速度逐年放缓,但是快递业务量却逐年增加;(4)635.2×(1+50%)=952.8,答:2020年的快递业务量为952.8亿件.故答案为:507.1,26.6,28.23.(8分)如图,在菱形ABCD中,点E,F分别是边AD,AB的中点.(1)求证:△ABE≌△ADF;(2)若BE=,∠C=60°,求菱形ABCD的面积.【分析】(1)由SAS证明△ABE≌△ADF即可;(2)证△ABD是等边三角形,得出BE⊥AD,求出AD即可.【解答】(1)证明:∵四边形ABCD是菱形,∴AB=AD,∵点E,F分别是边AD,AB的中点,∴AF=AE,在△ABE和△ADF中,,∴△ABE≌△ADF(SAS);(2)解:连接BD,如图:∵四边形ABCD是菱形,∴AB=AD,∠A=∠C=60°,∴△ABD是等边三角形,∵点E是边AD的中点,∴BE⊥AD,∴∠ABE=30°,∴AE=BE=1,AB=2AE=2,∴AD=AB=2,∴菱形ABCD的面积=AD×BE=2×=2.24.(8分)某学校为丰富同学们的课余生活,购买了一批数量相等的象棋和围棋供兴趣小组使用,其中购买象棋用了420元,购买围棋用了756元,已知每副围棋比每副象棋贵8元.(1)求每副围棋和象棋各是多少元?(2)若该校决定再次购买同种围棋和象棋共40副,且再次购买的费用不超过600元,则该校最多可再购买多少副围棋?【分析】(1)设每副围棋x元,则每副象棋(x﹣8)元,根据420元购买象棋数量=756元购买围棋数量列出方程并解答;(2)设购买围棋m副,则购买象棋(40﹣m)副,根据题意列出不等式并解答.【解答】解:(1)设每副围棋x元,则每副象棋(x﹣8)元,根据题意,得=.解得x=18.经检验x=18是所列方程的根.所以x﹣8=10.答:每副围棋18元,则每副象棋10元;(2)设购买围棋m副,则购买象棋(40﹣m)副,根据题意,得18m+10(40﹣m)≤600.解得m≤25.故m最大值是25.答:该校最多可再购买25副围棋.25.(10分)如图,将一副斜边相等的直角三角板按斜边重合摆放在同一平面内,其中∠CAB =30°,∠DAB=45°,点O为斜边AB的中点,连接CD交AB于点E.(1)求证:A,B,C,D四个点在以点O为圆心的同一个圆上;(2)求证:CD平分∠ACB;(3)过点D作DF∥BC交AB于点F,求证:BO2+OF2=EF•BF.【分析】(1)利用直角三角形斜边的中线等于斜边的一半,判断出OA=OB=OC=OD,即可得出结论;(2)利用等弧所对的圆周角相等,即可得出结论;(3)先判断出△DEF∽△BDF,得出DF2=BF•EF,再利用勾股定理得出OD2+OF2=DF2,即可得出结论.【解答】证明:(1)如图,连接OD,OC,在Rt△ABC中,∠ACB=90°,点O是AB 的中点,∴OC=OA=OB,在Rt△ABD中,∠ADB=90°,点O是AB的中点,∴OD=OA=OB,∴OA=OB=OC=OD,∴A,B,C,D四个点在以点O为圆心的同一个圆上;(2)由(1)知,A,B,C,D四个点在以点O为圆心的同一个圆上,且AD=BD,∴∠ACD=∠BCD,∴CD平分∠ACB;(3)由(2)知,∠BCD=45°,∵∠ABC=60°,∴∠BEC=75°,∴∠AED=75°,∵DF∥BC,∴∠BFD=∠ABC=60°,∵∠ABD=45°,∴∠BDF=180°﹣∠BFD﹣∠ABD=75°=∠AED,∵∠DFE=∠BFD,∴△DEF∽△BDF,∴,∴DF2=BF•EF,连接OD,则∠BOD=90°,OB=OD,在Rt△DOF中,根据勾股定理得,OD2+OF2=DF2,∴OB2+OF2=BF•EF,即BO2+OF2=EF•BF.26.(12分)如图,已知抛物线y=a(x+6)(x﹣2)过点C(0,2),交x轴于点A和点B (点A在点B的左侧),抛物线的顶点为D,对称轴DE交x轴于点E,连接EC.(1)直接写出a的值,点A的坐标和抛物线对称轴的表达式;(2)若点M是抛物线对称轴DE上的点,当△MCE是等腰三角形时,求点M的坐标;(3)点P是抛物线上的动点,连接PC,PE,将△PCE沿CE所在的直线对折,点P落在坐标平面内的点P′处.求当点P′恰好落在直线AD上时点P的横坐标.【分析】(1)将点C坐标代入抛物线解析式中,即可得出结论;(2)分三种情况:直接利用等腰三角形的性质,即可得出结论;(3)先判断出△PQE≌△P'Q'E(AAS),得出PQ=P'Q',EQ=EQ',进而得出P'Q'=n,EQ'=QE=m+2,确定出点P'(n﹣2,2+m),将点P'的坐标代入直线AD的解析式中,和点P代入抛物线解析式中,联立方程组,求解即可得出结论.【解答】解:(1)∵抛物线y=a(x+6)(x﹣2)过点C(0,2),∴2=a(0+6)(0﹣2),∴a=﹣,∴抛物线的解析式为y=﹣(x+6)(x﹣2)=﹣(x+2)2+,∴抛物线的对称轴为直线x=﹣2;(2)如图1,由(1)知,抛物线的对称轴为x=﹣2,∴E(﹣2,0),∵C(0,2),∴OC=OE=2,∴CE=OC=2,∠CED=45°,∵△CME是等腰三角形,∴①当ME=MC时,∴∠ECM=∠CED=45°,∴∠CME=90°,∴M(﹣2,2),②当CE=CM时,∴MM1=CM=2,∴EM1=4,∴M1(﹣2,4),③当EM=CE时,∴EM2=EM3=2,∴M2(﹣2,﹣2),M3(﹣2,2),即满足条件的点M的坐标为(﹣2,﹣2)或(﹣2,4)或(﹣2,2)或(﹣2,﹣2);(3)如图2,由(1)知,抛物线的解析式为y=﹣(x+6)(x﹣2)=﹣(x+2)2+,∴D(﹣2,),令y=0,则(x+6)(x﹣2)=0,∴x=﹣6或x=2,∴点A(﹣6,0),∴直线AD的解析式为y=x+4,过点P作PQ⊥x轴于Q,过点P'作P'Q'⊥DE于Q',∴∠EQ'P'=∠EQP=90°,由(2)知,∠CED=∠CEB=45°,由折叠知,EP'=EP,∠CEP'=∠CEP,∴△PQE≌△P'Q'E(AAS),∴PQ=P'Q',EQ=EQ',设点P(m,n),∴OQ=m,PQ=n,∴P'Q'=n,EQ'=QE=m+2,∴点P'(n﹣2,2+m),∵点P'在直线AD上,∴2+m=(n﹣2)+4①,∵点P在抛物线上,∴n=﹣(m+6)(m﹣2)②,联立①②解得,m=或m=,即点P的横坐标为或.。
2020年桂林中考数学试卷(后附解析)

2020年广西桂林中考数学试卷第I卷(选择题)一、选择题(本大题共12小题,共36.0分)1.有理数2,1,−1,0中,最小的数是()A. 2B. 1C. −1D. 02.如图,直线a,b被直线c所截,a//b,∠1=50°,则∠2的度数是()A. 40°B. 50°C. 60°D. 70°3.下列调查中,最适宜采用全面调查(普查)的是()A. 调查一批灯泡的使用寿命B. 调查漓江流域水质情况C. 调查桂林电视台某栏目的收视率D. 调查全班同学的身高4.下面四个几何体中,左视图为圆的是()A. B. C. D.5.若√x−1=0,则x的值是()A. −1B. 0C. 1D. 26.因式分解a2−4的结果是()A. (a+2)(a−2)B. (a−2)2C. (a+2)2D. a(a−2)7.下列计算正确的是()A. x⋅x=2xB. x+x=2xC. (x3)3=x6D. (2x)2=2x28.直线y=kx+2过点(−1,4),则k的值是()A. −2B. −1C. 1D. 29.不等式组{x−1>05−x≥1的整数解共有()A. 1个B. 2个C. 3个D. 4个10.如图,AB是⊙O的弦,AC与⊙O相切于点A,连接OA,OB,若∠O=130°,则∠BAC的度数是()A. 60°B. 65°C. 70°D. 75°11.参加足球联赛的每两支球队之间都要进行两场比赛,共要比赛110场,设参加比赛的球队有x支,根据题意,下面列出的方程正确的是()A. 12x(x+1)=110 B. 12x(x−1)=110C. x(x+1)=110D. x(x−1)=11012.如图,已知AB⏜的半径为5,所对的弦AB长为8,点P是AB⏜的中点,将AB⏜绕点A逆时针旋转90°后得到AB′⏜,则在该旋转过程中,点P的运动路径长是()A. √52π B. √5π C. 2√5π D. 2π第II卷(非选择题)二、填空题(本大题共6小题,共18.0分)13.2020的相反数是______.14.计算:ab⋅(a+1)=______.15.如图,在Rt△ABC中,∠C=90°,AB=13,AC=5,则cos A的值是______.16.一个正方体的平面展开图如图所示,任选该正方体的一面出现“我”字的概率是______.17.反比例函数y=kx(x<0)的图象如图所示,下列关于该函数图象的四个结论:①k>0;②当x<0时,y随x的增大而增大;③该函数图象关于直线y=−x对称;④若点(−2,3)在该反比例函数图象上,则点(−1,6)也在该函数的图象上.其中正确结论的个数有______个.18. 如图,在Rt △ABC 中,AB =AC =4,点E ,F 分别是AB ,AC 的中点,点P 是扇形AEF 的EF ⏜上任意一点,连接BP ,CP ,则12BP +CP 的最小值是______.三、解答题(本大题共8小题,共66.0分)19. 计算:(π+√3)0+(−2)2+|−12|−sin30°.20. 解二元一次方程组:{2x +y =1,①4x −y =5.②.21. 如图,在平面直角坐标系中,△ABC 的三个顶点分别是A(1,3),B(4,4),C(2,1).(1)把△ABC 向左平移4个单位后得到对应的△A 1B 1C 1,请画出平移后的△A 1B 1C 1;(2)把△ABC 绕原点O 旋转180°后得到对应的△A 2B 2C 2,请画出旋转后的△A 2B 2C 2;(3)观察图形可知,△A 1B 1C 1与△A 2B 2C 2关于点(______,______)中心对称.22.阅读下列材料,完成解答:材料1:国家统计局2月28日发布了2019年国民经济和社会发展统计公报,该公报中的如图发布的是全国“2015−2019年快递业务量及其增长速度”统计图(如图1).材料2:6月28日,国家邮政局发布的数据显示:受新冠疫情影响,快递业务量快速增长,5月份快递业务量同比增长41%(如图2).某快递业务部门负责人据此估计,2020年全国快递业务量将比2019年增长50%.(1)2018年,全国快递业务量是______亿件,比2017年增长了______%;(2)2015−2019年,全国快递业务量增长速度的中位数是______%;(3)统计公报发布后,有人认为,图1中表示2016−2019年增长速度的折线逐年下降,说明2016−2019年全国快递业务量增长速度逐年放缓,所以快递业务量也逐年减少.你赞同这种说法吗?为什么?(4)若2020年全国快递业务量比2019年增长50%,请列式计算2020年的快递业务量.23.如图,在菱形ABCD中,点E,F分别是边AD,AB的中点.(1)求证:△ABE≌△ADF;(2)若BE=√3,∠C=60°,求菱形ABCD的面积.24.某学校为丰富同学们的课余生活,购买了一批数量相等的象棋和围棋供兴趣小组使用,其中购买象棋用了420元,购买围棋用了756元,已知每副围棋比每副象棋贵8元.(1)求每副围棋和象棋各是多少元?(2)若该校决定再次购买同种围棋和象棋共40副,且再次购买的费用不超过600元,则该校最多可再购买多少副围棋?25.如图,将一副斜边相等的直角三角板按斜边重合摆放在同一平面内,其中∠CAB=30°,∠DAB=45°,点O为斜边AB的中点,连接CD交AB于点E.(1)求证:A,B,C,D四个点在以点O为圆心的同一个圆上;(2)求证:CD平分∠ACB;(3)过点D作DF//BC交AB于点F,求证:BO2+OF2=EF⋅BF.26.如图,已知抛物线y=a(x+6)(x−2)过点C(0,2),交x轴于点A和点B(点A在点B的左侧),抛物线的顶点为D,对称轴DE交x轴于点E,连接EC.(1)直接写出a的值,点A的坐标和抛物线对称轴的表达式;(2)若点M是抛物线对称轴DE上的点,当△MCE是等腰三角形时,求点M的坐标;(3)点P是抛物线上的动点,连接PC,PE,将△PCE沿CE所在的直线对折,点P落在坐标平面内的点P′处.求当点P′恰好落在直线AD上时点P的横坐标.答案和解析1.【答案】C【解析】解:根据有理数比较大小的方法,可得−1<0<1<2,∴在2,1,−1,0这四个数中,最小的数是−1.故选:C.有理数大小比较的法则:①正数都大于0;②负数都小于0;③正数大于一切负数;④两个负数,绝对值大的其值反而小,据此判断即可.此题主要考查了有理数大小比较的方法,要熟练掌握,解答此题的关键是要明确:①正数都大于0;②负数都小于0;③正数大于一切负数;④两个负数,绝对值大的其值反而小.2.【答案】B【解析】解:∵a//b,∴∠1=∠2,∵∠1=50°,∴∠2=50°,故选:B.根据平行线的性质和∠1的度数,可以得到∠2的度数,本题得以解决.本题考查平行线的性质,解答本题的关键是明确题意,利用数形结合的思想解答.3.【答案】D【解析】解:A、调查一批灯泡的使用寿命,由于具有破坏性,应当使用抽样调查,故本选项不合题意;B、调查漓江流域水质情况,应当采用抽样调查的方式,故本选项不合题意;C、调查桂林电视台某栏目的收视率,人数多,耗时长,应当采用抽样调查的方式,故本选项不合题意.D、调查全班同学的身高,应当采用全面调查,故本选项符合题意.故选:D.由普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似.本题考查了抽样调查和全面调查的区别,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大时,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.4.【答案】D【解析】解:下面四个几何体中,A的左视图为矩形;B的左视图为三角形;C的左视图为矩形;D的左视图为圆.故选:D.根据四个几何体的左视图进行判断即可.本题考查了简单几何体的三视图,解决本题的关键是掌握几何体的三视图.5.【答案】C【解析】解:∵√x−1=0,∴x−1=0,解得:x=1,则x的值是1.故选:C.利用算术平方根性质确定出x的值即可.此题考查了算术平方根,熟练掌握算术平方根的性质是解本题的关键.6.【答案】A【解析】解:原式=(a+2)(a−2),故选:A.利用平方差公式进行分解即可.此题主要考查了公式法分解因式,关键是掌握平方差公式a2−b2=(a+b)(a−b).7.【答案】B【解析】解:A.x⋅x=x2,故本选项不合题意;B.x+x=2x,故本选项符合题意;C.(x3)3=x9,故本选项不合题意;D.(2x)2=4x2,故本选项不合题意.故选:B.分别根据同底数幂的乘法法则,合并同类项法则,幂的乘方运算法则以及积的乘方运算法则逐一判断即可.本题主要考查了同底数幂的乘法,合并同类项以及幂的乘方与积的乘方,熟记相关运算法则是解答本题的关键.8.【答案】A【解析】解:∵直线y=kx+2过点(−1,4),∴4=−k+2,∴k=−2.故选:A.由直线y=kx+2过点(−1,4),利用一次函数图象上点的坐标特征可得出关于k的一元一次方程,解之即可得出k值.本题考查了一次函数图象上点的坐标特征,牢记直线上任意一点的坐标都满足函数关系式y=kx+b是解题的关键.9.【答案】C【解析】解:解不等式x−1>0,得:x>1,解不等式5−x≥1,得:x≤4,则不等式组的解集为1<x≤4,所以不等式组的整数解有2、3、4这3个,故选:C.分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集,从而得出答案.本题考查的是一元一次不等式组的整数解,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.10.【答案】B【解析】解:∵AC与⊙O相切于点A,∴AC⊥OA,∴∠OAC=90°,∵OA=OB,∴∠OAB=∠OBA.∵∠O=130°,∴∠OAB=180°−∠O2=25°,∴∠BAC=∠OAC−∠OAB=90°−25°=65°.故选:B.利用切线的性质及等腰三角形的性质求出∠OAC及∠OAB即可解决问题.本题考查切线的性质,等腰三角形的性质等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.11.【答案】D【解析】解:设有x个队参赛,则x(x−1)=110.故选:D.设有x个队参赛,根据参加一次足球联赛的每两队之间都进行两场场比赛,共要比赛110场,可列出方程.本题考查由实际问题抽象出一元二次方程,关键是根据总比赛场数做为等量关系列方程求解.12.【答案】B【解析】解:如图,设AB⏜的圆心为O,∵圆O半径为5,所对的弦AB长为8,点P是AB⏜的中点,根据垂径定理,得AC=12AB=4,PO⊥AB,OC=√OA2−AC2=3,∴PC=OP−OC=5−3=2,∴AP=√AC2+PC2=2√5,∵将AB⏜绕点A逆时针旋转90°后得到AB′⏜,∴∠PAP′=∠BAB′=90°,∴L PP′=90π×2√5180=√5π.则在该旋转过程中,点P的运动路径长是√5π.故选:B.根据已知AB⏜的半径为5,所对的弦AB长为8,点P是AB⏜的中点,利用垂径定理可得AC=4,PO⊥AB,再根据勾股定理可得AP的长,利用弧长公式即可求出点P的运动路径长.本题考查了轨迹、垂径定理、勾股定理、圆心角、弧、弦的关系、弧长计算、旋转的性质,解决本题的关键是综合运用以上知识.13.【答案】−2020【解析】解:2020的相反数是:−2020.故答案为:−2020.直接利用相反数的定义得出答案.本题考查相反数.熟练掌握相反数的求法是解题的关键.14.【答案】a2b+ab【解析】解:原式=a2b+ab,故答案为:a2b+ab.根据整式的运算法则即可求出答案.本题考查整式的运算,解题的关键是熟练运用整式的运算法则,本题属于基础题型.15.【答案】513【解析】解:在Rt△ABC中,cosA=ACAB =513,故答案为:513.根据余弦的定义解答即可.本题考查的是锐角三角函数的定义,掌握锐角A的邻边b与斜边c的比叫做∠A的余弦是解题的关键.16.【答案】13【解析】解:∵共有六个字,“我”字有2个,∴P(“我”)=26=13.故答案为:13.根据概率公式解答就可求出任选该正方体的一面出现“我”字的概率.此题考查了概率公式的应用.注意概率=所求情况数与总情况数之比.17.【答案】3【解析】解:观察反比例函数y=kx(x<0)的图象可知:图象过第二象限,∴k<0,所以①错误;因为当x<0时,y随x的增大而增大;所以②正确;因为该函数图象关于直线y=−x对称;所以③正确;因为点(−2,3)在该反比例函数图象上,所以k=−6,则点(−1,6)也在该函数的图象上.所以④正确.所以其中正确结论的个数为3个.故答案为3.观察反比例函数y=kx(x<0)的图象可得,图象过第二象限,然后根据反比例函数的图象和性质即可进行判断.本题考查了反比例函数图象上点的坐标特征、反比例函数的性质、轴对称的性质,解决本题的关键是掌握反比例函数的性质.18.【答案】√17【解析】解:在AB上取一点T,使得AT=1,连接PT,PA,CT.∵PA=2.AT=1,AB=4,∴PA2=AT⋅AB,∴PAAT =ABPA,∵∠PAT=∠PAB,∴△PAT∽△BAP,∴PTPB =APAB=12,∴PT=12PB,∴12PB+CP=CP+PT,∵PC+PT≥TC,在Rt△ACT中,∵∠CAT=90°,AT=1,AC=4,∴CT=√AT2+AC2=√17,∴12PB+PC≥√17,∴12PB+PC的最小值为√17.故答案为√17.在AB上取一点T,使得AT=1,连接PT,PA,CT.证明△PAT∽△BAP,推出PTPB =APAB=12,推出PT=12PB,推出12PB +CP =CP +PT ,根据PC +PT ≥TC ,求出CT 即可解决问题.本题考查胡不归问题,等腰直角三角形的性质,相似三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造相似三角形解决问题,属于中考常考题型. 19.【答案】解:原式=1+4+12−12=5.【解析】原式利用零指数幂、负整数指数幂法则,绝对值的代数意义,以及特殊角的三角函数值计算即可求出值.此题考查了实数的运算,零指数幂,以及特殊角的三角函数值,熟练掌握运算法则是解本题的关键. 20.【答案】解:①+②得:6x =6,解得:x =1,把x =1代入①得:y =−1,则方程组的解为{x =1y =−1.【解析】方程组利用加减消元法求出解即可.此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法. 21.【答案】−2 0【解析】解:(1)如图所示,△A 1B 1C 1即为所求;(2)如图所示,△A 2B 2C 2即为所求;(3)由图可得,△A 1B 1C 1与△A 2B 2C 2关于点(−2,0)中心对称.故答案为:−2,0.(1)依据平移的方向和距离,即可得到平移后的△A 1B 1C 1;(2)依据△ABC 绕原点O 旋转180°,即可画出旋转后的△A 2B 2C 2;(3)依据对称点连线的中点的位置,即可得到对称中心的坐标.此题主要考查了平移变换和旋转变换,正确根据题意得出对应点位置是解题关键.22.【答案】507.1 26.6 28【解析】解:(1)由材料1中的统计图可得:2018年,全国快递业务量是507.1亿件,比2017年增长了26.6%;(2)由材料1中的统计图可得:2015−2019年,全国快递业务量增长速度的中位数是28%;(3)不赞同,理由:由图1中的信息可得,2016−2019年全国快递业务量增长速度逐年放缓,但是快递业务量却逐年增加;(4)635.2×(1+50%)=852.82,答:2020年的快递业务量为852.82亿件.故答案为:507.1,26.6,28.(1)由材料1中的统计图中的信息即可得到结论;(2)由材料1中的统计图的信息即可得到结论;(3)根据统计图中的信息即可得到结论;(4)根据题意列式计算即可.本题考查了条形统计图,中位数的定义,正确的理解题意是解题的关键.23.【答案】(1)证明:∵四边形ABCD是菱形,∴AB=AD,∵点E,F分别是边AD,AB的中点,∴AF=AE,在△ABE和△ADF中,{AB=AD ∠A=∠A AE=AF,∴△ABE≌△ADF(SAS);(2)解:连接BD,如图:∵四边形ABCD是菱形,∴AB=AD,∠A=∠C=60°,∴△ABD是等边三角形,∵点E是边AD的中点,∴BE⊥AD,∴∠ABE=30°,∴AE=√33BE=1,AB=2AE=2,∴AD=AB=2,∴菱形ABCD的面积=AD×BE=2×√3=2√3.【解析】(1)由SAS证明△ABE≌△ADF即可;(2)证△ABD是等边三角形,得出BE⊥AD,求出AD即可.本题考查了菱形的性质、全等三角形的判定与性质、等边三角形的判定与性质、直角三角形的性质等知识;熟练掌握菱形的性质是解题的关键.24.【答案】解:(1)设每副围棋x元,则每副象棋(x−8)元,根据题意,得420x−8=756x.解得x=18.经检验x=18是所列方程的根.所以x−8=10.答:每副围棋18元,则每副象棋10元;(2)设购买围棋m副,则购买象棋(40−m)副,根据题意,得18m+10(40−m)≤600.解得m≤25.故m最大值是25.答:该校最多可再购买25副围棋.【解析】(1)设每副围棋x元,则每副象棋(x−8)元,根据420元购买象棋数量=756元购买围棋数量列出方程并解答;(2)设购买围棋m副,则购买象棋(40−m)副,根据题意列出不等式并解答.本题考查了分式方程的应用和一元一次不等式的应用,分析题意,找到关键描述语,找到合适的数量关系是解决问题的关键.25.【答案】证明:(1)如图,连接OD,OC,在Rt△ABC中,∠ACB=90°,点O是AB的中点,∴OC=OA=OB,在Rt△ABD中,∠ADB=90°,点O是AB的中点,∴OD=OA=OB,∴OA=OB=OC=OD,∴A,B,C,D四个点在以点O为圆心的同一个圆上;(2)连接OC,OD,由(1)知,OA=OC=OD,∴∠OCD=∠ODC,在Rt△ABC中,∠BAC=30°,∴∠ABC=∠BOC=60°,在Rt△ABD中,∠DAB=45°,∴∠ABD=45°=∠DAB,∴AD=BD,∵点O是AB的中点,∴OD⊥AB,∠ADB=45°,∴∠BOD=90°,∠ODB=12∴∠COD=150°,∴∠OCD=∠ODC=15°,∴∠BDC=∠ODB−∠ODC=30°,∵∠CBD=∠ABC+∠ABD=105°,∴∠BCD=180°−∠CBD−∠BDC=45°,∴∠ACD=90°−∠BCD=45°=∠BCD,∴CD平分∠ACB;(3)由(2)知,∠BCD=45°,∵∠ABC=60°,∴∠BEC=75°,∴∠AED=75°,∵DF//BC,∴∠BFD=∠ABC=60°,∵∠ABD=45°,∴∠BDF=180°−∠BFD−∠ABD=75°=∠AED,∵∠DFE=∠BFD,∴△DEF∽△BDF,∴DFBF =EFDF,∴DF2=BF⋅EF,连接OD,则∠BOD=90°,OB=OD,在Rt△DOF中,根据勾股定理得,OD2+OF2=DF2,∴OB2+OF2=BF⋅EF,即BO2+OF2=EF⋅BF.【解析】(1)利用直角三角形斜边的中线等于斜边的一半,判断出OA=OB=OC=OD,即可得出结论;(2)先求出∠COD=150°,利用等腰三角形的性质得出∠ODC=15°,进而求出∠BDC=30°,进而求出∠BCD=45°,即可得出结论;(3)先判断出△DEF∽△BDF,得出DF2=BF⋅EF,再利用勾股定理得出OD2+OF2=DF2,即可得出结论.此题是圆的综合题,主要考查了四点共圆的判断方法,相似三角形的判定和性质,直角三角形斜边的中线等于斜边的一半的性质,等腰三角形的判定和性质,勾股定理,三角形内角和定理,判断出∠BDF=∠AED 是解本题的关键.26.【答案】解:(1)∵抛物线y=a(x+6)(x−2)过点C(0,2),∴2=a(0+6)(0−2),∴a=−16,∴抛物线的解析式为y=−16(x+6)(x−2)=−16(x+2)2+83,∴抛物线的对称轴为直线x=−2;(2)如图1,由(1)知,抛物线的对称轴为x=−2,∴E(−2,0),∵C(0,2),∴OC=OE=2,∴CE=√2OC=2√2,∠CED=45°,∵△CME是等腰三角形,∴①当ME=MC时,∴∠ECM=∠CED=45°,∴∠CME=90°,∴M(−2,2),②当CE=CM时,∴MM1=CM=2,∴EM1=4,∴M1(−2,4),③当EM=CE时,∴EM2=EM3=2√2,∴M2(−2,−2√2),M3(−2,2√2),即满足条件的点M的坐标为(−2,−2)或(−2,4)或(−2,2√2)或(−2,−2√2);(3)如图2,由(1)知,抛物线的解析式为y=−16(x+6)(x−2)=−16(x+2)2+83,∴D(−2,83),令y=0,则(x+6)(x−2)=0,∴x=−6或x=2,∴点A(−6,0),∴直线AD的解析式为y=23x+4,过点P作PQ⊥x轴于Q,过点P′作P′Q′⊥DE于Q′,∴∠EQ′P′=∠EQP=90°,由(2)知,∠CED=∠CEB=45°,由折叠知,EP′=EP,∠CEP′=∠CEP,∴△PQE≌△P′Q′E(AAS),∴PQ=P′Q′,EQ=EQ′,设点P(m,n),∴OQ=m,PQ=n,∴P′Q′=n,EQ′=QE=m+2,∴点P′(n−2,2+m),∵点P′在直线AD上,∴2+m=23(n−2)+4①,∵点P在抛物线上,∴n=−16(m+6)(m−2)②,联立①②解得,m=−13−√2412(舍)或m=−13+√2412,即点P的横坐标为−13+√2412.【解析】(1)将点C坐标代入抛物线解析式中,即可得出结论;(2)分三种情况:直接利用等腰三角形的性质,即可得出结论;(3)先判断出△PQE≌△P′Q′E(AAS),得出PQ=P′Q′,EQ=EQ′,进而得出P′Q′=n,EQ′=QE=m+2,确定出点P′(n−2,2+m),将点P′的坐标代入直线AD的解析式中,和点P代入抛物线解析式中,联立方程组,求解即可得出结论.此题是二次函数综合题,主要考查了待定系数法,等腰三角形的性质,全等三角形的判定和性质,用分类讨论的思想解决问题是解本题的关键.。
2020年广西桂林中考数学试卷(含答案解析)
2020年广西桂林中考数学试卷副标题题号一二三总分得分一、选择题(本大题共12小题,共36.0分)1.有理数2,1,−1,0中,最小的数是()A. 2B. 1C. −1D. 02.如图,直线a,b被直线c所截,a//b,∠1=50°,则∠2的度数是()A. 40°B. 50°C. 60°D. 70°3.下列调查中,最适宜采用全面调查(普查)的是()A. 调查一批灯泡的使用寿命B. 调查漓江流域水质情况C. 调查桂林电视台某栏目的收视率D. 调查全班同学的身高4.下面四个几何体中,左视图为圆的是()A. B. C. D.5.若√x−1=0,则x的值是()A. −1B. 0C. 1D. 26.因式分解a2−4的结果是()A. (a+2)(a−2)B. (a−2)2C. (a+2)2D. a(a−2)7.下列计算正确的是()A. x⋅x=2xB. x+x=2xC. (x3)3=x6D. (2x)2=2x28.直线y=kx+2过点(−1,4),则k的值是()A. −2B. −1C. 1D. 29.不等式组{x−1>05−x≥1的整数解共有()A. 1个B. 2个C. 3个D. 4个10.如图,AB是⊙O的弦,AC与⊙O相切于点A,连接OA,OB,若∠O=130°,则∠BAC的度数是()A. 60°B. 65°C. 70°D. 75°11.参加足球联赛的每两支球队之间都要进行两场比赛,共要比赛110场,设参加比赛的球队有x支,根据题意,下面列出的方程正确的是()A. 12x(x+1)=110 B. 12x(x−1)=110C. x(x+1)=110D. x(x−1)=11012.如图,已知AB⏜的半径为5,所对的弦AB长为8,点P是AB⏜的中点,将AB⏜绕点A逆时针旋转90°后得到AB′⏜,则在该旋转过程中,点P的运动路径长是()A. √52π B. √5π C. 2√5π D. 2π二、填空题(本大题共6小题,共18.0分)13.2020的相反数是______.14.计算:ab⋅(a+1)=______.15.如图,在Rt△ABC中,∠C=90°,AB=13,AC=5,则cos A的值是______.16.一个正方体的平面展开图如图所示,任选该正方体的一面出现“我”字的概率是______.17.反比例函数y=kx(x<0)的图象如图所示,下列关于该函数图象的四个结论:①k>0;②当x<0时,y随x的增大而增大;③该函数图象关于直线y=−x对称;④若点(−2,3)在该反比例函数图象上,则点(−1,6)也在该函数的图象上.其中正确结论的个数有______个.18. 如图,在Rt △ABC 中,AB =AC =4,点E ,F 分别是AB ,AC 的中点,点P 是扇形AEF 的EF ⏜上任意一点,连接BP ,CP ,则12BP +CP 的最小值是______. 三、解答题(本大题共8小题,共66.0分) 19. 计算:(π+√3)0+(−2)2+|−12|−sin30°.20. 解二元一次方程组:{2x +y =1,①4x −y =5.②.21. 如图,在平面直角坐标系中,△ABC 的三个顶点分别是A(1,3),B(4,4),C(2,1).(1)把△ABC 向左平移4个单位后得到对应的△A 1B 1C 1,请画出平移后的△A 1B 1C 1; (2)把△ABC 绕原点O 旋转180°后得到对应的△A 2B 2C 2,请画出旋转后的△A 2B 2C 2; (3)观察图形可知,△A 1B 1C 1与△A 2B 2C 2关于点(______,______)中心对称.22.阅读下列材料,完成解答:材料1:国家统计局2月28日发布了2019年国民经济和社会发展统计公报,该公报中的如图发布的是全国“2015−2019年快递业务量及其增长速度”统计图(如图1).材料2:6月28日,国家邮政局发布的数据显示:受新冠疫情影响,快递业务量快速增长,5月份快递业务量同比增长41%(如图2).某快递业务部门负责人据此估计,2020年全国快递业务量将比2019年增长50%.(1)2018年,全国快递业务量是______亿件,比2017年增长了______%;(2)2015−2019年,全国快递业务量增长速度的中位数是______%;(3)统计公报发布后,有人认为,图1中表示2016−2019年增长速度的折线逐年下降,说明2016−2019年全国快递业务量增长速度逐年放缓,所以快递业务量也逐年减少.你赞同这种说法吗?为什么?(4)若2020年全国快递业务量比2019年增长50%,请列式计算2020年的快递业务量.23.如图,在菱形ABCD中,点E,F分别是边AD,AB的中点.(1)求证:△ABE≌△ADF;(2)若BE=√3,∠C=60°,求菱形ABCD的面积.24.某学校为丰富同学们的课余生活,购买了一批数量相等的象棋和围棋供兴趣小组使用,其中购买象棋用了420元,购买围棋用了756元,已知每副围棋比每副象棋贵8元.(1)求每副围棋和象棋各是多少元?(2)若该校决定再次购买同种围棋和象棋共40副,且再次购买的费用不超过600元,则该校最多可再购买多少副围棋?25.如图,将一副斜边相等的直角三角板按斜边重合摆放在同一平面内,其中∠CAB=30°,∠DAB=45°,点O为斜边AB的中点,连接CD交AB于点E.(1)求证:A,B,C,D四个点在以点O为圆心的同一个圆上;(2)求证:CD平分∠ACB;(3)过点D作DF//BC交AB于点F,求证:BO2+OF2=EF⋅BF.26.如图,已知抛物线y=a(x+6)(x−2)过点C(0,2),交x轴于点A和点B(点A在点B的左侧),抛物线的顶点为D,对称轴DE交x轴于点E,连接EC.(1)直接写出a的值,点A的坐标和抛物线对称轴的表达式;(2)若点M是抛物线对称轴DE上的点,当△MCE是等腰三角形时,求点M的坐标;(3)点P是抛物线上的动点,连接PC,PE,将△PCE沿CE所在的直线对折,点P 落在坐标平面内的点P′处.求当点P′恰好落在直线AD上时点P的横坐标.答案和解析1.【答案】C【解析】解:根据有理数比较大小的方法,可得−1<0<1<2,∴在2,1,−1,0这四个数中,最小的数是−1.故选:C.有理数大小比较的法则:①正数都大于0;②负数都小于0;③正数大于一切负数;④两个负数,绝对值大的其值反而小,据此判断即可.此题主要考查了有理数大小比较的方法,要熟练掌握,解答此题的关键是要明确:①正数都大于0;②负数都小于0;③正数大于一切负数;④两个负数,绝对值大的其值反而小.2.【答案】B【解析】解:∵a//b,∴∠1=∠2,∵∠1=50°,∴∠2=50°,故选:B.根据平行线的性质和∠1的度数,可以得到∠2的度数,本题得以解决.本题考查平行线的性质,解答本题的关键是明确题意,利用数形结合的思想解答.3.【答案】D【解析】解:A、调查一批灯泡的使用寿命,由于具有破坏性,应当使用抽样调查,故本选项不合题意;B、调查漓江流域水质情况,应当采用抽样调查的方式,故本选项不合题意;C、调查桂林电视台某栏目的收视率,人数多,耗时长,应当采用抽样调查的方式,故本选项不合题意.D、调查全班同学的身高,应当采用全面调查,故本选项符合题意.故选:D.由普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似.本题考查了抽样调查和全面调查的区别,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大时,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.4.【答案】D【解析】解:下面四个几何体中,A的左视图为矩形;B的左视图为三角形;C的左视图为矩形;D的左视图为圆.故选:D.根据四个几何体的左视图进行判断即可.本题考查了简单几何体的三视图,解决本题的关键是掌握几何体的三视图.5.【答案】C【解析】解:∵√x−1=0,∴x−1=0,解得:x=1,则x的值是1.故选:C.利用算术平方根性质确定出x的值即可.此题考查了算术平方根,熟练掌握算术平方根的性质是解本题的关键.6.【答案】A【解析】解:原式=(a+2)(a−2),故选:A.利用平方差公式进行分解即可.此题主要考查了公式法分解因式,关键是掌握平方差公式a2−b2=(a+b)(a−b).7.【答案】B【解析】解:A.x⋅x=x2,故本选项不合题意;B.x+x=2x,故本选项符合题意;C.(x3)3=x9,故本选项不合题意;D.(2x)2=4x2,故本选项不合题意.故选:B.分别根据同底数幂的乘法法则,合并同类项法则,幂的乘方运算法则以及积的乘方运算法则逐一判断即可.本题主要考查了同底数幂的乘法,合并同类项以及幂的乘方与积的乘方,熟记相关运算法则是解答本题的关键.8.【答案】A【解析】解:∵直线y=kx+2过点(−1,4),∴4=−k+2,∴k=−2.故选:A.由直线y=kx+2过点(−1,4),利用一次函数图象上点的坐标特征可得出关于k的一元一次方程,解之即可得出k值.本题考查了一次函数图象上点的坐标特征,牢记直线上任意一点的坐标都满足函数关系式y=kx+b是解题的关键.9.【答案】C【解析】解:解不等式x−1>0,得:x>1,解不等式5−x≥1,得:x≤4,则不等式组的解集为1<x≤4,所以不等式组的整数解有2、3、4这3个,故选:C.分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集,从而得出答案.本题考查的是一元一次不等式组的整数解,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.10.【答案】B【解析】解:∵AC与⊙O相切于点A,∴AC⊥OA,∴∠OAC=90°,∵OA=OB,∴∠OAB=∠OBA.∵∠O=130°,=25°,∴∠OAB=180°−∠O2∴∠BAC=∠OAC−∠OAB=90°−25°=65°.故选:B.利用切线的性质及等腰三角形的性质求出∠OAC及∠OAB即可解决问题.本题考查切线的性质,等腰三角形的性质等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.11.【答案】D【解析】解:设有x个队参赛,则x(x−1)=110.故选:D.设有x个队参赛,根据参加一次足球联赛的每两队之间都进行两场场比赛,共要比赛110场,可列出方程.本题考查由实际问题抽象出一元二次方程,关键是根据总比赛场数做为等量关系列方程求解.12.【答案】B【解析】解:如图,设AB⏜的圆心为O,∵圆O半径为5,所对的弦AB长为8,点P是AB⏜的中点,根据垂径定理,得AB=4,PO⊥AB,AC=12OC=√OA2−AC2=3,∴PC=OP−OC=5−3=2,∴AP=√AC2+PC2=2√5,∵将AB⏜绕点A逆时针旋转90°后得到AB′⏜,∴∠PAP′=∠BAB′=90°,∴L PP′=90π×2√5180=√5π.则在该旋转过程中,点P的运动路径长是√5π.故选:B.根据已知AB⏜的半径为5,所对的弦AB长为8,点P是AB⏜的中点,利用垂径定理可得AC= 4,PO⊥AB,再根据勾股定理可得AP的长,利用弧长公式即可求出点P的运动路径长.本题考查了轨迹、垂径定理、勾股定理、圆心角、弧、弦的关系、弧长计算、旋转的性质,解决本题的关键是综合运用以上知识.13.【答案】−2020【解析】解:2020的相反数是:−2020.故答案为:−2020.直接利用相反数的定义得出答案.本题考查相反数.熟练掌握相反数的求法是解题的关键.14.【答案】a2b+ab【解析】解:原式=a2b+ab,故答案为:a2b+ab.根据整式的运算法则即可求出答案.本题考查整式的运算,解题的关键是熟练运用整式的运算法则,本题属于基础题型.15.【答案】513【解析】解:在Rt△ABC中,cosA=ACAB =513,故答案为:513.根据余弦的定义解答即可.本题考查的是锐角三角函数的定义,掌握锐角A的邻边b与斜边c的比叫做∠A的余弦是解题的关键.16.【答案】13【解析】解:∵共有六个字,“我”字有2个,∴P(“我”)=26=13.故答案为:13.根据概率公式解答就可求出任选该正方体的一面出现“我”字的概率.此题考查了概率公式的应用.注意概率=所求情况数与总情况数之比.17.【答案】3【解析】解:观察反比例函数y=kx(x<0)的图象可知:图象过第二象限,∴k<0,所以①错误;因为当x<0时,y随x的增大而增大;所以②正确;因为该函数图象关于直线y=−x对称;所以③正确;因为点(−2,3)在该反比例函数图象上,所以k=−6,则点(−1,6)也在该函数的图象上.所以④正确.所以其中正确结论的个数为3个.故答案为3.观察反比例函数y=kx(x<0)的图象可得,图象过第二象限,然后根据反比例函数的图象和性质即可进行判断.本题考查了反比例函数图象上点的坐标特征、反比例函数的性质、轴对称的性质,解决本题的关键是掌握反比例函数的性质.18.【答案】√17【解析】解:在AB上取一点T,使得AT=1,连接PT,PA,CT.∵PA=2.AT=1,AB=4,∴PA2=AT⋅AB,∴PAAT =ABPA,∵∠PAT=∠PAB,∴△PAT∽△BAP,∴PTPB =APAB=12,∴PT=12PB,∴12PB+CP=CP+PT,∵PC+PT≥TC,在Rt△ACT中,∵∠CAT=90°,AT=1,AC=4,∴CT=√AT2+AC2=√17,∴12PB+PC≥√17,∴12PB+PC的最小值为√17.故答案为√17.在AB上取一点T,使得AT=1,连接PT,PA,CT.证明△PAT∽△BAP,推出PTPB =APAB=12,推出PT=12PB,推出12PB+CP=CP+PT,根据PC+PT≥TC,求出CT即可解决问题.本题考查胡不归问题,等腰直角三角形的性质,相似三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造相似三角形解决问题,属于中考常考题型.19.【答案】解:原式=1+4+12−12=5.【解析】原式利用零指数幂、负整数指数幂法则,绝对值的代数意义,以及特殊角的三角函数值计算即可求出值.此题考查了实数的运算,零指数幂,以及特殊角的三角函数值,熟练掌握运算法则是解本题的关键.20.【答案】解:①+②得:6x =6,解得:x =1,把x =1代入①得:y =−1,则方程组的解为{x =1y =−1.【解析】方程组利用加减消元法求出解即可.此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.21.【答案】−2 0【解析】解:(1)如图所示,△A 1B 1C 1即为所求;(2)如图所示,△A 2B 2C 2即为所求;(3)由图可得,△A 1B 1C 1与△A 2B 2C 2关于点(−2,0)中心对称.故答案为:−2,0.(1)依据平移的方向和距离,即可得到平移后的△A 1B 1C 1;(2)依据△ABC 绕原点O 旋转180°,即可画出旋转后的△A 2B 2C 2;(3)依据对称点连线的中点的位置,即可得到对称中心的坐标.此题主要考查了平移变换和旋转变换,正确根据题意得出对应点位置是解题关键. 22.【答案】507.1 26.6 28【解析】解:(1)由材料1中的统计图可得:2018年,全国快递业务量是507.1亿件,比2017年增长了26.6%;(2)由材料1中的统计图可得:2015−2019年,全国快递业务量增长速度的中位数是28%;(3)不赞同,理由:由图1中的信息可得,2016−2019年全国快递业务量增长速度逐年放缓,但是快递业务量却逐年增加;(4)635.2×(1+50%)=852.82,答:2020年的快递业务量为852.82亿件.故答案为:507.1,26.6,28.(1)由材料1中的统计图中的信息即可得到结论;(2)由材料1中的统计图的信息即可得到结论;(3)根据统计图中的信息即可得到结论;(4)根据题意列式计算即可.本题考查了条形统计图,中位数的定义,正确的理解题意是解题的关键.23.【答案】(1)证明:∵四边形ABCD是菱形,∴AB=AD,∵点E,F分别是边AD,AB的中点,∴AF=AE,在△ABE和△ADF中,{AB=AD ∠A=∠A AE=AF,∴△ABE≌△ADF(SAS);(2)解:连接BD,如图:∵四边形ABCD是菱形,∴AB=AD,∠A=∠C=60°,∴△ABD是等边三角形,∵点E是边AD的中点,∴BE⊥AD,∴∠ABE=30°,∴AE=√33BE=1,AB=2AE=2,∴AD=AB=2,∴菱形ABCD的面积=AD×BE=2×√3=2√3.【解析】(1)由SAS证明△ABE≌△ADF即可;(2)证△ABD是等边三角形,得出BE⊥AD,求出AD即可.本题考查了菱形的性质、全等三角形的判定与性质、等边三角形的判定与性质、直角三角形的性质等知识;熟练掌握菱形的性质是解题的关键.24.【答案】解:(1)设每副围棋x元,则每副象棋(x−8)元,根据题意,得420x−8=756x.解得x=18.经检验x=18是所列方程的根.所以x−8=10.答:每副围棋18元,则每副象棋10元;(2)设购买围棋m副,则购买象棋(40−m)副,根据题意,得18m+10(40−m)≤600.解得m≤25.故m最大值是25.答:该校最多可再购买25副围棋.【解析】(1)设每副围棋x元,则每副象棋(x−8)元,根据420元购买象棋数量=756元购买围棋数量列出方程并解答;(2)设购买围棋m副,则购买象棋(40−m)副,根据题意列出不等式并解答.本题考查了分式方程的应用和一元一次不等式的应用,分析题意,找到关键描述语,找到合适的数量关系是解决问题的关键.25.【答案】证明:(1)如图,连接OD,OC,在Rt△ABC中,∠ACB=90°,点O是AB的中点,∴OC=OA=OB,在Rt△ABD中,∠ADB=90°,点O是AB的中点,∴OD=OA=OB,∴OA=OB=OC=OD,∴A,B,C,D四个点在以点O为圆心的同一个圆上;(2)连接OC,OD,由(1)知,OA=OC=OD,∴∠OCD=∠ODC,在Rt△ABC中,∠BAC=30°,∴∠ABC=∠BOC=60°,在Rt△ABD中,∠DAB=45°,∴∠ABD=45°=∠DAB,∴AD=BD,∵点O是AB的中点,∴OD⊥AB,∴∠BOD=90°,∠ODB=12∠ADB=45°,∴∠COD=150°,∴∠OCD=∠ODC=15°,∴∠BDC=∠ODB−∠ODC=30°,∵∠CBD=∠ABC+∠ABD=105°,∴∠BCD=180°−∠CBD−∠BDC=45°,∴∠ACD=90°−∠BCD=45°=∠BCD,∴CD平分∠ACB;(3)由(2)知,∠BCD=45°,∵∠ABC=60°,∴∠BEC=75°,∴∠AED=75°,∵DF//BC,∴∠BFD=∠ABC=60°,∵∠ABD=45°,∴∠BDF=180°−∠BFD−∠ABD=75°=∠AED,∵∠DFE=∠BFD,∴△DEF∽△BDF,∴DFBF =EFDF,∴DF2=BF⋅EF,连接OD,则∠BOD=90°,OB=OD,在Rt△DOF中,根据勾股定理得,OD2+OF2=DF2,∴OB2+OF2=BF⋅EF,即BO2+OF2=EF⋅BF.【解析】(1)利用直角三角形斜边的中线等于斜边的一半,判断出OA=OB=OC=OD,即可得出结论;(2)先求出∠COD=150°,利用等腰三角形的性质得出∠ODC=15°,进而求出∠BDC= 30°,进而求出∠BCD=45°,即可得出结论;(3)先判断出△DEF∽△BDF,得出DF2=BF⋅EF,再利用勾股定理得出OD2+OF2= DF2,即可得出结论.此题是圆的综合题,主要考查了四点共圆的判断方法,相似三角形的判定和性质,直角三角形斜边的中线等于斜边的一半的性质,等腰三角形的判定和性质,勾股定理,三角形内角和定理,判断出∠BDF=∠AED是解本题的关键.26.【答案】解:(1)∵抛物线y=a(x+6)(x−2)过点C(0,2),∴2=a(0+6)(0−2),∴a=−16,∴抛物线的解析式为y=−16(x+6)(x−2)=−16(x+2)2+83,∴抛物线的对称轴为直线x=−2;(2)如图1,由(1)知,抛物线的对称轴为x=−2,∴E(−2,0),∵C(0,2),∴OC=OE=2,∴CE=√2OC=2√2,∠CED=45°,∵△CME是等腰三角形,∴①当ME=MC时,∴∠ECM=∠CED=45°,∴∠CME=90°,∴M(−2,2),②当CE=CM时,∴MM1=CM=2,∴EM1=4,∴M1(−2,4),③当EM=CE时,∴EM2=EM3=2√2,∴M2(−2,−2√2),M3(−2,2√2),即满足条件的点M的坐标为(−2,−2)或(−2,4)或(−2,2√2)或(−2,−2√2);(3)如图2,由(1)知,抛物线的解析式为y=−16(x+6)(x−2)=−16(x+2)2+83,∴D(−2,83),令y=0,则(x+6)(x−2)=0,∴x=−6或x=2,∴点A(−6,0),∴直线AD的解析式为y=23x+4,过点P作PQ⊥x轴于Q,过点P′作P′Q′⊥DE于Q′,∴∠EQ′P′=∠EQP=90°,由(2)知,∠CED=∠CEB=45°,由折叠知,EP′=EP,∠CEP′=∠CEP,∴△PQE≌△P′Q′E(AAS),∴PQ=P′Q′,EQ=EQ′,设点P(m,n),∴OQ=m,PQ=n,∴P′Q′=n,EQ′=QE=m+2,∴点P′(n−2,2+m),∵点P′在直线AD上,∴2+m=23(n−2)+4①,∵点P在抛物线上,∴n=−16(m+6)(m−2)②,联立①②解得,m=−13−√2412(舍)或m=−13+√2412,即点P的横坐标为−13+√2412.【解析】(1)将点C坐标代入抛物线解析式中,即可得出结论;(2)分三种情况:直接利用等腰三角形的性质,即可得出结论;(3)先判断出△PQE≌△P′Q′E(AAS),得出PQ=P′Q′,EQ=EQ′,进而得出P′Q′=n,EQ′=QE=m+2,确定出点P′(n−2,2+m),将点P′的坐标代入直线AD的解析式中,和点P代入抛物线解析式中,联立方程组,求解即可得出结论.此题是二次函数综合题,主要考查了待定系数法,等腰三角形的性质,全等三角形的判定和性质,用分类讨论的思想解决问题是解本题的关键.第15页,共21页。
2020年广西桂林市中考数学试卷(含详细解析)
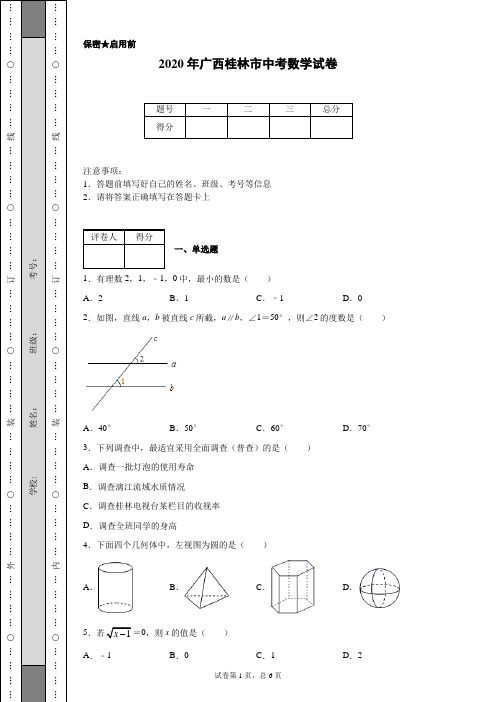
(1)2018年,全国快递业务量是亿件,比2017年增长了%;
(2)2015﹣2019年,全国快递业务量增长速度的中位数是%;
6.因式分解a2﹣4的结果是( )
A.(a+2)(a﹣2)B.(a﹣2)2C.(a+2)2D.a(a﹣2)
7.下列计算正确的是( )
A.x•x=2xB.x+x=2xC.(x3)3=x6D.(2x)2=2x2
8.直线y=kx+2过点(﹣1,4),则k的值是( )
A.﹣2B.﹣1C.1D.2
9.不等式组 的整数解共有( )
(1)把 向左平移4个单位后得到对应的 A1B1C1,请画出平移后的 A1B1C1;
(2)把 绕原点O旋转180°后得到对应的 A2B2C2,请画出旋转后的 A2B2C2;
(3)观察图形可知, A1B1C1与 A2B2C2关于点(,)中心对称.
22.阅读下列材料,完成解答:
材料1:国家统计局2月28日发布了2019年国民经济和社会发展统计公报,该公报中的如图发布的是全国“2015﹣2019年快递业务量及其增长速度”统计图(如图1).
参考答案
1.C
【解析】
【分析】
有理数大小比较的法则:①正数都大于0;②负数都小于0;③正数大于一切负数;④两个负数,绝对值大的其值反而小,据此判断即可.
【详解】
解:根据有理数比较大小的方法,可得
﹣1<0<1<2,
∴在2,1,﹣1,0这四个数中,最小的数是﹣1.
广西桂林市2020版中考数学试卷A卷

广西桂林市2020版中考数学试卷A卷姓名:________ 班级:________ 成绩:________一、选择题 (共8题;共16分)1. (2分)下列叙述正确的个数有:(3)无限小数都是无理数(4)有限小数都是有理数(5)实数分为正实数和负实数两类。
()A . 1个B . 2个C . 3个D . 4个2. (2分)下列计算正确的是()A . (a3)3=a6B . a6÷a3=a2C . 2a+3b=5abD . a2•a3=a53. (2分)一个几何体的三视图如下图所示,这个几何体是()A . 球B . 圆柱C . 长方体D . 圆锥4. (2分)为了解本地区老年人一年中生病次数,下列样本抽取方式最合适的是()A . 到公园里调查100名晨练老人B . 到医院调查100名老年病人C . 到某小区调查10名老年居民D . 利用户籍资料,按规则抽查10%的老年人5. (2分)式子在实数范围内有意义,则x的取值范围是()A . x<1B . x≤1C . x>1D . x ≥16. (2分)在Rt△ABC中,∠C=90°,a,b,c分别是∠A,∠B,∠C的对边,下列关系式中错误的是()A . b=c•cosBB . b=a•tanBC . a=c•sinAD . a=b•cotB7. (2分)下列命题中,真命题是()A . 对角线相等的四边形是矩形B . 对角线互相垂直平分的四边形是菱形C . 一组对边平行,另一组对边相等的四边形是平行四边形D . 一组邻边相等,并且有一个内角为直角的四边形是正方形8. (2分)小轩从如图所示的二次函数y=ax2+bx+c(a≠0)的图象中,观察得出了下面五条信息:①ab>0;②a+b+c<0;③b+2c>0;④a﹣2b+4c>0;⑤a=b.你认为其中正确信息的个数有()A . 2个B . 3个C . 4个D . 5个二、填空题 (共9题;共23分)9. (1分) (2016七上·凤庆期中) 若a、b互为相反数,c、d互为倒数,则2a+3cd+2b=________.10. (15分)(2019·盐城)(1)【生活观察】甲、乙两人买菜,甲习惯买一定质量的菜,乙习惯买一定金额的菜,两人每次买菜的单价相同,例如:①完成上表;②计算甲两次买菜的均价和乙两次买菜的均价.(均价=总金额÷总质量)(2)【数学思考】设甲每次买质量为m千克的菜,乙每次买金额为n元的菜,两次的单价分别是a元/千克、b元/千克,用含有m、n、a、b的式子,分别表示出甲、乙两次买菜的均价、 .比较、的大小,并说明理由.(3)【知识迁移】某船在相距为s的甲、乙两码头间往返航行一次,在没有水流时,船的速度为v所需时间为:如果水流速度为p时(p<v),船顺水航行速度为(v+p),逆水航行速度为(v-p),所需时间为请借鉴上面的研究经验,比较、的大小,并说明理由.11. (1分)(2019·营口模拟) 如图,两同心圆的圆心为O,大圆的弦AB切小圆于P,两圆的半径分别为2和1,若用阴影部分围成一个圆锥,则该圆锥的底面半径为________.12. (1分) (2016九上·武汉期中) 设a,b是方程x2+x﹣9=0的两个实数根,则a2+2a+b的值为________.13. (1分)如图,在△ABC中,∠BAC=90°,BC=5cm,AC=3cm,将△ABC绕顶点C按顺时针方向旋转45°至△A1B1C的位置,则线段AB扫过区域(图中阴影部分)的面积为________ cm2 .14. (1分)某市移动公司为了调查手机发送短信息的情况,在本区域的120位用户中抽取了10位用户来统计他们某周发信息的条数,结果如下表:手机用户序号12345678910发送短信息条数20192020211715232025本次调查中这120位用户大约每周一共发送________ 条短信息.15. (1分) (2017九下·福田开学考) 如图,已知⊙O的直径AB=6,E、F为AB的三等分点,M、N为上两点,且∠MEB=∠NFB=60°,则EM+FN=________.16. (1分) (2015七下·鄄城期中) 如果每盒钢笔有10支,总售价100元,那么购买钢笔的总钱数y(元)与所买支数x之间的关系式为________.17. (1分) (2018七上·郑州期末) 如图,长方形ABCD中有6个形状、大小相同的小长方形,根据图中所标尺寸,则图中阴影部分的面积之和为________三、解答题 (共11题;共106分)18. (5分)(2019·东台模拟) 计算:19. (10分)(2017·平南模拟) 计算下面各题(1)计算:| ﹣2|+20150﹣()+3tan30°;(2)解不等式组:,并将不等式组的解集在所给数轴上表示出来.20. (15分)某班实行小组量化考核制,为了了解同学们的学习情况,王老师对甲、乙两个小组连续六周的综合评价得分进行了统计,并将得到的数据制成如下的统计表:(1)请根据上表中的数据完成下表(注:方差的计算结果精确到0.1)(2)根据综合评价得分统计表中的数据,请在下图中画出乙组综合评价得分的折线统计图.(3)根据折线统计图中的信息,请你分别对甲、乙两个小组连续六周的学习情况作出简要评价.21. (5分)某演讲比赛中只有甲、乙、丙三位同学进行决赛,他们通过抽签决定演讲顺序,用列表法或画树状图法求:(1)第二个出场为甲的概率;(2)丙在乙前面出场的概率.22. (5分) (2017八下·藁城开学考) 如图,在四边形ABCD中,∠B=90°,DE∥AB交BC于E、交AC于F,∠CDE=∠ACB=30°,BC=DE.求证:△FCD是等腰三角形.23. (5分)如图,已知△ABC中,∠C=90°AD平分∠BAC,ED⊥BC交AB于E,DF∥AB交AC于F,求证:四边形AFDE是菱形.24. (20分) (2016九上·龙海期中) 如图所示,在平面直角坐标系中,过点A(﹣,0)的两条直线分别交y轴于B、C两点,且B、C两点的纵坐标分别是一元二次方程x2﹣2x﹣3=0的两个根(1)求线段BC的长度;(2)试问:直线AC与直线AB是否垂直?请说明理由;(3)若点D在直线AC上,且DB=DC,求直线BD的解析式;(4)在x轴上是否存在P,使以O、B、P三点为顶点的三角形与△ABC相似?若存在,请直接写出P点的坐标;若不存在,请说明理由.25. (10分)如图,分别是正方形、正五边形和正六边形,(1)试分别计算这三种正多边形的相邻两条对角线的夹角的度数;(2)探究正n边形相邻两条对角线的夹角满足的规律.26. (10分) (2017七下·蒙阴期末) 双蓉服装店老板到厂家购A、B两种型号的服装,若购A种型号服装9件,B种型号服装10件,需要1810元;若购进A种型号服装12件,B种型号服装8件,需要1880元。
2020年广西桂林市中考数学试卷(有解析)

∴2∠A=∠B,3∠A=∠C
∵∠A+∠B+∠C=180°,
∴∠A+2∠A+3∠A=180°
∴∠A=30°,
∴∠C=90°,
所以三角形为直角三角形.
三角形的三个角存在关系时,统一成同一个角,再根据内角和为180°,即可求出大小.
6.C
根据正数大于0,负数小于0,正数大于一切负数,两个负数,绝对值大的反而小比较即可.
A.对重庆市初中学生每天阅读时间的调查
B.对端午节期间市场上粽子质量情况的调查
C.对某批次手机的防水功能的调查
D.对某校九年级3班学生肺活量情况的调查
10.某班同学毕业时,都将自己的照片向全班其他同学各送一张表示留念,全班共送1892张照片,如果全班有x名同学,根据题意,列出方程为()
A.x(x+1)=1892B.x(x−1)=1892×2
C.x(x−1)=1892D.2x(x+1)=1892
11.如图,若 , , ,则 ()
A. B. C. D.
12.若整数 同时满足不等式 与 ,则该整数x是( ).
A.1B.2C.3D.2和3
二、填空题
13.式子“ ”读作________.
14.已知点A(2,﹣3)关于x轴的对称点A'在反比例函数y= 的图象上,则实数k的值为_____.
(2)说明△A2B2C2是由△A1B1C1经过怎样的平移得到的?
26.如图,在 中, , ,点 为 的中点, 为 的中点, ,垂足为点 ,求 , 的长.
参考答案
1.B
由题意可得,可将 看成一个整体,再运用平方差公式求解,经过化简即可求出
解:(3a+2b)2-(a-b)2
2020年广西桂林市中考数学试卷 (word版,含答案)
2020年广西桂林市中考数学试卷一、选择题(本大题共12小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.有理数2,1,﹣1,0中,最小的数是()A.2B.1C.﹣1D.02.如图,直线a,b被直线c所截,a∥b,∠1=50°,则∠2的度数是()A.40°B.50°C.60°D.70°3.下列调查中,最适宜采用全面调查(普查)的是()A.调查一批灯泡的使用寿命B.调查漓江流域水质情况C.调查桂林电视台某栏目的收视率D.调查全班同学的身高4.下面四个几何体中,左视图为圆的是()A.B.C.D.5.若=0,则x的值是()A.﹣1B.0C.1D.26.因式分解a2﹣4的结果是()A.(a+2)(a﹣2)B.(a﹣2)2C.(a+2)2D.a(a﹣2)7.(3分)下列计算正确的是()A.x•x=2x B.x+x=2x C.(x3)3=x6D.(2x)2=2x2 8.直线y=kx+2过点(﹣1,4),则k的值是()A.﹣2B.﹣1C.1D.29.不等式组的整数解共有()A.1个B.2个C.3个D.4个10.如图,AB是⊙O的弦,AC与⊙O相切于点A,连接OA,OB,若∠O=130°,则∠BAC 的度数是()A.60°B.65°C.70°D.75°11.参加足球联赛的每两支球队之间都要进行两场比赛,共要比赛110场,设参加比赛的球队有x支,根据题意,下面列出的方程正确的是()A.x(x+1)=110B.x(x﹣1)=110C.x(x+1)=110D.x(x﹣1)=11012.如图,已知的半径为5,所对的弦AB长为8,点P是的中点,将绕点A逆时针旋转90°后得到,则在该旋转过程中,点P的运动路径长是()A.πB.πC.2πD.2π二、填空题(本大题共6小题,每小题3分,共18分.请把答案填在题中的横线上)13.2020的相反数是.14.计算:ab•(a+1)=.15.如图,在Rt△ABC中,∠C=90°,AB=13,AC=5,则cos A的值是.16.一个正方体的平面展开图如图所示,任选该正方体的一面出现“我”字的概率是.17.反比例函数y=(x<0)的图象如图所示,下列关于该函数图象的四个结论:①k>0;②当x<0时,y随x的增大而增大;③该函数图象关于直线y=﹣x对称;④若点(﹣2,3)在该反比例函数图象上,则点(﹣1,6)也在该函数的图象上.其中正确结论的个数有个.18.如图,在Rt△ABC中,AB=AC=4,点E,F分别是AB,AC的中点,点P是扇形AEF 的上任意一点,连接BP,CP,则BP+CP的最小值是.三、解答题(本大题共8小题,共66分.解答应写出必要的文字说明、证明过程或演算步骤)19.(6分)计算:(π+)0+(﹣2)2+|﹣|﹣sin30°.20.(6分)解二元一次方程组:.21.(8分)如图,在平面直角坐标系中,△ABC的三个顶点分别是A(1,3),B(4,4),C(2,1).(1)把△ABC向左平移4个单位后得到对应的△A1B1C1,请画出平移后的△A1B1C1;(2)把△ABC绕原点O旋转180°后得到对应的△A2B2C2,请画出旋转后的△A2B2C2;(3)观察图形可知,△A1B1C1与△A2B2C2关于点(,)中心对称.22.(8分)阅读下列材料,完成解答:材料1:国家统计局2月28日发布了2019年国民经济和社会发展统计公报,该公报中的如图发布的是全国“2015﹣2019年快递业务量及其增长速度”统计图(如图1).材料2:6月28日,国家邮政局发布的数据显示:受新冠疫情影响,快递业务量快速增长,5月份快递业务量同比增长41%(如图2).某快递业务部门负责人据此估计,2020年全国快递业务量将比2019年增长50%.(1)2018年,全国快递业务量是亿件,比2017年增长了%;(2)2015﹣2019年,全国快递业务量增长速度的中位数是%;(3)统计公报发布后,有人认为,图1中表示2016﹣2019年增长速度的折线逐年下降,说明2016﹣2019年全国快递业务量增长速度逐年放缓,所以快递业务量也逐年减少.你赞同这种说法吗?为什么?(4)若2020年全国快递业务量比2019年增长50%,请列式计算2020年的快递业务量.23.(8分)如图,在菱形ABCD中,点E,F分别是边AD,AB的中点.(1)求证:△ABE≌△ADF;(2)若BE=,∠C=60°,求菱形ABCD的面积.24.(8分)某学校为丰富同学们的课余生活,购买了一批数量相等的象棋和围棋供兴趣小组使用,其中购买象棋用了420元,购买围棋用了756元,已知每副围棋比每副象棋贵8元.(1)求每副围棋和象棋各是多少元?(2)若该校决定再次购买同种围棋和象棋共40副,且再次购买的费用不超过600元,则该校最多可再购买多少副围棋?25.(10分)如图,将一副斜边相等的直角三角板按斜边重合摆放在同一平面内,其中∠CAB =30°,∠DAB=45°,点O为斜边AB的中点,连接CD交AB于点E.(1)求证:A,B,C,D四个点在以点O为圆心的同一个圆上;(2)求证:CD平分∠ACB;(3)过点D作DF∥BC交AB于点F,求证:BO2+OF2=EF•BF.26.(12分)如图,已知抛物线y=a(x+6)(x﹣2)过点C(0,2),交x轴于点A和点B (点A在点B的左侧),抛物线的顶点为D,对称轴DE交x轴于点E,连接EC.(1)直接写出a的值,点A的坐标和抛物线对称轴的表达式;(2)若点M是抛物线对称轴DE上的点,当△MCE是等腰三角形时,求点M的坐标;(3)点P是抛物线上的动点,连接PC,PE,将△PCE沿CE所在的直线对折,点P落在坐标平面内的点P′处.求当点P′恰好落在直线AD上时点P的横坐标.参考答案一、CBDDC ABACB DB二、13.﹣202014.a2b+ab15.16.17.318.三、19.解:原式=1+4+﹣=5.20.解:①+②得:6x=6,解得:x=1,把x=1代入①得:y=﹣1,则方程组的解为.21.解:(1)如图所示,△A1B1C1即为所求;(2)如图所示,△A2B2C2即为所求;(3)﹣2,0.22.解:(1)由材料1中的统计图可得:2018年,全国快递业务量是507.1亿件,比2017年增长了26.6%;(2)由材料1中的统计图可得:2015﹣2019年,全国快递业务量增长速度的中位数是28%;(3)不赞同,理由:由图1中的信息可得,2016﹣2019年全国快递业务量增长速度逐年放缓,但是快递业务量却逐年增加;(4)635.2×(1+50%)=852.82,答:2020年的快递业务量为852.82亿件.23.(1)证明:∵四边形ABCD是菱形,∴AB=AD,∵点E,F分别是边AD,AB的中点,∴AF=AE,在△ABE和△ADF中,,∴△ABE≌△ADF(SAS);(2)解:连接BD,如图:∵四边形ABCD是菱形,∴AB=AD,∠A=∠C=60°,∴△ABD是等边三角形,∵点E是边AD的中点,∴BE⊥AD,∴∠ABE=30°,∴AE=BE=1,AB=2AE=2,∴AD=AB=2,∴菱形ABCD的面积=AD×BE=2×=2.24.解:(1)设每副围棋x元,则每副象棋(x﹣8)元,根据题意,得=.解得x=18.经检验x=18是所列方程的根.所以x﹣8=10.答:每副围棋18元,则每副象棋10元;(2)设购买围棋m副,则购买象棋(40﹣m)副,根据题意,得18m+10(40﹣m)≤600.解得m≤25.故m最大值是25.答:该校最多可再购买25副围棋.25.证明:(1)如图,连接OD,OC,在Rt△ABC中,∠ACB=90°,点O是AB的中点,∴OC=OA=OB,在Rt△ABD中,∠ADB=90°,点O是AB的中点,∴OD=OA=OB,∴OA=OB=OC=OD,∴A,B,C,D四个点在以点O为圆心的同一个圆上;(2)连接OC,OD,由(1)知,OA=OC=OD,∴∠OCD=∠ODC,在Rt△ABC中,∠BAC=30°,∴∠ABC=∠BOC=60°,在Rt△ABD中,∠DAB=45°,∴∠ABD=45°=∠DAB,∴AD=BD,∵点O是AB的中点,∴OD⊥AB,∴∠BOD=90°,∠ODB=∠ADB=45°,∴∠COD=150°,∴∠OCD=∠ODC=15°,∴∠BDC=∠ODB﹣∠ODC=30°,∵∠CBD=∠ABC+∠ABD=105°,∴∠BCD=180°﹣∠CBD﹣∠BDC=45°,∴∠ACD=90°﹣∠BCD=45°=∠BCD,∴CD平分∠ACB;(3)由(2)知,∠BCD=45°,∵∠ABC=60°,∴∠BEC=75°,∴∠AED=75°,∵DF∥BC,∴∠BFD=∠ABC=60°,∵∠ABD=45°,∴∠BDF=180°﹣∠BFD﹣∠ABD=75°=∠AED,∵∠DFE=∠BFD,∴△DEF∽△BDF,∴,∴DF2=BF•EF,连接OD,则∠BOD=90°,OB=OD,在Rt△DOF中,根据勾股定理得,OD2+OF2=DF2,∴OB2+OF2=BF•EF,即BO2+OF2=EF•BF.26.解:(1)∵抛物线y=a(x+6)(x﹣2)过点C(0,2),∴2=a(0+6)(0﹣2),∴a=﹣,∴抛物线的解析式为y=﹣(x+6)(x﹣2)=﹣(x+2)2+,∴抛物线的对称轴为直线x=﹣2;(2)如图1,由(1)知,抛物线的对称轴为x=﹣2,∴E(﹣2,0),∵C(0,2),∴OC=OE=2,∴CE=OC=2,∠CED=45°,∵△CME是等腰三角形,∴①当ME=MC时,∴∠ECM=∠CED=45°,∴∠CME=90°,∴M(﹣2,2),②当CE=CM时,∴MM1=CM=2,∴EM1=4,∴M1(﹣2,4),③当EM=CE时,∴EM2=EM3=2,∴M2(﹣2,﹣2),M3(﹣2,2),即满足条件的点M的坐标为(﹣2,﹣2)或(﹣2,4)或(﹣2,2)或(﹣2,﹣2);(3)如图2,由(1)知,抛物线的解析式为y=﹣(x+6)(x﹣2)=﹣(x+2)2+,∴D(﹣2,),令y=0,则(x+6)(x﹣2)=0,∴x=﹣6或x=2,∴点A(﹣6,0),∴直线AD的解析式为y=x+4,过点P作PQ⊥x轴于Q,过点P'作P'Q'⊥DE于Q',∴∠EQ'P'=∠EQP=90°,由(2)知,∠CED=∠CEB=45°,由折叠知,EP'=EP,∠CEP'=∠CEP,∴△PQE≌△P'Q'E(AAS),∴PQ=P'Q',EQ=EQ',设点P(m,n),∴OQ=m,PQ=n,∴P'Q'=n,EQ'=QE=m+2,∴点P'(n﹣2,2+m),∵点P'在直线AD上,∴2+m=(n﹣2)+4①,∵点P在抛物线上,∴n=﹣(m+6)(m﹣2)②,联立①②解得,m=(舍)或m=,即点P的横坐标为.。
广西桂林市2020年中考数学试卷 解析版

2020年广西桂林中考数学试卷一、选择题(本大题共12小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.(3分)有理数2,1,﹣1,0中,最小的数是()A.2B.1C.﹣1D.02.(3分)如图,直线a,b被直线c所截,a∥b,∠1=50°,则∠2的度数是()A.40°B.50°C.60°D.70°3.(3分)下列调查中,最适宜采用全面调查(普查)的是()A.调查一批灯泡的使用寿命B.调查漓江流域水质情况C.调查桂林电视台某栏目的收视率D.调查全班同学的身高4.(3分)下面四个几何体中,左视图为圆的是()A.B.C.D.5.(3分)若=0,则x的值是()A.﹣1B.0C.1D.26.(3分)因式分解a2﹣4的结果是()A.(a+2)(a﹣2)B.(a﹣2)2C.(a+2)2D.a(a﹣2)7.(3分)下列计算正确的是()A.x•x=2x B.x+x=2x C.(x3)3=x6D.(2x)2=2x2 8.(3分)直线y=kx+2过点(﹣1,4),则k的值是()A.﹣2B.﹣1C.1D.29.(3分)不等式组的整数解共有()A.1个B.2个C.3个D.4个10.(3分)如图,AB是⊙O的弦,AC与⊙O相切于点A,连接OA,OB,若∠O=130°,则∠BAC的度数是()A.60°B.65°C.70°D.75°11.(3分)参加足球联赛的每两支球队之间都要进行两场比赛,共要比赛110场,设参加比赛的球队有x支,根据题意,下面列出的方程正确的是()A.x(x+1)=110B.x(x﹣1)=110C.x(x+1)=110D.x(x﹣1)=11012.(3分)如图,已知的半径为5,所对的弦AB长为8,点P是的中点,将绕点A逆时针旋转90°后得到,则在该旋转过程中,点P的运动路径长是()A.πB.πC.2πD.2π二、填空题(本大题共6小题,每小题3分,共18分.请把答案填在题中的横线上)13.(3分)2020的相反数是.14.(3分)计算:ab•(a+1)=.15.(3分)如图,在Rt△ABC中,∠C=90°,AB=13,AC=5,则cos A的值是.16.(3分)一个正方体的平面展开图如图所示,任选该正方体的一面出现“我”字的概率是.17.(3分)反比例函数y=(x<0)的图象如图所示,下列关于该函数图象的四个结论:①k>0;②当x<0时,y随x的增大而增大;③该函数图象关于直线y=﹣x对称;④若点(﹣2,3)在该反比例函数图象上,则点(﹣1,6)也在该函数的图象上.其中正确结论的个数有个.18.(3分)如图,在Rt△ABC中,AB=AC=4,点E,F分别是AB,AC的中点,点P是扇形AEF的上任意一点,连接BP,CP,则BP+CP的最小值是.三、解答题(本大题共8小题,共66分.解答应写出必要的文字说明、证明过程或演算步骤)19.(6分)计算:(π+)0+(﹣2)2+|﹣|﹣sin30°.20.(6分)解二元一次方程组:.21.(8分)如图,在平面直角坐标系中,△ABC的三个顶点分别是A(1,3),B(4,4),C(2,1).(1)把△ABC向左平移4个单位后得到对应的△A1B1C1,请画出平移后的△A1B1C1;(2)把△ABC绕原点O旋转180°后得到对应的△A2B2C2,请画出旋转后的△A2B2C2;(3)观察图形可知,△A1B1C1与△A2B2C2关于点(,)中心对称.22.(8分)阅读下列材料,完成解答:材料1:国家统计局2月28日发布了2019年国民经济和社会发展统计公报,该公报中的如图发布的是全国“2015﹣2019年快递业务量及其增长速度”统计图(如图1).材料2:6月28日,国家邮政局发布的数据显示:受新冠疫情影响,快递业务量快速增长,5月份快递业务量同比增长41%(如图2).某快递业务部门负责人据此估计,2020年全国快递业务量将比2019年增长50%.(1)2018年,全国快递业务量是亿件,比2017年增长了%;(2)2015﹣2019年,全国快递业务量增长速度的中位数是%;(3)统计公报发布后,有人认为,图1中表示2016﹣2019年增长速度的折线逐年下降,说明2016﹣2019年全国快递业务量增长速度逐年放缓,所以快递业务量也逐年减少.你赞同这种说法吗?为什么?(4)若2020年全国快递业务量比2019年增长50%,请列式计算2020年的快递业务量.23.(8分)如图,在菱形ABCD中,点E,F分别是边AD,AB的中点.(1)求证:△ABE≌△ADF;(2)若BE=,∠C=60°,求菱形ABCD的面积.24.(8分)某学校为丰富同学们的课余生活,购买了一批数量相等的象棋和围棋供兴趣小组使用,其中购买象棋用了420元,购买围棋用了756元,已知每副围棋比每副象棋贵8元.(1)求每副围棋和象棋各是多少元?(2)若该校决定再次购买同种围棋和象棋共40副,且再次购买的费用不超过600元,则该校最多可再购买多少副围棋?25.(10分)如图,将一副斜边相等的直角三角板按斜边重合摆放在同一平面内,其中∠CAB =30°,∠DAB=45°,点O为斜边AB的中点,连接CD交AB于点E.(1)求证:A,B,C,D四个点在以点O为圆心的同一个圆上;(2)求证:CD平分∠ACB;(3)过点D作DF∥BC交AB于点F,求证:BO2+OF2=EF•BF.26.(12分)如图,已知抛物线y=a(x+6)(x﹣2)过点C(0,2),交x轴于点A和点B (点A在点B的左侧),抛物线的顶点为D,对称轴DE交x轴于点E,连接EC.(1)直接写出a的值,点A的坐标和抛物线对称轴的表达式;(2)若点M是抛物线对称轴DE上的点,当△MCE是等腰三角形时,求点M的坐标;(3)点P是抛物线上的动点,连接PC,PE,将△PCE沿CE所在的直线对折,点P落在坐标平面内的点P′处.求当点P′恰好落在直线AD上时点P的横坐标.2020年广西桂林中考数学试卷参考答案与试题解析一、选择题(本大题共12小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.(3分)有理数2,1,﹣1,0中,最小的数是()A.2B.1C.﹣1D.0【分析】有理数大小比较的法则:①正数都大于0;②负数都小于0;③正数大于一切负数;④两个负数,绝对值大的其值反而小,据此判断即可.【解答】解:根据有理数比较大小的方法,可得﹣1<0<1<2,∴在2,1,﹣1,0这四个数中,最小的数是﹣1.故选:C.2.(3分)如图,直线a,b被直线c所截,a∥b,∠1=50°,则∠2的度数是()A.40°B.50°C.60°D.70°【分析】根据平行线的性质和∠1的度数,可以得到∠2的度数,本题得以解决.【解答】解:∵a∥b,∴∠1=∠2,∵∠1=50°,∴∠2=50°,故选:B.3.(3分)下列调查中,最适宜采用全面调查(普查)的是()A.调查一批灯泡的使用寿命B.调查漓江流域水质情况C.调查桂林电视台某栏目的收视率D.调查全班同学的身高【分析】由普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似.【解答】解:A、调查一批灯泡的使用寿命,由于具有破坏性,应当使用抽样调查,故本选项不合题意;B、调查漓江流域水质情况,应当采用抽样调查的方式,故本选项不合题意;C、调查桂林电视台某栏目的收视率,人数多,耗时长,应当采用抽样调查的方式,故本选项不合题意.D、调查全班同学的身高,应当采用全面调查,故本选项符合题意.故选:D.4.(3分)下面四个几何体中,左视图为圆的是()A.B.C.D.【分析】根据四个几何体的左视图进行判断即可.【解答】解:下面四个几何体中,A的左视图为矩形;B的左视图为三角形;C的左视图为矩形;D的左视图为圆.故选:D.5.(3分)若=0,则x的值是()A.﹣1B.0C.1D.2【分析】利用算术平方根性质确定出x的值即可.【解答】解:∵=0,∴x﹣1=0,解得:x=1,则x的值是1.故选:C.6.(3分)因式分解a2﹣4的结果是()A.(a+2)(a﹣2)B.(a﹣2)2C.(a+2)2D.a(a﹣2)【分析】利用平方差公式进行分解即可.【解答】解:原式=(a+2)(a﹣2),故选:A.7.(3分)下列计算正确的是()A.x•x=2x B.x+x=2x C.(x3)3=x6D.(2x)2=2x2【分析】分别根据同底数幂的乘法法则,合并同类项法则,幂的乘方运算法则以及积的乘方运算法则逐一判断即可.【解答】解:A.x•x=x2,故本选项不合题意;B.x+x=2x,故本选项符合题意;C.(x3)3=x9,故本选项不合题意;D.(2x)2=4x2,故本选项不合题意.故选:B.8.(3分)直线y=kx+2过点(﹣1,4),则k的值是()A.﹣2B.﹣1C.1D.2【分析】由直线y=kx+2过点(﹣1,4),利用一次函数图象上点的坐标特征可得出关于k的一元一次方程,解之即可得出k值.【解答】解:∵直线y=kx+2过点(﹣1,4),∴4=﹣k+2,∴k=﹣2.故选:A.9.(3分)不等式组的整数解共有()A.1个B.2个C.3个D.4个【分析】分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集,从而得出答案.【解答】解:解不等式x﹣1>0,得:x>1,解不等式5﹣x≥1,得:x≤4,则不等式组的解集为1<x≤4,所以不等式组的整数解有2、3、4这3个,故选:C.10.(3分)如图,AB是⊙O的弦,AC与⊙O相切于点A,连接OA,OB,若∠O=130°,则∠BAC的度数是()A.60°B.65°C.70°D.75°【分析】利用切线的性质及等腰三角形的性质求出∠OAC及∠OAB即可解决问题.【解答】解:∵AC与⊙O相切于点A,∴AC⊥OA,∴∠OAC=90°,∵OA=OB,∴∠OAB=∠OBA.∵∠O=130°,∴∠OAB==25°,∴∠BAC=∠OAC﹣∠OAB=90°﹣25°=65°.故选:B.11.(3分)参加足球联赛的每两支球队之间都要进行两场比赛,共要比赛110场,设参加比赛的球队有x支,根据题意,下面列出的方程正确的是()A.x(x+1)=110B.x(x﹣1)=110C.x(x+1)=110D.x(x﹣1)=110【分析】设有x个队参赛,根据参加一次足球联赛的每两队之间都进行两场场比赛,共要比赛110场,可列出方程.【解答】解:设有x个队参赛,则x(x﹣1)=110.故选:D.12.(3分)如图,已知的半径为5,所对的弦AB长为8,点P是的中点,将绕点A逆时针旋转90°后得到,则在该旋转过程中,点P的运动路径长是()A.πB.πC.2πD.2π【分析】根据已知的半径为5,所对的弦AB长为8,点P是的中点,利用垂径定理可得AC=4,PO⊥AB,再根据勾股定理可得AP的长,利用弧长公式即可求出点P的运动路径长.【解答】解:如图,设的圆心为O,∵圆O半径为5,所对的弦AB长为8,点P是的中点,根据垂径定理,得AC=AB=4,PO⊥AB,OC==3,∴PC=OP﹣OC=5﹣3=2,∴AP==2,∵将绕点A逆时针旋转90°后得到,∴∠P AP′=∠BAB′=90°,∴L PP′==π.则在该旋转过程中,点P的运动路径长是π.故选:B.二、填空题(本大题共6小题,每小题3分,共18分.请把答案填在题中的横线上)13.(3分)2020的相反数是﹣2020.【分析】直接利用相反数的定义得出答案.【解答】解:2020的相反数是:﹣2020.故答案为:﹣2020.14.(3分)计算:ab•(a+1)=a2b+ab.【分析】根据整式的运算法则即可求出答案.【解答】解:原式=a2b+ab,故答案为:a2b+ab.15.(3分)如图,在Rt△ABC中,∠C=90°,AB=13,AC=5,则cos A的值是.【分析】根据余弦的定义解答即可.【解答】解:在Rt△ABC中,cos A==,故答案为:.16.(3分)一个正方体的平面展开图如图所示,任选该正方体的一面出现“我”字的概率是.【分析】根据概率公式解答就可求出任选该正方体的一面出现“我”字的概率.【解答】解:∵共有六个字,“我”字有2个,∴P(“我”)==.故答案为:.17.(3分)反比例函数y=(x<0)的图象如图所示,下列关于该函数图象的四个结论:①k>0;②当x<0时,y随x的增大而增大;③该函数图象关于直线y=﹣x对称;④若点(﹣2,3)在该反比例函数图象上,则点(﹣1,6)也在该函数的图象上.其中正确结论的个数有3个.【分析】观察反比例函数y=(x<0)的图象可得,图象过第二象限,然后根据反比例函数的图象和性质即可进行判断.【解答】解:观察反比例函数y=(x<0)的图象可知:图象过第二象限,∴k<0,所以①错误;因为当x<0时,y随x的增大而增大;所以②正确;因为该函数图象关于直线y=﹣x对称;所以③正确;因为点(﹣2,3)在该反比例函数图象上,所以k=﹣6,则点(﹣1,6)也在该函数的图象上.所以④正确.所以其中正确结论的个数为3个.故答案为3.18.(3分)如图,在Rt△ABC中,AB=AC=4,点E,F分别是AB,AC的中点,点P是扇形AEF的上任意一点,连接BP,CP,则BP+CP的最小值是.【分析】在AB上取一点T,使得AT=1,连接PT,P A,CT.证明△P AT∽△BAP,推出==,推出PT=PB,推出PB+CP=CP+PT,根据PC+PT≥TC,求出CT 即可解决问题.【解答】解:在AB上取一点T,使得AT=1,连接PT,P A,CT.∵P A=2.AT=1,AB=4,∴P A2=AT•AB,∴=,∵∠P AT=∠P AB,∴△P AT∽△BAP,∴==,∴PT=PB,∴PB+CP=CP+PT,∵PC+PT≥TC,在Rt△ACT中,∵∠CAT=90°,AT=1,AC=4,∴CT==,∴PB+PC≥,∴PB+PC的最小值为.故答案为.三、解答题(本大题共8小题,共66分.解答应写出必要的文字说明、证明过程或演算步骤)19.(6分)计算:(π+)0+(﹣2)2+|﹣|﹣sin30°.【分析】原式利用零指数幂、负整数指数幂法则,绝对值的代数意义,以及特殊角的三角函数值计算即可求出值.【解答】解:原式=1+4+﹣=5.20.(6分)解二元一次方程组:.【分析】方程组利用加减消元法求出解即可.【解答】解:①+②得:6x=6,解得:x=1,把x=1代入①得:y=﹣1,则方程组的解为.21.(8分)如图,在平面直角坐标系中,△ABC的三个顶点分别是A(1,3),B(4,4),C(2,1).(1)把△ABC向左平移4个单位后得到对应的△A1B1C1,请画出平移后的△A1B1C1;(2)把△ABC绕原点O旋转180°后得到对应的△A2B2C2,请画出旋转后的△A2B2C2;(3)观察图形可知,△A1B1C1与△A2B2C2关于点(﹣2,0)中心对称.【分析】(1)依据平移的方向和距离,即可得到平移后的△A1B1C1;(2)依据△ABC绕原点O旋转180°,即可画出旋转后的△A2B2C2;(3)依据对称点连线的中点的位置,即可得到对称中心的坐标.【解答】解:(1)如图所示,△A1B1C1即为所求;(2)如图所示,△A2B2C2即为所求;(3)由图可得,△A1B1C1与△A2B2C2关于点(﹣2,0)中心对称.故答案为:﹣2,0.22.(8分)阅读下列材料,完成解答:材料1:国家统计局2月28日发布了2019年国民经济和社会发展统计公报,该公报中的如图发布的是全国“2015﹣2019年快递业务量及其增长速度”统计图(如图1).材料2:6月28日,国家邮政局发布的数据显示:受新冠疫情影响,快递业务量快速增长,5月份快递业务量同比增长41%(如图2).某快递业务部门负责人据此估计,2020年全国快递业务量将比2019年增长50%.(1)2018年,全国快递业务量是507.1亿件,比2017年增长了26.6%;(2)2015﹣2019年,全国快递业务量增长速度的中位数是28%;(3)统计公报发布后,有人认为,图1中表示2016﹣2019年增长速度的折线逐年下降,说明2016﹣2019年全国快递业务量增长速度逐年放缓,所以快递业务量也逐年减少.你赞同这种说法吗?为什么?(4)若2020年全国快递业务量比2019年增长50%,请列式计算2020年的快递业务量.【分析】(1)由材料1中的统计图中的信息即可得到结论;(2)由材料1中的统计图的信息即可得到结论;(3)根据统计图中的信息即可得到结论;(4)根据题意列式计算即可.【解答】解:(1)由材料1中的统计图可得:2018年,全国快递业务量是507.1亿件,比2017年增长了26.6%;(2)由材料1中的统计图可得:2015﹣2019年,全国快递业务量增长速度的中位数是28%;(3)不赞同,理由:由图1中的信息可得,2016﹣2019年全国快递业务量增长速度逐年放缓,但是快递业务量却逐年增加;(4)635.2×(1+50%)=852.82,答:2020年的快递业务量为852.82亿件.故答案为:507.1,26.6,28.23.(8分)如图,在菱形ABCD中,点E,F分别是边AD,AB的中点.(1)求证:△ABE≌△ADF;(2)若BE=,∠C=60°,求菱形ABCD的面积.【分析】(1)由SAS证明△ABE≌△ADF即可;(2)证△ABD是等边三角形,得出BE⊥AD,求出AD即可.【解答】(1)证明:∵四边形ABCD是菱形,∴AB=AD,∵点E,F分别是边AD,AB的中点,∴AF=AE,在△ABE和△ADF中,,∴△ABE≌△ADF(SAS);(2)解:连接BD,如图:∵四边形ABCD是菱形,∴AB=AD,∠A=∠C=60°,∴△ABD是等边三角形,∵点E是边AD的中点,∴BE⊥AD,∴∠ABE=30°,∴AE=BE=1,AB=2AE=2,∴AD=AB=2,∴菱形ABCD的面积=AD×BE=2×=2.24.(8分)某学校为丰富同学们的课余生活,购买了一批数量相等的象棋和围棋供兴趣小组使用,其中购买象棋用了420元,购买围棋用了756元,已知每副围棋比每副象棋贵8元.(1)求每副围棋和象棋各是多少元?(2)若该校决定再次购买同种围棋和象棋共40副,且再次购买的费用不超过600元,则该校最多可再购买多少副围棋?【分析】(1)设每副围棋x元,则每副象棋(x﹣8)元,根据420元购买象棋数量=756元购买围棋数量列出方程并解答;(2)设购买围棋m副,则购买象棋(40﹣m)副,根据题意列出不等式并解答.【解答】解:(1)设每副围棋x元,则每副象棋(x﹣8)元,根据题意,得=.解得x=18.经检验x=18是所列方程的根.所以x﹣8=10.答:每副围棋18元,则每副象棋10元;(2)设购买围棋m副,则购买象棋(40﹣m)副,根据题意,得18m+10(40﹣m)≤600.解得m≤25.故m最大值是25.答:该校最多可再购买25副围棋.25.(10分)如图,将一副斜边相等的直角三角板按斜边重合摆放在同一平面内,其中∠CAB =30°,∠DAB=45°,点O为斜边AB的中点,连接CD交AB于点E.(1)求证:A,B,C,D四个点在以点O为圆心的同一个圆上;(2)求证:CD平分∠ACB;(3)过点D作DF∥BC交AB于点F,求证:BO2+OF2=EF•BF.【分析】(1)利用直角三角形斜边的中线等于斜边的一半,判断出OA=OB=OC=OD,即可得出结论;(2)先求出∠COD=150°,利用等腰三角形的性质得出∠ODC=15°,进而求出∠BDC =30°,进而求出∠BCD=45°,即可得出结论;(3)先判断出△DEF∽△BDF,得出DF2=BF•EF,再利用勾股定理得出OD2+OF2=DF2,即可得出结论.【解答】证明:(1)如图,连接OD,OC,在Rt△ABC中,∠ACB=90°,点O是AB 的中点,∴OC=OA=OB,在Rt△ABD中,∠ADB=90°,点O是AB的中点,∴OD=OA=OB,∴OA=OB=OC=OD,∴A,B,C,D四个点在以点O为圆心的同一个圆上;(2)连接OC,OD,由(1)知,OA=OC=OD,∴∠OCD=∠ODC,在Rt△ABC中,∠BAC=30°,∴∠ABC=∠BOC=60°,在Rt△ABD中,∠DAB=45°,∴∠ABD=45°=∠DAB,∴AD=BD,∵点O是AB的中点,∴OD⊥AB,∴∠BOD=90°,∠ODB=∠ADB=45°,∴∠COD=150°,∴∠OCD=∠ODC=15°,∴∠BDC=∠ODB﹣∠ODC=30°,∵∠CBD=∠ABC+∠ABD=105°,∴∠BCD=180°﹣∠CBD﹣∠BDC=45°,∴∠ACD=90°﹣∠BCD=45°=∠BCD,∴CD平分∠ACB;(3)由(2)知,∠BCD=45°,∵∠ABC=60°,∴∠BEC=75°,∴∠AED=75°,∵DF∥BC,∴∠BFD=∠ABC=60°,∵∠ABD=45°,∴∠BDF=180°﹣∠BFD﹣∠ABD=75°=∠AED,∵∠DFE=∠BFD,∴△DEF∽△BDF,∴,∴DF2=BF•EF,连接OD,则∠BOD=90°,OB=OD,在Rt△DOF中,根据勾股定理得,OD2+OF2=DF2,∴OB2+OF2=BF•EF,即BO2+OF2=EF•BF.26.(12分)如图,已知抛物线y=a(x+6)(x﹣2)过点C(0,2),交x轴于点A和点B (点A在点B的左侧),抛物线的顶点为D,对称轴DE交x轴于点E,连接EC.(1)直接写出a的值,点A的坐标和抛物线对称轴的表达式;(2)若点M是抛物线对称轴DE上的点,当△MCE是等腰三角形时,求点M的坐标;(3)点P是抛物线上的动点,连接PC,PE,将△PCE沿CE所在的直线对折,点P落在坐标平面内的点P′处.求当点P′恰好落在直线AD上时点P的横坐标.【分析】(1)将点C坐标代入抛物线解析式中,即可得出结论;(2)分三种情况:直接利用等腰三角形的性质,即可得出结论;(3)先判断出△PQE≌△P'Q'E(AAS),得出PQ=P'Q',EQ=EQ',进而得出P'Q'=n,EQ'=QE=m+2,确定出点P'(n﹣2,2+m),将点P'的坐标代入直线AD的解析式中,和点P代入抛物线解析式中,联立方程组,求解即可得出结论.【解答】解:(1)∵抛物线y=a(x+6)(x﹣2)过点C(0,2),∴2=a(0+6)(0﹣2),∴a=﹣,∴抛物线的解析式为y=﹣(x+6)(x﹣2)=﹣(x+2)2+,∴抛物线的对称轴为直线x=﹣2;(2)如图1,由(1)知,抛物线的对称轴为x=﹣2,∴E(﹣2,0),∵C(0,2),∴OC=OE=2,∴CE=OC=2,∠CED=45°,∵△CME是等腰三角形,∴①当ME=MC时,∴∠ECM=∠CED=45°,∴∠CME=90°,∴M(﹣2,2),②当CE=CM时,∴MM1=CM=2,∴EM1=4,∴M1(﹣2,4),③当EM=CE时,∴EM2=EM3=2,∴M2(﹣2,﹣2),M3(﹣2,2),即满足条件的点M的坐标为(﹣2,﹣2)或(﹣2,4)或(﹣2,2)或(﹣2,﹣2);(3)如图2,由(1)知,抛物线的解析式为y=﹣(x+6)(x﹣2)=﹣(x+2)2+,∴D(﹣2,),令y=0,则(x+6)(x﹣2)=0,∴x=﹣6或x=2,∴点A(﹣6,0),∴直线AD的解析式为y=x+4,过点P作PQ⊥x轴于Q,过点P'作P'Q'⊥DE于Q',∴∠EQ'P'=∠EQP=90°,由(2)知,∠CED=∠CEB=45°,由折叠知,EP'=EP,∠CEP'=∠CEP,∴△PQE≌△P'Q'E(AAS),∴PQ=P'Q',EQ=EQ',设点P(m,n),∴OQ=m,PQ=n,∴P'Q'=n,EQ'=QE=m+2,∴点P'(n﹣2,2+m),∵点P'在直线AD上,∴2+m=(n﹣2)+4①,∵点P在抛物线上,∴n=﹣(m+6)(m﹣2)②,联立①②解得,m=(舍)或m=,即点P的横坐标为.。
广西桂林市2020年中考数学试卷B卷

广西桂林市2020年中考数学试卷B卷姓名:________ 班级:________ 成绩:________一、选择题 (共10题;共20分)1. (2分)如果|﹣2a|=﹣2a,则a的取值范围是()A . a>0B . a≥0C . a≤0D . a<02. (2分)如图,在空白网格内将某一个小正方形涂成阴影部分,且所涂的小正方形与原阴影图形的小正方形至少有一边重合.小红按要求涂了一个正方形,所得到的阴影图形恰好是轴对称图形的概率为()A .B .C .D .3. (2分)(2017·深圳模拟) 支付宝与“快的打车”联合推出优惠,“快的打车”一夜之间红遍大江南北.据统计,2016年“快的打车”账户流水总金额达到147.3亿用科学记数法表示为()A . 1.473×1010B . 14.73×1010C . 1.473×1011D . 1.473×10124. (2分)(2016·云南模拟) 下列计算错误的是()A .B . (﹣2)﹣2=4C .D . 20150=15. (2分) (2017九上·沂源期末) 用甲、乙两种原料配制成某种饮料,已知这两种原料的维生素C含量及购买这两种原料的价格如下表:甲种原料乙种原料维生素C含量(单位•千克)600100原料价格(元•千克)84现配制这种饮料10kg,要求至少含有4200单位的维生素C,若所需甲种原料的质量为x kg,则x应满足的不等式为()A . 600x+100(10﹣x)≥4200B . 8x+4(100﹣x)≤4200C . 600x+100(10﹣x)≤4200D . 8x+4(100﹣x)≥42006. (2分)若关于x的一元二次方程有两个不相等的实数根,则m的取值范围是A .B .C .D .7. (2分) (2016八上·平凉期中) 如图所示,在△ABC中,点D是BC上一点,∠BAD=80°,AB=AD=DC,则∠C的大小为()A . 50°B . 40°C . 20°D . 25°8. (2分)(2017·随州) 如图是某几何体的三视图,这个几何体是()A . 圆锥B . 长方体C . 圆柱D . 三棱柱9. (2分)如图,在菱形ABCD中,AB=2 ,∠C=120°,以点C为圆心的与AB,AD分别相切于点G,H,与BC,CD分别相交于点E,F,若用扇形CEF作一个圆锥的侧面,则这个圆锥的高是()A . 2B . 3C . 2D . 210. (2分)已知抛物线y=x2﹣x﹣1与x轴的一个交点为(m,0),则代数式m2﹣m﹣2013的值是()A . ﹣2012B . ﹣2013C . 2012D . 2013二、填空题 (共9题;共9分)11. (1分)甲乙两人进行射击比赛,在相同条件下各射击10次,他们平均成绩均为8环,10次射击成绩的方差分别是:S甲2=1.5,S乙2=1.2,则射击成绩较稳定的是________.(选填“甲”或“乙”)12. (1分)(2017·蒙自模拟) 函数y= 的自变量取值范围是________.13. (1分)(2017·曲靖模拟) 如图,平行四边形ABCD的对角线互相垂直,要使ABCD成为正方形,还需添加的一个条件是________(只需添加一个即可)14. (1分)(2017·营口模拟) 分解因式:3ax2﹣3ay2=________.15. (1分)(2017·昆都仑模拟) 如图,半径为3的⊙O与Rt△AOB的斜边AB切于点D,交OB于点C,连接CD交直线OA于点E,若∠B=30°,则线段AE的长为________.16. (1分)(2017·齐齐哈尔) 如图,在等腰三角形纸片ABC中,AB=AC=10,BC=12,沿底边BC上的高AD 剪成两个三角形,用这两个三角形拼成平行四边形,则这个平行四边形较长的对角线的长是________.17. (1分)如图,直线y=2x+1分别交于x、y轴于点A、C.P是该直线与双曲线y= (x>0)的交点,PB⊥x轴,B为垂足,设点M与点P在同一个反比例函数的图象上,且点M在直线PB在右则,作MN⊥x轴,N为垂足,当△MNB与△AOC相似时,点M的坐标是________.18. (1分) (2019九下·江都月考) 如图,已知点A的坐标为(,3),AB⊥x轴,垂足为B,连接OA,反比例函数y= (k>O,x>O)的图象与线段OA、OB分别交于点C、D,过点C作CE⊥x轴于E.若AB=3BD,则△COE的面积为________.19. (1分)(2019·贵阳模拟) 如图,将矩形ABCD绕其右下角的顶点按顺时针方向旋转90°至图①位置,继续绕右下角的顶点按顺时针方向旋转90°至图②位置,以此类推,这样连续旋转2017次.若AB=4,AD=3,则顶点A在整个旋转过程中所经过的路径总长为________.三、解答题 (共7题;共93分)20. (10分)(2017·景德镇模拟) 综合题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2020年桂林市初中毕业升学考试试卷数 学(考试用时:120分钟 满分: 120分)注意事项:1.试卷分为试题卷和答题卡两部分,在本试...题.卷上作答无效......。
2.答题前,请认真阅读答题..卡.上的注意事项。
3.考试结束后,将本试卷和答题......卡.一并交回。
一、选择题(共12小题,每小题3分,共36分.在每小题给出的四个选项中只有一项是符合要求的,用2B 铅笔把答题..卡.上对应题目的答案标号涂黑). 1.2011的倒数是( ).A .12011 B .2011 C .2011- D .12011- 2.在实数2、0、1-、2-中,最小的实数是( ).A .2B .0C .1-D .2-3.下面四个图形中,∠1=∠2一定成立的是( ).4.下列图形分别是桂林、湖南、甘肃、佛山电视台的台徽,其中为中心对称图形的是( ).5.下列运算正确的是( ).A . 22232x x x -= B .22(2)2a a -=-C .222()a b a b +=+ D .()2121a a --=--6.如图,已知Rt △ABC 中,∠C =90°,BC =3, AC =4, 则sinA 的值为( ).A .34B .43 C .35 D .457.如图,图1是一个底面为正方形的直棱柱;现将图1切割成图2的几何体,则图2的 俯视图是( ).8.直线1y kx =-一定经过点( ).A .(1,0)B .(1,k )C .(0,k )D .(0,-1) 9.下面调查中,适合采用全面调查的事件是( ).A .对全国中学生心理健康现状的调查.B .对我市食品合格情况的调查.C .对桂林电视台《桂林板路》收视率的调查.D .对你所在的班级同学的身高情况的调查.10.若点 P (a ,a -2)在第四象限,则a 的取值范围是( ). A .-2<a <0 B .0<a <2 C .a >2 D .a <0 11.在平面直角坐标系中,将抛物线223y x x =++绕着它与y 轴的交点旋转180°,所得抛物线的解析式是( ).A .2(1)2y x =-++ B .2(1)4y x =--+ C .2(1)2y x =--+ D .2(1)4y x =-++12.如图,将边长为a 的正六边形A 1 A 2 A 3 A 4 A 5 A 6在直线l 上由图1的位置按顺时针方向向右作无滑动滚动,当A 1第一次滚动到图2位置时,顶点A 1所经过的路径的长为( ). A .4233a π+ B . 8433a π+ C . 433a π+ D . 4236a π+二、填空题(共6小题,每小题3分,共18分,请将答案填在答题..卡.上). 13.因式分解:22a a += .14.我市在临桂新区正在建设的广西桂林图书馆、桂林博物馆、桂林大剧院及文化广场,建成后总面积达163500平方米,将成为我市“文化立市”和文化产业大发展的新标志,把163500平方米用科学记数法可表示为 平方米.15.当2x =-时,代数式21x x -的值是 .16.如图,等腰梯形ABCD 中,AB ∥DC,BE ∥AD , 梯形ABCD的周长为26,DE =4,则△BEC 的周长为 .17.双曲线1y 、2y 在第一象限的图像如图,14y x=, 过1y 上的任意一点A ,作x 轴的平行线交2y 于B , 交y 轴于C ,若1AOB S ∆=,则2y 的解析式是 . 18.若111a m=-,2111a a =-,3211a a =-,… ;则2011a 的值为 .(用含m的代数式表示)三、解答题(本大题共8题,共66分,请将答案写在答题..卡.上). 19.(本题满分6分)计算:01(21)22452tan -︒+--+-20.(本题满分6分)解二元一次方程组:35382x y y x =-⎧⎨=-⎩21.(本题满分8分)求证:角平分线上的点到这个角的两边距离相等.已知: 求证: 证明: 22.(本题满分8分)“初中生骑电动车上学”的现象越来越受到社会的关注,某校利用“五一”假期,随机抽查了本校若干名学生和部分家长对“初中生骑电动车上学”现象的看法,统计整理制作了如下的统计图,请回答下列问题: (1)这次抽查的家长总人数为 ; (2)请补全条形统计图和扇形统计图;(3)从这次接受调查的学生中,随机抽查一个学生恰好抽到持“无所谓”态度的概率是 .3.(本题满分8分)某市为争创全国文明卫生城,2020年市政府对市区绿化工程投入的资金是2020万元,2020年投入的资金是2420万元,且从2020年到2020年,两年间每年投入资金的年平均增长率相同.(1)求该市对市区绿化工程投入资金的年平均增长率;(2)若投入资金的年平均增长率不变,那么该市在2020年需投入多少万元? 24.(本题满分8分)某校志愿者团队在重阳节购买了一批牛奶到“夕阳红”敬老院慰问孤寡老人,如果给每个老人分5盒,则剩下38盒,如果给每个老人分6盒,则最后一个老人不足5盒,但至少分得一盒.(1)设敬老院有x 名老人,则这批牛奶共有多少盒?(用含x 的代数式表示). (2)该敬老院至少有多少名老人?最多有多少名老人?25.(本题满分10分)如图,在锐角△ABC 中,AC 是最短边;以AC 中点O 为圆心,12AC 长为半径作⊙O ,交BC 于E ,过O 作OD ∥BC 交⊙O 于D ,连结AE 、AD 、DC .(1)求证:D 是»AE 的中点; (2)求证:∠DAO =∠B +∠BAD ; (3)若12CEF OCD S S ∆∆=,且AC =4,求CF 的长.26.(本题满分12分)已知二次函数21342y x x =-+的图象如图. (1)求它的对称轴与x 轴交点D 的坐标;(2)将该抛物线沿它的对称轴向上平移,设平移后的抛物线与x 轴,y 轴的交点分别为A 、B 、C 三点,若∠ACB =90°,求此时抛物线的解析式;(3)设(2)中平移后的抛物线的顶点为M ,以AB 为直径,D 为圆心作⊙D ,试判断直线CM 与⊙D 的位置关系,并说明理由.① ②35382x y y x =-⎧⎨=-⎩ 2020年桂林市初中毕业升学考试数学参考答案及评分标准一、选择题: 题号 1 2 3 4 5 6 7 8 9 10 11 12 答案 A D BCAC CD D B B A二、填空题:13.(2)a a + 14.51.63510⨯ 15.43- 16.18 17.26y x =18.11m- 三、解答题:19.(本题满分 6分)解:原式=112122--⨯+ ………4分(求出一个值给1分) =12……………………6分20.(本题满分6分)解: 把①代入②得:382(35)y y =-- ……………………1分2y = ……………………3分把2y =代入①可得:325x =⨯- ……………………4分1x = ……………………5分所以此二元一次方程组的解为12x y =⎧⎨=⎩. ……………………6分21.(本题满分8分)已知:如图,OC 是∠AOB 的平分线,P 是OC 上任意一点,PE ⊥OA ,PF ⊥OB ,垂足分别为E 、F ……………2分求证:PE =PF …………………………………3分 证明:∵OC 是∠AOB 的平分线∴∠POE =∠POF …………………4分 ∵PE ⊥OA ,PF ⊥OB∴∠PEO =∠PFO ……………………5分 又∵OP =OP ………………6分∴△POE ≌△POF ……………………7分 ∴PE =PF ……………………8分22.(本题满分8分)解:(1)100 ; ………………2分(2)条形统计图:70, ………………4分扇形统计图:赞成:10﹪,反对:70﹪; ………………6分(3)25. ………………8分 23.(本题满分8分) 解:(1)设该市对市区绿化工程投入资金的年平均增长率为x , ………………1分根据题意得,22000(1)2420x += ……………3分得 110%x =,2 2.1x =-(舍去) …………5分答:该市对市区绿化工程投入资金的年平均增长率为10﹪. …………6分 (2)2020年需投入资金:22420(110%)2928.2⨯+=(万元) …………7分 答:2020年需投入资金2928.2万元. …………8分 24.(本题满分8分) 解:(1)牛奶盒数:(538)x +盒 …………1分 (2)根据题意得:5386(1)55386(1)1x x x x +--<⎧⎨+--≥⎩ …………4分∴不等式组的解集为:39<x ≤43 …………6分 ∵x 为整数∴x =40,41,42,43答:该敬老院至少有40名老人,最多有43名老人. …………8分25.(本题满分10分)证明:(1)∵AC 是⊙O 的直径∴AE ⊥BC …………1分 ∵OD ∥BC∴AE ⊥OD …………2分∴D 是»AE 的中点 …………3分 (2)方法一:如图,延长OD 交AB 于G ,则OG ∥BC …4分 ∴∠AGD =∠B∵∠ADO =∠BAD +∠AGD …………5分 又∵OA =OD∴∠DAO =∠ADO∴∠DAO =∠B +∠BAD …………6分 方法二:如图,延长AD 交BC 于H …4分 则∠ADO =∠AHC∵∠AHC =∠B +∠BAD …………5分 ∴∠ADO =∠B +∠BAD 又∵OA =OD∴∠DAO =∠B +∠BAD …………6分(3) ∵AO =OC ∴12OCD ACD S S ∆∆=∵12CEF OCD S S ∆∆= ∴14CEFACDSS ∆∆= …………7分 ∵∠ACD =∠FCE ∠ADC =∠FEC =90° ∴△ACD ∽△FCE …………………8分∴2()CEF ACD S CF S AC ∆∆= 即: 21()44CF = …………9分 ∴CF =2 …………10分26.(本题满分12分) 解: (1)由21342y x x =-+得 32bx a=-= …………1分 ∴D(3,0)…………2分(2)方法一:如图1, 设平移后的抛物线的解析式为21342y x x k =-++ …………3分则C (0,)k OC =k令0y = 即 213042x x k -++=得 1349x k =++ 2349x k =-+ …………4分∴A (349,0)k -+,B (349,0)k ++∴22(493349)1636AB k k k =++-++=+………5分222222(349)(349)AC BC k k k k +=+-+++++22836k k =++……………………6分 ∵222AC BC AB +=即: 228361636k k k ++=+得 14k = 20k =(舍去) ……………7分∴抛物线的解析式为213442y x x =-++ ……………8分方法二: ∵ 21342y x x =-+ ∴顶点坐标93,4⎛⎫⎪⎝⎭设抛物线向上平移h 个单位,则得到()0,C h ,顶点坐标93,4M h ⎛⎫+ ⎪⎝⎭…………3分 ∴平移后的抛物线: ()219344y x h =--++……………………4分 当0y =时, ()2193044x h --++=, 得 1349x h =-+ 1349x h =++∴ A (349,0)h -+ B (349,0)h ++……………………5分∵∠ACB =90° ∴△AOC ∽△COB ∴2OC =OA ·OB ……………………6分()()2493493h h h =+-++ 得 14h =,()20h =舍去…………7分∴平移后的抛物线: ()()22191253434444y x x =--++=--+…………8分(3)方法一:如图2, 由抛物线的解析式213442y x x =-++可得 A (-2 ,0),B (8,0) ,C (4,0) ,M 25(3,)4…………9分过C 、M 作直线,连结CD ,过M 作MH 垂直y 轴于H , 则3MH = ∴2225625()416DM ==22222252253(4)416CM MH CH =+=+-=在Rt △COD 中,CD =22345+==AD∴点C 在⊙D 上 …………………10分∵2225625()416DM ==2222225256255()16416CD CM +=+==……11分 ∴222DM CM CD =+∴△CDM 是直角三角形,∴CD ⊥CM ∴直线CM 与⊙D 相切 …………12分方法二:如图3, 由抛物线的解析式可得A (-2 ,0),B (8,0) ,C (4,0) ,M 25(3,)4…………9分 作直线CM ,过D 作DE ⊥CM 于E , 过M 作MH 垂直y 轴于H ,则3MH =,254DM =, 由勾股定理得154CM = ∵DM ∥OC∴∠MCH=∠EMD∴Rt △CMH ∽Rt △DME …………10分∴DE MDMH CM=得 5DE = …………11分 由(2)知10AB = ∴⊙D 的半径为5∴直线CM 与⊙D 相切 …………12分。
