最值问题(费马点)知识讲解
专题67 费马点中三线段模型与最值问题(解析版)

专题67 费马点中三线段模型与最值问题【专题说明】费马点”是指位于三角形内且到三角形三个顶点距高之和最短的点。
主要分为两种情况:(1)当三角形三个内角都小于120°的三角形,通常将某三角形绕点旋转60度,从而将“不等三爪图”中三条线段转化在同一条直线上,利用两点之间线段最短解决问题。
(2)当三角形有一个内角大于120°时,费马点就是此内角的顶点.费马点问题解题的核心技巧:旋转60° 构造等边三角形将“不等三爪图”中三条线段转化至同一直线上利用两点之间线段最短求解问题【模型展示】问题:在△ABC内找一点P,使得P A+PB+PC最小.APB C【分析】在之前的最值问题中,我们解决的依据有:两点之间线段最短、点到直线的连线中垂线段最短、作对称化折线段为直线段、确定动点轨迹求最值等.(1)如图,分别以△ABC中的AB、AC为边,作等边△ABD、等边△ACE.(2)连接CD、BE,即有一组手拉手全等:△ADC≌△ABE.(3)记CD、BE交点为P,点P即为费马点.(到这一步其实就可以了)(4)以BC 为边作等边△BCF ,连接AF ,必过点P ,有∠P AB =∠BPC =∠CP A =120°.在图三的模型里有结论:(1)∠BPD =60°;(2)连接AP ,AP 平分∠DPE .有这两个结论便足以说明∠P AB =∠BPC =∠CP A =120°.原来在“手拉手全等”就已经见过了呀,只是相逢何必曾相识!【精典例题】1、如图,四边形ABCD 是菱形,AB=4,且∠ABC=∠ABE=60°,G 为对角线BD (不含B 点)上任意一点,将∠ABG 绕点B 逆时针旋转60°得到∠EBF ,当AG+BG+CG 取最小值时EF 的长( )A . 2B .C . 3D . 3【答案】D【详解】解:如图,∠将∠ABG绕点B逆时针旋转60°得到∠EBF,∠BE=AB=BC,BF=BG,EF=AG,∠∠BFG是等边三角形.∠BF=BG=FG,.∠AG+BG+CG=FE+GF+CG.根据“两点之间线段最短”,∠当G点位于BD与CE的交点处时,AG+BG+CG的值最小,即等于EC的长,过E点作EF∠BC交CB的延长线于F,∠∠EBF=180°-120°=60°,∠BC=4,∠BF=2,,在Rt∠EFC中,∠EF2+FC2=EC2,∠∠CBE=120°,∠∠BEF=30°,∠∠EBF=∠ABG=30°,∠EF=BF=FG,∠EF=13, 故选:D .2、如图,将ABC ∆绕点A 逆时针旋转60°得到ADE ∆,DE 与BC 交于点P ,可推出结论:PA PC PE +=问题解决:如图,在MNG ∆中,6MN =,75M ∠=︒,MG =O 是MNG ∆内一点,则点O 到MNG ∆三个顶点的距离和的最小值是___________【答案】【详解】如图,将∠MOG 绕点M 逆时针旋转60°,得到∠MPQ ,显然∠MOP 为等边三角形,∠,OM +OG =OP +PQ ,∠点O 到三顶点的距离为:ON +OM +OG =ON +OP +PQ ,∠当点N 、O 、P 、Q 在同一条直线上时,有ON +OM +OG 最小,此时,∠NMQ =75°+60°=135°,过Q 作QA∠NM 交NM 的延长线于A ,则∠MAQ=90°,∠∠AMQ =180°-∠NMQ=45°,∠MQ =MG =∠AQ =AM =MQ•cos45°=4,∠NQ ==故答案为:3、如图,四边形 ABCD 是菱形,A B =6,且∠ABC =60° ,M 是菱形内任一点,连接AM ,BM ,CM ,则AM +BM +CM 的最小值为________.【答案】【详解】将∠BMN 绕点B 顺时针旋转60度得到∠BNE ,∠BM =BN ,∠MBN =∠CBE =60°,∠MN=BM∠MC=NE∠AM +MB +CM =AM +MN +NE .当A 、M 、N 、E 四点共线时取最小值AE .∠AB =BC =BE =6,∠ABH =∠EBH =60°,∠BH ∠AE ,AH =EH ,∠BAH =30°,∠BH =12AB =3,AH =∠AE =2AH =故答案为4、如图,∠ABC中,∠BAC=30°且AB=AC,P是底边上的高AH上一点.若AP+BP+CP的最小值为,则BC=_____.【详解】如图将∠ABP绕点A顺时针旋转60°得到∠AMG.连接PG,CM.∠AB=AC,AH∠BC,∠∠BAP=∠CAP ,∠PA=PA ,∠∠BAP∠∠CAP (SAS ),∠PC=PB ,∠MG=PB ,AG=AP ,∠GAP=60°,∠∠GAP 是等边三角形,∠PA=PG ,∠PA+PB+PC=CP+PG+GM ,∠当M ,G ,P ,C 共线时,PA+PB+PC 的值最小,最小值为线段CM 的长,∠AP+BP+CP 的最小值为,∠∠BAM=60°,∠BAC=30°,∠∠MAC=90°,∠AM=AC=2,作BN∠AC 于N .则BN=12AB=1,CN=25、如图,四边形ABCD 是正方形,∠ABE 是等边三角形,M 为对角线BD (不含B 点)上任意一点,将BM 绕点B 逆时针旋转60°得到BN ,连接EN 、AM 、CM.∠ 求证:∠AMB∠∠ENB ;∠ ∠当M 点在何处时,AM +CM 的值最小;∠当M 点在何处时,AM +BM +CM 的值最小,并说明理由;∠ 当AM +BM +CM 的最小值为13 时,求正方形的边长.【答案】(1)∠AMB∠∠ENB ,证明略。
加权费马点最值问题通法

加权费马点最值问题通法说起加权费马点这个话题,真是个让人又爱又恨的东西。
听起来高大上,其实就像吃了一口好吃的蜜饯,酸甜苦辣都有。
不过,你要知道,加权费马点最值问题就是找一个让大家都满意的位置,像是咱们选个合适的餐厅,总得让每个人都能吃得开心,对吧?想象一下,你和一群小伙伴去吃饭,大家的口味不同。
有人爱吃辣,有人偏爱清淡,有人则是“只要能填饱肚子就好”。
这就得讲究一下选择的艺术了。
我们把这堆人想象成几个点,咱们的目标是找一个“权重”最合适的点,简单说就是让每个人都尽量满意。
比如说,你有个朋友特别爱吃麻辣小龙虾,那他在你心中的“权重”就比其他人高。
于是,咱们就得在众多美食中找到那个最合适的位置,像是在寻宝一样,瞄准了就要狠狠抓住。
当我们在解决这个问题时,得考虑每个点的“重量”。
有些点的重要性就像天上掉下来的星星,闪闪发光,显得特别重要;而有些点呢,像是地上不起眼的小石头,重要性就差了那么一截。
可不是说这些小点就不重要,它们也有它们的位置,只是相对而言,没那么显眼而已。
再说说距离,简直就是个无形的魔咒,时刻在影响我们的选择。
比如说,咱们选餐厅时,不光要考虑菜品,还得看它离我们有多远。
谁愿意在外面转悠半天,结果还是没找到地方呢?所以,距离的概念在这儿就像个大Boss,得认真对待。
想象一下,你在规划一次旅行,心里想着“哎呀,去哪个地方最合适呢?”这时候,加权费马点就像你旅行计划里的GPS,给你指引方向。
选点的时候,脑海中不断回响的就是“这个点离我近,那个点有好吃的,咱们得好好算一算。
”于是,一路走来,数着每个地方的得失,找到了那个最合适的点,真是让人感到一阵欣喜。
搞清楚这些概念后,我们就能开始实践了。
你可以把这当成一次小小的实验,先在纸上标记出所有的点,像画地图一样,轻轻松松。
然后,把每个点的权重和距离都标出来,像在做一份特别的菜单。
这样,你就能清晰地看到哪个点更有优势,哪个又是个“空城计”,让你白白浪费时间。
费马点问题知识点

费马点问题知识点费马点问题是一个深奥而有趣的数学难题,涉及到费马大定理的相关内容。
费马大定理是说:对于任何大于2的整数n,不存在任何整数a、b、c,使得a^n +b^n = c^n成立。
这个问题最初由法国数学家费马在17世纪提出,并直到1994年才被英国数学家安德鲁·怀尔斯证明。
费马点问题是针对这个定理的一个特殊情况展开的。
费马点问题是指在三维空间中,给定一系列点,找出其中距离其他点最近的点。
换句话说,对于给定的点集合,找出其中的一个点,使得该点到其他点的距离最小。
这个问题在计算几何学中被广泛讨论和应用。
解决费马点问题的方法可以通过一步一步的思考来完成。
下面将介绍一种常见的解决方法:第一步:确定问题首先,我们需要明确问题的描述和要求。
费马点问题要求找到一个点,使得该点到其他点的距离最小。
第二步:理解问题在解决问题之前,我们需要理解问题的背景和相关知识。
费马点问题涉及到距离的计算和最小值的确定。
第三步:分析问题接下来,我们需要对问题进行分析。
费马点问题可以通过计算每个点到其他点的距离,并找到最小距离对应的点来解决。
这个过程可以使用数学公式和计算方法来完成。
第四步:解决问题在分析完问题之后,我们可以开始解决费马点问题。
首先,我们需要计算每个点到其他点的距离,可以使用欧几里得距离公式来计算。
然后,找到最小距离对应的点,并将其作为费马点。
第五步:验证解决方案解决问题之后,我们需要验证解决方案的准确性。
可以通过重新计算费马点到其他点的距离,并验证其是否是最小距离。
第六步:总结最后,我们需要总结问题的解决过程和结果。
费马点问题是一个有趣且复杂的数学难题,通过分析和计算,我们可以找到最佳解决方案。
这篇文章介绍了费马点问题的基本知识点和解决方法。
通过一步一步的思考和分析,我们可以解决这个有趣的数学难题。
费马点问题在计算几何学中有广泛的应用,对于理解和掌握相关知识具有重要意义。
希望本文对读者有所帮助,引起大家对数学问题的兴趣和思考。
费马点最值问题(解析版)

费马点最值问题一.模型例题(共4小题)1.问题的提出:如果点P 是锐角ABC ∆内一动点,如何确定一个位置,使点P 到ABC ∆的三顶点的距离之和PA PB PC ++的值为最小?问题的转化:把APC ∆绕点A 逆时针旋转60度得到△AP C '',连接PP ',这样就把确定PA PB PC ++的最小值的问题转化成确定BP PP P C +'+''的最小值的问题了,请你利用图1证明:PA PB PC BP PP P C ++=+'+''.问题的解决:当点P 到锐角ABC ∆的三顶点的距离之和PA PB PC ++的值为最小时,请你用一定的数量关系刻画此时的点P 的位置120APB APC ∠=∠=︒.问题的延伸:如图2是有一个锐角为30︒的直角三角形,如果斜边为2,点P 是这个三角形内一动点,请你利用以上方法,求点P 到这个三角形各顶点的距离之和的最小值.【解答】解:问题的转化:如图1,由旋转得:60PAP '∠=︒,PA P A '=,APP '∴∆是等边三角形,PP PA '∴=,PC P C '= ,PA PB PC BP PP P C ∴++=+'+''.问题的解决:满足:120APB APC ∠=∠=︒时,PA PB PC ++的值为最小;理由是:如图2,把APC ∆绕点A 逆时针旋转60度得到△AP C '',连接PP ',由“问题的转化”可知:当B 、P 、P '、C '在同一直线上时,PA PB PC ++的值为最小,120APB ∠=︒ ,60APP '∠=︒,180APB APP '∴∠+∠=︒,B ∴、P 、P '在同一直线上,由旋转得:120AP C APC ''∠=∠=︒,60AP P '∠=︒ ,180AP C AP P '''∴∠+∠=︒,P ∴、P '、C '在同一直线上,B ∴、P 、P '、C '在同一直线上,∴此时PA PB PC ++的值为最小,故答案为:120APB APC ∠=∠=︒;问题的延伸:如图3,Rt ACB ∆中,2AB = ,30ABC ∠=︒,1AC ∴=,BC =把BPC ∆绕点B 逆时针旋转60度得到△BP C '',连接PP ',当A 、P 、P '、C '在同一直线上时,PA PB PC ++的值为最小,由旋转得:BP BP '=,PBP '∠=,PC P C ''=,BC BC '=,BPP ∴∆'是等边三角形,PP PB '∴=,30ABC APB CBP APB C BP ''∠=∠+∠=∠+∠=︒ ,90ABC '∴∠=︒,由勾股定理得:AC '==,PA PB PC PA PP P C AC ''''∴++=++==则点P .2.如图,ABC ∆中,AB AC =,点P 为ABC ∆内一点,120APB BAC ∠=∠=︒.若4AP BP +=,则PC 的最小值为()A .2B .23C .5D .3【解答】解:把APB ∆绕点A 逆时针旋转120︒得到△AP C ',作AD PP ⊥'于D ,则AP AP =',120PAP ∠'=︒,120AP C APB ∠'=∠=︒,30AP P ∴∠'=︒,3PP ∴'=,90PP C ∠'=︒,4AP BP += ,4BP PA ∴=-,在Rt △PP C '中,22222(3)(4)4(1)12PC P P P C PA PA PA ='+'+--+,则PC 1223=,故选:B .3.如图,2的等边ABC ∆,平面内存在点P ,则3PA PB PC +的取值范围为大于22.【解答】解:如图,将BPC ∆绕点B 顺时针旋转120︒,得△BP C '',连接PP ',过点B 作BD PP ⊥'于点D ,ABC ∆ 是等边三角形,60ABC ∴∠=︒,AB BC BC =='=,AC AB BC ∴'=+'=120CBC PBP ∠'=∠'=︒ ,180ABC ABC CBC ∴∠'=∠+∠'=︒,∴点A ,B ,C '在同一条直线上,BP BP =' ,120PBP ∠'=︒,BD PP ⊥',30BPP BP P ∴∠'=∠'=︒,PD ∴=,2PP PD ∴'==,PA PP PC PA PC AC ∴+'+=++>',因为等边三角形的边长为PA PC ∴+的取值范围为大于等于故答案为:大于等于.4.问题探究将几何图形按照某种法则或规则变换成另一种几何图形的过程叫做几何变换.旋转变换是几何变换的一种基本模型.经过旋转,往往能使图形的几何性质明白显现.题设和结论中的元素由分散变为集中,相互之间的关系清楚明了,从而将求解问题灵活转化.问题提出:如图1,ABC ∆是边长为1的等边三角形,P 为ABC ∆内部一点,连接PA 、PB 、PC ,求PA PB PC ++的最小值.方法分析:通过转化,把由三角形内一点发出的三条线段(星型线)转化为两定点之间的折线(化星为折),再利用“两点之间线段最短”求最小值(化折为直).问题解决:如图2,将BPA ∆绕点B 逆时针旋转60︒至△BP A '',连接PP '、A C ',记A C '与AB 交于点D ,易知1BA BA BC '===,120A BC A BA ABC ''∠=∠+∠=︒.由BP BP '=,60P BP '∠=︒,可知△P BP '为正三角形,有PB P P '=.故PA PB PC P A P P PC A C '''++=++.因此,当A '、P '、P 、C 共线时,PA PB PC ++有最小值是学以致用:(1)如图3,在ABC ∆中,30BAC ∠=︒,4AB =,3CA =,P 为ABC ∆内部一点,连接PA 、PB 、PC ,则PA PB PC ++的最小值是5.(2)如图4,在ABC ∆中,45BAC ∠=︒,3AB CA ==,P 为ABC ∆内部一点,连接PA 、PB 、PC ,PB PC ++的最小值.(3)如图5,P 是边长为2的正方形ABCD 内一点,Q 为边BC 上一点,连接PA 、PD 、PQ ,求PA PD PQ ++的最小值.【解答】解:(1)如图3中,将APC ∆绕点A 逆时针旋转60︒得到AFE ∆,易知AFP ∆是等边三角形,90EAB ∠=︒,在Rt EAB ∆中,5BE ==,PA PB PC EF FP PB BE ++=++ ,5PA PB PC ∴++,PA PB PC ∴++的最小值为5.故答案为5.(2)如图4中,将APB ∆绕点A 逆时针旋转90︒得到AFE ∆,易知AFP ∆是等腰直角三角形,135EAB ∠=︒,作EH BA ⊥交BA 的延长线于H .在Rt EAH ∆中,90H ∠=︒ ,45EAH ∠=︒,AE AB ==2EH AH ∴==,在Rt EHC ∆中,EC ==PB PC FP EF PC CE ++=++,∴PB PC ++,∴PB PC ++(3)如图5中,将APD∆是等边三角形,∆绕点A逆时针旋转60︒得到AFE∆,则易知AFP作EH BC⊥于H,交AD于G.,PA PD PQ EF FP PQ EH++=++易知sin60=⋅︒=2EG AE==,GH AB∴=+EH2∴++,PA PD PQ2∴++2+.PA PD PQ二.同步练习(共20小题)5.法国数学家费马提出:在ABC∆内存在一点P,使它到三角形顶点的距离之和最小.人们称这个点为费马点,此时PA PB PC∆中,费马点P满足++的值为费马距离.经研究发现:在锐角ABCPC=,60∠=︒,则ABCPA=,4∆的费马点,且3APB BPC CPA120∠=∠=∠=︒,如图,点P为锐角ABC费马距离为7+【解答】解:如图:120APB BPC CPA∠=∠=∠=,60ABC∠=︒,1360∴∠+∠=︒,1260∠+∠=︒,2460∠+∠=︒,14∴∠=∠,23∠=∠,BPC APB∴∆∆∽∴PC PB PB PA=,即212PB=PB∴=.7PA PB PC∴++=+故答案为:7+.6.在ABC∆中,90ACB∠=︒,点P为ABC∆内一点.(1)如图1,连接PB,PC,将BCP∆沿射线CA方向平移,得到DAE∆,点B,C,P的对应点分别为点D,A,E,连接CE.如果BP CE⊥,3BP=,6AB=,则CE=(2)如图2,连接PA,PB,PC,当8AC BC==时,求PA PB PC++的最小值.【解答】解:(1)如图1,连接BD、CD,BCP ∆ 沿射线CA 方向平移,得到DAE ∆,//BC AD ∴且BC AD =,90ACB ∠=︒ ,∴四边形BCAD 是矩形,6CD AB ∴==,3BP = ,3DE BP ∴==,BP CE ⊥ ,//BP DE ,DE CE ∴⊥,∴在Rt DCE ∆中,CE ===;故答案为:(2)如图2所示,以点A 为旋转中心,将ABP ∆顺时针旋转60︒得到AMN ∆,连接BN .由旋转可得,AMN ABP ∆≅∆,MN BP ∴=,PA AM =,60PAM BAN ∠=︒=∠,AB AN =,PAM ∴∆、ABN ∆都是等边三角形,PA PM ∴=,PA PB PC CP PM MN ∴++=++,当8AC BC ==时,AB =,当C 、P 、M 、N 四点共线时,由CA CB =,NA NB =可得CN 垂直平分AB ,12AQ AB CQ ∴==,NQ ==,∴此时CN CP PM MN PA PB PC =++=++=+.即PA PB PC ++的最小值为+.7.如图,在ABC ∆中,3AB =,2AC =,60BAC ∠=︒,P 为ABC ∆内一点,则PA PB PC ++的最小值为【解答】解:如图,将ABP ∆绕着点A 逆时针旋转60︒,得到AEH ∆,连接EP ,CH ,过点C 作CN AH ⊥,交HA 的延长线于N ,ABP AHE ∴∆≅∆,BAP HAE ∴∠=∠,AE AP =,3AH AB ==,60BAH ∠=︒,60HAB EAP ∴∠=∠=︒,AEP ∴∆是等边三角形,AE AP EP ∴==,AP BP PC PC EP EH ∴++=++,∴当点H ,点E ,点P ,点C 共线时,PA PB PC ++有最小值HC ,18060CAN BAH BAC ∠=︒-∠-∠=︒ ,CN AN ⊥,30ACN ∴∠=︒,112AN AC ∴==,CN ==,4HN AH AN ∴=+=,HC ∴=,PA PB PC ∴++,8.如图,ABC ∆中,30ABC ∠=︒,5AB =,6BC =,P 是ABC ∆内部的任意一点,连接PA 、PB 、PC ,则PA PB PC ++【解答】解:如图,以BP 为边作等边三角形BPD ,将BPC ∆绕点B 顺时针旋转60︒,得到BDC '∆,连接AC ',BPD ∆ 是等边三角形,BP BD DP ∴==,60PBD ∠=︒,将BPC ∆绕点B 顺时针旋转60︒,PC C D '∴=,PBC DBC '∠=∠,6BC BC '==,603090ABC ABP PBD DBC PBD ABC PBC ''∴∠=∠+∠+∠=∠+∠+∠=︒+︒=︒,PA PB PC PA PD DC '++=++ ,∴当点A ,点P ,点D ,点C '共线时,PA PB PC ++有最小值为PC ',PC '∴===,9.如图,在ABC ∆中,90ACB ∠=︒,点P 为ABC ∆内一点,连接PA 、PB 、PC ,当3AC =,6AB =时,则PA PB PC ++的最小值是【解答】解:如图所示,以点A 为旋转中心,将ABP ∆顺时针旋转60︒得到ANM ∆,连接BN .由旋转可得,AMN APB ∆≅∆,MN BP ∴=,PA AM =,60PAM BAN ∠=︒=∠,AB AN =,PAM ∴∆、ABN ∆都是等边三角形,PA PM ∴=,PA PB PC CP PM MN ∴++=++,当3AC =,6AB =时,BC =,1sin 2ABC ∴∠=,30ABC ∴∠=︒,60ABN ∠=︒ ,90CBN ∴∠=︒当C 、P 、M 、N 四点共线时,PA PB PC ++的值最小,最小值CN ===,故答案为:.10.已知,如图在ABC ∆中,30ACB ∠=︒,5BC =,6AC =,在ABC ∆内部有一点D ,连接DA 、DB 、DC ,则DA DB ++【解答】解:如图,过点C 作CE CD ⊥,且CE CD =,连接DE ,将ADC ∆绕点C 逆时针旋转90︒得到FEC ∆,连接FB ,过点F 作FH BC ⊥,交BC 的延长线于H ,CE CD ⊥ ,CE CD =,DE ∴=,将ADC ∆绕点C 逆时针旋转90︒得到FEC ∆,EF AD ∴=,90ACF ∠=︒,6CF AC ==,DA DB DB EF DE ∴++=++,∴当点F ,点E ,点D ,点B 共线时,DA DB ++有最小值为FB ,18060FCH ACF ACB ∠=︒-∠-∠=︒ ,30CFH ∴∠=︒,132CH CF ∴==,FH ==,BF ∴==11.如图,在ABC ∆中,30BAC ∠=︒,AC =,8AB =,点D 在ABC ∆内,连接DA 、DB 、DC ,则DC DB ++的最小值是【解答】解:如图,将ADB ∆绕点A 顺时针旋转120︒得到AEF ∆,连接DE ,CF ,过点F 作FH CA ⊥交CA的延长线于H .AD AE = ,120DAE ∠=︒,BD EF =,DE ∴=,DC DB DA DC DE EF ∴++=++,CD DE EF CF ++ ,在Rt ABC ∆中,90ACB ∠=︒,8AB =,30BAC ∠=︒,cos30AB AB ∴=⋅︒=在Rt AFH ∆中,90H ∠=︒,8AF AB ==,30FAH ∠=︒,142FH AF ∴==,AH ==,CH AC AH ∴=+=,CF ∴===,CD DB ∴+,CF ∴的最小值为.故答案为:.12.如图,ABC ∆中,30ABC ∠=︒,4AB =,5BC =,P 是ABC ∆内部的任意一点,连接PA ,PB ,PC ,则PA PB PC ++【解答】解:如图,将ABP ∆绕着点B 逆时针旋转60︒,得到DBE ∆,连接EP ,CD ,ABP DBE∴∆≅∆ABP DBE ∴∠=∠,4BD AB ==,60PBE ∠=︒,BE PE =,AP DE =,BPE ∴∆是等边三角形EP BP∴=AP BP PC PC EP DE∴++=++∴当点D ,点E ,点P ,点C 共线时,PA PB PC ++有最小值CD30ABC ABP PBC∠=︒=∠+∠ 30DBE PBC ∴∠+∠=︒90DBC ∴∠=︒CD ∴==,13.如图,P 为正方形ABCD 内的动点,若2AB =,则PA PB PC ++【解答】解:将BPC ∆绕点B 顺时针旋转60︒,得到△BP C '',BP BP '∴=,60PBP '∠=︒,BPC ∆≅△BP C '',BPP '∴∆是等边三角形,PC P C ''=,PBC P BC ''∠=∠,2BC BC '==,BP PP '∴=,PA PB PC AP PP P C '''∴++=++,∴当AP ,PP ',P C ''在一条直线上,PA PB PC ++有最小值,最小值是AC '的长,60150ABP PBP P BC ABP PBC '''∠+∠+∠=︒+∠+∠=︒ ,30EBC ∴∠=︒,1EC '∴=,BE '==,2AE ∴=+,AF ∴===,14.如图,在边长为6的正方形ABCD 中,点M ,N 分别为AB 、BC 上的动点,且始终保持BM CN =.连接MN ,以MN 为斜边在矩形内作等腰Rt MNQ ∆,若在正方形内还存在一点P ,则点P 到点A 、点D 、点Q 的距离之和的最小值为3+【解答】解:设BM x =,则6BN x =-,222MN BM BN =+ ,2222(6)2(3)18MN x x x ∴=+-=-+,∴当3x =时,MN 最小,此时Q 点离AD 最近,3BM BN == ,Q ∴点是AC 和BD 的交点,22AQ DQ AD ∴===,过点Q 作QM AD '⊥于点M ',在ADQ ∆内部过A 、D 分别作30M DP M AP ∠'=∠'=︒,则120APD APQ DPQ ∠=∠=∠=︒,点P 就是费马点,此时PA PD PQ ++最小,在等腰Rt AQD ∆中,AQ DQ ==,QM AD '⊥,232AM QM AQ ∴='==,故cos30AM PA '︒=,解得:PA =PM '=故3QP =PD =,则233PA PD PQ ++=⨯+=+,∴点P 到点A 、点D 、点Q 的距离之和的最小值为3+,故答案为3+.15.如图,点D 为等边三角形ABC 内一点,且120BDC ∠=︒,则AD BD 的最小值为32.【解答】解:如图,将BCD ∆绕点C 顺时针旋转60︒得到ACE ∆,连接DE ,过点A 作AH DE ⊥于H .CD CE = ,60DCE ∠=︒,DCE ∴∆是等边三角形,60EDC DEC ∴∠=∠=︒,120BDC AEC ∠=∠=︒ ,60AED ∴∠=︒,BD AE = ,∴AD AD BD AE=,AH DE ⊥ ,AD AH ∴,∴ADAH BD AE,90AHE ∠=︒ ,60AEB ∠=︒,∴sin 60AH AE =︒=,∴AD BD ,∴AD BD 的最小值为32.16.如图,已知矩形ABCD ,4AB =,6BC =,点M 为矩形内一点,点E 为BC 边上任意一点,则MA MD ME ++的最小值为4+【解答】解:将AMD ∆绕点A 逆时针旋转60︒得到△AM D '',由性质的性质可知:MD M D ='',ADD ∆'和AMM ∆'均为等边三角形,AM MM ∴=',MA MD ME D M MM ME ∴++='+'+,D M ∴'、MM '、ME 共线时最短,由于点E 也为动点,∴当D E BC '⊥时最短,此时易求得4D E D G GE '='+=+,MA MD ME ∴++的最小值为4+17.如图,在直角三角形ABC ∆内部有一动点P ,90BAC ∠=︒,连接PA ,PB ,PC ,若6AC =,8AB =,求PA PB PC ++的最小值【解答】解:如图,将ACP ∆绕点C 顺时针旋转60︒得到ECF ∆,连接PF ,BE ,作EH BA ⊥交BA 的延长线于H .由旋转的旋转可知:PA EF =,PCF ∆,ACE ∆是等边三角形,PF PC ∴=,PA PB PC EF FP PB ∴++=++,EF FP PB BE ++ ,∴当B ,P ,F ,E 共线时,PA PB PC ++的值最小,90BAC ∠=︒ ,60CAE ∠=︒,180906030HAE ∴∠=︒-︒-︒=︒,EH AH ⊥ ,6AE AC ==,132EH AE ∴==.AH ==,BE ∴===,PA PB PC ∴++的最小值为故答案为18.若点P 为ABC ∆所在平面上一点,且120APB BPC CPA ∠=∠=∠=︒,则点P 叫做ABC ∆的费马点.当三角形的最大角小于120︒时,可以证明费马点就是“到三角形的三个顶点的距离之和最小的点”.即PA PB PC ++最小.(1)如图1,向ABC ∆外作等边三角形ABD ∆,AEC ∆.连接BE ,DC 相交于点P ,连接AP .①证明:点P 就是ABC ∆费马点;②证明:PA PB PC BE DC ++==;(2)如图2,在MNG ∆中,MN =,75M ∠=︒,3MG =.点O 是MNG ∆内一点,则点O 到MNG ∆三个顶点的距离和的最小值是【解答】(1)证明:①如图11-中,作AM CD ⊥于M ,AN BE ⊥于N 设AB 交CD 于O .ADB ∆ ,ACE ∆都是等边三角形,AD AB ∴=,AC AE =,60DAB CAE ∠=∠=︒,DAC BAE ∴∠=∠,()ADC ABE SAS ∴∆≅∆,CD BE ∴=,DAC ABE S S ∆∆=,ADC ABE ∠=∠,AM CD ⊥ ,AN BE ⊥,∴1122CD AM BE AN ⋅⋅=⋅⋅,AM AN ∴=,APM APN ∴∠=∠,AOD POB ∠=∠ ,60OPB DAO ∴∠=∠=︒,60APN APM ∴∠=∠=︒,120APC BPC APC ∴∠=∠=∠=︒,∴点P 是就是ABC ∆费马点.②在线段PD 上取一点T ,使得PT PA =,连接AT .60APT ∠=︒ ,PT PA =,APT ∴∆是等边三角形,60PAT ∴∠=︒,AT AP =,60DAB TAP ∠=∠=︒ ,DAT BAP ∴∠=∠,AD AB = ,()DAT BAP SAS ∴∆≅∆,PB DT ∴=,PD DT PT PA PB ∴=+=+,PA PB PC PD PC CD BE ∴++=+==.(2)解:如图2:以MG 为边作等边三角形MGD ∆,以OM 为边作等边OME ∆.连接ND ,作DF NM ⊥,交NM 的延长线于F.MGD ∆ 和OME ∆是等边三角形OE OM ME ∴==,60DMG OME ∠=∠=︒,MG MD =,GMO DME∴∠=∠在GMO ∆和DME ∆中,OM ME GMO DME MG MD =⎧⎪∠=∠⎨⎪=⎩,()GMO DME SAS ∴∆≅∆,OG DE∴=NO GO MO DE OE NO∴++=++∴当D 、E 、O 、N 四点共线时,NO GO MO ++值最小,75NMG ∠=︒ ,60GMD ∠=︒,135NMD ∴∠=︒,45DMF ∴∠=︒,3MG = 322MF DF ∴==,3211222NF MN MF ∴=+==,ND ∴=MO NO GO ∴++,,19.问题提出(1)如图①,在ABC ∆中,2BC =,将ABC ∆绕点B 顺时针旋转60︒得到△A B C ''',则CC '=2;问题探究(2)如图②,在ABC ∆中,3AB BC ==,30ABC ∠=︒,点P 为ABC ∆内一点,连接PA 、PB 、PC ,求PA PB PC ++的最小值,并说明理由;问题解决(3)如图③,在四边形ABCD 中,//AD BC ,6AB =,4AD =,60ABC BCD ∠=∠=︒.在四边形ABCD 内部有一点,满足120APD ∠=︒,连接BP 、CP ,点Q 为BPC ∆内的任意一点,是否存在一点P 和一点Q ,使得PQ BQ CQ ++有最小值?若存在,请求出这个最小值;若不存在,请说明理由.【解答】解:(1)如图①,由旋转的性质可知:BCC ∆'是等边三角形,2CC BC ∴'==,故答案为2.(2)如图②,将ABP ∆绕点B 逆时针旋转60︒得到BFE ∆,连接PF ,EC .由旋转的性质可知:PBF ∆是等边三角形,PB PF ∴=,PA EF = ,PA PB PC PC PF EF ∴++=++,PC PF EF EC ++ ,∴当P ,F 在直线EC 上时,PA PB PC ++的值最小,易证3BC BE BA ===,90CBE ∠=︒,EB BC ⊥ ,EC ∴==,PA PB PC ∴++的最小值为.(3)(3)如图③1-中,将PBQ ∆绕点B 逆时针旋转60︒得到EBG ∆,则PQ EG =,BQG ∆是等边三角形,BQ QG ∴=,PQ EG =,PQ BQ CQ EG GQ QC EC ∴++=++,EC ∴的值最小时,QP QB QC ++的值最小,如图③2-中,延长BA 交CD 的延长线于J ,作ADJ ∆的外接圆O ,将线段BO ,BP 绕点B 逆时针旋转60︒得到线段BO ',BE ,连接EO ',OB ,OP .易证()BEO BPO SAS ∆'≅∆,EO OP ∴'=,180APD AJD ∠+∠=︒ ,A ∴,P ,D ,J 四点共圆,OP ∴=,433EO ∴'=,∴点E 的运动轨迹是以O '为圆心,433为半径的圆,∴当点E 在线段CO '上时,EC 的值最小,最小值CO EO ='-',连接OO',延长OO'到R,使得O R OO'=',连接BR,则90OBR∠=︒,作RH CB⊥交CB的延长线于H,O T CH'⊥于T,OM BC⊥于M.在Rt OBM∆中,5BM=,OM=1433OB∴=,14BR∴==,由BHR OMB∆∆∽,∴RH BRBM OB=,RH∴=,////HR O T OM',OO RO'=',TM TH∴=,2RH OMO T+∴'==,3BT∴==,3CO∴'==,CO EO∴'-'=.QP QB QC∴++的最小值为.20.如图1,在ABC∆中,90ACB∠=︒,点P为ABC∆内一点.(1)连接PB,PC,将BCP∆沿射线CA方向平移,得到DAE∆,点B,C,P的对应点分别为点D,A,E,连接CE.①依题意,请在图2中补全图形;②如果BP CE⊥,3BP=,6AB=,求CE的长.(2)如图3,连接PA ,PB ,PC ,求PA PB PC ++的最小值.小慧的作法是:以点A 为旋转中心,将ABP ∆顺时针旋转60︒得到AMN ∆,那么就将PA PB PC ++的值转化为CP PM MN ++的值,连接CN ,当点P 落在CN 上时,此题可解.请你参考小慧的思路,在图3中证明PA PB PC CP PM MN ++=++.并直接写出当4AC BC ==时,PA PB PC ++的最小值.【解答】解:(1)①补全图形如图所示;②如图,连接BD 、CDBCP ∆ 沿射线CA 方向平移,得到DAE ∆,//BC AD ∴且BC AD =,90ACB ∠=︒ ,∴四边形BCAD 是矩形,6CD AB ∴==,3BP = ,3DE BP ∴==,BP CE ⊥ ,//BP DE ,DE CE ∴⊥,∴在Rt DCE ∆中,223692733CE CD DE =-=-==;(2)证明:如图所示,以点A 为旋转中心,将ABP ∆顺时针旋转60︒得到AMN ∆,连接BN .由旋转可得,AMN ABP ∆≅∆,MN BP ∴=,PA AM =,60PAM BAN ∠=︒=∠,AB AN =,PAM ∴∆、ABN ∆都是等边三角形,PA PM ∴=,PA PB PC CP PM MN ∴++=++,当4AC BC ==时,AB =,当C 、P 、M 、N 四点共线时,由CA CB =,NA NB =可得CN 垂直平分AB ,12AQ AB CQ ∴==,NQ ==,∴此时CN CP PM MN PA PB PC =++=++=+.21.(1)阅读材料:如图(1),四边形ABCD 是正方形,ABE ∆是等边三角形,M 为对角线BD (不含B 点)上任意一点,将BM 绕点B 逆时针旋转60︒得到BN ,连接EN 、AM 、CM ,①求证:AMB ENB ∆≅∆;②当M 点在何处时,AM CM +的值最小;③当M 点在何处时,AM BM CM ++的值最小,并说明理由;(2)根据阅读材料所提供的数学思想和方法,完成下面的题目:如图(2),A 、B 、C 、D 四个城市恰好为一个正方形的四个顶点,要建立一个公路系统,使每两个城市之间都有公路相通,并使整个公路系统的总长为最短,应当如何修建?请画出你的设计图.【解答】解:(1)① 四边形ABCD 是正方形,ABE ∆是等边三角形,AB BC BE ∴==,60ABE ∠=︒,将BM 绕点B 逆时针旋转60︒得到BN ,BN BM ∴=,60MBN ∠=︒,ABE MBN ∴∠=∠,EBN ABM ∴∠=∠,且AB BE =,MB NB =,()AMB ENB SAS ∴∆≅∆;②当M 点落在BD 的中点时,A 、M 、C 三点共线时,AM CM +的值最小;③如图1,连接CE ,当M 点位于BD 与CE 的交点处时,AM BM CM ++的值最小,理由如下:连接MN ,由(1)知,AMB ENB ∆≅∆,AM EN ∴=,60MBN ∠=︒ ,MB NB =,BMN ∴∆是等边三角形,BM MN ∴=,AM BM CM EN MN CM ∴++=++,根据“两点之间线段最短”,得EN MN CM EC ++=最短,∴当M 点位于BD 与CE 的交点处时,AM BM CM ++的值最小,即等于EC 的长;(2)如图2,作等边ABQ ∆和等边CDP ∆,等边CEH ∆,同理可证CHP CED ∆≅∆,则CH CE =,PH DE =,DE CE PH HE ∴+=+,∴点H ,点P ,点E 三点共线时,DE CE +的值最小值为PE ,同理,AF BF +的最小值为FQ ,DE CE EF AF BF PE FE FQ ∴++++++,∴点P ,点E ,点F ,点Q 共线时,并使整个公路系统的总长为最短,即最短距离为PQ ,∴设计图:(30)EDC ECD FAB FBA ∠=∠=∠=∠=︒22.已知,在ABC ∆中,30ACB ∠=︒(1)如图1,当2AB AC ==,求BC 的值;(2)如图2,当AB AC =,点P 是ABC ∆内一点,且2PA =,21PB =3PC =,求APC ∠的度数;(3)如图3,当4AC =,7()AB CB CA >,点P 是ABC ∆内一动点,则PA PB PC ++的最小值为43.【解答】解:(1)如图1中,作AP BC ⊥于P .AB AC = ,AP BC ⊥,BP PC ∴=,在Rt ACP ∆中,2AC = ,30C ∠=︒,cos303PC AC ∴=︒=2BC PC ∴==.(2)如图2中,将APB ∆绕点A 逆时针旋转120︒得到QAC ∆.AB AC = ,30C ∠=︒,120BAC ∴∠=︒,2PA AQ ∴==,PB QC ==,120PAQ ∠=︒ ,PQ ∴=222PQ PC QC ∴+=,90QPC ∴∠=︒,30APQ ∠=︒ ,3090120APC ∴∠=︒+︒=︒.(3)如图3中,将BCP ∆绕点C 逆时针旋转60︒得到△CB P '',连接PP ',AB ',则90ACB ∠'=︒.PA PB PC PA PP P B ++=+'+'' ,∴当A ,P ,P ',B '共线时,PA PB PC ++的值最小,最小值AB ='的长,由AB =4AC =,30C ∠=︒,可得BC CB ='=,AB ∴'=.23.阅读下列材料:小华遇到这样一个问题,如图1,ABC∆内部有一点P,连BC=,5AC=,在ABCACB∆中,30∠=︒,6接PA、PB、PC,求PA PB PC++的最小值.小华是这样思考的:要解决这个问题,首先应想办法将这三条端点重合于一点的线段分离,然后再将它们连接成一条折线,并让折线的两个端点为定点,这样依据“两点之间,线段最短”,就可以求出这三条线段和的最小值了.他先后尝试了翻折、旋转、平移的方法,发现通过旋转可以解决这个问题.他的做法是,如图2,将APC∆,连接PD、BE,则BE的长即为所求.∆绕点C顺时针旋转60︒,得到EDC(1)请你写出图2中,PA PB PC++(2)参考小华的思考问题的方法,解决下列问题:①如图3,菱形ABCD中,60∠=︒,在菱形ABCD内部有一点P,请在图3中画出并指明长度等于ABC++最小值的线段(保留画图痕迹,画出一条即可);PA PB PC②若①中菱形ABCD的边长为4,请直接写出当PA PB PC++值最小时PB的长.【解答】解:(1)如图2. 将APC∆绕点C顺时针旋转60︒,得到EDC∆,∴∆≅∆,APC EDC∠=︒,ACP ECD==,60PCD∴∠=∠,5AC EC∴∠+∠=∠+∠,ACP PCB ECD PCB∴∠+∠=∠=︒,30ECD PCB ACBBCE ECD PCB PCD∴∠=∠+∠+∠=︒+︒=︒.306090在Rt BCEBC=,5,6CE=,∆中,90∠=︒BCE∴==BE即PA PB PC++(2)①将APC∆,连接PE、DE,∆绕点C顺时针旋转60︒,得到DEC则线段BD 等于PA PB PC ++最小值的线段;②如图31-中,当B 、P 、E 、D 四点共线时,PA PB PC ++值最小,最小值为BD . 将APC ∆绕点C 顺时针旋转60︒,得到DEC ∆,APC DEC ∴∆≅∆,CP CE ∴=,60PCE ∠=︒,PCE ∴∆是等边三角形,PE CE CP ∴==,60EPC CEP ∠=∠=︒.菱形ABCD 中,1302ABP CBP ABC ∠=∠=∠=︒,603030PCB EPC CBP ∴∠=∠-∠=︒-∠︒=︒,30PCB CBP ∴∠=∠=︒,BP CP ∴=,同理,DE CE =,BP PE ED ∴==.连接AC ,交BD 于点O ,则AC BD ⊥.在Rt BOC ∆中,90BOC ∠=︒ ,30OBC ∠=︒,4BC =,cos 4BO BC OBC ∴=∠=⨯2BD BO ∴==,13BP BD ∴==即当PA PB PC ++值最小时PB24.已知抛物线2142y x bx =-++的对称轴为1x =,与y 交于点A ,与x 轴负半轴交于点C ,作平行四边形ABOC 并将此平行四边形绕点O 顺时针旋转90︒,得到平行四边形A B O C ''''.(1)求抛物线的解析式和点A 、C 的坐标;(2)求平行四边形ABOC 和平行四边形A B O C ''''重叠部分△OC D '的周长;(3)若点P 为AOC ∆内一点,直接写出PA PC PO ++的最小值(结果可以不化简)以及直线CP的解析式.【解答】解:(1)由已知得,112()2bx =-=⨯-,则1b =,抛物线的解析式为2142y x x =-++,(0,4)A ∴,令0y =,得21402x x -++=,12x ∴=-,24x =.(2)在ABCD 中,90OAB AOC ∠=∠=︒,则//AB CO,OB ∴==2OC OC '==,OC D OCA B ∴∠'=∠=∠,C OD BOA ∠'=∠,∴△C OD BOA '∆∽,∴C OD BOA C OC C OB '∆'=== AOB ∆的周长为6+,∴△C OD '的周长为565(6255+⨯=+;(3)此点位费马点,设三角形AOB 的三边为a ,b ,c ,2OC = ,4OA =,AC ==,PA PB PC ++==.直线CP解析式为1)2y x =-+-.。
旋转中的最值模型(费马点模型)(解析版)—2024-2025学年九年级数学上学期(人教版)
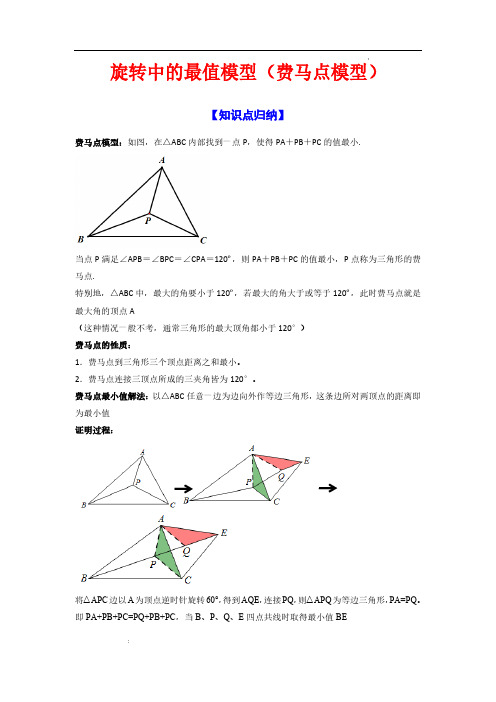
旋转中的最值模型(费马点模型)【知识点归纳】费马点模型:如图,在△ABC内部找到一点P,使得PA+PB+PC的值最小.当点P满足∠APB=∠BPC=∠CPA=120º,则PA+PB+PC的值最小,P点称为三角形的费马点.特别地,△ABC中,最大的角要小于120º,若最大的角大于或等于120º,此时费马点就是最大角的顶点A(这种情况一般不考,通常三角形的最大顶角都小于120°)费马点的性质:1.费马点到三角形三个顶点距离之和最小。
2.费马点连接三顶点所成的三夹角皆为120°。
费马点最小值解法:以△ABC任意一边为边向外作等边三角形,这条边所对两顶点的距离即为最小值证明过程:将△APC边以A为顶点逆时针旋转60°,得到AQE,连接PQ,则△APQ为等边三角形,PA=PQ。
即PA+PB+PC=PQ+PB+PC,当B、P、Q、E四点共线时取得最小值BE【例题精讲】例1.(等边三角形费马点)如图,在ABC V 中,3AB =,2AC =,60BAC Ð=°,P 为ABC V 内一点,则PA PB PC ++的最小值为 .【点睛】本题考查了全等三角形判定与性质,旋转的性质,以及等边三角形的性质和求线段最值的问题,掌握做辅助线是解题的关键.例2.(直角三角形费马点)如图,已知Rt △ABC 中,∠ABC =90°,∠ACB =30°,斜边AC =4,点P 是三角形内的一动点,则PA +PB +PC 的最小值是 .∵∠90,30ABC ACB °°=Ð=,AC 2,AB \=结AD,BE,CE.若AB=DE=BC=10,∠ABC=75°,则AD+BE+CE的最小值为.【点睛】本题考查轴对称求最短距离,熟练掌握轴对称的性质,通过构造平行四边形、旋转例4.(加权费马点)如图,Rt ABC △中,30CAB Ð=°,3BC =,点P 为ABC V 内一点,连接,,PA PB PC ,则PC PB +的最小值为 .++++的最小值为.AP BP PQ QC QD∴AP BP PQ CQ DQ ++++B P P P PQ QQ Q C ¢¢¢¢¢¢=++++,∴当,,,,,B P P Q Q C ¢¢¢¢六点共线时AP BP PQ CQ ++++连接,¢¢BB CC ,∵AB AB ¢=,60B AB ¢Ð=°,∴ABB ¢V 是等边三角形,∴1AB BB ¢¢==,∴B ¢在AB 的垂直平分线上,例6.(培优综合)在ABCD Y 中,45ABC Ð=°,连接AC ,已知AB AC ==E 在线段AC 上,将线段DE 绕点D 顺时针旋转 90° 为线段DF .(1)如图1,线段AC 与线段BD 的交点和点E 重合,连接EF ,求线段EF 的长度;(2)如图2,点G 为DC 延长线上一点,使得GC EC =,连接FG 交AD 于点H ,求证:CD =;(3)如图3,在(2)的条件下,平面内一点P ,当HP CP +最小时,求HPB △的面积.∵45BAC Ð=°,AB AC ==∴45ACB ABC Ð=Ð=°,BAC Ð∴2222BC AB ==´=,∵ABCD Y ,∴45DCG ABC Ð=Ð=°,CD∵90BAC Ð=°,AB CD ∥,∴AC GD ^,90GCA ECD Ð=Ð=°,又∵GC EC =,AC DC =,∴()SAS GCA ECD V V ≌,∴GA ED =,GAC EDC Ð=Ð,∵ED FD =,ED FD ^,∴GA FD =,90AGC GDF Ð+Ð=°-Ð由旋转的性质可得,2BC BC ¢==,∵AD BC ∥,∴90AIB Ð=°,45IAB ABC Ð=Ð=°,∴222122IB IA AB ===´=,在Rt IC H ¢V 中,12IC IB BC ¢¢=+=+22223213C H IC IH ¢¢=+=+=,∵1122BC H S C H BJ BC IH ¢¢¢=⋅=⋅V ,即:在Rt IBH V 中,221BH IB IH =+=在Rt BJH V 中,22JH BH BJ =-=【课后训练】1.如图,在ABC V 中,90,5,BAC AB AC Ð==°=P 为ABC V 内部一点,则点P 到ABC V 三个顶点之和的最小值是 .∴BAP HAE Ð=Ð,AE AP =,AH AB ==∴60HAB EAP Ð=Ð=°,∴AEP △是等边三角形,∴AE AP EP ==,∴AP BP PC EP EH PC ++=++,∴当点H 、E 、P 、C 共线时,AP BP PC ++∵18018060NAC BAH BAC Ð=°-Ð-Ð=°-条动线段MN BC ∥,且MN =,则AN BM CN ++的最小值为 .【点睛】本题考查了平行四边形的判定与性质,旋转变换,的一半,等边三角形的判定与性质,勾股定理,两点之间线段最短等知识,解题的关键是学会利用旋转法添加辅助线,构造全等三角形解决问题..如图,点M 是矩形ABCD 内一点,且,,MA MD MN ,则MA MD MN ++的最小值为 .【答案】7532+根据旋转的性质有:ADD ¢\△为等边三角形,同理AMM ¢V 为等边三角形,AM AM MM ¢==\MA MD MN +\+=\当线段M D ¢¢、MM 在矩形ABCD 中,D 即可知四边形ABEF 是矩形,ADD ¢QV 为等边三角形,\12AF FD AD ===\2D F D A AF ¢¢=-4.如图,P为正方形ABCD内的动点,若AB=2,则PA+PB+PC的最小值为.(1)如图1,已知150AOB Ð=°,120BOC Ð=°,将BOC V 绕点C 按顺时针方向旋转60°得ADC △.①DAO Ð的度数是 ;②用等式表示线段OA ,OB ,之间的数量关系,并证明;(2)设AOB a Ð=,BOC b Ð=.①当a ,b 满足什么关系时,OA OB OC ++有最小值?请在图2中画出符合条件的图形,并说明理由;②若等边ABC V 的边长为1,直接写出OA OB OC ++的最小值.QV ADC BOC \≌△△,OCD ÐCD OC \=,ADC BOC Ð=ÐOCD \△是等边三角形,OC OD CD \==,COD Ð=150AOB Ð=°Q ,120BOC Ð=90AOC \Ð=°,\O C OC ¢\=,O A OA ¢¢=,A C BC ¢=,A O C AOC ¢¢Ð=Ð.(1)如图1, 连接DE BE 、, 若5,3BCE ABE S S ==V V ,求BED S V ;(2)如图2, 若,DM BC DM BM ^=, 延长BE 交DM 于点N , 且NM MC =, 求证:AD DN =-;(3)如图3,若4,90AD AB ABD ==Ð=°,P 为BCD △内一点,请直接写出PD PC PB ++的最小值.∵,DM BC DM BM ^=,∴BDM V 是等腰直角三角形,∴222BD BM DM DM =+=∴BD BF =,∴45F BDM CBD Ð=Ð=Ð=∴90DBF Ð=°,∴2DF BD =,∴4CH BC ==,DCH BCD BCH Ð=Ð+Ð∴PG PC =,∴PD PC PB PD PG GH DH ++=++³即当点D ,P ,G ,H 四点共线时,PD 在Rt DCH △中,22DH CD CH =+=即PD PC PB ++的最小值为27.【点睛】本题主要考查了等边三角形的判定和性质,平行四边形的性质,勾股定理,图形的形ACFG ,点D 恰好在线段GF 上.(1)若AB的长度比BC少4,8V的面积;AC=,求ABC(2)求证:BG DG-;(3)已知点P是ABCV的顶点和边重合,在(1)的条件下,请直V内一动点,且P不与ABC接写出PA PB++的最小值.∵90BED HEG Ð=Ð=°,∴BED HED HEG Ð-Ð=Ð-即BEH DEG Ð=Ð,∵EMG BED EBG =Ð+Ð=∠∴EBG GDE Ð=Ð,∵90BAC Ð=°,∴1122ABC S AB AC BC AG =´=´△,∴6824105AB AC AG BC ´´===,针旋转90°交DC 的延长线于点F ,求证:AE CF =;(2)边长4AB =把边AB 沿BE 翻折.①如图2,若点P 落在对角线BD 上,则AE = ;②如图3,点G 在边CD 上,1DG =,连接AG 、BG ,当点P 落在ABG V 内部时(不含边上),线段AE 长度的取值范围为 ;(3)如图4,点M 是正方形ABCD 内一点,连接MA 、MC ,若5AB =,求MA MC +最小值;(4)如图5,点M 是矩形ABCD 内一点,连接,,MA MB MC ,若AB =4BC =,则MA MB MC ++最小值为 .当点P 落到BG 上,连接由折叠的性质可得,∴=EPG EDG ÐÐ∵1DG =,(3)①当A 、M AM MC AC +>,②当点A 、M 、C ∵AB BC =,ABC Ð(4)如图,将V ∴A M AM ¢¢=,BM 又∵60M BM ¢Ð=°∴M BM ¢V 是等边三角形,【点睛】本题考查正方形的性质、折叠的性质、旋转的性质、全等三角形的判定与性质、等腰直角三角形的性质与判定、勾股定理、等边三角形的判定与性质、切线的性质,熟练掌握相关性质是解题的关键.。
费马点最值问题的解法

费马点最值问题的解法数学运算部分一直花样百出,复杂多变,是很让考生头疼至极的。
一、和定最值问题题型特征未知几个量的和一定,谋某个量的最大值或最小值。
二、解题核心思想谋某个量最小,并使其他量尽可能大;谋某个量最轻,并使其他量尽可能小。
三、列方程依据将所有量用所设未知数x则表示出,按照总和一定列于一元一次方程。
四、例题展示1.人出席七项活动,未知每个人只出席一项活动,而且每项活动出席的人数都不一样。
那么出席第四多的活动最多存有几人出席?a.22b.21c.24d.23【解析】题干描述中“人参加7项活动”明显是7个量的和一定,最后所求也是问的最大值,所以很显然就是和定最值问题。
求第四多的活动最多有多少人,只要使其他量尽可能少即可,此时可以确定第五、六、七项活动的人数,分别是1,2,3人。
其余项没法直接确定,但我们可以确定要使第三项也尽可能小,再小也不能少于第四项的人数,再结合题干人数不一样,故第三项最小也得比第四项多1人,第二项比第三项多一人,第一项比第二项多1人。
故可设第四项位x,可得以下方程: (x+3)+ (x+2)+ (x+1)+x+3+2+1=,解得x=22,选择a项。
2.某单位年招录了65名毕业生,拟将分配至该单位的7个相同部门。
假设行政部门分给的毕业生人数比其他部门都多,问行政部门分给的毕业生人数至少就是多少人?a.10b.11c.12d.13【解析】题干描述中“65名毕业生,拟分配到该单位的7个不同部门”,且求最小值,故是和定最值问题。
问题所求为最大量的最小值,只要使其他部门分得的人数尽可能的多即可。
分得第二多部门的人数再多也不能多于行政部门,最多只能少1,其余的部门和第二多部门的人数相等即可达到最大值。
故可得方程:x+6(x-1)=65,解得x约等于10点几,因为问题所求是最小值,故x取不到10,只能取11,b项当选。
最值问题(费马点)资料讲解

最值问题(费马点)最值问题2(费马点)1、已知:P是边长为1的正方形ABCD内的一点,求PA+PB+PC的最小值.2、已知:P是边长为1的等边三角形ABC内的一点,求PA+PB+PC的最小值.图2图1A'PPA ABCBC3、(延庆)(本题满分4分)阅读下面材料:阅读下面材料:小伟遇到这样一个问题:如图1,在△ABC (其中∠BAC 是一个可以变化的角)中,AB=2,AC=4,以BC 为边在BC 的下方作等边△PBC ,求AP 的最大值。
小伟是这样思考的:利用变换和等边三角形将边的位置重新组合.他的方法是以点B 为旋转中心将△ABP 逆时针旋转60°得到△A ’BC,连接A A ',当点A 落在C A '上时,此题可解(如图2).请你回答:AP 的最大值是 .参考小伟同学思考问题的方法,解决下列问题:如图3,等腰Rt △ABC .边AB=4,P 为△ABC 内部一点, 则AP+BP+CP 的最小值是 .(结果可以不化简)图3ABP4、(朝阳二模)阅读下列材料:小华遇到这样一个问题,如图1, △ABC 中,∠ACB =30º,BC =6,AC =5,在△ABC内部有一点P ,连接PA 、PB 、PC ,求PA +PB +PC 的最小值.小华是这样思考的:要解决这个问题,首先应想办法将这三条端点重合于一点的线段分离,然后再将它们连接成一条折线,并让折线的两个端点为定点,这样依据“两点之间,线段最短”,就可以求出这三条线段和的最小值了.他先后尝试了翻折、旋转、平移的方法,发现通过旋转可以解决这个问题.他的做法是,如图2,将△APC 绕点C 顺时针旋转60º,得到△EDC ,连接PD 、BE ,则BE 的长即为所求.(1)请你写出图2中,PA +PB +PC 的最小值为 ; (2)参考小华的思考问题的方法,解决下列问题:①如图3,菱形ABCD 中,∠ABC =60º,在菱形ABCD 内部有一点P ,请在图3中画出并指明长度等于PA +PB +PC 最小值的线段(保留画图痕迹,画出一条即可);②若①中菱形ABCD 的边长为4,请直接写出当PA +PB +PC 值最小时PB 的长.B图2B图3C B图15、(海淀二模)如图. 在平面直角坐标系xOy 中. 点B 的坐标为(0,2). 点D 在x 轴的正半轴上. 30ODB ∠=︒. OE 为△BOD 的中线. 过B 、E 两点的抛物线236y ax x c =++与x 轴相交于A 、F 两点(A 在F 的左侧).(1) 求抛物线的解析式;(2)等边△OMN 的顶点M 、N 在线段AE 上. 求AE 及AM 的长;(3) 点P 为△ABO 内的一个动点. 设m PA PB PO =++.请直接写出m 的最小值, 以及m 取得最小值时, 线段AP 的长.(备用图)。
最值系列之费马点(1)课件

B
Dv
w
a
C
E
F
G
B
课堂小结
1.这节课你学到了什么?
2.对于本节课你还有什么困惑?
目录
课后练习
1.如图,向锐角△ABC外作等边△ABD、△AEC,连接BE,DC相交于点P,连
接AP.
(1)证明:点P是△ABC的费马点;
(2)证明:PA+PB+PC=BE=DC.
2.有甲乙丙三个村庄,要在中间建一供水站向三地送水,现要确定供水站
求平面上到这三个点的距离之和最短的
点的位置。
目录
费马与费马点
托里拆利成功地解决了费马的问题。他给出的答案是:
△ABC 三条边的张角都等于120°,即满足∠APB =∠BPC =∠CPA = 120°
的点P就是到点 A,B,C 的距离之和最小的点。
目录
后来人们就把平面上到一个三角形的三
个顶点 A,B,C 距离之和最小的点称为
A
P''
P''
P'
P
B
A
C'
C
P
P
B
C'
P'
C
作费马点
在△ABC(三个内角均小于120°)中作一点P,使点P到三角形三顶点
的距离之和最小。
A
回顾:
D
B
C
A
E
P
B
C
作费马点
在△ABC(三个内角均小于120°)中作一点P,使点P到三角形三顶点
D
的距离之和最小。
A
A
E
P
B
C
以三角形任意两边向外作等边三角形,
费马点与加权费马点详细总结(解析版)

费马点与加权费马点详细总结知识点梳理【常规费马点】【加权费马点】题型一普通费马点最值问题题型二加权费马点·单系数型题型三加权费马点·多系数型知识点梳理【常规费马点】【问题提出】如图△ABC所有的内角都小于120度,在△ABC内部有一点P,连接PA、PB、PC,当PA+PB+PC的值最小时,求此时∠APB与∠APC的度数.【问题处理】如图1,将△ACP绕着点C顺时针旋转60度得到△A'CP',则△ACP≌△A'CP',CP=CP',AP =A'P',又∵∠PCP'=60°,∴△PCP'是等边三角形,∴PP'=PC,∴PA+PB+PC=P'A'+PB+PP',如图2,当且仅当点B、P、P'、A'共线时,PA+PB+PC最小,最小值为A'B,此时∠BPC=∠APC=∠APB =120°【问题归纳】如费马点就是到三角形的三个顶点的距离之和最小的点.费马点结论:①对于一个各角不超过120°的三角形,费马点是对各边的张角都是120°的点,所以三角形的费马点也叫三角形的等角中心;②对于有一个角超过120°的三角形,费马点就是这个内角的顶点.【如何作费马点】如图3,连接AA',我们发现△ACA'为等边三角形,点P在A'B上,同理,我们可以得到等边△BAB',点P也在CB'上,因此,我们可以以△ABC三角形任意两边为边向外构造等边三角形,相应连线的交点即为费马点。
(最大角小于120°时)【例1】如图,在△ABC中,∠ACB=90°,AB=AC=1,P是△ABC内一点,求PA+PB+PC的最小值.【答案】6+2 2【分析】如图,以AC为边构造等边△ACD,连接BD,BD的长即为PA+PB+PC的最小值.至于点P的位置?这不重要!如何求BD?考虑到△ABC和△ACD都是特殊的三角形,过点D作DH⊥BA交BA的延长线于H点,根据勾股定理,即可得出结果.【练习1】如图,已知矩形ABCD,AB=4,BC=6,点M为矩形内一点,点E为BC边上任意一点,则MA+ MD+ME的最小值为______.【分析】依然构造60°旋转,将三条折线段转化为一条直线段.分别以AD、AM为边构造等边△ADF、等边△AMG,连接FG,易证△AMD≌△AGF,∴MD=GF∴ME+MA+MD=ME+EG+GF过F作FH⊥BC交BC于H点,线段FH的长即为所求的最小值.【加权费马点】如果所求最值中三条线段的系数有不为1的情况,我们把这类问题归为加权费马点问题,解决方法类似,也是通过旋转进行线段转化,只不过要根据系数的情况选择不同的旋转或放缩方法。
几何最值模型之费马点模型(解析版)

几何最值模型之费马点模型皮耶·德·费马,17世纪法国数学家,有“业余数学家之王”的美誉,之所以叫业余并非段位不够,而是因为其主职是律师,兼职搞搞数学.费马在解析几何、微积分等领域都有卓越的贡献,除此之外,费马广为人知的是以其名字命名的“费马小定理”、“费马大定理”等.费马点:三角形内的点到三个顶点距离之和最小的点。
费马点问题是由全等三角形中的手拉手模型衍生而来,主要考查转化与化归等的数学思想,在各类考试中都以中高档题为主。
本专题就最值模型中的费马点问题进行梳理及对应试题分析,方便掌握。
模型分析模型:费马点模型1.费马点模型概念:数学上称,到三角形3个顶点距离之和最小的点为费马点。
2.解题依据:旋转变换。
3.解题策略:构造等边三角形共顶点旋转,通过旋转把三条线段凑在一起顺次相连。
4.解题思路:化折为直,共线时求最值。
5.费马点的作法:分别以△ABC的AB、AC为一边向外作等边△ABE和等边△ACF,连接CE、BF,设交点为M,则点M即为△ABC的费马点。
模型展示模型①:费马点模型【模型解读】结论1:如图,点M为△ABC内任意一点,连接AM、BM、CM,当M与三个顶点连线的夹角为120°时,MA+MB+MC的值最小。
注意:上述结论成立的条件是△ABC的最大的角要小于120º,若最大的角大于或等于120º,此时费马点就是最大角的顶点A。
(这种情况一般不考,通常三角形的最大顶角都小于120°)【模型解析①】构造等边三角形共顶点旋转以AB为一边向外作等边三角形△ABE,将BM绕点B逆时针旋转60°得到BN,连接EN.∵△ABE 为等边三角形,∴AB =BE ,∠ABE =60°.而∠MBN =60°,∴∠ABM =∠EBN .在△AMB 与△ENB 中,∵AB =BE∠ABM =∠EBN BM =BN,∴△AMB ≌△ENB (SAS ).连接MN .由△AMB ≌△ENB 知,AM =EN .∵∠MBN =60°,BM =BN ,∴△BMN 为等边三角形.∴BM =MN .∴AM +BM +CM =EN +MN +CM .∴当E 、N 、M 、C 四点共线时,AM +BM +CM 的值最小.此时,∠BMC =180°-∠NMB =120°;∠AMB =∠ENB =180°-∠BNM =120°;∠AMC =360°-∠BMC -∠AMB =120°.【模型解析②】“手拉手模型”原理在△ABC 的外侧,分别作等边△ABT 、等边△ACE ,连接CT 、BE 相交于点P,此时∠BPT =60°,∠APB =∠BPC =∠CPA =120°(参见“手拉手模型-全等”),点P 就是△ABC 的费马点,费马距离等于CT 或BE .【模型解析③】费马点的作法如图,分别以△ABC 的AB 、AC 为一边向外作等边△ABE 和等边△ACF ,连接CE 、BF ,设交点为M ,则点M 即为△ABC 的费马点。
压轴密训之八:最值之费马点

中考考点-------费马点一、历史背景和定义【历史背景】皮埃尔·德·费马(Pierre De Fermat ),法国律师和业余数学家。
被誉为"业余数学家之王"。
曾提出关于三角形的一个有趣问题:若给定一个三角形△ABC的话,从这个三角形的费马点P到三角形的三个顶点A、B、C的距离之和比从其它点算起的都要小.这个特殊点对于每个给定的三角形都只有一个.【数学定义】(1)托里拆利的解法中提到:对于每一个角都小于120°的△ABC的每一条边为底边,向外作正三角形,然后作这三个正三角形的外接圆。
托里拆利指出这三个外接圆会有一个共同的交点,而这个交点就是所要求的点。
这个点因此也叫做托里拆利点。
(如下左图)(2)也可以,如上右图,分别以BC 、AC 为边向外侧作等边三角形ACE 、BCF ,连结AF 、BE 交于一点,则该点即为所求的P 点(即费马点).【证明过程】类似证明方法还有如下:(只提供图,过程同学们自己研究)E二、 实战演练先来一个正规的三角形的题吧!【例1】 (2019年龙岩市质检)如图,△ABC 中, ∠ABC =30°,AB =4,BC =5,P 是△ABC 内部的任意一点,连结P A ,PB ,PC ,则P A +PB +PC 的最小值为 .【解析】如图,将△ABP 绕着点B 逆时针旋转60°,得到△DBE ,连结EP 、AD 、CD ,∴△ABP ≌△DBE ,∴∠ABP =∠DBE ,BD =AB =4,∠PBE =∠ABD =60°,BE =PE ,AP =DE , ∴△BPE 是等边三角形,∴EP =BP , ∴AP +BP +PC =PC +EP +DE ≥CD , ∴当点D 、E 、P 、C 四点共线时,P A +PB +PC 有最小值CD ,∵∠ABC =30°, ∴∠DBC =∠ABD +∠ABC =90°,22224541CD BD C =+=+=做完一个题,那就来个灵魂三问?(1)如何作三角形的费马点? (2)为什么是这个点? (3)费马点怎么考?问题背景:如图1,将△ABC 绕点A 逆时针旋转60°得到△ADE ,DE 与BC交于点P ,可推出结论:P A +PC =PE .问题解决:如图2,在△MNG 中,MN =6,∠M =75°,MG =42,点O 是△MNG 内一点,则点O 到△MNG 三个顶点的距离和的最小值是______.OMNG图2图1ABCD EP下面这个题可能会给你一点想法正方形的题目也来一个!【例2】 (2019年中雅真题)如图,点P 为正方形ABCD 对角线BD 上一动点,2AB =,则AP BP CP ++的最小值为( ) A.25+B.26+C.4D.32【解析】利用旋转,费马点思维将ABP △绕着点A 顺时针旋转60︒,得''AB P △, ∵'AP AP =,'60PAP ∠=︒∴'APP △为等边三角形, ∴'AP PP =,又由旋转可知,''BP B P = ∴'''AP BP CP CP PP B P ++=++,当120APC ∠=︒时,∵'180APC APP ∠+=︒,''180AP P AP B ∠+=︒∴此时''C P P B 、、、四点共线, 此时AP BP CP ++的最小值为'B C ∵'2AB AB ==,且'60BAB =︒过B ’作AD BC 、的垂线分别交AD BC 、于G H 、,可知'30B AG ∠=︒,''13B G B H AG HB ====, ()()22'32184362B C =++=+=+62=+如图,四边形ABCD 是正方形,△ABE 是等边三角形,M 为对角线BD (不含B点)上任意一点,将BM 绕点B 逆时针旋转60°得到BN ,连接EN 、AM 、CM .(1)求证:△AMB ≌△ENB ;(2)①当M 点在何处时,AM +CM 的值最小; ②当M 点在何处时,AM +BM +CM 的值最小,并说明理由;(3)当AM +BM +CM 的最小值为31+时,求正方形的边长。
[数学]-专项07 图形旋转之费马点最值模型全攻略(原版)
![[数学]-专项07 图形旋转之费马点最值模型全攻略(原版)](https://img.taocdn.com/s3/m/92d9993330b765ce0508763231126edb6e1a7643.png)
专题07 图形旋转之费马点最值模型全攻略如何找一点P使它到△ABC三个顶点的距离之和PA+PB+PC最小?当B、P、Q、E四点共线时取得最小值费马点的定义:数学上称,到三角形3个顶点距离之和最小的点为费马点。
它是这样确定的:1. 如果三角形有一个内角大于或等于120°,这个内角的顶点就是费马点;2. 如果3个内角均小于120°,则在三角形内部对3边张角均为120°的点,是三角形的费马点。
费马点的性质:费马点有如下主要性质:1.费马点到三角形三个顶点距离之和最小。
2.费马点连接三顶点所成的三夹角皆为120°。
费马点最小值快速求解:费尔马问题告诉我们,存在这么一个点到三个定点的距离的和最小,解决问题的方法是运用旋转变换.秘诀:以△ABC任意一边为边向外作等边三角形,这条边所对两顶点的距离即为最小值类型一、基本费马点模型例题1.如图,P 是边长为1的等边ABC ∆内的任意一点,求t PA PB PC =++的取值范围.【变式训练1】已知正方形ABCD 内一动点E 到A 、B 、C的边长.【变式训练2】如图,ABCD 为矩形,AB=AD =4,EF 为ABCD 内两点,求(AF +DF +FE +CE +BE )的最小值.【变式训练3】如图,已知矩形ABCD ,AB =4,BC =6,点M 为矩形内一点,点E 为BC 边上任意一点,则MA +MD +ME 的最小值为______.【变式训练4】如图,P 为正方形ABCD 对角线BD 上一动点,若AB =2,则AP +BP +CP 的最小值为( )ABCDMEA .+B .+C .4D .3类型二、加权费马点模型例:如图,在Rt ABC 中,30,6,5ACB BC AC ∠=︒==,在ABC 内部有一点P ,连接PA 、PB 、PC .(加权费马点)求:(1)PA PB PC ++的最小值;(2)PA PB ++的最小值(3)PA PB ++的最小值;(4)2PA PB ++的最小值。
费马求最大值和最小值的方法

费马求最大值和最小值的方法
费马求最大值和最小值的方法是一种基于费马定理的数学方法,用于求解函数的最值问题。
费马定理指出,如果函数在某一点的导数为零,则该点可能是函数的最大值或最小值点。
费马求最大值和最小值的方法主要包括以下步骤:
1. 确定函数的定义域和导数。
2. 找到导数为零的点,这些点可能是函数的极值点。
3. 检查这些点的左右两侧的导数符号,如果左侧导数小于零,右侧导数大于零,则该点为函数的极小值点;如果左侧导数大于零,右侧导数小于零,则该点为函数的极大值点。
4. 如果函数在定义域内有多个极值点,则需要比较这些点的函数值,以确定函数的最小值和最大值。
需要注意的是,费马求最大值和最小值的方法只适用于可导函数,并且导数在极值点的左右两侧符号发生变化。
此外,该方法只能找到函数的局部最值点,而不能保证找到全局最值点。
中考数学专题复习37几何最值之费马点问题(全国通用解析版)

问题分析“费马点”指的是位于三角形内且到三角形三个顶点距高之和最短的点。
主要分为两种情况:(1)当三角形三个内角都小于120°的三角形.通常将某三角形绕点旋转60度.从而将“不等三爪图”中三条线段转化在同一条直线上.利用两点之间线段最短解决问题。
(2)当三角形有一个内角大于120°时.费马点就是此内角的顶点.费马点问题解题的核心技巧:旋转60° 构造等边三角形将“不等三爪图”中三条线段转化至同一直线上利用两点之间线段最短求解问题模型展示:如图.在△ABC内部找到一点P.使得PA+PB+PC的值最小.当点P满足△APB=△BPC=△CPA=120º.则PA+PB+PC的值最小.P点称为三角形的费马点.特别地.△ABC中.最大的角要小于120º.若最大的角大于或等于120º.此时费马点就是最大角的顶点A(这种情况一般不考.通常三角形的最大顶角都小于120°)费马点的性质:1.费马点到三角形三个顶点距离之和最小。
2.费马点连接三顶点所成的三夹角皆为120°。
最值解法:以△ABC任意一边为边向外作等边三角形.这条边所对两顶点的距离即为最小值。
证明过程:几何最值之费马点问题方法技巧将△APC 边以A 为顶点逆时针旋转60°.得到AQE.连接PQ.则△APQ 为等边三角形.PA=PQ 。
即PA+PB+PC=PQ+PB+PC.当B 、P 、Q 、E 四点共线时取得最小值BE【例1】如图.四边形 ABCD 是菱形.A B =6.且△ABC =60° .M 是菱形内任一点.连接AM .BM .CM .则AM +BM +CM 的最小值为________.【答案】63【详解】将△BMN 绕点B 顺时针旋转60度得到△BNE .△BM =BN .△MBN =△CBE =60°.△MN=BM△MC=NE△AM +MB +CM =AM +MN +NE .当A 、M 、N 、E 四点共线时取最小值AE .△AB =BC =BE =6.△ABH =△EBH =60°.△BH △AE .AH =EH .△BAH =30°.△BH =12AB =3.AH =3BH =33.△AE =2AH =63.故答案为63.题型精讲【例2】如图.四边形ABCD 是正方形.△ABE 是等边三角形.M 为对角线BD (不含B 点)上任意一点.将BM 绕点B 逆时针旋转60°得到BN.连接EN 、AM 、CM.(1)求证:△AMB△△ENB ;(2)△当M 点在何处时.AM +CM 的值最小; △当M 点在何处时.AM +BM +CM 的值最小.并说明理由;(3)当AM +BM +CM 的最小值为13 时.求正方形的边长.【答案】(1)△AMB△△ENB.证明略。
中考数学几何最值模型第5讲费马定理

过F作FH⊥BC交BC于H点,线段FH的长即为所求的最小值4 + 3 3.
课堂练习
2、如图,P为正方形ABCD对角线BD上一动点,若AB=2,则AP+BP+CP
A
的最小值为( B )
【解答】解:如图将△ABP绕点A顺时针旋转60度得到△AEF,
当E、F、P、C四点共线时,PA+PB+PC最小。
有且仅有点A1 ,1 ,,H四点共线,并且A1 ⊥BC时(因为点H是在
BC上的动点,点到直线的距离,垂线段最短)
5、费马定理-牛刀小试
【例题2】
1.如右图,某货运场为一个矩形场地ABCD,其中AB=500米,AD=800米,顶点A,D
为两个出口,现在想在货运广场内建一个货物堆放平台P,在BC边上(含B,C两点)开
过程如下:∵AP=AF,∠PAF=60°,
∴△PAF是等边三角形,
∴PA=PF=AE,EF=PB,
∴PA+PB+PC=EF+PF+PC,
∴当E、F、P、C共线时,PA+PB+PC最小,
作EM⊥DA交DA的延长线于M,ME的延长线交CB的延长线于N,则四边形ABNM是M
矩形,
在Rt△AME中,∵∠M=90°,∠MAE=30°,AE=2,
费马尔问题思考:
如何找到一点P,使它到△ABC三个顶点的距离之和PA+PB+PC最小?
+ + = + + ≥
当B、P、Q、E四点共线时,满足最小值
5、费马定理-牛刀小试
【例题1】
如图,矩形ABCD是一个长为1000米,宽为600米的货场,A、D是入
第09讲 最值问题之费马点与加权费马点

第9讲 最值问题之费马点与加权费马点知识点精讲到三个定理的三条线段之和最小,夹角都为120°.旋转与最短路程问题主要是利用旋转的性质转化为两点之间线段最短的问题,同时与旋转有关路程最短的问题,比较重要的就是费马点问题.皮耶·德·费马(Pieere de Fermat )是一个17世纪的法国律师,也是一位业余数学家.之所以称业余,是由于皮耶·德·费马具有律师的全职工作.他的姓氏根据法文与英文实际发音也常译为“费尔玛”.费马最后定理在中国习惯称为费马大定理,西方数学界原名“最后”的意思是:其它猜想都证实了,这是最后一个.著名的数学史学家贝尔(E .T .Bell )在 20世纪初所撰写的著作中,称皮耶·德·费马为“业余数学家之王” .贝尔深信,费马比皮耶·德·费马同时代的大多数专业数学家更有成就,然而皮耶·德·费马并未在其他方面另有成就,本人也渐渐退出人们的视野,考虑到17世纪是杰出数学家活跃的世纪,因而贝尔认为费马是17世纪数学家中最多产的明星.费马点问题最早是由法国数学家皮埃尔·德·费马在一封写给意大利数学家埃万杰利斯塔·托里拆利(气压计的发明者)的信中提出的.托里拆利最早解决了这个问题,而19世纪的数学家斯坦纳重新发现了这个问题,并系统地进行了推广,因此这个点也称为托里拆利点或斯坦纳点,相关的问题也被称作费马·托里拆利·斯坦纳问题,这一问题的解决极大推动了联合数学的发展,在近代数学史上具有里程碑式的意义.结论:(1)平面内一点P 到△ABC 三个顶点的之和为P A +PB +PC ,当点P 为费马点时,距离之和最小. 特殊三角形中:(2)三内角皆小于120°的三角形,分别以AB 、BC 、CA 为边,向三角形外侧作正三角形ABC 1,AB 1C , BCA 1,然后连接AA 1,BB 1,CC 1,则三线交于一点P ,则点P 就是所求的费马点.(3)若三角形有一内角大于或等于120°,则此钝角的顶点就是所求的费马点. (4)当△ABC 为等边三角形时,此时内心与费马点重合.下面简单说明如何找点P 使它到△ABC 三个顶点的距离之和P A +PB +PC 最小?这就是所谓的费尔马问题.这时∠BP A =180°-∠APP ´=180°-60°=120°,∠APC =∠AP ´C ´=180°-∠AP ´P =180°-60°=120°,∠BPC =360°-∠BP A -∠APC =360°-120°-120°=120°,因此,当△ABC 的每一个内角都小于120°时,所求的点P 对三角形每边的张角都是120°,可在AB 、BC 边上分别作120°的弓形弧,两弧在三角形内的交点就是P 点;当有一内角大于或等于120°时,所求的P 点就是钝角的顶点. 费尔马问题告诉我们,存在这么一个点到三个定点的距离之和最小,解决问题的方法是运用旋转变换.解析:如图1,把△APC 绕A 点逆时针旋转60°得到△AP ´C ´,连接PP ´,则△APP ´为等边三角形,AP =PP ´,P ´C =PC ,所以P A +PB +PC =PP ´+PB +P ´C ´.点C ´可看成是线段AC 绕A 点逆时针旋转60°而得的定点,BC ´为定长,所以当B 、P 、P ´、C ´四点在同一直线上时,P A +PB +PC 最小.加权费马点模型P BAP´CC´图1“加权”的意思就是“乘以权重”,即“乘以系数”的意思.加权费马点指三角形三个顶点的距离乘以系数时和的最小值问题.限于初中知识的局限性,加权费马点问题三角形三个顶点的距离乘以的系数是特殊的勾股系数,及他们的平方关系,而出题角度上由于最后计算部分只能是特殊角如120°,135°,150°的角度.通过旋转变换,可以改变线段的位置,优化图形的结构,将不规则图形变为规则图形,或将分散的条件集中在一起,以便挖掘隐含条件,使问题得以解决. 【模型解析】在△ABC 中有一点P ,连接AP ,BP ,CP ,求aP A +bPB +cPC 的最小值.数据处理原则求aP A +bPB +cPC 的最小值(a 、b 、c 为整数)①先将aP A +bPB +cPC 的系数化简成一个系数为一的系数,通常这条线段不作为旋转P 与另两个端点的三角形进行旋转特殊角度进行分析. ②常见角度处理原则∠ACB 为30°和旋转角∠ACA ´=60°形成∠BCA ´=90°; ∠ACB 为30°和旋转角∠ACA ´=90°形成∠BCA ´=120°; ∠ACB 为30°和旋转角∠ACA ´=120°形成∠BCA ´=150°; ∠ACB 为45°和旋转角∠ACA ´=90°形成∠BCA ´=135°; ∠ACB 为60°和旋转角∠ACA ´=60°形成∠BCA ´=120°; ∠ACB 为60°和旋转角∠ACA ´=90°形成∠BCA ´=150°; ∠ACB 为90°和旋转角∠ACA ´=60°形成∠BCA ´=150°.这些较为常见的特殊角组合,在初中的知识结构中能在直角三角形中进行求解线段长度.一般需要将加权的线段转化为首尾顺次相接,在运用两点之间线段最短解题.③【解题套路】处理数据aP A +bPB +cPC ,这里我们以左右同时除以b ,进行说明.处理后得abAP +BP +cbCP .以A ,C 为旋转中心,进行旋转,我们以C 为旋转中心为例,如上图△P ″A ″C ∽△P ´A ´C ,在得到P ″A ″与P A 的关系,由勾股定理与特殊三角形关系得到P ´P ″与PC 的关系,当B 、P ´、P ″、A ″共线时运BPAA´P´C´A´A´´用两点间线段最短进行求解. ④加权费马点模型典例等边三角形ABC 中,边长为m ,P 为△ABC 内部一点,求b a AP +BP +caCP 的最小值(a 、b 、c 为勾股数或相等b ≤a ≤c ).[解析]将△ACP 绕点C 旋转90°得△A ´CP ´,取CP ´和CA ´的点P ″,A ″使CP ″=baCP ´,A ″C =baA ´C ,连接PP ″. ∵△ACP 绕点C 旋转90°得△A ´CP ´,∴PC =P ´C ,∵∠ACB =60°,∠ACA ´=90°,∴∠A ´CB =150°,∴∠A ´CG =30°,∵CP ″=b a CP ´,A ″C =baA ´C ,∠A ´CP ´=∠A ´CP ´,∴△P ´A ´C ∽△P ″A ″C ,∴P ″A ″=b a P A ,∵AC =m ,∴A ″C =bm a ,CF,A ″F =2bm a ,∵在Rt △P ´CP ″中,CP ″=baCP ,∴PP ″=c a PC ,∴求b a AP +BP +caCP 的最小值为B 、P ´、P ″、A ″共线,∴最小值BA.典型例题【例1】阅读下列材料对于任意的△ABC ,若三角形内或三角形上有一点P 、若P A +PB +PC 有最小值,则取到小值时,点P 为该三角形的费马点.①若三角形内有一个内角大于或等于120°,这个内角的顶点就是费马点;②若三角形内角均小于120°,则满足条件∠APB =∠BPC =∠APC =120°时,点P 即为费马点. 解决问题: (1)如图,△ABC 中,三个内角均小于120°,分别以AB 、AC 为边向外作等边△ABD 、△ACE ,连接CD 、BE 交于点P .证明:点P 为△ABC 的费马点,(即证明∠APB =∠BPC =∠APC =120°)且P A +PB +PC =CD . (2)如图,点Q 为三角形内部异于点P 的一点,证明:QA +QC +QB >P A +PB +PC . (3)若∠ABC =30°,AB =3,BC =4,直接写出P A +PB +PC 的最小值.【答案】(1)详细证明过程略:[提示,如图]在线段CD 上取点F ,使得PF =BP . 第一阶段:如图以,先证明△ACD ≌△AEB ,可得CD =BE ,∠ADC =∠ABE ,因此∠BPD =∠BAD =60°,∴∠BPC =120°,得证明.第二阶段:如图二,因为PB =PF ,∠BPF =60°,可证△BPF 为等边三角形,则∠DFB =120°. 第三阶段:如图三,证明△ABP ≌△DBF ,则P A =DF ,∠BP A =∠DFB =120°,∴∠BPC =∠BP A =∠APC =120°,且CD =DF +PF +PC =P A +PB +PC .(2)详细证明过程略,如图四,以BQ 为边构造等边△BQG ,连接DG ,证明△BGD ≌△BQA ,则DG =QA ,根据两点之间线段最短,DG +QG +QC >DC ,则QA +QC +QB >P A +PB +PC . (3)最小值为5.【例2】在等边三角形ABC 中,边长为4,P 为三角形ABC 内部一点,求AP +BPPC 的最小值.ABCEPDQADBCEP图一EBCE图二B图三图四E图五[解析]过C作AC的垂线截取A´C=AC,过C作PC的垂线截取P´C=PC.∵PC⊥P´C,AC⊥A´C,∴∠ACA´=∠PCP´=90°,∴∠ACP=∠A´CP´,∵A´C=AC,∠ACP=∠A´CP´,P´C=PC,∴△ACP≌△A´CP´,∴AP=A´P´,∵PC⊥P´C,P´C=PC,∴PP,∴AP+BP的最小值为B、P、P´、A四点共线时取最小值为A´B,∵∠ACA´=90°,∠ACB=60°,∴∠BCA´=150°,∴∠A´CH=30°,∵A´C=4,∴A´H=2,CH=,∴A´B==【例3】在△ABC中,BC为4,AC=ACB=45°,P为三角形ABC内部一点,求AP+BPPC的最小值.ABPCA´A将△ACP绕点C旋转90°得△A´CP´,连接PP´.∵△ACP绕点C旋转90°得△A´CP´,∴PC=P´C,P A=P´A´,∵∠ACB=45°,∠ACA´=90°,∴∠A´CB=135°,∴∠A´CG=45°,∴P A=P´A´,∠PCP´=90°,∴PPPC,∵A´C=A´G=CG=3,∴求AP+BPPC的最小值为B、P、P´、A共线即可,∴最小值为BA【例4】在△ABC中,BC为4,AC=∠ACB=45°,P为三角形ABC内部一点,求12AP+BPPC的最小值.将△ACP绕点C旋转90°得△A´CP´,取CP´和CA´的中点P´´,A´´,则CP´´=12CP´,CA´´=12CA´,连接PP´´.∵△ACP绕点C旋转90°得△A´CP´,∴PC=P´C,∵∠ACB=45°,∠ACA´=90°,∴∠A´CB=135°,∴∠A´CG=45°,∵CP´´=12CP´,CA´´=12CA´,∠A´CP´=∠A´CP´,∴△P´A´C∽△P´´A´´C,∴P´´A´´=12P´A´,∵A´C=,∴A´´C,CF=A´´F=32,∵在Rt△PCP´´中,CP´´=12CP,∴PPPC,∴求12AP+BP的最小值为B、P、P´´、A´´共线即可,∴最小值为BA´´=.AB CP45°45°ABP【例5】在正△ABC中,边长为4,P为△ABC内部一点,求43AP+BP+53PC的最小值.[解析]将△ACP绕点C旋转90°得△A´CP´,在CP´和CA´上取点P´´,A´´,则CP´´=43CP´,CA´´=43CA´,连接PP´´、A´´P´´.∵△ACP绕点C旋转90°得△A´CP´,∴PC=P´C,∵∠ACB=60°,∠ACA´=90°,∴∠A´CB=150°,∴∠A´CG=30°,∵CP´´=43CP´,CA´´=43CA´,∠A´CP´=∠A´CP´,∴△P´A´C∽△P´´A´´C,∴P´´A´´=43P´A´=43P A,∵A´C=4,∴A´´C=5,CF,A´´F=52,∵在Rt△PCP´´中,CP´´=4 3CP,∴PP´´=53PC,∴求43AP+BP+53PC的最小值为B、P、P´´、A´´共线即可,∴最小值为BA´´3B43BPAC【例6】在△ABC中,BC为6,AC=4,∠ACB=30°,P为△ABC内部一点,求AP+BPPC的最小值.将△ACP绕点C旋转90°得△A´CP´,连接PP´´.∵△ACP绕点C旋转90°得△A´CP´,∴P A=P´A,PC=P´C,∵∠ACB=30°,∠ACA´=90°,∴∠A´CB=120°,∴∠A´CG=60°,∵A´C=4,A´G=CG=2,∵在Rt△PCP´´中,∠PCP´=90°,PC=P´C,PPC P,∴求AP+BPC的最小值为B、P、A´共线即可,∴最小值为BA´=【例7】在△ABC中,BC为6,AC=4,∠ACB=30°,P为△ABC内部一点,求12AP+BP PC的最小值.[解析]将△ACP绕点C旋转90°得△A´CP´,在CP´和CA´上取点P´´,A´´,则CP´´=12CP´,CA´´=12CA´,连接PP´´.∵△ACP绕点C旋转90°得△A´CP´,∴PC=P´C,∵∠ACB=30°,∠ACA´=90°,∴∠A´CB=120°,´´AB CPA´A´AB CP∴∠A´CG=60°,∵CP´´=12CP´,CA´´=12CA´,∠A´CP´=∠A´CP´,∴△P´A´C∽△P´´A´´C,∴P´´A´´=12P A,∵A´C=4,∴A´´C=2,CF=A´´FRt△PCP´´中,CP´´=12CP,∴PP´´=,∴求12AP+BPPC的最小值为B、P、P´´、A´´共线即可,∴最小值为BA【例8】在△ABC中,BC为6,AC=4,∠ACB=30°,P为△ABC内部一点,求34AP+BP+54PC的最小值(求3 AP+BP+5PC的最小值).将△ACP绕点C旋转90°得△A´CP´,在CP´和CA´上取点P´´,A´´,则CP´´=34CP´,CA´´=34CA ´,连接PP´´.∵△ACP绕点C旋转90°得△A´CP´,∴PC=P´C,∵∠ACB=30°,∠ACA´=90°,∴∠A´CB=120°,∴∠A´CG=60°,∵CP´´=34CP´,CA´´=34CA´,∠A´CP´=∠A´CP´,∴△P´A´C∽△P´´A´´C,∴P´´A´´=34P A,∵A´C=4,∴A´´C=3,CF=A´´F,∵在Rt△PCP´´中,CP´´=34CP,∴PP´´=54PC,P193—204A´A´APBC∴求34P A +BP +54PC 的最小值为BPP ″A ″共线即可.∴最小值BA =.【注意】求3P A +4BP +5PC 的最小值先求34P A +BP +54PC 的最小值即可,最后将最小值乘以4即可,3P A +4BP +5PC 的最小值为4×=【例9】如图,四边形ABCD 是正方形,△ABE 是等边三角形,M 为对角线BD (不含B 点)上任意一点,将BM 绕点B 逆时针旋转60°得到BN ,连接EN 、AM 、CM . (1)求证:△AMB ≌△ENB ;(2)①当M 点在何处时,AM +CM 的值最小;②当M 点在何处时,AM +BM +CM 的值最小,并说明理由;(3)当AM +BM +CM 1时,求正方形的边长.解析(1)证明:∵△ABE 是等边三角形,∴BA =BE ,∠ABE =60°. ∵∠MBN =60°,∴∠MBN -∠ABN =∠ABE -∠ABN .即∠MBA =∠NBE .又∵MB =NB ,∴△AMB ≌△ENB (SAS ).(2)如图,连接CE ,当M 点位于BD 与CE 的交点处时,AM +BM +CM 的值最小. 理由如下:连接MN ,由(1)知,△AMB ≌△ENB ,∴AM =EN ,∵∠MBN =60°,MB =NB ,∴△BMN 是等边三角形.∴BM =MN . ∴AM +BM +CM =EN +MN +CM . 根据“两点之间线段最短”,得EN +MN +CM =EC 最短.∴当M 点位于BD 与CE 的交点处时,AM +BM +CM 的值最小,即等于EC 的长. (3)过E 点作EF ⊥BC 交CB 的延长线于F , ∴∠EBF =∠ABF -∠ABE =90°=60°=30°.设正方形的边长为x ,则BF =2x ,EF =2x .在Rt △EFC 中,∵EF 2+FC 2=EC 2,∴222()()1)22xx x ++=.解得,x 1x 2(舍去负值)..【例10】如图,矩形纸片ABCD (AD >AB )中,将它折叠,使点A 与C 重合,在矩形ABCD 中,AB =600,BC =1000,P 是内部一点,Q 是BC 边上任意一点,试确定点P 、Q 的位置,使得P A +PD +PQ 最小,并求出这个最小值.解析点Q是BC边的中点,点P在AD的中垂线上且满足∠ADP=120°.最小值为600+【例11】已知O是△ABC内一点,∠AOB=∠BOC=∠COA=120°;P是△ABC内任一点,求证:P A+PB+PC≥OA+OB+OC.(O为费马点)解析以B为旋转中心,60°为旋转角,将点P、O、C分别旋转到点P′、O′、C′,连接OO′、PP′.则△POO′、△BPP′都是正三角形.∴OO′=OB,PP′=PB.显然△BO′C′≌△BOC,△BP′C′≌△BPC. 由于∠BO′C′=∠BOC=120°=180°-∠BO′O,∴A、O、O′、C′四点共线.【例12】已知正方形ABCD内一动点E到A、B、C,求此正方形的边长.解析 如图,连接AC ,把△AEC 绕点C 顺时针旋转60°,得到△GFC ,连接EF 、BG 、AG ,可知△EFC 、△AGC 都是等边三角形,则EF =CE .又FG =AE ,∴AE +BE +CE =BE +EF +FG . ∵点B 、点G 为定点(G 为点A 绕C 点顺时针旋转60°所得).∴线段BG 即为点E 到A 、B 、C 三点的距离之和的最小值,此时E 、F 两点都在BG 上.设正方形的边长为a ,那么BO =CO a ,GC a ,GO .∴BG =BO +GO a .∵点E 到A 、B 、C .∴2a +2,解得a =2. 相似巩固1.在边长为4的正△ABC 中有一点P ,连接P A 、PB 、PC ,求12P A +PB 的最小值.将△ACP 绕点C 旋转90°得△A ′CP ′,取CP ′和CA ′的中点P ″,A ″,连接PP ″.∵△ACP 绕点C 旋转90°得△A ′CP ′,∴PC =P ′C .∵∠ACB =60°,∠ACA ′=90°,∴∠A ′CB =150°,∴∠A ′CG =30°.∵取CP ′和CA ′的中点P ″,A ″,∴CP ″=12CP ,P ″A ″=12P A .∵A ′C =4,∴A ″C =2,CF ,A ″F =1,·∵在Rt △PCP ″中CP ″= 12CP ,∴PP .∴求12P A +PB +2PC 的最小值为BPP ″A ″共线,∴最小值为BA2.如图,点P 在边长为2的正方形ABCD 内,连结P A 、PB 、PC ,则P A +PB +PC 的最小值为 .【解析】△BPC 绕B 点顺时针旋转60度,可得△PBE 为等边三角形,若P A +PB +PC =AP +PE +EF 要使最小只要AP ,PE ,EF 在一条直线上,求出AF 的值即可.【详解】△BPC 绕B 点顺时针旋转60度,可得△PBE 为等边三角形.即得P A +PB +PC =AP +PE +EF 要使最小只要AP ,PE ,EF 在一条直线上,即如下图:可得最小P A +PB +PC =AF .此时∠EBC +∠CBP =∠FBE +∠EBC =60°=∠FBC ,所以∠ABF =90°+60°=150°,∠MBF =30°,BM MF =1,则AM =2,在△AMF 中,勾股定理得:AM 2+MF 2=AF 2,AF .4.如图,△ABC 中,∠BAC =30°,且AB =AC ,P 是底边上的高AH 上一点.若AP +BP +CP 的最小值为,则BC = .【解析】如图将△ABP 绕点A 顺时针旋转60°得到△AMG .连接PG ,CM .首先证明当M ,G ,P ,C 共线时,P A +PB +PC 的值最小,最小值为线段CM 的长,想办法求出AC 的长即可解决问题.【详解】如图将△ABP 绕点A 顺时针旋转60°得到△AMG .连接PG ,CM .∵AB =AC ,AH ⊥BC ,∴∠BAP =∠CAP ,∵P A =P A ,∴△BAP ≌△CAP (SAS ),∴PC =PB ,∵MG =PB ,AG =AP ,∠GAP =60°,∴△GAP 为等边三角形,∴P A =PG .∴P A +PB +PC =CP +PG +GM , ∴当M ,G ,P ,C 共线时,P A +PB +PC 的值最小,最小值为线段CM 的长,∵AP +BP +CP 的最小值为,∴CM =,∵∠BAM =60°,∠BAC =30°,∴∠MAC =90°, ∴AM =AC =1,作BN ⊥AC 于N ,则BN =12AB =1,ANCN =2∴BC.【点睛】本题考查轴对称—最短问题,等腰三角形的性质,等边三角形的判定和性质,解直角三角形等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,学会利用两点之间线段最短解决问题.5.如图,在平面直角坐标系中,点A 的坐标为(-6,0),点B 的坐标为(6,0),点C 的坐标为(),延长AC 至点D 使得CD =AC ,过点D 作DE ∥AB ,交BC 的延长线于点E ,设G 为y 轴上的一点,点P 从直线yx +y 轴的交点M 出发,先沿y 轴到达点G ,再沿GA 到达点A ,若点P 在y 轴上运动的速度是它在直线GA 上运动速度的2倍,试确定点G 的位置,使点P 按照上述要求到达A 所应的实际最短.解:∵t =2GM v +GA v =22GA GM v +,∴当2GA +GM 最小时,时间最短. 如图,假设在OM 上存在一点G ,则BG =AG ,∴MG +2AG =MG +AG +BG .把△MGB 绕点B 顺时针旋转60°,得到△M ′G ′B ,连接GG ′,MM ′.∴△GG ′B 、△MM ′B 都为等边三角形,则GG ′=G ′B =GB ,又M ′G ′=MG .∴MG +AG +BG =M ′G ′+GG ′+AG ,∵点A ,M ′为定点,∴AM ′与OM 的交点为G ,此时MG +AG +BG 最小,∴点G 的坐标为().126.A、B、C、D四个城市恰好为一个正方形的四个顶点,要建立一个公路系统使得每两个城市之间都有公路相通,并使整个公路系统的总长度最小,则应当如何修建?解:如图,将△ABP绕点N逆时针旋转60°,得到△EBM;同样,将△DCQ绕点C顺时针旋转60°,得到△FCN,连结AE、DF,则△ABE、△DCF均为等边三角形,连结PM、QN,则△BPM,△CQN均为等边三角形.所以当点E、M、P、Q、N、F共线时,整个公路系统的总长取到最小值,为线段EF的长,如图,此时点P、Q在EF上.7.如图,在△ABC中,∠ABC=60°,AB=5,BC=3,P是△ABC内一点,求P A+PB+PC的最小值,并确定当P A+PB+PC取得最小值时,∠APC的度数.答案:P A +PB +PC 的最小值为7,此时∠APC =120°.【提示】如图,将△APB 绕点B 逆时针旋转60°,得到△A ′BP ′,连结PP ′,A ′C .过点A ′作A ′E ⊥BC ,交CB 的延长线于点E ,解Rt △A ′EC 求A ′C 的长,所得即为P A +PB +PC 的最小值. 跟踪检测1.如图,在平面直角坐标系xoy 中,△ABC 三个顶点的坐标分别为A (-6,0),B (6,0),C (),延长AC 到点D ,使CD =12AC ,过点D 作DE ∥AB 交BC 的延长线于点E . (1)求D 点的坐标;(2)作C 点关于直线DE 的对称点F ,分别连结DF 、EF ,若过B 点的直线y =kx +b 将四边形CDFE 分成周长相等的两个四边形,确定此直线的解析式;(3)设G 为y 轴上一点,点P 从直线y =kx +b 与y 轴的交点出发,先沿y 轴到达G 点,再沿GA 到达A 点,若P 点在y 轴上运动的速度是它在直线GA 上运动速度的2倍,试确定G 点的位置,使P 点按照上述要求到达A 点所用的时间最短.分析和解:(1)D 点的坐标((过程略).(2)直线BM 的解析式为y +(过程略).(3)如何确定点G 的位置是本题的难点也是关键所在.设Q 点为y 轴上一点,P 在y 轴上运动的速度为v ,则P 沿M →Q →A 运动的时间为2MQ v +AQ v ,使P 点到达A 点所用的时间最短,就是12MQ +AQ 最小,或MQ +2AQ 最小,或MQ +2AQ 最小.解法1 ∵BQ =AQ ,∴MQ +2AQ 最小就是MQ +AQ +BQ 最小,就是在直线MO 上找到G 使他到A 、B 、M 三点的距离和最小.至此,再次发现这又是一个费尔马问题的变形,注意到题目中等边三角形的信息,考虑作旋转变换.把△MQB 绕点B 顺时针旋转60°,得到△M ′Q ′B ,连接QQ ′,MM ′(图5),可知△QQ ′B 、△MM ′B 都是等边三角形,则QQ ′=BQ .又M ′Q ′=MQ ,∴MQ +AQ +BQ =M ′Q ′+QQ ′+AQ .∵点A 、M ′为定点,所以当Q ,Q ′两点在线段AM ′上时,MQ +AQ +BQ 最小.由条件可证明Q ′点总在AM ′上,所以AM ′与OM 的交点就是所要的G 点(图6).可证OG =12MG .图5 图6 图7解法2 考虑12MQ +AQ 最小,过Q 作BM 的垂线交BM 于K ,由OB =6,OM =可得∠BMO =30°,所以QK =12MQ . 要使12MQ +AQ 最小,只需使AQ +QK 最小,根据“垂线段最短”,可推出当点A 、Q 、K 在一条直线上时,AQ +QK 最小,并且此时的QK 垂直于BM ,此时的点Q 即为所求的点G (图7).过A 点作AH ⊥BM 于H ,则AH 与y 轴的交点为所求的G 点.由OB =6,OM =,可得∠OBM =60°,∴∠BAH =30°.在Rt △OAG 中,OG =AO ·tan ∠BAH =∴G 点的坐标为()(G 点为线段OC 的中点).2.在△ABC 中,BC 为4,AC =,∠ACB =45°,P 为三角形ABC 内部一点,求AP BP PC 的最小值.分析由AP BP ,求2AP +BP +2即可.将△ACP 绕点C 旋转90°得△A ′CP ′,取CP ′和CA ′的点P ″,A ″使CP ″=2CP ′,A ″C =2A ′C ,连接PP ″. ∵△ACP 绕点C 旋转90°得△A ′CP ′,∴∠A ′CG =45°.∵CP ″=2CP ′,A ″C =2A ′C ,∠A ′CP ′=∠A ′CP ′,∴△P ′A ′C ∽△P ″A ″C ,∴P ″A ″=2P A .∵A ′C =,∴A ″C =3,CF =A ″F =2.∵在RT △PCP ″中,CP ″=2CP ,∴PP .+BP 的最小值为BPP ″A ″共线即可.∴最小值BA∴由AP BP PC .3.在边长为4的正△ABC 中有一点P ,连接P A 、PB 、PC ,求PB +54PC +34P A 的最小值.将△ACP绕点C旋转90°得△A′CP′,取CP′和CA′的点P″,A″,使CP″=34CP′,A″C=34A′C,连接PP″,∵△ACP绕点C旋转90°得△A′CP′,∴PC=P′C,∵∠ACB=60°,∠ACA′=90°,∴∠A′CB=150°,∴∠A′CG=30°,∵CP″=34CP′,A″C=34A′C,∠A′CP′=∠A′CP′,∴△P′A′C∽△P″A″C,∴P″A″=34P A.∵A′C=4,∴A″C=2,CF A″F=1.∵在RT△PCP″中,CP″=34CP,∴PP″=54PC.∴求PB+54PC+34P A的最小值为BPP″A″共线,∴最小值BA4.在△ABC中有一点P连接P A、PB、PC,AC=2,BC=P A+PB的最小值.(补充:在120°的等腰三角形中,三边比为1:1将△ACP绕点C旋转120°得△A′CP′,连接PP′.∵△ACP绕点C旋转120°得△A′CP′,∴PC=P′C.∵∠ACB=30°,∠ACA′=120°,∴∠A′CB =150°,∴∠A′CG=30°.∵A′C=2,∴CG A′G=1.∵在120°的等腰△PCP′中,∴PP PC.∴求P A+PB PC的最小值为BPP′A′共线,∴最小值BA.5.如图所示,在四边形ABCD中,AB=BC,∠ABC=60°,P为四边形ABCD内部一点,∠APD=120°,证明:P A+PD+PC≥BD.【答案】如图所示,在四边形ABCD外侧作等边△AB′D,由∠APD=120°可知四边形APDB′符合(1)的条件,连接B′P,则B′P=P A+PD.连接B′C,则易知B′C≤PB′+PC,即B′C≤P A+PD+PC.此时,解题的目标是证明BD=B′C.因为△AB′D是等边三角形,故AB′=AD,∠B′AD=60°.连接AC,易知△ABC为等边三角形,故AC=AB,∠BAC=60°.在△ABD和△ACB′中,∠BAD=∠CAD+∠BAC=∠CAD+∠DAB′=∠CAB′,AB=AC.AD=AB′,故△ABD≌△ACB′.从而BD=B′C.故P A+PD+PC≥BD.6.如图,已知两条直线a∥b,直线a、b间的距离为h,点M、N在直线a上,MN=x;点P在直线b上,并且x+h=40.(1)记△PMN的面积为S,①求S与x的函数关系式,并求出MN的长为多少时△PMN的面积最大?最大面积是多少?②当②PMN的面积最大时,能求出②PMN正切值吗?为什么?(2)请你用尺规作图的方法确定②PMN的周长最小时点P的位置(要求不写作法,但保留作图痕迹);并判断②PMN的形状;(3)请你在(2)②中得到的②PMN内求一点P,使得AP+AM+AN的和最小,求出AP+AM+AN和的最小值.【解析】试题分析:(1)②根据x+h=40得出h=40-x,再由三角形的面积公式即可得出结论;②因为只要MN=h=20,P在直线b上任意位置时,②PMN的面积取得最大值,因为不能确定P点位置,所以②PMN得大小无法确定,因此不能求出②PMN的正切值;(2)②作出②PMN,由图可知②PMN是以线段MN为底的等腰三角形;②根据勾股定理求出PN的长,进而可得出结论;(3)将②MP A绕点M顺时针旋转60°得到②MP’A’,根据图形旋转的性质得出P'A'A'=P A,②MA'P=120°.连接AA',则②MAA'是等边三角形.由此可得出P',A',A,N四点在一条直线上,故AP+AM+AN=P'A'+AA'+AN =P'N,所以AP+AM+AN和的最小值等于P'N的长,由此可得出结论.试题解析:(1)②:x+h=40,h=40-x,s=12x(40-x)=12x2+20x,∵s=-12(x-20)2+200,∴当MN=20时,△PMN的面积最大,最大面积为200;②不能.因为只要MN=h=20,P在直线b上任意位置时,△PMN的面积取得最大值,因为不能确定P点位置,所以么∠PMN得大小无法确定,因此不能求出②PMN的正切值;(2)如图1,△PMN是以线段MN为底的等腰三角形.图1图2(3)如图2,在等腰△PMN的顶角②MPN的平分线上取点A,使得②AMN=②ANM=30°,点A在此处可使得AP+AM+AN的和最小.∵此时②MAP=②NAP=②NAM=120°.将△MP A绕点M顺时针旋转60°得到△MP'A'.∴P'A'=P A,②MA'P'=120°,连接AA',则△MAA'是等边三角形.∴MA=AA',②MA'A=②NAA'=60°.∴∠MA'P+MAA'=MAA'+②MAN=180°.即P',A',A,N四点在一条直线上,∴AP+AM+AN=P'A'+AA'+AN=P'N,AP+AM+AN和的最小值等于P'N的长,此时,NA=MA=10÷cos30°AB=10×tan30∴AP+AM+AN的最小值为:20+考点:1.二次函数综合题:2.平行线之间的距离:3.轴对称一最短路线问题.7.如图,某货运场为一个矩形场地ABCD,其中AB=500米,AD=800米,顶点A,D为两个出口,现在想在货运广场内建一个货物堆放平台P,在BC边上(含B,C两点)开一个货物入口M,并修建三条专用车道P A PD,PM.若修建每米专用车道的费用为10000元,当M,P建在何处时,修建专用车道的费用最少?最少费用为多少?(结果保留整数)实际应用:如图,连接AM,DM,将②ADP绕点A逆时针旋转60°,得△AP'D',当M,P,P',D'在同一条直线上时,AP+PM+DP最小,最小值为D'M,∵M在BC上,∴当D'M⊥BC时,D'M取最小值,设D'M交AD于E,∵△ADD'是等边三角形,∴EM=AB=500,∴BM=400,PM=EM-PE=500∴D'E AD=∴D'M=,∴最少费用为10000×(=1000000(万元;∴M建在BC中点(BM=400米)处,点P在过M且垂直于BC的直线上,且在M上方(500米处,最少费用为1000000(万元.8.(1)如图1,△ABC和△CDE都是等边三角形,且B、C、D三点共线,联结AD、BE相交于点P,求证:BE=AD.(2)如图2,在△BCD中,②BCD<120°,分别以BC、CD和BD为边在△BCD外部作等边△ABC、等边△CDE和等边△BDF,联结AD、BE和CF交于点P,下列结论中正确的是_____________(只填序号即可)②AD=BE=CF;②②BEC=②ADC;②②DPE=②EPC=②CP A=60;(3)如图2,在(2)的条件下,求证:PB+PC+PD=BE.图1图2【答案】(1)证明:∵△ABC和△CDE都是等边三角形.∴BC=AC,CE=CD,②ACB=②DCE=60°,∴②BCE=②ACD,△BCE≌△ACD (SAS)∴BE=AD(2)②②②都正确(3)证明:在PE上截取PM=PC,联结CM由(1)可知,△BCE≌△ACD (SAS)∴∠1=∠2设CD与BE交于点G,在②CGE和②PGD中∴②1=②2,②CGE=②PGD∴②DPG=②ECG=60°同理②CPE=60°∴△CPM是等边三角形∴CP=CM,②PMC=60°∴②CPD=②CME=120°∵∠1=∠2,∴△CPD≌△CME(AAS)∴PD=ME∴BE=PB+PM+ME=PB+PC+PD.即PB+PC+PD=BE.9.已知:△ABC中,②A≥120°,P是不与A重合的定点,求证:P A+PB+PC>AB+AC.【答案】可考虑旋转某一个三角形,使AB和AC“接”成一条线段,再根据三角形中两边之和大于第三边去证明.将△P AB绕A点旋转,当按顺时针方向,旋转180°-②BAC时,到达右图的△P'AB的位置,此时AC、AB'互为反向延长线.于是PP'+P'B'+PC>CB'由于②P'AP=②B'AB=180°-②BAC≤60°,所以PP'≤P A=P'A;又P'B'=PB,故P A+PB+PC>CB'=AC+AB',即P A+PB+PC>AC+AB.。
第3讲 费马点与胡不归最值问题
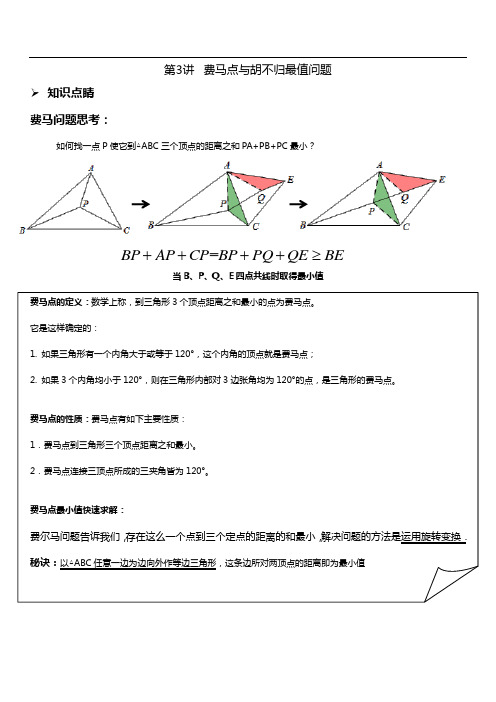
第3讲费马点与胡不归最值问题➢知识点睛费马问题思考:如何找一点P使它到△ABC三个顶点的距离之和PA+PB+PC最小?当B、P、Q、E四点共线时取得最小值费马点的定义:数学上称,到三角形3个顶点距离之和最小的点为费马点。
它是这样确定的:1. 如果三角形有一个内角大于或等于120°,这个内角的顶点就是费马点;2. 如果3个内角均小于120°,则在三角形内部对3边张角均为120°的点,是三角形的费马点。
费马点的性质:费马点有如下主要性质:1.费马点到三角形三个顶点距离之和最小。
2.费马点连接三顶点所成的三夹角皆为120°。
费马点最小值快速求解:费尔马问题告诉我们,存在这么一个点到三个定点的距离的和最小,解决问题的方法是运用旋转变换.秘诀:以△ABC任意一边为边向外作等边三角形,这条边所对两顶点的距离即为最小值=BP AP CP BP PQ QE BE++++≥➢ 精讲精练例1: 已知:△ABC 是锐角三角形,G 是三角形内一点 . ∠AGC=∠AGB=∠BGC=120°. 求证:GA+GB+GC 的值最小.练习1: 如图,P 是边长为1的等边ABC ∆内的任意一点,求t PA PB PC =++的取值范围.例2:已知正方形ABCD 内一动点E 到A 、B 、C 三点的距离之和的最小值为26+,求正方形的边长.练习2: 若P 为锐角△ABC 的费马点,且∠ABC =60°,PA =3,PC =4, 求PB 的值.例3: 如图,矩形ABCD 是一个长为1000米,宽为600米的货场,A 、D 是入口,现拟在货场内建一个收费站P ,在铁路线BC 段上建一个发货站台H ,设铺设公路AP 、DP 以及PH 之长度和为l ,求l 的最小值.600mDACPBH练习3: 如图,某货运场为一个矩形场地ABCD,其中AB=500米,AD=800米,顶点A,D为两个出口,现在想在货运广场内建一个货物堆放平台P,在BC边上(含B,C两点)开一个货物入口M,并修建三条专用车道PA,PD,PM.若修建每米专用车道的费用为10000元,当M,P建在何处时,修建专用车道的费用最少?最少费用为多少?(结果保留整数)例4:如图,在平面直角坐标系xOy中,△ABC三个顶点的坐标分别为A(﹣6,0),B(6,0),C(0,4),延长AC到点D,使CD=AC,过点D作DE∥AB交BC的延长线于点E.(1)求D点的坐标;(2)作C点关于直线DE的对称点F,分别连接DF、EF,若过B点的直线y=kx+b将四边形CDFE分成周长相等的两个四边形,确定此直线的解析式;(3)在第二问的条件下,设G为y轴上一点,点P从直线y=kx+b与y轴的交点出发,先沿y轴到达G 点,再沿GA到达A点,若P点在y轴上运动的速度是它在直线GA上运动速度的2倍,试确定G点的位置,使P点按照上述要求到达A点所用的时间最短.(要求:简述确定G点位置的方法,不要求证明)➢巩固练习1. 如图,已知矩形ABCD ,AB =4,BC =6,点M 为矩形内一点,点E 为BC 边上任意一点,则MA +MD +ME 的最小值为______.第1题图 第2题图第3题图2. 如图,P 为正方形ABCD 对角线BD 上一动点,若AB =2,则AP +BP +CP 的最小值为( ) A .+B .+C .4D .33.如图,四边形ABCD 是菱形,AB =4,且∠ABC =∠ABE =60°,M 为对角线BD (不含B 点)上任意一点,将BM 绕点B 逆时针旋转60°得到BN ,连接EN 、AM 、CM ,则AM +BM +CM 的最小值为 .4.将△ABC 放在每个小正方形的边长为1的网格中,点B 、C 落在格点上,点A 在BC 的垂直平分线上,∠ABC =30°,点P 为平面内一点. (1)∠ACB = 度;(2)如图,将△APC 绕点C 顺时针旋转60°,画出旋转后的图形(尺规作图,保留痕迹); (3)AP +BP +CP 的最小值为 .ABCDME5.如图,四个村庄坐落在矩形ABCD的四个顶点上,AB=10公里,BC=15公里,现在要设立两个车站E,F,则EA+EB+EF+FC+FD的最小值为公里.6.已知,在△ABC中,∠ACB=30°(1)如图1,当AB=AC=2,求BC的值;(2)如图2,当AB=AC,点P是△ABC内一点,且PA=2,PB=,PC=3,求∠APC的度数;(3)如图3,当AC=4,AB=(CB>CA),点P是△ABC内一动点,则PA+PB+PC的最小值为.7.如图l,在△ABC中,∠ACB=90°,点P为△ABC内一点.(1)连接PB,PC,将△BCP沿射线CA方向平移,得到△DAE,点B,C,P的对应点分别为点D、A、E,连接CE.①依题意,请在图2中补全图形;②如果BP⊥CE,BP=3,AB=6,求CE的长(2)如图3,以点A为旋转中心,将△ABP顺时针旋转60°得到△AMN,连接PA、PB、PC,当AC=3,AB =6时,根据此图求PA+PB+PC的最小值.胡不归最值模型➢ 知识点睛在前面的最值问题中往往都是求某个线段最值或者形如PA +PB 最值,除此之外我们还可能会遇上形如“PA +kPB ”这样的式子的最值,此类式子一般可以分为两类问题:(1)胡不归问题; (2)阿氏圆. 【故事介绍】从前有个少年外出求学,某天不幸得知老父亲病危的消息,便立即赶路回家.根据“两点之间线段最短”,虽然从他此刻位置A 到家B 之间是一片砂石地,但他义无反顾踏上归途,当赶到家时,老人刚咽了气,小伙子追悔莫及失声痛哭.邻居告诉小伙子说,老人弥留之际不断念叨着“胡不归?胡不归?…”然而如果先沿着驿道AC 先走一段,再走砂石地,会不会更早些到家?2驿道【模型建立】如图,一动点P 在直线MN 外的运动速度为1V ,在直线MN 上运动的速度为2V ,且21V V <,A 、B 为定点,点C 在直线MN 上,确定点C 的位置使21AC BCV V的值最小.2M【问题分析】121121=V AC BC BC AC V V V V ⎛⎫++ ⎪⎝⎭,记12V k V =,即求BC +kAC 的最小值.【问题解决】构造射线AD 使得sin ∠DAN =k ,即CHk AC=,CH =kAC .将问题转化为求BC +CH 最小值,过B 点作BH ⊥AD 交MN 于点C ,交AD 于H 点,此时BC +CH 取到最小值,即BC +kAC 最小.M【模型总结】在求形如“P A +kPB ”的式子的最值问题中,关键是构造与kPB 相等的线段,将“P A +kPB ”型问题转化为“P A +PC ”型.而这里的PB 必须是一条方向不变的线段,方能构造定角利用三角函数得到kPB 的等线段.M➢精讲精练例1: 如图,△ABC 中,AB =AC =10,tan A =2,BE ⊥AC 于点E ,D 是线段BE 上的一个动点,则55CD BD +的最小值是_______.练习1-1: 如图,平行四边形ABCD 中,∠DAB =60°,AB =6,BC =2,P 为边CD 上的一动点,则32PB PD +的最小值等于________.练习1-1: 如图,△ABC 中,∠BAC =30°且AB =AC ,P 是底边上的高AH 上一点.若AP +BP +CP 的最小值为2,则BC = .ABCDEABCDP例2: 等边三角形ABC的边长为6,将其放置在如图所示的平面直角坐标系中,其中BC边在x轴上,BC边的高OA在Y轴上.一只电子虫从A出发,先沿y轴到达G点,再沿GC到达C点,已知电子虫在Y轴上运动的速度是在GC上运动速度的2倍,若电子虫走完全程的时间最短,则点G的坐标为.练习2: 如图,△ABC在直角坐标系中,AB=AC,A(0,2),C(1,0),D为射线AO上一点,一动点P 从A出发,运动路径为A→D→C,点P在AD上的运动速度是在CD上的3倍,要使整个运动时间最少,则点D的坐标应为()A.(0,)B.(0,)C.(0,)D.(0,)例3: 直线y=与抛物线y=(x﹣3)2﹣4m+3交于A,B两点(其中点A在点B的左侧),与抛物线的对称轴交于点C,抛物线的顶点为D(点D在点C的下方),设点B的横坐标为t(1)求点C的坐标及线段CD的长(用含m的式子表示);(2)直接用含t的式子表示m与t之间的关系式(不需写出t的取值范围);(3)若CD=CB.①求点B的坐标;②在抛物线的对称轴上找一点F,使BF+CF的值最小,则满足条件的点F的坐标是.练习3: 如图1,在平面直角坐标系中将y=2x+1向下平移3个单位长度得到直线l1,直线l1与x轴交于点C;直线l2:y=x+2与x轴、y轴交于A、B两点,且与直线l1交于点D.(1)填空:点A的坐标为,点B的坐标为;(2)直线l1的表达式为;(3)在直线l1上是否存在点E,使S△AOE=2S△ABO?若存在,则求出点E的坐标;若不存在,说明理由.(4)如图2,点P为线段AD上一点(不含端点),连接CP,一动点H从C出发,沿线段CP以每秒1个单位的速度运动到点P,再沿线段PD以每秒个单位的速度运动到点D后停止,求点H在整个运动过程中所用时间最少时点P的坐标.例4: 已知抛物线y=a(x+3)(x﹣1)(a≠0),与x轴从左至右依次相交于A、B两点,与y轴相交于点C,经过点A的直线y=﹣x+b与抛物线的另一个交点为D.(1)若点D的横坐标为2,求抛物线的函数解析式;(2)若在(1)的条件下,抛物线上存在点P,使得△ACP是以AC为直角边的直角三角形,求点P的坐标;(3)在(1)的条件下,设点E是线段AD上的一点(不含端点),连接BE.一动点Q从点B出发,沿线段BE以每秒1个单位的速度运动到点E,再沿线段ED以每秒个单位的速度运动到点D后停止,问当点E 的坐标是多少时,点Q在整个运动过程中所用时间最少?练习4: 如图,已知抛物线y=﹣x2+bx+c交x轴于点A(2,0)、B(﹣8,0),交y轴于点C,过点A、B、C三点的⊙M与y轴的另一个交点为D.(1)求此抛物线的表达式及圆心M的坐标;(2)设P为弧BC上任意一点(不与点B,C重合),连接AP交y轴于点N,请问:AP•AN是否为定值,若是,请求出这个值;若不是,请说明理由;(3)延长线段BD交抛物线于点E,设点F是线段BE上的任意一点(不含端点),连接AF.动点Q从点A 出发,沿线段AF以每秒1个单位的速度运动到点F,再沿线段FB以每秒个单位的速度运动到点B后停止,问当点F的坐标是多少时,点Q在整个运动过程中所用时间最少?➢巩固练习1. 如图,在平面直角坐标系中,点()3,3A ,点P 为x 轴上的一个动点,当OP AP 21+最小时,点P 的坐标为___________.2. 如图,四边形ABCD 是菱形,AB=4,且∠ABC=60°,点M 为对角线BD (不含点B )上的一动点,则BM AM 21+的最小值为___________.3. 如图,在平面直角坐标系中,二次函数y =ax 2+bx +c 的图象经过点A (﹣1,0),B (0,﹣),C (2,0),其对称轴与x 轴交于点D . (1)求二次函数的表达式及其顶点坐标;(2)点M 为抛物线的对称轴上的一个动点,若平面内存在点N ,使得以A ,B ,M ,N 为顶点的四边形为菱形,求点M 的坐标;(3)若P 为y 轴上的一个动点,连接PD ,求PB +PD 的最小值.4. 【问题提出】如图①,已知海岛A到海岸公路BD距离为AB的长度,C为公路BD上的酒店,从海岛A到酒店C,先乘船到登陆点D,船速为a,再乘汽车,车速为船速的n倍,点D选在何处时,所用时间最短?【特例分析】若n=2,则时间t=+,当a为定值时,问题转化为:在BC上确定一点D,使得+的值最小.如图②,过点C做射线CM,使得∠BCM=30°.(1)过点D作DE⊥CM,垂足为E,试说明:DE=;(2)请在图②中画出所用时间最短的登陆点D′.【问题解决】(3)请你仿照“特例分析”中的相关步骤,解决图①中的问题.(写出具体方案,如相关图形呈现、图形中角所满足的条件、作图的方法等)【综合运用】(4)如图③,抛物线y=﹣x2+x+3与x轴分别交于A,B两点,与y轴交于点C,E为OB中点,设F为线段BC上一点(不含端点),连接EF.一动点P从E出发,沿线段EF以每秒1个单位的速度运动到F,再沿着线段FC以每秒个单位的速度运动到C后停止.若点P在整个运动过程中用时最少,请求出最少时间和此时点F的坐标.5. 如图,△ABC是等边三角形.(1)如图1,AH⊥BC于H,点P从A点出发,沿高线AH向下移动,以CP为边在CP的下方作等边三角形CPQ,连接BQ.求∠CBQ的度数;(2)如图2,若点D为△ABC内任意一点,连接DA,DB,DC.证明:以DA,DB,DC为边一定能组成一个三角形;(3)在(1)的条件下,在P点的移动过程中,设x=AP+2PC,点Q的运动路径长度为y,当x取最小值时,写出x,y的关系,并说明理由.6. 如图,已知抛物线y=(x+2)(x﹣4)(k为常数,且k>0)与x轴从左至右依次交于A,B两点,与y 轴交于点C,经过点B的直线y=﹣x+b与抛物线的另一交点为D.(1)若点D的横坐标为﹣5,求抛物线的函数表达式;(2)若在第一象限内的抛物线上有点P,使得以A,B,P为顶点的三角形与△ABC相似,求k的值;(3)在(1)的条件下,设F为线段BD上一点(不含端点),连接AF,一动点M从点A出发,沿线段AF 以每秒1个单位的速度运动到F,再沿线段FD以每秒2个单位的速度运动到D后停止,当点F的坐标是多少时,点M在整个运动过程中用时最少?7. 已如二次函数y=﹣x2+2x+3的图象和x轴交于点A、B(点A在点B的左侧),与y轴交于点C,(1)如图1,P是直线BC上方抛物线上一动点(不与B、C重合)过P作PQ∥x轴交直线BC于Q,求线段PQ 的最大值;(2)如图2,点G为线段OC上一动点,求BG+CG的最小值及此时点G的坐标;(3)如图3,在(2)的条件下,M为直线BG上一动点,N为x轴上一动点,连接AM,MN,求AM+MN的最小值.8. 如图,在Rt △ABC中,∠ACB =90°,∠B =30°,AB =4,点D 、F 分别是边AB ,BC 上的动点,连接CD ,过点A 作AE ⊥CD 交BC 于点E ,垂足为G ,连接GF ,则GF +FB 的最小值是( )A .B .C .D .9. 抛物线26236y x =+x 轴交于点A ,B (点A 在点B 的左边),与y 轴交于点C .点P 是直线AC 上方抛物线上一点,PF ⊥x 轴于点F ,PF 与线段AC 交于点E ;将线段OB 沿x 轴左右平移,线段OB 的对应线段是O 1B 1,当12PE EC +的值最大时,求四边形PO 1B 1C 周长的最小值,并求出对应的点O 1的坐标.E B 1O 1P A B CF yx O。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
最值问题2(费马点)
1、已知:P是边长为1的正方形ABCD内的一点,求PA+PB+PC的最小值.
2、已知:P是边长为1的等边三角形ABC内的一点,求PA+PB+PC的最小值.
图2
图1
A'
P
P
A A
B
C
B
C
3、(延庆)(本题满分4分)阅读下面材料:
阅读下面材料:
小伟遇到这样一个问题:如图1,在△ABC (其中∠BAC 是一个可以变化的角)中,AB=2,AC=4,以BC 为边在BC 的下方作等边△PBC ,求AP 的最大值。
小伟是这样思考的:利用变换和等边三角形将边的位置重新组合.他的方法是以点B 为旋转中心将△ABP 逆时针旋转60°得到△A ’BC,连接A A '
,当点A 落在C A '
上时,此题可解(如图2).
请你回答:AP 的最大值是 . 参考小伟同学思考问题的方法,解决下列问题:
如图3,等腰Rt △ABC .边AB=4,P 为△ABC 内部一点, 则AP+BP+CP 的最小值是 .(结果可以不化简)
图3
A
B
P
4、(朝阳二模)阅读下列材料:
小华遇到这样一个问题,如图1, △ABC 中,∠ACB =30º,BC =6,AC =5,在△ABC 内部有一点P ,连接P A 、PB 、PC ,求P A +PB +PC 的最小值.
小华是这样思考的:要解决这个问题,首先应想办法将这三条端点重合于一点的线段分离,然后再将它们连接成一条折线,并让折线的两个端点为定点,这样依据“两点之间,线段最短”,就可以求出这三条线段和的最小值了.他先后尝试了翻折、旋转、平移的方法,发现通过旋转可以解决这个问题.他的做法是,如图2,将△APC 绕点C 顺时针旋转60º,得到△EDC ,连接PD 、BE ,则BE 的长即为所求.
(1)请你写出图2中,P A +PB +PC 的最小值为 ; (2)参考小华的思考问题的方法,解决下列问题:
①如图3,菱形ABCD 中,∠ABC =60º,在菱形ABCD 内部有一点P ,请在图3
中画出并指明长度等于P A +PB +PC 最小值的线段(保留画图痕迹,画出一条即可);②若①中菱形ABCD 的边长为4,请直接写出当P A +PB +PC 值最小时PB 的长.
B
图
2
B
图
3
C B 图1
5、(海淀二模)如图. 在平面直角坐标系xOy 中. 点B 的坐标为(0,2). 点D 在x 轴的正半
轴上. 30ODB ∠=︒. OE 为△BOD 的中线. 过B 、E 两点的抛物线2
3
6
y ax x c =+
+与x 轴相交于A 、F 两点(A 在F 的左侧).
(1) 求抛物线的解析式;
(2) 等边△OMN 的顶点M 、N 在线段AE 上. 求AE 及AM 的长;
(3) 点P 为△ABO 内的一个动点. 设m PA PB PO =++.
请直接写出m 的最小值, 以及m 取得最小值时, 线段AP 的长. (备用图)。
