欧拉角的求取与互补滤波器在姿态解算中的应用
互补滤波算法姿态解算

互补滤波算法姿态解算互补滤波算法是一种常用的姿态解算方法,广泛应用于飞行控制系统、惯性导航系统和姿态测量装置等领域。
该算法通过融合加速度计和陀螺仪的测量数据,实现对目标物体的姿态估计。
下面将详细介绍互补滤波算法的原理和应用。
一、互补滤波算法原理互补滤波算法主要基于两个观察结果:加速度计测量的重力矢量与陀螺仪测量的角速度。
加速度计测量的重力矢量可以提供一个参考方向,而陀螺仪测量的角速度可以提供连续更新的姿态角度信息。
互补滤波算法通过将这两个信息进行互补,实现对目标物体的姿态解算。
互补滤波算法的核心思想是将陀螺仪测量的角速度逐步累加,计算出目标物体的旋转角度,并将该角度作为姿态角。
由于陀螺仪的测量存在漂移等误差,随着时间的增加,角度积分的误差会越来越大。
为了避免这个问题,互补滤波算法通过加速度计测量的重力矢量进行补偿。
具体地,互补滤波算法使用一个权衡参数α(取值范围为0到1)来控制加速度计和陀螺仪的权重。
在每次更新姿态角时,新的姿态角为上一次的角度加上陀螺仪积分得到的角度乘以α,再加上加速度计测量的角度乘以1-α。
姿态角更新公式如下:θ(n) = α * (θ(n-1) + Δθ(n)) + (1-α) * θ_acc(n)其中,θ(n)为当前的姿态角,θ(n-1)为上一次的姿态角,Δθ(n)为陀螺仪积分得到的角度变化,θ_acc(n)为加速度计测量的角度。
二、互补滤波算法应用飞行器的姿态控制需要实时获取飞行器的姿态信息,并根据预设的姿态稳定控制侧滑、上升/下降等动作。
互补滤波算法可以通过融合加速度计和陀螺仪的测量数据,快速准确地获取飞行器的姿态信息。
在飞行器的姿态控制中,将陀螺仪测量的角速度作为连续更新的角度信息,用于控制飞行器的姿态稳定。
同时,通过加速度计测量的重力矢量可以提供一个参考方向,以补偿陀螺仪测量的角速度的误差。
1.初始化姿态角为加速度计测量的角度。
2.按照一定的时间间隔,读取加速度计和陀螺仪的测量数据。
欧拉角法在扑翼飞行器姿态解算中需要经过的旋转和平移

欧拉角法在扑翼飞行器姿态解算中需
要经过的旋转和平移
欧拉角法是一种在三维空间中描述物体旋转的方法,它在扑翼飞行器姿态解算中起着至关重要的作用。
扑翼飞行器,作为一种特殊的飞行器,其姿态解算需要精确考虑飞行器的每一个细微动作,以确保其能够稳定飞行。
在扑翼飞行器的姿态解算中,欧拉角法需要经过的旋转主要包括绕X轴、Y轴和Z轴的旋转。
这些旋转是相互独立的,但在实际飞行中,它们会组合在一起,形成复杂的旋转动作。
绕X轴的旋转称为俯仰角,它决定了飞行器的前后倾斜程度;绕Y轴的旋转称为偏航角,它决定了飞行器的左右倾斜程度;绕Z轴的旋转称为滚动角,它决定了飞行器的左右翻滚程度。
除了旋转之外,平移也是扑翼飞行器姿态解算中需要考虑的因素。
平移是指飞行器在三维空间中的位置变化,通常由三个坐标轴上的位移来表示。
这些位移可以通过传感器数据来测量,并与旋转数据一起用于计算飞行器的当前姿态。
在欧拉角法中,旋转和平移是通过一系列的数学运算来实现的。
首先,需要获取飞行器的传感器数据,包括加速度计、陀螺仪等。
然后,通过这些数据计算出飞行器的旋转角度和平移距离。
最后,将这些数据结合起来,形成飞行器的完整姿态信息。
总之,欧拉角法在扑翼飞行器姿态解算中需要经过的旋转和平移是一个复杂而精细的过程。
通过精确的旋转和平移计算,可以确保扑翼飞行器在各种飞行状态下都能够保持稳定和准确的姿态,从而实现高效、安全的飞行。
imu数据处理公式

IMU(惯性测量单元)数据处理通常包括数据预处理、姿态解算和融合算法等步骤。
以下是一些常用的数据处理公式和方法:
1. 数据预处理:
零偏校正:将加速度计和陀螺仪的偏移量进行修正,常用的方法包括零偏校正和尺度因子校正。
2. 姿态解算:
四元数法:将IMU的测量值进行积分,得到姿态四元数,通过四元数来计算姿态角。
欧拉角法:将IMU的测量值进行积分,得到欧拉角,通过欧拉角来计算姿态角。
卡尔曼滤波法:将IMU的测量值和加速度计数据融合,通过卡尔曼滤波算法来估计姿态角。
3. 融合算法:
互补滤波器:将加速度计和陀螺仪数据按照一定的权重进行融合,得到姿态角。
常用的权重方法包括一阶互补滤波和二阶互补滤波等。
卡尔曼滤波器:将加速度计和陀螺仪数据融合,通过卡尔曼滤波算法来估计姿态角。
卡尔曼滤波器可以处理噪声和误差,提高数据精度。
4. 速度和位置计算:
基于IMU的数据,可以通过积分和滤波算法计算速度和位置信息。
常用的方法包括基于加速度计的积分、基于陀螺仪的积分、融合算法等。
以上是一些常见的IMU数据处理公式和方法,具体的实现方式可能因应用场景、传感器型号和数据处理需求而有所不同。
姿态解算方法(1)_一种互补滤波方法

姿态解算⽅法(1)_⼀种互补滤波⽅法姿态解算⽅法(1)_ ⼀种互补滤波⽅法本⽂内容主要是参考《An efficient orientation filter for inertial and inertial/magnetic sensor arrays 》此篇论⽂,由于其在普通飞控中的⼴泛运⽤,所以这⾥简单记录学习感受以期后续详细思索。
当然也是因为这篇⽐较易懂,正好可以锻炼⼀下我捉襟见肘的表述能⼒。
写到这⾥可能已经开始被骂了。
⼏个较好的博⽂链接如下:(1)(2)这是在博客园的第⼀篇博⽂,想来⾃⼰⼀直攒在电脑⾥的东西,不仅容易被弄没了,也没办法被⼤家纠错批评,故也就不在乎好坏把想到的都写下来。
⾔归正传,⾸先,需要了解下四元数的知识,这在维基(3)和(1)中都有很好的解释了,这⾥为了争取篇幅讲述算法核⼼部分就不再赘述。
(3)⾓加速度的事那么进⼊关于姿态确定的部分。
三轴陀螺仪模块可以测量传感器所在平⾯的⾓加速度,⼀般来说MPU6050模块返回的是三个⾓速度值。
如果初始姿态是已知的,时间的计量⼜是准确的,那么就可以积分出姿态了。
可惜的是⾓速度的测量准确度实在是不能积分出⼀个准确的位置值。
不过这⾥还是说⼀下这个积分过程。
sω=0ωxωyωzS E ˙q=12SEˆq⊗Sωsω为传感器获得的⾓速度值,再次提醒这⾥的值可能是不准确的。
SEˆq是表⽰传感器相对于地⾯坐标系的SO(3)变换四元数的估计,这⾥⽤于表⽰传感器姿态的估计。
⊗是四元数的⼀种运算⽅式,在上⽂的参考⽂献中可以找得到的。
差分的形式可以表⽰为:δS E qω,t=12SEˆqt−1⊗SωtSE qω,t=S E ˆqt−1+δSE qω,tΔtΔt是两次预测之间的时间差,准确的说是传感器上⼀次数据和这⼀次数据获取时间差。
其他的部分和连续的形式对应就不多说了。
基于场⽅向观测的姿态求解⾸先把姿态观测问题看做是⼀个求尽可能满⾜观测结果的姿态的优化问题。
EKF和互补滤波器在飞行姿态确定中的应用

2 1 陀螺数 学模 型 .
ME MS陀螺仪的漂 移误 差 由常值 漂移 、 时变 漂移 以及
随机 漂移 组成 。可采用 A l l n方 差分 析法 对其 进行分 析 。 a
从 图 1与 图 2可知 , 随着 电机 转速 增加 , 动频 率加 振
Aln 差是一种基 于时域的分 析方法 , l 方 a 能够容 易地对各种 类型误差源和整个 噪声统 计特性 进行 细致 的表征 与辨识 ,
0 O1
00 .0 0 1 0 2 0 3 O
声 等影响使以上姿态解算 方法 失效 , 了在各种 飞行 状态 为
OO .0 0
1 0
2 0
3 O
频率 / z H
频率 /z H () b 滤波后
() f rftrn b a e i eig t l
获得准确的姿态信息 , 可将上述 2 种姿态估计信息相融合 。
与实现的基 础上 , 行飞行器平台实验验证。研究结果表 明 2种算法均有效 , 进 且互 补滤波器相对经典 K — l a
m n滤波器更为简单 、 效。 a 有
关键词 :姿态测量 ; 展 K l a 扩 a n滤波器 ;互补滤波器 ; ln方差 m Al a 中图分类号 :V 4 . ;T 3 18 2 7 1 P 9 . 文献标 识码 :A 文章编号 :10 —7 7 2 1 ) 104 -4 0 0 98 ( 0 1 1- 190
at u e d tr n t n fr a h l o tr T e meh d l ge n i lme tt n o h t o ag r h a e w l t t d ee miai ei pe . h to oo is a d mp e n ai f t e w lo t ms r e l i o o c o i
欧拉角的求取与互补滤波器在姿态解算中的应用
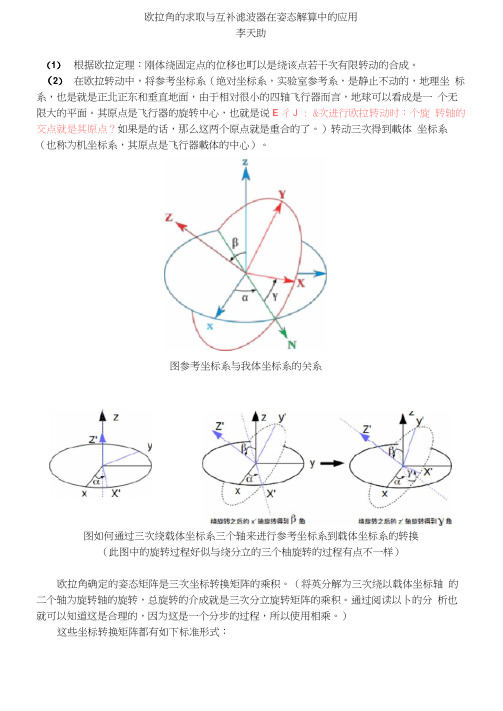
欧拉角的求取与互补滤波器在姿态解算中的应用李天助(1)根据欧拉定理:刚体绕固定点的位移也町以是绕该点若干次有限转动的合成。
(2)在欧拉转动中,将参考坐标系(绝对坐标系,实验室参考系,是静止不动的,地理坐标系,也是就是正北正东和垂直地面,由于相对很小的四轴飞行器而言,地球可以看成是一个无限大的平面。
其原点是飞行器的旋转中心,也就是说E彳J : &次进行欧拉转动时:个旋转轴的交点就是其原点?如果是的话,那么这两个原点就是重合的了。
)转动三次得到載体坐标系(也称为机坐标系,其原点是飞行器載体的中心)。
图参考坐标系与我体坐标系的关系图如何通过三次绕载体坐标系三个轴来进行参考坐标系到载体坐标系的转换(此图中的旋转过程好似与绕分立的三个柚旋转的过程有点不一样)欧拉角确定的姿态矩阵是三次坐标转换矩阵的乘积。
(将英分解为三次绕以载体坐标轴的二个轴为旋转轴的旋转,总旋转的介成就是三次分立旋转矩阵的乘积。
通过阅读以卜的分析也就可以知道这是合理的,因为这是一个分步的过程,所以使用相乘。
)这些坐标转换矩阵都有如下标准形式:'10 ocos 8 0 一 C0S0 Sill# 0" &(©) = 0COS0 sin0 &(0)= W 0 1 0 & (以_S1I10 cos?/ 0 0 ■ 一sin© cos 。
SLI10 ■ 0 cos 8 ■ 0 ■ 0 1 ■公式⑴上而的三个旋转矩阵分别是绕x 、y 、z 轴旋转得到的,其代体的推算过程是通过投影和 来实现的。
(具体推导过程可以参见周建龙等人编写的《几何与代数》中P118页例3.19)。
显然,我们知道矩阵的乘法是不满足交换律的,所以轴旋转的H 宇不凤比如x->y->z, 与x->z->y 是完全不一样的。
通过以上的分析,就可以知道姿态矩阵还有三次转动的顺序有关。
为了避免万向节锁(Gimbal Lock ),选择介适的转动顾序是十分关键的。
自适应显式互补滤波在六旋翼飞行器中的应用

自适应显式互补滤波在六旋翼飞行器中的应用刘洲;单修洋;谭芳【摘要】针对六旋翼飞行器的惯性传感器在测量过程中存在漂移的问题,提出了基于自适应显式互补滤波的姿态解算算法,并对该算法的原理和稳定性进行分析;搭建了六旋翼飞行器的实验测试装置,并进行机体的动、静态测试实验.在实验中,对自适应显式互补滤波算法、显式互补滤波算法以及陀螺仪传感器测量方法进行比较.实验结果表明:自适应显式互补滤波算法能够实现惯性传感器的解算姿态角误差收敛,且动态误差最小.%To solve the drift problem of inertial sensor of six-rotor aircraft during the measurement process,a attitude estimation algorithm based on adaptive explicit complementary filtering(AECF) is proposed.The principle and stability of the proposed algorithm are analyzed.A six-rotor aircraft experimental test device is set up to carry out static and dynamic experiment of the aircraft.Adaptive explicit complementary filtering algorithm,explicit complementary filtering algorithm and gyroscope sensor measurement are compared in the experiment.The experimental results show that the adaptive explicit complementary filtering algorithm can make the solution attitude error of sensor gradually converge and its dynamic error is the smallest.【期刊名称】《传感器与微系统》【年(卷),期】2017(036)005【总页数】4页(P157-160)【关键词】自适应显式互补滤波;六旋翼飞行器;姿态解算;惯性传感器;陀螺仪【作者】刘洲;单修洋;谭芳【作者单位】中南大学机电工程学院,湖南长沙410083;中南大学机电工程学院,湖南长沙410083;中南大学机电工程学院,湖南长沙410083【正文语种】中文【中图分类】V249六旋翼飞行器惯性测量单元IMU使用的是微机电系统(micro-electro-mechanical system,MEMS)类型传感器。
二阶互补滤波姿态求解器的设计

二阶互补滤波姿态求解器的设计南余荣;宛冬晴;潘帅;姚亚楠【摘要】为了降低小型四旋翼姿态解算的成本和提高姿态输出精度,采用了低成本MPU-9250作为IMU,设计了一种二阶互补滤波姿态求解器.二阶互补滤波算法所产生的计算量不大并且对处理芯片的性能要求不高,从而达到降低成本的目的.通过实际测试,以成品AHRS100作为航姿参考系统,得出姿态角度动态误差在3°以内.实验结果表明:所设计的姿态求解器能较精确地解算出四旋翼的姿态角度,满足了小型四旋翼对输出姿态精度的要求.%A second order complementary filter solver is designed in order to reduce the cost and improve the output precision of small quad-rotors in attitude calculation process.The Low-cost MPU-9250 is adopted as IMU in this paper.The second-order complementary filtering algorithm produces little computation and the performance requirement of the processing chip isn`t high.It will achieve the purpose of reducing cost.Through the practical test, using AHRS100 as attitude reference system, and the dynamic error of the attitude angl e is less than 3°.The experimental result show that the solver designed in this paper can calculate the attitude angle fairly accurately and meet the requirement of output precision of small quad-rotors.【期刊名称】《浙江工业大学学报》【年(卷),期】2017(045)004【总页数】5页(P416-420)【关键词】四旋翼;二阶互补滤波;姿态角度【作者】南余荣;宛冬晴;潘帅;姚亚楠【作者单位】浙江工业大学信息工程学院,浙江杭州 310023;浙江工业大学信息工程学院,浙江杭州 310023;浙江工业大学信息工程学院,浙江杭州 310023;浙江工业大学信息工程学院,浙江杭州 310023【正文语种】中文【中图分类】TP273随着科技的进步和时代的发展,无人机凭借自身特有的优势,在民用军事和农业中得到了广泛的应用[1],例如可以用无人机进行航拍摄影,电力巡检,新闻报告,喷洒农药,侦查敌情,还可以用无人机来送快递,在这些方面无人机有着人工所不具备的特有优势,无人机成为当下科技行业研究的热点.一直以来,在诸多研究问题中,飞行器的姿态解算问题都是研究的重点[2-3].在小型四旋翼姿态解算中一般采用低成本捷联惯性导航测量单元,主要由陀螺仪,磁力计和加速度计组成,陀螺仪具有很好的动态跟踪特性[4-5],在飞行器飞行过程中测得的角速度会比较准确,实际上单独用陀螺仪也能解算出四旋翼的姿态,但是由陀螺仪测量得到的积分角度会产生误差的累积,如果不加以补偿,长时间可能引起严重的偏差,所以笔者利用加速度计和磁力计对陀螺仪解算的角度进行误差补偿[6-7].计算四旋翼在三维空间的旋转有很多种等价的表示方法,常见的有方向余弦、四元数和欧拉角[8].欧拉角虽然简单易于表示和理解,但是由于其自身的姿态表示特点导致万向节死锁,不能全方位地解算出四旋翼的姿态方位,方向余弦法虽然能满足四旋翼全方位姿态解算的要求,但是需要的运算量太大[9-10],在采用低成本处理芯片的平台中,导致姿态不能实时输出.故笔者采用四元数来表示姿态变化,四元数有一些其他角位移表示方法所没有的优点如平滑插值,能和矩阵形式快速转换等[11-12].融合加速度计,陀螺仪和磁力计测得数据的方法有一阶互补滤波,二阶互补滤波和扩展卡尔曼滤波等[13],扩展卡尔曼算法虽然比较先进,解算出来的角度能很好地跟踪飞行器真实的角度,但其设计复杂,计算量大,在小型四旋翼中普遍使用的低成本惯性测量单元不满足其对IMU性能的要求[14].一阶互补滤波算法虽然设计简单,易于调试,只需调节一个参数,但解算精确度差.故笔者采用了二阶互补滤波算法,以STM32F103C8T6为CPU,IMU采用MPU-9250,这两个模块累计成本在30元左右,而卡尔曼滤波算法采用的CPU和IMU模块累计成本普遍在80~120元之间,加入PI环节补偿单独用陀螺仪测量所产生的误差,通过调节两个参数KP和Ki最终解算出了较精确的姿态[15-16],满足了小型低成本四旋翼飞行器求解姿态过程中对成本和精度的综合要求.对四旋翼进行姿态解算前首先要建立导航坐标系n系和机体坐标系b系,建立的导航坐标系坐标原点位于四旋翼的质心,xn轴指向北,yn指向东,zn指向地即东北地坐标系,三条轴之间都是俩俩垂直的,同理建立四旋翼的机体坐标系,机体坐标系和四旋翼固联,随着四旋翼的旋转而旋转,坐标系如图1所示.绕机体坐标系三条轴的任意旋转序列都可以确定四旋翼的方位,设横滚角α,俯仰角β,偏航角γ分别为绕xb轴,yb轴,zb轴旋转得到的角度值,一组角度值一共可表示12种不同的旋转方式.欧拉角与方向余弦矩阵之间的关系为四元数是一种高阶复数,能很方便地刻画飞行器绕任意轴的旋转,且计算量小.四元数q的表达式为其中四元数q和方向余弦矩阵之间的关系式为陀螺仪动态响应好,积分后可测倾角,但在解算姿态的过程中,会产生累积误差和零漂等,在低频段信号不好.磁力计和加速度在低频段表现优秀,但是瞬时特性很差,当四旋翼姿态剧烈变化时,不能满足四旋翼实时解算的要求.因此可以结合它们分别在高频段和低频段的优势,利用互补滤波原理对陀螺仪测得的姿态角度进行高通滤波,对磁力计和加速度计测得的姿态角度进行低通滤波,得到在高频段和低频段都较好的信号,滤波原理如图2所示.由图(2)可以进一步得到二阶互补滤波公式为式中:GH(s)=s2/(s2+Kps+Ki)为二阶高通滤波器;GL(s)=Kps+Ki/(s2+Kps+Ki)为二阶低通滤波器,GL(s)+GH(s)=1;wg为陀螺仪测量的角速度;为最终得到的姿态角度值;θa为将磁力计和加速度计测量值进行处理得到的角度值.选择适当的KP,Ki,利用式(4)即可得到较为精确的姿态数据.在解算过程中,传感器测得的原始数据是姿态角,因此先将姿态角转换为四元数,然后利用四元数进行姿态更新,最后还是要将四元数转换为姿态角.可求出四旋翼在初始时候的四元数,即在载体坐标系下,设加速度计测得的值为ab,磁力计测得的值为mb,将加速度和磁力计测得的值做归一化处理,方向不变,分别得到b和b,可将n系下的重力向量转到b系下,即总的误差向量e为式中:e1为加速度计测得的单位向量与从四元数那里获得的重力向量之间的误差向量;e2为磁力计测得的单位向量与从四元数那里得到的单位向量之间的误差向量.令δ=(Kp+Ki/s)·e,陀螺仪测得的角速度为wg,将δ与wg进行叠加得到修正后的角速度w,最后来更新四元数,得式中w=0+wxi+wyj+wzk,由式(8)可以得到四元数的迭代方程式为由式(9)可知:只需传入角速度在三个轴的分量和周期T即可求得下一周期的四元数值,将求得的四元数进行单位化,得到最终表示四旋翼姿态的欧拉角为详细的姿态解算过程,如图3所示.3.1 实验平台我们选用STM32F103C8T6为CPU,IMU采用MPU-9250,MPU-9250是一个QFN封装的复合芯片,它由两部分组成,一组是3轴加速度计和3轴陀螺仪,另一组则是AKM公司的AK896 3轴磁力计.采用AHRS100成品航姿系统作为参考系统进行对比,AHRS100在各种恶劣条件下均能精确解算出四旋翼的姿态.3.2 测试结果和分析将一阶互补滤波算法和二阶互补滤波算法的廉价IMU单元与AHRS100固定在四旋翼上并在实际场景下飞行,通过计算机串口同时读取3个测量单元的数据进行实时姿态解算,采样时间为60 s,以AHRS100成品航姿系统测得的姿态数据为参考标准进行MATLAB绘图.图4为一阶互补滤波姿态求解器、二阶互补滤波姿态求解器和参考航姿系统所测得的俯仰角输出对比情况,进一步利用MATLAB内置的计算工具,求出俯仰角误差,如图5所示,可以很明显看到大部分时间里一阶解算角度误差都是大于二阶解算角度误差,二阶解算角度误差第4 s和第6 s左右达到最大,接近2°.而一阶解算角度最大误差在第25 s达到了3.2°.图6为测得的横滚角输出对比情况,进一步绘制出横滚角误差(图7),可以很明显看到大部分时间里一阶解算角度误差都是大于二阶解算角度误差.在几个特殊的时间点由于飞行器姿态变化剧烈导致姿态求解角度和真实角度偏差较大,在第18 s左右二阶解算角度误差达到最大,达到2.3°.而一阶解算角度最大误差在第39 s左右达到了4.3°.图8为测得的偏航角输出对比情况,进一步绘制出偏航角误差,如图9所示,可以很明显看到大部分时间里一阶解算角度误差都是大于二阶解算角度误差.二阶解算角度误差大多在1.5°以内.而一阶解算角度误差在很多时刻都超过了1.5°,解算精度明显低于二阶解算精度.可以得到四旋翼在飞行过程中,无论是俯仰角,横滚角还是偏航角,一阶解算的精确度都是明显低于二阶解算的精确度.大多数时间内二阶解算俯仰角误差,横滚角误差和偏航角误差分别控制在2°,1.5°,1.5°以内,姿态角最大动态误差小于2.5°,满足小型低成本四旋翼飞行器对输出姿态精度的要求.针对小型四旋翼姿态解算这一问题进行了详细的分析,通过对比一阶互补滤波算法,卡尔曼滤波算法,二阶互补滤波算法最后设计了一种基于四元数的二阶互补滤波姿态求解器,并对解算的原理和流程做了详细介绍.以四旋翼飞行器为实验平台,通过实际飞行测试,对比二阶互补滤波姿态求解器和一阶互补滤波姿态求解器解算出的角度误差,得出了二阶解算精度明显高于一阶解算精度的结论,验证了笔者所设计的二阶互补滤波算法在提升输出姿态精度上的有效性.【相关文献】[1] 郭晓鸿,杨忠,陈喆,等.EKF和互补滤波在飞行姿态确定中的应用[J].传感器与微系统,2011,30(11):56-58.[2] 王立波.捷联惯导系统设计与数据处理技术研究[M].北京:科学出版社,2006.[3] 史智宁,韩波,徐玉,等.基于重力场自适应互补滤波的无人直升机水平姿态估计方法[J].传感技术学报,2009,22(7):993-996.[4] 方路平,高坤,潘清,等.基于陀螺仪的穿刺手术导航系统设计[J].浙江工业大学学报,2016,44(2):129-133.[5] 王宇,董辉,徐建明,等.一种新的智能小车控制策略[J].浙江工业大学学报,2012,40(2):217-221.[6] 胥芳,倪紫京,占红武.自平衡小车的模型分析与数据处理[J].浙江工业大学学报,2016,44(3):288-291.[7] 张荣辉,贾宏光,陈涛,等.基于四元数法的捷联惯性导航系统的姿态解算[J].光学精密工程.2008,16(10):1963-1970.[8] 张承岫,李铁鹰,王耀力.基于MPU6050和互补滤波的四旋翼飞控系统设计[J].传感技术学报,2016,29(7):1011-1015.[9] 蔡磊,牛小骥,张提升,等.MEMS惯导在四旋翼飞行器中导航性能的实验分析[J].传感技术学报,2016,29(5):711-715.[10] 彭孝东,张铁民,李继宇,等.基于传感器校正与融合的农用小型无人机姿态估计算法[J].自动化学报,2015,41(4):854-860.[11] 王延东,贾宏光.组合导航系统滤波器截断误差抑制方法[J].传感技术学报,2014,27(5):616-621.[12] 郑君里,杨为理,应启珩.信号与系统[M].北京:高等教育出版社,2000.[13] 文常保,高丽红,方吉善,等.基于改进型限幅平均滤波法的高精度称重系统研究[J].传感技术学报,2014,27(5):649-653.[14] 张洪涛.四旋翼微型飞行器位姿及控制策略的研究[D].哈尔滨:哈尔滨工业大学,2014.[15] 傅忠云,刘文波,孙金秋,等.自适应混合滤波算法在微型飞行器姿态估计中的应用[J].传感技术学报,2014,27(5):698-703.[16] 彭孝东,张铁民,李继宇,等.基于传感器校正与融合的农用小型无人机姿态估计算法[J].自动化学报,2015,41(4):854-860.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
公式(5) 当然也有形如以下的表达方式:
公式(6) 当 dt 趋近于 0 时,由公式(6)可以得到旋转矩阵的导数: 其中:
k 上式中的������������ ,������������ ,������������ 分别为 IMU(惯性测量单元)的陀螺仪测得的载体坐标系下 的机体的 x,y,z 轴的角速度。比较短的时间内间隔读取陀螺仪的数据,通过上述公式就可以 实现方向余弦矩阵随时间的传递,然而,MEMS(MEMS, Micro-Electro-Mechanical System, 微机电系统)陀螺仪会发生温度漂移,同时积分去处有累积误差(积分运算的误差从哪里体 现出来?) 。如果不加以补偿,在短时间内就会积累很大的姿态误差,导致四轴飞行器控制 失效。所以必须采用一定的姿态解算算法,融合各种传感器的数据,进行误差补偿以实现精 确的姿态解算。 (3)基于互补滤波器的姿态求解器设计 陀螺仪动态响应好,但计算姿态时,会产生累积误差(积分体现在哪里,通过积分得到 欧拉角?) 。数字罗盘(也叫做电子罗盘或是三轴磁感传场感器) ,和加速度传感器测量姿态 没有累积误差,但动态响应较差。因些,它们在频域上特性互补,可以采用互补滤波器材融 合这三种传感器的数据, 提高测量精度和系统的动态性能。 也就是即不会产生积分上的累积 误差导致偏差太大, 也不会因为动态特性太差而不会丢失了实时的特性, 无法做到实时的控 制。 R— — 真实姿态方向余弦矩阵 ������ — — 表示互补滤波器计算输出的姿态方向余弦矩阵 ������0 — — 代表由加速度传感器和数字罗盘观测到的姿态方向余弦矩阵 ������������ — — 表示������0 的高频观测噪声,则������0 = R + ������������ (动态特性太差,就是高频噪声被保留了下来,导致曲线的不平滑,从信号与系统的分析角 度上来看,动态变化太大,也就是信号变化速度快,这就是信号与系统中的高频分量过多) ������������ — — 代表陀螺仪数据计算得到的姿态 ������������ — — 表示������������ 的低频累积误差,则������������ = R + ������������ (低频太差,也就是信号中的低频分量太多) 由上面的分析可以知道,要得到好的,精确度高的 R 信号,要滤除加速度计和数字罗盘 中的高频分量,还有就是陀螺仪上的低频分量。 取������������
欧拉角的求取与互补滤波器在姿态解算中的应用 李天助 (1)根据欧拉定理:刚体绕固定点的位移也可以是绕该点若干次有限转动的合成。 (2)在欧拉转动中,将参考坐标系(绝对坐标系,实验室参考系,是静止不动的,地理坐 标系,也是就是正北正东和垂直地面,由于相对很小的四轴飞行器而言,地球可以看成是一 个无限大的平面。 其原点是飞行器的旋转中心, 也就是说飞行器每次进行欧拉转动时三个旋 转轴的交点就是其原点?如果是的话,那么这两个原点就是重合的了。 )转动三次得到载体 坐标系(也称为机坐标系,其原点是飞行器载体的中心) 。
������ 2������
。
在大于������������ 的高频段内,陀螺仪对解算结果起主要作用;在小于������������ 低频段,数字罗盘和加速计 对解算的结果起主要作用。此时对公式(8)进行 Laplace 反变换可得其在时域中的表达式:
公式(9) 为了消除静态偏差,取
kP 的大小决定互补滤波器的截止频率,kI 的大小决定了消除静态误差的时间,通常 kI 的大 小为 kP 的 0.01~0.1 倍。 加速度传感器测量载体坐标系下重力加速度矢量 g 的方向, 以校正横滚和俯仰的姿态角; 数字罗盘测量在参考坐标系 (也就是绝对坐标系) 下的航向角, 以校正飞行器的偏航姿态角。 通过分析可以知道, 通过分解重力加速度矢量到那个载体坐标系的三个轴上, 是完全可以确 定翻滚和俯仰的, 但是偏航是没有办法确定的, 这是因为偏航实质上就是绕着绝对坐标系的 z 轴在旋转,这样的话,不管偏航如何,那个重力加速度矢量到机体坐标系上的分量大小是 不会有任何的改变的。所以,引入电子罗盘的关键作用就是在于其能通过感知地磁场,来确 认绝对坐标系,通过与载机坐标系的比较,自然可以轻松的知道飞行器的偏航角。 (现在感觉以上所讨论的种种其实都是为了从传感器上获取精确的欧拉角的值, 而方向余弦 变换矩阵, 主要的目的似乎研究的是载体坐标系与绝对坐标系之间的变换关系, 而其中含有
公式(1) 上面的三个旋转矩阵分别是绕 x、y、z 轴旋转得到的,其具体的推算过程是通过投影和 来实现的。 (具体推导过程可以参见周建龙等人编写的《几何与代数》中 P118 页例 3.19) 。 显然,我们知道矩阵的乘法是不满足交换律的, 所以轴旋转的顺序不同, 比如 x->y->z, 与 x->z->y 是完全不一样的。 通过以上的分析,就可以知道姿态矩阵还有三次转动的顺序有关。为了避免万向节锁 (Gimbal Lock) ,选择合适的转动顺序是十分关键的。具体如何实现可以参考路洋学长的个 人网站——巧匠的四轴飞行器教程部分(/919/) ,其中有一个视 频谈论到了此问题。 若按 z->y->x 顺序来转动的话,其最终的姿态矩阵显然就是:
图参考坐标系与载体坐标系的关系
图如何通过三次绕载体坐标系三个轴来进行参考坐标系到载体坐标系的转换 (此图中的旋转过程好似与绕分立的三个轴旋转的过程有点不一样) 欧拉角确定的姿态矩阵是三次坐标转换矩阵的乘积。 (将其分解为三次绕以载体坐标轴 的三个轴为旋转轴的旋转, 总旋转的合成就是三次分立旋转矩阵的乘积。 通过阅读以下的分 析也就可以知道这是合理的,因为这是一个分步的过程,所以使用相乘。 ) 这些坐标转换矩阵都有如下标准形式:
其中,向量 g 就是加速度传感器测量的重力加速度矢量。 飞行器的航向是定义在参考坐标系的 x-y 平面内的, 所以偏航误差������������ 近似为数字罗盘测 量的航向矢量与互补滤波器估计的航向矢量,投影到参考坐标系 x-y 平面形成的 2 个单位矢 量的叉乘 c,再转换到载体坐标系下的向量:
公式(3) (3)方向余弦矩阵随时间的传递 在时间 t 内,当 t 为极小值的时候,姿态角的变化量dφ、dϕ、dθ皆趋近于 0,将这三 个值代入公式(2)中,并通过sinθ ≈ θ,cosθ ≈ 1,可以将旋转矩阵简化:
公式(4) 其实这个矩阵不是公式(3)真正退化的结果,但其实本质上是一样的。如果二阶无穷 小量再进一步简化就可以得到:
公式(7) 互补滤波器的优点就在于它同时滤除了低频和高频的干扰,方便实现传感器数据融合。 由
可以得到
(这一过程是怎么来的,我也搞不清楚,应该是信号与系统很相关。 ) 将此式代入公式(7)当中,就可以得到
ห้องสมุดไป่ตู้
公式(8) 根据这一式子,很容易通过直接模拟框图,得到互补滤波器的模型:
C(s)如果取固定常数 k,则设计的低通滤波器和高能滤波器的截止频率������������ =
的关键量就是欧拉角, 欧拉角其实就包含在了方向余弦变换矩阵当中, 而从方向余弦矩阵中 求解得到欧拉角也是可以完成的。 ) 由于加速度传感器和数字罗盘的响应时间是不相同的 kP 和 kI,最终设计的互补滤波器 的姿态求解器的结构如图:
飞行器的偏航不会影响重力加速度矢量的方向, 而且横滚角和俯仰角也不会影响飞行器 的航向,所以,两路校正之间是解耦的,不会相互干扰,分为两路是合理的。 (说的就是姿 态求解器中的那两路。 ) 四旋翼飞行器大部分时间处于悬停、 匀速飞行阶段, 此时加速度传感器只会机体高频振 荡的干扰,而且在起飞、降落和加减速阶段,其加速度相对重力加速度较小,而且持续时间 很短,最终会被互补滤波器滤除(毛刺可能会产生的地方) 。因此可以将加速度传感器的数 据作为机体重力加速度的测量结果。互补滤波器(通过加速度计和数字罗盘,配合陀螺仪计 ������ 算出来的旋转姿态矩阵)估计的重力加速度矢量为旋转矩阵������������ 的第 3 行,其与加速度传感 器测量的重力加速度矢量的偏差,即为俯仰和横滚角误差,其值为两个矢量的叉乘。 (这话 说的是毛线意思?)
������ =
������ (������ ) ������ +������ (������ )
,������������ ������ = 1 − ������������ ������ =
������
������ +������ (������ )
,如果 C(s)具有全通特性(你怎
么知道它有全通特性呢?) 。������������ ������ 具有低通滤波特性,������������ ������ 具有高通滤波特性。 则两者进行互补就可以得到
其中,������������ 为陀螺仪测量的角速度矢量。将ω代入公式(6) ,就可以得到随时间传送的准 确的旋转矩阵,进而由公式(3)求得各个姿态角。如此一来,姿态解算就算是结束了。通 过以上分析, 发现些姿态解算方法并没有使用到四元数, 而只用到了方向余弦矩阵与欧拉角 之间的转换关系。比较的简单易懂。其过程就是大概可以概括为: 1. 通过方向余弦可以进行参考坐标系与机体坐标系之间的变换,而方向余弦矩阵中又可以 求解出欧拉角,而欧拉角就是控制函数的输入变量。 2. 通过互补滤波器,感觉上就是对陀螺仪进行滤波,因为从方向余弦旋转矩阵角度而言, 如果说陀螺仪测得的数据是准确的话,那其实问题就解决了,但是事实是残酷的,所以 互补滤波器,就是通过数字罗盘和加速度计来补偿陀螺仪测量是所会产生的累积误差。 而通过互补滤波器之后,把得到的,新的,经过修正过的陀螺仪的值(此时的值是准确 可信的)送到方向余弦转换矩阵中去求得欧拉角。这样问题就得以解决了。 (顺便再说一个,通过设计的互补滤波器来等到融合的式子,这一个过程感觉是超过所 学的知识范畴了。但可以知道,要想得到互补之后的陀螺仪的结果,就必须经过这一个 过程。 ) 接下来就可以讨论一下 PID 的值的问题,如果说上面的互补滤波器得到的是传感器测量 并计算得到的一个可靠的实时的飞行器的姿态的话,那么就可以通过遥控器来给出一个 目标的姿态。其实这个目标的姿态就会决定飞行器的飞行轨迹了。而如何更加快速地到 达目标姿态,这个就是在自动控制领域中经常使用到的 PID 控制方式了。达到响应快的 目的。而在智能车的控制过程中,PID 的作用就是使智能车通过快速地启动,灵敏的过 弯以及减速。 罗鸿飞学长:陀螺仪部分相当于一个积分器加上高通滤波器,加速度计就是个低通滤波 器,然后两个合起来。 但是加权的意思是你一共只有两个输入,一个是根据陀螺仪和上次状态估算出的值,一 个加速度计的值,你肯定相信它们的比重不一样,如果完全相信加速度计它的权重就是 1,陀螺仪的权重就是 0,反之也一样。实际上两个东西的权重由它们信号的质量决定, 所以两个都有权重。
