小学奥数 容斥原理之数论问题 精选练习例题 含答案解析(附知识点拨及考点)
高斯小学奥数四年级下册含答案第19讲_容斥原理

第十九讲容斥原理这一讲我们主要学习和“包含”与“排除”有关的问题,这样的问题在生活中就有不少,比如吃瓜子.我们说吃掉了一斤瓜子,指的是带壳的瓜子,并非真的吃到肚子里一斤,因为这一斤中还“包含”着瓜子壳.如果要计算到底吃了多少,最简单的方法就是称一称瓜子壳,用原来的一斤“排除”掉瓜子壳的重量.瓜子的例子相对简单,一斤瓜子里一部分是瓜子仁,另一部分就是瓜子壳,两者各不相关.但本讲要学习的包含与排除问题要复杂一些,各部分之间会有重叠.比如一个办公室中每个人都至少爱喝茶或咖啡中的一种,已知有7个人爱喝茶,10个人爱喝咖啡,那能不能就说办公室里有17个人呢?显然不能,因为可能有一些人既爱喝茶也爱喝咖啡,如果直接将喝茶的人数和喝咖啡的人数相加,会把既爱喝茶又爱喝咖啡的人计算2次(如图所示),计算人数的时候要把这一部分减去才行.比如,如果有3个人既爱喝茶又爱喝咖啡,那总的人数就应该是710314+-=人.这就是我们今天要来研究的问题——有重叠的计数问题,即包含与排除问题.研究这种问题通常需要画出示意图(如喝茶与喝咖啡的图),这样的示意图又叫做文氏图,下面我们就用文氏图推导两个对象的容斥原理公式.№1. 简单容斥原理(两个对象)如右图所示,如果要计算三个部分的总数,直接计算A +B 就会算多了,而多算的正好是③部分,只要把多算的减掉就可以了.上述分析总结成公式就是:这个公式就是两个对象....的容斥原理. 既喝茶又喝咖啡的A例题1(1)一群小朋友共有50人,他们都喜欢吃辣椒或芥末中的一种或两种,喜欢吃辣椒的有36人,喜欢吃芥末的有20人,那么两者都喜欢吃的有多少人?(2)暑假里,小高和墨莫一起讨论金陵十八景.他们发现十八景中的每一处都有人去过,而且有五处是两人都去过的.如果小高去过其中的十二景,那么墨莫去过其中的几景?(3)在一群小朋友中,有12人看过动画片《黑猫警长》,有21人看过动画片《大闹天宫》,并且有8人两部动画片都看过.已知每个小朋友至少都看过其中的一部,那么有几个小朋友只看过这两部中的一部动画片?「分析」试着画一下文氏图分析一下吧!注意图中每一部分所代表的含义!练习1四年级同学参加语文、数学考试,每人至少有一门功课的成绩是优秀.其中语文成绩优秀的有42人,数学优秀的有56人,语文、数学都优秀的有15人,请问四年级共多少名同学?例题2渔乡小学举行长跑和游泳比赛,共305人参加.有150名男生和90名女生参加长跑比赛,有120名男生和70名女生参加游泳比赛,有110名男生两项比赛都参加了.请问:只参加游泳而没参加长跑的女生有多少人?「分析」题目中既有参加长跑的,又有参加游泳的,作图时可以画两个圆,分别表示“游泳”和“长跑”.但条件中还有男生、女生,那男生、女生该怎么表示呢?练习2某校参加数学竞赛的有120名男生、80名女生,参加语文竞赛的有120名女生、80名男生.已知该校总共有260名学生参加竞赛,其中75名男生两科竞赛都参加了,请问只参加一科竞赛的女生有多少人?№2. 复杂容斥原理(三个对象)例题3三位基金经理投资若干支股票.张经理买过其中66支,王经理买过其中40支,李经理买过其中23支.张经理和王经理都买过的有17支,王经理和李经理都买过的有13支,李经理和张经理都买过的有9支,三个人都买过的有6支.请问:这三位经理一共买过多少支股票? 「分析」我们还是画出文氏图来分析,题中的已知条件分别对应图中的哪个部分?怎样来求各个部分的数量呢?一定要记得将求出来的数及时填入图中适当的位置.怎么理解这个公式呢?我们还是利用文氏图来说明. 如图,我们在计算A B C++时,有一些部分被重复计算了:④、⑤、⑥被计算了两次,而⑦被计算了三次.因此我们需要把重复计算的去掉.需要注意的是,去掉A 、B 重叠,B 、C 重叠和A 、C 重叠的部分后,④、⑤、⑥重复计算的一次去掉了,但⑦被去掉了三次,还需要补上一次,这就得到了上面的公式.即把所有圆圈相加,减去两个圆圈重叠部分,再加上三个圆圈重叠的部分得到的就是总数.在使用这个公式时,请同学们一定要清楚公式中每一部分的含义,不能有丝毫的偏差.只有所有条件都和公式完全吻合时我们才能使用这个公式. 练习3卡莉娅用三块长方形桌布相互重叠地铺在一张长方形桌子上,正好将桌子完全覆盖.已知三块桌布的面积分别是40平方分米、36平方分米和27平方分米,其中第一块和第二块桌布重叠的面积为5平方分米,第二块和第三块重叠了7平方分米,而第一块和第三块则重叠了4平方分米.如果三块重叠的部分等于2平方分米,那么这张桌子的面积是多少?B文氏图才是体现条件的最基本最直观的方法,但是我们要灵活选择,不能随便套用公式.我们要先理解图中各部分的含义,再来看相加时每个部分“包含”了几次,然后把算重的部分减去.例题4课间,王老师出了三道脑筋急转弯让学生做,其中只答对第1道题的人有10人,只答对第2道题的人有6人,只答对第3道题的人有4人.至少答对两道题的学生有8人,还有5名同学一道题也没答对.(1)请问王老师的班上有多少名学生?(2)若既答对第1道又答对第2道题的同学有4人,三道题都答对的有1人,那么答对第3道题的同学有多少人?「分析」画出三个对象文氏图,仔细找找题中所描述的条件分别对应图中的哪些部分?这里需要指出的是,我们要留意题中的一些说法,比如“至少答对一道题”对应的是图中的什么区域?“至少答对两道题”对应的是图中的什么区域?“只答对一道题”呢?练习4高思学校有学生1000人,现有《中国少年报》、《少年文艺》和《数学报》三种报刊,其中只订阅一种报刊的有600人,只订阅两种报刊的有200人,三种报刊都订阅的有50人,请问:这个学校有多少人没有订报?例题5四年级一班有46名学生参加3项课外活动.其中有24人参加了数学小组,20人参加了语文小组,参加文艺小组的人数是既参加数学小组也参加文艺小组人数的4倍,又是3项活动都参加人数的8倍,既参加文艺小组也参加语文小组的人数相当于3项都参加的人数的3倍,既参加数学小组又参加语文小组的有10人.请问参加文艺小组的人数是多少?「分析」图中每一部分分别代表什么呢?题目给了几个倍数关系,我们不妨设份数计算一下.№3. 容斥原理中的最值问题例题6某班共有学生48人,其中27人会游泳,33人会骑自行车,40人会打乒乓球.那么,这个班至少有多少学生这三项运动都会?「分析」题目要我们求至少有多少人三项都会,那么也就是要会只两项的尽量多,此时文氏图很难进行分析,不妨画一下线段图试试吧!课堂内外文氏图文氏图,也叫“维恩图”,是由英国著名数学家Venn发明的.维恩(John Venn,公元1834年8月4日─公元1923年4月4日)十九世纪英国著名的数学家和哲学家,生于英国赫尔.他1883年获得理学博士学位,同年被选为英国皇家学会会员.维恩最主要的成就是系统解释并发展了几何表示的方法,也就是发明了文氏图.他作出一系列简单闭曲线(圆或更复杂的图形),将平面分为许多间隔.利用这种图表,维恩阐明了演绎推理的基本原理.为了进一步明确起见,他还引入了一些数学难题作为实例.虽然在维恩之前,莱布尼茨(Leibniz)已系统地运用过这类逻辑图,但今天这种逻辑图仍称作“维恩图”(Venn Diagram).另外,维恩在概率论和逻辑学方面也有很大贡献,他的著作——《机会逻辑》和《符号逻辑》,在19世纪末20世纪初曾享有很高的声誉.除了数学以外,维恩还有一较特别的技能——制作机器.他曾制作过一部板球发球机,当澳洲板球队在1909年到访剑桥大学时,维恩的机器依然运作正常,并使他们其中一位成员打空四次.作业1. 一个班有50个小学生,统计借课外书的情况是:全班学生都借有语文或数学课外书.借语文课外书的有39人,借数学课外书的有32人.请问:语文、数学两种课外书都借的有多少人?2. 六一班有学生46人,其中会骑自行车的17人,会游泳的14人,既会骑车又会游泳的4人,请问两样都不会的有多少人?3. 许、王、原三位老师走进一家蛋糕店,发现这里的每一种糕点至少被她们中的一个人吃过.她们分别数了一下,许老师吃过其中的15种,王老师吃过其中的10种,原老师吃过其中的6种,有8种糕点许、王两老师都吃过,有5种糕点许、原两老师都吃过,有3种糕点王、原两老师都吃过,有2种糕点这三位老师都吃过.那么这个面包店有多少种糕点?4. 五年级共有110人,其中92人参加了语文小组,51人参加了英语小组,58人参加了数学小组,至少参加2个小组的有80人,参加了三个小组的有20人.那么五年级有多少人没有参加小组?5.五年级共有150人,其中92人参加了语文小组,51人参加了英语小组,30人只.参加了数学小组,既参加语文也参加英语小组的人有35人.那么五年级有多少人没有参加小组?第十九讲 容斥原理1. 例题1答案:6;11;17 详解:画出两个对象的文氏图,找到相应的数字表示的区域. (1)3620506+-=人.(2)小高去过其中的12景,那么只有墨莫一个去过的景有18126-=景,墨莫共去过6511+=景.(3)这里要把重复的区域去掉两次才是只看过一部的,共有12218217+-⨯=人.2. 例题2答案:55详解:画出文氏图,游泳和长跑这两项比赛会有重叠,要区别游泳的男生和游泳女生,且这两部分不会重叠,这时我们用一条直线把一个区域分成两部分,这两部分没有重叠.如果不考虑性别,参加长跑比赛的人有15090240+=人,参加游泳比赛的人有12070190+=人.总人数是305人,那么游泳和长跑都参加的人有240190305125+-=人,其中男生有110人,那么两样都参加的女生有12511015-=人.那么只参加游泳的女生有701555-=人.此题的方法不唯一,也可以看图算出男生有120150110160+-=人,那么女生有305160145-=人.只参加游泳的人有1459055-=人.3. 例题3答案:96详解:首先画出文氏图,找到相应的数字所表示的区域.计算股票之和把张、王、李股票数相加664023129++=,其中129支股票中G 、E 、F 算了两次,H 算了三次.去掉这些重复计算的区域(G 、E 、F 去掉一次,H 去掉两次),1291713990---=,发现G 、E 、F 去掉了一次,但H 去掉了三次,最后还要把H 加上一次.90696+=90+6=96支.游泳长跑男生 女生 15090120 70110 305张66王40李231713 9 6 A B C E FGH4. 例题4答案:33人;9人详解:(1)难点是至少答对二道题的学生指的是哪个区域.至少答对二道题的区域是指这些重叠的区域A 、B 、C 、D ,那么王老师班上有10648533++++=人.(2)通过画文氏图,D =1,A =3, 835++=-=B D C ,答对第3道题的同学有549+=人.5. 例题5答案:24人详解:遇到倍数关系时,一般情况下设最小的为“1”,有倍数关系的就好办了.这里面设3项活动都参加的人数为“1”,那么文艺小组人数为“8”,既参加数学也参加文艺的人数为“2”,既参加文艺又参加语文小组人数为“3”.方法一:根据文氏图可求出总人数为2420"8""2""3"10"1"34"4"46++---+=+=,那么"1"3=人,文艺小组有"8"24=人.方法二:数学有24人参加,语文有20人参加,既参加数学又参加语文的有10人,所以参加语文和数学至少一门的人有24201034+-=人,那么只参加文艺的人有463412-=人,这部分人有"4"12=,"1"3=人,文艺小组有"8"24=人.6. 例题6答案:6根详解:要想三项都会的人尽量少,那么要让会游泳、骑自行车、乒乓球的人尽量分散开来.画图如下,最后可得至少有4名学生三项都会.第3道 第2道 10 64 BCA D第1道 数24语20文“8”“3”“2” “1”10 2748用直线长度表示会游泳的人数 ①7. 练习1答案:83简答:画出两个对象的文氏图,找到相应的数字表示的区域.42561583+-=人.8. 练习2答案:70简答:如果不考虑性别,参加数学竞赛的人有12080200+=人,参加语文竞赛的人有80120200+=人.总人数是260人,那么数学和语文都参加的人有200200260140+-=人,其中男生有75人,那么两样都参加的女生有1407565-=人.那么只参加一科竞赛的女生有()()80651206570-+-=人.数学语文男生 女生80120120 8075 260 48272112②骑自行车的人数尽量不和游泳的人重复,故接着游泳的后面画2721481236 4 同理,会乒乓球的人可再接着骑自行车的人后面画 ③9. 练习3答案:89平方分米简答:三个对象容斥原理:403627574289++---+=平方分米.10. 练习4答案:150人简答:如图,只订阅一种报刊的是E 、F 、G 三部分,共600人;只订阅两种报刊的是A 、B 、C 三部分,共200分,三种报刊都订阅的是D ,有50人,所以订报刊的人一共有60020050850++=人,学校有一共有1000人,所以没有订报的人有1000850150-=人.11. 作业1答案:21简答:利用容斥原理,32395021+-=人.12. 作业2答案:19简答:先求出至少会一样的人数,再求两样都不会的人数.()461417419-+-=人.13. 作业3答案:17简答:利用三个对象之间的容斥原理,共()151********++-+++=种糕点.14. 作业4答案:9简答:根据容斥原理,共有()11092515880209-++--=人.15. 作业5答案:12人简答:画出文氏图,先求出至少参加一个小组的人数.至少参加一个小组的人有92513035138++-=人.一个小组都没参加的有15013812-=人.数学报 文艺 E F G B C A D 少年报。
小学四年级奥数第35讲 容斥原理(含答案分析)

第35讲容斥原理一、专题简析:容斥问题涉及到一个重要原理——包含与排除原理,也叫容斥原理。
即当两个计数部分有重复包含时,为了不重复计数,应从它们的和中排除重复部分。
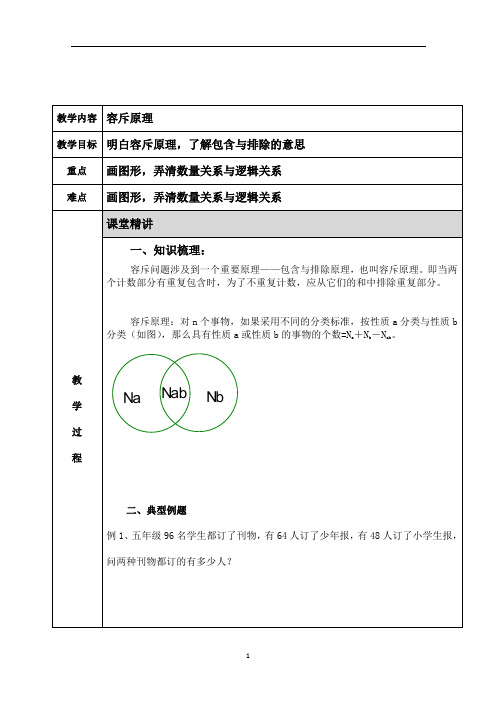
容斥原理:对n个事物,如果采用不同的分类标准,按性质a分类与性质b 分类(如图),那么具有性质a或性质b的事物的个数=N a+N b-N ab。
Nab NbNa二、精讲精练:例1:一个班有48人,班主任在班会上问:“谁做完语文作业?请举手!”有37人举手。
又问:“谁做完数学作业?请举手!”有42人举手。
最后问:“谁语文、数学作业都没有做完?”没有人举手。
求这个班语文、数学作业都完成的人数。
练习一1、五年级有122名学生参加语文、数学考试,每人至少有一门功课取得优秀成绩。
其中语文成绩优秀的有65人,数学优秀的有87人。
语文、数学都优秀的有多少人?2、四年级一班有54人,订阅《小学生优秀作文》和《数学大世界》两种读物的有13人,订《小学生优秀作文》的有45人,每人至少订一种读物,订《数学大世界》的有多少人?例2:某班有36个同学在一项测试中,答对第一题的有25人,答对第二题的有23人,两题都答对的有15人。
问多少个同学两题都答得不对?练习二1、五(1)班有40个学生,其中25人参加数学小组,23人参加科技小组,有19人两个小组都参加了。
那么,有多少人两个小组都没有参加?2、一个班有55名学生,订阅《小学生数学报》的有32人,订阅《中国少年报》的有29人,两种报纸都订阅的有25人。
两种报纸都没有订阅的有多少人?例3:某班有56人,参加语文竞赛的有28人,参加数学竞赛的有27人,如果两科都没有参加的有25人,那么同时参加语文、数学两科竞赛的有多少人?练习三1、一个旅行社有36人,其中会英语的有24人,会法语的有18人,两样都不会的有4人。
两样都会的有多少人?2、一个俱乐部有103人,其中会下中国象棋的有69人,会下国际象棋的有52人,这两种棋都不会下的有12人。
小学奥数之容斥原理(二)

容斥原理(二)【例题分析】例1. 有25人参加跳远达标赛,每人跳三次,每人至少有一次达到优秀。
第一次达到优秀的有10人,第二次达到优秀的有13人,第三次达到优秀的有15人,三次都达到优秀的只有1人。
只有两次达到优秀的有多少人?例2. 在一个炎热的夏日,几个小朋友去冷饮店,每人至少要了一样冷饮,其中有6人要了冰棍,6人要了汽水,4人要了雪碧,只要冰棍和汽水的有3人,只要冰棍和雪碧的没有,例3. 有28人参加田径运动会,每人至少参加两项比赛。
已知有8人没参加跑的项目,参加投掷项目的人数与参加跑和跳两项的人数都是17人。
问:只参加跑和投掷两项的有多少人?分析与解:“每人至少参加两项比赛”说明没有不参加的,也没有参加一项比赛的,我们可以在下图中参加一项的区域用0表示。
人参加,3人,既参加数学又参加英语和既参加英语又参加语文的人数均为质数,而三种全参加的只。
答:既参加英语又参加数学小组的为2人或7人。
例5. 某班同学参加升学考试,得满分的人数如下:数学20人,语文20人,英语20人,数学、英语两科满分者8人,数学、语文两科满分者7人,语文、英语两科满分者9人,三科都没得满分者3人。
问这个班最多多少人?最少多少人?整理后:全班人数=39+x39+x 表示全班人数,当x 取最大值时,全班人数就最多,当x 取最小值时,全班人数就最少。
x 是数学、语文、英语三科都得满分的同学,因而x 中的人数一定不超过两科得满分的人数,即x x ≤≤78,且x ≤9,由此我们得到x ≤7。
另一方面x 最小可能是0,即没有三科都得满分的。
当x 取最大值7时,全班有()39746+=人,当x 取最小值0时,全班有()390+=39人。
答:这个班最多有46人,最少有39人。
【模拟试题】(答题时间:30分钟)1. 六年级共有96人,两种刊物每人至少订其中一种,有23的人订《少年报》,有12的人订《数学报》,两种刊物都订的有多少人?2. 小明和小龙两家合住一套房子,门厅、厨房和厕所为公用,在登记住房面积时,两家他们住的一套房子共有多少平方米?3. 某班45名同学参加体育测试,其中百米得优者20人,跳远得优者18人,又知百米、跳远都得优者7人,跳高、百米得优者6人,跳高、跳远均得优者8人,跳高得优者22人,全班只有1名同学各项都没达优秀,求三项都是优秀的人数。
2021-2022学年五年级上册奥数培训专题——容斥原理(附答案)

2021-2022学年五年级上册奥数培训专题——容斥原理姓名:___________班级:___________考号:___________一、解答题1.一个班有小学生55人,订阅小学生数学报的有12人,订阅少年报的有9人,两种报纸都订的有5人,(1)订阅报纸的总人数是多少?(2)两种报纸都不订的有多少人?2.一个旅行社有36人,其中会英语的有24人,会法语的有18人,这两种语言都不会的有4人,这两种语言都会的有多少人?3.求在1~100的自然数中不是5的倍数也不是6的倍数的数有多少个?4.艺术节那天,学校画廊里展出了每个年级学生的图画作品,其中有23幅不是五年级的,有21幅不是六年级的,五六年级参展的共有8幅,其他年级参展的有多少幅?5.将边长为4厘米和5厘米的正方形纸片部分重叠,盖在桌面上,已知重叠的部分为9平方厘米,两块正方形纸片盖住桌面的总面积是多少?6.二(2)班有50人,下课后每人都至少做完了一门作业,其中做完语文作业的有35人,做完数学作业的有40人,两种作业都做完的有多少人?7.某艺术中心有62名学生,其中会弹钢琴的有11名,会吹长笛的有56名,两样都不会的有4名。
两样都会的有多少名?8.某校选出50名学生参加作文比赛和数学比赛,作文比赛获奖的有14人,数学比赛获奖的有12人,有3人两项比赛都获奖,两项比赛都没获奖的有多少人?9.四(1)班有40个学生,其中25人参加数学小组,23人参加航模小组,有19个人两个小组都参加了,那么有多少人两个小组都没参加?10.在一次数学测验中,所有同学都答了第1、2题,其中答对第一题的有35人,答对第2题的有28人,这两题都答对的有20人,没有人两题都打错。
问参加这次测验的有多少人?11.一个俱乐部里,会下中国象棋的有69人,会下国际象棋的有52人,两种都不会下的有12人,都会下的有30人这个俱乐部里有多少人?12.某班上体育课,全班排成4列(每列人数相等),从前往后数小芳第6个,从后往前数在第7个,这个班共有多少人?13.在1到200之间的全部自然数中,既不是8的倍数也不是5的倍数的数有几个?14.科技节那天,学校的科技室例展出了每个年级学生的作品,其中有114件不是一年级的,有96件不是二年级的,一二年级参展的作品共32件,其他年级参展的作品有多少件?试题答案1.16人;39人【分析】可将这55人分成4类,即只订阅小学生数学报,只订阅少年报,两种报纸都订阅,两种报纸都没有订阅,分别求出每一类的人数,再求出题目所求。
六年下册奥数试题- 容斥原理(二) 全国通用(含答案)

第10讲容斥原理(二)上一讲我们已经初步研究了简单的容斥原理,今天我们继续研究较复杂的容斥问题。
例1五年级一班有45名同学,每人都积极报名参加暑假体育训练班,其中报足球班的有25人,报篮球班的有20人,报游泳班的有30人,足球、篮球都报者有10人,足球、游泳都报者有10人,足球、篮球都报者有12人。
请问:三项都报的有多少人?分析:由于问题比较复杂,我们把它简化成下图.要计算阴影部分的面积,我们记A∩B 为圆A与圆B公共部分的面积,B∩C为圆B与圆C公共部分的面积,A∩C表示圆A与圆C 的公共部分的面积,x为阴影部分的面积则图形盖住的面积为:A+B+C-A∩B-B∩C-A∩C+X。
请同学们注意:阴影部分的面积先加了3次,然后又被减了3次,最后又加了1次。
解答:设三项都报的有x人,由容斥原理有30+25+20-10-10-12+x=45解得x=2。
答:三项都报名的有2人。
说明:在“A+B+C-A∩B-B∩C-A∩C+X”式中,A,B,C,A∩B,B∩C,A∩C,x和总量这8个数中,只要知道了7个数,就可通过列方程求出第8个数。
例2从1至1000这1000个自然数中,不能被3、5、7中任何一个自然数整除的数一共有多少个?分析:第一步先求出:能被3、5、7中任何一个自然数整除的数一共有多少个?第二步再求出:不能被3、5、7中任何一个自然数整除的数一共有多少个?能被3整除的自然数的个数+能被5整除的自然数的个数+能被7整除的自然数的个数-(既能被3整除又能被5整除的自然数的个数+既能被3整除又能被7整除的自然数的个数+既能被5整除又能被7整除的自然数的个数)+能同时被3、5、7整除的自然数的个数=能被3、5、7中任何一个自然数整除的数的个数。
解答:能被3整除的自然数有多少个?1000÷3=333……1 有333个。
能被5整除的自然数有多少个?1000÷5=200 有200个。
能被7整除的自然数有多少个?1000÷7=142……6 有142个。
四年级下奥数试题——第六讲包容与排斥(含答案)沪教版

精讲精练四年级思维数学 第六讲包容与排斥原理思维目标:根据题意,合理解决重叠部分的问题即包容与排斥原理。
数学目标:看谁算的巧思维: 两个图形分别用A 、B 表示,重叠部分用AB 表示,盖住的面积用N 表示,那么: N=A+B -AB ; AB= A+B -N ;A= N -B+AB ;B= N -A+AB 数学:先观察式子中的数字,然后进行合理巧算。
【例1】一个长为8厘米、宽为6厘米的长方形与一个边长为4厘米的正方形(如右图),放在桌子上。
它们盖住桌面的面积有多少平方厘米?金钥匙:A 面积:8×6=48(平方厘米)B 面积:4×4=16(平方厘米) AB 面积:3×3=9(平方厘米) N=A+B -AB = 48+16-9 =64-9=55(平方厘米)答:它们盖住桌面的面积有55平方厘米. 试金石:1、 四⑴班的每位学生都至少喜欢体育或文艺活动中的一种。
其中喜欢体育活动的有41人,喜欢文艺活动的有38人,两种活动都喜欢的有25人。
这个班共有学生多少人?学习目标 知识梳理AB2、某班从图书馆借来一批图书分给班上50位同学。
有30人各借到一本自然科学类书籍,有25人各借到一本文艺类书籍,既借了一本自然科学类书籍又借了一本文艺类书籍的学生有几人?【例2】某班40名学生在一次期中考试中每人至少有一门得优秀,语文得优秀的有14人,数学得优秀的有34人。
只有一门得优秀的各有多少人?金钥匙:根据题意,我们可以知道有些同学两门功课都得了优秀,在语文学科被算了一次,在数学学科也被算了一次,把两门学科得优秀的总人数去掉班级人数,多出的就是两门都得优秀的人数。
这样就能得出结果:34+14-40 数学一门:34-8=26(人)=48-40 语文一门:14-8=6(人)=8(人)答:数学一门得优秀的有26人,语文6人。
试金石:1、一次老师给全班同学做两道“动脑筋”的数学题,结果全班每人至少做对一题。
(小学奥数)容斥原理之数论问题

1. 瞭解容斥原理二量重疊和三量重疊的內容;2. 掌握容斥原理的在組合計數等各個方面的應用.一、兩量重疊問題 在一些計數問題中,經常遇到有關集合元素個數的計算.求兩個集合並集的元素的個數,不能簡單地把兩個集合的元素個數相加,而要從兩個集合個數之和中減去重複計算的元素個數,即減去交集的元素個數,用式子可表示成:A B A B A B =+-(其中符號“”讀作“並”,相當於中文“和”或者“或”的意思;符號“”讀作“交”,相當於中文“且”的意思.)則稱這一公式為包含與排除原理,簡稱容斥原理.圖示如下:A 表示小圓部分,B 表示大圓部分,C 表示大圓與小圓的公共部分,記為:A B ,即陰影面積.圖示如下:A 表示小圓部分,B 表示大圓部分,C 表示大圓與小圓的公共部分,記為:A B ,即陰影面積.包含與排除原理告訴我們,要計算兩個集合A B 、的並集AB 的元素的個數,可分以下兩步進行:教學目標知識要點1.先包含——A B +重疊部分A B 計算了2次,多加了1次;2.再排除——A B A B +-把多加了1次的重疊部分A B 減去.7-7-4 容斥原理之數論問題第一步:分別計算集合A B 、的元素個數,然後加起來,即先求A B +(意思是把A B 、的一切元素都“包含”進來,加在一起);第二步:從上面的和中減去交集的元素個數,即減去C AB =(意思是“排除”了重複計算的元素個數).二、三量重疊問題A 類、B 類與C 類元素個數的總和A =類元素的個數B +類元素個數C +類元素個數-既是A 類又是B 類的元素個數-既是B 類又是C 類的元素個數-既是A 類又是C 類的元素個數+同時是A 類、B 類、C 類的元素個數.用符號表示為:A B C A B C A B B C A C A B C =++---+.圖示如下:在解答有關包含排除問題時,我們常常利用圓圈圖(韋恩圖)來幫助分析思考.【例 1】 在1~100的全部自然數中,不是3的倍數也不是5的倍數的數有多少個?A B【考點】容斥原理之數論問題 【難度】2星 【題型】解答【解析】 如圖,用長方形表示1~100的全部自然數,A 圓表示1~100中3的倍數,B 圓表示1~100中5的倍數,長方形內兩圓外的部分表示既不是3的倍數也不是5的倍數的數.由1003331÷=可知,1~100中3的倍數有33個;由100520÷=可知,1~100中5的倍數有20個;由10035610÷⨯=()可知,1~100既是3的倍數又是5的倍數的數有6個.例題精講圖中小圓表示A 的元素的個數,中圓表示B 的元素的個數,大圓表示C 的元素的個數. 1.先包含:A B C ++ 重疊部分A B 、B C 、C A 重疊了2次,多加了1次. 2.再排除:A B C A B B C A C ++--- 重疊部分A B C 重疊了3次,但是在進行A B C ++- A B B C A C --計算時都被減掉了. 3.再包含:A B C A B B C A C A B C ++---+.由包含排除法,3或5的倍數有:3320647+-=(個).從而不是3的倍數也不是5的倍數的數有1004753-=(個).【答案】53【巩固】 在自然數1100~中,能被3或5中任一個整除的數有多少個?【考點】容斥原理之數論問題 【難度】2星 【題型】解答【解析】 1003331÷=,100520÷=,10035610÷⨯=().根據包含排除法,能被3或5中任一個整除的數有3320647+-=(個).【答案】47【巩固】 在前100個自然數中,能被2或3整除的數有多少個?【考點】容斥原理之數論問題 【難度】2星 【題型】解答【解析】 如圖所示,A 圓內是前100個自然數中所有能被2整除的數,B 圓內是前100個自然數中所有能被3整除的數,C 為前100個自然數中既能被2整除也能被3整除的數.前100個自然數中能被2整除的數有:100250÷=(個).由1003331÷=知,前100個自然數中能被3整除的數有:33個.由10023164÷⨯=()知,前100個自然數中既能被2整除也能被3整除的數有16個.所以A 中有50個數,B 中有33個數,C 中有16個數.因為A ,B 都包含C ,根據包含排除法得到,能被2或3整除的數有:50331667+-=(個).【答案】67【例 2】 在從1至1000的自然數中,既不能被5除盡,又不能被7除盡的數有多少個?【考點】容斥原理之數論問題 【難度】2星 【題型】解答【解析】 1~1000之間,5的倍數有10005⎡⎤⎢⎥⎣⎦=200個,7的倍數有10007⎡⎤⎢⎥⎣⎦=142個,因為既是5的倍數,又是7的倍數的數一定是35的倍數,所以這樣的數有100035⎡⎤⎢⎥⎣⎦=28個.所以既不能被5除盡,又不能被7除盡的數有1000-200-142+-28=686個.【答案】686【巩固】 求在1至100的自然數中能被3或7整除的數的個數.【考點】容斥原理之數論問題【難度】2星【題型】解答【解析】記A:1~100中3的倍數,1003331÷=,有33個;B:1~100中7的倍數,1007142÷=,有14個;A B:1~100中3和7的公倍數,即21的倍數,10021416÷=,有4個.依據公式,1~100中3的倍數或7的倍數共有3314443+-=個,則能被3或7整除的數的個數為43個.【答案】43【例 3】以105為分母的最簡真分數共有多少個?它們的和為多少?【考點】容斥原理之數論問題【難度】4星【題型】解答【解析】以105為分母的最簡真分數的分子與105互質,105=3×5×7,所以也是求1到105不是3、5、7倍數的數有多少個,3的倍數有35個,5的倍數有21個,7的倍數有15個,15的倍數有7個,21的倍數有5個,35的倍數有3個,105的倍數有1個,所以105以內與105互質的數有105-35-21-15+7+5+3-1=48個,顯然如果n與105互質,那麼(105-n)與n互質,所以以105為分母的48個最簡真分數可兩個兩個湊成1,所以它們的和為24.【答案】48個,和24【巩固】分母是385的最簡真分數有多少個?並求這些真分數的和.【考點】容斥原理之數論問題【難度】4星【題型】解答【解析】385=5×7×11,不超過385的正整數中被5整除的數有77個;被7整除的數有55個;被11整除的數有35個;被77整除的數有5個;被35整除的數有11個;被55整除的數有7個;被385整除的數有1個;最簡真分數的分子可以有385-77-55-35+5+11+7-1=240.對於某個分數a/385如果是最簡真分數的話,那麼(385-a)/385也是最簡真分數,所以最簡真分數可以每兩個湊成整數1,所以這些真分數的和為120.【答案】240個,120個【例 4】在1至2008這2008個自然數中,恰好是3、5、7中兩個數的倍數的數共有 個.【考點】容斥原理之數論問題 【難度】3星 【題型】填空【關鍵字】西城實驗【解析】 1到2008這2008個自然數中,3和5的倍數有200813315⎡⎤=⎢⎥⎣⎦個,3和7的倍數有20089521⎡⎤=⎢⎥⎣⎦個,5和7的倍數有20085735⎡⎤=⎢⎥⎣⎦個,3、5和7的倍數有200819105⎡⎤=⎢⎥⎣⎦個.所以,恰好是3、5、7中兩個數的倍數的共有1331995195719228-+-+-=個.【答案】228個【例 5】 求1到100內有____個數不能被2、3、7中的任何一個整除。
五年级下册数学试题 - 奥数第04讲:容斥定理 人教版(含答案)

第4讲 容斥定理内容概念:有重叠部分的若干对象的计数问题,能利用文氏图进行辅助分析,弄清文氏图中每部分的含义;结合文氏图理解两个对象和三个对象的容斥原理;灵活处理具有一些不确定性的计数问题,以及其他形式的重复计数问题。
典型问题:兴趣篇:1. 暑假里,小悦和冬冬一起讨论“金陵十八景”。
他们发现十八景中的每一处都有人去过,而且有五处是两人都去过的。
如果小悦去过其中的十二景,那么冬冬去过其中的几景?【分析】“十八景”剩余了18126-=景,所以冬冬去过其中的6+5=11景。
2.在一群小朋友中,有12人看过动画片《黑猫警长》,有21人看过动画片《大闹天宫》,并且有8人两部动画片都看过。
请问:至少看过其中一部的小朋友有多少人?【分析】至少看过一部的小朋友有:1221825+-=(人)3、 五年级一班45个学生参加期末考试。
成绩公布后,数学得满分的有10人,数学及语文均得满分的有3人,这两科都没有得满分的有29人。
请问:语文成绩得满分的有多少人?【分析】两科至少有一科得满分的有:452916-=(人),只有数学得满分的有:1037-=人,语文得满分的有:1679-=(人)。
4.某餐馆有27道招牌菜。
小悦吃过其中的13道,冬冬吃过其中的7道,而且有2道菜是两人都吃过的。
请问:有多少道招牌菜是两人都没有吃过的?【分析】两人都吃过的菜有:137218+-=道理,两人都没有吃过的有:27189-=(道)。
5.如图4-1,已知甲、乙、丙三个圆的面积均为30,甲与乙、乙与丙、甲与丙重合部分的面积分别为6、8、5,同时被这三个圆覆盖的部分的面积为2。
请问:(1)只被甲或乙覆盖,却不被丙覆盖的部分的面积是多少?(2)只被这3个圆中某一个圆覆盖的部分的面积是多少?【分析】(1)根据题意,有:6D G +=,则2G =,624D =-=;8F G +=,则有:826F =-=;5E G +=,则有:523E =-=;所以:()306321A =-+=;()308319B =-+=所以只被甲或者乙覆盖,却不被丙覆盖的是:2119343++=;(2)()306618C =-+=所以只被这3个圆中的某一个圆覆盖的部分的面积是:21191858++=。
(精品)小学奥数7-7-5 容斥原理之最值问题.专项练习及答案解析

1. 了解容斥原理二量重叠和三量重叠的内容;2. 掌握容斥原理的在组合计数等各个方面的应用.一、两量重叠问题 在一些计数问题中,经常遇到有关集合元素个数的计算.求两个集合并集的元素的个数,不能简单地把两个集合的元素个数相加,而要从两个集合个数之和中减去重复计算的元素个数,即减去交集的元素个数,用式子可表示成:A B A B A B =+-(其中符号“”读作“并”,相当于中文“和”或者“或”的意思;符号“”读作“交”,相当于中文“且”的意思.)则称这一公式为包含与排除原理,简称容斥原理.图示如下:A 表示小圆部分,B 表示大圆部分,C 表示大圆与小圆的公共部分,记为:A B ,即阴影面积.图示如下:A 表示小圆部分,B 表示大圆部分,C 表示大圆与小圆的公共部分,记为:A B ,即阴影面积.包含与排除原理告诉我们,要计算两个集合A B 、的并集A B 的元素的个数,可分以下两步进行:第一步:分别计算集合A B 、的元素个数,然后加起来,即先求A B +(意思是把A B 、的一切元素都“包含”进来,加在一起);第二步:从上面的和中减去交集的元素个数,即减去C A B =(意思是“排除”了重复计算的元素个数).二、三量重叠问题A 类、B 类与C 类元素个数的总和A =类元素的个数B +类元素个数C +类元素个数-既是A 类又是B 类的元素个数-既是B 类又是C 类的元素个数-既是A 类又是C 类的元素个数+同时是A 类、B 类、C 类的元素个数.用符号表示为:A B C A B C A B B C A C A B C =++---+.图示如下:教学目标知识要点7-7-5.容斥原理之最值问题1.先包含——A B +重叠部分A B 计算了2次,多加了1次;2.再排除——A B A B +-把多加了1次的重叠部分A B 减去.在解答有关包含排除问题时,我们常常利用圆圈图(韦恩图)来帮助分析思考.【例 1】 “走美”主试委员会为三~八年级准备决赛试题。
小学奥数7-7-5 容斥原理之最值问题.专项练习及答案解析

1.了解容斥原理二量重叠和三量重叠的内容;2. 掌握容斥原理的在组合计数等各个方面的应用.一、两量重叠问题 在一些计数问题中,经常遇到有关集合元素个数的计算.求两个集合并集的元素的个数,不能简单地把两个集合的元素个数相加,而要从两个集合个数之和中减去重复计算的元素个数,即减去交集的元素个数,用式子可表示成:A B A B A B =+-(其中符号“”读作“并”,相当于中文“和”或者“或”的意思;符号“”读作“交”,相当于中文“且”的意思.)则称这一公式为包含与排除原理,简称容斥原理.图示如下:A 表示小圆部分,B 表示大圆部分,C 表示大圆与小圆的公共部分,记为:A B ,即阴影面积.图示如下:A 表示小圆部分,B 表示大圆部分,C 表示大圆与小圆的公共部分,记为:AB ,即阴影面积.包含与排除原理告诉我们,要计算两个集合A B 、的并集A B 的元素的个数,可分以下两步进行: 第一步:分别计算集合A B 、的元素个数,然后加起来,即先求A B +(意思是把A B 、的一切元素都“包含”进来,加在一起);第二步:从上面的和中减去交集的元素个数,即减去C A B =(意思是“排除”了重复计算的元素个数).二、三量重叠问题A 类、B 类与C 类元素个数的总和A =类元素的个数B +类元素个数C +类元素个数-既是A 类又是B 类的元素个数-既是B 类又是C 类的元素个数-既是A 类又是C 类的元素个数+同时是A 类、B 类、C 类的元素个数.用符号表示为:A B C A B C A B B C A C A B C =++---+.图示如下:在解答有关包含排除问题时,我们常常利用圆圈图(韦恩图)来帮助分析思考.教学目标知识要点7-7-5.容斥原理之最值问题1.先包含——A B + 重叠部分A B 计算了2次,多加了1次;2.再排除——A B A B +-把多加了1次的重叠部分A B 减去. 图中小圆表示A 的元素的个数,中圆表示B 的元素的个数,大圆表示C 的元素的个数.1.先包含:A B C ++ 重叠部分A B 、B C 、C A 重叠了2次,多加了1次. 2.再排除:A B C A B B C A C ++--- 重叠部分A B C 重叠了3次,但是在进行A B C ++- A B B C A C --计算时都被减掉了. 3.再包含:A B C A B B C A C A B C ++---+.【例 1】 “走美”主试委员会为三~八年级准备决赛试题。
小学奥数 容斥原理 知识点+例题+练习 (分类全面)
5、在1到130的全部自然数中,既不是6的倍数又不是5的倍数的数有多少个?不是6的倍数或不是5的倍数的数有几个?
6、某班统计考试成绩,数学得90分上的有25人;语文得90分以上的有21人;两科中至少有一科在90分以上的有38人。问两科都在90分以上的有多少人?
巩固:刘老师、夏老师和胡老师共有书90本,其中刘老师和夏老师一共有70本,夏老师和胡老师共有50本,三位老师各有书多少本?
例5、在1至10000中不能被5或7整除的数共有多少个?既不能被5整除又不能被7整除的有多少个?
巩固:在1到200的全部自然数中,既不是5的倍数又不是8的倍数的数有多少个?不是5的倍数或不是8的倍数的数有几个?
巩固:某校的每个学生至少爱好体育和文娱中的一种活动,已知有900人爱好体育活动,有850人爱好文娱活动,其中260人两种活动都爱好。这个学校共有学生多少人?
例3、学校开展课外活动,共有250人参加。其中参加象棋组和乒乓球组的同学不同时活动,参加象棋组的有83人,参加乒乓球组的有86人,这两个小组都参加的有25人。问这250名同学中,象棋组、乒乓球组都不参加的有多少人?
课后作业
1、五年级有112人参加语文、数学考试,每人至少有一门功课得优,其中,语文得优的有65人,数学得优的有87人,问语文、数学都得优的有多少人?
2、某班在一次测验中有26人语文获优,有30人数学获优,其中语、数双优的有12人,另外还有8人语、数均未获优,这个班共有多少个学生?
3、五(1)班有学生50人,在一次测试中,语文90分以上的有30人,数学90分以上的35人,语文和数学都在90分以上的有20人,90分以下的有多少人?
四年级奥数题第35讲容斥原理

第 35 讲 容斥原理一、专题简析:容斥问题涉及到一个重要原理——包含与排除原理 , 也叫容斥原理。
即当两 个计数部分有重复包含时 , 为了不重复计数 , 应从它们的和中排除重复部分。
容斥原理:对 n 个事物, 如果采用不同的分类标准 , 按性质 a 分类与性质 b 分类(如图) , 那么具有性质 a 或性质 b 的事物的个数 =N a + N b -N ab 。
例 1:一个班有 48 人, 班主任在班会上问:“谁做完语文作业?请举手!”有 37 人举手。
又问: “谁做完数学作业?请举手!”有 42 人举手。
最后问:“谁 语文、数学作业都没有做完?”没有人举手。
求这个班语文、数学作业都完成 的人数。
练习一1、五年级有 122 名学生参加语文、数学考试 , 每人至少有一门功课取得优秀成 绩。
其中语文成绩优秀的有 65人,数学优秀的有 87 人。
语文、数学都优秀的有 多少人?2、四年级一班有 54 人 , 订阅《小学生优秀作文》和《数学大世界》两种读物的 有 13人, 订《小学生优秀作文》的有 45人, 每人至少订一种读物 ,订《数学大世 界》的有多少人?精讲精练:例2:某班有36 个同学在一项测试中, 答对第一题的有25 人, 答对第二题的有23 人, 两题都答对的有15 人。
问多少个同学两题都答得不对?练习二1、五(1)班有40 个学生, 其中25 人参加数学小组,23 人参加科技小组, 有19 人两个小组都参加了。
那么, 有多少人两个小组都没有参加?2、一个班有55 名学生, 订阅《小学生数学报》的有32 人, 订阅《中国少年报》的有29人, 两种报纸都订阅的有25人。
两种报纸都没有订阅的有多少人?例3:某班有56人, 参加语文竞赛的有28人, 参加数学竞赛的有27人, 如果两科都没有参加的有25人, 那么同时参加语文、数学两科竞赛的有多少人?练习三1、一个旅行社有36人,其中会英语的有24人, 会法语的有18人, 两样都不会的有4 人。
(奥数典型题)容斥原理--2024年六年级下册小升初数学思维拓展含答案

(奥数典型题)容斥原理--2024年六年级下册小升初数学思维拓展容斥原理【知识点归纳】在日常生活中,人们常常需要统计一些数量,在统计的过程中,往往会发现有些数量重复出现,为了使重复出现的部分不致被重复计算,人们研究出一种新的计数方法,既先不考虑重复的情况,把包含于某内容中的所有对象的数目先计算出来,然后再把计数时重复计算的数目排除出去,使计算的结果既无遗漏又无重复.这种计数方法称为包含排除法,也叫做容斥原理或重叠问题.一般方法:在解答有关包含排除问题时,我们常常利用圆圈图(韦恩图)来帮助分析思考.容斥原理1:两量重叠问题A类与B类元素个数的总和=A类元素的个数+B类元素个数﹣既是A类又是B类的元素个数用符号可表示成:A∪B=A+B﹣A∩B(其中符号“∪”读作“并”,相当于中文“和”或者“或”的意思,符号“∩”读作“交”,相当于中文“且”的意思).容斥原理2:三量重叠问题A类、B类与C类元素个数的总和=A类元素的个数+B类元素个数+C类元素个数﹣既是A类又是B类的元素个数﹣既是B类又是C类的元素个数﹣既是A类又是C类的元素个数+同时是A类、B类、C类的元素个数.用符号表示为:A∪B∪C=A+B+C﹣A∩B﹣B∩C﹣A∩C+A∩B∩C1.三年级共有80名同学参加书法兴趣小组和美术兴趣小组,其中参加书法组的有52人,参加美术组的有48人.那么,既参加书法组又参加美术组的有多少人?2.我们班参入调查了饭后吃水果情况:30人喜欢吃苹果,27人喜欢吃梨,10人两种都喜欢,问我们班有多少人?3.同学们收集图片.张明、李红、蔡正明、王丹、熊威、高伟、梅芳7个人收集了名山图片,吴凤、李红、王丹、戴月红、高伟这5人收集了河流图片,吴心怡、张冬、李可这3人收集了奥运图片.(1)收集名山图片和奥运图片的共有多少人?(2)收集名山图片和河流图片的共有多少人?4.在校运动会上,共有30人参加跳远和跳高。
参加跳远的有18人,参加跳高的有22人,既参加跳远又参加跳高的有多少人?5.三(1)班有48人,其中订《少年报》的有32人,订《数学报》的有38人,有25人两份报都订。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1. 了解容斥原理二量重叠和三量重叠的内容;2. 掌握容斥原理的在组合计数等各个方面的应用.一、两量重叠问题 在一些计数问题中,经常遇到有关集合元素个数的计算.求两个集合并集的元素的个数,不能简单地把两个集合的元素个数相加,而要从两个集合个数之和中减去重复计算的元素个数,即减去交集的元素个数,用式子可表示成:A B A B A B =+-(其中符号“”读作“并”,相当于中文“和”或者“或”的意思;符号“”读作“交”,相当于中文“且”的意思.)则称这一公式为包含与排除原理,简称容斥原理.图示如下:A 表示小圆部分,B 表示大圆部分,C 表示大圆与小圆的公共部分,记为:A B ,即阴影面积.图示如下:A 表示小圆部分,B 表示大圆部分,C 表示大圆与小圆的公共部分,记为:A B ,即阴影面积.包含与排除原理告诉我们,要计算两个集合A B 、的并集A B 的元素的个数,可分以下两步进行:第一步:分别计算集合A B 、的元素个数,然后加起来,即先求A B +(意思是把A B 、的一切元素都“包含”进来,加在一起);第二步:从上面的和中减去交集的元素个数,即减去C A B =(意思是“排除”了重复计算的元素个数).二、三量重叠问题A 类、B 类与C 类元素个数的总和A =类元素的个数B +类元素个数C +类元素个数-既是A 类又是B 类的元素个数-既是B 类又是C 类的元素个数-既是A 类又是C 类的元素个数+同时是A 类、B 类、C 类的元素个数.用符号表示为:A B C A B C A B B C A C A B C =++---+.图示如下:教学目标知识要点1.先包含——A B +重叠部分AB 计算了2次,多加了1次; A B A B +-1A B7-7-4 容斥原理之数论问题在解答有关包含排除问题时,我们常常利用圆圈图(韦恩图)来帮助分析思考.【例 1】 在1~100的全部自然数中,不是3的倍数也不是5的倍数的数有多少个?A B【考点】容斥原理之数论问题 【难度】2星 【题型】解答【解析】 如图,用长方形表示1~100的全部自然数,A 圆表示1~100中3的倍数,B 圆表示1~100中5的倍数,长方形内两圆外的部分表示既不是3的倍数也不是5的倍数的数.由1003331÷=可知,1~100中3的倍数有33个;由100520÷=可知,1~100中5的倍数有20个;由10035610÷⨯=()可知,1~100既是3的倍数又是5的倍数的数有6个.由包含排除法,3或5的倍数有:3320647+-=(个).从而不是3的倍数也不是5的倍数的数有1004753-=(个).【答案】53【巩固】 在自然数1100~中,能被3或5中任一个整除的数有多少个?【考点】容斥原理之数论问题 【难度】2星 【题型】解答【解析】 1003331÷=,100520÷=,10035610÷⨯=().根据包含排除法,能被3或5中任一个整除的数有3320647+-=(个).【答案】47【巩固】 在前100个自然数中,能被2或3整除的数有多少个?【考点】容斥原理之数论问题 【难度】2星 【题型】解答【解析】 如图所示,A 圆内是前100个自然数中所有能被2整除的数,B 圆内是前100个自然数中所有能被3整除的数,C 为前100个自然数中既能被2整除也能被3整除的数.前100个自然数中能被2整除的数有:100250÷=(个).由1003331÷=知,前100个自然数中能被3整除的数有:33个.由10023164÷⨯=()知,前100个自然数中既能被2整除也能被3整除的数有16个. 例题精讲 图中小圆表示A 的元素的个数,中圆表示B 的元素的个数,C1.先包含:A B C ++重叠部分A B 、B C 、C A 重叠了2次,多加了1次. 2.再排除:A B C A B B C A C ++--- A B C 3A B C ++-A B B C A C--A B C A B B C A C A B C ++---+所以A 中有50个数,B 中有33个数,C 中有16个数.因为A ,B 都包含C ,根据包含排除法得到,能被2或3整除的数有:50331667+-=(个).【答案】67【例 2】 在从1至1000的自然数中,既不能被5除尽,又不能被7除尽的数有多少个?【考点】容斥原理之数论问题 【难度】2星 【题型】解答【解析】 1~1000之间,5的倍数有10005⎡⎤⎢⎥⎣⎦=200个,7的倍数有10007⎡⎤⎢⎥⎣⎦=142个,因为既是5的倍数,又是7的倍数的数一定是35的倍数,所以这样的数有100035⎡⎤⎢⎥⎣⎦=28个. 所以既不能被5除尽,又不能被7除尽的数有1000-200-142+-28=686个.【答案】686【巩固】 求在1至100的自然数中能被3或7整除的数的个数.【考点】容斥原理之数论问题 【难度】2星 【题型】解答【解析】 记 A :1~100中3的倍数,1003331÷=,有33个; B :1~100中7的倍数,1007142÷=,有14个;A B :1~100中3和7的公倍数,即21的倍数,10021416÷=,有4个. 依据公式,1~100中3的倍数或7的倍数共有3314443+-=个,则能被3或7整除的数的个数为43个. 【答案】43【例 3】 以105为分母的最简真分数共有多少个?它们的和为多少?【考点】容斥原理之数论问题 【难度】4星 【题型】解答【解析】 以105为分母的最简真分数的分子与105互质,105=3×5×7,所以也是求1到105不是3、5、7倍数的数有多少个,3的倍数有35个,5的倍数有21个,7的倍数有15个,15的倍数有7个,21的倍数有5个,35的倍数有3个,105的倍数有1个,所以105以内与105互质的数有105-35-21-15+7+5+3-1=48个,显然如果n 与105互质,那么(105-n )与n 互质,所以以105为分母的48个最简真分数可两个两个凑成1,所以它们的和为24.【答案】48个,和24【巩固】 分母是385的最简真分数有多少个?并求这些真分数的和.【考点】容斥原理之数论问题 【难度】4星 【题型】解答【解析】 385=5×7×11,不超过385的正整数中被5整除的数有77个;被7整除的数有55个;被11整除的数有35个;被77整除的数有5个;被35整除的数有11个;被55整除的数有7个;被385整除的数有1个;最简真分数的分子可以有385-77-55-35+5+11+7-1=240.对于某个分数a/385如果是最简真分数的话,那么(385-a )/385也是最简真分数,所以最简真分数可以每两个凑成整数1,所以这些真分数的和为120.【答案】240个,120个【例 4】 在1至2008这2008个自然数中,恰好是3、5、7中两个数的倍数的数共有 个.【考点】容斥原理之数论问题 【难度】3星 【题型】填空【关键词】西城实验【解析】 1到2008这2008个自然数中,3和5的倍数有200813315⎡⎤=⎢⎥⎣⎦个,3和7的倍数有20089521⎡⎤=⎢⎥⎣⎦个,5和7的倍数有20085735⎡⎤=⎢⎥⎣⎦个,3、5和7的倍数有200819105⎡⎤=⎢⎥⎣⎦个.所以,恰好是3、5、7中两个数的倍数的共有1331995195719228-+-+-=个.【答案】228个【例 5】 求1到100内有____个数不能被2、3、7中的任何一个整除。
【考点】容斥原理之数论问题 【难度】3星 【题型】填空【关键词】学而思杯,4年级,第12题【解析】 被2整除的有50个,被3整除的有33个,被7整除的有14个同时被2和3整除的有16个,同时被2和7整除的有7个,同时被3和7整除的有4个同时被2和3和7整除的有2个,()100503314167421007228-++---+=-=个【答案】28个。
【例 6】 在从1到1998的自然数中,能被2整除,但不能被3或7整除的数有多少个?【考点】容斥原理之数论问题 【难度】3星 【题型】解答【解析】 a b ⎡⎤⎢⎥⎣⎦表示取商的整数部分.例如,732⎡⎤=⎢⎥⎣⎦.要注意的是,符号[]与+、-、⨯、÷符号一样,也是一种运算,叫取整运算.本题中,先求出能被2整除的数有多少个,再分别求出能被2和3、能被2和7分别整除的数的个数,那么用能被2整除的数的个数减去能被2和3整除的数的个数,再减去能被2和7整除的数的个数,所得的差是不是所求的得数呢?仔细想想你会发现不是的,因为它多减了能同时被2、3、7整除的数.故能被2整除的有:19982999÷=(个).能被2和3同时整除的有:[199823]333÷⨯=()(个).能被2和7同时整除的有:[199827]142÷⨯=().能被2、3、7同时整除的有:[1998237]47÷⨯⨯=()(个).所以,能被2整除,但不能被3或7整除的数有99933314247571--+=(个).【答案】571个【例 7】 50名同学面向老师站成一行.老师先让大家从左至右按1,2,3,…,49,50依次报数;再让报数是4的倍数的同学向后转,接着又让报数是6的倍数的同学向后转.问:现在面向老师的同学还有多少名?【考点】容斥原理之数论问题 【难度】3星 【题型】解答【关键词】华杯赛,初赛,第13题【解析】 在转过两次后,面向老师的同学分成两类:第一类是标号既不是4的倍数,又不是6的倍数;第二类是标号既是4的倍数又是6的倍数.1~50之间,4的倍数有504⎡⎤⎢⎥⎣⎦=12,6的倍数有506⎡⎤⎢⎥⎣⎦=8,即是4的倍数又是6的倍数的数一定是12的倍数,所以有5012⎡⎤⎢⎥⎣⎦=4.于是,第一类同学有50-12-8+4=34人,第二类同学有4人,所以现在共有34+4=38名同学面向老师.【答案】38名【例 8】 体育课上,60名学生面向老师站成一行,按老师口令,从左到右报数:1,2,3,…,60,然后,老师让所报的数是4的倍数的同学向后转,接着又让 所报的数是5的倍数的同学向后转,最后让所报的数是6的倍数的同学向后转,现在面向老师的学生有________人。
【考点】容斥原理之数论问题 【难度】3星 【题型】填空【关键词】希望杯,六年级,二试,第15题,4分【解析】 可知其中4的倍数有15个,5的倍数有12个,6的倍数有10个,同时是4和5的倍数的有3个,同时是5和6的倍数的有2个,同时是4和6的倍数的有5个,同时是4、5、6的倍数的数有1个,现在背向老师的有15+12+10-3-2-5+1=28个,面向老师的学生有60-28=32人。
