(完整版)小学奥数数论问题余数问题练习题【五篇】
四年级常考的奥数题:余数问题

四年级常考的奥数题:余数问题四年级常考的奥数题:余数问题导语:任何一个人,都要必须养成自学的习惯,即使是今天在学校的学生,也要养成自学的习惯,因为迟早总要离开学校的!自学,就是一种独立学习,独立思考的能力。
行路,还是要靠行路人自己。
下面是小编为大家整理的:奥数题。
希望对大家有所帮助,欢迎阅读,仅供参考,更多相关的知识,请关注CNFLA学习网!小学奥数题【例一】所谓同余问题,就是给出“一个数除以几个不同的数”的余数,反求这个数,称作同余问题。
首先要对这几个不同的数的最小公倍数心中有数,下面以4、5、6为例,请记住它们的最小公倍数是60。
1、差同减差:用一个数除以几个不同的`数,得到的余数,与除数的差相同,此时反求的这个数,可以选除数的最小公倍数,减去这个相同的差数,称为:“差同减差”。
例:“一个数除以4余1,除以5余2,除以6余3”,因为4-1=5-2=6-3=3,所以取-3,表示为60n-3。
【60后面的“n”请见4、,下同】2、和同加和:用一个数除以几个不同的数,得到的余数,与除数的和相同,此时反求的这个数,可以选除数的最小公倍数,加上这个相同的和数,称为:“和同加和”。
例:“一个数除以4余3,除以5余2,除以6余1”,因为4+3=5+2=6+1=7,所以取+7,表示为60n+7。
3、余同取余:用一个数除以几个不同的数,得到的余数相同,此时反求的这个数,可以选除数的最小公倍数,加上这个相同的余数,称为:“余同取余”。
例:“一个数除以4余1,除以5余1,除以6余1”,因为余数都是1,所以取+1,表示为60n+1。
4、最小公倍加:所选取的数加上除数的最小公倍数的任意整数倍(即上面1、2、3中的60n)都满足条件,称为:“最小公倍加”,也称为:“公倍数作周期”。
小学奥数题【例二】基本概念:对任意自然数a、b、q、r,如果使得a÷b=q……r,且0余数的性质:①余数小于除数。
②若a、b除以c的余数相同,则c|a-b或c|b-a。
五年级奥数题及答案-求余数问题

五年级奥数题及答案-求余数问题
编者小语:奥数教学不能单纯是传授数学知识,更重要的是培养学生数学意识、数学思想、独立获得和运用数学知识的能力和良好的数学学习习惯的过程。
让学生具备在未来的工作中科学地提出数学问题、探索数学问题、创造性地解决数学问题的能力。
为大家准备了小学五年级奥数题,希望小编整理的五年级奥数题及参考答案:求余数问题,可以帮助到你们,助您快速通往高分之路!!
求余数:
求437×319×2010+2010被7除的余数。
解答:437≡3(mod7),319≡5(mod7),2010≡1(mod7)
由"同余性质"可知:
437×319×2010≡3×5×1(mod7)=15(mod7)≡1(mod7)
所以:437×319×2010+2010≡1+1(mod7)=2(mod7)
即:437×319×2010+2010被7除的余数是2.这道题主要考察了同余性质。
必须注意的是同余性质只能用在加、减、乘。
五年级奥数.数论.中国剩余定理及弃九法(B级).学生版

五年级奥数.数论.中国剩余定理及弃九法(B级).学⽣版⼀、中国剩余定理——中国古代趣题1) 趣题⼀中国数学名著《孙⼦算经》⾥有这样的问题:“今有物,不知其数,三三数之,剩⼆,五五数之,剩三,七七数之,剩⼆,问物⼏何?”答⽈:“⼆⼗三。
”此类问题我们可以称为“物不知其数”类型,⼜被称为“韩信点兵”。
韩信点兵⼜称为中国剩余定理,相传汉⾼祖刘邦问⼤将军韩信统御兵⼠多少,韩信答说,每3⼈⼀列余1⼈、5⼈⼀列余2⼈、7⼈⼀列余4⼈、13⼈⼀列余6⼈……。
刘邦茫然⽽不知其数。
我们先考虑下列的问题:假设兵不满⼀万,每5⼈⼀列、9⼈⼀列、13⼈⼀列、17⼈⼀列都剩3⼈,则兵有多少?⾸先我们先求5、9、13、17之最⼩公倍数9945(注:因为5、9、13、17为两两互质的整数,故其最⼩公倍数为这些数的积),然后再加3,得9948(⼈)。
孙⼦算经的作者及确实著作年代均不可考,不过根据考证,著作年代不会在晋朝之后,以这个考证来说上⾯这种问题的解法,中国⼈发现得⽐西⽅早,所以这个问题的推⼴及其解法,被称为中国剩余定理。
中国剩余定理(Chinese Remainder Theorem )在近代抽象代数学中占有⼀席⾮常重要的地位。
2) 趣题⼆我国明朝有位⼤数学家叫程⼤位,他在解答“物不知其数”问题(即:有物不知其数,三三数之剩⼆,五五数之剩三,七七数之剩⼆,问物⼏何?)时⽤四句诗概括出这类问题的优秀解法:“三⼈同⾏七⼗稀,五树梅花廿⼀枝,七⼦团圆正⽉半,除百零五便得知.”这⾸诗就是解答此类问题的⾦钥匙,它被世界各国称为“中国剩余定理”(Chinese Remainder Theorem ),是我国古代数学的⼀项辉煌成果.诗中的每⼀句话都表⽰⼀个步骤:三⼈同⾏七⼗稀,是说除以3所得的余数⽤70乘.五树梅花廿⼀枝,是说除以5所得的余数⽤21乘.七⼦团圆正⽉半,是说除以7所得的余数⽤15乘.除百零五便得知,是说把上⾯乘得的3个积加起来,减去105的倍数,减得差就是所求的数.此题的中国剩余定理的解法是:⽤70乘3除所得的余数,21乘5除所得的余数,15乘7除所得的余数,把这3个结果加起来,如果它⼤于105,则减去105,所得的差如果仍⽐105⼤,则继续减知识框架中国剩余定理及弃九法去105,最后所得的整数就是所求.也就是270321215233-=++=,233105128-=,12810523为什么70,21,15,105有此神奇效⽤?70,21,15,105是从何⽽来?先看70,21,15,105的性质:70被3除余1,被5,7整除,所以70a是⼀个被3除余a⽽被5与7整除的数;21是5除余1,被3与7整除的数,因此21b是被5除余b,被3与7整除的数;同理15c是被7除余c,被3、5整除的数,105是3,5,7的最⼩公倍数.也就是说,702115++是a b c被3除余a,被5除余b,被7除余c的数,这个数可能是解答,但不⼀定是最⼩的,因此还要减去它们的公倍数.了解了“剩余定理”的秘密后,对类似于上⾯的题⽬,我们都可以⽤中国剩余定理来解答.3)核⼼思想和⽅法对于这⼀类问题,我们有⼀套看似繁琐但是⼀旦掌握便可⼀通百通的⽅法,下⾯我们就以《孙⼦算经》中的问题为例,分析此⽅法:今有物,不知其数,三三数之,剩⼆,五五数之,剩三,七七数之,剩⼆,问物⼏何?题⽬中我们可以知道,⼀个⾃然数分别除以3,5,7后,得到三个余数分别为2,3,2.那么我们⾸先构造⼀个数字,使得这个数字除以3余1,并且还是5和7的公倍数。
小学奥数题库《数论》余数问题中国剩余定理3星题(含解析)全国通用版

数论-余数问题-中国剩余定理-3星题课程目标知识提要中国剩余定理•概述中国剩余定理即我们常说的“物不知数”,是利用同余式组来求解的一类问题。
A、一个数分别除以两个数余数相同的时候,将原数减去这个余数之后可以整除那两个数B、上述情况下的余数虽有不同,但与各自对应的除数的差相同,将原数加上这个差之后便可以整除C、其他情况下,凑出相同余数之后,运用第一种情况的方法.精选例题中国剩余定理1. 某个自然数除以2余1,除以3余2,除以4余1,除以5也余1,则这个数最小是.【答案】41【分析】这个自然数除以2、4、5都余1,[2,4,5]=20,所以这个数应满足1+20n,同时除以3余2,所以最小是41.2. 一个大于10的自然数,除以5余3,除以7余1,除以9余4,那么满足条件的自然数最小为.【答案】148【分析】观察发现三个数中前两个数的除数与余数的和都是5+3=7+1=8,这样我们可以把余数都处理成8,即一个数除以5余3相当于除以5余8,除以7余1相当于除以7余8,所以满足前两个条件的自然数为a=35m+8,下一步只需要a除以9余4,35÷9=3⋯8,只需8+8m除以9余4,只需8m除以9余5,最小的m=4,因此满足所有条件的最小自然数为8+35×4=148.3. 有一筐苹果,甲班分,每人3个还剩11个;乙班分,每人4个还剩10个;丙班分,每人5个还剩12个.那么这筐苹果至少个.【答案】62【分析】设有x个苹果.因为11除以3余2,所以x除以3余2;因为10除以4余2,所以x除以4余2;因为12除以5余2,所以x除以5余2.又因为x大于12,x=[3,4,5]+2=60+2=62(个).4. 小明心里想了一个正整数.并且求出了它分别被14和21除后所得的余数,已知这两个余数的和是33,则该整数被42除的余数是.【答案】41【分析】该整数除以14的余数不大于13,除以21余数不大于20,所以这两个余数的和不大于33,而由题有这两个余数的和恰好是33,所以该整数除以14余数是13,除以21余数是20.这个数加上1就是14和21的倍数,而[14,21]=42,所以这个数可以表示成42k−1的形式,被42除的余数是41.5. 一个大于2的数,除以3余1,除以5余3,除以7余5,问满足条件的最小自然数是.【答案】103.【分析】我们发现两个算式除数与余数的差都相等,所以把他们都处理成都缺2能被整除,这样得[3、5、7]−2=103.6. 某数除以11余8,除以13余10,除以17余12,那么这个数的最小可能值是.【答案】998【分析】观察到11−8=13−10=3,因此除以11余8,除以13余10的最小自然数为11×13−3=140,设某数为a,则a=143m−3m为非零自然数,只需143m−3除以17余12,而143÷17=8⋯7,只需(7m−3)÷17=n⋯12,即7m−15是17的倍数所以,m=7,所以a=143×7−3=998.7. 一个大于3的数,除以7余4,除以9余6,除以11余8,问满足条件的最小自然数是.【答案】690.【分析】我们发现两个算式除数与余数的差都相等,所以把他们都处理成都缺3能被整除,这样得[7、9、11]−3=690.8. 一个大于10的数,除以5余3,除以7余1,问满足条件的最小自然数为.【答案】43.【分析】根据总结,我们发现两个数的除数与余数的和都是5+3=7+1=8,这样我们可以把余数都处理成都余8,所以[5、7]=35,所以这个数就是35+8=43.9. 我国南宋数学家杨辉在其《续古摘奇算法》上记载了这样一个问题:“二数余一,五数余二,七数余三,九数余四,问本数.”用现代语言表述就是:“有一个数用2除余1,用5除余2,用7除余3,用9除余4,问这个数是多少?”请将满足条件的最小的自然数写在这里.【答案】157【分析】(解法一)先考虑除以5余2,除以7余3,除以9余4;用剩余定理得5×7×5+5×9×1+7×9×4=472[5,7,9]=315,故472±315k都符合除以5余2,除以7余3,除以9余4最小是472−315=157,且也符合除以2余1.(解法二)除以2余1的数有:1,3,5,7,9,11,13,15,17,⋯;除以5余2的数有:2,7,12,17⋯;除以7余3的数有:3,10,17⋯;所以满足“用2除余1,用5除余2,用7除余3”的数的形式为[2,5,7]n+17=70n+17(n为自然数)此时只需要找一个最小的n,满足除以9余4即可.当n=2时,满足除以9余4,所以满足条件的最小的自然数为70⋯2+17=15710. 一个数,除以11余7,除以13余9,除以19余15,问满足条件的最小自然数是.【答案】2713.【分析】我们发现两个算式除数与余数的差都相等,所以把他们都处理成都缺4能被整除,这样得[11、13、19]−4=2713.11. 智慧老人到小明的年级访问,小明说他们年级共一百多名同学,老人请同学们按三人一行排队,结果多出一人,按五人一行排队,结果多出二人,按七人一行排队,结果多出一人,老人说我知道你们年级人数应该是人.【答案】127【分析】根据条件,该数除以3余1,除以5余2,除以7余1,逐级满足法,令该数为a,则a÷3⋯⋯1 ①a÷5⋯⋯2 ②a÷7⋯⋯1 ③符合条件①的有1,4,7,10,13,16,⋯.同时满足①、②的最小值为7,以后a=7+15m均满足①、②;现在来看(7+15m)除以7余1,则15m除以7余1,则m最小取1,符合,最小的符合的数为a=22.以后每隔[3,5,7]=105即符合.由于该年级有100多名学生,为22+105= 127.12. 一个大于2000数,除以11余5,除以13余3,除以17余16,问满足条件的最小自然数为.【答案】2447.【分析】根据题意,我们发现三个算式中两个数的除数与余数的和都是11+5=13+3= 16,这样我们可以把余数都处理成都余16,所以[11、13、17]=2431,所以这个数就是2431+16=2447.13. 某个两位数是2的倍数,加1是3的倍数,加2是4的倍数,加3是5的倍数,那么这个两位数是.【答案】62【分析】由题可知,此数是一个2的倍数,并且除以3、4、5都余2的数,这样的数最小是2,因为这个数是两位数,2+[3、4、5]=62.14. 5年级3班同学上体育课,排成3行少1人,排成4行多3人,排成5行少1人,排成6排多5人,问上体育课的同学最少人.【答案】59.【分析】分析题意知,这个班的人数除以3余2,除以4余3,除以5余4,除以6余5,凑缺相同,这个班人数为[3、4、5、6]−1=59(人).15. 有一堆水果糖,如果按8块一份来分,最后剩下2块;如果按9块一份来分,最后剩3块;如果按10块一份来分,最后剩下4块.这堆糖至少有块.【答案】354【分析】这堆水果糖的总数被8除余2,被9除余3,被10除余4,如果增加6块就刚好是8、9、10的公倍数,又8、、9、10的最小公倍数是360.所以这堆水果糖至少有360−6=354(块).16. 一个大于100的数,除以9余3,除以11余1,问满足条件的最小自然数为.【答案】111.【分析】据题意,我们发现两个数的除数与余数的和都是9+3=11+1=12,这样我们可以把余数都处理成都余12,所以[9、11]=99,所以这个数就是99+12=111.17. 一个大于10的自然数,除以5余3,除以7余1,除以9余8,那么满足条件的自然数最小为.【答案】323【分析】根据总结,我们发现三个数中前两个数的除数与余数的和都是5+3=7+1=8这样我们可以把余数都处理成8,即一个数除以5余3相当于除以5余8,除以7余1相当于除以7余8,所以可以看成这个数除以5、7、9的余数都是8,那么它减去8之后是5、7、9的公倍数.而[5,7,9]=315所以这个数最小为315+8=323.18. 一个大于10的数,除以5余3,除以7余1,除以9余8,问满足条件的最小自然数为.【答案】323.【分析】根据总结,我们发现三个数中两个数的除数与余数的和都是5+3=7+1=8,这样我们可以把余数都处理成都余8,所以[5、7、9]=315,所以这个数就是315+8=323.19. 红星小学组织学生划船.若乘坐大船,除1条船坐6人外,其余每船均坐17人;若乘小船,则除1条船坐2人外,其余每船均坐10人.如果学生的人数超过100、不到200,那么学生共有人.【答案】142【分析】除1条船坐6人外,其余每船均坐17人,说明总人数可以表示成17m+6的形式;除1条船坐2人外,其余每船均坐10人,说明总人数可以表示成10n+2的形式;那么有17m+6=10n+2,化简得17m+4=10n,经分析m的个位只能是8.又学生的人数超过100、不到200,所以m=8,学生的人数是17×8+6=142.20. 一个自然数能被11整除,除以13余12;除以15余13;这个数最小为.【答案】1078.【分析】n除以15余13:最小为13,通式为13+15k1;n除以13余12:k1最小为6,则有13+15×6=103,通式为103+[15,13]k2=103+195k2.n除以11余0:k2最小为5,则有103+195×5=1078.21. —个自然数被3除余2,被5除余4,并且这个数大于100且小于125,那么这个数是.【答案】104或119【分析】被3除余2,被5除余4,求出3和5的最小公倍数15,估算15的哪一个倍数大于100小于125,经计算可知,105和120介于100到125之间,再用105和120分别减1即可,这个自然数是104或119.22. 在1到100这100个数中,被2,3,5除都有非零的余数,且余数彼此不等的数有个.【答案】6【分析】根据余数不能比除数大.一个数除以2,余数只能是1.而要求余数彼此不等,所以,这些数除以3,余数只能是2.满足以上两个条件的数为6的倍数少1.有:5、11、17、23、29、35、41、47、53、59、65、71、77、83、89、95.再满足被5除有余数,且余数不为1和2,(个位不能为5、1、7).符合条件的数只有:23、29、53、59、83、89,共6个数.23. 有一个自然数用7除余3,用9除余4,请按照从小到大的顺序,将满足条件的前两个自然数写在这里.【答案】31,94【分析】除以7余3的数有:3,10,17,24,31⋯;除以9余4的数有:4,13,22,31⋯;所以满足“除以7余3,除以9余4”的数的形式为[7,9]n+31=63n+31(n为自然数)按照从小到大的顺序,将满足条件的前两个自然数为31,94.24. 有一个整数,用它分别去除157、234和324,得到的三个余数之和是100,这个整数是多少?【答案】41【分析】详解:157、234和324的和是715,减去100的差是615.615是这个整数的倍数.而615的约数有1、3、5、15、41、123、205、615,验证只有41满足余数和是100.25. 有三个连续自然数,其中最小的能被15整除,中间的能被17整除,最大的能被19整除,请写出一组这样的三个连续自然数.【答案】2430,2431,2432.【分析】设三个连续自然数中最小的一个为n,则其余两个自然数分别为n+1,n+2.依题意可知:15∣n,17∣(n+1),19∣(n+2),根据整除的性质对这三个算式进行变换:15∣n 17∣(n +1)19∣(n +2)→→→15∣2n 17∣(2n +2)19∣(2n +4)→→→15∣(2n −15)17∣(2n −15)19∣(2n −15)}⇒[15,17,19]∣(2n −15)从上面可以发现 2n −15 应为 15、17、19 的公倍数.由于 [15,17,19]=4845,所以 2n −15=4845(2k −1)(因为 2n −15 是奇数),可得 n =4845k −2415.当 k =1 时 n =2430,n +1=2431,n +2=2432,所以其中的一组自然数为 2430、2431、2432.26. 一个大于 10 的数,除以 3 余 1,除以 5 余 2,除以 11 余 7,问满足条件的最小自然数是多少?【答案】 172【分析】 法一:仔细分析可以发现 3×2+1=5+2=7,所以这个数可以看成被 3、5、11 除余 7,由于 [3,5,11]=165,所以这个数最小是 165+7=172.法二:事实上,如果没有“大于 10”这个条件,7 即可符合条件,所以只需要在 7 的基础上加上 3、5、11 的最小公倍数,得到 172 即为所求的数.27. 一个三位数除以 5 余 2,除以 7 余 3.这个三位数最小是多少?【答案】 122【分析】 使用逐步满足条件法,满足第一个条件的数依次为 2、7、12、17,而 17 除以 7 余 3.那么同时满足两个条件的数最小是 17.然后依次为 52、87、122.最小的三位数是 122.28. 一个布袋中装有 5000 多个小球,如果 10 个一包,最后还剩 9 个,如果 9 个一包,最后还剩 8 个 ⋯⋯ 如果 5 个一包,最后还剩 4 个,那么如果 13 个一包,最后还剩多少个?【答案】 8 个【分析】 简答:布袋中的小球数除以 10 余 9,除以 9 余 8,除以 8 余 7⋅⋯,除以 5 余 4,[5,6,7,8,9,10]=[5,7,8,9]=5×7×8×9=2520,所以,布袋中球数是 2520−1+2520=5039,5039÷13 余 8.29. (1)—个三位数除以 4 余 2,除以 6 余 2,那么这个三位数最小是多少?(2)—个三位数除以 3 余 1,除以 4 余 2,除以 6 余 4,那么这个三位数最小是多少?(3)—个数除以 9 余 2,除以 12 余 5,那么这个数最小是多少?【答案】 (1)110;(2)106;(3)29【分析】简答:(1)[4,6]=12,14+12×8=110;(2)按“差同”计算;(3)按“差同”计算.30. 一个自然数除以8、9、11后分别余2、7、3,而所得的三个商的和是622,这个数是多少?【答案】1906.【分析】设这个数为x.x除以8余2:最小为2,通式为2+8k1;x除以9余7:k1最小为4,则有2+8×4=34,通式为34+[8,9]k2=34+72k2.x除以11余3:k2最小为4,则有34+72×4=322.则x=322+[8,9,11]n=322+792n.322+792n−28+322+792n−79+322+792n−311=622 40+99n+35+88n+29+72n=622259n=518n=2x=322+792×2=1906.31. 已知自然数A除以11余5,除以9余7,除以13余3,这个数最小是多少?【答案】1303【分析】本题属于“物不知数”问题,可以运用中国剩余定理,但需要先要找出11与9的公倍数中除以13余1的数、11与13的公倍数中除以9余1的数以及9与13的公倍数中除以11余1的数.比较麻烦.实际上,观察可知11+5=9+7=13+3=16,也就是说这个数减去16后是11、9、13的公倍数,那么这个数最小就是11、9、13的最小公倍数加上16,为11×9×13+16=1303.32. 今有一堆石子,三个三个数余1个,五个五个数余3个,七个七个数余5个,这堆石子最少有多少个?【答案】103【分析】三个三个、五个五个、七个七个的数都是差两个,那借来两个石子,现在的就可以被3、5和7除得开,最小是3×5×7=105,归还那两块,总计最少103个.借来还去的思想.33. 有一个自然数,用它分别去除61、90、130都有余数,3个余数的和是26,这3个余数中最大的一个是多少?【答案】11【分析】.简答:61、90和130的和减去26得到255,255的约数中验证得满足条件的只有17,所以这个自然数是17,所以余数中最大的是130除以17的余数1134. 已知两个连续的两位数除以5的余数之和是5,除以6的余数之和是5,除以7的余数之和是1.求这两个两位数.【答案】77和78【分析】两个连续的两位数除以5的余数之和是5,则可以判断出第一个数除以5余2.除以6的余数之和是5,则可以判断出第一个数除以6余2或余5.除以7的余数之和是1,则可以判断出第一个数除以7余0.满足第一、三两个条件的数有7、42、77,再考虑第二个条件,只有77满足.因此这两个数为77和78.35. 有一个自然数,用它分别去除63,90,130都有余数,3个余数的和是25.这3个余数中最大的一个是多少?【答案】20【分析】设这个除数为M,设它除63,90,130所得的余数依次为a,b,c,商依次为A,B,C.63÷M=A⋯⋯aa+b+c=25,则(63+90+130)−(a+b+c)=(A+B+C)×M,即283−25=258=(A+B+C)×M.所以M是258的约数.258=2×3×43显然当除数M为2、3、6时,3个余数的和最大为3×(2−1)=3,3×(3−1)=6,3×(6−1)=15所以均不满足.而当除数M为43×2,43×3,43×2×3时,它除63的余数均是63,所以也不满足.那么除数M只能是43,它除63,90,130的余数依次为20,4,1,余数的和为25,满足.显然这3个余数中最大的为20.36. 一个小于200的数,它除以11余8,除以13余10,这个数是几?【答案】140.【分析】分析题意,我们发现这两个算式除数与余数的差都等于11−8=13−10=3,观察发现这个数加上3后就能同时被11和13整除,所以[11、13]=143,所以这个数是143−3=140.37. 有一个整数,用它去除63,90,130所得到的3个余数之和是25,那么这3个余数中最大的一个是多少?【答案】20【分析】设这个数为x,由题意可得:① $\left\{\begin{gathered}63 \div x = a \cdots {r_1} \hfill \\90 \div x = b \cdots {r_2} \hfill \\130 \div x = c \cdots {r_3} \hfill \\\end{gathered} \right. \Rightarrow 63 + 90 + 130 - 25 =258$ 为x的倍数;②258=2×3×43③枚举验证⇒x=43.所以 $\left\{ \begin{gathered}63 \div 43 \cdots 20 \hfill \\90 \div 43 \cdots 4 \hfill \\130 \div 43 \cdots 1 \hfill \\\end{gathered} \right.$,显然这3个余数中最大的一个是20.38. (1)一个三位数除以6余2,除以8余2,那么这个三位数最小是多少?(2)—个数除以3余2,除以5余4,除以7余6,那么这个数最小是多少?(3)—个数除以6余2,除以11余1,那么这个数最小是多少?【答案】(1)122;(2)104;(3)5639. 有一个自然数,除以2余1,除以3余2,除以4余3,除以5余4,除以6余5,除以7余6,则这个数最小是.【答案】419.【分析】分析题意知,这个数加1就能被2,3,4,5,6,7整除,所以这个数为[2、3、4、5、6、7]−1=420−1=419.40. 一个数除以3余2,除以5余3,除以7余4,问这个数是多少?【答案】53【分析】如果用剩余定理相信大家会做了,接下来看逐步满足法.第一个条件,除以3余2,最小是2;先记下2.第二个条件,除以5余3,原来已经有了2,要保持满足第一个条件不变,那么在2的基础上增加3的倍数,这样除以3余2不会变.2+3n的形式.这个数要满足第二个条件,除以5余3.在2+3n中,2已经余2了,3n需要余1,所以n=2即可.这样满足前两个条件的最小的数是8.第三个条件,除以7余4.8+3×5n的形式.3×5n=15n除以7要余4−1=3,15除以7余1,所以n最小是3,这个数是8+45=53满足题意.41. 今有物不知其数,三三数之剩一,四四数之剩三,五五数之剩二,问物几何?【答案】7【分析】40×1+45×3+36×2=247,3×4×5=60,247÷60=4⋯⋯7,最少是7.42. 一个三位数除以4余3,除以6也余3.这个三位数最大是多少?【答案】999【分析】这是一道余同的问题.满足条件的数可以表示为[4,6]×n+3,其中n为自然数.要求满足条件的最大三位数,应令n为83,即[4,6]×83+3=999.43. 一个数被5除余3,被7除余4,被9除余5,这个数最小是几?【答案】158【分析】7和9的公倍数9和5的公倍数5和7的公倍数6345351269070135105180140225175210245280⋯⋯⋯在7和9的公倍数中,除以5余1的最小数是126;在5和9的公倍数中,除以7余1的最小数是225;在5和7的公倍数中,除以9余1的最小数是280;那么126×3+225×4+280×5=2678.[5,7,9]=315.所以,最小的数为2678−315×8=158.44. 四年级的同学,每9人一排多5人,每7人一排多1人,每5人一排多2人,问这个年级至少有多少人?【答案】302【分析】这个题相当于是一个数被9除余5,被7除余1,被5除余2,这个数最小是几.9、7、5三个数两两互质。
小学奥数题库《数论》余数问题带余除法5星题(含解析)全国通用版
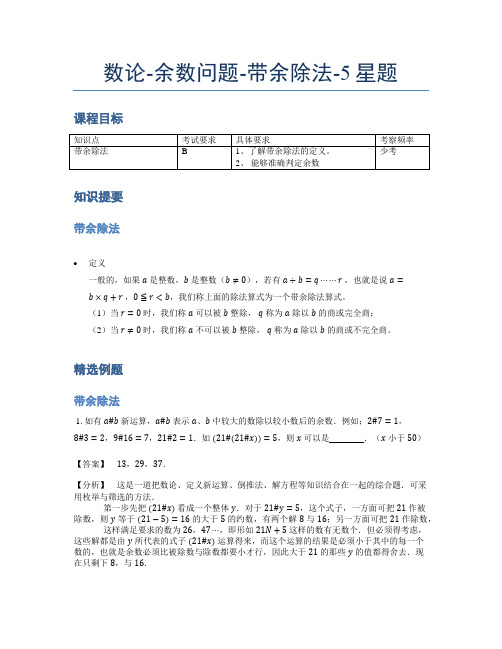
数论-余数问题-带余除法-5星题课程目标知识提要带余除法•定义一般的,如果a是整数,b是整数(b≠0),若有a÷b=q⋯⋯r,也就是说a=b×q+r,0≦r<b,我们称上面的除法算式为一个带余除法算式。
(1)当r=0时,我们称a可以被b整除,q称为a除以b的商或完全商;(2)当r≠0时,我们称a不可以被b整除,q称为a除以b的商或不完全商。
精选例题带余除法1. 如有a#b新运算,a#b表示a、b中较大的数除以较小数后的余数.例如;2#7=1,8#3=2,9#16=7,21#2=1.如(21#(21#x))=5,则x可以是.(x小于50)【答案】13,29,37.【分析】这是一道把数论、定义新运算、倒推法、解方程等知识结合在一起的综合题.可采用枚举与筛选的方法.第一步先把(21#x)看成一个整体y.对于21#y=5,这个式子,一方面可把21作被除数,则y等于(21−5)=16的大于5的约数,有两个解8与16;另一方面可把21作除数,这样满足要求的数为26,47⋯,即形如21N+5这样的数有无数个.但必须得考虑,这些解都是由y所代表的式子(21#x)运算得来,而这个运算的结果是必须小于其中的每一个数的,也就是余数必须比被除数与除数都要小才行,因此大于21的那些y的值都得舍去.现在只剩下8,与16.第二步求:(21#x)=8与(21#x)=16.对于(21#x)=8可分别解得,把21作被除数时:x=13,把21作除数时为:x=29,50,⋯形如21N+8的整数(N是正整数).对于(21#x)=16,把21作被除数无解,21作除数时同理可得:x=37,58⋯所有形如21N+16这样的整数.(N是正整数).所以符合条件的答案是13,29,37.2. 字母a,b,c,d,e,f,g分别代表1至7中的一个数字,若a+b+c=c+d+e=c+f+g,则c可取的值有个.【答案】3【分析】a+b+c=c+d+e=c+f+g,a+b+c+c+d+e+c+f+g=(a+b+c+d+e+f+g)+2c=(1+2+3+4+5+6+7)+2c=28+2c28+2c是3的倍数,28÷3⋯1,所以2c÷3⋯2,c=1或4或7都可满足;构造:当c=1时,(28+2)÷3=10,所以a+b=d+e=f+g=9,a=2,b=7,d=3,e=6,f=4,g=5;当c=4,(28+2×4)÷3=12,所以a+b=d+e=f+g=8,a=1,b=7,d=2,e=6,f=3,g=5;当c=7,(28+2×7)÷3=14,所以a+b=d+e=f+g=7,a=1,b=6,d=2,e=5,f=3,g=4.综上,共有3种情况.3. 1×3×5×⋯×1991的末三位数是多少?【答案】625【分析】首先,仅考虑后三位数字,所求的数目相当于1×3×5×⋯×991的平方再乘以993×995×997×999的末三位.而993×995×997×999=993×999×995×997=(993000−993)×(995000−995×3)=(993000−993)×(995000−2985),其末三位为7×15=105;然后来看前者.它是一个奇数的平方,设其为(5k)2(k为奇数),由于(5k)2=25k2=25+25(k2−1),而奇数的平方除以8余1,所以k2−1是8的倍数,则25(k2−1)是200的倍数,设25(k2−1)=200m,则(5k)2=25+25(k2−1)=25+200m,所以它与105的乘积(5k)2×105=(25+200m)×105=21000m+2625,所以不论m的值是多少,所求的末三位都是625.4. 如果某整数同时具备如下三条性质:(1)这个数与1的差是质数;(2)这个数除以2所得的商也是质数;(3)这个数除以9所得的余数是5.那么我们称这个整数为幸运数,求出所有的两位幸运数.【答案】14【分析】条件(1)也就是这个数与1的差是2或奇数,这个数只能是3或者是偶数,再根据条件(3),除以9余5,在两位的偶数中只有14,32,50,68,86,这五个数满足条件;其中86与50不符合(1),32与68不符合(2).三个条件都符合的只有14,所以这个数是14.5. 求证:可以找到一个各位数字都是4的自然数,它是1996的倍数.【答案】见解析.【分析】1996÷4=499,下面证明可以找到1个各位数字都是1的自然数,它是499的倍数.取500个数:1,11,111,⋯⋯,111⋯⋯1(500个1).用499去除这500个数,得到500个余数a1,a2,a3,⋯,a500.由于余数只能取0,1,2,⋯,498这499个值,所以根据抽屉原则,必有 2 个余数是相同的,这 2 个数的差就是 499 的倍数,差的前若干位是 1,后若干位是 0:11⋯100⋯0.又 499 和 10 是互质的,所以它的前若干位由 1 组成的自然数是 499 的倍数,将它乘以 4,就得到一个各位数字都是 4 的自然数,这是 1996 的倍数.6. 用 1、2、3、4、5 各一个可以组成 120 个五位数,你能否从这 120 个数里面找出 11 个数来,使得它们除以 11 的余数各不相同?如果五个数字是 1、3、4、6、8 呢?【答案】 不能;不能.【分析】 (1)不能.五位数有 3 个奇位数字和 2 个偶位数字,将 1、2、3、4、5 分到奇偶位有 C 52=10 种方法,那么形成的五位数最多只能产生 10 种除以 11 的余数,无法出现 11 种除以 11 的余数.(2)不能.与(1)同理.当然,想不到这个的同学一一枚举即可,(1)中很明显余数为 0 的是构造不出来的,此外,余数为 2、4、6 也无法构造出来.(2)中余数为 6、7、10 的是构造不出来的.7. 任意给定一个正整数 n ,一定可以将它乘以适当的整数,使得乘积是完全由 0 和 7 组成的数.【答案】 见解析.【分析】 考虑如下 n +1 个数:7,77,777,⋯⋯,77⋯7⏟n 位,77⋯7⏟n+1位,这 n +1 个数除以 n 的余数只能为 0,1,2,⋯⋯,n −1 中之一,共 n 种情况,根据抽屉原理,其中必有两个数除以 n 的余数相同,不妨设为 77⋯7⏟p 位和 77⋯7⏟q 位(p >q ),那么 77⋯7⏟p 位−77⋯7⏟q 位=77⋯7⏟(p−q)位00⋯0⏟q 位 是 n 的倍数,所以 n 乘以适当的整数,可以得到形式为 77⋯7⏟(p−q)位00⋯0⏟q 位的数,即由 0 和 7 组成的数.8. 两个不等的自然数 a 和 b ,较大的数除以较小的数,余数记为 a ⊙b ,比如 5⊙2=1,7⊙25=4,6⊙8=2.(1)求 1991⊙2000,(5⊙19)⊙19,(19⊙5)⊙5;(2)已知 11⊙x =2,而 x 小于 20,求 x ;(3)已知 (19⊙x)⊙19=5,而 x 小于 50,求 x .【答案】 (1)9;3;1;(2)x =3,9,13;(3)x =12,26,33,45.【分析】 (1)1991⊙2000=9;由5⊙19=4,得(5⊙19)⊙19=4⊙19=3;由19⊙5=4,得(19⊙5)⊙5=4⊙5=1.(2)我们不知道11和x哪个大(注意,x≠11),即哪个作除数,哪个作被除数,这样就要分两种情况讨论.①x<11,这时x除11余2,x整除11−2=9.又x⩾3(因为x应大于余数2),所以x=3或9.②x>11,这时11除x余2,这说明x是11的倍数加2,但x<20,所以x=11+2=13.因此(2)的解为x=3,9,13.(3)这个方程比(2)又要复杂一些,但我们可以用同样的方法来解.用y表示19⊙x,不管19作除数还是被除数,19⊙x都比19小,所以y应小于19.方程y⊙19=5,说明y除19余5,所以y整除19−5=14,由于y⩾6,所以y=7,14.当y=7时,分两种情况解19⊙x=7.①x<19,此时x除19余7,x整除19−7=12.由于x⩾8,所以x=12.②x>19,此时19除x余7,x是19的倍数加7,由于x<50,所以x=19+7= 26,x=19×2+7=45.当y=14时,分两种情况解19⊙x=14.①x<19,这时x除19余14,x整除19−14=5,但x大于14,这是不可能的.②x>19,此时19除x余14,这就表明x是19的倍数加14,因为x<50,所以x=19+14=33.总之,方程(19⊙x)⊙19=5有四个解,x=12,26,33,45.9. 箱子里面有两种珠子,一种每个19克,另一种每个17克,所有珠子的重量为2017克,求两种珠子的数量和所有可能的值.【答案】107,109,111,113,115,117【分析】设19克的珠子有a个,17克的珠子有b个,根据题意列方程得19a+17b=2017利用余数分析法解不定方程.由于2017÷19余3所以有17b÷19余3,解得b=8从而得出a=99,即19×99+17×8=2017,即找到一组解为{a=99b=8此时a+b=99+8=107,由于19和17互质,那么只需要将a顺次减少17,b顺次增大19即可得出其他解{a=82b=27{a=65b=46{a=48b=65{a=31b=84{a=14b=103对于a+b的和而言,共可算得6个答案,分别为:107,109,111,113,115,117.10. 一个自然数除以8得到的商加上这个数除以9的余数,其和是13.求所有满足条件的自然数.【答案】108,100,92,84,76,68,60,52,44.【分析】本题考査学生掌握带余除法及枚举筛选的综合能力.设所求的自然数为n,且设n除以8商x余r,n除以9商a余y,于是有n=8x+r=9a+y(其中x+y=13).又已知0⩽y⩽8,0⩽r⩽7,下面分类讨论:若y=0,则x=13,得8×13+r=9a,解出r=4,故n=8×13+4=108;若y=1,则x=12,得8×12+r=9a+1,解出r=4,故n=8×12+4=100;类似地,若y=2、3、4、5、6、7、8,则分别有x=11、10、9、8、7、6、5,解得r=4,故n=8×11+4=92;n=8×10+4=84;n=8×9+4=76;n=8×8+4=68;n=8×7+4=60;n=8×6+4=52;n=8×5+4=44.答:满足条件的然数共有9个:108、100、92、84、76、68、60、52、44.说明:本题也可以先确定r=4.由y=13−x代人可得8x+r=9a+(13−x),即9x−9a=13−r,于是13−r的差应是9的倍数,又0⩽r⩽7,故r=4.。
五年级奥数余数问题

五年级奥数余数问题一、题目。
1. 一个数除以3余2,除以5余3,除以7余2,求这个数最小是多少?解析:我们先列出除以3余2的数:2、5、8、11、14、17、20、23、26…再列出除以5余3的数:3、8、13、18、23、28…然后列出除以7余2的数:2、9、16、23、30…可以发现23同时满足这三个条件,所以这个数最小是23。
2. 有一个数,除以4余1,除以5余2,除以6余3,这个数最小是多少?解析:这个数加上3就能被4、5、6整除。
4、5、6的最小公倍数是4 = 2×2,5 = 5,6=2×3,最小公倍数LCM = 2×2×3×5 = 60。
所以这个数最小是60 3=57。
3. 一个数除以5余4,除以8余3,求这个数最小是多少?解析:设这个数为x。
根据除以5余4,可设x = 5a+4(a为整数)。
又因为除以8余3,所以5a + 4=8b+3(b为整数),即5a=8b 1。
通过试值法,当b = 2时,a = 3。
此时x=5×3 + 4=19,19除以8余3,所以这个数最小是19。
4. 一个数除以9余7,除以11余9,这个数最小是多少?解析:这个数加上2就能被9和11整除。
9和11互质,它们的最小公倍数是9×11 = 99。
所以这个数最小是99 2 = 97。
5. 某数除以7余1,除以8余2,除以9余3,求这个数最小是多少?解析:这个数加上6就能被7、8、9整除。
7、8、9的最小公倍数为7×8×9=504。
所以这个数最小是504 6 = 498。
6. 一个数除以3余1,除以5余2,除以7余3,这个数最小是多少?解析:中国剩余定理:先求5×7 = 35,35除以3余2,2×2 = 7,7除以3余1。
再求3×7=21,21除以5余1,1×2 = 2,2除以5余2。
然后求3×5 = 15,15除以7余1,1×3=3,3除以7余3。
小学奥数题及答案余数问题

小学奥数题及答案余数问题
小学奥数题及答案余数问题
1.应用题
用一根既细又直的竹竿测量游泳池的水深,把竹竿的一端插入水中(碰到池底)后,没浸湿的部分长120厘米,把竹竿掉过头来,再插入水中(也碰到池底),此时没浸湿的'部分长30厘米,问游泳池有多深?
解答:第二次浸湿的部分就是游泳池的深度,所以游泳池深为:120-30=90(厘米)
【小结】。
第一次浸湿的长度实际上也是游泳池的深度。
2.余数问题
人教版小学五年级奥数题及答案余数问题:一批图书,数量在20到30本之间,平均分给7个同学,结果剩余的图书每比个人分到的书多2本,那么这批图书有多少本?
解答:
【小结】先估算出每个人可能分到几本,再分情况依次考虑。
小学奥数数论问题余数问题练习题【五篇】

小学奥数数论问题余数问题练习题【五篇】分析:这个题没有告诉我们,这三个数除以这个数的余数分别是多少,但是因为所得的余数相同,根据性质2,我们能够得到:这个数一定能整除这三个数中的任意两数的差,也就是说它是任意两数差的公约数.101-45=56,101-59=42,59-45=14,(56,42,14)=14,14的约数有1,2,7,14,所以这个数可能为2,7,14.2.已知三个数127,99和一个小于30的两位数a除以一个一位数b的余数都是3,求a和b的值.分析:127-3=124,99-3=96,则b是124和96的公约数.而(124,96)=4,所以b=4.那么a的可能取值是11,15,19,23,27.3.除以99,余数是______.分析:所求余数与19×100,即与1900除以99所得的余数相同,所以所求余数是19.4.求下列各式的余数:(1)2461×135×6047÷11(2)19992000÷7分析:(1)5;(2)1999÷7的余数是4,19992000 与42000除以7 的余数相同.然后再找规律,发现4 的各次方除以7的余数的排列规律是4,2,1,4,2,1......这么3个一循环,所以由2000÷3 余2 能够得到42000除以7 的余数是2,故19992000÷7的余数是2 .【第二篇】(小学数学奥林匹克初赛)有苹果,桔子各一筐,苹果有240个,桔子有313个,把这两筐水果分给一些小朋友,已知苹果等分到最后余2个不够分,桔子分到最后还余7个桔子不够再分,求最多有多少个小朋友参加分水果分析:此题是一道求除数的问题.原题就是说,已知一个数除240余2,除313余7,求这个数为多少,我们能够根据带余除法的性质把它转化成整除的情况,从而使问题简化,因为240被这个数除余2,意味着240-2=238恰被这个数整除,而313被这个数除余7,意味着这313—7=306恰为这个数的倍数,我们只需求238和306的公约数便可求出小朋友最多有多少个了.240—2=238(个) ,313—7=306(个) ,(238,306)=34(人) .【第三篇】有一个大于1的整数,除45,59,101所得的余数相同,求这个数.分析:这个题没有告诉我们,这三个数除以这个数的余数分别是多少,但是因为所得的余数相同,根据性质2,我们能够得到:这个数一定能整除这三个数中的任意两数的差,也就是说它是任意两数差的公约数.101-45=56,101-59=42,59-45=14,(56,42,14)=14,14的约数有1,2,7,14,所以这个数可能为2,7,14.【第四篇】1.已知三个数127,99和一个小于30的两位数a除以一个一位数b的余数都是3,求a和b的值.分析:127-3=124,99-3=96,则b是124和96的公约数.而(124,96)=4,所以b=4.那么a的可能取值是11,15,19,23,27.2.除以99的余数是______.分析:所求余数与19×100,即与1900除以99所得的余数相同,所以所求余数是19.【第五篇】。
关于余数问题的小学奥数练习题

关于余数问题的小学奥数练习题关于余数问题的小学奥数练习题篇一2、小东在计算除法时,把除数87写成78,结果得到的商是54,余数是8,正确的余数是多少?3、a÷24=121……b,要使余数,被除数应该等于多少?4、奥数带余数的四则运算题:一个三位数被37除余17,被36除余3,那么这个三位数是多少?5、31453×68765×98657的积,除以4的余数是多少?6、如果时针现在表示的时间是18点整,那么分针旋转1990圈之后是几点钟?7、两数相除商8余16,被除数、除数、商、余数的和是463,被除数是多少?8、四位数8□98能同时被17和19整除,那么这个四位数是多少?9、222……22(2000个2)除以13所得的余数是多少?10、已知:a=19911991……1991(1991个1991),问:a除以13,余数是几?关于余数问题的小学奥数练习题篇二2、某数除以5余2,除以6少2,除以7少3,这个数最小是多少?3、有150到200个零件平均装入5个盒子,多1个,改用6个盒子装,多4个,若改用7个盒子装,最后多5个。
这批零件共有多少个?4、一篮苹果不足60个,平均分给5个小朋友,多1个;平均分给6个小朋友,多3个,若平均分给7人,最后多2个。
一共有多少个?5、有一堆球,3个3个的数,最后剩2个;5个5个的数,最后剩3个;7个7个的数,最后剩2个。
这些球一共有多少个?6、某数除以5余2,除以6余3,除以7余4,这个数至少是多少?7、一串彩灯,7个7个的数,最后多1盏;9个9个的数,最后多3盏;5个5个的数,刚好可数完。
这串彩灯至少有多少个?8、某数除以7余2,除以10少2,除以11余3,这个数至少是多少?9、一个奇数,分别用288和214除以这个奇数,所得的余数都是29,这个数是多少?10、一个整数,用300,262和205分别除以这个整数,得到的余数相同。
这个数应该是多少?关于余数问题的小学奥数练习题篇三2、A÷24=121……b,要使余数,被除数应该是多少?3、四位数8□98能同时被17和19整除,那么这个四位数所有的质因数是和是多少?4、31453×68765×987657的积,除以4的余数是多少?5、一串数1、2、4、7、11、16、22、29……这串数的组成规律是:第2个数比第1个数多1;第3个数比第2个数多2;第4个数比第3个数多3;以此类推,那么这串数左起的第1992个数除以5的余数是多少?6、如果现在表示的时间是18点整,那么分针旋转1990圈之后是几点钟?7、小明往一个大池子里扔石子,第一次扔1个石子,第二次扔2个石子,第三次扔3个石子……,他准备扔到池子里的石子的总数被106除,余数是0,那么小明要扔多少次?8、从7开始,把7的倍数依次写下去,一直写到994成为一个很大的数:71421……987994,这个数是几位数?9、用1~9的九个数字组成三个三位数,使其中的三位数被3除余2,且还尽可能地小;次大的三位数被3除余1;最小的三位数被3整除,那么的三位数是多少?10、100个7组成的一百位数,被13除后,余数是多少?分类精心精选精品文档,欢迎下载,所有文档经过整理后分类挑选加工,下载后可重新编辑,正文所有带XX或是空格类下载后可自行代入字词。
五年级奥数之余数问题

五年级奥数之余数问题余数问题例1、有一个数,除以3余2,除以4余1,问这个数除以12余几?例2、XXX在计算有余数的除法时,把被除数113错写成了131.结果商比原来多3,但余数恰巧相同,那么余数是多少?例3、444……4÷6,当商是整数时,余数是几?(100个4)例4、有一列数,前两个数是3和4,从第3个数开始,每一个数都是前两个数的和。
这一列数中第100个数除以4,余数是多少?例5、甲数除以9余7,乙数除以9余5.甲、乙两数的和除以9余数是几?甲乙两数的差除以9余数是几?甲、乙两数的积除以9余数是几?例6、一个自然数除以2余1,除以5余1,除以7余1,这个自然数最小是多少?例7、自然数、、除以m的余数相同,m最大是多少?例8、自然数2836、4582、5146、6522除以一个自然数,所得余数相同且为两位数,除数和余数的和为多少?例9、XXX玩具店有大小相同的红、黄、蓝、绿四种颜色的小球分别为344、277、411和555个。
现在要用一种精致的小盒分别去装这些小球,每只盒子里装的小球同样多,剩下的红、黄、蓝三色小球也恰好同样多。
剩下的绿球有多少个?例10、9练:1、一个数除以3余2,除以5余3,除以7余2,符合这些条件的最小数是多少?2010被7除余几?2、XXX计算有余数的除法时,把被除数137错写成173.商比原来多3,余数正好相同。
问除数、余数各是多少?3、555……55÷13,当商是整数时,余数是几?(2001个5)4、有一串数排成一行,个中第一个数是3,第二个数是10,从第三个数起,每一个数恰好是前两个数的和。
在这一串数中,第1991个数被3除,所得的余数是几?5、甲数除以5余3,乙数除以5余2.甲、乙两数的和除以5余数是几?甲乙两数的差除以5余数是几?甲、乙两数的积除以5余数是几?6、一个自然数除以3余2,除以5余1,除以7余1,这个自然数最小是多少?7、自然数1000、2001、967除以m的余数不异,那末m 是几何?8、一个自然数,除1200、1314、1048所得的余数不异且大于5,那末这个自然数与余数的和是几何?9、甲、乙、丙、丁四个学校划分有69人、85人、93人、97人游览。
小学奥数-余数问题-完整版题型训练

数论问题之余数问题教学目标余数问题是数论知识板块中另一个内容丰富,题目难度较大的知识体系,也是各大杯赛小升初考试必考的奥数知识点,所以学好本讲对于学生来说非常重要。
余数问题主要包括了带余除法的定义,三大余数定理(加法余数定理,乘法余数定理,和同余定理),及中国剩余定理和有关弃九法原理的应用。
三大余数定理:1、余数的加法定理a与b的和除以c的余数,等于a,b分别除以c的余数之和,或这个和除以c的余数。
例如:23,16除以5的余数分别是3和1,所以23+16=39除以5的余数等于4,即两个余数的和3+1.当余数的和比除数大时,所求的余数等于余数之和再除以c的余数。
例如:23,19除以5的余数分别是3和4,所以23+19=42除以5的余数等于3+4=7除以5的余数,即2.2、余数的乘法定理a与b的乘积除以c的余数,等于a,b分别除以c的余数的积,或者这个积除以c所得的余数。
例如:23,16除以5的余数分别是3和1,所以23×16除以5的余数等于3×1=3。
当余数的和比除数大时,所求的余数等于余数之积再除以c的余数。
例如:23,19除以5的余数分别是3和4,所以23×19除以5的余数等于3×4除以5的余数,即2.3.同余定理若两个整数a、b被自然数m除有相同的余数,那么称a、b对于模m同余,用式子表示为:a ≡b ( mod m ),左边的式子叫做同余式。
同余式读作:a同余于b,模m。
由同余的性质,我们可以得到一个非常重要的推论:若两个数a,b除以同一个数m得到的余数相同,则a,b的差一定能被m整除用式子表示为:如果有a≡b ( mod m ),那么一定有a-b=mk,k是整数,即m|(a-b)三、弃九法原理而我们在求一个自然数除以9所得的余数时,常常不用去列除法竖式进行计算,只要计算这个自然数的各个位数字之和除以9的余数就可以了,在算的时候往往就是一个9一个9的找并且划去,所以这种方法被称作“弃九法”。
(完整版)小学奥数数论问题余数问题练习题.doc

小学奥数数论问题余数问题练习题【五篇】分析:这个题没有告诉我们 ,这三个数除以这个数的余数分别是多少 ,但是因为所得的余数相同 ,根据性质 2,我们能够得到:这个数一定能整除这三个数中的任意两数的差 ,也就是说它是任意两数差的公约数 .101-45=56,101-59=42,59-45=14,(56,42,14)=14,14的约数有 1,2,7,14,所以这个数可能为 2,7,14.2.已知三个数 127,99 和一个小于 30 的两位数 a 除以一个一位数 b 的余数都是 3,求 a 和 b 的值 .分析: 127-3=124,99-3=96,则 b 是 124 和 96 的公约数 .而(124,96)=4,所以 b=4. 那么 a 的可能取值是 11,15,19,23,27.3.除以 99,余数是 ______.分析:所求余数与 19×100,即与 1900 除以 99 所得的余数相同 ,所以所求余数是 19.4.求下列各式的余数:(1)2461 × 135× 6047 ÷ 11(2)19992000 ÷ 7分析: (1)5;(2)1999÷7的余数是4,19992000与42000除以7的余数相同.然后再找规律 ,发现 4 的各次方除以 7 的余数的排列规律是4,2,1,4,2,1......这么 3 个一循环 ,所以由 2000÷3 余 2 能够得到 42000 除以 7 的余数是 2,故 19992000÷7的余数是 2.【第二篇】(小学数学奥林匹克初赛 )有苹果 ,桔子各一筐 ,苹果有 240 个,桔子有 313 个,把这两筐水果分给一些小朋友 ,已知苹果等分到最后余 2 个不够分 ,桔子分到最后还余 7 个桔子不够再分 ,求最多有多少个小朋友参加分水果分析:此题是一道求除数的问题.原题就是说 ,已知一个数除 240 余 2,除 313 余7,求这个数为多少,我们能够根据带余除法的性质把它转化成整除的情况,从而使问题简化 ,因为 240 被这个数除余 2,意味着 240-2=238恰被这个数整除 ,而 313被这个数除余 7,意味着这 313—7=306 恰为这个数的倍数 ,我们只需求 238 和 306 的公约数便可求出小朋友最多有多少个了 .240—2=238(个) ,313—7=306(个) ,(238,306)=34(人) .【第三篇】有一个大于 1 的整数 ,除 45,59,101 所得的余数相同 ,求这个数 .分析:这个题没有告诉我们 ,这三个数除以这个数的余数分别是多少 ,但是因为所得的余数相同 , 根据性质 2,我们能够得到:这个数一定能整除这三个数中的任意两数的差 ,也就是说它是任意两数差的公约数 .101-45=56,101-59=42,59-45=14,(56,42,14)=14,14的约数有1,2,7,14,所以这个数可能为 2,7,14.【第四篇】1.已知三个数 127,99 和一个小于 30 的两位数 a 除以一个一位数 b 的余数都是 3,求 a 和 b 的值 .分析: 127-3=124,99-3=96,则 b 是 124 和 96 的公约数 .而(124,96)=4,所以 b=4. 那么 a 的可能取值是 11,15,19,23,27.2.除以 99 的余数是 ______.分析:所求余数与 19×100,即与 1900 除以 99 所得的余数相同 ,所以所求余数是 19.【第五篇】199419941994(1994个 1994)除以 15 的余数是 ______.分析:法 1:从简单情况入手找规律,发现 1994÷15余14,19941994 ÷ 15余 4,199419941994 ÷余15 9,1994199419941994 ÷ 15余 14,......,发现余数 3 个一循环,1994 ÷3=664...2,19941994 1994(1994个1994)除以 15 的余数是 4;法 2:我们利用最后一个例题的结论能够发现199419941994能被 3 整除 ,那么19941994199400 0能被 15 整除 ,1994 ÷3=664...2,19941994 1994(1994个1994)除以 15 的余数是4.。
(完整版)二年级奥数有余数的除法典型问题

二年级奥数-------有余数的除法
一、余数要比除数小问题.
例1.计算有余数的除法,()一定要比()小。
巩固训练:
1.一个数除以4,如果有余数,余数可能是()。
2. 被除数最大是几?最小是几?( )÷6 =6……( )
3. ( )÷7 =( )……( )余数可以是几?最大是几?
4. ( ) ÷( ) =( )……5,除数最小是几?
二、拿去或者添加几个可以平均分问题。
例1.有37个,至少拿走几个,就使得7个小朋友分得一样多?每个小朋友分几个?
例2.老师拿来16朵红花,每名同学奖3朵,还剩1朵,老师奖给了多少名同学?
巩固练习:
1.老师拿出15颗小红星,每人奖励2颗,还余1颗,老师奖给了几位小朋友?
2.有28个梨,最少拿走几个,就使得6个小朋友分的一样多?
3.小文带5个小朋友中32棵树,平均每人种多少棵?小文要多种几棵才能完成任务
三、循环规律问题
例1. 节日街上挂彩灯,从第一盏灯开始,按红、黄、蓝、绿各一盏的顺序依次重复下去,问:第50盏灯是什么颜色?这50盏灯里红灯有几盏?
例2.一本童话书,每两页文字之间有3幅插图,那么第36页是文字还是插图?
四、分糖果问题
例1、有一些糖果不到20块。
平均分给3个小朋友或平均分给5个小朋友吃,都剩下1块。
想一想,一共有多少块糖果?
五、结果加“一”问题
例1、有22只鸟,每个笼子最多只能放4只,至少需要你几个笼子?例2、王老师和20名同学去划船,每条船最多坐5人,至少要租几条船?
巩固练习:
1、有33吨沙子,一辆货车每次可以运4吨,至少要运几次?。
(完整版)三年级奥数有余数的除法练习

把一些书平均分给几个小朋友,要使小朋友分得的本数最多,这本书分到最后会出现什么情况呢?一种是全部分完,还有一种是剩余,并且剩余的本数必须比小朋友的人数少,否则还可以继续分下去。
每次除得的余数必须比除数小。
解决这类应用题的关键是先确定余数,如果余数已知,就可以确定除数,然后再根据被除数与除数、商和余数的关系求出被除数。
在有余数的除法中,要记住:1、余数必须小于除数;2、被除数=商乂除数+余数练习题:(整数范围内)1、 ()—6 = 8 ...... (),被除数最大是几?2、 ()*()= 8 .............. 1中,被除数最小是几?3、 ()—4 = 7 ...... (),被除数最大是几?4、 ()*()= 3 .............. 2中,被除数最小是几?5、 ()—8 = 3 ...... (),被除数最小是几?6、 ()*() = 4............. 4中,被除数最小是几?7、28 *() = () .... 4中,除数最大是几?8、 ()—7 =() ..... ()中,商和余数相等,被除数最大是几?9、()+ () = ()……4中,商和余数相等,被除数最小是几?10、149除以一个两位数,余数是5,这个两位数是多少?11、一个三位数除以15,商和余数相等,请写出符合条件的最小的三位数。
12、有一个除法算式,它的余数是9,除数和商相等,被除数最小是几?★例2:算式□十6=口……□中,不告诉你被除数,商是多少,你能写出它的余数有哪几个吗?◊我试试:1、算式□十7=口……□中,你能写出它的余数有哪几个吗?2、算式□—9= 5 □中,被除数最大是几?最小是几?3、算式□ —□= 13 ....... 8中,除数最小是几?被除数最小是几?★例3: 23-□ = □……5中,除数和商各是多少?1、27-□ = □……3中,除数和商各是多少?21 2、□十8= 5……□中,被除数和余数各是多少?3、在一道有余数的除法中,商是最小的两位数,除数是最大的一位数,被除数和余数最大 是多少?最小是多少?一、填空:1、 下面算式中的余数可能是几? □ - 5=口……□ ( ) □ - 6=口……□ ( ) □ - 7=口……□()2、 要使商和余数相同,被除数是哪些数? □ - 9=口……□ ( ) □ - 6=口……□ ( )3、 下列算式中除数和商各是几?18 : □ — …4 除数( ) ,商( ) 33十口 = □… …3 除数( ) ,商( ) 35 •□一 □… …8 除数() ,商()二、判断题: 1、 在算式□十6= 8……□中,余数最大是 5。
小学六年级奥数题大全:余数问题

1.1111+2×1111+3×1111+…+1111×1111被7除所得的余数是 . ? 2.在所有的两位数中,⽤较⼤的⾃然数除以较⼩的⾃然数,得到的余数可以达到 .?? 3.⼀个⾃然数被9除余1,所得的商被8除也余1.再把第2次所得的商除以8得商为a余7.⼜知这个⾃然数被17除余4,所得的商被17除余15,商是a的2倍,这个⾃然数是 . 4.除以3余1,除以4,5,7不⾜2的三位数是 .?? 5.⽤某⾃然数a去除2002,得到的商是46,余数是r.则a= ,r= .?? 6.除以3余1,除以5余2,除以7余4的最⼩三位数是 .?? 7.两数相除商5余5,如果被除数扩⼤5倍,除数不变,则商是27,余数是3,原被除数是,除数是 .?? 8.7599除以⼀个质数,所得余数是9,这个质数最⼩是 .?? 9.678除以⼀个数,不完全商是13,并且除数与余数的差是8,除数是,余数是 .?? 10.⼀个三位数除以9余6,除以4余2,除以5余1,这样的数中的⼀个是 . 11.某三位数的各位数字都不为零,并且这个三位数被它的各位数字之和除,所得的商最⼩可能是 .?? 12.8.77÷5.3除到⼀位⼩数时,商是1.6,余数是___________.?? 13.在下⾯算式的⽅框内填数,使带余数的除法的余数.? □÷78=245…□ 14.⼀个数能被3、5、7整除,若⽤11去除则余1.这个数最⼩是 .? 15.某校五年级有学⽣若⼲⼈.? (1)若3⼈⼀⾏最后余2⼈,7⼈⼀⾏最后余2⼈,11⼈⼀⾏最后也余2⼈,五年级最少有学⽣多少⼈ (2)若3⼈⼀⾏最后余1⼈,7⼈⼀⾏最后余5⼈,11⼈⼀⾏最后余9⼈,五年级最少有学⽣多少⼈?。
带余数的除法奥数题道 带余数的除法奥数题及答案

带余数的除法奥数题道带余数的除法奥数题及答案题目1小明手上有45个苹果,要均分给他的3个朋友。
请问小明每人能分到几个苹果,还有剩余几个苹果?解答将45除以3得到商15,余数为0。
小明每人能分到15个苹果,没有剩余。
题目2小红收到了30本书,想要将它们平均分成4堆。
请问每堆书有几本,还有剩余几本书?解答将30除以4得到商7,余数2。
小红每堆书有7本,还剩下2本。
题目3小华手上有65只纸鹤,他想把它们放在3本相同大小的笔记本中。
请问每本笔记本里有几只纸鹤,还有剩余几只?解答将65除以3得到商21,余数2。
每本笔记本里有21只纸鹤,还剩下2只。
题目4有100个学生参加足球比赛,要将他们平均分到10个队中。
请问每个队有几个学生,还有剩余几个学生?解答将100除以10得到商10,余数0。
每个队有10个学生,没有剩余。
题目5小李有17本漫画书,要将它们分成5堆。
请问每堆有几本书,还有剩余几本?解答将17除以5得到商3,余数2。
每堆有3本书,还剩下2本。
题目6小明买了23根铅笔,要均分给他的4个朋友。
请问每人能分到几根铅笔,还有剩余几根?解答将23除以4得到商5,余数3。
每人能分到5根铅笔,还剩下3根。
题目7小华有98个糖果,他想将它们平均分给他的7个同学。
请问每个同学能分到几个糖果,还有剩余几个糖果?解答将98除以7得到商14,余数0。
每个同学能分到14个糖果,没有剩余。
题目8小红有53块巧克力,她想将它们分成4堆。
请问每堆有几块巧克力,还有剩余几块?解答将53除以4得到商13,余数1。
每堆有13块巧克力,还剩下1块。
题目9小李有63颗石头,他想将它们放在4个箱子中。
请问每个箱子里有几颗石头,还有剩余几颗?解答将63除以4得到商15,余数3。
每个箱子里有15颗石头,还剩下3颗。
题目10有30个学生参加篮球比赛,要将他们平均分到6个队中。
请问每个队有几个学生,还有剩余几个学生?解答将30除以6得到商5,余数0。
小学奥数数论专题--余数(六年级)竞赛测试.doc

小学奥数数论专题--余数(六年级)竞赛测试姓名:_____________ 年级:____________ 学号:______________题型选择题填空题简答题xx题xx题xx题总分得分一、xx题评卷人得分(每空xx 分,共xx分)【题文】号码分别为101,126,173,193的4个运动员进行乒乓球比赛,规定每两人比赛的盘数是他们号码的和被3除所得的余数.那么打球盘数最多的运动员打了多少盘?【答案】5【解析】因为两个数和的余数同余与余数的和.有101,126,173,193除以3的余数依次为2,0,2,1.则101号运动员与126,173,193号运动员依次进行了2,1,0盘比赛,共3盘比赛;26号运动员与101,173,193号运动员依次进行了2,2,1盘比赛,共5盘比赛;173号运动员与101,126,193号运动员依次进行了1,2,0盘比赛,共3盘比赛;193号运动员与101,126,173号运动员依次进行了0,1,0盘比赛,共1盘比赛.所以,打球盘数最多的运动是126号,打了5盘.【题文】自然数-1的个位数字是多少?【答案】7【解析】我们先计算出的个数数字,再减去1即为所求.(特别的如果是0,那么减去1后的个位数字因为借位为9)将一个数除以10,所得的余数即是这个数的个位数字.而积的余数等于余数的积.有2除以10的余数为2,2×2除以10的余数为4,2×2×2除以10的余数为8,2×2×2×2除以10的余数为6;2×2×2×2×2除以10的余数为2,除以10的余数为4,除以10的余数为8,除以10的余数为6;…… ……也就是说,n个2相乘所得的积除以10的余数每4个数一循环.因为67÷4=16……3,所以除以10的余数同余与2×2×2,即余数为8,所以-1除以8的余数为7.即-1的个位数字为7.评注:n个相同的任意整数相乘所得积除以10的余数每4个数一循环.【题文】算式7+7×7+…+计算结果的末两位数字是多少?【答案】56【解析】我们只用算出7+7×7+…+的和除以100的余数,即为其末两位数字.7除以100的余数为7,7×7除以100的余数为49,7×7×7除以100的余数为43,7×7×7×7除以100的余数等于43×7除以100的余数为1;而除以100的余数等于×7的余数,即为7,……这样我们就得到一个规律除以100所得的余数,4个数一循环,依次为7,49,43,1.1990÷4=497……2,所以7+7×7+…+的和除以100的余数同余与:497×(7+49+43+1)+7+49=49756,除以100余56.所以算式7+7×7+…+计算结果的末两位数字是56.【题文】除以9的余数是多少?【答案】2【解析】能被9整除的数的特征是其数字和能被9整除,如果这个数的数字和除以9余a,那么我们在减去a而得到的新数一定能被9整除,那么这个新数加上a后再除以9,所得的余数一定为a,即一个数除以9的余数等于其数字和除以9的余数.的数字和为20×(1+9+9+0)=380,380的数字和又是3+8=11,11除以9的余数为2,所以除以9的余数是2.【题文】将1,2,3,…,30从左往右依次排列成一个5l位数,这个数被11除的余数是多少?【答案】8【解析】1,2,3,...,30这30个数从左往右依次排列成一个51位数为:123456...910...17...192021...25 (2930)记个位为第1位,十位为第2为,那么:它的奇数位数字和为:0+9+8+7+6+…+1+9+8+7+6+…+1+9+7+5+3+1=115;它的偶数位数字和为:3+++8+6+4+2=53;它的奇数位数字和与偶数位数字和的差为115-53=62.而62除以11的余数为7.所以将原来的那个51位数增大4所得到的数123456…910…17…192021…25…2934就是11倍数,则将123456…910…17…192021…25…2934减去4所得到数除以11的余数为7.即这个51位数除以11的余数是7.评注:如果记个位为第1位,十位为第2位,那么一个数除以11的余数为其奇数位数字A和减去偶数位数字和B的差A-B=C,再用C除以11所得的余数即是原来那个数的余数.(如果减不开可将偶数位数字和B 减去奇数位数字和A,求得B-A=C,再求出C除以11的余数D,然后将11-D即为原来那个数除以11的余数) .如:123456的奇数位数字和为6+4+2=12,偶数位数字和为5+3+1=9,奇数位数字和与偶数位数字和的差位12-9=3,所以123456除以11的余数为3.又如:654321的奇数位数字和为1+3+5=9,偶数位数字和位2+4+6=12,奇数位数字和减不开偶数位数字和,那么先将12-9=3,显然3除以11的余数为3,然后再用11-3=8,这个8即为654321除以11的余数.【题文】一个1994位的整数,各个数位上的数字都是3.它除以13,商的第200位(从左往右数)数字是多少?商的个位数字是多少?余数是多少?【答案】2,7【解析】这个数即为,而整除13的数的特征是将其后三位与前面的数隔开而得到两个新数,将这两个新数做差,这个差为13的倍数.显然有能够被13类整除,而1994÷6=332……2,即==+33,而是13的倍数,所以除以13的余数即为33除以13的余数为7.有÷13=25641,而÷13=25641025641,所以除以13所得的商每6个数一循环,从左往右依次为2、5、6、4、1、0.200÷6=33……2,所以除以13所得商的第23位为5.除以13的个位即为33除以13的个位,为2.即商的第23位(从左往右数)数字是5,商的个位数字是2,余数是7.【题文】己知:a=.问:a除以13的余数是几?【答案】8【解析】因为199119911991能被13整除,而1991÷3=663……2.有a==199119911991×+199119911991×+199119911991×++199119911991×+…+199119911991×+19911991.所以a除以13的余数等于19911991除以13的余数8.【题文】有一个数,除以3余数是2,除以4余数是1.问这个数除以12余数是几?【答案】5【解析】我们将这个数加上7,则这个数能被3整除,同时也能被4整除,显然能被12整除,所以原来这个数除以12的余数为12-7=5.【题文】某个自然数被247除余63,被248除也余63.那么这个自然数被26除余数是多少?【答案】11【解析】我们将这个数减去63,则得到的新数能被247整除,也能被248整除,而相邻的两个整数互质,所以得到的新数能被247×248,显然能被26整除.于是将新数加上63除以26的余数等于63除以26的余数为11.所以这个自然数被26除余数是11.【题文】一个自然数除以19余9,除以23余7.那么这个自然数最小是多少?【答案】237【解析】这个自然数可以表达为19m+9,也可以表达为23n+7,则有19m+9=23n+7,即23n-19m=2,将未知数系数与常数对19取模,有4n≡2(mod 19) .n最小取10时,才有4n≡2(mod 19) .所以原来的那个自然数最小为23×10+7=237.评注:有时往往需要利用不定方程来清晰的表示余数关系,反过来不定方程往往需要利用余数的性质来求解.【题文】如图,在一个圆圈上有几十个孔(不到100个).小明像玩跳棋那样从A孔出发沿着逆时针方向,每隔几个孔跳一步,希望一圈以后能跳回到A孔.他先试着每隔2孔跳一步,结果只能跳到B孔.他又试着每隔4孔跳一步,也只能跳到B孔.最后他每隔6孔跳一步,正好回到A孔.问这个圆圈上共有多少个孔?【答案】91【解析】设这个圆圈有n个圆孔,那么有n除以3余1,n除以5余1,n能被7整除.则将n-1是3、5的倍数,即是15的倍数,所以n=15t+1,又因为n是7的倍数,即15t+1=7A,将系数与常数对7取模,有t-1≡0(mod 7),所以t取6或6与7的倍数和.对应孔数为15×6+1=91或91与105的倍数和,满足题意的孔数只有91.即这个圆圈上共有91个孔.【题文】某住宅区有12家住户,他们的门牌号分别是l,2,3,…,12.他们的电话号码依次是12个连续的六位自然数,并且每家的电话号码都能被这家的门牌号码整除.已知这些电话的首位数字都小于6,并且门牌号码是9的这一家的电话号码也能被13整除,问这一家的电话号码是什么数?【答案】388089【解析】设这12个连续的自然数为n+1,n+2,n+3,…,n+12,那么有它们依次能被1,2,3,…,12整除,显然有n能同时被1,2,3,…,12整除.即为1,2,3,…,12的公倍数.[1,2,3,…,12]=23×32×5×7×11=27720,所以n是27720的倍数,设为27720k.则有第9家的门牌号码为27720k+9为13的倍数,即27720k+9=13A,将系数与常数对13取模有:4k+9≡0(mod 13),所以k可以取1或1与13的倍数和.有要求n+1,n+2,n+3,…,n+12,为六位数,且首位数字都小于6,所以k只能取14,有n=27720×14=388080.那么门牌号码是9的这一家的电话号码是388080+9=388089.【题文】有5000多根牙签,可按6种规格分成小包.如果10根一包,那么最后还剩9根.如果9根一包,那么最后还剩8根.第三、四、五、六种的规格是,分别以8,7,6,5根为一包,那么最后也分别剩7,6,5,4根.原来一共有牙签多少根?【答案】5039【解析】设这包牙签有n根,那么加上1根后为n+1根,此时有n+1根牙签即可以分成10根一包,又可以分成9根一包,还可以分成8、7、6、5根一包.所以,n+1是10、9、8、7、6、5的倍数,即它们的公倍数.[10,9,8,7,6,5]=23×32×5×7=2520,即n+1是2520的倍数,在满足题意下只能是2520×2=5040,所以n=5039.即原来一共有牙签5039根.【题文】有一个自然数,用它分别去除63,90,130都有余数,3个余数的和是25.这3个余数中最大的一个是多少?【答案】20【解析】设这个自然数为☆,设它除63,90,130所得的余数依次为a,b,c,商依次为A,B,C.显然有63+90+130=☆×(A+B+C)+(a+b+c)=☆×(A+B+C)+25,所以☆×(A+B+C)=(63+90+130)-25=258,所以☆是258的约数.258=2×3×43,显然当除数☆为2、3、6时,3个余数的和最大为3×(2-1)=3,3×(3-1)=6,3×(6-1)=15,所以均不满足.而当除数☆为43×2,43×3,43×2×3时,它除以63的余数均是63,所以也不满足.那么除数☆只能是43,它除以63,90,130的余数依次为20,4,1,余数的和为25,满足.显然这3个余数中最大的为20.【题文】一个数去除55l,745,1133,1327这4个数,余数都相同.问这个数最大可能是多少?【答案】194【解析】这个数A除55l,745,1133,1327,所得的余数相同,所以有55l,745,1133,1327两两做差而得到的数一定是除数A的倍数.1327-1133=194,1133-745=388,745-551=194,1327-745=582,1327-551=776,1133-551=582.这些数都是A的倍数,所以A是它们的公约数,而它们的最大公约数(194,388,194,582,776,582)=194.所以,这个数最大可能为194.【题文】用某自然数去除,得到商是46,余数是,求和.【答案】43,14【解析】因为是的倍还多,得到,得,所以,.【题文】甲、乙两数的和是,甲数除以乙数商余,求甲、乙两数.【答案】1000,88【解析】(法1)因为甲乙,所以甲乙乙乙乙;则乙,甲乙.(法2)将余数先去掉变成整除性问题,利用倍数关系来做:从中减掉以后,就应当是乙数的倍,所以得到乙数,甲数.【题文】一个两位数除310,余数是37,求这样的两位数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
小学奥数数论问题余数问题练习题【五篇】
分析:这个题没有告诉我们,这三个数除以这个数的余数分别是多少,但是因为所得的余数相同,根据性质2,我们能够得到:这个数一定能整除这三个数中的任意两数的差,也就是说它是任意两数差的公约数.
101-45=56,101-59=42,59-45=14,(56,42,14)=14,14的约数有1,2,7,14,所以这个数可能为2,7,14.
2.已知三个数127,99和一个小于30的两位数a除以一个一位数b的余数都是3,求a和b的值.
分析:127-3=124,99-3=96,则b是124和96的公约数.而(124,96)=4,所以b=4.那么a的可能取值是11,15,19,23,27.
3.除以99,余数是______.
分析:所求余数与19×100,即与1900除以99所得的余数相同,所以所求余数是19.
4.求下列各式的余数:
(1)2461×135×6047÷11
(2)19992000÷7
分析:(1)5;(2)1999÷7的余数是4,19992000 与42000除以7 的余数相同.然后再找规律,发现4 的各次方除以7的余数的排列规律是4,2,1,4,2,1......这么3个一循环,所以由2000÷3 余2 能够得到42000除以7 的余数是2,故19992000÷7的余数是2 .
【第二篇】
(小学数学奥林匹克初赛)有苹果,桔子各一筐,苹果有240个,桔子有313个,把这两筐水果分给一些小朋友,已知苹果等分到最后余2个不够
分,桔子分到最后还余7个桔子不够再分,求最多有多少个小朋友参加
分水果
分析:此题是一道求除数的问题.原题就是说,已知一个数除240余2,除313余7,求这个数为多少,我们能够根据带余除法的性质把它转化成整除的情况,从而使问题简化,因为240被这个数除余2,意味着240-
2=238恰被这个数整除,而313被这个数除余7,意味着这313—7=306
恰为这个数的倍数,我们只需求238和306的公约数便可求出小朋友最多有多少个了.240—2=238(个) ,313—
7=306(个) ,(238,306)=34(人) .
【第三篇】
有一个大于1的整数,除45,59,101所得的余数相同,求这个数.
分析:这个题没有告诉我们,这三个数除以这个数的余数分别是多少,但是因为所得的余数相同,根据性质2,我们能够得到:这个数一定能整除这三个数中的任意两数的差,也就是说它是任意两数差的公约数.
101-45=56,101-59=42,59-45=14,(56,42,14)=14,14的约数有
1,2,7,14,所以这个数可能为2,7,14.
【第四篇】
1.已知三个数127,99和一个小于30的两位数a除以一个一位数b的
余数都是3,求a和b的值.
分析:127-3=124,99-3=96,则b是124和96的公约数.而(124,96)=4,所以b=4.那么a的可能取值是11,15,19,23,27.
2.除以99的余数是______.
分析:所求余数与19×100,即与1900除以99所得的余数相同,所以所求余数是19.
【第五篇】
19941994…1994(1994个1994)除以15的余数是______.
分析:法1:从简单情况入手找规律,发现1994÷15余
14,19941994÷15余4,199419941994÷15余9,
1994199419941994÷15余14,......,发现余数3个一循
环,1994÷3=664...2,19941994…1994(1994个1994)除以15的余数是4;法2:我们利用最后一个例题的结论能够发现199419941994能被3整除,那么19941994199400…0能被15整
除,1994÷3=664...2,19941994…1994(1994个1994)除以15的余数是4.。
