高中数学人教版双曲线上课课件PPT1
合集下载
3.2.1双曲线及其标准方程课件(人教版)(1)

方法归纳
(1)求双曲线标准方程的步骤:
①定位:确定与坐标系的相对位置,在标准方程的前提下,确定焦点位
于哪条坐标轴上,以确定方程的情势.
②定量:确定a2、b2的值,常由条件列方程组求解.
(2)双曲线标准方程的两种求法:
①定义法:根据双曲线的定义得到相应的a、b、c,再写出双曲线的标准
方程.
②待定系数法:先设出双曲线的标准方程,然后根据条件求出待定的
的点的轨迹叫做双曲线.
M
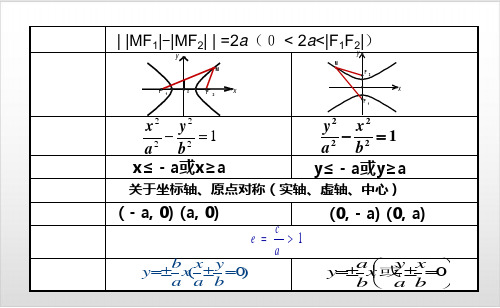
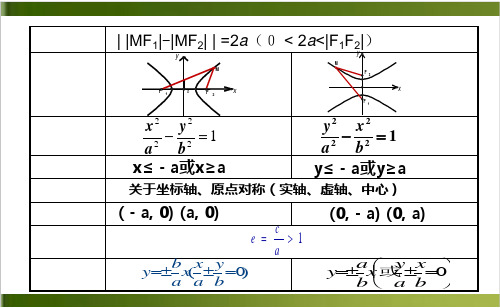
| |MF1| - |MF2| |= 2a (0<2a<|F1F2|)
这两个定点叫做双曲线的焦点,
两焦点间的距离叫做双曲线的焦距=2c,
焦距的一半称为半焦距.
F1
F2
概念辨析
思考:
(1)如果定义中去掉“绝对值”三个字会有什么影响?
如果不加绝对值,那得到的轨迹只是双曲线的一支.
使得|OB|=b吗?
新知探究
3.双曲线的标准方程
y
y
M
F1
O
•
F2 x
x2 y2
焦点在x轴上: 2 2 1(a 0, b 0)
a
b
焦点坐标:
F1(-c,0)、F2(c,0)
a,b,c关系: c2=a2+b2
M
F2
O
x
F1
y2 x2
焦点在y轴上: 2 2 1(a 0, b 0)
段PB为半径作圆.
(1)当点P在线段AB上运动时,如果|F1F2|>|AB|,两圆不相交,不存在
交点轨迹;
(2)如果|F1F2|<|AB|,那么两圆相交,其交点M的轨迹是 椭圆 .
l
A
双曲线的简单几何性质 第1课时(上课课件)

4
人A数学选择性必修第一册
返回导航 上页 下页
(3)设与双曲线x22-y2=1 有公共渐近线的双曲线方程为x22-y2=k(k≠0), 将点 M(2,-2)的坐标代入得 k=222-(-2)2=-2,∴双曲线的标准方 程为y22-x42=1.
人A数学选择性必修第一册
返回导航 上页 下页
2.求满足下列条件的双曲线的标准方程:
人A数学选择性必修第一册
返回导航 上页 下页
3.2.2 双曲线的简单几何性质 第一课时 双曲线的简单几何性质(1)
人A数学选择性必修第一册
返回导航 上页 下页
根据双曲线的方程研究其几何性质
标准方程
ax22-by22=1(a>0,b>0)
ay22-bx22=1(a>0,b>0)
性 图形
质
人A数学选择性必修第一册
人A数学选择性必修第一册
返回导航 上页 下页
3.若双曲线的渐近线方程为 y=±34x,则双曲线的离心率 为__54_或__53___.
―→
依题意列 出不等式
―→
求出e的 取值范围
人A数学选择性必修第一册
返回导航 上页 下页
[解析] 由题意可知直线 l 的方程为ax+by=1,即 bx+ay-ab=0.点(1,0)
到直线 l 的距离 d1= baa2-+1b2,点(-1,0)到直线 l 的距离 d2= baa2++1b2,
s=d1+d2= a22a+b b2=2acb,由 s≥45c,得2acb≥45c,
返回导航 上页 下页
标准方程
ax22-by22=1(a>0,b>0)
ay22-bx22=1(a>0,b>0)
人A数学选择性必修第一册
返回导航 上页 下页
(3)设与双曲线x22-y2=1 有公共渐近线的双曲线方程为x22-y2=k(k≠0), 将点 M(2,-2)的坐标代入得 k=222-(-2)2=-2,∴双曲线的标准方 程为y22-x42=1.
人A数学选择性必修第一册
返回导航 上页 下页
2.求满足下列条件的双曲线的标准方程:
人A数学选择性必修第一册
返回导航 上页 下页
3.2.2 双曲线的简单几何性质 第一课时 双曲线的简单几何性质(1)
人A数学选择性必修第一册
返回导航 上页 下页
根据双曲线的方程研究其几何性质
标准方程
ax22-by22=1(a>0,b>0)
ay22-bx22=1(a>0,b>0)
性 图形
质
人A数学选择性必修第一册
人A数学选择性必修第一册
返回导航 上页 下页
3.若双曲线的渐近线方程为 y=±34x,则双曲线的离心率 为__54_或__53___.
―→
依题意列 出不等式
―→
求出e的 取值范围
人A数学选择性必修第一册
返回导航 上页 下页
[解析] 由题意可知直线 l 的方程为ax+by=1,即 bx+ay-ab=0.点(1,0)
到直线 l 的距离 d1= baa2-+1b2,点(-1,0)到直线 l 的距离 d2= baa2++1b2,
s=d1+d2= a22a+b b2=2acb,由 s≥45c,得2acb≥45c,
返回导航 上页 下页
标准方程
ax22-by22=1(a>0,b>0)
ay22-bx22=1(a>0,b>0)
3.2.1双曲线及其标准方程课件(人教版)(1)

2 =5
2
则有 25 4
,解得 2
,双曲线的标准方程为 5 -y2=1.
− 2 = 1
=1
2
法二∵焦点在x轴上,c=
25
2
y2
6,∴设所求双曲线方程为 λ -6−λ=1(其中0<λ<6).
4
∴ λ -6−λ=1,∴λ=5或λ=30(舍去).
2
∴所求双曲线的标准方程是 5 -y2=1.
P到焦点F2的距离.
【错解一】
a=4,由|PF1|-|PF2|=8,即9-|PF2|=8,得|PF2|=1.
【错解二】
a=4,由双曲线的定义得||PF1|-|PF2||=8,所以|9-|PF2||=8,
所以|PF2|=1或17.
【错因】 错解一是对双曲线的定义中的差的绝对值掌握不够,是概念性的错误.错解二没有验证两解
将P、Q两点坐标代入可得
y2
225
9
−
=1
162
2
25
256
−
=1
2
92
2
2 =9
,解得 2
,
= 16
y2
2
(三)典型例题
1.求双曲线的标准方程
例1.根据下列条件,求双曲线的标准方程.
15
16
(1)经过点P(3, 4 ),Q(- 3 ,5).
2 y2
法二:设双曲线方程为 + =1(mn<0).
焦点
两个定点叫做双曲线的焦点
焦距
两焦点间的距离叫做双曲线的焦距
集合
语言
P={M|||MF1|-|MF2||=2a,0<2a<|F1F2|}
2
则有 25 4
,解得 2
,双曲线的标准方程为 5 -y2=1.
− 2 = 1
=1
2
法二∵焦点在x轴上,c=
25
2
y2
6,∴设所求双曲线方程为 λ -6−λ=1(其中0<λ<6).
4
∴ λ -6−λ=1,∴λ=5或λ=30(舍去).
2
∴所求双曲线的标准方程是 5 -y2=1.
P到焦点F2的距离.
【错解一】
a=4,由|PF1|-|PF2|=8,即9-|PF2|=8,得|PF2|=1.
【错解二】
a=4,由双曲线的定义得||PF1|-|PF2||=8,所以|9-|PF2||=8,
所以|PF2|=1或17.
【错因】 错解一是对双曲线的定义中的差的绝对值掌握不够,是概念性的错误.错解二没有验证两解
将P、Q两点坐标代入可得
y2
225
9
−
=1
162
2
25
256
−
=1
2
92
2
2 =9
,解得 2
,
= 16
y2
2
(三)典型例题
1.求双曲线的标准方程
例1.根据下列条件,求双曲线的标准方程.
15
16
(1)经过点P(3, 4 ),Q(- 3 ,5).
2 y2
法二:设双曲线方程为 + =1(mn<0).
焦点
两个定点叫做双曲线的焦点
焦距
两焦点间的距离叫做双曲线的焦距
集合
语言
P={M|||MF1|-|MF2||=2a,0<2a<|F1F2|}
3.2.2双曲线的简单几何性质(第1课时)课件-高二上学期数学人教A版(2019)选择性必修第一册

双曲线的渐近线方程?
=−
2 2
对于双曲线 2 − 2 = 1和它的渐近线 = ± ,
=
y
(, )
将方程中的与互换,就得到双曲线
即 = ± .
− 2 = 1 的渐近线方程 = ± ,
2
2
2
(−, )
规律方法:由双曲线方程求渐近线方程,只需把1变成0,
∴当 ∈
2
+
2
2
> 1.
=
(1, +∞)时,
∈
1+
2
(0, +∞),且增大, 也增大
b
离心率越大, 渐近线y x的斜率越大 双曲线的“张口”越大
a
新知探究
方程
2 2
− 2=1
2
2 2
− 2=1
2
图像
范围
对称性
≤ −,或 ≥
≤ −,或 ≥
≤ −,或 ≥
关于轴、轴、原点对称
( − ,),(,) (, − ),(,)
a
b
y x
y x
渐近线
b
a
= >
离心率
顶点
1. 求下列双曲线的实轴与虚轴的长, 顶点和焦点的坐标, 离心率, 渐近线方程.
2
2
x
y
2
2
2
2
2
2
(1) x 8 y 32; (2) 9 x y 81; (3) x y 4; (4)
=−
2 2
对于双曲线 2 − 2 = 1和它的渐近线 = ± ,
=
y
(, )
将方程中的与互换,就得到双曲线
即 = ± .
− 2 = 1 的渐近线方程 = ± ,
2
2
2
(−, )
规律方法:由双曲线方程求渐近线方程,只需把1变成0,
∴当 ∈
2
+
2
2
> 1.
=
(1, +∞)时,
∈
1+
2
(0, +∞),且增大, 也增大
b
离心率越大, 渐近线y x的斜率越大 双曲线的“张口”越大
a
新知探究
方程
2 2
− 2=1
2
2 2
− 2=1
2
图像
范围
对称性
≤ −,或 ≥
≤ −,或 ≥
≤ −,或 ≥
关于轴、轴、原点对称
( − ,),(,) (, − ),(,)
a
b
y x
y x
渐近线
b
a
= >
离心率
顶点
1. 求下列双曲线的实轴与虚轴的长, 顶点和焦点的坐标, 离心率, 渐近线方程.
2
2
x
y
2
2
2
2
2
2
(1) x 8 y 32; (2) 9 x y 81; (3) x y 4; (4)
人教高中数学必修《双曲线》精品PPT1

双曲线定义
平面内与两个定点F1,F2的距离的差 的绝对值等于常数(小于|F1F2|)的点的轨迹 叫做双曲线. ||MF1|-|MF2||=2a ① 两个定点F1、F2 ——双曲线的焦点; ② |F1F2|=2c——焦距. 说明:(1) 2a<2c;(2) 2a>0;
① |MF1|-|MF2|=|F2F|=2a ② |MF2|-|MF1|=|F1F|=2a 由①②可得:
2.3.1双曲线及其标准方程
1. 椭圆平: 面内与两定点F1、F2的距离的和 等于常数2a(2a>|F1F2|>0)的点的轨迹.
|MF1|+|MF2|=2a( 2a>2c>0) 点M的轨迹是椭圆
若2a=2c,
点M的轨迹是线段F1F2;
若2a<2c,
点M的轨迹不存在。
3.引入问题: 若把椭圆中的距离“和”改为距离”差”
[例2] 如果方程
x2
y2
1
2m m1
表示双曲线,求m的取值范围.
思考:
方程 x2 y2 1表示焦点在y轴
2m m1
双曲线时,则m的取值范围__________.
[例2] 如果方程
x2
y2
1
2m m1
表示双曲线,求m的取值范围.
思考:
方程 x2 y2 1表示焦点在y轴
2m m1
双曲线时,则m的取值范围___m_<_-__2___.
[例3] 已知A,B两地相距800m,在A地 听到炮弹爆炸声比在B地晚2s,且声速为 340m/s,求炮弹爆炸点的轨迹方程.
yP
x
A
B
[例3] 已知A,B两地相距800m,在A地 听到炮弹爆炸声比在B地晚2s,且声速为 340m/s,求炮弹爆炸点的轨迹方程.
人教A版高中数学《双曲线》PPT完美课件1
O
X
问题三: 人教A版高中数学《双曲线》PPT完美课件1
若直线y=kx-1与双曲线4x2-y2=1无公共点,实数k的取值 范围是什么?说明位置关系。
人教A版高中数学《双曲线》PPT完美 课件1
问题三: 人教A版高中数学《双曲线》PPT完美课件1
若直线y=kx-1与双曲线4x2-y2=1无公共点,实数k的取值 范围是什么?说明位置关系。
问题一:
直线y=kx-1与双曲线4x2-y2=1有且只有一个公共点,求直 线方程,说明位置关系。
解 : 联 立 4 y x 2 k y x 2 1 1 得 (4 - k 2 )x 2 + 2 k x - Y2 = 0
O
X
问题二
若直线y=kx-1与双曲线4x2-y2=1有两个不同公共点,实数 k的取值范围是什么?说明位置关系。
得到一元二次方程
计算判别式
>0
=0
<0
相交 相切 相离
人教A版高中数学《双曲线》PPT完美 课件1
练习:
1、已知直线y=kx-1与双曲线x2-y2=4,试讨论实数k的取值范围,使直 线与双曲线
(1)交于异支两点;
-1<k<1 ;
(2)与左支交于两点.
- 5 k 1 2
解 : x y 2 = -k y 2 由 - = x 1 4 得 x ( 2 , 1 -k 2 ) 2 k x 5 0
问题二: 人教A版高中数学《双曲线》PPT完美课件1
若直线y=kx-1与双曲线4x2-y2=1有两个不同公共点,实数 k的取值范围是什么?说明位置关系。
解 : 联 立 4 y x 2 k y x 2 1 1 得 (4 - k 2 )x 2 + 2 k x Y- 2 = 0
《双曲线》_PPT完整版人教版1

94
1.
a 3 ,b 2, c 9 4 5 . 4
2
4
2
∴ 离心率 e 5 . 3
《双曲线》教学分析人教版1-精品课 件ppt( 实用版)
《双曲线》教学分析人教版1-精品课 件ppt( 实用版)
变式1
求以椭圆
x2 13
y2 3
1的焦点为焦点,以直线
y
1 2
x为
渐近线的双曲线方程。
所求双曲线的渐近线为 x y 0 21
4 (2)焦点在 y 轴,焦距是 16, e 4 ;
3 (3)以椭圆 x2 y2 1 的焦点为顶点,以椭圆的顶点为焦点;
85
(4)一个焦点是 F1(-6,0)的等轴双曲线.
解:(1) 2a 8, c 5 , a4
a 4, c 5, b2 c2 a2 9. 故所求标准方程为:x2 y2 1.
例3 求与双曲线
x2 y2 1 共渐近线且过点 (2
16 9
3, 3)
的双曲线方程及离心率.
解:设与已知双曲线共渐近线的双曲线方程为 x2 y2 0
16 9
∵ 点 (2 3, 3)在双曲线上,
12 9 1
16 9 4 故所求双曲线方程为:x2 y2
16 9
1 4
即
y2 x2
2.3.2 双曲线的简单几何性质(1)
思考回顾 椭圆的简单几何性质 ?
①范围; ②对称性; ③顶点; ④离心率等
双曲线是否具有类似的性质呢?
图象
方程 性质
A1 F1
y B1
O
B2
M
A2
F2 x
范围
| x | a,| y | b
B1 A1 A2
B2
1.
a 3 ,b 2, c 9 4 5 . 4
2
4
2
∴ 离心率 e 5 . 3
《双曲线》教学分析人教版1-精品课 件ppt( 实用版)
《双曲线》教学分析人教版1-精品课 件ppt( 实用版)
变式1
求以椭圆
x2 13
y2 3
1的焦点为焦点,以直线
y
1 2
x为
渐近线的双曲线方程。
所求双曲线的渐近线为 x y 0 21
4 (2)焦点在 y 轴,焦距是 16, e 4 ;
3 (3)以椭圆 x2 y2 1 的焦点为顶点,以椭圆的顶点为焦点;
85
(4)一个焦点是 F1(-6,0)的等轴双曲线.
解:(1) 2a 8, c 5 , a4
a 4, c 5, b2 c2 a2 9. 故所求标准方程为:x2 y2 1.
例3 求与双曲线
x2 y2 1 共渐近线且过点 (2
16 9
3, 3)
的双曲线方程及离心率.
解:设与已知双曲线共渐近线的双曲线方程为 x2 y2 0
16 9
∵ 点 (2 3, 3)在双曲线上,
12 9 1
16 9 4 故所求双曲线方程为:x2 y2
16 9
1 4
即
y2 x2
2.3.2 双曲线的简单几何性质(1)
思考回顾 椭圆的简单几何性质 ?
①范围; ②对称性; ③顶点; ④离心率等
双曲线是否具有类似的性质呢?
图象
方程 性质
A1 F1
y B1
O
B2
M
A2
F2 x
范围
| x | a,| y | b
B1 A1 A2
B2
双曲线及其标准方程ppt课件

所以 2 mm 1 0 ,解得 m 2 或 m 1, 即实数 m 的取值范围是,2 1, .
总结一下
1.双曲线的定义 2.双曲线的标准方程
Fresh and simple general ppt template
谢谢观看
2.焦点在y轴上的双曲线的标准方程
如图,双曲线的焦距为 2c,焦点分别是
F1(0, c) , F2 (0,c) ,a,b 的意义同上,这时
双曲线的方程是
y2 a2
x2 b2
1(a
0, b
0)
,这个
方程也是双曲线的标准方程.
y
M
F2
x O
F1
双曲线标准方程
图形
y M x
F1 O F2
y M F2
3.2.1 双曲线及其标准方程
人教A版(2019)选择性必修一
学习目标
01 经历从具体情境中抽象出双曲线模型的过程 02 了解双曲线的定义、几何图形和标准方程
03 通过双曲线标准方程的推导过程理解数形结合思想
学习重点
双曲线的定义、标准方程
学习难点
双曲线标准方程的推导
新课导入
我们知道,平面内与两个定点F1,F2的距离的和等于常数的点的轨
由双曲线的定义,双曲线就是下列点的集合:
P {M || MF1 | | MF2 || 2a , 0 2a | F1F2 |} .
因为 | MF1 | (x c)2 y2 ,| MF2 | (x c)2 y2 , 所以 (x c)2 y2 (x c)2 y2 2a .①
类比椭圆标准方程的化简过程,化简①,得 (c2 a2 )x2 a2 y2 a2 (c2 a2 ) ,
x2 b2
1a
总结一下
1.双曲线的定义 2.双曲线的标准方程
Fresh and simple general ppt template
谢谢观看
2.焦点在y轴上的双曲线的标准方程
如图,双曲线的焦距为 2c,焦点分别是
F1(0, c) , F2 (0,c) ,a,b 的意义同上,这时
双曲线的方程是
y2 a2
x2 b2
1(a
0, b
0)
,这个
方程也是双曲线的标准方程.
y
M
F2
x O
F1
双曲线标准方程
图形
y M x
F1 O F2
y M F2
3.2.1 双曲线及其标准方程
人教A版(2019)选择性必修一
学习目标
01 经历从具体情境中抽象出双曲线模型的过程 02 了解双曲线的定义、几何图形和标准方程
03 通过双曲线标准方程的推导过程理解数形结合思想
学习重点
双曲线的定义、标准方程
学习难点
双曲线标准方程的推导
新课导入
我们知道,平面内与两个定点F1,F2的距离的和等于常数的点的轨
由双曲线的定义,双曲线就是下列点的集合:
P {M || MF1 | | MF2 || 2a , 0 2a | F1F2 |} .
因为 | MF1 | (x c)2 y2 ,| MF2 | (x c)2 y2 , 所以 (x c)2 y2 (x c)2 y2 2a .①
类比椭圆标准方程的化简过程,化简①,得 (c2 a2 )x2 a2 y2 a2 (c2 a2 ) ,
x2 b2
1a
第三章3.2.2第1课时双曲线的简单几何性质PPT课件(人教版)

4.双曲线x2-y2=1的顶点到其渐近线的距离等于
A.12
√B.
2 2
C.1
D. 2
解析 双曲线x2-y2=1的渐近线方程为x±y=0,顶点坐标为(1,0) 2.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
5.已知双曲线 C:ax22-by22=1(a>0,b>0)的离心率为 25,则双曲线 C 的渐近线方
∴b=2,∴-m1 =b2=4, ∴m=-41,故选 C.
12345
3.中心在原点,焦点在x轴上,且一个焦点在直线3x-4y+12=0上的等轴双曲
线的方程是
√A.x2-y2=8
B.x2-y2=4
C.y2-x2=8
D.y2-x2=4
解析 令y=0,得x=-4, ∴等轴双曲线的一个焦点为(-4,0), ∴c=4,a2=b2=21c2=21×16=8,故选 A.
实轴长2a=6,虚轴长2b=4,
离心率 e=ac= 313, 渐近线方程为 y=±bax=±23x.
延伸探究 求双曲线nx2-my2=mn(m>0,n>0)的实半轴长、虚半轴长、焦点坐标、离心 率、顶点坐标和渐近线方程.
解 把方程 nx2-my2=mn(m>0,n>0)化为标准方程为xm2-yn2=1(m>0,n>0), 由此可知,实半轴长 a= m,
所以双曲线的离心率为 1+ 2.
3 随堂演练
PART THREE
1.(多选)已知双曲线方程为x2-8y2=32,则
√A.实轴长为 8 2
√B.虚轴长为 4
C.焦距为 6
√D.离心率为3 4 2
解析 双曲线方程 x2-8y2=32 化为标准方程为3x22 -y42=1, 可得 a=4 2,b=2,c=6,
双曲线及其标准方程 课件(人教版)

()D.45
解析:(1)因为由双曲线的定义有|PF1|-|PF2|=|PF2| =2a=2 2,
所以|PF1|=2|PF2|=4 2, |PF1|2+|PF2|2-|F1F2|2
则 cos ∠F1PF2= 2|PF1|·|PF2| =
(4 22)×24+(2×2 22)2 2-42=34. 答案:C
解:(1)法一:由题意知双曲线的两焦点为 F1(0,-
3),F2(0,3). 设双曲线方程为ay22-xb22=1(a>0,b>0), 将点 A(4,-5)代入双曲线方程得2a52-1b62=1. 又 a2+b2=9,解得 a2=5,b2=4. 所以双曲线的标准方程为y52-x42=1.
法二:||AF1|-|AF2||=| 20- 80|=2 5=2a,
[迁移探究 2] (变换条件)上例中将条件“|PF1|= 2|PF2|”改为“P→F1·P→F2=0”,则△F1PF2 的面积是 ________.
解:不妨设点 P 在双曲线的右支上,则|PF1|-|PF2|
=2a=2 2, 由于P→F1·P→F2=0,所以P→F1⊥P→F2.
所以在△F1PF2 中,有|PF1|2+|PF2|2=|F1F2|2, 即|PF1|2+|PF2|2=16,所以|PF1|·|PF2|=4, 所以 S△F1PF2=12|PF1|·|PF2|=2. 答案:2
双曲线及其标准方程
1.双曲线的定义 把平面内与两个定点 F1、F2 的距离的差的绝对值等 于常数(小于|F1F2|)的点的轨迹叫做双曲线,这两个定点 叫做双曲线的焦点,两焦点间的距离叫做双曲线的焦距.
温馨提示 把定常数记为 2a,当 2a<|F1F2|时,其轨迹是双曲线; 当 2a=|F1F2|时,其轨迹是以 F1、F2 为端点的两条射线(包 括端点);当 2a>|F1F2|时,其轨迹不存在.
高二数学人教A版选修一《3.2双曲线》完整课件(85页)

)
A.[-4,1)
B.(-∞,-4)∪(1,+∞)
C.(-4,1)
D.(-∞,-4]∪[1,+∞)
解析:根据题意,若曲线k+x24+k-y2 1=1 表示双曲线,则有 (k+4)(k-1)<0,解得-4<k<1.
答案:C
题型三 双曲线标 (1)只有当双曲线的两焦点 F1,F2 在坐标轴上,并且线段 F1F2 的垂直平分线也是坐标轴时得到的方程才是双曲线的标准 方程. (2)标准方程中的两个参数 a 和 b,确定了双曲线的形状和大 小,是双曲线的定形条件,这里的 b2=c2-a2 与椭圆中的 b2=a2 -c2 相区别,且椭圆中 a>b>0,而双曲线中 a,b 大小不确定.
()
(3)方程 mx2+ny2=1(mn<0)表示双曲线.
()
答案:(1)× (2)× (3)√
2.双曲线1x02-y22=1 的焦距为
A.2 2
B.4 2
C.2 3
D.4 3
()
解析:因为 c2=10+2=12,所以 c=2 3,从而焦距为 4 3. 答案:D
3.已知双曲线的 a=5,c=7,则该双曲线的标准方程为( ) A.2x52-2y42 =1 B.2y52 -2x42=1 C.2x52-2y42 =1 或2y52 -2x42=1 D.2x52-2y42 =0 或2y52 -2x42=0
数 m 的取值范围是
()
A.m>2
B.m<1 或 m>2
C.-1<m<2
D.-1<m<1 或 m>2
(2)“3<m<5”是“方程mx-2 5+m2-ym2 -6=1 表示的图形为双曲
《双曲线》课件人教版1

《双曲线》课件人教版1
如何求双曲线的标准方程?
1. 建系. 以F1,F2所在的直线为X轴,线
段F1F2的垂直平分线为y轴,建立直 角坐标系Oxy
y
M
2.设点 设M(x , y),双曲线的焦
距为2c(c>0),F1(-c,0),F2(c,0) F1
o F2 x
常数=2a
3.列式.||MF1 |- |MF2||= 2a
y2 b2
1
y2 a2
x2 b2
1
(a0, b0)
c2 a2 b2
《双曲线》课件人教版1
《双曲线》课件人教版1
思考:如何判断双曲线的焦点在哪个轴上?
看 x 2 , y 2 前的系数,哪一个为正,
则在哪一个轴上
练习:写出以下双曲线的焦点坐标.
(1) x 2 - y 2 =1; 16 9
(5,0),(-5,0)
(2)常数要小于|F1F2|大于0
F1 o F2
0<2a<2c
①如图(A),
|PF1|-|PF2|=2a ②如图(B),
|PF2|-|PF1|=2a 由①②可得: | |PF1|-|PF2| | = 2a
(差的绝对值)
上面 两条合起来叫做双曲线
拉链画双曲线
双曲线定义
| |MF1| - |MF2| | = 2a 0<2a<2c
时,则m的取值范围___m_______2___.
P121 T4
《双曲线》课件人教版1
《双曲线》课件人教版1
小结
定义 | |MF1|-|MF2| | =2a(0 < 2a<|F1F2|)
图象
y
M
F1 o F2 x
选择性必修第一册3.2.1双曲线及其标准方程课件(人教版)

a>b>0, a2=b2+c2 a, b, c中a最大
双曲线
||MF1|-|MF2||=2a (a<c)
x2 a2
y2 b2
1(a
0, b
0)
y2 x2 a2 b2 1(a 0, b 0)
F1(-c, 0), F2(c, 0) F1(0, -c), F2(0, c)
a>0, b>0, c2=a2+b2 a, b, c中c最大
练习 已知1-x2k -|k|y-2 3 =-1,当 k 为何值时: (1)方程表示双曲线;(2)方程表示焦点在 x 轴上的双曲线.
解:(1)原方程可变形为|k|y-2 3 -1-x2k =1. 要使方程表示双曲线,必须满足(|k|-3)(1-k)>0, 即|1k-|-k3>>00, 或|1k-|-k3<<00,, 解得 k<-3 或 1<k<3.
们的斜率之积是 4 ,求点M的轨迹方程. 9
解:设M( x,
y ), 则k AM
kBM
4 ,
9
即
x
y 5
x
y 5
4(x 9
5).
A
y
M •
O
Bx
化简得 4x2 9 y2 100,即 x2 y2 1( x 5). 25 100
9
∴点M的轨迹方程为 x2 y2 1( x 5). 25 100
o A•
B• x
利用A, C( 或B, C) 两处测得的爆炸声的时间差 , 求爆炸点
所在的另一个双曲线的方程.
解这两个双曲线方程组成的方程组 , 就能确定爆炸点的准确位置 . 这是双曲
线的一个重要应用 .
双曲线
||MF1|-|MF2||=2a (a<c)
x2 a2
y2 b2
1(a
0, b
0)
y2 x2 a2 b2 1(a 0, b 0)
F1(-c, 0), F2(c, 0) F1(0, -c), F2(0, c)
a>0, b>0, c2=a2+b2 a, b, c中c最大
练习 已知1-x2k -|k|y-2 3 =-1,当 k 为何值时: (1)方程表示双曲线;(2)方程表示焦点在 x 轴上的双曲线.
解:(1)原方程可变形为|k|y-2 3 -1-x2k =1. 要使方程表示双曲线,必须满足(|k|-3)(1-k)>0, 即|1k-|-k3>>00, 或|1k-|-k3<<00,, 解得 k<-3 或 1<k<3.
们的斜率之积是 4 ,求点M的轨迹方程. 9
解:设M( x,
y ), 则k AM
kBM
4 ,
9
即
x
y 5
x
y 5
4(x 9
5).
A
y
M •
O
Bx
化简得 4x2 9 y2 100,即 x2 y2 1( x 5). 25 100
9
∴点M的轨迹方程为 x2 y2 1( x 5). 25 100
o A•
B• x
利用A, C( 或B, C) 两处测得的爆炸声的时间差 , 求爆炸点
所在的另一个双曲线的方程.
解这两个双曲线方程组成的方程组 , 就能确定爆炸点的准确位置 . 这是双曲
线的一个重要应用 .
双曲线及其标准方程ppt课件

课后提升
1.必做题:P127页课本习题3.2第1,2,5题
2. 思考题(选做):定位问题
某中心接到其正东、正西、正北方向三个观测点的报告,正西、
正北两个观测点同时听到了一声巨响,正东观测点听到的时间比其
它两个观测点晚4秒。已知各观测点到该中心的距离都是1020m,试
确定该巨响发生的位置。
(假定声音传播的速度为340m/s,相关各点均在同一平面内。)
−
= 令 = −
−
你能在y轴上找一点B,使得|OB|=b吗?
1
验证
设点
2
坐标法
4
化简
列式
3
绝对值
教学过程分析
3
通过图象,生成定义
绘制图象,合作探究
2
1
类比启发,方程推导
重
点
4
5
类比推理,举一反三
列表对比,加深理解
教学过程分析
方程推导
在学生脑海里留下更加深刻的印象。
通过学生的自主学习、小组合作、师生互
动,让学生学会交流、表达、质疑、反思。
04
01
02
03
谢
大
谢
家
5.及时练习,巩固所学
6.回顾小结,思维提升
7.课后延伸,探究发现
教学过程分析
复习回顾,课题导入
复习回顾:
椭圆及其标准方程
创设情境
导入课题:双曲线及其标准方程
教学过程分析
3
通过图象,生成定义
绘制图象,合作探究
2
1
类比启发,方程推导
4
类比推理,举一反三
5
《双曲线》ppt高中人教版1
Δ>0
直线与双曲线相交(两个交点)
Δ=0
直线与双曲线相切
Δ<0
直线与双曲线相离
人教A版数学选修2—1ቤተ መጻሕፍቲ ባይዱ2.3 直线与双曲线的位置关系
代数法判断直线与双曲线的位置关系: 人教A版数学选修2—1 2.3 直线与双曲线的位置关系
把直线方程代入双曲线方程
得到一元一次方程
直线与双曲线的 渐进线平行或重合
相交(一个交点)或相离
•
2.许地山这样说,也是这样做的,他 长大后 埋头苦 干,默 默奉献 ,成为 著名的 教授和 作家, 他也因 此取了 个笔名 叫落花 生,这 就是他 笔名的 由来。
•
3.在伟大庄严的教堂里,从彩色玻璃 窗透进 一股不 很明亮 的光线 ,沉重 的琴声 好像是 把人的 心都洗 淘了一 番似的 ,我感 到了我 自己的 渺小。
人教A版数学选修2—1 2.3 直线与双曲线的位置关系
问题二: 人教A版数学选修2—1 2.3直线与双曲线的位置关系
若直线y=kx-1与双曲线4x2-y2=1有两个不同公共点,实数 k的取值范围是什么?说明位置关系。
解 : 联 立 4 y x 2 k y x 2 1 1 得 (4 - k 2 )x 2 + 2 k x Y- 2 = 0
人教A版数学选修2—1 2.3 直线与双曲线的位置关系
yax或yx0 b a b
教学目标:
1.知识与能力: (1)理解并熟练掌握直线与双曲线的各种位置关系,
能类比直线与椭圆的位置关系进行判断求解, 培养分析、归纳、推理、类比的能力。 (2)掌握判断位置关系的两种思路:几何法、代数 法。 (3)加强运算能力的训练,培养良好的思维习惯。
2.过程与方法: 强化数形结合、函数方程、转化化归、分类讨论等数学思想方法在直线与双曲
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
【解析】 双曲线C1的一条渐近线方程为bx-ay=0, 圆心(2,0)到渐近线的距离为1,
即 a|22+b| b2=1,得a2=3b2,
Hale Waihona Puke 即ba=3 3.所以双曲线C1的渐近线方程为y=± 33x.故选D.
(2)(2020·唐山市第一次模拟)已知F是双曲线C:
x2 a2
-
y2 b2
=
1(a>0,b>0)的右焦点,M是C的渐近线上一点,且MF⊥x轴,过
第二课时 双曲线与抛物线小题
热点调研
一、基础知识 双曲线的方程与性质
标准方程
xa22-yb22=1(a>0,b>0) ya22-xb22=1(a>0,b>0)
图形
范围 x≥a或x≤-a,y∈R
x∈R,y≥a或y≤-a
对称轴:坐标轴 对称 对称性
中心:原点
顶点坐标:
顶点坐标:
顶点
A1(-a,0),A2(a,0)
押题一 双曲线
(1)(2020·百校联考)双曲线C1:xa22-yb22=1(a>0,b>0)的
渐近线与圆C2:(x-2)2+y2=1相切,则双曲线C1的渐近线方程 为( D )
A.y=±12x
B.y=±13x
C.y=±
2 2x
D.y=±
3 3x
【分析】 双曲线C1的一条渐近线方程为bx-ay=0,根据 渐近线与圆C2:(x-2)2+y2=1相切,则有 a|22+b| b2=1求解.
A1(0,-a),A2(0,a)
性 轴
实轴:线段A1A2,虚轴:B1B2
质 焦距
|F1F2|=2c
离心率
e=ca,e∈(1,+∞),e越大,开口越大
a,b,c 的关系
c2=a2+b2
渐近线
y=±bax
y=±bax
等轴双曲线 (1)定义:中心在原点,以坐标轴为对称轴,实半轴长与虚 半轴长相等的双曲线叫做等轴双曲线. (2)性质:①a=b;②e= 2;③渐近线互相垂直;④等轴双 曲线上任意一点到中心的距离是它到两焦点距离的等比中项.
共轭双曲线 (1)定义:如果一条双曲线的实轴和虚轴分别是另一条双曲 线的虚轴和实轴,那么这两条双曲线互为共轭双曲线. (2)性质:①它们有共同的渐近线;②它们的四个焦点共 圆;③它们的离心率的倒数的平方和等于1.
抛物线的标准方程和几何性质
标准 方程
y2=2px (p>0)
y2=-2px (p>0)
x2=2py (p>0)
x2=-2py (p>0)
图形
顶点 对称轴
焦点
准线
(0,0)
x轴
y轴
Fp2,0
F-p2,0
F0,p2
F0,-p2
x=-p2
x=p2
y=-p2
y=p2
二、常见方法结论
双曲线 (1)双曲线的焦点到其渐近线的距离为b. (2)若P是双曲线右支上一点,F1,F2分别为双曲线的左、右 焦点,则|PF1|min=a+c,|PF2|min=c-a. (3)同支的焦点弦中最短的为通径(过焦点且垂直于实轴的 弦),其长为2ab2;异支的弦中最短的为实轴,其长为2a. (4)若P是双曲线上不同于实轴两端点的任意一点,F1,F2分 别为双曲线的左、右焦点,则S△PF1F2= b2θ,其中θ为∠F1PF2.
关于抛物线的切线 (1)以焦点弦为直径的圆与准线相切;以焦半径为直径的圆 与y轴相切(开口向右). (2)过抛物线焦点弦的两个端点作抛物线的两条切线,则切 线互相垂直,且交点在抛物线准线上. (3)过抛物线的准线上任意一点作抛物线的两条切线,则切 线互相垂直,两切点与抛物线焦点共线.
如果OA,OB是抛物线y2=2px上的两条弦(O是原点),则
,
|AF| |BF|
=
1-cosθ 1+cosθ
,
1 |AF|
+
1 |BF|
=
2 p
,
|AB|=sin22pθ.
(2)过抛物线x2=2py(p>0)的焦点F作倾斜角为θ的直线交抛物 线于点A(x1,y1),B(x2,y2),其中x1<0<x2,则有|AF|= 1+spinθ,|BF|=1-spinθ,||ABFF||=11+-ssiinnθθ,|A1F|+|B1F|=2p,|AB| =co2sp2θ.
∵MN⊥ON,且kMN=
bac+b2ca c-2c
=
3b a
,kON=-
b a
,∴kMN·kON=-
3b2 a2
=-1,∴
b2 a2
=
1 3
,因此,双曲线C的离心率为e=
c a
=
a2+b2 a2
=
1+ba2=2 33.故选A.
(3)(2020·河南省鹤壁第二次模拟)已知双曲线C:
x2 a2
-
y2 b2
tan 2
(5)若P是双曲线
x2 a2
-
y2 b2
=1(a>0,b>0)右支上不同于实轴端点
的任意一点,F1,F2分别为双曲线的左、右焦点,I为△PF1F2内 切圆的圆心,则圆心I的横坐标为定值a.
(6)设F1,F2是双曲线
x2 a2
-
y2 b2
=1(a>0,b>0)的左、右焦点,
AB是过F1的弦,则|AF2|+|BF2|-|AB|=4a.
F作直线OM的平行线交C的渐近线于点N(O为坐标原点),若
MN⊥ON,则双曲线C的离心率是( A )
A.2 3 3
B. 3
6 C. 2
D.2
【解析】
设点M为双曲线C的渐近线y=
b a
x上的一点,易知点
F(c,0),所以点M
c,bac
,直线FN的方程为y=
b a
(x-c),联立
yy==-ba(baxx-,c),解得xy==-2c,b2ca,则点N2c,-2bac,
(1)若OA,OB互相垂直,则直线AB过定点(2p,0);
(2)若直线AB过定点(2p,0),则OA,OB互相垂直.
(1)过抛物线y2=2px(p>0)的焦点F作倾斜角为θ的直线交
抛物线于点A(x1,y1),B(x2,y2),其中y1<0<y2,则有|AF|=
p 1+cosθ
,|BF|=
p 1-cosθ
(7)AB为双曲线
x2 a2
-
y2 b2
=1(a>0,b>0)的弦,A(x1,y1),
B(x2,y2),弦中点M(x0,y0).则
①弦长l= 1+k2|x1-x2|= ②直线AB的斜率kAB=ba22yx00.
1+k12|y1-y2|;
关于抛物线的焦点弦 线段AB为抛物线y2=2px(p>0)的焦点弦,A(x1,y1),B(x2, y2),则 (1)x1x2=p42; (2)y1y2=-p2; (3)焦半径|AF|=x1+p2; (4)弦长l=x1+x2+p.当弦AB⊥x轴时,弦长最短为2p,此时 的弦又叫通径.
=
