结构动力学(单自由度体系的振动分析)
(结构动力学3)单自由度41解析

1 1 2 (0)] 2 EI E Ek Es k[u (0)] m[u 2 2
无阻尼体系自由振动过程中的总能量守恒,不随 时间变化,等于初始时刻输入的能量。
3.3自由振动过程中的能量
有阻尼体系中的能量: 在0至t时刻由粘性阻尼耗散的能量ED为:
)u dt cu dt ED f D du (cu
3.2 有阻尼自由振动
4.自由振动试验
解:
⑤ 阻尼系数c
c c c ccr 2mn 2 m k
0.0276 m 9.24t
c (2 km )
k 1460kN m
0.0276 2 1460 9.24 6.41kN s m
3.2 有阻尼自由振动
3.3自由振动过程中的能量
无阻尼体系中的能量:
u (t ) u (0) cos n t ( 0) u sin n t
Ek 1 (t )] 2 m[u 2 Es 1 k[u (t )] 2 2
n
(0) 1 u 2 E k m n [u(0) sin n t cos n t ]2 2 n (0) 1 u E s k [u(0) cos n t sin n t ]2 2 n
自振周期:Natural Period (of vibration) ——结构的重要动力特性
3.1 无阻尼自由振动
结构自振频率和自振周期及其关系
k 自振圆频率: n (单位:弧度/秒, rad/s) m
自振周期:
Tn
2
n
(单位:秒, sec)
自振频率:
n fn (单位:周/秒, 赫兹, Hz) 2
ui 1 ln 2j ui j
单自由度无阻尼自由振动的系统分析

单自由度无阻尼自由振动的系统分析在结构动力学之中,单自由度体系的振动是最简单的振动,但单自由度体系的频率计算在结构动力学计算中有着十分重要的意义,因为从中我们能得到关于振动理论的一些最基本的概念和分析方法同时也为更复杂的多质点多自由度体系振动问题奠定基础,同时现实工程中也有许多振动问题可以简化为单自由度问题近似的利用单自由度振动理论去分析解决。
在单层厂房、水塔等建筑物中得到有效的利用结构的自由振动是指结构受到扰动离开平衡位置后,不再受到任何外力影响的振动过程,此处动力系统是否有阻尼项,会直接影响到动力系统的反应。
在此,我们把自由振动分为无阻尼自由振动与有阻尼的自由振动。
一、无阻尼自由系统的振动分析目前,以弹簧-质量系统为力学模型,研究单自由度系统的振动具有非常普遍的实际意义,因为工程中许多问题简化后,用单自由度体系的振动理论就能得到很好的解决。
而对多自由度系统和连续振动,在特殊坐标的考察时,也会显示出与单自由度系统类似的振动。
进行无阻尼自由振动分析的主要目的是为了获得系统固有振动的特性,只有充分地了解系统的自身振动特性才能有效的计算系统的动力响应,目前在单质点单自由度无阻尼自由振动体系中我们的运动方程为:0)()(..=+t ku t um (1) 或 0u(t))(=+ωt u (2)其中的ω是振动圆频率,是反应系统动力的重要参数,其计算公式为:m k m ==δω12 (3)由上式可以看出,ω只和系统的刚度及质量有关,而与系统所受到的初始受力状态无关。
ω的量纲与角速度相同为rad/s ,它反映了系统自由振动的快慢。
自由振动系统的这一特性,我们在日常生活中司空见惯。
比如,键盘类乐器标定后,按动某一个琴键,不管你按动的轻重如何,琴键所发出的声音的频率是一定的,按得轻或按得重仅影响声音的强弱。
(2)式经过三角函数的转换可表示为:)sin()(νω+=t A t u (4)其通解为t A t A t u ωωsin cos )(21+= 常数A 1与A 2与初始条件有关,01χ=A ωχ/02 =A式(4)是标准的简谐方程其中A 是其振幅,则ν是其初相角,他们的计算公式2020)(ωx x A += ,00arctan x x v ω=对于质点振动系统,质量越大,则系统的固有频率越低;刚度越大,则系统的固有频率越高。
结构动力学课后习题答案

结构动力学课后习题答案结构动力学是研究结构在动态载荷作用下的响应和行为的学科。
它涉及到结构的振动、冲击响应、疲劳分析等方面。
课后习题是帮助学生巩固课堂知识、深化理解的重要手段。
以下内容是结构动力学课后习题的一些可能答案,供参考:习题1:单自由度系统自由振动分析解答:对于一个单自由度系统,其自由振动的频率可以通过以下公式计算:\[ f = \frac{1}{2\pi}\sqrt{\frac{k}{m}} \]其中,\( k \) 是系统的刚度,\( m \) 是系统的总质量。
系统自由振动的振幅随着时间的衰减可以通过阻尼比 \( \zeta \) 来描述,其衰减系数 \( \delta \) 可以通过以下公式计算:\[ \delta = \sqrt{1-\zeta^2} \]习题2:单自由度系统受迫振动分析解答:当单自由度系统受到周期性外力作用时,其受迫振动的振幅可以通过以下公式计算:\[ A = \frac{F_0}{\sqrt{(k-m\omega^2)^2+(m\zeta\omega)^2}} \] 其中,\( F_0 \) 是外力的幅值,\( \omega \) 是外力的角频率。
习题3:多自由度系统模态分析解答:对于多自由度系统,可以通过求解特征值问题来得到系统的模态。
特征值问题通常表示为:\[ [K]{\phi} = \lambda[M]{\phi} \]其中,\( [K] \) 是系统的刚度矩阵,\( [M] \) 是系统的质量矩阵,\( \lambda \) 是特征值,\( {\phi} \) 是对应的特征向量,即模态形状。
习题4:结构的冲击响应分析解答:对于结构的冲击响应分析,通常需要考虑冲击载荷的持续时间和冲击能量。
结构的冲击响应可以通过冲击响应谱(IRF)来分析,它描述了结构在不同频率下的响应。
冲击响应分析的结果可以用来评估结构的耐冲击性能。
习题5:疲劳分析解答:结构的疲劳分析需要考虑结构在重复载荷作用下的寿命。
结构力学课件15动力学(1)
能相差很大。反之,两个外形看来并不相同的结构,如果其
2自021振/7/2周3 期相近,则在动荷载作用下的动力性能基本一致。2
例4、图示三根单跨梁,EI为常数,在梁中点有集中质量m, 不考虑梁的质量,试比较三者的自振频率。
EI
l
w=
k11 =
3EI l3
+k
m
m
•对于静定结构一般计算柔度系数方便。
•如果让振动体系沿振动方向发生单位位移时,所有刚节点
都不能发生转动(如横梁刚度为∞刚架)计算刚度系数方便。
两端刚结的杆的侧移刚度为:
12 l
EI
3
一端铰结的杆的侧移刚度为:
2021/7/23
3 EI l3
5
五、阻尼对自由振动的影响
忽略阻尼影响时所得结果 大能体不上能 反映实际结构的振动规律。
忽略阻尼的振动规律
考虑阻尼的振动规律
结构的自振频率是结构的固有特性,与外因无关。
简谐荷载作用下有可能出现共振。
自由振动的振幅永不衰减。
自由振动的振幅逐渐衰减。
共振时的振幅趋于无穷大。 共振时的振幅较大但为有限值。
产生阻尼的原因:结构与支承之间的外摩擦;材料之间的内摩
擦;周围介质的阻力。
阻尼力的确定:总与质点速度反向;大小与质点速度有如下关系:
①与质点速度成反比(比较常用,称为粘滞阻尼)。
②与质点速度平方成反比(如质点在流体中运动受到的阻力)。
③与质点速度无关(如摩擦力)。
粘滞阻尼力的分析比较简单,(因为R(t)=-Cy ).
结构动力学单自由度

m3
例如: 例如:
m
m1
m2
mk
mN
− m1&&1 x x − m2&&2 − mk &&k x
x − mN &&N
2. 广义坐标法
假定具有分布质量的结构在振动时的位移曲线可用一系列 规定的位移曲线的和来表示: 规定的位移曲线的和来表示:
适用于质量分布比较均 匀,形状规则且边界条 件易于处理的结构。 件易于处理的结构。 例如: 例如:右图简支梁的变 形可以用三角函数的线 性组合来表示。 性组合来表示。
结构的自由振动与受迫振动 结构的自由振动与受迫振动
y
y
t
t
定义
结构受外部干扰后发生振动,而在干扰消失后继续振动, 结构受外部干扰后发生振动,而在干扰消失后继续振动, 这种振动称为结构的自由振动 自由振动。 这种振动称为结构的自由振动。 如果结构在振动过程中不断地受到外部干扰力作用, 如果结构在振动过程中不断地受到外部干扰力作用,这种 振动称为结构的强迫振动 又称受迫振动 强迫振动, 振动称为结构的强迫振动,又称受迫振动 。
结构的动力特性
数学模型
承受动力荷载的结构体系的主要物理特性: 承受动力荷载的结构体系的主要物理特性: 质量、弹性特性、阻尼特性、 质量、弹性特性、阻尼特性、外荷载 在最简单的单自由度体系模型中, 在最简单的单自由度体系模型中,所有特性都假定集结于 一个简单的基本动力体系模型 基本动力体系模型内 一个简单的基本动力体系模型内,每一个特性分别由一个 具有相应物理特性的元件表示: 具有相应物理特性的元件表示:
与结构静力学相比,动力学的复杂性主要表现在: 与结构静力学相比,动力学的复杂性主要表现在: • 动力问题具有随时间而变化的性质; 动力问题具有随时间而变化的性质; • • • • 数学解答不是单一的数值,而是时间的函数; 数学解答不是单一的数值,而是时间的函数; 惯性力是结构内部弹性力所平衡的全部荷载的一个重要部 分! 引入惯性力后涉及到二阶微分方程的求解; 引入惯性力后涉及到二阶微分方程的求解; 需考虑结构本身的动力特性:刚度分布、质量分布、 需考虑结构本身的动力特性:刚度分布、质量分布、阻尼 特性分布的影响; 特性分布的影响;
结构力学

自由振动的解
比较两式得:
A ( y 0 ) (v 0 / w )
2 2
arctan
wy0
v0
(a)没有初始速度,仅由初始位移引起的振动按 的 y0 coswt 的规律变化; (b)没有初始位移,仅由初始速度引起的振动按 的 v 0 sin wt 的规律变化; w (c)既有初始位移,又有初始速度引起的振动形态按 方程 y(t ) A sin(wt ) 进行。
能相差很大;
b、两个外表看来并不相同的结构,如果其自振周期相
近,则在动荷载作用下其动力性能基本一致。地震中常 出现这样的现象。
2009-12-3
单自由度系统的动力特性
圆频率的计算公式:
w
k m 1 m g W g st
圆频率也仅与结构参数k和m有关,即仅与结构体 系本身的固有性质有关,而与初始干扰无关,故称 为固有频率或自振频率。
y A sin(wt v)
则,系统振幅和初相角为:
A y
2 0
w
2 0 y 2
,
v arc tg
w y0
0 y
因物体落到C点后才开始振动,所以
y0 yst , 0 2gh y
2009-12-3
课后练习
于是
2 gh 2 A y yst 2hyst g / yst
2009-12-3
单自由度系统的动力特性
(3)工程频率f :
w, 单位为Hz。 f 2
计算自振周期的几种形式:
(1)由周期和圆频率的定义可知:
m T 2 k
(2)将
1 k
代入上式,得:
T 2 m
2009-12-3
结构力学-单自由度体系的自由振动

mh3 T 2 24 EI
Vibration Characteristic
y(t ) Asin( t )
Acceleration: Inertia Force:
(t ) A 2 sin(t ) y (t ) mA 2 sin(t ) I (t ) m y
这是一个齐次方程,其通解为
y(t ) C1 cost C2 sin t
C1 和 C2 可由初始条件确定,设初始位移和初始速度分别为
y(0) y0 C1 y0
(0) v0 y
C2
v0
v0
,
y (t ) y0 cos t
sin t
y (t ) y0 cos t
在无阻尼自由振动中,位移、加速度和惯性力都按正弦规律
变化,且作相位相同的同步运动,即它们在同一时刻均达极值,
而且惯性力的方向与位移的方向一致。
幅值产生于
sin(t ) 1 时,其值分别为:
y A
A 2 y
I mA
2
由于在运动的任一瞬时质体都处于平衡状态,在幅值出现时
l
1 m
EA ml
st Wl T 2 2 g EAg
例: 求图示结构自振频率 。(EI 为常数,杆件自身 质量不计) [分析] 图乘法求位移
A m C l h
1 1 2 2 1 2 h2 B ( h h hl h) (h l ) EI 2 3 2 3 3EI
y y
v0
sin t
T
0
t
y cos t
-y
y
结构动力学习题答案

结构动力学习题答案在结构动力学中,习题答案通常涉及对结构在动态载荷下的行为进行分析和计算。
这些习题可能包括自由振动分析、受迫振动分析、随机振动分析、模态分析、响应谱分析等。
以下是一些典型的结构动力学习题答案示例。
习题一:单自由度系统的自由振动问题:一个单自由度系统具有质量m=2kg,阻尼系数c=0.5N·s/m,弹簧刚度k=800N/m。
初始条件为位移x(0)=0.1m,速度v(0)=0。
求该系统自由振动的位移时间历程。
答案:首先,确定系统的自然频率ωn:\[ \omega_n = \sqrt{\frac{k}{m}} = \sqrt{\frac{800}{2}}\text{ rad/s} \]然后,计算阻尼比ζ:\[ \zeta = \frac{c}{2\sqrt{mk}} = \frac{0.5}{2\sqrt{2 \cdot 800}} \]由于ζ < 1,系统将进行衰减振动。
可以使用以下公式计算位移时间历程:\[ x(t) = A e^{-\zeta \omega_n t} \cos(\omega_d t + \phi) \] 其中,\( \omega_d = \sqrt{\omega_n^2 - \zeta^2 \omega_n^2} \) 是阻尼频率,A是振幅,\( \phi \)是相位角。
初始条件给出x(0)=0.1m,v(0)=0,可以解出A和\( \phi \)。
最终位移时间历程的表达式为:\[ x(t) = 0.1 e^{-\zeta \omega_n t} \cos(\omega_d t) \]习题二:单自由度系统的受迫振动问题:考虑上述单自由度系统,现在施加一个简谐力F(t)=F_0sin(ωt),其中F_0=100N,ω=10 ra d/s。
求系统的稳态响应。
答案:稳态响应可以通过傅里叶级数或直接应用受迫振动的公式来求解。
对于简谐力,系统的稳态响应为:\[ x_{ss}(t) = \frac{F_0}{k - m\omega^2} \sin(\omega t + \phi) \]其中,\( \phi \) 是相位差,可以通过以下公式计算:\[ \phi = \arctan\left(\frac{2\zeta\omega}{\omega_n^2 -\omega^2}\right) \]习题三:多自由度系统的模态分析问题:考虑一个二自由度系统,其质量矩阵M和刚度矩阵K如下:\[ M = \begin{bmatrix} m_1 & 0 \\ 0 & m_2 \end{bmatrix},\quad K = \begin{bmatrix} k_1 & -k_c \\ -k_c & k_2\end{bmatrix} \]其中,\( m_1 = 2kg \),\( m_2 = 1kg \),\( k_1 = 800N/m \),\( k_2 = 1600N/m \),\( k_c = 200N/m \)。
单自由度体系自由振动,速度相位与位移相位的关系

单自由度体系(Single Degree of Freedom System, SDOF)是工程动力学中的一个重要概念,它对于描述系统的振动特性有着重要的作用。
在自由振动过程中,速度相位与位移相位之间存在着密切的关系。
本文将从单自由度体系自由振动的基本原理入手,探讨速度相位与位移相位之间的关系,希望通过本文的介绍,读者能够对这一问题有更加清晰的认识。
一、单自由度体系自由振动的基本原理1. 自由振动的基本概念自由振动是指在没有外界干扰的情况下,系统在一定的初位移或初速度作用下,由于其自身的惯性和弹性特性而产生的振动现象。
在工程领域中,自由振动是一种非常常见的振动形式,因此研究自由振动对于工程设计和分析有着重要的意义。
2. 单自由度体系的定义单自由度体系是指系统中只有一个自由度可以自由变化的体系。
在动力学领域中,单自由度体系被广泛应用于描述各种机械、土木和航空航天结构的振动特性。
它是一种简化模型,但对于许多实际工程问题的分析具有较高的适用性。
3. 自由振动的基本方程单自由度体系的自由振动可以通过一阶微分方程来描述。
其基本方程可以表示为:\[m\ddot{x}+c\dot{x}+kx=0\]其中,\(m\)为系统的质量,\(c\)为系统的阻尼系数,\(k\)为系统的刚度,\(x\)为系统的位移函数,\(t\)为时间。
二、速度相位与位移相位的定义1. 速度相位的定义在振动过程中,速度相位是指速度\(v\)相对于位移\(x\)的相位差。
通常用一个角度来表示,它可以用来描述振动的快慢和超前滞后关系。
2. 位移相位的定义位移相位是指位移\(x\)相对于某一固定参考点的相位差。
它也通常用一个角度来表示,可以用来描述振动的相对位置。
三、速度相位与位移相位的关系速度相位与位移相位之间存在着密切的关系。
在自由振动过程中,它们之间满足以下关系:\[tan(\phi_v-\phi_x)=\frac{2\zeta}{1-\omega^2}\]其中,\(\phi_v\)为速度相位,\(\phi_x\)为位移相位,\(\zeta\)为系统的阻尼比,\(\omega\)为系统的固有频率。
结构动力学 -单自由度体系的振动

13
§2.2 无阻尼自由振动
自由振动(free vibration) :无外界干扰的体系振动形 态称为自由振动(free vibration)。振动是由初始位 移或初始速度或两者共同影响下所引起的。 无阻尼自由振动:如果阻尼系数等于零,则这种自由 振动称为无阻尼自由振动(undamped free vibration)。 假设由于外界干扰,质点离开平衡位置,干扰消失后, 质点将围绕静力平衡点作自由振动。
或:m y ( t) c y ( t) k ( t) y m y g ( t) P e( f t) f
Peff (t ) :等效荷载,即在地面加速度yg (t )影响下,结构的响
应就和在外荷载p (t )作用下的响应一样,只是外荷载 p (t )
等于质量和地面加速度的乘积。
干扰力的大小只能影响振幅A的大小,而对结构自
振周期T的大小没影响。
(2)自振周期与质量平方根成正比,质量越大,则
周期越大;自振周期与刚度的平方根成反比,刚度
越大,则周期越小。要改变结构的自振周期,只有
改变结构的质量或刚度。
24
§2.2 无阻尼自由振动
k g
m
st
(3)把集中质点放在结构上产生最大位移的地方,则可
1、位移以静力平衡位置作为基准的,而这样确定的位移 即为动力响应。
2、在求总挠度和总应力时,要把动力分析的结果与静
力分析结果相加。
9
§2.1运动方程的建立
3、支座运动的影响 结构的动位移和动应力既可以由动荷载引起,也
可以由结构支座的运动而产生。 1)由地震引起建筑物基础的运动; 2)由建筑物的振动而引起安置在建筑物内的设备 基底的运动等等。
结构动力学第二章 单自由度系统的振动2

0.39 0.66 0.73 1.00 1.05 1.20 1.42 1.55 1.69 1.76 2.00
23
24
解: 水塔的自振频率和周期分别为
k 29.4106 N / m 31.305rad / s
m
30103 kg
T 2 0.2007s
取微小时段 0.01s ,约相当于水塔自振
同理,积分项 B(t) 可用相同的方法进行计算。
16
因此,无阻尼体系动力响应的数值解: y(t) A(t) sin t B(t) cost
同理,也可求得有阻尼体系动力响应。 注:数值积分解答的精确度与计算中选择和微 小时段 有关,一般可取小于系统自振周期 的十分之一,便可得到较好的结果。
17
A yst
1
2
t1
2
( 1 cost1
) 2
t1
1/ 2
sint1
t1 T
0.371
动力系数只与 t1 有关,即只与 t1 T 有关
下表列出不同 t1 T 值时的动力系数。
表 不同 t1 T 值时的动力系数表
t1/T 0.125 0.20 0.25 0.371 0.40 0.50 0.75 1.00 1.50 2.00
用下式进行计算。
无阻尼:
( 0)
y(t) 1 t p( ) sin (t )d
m 0
有阻尼: y(t) 1
( 0)
md
t 0
p(
)e (t )
sin d
(t
)d
2)对于许多实际情况,如果荷载的变化规律是 用一系列离散数据表示(如试验数据),此时 的响应计算就必须借助于数值分析方法。
11
结构力学:结构动力学-1

k11
3EI l3
刚度系数
my(t)
3EI l3
y(t)
P(t)
运动方程
m P(t)
my(t) y(t)
y
k11 y
k11y(t) P(t) my(t)
一、刚度法
刚度法步骤: 1.在质量上沿位移正向加惯性力; 2.求发生位移y所需之力; 3.令该力等于体系外力和惯性力。
练习:列图示体系的运动方程。
m y(t)
P(t)
m
P(t) P(t)
my(t) P(t) 运动方程 P(t) my(t) 惯性力 P(t) P(t) 0
形式上的平衡方程,实质上的运动方程
y(t)
k
m
P(t)
ky(t)
m
P(t)
my(t) P(t) ky(t)
ky(t)
P(t)
my(t)
P(t) [my(t)] ky(t) 0
m
y(t)
=1 11
P(t)
y(t) P(t)
my(t)
l EI
l
EI
l
11
2l 3 3EI
my(t)
3EI 2l 3
y(t)
P(t)
练习: 列图示体系的运动方程。
l
11
2l 3 3EI
my(t)
3EI 2l 3
y(t)
P(t)
例9-3 列图示体系的运动方程。
m
y(t)
=1 11
P(t)
y(t) P(t)
my(t)
l EI
l
EI
l
11
2l 3 3EI
my(t)
3EI 2l 3
《结构力学》结构动力学(2)

为最大的动力位移与静力位移之比,称为位移动力系数。
简谐荷载作用下, 与 之间关系曲线分析。
1、无阻尼条件
(1) 0 时, 5.0
1, ymax ( t ) yst。
4.0
(2)0 1 0 时,
随着 增加 增大,
3.0
0
FP ( t ) FP sint。 y( t ) yst sint。
(3)当ξ=1时的阻尼称为临界阻尼;相应的 值称为
临界阻尼系数,用cr 表示,则
cr 2mk 2m ,
k 2mk 2m cr
阻尼比 即为阻尼系数 与临界阻尼系数 cr 之比。
§14-4 单自由度结构在简谐荷载作用下的强迫振动
当干扰力 F(t) 直接作用在质点上,质点的受力将如图14-10所示,
且 y( t )与FP ( t ) 同步。
2.0
(3) 1 时, 1.0
, ymax ( t ) , 共振。
(4)1 时,
1.0 2 2.0
3.0
随着 增加 减小,且 y( t )与 FP ( t ) 反向。
(5) 时, 0, 在静平衡位置附近作微小
振动 。
y0
cos 't
y0
ky0
'
sin
't
y bekt sin( 't ')
其中
b
y02
(ห้องสมุดไป่ตู้
y0
ky0
'
)2
tan ' ' y0
/ 为有阻尼自振频率。
y0 ky0
令 k ,称为阻尼比。
' 2 k2 1 ( k )2 1 2
通常当ξ<0.1时,则 ' 和 的差别很小。
于开平-结构动力学第二讲

(2) 阻尼力的功:
Wd A cos t dt c 2 / 1 cos 2 t cA2 2 dt 0 2 1 2 1 2 2 2 / cA2 2 cA cos 2 t dt 0 2 2
5 稳态响应振幅和相位
5.2 初始相位角 根据初相位角表达式
2 tg 1 2
可以画出初相位角随频率比的变化曲线,简称相频曲线:
在共振点,不管阻尼比多大,初相位角均为90度。
6 稳态响应复数解法及频响函数
之前将外载荷假设为正弦形式,其运动控制方程为:
������������ሷ 1 + ������������ሶ 1 + ������������1 = ������0 sin������������ 简谐激励的另一种典型形式为余弦形式,其运动控制方程写作: ������������ሷ 2 + ������ ������ሶ 2 + ������������2 = ������0 cos������������ (2) (1)
o o o
o
1 2 Fo A sin Fo A sin 2
6 稳态响应复数解法及频响函数
令方程特解为������ ������ = ������������ ������ ������������������ ,代入运动控制方程得: (−������2 ������������������ + ������������������������������ + ������������������ )������ ������������������ = ������0 ������ ������������������ 方程对任意时刻t恒等,则方程两边指数函数������ ������������������ 前系数相等,由此可得: ������������ = ������0 ������ − ������������ 2 + ������������������
结构动力学-2(哈工大结构动力学)

m y(t)
cy(t)
my(t) k11 y(t )
运动方程 my cy k11y 0
令 c / 2m y 2y 2 y 0
设 y(t) Aet
2 2 2 0 特征方程
根为 i 1 2 由初始条件
小阻尼情况
y(0) y0 , y(0) v0
1 (c 2m)
c1 (v0 y0 ) / D , c2 y0
k
k
k
PROBLEMS:
3.A mass m is at rest,partially supported by a spring and partially by stops.In the position shown,the spring force is mg/2. At time t=0 the stops are rotated,suddenly releasing the mass.Determine the motion of the mass.
第二章单自由度体系的振动分析
§2.1 自由振动
一. 无阻尼体系 运动方程
y(t) 11[my(t)] k11y(t) my(t) 令 2 k11 1
m m11
y(t) 2 y(t) 0
二阶线性齐次常微分方程
m
my(t)
y(t)
l EI
km
运动方程的通解 y(t) c1 cost c2 sin t
令 D 1 2
方程的通解为
y(t) Aet sin( Dt D )
A
y02
( v0
y0 D
)2
y(t) et (c1 sin Dt c2 cosDt) tan D y0D /(v0 y0 )
结构动力学之单自由度体系简谐荷载作用下的受迫振动
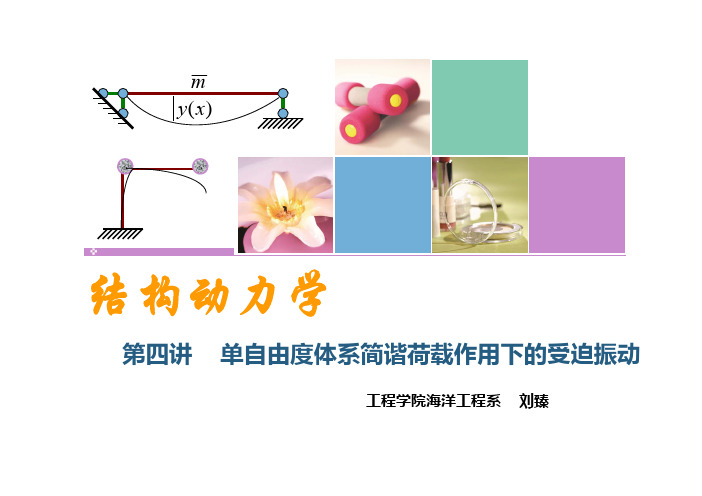
由初始条件确定 振动由两部分组成: 第一部分按荷载频率 θ 振动,为纯粹的强迫振动; 第二部分按自振频率 ω 振动,为外力引起的自由振动。
变换得: y 2 y
。
即把非直接作用于质体的荷载按照静力位移 等效的条件转换成直接作用于质体的荷载。
等效 12 F (t ) F( t ) 11
2013/12/10
课后练习
F 则运动方程的解为:y 0.6875 2 m 1 1
48 EI ml 3
b)当2 1.2
ymax
F 1 F ml 3 Fl 3 0.6875 0.6875 (2.2727) 0.0326 2 m 1 1.44 m 48EI EI
2013/12/10
有阻尼受迫振动方程解
在外力 p( t ) P sin t 作用下,并且考虑阻尼
2013/12/10
动力系数β
sin t P 即特解部分: y (t ) m 2 (1 2 2 )
令:
p y st p 2 m k
p
1 1Байду номын сангаас 2 / 2
yst为最大静位移,表示将荷载最大值P当作静荷 载作用时结构所产生的位移;
β为动力放大系数或动力系数,表示最大动位移 [y(t)]max 与最大静位移yst 的比值。
课后练习
例2:
F (t ) F sin t 图示跨中带有一质体的无重简支梁,动力荷载
作用在距离左端l/4处,若
2-1结构动力学(单自由度)解析

2. 有阻尼自由振动
cy ky FP (t ) m y
FP(t)=0
cy ky 0 m y
k c , 2 m m
2
2y y 0 y
2
2. 有阻尼自由振动
2 y 2y y 0
特征方程
y 0 y0 y 0 v0
y (t ) y 0 cost
v0
sin t
(1)方程的解
y(t ) y0 cost v0
sin t
y(t ) A sin t
振幅
(amplitude of vibration)
A
y0
2
0 y v0 2 = y0
m/2
EI EI EI
m
l
2 l3 11 3 EI
l
1 3 2l 3 m 2 3EI
EI ml 3
3. 质点重W,求图示体系的自振频率。
k11 k
EI k
3EI l3
l
m W / g
3EI k 3 l g W
4. 求图示体系的自振频率。
m
EI EI1=∞ EA l
g y st
y st m T 2 2 k g
频率只取决于体系的质量和刚度,而与外界因素 无关,是体系本身固有的属性,所以又称为固有频率
(natural frequency)。
(3)简谐自由振动的特性
y(t ) Asin( t )
(t ) A 2 sin(t ) y 加速度为: 惯性力为: FI (t ) m (t ) mA 2 sin(t ) y
10结构动力学概论

当 FP (t)为简谐荷载时,其解的形式为
第十章 结构动力学简介
y(t)
y0
cos ωt
ν0 ω
sin ωt
F
θ sin ωt
F
sin θt
m(ω2 θ 2 ) ω
m(ω2 θ 2 )
前两项为初始条件引起的自由振动;第三项为荷载(干扰力)引起的自由振 动,称为伴生自由振动。实际上,由于阻尼的存在,自由振动部分都很快 衰减掉。自由振动消失前的振动阶段称为过渡阶段。第四项为按荷载频率 进行的振动,此阶段为振动的平稳阶段,称为纯受迫振动或稳态振动。
2、平衡方程的建立
平衡方程的建立有两种方法:一是刚度法;一是柔度法。
my
y k
k
m
刚度法:根据达兰贝尔原理,沿位移正向,在质点上加上惯性力,列动态平 衡方程
ky my
k y ——总是与位移方向相反,指向平衡位置
平m衡y 方—程—与加速m度y方向相k反y 0
第十章 结构动力学简介
柔度法:在惯性力作用下,质点的位移等于实际位移
结构力学
STRUCTURAL MECHANICS
第十章 结构动力学简介
§10-1 概述
一、动力计算的内容
动力计算的内容:研究结构在动荷载作用下的动力反应的计算原理和方法。 涉及到内外两方面的因素: 1)确定动力荷载(外部因素,即干扰力); 2)确定结构的动力特性(内部因素,如结构的自振频率、周期、振型和 阻尼等等),类似静力学中的I、S等; 计算动位移及其幅值;计算动内力及其幅值。
纯受迫振动解的讨论请同学们课下自学完成!
第十章 结构动力学简介
三、阻尼对振动的影响
§10-3 单自由度体系的振动分析
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
c1 (v0 y0 ) / D , c2 y0
令 D 1 2
方程的通解为
y(t) et (c1 sin Dt c2 cosDt)
y(t) A
tan D
Aet sin( Dt D )
y02
( v0
y0 D
)2
y0D /(v0 y0 )
小阻尼情况
y(0) y0 , y(0) v0
c-----阻尼系数 (damping coefficient )
二、运动方程及其解
m y(t)
cy(t)
my(t) k11 y(t )
运动方程 my cy k11y 0
令 c / 2m y 2y 2 y 0
设 y(t) Aet
2 2 2 0 特征方程
二、运动方程及其解
Ak11 mA 2 2 k11 m
幅值方程
2.算例 例一.求图示体系的自振频率和周期.
解:
11
1 EI
(1 2
l
l
2 3
l
1 2
l
l
l
1l 2
l 2
l)
7 l3
12 EI
1
m11
12EI 7ml3
l/2
T 2 2 7ml3
12EI
m
EI EI
l
=1 11
l
l
=1
l
例二.求图示体系的自振频率和周期. m/2 m
Tmax
1 m(2l)2
2
1 m(l)2
2
m
l
EI m m
k
(t )
k
lll
1 m(2l)2 9 ml2 2 2
2
2
U max
1 k(l)2
2
1 k(2l)2
2
5 kl2 2
2
Tmax Umax
5k
9m
2.列幅值方程
MA 0
2l 2m
kl l 2m 2l 2m
A
2kl
2l 2m 2l kl l ml2 l 2lm2 2l 2lk 2l 0
Asin[ (t 2 ) ] y(t 2 )
T 2
自振周期
T 2 自振周期
1 2 自振园频率(自振频率)
T
A
振幅
初相位角
与外界无关,体系本身固有的特性
三.自振频率和周期的计算 1.计算方法
E(t)
1 2
my02
1 2
kv02
=常数
(1)利用计算公式
2 k11 1 m m11
9l 2 2m 5kl2 0
5k
9m
2.1.2 粘滞阻尼自由振动
一、阻尼假定 阻尼:使振动衰减的作用. 阻尼产生原因:材料的内摩擦,接触面等处的外摩擦及介质阻力等. 阻尼力:在振动分析当中用于代替阻尼作用的阻碍振动的力。 粘滞阻尼理论假定阻尼力大小与速度成正比,方向与速度相反。
R(t) cy(t)
2
2
E(t)
1 2
m
2[- y0sin
t
v0
cost]2
1 2
k[
y0cost
v0
sin
t]2
(3)利用振动规律
y(t) Asin( t ) y(t) A 2 sin( t ) I (t) my(t) mA 2 sin( t )
位移与惯性力同频同步.
m y(t)
l EI
mA 2 A
1
k11
y(t) Asin( t )
其中
A
y02
y02
2
tan
y0
y0
一.运动方程及其解
m my(t) y(t)
l EI
y(t) 11[my(t)]
k11y(t) my(t)
令
2 k11 1 m m11
y(t) 2 y(t) 0
二阶线性齐次常微分方程
其通解为 y(t) c1 cost c2 sin t
l
=1
解:
11
2 3
l3 EI
EI EI
l EI l
1 3 m 2l3
EI ml3
l
2 3EI
T 2 ml3
EI
例三.质点重W,求体系的频率和周期.
解:
k11
k
3EI l3
mW /g
k
3EI l3
g
3EI l2
W
EI
k
l
k11
1
k11
3EI
l3
k
例四.求图示体系的自振频率和周期.
解: 1.能量守恒
k11y(t) my(t)
令
2 k11 1 m m11
y(t) 2 y(t) 0
二阶线性齐次常微分方程
其通解为 y(t) c1 cost c2 sin t
由初始条件
y(0) y0 y(0) y0
可得 c1 y0 c2 y0 /
y(t)
y0
cost
y0
sin
t
令 y0 Asin y0 / Acos
1 (c 2m)
c1 (v0 y0 ) / D , c2 y0
令 D 1 2
方程的通解为
y(t) et (c1 sin Dt c2 cosDt)
y(t) A
tan D
Aet sin( Dt D )
y02
( v0
y0 D
)2
y0D /(v0 y0 )
临界阻尼情况
1(c 2m) y(t) et[(v0 y0 )t y0 ]
由初始条件
y(0) y0 y(0) y0
可得 c1 y0 c2 y0 /
y(t)
y0
cost
y0
sin
t
二.振动分析
令 y0 Asin y0 / Acos
y(t) Asin( t )
其中
A
y02
y02
2
tan
y0
y0
单自由度体系不计阻尼时的自由振动是简谐振动.
y(t) Asin( t ) Asin( t 2 )
m y(t)
cy(t)
my(t) k11 y(t )
运动方程 my cy k11y 0
令 c / 2m y 2y 2 y 0
设 y(t) Aet
2 2 2 0 特征方程
根为 i 1 2 由初始条件
小阻尼情况
y(0) y0 , y(0) v0
1 (c 2m)
W mg, st W11 2 g
st
T (t) 1 my 2 (t) 1 mA2 2 cos2 (t )
2
ቤተ መጻሕፍቲ ባይዱ
2
U
(t)
1 2
k11 y 2
(t)
1 2
k11 A2
sin
2
(t
)
(2)利用机械能守恒
Tmax Umax
EI
1 2
my02
1 2
kv02
E(t) 1 my 2 (t) 1 ky2 (t)
§2.单自由度体系的振动分析
§2.1 自由振动分析
自由振动---由初位移、初速度引起的,在振动中无动荷载作用的振动。
分析自由振动的目的---确定体系的动力特性:频率、周期。
阻尼---耗散能量的作用。
2.1.1 不计阻尼自由振动
一.运动方程及其解
m my(t) y(t)
l EI
y(t) 11[my(t)]
超阻尼情况
1(c 2m)
y(t)
et ( v0
y0 c
shct
y0ch ct )
c
2 1
c / 2m
1
cr 2m -----临界阻尼系数 c c -----阻尼比 cr 2m
