第五章补充_单自由度系统的振动讲解
单自由度振动系统

单自由度振动系统m质量,k刚度,c阻尼,有时有p激振力单自由度振动系统,指用一个独立参量便可确定系统位置的振动系统。
只要以它的平衡位置取为坐标原点,任一瞬时的质点坐标x(线位移)或 (角位移)就可以决定振动质点的瞬时位置。
根据牛顿定律:mx+cx+kx=F1.单自由度系统无阻尼自由振动mx+kx=0;x+kmx=0;令w m2=k/m,求微分方程的解,得x=c1e iw n t+c2e−iw n t=c1+c2cosw n t+i c1−c2sinw n t=b1cosw n t+b2sinw n t将其合成一个简谐振动,并代入初始条件:t=0时,x=x0,x=x0x=Asin(w n t+φ); A=x2+x02w n2; φ=tg−1x0w nx01.1固有频率系统的圆频率和频率只与系统本身的物理性质(弹性和惯性)有关,因此当振动系统的结构确定后,系统的振动频率就固定不变,而不管运动的初始条件如何,也和振幅的大小无关,因此成为固有圆频率和固有频率。
w n=km ;f n=12πkm1.2固有频率计算方法1)公式法。
根据公式w n=km计算2)静变形法。
根据质量块所处平衡位置的弹簧变形计算。
3)能量法。
根据能量守恒定律,由于无阻尼,无能量损失,12mx2+12kx2=E,将x的方程代入上式,系统的最大动能等于系统的最大弹性势能,计算求出。
4)瑞利法。
考虑到系统弹簧质量的计算方法,如假设系统的静态变形曲线作为假定的振动形式,根据推倒,得出系统的固有频率为w n=km+ρl3,式中加入的部分为“弹簧等效质量”不同振动系统的等效质量不同,只需先算出弹性元件的动能,根据T s =12m s x 2,计算即可。
1.3扭转振动根据扭转运动的牛顿定律 M =I θ,M 为施加到转动物体上的力矩,I 转动物体对于转动轴的转动惯量,θ角加速度。
圆盘转动惯量为I ,轴的转动刚度为kθ。
系统受到干扰后做扭转自由振动,振动时圆盘上受到一个由圆轴作用的与θ方向相反的弹性恢复力矩-K θθ。
单自由度系统的有阻尼自由振动

0.8 (e nTd ) 20 0.16
ln5 20 nTd 20 n 2 n 1 2
由于 很小,ln5 40
ln5 W W ln5 1502 c 2 m k 2 2 40 g st 40 1980 0.122( Ns/cm)
nt
2 t n2 n
C2 e
2 t n2 n
)
代入初始条件 (t 0时 , x x0 , x x 0 )
C1
2 0 ( n n 2 n x ) x0
2 n
2
2 n
; C2
2 0 ( n n 2 n ) x0 x 2 2 n 2 n
可见阻尼使自由振动的周期增大,频率降低。当阻尼小时, 影响很小,如相对阻尼系数为5%时,为1.00125,为20%时, 影响为1.02,因此通常可忽略。
14
振幅的影响: 为价评阻尼对振幅衰减快慢的影响,引入减 幅系数η ,定义为相邻两个振幅的比值。
Ai Aewnti wnti td ewntd Ai 1 Ae
5
也可写成
x Ae nt sin(d t )
2 d n n2
—有阻尼自由振动的圆频率
x 0 , 则 设 t 0 时, x x0 , x
2 2 2 x n ( x nx ) 0 n 2 A x0 0 2 02 ; tg1 0 nx0 n n x
16
例4 如图所示,静载荷P去除后质量块越过平衡位置的最大 位移为10%,求相对阻尼系数。
17
x(t ) e
wnt
0 wn x0 x ( x0 cos wd t sin wd t ) wd
18
12.3 单自由度体系的自由振动

各杆EI= 。 【例12-5】试求图示结构的ω。各杆 =C。 】
3l 4 B C D m B y A l l l 4 A l C D l
1
M1 图
解:
δ 11
7l 3 = 12 EI
1 12 EI EI = = 1.309 ω= 3 mδ11 7ml ml 3
All Rights Reserved 重庆大学土木工程学院®
【注二】惯性力 FI = −m&& = maω 2 sin(ωt + α ) = mω 2 y , 注二】 y FI 永远与位移方向一致,在数值上与位移成比例, 永远与位移方向一致,在数值上与位移成比例,其比例系 数为 mω 2 。
All Rights Reserved
重庆大学土木工程学院®
12.3.4 自振周期与自振频率
1.自振周期 自振周期 因
y = a sin (ωt + α ) = a sin (ωt + α + 2 π ) 2π = a sin ω t + + α = a sin[ω (t + T ) + α ] ω
所以自振周期
T =
2π
ω
表示体系振动一次所需要的时间,其单位为 ( 表示体系振动一次所需要的时间,其单位为s(秒) 。
式中, 为重力加速度 为重力加速度; 式中,g为重力加速度;W=mg为质点 为质点 的重力; 表示将重力W=mg 的重力;∆st=Wk11,表示将重力 施加于振动方向所产生的静位移。 施加于振动方向所产生的静位移。
All Rights Reserved 重庆大学土木工程学院®
T = 2π ∆st g
All Rights Reserved 重庆大学土木工程学院®
单自由度系统自由振动

取物块的静平衡位置为坐标原点 O , x 轴顺弹簧 变形方向铅直向下为正。当物块在静平衡位置 时,由平衡条件,得到
mg k st
弹簧的静变形
当物块偏离平衡位置为x距离时,物块的运动微 分方程为
mx mg k ( st x)
mx kx
k 固有圆频率 令 : 0 m 无阻尼自由振动微分方程 2018年9 月4日
周期 T 2
0
; 则
1 0 2 2f T
f 称为振动的频率,表示每秒钟振动的次数,单位为1/s或Hz
0 称为固有角(圆)频率(固有频率),表示每2秒内振动
2018年9月4日 《振动力学》
的次数,单位为rad/s,只与系统的质量m和刚度系数k有关。
8
1.单自由度系统自由振动-无阻尼自由振动
统固有的物理参数,称为固有频率,振幅取决 于初始扰动的大小。阻尼振动的固有频率小于 无阻尼情形。临界阻尼和大阻尼条件下的系统 作非往复的衰减运动。
2018年9月4日 《振动力学》
3
单自由度系统自由振动
教学内容
• 无阻尼自由振动 • 能量法 • 等效质量和等效刚度 • 阻尼自由振动
2018年9月4日 《振动力学》
c1 A sin ,
c2 A cos
x t A sin 0 t
2018年9月4日 《振动力学》
无阻尼自由振动是简谐振动.
7
1.单自由度系统自由振动-无阻尼自由振动
1.2 无阻尼自由振动的特点
(1)固有频率
无阻尼自由振动是简谐振动,是一种周期振动
0 ( t T ) 0t 2
振动不能维持等幅而趋于衰减,称为有阻尼自由
《单自由度系的振动》课件

主动控制技术广泛应用于航空航天、机械制造、土木工程等领域, 以减小或消除结构的振动。
优势与局限性
主动控制技术的优点在于能够快速响应并有效抑制振动,但需要外部 能源和复杂的控制系统,增加了系统的复杂性和成本。
被动控制技术
被动控制技术定义
被动控制技术是利用阻尼材料或结构来吸收或耗散振动能量的方 法。
弹性力学模型
描述弹性体的振动特性,适用于弹性体的振动。
振动分析的数值方法
有限元法
将系统离散化为有限个单元,求解每个单元的振动响应。
时域法
在时间域内直接求解系统的振动响应。
频域法
将系统振动问题转化为频率域内的问题,求解系统的振动特性。
04
单自由度系统的振动控 制
主动控制技术
主动控制技术定义
主动控制技术是一种通过向系统提供反向振动来抵消原始振动的方 法。
03
单自由度系统的振动分 析
振动分析的基本方法
解析法
通过数学公式推导,求解系统的振动特性。
实验法
通过实验测量系统的振动响应,分析其特性 。
数值法
利用数值计算方法,求解系统的振动响应。
振动分析的数学模型
线性模型
描述线性系统的振动特性,适用于小振幅振动。
非线性模型
描述非线性系统的振动特性,适用于大振幅振动 。
总结词
在机械系统中,振动控制是提高设备稳定性和延长使用寿命 的关键。
详细描述
机械系统中的许多设备,如发动机、压缩机、机床等,都容 易受到振动的影响。通过采用适当的控制策略,如主动或被 动隔振、阻尼减振等,可以有效减小振动对设备性能的影响 ,提高设备的稳定性和可靠性。
建筑结构中的振动控制
机械震动--单自由度体系的自由振动

y sy(t)机械振动分析------单自由度无阻尼系统的自由振动机械振动是物体(或物体的一部分)在平衡位置(物体静止时的位置)附近作的往复运动。
可分为自由振动、受迫振动。
又可分为无阻尼振动与阻尼振动。
常见的简谐运动有弹簧振子模型、单摆模型等。
振动在机械中的应用非常普遍,例如在振动筛分行业中基本原理系借电机轴上下端所安装的重锤(不平衡重锤),将电机的旋转运动转变为水平、垂直、倾斜的三次元运动,再把这个运动传达给筛面。
若改变上下部的重锤的相位角可改变原料的行进方向。
物体受到初干扰后,仅在系统的恢复力作用下在其平衡位置附近的振动称为无阻尼自由振动。
其中仅需用一个独立坐标就可确定振体位置的系统为单自由度系统。
单自由度系统的振动理论是振动理论的基础。
研究单自由度系统的振动有着非常普遍的实际意义,因为工程上有许多问题通过简化,用单自由度系统的振动理论就能得到满意的结果。
而同时对多自由度系统和连续系统的振动,在特殊坐标系中考察时,显示出与单自由度系统类似的性态。
因此,揭示单自由度振动系统的规律、特点,为进一步研究复杂振动系统奠定了基础。
影响振动作用的因素是振动频率、加速度和振幅。
现在我们就此方面展开对单自由度无阻尼振动的讨论。
主要包括两部分:单自由度无阻尼系统的自由振动和单自由度无阻尼系统的受迫振动。
一、单自由度无阻尼系统的自由振动如下图,设此梁上的集中质量为m ,其重量为W mg ,梁由于质量的重力引起的质量处的静力位移用s y 表示,与s y 相应的质量位置称为质量的静力平衡位置。
若此质量受到扰动离开了静力平衡位置,当扰动除去后,则体系将发生振动,这样的振动称为体系的自由振动。
由于振动的方向与梁轴垂直,故称为横向振动。
在此,只讨论微小振幅的振动,由振动引起的内力限于材料的弹性极限以内,用以表示质量运动的方程将为线性微分方程。
1、建立运动方程建立运动方程常用的基本原理是达朗伯原理(亦称惯性力法或动静法)。
单自由度体系的自由振动

令
ω2 = k
m
y + ω 2 y = 0
运动方程的解 y + ω 2 y = 0 可由振动的初 2
始条件来确定
常系数的线性齐次微分方程,其通解为
y(t) = A1 cosωt + A2 sinωt
若当 t = 0 时 y = y0 初位移
y(0) = y0 = A1 cosω × 0 + A2 sin ω × 0
因此,自振周期(或频率)的计算十分重 要。
例 计算自振频率
14
EI=常数
如果让振动体系沿振动方向发生单位位移时,所有刚 结点都不能发生转动(如横梁刚度为无穷大的刚架) 计算刚度系数方便。
两端刚结的杆的侧移刚度为:12EI
l3
一端铰结的杆的侧移刚度为:3EI
l3
例 计算自振频率
1
k11
EI=常数
12 EI l3
y = y0 初速度
y(0) = y0 = −ωA1 sinω × 0 + ωA2 cosω × 0
A1 = y0
A2
=
y0
ω
y(t)
=
y0
cosωt
+
y0
ω
sin ωt
位移的多项表达式
位移、速度的单项表达式
3
y(t)
=
y0
cosωt
+
y0
ω
sin ωt
若令
y(t) = a sinϕ cosωt + a cosϕ sin ωt
结构自振周期、频率
6
自振周期的倒数称为工程频率 f = 1
(或频率),记作 f
T
频率 f 表示单位时间内的振动次数,其常用单位
单自由度系统受迫振动

解得
B
h
(n2 2 )2 4 22
tan
2 h n2 2
幅频特性与相频---称为静力偏移 β 为振幅与静力偏移之比,称为振幅比(又称放大因子)。 s 是激励频率与固有频率之比,称为频率比。
由二部分组成: *第一部分振动的频率是自由振动频率 d;由于阻尼的作 用,这部分的振幅都时间而衰减。---瞬态振动
*第二部分以激励频率作简谐振动,其振幅不随时间衰减 -稳态受迫振动。
特解为: 代入方程
B 2 sin(t ) 2B cos(t ) n2B sin(t ) h sin t
arctan
1
1 s
2s3 2 (2s)
2
特系 性统 曲的 线幅
频 特 性 和 相 频
单自由度系统受迫振动/ 受迫振动的过渡阶段
受迫振动的过渡阶段
在系统受到激励开始振动的初始阶段,其自由振动伴随受迫 振动同时发生。系统的响应是暂态响应与稳态响应的叠加
回顾: mx cx kx F0 sin t 显含t,非齐次微分方程
m1
d2x dt 2
m2
d2 dt 2
(x
e sin t)
cx
kx
整理后得系统的微分方程为
(m1 m2 )x cx kx m2e 2 sin t
(m1 m2 )x cx kx m2e 2 sin t
引入 微分方程化为标准形式 解得
令
解得
其幅频特性和相频特性曲线
【例】图示为一测振仪的简图,其中物块质量为 m,弹簧刚度系数为k,阻力系数c。测振仪放在 振动物体表面,将随物体而运动。设被测物体的 振动规律为 xe e sin t 。求测振仪中物块的运动 微分方程及其受迫振动规律。
汽车振动分析之 单自由度

tg
2 1 2
简谐激励下的强迫振动稳态响应解为:
x2(t)
B0 sin(t ) (1 2)2 (2)2
简谐激励下的强迫振动稳态响应解为:
x2 (t)
B0 sin(t ) (1 2 )2 (2)2
强迫振动稳态响应的基本特点:
1、系统在简谐激励的作用下,其强迫振动稳态响应是简谐振动, 振动的频率与激励频率相同。
2.1 简谐激励引起的强迫振动
简谐激振力 f (t) P0 sin t
P 激振力幅值 0
激振力圆频 率
mx cx kx P0 sin t
令: p2 k , 2p c
m
m
x 2px p2x P0 sin t
m
x(t) x1(t) x2 (t)
通解 特解
通解:x1 ent (C1 cos pdt C2 sin pdt)
另一种形式 x Aent sin( pdt )
振幅
初 相
A
x02
(v0
nx0 )2 pd2
位 角
tan x0 pd
v0 nx0
Aent 为阻尼振动振幅
这种情形下,自由振动不是等幅简谐振动,是按负指数衰减的
衰减运动。衰减运动的频率为 pd,衰减速度取决于衰减系数n即
zp。当t→∞时,x→0,即振动最终将完全消失,如图。
程为: mx cx kx 0
x c x k x 0 mm
令 2n c p2 k
m
m
m x
c k
d2 x dt2
2n
dx dt
p2x
0
n c 2m
称为衰减系数
Hale Waihona Puke n 称为相对阻尼系数p
第五章 单自由度系统的振动

上式也可改写为
F (t ) c0 ck cos(kt k )
式中
c0 a 0 / 2 ck ak2 bk2 bk k arct an ak
Cx Kx c0 ck cos(kt k ) M x
k 1
k 1
若系统的质量、刚度和阻尼分别为M、K和C,则此时受迫振动的微分方程为
c0相当于一个静载荷,它不引起振动,而只改变系统的静平衡位置。若令
k k
则稳态响应可以写为
ck x k cos(k t k k ) k 1 K
x e ( x0 cosd t
at
也可改写为 式中
d x Aeat sin(d t )
0 ax0 x
0 ax0 x
sin d t )
2 A x0 (
d
)2
arctan
d x0
0 ax0 x
从上面的式子可以看出,这时系统的运动为周期性的振动。其 振动圆频率为d ,称为有阻尼振动的固有频率,它比无阻尼自由振 动的固有频率 n 略小。振幅Ae-at随时间成指数形式衰减。如图给 出了这种衰减振动的响应曲线。
x A sin(nt )
式中:A称为振幅; 称为初相位,单位为rad。 无阻尼自由振动是一个以固有频率为频率的简谐振动。
设初始时刻t=0时的位移为x0、速度为v0,则可得
2 A x0 (v0 / 0 ) 2
x00 arctan 0 x
2、工程实例 机器或结构中的构件受一静负荷后要产生变形,其内 部要产生应力,分别称为静变形和静应力。而当受冲击或 产生振动时,构件要产生动变形和动应力。
单自由度系统振动

(弹簧质量系统的固有频率和自激振动、自由振动、受迫震动)一、实验目的通过单自由度振动系统的弹簧刚度,掌握固有频率n??与振动质量m和系统弹簧刚度k 之间的一个极为重要的关系mk??n??。
演示自激振动现象及其与自由振动和强迫振动的区别。
因为平时人们往往常遇见或能理解的自由振动和强迫振动的现象比较多,如单摆的振动、汽车的振动、电机由于转子不平衡引起的振动等等。
但自激振动的现象又很难被人们所认识,如比较典型的自激振动有钟表、电铃等。
前者的摆轮和后者的摆锤的振动容易被理解是强迫振动。
因此,我们把演示自激振动作为理论力学一个实验从反面让学生搞清自激振动和强迫振动的概念。
二、实验原理(一)单自由度线性系统的自由振动由一个质量块及弹簧的系统,在受到初干扰(初位移或初速度)后,仅在系统的恢复力作用下在其平衡位置附近所作的振动称为自由振动。
其运动微分方程为:0kxxm(无阻尼)其解为:sinntA 其中:2n2020??vxA,00narctanvx (二)单自由度线性系统的强迫振动在随时间周期性变化的外力作用下,系统作持续振动称为强迫振动,该外力称为干扰力。
其振动微分方程为thxxnxmsin22n(有阻尼)方程全解为:sinsin220BtnAext 强迫振动的振幅B可以表示为2020220041 nBB 式中:kHhB200?? 称为静力偏移,表示系统在干扰力的幅值H 的静力作用下的偏移。
(三)自激振动的基本特性:自激振动是一种比较特殊的现象。
它不同于强迫振动,因为其没有固定周期性交变的能量输入,而且自激振动的频率基本上取决于系统的固有特性。
它也不同于自由振动,因为它并不随时间增大而衰减,系统振动时,维持振动的能量不象自由振动时一次输入,而是象强迫振动那样持续地输入。
但这一能源并不象强迫振动时通过周期性的作用对系统输入能量,而是对系统产生一个持续的作用,这个非周期性作用只有通过系统本身的振动才能不断输入振动才能变为周期性的作用,也只用成为周期性作用后,能量才能不断输入振动?低常 佣 窒低车淖约ふ穸 R虼耍 肭科日穸 囊桓鲋匾 鹪谟谙低趁挥谐跏荚硕 筒换嵋 鹱约ふ穸 科日穸 虿蝗弧?三、实验项目:(一).求单自由度系统的振动频率已知:高压输电模型的质量kgm138.0??,砝码规格分别为100克和200克。
单自由度体系的自由振动

【例10.1】 等截面简支梁[图10.9(a)]的跨长为l, 弯曲刚度EI 为常数,在距梁端A点处有一集中质量m,若 不计梁本身的质量,试求梁的自振频率和自振周期。
图10.9
【解】 该结构为单自由度体系。由式(10.12)求自振频
率ω时,须先求出体系的柔度系数 11 ,即求出在单位力
作用下体系所产生的位移。利用图乘法,由图10.9(b), 算得
结构力学
单自由度体系的自由振动
一、自由振动的微分方程
建立运动微分方程通常有两种方法,一种方法是根据达朗贝尔 原理,利用刚度系数列出平衡方程,这种方法称为刚度法;另 一种方法是根据位移条件,利用柔度系数列出位移方程,这种 方法称为柔度法。
1. 刚度法
图10.7
2. 柔度法
FI +Fe= 0
my(t) k11y(t) 0
y(t) Asin(t )
v0 A cos
y0 Asin
t an1 y0
v0
A
y02
(
v0
)2
图10.8
简谐振动 振幅 相位角 初相角
三、结构的自振周期与频率
T 就是结构的自振周期
T 2π
自振周期的倒数表示每秒钟内的振动次数,称为工程频率, 以f 表示
f 1
T 2π
ω称为圆频率
图10.10
【解】 由于横梁各质点的水平位移相同[图10.10(b)], 故结构为单自由度体系。
在本例中,体系的刚度系数较易计算。取横梁为研究 对象[图10.10(c)],由平衡方程,得
k11
3
3EI1 h3
9EI1 h3
结构的自振频率为
k11 gk11 3 gEI1
mW
单自由度系统无阻尼振动讲义

单自由度系统无阻尼振动
单自由度系统的自 由振动——简谐振
动
1 运动微分方程的建立
弹簧—质量系统放在竖直方向,质量运动方向有重力。
重力只影 响质量块 的平衡位 置,并不 影响其振 动规律。
以系统的静平衡位置o为坐标原点,以垂直向下为轴 正向,建立如图所示的坐标系。
在静平衡位置有:
当物体在任意位置x时:
当质量块m在某一瞬时的速度为 弹簧在x处的微段d x的相应速度为
设r为弹簧单位长度的质量,则弹簧的动能为:
单自由度系统无阻尼振动
弹簧质量 弹簧的等效质量
例7 在长为l,抗弯刚度为EJ的简支梁的中点放一重量为W的物 体,梁的单位长度的质量为r,当考虑梁的分布质量时,求系 统的固有频率。
解:首先假定梁的振型。假设梁在自由振 动时动挠度曲线和简支梁中间有集中静载 荷作用下的静挠度曲线一样。
B点的等效刚度:
N个弹簧串联:
两个弹簧并联,在B端施加力F后,两个弹簧均伸长xB: 两个弹簧受力不同,分别为:
并联弹簧的等效刚度是原来弹簧刚度的总和, 比原来各弹簧单自的由刚度系度统无都阻要尼振大动 。
混联弹簧
等效刚度:
单自由度系统无阻尼振动
设计系统时:若需要减小刚度,采用串联弹性元件; 若需要增大刚度,采用并联弹性元件。
平面运动的刚体 T12mvc2 12Jc2
常见物体的势能计算
拉伸弹簧
扭转弹簧
U x kxdx 1 kx2
U
x
0
Kd
2 1
K2
0
2
刚体的重力势能 U mgzc 单自由度系统无阻尼振动
K 为抗扭弹簧系数
例1 可绕水平轴转动的细长杆,下端附有重锤(直杆的重量和 锤的体积都可以不计),组成单摆,杆长为l,锤重为mg,试 求摆的运动微分方程。
《振动力学》2单自由度系统自由振动

单位:弧度/秒(rad/s)
则有 : &x& + ω02 x = 0
通解 : x(t) = c1 cos(ω0t) + c2 sin(ω0t) = Asin(ω0t + ϕ)
c1, c2: 任意常数,由初始条件决定
振幅 : A = c12 + c22
初相位 : ϕ = tg −1 c1
c2
4
单自由度系统自由振动
解法2:
平衡位置2
动能 T = 1 Iθ&2 = 1 ml2θ&2
最大位移位置,系统动 能为零,势能达到最大
ω0 = k / m
T +V = const
Tmax = Vmax
Tmax = 0
Vmax
=
1 2
kxm2 ax
m
k
最大位移位置
0
xmax
静平衡位置
x
x&max = ω0 xmax
x 是广义的 对于转动: θ&max = ω0θmax
x(t) = Asin(ω0t + ϕ) 30
无阻尼的质量弹簧系统受到初始扰动后,其自由振动是以 ω0 为频率的简谐振动,并且永无休止。
x
T = 2π / ω 0
初始条件的说明:
初始条件是外界能量输入的一 x0
A
种方式,有初始位移即输入了 弹性势能,有初始速度即输入 了动能。
ϕ0
ω0
t
9
单自由度系统自由振动
零初始条件下的自由振动:
x(t)
=
x0
&x& + ω02 x = 0
ω0 =
k m
单自由度系统振动
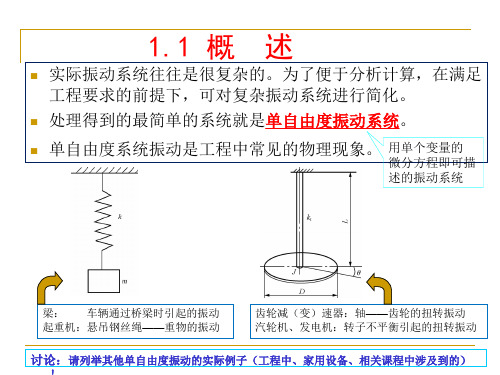
齿轮减(变)速器:轴——齿轮的扭转振动 汽轮机、发电机:转子不平衡引起的扭转振动
讨论:请列举其他单自由度振动的实际例子(工程中、家用设备、相关课程中涉及到的)
1.2 单自由度系统振动
单自由度振动系统类型:
1.无阻尼自由振动 2.有阻尼自由振动 3.有阻尼受迫振动 4.MATLAB数值仿真
动拉力与静拉力之比为动力放大系数
Fmax 64268 3.2134 G 20000
结论:当紧急制动时,起重机钢丝绳中的动拉力是正常提升时的3.2134倍
2.有阻尼自由振动解
单自由度有阻尼系统振动方程为:
cx kx 0 m x
其通解为: x e
n
n t
通解为: x Ae nt sin( 1 2 n t )
ξ>1时,称为强阻尼状态
2 1 ) n t
通解为: x c1e (
c2 e (
2 1 ) n t
ξ=1时,称为临界阻尼状态
n
V0 ( 2 1)n x0 c1 2n 2 1 V0 ( 2 1)n x0 c2 2n 2 1
1.无阻尼自由振动解
单自由度无阻尼系统振动方程为:
kx 0 m x 方程的通解为: x a sin n t b cos n t
k k 令 n 则固有频率为 n m m x 0 V0 若振动的初始条件: xt 0 x0 x
2
则其解为: x sin n t x0 cos n t
钢丝绳长度为 l 16m ,钢丝绳弹性模量 E 1.78105 MPa
03第三讲:单自由度系统的自由振动和强迫振动
自振周期和频率
k 1 w2 m md
(2)利用机械能守恒 (2) 利用机械能守恒
注意到
W mg Dst Wd
w2
g g Wd D st
EI EI
m
l
=1
d 11
l
T (t ) U (t ) 常数
Tmax U max
U (t ) 1 2 1 ky (t ) kA2 sin 2 (wt ) 2 2
计算频率和周期的几种形式
w
k 1 g m md Wd
g D st
T 2
m D st 2 k g
第三讲:单自由度系统的自由振动和强迫振动
一、无阻尼自由振动问题
频率和周期的计算方法
(1)利用计算公式 (1) 利用计算公式
第三讲:单自由度系统的自由振动和强迫振动
一、无阻尼自由振动问题 例.求图示体系的自振频率和周期.
单自由度体系对简谐荷载作用下的反应是结构动力学中的一个经典内容。 自由振动:体系在振动过程中没有动荷载的作用。 自由振动产生原因:体系在初始时刻(t=0)受到外界的干扰。
第三讲:单自由度系统的自由振动和强迫振动
一、无阻尼自由振动问题
1、 刚度法:研究作用于被隔离质量上的受力状 态,建立(动)平衡方程。 静平衡位置
2
cv kv 0 mv
特征方程:
2
c s sw2 0 m
当根式中的值为零时,对应的阻尼值称为临界阻尼,记作cc。显然, 应有cc/2m=w,即:
cc 2m w
2
∵
c 0则:
s
c c w 2 2m 2m
这时,对应的s 值为 :
单自由度振动系统的运动方程及其解析解

单自由度振动系统的运动方程及其解析解单自由度振动系统是指只有一个自由度的振动系统,其运动方程可以用一个二阶常微分方程表示。
在这篇文章中,我们将讨论单自由度振动系统的运动方程及其解析解。
1. 引言振动是自然界中一种常见的现象,也是物体在受到扰动后产生的周期性运动。
单自由度振动系统是研究振动现象的基本模型,它可以用来描述弹簧振子、摆锤等物理系统的振动。
2. 运动方程的建立对于单自由度振动系统,其运动方程可以通过牛顿第二定律推导而来。
假设系统的质量为m,位移为x,系统受到的外力为F,弹性系数为k,则可以得到如下的运动方程:m*x'' + k*x = F3. 简谐振动的解析解当外力为零时,即F=0,单自由度振动系统的运动方程简化为:m*x'' + k*x = 0这是一个常系数线性齐次二阶常微分方程,可以通过特征方程的方法求解。
假设解为x(t) = A*cos(ωt + φ),代入方程中可以得到:-m*ω^2*A*cos(ωt + φ) + k*A*cos(ωt + φ) = 0整理得到:(ω^2*m - k)*A*cos(ωt + φ) = 0由于A*cos(ωt + φ)不为零,所以可以得到特征方程:ω^2*m - k = 0解特征方程可以得到系统的固有频率:ω = sqrt(k/m)因此,单自由度振动系统的解析解为:x(t) = A*cos(ωt + φ)其中A和φ为待定常数,分别表示振幅和相位。
4. 非简谐振动的解析解当外力不为零时,即F≠0,单自由度振动系统的运动方程为:m*x'' + k*x = F这是一个非齐次线性二阶常微分方程,可以通过特解和通解的方法求解。
首先求解齐次方程,得到通解:x_h(t) = A*cos(ωt + φ)然后求解非齐次方程的特解,可以通过待定系数法或者复数法得到特解。
最后将通解和特解相加,得到系统的解析解:x(t) = x_h(t) + x_p(t)其中x_h(t)为齐次方程的通解,x_p(t)为非齐次方程的特解。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
利用欧拉公式: x(t) ent (c1 cosdt c2 sin dt),
初始条件: x(0) x0, x(0) x0
c1 x0 , c2 x0 n x0 d
d n 1 2
(有阻尼固有角频率)
c1=A1+A2 c2=j(A1-A2)
2
km 2mn 为临界阻尼系数。
化简后:
s1,2 n n 2 1
方程通解:
x(t) A1es1t A2es2t ,
3.1单自由度系统的自由振动
对ξ范围分三种情况讨论:
(1)欠阻尼
0 1
s1,2 n jn 1 2 x(t) ent ( A1e jdt A2e jdt ),
过x
阻
尼
单
自
由
度
系
统
自
由 响
O
t
应
3.2 单自由度系统的强迫振动
简谐激励下的响应 周期激励下的响应 任意激励下的响应
3.2 单自由度系统的强迫振动
3.2.1 简谐激励下的响应
激励力: 微分方程:
F = F0sinωt mx cx kx F0 sin t
解的形式:
x(t) = x1(t) + x2(t)
习题
1. 单摆
O
以角度θ为位移,建立运动方程,并求振动 θ
固有频率。
l
m
3.1单自由度系统的自由振动
2 . 升降机问题
升降机箱笼质量为m,由钢丝绳牵挂 以速度v0向下运动,钢丝绳刚度系数 为k,质量不计。如果升降机紧急刹 车,钢丝绳上端突然停止运动。 求此时钢丝绳受到的最大张力Tmax
(弹簧减振钩)
k T
m
v0
3.1单自由度系统的自由振动
3.1.2 有阻尼情形 (粘性阻尼)
微分方程:
mx cx kx 0
解的形式:
x(t) Aest,
特征方程:
ms2 cs k 0
特征根:
s1,2
c 2m
c
2
k
2m m
令:
c ccr
c 2mn
为阻尼比,ccr
欠
x
阻
尼
单
自
由
度
系
O
统
自
由
响
应
ent A
x(t) ent Asin dt
t
sin dt
3.1 单自由度系统的自由振动
(2)临界阻尼
1
s1,2 n
x(t) ent (c1 c2t)
c1、c2由初始条件决定: c1 x0 , c2 x0 n x0
3.2.1.1 稳态响应分析
用复数法求解x2:令 x2(t) Im( Xe jt )
代入微分方程 mx cx kx F0 sin t
得:
X
F0 m
n2
2
1
j2n
F0 k
1 2
1
j2
F0
1
e j Xe j
k (1 2 )2 (2)2
第三章:单自由度系统振动
单自由度系统的自由振动
无阻尼 有阻尼
单自由度系统的强迫振动
简谐激励下的响应 周期激励下的响应 任意激励下的响应
3.1单自由度系统的自由振动
3.1.1 无阻尼情形
微分方程:
mx kx 0
n
k —无阻尼固有角频率;
m
fn
1 2
得到:
k —固有频率;
m
x n2x 0
解的形式:
x(t) cest,
特征方程:
s2 n2 0
方程特征根:
s jn
k
其中c、s为常量。
3.1单自由度系统的自由振动
特征解:
x1 c1es1t ,
x2 c2es2t
根据线性系统叠加原理,方程的通解为两个特征解的线性叠加:
系统响应: x(t) ent[x0 (x0 n x0 )t]
系统处于将要振动又未振动的临界状态。(无振动)
3.1 单自由度系统的自由振动
(3)过阻尼
1
s1,2 n jn 1 2
x(t) ent (c1ent
c e 2 1
x1(t)
瞬态响应(通解) x1(t) ent (a1 cosdt a2 sin dt)
为对应齐次方程 mx cx kx 0 在欠阻尼情况下的解。
x2(t) 稳态响应(特解) x2(t) X sin( t )
为强迫振动下系统的特解。
3.2单自由度系统的强迫振动
其中
,(频率比) n
arctan
2 1 2
, (稳态响应初始相位)
X F0
1
,(稳态响应振幅)
k (1 2 )2 (2)2
3.2单自由度系统的强迫振动
简谐激励的稳态位移响应为:
x2(t) Im( Xe jt ) Im[ Xe j(t ) ] X sin( t )
x(t) c1es1t c2es2t
两个频率相同的简谐振动的合成仍然是一个简谐振动 (简谐振动的基本性质1)
x(t) Asin( nt 0 )
A、φ0 由初始条件决定 : x(0) x0, x(0) x0
A
x02
x0 2
n2
,
0
arctan
x0n
x0
3.1单自由度系统的自由振动
nt 2
2 1 ),
c1、c2由初始条件决定:
c1 x0 ( 2n
2 1)n x0 , 2 1
c2 x0 ( 2n
2 1)n x0 2 1
系统响应为一种振幅按指数规律衰减的非周期蠕动。(无振动)
3.1 单自由度系统的自由振动
简谐激励的稳态速度响应为:
v2 (t )
X
cos(t
)
X
sin(
t
2
)
简谐激励的稳态加速度响应为:
a2 (t )
2X
cos(t
2
)
2X
sin(
t
)
3.2单自由度系统的强迫振动
系统响应:
x(t)
Байду номын сангаас
e nt
( x0
cos d t
x0
n x0 d
sin
dt)
e nt
Asin
d t
A
x02
x0
n d
x0
2
arctan
x0
x0d n x0
系统响应为振幅按指数规律逐渐衰减的简谐振动。
3.1 单自由度系统的自由振动
