单自由度体系的振动分析(精选)
单自由度无阻尼自由振动的系统分析

单自由度无阻尼自由振动的系统分析在结构动力学之中,单自由度体系的振动是最简单的振动,但单自由度体系的频率计算在结构动力学计算中有着十分重要的意义,因为从中我们能得到关于振动理论的一些最基本的概念和分析方法同时也为更复杂的多质点多自由度体系振动问题奠定基础,同时现实工程中也有许多振动问题可以简化为单自由度问题近似的利用单自由度振动理论去分析解决。
在单层厂房、水塔等建筑物中得到有效的利用结构的自由振动是指结构受到扰动离开平衡位置后,不再受到任何外力影响的振动过程,此处动力系统是否有阻尼项,会直接影响到动力系统的反应。
在此,我们把自由振动分为无阻尼自由振动与有阻尼的自由振动。
一、无阻尼自由系统的振动分析目前,以弹簧-质量系统为力学模型,研究单自由度系统的振动具有非常普遍的实际意义,因为工程中许多问题简化后,用单自由度体系的振动理论就能得到很好的解决。
而对多自由度系统和连续振动,在特殊坐标的考察时,也会显示出与单自由度系统类似的振动。
进行无阻尼自由振动分析的主要目的是为了获得系统固有振动的特性,只有充分地了解系统的自身振动特性才能有效的计算系统的动力响应,目前在单质点单自由度无阻尼自由振动体系中我们的运动方程为:0)()(..=+t ku t um (1) 或 0u(t))(=+ωt u (2)其中的ω是振动圆频率,是反应系统动力的重要参数,其计算公式为:m k m ==δω12 (3)由上式可以看出,ω只和系统的刚度及质量有关,而与系统所受到的初始受力状态无关。
ω的量纲与角速度相同为rad/s ,它反映了系统自由振动的快慢。
自由振动系统的这一特性,我们在日常生活中司空见惯。
比如,键盘类乐器标定后,按动某一个琴键,不管你按动的轻重如何,琴键所发出的声音的频率是一定的,按得轻或按得重仅影响声音的强弱。
(2)式经过三角函数的转换可表示为:)sin()(νω+=t A t u (4)其通解为t A t A t u ωωsin cos )(21+= 常数A 1与A 2与初始条件有关,01χ=A ωχ/02 =A式(4)是标准的简谐方程其中A 是其振幅,则ν是其初相角,他们的计算公式2020)(ωx x A += ,00arctan x x v ω=对于质点振动系统,质量越大,则系统的固有频率越低;刚度越大,则系统的固有频率越高。
单自由度振动系统的运动方程解析解的应用案例分析

单自由度振动系统的运动方程解析解的应用案例分析单自由度振动系统是机械工程中非常重要的一类振动系统。
它的运动方程可用解析解表示,这在许多实际问题的解决中发挥着重要作用。
本文将通过分析两个应用案例,展示单自由度振动系统运动方程解析解的实际应用。
案例一:弹簧振子考虑一个弹簧振子系统,由一个质量为m的物体通过一个弹簧与固定支撑相连。
假设摩擦系数为零,物体只有沿水平方向的振动。
根据牛顿第二定律可以得到以下运动方程:m a=−aa其中a是物体的加速度,k是弹簧的劲度系数,x是物体的位移。
通过简单的求解可以得到该系统的解析解为:a = a cos(a_0 t + a)其中A和a分别是振幅和相位,a_0 是系统的固有角频率,有关常数可以通过初始条件来确定。
这个方程给出了振子在任意时间点的位移,通过振幅和相位可以描述振动的特征。
在实际应用中,我们可以利用这个方程来分析弹簧振子的运动规律,如计算特定时刻的位移、速度和加速度等。
案例二:简谐受迫振动考虑一个简谐受迫振动系统,它除了由弹簧力驱动外,还受到外部激励力F(t)的作用。
运动方程可以表示为:m a=−aa +F(t)其中F(t)是外部激励力的函数形式,可以是任意周期性函数。
在这种情况下,运动方程没有解析解,但我们可以通过变换方法将其转化为解析解出现的形式。
一个常见的方法是利用复指数形式的解,并通过计算使运动方程等号两边的实部和虚部相等。
通过求解可以得到:a = a cos(a_0 t + a) + a_p其中a_p是该系统的稳态解,表示受迫振动的特定解,由外部激励力决定,A和a是自由振动的振幅和相位。
这个方程描述了受迫振动系统的运动,可以用于分析系统在不同激励力下的响应,如共振频率、相位差等。
总结起来,单自由度振动系统运动方程解析解的应用案例分析有助于我们深入理解振动系统的运动行为。
通过解析解,我们可以更好地预测和控制系统的振动特性,为相关工程问题提供解决思路。
12.3 单自由度体系的自由振动

各杆EI= 。 【例12-5】试求图示结构的ω。各杆 =C。 】
3l 4 B C D m B y A l l l 4 A l C D l
1
M1 图
解:
δ 11
7l 3 = 12 EI
1 12 EI EI = = 1.309 ω= 3 mδ11 7ml ml 3
All Rights Reserved 重庆大学土木工程学院®
【注二】惯性力 FI = −m&& = maω 2 sin(ωt + α ) = mω 2 y , 注二】 y FI 永远与位移方向一致,在数值上与位移成比例, 永远与位移方向一致,在数值上与位移成比例,其比例系 数为 mω 2 。
All Rights Reserved
重庆大学土木工程学院®
12.3.4 自振周期与自振频率
1.自振周期 自振周期 因
y = a sin (ωt + α ) = a sin (ωt + α + 2 π ) 2π = a sin ω t + + α = a sin[ω (t + T ) + α ] ω
所以自振周期
T =
2π
ω
表示体系振动一次所需要的时间,其单位为 ( 表示体系振动一次所需要的时间,其单位为s(秒) 。
式中, 为重力加速度 为重力加速度; 式中,g为重力加速度;W=mg为质点 为质点 的重力; 表示将重力W=mg 的重力;∆st=Wk11,表示将重力 施加于振动方向所产生的静位移。 施加于振动方向所产生的静位移。
All Rights Reserved 重庆大学土木工程学院®
T = 2π ∆st g
All Rights Reserved 重庆大学土木工程学院®
第一章(单自由度系统的振动)

单自由度系统的振动方程
c
k
m
s k
c
o
u
m
u
f (t)
mu(t) k[u(t) s ] cu(t) mg f (t)
k (u s ) cu
m
mg
f (t)
mg k s
mu(t) cu(t) k u(t) f (t)(单自由度系统振动方程的一般形式)
结论:只要以系统静平衡位置为坐标原点,那么在列写系统运动方程 时就可以不考虑系统重力的作用。
问题2
k1
k2
k3
m
k4
k1 k3
k2
√
k4
问题2
k1
k2
k3
m
k4
k1
k3
k2
╳
k4 k1
k3
k2
m
k4
问题3
无质量弹性杆
刚性杆
k
m
等效
k
m
F
k F /
第一章:单自由度系统的振动
第二讲:
无阻尼单自由度系统的自由振动
•正确理解固有频率的概念 •会求单自由度无阻尼系统的固有频率
无阻尼单自由度系统的自由振动
4
o 势能:V mg(R r)(1 cos ) 1 mg(R r) 2
2
R
m 简谐运动: max sin(nt )
B
rC
Tmax
3m 4
(
R
r
)2
(n
max
)
2
A
D
mg
Vmax
1 2
mg
(
R
r
)m2 ax
Tmax Vmax
结构力学-单自由度体系的自由振动

mh3 T 2 24 EI
Vibration Characteristic
y(t ) Asin( t )
Acceleration: Inertia Force:
(t ) A 2 sin(t ) y (t ) mA 2 sin(t ) I (t ) m y
这是一个齐次方程,其通解为
y(t ) C1 cost C2 sin t
C1 和 C2 可由初始条件确定,设初始位移和初始速度分别为
y(0) y0 C1 y0
(0) v0 y
C2
v0
v0
,
y (t ) y0 cos t
sin t
y (t ) y0 cos t
在无阻尼自由振动中,位移、加速度和惯性力都按正弦规律
变化,且作相位相同的同步运动,即它们在同一时刻均达极值,
而且惯性力的方向与位移的方向一致。
幅值产生于
sin(t ) 1 时,其值分别为:
y A
A 2 y
I mA
2
由于在运动的任一瞬时质体都处于平衡状态,在幅值出现时
l
1 m
EA ml
st Wl T 2 2 g EAg
例: 求图示结构自振频率 。(EI 为常数,杆件自身 质量不计) [分析] 图乘法求位移
A m C l h
1 1 2 2 1 2 h2 B ( h h hl h) (h l ) EI 2 3 2 3 3EI
y y
v0
sin t
T
0
t
y cos t
-y
y
单自由度系统(自由振动)

第二章 单自由度系统的自由振动本章以阻尼弹簧质量系统为模型,讨论单自由度系统的自由振动。
§2-1 无阻尼系统的自由振动无阻尼单自由度系统的动力学模型如图1.1所示。
设质量为m ,单位是kg 。
弹簧刚度为K ,单位是N /m ,即弹簧单位变形所需的外力。
弹簧在自由状态位置如图中虚线所示。
当联接质量块后,弹簧受重力W=mg 作用而产生拉伸变形∆:,同时也产生弹簧恢复力K ∆,当其等于重力W 时,则处于静平衡位置,即 W=K ⋅∆若系统受到外界某种初始干扰,使系统静平衡状态遭到破坏.则弹簧力不等于重力,这种不平衡的弹性恢复力,便使系统产生自由振动。
首先建立座标,为简便起见,可选静平衡位置为座标原点,建立铅垂方向的座标x ,从原点算起,向下为正,向上为负,表示振动过程中质量块的位置。
现设质量m 向下运动到x ,此时弹簧恢复力为K(∆+x),显然大于重力W ,由于力不平衡,质量块在合力作用下,将产生加速度运动,故可按牛顿运动定律(作用于一个质点上所有力的合力,等于该质点的质量和沿合力方向的加速度的乘积),建立运动方程,取与x 正方向一致的力、加速度、速度为正,可列如下方程 改写为 0=+kx xm (1-1-1 令mkp =2(1-1-2)单自由度无阻尼系统自由振动运动方程为02=+x p x(1-1-3)设方程的特解为 ste x =将上式代入(1-1-3)处特征方程及特征根为ips p s ±==+2,1220则(1-1-3)的通解为ptD pt C e C e C x ipt ipt sin cos 11+=+=- (1-1-4)C 、D 为任意积分常数,由运动的初始条件确定,设t=0时00,x xx x == (1-1-5)()x m x k W F=+∆-=∑量位静平衡位置 一自由度弹簧—质量系统 ∆==k mgW xx)则pt pxpt x x sin cos 00 += (1-1-6)经三角变换,又可表示为)sin(α+=pt A x(1-1-7)其中 001220,x px tg p x x A -=⎪⎪⎭⎫ ⎝⎛+=α (1-1-8) 自由振动的振幅A 和初相位角α与系统的参数和初始条件有关。
《单自由度系的振动》课件

主动控制技术广泛应用于航空航天、机械制造、土木工程等领域, 以减小或消除结构的振动。
优势与局限性
主动控制技术的优点在于能够快速响应并有效抑制振动,但需要外部 能源和复杂的控制系统,增加了系统的复杂性和成本。
被动控制技术
被动控制技术定义
被动控制技术是利用阻尼材料或结构来吸收或耗散振动能量的方 法。
弹性力学模型
描述弹性体的振动特性,适用于弹性体的振动。
振动分析的数值方法
有限元法
将系统离散化为有限个单元,求解每个单元的振动响应。
时域法
在时间域内直接求解系统的振动响应。
频域法
将系统振动问题转化为频率域内的问题,求解系统的振动特性。
04
单自由度系统的振动控 制
主动控制技术
主动控制技术定义
主动控制技术是一种通过向系统提供反向振动来抵消原始振动的方 法。
03
单自由度系统的振动分 析
振动分析的基本方法
解析法
通过数学公式推导,求解系统的振动特性。
实验法
通过实验测量系统的振动响应,分析其特性 。
数值法
利用数值计算方法,求解系统的振动响应。
振动分析的数学模型
线性模型
描述线性系统的振动特性,适用于小振幅振动。
非线性模型
描述非线性系统的振动特性,适用于大振幅振动 。
总结词
在机械系统中,振动控制是提高设备稳定性和延长使用寿命 的关键。
详细描述
机械系统中的许多设备,如发动机、压缩机、机床等,都容 易受到振动的影响。通过采用适当的控制策略,如主动或被 动隔振、阻尼减振等,可以有效减小振动对设备性能的影响 ,提高设备的稳定性和可靠性。
建筑结构中的振动控制
第三讲单自由度系统的振动(阻尼)解读

nt i
两端取自然对数得 其中
ln ln e nTd
nT
δ称为对数减缩系数
Td
2
0 1 2
c 0 2 m k
n
对数减缩率δ与阻尼比ζ之间的关系为:
n
2
0 1
2
2 1
2
2
( 2<<1 )
上式表明:对数减缩率δ与阻尼比ζ之间只差2π倍,δ也是反映阻尼
x
这种振动的 振 幅 是 随 时 间 A x0 不断衰减的, 称为衰减振动。 衰减振动的运 动图线如图所 示。 d
Ae nt
衰减曲线的包络线
A1
A2
A3
t
Td
x
由衰减振动的表达式:
Ae
A x0
nt
x Ae
nt
sin(d t )
A1
A2
A3
这种振动不符合周期振 动 f (t ) f (t nT ) 的定
机械振动学
2.1.2.单自由度系统的有阻尼自由振动
1.阻尼
上节所研究的振动是不受阻力作用的,振动的振幅是不随
时间改变的,振动过程将无限地进行下去。
实际中的振动系统由于存在阻力,而不断消耗着振动的能 量,使振幅不断地减小,直到最后振动停止。 振动过程中的阻力习惯上称为阻尼。 阻尼类型: 1)介质阻尼; 2)结构阻尼; 3)库仑阻尼
ωd =ω0 , Td =T
阻尼对振幅的影响
nt 2 2 x Ae sin( n t ) 由衰减振动运动规律: 0
Ae-nt相当于振幅
设在某瞬时ti,振动达到的最大偏离值为Ai有: 经过一个周期 Td ,系统到达另一个 比前者略小的最大偏离值Ai+1
结构力学单自由度体系强迫振动

l3 4 EI
A16 FPl3 7 4EI.
3
FFPPssiinnω3 4t t
l
3mm 2
l 2
l
求质点处的最大动位移及最大动弯矩图,EI=常数
l3 4 EI
A1619FPl3 7 48EI .
FI 1298FPsint
FPsint
m
l/ 2
l/ 2
4 EI
3ml 3
求质点m处的最大动位移及最大动弯矩图,EI=常数
0
t<0
FP0
t
FP(t)= FP0 0<t<u
u
0 t> u
.
阶段Ⅰ: ( 0≤t ≤ u ) y(t) = yst (1- cosωt)
FP(t)
yt2yst
sint
2
2
FP0
u
.
阶段Ⅰ: ( 0≤t ≤ u )
yt2yst
sint
2
2
ytmax
2yst
2yst
sinu
2
2
.
U≥T/2 U≤T/2
FP(t)
• m ÿ+ k y = F P(t)
•y•(t)2yFPt
m
.
二、动荷载作用在结构的任意位置
FP(t)
••
m y
m
y
.
• 动位移方程:y(t)(m•y•)11FPt1P
若令等效荷载 FP'tFPt111P 只对质点位移等效
•y•(t)2yFP't 运动微分方程的标准
m 表达式(强迫振动)
2
3
A
l/2
l/2
2l3 3 EI
单自由度体系建立振动方程-精选文档

……………(a) m ( y y ) k ( y y ) W j d j d j 0 上式可以简化为 y kyj=W 及 m y ky 0 d d m y ky 0 .......... .......... .......... ......( b )
1
6i/L
R
4i 6i
r
6i/L
1
2i
K/2
18i/5L
VBA M图 24i/5L
84 EI K 5 L3
1
柔度法求 K 位移/力—柔度 力/位移—刚度
C
振动形态
y(t)
P(t)
EI
m EI1=∞ EI
C
振动形态
1
K K
6i L
6i L
K
24EI L3
6i L
P (t )
m y
Ky cy
m y c y Ky P ( t )
例题3----刚度法建立方程 试建立图示结构的振动方程,质点的质量都是m , EI=常数
B
m
EI
m y(t)
EA
EA y xy m y 2 L L m dx x 0 0 L2 2 L
2 L
M B 0
练习题2
器的阻尼系数为C
P(t)
EI
m
建立振动方程,阻尼
EI1=∞
EI
C
L
L
P(t)
EI
m EI1=∞ EI
要求K, 就要取水平力的平衡 因而,就要确定2个柱的剪力,这就要作出 结构在侧移为1 时的弯矩图。
K
Δ=1
第13例谐响应分析实例—单自由度系统的受迫振动

第13例谐响应分析实例—单自由度系统的受迫振动单自由度系统是动力学中的一个基本模型,用于描述质点或弹性系统在其中一方向上的振动。
在实际应用中,往往会遇到系统受到外力作用的情况,这时系统的运动方程称为受迫振动方程。
本文将基于第一章学习的单自由度系统的动力学原理,通过一个实际的例子,展示如何利用谐响应分析方法来解决单自由度系统的受迫振动问题。
假设一个质量为m的小球通过一根无摩擦的弹簧与固定点相连,并受到一个周期性外力的作用。
我们的目标是求解小球的运动方程,并分析系统在谐响应下的特性。
首先我们需要建立系统的动力学方程。
根据牛顿第二定律,可以得到受迫振动方程:m*a + c*v + k*x = F0*sin(ω*t)其中,m是小球的质量,a是小球的加速度,c是阻尼系数,v是小球的速度,k是弹簧的刚度,x是小球与平衡位置的位移,F0是外力的振幅,ω是外力的角频率,t是时间。
根据系统的初始条件,可以得到小球的初始位移和初始速度:x(0)=x0,为了求解受迫振动方程的特解,假设系统在稳态下的解为:x = A*sin(ωt + φ).将上式代入受迫振动方程,可以得到A和φ的关系式:A*[(-mω^2 + k)*sin(ωt + φ) + cω*cos(ωt + φ)] =F0*sin(ωt).由于上式中左右两侧的正弦项和余弦项的系数相等,根据同角正弦和余弦函数的和差公式,可以得到:A*[(-mω^2 + k)*sinφ + cω*cosφ] = F0,为了使得上述两个方程成立,可得到A和φ应满足的条件:解以上方程可以得到稳态下的解A和φ。
得到稳态解之后,我们可以分析系统的振动特性。
首先,可以计算出系统的谐响应函数:谐响应函数H(ω)描述了系统在不同外力频率下的响应强度。
图像的幅频响应特性被称为频率响应曲线。
为了绘制频率响应曲线,我们可以通过改变外力的频率ω来计算不同的稳态解A,进而得到H(ω)的数值。
其次,还可以分析系统的幅频特性。
单自由度体系的自由振动

令
ω2 = k
m
y + ω 2 y = 0
运动方程的解 y + ω 2 y = 0 可由振动的初 2
始条件来确定
常系数的线性齐次微分方程,其通解为
y(t) = A1 cosωt + A2 sinωt
若当 t = 0 时 y = y0 初位移
y(0) = y0 = A1 cosω × 0 + A2 sin ω × 0
因此,自振周期(或频率)的计算十分重 要。
例 计算自振频率
14
EI=常数
如果让振动体系沿振动方向发生单位位移时,所有刚 结点都不能发生转动(如横梁刚度为无穷大的刚架) 计算刚度系数方便。
两端刚结的杆的侧移刚度为:12EI
l3
一端铰结的杆的侧移刚度为:3EI
l3
例 计算自振频率
1
k11
EI=常数
12 EI l3
y = y0 初速度
y(0) = y0 = −ωA1 sinω × 0 + ωA2 cosω × 0
A1 = y0
A2
=
y0
ω
y(t)
=
y0
cosωt
+
y0
ω
sin ωt
位移的多项表达式
位移、速度的单项表达式
3
y(t)
=
y0
cosωt
+
y0
ω
sin ωt
若令
y(t) = a sinϕ cosωt + a cosϕ sin ωt
结构自振周期、频率
6
自振周期的倒数称为工程频率 f = 1
(或频率),记作 f
T
频率 f 表示单位时间内的振动次数,其常用单位
振动理论-第2章 单自由度系统的自由振动

c
l
解:梁重物处的静变形为
st
Wc2 (l c)2 3lEI
则:
3lEI k c2 (l c)2
1g f
2 st
例3. 已知:升降机吊笼,以等速 v0 下降,钢丝绳视为弹簧,
若A端突然停止,求钢绳所受到的最大应力。
W 10000lbf l 62 ft A 2.5in2 E 15106lbf / in2
4 等效质量和等效刚度
4 等效质量和等效刚度
4 等效质量和等效刚度
4 等效质量和等效刚度
4 等效质量和等效刚度
平行串联、并联弹簧的等效刚度
4 等效质量和等效刚度
平行串联、并联弹簧的等效刚度
4 等效质量和等效刚度
例1 A suspension system of a freight truck with a parallel-spring arrangement. Find the equivalent spring constant of the suspension if each of the three helical springs is made of G 80109 N / m2
(boom) to deform by an amount x2 x cos 45 and the spring k1
Eat 3 4b3
kr
AE l
d2E
4l
1 keq
1 kb
1 kr
4b3 Eat 3
4l d2
E
keq
E 4
at3d 2
d 2b3 lat3
4 等效质量和等效刚度
斜拉弹簧在某个位移方向上的等效弹簧刚度
Fx F cos F 为弹簧的伸长量
单自由度体系自由振动

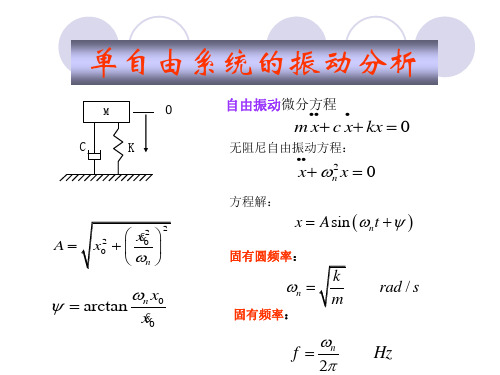
单自由度体系自由振动一、无阻尼振动单自由度体系自由振动可分为有阻尼和无阻尼振动两种。
在模型建立过程当中,可以直接进行建立。
在运行时,只需将c=0即可。
ω增加,单位时间内振动次数增加。
无阻尼振动是简谐振动,振幅和初相位仅取决于初位移和速度。
初始干扰反映了外部初始赋予体系能量的大小。
由于不考虑振动过程中体系能量的耗散,因而体系的总能量保持不变,这就表现为振幅A保持不变,永不衰减。
于是振动一旦发生便永不停息,但这仅是一种理想状态。
二、对阻尼自由振动的讨论当阻尼系数c不为0时,体系做阻尼运动。
由于有能量的耗散,体系的运动幅度会逐渐减小,最终停止振动。
有阻尼单自由度体系,自由振动的运动方程为ωξωm c m k t ky t y c t y m 2,0)()()(2===++∙∙∙, 则原式可变为022=++∙∙∙ωξωy y 。
解微分方程有如下结果:2.1 当1<ξ时,即小阻尼运动,方程的解为:)sin(A )sin cos ()(000ϕωωωξωωξωξω+=++=--t e t y v t y e t y d t d d d t 其中2200201)(ξωωωξω-=++=d d y v y A可画出小阻尼体系自由振动时的y-t曲线如图所示:是一条逐渐衰减的波动曲线2.2 当1>ξ时,即大阻尼的情况,方程的解为:⎥⎥⎦⎤⎢⎢⎣⎡-+--+=-t ch y t sh v y e t y o t ωξωξξξωωξ11)1()(20220 上式不含有简谐振动的因子,是因为体系受干扰后偏离平衡位置所积蓄起来的初始能量在恢复平衡位置的过程中全部消耗克服阻尼,由于阻尼很大,不足以引起振动。
当初始速度,初始位移都大于0时,可画出大阻尼体系自由振动时的y-t曲线如图所示:2.3 当1=ξ时,即临界阻尼的情况,方程的解为:[]t v t y e t y t 00)1)(++=-ωω(当初始速度,初始位移都大于0时,可画出临界阻尼体系自由振动时的y-t曲线如下图所示;当体系在临界阻尼时,其运动衰减的最快,即他能在最短时间内无振动的回到平衡位置。
振动理论03(1)-单自由度系统自由振动

42
2014/9/28
管中其中一个臂的水位升高1厘米,另一个臂的水位就
降低1厘米,因此就给出2厘米水柱的失衡重量,产生
-任意瞬时的位置与平衡位置 之间的距离)?
10
2014/9/28
弹簧力
阻尼力
作用在质量块的力总计 sin
应用牛顿第二定律: 单自由度系统运动微分方程
mx cx kx P0 sin t
惯性力 阻尼力 弹性力 外来的谐力
单自由度扭转系统振动方程
圆盘的惯性矩为 轴的抗扭刚度为 外加扭矩 0 用于转动物体的广义牛顿定律
弹簧-质量系统
研究系统的振动问题时,常常把它简化成由若干个“ 无质量”的弹簧和“无弹性”的质量所组成的模型, 称为弹簧-质量系统(spring mass system)
角振动(angular vibration):以角位移作为独立坐标的系 统。例如后面将要介绍的圆盘的扭振(Torsional vibration)。
用一根弹簧把一个质量m悬挂 在刚性天花板上。弹簧的刚度 由弹性系数 表示
在质量和刚性天花板之间有油 或者空气缓冲器机构
质量静止时,缓冲器不传递力 质量运动时,缓冲器的阻尼力与
速度成正比,即 c:阻尼常数或粘性阻尼常数
9
2014/9/28
假设一个交变外力作用在质 量上
计算外力造成的质量的运动 ,即求出质量运动距离 的时 间函数
振动理论(3) 第3章 单自由度系统自由振动
自由度
自由度
单自由度振动系统的运动方程及其解析解

单自由度振动系统的运动方程及其解析解单自由度振动系统是指只有一个自由度的振动系统,其运动方程可以用一个二阶常微分方程表示。
在这篇文章中,我们将讨论单自由度振动系统的运动方程及其解析解。
1. 引言振动是自然界中一种常见的现象,也是物体在受到扰动后产生的周期性运动。
单自由度振动系统是研究振动现象的基本模型,它可以用来描述弹簧振子、摆锤等物理系统的振动。
2. 运动方程的建立对于单自由度振动系统,其运动方程可以通过牛顿第二定律推导而来。
假设系统的质量为m,位移为x,系统受到的外力为F,弹性系数为k,则可以得到如下的运动方程:m*x'' + k*x = F3. 简谐振动的解析解当外力为零时,即F=0,单自由度振动系统的运动方程简化为:m*x'' + k*x = 0这是一个常系数线性齐次二阶常微分方程,可以通过特征方程的方法求解。
假设解为x(t) = A*cos(ωt + φ),代入方程中可以得到:-m*ω^2*A*cos(ωt + φ) + k*A*cos(ωt + φ) = 0整理得到:(ω^2*m - k)*A*cos(ωt + φ) = 0由于A*cos(ωt + φ)不为零,所以可以得到特征方程:ω^2*m - k = 0解特征方程可以得到系统的固有频率:ω = sqrt(k/m)因此,单自由度振动系统的解析解为:x(t) = A*cos(ωt + φ)其中A和φ为待定常数,分别表示振幅和相位。
4. 非简谐振动的解析解当外力不为零时,即F≠0,单自由度振动系统的运动方程为:m*x'' + k*x = F这是一个非齐次线性二阶常微分方程,可以通过特解和通解的方法求解。
首先求解齐次方程,得到通解:x_h(t) = A*cos(ωt + φ)然后求解非齐次方程的特解,可以通过待定系数法或者复数法得到特解。
最后将通解和特解相加,得到系统的解析解:x(t) = x_h(t) + x_p(t)其中x_h(t)为齐次方程的通解,x_p(t)为非齐次方程的特解。
141单自由度振动

O
R 固定
r
E
C
例2
解
完整、理想约束系统
O
vC (R r)
R
vC R r
rr
固定
r
E
C
T
1 2
mvC2
1 2
JC2
3 4
m(R r)22
V
mg(R r)(1 cos )
1 2
mg ( R
r)2
L T V 3 m(R r)22 1 mg(R r)2
4
2
代入拉格朗日方程得:
23
2
23
V 1 kh2 tan2 mg 1 l(1 cos ) 1 (kh2 1 mgl) 2
2
2
2
2
d dt
L
L
0
(1 ml2 Mh2 ) (kh2 1 mgl) 0
3
2
2 0
6kh2 3mgl
2ml2 6Mh2
例2
已知:m, r, R; 求:匀质圆柱体微摆动的周期。
例1
质量为m长为l的均质杆OA悬挂在O点处, 可绕O轴摆动。质量为M的滑块用刚度系数 为k的弹簧连接,并可沿杆OA滑动,如所示。 杆OA铅直位置是系统的平衡位置。忽略摩 擦力。求系统微幅振动的固有频率。
例1
解
取为广义坐标。
x h tan x hsec2
T 1 1 ml2 2 1 Mh2 2 sec4 1 (1 ml2 Mh2 ) 2
单自由度系统的微振动
微振动 — 质系在它的稳定平衡位形附近的 微幅振动。也称为线性振动。
单自由度定常保守系统的平衡位形q = q0:
V q
V (q) 0
在考虑微振动时,可以认为q - q0和 q 都是一阶 小量。
3-单自由度强迫振动解析

前面已经得出方程
x
的全解为:
2wnx
x
wn2 x
F0 m
sin wt
x
exwnt
x0
xwn wd
x0
sin wd t
x0
cos wd t
X
exwnt
0
xwn
sin
wd
w
cos
sin
wd t
sin
cos
wd t
X0 sin(w t )
第3章 单自由度系统强迫振动
3.1 单自由度系统在谐和激振下的强迫振动
Rmax=
2x
1
1x2
而r=1时
R= 1
2x
由此看出:当r=1,x很小时的R和Rmax相 差很小,所以在工程中仍认为当w=wn 时发
生共振。
第3章 单自由度系统强迫振动
3.1 单自由度系统在谐和激振下的强迫振动
28
3. 相频特性曲线(P37)
以x为参 数,画出f- r 曲线即 f
相频特性曲 线,表明了阻 尼和激振频 率对相位差 的影响。
1 r2
分别取 z*式的实部和虚部就是对应于
余弦和正弦激励的稳态响应。
第3章 单自由度系统强迫振动
3.1 单自由度系统在谐和激振下的强迫振动
21
稳态响应分析(P34-39)
1. 稳态响应xp=X0sin(wt-f)的性质(P34)
(1)在谐和激振条件下,响应也是谐和的, 其频率与激振频率相同; (2)谐和激励强迫振动的振幅X0和相位角φ 决定于系统本身的物理性质和激振力的大小 和频率,与初始条件无关;
• r →∞时,f→p,系统平稳运行。
第3章 单自由度系统强迫振动
第二章 单自由度系统
其中: n=1,2, … t0可以任意选取 ω=2π/T为周期激励的基频
2 t0 +T bn = ∫ F (t )sin nωtdt T t0
(一)周期激励作用下的强迫振动
对于线性系统,应用叠加原理,各激励力共同作用所引起的 系统稳态响应等于各激励力单独作用时引起的系统各稳态响应的 ∞ 和。 a
F (t)=
相位差 π 2
•
Fs
和Fd 频率相同
传给地基的力的最大值
FT = (kX ) 2 + (cω X ) 2 = kX 1 + (2ξγ ) 2
积极隔振
由于在 F sin ωt 作用下,系统稳态响应的振幅为
X=
则
F k (1 − γ 2 ) 2 + (2ξγ ) 2
FT = kX 1 + (2ξγ ) 2 =
M= X 1 = X0 (1 − γ 2 ) 2 + (2ξγ ) 2
γ = ω / ωn
等效静位移
X0 = F k
简谐激励下的强迫振动
共振条件
dM =0 dγ
γ * = 1 − 2ξ 2 ≈ 1
M max = M ( γ * ) = 1 2ξ 1 − ξ 2
旋转不平衡质量引起的强迫振动
系统的振动微分方程
解的讨论: 解的讨论:
λ1, 2 = − ξ ±
(
ξ 2 −1 ωn
)
当ξ = 1时,λ1 = λ2 = −ωn
x = ( B1 + B2t ) e −ωnt
不属于振动
当ξ > 1时,λ1、λ2都是负实数
x = B1e + B2 e
λ1t λ2 t
( −ξ + = Be
