用平面二连杆机器人为例贯穿运动学、雅可比、动力学、轨迹规划甚至控制与编程
二连杆机械臂的拉格朗日动力学推导式

高质量的文章撰写需要精细的研究和深入的思考,以下是一篇对于二连杆机械臂的拉格朗日动力学推导式的文章:1. 介绍二连杆机械臂是工业自动化中常见的一种机械结构,其运动特点复杂,控制困难。
为了对二连杆机械臂的运动进行有效的控制和分析,需要建立其动力学模型。
拉格朗日方法是一种描述系统动力学行为的有效方法,本文将使用拉格朗日方法推导二连杆机械臂的动力学方程。
2. 机械臂建模为了推导二连杆机械臂的动力学方程,首先需要对机械臂进行建模。
假设两个连杆的长度分别为l1和l2,质量分别为m1和m2,重心到旋转轴的距离分别为r1和r2,角度分别为θ1和θ2,推导用于描述系统的广义坐标和广义速度。
3. 拉格朗日动力学一般来说,拉格朗日方程可以表示为T-V=Q,其中T为系统的动能,V为系统的势能,Q为系统的外力。
首先计算系统的动能和势能,进而得到系统的拉格朗日方程。
4. 系统的动能对于二连杆机械臂而言,系统的动能包括了两个连杆的动能以及它们之间的相对动能。
根据运动学关系和动能的定义,可以得到系统的动能表达式。
5. 系统的势能与系统的动能类似,系统的势能也需要考虑两个连杆的势能以及它们之间的相对势能。
根据重力势能的定义和相对位置关系,可以得到系统的势能表达式。
6. 系统的拉格朗日方程将系统的动能和势能代入拉格朗日方程中,可以得到描述系统动力学行为的拉格朗日方程。
在此过程中,需要注意计算各项的偏导,并且考虑到其中一些项可能是不显式的。
7. 系统的控制通过建立系统的动力学方程,可以对二连杆机械臂的控制进行分析和设计。
可以通过对拉格朗日方程进行求解,得到系统的运动方程,并设计合适的控制器实现对机械臂的控制。
8. 结论通过本文对二连杆机械臂的拉格朗日动力学推导式的分析,可以得到系统的动力学方程,这对于机械臂的控制和设计具有重要意义。
在未来的研究和应用中,可以在此基础上进行更深入的分析和探索。
总结:本文通过拉格朗日动力学的方法推导了二连杆机械臂的动力学方程,这为机械臂的控制和设计提供了重要的理论基础。
空间二连杆机器人的动力学建模及其动态过程仿真

空间二连杆机器人的动力学建模及其动态过程仿真作者:td一引言1.机器人机械臂的运动学与动力学分析方法目录空间二连杆机器人的动力学建模 (1)及其动态过程仿真 (1)作者:td (1)一引言 (1)1.1用户界面模块(ADAMS/View) (4)1.2求解器模块(ADAMS/Solver) (5)1.3后处理模块(ADAMS/PostProcessor) (6)二.空间二连杆机器人adams建模仿真 (6)2.1空间二连杆串联机器人 (6)在ADAMS中用长方形连杆模拟机械臂,对两自由度的机械臂分别进行运动学分析动力学分析。
(6)2.1.1运动学分析 (6)2.1.2运动学分析 (9)机器人的运动学和动力学既包含有一般机械的运动学、动力学内容,又反映了机器人的独特内容。
工业机器人的运动学主要讨论了运动学的正问题和逆问题。
假设一个构型已知的机器人,即它的所有连杆长度和关节角度()1q t ,()2q t ,()3q t …()n q t ,…都是已知的,其中n 为自由度数,那么计算机器人末端执行器相对于参考坐标系的位姿就称为运动学的正问题分析。
换言之,如果已知机器人所有的关节变量,用正运动学方程就能计算任一瞬间机器人的位姿。
然而,如果希望机器人的末端执行器到达一个期望的位姿,就必须要知道机器人操作臂每一个连杆的几何参数和所有关节的角矢量()12,,T n q q q q =⋅⋅⋅利用操作臂连杆几何参数和末端执行器期望的位姿来求解关节角矢量是运动学逆问题。
运动学正问题可以利用齐次变换法来求解。
设i 杆坐标系相对于基座坐标系的位姿齐次变换矩阵是b i T ,则1231b i n n T A A A A A -=⋅⋅⋅⋅⋅⋅ ()11-式中i A 为i 杆坐标系相对于1i -杆坐标系的坐标变换矩阵。
相对于正运动学方程,机器人逆运动学方程显得更为重要。
由于按给定末端执行器的位姿求解关节变量是在关节空间中进行非线性方程的求解,其中涉及多值性和奇异现象,因此,这一逆问题成为机器人运动学中的一个重要内容。
用平面二连杆机器人为例贯穿运动学、雅可比、动力学、轨迹规划甚至控制与编程分析

一、平面二连杆机器人手臂运动学平面二连杆机械手臂如图1所示,连杆1长度1l ,连杆2长度2l 。
建立如图1所示的坐标系,其中,),(00y x 为基础坐标系,固定在基座上,),(11y x 、),(22y x 为连体坐标系,分别固结在连杆1和连杆2上并随它们一起运动。
关节角顺时针为负逆时针为正。
图1平面双连杆机器人示意图 1、用简单的平面几何关系建立运动学方程连杆2末段与中线交点处一点P 在基础坐标系中的位置坐标:)sin(sin )cos(cos 2121121211θθθθθθ++=++=l l y l l x p p (1)2、用D-H 方法建立运动学方程假定0z 、1z 、2z 垂直于纸面向里。
从),,(000z y x 到),,(111z y x 的齐次旋转变换矩阵为:⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=100010000cos sin 00sin cos 111101θθθθT (2) 从),,(111z y x 到),,(222z y x 的齐次旋转变换矩阵为:⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=100010000cos sin 0sin cos 2212212θθθθl T (3) 从),,(000z y x 到),,(222z y x 的齐次旋转变换矩阵为:⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡+++-+=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-⋅⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=⋅=10000100sin 0)cos()sin(cos 0)sin()cos(1000010000cos sin 0sin cos 1000010000cos sin 00sin cos 112121112121221221111120102θθθθθθθθθθθθθθθθθθl l l T T T (4)那么,连杆2末段与中线交点处一点P 在基础坐标系中的位置矢量为:⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡++++=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⋅⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡+++-+=⋅=110)sin(sin )cos(cos 10010000100sin 0)cos()sin(cos 0)sin()cos(212112121121121211121212020p p p z y x l l l l l l l P T P θθθθθθθθθθθθθθθθ (5)即,)sin(sin )cos(cos 2121121211θθθθθθ++=++=l l y l l x p p (6)与用简单的平面几何关系建立运动学方程(1)相同。
机器人运动学雅可比矩阵

05 雅可比矩阵的优化与改进
雅可比矩阵的稳定性分析
稳定性分析的重要性
在机器人运动控制中,雅可比矩阵的稳定性对机器人的运动性能 和动态响应具有重要影响。
稳定性判据
通过分析雅可比矩阵的特征值和特征向量,可以确定机器人的运动 稳定性,并为其运动控制提供依据。
通常使用齐次变换矩阵来表示机器人的位姿,该矩阵包含 了平移和旋转信息,能够完整地描述机器人在空间中的位 置和方向。
坐标系与变换
01
坐标系是用来描述物体在空间中位置和姿态的参照框架。
02
在机器人学中,通常使用固连于机器人基座的坐标系作为全局 参考坐标系,以及固连于机器人末端执行器的坐标系作为局部
参考坐标系。
THANKS FOR WATCHING
感谢您的观看
雅可比矩阵的物理意义
雅可比矩阵描述了机械臂末端执行器 的位置和姿态随关节变量变化的规律, 是机械臂运动学分析中的重要概念。
通过雅可比矩阵,可以分析机械臂的 可达工作空间、奇异性、运动速度和 加速度等运动学性能。
雅可比矩阵的计算方法
雅可比矩阵可以通过正向运动学和逆 向运动学两种方法计算得到。
在计算雅可比矩阵时,需要使用到线 性代数、微分方程等数学工具。
正向运动学是根据关节变量求解末端 执行器在参考坐标系中的位置和姿态; 逆向运动学是根据末端执行器的位置 和姿态求解关节变量。
04 雅可比矩阵在机器人运动 学中的应用
机器人的关节与连杆
关节
机器人的每个关节都有一个自由 度,决定了机器人的运动方式。 常见的关节类型包括旋转关节和 移动关节。
连杆
(完整版)用平面二连杆机器人为例贯穿运动学、雅可比、动力学、轨迹规划甚至控制与编程

一、平面二连杆机器人手臂运动学平面二连杆机械手臂如图1所示,连杆1长度1l ,连杆2长度2l 。
建立如图1所示的坐标系,其中,),(00y x 为基础坐标系,固定在基座上,),(11y x 、),(22y x 为连体坐标系,分别固结在连杆1和连杆2上并随它们一起运动。
关节角顺时针为负逆时针为正。
图1平面双连杆机器人示意图 1、用简单的平面几何关系建立运动学方程连杆2末段与中线交点处一点P 在基础坐标系中的位置坐标:)sin(sin )cos(cos 2121121211θθθθθθ++=++=l l y l l x p p (1)2、用D-H 方法建立运动学方程假定0z 、1z 、2z 垂直于纸面向里。
从),,(000z y x 到),,(111z y x 的齐次旋转变换矩阵为:⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=100010000cos sin 00sin cos 111101θθθθT (2) 从),,(111z y x 到),,(222z y x 的齐次旋转变换矩阵为:⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=100010000cos sin 0sin cos 2212212θθθθl T (3) 从),,(000z y x 到),,(222z y x 的齐次旋转变换矩阵为:⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡+++-+=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-⋅⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=⋅=10000100sin 0)cos()sin(cos 0)sin()cos(1000010000cos sin 0sin cos 1000010000cos sin 00sin cos 112121112121221221111120102θθθθθθθθθθθθθθθθθθl l l T T T (4)那么,连杆2末段与中线交点处一点P 在基础坐标系中的位置矢量为:⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡++++=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⋅⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡+++-+=⋅=110)sin(sin )cos(cos 10010000100sin 0)cos()sin(cos 0)sin()cos(212112121121121211121212020p p p z y x l l l l l l l P T P θθθθθθθθθθθθθθθθ (5)即,)sin(sin )cos(cos 2121121211θθθθθθ++=++=l l y l l x p p (6)与用简单的平面几何关系建立运动学方程(1)相同。
用平面三连杆机器人为例贯穿运动学、雅可比、动力学、轨迹规划甚至控制与编程
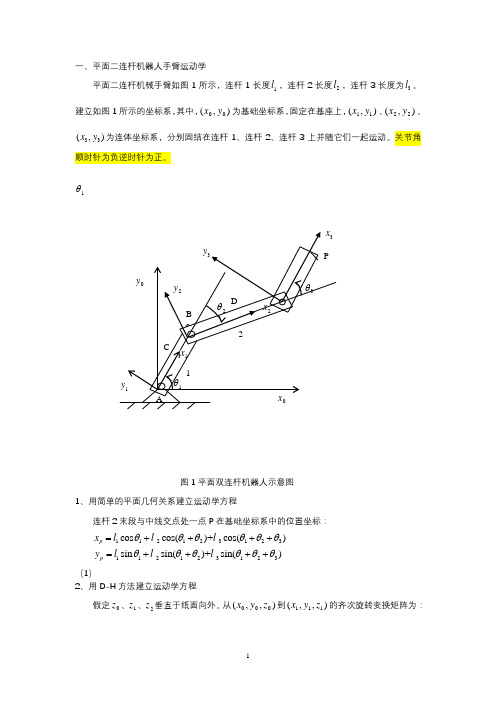
一、平面二连杆机器人手臂运动学平面二连杆机械手臂如图1所示,连杆1长度1l ,连杆2长度2l ,连杆3长度为3l 。
建立如图1所示的坐标系,其中,),(00y x 为基础坐标系,固定在基座上,),(11y x 、),(22y x 、33(,)x y 为连体坐标系,分别固结在连杆1、连杆2、连杆3上并随它们一起运动。
关节角顺时针为负逆时针为正。
1θ图1平面双连杆机器人示意图 1、用简单的平面几何关系建立运动学方程连杆2末段与中线交点处一点P 在基础坐标系中的位置坐标:112123123112123123cos cos()+cos()sin sin()+sin()p p x l l l y l l l θθθθθθθθθθθθ=++++=++++(1)2、用D-H 方法建立运动学方程假定0z 、1z 、2z 垂直于纸面向外。
从),,(000z y x 到),,(111z y x 的齐次旋转变换矩阵为:⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=100010000cos sin 00sin cos 111101θθθθT (2) 从),,(111z y x 到),,(222z y x 的齐次旋转变换矩阵为:⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=100010000cos sin 0sin cos 2212212θθθθl T (3) 从222(,,)x y z 到333(,,)x y z 的齐次旋转变换矩阵为:3323312cos sin 0sin cos 000010001l T θθθθ-⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦(3)从),,(000z y x 到333(,,)x y z 的齐次旋转变换矩阵为:11221332112233001231231231231121cos sin 00cos sin 0cos sin 0sin cos 00sin cos 00sin cos 00001000100010000100010001cos()sin()0cos cos(l l T T T T l l θθθθθθθθθθθθθθθθθθθθ---⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥=⋅⋅=⋅⋅⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦++-+++=212312311212)sin()cos()0sin sin()00100001l l θθθθθθθθθθ+⎡⎤⎢⎥++++++⎢⎥⎢⎥⎢⎥⎣⎦(4)那么,连杆2末段与中线交点处一点P 在基础坐标系中的位置矢量为:12312311212312312311212003311212312311212cos()sin()0cos cos()sin()cos()0sin sin()00010000011cos cos()cos()sin sin()l l l l l P T P l l l l l θθθθθθθθθθθθθθθθθθθθθθθθθθθ++-++++⎡⎤⎡⎤⎢⎥⎢⎥++++++⎢⎥⎢⎥=⋅=⋅⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦+++++++=3123sin()011p p p x l y z θθθ⎡⎤⎡⎤⎢⎥⎢⎥+++⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦(5) 即,112123123112123123cos cos()+cos()sin sin()+sin()p p x l l l y l l l θθθθθθθθθθθθ=++++=++++ (6)结论:(6)与用简单的平面几何关系建立运动学方程(1)相同。
机器人雅可比矩阵

机器人雅可比矩阵简介机器人雅可比矩阵(Robot Jacobian Matrix)是机器人运动学中的重要概念之一。
它描述了机器人末端执行器的速度与关节速度之间的关系,是机器人运动方程求解、运动规划和控制的基础。
本文将详细介绍机器人雅可比矩阵的定义、性质以及它在机器人学中的应用。
定义在介绍机器人雅可比矩阵之前,我们先回顾一下机器人运动学的基本概念。
假设有一个机器人系统,它由n个自由度的关节组成,每个关节的转动由关节角度表示。
而机器人的末端执行器的位置和姿态可以通过正向运动学求解得到,位置用笛卡尔坐标表示,姿态用旋转矩阵或四元数表示。
机器人雅可比矩阵描述了机器人末端执行器的速度与关节速度之间的关系。
具体来说,设机器人关节速度为q_dot,末端执行器速度为x_dot,机器人雅可比矩阵为J,那么雅可比矩阵满足以下关系:x_dot = J * q_dot性质机器人雅可比矩阵具有以下几个重要的性质:1.雅可比矩阵的维度为6×n,其中6表示笛卡尔坐标的维度,n表示机器人的自由度数。
2.雅可比矩阵是一个矩阵函数,它的元素可以表示为:J_ij = ∂f_i / ∂q_j其中,f_i表示末端执行器的第i个度量值,q_j表示第j个关节角度。
3.雅可比矩阵的每一列表示末端执行器在各个关节速度方向上的运动灵敏度。
如果某列的元素值较大,说明在该关节角度变化时,末端执行器的运动会更加敏感。
4.雅可比矩阵的秩决定了机器人在不同姿态下所能达到的运动自由度。
如果雅可比矩阵的秩小于n,那么机器人在某些姿态下会出现奇异配置,并且无法实现所需的末端执行器速度。
应用机器人雅可比矩阵在机器人学中有着广泛的应用。
下面介绍几个常见的应用场景:逆运动学求解在机器人学中,逆运动学是指已知末端执行器的位置和姿态,求解机器人关节角度的过程。
雅可比矩阵在逆运动学求解中起到了关键作用。
通过雅可比矩阵的逆矩阵,可以将末端执行器的速度映射到关节速度空间中,进而求解出关节速度。
二连杆平面机器人

4-2 引入平面矢量
我们都知道矢量是一个数学概念,它用于表示一个具有 大小和方向的物理量。简单地说,一个位移矢量表空间 任意两点之间的有向距离。为了进行机构分析,机构中 每一根连杆都可以表示为一个位移矢量,矢量的起点就 是连杆的某一端点,而其另一端点就是矢量的终点。这 个位移矢量的大小就是连杆的长度,矢量与x轴正向间的 夹角就是连杆的夹角。 矢量方程 那么显而易见对于简单的平面两连杆机器人的矢量方程 可以写为:
RP1=R1 +R2
2021年3月31日6时57分
y
R2
Rp1
2
R1
1
x
那么该平面坐标系对应的x和y的标量方程如下:
x=r1 cosθ1+r2 cos θ2 y=r1 sinθ1 + r2 sinθ2
1式
2021年3月31日6时57分
那么对上式求一阶导(位移的一阶导为速度) 然后转化为雅可比矩阵则有:
x′ - r1 sinθ1 -r2 sinθ2
W1
y′ r1 cosθ1+r2 cos θ2 W2
2式
对其再求二阶导则为加速度:
x〝 = -a1r1 sinθ1 –w1 2sinθ1- r1 w1cos θ1 –a1 r2 sinθ2-w22 sinθ2 -a2 r2 cos θ2
y〝 = a1 r1 cosθ1+ w1 2 cosθ1-w1 r1 sinθ1 +a2 r2 cosθ2 +w22 cos θ2 w2r2 sinθ2
研究操作机器人的运动,不仅涉及机械手本身,而且 涉及各物体间以及物体与机械手的关系。我们将要讨论 的齐次坐标及其变换,就是用来表达这些关系的。齐次 坐标变换不仅能够表示动力学问题,而且能够表达机器 人控制算法、计算机视觉和计算机图形学等问题。因此, 我们对这种数学表示方法特别感兴趣。
并联机器人的雅可比,可操作性,条件数和精度

并联机器人的雅可比,可操作性,条件数和精度(翻译论文)虽然在最早的机器人研究中就已经有了雅可比矩阵的概念、可操纵性、条件数的概念,但是它们的真正意义并不是很好理解。
在本文中,我们重新审视这些作为并联机器人优化设计精度指标的概念。
首先,我们指出,通常的雅可比矩阵的输入—输入方程可能不足以分析平台的定位误差。
然后我们检验可操纵性的概念,表明其经典的解释是错误的。
我们考虑各种常见的局部灵巧指数,其中大部分是基于雅可比矩阵的条件数。
值得注意的是,即使对于一个给定的机器人,在一个特定的姿态也会有各种各样的条件数,这些条件数之间都不一致,和我们想得到的精度指标也不一致。
然后考虑了全局调节指数。
除了存在基于错误的局部准确性指数的问题外,还有一个忽略了大部分时间而进行计算的计算问题。
最后,我们检验了其他哪些指标可用于优化设计,并且介绍了计算它们的难度。
1 引言我们将使用一个相对通用的非冗余并联机构的定义。
当一个机构用至少两个运动链来控制自由度n<6的末端执行器时,我们定义它为并联机构,而其他的6-n 个自由度是一个恒定值通过单自由度驱动关节控制。
此外,如果将驱动器锁定,则末端执行器的自由度为0,非驱动关节有一个单自由度。
这样的定义涵盖了经典的六自由度机器人,比如Gough 和Hexa 平台,还有少于六自由度的机构,如Delta 和3-UPU 机构。
如今,并联机构的应用领域越来越广,如望远镜、精定位装置、包装速度快、机床、医疗。
对尺寸非常的敏感是并联机构优化设计的一个关键问题。
最优设计的方法有静力学性能指标。
精度显然是许多应用中的一个关键问题。
并联机构也有串联机构的一些关键问题,因此,针对这些问题做了很多广泛的研究,定义除了很多准确性指标,这些结果已经应用到并联机构上。
本文的目的是检验这些指标是否适用于并联机构。
雅可比矩阵和逆雅可比矩阵用于研究末端执行器的定位精度的,为了这个目的,很有必要研究它们的概念。
机器人动力学 雅克比-概念解析以及定义

机器人动力学雅克比-概述说明以及解释1.引言1.1 概述机器人动力学是研究机器人运动过程中的力学和动力学特性的学科,主要涉及机器人的姿态、速度、加速度、力和力矩等相关物理量。
机器人动力学一直以来都是机器人领域的关键问题之一,对于机器人的运动控制和路径规划具有重要的指导意义。
雅克比矩阵是机器人动力学中一项关键的工具,用于描述机器人多自由度系统中各关节之间的运动传递关系。
通过雅克比矩阵,我们可以计算出机器人末端执行器在给定关节角速度下的线速度和角速度,从而实现对机器人运动的精确控制。
机器人动力学的研究在实际应用中有着广泛的意义。
首先,深入理解机器人的动力学特性可以帮助我们设计出更加高效、灵活的机器人控制算法,从而提升机器人的运动精度和速度。
其次,机器人动力学的研究还可以为机器人路径规划、障碍物避障等问题提供重要的理论支持和指导。
此外,随着机器人应用领域的拓展,如医疗、教育、家庭服务等,机器人动力学的研究也将在未来发挥更加重要的作用。
总结起来,机器人动力学是研究机器人运动特性的学科,雅克比矩阵则是机器人动力学中的重要工具。
通过研究和应用机器人动力学,我们可以实现对机器人运动的精确控制,提升机器人的运动效率和准确性,并且为机器人的应用和发展打下坚实的基础。
未来,机器人动力学的研究将随着机器人技术的不断发展而不断探索新的方向,并为更广泛的机器人应用提供理论支持和指导。
1.2 文章结构文章结构部分的内容应当包括对整篇文章的组织和章节安排进行介绍。
可以按照以下方式编写文章结构的内容:2. 文章结构本文共分为以下几个部分:引言、正文和结论。
2.1 引言部分将对机器人动力学的概念进行概述,介绍机器人动力学的背景和意义。
在此部分还将阐述本文的目的和结构。
2.2 正文部分将重点讨论雅克比矩阵的概念和应用。
首先,将介绍雅克比矩阵的定义和性质,以及其在机器人动力学中的重要作用。
接着,将探讨雅克比矩阵在路径规划、运动控制和力学分析等方面的应用。
逆运动学雅可比矩阵

逆运动学雅可比矩阵逆运动学雅可比矩阵是机器人学中的重要概念,用于描述机器人末端执行器的运动学性质。
通过逆运动学雅可比矩阵,我们可以推导出机器人在给定末端执行器速度时,关节的运动速度。
本文将介绍逆运动学雅可比矩阵的定义、推导方法和应用场景。
逆运动学雅可比矩阵是描述机器人末端执行器速度与关节速度之间关系的矩阵。
在机器人学中,关节速度是指机器人各个关节的运动速度,末端执行器速度是指机器人末端执行器在笛卡尔坐标系下的速度。
逆运动学雅可比矩阵将这两种速度联系起来,帮助我们理解机器人的运动学特性。
逆运动学雅可比矩阵的定义如下:假设机器人有n个关节,末端执行器在笛卡尔坐标系下的速度为v,关节速度为q̇,则逆运动学雅可比矩阵J的定义如下所示:J = (∂f/∂q̇)⁻¹其中,f表示末端执行器的位置和姿态函数,∂f/∂q̇表示末端执行器速度对关节速度的偏导数。
逆运动学雅可比矩阵的维度为6xN,其中N表示机器人关节数量。
在推导逆运动学雅可比矩阵时,我们可以使用几何法或微分法。
几何法是基于坐标变换和几何关系的推导方法,而微分法则是基于微分运算的推导方法。
这两种方法在不同情况下都有其适用性。
逆运动学雅可比矩阵在机器人学中有广泛的应用。
首先,逆运动学雅可比矩阵可以用于机器人轨迹规划和路径优化。
通过计算机器人末端执行器速度和关节速度的关系,我们可以优化机器人的运动轨迹,使其更加平滑和高效。
逆运动学雅可比矩阵还可以用于机器人的运动控制和力控制。
通过控制机器人的关节速度,我们可以实现对机器人末端执行器的精确控制。
在力控制中,逆运动学雅可比矩阵可以帮助我们估计机器人末端执行器受到的外部力和力矩,并进行相应的控制。
逆运动学雅可比矩阵还可以用于机器人的碰撞检测和避障。
通过计算机器人末端执行器速度和关节速度的关系,我们可以判断机器人是否会与周围环境发生碰撞,并采取相应的避障策略。
总结起来,逆运动学雅可比矩阵是机器人学中的重要概念,用于描述机器人末端执行器的运动学性质。
二连杆机器人动力学方程

二连杆机器人动力学方程二连杆机器人是一种简单的机器人系统,由两根连接在一起的连杆构成,可以用于模拟人体运动、机器人运动等。
其动力学方程可以通过Lagrange方法进行推导。
首先,定义系统的广义坐标,例如,可以选择两个连杆的角度(θ₁、θ₂)以及两个连杆的角速度(ω₁、ω₂)作为广义坐标。
然后,定义连杆的质量(m₁、m₂)、长度(l₁、l₂)、重心距离(d₁、d₂)等参数。
接下来,可以利用Lagrange方法推导出机器人的动力学方程。
Lagrange方法是一种基于能量的方法,用于描述系统的动力学。
步骤如下:1.计算连杆的动能(T)和势能(V)。
连杆的动能等于其质点的动能之和,连杆的势能等于其质点的势能之和。
2.根据广义坐标,构建系统的Lagrange函数(L = T - V)。
3.使用Euler-Lagrange方程,对Lagrange函数取关于广义坐标的偏导数,得到广义力(F)。
4.对广义力进行整理和简化,推导出动力学方程。
最终的动力学方程可以写成类似于以下形式的方程:(M(q) \cdot \ddot{q} + C(q, \dot{q}) \cdot \dot{q} + G(q) = \tau) 其中,(M(q))是系统的惯性矩阵,描述了系统的质量和几何特性;(\ddot{q})是广义加速度的二阶导数;(C(q, \dot{q}))是科里奥利力-禧维特力矩阵,描述了由于速度和加速度引起的惯性力效应;(G(q))是重力矩阵,描述了由于重力作用而引起的力矩;(\tau)是外部施加的关节力矩。
这样, 通过求解动力学方程,可以得到机器人系统在给定的广义力矩下的运动变化情况。
需要注意的是,具体的推导过程以及方程的形式会根据系统结构和约束条件的不同而有所差异。
雅可比矩阵和动力学分析

雅可比各列旳计算公式:
6 x
6 y
n x ny nz ( p n)x o x oy oz ( p o)x
6 z
6 x
a x 0
ay 0
az 0
( pa)x nx
6 y
6 z
0 0
0 0
0 0
ox ax
( p n)y ( p o)y
( p n)z ( p o)z
i x
i y
(2) 内部奇异形位:两个或两个以上关节轴线重叠时,机 器人各关节运动相互抵消,不产生操作运动。相应旳机器 人形位叫做内部奇异形位。
当机器人处于奇异形位时会产生退化现象,丧失一种或更 多旳自由度。这意味着在工作空间旳某个方向上,不论怎 样选择机器人关节速度,手部也不可能实现移动。
当l1l2s2=0时无解,机器人逆速度雅可比J-1奇异。 因l10,l20,所以,在2=0或2=180时,机器 人处于奇异形位。
2
Y
2
d1 d2
写成矩阵形式为
X
dX dY
1
Y
1
X
2
Y
2
d1 d2
X X
令
J
1
2
Y Y
1
2
简写为: dX=J dθ
关节空间微小运 动dθ与手部作业 空间微小位移 dX旳关系。
2R机器人旳速度雅可比矩阵为:
J
l1s1 l2s12
l1c1
l2c12
当雅可比不是满秩矩阵时,J旳行列式为0。
当雅可比不是满秩矩阵时,可能出现奇异解,机器人旳奇 异形位,相应操作空间旳点为奇异点。
机器人旳奇异形位分为两类:
(1) 边界奇异形位:当机器人臂全部伸展开或全部折回时, 手部处于机器人工作空间旳边界上或边界附近,逆雅可比 奇异。相应旳机器人形位叫做边界奇异形位。
(完整word版)平面双连杆机械臂动态模型(word文档良心出品)

构建平面双连杆机械臂动态模型1. 平面双连杆机械臂的分析图1 平面双连杆机械臂平面双连杆机械臂如图1,图中θ1 为关节1 转角,θ2 为关节2 转角,l1 为杆1 的长度,l2为杆2 的长度,r1 为关节1 到杆1 质心的距离,r2 为关节2 到杆2 质心的距离,M1为负载质量。
以图中的O 为原点的00y x -为基坐标。
2. 数学建模2.1寻找动力学末端坐标)cos(cos 21211θθθ++=l l x pl )sin(sin 21211θθθ++=l l y pl根据雅克比矩阵的形式⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=2121θθθθdy dy dx dx J对末端坐标进行微分得到末端速度方程)sin()(sin 21212111θθωωθω++--=l l x pl & )cos()(cos 21212111θθωωθω+++-=l l y pl &其中11θω&=,22θω&=,将(3)、(4)两式联立整理成速度雅克比矩阵形式 ⎥⎦⎤⎢⎣⎡+---=1221221112212211c l c l c l s l s l s l J其中1s =1sin θ,1c =1cos θ,22sin θ=s ,22cos θ=c ,12s =)sin(21θθ+,12c =)cos(21θθ+。
在机器人基础坐标系中的速度与各关节速度间的关系以及手部与外界接触力与对应各关节间的关系可以利用雅克比矩阵来建立。
对机械臂末端速度方程(3) 、方程(4) 进行求导得到末端加速度方程如下[]1221222122211221121221122112)()(c l c l c l c l s l s l s l x pl ωωωωαα+++-=+++&& []1221222122211221121221122112)()(s l s l s l sl s l s l s l y pl ωωωωαα+++-=+++&&其中1α=1θ&&,2α=2θ&&,上述推导的方程构成了进行动力学仿真的基础,它们表明了有效负荷的加速度与 两节点处电动机的角速度和角加速度之间的关系。
平面并联机器人的运动学和动力学研究

平面2自由度并联机器人的运动学和动力学研究林协源1刘冠峰1(1.广东工业大学广州)摘要:本文面向高速高精LED电子封装设备设计了一种高速高精2自由度平面并联机构(2-PPa并联机器人)。
该机构由一个动平台和两个对称分布的完全相同的支链组成,每个支链中都有一个移动副(驱动关节)和一个由平面平行四边形组成的特殊转动动副。
首先推导出该机器人的运动学模型包括正反解;其次结合焊线机实际工艺要求提出多项机构性能指标对该机构的几何参数进行多目标优化;然后基于Euler-Lagrange 方程建立该机器人的动力学方程,最后通过算例分析两个移动副在动平台按照一定轨迹运动时其速度、加速度和驱动力的变化规律。
这些为接下来研究该机器人的动态性能和系统解耦控制等都具有重要意义。
关键词:2自由度平面并联机器人运动学动力学Kinematic and Dynamic Analysis of a PlanarTwo-degree-freedom Parallel ManipulatorLIN Xieyuan1LIU Guanfeng1(1.Guangdong University of Technology Guangzhou )Abstract:In this paper,a type of planar 2-DOF parallel manipulator is proposed for uses in design of high- speed and high-accuracy LED packaging machines. The manipulator consists of a moving platform and two identical subchains. Each subchain is made of a prismatic joint (actuator) and a parallelogram with four passive revolute joints. We first derive the kinematic model of the manipulator. Then, we determine the optimal geometric parameters of the manipulator by solving a multi-goal optimization problem based on performance indices. We compute the dynamic equation use Euler-Lagrange formulation and use it to analyze the relationship between velocity, acceleration and driving torque of joints. This analysis is important for further study of the dynamic performance and the decoupling control methods for the manipulator.Key words:2-DOF Planar parallel manipulator Kinematics Dynamics0 前言在电子、包装和食品等轻工业场合中,机器人只需要3到4个自由度即可满足使用要求。
二连杆机器人动力学方程

二连杆机器人动力学方程简介二连杆机器人是一种常见的机器人结构,由两个连接在一起的杆件组成,类似人的上肢结构。
动力学方程是描述机器人运动的重要工具,可以用于控制机器人的运动以及研究机器人的力学性能。
本文将介绍二连杆机器人的动力学方程,并对其推导过程进行详细阐述。
动力学方程的推导首先,我们需要定义二连杆机器人的几何参数和状态变量。
假设机器人的两个杆件的长度分别为L1和L2,重力加速度为g。
假设机器人的关节角度分别为θ1和θ2,关节角速度分别为ω1和ω2,关节角加速度分别为α1和α2。
接下来,我们需要推导机器人的运动学方程。
根据运动学关系,可以得到杆件末端的位置坐标为:x = L1cos(θ1) + L2cos(θ1+θ2) y = L1sin(θ1) + L2sin(θ1+θ2)其次,我们需要推导机器人的动力学方程。
根据牛顿第二定律,可以得到机器人的动力学方程为:M1α1 + M2α2 + C1ω1 + C2ω2 + G1 + G2 = τ1 I1α1 + I2α2 + C3ω1 + C4ω2 + G3 + G4 = τ2其中M1和M2分别为杆件1和杆件2的质量,I1和I2分别为杆件1和杆件2的转动惯量,C1、C2、C3和C4分别为相关的离心力和科里奥利力系数,G1、G2、G3和G4分别为相关的重力分量,τ1和τ2分别为关节的扭矩。
重力分量的计算可以根据重力加速度和杆件的质量进行计算:G1 = (m1 + m2)g L1sin(θ1) + m2g L2sin(θ1+θ2) G2 = m2g L2*sin(θ1+θ2) G3 = 0 G4 = 0离心力和科里奥利力的计算可以根据关节角速度进行计算:C1 = -0.5m1L1ω1sin(2θ1) - m2L1ω1sin(2θ1) - 0.5m2L2ω2sin(2(θ1+θ2)) C2 = -0.5m2L2ω2sin(2(θ1+θ2)) C3 = 0.5m1L1ω1sin(2θ1) + m2L1ω1sin(2θ1) +0.5m2L2ω2sin(2(θ1+θ2)) C4 = 0.5m2L2ω2sin(2(θ1+θ2))最后,我们可以将运动学方程和动力学方程联立,得到关于加速度的线性方程组,即动力学方程。
两自由度串联机器人分析与设计综述

机器人技术基础三级项目报告设计题目:两自由度串联机器人分析与设计指导教师:赵永杰学生姓名:citycars学号:********邮箱:****************.cn院系:机械电子工程系汕头大学机械电子工程系2012年 6 月 17 日目录1.前言 (3)2.运动学模型 (4)3.机器人的位置及速度分析 (5)3.1 建立机器人位置输入输出方程 (5)3.2 建立机器人的速度关系及推导出雅可比矩阵 (5)3.3 机器人的位置反解 (5)3.4 机器人的速度反解 (7)4.机器人的速度各项同性分析及设计 (8)4.1 速度各项同性分析 (8)4.2 速度各向同性设计求解 (10)4.3 求解及分析 (10)4.4 综合分析 (12)5.结语 (13)6 附录 (13)附录1:位置反解程序 (14)附录2:速度反解程序 (15)附录3:速度各向同性程序 (15)两自由度串联机器人分析与设计【摘要】通过建立两自由度串联机器人位置输入输出方程,建立两自由度串联机器人的速度关系,推导出雅可比矩阵,分析两自由度串联机器人的速度各向同性的条件,设计出一各向同性的构型。
关键词位置方程速度关系雅可比矩阵各向同性1.前言随着现代科学技术的迅猛发展,特别是由于微电子技术、电子计算机技术的迅猛发展,机器人更加广泛地应用于各个领域。
工业机器人靠自身动力控制能力来实际各种功能,大都用于简单、重复、繁重的工作,如上、下料,搬运等,以及工作环境恶劣的场所,如喷漆、焊接、清砂和清理核废料等。
本课程设计旨在通过工业机器人的一个小分支-----两自由度串联机器人,其输入输出方程、雅可比等的分析,以及对于速度各向同性的分析和设计,对工业机器人有初步的了解,为以后从事工业机器人相关工作奠定基础。
2.运动学模型图1 平面两自由度串联机械人如图1所示,为一平面两自由度串联机械人,由两个关节组成,两连杆长度分别a1和a2,两旋转关节轴平行,关节1运动范围为0-180。
用平面二连杆机器人为例贯穿运动学、雅可比、动力学、轨迹规划甚至控制与编程分析

定义:根据目标位置和姿态,求解关节角度的过程 计算方法:利用几何学和逆运动学方程求解 意义:在机器人轨迹规划和运动控制中具有重要应用 适用范围:适用于具有完整运动学模型的机器人系统
定义:描述机器人末端执行器相对于机座标系的位置和姿态
建立坐标系:建立机器人末端执行器相对于机座标系的坐标系,以便进行运动学分析
编程语言选择:根据需求选择合适 的编程语言,如Python、C++等。
控制系统算法设计:设计控制算法, 如PID控制、模糊控制等。
添加标题
ห้องสมุดไป่ตู้添加标题
添加标题
添加标题
控制系统建模:建立平面二连杆机 器人的数学模型,包括运动学、动 力学等。
控制系统仿真与调试:通过仿真软 件对控制系统进行仿真和调试,确 保控制效果达到预期目标。
组成:控制系统由传感器、控制器和执行器 三部分组成。
分类:根据控制方式的不同,控制系统可以 分为开环控制系统和闭环控制系统。
线性二次型调节器 (LQR):通过优化二 次代价函数来设计控制 器,实现最优控制。
比例积分微分(PID)控 制器:通过比例、积分 和微分环节来减小误差, 实现系统的稳态和动态 性能。
度之间的关系,即 d/dt(末端执行器的位 置和姿态)=J(关节变
量)d/dt(关节变量)
添加标题
计算方法:通过微分 几何和线性代数的知 识,将关节变量和末 端执行器的位置和姿 态之间的关系进行计 算,得到雅可比矩阵
添加标题
作用:雅可比矩阵是 机器人运动学和动力 学分析中的重要工具, 通过它可以推导机器 人的运动方程,实现 机器人的轨迹规划和
运动学方程:建立机器人末端执行器的位置和姿态与关节角度之间的关系,得到运动学方程 运动学分析方法:采用解析法或数值法对运动学方程进行分析,得到机器人末端执行器的位 置和姿态随时间的变化规律
平面2R机械臂运动学分析

文 献 标 识 码 :A
〇 引言 在 实 际 工 程 领 域 ,很 多 应 用 场 合 下 不 总 是 需 要 多
自由度机器人的复杂运动,因此自由度少、结 构简单、 经济实用的串联机构早已引起国内外研究者的浓厚兴 趣 。随着科技的进步,人们涉足的领域越来越广,这就 必然要求我们对知识和理论不断进行创新[1]。 目前, 机 器 人 的 运 动 学 分 析 有 两 个 问 题 需 要 解 决 :运 动 学 正 问题,即根据关节位移、速 度 、加速度和臂长求末端点 的运动状态;动力学逆问题,即已知末端点运动轨迹和 臂长求解对应的关节位移、速度和加速度[2]。平 面 2R 串 联 机 械 臂 的 运 动 学 分 析 至 关 重 要 ,它 可 以 为 多 自 由 度的复杂结构机器人的运动学分析、动力学分析、轨迹 规划和控制方法的研究提供理论基础。 1 平 面 2R 机械臂结构
将 平 面 2R 机械臂机构简化为数学模型并建立坐 标 系 ,如 图 2 所 示 。
图 2 中,贫 和兔均为矢量,规定逆时针方向为正,顺时
针方向为负。贫>〇 为逆时针方向,氏<〇 为顺时针方向。 在 平 面 2R 机械臂机构的坐标系中,坐标 系 {2}的
原点和坐标系{〇}的原点不重合,坐标系{2}的方位和
2018年 第 1 期
将复合变换写成矩阵形式:
° P = l T 2p .
(2)
其 中 :齐 次 变 换 矩 阵 纟 T 是 4 X 4 方 阵 :
〇T = r ^
°m _
2 L〇 〇 〇 1 _
依 据 D e n a v i t -H t e n b e r g 法 ,用 4 X 4 的 齐 次 变 换 矩 阵 描 述 相 邻 两 连 杆 的 空 间 关 系 ,得 到 平 面 2 R 机 械
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、平面二连杆机器人手臂运动学平面二连杆机械手臂如图1所示,连杆1长度1l ,连杆2长度2l 。
建立如图1所示的坐标系,其中,),(00y x 为基础坐标系,固定在基座上,),(11y x 、),(22y x 为连体坐标系,分别固结在连杆1和连杆2上并随它们一起运动。
关节角顺时针为负逆时针为正。
图1平面双连杆机器人示意图 1、用简单的平面几何关系建立运动学方程连杆2末段与中线交点处一点P 在基础坐标系中的位置坐标:)sin(sin )cos(cos 2121121211θθθθθθ++=++=l l y l l x p p (1)2、用D-H 方法建立运动学方程假定0z 、1z 、2z 垂直于纸面向里。
从),,(000z y x 到),,(111z y x 的齐次旋转变换矩阵为:⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=100010000cos sin 00sin cos 111101θθθθT (2) 从),,(111z y x 到),,(222z y x 的齐次旋转变换矩阵为:⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=100010000cos sin 0sin cos 2212212θθθθl T (3) 从),,(000z y x 到),,(222z y x 的齐次旋转变换矩阵为:⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡+++-+=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-⋅⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=⋅=10000100sin 0)cos()sin(cos 0)sin()cos(1000010000cos sin 0sin cos 1000010000cos sin 00sin cos 112121112121221221111120102θθθθθθθθθθθθθθθθθθl l l T T T (4)那么,连杆2末段与中线交点处一点P 在基础坐标系中的位置矢量为:⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡++++=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⋅⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡+++-+=⋅=110)sin(sin )cos(cos 10010000100sin 0)cos()sin(cos 0)sin()cos(212112121121121211121212020p p p z y x l l l l l l l P T P θθθθθθθθθθθθθθθθ (5)即,)sin(sin )cos(cos 2121121211θθθθθθ++=++=l l y l l x p p (6)与用简单的平面几何关系建立运动学方程(1)相同。
建立以上运动学方程后,若已知个连杆的关节角21θθ、,就可以用运动学方程求出机械手臂末端位置坐标,这可以用于运动学仿真。
3、平面二连杆机器人手臂逆运动学建立以上运动学方程后,若已知个机械臂的末端位置,可以用运动学方程求出机械手臂二连杆的关节角21θθ、,这叫机械臂的逆运动学。
逆运动学可以用于对机械臂关节角和末端位置的控制。
对于本例中平面二连杆机械臂,其逆运动学方程的建立就是已知末端位置),(p p y x 求相应关节角21θθ、的过程。
推倒如下。
(1)问题已知末端位置坐标),(p p y x ,求关节角21θθ、。
(2)求1θ 由(6)式得到:22211211)sin ()cos (l l y l x p p =-+-θθ (7)整理得到:)sin cos (2111222122θθp p p p y x l l l y x +=-++ (8)令pp p pp tg y x θθθcos sin == (9)由(8)式得到:)cos(cos 211222122p pp p p x l l l y x θθθ-=-++ (10)由此可解出1θ。
p p p p p p x y arctg x l l l y x +⎥⎥⎦⎤⎢⎢⎣⎡-++=θθcos 2arccos 12221221 (11)(3)求2θ 由(6)式得到:2122122212)]sin([)]cos([l l y l x p p =+-++-θθθθ (12)整理得到:)]sin()cos([221212212222θθθθ+++=-++p p p p y x l l l y x (13) 令pp p pp tg y x θθθcos sin == (14)由(14)式得到:)cos(cos 2]sin )sin(cos )[cos(cos 221221212212222p pp p p p p p p x l x l l l y x θθθθθθθθθθθ-+=+++=-++ (15)由此可解出2θ。
122122222cos 2arccos θθθ-+⎥⎥⎦⎤⎢⎢⎣⎡-++=p p p p p p x y arctg x l l l y x (16)二、平面二连杆机器人手臂的速度雅可比矩阵速度雅可比矩阵的定义:从关节速度向末端操作速度的线性变换。
现已二连杆平面机器人为例推导速度雅可比矩阵。
上面的运动学方程两边对时间求导,得到下面的速度表达式:)()cos(cos )()sin(sin 2121211121212111θθθθθθθθθθθθ +⋅++⋅=+⋅+-⋅-=l l dtdy l l dt dx p p (17)把上式写成如下的矩阵形式:⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡++++-+--=⎥⎦⎤⎢⎣⎡212122121121221211)cos()cos(cos )sin()sin(sin θθθθθθθθθθθθ l l l l l l y x p p (18) 令上式中的末端位置速度矢量Xy x p p =⎥⎦⎤⎢⎣⎡, 关节角速度矢量Θ=⎥⎦⎤⎢⎣⎡ 21θθ, 矩阵),()cos()cos(cos )sin()sin(sin 212122121121221211θθθθθθθθθθθθJ l l l l l l =⎥⎦⎤⎢⎣⎡++++-+-- ),(21θθJ 就是速度雅可比矩阵,实现从关节角速度向末端位置速度的转变。
(18)式可以写成:速度雅可比矩阵可以进一步写成:⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡++++-+--=22211211212212112122121121)cos()cos(cos )sin()sin(sin ),(J J Jl l l l l l J J θθθθθθθθθθθθ (19)其中,)cos()cos(cos )sin()sin(sin 2122222121112121221221211111θθθθθθθθθθθθθθ+=∂∂=++=∂∂=+-=∂∂=+--=∂∂=l y J l l y J l x J l l x J p p p p (20)由此可知雅可比矩阵的定义:⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡∂∂∂∂∂∂=⎥⎦⎤⎢⎣⎡=21212221121121),(θθθθθθp p p pJ y y x x J J J J (21)三、平面二连杆机器人手臂的动力学方程推倒动力学方程的方法很多,各有优缺点。
拉格朗日方法思路清晰、不考虑连杆之间的内力,是推倒动力学方程的常用方法。
下面推导图1所示的平面双连杆机器人的动力学方程。
图1中所示连杆均为均质杆,其转动惯量分别是1I 和2I 。
1、求两连杆的拉格朗日函数 (1)求系统总动能连杆1的动能为:212112121121161)31(2121θθθ l m l m I K A ===(21)求连杆2质心D 处的线速度:对连杆2质心位置求导得到其线速度。
连杆2质心位置为:)sin(21sin )cos(21cos 2121121211θθθθθθ++=++=l l y l l x D D (22)连杆2质心速度为:)()cos(21cos )()sin(21sin 2121211121212111θθθθθθθθθθθθ +⋅++⋅=+⋅+-⋅-=l l Y l l x D D (23)(24) 连杆2的动能:21221222222222122122212212212222222122122212221222222212)cos 32(2161)cos 31(21])cos 21(41)cos 41[(21))(121(2121)(21θθθθθθθθθθθθθθθθ l l l m l m l l l l m l l l l l l l l m l m V m I K D D +++++=+++++++=++=(25) 系统总动能:212212222222222122122222112122122122222222212212221221)cos 2131(61)cos 21616121()cos 32(2161)cos 31(21θθθθθθθθθθθθ l l m l m l m l l m l m l m l m l l l m l m l l l l m K K K ++++++=+++++=+= (26)(2)求系统总势能 系统总势能为:))sin(21sin (sin 21212112111θθθθ+++=l l g m gl m P (27) (3)求拉格朗日函数)]sin(21sin [sin 21)cos 2131(61)cos 21616121(21211211121221222222222212212222211212θθθθθθθθθθ++--++++++=-=l l g m gl m l l m l m l m l l m l m l m l m PK L (28) (4)列写动力学方程按照拉格朗日方程,对应关节1、2的驱动力矩分别为:222111θθτθθτ∂∂-∂∂∂∂=∂∂-∂∂∂∂=LL t LL t (29))cos(21cos )21(sin 21sin )cos 2131()cos 3131(2122112122221221221222212222122122222112121θθθθθθθθθθθθτ++++--+++++=gl m gl m m l l m l l m l l m l m l l m l m l m l m (30)同理:)cos(21sin 2131)cos 2131(21222122122222122122222θθθθθθθτ+++++=gl m l l m l m l l m l m (31)联合(30)、(31)式,将动力学方程写成如下矩阵形式:(32) 四、平面二连杆机器人手臂的轨迹规划轨迹规划就是已知起点和终点的位置速度加速度等参数确定中间点的相应参数的过程。
轨迹规划是机器人完成规定任务所必需的。
它分为关节空间的轨迹规划和直角坐标空间的轨迹规划、以及基于动力学的轨迹规划等几种类型。
