神经网络预测控制大全
神经网络PID控制
NNI
十
十
x₁(k)=e(k)x₂(k)=△e(k)=e(k)-e(k-1)x₃(k)=△²e(k)=e(k)-2e (k-1)+e(k-2)e(k)=r(k)-y(k)NNC 的输出为:△u(k)=k₁x₁(k)+k₂x₂(k)+k₃x₃(k)式中,}i=1,2,3 为权系数,△u(k) 为输入信号的加权和。由此可见,NNC 具有增量D 控制的结构
i=1,2,…,Q-1
BP网络的输入层节点的输为
网络的隐含层输入、输为
·神经网络PID控制 20
o(k)=1
(13)
(14)
式中o 为输出层权系数 阈值,
网络的输出层的输入输出为
·神经网络PID控制 21
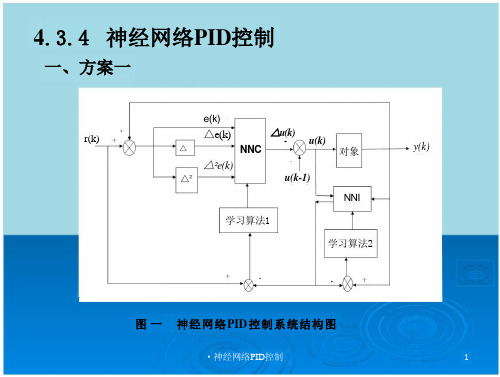
图二 神经网络PID控制系统结构图
·神经网络PID控制 17
二、方案二
被控对象
u
个
经典PID控制算式为u(k)=u(k-1)+Kp[e(k)-e(k-1)]+K,e(k)+K,[e(k)-2e(k-1) + e(k-2)1
7.由(20)式,计算修正输出层敝系数。(k);8.由(21)式,计算修正隐含层敝系数。)(k);9.置k=k+1, 返回到“3”,直到性能指标J 满足要求。
·神经网络PID控制 26
系数a(k)是慢时变的,a(k)=1.2(1-0.8e -01k),神经网络结构为4—5—3,输入层的个神经元分别为模型翰入r(k)、 输 出(k)、误 差(k)和常量。学习速率=0.25,动量系数=0.05,加权系数初始值取随[=0.50.5]上的随机数。当输入信号为幅值是的正弦信号(t)sin(2πt)时,取采样时间为.001s,仿真结果如图所示。·神经网络PID控制 27
神经网络预测控制综述

( ) 数模 型为预测模型的预测控制算法 。参数模型分为差分方 2以参
程模型和离散状 态空间模型 [] 1 o 。差分方程模型是一种离散时间动态模 型, 它分为确定性差分方程和随机性差分方程 。 通常 , 预测控制采用随机 差分方 程( C R A模型 、A I A模型 )状态空间模型是一种描述动 如 A M C RM 。 态系统 的完整模 型 , 它不仅反 映系统 的输入输 出关 系 , 而且还 能揭示系 统 内部 , 以及 内部与外部的联系 , 型由状 态方程 和输 出方程组成。 该模 基 于参数模 型的预测控 制算法( 括 G C G P 吸取 了 D C的滚 动优化 包 P ,P) M 策略 , 在预测模 型和反馈机制等 方面保留了 自校正控制 的优点 , 同时克
多采用这类模 型 ,如 S l石油公 司的 Q M e l D C和 St i 公 司 的 I C M eot pn DO 软件包 等。文献I ] 中有 I C M软件包成功应用于一个 2 0M 汽轮发 s DO 5 W 电机组控 制的例子 , 它的基础算 法是 M C算法 , A 但根据控制与辨识在算
维普资讯
S I E H I F R A I ND V L P E T&E O O Y C - C O M TO E E O M N T N CNM
文章编号 :0 5 6 3 ( 0 7 1 — 15 0 10 — 0 3 2 0 )5 0 5 — 3
20 年 07
第 1 卷 第 1 期 7 5
收稿 日期:O 7 0 - 0 2o—32
神 经 网 络 预 测 控 制 综 述
代正梅 , 田建艳
( 太原 理工大学信息工程学院 , 山西太原 ,30 4 002 )
摘
基于神经网络的广义预测控制综述

基于神经网络的广义预测控制综述第18卷第3期2005年6月常州工学院JournalofChangzhouInstituteofTechnologyV o1.18NO.3Jun.2005基于神经网络的广义预测控制综述李东侠张忠禄(常州T学院电子信息与电气工程学院,江苏常州213002)摘要:概括叙述了广义预测控制的发展现状,对具有误差校正的预测控制方法进行了概括,介绍了与神经网络相结合的非线性系统的预测控制方法,并在此基础上讨论了神经网络非线性预测控制中存在的问题及进一步研究的方向.关键词:预测控制;误差校正;神经网络;非线性系统中图分类号:TPI83文献标识码:A文章编号:1671—0436(2005)03—0012—041广义预测控制的发展现状广义预测控制是随着自适应控制的研究而发展起来的一种预测控制方法.GPC基于参数模型,引入了不相等的预测水平和控制水平,系统设计灵活方便,具有预测模型,滚动优化和在线反馈校正等特征,呈现出优良的控制性能和鲁棒性.到现在为止,人们已经对该控制算法作了大量的研究,并且取得了许多研究成果.1.1广义预测控制的间接算法广义预测控制算法有两类主要算法,即问接算法和直接算法(也称为显式算法和隐式算法). 间接算法在被控对象参数未知时,必须首先辨识被控对象的参数,然后利用辨识出来的参数计算求解控制律所需要的中问参数,最后才计算控制量.问接算法中需要进行Diophanfine方程的求解,矩阵求逆,递推最小二乘法的求解,计算量较大.为了减少在线计算量,针对这一问题,提出了许多改进方法.文[1]给出了Diophantine方程递推求解的方法;文[2]利用参数辨识的结果直接求解控制器,不用求解Diophantine方程,减少了计算量;文[3]采用递推的方法建立预测模型,避免了求解Diophantine方程,而且不受多项式稳定的限制;文[4]利用待求逆矩阵中下三角矩阵元收稿日期:2005-03—30素的特点,给出了一种递推求解逆矩阵的方法;文[5]提出了并行结构分解的算法,提高了在线计算效率;文[6]分别针对状态空间模型和输入输出模型,采用递推的方法,将GPC化为解Riccafi 方程,基于脉冲阵列结构提出了参数辨识的并行方法.1.2广义预测控制的直接算法同问接方法相比较,直接算法不需要求解Di. ophantine方程和逆矩阵,直接估计控制器的参数.文[7]在假定被控对象的阶跃响应前Ⅳ项已知的情况下,给出了一种直接算法和全局收敛性分析;文[8]使用带死区的参数估计方法估计控制器参数;文[9]引入等价性能指标,采用两个辨识器,先辨识被控对象的参数,得到广义输出,然后再用改进的最小二乘法估计控制器的参数;文[10]通过求性能指标的等值曲面,分析了受幅度和变化率约束下的优化问题,给出了一种基于几何分析的约束直接广义预测控制算法;文[11]分析了被控对象的开环参数,闭环参数和控制器参数之问的关系,采用三个辨识器,通过辨识开环系统的参数来递推计算系统的预测输出和参考轨迹,通过辨识闭环系统得到系统的广义输出,在此基础上辨识控制器的参数.除了上述基于受控自回归积分滑动平均模型第3期李东侠,张忠禄:基于神经网络的广义预测控制综述13 (CARIMA)的间接算法和直接算法以外,还有许多其他的广义预测控制算法,如与PID相结合的广义预测控制算法¨,与模糊控制相结合的GPC算法¨,变结构的预测控制算法和有约束的广义预测控制算法儿"等,许多学者还提出了一些改进算法,如加权控制律的GPC算法161,增量型广义预测控制…等.2基于神经网络误差校正的广义预测控制2.1误差校正原理对预测控制来说,核心问题是怎样根据对象的已知信息做出较好的预测.由于对象的验前信息的不充分性,基于此类信息集合得到的预测模型,用于在线预测时,其预测值与实测值之间一定存在一个偏差,我们称其为预测误差.预测误差越大,控制效果越差.当前采用的各种预测控制方法,不管是间接算法,还是直接算法,一般其预测输出的预测模型都是建立在数学模型的基础上,都没有考虑建模误差的影响.虽然一般的广义预测控制算法对模型失配有一定的抑制作用, 但目前的算法对模型失配的抑制能力是有限的, 当建模误差较大时,随着预测长度的增加,预测误差必然也会急剧增加,从而有可能破坏预测控制系统的鲁棒性,只有根据实测信息不断进行反馈校正,才能保证预测趋于准确.为了克服这一缺点,考虑引入预测误差对预测输出进行校正,即: 利用预测误差的过去信息建立误差的预测模型, 通过对误差的预测修正系统的预测输出,进一步克服模型失配的影响,提高控制系统的鲁棒性. 引入预测误差以后,系统的预测输出可以表示为: Y(t+k/t)=Y(t+k/t)+Y(t+k/t)(1)其中,Y(t+k/t)表示在t时刻对t+时刻系统输出的预测,Y(t+k/t)表示系统基于数学模型的输出预测,Y,(t+k/t)是根据预测误差的历史数据对模型预测的修正.2.2建立误差预测模型的方法为了克服建模误差的影响,增强预测控制的鲁棒性,许多学者对误差的预测进行了研究.传统方法是用时刻已知的模型输出误差e(k)=Y(k)一Y(k)来修正,文[18]中提出了利用预测误差的历史数据建立误差预测模型,通过对误差的预测修正纯粹基于数学模型的预测,采用时序分析里的AR模型,利用参数辨识的最小二乘法递推估计误差模型参数,建立误差的预测模型.由于神经网络能够逼近任意复杂的非线性函数关系,采用并行分布式信息处理方法,可同时综合定量和定性信息,既可在线学习也可离线计算, 灵活性大,所以用神经网络建立误差预测模型的方法有很大的发展空间.文[19]采用与神经网络相结合的方式,基于BP结构神经网络,对系统的建模误差进行预测, 建立误差的预测模型,取得了较好的控制效果.网络的输入向量为X=[Y(t),Y(t一1),…Y(t一),H(t—1),…,"(t一七一1)],其中Y(?)为系统的输出值,U(?)为系统的控制量,网络的输出向量为Y=[Y(t),…,Y(t—k)],而Y(t一七)Ay(t一七)一Y(t—k/t—k—),k=1,2,…,P(2)其中,Y(t—k)是t—k时刻系统的输出值,Y (t—k/t—k—d)是在t—k—d时刻基于数学模型对Y(t—k)的预测值,d为系统时滞,P为训练样本数.文[2O]提出了一种改进的全局寻优自适应快速BP算法,并应用于广义预测控制算法中, 用该网络建立误差预测模型,解决了限制GPC实时控制的快速性问题.文[21]采用动态BP网络对模型预测误差进行在线补偿,提高了预测精度. 文[22]中提出了利用径向基函数神经网络(RBFNN)来补偿由系统的非线性和外界干扰引起的预测误差,也取得了较好的控制效果.3基于神经网络的非线性系统的广义预测控制实际中的控制对象都带有一定的非线性,大多数具有弱非线性的对象可用线性化模型近似, 并应用已有的线性控制理论的研究成果来获得较好的控制效果.而对具有强非线性的系统的控制则一直是控制界研究的热点和难点,模型线性化无法满足系统控制要求,在某些极端情况下,线性化的参考模型甚至会导致控制系统稳定性的丧失,将广义预测控制对线性系统的良好控制作用l4常州工学院2005正推广到非线性系统,也是预测控制研究的方向之一.就预测控制的基本原理而言,只要从被控对象能够抽取出满足要求的预测模型,它便可以应用于任何类型的系统,包括线性和非线性系统.但由于非线性系统的复杂多样性,在实现的技术上和理论分析上难度比线性系统要大得多.近年来人们对非线性系统的预测控制做了大量的研究,并提出了不少有意义的方法.与神经网络,多模型控制,微分集合理论和微分代数理论等算法相结合,是非线性系统的GPC研究的有效途径之一.由于神经网络理论在求解非线性方面的巨大优势,很快被应用于非线性预测控制中,并形成许多不同的算法.如神经网络的内模控制,神经网络的增量型模型算法控制等,近来一些学者对有约束神经网络的预测控制也作了相应的研究.基于神经网络的非线性GPC研究还处于起步阶段, 这方面的研究成果很少,其主要原因是利用神经网络进行多步预测还没有直接有效的方法.文[24]设计了多层前馈神经网络,使控制律离线求解.文[25]采用两个网络进行预测,但结构复杂,距实际应用还有一定的距离,文[26]利用递阶遗传算法,经训练得出离线神经网络模型,经多步预测得出对象的预测模型,给出了具有时延的非线性系统的优化预测控制.将神经网络用于GPC的研究成果有利用Tank—Hopfield网络处理GPC矩阵求逆的算法,基于神经网络误差修正的GPC算法,利用小脑模型进行提前计算的GPC算法,基于GPC的对角递归神经网络控制方法以及用神经网络处理约束情形的预测控制算法.非线性系统的GPC研究成果还有基于双线性模型的GPC算法等,但算法都具有一定的局限性.4基于神经网络的预测控制中存在的问题众所周知,评价一个神经网络的主要性能指标是学习收敛速度和泛化能力.前者表现在以一定的精度逼近学习样本所需的时间,而后者表现在对学习样本集外的样本的逼近程度.采用Sigmoid函数作为网络单元函数的多层前馈网络(BPN)是当今应用最广的一种网络.这类网络采用反向传播(BP)学习算法.虽然BP网络是应用最多的一种神经网络,但它仍存在一些缺陷:(1)学习速度慢,即使一个比较简单的问题,也需要几百次甚至几千次的学习才能收敛;(2)不能保证收敛到全局最小点; (3)网络隐含层的层数及隐含层的单元数的选取尚无理论上的指导,而是根据经验确定.因此,网络往往有很大的冗余性,无形中增加了网络学习的时间;(4)网络的学习,记忆具有不稳定性.所以以下问题有待进一步完善:(1)神经网络的收敛速度一直是限制其应用的主要问题,要进一步提高神经网络的收敛速度及泛化能力,提高神经网络的实用性.(2)利用神经网络进行多步预测还没有直接有效的方法.(3)对非线性系统的预测控制还没有很好的解决,由于广义预测控制算法本身的特殊性和非线性系统的复杂多样,这方面的研究成果也较少.目前在非线性预测控制中使用的神经网络大多为静态的网络,限制了神经网络的非线性表达能力,并且网络结构复杂计算量大,快速有效的预测控制方法有待进一步研究.[参考文献][1]ClarkeD.W.andMohtadi,C.andTufts,P.S,mGeneralized PredictiveContro1.PartI.TheBasicAlgorithmic.PartIIExtcn—sionsandInterpretations[J].Automatic,1987,23(2):137一l6O.[2]袁着祉,崔保民.新型随机广义预测自校正控制器[J].自动化,1992,18(3):282—289.[3]金元郁.预测控制算法研究[D].沈阳:东北工学院博士学位论文,1990.[4]郭庆鼎,金元郁,胡耀华.求解GPC中逆矩阵的递推算法[J].控制与决策,1996,11(4):510—513.[5]扬健,席裕庚,张钟俊.预测控制滚动优化的时间分解方法[J].自动化,1995,21(5):555—561.[6]慕德俊,戴冠中.基于状态空间模型广义预测控制的并行算法[J].控制理论与应用,1995,12(5):646—652.[7]王伟.广义预测控制自适应控制的直接算法和全局收敛性分析[J].自动化,1995,21(1):57—62.【8]Wangwei.ADirectAdaptiveGeneralizedPredictiveControlAb gorithmwithGuaranteedStabillity[J].Int.J.ofAdaptiveControl&SignalProcessing,1994,8(3):211—227.第3期李东侠,张忠禄:基于神经网络的广义预测控制综述[9]舒迪前,石中锁.隐式自适应广义预测控制器及全局收敛性分析[J].自动化,1995,21(5):545—554.[10]张峻,席裕庚.基于几何分析的约束预测控制直接算法[J].控制与决策,1997,12(2):184—187.[11]胡耀华,贾欣乐.广义预测控制的直接算法[J].控制与决策,2000,15(2):221—223.[12]陈增强,车海平,袁着祉.具有比例积分结构的广义预测自校正控制器[J].控制与决策,1994,9(2):105—110.[13]张化光,吕剑虹,陈来九.模糊广义预测控制及其应用[J].自动化,1993,19(1):9—17.[14]毛志忠,杨琳.一种解决预测控制输入信号受约束问题的方法[J].控制与决策,1994,9(3):230—233.[15]LimKW,HoWK,LeeTH,LingKV,XuW.Generalized PredictiveControllerwithPoleRestriction[J].IEEProc—D, 1998,145(2):219—225.[16]周德云,陈新海.采用加权控制律的自适应广义预测控制器[J].控制与决策,1991,6(1):7—13.[17]孙明玮,陈增强,袁着祉.增量型广义预测控制[J].控制理论与应用,2000,17(2):165—168.[18]古钟璧,王祯学,王苇.具有误差预测修正的预测控制算法[J].控制与决策,1992,7(6):432—436.[19]李少远,刘浩,袁着祉.基于神经网络误差修正的广义预测控制[J].控制理论与应用,1996,13(5):677—680.[20]王一晶,左志强.基于改进BP网络的广义预测控制快速算法[J].基础自动化,2002,9(2):l0一l2.[21]刘晓华,王秀红,杨振光.基于动态BP网络误差修正的广义预测控制[J].青岛大学,2002,15(1):34—39.[22]张彬,李平,陈红艳.基于径向基函数神经网络偏差补偿的预测函数控制[J].哈尔滨理工大学,2003,8(1):46—49.[23]席裕庚.预测控制[M].北京:国防丁业出版社.1993.[24]ParisiniT,SanguinetiandZoppoliR.Nonlinearstabilizationby receding—hodzonneuralregulator[J].Int.J.Control,1998,70(3):341—362.[25]SchenkerB.AgarwalM.LongRangePredictiveControlfor PoorlyKnownSystems[J].Int.J.Control,1990,62(1):227—238.[26]刘宝坤,王慧,曹明,李光良.基于神经网络模型直接优化预测控制[J].信息与控制,1998,27(5):386—390.[27]胡耀华,贾欣乐.广义预测控制综述[J].信息与控制,2000,29(3):248—256.[28]史国栋,王洪元,薛国新.基于径向基函数模型的非线性预测控制策略研究[J].模式识别与人工智能,2000,13(4):361—365.[29]PhilipDWasserman.NeuralComputingTheoryandPractice[M].NewY ork:VanNostrandReinhold.1989.124—129. SummarizationofGeneralizedPredictiveControlBasedonNeuralNetworkLIDong?-xiaZHANGZhong?-lu(SchoolofElectronicInformation&ElectricEngineering,ChangzhouInstituteofTech nology,Changzhou213002)Abstract:ThispapersummarizestheactualityofGeneralizedPredictiveControl(GPC).The predic.tivecontrolmethodwitherrorcorrectionissummedup.Thenitrecommendsthepredictiveme thodscom.binedwithneuralnetworkofnonlinearsystem.Basedonthisitpresentstheproblemsexistingi nthepredic. tivecontrolofnonlinearsystemandfurtherresearchtrendsarealsodiscussed. Keywords:predictivecontrol;errorcorrection;neuralnetwork;nonlinearsystem责任编辑:张秀兰。
神经网络控制(RBF)

神经网络控制(RBF)神经网络控制(RBF)是一种基于径向基函数(RBF)的神经网络,用于控制系统,其主要功能是通过对输入信号进行处理来实现对系统输出的控制。
通过神经网络控制,控制器可以学习系统的动态行为和非线性模型,从而使得控制器能够自适应地进行调整和优化,实现对系统的精确控制。
RBF 网络通常由三层组成:输入层、隐藏层和输出层。
输入层接受系统的输入信号,并将其传递到隐藏层,隐藏层对输入数据进行处理并输出中间层的值,其中每个中间层神经元都使用一个基函数来转换输入数据。
最后,输出层根据隐藏层输出以及学习过程中的权重调整,计算并输出最终的控制信号。
RBF 网络的核心是数据集,该数据集由训练数据和测试数据组成。
在训练过程中,通过输入训练数据来调整网络参数和权重。
训练过程分为两个阶段,第一阶段是特征选择,该阶段通过数据挖掘技术来确定最优的基函数数量和位置,并为每个基函数分配一个合适的权重。
第二阶段是更新参数,该阶段通过反向传播算法来更新网络参数和权重,以优化网络的性能和控制精度。
RBF 网络控制的优点在于其对非线性控制问题具有优秀的适应性和泛化性能。
另外,RBF 网络还具有强大的学习和自适应调整能力,能够学习并预测系统的动态行为,同时还可以自动调整参数以提高控制性能。
此外,RBF 网络控制器的结构简单、易于实现,并且具有快速的响应速度,可以满足实时控制应用的要求。
然而,RBF 网络控制也存在一些局限性。
首先,RBF 网络需要大量的训练数据来确定最佳的基函数数量和位置。
此外,由于网络参数和权重的计算量较大,实时性较低,可能存在延迟等问题。
同时,选择合适的基函数以及与其相应的权重也是一项挑战,这需要在控制问题中进行深入的技术和经验探索。
总体而言,RBF 网络控制是一种非常有效的控制方法,可以在广泛的控制问题中使用。
其结构简单,性能稳定,具有很强的适应性和泛化性能,可以实现实时控制,为复杂工业控制问题的解决提供了一个重要的解决方案。
如何利用神经网络进行预测分析(Ⅰ)

神经网络是一种模仿人脑神经元之间相互连接的数学模型,可以用来进行复杂的数据处理和预测分析。
利用神经网络进行预测分析是一种常见的应用,可以用于股票价格预测、天气预测、人口增长预测等多个领域。
本文将探讨如何利用神经网络进行预测分析,并介绍一些常用的方法和技巧。
1. 数据收集在利用神经网络进行预测分析之前,首先需要收集相关的数据。
数据可以来自各种渠道,如历史数据、实时数据、传感器数据等。
例如,如果要预测股票价格,可以收集历史的股票交易数据;如果要预测天气,可以收集气象局的观测数据。
数据的质量和数量对预测结果有很大的影响,因此在收集数据时需要尽量确保数据的完整性和准确性。
2. 数据预处理在收集到数据后,需要对数据进行预处理以便神经网络进行分析。
数据预处理包括数据清洗、数据标准化、数据归一化等步骤。
数据清洗是指去除数据中的噪声和异常值,以确保数据的质量;数据标准化是指将数据按照一定的规则进行转换,使得数据具有统一的尺度和分布;数据归一化是指将数据按照一定的比例进行缩放,以便神经网络更好地学习和训练。
3. 神经网络模型选择选择合适的神经网络模型是进行预测分析的关键一步。
常用的神经网络模型包括前馈神经网络、循环神经网络、卷积神经网络等。
不同的神经网络模型适用于不同的预测分析任务,需要根据具体的问题选择合适的模型。
例如,对于时间序列数据的预测分析,循环神经网络通常是一个较好的选择;对于图像识别和语音识别等任务,卷积神经网络通常是更合适的模型。
4. 数据分割和训练在选择了合适的神经网络模型之后,需要将数据分割成训练集和测试集,并对神经网络进行训练。
训练集用于训练神经网络模型,测试集用于评估模型的性能。
在训练神经网络时,需要选择合适的优化算法和损失函数,以使得神经网络能够更好地拟合数据并进行预测分析。
5. 参数调整和模型评估在训练神经网络模型过程中,需要对模型的参数进行调整,并对模型的性能进行评估。
参数调整包括学习率的选择、隐藏层节点数的选择等。
现代控制工程第13章神经网络控制

13.3.2 BP学习算法
▪ 两个问题:
(1)是否存在一个BP神经网络能够逼近给定的样本或者函数。
( 2)如何调整BP神经网络的连接权,使网络的输入与输出与 给定的样本相同。
1986年,鲁梅尔哈特(D. Rumelhart)等提出BP学习算法。
13.3.2 BP学习算法
1. 基本思想
目标函数:
x1
y1m
x2
y2m
x p1
y
m pm
13.3.2 BP学习算法
2. 学习算法
d y wikj1
k i
k 1 j
d y y u m ( i
m
i
)
si
fm
(
m)
i
——输出层连接权调整公式
d u d k i
fk (
k)
i
w k 1 k
l
li
l
——隐层连接权调整公式
13.3.2 BP学习算法
2. 学习算法
13.2 神经元与神经网络
13.2.1 生物神经元的结构
人脑由一千多亿(1011亿- 1014 亿)个神经细胞(神经元)交织 在一起的网状结构组成,其中大 脑皮层约140亿个神经元,小脑皮 层约1000亿个神经元。
神经元约有1000种类型,每个神经元大约与103- 104个其他 神经元相连接,形成极为错综复杂而又灵活多变的神经网络。 人的智能行为就是由如此高度复杂的组织产生的。浩瀚的宇 宙中,也许只有包含数千忆颗星球的银河系的复杂性能够与大 脑相比。
13.2.1 生物神经元的结构
神经网络(neural networks,NN)
▪ 生物神经网络( natural neural network, NNN): 由中枢神经系 统(脑和脊髓)及周围神经系统(感觉神经、运动神经等)所 构成的错综复杂的神经网络,其中最重要的是脑神经系统。 ▪人工神经网络(artificial neural networks, ANN): 模拟人脑神经 系统的结构和功能,运用大量简单处理单元经广泛连接而组成 的人工网络系统。
神经网络在预测模型和控制系统中的应用

神经网络在预测模型和控制系统中的应用神经网络是一种模拟人脑神经系统运行的数学模型,在机器学习和人工智能领域有着广泛的应用。
作为一种高度自适应的算法,神经网络在预测模型和控制系统中发挥了重要作用。
神经网络在预测模型中的应用预测模型包括了诸如时间序列预测、金融市场预测、自然灾害预测等各种领域,对于提高决策的准确性和效率都有很大的帮助。
而神经网络则是其中的重要一环。
神经网络可以通过学习过去的数据,提取出其中的规律,并利用这些规律来预测未来的数据。
以时间序列预测为例,神经网络可以利用历史上同期的数据,进行训练,并得到一个预测模型。
这个预测模型可以用来预测未来时期的数据。
相比于传统的模型,神经网络可以更好地处理非线性数据关系,同时也可以更好地处理多个变量之间的影响关系。
除了时间序列预测,在金融市场预测中,神经网络也发挥了重要作用。
金融市场的波动性很高,而神经网络可以很好地处理这种波动。
通过学习历史上的股市数据,神经网络能够建立出股市走势的预测模型。
这个预测模型可以用来预测股市的未来发展趋势。
在实际的投资决策中,这些预测结果可以帮助投资者更好地理解市场,作出正确的投资决策。
神经网络在控制系统中的应用控制系统是一种可以监控、管理和控制工程和科学系统的集成体系。
控制系统通常需要利用大量的数据来进行监控和控制。
而神经网络可以帮助实现控制系统的智能化。
在控制系统中,神经网络可以利用历史上的数据,建立出一个预测模型。
这个预测模型可以用来预测未来的结果。
比如,对于一个复杂的航空控制系统,神经网络可以对机器状态进行监控,并预测出机器的可能故障。
这些预测结果可以提前告知维修人员,帮助他们事先准备好所需的维修工具和零件。
在制造业中,神经网络也可以用来进行过程控制。
利用多个神经网络,可以对制造过程中的各种参数进行监控和控制,从而实现制造过程的优化。
比如,在纺织生产中,神经网络可以对生产过程中的温度、湿度等参数进行监控。
通过对过去数据的学习,神经网络可以建立出一个精准的控制模型,并自动调整参数,从而实现制造过程的优化。
神经网络控制

从而使神经网络控制器逐渐在控制作用中占据主
导地位,最终取消反馈控制器的作用;
✓
一旦系统出现干扰,反馈控制器重新起作用。
✓
可确保控制系统的稳定性和鲁棒性,有效提高系
统的精度和自适应能力。
神经网络
控制器
期望输出
()
−1
()
+
-
()
传统控
网络实现;可进行离线辨识,也可进行在线辨识。
+
-
逆向建模
一般而言,建立逆模型对神经网络控制意义重大。
直接逆建模简化结构图:
可用于离线辨识,也可
用于在线辨识。
对 象
+
神经网络
逆模型
缺点:不是目标导向的,系统输入也不可能预先定义。
实际常采用正-逆建模结构。
正-逆建模
神经网络
逆模型
对 象
第3章 神经网络控制
第2部分 控制基础
3.5 神经网络控制基础
3.5.1 神经网络控制的优越性
神经网络可以处理那些难以用模型或规则描述的过
程或系统。
神经网络采用并行分布式信息处理,具有很强的容
错性。
神经网络是本质非线性系统,可实现任意非线性映
射。
神经网络具有很强的信息综合能力,能同时处理大
期望输出
()
稳定的参
考模型
参考模
型输入
()
+
()
()
+
-
神经网络
控制器
()
对象
()
基于神经网络的模型预测控制问题研究

基于神经网络的模型预测控制问题研究随着现代科技的发展和计算机技术的日新月异,神经网络技术已经被广泛应用于各个领域。
其中,在控制领域中,基于神经网络的模型预测控制(MPC)已经展现了很大的优势,成为了一种新型的控制技术。
在传统的控制方法中,我们需要建立完整的模型来进行控制。
而在基于神经网络的控制中,则是通过训练神经网络来逼近这个模型,从而实现智能化的控制。
由于神经网络具有非线性、自适应、泛化性强等优点,因此在处理复杂的、非线性的控制问题时,其优势更加明显。
在基于神经网络的MPC中,我们首先需要通过对控制对象进行建模,得到一个预测模型。
然后,通过神经网络对这个预测模型进行学习和逼近,得到一个更加精准的预测模型。
在此基础上,我们就可以将其应用于控制环节中,对需要控制的过程进行智能化的预测和控制。
需要注意的是,在使用神经网络进行MPC时,我们需要考虑许多因素。
首先是网络的架构。
不同的网络架构对MPC的性能和效果有着不同的影响。
因此,我们需要针对具体的控制问题选择合适的网络结构,以获得最佳的控制效果。
另外,在神经网络的训练过程中,我们需要考虑如何选择合适的学习算法和目标函数。
这些选择同样对神经网络的性能和训练效果产生着极大的影响。
因此,在进行神经网络的训练时,选择合适的学习算法和目标函数是非常必要的。
此外,在使用MPC进行实时控制时,我们还需要考虑计算时间和计算能力的问题。
因为MPC需要进行实时的预测和控制,所以控制系统的计算性能对其稳定性和效果具有重要影响。
因此,在进行MPC系统设计时,需要有足够的计算能力支撑控制系统的实时运行,并对计算时间进行充分的考虑。
总之,基于神经网络的MPC是一种新型的控制技术,可以在非线性、复杂的控制问题中展现出其优势。
但是,在进行具体的应用时,需要对网络架构、学习算法、目标函数等进行合理的选择,并考虑计算时间和计算能力的问题,才能获得最佳的控制效果。
随着神经网络技术的持续发展和应用,相信基于神经网络的MPC 在实际工程领域中将会得到更加广泛的应用和发展。
神经网络预测控制综述

神经网络预测控制综述摘要:近年来,神经网络预测控制在工业过程控制中不仅得到广泛的应用,而且其理论研究也取得了很大进展。
对当前各种神经刚络预测控制方法的现状及其工业应用进行了较深入地分析,并对其存在的问题和今后可能的发展趋势作了进一步探讨。
关键词:神经网络;预测控制:非线性系统;工业过程控制Abstract: In recent years, neural network predictive control has not only been widely used in industrial process control, but also has made great progress in theoretical research. The current status of various neural network prediction control methods and their industrial applications are analyzed in depth, and the existing question and possible future development trends are further discussed.Keywords: neural network; predictive control: nonlinear system; industrial process control20世纪70年代以来,人们从工业过程的特点出发,寻找对模型精度要去不高而同样能实现高质量控制性能的方法,预测控制就是在这种背景下发展起的[1]。
预测控制技术最初山Richalet和Cutler提出[2],具有多步预测、滚动优化、反馈校正等机理,因此能够克服过程模型的不确定性,体现出优良的控制性能,在工业过程控制中取得了成功的应用。
如Shell公司、Honeywell公司、Centum 公司,都在它们的分布式控制系统DCS上装备了商业化的预测控制软件包.并广泛地将其应用于石油、化工、冶金等工业过程中[3]。
神经网络控制系统教程PPT(MATLAB基于Simulink的三种典型神经网络控制系统学习资料)

1. 基于传统控制理论的神经控制将神经网络作为传统控制系统中的一个或几个部分,用以充当辨识器,或对象模型,或控制器,或估计器,或优化计算等。这种方式很多,常见的一些方式归纳如下:
22
(a)
(b)
图3-3 神经直接逆动态控制系统
1).神经直接逆动态控制神经直接逆动态控制采用受控对象的一个逆模型,它与受控对象串联,以便使系统在期望响应(网络输入
22
(2)神经间接自校正控制间接自校正控制一般称为自校正控制。自校正控制是一种利用辨识器将对象参数进行在线估计,用控制器实现参数的自动整定相结合的自适应控制技术,它可用于结构已知而参数未知但恒定的随机系统,也可用于结构已知而参数缓慢变化的随机系统。
图3-4 神经自校正控制系统
22
神经自校正控制结构如图3-4所示,它由一个自校正控制器和一个能够在线辨识的神经网络辨识器组成。自校正控制器与被控对象构成反馈回路,根据神经网 络辨识器和控制器设计规则,以得到控制器的参数。 可见,辨识器和自校正控制器的在线设计是自校正控 制实现的关键。
22
上述两种分类并无本质差别,只是后者划分更细一些,几乎涉及到传统控制、系统辨识。滤波和预报等所有方面,这也间接地反映了随着神经网络理论和应用研究的深入,将向控制领域、信息领域等进一步透。为了更能从本质上认识神经网络在实现智能控制中的作用和地位。1998年李士勇将神经网络控制从它与传统控制和智能控制两大门类的结合上考虑分为两大类:即基于传统控制理论的神经控制和基于神经网络的智能控制两大类。
神经网络控制系统
1
神经网络控制理论基于Simulink的三种典型神经网络控制系统
神经网络发展至今已有半个多世纪的历史,概括起来经历了三个阶段:20世纪40 60年代的发展初期; 70年代的研究低潮期;80年代,神经网络的理论研究取得了突破性进展。神经网络控制是将神经网络在相应的控制系统结构中当做控制器或辨识器。神经网络控制的发展,虽仅有十余年的历史,但已有了多种控制结构。
预测控制算法范文

预测控制算法范文预测控制算法是一种基于过去的观测数据来预测未来系统行为的控制方法。
它可以用于各种领域,如工业控制、金融市场预测、天气预报等。
本文将介绍几种常用的预测控制算法,包括递推最小二乘法、基于神经网络的算法和基于深度学习的算法。
1. 递推最小二乘法(Recursive Least Squares, RLS):递推最小二乘法是一种经典的预测控制算法。
它通过不断更新一个递推系数来预测未来系统行为。
具体而言,它通过最小化观测数据与预测输出之间的误差平方和来更新递推系数。
递推最小二乘法在实际应用中被广泛使用,因为它具有较好的收敛性和计算效率。
2.基于神经网络的算法:基于神经网络的预测控制算法基于一种称为前馈神经网络的模型,该模型可以学习和预测复杂的非线性系统行为。
算法首先使用一组历史观测数据来训练神经网络模型,然后使用该模型来预测未来系统行为。
该算法的优点是能够处理复杂系统并具有较高的预测精度,但需要大量的训练数据和计算资源。
3.基于深度学习的算法:基于深度学习的预测控制算法是近年来新兴的算法。
它使用一种称为深度神经网络的模型来学习和预测系统行为。
与传统的神经网络不同,深度神经网络拥有多个隐藏层,可以学习更加复杂的系统关系。
该算法在处理大规模数据集和高维数据方面具有很大优势,并在图像识别、语音识别等领域取得了显著的成果。
4.其他预测控制算法:除了上述提到的算法外,还有许多其他预测控制算法可供选择。
例如,基于卡尔曼滤波的算法可以处理系统中的噪声和不确定性,并提供准确的预测。
遗传算法可以通过模拟进化过程来最优的控制参数。
模糊控制算法可以处理模糊和模糊输入,适用于复杂和不确定的系统。
综上所述,预测控制算法在实际应用中起到了重要的作用。
根据不同的应用场景和需求,我们可以选择合适的算法来进行预测和控制。
未来随着科技的发展和算法的改进,预测控制算法将能够更好地处理复杂系统和大规模数据,并提供更准确的预测和控制结果。
神经网络广义Backstepping预测控制

为提 高 系统 的鲁 棒 性 ,广 义 B cs pig控 制 策 略需 与鲁 棒 自适 应 技 术 相 结 合 .自适 应 鲁 棒 技 akt pn e 术 [ 的缺 点是含 有不 确定 参数 的非 线 性 函数 项 必 须 满 足参 数 可 线性 化 条 件 , 不 易确 定 递 归 矩 阵. 1 且 而参 数可 线性化 的假 设在 许 多实 际应用 中并不 成立 ,如机 电运 动 系统 和机 器人 控 制 中 的摩擦 项 .近年 来 , 经 网络 预测 模 型广泛应 用 于系统 辨识 ,由于神 经 网络对非 线性 函数 的逼 近能力 ,因此 不需 进 神 引
smu a in x e me t i lt se p r n. o i
K ywo d e rs:g n r l e a k tp ig e eai d B c s pn ;RB e rln t ok ;p e it ec nrl z e F n ua ew rs rdci o t v o
第4 8卷
第5 期
吉 林 大 学 学 报 (理 学 版 ) Junl f inU i ri (cec dtn ora o Ji nv sy Si eE io ) l e t n i
Vo . 8 No
Sp 2 1 e 00
神 经 网络 广 义 B c s p ig预 测 控 制 ak t pn e
王 彦 全 赵 衍 辉 杨 晓翠 , , ,王海 洋 ,王 江 熙 乐 ,魏
( .白城师 范学 院 机械 电子工程 系,吉林 白城 170 ; .白城师范学院 物理系 , 1 300 2 吉林 白城 17 0 ; 30 0 3 .天津 大学 电气 与 自动化工程学 院,天津 30 7 ) 0 0 2
Ab t c :T e a t o s p o o e a g n r l e a k t p i g o t l ag r h a d s r t h u h r r p s d e e ai d B c s p n c nr l o t m n RB e r l n t r s a z e o i F n u a ewo k p e it e c nr lsr tg ,a d a ay e h y p n v s n e s b l y a d e r r f t e u i r y ut tl rd c i o t t e y n n lz d t e L a u o e s t i t n ro s o h n f ml l ma ey v o a a i o i
神经网络控制多种结构

神经间接模型参考自适应控制
构造一个参考模型,使其输出为期望输出,控制的目的,是使y跟踪yM。 对象特性非线性、不确定、不确知时采用。
参考模型
yM
e2
r NNC u 对象 y
e1
NNI
-
ˆ y
神经间接模型参考自适应控制
6
神经网络控制的多种结构
神经内模控制
具有结构简单、性能良好的优点。
r e
_
滤波器
F (z )
动作—评价学习神经控制
依据被控对象的当前状态与再励反馈信号,给出评价信号,对当前的控制 进行评价,确定下步的控制。
评价网络
P(x)
控制 网络
ˆ re (k )
u (k )
re (k )
对象
x(k ) 动作—评价学习神经控制
12
神经网络控制的多种结构
神经预测控制
预测控制是一种基于模型的控制, 特点:预测模型、滚动优化和反馈校正。 神经预测控制由神经网络实现预测模型NNP。
PID神经网络多变量控制
PID神经网络控制器NNC与多变量对象一起作为广义网络 ,不需辨识复杂 的非线性被控对象,可对其实现有效的控制。
9
神经网络控制的多种结构
CMAC直接逆运动控制
CMAC用于逆运动控制例——机械手控制问题。
x
ˆ f 1 (x)
末端位置 理想轨迹 CMAC
ˆ
ˆ x
机械手
g
内模 控制器
D (z )
u
对象
P (z )
y ˆ y
内部模型 e1
ˆ P( z )
神经内模控制
7
神经网络控制的多种结构
PID神经网络单变量控制
控制系统神经网络控制技术

控制系统神经网络控制技术控制系统是现代工业发展的重要组成部分,其作用是监测和控制工业系统的各种参数,以确保系统能够稳定可靠地运行。
而神经网络控制技术是一种新型的控制系统方法,它基于神经网络理论,利用具有自适应性和非线性特性的神经网络来控制系统,以提高系统的性能和鲁棒性。
下面将详细介绍神经网络控制技术在控制系统中的应用及其优越性。
一、神经网络控制技术的基本原理1.1神经网络理论概述神经网络理论是计算机科学中一个基础的研究领域,它是由生物学中的神经元学说发展而来。
神经网络是由一组相互连接的人工神经元构成的,这些神经元之间的连接可以传递信息,进而模拟人脑的神经网络。
1.2神经网络控制技术的原理神经网络控制技术利用具有自适应性和非线性特性的神经网络来控制系统,并通过反馈机制控制系统的输出变量,以保持系统的稳定性和精度。
神经网络控制技术具有很强的适应性,可以对系统中的各种复杂非线性因素进行在线学习和自适应调节,以达到最优控制效果。
二、神经网络控制技术在控制系统中的应用神经网络控制技术可以应用于各种控制系统中,如航空控制系统、机器人控制系统、电力系统等。
它在控制系统中的应用主要有以下几个方面:2.1预测控制神经网络可以对待控制变量的未来变化进行预测,以便根据预测结果采取相应的控制策略。
利用神经网络预测控制技术,可以在短时间内完成复杂系统的控制和优化调节,提高系统的响应速度和稳定性。
2.2优化控制神经网络可以对系统进行非线性建模和状态优化,以使得系统满足给定的控制要求。
利用神经网络优化控制技术,可以使系统的控制过程更加稳定、快速和准确,从而提高系统的控制质量和性能。
2.3非线性逆控制神经网络可以利用其非线性自适应特性,在控制系统中实现非线性逆控制,从而实现对系统的精确控制。
利用神经网络非线性逆控制技术,可以有效地克服系统建模中的误差和不确定性,提高系统的控制精度和可靠性。
三、神经网络控制技术的优越性相对于传统的控制技术,神经网络控制技术具有以下几个优越性:3.1 自适应性强神经网络控制技术可以根据系统实时的状态和环境信息进行自适应调节,从而保持系统的稳定性和可靠性。
基于神经网络的预测控制方法研究

基于神经网络的预测控制方法研究一、本文概述随着技术的快速发展,神经网络在各个领域中的应用逐渐显现出其独特的优势。
特别是在预测控制领域,神经网络以其强大的非线性映射能力和自学习能力,成为了研究热点。
本文旨在探讨基于神经网络的预测控制方法,并对其在实际应用中的效果进行深入分析。
本文首先将对神经网络的基本原理和常用模型进行简要介绍,为后续研究提供理论基础。
随后,重点研究基于神经网络的预测控制方法,包括其基本原理、设计流程、优化算法等方面。
通过理论分析和实验研究,本文旨在揭示神经网络在预测控制中的优势与不足,并提出相应的改进策略。
在研究方法上,本文将采用理论分析和实验研究相结合的方法。
在理论分析方面,通过对神经网络和预测控制理论的研究,建立基于神经网络的预测控制模型,并对其性能进行分析。
在实验研究方面,将采用实际数据对模型进行训练和测试,验证模型的有效性和泛化能力。
本文的研究对于推动神经网络在预测控制领域的应用具有重要意义。
通过对基于神经网络的预测控制方法的研究,可以为实际工程应用提供有力支持,提高控制系统的性能和稳定性。
本文的研究也有助于推动技术在其他领域的应用和发展。
二、神经网络基础神经网络是一种模拟人脑神经元网络结构和功能的计算模型,具有强大的自学习、自适应和非线性映射能力。
其基本结构由大量的神经元相互连接而成,每个神经元接收来自其他神经元的输入信号,并根据其权重和激活函数计算输出。
神经网络的核心在于其通过反向传播算法不断调整权重,使得网络输出逐渐逼近期望结果。
神经网络可以分为多种类型,如多层感知器(MLP)、卷积神经网络(CNN)、循环神经网络(RNN)等。
多层感知器是最基本的神经网络形式,由输入层、隐藏层和输出层组成,可以处理各种复杂的非线性问题。
卷积神经网络则特别适用于处理图像等具有网格结构的数据,通过卷积和池化等操作提取图像特征。
循环神经网络则适用于处理序列数据,如时间序列预测、自然语言处理等。
《神经网络控制》课件

神经网络控制需要大量的数据和计算资源,对模型的训练和调整要求较高。
2 神经网络控制的挑战
在复杂系统的实时控制和稳定性问题上,神经网络控制仍然面临挑战。
3 神经网络控制未来发展的方向
未来,神经网络控制将更加注重与其他控制技术的结合,如模糊控制、强化学习等。
总结
神经网络控制的优势 和局限性
《神经网络控制》PPT课 件
# 神经网络控制PPT课件
介绍神经网络控制
定义神经网络控制
神经网络控制是利用神经网络模型来设计控制器,实现对系统的控制和优化。
神经网络控制的作用和优势
神经网络控制具有非线性建模能力和适应性,可以处理复杂系统和非线性控制问题。
神经网络控制的发展历程
神经网络控制起源于20世纪80年代,经历了多个阶段的发展,如BP神经网络、RBF神经网络 等。
神经网络控制具有非线性建模 能力和适应性,但对数据和计 算资源要求较高。
神经网络控制的发展 前景
神经网络控制在自动化控制领 域有着广阔的应用前景,将与 其他技术相结合。
未来研究方向
进一步研究神经网络控制与其 他控制技术的融合,提高控制 系统的稳定性和性能。
神经网络的基本单元是神经元,其模型
前馈神经网络和反馈神经网络
2
和激活函数决定了神经网络的行为和表 达能力。
前馈神经网络是一种信息传递方向单一
的网络结构,而反馈神经网络具有循环
连接,在动态系统的控制中应用广泛。
3
训练神经网络的方法
常见的神经网络训练方法包括反向传播 算法、遗传算法、粒子群优化等,用于 调整网络参数以实现优化和学习。
神经网络控制实例
倒立摆控制
自适应神经网络PID
基于神经网络的预测控制方法研究与应用

基于神经网络的预测控制方法研究与应用随着机器学习技术的不断发展,神经网络作为其中重要的一种技术已经得到了广泛的应用。
在控制领域,基于神经网络的预测控制方法也逐渐成为研究的热点。
本文旨在对基于神经网络的预测控制方法进行探讨,并介绍其在实际应用中的优势和发展趋势。
一、神经网络的基本概念和原理神经网络是指模拟人类大脑神经元之间相互连接的计算模型,其主要组成部分包括输入层、隐藏层以及输出层。
其中,输入层接收来自外界的输入信息,输出层则输出神经网络的计算结果,而隐藏层则负责对输入信息进行计算、处理和转换。
神经网络的训练过程基于反向传播算法,通过反复迭代,不断优化神经网络的权重和偏置,使得其预测结果与实际结果更加接近。
二、基于神经网络的预测控制方法基于神经网络的预测控制方法是一种模型预测控制方法,其基本思想是利用神经网络对物理系统进行建模,并通过神经网络对未来状态进行预测,从而制定相应的控制策略。
与传统的基于模型的预测控制方法相比,基于神经网络的方法具有以下特点:1.对非线性系统建模能力强由于神经网络能够处理非线性问题,因此基于神经网络的预测控制方法可以较好地适用于非线性系统,并能够对其进行较为准确的建模。
2.不需要精确的数学模型对于某些复杂的系统,其数学模型可能很难建立或者不够准确,此时传统的基于模型的方法就显得不够有效。
而基于神经网络的预测控制方法则不需要求解精确的数学模型,仅需要利用神经网络对系统进行学习和预测即可。
3.对环境变化和干扰具有强鲁棒性在实际控制中,系统往往受到各种环境变化和干扰的影响,因此在控制过程中需要具备一定的鲁棒性。
基于神经网络的预测控制方法通过不断学习和训练,能够对环境变化和干扰进行自适应调节,从而具有较强的鲁棒性。
三、基于神经网络的预测控制方法在实际应用中的优势1.在控制复杂系统方面具有独到优势由于基于神经网络的预测控制方法具有对非线性系统建模能力强、不需要精确的数学模型、对环境变化和干扰具有强鲁棒性等特点,在控制复杂系统方面具有独到优势。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Wa 2( s )
1 1 (1 ), Wa1( s ) 25 0.5 74s
四.应用
四.应用
图9 主蒸汽温度设定值阶跃输入下的仿 真比较
四.应用
图十 时间常数改变后的仿真比较
四.应用
图十一 增益改变后的仿真比较
四.应用
图十二加入烟气扰动后的PID控制结构图
四.应用
图十三
加入烟气扰动后的对比曲线
四.应用
图十四 加10秒纯滞后以后的仿真结果图
四.结论
Байду номын сангаас
(1)本文提出的基于单元模型的神经网络预测控 制主蒸汽温度控制策略既可保证对主蒸汽温度 快而稳的调节,又使得所消耗的减温水量大大 降低,可明显提高控制策略的安全性和经济性, 符合火电厂机组运行的客观需求。 (2)时间常数鲁棒性很强,而增益鲁棒性较弱, 但适应能力很强。可在较短时间内适应参数的 变化。 (3)能很好地克服纯滞后并有较强的抗干扰能力。
五.参考文献
[1] 陈铁军,链系统方法及其应用, 河南科技出版社, 1993. [2] 陈铁军.并行预测系统与算法. [3] 李果勇.智能控制及其MATLAB实现,电子工业出版社,2005 [4] 杨献勇.热工过程自动控制I-M].北京:清华大学出版社, 2000. [5] 彭钢.热工PID控制算法的适应性与局限性分析[J].河北电力 技术,1997,(6):6—8. [7] 范伊波,等.基于自适应神经元网络的过热汽温智能控制 [J].动力工程,1998,(2):7—10. [8] 于渤.现代控制理论[M].北京:水利电力出版社,1995.
2 2 2 2 2 y k j ym k j5j u k j j u k j 2i
r
N2
NU
j 1
j 1
三.神经网络模型预测控制简介
图四为模型预测控制的过程。控制器由 神经网络模型和最优化方块组成,最优 化模块确定u(通过最小化J),最优u值 作为神经网络模型的输入
基于单元的模型是一种多输入单输出系统,通 过关联与其他相关单元相关联。通过自身动态 变化和单元间相互影响过程,共同描述对象的 整体运动特性。针对每个单元设计单元预测系 统和控制系统,它通过接受本单元相关信息和 直接关联的单元的测量和预测信息,预测该单 元的运动趋势,并分析判断,作出该单元的控 制决策。
二.单元控制的基本思想
传统的预测控制系统以整体系统模型为 基础,所设计的预测算法是集中式的, 随着系统规模的扩大,计算量迅速增加, 因此影响到其实时性。另外,很难用一 个同质的,单一的集中模型来描述复杂 系统,这就需要新的分析方法。
二.单元控制的基本思想
单元控制是用单元模型系统描述对象的动态过 程,为受控对象建立一种结构分散化模型,它 吸收了人工分析系统的经验知识,由定性的结 构模型和定量的模型给出单元模型。既含有整 体系统的因果结构,又包含单元间的相互关联。 此具有网状结构的模型,按照一定意义下的主 要因果关系,被抽象出一种链状结构,我们称 之为单元模型系统。这种模型比一般多输入多 输出系统含有更多的信息量,可以用来设计具 有高可靠性和强鲁棒性要求的控制系统。
一.引言
目前该系统控制的主导设计方案是PID律, 虽然一些先进控制技术近年来尝试在火 电厂自动化中应用,但由于理论上的局 限性和实现上的具体困难,均未能得到 广泛应用。
一.引言
本文根据单元控制的思想,并运用神经 网络预测控制的方法,应用于过热蒸汽 温度控制中。使单元控制的思想得以实 现,神经网络更接近生物神经网络的结 构,神经网络的优势得以更好发挥。设 计出了具有较高可靠性和较强鲁棒性的 控制系统。
三.神经网络模型预测控制简介
模型预测的第一步就是训练神经网络未来表示 网络的动态机制。模型输出与神经网络输出之 间的预测误差,用来作为神经网络的训练信号。 该过程如图二所示。
对象
u
神经网络模型
_
+
ym
e
学习算法
三.神经网络模型预测控制简介
神经网络模型利用当前输入和输出预测 神经网络未来输出值。神经网络模型结 构如图三所示。该网络可以采用批量在 线训练。
二.单元控制的基本思想
Zj , j Ni
Zj , jNi Zj , jNi
c
i i i
c
Zi
Zi
c
Zi
边界
h h h
c
Zh
s s s
c
Zs
Zh
c
Zs
c
Zh
Zs
三.神经网络模型预测控制简介
神经网络模型预测控制是使用非线性神 经网络模型来预测未来模型性能。控制 器计算控制输入,而控制输入在未来一 段指定的时间内将最优化模型性能。模 型预测第一步是要建立神经网络模型 (系统辨识);第二步是使用控制器来 预测未来神经网络性能。
各单元预测系统按照研究对象的关联模式相互关 联,并经由关联传递单元预测信息,共同完成对 整体系统未来一定时间动态特性的预测,而各单 元控制系统也经由关联传递控制信息,从而完成 对整体系统的控制。单元预测系统的设计和计算 是独立的和并行的,单元系统可以是不同性质和 不同模式的,能够适用于大型复杂系统地分析预 测。
控制器
yr
u*
优化 神经网络模型
ym
u
对象
y
四.应用
四.应用
常规主蒸汽温度控制方案(串级PID)
四.应用
其中
W 01( s )
1( s )
W ( s)
8 (1 15s ) 2
W 02( s )
2( s ) 1.125 1( s) (1 25s)3
WH 1(s) WH 2(s) 0.1
输入 第一层 第二层
y(k) u(k)
TDL
LW1.1 LW2.1
ym(k 1)
+
TDL
LW1.2
+
1 1
b1
b2
S1
三.神经网络模型预测控制简介
模型预测方法是水平后退的方法,神经 网络模型预测在指定时间内预测模型响 应。预测是用数字最优化程序来确定控 制信号,通过最优化如下的性能准则函 数,即
基于单元模型的神经网络预测控制 在过热蒸汽温度控制中的应用
电气工程学院:何一文
一.引言
火电厂锅炉的过热蒸汽温度是其运行质量的重 要指标之一,过热蒸汽温度过高或过低都 会影响电厂的安全经济运行,但汽温调节对 象是一个多容环节,它的纯延迟时间和时间 常数都比较大,干扰因素多,对象模型不确 定,在锅炉自动调节系统中属于可控性最差 的一个调节系统。
