DSP第四章课后答案
DSP应用技术教程部分习题答案

《TMS320C54x DSP应用技术教程》部分习题答案注意:未提供的参考答案习题(因考试为开卷形式.部分在课堂讲过.部分需要自行思考归纳总结或编程).请参考PPT和书上示例.自行解答。
第1章绪论1.简述Digital Signal Processing 和Digital Signal Processor 之间的区别与联系。
答:前者指数字信号处理的理论和方法.后者则指用于数字信号处理的可编程微处理器.简称数字信号处理器。
数字信号处理器不仅具有可编程性.而且其数字运算的速度远远超过通用微处理器.是一种适合于数字信号处理的高性能微处理器。
数字信号处理器已成为数字信号处理技术和实际应用之间的桥梁.并进一步促进了数字信号处理技术的发展.也极大地拓展了数字信号处理技术的应用领域。
2.什么是DSP技术?答:DSP技术是指使用通用DSP处理器或基于DSP核的专用器件.来实现数字信号处理的方法和技术.完成有关的任务。
5.数字信号处理的实现方法有哪些?答:参见P3-4 1.1.3节。
6.DSP的结构特点有哪些?答:哈佛结构和改进的哈佛结构、多总线结构、流水线技术、多处理单元、特殊的DSP指令、指令周期短、运算精度高、硬件配置强。
7.什么是哈佛结构和冯洛伊曼结构?它们有什么区别?答:参见P5-6 1.2.2节。
8.什么是哈佛结构和冯.诺依曼结构?它们有什么区别?答:DSP处理器将程序代码和数据的存储空间分开.各空间有自己独立的地址总线和数据总线.可独立编址和独立访问.可对程序和数据进行独立传输.这就是哈佛结构。
以奔腾为代表的通用微处理器.其程序代码和数据共用一个公共的存储空间和单一的地址和数据总线.取指令和取操作数都是通过一条总线分时进行的.这样的结构称为冯·诺伊曼结构。
采用哈佛结构.可同时取指令和取操作数.并行地进行指令和数据的处理.从而可以大大地提高运算的速度.非常适合于实时的数字信号处理。
而冯·诺伊曼结构当进行高速运算时.取指令和取操作数是分时操作的.这样很容易造成数据传输通道的瓶颈现象.其工作速度较慢。
DSP第四章 TMS320C20X系列的寻址方式及汇编指令

LT *0+
执行指令前: ARP=1, (AR1)=100H,(AR0)=3 执行操作: 用AR1所指的数据存储器100H内 容装载暂时寄存器; 执行指令后: ARP=1,(AR1)=103H
⑤减去索引量
方法
举例
指令使用AR内容作
LT *0-
为数据存储器地址,
执行指令后AR内容 执行指令前:
自动减去ARO的内容。 ARP=1, (AR1)=100H,(AR0)=3
执行操作:
用AR1所指的数据存储器100H内
容装载暂时寄存器;
执行指令后:
ARP=1,(AR1)=FEH
⑥加上索引量,反向进位
方法
举例
指令使用AR内容作为 数据存储器地址,执 行指令后AR内容自动 加上AR0的内容,该 加法采用反向进位方 法。 注:主要用于FFT算 法
LT *BR0+
把AR0加到辅助寄存器中时,地址以位倒序的方 式产生,即进位是从左向右,而不是从右向左进位。
LTP ind [,ARn]
MAC MAC pma , dma
乘且累加
MAC pma, ind [ , ARn]
MACD MACD pma, dma
乘且累加,并将被寻址数据移至下一单元
MACD pma, ind [, ARn]
MPY MPY dma
MPY ind [, ARn]
MPYA/MPYS
累加前次乘积,再将TREG与被寻址数相乘
PAC PAC
PREG转入累加器ACC
SPH
存储PREG高16位,直接或间接寻址
SPL
存储PREG低16位,直接或间接寻址
例1:MAC
0FF00H,02H ;DP=6,地址300H~37FH,PM=0, CNF=1
DSP芯片的原理与开发技术课后题部分答案

DSP课后习题答案总结第一章:概述1.2 简述DSP应用系统的典型结构和特点答:DSP系统的典型结构和工作过程:①对输入信号进行带限滤波和抽样;②进行A/D变换,将信号变换成数字比特流;③根据系统要求,DSP芯片对输入信号按照特定算法进行处理;④D/A转换,将处理后的数字样值转换为模拟信号;⑤平滑滤波,得到连续的模拟信号波形。
DSP系统的特点:接口方便、编程方便、稳定性好、精度高、可重复性好、集成方便等。
1.3 简述DSP应用系统的一般设计过程。
答:1.定义系统性能指标2.采用高级语言进行性能模拟3.设计实时DSP应用系统4.借助开发工具进行软硬件调试5.系统集成与独立系统运行1.8 设计DSP应用系统时,如何选择合适的DSP芯片。
答:根据实际应用系统的需要选择,以达到系统的最优化设计。
一般来说,需要考虑:DSP芯片的运算速度:DSP芯片的运算速度衡量指标:①指令周期;②MAC时间;③FFT执行时间;④MIPS;⑤MOPS;⑥MFLOPS;⑦BOPSDSP芯片的价格:DSP芯片的硬件资源DSP芯片的运算精度:一般字长为16bits,浮点芯片一般为32bitsDSP芯片的开发工具DSP芯片的功耗其他因素:例如,DSP芯片的封装形式、质量标准、供货情况、生命周期等。
1.11 中英文全称对照:DSP:Digital Signal ProcessingTI:Texa InstrumentsMAC:Multillier and AccumulatorMIPS:Million Istructions Per SecondMOPS: Million Operations Per SecondMFLOPS: Million Floating-point Operations Per SecondBOPS:Billion Operations Per secondDIP:Dual In-line PackagePGA:Pin Grid ArryPLCC:Plastic Leaded Chip CarrierPQFP:Plastic Quad Flat PackPWM:Pulse Width Modulation第二章:DSP芯片的基本结构和特性2.2 ALU和累加器的区别。
DSP 第四章 思考题

参考P40, 参考P40,图4.2.1
思考题
4.4 欲实现通过定时器周期中断的方法,形成每 0.1s触发一次XF端反转,请配置定时器的相关寄存 器,并说明配置理由。假设CPU时钟频率为20MHZ。
0.1s=100ms=100*10^6ns CLKOUT主频 CLKOUT主频f=20MHz,T=50ns 主频f=20MHz, 时钟数100*10^6ns/50ns=2 时钟数100*10^6ns/50ns=2 000 000 根据定时长度计算公式:Tt=T* (TDDR+1) * (PRD+1) 根据定时长度计算公式: 给定TDDR=15,PRD=62449,CLKOUT主频 给定TDDR=15,PRD=62449,CLKOUT主频 f=20MHz, f=20MHz,T=50ns Tt=50*(15+1)*(62449+1)=50*1,000,000(ns)=50(ms)
9~6
1
5
0
4
1111
3~0
TDR 0026h
保留
Soft
Free
PSC
TRB
TSS
TDDR
保留位
软件调试控制位
预定标 计数器
重新 加载位
停止 状态位
分 频 系 数
第4章 TMS320C54x的片内外设、接口及应用 TMS320C54x的片内外设、 的片内外设
3. 定时控制寄存器TCR 定时控制寄存器TCR 16位存储器映像寄存器, 16位存储器映像寄存器,包含定时器的控制位 位存储器映像寄存器 和状态位。 和状态位。
思考题
4.3 试分别说明下列中断语句的功能。 (1)STM (H,IMR
;清除INT2中断标志 清除INT2中断标志 ;放开(许可)TINT1 放开(许可)
DSP课后习题答案李建

第一章:一、数字信号处置的实现方式一样有哪几种?(1) 在通用的运算机上用软件实现(2) 在通用运算机系统中加上专用的加速处置机实现(3) 用通用的单片机实现,这种方式可用于一些不太复杂的数字信号处置(4) 用通用的可编程 DSP 芯片实现,可用于复杂的数字信号处置算法(5) 用专用的 DSP 芯片实现(6) 用基于通用 dsp 核的asic 芯片实现二、简单的表达一下 dsp 芯片的进展概况?答:第一时期, DSP 的雏形时期( 1980 年前后)代表产品: S2811。
要紧用途:军事或航空航天部门第二时期, DSP 的成熟时期( 1990 年前后)代表产品: TI 公司的 TMS320C20 要紧用途:通信、运算机领域第三时期, DSP 的完善时期( 2000 年以后)代表产品:TI 公司的 TMS320C54 要紧用途:各行业领域3、可编程 dsp 芯片有哪些特点?(1)采纳哈佛结构:冯.诺依曼结构,哈佛结构,改良型哈佛结构(2)采纳多总线结构(3)采纳流水线技术(4) 配有专用的硬件乘法-累加器(5) 具有特殊的 dsp 指令(6) 快速的指令周期(7) 硬件配置强(8) 支持多处置器结构(9) 省电治理和低功耗4、什么是哈佛结构和冯.诺依曼结构?它们有什么区别?哈佛结构:该结构采纳双存储空间,程序存储器和数据存储器分开,有各自独立的程序总线和数据总线,可独立编址和独立访问,可对程序和数据进行独立传输,使取指令操作、指令执行操作、数据吞吐并行完成,大大地提高了数据处置能力和指令的执行速度,超级适合于实时的数字信号处置。
冯.诺依曼结构:该结构采纳单存储空间,即程序指令和数据共用一个存储空间,使用单一的地址和数据总线,取指令和取操作数都是通过一条总线分时进行。
当进行高速运算时,不但不能同时进行取指令和取操作数,而且还会造成数据传输通道的瓶颈现象,其工作速度较慢。
区别:哈佛:该结构采纳双存储空间,程序存储器和数据存储器分开,有各自独立的程序总线和数据总线,可独立编址和独立访问,可对程序和数据进行独立传输,使取指令操作、指令执行操作、数据吞吐并行完成,大大地提高了数据处置能力和指令的执行速度,超级适合于实时的数字信号处置。
DSP简答题答案.WOC

复习大纲第一章绪论教学内容:DSP芯片的特点;DSP芯片的发展;DSP芯片的应用。
基本要求:掌握:DSP芯片的特点;了解:DSP芯片的发展;DSP芯片的应用。
第二章TMS320C54X的硬件结构教学内容:总线结构;中央处理器;中央存储器;复位电路。
基本要求:掌握:各类存储器的特点;理解:中央处理器中各部件的主要功能;了解:了解各总线的用途和复位电路。
第三章TMS320C54X的指令系统教学内容:寻址方式;指令系统;流水线。
基本要求:掌握:各寻址方式的特点;理解:指令系统中各指令的意义;不同指令的流水线特点。
第四章TMS320C54X应用系统开发过程教学内容:汇编,链接,COFF文件格式。
基本要求:掌握:常用汇编伪指令的使用、汇编器的使用;链接伪指令的使用、链接器的使用;理解:COFF文件格式。
第五章汇编语言程序设计教学内容:程序的控制与转移;堆栈的使用;加减法和乘法运算;重复操作;数据块传送;双操作数乘法;长字运算和并行运算;小数运算;除法运算;浮点运算。
第一章DSP技术概述1. DSP应用系统模型包括哪些主要部分?答:典型的DSP系统为:2. DSP系统有何特点?答:(1)精度高(2)可靠性强(3)集成度高(4)接口方便(5)灵活性好(6)保密性好(7)时分复用3. 试列举DSP芯片的特点。
答:(1)哈佛结构(2)多总线结构和多处理单元(3)流水线技术(4)特殊的DSP指令(5)指令周期短(6)运算精度高(7)硬件配置强(8)耗电省第二章DSP芯片结构介绍1. TMS320C54x芯片存储器采用什么结构?有何特点?答:1)采用改善的哈佛结构和存储器分区特点:改善的哈佛结构特点是:将程序和数据存储在不同的存储空间(即程序存储器和数据存储器是两个相互独立的存储器)存储器分区特点是:存储器分为3个可单独选择的空间后,在任何一个存储空间,RAM、ROM、EPROM、EEPROM或存储器影响外围设备,都可以驻留在片内或片外2. TMS320C54x芯片的总线有哪些?它们各自的作用和区别是什么?答:在TMS320C54x内部有P、C、D、E四种16位总线:(1)程序总线(PB)C54x用1条程序总线传送取自程序存储器的指令代码和立即操作数。
DSP实验答案Solution_lab4
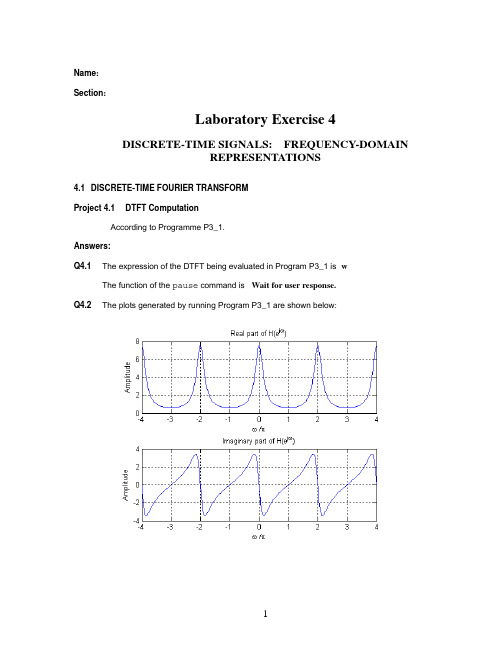
Name:Section:Laboratory Exercise 4DISCRETE-TIME SIGNALS: FREQUENCY-DOMAINREPRESENTATIONS4.1 DISCRETE-TIME FOURIER TRANSFORMProject 4.1 DTFT ComputationAccording to Programme P3_1.Answers:Q4.1 The expression of the DTFT being evaluated in Program P3_1 is -wThe function of the pause command is - Wait for user response.Q4.2 The plots generated by running Program P3_1 are shown below:The DTFT is a _____ periodic______ function of ω.Its period is - 2*piThe types of symmetries exhibited by the four plots are as follows:symmetryeven symmetry oddProject 4.2 DTFT PropertiesAnswers:Q4.6 The modified Program P3_2 created by adding appropriate comment statements, and adding program statements for labeling the two axes of each plot being generated by the program is given below:% Program P3_2% Time-Shifting Properties of DTFTclf;w = -pi:2*pi/255:pi; wo = 0.4*pi; D = 10;num = [1 2 3 4 5 6 7 8 9];h1 = freqz(num, 1, w);h2 = freqz([zeros(1,D) num], 1, w);subplot(2,2,1)plot(w/pi,abs(h1));gridtitle('Magnitude Spectrum of Original Sequence')subplot(2,2,2)plot(w/pi,abs(h2));gridtitle('Magnitude Spectrum of Time-Shifted Sequence')subplot(2,2,3)plot(w/pi,angle(h1));gridtitle('Phase Spectrum of Original Sequence')subplot(2,2,4)plot(w/pi,angle(h2));gridtitle('Phase Spectrum of Time-Shifted Sequence')The parameter controlling the amount of time-shift is – DQ4.7The plots generated by running the modified program are given below:From these plots we make the following observations:Q4.8Program P3_2 was run for the following value of the time-shift - 20 The plots generated by running the modified program are given below:From these plots we make the following observations:Q4.9 Program P3_2 was run for the following values of the time-shift and for the following values of length for the sequence – D=5 w = -pi:2*pi/511:piThe plots generated by running the modified program are given below:From these plots we make the following observations:Q4.10 The modified Program P3_3 created by adding appropriate comment statements, and adding program statements for labeling the two axes of each plot being generated by the program is given below:subplot(2,2,1)plot(w/pi,abs(h1));gridtitle('Magnitude Spectrum of Original Sequence')xlabel('\omega /\pi');ylabel('Amplitude');subplot(2,2,2)plot(w/pi,abs(h2));gridtitle('Magnitude Spectrum of Frequency-Shifted Sequence')xlabel('\omega /\pi');ylabel('Amplitude');subplot(2,2,3)plot(w/pi,angle(h1));gridtitle('Phase Spectrum of Original Sequence')xlabel('\omega /\pi');ylabel('Phase in radians');subplot(2,2,4)plot(w/pi,angle(h2));gridtitle('Phase Spectrum of Frequency-Shifted Sequence')xlabel('\omega /\pi');ylabel('Phase in radians');The parameter controlling the amount of frequency-shift is - woQ4.11The plots generated by running the modified program are given below:From these plots we make the following observations:Q4.12Program P3_3 was run for the following value of the frequency-shift - wo = 0.1*pi;The plots generated by running the modified program are given below:From these plots we make the following observations:4.2 DISCRETE FOURIER TRANSFORMProject 4.3 DFT and IDFT ComputationsAnswers:Q4.23 The MATLAB program to compute and plot the L-point DFT X[k] of a length-N sequence x[n] with L ≥ N and then to compute and plot the IDFT of X[k] is given below:n=1:10;l=15;x=fft(n,l);y=ifft(x);subplot(211)stem(x);title('fft');subplot(212)stem(y);title('ifft');The DFT and the IDFT pairs generated by running the program for sequences of different lengths N and for different values of the DFT length L are shown below:From these plots we make the following observations:Project 4.4 DFT PropertiesAnswers:Q4.30 The modified Program P3_7 created by adding appropriate comment statements, and adding program statements for labeling each plot being generated by the program is given below: clf;M = 6;a = [0 1 2 3 4 5 6 7 8 9];b = circshift(a,M);L = length(a)-1;n = 0:L;subplot(2,1,1);stem(n,a);axis([0,L,min(a),max(a)]);title('Original Sequence');subplot(2,1,2);stem(n,b);axis([0,L,min(a),max(a)]);title(['Sequence Obtained by Circularly Shifting by ',num2str(M),' Samples']);The parameter determining the amount of time-shifting is - MIf the amount of time-shift is greater than the sequence length then - Q4.31 The plots generated by running the modified program are given below:From these plots we make the following observations:4.3 z-TRANSFORMProject 4.5 Analysis of z-TransformsAnswers:Q4.46The frequency response of the z-transform obtained using Program P3_1 is plotted below:Q4.47The MATLAB program to compute and display the poles and zeros, to compute and display the factored form, and to generate the pole-zero plot of a rational z-transform is given below: num = [2 5 9 5 3];den = [5 45 2 1 1];zplane(num,den);[z,p,k]=tf2zp(num,den)sos=zp2sos(z,p,k);Using this program we obtain the following results on the z-transform G(z)of Q4.46:Q4.49The MATLAB program to compute and display the rational z-transform from its zeros, poles and gain constant is given below:z =[0.3 2.5 -0.2 + 0.4i -0.2-0.4i]';p =[0.5 -0.75 0.6+0.7i 0.6-0.7i]';k =3.9;[num,den]=zp2tf(z,p,k);h = zpk(z,p,k)The rational form of a z-transform with the given poles, zeros, and gain is found to be –Zero/pole/gain:3.9 (s-0.3) (s-2.5) (s^2 + 0.4s + 0.2)---------------------------------------(s-0.5) (s+0.75) (s^2 - 1.2s + 0.85)4.4SPECTRUM OF SPEECH SINGALQ 4.50a. get a section of vowel using the command:[x,fs]=wavread('six.wav',[24120 25930]);b. Plot the waveform x using the plot() command and listen to it using the soundsc() command.c. do fourier transform of windowed signal using ‘hanning’ ,and plot spectrum of bottom 5000Hzd. try again by choosing another section of vowel with different length , and explain the difference.% get a section of vowel[x,fs]=wavread('six.wav',[24120 25930]);% plot waveformt=(0:length(x)-1)/fs; % times of sampling instants subplot(2,1,1);plot(t,x);legend('Waveform');xlabel('Time (s)');ylabel('Amplitude');% do fourier transform of windowed signalY=fft(x.*hamming(length(x)));% plot spectrum of bottom 5000Hzhz5000=5000*length(Y)/fs;f=(0:hz5000)*fs/length(Y);subplot(2,1,2);plot(f,20*log10(abs(Y(1:length(f)))+eps));legend('Spectrum');xlabel('Frequency (Hz)');ylabel('Magnitude (dB)');Q 4.51a. Load the supplied speech signal into MATLAB using the command:[y,fs,nbits] = wavread('oilyrag.wav');b. Plot the spectrum of a section of voiced speech and unvoiced speech respectively, and unwrap them respectively.%=================读取语音,画图[y,fs,nbits] = wavread('oilyrag.wav');len=length(y);x=1:len;plot(x,y);title('orial speech');grid%=================清音的短时谱x=y(6000:7000);specnuvoic=shotspect(x,fs);%===================浊音的短时谱x=y(3000:4500);specvoic=shotspect(x,fs);step=fs/length(x);function z=shotspect(x,fs)%====计算x的短时谱% do fourier transform of windowed signalY=fft(x.*hamming(length(x)));% plot spectrum of bottom 2000Hzstep=fs/length(Y);f=0:step:2000;z=20*log10(abs(Y(1:length(f)))+eps); %分贝figure,plot(f,z);grid minorlegend('Spectrum');xlabel('Frequency (Hz)');ylabel('Magnitude (dB)');c. According to the spectrum of a section of voiced speech to estimate the pitch of the unvoiced speech and compare it with Q2.21.(1) spectrum:f= 106.5956;(2) waveform:f=105.2632%计算基音%频域计算index=period(specvoic(45:55),specvoic(55:65))+10;fvoic=step*index%时域计算Tvoice=period(y(3100:3200),y(3250:3350))+150; T=Tvoice/fs;fvoice=fs/Tvoicefunction z=period(x1,x2)[y1,I1]=max(x1);[y2,I2]=max(x2);z=abs(I2-I1);Date: Signature:。
DSP原理及应用-(修订版)--课后习题答案

第一章:1、数字信号处理的实现方法一般有哪几种?答:数字信号处理的实现是用硬件软件或软硬结合的方法来实现各种算法。
(1) 在通用的计算机上用软件实现;(2) 在通用计算机系统中加上专用的加速处理机实现;(3) 用通用的单片机实现,这种方法可用于一些不太复杂的数字信号处理,如数字控制;(4)用通用的可编程 DSP 芯片实现。
与单片机相比,DSP 芯片具有更加适合于数字信号处理的软件和硬件资源,可用于复杂的数字信号处理算法;(5) 用专用的 DSP 芯片实现。
在一些特殊的场合,要求的信号处理速度极高,用通用 DSP 芯片很难实现( 6)用基于通用 dsp 核的asic 芯片实现。
2、简单的叙述一下 dsp 芯片的发展概况?答:第一阶段, DSP 的雏形阶段( 1980 年前后)。
代表产品: S2811。
主要用途:军事或航空航天部门。
第二阶段, DSP 的成熟阶段( 1990 年前后)。
代表产品: TI 公司的 TMS320C20主要用途:通信、计算机领域。
第三阶段, DSP 的完善阶段( 2000 年以后)。
代表产品:TI 公司的 TMS320C54 主要用途:各个行业领域。
3、可编程 dsp 芯片有哪些特点?答: 1、采用哈佛结构( 1)冯。
诺依曼结构,( 2)哈佛结构( 3)改进型哈佛结构2、采用多总线结构 3.采用流水线技术4、配有专用的硬件乘法-累加器5、具有特殊的 dsp 指令6、快速的指令周期7、硬件配置强8、支持多处理器结构9、省电管理和低功耗4、什么是哈佛结构和冯。
诺依曼结构?它们有什么区别?答:哈佛结构:该结构采用双存储空间,程序存储器和数据存储器分开,有各自独立的程序总线和数据总线,可独立编址和独立访问,可对程序和数据进行独立传输,使取指令操作、指令执行操作、数据吞吐并行完成,大大地提高了数据处理能力和指令的执行速度,非常适合于实时的数字信号处理。
冯。
诺依曼结构:该结构采用单存储空间,即程序指令和数据共用一个存储空间,使用单一的地址和数据总线,取指令和取操作数都是通过一条总线分时进行。
DSP课后习题与思考题

第一章习题与思考题一、填空:1.Instruction Cycle(指令周期)是执行一条指令所需的时间,指令周期的单位是(nS纳秒)。
所以DSP单周期指令的周期也是(时钟周期)。
2.选择DSP芯片所需考虑的因素有(DSP芯片性能)、(片内硬件资源)、(价格)、(DSP芯片的开发工具)等。
3.TMS320LF2407A控制器是专门为基于(控制)的应用而设计的。
其运算速度最大可为(40MIPS),最小指令周期为(25nS)。
4.TMS320LF2407ADSP控制器有强大的外设功能,包括(时间管理器EVA,EVB)、(控制器局域网CAN)、(串行接口SPI,SCI)、(模/数转换器ADC)、(看门狗定时器)。
5.TMS320LF2407ADSP芯片有RAM:(DARAM)、(SARAM),是(16)位。
二、思考题:1. 根据TI公司对DSP命名的方法。
解释给出芯片型号的各个字段的意义。
TMS 320 LF 2407APGE2. 为何将TMS320x2000系列的DSP也称作DSP数字信号控制器或DSP单片机。
3. 与TMS320x240x系列器件相比,TMS320x240xA器件增加了那些新特点。
运行速度加快30MHz——40MHz片上Flash/Rom中的代码可以加密;PDPINTX、CAPn、XINTn、和ADCSOC管脚有输入保护电路;PDPINTx管脚的状态反映在COMCONx寄存器中。
第二章习题与思考题一、填空:1.TMS320LF240xA系列DSP控制器采用了改进的(哈佛结构)总线,具有分离的(程序总线)和(数据总线),使用(四)级流水线作业。
2.TMS320LF240xA系列DSP控制器具有两套相互独立的(程序操作总线)和(数据操作总线),共有6套16位的内部总线构成,分别为(程序读总线PRDB、程序地址总线PAB、数据读总线DRDB、数据写总线DWDB、数据读地址总线DRAB、数据写地址总线DWAB)。
西工大DSP第4章习题答案

习题与程序题一、填空:1.寻址方式是指寻找指令中(操作数地址)的方式。
TMS320LF2000汇编指令采用3种存储器寻址方式:(立即寻址方式)、(直接寻址方式)、(间接寻址方式)。
2.立即寻址方式分两种类型:(短立即寻址方式)和(长立即寻址方式)。
3.直接寻址方式的寻址对象是64K字的数据存储器,具体操作是将64K字的数据存储器分为(512)个数据页,每个数据页中包括(128字)单元。
4.间接寻址方式的寻址对象是64K字的数据存储器。
它是利用CPU内部8个16位的(辅助寄存器)(AR0~AR7)中任意一个辅助寄存器Rn的内容作为一个16位地址,来访问64K数据存储器中的任意单元。
5.汇编语言程序的语句除汇编指令以外,还可以由(伪指令)和(宏指令)组成。
6.一条源语句包含有4个有序的域,依次为:(标号域),(助记符域),(操作数域)和(注释域)。
7.一个完整的汇编文件应包含:(汇编源程序文件)、(头文件)、(命令文件)。
二、完成下列指令及注释:1. ⑴LDP #6 ;设置数据页为6(0300h~037Fh)ADD 5h,2 ;将0305h单元的内容左移2位;累加器,结果存入累加器指令执行前指令执行后dma:305h dma:305hC C⑵ADD *+,AR0 ;当前辅助寄存器AR4所指定的;器单元的内容加至累加器;当前辅助寄存器的内容加1;AR0设定为下一个辅助寄存器指令执行前指令执行后ARP ARPAR4 AR4dma:302h dma:302hC C2. 设OVM=0,ADDC *+,AR3 ;累加器结果正常;当前辅助寄存器AR0指定的数据存储单元15h;的内容与ACC和C的内容相加,结果存入CC;AR0的内容加1,指定AR3为下次辅助寄存器指令执行前指令执行后ARP ARPAR0 AR0dma:315h dma:315hC COV OV3. AND *- ;当前辅助寄存器AR2指定的数;的内容与ACC的低位字逻辑“;的低位字,ACC的高位字清零;AR1的内容减1指令执行前指令执行后ARP ARPAR1 AR1dma:315h dma:315hC C4. CALL 300h,*-,AR1 ;PC+2→TOS.程序存储器地址;入程序计数器(PC),并从该地;当前辅助寄存器的内容减1.;一个辅助寄存器指令执行前指令执行后5. CMPR 1 ;(当前AR)<(AR0)?,1表示指令执行前指令执行后6. LDP #0 ;(DP=0)LACL 60h ;60h单元的内;累加器的高16位填0指令执行前指令执行后dma:60h dma:60hACCC C7. LAR AR2,*+ ;将当前辅助寄存器所指的数据存;;容增1指令执行前指令执行后8. LST #1,0h ;(DP=4),ARB被装入新的A指令执行前指令执行后9.⑴NEG ;(OVM=1)OVM=1)累加器求负指令执行前指令执行后ACCC COV OV⑵NEG ;(OVM=0)指令执行前指令执行后ACCC COV OV10. POP ;PC增1.(TOS)→ACC(15:0);堆栈弹出一级指令执行前指令执行后C C堆栈11. PUSH ;PC;推一级.ACC(15:0)→TOS指令执行前指令执行后C C堆栈堆栈12.LDP #6SACL 29h,2 ;PC增1.(ACC)左移2位送入数据;存储单元329h处指令执行前指令执行后ACC ACCC C329h 329h13. SAR AR1,*- ;将AR1的内容存入当前辅;定的存储单元205h指令执行前指令执行后14. SBRK #8Eh ;当前辅助寄存器的值减去靠右对齐;正整数(无符号算术运算)指令执行前指令执行后15. SPLK #ABCDh,*+,AR1 ;将16位立即数ABCDh写入当前;所指定的数据存储单元320h.;当前辅助寄存器的内容增1;AR1被指定为下一个辅助寄存器指令执行前 指令执行后16. SUB *-,1,AR5 ;ACC 的内容减去当前辅助寄存器A;指定的数据存储单元02FEh 的内容;1位后的值(移位时高位填零), ;结果存入ACC 。
DSP应用技术教程 部分习题答案

《TMS320C54x DSP应用技术教程》部分习题答案注意:未提供的参考答案习题(因考试为开卷形式,部分在课堂讲过,部分需要自行思考归纳总结或编程),请参考PPT和书上示例,自行解答。
第1章绪论1.简述Digital Signal Processing 和Digital Signal Processor 之间的区别与联系。
答:前者指数字信号处理的理论和方法,后者则指用于数字信号处理的可编程微处理器,简称数字信号处理器。
数字信号处理器不仅具有可编程性,而且其数字运算的速度远远超过通用微处理器,是一种适合于数字信号处理的高性能微处理器。
数字信号处理器已成为数字信号处理技术和实际应用之间的桥梁,并进一步促进了数字信号处理技术的发展,也极大地拓展了数字信号处理技术的应用领域。
2.什么是DSP技术?答:DSP技术是指使用通用DSP处理器或基于DSP核的专用器件,来实现数字信号处理的方法和技术,完成有关的任务。
5.数字信号处理的实现方法有哪些?答:参见P3-4 1.1.3节。
6.DSP的结构特点有哪些?答:哈佛结构和改进的哈佛结构、多总线结构、流水线技术、多处理单元、特殊的DSP指令、指令周期短、运算精度高、硬件配置强。
7.什么是哈佛结构和冯洛伊曼结构?它们有什么区别?答:参见P5-6 1.2.2节。
8.什么是哈佛结构和冯.诺依曼结构?它们有什么区别?答:DSP处理器将程序代码和数据的存储空间分开,各空间有自己独立的地址总线和数据总线,可独立编址和独立访问,可对程序和数据进行独立传输,这就是哈佛结构。
以奔腾为代表的通用微处理器,其程序代码和数据共用一个公共的存储空间和单一的地址和数据总线,取指令和取操作数都是通过一条总线分时进行的,这样的结构称为冯·诺伊曼结构。
采用哈佛结构,可同时取指令和取操作数,并行地进行指令和数据的处理,从而可以大大地提高运算的速度,非常适合于实时的数字信号处理。
而冯·诺伊曼结构当进行高速运算时,取指令和取操作数是分时操作的,这样很容易造成数据传输通道的瓶颈现象,其工作速度较慢。
DSP习题答案-4(2017)

第四章习题参考答案1、连续时间信号g a (t )的Nyquist 频率为Ωm ,求以下由g a (t )衍生出的连续时间信号的Nyquist 频率。
a 、由y 1(t )=g a (t )g a (t )可知:解:111()()*()()()22,-2m m mY j G j G j G G d θθθππθθ∞-∞Ω=ΩΩ=Ω-<ΩΩ<Ω∴Ω<Ω⎰且b 、y 2(t )=g a (t/3)解:1()3(3)33mmY j Ga j Ω=Ω<ΩΩ∴Ω<Ωc 、y 3(t )=g a (3t )解:311()()33133m mY j Ga j Ω=Ω<Ω∴Ω<ΩΩ d 、y 4(t )=∫g a (t −τ)∞−∞g a (τ)dτ解: ()().()mY j Ga j Ga j Ω=ΩΩΩ<Ω有抽样定理知: e 、y 5(t )=dg a (t )dt解: 时域微分Y 5(jΩ)=jΩG a (jΩ),Y 5(jΩ)的Nyquist 频率是Ωm2、对于一段长2.5s 的连续时间信号进行无混叠的均匀采样,产生一段包含5001个采样点的有限序列,连续时间序列中存在的最高频率成分是什么?2.51200020001000500022s s H f Ts f Hz f Hz Ts =∴=====解:(秒),,3、连续时间的信号()a x t 是频率为300Hz ,500Hz ,1.2KHz ,2.15KHz 和3.5KHz 的正弦信号的线性组合,以 2.0KHz 采样率对()a x t 进行采样,采样所得的序列通过一个截止频率为900Hz 的理想低通滤波器,从而得到一个连续时间信号()a y t ,输出()a y t 的频率分量是什么?解:因为输入是正弦信号,所以在频谱中都有对应频率的两个冲激,经2000HZ 采样后,并形成周期性的拓展,得到/2f π=Ω :(以下只列出正频率部分,单位Hz )300,-300+2000=1700,300+2000=2300,…500,-500+2000=1500,500+2000=2500,…1200,-1200+2000=800,1200+2000=3200,…2150,2150-2000=150,2000+2150=4150,…3500,4000-3500=500,3500-2000=1500,6000-3500=2500,2000+3500=5500,… 所以,通过信号频率为150 Hz ,300Hz ,500 Hz ,800 Hz 。
数字信号处理第4章习题解答教材

DFT [x2 (n)]
DFT {Im[ w(n )]}
1 j Wop (k )
1 2j
[W
((k )) N
W
* (( N
k )) N
]RN
(k)
解:由题意 X k DFT xn,Y k DFT y n 构造序列 Z k X k jY k 对Z k 作一次N点IFFT可得序列z n z(n) IDFT Z k
Re[w(n)] j Im[w(n)]
Wep (k) Wop (k)
由x1(n) Re[w(n)]得
X1(k) DFT[x1(n)] DFT{Re[w(n)]} Wep (k)
1 2
[W
((k
))
N
W *((N
k ))N
]RN
(k)
由x2 (n) Im[w(n)]得
X 2 (k )
(2) 按频率抽取的基-2FFT流图
同样共有L = 4级蝶形运算,每级N / 2 = 8个蝶形运算
基本蝶形是DIT 蝶形的转置
X m1(k )
X m1( j)
WNr
-1
X m (k ) Xm( j)
每个蝶形的两节点距离为2Lm ,即从第一级到 第四级两节点距离分别为8,4,2,1。
系数WNr的确定:r (k )2 2m1 即k的二进制左移m 1位补零
3. N=16 时,画出基 -2 按时间抽取法及按频率抽取法 的 FFT 流图(时间抽取采用输入倒位序,输出自然数 顺序,频率抽取采用输入自然顺序,输出倒位序)。
解: 自然序
倒位序
0 0000 0000 0 1 0001 1000 8 2 0010 0100 4 3 0011 1100 12 4 0100 0010 2 5 0101 1010 10 6 0110 0110 6 7 0111 1110 14
DSP第四章课后答案
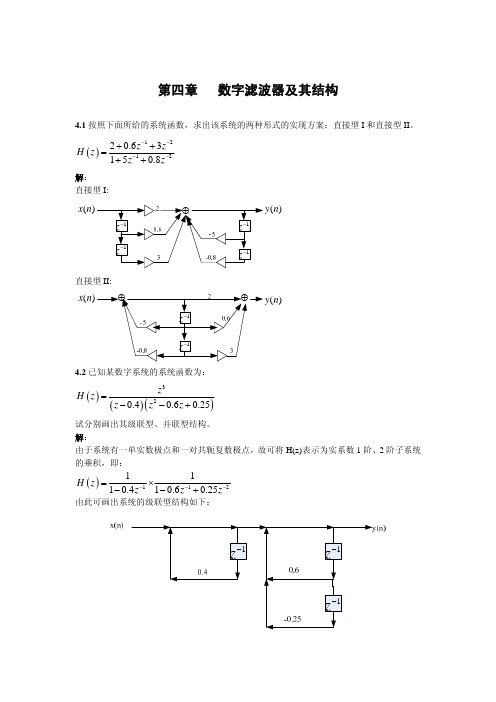
r cos x ( n) x1 z 1 r sin z 1 r sin
解:根据图中所设节点:
y ( n)
r cos
X 1 ( z ) X ( z ) rz 1Y ( z ) sin rz 1 X 1 ( z ) cos
解: 先写出网络中每个加法器的节点方程,节点标注如下:
x(n) b(0) b(1) b(2) y(n)
z 1
a(1)
z 1
a(2)
节点1
节点2
节点3
用 w1 (n), w2 ( n), w3 ( n) 表示 3 个节点的输出,则有以下 3 个方程:
w1 (n) b(0) x(n) a(1) y (n) w2 (n) b(1) x(n) w1 (n 1) a(2) y (n) w3 (n) b(2) x(n) w2 (n 1) y (n)
题(2) : 由(1) ,根据等比数列的前n项和,即可得到
1 1 a8 z 8 H ( z ) (1 a z ) 1 az 1 1 az 1
8 8
由此可画出由 FIR 系统和 IIR 系统级联而成的结构图,如下所示:
z8
a8
a
z 1
题(3) : (2)中的实现需要延迟器较多, (1)中的实现需要运算次数较多。
对上述方程作 z 变换,最终得到
1 2 1 2 W ( z) 1 a(1) z a (2) z a(3) z a(4) z V ( z)
所以, G ( z )
W ( z) a (3) z 1 a (4) z 2 , V ( z ) 1 a (1) z 1 a (2) z 2
DSP原理与应用课后答案(电子工业出版社)共12页word资料

第一章绪论1、简述DSP系统的构成和工作过程。
答:DSP系统的构成:一个典型的DSP系统应包括抗混叠滤波器、数据采集A/D转换器、数字信号处理器DSP、D/A转换器和低通滤波器等。
DSP系统的工作过程:①将输入信号x(t)经过抗混叠滤波,滤掉高于折叠频率的分量,以防止信号频谱的混叠。
②经过采样和A/D转换器,将滤波后的信号转换为数字信号x(n)。
③数字信号处理器对x(n)进行处理,得数字信号y(n)。
④经D/A转换器,将y(n)转换成模拟信号;⑤经低通滤波器,滤除高频分量,得到平滑的模拟信号y(t)。
9、简述DSP系统的设计步骤。
答:①明确设计任务,确定设计目标。
②算法模拟,确定性能指令。
③选择DSP芯片和外围芯片。
④设计实时的DSP芯片系统。
⑤硬件和软件调试。
⑥系统集成和测试。
第二章 TMS320C54x硬件结构1、 TMS320C54X芯片的基本结构都包括哪些部分?答:①中央处理器②内部总线结构③特殊功能寄存器④数据存储器RAM⑤程序存储器ROM⑥I/O口⑦串行口⑧主机接口HPI⑨定时器⑩中断系统2、TMS320C54X芯片的CPU主要由哪几部分组成?答:①40位的算术运算逻辑单元(ALU)。
②2个40位的累加器(ACCA、ACCB)。
③1 个运行-16至31位的桶形移位寄存器。
④17×17位的乘法器和40位加法器构成的乘法器-加法器单元(MAC)。
⑤比较、选择、存储单元(CSSU)。
⑥指令编码器。
⑦CPU状态和控制寄存器。
3、TMS320VC5402共有多少可屏蔽中断?它们分别是什么?RS和NMI属于哪一类中断源?答:TMS320VC5402有13个可屏蔽中断,RS 和NMI 属于外部硬件中断。
4、试分析下列程序的流水线冲突,画出流水线操作图。
如何解决流水冲突?STLM A ,AR0 STM #10,AR1 LD *AR1,B 解:流水线图如下图:1 2 3 4 5 6 789预取指取指 译码 寻址 读数 执行STLM A,AR0预取指取指 译码 寻址 读数 执行STM#10,AR1 (1st Word)预取指取指 译码寻址 读数 执行STM #10,AR1(2nd Word)预取指取指译码寻址读数执行LD *AR1,B解决流水线冲突:最后一条指令(LD *AR1,B)将会产生流水线冲突,在它前面加入一条NOP 指令可以解决流水线冲突。
(南京邮电大学)DSP习题答案汇总~~

(南京邮电⼤学)DSP习题答案汇总~~第⼀章习题1.1 在⼀间暗室⾥通过⼀个闪光频率为8Hz 的闪光灯观察⼀个以6Hz 为频率旋转的转轮。
求转轮表现出的转速并判断观察者对转轮旋转⽅向的判断正误。
若闪光灯频率变为12Hz ,16Hz 或24Hz ,重复上述问题。
本题涉及了转轮的问题,⽤到了公式)mod(s a f f f =,当a f 和f 符号相同时,观察者能观察到正确的转动⽅向;当a f 和f 符号相反时,观察者观察到的是错误的转动⽅向;否则,观察者不能辨别转轮的⽅向。
参考课本28页例题1.4.10。
1.2 对模拟信号x(t)=10sin(2πt)+10sin(8πt)+5sin(12πt) (其中t 以秒为单位)进⾏采样,采样频率s f =5Hz ,求x(t)的重建信号)(t x a 的表达式;证明两个信号具有相同的采样值,即)()(nT x nT x a =。
若采样率s f =10Hz ,重复上述问题。
本题通过证明说明了当a f1.3 以3Hz 的频率对信号x(t)=cos(5πt)+4sin(2πt)sin(3πt)进⾏抽样(其中t 以毫秒为单位)。
求(1)x(t)的重建信号)(t x a ;(2)写出重建信号是)(t x a ,但⼜不同于x(t)的另外两个信号x 1(t)和x 2(t)。
⽤到了公式)mod(s a f f f =,参见课本19页例1.4.7。
1.9 Consider the following sound wave, where t is in millisecond: x(t )=sin(10πt )+sin(20πt )+sin(60πt )+sin(90πt )This signal is prefiltered by an analog antialiasing prefilter H (f ) and then sampled at audio rate of 40kHz.The resulting samples are immediately reconstructed using an ideal reconstructor. Determine the output ya(t ) of the reconstructor in the following cases and compare it with the audible part of x(t ):a. When there is no prefilter ,that is, H(f )≡1.b. When H(f ) is an ideal prefilter with cutoff of 20kHz.c. When H(f ) is a practical prefilter that has a flat passband up to 20kHz and attenuates at arate of 48db?ocate beyond 20kHz.(You may ignore the effects of the phase response of the filter.)1.11 Give Eq.(1.5.4), prove the inverse DTFT property (1.5.5),that is,)(f X ∧=∞-∞=∑n x(nT)ejfTnπ-2 => x(nT)=-221fs fs sf )(f X ∧ejfTnπ2df1.12 Consider a pure sinusoid of frequency f 0 , x (t )=cos(2πf 0t ). Show that the spectrum of the sampled sinusoid x (n T) is : )(f X ∧=)]()([2100s s m mf f f mf f f T ++δ+--δ∑∞-∞=第⼆章习题2.1考虑⼀个3⽐特长的双极性⼆进制补码的逐次逼近A/D 转换器,其中满量程幅度为R =16V 。
DSP习题答案

第一章F28x简介1. 什么是DSP,它有什么用处?答:DSP是数字信号处理器(Digital Signal Processor ),是特别适合于实现各种数字信号处理运算的微处理器。
主要应用场合:(1)数字信号处理运算,(2)通信,(3)网络控制及传输设备,(4)语音处理,(5)电机和机器人控制,(6)激光打印机、扫描仪和复印机,(7)自动测试诊断设备及智能仪器仪表、虚拟仪器,(8)图像处理,(9)军事,(10)自动控制等。
2. 写出以下缩写词的中英文全称DSP、MIPS、MOPS、MFLOPS、MACS、XINTF、JTAG、MSPS、UART 答:DSP :Digital Signal Processor,数字信号处理器。
MIPS:Millions of Instruction Per Second,即每秒执行的百万条指令MOPS:Millions of Operation Per Second,每秒执行的百万条操作MFLOPS:Millions of Float Operation Per Second,每秒执行的百万次浮点运算MACS:MACS是指DSP在1秒内完成乘-累加运算的次数XINTF:External Interface ,外部接口。
JTAG:Jiont Testable Action Group,联合测试行动组。
MSPS:Million Samples per Second,每秒采样的百万次数。
UART:Universal Asynchronous Receiver/Transmitter,通用异步接收/发送器。
3. 什么是定点DSP芯片和浮点DSP芯片,各有什么优缺点?答:定点DSP芯片按照定点的数据格式进行工作,其数据长度通常为16位、24位、32位。
定点DSP的特点:体积小、成本低、功耗小、对存储器的要求不高;但数值表示范围较窄,必须使用定点定标的方法,并要防止结果的溢出。
DSP原理及应用课后答案

第二章3、处理器工作方式状态寄存器PMST 中的MP/MC、OVLY 和DROM 三个状态位对C54x的存储空间结构各有何影响?当OVLY= 0 时,程序存储空间不使用内部RAM。
当OVLY= 1 时,程序存储空间使用内部RAM。
内部RAM 同时被映射到程序存储空间和数据存储空间。
当MP/ MC=0 时,4000H~EFFFH 程序存储空间定义为外部存储器;F000H~FEFFH 程序存储空间定义为内部ROM;当MP/ MC=1 时,4000H~FFFFH 程序存储空间定义为外部存储。
DROM=0:0000H~3FFFH——内部RAM ;4000H~FFFFH——外部存储器;DROM=1 :0000H~3FFFH——内部RAM;4000H~EFFFH——外部存储器;F000H~FEFFH——片内ROM;FF00H~FFFFH——保留。
4 、TMS320C54x 芯片的片内外设主要包括哪些电路?①通用I/O 引脚②定时器③时钟发生器④主机接口HPI⑤串行通信接口⑥软件可编程等待状态发生器⑦可编程分区转换逻辑5、TMS320C54x 芯片的流水线操作共有多少个操作阶段?每个阶段执行什么任务?完成一条指令都需要哪些操作周期?六个操作阶段:①预取指P;将PC 中的内容加载PAB ②取指F; 将读取到的指令字加载PB③译码D; 若需要,数据1 读地址加载DAB;若需要,数据2 读地址加载CAB;修正辅助寄存器和堆栈指针④寻址A; 数据1 加载DB;数据2 加载CB;若需要,数据3 写地址加载EAB⑤读数R; 数据1 加载DB;数据2 加载CB;若需要,数据3 写地址加载EAB;⑥执行X。
执行指令,写数据加载EB。
6、TMS320C54x 芯片的流水线冲突是怎样产生的?有哪些方法可以避免流水线冲突?答:’C54x 的流水线结构,允许多条指令同时利用CPU 的内部资源。
由于CPU 的资源有限,当多于一个流水线上的指令同时访问同一资源时,可能产生时序冲突。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
由此可画出系统的并联型结构,如下图所示:
0.4 x(n)
z 1
y(n) 0.0588
0.6
z 1
z 1
0.5882
-0.25 4.3 已知 FIR 滤波器的单位脉冲响应为
h(n) (n) 0.3 (n 1) 0.72 (n 2) 0.11 (n 3) 0.12 (n 4)
4.8 一个线性时不变系统的单位脉冲响应为
a n h( n) 0
0n7 其他
(1) 画出该系统的直接型 FIR 结构图。 (2) 证明该系统的系统函数为
1 a8 z 8 H ( z) 1 az 1
并由该系统函数画出由 FIR 系统和 IIR 系统级联而成的结构图。 (3) 比较(1)和(2)两种系统实现方法,哪一种需要较多的延迟器?哪一种实现需要较多 的运算次数? 解: 题(1) :
所以有
y (n) b(2) x(n) b(1) x(n 1) b(0) x(n 2) a(1) y (n 2) a(2) y (n 1)
故该系统直接Ⅱ型结构如下:
z 1 z 1
4.7
求下面网络的系统函数, 确定要保证系统稳定系数 a (1), a (2), a (3), a (4) 应满足的条件。
z 1
x ( n)
y ( n)
z 1
z 1
4.2 已知某数字系统的系统函数为:
H z
z3 z 0.4 z 2 0.6 z 0.25
试分别画出其级联型、并联型结构。 解: 由于系统有一单实数极点和一对共轭复数极点,故可将 H(z)表示为实系数 1 阶、2 阶子系统 的乘积,即:
H(z)=
Y(z) rz 1 sin X ( z ) 1-2rz 1 cos +r 2 z 2
其对应的差分方程为: y(n)=r sin x(n 1) 2r cos y (n 1) r 2 y (n 2)
4.6 求以下网络的直接Ⅱ型实现方式:
z 1
z 1
得:
X ( z ) rz 1Y ( z ) sin X1 ( z) 1 rz 1 cos
而:
Y(z)=rz 1 X 1 ( z ) sin rz 1Y(z)cos 1 rz 1 cos Y(z) rz 1 sin X ( z ) rz 1Y ( z ) sin 1 rz 1 cos Y 则: (z)= rz 1 sin 1 rz 1 cos (1-2rz 1 cos +r 2 z 2 cos 2 )Y(z)=rz 1 sin X ( z )-r 2 z 2 sin 2 Y(z) X1 ( z)
4.5 写出下图所示结构的系统函数及差分方程:
r cos x ( n) x1 z 1 r sin z 1 r sin
解:根据图中所设节点:
y ( n)
r cos
X 1 ( z ) X ( z ) rz 1Y ( z ) sin rz 1 X 1 ( z ) cos
(1)试求该滤波器的系统函数。 (2)试分别画出其直接型、级联型结构。 解: 题(1) : 根据 H ( z )
h( n) z
n 0
N 1
n
,得
H z 1 0.3z 1 0.72 z 2 0.11z 3 0.12 z 4 (1 0.2 z 1 0.3 z 2 )(1 0.1z 1 0.4 z 2 )
H ( z ) h(n) z n 1 az 1 a 2 z 2 a 3 z 3 a 4 z 4 a 5 z 5 a 6 z 6 a 7 z 7
n 0
7
直接型 FIR 结构图如下所示:
z 1
a
z 1
a2
z 1
a3
z 1
a4
z 1
a5
第四章
数字滤波器及其结构
4.1 按照下面所给的系统函数,求出该系统的两种形式的实现方案:直接型 I 和直接型 II。
H z
解: 直接型 I:
2 0.6 z 1 3z 2 1 5 z 1 0.8 z 2
x ( n)
z 1
y ( n) z 1
z 1
直接型 II:
H z
1 1 1 1 1 0.4 z 1 0.6 z 0.25 z 2
由此可画出系统的级联型结构如下:
z 1
z 1 z 1
将 H(z)表示为实系数 1 阶、2 阶子系统之和,即:
H z
0.9412 0.0588 0.5882 z 1 1 0.4 z 1 1 0.6 z 1 0.25 z 2
解: 先写出网络中每个加法器的节点方程,节点标注如下:
x(n) b(0) b(1) b(2) y(n)
z 1
a(1)
z 1
a(2)
节点1
节点2
节点3
用 w1 (n), w2 ( n), w3 ( n) 表示 3 个节点的输出,则有以下 3 个方程:
w1 (n) b(0) x(n) a(1) y (n) w2 (n) b(1) x(n) w1 (n 1) a(2) y (n) w3 (n) b(2) x(n) w2 (n 1) y (n)
题(2) : 根据(1) ,它的直接型结构为:
z 1
z 1
z 1
z 1
级联型结构为:
z 1 z 1
4.4 求下列各图所示各系统的单位脉冲响应。 (1)
x(n) 1
z 1
z 1
z 1
-2
z 1
4
z 1
3
z 1
-1
z 1
1 y(n)
(2)
x(n)
z 1
z 1
z 1 z 1
z 1
2 y(n)
解: 题(1) :
z 1
1 -1
z 1
3
h(n) (n) 2 (n 1) 4 (n 2) 3 (n 3) (n 4) (n 5)
题(2) :
h(n) 2 (n) 3 (n 1) (n 2) (n 3) (n 4) (n 5) 3 (n 6) 2 (n 7)
1 1 a (1) z 1 a(2) z 2 H ( z) 1 G ( z ) 1 a(1) a(3) z 1 a(2) a(4) z 2
(2)稳定条件: 要求极点均在单位圆内:
f ( z ) z 2 a (1) a (3) z a (2) a (4) 0 f (1) 0, f (1) 0 0 a (1) a (3) 1 a(2) a(4) x1 x2 1 1 a (1) a (3) 1 a (2) a (4) 1 2 0 0 or x1 x2 1 a(2) a(4) 1 实际上 0时也有f (1) 0 f (1) 0,综合得: a (1) a (3) 1 a (2) a (4) a (2) a (4) 1
对上述方程作 z 变换,最终得到
1 2 1 2 W ( z) 1 a(1) z a (2) z a(3) z a(4) z V ( z)
所以, G ( z )
W ( z) a (3) z 1 a (4) z 2 , V ( z ) 1 a (1) z 1 a (2) z 2
z 1
a6
z 1
a7
题(2) : 由(1) ,根据等比数列的前n项和,即可得到
1 1 a8 z 8 H ( z ) (1 a z ) 1 az 1 1 az 1
8 8
由此可画出由 FIR 系统和 IIR 系统级联而成的结构图,如下所示:
z8
a8
a
z 1
题(3) : (2)中的实现需要延迟器较多, (1)中的实现需要运算次数较多。
z 1 z 1
解: 该系统是一个反馈网络,
其中 G(z)是一个二阶系统,如下
z 1
u ( n) z1来自H ( z) 1 1 G( z)
下面求 G ( z ) ,网络方程如下:
u1 (n) a(3)v(n) u2 (n 1) a(1) w(n) u2 (n) a (4)v(n) a(2) w(n) w(n) u1 (n 1)
