正态分布伪随机数生成方法总结
正态分布随机数公式

正态分布随机数公式正态分布随机数公式是统计学中一个相当重要的概念。
在我们的日常生活和学习中,它的应用其实比你想象的还要广泛呢!先来说说正态分布到底是个啥。
想象一下,你在学校组织的考试中,大部分同学的成绩都集中在一个中间的分数段,只有少数同学特别优秀或者特别差。
这种成绩的分布情况就很接近正态分布啦。
那正态分布随机数公式又是啥呢?它其实就是用来生成符合正态分布特征的随机数的工具。
比如说,我们在做一些模拟实验的时候,需要生成一些看起来像是符合正态分布的数据,这时候这个公式就派上用场啦。
我给您讲讲我曾经遇到的一件事儿吧。
有一次,我们学校要组织一场数学竞赛,老师为了让我们提前适应竞赛的难度,就自己用正态分布随机数公式生成了一套模拟试题的分数。
结果呢,大家拿到分数的时候都觉得特别神奇,因为大部分人的分数都在一个相对集中的区间内,只有几个同学特别突出或者特别落后,跟平时考试的分布情况还真有点像。
回到正态分布随机数公式本身,它的数学表达式看起来可能有点复杂,但其实理解起来也没那么难。
它主要涉及到一些数学参数,比如均值和标准差。
均值决定了正态分布的中心位置,标准差则决定了数据的分散程度。
比如说,如果均值是 50,标准差是 10,那么生成的随机数就会围绕着 50 这个中心,并且大部分会在 40 到 60 之间。
要是标准差变小,比如变成 5,那数据就会更加集中在 50 附近;反之,标准差变大,数据就会更分散。
在实际应用中,正态分布随机数公式可有用啦!比如在金融领域,分析股票价格的波动;在医学研究中,评估药物的疗效;在工程设计中,预测产品的可靠性等等。
就拿金融来说吧,股票价格的涨跌很多时候就呈现出正态分布的特点。
分析师们会用正态分布随机数公式来模拟股票价格的未来走势,帮助投资者做出更明智的决策。
在医学研究里,研究人员可能会用这个公式来模拟某种疾病的症状出现的概率,或者药物副作用的发生情况。
在工程方面,假设我们要设计一款新的汽车发动机,工程师们可以用正态分布随机数公式来模拟发动机零部件的寿命,从而更好地优化设计,提高产品的质量和可靠性。
rand系列函数

1,rand生成均匀分布的伪随机数。
分布在(0~1)之间主要语法:rand(m,n)生成m行n列的均匀分布的伪随机数rand(m,n,'double')生成指定精度的均匀分布的伪随机数,参数还可以是'single'rand(RandStream,m,n)利用指定的RandStream(我理解为随机种子)生成伪随机数rand(n):生成0到1之间的n阶随机数方阵rand(m,n):生成0到1之间的m×n的随机数矩阵2,randn生成标准正态分布的伪随机数(均值为0,方差为1)主要语法:和上面一样3, randi生成均匀分布的伪随机整数主要语法:randi(iMax)在闭区间[1,iMax]生成均匀分布的伪随机整数randi(iMax,m,n)在闭区间[1,iMax]生成mXn型随机矩阵randi([iMin,iMax],m,n)在闭区间[iMin,iMax]生成mXn型随机矩阵4,randperm随机打乱一个数字序列randperm(n):产生一个1到n的随机顺序。
>> randperm(10)ans =6 4 8 9 3 57 10 2 1p = randperm(n,k) 返回一行从1到n的整数中的k个,而且这k个数也是不相同的。
randperm完成的是不重复的重排采样(k-permutations),如果结果中的数需要重复多次出现的情况,则可以用:randi(n,1,k)。
5,randerr函数randerr(20,7)产生什么矩阵?产生一个20×7的矩阵,矩阵每一行随机有一个元素为1,其余的为0out2 = randerr(8,7,[0 2; .25 .75])每行出现零个错误的概率是25%出现2个错误的概率是75%(值为1表示出现错误)(1)产生随机矩阵,并返回制定范围内的元素>a = randi([-50 50], 1, 100);>b = find(a > 20 & a < 40)2(2)产生一个元素为0和1,size为100×5的随机矩阵,返回元素全为1的行。
产生正态分布随机数的matlab方法random

产生正态分布随机数的matlab方法random在Matlab中生成正态分布随机数有多种方法,下面将介绍其中几种常用的方法,并对它们进行全面评估。
1. 使用randn函数生成正态分布随机数- randn函数是Matlab中用于生成符合标准正态分布的随机数的函数。
- 该方法的优点是简单易用,一行代码就可以生成所需的随机数序列。
- 但是,这种方法生成的随机数序列可能不够随机,存在一定的偏差。
2. 使用Box-Muller变换生成正态分布随机数- Box-Muller变换是一种经典的生成正态分布随机数的方法,通过均匀分布的随机数生成正态分布的随机数。
- 这种方法生成的随机数更加符合正态分布的特性,具有更好的随机性和分布性。
- 但是,实现Box-Muller变换需要一定的数学基础和编程技巧,相对复杂一些。
3. 使用truncated normal distribution生成截尾正态分布随机数- 有时候我们需要生成一定范围内的正态分布随机数,这时可以使用truncated normal distribution方法。
- 这种方法可以有效地控制生成的随机数范围,使其符合实际应用需要的要求。
- 但是,对于一些特殊情况,需要考虑truncated normal distribution生成的随机数是否符合实际问题的分布需求。
总结回顾:在Matlab中生成正态分布随机数有多种方法,每种方法都有各自的优点和局限性。
根据实际需求,选择合适的方法是非常重要的。
在编写程序时,需要根据具体情况综合考虑随机性、分布性和实际应用需求,选择最合适的方法来生成正态分布随机数。
个人观点和理解:在实际编程中,生成符合实际需求的随机数是非常重要的。
对于正态分布随机数的生成,需要考虑到数据的随机性和分布特性,才能更好地应用于实际问题中。
也要注意选择合适的方法,并在实际应用中进行验证和调整,以确保生成的随机数符合实际需求。
正态分布是自然界和社会现象中广泛存在的一种分布形式,它具有许多重要的统计特性,如均值、标准差和形态等。
产生正态分布随机数及M序列

1. 编制两种方法产生正态分布随机数的程序并进行验证分析; 编程思路:产生正态分布随机数的两种方法:(1) 统计近似抽样法:a.设{i y }是(0,1)均匀分布的随机数序列,则{}1()0.5y i i i i E y y p y dy μ===⎰1220()()1/12y i y i i y p y dy σμ=-=⎰b.根据中心极限定理,当N →∞时,112()2()~(0,1)/12NNi yi i i yNy k N y x k N N N μσ==--==∑∑c.如需产生均值为x μ,方差为2x σ的正态分布随机变量x ,只需如下计算:212~(,)/12Ni i x x x x N y x N N μσμσ=-=+∑,试验证明12N =时,x 的统计性质就比较理想了。
(2) 变换抽样法:设12,y y 是两个相互独立的(0,1)均匀分布的随机变量,则新变量1/21121/2212(2log )cos(2)(2log )sin(2)x y y x y y ππ⎧=-⎨=-⎩ 是相互独立的,服从(0,1)N 分布的随机变量。
利用统计近似抽样法和变换抽样法的定义及之前产生(0,1)均匀分布的随机数的基本方法如乘同余法、混合同余法等产生正态分布随机数。
调试过程遇到的问题:(1)在用统计近似抽样法产生正态分布随机数时,给定,μσ,然后用Matlab 自带函数检验结果,感觉数据老对不上?解决方法:自己设定的,μσ分别是均值,标准差,利用Matlab 自带函数mean(),var()计算出来的分别是均值,方差,总觉得方差老对不上,其实是自己理解问题,var()计算出来的方差数值肯定是自己设定的标准差的平方大小左右。
(2)Matlab 下标从1开始;做运算两个矩阵的尺寸大小得对应上,还有调用的值一定得有值。
程序运行结果分析得到的结论:(1)统计近似抽样法:50010001500200025003000350040004500-50510统计近似抽样法(1)-4-202468050100150200 050100150200250300350-4-20246统计近似抽样法(2)-3-2-101234567010203040统计近似抽样法中要用产生的(0,1)序列的12个数的和,但具体哪12个,不太清楚,图(1)是:z(1)用的是x(1)~x(12),z(2)用的是x(2)~x(13),以此类推。
excel正态分布随机数生成公式

excel正态分布随机数生成公式Excel是一款功能强大的电子表格软件,除了常见的数据处理和计算功能外,它还提供了一些高级的统计分析功能,其中包括生成符合正态分布的随机数。
正态分布是统计学中常用的一种概率分布,也被称为高斯分布。
在Excel中,我们可以使用一条简单的公式来生成符合正态分布的随机数。
本文将介绍这个公式的原理和使用方法。
在Excel中,我们可以使用NORM.INV函数来生成符合正态分布的随机数。
NORM.INV函数的语法如下:NORM.INV(probability, mean, standard_dev)其中,probability是一个介于0和1之间的概率值,表示所要生成的随机数的累积概率;mean是正态分布的均值;standard_dev是正态分布的标准差。
为了更好地理解这个公式的原理,我们来举一个例子。
假设我们要生成100个符合均值为0,标准差为1的正态分布随机数。
我们可以使用下面的公式:=NORM.INV(RAND(), 0, 1)在这个公式中,RAND函数用于生成一个介于0和1之间的随机数。
然后,NORM.INV函数将这个随机数转化为符合均值为0,标准差为1的正态分布随机数。
我们可以将这个公式填充到一个100行1列的区域中,就可以得到100个符合正态分布的随机数。
除了生成100个符合正态分布的随机数,我们还可以根据自己的需要生成不同均值和标准差的正态分布随机数。
例如,如果我们要生成均值为10,标准差为2的正态分布随机数,可以使用下面的公式:=NORM.INV(RAND(), 10, 2)通过调整公式中的均值和标准差的值,我们可以得到不同的正态分布随机数。
在实际应用中,生成符合正态分布的随机数对于模拟和统计分析非常有用。
例如,我们可以使用这些随机数来模拟股票价格的变动、人口增长的模式等。
同时,正态分布也是许多统计方法的基础,生成符合正态分布的随机数可以帮助我们进行各种统计分析。
随机数的产生

随机数的产生摘要本文研究了连续型随机数列的产生,先给出了均匀分布的随机数的产生算法,在通过均匀分布的随机数变换得到其他连续型随机数的产生算法.在v c 环境下,我们给出了产生均匀分布随机数的算法,然后探讨了同余法的理论原理.通过均匀随机数产生其他分布的随机数,我们列举了几种通用算法,并讨论各个算法的优缺点,最后以正态分布为例验证高效舍选法的优势. 正文一、 随机数与伪随机数随机变量η的抽样序列12,,n ηηη ,…称为随机数列.如果随机变量η是均匀分布的,则η的抽样序列12,,n ηηη ,…称为均匀随机数列;如果随机变量η是正态分布的随机变量则称其抽样序列为正态随机数列.比如在掷一枚骰子的随机试验中出现的点数x 是一个随机变量,该随机变量就服从离散型均匀分布,x 取值为1,2,3,4,5,6,取每个数的概率相等均为1/6.如何得到x 的随机数?通过重复进行掷骰子的试验得到的一组观测结果12,,,n x x x 就是x 的随机数.要产生取值为0,1,2,…,9的离散型均匀分布的随机数,通常的操作方法是把10个完全相同的乒乓球分别标上0,1,2,…,9,然后放在一个不透明的袋中,搅拦均匀后从中摸出一球记号码1x 后放回袋中,接着仍将袋中的球搅拌均匀后从袋中再摸出一球记下号码2x 后再放回袋中,依次下去,就得到随机序列12,,,n x x x .通常称类似这种摸球的方法产生的随机数为真正的随机数.但是,当我们需要大量的随机数时,这种实际操作方法需要花费大量的时间,通常不能满足模拟试验的需要,比如教师不可能在课堂上做10000次掷硬币的试验,来观察出现正面的频率.计算机可以帮助人们在很短时间产生大量的随机数以满足模拟的需要,那么计算机产生的随机数是用类似摸球方法产生的吗?不是.计算机是用某种数学方法产生的随机数,实际上是按照一定的计算方法得到的一串数,它们具有类似随机数的性质,但是它们是依照确定算法产生的,便不可能是真正的随机数,所以称计算机产生的随机数为伪随机数.在模拟计算中通常使用伪随机数.对这些伪随机数,只要通过统计检验符合一些统计要求,如均匀性、随机性等,就可以作为真正的随机数来使用,我们将称这样产生的伪随机数为随机数.在计算机上用数学方法产生随机数的一般要求如下:1)产生的随机数列要有均匀性、抽样的随机性、试验的独立性和前后的一致性.2)产生的随机数列要有足够长的周期,以满足模拟实际问题的要求.3)产生随机数的速度要快,占用的内存少.计算机产生随机数的方法内容是丰富的,在这里我们介绍几种方法,计算机通常是先产生[0,1]区间上均匀分布的随机数,然后再产生其他分布的随机数.二、均匀分布随机数的产生2.1 算法1在v c的环境下,为我们提供了库函数rand()来产生一个随机的整数.该随机数是平均在0~RAND_MAX之间平均分布的,RAND_MAX是一个常量,在VC6.0环境下是这样定义的:#define RAND_MAX 0x7fff它是一个short 型数据的最大值,如果要产生一个浮点型的随机数,可以将rand()/1000.0这样就得到一个0~32.767之间平均分布的随机浮点数.如果要使得范围大一点,那么可以通过产生几个随机数的线性组合来实现任意范围内的平均分布的随机数.例如要产生-1000~1000之间的精度为四位小数的平均分布的随机数可以这样来实现.先产生一个0到10000之间的随机整数.方法如下:int a = rand()%10000;然后保留四位小数产生0~1之间的随机小数:double b = (double)a/10000.0;然后通过线性组合就可以实现任意范围内的随机数的产生,要实现-1000~1000内的平均分布的随机数可以这样做:double dValue =(rand()%10000)/10000.0*1000-(rand()%10000)/10000.0*1000;则dValue就是所要的值.但是,上面的式子化简后就变为:double dValue = (rand()%10000)/10.0-(rand()%10000)/10.0;这样一来,产生的随机数范围是正确的,但是精度不正确了,变成了只有一位正确的小数的随机数了,后面三位的小数都是零,显然不是我们要求的,什么原因呢,又怎么办呢.先找原因,rand()产生的随机数分辨率为32767,两个就是65534,而经过求余后分辨度还要减小为10000,两个就是20000而要求的分辨率为1000*10000*2=20000000,显然远远不够.下面提供的方法可以实现正确的结果:double a = (rand()%10000) * (rand()%1000)/10000.0;double b = (rand()%10000) * (rand()%1000)/10000.0;double dValue = a-b;则dValue就是所要求的结果.在下面的函数中可以实现产生一个在一个区间之内的平均分布的随机数,精度是4位小数.double AverageRandom(double min,double max){int minInteger = (int)(min*10000);int maxInteger = (int)(max*10000);int randInteger = rand()*rand();int diffInteger = maxInteger - minInteger;int resultInteger = randInteger % diffInteger + minInteger;return resultInteger/10000.0;}但是有一个值得注意的问题,随机数的产生需要有一个随机的种子,因为用计算机产生的随机数是通过递推的方法得来的,必须有一个初始值,也就是通常所说的随机种子,如果不对随机种子进行初始化,那么计算机有一个缺省的随机种子,这样每次递推的结果就完全相同了,因此需要在每次程序运行时对随机种子进行初始化,在v c中的方法是调用srand(int)这个函数,其参数就是随机种子,但是如果给一个常量,则得到的随机序列就完全相同了,因此可以使用系统的时间来作为随机种子,因为系统时间可以保证它的随机性.调用方法是srand(GetT ickCount()),但是又不能在每次调用rand()的时候都用srand(GetT ickCount())来初始化,因为现在计算机运行时间比较快,当连续调用rand()时,系统的时间还没有更新,所以得到的随机种子在一段时间内是完全相同的,因此一般只在进行一次大批随机数产生之前进行一次随机种子的初始化.下面的代码产生了400个在-1~1之间的平均分布的随机数. double dValue[400];srand(GetTickCount());for(int i= 0;i < 400; i++){double dValue[i] = AverageRandom(-1,1);}用该方法产生的随机数运行结果如图1所示:图1 400个-1~1之间平均分布的随机数2.2 算法2:用同余法产生随机数同余法简称为LCG(Linear Congruence Gener-ator),它是Lehmer 于1951年提出来的.同余法利用数论中的同余运算原理产生随机数.同余法是目前发展迅速且使用普遍的方法之一.同余法(LCG)递推公式为1()(mod )n n x ax c m -=+ (n=1,2,…), (1)其中n x ,a ,c 均为正整数.只需给定初值x.,就可以由式(1)得到整数序列{n x },对每一n x ,作变换n u =n x /m ,则{n u }(n=1,2,…)就是[0,1)上的一个序列.如果{n u }通过了统计检验,那么就可以将n u 作为[0,1)上的均匀分布随机数.在式(1)中,若c=0,则称相应的算法为乘同余法,并称口为乘子;若c ≠0,则称相应的算法为混合同余法.同余法也称为同余发生器,其中0x 称为种子.由式(1)可以看出,对于十进制数,当取模m=10k(k 为正整数)时,求其同余式运算较简便.例如36=31236(mod102),只要对21236从右截取k=2位数,即得余数36.同理,对于二进制数,取模m=2k 时,求其同余式运算更简便了.电子计算机通常是以二进制形式表示数的.在整数尾部字长为L 位的二进制计算机上,按式(1)求以m 为模的同余式时,可以利用计算机具有的整数溢出功能.设L 为计算机的整数尾部字长,取模m=2L ,若按式(1)求同余式时,显然有11111;[()/].n n n n n n n ax c m x ax c ax c m x ax c m ax c m -----+<=++≥=+-+当时,则当时,则这里[x]是取x 的整数部分.在电子计算机上由1n x -求n x 时,可利用整数溢出原理.不进行上面的除法运算.实际上,由于计算机的整数尾部字长为L ,机器中可存放的最大整数为2L -1,而此时a 1n x -+c ≥m ≥2L -1,因此a 1n x -+c 在机器里存放时占的位数多于L 位,于是发生溢出,只能存放n x 的右后L 位.这个数值恰是模m=2L 的剩余,即n x .这就减少了除法运算,而实现了求同余式.经常取模m=2L (L 为计算机尾部字长),正是利用了溢出原理来减少除法运算.由式(1)产生的n x (n=1,2,……),到一定长度后,会出现周而复始的周期现象,即{n x }可以由其某一子列的重复出现而构成,这种重复出现的子列的最短长度称为序列n x 的周期.由式(1)不难看出,{n x }中两个重复数之间的最短距离长度就是它的周期,用T 代表周期.周期性表示一种规律性,它与随机性是矛盾的.因此,通常只能取{n x }的一个周期作为可用的随机序列.这样一来,为了产生足够多的随机数,就必须{n x }的周期尽可能地大.由前所述,一般取m=2L ,这就是说模m 已取到计算机能表示的数的最大数值,意即使产生的随机数列{n x }的周期达到可能的最大数值,如适当地选取参数0x ,a ,c 等,还可能使随机数列{n x }达到满周期.三、非均匀分布随机数的产生3.1 一般通用方法 3.1.1组合法组合法的基本思想是把预定概率密度函数f ( x ) 表为其它一些概率密度的线性组合.而这些概率密度的随机抽样容易产生.通过这种避难就易的手段我们也许可以达到较高的输出速度和较好的性能.若分布密度函数f ( x ) 能表为如下式(2)所示的函数项级数的和,1()()i i i f x p f x ∞==∑(2)其 中1i i p ∞=∑,诸f( x )皆为概率密度函数.则依如下步骤可产生分布为f ( x )一次抽样.( 1 ) 产生一个随机自然数I , 使I 服从如下分布律:P ( I = i ) = p i i = 1 , 2 , 3……( 2 ) 产生服从f I ( x )的随机数0X 证明利用全概率公式,有:11()()()()()i i i i P x X x dx P Ii P x X x dx I i p f x dxf x dx∞=∞=<≤+==<≤+|===∑∑故X 服从f ( x ) 分布.我们以产生双指数(或拉普拉斯)分布的随机数为例来简单说明这种方法.双指数分布具有 概率密度函数f ( x ) = 0 . 5xe-, 如图2 :图2 双指数密度函数 f ( x ) 可表为:()0.5()0.5()l r f x f x f x =+ (3)其中()r f x 是指数分布,()l f x 是指数分布的对称分布.故产生双指数分布的抽样可按如下方法: 产生U 1 , U 2~U ( 0 , 1 ) ;若U 1 > 0 . 5 , 则令X = I n U 2,否则X = - I n U 2. 在式(2) 中, 若i →∞, 有p i → 0 ,则可用函数列{()}i i p f x 的前有限项和逼近f ( x ).这是一种近似的方法,与通常的函数逼近原理相同.只要近似的精度 ( 在某种“精度”的意义之下) 达到要求,我们就可以采用近似的方法 .使用组合法时,各f i ( x ) 的抽样应该容易产生,故选用合适的概率密度函数族{ f i ( x )}把任意连续分布表为式(2) ,乃是使用组合法的关键.3.3.2 概率密度变换法这是一种比较新的通用随机数产生方法.其主要的目的是对一般的f(x)找出较好的覆盖函数以达到较高的效率.我们知道,对某一特定的概率密度f(x),我们可以使用最优化技术找到好的覆盖函数.但对于一般情况,我们只能期望产生效率尚可的覆盖函数. H O R M A N N 用概率密度变换的方法生成一曲边梯形作为覆盖函数.其原理如下:使用一个变换函数T (x)把预定密度函数f ( x ) 变换为h ( x ) = T ( f ( x ) ) ,用一个分段线性函数l ( x )覆盖h ( x ),如图2 - 4 左图; h ( x ) 若是上凸的,则T 1-( l ( x ) )将是f ( x ) 的一个较好的覆盖函数,图3 概率密度变换法原理图这个方法在选择合适的T ( x ) ( l o g ( x ) 或1 / x a等) 后,能产生随机数包括了较多的分布类型.这个方法有较短的预处理时间,但需要较多的函数计算,不太适合硬件实现.此外,A h r e n s l用每段为常数的分段函数作为覆盖函数.L e y d o l d基于r a t i o - o f - u n i f o r m s 的方法也是一个通用算法.还有一种近似的方法,其产生的随机数与指定分布的随机数具有相同的前四阶矩,但概率分布不一定相同.这里就不详细介绍了.3.2 我们的方法当前的通用算法的问题是效率不能任意提高,不够灵活. 通常产生每个所需随机数X需以较大的概率计算f ( x )等函数.我们认为在速度要求非常高的场合,计算f ( x )是不利的,尤其以硬件进行函数计算是十分不利的.针对己有通用算法的不足,我们提出了基于组合法的通用算法.主要目的是尽可能地减少三角、指数、对数等超越函数的计算,以便硬件实现.产生任意连续分布随机数的高效舍选算法本文提出一种通用算法,可视需要使效率接近1 , 而且f ( x ) 的计算概率可任意小. 这些优点的取得是以长的预处理时间为代价的.在需要产生大量随机样本的场合( 例如通信系统的误码率测试,可能需要数小时乃至数天的仿真时间) ,本算法将有很大的优势,尽管有看法认为只有能用简单代码实现的算法才会被经常使用.3.2.1 算法原理假定预定的连续概率密度函数f ( x ) 为单峰的( 这是实际的大多数情况) ,已知其峰值点为m .一般f ( x ) 不关于x =m 对称,如图2 -5 .我们假定f ( x ) 定义在有界的区间[ a , b ] 上( 上文说过,对正态分布这类定义区间无限的情况,我们把这个区间取得足够大就可以了) . 直线X=m把f ( x ) 曲线与X轴所围面积分为左右两部分,我们把左右两部分各等分为K份,一共得到2 K个曲边梯形.并用2 K个矩形各自覆盖相应的曲边梯形.如图4所示( 图中各均分为四份) .R i , L i ( i = 1 , 2 , . . . , K -1 )是分点.并令R0=L=m,Lk = a,Rk= b .图4 均分f ( x ) 曲 线与X 轴所围面积我们的想法是利用舍选法的几何意义,分别在上述 2 K 个曲边梯形内均匀投点,从而使随机点在f ( x ) 曲线与x 轴所围的整个区域中均匀分布,这样即可产生f ( x ) 的抽样X . 而在曲边梯形内均匀投点可使用简单舍选法:先在各个矩形内均匀投点,再选出落于相应曲 边梯形内的点. 这种投点法浪费的点只位于各个矩形的一角, 显然效率大大高于简单舍选法.最为重要的是:随着K 的增大,效率会不断提高.另外,只有当投点位于曲边梯形的曲边之下时, 才需计算f ( x ) ,而且计算f ( x ) 概率是随着K 的增加而减小的. 我们每次“ 按概率”随机选中一个曲 边梯形进行投点. 这需要两步完成:先选择左边还是右边,再于此边的K 个曲边梯形中选择一个.这里的概率显然就是面积,这可以从以下的推导中看出来.为清晰起见,我们先阐述随机数的产生法,而把面积的均分这个预处理过程置于随后. 3.2.2 算法推导令()mP f x dx -∞=⎰为左边面积.则左边各曲边梯形面积皆为 P / K ,右边各曲边梯形面积皆为( ( I -P ) / K . f ( x ) 可表为:12111()()()KKi i i i P P f x f x f x KK==-=+∑∑(4)诸ji f ( x ) ( j = 1 , 2 ; i = 1 , 2 . . . k ) 皆为一腰为曲边的梯形形状的概率密度函数.依如下步骤可产生分布为f ( x ) 的一次抽样:S t e p l :产生一个随机自然数J ,使J 服从如下两点分布: P ( J = 1 ) = P , P ( J = 2 ) = 1 - P : S t e p 2 :产生一个随机自然数I , 使I 服从如下均匀分布律:P ( I = i ) = 1 / K , i = 1 , 2 . . . . K ; S t e p 3 : 用基本舍选法产生概率密度为f ( x ) 的随机数X . 证明利用全概率公式,有:2111211()()()(,)1(()())()Kj i KKi i i i P x X x dx P Jj P I i P x X x dx J j I i P P f x f x dxKKf x dx====<≤+===<≤+∣==-=+=∑∑∑∑故x 服从 f ( x ) 分布.下面完整地描述这个方法: S t e p l( 产生J ) :S t e p l . l 产生[ 0 , 1 ] 上的均匀随机数U 1 ;S t e p 1 . 2若U 1 < P ,则返回J = 1 , 否则返回J = 2 ; S t e p 2( 产生I ) :S t e p 2 . l 产生 [ 0 , I ] 上的均匀随机数U 2 ;S t e p 2 . 2 21;I kU x =+⎢⎥⎢⎥⎣⎦⎣⎦表示不大于x 的最大整数.产生 ji f ( x ) 的样本需区别j = 1 与j = 2 两种情况. 图2 - 6 示出j = 2 时一 典型的ji f ( x ) , 用简单舍选法产生其抽样,覆盖函数为矩形. 首先产生一个[ 0 , R i ] 的均匀数, 如它属于[ 0 , R 1i -] 小无需再产生y 轴方向的均匀随机数,接受此均匀数即可;否则还需产生一个Y 轴方向的均匀随机数进行投点,那些落在曲边下方的点被接受,投在矩形右上角的点被舍弃.同理易得j = 1 时的产生法.图5 典型的ji f ( x ) j=2整个S t e p 3 如下: S t e p 3( 产生X ) : i f J = =1{ l o o p :产生[ 0 , 1 ] 上的均匀随机数U 3 , W = ( L 0 - L 1 ) U 3 + L 1 : i f W> L1i -,返回 X = W;e l s e { 产生[ O , l ] 上的均匀随机数V ; if f ( W) - f ( L 1) < ( f ( L1j - ) - f ( L 1 ) ) V 返回X = W;e l s e 舍弃W ,重复l o o p ;} } e l s e{ l o o p : 产生[ 0 , 1 ] 上的 均匀随机数U 3 , W = ( R 1 - R o ) U 3 + R o ;i f W< R 1i -,返回 X = W; e l s e {产生[ 0 , 1 ] 上的均匀随机数V ;i f f ( W) - f ( R 1) C ( f ( R 1I - ) - f ( R 1) ) V , 返回X = W; e l s e 舍弃W ,重复l o o p ;} } 均匀随机数U 2 实际上可由U 1 变换得到, U 3 可由均匀数U2变换得到. 例如从U1 产生U 2 的方法是:当J = l 时, U 1 在[ 0 , P ] 上均匀分布, 故可令U 2 = U l / P ;当J = 2 时, U 1在[ P , 1] 上均匀分布, 故可令U 2 = ( U 1 - P ) / ( 1 - P ) . 从U 2 产生U 3 的方法是:当I = i 时, U 2 在 [ i / K , ( i + l ) / K ]上均匀分布, 故可令U 3 = K ( U 2 - i / K ) . 这样的做法节省了均匀随机数,增加了一些乘法和除法运算.对F P G A 等并行处理的硬件来说,产生均匀随机数是便宜的,除法运算是耗费的,所以我们不提倡减少均匀数的做法. 而对有C P U 的硬件来说, 减少均匀随机数意味着减少了过程调用,也许是值得的. 再介绍预处理过程.各分点需解下列递推方程求得:从i=1开始求解,直至i = K - 1 .这些方程可事先利用软件求解. 3.2.3 算法性能分析影响随机数产生速度的主要因素之一是f ( x ) 的计算,故把产生每个抽样平均计算f ( x )的次数 ( 计算概率)做为一个性能指标.另外舍选法的平均效率也作为一个性能指标,这个指标反映了每产生一个随机数所需的均匀数个数.产生每个样点X 需计算f ( x ) 的平均概率P f 可利用全概率公式计算:其中10i i iL L L L ---的分母是左边第i 个曲边梯形的下底长,分子是下底与上底的差,这个比值就是在此曲边梯形内投点时计算f ( x ) 的概率.10i i i R R R R ---的意义相仿.舍选法的平均效率” 可利用全概率公式计算:11()()11(1)()()L R KKi i L R A i A i P P K B i K B i η===+-∑∑诸(),(),(),()L L R R A i B i A i B i 分别表示左边各曲边梯形面积、左边各矩形面积、右边各曲边梯形面积和右边各矩形面积.在不同的K 值下,计算了算法用于产生正态分布、 指数分布、 瑞利分布三种标准分布时的上述两个性能参数.各个概率密度函数如下: 正态分布:2())2xf x =-指数分布:()xf x e-=瑞利分布:2()exp()48x xf x =-结果如下图6 :左图反映出概率密度函 数的计算概率P f 随K 的增大而减小, 最终趋于零,例如当K = 1 0 2 4 时, P f 已 非常小;右图反映出 舍选法的平均效率随K 的 增加而提高, 最终趋于 1 , 也就是三个均匀随机数产生一个预期的随机数.我们可根据实际情况选择合适的K 值.图6 计算概率密度函数的概率3.3正态分布的随机数的产生下面提出了一种已知概率密度函数的分布的随机数的产生方法,以典型的正态分布为例来说名任意分布的随机数的产生方法.如果一个随机数序列服从一维正态分布,那么它有有如下的概率密度函数:22()2()xf xμσ--=其中μ,σ(>0)为常数,它们分别为数学期望和均方差,如果读者对数学期望和均方差的概念还不大清楚,请查阅有关概率论的书.如果取μ =0,σ =0.2,则其曲线为图7 正态分布的概率密度函数曲线从图中可以看出,在μ附近的概率密度大,远离μ的地方概率密度小,我们要产生的随机数要服从这种分布,就是要使产生的随机数在μ附近的概率要大,远离μ处小,怎样保证这一点呢,可以采用如下的方法:在图7的大矩形中随机产生点,这些点是平均分布的,如果产生的点落在概率密度曲线的下方,则认为产生的点是符合要求的,将它们保留,如果在概率密度曲线的上方,则认为这些点不合格,将它们去处.如果随机产生了一大批在整个矩形中均匀分布的点,那么被保留下来的点的横坐标就服从了正态分布.可以设想,由于在μ处的f(x)的值比较大,理所当然的在μ附近的点个数要多,远离μ处的少,这从面积上就可以看出来.我们要产生的随机数就是这里的横坐标.基于以上思想,我们可以用程序实现在一定范围内服从正态分布的随机数.程序如下:double Normal(double x,double miu,double sigma) //概率密度函数{return 1.0/sqrt(2*PI*sigma) *exp(-1*(x-miu)*(x-miu)/(2*sigma*sigma));}double NormalRandom(double miu,double sigma,double min,double max)//产生正态分布随机数{double x;double dScope;double y;do{x = AverageRandom(min,max);y = Normal(dResult, miu, sigma);dScope = AverageRandom(0, Normal(miu,miu,sigma));}while( dScope > y);return x;}参数说明:double m iu:μ,正态函数的数学期望double s igma:σ,正态函数的均方差double m in,double max,表明产生的随机数的范围用如上方法,取μ=0,σ=0.2,范围是-1~1产生400个正态随机数如图8所示:图8 μ=0,σ=0.2,范围在-1~1时的400个正态分布的随机数分布图取μ=0,σ=0.05,范围是-1~1产生400个正态随机数如图9所示:图9 μ=0,σ=0.05,范围在-1~1时的400个正态分布的随机数分布图从图8和图9的比较可以看出,σ越小,产生的随机数靠近μ的数量越多,也说明了产生的随机数靠近μ的概率越大.我们,先产生4000个在0到4之间的正态分布的随机数,取μ=0,σ=0.2,再把产生的数据的数量做个统计,画成曲线,如下图10所示:图10 μ=0,σ=0.2,范围在0~4时的4000个正态分布的随机数统计图从图10中也可以看出,在靠近2处的产生的个数多,远离2处的产生的数量少,该图的轮廓线和概率密度曲线的形状刚好吻合.也就验证了该方法的正确性.有了以上基础,也就用同样的方法,只要知道概率密度函数,也就不难产生任意分布的随机数,方法都是先产生一个点,然后进行取舍,落在概率密度曲线下方的点就满足要求,取其横坐标就是所要获取的随机数参考文献:[1] 肖云茹.概率统计计算方法[M].天津:南开大学出版社,1994.[2]程兴新.曹敏.统计计算方法EM3.北京:北京大学出版社,1989.[3]王永德等.随机信号分析基础.北京:电子工业出版社,2 0 0 3.[4]皇甫堪等. 现代数字信号处理. 国防科技大学电子科学与工程学院内部印刷,2 0 0 2.。
matlab中随机信号的产生
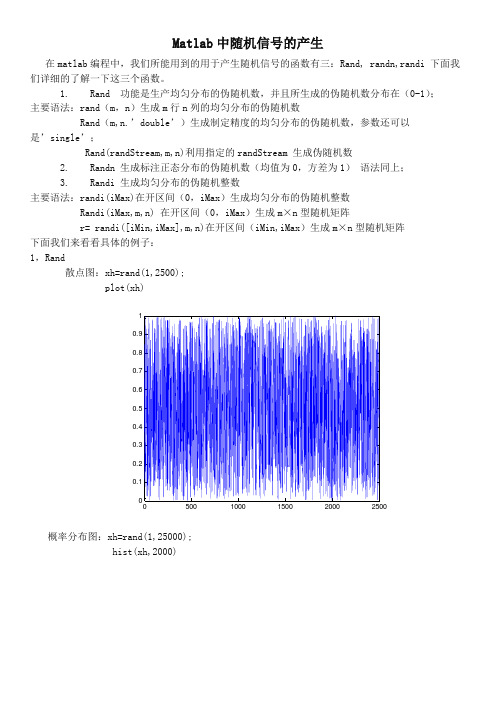
Matlab 中随机信号的产生在matlab 编程中,我们所能用到的用于产生随机信号的函数有三:Rand, randn,randi 下面我们详细的了解一下这三个函数。
1. Rand 功能是生产均匀分布的伪随机数,并且所生成的伪随机数分布在(0-1); 主要语法:rand (m ,n )生成m 行n 列的均匀分布的伪随机数Rand (m,n.’double’)生成制定精度的均匀分布的伪随机数,参数还可以是’single’; Rand(randStream,m,n)利用指定的randStream 生成伪随机数2. Randn 生成标注正态分布的伪随机数(均值为0,方差为1) 语法同上;3. Randi 生成均匀分布的伪随机整数主要语法:randi(iMax)在开区间(0,iMax )生成均匀分布的伪随机整数Randi(iMax,m,n) 在开区间(0,iMax )生成m ×n 型随机矩阵r= randi([iMin,iMax],m,n)在开区间(iMin,iMax )生成m ×n 型随机矩阵 下面我们来看看具体的例子:1,Rand散点图:xh=rand(1,2500);plot(xh)概率分布图:xh=rand(1,25000);hist(xh,2000)00.10.20.30.40.50.60.70.80.912,Randn散点图:xh=randn(1,400000);plot(xh)概率分布图:xh=randn(1,400000);hist(xh,2000)00.51 1.52 2.53 3.54x 105-5-4-3-2-1123453,Randi散点图:r= randi([12,214],1,144);plot(r)概率分布图:r= randi([12,214],1,144);hist(r,10000)对于随机种子,伪随机数的重复生成,在正常情况下每次调用相同指令生成的伪随机数是不同的例如:rand(1,4)rand(1,4)输出结果为:ans = 0.0428 0.2402 0.0296 0.0398ans = 0.7753 0.4687 0.3378 0.0074在一些特殊的情况下我们会用到相等的随机数,那我们该如何呢使两个语句生成的随机数相等呢?在Matlab中rand 、randn,和randi 从一个基础的随机数流中得到随机数,叫做默认流。
蒙特卡罗法生成服从正态分布的随机数

《蒙特卡罗法生成服从正态分布的随机数》一、引言“蒙特卡罗法”这一词汇,源自于蒙特卡罗赌场,是一种通过随机抽样和统计模拟来解决问题的方法。
而生成服从正态分布的随机数,是在数理统计、金融工程、风险管理等领域中常常遇到的问题。
在本文中,我们将探讨如何利用蒙特卡罗法生成服从正态分布的随机数,从而可以更深入地理解这一方法并应用于实际问题中。
二、蒙特卡罗法的基本原理蒙特卡罗法是一种基于随机抽样的方法,通过对概率模型进行模拟实验来获取近似解。
对于生成服从正态分布的随机数,我们可以利用蒙特卡罗法来模拟正态分布的概率密度函数,从而得到符合正态分布的随机数。
在生成正态分布的随机数时,我们可以采用以下步骤:1. 生成服从均匀分布的随机数2. 利用反函数法将均匀分布的随机数转化为正态分布的随机数3. 进行模拟实验,不断调整参数,直至生成的随机数符合所需的正态分布三、蒙特卡罗法生成正态分布的随机数的具体步骤1. 生成服从均匀分布的随机数我们可以利用随机数发生器生成服从均匀分布的随机数。
均匀分布的概率密度函数为f(x) = 1,x∈[0,1]。
我们可以生成若干个0到1之间的随机数作为初始值。
2. 利用反函数法将均匀分布的随机数转化为正态分布的随机数利用反函数法,我们可以将服从均匀分布的随机数转化为服从正态分布的随机数。
正态分布的累积分布函数为Φ(x) = ∫(-∞,x) (1/√(2π) * exp(-t^2/2)dt,而其反函数可以通过查表或近似计算得到。
利用反函数法,我们可以将生成的均匀分布的随机数通过正态分布的反函数转化为符合正态分布的随机数。
3. 进行模拟实验,不断调整参数,直至生成的随机数符合所需的正态分布在生成的随机数不符合所需的正态分布时,我们可以不断地调整参数、增加模拟实验的次数,直至得到符合所需的正态分布的随机数。
四、总结与回顾通过蒙特卡罗法生成服从正态分布的随机数,我们可以发现这一方法的灵活性和强大性。
一维正态分布随机数序列产生的几种方法介绍

一维正态分布随机数序列产生的几种方法介绍【摘要】正态分布在数理统计中具有基础性的作用,因此产生高质量的正态分布有重要的意义。
我们将介绍几种数值方法求正态分布:中心极限定理,Hasiting 有理逼近法,统计工具箱,反函数法,舍选法,R 软件及一维正态随机数的检验。
【关键词】正态分布;一维;随机数。
一.利用中心极限定理中心极限定理:(一般 n≥10),产生服从N(μ,σ2)的算法步骤:(1)产生n 个RND 随机数:r 1,r 2,…,r n ;(2) (3) 计算 y =σx +μ ,y 是服从 N(μ,σ2) 分布的随机数。
原理分析:设ζ1,ζ2,…,ζn 是n 个相互独立的随机变量,且ζi ~U(0,1), i = 1,2, …,n, 由中心极限定理知 : ,渐近服从正态分布N(0, l )。
注意:我们现在已经能产生[0,1]均匀分布的随机数了,那么我们可以利用这个定理来产生标准正态分布的随机数。
现在我们产生n 个[0,1]均匀分布随机数,我们有: 为方便起见,我们特别选 n = 12,则 : 这样我们很方便地就把标准正态分布随机数计算出来了。
在C 语言中表示为:例1:利用中心极限定理产生标准正态分布随机数并检验% example 1n r r r ,,,21 ⎪⎪⎭⎫ ⎝⎛-=∑=211121n i i r n n u ∑=-=1216i i r u ;/)(1122∑=-=n i n n i r x 计算,121)()(21==i i D E ζζ,有∑=-=ni n n i 1122/)(ζηclc,clearfor i=1:1000R=rand(1,12);X(i)=sum(R)-6;endX=X';m=mean(X)v=var(X)subplot(1,2,1),cdfplot(X)subplot(1,2,2),histfit(X)h=kstest(X, [X normcdf(X, 0,1)])结果为:H=0, 接受原假设,变换后的确为标准正态分布。
生成正态分布-概述说明以及解释

生成正态分布-概述说明以及解释1.引言1.1 概述概述部分的内容如下:正态分布,也被称为高斯分布或钟形曲线,是统计学和概率论中最重要的分布之一。
它在自然界、社会科学和经济学等领域都有广泛应用。
正态分布的形状呈现出对称的钟形曲线,其特点是均值处有最大密度,随着离均值的距离增加,密度逐渐减小。
其概率密度函数是通过一个简单的数学公式来描述的。
生成正态分布的方法有多种,其中一种常用的方法是使用随机数生成器。
通过使用特定的算法和随机种子,可以生成服从正态分布的随机数。
另一种常用的方法是利用中心极限定理,当多个独立同分布的随机变量相加时,其分布趋近于正态分布。
这种方法在模拟实验和推断统计中经常被使用。
本文将详细介绍正态分布的概念和性质,并探讨生成正态分布的方法。
在正文部分,我们将从数学和统计的角度解释正态分布的含义,并介绍其重要的特性,如均值和标准差。
然后,我们将详细介绍生成正态分布的方法,包括随机数生成器和中心极限定理的原理和应用。
总结部分将对文章进行总结,并探讨正态分布的应用前景。
正态分布在各个领域都有广泛的应用,如自然科学中的测量误差分析、社会科学中的人口统计和经济学中的金融市场分析等。
正态分布的生成方法对于模拟实验、数据分析和统计推断都具有重要的意义。
通过深入了解正态分布的生成方法,我们可以更好地理解和应用这一重要的概率分布。
综上所述,本文旨在介绍正态分布及其生成方法,并探讨其应用前景。
通过阅读本文,读者将对正态分布有更深入的理解,并能够灵活运用生成正态分布的方法进行数据分析和模拟实验。
1.2文章结构文章结构是指文章整体的布局和组织方式。
一个良好的文章结构可以使读者更好地理解文章内容,并且有助于文章的逻辑性和连贯性。
本文的结构如下:1. 引言1.1 概述引言部分将简要介绍正态分布的基本概念和重要性,引起读者的兴趣,并提出本文的研究目的。
1.2 文章结构本文将主要分为引言、正文和结论三个部分。
其中,引言部分将介绍本文的研究背景和目的;正文部分将详细探讨正态分布的定义、性质以及生成正态分布的方法;结论部分将总结文章的主要内容并展望正态分布的未来应用前景。
转:随机数产生原理及应用

转:随机数产⽣原理及应⽤摘要:本⽂简述了随机数的产⽣原理,并⽤C语⾔实现了迭代取中法,乘同余法等随机数产⽣⽅法,同时,还给出了在符合某种概率分布的随机变量的产⽣⽅法。
关键词: 伪随机数产⽣,概率分布1前⾔:在⽤计算机编制程序时,经常需要⽤到随机数,尤其在仿真等领域,更对随机数的产⽣提出了较⾼的要求,仅仅使⽤C语⾔类库中的随机函数已难以胜任相应的⼯作。
本⽂简单的介绍随机数产⽣的原理及符合某种分布下的随机变量的产⽣,并⽤C语⾔加以了实现。
当然,在这⾥⽤计算机基于数学原理⽣成的随机数都是伪随机数。
注:这⾥⽣成的随机数所处的分布为0-1区间上的均匀分布。
我们需要的随机数序列应具有⾮退化性,周期长,相关系数⼩等优点。
2.1迭代取中法:这⾥在迭代取中法中介绍平⽅取中法,其迭代式如下:Xn+1=(Xn^2/10^s)(mod 10^2s)Rn+1=Xn+1/10^2s其中,Xn+1是迭代算⼦,⽽Rn+1则是每次需要产⽣的随机数。
第⼀个式⼦表⽰的是将Xn平⽅后右移s位,并截右端的2s位。
⽽第⼆个式⼦则是将截尾后的数字再压缩2s倍,显然:0=<Rn+1<=1.这样的式⼦的构造需要深厚的数学(代数,统计学,信息学)功底,这⾥只是拿来⽤⼀下⽽已,就让我们站在⼤师的肩膀上前⾏吧。
迭代取中法有⼀个不良的性就是它⽐较容易退化成0.平⽅取中法的实现:View Code#include <stdio.h>#include <math.h>#define S 2float Xn=12345;//Seed & Iterfloat Rn;//Return Valvoid InitSeed(float inX0){Xn=inX0;}/*Xn+1=(Xn^2/10^s)(mod 10^2s)Rn+1=Xn+1/10^2s*/float MyRnd(){Xn=(int)fmod((Xn*Xn/pow(10,S)),pow(10,2*S));//here can's use %Rn=Xn/pow(10,2*S);return Rn;}/*测试主程序,注意,这⾥只列举⼀次测试主程序,以下不再重复*/int main(){int i;FILE * debugFile;if((debugFile=fopen("outputData.txt","w"))==NULL){fprintf(stderr,"open file error!");return -1;}printf("\n");for(i=0;i<100;i++){tempRnd=MyRnd();fprintf(stdout,"%f ",tempRnd);fprintf(debugFile,"%f ",tempRnd);}getchar();return0;}前⼀百个测试⽣成的随机数序列:0.399000 0.920100 0.658400 0.349000 0.180100 0.243600 0.934000 0.235600 0.550700 0.327000 0.692900 0.011000 0.012100 0.014600 0.021300 0.045300 0.205200 0.210700 0.439400 0.307200 0.437100 0.105600 0.115100 0.324800 0.549500 0.195000 0.802500 0.400600 0.048000 0.230400 0.308400 0.511000 0.112100 0.256600 0.584300 0.140600 0.976800 0.413800 0.123000 0.512900 0.306600 0.400300 0.024000 0.057600 0.331700 0.002400 0.000500 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000容易看出其易退化成0的缺点.2.2乘同余法:乘同余法的迭代式如下:Xn+1=Lamda*Xn(mod M)Rn+1=Xn/M各参数意义及各步的作⽤可参2.1当然,这⾥的参数的选取是有⼀定的理论基础的,否则所产⽣的随机数的周期将较⼩,相关性会较⼤。
matlab伪随机数生成算法

matlab伪随机数生成算法
Matlab中的伪随机数生成算法是基于梅森旋转算法(Mersenne Twister)的。
梅森旋转算法是一种高质量的伪随机数生成器,具有较长的周期和良好的统计性质。
在Matlab中,可以使用rand函数生成伪随机数。
该函数返回一个0到1之间的均匀分布的伪随机数。
具体来说,Matlab使用了叫做梅森旋转算法的算法来生成这些伪随机数。
梅森旋转算法是一种递归算法,它使用一个624维的状态向量来生成伪随机数。
每次调用rand函数时,梅森旋转算法会根据状态向量中的值计算出一个新的伪随机数,并更新状态向量的值。
当状态向量的值用尽后,梅森旋转算法会重新计算一组新的状态向量。
由于梅森旋转算法具有较长的周期,因此在Matlab中生成的伪随机数具有较好的随机性和统计性质。
但需要注意的是,由于是伪随机数生成算法,因此生成的随机数序列是确定性的,即给定相同的种子,生成的随机数序列是相同的。
如果需要更高质量的伪随机数生成算法,可以使用Matlab中的randn函数生成服从标准正态分布的伪随机数,或使用其他高级随机数生成函数如randperm、randi等。
matlab随机信号分析常用函数

随机信号分析常用函数及示例1、熟悉练习使用下列MATLAB函数,给出各个函数的功能说明和内部参数的意义,并给出至少一个使用例子和运行结果。
rand():函数功能:生成均匀分布的伪随机数使用方法:r = rand(n)生成n*n的包含标准均匀分布的随机矩阵,其元素在(0,1)内。
rand(m,n)或rand([m,n])生成的m*n随机矩阵。
rand(m,n,p,...)或rand([m,n,p,...])生成的m*n*p随机矩数组。
rand ()产生一个随机数。
rand(size(A))生成与数组A大小相同的随机数组。
r = rand(..., 'double')或r = rand(..., 'single')返回指定类型的标准随机数,其中double指随机数为双精度浮点数,single 指随机数为单精度浮点数。
例:r=rand(3,4);运行结果:r= 0.4235 0.4329 0.7604 0.20910.5155 0.2259 0.5298 0.37980.3340 0.5798 0.6405 0.7833randn():函数功能:生成正态分布伪随机数使用方法:r = randn(n)生成n*n的包含标准正态分布的随机矩阵。
randn(m,n)或randn([m,n])生成的m*n随机矩阵。
randn(m,n,p,...)或randn([m,n,p,...])生成的m*n*p随机矩数组。
randn ()产生一个随机数。
randn(size(A))生成与数组A大小相同的随机数组。
r = randn(..., 'double')或r = randn(..., 'single')返回指定类型的标准随机数,其中double指随机数为双精度浮点数,single 指随机数为单精度浮点数。
例:产生一个均值为1,标准差为2的正态分布随机值:r=1+2.*randn(10,1);运行结果:r= -1.37563.40462.9727-0.03731.65471.46811.0429-1.0079-0.89430.2511normrnd()函数功能:生成正态分布的随机数使用方法:R = normrnd(mu,sigma)生成服从均值参数为mu和标准差参数sigma的正态分布的随机数。
正态分布的随机数

正态分布的随机数⼀、功能产⽣正态分布N(µ,σ2)。
⼆、⽅法简介正态分布的概率密度函数为f(x)=1√2πσe−(x−µ)2/2σ2通常⽤N(µ,σ2)表⽰。
式中µ是均值,σ2是⽅差。
正态分布也称为⾼斯分布。
设r1,r2, ...,r n为(0,1)上n个相互独⽴的均匀分布的随机数,由于E(r i)=12,D(ri)=112,根据中⼼极限定理可知,当n充分⼤时x=12ni=1∑n r i−n2的分布近似正态分布N(0, 1)。
通常取n=12,此时有x=i=1∑12r i−6最后,再通过变换y=µ+σx,便可得到均值µ、⽅差为σ2的正态分布随机数y。
三、使⽤说明使⽤C语⾔编程⽣成正态分布函数N(0, 1)/************************************a ---给定区间下限b ---给定区间上限seed ---随机数种⼦************************************/#include "uniform.c"double gauss(double mean, double sigma, long int *s){int i;double x;double y;for(x = 0, i = 0; i < 12; i++){x += uniform(0.0, 1.0, s);}x = x - 6.0;y = mean + x * sigma;return(y);}uniform.c⽂件参见√() Loading [MathJax]/jax/output/HTML-CSS/fonts/TeX/fontdata.js。
高斯随机数产生原理及代码_笔记

一:随机数的产生C++中不提供random函数,但是提供了rand函数,产生0~RAND_MAX之间的整数,但严格意义上来讲生成的只是伪随机数(pseudo-random integral number).生成随机数时需要指定一个种子,如果在程序内循环,那么下一次生成随机数时调用上一次的结果作为种子。
但如果分两次执行程序,那么由于种子相同,生成的“随机数”也是相同的。
rand()函数不接受参数,默认以1为种子(即起始值)。
若随机数生成器总是以相同的种子开始,所以形成的伪随机数列也相同,失去了随机意义。
(但这样便于程序调试).C++中另一函数srand(),可以指定不同的数(无符号整数变元)为种子。
但是如果种子相同,伪随机数列也相同。
一个办法是让用户输入种子,但是仍然不理想。
比较理想的是用变化的数,比如时间来作为随机数生成器的种子。
time的值每时每刻都不同。
所以种子不同,所以,产生的随机数也不同。
rand函数产生随机数的方法:1>如果要产生0~10的10个整数,可以表达为:int N = rand() % 11;这样,N的值就是一个0~10的随机数,如果要产生1~10,则是这样:int N = 1 + rand() % 11;总结来说,可以表示为:a + rand()%(b-a+1)其中的a是起始值,(b-a+1)是整数的范围。
若要0~1的小数,则可以先取得0~10的整数,然后均除以10即可得到随机到十分位的10个随机小数,若要得到随机到百分位的随机小数,则需要先得到0~100的10个整数,然后均除以100,其它情况依此类推。
当要求的精度较高的时候,使用RAND_MAX作为分母。
如果要求左闭右开的话,分母设置为RAND_MAX+1即可。
精度要求高时形式如下:x=a+((rand()%RAND_MAX)/(double)RAND_MAX)*(b-a); /*x belong [a,b] */ 通常rand()产生的随机数在每次运行的时候都是与上一次相同的,这是有意这样设计的,是为了便于程序的调试。
如何产生已知均数和方差的正态分布随机数

如何产生已知均数和方差的正态分布随机数
前段时间看到SASOR论坛上一位网友发了“如何产生已知均数和方差的正态分布随机数”的问题,当时我是给他回复了,但现在想了半天也不知道当时是如何做出来了,所以又对着SAS做了半天,终于又想出来了,真是的,还是把它留在这里作个记号才好,否则过了一段时间又忘了,真是南无阿弥托佛啊!
应当有两种方法,其实都是一回事,假设其平均数为25,方差为5,方法一如下:
data homestay;
retain seed 1;/* 赋予seed变量初始值
do i=1 to 100;/*产生100个随机值
call rannor(seed, x);/*call语句
y=25+sqrt(5)*rannor(seed);/*Y值为均值为25,方差为5的随机产生的数值
output;
end;
proc print;
run;
方法二:
data homestay;
retain seed 1;
do i=1 to 100;
x=rannor(seed);
y=25+sqrt(5)*rannor(seed);
output;
end;
proc print;
run;
这样就可以产生均数为25、方差为5的100个正态分布的随机数了!。
