最小二乘法曲线拟合_原理及matlab实现
曲线拟合线性最小二乘法及其MATLAB程序

1 曲线拟合的线性最小二乘法及其MATLAB 程序例7.2.1 给出一组数据点列入表),(i i y x 7–2中,试用线性最小二乘法求拟合曲线,并用(7.2),(7.3)和(7.4)式估计其误差,作出拟合曲线.表7–2 例7.2.1的一组数据),(y x解 (1)在MATLAB 工作窗口输入程序>> x=[-2.5 -1.7 -1.1 -0.8 0 0.1 1.5 2.7 3.6];y=[-192.9 -85.50 -36.15 -26.52 -9.10 -8.43 -13.12 6.50 68.04];plot(x,y,'r*'),legend('实验数据(xi,yi)')xlabel('x'), ylabel('y'),title('例7.2.1的数据点(xi,yi)的散点图')运行后屏幕显示数据的散点图(略).(3)编写下列MA TLAB 程序计算在)(x f ),(i i y x 处的函数值,即输入程序>> syms a1 a2 a3 a4x=[-2.5 -1.7 -1.1 -0.8 0 0.1 1.5 2.7 3.6];fi=a1.*x.^3+ a2.*x.^2+ a3.*x+ a4运行后屏幕显示关于a 1,a 2, a3和a4的线性方程组fi =[ -125/8*a1+25/4*a2-5/2*a3+a4,-4913/1000*a1+289/100*a2-17/10*a3+a4,-1331/1000*a1+121/100*a2-11/10*a3+a4,-64/125*a1+16/25*a2-4/5*a3+a4,a4, 1/1000*a1+1/100*a2+1/10*a3+a4,27/8*a1+9/4*a2+3/2*a3+a4, 19683/1000*a1+729/100*a2+27/10*a3+a4, 5832/125*a1+324/25*a2+18/5*a3+a4]编写构造误差平方和的MA TLAB 程序>> y=[-192.9 -85.50 -36.15 -26.52 -9.10 -8.43 -13.12 6.5068.04];fi=[-125/8*a1+25/4*a2-5/2*a3+a4,-4913/1000*a1+289/100*a2-17/10*a3+a4,-1331/1000*a1+121/100*a2-11/10*a3+a4, -64/125*a1+16/25*a2-4/5*a3+a4, a4,1/1000*a1+1/100*a2+1/10*a3+a4,27/8*a1+9/4*a2+3/2*a3+a4,19683/1000*a1+729/100*a2+27/10*a3+a4,5832/125*a1+324/25*a2+18/5*a3+a4];fy=fi-y; fy2=fy.^2; J=sum(fy.^2)运行后屏幕显示误差平方和如下J=(-125/8*a1+25/4*a2-5/2*a3+a4+1929/10)^2+(-4913/1000*a1+289/100*a2-17/10*a3+a4+171/2)^2+(-1331/1000*a1+121/100*a2-11/10*a3+a4+723/20)^2+(-64/125*a1+16/25*a2-4/5*a3+a4+663/25)^2+(a4+91/10)^2+(1/1000*a1+1/100*a2+1/10*a3+a4+843/100)^2+(27/8*a1+9/4*a 2+3/2*a3+a4+328/25)^2+(19683/1000*a1+729/100*a2+27/10*a3+a4-13/2)^2+(5832/125*a1+324/25*a2+18/5*a3+a4-1701/25)^2为求使达到4321,,,a a a a J 最小,只需利用极值的必要条件0=∂∂ka J )4,3,2,1(=k ,得到关于的4321,,,a a a a 线性方程组,这可以由下面的MA TLAB 程序完成,即输入程序>> syms a1 a2 a3 a4J=(-125/8*a1+25/4*a2-5/2*a3+a4+1929/10)^2+(-4913/1000*a1+289/100*a2-17/10*a3+a4...+171/2)^2+(-1331/1000*a1+121/100*a2-11/10*a3+a4+723/20)^2+(-64/125*a1+16/25*a2-4/5*a3+a4+663/25)^2+(a 4+91/10)^2+(1/1000*a1+1/100*a2+1/10*a3+a4+843/100)^2+(27/8*a1+9/4*a2+3/2*a3+a4+328/25)^2+(19683/1000*a1+729/100*a2+27/10*a3+a4-13/2)^2+(5832/125*a1+324/25*a2+18/5*a3+a4-1701/25)^2;Ja1=diff(J,a1); Ja2=diff(J,a2); Ja3=diff(J,a3); Ja4=diff(J,a4);Ja11=simple(Ja1), Ja21=simple(Ja2), Ja31=simple(Ja3), Ja41=simple(Ja4),运行后屏幕显示J 分别对a 1, a 2 ,a 3 ,a4的偏导数如下Ja11=56918107/10000*a1+32097579/25000*a2+1377283/2500*a3+23667/250*a4-8442429/625Ja21 =32097579/25000*a1+1377283/2500*a2+23667/250*a3+67*a4+767319/625Ja31 =1377283/2500*a1+23667/250*a2+67*a3+18/5*a4-232638/125Ja41 =23667/250*a1+67*a2+18/5*a3+18*a4+14859/25解线性方程组Ja11 =0,Ja 21 =0,Ja 31 =0,Ja 41 =0,输入下列程序>>A=[56918107/10000, 32097579/25000, 1377283/2500, 23667/250; 32097579/25000, 1377283/2500, 23667/250, 67; 1377283/2500, 23667/250, 67, 18/5; 23667/250, 67, 18/5, 18];B=[8442429/625, -767319/625, 232638/125, -14859/25];C=B/A, f=poly2sym(C)运行后屏幕显示拟合函数f 及其系数C 如下C = 5.0911 -14.1905 6.4102 -8.2574f=716503695845759/140737488355328*x^3-7988544102557579/562949953421312*x^2+1804307491277693/281474976710656*x-4648521160813215/562949953421312故所求的拟合曲线为8.25746.410214.19055.0911)(23-+-=x x x x f .(4)编写下面的MATLAB 程序估计其误差,并作出拟合曲线和数据的图形.输入程序>> xi=[-2.5 -1.7 -1.1 -0.8 0 0.1 1.5 2.7 3.6];y=[-192.9 -85.50 -36.15 -26.52 -9.10 -8.43 -13.12 6.50 68.04];n=length(xi);f=5.0911.*xi.^3-14.1905.*xi.^2+6.4102.*xi -8.2574;x=-2.5:0.01: 3.6;F=5.0911.*x.^3-14.1905.*x.^2+6.4102.*x -8.2574;fy=abs(f-y); fy2=fy.^2; Ew=max(fy),E1=sum(fy)/n, E2=sqrt((sum(fy2))/n)plot(xi,y,'r*'), hold on, plot(x,F,'b-'), hold offlegend('数据点(xi,yi)','拟合曲线y=f(x)'),xlabel('x'), ylabel('y'),title('例7.2.1的数据点(xi,yi)和拟合曲线y=f(x)的图形')运行后屏幕显示数据与),(i i y x 拟合函数f 的最大误差E w ,平均误差E 1和均方根误差E2及其数据点和),(i i y x 拟合曲线y=f (x )的图形(略).Ew = E1 = E2 =3.105 4 0.903 4 1.240 97.3 函数的选取)(x r k 及其MATLAB 程序例7.3.1 给出一组实验数据点的),(i i y x 横坐标向量为x =(-8.5,-8.7,-7.1,-6.8,-5.10,-4.5,-3.6,-3.4,-2.6,-2.5, -2.1,-1.5, -2.7,-3.6),纵横坐标向量为y =(459.26,52.81,198.27,165.60,59.17,41.66,25.92, 22.37,13.47, 12.87, 11.87,6.69,14.87,24.22),试用线性最小二乘法求拟合曲线,并用(7.2),(7.3)和(7.4)式估计其误差,作出拟合曲线.解 (1)在MATLAB 工作窗口输入程序>>x=[-8.5,-8.7,-7.1,-6.8,-5.10,-4.5,-3.6,-3.4,-2.6,-2.5,-2.1,-1.5, -2.7,-3.6];y=[459.26,52.81,198.27,165.60,59.17,41.66,25.92,22.37,13.47, 12.87, 11.87,6.69,14.87,24.22];plot(x,y,'r*'),legend('实验数据(xi,yi)')xlabel('x'), ylabel('y'),title('例7.3.1的数据点(xi,yi)的散点图')运行后屏幕显示数据的散点图(略).(3)编写下列MA TLAB 程序计算在)(x f ),(i i y x 处的函数值,即输入程序>> syms a bx=[-8.5,-8.7,-7.1,-6.8,-5.10,-4.5,-3.6,-3.4,-2.6,-2.5,-2.1,-1.5,-2.7,-3.6]; fi=a.*exp(-b.*x)运行后屏幕显示关于a 和b 的线性方程组fi =[ a*exp(17/2*b), a*exp(87/10*b), a*exp(71/10*b),a*exp(34/5*b), a*exp(51/10*b), a*exp(9/2*b), a*exp(18/5*b), a*exp(17/5*b), a*exp(13/5*b), a*exp(5/2*b), a*exp(21/10*b), a*exp(3/2*b), a*exp(27/10*b), a*exp(18/5*b)]编写构造误差平方和的MA TLAB 程序如下>>y=[459.26,52.81,198.27,165.60,59.17,41.66,25.92,22.37,13.47,12.87, 11.87, 6.69,14.87,24.22];fi =[ a*exp(17/2*b), a*exp(87/10*b), a*exp(71/10*b), a*exp(34/5*b), a*exp(51/10*b), a*exp(9/2*b), a*exp(18/5*b), a*exp(17/5*b), a*exp(13/5*b), a*exp(5/2*b), a*exp(21/10*b), a*exp(3/2*b), a*exp(27/10*b), a*exp(18/5*b)];fy=fi-y;fy2=fy.^2;J=sum(fy.^2)运行后屏幕显示误差平方和如下J =(a*exp(17/2*b)-22963/50)^2+(a*exp(87/10*b)-5281/100)^2+(a*exp(71/10*b)-19827/100)^2+(a*exp(34/5*b)-828/5)^2+(a*exp(51/10*b)-5917/100)^2+(a*exp(9/2*b)-2083/50)^2+(a*exp(18/5*b)-648/25)^2+(a*exp(17/5*b)-2237/100)^2+(a*exp(13/5*b)-1347/100)^2+(a*ex p(5/2*b)-1287/100)^2+(a*exp(21/10*b)-1187/100)^2+(a*exp(3/2*b)-669/100)^2+(a*exp(27/10*b)-1487/100)^2+(a*exp(18/5*b)-1211/50)^2为求使达到b a ,J 最小,只需利用极值的必要条件,得到关于的b a ,线性方程组,这可以由下面的MA TLAB 程序完成,即输入程序>> syms a bJ=(a*exp(17/2*b)-22963/50)^2+(a*exp(87/10*b)-5281/100)^2+(a*exp(71/10*b)-19827/100)^2+(a*exp(34/5*b)-828/5)^2+(a*exp(51/10*b)-5917/100)^2+(a*exp(9/2*b)-2083/50)^2+(a*exp(18/5*b)-648/25)^2+(a*exp(17/5*b)-2237/100)^2+(a*exp(13/5*b)-1347/100)^2+(a*exp(5/2*b)-1287/100)^2+(a*exp(21/10*b)-1187/100)^2+(a*exp(3/2*b)-669/100)^2+(a*exp(27/10*b)-1487/100)^2+(a*exp(18/5*b)-1211/50)^2;Ja=diff(J,a); Jb=diff(J,b);Ja1=simple(Ja), Jb1=simple(Jb),运行后屏幕显示J 分别对的偏导数b a ,如下Ja1 =2*a*exp(3*b)+2*a*exp(17*b)+2*a*exp(87/5*b)+2*exp(68/5*b)*a+2*exp(9*b)*a+2*a*exp(34/5*b)-669/50*exp(3/2*b)-1487/50*exp(27/10*b)-2507/25*exp(18/5*b)-22963/25*exp(17/2*b)-5281/50*exp(87/10*b)-19827/50*exp(71/10*b)-2237/50*exp(17/5*b)-1656/5*exp(34/5*b)-1347/50*exp(13/5*b)-5917/50*exp(51/10*b)-1287/50*exp(5/2*b )-2083/25*exp(9/2*b)-1187/50*exp(21/10*b)+4*a*exp(36/5*b)+2*a*e xp(26/5*b)+2*a*exp(71/5*b)+2*a*exp(51/5*b)+2*a*exp(5*b)+2*a*exp (21/5*b)+2*a*exp(27/5*b)Jb1 =1/500*a*(2100*a*exp(21/10*b)^2+8500*a*exp(17/2*b)^2+6800*a*exp(34/5*b)^2-10035*exp(3/2*b)-40149*exp(27/10*b)-180504*exp (18/5*b)-3903710*exp(17/2*b)-459447*exp(87/10*b)-1407717*exp(71/10*b)-76058*exp(17/5*b)-1126080*exp(34/5*b)-35022*exp(13/5*b)-301767*exp(51/10*b)-32175*exp(5/2*b)-187470*exp(9/2*b)-24927*ex p(21/10*b)+7100*a*exp(71/10*b)^2+5100*a*exp(51/10*b)^2+4500*a*e xp(9/2*b)^2+7200*a*exp(18/5*b)^2+3400*a*exp(17/5*b)^2+2600*a*ex p(13/5*b)^2+2500*a*exp(5/2*b)^2+1500*a*exp(3/2*b)^2+2700*a*exp(27/10*b)^2+8700*a*exp(87/10*b)^2)用解二元非线性方程组的牛顿法的MATLAB 程序求解线性方程组J a1 =0,J b1 =0,得a = b=2.811 0 0.581 6故所求的拟合曲线(7.13)为0811.2)(=x f e x 5816.0-. (7.14)(4)根据(7.2),(7.3),(7.4)和(7.14)式编写下面的MA TLAB 程序估计其误差,并做出拟合曲线和数据的图形.输入程序>> xi=[-8.5 -8.7 -7.1 -6.8 -5.10 -4.5 -3.6 -3.4 -2.6 -2.5-2.1 -1.5 -2.7 -3.6];y=[459.26 52.81 198.27 165.60 59.17 41.66 25.92 22.3713.47 12.87 11.87 6.69 14.87 24.22];n=length(xi); f=2.8110.*exp(-0.5816.*xi); x=-9:0.01: -1;F=2.8110.*exp(-0.5816.*x); fy=abs(f-y); fy2=fy.^2;Ew=max(fy),E1=sum(fy)/n, E2=sqrt((sum(fy2))/n), plot(xi,y,'r*'), hold on plot(x,F,'b-'), hold off,legend('数据点(xi,yi)','拟合曲线y=f(x)')xlabel('x'), ylabel('y'),title('例7.3.1的数据点(xi,yi)和拟合曲线y=f(x)的图形')运行后屏幕显示数据与),(i i y x 拟合函数f 的最大误差E w = 390.141 5,平均误差E 1=36.942 2和均方根误差E 2=106.031 7及其数据点和拟合曲),(i i y x 线y =f (x )的图形(略).7.4 多项式拟合及其MATLAB 程序例7.4.1 给出一组数据点列入表),(i i y x 7–3中,试用线性最小二乘法求拟合曲线,并用(7.2),(7.3)和(7.4)式估计其误差,作出拟合曲线.表7–3 例7.4.1的一组数据),(y x解 (1)首先根据表7–3给出的数据点),(i i y x ,用下列MATLAB 程序画出散点图. 在MATLAB 工作窗口输入程序>> x=[-2.9 -1.9 -1.1 -0.8 0 0.1 1.5 2.7 3.6];y=[53.94 33.68 20.88 16.92 8.79 8.98 4.17 9.1219.88];plot(x,y,'r*'), legend('数据点(xi,yi)')xlabel('x'), ylabel('y'),title('例7.4.1的数据点(xi,yi)的散点图')运行后屏幕显示数据的散点图(略).(3)用作线性最小二乘拟合的多项式拟合的MAT LAB 程序求待定系数k a )3,2,1(=k .输入程序>> a=polyfit(x,y,2)运行后输出(7.16)式的系数a =2.8302 -7.3721 9.1382故拟合多项式为2138.91372.72830.2)(2+-=x x x f .(4)编写下面的MATLAB 程序估计其误差,并做出拟合曲线和数据的图形.输入程序>> xi=[-2.9 -1.9 -1.1 -0.8 0 0.1 1.5 2.7 3.6];y=[53.94 33.68 20.88 16.92 8.79 8.98 4.17 9.12 19.88];n=length(xi); f=2.8302.*xi.^2-7.3721.*xi+9.1382x=-2.9:0.001:3.6;F=2.8302.*x.^2-7.3721.*x+8.79;fy=abs(f-y); fy2=fy.^2; Ew=max(fy), E1=sum(fy)/n,E2=sqrt((sum(fy2))/n), plot(xi,y,'r*', x,F,'b-'),legend('数据点(xi,yi)','拟合曲线y=f(x)')xlabel('x'), ylabel('y'),title('例7.4.1 的数据点(xi,yi)和拟合曲线y=f(x)的图形')运行后屏幕显示数据与),(i i y x 拟合函数f 的最大误差E w ,平均误差E 1和均方根误差E2及其数据点(x i ,y i )和拟合曲线y =f (x )的图形(略).Ew = E1 = E2 =0.745 7, 0.389 2, 0.436 37.5 拟合曲线的线性变换及其MATLAB 程序例7.5.1 给出一组实验数据点的),(i i y x 横坐标向量为x =(7.5 6.8 5.10 4.53.6 3.4 2.6 2.5 2.1 1.5 2.7 3.6),纵横坐标向量为y =(359.26 165.60 59.17 41.66 25.92 22.37 13.47 12.87 11.87 6.69 14.87 24.22),试用线性变换和线性最小二乘法求拟合曲线,并用(7.2),(7.3)和(7.4)式估计其误差,作出拟合曲线.解 (1)首先根据给出的数据点),(i i y x ,用下列MATLAB 程序画出散点图.在MATLAB 工作窗口输入程序>> x=[7.5 6.8 5.10 4.5 3.6 3.4 2.6 2.5 2.1 1.5 2.73.6];y=[359.26 165.60 59.17 41.66 25.92 22.37 13.47 12.87 11.87 6.69 14.87 24.22];plot(x,y,'r*'), legend('数据点(xi,yi)')xlabel('x'), ylabel('y'),title('例7.5.1的数据点(xi,yi)的散点图')运行后屏幕显示数据的散点图(略).(2)根据数据散点图,取拟合曲线为a y =e bx )0,0(≠>b a , (7.19)其中是待定b a ,系数.令b B a A y Y ===,ln ,ln ,则(7.19)化为Bx A Y +=.在MATL AB 工作窗口输入程序>> x=[7.5 6.8 5.10 4.5 3.6 3.4 2.6 2.5 2.1 1.5 2.73.6];y=[359.26 165.60 59.17 41.66 25.92 22.37 13.47 12.87 11.87 6.69 14.87 24.22];Y=log(y); a=polyfit(x,Y,1); B=a(1);A=a(2); b=B,a=exp(A)n=length(x); X=8:-0.01:1; Y=a*exp(b.*X); f=a*exp(b.*x);plot(x,y,'r*',X,Y,'b-'), xlabel('x'),ylabel('y')legend('数据点(xi,yi)','拟合曲线y=f(x)')title('例7.5.1 的数据点(xi,yi)和拟合曲线y=f(x)的图形')fy=abs(f-y); fy2=fy.^2; Ew=max(fy), E1=sum(fy)/n,E2=sqrt((sum(fy2))/n)运行后屏幕显示e 的系a y =bx 数b =0.624 1,a =2.703 9,数据与拟合),(i i y x 函数f 的最大误差Ew =67.641 9,平均误差E 1=8.677 6和均方根误差E 2=20.711 3及其数据点和拟合曲),(i i y x 线e 的图形9703.2)(=x f x 1624.0(略).7.6 函数逼近及其MATLAB 程序最佳均方逼近的MATLAB 主程序function [yy1,a,WE]=zjjfbj(f,X,Y,xx)m=size(f);n=length(X);m=m(1);b=zeros(m,m); c=zeros(m,1);if n~=length(Y)error('X 和Y 的维数应该相同')endfor j=1:mfor k=1:mb(j,k)=0;for i=1:nb(j,k)=b(j,k)+feval(f(j,:),X(i))*feval(f(k,:),X(i));endendc(j)=0;for i=1:nc(j)=c(j)+feval(f(j,:),X(i))*Y(i);endenda=b\c;WE=0;for i=1:nff=0;for j=1:mff=ff+a(j)*feval(f(j,:),X(i));endWE=WE+(Y(i)-ff)*(Y(i)-ff);endif nargin==3return ;endyy=[];for i=1:ml=[];for j=1:length(xx)l=[l,feval(f(i,:),xx(j))];endyy=[yy l'];endyy=yy*a; yy1=yy'; a=a';WE;例7.6.1 对数据X 和Y , 用函数进行2,,1x y x y y ===逼近,用所得到的逼近函数计算在处的函 6.5=x 数值,并估计误差.其中X =(1 3 4 5 6 7 8 9); Y =(-11 -13 -11 -7 -1 7 17 29).解 在MATLAB 工作窗口输入程序>> X=[ 1 3 4 5 6 7 8 9]; Y=[-11 -13 -11 -7 -1 7 17 29];f=['fun0';'fun1';'fun2']; [yy,a,WE]=zjjfbj(f,X,Y,6.5)运行后屏幕显示如下yy =2.75000000000003a =-7.00000000000010 -4.99999999999995 1.00000000000000WE =7.172323350269439e-027例7.6.2 对数据X 和Y ,用函数2,,1x y x y y ===,x y cos =,=y e x,x y sin =进行逼近,其中X =(0 0.50 1.00 1.50 2.00 2.50 3.00),Y =(0 0.4794 0.8415 0.9815 0.9126 0.5985 0.1645).解 在MATLAB 工作窗口输入程序>> X=[ 0 0.50 1.00 1.50 2.00 2.50 3.00];Y=[0 0.4794 0.8415 0.9815 0.9126 0.5985 0.1645];f=['fun0';'fun1';'fun2';'fun3';'fun4';'fun5'];xx=0:0.2:3;[yy,a,WE]=zjjfbj(f,X,Y, xx), plot(X,Y,'ro',xx,yy,'b-')运行后屏幕显示如下(图略)yy = Columns 1 through 7-0.0005 0.2037 0.3939 0.5656 0.7141 0.8348 0.9236Columns 8 through 140.9771 0.9926 0.9691 0.9069 0.8080 0.6766 0.5191Columns 15 through 160.3444 0.1642a = 0.3828 0.4070 -0.3901 0.0765 -0.4598 0.5653 WE = 1.5769e-004即,最佳逼近函数为y=0.3828+0.4070*x-0.3901*x^2+0.0765*exp(x) -0.4598*cos(x) +0.5653*sin(x). 7.7 三角多项式逼近及其MATLAB 程序计算三角多项式的MATLAB 主程序function [A,B,Y1,Rm]=sanjiao(X,Y,X1,m)n= length(X)-1;max1=fix((n-1)/2);if m > max1m=max1;endA=zeros(1,m+1);B=zeros(1,m+1);Ym=(Y(1)+Y(n+1))/2; Y(1)=Ym; Y(n+1)=Ym; A(1)=2*sum(Y)/n;for i=1:mB(i+1)=sin(i*X)*Y'; A(i+1)=cos(i*X)*Y';endA=2*A/n; B=2*B/n; A(1)=A(1)/2;Y1=A(1);for k=1:mY1=Y1+A(k+1)*cos(k*X1)+ B(k+1)*sin(k*X1);Tm=A(1)+A(k+1).*cos(k*X)+ B(k+1).*sin(k*X); k=k+1;endY;Tm; Rm=(sum(Y-Tm).^2)/n;例7.7.1 根据上的个],[ππ-350,60,13=n 等距横坐标点ni x i π+π-=2 ),,2,1,0(n i =和函数3sin 2)(x x f =. (1)求的6阶三)(x f 角多项式逼近,计算均方误差;(2)将这三个三角多项式分别与的傅里)(x f 叶级数nx n n x f n n sin 19)1(318)(121∑∞=+--π= 的前6项进行比较;(3)利用三角多项式分别计算X i = -2, 2.5的值;(4)在同一坐标系中,画出函数)(x f ,350,60,13=n 的三角多项式和数据点的图形.解 (1)输入程序>> X1=-pi:2*pi/13:pi;Y1=2*sin(X1/3);X1i=[-2,2.5];[A1,B1,Y11,Rm1]=sanjiao(X1,Y1,X1i,6),X2=-pi:2*pi/60:pi;Y2=2*sin(X2/3);[A2,B2,Y12,Rm2]=sanjiao(X2,Y2,X1i,6)X3=-pi:2*pi/350:pi;Y3=2*sin(X3/3);[A3,B3,Y13,Rm3]=sanjiao(X3,Y3,X1i,6)X1i=[-2,2.5];Y1=2*sin(X1i/3)for n=1:6bi=(-1)^(n+1)*18*sqrt(3)*n/(pi*(9*n^2-1))end(2)画图,输入程序>>X1=-pi:2*pi/13:pi;Y1=2*sin(X1/3);Xi=-pi:0.001:pi; f=2*sin(Xi/3);[A1,B1,Y1i,R1m]=sanjiao(X1,Y1,Xi,6);X2=-pi:2*pi/60:pi;Y2=2*sin(X2/3); X3=-pi:2*pi/350:pi;Y3=2*sin(X3/3);[A2,B2,Y2i,R2m]=sanjiao(X2,Y2,Xi,6);[A3,B3,Y3i,R3m]=sanjiao(X3,Y3,Xi,6);plot(X1,Y1,'r*', Xi, Y1i,'b-',Xi, Y2i,'g--', Xi, Y3i, 'm:',Xi, f, 'k-.')xlabel('x'),ylabel('y')legend('数据点(xi,yi)','n=13的三角多项式','n=60的三角多项式','n=350的三角多项式','函数f(x)')title('例7.7.1 的数据点(xi,yi)、n=13,60,350的三角多项式T3和函数f(x)的图形')运行后图形(略).7.8 随机数据点上的二元拟合及其MATLAB 程序例7.8.1 设节点(X,Y,Z )中的X 和Y 分别是在区间和上的5]3,3[-]5.3,5.2[-0个随机数,Z 是函数Z =7-3x3e 在22y - -x (X,Y )的值,拟合点(X I ,Y I )中的X I =-3:0.2:3, Y I =-2.5:0.2:3.5.分别用二元拟合方法中最近邻内插法、三角基线性内插法、三角基三次内插法和MATLAB 4网格化坐标方法计算在(X I ,Y I )处的值,作出它们的图形,并与被拟和曲面进行比较.解 (1)最近邻内插法.输入程序>> x=rand(50,1);y=rand(50,1); %生成50个一元均匀分布随机数x 和y , x ,y .X=-3+(3-(-3))*x;%利用x 生成的随机变量.Y=-2.5+(3.5-(-2.5))*y; %利用y 生成的随机变量.Z=7-3* X.^3 .* exp(-X.^2 - Y.^2); %在每个随机点(X,Y )处计算Z的值.X1=-3:0.2:3;Y1=-2.5:0.2:3.5;[XI,YI] = meshgrid(X1,Y1); %将坐标(XI,YI )网格化.ZI=griddata(X,Y,Z,XI,YI, 'nearest') %计算在每个插值点(XI,YI )处的插值ZI.mesh(XI,YI, ZI) %作二元拟合图形.xlabel('x'), ylabel('y'), zlabel('z'),title('用最近邻内插法拟合函数z =7-3 x^3 exp(-x^2 - y^2) 的曲面和节点的图形')%legend('拟合曲面','节点(xi,yi,zi)')hold on %在当前图形上添加新图形.plot3(X,Y,Z, 'bo') %用兰色小圆圈画出每个节点(X,Y,Z). hold of %结束在当前图形上添加新图形.运行后屏幕显示用最近邻内插法拟合函数Z =7-3x3e 在22y - -x 两组不同节点处的曲面及其插值Z I (略).(2)三角基线性内插法.输入程序>> x=rand(50,1);y=rand(50,1); %生成50个一元均匀分布随机数x 和y , x ,y .X=-3+(3-(-3))*x;%利用x 生成 上的随机变量.Y=-2.5+(3.5-(-2.5))*y; %利用y 生成 上的随机变量.Z=7-3* X.^3 .* exp(-X.^2 - Y.^2); %在每个随机点(X,Y )处计算Z的值.X1=-3:0.2:3;Y1=-2.5:0.2:3.5;[XI,YI] = meshgrid(X1,Y1); %将坐标(XI,YI )网格化.ZI=griddata(X,Y,Z,XI,YI, 'linear') %计算在每个插值点(XI,YI )处的插值ZI.mesh(XI,YI, ZI) %作二元拟合图形.xlabel('x'), ylabel('y'), zlabel('z'),title('用三角基线性内插法拟合函数z =7-3 x^3 exp(-x^2 - y^2) 的曲面和节点的图形')%legend('拟合曲面','节点(xi,yi,zi)')hold on %在当前图形上添加新图形.plot3(X,Y,Z, 'bo') %用兰色小圆圈画出每个节点(X,Y,Z). hold of %结束在当前图形上添加新图形.运行后屏幕显示用三角基线性内插法拟合函数Z =7-3x3e 在22y - -x 两组不同节点处的曲面和节点的图形及其插值Z I (略).(3)三角基三次内插法.输入程序>> x=rand(50,1);y=rand(50,1); %生成50个一元均匀分布随机数x 和y , x ,y .X=-3+(3-(-3))*x;%利用x 生成 上的随机变量.Y=-2.5+(3.5-(-2.5))*y; %利用y 生成 上的随机变量.Z=7-3* X.^3 .* exp(-X.^2 - Y.^2); %在每个随机点(X,Y )处计算Z的值.X1=-3:0.2:3;Y1=-2.5:0.2:3.5;[XI,YI] = meshgrid(X1,Y1); %将坐标(XI,YI )网格化.ZI=griddata(X,Y,Z,XI,YI, 'cubic') %计算在每个插值点(XI,YI )处的插值ZI.mesh(XI,YI, ZI) %作二元拟合图形.xlabel('x'), ylabel('y'), zlabel('z'),title('用三角基三次内插法拟合函数z =7-3 x^3 exp(-x^2 - y^2) 的曲面和节点的图形')%legend('拟合曲面','节点(xi,yi,zi)')hold on %在当前图形上添加新图形.plot3(X,Y,Z, 'bo') %用兰色小圆圈画出每个节点(X,Y,Z). hold of %结束在当前图形上添加新图形.运行后屏幕显示用三角基三次内插法拟合函数Z =7-3x3e 在22y - -x 两组不同节点处的曲面和节点的图形及其插值Z I (略).(4)MATLAB 4网格化坐标方法.输入程序>> x=rand(50,1);y=rand(50,1); %生成50个一元均匀分布随机数x 和y , x ,y .X=-3+(3-(-3))*x;%利用x 生成 上的随机变量.Y=-2.5+(3.5-(-2.5))*y; %利用y 生成 上的随机变量.Z=7-3* X.^3 .* exp(-X.^2 - Y.^2); %在每个随机点(X,Y )处计算Z的值.X1=-3:0.2:3; Y1=-2.5:0.2:3.5;[XI,YI] = meshgrid(X1,Y1); %将坐标(XI,YI )网格化.ZI=griddata(X,Y,Z,XI,YI, 'v4') %计算在每个插值点(XI,YI )处的插值ZI.mesh(XI,YI, ZI) %作二元拟合图形.xlabel('x'), ylabel('y'), zlabel('z'),title('用MATL AB 4网格化坐标方法拟合函数z =7-3 x^3 exp(-x^2 - y^2) 的曲面和节点的图形')%legend('拟合曲面','节点(xi,yi,zi)')hold on %在当前图形上添加新图形.plot3(X,Y,Z, 'bo') %用兰色小圆圈画出每个节点(X,Y,Z). hold of %结束在当前图形上添加新图形.运行后屏幕显示用MA TLAB 4网格化坐标方法拟合函数Z =7-3x3e 在22y - -x 两组不同节点处的曲面和节点的图形及其插值ZI (略).(5)作被拟合曲面Z =7-3x3e 和22y - -x 节点的图形.输入程序>> x=rand(50,1);y=rand(50,1); %生成50个一元均匀分布随机数x 和y , x ,y .X=-3+(3-(-3))*x;%利用x 生成随机变量.Y=-2.5+(3.5-(-2.5))*y; %利用y 生成随机变量.Z=7-3* X.^3 .* exp(-X.^2 - Y.^2); %在每个随机点(X,Y )处计算Z的值.X1=-3.:0.1:3.;Y1=-2.5:0.1:3.5;[XI,YI] = meshgrid(X1,Y1); %将坐标(XI,YI )网格化.ZI=7-3* XI.^3 .* exp(-XI.^2 - YI.^2);mesh(XI,YI, ZI) %作二元拟合图形.xlabel('x'), ylabel('y'), zlabel('z'),title('被拟合函数z =7-3 x^3 exp(-x^2 - y^2) 的曲面和节点的图形')%legend('被拟合函数曲面','节点(xi,yi,zi)')hold on %在当前图形上添加新图形.plot3(X,Y,Z, 'bo') %用兰色小圆圈画出每个节点(X,Y,Z). hold of %结束在当前图形上添加新图形.运行后屏幕显示被拟合函数Z =7-3x3e 的22y - -x 曲面和节点的图形及其函数值ZI (略).7.9 随机数据点上的元拟合n 及其MATLAB 程序例7.9.1 首先利用M ATLAB 函数ran d 产生随机数据X 1,Y 1,Z 1,然后用线性变换b at u += (其中5,5-==b a )将随机数据X 1,Y 1 ,Z 1 变换为节点坐标(X,Y,Z ),再用函数e )1(373+-=z y x w 222z y x ---生成数据W, 用三元最近邻内插法方法计算函数w 在插值点x i ,10:5.0:3-= y i ,13:5.0:2-=z i =y i 处拟合数据的值,并作其图形.解 输入程序>> X1=-5+5*rand(10,1);Y1=-5+5*rand(10,1);Z1=Y1;[X,Y,Z] = meshgrid(X1,Y1,Z1);W=7-3* X.^3 .* Y.*(Z+1).* exp(-X.^2 - Y.^2- Z.^2);xi=-3:0.5:10;yi=-2:0.5:13;zi=yi;[XI,YI,ZI] = meshgrid(xi,yi,zi);W1=griddata3(X, Y, Z, W, XI, YI, ZI, 'nearest');slice(XI,YI,ZI,W1,[-2 4 9.5],9,[-2 2 9]),%shading flat%lighting flatxlabel('x'), ylabel('y'), zlabel('z'),title('被拟合函数W=7-3X^3Y(Z+1)exp(-X^2 - Y^2- Z^2) ');hold oncolorbar('horiz')view([-30 45])运行后屏幕显示三元线性拟合值及其图形(略).例7.9.2 设节点(X,Y,Z,W )中的X,Y 和Z 分别是在区间和]3,3[-]5.3,5.2[-,Y =Z 上的15个随机数,W 是函数e x w +=2222z y x ---在(X,Y,Z )的值,拟合点(x i ,y i ,z i )中的x i =-3:0.2:3, y i =-2.5:0.2:3.5,z i =y i , 用'linear '方法计算拟合数据的值,并作其图形.解 输入程序>> x=rand(15,1); y=rand(15,1);X1=-3+(3-(-3))*x;Y1=-2.5+(3.5-(-2.5))*y;Z1=Y1;[X,Y,Z] = meshgrid(X1,Y1,Z1);W=2+X.* exp(-X.^2 - Y.^2- Z.^2);xi=-3:0.2:3; yi=-2.5:0.2:3.5; zi=yi;[X2,Y2,Z2]=meshgrid(xi,yi,zi);W1=griddata3(X, Y, Z, W, X2,Y2,Z2,'linear');slice(X2,Y2,Z2,W1,[-1 0 1.5],2,[-2 3]),shading flat,lighting flat,xlabel('x'), ylabel('y'), zlabel('z'),title('被拟合函数W=2+X exp(-X^2 - Y^2- Z^2)');hold on,colorbar('horiz'), view([-3 5])运行后屏幕显示三元线性拟合值及其图形(略).。
最小二乘曲线拟合及MATLAB实现_测绘专业论文 精品

内蒙古科技大学本科生毕业设计说明书(毕业论文)题目:最小二乘曲线拟合及MATLAB实现学生姓名:李亚学号:0972143230专业:测绘工程班级:2009测绘2班指导教师:孙同贺讲师最小二乘曲线拟合及MATLAB实现摘要介绍曲线拟合的基本理论,对最小二乘原理进行了全方位的理论阐述,同时也阐述了曲线拟合的基本原理及多项式曲线拟合模型的建立。
详细的解答了曲线拟合中的最小二乘法,并介绍了部分的正交最小二乘法理论。
重点讲解多项式拟合的具体步骤,同时也介绍了非线性方程的最小二乘拟合,在建立理论的基础上对最小二乘曲线拟合法的MATLAB实现方法进行研究,利用MATLAB2012b的平台对测量数据进行最小二乘曲线拟合,介绍MATLAB的具体构造和曲线拟合工具。
利用MATLAB中的ployfit函数对实测数据进行多项式曲线拟合,并给出曲线拟合MATLAB实现的源程序,给出拟合曲线,并评定拟合的精度证明该方法是行之有效的。
关键词:最小二乘法,曲线拟合,MATLAB,测量数据Curve Fitting in Least-Square Methodand Its Realization with MatlabAbstractTo introduce the basic theory of curve fitting and discuss the least squares principle in this paper, what’s more, we also discuss the basic principle of curve fitting and the establishment of polynomial curve fitting model. Meanwhile, we also introduce the least-square method of curve fitting in detail and part of the theory of orthogonal least square method. We mainly discuss the specific steps of polynomial fitting, and also introduces the nonlinear equation of the least squares fitting at the same time, which established on the theory of least squares curve fitting in MATLAB in order to realize the method to do research. Using MATLAB2012b platform to achieve the goal of measuring data and introducing the special structure of MATLAB and curve fitting tool. We can use ployfit function in MATLAB to polynomial curve fitting of experimental data, and get the MATLAB source program about curve fitting and the fitting curve. Finally, we need to prove the method of assessing the precision of the fitting is effective.Key words: least square method; curve fitting; MATLAB, metrical data最小二乘曲线拟合及MATLAB实现 (I)摘要 (I)CURVE FITTING IN LEAST-SQUARE METHOD AND ITS REALIZATION WITH MATLAB (II)ABSTRACT (II)第一章引言 (1)1.1研究背景 (1)1.1.1 历史理论原理 (1)1.1.2 现代研究 (1)1.2问题定义 (2)1.2.1 曲线拟合的思想 (2)1.2.2 多项式拟合 (3)1.2.3 利用Matlab的polyfit函数进行多项式拟合 (3)1.3论文结构 (3)第二章数据曲线拟合 (4)2.1测量数据 (4)2.2拟合模型 (4)2.3最小二乘原理 (5)2.3.1最小二乘法 (5)2.3.2最小二乘估计与极大似然估计 (7)2.4.1曲线拟合理论 (9)2.4.2最小二乘法线性拟合原理 (10)2.4.3最小二乘非线性拟合 (12)2.4.4正交多项式 (13)2.4.5正交最小二乘曲线拟合 (15)2.5曲线拟合精度评定 (17)第三章MATLAB (19)3.1MATLAB概述 (19)3.1.1MATLAB简介 (19)3.1.2MATLAB的主要组成部分 (21)3.2MATLAB2012B的运行简介 (23)3.2.1启动和退出MATLAB2012b (23)3.2.2MATLAB2012b桌面系统 (24)3.2.3MATLAB函数调用系统 (26)3.2.4MATLAB2012b的帮助系统 (27)3.2.5附件管理系统 (28)3.2.6数据交换系统 (28)3.2.7MATLAB 中的其他系统 (29)3.3最小二乘曲线拟合法的MATLAB实现 (30)第四章最小二乘法曲线拟合的MATLAB实现 (32)4.1使用POLYFIT函数实现多项式拟合 (32)4.3三次多项式的曲线拟合 (34)4.4四次多项式曲线拟合 (35)4.5数据处理和精度评定 (36)第五章总结 (40)参考文献 (41)附录1: (43)MATLAB语言编程源代码 (43)附录2: (45)各次拟合的拟合曲线方程 (45)致谢 (46)外文翻译 (47)外文部分 (47)翻译部分 (54)第一章 引 言1.1研究背景1.1.1 历史理论原理Weierstrass 第一逼近定理[1]对任意函数()f C[a,b]x ∈和任意给定的0ε>,都存在n 次代数多项式()n p x ,满足()()[,]||<max nx a b f x p x ε∈- (1-1-1) Bernstein 多项式(bernstein polynomial )[1]前苏联数学家Bernstein 曾经给出这样的多项式序列:0(,)(1)n k n k n k n k B f x f x x k n -=⎛⎫⎛⎫=- ⎪ ⎪⎝⎭⎝⎭∑ (1-1-2)在整体上一致逼近()f x ,但它的收敛缓慢,要达到一定的精度,则n 要取很大,计算量大,所以研究如何在给定的精度下,对()f x 进行整体逼近,成为逼近论中的一个重要问题。
最小二乘法曲线拟合_原理及matlab实现

曲线拟合(curve-fitting ):工程实践中,用测量到的一些离散的数据},...2,1,0),,{(m i y x i i =求一个近似的函数)(x ϕ来拟合这组数据,要求所得的拟合曲线能最好的反映数据的基本趋势(即使)(x ϕ最好地逼近()x f ,而不必满足插值原则。
因此没必要取)(i x ϕ=i y ,只要使i i i y x -=)(ϕδ尽可能地小)。
原理:给定数据点},...2,1,0),,{(m i y x i i =。
求近似曲线)(x ϕ。
并且使得近似曲线与()x f 的偏差最小。
近似曲线在该点处的偏差i i i y x -=)(ϕδ,i=1,2,...,m 。
常见的曲线拟合方法:1.使偏差绝对值之和最小2.使偏差绝对值最大的最小3.使偏差平方和最小最小二乘法:按偏差平方和最小的原则选取拟合曲线,并且采取二项式方程为拟合曲线的方法,称为最小二乘法。
推导过程:1. 设拟合多项式为:2. 各点到这条曲线的距离之和,即偏差平方和如下:3. 问题转化为求待定系数0a ...k a 对等式右边求i a 偏导数,因而我们得到了: .......4、 把这些等式化简并表示成矩阵的形式,就可以得到下面的矩阵:5. 将这个范德蒙得矩阵化简后可得到:6. 也就是说X*A=Y ,那么A = (X'*X)-1*X'*Y ,便得到了系数矩阵A ,同时,我们也就得到了拟合曲线。
MATLAB 实现:MATLAB 提供了polyfit ()函数命令进行最小二乘曲线拟合。
调用格式:p=polyfit(x,y,n)[p,s]= polyfit(x,y,n)[p,s,mu]=polyfit(x,y,n)x,y 为数据点,n 为多项式阶数,返回p 为幂次从高到低的多项式系数向量p 。
x 必须是单调的。
矩阵s 包括R (对x 进行QR 分解的三角元素)、df(自由度)、normr(残差)用于生成预测值的误差估计。
matlab最小二乘法曲线拟合

matlab最小二乘法曲线拟合最小二乘法是一种常用的曲线拟合方法,它通过最小化实际观测值与拟合曲线之间的平方误差来确定最佳拟合曲线的参数。
给定一组实际观测数据点(xi, yi),我们希望找到一个拟合曲线y=f(x;θ),其中θ表示曲线的参数。
最小二乘法的目标是使误差的平方和最小化,即使得下述损失函数最小化:L(θ) = ∑(yi - f(xi;θ))^2其中,∑表示求和运算,L(θ)是损失函数,yi是第i个观测数据点的输出值,f(xi;θ)是根据参数θ计算得到的拟合曲线在第i个观测点的预测值。
为了找到最佳的参数θ,我们通过最小化损失函数来求解优化问题:minimize L(θ)这个问题可以通过求解等式∂L/∂θ = 0 来得到最优参数θ的闭式解。
具体的求解方法,可以通过矩阵和向量的运算来实现。
在Matlab中,可以使用“polyfit”函数进行最小二乘法的曲线拟合。
该函数可以拟合出一条多项式曲线,通过指定最佳拟合的次数,即多项式的阶数。
拟合结果包括最佳参数和拟合误差等信息。
使用方法如下:```% 输入观测数据x = [x1, x2, x3, ...]';y = [y1, y2, y3, ...]';% 拟合曲线order = 1; % 最佳拟合的次数(如一次线性拟合)p = polyfit(x, y, order);% 最佳参数coefficients = p;% 拟合曲线curve = polyval(p, x);% 绘制拟合曲线和观测数据plot(x, y, 'o', x, curve)```这样,就可以使用Matlab的最小二乘法曲线拟合方法来得到最佳的拟合曲线。
最小二乘法曲线拟合-原理及matlab实现

曲线拟合(curve-fitting ):工程实践中,用测量到的一些离散的数据},...2,1,0),,{(m i y x i i =求一个近似的函数)(x ϕ来拟合这组数据,要求所得的拟合曲线能最好的反映数据的基本趋势(即使)(x ϕ最好地逼近()x f ,而不必满足插值原则。
因此没必要取)(i x ϕ=i y ,只要使i i i y x -=)(ϕδ尽可能地小)。
原理:给定数据点},...2,1,0),,{(m i y x i i =。
求近似曲线)(x ϕ。
并且使得近似曲线与()x f 的偏差最小。
近似曲线在该点处的偏差i i i y x -=)(ϕδ,i=1,2,...,m 。
常见的曲线拟合方法:1.使偏差绝对值之和最小2.使偏差绝对值最大的最小3.使偏差平方和最小最小二乘法:按偏差平方和最小的原则选取拟合曲线,并且采取二项式方程为拟合曲线的方法,称为最小二乘法。
推导过程:1. 设拟合多项式为:kk x a x a a x +++=...)(10ϕ2. 各点到这条曲线的距离之和,即偏差平方和如下:3. 问题转化为求待定系数0a ...k a 对等式右边求i a 偏导数,因而我们得到了:.......4、 把这些等式化简并表示成矩阵的形式,就可以得到下面的矩阵:5. 将这个范德蒙得矩阵化简后可得到:6. 也就是说X*A=Y ,那么A = (X'*X)-1*X'*Y ,便得到了系数矩阵A ,同时,我们也就得到了拟合曲线。
MATLAB实现:MATLAB提供了polyfit()函数命令进行最小二乘曲线拟合。
调用格式:p=polyfit(x,y,n)[p,s]= polyfit(x,y,n)[p,s,mu]=polyfit(x,y,n)x,y为数据点,n为多项式阶数,返回p为幂次从高到低的多项式系数向量p。
x 必须是单调的。
矩阵s包括R(对x进行QR分解的三角元素)、df(自由度)、normr(残差)用于生成预测值的误差估计。
matlab最小二乘法拟合二次曲线

标题:探索MATLAB最小二乘法:拟合二次曲线的深度与广度近年来,MATLAB的最小二乘法在数据分析和拟合曲线中逐渐成为研究和工程实践中的热门话题。
具体来说,通过最小二乘法可以拟合出最优的二次曲线,从而更精准地分析和预测各种实际数据。
在本文中,我将利用最小二乘法拟合二次曲线这一主题,结合MATLAB的相关知识和理论基础,进行深度与广度兼具的探索和阐述。
希望通过这篇文章,可以让读者更全面、深入地了解MATLAB最小二乘法在拟合二次曲线中的应用和意义。
1. MATLAB最小二乘法概述MATLAB作为数据分析和数值计算的重要工具之一,其最小二乘法在拟合曲线中具有广泛的应用。
最小二乘法的核心思想是通过最小化误差的方式,找到一条最符合实际数据的曲线。
在MATLAB中,可以利用polyfit函数实现最小二乘法拟合二次曲线,其原理和实现方式将在后文详细说明。
2. 深入理解最小二乘法最小二乘法不仅仅是一种拟合曲线的技术,更是一种数学原理和计算方法。
在拟合二次曲线中,我们需要理解误差的来源及其产生的原因,掌握最小二乘法拟合的数学模型和计算过程。
通过深入理解最小二乘法,我们可以更准确地分析和解释拟合结果,为实际问题的研究和解决提供更为可靠的依据。
3. MATLAB实例分析接下来,我们将以一个实际的数据集为例,利用MATLAB进行最小二乘法拟合二次曲线。
通过具体的数据分析和计算实例,我们可以更直观地了解最小二乘法的应用过程和拟合效果。
也可以探讨和比较不同参数对拟合结果的影响,从而更全面地认识最小二乘法在拟合二次曲线中的灵活性和可操作性。
4. 总结与展望在本篇文章中,我们对MATLAB最小二乘法在拟合二次曲线中的深度与广度进行了探索和阐述。
通过对最小二乘法原理的解析和MATLAB 实例的分析,我们希望读者能够更全面、深入地理解其在数据分析和拟合曲线中的重要性和实际应用。
也希望能够引发更多关于最小二乘法的讨论和研究,为其在实际工程和科研中的进一步应用提供更多可能性。
曲线拟合的最小二乘法matlab举例

学院:光电信息学院 姓名:赵海峰 学号:1001一、曲线拟合的最小二乘法原理:由已知的离散数据点选择与实验点误差最小的曲线)(...)()()(1100x a x a x a x S n n ϕϕϕ+++=称为曲线拟合的最小二乘法。
若记),()()(),(0i k i j mi i k j x x x ϕϕωϕϕ∑==k i k i mi i k d x x f x f ≡=∑=)()()(),(0ϕωϕ上式可改写为),...,1,0(;),(n k d a k j noj j k -=∑=ϕϕ这个方程成为法方程,可写成距阵形式d Ga =其中,),...,,(,),...,,(1010T n T n d d d d a a a a ==⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=),(),(),()(),(),(),(),(),(101110101000n n n n n n G ϕϕϕϕϕϕϕϕϕϕϕϕϕϕϕϕϕϕΛM M M ΛΛ。
它的平方误差为:.)]()([)(||||2022i i mi i x f x S x -=∑=ωδ二、数值实例:下面给定的是乌鲁木齐最近1个月早晨7:00左右(新疆时间)的天气预报所得到的温度数据表,按照数据找出任意次曲线拟合方程和它的图像。
下面应用Matlab编程对上述数据进行最小二乘拟合三、Matlab程序代码:x=[1:1:30];y=[9,10,11,12,13,14,13,12,11,9,10,11,12,13,14,12,11,10,9,8,7,8,9,11,9,7,6,5,3,1 ];a1=polyfit(x,y,3) %三次多项式拟合%a2= polyfit(x,y,9) %九次多项式拟合%a3= polyfit(x,y,15) %十五次多项式拟合%b1=polyval(a1,x)b2=polyval(a2,x)b3=polyval(a3,x)r1= sum((y-b1).^2) %三次多项式误差平方和%r2= sum((y-b2).^2) %九次次多项式误差平方和%r3= sum((y-b3).^2) %十五次多项式误差平方和%plot(x,y,'*') %用*画出x,y图像%hold onplot(x,b1, 'r') %用红色线画出x,b1图像%hold onplot(x,b2, 'g') %用绿色线画出x,b2图像%hold onplot(x,b3, 'b:o') %用蓝色o线画出x,b3图像%四、数值结果:不同次数多项式拟和误差平方和为:r1 =r2 =r3 =r1、r2、r3分别表示三次、九次、十五次多项式误差平方和。
matlab加权最小二乘法拟合编程

一、概述最小二乘法(Least Squares Method)是一种常用的数学优化方法,通过最小化残差的平方和来拟合实际数据与理论模型之间的关系。
在实际应用中,我们常常需要对数据进行加权处理,以提高拟合效果和准确度。
而Matlab作为一种强大的数学建模和仿真软件,提供了丰富的函数和工具来实现加权最小二乘法的拟合编程。
二、加权最小二乘法原理1. 最小二乘法原理最小二乘法是一种常用的拟合方法,通过最小化实际观测值和理论值之间的误差来寻找最佳拟合曲线或曲面。
其数学表达为:minimize ||Ax - b||^2其中A为设计矩阵,x为拟合参数,b为观测值向量。
最小二乘法可以看作是一种优化问题,通过求解参数x的最优值来实现最佳拟合。
2. 加权最小二乘法原理在实际情况下,我们往往会遇到观测值有不同的权重或方差的情况,此时可以使用加权最小二乘法来提高拟合效果。
加权最小二乘法的数学表达为:minimize ||W^(1/2)(Ax - b)||^2其中W为权重矩阵,将不同观测值的权重考虑在内,通过加权的方式来优化拟合效果。
三、Matlab实现加权最小二乘法1. 数据准备在进行加权最小二乘法的拟合编程前,首先需要准备实际观测数据和设计矩阵A。
还需要考虑观测值的权重矩阵W,根据实际情况来确定不同观测值的权重。
2. 加权最小二乘法函数Matlab提供了丰富的函数和工具来实现加权最小二乘法的拟合。
其中,可以使用lsqcurvefit或lsqnonlin等函数来进行加权最小二乘法的拟合计算。
通过传入设计矩阵A、观测值向量b和权重矩阵W,以及拟合参数的初始值,来实现加权最小二乘法的拟合计算。
3. 拟合结果评估完成加权最小二乘法的拟合计算后,我们需要对拟合结果进行评估。
主要包括残差分析、拟合效果的可视化等方面。
通过分析残差的分布和拟合曲线与实际观测值的符合程度,来评估拟合效果的优劣。
四、实例分析1. 示例一:线性模型拟合假设我们有一组线性关系的实际观测数据,且各观测值具有不同的权重。
基于Matlab实现最小二乘曲线拟合

基于Matlab实现最小二乘曲线拟合一、本文概述在数据分析和科学计算中,曲线拟合是一种常见且重要的技术。
通过拟合,我们可以根据已知数据建立数学模型,预测未知数据,以及深入理解数据背后的规律。
最小二乘法是曲线拟合中最常用的一种方法,其原理是通过最小化预测值与实际值之间的平方误差来寻找最佳拟合曲线。
本文旨在介绍如何使用Matlab这一强大的数学计算软件,实现最小二乘曲线拟合,包括其理论基础、实现步骤以及实际应用案例。
通过本文的学习,读者将能够掌握在Matlab环境中进行最小二乘曲线拟合的基本方法,提高数据处理和分析能力。
二、最小二乘曲线拟合原理最小二乘法(Least Squares Method)是一种数学优化技术,它通过最小化误差的平方和来寻找数据的最佳函数匹配。
在曲线拟合中,最小二乘法被广泛应用于通过一组离散的数据点来估计一个连续函数的形状。
这种方法的基本思想是通过选择一个模型函数(通常是多项式、指数函数、对数函数等),使得该模型函数与实际数据点之间的差距(即残差)的平方和最小。
假设我们有一组数据点 ((x_1, y_1), (x_2, y_2), \ldots,(x_n, y_n)),我们希望通过一个模型函数 (y = f(x, \mathbf{p})) 来拟合这些数据点,其中 (\mathbf{p}) 是模型的参数向量。
最小二乘法的目标就是找到最优的参数向量 (\mathbf{p}^*),使得残差平方和 (S(\mathbf{p})) 最小:S(\mathbf{p}) = \sum_{i=1}^{n} [y_i - f(x_i,\mathbf{p})]^2]为了使 (S(\mathbf{p})) 达到最小,我们需要对(S(\mathbf{p})) 求偏导数,并令其等于零。
这样,我们就得到了一个关于 (\mathbf{p}) 的方程组。
解这个方程组,就可以得到最优的参数向量 (\mathbf{p}^*)。
Matlab实验报告七(最小二乘拟合曲线拟合)

4.结论及分析
经过实验验证,结果正确,实验无误。
三、实验小结
通过本次实验我发现matlab的用处很广范,能解决生活中的很多问题,预测一些还未发生的事情,越来越感觉这门课用处很大,也渐渐地喜欢这门课了。
t Q K L
1900 1.05 1.04 1.05
1901 1.18 1.06 1.08
1902 1.29 1.16 1.18
1903 1.30 1.22 1.22
1904 1.30 1.27 1.17
1905 1.42 1.37 1.30
1906 1.50 1.44 1.39
1907 1.52 1.53 1.47
Qdata=[1.05 1.18 1.29 1.30 1.30 1.42 1.50 1.52 1.46 1.60 1.69 1.81 1.93 1.95 2.01 2.00 2.09 1.96 2.20 2.12 2.16 2.08 2.24 2.56 2.34 2.45 2.58];
x0=[0.2 0.3 0.3];
2.y=polyval(Βιβλιοθήκη ,x):可用以计算多项式在x处的值y。
3.x = lsqcurvefit (‘fun’,x0,xdata,ydata):用以求含参量x(向量)的向量值函数。
4.x= lsqnonlin (‘fun’,x0,options):用以求含参量x(向量)的向量值函数。
【实验环境】
MatlabR2010b
用Q,K,L分别表示产值、资金、劳动力,要寻求的数量关系 。经过简化假设与分析,在经济学中,推导出一个著名的Cobb-Douglas生产函数:
(*)
式中 要由经济统计数据确定。现有美国马萨诸塞州1900—1926年上述三个经济指数的统计数据,如下表,试用数据拟合的方法,求出式(*)中的参数 。
matlab 最小二乘法拟合曲线

matlab 最小二乘法拟合曲线最小二乘法(Least Squares Method)是一种常用的数据拟合技术,在数学建模、统计学以及工程领域中被广泛应用。
该方法通过最小化实际观测值与拟合模型之间的平方误差和,从而找到一个最佳的拟合曲线。
首先,我们来了解一下最小二乘法的基本原理。
假设我们有一组n组数据点{(x1, y1), (x2, y2), ..., (xn, yn)},我们希望找到一个函数f(x)来拟合这些数据。
为了简便计,我们假设函数f(x)是一个线性函数,即f(x) = ax + b。
要使用最小二乘法来进行拟合,我们需要构造一个目标函数,该函数是残差平方和(Sum of Squared Residuals,SSR)。
残差表示实际数据点与拟合曲线之间的差异,而残差平方和则是将所有残差平方相加得到的一个值。
目标函数可以表示为:SSR = Σ(yi - f(xi))^2最小二乘法的核心思想就是通过调整拟合函数中的参数a和b,使得目标函数SSR达到最小值。
为了实现这一目标,我们需要对目标函数求导,并令导数为0。
这样做可以得到一组线性方程组,可以使用线性代数中的方法求解这个方程组,从而得到a和b的值。
推导过程略去不表,最终我们可以得到最佳的拟合曲线方程:f(x) = (Σxiyi - n * x_mean * y_mean) / (Σxi^2 - n *x_mean^2) * x + (y_mean - (Σxiyi - n * x_mean * y_mean) / (Σxi^2 - n * x_mean^2) * x_mean)其中,x_mean和y_mean分别表示x和y的平均值,n表示数据点的数量。
通过以上公式,我们可以得到一个最佳的线性拟合曲线,该曲线可以最小化数据点与拟合曲线之间的距离。
当然,在实际应用中,我们会遇到更复杂的拟合函数,而不仅仅是线性函数。
但不论函数形式如何,最小二乘法的思想都是相同的——将观测值与模型之间的误差最小化。
matlab最小二乘法拟合曲线并计算拟合曲线的总长度

matlab最小二乘法拟合曲线并计算拟合曲线的总长度在MATLAB中,你可以使用最小二乘法拟合曲线,然后使用积分的方法计算拟合曲线的总长度。
下面是一种可能的方法:1. 首先,使用MATLAB的`polyfit`函数进行最小二乘法拟合。
这个函数可以拟合多项式到一组数据。
```matlabx = [x1, x2, ... , xn]; % 输入数据y = [y1, y2, ... , yn]; % 输出数据p = polyfit(x, y, n); % n是多项式的阶数,比如2代表二次函数```这将返回一个向量p,代表多项式的系数,从最高阶到最低阶。
2. 然后,你可以使用`polyval`函数来评估拟合的曲线。
```matlabyfit = polyval(p, x); % 计算拟合的y值```3. 计算拟合曲线的总长度。
你可以使用数值积分的方法,例如`integral`函数。
你需要知道曲线在[a, b]之间的长度。
例如,如果你的数据在[-10, 10],你可以这样做:```matlaba = -10; % 积分下限b = 10; % 积分上限L = integral((x) abs(diff(polyval(p, x))), a, b); % 计算长度```这里我们使用`diff`函数来计算拟合曲线的导数(即曲线的斜率),然后乘以x的差分(即dx)。
最后,我们使用`integral`函数来计算这个函数的积分,也就是曲线的长度。
注意,我们使用`abs`函数来确保每一段都是正的,因为曲线可能向上或向下弯曲。
注意:这种方法只适用于连续且可微的函数。
如果你的数据包含噪声或者有突变,那么这种方法可能不准确。
matlab最小二乘法曲线拟合

matlab最小二乘法曲线拟合在数据处理和拟合曲线中,最小二乘法是一种常用的数学方法。
通过最小化数据点到拟合曲线的垂直距离的平方和,最小二乘法可以在给定数据集上拟合出一条曲线。
在MATLAB中,最小二乘法曲线拟合可以通过使用polyfit函数来实现。
最小二乘法原理最小二乘法的目标是找到一条曲线,使得曲线上的点到原始数据点的垂直距离的平方和最小。
具体而言,对于给定的数据集{(x1, y1), (x2, y2), ... , (xn, yn)},最小二乘法拟合的目标是找到一个多项式函数y =f(x) = a0 + a1*x + a2*x^2 + ... + an*x^n,其中a0, a1, a2, ... , an为待定系数,使得下述式子最小化:这里,ei表示第i个数据点的观测误差。
在MATLAB中使用最小二乘法进行曲线拟合MATLAB提供了polyfit函数来进行最小二乘法曲线拟合。
polyfit函数采用两个输入参数:x和y,分别表示数据点的横坐标和纵坐标。
此外,用户还需要指定多项式的阶数n。
polyfit将返回一个包含拟合多项式系数的向量p。
用户可以使用polyval函数来计算拟合曲线上的点的纵坐标,具体使用如下:p = polyfit(x, y, n);y_fit = polyval(p, x);下面我们通过一个例子来演示如何使用MATLAB进行最小二乘法曲线拟合。
假设我们有如下数据集,表示了一个函数y = f(x) = 2x^3 + 3x^2 - 5x + 2上的一些离散数据点:x = [0, 1, 2, 3, 4, 5];y = [2, 3, 4, 5, 6, 7];我们可以使用polyfit函数进行二次多项式曲线拟合,代码如下:p = polyfit(x, y, 2);y_fit = polyval(p, x);接下来,我们可以绘制原始数据点和拟合曲线,代码如下:plot(x, y, 'o');hold on;plot(x, y_fit, '-');xlabel('x');ylabel('y');legend('原始数据', '拟合曲线');在图中,原始数据点以圆圈表示,拟合曲线以实线表示。
最小二乘法原理及其MATLAB实现

最小二乘法原理及其MATLAB实现一、本文概述最小二乘法是一种广泛应用于数学、统计学、工程学、物理学等众多领域的数学优化技术。
其核心原理在于通过最小化误差的平方和来寻找最佳函数匹配,从而实现对数据的最佳逼近。
本文将对最小二乘法的原理进行详细阐述,并通过MATLAB编程实现,帮助读者深入理解并掌握这一强大的数据分析工具。
文章将首先介绍最小二乘法的基本原理,包括其历史背景、基本概念以及数学模型的构建。
然后,通过实例分析,展示如何应用最小二乘法进行线性回归模型的拟合,以及如何处理过拟合和欠拟合等问题。
接着,文章将详细介绍如何在MATLAB中实现最小二乘法,包括数据准备、模型构建、参数估计以及结果可视化等步骤。
文章还将对最小二乘法的优缺点进行讨论,并探讨其在不同领域的应用前景。
通过本文的学习,读者将能够全面理解最小二乘法的原理和应用,掌握其在MATLAB中的实现方法,为实际工作中的数据处理和分析提供有力支持。
二、最小二乘法原理最小二乘法(Least Squares Method)是一种数学优化技术,它通过最小化误差的平方和寻找数据的最佳函数匹配。
这种方法起源于19世纪的统计学,由数学家阿德里安-马里·勒让德(Adrien-Marie Legendre)和卡尔·弗里德里希·高斯(Carl Friedrich Gauss)分别独立发展。
建立模型:我们需要建立一个描述数据关系的数学模型。
这通常是一个线性方程,如 y = ax + b,其中 a和b是待求解的参数。
误差计算:对于给定的数据集,我们可以将每个数据点代入模型中进行计算,得到预测值。
预测值与真实值之间的差异就是误差。
平方误差和:为了衡量模型的拟合程度,我们需要计算所有误差的平方和。
这是因为平方误差和能够更好地反映误差的大小,尤其是在误差较大时。
最小化平方误差和:最小二乘法的核心思想是找到一组参数,使得平方误差和达到最小。
这通常通过求导和令导数等于零来实现,从而找到使平方误差和最小的参数值。
matlab最小二乘法拟合函数分段拟合

一、概述在数据分析和曲线拟合中,最小二乘法是一种常用的数据拟合方法。
它通过最小化实际观测值与拟合曲线之间的残差平方和来求得最优拟合曲线的参数。
而在MATLAB中,有专门的函数可以帮助我们进行最小二乘法拟合,实现不同类型的数据拟合。
本文将从最小二乘法的原理和MATLAB的使用角度,介绍如何在MATLAB中使用最小二乘法进行函数分段拟合。
二、最小二乘法原理1. 残差的定义在进行数据拟合时,我们经常会遇到实际观测值与拟合曲线之间存在一定的偏差,这种偏差即为残差。
对于第i个观测点,其残差可以表示为:\[e_{i} = y_{i} - F(x_{i}, \theta)\]其中\(y_{i}\)为实际观测值,\(F(x_{i}, \theta)\)为拟合曲线在\(x_{i}\)处的取值,\(\theta\)为拟合曲线的参数。
2. 最小二乘法的原理最小二乘法的目标是找到一组参数\(\theta^*\),使得实际观测值与拟合曲线的残差平方和最小,即\[\min_{\theta} \sum_{i=1}^{n} e_{i}^{2}\]通过对残差平方和的求导等于0,可以得到最优参数\(\theta^*\)的表达式,这样就得到了最优的拟合曲线。
三、MATLAB中的最小二乘法函数在MATLAB中,有专门用于最小二乘法拟合的函数lsqcurvefit。
该函数可以实现对一般形式的非线性方程进行最小二乘法拟合,在进行分段函数拟合时,也可以适用。
下面将介绍lsqcurvefit函数的基本用法。
1. 函数参数lsqcurvefit函数的基本参数包括:- fun:拟合函数的句柄,用于计算拟合曲线在给定x处的取值- x0:拟合曲线的初始参数- xdata:实际观测点的x坐标- ydata:实际观测点的y坐标- lb、ub:参数的取值范围约束2. 示例代码下面是一个使用lsqcurvefit函数进行分段线性函数拟合的示例代码:```matlab定义拟合函数fun = (x, xdata) x(1)*xdata.*(xdata<=3) + x(2)*xdata.*(xdata>3);初始化参数x0 = [1, 2];定义实际观测点xdata = [1, 2, 3, 4, 5];ydata = [3, 5, 7, 9, 11];进行最小二乘法拟合x = lsqcurvefit(fun, x0, xdata, ydata);```通过以上示例代码,可以实现对分段线性函数进行最小二乘法拟合,得到最优的拟合参数x。
最小二乘曲线拟合及其MATLAB实现
MCB 的使用频率:MCB 的设计和使用是针 对 50~60Hz 交流电网的,由于磁脱扣器的电磁 力与电源频率、动作电流有关,因此对于在交流 电压下使用的 MCB 用于直流电路或其它电源 频率场合的保护时,磁脱扣器的动作电流是不 同的。一般应根据制造厂商提供的磁脱扣动作 电流同电源频率变化系数来换算。
线性最小二乘曲线拟合的含有待定参数的函
数形式为:
(f x;a1,a2,…,am)=a1r(1 x)+a2r(2 x)+…+amr(m x) 其中 r(k x)为事先选定的一组已知函数,ak 为 待定系数,k=1,2,…,n,m<n。为寻求 a1,a2,…,am 使 反映偏离程度的函数 (J a1,a2,…,am)最小,只需要
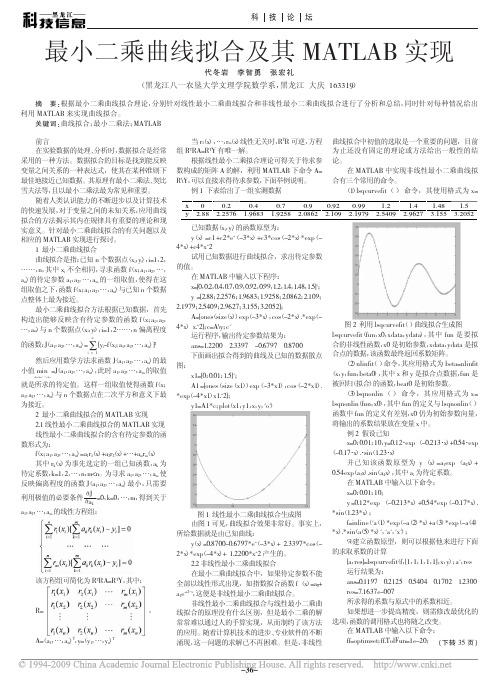
所给数据就是由已知曲线:
*x).*sin(a(5)*x)','a','x');
y(x)=0.8700-0.6797*e(^ -3*x)+ 2.3397*co(s -
%建立函数原型,则可以根据他来进行下面
2*x)*exp(-4*x)+ 1.2200*x^2 产生的。
的求取系数的计算
2.2 非线性最小二乘曲线拟合
4*x)+c4*x^2
试用已知数据进行曲线拟合,求出待定参数
的值。
在 MATLAB 中输入以下程序:
x=[0,0.2,0.4,0.7,0.9,0.92,0.99,1.2,1.4,1.48,1.5]';
y =[2.88;2.2576;1.9683;1.9258;2.0862;2.109;
2.1979;2.5409;2.9627;3.155;3.2052];
matlab最小二乘法拟合曲线代码

在Matlab中使用最小二乘法进行曲线拟合是一项非常常见的任务。
最小二乘法是一种数学优化技术,用于对一组数据进行曲线拟合,以便找到最能代表数据趋势的曲线。
在本文中,我将深入探讨Matlab中最小二乘法拟合曲线的代码实现,并共享我对这一主题的个人理解。
让我们来了解一下什么是最小二乘法。
最小二乘法是一种数学优化技术,用于寻找一组数据的最佳拟合曲线。
在Matlab中,可以使用内置的polyfit函数来实现最小二乘法曲线拟合。
这个函数的基本语法是:```matlabp = polyfit(x, y, n)```其中,x和y分别是数据点的横纵坐标,n是要拟合的多项式次数。
这个函数将返回多项式系数向量p,使得拟合多项式最小化了实际数据点与拟合曲线之间的误差平方和。
举个例子,假设我们有一组数据点(x, y),我们可以使用polyfit函数来进行二次多项式拟合:```matlabx = [1, 2, 3, 4, 5];y = [2, 3, 4, 3, 5];p = polyfit(x, y, 2);```在这个例子中,p将会是一个包含三个元素的向量,分别代表二次多项式的系数a、b和c。
通过这些系数,我们就可以得到拟合的二次多项式方程。
除了使用polyfit函数,我们还可以使用polyval函数来计算拟合曲线上的点。
其基本语法形式是:```matlaby_fit = polyval(p, x)```在这个例子中,p是通过polyfit得到的多项式系数向量,x是我们要计算拟合曲线上的点的横坐标,y_fit将是这些点的纵坐标。
另外,Matlab还提供了许多其他的拟合函数和工具箱,用于不同类型的数据和曲线拟合需求。
通过调用这些函数和工具箱,我们可以实现更复杂的曲线拟合任务,满足不同数据类型和拟合目标的需求。
总结来说,Matlab提供了丰富的工具和函数,用于实现最小二乘法曲线拟合。
通过调用polyfit函数和其他拟合工具箱,我们可以轻松地对一组数据进行曲线拟合,从而得到最能代表数据趋势的曲线。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
曲线拟合(curve-fitting ):工程实践中,用测量到的一些离散的数据},...2,1,0),,{(m i y x i i =求一个近似的函数)(x ϕ来拟合这组数据,要求所得的拟合曲线能最好的反映数据的基本趋势(即使)(x ϕ最好地逼近()x f ,而不必满足插值原则。
因此没必要取)(i x ϕ=i y ,只要使i i i y x -=)(ϕδ尽可能地小)。
原理:给定数据点},...2,1,0),,{(m i y x i i =。
求近似曲线)(x ϕ。
并且使得近似曲线与()x f 的偏差最小。
近似曲线在该点处的偏差i i i y x -=)(ϕδ,i=1,2,...,m 。
常见的曲线拟合方法:1.使偏差绝对值之和最小2.使偏差绝对值最大的最小3.使偏差平方和最小最小二乘法:按偏差平方和最小的原则选取拟合曲线,并且采取二项式方程为拟合曲线的方法,称为最小二乘法。
推导过程:1. 设拟合多项式为:kk x a x a a x +++=...)(10ϕ2. 各点到这条曲线的距离之和,即偏差平方和如下:3. 问题转化为求待定系数0a ...k a 对等式右边求i a 偏导数,因而我们得到了:.......4、 把这些等式化简并表示成矩阵的形式,就可以得到下面的矩阵:5. 将这个范德蒙得矩阵化简后可得到:6. 也就是说X*A=Y,那么A = (X'*X)-1*X'*Y,便得到了系数矩阵A,同时,我们也就得到了拟合曲线。
MATLAB实现:MATLAB提供了polyfit()函数命令进行最小二乘曲线拟合。
调用格式:p=polyfit(x,y,n)[p,s]= polyfit(x,y,n)[p,s,mu]=polyfit(x,y,n)x,y为数据点,n为多项式阶数,返回p为幂次从高到低的多项式系数向量p。
x 必须是单调的。
矩阵s包括R(对x进行QR分解的三角元素)、df(自由度)、normr(残差)用于生成预测值的误差估计。
[p,s,mu]=polyfit(x,y,n)在拟合过程中,首先对x进行数据标准化处理,以在拟合中消除量纲等影响,mu包含标准化处理过程中使用的x的均值和标准差。
polyval( )为多项式曲线求值函数,调用格式:y=polyval(p,x)[y,DELTA]=polyval(p,x,s)y=polyval(p,x)为返回对应自变量x在给定系数P的多项式的值。
[y,DELTA]=polyval(p,x,s) 使用polyfit函数的选项输出s得出误差估计Y DELTA。
它假设polyfit函数数据输入的误差是独立正态的,并且方差为常数。
则Y DELTA将至少包含50%的预测值。
如下给定数据的拟合曲线:x=[,,,,,],y=[,,,,,]。
解:MATLAB程序如下:x=[,,,,,];y=[,,,,,];p=polyfit(x,y,2)x1=::;y1=polyval(p,x1);plot(x,y,'*r',x1,y1,'-b')运行结果如图1计算结果为:p =即所得多项式为y=^2++0.51 1.52 2.53图1 最小二乘法曲线拟合示例对比检验拟合的有效性:例:在[0,π]区间上对正弦函数进行拟合,然后在[0,2π]区间画出图形,比较拟合区间和非拟合区间的图形,考察拟合的有效性。
在MATLAB中输入如下代码:clearx=0::pi;y=sin(x);[p,mu]=polyfit(x,y,9)x1=0::2*pi;y1=sin(x1);%实际曲线y2=polyval(p,x1);%根据由区间0到pi上进行拟合得到的多项式计算0到2pi上的函数值,%需要注意的是polyval()返回的函数值在pi到2pi上并没有进行拟合plot(x1,y2,'k*',x1,y1,'k-')运行结果:p =mu =R: [10x10 double]df: 22normr:MATLAB的最优化工具箱还提供了lsqcurvefit()函数命令进行最小二乘曲线拟合(Solve nonlinear curve-fitting (data-fitting) problems in least-squares sense)。
调用格式:x = lsqcurvefit(fun,x0,xdata,ydata)x = lsqcurvefit(fun,x0,xdata,ydata,lb,ub)x = lsqcurvefit(fun,x0,xdata,ydata,lb,ub,options)x = lsqcurvefit(problem)[x,resnorm] = lsqcurvefit(...)[x,resnorm,residual] = lsqcurvefit(...)[x,resnorm,residual,exitflag] = lsqcurvefit(...)[x,resnorm,residual,exitflag,output] = lsqcurvefit(...)[x,resnorm,residual,exitflag,output,lambda] = lsqcurvefit(...)[x,resnorm,residual,exitflag,output,lambda,jacobian] =x0为初始解向量;xdata,ydata为满足关系ydata=F(x, xdata)的数据;lb、ub为解向量的下界和上界,若没有指定界,则lb=[ ],ub=[ ];options为指定的优化参数;fun为拟合函数,其定义方式为:x = lsqcurvefit(@myfun,x0,xdata,ydata),其中myfun已定义为function F = myfun(x,xdata)F = …% 计算x处拟合函数值fun的用法与前面相同;resnorm=sum ((fun(x,xdata)-ydata).^2),即在x处残差的平方和; residual=fun(x,xdata)-ydata,即在x处的残差;exitflag为终止迭代的条件;output为输出的优化信息;lambda为解x处的Lagrange乘子;jacobian为解x处拟合函数fun的jacobian矩阵。
例:lsqcurvefit()优化程序Data = ...[];t = Data(:,1);y = Data(:,2);% axis([0 2 6])plot(t,y,'ro')title('Data points')%We would like to fit the function y = c(1)*exp(-lam(1)*t) + c(2)*exp(-lam(2)*t) to the data %The lsqcurvefit function solves this type of problem easily.%To begin, define the parameters in terms of one variable x:%x(1) = c(1)%x(2) = lam(1)%x(3) = c(2)%x(4) = lam(2)%Then define the curve as a function of the parameters x and the data t:F = @(x,xdata)x(1)*exp(-x(2)*xdata) + x(3)*exp(-x(4)*xdata);x0 = [1 1 1 0];[x,resnorm,~,exitflag,output] = lsqcurvefit(F,x0,t,y)hold onplot(t,F(x,t))hold offFsumsquares = @(x)sum((F(x,t) - y).^2);opts = optimset('LargeScale','off');[xunc,ressquared,eflag,outputu] = ...fminunc(Fsumsquares,x0,opts)fprintf(['There were %d iterations using fminunc,' ...' and %d using lsqcurvefit.\n'], ...,fprintf(['There were %d function evaluations using fminunc,' ...' and %d using lsqcurvefit.'], ...,type fitvectorx02 = [1 0];F2 = @(x,t) fitvector(x,t,y);[x2,resnorm2,~,exitflag2,output2] = lsqcurvefit(F2,x02,t,y)fprintf(['There were %d function evaluations using the 2-d ' ...'formulation, and %d using the 4-d formulation.'], ...,x0bad = [5 1 1 0];[xbad,resnormbad,~,exitflagbad,outputbad] = ...lsqcurvefit(F,x0bad,t,y)hold onplot(t,F(xbad,t),'g')legend('Data','Global fit','Bad local fit','Location','NE')hold offfprintf(['The residual norm at the good ending point is %f,' ...' and the residual norm at the bad ending point is %f.'], ...resnorm,resnormbad)displayEndOfDemoMessage(mfilename)拟合效果如下:Data points00.20.40.60.81 1.2 1.4 1.6 1.82直线的最小二乘拟合:y=a+bx式中有两个待定参数,a代表截距,b代表斜率。
对于等精度测量所得到的N组数据(xi,yi),i=1,2……,N,xi值被认为是准确的,所有的误差只联系着yi。
