Matlab对电磁学中等量异种点电荷电场线的不完整演示
点电荷系电场线与等势面的MATLAB仿真
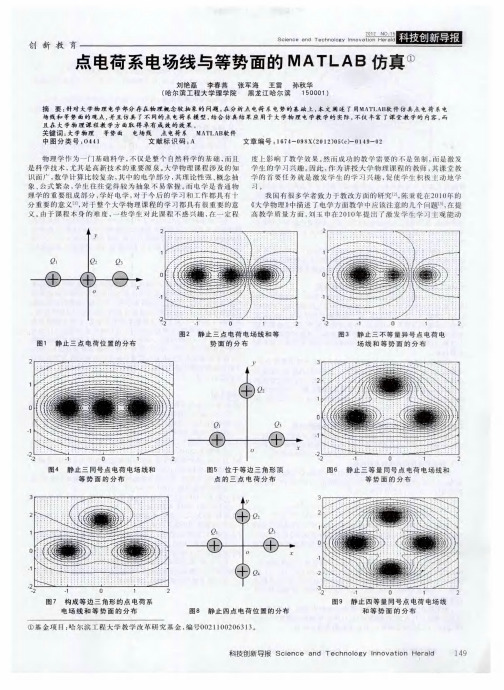
() 3
4。 —) 4。 z + 船√ a+ a√ + f z - e
取 四点 电荷 同号 , =Q =Q = 、 =l 用MATI 软 件 仿真 Q Q =1 a , AB 得到 的 四 等 量 同 号 点 电荷 电场 线 和 等势 面 分 布 如 图9 示 。 所 改变 电
鱼
Sci nce e an Techn o i ovaton d ol gy nn i Her l ad
创 新 教 育
U :— — — — 一 +一 一 +一一
4。 a+ 4。 √ 4。 一 z a√+) z√ 一j 肥√ + '( 6 s + f )
图7 示 。 所
2. 静 止 四点 电荷构 成 的点 电荷 系 2 静 止 四 点 电荷 构 成 的 点 电荷 系统 如 图8 示 。 所
点 电荷 的 电量 分 别 为Q 、 、 Q , Q,Q 、 分别 位 于 边 长为 2 的 正 方 a
图1 静 止 四 等量 异 号点 电荷 电场 线和 等 势 面 的分 布 0
学过程中 , 力于增加学生的学习兴趣 , 高课堂教学的效果 。 致 提
3 结 语
由此可见, 用M A AB 件 仿 真 点 电荷 系的 电场 线 和 等 势 面 TL 软 分 布 是 可 行 的 , 用 此 软 件 可 以 仿 真 不 同 类 型 的 点 电 荷 系 的 电 场 利 线 和 等 势 面分 布 , 只要 是 点 电荷 系电荷 分 布 已知 , 系统 的 电势 函数 能 够 用 理 论 公 式 表 示 出来 。 则将 很 容 易 的 用M ATL 软 件 仿 真 。 AB 得到 的分 布 图 可 以 使 教学 过 程 更 生 动 和 形 象 化 , 学 生 消 除 对 电 让 学 部 分 学 习 的 恐惧 。 师 在 上 课 前 可 将 点电 荷 系的 模 型 与 仿 真 结 教 果作 好 , 并且 一 旦 模 型建 立 , 师 在 课堂 授 课 时 可随 意 更 改 电 荷 的 教 电 量 与位 置 坐 标 参 数 , 时 只 需 几 分 钟 , 用 重新 仿 真也 只需 1 钟 左 分 右 。 果需 要将 电荷 的 电量 与 位 置坐 标 变 化 对 电场 线 和 等 势 面 分 如 布 的影 响 做 得 更生 动 性 形 象 , 则可 用 现 有 的g tr me e fa 函数 , 其 分 对
讲稿版利用Matlab模拟点电荷电场的分布

利用MATLAB 模拟点电荷电势的分布一、目的1.熟悉单个点电荷及一对点电荷的电势分布情况;2.学会使用MATLAB 进行数值计算,并绘出相应的图形;二、原理根据库仑定律:在真空中,两个静止点电荷之间的作用力与这两个电荷的电量乘积成正比,与它们之间距离的平方成反比,作用力的方向在两个电荷的连线上,两电荷同号为斥力,异号为吸引力,它们之间的力F 满足:R RQ Q k F 221=(式1) 由电场强度E 的定义可知:R RkQ E 2=(式2) 对于点电荷,根据场论基础中的定义,有势场E 的势函数为R kQ U =(式3) 在MATLAB 中,由以上公式算出各点的电势U ,可以用MATLAB 自带的库函数绘出相应的电势分布情况。
三、MATLAB 基本语法(一)标识符与数标识符是标志变量名、常量名、函数名和文件名的字符串的总称。
(二)矩阵及其元素的赋值赋值就是把数赋予代表常量或变量的标识符。
MATLAB 中的变量或常量都代表矩阵,标量应看作1×1价的矩阵。
赋值语句的一般形式为变量=表达式(或数)列如,输入语句a=[1 2 3;4 5 6;7 8 9]则显示结果为a=1 2 34 5 67 8 9输入 x=[1 2 3 4 5 6 7 8 9]结果为x= 1 2 3 4 5 6 7 8 9可以看出,矩阵的值放在方括号中,同一行中各元素之间以逗号或空格分开,不同行的元素以分号隔开。
语句的结尾可用回车或逗号“,”,此时会立即显示运算结果;如果不希望显示结果,就以分号“;”结尾再回车,此时运算仍然执行,只是不作显示。
变量的元素用圆括号“()”中的数字(也称为下标)来注明,一维矩阵(也称数组)中的元素用一个下标表示,二维矩阵可有两个下标数,以逗号分开。
在MATLAB中可以单独给元素赋值,例如,a(2,3)=6,x(2)=2等。
(三)元素群运算把n×m矩阵中的每个元素当作对象,成群地执行某种运算,称为元素群运算。
matlab表示等量异号电荷电势分布

matlab表示等量异号电荷电势分布
等量异号电荷电势分布是一种物理现象,它描述了两个不同电荷的电势分布。
电荷的电势分布是由电荷的数量和位置决定的,它可以用来描述电荷的分布情况。
Matlab是一种非常强大的数学软件,它可以用来模拟等量异号电荷电势分布。
Matlab可以用来模拟电荷的位置和数量,并且可以计算出电荷的电势分布。
Matlab可以用来模拟不同类型的电荷,包括正电荷、负电荷和中性电荷。
Matlab可以用来模拟等量异号电荷电势分布的变化情况。
它可以模拟电荷的
位置和数量的变化,以及电荷的电势分布的变化。
Matlab可以用来模拟不同类型
的电荷,以及不同类型电荷的电势分布。
Matlab可以用来模拟等量异号电荷电势分布的变化情况,这对于研究电荷的
电势分布非常有用。
Matlab可以用来模拟不同类型的电荷,以及不同类型电荷的
电势分布,这有助于我们更好地理解电荷的电势分布。
Matlab可以用来模拟等量
异号电荷电势分布,这有助于我们更好地理解电荷的电势分布,以及电荷的分布情况。
Matlab对电磁学中等量异种点电荷电场线的不完整演示

Matlab对电磁学中等量异种点电荷电场线的不完整演示Matlab对电磁学中等量异种点电荷电场线的不完整演示——总结分析——09物本——薛花——090501410581、实验目的:利用matlab对等量异种点电荷电场线的绘制的演示,加深了解等量异种点电荷电场线的分布情况,同时熟悉matlab在电磁学中的应用。
2、实验原理物理推导:首先建立电场线的微分方程,因为电场中任意一点的电场方向都沿该电场线的切线方向,所以满足:dy/dx=Ey/Ex引入参变量t得到:dx/Ex=dy/Ey=dt设二点电荷位于(-1,0)(1,0),二点电荷“电量”为q1,q2,由库仑定律和电场的叠加原理,得出下列微分方程:x’=dx/dt=Ex=q1(x+2)/[(x+2)2 +y2 +0.01]3/2+ q2(x-2)/[(x-2)2 +y2 +0.01]3/2 y’=dy/dt=Ey=q1y/[(x+2)2 +y2+0.01]3/2+ q2y/[(x-2)2 +y2+0.01]3/23、程序:微分方程的函数文件:function ydot=dcxlfun(t,y,flag,p1,p2) %p1,p2是参量,表示电量ydot=[p1*(y(1)+2)/(sqrt(((y(1)+2).^2+y(2).^2)+0.01 ).^3)-...p2*(y(1)-2)/(sqrt((( (y(1)-2).^2+y(2).^2)+0.01 ).^3); %dx/dt=Exp1*y(2)/(sqrt(( (y(1)+2).^2+y(2).^2)+0.01 ).^3)-...p2*y(2)/(sqrt(( (y(1)-2).^2+y(2).^2)+0.01).^3)]; %dy/dt=Ey这里的y是微分方程的解矢量,它包含俩个分量,y(1)表示x,y(2)表示y,解出y后就得到了x与y的关系,即可依次绘制出电场线。
微分方程的主程序:p1=1;p2=1; %点电荷所带电量axis([-5,5,-5,5]); %设定坐标轴范围hold on %图形控制,不可擦出模式plot(1,0,'*r'); plot(-1,0,'*r') %绘制两源电荷a=(pi/24):pi/12:(2*pi-pi/24); %圆周上电场线起点所对应的角度b=0.1*cos(a);c=0.1*sin(a); %电场线起点所对应的相对坐标b1=-1+b;b2=1+b; %把起点圆周的圆心放在源电荷处b0=[b1 b2]; c0=[c c]; %初始条件,所有电场线的起点for i=1:48 %循环求解48次方程[t,y]=ode45('dcxlfun',[0:0.05:40],[b0(i),c0(i)],[],p1,p2);%调用ode45求解,对应一个初条件(起点),求解一条电场线plot(y(:,1),y(:,2),'b') %绘制出此条电场线end %结束循环4、程序图:由于学习不够深入,没有做出正确到位的程序,程序图没有运行出来,所以没有程序图。
电磁场 点电荷 电场线 电势 MATLAB 仿真 中南大学

电磁场理论 实验一——利用Matlab 模拟点电荷电场的分布一.实验目的:1.熟悉单个点电荷及一对点电荷的电场分布情况;2.学会使用Matlab 进行数值计算,并绘出相应的图形;二.实验原理:根据库伦定律:在真空中,两个静止点电荷之间的作用力与这两个电荷的电量乘积成正比,与它们之间距离的平方成反比,作用力的方向在两个电荷的连线上,两电荷同号为斥力,异号为吸力,它们之间的力F 满足: R RQ Q k F ˆ212= (式1)由电场强度E 的定义可知:R RkQ E ˆ2= (式2)对于点电荷,根据场论基础中的定义,有势场E 的势函数为 (式3)而 U E -∇= (式4) 在Matlab 中,由以上公式算出各点的电势U ,电场强度E 后,可以用Matlab 自带的库函数绘出相应电荷的电场分布情况.三.实验内容:1. 单个点电荷点电荷的平面电力线和等势线真空中点电荷的场强大小是E=kq /r^2 ,其中k 为静电力恒量, q 为电量, r 为点电荷到场点P(x,y)的距离.电场呈球对称分布, 取电量q> 0, 电力线是以电荷为起点的射线簇.以无穷远处为零势点, 点电荷的电势为U=kq /r,当U 取常数时, 此式就是等势面方程.等势面是以电荷为中心以r 为半径的球面.●平面电力线的画法在平面上, 电力线是等角分布的射线簇, 用MATLAB 画射线簇很简单.取射线的半径为( 都取国际制单位) r0=0.12, 不同的角度用向量表示( 单位为弧度)th=linspace(0,2*pi,13).射线簇的终点的直角坐标为: [x,y]=pol2cart(th,r0).插入x 的起始坐标x=[x; 0.1*x].同样插入y 的起始坐标, y=[y; 0.1*y], x 和y 都是二维数组, 每一列是一条射线的起始和终止坐标.用二维画线命令plot(x,y)就画出所有电力线.●平面等势线的画法在过电荷的截面上, 等势线就是以电荷为中心的圆簇, 用MATLAB 画等势线更加简单.静电力常量为k=9e9, 电量可取为q=1e- 9; 最大的等势线的半径应该比射线的半径小一点? r0=0.1.其电势为u0=k8q /r0.如果从外到里取7 条等势线, 最里面的等势线的电势是最外面的3 倍, 那么各条线的电势用向量表示为:u=linspace(1,3,7)*u0.从- r0 到r0 取偶数个点, 例如100 个点, 使最中心点的坐标绕过0, 各点的坐标可用向量表示: x=linspace(- r0,r0,100), 在直角坐标系中可形成网格坐标: [X,Y]=meshgrid(x).各点到原点的距离为: r=sqrt(X.^2+Y.^2), 在乘方时, 乘方号前面要加点, 表示对变量中的元素进行乘方计算.各点的电势为U=k8q. /r, 在进行除法运算时, 除号前面也要加点, 同样表示对变量中的元素进行除法运算.用等高线命令即可画出等势线contour(X,Y,U,u), 在画等势线后一般会把电力线擦除, 在画等势线之前插入如下命令hold on 就行了.平面电力线和等势线如图1, 其中插入了标题等等.越靠近点电荷的中心, 电势越高, 电场强度越大, 电力线和等势线也越密.-0.2-0.15-0.1-0.0500.050.10.15-0.2-0.15-0.1-0.0500.050.10.15xy单个点电荷的电场线与等势线图1● 点电荷的立体电力线和等势面 立体电力线的画法先形成三维单位球面坐标, 绕z 轴一周有8 条电力线[X,Y,Z]=sphere(8),每维都是9×9 的网格矩阵, 将X 化为行向量, 就形成各条电力线的终点x 坐标x=r 0=X(:)′, 其他两个坐标也可同样形成终点坐标y=r 0+Y(:)' , z=r 0+Z(:)' .对x 坐标插入原点x=[x(zeros(size(x))], 其他两个坐标如下形成y=[y(zeros(size(y))], z=[z(zeros(size(z))], 用三维画线命令plot3(x,y,z), 就画出所有电力线.● 立体等势面的画法画5 条等势面时, 各面的电势为u=linspace(1,3,5)+u0, 各等势面的半径为r=k6q. /u, 其中第一个球面的半径为rr=r(1).三维单位球面的坐标可由[X,Y,Z]=sphere 命令形成, 每维都是21×21 的网格矩阵, 由于外球会包围内球, 因此把球面的四分之一设为非数, 表示割去该部分Z(X<0&Y<0)=nan. 用曲面命令可画出第一个曲面surf(rr6X,rr6Y,rr6Z), 只要取不同的半径就能画出不同的等势面.为了使等势面好看, 可设置一个颜色浓淡连续变化的命令shading interp.点电荷的立体电力线和等势面如图2, 旋转图片可从不同的角度观察.0.2x正电荷电场线等势面的三维图形yz图22 一对点电荷● 平面等势线的画法仍然用MATLAB 的等高线命令画等势线.对于正负两个点电荷, 电量不妨分别取q1=2e- 9,q2=- 1e- 9, 正电荷在x 轴正方, 负电荷在x 轴负方, 它们到原点的距离定为a=0.02; 假设平面范围为xx0=0.05,yy0=0.04, 两个坐标向量分别x=linspace(- xx0,xx0,20)和y=linspace(- yy0,yy0,50).设置平面网格坐标为[X,Y]=meshgrid(x), 各点到两电荷的距离分别为r1=sqrt((X- a).^2+Y .^2)和r2=sqrt((X+a).^2+Y .^2).各点的电势为U=k6q1. /r1+k6q2. /r2, 取最高电势为u0=50, 最低电势取其负值.在两者之间取11 个电势向量u=linspace (u0,- u0,11), 等高线命令contour(X,Y ,U,u,'k- ' )用黑实线, 画出等势线如图4所示, 其中, 左边从里到外的第6 条包围负电荷的等势线为零势线.● 平面电力线的画法利用MATLAB 的箭头命令, 可用各点的电场强度方向代替电力线.根据梯度可求各点的场强的两个分量[Ex,Ey]=gradient(- U),合场强为E=sqrt(Ex.^2+Ey.^2).为了使箭头等长, 将场强Ex=Ex. /E,Ey=Ey. /E 归一化, 用箭头命令quiver(X,Y,Ex,Ey)可标出各网点的电场强度的方向,异号点电荷对的场点方向如图3 所示.为了画出连续的电力线, 先确定电力线的起点.电荷的半径可取为r 0=0.002, 如图4 所示, 假设第一条电力线的起始角为30 度, 其弧度为q=30+pi /180, 起始点到第一个点电荷的坐标为x1=r0+cos(q),y=r0+sin(q), 到第二个点电荷的坐标只有横坐标x2=2+a+x1 不同.用前面的方法可求出该点到两个电荷之间的距离r1 和r2, 从而计算场强的两个分量以及总场强Ex=q1+x1 /r1^3 +q2+x2 /r2^3, Ey=q1+y/r1^3+q2+y/r2^3, E=sqrt(Ex6Ex+Ey6Ey).下面只要用到场强分量与总场强的比值, 在计算场强分量时没有乘以静电力常量k.由于电力线的方向与场强的切线方向相同, 取线段为s=0.0001,由此可求出终点的坐标为x1=x1+s#Ex/E,y=y+s+Ey/E, 从而计算x2.以终点为新的起点就能计算其他终点.当终点出界时或者到达另一点电荷时, 这个终点可作为最后终点. 这种计算电力线的方法称为切线法.xy一对点电荷的电场分布图-0.05-0.04-0.03-0.02-0.010.010.020.030.040.05-0.05-0.04-0.03-0.02-0.0100.010.020.030.040.05图3xy一对不相等的电荷的等势线图和电场线图图4-10-5510点电荷电场分布的3-D 图图5部分M-file;1. 点电荷的平面电力线和等势线%点电荷的平面电力线和等势线%平面电力线的画法q=1e-9;r0=0.12;th=linspace(0,2*pi,13);[x,y]=pol2cart(th,r0);x=[x;0.1*x];y=[y;0.1*y];plot(x,y);grid onhold onplot(0,0,'o','MarkerSize',12) xlabel('x','fontsize',16)ylabel('y','fontsize',16)title('单个点电荷的电场线与等势线','fontsize',20)%平面等势线的画法k=9e9;r0=0.1;u0=k*q/r0;u=linspace(1,3,7)*u0;x=linspace(-r0,r0,100);[X,Y]=meshgrid(x);r=sqrt(X.^2+Y.^2);U=k*q./r;hold on;contour(X,Y,U,u)2. 一对电荷平面等势线和电场线图%一对电荷平面等势线和电场线图clear all;clf;%平面等势线的画法q1=2e-9;q2=-1e-9;a=0.02;%到原点的距离xx0=0.05;yy0=0.04;k=9e9;x=linspace(-xx0,xx0,20);y=linspace(-yy0,yy0,50);[X,Y]=meshgrid(x);r11=sqrt((xx0/1.7-a)^2+(yy0/1.7)^ 2);r22=sqrt((xx0/1.7+a)^2+(yy0/1.7)^ 2);r1=sqrt((X-a).^2+Y.^2);%各点到点电荷的距离r2=sqrt((X+a).^2+Y.^2);U=k*q1./r1+k*q2./r2;%各点的电势u0=k*q1/r11+k*q2/r22;u=linspace(u0,-u0,11); %取21个等势向量contour(X,Y,U,u,'k-');hold ongrid onplot(a,0,'o','MarkerSize',12);plot(-a,0,'o','MarkerSize',12);xlabel('x','fontsize',16);ylabel('y','fontsize',16);%平面电力线的画法[Ex,Ey]=gradient(-U);E=sqrt(Ex.^2+Ey.^2);Ex=Ex./E;Ey=Ey./E;hold on;quiver(X,Y,Ex,Ey);title('一对不相等的电荷的等势线图和电场线图','fontsize',20)clear;3. 立体电力线的画法%立体电力线的画法q=1e-9;[X,Y,Z]=sphere(8);r0=0.18;r1=0.2;k=9e9;u0=k*q/r0;x=r1*X(:)';y=r1*Y(:)';z=r1*Z(:)';x=[x;zeros(size(x))];y=[y;zeros(size(y))];z=[z;zeros(size(z))];plot3(x,y,z)hold on;%立体等势线之画法u=linspace(1,3,5)*u0;%画5 条等势面时, 各面的电势为u=linspace(1,3,5)+u0,r=k*q./u;%各等势面的半径为r=k6q. /u[X,Y,Z]=sphere;Z(X<0&Y<0)=nan;surf(r(1)*X,r(1)*Y,r(1)*Z);%第一到第五个球面surf(r(2)*X,r(2)*Y,r(2)*Z);surf(r(3)*X,r(3)*Y,r(3)*Z);surf(r(4)*X,r(4)*Y,r(4)*Z);surf(r(5)*X,r(5)*Y,r(5)*Z);shading interp %个颜色浓淡连续变化的命令shading interp.xlabel('x','fontsize',16);ylabel('y','fontsize',16);zlabel('z','fontsize',16);title('正电荷电场线等势面的三维图形','fontsize',20);clear;4.clear all;clf;q1=1;q2=1;a=0.02;xx0=0.05;yy0=0.04;k=9e9;x=linspace(-xx0,xx0,20);y=linspace(-yy0,yy0,50);[X,Y]=meshgrid(x);r11=sqrt((xx0/1.7-a)^2+(yy0/1.7)^ 2);r22=sqrt((xx0/1.7+a)^2+(yy0/1.7)^ 2); r1=sqrt((X-a).^2+Y.^2);r2=sqrt((X+a).^2+Y.^2);U=k*q1./r1+k*q2./r2;u0=k*q1/r11+k*q2/r22;u=linspace(u0,-u0,11);contour(X,Y,U,u,'k-');hold on[Ex,Ey]=gradient(-U);E=sqrt(Ex.^2+Ey.^2);Ex=Ex./E;Ey=Ey./E;dth1=20;th1=(dth1:dth1:180-dth1)*pi/180; r0=a/5;x1=r0*cos(th1)+a;y1=r0*sin(th1);streamline(X,Y,Ex,Ey,x1,y1);streamline(-X,-Y,-Ex,-Ey,x1,-y1);q=abs(q1/q2);dth2=dth1/q;th2=(180-dth2:-dth2:dth2)*pi/180;x2=r0*cos(th2)-a;y2=r0*sin(th2);streamline(X,Y,Ex,Ey,x2,y2);streamline(X,-Y,Ex,-Ey,x2,-y2);grid onplot(a,0,'o','MarkerSize',12);plot(-a,0,'o','MarkerSize',12);xlabel('x','fontsize',16);ylabel('y','fontsize',16);title('一对点电荷的电场分布图');clear;clear all;clf;q1=1;q2=1;a=0.02;xx0=0.05;yy0=0.04;k=9e9;x=linspace(-xx0,xx0,20);y=linspace(-yy0,yy0,50);[X,Y]=meshgrid(x);r11=sqrt((xx0/1.7-a)^2+(yy0/1.7)^ 2);r22=sqrt((xx0/1.7+a)^2+(yy0/1.7)^2);r1=sqrt((X-a).^2+Y.^2);r2=sqrt((X+a).^2+Y.^2);U=k*q1./r1+k*q2./r2;u0=k*q1/r11+k*q2/r22;u=linspace(u0,-u0,11);contour(X,Y,U,u,'k-');hold on[Ex,Ey]=gradient(-U);E=sqrt(Ex.^2+Ey.^2);Ex=Ex./E;Ey=Ey./E;dth1=20;th1=(dth1:dth1:180-dth1)*pi/180;r0=a/5;x1=r0*cos(th1)+a;y1=r0*sin(th1);streamline(X,Y,Ex,Ey,x1,y1);streamline(-X,-Y,-Ex,-Ey,x1,-y1);q=abs(q1/q2);dth2=dth1/q;th2=(180-dth2:-dth2:dth2)*pi/180;x2=r0*cos(th2)-a;y2=r0*sin(th2);streamline(X,Y,Ex,Ey,x2,y2);streamline(X,-Y,Ex,-Ey,x2,-y2);grid onplot(a,0,'o','MarkerSize',12);plot(-a,0,'o','MarkerSize',12);xlabel('x','fontsize',16);ylabel('y','fontsize',16);title('一对点电荷的电场分布图');clear;5.[x,y]=meshgrid(-2:0.1:2,-2:0.1:2);%建立数据网格z=1./sqrt(x.^2+(y-1).^2+0.01)-1./sqrt(x.^2+(y+1).^2+0.01);%电势的表达式surfl(x,y,z);%三维曲面绘图shading interp %平滑i维曲面title('点电荷电场分布的3-D图')。
用Matlab研究电磁场的可视化PPT课件

2021/6/7
25
部分资料从网络收集整 理而来,供大家参考,
感谢您的关注!
V=c0*e./sqrt((X+0.2).^2+Y.^2)+c0.*q(i)./sqrt((X-0.2).^2+Y.^2); [Ex,Ey]=gradient(-V,h); figure(i) contour(X(:,:,1),Y(:,:,1),V,...
[20,-20,19,-19,18,-18,17,-17,... 16,-16,15,-15,14,-14,13,-13,... 12,-12,11,-11,10,-10]); axis([-0.38,0.38,-0.28,0.28]) hold on
E (3-1)V 根据题意,真空中若以无穷远为电势零点,则在两个点电 荷的电场中,空间的电势分布为:
VV1V(23-24)q10r14q20r2
2021/6/7
14
程序实现: clear all ep0=8.85*1e-12; c0=1/(4*pi*ep0); e=1.60e-10; h=0.018; x=-0.5:h:0.5; y=-0.5:h:0.5; [X,Y]=meshgrid(x,y); q=[e;1.9*e]; for i=1:2
Matlab是国际公认的最优秀的科技应用软件。将Matlab引入电磁学, 可以利用其可视化功能对电磁学现象进行计算机模拟。本论文就是利用 Matlab软件来研究静电场的分布、磁场的分布和带电粒子在电磁场中的 运动等问题的可视化。
2021/6/7
2
主要内容
• Matlab简介 • 相关电磁场知识 • Matlab在电磁场中的应用
、~=不等于 例如:2+2 ~= 4 ans = 0; 2+2 = 4 ans = 1 2)逻辑运算 逻辑运算符: & 与, | 或, ~ 非。 例如: a=[1 2];
异种不等量电荷的电场线及电势线

.问题分析:研究双电荷静电系统的电力线和等势线的分布,设在(-a ,0)处有一正电荷q 1,在(a ,0)处有一负电荷q 2,则在电荷所在平面内任意一点(坐标为(x ,y ))的电势和场强分别为:1212(,)44q q V x y r r πεπε=+, E V =-∇. 其中:r1=y a x 22++)( r2=y a -x 22+)(二.问题解决: 为简化模型,可令114πε=,a=3,MatlAB 语言描述如下:clear allclcclose allq1=input('请输入q1: ');q2=input('请输入q2: ');a=3;[X,Y]=meshgrid(-10:0.7:10,-10:0.7:10);rm=sqrt((X-a).^2+Y.^2);rp=sqrt((X+a).^2+Y.^2);V=q1*(1./rp)+q2*(1./rm);[Ex,Ey]=gradient(-V);E=sqrt(Ex.^2+Ey.^2);Ex=Ex./E;Ey=Ey./E;cv=linspace(min(min(V)),max(max(V)),100);contour(X,Y,V,cv, 'r-');%用红线画等势线;hold onquiver(X,Y,Ex,Ey,1,'b');%用蓝线画电场线;title('\fontname{宋体}\fontsize{15}双电荷静电系统的电场线和电势线')hold off(1)请输入q1: 5 请输入q2: -1此时绘出图形为:(2)请输入q1: 3 请输入q2: -1此时绘出图形为:三.思考感悟:由以上描绘的电场线以及等势线明显可看到:异种电荷形成电场时,电荷量越小,其周围等势线越稀疏,电场线越密集;电荷量越大,其周围等势线越密集,电场线越稀疏。
与理论分析一致。
(资料素材和资料部分来自网络,供参考。
电磁场matlab仿真实验

电磁场matlab 仿真实验一实验一:[例7-5]试分析一对等量异号的电荷周围空间上的电位和电场分布情况。
分析:将等量异号的电荷的几何中心放置于坐标原点位置,则它们在空间某点p 处产生的点位为:()G q g g q r r q r q r q02102102010*******πξπξπξπξπξϕ=-=⎪⎪⎭⎫ ⎝⎛-=-=其中G 为格林函数()()22222cos 2/cos 2/1r dr d r r dr d r +-=+-=θθ将G 用片面积坐标表示为⎪⎪⎭⎫⎝⎛=12ln g g G 在编程时,将G 当作点位函数处理,并利用梯度求出唱腔E=-▽φ。
用matlab 的m 语言编写的程序如下:[x,y]=meshgrid(-10:0.1:10);[Q,R]=cart2pol(x,y);R(R<=1)=NaN;q=input('请输入电偶极子的电量q =')%原程序有误,以此为准d=input('请输入电偶极子的间距d =')%原程序有误,以此为准E0=8.85*1e-12;K0=q/4/pi/E0;g1=sqrt((d./2).^2-d.*R.*cos(Q)+R.^2);%原程序有误,以此为准g2=sqrt((d./2).^2+d.*R.*cos(Q)+R.^2);%原程序有误,以此为准G=log(K0*g2./g1);contour(x,y,G,17,'g');hold on[ex,ey]=gradient(-G);tt=0:pi/10:2*pi;%原程序未定义tt ,以此为准sx=5*sin(tt);sy=5*cos(tt);streamline(x,y,ex,ey,sx,sy);xlabel('x');ylabel('y');hold off;当运行此程序后,按提示输入电偶极子电量和嗲耨集子间距如下:请输入电偶极子的电量q =0.5*1e-10请输入电偶极子的间距d =0.01即可汇出入图说使得嗲耨集资周围的长的分布图。
基于Matlab模拟点电荷电场线和等势线

基于Matlab模拟点电荷电场线和等势线作者:张雷来源:《科技视界》2019年第34期【摘要】在静电场中引入电场强度和电势后,通过等电势线图和场强分布图可以具体的描述静电场这种抽象的物质场。
利用计算机技术来模拟静电场等物质场逐渐成为趋势,本文介绍了如何利用Matlab软件模拟点电荷的电场线和等势线。
【关键词】点电荷;电场线;等势线;Matlab中图分类号: O441.1-4;G642 文献标识码: A 文章编号: 2095-2457(2019)34-0070-001DOI:10.19694/ki.issn2095-2457.2019.34.028Simulation of Electric Field and Equipotential line of Point Charge with MatlabZHANG Lei(School of mechanical and material engineering,xi’an university of arts and s ciences,Xi’an Shaanxi 710065, China)【Abstract】The electrostatic field which is a matter field so the abstract to understand can be described in specific equipotential line and electric field line. The use of computer technology to simulate the electrostatic field gradually become a trend. This paper introduces how to use Matlab software to simulate point charge electric field lines and equipotential line.【Key words】Point charge; The electric field lines; Equipotential line; Matlab1 点电荷的电场点电荷是电磁学中最简单的一种理想化模型。
MATLAB在电磁学中的应用

电磁学1、点电荷的电场研究真空中,两个带正电的点电荷,在电量相同和电量不同情况下的电场分布。
V=V i+V2= q i+—^ ,E=-▽ V小%* 4“0「22、程序实现主程序文件名为point.mclear allep0=8.85*le-12; %真空中的电容率cO=F(4*pi*epO);e=1.6e-10;h=0.018;x=-0.5:h:0.5;y=-0.5:h:0.5;str{1}=两同号等量点电荷'str{2}=两同号不等量点电荷'[X,Y]=meshgrid(x,y);q=[e;1.9*e];for i=1:2V=c0*e./sqrt((X+0.2).A2+Y.A2)+c0.*q(i)./sqrt((X-0.2).A2+Y.A2); %求电势[Ex,Ey]=gradie nt(-V,h); % 求电场figure(i)cou nter(X(:,:,1),Y(:,:,1),V;・%等势面[20,-20,19,-19,18,-18,17,-17,16,-16,15,-15,14,-14,13,-13,12,-12,11,-11,10,-10"; Axis([-0.38,0.38,-0.28,0.28])hold onphi=0:pi/17:2*pi; %以下画电场线sx1=0.2+0.01*cos(phi);sy 1=0.01*si n( phi);streamli ne(X(:,:,1),Y(:,:,1),Ex,Ey,sx1,sy1);hold onsx2=-0.2+0.01*cos(phi);sy2=0.01*si n( phi);streamli ne(X(:,:,1),Y(:,:,1),Ex,Ey,sx2,sy2);title(str(i))text(-0.215,0,'+:'fo ntsize;20); %标示点电荷text(0.185,0,'+:'fo ntsize,20);end二、带电细棒的电场1、若电荷Q均匀分布在长为L的细棒上,求真空中,带电细棒的电场在xy平面内的分布情况。
基于Matlab模拟点电荷电场线和等势线

基于Matlab模拟点电荷电场线和等势线电场线和等势线是理解电场分布的一个重要工具。
在Matlab中,我们可以使用特定的函数和工具箱来模拟和绘制电场线和等势线。
要模拟电场线和等势线,首先需要定义电场中的点电荷和电荷的分布。
对于一个点电荷,在Matlab中可以使用"charge()"函数定义其位置和大小。
例如,我们可以定义一个正电荷位于(0,0)处,并设置其电荷量为1:charge([0 0],1)对于分布在空间中的多个电荷,可以使用矢量或矩阵来存储其位置和大小。
例如,我们定义了三个电荷,分别位于(-1,0)、(1,0)和(0,1),且其电荷量依次为1、2、3:pos=[-1 0;1 0;0 1];charge=[1 2 3];charge(pos,charge)定义好电荷后,就可以计算电场线和等势线的分布。
在Matlab中,可以使用"streamline()"函数和"contour()"函数来分别计算和绘制电场线和等势线。
[X,Y]=meshgrid(-2:.2:2,-2:.2:2); %定义网格点Ex=@(x,y)x./((x+1).^2+y^2).^(1/2)-x./((x-1).^2+y^2).^(1/2); %定义库仑电场x方向分量Ey=@(x,y)y./((x+1).^2+y^2).^(1/2)-y./((x-1).^2+y^2).^(1/2); %定义库仑电场y方向分量startx=[0]; %定义起始点x坐标starty=[0]; %定义起始点y坐标streamline(X,Y,Ex,Ey,startx,starty);对于等势线的绘制,可以使用"contour()"函数。
该函数需要定义等势线函数(在这里,我们使用库仑势能定义等势线)和不同等势线对应的值。
例如,我们定义一个库仑势能,由两个位于(-1,0)和(1,0)的单位电荷产生:V=@(x,y)1./((x+1).^2+y^2).^(1/2)+1./((x-1).^2+y^2).^(1/2); %定义库仑势能 contour(X,Y,V([-5:.5:5; -5:.5:5])) %绘制等高线此外,我们还可以使用"quiver()"函数来绘制电场的矢量图,以更直观地展示电场的分布情况。
用MATLAB模拟双点电荷的电场和等位线

中图分类号 TP391.7
文献标识码 A 文章编号: 1002- 2422( 2007) 02- 0042- 02
Simulating the Electr ic Field and Isoelectr ic Line of ″Double Point Char ges″in MATLAB
Mo Zhao Hu Qiguang
q1 和 q2 分别代表双″点电荷″中两个点电荷的电量。 (q1x,q1y)代表点电荷 q1 的坐标位置,(q2x,q2y)代 表点电荷 q2 的坐标位置。 r1 为平面上任意一点到点电荷 q1 的距离,r2 为平面上 任意一点到点电荷 q2 的距离。
Ey=Ey./AEB cv=linspace(min(min(V)),max(max(V)),49)B 电位 contourf(X,Y,V,cv,' k- ' ) %画等位线 axis(' square' ) %图形标题
Abstr act Keywor d
The method of simulating the electric field and isoelectric line of ″Double Point Charges″is introduced,and the mathematic model is discussed.The program codes are also given in the paper. MATLAB Electric Field Isoelectric Line
版社,2002. [2] 梁灿彬. 电磁学. 北京:高等教育出版社,1992.
模拟图如图 2 所示。
* 张卫国 山东省东营职业学院中专部讲师(257091),研究方向:计算机网络和数据库应用
利用Matlab模拟点电荷系的电场线和等势面

利用Matlab模拟点电荷系的电场线和等势面陈伟;易志俊;丁益民【摘要】根据电场叠加原理,利用Matlab的绘图功能,绘出二维平面内点电荷系的等势面和电场线.以三个点电荷为例,模拟了它们的电场线和等势面,并通过改变电荷的位置和电荷量的大小对电场的分布情况进行分析比较,在教学中能起到很好的演示作用.【期刊名称】《大学物理实验》【年(卷),期】2014(027)003【总页数】3页(P94-96)【关键词】等势面;电场线;Matlab【作者】陈伟;易志俊;丁益民【作者单位】湖北大学,湖北武汉430062;湖北大学,湖北武汉430062;湖北大学,湖北武汉430062【正文语种】中文【中图分类】O4-39电场线和等势面是描述电场性质的重要的物理量,在物理教学中,通常需要绘制点电荷系的电场线和等势面,因此研究用计算机绘制电场线和等势面具有重要的现实意义。
Matlab是一种广泛应用于科研、工程计算和数值分析的高级语言,它以矩阵为基本的数据操作对象,进行高性能的数值计算和符号计算,并拥有强大的绘图功能。
在物理仿真中具有明显的优势。
近年来许多老师对用Matlab模拟点电荷电场进行了研究。
莫照等人通过数学建模的过程,将物理问题变成了数学问题,进而用Matlab模拟了双“点电荷”的电场和等位线[1];王明美也通过Matlab模拟了两个点电荷体系的电场线和等势线[2-3];向罗杰等人结合电场方程和泰勒展开式,分析电场线的性质,利用Mathematica模拟了共线的三个点电荷电场线的分布[4]。
本文首先计算出点电荷系在平面某点的电势叠加,利用Matlab的命令绘出等势面,然后结合电场线和等势面的垂直关系,绘出电场线。
这里对点电荷的分布以及电荷量没有特殊要求,由用户自己根据实际需要在一定范围内输入点电荷系的位置和电荷量,即可显示出其电场线和等势面,具有良好的普遍性和交互性,便于学生对点电荷系电场的规律进行探究式的学习。
电磁场的matlab仿真实验--m语言1

实验三:等量异号点电荷的电势分布一、实验目的与要求1.掌握命令窗口中直接输入语句,进行编程绘制等量异号点电荷的电势分布图;2.掌握二维网格和三维曲面绘图的语句。
二、实验类型设计三、实验原理及说明这里在命令窗口中直接输入简单的语句进行编程设计。
MATLAB有几千个通用和专用五、实验内容和步骤(一)建立等量异号点电荷的电势方程物理情景是oxy平面上在x=2,y=0处有一正电荷,x= -2,y=0处有一负电荷,根据计算两点电荷电场中电势的分布,由于(二)利用MA TLAB的函数, 绘制等量异号点电荷的电势分布图首先选定一系列的x和y后,组成了平面上的网络点,再计算对应每一点上的z值。
例如-5:0.2:5,-4:0.2:4分别是选取横坐标与纵坐标的一系列数值,meshgrid是生成数据网格的命令,[x,y]是xy平面上的坐标网格点。
z是场点(x ,y)的电势,要求写出z的表达式。
这里用到MA TLAB的函数mesh()描绘3D网格图,meshgrid()描绘在3D图形上加坐标网格,sqrt()求变量的平方根。
mesh()是三维网格作图命令,mesh(x,y,z)画出了每一个格点(x,y)上对应的z值(电势)。
在命令窗口中直接输入简单的语句,如下。
解1解2当场点即在电荷处时,会出现分母为零的情况,因此在r里加了一个小量0.01,这样既可以完成计算,又不会对结果的正确性造成太大影响。
另外需要注意的是表达式中的“./ ”、“.^ ”是对数组运算的算符,含义与数值运算中的“./ ”、“.^ ”相同,不同之处是后者只对单个数值变量进行运算,而前者对整个数组变量中的所有元素同时进行运算。
解2为了减少计算量,增加精确度,与先前的示例相比,计算范围由原先的-5<x<5 ,-4<y<4改为-2<x<2 ,-2<y<2 ;步长由0.5改为0.1,电荷位置也改在(-1,0)和(1,0)处。
用Matlab解决静电场中的问题

用M a t l a b解决静电场中的问题Last revision on 21 December 2020用M a t l a b 解决静电场中的问题【摘要】:Matlab 是一种用于算法开发,数据可视化,数值分析及数值图形生成的高级工具语言,它主要被应用于信号和图像处理,通讯,控制系统设计,测试和测量等广泛领域。
在本文中,我用Matlab 的功能使静电场里的某些模型(电场强度电势、电场线、等势线、等势面)可视化,方便了我们对有关静电场的知识的学习,提高了我们对知识的理解和运用能力,本文主要是从图像处理功能方面介绍了Matlab 语言在静电场一些问题中的应用。
【关键字】:Mtalab 电场强度 电势 电场线 等势线 等势面一、引言Matlab 是美国Mathworks 公司开发1984年推出的一套高性能的数值计算和可视化软件。
它是一种以矩阵运算为基础的交互式程序语言,其应用范围涵盖了当今几乎所有的工业应用与科学研究领域,,集数值分析、矩阵运算、信号处理和图形显示于一体。
.此外,Matlab 更强大的功能还表现在其有大量的工具箱(Toolbox),如:控制系统、数值模拟、信号处理及偏微分方程等工具箱。
因此,Matlab 已成为美国和其它发达国家大学教育和科学研究中必不可少的工具。
静电场中的电场线,等势线,等势面等图形是一种抽象的模型,在现实世界不具可视化的空间场的物体。
所以,形象的模拟出以上问题的图形,对于更进一步学习与研究电场知识有很大的意义。
静电场的问题学习与理解起来具有一定的特殊性:它既有理论数值的计算,又有图形图像的辅助处理与理解。
例如:形象的模拟出电场线,等势线,等势面,这能在教学中解决教师的授课难题,又能解决学生的理解上的困难。
近年来,一直有人在不断的探索这方面的问题,并且取得一定的成绩。
但还存在一定的缺陷,而Matlab 恰好解决了这些问题!这使得这些抽象问题能有一门精确的工具软件来处理完成。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Matlab对电磁学中等量异种点电荷电场线的不完整演示
——总结分析
——09物本
——薛花
——09050141058
1、实验目的:
利用matlab对等量异种点电荷电场线的绘制的演示,加深了解等量异种点电荷电场线的分布情况,同时熟悉matlab在电磁学中的应用。
2、实验原理物理推导:
首先建立电场线的微分方程,因为电场中任意一点的电场方向都沿该电场线的切线方向,所以满足:
dy/dx=Ey/Ex
引入参变量t得到:
dx/Ex=dy/Ey=dt
设二点电荷位于(-1,0)(1,0),二点电荷“电量”为q1,q2,由库仑定律和电场的叠加原理,得出下列微分方程:
x’=dx/dt=Ex=q1(x+2)/[(x+2)2 +y2 +0.01]3/2+ q2(x-2)/[(x-2)2 +y2 +0.01]3/2 y’=dy/dt=Ey=q1y/[(x+2)2 +y2+0.01]3/2+ q2y/[(x-2)2 +y2+0.01]3/2
3、程序:
微分方程的函数文件:
function ydot=dcxlfun(t,y,flag,p1,p2) %p1,p2是参量,表示电量
ydot=[p1*(y(1)+2)/(sqrt(((y(1)+2).^2+y(2).^2)+0.01 ).^3)-...
p2*(y(1)-2)/(sqrt((( (y(1)-2).^2+y(2).^2)+0.01 ).^3); %dx/dt=Ex
p1*y(2)/(sqrt(( (y(1)+2).^2+y(2).^2)+0.01 ).^3)-...
p2*y(2)/(sqrt(( (y(1)-2).^2+y(2).^2)+0.01).^3)]; %dy/dt=Ey
这里的y是微分方程的解矢量,它包含俩个分量,y(1)表示x,y(2)表示y,解出y后就得到了x与y的关系,即可依次绘制出电场线。
微分方程的主程序:
p1=1;p2=1; %点电荷所带电量
axis([-5,5,-5,5]); %设定坐标轴范围
hold on %图形控制,不可擦出模式
plot(1,0,'*r'); plot(-1,0,'*r') %绘制两源电荷
a=(pi/24):pi/12:(2*pi-pi/24); %圆周上电场线起点所对应的角度
b=0.1*cos(a);c=0.1*sin(a); %电场线起点所对应的相对坐标
b1=-1+b;b2=1+b; %把起点圆周的圆心放在源电荷处
b0=[b1 b2]; c0=[c c]; %初始条件,所有电场线的起点
for i=1:48 %循环求解48次方程
[t,y]=ode45('dcxlfun',[0:0.05:40],[b0(i),c0(i)],[],p1,p2);
%调用ode45求解,对应一个初条件(起点),求解一条电场线plot(y(:,1),y(:,2),'b') %绘制出此条电场线
end %结束循环
4、程序图:由于学习不够深入,没有做出正确到位的程序,程序图没有运行出来,所以没有程序图。
5、结果总结分析:正负和正正电荷电场线有许多不同,要注意初始值和间距的大小,以及方程中分母的值(不为0,加一个小小数0.01),善于研究,深入学习matlab,最终做出正确的程序,演示出符合正负点电荷的电场线分布的图形。
