等量及不等量电荷连线及中垂线场强电势
等量电荷电场线与等势线分布特点(简洁)

二.两点电荷连线的中垂线上,电场线方向均相 同,即场强方向均相同,且总与中垂线垂 直.在中垂线上到O点等距离处各点的场强相 等(O为两点电荷连线中点).
三.等量异种点电荷连线上以中点O场强最小, 中垂线上以中点O的场强为最大;
四.等量异种点电荷连线、中垂线上关于中于中点对称 处的场强大小相等、方向相反.
在连线的延长 线上,关于某 电荷对称的两 点电势不相等, 连线上的电势 高于延长线上 的电势
等量同种点电荷的等势线:是两簇对称曲线, 在AA′线上O点电势最低;在中垂线上O点电 势最高,向两侧电势逐渐降低,A、A′和B、 B′对称等势.
2
电荷对称的两点,延长线上的电势比连线上的电势低。
两点电荷连线中点O处场强为零,此处无电场 线.
中点O附近的电场线非常稀疏,但场强并不为 零.
两点电荷连线中垂线上,场强方向总沿线远离 O(等量正电荷).
在中垂线上从O点到无穷远,电场线先变密后 变疏,即场强先变强后变弱.
等量同种点电荷连线上以中点电场强度最小, 等于零.因无限远处场强E∞=0,则沿中垂线 从中点到无限远处,电场强度先增大后减小, 之间某位置场强必有最大值.
0 1
在中垂线上的电荷受到的静电力的方向总与中垂线垂直,因此,在中 垂线
上移动电荷时静电力不做功.中垂线为等势线且电势 为0(2).关于连线 对称的两点,电场强度大小相等,电势相同。关于中垂线对称的两点,电场 强度大小相等,电势不同。
0
关于正电荷对称的两点,延长线上的电势比连线上的电势高,关于负
等量电荷电场线的分布及电场强度、电势的特点分析

等量电荷电场线的分布及电场强度、电势的特点分析作者:廖贵生来源:《求知导刊》2014年第04期高二物理选修3-1教材中,在静电场中,“电场”这个概念很抽象,特别是对初学者来说,对等量电荷电场线分布及场强、电势特点模糊不清,以至在应用过程中经常出错。
1.等量电荷电场线分布电场线的特点:①电场线从正电荷或无限远出发,终止无限远或负电荷;②电场线在电场中不相交,这是因为在电场任意一点的场强不可能有两个方向;③在同一幅图中,可以用电场线的疏密来表示场强的大小:即电场线密的地方场强大,电场线疏的地方场强小。
2.等量电荷的场强(1)等量正、负点电荷。
等量正、负点的场强的大小用点的电荷的场强公式E=k—来计算。
根据公式可知,离场源电荷越远,场强越小;与场源电荷等距的各点组成球面上的场强大小相等。
方向:正点电荷的场强方沿着电场线的方向向外,负点电荷的场强方向沿着电场线向内。
(2)等量异种、同种电荷的场强。
在实际应用中,主要考查等量异种、同种电荷两条特殊线的场强,下面就等量异种、同种电荷两条特殊线(两电荷的连线上和两电荷连线上的中垂线)的场强进行分析。
等量异种电荷:例一:两电荷连线上。
如图1所示,在两电荷连线上任取一点G,设AG 长度为x,则G点场强EG为两点电荷分别在该点的场强EA、EB的矢量和,方向从A指向B (由正电荷指向负电荷一侧),由点电荷场强公式知:EG=EA+ EB=—+—=—∵x+(L-x)等于定值L,∴当x=(L-x),即x=—时,x与(L-x)乘积最大∴这时EG有最小值,即在两电荷连线中点O处场强最小,将x=—带入上式,可求得EG 最小值EGmin=——,方面由A指向B。
从O点向两侧逐渐增大,数值关于O点对称。
小结:等量异种电荷连线中点场强最小,靠近点电荷场强渐强,方向从正点荷指向负电荷。
例二:中垂线上。
如图2所示,在中垂线上,任取一点H,设OH=x,根据对称性知:EH 沿水平方向向右,即在中垂线上各点场强水平向右(垂直于中垂线指向负电荷一侧),沿中垂线移动电荷,电场力不做功,由电势差定义知:中垂线为一等势线,与无限远处等势,即各点电势为零。
等量同种、异种电荷电场强度和电势的定量比较

等量同种、异种电荷电场强度和电势的定量比较作者:杨杰来源:《理科考试研究·高中》2015年第02期平常教学中,关于等量同种、异种电荷连线上电场强度和电势的比较,往往更多地根据电场线的方向和分布定性地说明.由于电场线本身并不是客观存在的,而是人为引入的,再加上电场概念本身又比较抽象,不少同学对结论心存疑惑,更希望能够通过定量计算得出更具说服力的结论.笔者尝试着进一步分析发现,的确也可以通过定量计算进行说明,教学中也收到了理想的效果.一、等量同种电荷的电场强度和电势1.等量同种电荷的连线上①电场强度从电场线分布定性分析,a→o→b,由于电场线先变疏,后变密,所以电场强度先减小后增大.定量计算:设︱ab︱=L,︱aA︱=x,EA=kQx2,kQ(L-x)2,a→o过程中(x≤L2),x 变大, kQx2减小,kQ(L-x)2增大,∴EA减小.当x=L2时,Emin=Eo=0.由对称性可知,o→b过程中,电场强度不断增大.所以,a→o→b电场强度先减小后增大.②电势从电场方向定性分析,a→o,电场方向向右,o→b,电场方向向左.沿电场线方向电势降低.所以a→o→b,电势先减小后增大.定量计算:取无穷远处Ep=0,WA→∞=EPA-0,距电荷+Q距离为r处的A点的点电荷+q 的电势能,等于把它从这点移动到零势能位置时静电力做的功.EPA=WA→∞=∫∞rkQqr2dr=kQqr,则A点的电势φA=kQr.所以,到点电荷Q距离为r处的电势为φ=kQr(Q含正负,即正电荷在其周围产生的电势为正,负电荷在其周围产生的电势为负).在A点,a处的+Q在A点产生的电势为φ=kQx,b处的+Q在C点产生的电势为φ=kQL-x,所以等量同种电荷连线上的A点的电势φA=kQx+kQL-x=kQLx(L-x)=kQLL24-(L2-x)2,a→o过程中(x≤L2),x变大,φA减小,当x=L2时,φmin=4kQL.由对称性可知,o→b过程中,电势不断增大.所以,a→o→b,电势先减小后增大.2.等量同种电荷的中垂线上①电场强度从电场线分布定性分析,o→∞,电场线先变密,后变疏,所以,电场强度先增大后减小.定量计算:EC=2E1cosθ=8kQL2sin2θcosθ=42kQL22cos2θsin2θsin2θ.当2cos2θ=sin2θ时,即tanθ=2,场强有最大值Emax=1630kQL2.所以o→∞,电场强度先增大后减小.②电势从电场方向定性分析,电场方向沿o→∞方向.o→∞,电势降低.定量计算:a、b处的+Q在C点产生的电势均为kQL2sinθ=2kQsinθL所以φC=4kQsinθL,θ减小,φC减小,当θ=90°时,电势最高,φ0=φmax4kQL.所以o→∞,电势一直减小.二、等量异种电荷的电场强度和电势1.等量异种电荷的连线上①电场强度从电场线分布定性分析,a→o→b,由于电场线先变疏,后变密,所以电场强度先减小后增大.定量计算:同样设︱ab︱=L,︱aA︱=x,则EA-EO=kQx2 +kQ(L-x)2-8k QL2≥kQ[2x (L-x)2-8L2]=2kQ(L-2x)2x(L-x)L2≥0,所以EA≥EO,o点的电场强度最小,由对称性可知,a→o→b电场强度先减小后增大.②电势从电场方向定性分析,电场方向沿a→b方向,所以,a→b电势一直减小.定量计算:+Q在A点产生的电势为φ=kQx,-Q在C点产生的电势为φ=-kQL-x,所以φA=-kQx-kQL-x=kQ(L-2x)x(L-x),x增大,x(L-x)增大,(L-2x)减小,φA减小.所以,a→b电势一直减小.2.等量异种电荷的中垂线上①电场强度从电场线分布定性分析,o→∞,由于电场线越来越疏,所以,电场强度一直减小.定量计算:中垂线上任取一点C,Ec=8kQL2sin3θ,θ越小,EC越小.∴o→∞,E一直减小.②电势从电场方向定性分析,电场方向垂直于中垂线,沿o→∞方向移动电荷,电场力不做功,所以,o→∞,电势不变,且与无穷远处电势相等(电势为零).定量计算:+Q在C点产生的电势为φ=2kQsinθL,-Q在C点产生的电势为φ=-2kQsinθL.所以φC=0,o→∞,电势始终为0,中垂线为等势线.由此可见,无论通过定量计算还是定性分析,都会得出同样的结论.而定量分析能让学生经历概念规律的探究过程,使得原本抽象难懂的知识真实地呈现在学生眼前,加深了学生对同种、等量异种电荷的电场强度和电势的理解,有助于学生更好地解决与此相关的各类问题.下面笔者以一道典型的高考题为例,说明相关知识在解决实际问题中的重要作用.例1(2010年江苏单科第5题)空间有一沿x轴对称分布的电场,其电场强度E随x变化的图象如图所示.下列说法中正确的是().A.O点的电势最低B.x2点的电势最高C.x1和-x1两点的电势相等D.x1和x3两点的电势相等解析由题图知,该图象所反映的电场的特点:①在O处,场强为零,但电势最高;②在x1和-x1两点处,场强大小相等,方向相反,电势相等;③在x1和x3两点处,场强相同,但电势不同.由此可知,这个电场不是一个点电荷的电场,可能是两个点电荷形成的电场;从x=0到正负无穷远,场强有一个最大值,电势逐渐减小;当x趋近于正负无穷远时,场强和电势均为零.说明这是两个等量同种正电荷中垂线上的电场分布(如图所示).如果画出图象如右图所示,这就是09年江苏高考的第8题.同一个物理情境可以从不同的角度考查,但只要对等量同种、异种点电荷的电场、电势有准确的理解,问题自然就迎刃而解.答案C例2(2013年天津理综第6题)两个带等量正电的点电荷,固定在图中P、Q两点,MN 为PQ连线的中垂线,交PQ于O点,A点为MN上的一点.一带负电的试探电荷q,从A点由静止释放,只在静电力作用下运动.取无限远处的电势为零,则().A.q由A向O的运动是匀加速直线运动B.q由A向O运动的过程电势能逐渐减小C.q运动到O点时的动能最大D.q运动到O点时电势能为零解析等量正电荷连线的中垂线上,电场方向由O指向A,o→∞,电场强度先变大后变小,O点电场强度为零,A点电场强度大于零.又由于A点是中垂线上的任意一点,不一定是电场最强的特殊点,所以A到O的过程加速度是变化的,但不能确定是如何变化的,可能是一直减小,也可能先增大后减小.所以,A错误.带负电的试探电荷q,从A点由静止释放,所受静电力由A指向O,只在静电力作用下运动,A向O运动,电场力做正功,动能增加,电势能减小.取无限远处的电势为零,到O点时电势能为负,动能最大,所以,选项D错误,BC 正确.电场力减小,加速度逐渐减小的加速运动,q由A向O运动的过程电势能逐渐减小,q运动到O点时的动能最大,电势能不为零,AD错误.答案BC。
等量电荷的电场和电势分布

精心整理
精心整理 等量电荷的电场分布
等量正电荷等量负电荷等量异种电荷
等量异种与等量同种点电荷连线和中垂线上场强的变化规律:
(1)等量异种点电荷连线上中点场强最小,中垂线上各点中点的场强最大;等量同种点电荷连线上中点场强最小,等于零。
因为无穷远处场强为零,则沿等量同种点电荷中垂线从中点到无穷远处,电场强度先增大后减小,中间某位置必有最大值。
(2)等量异种点电荷连线和中垂线上关于中点对称处的场强相同;等量同种点电荷连线和中垂线
(1(2
)等量异种点电荷的连线上,从正电荷到负电荷电势越来越低,中垂线是一等势线,若沿中垂线移动电荷至无穷远,电场力不做功,因此若取无穷远处电势为零,则中垂线上各点的电势也为零.因此从中垂线上某点不沿中垂线移动电荷到无穷远,电场力做功仍为零.。
两等量点电荷的场强、电势、电势能的情况分析

两等量点电荷连线及中垂线上的场强、电势和电势能的情况分析1.等量同种电荷(1)两点电荷的连线上分析:在其连线上的中点,由于Q 相等,r相等,即E 大小相等,而两点电荷在的场强方向相反,故合场强为零,由||||212212r Q k r Q k E E E -=-=知,从中点往两边合场强增大,且关于中点对称。
(2)两点电荷的中垂线上分析:中垂线上的某点的场强由两点电荷分别在该点的场强叠加而成。
由于中垂线上的点到线两端的距离相等,由2rQ k E =知|E 1|=|E 2|,即大小相等,方向如图2所示:把E 1、E 2进行合成,故合场强E 如图所示。
所以从中垂线上中点往两边场强先是由零增大,但由2r Q k E =可知。
r 越大,E 减小,所以合场强又开始减小。
2.等量异种电荷(1)两点电荷的连线上分析:可根据电场线的疏密直接知中点最稀疏,故中点场强最小,往两边越密场强越大。
方向从正点荷指向负电荷。
(2)两点电荷的中垂线上分析:把正点荷、负点荷在中垂线上某点场强进行合成,合场强方向在连线上且由正电荷指向负电荷。
当A 点离中垂线中点越远,E 1、E 2大小越小,且夹角越大,所以合场强越小,又因为两边对称,可以中垂线上从中点经两边场强减小,方向与两点电荷的连线平行且由正电荷指向负电荷。
1.正电核电场线向外发散,负电荷电场线向内收缩,等势线总是和电场线垂直,在同一等势线上移动电荷,电场力不做功;2.电场力做正功,电势能减少,动能增加;电场力做负功,电势能增加,动能减少(不分正负电荷,通用)3.沿电场线方向,电势降落;沿电场线方向,电势降落最快。
(完整版)电荷电场线分布示意图及场强电势特点

等量同种负点电荷电场线大部分是曲线,起于无穷远,终止于负电荷;有两条电场线是直线。
电势每点电势为负值。
连线上场强以中点最小为零;关于中点对称的任意两点场强大小相等,方向相反,都是背离中点;由连线的一端到另一端,先减小再增大。
电势由连线的一端到另一端先升高再降低,中点电势最高不为零。
中垂线上场强以中点最小为零;关于中点对称的任意两点场强大小相等,方向相反,都沿着中垂线指向中点;由中点至无穷远处,先增大再减小至零,必有一个位置场强最大。
电势中点电势最低,由中点至无穷远处逐渐升高至零。
等量同种正点电荷电场线大部分是曲线,起于正电荷,终止于无穷远;有两条电场线是直线。
电势每点电势为正值。
连线上场强以中点最小为零;关于中点对称的任意两点场强大小相等,方向相反,都是指向中点;由连线的一端到另一端,先减小再增大。
电势由连线的一端到另一端先降低再升高,中点电势最低不为零。
中垂线上场强以中点最小为零;关于中点对称的任意两点场强大小相等,方向相反,都沿着中垂线指向无穷远处;由中点至无穷远处,先增大再减小至零,必有一个位置场强最大。
电势中点电势最高,由中点至无穷远处逐渐降低至零。
等量异种点电荷电场线大部分是曲线,起于正电荷,终止于负电荷;有三条电场线是直线。
电势中垂面有正电荷的一边每一点电势为正,有负电荷的一边每一点电势为负。
连线上场强以中点最小不等于零;关于中点对称的任意两点场强大小相等,方向相同,都是由正电荷指向负电荷;由连线的一端到另一端,先减小再增大。
电势由正电荷到负电荷逐渐降低,中点电势为零。
中垂线上场强以中点最大;关于中点对称的任意两点场强大小相等,方向相同,都是与中垂线垂直,由正电荷指向负电荷;由中点至无穷远处,逐渐减小。
电势中垂面是一个等势面,电势为零(以无穷远处为零电势点,场强为零)(以无穷远处为零电势点,场强为零)注意:电场线、等势面的特点和电场线与等势面间的关系:①电场线的方向为该点的场强方向,电场线的疏密表示场强的大小。
关于等量点电荷周围场强和电势的分布特点

关于等量点电荷周围场强和电势的分布特点作者:田军来源:《试题与研究·教学论坛》2017年第24期等量点电荷在空间的场强分布比较复杂,但在两条线(点电荷连线及其中垂线)上仍有其规律性,为研究方便,设它们带电量为Q,两电荷连线AB长度为L,中点为O。
一、等量的同种电荷形成的电场的特点1.场强特点①两点电荷连线上:任取一点P,设AP长度为x,则P点场强EP为两点电荷在该点的场强EA、EB的矢量和,方向沿AB连线,O点左侧从A指向B,右侧从B指向A(沿两电荷连线指向较远一侧电荷,若两电荷为等量负电荷则反之)。
P点电场强度大小知:EP=,∴当x=时,EP=0,即在两电荷连线中点O处场强最小,从O点向两侧逐渐增大,数值关于O点对称,方向相反。
②两点电荷连线的中垂线上:在O点两侧,电场强度方向均沿中垂线方向从O点指向无限远(若两电荷为等量负电荷则反之),由极限分析法易得:在O点处,E=0;在距O点无限远处,E=0。
说明中间某位置有极大值,可见:合电场强度的大小随着距O点的距离增大,先从零增大到最大,然后逐渐减小。
在中垂线上,任取一点P,设OP=x,由点电荷场强公式,P 点场强EP=2EAcosθ==运用数学方法,令y=,求导可得:y=令y′=0,则x2+2=3x2x2+2,即x2+2=3x2,∴当x=±L时,EP有最大值,∴从中点沿中垂线向两侧,电场强度的数值先增大后减小,两侧方向相反,关于O点对称的点数值相等。
2.电势特点①中点O点处的电势:φO=φA+φB=4>0②两点电荷连线上任意一点P处的电势:总结:在两个等量正电荷的连线上,由A点向B点方向,电势先减后增,在rA=R/2(即中点O处)电势最小,但电势总为正。
③两点电荷连线的中垂线上任意一点Q处的电势:总结:在两个等量正电荷的连线的中垂线上,由O点向N(M)点方向,电势一直减小且大于零,即O点最大,N(M)点为零。
二、等量的异种电荷形成的电场的特点1.场强特点①两电荷连线上任取一点G,设AG长度为x,则G点场强EG为两点电荷分别在该点的场强EA、EB的矢量和,方向从A指向B(由正电荷指向负电荷一侧),由点电荷场强公式知:∵x+(L-x)等于定值L,∴当x=(L-x),即x=时,x与(L-x)乘积最大,EG有最小值,即在两电荷连线中点O处场强最小,从O点向两侧逐渐增大,数值关于O点对称。
两个点电荷在其连线及中垂线上产生的场强电势

电势电势能电势差场强之间的关系场强(矢量)——对应的是力;电势(标量)——对应的是能;两者通过力做功——造成能量变化,而联系在一起;-------------电场线与场强的关系:电场线越密的地方表示场强越大,电场线上每点的切线方向表示该点的场强方向。
电场线与电势的关系:沿着电场线方向,电势越来越低。
电场线与等势面的关系:电场线越密的地方等势面也越密,电场线与通过该处的等势面垂直。
场强数值与电势数值无直接关系:场强大(或小)的地方电势不一定大(或小),零电势可人为选取,而场强是否为零则由电场本身决定。
从电势和电势能的关系来看:ε=Uq由于通常规定无穷远处的电势为零,正的场电荷电场中的各点电势都为正值,负的场电荷的电场中的各点电势都为负值。
这一点与检验电荷的电性和电量无关。
这样,我们知道:ε=Uq1)正的场源电荷电场中:U>0,负检验电荷在场中,电量为负值,因此它的电势能为负值;正检验电荷在场中,电量为正值,因此它的电势能为正值;2)负的场源电荷电场中:U<0,负检验电荷在场中,电量为负值,因此它的电势能为正值;正检验电荷在场中,电量为正值,因此它的电势能为负值;从电势能的特点来看,正电荷在正电荷的电场中电势能为正值,负电荷在负电荷的电场中电势能也为正值,同种电荷之间为斥力的作用,其势能为斥力势能,斥力势能大于零,相当于若规定地球上的海平面为重力势能的零点,物体在海拔高于海平面处(高山)的重力势能则为正值一样;另一方面,正电荷在负电荷的电场中电势能为负值,负电荷在正电荷电场中电势能也为负值,异种电荷之间为引力的作用,其势能为引力势能,引力势能小于零,相当于若规定地球上的海平面为重力势能的零点,物体在海拔低于海平面处(盆地)的重力势能则为负值一样。
二、电势差。
电场中两点间的电势的差值叫做电势差,即:UAB =UA-UB,UBA=UB-UA,在电场中A、B两点间移动电荷时,电场力的功等于电量q和这两点间的电势差UAB 的乘积。
对两个等量点电荷连线及中垂线上电场强度的讨论

对两个等量点电荷连线及中垂线上电场强度的讨论作者:胡方银来源:《中学教学参考·理科版》2010年第12期由于图像能直观、形象地表达物理规律,反映物理量之间的相互关系及变化趋势,因此图像在中学物理教学中有着广泛的应用,以图像及其运用为背景的问题也成为历届高考的热点。
本文利用图像分析两个等量电荷连线及中垂线上电场强度的分布情况,供大家参考。
一、两个等量的同种电荷题设:真空中有两个点电荷、,且,与之间的距离为2a。
1.中垂线上图1如图1所示,取连线中点为坐标原点O,向上为x轴正方向,建立一维坐标系,设x轴上的P点到O点为x,则在P点的场强:(a2+x2),方向:由指向P。
在P点的场强:,方向:由指向P。
因为,所以P点的合场强大小:,方向:沿x轴正方向。
为了直观地表示出电场强度E随x的变化规律,可以用几何画板作出函数f(x)的图像,从而可以定性地画出中垂线上电场强度E随位置x变化的图像,如图2所示。
图2、之间如图3所示,取、连线的中点为坐标原点O,向右方向为x轴的正方向,设P 点到O点的距离为x则:在P点的场强:方向:沿x轴正方向;在P点的场强:-x)2,方向:沿x轴负方向;则P点的合场强:E=kQ(a-x)2-kQ(a+x)2(0<x<a),方向:沿x轴负方向。
图3讨论:1.当x=0时,P点合场强E=0;2.当-a<x<0时,场强大小对称,但方向沿x轴正方向。
图4所以利用几何画板作函数f(x)=-(1(2-x)2-1(2+x)2)的图像,然后就可以确定连线间电场强度E随位置x的变化规律如图4所示。
二、两个等量的异种电荷题设:真空中有两个点电荷、-,且,与之间的距离为2a。
1.中垂线上图5如图5所示,取连线中点为坐标原点O,向上为x轴正方向,建立一维坐标系,设x轴上的P点距O点为x则:在P点的场强:方向:由指向P;在P点的场强:),方向:由P指向。
因为,所以P点的合场强大小:方向:水平向右。
利用几何画板作出函数f(x)的图像,便可画出中垂线上场强E随位置x的变化规律如图6所示:图6之间如图7所示,取、连线的中点为坐标原点O,向右方向为x轴的正方向,设P 点到O点的距离为x则:在P点的场强:方向:沿x轴正方向;在P点的场强:-x)2,方向:沿x轴正方向;则P点的合场强:E=kQ(a-x)2+kQ(a+x)2(0≤x<a),方向:沿x轴正方向,在-a<x<0上对称。
几种典型电场线分布示意图及场强电势特点表
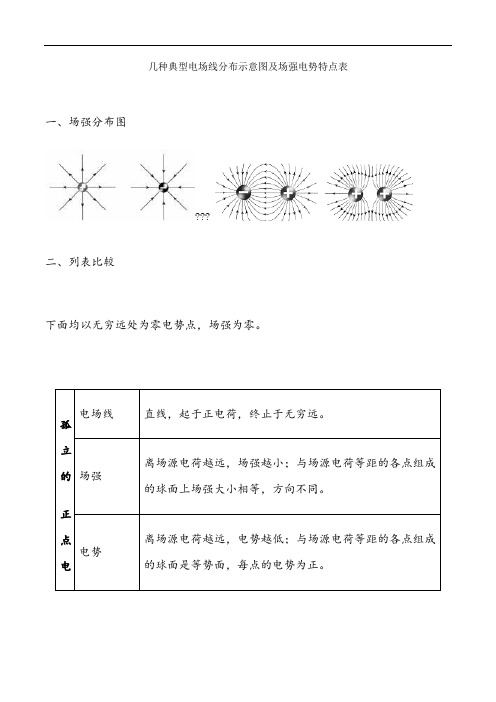
几种典型电场线分布示意图及场强电势特点表一、场强分布图
???
二、列表比较
下面均以无穷远处为零电势点,场强为零。
孤立的正点电电场线直线,起于正电荷,终止于无穷远。
场强
离场源电荷越远,场强越小;与场源电荷等距的各点组成
的球面上场强大小相等,方向不同。
电势
离场源电荷越远,电势越低;与场源电荷等距的各点组成
的球面是等势面,每点的电势为正。
等势面
(1)定义:电场中电势相等的点构成的面
(2)等势面的性质:
①在同一等势面上各点电势相等,所以在同一等势面上移动电荷,电场力不做功
②电场线跟等势面一定垂直,并且由电势高的等势面指向电势低的等势面。
③等势面越密,电场强度越大
④等势面不相交,不相切
(3)等势面的用途:由等势面描绘电场线,判断电场中电势的高低。
(4)几种电场的电场线及等势面
①点电荷电场中的等势面:以点电荷为球心的一簇球面如图l所示。
②
等量异种点电荷电场中的等势面:是两簇对称曲面,如图2所示。
③等量同种点电荷电场中的等势面:是两簇对称曲面,如图3所示。
④匀强电场中的等势面是垂直于电场线的一簇平面,如图4所示。
⑤形状不规则的带电导体附近的电场线及等势面,如图5所示。
注意:带方向的线表示电场线,无方向的线表示等势面。
图中的等势“面”画成了线,即以“线”代“面”。
图1 图2 图3 图5图4。
等量异种电荷中垂线上场强变化

等量异种电荷中垂线上场强变化
垂线上等量异种电荷的场强变化可以通过考虑两个电荷之间的相互作用来分析。
假设垂线上有两个电荷,一个正电荷和一个负电荷。
当距离正负电荷较远时,由于电荷之间的相互作用很小,可以近似认为电场是由单个电荷产生的。
在离质点较远的地方,电场强度不会有很大变化,因此垂线上的场强变化较小。
然而,当距离正负电荷较近时,由于电荷之间的相互作用增大,场强会出现较大的变化。
两个异种电荷之间的相互作用会导致电场线收束,从而增大电场强度。
具体来说,负电荷附近的电场强度会增大,正电荷附近的电场强度会减小。
因此,等量异种电荷中垂线上的场强变化主要由电荷之间的相互作用引起。
当两个电荷之间距离较近时,场强变化较大;当两个电荷之间距离较远时,场强变化较小。
等量电荷两条特殊线上的场强、电势分布特点

等量电荷两条特殊线上的场强、电势分布特点一、等量异种电荷1、两电荷连线上如图1所示,在两电荷连线上任取一点G ,设AG 长度为x ,则G 点场强E G 为两点电荷分别在该点的场强E A 、E B 的矢量和,方向从A 指向B (由正电荷指向负电荷一侧)E G = E A + E B =()[]()[]22222)(xL x xx L L kQ x L kQ x kQ ---=-+∵x+(L-x)等于定值L ,∴当x=(L-x),即x=2L时,x 与 (L-x)乘积最大 ∴这时E G 有最小值,即在两电荷连线中点O 处场强最小,将x=2L带入上式,可求得E G 最小值E Gmin =28L kQ,方面由A 指向B 。
从O 点向两侧逐渐增大,数值关于O 点对称。
小结;等量异种电荷连线中点场强最小,靠近点电荷场强渐强,方向从正点荷指向负电荷。
2、中垂线上如图2所示,在中垂线上,任取一点H ,设OH=x ,根据对称性知:E H 沿水平方向向右,即在中垂线上各点场强水平向右(垂直于中垂线指向负电荷一侧),沿中垂线移动电荷,电场力不做功,由电势差定义知:中垂线为一等势线,与无限远处等势,即各点电势为零。
H 点的场强图1GO B图2E H=232222222222222cos 22⎥⎥⎦⎤⎢⎢⎣⎡+⎪⎭⎫ ⎝⎛=+⎪⎭⎫ ⎝⎛⋅+⎪⎭⎫ ⎝⎛=⋅+⎪⎭⎫ ⎝⎛x L kQL x L L x L kQ x L kQ θ∴在O 点,即x=0处,E H 最大,x 越大,即距O 点越远E H 越小,两侧电场强度数值关于O 点对称。
小结:等量异种电荷的中垂线上电场强度由中点向上向下减小,方向与两点电荷的连线平行且由正电荷指向负电荷。
1)连线上:由于沿着电场线的方向电势降低,所以连线上从正点电荷到负点电荷电势降低。
(2)两点电荷连线中垂线上:由于中垂线上场强方向与中垂线垂直,所以某检验荷在中垂线上移动时,电场力不做功,由0==qW U AB AB 知,中垂线上任意两点的电势差为零,即中垂线上电势均为零。
两等量点电荷的场强、电势、电势能的情况分析

两等量点电荷连线及中垂线上的场强、电势和电势能的情况分析高中物理“电场”这个内容的概念很抽象,学生往往感到很困惑,导致对两点电荷连线及中垂线上的电场强度、电势、电势能的变化情况感到模糊不清,现就将我对这个问题的分析小结如下:这里所指的两点电荷是指靠得很近的两等量同种点电荷和等量异种点电荷。
一、两正点电荷连线及中垂线上的电场强度、电势、电势能的变化1、电场强度(1)两点电荷的连线上两点电荷在空间的电场是由这两个点电荷分别在该点的场强叠加而成。
根据电场强度的决定式2rQ k E =,可知E 与r 2成反比,与Q 成正比,而对于正电荷E 的方向背离点电荷。
在其连线上的中点,由于Q 相等,r 相等,即E 大小相等,而两点电荷在的场强方向相反,故合场强为零,如图1所示。
图1由||||212212r Q k r Q k E E E -=-=知,从中点往两边合场强增大,且关于中点对称。
小结:连线中点场强为零,靠近点电荷场强渐强,且关于中点对称,场强方向沿较近点电荷的场强方向。
(2)两点电荷的中垂线上中垂线上的某点的场强由两点电荷分别在该点的场强叠加而成。
由于中垂线上的点到线两端的距离相等,由2r Q kE =知|E 1|=|E 2|,即大小相等,方向如图2所示:图2分别把E 1、E 2分解在连线上和中垂线上,连线上的分量大小相等,方向相反,相互抵消,故合场强E 如图2所示。
所以从中垂线上中点往两边场强先是由零增大,但由2rQ k E =可知。
r 越大,E 减小,所以合场强又开始减小。
小结:两正电荷的中垂线上电场强度先从中点时的零逐渐增大,当增大到某个值时,又逐渐减小,且两边对称。
2、电势(1)可根据电势与电场线的关系(沿着电场线的方向电势降低)直接判断:连接上,从中点往两边电势升高;中垂线上从中点往两边电势降低。
电场线的分布如图3所示。
图3(2)也可由电势差的定义qW U AB AB =判断。
先看两点电荷的连线上:设一正检验电荷由连线上某点A 向中点O 运动时,如图4所示图4根据W=FS cos θ知,F 与S 的方向相同,故F 做正功,q 又为正电荷,所以 0>=qW U AO AO 即 0>-=O A Ao U ϕϕ故 O A ϕϕ>可知连线上从O 到点电荷电势升高,又由于两边对称,故连线上O 点电势最低。
等量的点电荷形成的电场中的场强和电势特点

等量的点电荷形成的电场中的场强和电势特点在等量的点电荷形成的电场中,场强表征电场的力量或效应的大小。
场强的计算公式为场强等于电荷的大小除以距离的平方。
对于等量的点电荷,它们的大小相等,因此它们在同一距离处产生的场强也是相等的。
这意味着在等量的点电荷形成的电场中,场强的大小在空间中保持均匀分布。
这是因为电场中的每个点电荷都会对周围的空间产生相同大小和方向的力,使得场强保持一致。
此外,等量的点电荷形成的电场中,场强的方向呈放射性。
场强的方向从正电荷指向负电荷,与指向统一矢量相反。
这是因为正电荷和负电荷之间存在电力线,电力线是场强的方向标志。
在等量的点电荷形成的电场中,电力线从正电荷出发,沿着放射线向外发散,指向负电荷。
由于等量的点电荷的方向是相同的,所以电力线和场强的方向也是相同的,呈放射性分布。
除了场强,另一个特点是电势。
电势是描述电场中的能量转换的量。
在等量的点电荷形成的电场中,电势的大小与电荷的大小和距离有关。
在距离电荷较远的地方,电势较小,而在距离电荷较近的地方,电势较大。
这是因为电荷会使空间中的能量分布发生变化,能量在电场中沿着电势梯度的方向传递。
在等量的点电荷形成的电场中,电势呈球对称形态,类似于一个球面。
球面上的每个点的电势是相等的,而且与距离电荷的距离成反比。
由于点电荷的大小相同,所以球面上每个点到电荷的距离相同,因此电势在整个球面上保持均匀。
此外,电势的方向是从正电荷指向负电荷的。
电势与电力线的方向相同,都是从正电荷指向负电荷。
这是因为电场中的能量转换主要是由正电荷向负电荷转移的。
综上所述,等量的点电荷形成的电场中,场强呈放射性分布,大小均匀;而电势呈球对称分布,大小与距离成反比。
这些特点揭示了等量的点电荷形成的电场的规律性和对电场中物体的作用效应。
等量双电荷连线及中垂线上场强与电势的变化规律

等量双电荷连线及中垂线上场强与电势的变化规律作者:司德平来源:《中学物理·高中》2014年第03期(郑州外国语学校河南郑州450001)真空中两个等量异(同)种点电荷的连线及中垂线上场强或电势的变化规律是历年高考考查的热点.这类“双电荷”问题体现了叠加、对称与极限思维,学生看起来似曾熟悉,但往往较难做出正确解答,究其原因,主要是没有真正理解这类“双电荷”电场的特点与规律.本文就来探讨真空中等量双电荷连线及中垂线上场强与电势的变化规律.1等量异种双电荷的连线及中垂线上场强与电势的变化规律1.1场强的变化规律(1)中垂线上场强的变化规律如图1所示,真空中两个等量异种点电荷的电量分别为+Q和-Q,连线为线段AB,MN为AB的中垂线,垂足为O.在中垂线MN上任取一点C,令OC=y,AB=L,在Rt△AOC和Rt△BOC中,有AC=BC=(L2)2+y2,cosθ=L2(L2)2+y2.+Q和-Q分别在C点处产生场强的大小为EA=EB=kQ(L2)2+y2.由平行四边形定则可知,C点处的合场强EC平行于连线AB指向-Q一侧,且EC=2EAcosθ=kQL[(L2)2+y2]3/2(1)(1)式中k、Q、L是常量,由(1)式可知,当y=0时,EC有最大值,且ECmax=8kQL2,即中垂线上垂足O处的场强最大;当y变大时,上式分母[(L2)2+y2]3/2逐渐变大,则EC的值因单调递减而逐渐变小;当y→∞时,EC→0,即中垂线上距O点无穷远处几乎不存在电场,场强为零.可见,真空中两个等量异种点电荷的连线中垂线上,垂足处的场强最大,沿中垂线向两侧、关于垂足对称场强逐渐减小,无穷远处场强为零,场强的方向始终垂直于中垂线指向负场源点电荷一侧.如图2所示.(2)连线上场强的变化规律如图1所示,在连线AB上任取一点D,令AD=x,AB=L,则BD=L-x.+Q在D点产生的场强为EA′=kQx2,-Q在D点产生的场强为EB′=kQ(L-x)2,由场强矢量的叠加原理可知,D点的合场强为ED=EA′+EB′=kQ[1x2+1(L-x)2](2)外接法、电流表内接法几种形式,如图3所示,构成“A-a、A-b、B-a、B-b”4种组合方式.对于同一个基本原理,也可能有多种实验处理的方法和替换方式,以伏安法测电阻(外接法)为例,如图4所示,其中(1)和(2)分别是改装了电流表和电压表,这两种情景是在基本伏安法的基础上进行了电表改装的拓展,本质与原设计是一致的;如果总电压恒定不变,可以变图(1)为图(3),变图(2)为图(4)或(5),引导学生进行归类能够将头脑中的电学实验有机的融合到一块.物理实验教学培养学生创新能力的重要途径,无论是演示实验还是学生分组实验,学生是主体,我们教师要充分发挥主导性作用,对教材中的实验内容和实验装置进行必要的改进和重组,提高物理实验的探究性和思考性,激发学生的正向思维,引导学生在思考、设计、探究的一系列过程中实现知识的累积和方法的沉淀,同时自身的创新意识和创新能力得到提高.为了讨论ED随x的变化规律,对(2)式求导可得ED′=kQ[-2x-3+2(L-x)-3]=2kQ[1(L-x)3-1x3](3)由(3)式可知,当x<L2时,ED′<0,则原函数ED在(0,L2]上为递减函数,即线段AO 上,沿AO方向各点的合场强具有随x增大而减小的变化规律;当x>L2时,ED′>0,则原函数ED在[L2,L)上为递增函数,即线段OB上,沿OB方向各点的合场强具有随x增大而增大的变化规律;当x=L2时,ED′=0,则原函数ED有最小值,即EDmin=8kQL2.场强的变化规律如图3所示.可见,在真空中两个等量异种点电荷的连线上,两端点处的场强最大,中点O处场强最小(但不等于零),连线上其他各点场强的大小总是沿连线从中点O向两场源电荷场强逐渐增大,其中关于中点O对称点的场强大小相等,方向相同,沿连线指向负场源点电荷一侧.此规律也可利用分子动理论中分子力随距离变化的规律进行类比.另外,也可根据两个等量异种点电荷的连线周围电场线的疏密变化,定性知道场强沿连线先变小后变大.1.2电势的变化规律真空中两个等量异种点电荷的连线位于一条由正场源点电荷指向负场源点电荷的电场线上,沿着电场线电势逐渐降低,其中连线的中垂线正场源点电荷一侧的电势大于零,连线的中垂线负场源点电荷一侧的电势小于零,连线与中垂线的交点(垂足)处的电势等于零,如图4所示;因为连线的中垂线上的场强方向始终垂直于中垂线指向负场源点电荷一侧,因此,沿中垂线移动电荷至无穷远时,电场力不做功,即中垂线为一条等势线.若取无穷远处电势为零,则中垂线上各点的电势均为零.2等量同种双电荷的连线及中垂线上场强与电势的变化规律2.1场强的变化规律(1)中垂线上场强的变化规律如图5所示,真空中两个等量同种点电荷的带电量均为+Q,连线AB的长度为L,连线与中垂线的交点(垂足)为O.在中垂线上任取一点C,设∠CAB=θ.两场源正点电荷分别在C点产生的场强为E1=E2=kQ(L2cosθ)2=4kQcos2θL2,由平行四边形定则可知,C点处的合场强E沿中垂线背离O点,且E=2E1sinθ=8kQL2cos2θsinθ(4)在(4)式中,令y=sinθcos2θ,对y求导得y′=cosθ-3sin2θcosθ=cosθ(1-3sinθ)·(1+3sinθ),则当sinθ=±33时,y′=0,即当θ=arcsin33=35.26°时,ymax=239,而θ=arcsin(-33)体现了中垂线上关于O点两侧电场的对称性.则中垂线上C点处合场强的最大值为Emax=8kQL2ymax=163kQ9L2.由(4)式可知,当θ=0°时,即在O点,场强E=0;当θ=90°时,即无穷远处,场强E=0;当θ=arcsin33=35.26°时,场强E有最大值Emax=163kQ9L2.可见,在真空中两个带电量均为+Q的等量同种点电荷连线的中垂线上,场强关于连线的中点O对称,先逐渐增大,后逐渐减小,场强的方向相反,始终沿中垂线背离O点.而在真空中两个带电量均为-Q的等量同种点电荷连线的中垂线上,只是相反的场强方向始终沿中垂线指向O点,其它则与上述结论相同.即等量同种点电荷连线的中垂线上的场强E随x变化的规律如图6所示.(2)连线上场强的变化规律与真空中两个等量异种点电荷连线上场强的变化规律类似,真空中两个等量同种点电荷连线中点O处的场强最小,且为零,沿连线从中点O向两场源电荷场强逐渐增大,两端点处的场强最大,且关于中点O对称点的场强大小相等,方向相反.场强大小的变化规律如图7所示.2.2电势的变化规律真空中两等量正电荷的连线上,场强的方向沿连线背离场源电荷,沿场强方向电势逐渐降低,因此,连线中点O处的电势最低,沿连线从中点O向两场源电荷电势逐渐升高,两端点处的电势最高,且电势大小关于中点O对称,如图8所示;真空中两等量正电荷的中垂线上,场强的方向始终沿中垂线背离O点,沿场强方向电势逐渐降低,因此O点处的电势最高,沿中垂线背离O点电势逐渐降低,无穷远处电势降为零,且电势大小关于O点对称.而真空中两等量负电荷恰好相反,连线中点O处的电势最高,沿连线从中点O向两场源电荷电势逐渐降低,两端点处的电势最低,且电势大小关于中点O对称;中垂线上O点处的电势最低,沿中垂线指向O点电势逐渐降低,且电势大小关于O点对称.2.3规律拓展如果真空中两同种点电荷的带电量不相等,则在两点电荷的连线上一定存在一点O′,在O′处的合场强为零,两点电荷连线上过O′点的垂线上的场强与电势的分布规律与上述结论类似,也存在一个极值点.由n个固定在一条直线上的同种点电荷产生的电场中,垂足处场强为零的这一直线的垂线上的场强与电势的分布规律也与上述结论类似.。
几种典型电场线分布示意图及场强、电势的特点

电场线等电势量连场强异线种上电势点电中荷场强垂线上电势电场线等电势量连同场强线种上正电势点电中场强荷垂线上电势电场线等电势量连同场强线种上负电势点电中场强荷垂线上电势孤电场线立的场强正点电势电荷等势面大多数是曲线,起于正电荷,停止于负电荷孤电场线;有三条电场线是直线。
立中垂面有正电荷的一边每一点电势为的正,有负电荷的一边每一点电势为负。
场强负中点 E 最小且不等于零;对于中点对称的点点电势E 大小相等,方向同样, E电荷等势面方向由正电荷指向负电荷;由连线的一端到另一端, E 先减小再增大。
由正电荷到负电荷渐渐降低,中点电势为零。
中点 E 最大且不等于零;对于中点对称的点 E 大小相等,方向同样,且都与中垂线垂直由正电荷指向负电荷;由中点至无量远处,渐渐减小。
中垂面是一个等势面,电势为零。
大多数是曲线,起于正电荷,停止于无量远;有两条电场线是直线。
每点电势为正当。
中点 E 最小且为零;对于中点对称的点 E 大小相等,方向相反, E 方向沿连线指向中点;由连线的一端到另一端 E 先减小再增大。
由连线的一端到另一端先降低再高升,中点电势最低不为零。
中点 E 最小且为零;对于中点对称的点 E 大小相等,方向相反, E 方向沿中垂线背叛中点;由中点至无量远处, E 先增大再减小至零。
中点电势最高,由中点至无量远处渐渐降低至零。
大多数是曲线,起于无量远,停止于负电荷;有两条电场线是直线。
每点电势为负值。
中点 E 最小且为零;对于中点对称的点 E 大小相等,方向相反, E 方向沿连线背叛中点;由连线的一端到另一端 E 先减小再增大。
由连线的一端到另一端先高升再降低,中点电势最高不为零。
中点 E 最小且为零;对于中点对称的点 E 大小相等,方向相反, E 方向沿中垂线指向中点;由中点至无量远处, E 先增大再减小至零。
中点电势最低,由中点至无量远处渐渐高升至零。
孤.电场线直线,起于正电荷场,线终是止直于线无,穷起远于。
两个点电荷在其连线及中垂线上产生的场强 电势(有静心绘制的示意图)

电势电势能电势差场强之间的关系场强(矢量)——对应的是力;电势(标量)——对应的是能;两者通过力做功——造成能量变化,而联系在一起;-------------电场线与场强的关系:电场线越密的地方表示场强越大,电场线上每点的切线方向表示该点的场强方向。
电场线与电势的关系:沿着电场线方向,电势越来越低。
电场线与等势面的关系:电场线越密的地方等势面也越密,电场线与通过该处的等势面垂直。
场强数值与电势数值无直接关系:场强大(或小)的地方电势不一定大(或小),零电势可人为选取,而场强是否为零则由电场本身决定。
从电势和电势能的关系来看:ε=Uq由于通常规定无穷远处的电势为零,正的场电荷电场中的各点电势都为正值,负的场电荷的电场中的各点电势都为负值。
这一点与检验电荷的电性和电量无关。
这样,我们知道:ε=Uq1)正的场源电荷电场中:U>0,负检验电荷在场中,电量为负值,因此它的电势能为负值;正检验电荷在场中,电量为正值,因此它的电势能为正值;2)负的场源电荷电场中:U<0,负检验电荷在场中,电量为负值,因此它的电势能为正值;正检验电荷在场中,电量为正值,因此它的电势能为负值;从电势能的特点来看,正电荷在正电荷的电场中电势能为正值,负电荷在负电荷的电场中电势能也为正值,同种电荷之间为斥力的作用,其势能为斥力势能,斥力势能大于零,相当于若规定地球上的海平面为重力势能的零点,物体在海拔高于海平面处(高山)的重力势能则为正值一样;另一方面,正电荷在负电荷的电场中电势能为负值,负电荷在正电荷电场中电势能也为负值,异种电荷之间为引力的作用,其势能为引力势能,引力势能小于零,相当于若规定地球上的海平面为重力势能的零点,物体在海拔低于海平面处(盆地)的重力势能则为负值一样。
二、电势差。
电场中两点间的电势的差值叫做电势差,即:UAB =UA-UB,UBA=UB-UA,在电场中A、B两点间移动电荷时,电场力的功等于电量q和这两点间的电势差UAB 的乘积。
等量双电荷连线及中垂线上场强与电势的变化规律

等量双电荷连线及中垂线上场强与电势的变化规律等量双电荷连线及中垂线上场强与电势的变化规律序1. 引言2. 等量双电荷连线的定义和特点3. 中垂线的定义和特点4. 等量双电荷连线和中垂线的物理意义5. 等量双电荷连线及中垂线上场强的变化规律6. 等量双电荷连线及中垂线上电势的变化规律7. 个人观点与理解8. 总结引言等量双电荷连线及中垂线是电荷分布和电势分布的描述工具,在电磁学中有着重要的应用。
本文将深入探讨等量双电荷连线及中垂线上场强与电势的变化规律,并分享个人观点与理解。
等量双电荷连线的定义和特点等量双电荷连线是指在电荷分布中,连接两个等量异号电荷的曲线。
它描述了两个电荷之间的相互作用,并且在中垂线上存在一点,该点的场强和电势具有特殊的性质。
中垂线的定义和特点中垂线是指连接等量双电荷连线上两个电荷之间的中点,并与等量双电荷连线的切线垂直。
它表示了电荷分布的对称性,并且在中垂线上存在一点,该点的场强和电势与两个电荷的场强和电势之和有关。
等量双电荷连线和中垂线的物理意义等量双电荷连线和中垂线的存在具有重要的物理意义。
等量双电荷连线反映了两个电荷的相互作用方式,表征了电荷分布的复杂性。
中垂线则说明了电荷分布的对称性,反映了电荷之间的平衡状态。
等量双电荷连线及中垂线上场强的变化规律在等量双电荷连线上,场强随着距离的增加而减小。
这是因为电荷之间的相互作用力随着距离的增加而减弱。
在中垂线上,场强也随着距离的增加而减小,但它的变化规律与等量双电荷连线不同。
中垂线上的场强在开始时增大,到达最大值后逐渐减小。
等量双电荷连线及中垂线上电势的变化规律电势是描述电荷分布中电势能的物理量。
在等量双电荷连线上,电势随着距离的增加而减小。
这是因为电势能随着距离的增加而减小。
在中垂线上,电势也随着距离的增加而减小,但它的变化规律与等量双电荷连线不同。
中垂线上的电势在开始时增大,到达最大值后逐渐减小。
个人观点与理解等量双电荷连线及中垂线对于理解电荷分布和电势分布的规律具有重要意义。
等量异种电荷中垂线场强变化

等量异种电荷中垂线场强变化《等量异种电荷中垂线场强那些事儿》嘿,朋友们!今天咱来聊聊等量异种电荷中垂线场强的奇妙世界。
想象一下啊,有这么两个电荷,一个带正电,一个带负电,它们就像两个小家伙在那儿较着劲呢。
而它们中间的那条垂线,可有着大文章。
你看啊,从正电荷出发,沿着中垂线往前走,一开始场强还挺大的呢,就好像你刚开始爬山,坡特别陡。
然后呢,越往前走,场强就慢慢变小啦,就跟爬山爬到一半,坡变缓了似的。
等走到中间那个点的时候,嘿,场强居然变成零啦!这多有意思,就好像你到了山顶,一下子平坦了,没了那种爬坡的压力。
再接着往前走,到了负电荷那边,场强又开始变大啦,不过是反过来的方向哦,就像下山的时候,坡又开始变陡了。
这中间的变化啊,可真是充满了趣味。
就好像我们的生活一样,有时候会遇到一些困难,感觉压力山大,就像场强大的时候。
但慢慢坚持走下去,可能就会迎来一段轻松的时光,就像场强为零的时候。
可别高兴太早哦,后面可能又会有新的挑战等着我们,就像场强又变大了。
我们不能害怕这些变化,反而要去感受它,理解它。
就像我们了解等量异种电荷中垂线场强的变化一样,知道它的规律,就能更好地应对。
而且啊,这不仅仅是物理学上的知识,它还能给我们很多启示呢。
比如在面对困难的时候,我们要知道,困难不会一直持续,总会有缓解的时候。
我们要保持信心,坚持走下去。
总之呢,等量异种电荷中垂线场强的变化看似复杂,其实很有趣,也很有意义。
它就像生活中的起起落落,让我们的世界变得丰富多彩。
我们要像探索这个奇妙的物理现象一样,去积极地面对生活中的每一个变化,每一个挑战,让自己的人生更加精彩!。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
B.四点中c点处的电势最低
C.b、d两点处的电场强度相同 NhomakorabeaD.将一试探电荷+q沿圆周由a点移至c点,+q的电 势能减小
(15江苏卷)两个相同的负电荷和一个正电荷附近 的电场线分布如图所示,c时两负电荷连线的中点, d点在正电荷的正上方,c、d到正电荷的距离相等, 则( )
所以:中垂线上电势一定为零,其他位置的电势值 也可以计算。
连线:
场强: 1.单调增:用求导方法可以知道,从o点往两边走,
场强都会增大,所以,在两电荷之间”两大夹小”,可 以代入数字验证。由于两电荷之外场强作差,所以是 “内大外小”。
2.偶函数:关于中点o对称位置场强相等。 分布图像:
电势: 中点O左侧都为正,右边都为负(正正负负)
A.O点电场强度为零
B.D点电场强度为零
C.若将点电荷+q从O移向C,电势能增大
D.若将点电荷-q从O移向C,电势能增大
(13山东理综)如图所示,在x轴相距为L的两点固 定两个等量异种点电荷+Q、-Q,虚线是以+Q所在 点为圆心、L/2为半径的圆,a、b、c、d是圆上的 四个点,其中a、c两点在x轴上,b、d两点关于x轴 对称。下列判断正确的是()
A.a点的电场强度比b点的大
B.a点的电势比b点的高
C.c点的电场强度比d点的大
D.c点的电势比d点的低
4.等量及不等量电荷连线及中垂线场强电势
一、矢量叠加(合成与分解) 1.平行四边形法则: 除了力、速度、位移,还包括场强(E,B). 2.电势的叠加(代数和)
二、等量异种电荷:
中垂线:场强具有单调性,近大远小。电势恒为零。
补充:电势的一般表达式(取无穷远处电势为零): ϕ=kq/r. 强调: 1.此处没有负号,但电荷量q要代入正负。 所以:正电荷周围的电势都为正,负电荷周围的电 势都为负。(口诀:正正负负) 2.计算电势能时,需要代入试探电荷的正负。
分布图像:
三、等量同种电荷:
场强: 1.中垂线上分布:零大零(先增大后减小) 2.连线上分布:两大夹零,内小外大(两电荷之间 相抵消,之外相加)。 电势: 连小中垂大(对于中点0,从连线上各点比较是最小 的,从中垂线上比较是最大电势点)。
(08山东)如图所示,在y轴上关于O点对称的A、 B两点有等量同种点电荷+Q,在x轴上C点有点电荷Q且CO=OD,∠ADO=600。下列判断正确的是()
