如何绘制伯德图.

新版本matlab中绘制bode图技巧

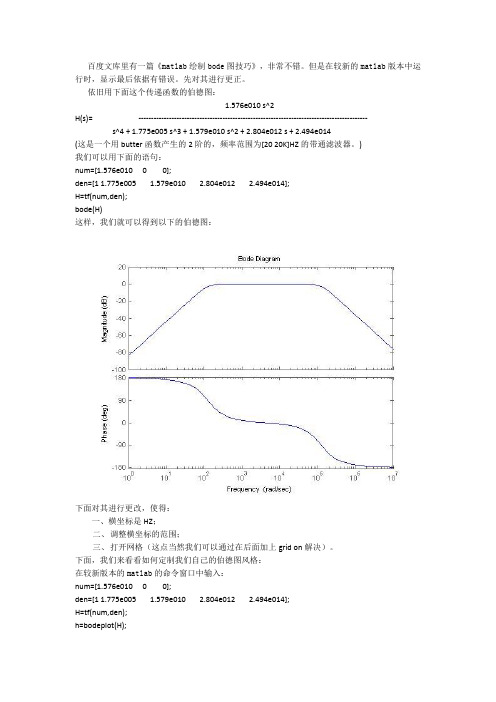
百度文库里有一篇《matlab绘制bode图技巧》，非常不错。

但是在较新的matlab版本中运行时，显示最后依据有错误。

先对其进行更正。

依旧用下面这个传递函数的伯德图：1.576e010 s^2H(s)= ------------------------------------------------------------------------------------------s^4 + 1.775e005 s^3 + 1.579e010 s^2 + 2.804e012 s + 2.494e014(这是一个用butter函数产生的2阶的，频率范围为[20 20K]HZ的带通滤波器。

)我们可以用下面的语句：num=[1.576e010 0 0];den=[1 1.775e005 1.579e010 2.804e012 2.494e014];H=tf(num,den);bode(H)这样，我们就可以得到以下的伯德图：下面对其进行更改，使得：一、横坐标是HZ；二、调整横坐标的范围；三、打开网格（这点当然我们可以通过在后面加上grid on解决）。

下面，我们来看看如何定制我们自己的伯德图风格：在较新版本的matlab的命令窗口中输入：num=[1.576e010 0 0];den=[1 1.775e005 1.579e010 2.804e012 2.494e014];H=tf(num,den);h=bodeplot(H);p=getoptions(h);p.Grid=’on’;p.XLim={[10 40000]};p.XLimMode={'manual'};p.FreqUnits='Hz';setoptions(h,p);这时，我们可以得到以下的伯德图：。

绘制伯德图

幅频和相频特性为：
A( ) (1 T 2 2 )2 (2 T )2， ( ) tg 1
1 T 1 ，o ，称为转折频率或交换频率。 T
Monday, March 09, 2015
可以用这两段渐近线近似的表示惯性环节的对数幅频特性。
3
惯性环节的Bode图
10 渐近线 0 -10 -20 0° -45° -90° 1 20T
20dB / Dec
图中，红、绿线分别是低频、高频渐近线，蓝线是实际曲线。
T
( )
2.0
-63.4
3.0
-71.5
4.0
-76
5.0
-78.7
7.0
-81.9
10
-84.3
20
-87.1
50
-88.9
100
-89.4
1 1 当 0时， (0) 0;当时， ( ) ;当时， () 。 T T 4 2 由图不难看出相频特性曲线在半对数坐标系中对于(0, －45°) 点是斜对称的，这是对数相频特性的一个特点。
当时间常数T 变化时，对数幅频特性和对数相频特性的形状都不变，仅仅是根据转折频率1/T 的大小整条曲线向左或向右平移即可。而当增益改变时，相频特性不变，幅频特性上下平移。
Monday, March 09, 2015 6
振荡环节的频率特性
K Kn 2 ⒋ 振荡环节的频率特性： G( s) 2 2 T s 2Ts 1 s 2 n s n 2
0 L( ) 20 lg K 0 0
K 1 K 1 0 K 1
( )
180
K 0
log

15 第十五讲伯德图

1
(1−ω
2
/ω
2 2 n
)
+ 4ς ω / ω
2 2 2 2 2
2 n
Mdb = −20log10
−1
(1−T ω
)
+ 4ς 2T 2ω2
2ςTω ϕ (ω) = − tan 1−ω2Tω2
1) 低频渐近线:
当ωT << 1时，即 ω << 1/T， 1/T→转折频率 MdB = 0dB
Mdb -40db/dec ω
• 步骤 1: 计算转折频率。
1+ s → ωb =1rad / s
1 → ωb =1rad / s s 1 → ωb = 2 rad / s 1 1+ s 2
Kdb = 20lg 10 = 20 dB
步骤 2: 确定要画的频率范围。所有转折频率都在1~10rad/s的这个十倍频程内，所以此伯德图将在以下范围内绘制：
0.1 1.0 10
ω
φ
+90
1+s
+45
0 10
-45
1 s
-90
1 1 1+ s 2
图.SP.15.1.6
步骤8: 将所有环节的相角相叠加。
φ
+90
0.1 1.0 10
ω
+45
0
合成相位i
-45
-90
图.SP.15.1.6
MATLAB 仿真
10(1+ s) G(s) = 1 s1+ s 2
sys=tf([10 10],[0.5 1 0]); bode(sys) pause
H(s) =1

5-3 频域：伯德图12

说明
为二阶系统 (振荡环节) 的转角角频率。
24
5.2.4 基本因子的伯德图
渐进线与实际曲线的误差与阻尼比ζ有关，当ζ＜ 0.707时必须考虑ζ对L(ω)的影响，对转角角频率ω=ωn附近的L(ω)曲线进行修正。
当频率接近 ω=ωn时，将产生谐振峰。阻尼比的大小决定了谐振峰值的幅值。
25
2ζ/n ω arctan 1 (/n ) 2
得到系统的对数幅频特性、相频特性。
9
5.2.3 对数频率特性图（伯德图）
典型环节归纳为四类基本因子：
常数增益K
在原点的极点(或零点) (jω)±1
实极点(或零点) ( jωτ +1)±1
复极点(或零点) [(jω/ω n )2+2ζ( jω/ω n ) +1]
±1
10
5.2.4 基本因子的伯德图
当 ω 1 / T 时，是一条斜率为-20dB/dec的直线
18
两条渐近线相交处的角频率 ω 1/ T 称为转角角频率。用两条渐近线近似惯性环节的对数幅频特性,最大误差出现在转角角频率处,
L( ) 20lg 1 ω 2 T 2
L ( )
1 / T
3 dB
L ( )
ω 90
20 0 0.1
20
1
10

20
( )
90
0
0.1
1
10

15
若在原点有多重零点 (jω)v
G jω ( jω) v
Lω 20lg G jω v 20lgω
ω v 90
16
3.实极点(或零点) (jωτ+1) ±1的伯德图

绘制伯德图

L2 () 40lg 2.85 ，从而， L2 (0.27) 40lg0.27 2.85 19.9dB
1 1 1 x ct an arg tan x 1 10 5 x 5 2 x 50, x 7.07
计算（6）
G2 ( j 0.01) arctan 3.7 0.01 900 arctan 0.1 0.01 arctan 0.2 0.01 arctan 41 0.01 2.12 90 0.06 0.12 22.29 110.350 G2 ( j 0.05) arctan 3.7 0.05 900 arctan 0.1 0.05 arctan 0.2 0.05 arctan 41 0.05 10.48 90 0.29 0.57 64 144.380 G2 ( j 0.1) arctan 3.7 0.1 900 arctan 0.1 0.1 arctan 0.2 0.1 arctan 41 0.1 20.3 90 0.57 1.15 76.29 147.710 G2 ( j 0.27) arctan 3.7 0.27 900 arctan 0.1 0.27 arctan 0.2 0.27 arctan 41 0.27 44.97 90 1.55 3.09 84.84 134.510 G2 ( j1) arctan 3.7 1 900 arctan 0.1 1 arctan 0.2 1 arctan 41 1 74.87 90 5.71 11.31 88.6 120.750 G2 ( j 2.67) arctan 3.7 2.67 900 arctan 0.1 2.67 arctan 0.2 2.67 arctan 41 2.67 82.22 90 14.95 28.1 89.47 140.30 G2 ( j 6.85) arctan 3.7 6.85 900 arctan 0.1 6.85 arctan 0.2 6.85 arctan 41 6.85 87.74 90 34.41 53.87 89.80 180.34 0

《典型环节伯德图》课件

Maya：一汇报人：
稳定性分析
稳定性定义：系统在受到扰动后能够恢复到其原始状态的能力
稳定性分类：稳定、不稳定、临界稳定
稳定性分析方法：伯德图分析、奈奎斯特图分析、根轨迹分析等
伯德图分析：通过绘制伯德图，观察系统在不同频率下的增益和相位变化，判断系统的稳定性。
动态性能分析
伯德图：描述系统动态性能的图形工具频率响应：系统对不同频率信号的响应相位裕度：系统稳定性的指标增益裕度：系统放大能力的指标动态性能分析方法：如根轨迹法、频率响应法等
MATLAB还提供了丰富的函数库，可以方便地进行各种数学计算和仿真。
Simulink软件介绍
软件名称： Simulink
开发商： MathWorks
公司
软件功能：用于建模、仿真和分析动态系
统
应用领域：广泛应用于控制工程、信号处理、通信等领
域
软件特点：图形化界面，易于操作，支持多种编程语言
软件版本：最新版本为 Simulink 2022a
其他绘制软件介绍
AutoCAD：一款专业的CAD软件，可以绘制各种类型的伯德图
SolidWorks：一款三维设计软件，可以绘制伯德图
Inventor：一款三维设计软件，可以绘制伯德图
SketchUp：一款三维设计软件，可以绘制伯德图
Blender：一款三维设计软件，可以绘制伯德图
幅频特性的分析
幅频特性的定义：描述信号在频率域上的分布特性幅频特性的表示方法：通常采用伯德图或奈奎斯特图幅频特性的应用：用于分析信号的频率响应、滤波器设计等幅频特性的测量方法：通过频谱分析仪或示波器等仪器进行测量
相频特性的分析
相频特性的定义：描述信号频率与相位之间的关系相频特性的表示方法：通常用相频特性曲线表示相频特性的应用：在信号处理、通信等领域有广泛应用相频特性的测量方法：通过实验或仿真进行测量

Matlab中Bode图的绘制技巧(精)

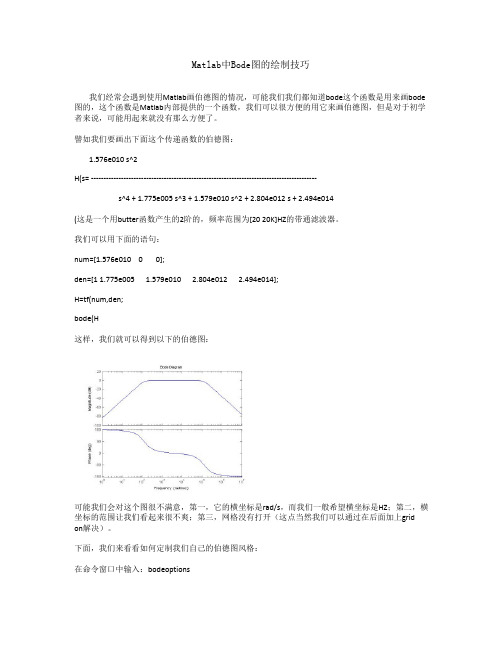
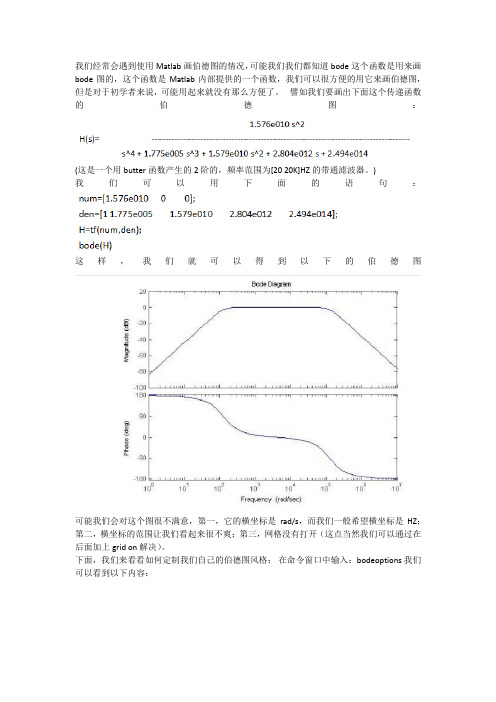
Matlab中Bode图的绘制技巧我们经常会遇到使用Matlab画伯德图的情况，可能我们我们都知道bode这个函数是用来画bode 图的，这个函数是Matlab内部提供的一个函数，我们可以很方便的用它来画伯德图，但是对于初学者来说，可能用起来就没有那么方便了。

譬如我们要画出下面这个传递函数的伯德图：1.576e010 s^2H(s= ------------------------------------------------------------------------------------------s^4 + 1.775e005 s^3 + 1.579e010 s^2 + 2.804e012 s + 2.494e014(这是一个用butter函数产生的2阶的，频率范围为[20 20K]HZ的带通滤波器。

我们可以用下面的语句：num=[1.576e010 0 0];den=[1 1.775e005 1.579e010 2.804e012 2.494e014];H=tf(num,den;bode(H这样，我们就可以得到以下的伯德图：可能我们会对这个图很不满意，第一，它的横坐标是rad/s，而我们一般希望横坐标是HZ；第二，横坐标的范围让我们看起来很不爽；第三，网格没有打开（这点当然我们可以通过在后面加上grid on解决）。

下面，我们来看看如何定制我们自己的伯德图风格：在命令窗口中输入：bodeoptions我们可以看到以下内容：ans =Title: [1x1 struct] XLabel: [1x1 struct] YLabel: [1x1 struct] TickLabel: [1x1 struct] Grid: 'off'XLim: {[1 10]} XLimMode: {'auto'} YLim: {[1 10]} YLimMode: {'auto'} IOGrouping: 'none' InputLabels: [1x1 struct] OutputLabels: [1x1 struct] InputVisible: {'on'} OutputVisible: {'on'} FreqUnits: 'rad/sec' FreqScale: 'log' MagUnits: 'dB' MagScale: 'linear' MagVisible: 'on' MagLowerLimMode: 'auto' MagLowerLim: 0 PhaseUnits: 'deg' PhaseVisible: 'on' PhaseWrapping: 'off'PhaseMatching: 'off'PhaseMatchingFreq: 0PhaseMatchingValue: 0我们可以通过修改上面的每一项修改伯德图的风格，比如我们使用下面的语句画我们的伯德图：P=bodeoptions;P.Grid='on';P.XLim={[10 40000]};P.XLimMode={'manual'};P.FreqUnits='HZ';num=[1.576e010 0 0];den=[1 1.775e005 1.579e010 2.804e012 2.494e014];H=tf(num,den;bode(H,P这时，我们将会看到以下的伯德图：上面这张图相对就比较好了，它的横坐标单位是HZ，范围是[1040K]HZ，而且打开了网格，便于我们观察-3DB处的频率值。

(完整版)Matlab中Bode图的绘制技巧(精)

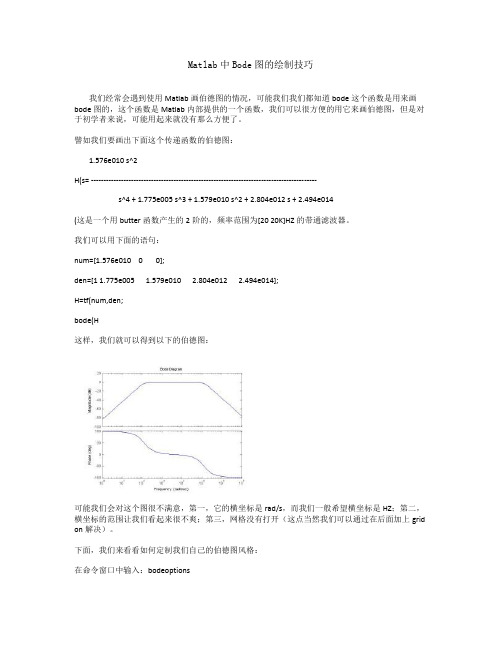
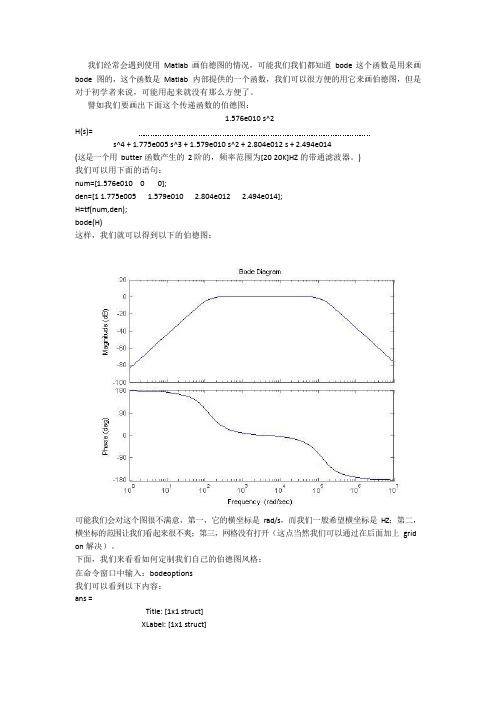
Matlab中Bode图的绘制技巧我们经常会遇到使用Matlab画伯德图的情况，可能我们我们都知道bode这个函数是用来画bode图的，这个函数是Matlab内部提供的一个函数，我们可以很方便的用它来画伯德图，但是对于初学者来说，可能用起来就没有那么方便了。

譬如我们要画出下面这个传递函数的伯德图：1.576e010 s^2H(s= ------------------------------------------------------------------------------------------s^4 + 1.775e005 s^3 + 1.579e010 s^2 + 2.804e012 s + 2.494e014(这是一个用butter函数产生的2阶的，频率范围为[20 20K]HZ的带通滤波器。

我们可以用下面的语句：num=[1.576e010 0 0];den=[1 1.775e005 1.579e010 2.804e012 2.494e014];H=tf(num,den;bode(H这样，我们就可以得到以下的伯德图：可能我们会对这个图很不满意，第一，它的横坐标是rad/s，而我们一般希望横坐标是HZ；第二，横坐标的范围让我们看起来很不爽；第三，网格没有打开（这点当然我们可以通过在后面加上grid on解决）。

下面，我们来看看如何定制我们自己的伯德图风格：在命令窗口中输入：bodeoptions我们可以看到以下内容：ans =Title: [1x1 struct] XLabel: [1x1 struct] YLabel: [1x1 struct] TickLabel: [1x1 struct] Grid: 'off'XLim: {[1 10]} XLimMode: {'auto'} YLim: {[1 10]} YLimMode: {'auto'} IOGrouping: 'none' InputLabels: [1x1 struct] OutputLabels: [1x1 struct] InputVisible: {'on'} OutputVisible: {'on'} FreqUnits: 'rad/sec' FreqScale: 'log' MagUnits: 'dB' MagScale: 'linear' MagVisible: 'on' MagLowerLimMode: 'auto' MagLowerLim: 0 PhaseUnits: 'deg' PhaseVisible: 'on' PhaseWrapping: 'off'PhaseMatching: 'off'PhaseMatchingFreq: 0PhaseMatchingValue: 0我们可以通过修改上面的每一项修改伯德图的风格，比如我们使用下面的语句画我们的伯德图：P=bodeoptions;P.Grid='on';P.XLim={[10 40000]};P.XLimMode={'manual'};P.FreqUnits='HZ';num=[1.576e010 0 0];den=[1 1.775e005 1.579e010 2.804e012 2.494e014];H=tf(num,den;bode(H,P这时，我们将会看到以下的伯德图：上面这张图相对就比较好了，它的横坐标单位是HZ，范围是[10 40K]HZ，而且打开了网格，便于我们观察-3DB处的频率值。

Matlab画伯德图

我们经常会遇到使用Matlab画伯德图的情况，可能我们我们都知道bode这个函数是用来画bode图的，这个函数是Matlab内部提供的一个函数，我们可以很方便的用它来画伯德图，但是对于初学者来说，可能用起来就没有那么方便了。

譬如我们要画出下面这个传递函数的伯德图：
(这是一个用butter函数产生的2阶的，频率范围为[2020K]HZ的带通滤波器。

)
我们可以用下面的语句：这样，我们就可以得到以下的伯德图
可能我们会对这个图很不满意，第一，它的横坐标是rad/s，而我们一般希望横坐标是HZ；第二，横坐标的范围让我们看起来很不爽；第三，网格没有打开（这点当然我们可以通过在后面加上grid on解决）。

下面，我们来看看如何定制我们自己的伯德图风格：在命令窗口中输入：bodeoptions我们可以看到以下内容：。

开环伯德图绘制

于是有： ω = K ⇒ ω0 = K ν
ν
75
《自动控制原理》电子教案
（5）绘制中频段首先在横坐标轴上将转折频率按从低到高的顺序标出各转折频率。然后，依次在各转折频率处改变直线的斜率，改变的多少取决于转折处环节的性质，如惯性环节的斜率为 − 20dB dec ，振荡环节为
− 40dB dec ，一阶微分环节为 + 20dB dec ，二阶微分环节为 + 40dB dec 等等。例：已知单位反馈控制系统的开环传递函数为 GK ( s) = 100( s + 2) s( s + 1)(s + 20) ，试绘制其开环
ω
2
由图可知：解得wc=4，
小结丗对最小相位系统、幅频特性与相频特性的关系
如果幅频特性的斜率为－１对应的相角为－ｐｉ／２；如果幅频特性的斜率为－ｋ对应的相角为－ｐｉ＊ｋ／２．
77
L(ω ) = 20 lg K − 20 ×ν × lg ω ω =1 = 20 lg K
③低频段直线（或其延长线）与零分贝线（横轴）的交点频率为 ω0 = K ，对于 I 型系统交点频
ν
1
率为 ω0 = K ，II 型系统交点频率为 ω0 =
1
K ；这是因为由低频段的幅频方程，可得到
L(ω ) = 20 lg K − 20 ×ν × lg ω = 0 ⇒ 20 lg K = 20 ×ν × lg ω = 20 lg ων
⎧ L (ω ) = −20 lg 1 + ω 2 − 20 lg lg 1 + 4ω 2 ⎧ϕ (ω ) = arctgω − arctg 2ω ⎪ 1 1 ，⎨ ⎨ 2 2 ⎩ϕ 2 (ω ) = −arctgω − arctg 2ω ⎪ L2 (ω ) = −20 lg 1 + ω − 20 lg lg 1 + 4ω ⎩

开环系统的频率特性绘制伯德图

1
s(1 s)(1 5s)
G(s)
10
s(1 s)(1 5s)
[具有积分环节的系统的频率特性的特点]：
m
频率特性可表示为：G(
j )
(
1
j )
i 1 n
(1 i s)
(1 Tj s)
j 1
m
其相角为： ( ) tg 1i
i 1
2
n j 1
tg 1Tj
当
0 时，(0)
,G(0)
比较开环系统极坐标方法，用伯德图表示的频率特性有如下优点：（1）把幅频特性的乘除运算转变为加减运算。
（2）在对系统作近似分析时，一般只需要画出对数幅频特性曲线的渐近线，从而大大简化了图形的绘制。
（3）在采用实验方法时，可将测得系统（或环节）频率响应的数据画在半对数坐标纸上。
开环系统频率特性为：
j )
K
1 1
jT2 jT1
两个系统的幅频特性完全相同。而它们的相频特性则有很大的区
别。由系统a、b的相频表达式：
a ( ) tan 1 T2 tan 1 T1 b ( ) tan 1 T2 tan 1 T1
40 35 30 25 20
0
a
-90
b
180
10-1
100
101
(K=100,T1=1,T2=0.1)
且有： (0)
2
, ()
(n
m)
2
。n
n1
2n2 ,
m
m1
2m2
由以上的分析可得到开环系统对数频率特性曲线的绘制方法：先画出每一个典型环节的波德图，然后相加。
[例]：开环系统传递函数为：G(s) 画出该系统的波德图。

3.1.2波特图的绘制(精)

图 1 波特图的横坐标和纵坐标
��/��，即横轴对lg�将是等分的，如图 1 横轴对照图所示。 ��与��的对应关系如图 1 纵轴对照图所示。
由于习惯上都以频率�作为自变量，因此横轴为对数坐标，标以自变量而波特图纵轴以等分坐标来标定��，其单位是分贝��，而且是20lgM��，由图可见，波特图是画在纵轴位等分坐标、横轴为对数坐标的特殊Байду номын сангаас标纸上，
波特图的绘制
波特图（Bode 图）又叫伯德图。引入对数幅频特性��，可以使串联环节的幅值相乘转化为对数幅频特性
的相加；而��或它的渐近线大多与��成线性关系，因此，若以��为纵轴，单位长度， �将变化 10 倍[以后称这个为一个 “10 倍频程” （decade），记为 dec]。波特图的横坐标和纵坐标示意图如图 1 所示。 ��为横轴，则其图线将为直线。另一方面，若以��为横轴，则��每变化一个
特性��也画在与��完全相同的半对数坐标纸上，其横轴的取值与对数幅频特性坐标相同，画在半对数坐标纸上的��称为对数相频特性。
这种坐标纸叫“半对数坐标纸” 。注意： 1、对数坐标是不均匀坐标，是由疏到密周期性变化排列的，因此，不能像等分坐标那样任意取值、任意移动，在对数坐标上的取值和移动是以“级”为单位的。 2、对数坐标的每一级代表 10 倍频程，即每个等分的级的频率差 10 倍，若第一个“1”处为 0.1，则以后的“1”处便分别为 1、10、100、1000 等。究竟第一个“1”处的频率值取为多少，要视研究的系统所需要的频率段而定。在一般的调速系统和随动系统中，第一个“1”处的频率值通常在 0.01、0.1、1 三个数值中取值。由于对数幅频特性��是画在半对数坐标纸上的，为便于比较对照，相频

matlab绘制bode图技巧(可编辑修改word版)

我们经常会遇到使用Matlab 画伯德图的情况，可能我们我们都知道bode 这个函数是用来画bode 图的，这个函数是Matlab 内部提供的一个函数，我们可以很方便的用它来画伯德图，但是对于初学者来说，可能用起来就没有那么方便了。

譬如我们要画出下面这个传递函数的伯德图：1.576e010 s^2H(s)=s^4 + 1.775e005 s^3 + 1.579e010 s^2 + 2.804e012 s + 2.494e014(这是一个用butter 函数产生的2 阶的，频率范围为[20 20K]HZ 的带通滤波器。

)我们可以用下面的语句：num=[1.576e010 0 0];den=[1 1.775e005 1.579e010 2.804e012 2.494e014];H=tf(num,den);bode(H)这样，我们就可以得到以下的伯德图：可能我们会对这个图很不满意，第一，它的横坐标是rad/s，而我们一般希望横坐标是HZ；第二，横坐标的范围让我们看起来很不爽；第三，网格没有打开（这点当然我们可以通过在后面加上grid on 解决）。

下面，我们来看看如何定制我们自己的伯德图风格：在命令窗口中输入：bodeoptions我们可以看到以下内容：ans =Title: [1x1 struct]XLabel: [1x1 struct]YLabel: [1x1 struct]TickLabel: [1x1 struct]Grid: 'off'XLim: {[1 10]}XLimMode: {'auto'}YLim: {[1 10]}YLimMode: {'auto'}IOGrouping: 'none'InputLabels: [1x1 struct]OutputLabels: [1x1 struct]InputVisible: {'on'}OutputVisible: {'on'}FreqUnits: 'rad/sec'FreqScale: 'log'MagUnits: 'dB'MagScale: 'linear'MagVisible: 'on'MagLowerLimMode: 'auto'MagLowerLim: 0PhaseUnits: 'deg'PhaseVisible: 'on'PhaseWrapping: 'off'PhaseMatching: 'off'PhaseMatchingFreq: 0PhaseMatchingValue: 0我们可以通过修改上面的每一项修改伯德图的风格，比如我们使用下面的语句画我们的伯德图：P=bodeoptions;P.Grid='on';P.XLim={[10 40000]};P.XLimMode={'manual'};P.FreqUnits='HZ';num=[1.576e010 0 0];den=[1 1.775e005 1.579e010 2.804e012 2.494e014];H=tf(num,den);bode(H,P)这时，我们将会看到以下的伯德图：上面这张图相对就比较好了，它的横坐标单位是HZ，范围是[10 40K]HZ，而且打开了网格，便于我们观察-3DB 处的频率值。

Matlab中Bode图的绘制技巧

。。 1

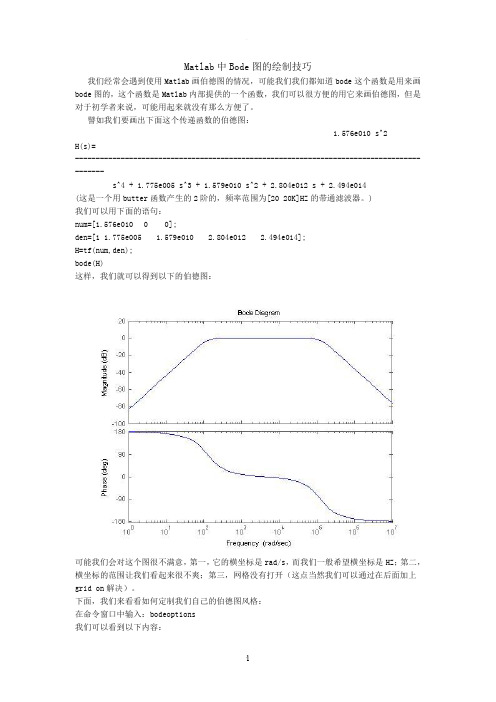
Matlab中Bode图的绘制技巧我们经常会遇到使用Matlab画伯德图的情况，可能我们我们都知道bode这个函数是用来画bode图的，这个函数是Matlab内部提供的一个函数，我们可以很方便的用它来画伯德图，但是对于初学者来说，可能用起来就没有那么方便了。譬如我们要画出下面这个传递函数的伯德图： 1.576e010 s^2 H(s)= ------------------------------------------------------------------------------------------ s^4 + 1.775e005 s^3 + 1.579e010 s^2 + 2.804e012 s + 2.494e014 (这是一个用butter函数产生的2阶的，频率范围为[20 20K]HZ的带通滤波器。) 我们可以用下面的语句： num=[1.576e010 0 0]; den=[1 1.775e005 1.579e010 2.804e012 2.494e014]; H=tf(num,den); bode(H) 这样，我们就可以得到以下的伯德图：

可能我们会对这个图很不满意，第一，它的横坐标是rad/s，而我们一般希望横坐标是HZ；第二，横坐标的范围让我们看起来很不爽；第三，网格没有打开（这点当然我们可以通过在后面加上grid on解决）。下面，我们来看看如何定制我们自己的伯德图风格：在命令窗口中输入：bodeoptions 我们可以看到以下内容：。。 2

ans = Title: [1x1 struct] XLabel: [1x1 struct] YLabel: [1x1 struct] TickLabel: [1x1 struct] Grid: 'off' XLim: {[1 10]} XLimMode: {'auto'} YLim: {[1 10]} YLimMode: {'auto'} IOGrouping: 'none' InputLabels: [1x1 struct] OutputLabels: [1x1 struct] InputVisible: {'on'} OutputVisible: {'on'} FreqUnits: 'rad/sec' FreqScale: 'log' MagUnits: 'dB' MagScale: 'linear' MagVisible: 'on' MagLowerLimMode: 'auto' MagLowerLim: 0 PhaseUnits: 'deg' PhaseVisible: 'on' PhaseWrapping: 'off' PhaseMatching: 'off' PhaseMatchingFreq: 0 PhaseMatchingValue: 0 我们可以通过修改上面的每一项修改伯德图的风格，比如我们使用下面的语句画我们的伯德图： P=bodeoptions; P.Grid='on'; P.XLim={[10 40000]}; P.XLimMode={'manual'}; P.FreqUnits='HZ'; num=[1.576e010 0 0]; den=[1 1.775e005 1.579e010 2.804e012 2.494e014]; H=tf(num,den); bode(H,P) 这时，我们将会看到以下的伯德图：。