开环伯德图绘制

合集下载

典型环节的Bode图

控制系统的开环频率特性目的：掌握开环Bode 图的绘制根据Bode 图确定最小相位系统的传递函数重点：开环Bode 图的绘制、根据Bode 图确定最小相位系统的传递函数1 开环伯德图手工作图的一般步骤：1）将开环传递函数表示为时间常数表达形式，计算各个典型环节的交接频率2）求20lgK 的值，并明确积分环节的个数ν 3）通过（1,20lgK ）绘制斜率为-20vdB/dec 低频段 4）随着频率增加，每遇到一个典型环节的交接频率，就改变一次斜率最小相位系统定义：递函数的零点、极点全部位于S 左半平面，同时又无纯滞后环节的系统称为最小相位系统。

否则就是非最小相位系统。

对数幅频特性与相频特性之间存在确定的对应关系。

对于一个最小相位系统，我们若知道了其幅频特性，它的相频特性也就唯一地确定了。

也就是说：只要知道其幅频特性，就能写出此最小相位系统所对应的传递函数，而无需再画出相频特性。

非最小相位系统高频时相角迟后大，起动性能差，响应缓慢。

对响应要求快的系统，不宜采用非最小相位元件。

2 典型环节的伯德图绘制曲线在MA TLAB 中实现，利用下述的程序段：num=[b2 b1 b0]; den=[1 a2 a1 a0]; H=tf(num,den); bode(H) margin(H) hold on2.1 比例环节传递函数：()G s K = 频率特性：()G j K ω=对数幅频特性：()20lg L j K ω= 对数相频特性：()0ϕω=程序段：num=[0 10]; den=[0 1]; H=tf(num,den); bode(H)margin(H) holdon结论：放大环节的对数幅频特性是一条幅值为20lgK 分贝，且平行于横轴的直线，相频特性是一条和横轴重合的直线。

K>1时，20lgK>0dB ；K<1时，20lgK<0dB 。

2.2 惯性环节（低通滤波特性）传递函数：1()1G s sτ=+频率特性：()()()j G j A e ϕωωω=对数幅频特性：21()20lg 1()L ωτω=+对数相频特性：()arctan ϕωτω=-绘制1()10.1G s s=+的Bode 图程序段：num=[0 1]; den=[0.1 1];H=tf(num,den); bode(H) margin(H) holdon结论：惯性环节的对数幅频特性可以用在1ωτ= 处相交于0分贝的两条渐近直线来近似表示：当1ωτ时，是一条0分贝的直线；当1ωτ时，是一条斜率为-20dB/dec 的直线。

如何绘制伯德图

????tjtjg21122???22222241lg20lg20????ttjg????t1???041lg20222222dbtt???????t1???lg4041lg20222222dbttt?????????t1t1t1五振荡环节t1150decdb40?40?20?db?l高频渐近线t1101t1t110?低频渐近线图517振荡环节渐进线对数幅频特性?振荡环节的相频特性是?5832212????ttarctgjg????16当时
5-14，可知，一阶微分环节与惯性环节的对数幅频特性和相频特性是
900 ( )
度
1 1 100
1 1 10
1 1 10 渐近特性
100
1

450
00
45o / dec
1 1 100
1 1 10
1
10
1
100
1

以横轴（ω 轴）为对称的。
图5-16 一阶微分环节的Bode图
振荡环节对数幅频特性的渐近线，它们的转折频率为
幅频特性曲线的渐近线如图5-17所示。
T
。对数
14
dB
L( )
1 1 10 T 1 T
低频渐近线
10
0
1 T
40 dB /dec
20

40
高频渐近线
图5-17 振荡环节渐进线对数幅频特性
•振荡环节的相频特性是 2 T G ( j ) arctg 2 2） • （ 5-83 1 T
（三）惯性环节惯性环节的频率特性是
G ( j)
其对数幅频特性是
1 jT 1
(5-73)
1
20 lg G ( j ) 20 lg 20 lg 1T22

典型环节的Bode图

控制系统的开环频率特性目的：掌握开环Bode图的绘制根据Bode图确定最小相位系统的传递函数重点：开环Bode图的绘制、根据Bode图确定最小相位系统的传递函数1 开环伯德图手工作图的一般步骤：1）将开环传递函数表示为时间常数表达形式，计算各个典型环节的交接频率2）求20lgK的值，并明确积分环节的个数ν3）通过（1,20lgK）绘制斜率为-20vdB/dec低频段4）随着频率增加，每遇到一个典型环节的交接频率，就改变一次斜率最小相位系统定义：递函数的零点、极点全部位于S 左半平面，同时又无纯滞后环节的系统称为最小相位系统。

否则就是非最小相位系统。

对数幅频特性与相频特性之间存在确定的对应关系。

对于一个最小相位系统，我们若知道了其幅频特性，它的相频特性也就唯一地确定了。

也就是说：只要知道其幅频特性，就能写出此最小相位系统所对应的传递函数，而无需再画出相频特性。

非最小相位系统高频时相角迟后大，起动性能差，响应缓慢。

对响应要求快的系统，不宜采用非最小相位元件。

Tf函数用来建立实部或复数传递函数模型或将状态方程、或零级增益模型转化成传递函数形式。

sys = tf(num,den)命令可以建立一个传递函数，其中分子和分母分别为num和den。

输出sys 是储存传递函数数据的传递函数目标。

单输入单输出情况下，num和den是s的递减幂级数构成的实数或复数行向量。

这两个向量并不要求维数相同。

如h = tf([1 0],1)就明确定义了纯导数形式h(s)=s。

若要构建多输入多输出传递函数，要分别定义每一个单输入单输出系统的端口的分子与分母。

2 典型环节的伯德图绘制曲线在MA TLAB中实现，利用下述的程序段：num=[b2 b1 b0];den=[1 a2 a1 a0];H=tf(num,den);bode(H)margin(H)hold on2.1 比例环节传递函数：()G s K=频率特性：()G j Kω=对数幅频特性：()20lgL j Kω=对数相频特性：()0ϕω=程序段：num=[0 10]; den=[0 1]; H=tf(num,den);bode(H)margin(H) holdon结论：放大环节的对数幅频特性是一条幅值为20lgK分贝，且平行于横轴的直线，相频特性是一条和横轴重合的直线。

BODE图的讲解

L() 20 lg () *90
共二十三页
( )
§5.3.1 典型环节的Bode图
§5.3.1 典型(diǎnxíng)环节的Bode图
⑶ 积分(jīfēn) G( j ) 1
环节
j
L() 20lg () 90
当 G( j) ( 1 ) j
L() 20 lg () 90*
⑷ 惯性环节
§5.3.1 典型(diǎnxíng)环节的Bode图
⑹ 节
振荡(zhèndàng)G环(s)
n2 s2 2ns n2
G(
j )
1
2
2 n
1
j2
n
L( ) 20lg
[1
2 n2
]2
[2
n
]2
( )
arctan 2
n
1 -
2
2 n
1
n
1
n
L() 0 () 0
L( ) 40lg n
第一转折频率之左的特性及其延长线
共二十三页
内容(nèiróng)总结
1)由开环频率特性求出幅频特性和相频特性，或实频特性和虚频特性。不含零点时，模值和相位一般会单调收缩，当有零点时，曲线可能会扭曲。(4) (非直线）特性曲线可以绘制渐近对数(duìshù)幅频特性，进一步简化绘制过程。是一条斜率为＋ 20db/dec，过（1,0)点的直线，记作〔＋20〕。谐振频率wr 和谐振峰值Mr。① 两惯性环节转折频率很接近时
30dB
20( lgc
lg
2)
20 lg
c
2
lg c 30 1.5
2 20
c 2 101.5 63.2 rad s

如何绘制伯德图

20 lg 10 20(dB)
。
6
设 ' 10 ，则有
20 lg 20 lg 10 20 20 lg
'
(5-68)
dB L( )
可见，其对数幅频特性是一条在 ω =1（弧度/秒）处穿过零分贝线（ ω 轴），且以每增加十倍频降低 20 分贝的速度（ -20dB/dec ）变化的直线。积分环节的相频特性是
对数幅频特性为
20 lg G( j ) 20 lg K
（5-61）
当K>1时，20lgK>0，位于横轴上方；
当K=1时，20lgK=0，与横轴重合；
当K<1时，20lgK<0，位于横轴下方。
4
放大环节的对数幅频特性如图5-11所示，它是一条与角频率ω 无关且平行于横轴的直线，其纵坐标为20lgK。
0
100
1000

（5-63）
180
0
放大环节的相频特性是
G( j ) 0
0
图5-11 放大环节的Bode图
（5-64）如图5-11所示，它是一条与角频率ω无关且与ω轴重合的直线。
5
（二）积分环节积分环节的频率特性是
G ( j ) 1 j j 1

1

e
j 90
2 2 2
（5-85）
相频特性是
G ( j ) arctg 2 1
2 2
dB
40
（5-86）20
0
1 1 10
0
精确特性
40dB / dec
二阶微分环节与振荡节的Bode
1
图关于ω 轴对称，如图5-21 。

系统开环频率特性的绘制

20lg G1( j)
v 20 lg
Kv
j
20lg Kv 20lg v 0
v
和
20lg G2 ( j)
a
20 lg
Ka
2
a
20 lg
Ka
20 lg
2 a
0
(5-95)
(5-96)
8
由上面两式分别得到
v Kv
（5-97）
a
Ka 或Ka
2 a
（5-98）
通过上面的分析，在绘制传递函数为式（5-93）和（5-94）的对数幅频特性时，可用下述两种方法之一进行。
1
一、绘制系统开环频率特性极坐标图的步骤
1. 将系统开环传递函数分解成若干典型环节的串联形式； 2.典型环节幅频特性相乘得到系统开环幅频特性， 3.典型环节相频特性相加得到系统开环相频特性； 4.如幅频特性有渐近线，则根据开环频率特性表达式的实部和
虚部，求出渐近线； 5.最后在G(jω)H(jω)平面上绘制出系统开环频率特性的极坐标图。
dB
dB
a
A
20dB / dec
0 20log KV
1
V
图5-26 KV与V的关系
a
A
0 20log Ka
40dB / dec
1 a
图5-27 Ka 与 a的关系
9
方法一：对于式（5-93），先过横轴上ω=1点作横轴的垂直线，过纵轴上20lgKv点作横轴的平行线，这两条直线交于A 点，然后过A点作斜率为 -20dB/dec的直线即为所求的对数幅频特性（图5-26）；对于式（ 5-94），过横轴上ω=1 点作横轴的垂线过纵轴上20lgKa 点作横轴的平行线，这两条直线交于A点，然后过A点作斜率为-40dB/dec的直线即为所求的对数幅频特性（图5-27）。

第五章_开环伯德图

20lg 1 jω T 20lg 1 ω 2 T 2
ω tg1ω T
11
L ( )
dB
20
20 0
( )
90
1 10T
1 T
10 T

45 0
1 10T
1 T
10 T

一阶微分环节高频渐近线的斜率是+20dB/dec，其相位变化范围由0°（ω=0）经+45°至90°（ω=∞）
0.7
0.3 0.2
( )
180 90 0

0.7
0.3 0.2
1 10T
1 T
10 T

20
8．延迟环节
幅频特性相频特性
( )
0 100 200 300 400
1 10T
e jω
T
Lω 20lgG jω 20lg1 0 dB
1 T 2ω 2
即二阶微分环节的幅频和相频特性分别与振荡环节的相应特性是关于横轴对称。此时，其对数幅频特性的高频渐近线的斜率为 +40dB/dec而相频由0°（对应ω=0）经 1 90°ω ω T ，最后趋于180°（ω→∞）。
n
19
L( )
40 20
0dBBiblioteka 409000.1
1
10

6
4. 惯性环节
惯性环节的幅频特性为
G jω 1 1 jω T
惯性环节的幅频特性
20 lg 1 1 20 lg 20 lg 1 2T 2 1 jT 1 2T 2
1 在 ω T 时（低频段）：
20lg 1 ω2T 2 20lg1 0 dB

§5-3系统开环频率特性的绘制(精)

G ( j ) H ( j ) K 1 T12 2 1 1 T22 2 1
(T1 T2 ) G ( j ) H ( j ) arctgT1 arctgT2 arctg 1 T1T2 2
4
（1）极坐标图
当 0 时， G( j ) H ( j ) K , G( j ) H ( j ) 00 当
1 1 1 1 和，且 T1 T2 T2 T1
L ( ) dB L ( )
A
20 log K
0
B
渐近特性
，将它们
20dB / dec
1 T1
精确特性
在ω 轴上标出（图5-25）；在纵坐标上找到 20lgK 的点 A ，过 A 点作平行于横轴的直线 AB ，这条平行线对应放大环节的幅频特性；
C
1 T2

40dB / dec
(1)
度
( 2)
D
(3)
0 1 在交接频率 T 处作ω 轴的垂线 1 450

（虚线）交平行线AB于B点，以B 为起点作斜率为-20dB/dec的斜
1 线BC，C点对应交接频率，折线 T2
( 4)
ABC对应放大环节K和惯性环节 1 的叠加； Ts 1
图5-25 开环系统Bode图
8
由上面两式分别得到
v Kv
a
2 K a 或K a a
（5-97）
（5-98）
通过上面的分析，在绘制传递函数为式（5-93）和（5-94）的对数幅频特性时，可用下述两种方法之一进行。
dB
dB
a
0
20 log KV
A
20dB / dec

开环伯德图的绘制

0.1
arctg

20
g 20

幅值裕度 c 1
(c ) 90 arctg
177.15
c
0
90

0.1
arctg
c
20
180 (c ) 2.85
180
270
相角裕度 g 1.5
1 1 h 2.26 A(g ) G( j1.5)
60dB / dec
开环伯德图（习题五）
单位负反馈系统传递函数如下，画出幅相曲线，并求稳定裕度 s 100( 1) 100(0.5 j 1) 2 G( j ) G( s) j( j 1)(0.1 j 1)(0.05 j 1) s s s( s 1)( 1)( 1) L( ) 10 20
相频特性曲线的绘制
1. 在确定转角频率之后，找到对应转角频率的相位角
2.
在中间选出一些特殊点，计算对应相位角，最后画出草图
2
开环伯德图的绘制 L( )
G( s) 50( s 2) s( s 1)
50( j 2) j ( j 1)
40 20
20dB / dec
40dB / dec 20dB / dec
60dB / dec
7
L( )
40
0
40
开环伯德图（习题二）
G( j ) 10 1 1 1 10 j (10 j 1)(0.05 j 1) j (10 j 1) (0.05 j 1)
(c ) 90 arctg
( )
0.1
自动控制原理
潘剑飞
2653-4850（办公室）

伯徳图的画法和在判稳中的应用

例：开环特征方程有两个右根，P=2，试判定闭环系统的稳定性。解：
P=2
正负穿越数之差（N+-N-）为1
Z=P-2N=2-2=0 系统闭环稳定
例：开环特征方程无右根，P=0，试判定闭环系统的稳定性。解：
P=0
正负穿越数之差为0
系统闭环稳定
§ 5.4 稳定裕度
♣ ♣ ♣
K值较小时，系统稳定； K值较大时，系统不稳定的； K取某个值时，Nyquist曲线通过 (-1,j0)点，系统处于临界稳定状态。
c ——Nyquist曲线与单位圆交点处(此处幅值为1）的称为截止频率(又称剪切频率)，记为 c 。
G( jωc ) H ( jωc ) 1
相角裕度 180 G( jc ) H ( jc ) 含义：如果系统对频率为截止频率的信号的相角滞后再增大度，则系统处于临界稳定状态。稳定系统的 > 0 , 越大,系统相对稳定性越高。
(5) 系统开环对数相频特性表达式为
( ) arctan0.5 900 arctan arctan0.05
逐点计算结果
系统开环相频特性数据
－20dB/dec
20
－20dB/dec －40dB/dec －40dB/dec
例：
L(1) 20lg 7.5 17.5
2. Bode图上的稳定判据
闭环系统稳定的充要条件是：当ω 由0变到 +∞ 时，在开环对数幅频特性 L(ω)≥0 的频段内，相频特性φ(ω) 穿越-π线的次数（正穿越与负穿越次数之差）为p/2，p为s平面右半部的开环极点数。若开环传递函数无极点分布在S右半平面，即 P 0 ，则闭环系统稳定的充要条件是：在L(ω)≥0 的频段内，相频特性φ(ω) 在-π线上正负穿越次数代数和为零，或者不穿越 -π线。 Nyquist图 Bode图

bode图 nyquist图

系统开环Bode图的绘制

单回路开环系统Bode图的绘制步骤
确定各环节的转折频率并由小到大标示在对数频率轴上；计算20lgK，在ω＝1 rad/s处找到纵坐标等于20lgK 的点，过该点作斜率等于 -20v dB/dec的直线，向左延长此线至所有环节的转折频率之左，得到最低频段的渐近线。向右延长最低频段渐近线，每遇到一个转折频率改变一次渐近线斜率；对惯性环节，- 20dB/dec 振荡环节， - 40dB/dec 一阶微分环节，+20dB/dec 二阶微分环节，+40dB/dec 对渐近线进行修正以获得准确的幅频特性；相频特性曲线由各环节的相频特性相加获得。
延迟环节是不是最小相位环节？
系统开环Bode图的绘制

Bode图的绘制举例
系统开环Bode图的绘制

单回路开环系统Bode图的绘制
系统开环Nyquist图的绘制

概述
K ( n s 1) ( k s 2 k k s 1)
2 2

G( s) s
v
n 1
k 1
2 2 i 1 j 1

系统开环Nyquist图的绘制

概述
G( s ) G1 ( s )G2 ( s )...Gn ( s )
G( j ) A1 ( )e
j1 ( )
A2 ( )e
j 2 ( )
.. An ( )e
j n ( )
A( ) A1 ( ) A2 ( )... An ( )
系统开环Bode图的绘制

最小相位环节的频率特性
（1）定义
凡在右半S 平面上有开环零点或极点的系统，称为非最小相位系统。 “最小相位” 是指，具有相同幅频特性的一些环节，其中相角位移有最小可能值的，称为最小相位环节；反之，其中相角位移大于最小可能值的环节称为非最小相位环节；后者常在传递函数中包含右半S平面的零点或极点。

典型环节的Bode图

典型环节的B o d e图-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN控制系统的开环频率特性目的：掌握开环Bode图的绘制根据Bode图确定最小相位系统的传递函数重点：开环Bode图的绘制、根据Bode图确定最小相位系统的传递函数1 开环伯德图手工作图的一般步骤：1）将开环传递函数表示为时间常数表达形式，计算各个典型环节的交接频率2）求20lgK的值，并明确积分环节的个数ν3）通过（1,20lgK）绘制斜率为-20vdB/dec低频段4）随着频率增加，每遇到一个典型环节的交接频率，就改变一次斜率最小相位系统定义：递函数的零点、极点全部位于S 左半平面，同时又无纯滞后环节的系统称为最小相位系统。

否则就是非最小相位系统。

对数幅频特性与相频特性之间存在确定的对应关系。

对于一个最小相位系统，我们若知道了其幅频特性，它的相频特性也就唯一地确定了。

也就是说：只要知道其幅频特性，就能写出此最小相位系统所对应的传递函数，而无需再画出相频特性。

非最小相位系统高频时相角迟后大，起动性能差，响应缓慢。

对响应要求快的系统，不宜采用非最小相位元件。

2 典型环节的伯德图绘制曲线在MATLAB中实现，利用下述的程序段：num=[b2 b1 b0];den=[1 a2 a1 a0];H=tf(num,den);bode(H)margin(H)hold on比例环节传递函数：()G s K=频率特性：()G j Kω=对数幅频特性：()20lgL j Kω=对数相频特性：()0ϕω=程序段：num=[0 10]; den=[0 1]; H=tf(num,den);bode(H)margin(H) hold on结论：放大环节的对数幅频特性是一条幅值为20lgK分贝，且平行于横轴的直线，相频特性是一条和横轴重合的直线。

K>1时，20lgK>0dB；K<1时，20lgK<0dB。

典型环节的Bode图

控制系统的开环频率特性目的：掌握开环Bode图的绘制根据Bode图确定最小相位系统的传递函数重点：开环Bode图的绘制、根据Bode图确定最小相位系统的传递函数1 开环伯德图手工作图的一般步骤：1）将开环传递函数表示为时间常数表达形式，计算各个典型环节的交接频率2）求20lgK的值，并明确积分环节的个数ν3）通过（1,20lgK）绘制斜率为-20vdB/dec低频段4）随着频率增加，每遇到一个典型环节的交接频率，就改变一次斜率最小相位系统定义：递函数的零点、极点全部位于S 左半平面，同时又无纯滞后环节的系统称为最小相位系统。

否则就是非最小相位系统。

对数幅频特性与相频特性之间存在确定的对应关系。

对于一个最小相位系统，我们若知道了其幅频特性，它的相频特性也就唯一地确定了。

也就是说：只要知道其幅频特性，就能写出此最小相位系统所对应的传递函数，而无需再画出相频特性。

非最小相位系统高频时相角迟后大，起动性能差，响应缓慢。

对响应要求快的系统，不宜采用非最小相位元件。

Tf函数用来建立实部或复数传递函数模型或将状态方程、或零级增益模型转化成传递函数形式。

sys = tf(num,den)命令可以建立一个传递函数，其中分子和分母分别为num和den。

输出sys 是储存传递函数数据的传递函数目标。

单输入单输出情况下，num和den是s的递减幂级数构成的实数或复数行向量。

这两个向量并不要求维数相同。

如h = tf([1 0],1)就明确定义了纯导数形式h(s)=s。

若要构建多输入多输出传递函数，要分别定义每一个单输入单输出系统的端口的分子与分母。

2 典型环节的伯德图绘制曲线在MA TLAB中实现，利用下述的程序段：num=[b2 b1 b0];den=[1 a2 a1 a0];H=tf(num,den);bode(H)margin(H)hold on2.1 比例环节传递函数：()G s K=频率特性：()G j Kω=对数幅频特性：()20lgL j Kω=对数相频特性：()0ϕω=程序段：num=[0 10]; den=[0 1]; H=tf(num,den);bode(H)margin(H) holdon结论：放大环节的对数幅频特性是一条幅值为20lgK分贝，且平行于横轴的直线，相频特性是一条和横轴重合的直线。

典型环节传递函数及伯德图

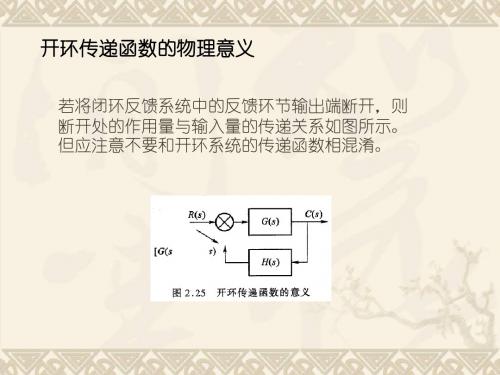
( )(度)

0
0.1
1
10

２.积分环节

积分环节的特点：输出量与输入量的积分成正比例，即输出量取决于输入量对时间的积累过程。积分环节的微分方程:

积分环节的传递函数:

积分环节的单位阶跃响应：
２.积分环节
积分环节也是自动控制系统中最常见的环节之一，凡是输出量对输入量具有贮存和积累特点的元件一般都含有积分环节，例如机械运动中位移与转速、转速与转矩、速度与加速度、电容的电压与电流、水箱的水位与水流量等。下面介绍几个常见的积分环节。 (１)电动机
６.振荡环节
G jω 1 2 2 L ω 20lg 1 T ω 2 2 T jω 2ζ T jω 1

2ζ Tω
2
2
ω t g1
2ζ Tω 2 2 1 T ω
低频段，即ω T<<1时
10
Lω 20lg1 ＝0 dB
1 T
10 T

式中，T为惯性时间常数。惯性环节的传递函数:

惯性环节的单位阶跃响应：
４.惯性环节（一阶输出的微分环节，是一个相位滞后环节）
自动控制系统中经常含有这种环节，这种环节含有一个储能元件（如储存磁场能的电感、储存电场能的电容、储存弹性势能的弹簧和储存动能的机械负载等）和一个耗能元件（如电阻、阻尼器等）。下面通过两个实例来加以说明。

电动机转速和转矩、角位移和转速都是积分关系。当不考虑负载转矩时，电动机的转矩与转速的关系如下

对上式进行拉氏变换得

而电动机的角位移与转速关系如下

对上式进行拉氏变换可得

5.3.2开环系统bode图的绘制

5.3.2 开环系统Bode 图的绘制将开环传递函数()G s 表示成式(5-48)形式的典型环节组合形式，有12121212()20lg ()20lg[()()()]20lg ()20lg ()20lg ()()()()()()()()l l l l L A A A A A A A L L L ω=ω=ωωω⎧⎪=ω+ω++ω⎪⎨=ω+ω++ω⎪⎪ϕω=ϕω+ϕω+ϕω⎩ （5-58）式中，)(ωi L 和)(ωϕi 分别表示各典型环节的对数幅频特性和对数相频特性。

式（5-58）表明，只要能作出)(ωj G 所包含的各典型环节的对数幅频和对数相频曲线，将它们进行代数相加，就可以求得开环系统的Bode 图。

实际上，在熟悉了对数幅频特性的性质后，可以采用更为简捷的办法直接画出开环系统的Bode 图，具体步骤如下。

(1) 将开环传递函数写成尾1标准形式：()211()2211(1)[()21]()(1)[()21]m p pzh i h i zh zh n q v qv pk j k j pk pks s s K z G s s s s s p -==--==+++=+++∏∏∏∏ξωωξωω 确定系统开环增益K 和型别v ，把各典型环节的转折频率由小到大依次标在频率轴上。

(2) 绘制开环对数幅频特性低频段的渐近线。

由于低频段渐近线的频率特性为()v K j ω，所以它就是过点（K lg 20,1）、斜率为20dB/dec v -的直线。

(3) 在低频段渐近线的基础上，沿频率增大的方向每遇到一个转折频率就改变一次斜率，其规律是遇到惯性环节的转折频率，斜率变化20dB/dec -；遇到一阶复合微分环节的转折频率，斜率变化20dB/dec ；遇到二阶复合微分环节的转折频率，斜率变化40dB/dec ；遇到振荡环节的转折频率，斜率变化40dB/dec -；直到所有转折全部进行完毕。

最右端转折频率之后的渐近线斜率应该是20()dB/dec n m --，其中，m n ,分别为)(s G 分母、分子的阶数。

自动控制理论-19开环对数频率特性曲线的绘制

针转一圈时，在F(s)平面上，ΓF曲线从B点开始绕原点反时针转一圈。
定理如下：
•如果封闭曲线 s 内有Z个F(s)的零点，有P个F(s)的极点，则s依 s 顺时针转一圈时，在F(s)平面上， F(s)曲线绕原点反时针转的圈数R为P 和Z之差，即R＝P－Z
•若R为负,表示F(s)曲线绕原点顺时针转过的圈数。
例已知单位负反馈系统如图所示，试做出系统的开环伯德图。
解：作L():
(1) G s 40 40 / 4 10 K
s(s 4)
s
1 4
s
1
s
1 4
s
1
s(Ts 1)
因此，开环增益 K=10
转折频率
1
1 T
4 (1/ s)
20lg K 20 dB
L()/dB
40
-20 dB/dec
辅助函数F(s)具有如下特点： ①其零点和极点分别是闭环和开环的特征根。 ②其零点的个数与极点的个数相同。 ③辅助函数与系统开环传递函数只差常数1。
1.辐角原理（柯西）
设S为复变量，F(S)为S的有理分式函数，对于S平面上任一变
量点，通过复变函数F(S)的映射关系，在F(S)平面上可确定关于变
量的象。
反馈控制系统
开环传递函数
GsH s

M1sM 2 s N1sN2 s
闭环传递函数
(s)
1
Gs GsH s
M1sN2 s N1sN2 s M1sM 2 s
令 Fs 1 GsH s
N1sN2 s M1sM 2 s N1sN2 s
将F(s)写成零、极点形式，有
n
s zi
F s i1 n s pi i 1

开环伯德图绘制

于是有： ω = K ⇒ ω0 = K ν
ν
75
《自动控制原理》电子教案
（5）绘制中频段首先在横坐标轴上将转折频率按从低到高的顺序标出各转折频率。然后，依次在各转折频率处改变直线的斜率，改变的多少取决于转折处环节的性质，如惯性环节的斜率为 − 20dB dec ，振荡环节为
− 40dB dec ，一阶微分环节为 + 20dB dec ，二阶微分环节为 + 40dB dec 等等。例：已知单位反馈控制系统的开环传递函数为 GK ( s) = 100( s + 2) s( s + 1)(s + 20) ，试绘制其开环
ω
2
由图可知：解得wc=4，
小结丗对最小相位系统、幅频特性与相频特性的关系
如果幅频特性的斜率为－１对应的相角为－ｐｉ／２；如果幅频特性的斜率为－ｋ对应的相角为－ｐｉ＊ｋ／２．
77
L(ω ) = 20 lg K − 20 ×ν × lg ω ω =1 = 20 lg K
③低频段直线（或其延长线）与零分贝线（横轴）的交点频率为 ω0 = K ，对于 I 型系统交点频
ν
1
率为 ω0 = K ，II 型系统交点频率为 ω0 =
1
K ；这是因为由低频段的幅频方程，可得到
L(ω ) = 20 lg K − 20 ×ν × lg ω = 0 ⇒ 20 lg K = 20 ×ν × lg ω = 20 lg ων
⎧ L (ω ) = −20 lg 1 + ω 2 − 20 lg lg 1 + 4ω 2 ⎧ϕ (ω ) = arctgω − arctg 2ω ⎪ 1 1 ，⎨ ⎨ 2 2 ⎩ϕ 2 (ω ) = −arctgω − arctg 2ω ⎪ L2 (ω ) = −20 lg 1 + ω − 20 lg lg 1 + 4ω ⎩

典型环节的Bode图

控制系统的开环频率特性目的：掌握开环Bode图的绘制根据Bode图确定最小相位系统的传递函数重点：开环Bode图的绘制、根据Bode图确定最小相位系统的传递函数1 开环伯德图手工作图的一般步骤：1）将开环传递函数表示为时间常数表达形式，计算各个典型环节的交接频率2）求20lgK的值，并明确积分环节的个数ν3）通过（1,20lgK）绘制斜率为-20vdB/dec低频段4）随着频率增加，每遇到一个典型环节的交接频率，就改变一次斜率最小相位系统定义：递函数的零点、极点全部位于S 左半平面，同时又无纯滞后环节的系统称为最小相位系统。

否则就是非最小相位系统。

对数幅频特性与相频特性之间存在确定的对应关系。

对于一个最小相位系统，我们若知道了其幅频特性，它的相频特性也就唯一地确定了。

也就是说：只要知道其幅频特性，就能写出此最小相位系统所对应的传递函数，而无需再画出相频特性。

非最小相位系统高频时相角迟后大，起动性能差，响应缓慢。

对响应要求快的系统，不宜采用非最小相位元件。

Tf函数用来建立实部或复数传递函数模型或将状态方程、或零级增益模型转化成传递函数形式。

sys = tf(num,den)命令可以建立一个传递函数，其中分子和分母分别为num和den。

输出sys 是储存传递函数数据的传递函数目标。

单输入单输出情况下，num和den是s的递减幂级数构成的实数或复数行向量。

这两个向量并不要求维数相同。

如h = tf([1 0],1)就明确定义了纯导数形式h(s)=s。

若要构建多输入多输出传递函数，要分别定义每一个单输入单输出系统的端口的分子与分母。

2 典型环节的伯德图绘制曲线在MA TLAB中实现，利用下述的程序段：num=[b2 b1 b0];den=[1 a2 a1 a0];H=tf(num,den);bode(H)margin(H)hold on2.1 比例环节传递函数：()G s K=频率特性：()G j Kω=对数幅频特性：()20lgL j Kω=对数相频特性：()0ϕω=程序段：num=[0 10]; den=[0 1]; H=tf(num,den);bode(H)margin(H) holdon结论：放大环节的对数幅频特性是一条幅值为20lgK分贝，且平行于横轴的直线，相频特性是一条和横轴重合的直线。

实验二：绘制控制系统的Bode图(学生用)

实验二：绘制控制系统的Bode图Bode Graphics of Controlling System一、实验目的1.利用计算机做出开环系统的伯德图；2.观察记录控制系统的开环频域性能；3.控制系统的开环频率特性分析。

二、实验步骤1.在Windows界面上双击matlab图标，即可打开MATLAB命令平台。

2.练习相关M函数（1）伯德图绘图函数：bode(sys)bode(sys,{wmin,wmax})bode(sys,w)[m,p,w]=bode(sys)函数功能：对数频率特性作图函数，即伯德图作图。

格式1：给定开环系统的数学模型对象sys作伯德图，频率向量w自动给出。

格式2：给定变量w的绘图区间为{wmin,wmax}。

格式3：频率向量w由人工给出。

w的单位为[弧度]/秒，可以由命令logspace得到对数等分的w值。

格式4：返回变量格式，不作图。

m为频率特性G(jω)的幅值向量，m=︱G(j)︳。

p为频率特性G(jω)的幅角向量，p=arg[G(jω)]，单位为角度（°）。

w为频率向量，单位为[弧度]/秒。

更详细的命令说明，可键入“help bode”在线帮助查阅。

例如，系统开环传递函数为作图程序为num=[10];den=[1 2 10];sys=tf(num,den);bode(sys);grid on上面两句或者直接换为：bode(num,den);绘制伯德图如图1所示。

或者给定人工变量w=logspace(-1,1,32); % w范围和点数n ，下面对该函数做了详细的说明bode(num,den,w); %或者sys=tf(num,den); bode(sys,w);grid on绘制伯德图如图2所示。

图3 伯德图图4 伯德图（2）对数分度函数：logspace(d1,d2)logspace(d1,d2,n)函数功能：产生对数分度向量。

格式1：从10d1到10d2之间作对数等分分度，产生50个元素的对数等间隔向量。