加拿大国家中小学数学竞赛( kangaroo math 袋鼠竞赛)2018年三四年级(含答案)
加拿大国际袋鼠数学竞赛试题及答案-2016年ParentsQuestions

加拿⼤国际袋⿏数学竞赛试题及答案-2016年ParentsQuestionsCanadian Math Kangaroo ContestPart A: Each correct answer is worth 3 points1.Which letter on the board is not in the word "KOALA"?(A) R (B) L (C) K (D) N (E) O2.In a cave, there were only two seahorses, one starfish and three turtles. Later, five seahorses, three starfishand four turtles joined them. How many sea animals gathered in the cave?(A) 6 (B) 9 (C) 12 (D) 15 (E) 183.Matt had to deliver flyers about recycling to all houses numbered from 25 to 57. How many houses got theflyers?(A) 31 (B) 32 (C) 33 (D) 34 (E) 354.Kanga is 1 year and 3 months old now. In how many months will Kanga be 2 years old?(A) 3 (B) 5 (C) 7 (D) 8 (E) 95.(A) 24 (B) 28 (C) 36 (D) 56 (E) 806. A thread of length 10 cm is folded into equal parts as shown in the figure.The thread is cut at the two marked places. What are the lengths of the three parts?(A) 2 cm, 3 cm, 5 cm (B) 2 cm, 2 cm, 6 cm (C) 1 cm, 4 cm, 5 cm(D) 1 cm, 3 cm, 6 cm (E) 3 cm, 3 cm, 4 cm7.Which of the following traffic signs has the largest number of lines of symmetry?(A) (B) (C) (D) (E)8.Kanga combines 555 groups of 9 stones into a single pile. She then splits the resulting pile into groups of 5 stones. How many groups does she get?(A) 999 (B) 900 (C) 555 (D) 111 (E) 459.What is the shaded area?(A) 50 (B) 80 (C) 100 (D) 120 (E) 15010.In a coordinate system four of the following points are the vertices of a square. Which point is not a vertexof this square?(A) (?1;3)(B) (0;?4)(C) (?2;?1)(D) (1;1)(E) (3;?2)Part B: Each correct answer is worth 4 points11.There are twelve rooms in a building and each room has two windows and one light. Last evening, eighteen windows were lighted. In how many rooms was the light off?(A) 2 (B) 3 (C) 4 (D) 5 (E) 612.Which three of the five jigsaw pieces shown can be joined together to form a square?(A) 1, 3 and 5 (B) 1, 2 and 5 (C) 1, 4 and 5 (D) 3, 4 and 5 (E) 2, 3 and 513.John has a board with 11 squares. He puts a coin in each of eight neighbouring squareswithout leaving any empty squares between the coins. What is the maximum numberof squares in which one can be sure that there is a coin?(A) 1 (B) 3 (C) 4 (D) 5 (E) 614.Which of the following figures cannot be formed by gluing these two identical squares of paper together?(A) (B) (C) (D) (E)15.Each letter in BENJAMIN represents one of the digits 1, 2, 3, 4, 5, 6 or 7. Different letters represent different digits. The number BENJAMIN is odd and divisible by 3. Which digit corresponds to N?(A) 1 (B) 2 (C) 3 (D) 5 (E) 716.Seven standard dice are glued together to make the solid shown. The faces of the dice thatare glued together have the same number of dots on them. How many dots are on the surfaceof the solid?(A) 24 (B) 90 (C) 95 (D) 105 (E) 12617.Jill is making a magic multiplication square using the numbers 1, 2, 4, 5, 10, 20, 25, 50 and 100. The productsof the numbers in each row, in each column and in the two diagonals should all be the same. In the figure you can see how she has started. Which number should Jill place in the cell with the question mark?(A) 2 (B) 4 (C) 5 (D) 10 (E) 2518.What is the smallest number of planes that are needed to enclose a bounded part in three-dimensional space?(A) 3 (B) 4 (C) 5 (D) 6 (E) 719.Each of ten points in the figure is marked with either 0 or 1 or 2. It is known thatthe sum of numbers in the vertices of any white triangle is divisible by 3, while thesum of numbers in the vertices of any black triangle is not divisible by 3. Three ofthe points are marked as shown in the figure. What numbers can be used to markthe central point?(A) Only 0. (B) Only 1. (C) Only 2. (D) Only 0 and 1. (E) Either 0 or 1 or 2.20.Betina draws five points AA,BB,CC,DD and EE on a circle as well as the tangent tothe circle at AA, such that all five angles marked with xx are equal. (Note thatthe drawing is not to scale.) How large is the angle ∠AABBDD ?(A) 66°(B) 70.5°(C) 72°(D) 75°(E) 77.5°Part C: Each correct answer is worth 5 points21.Which pattern can we make using all five cards given below?(A) (B) (C) (D) (E)22.The numbers 1, 5, 8, 9, 10, 12 and 15 are distributed into groups with one or more numbers. The sum of thenumbers in each group is the same. What is the largest number of groups?(A) 2 (B) 3 (C) 4 (D) 5 (E) 623.My dogs have 18 more legs than noses. How many dogs do I have?(A) 4 (B) 5 (C) 6 (D) 8 (E) 924.In the picture you see 5 ladybirds.Each one sits on its flower. Their places are defined as follows: the difference of the dots on their wings is the number of the leaves and the sum of the dots on their wings is the number of the petals. Which of the following flowers has no ladybird?(A) (B) (C) (D) (E)25.On each of six faces of a cube there is one of the following six symbols: ?, ?, ?, ?, ? and Ο. On each face there is a different symbol. In the picture we can see this cube shown in two different positions.Which symbol is opposite the ??(A) Ο(B)?(C) ?(D) ?(E) ?26.What is the greatest number of shapes of the form that can be cut out from a5 × 5 square?(A) 2 (B) 4 (C) 5 (D) 6 (E) 727.Kirsten wrote numbers in 5 of the 10 circles as shown in the figure. She wants to writea number in each of the remaining 5 circles such that the sums of the 3 numbers alongeach side of the pentagon are equal. Which number will she have to write in the circlemarked by XX?(A) 7 (B) 8 (C) 11 (D) 13 (E) 1528. A 3×3×3 cube is built from 15 black cubes and 12 white cubes. Five faces of the larger cube are shown.Which of the following is the sixth face of the large cube?(A) (B) (C) (D) (E)29.Jakob wrote down four consecutive positive integers. He then calculated the four possible totals made bytaking three of the integers at a time. None of these totals was a prime. What is the smallest integer Jakob could have written?(A) 12 (B) 10 (C) 7 (D) 6 (E) 330.Four sportsmen and sportswomen - a skier, a speed skater, a hockey player and a snowboarder - had dinnerat a round table. The skier sat at Andrea's left hand. The speed skater sat opposite Ben. Eva and Filip sat next to each other.A woman sat at the hockey player`s left hand. Which sport did Eva do?(A) speed skating (B) skiing (C) ice hockey (D) snowboarding(E) It`s not possible to find out with the given information.International Contest-Game Math Kangaroo Canada, 2016Answer KeyParents Contest。
加拿大国家中小学数学竞赛( kangaroo math 袋鼠竞赛)2017年五六年级(含答案)

I N T ER N A T I ON A L CO N T E S T-GA M EM A TH KA N GA RO OC A N A DA, 2017INSTRUCTIONSGRADE 5-61.You have 75 minutes to solve 30 multiple choice problems. For each problem, circle onlyone of the proposed five choices. If you circle more than one choice, your response will be marked as wrong.2.Record your answers in the response form. Remember that this is the only sheet that ismarked, so make sure you have all your answers transferred here by the end of the contest.3.The problems are arranged in three groups. A correct answer of the first 10 problems isworth 3 points. A correct answer of problems 11-20 is worth 4 points. A correct answer of problems 21-30 is worth 5 points. For each incorrect answer, one point is deducted from your score. Each unanswered question is worth 0 points. To avoid negative scores, you start from 30 points. The maximum score possible is 150.4.Calculators and graph paper are not permitted. You are allowed to use rough paper for draftwork.5.The figures are not drawn to scale. They should be used only for illustration.6.Remember, you have about 2-3 minutes for each problem; hence, if a problem appears tobe too difficult, save it for later and move on to the other problems.7.At the end of the allotted time, please submit the response form to the contest supervisor.Please do not forget to pick up your Certificate of Participation!Good luck! Canadian Math Kangaroo Contest team2017 CMKC locations: Algoma University; Bishop's University; Brandon University; Brock University; Carlton University; Concordia University; Concordia University of Edmonton; Coquitlam City Library; Dalhousie University; Evergreen Park School; F.H. Sherman Recreation & Learning Centre; GAD Elementary School; Grande Prairie Regional College; Humber College; Lakehead University (Orillia and Thunder Bay); Laurentian University; MacEwan University; Memorial University of Newfoundland; Mount Allison University; Mount Royal University; Nipissing University; St. Mary’s University (Calgary); St. Peter’s College; The Renert School at Royal Vista; Trent University; University of Alberta-Augustana Campus; University of British Columbia (Okanagan); University of Guelph; University of Lethbridge; University of New Brunswick; University of Prince Edward Island; University of Quebec at Chicoutimi; University of Quebec at Rimouski; University of Regina; University of Toronto Mississauga; University of Toronto Scarborough; University of Toronto St. George; University of Windsor; The University of Western Ontario; University of Winnipeg; Vancouver Island University; Walter Murray Collegiate, Wilfrid Laurier University; YES Education Centre; York University; Yukon College.2017 CMKC supporters: Laurentian University; Canadian Mathematical Society; IEEE; PIMS.Canadian Math Kangaroo ContestPart A: Each correct answer is worth 3 points1.A fly has 6 legs, a spider has 8 legs. Together, 3 flies and 2 spiders have as many legs as 9 chickens andseveral cats. How many cats are there?(A) 2 cats (B) 3 cats (C) 4 cats (D) 5 cats (E) 6 cats2.Alice has 4 pieces of this shape: . Which picture can she not make from these four pieces?(A) (B) (C)(D) (E)3.Kalle knows that 1111 × 1111 = 1234321. What is the answer of 1111 × 2222?(A) 3456543 (B) 2346642 (C)2457642 (D) 2468642 (E) 43212344.There are 10 islands and 12 bridges, as depicted in the figure. All bridgesare open for traffic right now. What is the smallest number of bridges thatmust be closed in order to stop the traffic between A and B?(A) 1 (B) 2 (C) 3 (D) 4 (E) 55.Martin wants to colour the squares of the rectangle so that 1/3 of allsquares are blue and half of all squares are yellow. The rest of the squaresare to be coloured red.How many squares will he colour red?(A) 1 (B) 2 (C) 3 (D) 4 (E) 56.When the car wheels make one full rotation the car moves forward by about 1.8 meters. Approximatelyhow many kilometres will the car move forward after 10,000 full rotations of the wheels?(A) 1.8 (B) 18 (C) 180 (D) 1 800 (E) 18 0007.There are 32 students in Mrs. Vicky’s class. Part of the students took one pencil each from the box withpencils on the teacher’s desk. Then a third of the remaining students took 3 pencils each, and there were no more pencils left in the box. How many pencils were there in the box at first?(A) 16 (B) 24 (C) 32 (D) 43 (E) 648.Three rhinoceroses Jane, Kate and Lynn go for a walk: Jane first, Kate in the middle, and Lynn – last. Janeweighs 500 kg more than Kate. Kate weighs 1000 kg less than Lynn. Which of the following pictures may show Jane, Kate and Lynn in the order they walked?(A) (B)(C) (D)(E)9.Peter and Nick are both working on "Kangaroo" contest problems. For every two problems that Petersolves, Nick manages to solve three problems. In total, the boys solved 30 problems. How many problems did Nick solve more than Peter?(A) 5 (B) 6 (C) 7 (D) 8 (E) 910.Bob folded a piece of paper, used a hole puncher and punched exactly one hole in the folded paper.Then, he unfolded the piece of paper, which looked as shown below.Which of the following pictures shows the lines along which Bob folded the piece of paper?(A) (B) (C) (D) (E)Part B: Each correct answer is worth 4 points11.A special die has a number on each of its six faces. The sums of the numbers on opposite faces are all equal. Five of the numbers are 5, 6, 9, 11 and 14. What number is on the sixth face? (A) 4 (B) 7 (C) 8 (D) 13 (E) 15 12.Tom wrote all the numbers from 1 to 20 in a row and obtained the 31‐digit number1234567891011121314151617181920.Then he deleted 24 of the 31 digits, so that the remaining number was as large as possible. Which number was it? (A) 9671819 (B) 9567892 (C) 9781920 (D) 9912345 (E) 981819213.Peter went hiking in the mountains for 5 days. He started on Monday and his last trip was on Friday. Each day he walked 2km more than the day before. The total distance he walked during the five days was 70km. What distance did Peter walk on Thursday? (A) 12 km (B) 13 km (C) 14 km (D) 15 km (E) 16 km14.In a chocolate store, one chocolate costs $3. One day the store had a deal: “Buy two and get a third one free” and Adam decided to take 49 chocolates. How much did he pay for the chocolates? (A) $75 (B) $98 (C) $99 (D) $102 (E) $14715.Eight kangaroos stood in a line as shown in the diagram.At some point, two kangaroos standing side by side and facing each other exchanged places by jumping past each other. This was repeated until no further jumps were possible. How many exchanges were made? (A) 2 (B) 10 (C) 12 (D) 13 (E) 1616.The Modern Furniture store is selling sofas, loveseats, and chairs made from identical modular pieces as shown in the picture. Including the armrests, the width of the sofa is 220 cm and the width of the loveseat is 160 cm.What is the width of the chair? (A) 60 cm (B) 80 cm (C) 90 cm(D) 100 cm(E) 120 cmsofa loveseatchair220 cm160cm17.There are five padlocks and 5 keys – one for each of them (see the figure). The number code on each key has been modified into a letter code on the corresponding padlock. Equal digits have been replaced by the same letter, and different digits – by different letters. What is the number code on the fifth key?(A) 382(B) 282 (C) 284 (D) 823 (E) 82418.Boris has an amount of money and three magic wands that he can use only once. Wand A adds $1. Wand S subtracts $1. Wand D doubles the amount. In which order must he use these wands to obtain the largest amount of money? (A) DAS (B) ASD (C) DSA (D) ADS (E) SAD19.A vase weighs 600 g when one third of it is filled with water. The same vase weighs 800 g when two thirds of it are filled with water. What is the weight of the vase when it is empty? (A) 100 g (B) 200 g (C) 300 g (D) 400 g (E) 500 g20.Rafael has three squares. The first one has side length 2 cm. The second one has side length 4 cm and a vertex is placed in the centre of the first square. The last one has side length 6 cm and a vertex is placed in the centre of the second square, as shown in the picture. What is the area of the figure? (A) 32 cm 2 (B) 51 cm 2 (C) 27 cm 2 (D) 16 cm 2 (E) 6 cm 2Part C: Each correct answer is worth 5 points21.The natural numbers are arranged in the form of a triangle: 1 is in the first row, 2 and 3 are in the second row, 4, 5 and 6 are in the third row, and so on. What is the sum of the numbers written in the 10‐th row?(A) 490(B) 495 (C) 500(D) 505 (E) 5101 2 3 456.. .22.There are eight balls numbered with the numbers 40, 80, 100, 101, 190, 200, 260 and 292 in a bag.Martina takes four balls out of the bag and calculates the sum of the numbers on these balls. It appears that this sum is half of the sum of the numbers on the balls that remain in the bag. What is the greatest number written on the balls taken out?(A) 101 (B) 200 (C) 260 (D) 190 (E) 29223.The structure on the figure is made of unit cubes glued together. Morten wants toput it into a rectangular box. What are the dimensions (length, width and height)of the smallest box he can use?(A) 3 × 3 × 4 (B) 3 × 5 × 5 (C) 3 × 4 × 5 (D) 4 × 4 × 4 (E) 4 × 4 × 524.Four players scored goals in a handball game. All of them scored a different number of goals. One of theplayers, Mike, scored the least number of goals. The other three players scored 20 goals in total. What is the largest number of goals Mike could have scored?(A) 2 (B) 3 (C) 4 (D) 5 (E) 625.Ala likes even numbers, Beata likes numbers divisible by 3, Celina likes numbers divisible by 5. Each ofthese three girls went separately to a basket containing 8 balls with numbers written on them, and took all the balls with numbers she liked. It turned out that Ala collected balls with numbers 32 and 52, Beata ‐ 24,33 and 45, Celina ‐ 20, 25 and 35. In what order did the girls approach the basket?(A) Ala, Celina, Beata (B) Celina, Beata, Ala (C) Beata, Ala, Celina(D) Beata, Celina, Ala (E) Celina, Ala, Beata26.The picture of a kangaroo in the first (leftmost) triangle was reflected across the dotted lines, as in mirrors.The first two reflections are shown.What does the reflection look like in the shaded triangle?(A) (B) (C) (D) (E)27.The numbers 1, 2, 3, 4, and 5 must be written in the five cells in the figure, respecting the following rules:-If a number is just below another number, it must be greater.-If a number is just to the right of another number, it must be greater.In how many ways can this be done?(A) 3 (B) 4 (C) 5 (D) 6 (E) 828.John wrote a natural number in each of the four boxes in the bottom row of the diagram. Then he wrote ineach of the other boxes the sum of the two numbers in the boxes immediately underneath. What is the largest number of odd numbers that could appear in the completed diagram?(A) 4 (B) 5 (C) 6 (D) 7 (E) 829.Julia has four pencils of different colours and wants to use some or all of them to paint the map of anisland divided into four countries, as in the picture. Any two countries with a common border must be coloured differently on the map. How many different colourings of this map are possible? (Twocolourings are considered different if at least one of the countries is coloured differently).(A) 12 (B) 18 (C) 24 (D) 36 (E) 4830.A bar consists of two grey cubes and one white cube glued together as shown in the figure.Which cube can be built from nine such bars?(A) (B) (C) (D) (E)International Contest-GameMath Kangaroo Canada, 2017Answer KeyGrade 5-61 A B C D E 11 A B C D E21 A B C D E2 A B C D E12 A B C D E 22 A B C D E3 A B C D E 13 A B C D E23 A B C D E4 A B C D E 14 A B C D E 24 A B C D E5 A B C D E 15 A B C D E 25 A B C D E6 A B C D E 16 A B C D E 26 A B C D E7 A B C D E 17 A B C D E 27 A B C D E8 A B C D E 18 A B C D E 28 A B C D E9 A B C D E 19 A B C D E 29 A B C D E10 A B C D E 20 A B C D E 30 A B C D E。
2018年度国外数学竞赛试题翻译汇编

(升级版)
赵力 2019 - 06 - 19
时间,就像高铁,一眨眼,就过站了……
人生很简单 总有一些风景,注定要错过 与其执着,不如随缘 只要懂得“珍惜、知足、感恩”就可以了!
笑看世事繁华,淡定人生心态 不索不可取,不求不可得 学会感恩,做人做事,无憾我心 不再奢望浮华之梦,不再……
v
纯属公益, 免费使用分享, 只送不卖
2018 年亚太地区数学奥林匹克试题
时间,一点不像高铁,过了站,居然买不到回来的车票!
生命,不就如一场雨吗 你曾无知地在其间雀跃,曾痴迷地在其间沉吟 但更多时候 你得忍受那些寒冷与潮湿,那些无奈与寂寞 并且以晴日的幻想来度日
当你握紧双手,里面什么也没有 当你打开双手,世界就在你手中
纯属公益, 免费使用分享, 只送不卖
目录
2018 年亚太地区数学奥林匹克 ……………………………………… 1 2018 年波罗的海地区数学奥林匹克 ………………………………… 2 2018 年第 10 届 Benelux 数学奥林匹克 ……………………………… 5 2018 年巴尔干地区数学奥林匹克 …………………………………… 6 2018 年巴尔干地区数学奥林匹克预选题…………………………… 7 2018 年巴尔干地区初中数学奥林匹克 ……………………………… 10 2018 年高加索地区数学奥林匹克 …………………………………… 11 2018 年中美洲及加勒比地区数学奥林匹克 ………………………… 13 2018 年 Cono Sur 数学奥林匹克 ……………………………………… 14 2018 年捷克-波兰-斯洛伐克联合数学竞赛 ………………………… 15 2018 年捷克和斯洛伐克数学奥林匹克 ……………………………… 16 2018 年多瑙河地区数学奥林匹克 …………………………………… 17 2018 年欧洲女子数学奥林匹克 ……………………………………… 19 2018 年欧洲数学杯奥林匹克 ………………………………………… 21 2018 年拉丁美洲数学奥林匹克 ……………………………………… 23 2018 年国际大都市数学竞赛(IOM) ………………………………… 24 2018 年第 2 届 IMO 复仇赛 …………………………………………… 25 2018 年第 5 届伊朗几何奥林匹克 …………………………………… 26 2018 年第 17 届基辅数学节竞赛 …………………………………… 30 2018 年地中海地区数学竞赛 ………………………………………… 32 2018 年中欧数学奥林匹克 …………………………………………… 33 2018 年北欧数学奥林匹克 …………………………………………… 35 2018 年泛非数学奥林匹克 …………………………………………… 36 2018 年泛非数学奥林匹克预选题 …………………………………… 38 2018 年罗马尼亚大师杯数学奥林匹克 ……………………………… 42
袋鼠数学竞赛

一年一度的的英国高级数学袋鼠竞赛(Senior Kangaroo)和奥林匹克数学竞赛第一轮(British Mathematical Olympiad Round 1 ,简称BMO1)一般同时进行。
今年的比赛是在11月16日,竞赛由 UKMT 主办。
The UK Mathematics Trust (UKMT) 是注册的慈善机构,主要为青少年提供数学教育,是全英国最大的数学竞赛组织。
英国奥数竞赛BMO和高级袋鼠竞赛(Senior Kangaroo)都是为英格兰和威尔士 13年级或以下的学生设计的比赛(北爱尔兰是14年级或以下,苏格兰是S6或以下)。
所以一般来说是读A Level的12-13年级(17-18岁)的学生参加,也有数学成绩优异的11年级或更小的学生参加。
今年是在英国高级数学挑战赛SMC 中取得100分以上的(约1000人)有资格晋级英国奥数竞赛第一轮(BMO1), 76分以上的(约6000人)晋级高级袋鼠赛(Senior Kangaroo)。
英国高级袋鼠赛(Senior Kangaroo),一个小时,20道填空题,每题5分,满分100分。
直接写答案即可,不用写过程,做错不扣分。
得分最高的25%可以得到Merit证书,2022年分数达到40分以上的可以得到Merit证书。
英国奥数竞赛第一轮( BMO1),3.5小时,六道大题,每题10分,要求写出详细的演算过程,满分60分。
成绩最好的100名学生将被邀请参加第二轮(BMO2)的决赛。
详情请点:英国奥数竞赛真题及答案。
英国奥数竞赛第二轮( BMO2)将在2023年1月25日进行,3.5小时,四道大题,每题10分,要求写出详细的演算过程。
2022年17分以上可获得优异(Distinction)证书,10分以上获得良好(Merit)证书。
之后会从中选拔出最优秀的几十人参加集训,准备国际奥林匹克数学竞赛(International Mathematical Olympiad,简称IMO)和其它国际赛事。
澳大利亚kangaroo袋鼠数学竞赛试题及答案grade1-11 2015年

(A) 16
(B) 15
(C) 12
(D) 8
(E) 7
Mathematical Kangaroo 2015 Group Ecolier (Grade 3 and 4)
Austria – 23. 3. 2015
‐ 3 point questions ‐
1.
(A) 6
(B) 7
(C) 8
(D) 10
(A) 24 meters (B) 48 meters (C) 72 meters (D) 80 meters (E) 88 meters
15. Some pirates are climbing onto a ship one after the other using a rope. Their leader is exactly in the middle. He is the eighth pirate to climb onto the ship. How many pirates board the ship?
(C)
(D)
(E)
2. How many triangles can you find in the picture?
(A) 7 (B) 6 (C) 5 (D) 4
(E) 3
3. Which part of the house is missing?
(A)
(B)
(C)
(D)
(E)
4. How many dots do all ladybirds have together? (A) 17 (B) 18 (C) 19 (D) 20 (E) 21
(A) 10
(B) 12
(C) 13
(D) 14
袋鼠数学2018真题(3-4年级)

has one of the digits:0,1,2,3,4,5,6,7,8below.How many stamps does she use?salah satu digit berikut:0,1,2,3,4,Kangaroo seperti berikut.Berapakah bilangan cop yang digunakan?Leonie有10个橡皮图章。
每个图章拥有0,1,2,3,4,5,6,7,8,9的其中一个数字。
如下图所示,她把Kangaroo比赛的日期印了出来。
请问她一共用了多少个图章?85032011(A)5(B)6(C)7(D)9(E)10#2.The picture shows3flying arrows and9fixed balloons.When an arrow hits a balloon, the balloon bursts and the arrowflies further in the same direction.How many balloons in total are hit by arrows?Gambar berikut menunjukkan3anak panah yang berterbangan dan9belon yang tidak bergerak.Apabila suatu anak panah mengenai suatu belon,belon tersebut akan pecah dan anak panah tersebut akan terus terbang pada arah yang sama.Berapakah jumlah bilangan belon yang akan dipecahkan oleh anak panah?下图显示3支飞箭和9粒固定的气球。
当一支箭击中一粒气球,那粒气球会爆裂,而箭会继续往同样的方向飞行。
canadamo数学竞赛知识点

在撰写这篇文章之前,我首先要对“canadamo数学竞赛知识点”进行全面评估,以确保文章的深度和广度兼具。
在这篇文章中,我将从简到繁地分析并探讨canadamo数学竞赛的知识点,帮助你更深入地理解这个主题。
canadamo是加拿大数学奥林匹克(Canadian Mathematical Olympiad)的缩写,是加拿大国内最具权威性和影响力的数学竞赛之一。
参加canadamo数学竞赛,不仅能锻炼学生的数学能力,更能培养学生的逻辑思维和解决问题的能力。
我将从基础知识点开始,逐步深入,全面探讨canadamo数学竞赛的重要知识点。
1. 数论- 数论是canadamo数学竞赛中的重要知识点之一。
它涉及整数的性质、因数分解、同余方程等内容。
在canadamo数学竞赛中,数论题目常常涉及数字性质的推导和证明,考查选手的数学逻辑推理能力。
2. 几何- 几何是canadamo数学竞赛的另一个重要知识点。
它包括平面几何和立体几何两部分,涉及角度、边长、面积、体积等概念。
在canadamo数学竞赛中,几何题目常常涉及图形的性质和相似性的判断,考查选手的几何分析能力和空间想象能力。
3. 代数- 代数是canadamo数学竞赛的核心知识点之一。
它涉及方程、不等式、多项式、数列等内容。
在canadamo数学竞赛中,代数题目常常涉及函数的性质和变量的关系,考查选手的代数运算能力和推理能力。
4. 组合数学- 组合数学是canadamo数学竞赛的另一个重要知识点。
它包括排列、组合、概率等内容。
在canadamo数学竞赛中,组合数学题目常常涉及排列组合的计算和概率问题的推导,考查选手的组合分析能力和概率计算能力。
总结回顾:通过对canadamo数学竞赛知识点的全面评估,我们可以看到,数论、几何、代数和组合数学是其重要的知识点。
参加canadamo数学竞赛不仅需要掌握这些知识点,还需要灵活运用,并具备深入思考和解决问题的能力。
加拿大国际袋鼠数学竞赛试题 -2004年

Back to All Problems PageMATH KANGAROO 2004 in USALevel of Grades 3 - 43 points each1. 2001+ 2002 + 2003 + 2004 + 2005 =A) 1,015 B) 5,010 C) 10,150 D) 11,005 E) 10,0152. Marek was 4 years old when his sister was born. Today he blew out all 9 candles on his birthday cake. What is the difference between Marek’s and his sister’s age today?A) 4 years B) 5 years C) 9 years D) 13 years E) 14 years3. The picture below shows a road from town A to town B (indicated by solid line) and a detour (marked by a dash line) caused by renovation of the section CD. How many kilometres longer is the road from town A to town B because of the detour now?A) 3 km B) 5 km C) 6 km D) 10 km E) This cannot be calculated.4. Which of the results below is not identical to the difference 671 – 389?A) 771 – 489 B) 681 – 399 C) 669 – 391 D) 1871 – 1589 E) 600 –3185. There were some birds sitting on the telegraph wire. At one moment, 5 of them flied away and after some time, 3 birds came back. At that time there were 12 birds sitting on the wire. How many birds were there at the very beginning?A) 8 B) 9 C) 10 D) 12 E) 146. Which numbers are inside a rectangle and inside a circle but not inside a triangle at the same time?A) 5 and 11 B) 1 and 10 C) 13 D) 3 and 9 E)6, 7 and 47. Buildings on Color Street are numbered from 1 to 5 (see the picture).Each building is colored with one of the following colors: blue, red,yellow, pink, and green. It is known that:– The red building neighbours with the blue one only.– The blue building is between the red one and the green one.What is the color of the building numbered with 3?A) Blue B) Red C) Yellow D) Pink E) Green8. How many white squares need to be shaded so that the number ofshaded squares equals exactly to half of the number of white squares?A) 2 B) 3 C) 4 D) 6 E) It isimpossible to calculate it.4 points each9. Five identical sheets of a plastic rectangles were dividedinto white and black squares. Which of the sheets from A to Ehas to be covered with the sheet to the right in order to gettotally black rectangle?A: B: C: D:E:10. The scales in the pictures had been balanced. There are pencils and a pen on the arms of the scales. What is the weight of the pen in grams?A) 6 g B) 7 g C) 8 g D) 9 g E) 10 g11. I notice four clocks on the wall (see the picture). Only one of them shows correct time. One of them is 20 minutes ahead, another is 20 minutes late, and the other is stopped. What is the time at the moment?among them. There are 14 students on Mathew’s left, and Maria is among them. There are 7 students between Maria and Mathew. How many students are in this class?A) 37 B) 30 C) 23 D) 22 E) 1620. The sum of the digits of the 10-digit number is 9.What is the product of the digits of this number?A) 0 B) 1 C) 45 D) 9 x 8 x 7 x…..x 2 x 1E) 1021. Out of 125 small, white and black cubes, the big cube was formed (see the picture). Every twoadjacent cubes have different colors. The vertices of the big cube are black. How many white cubesdoes the big cube contain?A) 62 B) 63 C) 64 D) 65 E) 6822. A lottery-ticket was 4 dollars. Three boys: Paul, Peter, and Robert made a contribiution and bought two tickets. Paul gave 1 dollar, Peter gave 3 dollars, and Robert gave 4 dollars. One of the tickets they bought was worth 1000 dollars. Boys shared the award fairly, meaning, proportionally to their contributions. How much did Peter receive?A) 300 B) 375 C) 250 D) 750 E) 42523. In three soccer games the Dziobak’s team scored three goals and lost one. For every game won the team gets 3 points, fora tie it gets 1 point, and for the game lost it gets 0 points. For sure, the number of points the team earned in those three games was not equal to which of the following numbers?A) 7 B) 6 C) 5 D) 4 E) 324. In every white section of a diagram, the products of two numbers from grey sections – one fromabove and one from the left – was placed (for example: 42 = 7 • 6 ). Some of these products arerepresented by letters. Which two letters represent the same number?A) L and M B) T and N C) R and P D) K and P E) M and Sback to all problems page。
加拿大国家中小学数学竞赛( kangaroo math 袋鼠竞赛)2018年一二年级(含答案)

I N T E R N A T I O N A L C O N T E S T-G A M EM A T H K A N G A R O OC A N AD A,2018I N S T R U C T I O N SG R A D E1-21.You have 45 minutes to solve 18 multiple choice problems. For eachproblem, circle only one of the proposed five choices. If you circle more than one choice, your response will be marked as wrong.2.Record your answers in the response form. Remember that this is the onlysheet that is marked, so make sure you have all your answers transferred to the response form before giving it back to the contest supervisor.3.The problems are arranged in three groups. A correct answer of the first 6problems is worth 3 points. A correct answer of the problems 7-12 is worth4 points. A correct answer of the problems 13-18 is worth5 points. Foreach incorrect answer, one point is deducted from your score. Each unanswered question is worth 0 points. To avoid negative scores, you start from 18 points. The maximum score possible is 90.4.The use of external material or aid of any kind is not permitted.5.The figures are not drawn to scale. They should be used only for illustrationpurposes.6.Remember, you have about 2 to 3 minutes for each problem; hence, if aproblem appears to be too difficult, save it for later and move on to another problem.7.At the end of the allotted time, please give the response form to thecontest supervisor.8.Do not forget to pick up your Certificate of Participation on your way out!Good luck!Canadian Math Kangaroo Contest teamCanadian Math Kangaroo ContestPart A: Each correct answer is worth 3 points1.Which shape cannot be formed using and ?(A) (B) (C) (D) (E)2.At least how many 4-ray stars like this are glued together tomake this shape ?(A) 5 (B) 6 (C) 7 (D) 8 (E) 93.This pizza was divided into equal slices.How many slices are missing?(A) 1 (B) 2 (C) 3 (D) 4 (E) 54.How many kangaroos must be moved from one park to the other in order toget the same number of kangaroos in each park?(A) 4 (B) 5 (C) 6 (D) 8 (E) 95.Which of these ladybugs has to fly away so that the rest of them have 20dots in total?(A) (B) (C) (D) (E)6.Emilie builds towers in the following patternWhich one will be the tower number 6?(A) (B) (C) (D) (E)Part B: Each correct answer is worth 4 points7.If ◊+ ◊ = 4 and ∆ + ∆ + ∆ = 9, what is the value of ◊ + ∆ = ?(A) 2 (B) 3 (C) 4 (D) 5 (E) 68.Lisa has 4 pieces , but she only needs 3 forcompleting her puzzle frame . Which piece will be left over?(A)(B)(C)(D) (E)or9.How many right hands are in this picture?(A) 3 (B) 4 (C) 5 (D) 6 (E) 710.The dog went to its food following a path. In total it made 3 right turns and2 left turns. Which path did the dog follow?(A) (B) (C)(D) (E)11.What number is in the box marked "?" ?(A) 6 (B) 13 (C) 24 (D) 29 (E) Some other number12.Charles cut a rope in three equal pieces and then made some equal knotswith them. Which figure correctly shows the three pieces with the knots?(A) (B)(C) (D)(E)Part C: Each correct answer is worth 5 points13.How many circles and how many squares are covered by the blot in thepicture?(A) 1 circle and 3 squares(B) 2 circles and 1 square(C) 3 circles and 1 square(D) 1 circles and 2 squares(E) 2 circles and 2 squares14.Diana shoots three arrows at a target.On her first try, she gets 6 points and the arrows land like this: 6 pointsOn her second try, she gets 8 points and the arrows land like this: 8 pointsOn her third try, the arrows land like this:? points How many points will she get the third time?(A) 8 (B) 10 (C) 12 (D) 14 (E) 1615.How many different numbers greater than 10 and smaller than 25 with distinct digits can we make by using any two of the digits 2, 0, 1, and 8?(A) 4 (B) 5 (C) 6 (D) 7 (E) 816.Mark had some sticks of length 5 cm and width 1 cm.With the sticks he constructed the fence below.What is the length of the fence?(A) 20 cm(B) 21 cm(C) 22 cm (D) 23 cm (E) 25 cmlength17.The road from Anna's house to Mary's house is 16 km long.The road from Mary's house to John's house is 20 km long.The road from the crossroad to Mary's house is 9 km long.How long is the road from Anna’s house to John's house?(A) 7 km (B) 9 km (C) 11 km (D) 16 km (E) 18 km18.There are four ladybugs on a 4×4 board. Two are asleep and do not move.The other two ladybugs move one square every minute (up, down, left, or right). Here are pictures of the board for the first four minutes:Minute 1 Minute 2 Minute 3 Minute 4Which of these is a picture of the fifth minute (Minute 5)?(A) (B) (C) (D) (E)International Contest-GameMath Kangaroo Canada, 2018Answer KeyGrade 1-21 A B C D E 7 A B C D E 13 A B C D E2 A B C D E 8 A B C D E 14 A B C D E3 A B C D E 9 A B C D E 15 A B C D E4 A B C D E 10 A B C D E 16 A B C D E5 A B C D E 11 A B C D E 17 A B C D E6 A B C D E 12 A B C D E 18 A B C D E。
2019年袋鼠数学竞赛L3
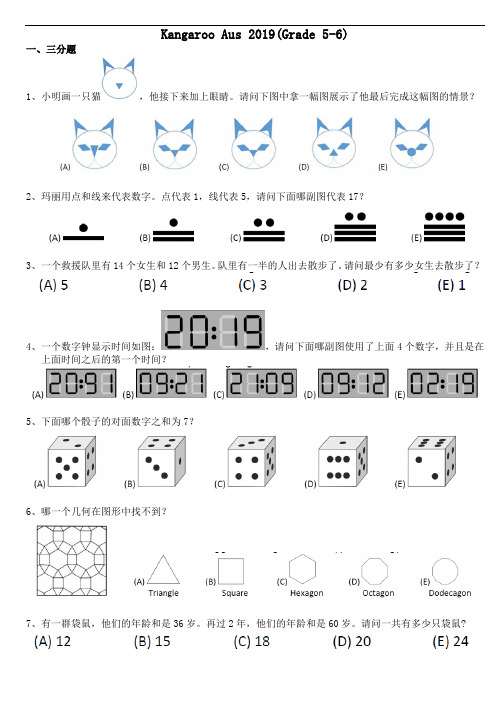
Kangaroo Aus 2019(Grade 5-6)一、三分题1、小明画一只猫,他接下来加上眼睛。
请问下图中拿一幅图展示了他最后完成这幅图的情景?2、玛丽用点和线来代表数字。
点代表1,线代表5,请问下面哪副图代表17?3、一个救援队里有14个女生和12个男生。
队里有一半的人出去散步了。
请问最少有多少女生去散步了?4、一个数字钟显示时间如图:,请问下面哪副图使用了上面4个数字,并且是在上面时间之后的第一个时间?5、下面哪个骰子的对面数字之和为7?6、哪一个几何在图形中找不到?7、有一群袋鼠,他们的年龄和是36岁。
再过2年,他们的年龄和是60岁。
请问一共有多少只袋鼠?8、劳拉想在图中给一个2×2的正方形涂色。
请问有多少种方法?二、四分题9、每一张卡片上都有一位三位数。
这三个三位数的和是826。
那么隐藏的两个数字之和是多少?10、大卫把6个最小的奇数写在骰子上。
然后,他抛了3次,这3次的和不可能为?11、吉姆有一个可以折叠的由10根相同长度的小棒连成的棒子。
以下哪个图形不能用这个棒子做成?12、哪一幅图的黑色面积最大?13、一个小院子里有30只小动物(狗、猫、老鼠)。
牧师把6只狗变为6只猫,然后再把5只猫变为5只老鼠。
这个时候,狗、猫、老鼠的只数一样多。
请问最开始有多少只猫?14、大卫用1cm×1cm×2cm的砖头搭建城堡。
如图;他搭的最后一个塔共用了28块砖。
请问最后他搭的那个塔是多高?15、吉姆按照如图方式把纸折碟,然后再按照图示的方法,沿着两条线把这个纸剪开。
请问,他最后得到了多少张纸块?16、每一张图上都画了一条线。
现在我们把他们叠成一个正方体。
请问哪一幅图在折叠成正方体后,它上面的线是一个封闭的图形?三、五分题17、骰子的每一面都写了一个数字。
如图。
已知每个对面的数字积都相等。
请问6个面的数字都加起来和最小为多少?18、如图,三个黑色的小球加上一个白色的小球放在天平左端,右端放一块30克的冰和一个黑色的球。
2018 -美国袋鼠数学一二年级竞赛练习题

SAMPLE QUESTION FOR 3 POINTSAlice draws a figure connecting all the ladybugs in the order of increasing number of dots. She starts with the ladybug with one dot. Which figure will she get?SAMPLE QUESTION FOR 4 POINTSPeter drew a pattern twice, as in the picture. Which point will he reach when he draws the third pattern?A) A B) B C) C D) D E) ESAMPLE QUESTION FOR 5 POINTSThe number of dwarfs that can fit under a mushroom is equal to the number of dots on the mushroom cap. The picture below shows one side of each mushroom. The number of dots on the other side is the same. If 30 dwarfs are seeking shelter from the rain, how many dwarfs will get wet?A) 2 B) 3 C) 4 D) 5 E) 6SAMPLE QUESTION FOR 3 POINTSAlice draws a figure connecting all the ladybugs in the order of increasing number of dots. She starts with the ladybug with one dot. Which figure will she get?SAMPLE QUESTION FOR 4 POINTSPeter drew a pattern twice, as in the picture. Which point will he reach when he draws the third pattern?A) A B) B C) CD) DE) ESAMPLE QUESTION FOR 5 POINTSThe number of dwarfs that can fit under a mushroom is equal to the number of dots on themushroom cap. The picture below shows one side of each mushroom. The number of dots on the other side is the same. If 30 dwarfs are seeking shelter from the rain, how many dwarfs will get wet?A) 2 B) 3 C) 4 D) 5E) 6SAMPLE QUESTION FOR 3 POINTSThe picture shows 3 arrows that are flying and 9 balloons that can't move. When an arrow hits a balloon, the balloon pops, and the arrow keeps flying in the same direction. How many balloons will be hit by the flying arrows?A) 2 B) 3 C) 4 D) 5 E) 6SAMPLE QUESTION FOR 4 POINTSToby glues 10 cubes together to make the structure shown to the right. He paints the whole structure, even the bottom. How many cubes are painted on exactly 4 of their faces?A) 6 B) 7 C) 8 D) 9 E) 10SAMPLE QUESTION FOR 5 POINTSLeon wants to write the numbers from 1 to 7 in the grid shown. Two consecutive numbers cannot be written in two neighboring cells. Neighboring cells are those that meet at the edge or at a corner. What numbers can he write in the cell marked with the question mark?A) all seven numbersB) all of the odd numbersC) all of the even numbersD) only the number 4E) only the numbers 1 or 7SAMPLE QUESTION FOR 3 POINTSThe picture shows 3 arrows that are flying and 9 balloons that can't move. When an arrow hits a balloon, the balloon pops, and the arrow keeps flying in the same direction. How many balloons will be hit by the flying arrows?A) 2 B) 3 C) 4 D) 5 E) 6SAMPLE QUESTION FOR 4 POINTSToby glues 10 cubes together to make the structure shown to the right. He paints the whole structure, even the bottom. How many cubes are painted on exactly 4 of their faces?A) 6 B) 7 C) 8D) 9 E) 10SAMPLE QUESTION FOR 5 POINTSLeon wants to write the numbers from 1 to 7 in the grid shown. Two consecutive numbers cannot be written in two neighboring cells. Neighboring cells are those that meet at the edge or at a corner. What numbers can he write in the cell marked with the question mark?A) all seven numbersB) all of the odd numbersC) all of the even numbersD) only the number 4E) only the numbers 1 or 7SAMPLE QUESTION FOR 3 POINTSAlice subtracted two 2-digit numbers. Then she paintedtwo cells. What is the sum of the two digits in the painted cells?A)8 B) 9 C) 12 D) 13 E) 15SAMPLE QUESTION FOR 4 POINTSEmily wants to enter a number into each cell of the triangular table. The sum of the numbers in any two cells with a common edge must be the same. She has already entered two numbers. What is the sum of all the numbers in the table?A) 18 B) 20 C) 21 D) 22 E) impossible to determineSAMPLE QUESTION FOR 5 POINTSFive balls, A, B, C, D, and E, weigh 30 g, 50 g, 50 g, 50 g, and 80 g each, not necessarily in that order. Which ball weighs 30 g?A) A B) B C) C D) D E) ESAMPLE QUESTION FOR 3 POINTSAlice subtracted two 2-digit numbers. Then she painted two cells. What is the sum of the two digits in the painted cells?B)8 B) 9 C) 12 D) 13E) 15SAMPLE QUESTION FOR 4 POINTSEmily wants to enter a number into each cell of the triangular table. The sum of the numbers in any two cells with a common edge must be the same. She has already entered two numbers. What is the sum of all the numbers in the table?A) 18 B) 20 C) 21D) 22 E) impossible to determineSAMPLE QUESTION FOR 5 POINTSFive balls, A, B, C, D, and E, weigh 30 g, 50 g, 50 g, 50 g, and 80 g each, not necessarily in that order. Which ball weighs 30 g?A) A B) B C) C D) D E) ESAMPLE QUESTION FOR 3 POINTSWhen the letters of the word MAMA are written vertically above one another, the word has a vertical line of symmetry. Which of these words also has a vertical line of symmetry when written in the same way?A) ROOT B) BOOM C) BOOT D) LOOT E) TOOTSAMPLE QUESTION FOR 4 POINTSA rectangle is divided into 40 identical squares. The rectangle contains more than one row of squares. Andrew found the middle row of squares and colored it in. How many squares did he not color?A) 20 B) 30 C) 32 D) 35 E) 39SAMPLE QUESTION FOR 5 POINTSDomino tiles are said to be arranged correctly if the number of dots at the ends that touch are the same. Peter laid six dominoes in a line as shown in the diagram. He can make a move by either swapping the position of any two dominoes or by rotating one domino. What is the smallest number of moves he needs to make to arrange all the tiles correctly?A) 1 B) 2C) 3D) 4E) It is impossible to do.SAMPLE QUESTION FOR 3 POINTSWhen the letters of the word MAMA are written vertically above one another, the word has a vertical line of symmetry. Which of these words also has a vertical line of symmetry when written in the same way?A) ROOT B) BOOM C) BOOT D) LOOT E) TOOTSAMPLE QUESTION FOR 4 POINTSA rectangle is divided into 40 identical squares. The rectangle contains more than one row of squares. Andrew found the middle row of squares and colored it in. How many squares did he not color?A) 20 B) 30 C) 32 D) 35 E) 39SAMPLE QUESTION FOR 5 POINTSDomino tiles are said to be arranged correctly if the number of dots at the ends that touch are the same. Paulius laid six dominoes in a line as shown in the diagram. He can make a move by either swapping the position of any two dominoes or by rotating one domino. What is the smallest number of moves he needs to make to arrange all the tiles correctly?A) 1 B) 2C) 3D) 4E) It is impossible to do.SAMPLE QUESTION FOR 3 POINTSIn my family each child has at least two brothers and at least one sister. What is the smallest possible number of children in my family?A) 3 B) 4 C) 5 D) 6 E) 7SAMPLE QUESTION FOR 4 POINTSEight congruent semicircles are drawn inside a square with a side length of 4. What is the area of the non-shaded part of the square?A) 2πB) 8 C) 6 + πD) 3π– 2 E) 3πSAMPLE QUESTION FOR 5 POINTSDiana draws a rectangular grid of 12 squares on squared paper. Some of the squares are painted black. In each blank square she writes the number of black squares that share a side with it. The figure shows an example. Now she does the same in a rectangular grid with 2018 squares. What is the maximum value that she can obtain as the result of the sum of all the numbers in the grid?A) 1262 B) 2016 C) 2018 D) 3025 E) 3027SAMPLE QUESTION FOR 3 POINTSIn my family each child has at least two brothers and at least one sister. What is the smallest possible number of children in my family?A) 3 B) 4 C) 5D) 6 E) 7SAMPLE QUESTION FOR 4 POINTSEight congruent semicircles are drawn inside a square with a side length of 4. What is the area of the non-shaded part of the square?A) 2πB) 8C) 6 + πD) 3π– 2 E) 3πSAMPLE QUESTION FOR 5 POINTSDiana draws a rectangular grid of 12 squares on squared paper. Some of the squares are painted black. In each blank square she writes the number of black squares that share a side with it. The figure shows an example. Now she does the same in a rectangular grid with 2018 squares. What is the maximum value that she can obtain as the result of the sum of all the numbers in the grid?A) 1262 B) 2016 C) 2018 D) 3025E) 3027LEVELS 11 AND 12SAMPLE QUESTION FOR 3 POINTSThe figure shows the floor plan of Renate's house. Renate enters her house from the porch and walks through each door exactly once. In which room does she end up?A) 1 B) 2 C) 3 D) 4 E) 5SAMPLE QUESTION FOR 4 POINTSA vase is filled up to the top with water, at a constant rate. The graph shows the height h of the water as a function of time t.Which of the following can be the shape of the vase?A) B) C) D) E)SAMPLE QUESTION FOR 5 POINTSThere are 40% more girls than boys in a class. How many pupils are in this class if the probability that a two-person delegation selected at random consists of a girl and a boy equals 1/2?A) 20 B) 24 C) 36 D) 38 E) This situation is not possible.LEVELS 11 AND 12 ANSWERSSAMPLE QUESTION FOR 3 POINTSThe figure shows the floor plan of Renate's house. Renate enters her house from the porch and walks through each door exactly once. In which room does she end up?A) 1 B) 2C) 3 D) 4 E) 5SAMPLE QUESTION FOR 4 POINTSA vase is filled up to the top with water, at a constant rate. The graph shows the height h of the water as a function of time t.Which of the following can be the shape of the vase?B) B) C) D) E)SAMPLE QUESTION FOR 5 POINTSThere are 40% more girls than boys in a class. How many pupils are in this class if the probabilitythat a two-person delegation selected at random consists of a girl and a boy equals 1/2?A) 20 B) 24 C) 36D) 38 E) This situation is not possible.。
加拿大国际袋鼠数学竞赛试题-2013年

加拿⼤国际袋⿏数学竞赛试题-2013年Grade 1-2International Contest-Game MATH KANGAROOPart A: Each correct answer is worth 3 points. 1. Which digits are missing?Year 2013(A) 3 and 5 (B) 4 and 8(C) 2 and 0(D) 6 and 9(E) 7 and 12. There are twelve books on a shelf and four children in a room. Howmany books will be left on the shelf if each child takes one book?(A) 12(B) 8(C) 4(D) 2(E) 03. Which of the dresses has less than seven dots, but more than five dots?(A)(B)(C)(D)(E)Grade 1-2Year 20134. A lot of babies were born in the zoo last year: two baby lions, three baby dolphins and four baby eagles. How many legs do all these babies have altogether?(A) 20(B) 18(C) 16(D) 14(E) 125. Several students want to plant 20 tulips in the school garden. It takes ten minutes for them to plant five tulips. They started at 9:00 in the morning. At what time will they finish planting all 20 tulips?(A) At 9:10(B) At 9:20 (C) At 9:40(D) At 9:50(E) At 10:006. How many more bricks are there in the larger stack?(A) 4(B) 5(C) 6(D) 7Part B: Each correct answer is worth 4 points.(E) 107. Ann has. Barb gave Eve. Jim has. Bob has. Who is Barb?(A)(B)(C)8. There is a path with square tiles.(D)(E)How many tiles fit in the area inside?(A) 5(B) 6(E) 9Grade 1-2Year 20139. Cat and Mouse are moving to the right. When Mouse jumps 1 tile, Cat jumps 2 tiles at the same time.On which tile does Cat catch Mouse?(A) 1(B) 2(C) 3(D) 4(E) 510. I am a number. If you count by tens you will say my name. I am not ten. If you add me to 30, you will get anumber less than 60. Who am I?(A) 20(B) 30(C) 40(D) 50(E) 6011. There is a house on each corner of the streets. The housesare shown on the map. Two new houses will be built oneach street between the corner houses. How many houseswill there be in all?(A) 8(B) 12(C) 16(D) 20(E) Other answer12. Kasia has 3 brothers and 3 sisters. How many brothers and how many sisters does her brother Mike have?(A) 3 brothers and 3 sisters(B) 3 brothers and 4 sisters(C) 2 brothers and 3 sisters(D) 3 brothers and 2 sisters(E) 2 brothers and 4 sistersPart C: Each correct answer is worth 5 points.13. Ania makes a large cube from 27 small white cubes. She paints all the faces of the large cube. Then Ania removes four small cubes from four of the corners, as shown. While the paint is still wet, she stamps each of the new faces onto a piece of paper. How many of the following stamps can Ania make?(A) 1(B) 2(C) 3(D) 4(E) 514. Ann has a lot of these pieces:She tries to put them in the square, as many as possible. How many cells shall be left empty?(A) 0(B) 1(C) 2(D) 3(E) 4Grade 1-215. In a game it is possible to make the following exchanges:Year 2013Adam has 6 pears. How many strawberries will Adam have, when he trades all his pears for juststrawberries?(A) 12(B) 36(C) 1816. Sophie makes a row of 10 houses with matchsticks. In the picture you can see the beginning of the row. How many matchsticks does Sophie need altogether?(A) 50(B) 51(C) 55(D) 60(E) 6217. A square box is filled with two layers of identical square pieces of chocolate. Kirill has eaten all 20 pieces in the upper layer, which are along the walls of the box. How many pieces of chocolate are left in the box?(A) 16(B) 30(C) 50(D) 52(E) 7018. In a park there are babies in four-wheel strollers and children on two-wheel bikes. Paula counted wheels and the total was 12. When she added the number of strollers to the number of bikes, the total was 4. How many two-wheel bikes are there in the park?(A) 1(B) 2(C) 3(D) 4(E) Other numberGrade 3-4Year 2013International Contest-Game MATH KANGAROOPart A: Each correct answer is worth 3 points. 1. In which figure is the number of black kangaroos bigger than the number of white kangaroos?(A)(B)(C)(D)(E)2. Aline writes a correct calculation. Then she covers two digits which are the same with a sticker:Which digit is under the stickers?(A)(B)(C)(D)(E)3. Monica arrived in the Kangaroo Camp on July 25th in the morning and left the camp on August 3rd inthe afternoon. How many nights did she sleep in the camp?(A) 7(B) 9(C) 10(D) 30(E) 84. How many triangles of all sizes can be seen in the picture below?(A) 9(B) 10(C) 11(D) 13(E) 125. In London 2012, the USA won the most medals: 46 gold, 29 silver and 29 bronze. China was secondwith 38 gold, 27 silver and 23 bronze. How many more medals did the USA win compared to China?(A) 6(B) 14(C) 16(D) 24Grade 3-4Year 20136. There are three families in my neighbourhood with three children each; two of the families havetwins. All twins are boys. At most how many girls are in these families?(A) 2(B) 3(C) 4(D) 5(E) 67. Vero's mother prepares sandwiches with two slices of bread each. A package of bread has 24 slices.How many sandwiches can she prepare from two and a half packages of bread?(A) 24(B) 30(C) 48(D) 34(E) 268. About the number 325, five boys said:Andrei: "This is a 3-digit number"Boris: "All digits are distinct"Vick: "The sum of the digits is 10"Greg: "The units digit is 5"Danny: "All digits are odd"Which of the boys was wrong?(A) Andrei(B) Boris(C) Vick(D) Greg(E) DannyPart B: Each correct answer is worth 4 points. 9. The rectangular mirror was broken.Which of the following pieces is the missing part of the broken mirror?(A)(B)(C)(D)(E)10. When Pinocchio lies, his nose gets 6 cm longer. When he tells the truth, his nose gets 2 cm shorter. When his nose was 9 cm long, he told three lies and made two true statements. How long was Pinocchio's nose afterwards?(A) 14 cm(B) 15 cm(C) 19 cm(D) 23 cm(E) 31 cmGrade 3-4Year 201311. John is 33 years old. His three sons are 5, 6 and 10 years old. In how many years will the three sons together be as old as their father?(A) 4(B) 6(C) 8(D) 10(E) 1212. On the map, white lines represent streets. There are pictograms on some intersections (for example, trafic light, basket, tram). Ann started walking at the beginning of the middle vertical street in the direction of the arrow. At every intersection of streets she turned either to the right or to the left. First she turned right, then left, then again left, then right, then left, and finally again left. Which of the landmarks did Ann approach in the end?(A)(B)(E)13. Schoolmates Andy, Betty, Cathie and Dannie were born in the same year. Their birthdays were on February 20th, April 12th, May 12th and May 25th, not necessarily in this order. Betty and Andy were born in the same month. Andy and Cathie were born in the same day of different months. Who of these schoolmates is the oldest?(A) Andy(B) Betty(C) Cathie (D) Dannie (E) impossible to determine14. In the Adventure Park, 30 children took part in two of the adventures. 15 of them participated in the "moving bridge" contest, and 20 of them went down the zip-wire. How many of the children took part in both adventures?(A) 25(B) 15(C) 30(D) 10(E) 515. Which of the five pieces in the answers fits with the piece in the separate picture, so that together they form a rectangle?(A)(B)(C)(D)(E)16. Children in the school club had to arrange fitness balls according to their size from the biggest to the smallest one. Rebecca was comparing them and said: the red ball is smaller than the blue one, the yellow one is bigger than the green one, and the green one is bigger than the blue one. What is the correct order of the fitness balls?(A) green, yellow, blue, red (D) yellow, green, blue, red(B) red, blue, yellow, green (E) blue, yellow, green, red(C) yellow, green, red, blueGrade 3-4Year 2013Part C: Each correct answer is worth 5 points.17. In the shown triangle, first we join the midpoints of all the three sides. This way, we form a smaller triangle. We repeat this one more time with the smaller triangle, forming a new even smaller triangle, which we colour in red. How many triangles of the size of the red triangle are needed to cover completely the original triangle, without overlapping?Note: Midpoint of a side is the point that divides the side in two parts of the same length.(A) 5(B) 8(C) 10(D) 16(E) 3218. There are oranges, apricots and peaches in a big basket. How many fruits are there in the basket if the peaches and the apricots together are 18, the oranges and the apricots together are 28 and 30 fruits are not apricots?(A) 46(B) 20(C) 40(D) 38(E) 2919. In December Tom-the-cat slept for exactly 3 weeks. Which calculations should we do in order to find how many minutes he stayed awake during this month?(A) (31 – 7) × 3 × 24 × 60(B) (31 – 7 × 3) × 24 × 60(C) (30 – 7 × 3) × 24 × 60(D) (31 – 7 ) × 24 × 60(E) (31 – 7 × 3) × 24 × 60 × 6020. Basil has several domino tiles, as shown in the figure. He wants to arrange them in a line according to the well-known "domino rule": in any two tiles that are next to each other, the squares that touch must have the same number of points. What is the largest number of tiles he can arrange in this way?(A) 3(B) 4(C) 521. Cristi has to sell 10 glass bells that vary in price: 1 euro, 2 euro, 3 euro, 4 euro, 5 euro, 6 euro, 7 euro, 8 euro, 9 euro, 10 euro. In how many ways can Cristi divide all the glass bells in three packages so that all the packages have the same price?(A) 1(B) 2(C) 3(D) 4(E) Such a division is not possible.Grade 3-4Year 201322. Nancy bought 17 cones of ice-cream for her three children. Misha ate twice as many cones as Ana. Dan ate more ice-cream than Ana but less than Misha. How many cones of ice-cream did Dan eat?(A) 4(B) 5(C) 6(D) 7(E) 823. Peter bought a carpet 36 dm wide and 60 dm long. The figure shows part of this carpet. As seen, the carpet has a pattern of small squares containing either a sun or a moon. You can count that along the width there are nine squares. When the carpet is fully unrolled, how many moons will be seen?(A) 68(B) 67(C) 65(D) 63(E) 6024. Beatrice has a lot of pieces like the grey one in the picture. At least how many of these grey pieces will she need to makea grey square?(A) 3(B) 4(C) 6(D) 8(E) 16Grade 11-12International Contest-Game MATH KANGAROOPart A: Each correct answer is worth 3 points.Year 20131. Which of the following numbers is the largest?(A) 2013(B) 20+13(C) 2013(D) 2013(E) 20 × 132. Four circles of radius 1 are touching each other and a smaller circle as seen in the picture. What is the radius of the smaller circle?(A) 2 ?11 (B)23 (C)43 (D)47 (E)163. A three-dimensional object bounded only by polygons is called a polyhedron. What is the smallestnumber of polygons that can bind a polyhedron, if we know that one of the polygons has 12 sides?(A) 12(B) 13(E) 244. The cube root of 333 is equal to(A) 33(B) 333 ?1(C) 323(D) 332(E) ( 3)35. The year 2013 has the property that its number is made up of the consecutive digits 0, 1, 2 and 3.How many years have passed since the last time a year was made up of four consecutive digits?(A) 467(B) 527(C) 581(D) 693(E) 9906. Let f be a linear function for which f(2013) – f(2001) = 100. What is f(2031) – f(2013)?(A) 75(B) 100(C) 120(D) 150(E) 1807. Given that 2 < x < 3, how many of the following statements are true?4 < x2 < 94 < 2x < 96 < 3x < 9 0 < x2 ? 2x < 3(A) 0(B) 1(C) 2(D) 3(E) 48. Six superheroes capture 20 villains. The first superhero captures one villain, the second capturestwo villains and the third captures three villains. The fourth superhero captures more villains thanany of the other five. What is the smallest number of villains the fourth superhero must havecaptured?(A) 7(B) 6(C) 5(D) 4(E) 3Grade 11-12Year 20139. In the cube to the right you see a solid, non-transparent pyramid ABCDS with base ABCD, whose vertex S lies exactly in the middle of an edge of the cube. You look at this pyramid from above, from below, from behind, from ahead, from the right and from the left. Which view does not arise?(A)(B)(C)(D)(E)10.Whena certainsolid substancemelts,itsvolume increasesby1 12.By how much doesitsvolumedecrease when it solidifies again?(A)1 10(B)1 11(C)1 12(D)1 13(E)1 14Part B: Each correct answer is worth 4 points.11. The diagram shows two squares of equal side length placed so thatthey overlap. The squares have a common vertex and the sides make anangle of 45 degrees with each other, as shown. What is the area of theoverlap as a fraction of the area of one square?1 (A)21 (B)2(C) 1? 1 2(D) 2 ?12 ?1 (E)212.How many positive integers n exist such that bothn 3and 3nare three-digit integers?(A) 12(B) 33(C) 34(D) 100(E) 30013. A circular carpet is placed on a floor of square tiles. All the tiles which have more than one point in common with the carpet are marked grey. Which of the following is an impossible outcome?(A)(B)(C)(D)(E)14. Consider the following statement about a function f on the set of integers: "For any even x, f(x) is even." What would be the negation of this proposition?(A) For any even x, f(x) is odd(B) For any odd x, f(x) is even(C) For any odd x, f(x) is odd(D) There exists an even number x such that f(x) is odd(E) There exists an odd number x such that f(x) is oddGrade 11-12Year 201315. How many pairs (x,y) of positive integers satisfy the equation x2 y3 = 612 ?(A) 6(B) 8(C) 10(D) 12(E) Another number.16. Given a function W (x) = (a ? x)(b ? x)2 , where a < b. Its graph is in one of the following figures. In which one?(A)(B)(C)(D)(E)17. Consider a rectangle, one of whose sides has a length of 5. The rectangle can be cut into a squareand a rectangle, one of which has the area 4. How many such rectangles exist?(A) 1(B) 2(C) 3(D) 4(E) 518. Assume that x2 ? y2 = 84 , where x and y are positive integers. How many values may theexpression x2 + y2 have?(A) 1(B) 2(C) 3(D) 5(E) 619. In the triangle ABC the points M and N on the side AB are such that AN = ACand BM = BC. Find ∠ACB if ∠MCN = 43°.(A) 86°(B) 89°(C) 90°(D) 92°(E) 94°20. A box contains 900 cards numbered from 100 to 999. Any two cards have different numbers.Fran?ois picks some cards and determines the sum of the digits on each of them. At least how manycards must he pick in order to be certain to have three cards with the same sum?(A) 51(B) 52(C) 53(D) 54(E) 55Part C: Each correct answer is worth 5 points.21. How many pairs (x,y) of integers with x ≤ y exist such that their product equals 5 times their sum?(A) 4(B) 5(C) 6(D) 7(E) 822. Let f (x), x ∈ R be the function defined by the following properties: f is periodic with period 5 andf (x) = x2 when x ∈[?2,3) . What is f(2013) ?(A) 0(B) 1(C) 2(D) 4(E) 923. We have many white cubes and many black cubes, all of the same size. We want to build a rectangular prism composed by exactly 2013 of these cubes so that they are placed alternating a white cube and a black cube in all directions. If we start putting a black cube in one of the eight corners of the prism, how many black squares will we see on the exterior surface of the solid?(A) 887(B) 888(C) 890(E) It depends on the dimensions of the prism(D) 892Grade 11-12Year 201324. How many solutions (x,y), where x and y are real numbers, does the equation x2 + y2 = x + yhave? (A) 1(B) 5(C) 8(D) 9(E) Infinitely many.25. There are 2013 points marked inside a square. Some of them are connected to the vertices of thesquare and with each other so that the square is divided into non-overlapping triangles. All markedpoints are vertices of these triangles. How many triangles are formed this way?(A) 2013(B) 2015(C) 4026(D) 4028(E) impossible to determine26. There are some straight lines drawn on the plane. Line a intersects exactly three other lines and lineb intersects exactly four other lines. Linec intersects exactly n other lines, with n ≠ 3, 4 .Determine the number of lines drawn on the plane.(A) 4(B) 5(C) 6(D) 7(E) Another number.27. The sum of the first n positive integers is a three-digit number in which all of the digits are thesame. What is the sum of the digits of n?(A) 6(B) 9(C) 12(D) 15(E) 1828. On the island of Knights and Knaves there live only two types of people: Knights (who always speak the truth) and Knaves (who always lie). I met two men who lived there and asked the taller man if they were both Knights. He replied, but I could not figure out what they were, so I asked the shorter man if the taller was a Knight. He replied, and after that I knew which type they were. Were the men Knights or Knaves?(A) They were both Knights.(B) They were both Knaves.(C) The taller was a Knight and the shorter was a Knave.(D) The taller was a Knave and the shorter was a Knight.(E) Not enough information is given.29. Julian has written an algorithm in order to create a sequence of numbers as a1 = 1,am+n = am + an + mn , where m and n are natural numbers. Find the value of a100.(A) 100(B) 1000(C) 2012(D) 4950(E) 505030. The roundabout shown in the picture is entered by 5 cars at the same time, eachone from a different direction. Each of the cars drives less than one round and notwo cars leave the roundabout in the same direction. How many differentcombinations are there for the cars leaving the roundabout?(A) 24(B) 44(C) 60(D) 81(E) 120Year 2013Grade 1 and 2 DBACCB DEDABE DACBDBGrade 3 and 4 DDBBCDBE BDBADEBD DDBCEBBBGrade 5 and 6 ECCBEBBECD CCDBADDACD ADBABDBBDBGrade 7 and 8 DBACEECEAC DEBCBAABBC AEDCCABDBCGrade 9 and 10 DBCCBAECBC DBDADDBCEB DCCEEDCCBBGrade 11 and 12 CABDCDEBED DAEDEADBEC ADCED*CBDEB*Answer E was also accepted as correct for Q25 Answers。
澳大利亚kangaroo袋鼠数学竞赛试题及答案grade1-11 2018年

Känguru der Mathematik 2018Level Felix (Grade 1 and 2)Austria – 15. 3. 2018– 3 Point Examples –1. Alice draws lines between the beetles. She starts with the beetle with the fewest points.Then she continues drawing to the beetle with one more point.Which figure is formed?(A)(B)(C)(D)(E)2. The same amount of kangaroos should be in both parks. How many kangaroos have to be moved from the left parkto the right park for that to happen?(A) 4 (B) 5 (C) 6 (D) 8 (E) 93. Which beetle has to fly away so that the remaining beetles have 20 dots altogether?(A) Beetle with 4 points (B) Beetle with 7 points (C) Beetle with 5 points (D) Beetle with 6 points (E) no beetle4. Peter has drawn this pattern:He draws exactly the same pattern once more.Which point is on his drawing?(A) A (B) B (C) C (D) D (E) E5. Theodor has built this tower made up of discs. He looks at the tower from above.How many discs does he see?(A) 1 (B) 2 (C) 3 (D) 4 (E) 56. This diagram shows two see-through sheets. You place the sheets on top of each other.Which pattern do you get?(A) (B) (C) (D) (E)7. In order to get to his bone, the dog has to follow the black line. In total he turns 3-times to the right and 2-times tothe left.Which path does he take?(A) (B) (C) (D) (E)8. Lisa needs exactly 3 pieces to complete her jigsaw.Which of the 4 pieces is left over?(A) A (B) B (C) C (D) D (E) C or D9. Charles cuts a rope into 3 equally long pieces. Then he makes one knot in one of the pieces, 2 in the next and in thethird piece 3 knots. Then he lays the three pieces down in a random order.Which picture does he see?(A) (B) (C) (D) (E)10. H ow many of the hands pictured show a right hand?(A) 3 (B) 4 (C) 5 (D) 6 (E) 711. T he number of spots on the fly agarics (toadstools) shows how many dwarfs fit under it. We can see one side of thefungi. The other side has the same amount of spots. When it rains 36 dwarfs are trying to hide under the fungi.How many dwarfs get wet?(A) 2 (B) 3 (C) 4 (D) 5 (E) 612. Y ou are forming two-digit numbers using the digits 2, 0, 1 or 8. They have to be bigger than 10 and smaller than 25.Every number is made up of two different digits.How many different numbers to you get?(A) 4 (B) 5 (C) 6 (D) 7 (E) 813. A lice has 3 white, 2 black and 2 grey pieces of paper. First she cuts every piece of paper that is not black into twopieces. Then she halves every piece of paper that is not white.How many pieces of paper does she obtain in total?(A) 14 (B) 16 (C) 17 (D) 18 (E) 2014. S usi makes this pattern using ice-lolly sticks. Each stick is 5 cm long and 1 cm wide.How long is Susi’s pattern?(A) 20 cm (B) 21 cm (C) 22 cm (D) 23 cm (E) 25 cm15. T he road from Anna’s to Mary’s house is 16 km long. The road from Mary’s to John’s house is 20 km long.The road from the crossing to Mary’s house is 9 km long.How long is the road from Anna’s to John’s house?(A) 7 km (B) 9 km (C) 11 km (D) 16 km (E) 18 kmKänguru der Mathematik 2018Level Ecolier (Grade 3 and 4)Austria – 15. 3. 2018- 3 Point Examples -1. As seen in the diagram, 3 darts are flying towards 9 fixedballoons. If a balloon is hit by a dart, it bursts and the dartcontinues in the same direction it had beforehand.How many balloons are hit by the darts?(A) 2(B) 3(C) 4(D) 5(E) 62. Susanne is 6 years old. Her sister Lisa is 2 years younger. Brother Max is 2 years older than Susanne.How old are the 3 siblings altogether?(A) 15 (B) 16 (C) 17 (D) 18 (E) 193. The diagram shows a wooden block with 5 screws. 4 of which are equally long, onescrew is shorter.Which is the shorter screw?(A) 1 (B) 2 (C) 3 (D) 4 (E) 54. Leonie has one stamp for each of the digits 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.Using them, she stamps the date of the kangaroo-competition.How many of the stamps does Leonie use to do that?(A) 5(B) 6(C) 7(D) 9(E) 105. On the right you can see a picture of ladybird Sophie.Sophie turns.Which of the pictures below is not Sophie?(A) (B) (C) (D) (E)6. Lucy folds a piece of paper exactly half way and then cuts out a figure:Then she unfolds the paper again.Which of the five pictures can she see?(A) (B) (C) (D) (E)7. Mike sets the table for 8 people: The fork has to lie to the left and theknife to the right of the plate.For how many people is the cutlery set correctly?(A) 5 (B) 4 (C) 6 (D) 2 (E) 38. Using these tiles Robert makes different patterns.How many of the patterns shown below can he make?(A) 1 (B) 2 (C) 3 (D) 4 (E) 5- 4 Point Examples -9. Diana shoots 3 darts, three times at a target board with two fields.The first time she scores 12 points, the second time 15.The number of points depends on which field she has hit.How many points does she score the third time?(A) 18 (B) 19 (C) 20 (D) 21 (E) 2212 Points 15 Points ? 10.Albert places these 5 figures , , , , on a 5x5-grid.Each figure is only allowed to appear once in every column and in everyrow.Which figure does Albert have to place on the field with the questionmark?(A) (B) (C) (D) (E)11. T om wants to completely cover his paper boat using the shapesand .What is the smallest number of shapes he needs for that?(A) 5 (B) 6 (C) 7 (D) 8 (E) 912. T he two colours of this picture are swapped.Then the picture is turned.Which of the pictures below is obtained?(A) (B) (C) (D) (E)13. Felix the rabbit has 20 carrots. Every day he eats 2 of them.He has eaten the 12th carrot on a Wednesday.On which day of the week did he start eating the carrots?(A) Monday (B) Tuesday (C) Wednesday (D) Thursday (E) Friday14. A rose bush has 8 flowers on which butterflies and dragonflies are sitting.On every flower there is at most one insect sitting on it. More than half of theflowers are occupied.The number of butterflies is twice as big as the number of dragonflies.How many butterflies are sitting on the rose blossoms?(A) 2 (B) 3 (C) 4 (D) 5 (E) 615.The map shows the roundtrip that Captain Bluebearcovers during his journey. Three distances are given onthe map.He sails from island to island and starts at the islandBerg. In total he covers a distance of 100 km. Thedistances between the islands Wüste and Wald is equalto the distance between the islands Berg and Blume viaVulkan.How big is the distance between Berg and Wald?(A) 17 km (B) 23 km (C) 26 km (D) 33 km (E) 35 km16. T obias glues 10 cubes together so that the following object is formed:He paints all of it, even the bottom.How many cubes then have exactly 4 faces coloured in?(A) 6 (B) 7 (C) 8 (D) 9 (E) 10- 5 Point Examples -17. T he big rectangle consists of various squares of different sizes.Each of the three smallest squares has area 1.How big is the area of the big rectangle?(A) 65 (B) 71 (C) 77 (D) 87 (E) 9818. I n order to slay a dragon, Mathias has to cut off all of its heads. As soon as he has cut off 3 heads, a new onegrows back immediately. After Mathias has cut off 13 heads the dragon is dead.How many heads did the dragon have initially?Start(A) 8 (B) 9 (C) 10 (D) 11 (E) 1219. T he rooms in Kanga’s house are numbered. Eva enters the house through themain entrance. Eva has to walk through the rooms in such a way that each roomthat she enters has a number higher than the previous one.Through which door does Eva leave the house?(A) A (B) B (C) C (D) D (E) E20. T he symbols stand for one of the digits 1, 2, 3, 4 or 5.It is known thatWhich symbol stands for the digit 3?(A) (B) (C) (D) (E)21. A belt can be joined together in 5 different ways.How many cm is the belt longer if it is only closed in the first hole instead of in all 5 holes?(A) 4 cm (B) 8 cm (C) 10 cm (D) 16 cm (E) 20 cm22. A decorated glass tile is mirrored several times along the boldly printed edge. The first mirror image is shown.spiegelnWhat does the tile on the far right look like after the third reflection?(A) (B)(C) (D) (E)23. L ea should write the numbers 1 to 7 in the fields of the given figure. There is only onenumber allowed in every field.Two consecutive numbers are not allowed to be in adjacent fields. Two fields areadjacent if they have one edge or one corner in common.Which numbers can she write into the field with the question mark?(A) all 7 numbers (B) only odd numbers (C) only even numbers (D) the number 4 (E) the numbers 1or 724. E ach of the four balls weighs either 10 or 20 or 30 or 40 grams.Which ball weighs 30 grams?(A) A (B) B (C) C (D) D (E) It can be A or B.Känguru der Mathematik 2018Group Benjamin (Grade 5 and 6)Austria – 15. 3. 2018- 3 Points Examples -1. As seen in the diagram, three darts are thrown at nine fixedballoons. If a balloon is hit it will burst and the dart continues in thesame direction it had beforehand. How many balloons will not behit by a dart?(A) 2 (B) 3 (C) 4 (D) 5 (E) 62. Peter places threebuilding blocks on a table, asshown.What does he see when he islooking at them from above?(A) (B) (C) (D) (E)3. If you hit the target board, you score points.The number of points depends on which one of the three areas youhit. Diana throws two darts, three times at the target board. On thefirst attempt she scores 14 points and on the second 16 points.How many points does she score on the third attempt?(A) 17 (B) 18 (C) 19 (D) 20 (E) 22 14 Points 16 Points ???4. A garden is split into equally sized square-shaped lots. A fast and a slow snail crawl in different directions along the outside edge of the garden. Both start at the corner S. The slowsnail crawls 1 m in one hour and the fast one crawls 2 m in one hour.In which position will the two snails meet for the first time?(A) A (B) B (C) C (D) D (E) E5. A star consist of a square and four triangles. Allsides of the triangles are equally long. The perimeter of the square is 36 cm. What is the perimeter ofthe star?(A) 144 cm (B) 120 cm (C) 104 cm (D) 90 cm (E) 72 cm6. A big spot of ink covers most of a calendar page of a certain month.Which day of the week does the 25th day of that month fall on?(A) Monday (B) Wednesday (C) Thursday (D) Saturday (E) Sunday7. How many times do you have to roll an ordinary die in order to be certain that at least onenumber is rolled twice?(A) 5 (B) 6 (C) 7 (D) 12 (E) 188. A figure is made up of three squares. The side length of the smallest square is 6 cm. How longis the side length of the biggest square?(A) 8 cm (B) 10 cm (C) 12 cm (D) 14 cm (E) 16 cm- 4 Point Examples -9. Alice subtracts one two-digit number from another two-digit number.Afterwards she paints over two digits in the calculation.How big is the sum of the two painted digits?(A) 8 (B) 9 (C) 12 (D) 13 (E) 1510. In the diagram the circles represent light bulbs which are connected to someother light bulbs. Initially all light bulbs are switched off. If you touch a light bulbthen that light bulb and all directly adjacent light bulbs switch themselves on. Whatis the minimum number of light bulbs you have to touch in order to switch on allthe light bulbs?(A)2 (B) 3 (C) 4 (D) 5 (E) 611. Four equally big squares are partiallycoloured in black.In which of the four squares is the totalarea of the black parts biggest?(A) A (B) B (C) C (D)D (E) The total area of the black parts is always equally big.12. The four smudges hide four of the numbers 1, 2, 3, 4, 5. The calculationsalong the two arrows are correct.Which number hides behind the smudge with the star?(A) 1 (B) 2 (C) 3 (D) 4 (E) 513. A lion hides in one of three rooms. On the door to room number 1 a note reads: …The lion is not here“. On the door to room number 2 a note reads: …The lion is here“. On the door to room number 3 a note reads: …2 + 3 = 5“. Exactly one of the three notes is true. In which room is the lion?(A) Room 1 (B) Room 2 (C) Room 3(D) It can be in any room. (E) It is either in room 1 or room 2.14. The two girls Eva and Olga and the three boys Adam, Isaac and Urban play together with a ball. If a girl has the ball she throws it either to the second girl or to a boy. Every boy only throws the ball to another boy, however not to the one where the ball has just come from. The first throw is made by Eva to Adam. Who makes the 5th throw?(A) Adam (B) Eva (C) Isaac (D) Olga (E) Urban15. The faces of a die are either white, grey or black. Opposite faces are always a different colour. Which of the following nets does not belong to such a die?(A) (B) (C) (D) (E)16. From a list with the numbers 1, 2, 3, 4, 5, 6, 7, Monika chooses 3 different numbers whose sum is 8. From the same list Daniel chooses 3 different numbers whose sum is 7. How many of the numbers were chosen by both Monika and Daniel?(A) none (B) 1 (C) 2 (D) 3 (E) It cannot be determined.- 5 Point Examples - 17. Emily wants to write a number into every free small triangle. The sum of the numbers in two triangles with a common side should always be the same. Two numbers are alreadygiven. How big is the sum of all numbers in the figure?(A) 18 (B) 20 (C) 21 (D) 22 (E) it cannot be calculated18. Instead of digits Hannes uses the letters A, B, C and D in a calculation. Different letters stand fordifferent digits. Which digit does the letter B stand for?(A) 0 (B) 2 (C) 4 (D) 5 (E) 619. Four ladybirds each sit on adifferent cell of a 4 x 4 grid. One isasleep and does not move. On awhistle the other three each move toan adjacent free cell.They can crawl up, down, to the rightor to the left but are not allowed on any account to move back to the cell that they have just come from.Where could the ladybirds be after the fourth whistle? (A)(B) (C) (D) (E)20. The five balls weigh 30 g,50 g, 50 g, 50 g and 80 g.Which of the balls weighs30 g?(A) A (B) B (C) C (D) D (E) E21. Three different digits A, B and C are chosen. Then the biggest possible six-digit number is built where the digit A appears 3 times, the digit B 2 times and the digit C 1 time.Which representation is definitely not possible for this number?(A) AAABBC (B) CAAABB (C) BBAAAC (D) AAABCB (E) AAACBB22. The sum of Kathi ’s age and the age of her mother is 36. The sum of the age of her mother and the age of her grandmother is 81. How old was Kathi ’s grandmother when Kathi was born?(A) 28 (B) 38 (C) 45 (D) 53 (E) 5623. Nick wants to split the numbers 2, 3, 4, 5, 6, 7, 8, 9, 10 into some groups so that the sum of the numbers in each group is equally big. What is the biggest number of groups he can build this way?(A) 2 (B) 3 (C) 4 (D) 6 (E) another number24. The figure shown on the right consists of one square part and eight rectangular parts. Eachpart is 8 cm wide. Peter assembles all parts to form one long, 8 cm wide rectangle. How long isthis rectangle?(A) 150 cm (B) 168 cm (C) 196 cm (D) 200 cm (E) 232 cmInitial position After the first whistle After the second whistle After the third whistle- 3 Point Examples - 1. Which result is obtained by the calculation (20+18)∶(20−18)?(A) 18 (B) 19 (C) 20 (D) 34 (E) 362. If the letters of the Word MAMA are written underneath each other then the word has a vertical axis of symmetry. For which of these words does that also hold true?(A) ADAM (B) BAUM (C) BOOT (D) LOGO (E) TOTO3. A triangle ABC has side lengths 6 cm, 10 cm and 11 cm. An equilateral triangle XYZ has the same perimeter as the triangle ABC. What are the side lengths of the triangle XYZ?(A) 6 cm (B) 9 cm (C) 10 cm (D) 11 cm (E) 27 cm4. Which number has to replace the ✩ in the calculation so that it is true? (A) 8(B) 9 (C) 10 (D) 12 (E) 155. The fence on the right has many holes. One morning the fence falls over and lies on thefloor. Which of the following pictures shows the fallen down fence? (A)(B)(C) (D)(E)6.Bernd produces steps for a staircase which are 15 cm high and 15 cm deep (see diagram). The staircase should reachfrom the ground floor to the first floor which is 3 m higher.How many steps does Bernd have to produce?(A) 8(B) 10(C) 15(D)20(E) 257.In a game of luck, A ball rolls downwards towards hammered nails and is diverted either tothe right or the left by a nail immediately below it. One possible path is shown in the diagram. How many different ways are there for the ball to reach the second compartment from theleft?(A) 2 (B) 3 (C) 4 (D) 5 (E) 68. A large rectangle is made up of 9 equally big rectangles. The longer side of each smallrectangle is 10 cm long. What is the perimeter of the large rectangle?(A) 40 cm (B) 48 cm (C) 76 cm (D) 81 cm (E) 90 cm9. Two circles are inscribed into an 11 cm long and 7 cm wide rectangle so that they eachtouch three sides of the rectangle. How big is the distance between the centres of the twocircles?(A) 1 cm (B) 2 cm (C) 3 cm (D) 4 cm (E) 5 cm10. The square ABCD has side length 3 cm. The points M and N, which lie on the sides AD and ABrespectively, are joined to the corner C. That way the square is split up into three parts withequal area. How long is the line segment DM?(A) 0.5 cm (B) 1 cm (C) 1.5 cm (D) 2 cm (E) 2.5 cmKänguru der Mathematik 2018 Level Kadett (Grade 7 and 8) Austria – 15. 3. 20182 ⋅ 18 ⋅ 14 = 6 ⋅ ✩ ⋅ 7- 4 Point Examples -11. Martina multiplies two, two-digit numbers and then paints over some ofthe digits. How big is the sum of the three digits that Martina has painted over?(A) 5 (B) 6 (C) 9 (D) 12 (E) 1412. A rectangle is split up into 40 equally big squares. The rectangle consists of more than one row of squares. Andreas colours in all squares of the middle row. How many squares did he not colour in?(A) 20 (B) 30 (C) 32 (D) 35 (E) 3913. Philipp wants to know how much his book weighs correct to half a gram. However, his scale only shows correct to 10 g and therefore he weighs several identical books all together. What is the minimum number of identical books he has to put on the scale in order to reach his aim?(A) 5 (B) 10 (C) 15 (D) 20 (E) 5014. A lion hides in one of three rooms. On the door to room number 1 a note reads: …The lion is here“. On the door to room number 2 a note reads: …The lion is not here“. On the door to room number 3 a note reads: …2 + 3 = 2 x 3“. Exactly one of the three notes is true. Which room is the lion in?(A) Room 1 (B) Room 2 (C)Room 3(D) It can be in any room. (E) It is either in room 1 or room 2.15. Valentin draws a zig-zag line insidea rectangle as shown in the diagram. For that he uses the angles 10°, 14°, 33°and 26°. How big is angle ?(A) 11° (B) 12° (C) 16° (D) 17° (E) 33°16. Alice writes down three prime numbers that are all less than 100. Sheonly uses the digits 1, 2, 3, 4 and 5, in fact she uses each digit exactly once.Which of the following prime numbers did she definitely write down?(A) 2 (B) 5 (C) 31 (D) 41 (E) 5317. A hotel in the carribean correctly advertises using the slogan: …350 days of sun in the year!” How many days does Mr. Happy have to spend in the hotel in a year with 365 days to be guaranteed to have two consecutive days of sunshine to enjoy?(A) 17 (B) 21 (C) 31 (D)32 (E) 3518. The diagram shows a rectangle and a straight line x, which is parallel to oneof the sides of the rectangle. There are two points A and B on x inside therectangle. The sum of the areas of the two triangles shaded in grey is 10 cm².How big is the area of the rectangle?(A) 18 cm2(B)20 cm2(C) 22 cm2(D) 24 cm2(E) It depends on the position of the points A and B.19. Jakob writes one of the natural numbers 1 to 9 into each cell of the 3x3-table. Then he worksout the sum of the numbers in each row and in each column. Five of his results are 12, 13, 15, 16and 17. What is the sixth sum?(A) 17 (B) 16 (C) 15 (D) 14 (E) 1320. 11 points are marked left to right on a straight line and their distances recorded. The sum of the distances from the first point to every other point is 2018. The sum of all distances from the second point to every other point, including the first point, is 2000. What is the distance between the first and the second point?(A) 1 (B) 2 (C) 3 (D) 4 (E) 5- 5 Point Examples -21. At an election for student representatives there are three candidates. 130 students have voted. The candidate that has the most votes wins. Currently Samuel has 24, Kevin 29 and Alfred 37 votes. How many of the currently not yet counted votes does Alfred need to get in order to definitely win the election?(A) 13(B) 14(C) 15(D) 16(E) 1722. The diagram shows the net of a box consisting onlyof rectangles. How big is the volume of the box?(A) 43 cm3(B) 70 cm3(C) 80 cm3(D) 100 cm3(E) 1820 cm323. Rita wants to write a number into everysquare of the diagram shown. Every numbershould be equal to the sum of the twonumbers from the adjacent squares. Squaresare adjacent if they share one edge. Two numbers are already given. Which number isshe going to write into the square marked with x?(A) 10(B) 7(C) 13(D) −13(E) −324. Simon runs along the edge round a 50 m long rectangular swimming pool, while at the sametime Jan swims lengths in the pool. Simon runs three times as fast as Jan swims. While Jan swims6 lengths, Simon manages 5 rounds around the pool. How wide is the swimming pool?(A) 25 m (B) 40 m (C) 50 m (D) 80 m (E) 180 m25. Lisas aviation club designs a flag with a flying …dove“ on a 4x6-grid. The area of the…dove“ is 192 cm2. The perimeter of the …dove“ is made up of straight lines and circulararcs. What measurements does the flag have?(A) 6 cm x 4 cm (B) 12 cm x 8 cm (C) 20 cm x 12 cm(D) 24 cm x 16 cm (E) 30 cm x 20 cm26. The points N, M and L lie on the sides of an equilateral triangle ABC so thatNM ⊥ BC, ML ⊥ AB and LN ⊥ AC holds true. The area of the triangle ABC is 36 cm2.What is the area of the triangle LMN?(A) 9 cm² (B) 12 cm² (C) 15 cm² (D) 16 cm² (E) 18 cm²27. Anna, Bettina and Claudia go shopping. Bettina spends 85% less than Claudia.Anna spends 60% more than Claudia. Together they spend 55 €. How much moneydoes Anna spend?(A) 3 €(B) 20 € (C) 25 € (D) 26 € (E) 32 €28. Viola practices long-jumping. On average she has jumped 3.80 m so far. On the next jump she reaches 3.99 m and thus the mean increases to 3.81 m. How far does she have to jump on her next attempt in order to increase her mean to 3.82 m?(A) 3.97 m (B) 4.00 m (C) 4.01 m (D) 4.03 m (E) 4.04 m29. In the isosceles triangle ABC (with base AC) the points K and L are added on the sidesAB and BC respectively so that AK = KL = LB and KB = AC. How big is the angle ∠ ABC?(A) 30° (B) 35° (C) 36° (D) 40° (E) 44°30. In a game of dominoes the tiles always have to be placed so that the touching halves oftwo adjacent domino tiles show the same number of dots. Paul has six domino tiles in front of him (see diagram).In several steps Paul tries to arrange them in a correct order. In each step he is either allowed to swap any two domino tiles or he is allowed to turn one domino tile 180° around. What is the minimum number of steps he needs in order to arrange the domino tiles correctly?(A) 1 (B) 2 (C) 3 (D) 4 (E) This is impossible.Känguru der Mathematik 2018Level Junior (Grade 9 and 10)Austria – 15.3.2018- 3 Point Examples -1. Every child in my family has at least two brothers and at least one sister. What is theminimum number of children in my family?(A) 3 (B) 4 (C) 5 (D) 6 (E) 72. The rings shown are partially interlinked. How long is the longest chain built this waywhich also contains the thick light ring?(A) 3 (B) 4 (C) 5 (D) 6 (E) 73. In a triangle one side has length 5 and another side has length 2. The length of the third side is an odd whole number. Determine the length of the third side.(A) 3 (B) 4 (C) 5 (D) 6 (E) 74. The distance between the top of the cat that is sitting onthe table to the top of the cat that is sleeping on the floor is150 cm. The distance from the top of the cat that is sleepingon the table to the top of the cat that is sitting on the floor is110 cm. How high is the table?(A) 110 cm (B) 120 cm (C) 130 cm (D) 140 cm (E) 150 cm5. The sum of 5 consecutive whole numbers is 102018. What is the middle number of those numbers?(A) 102013(B) 52017(C) 102017(D) 22018(E) 2∙ 1020176. In the three regular hexagons shown, X, Y and Z describe in this orderthe areas of the grey shaded parts. Which of the following statementsis true?(A)X=Y=Z(B) Y=Z≠ X(C) Z=X≠ Y(D) X=Y≠ Z(E) Each of the areas has a different value.7. Maria wants to divide 42 apples, 60 peaches and 90 cherries fairly amongst her friends. In order to do so she divides the entire fruit into baskets, each with the same amount of apples, peaches and cherries, to then give each of her friends one such basket with fruit. At most, how many baskets of fruit can she fill this way?(A) 3 (B) 6 (C) 10 (D) 14 (E) 428. In the (correct) calculation shown, some of the digits were replaced by the letters P, Q, R and S.What is the value of P + Q + R + S?(A) 14 (B)15 (C) 16 (D) 17 (E) 249. How big is the sum of 25 % of 2018 and 2018 % of 25?(A)1009 (B) 2016 (C) 2018 (D) 3027 (E) 504510. In the diagram shown, you should follow the arrows to get from A to B.How many different ways are there that fulfill this condition?(A) 20(B)16(C) 12(D) 9(E) 611. The entrances of two student halls lie in a plain street 250 m apart from each other. There are 100 students in the first one and 150 students in the second one. Where should a bus stop be built if the total sum of the distances that each student of both halls has to cover to get to the bus stop should be a minimum?(A) directly in front of the first hall (B) 100 m away from the entrance of the first hall(C) 100 m away from the entrance of the second hall (D) directly in front of the second hall(E) in any place between the two hall entrances12. 105 numbers are written in a row: 1,2,2,3,3,3,4,4,4,4,5,5,5,5,5,...Where each number n is written exactly n-times. How many of those numbers are divisible by 3?(A) 4 (B) 12 (C) 21 (D) 30 (E) 4513. Eight congruent semi-circles are drawn inside a square with side length 4. How big is thearea of the white part?(A) 2π(B)8(C) 6+π(D) 3π−2(E) 3π14. On one particular day there are a total of 40 trains from one of the towns M, N, O, P and Q to exactly one other of those towns. There are 10 trains either from or to M. There are 10 trains either from or to N. There are 10 trains either from or to O. There are 10 trains either from or to P. How many trains are there either from or to Q?(A) 0 (B) 10 (C) 20 (D) 30 (E) 4015. At a humanistic university you can study languages, history and philosophy. Some of the students there study exactly one language. (Nobody studies several languages at the same time.) Amongst those, 35 % study English. Amongst all students of the university 13 % study a language other than English. Which percentage of the students studies a language?(A) 13 % (B)20 % (C) 22 % (D) 48 % (E) 65 %16. Peter wants to buy a book but has no money. He can only buy this book with his father's and his two brother's help. His father gives him half as much money as his brothers give him jointly. His older brother gives him a third of the sum that the two others give him. The youngest brother gives him 10 €. How expensive is the book?(A)24 €(B) 26 €(C) 28 €(D) 30 €(E) 32 €17. How many three-digit numbers are there with the property that the two-digit number obtained by deleting the middle number is exactly a ninth of the original number?(A) 1 (B) 2 (C) 3 (D)4 (E) 518. How often does the summand 2018² appear under the root, if the following statement is correct?√20182 + 20182 + … + 20182=201810(A) 5(B) 8(C) 18(D) 20188(E)201818∙ 102018 ∙ (102018−1)?19. How many digits has the final result of the calculation 19(A) 2017 (B) 2018 (C) 4035 (D)4036 (E) 403720. In a regular 2018-sided shape the vertices are numbered 1 to 2018 in order. Two diagonals of the polygon are drawn in, where one of them connects the vertices 18 and 1018 and the other one the vertices 1018 and 2000. How many vertices do the three resulting polygons have?(A)38, 983, 1001 (B) 37, 983, 1001 (C) 38, 982, 1001 (D) 37, 982, 1000 (E) 37, 983, 1002。
2017年5-6年级袋鼠数学竞赛试题

假设每组的和是x,3组数的和就是3x。
6个数的和是3的倍数。 5+6+9+11+14=55
55+4=59,59不是3的倍数 55+7=62,62不是3的倍数
55+8=63,63是3的倍数 55+13=68,68不是3的倍数 55+15=63,70不是3的倍数
8.Martin把下图长方形中1/3的小正方形涂上了蓝色,一半的小正方形涂
(D) 16 cm2
(E) 6 cm2
2×2+4×4+6×6=56(cm2 )
56-1×1-2×2=51(cm2)
16. 四位球员在一场手球比赛中都有进球。他们所有人的进球数量都不同。
在四位当中,Mike 获得的进球数量最少。其余的三位总共进了 20球。
请问Mike的进球数量最大可能为多少?
(A) 2
2km 2km 2km 2km 2km 2km 2km 2km 2km 2km
70km
70-2×10=50(km) 50÷5=10(km) 10+2×3=16(km)
14. 如图所示,第一个三角形里有一只袋鼠。将虚线当作镜子。 前2个镜子的倒影已被显示 出来。 请问哪项是涂黑三角形里的袋鼠的方向?
√
4.Kalle 知道 1111 x 1111 = 1234321。请问 1111 x 2222 等于多少?
√ (A) 3456543 (B) 2345432 (C) 2234322 (D) 2468642 (E) 4321234 1 1 11×2 2 2 2 =(1 1 1 1×1 1 1 1)×2 =1 2 3 4 3 2 1×2 =24 6 8 6 4 2
从右面看: 可以确定盒子宽是4
新加坡kangaroo袋鼠数学竞赛试题及答案grade1-12 2015年

(B) 14 hours 39 minutes (D) 13 hours 21 minutes
24. The numbers 3, 5, 7, 8 and 9 are written into the squares (see fig.) so that the sum of the numbers in the row is equal to the sum of the numbers in the column. Which number is written in the central square?
He has screwed pairs of them together into five long strips.
Which strip is the longest?
(A) A
(B) B
(C) C
3. Which number is hidden behind the square?
(D) D
(A) 14
(B) 30
(C) 42
(D) 48
(E) 54
22. Nick built a cube using gray and white cubes (see fig.). The cubes with the same color do not have a common face. Which statement describes the number of used cubes?
(A) 2
(B) 3
(C) 4
Байду номын сангаас(D) 5
(E) 6
12. Six towers are built with grey cubes and white cubes. Each tower is made with five cubes. Cubes of the same colors do not touch. How many white cubes are there?
2023年9月份四年级袋鼠数学竞赛题

2023年9月份四年级袋鼠数学竞赛题1. 背景介绍2023年9月份四年级袋鼠数学竞赛是一项面向小学四年级学生的全球性数学竞赛活动。
该竞赛由澳大利亚的数学教育专家和机构主办,旨在激发学生对数学的兴趣,培养他们的数学思维和解决问题的能力。
竞赛题目涵盖了数学的多个领域,包括逻辑推理、运算技巧、几何图形等,考察学生的综合数学能力。
2. 竞赛题目解析2023年9月份四年级袋鼠数学竞赛题目涵盖了多个数学知识点,以多种形式展现,如选择题、填空题、解答题等。
我们来看看其中的选择题部分:1) 选择题题目1:小美有3个苹果,她拿走了1个,然后又拿走了2个,她现在手里还有几个苹果?A. 0个B. 1个C. 2个D. 3个这道题主要考察了学生对于简单的减法运算的掌握能力,以及对物品数量变化的理解。
通过简单的计算便可得出答案,但在实际竞赛中,考生需要理清思路,准确作答。
题目2:根据下图,以下哪个图形是一个正方形?A. □B. △C. ☆D. ○这道题目考察了学生对几何图形的识别能力,需要考生通过观察和辨别,找出符合条件的几何图形。
除了选择题外,还存在填空题和解答题部分,题目形式更加多样,从而全面考察学生的数学综合能力。
2) 填空题题目3:8 + __ = 15题目4:3 × 4 = __题目5:3的平方是__.这些填空题旨在考察学生的基础运算技能和数学运算规律的掌握程度,同时也培养了学生的逻辑思维能力。
3) 解答题题目6:小明有10元钱,他买了一本书花了3元,买了一支钢笔花了2元,剩下的钱还有多少?题目7:请依次写出3的前5个倍数。
解答题部分则更加注重学生的综合运用能力,需要学生将所学的知识进行整合并应用于实际问题的解决中,从而培养了学生的问题解决能力。
3. 总结与展望通过对2023年9月份四年级袋鼠数学竞赛题目的详细解析可见,该竞赛题目涵盖了数学的多个领域,考察了学生的综合数学能力。
在解答这些题目的过程中,学生不仅需要具有较高的数学基础知识,还需要有较强的逻辑思维和问题解决能力。
袋鼠数学-3年级-Kangroo sample Primary-3 2018

Singapore Math Kangaroo Contest 2018Rough Working–0points|Wrong–deduct1point)has one of the digits:0,1,2,3,4,5,6,7,8and9.Sheas shown below.How many stamps does she use?810320(A)5(B)6(C)7(D)9(E)10Question2The picture shows3flying arrows and9fixed balloons.When an arrow hits a balloon,it bursts, and the arrowflies further in the same direction.How many balloons will be hit by the arrows?(A)2(B)3(C)4(D)5(E)6Question3Susan is6years old.Her sister is one year younger and her brother is one year older.What is the sum of the ages of the three siblings?(A)10(B)15(C)18(D)21(E)30Question4The picture showsfive screws in a block.Among the5screws,only1of them is shorter than the other4screws.Which screw is the shortest?(A)1(B)2(C)3(D)4(E)5Question5The picture of the ladybird is shown below.Which option is not the same ladybird?(A)(B)(C)(D)(E)Question6Lucy folds a sheet of paper in half.Then she cuts a piece out of it as shown in the picture below. What will she see when she unfolds the paper?(A)(B)(C)(D)(E)Question7In herfirst try,Diana scores12points in total with three arrows.On her second try she scores15 points.How much points does(A)18(B)19(C)20(D)21(E)22Question8Mike sets the table for8guests as shown in the picture below.He wants to serve each guest with the correct arrangement,which means a fork on the left of each plate and a knife on the right.How many guest will have the correct(A)5(B)4(C)6(D)2(E)3|Wrong–deduct1point)Question9Roberto makes designs using tiles like this.How many of the5designs can he make?(A)1(B)2(C)3(D)4(E)5Question10Albertfills the grid below withfivefigures.Eachfigure appears exactly once in every column and every row.Whichfigure must mark?(A(B)(C)(D)(E)Question11Tom wants to cover the boat completely using the2types of shapes,a square and a trapezium as shown in the picture below.If no shapes can overlap each other,what is the least number of square and trapezium pieces does Tom needs to cover the boat completely?(A)5(B)6(C)7(D)8(E)9The colours in the picture below are inverted.Then the picture was rotated.What does the new picture looklike?(A )11111Question 13A rabbit has 20carrots.It eats 2carrots every day.If it ate the 12th carrot on Wednesday,which day did the rabbit start eating the carrots?(A )Monday (B )Tuesday (C )Wednesday (D )Thursday (E )Friday Question 14Toby glues 10cubes together to make the structure shown below.He paints the surface of the structure,including the bottom.How many cubes 4faces painted?(A )6(B )7(C )8(D )9(E )10Question 15There are 8flowers on a rose bush.There are no more than one insect per flower.More than half of the flowers are occupied.The number of butterflies on the flowers is twice the number of dragonflies on the flowers.How many butterflies are on the flowers?(A )2(B )3(C )4(D )5(E )6Kook wants to sail from the island called Easter through every island on the map and back to The total journey is 100km long.Some of the distances between each island have been written in the picture as shown below.For example,the distance between Easter Island andVolcano Island is 17km.The distance between Desert Island and Lake Island is the sameas the distance between Easter Island and Flower Island through Volcano Island.What is the distance between Easter Island and Lake Island?(A )17km (B )23km (C )26km (D )33km (E )35kmSection C (Correct –5points |Unanswered –0points |Wrong –deduct 1point)Question 17The rooms in Kanga’s house are numbered from 1to 14.Baby Roo enters the main door as indicated by the arrow show in the picture below.He passes through some rooms before leaving the house in one of the doors labeled A,B,C,D and E.The numbers of the rooms that he visits are always increasing.Through which door does he leave the house?(A )A (B )B (C )C (D )D (E )EQuestion 18Four balls each weigh 10,weighs 30?(A )A(B )B (C )C (D )D(E )It could be A or B2018–Primary 3/Grade 3in five ways.How much longer is the band fastened (A )4cm (B )8cm (C )10cm (D )16cm (E )20cmQuestion 20In an ancient language the symbolsIt is knownthat:represent the followingnumbers 1,2,3,4,and 5.Nobody knows which symbol represents which number.We know that:It is known that:Which (A )t is known that:It is known that:It is known that:It is known that:)It is known that:(A )(B )(C )(D )(E )Singapore Math Kangaroo Contest 2018–Primary 3/Grade 3Question 22The large rectangle is made up of different sized squares as shown in the picture below.The 3small squares each have an area of 1.1(A )165(B )176(C )187(D )198(E )200Question 23Loes wants to write the numbers from 1to 7in the boxes shown below.Two consecutive numbers cannot be written in twoneighbouring boxes.Neighbouring boxes share a common side.What numbers can she write in the box marked with a question mark?(A )all seven numbers (B )only odd numbers (C )only even numbers (D )only number 4(E )only the numbers 1or 7Question 24To defeat a dragon Mathias has to cut offall the dragon’s heads.If he can cut off3dragon’s heads,one new head immediately grows.Mathias defeats the dragon by cutting off13heads in total.How many heads did the dragon have in the beginning?(A )8(B )9(C )10(D )11(E )12Rough Working。
2018年度国外数学竞赛试题翻译汇编

纯属公益, 免费使用分享, 只送不卖
2018 年巴西数学奥林匹克复仇赛 …………………………………… 114 2017/2018 英国数学竞赛 …………………………………………… 115 2018 年保加利亚数学奥林匹克 ……………………………………… 117 2018 年保加利亚 JBMO 代表队选拔考试 …………………………… 118 2018 年加拿大数学奥林匹克 ………………………………………… 119 2018 年塞浦路斯 IMO 代表队选拔考试 …………………………… 120 2018 年塞浦路斯 JBMO 代表队选拔考试 …………………………… 122 2018 年丹麦数学奥林匹克(第二轮) ………………………………… 125 2018 年法国 JBMO 代表队选拔考试 ………………………………… 126 2018 年德国数学奥林匹克(联邦级) ………………………………… 128 2018 年德国数学奥林匹克(12 年级决赛) …………………………… 130 2018 年希腊数学奥林匹克 …………………………………………… 131 2018 年希腊 IMO 代表队选拔考试 ………………………………… 133 2018 年希腊 JBMO 代表队选拔考试 ………………………………… 134 2018 年香港数学奥林匹克 …………………………………………… 135 2018 年香港 IMO 代表队选拔考试 ………………………………… 136 2018 年匈牙利库尔沙克数学竞赛 …………………………………… 138 2018 年印度全国数学奥林匹克 ……………………………………… 139 2018 年印度 IMO 代表队选拔考试 ………………………………… 140 2018 年伊朗数学奥林匹克 …………………………………………… 143 2018 年伊朗 IMO 代表队选拔考试 ………………………………… 146 2018 年爱尔兰数学奥林匹克 ………………………………………… 149 2018 年意大利数学奥林匹克 ………………………………………… 151 2018 年哈萨克斯坦数学奥林匹克(11 年级决赛) …………………… 152 2018 韩国数学奥林匹克 ……………………………………………… 153 2018 年韩国数学冬令营训练题 ……………………………………… 156 2018 年科索沃 IMO 培训考试 ……………………………………… 157 2018 年马其顿数学奥林匹克 ………………………………………… 158 2018 年马其顿 JBMO 代表队选拔考试 ……………………………… 159
加拿大国际袋鼠数学竞赛试题 -2011年

3point problemsPROBLEM 01Basil wants to paint the word KANGAROO. He paints one letter each day. He starts on Wednesday.On what day will he paint the last letter?(A) Monday(B) Tuesday(C) Wednesday(D) Thursday(E) FridayPROBLEM 02A caveman wants to balance the two set of stones shown in the picture. Which extra stone should he put on the right-hand side to make both sides equally heavy?(B)(D) (E)PROBLEM 03A toy kangaroo is on one square of a board, as shown in the picture.A child moves the toy from one square to a neighbouring square. He uses the following order: first to the right, then upwards, then to the left, then downwards, and then to the right. Which of the following pictures shows where the toy will be at the end?(C)(D)PROBLEM 04Simon got up one hour and a half ago. In three hours and a half, he will take the train to grandmother's. How long before the train departure did he get up?(A) 2 hours (B) 3 and a halfhours(C) 4 hours (D) 4 and a halfhours(E) 5 hoursMaria described one of the five figures below in the following way. ``It is not a square. It is grey. It is(A) A(B) B(C) C(D) D(E) E PROBLEM 06Lenka paid 1 euro and 50 cents for three scoops of ice-cream. Miso paid 2 euros and 40 cents for two cakes. How much did Igor pay for one scoop of ice-cream and one cake?(A) 1 euro 70cents(B) 1 euro 90cents(C) 2 euro 20cents(D) 2 euro 70cents(E) 3 euro 90cents PROBLEM 07A tower clock strikes on the hour (that is, at 8:00, 9:00, 10:00 and so on) as many times as the hour. The clock also strikes once when the time is half past an hour (that is, at 8:30, 9:30, 10:30 and so on). How many times did the clock strike from 7:55 to 10:45?(A) 6(B) 18(C) 27(D) 30(E) 33 PROBLEM 08Which figure has the largest area?(A) (B) (C) (D) (E)4point problemsPROBLEM 09The poulterer has boxes of 6 eggs and boxes of 12 eggs. What is the smallest number of boxes he needs in order to store 66 eggs?(A) 5(B) 6(C) 9(D) 11(E) 13In a school class all pupils have at least one pet and at most two pets. The pupils have recorded howmany pupils are there in this class?(A) 11(B) 12(C) 13(D) 14(E) 17 PROBLEM 11There are 13 coins in John's pocket. Each coin is either 5 or 10 cents. Which of the following cannot be the total value of John's coins?(A) 80 cents(B) 60 cents(C) 70 cents(D) 115 cents(E) 125 cents PROBLEM 12The sheet shown in the picture is folded along the thick line.(A) A(B) B(C) C(D) D(E) E PROBLEM 13Ann, Bob, Cleo, Dido, Eef, and Fer each roll a die. They all get different numbers.The number Ann rolled is twice Bob's number.The number Ann rolled is three times Cleo's.The number Dido rolled is four times Eef's.What number did Fer roll?(A) 2(B) 3(C) 4(D) 5(E) 6 PROBLEM 14A quiz show has the following rules. Every participant has 10 points at the beginning and has to answer 10 questions. For a correct answer 1 point is added and for an incorrect answer 1 point is taken away. Mrs Smith had 14 points at the end of the quiz show. How many incorrect answers did she give?(A) 3(B) 4(C) 5(D) 6(E) 7The picture shows a magic maze.At each square of the maze there is a piece of cheese. Mouse Ron enters the maze and wants to leave with as many pieces of cheese as he can. He cannot step on any square twice. What is the largest number of pieces of cheese he can get?(A) 17(B) 33(C) 37(D) 41(E) 49 PROBLEM 16During a party each of two identical cakes was divided into four equal parts. Then each of these parts was divided into three equal slices. Each person at the party got a slice of cake and three slices were left over. How many people were at the party?(A) 24(B) 21(C) 18(D) 27(E) 135point problemsPROBLEM 17Four girlfriends Masha, Sasha, Dasha and Pasha sit on a bench as seen.First Masha exchanged places with Dasha.Then Dasha exchanged places with Pasha.At the end the girls sat on the bench in the following order from left to right, as shown in the picture: Masha, Sasha, Dasha, Pasha.(A) Masha, Sasha, Dasha, Pasha (B) Masha, Dasha,Pasha, Sasha(C) Dasha, Sasha,Pasha, Masha(D)Sasha, Masha,Dasha, Pasha(E) Pasha, Masha,Sasha, DashaThe digital watch in the picture shows two different digits.How many times a day does this watch show the same digit in all four positions?(A) 1 (B) 24 (C) 3 (D) 5(E) 12PROBLEM 19The picture shows an arrangement of four identical dice.On each die, the total number of pips on each pair of opposite faces is 7. What does the arrangement look like from behind? (A) (B) (C) (D) (E)PROBLEM 20You have the three cards shown in the picture.You can form different numbers with them, for example 989 or 986.Altogether, how many different 3-digit numbers can you form with these three cards? (A) 4(B) 6(C) 8(D) 9(E) 12The pieces cannot cover each other. Which of the following pieces cannot be used by Andra to make the pattern?PROBLEM 22How many cubes were used to build the castle?(A) 56(B) 60(C) 64(D) 68(E) 72 PROBLEM 23He now writes each of the numbers 1, remaining circles so that the sum of the numbers along each side of the square is equal to 13. What will be the sum of the numbers in the shaded circles?(A) 12(B) 13(C) 14(D) 15(E) 16PROBLEM 24Sylvia drew three shapes made from hexagons, as shown in the picture.She continues with this pattern. How many hexagons will the fifth figure contain?(A) 37(B) 49(C) 57(D) 61(E) 64Math Kangaroo2011March17,2011Levels1and2Kangourou Sans Fronti`e resMathematics Promotion Society Math Kangaroo in USAMath Kangaroo2011in USAInternational Competition in MathematicsThursday,March17,2011Levels1and2This test consists of24questions on4pages.You have75minutes to complete it.Calculators are not allowed!Please enter your answers on the answer form provided.Please put your name and ID number on the line below.3Point Problems1.Consecutive positive numbers were placed in the cells of the table below.What number is missing from the middle cell?12?45A)0B)1C)3D)62.6+2=A)5B)6C)7D)83.Sharon had10dolls.She gave Betty one of her dolls.How many dolls does Sharon have now?A)6B)7C)8D)94.There are2boys and2dogs and nobody else on the playground.How many legsare there on this playground?A)12B)10C)8D)45.Which month sometimes has only29days?A)January B)February C)March D)April6.7students and a teacher are ready for a snack.There are7glasses ofmilk,8candy bars and1cup of coffee ready for them.Each student willhave the same snack.How many candy bars will the teacher get with hiscoffee?A)0B)1C)2D)3c Math Kangaroo in USA,NFP Math Kangaroo2011March17,2011Levels1and27.What is the sum of the digits in the number2011?A)202B)31C)4D)138.Katie’s doll is wearing a dress,has two braids and is holding oneflower in her hand.Which picture shows Katie’s doll?4Point Problems9.At the end of the skiing season,there were12pairs of ski boots left at the store.How many ski boots counted one-by-one were left at the store?A)6B)12C)24D)410.The picture below shows a puzzle with one piece miss-ing.Which of the pieces below needs to be added to thepuzzle in order for it to make a picture of a cat?A)B)C)D)11.Today is3/12/2011.No item can be sold after the date shown below it.Which of the items cannot be sold?A)9/15/2011B)3/4/2012C)7/11/2011D)2/25/201112.In36years,Mark’s grandmother will celebrate her100th birthday.How old is Mark’s grand-mother now?A)74B)64C)66D)3613.Anne has several dogs and4cats.The number of her cats’ears is equal to the number of her dogs’paws.How many dogs does Anne have?A)8B)2C)4D)6 c Math Kangaroo in USA,NFP Math Kangaroo2011March17,2011Levels1and2 14.Tofind her toy,Marie needs to follow the path which is marked by the following signs in this order:,,,,,,,,.Which toy belongs to Marie?5Point Problems15.The picture below shows part of a train schedule.Right now,it’s8:45.Mr.Smith will go from Chicago to Indianapolis on the next train.The trip will take2hours and45minutes.What time will Mr.Smith arrive in Indianapolis?CHICAGO–DeparturesINDIANAPOLIS6:558:309:1511:1512:50A)11:30B)12:00C)11:15D)12:1516.Katie bought three identical pencils,two identical pens and two identical erasers,and paid $11.60.Hannah bought one pencil,two pens and two erasers,and she paid$8.40.How much does one pencil cost?A)$1.20B)$1.50C)$1.60D)$3.2017.Natalie folded a piece of paper in half and cut out a shape,as shown in thepicture to the right.Which of the pictures below shows the piece of paper after itwas unfolded?A)B)C)D)18.Mr.and Mrs.Taylor have three daughters.The youngest is5years old.The middle daughter is4years younger than the oldest daughter and6years older than the youngest daughter.How old is the Taylors’oldest daughter?A)10B)11C)9D)15 c Math Kangaroo in USA,NFP Math Kangaroo 2011March 17,2011Levels 1and 219.The flowers in the flower shop were kept in three vases.There were 16flowers in the first vase,11flowers in the second vase,and 17flowers in the third vase.The owner decided to sell only bouquets of 5flowers each.After selling some bouquets,she noticed that she did not have enough flowers to make another bouquet.How many flowers did she have left?A)1B)2C)3D)420.Simon has two identical aquariums.There are 26quarts of water in one,and 42quarts of water in the other.How many quarts of water does Simon need to pour from the second aquarium into the first in order to have the same amount of water in both?A)6B)16C)10D)821.Fido the Dog,Philemon the Cat and 4monkeys together weigh 24lbs.Fido and one monkey together weigh 11lbs.Philemon and 2monkeys together weigh 1lb less than Fido and one monkey weigh together.Each of the monkeys weighs the same.How much does Philemon weigh?A)3lbs B)4lbs C)5lbs D)6lbs22.Anita,Clara,Michael and Daniel had an apple eating contest.The person who ate the most apples won.Daniel ate more apples than Clara,and Michael ate fewer apples than Anita.We also know that Daniel did not win.Who ate the most apples?A)Anita B)Clara C)Michael D)We cannot know.23.What number do we need to put in the first square in order to get 100as the result after doing all the operations shownbelow?A)11B)9C)14D)1224.Paul and Jon were building using identical cube blocks.Paul made the building shown in Picture 1.Picture 2shows Paul’s building as seen from above.Picture 3shows Jon’s building as seen from above.(Note:The numbers in each square indicate how many blocks are placed one on top of another in that place.)Which of the answers shows Jon’sbuilding?Picture 1.1111123Picture 2.1112223Picture 3.A)B)C)D)c Math Kangaroo in USA,NFP Page 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
I N T E R N A T I O N A L C O N T E S T-G A M EM A T H K A N G A R O OC A N AD A,2018I N S T R U C T I O N SG R A D E3-41.You have 60 minutes to solve 24 multiple choice problems. For each problem,circle only one of the proposed five choices. If you circle more than one choice, your response will be marked as wrong.2.Record your answers in the response form. Remember that this is the only sheetthat is marked, so make sure you have all your answers transferred to the response form before giving it back to the contest supervisor.3.The problems are arranged in three groups. A correct answer of the first 8problems is worth 3 points. A correct answer of the problems 9-16 is worth 4 points. A correct answer of the problems 17-24 is worth 5 points. For each incorrect answer, one point is deducted from your score. Each unanswered question is worth 0 points. To avoid negative scores, you start from 24 points. The maximum score possible is 120.4.The use of external material or aid of any kind is not permitted.5.The figures are not drawn to scale. They should be used only for illustrationpurposes.6.Remember, you have about 2 to 3 minutes for each problem; hence, if a problemappears to be too difficult, save it for later and move on to another problem.7.At the end of the allotted time, please give the response form to the contestsupervisor.8.Do not forget to pick up your Certificate of Participation on your way out!Good luck!Canadian Math Kangaroo Contest teamCanadian Math Kangaroo Contest Part A: Each correct answer is worth 3 points1.Lea has 10 rubber stamps. Each stamp has one of the digits:0, 1, 2, 3, 4, 5, 6, 7, 8, 9.She prints the date of St. Patrick’s Day 2018:How many different stamps does she use?(A) 5(B) 6 (C) 7 (D) 9 (E) 102.The picture shows three flying arrows and nine fixedballoons. When an arrow hits a balloon, it bursts,and the arrow flies further in the same direction.How many balloons will be hit by the arrows?(A) 2 (B) 3 (C) 4(D) 5 (E) 63.Susan is six years old. Her sister is one year younger, and her brother is one yearolder. What is the sum of the ages of the three siblings?(A) 10 (B) 15 (C) 18 (D) 21 (E) 304.Here is a picture of Sophie the ladybug. She turns around. Which picture ofthe ladybugs below is not Sophie?(A)(B)(C)(D)(E)5.Lucy folds a sheet of paper in half. Then she cuts a piece out of it. What willshe see when she unfolds the paper?(A) (B) (C) (D)(E)1 70320186. A table is set for 8 people.How many settings have the fork to the left of the plate and the knife to the right of the plate?(A) 5(B) 4 (C) 6 (D) 2 (E) 3 7.Emily added two 2-digit numbers correctly on paper. Then she painted out two cells,as shown below.What is the sum of two digits in the painted cells?(A) 5(B) 7 (C) 8 (D) 9 (E) 13 8.First, Diana scores 12 points in total with three arrows. On her second turn shescores 15 points.How many points does she score on her third turn?(A) 18 (B) 19 (C) 20 (D) 21 (E) 22 Part B: Each correct answer is worth 4 points9.How many different numbers greater than 12 and smaller than 58 with distinct digitscan we make by using any two of the digits 0, 1, 2, 5, and 8?(A) 3(B) 5(C) 7 (D) 8 (E) 912 points15 points ? points10.Roberto makes designs using tiles like this .How many of the following five designs can he make?(A) 1 (B) 2 (C) 3 (D) 4 (E) 511.Each of these five figures ,, , , , appears exactly once in everycolumn and every row of the given table.Which figure must we put in the cell with the question mark?(A) (B) (C) (D) (E)12.Toby glues 10 cubes together to make the structure shown.He paints the whole structure, even the bottom.How many cubes are painted on exactly four of their faces?(A) 6 (B) 7 (C) 8 (D) 9 (E) 1013.The opposite faces of a cube are identical, being dark, bright or patterned.Which picture below is the unfolded net of this cube?(A)14.Tom cuts two types of pieces out of grid paper.What is the smallest number of pieces identical to the ones shown that Tom needs to build the boat in the picture?(A) 5 (B) 6 (C) 7 (D) 8 (E) 915.The rooms in Kanga's house are numbered. Baby Roo entersthe main door, passes through some rooms and leaves thehouse. The numbers of the rooms that he visits are alwaysincreasing. Through which door does he leave the house?(A) A (B) B (C) C (D) D (E) E16.Peta rabbit had 20 carrots. She ate two carrots every day. She ate the twelfth carroton Wednesday. On which day did she start eating the carrots?(A) Monday (B) Tuesday (C) Wednesday (D) Thursday (E) FridayPart C: Each correct answer is worth 5 points17.The belt shown in the drawing can be fastened in five ways.How much longer is the belt fastened in one hole than the belt fastened in all five holes?(A) 4 cm (B) 8 cm (C) 10 cm (D) 16 cm (E) 20 cm18.In an ancient writing the symbols represent thenumbers 1, 2, 3, 4, and 5. Nobody knows which symbol represents which number.We know thatWhich symbol represents the number 3?(A)(B) (C) (D) (E)19. A stained-glass tile is flipped along the black line. The figure shows the tile after thefirst flip.What will the stained-glass tile look like after the third flip (at the far right)?(A)(B)(C)(D)(E)20.The large rectangle is made up of squares of varied sizes. The three smallest squareseach have an area of 1, as shown.What is the area of the largest square?(A) 81 (B) 100 (C) 110 (D) 121 (E) 14421.Five ducklings walk behind the mother duck in a row from the oldest to the youngestlike this: Dina and Becca walk right one after the other, Mingo walks behind Lisa butin front of Becca, Becca walks directly in front of Pip. What is the name of theyoungest duckling?(A) Dina (B) Pip (C) Becca (D) Lisa (E) Mingo22.Four balls each weigh 10, 20, 30 and 40 grams. Which ball weighs 30 grams?(A) A (B) B (C) C (D) D (E) it could be A or B23.Lois wants to write the numbers from 1 to 7 in the grid shown.Two consecutive numbers cannot be written in two neighbouringcells. Neighbouring cells meet at the edge or at a corner. Whatnumbers can she write in the cell marked with a question mark?(A) all seven numbers (B) only odd numbers(C) only even numbers (D) only number 4(E) only the numbers 1 or 7 24.The distance from Anna's to Mary's house is 16 kilometers along the shown road.The distance from Mary's to Nick's house is 20 kilometers.The distance from Nick's to John's house is 19 kilometers.How far is Anna's house from John's?(A) 15 (B) 16(C) 18(D) 19 (E) 20 ?International Contest-GameMath Kangaroo Canada, 2018Answer KeyGrade 3-41 A B C D E 9 A B C D E17 A B C D E2 A B C D E10 A B C D E 18 A B C D E3 A B C D E 11 A B C D E 19 A B C D E4 A B C D E 12 A B C D E 20 A B C D E5 A B C D E 13 A B C D E21 A B C D E6 A B C D E 14 A B C D E 22 A B C D E7 A B C D E 15 A B C D E 23 A B C D E8 A B C D E 16 A B C D E24 A B C D E。
