4遗传模型
线粒体基因突变的模型

线粒体基因突变的模型
1. 遗传模型,线粒体基因突变可以通过遗传方式传递给后代。
母亲的线粒体DNA会通过卵子传递给下一代,因此线粒体基因突变主要由母系遗传。
这种遗传模型被称为线粒体遗传。
2. 突变类型,线粒体基因突变可以包括点突变、插入突变、缺失突变等多种类型。
这些突变可能导致线粒体基因的编码产物发生结构或功能上的改变,进而影响线粒体的正常功能。
3. 疾病模型,线粒体基因突变与一些疾病密切相关,如线粒体疾病、神经退行性疾病等。
研究人员通过建立相关的动物模型,如小鼠模型或转基因模型,来模拟线粒体基因突变对机体的影响,以便深入研究疾病的发病机制和寻找治疗方法。
4. 细胞模型,科研人员也会利用细胞培养模型来研究线粒体基因突变。
通过将突变的线粒体DNA导入细胞中,观察细胞的生理功能和代谢活动是否发生改变,从而揭示线粒体基因突变对细胞功能的影响。
5. 治疗模型,针对线粒体基因突变相关疾病的治疗模型也备受
关注。
包括基因治疗、药物治疗、细胞治疗等多种手段,科研人员希望通过这些模型找到有效的治疗手段,改善患者的生活质量。
总的来说,线粒体基因突变的模型涉及遗传学、分子生物学、细胞生物学等多个领域,通过建立不同的模型来全面研究线粒体基因突变对生物体的影响及相关疾病的发病机制,为未来的治疗提供理论基础和实验依据。
基因组选择育种遗传评估模型

基因组选择育种遗传评估模型
基因组选择育种遗传评估模型是一种基于全基因组信息进行选择育种的模型,通过对个体的基因组信息进行精确测量和分析,预测其表型表现和育种价值。
该模型主要分为三个步骤:
1. 基因型数据准备:对个体的基因组进行测序或基因分型,获取个体的基因型数据。
2. 关联分析:通过关联分析方法,将基因型数据与表型数据进行关联,找出与表型性状相关的基因位点。
3. 预测育种值:利用与表型性状相关联的基因位点信息,构建预测模型,对个体的育种值进行预测。
基因组选择育种遗传评估模型具有以下优点:
1. 高精度:通过对全基因组信息的分析,可以更准确地预测个体的表型表现和育种价值。
2. 高效率:相较于传统的育种方法,基因组选择育种遗传评估模型可以大大缩短育种周期和成本。
3. 广泛应用:该模型适用于各种农作物和动物,具有广泛的应用前景。
总的来说,基因组选择育种遗传评估模型是一种基于全基因组信息进行精确育种的模型,具有高精度、高效率和广泛应用等优点。
未来随着基因组学技术的发展,该模型将得到更广泛的应用和推广。
方差分析的遗传模型

方差分析的遗传模型方差分析的遗传模型:揭示和利用遗传多样性的潜能。
概述方差分析的遗传模型是一种强大的统计分析方法,用于研究遗传因素,它被广泛应用于研究遗传变异的形成、遗传基因关系的研究以及遗传疾病的形成机制。
该模型综合分析了遗传因素、环境因素和它们之间的相互作用,以梳理遗传变量文献中建议的模型,可以分析个体间的亲缘变异和环境变异,进而探索深层次的遗传因素。
结构方差分析的遗传模型包括两个分析过程:单位变量分析和综合变量分析。
单位变量分析是指将研究对象分为几个类别,单独计算每个类别的方差,以及比较各个类别之间的方差情况,这样就可以推断出各个类别之间是否存在遗传变异。
综合变量分析是指将所有研究对象视为一个整体,计算所有数据集中变量的方差爱这些变量在综合变量分析中称之为因子,然后将每个变量的方差都拆分为两部分,一部分是多样性变量,另一部分是因子变量。
其中,多样性变量表示变量之间的因素间变量,而因子变量表示因素内部变量(单位变量)。
工作流程方差分析的遗传模型的工作流程如下:1.数据采集:获取相关性评价、实验数据、相关技术参数等数据;2.数据处理:对数据进行清洗、标准化和离散化等处理;3.单因素方差分析:对所获取的单独变量或因子变量进行方差分析,计算变量与变量之间的关系;4.多变量分析:根据单因素方差分析结果,进行多变量方差分析,研究不同变量之间的复杂关系;5.分析结果:对分析结果进行判断和解释,研究不同变量之间的因果关系。
应用方差分析的遗传模型在研究人口遗传学领域有着广泛的应用。
例如,可以应用该模型来研究遗传性疾病具有遗传特征,以及家族中共性遗传疾病的发病机制;另外,也可以用该模型对人口遗传变化进行模拟,以及在两个不同人口之间进行交叉研究,从而了解不同人群之间遗传变异的情况和差异。
此外,还可以应用该方法进行基因功能研究,以及植物及动物的育种研究。
优势方差分析的遗传模型具有多重优势,首先,其可以对具有遗传特征的变量进行综合性分析,从而更好地探索探究遗传变异;其次,它可以从多个变量之间的关系出发,更有效地展示变量之间的复杂关系;最后,其还可以建立模拟的模型,从而更好地计算和识别基因独特的功能,为未来的研究奠定良好的基础。
简单遗传算法模型

简单遗传算法模型1. 概述遗传算法(GA)是一种启发式搜索算法,它受进化论中自然选择和遗传机制的启发而设计。
GA是一种非常强大的算法,它可以用来解决各种各样的优化问题。
2. 基本原理GA的基本原理是通过选择、交叉和变异操作,不断地优化一个种群的个体,最终使种群收敛到最优解。
选择:选择是GA中最关键的操作之一,它决定了哪些个体会进入下一代。
常用的选择方法有轮盘赌选择、锦标赛选择和精英选择等。
交叉:交叉是GA中另一个重要的操作,它通过交换两个个体的基因来生成新的个体。
交叉可以增加种群的多样性,提高GA的搜索能力。
常用的交叉方法有单点交叉、双点交叉和均匀交叉等。
变异:变异是GA中的一种随机操作,它通过改变个体的基因来产生新的个体。
变异可以防止种群过早收敛到局部最优解,提高GA的全局搜索能力。
常用的变异方法有比特翻转变异、均匀变异和高斯变异等。
3. 算法流程GA的算法流程如下:1. 初始化种群:随机生成一个种群,每个个体由一组基因组成。
2. 评估种群:计算每个个体的适应度值。
3. 选择:根据个体的适应度值,选择一部分个体进入下一代。
4. 交叉:对选出的个体进行交叉操作,生成新的个体。
5. 变异:对新的个体进行变异操作,生成最终的种群。
6. 重复步骤2-5,直到达到终止条件。
4. 优点和缺点GA具有以下优点:能够解决各种各样的优化问题。
不需要对问题做任何假设,也不需要任何先验知识。
能够找到全局最优解,而不是局部最优解。
GA也存在以下缺点:计算量大,尤其是当问题规模较大时。
容易陷入局部最优解,尤其是当问题具有多个局部最优解时。
难以确定合适的参数,例如种群规模、交叉率和变异率等。
5. 应用GA已被广泛应用于各种各样的领域,包括:组合优化:旅行商问题、背包问题、车辆路径问题等。
机器学习:神经网络训练、支持向量机训练、决策树学习等。
进化计算:遗传规划、进化策略、进化编程等。
6. 总结GA是一种非常强大的算法,它可以用来解决各种各样的优化问题。
遗传病发病率的数学模型高考生物计算题真题解析

遗传病发病率的数学模型高考生物计算题真题解析在生物学的学习中,数学模型的应用是必不可少的一部分。
遗传病发病率的数学模型是其中的一种重要的应用。
在高考生物考试中,经常会出现与遗传病发病率相关的计算题。
本文将对遗传病发病率的数学模型进行解析。
一、遗传病发病率的定义遗传病发病率是指在一定种群中,某种遗传病在一定时间内新发病的率。
通常以千分之几或者百分之几来度量。
二、遗传病发病率的数学模型在遗传病发病率的计算中,常用的数学模型有“剧毒遗传树”的模型、受体率模型和费歇卡模型等。
1. “剧毒遗传树”模型这个模型用于计算某种遗传病在家族中新发病的概率。
根据遗传病的类型,可以绘制出遗传病在家族中的传递路径,即“剧毒遗传树”。
通过剧毒遗传树,可以计算某一代或多代的发病率。
2. 受体率模型受体率模型适用于计算某种常染色体显性疾病的发病率。
该模型根据遗传病基因的传递方式,计算家族中某一世代的发病率。
3. 费歇卡模型费歇卡模型适用于计算某种常染色体隐性疾病的发病率。
该模型根据遗传病基因的传递方式,计算家族中某一世代的发病率。
三、数学模型的应用举例以下是一个实际的应用题,来看一下如何使用数学模型计算遗传病发病率。
某地需要对一种遗传病进行筛查,该遗传病为常染色体隐性疾病,发病率为1%。
假设筛查区域的人口为10万人,请计算该地区有该遗传病的携带者人数和患病儿童的数目。
解答:根据费歇卡模型,假设该地区该遗传病的携带者频率为p,正常基因的频率为q,则有p+q=1。
由题意可知,发病率为1%,即患病个体的频率为0.01,而携带者个体的频率为2pq。
根据人口数量,我们可以设定有N个个体,则正常的基因型频率为q^2,即q^2=N*q,从而可以得到q=N/(N+1)。
而遗传病的携带者频率为2pq,即2pq=N(N+1)。
根据题意可得:2pq=0.01N(N+1)2q(N-(N+1))=0.01N(N+1)q(N+1-N)=0.005(N^2+N)q=0.005(N+1)代入已知的人口数量N=10万,可得到q=0.005*1.01=0.00505。
5遗传模型——精选推荐

遗传模型随着人类的进化,人们为了揭示生命的奥妙,越来越注重遗传学的研究,特别是遗传特征的逐代传播,引起人们更多的注意。
无论是人,还是动、植物都会将本身的特征遗传给下一代,这主要是因为后代继承了双亲的基因,形成自己的基因对,基因对确定了后代所表现的特征。
下面,我们将研究两种类型的遗传:常染色体遗传和x一链遗传。
根据亲体基因遗传给后代的方式,建立矩阵模型,利用这些模型可以逐代研究一个总体的基因型的分布。
1.常染色体遗传模型在常染色体遗传中,后代是从每个亲体的基因对中各继承一个基因,形成自己的基因对,基因对也称为基因型。
如果我们所考虑的遗传特征是由两个基因A和a控制的,那么就有三种基因对,记为AA,Aa,aa。
例如,金鱼草是由两个遗传基因决定它的花的颜色,基因型是AA的金鱼草开红花,Aa型的开粉红色花,而aa型的开白花。
又如人类眼睛的颜色也是通过常染色体遗传控制的。
基因型是AA 或Aa的人,眼睛为棕色,基因型是aa的人,眼睛为蓝色。
这里因为Aa和AA都表示了同一外部特征,我们认为基因A支配基因a,也可认为基因a对于A来说是隐性的。
当一个亲体的基因型为Aa,而另一个亲体的基因型是aa,那么后代可以从aa型中得到基因a,从Aa型中得到基因A,或得到基因a。
这样,后代基因型为Aa或aa的可能性相等,下面给出双亲体基因型的所有可能的结合,使其后代形成每种基因型的概率:例农场的植物园中某种植物的基因型为AA,Aa和aa。
农场计划采用AA型的植物与每种基因型植物相结合的方案培育植物后代。
那么经过若干年后,这种植物的任一代的三种基因型分布如何?假设:(1)设a n,b n和c n。
分别表示第n代植物中,基因型为AA,Aa和aa的植物占植物总数的百分率。
令x(n)为第n代植物的基因型分布:()n n n n a x b c ⎛⎫ ⎪= ⎪ ⎪⎝⎭x (0)表示植物基因型的初始分布(即培育开始时的分布),显然有 a n +b n +c n =1(ii)第n-1代的分布与第n 代的分布关系是通过表3一l 确定的: 建模: 根据假设(ii),先考虑第n 代中的AA 型。
利用重组自交系(RILs)群体进行质量数量性状的遗传分析遗传模型和小麦产量性状遗传

照互补、抑制、重叠、积加、显性上位、隐性上位及协调作用等控制质量性状基因的互作方
式, 在微效基因背景下进行了建模, 探讨了两个位点主基因控制的质量 数量性状的遗传
模型和分析方法。但作为控制质量 数量性状的主基因, 这些作用方式只是一些特例。以
上模型大多是对分离世代个体 (或株系) 进行分析, 会受环境影响较大而导致不易准确鉴定其
R IL s 群体对由 1 对或 2 对主基因和微效基因共同控制的质量 析方法进行探讨。并采用该方法对小麦产量性状进行分析。
数量性状的遗传模型和分
1 遗传模型
根据遗传学原理, 主基因效应较大, 控制的性状呈现明显的不连续分布; 由大量的微效 基因控制的性状呈正态分布。某一主基因型在微效基因背景下, 呈现以该主基因型值为均数 的正态分布。同一群体若有多个不同的主基因型值, 微效基因对每个主基因型值的影响是相 同 的, 因此多个正态分布的方差 (Ρ2) 相同, 该群体的分布则是各个正态分布的联合分布。 R IL s 群体是由一系列相对纯合的系组成, 从理论上讲, 若某个 R IL s 群体涉及 1 对主基因 A —a (A , a 分别表示增减效) 差异, 则 R IL s 群体中有 2 种不同的主基因型: AA、aa, 各占 1 2; 若涉及 2 对主基因A —a、B —b 差异, 则有 4 种不同的主基因型: AABB、AA bb、aaBB、
经典观点认为生物的性状分为质量性状和数量性状, 质量性状受少数主基因控制, 而数
ቤተ መጻሕፍቲ ባይዱ
量性状受大量微效基因控制。事实上, 作物的许多经济性状既有可分组的趋势, 又呈现连续 变异, 同时表现出质量性状和数量性状两者的特征, 莫惠栋称之为质量 数量性状 (Q Q 性状) [1, 2], 这类性状是由主基因 多基因混合遗传体系[3]控制的。有些性状被认为属数 量性状的范畴, 越来越多的Q TL s (guan tita tive tra it lines) 分子标记定位结果表明其存在作用 较大的主基因[4~ 11]; 而有些被认为属质量性状的范畴, 实际上也表现出连续变异的特征, 又 有微效基因的作用。质量 数量性状是较广泛地存在的。不少学者[1~ 3, 12~ 19 ]对质量 数
常见的炎症模型的造模方法有哪些

常见的炎症模型的造模方法有哪些炎症是人体对于外部刺激或内部损伤的一种自我保护反应,通常会伴随一系列的症状,例如红肿、疼痛、发热等。
炎症模型是用来研究这个生理过程的工具,可以有助于我们理解炎症的机制和寻找治疗炎症相关疾病的方法。
下面将介绍一些常见的炎症模型的造模方法。
1. 细菌或病毒感染模型:这是最常见的炎症模型之一。
通过给动物注射或感染细菌、病毒或其他微生物,可以模拟真实感染情况下的炎症反应。
例如,在小鼠中注射细菌,可以观察到炎性细胞浸润、组织纤维化等反应,并通过分析炎症介质的表达来进一步研究炎症的机制。
2. 激素介导的炎症模型:某些激素(如肾上腺皮质激素)可以诱导炎症反应。
通过给动物注射这些激素,可以在短时间内引发炎症反应,研究其发生机制和治疗方法。
例如,给小鼠注射肾上腺素可以引发全身性炎症反应,并观察其炎症介质的变化和症状的表现。
3. 实体和组织损伤模型:通过物理或化学方法对动物的组织或器官进行损伤,可以模拟外伤引发的炎症反应。
例如,通过切割或压迫动物的皮肤或组织,可以引起局部炎症反应,观察炎性细胞的浸润和炎症介质的表达。
4. 致敏模型:在动物中引入过敏原,例如在小鼠中注射抗原,可以引发过敏反应并诱导炎症反应。
通过分析过敏反应的机制和研究炎症介质的变化,可以帮助我们了解过敏和炎症之间的关系。
5. 自身免疫模型:自身免疫性疾病与炎症有密切关系。
通过给动物注射自身抗原,例如在小鼠中注射胸腺提取物,可以触发自身免疫反应并引起炎症。
通过研究这些模型,可以深入了解自身免疫疾病的发生机制和炎症调节的方法。
6. 遗传模型:研究表明,一些基因的突变或缺陷与炎症相关的疾病有关。
通过培育具有特定基因突变的动物模型,可以模拟这些疾病,并研究其炎症反应的变化,以及借此寻找治疗方法。
7. 让步模型:炎症调控的研究中,为了便于实验操作,常常使用让步模型。
通过给动物注射低剂量的炎症介质,例如注射低剂量的细菌成分(如脂多糖),来模拟炎症反应,并研究其机制。
生物学中的模型

生物学中的模型生物学中的模型生物学是研究生命的科学,它关注生命如何从简单的化学反应和分子间相互作用演化成了复杂的生命形态,以及生命如何在不同层次上运作和交互。
为了更好地理解和研究生命,生物学家们常常使用模型来描述和解释生命的过程及其相互作用。
本文将介绍几种在生物学中常用的模型。
1. 生态系统模型生态系统模型是研究生态系统结构和功能的一种方法。
它通过在计算机上构建生态系统,来模拟生态系统中不同种群之间的相互作用,以及环境因素对生态系统的影响。
这种模型可以用来预测生态系统的响应,例如生物多样性损失、自然灾害和气候变化等。
同样的,生态系统模型也可以用来研究人为干扰对生态系统的影响,例如城市化、农业和工业污染等。
2. 分子模拟模型分子模拟模型是用来描述生物分子结构和功能的一种方法。
它基于物理化学原理,通过计算机程序模拟生物分子间的相互作用和运动。
这种模型可以用来研究许多生物分子的结构和功能,例如蛋白质、核酸和脂质等。
通过分子模拟模型,生物学家可以研究许多生物过程,例如生物催化、药物设计和分子信号传导等。
3. 细胞模型细胞模型是描述和解释细胞生物学过程的一种方法。
它通过计算机程序模拟细胞内各种分子和结构的相互作用和运动。
这种模型可以用来研究细胞的生长、分裂、代谢和信号传导等过程。
细胞模型可以帮助生物学家更好地理解细胞的功能和机制,同时也可以用来研究人类疾病的发生和治疗。
4. 人口遗传模型人口遗传模型是研究人类遗传学的一种方法。
它基于人口遗传学的理论,把人类作为一个群体来研究不同基因型和表型之间的相互作用。
这种模型可以用来研究人类基因的分布和变异,以及不同群体之间的遗传差异。
人口遗传模型也可以用来研究人类基因和疾病之间的关系,例如遗传性疾病的传播和流行。
总的来说,生物学中的模型是用来描述和解释生命过程及其相互作用的方法。
这些模型可以帮助生物学家更好地理解生命的机制和规律,同时也可以应用于医学和生物工程等领域,为人类提供更好的生活质量和健康保障。
回交自交系(BIL)群体4对主基因加多基因混合遗传模型分离分析方法的建立

作物学报ACTA AGRONOMICA SINICA 2013, 39(2): 198−206 /zwxb/ ISSN 0496-3490; CODEN TSHPA9E-mail: xbzw@DOI: 10.3724/SP.J.1006.2013.00198回交自交系(BIL)群体4对主基因加多基因混合遗传模型分离分析方法的建立王金社赵团结盖钧镒*南京农业大学大豆研究所 / 国家大豆改良中心 / 农业部大豆生物学与遗传育种重点实验室(综合) / 作物遗传与种质创新国家重点实验室, 江苏南京 210095摘要: 主基因加多基因混合遗传模型是用于分析数量性状表型数据的统计分析方法, 该方法便于育种工作者利用杂种分离世代的数据对育种性状的遗传组成初步判断,制定相应的育种策略,也可用于校验QTL定位所揭示的数量性状的性状遗传组成。
回交自交系(BIL)群体是永久性群体, 可以进行有重复的比较试验, 适用于受环境影响较大的复杂性状的遗传研究。
本研究以BIL群体为对象构建了4对主基因、主基因加多基因分离分析方法的遗传模型, 包括2类11个遗传模型。
利用基于IECM (iterative expectation conditional maximization)算法的极大似然分析方法估算各个混合遗传模型中的分布参数, 用AIC值和一组适合性测验结果选取最优模型, 并从入选模型的分布参数通过最小二乘法估计遗传参数。
由1个模拟的随机区组试验对模型进行验证, 模拟群体中遗传参数的估计值与设定值之间具有很好的一致性。
利用本文建立的模型重新分析大豆回交自交系群体(Essex×ZDD2315)及其亲本对胞囊线虫(Hetero-dera glycines Ichinohe) 1号生理小种的抗性数据后发现4对主基因模型优于原报道的3对主基因模型, 说明本方法的有效性和正确性。
关键词:回交自交家系群体(BIL); 主基因加多基因混合遗传; 分离分析Establishment of Segregation Analysis of Mixed Inheritance Model with Four Major Genes Plus Polygenes in Backcross Inbred Lines (BIL) Populations WANG Jin-She, ZHAO Tuan-Jie, and GAI Jun-Yi*Soybean Research Institute of Nanjing Agricultural University / National Center for Soybean Improvement / Key Laboratory for Biology and Genetic Improvement of Soybean (General), Minister of Agriculture / National Key Laboratory for Crop Genetics and Germplasm Enhancement, Nanjing 210095, ChinaAbstract: The segregation analysis of major genes plus polygenes is a statistical method for genetic analysis of quantitative traits. The method is particularly valuable for plant breeders to use their data accumulated from segregation populations to estimate the genetic system of target traits, which is necessary for designing breeding strategies and also useful for validating the results of QTL mapping. The backcross inbred line (BIL) population is one of the permanent populations, which is suitable for genetic analysis of complex traits and can be used in replicated experiments. For BIL population, the analytical procedures of three and less major genes plus polygenes mixed inheritance models have been established. The objective of the present study was to estab-lish the analytical procedures of segregation analysis for four major genes plus polygenes mixed inheritance models in BIL popu-lation. Eleven genetic models with four additive and (or) epistatic major genes including those without and with polygenes were established. The component distribution parameters were solved and estimated by using maximum likelihood method based on IECM (Iterative Expectation Conditional Maximization) algorithm. Among the possible models, the best one was chosen accord-ing to Akaike’s Information Criterion (AIC) and a set of tests for goodness of fit. Then the genetic parameters of the optimal model were estimated through the least square method. For demonstration of the established procedures, a simulated data set of a本研究由国家重点基础研究发展计划(973计划)项目(2009CB1184, 2010CB1259, 2011CB1093), 国家高新技术研究发展计划(863计划)项目(2011AA10A105, 2012AA101106), 国家自然科学基金资助项目(31071442, 32671266), 农业部公益性行业专项(200803060), 江苏省优势学科建设工程专项和国家重点实验室自主课题项目资助。
遗传算法模型公式

遗传算法模型公式遗传算法是一种模拟生物进化过程的优化算法,它模拟了自然界中生物进化的过程,通过选择、交叉和变异等操作来搜索最优解。
遗传算法的核心是遗传操作,其基本公式如下:1. 初始化种群遗传算法首先需要初始化一个种群,种群中的每个个体都代表了问题的一个解。
个体的表示方式可以是二进制、十进制或其他形式,具体根据问题的特点而定。
2. 评估适应度对每个个体进行适应度评估,以确定其在问题中的优劣程度。
适应度函数的选择很关键,它应能准确地评估个体的性能,使优秀个体具有较高的适应度值。
3. 选择操作根据适应度值选择优秀个体作为父代,采用轮盘赌选择、竞争选择或其他选择策略,使适应度较高的个体有更大的概率被选中。
4. 交叉操作选中的父代个体通过交叉操作产生新的个体。
交叉操作可以是单点交叉、多点交叉、均匀交叉等,不同的交叉方式会对个体的基因组合方式产生影响。
5. 变异操作对新个体进行变异操作,以增加种群的多样性。
变异操作可以是位变异、插入变异、倒位变异等,通过改变个体的某些基因值来引入新的解。
6. 新种群生成通过选择、交叉和变异操作,生成新的种群。
新种群中的个体包括父代个体和经过交叉变异产生的子代个体。
7. 重复迭代重复进行评估适应度、选择、交叉和变异操作,直到满足终止条件。
终止条件可以是达到最大迭代次数、找到满意解或达到一定的收敛条件。
遗传算法模型公式的应用范围广泛,可以用于解决各种优化问题,如旅行商问题、背包问题、排课问题等。
通过模拟生物进化的过程,遗传算法能够在解空间中搜索到全局最优解或接近最优解的解。
总结起来,遗传算法模型公式包括了初始化种群、评估适应度、选择操作、交叉操作、变异操作和新种群生成等步骤。
通过不断的迭代优化,遗传算法能够搜索到问题的最优解。
遗传算法作为一种启发式算法,在解决复杂问题时具有很高的效率和鲁棒性。
在实际应用中,可以根据问题的特点灵活选择适当的遗传算法参数和操作策略,以获得更好的优化结果。
生物种群进化中的群体遗传学模型分析

生物种群进化中的群体遗传学模型分析生物种群进化的过程是非常复杂和多样的,各种因素不断地相互作用,导致了每个物种的特征和适应度的不同。
在这个进化中,遗传学的作用不可避免,而群体遗传学模型分析是一种重要的方法来解析这些作用。
本文将介绍群体遗传学模型分析的基本原理和概念,并通过一些例子来说明它们在生物进化过程中的应用。
基本原理和概念群体遗传学模型分析的基本原理是利用数学模型来分析生物种群内遗传变异的动态过程。
它需要考虑到不同的基因型在遗传性状、亲缘关系和环境变量等方面的相互作用,以及这些作用在时间和空间上的变化。
常见的群体遗传学模型包括Hardy-Weinberg平衡和Wright-Fisher模型等。
Hardy-Weinberg平衡是一种理论模型,它描述了在一定条件下,一个群体中的基因型频率保持稳定的情况。
这些条件包括:1、群体足够大;2、无选择、无突变、无基因流、无偏好交配、无遗传漂变等;3、基因分离符合孟德尔定律。
根据Hardy-Weinberg平衡,可以推导出一些基因型频率的关系式,如p2+2pq+q2=1,其中p和q分别代表两种等位基因的频率。
这些关系式对于群体遗传学模型的分析非常重要,因为它们提供了基本的背景知识和基准值。
Wright-Fisher模型是一种基于多代群体的离散模型,它考虑了随机性和无偏性等方面的因素。
在Wright-Fisher模型中,群体中的个体数量和基因型分布会随机变化,从而导致遗传变异的动态过程。
这个过程中涉及到的因素包括:1、繁殖;2、无选择、无突变、无基因流、无偏好交配、无遗传漂变等;3、个体之间的亲缘关系和环境变量。
通过对这些因素的建模和仿真,可以得到关于遗传变异和适应度变化的预测和解释。
应用示例群体遗传学模型分析在生物学中有着广泛的应用,它可以用于研究不同类型的生物种群的进化过程和机制。
以下是一些应用示例:1、自然选择自然选择是生物进化中的一个核心概念,它指的是优胜劣汰的过程,即适应度高的个体在群体中更容易繁殖,适应度低的个体则更容易被淘汰。
数量性状的遗传模型

质量性状与数量性状比较
基因控制 变异分布 表型分布 受环境影响 遗传规律 数量性状 多基因 正态分布 连续 大 非孟德尔遗传 质量性状 单基因 二项分布 分散 小 孟德尔遗传
性状特点 研究对象 易量度 群体 不易量度 个体和群体
•某些性状既有数量性状特点,又有质量性状特点,因区 分的着眼点不同而异。
第三章 数量性状的数学模型
1
一、质量性状和数量性状
(qualitative and quantitative character)
质量性状
性状间差别明显,一般没有中间过渡类 型;这种呈现不连续变异的性状叫做质 量性状。
数量性状
性状间只有数量的不同,没有明显的质 的差别,其间有一系列的过渡类型;这 种表现连续变异的性状叫做数量性状。
2 pBqB dB
B2B2
q B2
aB
VG VA VD VI
VA
2
pAqA
2 A
2
pBqB
2 B
VD (2 pAqAd A)2 (2 pBqBdB )2
环境效应 (environmental effect)
系统 (systematic) 环境效应 – 同时对多个个体产生相同影响的环境因素
(2 pqd)2
多基因座模型
群体平均基因型值
ai ( pi qi ) 2 piqidi
个体育种值
A Ai
VA 2 piqii2
个体显性离差
D Di
VD (2 piqidi )2
多基因座模型
上位离差(epistatic deviation)
多个基因座位上总的基因型值与各个座位的基 因型值之和的离差
21=2q
2q2d
八年级上册生物模型

八年级上册生物模型
在八年级上册的生物学课程中,我们可能会涉及到一些生物模型,以下是一些可能的例子:
1. 细胞模型,细胞是生物体的基本单位,通过建立细胞模型,
我们可以更好地了解细胞的结构和功能,例如细胞膜、细胞核、线
粒体等。
2. 遗传模型,遗传是生物学中重要的概念,通过建立遗传模型,我们可以更好地理解基因的传递和表达,例如孟德尔的豌豆杂交模型。
3. 生态模型,生态学是生物学的一个重要分支,通过建立生态
模型,我们可以更好地理解生物在环境中的相互作用和生态系统的
结构与功能。
4. 消化系统模型,通过建立消化系统模型,我们可以更好地了
解人体消化系统的结构和功能,例如口腔、食道、胃等器官的作用。
5. 光合作用模型,光合作用是植物进行能量转换的重要过程,
通过建立光合作用模型,我们可以更好地理解光合作用的原理和过程。
这些只是一些可能的例子,实际上在八年级上册的生物学课程中,还会涉及到更多的生物模型。
通过建立和学习这些模型,我们可以更好地理解和应用生物学的知识,提高对生物世界的认识和理解能力。
动物模型的分类

动物模型的分类动物模型是指以动物作为实验对象来研究和验证科学问题的工具。
根据不同的研究目的和实验需求,动物模型可以分为多种分类。
本文将就动物模型的分类进行详细介绍。
一、按照研究目的分类1. 疾病模型:用于研究特定疾病的发生机制、诊断方法和治疗策略。
例如,使用小鼠模型研究癌症的发生和治疗方法。
2. 行为模型:用于研究动物的行为特征、学习记忆、情绪等。
例如,使用大鼠模型研究抑郁症的行为表现和机制。
3. 发育模型:用于研究动物的胚胎发育过程、器官形成和功能发育。
例如,使用斑马鱼模型研究胚胎发育的遗传机制。
4. 药效学模型:用于评估药物的安全性和有效性。
例如,使用猕猴模型评估新药的药代动力学和毒性。
5. 遗传模型:用于研究基因对生物特征和疾病的影响。
例如,使用果蝇模型研究遗传突变对生命活动的影响。
二、按照实验动物种类分类1. 哺乳动物模型:包括人类近缘动物和实验室动物。
人类近缘动物如猴类、猿类等,其遗传与生理特征较接近人类,可以更准确地预测人类的反应。
实验室动物如小鼠、大鼠等,其繁殖能力强,容易获取,成本较低。
2. 禽类模型:包括鸡、鸭、鹅等。
禽类具有独特的生理特征,如鸡蛋的孵化过程、鸟类的迁徙行为等,可以用于研究特定的生物学问题。
3. 水生动物模型:包括斑马鱼、鲤鱼、鳗鱼等。
水生动物具有透明胚胎和容易获取的特点,适用于观察胚胎发育和遗传变异。
4. 爬行动物模型:包括蜥蜴、蛇、乌龟等。
爬行动物的生理特征与哺乳动物有所不同,可以用于研究特定的生物学问题,如蜥蜴的再生能力。
三、按照动物模型的应用领域分类1. 医学研究:用于研究疾病的发生机制、诊断方法和治疗策略。
例如,使用小鼠模型研究心脏病的发生机制和新药的疗效。
2. 药物研发:用于评估药物的安全性和有效性。
例如,使用猕猴模型评估新药的药代动力学和毒性。
3. 农业科学:用于提高农作物的产量和品质。
例如,使用水稻模型研究抗虫性和耐旱性的改良。
4. 环境科学:用于评估环境污染对生物的影响。
玉米品质性状遗传分析

淮南工业学院硕士学位论文玉米品质性状遗传分析姓名:***申请学位级别:硕士专业:作物遗传育种指导教师:***2001.7.1摘要本试验采用2套自交系P。
和P。
(Pf为4个自交系,做母本:P。
为6个自交系,做父本),按不完全双列杂交配成24个组合。
分析了玉米4个品质性状(淀粉含量、油分含量、蛋白质含量、赖氨酸含量)的杂种优势、性状相关和亲子相关。
估算其一般配合力、特殊配合力及其相关。
研究了4个品质性j状的遗传模型,并对遗传参数和遗传力进行了估算。
研究结果表明:油分含量的杂种优势最高,其次是淀粉含量,而蛋白质和赖氨酸含量出现负杂种优势,油分含量与赖氨酸含量相关显著。
除蛋白质含量外,其余3个品质性状的亲子相关达到极显著或显著。
赖氨酸含量的遗传符合加性一显性模型,淀粉含量、油分含量、蛋白质含量还有上位性效应,4个品质性状的遗传方式均以加性效应为主。
同一品质性状不同亲本的一般配合力差异较大,同一自交系不同品质性状的一般配合力也有差异,同一品质性状因组合不同而特殊配合力也不一样。
亲本自交系的GCA和SCA对杂种的品厨}生状有重要作用,二者不能互相代替。
关键词:玉米:品质性状;杂种优势;相关分析:配合力:遗传模型日U舌玉米在吉林省粮食生产中占有重要的位置,玉米的品质对粮食生产、饲料生产和加工产品都有很大影响。
玉米的用途不同,对它的品质性状的要求也不一样。
玉米用途的广泛性决定了玉米品质育种的多样性。
通过玉米育种工作者的辛勤工作,已经培育出了许多高产稳产品种。
但由于绝大多数玉米育种工作者的育种目标就是高产,导致提高单产和其他农艺性状的同时却降低了营养物质的含量。
现在,这种状况有所改善,世界各国都在进行提高玉米品质性状的基础性和应用方面的研究工作¨”l。
玉米育种工作正在由数量型向质量型、专用型转变。
玉米杂交育种的生产实践表明,玉米的重要品质性状,如淀粉、油分、蛋白质和赖氨酸含量是由多个微效基因控制的,属数量性状范畴。
肿瘤动物模型常用建立方法

肿瘤动物模型常用建立方法肿瘤动物模型是用于研究和测试肿瘤发生、发展和治疗的工具。
建立适当的肿瘤动物模型对于揭示肿瘤的生物学特性和评估各种治疗方法的有效性至关重要。
以下是常用的肿瘤动物模型建立方法。
1. 移植瘤模型:这是最常见和简化的动物模型建立方法之一。
它涉及在动物体内或体外移植人类或动物来源的肿瘤细胞株。
这些细胞可以从肿瘤组织中分离得到,并在实验室中培养。
移植瘤模型的优点是易于建立和控制,但它不能反映肿瘤的整个发展过程。
2. 转基因模型:转基因动物模型是通过将特定的基因突变导入小鼠或其他动物体内来模拟肿瘤。
这些基因突变可以是人类肿瘤相关基因的突变,也可以是具有肿瘤形成潜能的其他基因的突变。
转基因模型可以提供更真实的肿瘤发展和治疗反应,但其建立过程相对复杂和耗时。
3. 化学诱发模型:这种方法通过给动物暴露于化学物质,如化学致癌物质或腺病毒,来诱发肿瘤的发生。
这些化学物质可以引起DNA损伤或基因突变,从而促进肿瘤的形成。
化学诱导模型可以提供与人类肿瘤相似的病理特征,但其应用范围受到化学物质的选择和剂量的限制。
4. 遗传模型:遗传模型使用特定品系的小鼠或其他动物,这些动物因其自身的遗传缺陷而具有高发生肿瘤的风险。
这些遗传模型可以是自然突变品系,也可以是通过基因工程技术引入的遗传缺陷。
遗传模型可以提供对特定肿瘤类型和易感因素的研究,但其适用范围受到特定品系的限制。
以上是常见的肿瘤动物模型建立方法。
根据具体研究目的和研究条件的不同,选择合适的肿瘤动物模型对于取得可靠的研究结果至关重要。
不同模型的优劣势需要综合考虑,并根据研究的需要进行合理选择。
遗传算法优化模型参数方法讨论和应用

遗传算法优化模型参数方法讨论和应用摘要遗传算法是一种通过模拟生物进化过程来优化问题解决方案的算法。
在应用遗传算法优化模型参数时,需要选择合适的编码方式、适应度函数和交叉、变异等操作方法。
本文将讨论遗传算法优化模型参数的原理,介绍常用的优化方法,并探讨其在实际应用中的效果。
引言模型参数的优化是很多机器学习和优化问题的核心。
遗传算法作为一种全局优化方法,已经被广泛应用于参数优化领域。
在遗传算法中,通过随机选择和进化操作来搜索最优解。
其优点包括对于问题形式的通用性、可并行处理以及能够找到局部最优解等。
一、遗传算法的原理遗传算法的核心思想是通过模拟自然界的进化过程来搜索最优解。
它模仿了遗传信息的传递、变异和自然选择等自然过程。
1. 编码方式的选择遗传算法的第一步是对问题进行适当的编码,将问题的解表示为一个基因型。
常用的编码方式包括二进制编码、实数编码和排序编码等。
二进制编码适合优化问题,实数编码适合连续优化问题,排序编码适合离散优化问题。
2. 个体的表示和适应度函数的定义在遗传算法中,个体表示一个潜在的解,而适应度函数用于评估个体的好坏程度。
适应度函数需要与问题相匹配,并且能够准确衡量个体的适应性。
适应度函数的定义对优化结果有重要影响。
3. 选择操作选择操作是从选择池中挑选适应度较好的个体作为交叉和变异的父代。
常用的选择操作方法包括轮盘赌选择、锦标赛选择和排名选择等。
轮盘赌选择将个体的适应度转换为选择概率,然后按照概率选择个体。
锦标赛选择从选择池中随机选择一部分个体,然后选择适应度最好的个体作为父代。
排名选择将个体按照适应度从高到低排序,然后选择适应度高的个体作为父代。
4. 交叉和变异操作交叉操作是指将两个父代的染色体部分互换,从而产生新的后代。
变异操作是指对染色体的部分基因进行随机变化。
交叉和变异操作是引入新解的机制,使得优化过程可以跳出局部最优解。
二、常用的遗传算法优化方法在实际应用中,遗传算法经常被用来优化模型参数。
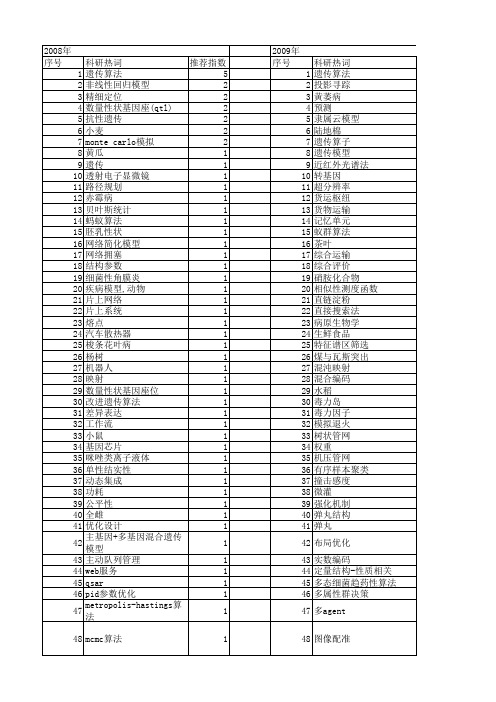
【江苏省自然科学基金】_遗传模型_期刊发文热词逐年推荐_20140815
1 1 1 1 1 1 1 1 1 1 1 1 1 1
53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100
2010年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51
2009年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52
53 54 55 56 57 58 59法 内弹道 免疫遗传算法(iga) 免疫算法 偏最小二乘法 优化设计 优化模型 优化 任务分配 不可行度 rva谱 qtl作图 bp网络 2型猪链球菌
推荐指数 7 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2008年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
常染色体遗传模型
• 假设:(1)设an,bn和cn分别表示第n代植 物中,基因型为AA,Aa和aa的植物占 植物总数的百分率。令x(n)为第n代植物 的基因型分布:
an
x(n)
bn
cn
x(0)表示植物基因型的初始分布(即培育开 始时的分布),显然有 an+bn+cn=1
常染色体遗传模型
• (ii)第n-1代的分布与第n代的分布关系 是通过上表确定的.
常染色体遗传模型
• 建模: 根据假设(ii),先考虑第n代中的 AA型。由于第n-1代的AA型与AA型结 合,后代全部是AA型;第n-l代的Aa型 与AA型结合,后代是AA型的可能性为 1/2,而第n-l代的aa型与AA型结合,后 代不可能是AA型。因此 an=1an-1 +1/2bn-1+0cn-1 …………
常染色体遗传模型
an=1an-1 +1/2bn-1+0cn-1 bn=0an-1 +1/2bn-1+1cn-1 cn=0an-1 + 0bn-1+ 0cn-1
x(n) Mx(n1)
1
1 2
0
M
=
0
1 2
1
0 0 0
常染色体遗传模型
• 模型讨论:
• 若在上述问题中,不选用因型AA植物 与每一植物结合,而是将具有相同基因 型植物相结合,那么后代所具有三种基 因型的概率由下表给出:
• 假设
• (i)常染色体遗传的正常基因记为A,不 正常基因记为a,并以AA,Aa,aa分别 表示正常人,隐性患者,显性患者的基 因型
• (ii)设an,bn分别表示第n代中基因型为 AA,Aa 占总人数的百分数,记
x(n)
an
bn
常染色体隐性病模型
• (iii)为使每个儿童至少有一个正常的父 亲或母亲,因此正常人或隐性患者必须 与正常人结合,其后代的基因型概率由 表给出:
常染色体遗传模型
• 在常染色体遗传中,后代是从每个亲体 的基因对中各继承一个基因,形成自己 的基因对,基因对也称为基因型。如果 我们所考虑的遗传特征是由两个基因A 和a控制的,那么就有三种基因对,记 为AA,Aa,aa。
常染色体遗传模型
• 例如,金鱼草是由两个遗传基因决定它 的花的颜色,基因型是AA的金鱼草开 红花, Aa型的开粉红色花,而aa型的 开白花。又如人类眼睛的颜色也是通过 常染色体遗传控制的。基因型是AA或 Aa的人,眼睛为棕色,基因型是aa的人, 眼睛为蓝色。
后 代 AA 基因
型 Aa
aa
父体——母体的基因型
AA-AA Aa-Aa
aa-aa
1
1/4
0
0
1/2
0
0
1/4
1
常染色体隐性病模型
• 现在世界上已经发现的遗传病将近4000 种。在一般情况下,遗传疾病是与特殊 的种族、部落及群体有关。例如,遗传 病库利氏贫血症的患者以居住在地中海 沿岸为多,镰状网性贫血症一般流行在 黑人中,家族黑蒙性白痴症则流行在东 欧犹太人中间。患者经常未到成年就痛 苦地死去,而他们的父母则是疾病的病 源。
任选雌雄各一个成配偶,然后在它们产生的 后代中任选两个结成配偶。如此继续下去。 • (ii)父体与母体的基因型组成同胞对,同胞对 的形式有(A,AA),(A,Aa),(A,aa),(a, AA),(a,Aa),(a,aa)。初始一对雌雄的同 胞对,是这六种类型中的任一种,其后代的 基因型由表给出。
X—链遗传模型
常染色体遗传模型
• 这里因为Aa和AA都表示了同一外部特 征,我们认为基因A支配基因a,也可认 为基因a对于A来说是隐性的。当一个亲 体的基因型为Aa,而另一个亲体的基因 型是aa,那么后代可以从aa型中得到基 因a,从Aa型中得到基因A,或得到基 因a。这样,后代基因型为Aa或aa的可 能性相等
父体——母体的基因型
AA 后代
基因
型
Aa
aa
AA-AA 1
0 0
AA-Aa 1/4
1/2 1/4
常染色体隐性病模型
• 建模 • 由假设(iii),从第n-1代到第n代基因
型分布的变化取决于方程……
常染色体隐性病模型
• 模型讨论 • 研究在随机结合的情况下,隐性患者
的变化是很有意思的,但随机结合导致 了非线性化问题,超出范围,
X—链遗传模型
• (iv)如果第n-1代配偶的同胞对是(A, Aa) 型,那么它们的雄性后代将等可能地得 到基因A或a,它们的雌性后代的基因型 将等可能地是AA或A. 又由于第n代雌雄 结合是随机的,那么第n代配偶的同胞 对将等可能地为四种类型(A,AA),(A, Aa),(a,AA),(a,Aa)之一。其他类似 可分析
遗传模型
1.常染色体遗传 2.X—链遗传
遗传模型
• 随着人类的进化,人们为了揭示生命的 奥妙,越来越注重遗传学的研究,特别 是遗传特征的逐代传播,引起人们更多 的注意。无论是人,还是动、植物都会 将本身的特征遗传给下一代,这主要是 因为后代继承了双亲的基因,形成自己 的基因对,基因对确定了后代所表现的 特征。
父体一母体的基因型
(A,AA) (A,Aa) (A,aa) (a,AA) (a,Aa) (a,aa)
A
1
1/2
0
1
1/2
0
a
0
1/2
1
0
1/2
1
后
代
基 AA
1
1/2
0
0
0
0
因
型
Aa
0
1/2
1
1
1/2
0
aa
0
0
0
0
1Байду номын сангаас2
1
X—链遗传模型
• (iii)在每一代中,配偶的同胞对也是六 种类型之一,并有确定的概率。为计算 这些概率,设an,bn,cn,dn,en和fn分 别是第n代中,配偶的同胞对为(A,AA), (A,Aa),(A,aa),(a,AA),(a,Aa), (a,aa)型的概率。令 x(n)=(an, bn, cn, dn, en, fn)T, n=0,1,2,…
X—链遗传模型
• X—链遗传是指雄性具有一个基因A或a, 雌性具有两个基因AA,或Aa,或aa。 其遗传规律是雌性后代以相等概率得到 母体两个基因中的一个,雌性后代从父 体中得到一个基因,并从母体的两个基 因中等可能地得到一个。下面,研究与 X—链遗传有关的近亲繁殖过程。
X—链遗传模型
• 假设 • (i)从一对雌雄结合开始,在它们的后代中,
常染色体遗传模型
• 下面给出双亲体基因型的所有可能的结 合,使其后代形成每种基因型的概率:
父体——母体的基因型
AA-AA AA-Aa AA-aa Aa-Aa Aa-aa aa-aa
AA
1
后
代
基 Aa
0
因
型
aa
0
1/2
0
1/2
1
0
0
1/4
0
0
1/2
1/2
0
1/4
1/2
1
常染色体遗传模型
• 农场的植物园中某种植物的基因型为 AA,Aa和aa。农场计划采用AA型的植 物与每种基因型植物相结合的方案培育 植物后代。那么经过若干年后,这种植 物的任一代的三种基因型分布如何?
常染色体隐性病模型
• 假若我们能识别这些疾病的隐性患者, 并且规定隐性患者不能结合(因为两个隐 性病患者结合,他们的后代就可能成为 显性患者),那么未来的儿童,虽然有可 能是隐性患者,但绝不会出现显性特征, 不会受到疾病的折磨。现在,我们考虑 在控制结合的情况下,如何确定后代中 隐性患者的概率。
常染色体隐性病模型
