精品课件-一次函数第一课时PPT
合集下载
《一次函数》PPT课件(第1课时)

③ y=0.5x,
④y=x-6.
③
(1)其中过原点的直线是________;
④
( 2)函数y随x的增大而增大的是_______;
②
(3)函数y随x的增大而减小的________;
①
(4)图象在第一、二、三象限的________
.
(1.5,0)
3.直线y =2x-3 与x 轴交点的坐标为________;与y
2 了解分段函数的表示及其图象.
1
3
能初步应用一次函数模型解决现实生活中的
问题,体会一次函数的应用价值.(难点)
新课导入
1.复习
3
y
2
x
画出函数
和 y x 3 的图象.
2
2.反思
你在作这两个函数图象时,分别描了几个点?
你为何选取这几个点?有不同的取法吗?
3.思考
反过来,已知一个一次函数的图象经过
数学课件:www.1ppt.c om/keji an/shuxue/
美术课件:www.1ppt.c om/keji an/mei shu/
物理课件:www.1ppt.c om/keji an/wuli /
生物课件:www.1ppt.cc om/keji an/lishi /
科学课件:/keji an/kexue/
化学课件:/keji an/huaxue/
地理课件:/keji an/dili/
PPT素材:/s ucai/
PPT图表:/tubiao/
PPT教程: /powerpoint/
手抄报:/shouc haobao/
语文课件:/keji an/yuwen/
英语课件:/keji an/ying yu/
④y=x-6.
③
(1)其中过原点的直线是________;
④
( 2)函数y随x的增大而增大的是_______;
②
(3)函数y随x的增大而减小的________;
①
(4)图象在第一、二、三象限的________
.
(1.5,0)
3.直线y =2x-3 与x 轴交点的坐标为________;与y
2 了解分段函数的表示及其图象.
1
3
能初步应用一次函数模型解决现实生活中的
问题,体会一次函数的应用价值.(难点)
新课导入
1.复习
3
y
2
x
画出函数
和 y x 3 的图象.
2
2.反思
你在作这两个函数图象时,分别描了几个点?
你为何选取这几个点?有不同的取法吗?
3.思考
反过来,已知一个一次函数的图象经过
数学课件:www.1ppt.c om/keji an/shuxue/
美术课件:www.1ppt.c om/keji an/mei shu/
物理课件:www.1ppt.c om/keji an/wuli /
生物课件:www.1ppt.cc om/keji an/lishi /
科学课件:/keji an/kexue/
化学课件:/keji an/huaxue/
地理课件:/keji an/dili/
PPT素材:/s ucai/
PPT图表:/tubiao/
PPT教程: /powerpoint/
手抄报:/shouc haobao/
语文课件:/keji an/yuwen/
英语课件:/keji an/ying yu/
一次函数的图象ppt课件

3
探究新知
正比例函数的图象
知识点
探究1:画出正比例函数y=2x的图象
怎样画出给定函数的图象?一般可以分为哪几个步骤?
“描点法”,分成“列表、描点、连线”三个步骤.
(1) 列表:
x
… -3
-2
-1
0
1
2
3
…
y=2x
… -6
-4
-2
0
2
4
6
…
4
4
探究新知
探究1:画出正比例函数y=2x的图象
y=-2x
交点的坐标:y=3x 和y=-3x+2.
解:对于函数y=3x,取x=0,得y=0,
得到点(0,0);取x=1,得y=3,
得到点(1,3).
过点(0,0),(1,3)画直线,
就得到函数y=3x的图象,它与坐标
轴的交点是原点(0,0).
y
5
4
3
2
1
y=3x
-3 -2 -1 O1 2 3 x
-1
-2
பைடு நூலகம்-3
-4
2
它与x轴的交点是( 3 ,0),与y轴
的交点是(0,2).
y
5
4
3
2
1
y=3x
-3 -2 -1 O1 2 3 x
-1
-2
-3
-4
y=-3x+2
-5
15
15
探究新知
例3 画出一次函数y=2x-1与y=-0.5x+1的图象,并求出它们与
坐标轴的交点坐标.
y
y=2x-1
解:列表:
x
y=2x-1
y=-0.5x+1
一次函数说课课件(共19张PPT)

小结: 这节课的收获:
怎样的函数是一次函数?
一般地,形如y=kx+b(k,b是常数,k≠0) 的函数,叫做一次函数。
当b=0时,y=kx+b就变成了 y=kx(k≠0),所以说正比例函数是一种特 殊的一次函数。
作业
• 完成课本90页练习1、2、3
再 见!
函数关系式 函数 自 变量 变 量
常数
y =-300x+3000 y x 3000 , -300
S=-95t+570 S t 570 , -95
y=8x+9
y x 9,8
y=12x+50 y x 50 , 12
一次函数的概念:
一般地,若两个变量 x、y之间的关系可以表示成: y=kx+b(k,b是常数,k≠0)的形式,则称 y是x的 一次函数。(x为自变量,y为因变量。)
(3)汽车油箱中原有油50升,如果行驶中每小时 用油5升,求油箱中的油量y(单位:升)随行驶 时间x(单位:时)变化的函数关系式.并写出
自变量x的取值范围,y是x的一次函数吗?
解:汽车每小时用油5升,x个小时用油5x升, 因而 y=50-5x (即y=-5x+50) ∵y≥0 ∴0≤x≤10 即自变量x的取值范围是0≤x≤10 (y是x的一次函数,但不是x的正比例函数。)
三、教学重点、难点
• 教学重点:掌握一次函数的概念,学会 如何判断一次函数.
• 教学难点:能结合实际问题中的数量关 系求出一次函数的解析式,即学会做一 次函数有关的应用题.
四、教学过程
• 回顾旧知识 • 创设情境,引入问题 • 新知识讲解 • 反馈练习 • 课堂小结
一﹑
正比例函数的定义:
一次函数课件ppt

掌握如何根据直线的方程求解一次函数,并了解直线的性质。
一次函数与两直线的交点
了解如何通过两直线的交点求解一次函数的解析式。
一次函数与抛物线的交点
了解如何通过抛物线的交点求解一次函数的解析式。
一次函数在实际问题中的应用
一次函数与最值问题
掌握如何利用一次函数解决最值问题。
一次函数与不等式问题
了解如何利用一=kx+b(k,b是常数,k≠0)中,当b=0时, y=kx(k是常数,k≠0),此时称y是x的正比例函 数。
一次函数的表达式
表达式
y=kx+b(k,b是常数,k≠0)
变量的取值范围
当k>0时,y随x的增大而增大;当k<0时,y随x的增大而 减小。
截距的意义
b是常数项,表示与y轴的交点坐标。当b>0时,交点在y 轴的正半轴上;当b<0时,交点在y轴的负半轴上;当 b=0时,交点在原点。
03 一次函数的应用
一次函数在代数中的应用
一次函数与一元一次方程的关系
01
了解如何用一次函数解决一元一次方程的问题。
一次函数的单调性
02
掌握如何根据函数的单调性求解函数的值域和定义域。
一次函数的零点
03
了解如何通过零点将函数进行分类,并求解函数的零点。
一次函数在几何中的应用
直线方程与一次函数的关系
一次函数的图像
图像的绘制
描点法,先确定自变量x的取值范 围,然后分别在坐标系中找出对
应的y值,描点、连线即可得到一 次函数的图像。
图像的性质
当k>0时,直线呈上升趋势;当 k<0时,直线呈下降趋势。截距b 的取值决定了直线与y轴交点的位 置。
一次函数与两直线的交点
了解如何通过两直线的交点求解一次函数的解析式。
一次函数与抛物线的交点
了解如何通过抛物线的交点求解一次函数的解析式。
一次函数在实际问题中的应用
一次函数与最值问题
掌握如何利用一次函数解决最值问题。
一次函数与不等式问题
了解如何利用一=kx+b(k,b是常数,k≠0)中,当b=0时, y=kx(k是常数,k≠0),此时称y是x的正比例函 数。
一次函数的表达式
表达式
y=kx+b(k,b是常数,k≠0)
变量的取值范围
当k>0时,y随x的增大而增大;当k<0时,y随x的增大而 减小。
截距的意义
b是常数项,表示与y轴的交点坐标。当b>0时,交点在y 轴的正半轴上;当b<0时,交点在y轴的负半轴上;当 b=0时,交点在原点。
03 一次函数的应用
一次函数在代数中的应用
一次函数与一元一次方程的关系
01
了解如何用一次函数解决一元一次方程的问题。
一次函数的单调性
02
掌握如何根据函数的单调性求解函数的值域和定义域。
一次函数的零点
03
了解如何通过零点将函数进行分类,并求解函数的零点。
一次函数在几何中的应用
直线方程与一次函数的关系
一次函数的图像
图像的绘制
描点法,先确定自变量x的取值范 围,然后分别在坐标系中找出对
应的y值,描点、连线即可得到一 次函数的图像。
图像的性质
当k>0时,直线呈上升趋势;当 k<0时,直线呈下降趋势。截距b 的取值决定了直线与y轴交点的位 置。
初中数学-19.2.2一次函数第1课时课件

思考: 正比例函数与一次函数有什么
区别和联系呢?
区别: 一次函数有常数项,正比例函 数没有常数项。
联系: 正比例函数是特殊的一次函数, 一次函数不一定是正比例函数。
一次函数 正比例函数
例1.下列函数关系式中,哪些是一次函数? 哪些是正比例函数?
(1)y=2πx
(3)y 1 x
(2)y=-x-4 (4)y=x2 -3x
复习:Байду номын сангаас
正比例函数y=kx(k是常数,k≠0) 的图象和性质
k的正负性
k>0
k<0
y=kx(k是常数, k≠0)的图像
直线y=kx经过 的象限
性质
一、三象限 y随x的增大而增大
二、四象限 y随x的增大而减小
图象必经过的点 图象必经过(0,0)和(1,k)这两个点
概念:
一般地,形如y=kx+b(k,b是常数,k≠0) 的函数,叫做一次函数。
3 3
m 3
∴一次函数的表达式为 y 6x 3
注意:利用定义求一次函数 y kx b 表达式时,
必须保证:(1)k ≠ 0,
(2)自变量x的指数是“1”
1、在一次函数y=-3x-5中,k =_-_3_,b =__-_5_.
2、若函数y=(m-3)x+2-m是一次函数,则 m_≠__3___ .
3、在一次函数y=-2x+3中,当x=3时,y=_-_3_ ; 当x=__-1__时,y=5。
4.若函数y=mx-(4m-4)的图象过原点,则 m=_1__,此时函数是 _正_比__例__函数.若函数 y=mx-(4m-4)的图象经过(1,3)点, 则m=__1_/_3__,此时函数是_一__次___函数.
一次函数1-PPT资料16页

当b=0时,y=kx(k是常数,且k≠0称y是x的正比例函数
正比例函数是 一次函数的特例
函数 正比例函数
一次函数
概念说明
特别注意:
一个关自键变点量:的次数是1次 两个控制器:一次项系数k,常数项b
概念辨析
判断下列函数是不是一次函数,如果是一次函数,
是不是正比例函数?
(1)y=
3 2
x-1
是一次函数,不是正比例函数
(6)某种汽油8元/L,加油应付油费y元随加油量xL面所列出的函数式进行分类吗?
自觉感悟
y=40-5x
y=10-x
L=4x
y=8x
• 你能把上面所列出的函数式进行分类吗?
是一次函数
不是一次函数
概念产生
一般地,如果2个变量x与y之间的函数关系, 可以表示为y=kx+b(k、b为常数,且k≠0)的 形式,那么称y是x的一次函数.
小试牛刀
1.若y=(m-1)x+5是一次函数,
则m ≠1 。
2.若y=2x m2-3 - 4是一次函数,
则m =±2 。
小试牛刀
课堂小结 通过本节课的学习,你有哪些收获?
谢谢你的阅读
知识就是财富 丰富你的人生
(2)y=3x2+2 不是一次函数
(3)m=-5n 是一次函数, 是正比例函数
(4)y=6 - 3x 是一次函数,不是正比例函数
(5)y=2(t-5) 是一次函数,不是正比例函数 (6)2y=x-1 是一次函数,不是正比例函数
概念辨析
是 是 否 是 是
是
-1 0
是
0
否
3 -3
否
12
典型例题
例:已知函数 y(m1)xm21 (1)m取何值时,该函数是一次函数? (2) m取何值时,该函数是正比例函数?
正比例函数是 一次函数的特例
函数 正比例函数
一次函数
概念说明
特别注意:
一个关自键变点量:的次数是1次 两个控制器:一次项系数k,常数项b
概念辨析
判断下列函数是不是一次函数,如果是一次函数,
是不是正比例函数?
(1)y=
3 2
x-1
是一次函数,不是正比例函数
(6)某种汽油8元/L,加油应付油费y元随加油量xL面所列出的函数式进行分类吗?
自觉感悟
y=40-5x
y=10-x
L=4x
y=8x
• 你能把上面所列出的函数式进行分类吗?
是一次函数
不是一次函数
概念产生
一般地,如果2个变量x与y之间的函数关系, 可以表示为y=kx+b(k、b为常数,且k≠0)的 形式,那么称y是x的一次函数.
小试牛刀
1.若y=(m-1)x+5是一次函数,
则m ≠1 。
2.若y=2x m2-3 - 4是一次函数,
则m =±2 。
小试牛刀
课堂小结 通过本节课的学习,你有哪些收获?
谢谢你的阅读
知识就是财富 丰富你的人生
(2)y=3x2+2 不是一次函数
(3)m=-5n 是一次函数, 是正比例函数
(4)y=6 - 3x 是一次函数,不是正比例函数
(5)y=2(t-5) 是一次函数,不是正比例函数 (6)2y=x-1 是一次函数,不是正比例函数
概念辨析
是 是 否 是 是
是
-1 0
是
0
否
3 -3
否
12
典型例题
例:已知函数 y(m1)xm21 (1)m取何值时,该函数是一次函数? (2) m取何值时,该函数是正比例函数?
一次函数(1)PPT教学课件
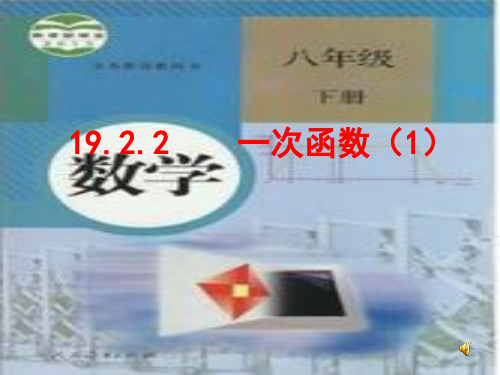
y=k1x+ k2(x-2)
当x=1时,y=0,得:0=k1+k2(1-2)
①
当x=-3时,y=4,得:4=-3k1+k2(-3-2) ②
2020/12/10
16
①②组合得:
0k1k2(1-2) 4-31k k2(--32)
解之得:
k
1
-1 2
k2
-1
2
∴ y与x之间的函数关系式为: y=- x+1
y=0.3x+5
思考:这个函数是正比例函数吗?
2020/12/10
3
学习目标:
1、掌握一次函数解析式的特点及意义; 2、理解一次函数与正比例函数的关系。
2020/12/10
4
二、自主预习
1、正比例函数一般式: y=kx(k是常数,k≠0)
2、正比例函数的图象:
一条经过原点和(1,k)的直线
y y= kx (k>0)
( 3) y=-0.5x-1
( 4) y=5x26
2、下列说法正确的是 ① ③ (填序号)
①正比例函数一定是一次函数;
②一次函数一定是正比例函数;
③若y-1与x成正比例,则y是x的一次函数;
④若y=kx+b,则y是x的一次函数。
2020/12/10
13
3、 已知方程3x-2y=1,把它写成y是x的一次函数的形 式是_y__=_1.5x-_0_._5_ ,当 x = 1时, y =__1__;当 y = 4 时, x =__3__。
9
(3)某城市的市内电话的月收费额y(单位: 元)包括月租费22元和拨打电话x min的计时费
(按0.1元/min收取).
y = 0.1x + 22
一次函数的图像(第1课时)同步课件

列表法: 把自变量的值和对应的函数值列成表格来表示函数关系的方法叫做列表法.
函数表达式法: 表示两个变量之间函数关系的式子称为函数表达式.
图像法: 在平面直角坐标系中,以函数的自变量的值为横坐标、对应的函数值为纵
坐标的点所组成的图形叫做这个函数的图像.
2.什么是一次函数?
一般地,形如y=kx+b(k、b 是常数,且k≠0)的函数,叫做一次函数,其中x是自变量,
y
y=-2x+3 5
解:
=+,
(2)
=-+ ,
∴
=
=
,
.
∴交点
坐标为( , )
y=x+2
4
3
2
1
-6 -5 -4 -3 -2 -1 O 1 2 3 4 5
-1
-2
-3
-4
-5
x
新知巩固
2.已知一次函数y=x+2与y=-2x+3 ,
(3)求这两条直线与坐标轴所围成的图形面积.
在平面直角坐标系中描出相应的点;
③连线:顺次连接描出的各点.
5
4
3
2
1
-2 -1 O 1 2 3 4 5
-1
-2
-3
x
尝试与交流
仿照上述方法,在下图中画出y=-x+2的图像.
判断点(0,2)、(2,0)、(3,1)、(-1,3)是否在此函数图像上.
y
①列表:
x
··· -2
-1
0
1
2
···
y
···
3
3
3
平行
6. 直线y=2x+3与直线y=2x-1的位置关系是________.
函数表达式法: 表示两个变量之间函数关系的式子称为函数表达式.
图像法: 在平面直角坐标系中,以函数的自变量的值为横坐标、对应的函数值为纵
坐标的点所组成的图形叫做这个函数的图像.
2.什么是一次函数?
一般地,形如y=kx+b(k、b 是常数,且k≠0)的函数,叫做一次函数,其中x是自变量,
y
y=-2x+3 5
解:
=+,
(2)
=-+ ,
∴
=
=
,
.
∴交点
坐标为( , )
y=x+2
4
3
2
1
-6 -5 -4 -3 -2 -1 O 1 2 3 4 5
-1
-2
-3
-4
-5
x
新知巩固
2.已知一次函数y=x+2与y=-2x+3 ,
(3)求这两条直线与坐标轴所围成的图形面积.
在平面直角坐标系中描出相应的点;
③连线:顺次连接描出的各点.
5
4
3
2
1
-2 -1 O 1 2 3 4 5
-1
-2
-3
x
尝试与交流
仿照上述方法,在下图中画出y=-x+2的图像.
判断点(0,2)、(2,0)、(3,1)、(-1,3)是否在此函数图像上.
y
①列表:
x
··· -2
-1
0
1
2
···
y
···
3
3
3
平行
6. 直线y=2x+3与直线y=2x-1的位置关系是________.
《一次函数》PPT课件(第1课时)

探究新知 观察以上出现的四个函数解析式,它们是不是正比例函
数,那么它们共同的特征如何表示呢? (1) c = 7 t - 35 (2) G = h -105 (3) y = 0.1 x + 22 (4) y = -5 x + 50
y = k(常数)x + b(常数)
探究新知
一般地,形如y=kx+b (k, b 是常数,k≠0)的函数,叫 做一次函数.
(2)由题意得:m+1=0 , 解得m= -1.
探究新知
知识点 2 利用一次函数解答实际问题
汽车油箱中原有油50升,如果汽车每行驶50千米耗油9升,
求油箱的油量y(单位:升)随行驶路程x(单位:千米)变化的
函数关系式,并写出自变量的取值范围,y 是 x 的一次函数吗?
解:油量y与行驶时间x的函数关系式为:y
50
9 50
x,
自变量x的取值范围是0≤x≤
2500 9
.
函数
y
50
9x 50
,是x的一次函数.
巩固练习
如果长方形的周长是30cm,长是xcm,宽是ycm. (1)写出y与x之间的函数解析式,它是一次函数吗? (2)若长是宽的2倍,求长方形的面积.
解:(1)y=15-x,是一次函数. (2)由题意可得x=2(15-x). 解得x=10,所以y=15-x=5. ∴长方形的面积为10×5=50(cm2).
课堂检测
拓广探索题
如图,△ABC是边长为x的等边三角形.
(1)求BC边上的高h与x之间的函数解析式.h是x的一次函数吗?
如果是,请指出相应的k与b的值.
A
解: (1)∵BC边上的高AD也是BC边上的中线,
一次函数的图象(第1课时)课件

上的点(x,y)都满足关系式y=–2x+5吗?
y
9 8 7 6 5 4 3 2 1
–7 –6 –5 –4 –3 –2 –1 0 1 2 3 4 5 6 7 8
x
–1
A
–2
–3
B
–4
–5
–6
–7
答:(1)点B坐标(4,-3) 当x=4时,y=-2x4+5=-3
故(4,-3)满足关系式 y=-2x+5
(2)一次函数y=–2x+5的 图象上的点(x,y)满足关系 式y=–2x+5
北师大版 八年级 上册(第四章)
3.一次函数的图象
(第1课时)
引例
已知一次函数y=2x , <1> 当x= 1 时,y = 2
当x= 2 时,y = 4 <2> 当x= –3时,y = – 6
当x= –4时,y = – 8 <3>以x为点的横坐标,相应的y的值为点 的纵坐标,可得点
(1, 2) ;(2,4) ;(-3,-6);(-4,-8) <4>再找一些满足同样要求的点
<4>作函数的一般步骤应怎样?
答: A:一次函数y=-3x的图象应是一条直线
B:作函数的一般步骤:列表,描点,连线
例 作出一次函数y=-3x的图象
解: x … -2 -1 0 1 2 … y
y=2x+1 … 6 3 0 -3 -6 … 5
4
作函数图象的一般步骤: 列表:找到一些满足条件的点。 描点:以表中各组对应值作为点的坐
1 2 34567 8
A
B
答: (1)当x=3, y=–2x3+5=-1 所对应的点(3,–1)在一次函数 y=–2x+5的图象上。
y
9 8 7 6 5 4 3 2 1
–7 –6 –5 –4 –3 –2 –1 0 1 2 3 4 5 6 7 8
x
–1
A
–2
–3
B
–4
–5
–6
–7
答:(1)点B坐标(4,-3) 当x=4时,y=-2x4+5=-3
故(4,-3)满足关系式 y=-2x+5
(2)一次函数y=–2x+5的 图象上的点(x,y)满足关系 式y=–2x+5
北师大版 八年级 上册(第四章)
3.一次函数的图象
(第1课时)
引例
已知一次函数y=2x , <1> 当x= 1 时,y = 2
当x= 2 时,y = 4 <2> 当x= –3时,y = – 6
当x= –4时,y = – 8 <3>以x为点的横坐标,相应的y的值为点 的纵坐标,可得点
(1, 2) ;(2,4) ;(-3,-6);(-4,-8) <4>再找一些满足同样要求的点
<4>作函数的一般步骤应怎样?
答: A:一次函数y=-3x的图象应是一条直线
B:作函数的一般步骤:列表,描点,连线
例 作出一次函数y=-3x的图象
解: x … -2 -1 0 1 2 … y
y=2x+1 … 6 3 0 -3 -6 … 5
4
作函数图象的一般步骤: 列表:找到一些满足条件的点。 描点:以表中各组对应值作为点的坐
1 2 34567 8
A
B
答: (1)当x=3, y=–2x3+5=-1 所对应的点(3,–1)在一次函数 y=–2x+5的图象上。
一次函数(第一课时)课件.ppt

形成概念
定义:一般地,形如y=kx+b(k,b是 常数,k≠0)的函数,叫做一 次函数. 当b=0时, y=kx+b即变成y=kx,
所以说正比例函数是一种特殊的一 次函数.
课堂练习
练习1 下列函数中哪些是一次函数,哪些又是正
比例函数?
(1)y=-8x
(2)y=
-8 x
(3)y=5x2 +6
(4)y=-0.5x-1 (5)y= x -1
y = 5 - 6x 也可以写为 y = -6x + 5
(2)登山队员向上登高多少千米时,他们所 在位置的气温是0 ℃ 呢?
当y=0时,0=-6x+5 所以x=5 /6(km)
问题1
某登山队大本营所在地的气温为5 ℃,海拔每升高1 km 气温下降6 ℃.登山队员由大本营向上登高x km时, 他们所处位置的气温是 y ℃. 试用函数解析式表示 y 与 x 的关系.
(4)把一个长10 cm,宽5 cm的矩形的长减少 x cm, 宽不变,矩形面积 y(单位:cm2)随x的值而变化.
问题3
观察以上出现的四个函数解析式,分别说出哪些是 自变量、自变量的函数和常数.
函数解析式 自变量的函数 自变量 常数
(1)c=7t-35
c
t
7,35
(2)G=h-105
G
h
-105
(3)y=0.1x+22
y
x
0.1,22
(4)y= -5x+50
y
x
-5,50
思考:上面这些函数解析式有什么共同特征呢? 它们都是常数与自变量的乘积与另一常数的和的形式.
形成概念
定义:一般地,形如y=kx+b(k,b是 常数,k≠0)的函数,叫做一 次函数.
一次函数的图象和性质(第1课时)PPT课件
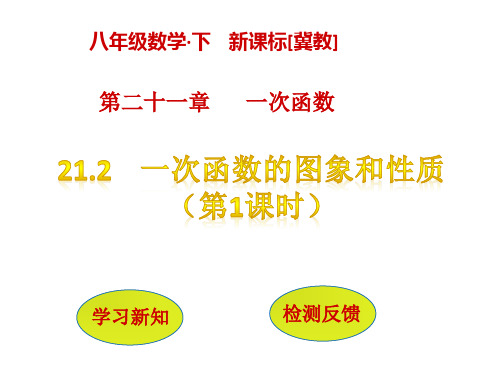
7.若一次函数y=kx+4的图像经过点(1,2).
(1)求k的值;
(2)在所给直角坐标系中画出此函数的图像;
(3)根据图像回答:当x
时,y>0.
解析:(1)把点(1,2)代入函数解析式,利用方程来求得k的值;(2)由 两点确定一条直线进行作图;(3)根据图像解答即可.
解:(1)依题意,得2=k+4,解得k=-2,即k的值是-2.
A.x<-2
B.x>-2
C.x<2
D.x>2
解析:由图像可得一次函数的图像与x轴的 交点为(-2,0),当y<0时,x<-2.故选A.
6.连降6天大雨,某水库的蓄水量随时间的增加而直线上升.若
该水库的蓄水量v(万米3)与降雨的时间t(天)的关系如图所示,
则下列说法正确的是
( B)
A.降雨后,蓄水量每天减少5万米3
达成共识. 1.图像为一条直线. 2.由画图过程,知一次函数y=2x-1的图像是由所有满足关系式y=2x-1 的点(x,y)连线而得到的.因此,凡满足关系式y=2x-1的x,y的值所对应 的点都在一次函数y=2x-1的图像上.
因为一次函数的图像是一条直线,所以也把一次函数y=kx+b 的图像称为直线y=kx+b.
为(0,2),与x轴的交点为
2 3
,0
.故选C.
4.函数
yk x
的图像经过点(1,-1),则函数y=kx-2的图像是
图中的
(A)
解析:∵
y
k x
的图像经过点(1,-1),∴k=xy=-1,∴函数解析式
为y=-x-2,所以函数图像经过(-2,0)和(0,-2).故选A.
【人教版】一次函数完整版PPT1

分析:由表格知x=0时,y=1;x=1时,y=0得 y与x的函数关系式为y=-x+1.所以当x=-1时, y=2.所以空格中原来填的数是2
你会用所学知识解决生活中的问题吗?
生物学家研究表明: 某种蛇的长度y(cm)是其尾长x(cm)的一次函数; 当蛇的尾长为 14cm时, 蛇的长为105.5cm; 当蛇的尾长为6 cm时, 蛇的长为45.5 cm; 当蛇的尾长为10 cm时,这条蛇的长度是多少?
2、如图所示:分别求出直线a、b的解析式为 .
y
a
4
y
4
b
-2 0
2
x
0
6
x
(人教版)一次函数课件下载1
巩固加深:
1、 若一次函数y=3x+b的图象经过点P(1,4),
则该函数图象的解析式为 y=3x+1 .
2、 已知一次函数y=kx+2,当x=5时,y的值
2
为4,则k=
.
5
3、已知直线 y=kx+b 经过点(9,0)和(24,20),
求k、b的值.
巩固加深:
4、若直线y=kx+b平行直线y=3x+2且在
y轴上的的交点坐标为 (0, 5) 则k=3 , b= 5 .
5、已知y+b与x成正比例,并且当x=1时,y=3 ; 当x=-2时,y=-6,求这个函数的解析式。
拓展练习:
小明根据某个一次函数关系式填写了下表:
其中有一格不慎被墨汁遮住了,想想看,该空格 里原来填的数是多少?解释你的理由。
(人教版)一次函数课件下载1
y
大家能否通过取直线上的
这两个点来求这条直线的
8
解析式呢?
7
你会用所学知识解决生活中的问题吗?
生物学家研究表明: 某种蛇的长度y(cm)是其尾长x(cm)的一次函数; 当蛇的尾长为 14cm时, 蛇的长为105.5cm; 当蛇的尾长为6 cm时, 蛇的长为45.5 cm; 当蛇的尾长为10 cm时,这条蛇的长度是多少?
2、如图所示:分别求出直线a、b的解析式为 .
y
a
4
y
4
b
-2 0
2
x
0
6
x
(人教版)一次函数课件下载1
巩固加深:
1、 若一次函数y=3x+b的图象经过点P(1,4),
则该函数图象的解析式为 y=3x+1 .
2、 已知一次函数y=kx+2,当x=5时,y的值
2
为4,则k=
.
5
3、已知直线 y=kx+b 经过点(9,0)和(24,20),
求k、b的值.
巩固加深:
4、若直线y=kx+b平行直线y=3x+2且在
y轴上的的交点坐标为 (0, 5) 则k=3 , b= 5 .
5、已知y+b与x成正比例,并且当x=1时,y=3 ; 当x=-2时,y=-6,求这个函数的解析式。
拓展练习:
小明根据某个一次函数关系式填写了下表:
其中有一格不慎被墨汁遮住了,想想看,该空格 里原来填的数是多少?解释你的理由。
(人教版)一次函数课件下载1
y
大家能否通过取直线上的
这两个点来求这条直线的
8
解析式呢?
7
一次函数(第1课时)PPT课件

随
是t的7倍与35的差. c=7t-35(20≤t≤25) 机
问 (2)一种计算成年人标准体重G(单位:kg)
的方法是:以厘米为单位量出身高值h,再减常数
答
105,所得差是G的值.
G=y(单位:
元)包括月租费22元和拨打电话x min的计时费(按
0.1元/min收取).
The foundation of success lies in good habits
10
结束语
当你尽了自己的最大努力时,失败也是伟大的, 所以不要放弃,坚持就是正确的。
When You Do Your Best, Failure Is Great, So Don'T Give Up, Stick To The End 演讲人:XXXXXX 时 间:XX年XX月XX日
y=0.1x+22
(4)把一个长10 cm、宽5 cm的长方形的长减
少xcm,宽不变,长方形的面积y(单位:cm2)随x
的变化而变化. y=-5x+50 (0≤t≤10)
y=-6x+5
c=7t-35
G=h-105 我们都长这样 y=kx+b (其中k、b为常数,且k≠0)
y=0.1x+22
y=-5x+50
一次函数
第1课时
随机答题环节:
正比例函数你了解多少?
课堂导入:
某登山队大本营所在地的 气温为5℃,海拔每升高1km气
y=5-6x 温下降6℃.登山队员由大本营
向上登高x km时,他们所在位 置的气温是y℃.试用函数解析 式表示y与x的关系.
这个函数与我们 学过的正比例函数有
什么相同&不同吗?
一次函数ppt课件

-13-
21.1 一次函数
[易错分析]
■混淆一次函数与正比例函数的概念
例 已知 y 关于 x 的函数表达式为 y= +k-3. 若函数是一次函数,
则 k=________;若函数是正比例函数,则 k=________.
解析:若函数 y=
+k-3 是一次函数,则 k2-8=1,所以 k=±3;若函
数 y=
+k-3 是正比例函数,则 k2-8=1,且 k-3=0,所以 k=3.
答案:±3 3
易错:3 ±3
错因:记混一次函数与正比例函数的概念导致错解.
易错警示:要牢记正比例函数与一次函数的关系,正比例函数是一次函数
的特殊形式,即正比例函数是一次函数,但一次函数不一定是正比例函数.
-14-
21.1 一次函数
答案:D
题型解法:根据正比例函数的定义确定字母的值时,需使比例系数和自
变量的指数同时符合条件.
-7-
21.1 一次函数
■题型二 应用正比例函数的图像和性质比较比例系数的大小 例 2 如图,三个正比例函数的图像分别对应函数关系式:①y=ax,
②y=bx,③y=cx,将 a,b,c 从小到大排列并用“<”连接为 ( )
④y=2x2+1,自变量 x 的次数不为 1,故不是一次函数.综上,是一次函数的
有①②③,共 3 个.
答案:B
易错:C
错因:误认为②不是一次函数.②是正比例函数,正比例函数也是一次函数.
满分备考:判断函数是否为一次函数时,首先将函数关系式化简整理,看
是否满足 y=kx+b 的形式,其次辨别比例系数 k 是否等于 0,另外需注意,来自-4-21.1 一次函数
21.1 一次函数
[易错分析]
■混淆一次函数与正比例函数的概念
例 已知 y 关于 x 的函数表达式为 y= +k-3. 若函数是一次函数,
则 k=________;若函数是正比例函数,则 k=________.
解析:若函数 y=
+k-3 是一次函数,则 k2-8=1,所以 k=±3;若函
数 y=
+k-3 是正比例函数,则 k2-8=1,且 k-3=0,所以 k=3.
答案:±3 3
易错:3 ±3
错因:记混一次函数与正比例函数的概念导致错解.
易错警示:要牢记正比例函数与一次函数的关系,正比例函数是一次函数
的特殊形式,即正比例函数是一次函数,但一次函数不一定是正比例函数.
-14-
21.1 一次函数
答案:D
题型解法:根据正比例函数的定义确定字母的值时,需使比例系数和自
变量的指数同时符合条件.
-7-
21.1 一次函数
■题型二 应用正比例函数的图像和性质比较比例系数的大小 例 2 如图,三个正比例函数的图像分别对应函数关系式:①y=ax,
②y=bx,③y=cx,将 a,b,c 从小到大排列并用“<”连接为 ( )
④y=2x2+1,自变量 x 的次数不为 1,故不是一次函数.综上,是一次函数的
有①②③,共 3 个.
答案:B
易错:C
错因:误认为②不是一次函数.②是正比例函数,正比例函数也是一次函数.
满分备考:判断函数是否为一次函数时,首先将函数关系式化简整理,看
是否满足 y=kx+b 的形式,其次辨别比例系数 k 是否等于 0,另外需注意,来自-4-21.1 一次函数
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例 一个小球由静止开始沿一个斜坡向下滚动,其 速度每秒增加2 m/s.
(1)求小球速度v(单位:m/s)关于时间t(单位: s)的函数解析式.它是一次函数吗?
(2)求第2.5 s 时小球的速度; (3)时间每增加1 s,速度增加多少,速度增加量是 否随着时间的变化而变化?
这节课的收获:
怎样的函数是一次函数?
y=-5x+50(0≤x≤10)
观察以上出现的四个函数解析式, 很显然它们不是正比例函数,这些 函数关系式有什么特点?
(1) c = 7t-35 (2) G=h-105
(3) y=0.1x+22 (4) y=-5x+50
这些函数都是用自变量的K(常数)倍与 一个常数的和来表示。
一般地,形如y=kx+b (k, b -x-4 (4)y=x2 -3x
(5) y=8x2+x(1-8x)
试一试 下列函数中哪些是一次函数,哪些又 是正比例函数?
(1)y8x (2)y5x26
(3) y 8 (4)y0.5x1
(5) y
x
x
1
2
(7)y=2(x-4)
y=5-6x
这个函数也可以写成
y=-6x+5
当登山队员由大本营向上登高0.5千米时, 他们所在位置的气温是多少?
当x=0.5时,y=-6×0.5+5=2
y=-6x+5
这个函数是正比例函数吗? 它与正比例函数有什么不同? 这种形式的函数还会有吗?
问题2 下列问题中,变量之间的对应关系是函数关 系吗?如果是,请写出函数解析式,这些函数解析式有 哪些共同特征?
系吗?如果是,请写出函数解析式,这些函数解析式有
哪些共同特征?
(3)某城市的市内电话的月收费额 y(单位:元)包
括月租费22元和拨打电话 x min 的计时费(按0.1元/min
收取);
y=0.1x+22
(4)把一个长10 cm,宽5 cm的矩形的长减少 x cm, 宽不变,矩形面积 y(单位:cm2)随x的值而变化.
函数值增加的值是变化的还是不变的?
课后作业
作业:教科书第99页第3,6题; 其中,第6 题增加以下两个小题:
(1)当x 取-3,-2,-1,0,1,2,3,4 时,求对 应的函数值,并列表表示对应关系;
(2)从表中观察,当自变量的值每增加1 时,对应 的函数值怎样变化?当自变量的值每增加2呢?
m 3 0
m 3
m
3
m3
∴一次函数的表达式为 y3x3
注意:利用定义求一次函数 y kxb表达式时,要
保证 k ≠ 0,自变量x的指数是“1”
课堂练习
练习3 已知一次函数 y=kx+b,当 x=1时,y=5;当 x=-1时,y=1.求 k 和 b 的值.
一次函数第一课时PPT
正比例函数
解析式:y=kx(k是常数,k≠0) 图象:一条经过原点和(1,k)的直线
y=kx(k<0) y y=kx (k>0)
性质:
x
当k>0时,直线y=kx经过第一、三象限,从左向 右上升,即随着x的增大y也增大;
当k<0时,直线y=kx经过第二、四象限,从左向
右下降,即随着x的增大y反而减小。
一般地,形如y=kx+b(k,b是常数,k≠0) 的函数,叫做一次函数。
当b=0时,y=kx+b就变成了y=kx,所以 说正比例函数是一种特殊的一次函数。
课堂小结
(1)什么叫一次函数? (2)一次函数与正比例函数有什么联系? (3)对于一次函数,需要变量的几对对应值才能确
定函数解析式?怎样求函数解析式? (4)一次函数中,当自变量每增加一个相同的值,
(1)有人发现,在20 ℃~25 ℃时蟋蟀每分鸣叫次数
c 与温度 t(单位:℃)有关,且 c 的值约是 t 的7 倍与35
的差;
c=7t-35(20≤t≤25)
(2)一种计算成年人标准体重G(单位:kg)的方
法是,以厘米为单位量出身高值 h ,再减常数105,所得
差是G 的值;
G=h-105
问题2 下列问题中,变量之间的对应关系是函数关
(6)y 2 13 x
(8) y x3 2
你能举出一些一次函数的例子吗?
课堂练习
练习2 请写出若干个变量 y 与 x 之间的函数解析 式,让同桌判断是否是一次函数;如果是,请说出其一 次项系数与常数项.
例2.已知函数 y(m3)xm283
是一次函数,求其解析式。
解:
由题意得: m 2 8 1
k≠0)的函数,叫做一次函数。
特别注意:k ≠ 0,自变量x的指数是“1”
思考:一次函数与正比例函数有什么不同?
概念:
一般地,形如y=kx+b(k,b是常数,k≠0) 的函数,叫做一次函数。
当b=0时,y=kx+b就变成了y=kx,所以 说正比例函数是一种特殊的一次函数。
一次函数 正比例函数
例1.下列函数关系式中,那些是一次函数? 哪些是正比例函数?
课件说明
• 学习目标: 1.结合具体情境理解一次函数的意义,能结合实际 问题中的数量关系写出一次函数的解析式; 2.能辨别正比例函数与一次函数的区别与联系; 3.初步体会用待定系数法求一次函数解析式的方法.
• 学习重点: 一次函数的概念.
• 问题1 某登山队大本营所在地的气温为5℃,
海拔每升高1㎞气温下降6 ℃,登山队员由大本 营向上登高x㎞时,他们所在位置的气温是y ℃ ,试用解析式表示y与x的关系。
