密度碰撞恢复系数测量

合集下载

一种快速测定物体碰撞恢复系数的测量装置和方法[发明专利]

专利名称：一种快速测定物体碰撞恢复系数的测量装置和方法专利类型：发明专利
发明人：李同清,张亚琛,贺毅强,黄威,徐天兵
申请号：CN202011126242.7
申请日：20201020
公开号：CN112129649A
公开日：
20201225
专利内容由知识产权出版社提供
摘要：本发明公开了一种快速测定物体碰撞恢复系数的测量装置，属于材料实验技术领域。

该快装置包括吸附机构，碰撞机构和信息采集机构；吸附机构包括真空负压泵与其通过气管连接的吸嘴；碰撞机构包括支撑架和滑杆，支撑架的底部中央固定安装有碰撞板；信息采集机构包括若干个声发射传感器，DS2型全信息声发射测量仪，激光测距仪和微型计算机。

本发明还公开了测定物体碰撞恢复系数的测量方法，使用以上的测量装置，准确地测量处物体的释放高度，进而测定其碰撞恢复系数。

本发明在搭建方便的基础上能够精准测量待测物体释放高度，同时还能避免释放过程中待测物体发生旋转，进一步保障测量结果的准确性，实现快速、准确的测定物体碰撞恢复系数。

申请人：江苏海洋大学,连云港市沃鑫高新材料有限公司
地址：222000 江苏省连云港市高新区苍梧路59号
国籍：CN
代理机构：连云港润知专利代理事务所
代理人：刘喜莲
更多信息请下载全文后查看。

离散元法中所用土壤参数测量及标定方法研究

离散元法中所用土壤参数测量及标定方法研究庞靖１，２，林晓君１，陈松涛３，耿令新１，周浩１，金鑫１，２㊀（１．河南科技大学农业装备工程学院，河南洛阳４７１００３；２．河南省机械装备先进创造协同中心，河南洛阳４７１００３；３．潍柴动力股份有限公司，山东潍坊２６１０００）摘要㊀［目的］针对离散元仿真软件涉及的土壤参数进行测量及标定㊂［方法］基于Ｈｅｒｔｚ－ＭｉｎｄｌｉｎｗｉｔｈＪＫＲ黏结模型，通过直接测量法测量土壤的固体密度㊁弹性模量和泊松比，并用堆积角和滑动摩擦角来标定土壤接触参数㊂通过中心组合试验，采用Ｄｅｓｉｇｎ－Ｅｘｐｅｒｔ８．０．６软件，以土壤休止角㊁土壤与６５Ｍｎ钢滑动摩擦角的仿真值与实测值的相对误差为优化目标进行回归分析㊂［结果］通过分析获得最优的离散元接触参数组合为土壤间恢复系数０．２８㊁静摩擦系数０．４９㊁滚动摩擦系数０．２４㊁土壤表面能０．０４Ｊ／ｍ２，土壤与６５Ｍｎ钢间恢复系数０．５９㊁静摩擦系数０．６７㊁滚动摩擦系数０．１３㊂在所测土壤参数及最优标定参数下，采用离散元仿真模拟探针入土行为，获得探针在８ｍｍ／ｓ的贯入速度下，贯入２０㊁４０㊁６０㊁８０和１００ｍｍ处仿真试验和土槽试验探针阻力相对误差分别为８．５９％㊁９．８８％㊁９．７２％㊁０．１５％㊁６．９８％，误差在可接受范围内㊂［结论］参数测量和标定方法准确可靠性，可为松软土壤的离散元仿真提供参考㊂关键词㊀离散元法；松软土壤；参数测量；参数标定；探针贯入中图分类号㊀Ｓ１５２．９㊀㊀文献标识码㊀Ａ㊀㊀文章编号㊀０５１７－６６１１（２０２３）１８－０００６－０６ｄｏｉ：１０．３９６９／ｊ．ｉｓｓｎ．０５１７－６６１１．２０２３．１８．００２㊀㊀㊀㊀㊀开放科学（资源服务）标识码（ＯＳＩＤ）：ＳｔｕｄｙｏｎＭｅａｓｕｒｅｍｅｎｔａｎｄＣａｌｉｂｒａｔｉｏｎＭｅｔｈｏｄｓｏｆＳｏｉｌＰａｒａｍｅｔｅｒｓＵｓｅｄｉｎＤｉｓｃｒｅｔｅＥｌｅｍｅｎｔＭｅｔｈｏｄＰＡＮＧＪｉｎｇ１，２，ＬＩＮＸｉａｏ⁃ｊｕｎ１，ＣＨＥＮＳｏｎｇ⁃ｔａｏ３ｅｔａｌ㊀（１．ＣｏｌｌｅｇｅｏｆＡｇｒｉｃｕｌｔｕｒａｌＥｎｇｉｎｅｅｒｉｎｇ，ＨｅｎａｎＵｎｉｖｅｒｓｉｔｙｏｆＳｃｉｅｎｃｅａｎｄＴｅｃｈｎｏｌｏ⁃ｇｙ，Ｌｕｏｙａｎｇ，Ｈｅｎａｎ４７１００３；２．ＨｅｎａｎＭａｃｈｉｎｅｒｙａｎｄＥｑｕｉｐｍｅｎｔＡｄｖａｎｃｅｄＣｒｅａｔｉｏｎＣｏｏｒｄｉｎａｔｉｏｎＣｅｎｔｅｒ，Ｌｕｏｙａｎｇ，Ｈｅｎａｎ４７１００３；３．ＷｅｉｃｈａｉＰｏｗｅｒＣｏ．，Ｌｔｄ．，Ｗｅｉｆａｎｇ，Ｓｈａｎｄｏｎｇ２６１０００）Ａｂｓｔｒａｃｔ㊀［Ｏｂｊｅｃｔｉｖｅ］Ｔｏｍｅａｓｕｒｅａｎｄｃａｌｉｂｒａｔｅｓｏｉｌｐａｒａｍｅｔｅｒｓｉｎｖｏｌｖｅｄｉｎｄｉｓｃｒｅｔｅｅｌｅｍｅｎｔｓｉｍｕｌａｔｉｏｎｓｏｆｔｗａｒｅ．［Ｍｅｔｈｏｄ］ＢａｓｅｄｏｎＨｅｒｔｚＭｉｎｄｌｉｎｗｉｔｈＪＫＲｂｏｎｄｍｏｄｅｌ，ｓｏｉｌｓｏｌｉｄｄｅｎｓｉｔｙ，ｅｌａｓｔｉｃｍｏｄｕｌｕｓａｎｄＰｏｉｓｓｏｎｓｒａｔｉｏｗｅｒｅｍｅａｓｕｒｅｄｂｙｄｉｒｅｃｔｍｅａｓｕｒｅｍｅｎｔｍｅｔｈｏｄ，ａｎｄｓｏｉｌｃｏｎｔａｃｔｐａｒａｍｅｔｅｒｓｗｅｒｅｃａｌｉｂｒａｔｅｄｂｙｓｔａｃｋｉｎｇａｎｇｌｅａｎｄｓｌｉｄｉｎｇｆｒｉｃｔｉｏｎａｎｇｌｅ．［Ｒｅｓｕｌｔ］Ｔｈｒｏｕｇｈａｎａｌｙｓｉｓ，ｔｈｅｏｐｔｉｍａｌｃｏｍｂｉｎａｔｉｏｎｏｆｄｉｓｃｒｅｔｅｅｌｅｍｅｎｔｃｏｎｔａｃｔｐａｒａｍｅｔｅｒｓｗａｓｏｂｔａｉｎｅｄａｓｆｏｌｌｏｗｓ：ｔｈｅｅｑｕａｔｉｏｎｗａｓｏｐｔｉｍｉｚｅｄｔｏｏｂｔａｉｎｔｈｅｏｐｔｉｍａｌｄｉｓｃｒｅｔｅｅｌｅｍｅｎｔｃｏｎｔａｃｔｐａｒａｍｅｔｅｒｃｏｍｂｉ⁃ｎａｔｉｏｎａｓｆｏｌｌｏｗｓ：ｔｈｅｃｏｅｆｆｉｃｉｅｎｔｏｆｒｅｓｔｉｔｕｔｉｏｎｂｅｔｗｅｅｎｓｏｉｌｐａｒｔｉｃｌｅｓｗａｓ０．２８，ｔｈｅｃｏｅｆｆｉｃｉｅｎｔｏｆｓｔａｔｉｃｆｒｉｃｔｉｏｎｗａｓ０．４９，ｔｈｅｃｏｅｆｆｉｃｉｅｎｔｏｆｒｏｌｌｉｎｇｆｒｉｃｔｉｏｎｗａｓ０．２４，ｔｈｅｓｏｉｌｓｕｒｆａｃｅｅｎｅｒｇｙｗａｓ０．０４Ｊ／ｍ２，ａｎｄｔｈｅｃｏｅｆｆｉｃｉｅｎｔｏｆｒｅｓｔｉｔｕｔｉｏｎｂｅｔｗｅｅｎｓｏｉｌａｎｄ６５Ｍｎｓｔｅｅｌｉ１３１１０．５９，ｔｈｅｃｏｅｆｆｉ⁃ｃｉｅｎｔｏｆｓｔａｔｉｃｆｒｉｃｔｉｏｎｗａｓ０．６７，ｔｈｅｃｏｅｆｆｉｃｉｅｎｔｏｆｒｏｌｌｉｎｇｆｒｉｃｔｉｏｎｗａｓ０．１３．Ｕｎｄｅｒｔｈｅｃｏｍｂｉｎａｔｉｏｎｏｆｔｈｅｍｅａｓｕｒｅｄｓｏｉｌｐａｒａｍｅｔｅｒｓａｎｄｔｈｅｏｐｔｉ⁃ｍａｌｃａｌｉｂｒａｔｉｏｎｐａｒａｍｅｔｅｒｓ，ｄｉｓｃｒｅｔｅｅｌｅｍｅｎｔｓｉｍｕｌａｔｉｏｎｗａｓｕｓｅｄｔｏｓｉｍｕｌａｔｅｔｈｅｐｒｏｂｅｓｐｅｎｅｔｒａｔｉｏｎｂｅｈａｖｉｏｒｉｎｔｏｔｈｅｓｏｉｌ．Ｔｈｅｒｅｌａｔｉｖｅｅｒｒｏｒｓｏｆｔｈｅｐｒｏｂｅｒｅｓｉｓｔａｎｃｅｉｎｔｈｅｓｉｍｕｌａｔｉｏｎｔｅｓｔａｎｄｓｏｉｌｔａｎｋｔｅｓｔａｔ２０，４０，６０，８０ａｎｄ１００ｍｍｐｅｎｅｔｒａｔｉｏｎｓｐｅｅｄｓｏｆ８ｍｍ／ｓｗｅｒｅ８．５９％，９．８８％，９．７２％，０．１５％ａｎｄ６．９８％，ｒｅｓｐｅｃｔｉｖｅｌｙ，ｗｉｔｈａｃｃｅｐｔａｂｌｅｅｒｒｏｒｓ．［Ｃｏｎｃｌｕｓｉｏｎ］Ｔｈｅｐａｒａｍｅｔｅｒｍｅａｓｕｒｅｍｅｎｔａｎｄｃａｌｉｂｒａｔｉｏｎｍｅｔｈｏｄｄｅｓｃｒｉｂｅｄｗａｓａｃｃｕｒａｔｅａｎｄｒｅｌｉａｂｌｅ，ｗｈｉｃｈｃａｎｐｒｏｖｉｄｅａｒｅｆｅｒｅｎｃｅｆｏｒｄｉｓｃｒｅｔｅｅｌｅｍｅｎｔｓｉｍｕｌａｔｉｏｎｏｆｓｏｆｔｓｏｉｌ．Ｋｅｙｗｏｒｄｓ㊀Ｄｉｓｃｒｅｔｅｅｌｅｍｅｎｔｍｅｔｈｏｄ；Ｓｏｆｔｓｏｉｌ；Ｐａｒａｍｅｔｅｒｍｅａｓｕｒｅｍｅｎｔ；Ｐａｒａｍｅｔｅｒｃａｌｉｂｒａｔｉｏｎ；Ｐｒｏｂｅｐｅｎｅｔｒａｔｉｏｎ基金项目㊀国家重点研发计划项目（２０１７ＹＦＤ０７００３００）㊂作者简介㊀庞靖（１９７７），男，河南洛阳人，副教授，博士，从事农业装备作业环境与作业质量检测技术研究㊂收稿日期㊀２０２２－０９－０６；修回日期㊀２０２３－０２－２８㊀㊀我国农业土壤种类多样，在离散元仿真软件里要涉及很多土壤参数，而明确土壤参数是进行正确仿真的前提㊂部分科研工作者或学者没有合适的测量工具测量土壤参数，因此选择合适的土壤参数测量和标定方法可以有效解决这一问题㊂离散元是一种可以将介质整体视为若干颗粒单元集合的数值模拟方法［１］，在散落物料流动性㊁固体破碎及机器－土壤相互作用方面具有广泛应用［２－３］㊂由于土壤特性复杂，有限元土壤模型准确性不高，且只能模拟土壤破坏行为，无法模拟土壤运动过程［４］，而离散元可以解决散粒之间及边界间的接触作用，利用黏连颗粒模拟生成土壤团聚体，极大提高了土壤模型的准确性［５］㊂目前，土壤的本征参数如固体密度㊁剪切模量和泊松比等可以通过仪器进行测量，而接触参数难以通过常规测量方法获得，因此很多学者通过离散元对物料参数进行标定的方法获得，主要包括以堆积角和滑动摩擦角为指标的参数标定法㊂冯俊小等［６］㊁刘文政等［７］㊁郝建军等［８］㊁王黎明等［９］采用离散元法分别对秸秆㊁马铃薯㊁油葵籽㊁猪粪进行了分析和标定㊂孙景彬等［１０］以坡地黏壤土为研究对象，针对Ｈｅｒｔｚ－ＭｉｎｄｌｉｎｗｉｔｈＪＫＲＣｏｈｅｓｉｏｎ接触模型，以土壤颗粒的仿真堆积角为响应值标定了土壤颗粒间接触参数，通过静摩擦㊁斜板及碰撞等试验得到了土壤与６５Ｍｎ钢之间静摩擦因数㊁滚动摩擦因数和恢复系数的范围；宋少龙等［１１］用Ｈｅｒｔｚ－Ｍｉｎｄｌｉｎ（ｎｏｓｌｉｐ）作为接触模型，通过土壤堆积和滑落试验标定土壤间和土壤与６５Ｍｎ钢间的系数；张晋［１２］用烘干法测土壤含水率，用筛分法测土壤质地，针对Ｈｅｒｔｚ－Ｍｉｎｄｌｉｎｗｉｔｈｂｏｎｄｉｎｇ模型，测土壤堆积角和坚实度来标定土壤之间及土壤与其他部件间的参数㊂不同的物料以及不同的土壤接触参数都存在一定的差异，标定所用的接触模型不同得到的结果也会有差距，对于坚实度特别小的松软土壤如耕后土壤，上述研究结果已经不适用㊂为了提高离散元法针对松软土壤研究的适应性和准确性，该研究选用Ｈｅｒｔｚ－ＭｉｎｄｌｉｎｗｉｔｈＪＫＲ黏结模型作为土壤接触模型，对于该模型所涉及的土壤泊松比㊁固体密度㊁剪切模量进行参数测量；采用堆积角和滑动摩擦角试验方法，对土壤间及土壤与触土部件间的恢复系数㊁动静摩擦系数和土壤表面能进行参数标定及优化，在优化后的参数下建立土槽仿真模型，并进行贯入阻力的室内试验与仿真试验对比，验证所测参数和标定参数的准确性，为松软土壤的仿真参数设置㊀㊀㊀安徽农业科学，Ｊ．ＡｎｈｕｉＡｇｒｉｃ．Ｓｃｉ．２０２３，５１（１８）：６－１１提供参考㊂１㊀土壤本征参数测量该研究以河南孟津林沟村（３４ʎ３９ᶄ４７ᵡＮ㊁１１２ʎ２６ᶄ０４ᵡＥ）的土壤为试验对象，通过比重计法测量，得到土壤颗粒直径小于０．０１ｍｍ的占１１％，土壤颗粒直径在０．０１＜０．０５ｍｍ的为２８％，土壤颗粒直径在０．０５＜１．００ｍｍ的为４９％，ȡ１．００ｍｍ的为１２％，根据土壤质地分类表得到土壤质地为砂壤土㊂由于土壤泊松比㊁剪切模量等参数受土壤含水率的影响，因此该研究所测土壤均在含水率为（１５ʃ１）％的条件下测量，其他含水率下的测量方法与此相同㊂１．１㊀固体密度的测量㊀土壤密度分为固体密度和体积密度，体积密度含有孔隙和空气，与压实程度有关，而固体密度是土壤本身的密度，与压实和空气无关㊂仿真软件ＥＤＥＭ所涉及的土壤密度为固体密度，该研究通过体积置换法［１７］测量土壤的固体密度，如图１所示㊂图１㊀体积置换法Ｆｉｇ．１㊀Ｖｏｌｕｍｅｄｉｓｐｌａｃｅｍｅｎｔｍｅｔｈｏｄ㊀㊀取少量土壤并将土壤充分烘干，得到土的质量（Ｍｓ）为１２３．２ｇ，所用容器的体积（Ｖｒ）为４００ｃｍ３㊂先将水注满容器，得到水的质量（Ｍｗ）为４１０ｇ，由此得到水的密度：ρｗ＝ＭｗＶｒ（１）式中：ρｗ为水的密度（ｇ／ｃｍ３）；Ｍｗ为注满水的质量（ｇ）；Ｖｒ为容器体积（ｃｍ３）㊂将烘干的土壤放入容器中，再将容器注满水，用水置换出烘干土壤中的间隙和空气㊂称量注满水后土壤颗粒与水的总质量（Ｍᵡ）为４８４ｇ，因此得到补充水的质量（总空隙充水质量）和体积：Ｍᶄｗ＝Ｍᵡ－Ｍｓ（２）Ｖᶄｗ＝Ｍᶄｗρｗ（３）式中：Ｍᶄｗ为补充水的质量（ｇ）；Ｍᵡ为土壤与水的总质量（ｇ）；Ｍｓ为土壤的质量（ｇ）；Ｖᶄｗ为补充水的体积（ｃｍ３）㊂恒容容器的总体积与补充水的体积之差得到土壤的体积和固体密度：Ｖｓ＝Ｖｒ－Ｖᶄｗ（４）ρｓ＝ＭｓＶｓ（５）式中：Ｖｓ为土壤体积（ｃｍ３）；ρｓ为土壤固体密度（ｇ／ｃｍ３）㊂土壤密度一般在２．６２．８ｇ／ｃｍ３［１３－１４］，将该试验所用土壤通过体积置换法得到土壤的固体密度为２．５６６ｇ／ｃｍ３，符合基本的土壤密度㊂１．２㊀泊松比㊀泊松比是反映材料横向正应变与轴向正应变的绝对值的比值，通过直接剪切试验（图２）可以测量土壤泊松比㊂图２㊀直剪试验Ｆｉｇ．２㊀Ｄｉｒｅｃｔｓｈｅａｒｔｅｓｔ通过绘制抗剪强度与垂直压力的关系曲线图，得到土壤的内摩擦角（ϕ）为２６ʎ，通过公式（６）和（７）得到土壤泊松比为０．３６㊂Ｋ＝１－ｓｉｎϕ（６）ｖ＝Ｋ１＋Ｋ（７）式中：Ｋ为土壤测压力系数；ϕ为土壤的内摩擦角（ʎ）；ｖ为土壤泊松比㊂１．３㊀弹性模量与剪切模量㊀弹性模量是衡量材料抵抗弹性变形能力大小的标尺㊂试验时先将土壤做成标准大小的圆柱形土样，土样的直径（Ｄ）和高（Ｌ）均为５０ｍｍ，用万能试验机（ＤＮＳ０２－１ＫＷ）以１ｍｍ／ｓ的速度对土样施加载荷，并读取力（Ｆ）和变形（ΔＬ）的数据，直至土壤应力呈下降趋势达到压溃效果，共做５组试验，由公式（８）（１０）计算出土壤弹性模量的平均值为８ＭＰａ，并由公式（１１）得到土的剪切模量为２．９９ＭＰａ，试验过程如图３所示㊂ε＝ΔＬＬ（８）Ａ＝πＤ２æèçöø÷２（９）Ｅ＝ＦＡˑε（１０）Ｇ＝Ｅ２ˑ（１＋ｖ）（１１）式中：ΔＬ为土样受压后的变形量（ｍ）；Ｌ为土样原来高度（ｍ）；Ｄ为土样直径（ｍ）；Ａ为土样接触面积（ｍ２）；Ｆ为土样受到的轴向载荷（Ｎ）；Ｅ为弹性模量（Ｐａ）；Ｇ为剪切模量（Ｐａ）㊂图３㊀土样压溃试验Ｆｉｇ．３㊀Ｃｒｕｓｈｉｎｇｔｅｓｔｏｆｓｏｉｌｓａｍｐｌｅ７５１卷１８期㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀庞靖等㊀离散元法中所用土壤参数测量及标定方法研究２㊀土壤参数仿真标定２．１㊀土壤堆积试验㊀通过测量堆积角，可以用来标定土壤颗粒间的碰撞恢复系数㊁静摩擦系数㊁动摩擦系数和土壤表面能㊂采用漏斗测定土壤颗粒的堆积角，如图４所示，漏斗的出口直径为２７ｍｍ，出口距水平面的高度为７５ｍｍ，试验中对土壤颗粒进行５组试验，每组试验都从４个方向测量角度并求平均值，最后得到５组试验的平均值作为休止角，通过试验测得含水率为（１５ʃ１）％时土壤休止角为３６．４３ʎ㊂图４㊀堆积试验Ｆｉｇ．４㊀Ｓｔａｃｋｉｎｇｔｅｓｔ土壤颗粒直径大小不一，土壤粒径是非常小的，在仿真计算时土壤模型的尺寸一般会比真实的土壤颗粒大，根据工况可以将土壤粒径放大１０５０倍，在此设定土壤颗粒粒径在０．５１．５ｍｍ㊂通过文献［１５－１７］以及ＥＤＥＭ里的ＧＥＭＭＷｉｚａｒｄ材料库，设定土壤颗粒间的恢复系数Ａ（０．２０．６）㊁静摩擦系数Ｂ（０．３０．７）㊁动摩擦系数Ｃ（０．１０．４）㊁土壤表面能Ｄ（０．０２０．１０Ｊ／ｍ２）㊂最陡爬坡试验可以较快地确定因素最优值所在区间，由表１可知，随着参数的增大，堆积角呈增大趋势，２号水平最接近试验结果，因此选择１㊁２㊁３组试验所选的水平进行中心组合试验（ＣＣＤ）㊂试验因素和水平编码如表２所示，根据试验设计，确定编码系数γ为２，中心组合试验结果如表３所示，其中相对误差（δ）的计算方法由下式确定：δ＝ａ－ａ１ａˑ１００％（１２）式中：ａ为休止角的试验值；ａ１为休止角的仿真值；δ为相对误差㊂表１㊀最陡爬坡试验方案及结果Ｔａｂｌｅ１㊀Ｔｅｓｔｓｃｈｅｍｅａｎｄｒｅｓｕｌｔｓｏｆｓｔｅｅｐｅｓｔｃｌｉｍｂｉｎｇ试验序号ＴｅｓｔＮｏ．ＡＢＣＤＪ／ｍ２堆积角Ｓｔａｃｋｉｎｇａｎｇｌｅʊʎ１０．２０．３０．１０．０２１６．３９２０．３０．４０．２０．０４３４．４７３０．４０．５０．３０．０６４３．０３４０．５０．６０．４０．０８４９．１２５０．６０．７０．５０．１０５７．３１㊀㊀应用软件ＤｅｓｉｇｎＥｘｐｅｒｔ８．０．６对试验结果进行分析，得到二次回归的模型㊂该二次回归模型的方差分析如表４所示，该回归模型Ｐ＜０．０００１，说明休止角相对误差与所得回归方程关系是十分显著，失拟项Ｐ＝０．４５２３＞０．０５，说明所得回归方程的非正常误差所占比例很小㊂该试验的相关系数（ｒ）为０．９９５７，因此所得回归方程可靠度较高㊂表２㊀中心组合试验因素水平编码Ｔａｂｌｅ２㊀Ｆａｃｔｏｒｌｅｖｅｌｃｏｄｉｎｇｏｆｃｅｎｔｒａｌｃｏｍｂｉｎａｔｉｏｎｔｅｓｔ编码ＣｏｄｅＡＢＣＤʊＪ／ｍ２２０．４００．５００．３００．０６１０．３５０．４５０．２５０．０５００．３００．４００．２００．０４－１０．２５０．３５０．１５０．０３－２０．２００．３００．１００．０２表３㊀中心组合试验及结果Ｔａｂｌｅ３㊀Ｃｅｎｔｅｒｃｏｍｂｉｎａｔｉｏｎｔｅｓｔａｎｄｒｅｓｕｌｔｓ试验序号ＴｅｓｔＮｏ．ＡＢＣＤＪ／ｍ２相对误差（δ）ʊ％１０．２５０．３５０．１５０．０３２８．７４２０．３５０．３５０．１５０．０３２７．４８３０．２５０．４５０．１５０．０３２６．６５４０．３５０．４５０．１５０．０３２９．１８５０．２５０．３５０．２５０．０３－２．３６６０．３５０．３５０．２５０．０３－８．９９７０．２５０．４５０．２５０．０３－１．９９８０．３５０．４５０．２５０．０３－７．８４９０．２５０．３５０．１５０．０５２１．０７１００．３５０．３５０．１５０．０５２１．８５１１０．２５０．４５０．１５０．０５２４．１１１２０．３５０．４５０．１５０．０５２４．９２１３０．２５０．３５０．２５０．０５－４．３２１４０．３５０．３５０．２５０．０５－７．９１１５０．２５０．４５０．２５０．０５－５．８２１６０．３５０．４５０．２５０．０５－３．１２１７０．２００．４００．２００．０４７．０３１８０．４００．４００．２００．０４１０．５１１９０．３００．３００．２００．０４８．８５２００．３００．５００．２００．０４１１．６０２１０．３００．４００．１００．０４４７．９８２２０．３００．４００．３００．０４－１１．８３２３０．３００．４００．２００．０２１０．７９２４０．３００．４００．２００．０６３．１２２５０．３００．４００．２００．０４６．６８２６０．３００．４００．２００．０４７．７７２７０．３００．４００．２００．０４３．７１２８０．３００．４００．２００．０４６．１２２９０．３００．４００．２００．０４６．６４３００．３００．４００．２００．０４８．８７㊀㊀通过回归分析得到的误差回归方程为δ＝２３４．０３－１８２．４３Ａ－３４４．４２Ｂ－７０８．３５Ｃ－１４５４．７５Ｄ＋２７２．２５ＡＢ－４０５．７５ＡＣ＋１４８８．７５ＡＤ－２２．７５ＢＣ＋１０３３．７５ＢＤ＋２５１３．７５ＣＤ＋１５３．６３Ａ２＋２９９．１３Ｂ２＋１０８４．１２Ｃ２－６９６．８８Ｄ２８㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀安徽农业科学㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀２０２３年表４㊀中心组合试验回归模型方差分析Ｔａｂｌｅ４㊀Ｖａｒｉａｎｃｅａｎａｌｙｓｉｓｏｆｒｅｇｒｅｓｓｉｏｎｍｏｄｅｌｏｆｃｅｎｔｒａｌｃｏｍｂｉｎａｔｉｏｎｔｅｓｔ方差来源Ｓｏｕｒｃｅｏｆｖａｒｉａｎｃｅ平方和ＳＳ自由度ＤＦ均方ＭＳＦ值ＦｖａｌｕｅＰ值Ｐｖａｌｕｅ模型Ｍｏｄｅｌ５９１８．７６１４４２２．７７１２４．７３＜０．０００１Ａ７．３７１７．３７２．１７０．１６１０Ｂ２１．７７１２１．７７６．４２０．０２２９Ｃ１３０．３３１１３０．３３３８．４５＜０．０００１Ｄ２１．９９１２１．９９６．４９０．０２２３ＡＢ７．４１１７．４１２．１９０．１５９９ＡＣ１６．４６１１６．４６４．８６０．０４３６ＡＤ８．８７１８．８７２．６２０．１２６７ＢＣ０．０５１０．０５０．０２０．９０３３ＢＤ４．２７１４．２７１．２６０．２７９１ＣＤ２５．２８１２５．２８７．４６０．０１５５Ａ２４．０５１４．０５１．１９０．２９１８Ｂ２１５．３４１１５．３４４．５３０．０５０４Ｃ２２０１．４８１２０１．４８５９．４４＜０．０００１Ｄ２０．１３１０．１３０．０４０．８４５５残差Ｒｅｓｉｄｕａｌ５０．８４１５３．３９失拟项Ｍｉｓｓｉｎｇｉｔｅｍ３５．７４１０３．５７１．１８０．４５２３㊀㊀应用ＤｅｓｉｇｎＥｘｐｅｒｔ８．０．６软件以休止角的相对误差为目标对回归方程求解寻优，得到土壤间相关系数（ｒ）的最优值，土壤－土壤恢复系数Ａ为０．２８，土壤－土壤静摩擦系数Ｂ为０．４９，土壤－土壤动摩擦系数Ｃ为０．２４，土壤表面能Ｄ为０．０４Ｊ／ｍ２㊂２．２㊀土壤滑落试验㊀通过土壤滑落试验（图５），测量滑动摩擦角可以标定土壤与触土部件的碰撞恢复系数㊁静摩擦系数和动摩擦系数㊂采用的钢板长２５０ｍｍ㊁宽１９０ｍｍ，在钢板一侧放置少量的土壤颗粒，斜面沿转轴缓慢旋转，当土壤由一侧滑落到另一侧时，测定土壤的滑动摩擦角㊂试验中进行５组试验，求平均值得到土壤滑动摩擦角为３２．６３ʎ㊂㊀㊀在仿真中为了平衡仿真时间仍将土壤颗粒半径设置为０．５１．５ｍｍ，根据文献［１８－２１］设定土壤与触土部件的恢复系数Ｅ（０．２０．６）㊁静摩擦系数Ｆ（０．３０．７）㊁动摩擦系数Ｇ（０．０１０．２０）㊂由表５可知，４号水平最接近试验结果，因此选择３㊁４㊁５组试验所选的水平进行中心组合试验（ＣＣＤ）㊂试验因素水平编码如表６所示，编码系数γ为１．６８２㊂图５㊀土壤滑落试验Ｆｉｇ．５㊀Ｓｏｉｌｓｌｉｄｉｎｇｔｅｓｔ表５㊀最陡爬坡试验方案及结果Ｔａｂｌｅ５㊀Ｔｅｓｔｓｃｈｅｍｅａｎｄｒｅｓｕｌｔｓｏｆｓｔｅｅｐｅｓｔｃｌｉｍｂｉｎｇ试验序号ＴｅｓｔＮｏ．ＥＦＧ滑动摩擦角Ｓｌｉｄｉｎｇｆｒｉｃｔｉｏｎａｎｇｌｅʊʎ１０．２０．３０．０１１９．４８２０．３０．４０．０６２３．７８３０．４０．５０．１１２８．３６４０．５０．６０．１６３２．０９５０．６０．７０．２１３７．５３㊀㊀中心组合试验结果如表７所示，其中相对误差（δ）的计算方法与休止角的计算方法一致㊂应用软件ＤｅｓｉｇｎＥｘｐｅｒｔ８．０．６对试验结果进行分析，得到中心组合试验的回归模型㊂该回归模型的方差分析结果如表８所示，可以看出回归模型的Ｐ＜０．０００１，说明滑动摩擦角的相对误差与所得回归方程关系是显著的；失拟项Ｐ＝０．０６０２＞０．０５，说明所得回归方程的非正常误差所占比例很小㊂该试验的相关系数（ｒ）为０．９７９０，因此所得回归方程可靠度较高㊂㊀㊀通过回归分析得到的误差回归方程为δ＝５１．７８＋３９０．４８Ｅ－４２３．９７Ｆ＋１６９．９１Ｇ－２４１．６７ＥＦ－２４０．２８ＥＧ－３１２．５０ＦＧ－２０６．４４Ｅ２＋４２５．０６Ｆ２＋１３８．２４Ｇ２表６㊀中心组合试验因素水平编码Ｔａｂｌｅ６㊀Ｆａｃｔｏｒｌｅｖｅｌｃｏｄｉｎｇｏｆｃｅｎｔｒａｌｃｏｍｂｉｎａｔｉｏｎｔｅｓｔ编码ＣｏｄｅＥＦＧ１．６８２０．６００．７００．２１１０．５６０．６６０．１９００．５００．６００．１６－１０．４４０．５４０．１３－１．６８２０．４００．５００．１１㊀㊀应用ＤｅｓｉｇｎＥｘｐｅｒｔ８．０．６软件以滑动摩擦角的相对误差为目标对回归方程求解寻优，得到土壤与钢的相关系数（ｒ）的最优值，土壤－６５Ｍｎ钢恢复系数Ｅ为０．５９，土壤－６５Ｍｎ钢静摩擦系数Ｆ为０．６７，土壤－６５Ｍｎ钢动摩擦系数Ｇ为０．１３㊂３㊀验证试验３．１㊀堆积角和滑动摩擦角验证试验㊀通过ＤｅｓｉｇｎＥｘｐｅｒｔ８．０．６软件对土壤的接触参数及土壤与６５Ｍｎ钢的接触参数寻优，用最优结果进行仿真试验，通过５组重复的仿真试验，得到仿真值与实际值的对比，如表９所示㊂９５１卷１８期㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀庞靖等㊀离散元法中所用土壤参数测量及标定方法研究表７㊀中心组合试验及结果Ｔａｂｌｅ７㊀Ｃｅｎｔｅｒｃｏｍｂｉｎａｔｉｏｎｔｅｓｔａｎｄｒｅｓｕｌｔｓ试验序号ＴｅｓｔＮｏ．ＥＦＧ相对误差（δ）ʊ％１０．５６０．６６０．１９－５．８２２０．５６０．６６０．１３３．８６３０．５６０．５４０．１９６．９３４０．５６０．５４０．１３１２．１４５０．４４０．６６０．１９－２．７６６０．４４０．６６０．１３２．９７７０．４４０．５４０．１９４．２９８０．４４０．５４０．１３９．９９９０．４００．６００．１６１．６５１００．６００．６０．１６０．３７１１０．５００．５００．１６１７．４７１２０．５００．７００．１６－２．８２１３０．５００．６００．１１６．９３１４０．５００．６００．２１－０．０９１５０．５００．６００．１６４．７２１６０．５００．６００．１６２．５４１７０．５００．６００．１６２．５４１８０．５００．６００．１６３．４３１９０．５００．６００．１６２．５４２００．５００．６００．１６２．５４表８㊀中心组合试验回归模型方差分析Ｔａｂｌｅ８㊀Ｖａｒｉａｎｃｅａｎａｌｙｓｉｓｏｆｒｅｇｒｅｓｓｉｏｎｍｏｄｅｌｏｆｃｅｎｔｒａｌｃｏｍｂｉｎａｔｉｏｎｔｅｓｔ方差来源Ｓｏｕｒｃｅｏｆｖａｒｉａｎｃｅ平方和ＳＳ自由度ＤＦ均方ＭＳＦ值ＦｖａｌｕｅＰ值Ｐｖａｌｕｅ模型Ｍｏｄｅｌ５１１．０２９５６．７８２５．６１＜０．０００１Ｅ１５．２８１１５．２８６．８９０．０２５４Ｆ１５．８５１１５．８５７．１５０．０２３３Ｇ０．８８１０．８８０．４００．５４１７ＥＦ６．０６１６．０６２．７３０．１２９４ＥＧ１．５０１１．５００．６８０．４３０５ＦＧ２．５３１２．５３１．１４０．３１０４Ｅ２７．７５１７．７５３．５００．０９１１Ｆ２３２．８５１３２．８５１４．８２０．００３２Ｇ２０．２２１０．２２０．１００．７６０７残差Ｒｅｓｉｄｕａｌ２２．１７１０２．２２失拟项Ｍｉｓｓｉｎｇｉｔｅｍ１８．１９５３．６４４．５８０．０６０２表９㊀试验结果对比Ｔａｂｌｅ９㊀Ｃｏｍｐａｒｉｓｏｎｏｆｔｅｓｔｒｅｓｕｌｔｓ试验Ｔｅｓｔ堆积角Ｓｔａｃｋｉｎｇａｎｇｌｅʊʎ滑动摩擦角Ｓｌｉｄｉｎｇｆｒｉｃｔｉｏｎａｎｇｌｅʊʎ仿真试验Ｓｉｍｕｌａｔｉｏｎｔｅｓｔ３５．８８３３．５３室内试验Ｉｎｄｏｏｒｔｅｓｔ３６．４３３２．６３相对误差Ｒｅｌａｔｉｖｅｅｒｒｏｒʊ％１．５１２．７３㊀㊀将仿真结果与实际堆积结果进行对比，如图６所示，结果显示优化后土壤的仿真堆积角与实际堆积角的角度差距较小，表明该组仿真设置有一定的准确性㊂３．２㊀探针贯入验证试验㊀为了进一步验证土壤参数的准确性，采用ＥＤＥＭ软件对探针贯入土壤过程进行仿真模拟，土壤颗粒半径仍设置为０．５１．５ｍｍ，土壤的接触模型为Ｈｅｒｔｚ－ＭｉｎｄｌｉｎｗｉｔｈＪＫＲ黏结模型，仿真参数设定以测量和标定结果为准，探针仿真模型采用ＳｏｌｉｄＷｏｒｋｓ软件创建的．ｘ＿ｔ文件直接导入，土壤为直径８０ｍｍ㊁高１５０ｍｍ的圆柱形，设置探针入土深度为１００ｍｍ，入土速度为８ｍｍ／ｓ，仿真时间为１２．５ｓ，瑞丽时间步长为１０％㊂在所测土壤参数和最优标定参数组合下的探针贯入１㊁５和１０ｃｍ的试验过程如图７所示㊂从图７可以看出，随着探针入土深度的增加，土壤扰动范围增大，与孙文峰等［２２－２４］的研究结果相似㊂因为探针尖头部分直径大于探杆直径，因此土壤扰动区域基本分布在探针尖头部分㊂㊀㊀室内试验如图８所示，所用到的设备有万能试验机（ＤＮＳ０２－１ＫＷ）㊁探针（尖头最粗直径１４ｍｍ）㊁桶（直径８０ｍｍ，高度４００ｍｍ）㊂将含水率为（１５ʃ１）％的土壤装入桶内，装入深度为１５０ｍｍ，不经过压实作用，体积密度约为１．１５ｇ／ｃｍ３㊂利用万能试验机设置探针入土速度与仿真速度一致，在８ｍｍ／ｓ速度下贯入，贯入深度为１００ｍｍ，将探针的受力情况传到电脑存储，试验重复３次，分别记下探针入土深度为２０㊁４０㊁６０㊁８０和１００ｍｍ处的阻力值，最后取平均值为阻力值，试验结果见表１０所示㊂由表１０可知，随着探针入土深度的增加，探针阻力在逐渐增加，且仿真结果和室内试验结果的阻力增加幅度大致相同㊂图６㊀实际试验（ａ）和仿真试验（ｂ）对比Ｆｉｇ．６㊀Ｃｏｍｐａｒｉｓｏｎｂｅｔｗｅｅｎａｃｔｕａｌｔｅｓｔ（ａ）ａｎｄｓｉｍｕｌａｔｉｏｎｔｅｓｔ（ｂ）４㊀结论（１）针对土壤的本征参数（固体密度㊁弹性模量㊁剪切模量和泊松比），用体积置换法㊁直剪试验和土样压溃试验直接测量得到㊂（２）针对土壤间的接触参数㊁表面能以及土壤与６５Ｍｎ钢的接触参数，采用ＥＤＥＭ软件进行土壤堆积仿真模拟和土壤在６５Ｍｎ钢板的滑落试验模拟㊂以堆积角和滑动摩擦角为指标，通过中心组合试验标定接触参数和表面能，获得土壤间的恢复系数０．２８㊁静摩擦系数０．４９㊁动摩擦系数０．２４和表面能０．０４Ｊ／ｍ２，土壤与６５Ｍｎ钢的恢复系数０．５９㊁静摩擦系数０１㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀安徽农业科学㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀２０２３年０．６７㊁动摩擦系数０．１３㊂图７㊀探针贯入过程Ｆｉｇ．７㊀Ｐｒｏｂｅｐｅｎｅｔｒａｔｉｏｎｐｒｏｃｅｓｓ图８㊀探针贯入室内试验Ｆｉｇ．８㊀Ｉｎｄｏｏｒｔｅｓｔｏｆｐｒｏｂｅｐｅｎｅｔｒａｔｉｏｎ表１０㊀贯入试验验证结果Ｔａｂｌｅ１０㊀Ｖｅｒｉｆｉｃａｔｉｏｎｒｅｓｕｌｔｓｏｆｐｅｎｅｔｒａｔｉｏｎｔｅｓｔ深度Ｄｅｐｔｈｍｍ探针阻力ＰｒｏｂｅｒｅｓｉｓｔａｎｃｅʊＮ室内试验Ｉｎｄｏｏｒｔｅｓｔ仿真试验Ｓｉｍｕｌａｔｉｏｎｔｅｓｔ相对误差Ｒｅｌａｔｉｖｅｅｒｒｏｒʊ％２０１．９８２．１５８．５９４０６．４８５．８４９．８８６０１０．０８９．１０９．７２８０１３．０５１３．０３０．１５１００１５．９１１７．０２６．９８㊀㊀（３）为验证土壤参数的准确性，分别对土壤堆积角和滑动摩擦角的实际试验与仿真试验进行对比，得到两者相对误差分别为１．５１％和２．７３％㊂在所测参数和标定最优参数组合下进行了探针贯入试验的仿真模拟和室内试验，获得探针在贯入深度为２０㊁４０㊁６０㊁８０和１００ｍｍ处的阻力相对误差分别为８．５９％㊁９．８８％㊁９．７２％㊁０．１５％㊁６．９８％，仿真试验与实际的探针贯入试验效果基本一致，证明了参数测量和标定方法的准确性㊂参考文献［１］谢方平，吴正阳，王修善，等．基于无侧限抗压强度试验的土壤离散元参数标定［Ｊ］．农业工程学报，２０２０，３６（１３）：３９－４７．［２］ＭＡＲＴＩＮＣＬ，ＢＯＵＶＡＲＤＤ，ＳＨＩＭＡＳ．ＳｔｕｄｙｏｆｐａｒｔｉｃｌｅｒｅａｒｒａｎｇｅｍｅｎｔｄｕｒｉｎｇｐｏｗｄｅｒｃｏｍｐａｃｔｉｏｎｂｙｔｈｅＤｉｓｃｒｅｔｅＥｌｅｍｅｎｔＭｅｔｈｏｄ［Ｊ］．Ｊｏｕｒｎａｌｏｆｔｈｅｍｅｃｈａｎｉｃｓａｎｄｐｈｙｓｉｃｓｏｆｓｏｌｉｄｓ，２００３，５１（４）：６６７－６９３．［３］ＳＷＥＩＪＥＮＴ，ＨＡＳＳＡＮＩＺＡＤＥＨＳＭ，ＡＳＬＡＮＮＥＪＡＤＨ，ｅｔａｌ．Ｔｈｅｅｆｆｅｃｔｏｆｐａｒｔｉｃｌｅｓｈａｐｅｏｎｐｏｒｏｓｉｔｙｏｆｓｗｅｌｌｉｎｇｇｒａｎｕｌａｒｍａｔｅｒｉａｌｓ：Ｄｉｓｃｒｅｔｅｅｌｅｍｅｎｔｍｅｔｈｏｄａｎｄｔｈｅｍｕｌｔｉ⁃ｓｐｈｅｒｅａｐｐｒｏｘｉｍａｔｉｏｎ［Ｊ］．Ｐｏｗｄｅｒｔｅｃｈｎｏｌｏｇｙ，２０２０，３６０：１２９５－１３０４．［４］王宪良，胡红，王庆杰，等．基于离散元的土壤模型参数标定方法［Ｊ］．农业机械学报，２０１７，４８（１２）：７８－８５．［５］ＭＩＬＫＥＶＹＣＨＶ，ＭＵＮＫＨＯＬＭＬＪ，ＣＨＥＮＹ，ｅｔａｌ．Ｍｏｄｅｌｌｉｎｇａｐｐｒｏａｃｈｆｏｒｓｏｉｌｄｉｓｐｌａｃｅｍｅｎｔｉｎｔｉｌｌａｇｅｕｓｉｎｇｄｉｓｃｒｅｔｅｅｌｅｍｅｎｔｍｅｔｈｏｄ［Ｊ］．Ｓｏｉｌ＆ｔｉｌｌａｇｅｒｅｓｅａｒｃｈ，２０１８，１８３：６０－７１．［６］冯俊小，林佳，李十中，等．秸秆固态发酵回转筒内颗粒混合状态离散元参数标定［Ｊ］．农业机械学报，２０１５，４６（３）：２０８－２１３．［７］刘文政，何进，李洪文，等．基于离散元的微型马铃薯仿真参数标定［Ｊ］．农业机械学报，２０１８，４９（５）：１２５－１３５，１４２．［８］郝建军，魏文波，黄鹏程，等．油葵籽粒离散元参数标定与试验验证［Ｊ］．农业工程学报，２０２１，３７（１２）：３６－４４．［９］王黎明，范盛远，程红胜，等．基于ＥＤＥＭ的猪粪接触参数标定［Ｊ］．农业工程学报，２０２０，３６（１５）：９５－１０２．［１０］孙景彬，刘琪，杨福增，等．黄土高原坡地土壤与旋耕部件互作离散元仿真参数标定［Ｊ］．农业机械学报，２０２２，５３（１）：６３－７３．［１１］宋少龙，汤智辉，郑炫，等．新疆棉田耕后土壤模型离散元参数标定［Ｊ］．农业工程学报，２０２１，３７（２０）：６３－７０．［１２］张晋．旋耕机正转深旋节能技术研究［Ｄ］．北京：中国农业科学院，２０２１．［１３］马玉莹，雷廷武，庄晓晖．测量土壤颗粒密度的体积置换法［Ｊ］．农业工程学报，２０１４，３０（１５）：１３０－１３９．［１４］朱红区．免耕施肥播种机开沟工作部件仿真与试验研究［Ｄ］．广州：华南农业大学，２０１６．［１５］王金武，李响，高鹏翔，等．胡萝卜联合收获机高效减阻松土铲设计与试验［Ｊ］．农业机械学报，２０２０，５１（６）：９３－１０３．［１６］樊昱．基于离散元法的马铃薯挖掘机理研究及仿生铲设计［Ｄ］．沈阳：沈阳农业大学，２０２０．［１７］杜俊，张文良，祝英豪，等．基于离散元法的旋埋刀辊功率分配特性研究［Ｊ］．安徽农业大学学报，２０２０，４７（６）：１０３１－１０３７．［１８］胡建平，赵军，潘浩然，等．基于离散元的双轴旋耕机功耗预测模型［Ｊ］．农业机械学报，２０２０，５１（Ｓ１）：９－１６．［１９］颜丙新，武广伟，付卫强，等．基于ＥＤＥＭ的玉米精播高位投种着床位置影响因素研究［Ｊ］．农业机械学报，２０２０，５１（Ｓ２）：４７－５４．［２０］戴飞，宋学锋，赵武云，等．全膜双垄沟覆膜土壤离散元接触参数仿真标定［Ｊ］．农业机械学报，２０１９，５０（２）：４９－５６，７７．［２１］郭文松，贺小伟，王龙，等．梳齿起膜气力脱膜式耕层残膜回收机研制［Ｊ］．农业工程学报，２０２０，３６（１８）：１－１０．［２２］孙文峰，付天鹏，何跃，等．水田带状复式整地机关键部件设计与试验［Ｊ］．农业机械学报，２０２２，５３（１）：５０－６２．［２３］张智泓，甘帅汇，左国标，等．以砂鱼蜥头部为原型的仿生深松铲尖设计与离散元仿真［Ｊ］．农业机械学报，２０２１，５２（９）：３３－４２．［２４］于从羊．刀辊－麦秆－土壤多相耦合仿真模型构建及验证［Ｄ］．合肥：安徽农业大学，２０２１．１１５１卷１８期㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀庞靖等㊀离散元法中所用土壤参数测量及标定方法研究。

水稻密度碰撞恢复系数测量

0.493
0.472
0.475
0.435
0.462
0.456ຫໍສະໝຸດ 下落高度 H 为 35cm，平均值 e=0.4387，下落高度 H 为 20cm，平均值为 e=0.4518。
表 3 碰撞材料为铁板的恢复系数
水稻种子颗粒下落高度 H/cm
碰撞恢复系数
35
0.425
0.526
0.476
0.415
0.552
图 4 高速摄影整体示意图
84 2017, Vol.37, No.19
农业与技术
※ 农机水利
4 所示，调整高速摄像的焦距使高速摄像所拍到的影像在电脑显示器上清楚的呈现出来，使水稻种子按 20cm、 35cm 的高度自由下落与碰撞材料接触后弹起，通过高速摄像仪所拍到的影像测量水稻种子弹起的高度。
[2] 赵英霞 . 基于食品安全的农业全产业链模式研充 [J]. 中国市场 ,2012(36):44-45
[3] 李政权 . 基于离散元法的小麦排种器的数字化设计方法研究 [D]. 长春 : 吉林大学 ,2009(6).
旱稻 502 的密度为 0.477g/mL。碰撞材料不同碰撞恢复系数不同，铝合金大于铁板大于有机玻璃，随着由于变形量和空气阻力的影响，高度越高碰撞恢复系数越小。
本文选取水稻品种为旱稻 502。
关键词：密度；碰撞恢复系数
中图分类号：S223
文献标识码：A
DOI：10.11974/nyyjs.20171032032
引言
水稻是我国重要的粮食作物，是粮食生产加工和大众消费中的主要粮食作物，因此水稻的产量是我国粮食安全的保障，国家必须继续加大力度发展扩大生产水稻才可保障粮食安全生产 [1]。我国有 65% 左右的人口以食水稻为主，可见水稻在我国的粮食安全中有着重要战略地位 [2]。但对于水稻种植方式中运用排种器的比重不高，本文用仿真软件 Edem 仿真排种器工作时种子在排种器中的运动状态，所测的水稻的密度、碰撞恢复都是 Edem 仿真时所需要的，为更加真实准确的模仿水稻种子在排种器中的运动状态提供基础。

一种确定金属材料接触碰撞中恢复系数的试验方法[发明专利]

专利名称：一种确定金属材料接触碰撞中恢复系数的试验方法专利类型：发明专利
发明人：赖雄鸣,赖琴芳,黄河,王成,张勇,杨建红,房怀英
申请号：CN201610696427.9
申请日：20160819
公开号：CN106353186A
公开日：
20170125
专利内容由知识产权出版社提供
摘要：本发明公开一种确定金属材料接触碰撞中恢复系数的试验方法，包括以下步骤：S1试验准备，准备试验材料金属球、金属板、速度传感器和采集卡；S2试验过程，释放金属球，使其从与金属板距离H的高处落下，在金属球第一次碰撞金属板直至停止于金属板的过程中，速度传感器获取金属球在金属板上每次碰撞后的加速度值和碰撞时间值，记第i次采集的加速度为a，a对应的时间值t；采集卡采集该加速度值和时间值；S3试验数据处理，包括S31根据加速度值和加速度所对应的时间值制作加速度随时间变化的曲线图；S32依次求出Δt、T和T；S33求出恢复系数。

本发明易操作，通过测试金属材料接触碰撞过程中加速度随的时间变化，获得精确的碰撞恢复系数，提高了测量精度。

申请人：华侨大学,福建南方路面机械有限公司
地址：362000 福建省泉州市丰泽区城东华侨大学
国籍：CN
代理机构：泉州市文华专利代理有限公司
代理人：戴中生
更多信息请下载全文后查看。

乒乓球碰撞恢复系数测量实验报告

乒乓球碰撞恢复系数测量实验报告
实验目的：研究弹性球与地面的碰撞过程，测量小球的入射速度和反弹速度，计算每次碰撞的恢复系数；了解智能手机内置传感器及相关软件的使用方法；学习基本的数据处理分析方法实验仪器材料：米尺、乒乓球、带有Phyphox软件的手机、木质桌面、水泥地面
实验方案设计：
<思路>
球与地板每次碰撞都伴随有声音发出，通过“听音”可测量碰撞的时间间隔，即球的飞行时间，忽略空气阻力影响，由此计算出每次碰撞的入射速度和反弹速度，求出每次碰撞时的恢复系数参考时，麻烦注意数据和格式的替换。

实验过程：<实验步骤>
1.打开Phyphox软件，使用计时器下的声学秒表中的多任务，连续记录碰撞的时间间隔
2.将乒乓球置于离木质桌面32cm的高度，无初速度地垂直落下
3.待五次结果记录完毕后，结束该部分实验
4.将桌面换成水泥地面，重复上述步骤参考时，麻顺注意数据和格式的替换，楼主也是学生党，这是我自己的实验报告
<出现的问题及解决方法>
问题：乒乓球不断落下的过程中，落点会有偏移，声音难以采集完全；办法：适当降低初始位置的高度，减少其处于空中的时间。

碰撞恢复系数测量

碰撞恢复系数测量一、引言在交通工程和汽车工程领域，碰撞安全性的研究一直是重要课题。

在车辆碰撞过程中，碰撞恢复系数的测量对于理解碰撞的能量吸收和恢复特性具有关键意义。

本文将深入探讨碰撞恢复系数的定义、意义、测量方法、设备原理，以及影响测量精度的因素和控制方法。

二、碰撞恢复系数的定义及意义碰撞恢复系数，也称为碰撞加速度系数或碰撞减速度系数，是指在车辆碰撞过程中，车辆恢复速度与冲击速度的比值。

它是评估车辆碰撞安全性能的重要参数，用于衡量车辆在碰撞后能够吸收的能量和恢复的能力。

三、碰撞恢复系数的测量方法1.直接测量法：通过在车辆上安装加速度计或减速度计，直接测量车辆在碰撞过程中的减速度值。

这种方法可以获取实时的碰撞数据，但对于实验环境和测试条件要求较高。

2.模拟仿真法：利用计算机仿真技术，模拟车辆在不同碰撞条件下的碰撞过程，并计算碰撞恢复系数。

这种方法可以模拟各种复杂的碰撞情况，但需要高精度的仿真模型和参数。

四、测量设备及原理1.加速度计/减速度计：是一种常用的测量设备，用于直接测量车辆在碰撞过程中的加速度或减速度。

其原理基于牛顿第二定律，通过测量物体的质量和加速度/减速度，计算碰撞过程中的力。

2.数据采集系统：用于实时采集和处理加速度计/减速度计的数据。

数据采集系统通常包括传感器、放大器、模数转换器和计算机等部分，能够将物理信号转换为数字信号，并进行存储和分析。

五、影响测量精度的因素及控制方法1.传感器精度：传感器的精度直接影响测量结果的准确性。

为提高测量精度，应选择高精度、低漂移的传感器，并进行定期校准和维护。

2.测试环境：测试环境如温度、湿度、振动等都会影响测量结果的准确性。

为减小环境因素的影响，应确保测试环境稳定并符合实验要求。

3.安装位置：传感器的安装位置也会影响测量结果。

为减小安装位置对测量的影响，应选择合适的安装位置，并确保传感器安装牢固、稳定。

4.数据处理方法：数据处理方法的准确性也会影响测量结果。

参种千粒重密度碰撞恢复系数的测量

参种千粒重密度碰撞恢复系数的测量
文正彪;刘宽厚;王婧;王新阳;张亮
【期刊名称】《农业与技术》
【年(卷),期】2017(037)017
【摘要】为深入探讨气吸式人参播种机播种的运动情况,通过软件进行仿真效果,需测出人参种的基本物理参数:千粒重、密度、碰撞恢复系数等.以期为气吸式播种机的运动情况提供借鉴.选取东北长白山地区参农常种植的人参为样本,做西洋参、林下参、园参的参数测量试验.
【总页数】4页(P55-58)
【作者】文正彪;刘宽厚;王婧;王新阳;张亮
【作者单位】吉林省农业机械研究院,吉林长春 130022;吉林省农业机械研究院,吉林长春 130022;吉林省农业机械研究院,吉林长春 130022;吉林省农业机械研究院,吉林长春 130022;吉林省农业机械研究院,吉林长春 130022
【正文语种】中文
【中图分类】S-3
【相关文献】
1.密度碰撞恢复系数测量
2.水稻密度碰撞恢复系数测量
3.基于压电传感器的一维弹性碰撞恢复系数测量系统研究
4.一种基于变恢复系数的接触碰撞力模型
5.脆性物质碰撞恢复系数e的测量
因版权原因，仅展示原文概要，查看原文内容请购买。

恢复系数的不同定义及其适用性分析

恢复系数的不同定义及其适用性分析李逸良;邱信明;张雄【摘要】本文归纳了恢复系数的速度、冲量、能量3种不同定义方式,并针对质点、刚体、质点系和弹性体4种不同研究对象,在具体的碰撞过程中详细计算了不同定义下的恢复系数数值.通过比较其差别与联系,逐一检验了各种定义方式的适用性.结果表明质心速度定义的恢复系数在非质点碰撞问题中是有缺陷的.【期刊名称】《力学与实践》【年(卷),期】2015(037)006【总页数】5页(P773-777)【关键词】恢复系数;碰撞;质心;接触点;机械能【作者】李逸良;邱信明;张雄【作者单位】清华大学航天航空学院,北京 100084;清华大学航天航空学院,北京100084;清华大学航天航空学院,北京 100084【正文语种】中文【中图分类】O313.4恢复系数是弹塑性体碰撞的一个重要的指标，在许多学科中都有广泛的应用［1］.如常被用做交通事故控制和校验的标准［2］；被用来研究岩土体物理力学性质等［3］.恢复系数有几种不同的定义方式，但各自的适用范围较为模糊，容易产生误用.在不考虑碰撞界面摩擦的情况下，本文拟对恢复系数的不同定义方式进行归纳，并在具体碰撞算例中分析其适用范围和相容性.恢复系数的初始定义是用来表征两个质点碰撞时能量耗散的程度，后来也被广泛用来描述刚体和弹性体的碰撞.恢复系数有如下3种定义方式：2.1 按速度定义恢复系数的速度定义是碰撞后法向相对分离速度v nr和碰撞前相对接近速度v n0的比值这一定义始于牛顿对质点碰撞的研究［4］.近来采用此定义的研究有Evans等［5］、Budetta等［6］和李士龙［7］.按选取的速度参考点不同，此定义细分为两小类：以物体质心为速度参考点，如Karthikeyan等［8］；以碰撞接触点为速度参考点，如Hurmuzlu等［9］和Stronge［10］.2.2 按冲量定义恢复系数的冲量定义是19世纪初由Poisson提出来的.如图1所示，碰撞时由于物体相互挤压而导致作用力增大的过程是压缩阶段，作用力达到峰值后开始减少直到物体脱离接触的过程是恢复阶段.恢复系数的冲量定义是恢复阶段法向冲量I r与压缩阶段的法向冲量I0之比使用这一定义的有Stronge［10］和Routh［11］.2.3 能量定义Stronge［10］于1990年给出了恢复系数的能量定义.在能量定义中，恢复系数的平方e2为恢复阶段弹性变形所释放的能量E r与压缩阶段储存的能量E0之比使用这一定义的有Vu-Quoc等［12］和Karthikeyan等［8］.不难证明，以上3种恢复系数的定义方式在质点的碰撞中是相互等价的.但实际问题中，参与碰撞的对象常常不能被简化为质点，因此不同定义的适用性就需要仔细分析.下面将在刚体、质点系以及弹性体的碰撞算例中分别使用3种定义进行计算和讨论.如图2所示，设长为l，质量为m的均匀细杆，以初速度v0与光滑地面发生倾角为θ的碰撞，碰撞过程无机械能损失.若碰撞中地面给细杆的总冲量为I，碰撞后细杆质心速度为v cr，角速度为ω，由动量定理和对杆质心的角动量定理，有由碰撞前后机械能守恒，有联立式（4）和式（5）解得计算杆碰撞点与地面的法向相对分离速度得v ir= v cr+ωl sinθ/2=v0.计算速度定义的恢复系数：取质心为参考点，；取碰撞点为参考点，e1=1.在最大压缩状态，杆碰撞点的法向速度为零，设此时杆质心速度v2（向下），角速度ω2.若压缩冲量为I0，根据动量定理m v0-m v2=I0和角动量定理ml2ω2/12=I0 l sinθ/2，及接触点速度v2-ω2 l sinθ/2=0，可得压缩冲量和恢复冲量分别为I0=m v0/¡1+3 sin2θ¢，I r=I-I0=I0.因此，按冲量定义的恢复系数是e2=1.此外，由于碰撞前后无动能损失，显然能量定义的恢复系数e3=1.可见，由碰撞点的速度、冲量和能量定义这3种方法得到的恢复系数是相同的，均为e=1，对应完全弹性碰撞.只有以质心做参考点的速度定义的恢复系数值不同.因此有理由认为，接触点速度、冲量、能量定义的恢复系数很好地刻画了物体碰撞性质，而质心速度的定义有些情况下不够准确.下面来看一个质点系碰撞的例子.如图3所示，光滑平面上两个相同的质点系，各由两个质量为m的质点和弹性系数为k的弹簧组成.一个质点系以初速度v0向右，与初始静止的另一质点系发生碰撞.若碰撞前弹簧为自然长度，考察碰撞后的运动状态和恢复系数.4.1 首次碰撞分析球B和球M首先发生碰撞，碰撞时弹簧的形变可忽略不计.因二球质量相同，碰撞后将发生速度交换，即vB=0，vM=v0，两质系的质心速度均变为0.5v0.计算速度定义的恢复系数.取质心为参考点，e=0；取接触点为参考点，e1=1.计算冲量定义的恢复系数.因碰撞实为两质点的碰撞，故e2=1.计算能量定义的恢复系数.碰撞前系统总动能为E0=m v，碰撞后球B和球N静止，弹簧无变形，系统总能量仍为E r=m v，故e3=1.可见，由接触点速度、冲量、能量定义仍然给出了相同的恢复系数.4.2 二次碰撞分析若首次碰撞结束于t=0时刻，之后小球将在弹簧弹力的作用下运动.在第二次碰撞前，左边质系中球A和球B的质心坐标系下的坐标分别为，以弹簧无压缩状态为两坐标零点，由牛顿定律得到质心参考系下的相对运动学方程利用初始条件x（0）=x（0）=0,且（0）= -（0）=v0/2，可解得对于球M和球N，同样可得回到地面坐标系.由于两个质系的质心速度均为v0/2，且t=0时刻有xB=xM，则球B和球M的绝对运动方程为由式（9）发现，当时，又会有xB=xM，且此时各球速度（t1）=0，（t1）=v0，（t1）=0，（t1）=v0.这表明球B与球M将发生二次碰撞，碰撞后两球速度再次交换.二次碰撞后球A和球B静止，球M和球N速度均为v0.此时两系统的弹簧均处于原长，之后左边质系静止，右边质系以速度v0向右运动.两次碰撞后，两个的质心发生了速度交换.类似第一次碰撞的计算，二次碰撞过程中按接触点速度、冲量、能量定义得到的恢复系数均为e=1.而以质心为参考点，将得到e→∞.以这个比较极端的例子容易发现，以质心做参考点的速度定义的p恢复系数是不合适的.但若弹簧的刚度系数很大，，则两次碰撞的时间间隔，近似于一次碰撞.两质系的质心速度碰撞前为v c1=v0，v c2=0；碰撞后为v cr1=0，v cr2=v0，由质心速度定义方式得到恢复系数e′1=1，是正确的结果.实际上，弹簧刚度系数很大时，质系在碰撞中发生的形变远小于系统尺度，可以忽略.此时质系的碰撞也已经退化成为刚体的碰撞了.需要指出的是，本文的例子为质系的正碰.在多刚体的碰撞中，如果考虑斜碰撞和摩擦，可能存在能量扩散效应而导致能量定义失效［14］.我们用有限元计算来分析弹性体的碰撞过程.半径为20m的球，以初速度20m/s正碰刚性平面.设线弹性材料的泊松比为0.3，密度ρ= 2700kg/m3，分别采用3种弹性模量E=10GPa，90GPa，1000GPa进行计算.得到的质心速度、接触力、动能随时间变化曲线如图4.显然，弹性模量大时，碰撞力峰值出现早，接触时间更短，碰撞后能量的损失更小，即碰撞更接近刚体.表1给出了各物理量随弹性模量的变化规律.则由质心速度，冲量和能量定义的恢复系数应为，计算出的恢复系数如表2所示. 可见对于不同的弹性模量，冲量恢复系数e2和能量恢复系数e3一直十分接近，但质心恢复系数e在弹性模量较小时误差较大，只有模量很大时才接近e3.这是因为在高弹性模量时，球已经十分接近一个刚体的缘故.此外从数值上看，即使是完全弹性材料的碰撞，恢复系数也无法达到e=1，因为弹性球脱离刚性面后，由于球内残余弹性应力波的存在，变形能不能完全恢复成弹性体的动能.有限元计算需要对物体数值离散，其中的接触算法定义的是面和面接触，没有几何意义上的接触点.因此，计算中接触区域的速度有大幅度的震荡，找不出分离速度和接近速度，故无法计算接触点速度定义的恢复系数e1.因此，对于弹性体的碰撞，机械能（动能+应变能）是表征碰撞性质的最准确参数，冲量定义的恢复系数也仍然适用，虽然两种方法的实验数据获得都比较困难.由于弹性体自身的变形，无论参考点是质心还是接触点，速度定义的恢复系数都有局限性.接触点定义的局限性体现于无法获得准确的接触点速度；质心的定义简便易行，但计算恢复系数只能针对变形很小的情况适用.本文总结了历史上恢复系数的3种不同定义方法，并逐一验证了它们在质点碰撞、刚体碰撞、质点系碰撞以及弹性体碰撞中的适用性.结果表明，恢复系数表征着物体碰撞前后能量的变化情况，所以能量的定义是恢复系数最为准确的定义.对于质点碰撞，3种定义都适用且完全等价.对于刚体、质点系的碰撞，接触点速度、冲量、能量的定义方式都适用，但质心速度的定义方式一般不再适用，只可作为弹簧刚度系数很大、物体尺寸可忽略时的近似.对于弹性体的碰撞，用能量和冲量方式定义的恢复系数仍然适用，而速度定义则不再适用.在实际应用中，考虑到测量的简便，质心速度定义的恢复系数通常是最容易被采用的方式，而作者在这里用几个简单算例说明，恢复系数定义的使用需要与采用的力学模型相匹配，否则容易引起误用.【相关文献】1董富祥，洪嘉振.多体系统动力学碰撞问题研究综述.力学进展，2009，39（3）：352-3592都雪静，许洪国，常胜等.材料性能对汽车碰撞散落物运动特性的影响.系统仿真学报，2008，20（21）：5999-60013章广成，向欣，唐辉明.落石碰撞恢复系数的现场试验与数值计算.岩石力学与工程学报，2011，（06）：1266-12734 Newton I.Philosophiae Nuturalis Principia Mathematica. London：Reg Soc Preases，16865 Evans SG，Hungr O.The assessment of rockfall hazard at the base of talusslopes.Canadian Geotechnical Journal，1993，30（4）：620-6366 Budetta P，Santo A.Morphostructural evolution and related kinematics of rockfalls in Campania（southern Italy）：a case study.Engineering Geology，1994，36（3）：197-2107李士龙.薄壁圆环的弹塑性碰撞.［硕士论文］.杭州：浙江大学，20138 Karthikeyan K，Russell B，Deshpande V，et al.Multihit armour characterisation of metal-composite bi-layers. Journal of Mechanics of Materials and Structures，2013，7（7）：721-7349 Hurmuzlu Y，Marghitu DB.Rigid body collisions of planar kinematic chains with multiple contact points.The International Journal of Robotics Research，1994，13（1）：82-9210 Stronge WJ.Rigid body collisions with friction.Proceedings of the Royal Society ofLondon.Series A：Mathematical and Physical Sciences，1990，431（1881）：169-18111 Routh EJ.Dynamics of a System of Rigid Bodies.London：MacMillan，186012 Vu-QuocL，ZhangX，LesburgL.A normalforcedisplacement model for contacting spheres accounting for plastic deformation：force-driven formulation.Journal of Applied Mechanics，2000，67（2）：363-37113 Strong WJ.Impact Mechanics.Cambridge：Cambridge University Press，200014姚文莉，陈滨，徐鉴.基于能量恢复系数的多刚体系统的摩擦碰撞.北京大学学报（自然科学版），2007，43（5）：585-591。

理论力学实验三碰撞试验数据处理

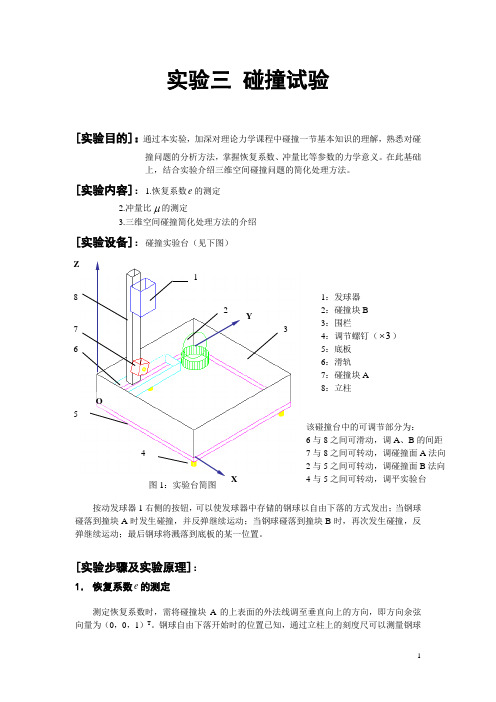
实验三碰撞试验[实验目的]：通过本实验，加深对理论力学课程中碰撞一节基本知识的理解，熟悉对碰撞问题的分析方法，掌握恢复系数、冲量比等参数的力学意义。

在此基础上，结合实验介绍三维空间碰撞问题的简化处理方法。

[实验内容]：1.恢复系数e 的测定2.冲量比μ的测定3.三维空间碰撞简化处理方法的介绍[实验设备]：碰撞实验台（见下图）按动发球器1右侧的按钮，可以使发球器中存储的钢球以自由下落的方式发出；当钢球碰落到撞块A 时发生碰撞，并反弹继续运动；当钢球碰落到撞块B 时，再次发生碰撞，反弹继续运动；最后钢球将溅落到底板的某一位置。

[实验步骤及实验原理]：1．恢复系数e 的测定测定恢复系数时，需将碰撞块A 的上表面的外法线调至垂直向上的方向，即方向余弦向量为（0，0，1）T 。

钢球自由下落开始时的位置已知，通过立柱上的刻度尺可以测量钢球1：发球器 2：碰撞块B 3：围栏 4：调节螺钉（3⨯） 5：底板 6：滑轨 7：碰撞块A 8：立柱该碰撞台中的可调节部分为： 6与8之间可滑动，调A 、B 的间距 7与8之间可转动，调碰撞面A 法向 2与5之间可转动，调碰撞面B 法向 4与5之间可转动，调平实验台碰撞后的反弹高度，从而可以计算出碰撞中的恢复系数。

见图2。

设初始高度为0h ，碰撞前速度为1v *，碰撞后钢球反弹的最高位置为max h ，碰撞后钢球的质心速度为1V 。

则：，012gh v =， max 12gh V -= （负号说明方向为-Z 方向）恢复系数的定义为：AAv v V V e ---=11，碰撞块A 的碰撞前和碰撞后速度均为0，可得：maxh h e =（1）测出max h 的值便可以由式（1）计算出恢复系数e2．冲量比μ的测定测定冲量比时，同样需将碰撞块A 的上表面的外法线调至垂直向上的方向，另外还要取下碰撞块B ，这时钢球经过第一次碰撞将直接溅落在底板上。

通过测量其溅落位置并结合已测定的恢复系数可以得到冲量比的测定结构。

碰撞恢复系数测量实验报告

碰撞恢复系数测量实验报告引言：碰撞恢复系数是描述碰撞过程中动能转移和损失的一个重要参数。

本实验旨在通过测量碰撞前后物体的速度变化，计算出碰撞恢复系数，并探讨不同物体在碰撞过程中的能量转移情况。

实验目的：1. 测量不同物体在碰撞过程中的速度变化；2. 计算不同物体的碰撞恢复系数；3. 探究不同物体在碰撞过程中能量转移的特点。

实验器材：1. 两个小球（可选择不同材质的小球）；2. 直尺；3. 计时器；4. 平滑的水平桌面。

实验步骤：1. 将两个小球放在桌面上，使它们距离适当，确保碰撞过程中不会相互阻挡；2. 用直尺测量两个小球的直径，并记录下来；3. 给其中一个小球一个初始速度，可通过手动推动或利用斜面等方式；4. 观察碰撞过程，并用计时器记录下两个小球的碰撞时间；5. 计算碰撞前后两个小球的速度，并计算碰撞恢复系数。

实验数据：根据实验步骤所获得的数据，我们可以计算出碰撞前后两个小球的速度，并据此计算碰撞恢复系数。

以下是一组示例数据：小球A质量：m1 = 0.1 kg小球B质量：m2 = 0.2 kg小球A初始速度：v1i = 2.5 m/s小球B初始速度：v2i = 0.5 m/s碰撞时间：t = 0.05 s根据动量守恒定律和动能守恒定律，可以得到以下计算公式：碰撞前小球A的速度：v1f = (m1 - m2) * v1i / (m1 + m2) + 2 * m2 * v2i / (m1 + m2)碰撞前小球B的速度：v2f = 2 * m1 * v1i / (m1 + m2) + (m2 - m1) * v2i / (m1 + m2)碰撞恢复系数：e = (v1f - v2f) / (v1i - v2i)根据以上公式，我们可以计算出碰撞恢复系数为：e = (v1f - v2f) / (v1i - v2i) = (0.6 - 0.4) / (2.5 - 0.5) = 0.1实验结果与讨论：根据实验数据和计算结果，我们可以得出碰撞恢复系数为0.1。

颗粒间碰撞恢复系数

颗粒间碰撞恢复系数
在实际应用中，颗粒间碰撞恢复系数对于粒子物理、材料科学、地质学等领域的研究都具有重要意义。

例如，研究颗粒在空气中的行为时，颗粒间碰撞恢复系数可以用来描述颗粒之间的能量转移和散失情况，进而推导出颗粒的运动特性。

在材料科学领域，颗粒间碰撞恢复系数可以用于评估材料的弹性和强度。

通过测量材料中颗粒间碰撞的恢复系数，可以推断材料的压缩性能和抗拉强度等重要指标。

此外，在地质学领域，颗粒间碰撞恢复系数也被广泛应用于研究地下岩层的物理性质。

通过对岩层中颗粒间碰撞恢复系数的测量和分析，可以推断出岩层的孔隙度和渗透性等参数，进而为地下资源勘探和开发提供重要的科学依据。

- 1 -。

颗粒物料恢复系数简易测量方法及其应用

颗粒物料恢复系数简易测量方法及其应用
颗粒物料恢复系数简易测量方法及其应用
杨明金，杨玲，李庆东
【摘要】介绍了一种简易的基于运动学原理的颗粒物料恢复系数测量方法。

通过调整碰撞板被碰撞点离底座上表面的高度测量得到两种不同高度所对应的投射距离，从而计算出颗粒物料在不同条件下的恢复系数。

以杂交水稻稻种为例，测量了3种稻种在不同影响因素及水平条件下的恢复系数，效果较好。

通过正交表的工程平均，并进行回归分析，得到了一定含水率稻种的恢复系数与下落高度之间的回归方程。

【期刊名称】农机化研究
【年(卷),期】2009(031)010
【总页数】3
【关键词】颗粒物料；恢复系数；测量原理；运动学；应用
0 引言
颗粒物料在自然界中普遍存在，在工程领域中应用广泛。

颗粒物料的物理特性是设计和研究与之相关装备的基础数据，许多颗粒物料的动态仿真结果极大地依赖于颗粒物料的物理特性[1]。

颗粒物料的恢复系数表示了颗粒物料被碰撞后能恢复到其原始状态(碰撞前)的性能，从而在农业工程和化学工程等领域中广泛应用。

例如，设计播种机时确定种子落入种植沟底的碰撞、跳跃和弹射，种子在刮种器和投种器中各种形态的碰撞和弹射，种子在成穴过程中承受的投掷作用等，都需要种子的恢复系数[2]。

在确定颗粒物料或散粒物料的流体动力学仿真的壁面边界条件时，需要该颗粒物料的恢复系数[3]。

颗粒物料恢复系数的测量可以利用高速CCD相机拍下物料碰撞前后的运动轨迹，并通过计算获得，。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

密度碰撞恢复系数测量
作者：顾炳龙杨亚洲张玉虎
来源：《农业与技术》2017年第05期
摘要：为了深入探讨花生脱壳机脱壳过程中花生的运动情况，通过离散元软件Edem的颗粒仿真效果，测花生参数：密度、碰撞恢复系数，建立颗粒模型加以仿真，导出其工作过程图像，以期为花生脱壳机的运动情况提供借鉴。

选取品种为大白沙和花育23的花生做参数测量试验。

关键词：密度；摩擦系数；刚度系数；弹性系数；碰撞恢复系数
中图分类号：S23 文献标识码：A DOI：10.11974/nyyjs.20170332018
引言
花生的种植历史悠久，地域广阔，在世界上种植面积仅次于油菜，而在世界油料生产和国际贸易中也是仅次于大豆，同样居于第2位。

花生是我国重要的油料作物和优质蛋白资源。

脱壳是花生种植及油用、食用加工前的必经工序，是影响花生果仁及其制品品质和商品性的关键[1-3]。

机械化脱壳加工技术由于脱净率低、破损率高，改善脱壳部件，提高效率尤为迫切；用软件可以在部件改进时进行大量仿真，达到节约成本的目的。

本文通过对Edem前期数据的测量，以期用Edem为花生部件改进、花生实际效果对比做出准备工作。

1 密度的测量
1.1 试验设备
量程为250mL细直量筒、精度为0.01g的电子天平。

1.2 试验方法
每种花生选取30粒，分3组，每组10粒，分别测其壳重与仁重。

在刻度为250mL量筒中先装入150mL的水，然后分别把壳和仁浸入水中，测其体积。

通过公式
求出其体积，由于每种花生得出3个值，求平均。

下图所选花生为花育23。

1.3 试验结果分析
花育23壳密度为0.445g/mL，仁密度为0.982g/mL；大白沙壳密度为0.307g/mL，仁密度为0.911g/mL。

2 碰撞恢复系数的测量
2.1 试验设备
2.2 试验方法
首先调节好设备，在桌面上调节好设备。

首先在桌面上放好花生碰撞材料（铁板、尼龙、花生壳），然后按照30cm、40cm、50cm的高度向下投放花生壳或仁，测出花生壳或仁弹起的高度。

由牛顿碰撞定律知，对于材料一定的两物体，它们碰撞后开开的相对速度v2-v1余碰撞前接近的相对速度v10-v20成正比，比值e称为恢复系数，即：
2.3 试验结果分析
见表1和表2。

对于高度而言，种子的碰撞系数呈现先增大后减小的趋势，这是由于花生在运动过程中损耗了能量。

对于花生而言，花生仁与其它材料的碰撞系数高于花生壳和花生整体的碰撞系数，这是由于花生仁的密度比花生壳和花生整体大，使碰撞能量更加集中。

3 总结
花育23壳密度为0.445g/mL，仁密度为0.982g/mL；大白沙壳密度为0.307g/mL，仁密度为0.911g/mL。

不同的花生品种对碰撞恢复系数影响不大；高度对碰撞系数的影响呈现先增大后减小的趋势；仁的碰撞系数高于壳和花生整体的碰撞恢复系数。

参考文献
[1]吕小莲，胡志超，于向涛，刘敏基，于昭洋.花生种子挤压破碎机理的试验研究[J].2013（4）.
[2]尚书旗，刘曙光，王方艳，等.花生生产机械的研究现状与进展分析[J].农业机械学报，2005（03）：143-147.
[3]程献丽，高连兴，刘明国，王瑞丽，那雪姣. 花生冲击脱壳的力学特性试验[J].2009-02，40（1）：111-113.
[4]李政权.基于离散元法的小麦排种器的数字化设计方法研究[D].长春：吉林大学，2009（6）.。