斯坦纳树问题及其推广
斯坦纳树算法

斯坦纳树算法
斯坦纳树是一棵连接所有图节点的生成树,其边权和最小。
斯坦纳树问题是NP难问题,因此通常需要使用近似算法进行求解。
斯坦纳树算法的基本思想是:将原图中的所有边分解为若干个小图,然后对每个小图分别求解最小生成树。
最后,将所有小图的最小生成树通过一些边连接起来,形成最小斯坦纳树。
斯坦纳树算法的时间复杂度为O(2^n * n^2),其中n为图中节点的数量。
该算法适用于节点数量较少的图,但对于大规模的图来说,其运行时间会非常长,因此需要结合其他算法进行优化。
- 1 -。
图的steiner最小树问题及其求解

图的steiner最小树问题及其求解摘要:斯坦纳树问题是组合优化学科中的一个问题。
属于NP-难问题,即无法在多项式时间内得到最优解。
本文主要讨论了图的steiner最小树问题,并给出了近似算法,该算法是在破圈法的基础上进行了改进,并且引用了agent的思想。
最后对算法进行了分析。
关键词:Steiner最小树NP-难题破圈法中图分类号:TP312文献标识码:A文章编号:1009-3044(2009)25-7312-02Graphical Steiner Minimum Tree Problem and SolusionYANG Ling-yun(College of Computer and Information Engineering, Henan University, Kaifeng 475001,China)Abstract: Steiner tree problem is one of the subject of combinatorial optimization problem. It belongs to NP-hard problems that cann’t find the optimal solution in polynomial time. This article discusses the minimum steiner tree problem in graphs, and gives the approximate algorithm, which is improved on loop damage method, and quoted the agent's thinking. Finally, an analysis of the algorithm.Key words: steiner minimum tree; NP-hard problem; loopdamage method现实生活中经常要求解决这样的问题,即将若干给定点相连并使连线的总长最短。
9A1 最小瓶颈支撑树和斯坦纳树

最小瓶颈支撑树和斯坦纳树MBST and Steiner Tree设( G, W ) 是无向连通赋权图,G的所有支撑树中权值最大的边的权值最小的支撑树称为G的最小瓶颈支撑树(minimal bottleneck spanning tree, MBST)AE C D 235910F B 478A E C D 2359F B 4AE C D 239F B 78A E C D 59F B 478MST⏹定理❑无向连通赋权图的最小支撑树一定是最小瓶颈支撑树,但最小瓶颈支撑树不一定是最小支撑树⏹证明 —— MST 一定是MBST❑假设最小支撑树 T 不是最小瓶颈支撑树,设 T 的最大权值边为 e ,则最小瓶颈支撑树 T b 的所有边的权值都小于 w (e )❑删除 T 中的 e 形成两棵数 T 1 和 T 2 ❑由于 T b 连通,因此存在 T b 的边 e ',连接 T 1 中某顶点和 T 2 中某顶点。
于是用 e ' 连接 T 1 和 T 2 后得到得到新的支撑树,但其总权值小于 T ,与 T 是最小支撑树产生矛盾 e T 2 e'T 1⏹证明—— MBST不一定是MST❑考虑一个无向连通赋权图,图中仅存在一条桥而且权值最大,则图中每个支撑树(无论是否最小支撑树)都是最小瓶颈支撑树w⏹设( G=(V, E), W ) 是无向连通赋权图,R V,在G的所有包含R中所有顶点的子图中,总权值最小的树称为G的斯坦纳树(Steiner tree)⏹当R = V时,斯坦纳树问题即是最小支撑树问题adc b21 1 12 2 a d cb 1 1 1adc b43 3 34 4 a d c b 4 4⏹虽然斯坦纳树问题与最小支撑树问题具有相似之处,然而斯坦纳树问题则难得多❑属于NPC问题,事实上,它是卡普(Richard Manning Karp)证明的第一批21个NPC问题之一E nd。
斯坦纳树模型在含DG配电网规划中的应用

斯坦纳树模型在含DG配电网规划中的应用韩翔宇;刘涤尘;廖清芬;贾骏;朱正;胡静竹【摘要】不确定性分布式电源的接入,给配电网规划带来新的挑战.首先将含分布式电源的配电网规划归纳为求解斯坦纳树问题,提出了一种新的配电网规划建模方法.其次通过DG供电分区的划定,将分区内的负荷节点处理为一个不接DG的负荷节点,消除DG对配电网规划的影响.针对斯坦纳树问题传统解法求解时间会随着斯坦纳点的规模成倍增加的缺陷,采用一种改进的粒子群优化(PSO)算法解决斯坦纳树N-P完全问题.结合54节点算例并与传统方法计算结果比较,验证了该方法的有效性.【期刊名称】《电力系统及其自动化学报》【年(卷),期】2016(028)006【总页数】6页(P62-67)【关键词】分布式电源;配电网规划;斯坦纳树;供电分区;改进粒子群优化算法【作者】韩翔宇;刘涤尘;廖清芬;贾骏;朱正;胡静竹【作者单位】武汉大学电气工程学院,武汉430072;武汉大学电气工程学院,武汉430072;武汉大学电气工程学院,武汉430072;武汉大学电气工程学院,武汉430072;武汉大学电气工程学院,武汉430072;武汉大学电气工程学院,武汉430072【正文语种】中文【中图分类】TM715分布式电源DG(distributed generation)是直接接在用户附近或配网中的小型发电设备,它能使清洁能源和分散能源得到充分利用,缓解能源危机。
配电网规划是带有约束条件的非线性混合整数优化问题,DG的加入使规划难度增加。
所以含DG的配电网规划也就成为配电网规划中的一个难点。
含DG的配电网规划可划分为两部分:DG对配电网及规划的影响研究[1]和计及DG的配电网协调规划研究。
目前协调规划的主流求解算法有启发式算法[2]、数学规划算法[3]、随机优化算法[4]等。
启发式算法计算无法保证结果的最优性,数学规划算法无法逃避随着求解规模的增大算法难收敛的问题,以遗传算法[5-6]、蚁群算法与禁忌搜索[7]、粒子群算法[8]等或相应的改进算法为代表的随机优化算法是目前的研究热点。
最小斯坦纳树学习笔记
最⼩斯坦纳树学习笔记定义摘⾃百度百科的定义:斯坦纳树问题是组合优化问题,与最⼩⽣成树相似,是最短⽹络的⼀种。
最⼩⽣成树是在给定的点集和边中寻求最短⽹络使所有点连通。
⽽最⼩斯坦纳树允许在给定点外增加额外的点,使⽣成的最短⽹络开销最⼩。
可以这么理解:⼀个图的⽣成树是构造⼀棵树把所有点给联通,⽽斯坦纳树则是构造⼀棵树把给定的⼏个点联通。
如同⽣成树有最⼩的⼀棵,斯坦纳树也有最⼩的。
如何求最⼩斯坦纳树,是我们今天要探讨的话题。
实现例题:Luogu P6192【模板】最⼩斯坦纳树给定⼀个包含n个结点和m条带权边的⽆向连通图G=(V,E)。
再给定包含k个结点的点集S,选出G的⼦图G′=(V′,E′),使得:S⊆V′G′为连通图;E′中所有边的权值和最⼩。
你只需要求出E′中所有边的权值和。
n≤100,m≤500,k≤10。
求最⼩斯坦纳树,我们使⽤的是状压DP。
⾸先⾮常显然的是,这个选出来的⼦图G′⼀定是个树。
令f i,S表⽰当前这个树的根为i,选出的点的集合为S(注意这⾥选出的点专指那k个点中的点),这⾥的S在 dp 中是被状压的。
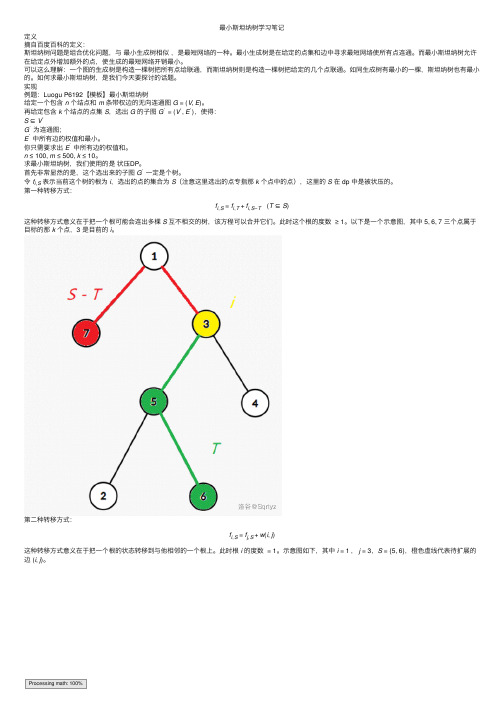
第⼀种转移⽅式:f i,S=f i,T+f i,S−T (T⊆S)这种转移⽅式意义在于把⼀个根可能会连出多棵S互不相交的树,该⽅程可以合并它们。
此时这个根的度数≥1。
以下是⼀个⽰意图,其中 5,6,7 三个点属于⽬标的那k个点,3 是⽬前的i。
第⼆种转移⽅式:f i,S=f j,S+w(i,j)这种转移⽅式意义在于把⼀个根的状态转移到与他相邻的⼀个根上。
此时根i的度数=1。
⽰意图如下,其中i=1,j=3,S={5,6},橙⾊虚线代表待扩展的边 (i,j)。
Processing math: 100%考虑 dp 顺序,显然S从⼩到⼤枚举即可。
对于第⼀种转移⽅式,只需枚举S的⼦集T。
对于第⼆种转移⽅式,注意到这玩意⼉是个三⾓不等式,联想到最短路也是如此——没错,⽤最短路跑⼀遍就⾏了。
参考代码int n, m, k, f[Maxn][1 << Maxk];struct Edge {int next, to, dis;}edge[Maxm * 2];int head[Maxn], edge_num;void add_edge(int from, int to, int dis) {edge[++edge_num].next = head[from];edge[edge_num].to = to;edge[edge_num].dis = dis;head[from] = edge_num;}queue <int> Q; int dist[Maxn]; bool inq[Maxn];void SPFA(int S) {memset(inq, 0, sizeof(inq));for(int i = 1; i <= n; ++i) {dist[i] = f[i][S];if(dist[i] != 1061109567) Q.push(i), inq[i] = 1;}while(Q.size()) {int u = Q.front();Q.pop();inq[u] = 0;for(int i = head[u]; i; i = edge[i].next) {int v = edge[i].to;if(dist[v] > dist[u] + edge[i].dis) {dist[v] = dist[u] + edge[i].dis;if(!inq[v]) {inq[v] = 1;Q.push(v);}}}}for(int i = 1; i <= n; ++i) f[i][S] = dist[i];}int main() {n = read(); m = read(); k = read();int u, v, w;for(int i = 1; i <= m; ++i) {u = read(); v = read(); w = read();add_edge(u, v, w);add_edge(v, u, w);}memset(f, 63, sizeof(f));for(int i = 1; i <= k; ++i) {u = read();f[u][1 << (i - 1)] = 0;}for(int i = 1; i <= n; ++i) f[i][0] = 0;for(int S = 0; S < (1 << k); ++S) {for(int i = 1; i <= n; ++i)for(int T = S & (S - 1); T; T = S & (T - 1))f[i][S] = min(f[i][S], f[i][T] + f[i][T ^ S]);SPFA(S);}int ans = 2e9;for(int i = 1; i <= n; ++i) ans = min(ans, f[i][(1 << k) - 1]);cout << ans << endl;return 0;}例题[WC2008] 游览计划考虑把每个⽅格当成⼀个点,最⼩斯坦纳树搞它就完了。
图的steiner最小树问题及其求解

图的steiner最小树问题及其求解作者:杨凌云来源:《电脑知识与技术》2009年第25期摘要:斯坦纳树问题是组合优化学科中的一个问题。
属于NP-难问题,即无法在多项式时间内得到最优解。
本文主要讨论了图的steiner最小树问题,并给出了近似算法,该算法是在破圈法的基础上进行了改进,并且引用了agent的思想。
最后对算法进行了分析。
关键词:Steiner最小树 NP-难题破圈法中图分类号:TP312文献标识码:A文章编号:1009-3044(2009)25-7312-02Graphical Steiner Minimum Tree Problem and SolusionYANG Ling-yun(College of Computer and Information Engineering, Henan University, Kaifeng 475001,China)Abstract: Steiner tree problem is one of the subject of combinatorial optimization problem. It belongs to NP-hard problems that cann’t find the optimal solution in polynomial time. This article discusses the minimum steiner tree problem in graphs, and gives the approximate algorithm, which is improved on loop damage method, and quoted the agent's thinking. Finally, an analysis of the algorithm.Key words: steiner minimum tree; NP-hard problem; loop damage method现实生活中经常要求解决这样的问题,即将若干给定点相连并使连线的总长最短。
几类特殊的斯坦纳最小树问题

几类特殊的斯坦纳最小树问题【基金项目】2010 年度浙江省大学生科技创新活动计划 (新苗人才计划)【立项项目】“几类特殊斯坦纳最小树问题的研究”研究成果( 2010R424038).一、斯坦纳最小树的性质1.已知3 点的斯坦纳最小树关于斯坦纳最小树问题,17 世纪法国数学家费马曾有过类似的研究.他提出了费马点问题:“在平面上,任给△ ABC试求一点S,使它到A,B, C三点的距离之和最小•”这个问题在费马提出后不久就被托里拆利解决了,并得到了相关的结论:在△ ABC中,/A为其最大角,S是平面上的点.(1)当/A>xO=[0,1 : >>x=fminunc(f,x0)用MATLAB^件运行,得结果是:x1=1.9671 , x2=1.57,最小距离为5.393.对于4 个点的斯坦纳最小树,如果这4 个点构成凸四边形,类似于正方形,其斯坦纳最小树有2个斯坦纳点S1,S2;如果4个点构成凹四边形,当/ ADB h BDC h CDA=120时,连线段AD,DB,DC即为其斯坦纳最小树,不必添加斯坦纳点.而当/ ADB,Z BDC,Z CDA不全相等时,不妨设/ CDA最小,那么其斯坦纳最小树中斯坦纳点只有1个,该点必为△ ADC的费马点S.其实数学家已经证明了此类问题目前尚未找到有效的算法,即它是个“ NP问题” •例如寻找1个由4点构成的正方形的斯坦纳点的程序:f=(x)sqrt((x(1)-0)八2+(x(2)-0)八2)+sqrt((x(1)-0)八2+(x(2)-1)八2)+sqrt((x(3)-1)八2+(x(4)-0)八2)+sqrt((x(3)-1)八2+(x(4)-1)A2)+sqrt((x(1) -x(3))八2+(x (2)-x(4))A2);>>x0=[0,1,2,3 ]>>x=fminunc(f,x0)用MATLAB^件运行,得结果(即最优解)是:x1=0.2887,x2=0.5,x3=0.7113,x4=0.5 ,连线总长度最小为d=2.7321.上述研究仅是用初等方法给出了不多于4 个点的斯坦纳最小树及其算法,那么5 点甚至更多点的斯坦纳最小树及其算法值得我们进一步研究.。
steiner树问题的近似算法

steiner树问题的近似算法
马绍汉;王锐
【期刊名称】《计算机学报》
【年(卷),期】1989(012)007
【摘要】著名的Steiner树问题是,给定图G=(V、E),QV,在边集E上定义权函数f:E→Z^+,要求在图G上找一子树T=(Y,U),使得QY且∑_(c∈U)f(e)达到极小以后,我们称该问题为ST问题,R.M.Karp曾证明ST问题为NP-完全的,本文作者曾提出图上Steiner树问题:在图G=(V,E),QV上,要求一子树T=(Y,
【总页数】3页(P558-560)
【作者】马绍汉;王锐
【作者单位】不详;不详
【正文语种】中文
【中图分类】TP311.12
【相关文献】
1.改进的基于拓扑分析的Steiner树近似算法 [J], 高磊;张德运;王晓东;安智平
2.关于满Steiner树问题的一个近似算法 [J], 罗美菊;赵传立;唐恒永
3.多材料Terminal Steiner树拼接问题的近似算法研究 [J], 文永松;朱淑娟;庞一成
4.近乎最佳的Manhattan型Steiner树近似算法 [J], 马军;杨波;马绍汉
5.图的Steiner树问题的改进的快速近似算法 [J], 吕其诚
因版权原因,仅展示原文概要,查看原文内容请购买。
Steiner树

HPM&S
(1) Steiner点的由来
19世纪中期,瑞士数学家J.Steiner将三点Fermat问题推广
到n个顶点,即Euclid平面上给定n给点v1,v2,…vn',在平面上 ' V V,…,v 的 总 距 离 求 一 , 使 得 到 v1,v2 n ' ' v1v v2v vnv' 最短。
(1)求给定的n个点上的最小生成树,记录其费用 ; (2)取一个可能的Steiner点加入,求最小生成树 ; (3)若该树的费用小于当前的最小费用,则记录此 树并更新费用;
(4)重复(2)到(4)直到已有n-2个Steiner点, 或任何剩余的Steiner点加入都不能减少费用。
HPM&S
5.5.3 贪婪算法
典型应用:组播树
单播模型中,数据包通过网络沿着单一路径从源主机向目标主机传 递;
组播模型中,组播源向某一组地址传递数据包,而这一地址却代表 一个主机组。为了向所有接收者传递数据,一般采用组播分布树描述 IP组播在网络里经过的路径。
返回
HPM&S
3.活动简介
所需材料
钉子、线(橡皮绳)、直尺(卷尺)、笔和纸
如果∠B≥ 如果∠B<
120 ,则点U是Fermat点;
120 ,则AC是大边。以AC为一边,在
△ABC的另一侧做等边三角形△ACD,连接BD, 交 △ ACD 的 外 接 圆 于 U , 则 ∠AUB=∠BUC=∠AUC= ,因此U是Fermat点, 120 而AU,BU,CU为最小总距离上三条线段。 返回
4)从m个点中另取s个点重复2),3)直到穷尽m个点中所有可能的点组合。
HPM&S
Steiner最小树问题及其应用

第8卷 第15期 2008年8月1671-1819(2008)15-4238-09科 学 技 术 与 工 程Science T echno logy and Eng i neeringV ol 18 N o 115 A ug . 2008Z 2008 Sci 1T ech 1Engng 1综 述数 学Steiner 最小树问题及其应用张 瑾1,2马 良1*(上海理工大学管理学院1,上海200093;河南大学计算机与信息工程学院2,开封475001)摘 要 Ste i ner 最小树问题是一个历史悠久的经典的组合优化问题,由于应用广泛,多年来一直受到研究者的广泛关注。
介绍了各种S teine r 树问题及其求解算法和实际应用。
关键词 Ste i ner 最小树 精确算法 启发式算法 应用中图法分类号 O 224; 文献标志码 A2008年4月21日收到国家自然科学基金项目(70471065)、上海市重点学科建设项目(T0502)资助第一作者简介:张 瑾(1974)),女,河南开封人,博士生1研究方向:系统工程、智能优化。
*通信作者简介:马 良(1964)),男,上海人,博士,教授,博士生导师1研究方向:智能优化。
现实生活中经常要求解决这样的问题,即将若干给定点相连并使连线的总长最短。
在网络通信领域中,该问题被一般化地提为:如果要在n 个区域间铺设通信网,使得各区域之间能实现信息的共享,那么应如何铺设才能使通信线路的总长最短?一般首先想到的可能就是求连接这n 个点的最小生成树(M i n i m um Spann i n g Tree )M ST )这种做法,但如果不拘泥于这n 个点,而引入除这n 个点之外的另外几个点的话,则有可能使连接各区域的通信线路的总长更短。
这是Steiner 最小树问题(Steiner M i n i m u m Tree Prob le m ,简记为S MTP)的来源。
S teiner 最小树问题是经典的组合优化问题,最早可以追溯到17世纪初。
定直线的欧式2-斯坦纳树问题

定直线的欧式2-斯坦纳树问题全文共四篇示例,供读者参考第一篇示例:欧式2-斯坦纳树问题是图论中的一个经典问题,也是计算机科学领域中的一个重要研究课题。
该问题的目标是找到一个连接给定点集合中所有点的最小生成树,且这个生成树中只包含给定的点和连接这些点的边。
欧式2-斯坦纳树问题是在斯坦纳树问题的基础上进行了扩展和优化。
在斯坦纳树问题中,给定一组点和一个连接这些点的权重边集合,需要找到一个包含所有给定点的生成树,使得生成树的总权重最小。
而在欧式2-斯坦纳树问题中,不仅需要考虑点之间的欧式距离,还需要考虑连接这些点的边的长度,以及生成树的总长度。
欧式2-斯坦纳树问题在实际应用中有着广泛的应用场景,比如在通信网络中优化网络拓扑结构、在城市规划中设计最优交通路线、在社交网络中提高信息传播效率等。
研究和解决这个问题对于优化现实生活中的各种问题具有重要意义。
在解决欧式2-斯坦纳树问题时,可以采用多种算法和方法。
其中最常用的算法之一就是最小生成树算法,比如Prim算法和Kruskal算法。
这些算法可以在给定点和边的情况下找到一个最小生成树,保证了生成树的总长度最小。
在解决欧式2-斯坦纳树问题时,还可以考虑使用近似算法或者启发式算法来求解。
这些算法虽然不能保证找到最优解,但可以在较短的时间内找到一个接近最优解的解。
可以使用贪心算法、遗传算法、模拟退火算法等来求解欧式2-斯坦纳树问题。
除了算法和方法的选择,还需要考虑如何设计合适的数据结构来表示图、点和边。
在欧式2-斯坦纳树问题中,图可以用邻接矩阵或邻接链表来表示,点可以用坐标表示,边可以用权重表示。
通过合理设计数据结构,可以简化算法的实现,提高算法的效率。
欧式2-斯坦纳树问题是一个复杂且具有挑战性的问题,但是通过合理选择算法和数据结构,可以有效地解决这个问题。
在实际应用中,可以根据具体的需求和场景来选择合适的算法和方法,从而优化解决方案。
希望通过不断地研究和探索,可以进一步提高欧式2-斯坦纳树问题的求解效率和准确度,为实际问题的优化提供更好的方案。
最小斯坦纳树解决最优布线问题

用最小斯坦纳模型解决布线问题[问题描述]给出平面上若干个点(不超过10个),用一些水平或者竖直的线段(线段的端点不一定是这些要连接的点)将这些点连接起来,要求线段的总长度最小。
如下图所示,其中由红色圆环和黄色实心构成的圆形表示需要连接的点。
它们的坐标就是程序的输入信息。
绿色的线条表示程序经过计算得到的最优布线方案。
注意到,图中还有一些黄色的点。
这些点是程序在运行过程中计算出来的点,这些点的位置正好是某一个需要连接的点在这些横着或竖着的线段上的投影。
我们可以看到,线段的端点可以是黄色的点也可以是必须要连接的点。
[算法分析]观察上图,我们发现每一条线段上都有若干个点,这些点可能是黄色的点也有可能是需要连接的点。
每一条线段上的点将这条线段分为一个一个的小线段。
这些小线段之间的交点只可能是小线段的端点。
现在我们的问题变为,给出平面上一些需要连接的点集A。
在平面上选择一些不属于A的点,这些点组成的集合称为B。
设。
我们找一些的水平或竖直的并且端点都属于C的线段,能将C中所有的点连接起来,并且线段的总长度最小。
我们称这个问题为问题二。
显然问题二和原问题是等价的。
我们先来分析一下为使线段的总长度最小,B集合内点的选取可以缩小到什么范围。
我们有如下结论:B集合中每一个点的横坐标一定是A集合中某个点的横坐标;B集合中每一个点的总坐标一定是A集合中某个点的纵坐标。
为了说明这个结论,我们观察上图。
我们能够发现,B集合(所有黄色的点)中任意一个点,对于经过它的水平直线一定穿过至少一个A集合中的点;对于经过它的竖直直线一定穿过至少一个A集合中的点。
这个结论的证明思路比较简单,所以这里略去。
有了上面这个结论,我们可以对问题二进行初步的处理。
对于输入的需要连接的同一平面上的点集A,我们考虑将每个A中的点用一条水平的直线和一条竖直的直线穿过。
如果平面上某个点是某一条水平直线和某一条竖直直线的交点,并且这个点不是A中的点,那么我们将这个点加入集合D。
斯坦纳树入门小记

斯坦纳树⼊门⼩记
前⾔
普通的最⼩⽣成树,是⽤于求使给定点集连通的最⼩代价。
⽽斯坦纳树的不同点就在于,除了必选点之外,它还可以选择⼀些不必连通的辅助点,起到减⼩代价的作⽤。
⼤致思想
考虑最朴素的状压DP,设f S表⽰连通点集S的最⼩代价。
但是,斯坦纳树的题⽬⼀般都是必选点数量很⼩,辅助点数量却可能很多。
因此我们不得不改变状态的设⽴⽅式:f i,S表⽰以i为根、连通必选点点集S的最⼩代价。
说是以i为根,实际上这个根并没有什么具体意义,只是单纯⽅便转移⽽已。
然后转移就⽤两种⽅式:
根据点转移:枚举S的⼀个⼦集T,得到f i,S=f i,T+f i,S xor T−a i。
即把凭借a i连通的两个连通块合并起来,减去a i是因为它在两个连通块中都有贡献,计算重复了。
根据边转移:枚举⼀条边(u,v),得到f v,S=f u,S+a v。
不难发现这就相当于是⼀个最短路的式⼦,直接SPFA即可。
例题
板⼦题:。
Processing math: 100%。
06程序游戏

其它包含重要概念的谜题有:解决了河马称重问题的阿基米德浮体定律;在决策理论中尚未解决的诸如分配家务劳动的问题;一些由窃贼或强盗提起的组合问题;一个由“懒惰的情人”提起的重要的曲线理论问题。
“曲线理论”是关于曲线连接的一系列点的研究。许多操作研究中的实际问题都可以用曲线表示出来,有些可有简洁的结果。如我们知道的如何用“克拉斯考运算法”排列树的最小间隔。另一个与此密切相关的问题,即“斯坦纳的树排问题”在总体上尚未解决。由于“斯坦纳树”问题有许多实际应用,关于开发解决这一问题的高效计算机运算法的大量研究工作正在进行。
有可能改变划井游戏的规则,在允许获得四个单元的模式而不是直行的情况下,在两个游戏之间建立起同型性吗?
上一页 下一页
河马难题
a.很多年以前,某个部落的首领十分尊崇神圣的河马。
b.每年在首领生日的这天,首领和他的收税官都要用王室的驳船载着河马到收税站去。
d.卡内先生:你放镍币,我放银币。谁先放了三个相加等于15的不同数字,谁就可得到案子上所有的钱。
e.让我们看一个典型的玩法。这位妇人先把一枚镍币放在7上。由于7已被放上,其他人就不能再放了。对其它数字也是如此。
f.设盘者把一枚银币放在8上。
g.妇人下一次将把镍币放在2上,这样再放一次6,三个数字相加为15,就可以赢了。
“妙”是指一种算法能在最短的时间内解决问题。使用计算机需要花钱,就像雇工干活需要花钱一样。因此,具有高效(好)的算法,就具有很大的实际优势。一种被称为“操作研究”的数学热门分科,就是开发解决复杂问题的最高效方法。
尽管本部分的程序问题出于娱乐而作了选择,你还是可以很容易地了解许多深奥的数学概念。如第一个谜题,生动地表明数学家们把两个看似不相关的问题称为“同型”的含义。游艺活动中有关数字的打赌比赛实际上含有与玩“划井游戏”相同的计谋。这与由加拿大数学家利奥·摩瑟发明的聪明的数学游戏以及用于网络系统的游戏是“同型的”。这些游戏的计谋都是基于3—3数字魔方,这是一种最古老的奇妙组合之一。
关于求解费马点问题的多种方法探究与综述

关于求解费马点问题的多种方法探究与综述作者:李静爽来源:《教育教学论坛》2016年第21期摘要:本文主要针对经典的三角形费马点问题及其加权推广问题,对几种方法(两种数学和两种物理解法)进行综述和扩展,展现不同解法的不同知识层次和逻辑思维方式,为不同的教育工作者都能提供一个较好的教学案例。
关键字:费马点;加权费马点;二元极值;最小势能;光行最速中图分类号:G642.0 文献标志码:A 文章编号:1674-9324(2016)21-0231-03费马点问题的原型为生产实践中经常遇到的一类问题——选址问题。
例如在三个城市之间建造一个垃圾场,如何选择垃圾场的位置,使其到三个城市的距离之和最小,这就是经典的三角形费马点问题。
进一步地,若从三个城市向垃圾场运送垃圾的代价不同,且与其距离成正比,如何选择垃圾场的位置使其总代价最小,那么就变为一个加权费马点问题。
费马点问题是17世纪时,由法国数学家费马在写给意大利数学家托里折利的一封信中最早提出,最早由托里拆利解决。
因此该问题后来被称为费马点问题。
有关费马点的研究很多,推广应用也很多。
主要是费马点问题具有多层次性,可以用初等数学知识求解,也可用高等数学知识求解,还可与物理知识结合求解。
题目可变换多种形式和深度,设计为中学题目,竞赛题目,可作为大学课堂例题,也可作为研究性课题,甚至是推广到组合优化中的斯坦纳树问题。
本文主要针对经典的三角形费马点问题及其加权推广问题,对几种方法进行综述和拓展,展现不同解法的不同知识层次和不同的逻辑思维方式,为不同的教育工作者均能提供一个较好的素材。
本文详细阐述和推导了求解三角形费马点问题的四种方法,并且每种方法均推广到了求解加权费马点的问题。
二元极值法需要利用高等数学中多元微分的知识,方法严谨,但不利于观察其中的几何特征;梯度法同样需要高等数学知识,方法简洁,且与几何特征相联系,是学习梯度时较好的课堂案例;最小势能解法和光行最速解法为物理解法,构思巧妙,学科交叉,启发思维,可以作为数学教学的案例,更可以作为物理应用的教学案例,都有助于培养学生的创造性思维。
浅析算法——斯坦纳树

浅析算法——斯坦纳树
斯坦纳树
⽤途
给⼀个图,求最⼩⽣成树?
这个很简单,prim/kruskal 搞⼀搞。
如果只要求联通某⼏个点,⽽不强制要求其他点的联通?
这个prim/kruskal 就不好做了。
那怎么求这个呢?
当然是要⽤到斯坦纳树啊。
计算⽅法
假设表⽰最后⼀个联通的是,当前要求点的联通性为(状态压缩),那么有两种状态转移:1. ,其中是的⼦集。
2. ,其中之间有边相连。
第⼀个⽅程是很好维护的,关键是第⼆个⽅程。
观察到,第⼆个⽅程与spfa 的⽅程很相似。
那么我们就可以⽤spfa 维护第⼆个⽅程啦!
例题
斯坦纳森林
⽤途
给⼀个图,求最⼩⽣成树?
这个很简单,prim/kruskal 搞⼀搞。
如果只要求联通某⼏个点,⽽不强制要求其他点的联通?
这个很简单,斯坦纳树可以解决这个问题。
如果只要求某⼏个集合中的点互相联通,⽽分属两个不同集合的点没有要求,可以共⽤边?这个就需要⽤斯坦纳森林了。
计算⽅法
把所有的集合放在⼀起,做⼀遍斯坦纳树,然后对所有集合做⼀遍⼦集合并dp 。
例题f i ,sta i sta =+f i ,sta f i ,s f i ,sta −s s sta =+va f i ,sta f u ,sta l u ,i u ,i =+va d v d u l u ,v。
平面上具有边长限制的斯坦纳树问题

平面上具有边长限制的斯坦纳树问题先来说说啥是斯坦纳树啊。
想象一下,你有几个点分布在一个平面上,就好像是地图上的几个小村庄。
现在呢,你要把这些村庄用道路连接起来,让大家可以互相往来。
普通的连接方法可能就是直接把每个村庄两两相连,这就好比是给每两个村庄都修一条直达的路。
但斯坦纳树可没那么简单,它是要找一种更巧妙的连接方式,可能会在这些村庄之外再找几个合适的点,然后通过这些新点和原来的村庄一起构建一个网络,使得总的道路长度最短。
这就像是在规划交通网络的时候,除了连接已有的城镇,还会考虑在一些关键位置设置中转站或者枢纽,让整个交通更高效。
那什么是边长限制呢?这就好比是给修路加了个条件。
比如说,咱们修的路不能太长,每一段路都有个长度上限。
这就像是规定了每一条路不能修得超过某个距离,不然成本太高啦,或者是有一些地理条件限制,没办法修太长的路。
解决这个问题可不容易啊。
你得考虑好多因素。
要找到那些合适的额外的点,也就是斯坦纳点,它们的位置得恰到好处,既能帮助减少总的连接长度,又不能让某一段路超过规定的边长限制。
这就像是找一个最佳的中转站位置,既要方便各个小区,又不能离得太远。
而且,不同的点的分布情况会对结果产生很大的影响。
如果这些点比较集中,那可能相对好规划一些;但要是点很分散,又有边长限制,那就得绞尽脑汁去设计方案了。
有时候,可能看似找到了一个不错的方案,但稍微调整一下某个点的位置或者连接方式,就会发现又有更好的方案出现。
在数学领域,好多聪明的脑袋都在研究这个问题。
他们用各种算法和方法去尝试找到最优解。
有的算法就像是在平面上一步一步地试探,看看哪个方向、哪个位置能让总的长度最短,同时又不违反边长限制;有的则是通过一些数学模型和公式来分析计算,试图从理论上找到最好的答案。
不过呢,虽然这个问题很有挑战性,但研究它也很有意义。
在实际生活中,除了刚才说的城市规划、管道铺设,像通信网络的布局、电路设计等很多方面都会用到相关的知识。
对于堵,黄的“也谈Steiner树问题”一文的答复

对于堵,黄的“也谈Steiner树问题”一文的答复
越民义
【期刊名称】《运筹学杂志》
【年(卷),期】1996(015)001
【摘要】前面发表的是堵丁柱和黄光明两教授所写的'也谈 Steiner 树问题'的文章(下面简称'也谈').文章对我在本刊1995年第一期发表的文章中对他们在1992年在 Algorithmica 第七期上关于 Steiner 树的文章(下面简称'文章')所提的一些问题作了答复,对此我在此表示感谢.下面我将进一步阐明我所提出的问题,并对'文章'和'也谈'提出一些看法.一、我在上期文章中所提出的第一个问题是针对'文章'中的引理10的证明来说的.为了将我的问题说得更清楚一些。
【总页数】2页(P71-72)
【作者】越民义
【作者单位】中国科学院应用数学研究所
【正文语种】中文
【中图分类】O224
【相关文献】
1.对<热辐射光谱"蓝移"问题的商榷>一文的答复 [J], 冯炽焘;王忆锋
2.南岭骑田岭花岗岩基属印支期侵位的岩浆动力学佐证:对《关于南岭花岗岩侵位年龄问题》一文的答复与讨论 [J], 章邦桐;吴俊奇;凌洪飞;陈培荣
3.深埋隧道外水压力计算中几个问题的探讨——对"读《深埋隧道外水压力计算的解析-数值法》一文随笔"的答复 [J], 王建秀
4.对郭立田同志《也谈唯物辩证法的三个基本规律》一文的答复 [J], 庞长富
5.汉语史研究中的概念、材料、方法与理论问题——对“《汉语语法化的历程》商兑”一文的答复 [J], 石毓智
因版权原因,仅展示原文概要,查看原文内容请购买。
