斯坦纳最小树
图的steiner最小树问题及其求解

图的steiner最小树问题及其求解摘要:斯坦纳树问题是组合优化学科中的一个问题。
属于NP-难问题,即无法在多项式时间内得到最优解。
本文主要讨论了图的steiner最小树问题,并给出了近似算法,该算法是在破圈法的基础上进行了改进,并且引用了agent的思想。
最后对算法进行了分析。
关键词:Steiner最小树NP-难题破圈法中图分类号:TP312文献标识码:A文章编号:1009-3044(2009)25-7312-02Graphical Steiner Minimum Tree Problem and SolusionYANG Ling-yun(College of Computer and Information Engineering, Henan University, Kaifeng 475001,China)Abstract: Steiner tree problem is one of the subject of combinatorial optimization problem. It belongs to NP-hard problems that cann’t find the optimal solution in polynomial time. This article discusses the minimum steiner tree problem in graphs, and gives the approximate algorithm, which is improved on loop damage method, and quoted the agent's thinking. Finally, an analysis of the algorithm.Key words: steiner minimum tree; NP-hard problem; loopdamage method现实生活中经常要求解决这样的问题,即将若干给定点相连并使连线的总长最短。
【浙江省自然科学基金】_城市设计_期刊发文热词逐年推荐_20140812

推荐指数 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2009年 序号 1 2 3 4 5 6 7 8
科研热词 行为模式 维修管理系统 社区公园 时空推理 建模 建成环境评价 多agent系统定性推理 城市轨道交通
推荐指数 1 1 1 1 1 1 1 1
2010年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
2012年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52
2008年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18
科研热词 高效建模 飞灰 通用分组无线业务 水泥 气象条件 无线监控 无标度 指数分布 建筑模型模板库 嵌入式系统 小世界 实时绘制 复杂网络 城市污水排放 城市场景 土壤聚合物 固化 公共交通网络
推荐指数 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2013年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52
最小斯坦纳树学习笔记
最⼩斯坦纳树学习笔记定义摘⾃百度百科的定义:斯坦纳树问题是组合优化问题,与最⼩⽣成树相似,是最短⽹络的⼀种。
最⼩⽣成树是在给定的点集和边中寻求最短⽹络使所有点连通。
⽽最⼩斯坦纳树允许在给定点外增加额外的点,使⽣成的最短⽹络开销最⼩。
可以这么理解:⼀个图的⽣成树是构造⼀棵树把所有点给联通,⽽斯坦纳树则是构造⼀棵树把给定的⼏个点联通。
如同⽣成树有最⼩的⼀棵,斯坦纳树也有最⼩的。
如何求最⼩斯坦纳树,是我们今天要探讨的话题。
实现例题:Luogu P6192【模板】最⼩斯坦纳树给定⼀个包含n个结点和m条带权边的⽆向连通图G=(V,E)。
再给定包含k个结点的点集S,选出G的⼦图G′=(V′,E′),使得:S⊆V′G′为连通图;E′中所有边的权值和最⼩。
你只需要求出E′中所有边的权值和。
n≤100,m≤500,k≤10。
求最⼩斯坦纳树,我们使⽤的是状压DP。
⾸先⾮常显然的是,这个选出来的⼦图G′⼀定是个树。
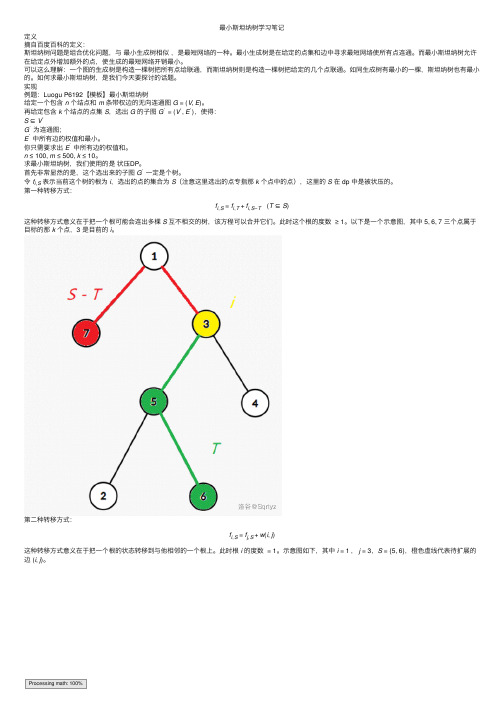
令f i,S表⽰当前这个树的根为i,选出的点的集合为S(注意这⾥选出的点专指那k个点中的点),这⾥的S在 dp 中是被状压的。
第⼀种转移⽅式:f i,S=f i,T+f i,S−T (T⊆S)这种转移⽅式意义在于把⼀个根可能会连出多棵S互不相交的树,该⽅程可以合并它们。
此时这个根的度数≥1。
以下是⼀个⽰意图,其中 5,6,7 三个点属于⽬标的那k个点,3 是⽬前的i。
第⼆种转移⽅式:f i,S=f j,S+w(i,j)这种转移⽅式意义在于把⼀个根的状态转移到与他相邻的⼀个根上。
此时根i的度数=1。
⽰意图如下,其中i=1,j=3,S={5,6},橙⾊虚线代表待扩展的边 (i,j)。
Processing math: 100%考虑 dp 顺序,显然S从⼩到⼤枚举即可。
对于第⼀种转移⽅式,只需枚举S的⼦集T。
对于第⼆种转移⽅式,注意到这玩意⼉是个三⾓不等式,联想到最短路也是如此——没错,⽤最短路跑⼀遍就⾏了。
参考代码int n, m, k, f[Maxn][1 << Maxk];struct Edge {int next, to, dis;}edge[Maxm * 2];int head[Maxn], edge_num;void add_edge(int from, int to, int dis) {edge[++edge_num].next = head[from];edge[edge_num].to = to;edge[edge_num].dis = dis;head[from] = edge_num;}queue <int> Q; int dist[Maxn]; bool inq[Maxn];void SPFA(int S) {memset(inq, 0, sizeof(inq));for(int i = 1; i <= n; ++i) {dist[i] = f[i][S];if(dist[i] != 1061109567) Q.push(i), inq[i] = 1;}while(Q.size()) {int u = Q.front();Q.pop();inq[u] = 0;for(int i = head[u]; i; i = edge[i].next) {int v = edge[i].to;if(dist[v] > dist[u] + edge[i].dis) {dist[v] = dist[u] + edge[i].dis;if(!inq[v]) {inq[v] = 1;Q.push(v);}}}}for(int i = 1; i <= n; ++i) f[i][S] = dist[i];}int main() {n = read(); m = read(); k = read();int u, v, w;for(int i = 1; i <= m; ++i) {u = read(); v = read(); w = read();add_edge(u, v, w);add_edge(v, u, w);}memset(f, 63, sizeof(f));for(int i = 1; i <= k; ++i) {u = read();f[u][1 << (i - 1)] = 0;}for(int i = 1; i <= n; ++i) f[i][0] = 0;for(int S = 0; S < (1 << k); ++S) {for(int i = 1; i <= n; ++i)for(int T = S & (S - 1); T; T = S & (T - 1))f[i][S] = min(f[i][S], f[i][T] + f[i][T ^ S]);SPFA(S);}int ans = 2e9;for(int i = 1; i <= n; ++i) ans = min(ans, f[i][(1 << k) - 1]);cout << ans << endl;return 0;}例题[WC2008] 游览计划考虑把每个⽅格当成⼀个点,最⼩斯坦纳树搞它就完了。
【浙江省自然科学基金】_设计层次_期刊发文热词逐年推荐_20140813

科研热词 推荐指数 层次分析法 2 铁路集装箱 1 配置需求 1 遗传算法 1 资源描述框架 1 调度自动化 1 融合蛋白 1 自适应策略 1 脂联素 1 肿瘤坏死因子α 拮抗剂 1 网络化 1 网构软件 1 编码体系 1 结构对称性 1 系统评价 1 粒子群算法 1 神经网络技术 1 真核表达 1 流程设计 1 模糊多属性决策 1 模型驱动 1 机械对称性 1 景观栅格 1 拆卸熵 1 抽象状态机(asm) 1 对称性应用 1 多粒度 1 复杂产品 1 城市景观 1 可溶性肿瘤坏死因子受体ii 1 可拆卸性评价 1 原理对称性 1 动态自适应 1 功能对称性 1 公共信息模型 1 优先指数 1 仓单质押贷款 1 主成分分析法 1 peer-to-peer(p2p) 1 agent 1
推荐指数 2 2 2 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
53 54 55 56 57 58 59 60 61 62 63 64 65
功能对称 内在属性特征 企业服务总线 人机交互 人事档案管理 产品族 云制造 一体化 laov网络 kronecker叉积 ifs aov网络 abo血型
科研热词 逻辑层次密钥 组密钥管理 产品设计 wsn tinyos 风格意象 风景园林 面向服务 非规则分形组织 非真实感渲染 设计过程 设计层次 血液病 腓肠动脉 聚合物 网格工作流 绿色街道 织物 细节设计 组织设计 穿支皮瓣 电子服务 灰度渐变 活动理论 水墨绘制 模块化 染色体 架构理论 架构创新 杂合性缺失 智能响应 景观设计 显微外科手术 时空对称 数字化解剖 效用对称 提花丝织物 拓扑排序 感性工学 微粒与细胞相互作用 微粒 广义功能 平纹组织模型 工业设计 层次 对称 多层次框架 复杂系统 基因/药物传递 基因 图像数据 单色显像
图的steiner最小树问题及其求解

图的steiner最小树问题及其求解作者:杨凌云来源:《电脑知识与技术》2009年第25期摘要:斯坦纳树问题是组合优化学科中的一个问题。
属于NP-难问题,即无法在多项式时间内得到最优解。
本文主要讨论了图的steiner最小树问题,并给出了近似算法,该算法是在破圈法的基础上进行了改进,并且引用了agent的思想。
最后对算法进行了分析。
关键词:Steiner最小树 NP-难题破圈法中图分类号:TP312文献标识码:A文章编号:1009-3044(2009)25-7312-02Graphical Steiner Minimum Tree Problem and SolusionYANG Ling-yun(College of Computer and Information Engineering, Henan University, Kaifeng 475001,China)Abstract: Steiner tree problem is one of the subject of combinatorial optimization problem. It belongs to NP-hard problems that cann’t find the optimal solution in polynomial time. This article discusses the minimum steiner tree problem in graphs, and gives the approximate algorithm, which is improved on loop damage method, and quoted the agent's thinking. Finally, an analysis of the algorithm.Key words: steiner minimum tree; NP-hard problem; loop damage method现实生活中经常要求解决这样的问题,即将若干给定点相连并使连线的总长最短。
斯坦纳树解法-概述说明以及解释

斯坦纳树解法-概述说明以及解释1.引言1.1 概述概述部分是文章的开篇部分,用于介绍主题和问题背景。
下面是一个示例:概述斯坦纳树(Steiner Tree)是图论中的一个经典问题,旨在找到一个具有最小总权重的联通子图,以连接给定一组节点。
斯坦纳树问题在实际生活中有着广泛的应用,例如通信网络设计、电力系统规划和生物信息学等领域。
本文将详细介绍斯坦纳树的概念、应用领域以及解法的基本原理。
首先,我们将给出斯坦纳树的定义和问题描述,以便读者对该问题有一个清晰的认识。
然后,我们将探讨斯坦纳树在不同领域中的应用,以展示它在实际问题中的重要性。
接下来,我们将介绍一些经典的斯坦纳树解法,包括近似算法和精确算法,并详细讨论它们的基本原理和优缺点。
通过本文的阅读,读者将能够了解斯坦纳树问题的背景和意义,掌握不同领域中的应用案例,并对斯坦纳树解法的基本原理有一定的了解。
此外,我们还将对斯坦纳树解法的优点和局限性进行讨论,并展望未来在这一领域的发展方向。
接下来,在第二节中,我们将开始具体介绍斯坦纳树的概念和应用领域。
1.2 文章结构【文章结构】本文主要分为引言、正文和结论三个部分。
下面将对每个部分进行详细介绍。
1. 引言引言部分主要包括概述、文章结构和目的三个方面的内容。
在概述部分,将简要介绍斯坦纳树解法的背景和重要性。
2. 正文正文部分是文章的核心部分,主要包括斯坦纳树的概念、应用领域和解法的基本原理三个方面的内容。
2.1 斯坦纳树的概念在本小节中,将详细解释什么是斯坦纳树,斯坦纳树的定义和特点。
2.2 斯坦纳树的应用领域本小节将介绍斯坦纳树的应用领域,包括网络通信、电力系统、交通规划等方面的应用案例。
2.3 斯坦纳树解法的基本原理在本小节中,将详细介绍斯坦纳树解法的基本原理和算法,包括构建斯坦纳树的思路和具体步骤。
同时,可以提及一些经典的斯坦纳树解法算法和优化方法。
3. 结论结论部分对斯坦纳树解法的优点和局限性进行总结,并对未来的发展方向进行展望。
3通讯网络的最小生成树(可编辑)

§3 通讯网络的最小生成树* * 无圈图称为森,连通的无圈图称为树。
若G1是连通图G2的生成子图,且G1本身是树,则称为G1为G2的生成树。
树是最简单但又是十分重要的一类图。
由于其结构简单,它常用来验证图论的某些猜想。
它在许多学科领域中有广泛的应用,例如分子结构,电网络分析等。
最短连接问题与树有关,学科分类和一些决策过程也往往可以用树的形式表示。
树有许多很好的性质:图 T=(V,E),|V|=n,|E|=m,则下面关于树的命题是等价的。
(1)T是一个树。
(2)T无圈,且m=n-1。
(3)T连通,且m = n-1。
(4)T无圈,但加一新边即得唯一一个圈。
(5)T连通,但舍去一边就不连通。
(6)T中任意两点,有唯一链相连。
上述性质中每一个命题均可作为树的定义,它们对判断和构造树将极为方便。
对图G=(V,E)的每一条边e E赋以相应的实数权 W(e),得到一个网络,记为N=(V,E,W)。
设T=(V,E’)是N 的一个生成树,令 W(T)= , 则W(T)称为T的权,N 中权最小的生成树称为N的最小生成树。
许多实际问题,如在若干个城市之间建造铁路网、输电网或通信网等,都可归纳为寻求连通赋权图(网络)(eij 的最小生成树问题。
例如已知城市v和v间的直通线路的造价为Wij=w(eij)=(vi,vj)),要求一个总造价为最小的设计方案。
又如一个城市中,对若干新建居民点供应自来水和煤气,已测知连接各点间的直通管道的造价,要求给出一个总造价最小的铺设方案等等。
下面介绍在给定网络N =(V,E,W)内求最小生成树的两种算法。
设网络点数为n,此时最小生成树的边数为n-1。
算法1 (克鲁斯凯尔,Kruskal)算法I的中心思想是每次添加权尽可能小的边,使新的图无圈,直到生成最小生成树为止。
也形象地简称“最小边的加入法”。
其步骤如下:(1)把N内的所有边按照权的非减次序排列。
(2)按(1)排列的次序检查N中的每一条边,如果这条边与已得到的边不产生圈,则取这一条边为解的一部分。
Steiner最小树问题及其应用

第8卷 第15期 2008年8月1671-1819(2008)15-4238-09科 学 技 术 与 工 程Science T echno logy and Eng i neeringV ol 18 N o 115 A ug . 2008Z 2008 Sci 1T ech 1Engng 1综 述数 学Steiner 最小树问题及其应用张 瑾1,2马 良1*(上海理工大学管理学院1,上海200093;河南大学计算机与信息工程学院2,开封475001)摘 要 Ste i ner 最小树问题是一个历史悠久的经典的组合优化问题,由于应用广泛,多年来一直受到研究者的广泛关注。
介绍了各种S teine r 树问题及其求解算法和实际应用。
关键词 Ste i ner 最小树 精确算法 启发式算法 应用中图法分类号 O 224; 文献标志码 A2008年4月21日收到国家自然科学基金项目(70471065)、上海市重点学科建设项目(T0502)资助第一作者简介:张 瑾(1974)),女,河南开封人,博士生1研究方向:系统工程、智能优化。
*通信作者简介:马 良(1964)),男,上海人,博士,教授,博士生导师1研究方向:智能优化。
现实生活中经常要求解决这样的问题,即将若干给定点相连并使连线的总长最短。
在网络通信领域中,该问题被一般化地提为:如果要在n 个区域间铺设通信网,使得各区域之间能实现信息的共享,那么应如何铺设才能使通信线路的总长最短?一般首先想到的可能就是求连接这n 个点的最小生成树(M i n i m um Spann i n g Tree )M ST )这种做法,但如果不拘泥于这n 个点,而引入除这n 个点之外的另外几个点的话,则有可能使连接各区域的通信线路的总长更短。
这是Steiner 最小树问题(Steiner M i n i m u m Tree Prob le m ,简记为S MTP)的来源。
S teiner 最小树问题是经典的组合优化问题,最早可以追溯到17世纪初。
【浙江省自然科学基金】_最优决策_期刊发文热词逐年推荐_20140811
科研热词 推荐指数 闭环dna计算模型 1 约柬线性描述分析 1 白化变换 1 正交子空间投影 1 有目的的终止技术 1 支持(反对、中立)目标集 1 指派问题 1 投影法 1 批接入实验 1 奇异值分解 1 多属性决策 1 区间数 1 区间型理想点 1 动态多目标决策 1 人脸识别 1 vague集相似度 1 vague集 1
2009年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13
科研热词 衰减信道 绿色服装 神经网络 生产型企业 生产决策 正态分布 条件风险值 无线链路 无线传感器网络 多目标 信息融合 bp算法 6r
推荐指数 1 1 1 1 1 1 1 1 1 1 1 1 1
2010年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19
2014年 序号 1 2 3 4 5 6 7
53 lévy过程 54 levy过程 55 cvar
1 1 1
2014年 科研热词 最优决策 运输 订货 提前期 品牌资产 供应链 产品伤害危机 推荐指数 2 1 1 1 1 1 1
2011年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
2011年 科研热词 供应链管理 集值统计 网络方案 指标体系 投资决策 承诺契约 库存决策 层次分析法 客户战略选择行为 多目标 口碑 企业战略 交叉规划 s-最优联合解 推荐指数 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2012年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34
组合优化及算法

背包问题
• 给定n个容积分别为ai,价值分别为ci的物 品.设有一个容积为b的背包,如何以最大 的价值装包?
平行机排序问题
• M个完全相同的机器,n个相互独立的工件, 加工时间互不相同,每个工件只需在任一 台机器上不中断建工一次,如果安排加工 方案,才能使预定的加工时间最短?
定义 若存在一个多项式函数g(x)和一个验证算法H,对一类判 定问题A的任何一个“是” 实例I,都存在一个字符串S是I的 可行解,满足其输入长度d(S)不超过g(d(I)),其中d(I)为I的输 入长度,且算法H验证S为实例I的可行解的计算时间f(H)不超 过g(d(I)),则称判定问题A是非确定多项式的。
计算复杂性的概念
多项式时间算法 例 构造算法将n个自然数从小到大排列起来
算法 输入自然数a(1),a(2),…,a(n). for (i=1;i<n;i++) for (j=i+1;j<=n;j++) if (a(i)>a(j)){ k=a(i);a(i)=a(j);a(j)=k; }
基本运算的总次数(最坏情形):2n(n-1)=O(n2)
例 线性规划问题(LP)的判定形式——LP判定问题:
给定一个实数值z,(LP)是否有可行解使其目标值不超过z? 即:给定z,是否有 {x|cT x z, Ax b, x 0}?
对任何一个优化问题, 可以考虑其三种形式:
最优化形式(原形:最优解) 计值形式(最优值)
难度降低
判定形式(上界)
就有效算法的存在性而言,通常认为三种形式等价!
算法 – 定义
定义:算法是指一步步求解问题的通用程序,它是 解决问题的程序步骤的一个清晰描述.
组合数学课程介绍

12
• 斯坦福数学系的教授研究了这个问题, 设立了一个小小的奖项来征集答案, 100美金.
• 数学家和计算机学者都来参与了 • 谁赢了呢?
– 伊利诺大学计算机系的比尔.卡特勒借助计算机 得出的答案是17152种拼法
– 数学家用纸和笔对排列进行分类,共24个基本 族,基本解法是536种,考虑旋转32种,答案 也是17152种。
大禹(2205BC -2105BC)
492 357 816
10
• 组合数学中有许多象幻方这样精巧的结构。
• 1977年美国旅行者1号、2号宇宙飞船就带 上了幻方以作为人类智慧的信号。
2200BC
4 9 2神 3 5 7农
幻
8 1 6方
15世纪
1 15 14 4 4 12 6 7 9 阶
幻 8 10 11 5 方
31
• “6度分离” —对每个人来说,平均大约只需要通过6 个人就能将信寄到目的地。
• 研究无尺度网络,对于防备黑客攻击、防治流行病、和 开发新药等,都具有重要的意义。
• 在1999年,Barab´asi et al.发现在因特网上,任意两个 网页间的链接即网页之间的“距离”平均为18.59 。从 任意一个网页出发, 原则上可以通过不超过19次链接到 达互联网中的任何网页。 (Nature 401, 1999)
/zh-cn/%E7%BB%84%E5%90%88%E6%95%B0%E5%AD%A6
Combinatorics: Combinatorics is a branch of pure mathematics concerning the study of discrete (and usually finite) objects. It is related to many other areas of mathematics, such as algebra, probability theory, ergodic theory and geometry, as well as to applied subjects in computer science and statistical physics.
【浙江省自然科学基金】_管理层次_期刊发文热词逐年推荐_20140812
科研热词 非营利组织 遗传算法 财务危机 评价和选择方法 设备运行性能 设备诊断 行业协会 群决策 网站测评 系统生命周期 移动ip 灰色综合评价 服装供应商 影响机制 层次分析法 定性指标体系 多步寻呼 动态能力 信息熵 企业家能力 企业家学习 topsis法 ip寻呼
2012年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23
科研热词 逻辑层次密钥 组密钥管理 wsn tinyos 风景园林 面向服务 设计过程 设计层次 网络位置 绿色街道 细节设计 模块化 架构理论 架构创新 景观设计 多层次框架 复杂系统 创新绩效 关系嵌入 全球制造网络 企业服务总线 人事档案管理 一体化
推荐指数 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2009年 序号 1 2 3 4 5 6 7
科研热词 顾客满意度 社会资本 灰色评价 双维层次 劳动力市场分割 剩余劳动力转移 人力资本
推荐指数 1 1 1 1 1 1 1
2010年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17
科研热词 推荐指数 知识搜索 3 层次分析法 3 创新绩效 3 非平衡最小二乘支持向量机 2 船舶 2 网络位置 2 粗糙集 2 本地集群网络 2 客户流失预测 2 团队创造力 2 启发式算法 2 可靠性 2 全球制造网络 2 人因可靠性评估方法 2 跨层次研究 1 行业差异 1 网络中心性 1 粒子群优化算法 1 碳排量 1 碳强度 1 知识缄默性 1 知识异质性 1 模糊综合评价 1 模拟植物生长算法 1 桥梁 1 权重 1 最优布局 1 斯坦纳最小树 1 效能感 1 探索性学习 1 指标分析 1 技术学习策略 1 应急管理 1 帕累托最优解 1 层次分析法(ahp) 1 多目标优化 1 城市灾害 1 城市地下物流 1 团队学习 1 因子分析法 1 商业模式 1 利用性学习 1 分插机构 1 农业机械 1 全寿命周期评价 1 伙伴选择 1 企业社会责任水平 1 产业集群 1 交互记忆系统 1 互补度 1 个体创造力 1 topsis法 1
组合图论图论及其算法课件

4. 实例:求下列赋权完全图的最优Hamilton回路.
A
解:ACEBDA: 权和 25 BACEDB: 权和 25 CABEDC: 权和 22 DACEBD: 权和 25 EACDBE: 权和 27
21 B
9 10
34 5E 7 6
C8D 所选初始点不同,得到的近似解也不同.
5. 修改方法:最邻近插入法
(2)不允许高速路在所研究的城市以外的某点 处连接.
最短网络问题: 如何用最短的线路将三部电话连起来?
A
B
C
此问题可抽象为设△ABC为等边三角形,,连接三 顶点的路线(称为网络)。这种网络有许多个, 其中最短路线者显然是二边之和(如AB∪AC).
❖ 但若增加一个周转站(新点P),连接4点的新网 络的最短路线为PA+PB+PC。最短新路径之长N 比原来只连三点的最短路径O要短。
3). 重复2)过程直到汇y被标号,或不再有顶点可以标号为止. 若y得到标号,说明存在一条x y增广路P,进入步骤2调整过程; 若y未得到标号,标号过程无法进行,说明f 即为最大流.
(2) 调整过程
1).
令
min{ min (vi ,v j )P
(Cij
f
ij
),
(
min
vi ,v j )P
f ji},调整增广路P中
三. 中国邮递员问题(1962,管梅谷)
1. 问题:邮递员每天从邮局选好邮件,送到他所管辖 的邮区的客户手中,再返回邮局,他每天必须走过每 条街道至少一次,问如何选择邮递路线,使得他走过 的投递总行程最短?
2. 模型:非负赋权图G: 顶点----交叉口或终端,边----街道,权-----街道长 度,此即求图的通过每条边至少一次的闭途径,称为G 的环游.
【浙江省自然科学基金】_植物模拟_期刊发文热词逐年推荐_20140813

科研热词 推荐指数 二层规划 3 非线性二层规划 2 模拟植物生长算法(pgsa) 2 模拟植物生长算法 2 非常规突发事件 1 长江口 1 遮光率 1 迭代函数系统 1 近似拟合 1 运筹学 1 褐飞虱 1 营养盐 1 耐受性 1 线性二层规划 1 生长 1 现场培养 1拟 1 植物吸收 1 植物优化配置 1 植物乳杆菌lpb1 1 植物 1 森林演化 1 树木模拟 1 暴露面积 1 智能算法 1 投资组合 1 技术联盟 1 情景 1 干旱 1 夏蜡梅 1 增温 1 基质氮 1 响应曲面分析 1 咸淡水混合 1 叶绿素荧光参数 1 叶绿素相对含量 1 取食行为 1 反硝化 1 分形几何 1 光照指数 1 光照度 1 光合特性 1 产卵选择性 1 丢番图方程 1 l系统 1 ifs 1 gpu 1 fon模型 1
2012年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51
推荐指数 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2009年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
科研热词 葎草 细胞活性 磷 热冲击 浮游植物 氯 氮 植物修复 核酮糖1,5-二磷酸羧化酶 富营养化水体 叶绿素a 冷胁迫 冷却系统 光抑制 光合作用 佛手
2008年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18
科研热词 阿特拉津氯水解酶基因 阿特拉津 遗传算法 遗传偏最小二乘法 转基凶烟草 虚拟植物生长模型 茉莉酸类化合物 番茄 用户动态交互 生物降解 环境生物技术 模块化 植物修复 层次化 定量结构-性质关系 动态生长 作物栽培管理 专家系统
Flute斯坦纳最小树构造算法

HOW—最小线长计算加速
• 正常的计算POWVs线长 • 但是同一个group间的计算是有很多重复点的,
每个POWV单独计算浪费很多时间。 • POWV之间可以有依赖性的依次计算,其实这
是一个最小生长树的问题。 • 对于一个Group中q个POWVs,建立一个q+1个
节点的完全图,多出的一点对应于线长数组 (HPWL),图中边权为两个相邻线长数组的 边际距离。 • 从HPWL点开始宽搜建立最小生长树,叶子节 点为图中的node
堆边的集合,由此线长即可以由hi,vi组成的向 量表示。 • 右下图的线长可依次表示为(1, 2, 1, 1, 1, 2), (1, 1, 1, 1, 2, 3), (1, 2, 1, 1, 1, 1) • 虽然斯坦纳树数量是巨大的,但是上述的线长 向量数量要小很多,并且可以略过许多一定大 的向量,如a,c中a可以无视。 • 那么由此得到的最小的那些不可以被无视的向 量就组成了POWVs,对于一个端点很少的线网 而言,POWV是十分少的。
Chris Chu and Yiu-Chung Wong
Review By Carelife
What—FLUTE
• 基于快速查找表的矩形斯坦纳最小树构造算法 • 所有N点线网根据pin脚位置都可划分到n!个group中,每
个group中存有POWV,对于一个线网最优线长可由 POWV来获得,FLUTE算法首先会预计算这些POWV形成 一个查找表。与POWV一起存储的还有POST,一个 POWV对应多个POST,一个POST只有一个POWV。 • POWV:potentially optimal wirelength vectors • POST:potentially optimal Steiner tree • 基于此,要得到一颗RSMT,只需计算线网所在组对应 的POWV的线长,然后返回对应的POST即可。 • 上述查找表算法最高支持9点线网,对于9点以上的需要 递归的切分线网。 • FLUTE算法的复杂度依旧是O(nlogn)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
问题
假定要设计一个有9个通 讯站点的局部网络,使 其造价最低。这9个站的 直角坐标为: a(0,15), b(5,20), c(16,24), d(20,20), e(33,25), f(23,11), g(35,7), h(25,0), i(10,3)。 求出联结这9个通讯站的 最小Steiner树。
(5)修正的Prim启发式算法
受到求最小生成树的Prim算法的启发,根 据Prim算法的思想,构造出下面的求最小 直角折线Steiner树的方法。 先引入一些记号: Z: 给定的通讯站点集合; G: 给定通信站点的x坐标线,y坐标线 形成的格点全体构成的集合; T: 当前Steiner树的顶点集; S=G-Z; 算法步骤: 1)选取Z中距离最近的两点zi=(xi,yi), zj=(xj,yj);
提示: 最小Steiner树问题是NP难题。 前面介绍的方法,除穷举法之外,每个算 法都是有效算法,但不一定能得到最优解, 一般需要对解的近似程度进行分析。 对算法的好坏,可随机给出一些通讯站, 用这些方法来求解,对算法给出的解进行 比较,看哪个算法效果最佳。
编写贪婪试探算法、改进型试探算法 的MATLAB程序,求给定的9个通讯站 的最小Steiner树。 用手工操作的方式,由修正的Prim启 发式算法求给定的9个通讯站的最小 Steiner树,体会该算法的思想。
(2)贪婪试探算法
图13.5的最小生成树如图13.8(a),顶点按 直角坐标之定位放置,右边的图是把边画成直 角折线,该图称为其三个点的最小直角折线支 撑树。若将图13.8的右边图中重边的端点d作 为虚设站加入,则4个点的最小生成树的权减 少了2。
图13.8
一般情况下,可把最小直角折线支撑树中重 边的端点作为Steiner点的侯选点。结合贪 婪法的思想,可构造出如下的试探法,能否 得到正确解,需要证明。 1)输入给定的n个通信站点的坐标; 2)计算最小直角折线支撑树; 3)找重边,则重边的端点便是Steiner点 的侯选点; 4)分别计算出每个侯选点作为Steiner点加 入后所减少的费用,该费用称为此点的价值; 5)把最大价值的侯选点也作为一个给定点, 重复2)到5)直到没有正价值的侯选点。
次。假设每次迭代只需用1/60秒的时间, 3572224次迭代需要大约17个小时。
9个给定 点和31 个可能的 Steiner 点 a(0,15), b(5,20), c(16,24), d(20,20), e(33,25), f(23,11), g(35,7), h(25,0), i(10,3)
用模拟退火法来求图13.4所给出的9个点的 最小Steiner树,在25MHz型386计算机上 运行,大约1.5分中便可得到了最优解。 对应于随机数产生器的不同种子的不同运 行,可给出全部五个不同的最优解。 在上百次运行中,模拟退火法都总是收敛 到五个最优解中的一个。 计算时间方面的优越性表明当该问题的规 模较大,穷举法不可行时,模拟退火法的 价值。
(3)改进型试探算法
如果每次迭代,都按照随意的顺序加入“虚设站”, 并使得到的最小生成树费用有所减少,直到已加入 n-2个“虚设站”,或加入任何一个剩余的可能的 Steiner点都不能使费用减少为止。按步骤描述如 下 1)求给定的n个点的最小生成树,记录其费用; 2)取一个可能的Steiner点加入,求最小生成树, 若该树的费用小于当前的费用,则记录此树并更新 费用; 3)重复2)直到已有n-2个Steiner点,或任何剩余 的Steiner点加入都不能减少费用。 贪婪试探算法和改进型试探算法都是近似算法,对 一般的问题未必能得到最优解。
在下述四类区域中不含Steiner点
D 1 {( x , y ) | x x 00 ( k ), y y k }; D 3 {( x , y ) | x x 10 ( k ), y y k }; D 2 {( x , y ) | x x 01 ( k ), y y k }; D 4 {( x , y ) | x x 11 ( k ), y y k };
求V0的最小Steiner树可分解为两个问题: 1)求Steiner点;2)求最小生成树。 根据提示“最小Steiner树最多只需n-2个虚 设站(ቤተ መጻሕፍቲ ባይዱteiner点)”, Vs :表示Vp中任意s个点的集合。 对满足0≤s≤n-2的整数s和点集Vs Vp,以 V= Vs∪V0为顶点集的加权完全图Ks+n的 最小生成树记为Ts, 所有Ts 中权最小者记为 T*,T*即为所要求的最小Steiner树。
e)若dist1<dist2, 则加入path1, 若dist2<dist1, 则加入path2, 若dist1=dist2, 则对下一个最近点 重复(2)a到(2)e, 直到dist1¹ dist2, 或穷 尽了Z中所有顶点(此时任意选择); 3)取ziZ∩(G-T),zjT,使zi,zj尽可能 近; 4)重复2),3)直到Z中的顶点均在 T中。
范例2 通讯网络的最佳Steiner树
1.问题 2.假设 3.问题分析及模型 4.问题求解
穷举法 贪婪试探算法 改进型试探算法 模拟退火法 修正的Prim启发式算法
5.结果
1.问题
给定平面上若干通讯站,两通讯站之间的线 路长度为两点间的直角折线距离,即 d=|x1-x2|+|y1-y2| 两点间的线路费用正比于线路的长度。 ①如何布线使连接通信站的线网费用最低? ②如何构造最小Steiner树,即最低费用的 Steiner树?
2.假设
1)通信站点集合V0是整数坐标的平面 点集; 2)两点间的距离为直角折线距离,线 路费用正比于线路长度; 3)允许通讯线在非站点处连接。
3.问题分析及模型
给定n个通讯站点,用通讯线把这些站点联 结起来,允许通讯线在非站点处连接,如何 连接,可使连接通信站的线网费用最低? 允许通讯线在站点以外的点(即“虚设站” 或Steiner点)连接,这样可以使线网费用 降低,但问题要复杂得多。 如,有三个通讯站,直角坐标分别为a(0,0), b(4,3),c(6,0)
如图13.7,星号点是给定的9个通讯站点。共 有n(n-1)=72个Steiner点的可能位置,它们 位于过9个点的水平线与垂直线的交点上。 且由于区域D1,D2,D3和D4内不含Steiner点, 72个可能的Steiner点位置可减少到31个 (图4中小圆圈所示的31个位置)。 31 31 31 m=31,迭代次数减少到 0 1 7 3572224
(4)模拟退火法
这是一种通用的随机搜索法,是解决NPH 问题的比较有效的方法。 1)给定点集连同一些虚设点一起构成点集 Z,求Z的最小支撑树,其费用记为C,置 k=0; 2)产生新的点集S 从以下几种方式中随机选择一种: ·加入一个新的虚设点 ·去掉一个存在的虚设点 ·移动一个现有的虚设点到一个随机的允 许位置
3)确定新点集S的最小支撑树,其费 用记为C1,
若C1≤C,则更新C为C1,更新当前点集 Z为S, 当k=M时停止,否则k=k+1,转2); 若C1>C,则仅以一定的概率(可取为 exp{-(C1-C)/T(k)},其中T为一控制参数, 称为温度,随k的增大而减小,比如取 T(k)=T(0)/k,称为冷却方案)接受S作为 当前点集Z,转2)。
2)这两点的x坐标或y坐标相同,则将两点连接起 来,并把该路径上所有在G中的点以及zi,zj加入T, 否则 a)构造过(xi,yj)的连接zi,zj的直角折线路径 path1,将path1上所有属于G的点以及zi,zj加入T; b)在Z-T中找到与当前树距离最近的顶点z,其 距离记为dist1,然后删掉树中的path1; c)构造过(xi,yj)的连接zi,zj的直角折线路径 path1, 将path1上所有属于G的点以及zi,zj加入T; d)在Z-T中找到与当前树距离最近的顶点z,其 距离记为dist2,然后删掉树中的path2;
(1)穷举法
求最小Steiner树问题是NP难题,点数较小 的问题可用穷举法,但若规模较大,应寻 求近似算法。 由于费用最少的Steiner树T*上最多只需引 入n-2个虚设点,因此可从m≤n(n-1)个可能 的Steiner点位置中任取s个点, s=0,1,2,…,n-2,连同给定的n个点一起, 用Kruskal算法,求由这n+s个点确定的赋 权完全图(图中边权取为两点间的直角折 线距离)的最小生成树Ts。 若m不大,此法可行,若m大,此法将无效。
Steiner树:
Steiner树——通过加入若干“虚设站”后,构造 出由原站点和虚设站生成的最小生成树。若虚设站 设置得恰当,就可降低由原站点生成的最小生成树 所需的费用。用这种方法可降低费用多达13.4% 注意: 1)Steiner树允许线路在通讯站点以外连接,这种 连接点即为虚设站。 2)为构造一个有n个站的网络,最低费用的 Steiner树最多只需n-2个虚设站,这些虚设站称为 Steiner点。Steiner 点位于给定通信站点的x坐标 线,y坐标线形成的格点上。
结果
用穷举法可得到给定的9个通讯站的最 小Steiner树,共有5个,费用为94。 图13.9给出了这5个最小Steiner树, 其中每个Steiner树都含4个或5个 Steiner点。因此可按图13.9中任何一 个Steiner树来设计给定9个站的费用 最少的局部网络。
图13.9
图13.5
图13.6
“虚设站”(即Steiner点)的个数和位置是解决问 题的关键。 “Steiner点位于给定通信站点的x坐标线,y坐标 线形成的格点上”,最多有n2-n=n(n-1)个Steiner 点的可能位置,这些位置就是Steiner点的候选点. 当n=9时,有n(n-1)=72个Steiner点的可能位置 V0 :给定的n个通信站点的集合; Vp : Steiner点的候选点集合,设其点数为p, Vp∩V0=φ; 以V= Vp∪V0为顶点集作一个加权完全图Kp+n,其 中的边(u,v)的权取为点u与v之间的直角折线距离。 问题成为:求加权完全图Kp+n中包含V0(也允许包 含V中的其他点)的权最小的子树。此即求加权完 全图Kp+n中,V0的最小Steiner树问题。
