第四节最小树问题
运筹学4

练习:应用破圈法求最小树
v1 23 20 v2 4 v7 9 16 17 v4 15
Page 1
1
36
v6
28
v3
3
25
v5
树与图的最小树
v1 23 v6 28 v5 36 25 17 16 v4
Page 2
20
v2 4
15 9 v3 3
1
v7
树与图的最小树
v1 23 v6 28 v5 25 17 16 v4 1 v7 9 v3 3
最短路问题
定义:
Page 27
1)人—M(Man),狼—W(Wolf), 羊—G(Goat), 草—H(Hay) 2) 点—— vi 表示河岸的状态 3) 边—— ek 表示由状态 vi 经一次渡河到状态 vj
4) 权——边 ek 上的权定为 1
我们可以得到下面的加权有向图
最短路问题
状态说明: v1,u1 =( M,W,G,H ); v2,u2 =(M,W,G); v3,u3 =(M,W,H); v4,u4=(M,G,H); v5,u5 =(M,G)
v1
v2
v3
v4
v5
v6
最短路问题
把所有弧的权数计算如下表,把权数赋到图中,再用 Dijkstra算法求最短路。
1 1 2 3 4 5 6 2 16 3 22 16 4 30 22 17 5 41 30 23 17 6 59 41 31 23 18
Page 46
59 22 v1 16 v2 30 41 v4 23 41 23 17 v5 31 18 v6
①
4 s 4 1
4
③
7
t 9
6 2 ④
最小支撑树问题

§6.2 最小支撑树问题
Minimum Spanning Tree Problem
Ch6 Graph and Network
2012年4月20日星期五 Page 2 of 5
求最小树的方法:破圈法和避圈法 破圈法:任取一圈,去掉圈中最长边,直到无圈。 v1 v3 7 v5 8 5 4 5 8 1 2 v2 v1 4 2 v2 3 v4 v6 3 v4 v3 6 5 1 v6 v5
§6.2 最小支撑树问题
Minimum Spanning Tree Problem
Ch6 Graph and Network
2012年4月20日星期五 Page 5 of 5
作业: 作业:P283 10.4 10.5
最短路问题
Exit
Ch6 Graph and Network
2012年4月20日星期五 Page 4 of 5
加边法:去掉G中所有边,得到n个孤立点;然后加边; 加边的原则:从最短边开始添加,加边的过程中不能形 成圈,直到连通(n-1条边)。 v1 v3 7 v5 8 5 4 5 8 1 2 v2 v1 4 2 v2 3 v4 v6 3 v4 v3 5 1 Min C(T)=15 6 v6 v5
§6.2 最小支撑树问题
Minimum Spanning Tree Problem
Ch6 Graph and Network
2012年4月20日星期五 Page 3 of 5
得到最小树: v1 4 2 v2 3 v4 v6 v3 5 1 v5
Min C(T)=15
§6.2 最小支撑树问题
Spanning Tree Problem
§6.2 最小支撑树问题
Minimum Spanning Tree Problem
最小树问题

6.3.1 狄克斯特拉算法 (Dijkstra algorithm, 1959) 计算两节点之间或一个节点到所有节点之间的最短路 令 dij 表示 vi vj 的直接距离(两点之间有边),若两点之间 没有边,则令 dij = ,若两点之间是有向边,则 dji = ; 令 dii = 0,s 表示始点,t 表示终点 • 对每个节点,用两种标号:T和P,表示从始点到该节点的距 离,P是最短距离(权),为永久标号,T是目前路径的距离,是 临时标号。 • 通过不断改进T值,当其最小时,将其改为P标号。 • 开始时,令始点有P=0的P标号,其它节点为T=+ .
•(3)Kruskal 算法:将图中所有边 v1 按权值从小到大排列,依次选 1 所剩最小的边加入边集 T,只 v8 要不和前面加入的边构成回路, 5 直到 T 中有 n1 条边,则 T 是最小生成树
v7
4
v2
1
v3
2
4 5
1
3
4
1
v4 5 v5
v0 2 3 v6 2 4
图的矩阵表示
将图的几何形状转化为代数矩阵形式,可大 大方便计算机对图的处理与运算。 1、无权图的矩阵表示:
6.2.3 最小生成树
v5 9 v6 17 10 8 7 11 v4 16 v3 9.5 v2 v1 10
12 7 19.5
10 16 11 10 17 10 9.5 19.5 16 9.5 7 12 7 8 7 11 10 8 9 17 19.5 12 7 9
寻找连通图支撑树的方法有“破圈法”。就是从图中 任取一个圈,去掉一条边。再对剩下的图重复以上步 骤,直到不含圈时为止,这样就得到一个支撑树。 例4 用破圈法求出下图的一个支撑树。 v2 e1 v1 e2 v3 e3 e4 e7 e8 e6 v5
最小树

∑
),W 弧e =(i,j)上的权常记为 (e), e 或w(e),wij等 , )上的权常记为W( ), ( ) 如果T*是 的一棵生成树 且对G的任何一棵生成树 的一棵生成树, 的任何一棵生成树T都有 如果 是G的一棵生成树,且对 的任何一棵生成树 都有 W( T* )≤W(T),则T*称为网络 的最小支撑树或者最小生 ),则 称为网络 称为网络G的最小支撑树或者最小生 ( ( ), 成树( ),或者简称最小树 成树(MST:minimum spanning tree),或者简称最小树 : ),或者简称最小树. 图的最小树一般不唯一
{
}
11
SOLLIN 算法 (1961) 基本思想:前面介绍的两种算法的综合。每次迭代同 基本思想:前面介绍的两种算法的综合。 时扩展多棵子树, 时扩展多棵子树,直到得到最小树 T.
STEP0 中任意一个顶点i, STEP0. 对N中任意一个顶点 ,定义 i={i}. 令T= 。 中任意一个顶点 定义N STEP1 如果T 中已有n-1条弧 条弧, 的最小树; STEP1. 如果 中已有 条弧,则T为G的最小树;否则,对T 中的所有子树 为 的最小树 否则, * 节点集合N 中的最小弧, 节点集合 k,计算边割 [ N k , N k ] 中的最小弧,即计算 w(ek ) = min w(e), 其中 e
该图正好含有一个圈.
5
最小树
定义2 为权函数, 定义 G=(N,E,W)为一个无向网络,W为权函数 即W: ( , , )为一个无向网络, 为权函数 E→R (这里 表示实数集合). G中权最小(大)的弧称为最小 这里R表示实数集合 表示实数集合) 中权最小 中权最小( (大)弧. 如果H=( 的一个子图, 的权定义为H所包含 如果 (N1,E1)为G的一个子图,子图 的权定义为 所包含 的一个子图 子图H的权定义为 的所有弧的权之和,记为W(H),即W(H)= 的所有弧的权之和,记为 , ( ) W ( e) .
教学课件:第五章-最小树问题

最小树问题在现实生活中具有广泛的应用,如电路设计、网络路由、物流配送等。通过解 决最小树问题,可以优化网络结构、降低成本、提高效率,为实际问题的解决提供重要的 理论支持和实践指导。
最小树问题的未来研究方向
算法优化与改进
尽管已经存在许多有效的算 法用于解决最小树问题,但 随着问题规模的扩大和复杂 度的增加,需要进一步优化 和改进现有算法,以提高求 解速度和精度。
04 最小小生成树问题是在最小生成树问题的基础上,给 每条边赋予一个权重值,目标是寻找一棵权值最小的生成树 。
详细描述
在带权重的最小生成树问题中,每条边都有一个关联的权重 ,表示该边的长度或代价。算法需要选择一组边,这些边能 够连接所有节点并且总权值最小。常见的带权重的最小生成 树算法有普里姆算法和克鲁斯卡尔算法。
理论分析与证明
对于最小树问题的求解算法 ,需要深入的理论分析和证 明,以揭示算法的内在机制 和性能。未来可以进一步研 究算法的理论基础和数学证 明,为算法的设计和分析提 供更严格的依据。
THANKS FOR WATCHING
感谢您的观看
05 总结与展望
最小树问题的研究现状与成果
最小树问题的定义和性质
最小树问题是一类组合优化问题,旨在寻找一棵具有最小权值的树,该树连接给定的顶点 集。最小树问题在计算机科学、运筹学和图论等领域具有广泛的应用。
最小树问题的研究进展
近年来,最小树问题的研究取得了重要的进展。研究者们提出了许多有效的算法和近似算 法,用于解决最小树问题及其变种。这些算法在理论和实践方面都取得了重要的突破,为 解决实际问题提供了有效的工具。
教学课件:第五章-最小树问
目录
• 引言 • 最小树问题的算法 • 最小树问题的实例分析 • 最小树问题的扩展问题 • 总结与展望
10.2_最小树问题
+50+60 = 290(米)
所以,排污管道最小建设
3
30
成本 = 290×500 = 145000 元 60
1
4
40
5
30 30
7 处理中心A
50
30 20
6
8
12
OR:SM
本章小结
树是图论中应用比较活跃的领域,在各个学科中都有广 泛的应用。
例如在一些地区之间架设电话线路或铺设铁路线,修公 路等施工方案的确定,都可以采用最小树的方法求得最 佳施工方案。
60
100
70
50
2栋
40
30
0
80
30
60
120
3栋
100
60
0
60
180
90
120
4栋
80
60
0
40
80
100
5栋
60
100
30
180
40
0
30
80
6栋
150
60
90
80
0
50
70
7栋
70
120
30
50
0
8栋
20
50
120
100
80
70
0
表中空格表示由于特殊原因无法铺设管道。
10
OR:SM
三、最小树问题应用案例
树图:无圈的连通图称为树。
4
OR:SM
二、树及性质
性质1 如果树T的点数不小于2,那么至少有两个悬挂点。
性质2 如果一个图G具有n个顶点,那么图G是一个树的 充分必要条件是图G不含圈且恰有n-1条边。
最小树问题VS最短路问题

2
i 1 j 1 8 8
a67
x12 x13 x24 x34 3; x34 x36 x47 x67 3; x47 x45 x78 x58 3; x x x x x x 5; 12 13 24 47 36 67 st x x x x x x 5; 36 34 45 58 78 67 x12 x13 x36 x67 x78 x58 x45 x24 7; x 7; ij ij xij 8; j=1ٛ 8) 0或1;(i=1ٛ
最小树问题 • 已知有六个城市,它们之间 要 架设电话线,要求任意两个城 市均可以互相通话,并且电话 线的总长度最短
最短路问题(SPP-Shortest Path Problem)
• 一名货柜车司机奉命在最短的时间内将一 车货物从甲地运往乙地. 从甲地到乙地的公 路网纵横交错,因此有多种行车路线,这 名司机应选择哪条线路呢? • 假设货柜车的运行速度是恒定的,那么这 一问题相当于需要找到一条从甲地到乙地 6 B D 的最短路. 6 5
A 7 C 4至v7点的最短路问题归结为求解整数规划问题。 1
v2
v5 v4 2 3 3 4 v6 4 v7
最短路问题
• 城市中的管道铺设,线路安排,工 厂布局,设备更新,选址问题
min Z aij xij
i 1 j 1 7 7
9
v1
5 v3
2 8
8
1, 最短路径弧(i, j ); 解:设xij 0, 否则
7
x12 x13 1; x12 x 23 x 24 x 25; x13 x 23 x34 x36; x 24 x34 x 45 x 46; st x 25 x 45 x65 x57; x36 x 46 x65 x 67; x57 x67 1; xij 0或1, (i 1…7;j=1
最小树与最小树形图(数学建模)讲解

最小树与最小树形图(数学建模)讲解一、最小树的定义及性质1. 定义:最小树,又称最小树,是指在给定的带权无向图中,包含图中所有顶点的一个树形结构,且树中所有边的权值之和最小。
2. 性质:(1)最小树中不存在回路;(2)对于最小树中的任意两个顶点,它们之间有且仅有一条路径;(3)最小树中边的数量等于顶点数量减一;(4)在最小树中添加任意一条边,都会形成一条回路;(5)最小树不唯一,但权值之和相同。
二、求解最小树的方法1. Prim算法Prim算法是一种贪心算法,其基本思想是从图中的一个顶点开始,逐步添加边和顶点,直到形成最小树。
具体步骤如下:(1)初始化:选择一个顶点作为最小树的起点,将其加入最小树集合;(2)迭代:在最小树集合和非最小树集合之间,寻找一条权值最小的边,将其加入最小树集合;(3)重复步骤2,直到所有顶点都加入最小树集合。
2. Kruskal算法Kruskal算法同样是一种贪心算法,其基本思想是将图中的所有边按权值从小到大排序,然后依次选择权值最小的边,判断是否形成回路,若不形成回路,则将其加入最小树集合。
具体步骤如下:(1)初始化:将所有顶点视为独立的树;(2)按权值从小到大排序所有边;(3)迭代:选择权值最小的边,判断其是否形成回路,若不形成回路,则将其加入最小树集合;(4)重复步骤3,直到所有顶点都在同一棵树中。
三、最小树形图的定义及求解方法1. 定义:最小树形图,又称最优树形图,是指在给定的有向图中,找到一个包含所有顶点的树形结构,使得树中所有边的权值之和最小。
2. 求解方法:朱刘算法(Edmonds' Algorithm)朱刘算法是一种用于求解最小树形图的算法,其基本思想是通过寻找图中的最小权值环,进行收缩和扩展操作,最终得到最小树形图。
具体步骤如下:(1)寻找最小权值环;(2)对最小权值环进行收缩操作,将环中的顶点合并为一个新顶点;(3)在新图中寻找最小树形图;(4)将新图中的最小树形图扩展回原图,得到原图的最小树形图。
Steiner最小树问题及其应用

第8卷 第15期 2008年8月1671-1819(2008)15-4238-09科 学 技 术 与 工 程Science T echno logy and Eng i neeringV ol 18 N o 115 A ug . 2008Z 2008 Sci 1T ech 1Engng 1综 述数 学Steiner 最小树问题及其应用张 瑾1,2马 良1*(上海理工大学管理学院1,上海200093;河南大学计算机与信息工程学院2,开封475001)摘 要 Ste i ner 最小树问题是一个历史悠久的经典的组合优化问题,由于应用广泛,多年来一直受到研究者的广泛关注。
介绍了各种S teine r 树问题及其求解算法和实际应用。
关键词 Ste i ner 最小树 精确算法 启发式算法 应用中图法分类号 O 224; 文献标志码 A2008年4月21日收到国家自然科学基金项目(70471065)、上海市重点学科建设项目(T0502)资助第一作者简介:张 瑾(1974)),女,河南开封人,博士生1研究方向:系统工程、智能优化。
*通信作者简介:马 良(1964)),男,上海人,博士,教授,博士生导师1研究方向:智能优化。
现实生活中经常要求解决这样的问题,即将若干给定点相连并使连线的总长最短。
在网络通信领域中,该问题被一般化地提为:如果要在n 个区域间铺设通信网,使得各区域之间能实现信息的共享,那么应如何铺设才能使通信线路的总长最短?一般首先想到的可能就是求连接这n 个点的最小生成树(M i n i m um Spann i n g Tree )M ST )这种做法,但如果不拘泥于这n 个点,而引入除这n 个点之外的另外几个点的话,则有可能使连接各区域的通信线路的总长更短。
这是Steiner 最小树问题(Steiner M i n i m u m Tree Prob le m ,简记为S MTP)的来源。
S teiner 最小树问题是经典的组合优化问题,最早可以追溯到17世纪初。
最小生成树问题(共7张PPT)

个,所以支撑树是有不唯一]。
C n1 m
求最小树的Kruskal算法
赋权的连通图G=(V,E)中m=|E|,n=|V|,
S1:对E中各边的权排序,设 w1≤w2≤…≤wm,wi=w(ei)
S2:初始化: w←0,T←φ,k←1,t←0
S3:若t=n-1则转S6,否则转S4
Y
N
T’←T∪{ek}
T’成圈? N END
Y
T←T+ {ek},
k←k+1 w←w+wk,
t←t+1,k←k+1
用Kruskal算法求最小树
用Kruskal算法(避圈法)求赋权连通图G的最小树
V2
5
V6
Kruskal法盯住边,而Prim法更注意顶点:
T为最小树,w为T的权。
4
T={v1,v2,v3,v5}
Prim法求最小支撑树 E的权排序w1≤w2≤…≤wm w←0,T←φ,k←1,t←0
对要m让条程边序的读边懂长“图排”,序S程3,:序m如个何元判素断排是序否较成好“的圈算”?法谈是何基容于易分,治时策间略、的空快间速复排杂序性(Q绝u不ick应S小or看ting),其时间复杂性是O(m㏒m)。
min S2:初始化:w←0,T←φ,k←1,t←0 设: {w(vv )}w(vv ) 简对称m条最边小的树边或长最排短序树,[管vvm线ij个 铺ST 元设素]。排序较好的i算法j是基于分治策略的快l速排k序(Quick Sorting),其时间复杂性是O(m㏒m)。
S4:若T∪{ek}有圈则k←k+1转S4,否则 转S5
S5: T←T∪{ek},w←w+wk, t←t+1, k←k+1,转S3
§6.4 最小树

§6.4 最小树1、最小树及其性质支撑树T 的权(或长):∑'∈=E e e W T W )()(最小支撑树:G 中权最小的支撑树定理6.4.1 设T 是G 的支撑树, 则T 是G 的最小树当且仅当对任意边*T e ∈有)(max )()(e W e W e C e '=∈'其中e T e C +⊆)(为一个唯一的回路。
定理6.4.2 设T 是G 的支撑树, 则T 是G 的最小树当且仅当对任意边T e ∈有)(min )()(e W e W e e '=Ω∈'其中e T e +⊆Ω*)(为一个唯一割集。
定理6.4.3 设T 是G 的支撑树,则T 是G 的唯一最小树当且仅当对任意边T G e \∈,e 是C (e )中的唯一最大边。
定理6.4.4 设T 是G 的支撑树,则T 是G 的唯一最小树当且仅当对任意边T e ∈,e 是)(e Ω中的唯一最大边。
2、求最小树的Kruskal 算法(贪心算法或避圈法)基本思想:从图G 的m 条边中选取1-n 条权尽量小的边,并且使它们不构成回路。
理论基础:定理6.4.1具体步骤:首先选出一条权最小的边,再从剩下的边中选出一条权最小的, 并且与前面已经选出的边不构成回路。
如此选下去,直到选出1-n 条边为止。
第1步 开始把边按权的大小由小到大排列起来,即m a a a ,...,,21置 φ=S ,0=i ,1=j 。
第2步 若1||-==n i S ,则停。
这时T S G =][即为所求;否则, 转向第3步。
第3步 若}]{[j a S G Y 不构成回路,则置j i a e =+1,}{1+=i e S S Y ,1+=i i ,1+=j j ,转向第2步;否则,置1+=j j ,转向第2步。
例:求图6.4.1的最小树T 。
解:83221)(=+++=T w3、求最小树的破圈法具体步骤:任意选出图G 的一条回路,从中去掉一条权最大的边。
最小树问题.

W T ' W T w e w e '
证明:(1)→(2) 由于T是树,由定义知T连通且无圈。只须证明m=n-1。 归纳法:当n=2时,由于T是树,所以两点间显然有且 仅有一条边,满足m=n-1。 假设 n=k-1时命题成立,即有k-1个顶点时,T有 k-2条边。 当n=k时,因为T连通无圈,k个顶点中至少有一 个点次为1。设此点为u,即u为悬挂点,设连接点u的 悬挂边为[v,u],从T中去掉[v,u]边及点u ,不会影 响T的连通性,得图T’,T’为有k-1个顶点的树,所以 T’有k-2条边,再把( v,u)、点u加上去,可知当T 有k个顶点时有k-1条边。
第2步:在Xi 确定的割集(Xi)中选一条最小权边ek, ek=[v’,vk], v’∈Xi ,vk ∈ Xi , Ei-1= Ei∪ek
Xi+1= Xi ∪﹛vk﹜,Xi+1= Xi \ ﹛vk﹜
第3步:若Xi+1=V,结束,(V,Ei+1)是所求的最 小树。否则,把i换成i+1,返回第2步。
例:
定理3:图T是树的充分必要条件是任意两个顶点之间恰 有一条链。
证明:必要性 因T是连通的,故任两个点之 间至少有一条链。但如果某两个点之间有两条链 的话,那么图T中含有圈,这与树的定义矛盾, 从而任两个点之间恰有一条链。
充分性 设图T中任两个点之间恰有一条链, 那么易见T是连通的,如果T中含有圈,那么这个 圈上的两个顶点之间有两条链,这与假设矛盾, 故T不含圈,于是T是树。
图论经典问题
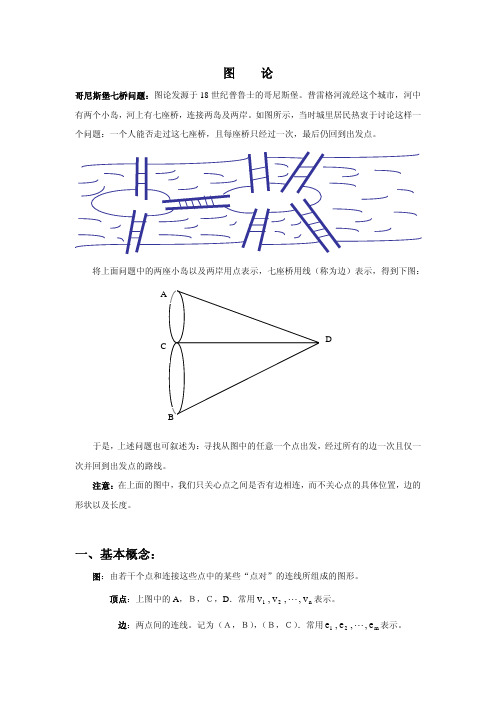
图 论哥尼斯堡七桥问题:图论发源于18世纪普鲁士的哥尼斯堡。
普雷格河流经这个城市,河中有两个小岛,河上有七座桥,连接两岛及两岸。
如图所示,当时城里居民热衷于讨论这样一个问题:一个人能否走过这七座桥,且每座桥只经过一次,最后仍回到出发点。
将上面问题中的两座小岛以及两岸用点表示,七座桥用线(称为边)表示,得到下图:于是,上述问题也可叙述为:寻找从图中的任意一个点出发,经过所有的边一次且仅一次并回到出发点的路线。
注意:在上面的图中,我们只关心点之间是否有边相连,而不关心点的具体位置,边的形状以及长度。
一、基本概念:图:由若干个点和连接这些点中的某些“点对”的连线所组成的图形。
顶点:上图中的A ,B,C,D .常用表示。
n 21 v , , v , v 边:两点间的连线。
记为(A,B),(B,C).常用表示。
m 21e , , e , e次:一个点所连的边数。
定点v的次记为d(v).图的常用记号:G=(V,E),其中,}{v V i =,}{e E i =子图:图G的部分点和部分边构成的图,成为其子图。
路:图G中的点边交错序列,若每条边都是其前后两点的关联边,则称该点边序列为图G的一条链。
圈(回路):一条路中所含边点均不相同,且起点和终点是同一点,则称该路为圈(回路)。
有向图:,其中(,)G N A =12{,,,}k N n n n = 称为的顶点集合,A a 称为G 的弧集合。
G {(,)ij i j }n n ==若,则称为的前驱, 为n 的后继。
(,)ij i j a n n =i n j n j n i 赋权图(网络):设是一个图,若对G 的每一条边(弧)都赋予一个实数,称为边的权,。
记为。
G (,,)G N E W =两个结论:1、图中所有顶点度数之和等于边数的二倍; 2、图中奇点个数必为偶数。
二、图的计算机存储:1. 关联矩阵简单图:,对应(,)G N E =N E ×阶矩阵()ik B b =10ik i k b ⎧=⎨⎩点与边关联否则简单有向图:,对应(,)G N A =N A ×阶矩阵()ik B b =110ik ik ik a i b a i ⎧⎪=−⎨⎪⎩弧以点为尾弧以点为头否则2. 邻接矩阵简单图:,对应(,)G N E =N N ×阶矩阵()ij A a =10ij i j a ⎧=⎨⎩点与点邻接否则简单有向图:,对应(,)G N A =N N ×阶矩阵()ij A a =10ij i ja ⎧=⎨⎩有弧从连向否则5v 34v01010110100101011110101000110111101065432166654321⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=×v v v v v v A v v v v v v3. 权矩阵:简单图:,对应(,)G N E =N N ×阶矩阵()ij A a =ij ij i j a ω⎧=⎨∞⎩点与点邻接否则123456781234567802130654.5061002907250473080 v v v v v v v v v v v v v v v v 48∞∞∞∞⎡⎤⎢⎥∞∞∞∞∞⎢⎥⎢⎥∞∞∞∞∞⎢⎥∞∞∞∞∞⎢⎥⎢⎥∞∞∞∞⎢⎥∞∞∞∞⎢⎥⎢⎥∞∞∞∞⎢⎥∞∞∞∞∞∞⎢⎥⎣⎦三、图的应用:例:如图,用点代表7个村庄,边上的权代表村庄之间的路长,现在要在这7个村庄中布电话线,如何布线,使材料最省?分析:需要将图中的边进行删减,使得最终留下的图仍然连通,并且使总的权值最小。
西交《运筹学》重要知识点解析和例题分析第六部分

《运筹学》重要知识点解析和例题分析第六部分一.图的基本概念 定义一个图G 是指一个二元组(V(G),E(G)).即图是由点及点之间的联线所组成。
其中: 1)图中的点称为图的顶点(vertex).记为:v2)图中的连线称为图的边(edge).记为:,i j e v v ⎡⎤=⎣⎦.,i j v v 是边 e 的端点。
3)图中带箭头的连线称为图的弧(arc).记为:(),i j a v v =.,i j v v 是弧 a 的端点。
—— 要研究某些对象间的二元关系时.就可以借助于图进行研究 分类▪ 无向图:点集V 和边集E 构成的图称为无向图(undirected graph).记为: G(V.E)—— 若这种二元关系是对称的.则可以用无向图进行研究▪ 有向图:点集V 和弧集A 构成的图称为有向图(directed graph) .记为:D(V.A)—— 若这种二元关系是非对称的.则可以用有向图进行研究▪ 有限图: 若一个图的顶点集和边集都是有限集.则称为有限图.只有一个顶点的图称为平凡图.其他的所有图都称为非平凡图.图的特点:1 图反映对象之间关系的一种工具.与几何图形不同。
2 图中任何两条边只可能在顶点交叉.在别的地方是立体交叉.不是图的顶点。
3 图的连线不用按比例画.线段不代表真正的长度.点和线的位置有任意性。
4 图的表示不唯一。
如:以下两个图都可以描述“七桥问题”。
点(vertex)的概念1 端点:若e =[u.v] ∈E.则称u.v 是 e 的端点。
2 点的次:以点 v 为端点的边的个数称为点 v 的次.记为:()d v 。
在无向图G 中.与顶点v 关联的边的数目(环算两次),称为顶点v 的度或次数.记为()d v 或 dG(v).在有向图中.从顶点v 引出的边的数目称为顶点v 的出度.记为d+(v).从顶点v 引入的边的数目称为v 的入度.记为d -(v). 称()d v = d+(v)+d -(v)为顶点v 的度或次数. 3 奇点:次为奇数的点。
实验4Lingo求解最短路最小树问题

u(1)=0;
@for(link:@bin(x));
@for(city(k)|k #GT# 1:@sum(city(i)|i #ne# k:x(i,k))=1;
@for(city(j)|j #gt# 1 # and # j #ne# k:u(j)>=u(k)+x(k,j)-(n-2)*(1-
x(k,j))+(n-3)*x(j,k);););
若G' 是包含 G 的全部顶点的子图,它又是树,则称G' 的生
成树。若图 G(V , E) 是一个连通赋权图,T 是 G 的一颗生成树,
T 的每条边所赋权的和称为树 T 的权,称具有最小权的生成
v 树为 G 的最小生成树。
1
v2
v3 v4
v5 v6
例1-2 假设某电力公司在7个村庄之间架设电线, 各村庄之间的距离如下图所示,试求出使电线总长度最 小的架线方案。
roads(cities, cities)/
A,B1 A,B2 B1,C1 B1,C2 B1,C3 B2,C1 B2,C2
B2,C3
C1,D C2,D C3,D/: w, x; endsets
min
wij xij
(Vi ,V j )E
data: w = 2 4 3 3 1 2 3 1 1 3 4; enddata n=@size(cities);
1.000000 1.000000 1.000000 1.000000 1.000000 1.000000
3.000000 3.000000 2.000000 2.000000 1.000000 2.000000
从上述求解报告得到最优架设线路 为1-2-3,2-4-5-6-7,总长度为13。
最小树与最短路问题

常记:V = {v1, v2, … , vn}, |V | = n ; E = {e1, e2, … , em}(ek=vivj ) , |E | = m.
图的一些基本概念
有边联结的两个点称为相邻的点, 有一个公共端点的 边称为相邻边. 边和它的端点称为互相关联. 常用d(v) 表示图G中与顶点v关联的
291.1 303.8 248.8 106.5
问题分析与建模 • 用v1,v2,v3,v4,v5,v6,v7,v8表示8个学院的地理位置,因 为各学院之间的距离都是固定的,则我们得一赋 权图。 • 要使各学院都可以用网络通讯,这样的图一定为连 通的,其次若图中有圈,则可以划去一条以节省一 条光缆,因而计算机网络一定为一棵树。 • 考虑到使用光缆最少,所以要在赋权图中找到一 边权之和最小的树。即:最小树。 问题归结为:求一赋权图的最小树问题。
2、最小生成树模型
一个无圈的连通图称为树。 设图G为具有n顶点的树,则下列6个结论等价 ①、G为无圈的连通图。
②、G为连通的且具有n-1条边。 ③、G为连通的且每条边为一割集。
④、G无圈且具有n-1条边。 ⑤、G任意两个顶点之间恰有一条路。 ⑥、G为最小连通图。
若图T=(V,E')是图G=(V,E)的生成子图,且T是一棵 树,则称T是G的一棵生成树。
最小生成树
设G=(V,E)是一个非负赋权图,设T=(V,E') 是G的一棵生成树,记生成树的边权之和为:
w(T )
称为生成树的权。
( vi ,v j )T
w
ij
若G的一生成树T*,其权w(T*)是G所有生成树权 最小者,则称T*为最小生成树。
一个实际的例子
问题提出:
SU大学有8个学院,其中A为 学校行政部门(如图所示)。 该大学现在需要设计一个电 脑网络系统,使得A到每个系 都有光缆相连.SU 大学主管 部门希望连接用的光缆量尽 量的少,为便于管理,要求光 缆连接点必须设在各学院处, 施工部门测得各学院的位置 坐标如下:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
所以,总的计算量约为O(n2)
证明
W (e) max W (e) eC ( e )
最小树及其性质 续
定理 6.4.2 设 T 是 G 的支撑树,则 T 是 G 的最小树当 且仅当对任意边 eT 有
W (e) min W (e) eΩ ( e )
其中 Ω(e) T * + e 为一个唯一割集。
证明 定理6.4.3 设T是G的支撑树,则T是G的唯一最小树当且仅 当对任意边e∈G\T,e是C(e)中的唯一最大边。
在第3步中,判定加边后是否构成回路总共约需m次 比较,而加边后点的重新标号最多需n(n-1)次比较
所以,总的计算量为 mlog2m+n+m+n(n-1)~O(n2log2n)
Dijkstra算法的步骤
第1步 置uj=w1j,T=Φ,R={1},S={2,3, …,n}
第2步
取 uk
min{u jS
第四节 最小树问题
最小树及其性质 求最小树的Kruskal算法
算法步骤 算法复杂性
求最小树的Dijkstra算法
算法步骤 算法复杂性
最小树及其性质
支撑树T的权(或长):W (T ) W (e) eE
最小树:G中权最小的支撑树
定理6.4.1 设T是G的一个支撑树,则T是G的最小树 当且仅当对任意边e∈T*有
j
}
wik
,置T
=T
U {eik } ,
ቤተ መጻሕፍቲ ባይዱ
R = R U{k} , S = S \ {k} ;
第3步
若 S = Φ ,则停止;否则,置
uk
=
min{u jS
j
,w
kj
},
j S ,返回第 2 步。
例
Dijkstra算法的复杂性
执行第2步时,第一次是(n-2)次比较, 第二次为(n-3)次比较, 第三次为(n-4)次比较,…, 因此总的比较为(n-1)(n-2)/2次
定理6.4.4 设T是G的支撑树,则T是G的唯一最小树当且仅
当对任意边e∈T ,e是Ω(e)中的唯一最小边。
Kruskal算法的步骤
第1步 开始把边按权的大小由小到大排列,即将图的 边排序为a1,a2, …,am,使W(a1) ≤W(a2)≤…≤W(am) 置 S=Φ,i=0,j=1。
第2步 若|S|=i=n-1,则停止。这时G[S]=T即为所求; 否则,转向第3步。
第3步 若G[S∪{aj}]不构成回路,则置ei+1=aj, S=S∪{ei+1} ,i:=i+1,j:=j+1,转向第2步;否则,置 j:=j+1,转向第2步。
例
Kruskal算法的复杂性
首先,在第1步中把边按权的大小由小到大排列起来, 这约需mlog2m次比较(m为此网络的边数) 其次,第2步最多循环n次
