中考数学复习指导：一道几何旋转变换题的变式训练.doc
2023年 九年级数学中考复习 几何图形变换综合压轴题 专题训练(含答案)
2023年春九年级数学中考复习《几何图形变换综合压轴题》专题训练（附答案）1．如图，△ABC和△ECD都是等边三角形，直线AE，BD交于点F．（1）如图1，当A，C，D三点在同一直线上时，∠AFB的度数为，线段AE与BD的数量关系为．（2）如图2，当△ECD绕点C顺时针旋转α（0°≤α＜360°）时，（1）中的结论是否还成立？若不成立，请说明理由；若成立，请就图2给予证明．（3）若AC＝4，CD＝3，当△ECD绕点C顺时针旋转一周时，请直接写出BD长的取值范围．2．如图1，在Rt△ABC中，∠BAC＝90°，AB＝AC，D、E两点分别在AC、BC上，且DE∥AB，将△CDE绕点C按顺时针方向旋转，记旋转角为α．（1）问题发现：当α＝0°时，的值为；（2）拓展探究：当0°≤α＜360°时，若△EDC旋转到如图2的情况时，求出的值；（3）问题解决：当△EDC旋转至A、B、E三点共线时，若CE＝5，AC＝4，直接写出线段AD的长．3．已知：如图1，线段AD＝5，点B从点A出发沿射线AD方向运动，以AB为底作等腰△ABC，使得AC＝BC＝AB．（1）如图2，当AB＝10时，求证：CD⊥AB；（2）当△BCD是以BC为腰的等腰三角形时，求BC的长；（3）当AB＞5时，在线段BC上是否存在点E，使得△BDE与△ACD全等，若存在，求出BC的长；若不存在，请说明理由；（4）作点A关于直线CD的对称点A′，连接CA′当CA′∥AB时，CA′＝（请直接写出答案）．4．如图1，在△ABC中，AE⊥BC于点E，AE＝BE，D是AE上的一点，且DE＝CE，连接BD，CD．（1）试判断BD与AC的位置关系是：；数量关系是：；（2）如图2，若将△DCE绕点E旋转一定的角度后，试判断BD与AC的位置关系和数量关系是否发生变化，并说明理由；（3）如图3，若将（2）中的等腰直角三角形都换成等边三角形，其他条件不变．①试猜想BD与AC的数量关系为：；②你能求出BD与AC的夹角度数吗？如果能，请直接写出夹角度数；如果不能，请说明理由．5．如图，平面直角坐标系中O为原点，Rt△ABC的直角顶点A在y轴正半轴上，斜边BC 在x轴上，已知B、C两点关于y轴对称，且C（﹣8，0）．（1）请直接写出A、B两点坐标；（2）动点P在线段AB上，横坐标为t，连接OP，请用含t的式子表示△POB的面积；（3）在（2）的条件下，当△POB的面积为24时，延长OP到Q，使得PQ＝OP，在第一象限内是否存在点D，使得△OQD是等腰直角三角形，如果存在，求出D点坐标；如果不存在，请说明理由．6．如图1，已知△ABC中，∠ACB＝90°，AC＝BC＝6，点D在AB边的延长线上，且CD ＝AB．（Ⅰ）求BD的长度；（Ⅱ）如图2，将△ACD绕点C逆时针旋转α（0°＜α＜360°）得到△A'CD'．①若α＝30°，A'D'与CD相交于点E，求DE的长度；②连接A'D、BD'，若旋转过程中A'D＝BD'时，求满足条件的α的度数．（Ⅲ）如图3，将△ACD绕点C逆时针旋转α（0°＜α＜360°）得到△A'CD'，若点M 为AC的中点，点N为线段A'D'上任意一点，直接写出旋转过程中线段MN长度的取值范围．7．如图①，将两个等腰直角三角形纸片OAB和OCD放置在平面直角坐标系中，点O（0，0），点A（0，+1），点B（+1，0），点C（0，1），点D（1，0）．（Ⅰ）求证：AC＝BD；（Ⅱ）如图②，现将△OCD绕点O顺时针方向旋转，旋转角为α（0°＜α＜180°），连接AC，BD，这一过程中AC和BD是否仍然保持相等？说明理由；当旋转角α的度数为时，AC所在直线能够垂直平分BD；（Ⅲ）在（Ⅱ）的情况下，将旋转角α的范围扩大为0°＜α＜360°，那么在旋转过程中，求△BAD的面积的最大值，并写出此时旋转角α的度数．（直接写出结果即可）8．在△ABC中，AB＝AC，∠BAC＝α，过点A作直线l平行于BC，点D是直线l上一动点，连接CD，射线DC绕点D顺时针旋转α交直线AB于点E．（1）如图1，若α＝60°，当点E在线段AB上时，请直接写出线段AC，AD，AE之间的数量关系，不用证明；（2）如图2，若α＝60°，当点E在线段BA的延长线上时，（1）中的结论是否成立？若成立，请证明；若不成立，请写出正确结论，并证明．（3）如图3，若α＝90°，BC＝6，AD＝，请直接写出AE的长．9．有一根直尺短边长4cm，长边长10cm，还有一块锐角为45°的直角三角形纸板，它的斜边长为16cm，如图甲，将直尺的短边DE与直角三角形纸板的斜边AB重合，且点D 与点A重合．将直尺沿射线AB方向平移，如图乙，设平移的长度为xcm，且满足0≤x ≤12，直尺和三角形纸板重叠部分的面积为Scm2．（1）当x＝0cm时，S＝；当x＝12cm时，S＝．（2）当0＜x＜8（如图乙、图丙），请用含x的代数式表示S．（3）是否存在一个位置，使重叠部分面积为28cm2？若存在求出此时x的值．10．如图①，C为线段BD上的一点，BC≠CD，分别以BC，BD为边在BD的上方作等边△ABC和等边△CDE，连接AE，F，G，H分别是BC，AE，CD的中点，连接FG，GH，FH．（1）△FGH的形状是；（2）将图①中的△CDE绕点C顺时针旋转，其他条件不变，（1）的结论是否成立？结合图②说明理由；（3）若BC＝2，CD＝4，将△CDE绕点C旋转一周，当A，E，D三点共线时，直接写出△FGH的周长．11．已知，射线AB∥CD，P是直线AC右侧一动点，连接AP，CP，E是射线AB上一动点，过点E的直线分别与AP，CP交于点M，N，与射线CD交于点F，设∠BAP＝∠1，∠DCP＝∠2．（1）如图1，当点P在AB，CD之间时，求证：∠P＝∠1+∠2；（2）如图2，在（1）的条件下，作△PMN关于直线EF对称的△P'MN，求证：∠3+∠4＝2（∠1+∠2）；（3）如图3，当点P在AB上方时，作△PMN关于直线EF对称的△P'MN，（1）（2）的结论是否仍然成立，若成立，请说明理由；若不成立，请直接写出∠P，∠1，∠2之间数量关系，以及∠3，∠4与∠1，∠2之间数量关系．12．（1）如图1，平面直角坐标系中A（0，a），B（a，0）（a＞0）．C为线段AB的中点，CD⊥x轴于D，若△AOB的面积为2，则△CDB的面积为．（2）如图2，△AOB为等腰直角三角形，O为直角顶点，点E为线段OB上一点，且OB＝3OE，C与E关于原点对称，线段AB交x轴于点D，连CD，若CD⊥AE，试求的值．（3）如图3，点C、E在x轴上，B在y轴上，OB＝OC，△BDE是以B为直角顶点的等腰直角三角形，直线CB、ED交于点A，CD交y轴于点F，试探究：是否为定值？如果是定值，请求出该定值；如果不是，请求出其取值范围．13．在△ABC中，AB＝AC，∠BAC＝90°．（1）如图1，点P，Q在线段BC上，AP＝AQ，∠BAP＝15°，求∠AQB的度数；（2）点P，Q在线段BC上（不与点B，C重合），AP＝AQ，点Q关于直线AC的对称点为M，连接AM，PM．①依题意将图2补全；②用等式表示线段BP，AP，PC之间的数量关系，并证明．14．【问题背景】如图1，在Rt△ABC中，AB＝AC，D是直线BC上的一点，将线段AD绕点A逆时针旋转90°至AE，连接CE，求证：△ABD≌△ACE；【尝试应用】如图2，在图1的条件下，延长DE，AC交于点G，BF⊥AB交DE于点F，求证：FG＝AE；【拓展创新】如图3，A是△BDC内一点，∠ABC＝∠ADB＝45°，∠BAC＝90°，BD ＝，直接写出△BDC的面积为．15．在平面直角坐标系中，A（a，0），B（0，b）分别是x轴负半轴和y轴正半轴上一点，点C与点A关于y轴对称，点P是x轴正半轴上C点右侧一动点．（1）当2a2+4ab+4b2+2a+1＝0时，求A，B的坐标；（2）当a+b＝0时，①如图1，若D与P关于y轴对称，PE⊥DB并交DB延长线于E，交AB的延长线于F，求证：PB＝PF；②如图2，把射线BP绕点B顺时针旋转45o，交x轴于点Q，当CP＝AQ时，求∠APB的大小．16．已知：在Rt△ABC中，∠C＝90°，∠B＝30°，BC＝6，左右作平行移动的等边三角形DEF的两个顶点E、F始终在边BC上，DE、DF分别与AB相交于点G、H．（1）如图1，当点F与点C重合时，点D恰好在斜边AB上，求△DEF的周长；（2）如图2，在△DEF作平行移动的过程中，图中是否存在与线段CF始终相等的线段？如果存在，请指出这条线段，并加以证明；如果不存在，请说明理由；（3）假设C点与F点的距离为x，△DEF与△ABC的重叠部分的面积为y，求y与x的函数关系式，并写出定义域．17．在△ABC中，∠C＝90°，AC＝2，BC＝2，点D为边AC的中点（如图），点P、Q 分别是射线BC、BA上的动点，且BQ＝BP，联结PQ、QD、DP．（1）求证：PQ⊥AB；（2）如果点P在线段BC上，当△PQD是直角三角形时，求BP的长；（3）将△PQD沿直线QP翻折，点D的对应点为点D'，如果点D'位于△ABC内，请直接写出BP的取值范围．18．定义：如图1，点M，N把线段AB分割成AM，MN和BN，若以AM，MN，BN为边的三角形是一个直角三角形，则称点M，N是线段AB的勾股分割点．（1）已知点M，N是线段AB的勾股分割点，若AM＝2，MN＝3，求BN的长．（2）如图2，在等腰直角△ABC中，AC＝BC，∠ACB＝90°，点M，N为边AB上两点满足∠MCN＝45°，求证：点M，N是线段AB的勾股分割点；阳阳同学在解决第（2）小题时遇到了困难，陈老师对阳阳说：要证明勾股分割点，则需设法构造直角三角形，你可以把△CBN绕点C逆时针旋转90°试一试．请根据陈老师的提示完成第（2）小题的证明过程．19．问题背景如图（1），△ABD，△AEC都是等边三角形，△ACD可以由△AEB通过旋转变换得到，请写出旋转中心、旋转方向及旋转角的大小．尝试应用如图（2），在Rt△ABC中，∠ACB＝90°，分别以AC，AB为边，作等边△ACD和等边△ABE，连接ED，并延长交BC于点F，连接BD．若BD⊥BC，求的值．拓展创新如图（3），在Rt△ABC中，∠ACB＝90°，AB＝2，将线段AC绕点A顺时针旋转90°得到线段AP，连接PB，直接写出PB的最大值．20．【教材呈现】如图是苏科版九年级下册数学教材第92页的第17题．一块直角三角形木板，它的一条直角边AC长为1.5m，面积为1.5m2．甲乙两人分别按图1、图2把它加工成一个正方形的桌面，请说明哪个正方形的面积较大．【解决问题】（1）记图1、图2中的正方形面积分别为S1，S2，则S1S2．（填“＞”、“＜”或“＝”）．【问题变式】若木板形状是锐角三角形A1B1C1．某数学兴趣小组继续思考：按图3、图4、图5三种方式加工，分别记所得的正方形面积为S3、S4、S5，哪一个正方形的面积最大呢？（2）若木板的面积S仍为1.5m2．小明：记图3中的正方形为“沿B1C1边的内接正方形”，图4中的正方形为“沿A1C1边的内接正方形”，依此类推．以图3为例，求“沿B1C1边的内接正方形DEFG”的面积．设EF ＝x ，B 1C 1＝a ，B 1C 1边上的高A 1H ＝h ，则S ＝ah ．由“相似三角形对应高的比等于相似比”易得x ＝；同理可得图4、图5中正方形边长，再比较大小即可．小红：若要内接正方形面积最大，则x 最大即可；小莉：同一块木板，面积相同，即S 为定值，本题中S ＝1.5，因此，只需要a +h 最小即可．我们可以借鉴以前研究函数的经验，令y ＝a +h ＝a +＝a +（a ＞0）．下面来探索函数y ＝a +（a ＞0）的图象和性质．①根据如表，画出函数的图象：（如图6）a… 1 2 3 4 … y … 12 9 6 4 3 3 4 4…②观察图象，发现该函数有最小值，此时a 的取值 ；A ．等于2；B ．在1～之间；C ．在～之间；D ．在～2之间．（3）若在△A 1B 1C 1中（如图7），A 1B 1＝5，A 1C 1＝，高A 1H ＝4．①结合你的发现，得到S 3、S 4、S 5的大小关系是 （用“＜”连接）． ②小明不小心打翻了墨水瓶，已画出最大面积的内接正方形的△A 1B 1C 1原图遭到了污损，请用直尺和圆规帮他复原△A 1B 1C 1．（保留作图痕迹，不写作法）参考答案1．解：（1）∵△ABC是等边三角形，∴AC＝BC，∠BAC＝∠ACB＝60°，∵△ECD是等边三角形，∴CE＝CD，∠DCE＝60°，∴∠ACB＝∠DCE＝60°，∴∠ACB+∠BCE＝∠DCE+∠BCE，即∠ACE＝∠BCD，在△ACE和△BCD中，，∴△ACE≌△BCD（SAS），∴AE＝BD，∠CAE＝∠CBD，在△ABF中，∠AFB＝180°﹣（∠BAF+∠ABF）＝180°﹣（∠BAF+∠CBF+∠ABC）＝180°﹣（∠BAC+∠ABC）＝180°﹣（60°+60°）＝60°，∴∠AFB＝60°，故答案为：∠AFB＝60°，AE＝BD；（2）（1）中结论仍成立，证明：∵△ABC是等边三角形，∴AC＝BC，∠BAC＝∠ACB＝60°，∵△ECD是等边三角形，∴CE＝CD，∠DCE＝60°，∴∠ACB＝∠DCE＝60°，∴∠ACB+∠BCE＝∠DCE+∠BCE，即∠ACE＝∠BCD，在△ACE和△BCD中，，∴△ACE≌△BCD（SAS），∴AE＝BD，∠CAE＝∠CBD，∵∠AFB+∠CBD＝∠ACB+∠CAE，∴∠AFB＝∠ACB，∵∠ACB＝60°，∴∠AFB＝60°；（3）在△BCD中，BC+CD＞BD，BC﹣CD＜BD，∴点D在BC的延长线上时，BD最大，最大为4+3＝7，当点D在线段BC上时，BD最小，最小为4﹣3＝1，∴1≤BD≤7，即BD长的取值范围为1≤BD≤7．2．解：（1）∵∠BAC＝90°，AB＝AC，∴△ABC为等腰直角三角形，∠B＝45°，∵DE∥AB，∴∠DEC＝∠B＝45°，∠CDE＝∠A＝90°，∴△DEC为等腰直角三角形，∴cos∠C＝＝，∵DE∥AB，∴＝＝，故答案为：；（2）由（1）知，△BAC和△CDE均为等腰直角三角形，∴＝＝，又∠BCE＝∠ACD＝α，∴△BCE∽△ACD，∴＝＝，即＝；（3）①如图3﹣1，当点E在线段BA的延长线上时，∵∠BAC＝90°，∴∠CAE＝90°，∴AE＝＝＝3，∴BE＝BA+AE＝4+3＝7；由（2）知，＝．故AD＝．②如图3﹣2，当点E在线段BA上时，AE＝＝＝3，∴BE＝BA﹣AE＝4﹣3＝1，由（2）知，＝．故AD＝．综上所述，AD的长为或，故答案为：或．3．解：（1）如图2中，∵AB＝10，AD＝5，∴AD＝DB，∵CA＝CB，AD＝DB，∴CD⊥AB．（2）如图1中，当AB＜AD时，BC＝BD．设AB＝10k，则AC＝BC＝6k，∵AD＝5，∴10k+6k＝5，∴k＝，∴BC＝6k＝．如图1﹣1中，当AB＞AD时，BC＝BD，同法可得10k﹣6k＝5，解得k＝，∴BC＝6k＝，综上所述，BC的值为或．（3）如图3﹣1中，当△ADC≌△BED时，BD＝AC＝BC，由（2）可知，BC＝．如图3﹣2中，当△ADC≌△BCE时，点E与C重合，此时AB＝10k＝10，∴k＝1，BC＝6k＝6．综上所述，BC的值为或6．（4）如图3中，当CA′∥AB时，∵CA′∥AB，∴∠ADC＝∠A′CD，由翻折可知，∠A′CD＝∠ACD，∴∠ACD＝∠ADC，∴AC＝AD＝5，∴CA′＝CA＝5．故答案为5．4．解：（1）结论：BD＝AC，BD⊥AC．理由：延长BD交AC于F．∵AE⊥CB，∴∠AEC＝∠BED＝90°．在△AEC和△BED中，，∴△AEC≌△BED（SAS），∴AC＝BD，∠CAE＝∠EBD，∵∠AEC＝90°，∴∠ACB+∠CAE＝90°，∴∠CBF+∠ACB＝90°，∴∠BFC＝90°，∴AC⊥BD，故答案为：BD⊥AC，BD＝AC．（2）如图2中，不发生变化，设DE与AC交于点O，BD与AC交于点F．理由是：∵∠BEA＝∠DEC＝90°，∴∠BEA+∠AED＝∠DEC+∠AED，∴∠BED＝∠AEC，在△BED和△AEC中，，∴△BED≌△AEC（SAS），∴BD＝AC，∠BDE＝∠ACE，∵∠DEC＝90°，∴∠ACE+∠EOC＝90°，∵∠EOC＝∠DOF，∴∠BDE+∠DOF＝90°，∴∠DFO＝180°﹣90°＝90°，∴BD⊥AC；（3）①如图3中，结论：BD＝AC，理由是：∵△ABE和△DEC是等边三角形，∴AE＝BE，DE＝EC，∠BEA＝∠DEC＝60°，∴∠BEA+∠AED＝∠DEC+∠AED，∴∠BED＝∠AEC，在△BED和△AEC中，，∴△BED≌△AEC（SAS），∴BD＝AC，故答案为：BD＝AC．②能；设BD与AC交于点F，由①知，△BED≌△AEC，∴∠BDE＝∠ACE，∴∠DFC＝180°﹣（∠BDE+∠EDC+∠DCF）＝180°﹣（∠ACE+∠EDC+∠DCF）＝180°﹣（60°+60°）＝60°，即BD与AC的夹角中的锐角的度数为60°．5．解：（1）∵B、C两点关于y轴对称，且C（﹣8，0），∴点B（8，0），BO＝CO，又∵AO⊥BC，∴AC＝AB，∵∠CAB＝90°，AC＝AB，CO＝BO，∴AO＝CO＝BO＝8，∴点A（0，8）；（2）如图1，过点P作PM⊥OB于M，∵点P的横坐标为t，∴OM＝t，∴MB＝8﹣t，∵∠CAB＝90°，AC＝AB，∴∠ABO＝45°，∴∠BPM＝∠ABO＝45°，∴PM＝MB＝8﹣t，∴S△POB＝×OB×PM＝×8×（8﹣t）＝32﹣4t；（3）∵△POB的面积为24，∴32﹣4t＝24，∴t＝2，∴点P（2，6），如图2，当点Q为直角顶点时，过点Q作HG⊥y轴，过点D作DG⊥HG于点G，∵PQ＝OP，点P（2，6），∴点Q（4，12），∵∠OQD＝90°＝∠OHQ＝∠QGD，∴∠OQH+∠DQG＝90°＝∠OQH+∠HOQ，∴∠HOQ＝∠GQD，又∵OQ＝QD，∴△OHQ≌△QGD（AAS），∴OH＝QG＝12，HQ＝GD＝4，∴HG＝16，∴点D（16，8）；当点D为直角顶点时，过点Q作HG⊥y轴，过点D作DG⊥HG于点G，过点D作DN ⊥y轴于N，同理可求△QDG≌△ODN，∴ON＝QG，DN＝DG，∵DN＝QG+HQ＝4+QG，DG＝HN＝12﹣ON，∴ON＝QG＝4，DN＝DG＝8，∴点D（8，4），综上所述：点D（16，8）或（8，4）．6．解：（Ⅰ）如图1，过点C作CH⊥AB于H，∵∠ACB＝90°，AC＝BC＝6，CH⊥AB，∴AB＝CD＝6，CH＝BH＝AB＝3，∠CAB＝∠CBA＝45°，∴DH＝＝＝3，∴BD＝DH﹣BH＝3﹣3；（Ⅱ）①如图2，过点E作EF⊥CD'于F，∵将△ACD绕点C逆时针旋转α（0°＜α＜360°）得到△A′CD′，∴CD＝CD'＝6，∠DCD'＝30°＝∠CDA＝∠CD'A'，∴CE＝D'E，又∵EF⊥CD'，∴CF＝D'F＝3，EF＝，CE＝2EF＝2，∴DE＝DC﹣CE＝6﹣2；②如图2﹣1，∵∠ABC＝45°，∠ADC＝30°，∴∠BCD＝15°，∴∠ACD＝105°，∵将△ACD绕点C逆时针旋转α（0°＜α＜360°）得到△A′CD′，∴AC＝A'C，CD＝CD'，∠ACA'＝∠DCD'＝α，∴CB＝CA'，又∵A′D＝BD′，∴△A'CD≌△BCD'（SSS），∴∠A'CD＝∠BCD'，∴105°﹣α＝15°+α，∴α＝45°；如图2﹣2，同理可证：△A'CD≌△BCD'，∴∠A'CD＝∠BCD'，∴α﹣105°＝360°﹣α﹣15°，∴α＝225°，综上所述：满足条件的α的度数为45°或225°；（Ⅲ）如图3，当A'D'⊥AC时，N是AC与A'D'的交点时，MN的长度最小，∵∠A'＝45°，A'D'⊥AC，∴∠A'＝∠NCA'＝45°，∴CN＝A'N＝3，∵点M为AC的中点，∴CM＝AC＝3，∴MN的最小值＝NC﹣CM＝3﹣3；如图4，当点A，点C，点D'共线，且点N与点D'重合时，MN有最大值，此时MN＝CM+CN＝6+3，∴线段MN的取值范围是3﹣3≤MN≤6+3．7．解：（Ⅰ）∵点A（0，+1），点B（+1，0），点C（0，1），点D（1，0），∴OA＝+1，OB＝+1，OC＝1，OD＝1，∴AC＝OA﹣OC＝+1﹣1＝，BD＝+1﹣1＝，∴AC＝BD；（Ⅱ）由题意知，OA＝OB，OC＝OD，∠AOB＝∠COD＝90°，∴∠AOC＝∠AOB﹣∠COB＝90°﹣∠COB，∠BOD＝∠COD﹣∠COB＝90°﹣∠COB，∴∠AOC＝∠BOD，∴△AOC≌△BOD（SAS），∴AC＝BD，∠OAC＝∠OBD，如图1（注：点C在x轴上，为了不要出现误解，点C没画在x轴上），延长AC交BD 于D，连接BC，在Rt△AOB中，OA＝OB，∴∠OAB＝∠OBA＝45°，∴∠CAB+∠ABD＝∠OAB﹣∠OAC+∠ABO+∠BOD＝∠OAB+∠OBA＝90°，∴AC⊥BD，∵AC垂直平分BD，∴CD＝BC，设点C的坐标为（m，n），∴m2+n2＝1①，由旋转知，CD＝＝，∵B（+1，0），[m﹣（+1）]2+n2＝2②，联立①②解得，m＝1，n＝0，∴点C在x轴上，∴旋转角为∠AOC＝90°，故答案为：90°；（Ⅲ）如图2，∵OA＝OB＝+1，∴AB＝OA＝2+，过点O作OH⊥AB于H，∴S△AOB＝OA•OB＝AB•OH，∴OH＝＝＝＝，过点D作DG⊥AB于G，S△ABD＝AB•DG＝（2+）DG，要使△ABD的面积最大，则DG最大，由旋转知，点D是以O为圆心，1为半径的圆上，∴点D在HO的延长线上时，DG最大，即DG的最大值为D'H＝OD'+OH＝1+＝，∴S△ABD最大＝AB•D'H＝（2+）×＝，在Rt△AOB中，OA＝OB，OH⊥AB，∴∠BOH＝45°，∴旋转角∠BOD'＝180°﹣45°＝135°．8．解：（1）AC＝AE+AD．证明：连接CE，∵线段DC绕点D顺时针旋转α交直线AB于点E，α＝60°，∵AB＝AC，∠BAC＝60°，∴CB＝CA＝AB，∠ACB＝60°，∵AD∥BC，∴∠DAF＝∠ACB＝60°，∵∠FDC＝∠EAF＝60°，∠AFE＝∠DFC，∴△AFE∽△DFC，∴，∴，∵∠AFD＝∠EFC，∴△AFD∽△EFC，∴∠DAF＝∠FEC＝60°，∴△DEC是等边三角形，∴CD＝CE，∠ECD＝60°，∴∠BCE＝∠ACD，∴△BCE≌△ACD（SAS），∴BE＝AD，∴AB＝AE+BE＝AE+AD，∴AC＝AE+AD；（2）不成立，AD＝AC+AE．理由如下：在AC的延长线上取点F，使AF＝AD，连接DF，当α＝60°时，∠BAC＝∠EDC＝60°，∵AB＝AC，∴△ABC是等边三角形，∴AB＝AC＝BC∠BCA＝60°，∵l∥BC，∴∠DAC＝∠BCA＝60°，∠EAD＝∠ABC＝60°，∵AF＝AD，∴∠ADF＝∠AFD＝60°，AD＝FD＝AF，∴∠EDC＝∠ADF＝60°，∴∠EDC﹣∠ADC＝∠ADF﹣∠ADC，即∠EDA＝∠CDF，∵AD＝FD，∠EAD＝∠AFD＝60°，∴△EAD≌△CFD（ASA），∴AE＝CF，∴AD＝AF＝AC+CF＝AC+AE；（3）AE的长为或．当点E在线段AB上，过点D作直线l的垂线，交AC于点F，如图3所示．∵△ABC中，∠BAC＝90°，AC＝AB，∴∠ACB＝∠B＝45°．∵直线l∥BC，∴∠DAF＝∠ACB＝45°．∵FD⊥直线l，∴∠DAF＝∠DF A＝45°．∴AD＝FD．∵∠EDC＝∠ADF＝90°，∴∠ADE＝∠FDC．由（1）可知DC＝DE，∴△ADE≌△FDC（SAS），∴AE＝CF．∵AD＝，∴AF＝2，∵BC＝6，∴AC＝AB＝3，∴AE＝AC﹣AF＝3﹣2．当点E在线段AB的延长线上时，如图4所示．过点D作直线l的垂线，交AB于点M，同理可证得△ADC≌△MDE（SAS），∴AC＝EM＝3，∵AD＝，∴AM＝2，∴EM+AM＝3+2．综合以上可得AE的长为3+2或3﹣2．9．解：（1）当x＝0cm时，S＝4×4÷2＝8cm2；当x＝12cm时，S＝4×4÷2＝8cm2．故答案为：8cm2；8cm2．（2）①当0＜x＜4时，∵△CAB为等腰直角三角形，∴∠CAB＝45°，∴△ADG和△AEF都是等腰直角三角形，∴AD＝DG＝x，AE＝EF＝x+4，∴梯形GDEF的面积＝×（GD+EF）×DE＝×（x+x+4）×4＝4x+8．②如图所示：过点C作CM⊥AB于点M．当4＜x＜8时，梯形GDMC的面积＝（GD+CM）×DM＝（x+8）（8﹣x）＝﹣x2+32，梯形CMEF的面积＝（EF+CM）×ME＝[16﹣（x+4）+8][（x+4）﹣8]＝（20﹣x）（x﹣4）＝﹣x2+12x﹣40，S＝梯形GDMC的面积+梯形CMEF的面积＝（﹣x2+32）+（﹣x2+12x﹣40）＝﹣x2+12x ﹣8．综合以上可得，S＝．（3）当0＜x＜4时s最大值小于24，当x＝4时，S＝24cm2，所以当S＝28cm2时，x必然大于4，即﹣x2+12x﹣8＝28，解得x1＝x2＝6，当x＝6cm时，阴影部分面积为28cm2．当8＜≤12时，由对称性可知s的最大值也是小于24，不合题意舍去．∴当x＝6cm时，阴影部分面积为28cm2．10．解：（1）∵△ABC和△CDE都是等边三角形，∴∠B＝∠DCE＝60°，AB＝BC，CE＝CD，∴CE∥AB，∵BC≠CD，∴CE≠AB，∴四边形ABCE是梯形，∵点F，G分别是BC，AE的中点，∴FG是梯形ABCE的中位线，∴FG∥AB，∴∠GFC＝60°，同理：∠GHB＝60°，∴∠FGH＝180°﹣∠GFC﹣∠GHB＝60°＝∠GFC＝∠GHB，∴△FGH是等边三角形，故答案为：等边三角形；（2）成立，理由如下：如图1，取AC的中点P，连接PF，PG，∵△ABC和△CDE都是等边三角形，∴AB＝BC，CE＝CD，∠BAC＝∠ACB＝∠ECD＝∠B＝60°，又F，G，H分别是BC，AE，CD的中点，∴FP＝AB，FC＝BC，CH＝CD，PG＝CE，PG∥CE，PF∥AB，∴FP＝FC，PG＝CH，∠GPC+∠PCE＝180°，∠FPC＝∠BAC＝60°，∠PFC＝∠B＝60°，∴∠FPG＝∠FPC+∠GPC＝60°+∠GPC，∠GPC＝180°﹣∠PCE，∴∠FCH＝360°﹣∠ACB﹣∠ECD﹣∠PCE＝360°﹣60°﹣60°﹣（180°﹣∠GPC）＝60°+∠GPC，∴∠FPG＝∠FCH，∴△FPG≌△FCH（SAS），∴FG＝FH，∠PFG＝∠CFH，∴∠GFH＝∠GFC+∠CFH＝∠GFC+∠PFG＝∠PFC＝60°，∴△FGH为等边三角形；（3）①当点D在AE上时，如图2，∵△ABC是等边三角形，∴∠ACB＝60°，AC＝BC＝2，∵△CDE是等边三角形，∴∠CED＝∠CDE＝60°，CE＝CD＝DE＝4，过点C作CM⊥AE于M，∴DM＝EM＝DE＝2，在Rt△CME中，根据勾股定理得，CM＝＝＝2，在Rt△AMC中，根据勾股定理得，AM＝＝＝4，∴AD＝AM﹣DM＝4﹣2＝2，∵∠ACB＝∠DCE＝60°，∴∠ACB﹣∠DCB＝∠DCE﹣∠DCB，∴∠ACD＝∠BCE，连接BE，在△ACD和△BCE中，，∴△ACD≌△BCE（SAS），∴BE＝AD＝2，∠ADC＝∠BEC，∵∠ADC＝180°﹣∠CDE＝120°，∴∠BEC＝120°，∴∠BEA＝∠BEC﹣∠CED＝60°，过点B作BN⊥AE于N，∴∠BNE＝90°，在Rt△BNE中，∠EBN＝90°﹣∠BEA＝30°，∴EN＝BE＝1，∴BN＝EN＝，DN＝DE﹣EN＝3，连接BD，根据勾股定理得，BD＝＝＝2，∵点H是CD的中点，点F是BC的中点，∴FH是△BCD的中位线，∴FH＝BD＝，由（2）知，△FGH是等边三角形，∴△FGH的周长为3FH＝3，②当点D在AE的延长线上时，如图3，同①的方法得，FH＝，∴△FGH的周长为3FH＝3，即满足条件的△FGH的周长为3或3．11．（1）证明：如图1中，过点P作PT∥AB．∵AB∥CD，AB∥PT，∴AB∥PT∥CD，∴∠1＝∠APT，∠2＝∠CPT，∴∠APC＝∠APT+∠CPT＝∠1+∠2．（2）证明：如图2中，连接PP′．∵∠3＝∠MPP′+∠MP′P，∠4＝∠NPP′+∠NP′P，∠APC＝∠MP′N，∴∠3+∠4＝2∠APC，∵∠APC＝∠1+∠2，∴∠3+∠4＝2（∠1+∠2）．（3）结论不成立．结论是：∠P＝∠2﹣∠1，∠4﹣∠3＝2（∠2﹣∠1）．理由：如图3中，设PC交AB于E，AP交NP′于F．∵AB∥CD，∴∠PEB＝∠2，∵∠PEB＝∠1+∠P，∴∠2＝∠P+∠1，∴∠P＝∠2﹣∠1．∵∠4＝∠P+∠PFN，∠PFN＝∠3+∠P′，∠P＝∠P′，∴∠4＝∠P+∠3+∠P，∴∠4﹣∠3＝2∠P＝2（∠2﹣∠1），∴∠4﹣∠3＝2（∠2﹣∠1）．12．解：（1）∵A（0，a），B（a，0）（a＞0），∴OA＝a，OB＝a，∵△AOB的面积为2，∴S△AOB＝×a×a＝2，∴a＝2（负值舍去），∴A（0，2），B（2，0），∵C为线段AB的中点，∴C（1，1），∴OD＝BD＝CD＝1，∴S△CDB＝×1×1＝．故答案为：．（2）连AC，过点D作DM⊥BC于M，∵△AOB是等腰直角三角形，∴AO⊥BO，AO＝BO，∠B＝∠OAB＝45°，又CO＝EO，∴AO是CE的垂直平分线，∴AE＝AC，不妨设AE、CD交于F，AO、CD交于G，∴∠CGA＝∠OAE+∠AFC＝∠OCD+∠COA，∵∠AFC＝∠COA＝90°，∴∠OAE＝∠OCD＝∠OAC，又∵∠CAD＝∠CAO+∠OAB＝∠OCD+∠B＝∠CDA，∴CD＝CA＝EA，∴△AOE≌△CMD（AAS），∴OE＝DM，∴＝＝＝3，∴＝2；（3）＝2，理由如下：作点C关于y轴的对称点N，连接BN，作DM∥BC交y轴于M，∵OB＝OC＝ON，∠BON＝90°，∴△BON等腰直角三角形，∴∠BNO＝∠BMD＝45°，∴∠MBD＝∠OBE+∠DBE＝∠OBE+∠BOE＝∠BEN，又∵BD＝BE，∴△BMD≌△ENB（AAS），∴EN＝BM，BN＝DM＝BC，又∵∠BFC＝∠DFM，∠BCF＝∠FDM，∴△BCF≌△MDF（AAS），∴BF＝MF，∴CO﹣EO＝NO﹣EO＝NE＝BM＝2BF，即＝2．13．解：（1）∵在△ABC中，AB＝AC，∠BAC＝90°，∴∠B＝∠C＝45°，∵∠APQ是△ABC的一个外角，∴∠APQ＝∠B+∠BAP，∵∠BAP＝15°，∴∠APQ＝60°，∵AP＝AQ，∴∠APQ＝∠AQB＝60°．（2）①图形如图2所示．②解：结论：PC2+BP2＝2AP2．理由：连接MC．∵AB＝AC，∠BAC＝90°，∴∠B＝∠ACB＝45°，∵AP＝AQ，∴∠APQ＝∠AQP，∴∠BAP＝∠CAQ，∴△ABP≌△ACQ（SAS），∴BP＝CQ，∵点Q关于直线AC的对称点为M，∴AQ＝AM，CQ＝CM，∠CAM＝∠CAQ，∠ACM＝∠ACQ＝45°，∴AP＝AM，∠B＝∠ACM＝45°，∠BAP＝∠CAM，BP＝CM，∴∠BAC＝∠P AM＝90°，在Rt△APM中，AP＝AM，∠P AM＝90°，∴PM＝，∵∠ACQ＝∠ACM＝45°，∴∠PCM＝90°，在Rt△PCM中，∠PCM＝90°，∴PC2+CM2＝PM2，∴PC2+BP2＝2AP2．14．【问题背景】证明：如图1，∵∠BAC＝∠DAE＝90°，∴∠DAB＝∠EAC，在△ABD和△ACE中，，∴△ABD≌△ACE（SAS）．【尝试应用】证明：如图2，过点D作DK⊥DC交FB的延长线于K．∵DK⊥CD，BF⊥AB，∴∠BDK＝∠ABK＝90°，∵AB＝AC，∠BAC＝90°，∴∠ABC＝∠ACB＝45°，∴∠DBK＝∠K＝45°，∴DK＝DB，∵△ABD≌△ACE，∴∠ABD＝∠ACE＝135°，DB＝EC＝DK，∴∠ECG＝45°，∵BF⊥AB，CA⊥AB，∴AG∥BF，∴∠G＝∠DFK，在△ECG和△DKF中，，∴△ECG≌△DKF（AAS），∴DF＝EG，∵DE＝AE，∴DF+EF＝AE，∴EG+EF＝AE，即FG＝AE．【拓展创新】解：如图3中，过点A作AE⊥AD交BD于E，连接CE．．∵∠ADB＝45°，∠DAE＝90°，∴△ADE与△ABC都是等腰直角三角形，同法可证△ABD≌△ACE，∴CE＝BD＝2，∵∠AEC＝∠ADB＝45°，∴∠CED＝∠CEB＝90°，∴S△BDC＝•BD•CE＝×2×2＝6．故答案为：6．15．解：（1）∵2a2+4ab+4b2+2a+1＝0，∴（a+2b）2+（a+1）2＝0，∵（a+2b）2≥0 （a+1）2≥0，∴a+2b＝0，a+1＝0，∴a＝﹣1，b＝，∴A（﹣1，0）B（0，）．（2）①证明：如图1中，∵a+b＝0，∴a＝﹣b，∴OA＝OB，又∵∠AOB＝90°，∴∠BAO＝∠ABO＝45°，∵D与P关于y轴对称，∴BD＝BP，∴∠BDP＝∠BPD，设∠BDP＝∠BPD＝α，则∠PBF＝∠BAP+∠BP A＝45°+α，∵PE⊥DB，∴∠BEF＝90°，∴∠F＝90o﹣∠EBF，又∠EBF＝∠ABD＝∠BAO﹣∠BDP＝45°﹣α，∴∠F＝45o+α，∴∠PBF＝∠F，∴PB＝PF．②解：如图2中，过点Q作QF⊥QB交PB于F，过点F作FH⊥x轴于H．可得等腰直角△BQF，∵∠BOQ＝∠BQF＝∠FHQ＝90°，∴∠BQO+∠FQH＝90°，∠FQH+∠QFH＝90°，∴∠BQO＝∠QFH，∵QB＝QF，∴△FQH≌△QBO（AAS），∴HQ＝OB＝OA，∴HO＝AQ＝PC，∴PH＝OC＝OB＝QH，∴FQ＝FP，又∠BFQ＝45°∴∠APB＝22.5°．16．解：（1）在Rt△ABC中，∠C＝90°，∠B＝30°，BC＝6，∴AC＝2，∠A＝60°，∵△DEF是等边三角形，∴∠DCE＝60°，∴∠ACD＝30°，∴∠ADC＝90°，∴CD＝AC＝3，∴△DEF的周长＝9；（2）解：结论：CF＝DG．理由：∵BC＝6，EF＝DF＝DE＝3，∴CF+BE＝BC﹣EF＝6﹣3＝3，∵△DEF是等边三角形，∴∠DEF＝60°，∵∠DEF＝∠B+∠EGB，∴∠B＝∠EGB＝∠DGE＝30°，∴EG＝BE，∵EG+DG＝CF+BE＝3，∴CF＝DG；（3）∵S△DEF＝×32＝，S△DGH＝•GH•DH＝•x•x＝x2，y＝S△DFE﹣S△DHG＝﹣x2（0≤x≤3）．17．解：（1）在Rt△ABC中，AC＝2，BC＝2，根据勾股定理得，AB＝＝＝4，∴＝，∵BQ＝BP，∴＝，∴，∵∠QBP＝∠CBA，∴△BPQ∽△BAC，∴∠BQP＝∠ACB＝90°，∴PQ⊥AB；（2）∵点D是AC的中点，∴AD＝CD＝AC＝1，由（1）知，PQ⊥AB，∴∠AQP＝90°，∴∠PQD＜90°，∵△PQD是直角三角形，∴①当∠DPQ＝90°时，如图1，在Rt△ABC中，AC＝2，AB＝4，∴sin∠ABC＝＝，∴∠ABC＝30°，∴∠QPB＝90°﹣∠ABC＝60°，∴∠DPC＝90°﹣∠BPQ＝30°，∴CP＝＝＝，∴BP＝BC﹣CP＝，②当∠PDQ＝90°时，∴∠ADQ+∠PDC＝90°，如图2，过Q作QE⊥AC于E，∴∠DEQ＝90°＝∠ACB，∴∠ADQ+∠DQE＝90°，∴∠DQE＝∠PDC，∴△EQD∽△CDP，∴，∴，设BP＝t，则CP＝BC﹣BP＝2﹣t，在Rt△BQP中，BQ＝BP cos30°＝t，∴AQ＝AB﹣BQ＝4﹣t，在Rt△AEQ中，QE＝AQ cos30°＝（4﹣t）•＝2﹣t，AE＝AQ＝2﹣t，∴DE＝AD﹣AE＝t﹣1，∴，∴t＝或t＝（大于2，舍去）∴BP＝；即BP＝或；（3）；理由：如图3，①当点D'恰好落在边BC上时，由折叠知，PD'＝PD，PQ⊥DD'，由（1）知，PQ⊥AB，∴DD'∥AB，∴∠DD'C＝∠ABC＝30°，∴CD'＝CD＝，设BP＝m，则CP＝BC﹣BP＝2﹣m，∴DP＝D'P＝CD'﹣CP＝m﹣，在Rt△CDP中，根据勾股定理得，DP2＝CP2+CD2，∴（m﹣）2＝（2﹣m）2+1，∴m＝，②当点D'落在D时，即PQ过点D，在Rt△CDP'中，∠P'＝90°﹣∠DD'P'＝30°，∴CP'＝＝＝，∴BP'＝BC+CP'＝，综上：．18．（1）解：当MN最长时，BN＝＝＝；当BN最长时，BN＝＝＝，综合以上可得BN的长为或；（2）证明：如图，把△CBN绕点C逆时针旋转90°，得到△CAN'，连接MN'，∴△AN'C≌△BNC，∴CN'＝CN，∠ACN'＝∠BCN，∠CBN＝∠CAN'，∵∠MCN＝45°，∴∠N'CA+∠ACM＝∠ACM+∠BCN＝45°，∴∠MCN'＝∠BCM，∴△MN'C≌△MNC（SAS），∴MN'＝MN，∵AC＝BC，∠ACB＝90°，∴∠B＝∠CAM＝45°，∴∠CAN'＝45°，∴∠MAN'＝∠CAN'+∠CAM＝45°+45°＝90°，在Rt△MN'A中，AN'2+AM2＝N'M2，∴BN2+AM2＝MN2，∴点M，N是线段AB的勾股分割点．19．问题背景解：∵△ABD，△AEC都是等边三角形，∴∠BAD＝60°，∠CAE＝60°，AD＝AB，AC＝AE，∴∠BAD+∠BAC＝∠CAE+∠BAC，∴∠DAC＝∠BAE，∴△ACD≌△AEB（SAS），∴△ACD可以由△AEB绕点A顺时针旋转60°得到，即旋转中心是点A，旋转方向是顺时针，旋转角是60°；尝试应用∵△ACD和△ABE都是等边三角形，∴AC＝AD，AB＝AE，∠CAD＝∠BAE＝60°，∴∠CAB＝∠DAE，∴△ADE≌△ACB（SAS），∴∠ADE＝∠ACB＝90°，DE＝CB，∵∠ADE＝90°，∴∠ADF＝90°，∵∠ADC＝∠ACD＝60°，∴∠DCF＝∠CDF＝30°，∴CF＝DF，∵BD⊥BC，∴∠BDF＝30°，∴BF＝DF，设BF＝x，则CF＝DF＝2x，DE＝3x，∴；拓展创新∵∠ACB＝90°，∴点C在以AB为直径的圆上运动，取AB的中点D，连接CD，∴CD＝AB＝1，如图，过点A作AE⊥AB，且使AE＝AD，连接PE，BE，∵将线段AC绕点A顺时针旋转90°得到线段AP，∴∠P AC＝90°，P A＝AC，∵∠EAD＝90°，∴∠P AE＝∠CAD，∴△CAD≌△P AE（SAS），∴PE＝CD＝1，∵AB＝2，AE＝AD＝1，∴BE＝＝＝，∴BP≤BE+PE＝+1，当且仅当P、E、B三点共线时取等号，∴BP的最大值为+1．20．解：（1）由AC长为1.5m，△ABC的面积为1.5m2，可得BC＝2m，如图①，设加工桌面的边长为xcm，∵DE∥CB，∴△ADE∽△ACB，∴＝，即＝，解得：x＝；如图②，设加工桌面的边长为ym，过点C作CM⊥AB，分别交DE、AB于点N、M，∵AC＝1.5m，BC＝2m，∴AB＝＝＝2.5（m），∵△ABC的面积为1.5m2，∴CM＝m，∵DE∥AB，∴△CDE∽△CAB，∴＝，即＝，解得：y＝，∴x＞y，即S1＞S2，故答案为：＞．（2）①函数图象如图6所示：②观察图象，发现该函数有最小值，此时a的取值～2之间．故选D．（3）①由（2）可知，S5＜S4＜S3．故答案为：S5＜S4＜S3．②如图7，△A1B1C1即为所求作．。
2022年中考数学几何模型之几何图形的旋转变换(讲+练)(原卷版)
专题09 几何图形的旋转变换知识点：（1）旋转后的图形与原图形是全等的；（进而得到相等的线段、相等的角） （2）旋转前后两个图形对应点到旋转中心的距离相等；（进而得到等腰三角形） （3）对应点与旋转中心所连线段的夹角都等于旋转角；（若特殊角则得到等边三角形、等腰直角三角形） 题型一、求点的坐标例1.如图，在平面直角坐标系中，A （1，0），B （﹣2，4），AB 绕点A 顺时针旋转90°得到AC ，则点C 的坐标是（ ）A ．（4，3）B ．（4，4）C ．（5，3）D ．（5，4）例2.如图，Rt △AOB 中，∠AOB ＝90°，OA ＝3，OB ＝4，将△AOB 沿x 轴依次以三角形三个顶点为旋转中心顺时针旋转，分别得图②，图③，则旋转到图⑩时直角顶点的坐标是（ ）A ．（28，4）B ．（36，0）C ．（39，0）D ．（912，32√3）【变式训练1】如图在平面直角坐标系xOy 中，点B 的坐标为（1，2），过点B 作BA ⊥y 轴于点A ，连接OB 将△AOB 绕点O 按顺时针方向旋转45º，得到△A ’OB ’，则点B 的坐标为（ ）A .B .C .D .【变式训练2】如图，在平面直角坐标系中，△AOB的顶点B在第一象限，点A在y轴的正半轴上，AO＝AB＝2，∠OAB＝120°，将△AOB绕点O逆时针旋转90°，点B的对应点B′的坐标是（）A．（﹣2−√32，√3）B．（﹣2−√32，2−√32）C．（﹣3，2−√32）D．（﹣3，√3）【变式训练3】如图，△AOB为等腰三角形，顶点A的坐标底边OB在x轴上。
将△AOB绕点B按顺时针方向旋转一定角度后得△A’O'B，点A的对应点A’在x轴上，则点O’的坐标为（）A. B. C. D.【变式训练4】如图，在平面直角坐标系中，将正方形OABC绕点O逆时针旋转45°后得到正方形OA1B1C1，依此方式，绕点O连续旋转2020次得到正方形OA2020B2020C2020，如果点A的坐标为（1，0），那么点B2020的坐标为（）A．（﹣1，1）B．(−√2，0)C．（﹣1，﹣1）D．(0，−√2)模型二、几何图形的旋转例1.如图1，已知点B、C、D在同一条直线上，△ABC和△CDE都是等边三角形，BE交AC于点F，AD交CE于点H．（1）求出∠ACE的度数；（2）请在图1中找出一对全等的三角形，并说明全等的理由；（3）若将△CDE绕C点转动到如图2所示的位置，其余条件不变，（2）中的结论是否还成立，说明理由．例2.如图1，正方形ABCD 与正方形AEFG 的边AB 、AE （AB AE <）在一条直线上，正方形AEFG 以点A 为旋转中心逆时针旋转，设旋转角为α．在旋转过程中，两个正方形只有点A 重合，其它顶点均不重合，连接BE 、DG ．（1）当正方形AEFG 旋转至如图2所示的位置时，求证：BE DG =； （2）当点C 在直线BE 上时，连接FC ，直接写出FCD ∠的度数； （3）如图3，如果45α=︒，2AB =，AE =G 到BE 的距离．例3.在Rt △ABC 中，AC ⊥AB ，D 为内平面内一动点，CD ＝a ，CB ＝b ，其中a ，b 为常数，且a <b ，将△ADC 沿射线AB 方向平移，得到△BEF ，点A 、C 、D 的对应点分别为点B 、E 、F ，连接AF .（1）如图，若D 在△ABC 内部，请在图中画出△BEF ；（2）在（1）的条件下，若CD ⊥AF ，求AF 的长（用含a ，b 的式子表示）；（3）若∠ABC ＝试探究当线段AF 的长度取最小值时∠ACD 的大小（用含的式子表示）.【变式训练1】已知：在Rt △ABC 中，∠ACB ＝90º，AC ＝BC ，D 是线段AB 上一点，连结CD ，将线段CD 绕点C 逆时针旋转90º得到线段CE ，连结DE ，BE. （1）依题意补全图形； （2）若∠ACD ＝，用含的代数式表示∠DEB ；（3）若△ACD 的外心在三角形的内部，请直接写出的取值范围.A BCD E FG图2A BC D E FG图3GFED CBA 图1【变式训练2】阅读下面材料，并解决问题：（1）如图①等边△ABC 内有一点P ，若点P 到顶点A 、B 、C 的距离分别为3，4，5，求∠APB 的度数．为了解决本题，我们可以将△ABP 绕顶点A 旋转到△ACP ′处，此时△ACP ′≌△ABP ，这样就可以利用旋转变换，将三条线段P A 、PB 、PC 转化到一个三角形中，从而求出∠APB ＝ 150° ； （2）基本运用请你利用第（1）题的解答思想方法，解答下面问题已知如图②，△ABC 中，∠CAB ＝90°，AB ＝AC ，E 、F 为BC 上的点且∠EAF ＝45°，求证：EF 2＝BE 2+FC 2； （3）能力提升如图③，在Rt △ABC 中，∠C ＝90°，AC ＝1，∠ABC ＝30°，点O 为Rt △ABC 内一点，连接AO ，BO ，CO ，且∠AOC ＝∠COB ＝∠BOA ＝120°，求OA +OB +OC 的值．【变式训练3】在ABC △中，AC BC =，在AED △中，AD ED =，点D 、E 分别在CA 、AB 上．（1）如图①，若90ACB ADE ∠=∠=︒，则CD 与BE 的数量关系是_________；（2）若120ACB ADE ∠=∠=︒，将AED △绕点A 旋转至如图②所示的位置，则CD 与BE 的数量关系是_________；（3）若2(090)ACB ADE αα∠=∠=<<︒，将AED △绕点A 旋转至如图③所示的位置，探究线段CD 与BE 的数量关系，并加以证明（用含α的式子表示）．课后训练1.如图，在平面直角坐标系中，长方形ABCD 的顶点B 在坐标原点，顶点A 、C 分别在y 轴、x 轴的负半轴上，其中A （0，﹣4），C （﹣2，0），将矩形ABCD 绕点D 逆时针旋转得到矩形A 'B 'C 'D ，点B '恰好落在x 轴上，线段B 'A '与CD 交于点E 的坐标为（ ）A ．（﹣2，−32）B ．（﹣2，−34）C ．（﹣2，﹣2）D ．（﹣2，−54）2.如图，在平面直角坐标系中，点P 1的坐标为（√22，√22），将线段OP 1绕点O 按顺时针方向旋转45°，再将其长度伸长为OP 1的2倍，得到线段OP 2；又将线段OP 2绕点O 按顺时针方向旋转45°，长度伸长为OP 2的2倍，得到线段OP 3；如此下去，得到线段OP 4，OP 5，…，OP n （n 为正整数），则点P 2020的坐标是 ．3.如图，在△ADE中，∠DAE＝80º，将△ADE绕点A顺时针旋转得△ABC，若AC平分∠DAE，则＝；若AC平分∠BAE，则＝.4.如图，在△ABC中，∠BAC＝90º，B＝AC＝10，点D为△ABC内一点，∠BAD＝15º，AD＝6，连接BD，将△ABD绕点A按逆时针方向旋转，使AB与AC重合，点D的对应点为点E，连接DE，DE交AC于点F，则CF的长为.5.如图，△ABC中，∠ABC＝45º，AH⊥BC于点H，点D在AH上，且DH＝CH，连结BD，将△BHD绕点H旋转，得到△EHF（点B、D分别与点E、F对应），连结AE，当点F落在AC上时（F不与C重合），若BC＝4，tanC＝3，则AE的长为.6.如图，在ABC △中，AB AC =，且30BAC ∠=︒，以AB 为腰作等腰直角三角形ABD ,以AC 为斜边作等腰直角三角形ACE ，连接CD BE 、交于点F ，求DFB ∠的度数．7.如图1，已知ABC △是等腰直角三角形，90BAC ∠=︒，点D 是BC 的中点．作正方形DEFG ，使点A 、C 分别在DG 和DE 上，连接AE ，BG ． （1）试猜想线段BG 和AE 的数量关系是__________； （2）将正方形DEFG 绕点D 逆时针方向旋转(0360)αα︒<<︒， ①判断（1）中的结论是否仍然成立？请利用图2证明你的结论； ②若4BC DE ==，当AE 取最大值时，求AF 的值．8.阅读下面材料，并解决问题：（1）如图①等边△ABC 内有一点P ，若点P 到顶点A 、B 、C 的距离分别为3，4，5，求∠APB 的度数．为了解决本题，我们可以将△ABP 绕顶点A 旋转到△ACP ′处，此时△ACP ′≌△ABP ，这样就可以利用旋转变换，将三条线段P A 、PB 、PC 转化到一个三角形中，从而求出∠APB ＝ 150° ；F EDCBA（2）基本运用请你利用第（1）题的解答思想方法，解答下面问题已知如图②，△ABC中，∠CAB＝90°，AB＝AC，E、F为BC上的点且∠EAF＝45°，求证：EF2＝BE2+FC2；（3）能力提升如图③，在Rt△ABC中，∠C＝90°，AC＝1，∠ABC＝30°，点O为Rt△ABC内一点，连接AO，BO，CO，且∠AOC＝∠COB＝∠BOA＝120°，求OA+OB+OC的值．9.在等腰Rt△ABC中，AB＝AC，∠BAC＝90º.（1）如图1，D、E是等腰Rt△ABC斜边BC上两动点，且∠DAE＝45º，将△ABE绕点A 逆时针旋转90º后，得到△AFC，连接DF.①求证：△AED≌△AFD；②当BE＝3，CE＝7时，求DE的长；（2）如图2，点D是等腰Rt△ABC斜边BC所在直线上的一动点，连接AD，以点A为直角顶点作等腰Rt△ADE，当BD＝3，BC＝9时，求DE的长.。
中考数学复习初中数学 旋转专项综合练及答案
中考数学复习初中数学旋转专项综合练及答案一、旋转1．操作与证明：如图1，把一个含45°角的直角三角板ECF和一个正方形ABCD摆放在一起，使三角板的直角顶点和正方形的顶点C重合，点E、F分别在正方形的边CB、CD上，连接AF．取AF中点M，EF的中点N，连接MD、MN．（1）连接AE，求证：△AEF是等腰三角形；猜想与发现：（2）在（1）的条件下，请判断MD、MN的数量关系和位置关系，得出结论．结论1：DM、MN的数量关系是；结论2：DM、MN的位置关系是；拓展与探究：（3）如图2，将图1中的直角三角板ECF绕点C顺时针旋转180°，其他条件不变，则（2）中的两个结论还成立吗？若成立，请加以证明；若不成立，请说明理由．【答案】（1）证明参见解析；（2）相等，垂直；（3）成立，理由参见解析.【解析】试题分析：（1）根据正方形的性质以及等腰直角三角形的知识证明出CE=CF，继而证明出△ABE≌△ADF，得到AE=AF，从而证明出△AEF是等腰三角形；（2）DM、MN的数量关系是相等，利用直角三角形斜边中线等于斜边一半和三角形中位线定理即可得出结论.位置关系是垂直，利用三角形外角性质和等腰三角形两个底角相等性质，及全等三角形对应角相等即可得出结论；（3）成立，连接AE，交MD于点G，标记出各个角，首先证明出MN∥AE，MN=AE，利用三角形全等证出AE=AF，而DM=AF，从而得到DM，MN数量相等的结论，再利用三角形外角性质和三角形全等，等腰三角形性质以及角角之间的数量关系得到∠DMN=∠DGE=90°．从而得到DM、MN的位置关系是垂直.试题解析：（1）∵四边形ABCD是正方形，∴AB=AD=BC=CD，∠B=∠ADF=90°，∵△CEF 是等腰直角三角形，∠C=90°，∴CE=CF，∴BC﹣CE=CD﹣CF，即BE=DF，∴△ABE≌△ADF，∴AE=AF，∴△AEF是等腰三角形；（2）DM、MN的数量关系是相等，DM、MN的位置关系是垂直；∵在Rt△ADF中DM是斜边AF的中线，∴AF=2DM，∵MN 是△AEF的中位线，∴AE=2MN，∵AE=AF，∴DM=MN；∵∠DMF=∠DAF+∠ADM，AM=MD，∵∠FMN=∠FAE，∠DAF=∠BAE，∴∠ADM=∠DAF=∠BAE，∴∠DMN=∠FMN+∠DMF=∠DAF+∠BAE+∠FAE=∠BAD=90°，∴DM⊥MN；（3）（2）中的两个结论还成立，连接AE，交MD于点G，∵点M为AF的中点，点N为EF的中点，∴MN∥AE，MN=AE，由已知得，AB=AD=BC=CD，∠B=∠ADF，CE=CF，又∵BC+CE=CD+CF，即BE=DF，∴△ABE≌△ADF，∴AE=AF，在Rt△ADF中，∵点M为AF的中点，∴DM=AF，∴DM=MN，∵△ABE≌△ADF，∴∠1=∠2，∵AB∥DF，∴∠1=∠3，同理可证：∠2=∠4，∴∠3=∠4，∵DM=AM，∴∠MAD=∠5，∴∠DGE=∠5+∠4=∠MAD+∠3=90°，∵MN∥AE，∴∠DMN=∠DGE=90°，∴DM⊥MN．所以（2）中的两个结论还成立.考点：1.正方形的性质；2.全等三角形的判定与性质；3.三角形中位线定理；4.旋转的性质．2．如图1，在平面直角坐标系xOy中，抛物线C：y=ax2+bx+c与x轴相交于A，B两点，顶点为D（0，4），AB=42，设点F（m，0）是x轴的正半轴上一点，将抛物线C绕点F 旋转180°，得到新的抛物线C′．（1）求抛物线C的函数表达式；（2）若抛物线C′与抛物线C在y轴的右侧有两个不同的公共点，求m的取值范围．（3）如图2，P是第一象限内抛物线C上一点，它到两坐标轴的距离相等，点P在抛物线C′上的对应点P′，设M是C上的动点，N是C′上的动点，试探究四边形PMP′N能否成为正方形？若能，求出m的值；若不能，请说明理由．【答案】（1）2142y x =-+；（2）2＜m＜3）m =6或m3． 【解析】试题分析：（1）由题意抛物线的顶点C （0，4），A（，0），设抛物线的解析式为24y ax =+，把A（0）代入可得a =12-，由此即可解决问题； （2）由题意抛物线C ′的顶点坐标为（2m ，﹣4），设抛物线C ′的解析式为()2142y x m =--，由()22142142y x y x m ⎧=-+⎪⎪⎨⎪=--⎪⎩，消去y 得到222280x mx m -+-=，由题意，抛物线C ′与抛物线C 在y 轴的右侧有两个不同的公共点，则有()222(428020280m m m ⎧-->⎪⎪>⎨⎪->⎪⎩，解不等式组即可解决问题；（3）情形1，四边形PMP ′N 能成为正方形．作PE ⊥x 轴于E ，MH ⊥x 轴于H ．由题意易知P （2，2），当△PFM 是等腰直角三角形时，四边形PMP ′N 是正方形，推出PF =FM ，∠PFM =90°，易证△PFE ≌△FMH ，可得PE =FH =2，EF =HM =2﹣m ，可得M （m +2，m ﹣2），理由待定系数法即可解决问题；情形2，如图，四边形PMP ′N 是正方形，同法可得M （m ﹣2，2﹣m ），利用待定系数法即可解决问题．试题解析：（1）由题意抛物线的顶点C （0，4），A（，0），设抛物线的解析式为24y ax =+，把A（0）代入可得a =12-，∴抛物线C 的函数表达式为2142y x =-+．（2）由题意抛物线C ′的顶点坐标为（2m ，﹣4），设抛物线C ′的解析式为()2142y x m =--，由21421(42x y x y ⎧=-+⎪⎪⎨⎪=-⎪⎩，消去y 得到222280x mx m -+-= ，由题意，抛物线C ′与抛物线C 在y 轴的右侧有两个不同的公共点，则有()222(428020280m m m ⎧-->⎪⎪>⎨⎪->⎪⎩，解得2＜m＜，∴满足条件的m 的取值范围为2＜m＜ （3）结论：四边形PMP ′N 能成为正方形．理由：1情形1，如图，作PE ⊥x 轴于E ，MH ⊥x 轴于H ．由题意易知P （2，2），当△PFM 是等腰直角三角形时，四边形PMP ′N 是正方形，∴PF =FM ，∠PFM =90°，易证△PFE ≌△FMH ，可得PE =FH =2，EF =HM =2﹣m ，∴M （m +2，m ﹣2），∵点M 在2142y x =-+上，∴()212242m m -=-++，解得m =17﹣3或﹣17﹣3（舍弃），∴m =17﹣3时，四边形PMP ′N 是正方形．情形2，如图，四边形PMP ′N 是正方形，同法可得M （m ﹣2，2﹣m ），把M （m ﹣2，2﹣m ）代入2142y x =-+中，()212242m m -=--+，解得m =6或0（舍弃），∴m =6时，四边形PMP ′N 是正方形．综上所述：m =6或m 17﹣3时，四边形PMP ′N 是正方形．3．在正方形ABCD 中，点E ，F 分别在边BC ，CD 上，且∠EAF=∠CEF=45°. (1)将△ADF 绕着点A 顺时针旋转90°，得到△ABG(如图①)，求证：△AEG ≌△AEF ； (2)若直线EF 与AB ，AD 的延长线分别交于点M ，N(如图②)，求证：EF 2=ME 2+NF 2； (3)将正方形改为长与宽不相等的矩形，若其余条件不变(如图③)，请你直接写出线段EF ，BE ，DF 之间的数量关系.【答案】（1）证明见解析；（2）证明见解析；（3）EF2=2BE2+2DF2.【解析】试题分析：（1）根据旋转的性质可知AF=AG，∠EAF=∠GAE=45°，故可证△AEG≌△AEF；（2）将△ADF绕着点A顺时针旋转90°，得到△ABG，连结GM．由（1）知△AEG≌△AEF，则EG=EF．再由△BME、△DNF、△CEF均为等腰直角三角形，得出CE=CF，BE=BM，NF=DF，然后证明∠GME=90°，MG=NF，利用勾股定理得出EG2=ME2+MG2，等量代换即可证明EF2=ME2+NF2；（3）将△ADF绕着点A顺时针旋转90°，得到△ABG，根据旋转的性质可以得到△ADF≌△ABG，则DF=BG，再证明△AEG≌△AEF，得出EG=EF，由EG=BG+BE，等量代换得到EF=BE+DF．试题解析：（1）∵△ADF绕着点A顺时针旋转90°，得到△ABG，∴AF=AG，∠FAG=90°，∵∠EAF=45°，∴∠GAE=45°，在△AGE与△AFE中，，∴△AGE≌△AFE（SAS）；（2）设正方形ABCD的边长为a．将△ADF绕着点A顺时针旋转90°，得到△ABG，连结GM．则△ADF≌△ABG，DF=BG．由（1）知△AEG≌△AEF，∴EG=EF．∵∠CEF=45°，∴△BME、△DNF、△CEF均为等腰直角三角形，∴CE=CF，BE=BM，NF=DF，∴a﹣BE=a﹣DF，∴BE=DF，∴BE=BM=DF=BG，∴∠BMG=45°，∴∠GME=45°+45°=90°，∴EG2=ME2+MG2，∵EG=EF ，MG=BM=DF=NF，∴EF2=ME2+NF2；（3）EF2=2BE2+2DF2．如图所示，延长EF交AB延长线于M点，交AD延长线于N点，将△ADF绕着点A顺时针旋转90°，得到△AGH，连结HM，HE．由（1）知△AEH≌△AEF，则由勾股定理有（GH+BE）2+BG2=EH2，即（GH+BE）2+（BM﹣GM）2=EH2又∴EF=HE，DF=GH=GM，BE=BM，所以有（GH+BE）2+（BE﹣GH）2=EF2，即2（DF2+BE2）=EF2考点：四边形综合题4．平面上，Rt△ABC与直径为CE的半圆O如图1摆放，∠B＝90°，AC＝2CE＝m，BC＝n，半圆O交BC边于点D，将半圆O绕点C按逆时针方向旋转，点D随半圆O旋转且∠ECD始终等于∠ACB，旋转角记为α（0°≤α≤180°）（1）当α＝0°时，连接DE ，则∠CDE ＝ °，CD ＝ ；（2）试判断：旋转过程中BDAE的大小有无变化？请仅就图2的情形给出证明； （3）若m ＝10，n ＝8，当α＝∠ACB 时，求线段BD 的长；（4）若m ＝6，n ＝2，当半圆O 旋转至与△ABC 的边相切时，直接写出线段BD 的长．【答案】（1）90°，2n ；（2）无变化；（3）55；（4）BD=101143． 【解析】试题分析：（1）①根据直径的性质，由DE ∥AB 得CD CECB CA=即可解决问题．②求出BD 、AE 即可解决问题．（2）只要证明△ACE ∽△BCD 即可．（3）求出AB 、AE ，利用△ACE ∽△BCD 即可解决问题．（4）分类讨论：①如图5中，当α=90°时，半圆与AC 相切，②如图6中，当α=90°+∠ACB 时，半圆与BC 相切，分别求出BD 即可． 试题解析：（1）解：①如图1中，当α=0时，连接DE ，则∠CDE =90°．∵∠CDE =∠B =90°，∴DE ∥AB ，∴CE CD AC CB ==12．∵BC =n ，∴CD =12n ．故答案为90°，12n ． ②如图2中，当α=180°时，BD =BC +CD =32n ，AE =AC +CE =32m ，∴BD AE =n m．故答案为nm． （2）如图3中，∵∠ACB =∠DCE ，∴∠ACE =∠BCD ．∵CD BC nCE AC m==，∴△ACE ∽△BCD ，∴BD BC nAE AC m==．（3）如图4中，当α=∠ACB 时．在Rt △ABC 中，∵AC =10，BC =8，∴AB =22AC BC -=6．在Rt △ABE 中，∵AB =6，BE =BC ﹣CE =3，∴AE =22AB BE +=2263+=35，由（2）可知△ACE ∽△BCD ，∴BD BCAE AC=，∴35=810，∴BD =125．故答案为125． （4）∵m =6，n =42，∴CE =3，CD =22，AB =22CA BC -=2，①如图5中，当α=90°时，半圆与AC 相切．在Rt △DBC 中，BD =22BC CD +=224222+（）（）=210． ②如图6中，当α=90°+∠ACB 时，半圆与BC 相切，作EM ⊥AB 于M ．∵∠M =∠CBM =∠BCE =90°，∴四边形BCEM 是矩形，∴342BM EC ME ===，，∴AM =5，AE =22AM ME +=57，由（2）可知DB AE =223，∴BD =2114． 故答案为210或2114．点睛：本题考查了圆的有关知识，相似三角形的判定和性质、勾股定理等知识，正确画出图形是解决问题的关键，学会分类讨论的思想，本题综合性比较强，属于中考压轴题．5．如图，矩形OABC 的顶点A 在x 轴正半轴上，顶点C 在y 轴正半轴上，点B 的坐标为（4，m ）（5≤m≤7），反比例函数y ＝16x（x ＞0）的图象交边AB 于点D ． （1）用m 的代数式表示BD 的长；（2）设点P 在该函数图象上，且它的横坐标为m ，连结PB ，PD①记矩形OABC面积与△PBD面积之差为S，求当m为何值时，S取到最大值；②将点D绕点P逆时针旋转90°得到点E，当点E恰好落在x轴上时，求m的值．【答案】（1）BD＝m﹣4（2）①m＝7时，S取到最大值②m＝5【解析】【分析】（1）先确定出点D横坐标为4，代入反比例函数解析式中求出点D横坐标，即可得出结论；（2）①先求出矩形OABC的面积和三角形PBD的面积得出S＝﹣12（m﹣8）2+24，即可得出结论；②利用一线三直角判断出DG＝PF，进而求出点P的坐标，即可得出结论．【详解】解：（1）∵四边形OABC是矩形，∴AB⊥x轴上，∵点B（4，m），∴点D的横坐标为4，∵点D在反比例函数y＝16x上，∴D（4，4），∴BD＝m﹣4；（2）①如图1，∵矩形OABC的顶点B的坐标为（4，m），∴S矩形OABC＝4m，由（1）知，D（4，4），∴S△PBD＝12（m﹣4）（m﹣4）＝12（m﹣4）2，∴S＝S矩形OABC﹣S△PBD＝4m﹣12（m﹣4）2＝﹣12（m﹣8）2+24，∴抛物线的对称轴为m＝8，∵a＜0，5≤m≤7，∴m＝7时，S取到最大值；②如图2，过点P作PF⊥x轴于F，过点D作DG⊥FP交FP的延长线于G，∴∠DGP＝∠PFE＝90°，∴∠DPG+∠PDG＝90°，由旋转知，PD＝PE，∠DPE＝90°，∴∠DPG+∠EPF＝90°，∴∠PDG＝∠EPF，∴△PDG≌△EPF（AAS），∴DG＝PF，∵DG＝AF＝m﹣4，∴P（m，m﹣4），∵点P在反比例函数y＝16，x∴m（m﹣4）＝16，∴m＝2+25或m＝2﹣25（舍）．【点睛】此题是反比例函数综合题，主要考查了待定系数法，矩形的性质，三角形的面积公式，全等三角形的判定，构造出全等三角形是解本题的关键．6．（12分）如图1，在等边△ABC中，点D，E分别在边AB，AC上，AD=AE，连接BE，CD，点M、N、P分别是BE、CD、BC的中点．（1）观察猜想：图1中，△PMN的形状是；（2）探究证明：把△ADE绕点A逆时针方向旋转到图2的位置，△PMN的形状是否发生改变？并说明理由；（3）拓展延伸：把△ADE绕点A在平面内自由旋转，若AD=1，AB=3，请直接写出△PMN 的周长的最大值．【答案】(1) 等边三角形；(2) △PMN的形状不发生改变，仍然为等边三角形,理由见解析；（3）6【解析】分析：（1）如图1，先根据等边三角形的性质得到AB=AC，∠ABC=∠ACB=60°，则BD=CE，再根据三角形中位线性质得PM∥CE，PM=12CE，PN∥AD，PN=12BD，从而得到PM=PN，∠MPN=60°，从而可判断△PMN为等边三角形；（2）连接CE、BD，如图2，先利用旋转的定义，把△ABD绕点A逆时针旋转60°可得到△CAE，则BD=CE，∠ABD=∠ACE，与（1）一样可得PM=PN，∠BPM=∠BCE，∠CPN=∠CBD，则计算出∠BPM+∠CPN=120°，从而得到∠MPN=60°，于是可判断△PMN为等边三角形．（3）利用AB﹣AD≤BD≤AB+AD（当且仅当点B、A、D共线时取等号）得到BD的最大值为4，则PN的最大值为2，然后可确定△PMN的周长的最大值．详解：（1）如图1．∵△ABC为等边三角形，∴AB=AC，∠ABC=∠ACB=60°．∵AD=AE，∴BD=CE．∵点M、N、P分别是BE、CD、BC的中点，∴PM∥CE，PM=12CE，PN∥AD，PN=12BD，∴PM=PN，∠BPM=∠BCA=60°，∠CPN=∠CBA=60°，∴∠MPN=60°，∴△PMN为等边三角形；故答案为等边三角形；（2）△PMN的形状不发生改变，仍然为等边三角形．理由如下：连接CE、BD，如图2．∵AB=AC，AE=AD，∠BAC=∠DAE=60°，∴把△ABD绕点A逆时针旋转60°可得到△CAE，∴BD=CE，∠ABD=∠ACE，与（1）一样可得PM∥CE，PM=12CE，PN∥AD，PN=12BD，∴PM=PN，∠BPM=∠BCE，∠CPN=∠CBD，∴∠BPM+∠CPN=∠CBD+∠CBD=∠ABC﹣∠ABD+∠ACB+∠ACE=60°+60°=120°，∴∠MPN=60°，∴△PMN为等边三角形．（3）∵PN=12BD，∴当BD的值最大时，PN的值最大．∵AB﹣AD≤BD≤AB+AD（当且仅当点B、A、D共线时取等号）∴BD的最大值为1+3=4，∴PN的最大值为2，∴△PMN的周长的最大值为6．点睛：本题考查了旋转的性质：对应点到旋转中心的距离相等；对应点与旋转中心所连线段的夹角等于旋转角；旋转前、后的图形全等．也考查了等边三角形的判定与性质和三角形中位线性质．7．在平面直角坐标中，边长为2的正方形OABC的两顶点A、C分别在y轴、x轴的正半轴上，点O在原点.现将正方形OABC绕O点顺时针旋转，当A点一次落在直线y x=上时停止旋转，旋转过程中，AB边交直线y x=于点M，BC边交x轴于点N（如图）.（1）求边OA在旋转过程中所扫过的面积；（2）旋转过程中，当MN和AC平行时，求正方形OABC旋转的度数；（3）设MBN∆的周长为p，在旋转正方形OABC的过程中，p值是否有变化？请证明你的结论.【答案】（1）π/2（2）22.5°(3)周长不会变化，证明见解析【解析】试题分析：（1）根据扇形的面积公式来求得边OA在旋转过程中所扫过的面积；（2）解决本题需利用全等，根据正方形一个内角的度数求出∠AOM的度数；（3）利用全等把△MBN的各边整理到成与正方形的边长有关的式子．试题解析：（1）∵A点第一次落在直线y=x上时停止旋转，直线y=x与y轴的夹角是45°，∴OA旋转了45°．∴OA在旋转过程中所扫过的面积为24523602ππ⨯=．（2）∵MN ∥AC ，∴∠BMN=∠BAC=45°，∠BNM=∠BCA=45°． ∴∠BMN=∠BNM ．∴BM=BN ． 又∵BA=BC ，∴AM=CN ．又∵OA=OC ，∠OAM=∠OCN ，∴△OAM ≌△OCN ． ∴∠AOM=∠CON=12（∠AOC-∠MON ）=12（90°-45°）=22.5°． ∴旋转过程中，当MN 和AC 平行时，正方形OABC 旋转的度数为45°-22.5°=22.5°． （3）在旋转正方形OABC 的过程中，p 值无变化． 证明：延长BA 交y 轴于E 点，则∠AOE=45°-∠AOM ，∠CON=90°-45°-∠AOM=45°-∠AOM ， ∴∠AOE=∠CON ．又∵OA=OC ，∠OAE=180°-90°=90°=∠OCN ． ∴△OAE ≌△OCN ． ∴OE=ON ，AE=CN ．又∵∠MOE=∠MON=45°，OM=OM ， ∴△OME ≌△OMN ．∴MN=ME=AM+AE ． ∴MN=AM+CN ，∴p=MN+BN+BM=AM+CN+BN+BM=AB+BC=4． ∴在旋转正方形OABC 的过程中，p 值无变化． 考点：旋转的性质.8．如图1，菱形ABCD ，AB 4=，ADC 120∠=o ，连接对角线AC 、BD 交于点O ，()1如图2，将AOD V 沿DB 平移，使点D 与点O 重合，求平移后的A'BO V 与菱形ABCD重合部分的面积．()2如图3，将A'BO V 绕点O 逆时针旋转交AB 于点E'，交BC 于点F ，①求证：BE'BF 2+=； ②求出四边形OE'BF 的面积．【答案】() 13?2①证明见解析3【解析】 【分析】(1)先判断出△ABD 是等边三角形，进而判断出△EOB 是等边三角形，即可得出结论； (2)先判断出 ≌△OBF ，再利用等式的性质即可得出结论； (3)借助①的结论即可得出结论． 【详解】()1Q 四边形为菱形，ADC 120∠=o ，ADO 60∠∴=o ，ABD ∴V 为等边三角形，DAO 30∠∴=o ，ABO 60∠=o ，∵AD//A′O ， ∴∠A′OB=60°，EOB ∴V 为等边三角形，边长OB 2=，∴重合部分的面积：343⨯=，()2①在图3中，取AB 中点E ，由()1知，∠EOB=60°，∠E′OF=60°， ∴∠EOE′=∠BOF ，又∵EO=BO ，∴∠OEE′=∠OBF=60°， ∴△OEE′≌△OBF ， ∴EE′=BF ，∴BE′+BF=BE′+EE′=BE=2；②由①知，在旋转过程中始终有△OEE′≌△OBF ，∴S △OEE′=S △OBF ，∴S 四边形OE′BF =OEB S 3=V【点睛】本题考查了菱形的性质、全等三角形的判定与性质，等边三角形的判定与性质，综合性较强，熟练掌握相关内容、正确添加辅助线是解题的关键.9．在平面直角坐标系中，O 为原点，点A （8，0），点B （0，6），把△ABO 绕点B 逆时针旋转得△A′B′O′，点A 、O 旋转后的对应点为A′、O′，记旋转角为α． （1）如图1，若α=90°，则AB= ，并求AA′的长； （2）如图2，若α=120°，求点O′的坐标；（3）在（2）的条件下，边OA上的一点P旋转后的对应点为P′，当O′P+BP′取得最小值时，直接写出点P′的坐标．【答案】（1）10，102；（2）（33，9）；（3）12354 55（，）【解析】试题分析：(1)、如图①，先利用勾股定理计算出AB=5，再根据旋转的性质得BA=BA′，∠ABA′=90°，则可判定△ABA′为等腰直角三角形，然后根据等腰直角三角形的性质求AA′的长；(2)、作O′H⊥y轴于H，如图②，利用旋转的性质得BO=BO′=3，∠OBO′=120°，则∠HBO′=60°，再在Rt△BHO′中利用含30度的直角三角形三边的关系可计算出BH和O′H的长，然后利用坐标的表示方法写出O′点的坐标；(3)、由旋转的性质得BP=BP′，则O′P+BP′=O′P+BP，作B点关于x轴的对称点C，连结O′C交x轴于P点，如图②，易得O′P+BP=O′C，利用两点之间线段最短可判断此时O′P+BP的值最小，接着利用待定系数法求出直线O′C的解析式为y=x﹣3，从而得到P（，0），则O′P′=OP=，作P′D⊥O′H于D，然后确定∠DP′O′=30°后利用含30度的直角三角形三边的关系可计算出P′D 和DO′的长，从而可得到P′点的坐标．试题解析：(1)、如图①，∵点A（4，0），点B（0，3），∴OA=4，OB=3，∴AB==5，∵△ABO绕点B逆时针旋转90°，得△A′BO′，∴BA=BA′，∠ABA′=90°，∴△ABA′为等腰直角三角形，∴AA′=BA=5；(2)、作O′H⊥y轴于H，如图②，∵△ABO绕点B逆时针旋转120°，得△A′BO′，∴BO=BO′=3，∠OBO′=120°，∴∠HBO′=60°，在Rt△BHO′中，∵∠BO′H=90°﹣∠HBO′=30°，∴BH=BO′=，O′H=BH=，∴OH=OB+BH=3+，∴O′点的坐标为（）；（3）∵△ABO绕点B逆时针旋转120°，得△A′BO′，点P的对应点为P′，∴BP=BP′，∴O′P+BP′=O′P+BP，作B点关于x轴的对称点C，连结O′C交x轴于P点，如图②，则O′P+BP=O′P+PC=O′C，此时O′P+BP的值最小，∵点C与点B关于x轴对称，∴C（0，﹣3），设直线O′C的解析式为y=kx+b，把O′（），C（0，﹣3）代入得，解得，∴直线O′C的解析式为y=x﹣3，当y=0时，x﹣3=0，解得x=，则P（，0），∴OP=，∴O′P′=OP=，作P′D⊥O′H于D，∵∠BO′A=∠BOA=90°，∠BO′H=30°，∴∠DP′O′=30°，∴O′D=O′P′=，P′D=，∴DH=O′H﹣O′，∴P′点的坐标为（，）．考点：几何变换综合题10．在平面直角坐标系中，O为原点，点A（0，4），点B（﹣2，0），把△ABO绕点A 逆时针旋转，得△AB′O′，点B、O旋转后的对应点为B′、O′．（1）如图①，若旋转角为60°时，求BB′的长；（2）如图②，若AB′∥x轴，求点O′的坐标；（3）如图③，若旋转角为240°时，边OB上的一点P旋转后的对应点为P′，当O′P+AP′取得最小值时，求点P′的坐标（直接写出结果即可）【答案】（1）252）点O′8545）；（3）点P′的坐标为（﹣835，365． 【解析】分析：（1）由点A 、B 的坐标可得出AB 的长度，连接BB ′，由旋转可知：AB =AB ′，∠BAB ′=60°，进而可得出△ABB ′为等边三角形，根据等边三角形的性质可求出BB ′的长； （2）过点O ′作O ′D ⊥x 轴，垂足为D ，交AB ′于点E ，则△AO ′E ∽△ABO ，根据旋转的性质结合相似三角形的性质可求出AE 、O ′E 的长，进而可得出点O ′的坐标；（3）作点A 关于x 轴对称的点A ′，连接A ′O ′交x 轴于点P ，此时O ′P +AP ′取最小值，过点O ′作O ′F ⊥y 轴，垂足为点F ，过点P ′作PM ⊥O ′F ，垂足为点M ，根据旋转的性质结合解直角三角形可求出点O ′的坐标，由A 、A ′关于x 轴对称可得出点A ′的坐标，利用待定系数法即可求出直线A ′O ′的解析式，由一次函数图象上点的坐标特征可得出点P 的坐标，进而可得出OP 的长度，再在Rt △O ′P ′M 中，通过解直角三角形可求出O ′M 、P ′M 的长，进而可得出此时点P ′的坐标．详解：（1）∵点A （0，4），点B （﹣2，0），∴OA =4，OB =2，∴AB 22OA OB 5． 在图①中，连接BB ′．由旋转可知：AB =AB ′，∠BAB ′=60°，∴△ABB ′为等边三角形，∴BB ′=AB 5 （2）在图②中，过点O ′作O ′D ⊥x 轴，垂足为D ，交AB ′于点E ． ∵AB ′∥x 轴，O ′E ⊥x 轴，∴∠O ′EA =90°=∠AOB ．由旋转可知：∠B ′AO ′=∠BAO ，AO ′=AO =4，∴△AO ′E ∽△ABO ，AE AO ='O E BO ='AO AB，即4AE ='2O E 25∴AE 85，O ′E 45∴O ′D 45+4，∴点O ′的坐标为（85555，+4）． （3）作点A 关于x 轴对称的点A ′，连接A ′O ′交x 轴于点P ，此时O ′P +AP ′取最小值，过点O ′作O ′F ⊥y 轴，垂足为点F ，过点P ′作PM ⊥O ′F ，垂足为点M ，如图3所示．由旋转可知：AO′=AO=4，∠O′AF=240°﹣180°=60°，∴AF=12AO′=2，O′F=32AO′=23，∴点O′（﹣23，6）．∵点A（0，4），∴点A′（0，﹣4）．设直线A′O′的解析式为y=kx+b，将A′（0，﹣4）、O′（﹣23，6）代入y=kx+b，得：4236bk b=-⎧⎪⎨-+=⎪⎩，解得：534kb⎧=-⎪⎨⎪=-⎩，∴直线A′O′的解析式为y=﹣53x﹣4．当y=0时，有﹣53x﹣4=0，解得：x=﹣43，∴点P（﹣43，0），∴OP=O′P′=43．在Rt△O′P′M中，∠MO′P′=60°，∠O′MP′=90°，∴O′M=12O′P′=23，P′M=32O′P′=65，∴点P′的坐标为（﹣23+235，6+65），即（﹣833655，）．点睛：本题考查了函数图象及旋转变换、待定系数法求一次函数解析式、等边三角形的判定与性质、一次函数图象上点的坐标特征以及解直角三角形，解题的关键是：（1）利用等边三角形的性质找出BB′的长；（2）通过解直角三角形求出AE、O′E的长；（3）利用两点之间线段最短找出当O′P+AP′取得最小值时点P的位置．11．如图①，在ABCD中，AB=10cm，BC=4cm，∠BCD=120°，CE平分∠BCD交AB于点E.点P从A点出发，沿AB方向以1cm/s的速度运动，连接CP，将△PCE绕点C逆时针旋转60°，使CE与CB重合，得到△QCB，连接PQ.（1）求证：△PCQ是等边三角形；（2）如图②，当点P在线段EB上运动时，△PBQ的周长是否存在最小值？若存在，求出△PBQ周长的最小值；若不存在，请说明理由；（3）如图③，当点P在射线AM上运动时，是否存在以点P、B、Q为顶点的直角三角形？若存在，求出此时t的值；若不存在，请说明理由.（1）（2）（3）【答案】（1）证明见解析；（2）存在，理由见解析；（3）t为2s或者14s.【解析】分析：（1）根据旋转的性质，证明△PCE≌△QCB，然后根据全等三角形的性质和等边三角形的判定证明即可；（2）利用平行四边形的性质证得△BCE为等边三角形，然后根据全等三角形的性质得到△PBQ的周长为4+CP，然后垂线段最短可由直角三角形的性质求解即可；（3）根据点的移动的距离，分类讨论求解即可.详解：（1）∵旋转∴△PCE≌△QCB∴CP=CQ，∠PCE =∠QCB，∵∠BCD=120°，CE平分∠BCD，∴∠PCQ=60°，∴∠PCE +∠QCE=∠QCB+∠QCE=60°，∴△PCQ为等边三角形.（2）存在∵CE平分∠BCD，∴∠BCE=60 ，∵在平行四边形ABCD 中，∴AB∥CD∴∠ABC=180°﹣120°=60°∴△BCE为等边三角形∴BE=CB=4∵旋转∴△PCE≌△QCB∴EP=BQ，∴C△PBQ=PB+BQ+PQ=PB+EP+PQ=BE+PQ=4+CP∴CP⊥AB时，△PBQ周长最小当CP⊥AB时，CP=BCsin60°=∴△PBQ周长最小为4＋（3）①当点B与点P重合时，P,B,Q不能构成三角形②当0≤t＜6时，由旋转可知，∠CPE=∠CQB，∠CPQ=∠CPB+∠BPQ=60°则：∠BPQ+∠CQB＝60°，又∵∠QPB+∠PQC+∠CQB+∠PBQ=180°∴∠CBQ=180°—60°—60°=60°∴∠QBP=60°，∠BPQ＜60°，所以∠PQB可能为直角由（1）知，△PCQ为等边三角形，∴∠PBQ=60°，∠CQB＝30°∵∠CQB＝∠CPB∴∠CPB=30°∵∠CEB＝60°，∴∠ACP＝∠APC=30°∴PA=CA=4，所以AP=AE-EP=6-4=2÷=s所以t＝212③当6＜t＜10时，由∠PBQ＝120°＞90°，所以不存在④当t＞10时，由旋转得：∠PBQ=60°，由（1）得∠CPQ=60°∴∠BPQ=∠CPQ+∠BPC=60°+∠BPC，而∠BPC＞0°，∴∠BPQ＞60°∴∠BPQ=90°，从而∠BCP=30°，∴BP=BC=4所以AP=14cm所以t=14s综上所述：t为2s或者14s时，符合题意。
2020初中数学中考专题复习——图形变换旋转综合题专项训练(附答案详解)
A．1 个
B．2 个
C．3 个
D．4 个
15．在 Rt△ ABC 中，AC＝BC，点 D 为 AB 中点．∠GDH＝90°，∠GDH 绕点 D 旋转，
DG，DH 分别与边 AC，BC 交于 E，F 两点．下列结论：①AE+BF＝AC，②AE2+BF2
＝EF2，③S ＝ 四边形 CEDF 1 S△ ABC，④△DEF 始终为等腰直角三角形．其中正确的是(
A．45°
B．60°
C．70°
D．90°
14．如图，把 Rt△ ABC 绕顶点 C 顺时针旋转 90°得到 Rt△ DFC，若直线 DF 垂直平分
AB，垂足为点 E，连接 BF，CE，且 BC=2，下面四个结论：①BF= 2 2 ；②∠CBF=45°；
③△BEC 的面积=△ FBC 的面积；④△ECD 的面积为 2 2 3 ，其中正确的结论有（ ）
经过的路径为 BD ，则图中阴影部分的面积是（ ）
A． 2 3
B． 4 3
C．4π
D．条件不足，无法计算
21．如图，平面直角坐标系中，矩形 OABC 的顶点 A（﹣6，0），C（0，2 3 ）．将矩
形 OABC 绕点 O 顺时针方向旋转，使点 A 恰好落在 OB 上的点 A1 处，则点 B 的对应 点 B1 的坐标为_____．
2020 初中数学中考专题复习——图形变换旋转综合题专项训练（附答案详解） 1．已知正方形 MNKO 和正六边形 ABCDEF 边长均为 1，把正方形放在正六边形外边， 使 OK 边与 AB 边重合，如图所示．按下列步骤操作： 将正方形在正六边形外绕点 B 顺时针旋转，使 KN 边与 BC 边重合，完成第一次旋转；再绕点 C 顺时针旋转，使 NM 边与 CD 边重合，完成第二次旋转；……在这样连续 6 次旋转的过程中，点 M 在图中 直角坐标系中的纵坐标可能是（ ）
浙江省中考数学复习第二部分题型研究题型五几何探究题类型四旋转变换问题针对演练(2021年整理)
浙江省2018年中考数学复习第二部分题型研究题型五几何探究题类型四旋转变换问题针对演练编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（浙江省2018年中考数学复习第二部分题型研究题型五几何探究题类型四旋转变换问题针对演练）的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。
本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为浙江省2018年中考数学复习第二部分题型研究题型五几何探究题类型四旋转变换问题针对演练的全部内容。
第二部分题型研究题型五几何探究题类型四旋转变换问题针对演练1。
如图,在锐角△ABC中,AB＝4,BC＝5，∠ACB＝45°，将△ABC绕点B按逆时针方向旋转，得到△A1BC1.（1)如图①，当点C1在线段CA的延长线上时，求∠CC1A1的度数；(2）如图②，连接AA1,CC1.若△ABA1的面积为4,求△CBC1的面积；(3)如图③,点E为线段AB中点，点P是线段AC上的动点，在△ABC绕点B按逆时针方向旋转过程中，点P的对应点是点P1，求线段EP1长度的最大值与最小值．第1题图2. 如图，在菱形ABCD中，AB＝2，∠BAD＝60°，过点D作DE⊥AB于点E，DF⊥BC于点F。
（1）如图①，连接AC分别交DE、DF于点M、N，求证：MN＝错误!AC;（2）如图②,将∠EDF以点D为旋转中心旋转,其两边DE′、DF′分别与直线AB、BC相交于点G、P，连接GP，当△DGP的面积等于33时,求旋转角的大小并指明旋转方向．第2题图3。
如图，在平面直角坐标系中，O为坐标原点，点A的坐标为(5，0）,菱形OABC的顶点B，C都在第一象限，tan∠AOC＝错误!，将菱形绕点A按顺时针方向旋转角α(0°＜∠α＜∠AOC)得到菱形FADE（点O的对应点为点F），ED与BP交于点D，EF与OC交于点G，连接AG.（1）求点B的坐标；（2)当OG＝4时，求AG的长;（3）求证：GA平分∠OGE；(4）连接BD并延长交x轴于点P，当点P的坐标为（12，0）时，求点G的坐标．第3题图答案1。
2020初中数学中考专题复习——图形变换旋转综合题专项训练1(附答案详解)
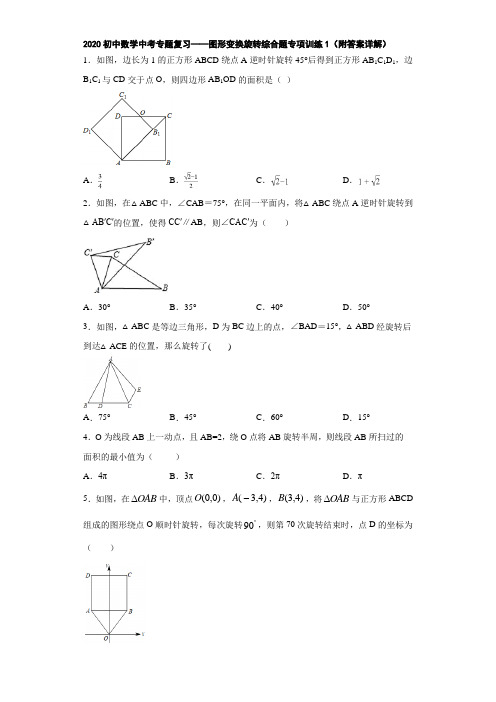
2020初中数学中考专题复习——图形变换旋转综合题专项训练1（附答案详解） 1．如图，边长为1的正方形ABCD 绕点A 逆时针旋转45°后得到正方形AB 1C 1D 1，边B 1C 1与CD 交于点O ，则四边形AB 1OD 的面积是（ ）A ．B ．C ．D ． 2．如图，在△ABC 中，∠CAB ＝75°，在同一平面内，将△ABC 绕点A 逆时针旋转到△AB′C′的位置，使得CC′∥AB ，则∠CAC′为（ ）A ．30°B ．35°C ．40°D ．50°3．如图，△ABC 是等边三角形，D 为BC 边上的点，∠BAD ＝15°，△ABD 经旋转后到达△ACE 的位置，那么旋转了( )A ．75°B ．45°C ．60°D ．15°4．O 为线段AB 上一动点，且AB=2，绕O 点将AB 旋转半周，则线段AB 所扫过的面积的最小值为（ ）A ．4πB ．3πC ．2πD ．π5．如图，在OAB ∆中，顶点(0,0)O ，(3,4)A -，(3,4)B ，将OAB ∆与正方形ABCD 组成的图形绕点O 顺时针旋转，每次旋转90︒，则第70次旋转结束时，点D 的坐标为（ ）A ．(10,3)B ．(3,10)-C ．(10,3)-）D ．(3,10)- 6．如图，在等边ABC ∆中，D 是边AC 上一点，连接BD ，将BCD ∆绕点B 逆时针旋转60︒得到BAE ∆，连接ED ，若6BC =，4BD =，则有以下四个结论：①BDE ∆是等边三角形；②//AE BC ；③ADE ∆的周长是10；④ADE BDC ∠=∠．其中正确结论的序号是（ ）A ．②③④B ．①③④C ．①②④D ．①②③ 7．如图，矩形 ABCD 中，AB=8，BC=6，将矩形 ABCD 绕点 A 逆时针旋转得到矩形 AEFG ，AE ，FG 分别交射线CD 于点 PH ，连结 AH ，若 P 是 CH 的中点，则△APH的周长为（ ）A ．15B ．18C ．20D ．248．如图，等边三角形ABC 的边长是2，M 是高CH 所在直线上的一个动点，连接MB ，将线段BM 绕点B 逆时针旋转60°得到BN ，连接MN ，则在点M 运动过程中，线段MN 长度的最小值是（ ）A ．12B ．1C ．3D ．3 9．如图，将△ABC 绕点A 旋转至△ADE 的位置，使点E 落在BC 边上，则对于结论：①DE ＝BC ；②∠EAC ＝∠DAB ；③EA 平分∠DEC ；④若DE ∥AC ，则∠DEB ＝60°；其中正确结论的个数是（ ）A ．4B ．3C ．2D ．110．如图，将边为3的正方形ABCD 绕点A 逆时针方向旋转30°后得到正方形AEFH ，则图中阴影部分的面积为（ ）A ．332-B ．33-C ．23-D ．33- 11．如图，点A 是抛物线24y x x =-对称轴上的一点，连接OA ，以A 为旋转中心将AO 逆时针旋转90°得到AO ′，当O ′恰好落在抛物线上时，点A 的坐标为______________．12．如图，将矩形ABCD 绕点A 旋转至矩形AB ′C ′D ′位置，此时AC ′的中点恰好与D 点重合，AB ′交CD 于点E ．若AB ＝3，则△AEC 的面积为_____．13．如图，点 A 的坐标是（﹣2，0），点 B 的坐标是（0，6），C 为 OB 的中点，将△ABC 绕点 B 逆时针旋转 90°后得到△A′B′C′．若反比例函数 y =k x的图象恰好经过 A′B 的中点 D ，则k _________．14．如图，正方形 ABCD 中，点 E ，F 分别在 BC 和 AB 上，BE ＝3，AF ＝2，BF＝4，将△ BEF 绕点 E 顺时针旋转，得到△GEH ，当点 H 落在 CD 边上时，F ，H 两点之间的距离为_____．15．把一副三角板如图1放置其中∠ACB =∠DEC =90°，∠A =45°，∠D =30°，斜边AB =6，CD =8，把三角板DCE 绕点C 顺时针旋转15︒得到三角形1D CE (如图2)，此时AB 与1CD 交于点O ，则线段1AD 的长度为_______．16．如图，等腰Rt ABC ∆与等腰Rt CDE ∆，AC BC =，CD DE =，212AC CD ==，DH AE ⊥，垂足为H ，直线HD 交BE 于点O .将CDE ∆绕点C 顺时针旋转，则OA 的长的最大值是______.17．如图，△ABC ，△ADE 均为等腰直角三角形，∠BAC=∠DAE=90°，将△ADE 绕点A 在平面内自由旋转，连接DC ，点M ，P ，N 分别为DE ，DC ，BC 的中点，若AD=3，AB=7，则线段MN 的取值范围是______．18．如图：已知Rt ABC ∆，对应的坐标如下，请利用学过的变换（平移、旋转、轴对称）知识经过若干次图形变化，使得点A 与点E 重合、点B 与点D 重合，写出一种变化的过程_____．19．如图，在菱形ABCD 中，2,60AB BAD =∠=︒，将菱形ABCD 绕点A 逆时针方向旋转，对应得到菱形AEFG ，点E 在AC 上，EF 与CD 交于点P ，则DP 的长是_____．20．如图，在ABC V 中，90ACB ∠=︒，10AC BC ==，在DCE V 中，90DCE ∠=︒，6DC EC ==，点D 在线段AC 上，点E 在线段BC 的延长线上．将DCE V 绕点C 顺时针方向旋转60°得到D CE ''△（点D 的对应点为D ¢，点E 的对应点为点E '），连接AD '、BE '，过点C 作CN BE '⊥，垂足为N ，直线CN 交线段AD '于M ，则MN 的长为__________．21．如图乙，ABC V 和ADE V 是有公共顶点的等腰直角三角形，90BAC DAE ∠=∠=︒，点P 为射线BD ，CE 的交点．（1）如图甲，将ADE V 绕点A 旋转，当C 、D 、E 在同一条直线上时，连接BD 、BE ，则下列给出的四个结论中，其中正确的是哪几个 ；（回答直接写序号） ①BD CE =；②BD CE ⊥；③45∠+∠=︒ACE DBC ；④()2222=+BE AD AB（2）若6AB =，3AD =，把ADE V 绕点A 旋转．①当90CAE ∠=︒时，求PB 的长；②直接写出旋转过程中线段PB 的最大值和最小值．22．如图，点E 是正方形ABCD 内的一点，将△BEC 绕点C 顺时针旋转至△DFC ． （1）请问最小旋转度数为多少？（2）指出图中的全等图形以及它们的对应角？（3）若∠EBC=30°，∠BCE=80°，求∠F 的度数．23．如图，四边形ABCD 中，AC ，BD 是对角线，△ABC 是等边三角形．线段CD 绕点C 顺时针旋转60°得到线段CE ，连接AE ．（1）求证：AE ＝BD ；（2）若∠ADC ＝30°，AD ＝3，BD ＝42．求CD 的长．24．如图，△ABC 中，AB ＝AC ，∠BAC ＝50°，P 是BC 边上一点，将△ABP 绕点A逆时针旋转50°，点P旋转后的对应点为点P′.(1)画出旋转后的三角形；(2)连接PP′，若∠BAP＝20°，求∠PP′C的度数．25．综合与实践﹣四边形旋转中的数学“智慧”数学小组在课外数学活动中研究了一个问题，请帮他们解答．任务一：如图1，在矩形ABCD中，AB=6，AD=8，E，F分别为AB，AD边的中点，四边形AEGF为矩形，连接CG．（1）请直接写出CG的长是______．（2）如图2，当矩形AEGF绕点A旋转（比如顺时针旋转）至点G落在边AB上时，请计算DF与CG的长，通过计算，试猜想DF与CG之间的数量关系．（3）当矩形AEGF绕点A旋转至如图3的位置时，（2）中DF与CG之间的数量关系是否还成立？请说明理由．任务二：“智慧”数学小组对图形的旋转进行了拓展研究，如图4，在▱ABCD中，∠B=60°，AB=6，AD=8，E，F分别为AB，AD边的中点，四边形AEGF为平行四边形，连接CG．“智慧”数学小组发现DF与CG仍然存在着特定的数量关系．（4）如图5，当▱AEGF绕点A旋转（比如顺时针旋转），其他条件不变时，“智慧”数学小组发现DF与CG仍然存在着这一特定的数量关系．请你直接写出这个特定的数量关系．26．综合与探究问题情境在综合实践课上，老师让同学们探究“平面直角坐标系中的旋转问题”．如图，在平面直角坐标系中，四边形AOBC 是矩形，点()0,0O ，点()5,0A ，点()0,3B ． 操作发现以点A 为中心，顺时针旋转矩形AOBC ，得到矩形ADEF ，点O ，B ，C 的对应点分别为D ，E ，F ．（1）如图①，当点D 落在BC 边上时，求点D 的坐标；继续探究（2）如图②，当点D 落在线段BE 上时，AD 与BC 交于点H ．①求证ADB AOB ∆≅∆；②求点H 的坐标．拓展探究（3）如图①，点M 是x 轴上任意一点，点N 是平面内任意一点，是否存在点N 使以A 、D 、M 、N 为顶点的四边形是菱形？若存在，请直接写出点N 的坐标；若不存在，请说明理由．27．（1）如图1，点A 为线段BC 外一动点，且BC a =，AB b =，填空：当点A 位于__________时，线段AC 的长取到最大值__________，且最大值为；（用含a 、b 的式子表示）．（2）如图2，若点A 为线段BC 外一动点，且6BC =，3AB =，分别以AB ，AC 为边，作等边ABD △和等边ACE △，连接CD ，BE ．①图中与线段BE 相等的线段是线段__________，并说明理由；②直接写出线段BE 长的最大值为__________．（3）如图3，在平面直角坐标系中，点A 的坐标为(40)，，点B 的坐标为(100)，，点P 为线段AB 外一动点，且4PA =，PM PB =，90BPM ∠=︒，请直接写出线段AM 长的最大值为__________，及此时点P 的坐标为__________．（提示：等腰直角三角形的三边长a 、b 、c 满足::1:1:2a b c =）28．如图，在△ABC 和△ADE 中，AB ＝AC ，AD ＝AE ，∠BAC ＋∠EAD ＝180°，△ABC 不动，△ADE 绕点A 旋转，连接BE ，CD ，F 为BE 的中点，连接AF.(1)如图①，当∠BAE ＝90°时，求证：CD ＝2AF ；(2)当∠BAE≠90°时，(1)的结论是否成立？请结合图②说明理由．29．如图1，矩形ABCD 中，E 是AD 的中点，以点E 直角顶点的直角三角形EFG 的两边EF ，EG 分别过点B ，C ，∠F ＝30°. （1）求证：BE ＝CE（2）将△EFG 绕点E 按顺时针方向旋转，当旋转到EF 与AD 重合时停止转动.若EF ，EG 分别与AB ，BC 相交于点M ，N.（如图2）①求证：△BEM ≌△CEN ；②若AB ＝2，求△BMN 面积的最大值；③当旋转停止时，点B恰好在FG上（如图3），求sin∠EBG的值.30．如图1，将两个完全相同的三角形纸片ABC和DEC重合放置，其中∠C=90°．若固定△ABC，将△DEC绕点C旋转．（1）当△DEC统点C旋转到点D恰好落在AB边上时，如图2．①当∠B=∠E=30°时，此时旋转角的大小为；②当∠B=∠E=α时，此时旋转角的大小为(用含a的式子表示)．（2）当△DEC绕点C旋转到如图3所示的位置时，小杨同学猜想：△BDC的面积与△AEC的面积相等，试判断小杨同学的猜想是否正确，若正确，请你证明小杨同学的猜想．若不正确，请说明理由．参考答案1．C【解析】【分析】连接AC1，AO，根据四边形AB1C1D1是正方形，得出∠C1AB1=∠AC1B1=45°，求出∠DAB1=45°，推出A、D、C1三点共线，在Rt△C1D1A中，由勾股定理求出AC1，进而求出DC1=OD，根据三角形的面积计算即可．【详解】连接AC1，∵四边形AB1C1D1是正方形，∴∠C1AB1=×90°=45°=∠AC1B1，∵边长为1的正方形ABCD绕点A逆时针旋转45°后得到正方形AB1C1D1，∴∠B1AB=45°，∴∠DAB1=90°-45°=45°，∴AC1过D点，即A、D、C1三点共线，∵正方形ABCD的边长是1，∴四边形AB1C1D1的边长是1，在Rt△C1D1A中，由勾股定理得：AC1=，则DC1=-1，∵∠AC1B1=45°，∠C1DO=90°，∴∠C1OD=45°=∠DC1O，∴DC1=OD=-1，∴S△ADO=×OD•AD=，∴四边形AB1OD的面积是=2×=-1，故选C．2．A【解析】【分析】根据旋转的性质可得AC=AC,∠BAC=∠BAC',再根据两直线平行,内错角相等求出∠ACC=∠CAB,然后利用等腰三角形两底角相等求出∠CAC,再求出∠BAB=∠CAC,从而得解【详解】∵CC′∥AB，∠CAB＝75°，∴∠C′CA＝∠CAB＝75°，又∵C、C′为对应点，点A为旋转中心，∴AC＝AC′，即△ACC′为等腰三角形，∴∠CAC′＝180°﹣2∠C′CA＝30°．故选A．【点睛】此题考查等腰三角形的性质，旋转的性质和平行线的性质，运用好旋转的性质是解题关键3．C【解析】【分析】首先根据题意寻找旋转后的重合点，根据重合点来找到旋转角.【详解】根据题意△ABC是等边三角形∴=AB AC∴可得B点旋转后的点为C∴旋转角为60∠=BAC︒故选C.【点睛】本题主要考查旋转角的计算，关键在于根据重合点来确定旋转角.4．D【解析】【分析】当O 是AB 中点时，线段AB 所扫过的面积的最小；【详解】解：当O 是AB 中点时，线段AB 所扫过的面积的最小，最小面积=π•12=π，故选D ．【点睛】本题考查扇形面积的计算、旋转变换的性质等知识，解题的关键是理解题意，灵活运用所学知识解决问题，属于中考常考题型．5．D【解析】【分析】先求出6AB =，再利用正方形的性质确定(3,10)D -，由于704172=⨯+，所以第70次旋转结束时，相当于OAB ∆与正方形ABCD 组成的图形绕点O 顺时针旋转2次，每次旋转90︒，此时旋转前后的点D 关于原点对称，于是利用关于原点对称的点的坐标特征可出旋转后的点D 的坐标．【详解】解：(3,4)A -Q ，(3,4)B ，336AB ∴=+=，Q 四边形ABCD 为正方形，6AD AB ∴==，(3,10)D ∴-，704172=⨯+Q ，∴每4次一个循环，第70次旋转结束时，相当于OAB ∆与正方形ABCD 组成的图形绕点O 顺时针旋转2次，每次旋转90︒，∴点D 的坐标为(3,10)-．【点睛】本题考查了坐标与图形变化﹣旋转：图形或点旋转之后要结合旋转的角度和图形的特殊性质来求出旋转后的点的坐标．常见的是旋转特殊角度如：30︒，45︒，60︒，90︒，180︒．6．D【解析】【分析】先由△BCD绕点B逆时针旋转60°，得到△BAE，可知：BD=BE，∠DBE=60°，则可判断△BDE是等边三角形；根据等边三角形的性质得BA=BC，∠ABC=∠C=∠BAC=60°，再根据旋转的性质得到∠BAE=∠BCD=60°，从而得∠BAE=∠ABC=60°，根据平行线的判定方法即可得到AE∥BC；根据等边三角形的性质得∠BDE=60°，而∠BDC>60°，则可判断∠ADE≠∠BDC；由△BDE是等边三角形得到DE=BD=4，再利用△BCD绕点B逆时针旋转60°，得到△BAE，则AE=CD，△AED的周长=AE+AD+DE=CD+AD+DE=AC+BD=BC+BD=10．【详解】∵△BCD绕点B逆时针旋转60°，得到△BAE，∴BD=BE，∠DBE=60°，∴△BDE是等边三角形，∴①正确；∵△ABC为等边三角形，∴BA=BC，∠ABC=∠C=∠BAC=60°，∵△BCD绕点B逆时针旋转60°，得到△BAE，∴∠BAE=∠BCD=60°，∴∠BAE=∠ABC，∴AE∥BC，∴②正确；∵△BDE是等边三角形，∴DE=BD=4，∵△BCD绕点B逆时针旋转60°，得到△BAE，∴△AED的周长=AE+AD+DE=CD+AD+DE=AC+BD=BC+BD=6+4=10，∴③正确；∵△BDE是等边三角形，∴∠BDE=60°，∵∠BDC=∠BAC+∠ABD＞60°，∴∠ADE=180°-∠BDE-∠BDC＜60°，∴∠ADE≠∠BDC，∴④错误．故选D．【点睛】本题主要考查旋转得性质，等边三角形的判定和性质定理，掌握旋转的性质以及等边三角形的性质定理，是解题的关键．7．C【解析】【分析】连结AC，先由△AGH≌△ADH得到∠GHA＝∠AHD，进而得到∠AHD＝∠HAP，所以△AHP是等腰三角形，所以PH＝PA＝PC，所以∠HAC是直角，再在Rt△ABC中由勾股定理求出AC的长，然后由△HAC∽△ADC，根据＝求出AH的长，再根据△HAC∽△HDA求出DH的长，进而求得HP和AP的长，最后得到△APH的周长.【详解】∵P是CH的中点，PH＝PC，∵AH＝AH，AG＝AD，且AGH与ADH都是直角，∴△AGH≌△ADH，∴∠GHA＝∠AHD，又∵GHA＝HAP，∴∠AHD＝∠HAP，∴△AHP 是等腰三角形，∴PH＝PA＝PC，∴∠HAC是直角，在Rt△ABC中，AC＝＝10，∵△HAC∽△ADC，∴＝，∴AH＝＝＝7.5，又∵△HAC∽△HAD，＝，∴DH＝4.5，∴HP＝＝6.25，AP＝HP＝6.25，∴△APH的周长＝AP＋PH＋AH＝6.25＋6.25＋7.5＝20.【点睛】本题主要考查直角三角形的性质以及相似三角形的性质，解题的关键是清楚直角三角形斜边上的中线是斜边的一半以及会运用相似三角形线段成比例求出各边长的长.8．B【解析】【分析】由旋转的特性以及∠MBN=60°，可知△BMN是等边三角形，从而得出MN=BN，再由点到直线的所有线段中，垂线段最短可得出结论．【详解】由旋转的特性可知，BM=BN．又∵∠MBN=60°，∴△BMN为等边三角形，∴MN=BM．∵点M是高CH所在直线上的一个动点，∴当BM⊥CH时，MN最短（到直线的所有线段中，垂线段最短）．又∵△ABC为等边三角形，且AB=BC=CA=2，∴当点M和点H重合时，MN最短，且有MN=BM=BH=12AB=1．故选B．【点睛】本题考查了旋转的特性、垂线段最短以及等边三角形的判定与性质．解题的关键是：得到当BM⊥CH时，MN最短．9．A【解析】【分析】由旋转的性质可知，△ABC≌△ADE，DE＝BC，可得①正确；∠CAE＝∠CAB﹣∠BAE，∠DAB＝∠DAE﹣∠BAE，可得∠EAC＝∠DAB，可判定②正确；AE＝AC，则∠AEC＝∠C，再由∠C＝∠AED，可得∠AEC＝∠AED；可判定③正确；根据平行线的性质可得可得∠C ＝∠BED，∠AEC＝∠AED=∠C，根据平角的定义可得∠DEB＝60°；综上即可得答案．【详解】∵将△ABC绕点A旋转至△ADE的位置，使点E落在BC边上，∴△ABC≌△ADE，∴DE＝BC，AE=AC，∠BAC＝∠DAE，∠C＝∠AED，故①正确；∴∠CAE＝∠CAB﹣∠BAE，∠DAB＝∠DAE﹣∠BAE，∴∠EAC＝∠DAB；故②正确；∵AE＝AC，∴∠AEC＝∠C，∴∠AEC＝∠AED，∴EA平分∠DEC；故③正确；∵DE∥AC，∴∠C＝∠BED，∵∠AEC＝∠AED=∠C，∴∠DEB＝∠AEC＝∠AED =60°，故④正确；综上所述：正确的结论是①②③④，共4个，故选：A．【点睛】本题考查旋转的性质，旋转前、后的两个图形全等，对应边、对应角相等，对应点与旋转中心所连线段的夹角等于旋转角．10．B【解析】【分析】根据正边形的性质求出DM的长，再求得四边形ADMB′的面积，然后由旋转的性质求得阴影部分面积．【详解】解：设CD、B′C′相交于点M，连接AM，DM＝x，∵ABCD绕点A逆时针方向旋转30°后得到正方形AEFH，∴∠MAD＝30°，AM＝2x，在△ADM中，x2+3＝4x2，解得：x＝1，∴S ADMB′＝3，∴图中阴影部分面积为：3﹣3．故选：B．【点睛】本题要把旋转的性质和正方形的性质结合求解．旋转变化前后，对应线段、对应角分别相等，图形的大小、形状都不改变，注意方程思想的运用．11．（2，2）或（2，-1）【解析】∵抛物线y=x2-4x对称轴为直线x=-42 2-=∴设点A坐标为（2，m），如图所示，作AP⊥y轴于点P，作O′Q⊥直线x=2，∴∠APO=∠AQO′=90°，∴∠QAO′+∠AO′Q=90°，∵∠QAO′+∠OAQ=90°，∴∠AO′Q=∠OAQ，又∠OAQ=∠AOP，∴∠AO′Q=∠AOP，在△AOP和△AO′Q中，APO AQO AOP AO QAO AO ∠∠'⎧⎪∠∠'⎨⎪'⎩＝＝＝∴△AOP ≌△AO′Q （AAS ），∴AP=AQ=2，PO=QO′=m ，则点O′坐标为（2+m ，m-2），代入y=x 2-4x 得：m-2=（2+m ）2-4（2+m ），解得：m=-1或m=2，∴点A 坐标为（2，-1）或（2，2），故答案是：（2，-1）或（2，2）．【点睛】本题考查了坐标与图形的变换-旋转，全等三角形的判定与性质，函数图形上点的特征，根据全等三角形的判定与性质得出点O′的坐标是解题的关键．12．3【解析】【分析】先求出∠ACD =30°，进而可算出CE 、AD ，再算出△AEC 的面积．【详解】如图，由旋转的性质可知：AC =AC '，∵D 为AC '的中点，∴AD =1122AC AC ='， ∵ABCD 是矩形，∴AD ⊥CD ，∴∠ACD=30°，∵AB∥CD，∴∠CAB=30°，∴∠C'AB'=∠CAB=30°，∴∠EAC=30°，∴AE=EC，∴DE=1122AE EC=，∴CE=222 33CD AB==，DE=11 3AB=，AD=3，∴132AECS EC AD==nn．故答案为：3．【点睛】本题考查了旋转的性质、矩形的性质、直角三角形中30度角的性质，三角形面积计算等知识点，难度不大．清楚旋转的“不变”特性是解答的关键．13．15【解析】【分析】作A′H⊥y轴于H．证明△AOB≌△BHA′（AAS），推出OA＝BH，OB＝A′H，求出点A′坐标，再利用中点坐标公式求出点D坐标即可解决问题．【详解】作A′H⊥y轴于H．∵∠AOB＝∠A′HB＝∠ABA′＝90°，∴∠ABO＋∠A′BH＝90°，∠ABO＋∠BAO＝90°，∴∠BAO＝∠A′BH，∵BA＝BA′，∴△AOB≌△BHA′（AAS），∴OA＝BH，OB＝A′H，∵点A的坐标是（−2，0），点B的坐标是（0，6），∴OA＝2，OB＝6，∴BH＝OA＝2，A′H＝OB＝6，∴OH＝4，∴A′（6，4），∵BD＝A′D，∴D（3，5），∵反比例函数y＝kx的图象经过点D，∴k＝15．故答案为：15．【点睛】本题考查反比例函数图形上的点的坐标特征，坐标与图形的变化−旋转等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题，属于中考选择题中的压轴题．14．6【解析】【分析】先确定正方形ABCD的边长AB＝6，则CE＝3，再利用勾股定理计算出EF＝5，根据旋转的性质得EF＝EH＝5，接着计算出CH＝4，从而可得到CH＝BF，于是可判定四边形BCHF 为矩形，然后利用矩形的性质确定FH的长．【详解】正方形ABCD的边长AB＝6,而BE＝3，则CE＝3,在Rt△BEF中，EF5==,∵△BEF绕点E顺时针旋转，得到△GEH,∴EF＝EH＝5,在Rt△EHC中，CH＝22-=,534∴CH＝BF＝4，∴四边形BCHF为矩形，∴FH＝BC＝6．故答案为6．【点睛】本题考查了旋转的性质：对应点到旋转中心的距离相等；对应点与旋转中心所连线段的夹角等于旋转角；旋转前、后的图形全等．也考查了正方形的性质．15．34【解析】【分析】首先由旋转的角度为15°，可知∠ACD1=45°..已知∠CAO=45°，即可得AO⊥CD1，然后可在Rt△AOC和Rt△AOD1中，通过解直角三角形求得AD1的长．【详解】解：如图，∵∠A=45°，∠D=30°，若旋转角度为15°，则∠ACO=30°+15°=45°，∴∠AOC=180°−∠ACO−∠CAO=90°，在等腰Rt△ABC中，AB=6，则AC=BC=32同理可得：AO=OC=3，在Rt△AOD1中，OA=3，OD1=CD1−OC=5，由勾股定理得：AD122+3435故答案为34．【点睛】此题主要考查了旋转的性质以及解直角三角形的综合应用，能够发现AO⊥OC是解决此题的关键．16．6532+【解析】【分析】延长ED到N，使得DN=DE，连接CN，BN，延长BN交AE于M．取BC的中点F，连接AF，OF．利用矩形的性质证明OD∥BN，推导出OB=OE，求出OF，AF即可解决问题．【详解】如图，延长ED到N，使得DN=DE，连接CN，BN，延长BN交AE于M．取BC的中点F，连接AF，OF．∵CD⊥EN，DN=DE，∴CN=CE，∵DC=DE，∠CDE=90°，∴∠DCE=∠DCN=45°，∴∠ACB=∠NCE=90°，∴∠BCN=∠ACE，在△BCN和△ACE中，CB CABCN ACECN CE=⎧⎪∠=∠⎨⎪=⎩，∴△BCN≌△ACE（SAS），∴∠BNC=∠AEC，∵∠BNC+∠CNM=180°，∴∠CNM+∠AEC=180°，∴∠ECN+∠NME=180°，∵∠ECN=90°，∴∠NME=90°，∵DH⊥AE，∴∠NME=∠DHE=90°，∴OD∥BN，∵DN=DE，∴OB=OE，∵BF=CF，∴OF=12 EC，∵CD=DE=6，∠CDE=90°，∴，∴，在Rt△ACF中，∵AC=12，CF=6，∴AF==∵OA≤AF+OF，∴，∴OA的最大值为．故答案为【点睛】本题考查旋转变换，等腰直角三角形的性质，三角形的中位线定理，全等三角形的判定和性质等知识，题目综合性较强，难度较大，属于中考填空题中的压轴题．解题的关键是学会添加常用辅助线，构造全等三角形解决问题，17．【解析】【分析】根据中位线定理和等腰直角三角形的判定证明△PMN是等腰直角三角形，求出MN=2BD，然后根据点D在AB上时，BD最小和点D在BA延长线上时，BD最大进行分析解答即可．【详解】∵点P，M分别是CD，DE的中点，∴PM=12CE，PM∥CE，∵点P，N分别是DC，BC的中点，∴PN=12BD，PN∥BD，∵△ABC，△ADE均为等腰直角三角形，∴AB=AC，AD=AE，∠BAC=∠DAE=90°，∴∠BAD=∠CAE，∴△ABD≌△ACE（SAS），∴BD=CE，∴PM=PN，∴△PMN是等腰三角形，∵PM∥CE，∴∠DPM=∠DCE，∵PN∥BD，∴∠PNC=∠DBC，∵∠DPN=∠DCB+∠PNC=∠DCB+∠DBC，∴∠MPN=∠DPM+∠DPN=∠DCE+∠DCB+∠DBC=∠BCE+∠DBC=∠ACB+∠ACE+∠DB C=∠ACB+∠ABD+∠DBC=∠ACB+∠ABC，∵∠BAC=90°，∴∠ACB+∠ABC=90°，∴∠MPN=90°，∴△PMN是等腰直角三角形，∴PM=PN=12 BD，∴MN=2BD，∴点D在AB上时，BD最小，∴BD=AB-AD=4，MN的最小值；点D在BA延长线上时，BD最大，∴BD=AB+AD=10，MN的最大值为，∴线段MN的取值范围是故答案为：．【点睛】此题考查了旋转的性质，三角形中位线定理，全等三角形的判定和性质，等腰直角三角形的判定和性质等，关键是根据全等三角形的判定和等腰直角三角形的判定证明△PMN是等腰三角形．18．答案不唯一（例：先将△ABC以点B为旋转中心顺时针旋转90，再将得到的图形向右平移2个单位向下平移2个单位即可）．【解析】【分析】根据“平移”、“轴对称”和“旋转”的性质进行分析解答即可．【详解】解：根据题意，可按下列方式变换使点A与点E重合，点B与点D重合：（1）先将△ABC以点B为旋转中心顺时针旋转90，再将得到的图形向右平移2个单位，并向下平移2个单位即可；（2）先将△ABC向右平移2个单位，再向下平移2个单位，然后将所得△ABC绕点B顺时针旋转90°即可；……故答案为：本题答案不唯一，如：先将△ABC以点B为旋转中心顺时针旋转90，再将得到的图形向右平移2个单位向下平移2个单位即可．【点睛】本题考查熟悉“平移”、“轴对称”和“旋转”这三种图形变换的性质，并认真观察所给图形的位置特征，是正确解答这类题的关键．191【解析】【分析】连接BD 交AC 于O ，由菱形的性质得出2,60CD AB BCD BAD ==∠=∠=︒，1302ACD BAC BAD ∠=∠=∠=︒，,OA OC AC BD =⊥，由直角三角形的性质求出112OB AB ==，OA ==，得出AC =2,60AE AB EAG BAD ==∠=∠=︒，得出2CE AC AE =-=，证出90CPE ∠=︒，由直角三角形的性质得出112PE CE ==，3PC ==，即可得出结果．【详解】解：连接BD 交AC 于O ，如图所示：∵四边形ABCD 是菱形，∴2,60CD AB BCD BAD ==∠=∠=︒， 1302ACD BAC BAD ∠=∠=∠=︒，,OA OC AC BD =⊥， ∴112OB AB ==，∴OA ==，∴AC =由旋转的性质得：2,60AE AB EAG BAD ==∠=∠=︒，∴2CE AC AE =-=，∵四边形AEFG 是菱形，∴EF AG ∕∕，∴60CEP EAG ∠=∠=︒，∴90CEP ACD ∠+∠=︒∴90CPE ∠=︒， ∴1312PE CE ==-，333PC PE ==-， ∴2(33)31DP CD PC =-=--=-； 故答案为：31-．【点睛】考核知识点：菱形性质，旋转性质.解直角三角形是关键.20．7+ 1537. 【解析】【分析】先画出图形，过点B 作E′C 的垂线交其延长线于F 点，过点D′作CM 的垂线交CM 于H 点，过A 点作CM 的垂线交其延长线于G 点．在Rt △BFC 求出BF ，再在△BE′F 用“面积法”求CN ，证明△ACG ≌△BCN ，△CD′H ≌△CE′N ，将有关线段转化，可求CM ，从而可求MN ．【详解】解：如图，若将△DCE 绕点C 顺时针旋转60°得到△D′CE′，过点B 作E′C 的垂线交其延长线于F 点，过点D′作CM 的垂线交CM 于H 点，过A 点作CM 的垂线交其延长线于G 点．∵∠ACD′=60°，∠ACB=∠D′CE′=90°，∴∠BCE′=360°-∠ACD′-∠ACB-∠D′CE′=120°．∴∠BCF=180°-∠BCE′=60°，∴∠FBC=30°，∴FC=5，∴BF= =，∴S △BCE′=12BF•CE′= 162⨯⨯= ∵∠ACG+∠BCN=90°，∠BCN+∠CBN=90°，∴∠ACG=∠CBN ，又∵AC=BC ，∴Rt △ACG ≌Rt △CBN ，∴AG=CN ，CG=BN ．同理△CD′H ≌△E′CN ，D′H=CN ，CH=NE′．∴AG=D′H ，在△AMG 和△D′MH 中，90AGM D HM AMG D MHAG D H ︒⎧∠=∠=⎪∠=∠''⎨='⎪⎩， ∴△AMG ≌△D′MH ，∴HM=MG ，∴M 为GH 中点，CM= ()111()222CG CH NB NE BE ''+=+=， 又∵BF= ，∠BCF=60°，∴CF=5，FE′=CF+CE′=11，∴14==，∴CM=12BE′=7． 又∵S △BCE′=12CN•BE′， ∴CN=2S △BCE′÷BE′= 7∴MN=CM+CN=7+ .故答案是：7+ 153.【点睛】本题考查了旋转的性质、三角形全等的判定和性质、勾股定理的运用，通过作辅助线构造全等三角形是解题的关键．21．（1）①②③；（2）①655=PB或1855；②PB长的最小值是333-，最大值是333+．【解析】【分析】(1)①由条件证明△ABD≌△ACE，就可以得到结论②由△ABD≌△ACE就可以得出∠ABD=∠ACE，就可以得出∠BDC=90°，进而得出结论；③由条件知∠ABC=∠ABD+∠DBC=45°，由∠ABD=∠ACE就可以得出结论；④△BDE为直角三角形就可以得出BE2=BD2+DE2，由△DAE和△BAC是等腰直角三角形就有DE2=2AD2，BC2=2AB2，就有BC2=BD2+CD2≠B D2就可以得出结论．(2)①分两种情形a、如图2中，当点E在AB上时，BE=AB-AE=3，由△PEB∽△AEC，得PB BEAC EC=，由此即可解决问题．b、如图3中，当点E在BA延长线上时，BE=9，解法类似；②a、如图4中，以A为圆心AD为半径画圆，当CE在⊙A上方与⊙A相切时，PB的值最大．b、如图5中，以A为圆心AD为半径画圆，当CE在⊙A下方与⊙A相切时，PB的值最小，分别求出PB即可．【详解】(1)解：如图甲：①∵∠BAC=∠DAE=90°，∴∠BAC+∠DAC=∠DAE+∠DAC ，即∠BAD=∠CAE ．在△ABD 和△ACE 中，AD AE BAD CAE AB AC ⎧⎪∠∠⎨⎪⎩＝＝＝，∴△ABD ≌△ACE(SAS)，∴BD=CE ，∴①正确；②∵△ABD ≌△ACE ，∴∠ABD=∠ACE ．∵∠CAB=90°，∴∠ABD+∠AFB=90°，∴∠ACE+∠AFB=90°．∵∠DFC=∠AFB ，∴∠ACE+∠DFC=90°，∴∠FDC=90°．∴BD ⊥CE ，∴②正确；③∵∠BAC=90°，AB=AC ，∴∠ABC=45°，∴∠ABD+∠DBC=45°．∴∠ACE+∠DBC=45°，∴③正确；④∵BD ⊥CE ，∴BE 2=BD 2+DE 2，∵∠BAC=∠DAE=90°，AB=AC ，AD=AE ，∴DE 2=2AD 2，BC 2=2AB 2，∵BC 2=BD 2+CD 2≠BD 2，∴2AB 2=BD 2+CD 2≠BD 2，∴BE 2≠2(AD 2+AB 2)，∴④错误．故答案为①②③．(2)①解：a ．如图2中，当点E 在AB 上时，3=-=BE AB AE ．∵90∠︒=EAC ， ∴2222335CE AE AC 6=+=+=，同(1)可证△≌△ADB AEC ，∴∠=∠DBA ECA ，∵∠=∠PEB AEC ，∴△∽△PEB AEC ，∴=PB BE AC EC， ∴635=PB ， ∴65PB =； b ．如图3中，当点E 在BA 延长线上时，639BE AB AE =+=+=,∵90∠︒=EAC ，∴22226353CE AE AC =+=+=，同(1)可证△≌△ADB AEC ，∴∠=∠DBA ECA ，∵∠=∠BEP CEA ，∴△∽△PEB AEC ，∴=BP BE AC EC， ∴635=BP ， ∴185=PB ，综上，65=PB 或185； ②解：a ．如图4中，以A 为圆心AD 为半径画圆，当CE 在A e 下方与A e 相切时，PB 的值最小．理由：此时BCE ∠最小，由(1)可知PBC V 是直角三角形，斜边BC 为定值，BCE ∠最小，因此PB 最小，∵⊥AE EC ， ∴22226333EC AC AE =-=-=，由(1)可知，ABD ACE △≌△，∴90∠=∠=︒ADB AEC ，33==BD CE∴90∠=∠=∠=︒ADP DAE AEP ，且AD=AE=3，∴四边形AEPD 是正方形，∴3==PD AE ，∴333=-=PB BD PD ；b ．如图5中，以A 为圆心AD 为半径画圆，当CE 在A e 上方与A e 相切时，PB 的值最大．理由：此时BCE ∠最大，因此PB 最大，(同理，PBC V 是直角三角形，斜边BC 为定值，BCE ∠最大，因此PB 最大)∵⊥AE EC ， ∴2233-=EC AC AE ，由(1)可知，ABD ACE △≌△，∴90∠=∠=︒ADB AEC ，33==BD CE∴90∠=∠=∠=︒ADP DAE AEP ，且AD=AE=3，∴四边形AEPD 是正方形，∴3==PD AE ， ∴333=+=PB BD PD ．综上所述，PB 长的最小值是333，最大值是333．【点睛】本题属于几何变换综合题，考查了等腰直角三角形的性质、旋转变换、全等三角形的判定和性质、相似三角形的判定和性质、圆的有关知识，解题的关键是灵活运用这些知识解决问题，学会分类讨论的思想思考问题，学会利用图形的特殊位置解决最值问题，属于中考压轴题．22．（1）90°；（2）△BCE ≌△DCF ，对应角为：∠CBE 与∠CDF ，∠BCE 与∠DCF ，∠BEC 与∠DFC ；（3）70°．【解析】试题分析：（1）根据正方形的性质得CB=CA ，∠BCA=90°，然后根据旋转的定义得到△BEC绕点C 顺时针旋转得到△DFC 的最小旋转度数为90°；（2）根据旋转的性质得△BCE ≌△DCF ，再根据全等的性质写出对应角；（3）先根据三角形内角和定理计算出∠BEC=70°，然后根据（2）中的结论求解． 试题解析：（1）∵四边形ABCD 为正方形，∴CB=CA，∠BCA=90°，∴△BEC绕点C顺时针旋转90°可得到△DFC，∴最小旋转度数为90°；（2）△BCE≌△DCF，对应角为：∠CBE与∠CDF，∠BCE与∠DCF，∠BEC与∠DFC；（3）∵∠EBC=30°，∠BCE=80°，∴∠BEC=180°-30°-80°=70°，∴∠F=∠BEC=70°．23．（1）见解析；（2【解析】【分析】(1)根据AC=BC、∠DCE+∠ACD=∠ACB+∠ACD、CE=CD证△ACE≌△BCD即可；(2)连接DE，可得△DCE是等边三角形，即∠CDE=60°、DC=DE，继而在Rt△ADE中，由勾股定理可得DE的长，即可求得CD．【详解】(1)∵△ABC是等边三角形，∴AC=BC，∠ACB=60°，由旋转的性质可得：CE=CD，∠DCE=60°，∴∠DCE+∠ACD=∠ACB+∠ACD，即∠ACE=∠BCD．在△ACE和△BCD中，∵AC BCACE BCDCE CD=⎧⎪∠=∠⎨⎪=⎩，∴△ACE≌△BCD(SAS)，∴AE=BD；(2)连接DE．∵CD=CE ，∠DCE=60°，∴△DCE 是等边三角形．∴∠CDE=60°，DC=DE ．∵∠ADC=30°，∴∠ADC+∠CDE=90°．∵AD=3，2，∴2．在Rt △ADE 中，由勾股定理， 可得()222242323DE AE AD =-=-= ∴23【点睛】本题主要考查旋转的性质、全等三角形的判定与性质及勾股定理的应用，连接DE 发现等边三角形与直角三角形是解题的关键．24．（1）画图见解析；（2）∠PP′C ＝30°. 【解析】【分析】（1）如图，作∠PAP ′=50°，且AP=AP′，连接PP′，△ACP′即为所求；（2），连接PP′，由旋转的性质可得，∠PAP′＝∠BAC ＝50°，AP ＝AP′，△ABP ≌△ACP′，根据等腰三角形的性质及三角形的内角和定理可得∠APP′＝∠AP′P ＝65°，根据全等三角形的性质可得∠AP′C ＝∠APB ，在△ABC 中，∠BAC ＝50°，AB ＝AC ，可求得∠B ＝65°，再由∠BAP ＝20°，根据三角形的内角和定理求得∠APB ＝95°＝∠AP′C ，所以∠PP′C ＝∠AP′C －∠AP′P ＝30°. 【详解】(1)旋转后的△ACP′如图所示．(2)如图，连接PP′.由旋转可得，∠PAP′＝∠BAC＝50°，AP＝AP′，△ABP≌△ACP′，∴∠APP′＝∠AP′P＝65°，∠AP′C＝∠APB，∵∠BAC＝50°，AB＝AC，∴∠B＝65°，又∵∠BAP＝20°，∴∠APB＝95°＝∠AP′C，∴∠PP′C＝∠AP′C－∠AP′P＝95°－65°＝30°.【点睛】本题主要考查了旋转的性质，熟练运用旋转的性质、等腰三角形的性质及三角形的内角和定理是解决本题的关键.25．5【解析】【分析】（1）如图1中，由此EG交CD于H，则四边形FGHD是矩形．在Rt△CGH中，利用勾股定理即可解决问题；（2）如图2中，作FP⊥AD于P．利用勾股定理相似三角形的性质，分别求出CG、DF即可解决问题；（3）成立．连接AG、AC．只要证明△ADF∽△ACG，可得45DF ADCG AC==即可解决问题；（4）在图4中，通过计算即可解决问题；【详解】（1）如图1中，由此EG交CD于H，则四边形FGHD是矩形．在Rt△CGH中，GH=DF=4，CH=DH=AE=3，∴CG=22CH GH+=5．故答案为：5．（2）如图2中，作FP⊥AD于P．在矩形AEGF中，∵AE=3，EG=4，∴AG=5，BG=AB-AG=1，在Rt△CBG中，CG=228165+=，由△APF∽△AEG，可得AP PE AF AE EG AG==，∴4 345 AP PF==，∴AP=125，PF=165，DP=AD﹣AP=8﹣122855=，在Rt△PDF中，DF=22PD PF+=22465 5PD PF+=，∴DF=45 CG．（3）成立．理由如下：连接AG、AC．由旋转可知：∠DAF=∠CAG，由勾股定理可知：2210AD CD+=，AG=5，∵84105ADAC==，45AFAG=，。
2020初中数学中考专题复习——图形变换旋转综合题专项训练4(附答案详解)
2020初中数学中考专题复习——图形变换旋转综合题专项训练4（附答案详解）1．如图示，若△ABC内一点P满足∠PAC=∠PBA=∠PCB，则点P为△ABC的布洛卡点．三角形的布洛卡点（Brocard point）是法国数学家和数学教育家克洛尔（A．L．Crelle 1780﹣1855）于1816年首次发现，但他的发现并未被当时的人们所注意，1875年，布洛卡点被一个数学爱好者法国军官布洛卡（Brocard 1845﹣1922）重新发现，并用他的名字命名．问题：已知在等腰直角三角形DEF中，∠EDF=90°，若点Q为△DEF的布洛卡点，DQ=1，则EQ+FQ=（）A．5 B．4 C．3+2D．2+22．如图，将△ABC绕点A逆时针旋转110°，得到△ADE，若点D落在线段BC的延长线上，则∠B大小为()A．30°B．35°C．40°D．45°3．如图，边长为12的等边三角形ABC中，M是高CH所在直线上的一个动点，连结MB，将线段BM绕点B逆时针旋转60°得到BN，连结HN．则在点M运动过程中，线段HN长度的最小值是（）A．6 B．3 C．2 D．1．54．如图，△ABC中，∠C＝90°，∠B＝30°，AC7，D、E分别在边AC、BC上，CD＝1，DE∥AB，将△CDE绕点C旋转，旋转后点D、E对应的点分别为D′、E′，当点E′落在线段AD′上时，连接BE′，此时BE′的长为（）A ．23B ．33C ．27D ．37 5．如图，边长为24的等边三角形ABC 中，M 是高CH 所在直线上的一个动点，连结MB ，将线段BM 绕点B 逆时针旋转60°得到BN ，连结HN ．则在点M 运动过程中，线段HN 长度的最小值是（ ）A ．12B ．6C ．3D ．16．如图，将ABC ∆绕点C 顺时针旋转得到DEC ∆，使点A 的对应点D 恰好落在边AB 上，点B 的对应点为E ，连接BE ，其中有：①AC AD =；②AB EB ⊥；③BC DE =；④A EBC ∠=∠，四个结论，则结论一定正确的有（ ）个A ．1个B ．2个C ．3个D ．4个 7．如图，点O 是边长为1的等边三角形ABC 的中心，将ABC ∆绕点O 逆时针方向旋转180︒，得到111A B C ∆，则111A B C ∆与ABC ∆重叠部分（图中阴影部分）的面积为（ ）A ．38B ．36C 3D ．138．如图，将△ABC 绕点A 逆时针旋转一定角度，得到△ADE ，若∠CAE=65°，∠E=70°，且AD⊥BC，∠BAC的度数为（）．A．60 °B．75°C．85°D．90°9．如图，直线323y x=-+与x轴、y轴分别交于A、B两点，把△AOB绕点A顺时针旋转60°后得到△AO′B′，则点B'的坐标是（）A．（4，23）B．（23，4）C．（3，3）D．（232+，23）10．如图，曲线C2是双曲线C1：y=6x（x＞0）绕原点O逆时针旋转45°得到的图形，P是曲线C2上任意一点，点A在直线l：y=x上，且PA=PO，则△POA的面积等于（）A．6B．6 C．3 D．1211．已知A、B是线段MN上的两点，MN=4，MA=1，MB＞1．以A为中心顺时针旋转点M，以B为中心逆时针旋转点N，使M、N两点重合成一点C，构成△ABC．设AB=x，请解答：（1）x的取值范围______；（2）若△ABC是直角三角形，则x的值是______．12．如图，将正方形ABCD 绕点A 逆时针旋转30至正方形'''AB C D ，边''B C 交CD 于点E ，若正方形ABCD 的边长为3，则DE 的长为________．13．如图，直线//PQ MN ，点A 在PQ 上，直角BEF 的直角边 BE 在MN 上，且90°，B ∠=BEF ∠=30．现将 BEF 绕点B 以每秒1︒的速度按逆时针方向旋转（E F ，的对应点分别是 E F ''，）， 同时，射线 AQ 绕点A 以每秒4︒的速度按顺时针方向旋转（ Q 的对应点是 Q '）.设旋转时间为t 秒，（045≤≤t ）在旋转的过程中，若射线AQ '与边E F ''平行时，则t 的值为_____．14．将一副三角板按图所示的方式叠放在一起，使直角的顶点重合于点O ，并能使O 点自由旋转，设AOC α∠=，BOD β∠=，则α与β之间的数量关系是__________．15．如图，正方形ABCD 绕点B 逆时针旋转30°后得到正方形BEFG ，EF 与AD 相交于点H ，延长DA 交GF 于点K ．若正方形ABCD 3AK= ．16．将一个含45°角的三角板ABC，如图摆放在平面直角坐标系中，将其绕点C顺时针旋转75°，点B的对应点'B恰好落在轴上，若点C的坐标为(1,0)，则点'B的坐标为____________．17．如图，在△ABC中，∠BAC=75°，以点A为旋转中心，将△ABC绕点A逆时针旋转，得△AB'C'，连接BB'，若BB'∥AC'，则∠BAC′ 的度数是______________.18．如图①，O为直线AB上一点作射线OC，使∠AOC＝120°，将一个直角三角尺如图摆放，直角顶点在点O处，一条直角边OP在射线OA上，将图①中的三角尺绕点O 以每秒5°的速度按逆时针方向旋转(如图②所示)，在旋转一周的过程中第t秒时，OQ所在直线恰好平分∠BOC，则t的值为______．19．如图，在△ABC中，∠C＝90°，BC＝3，AC＝5，点D为线段AC上一动点，将线段BD绕点D逆时针旋转90°，点B的对应点为E，连接AE，则AE长的最小值为_____．20．如图，在矩形ABCD中，AB＝15，BC＝17，将矩形ABCD绕点D按顺时针方向旋转得到矩形DEFG，点A落在矩形ABCD的边BC上，连接CG，则CG的长是_____．21．如图，点P是正方形ABCD内一点，点P到点A，B和D的距离分别为1，22，10.△ADP沿点A旋转至△ABP′，连接PP′，并延长AP与BC相交于点Q.(1)求证：△APP′是等腰直角三角形；(2)求∠BPQ的大小．22．一副三角板如图1所置，其中AC边与等腰Rt△EBD斜边上的中线EC共线，以C 点为旋转中心，顺时针转动△ACB，B、A两点分别于G、F两点对应，CG交BE边于点M，CF交DE边于N，已知旋转角为α，BC＝2．（问题发现）（1）如图2所示，若旋转角α（0°＜α＜30°）时，猜想CM与CN的数量关系，并写出你的推断过程；（类比探究）（2）如图3所示，若旋转角α＝75°时，（1）中的结论是否还成立？，此时连接MN，请直接写出MN的长度为；（拓展延伸）（3）在图3的基础上将△GCF向左平移至△GHF的位置，若DH＝k•BH，猜想线段HN与HM的数量关系．23．问题背景：图1，等腰△ABC中，AB=AC，∠BAC=120°，过点A作AD⊥BC于点D，则D为BC的中点，∠BAD=12∠BAC=60°；于是BC AB =2BD AB=3；（1）迁移应用：如图2，△ABC 和△ADE 都是等腰三角形，∠BAC=∠DAE=120°，D ，E ，C 三点在同一条直线上，连接BD ．求证：CD=3AD+BD ；（2）拓展延伸如图图3，在菱形ABCD 中，∠ABC=120°，在∠ABC 内作射线BM ，作点C 关于BM 的对称点E ，连接AE 并延长交BM 于点F ，连接CE ，CF ．若AE=5，CE=2，求BF 的长．24．如图，在Rt △ABC 中，∠ACB=90°，AB=35cm ，AC=6cm ，将△ABC 绕点C 逆时针旋转90°后得到△A 1B 1C ，再将△A 1B 1C 沿CB 向右平移，使点B 2恰好落在斜边AB 上，A 2B 2与AC 相交于点D ．（1）判断四边形A 1A 2B 2B 1的形状，并说明理由；（2）求△A 2CD 的面积．25．如图1，O 为正方形ABCD 的中心，分别延长OA 、OD 到点,F E ，使OF=2OA ，OE 2OD =，连接EF ，将FOE ∆绕点O 按逆时针方向旋转角α得到F OE ''∆，连接,AE BF ''（如图2）．（1）探究AE '与BF '的数量关系，并给予证明；（2）当30α=︒时，求证：AOE '为直角三角形．26．我们定义：如图1，在ABC ∆中，把AB 绕点A 按顺时针方向旋转α得到AB '，把AC 绕点A 按逆时针方向旋转β得到AC '，连接B C ''.当180αβ+=︒时，我们称AB C ''△是ABC ∆的“旋补三角形”，边B C ''上的中线AD 叫做ABC ∆的“旋补中线”，点A 叫做“旋补中心”．特例感知（1）在图2、图3中，AB C ''∆是△ABC 的“旋补三角形”，AD 是的“旋补中线”． ①如图2，当ABC ∆为等边三角形时，AD 与BC 的数量关系为AD= BC ； ②如图3，当90,8BAC BC ∠=︒=时，则AD 长为 ．猜想论证(2)在图1中，当ABC ∆为任意三角形时，猜想AD 与BC 的数量关系，并给予证明． 拓展应用(3)如图4，在四边形ABCD 中，90,150,12,23,6C D BC CD DA ∠=︒∠=︒===.在四边形内部是否存在点P ，使PDC ∆是PAB ∆的“旋补三角形”?若存在，求PAB ∆的“旋补中线”长；若不存在，说明理由．27．如图，在菱形ABCD 中，对角线AC 、BD 交于点O ，已知AC=25，AB=5．（1）求BD 的长；（2）点E 为直线AD 上的一个动点，连接CE ，将线段EC 绕点C 顺时针旋转∠BCD 的角度后得到对应的线段CF （即∠ECF=∠BCD ），EF 交CD 于点P ．①当E 为AD 的中点时，求EF 的长；②连接AF 、DF ，当DF 的长度最小时，求△ACF 的面积．28．如图，△ABC 是等腰直角三角形，D 是底边AB 上一点（不与A ，B 重合），连接CD ，将线段CD 绕点C 逆时针方向旋转90°得线段CE ，连接BE ，DE .（1）根据题意补全图形；（2）求证：AD ＝BE .29．在ABC 中，90ACB ∠=︒，30ABC ∠=︒，将ABC 绕顶点C 顺时针旋转，旋转角为00(80)1θ︒<<︒，得到''A B C ．（1）如图1，当'AB CB ∥时，设''A B 与CB 相交于点D ，求证'A CD 是等边三角形；（2）如图2，设AC 中点为E ，''A B 中点为P ，AC a =，连接EP ．在旋转过程中，线段EP 的长度是否存在最大值？如果存在，请求出这个最大值并说明此时旋转角θ的度数，如果不存在，请说明理由．30．一次函数323y x =+的图像与x 轴、y 轴分别交于点A 、B ，以AB 为边在第二象限内作等边ABC ．（1）求C 点的坐标；（2）在第二象限内有一点(),1M m ，使ABM ABC S S =△△，求M 点的坐标；（3）将ABC 沿着直线AB 翻折，点C 落在点E 处；再将ABE △绕点E 顺时针方向旋转15°，点B 落在点F 处，过点F 作FG y ⊥轴于G ．求EFG 的面积．参考答案1．D【解析】【详解】解：如图，在等腰直角三角形△DEF 中，∠EDF=90°，DE=DF ，∠1=∠2=∠3， ∵∠1+∠QEF=∠3+∠DFQ=45°，∴∠QEF=∠DFQ ，∵∠2=∠3，∴△DQF ∽△FQE ，∴2DQ FQ DF FQ QE EF ===， ∵DQ=1，∴2，EQ=2，∴2，故选D【点睛】本题考查旋转的性质；平行线的判定与性质；等腰直角三角形．2．B【解析】【分析】由旋转性质等到△ABD 为等腰三角形,利用内角和180°即可解题.【详解】解：由旋转可知,∠BAD=110°,AB=AD ∴∠B=∠ADB,∠B=（180°-110°）÷2=35°, 故选B.【点睛】本题考查了等腰三角形的性质,三角形的内角和,属于简单题,熟悉旋转的性质是解题关键. 3．B【解析】【分析】取CB 的中点G ，连接MG ，根据等边三角形的性质可得BH=BG ，再求出∠HBN=∠MBG ，根据旋转的性质可得MB=NB ，然后利用“边角边”证明△MBG ≌△NBH ，再根据全等三角形对应边相等可得HN=MG ，然后根据垂线段最短可得MG ⊥CH 时最短，再根据∠BCH=30°求解即可．【详解】解：如图，取BC 的中点G ，连接MG ，∵旋转角为60°，∴∠MBH+∠HBN=60°，又∵∠MBH+∠MBC=∠ABC=60°，∴∠HBN=∠GBM ，∵CH 是等边△ABC 的对称轴，∴HB=12AB ， ∴HB=BG ，又∵MB 旋转到BN ，∴BM=BN ，在△MBG 和△NBH 中，BG BH MBG NBH MB NB =⎧⎪∠=∠⎨⎪=⎩， ∴△MBG ≌△NBH （SAS ），∴MG=NH ，根据垂线段最短，当MG ⊥CH 时，MG 最短，即HN 最短，此时∠BCH=12×60°=30°，CG=12AB=12×12=6， ∴MG=12CG=12×6=3，∴HN=3；故选：B．【点睛】本题考查了旋转的性质，等边三角形的性质，全等三角形的判定与性质，垂线段最短的性质，作辅助线构造出全等三角形是解题的关键，也是本题的难点．4．B【解析】【分析】如图，作CH⊥BE′于H，设AC交BE′于O．首先证明∠CE′B＝∠D′＝60°，解直角三角形求出HE′，BH即可解决问题．【详解】解：如图，作CH⊥BE′于H，设AC交BE′于O．∵∠ACB＝90°，∠ABC＝30°，∴∠CAB＝60°，∵DE∥AB，∴CDCA＝CECB，∠CDE＝∠CAB＝∠D′＝60°∴'CDCA＝'CECB，∵∠ACB＝∠D′CE′，∴∠ACD′＝∠BCE′，∴△ACD′∽△BCE′，∴∠D′＝∠CE′B＝∠CAB，在Rt△ACB中，∵∠ACB＝90°，AC，∠ABC＝30°，∴AB＝2AC＝，BC AC∵DE∥AB，∴CDCA＝CECB，，∴CE∵∠CHE′＝90°，∠CE′H＝∠CAB＝60°，CE′＝CE＝3∴E′H＝12CE′＝32，CH＝3HE′＝32，∴BH＝22BC CH-＝9214-＝532∴BE′＝HE′+BH＝33，故选：B．【点睛】本题考查了相似三角形的综合应用题，涉及了旋转的性质、平行线分线段成比例、相似三角形的性质与判定等知识点，解题的关键是灵活运用上述知识点进行推理求导．5．B【解析】【分析】取CB的中点G，连接MG，根据等边三角形的性质可得BD＝BG，再求出∠HBN＝∠MBG，根据旋转的性质可得MB＝NB，然后利用“边角边”证明△MBG≌△NBH，再根据全等三角形对应边相等可得HN＝MG，然后根据垂线段最短可得MG⊥CH时最短，再根据∠BCH＝30°求解即可．【详解】如图，取BC的中点G，连接MG，∵旋转角为60°，∴∠MBH+∠HBN ＝60°，又∵∠MBH+∠MBC ＝∠ABC ＝60°，∴∠HBN ＝∠GBM ，∵CH 是等边△ABC 的对称轴，∴HB ＝12AB ， ∴HB ＝BG ，又∵MB 旋转到BN ，∴BM ＝BN ，在△MBG 和△NBH 中，BG BH MBG NBH MB NB =⎧⎪∠=∠⎨⎪=⎩，∴△MBG ≌△NBH （SAS ），∴MG ＝NH ，根据垂线段最短，当MG ⊥CH 时，MG 最短，即HN 最短，此时∠BCH ＝12×60°＝30°，CG ＝12AB ＝12×24＝12， ∴MG ＝12CG ＝12×12＝6， ∴HN ＝6，故选B ．【点睛】本题考查了旋转的性质，等边三角形的性质，全等三角形的判定与性质，垂线段最短的性质，作辅助线构造出全等三角形是解题的关键，也是本题的难点．6．A【解析】【分析】由旋转的性质即可判定①③结论错误，②无法判定，通过等角转换即可判定④正确.【详解】由旋转的性质，得AC=CD ，AC≠AD ，此结论错误；由题意无法得到AB EB ⊥，此结论错误；由旋转的性质，得BC=EC ，BC≠DE ，此结论错误；由旋转的性质，得∠ACB=∠DCE ，∵∠ACB=∠ACD+∠DCB ，∠DCE=∠ECB+∠DCB ，∴∠ACD=∠ECB∵AC=CD ，BC=CE∴∠A=∠CDA=12（180°-∠ECB ），∠EBC=∠CEB=12（180°-∠ECB ） ∴A EBC ∠=∠，此结论正确；故选：A.【点睛】此题主要考查旋转的性质，熟练掌握，即可解题.7．B【解析】【分析】观察图形并根据旋转的性质,可知图中空白小三角形也是等边三角形,且边长为13,根据相似的性质,其面积为大等边三角形的19,这样求出大三角形的面积再减去三个小空白三角形的面积即可得到答案.【详解】解:设等边三角形ABC 的高为h ,则1sin 60h =⨯︒=11224ABC S =⨯⨯=1=34946S -⨯⨯=阴影. 故答案选:B.【点睛】本题主要考查了旋转的性质,等边三角形的性质与面积等知识点,熟练掌握这些性质是解答关键.8．C【解析】试题分析：根据旋转的性质知，∠EAC=∠BAD=65°，∠C=∠E=70°．如图，设AD ⊥BC 于点F ．则∠AFB=90°，∴在Rt △ABF 中，∠B=90°-∠BAD=25°，∴在△ABC 中，∠BAC=180°-∠B-∠C=180°-25°-70°=85°，即∠BAC 的度数为85°．故选C ． 考点: 旋转的性质.9．B【解析】∵点B 是直线与y 轴的交点，又∵当x =0时，3022y =+=， ∴点B 的坐标为(0, 2)，∴OB =2.∵点A 是直线与x 轴的交点， 又∵当y =0时，320+=， ∴23x =∴点A 的坐标为(3，∴OA =23∴在Rt △AOB 中，()22222324AB OA OB =+=+=. ∵在Rt △AOB 中，AB =4，OB =2，即12OB AB =， ∴∠OAB =30°.∵△AOB 绕点A 顺时针旋转60°后得到△AO'B'，∴∠BAB'=60°，AB'=AB=4.∴∠OAB'=∠OAB+∠BAB'=30°+60°=90°.∴点B'的横坐标与点A的横坐标相等，即点B'的横坐标为∵AB'=4，∠OAB'=90°，∴点B'的纵坐标为4.∴点B'的坐标为(故本题应选B.点睛：本题考查了一次函数和旋转变换的相关知识. 旋转变换是全等变换，与旋转变换相关的题目中全等图形性质的应用是考查的重点. 旋转角的确定和运用是解决与旋转相关的题目的关键和难点. 另外，利用一次函数的解析式与图象的关系以及直角三角形的相关知识确定相关角的度数也是解题的重要环节.10．B【解析】【分析】将双曲线逆时针旋转使得l与y轴重合，等腰三角形△PAO的底边在y轴上，应用反比例函数比例系数k的性质解答问题．【详解】如图，将C2及直线y=x绕点O逆时针旋转45°，则得到双曲线C3，直线l与y轴重合．双曲线C3，的解析式为y=-6x，过点P作PB⊥y轴于点B，∵PA=PO，∴B为OA中点．∴S△PAB=S△POB，由反比例函数比例系数k的性质，S△POB=3，∴△POA的面积是6.故选B ．【点睛】本题为反比例函数综合题，考查了反比例函数的轴对称性以及反比例函数比例系数k 的几何意义．11．1＜x ＜2 x 53=或x 43=． 【解析】【分析】（1）因为所求AB 或x 在△ABC 中，所以可利用三角形三边之间的关系即两边之和大于第三边，两边之差小于第三边进行解答．（2）应该分情况讨论，因为不知道在三角形中哪一个是作为斜边存在的．所以有三种情况，即：①若AC 为斜边，则1=x2+（3-x ）2，即x2-3x+4=0，无解；②若AB 为斜边，则x 2=(3﹣x )2+1，解得x 53=，满足1<x<2；③若BC 为斜边，则(3﹣x )2=1+x 2，解得：x 43=，满足1＜x ＜2；【详解】解：（1）∵MN =4，MA =1，AB =x ，∴BN =4﹣1﹣x =3﹣x ，由旋转的性质得：MA =AC =1，BN =BC =3﹣x ，由三角形的三边关系得 3131x x x x--⎧⎨-+⎩＜＞， ∴x 的取值范围是1＜x ＜2．故答案为：1＜x ＜2；（2）∵△ABC 是直角三角形，∴若AC 为斜边，则1=x 2+(3﹣x )2，即x 2﹣3x +4=0，无解，若AB 为斜边，则x 2=(3﹣x )2+1，解得：x 53=，满足1＜x ＜2， 若BC 为斜边，则(3﹣x )2=1+x 2，解得：x 43=，满足1＜x ＜2， 故x 的值为：x 53=或x 43=． 故答案为：x 53=或x 43=． 【点睛】本题主要考查了旋转的性质，一元一次不等式组的应用，三角形的三边关系，掌握一元一次不等式组的应用，旋转的性质，三角形的三边关系是解题的关键.12【解析】【分析】连接AE ，由旋转性质知AD ＝AB′＝3、∠BAB′＝30°、∠B′AD ＝60°，证Rt △ADE ≌Rt △AB′E得∠DAE ＝12∠B′AD ＝30°，由DE ＝ADtan ∠DAE 可得答案． 【详解】解：如图，连接AE ，∵将边长为3的正方形ABCD 绕点A 逆时针旋转30°得到正方形AB'C′D′，∴AD ＝AB′＝3，∠BAB′＝30°，∠DAB ＝90°∴∠B′AD ＝60°，在Rt △ADE 和Rt △AB′E 中， AD AB AE AE'⎧=⎨=⎩， ∴Rt △ADE ≌Rt △AB′E （HL ），∴∠DAE ＝∠B′AE ＝12∠B′AD ＝30°，∴DE ＝ADtan ∠DAE ＝3×3，【点睛】此题主要考查全等、旋转、三角函数的应用，解题的关键是熟知旋转的性质及全等三角形的判定定理．13．6s或42s【解析】【分析】有两种情况：利用数形结合，画图后作辅助线，构建平行线的性质和外角的性质可得结论．【详解】解：①如图2，AQ'∥E'F'，延长BE'交AQ'于C，则∠F'E'B=∠ACB=30°，由题意得：∠EBE'=t°，∠QAQ'=4t°，∴t°+4t°=30°，∴t=6；②如图3，AQ'∥E'F'，延长BE'，交PQ于D，交直线AQ'于C，则∠F'E'B=∠ACD=30°，由题意得：∠NBE'=t°，∠QAQ'=4t°，∴∠ADB=∠NBE'=t°，∵∠ADB=∠ACD+∠DAC ，∴30°+180°-4t°=t°， ∴t=42，综上，在旋转的过程中，若射线AQ′与边E′F′平行时，则t 的值为6秒或42秒；故答案为：6秒或42秒．【点睛】本题考查的是旋转变换和平行线的性质，熟练掌握旋转的性质是关键，在解答（2）时，要采用分类讨论的思想，作延长线构建出平行线的截线，从而可得同位角相等解决问题． 14．180αβ+=︒【解析】【分析】分重叠和不重叠两种情况讨论，由旋转的性质，即可求解．【详解】如图，由题意得：90AOB COD ∠=∠=︒，AOC α=，BOD β∠=，AOC BOD αβ∴+=∠+∠AOC BOC COD =∠+∠+∠9090180AOB COD ︒︒︒=∠+∠=+=9090=︒+︒180=︒．如图，由题意得：90AOB COD ∠=∠=︒，AOC α∠=，BOD β∠=，360AOC COD BOD AOB ︒∠+∠+∠+∠=，AOC BOD αβ∴+=∠+∠360AOB COD -∠+∠︒=3609090=︒-︒-︒180=︒．综上所述，180αβ+=︒，故答案为：180αβ+=︒．【点睛】本题考查了旋转的性质，灵活运用旋转的性质是本题的关键．15．233．【解析】【详解】连接BH ，如图所示：∵四边形ABCD 和四边形BEFG 是正方形，∴∠BAH=∠ABC=∠BEH=∠F=90°，由旋转的性质得：AB=EB ，∠CBE=30°，∴∠ABE=60°，在Rt △ABH 和Rt △EBH 中，∵BH=BH ，AB=EB ，∴Rt △ABH ≌△Rt △EBH （HL ），∴∠ABH=∠EBH=12∠ABE=30°，AH=EH ，∴AH=AB•tan ∠ABH=333⨯=1， ∴EH=1，∴FH=31-， 在Rt △FKH 中，∠FKH=30°，∴KH=2FH=2(31)-，∴AK=KH ﹣AH=2(31)1--=233-；故答案为233-．考点：旋转的性质．16．()12,0+【解析】【分析】先求得∠ACO=60°，得出∠OAC=30°，求得AC=2OC=2，解等腰直角三角形求得直角边为2，从而求出B′的坐标．【详解】解：∵∠ACB=45°，∠BCB′=75°，∴∠ACB′=120°，∴∠ACO=60°，∴∠OAC=30°，∴AC=2OC ，∵点C 的坐标为（1，0），∴OC=1，∴AC=2OC=2，∵△ABC 是等腰直角三角形，AB BC ∴==B C A B '''∴==1OB '∴=+∴B′点的坐标为(1+【点睛】此题主要考查了旋转的性质及坐标与图形变换，同时也利用了直角三角形性质，首先利用直角三角形的性质得到有关线段的长度，即可解决问题．17．105°【解析】【分析】根据旋转的性质得AB′=AB ，∠B′AB=∠C′AC ，再根据等腰三角形的性质得∠AB′B=∠ABB′，然后根据平行线的性质得到∠AB′B=∠C′AB′=75°，于是得到结论．【详解】解：∵△ABC 绕点A 逆时针旋转到△AB′C′，∴AB′=AB ，∠B′AB=∠C′AC ，∠C′AB′=∠CAB=75°，∴△AB′B 是等腰三角形，∴∠AB′B=∠ABB′∵BB'∥AC ，∴∠A B′B=∠C′AB′=75°，∴∠C′AC=∠B′A B =180°-2×75°=30°，∴∠BAC′=∠C′AC+∠BA C =30°+75°=105°，故答案为：105°．【点睛】本题考查了旋转的性质：旋转前后两图形全等；对应点到旋转中心的距离相等；对应点与旋转中心的连线段的夹角等于旋转角．也考查了平行线的性质．18．24或60【解析】【分析】先根据题目中的要求，找出OQ平分∠BOC的两种状态，分别得出结果.【详解】解：已知∠AOC＝120°，三角尺绕点O以每秒5°的速度按逆时针方向旋转，要使OQ所在直线恰好平分∠BOC，有两种情况，OQ所在的直线平分和延长线平分∠BOC，所以第一种情况时，t为24，第二种情况时，t为60,故答案为24或60【点睛】此题重点考察学生对图形平移的理解，抓住平移前后的变化是解题的关键.19．2【解析】【分析】由旋转的性质可知BD＝DE，∠C＝90°，则容易想到构造一个直角三角形与Rt△BCD全等，即过E点作EH⊥AD于点H，设CD＝x，则可用x表示AE的长，从而判断什么时候AE取得最小值．【详解】设CD＝x，则AD＝5﹣x，过点E作EH⊥AD于点H，如图：由旋转的性质可知BD＝DE，∵∠ADE+∠BDC＝90°，∠BDC+∠CBD＝90°，∴∠ADE＝∠CBD，又∵∠EHD＝∠C，∴△BCD≌△DHE，∴EH＝CD＝x，DH＝BC＝3．∵AD＝5﹣x，∴AH＝AD﹣DH＝5﹣x﹣3＝2﹣x，∵在Rt△AEH中，AE2＝AH2+EH2＝（2﹣x）2+x2＝2x2+4x+4＝2（x﹣1）2+2，所以当x＝1时，AE2取得最小值2，即AE取得最小值2．故答案是：2．【点睛】考查了全等三角形的性质和判定，解此题的关键灵活其相关的知识点进行推理证明．20．4534 17【解析】【分析】连接AE，由旋转变换的性质可知，∠ADE＝∠CDG，AD＝BC＝DE＝17，AB＝CD＝DG＝15，由勾股定理得，CE＝228DE CD-=，得出BE＝BC−CE＝9，则AE＝22334AB BE+=，进一步证明△ADE∽△CDG，得出DC1517CGAE AD==，然后即可得出结果．【详解】连接AE，如图所示：由旋转变换的性质可知，∠ADE＝∠CDG，AD＝BC＝DE＝17，AB＝CD＝DG＝15，由勾股定理得，CE228DE CD-=，∴BE＝BC﹣CE＝17﹣8＝9，则AE22334AB BE+=∵AD DEDC DG=，∠ADE＝∠CDG，∴△ADE∽△CDG，∴DC1517 CGAE AD==，解得，CG【点睛】本题主要考查了旋转图形中相似三角形性质与判定的综合运用，熟练掌握相关概念是解题关键.21．（1）证明见解析；（2）∠BPQ=45°．【解析】【分析】（1）根据旋转的性质可知，△APD≌△AP′B，所以AP=AP′，∠PAD=∠P′AB，因为∠PAD+∠PAB=90°，所以∠P′AB+∠PAB=90°，即∠PAP′=90°，故△APP′是等腰直角三角形；（2）根据勾股定理逆定理可判断△PP′B是直角三角形，再根据平角定义求出结果.【详解】（1）证明：∵四边形ABCD为正方形，∴AB=AD，∠BAD=90°，∵△ADP沿点A旋转至△ABP′，∴AP=AP′，∠PAP′=∠DAB=90°，∴△APP′是等腰直角三角形；（2）∵△APP′是等腰直角三角形，∴，∠APP′=45°，∵△ADP沿点A旋转至△ABP′，∴，在△PP′B中，，，∵）2+（）2=）2，∴PP′2+PB2=P′B2，∴△PP′B 为直角三角形，∠P′PB=90°，∴∠BPQ=180°﹣∠APP′﹣∠P′PB=180°﹣45°﹣90°=45°．【点睛】本题主要考查了旋转的性质、等腰三角形的判定与性质、勾股定理及逆定理的综合运用，有一定难度，关键是明确旋转的不变性．22．（1）CM ＝CN ，证明详见解析；（2）成立，3；（3）HN ＝k •HM ． 【解析】【分析】（1）根据等腰三角形的性质得到EC ⊥CD ，EC ＝CD ＝BC ，证明△BCM ≌△ECN ，根据全等三角形的性质证明结论；（2）作CP ⊥BE 于点P ，根据等腰直角三角形的性质求出PC ，根据余弦的定义求出CM ，根据等腰直角三角形的性质计算，得到答案；（3）作HQ ∥EC ，证明△MHQ ∽△NHD ，根据相似三角形的性质解答即可．【详解】解：（1）CM ＝CN ，理由如下：在Rt △BED 中，EB ＝ED ，BC ＝CD ，∴EC ⊥CD ，EC ＝CD ＝BC ，∠BEC ＝∠DEC ＝∠B ＝∠D ＝45°，∵∠BCM+∠ECM ＝90°，∠ECN+∠ECM ＝90°，∴∠BCM ＝∠ECN ，在△BCM 和△ECN 中， B CEN BC ECBCM ECN ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△BCM ≌△ECN （ASA ）∴CM ＝CN ；（2）（1）中的结论成立，MN =， 理由如下：作CP ⊥BE 于点P ，（1）中的结论成立，证明过程同（1）相同，在Rt△BCP中，∠B＝45°，∴PC＝BC•sinB＝2，∵∠BCM＝75°，∠BCP＝45°，∴∠PCM＝30°，∴CM＝PCcos PCl＝263，在等腰直角三角形MCN中，MN＝2PC＝433，故答案为：成立；433；（3）HN＝k•HM，理由如下：过点H作HQ∥EC交BE于点Q，则△BHQ为等腰直角三角形，∴BH＝HQ，∵DH＝k•BH，∴DH＝k•QH，∵∠MHQ+∠QHF＝90°，∠NHD+∠QHF＝90°，∴∠MHQ＝∠NHD，又∠MQH＝∠NDH，∴△MHQ∽△NHD，∴HNHII＝HDHQ＝k，即HN＝k•HM．【点睛】本题考查了全等三角形的判定与性质、相似三角形的判定与性质、解直角三角形、勾股定理等知识，此题综合性强，有一定难度，证明三角形相似是解决问题的关键．23．（1）见解析；（2）【解析】【分析】AD，（1）作AH⊥CD于H，易证△DAB≌△EAC，得BD=CE，由∠ADH=30°，得DH=2结合DH=HE，即可得到结论；（2）作BH⊥AE于H，连接BE，易得BC=BE=BD=BA，从而得A、D、E、C四点共圆，进而得△EFC是等边三角形，可得FH=4.5，结合∠BFH=30°，即可求解．【详解】（1）如图2中，作AH⊥CD于H．∵△ABC和△ADE都是等腰三角形，∠BAC=∠DAE=120°，∴AD=AE，AB=AC，∠DAB=∠EAC，∴△DAB≌△EAC（SAS），∴BD=CE，∵∠ADH=(180°-120°)÷2=30°，AD，∴在Rt△ADH中，DH=2∵AD=AE，AH⊥DE，∴DH=HE，∵；（2）如图3中，作BH⊥AE于H，连接BE．∵四边形ABCD是菱形，∠ABC=120°，∴△ABD，△BDC是等边三角形，∴BA=BD=BC，∵E、C关于BM对称，∴BC=BE=BD=BA，FE=FC，∴A、D、E、C四点共圆，∴∠ADC=∠AEC=120°，∴∠FEC=60°，∴△EFC 是等边三角形， ∴EC=EF=2， ∵AE=5， ∴AH=HE=2.5， ∴FH=4.5，∵在Rt △BHF 中，∠BFH=30°， ∴HFBF=cos30°， ∴BF=4.5÷32=33．【点睛】本题主要考查全等三角形，等腰三角形，菱形以及圆的基本性质的综合，掌握含120°的等腰三角形的性质，三角形全等的判定和性质，菱形的性质以及圆周角定理，是解题的关键． 24．（1）四边形A 1A 2B 2B 1是平行四边形，理由见解析；（2）2A CD S =8116cm 2． 【解析】 【分析】（1）根据平移的性质以及平行四边形的判定定理，即可得到结论； （2）根据勾股定理得BC=3cm ，进而得CB 1=3cm ，AB 1=3cm ，B 1B 2 =32cm ，A 1 A 2=32cm ，CA 2=92cm ，由A 1B 1∥A 2B 2，得1CD CB =21CA CA ，从而得CD=94cm ，进而即可求解．【详解】（1）四边形A 1A 2B 2B 1是平行四边形，理由如下：∵将△ABC 绕点C 逆时针旋转90°后得到△A 1B 1C ，再将△A 1B 1C 沿CB 向右平移得△A 2B 2C 2，∴A 1B 1∥A 2B 2，A 1B 1=A 2B 2， ∴四边形A 1A 2B 2B 1是平行四边形； （2）在Rt △ABC 中，=3cm ，由题意：BC=CB 1=3cm ，A 1C=AC=6cm ， ∴AB 1=3cm ，∵B 1B 2∥BC ，AB 1=CB 1， ∴AB 2=B 2B ，∴B 1B 2=12BC=32cm ， ∴A 1 A 2= B 1B 2 =32cm ，∴CA 2=6-32=92cm ， ∵A 1B 1∥A 2B 2， ∴1CD CB =21CA CA ， ∴3CD =926，∴CD=94cm ，∴2A CD S=12•CA 2•CD=12×92×94=8116cm 2． 【点睛】本题主要考查平移，旋转的性质，平行四边形的判定定理，平行线截线段定理，掌握平行线截得的线段对应成比例，是解题的关键． 25．(1)AE BF ''=，理由见解析；(2)见解析 【解析】 【分析】（1）根据正方形的性质以及旋转的性质证明F OB E OA ''≅即可；（2）作E OA '的中线AM ，通过正方形的性质以及已知条件得出△AOM 为等边三角形，再根据等腰三角形的性质得出30E AM '∠=︒，从而得出90E AM OAM '∠+∠=︒即可． 【详解】 （1）AE BF ''=理由如下：∵O 为正方形ABCD 的中心， ∴AO=DO=BO=CO ，∠AOD=∠AOB=90°， ∵OF=2OA ，OE 2OD =， ∴OF=OE ，又∵F OE ''∆是△EOF 旋转得到， ∴OF OE ''=，90E OF ''∠=︒，∴90F OB AOF E OA AOF ''''∠+∠=∠+∠=︒， ∴F OB E OA ''∠=∠∴在F OB '与E OA ' 中，BO AOF OB E OA OF OE ''=⎧⎪∠=''∠⎨⎪=⎩，∴F OB E OA ''≅（SAS ） ∴AE BF ''=；(2)如图，作E OA '的中线AM ， 则222OE OM OD OA '===，OA OM ∴=，∵30α=︒，∴∠AOM=60°，∴△AOM 为等边三角形，MA MO ME '∴==，AE M E AM ''∴∠=∠又∵60AMO OAM ∠=∠=︒30E AM '∴∠=︒， 90E AM OAM '∴∠+∠=︒即90E AO '∠=︒， ∴AOE '为直角三角形．【点睛】本题考查了正方形与旋转的综合题型，涉及了全等三角形的判定与性质、旋转的性质、正方形的性质以及等腰三角形的性质，解题的关键是作出辅助线，灵活运用几何中的边角关系． 26．（1）①12；②4 ；（2）12，证明见解析；（339 【解析】 【分析】（1）①首先证明ADB '是含有30°的直角三角形，可得12AD AB '=即可解决问题； ②首先证明BAC B AC ''≅，根据直角三角形斜边上的中线的性质即可解决问题； （2）如图所示作出辅助线，首先证明四边形AC MB ''是平行四边形，再证明BAC AB M '≅，即可解决问题；（3）如图所示作出辅助线，证明PA=PD ，PB=PC ，再证明∠APD+∠BPC=180°即可． 【详解】解：（1）①在图2中， ∵△ABC 是等边三角形， ∴AB=BC=AC=AB AC ''=， ∵DB DC ''=， ∴AD ⊥B C ''，∵∠BAC=60°，∠BAC+180B AC ''∠=︒， ∴120B AC ''∠=︒， ∴30B C ''∠=∠=︒，∴1122AD AB BC '==， 故答案为：12；②在图3中，∵∠BAC=90°，∠BAC+180B AC ''∠=︒， ∴90BAC B AC ''∠=∠=︒， ∵AB AB '=，AC AC '=， ∴BAC B AC ''≅， ∴BC B C ''=， ∵B D DC ''= ∴11422AD B C BC ''===， 故答案为：4； （2）结论为：12AD BC =理由：如下图，延长AD 到点M ，使得AD=DM ，连接B M '，C M '， ∵B D DC ''=，AD=DM ， ∴四边形AC MB ''是平行四边形， ∴AC B M AC ''==，∵∠BAC+180B AC ''∠=︒，180B AC AB M '''∠+∠=︒ ∴BAC AB M '∠=∠， ∵AB AB '=∴BAC AB M '≅（SAS ） ∴BC=AM ∴12AD BC =；（3）存在，理由：如图4中，延长AD 交BC 的延长线于点M ，作BE ⊥AD 于点E ，作线段BC 的垂直平分线交BE 于点P ，交BC 于点F ，连接PA 、PD 、PC ，作△PCD 的中线PN ，连接DF 交PC 于点O ．∵∠ADC=150°，∴∠MDC=30°，在Rt△DCM中，∵CD=，∠DCM=90°，∠MDC=30°，∴CM=2，DM=4，∠M=60°，在Rt△BEM中，∵∠BEM=90°，BM=14，∠MBE=30°，∴EM=17 2BM=，∴DE=EM-DM=3，∵AD=6，∴AE=DE，∵BE⊥AD，∴PA=PD，PB=PC，在Rt△CDF中，∵CD=CF=6，∴tan CDF∠=∴∠CDF=60°=∠CPF，∴△FCP≌△CFD，∴CD=PF，又∵CD∥PF∴四边形CDPF是矩形，∴∠CDP=90°，∴∠ADP=∠ADC-∠CDP=60°，∴△ADP是等边三角形，∴∠ADP=60°，∵∠BPF=∠CPF=60°，∴∠BPC=120°，∴∠APD+∠BPC=180°，∴△PCD是△PAB的“旋补三角形”，在Rt△PDN中，∵∠PDN=90°，PD=AD=6，PN=()22223639DN PD +=+=．【点睛】本题考查了四边形综合题、全等三角形的判定和性质、平行四边形的判定和性质、含30°直角三角形的性质、等边三角形的判定和性质、矩形的判定和性质等知识点，解题的关键是灵活运用所学知识解决问题，学会添加辅助线，构造全等三角形解决问题，属于几何压轴题． 27．（1）5（2）①13②当DF 的长度最小时，△ACF 的面积为14． 【解析】 【分析】（1）由菱形的性质得出AD=AB=BC=CD=5，AC ⊥BD ，15,2OA OC AC OB OD ====由勾股定理求出OB ，即可得出BD 的长；（2）①过点C 作CH ⊥AD 于H ，由菱形的性质和三角函数得出5AH OA AC AB =求出AH=2，由勾股定理求出224CH AC AH =-=求出12HE AE AH =-=再由勾股定理求出65EC =△BCD ∽△ECF ，得出EC BC EF BD =即可得出结果； ②先证明△BCE ≌△DCF ，得出BE=DF ，当BE 最小时，DF 就最小，且BE ⊥DE 时，BE 最小，此时∠EBC=∠FDC=90°，BE=DF=4，△EBC 的面积=△ABC 的面积=△DCF 的面积，则四边形ACFD 的面积=2△ABC 的面积=20，过点F 作FH ⊥AD 于H ，过点C 作CP ⊥AD 于P ，则∠CPD=90°，证明△PCD ∽△HDF ，得出35HF PD FD CD ==求出121,652ADFHF S AD FH ==⋅=即可得出△ACF 的面积． 【详解】（1）∵四边形ABCD 是菱形，∴AD=AB=BC=CD=5，AC ⊥BD ，OA=OC=125OB=OD ， 在Rt △ABO 中，由勾股定理得：22AB OA -225(5)-5∴BD=2OB=45；（2）①过点C 作CH ⊥AD 于H ，如图1所示：∵四边形ABCD 是菱形， ∴∠BAC=∠DAC ， ∴cos ∠BAC=cos ∠DAC ， ∴AH AC =OA AB 5255，∴AH=2， ∴22AC AH -，∵E 为AD 的中点， ∴AE=12AD=52， ∴HE=AE-AH=12， 在Rt △CHE 中，由勾股定理得：221()42+=652， 由旋转的性质得：∠ECF=∠BCD ，CF=CE ， ∴BC EC =CDCF， ∴△BCD ∽△ECF ， ∴EC BCEF BD=，即652EF45， 解得：13 ②如图2所示：∵∠BCD=∠ECF，∴∠BCD-DCE=∠ECF-∠DCE，即∠BCE=∠DCF，在△BCE和△DCF中，BC DCBCE DCFCE CF=⎧⎪∠=∠⎨⎪=⎩，∴△BCE≌△DCF（SAS），∴BE=DF，当BE最小时，DF就最小，且BE⊥DE时，BE最小，此时∠EBC=∠FDC=90°，BE=DF=4，△EBC的面积=△ABC的面积=△DCF的面积，则四边形ACFD的面积=2△ABC的面积=5×4=20，过点F作FH⊥AD于H，过点C作CP⊥AD于P，则∠CPD=90°，∴∠PCD+∠PDC=90°，∵∠FDC=90°，∴∠PDC+∠HDF=90°，∴∠PCD=∠HDF，∴△PCD∽△HDF，∴HFFD=PDCD=35，∴HF=4×35=125，∴△ADF的面积=12AD•HF=12×5×125=6，∴△ACF的面积=四边形ACFD的面积-△ADF的面积=20-6=14，即当DF的长度最小时，△ACF的面积为14．【点睛】本题是四边形综合题目，考查了菱形的性质、勾股定理、全等三角形的判定与性质、相似三角形的判定与性质、三角函数、三角形面积公式等知识；本题综合性强，证明三角形相似是。
中考数学总复习--几何变换之翻折探究专题(含答案).doc
最新中考数学总复习“几何变换之翻折探究专题思考与解决几何图形的问题，主要是借助基本图形的性质（定义，定理等）和图形之间的关系.许多基本图形的性质都源于这个图形本身的“变换特征J而最为重要和最为常用的图形关系“全等三角形"很多的情况也是同样具有“变换勺孩式的联系.本来两个三角形全等是指它们的形状和大小都一样，和相互间的位置没有肓接关系，但是，在同一个问题中涉及到的两个全等三角形，绝大多数都有一定的位置关系，或成轴对称关系，或成平移关系, 或成旋转的关系（包括中心对称）.这样，在解决具体的儿何图形问题时，图形本身所显示或暗示的“变换特征J对我们识别出、构造出基本图形和图形关系（如全等三角形），有着极为重耍的启发和引导的作用.图形的翻折问题本质上是轴对称问题，满足轴对称的性质，即:1.折叠图形关于折痕对称2.对应边.角相等3・对应点的连线被折痕垂直平分我们解决翻折问题一般也是从以上性质出发解决的.先讲翻折题的三种常见方法【题目】（16年秋锡山区期屮）如图，在平面直角坐标系屮，矩形ABCO的边0A在x轴上，边0C在y轴上，点B的坐标为（1, 3）,将矩形沿对角线AC翻折，点B落在点D的位置，且AD交y轴于点E,那么点D的坐标为_________________________ ・法一：求定点关于定真线的对称点（万能方法）如答图1,连BD,处AC 于G,贝UABC^AAGB^ABFD,.•.BD = 2BG = AB -«2=3x- x2= , DF=BD- 1x . E \/To io io ioBF=3DF=-,5 95・・・D （-L匕5 5法二：由直角翻折主动寻求K型相似（特殊技巧）• •••••••• • •••如答图1, l±l ZADC=90°=>A ADN^ADCF,相似比为3： 1,设ON=CF=x,则DN=3x, DF=3-3x,由AN = 3DF 得x+l=3 (3-3x),解得x=4,_.・.D (—°,_以2_5 5 5法三:电翻折主动寻求等腰二角形（特殊技巧）如答图2,延长CD交x轴于H,可得CH=AH,设DH = y,则AH = y,在RtAADH +用勾股定理耳［得y=4易得DM=-, AD-）5 5 5法四：出翻折主勿寻求等腰三角形（特殊技巧）如答图2,设CE=AE=a,则OE=3—a,在RtAAOE 中用勾股定理可得a=-,由比例关系可得OM=-, /.D （-1，55 5 5【例题剖析】题型一：利用对应边相等，对应角相等例1一1、（2015 年无锡）10・如图，RtAABC 中，ZACB = 90°, AC= 3, BC=4,将边AC沿CE翻折，使点A落在AB上的点D处；再将边BC沿CF翻折，使点B落在CD的延长线上的点B处，两条折痕与斜边AB分别交于点E、F,贝U线段BF的长为（）人3 4 2 3A. 一B. -C. - r> —【解答】选BK点评》本题的关键点在于发现并证明ZBTB是直角，由翻折可知ZA=ZADC=ZBQF,又ZB=ZB f=—< ZBTB是肓角=>AB f DF是“345"的三角形乂由翻折可知B，C = BC=4, CD = AC = 3,例1一2、（18年4月锡山区二模）17.如图，在“ABC 中，ZACB=90°，点、D, E 分别在 AC, BC±,且ZCDE=ZB,将ZkCDE 沿DE 折叠，点C 恰好落在AB 边上的点F 处.若AC=8, AB=\O ，则CD 的长为 ___________ ・母子三角形K 点评』本题的关键点在于发现并证明F 是AB 的中点，如答图，由翻折=CF 丄DE===== < Z1 = Z2-= < Z2= ZB=>CF=BF 二=========<F 是AB 中点 木题也可以根据90度翻折构造K 型相似来解决，如答图2K 针对练习》1、（18年4刀宜兴一模）16・如图，在矩形ABCD 中，AB=4, BC=6, E 是BC 的中点, 连结AE,将ZkABE 沿AE 折叠，点B 落在点F 处，连结CF,则sinZEFC= ________________ .【解答】CD=；【解答】；§型二：利用（或构造）等腰三角形例2—1、（18年4月宜兴一模）10. —张矩形纸片ABCD,其中AD = 8cm, AB=6cm,先沿对角线BD对折，点C落在点C的位置，BC交AD于点G （图1）；再折叠一次，使点D与点A 重合，得折痕EN, EN交AD于点M （图2）,则EM的长为（7 —A. 2B.丄C・ 0 D.【解答】选DK点评》木题的关键点在于发现并利用ADEN是等腰三角形，由翻折=>ZCDB = ZEDB, 作高EHEN 是折痕=>EN〃CDnZEND=ZBDC=>ZEND=ZEDN=>EN=ED== v^DEN 是“556”的三角形例2—2、(12年南长区一模)已知正方形ABCD 的边长为6cm,点E 是射线BC 上的一个动【解答】当E 点在BC 边上时，sinZDAB r =5,当E 点在BC 的延长线上时，sinZDAB r 13_3 —, 5K 点评》本题三种方法都可以，方运一：如答图1,构造箏腰三角形AGF,再由勾股定理得到方程x 2+62= (9-x) 2解得 x=,所以sinZDAB r ='2 13 方法二 如答圏2, A ABE^AAHB^AB Z GB,三边之比都为2： 3： 甄 ABH=2B E= 2<4= u_=>BB f =2BH=_=>BG= lBB z =-=>AG=-=>sinZ yrr /TJ /TJ yi3 y/H 13 13 DAB ，=L 13方法三：如答图3，构造相似三角形厶ABT S /XEEG ,且相似比为3： 2,可得方程组[3x+2y=6 ,解得卜=勺 所以sinZDAB z =-l(3x)2 + 0y M6 [y=*另一种情况类似，参考答图4 ' 答图4点，连接AE 交射线DC 于点F,将ZkABE 沿直线AE 翻折，点B 落在点B 处.(1) cm ； 求sinZDAB r 的值；D^-=1 时，CF=DC答图3 答图1 答图2例2—3、（17 年滨湖二模）18・如图，在RtAABC 中，ZC=90°, AC=3cm, BC=4cm,点 E 从C 点出发向终点B 运动，速度为lcm/秒，运动时间为t 秒，作EF 〃AB,点P 是点C 关K 点评为本题的关键点在于CP 与折痕EF 垂直，也即与AB 垂直，在ZAPE=90°Bj,可得 等腰三角形ABE 。
初三数学旋转试题及答案
初三数学旋转试题及答案在解答初三数学旋转试题时，我们首先需要理解旋转的概念和性质，然后应用这些知识来解决具体的几何问题。
以下是一些典型的旋转试题及其答案。
1. 题目：在平面直角坐标系中，点A的坐标为(3,4)，若将点A绕原点O逆时针旋转90°，求旋转后点A的新坐标。
答案：首先，我们需要知道逆时针旋转90°后，点的坐标变换规则是(x, y)变为(-y, x)。
因此，点A(3,4)旋转后的新坐标为(-4, 3)。
2. 题目：已知三角形ABC，其中∠A=30°，∠B=60°，∠C=90°，边AB的长度为6，边BC的长度为4，求将三角形ABC绕点C逆时针旋转90°后，点A的新位置。
答案：由于三角形ABC是一个直角三角形，且∠C=90°，旋转后点A 将位于点B的正上方，且与点B的距离等于AB的长度。
因此，点A的新位置可以通过计算得到，即点A的新坐标为(4, 6)。
3. 题目：在平面直角坐标系中，点P的坐标为(2, -1)，若将点P绕点Q(1, 2)顺时针旋转45°，求旋转后点P的新坐标。
答案：首先，我们需要计算点P相对于点Q的向量，即(2-1, -1-2)=(1, -3)。
然后，将这个向量顺时针旋转45°，可以通过旋转矩阵来实现。
旋转矩阵为：\[\begin{bmatrix}\cos(-45°) & -\sin(-45°) \\\sin(-45°) & \cos(-45°)\end{bmatrix}=\begin{bmatrix}\frac{\sqrt{2}}{2} & \frac{\sqrt{2}}{2} \\-\frac{\sqrt{2}}{2} & \frac{\sqrt{2}}{2}\end{bmatrix}\]将向量(1, -3)与旋转矩阵相乘，得到新的向量为(\(\frac{\sqrt{2}}{2} - \frac{3\sqrt{2}}{2}\), \(-\frac{\sqrt{2}}{2} - \frac{3\sqrt{2}}{2}\))。
中考数学专题复习旋转变换题三例试题
无棣县埕口中学中考数学专题复习旋转变换题三例新人教版创作单位：*ＸＸＸ创作时间：2022年4月12日创作编者：聂明景一、在旋转中酝酿与发现例1：〔2021)如图，在Rt△ABC中，∠ACB=90°, ∠B =60°，BC=2．点0是AC的中点，过点0的直线l从与AC重合的位置开场，绕点0作逆时针旋转，交AB边于点D.过点C作CE∥AB交直线l于点E，设直线l的旋转角为α.(1)①当α=________度时，四边形EDBC是等腰梯形，此时AD的长为_________；②当α=________度时，四边形EDBC是直角梯形，此时AD的长为_________；(2)当α=90°时,判断四边形EDBC是否为菱形，并说明理由．思路点拨：直线l绕AC的中点O旋转，始终保持着△AOD和△EOC全等，探究四边形EDBC是等腰梯形的条件，执果索因，应让∠B =∠EDB=60°或者ED=BC=2，所以当直线l的旋转角α为30°时，便有∠EDB=60°；此时AD=1；探究四边形EDBC是直角梯形，那么只需让∠EDB=90°即可，所以当直线l的旋转角α为60°时便成立；当直线l的旋转角α=90°时,便可得DE∥CB，便不难发现和证明四边形EDBC为菱形解析：〔1〕①30，1；②60，1.5；〔2〕当∠α=900时，四边形EDBC 是菱形.∵∠α=∠ACB=900，∴BC //ED . ∵CE //AB , ∴四边形EDBC 是平行四边形. 在Rt △ABC 中，∠ACB =900，∠B =600,BC =2,∴∠A =300.∴AB =4,AC.∴AO =12AC. 在Rt △AOD 中，∠A =300，∴AD =2.∴BD =2.∴BD =BC .又∵四边形EDBC 是平行四边形， ∴四边形EDBC 是菱形点评：解决直线绕某一点旋转的动态问题的关键是树立联络，开展的动态观点，整体地把握命题的条件，抓住在运动变化过程中暂时静止的某一瞬间 ，动中求静，寻找和确定某些特殊图形或者位置，进展观察联想，猜测，分析，归纳，总结，寻找出变量关系式，从而使问题得到打破和解决。
2024年中考数学高频考点专题复习——旋转综合题(含解析)
2024年中考数学高频考点专题复习——旋转综合题1．如图，△ABC 和△DEF 关于某点对称（1）在图中画出对称中心O ；（2）连结AF 、CD ，判断四边形ACDF 的形状，并说明理由．2．在平面直角坐标系中的位置如图所示，其中每个小正方形的边长为1个单位．（1）画出关于原点O 的中心对称图形；（2）在（1）的条件下，请分别写出点A 、B 、C 的对应点、、的坐标．ABC ABC 111A B C 1A 1B 1C3．如图1，图2，△ABC 是等边三角形，D 、E 分别是AB 、BC 边上的两个动点（与点A 、B 、C 不重合），始终保持BD=CE.（1）当点D 、E 运动到如图1所示的位置时,求证：CD=AE.（2）把图1中的△ACE 绕着A 点顺时针旋转60°到△ABF 的位置（如图2），分别连结DF 、EF.①找出图中所有的等边三角形(△ABC 除外)，并对其中一个给予证明；②试判断四边形CDFE 的形状,并说明理由.4．如图，矩形 中， ，将矩形 绕点C 顺时针旋转得到矩形 .设旋转角为 ，此时点 恰好落在边 上，连接 .（1）当 恰好是 中点时，此时 ；（2）若 ，求旋转角 及 的长.5．将线段AB 绕点A 逆时针旋转60°得到线段AC ，继续旋转α（0°＜α＜120°）得到线段AD ，连接CD 、BD ．（1）如图，若α=80°，则∠BDC 的度数为 ；（2）请探究∠BDC 的大小是否与角α的大小有关，并说明理由．ABCD 4BC =ABCD A B C D ''''αB 'AD B B 'B 'AD α=75AB B ︒∠='αAB6．在平面直角坐标系中，小方格都是边长为1的正方形，△ABC ≌△DEF ，其中点A 、B 、C 、都在格点上，请你解答下列问题：（1）如图（a ）在方格纸中，选择标有序号①②③④中的一个小正方形涂黑，与图中阴影部分构成中心对称图形，涂黑的小正方形的序号为 ．（2）画出△ABC 关于y 轴对称的△A 1B 1C 1；画出△ABC 绕点P （1，﹣1）顺时针旋转90°后的△A 2B 2C 2；（3）△A 1B 1C 1与△A 2B 2C 2成中心对称吗？若成中心对称请你求出对称中心的坐标；若不成，则说明理由．7．图1是某小型汽车的侧面示意图，其中矩形 表示该车的后备箱，在打开后备箱的过程中，箱盖 可以绕点A 逆时针方向旋转，当旋转角为 时，箱盖 落在 的位置（将后备箱放大后如图2所示）．已知 厘米， 厘米， 厘米．在图2中求： （1）点 到 的距离（结果保留根号）；（2）E 、 两点的距离（结果保留根号）．ABCD ADE 60︒ADE AD E ''90AD =30DE =40EC =D 'BC E '8．如图， 是等腰直角三角形， 是直角三角形， ，点 为边 中点将 绕点 顺时针旋转，旋转角记为 ，点 为边 的中点．（1）如图，求初始状态时 的大小；（2）如图，在旋转过程中，若点 构成平行四边形，请直接写出此时 的值；（3）在旋转过程中，若点 和点 重合，请在图中画出 并连接 ，判断此时是否有 ?如果成立，请证明；如果不成立，请说明理由．ABC 90,ABC BDE ∠=︒ 30E ∠=︒D BC BDE D (0360)αα<<︒F BE AEC ∠,,,B D F B 'a F B ,B DE ' AE AE ED ⊥9．如图，在菱形 中， ，将边 绕点 逆时针旋转至 ，记旋转角为 ．过点 作 于点 ，过点 作 直线 于点 ，连接 ．（1）（探索发现）填空：当 时， = ．的值是 （2）（验证猜想）当 时，（1）中的结论是否仍然成立?若成立，请仅就图2的情形进行证明；若不成立，请说明理由；（3）（拓展应用）在（2）的条件下，若 ，当 是等腰直角三角形时，请直接写出线段 的长．ABCD 120BAD ∠= AB A 'AB αD DF BC ⊥F B BE ⊥'B D E EF 60α= 'EBB ∠ 'EF DB 0360α<< AB =BDE ∆EF10．如图(1),在△ABC中,AB=BC,P为AB边上一点,连接CP,以PA、PC为邻边作APCD，AC与PD 相交于点E，已知∠ABC=∠AEP= (0°< <90°).（1）求证: ∠EAP=∠EPA;（2）APCD是否为矩形?请说明理由;（3）如图(2),F为BC中点,连接FP,将∠AEP绕点E顺时针旋转适当的角度,得到∠MEN(点M、N分别是∠MEN的两边与BA、FP延长线的交点).猜想线段EM与EN之间的数量关系，并证明你的结论.αα11．定义：有一组邻边相等，且它们的夹角为60°的四边形叫做半等边四边形．（1）已知在半等边四边形ABCD 中，AB=AD ，∠BAD=60°，∠BCD=120°．①如图1，若∠B=∠D ，求证：BC=CD ；②如图2，连结AC ，探索线段AC 、BC 、CD 之间的数量关系，并说明理由；（2）如图3，已知∠MAC=30°，AC=10+10，点D 是射线AM 上的一个动点，记∠DCA=a ，点B 在直线AC 的下方，若四边形ABCD 是半等边四边形，且CB=CD ．问：当点D 在15°≤a≤45°的变化过程中运动时，点B 也随之运动，请直接写出点B 所经过的路径长．12．已知，把45°的直三角板的直角顶点E 放在边长为6的正方形ABCD 的一边BC 上，直三角板的一条直角边经过点D ，以DE 为一边作矩形DEFG ，且GF 过点A ，得到图1.（1）求矩形DEFG 的面积；（2）若把正方形ABCD 沿着对角线AC 剪掉一半得到等腰直角三角形ABC ，把45°的直三角板的一个45°角的顶点与等腰直角三角形ABC 的直角顶点B 重合，直三角板夹这个45°角的两边分别交CA 和CA 的延长线于点H 、P ，得到图2.猜想：CH 、PA 、HP 之间的数量关系，并说明理由；（3）若把边长为6的正方形ABCD 沿着对角线AC 剪掉一半得到等腰直角三角形ABC ，点M 是Rt △ABC 内一个动点，连接MA 、MB 、MC ，设MA+MB+MC ＝y ，直接写出 的最小值.2y13．（1）观察猜想：如图①，在Rt △ABC 和Rt △BDE 中，∠ABC ＝∠EBD ＝90°，AB ＝BC ，BE ＝BD ，连接AE ，点F 是AE 的中点，连接CD 、BF ，当点D 、B 、C 三点共线时，线段CD 与线段BF 的数量关系是 ，位置关系是 .（2）探究证明：在（1）的条件下，将Rt △BDE 绕点B 顺时针旋转至图②位置时，（1）中的结论是否仍然成立？如果成立，请你就图②的情形进行证明；如果不成立，请说明理由；（3）拓展延伸：如图③，在Rt △ABC 和Rt △BDE 中，∠ABC ＝∠EBD ＝90°，BC ＝2AB ＝8，BD ＝2BE ＝4，连接AE ，点F 是AE 的中点，连结CD 、BF ，将△BDE 绕点B 在平面内自由旋转，请直接写出BF 的取值范围，14．请认真阅读下面的数学小探究系列，完成所提出的问题：（1）探究1，如图1，在等腰直角三角形ABC 中， ， ，将边AB 绕点B 顺时针旋转90°得到线段BD ，连接CD ，过点D 作BC 边上的高DE ，则DE 与BC 的数量关系是 ， 的面积为 ；（2）探究2，如图2，在一般的 中， ，（ ， ），将边AB 绕点B 顺时针旋转90°得到线段BD ，连接CD ，请用含m ，n 的式子表示 的面积，并说明理由.（3）探究3：如图3，在等腰三角形ABC 中， ， （ ，， ），将边AB 绕点B 顺时针旋转90°得到线段BD ，连接CD ，试探究用含a ，b ，c 的式子表示 的面积，要有探究过程.90ACB ∠=︒5BC =BCD Rt ABC 90ACB ∠=︒22()()BC m n m n =+--0m >0n >BCD AB AC =BC a b c =++0a >0b >0c >BCD15．如图1，在△ABC中，∠A＝120°，AB＝AC，点D，E分别在边AB，AC上，AD＝AE，连接BE，点M，N，P分别为DE，BE，BC的中点，连接NM，NP.（1）图1中，线段NM，NP的数量关系是 ，∠MNP的度数为 ；（2）把△ADE绕点A顺时针旋转到如图2所示的位置，连接MP.求证：△MNP是等边三角形；（3）把△ADE绕点A在平面内旋转，若AD＝2，AB＝5，请直接写出△MNP面积的最大值.16．（1）问题发现：如图①，正方形ABCD的边长为4，对角线AC、BD相交于点O，E是AB上点（点E不与A、B重合），将射线OE绕点O逆时针旋转90°，所得射线与BC交于点F，则四边形OEBF的面积为 .（2）问题探究：如图②，线段BQ＝10，C为BQ上点，在BQ上方作四边形ABCD，使∠ABC＝∠ADC＝90°，且AD ＝CD，连接DQ，求DQ的最小值；（3）问题解决：“绿水青山就是金山银山”，某市在生态治理活动中新建了一处南山植物园，图③为南山植物园花卉展示区的部分平面示意图，在四边形ABCD中，∠ABC＝∠ADC＝90°，AD＝CD，AC＝600米.其中AB、BD、BC为观赏小路，设计人员考虑到为分散人流和便观赏，提出三条小路的长度和要取得最大，试求AB+BD+BC的最大值.17．如图14-1，在平面直角坐标系xOy 中，直线l 2：y=与x 轴交于点B ，与直线l 1交于点c ，c点到x 轴的距离CD 为2 ，直线1交x 轴于点A(-3，0) ．（1）求直线l 1的函数表达式；（2）如图14-2，y 轴上的两个动点E 、F(E 点在F 点上方)满足线段EF 的长为 ，连接CE 、AF ，当线段CE+EF+AF 有最小值时，求出此时点F 的坐标，以及CE+EF+AF 的最小值；（3）如图14-3，将△ACB 绕点B 逆时针方向旋转60°，得到△BGH ，使点A 与点H 重合，点C 与点G 重合(C 、G 两点恰好关于x 轴对称)，将ABGH 沿直线BC 平移，记平移中的△BGH 为△B'G'H'，在平移过程中，设直线B'H'与x 轴交于点M ，是否存在这样的点M ，使得△B'MG'为等腰三角形？若存在，请直接写出此时点M 的坐标；若不存在，说明理由．18．如图（1）问题发现：如图1，已知点C 为线段 上一点，分别以线段 为直角边作两个等腰直角三角形， ，连接 ，线段 之间的数量关系为 ；位置关系为 .（2）拓展研究：如图2，把 绕点C 逆时针旋转，线段 交于点F ，则 之间的关系是否仍然成立，说明理由；x AB ,AC BC 90,,ACD CA CD CB CE ︒∠===,AE BD ,AE BD Rt ACD ∆,AF BD ,AE BD（3）解决问题：如图3，已知 ，连接 ，把线段AB 绕点A 旋转，若 ，请直接写出线段 的取值范围.19．如图1，在 中， , ，点 分别是 的中点，连接 .（1）探索发现：图1中，的值为 ； 的值为 ；（2）拓展探究若将 绕点 逆时针方向旋转一周，在旋转过程中的大小有无变化，请仅就图2的情形给出证明；（3）问题解决当 旋转至 三点在同一直线时，直接写出线段 的长.,,90AC CD BC CE ACD BCE ︒==∠=∠=,,AB AE AD 7,5AB AC ==AE ABC 2AB AC ==120BAC ∠=︒,D E ,AC BC DE AB BC AD BE CDE C AD BECDE ,,A D E BE20．有两个形状、大小完全相同的直角三角板ABC 和CDE ，其中∠ACB ＝∠DCE ＝90°．将两个直角三角板ABC 和CDE 如图①放置，点A ，C ，E 在直线MN 上．（1）三角板CDE 位置不动，将三角板ABC 绕点C 顺时针旋转一周，①在旋转过程中，若∠BCD ＝35°，则∠ACE ＝ ▲ °；②在旋转过程中，∠BCD 与∠ACE 有怎样的数量关系？请依据图②说明理由．（2）在图①基础上，三角板ABC 和CDE 同时绕点C 顺时针旋转，若三角板ABC 的边AC 从CM 处开始绕点C 顺时针旋转，转速为12°/秒，同时三角板CDE 的边CE 从CN 处开始绕点C 顺时针旋转，转速为2°/秒，当AC 旋转一周再落到CM 上时，两三角板都停止转动．如果设旋转时间为t 秒，则在旋转过程中，当∠ACE ＝2∠BCD 时，t 为多少秒？21．我们做如下的规定：如果一个三角形在运动变化时保持形状和大小不变，则把这样的三角形称为三角形板.把两块边长为4的等边三角形板 和 叠放在一起，使三角形板 的顶点 与三角形板 的AC 边中点 重合，把三角形板 固定不动，让三角形板 绕点 旋转，设射线 与射线 相交于点M ，射线 与线段 相交于点N.ABC DEF DEF D ABC O ABC DEF O DE AB DF BC（1）如图1，当射线 经过点 ，即点N 与点 重合时，易证△ADM ∽△CND.此时，AM·CN= .（2）将三角形板 由图1所示的位置绕点 沿逆时针方向旋转，设旋转角为 .其中 ，问AM·CN 的值是否改变？说明你的理由.（3）在（2）的条件下，设AM= x ，两块三角形板重叠面积为 ，求 与 的函数关系式.（图2，图3供解题用）22．已知抛物线（，，是常数，）的顶点为，与轴相交于，两点（点在点的左侧），与轴相交于点．（1）若点，求点和点的坐标；（2）将点绕点逆时针方向旋转，点的对应点为，若，两点关于点中心对称，求点的坐标和抛物线解析式：（3）在（1）的条件下，点为直线下方抛物线上的一个动点，过点作轴，与相交于点，过点作轴，与轴相交于点，求的最大值及此时点的坐标．DF B B DEF O α090α<< y y x 2y ax bx c =++a b c 0a ≠()14M -，x A B A B y C ()03C -，A B A B 90︒A 1A A 1A M 1A P BC P PD x BC D P PE y x E PD PE +P答案解析部分1．【答案】（1）解：对称中心O 如图所示；（2）解：∵A 与F ，C 与D 是对应点，∴AO=DO ，CO ＝FO ，∴四边形ACDF 是平行四边形．2．【答案】（1）解：如图所示：（2）解：由图可知：，，．3．【答案】（1）证明：∵△ABC 是正三角形，∴BC=CA ，∠B=∠ECA=60°.又∵BD=CE ，∴△BCD ≌△CAE.∴CD=AE.（2）解：① 图中有2个正三角形，分别是△BDF ，△AFE.由题设，有△ACE ≌△ABF ，∴CE=BF ，∠ECA=∠ABF=60°又∵BD=CE ，∴BD=CE=BF ，∴△BDF 是正三角形，∵AF=AE ，∠FAE=60°，∴△AFE 是正三角形.1(12)A -，1(33)B -，1(40)C ，② 四边形CDFE 是平行四边形.∵∠FDB=∠ABC =60°∴FD ∥EC.又∵FD=FB=EC ，∴四边形CDFE 是平行四边形.4．【答案】（1）60°（2）解：∵四边形 是矩形，∴ ，∴ .由旋转的性质得 ，∴ ，∴ ，即旋转角 为30°.作 于点E.则 .5．【答案】（1）30°（2）解：无关．理由如下：由旋转变换可知：∠BAC=60°，∠CAD=α， = ， AB=AC=AD ，∴ ，，ABCD //AD BC 75CBB AB B ︒'∠=∠='CB CB ='75CB B CBB ︒∠'=∠='180757530BCB ︒︒︒︒∠--='=αB E BC '⊥122AB B E CB '='==()1180602ADB α∠=︒-+︒⎡⎤⎣⎦1202α︒-()11802ADC α∠=︒-()11202ADB α︒∠=-∴∠BDC=∠ADC-∠ADB= - =30° ，∴∠BDC 的大小与ɑ的度数无关．6．【答案】（1）②（2）解：如图（3）解：如图所示：△A 1B 1C 1与△A 2B 2C 2成中心对称图形，对称中心的坐标为：（1，0）．7．【答案】（1）解：过点 作 ，垂足为点H ，交 于点F ．由题意得 （厘米）， ．∵四边形 是矩形，∴ ， ．在 中， 又∵ ， ，∴ ．∴ （厘米）答：点 到 的距离是 （厘米）．（2）解：连结 、 、 ．()11802α︒-()11202α︒-D 'D H BC '⊥AD 90AD AD =='60DAD ∠='︒ABCD AD BC 90AFD BHD ∠'=∠='︒Rt AD F ∆'sin 90sin 60D F AD DAD ︒=⋅∠=⋅='''40CE =30DE =70FH=70)D H D F FH ='++'=D 'BC ()70+AE AE 'EE '由题意得 ， ．∴ 是等边三角形．∴ ．∵四边形 是矩形，∴ ．在 中， ， ，∴（厘米）答：E 、 两点的距离是厘米．8．【答案】（1）解：∵∠BED ＝30°，△BDE 是直角三角形，∴∠EBD ＝90°－∠BED ＝60°．又∵D 是BC 的中点，∴DE 是BC 的垂直平分线．∵BE ＝CE ，∠BEC ＝60°，∴△BCE 是等边三角形．∴BC ＝BE ．∵△ABC 是等腰三角形，∠ABC ＝90°，∴AB ＝BC ．∴BE ＝AB ．∵AB ⊥BC ，DE ⊥BC ，∴AB ∥DE ，∴∠ABE ＝∠BED ＝30°．∴∠BAE ＝∠BEA ＝ (180°－∠ABE)＝75°．∴∠AEC ＝∠BAE ＋∠BEC ＝135°．（2）解：∵四边形BDFB ＇是平行四边形，∠FB ＇D ＝60°∴B ＇F ∥BD ，∴∠B D B ＇＝∠FB ＇D ＝60°AE AE ='60EAE ∠='︒AEE ∆'EE AE '=ABCD 90ADE ∠=︒Rt ADE ∆90AD =30DE =AE ===E '12即 ＝60°．（3）解：△B ＇DE 如图所示，AE ⊥DE 不成立，理由如下：DE 与AB 相交于点G ，假设AE ⊥DE ，则△AEG ∽△DBG ，设BG ＝a ，∠BDG ＝30°，∴DG ＝2a ，BD ＝ a ，AB ＝2 BD ＝ a ．∴AG ＝AB －BG ＝（－1）a ，B ＇D ＝BD ＝a ．∴DE ＝ ＝3a．∴GE ＝DE －DG＝3a －2a ＝a ．∴ ， ．∴ 与假设矛盾．∴AE ⊥DE 不成立．9．【答案】（1）30（2）解：当 时， （1）中的结论仍然成立．证明：如图1，连接 ．a tan 30B D＇AG DG ==1GE a GB a ==AG GE DG GB≠0360α<< BD，， ． ， ． ． ．，即 ． ，， ． ．，（3）解：线段 的长为 或 ．连接 ， 交于点 ．，， ，，∵DE=BE ，∠DEB=90°，∴∠EDB=∠EBD=45°，． ，∠B′EB=90°，， ． ， ． ．'AB AD AB == 1'(180)9022AB B αα∴∠=︒-=︒-1'[180(120)]3022AB D αα∠=︒-︒-=︒+'180''180(90)(306022EB B AB D AB B αα∴∠=︒-∠-∠=︒-︒--︒+=︒'30EBB ∴∠=︒11(180)3022CBD ABC BAD∠=∠=︒-∠=︒ 'EBB CBD ∴∠=∠'''EBB FBB CBD FBB ∴∠+∠=∠+∠'DBB EBF ∠=∠cos BF DBF BD ∠== cos ''BE EBB BB ∠=='BF BE BD BB ∴='DBB FBE ∆∆∽''EF BE DB BB ∴==EF 3+3-AC BD O AC DB ⊥ 1602BAO BAD ∠=∠=︒sin OB AB BAO ∴=⋅∠=2BD OB ∴==sin DE BE BD DBE ∴==⋅∠=='AB AD AB == 1'(180)9022AB B αα∴∠=︒-=︒-1'[180(120)]3022AB D αα∠=︒-︒-=︒+'180''180(90)(306022EB B AB D AB B αα∴∠=︒-∠-∠=︒-︒--︒+=︒'30EBB ∴∠=︒'tan '2EB BE EBB ∴=⋅∠==分两种情况： 如图，，∵∠B′BE=∠DBF=30°，∴cos ∠B′BE=cos ∠DBF=，又∵∠B′BE+∠EBD=∠EBD+∠DBF ，∴∠B′BD=∠EBF ，∴△B′BD ∽△EBF ，∴ ， ． 如图，．①''2B D DE BE =+=+EB FB B B DB ='=EB FB EF B B DB B D '='2)3EF D '∴==+=②''2B D DE B E =-=∵∠B′BE=∠DBF=30°，∴cos ∠B′BE=cos ∠DBF=，又∵∠B′BE-∠FBB′=∠DBF-∠FBB′，∴∠B′BD=∠EBF ，∴△B′BD ∽△EBF ，∴ ，．综上所述，线段 的长为或 ．10．【答案】（1）证明：(1)在△ABC 和△AEP 中,∠ABC=∠AEP,∠BAC=∠EAP, ∠ACB=∠APE,在△ABC 中,AB=BC. ∠ACB=∠BAC,∠EPA=∠EAP,（2）解： APCD 是矩形.四边形APCD 是平行四边形,AC=2EA,PD=2EP.由(1)知, ∠EPA=∠EAP.EA=EP ，进而AC=PDAPCD 是矩形.（3）解：EM=ENEA=EP, ∠EPA=90° - ∠EAM=180°-∠EAP =180°-∠EPA= 180°-(90°-)=90°+ 由(2)知, ∠CPB=90°,F 是BC 的中点, FP=FB,∠FPB=∠ABC= ，∠EPN=∠EPA+∠APN=∠EPA+∠FPB=90° -+ =90°+ ∠EAM=∠EPN∠AEP 绕点E 顺时针旋转适当的角度，得到∠MEN ，EB FB B B DB ='=EB FB EF B B DB B D '='2)3EF B D ∴===-'EF 33 ∴∴∴ ∴∴∴ ∴12α∴12α12α∴∴α∴12αα12α∴∠AEP-∠AEN =∠MEN-∠AEN,即∠MEA=∠NEP.△EAM ≌△EPN,EM=EN.11．【答案】（1）解：①证明：连结AC ，∵∠A+∠B+∠C+∠D=360°，且∠A=60°，∠C=120°，∴∠B+∠D=180°，且∠B=∠D ，∴∠B=∠D=90°，∵AB=AD ，AC=AC ，∴△ABC ≌△ADC （HL ），∴BC=DC ；②解：延长CB ，使得CD=BE ，∵∠BAD=60°，∠BCD=120°，∴∠ABC+∠D=180°，且∠ABC+∠ABE=180°，∴∠D=∠ABE ，又∵AB=AD∴△ABE ≌△ADC ，∴AE=AC，∴∴∴∠BAE=∠DAC ，∴∠EAC=∠BAE+∠BAC=∠DAC+∠BAC=∠BAD=60°，∴△ACE 是等边三角形，∴AC=CE=CB+BE=CB+CD（2）解：如图，设∠ACD=15°，∠DCD‘=30°，作CM ⊥AD ，D‘H ⊥AC ，由旋转图形的特点可知，CB=CD ，CB‘=CD’，∠BCB'=DCD‘=30°，∴△∠BCB'≌△DCD‘，BB'=DD’，设D'H=x ，由勾股定理得：， HC=x，则，解得x=10， 即D'H=10，得，AD’=20，在Rt △AMC 中，∵，∠DAC=30°，∴，AM=（，-5，，∴DD’为D 点的运动路程，则BB‘的运动路程也为10 .12．【答案】（1）解：∵四边形ABCD 是正方形，∴∠ADC ＝∠DCE ＝90°，∵四边形DEFG 是矩形，∴∠AGD ＝∠GDE ＝90°，∴∠DCE ＝∠AGD ＝90°，∠ADC ＝∠GDE ＝90°，∴∠ADC ﹣∠ADE ＝∠GDE ﹣∠ADE ，∴∠EDC ＝∠ADG ，∵∠EDC ＝∠ADG ，∠DCE ＝∠AGD ＝90°，∴△ECD ∽△AGD ，∴ ，∴DG•DE ＝DC•DA ＝6×6＝36，∴矩形DEFG 的面积＝DG•DE ＝36；（2）解： ，证明：把△BAP 绕着点B 顺时针旋转90°得到△BCK ，连接KH ，由旋转得△BAP ≌△BCK ，∴BK ＝BP ，∠PBA ＝∠KBC ，∠BCK ＝∠BAP ＝ ，∴∠HCK ＝ ＝ ，∴由勾股定理得， ，∵∠PBE ＝45°，∴∠PBA+∠ABE ＝45°，∵∠PBA ＝∠KBC ，∴∠KBC+∠ABE ＝45°，∵∠ABC ＝90°，∴∠HBK ＝45°，∵∠PBE ＝45°，∴∠HBK ＝∠PBE ＝45°，∵BK ＝BP ，∠HBK ＝∠PBE ，BH ＝BH ，∴△BHP ≌△BHK （SAS ），CD DE DG DA=222CH PA HP +＝18045135︒-︒=︒BCK BCA ∠-∠1354590︒-︒=︒222CH PA KH +＝∴HK ＝HP ，∵ ，∴ ；（3）解：把△BMC 绕着点B 顺时针旋转60°得到△BKN ，连接MK ，BN ，NC ，由旋转得，△BMC ≌△BKN ，∴MC ＝KN ，BM ＝BK ，∵BM ＝BK ，∠MBK ＝60°，∴△BKM 是等边三角形，∴MK ＝BM ，∴MA+MB+MC ＝AM+MK+KN ，当A ，M ，K ，N 四点共线时，AN 就是所求的MA+MB+MC 的最小值，过N 作NQ ⊥AB 交AB 的延长线于Q ，∵ ，∠BQN ＝90°，∴QN ＝BN•sin30°＝6× ＝3，BQ ＝BN•cos30°＝ ，∴AQ ＝AB+BQ ＝，在Rt △AQN 中，由勾股定理得，，∴ 的最小值为 .13．【答案】（1）CD=2BF ；BF ⊥CD（2）解：BF ⊥CD ，CD=2BF 成立，证明：∵△ABC 与△DBE 都是等腰直角三角形，∴AB=BC ，DB=EB ，∠ABC=∠DBE=90°，222CH PA KH +＝222CH PA HP +＝180906030NBQ ∠︒-︒-︒=︒＝126=6+(222226372AN AQ QN +=++=+＝2y 72+如图②，将△ABE 绕点B 顺时针旋转90°得到△CBG ，点E 、F 的对应点分别是G 、H ，连BH ， 则△ABE ≌△CBG ，BE=BG ，AE=CG ，BF=BH ，∠FBH=∠EBG=90°，AF=CH ，EF=GH ， ∴BF ⊥BH ，∵AF=EF ，∴CH=GH ，∵∠DBE=90°，∴∠DBE+∠EBG=180°，∴D 、B 、G 三点共线，∴BH ∥CD ，，∴BF ⊥CD ，，即CD=2BF ，∴BF ⊥CD ，CD=2BF 成立；（3）14．【答案】（1）DE=BC ；12.5（2）解：过点D 作BC 边上的高DE ，如图，∵∠ABC+∠A=90°，∠ABC+∠DBE=90°，∴∠A=∠DBE ，又∵∠ACB=∠E=90°，AB=BD ，∴ ，∴，12BH CD =12BF CD =13BF ≤≤ACB BED ≌BC DE =又 .∴ 的面积为：.（3）解：作 于G ，过点D 作BC 边上的高DE ，如图，由（2）同理，可证 ，∴ ，又 ，∵AB=AC ， ，∴ .∴ 的面积为： .15．【答案】（1）NM=NP ；60°（2）证明：由旋转得：∠BAD=∠CAE ，又∵AB=AC ，AD=AE ，∴△ABD ≌△ACE （SAS ），∴BD=CE ，∠ABD=∠ACE ，∵点M ，N ，P 分别为DE ，BE ，BC 的中点，∴MN= BD ，PN= CE ，MN ∥BD ，PN ∥CE ，∴MN=PN ，∠ENM=∠EBD ，∠BPN=∠BCE ，∴∠ENP=∠NBP+∠NPB=∠NBP+∠ECB ，∵∠EBD=∠ABD+∠ABE=∠ACE+∠ABE ，∴∠MNP=∠MNE+∠ENP=∠ACE+∠ABE+∠EBC+∠EBC+∠ECB=180°-∠BAC=60°，∴△MNP 是等边三角形；（322()()4mn BC m n m n =+--=BCD 221448m n 2mn mn ⨯⨯=AGB BED ≌BG DE =BC a b c =++BC a b c =++11()22BG BC a b c ==++BCD 2111()()()224a b c a b c a b c ⨯++⨯++=++121216．【答案】（1）4（2）解：如图②中，连接BD ，取AC 的中点O ，连接OB ，OD.∵∠ABD ＝∠ADC ＝90°，AO ＝OC ，∴OA ＝OC ＝OB ＝OD ，∴A ，B ，C ，D 四点共圆，∴∠DBC ＝∠DAC ，∵DA ＝DC ，∠ADC ＝90°，∴∠DAC ＝∠DCA ＝45°，∴∠DBQ ＝45°，根据垂线段最短可知，当QD ⊥BD 时，QD 的值最短，DQ 的最小值＝BQ ＝5 .（3）解：如图③中，将△BDC 绕点D 顺时针旋转90°得到△EDA ， ∵∠ABC+∠ADC ＝180°，∴∠BCD+∠BAD ＝∠EAD+BAD ＝180°，∴B ，A ，E 三点共线，∵DE ＝DB ，∠EDB ＝90°，∴BE ＝ BD ，∴AB+BC ＝AB+AE ＝BE ＝BD，∴BC+BC+BD ＝（ +1）BD ，∴当BD 最大时，AB+BC+BD 的值最大，∵A ，B ，C ，D 四点共圆，∴当BD 为直径时，BD 的值最大，∵∠ADC ＝90°，∴AC 是直径，∴BD ＝AC 时，AB+BC+BD 的值最大，最大值＝600（ +1）.17．【答案】（1）解：∵点C 的纵坐标为2 ，点c 在直线l 2：y= ∴点C(-1，2 )设l 1的表达式为y= kx+ b将A(-3，0)、C(-1，2)代入， 解得故直线l 1的表达式为：y=x+3 （2）解：作点a关于y 轴的对称点A(3，0)，将点a4向上平移个单位长度得E (3，)连接E'C 交y 轴于点E ，在E下方取EF= ，则点F是所求点，将点C 、E' 的坐标代入一次函数表达式，同理可得： CE' 的函数表达式为：y= 故点E(0，)，点F(0，)CE+EF+4F 的最小值=FE+CE'= +．（3）M(5+8，0)或(5-8，0)或(-3，0)或(-19，0) x +03k bk b=-+⎧⎪⎨=-+⎪⎩k b ⎧=⎪⎨=⎪⎩x +18．【答案】（1）AE=BD ；AE ⊥BD（2）解： 仍然成立.由题意得，∵△ACD 和△BCE 是等腰直角三角形即 ，∴∴ .∴∴ .（3）解： 连接BD.由（2）可知，AE=BD ，在△ABD 中，且 ，所以 即 在AB 绕点A 旋转过程中，当A ，B ，D 三点在一条直线上时， 或者,AE BD AE BD =⊥90ACD DCE ECB DCE DCE ︒∴∠+∠=∠+∠=+∠,,ACE DCB AC CD EC CB ∠=∠==ACE DCB∆≅∆,12AE DB =∠=∠180(4512)90EFB ︒︒︒∠=--∠+∠=AE BD⊥77AE -≤≤7AD AB ===77BD <<+77AE -<<+7AE =7AE =∴ ≤AE≤ 19．【答案】（1（2）解：无变化,理由: 由(1)知,CD=1, ,∴,∴ ,由(1)知,∠ACB=∠DCE=30°,∴∠ACD=∠BCE,∴△ACD ∽△BCE,∴,（3）解：线段BE 的长为或 ，理由如下： 当点D 在线段AE 上时,如图2,过点C 作CF ⊥AE 于F,∠CDF=180°﹣∠CDE=60°,∴∠DCF=30°,∴ ,∴,7-7+CE BE ==CD CE =AC BC =CD AC CE BC ==AD AC BE BC ==1122DF CD ==CF ==在Rt △AFC 中,AC=2,根据勾股定理得, ,∴AD=AF+DF=,由(2)知, ,∴当点D在线段AE 的延长线上时,如图3,过点C 作CG ⊥AD 交AD 的延长线于G,∵∠CDG=60°,∴∠DCG=30°,∴ ,∴ ,在Rt △ACG 中,根据勾股定理得,,∴ ,由(2)知,,∴即:线段BE 的长为或.AF ==AD BE =BE ==1122DG CD ==CG ==AG =AD AG DG =-=AD BE =BE ==20．【答案】（1）①145；②∠BCD+∠ACE ＝180°，理由如下：∵∠ACE ＝∠ACB+∠BCE ，∴∠BCD+∠ACE ＝∠BCD+∠ACB+∠BCE ＝∠ACB+∠DCE ＝90°+90°＝180°；（2）解：三角板ABC 和CDE 重合之前，∠ACE ＝180°-10°t ，∠BCD ＝10°t ，依题意有180°-10°t ＝2×10°t ，解得t ＝6；三角板ABC 和CDE 重合之后，∠ACE ＝10°t-180°，∠BCD ＝360°-10°t ，依题意有10°t-180°＝2×（360°-10°t ），解得t ＝30．故当t ＝6或30秒时，有∠ACE ＝2∠BCD ．故答案为：6或30．21．【答案】（1）4（2）解：AM•CN 的值不会改变.连接BD ，在△ADM 与△CND 中，∵∠A=∠C=60°，∠DNC=∠DBN+∠BDN=30°+α，∠ADM=30°+α，∴∠ADM=∠CND ，∴△ADM ∽△CND∴ ，∴AM•CN=AD•CD=2×2=4，∴AM•CN 的值不会改变；（3）解：情形1，当0°＜α＜60°时，1＜AM ＜4，即1＜x ＜4，此时两三角形板重叠部分为四边形AD AM CN CD如图2，过D 作DQ ⊥AB 于Q ，DG ⊥BC 于G ，∴DQ=DG= ，由（2）知，AM•CN=4，得CN=，于是y=（1＜x ＜4）； 情形2，当60°≤α＜90°时，AM≥4时，即x≥4，此时两三角形板重叠部分为△DPN ，如图3，过点D 作DH ∥BC 交AM 于H ，易证△MBP ∽△MHD ，∴ ，又∵MB=x-4，MH=x-2，DH=2,∴BP=，∴PN=4－ ，于是y= ，综上所述，1＜x ＜4时，y=；x≥4时，y= 22．【答案】（1）解：设抛物线解析式为，将点代入得，4x 21122AB AM DQ CN DG x -⋅-⋅=BP MB DH MH=282x x --4282x x x ---114284222x PN DG x x -⎛⎫⋅=--= ⎪-⎝⎭x ()214y a x =--()03C -，解得：∴抛物线解析式为当时，解得：，∵点在点的左侧，∴，；（2）解：∵，抛物线，与轴相交于，两点∴，对称轴为直线，设，则，∴∵点绕点逆时针方向旋转得到，则点一定在第四象限，如图所示，则，，∵，两点关于点中心对称，∴解得：，则∴，1a =()214y x =--0y =()2140x --=1213x x =-=，A B ()10A -，()30B ，()14M -，2y ax bx c =++x A B 0a >1x =()0A m ，()20B m -，222AB m m m=--=-A B 90︒A 'A '22BA BA m ='=-()222A m m '--，A 1A M 228m -=-3m =-()58A '-，()30A -，()50B ，将点代入得，解得：∴抛物线解析式为；（3）解：如图所示，设交于点，由（1）可得，，设直线的解析式为，将点代入得，解得所以直线的解析式为，∵抛物线解析式为，设，则，∴，∵轴，轴，由∵则是等腰直角三角形，∴()30A -，()214y a x =--1640a -=14a =()21144y x =--PE BC F ()30B ，()03C -，BC 3y kx =-()30B ，330k -=1k =BC 3y x =-()221423y x x x =--=--()223P t t t --，()0E t ，()3F t t -，223233FP t t t t t =--++=-+223PE t t =-++PD x PE y OC OB=OCB 45FDP OBC ∠=∠=︒∴也是等腰直角三角形，∴∴∴当时，取得最大值此时，即．PDF PD PF=PD PE+22323t t t t =-+-++2253t t =-++252525232168t t ⎛⎫=--+++ ⎪⎝⎭2549248t ⎛⎫=--+ ⎪⎝⎭54t =PD PE +498225632314416t t ⎛⎫--=--=- ⎪⎝⎭563416P ⎛⎫- ⎪⎝⎭。
矿产
矿产资源开发利用方案编写内容要求及审查大纲
矿产资源开发利用方案编写内容要求及《矿产资源开发利用方案》审查大纲一、概述
㈠矿区位置、隶属关系和企业性质。
如为改扩建矿山, 应说明矿山现状、
特点及存在的主要问题。
㈡编制依据
(1简述项目前期工作进展情况及与有关方面对项目的意向性协议情况。
(2 列出开发利用方案编制所依据的主要基础性资料的名称。
如经储量管理部门认定的矿区地质勘探报告、选矿试验报告、加工利用试验报告、工程地质初评资料、矿区水文资料和供水资料等。
对改、扩建矿山应有生产实际资料, 如矿山总平面现状图、矿床开拓系统图、采场现状图和主要采选设备清单等。
二、矿产品需求现状和预测
㈠该矿产在国内需求情况和市场供应情况
1、矿产品现状及加工利用趋向。
2、国内近、远期的需求量及主要销向预测。
㈡产品价格分析
1、国内矿产品价格现状。
2、矿产品价格稳定性及变化趋势。
三、矿产资源概况
㈠矿区总体概况
1、矿区总体规划情况。
2、矿区矿产资源概况。
3、该设计与矿区总体开发的关系。
㈡该设计项目的资源概况
1、矿床地质及构造特征。
2、矿床开采技术条件及水文地质条件。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
矿产资源开发利用方案编写内容要求及审查大纲
矿产资源开发利用方案编写内容要求及《矿产资源开发利用方案》审查大纲一、概述
㈠矿区位置、隶属关系和企业性质。
如为改扩建矿山, 应说明矿山现状、
特点及存在的主要问题。
㈡编制依据
(1简述项目前期工作进展情况及与有关方面对项目的意向性协议情况。
(2 列出开发利用方案编制所依据的主要基础性资料的名称。
如经储量管理部门认定的矿区地质勘探报告、选矿试验报告、加工利用试验报告、工程地质初评资料、矿区水文资料和供水资料等。
对改、扩建矿山应有生产实际资料, 如矿山总平面现状图、矿床开拓系统图、采场现状图和主要采选设备清单等。
二、矿产品需求现状和预测
㈠该矿产在国内需求情况和市场供应情况
1、矿产品现状及加工利用趋向。
2、国内近、远期的需求量及主要销向预测。
㈡产品价格分析
1、国内矿产品价格现状。
2、矿产品价格稳定性及变化趋势。
三、矿产资源概况
㈠矿区总体概况
1、矿区总体规划情况。
2、矿区矿产资源概况。
3、该设计与矿区总体开发的关系。
㈡该设计项目的资源概况
1、矿床地质及构造特征。
2、矿床开采技术条件及水文地质条件。