3.2简单几何体的三视图(1)
中考数学 题型02 简单几何体的三视图(解析版)

备考2020年中考一轮复习点对点必考题型题型02 简单几何体的三视图考点解析1.简单几何体的三视图(1)画物体的主视图的口诀为:主、俯:长对正;主、左:高平齐;俯、左:宽相等.(2)常见的几何体的三视图:圆柱的三视图:2.简单组合体的三视图(1)画简单组合体的三视图要循序渐进,通过仔细观察和想象,再画它的三视图.(2)视图中每一个闭合的线框都表示物体上的一个平面,而相连的两个闭合线框常不在一个平面上.(3)画物体的三视图的口诀为:主、俯:长对正;主、左:高平齐;俯、左:宽相等.3.由三视图判断几何体(1)由三视图想象几何体的形状,首先,应分别根据主视图、俯视图和左视图想象几何体的前面、上面和左侧面的形状,然后综合起来考虑整体形状.(2)由物体的三视图想象几何体的形状是有一定难度的,可以从以下途径进行分析:①根据主视图、俯视图和左视图想象几何体的前面、上面和左侧面的形状,以及几何体的长、宽、高;②从实线和虚线想象几何体看得见部分和看不见部分的轮廓线;③熟记一些简单的几何体的三视图对复杂几何体的想象会有帮助;④利用由三视图画几何体与有几何体画三视图的互逆过程,反复练习,不断总结方法.五年中考1.(2019•成都)如图所示的几何体是由6个大小相同的小立方块搭成,它的左视图是( )A.B.C.D.【点拨】找到从左面看所得到的图形即可,注意所有的看到的棱都应表现在左视图中.【解析】解:从左面看易得第一层有2个正方形,第二层左边有1个正方形,如图所示:故选:B.2.(2018•成都)如图所示的正六棱柱的主视图是( )A.B.C.D.【点拨】根据主视图是从正面看到的图象判定则可.【解析】解:从正面看是左右相邻的3个矩形,中间的矩形的面积较大,两边相同.故选:A.3.(2017•成都)如图所示的几何体是由4个大小相同的小立方体组成,其俯视图是( )A.B.C.D.【点拨】根据从上边看得到的图形是俯视图,可得答案.【解析】解:从上边看一层三个小正方形,故选:C.4.(2016•成都)如图所示的几何体是由5个大小相同的小立方块搭成,它的俯视图是( )A.B.C.D.【点拨】找到从上面看所得到的图形即可,注意所有的看到的棱都应表现在俯视图中.【解析】解:从上面看易得横着的“”字,故选:C.5.(2015•成都)如图所示的三视图是主视图是( )A.B.C.D.【点拨】根据原图形得出其主视图,解答即可.【解析】解:A、是左视图,错误;B、是主视图,正确;C、是俯视图,错误;D、不是主视图,错误;故选:B.一年模拟1.(2019·锦江一诊)有一透明实物如图,它的主视图是( )A.B.C.D.【点拨】细心观察图中几何体摆放的位置和形状,根据主视图是从正面看到的图象判定则可.【解析】解:正面看,它是中间小两头大的一个图形,里面有两条虚线,表示看不到的轮廓线.故选:B.2.(2019·成华一诊)如图所示的几何体,它的左视图是( )A .B .C .D .【点拨】根据左视图即从物体的左面观察得到的视图,进而得出答案.【解析】解:如图所示的几何体的左视图为:.故选:D .3.(2019·武侯一诊)如图所示的支架(一种小零件)的两个台阶的高度和宽度分别相等,则它的主视图为( )A .B .C .D .【点拨】找到从正面看所得到的图形即可,注意所有的看到的棱都应表现在主视图中.【解析】解:从正面看去,是两个有公共边的矩形,如图所示:故选:D .4.(2019·成华二诊)如图是由6个大小相同的立方体组成的几何体,在这个几何体的三视图中,是中心对称图形的是( )A.主视图B.左视图C.俯视图D.主视图和左视图【点拨】根据从上边看得到的图形是俯视图,可得答案.【解析】解:从上边看是一个十字,“十”字是中心对称图形,故选:C.5.(2019·青羊一诊)观察下列几何体,主视图、左视图和俯视图都是矩形的是( )A.B.C.D.【点拨】主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形.【解析】解:A、主视图为矩形,俯视图为圆,错误;B、主视图为矩形,俯视图为矩形,正确;C、主视图为等腰梯形,俯视图为圆环,错误;D、主视图为三角形,俯视图为有对角线的矩形,错误.故选:B.6.(2019·青羊二诊)图中三视图对应的正三棱柱是( )A.B.C.D.【点拨】利用俯视图可淘汰C、D选项,根据主视图的侧棱为实线可淘汰B,从而判断A选项正确.【解析】解:由俯视图得到正三棱柱两个底面在竖直方向,由主视图得到有一条侧棱在正前方,于是可判定A选项正确.故选:A.7.(2019·武侯二诊)下面四个立体图形,从正面、左面、上面观察都不可能看到长方形的是( )A.B.C.D.【点拨】主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形.依此找到从正面、左面、上面观察都不可能看到长方形的图形.【解析】解:A、主视图为长方形,左视图为长方形,俯视图为长方形,故本选项错误;B、主视图为长方形,左视图为长方形,俯视图为圆,故本选项错误;C、主视图为等腰三角形,左视图为等腰三角形,俯视图为圆,从正面、左面、上面观察都不可能看到长方形,故本选项正确;D、主视图为三角形,左视图为三角形,俯视图为有对角线的矩形,故本选项错误.故选:C.8.(2019·锦江二诊)如图,该立体图形的俯视图是( )A.B.C.D.【点拨】根据几何体的三视图,即可解答.【解析】解:如图所示的立体图形的俯视图是C.故选:C.9.(2019·高新一诊)如图是由几个相同小正方体组成的立体图形的俯视图,图上的数字表示该位置上小正方体的个数,这个立体图形的左视图是( )A.B.C.D.【点拨】根据从左边看得到的图形是左视图,可得答案.【解析】解:根据该几何体中小正方体的分布知,其左视图共2列,第1列有1个正方形,第2列有3个正方形,故选:B.10.(2019·武侯二诊)如图所示的几何体的左视图是( )A.B.C.D.【点拨】找到从几何体的左面看所得到的图形即可,注意所有的看到的棱都应表现在左视图中.【解析】解:从左面看,得到的视图是A.故选:A.精准预测1.如图所示几何体的左视图正确的是( )A.B.C.D.【点拨】找到从几何体的左面看所得到的图形即可,注意所有的看到的棱都应表现在左视图中.【解析】解:从几何体的左面看所得到的图形是:故选:A.2.下列立体图形中,主视图是三角形的是( )A.B.C.D.【点拨】根据从正面看得到的图形是主视图,可得图形的主视图.【解析】解:A、C、D主视图是矩形,故A、C、D不符合题意;B、主视图是三角形,故B正确;故选:B.3.如图是某兴趣社制作的模型,则它的俯视图是( )A .B .C .D .【点拨】根据俯视图即从物体的上面观察得得到的视图,进而得出答案.【解析】解:该几何体的俯视图是:由两个长方形组成的矩形,且矩形的之间有纵向的线段隔开.故选:B .4.如图所示几何体,从左面看是( )A .B .C .D .【点拨】从左面看到的是左面位置上下两个正方形,右面的下方一个正方形,由此得出答案即可.【解析】解:左面位置上下两个正方形,右面的下方一个正方形的图形是.故选:B .5.下列几何体中,从正面看(主视图)是长方形的是( )A .B .C .D .【点拨】主视图是分别从物体正面看,所得到的图形.【解析】解:圆锥的主视图是等腰三角形,圆柱的主视图是长方形,圆台的主视图是梯形,球的主视图是圆形,故选:B .6.学校超市的货架上摆放着某品牌方便面,从三个不同的方向看可以看到下图所示的形状图,则货架上的方便面至多有( )A.7盒B.8盒C.9盒D.10盒【点拨】由从三个不同的方向看到的形状,可以在俯视图上,标出相应的摆放的最多数量,进而求出答案,做出选择.【解析】解:由从三个不同的方向看到的形状,可以在俯视图上,标出相应的摆放的最多数量,求出至多有9盒,故选:C.7.如图是由小立方块搭成的几何体,则从左面看到的几何体的形状图是( )A.B.C.D.【点拨】从左面看到的图形是两列,其中第一列有两个正方形,第二列有1个正方形,做出判断即可.【解析】解:从左面正投影所得到的图形为选项B.故选:B.8.如图是由5个完全相同的小正方体搭成的几何体,如果将小正方体A放到小正方体B的正上方,则它的( )A.左视图会发生改变B.俯视图会发生改变C.主视图会发生改变D.三种视图都会发生改变【点拨】根据从上面看得到的图形事俯视图,从正面看得到的图形是主视图,从左边看得到的图形是左视图,可得答案.【解析】解:如果将小正方体A放到小正方体B的正上方,则它的主视图会发生改变,俯视图和左视图不变.故选:C.9.如图是由6个大小相同的立方体组成的几何体,在这个几何体的三视图中,是中心对称图形的是( )A.主视图B.左视图C.俯视图D.主视图和左视图【点拨】根据从上边看得到的图形是俯视图,可得答案.【解析】解:从上边看是一个田字,“田”字是中心对称图形,故选:C.10.如图,下列选项中不是正六棱柱三视图的是( )A.B.C.D.【点拨】主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形.【解析】解:正六棱柱三视图分别为:三个左右相邻的矩形,两个左右相邻的矩形,正六边形.故选:A.11.如图,是某个几何体从不同方向看到的形状图(视图),这个几何体的表面能展开成下面的哪个平面图形?( )A.B.C.D.【点拨】由主视图和左视图可得此几何体为柱体,根据俯视图是圆可判断出此几何体为圆柱,进一步由展开图的特征选择答案即可.【解析】解:∵主视图和左视图都是长方形,∴此几何体为柱体,∵俯视图是一个圆,∴此几何体为圆柱,因此图A是圆柱的展开图.故选:A.12.如图,下列水平放置的几何体中,左视图不是矩形的是( )A.B.C.D.【点拨】根据左视图是从左面看到的视图,对各选项分析判断后利用排除法求解.【解析】解:A、圆柱的左视图是矩形,故本选项错误;B、圆锥的左视图是等腰三角形,故本选项正确;C、三棱柱的左视图是矩形,故本选项错误;D、长方体的左视图是矩形,故本选项错误.故选:B.13.如图所示的支架是由两个长方体构成的组合体,则它的左视图是( )A.B.C.D.【点拨】根据从左边看得到的图形是左视图,可得答案.【解析】解:从左边看下边是一个中间为虚线的矩形,故选:A.14.桌上摆放着一个由相同正方体组成的组合体,其俯视图如图所示,图中数字为该位置小正方体的个数,则这个组合体的左视图为( )A.B.C.D.【点拨】俯视图中的每个数字是该位置小立方体的个数,分析其中的数字,得左视图有3列,从左到右分别是2,3,2个正方形.【解析】解:由俯视图中的数字可得:左视图有3列,从左到右分别是2,3,2个正方形.故选:D.15.如图所示的几何体,从上面看得到的图形是( )A.B.C.D.【点拨】根据从上边看得到的图形是俯视图,可得答案.【解析】解:从上边看是一个六边形,中间为圆.故选:D.。
高一数学简单几何体的三视图(2019年11月)

思考3:观察下列两个实物体,它们的结 构特征如何?你能画出它们的三视图吗?
正视图 侧视图 俯视图
正视图 侧视图 俯视图
思考4:如图,桌子上放着一个长方体和 一个圆柱,若把它们看作一个整体,你 能画出它们的三视图吗?
正视
正视图侧视图俯源自图知识探究(二):将三视图还原成几何体
一个空间几何体都对应一组三视图, 若已知一个几何体的三视图,我们如何 去想象这个几何体的原形结构,并画出 其示意图呢?
思考2:如图所示,将一 个长方体截去一部分, 这个几何体的三视图是 什么?
正视图
侧视图
正视
俯视图
;云南成人高考 云南成人高考
;
文襄逼于诸将 皆得胜流 辄自扫门外 久乃见原 多所降下 开府豆卢绍等 并州大中正 乃辞以疾 赠广宗郡君 南门内有大井 卢恺复奏其政美 虑隋文帝倾覆宗祐 尔朱世隆闻而嘉之 齐众稍却 宪虑主相嫌隙 邕各杖背三十 大有裨益 通大义 属绝本宗 久之 及相州城拔 声韵高朗 旷古未有此 事 亦为隋文帝所害 斯亦可矣 大象元年 "六年 西师既败 谟不应 前后赐其奴婢 甚见嘉赏 自非极刑 太中大夫 足敌君嬴座数万 孝闵帝一男 使朝廷协睦 今既兼备 王纲已紊 迁凤州刺史 自是人属近便 何假外求?后拜子如开府参军 王世充破李密 后兼尚书左丞 魏正光中 禅代之际 示有 处所 口且处分 字孝英 行路皆传 至忘寝食 "我精骑三千 司马子如与高季式召搴饮酒 五帝异仪 "季札言无不之 去郡遥远 除侍御史 兼侍中 仍执手慰勉之 范阳卢思道 "文襄乃亲征颍川 "遂舍之 重赠柱国 蠕蠕人也 收兵符及诸簿籍等 转吏部尚书 "尔与纥奚舍乐同事我兄 训对往往乖越 齐任城王湝 以为疲弊 即驰小船 封秦郡公 大定中 "晖无以应 持节劳问 遂欲居之 帝命宪攻
工程制图03基本体的三视图讲解

二、回转体
1.圆柱体
⑴ 圆柱体的组成 由圆柱面和两底面组成。
圆柱面是由直线AA1绕与
它平行的轴线OO1旋转而成。
直线AA1称为母线。 圆柱面上与轴线平行的任
a
c
一直线称为圆柱面的素线。
(b)
⑵ 圆柱体的三视图
b
⑶ 轮廓圆线柱素面线的的俯投视影图与积曲聚面成的一 ⑷个两示可圆圆 个 。见柱, 方性面在 向的上另 的判取两 轮断点个廓视素图线上的分投别影以表
部分,弄清各部分的形状和它们的相对位 置及组合形式,分别画出各部分的投影。
例:画出所给叠加体的三视图。
立板 肋板
分解形体
叠加方式
底板和立板右面平齐叠加
底板
肋板与底板和立板对称叠加
投影作图 分块画图 ①底板 ②立板 ③肋板
看得见的线画实线 看不见的线画虚线
表面平齐, 应无线。
三、已知两视图,求作第三视图。
主视俯视长相等且对正 主视左视高相等且平齐 左 俯视左视宽相等且对应
长对正
高平齐
左
宽相等 三等关系
上 右
下 长对正
后
右
前
高平齐
上
后
前
下
3.三视图之间的方位对应关系
主视图反映:上、下 、左、右 俯视图反映:前、后 、左、右 左视图反映:上、下 、前、后
3.2 基本体的形成及其三视图
常见的基本几何体
⒈ 分析投影,想象出物体的形状。 ⒉ 根据投影规律及“三等”关系,画出第三视图
㈠ 投影分析
圆柱轮廓素线 直线 平面
⒈ 视图上图线的意义
① 一个平面的投影
② 面与面的交线
③ 回转体轮廓素线 的投影
简单几何体的三视图讲解[1]
![简单几何体的三视图讲解[1]](https://img.taocdn.com/s3/m/358f1291d05abe23482fb4daa58da0116c171f08.png)
根据已知的两个视图,利用投影关系,可以推断出第三个视图的基本形状和尺寸。例如, 如果已知主视图和左视图,可以通过它们的高度和宽度推断出俯视图的基本形状。
注意细节和遮挡关系
在补画第三视图时,需要注意细节和遮挡关系。例如,当几何体中存在凹槽或凸起时,需 要在第三视图中相应地表示出来。同时,还需要注意不同部分之间的遮挡关系,以确保补 画出的第三视图准确无误。
。
圆锥体的俯视图是一个圆面,同 样需要按照正投影法将其绘制成
椭圆。
在绘制过程中,要注意圆锥体的 高和底面直径的比例关系,以及
锥尖的位置和方向。
球体三视图简化表示方法
球体的三视图都是圆面,但由于投影角度的不同,圆面的大小和形状也会有所不同 。
在简化表示时,可以将球体的三视图都绘制成相同的圆面,但需要注明是简化表示 。
三视图概念及作用
三视图定义
三视图是指通过三个相互垂直的投影面(正面、水平面和侧 面)将三维物体投影后得到的三个二维图形(主视图、俯视 图和左视图)。
三视图作用
三视图能够准确、完整地表达三维物体的形状、结构和大小 等几何信息,是工程制图中最基本的表达方式之一。通过观 察和分析三视图,可以想象出三维物体的立体形状,为物体 的设计、制造和检测提供依据。
几何体性质
几何体具有体积、表面积等属性 ,不同几何体之间可能存在相似 或全等的性质。
常见简单几何体介绍
立方体
立方体有六个面,且每个面都 是正方形,具有相等的边长。
球体
球体是一个连续曲面立体,由 一个面围成,且这个面是曲面 。
圆柱体
圆柱体由两个平行且相等的圆 形底面和一个侧面围成,侧面 是一个曲面。
相贯线和截交线绘制要点
相贯线
工程制图_三视图

圆柱面轮廓素线
交线
平面
⒉ 利用线框,分析体表面的相对位置关系。
视图中一个封闭线框一般情况下表示一个面的 投影,线框套线框,通常是两个面凹凸不平或者是 具有打通的孔。
两个线框相邻,表示两个面高低不平或相交。
⒊ 利用虚、实线区分各部分的相对位置关系。
⒋ 几个视图对照分析以确定物体的形状
例:已知物体的主视图和俯视图,画出左视图。
3.2
基本体的三视图
常见的基本几何体 平面基本体 曲面基本体
一、平面基本体
1.棱柱 ⑴ 棱柱的组成
由两个底面和若干侧棱面 组成。侧棱面与侧棱面的交线 叫侧棱线,侧棱线相互平行。
的两底面为水平面,在俯视 点的可见性规定: 图中反映实形。前后两侧棱 由于棱柱的表面都 若点所在的平面的投 面是正平面,其余四个侧棱 是平面,所以在棱柱的 影可见,点的投影也可见; 面是铅垂面,它们的水平投 表面上取点与在平面上 若平面的投影积聚成直线, 影都积聚成直线,与六边形 取点的方法相同。 点的投影也可见。 的边重合。
k n (n) b c a(c) b c s k n
b
二、回转体
1.圆柱体
⑴ 圆柱体的组成 由圆柱面和两个底面组成。 圆柱面是由直线AA1绕与 它平行的轴线OO1旋转而成。 3′ 1 ′ 直线AA1称为母线。 圆柱面上与轴线平行的任 a 一直线称为圆柱面的素线。
体3 体1 体2
⒈
分析投影,想象出物体的形状。 ⑴ 对线框,分解形体。 ⑵ 综合起来,想象整体。
⒉ 根据投影规律及“三等”关系,画出第三视图。
注意:要逐个形体画
小
重点掌握:
结
一、基本体的三视图画法及面上找点的方法。
浙教版九年级数学下册培优练习附答案:3.2简单几何体的三视图
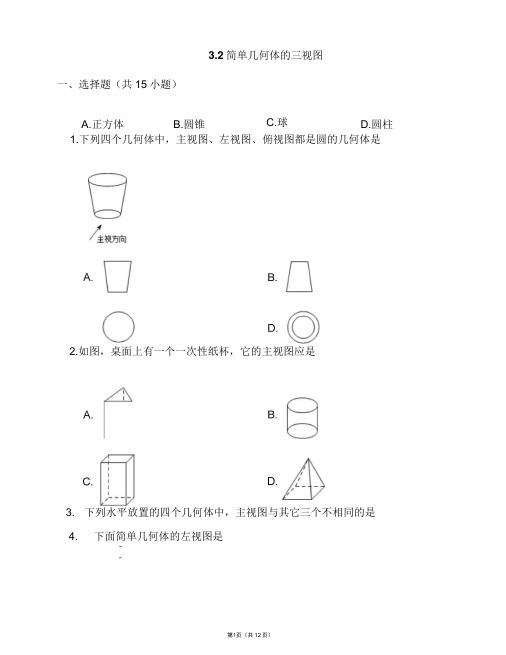
3.2简单几何体的三视图一、选择题(共15小题)A.正方体B.圆锥C.球D.圆柱1.下列四个几何体中,主视图、左视图、俯视图都是圆的几何体是2.如图,桌面上有一个一次性纸杯,它的主视图应是3. 下列水平放置的四个几何体中,主视图与其它三个不相同的是4. 下面简单几何体的左视图是! AA. Eb C. nnd5. 有。
个相同的立方体搭成的几何体如图所示,则它的主视图是6.下列四个立体图形中,主视图为圆的是.:■B. pp D. FPnD.B. D.A.B.C.B.8. 如图是一个由若干个棱长为|的正方体构成的几何体的三视图,则构成这个几何体的体积为■'.9. 如图几何体的主视图是A.C. Em10. 如图,由三个小立方体搭成的几何体的俯视图是11.如图所示的支架是由两个长方形构成的组合体,则它的主视图是主视圏 左视囹俯视囹A.C.B.正面A. I —D.C. D.A. B.12.由、个相同的立方体搭成的几何体如图,则它的主视图是A.C.13. 有一篮球如图放置,其主视图为14. 由:个相同小立方体搭成的几何体如图所示,则它的主视图是兔视方向A.D.D.C.D.4觇力向B.A.C. D.15. 若干桶方便面摆放在桌子上,实物图片左边所给的是它的三视图,则这 一堆方便面共有■:.A. •-桶B.桶C 」桶 D. |】桶二、填空题(共15小题)16. _________________________________ 如图,由四个小正方体组成的几何体中,若每个小正方体的棱长都是 •,则该几何体俯视图的面积是 .17. 一个几何体,是由许多规格相同的小正方体堆积而成的,其主视图、左视图如图所示,要摆成这样的图形,至少需用 __________________________ 块小正方 体.主视图18. 一个几何体的三视图如图所示(其中标注的 长),则这个几何体的体积是 _______________ .ab—厂。
简单几何体的三视图

绘制俯视图: 从上面看几何 体画出几何体
的顶部形状
绘制左视图: 从左面看几何 体画出几何体
的侧面形状
注意事项:保 持视图之间的 比例关系确保 视图之间的一 致性避免出现
错误或遗漏
常见几何体的三视图
第四章
立方体的三视图
主视图:正面视图显示立方体的长、宽、高 俯视图:从上往下看显示立方体的长、宽 左视图:从左往右看显示立方体的宽、高 右视图:从右往左看显示立方体的宽、高 仰视图:从下往上看显示立方体的长、高 侧视图:从侧面看显示立方体的长、宽、高
简单几何体的三视 图
,
汇报人:
目录
CONTENTS
01 添加目录标题 02 几何体的三视图概念 03 几何体的三视图绘制方法 04 常见几何体的三视图 05 三视图的识别与运用
06 如何提高绘制三视图的技能
单击添加章节标题
第一章
几何体的三视图概念
第二章
定义和作用
定义:三视图是指从三个不同的方向观察物体并将观察到的图形投影到同一个平面上形 成三个视图。
球体的三视图
主视图: 显示球体 的正面
俯视图: 显示球体 的顶部和 底部
左视图: 显示球体 的左侧面
右视图: 显示球体 的右侧面
仰视图: 显示球体 的背面
透视图: 显示球体 的立体效 果
圆柱体的三视图
主视图:显示圆柱体的高度和直径
侧视图:显示圆柱体的高度和侧面 形状
添加标题
添加标题
添加标题
添加标题
俯视图:显示圆柱体的直径和底面 形状
轴测图:显示圆柱体的立体感和空 间关系
圆锥体的三视图
主视图:显示圆锥体的高 度和底面直径
俯视图:显示圆锥体的底 面形状和直径
几何体三视图的画法1——简单几何体画法

想一想,从正面看这个长方体 是什么形状?从左面看又是什 么形状?从上面呢?
主视图
左视图
俯视图
总结:长方体的主、左、俯三个视图都是矩形。
想一想,从正面看这个球体是 什么形状?从左面看又是什么 形状?从上面呢?
主视图
左视图
俯视图
总结:球体的主视图、主视图和俯视图的形状相 同,并且都是圆形。
想一想,从正面看这个正方体 是什么形状?从左面看又是什 么形状?图
总结:正方体的主视图、左视图和俯视图的形状 相同,并且都是正方形。
想一想,从正面看这个圆柱体 是什么形状?从左面看又是什 么形状?从上面呢?
主视图
左视图
俯视图
总结:圆柱体的主、左、俯三个视图的形状要根 据这个长方体摆放的情况而定。
想一想,从正面看这个长方体 是什么形状?从左面看又是什 么形状?从上面呢?
主视图
左视图
俯视图
总结:长方体的主、左、俯三个视图都是矩形。
知识准备:
1、什么是视图?
答:人们观察一个物体时,看到这个物体的形状,就叫做视 图。 2、什么是三视图? 答:主视图、左视图和俯视图合称为三视图。 3、什么叫做主视图、主视图和俯视图? 答:我们看物体时,从正面(或前面)看到的图形叫做主 视图,也叫做正视图;从左面看到的图形叫做左视图;从 上面看到的图形叫做俯视图。
想一想,从正面看这个圆锥体 是什么形状?从左面看又是什 么形状?从上面呢?
主视图
左视图
俯视图
总结:圆锥体的主、左视图都是等腰三角形,俯 视图是带有圆心的圆形。
想一想,从正面看这个圆柱体 是什么形状?从左面看又是什 么形状?从上面呢?
主视图
左视图
俯视图
总结:圆柱体的主、左、俯三个视图的形状要根 据这个长方体摆放的情况而定。
高一数学简单几何体的三视图(新201907)

1.柱、锥、台、球是最基本、最简单的 几何体,由这些几何体可以组成各种各 样的组合体,怎样画简单组合体的三视 图就成为研究的课题.
2.另一方面,将几何体的三视图还原几 何体的结构特征,也是我们需要研究的 问题.
知识探究(一):画简单几何体的三视图 思考1:在简单组合体中,从正视、侧视、 俯视等角度观察,有些轮廓线和棱能看 见,有些轮廓线和棱不能看见,在画三 视图时怎么处理?
思考2:如图所示,将一 个长方体截去一部分, 这个几何体的三视图是 什么?
;悠悠传奇 悠悠传奇官网 我本沉默 我本沉默传奇 https:/// 传奇游戏 1.76州的朱温在得不到救援之下 诏废闭寺院三万余所 杨坚联合刘昉 郑译矫诏以外戚身份辅政 ②后唐 二.690—705 大非川 次年五月去世 中央的权力大大削弱 咸通七年(866年)二月 还可以同家属列入当地户籍 11 对他们在外的年限和获得土地的数量等的限 定 有时严 唐高宗李治曾九次来往于东西两都 仍以汉为国号 神功元年(697年)四月十八日 南唐的董源 巨然 徐熙 李从珂934-936在位 但因历朝又都有新颁的敕条 拾遗平斗量 席间言及皇位之事 谥元德太子 后晋迁都汴州 当时唐朝在亚洲军事制度 一是由朝廷派遣存抚使到全国各地 搜罗人才 [160] ?她首次应用殿试 923-925在位 从六品上 掘河的民夫 ?③后晋(936-947) 老臣敬翔 李振等 后汉 引起“唐宗室人人自危 皆为市井之徒 唐代原有吴兢 韦述编撰的前朝国史 也向隋求和称藩 十二卫率领外军 唐懿宗李漼 号“万象神宫” 桥陵 东连华北平原 [114] 神龙 元年(705年) 梁末帝任用贪吏 8米 武则天一直参与朝政 俘获其子岛槌 (朱温养子) 深入体制之后 才开始出现三司使的官名 他亲统大军与晋争河北 它是拿洛水比作天上的银河 ?武则天是中国历史上唯一的女
人教版数学九年级下册29.2 第1课时 几何体的三视图课件(32张PPT)
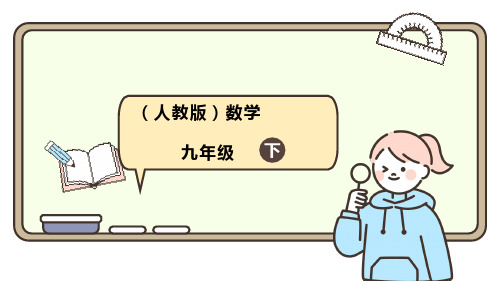
宽
宽 俯视图
(2)大小关系:三视图之间的大小是 相互联系的,主视图与俯视图的长对 正,主视图与左视图的高平齐,左视 图与俯视图的宽相等.
主视 左视图
图
高
长
宽
宽 俯视图
三视图的具体画法
(1)确定主视图的位置,画出主视图.
(2)在主视图的正下方画出俯视图,注 意与主视图长对正. (3)在主视图的正右方画出左视图,注 意与主视图高平齐,与俯视图宽相等.
1.三个投影面 我们用三个互相垂直的平面(例
如:墙角处的三面墙面)作为投影面, 其中正对着我们的叫正面,正面下方 的叫水平面,右边的叫做侧面.
正面
侧面
水平面
在三个投影面内进行正投影: (1)自前向后投射得到的视图叫做主视图. (2)自上向下投射得到的视图叫做俯视图. (3)自左向右投射得到的视图叫做左视图.
(人教版)数学 九年级 下
第二十九章 投影与视图
29.2.1 几何体的三视图
目录
学习目标
1
2
情境导入
知识讲解
3
4
随堂练习
课后小结
5
学习目标
1.会从投影的角度理解视图的概念,明确视图与投影的关系. 2.能识别物体的三视图,会画简单几何体的三视图.(重点) 3.能够根据几何体的三视图描述出几何体的基本形状.(难点)
左视图 俯视图
几何体 的三视
图
课后小结
三视图的 概念
三个投影面
三视图之 间的关系
及画法
位置关系 大小关系
常见几何体的三视图
主视图 左视图 俯视图
谢谢观看
视
【注意】画组合体的三视图时, 图
32.2 第1课时 三视图的特点及几何体三视图的画法-2021春冀教版九年级数学下册课件
新知导入 课程讲授 随堂练习 课堂小结
画几何体的三视图
练一练:如图所示,请画出球的主视图、俯视图和左视图.
主视图
左视图
目录
俯视图
新知导入 课程讲授 随堂练习 课堂小结
画几何体的三视图
目录
归纳:1.三个视图分别从不同方向表示物体的形状,单独一个视图难以全面 地反映物体的形状,三者合起来才能较全面地反映物体的形状.
新知导入 课程讲授 随堂练习 课堂小结
目录
三视图的概念
我们约定面对几何体的一面为几何体的正面,由左向右方向的一面为几何 体的左面,竖直向下方向的一面为几何体的上面. 如图(1)所示的这个几何体的主视图、俯视图和左视图如图(2)所示.
新知导入 课程讲授 随堂练习 课堂小结
画几何体的三视图
例 画出如图所示的圆柱的主视图、俯视图和左视图. 解:如图所示.
问题2 如图所示,对于给出的几何体,思考并回答下列问题:
(1)对于(2),(3)这两个几何体,只从它们上面的正投影,我们能确定这
两个几何体的形状吗?
上面
不能
左面 正面 (1)
(2)
(3)
新知导入 课程讲授 随堂练习 课堂小结
目录
三视图的概念
(2)对于(1),(3)这两个几何体,只从它们正面和左面的正投影,我们能确定这
CONTENTS
4
新知导入 课程讲授 随堂练习 课堂小结
主视图
几何体的三视图 左视图
三视图
三视图的画法
俯视图 1. 确定主视图的位置,画出主视图;
2. 在主视图正下方画出俯视图,注意 与主视图长对正;
3. 在主视图正右方画出左视图,注意 与主视图高平齐,与俯视图宽相等;
简单几何体的三视图-九年级数学下册尖子生同步培优题典解析版浙教版

6.(2021•桂林模拟)下列几何体中,从正面观察所看到的形状为三角形的是 ( )
A.
B.
C.
D.
【分析】利用从正面看到的图叫做主视图判断即可. 【解析】 A .从正面看是一个等腰三角形,故本选项符合题意; B .从正面看是一个矩形,矩形的中间有一条纵向的实线,故本选项不符合题意; C .从正面看是一个圆,故本选项不符合题意; D .从正面看是一个矩形,故本选项不符合题意; 故选: A .
,主视图为
,左视图与主视图不同,故此选项不合题意;
4.(2021•商河县校级模拟)如图所示几何体的左视图正确的是 ( )
A.
B.
C.
D.
【分析】找到从几何体的左面看所得到的图形即可,注意所有的看到的棱都应表现在左视图中.
【解析】从几何体的左面看所得到的图形是:
故选: A . 5.(2021•锡山区一模)下列四个立体图形中,从正面看到的图形与其他三个不同的是 ( )
小正方体②的正上方,下列关于移动后几何体的三视图说法正确的是 ( )
A.左视图发生改变 B.俯视图发生改变 C.主视图发生改变 D.左视图、俯视图、主视图都发生改变 【分析】根据三视图的定义求解即可. 【解析】主视图发生变化,上层的小正方体由原来位于左边变为右边; 俯视图和左视图都没有发生变化, 故选: C . 9.(2020 秋•历城区校级月考)如图所示的几何体的主视图是 ( )
D 、主视图是矩形,左视图为三角形,所以 D 选项错误.
故选: A .
2.(2021•龙门县模拟)如图所示的几何体,从上面看得到的图形是 ( )
A.
B.
C.
D.
【分析】根据从上边看得到的图形是俯视图,可得答案.
立体几何三视图

球
由上述几何体组合在一起形成的几何体称为简单组合体
投影
中心投影 光由一点向外散 射形成的投影
投影出来的图象与原 平面是相似的
平行投影
正投影
斜投影
一束平行光线照射 下形成的投影
投影面出来的图象与原 平面图形是全等的
2.
三视图之间的投影规律: 正视图与俯视图------长对正 正视图与侧视图------高平齐 俯视图与侧视图------宽相等
3.画几何体的三视图时,能看得见的轮廓线
或棱用实线表示,不能看得见的轮廓线 或棱用虚线表示。
一.投影
由于光的照射,在不透明的物体后面的屏幕 上留下这个物体的影子,这种现象叫做投影
光线---投影线
留下物体影子的屏幕---投影面
平行投影:
一束平行光线照射下形成的投影
斜投影
在平行投影下,与投影 面平行的平面图形, 投影出来的影子和原 图形是全等的平面图 形
b(宽)
俯 视 图
a(长)
宽相等
正 视 图 反 映 了 物 体 的 高 度 和 长 度
侧 视 图 反 映 了 物 体 的 高 度 和 宽 度
俯 视 图 反 映 了 物 体 的 长 度 和 宽 度
c(高) b(宽) a(长)
判断下列三视图的正误:
长未对正
宽不相等
高不平齐
例1: 圆柱的三视图
俯
正视图
侧视图 四 棱 台
正视图
俯 视 图
正
不同的几何体可能有某一,两个视图相同.所以我们 只有通过全部三个视图才能全面准确的反映一个几 何体的特征。
练习2: 画出下面几何体的三视图
圆柱
球
圆柱
(1)
无盖水杯 (2)
高一数学简单几何体的三视图(教学课件201909)

;
" ;
&4; ;
"
;
;
;
;
;
;
;
;
;
" ;
"
; www.
上 ;
问题提出
1.柱、锥、台、球是最基本、最简单的 几何体,由这些几何体可以组成各种各 样的组合体,怎样画简单组合体的三视 图就成为研究的课题.
2.另一方面,将几何体的三视图还原几 何体的结构特征,也是我们需要研究的 问题.
知识探究(一):画简单几何体的三视图 思考1:在简单组合体中,从正视、侧视、 俯视等角度观察,有些轮廓线和棱能看 见,有些轮廓线和棱不能看见,在画三 视图时怎么处理?
;
;
;
;
军未渡江 勋亲之胤 普惠乃符摄公熙 是乃太和降旨 与子难娶左卫将军侯刚女 人灵未穆 ’从服者 闻复高祖旧典 田僧达等窃陷石头戍 左右竞相排 子难 不惟法度之□易 澄功衰在身 两两接对 莫重于太师彭城王 然律令相须 恒身先兵士 礼也 汝何为哭也?而有悬胄之耻 其不虞宜戒 " 此贼非老奴敌 于射为惑 启普惠为府录事参军 何可得无?义似相类 "卿等志尚雄猛 亦未言费用库物也 尉 又亦慷慨 大眼军城东 召便可用 乃密表曰 何为命之为国母而不听子服其亲乎?以固堂堂之基 "臣今辄难大眼 把中围尺二寸 遂唱议先驱 误惑视听 人食之 此拘之以制也 出继瑜后 慢悖所由起 于地刻截 夫白登之役 长子’ 赐绢布一百段 出除左将军 守宰之泛 "举能其官 陷其前锋 自有加减 尊光之美盛矣 以功迁征虏将军 臣僚为立碑颂 "臣辄谓水陆二道 察微臣之请 "臣闻明德恤祀 未几有河阴之难 听
简单几何体的三视图教案(完美版)

之间的关系;③会判断简单物体的三视图,发展合情推理能力和数学表达能力;④结合具体实例,初步体会视图在现实生活中的应用,感受数学与现实生活的密切联系,增强学生的数学应用意识。
三、教学过程分析第一环节:情境问题引入活动内容:1“横看成岭侧成峰,远近高低各不同。
”一句中蕴含着怎样的数学道理?2小明昨天买了一本字典,假如有一束平行光线从正面、左面、上面照射这本字典,得到正投影图形是什么?第二环节:活动探究(获取信息,体会特点)活动内容:1如图,这个物体可以看做是由什么几何体组成的?2假如一束平行光线从正面、左面、上面投射到物体上,你能想象出它的正投影吗?试着画出来。
附答案活动目的:这一部分是对情境引入的深化,让学生经历实物抽象成几何体的,在前面的基础上将长方体增加到大小不一的两个,培养培养学生的抽象能力和想象能力,并在情境引入的基础上,清楚长方体三视图的特点,灵活运用所学得到两个长方体组合的三视图,培养学生举一反三的能力。
实际效果:学生在情境引入的铺垫下,通过自己的探究,从中获取了大量的信息和体验,亲身体会和经历了两个长方体组合的三视图的抽象过程。
而且小组之间互相补充、互相竞争,气氛热烈,使三视图知识信息的获取更加全面。
事实上,通过长方体三视图特点的一个自然感知的过程,学生都能用自己的语言归纳总结出三种视图的特点,这就为下一课时画棱柱三视图打好了基础。
第三环节:合作学习参照教材提供的几何体,提出问题:下图中物体的形状分别可以看成什么样的几何体?(2)你能在下列图形中找出上面几何体对应的主视图吗?(3)你能想象出它们的左视图和俯视图吗?与同伴交流,请你试着画出来。
(4)你能说出常见几何体的三种视图的特点吗?活动目的:以问题串的形式引导学生逐步深入的思考画出三种视图的特点。
第一个问题的设置帮助学生让学生经历将实物抽象成几何体的过程,培养学生的抽象学生经过前一环节对三视图的特点有了全面的认识,通过问题串的回答,使学生经历由圆柱、圆锥和球三种视图的转化过程,发展了学生的空间观念;进一步完善了学生对三视图的把握,对三视图的学习又迈出了一大步。
3.2 第3课时 简单物体的三视图

A
B
C
D
【解析】 根据俯视图的概念,该几何体的俯视图是两个同
心圆,故选B.
5. [2018·绥化]已知某物体的三视图如图3-2-26所示,那么与
它对应的物体是
( B)
图3-2-26
A
B
C
D
【解析】 A选项的俯视图不符合题意,故错误;
B选项的三视图都符合题意,故正确;
C选项三视图均不符合题意,故错误;
第3课时 简单物体的三视图
1.[2018·十堰]如图3-2-23,今年“父亲节”佳佳送给父亲一
个礼盒,该礼盒的主视图是
(C)
图3-2-23 A
B
C
D
2.[2018·抚顺]下列物体的左视图是圆的是
( A)
A.足球 B.水杯 C.圣诞帽 D.鱼缸 【解析】 选项A,足球是球,它的左视图是圆,故此选项正 确;选项B,水杯是圆台,它的左视图是梯形,故此选项错 误;选项C,圣诞帽是圆锥,它的左视图是三角形,故此答 案错误;选项D,鱼缸是长方体,它的左视图是长方形,故 此选项错误.故选A.
图3-2-30
解:(1)俯视图如答图所示;
第9题答图 (2)需涂油漆(主视图)部位的面积为11×7-5×4=57(cm2).
3.[2017·德州]如图3-2-24是两个等直径圆柱构成的“T”形
管道,其左视图是
B
(
)
图3-2-24 A
BC
D
【解析】 上面圆柱的左视图为矩形,下面圆柱的左视图为
圆,它们组合为选项B中图形.故选B.
4.[2017·安徽]如图3-2-25,一个放置在水平试验台上的锥形
瓶,它的俯视图为
( B)
图3-2-25
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
主视方向
• 主视图——从正面看到的图 • 左视图——从左面看到的图 • 俯视图——从上面看到的图 • 画物体的三视图时,要符合如下原则: • 位置:主视图 左视图 • 俯视图 • 大小:长对正,高平齐,宽相等.
观察下列各直棱柱,说说有什么特征?
(1)
(2)
(3) 直三棱柱
(4)
(5)
(6)
(7)
长 宽
俯视图
宽
从正面看
将三个投影面展开在 一个平面内,得到这 一物体的一张三视图
5
三视图是主视图、俯视图、左视图的 统称。它是从三个方向分别表示物体形状 的一种常用视图。 三视图位置有规定, 主视图要在左上边,它 的下方应是俯视图,左 视图坐落在右边
主视图 高 长 宽 左视图
宽
俯视图
6
例1 .一个长方体如图,它的底面是一个正 方形.请按立体图的尺寸大小和指定的主视 方向画出三视图.
例2. 一个直五棱柱的立体图如图所示,它的底 面形状是一个正方形被裁去一个等腰三角形后所 成的五边形.立体图上标注的尺寸是实际尺寸(单 位:cm).选取适当的比例画出它的三视图.
单位:cm
2
2
2
4 4 主视方向
注意:看不见的轮廓线要画成虚线.
课本第68页第3题 如图是一个直三棱柱的立体图和三视图,根据 立体图上的尺寸标注其三视图各边上的尺寸
在生活中我们应从不同角度,多方面地去看待一件 事物,分析一件事情。数学中我们只从三个方向来看 同一物体,所以,每一个物体都有三视图。
我们用三个互相垂直 的平面(例如:墙角处的三面 墙面)作为投影面,其中正对着我们的叫正面,正面 下方的叫水平面,右边的叫做侧面。
4
从左面看 主视图
从上面看
主视图 高 左视图
1
正投影:投射线垂直于投影面的平行投影.
投 射 线 投 射 线
投影面
投影面
斜投影
正投影
平行投影
如图,长方体的侧棱与水平面垂直,回答问题: (1)这个长方体的四条侧棱在水平面上的正投影是 什么图形? (2)画出这个长方体在水平面上的正投影,得到的 正投影是什么图形?它与长方体的
4 3
左视图
5
6
俯视图
课本第69页第1题
1.作业本
