专题20 半角模型(解析版)
半角模型专题训练含解析

半角模型专题训练一、解答题1.(探索发现)如图①,四边形ABCD 是正方形,M ,N 分别在边CD 、BC 上,且45MAN=∠︒,我们把这种模型称为“半角模型”,在解决“半角模型”问题时,旋转是一种常用的方法.如图①,将ADM ∆绕点A 顺时针旋转90︒,点D 与点B 重合,得到ABE ∆,连接AM 、AN 、MN .(1)试判断DM ,BN ,MN 之间的数量关系,并写出证明过程.(2)如图②,点M 、N 分别在正方形ABCD 的边BC 、CD 的延长线上,45MAN=∠︒,连接MN ,请写出MN 、DM 、BN 之间的数量关系,并写出证明过程.(3)如图③,在四边形ABCD 中,AB=AD ,120BAD=∠︒,180B+D=∠∠︒,点N ,M 分别在边BC ,CD 上,60MAN=∠︒,请直接写出线段BN ,DM ,MN 之间的数量关系.2.如图,等腰直角三角形ABC 中,∠BAC = 90°,AB =AC ,点M ,N 在边BC 上,且∠MAN =45°.若BM = 1,CN =3,求MN 的长.3.问题背景:如图1,在四边形ABCD 中,90BAD ︒∠=,90BCD ︒∠=,BA BC =,120ABC ︒∠=,60MBN ︒∠=,MBN ∠绕B 点旋转,它的两边分别交AD 、DC 于E 、F .探究图中线段,,AE CF EF 之间的数量关系.小李同学探究此问题的方法是:延长FC 到G ,使CG AE =,连接BG ,先证明BCG BAE △≌△,再证明BGF BEF △≌△,可得出结论,他的结论就是______________;探究延伸:如图2,在四边形ABCD 中,BA BC =,180BAD BCD ︒∠+∠=,2ABC MBN ∠=∠,MBN ∠绕B 点旋转,它的两边分别交AD 、DC 于E 、F .上述结论是否仍然成立?并说明理由.实际应用:如图3,在某次军事演习中,舰艇甲在指挥中心(O 处)北偏西30°的A 处舰艇乙在指挥中心南偏东70°的B 处,并且两舰艇到指挥中心的距离相等接到行动指令后,舰艇甲向正东方向以75海里/小时的速度前进,同时舰艇乙沿北偏东50°的方向以100海里/小时的速度前进,1.2小时后,指挥中心观测到甲、乙两舰艇分别到达E 、F 处,且指挥中心观测两舰艇视线之间的夹角为70°,试求此时两舰艇之间的距离.4.如图,AB AD BC DC ===,90C D ABE BAD ∠=∠=∠=∠=︒,点E 、F 分别在边BC 、CD 上,45EAF ∠=︒,过点A 作GAB FAD ∠=∠,且点G 在CB 的延长线上.(1)GAB ∆与FAD ∆全等吗?为什么?(2)若2DF =,3BE =,求EF 的长.5.如图,在四边形ABCD 中,90B D ∠=∠=︒,E ,F 分别是BC ,CD 上的点,连接AE ,AF ,EF .(1)如图①,AB AD =,120BAD ∠=︒,60EAF ∠=︒.求证:EF BE DF =+;(2)如图②,120BAD ∠=︒,当AEF 周长最小时,求AEF AFE +∠∠的度数; (3)如图③,若四边形ABCD 为正方形,点E 、F 分别在边BC 、CD 上,且45EAF ∠=︒,若3BE =,2DF =,请求出线段EF 的长度.6.如图,ABC 是边长为2的等边三角形,BDC 是顶角为120°的等腰三角形,以点D 为顶点作60MDN ∠=︒,点M 、N 分别在AB 、AC 上.(1)如图①,当//MN BC 时,则AMN 的周长为______;(2)如图②,求证:BM NC MN +=.7.问题背景如图①,在四边形ABCD 中,AB AD =,120BAD ∠=︒,90B ADC ∠=∠=︒,点E ,F 分别是BC ,CD 上的点,且60EAF ∠=︒,连接EF ,探究线段BE ,EF ,DF 之间的数量关系.探究发现(1)小明同学的方法是将ABE △绕点A 逆时针旋转120︒至ADG 的位置,使得AB 与AD 重合,然后再证明AFE AFG △≌△,从而得出结论:______;拓展延伸(2)如图②,在四边形ABCD 中,AB AD =,180B D ∠+∠=︒,点E ,F 分别是边BC ,CD 上的点,且12EAF BAD ∠=∠,连接EF .(1)中的结论是否仍然成立?若成立,请写出证明过程;若不成立,请说明理由;(3)如图③,在正方形ABCD 中,点E ,F 分别是边BC ,CD 上的点,且45EAF ∠=︒,连接EF ,已知3BE =,2DF =,求正方形ABCD 的边长.8.如图,ABC 是边长为3的等边三角形,BDC 是等腰三角形,且120BDC ∠=︒,以D 为顶点作一个60︒角,使其两边分别交AB 于点M ,交AC 于点N ,连接MN ,求AMN 的周长.9.如图,已知:正方形ABCD ,点E ,F 分别是BC ,DC 上的点,连接AE ,AF ,EF ,且45EAF ∠=︒,求证:BE DF EF +=.10.(1)如图1,在四边形ABCD 中,AB =AD ,∠BAD =100°,∠B =∠ADC =90°.E ,F 分别是BC ,CD 上的点.且∠EAF =50°.探究图中线段EF ,BE ,FD 之间的数量关系.小明同学探究的方法是:延长FD 到点G ,使DG =BE ,连接AG ,先证明△ABE ≌△ADG ,再证明△AEF ≌△AGF ,可得出结论,他的结论是 (直接写结论,不需证明); (2)如图2,若在四边形ABCD 中,AB =AD ,∠B +∠D =180°,E ,F 分别是BC ,CD 上的点,且2∠EAF =∠BAD ,上述结论是否仍然成立,若成立,请证明,若不成立,请说明理由;(3)如图3,四边形ABCD 是边长为7的正方形,∠EBF =45°,直接写出△DEF 的周长.11.如图,正方形ABCD中,E、F分别在边BC、CD上,且∠EAF=45°,连接EF,这种模型属于“半角模型”中的一类,在解决“半角模型”问题时,旋转是一种常用的分析思路.例如图中△ADF与△ABG可以看作绕点A旋转90°的关系.这可以证明结论“EF =BE+DF”,请补充辅助线的作法,并写出证明过程.(1)延长CB到点G,使BG=,连接AG;(2)证明:EF=BE+DF12.(2019秋•东台市期末)在等边△ABC的两边AB、AC所在直线上分别有两点M、N,D为△ABC外一点,且∠MDN=60°,∠BDC=120°,BD=DC.探究:当M、N分别在直线AB、AC上移动时,BM、NC、MN之间的数量关系及△AMN的周长Q与等边△ABC 的周长L的关系.(1)如图1,当点M、N边AB、AC上,且DM=DN时,BM、NC、MN之间的数量关系是;此时QL;(2)如图2,点M、N在边AB、AC上,且当DM≠DN时,猜想(I)问的两个结论还成立吗?若成立请直接写出你的结论;若不成立请说明理由.(3)如图3,当M、N分别在边AB、CA的延长线上时,探索BM、NC、MN之间的数量关系如何?并给出证明.参考答案1.(1)MN DM BN =+,证明见解析;(2)MN BN DM =-,证明见解析;(3)MN DM BN =+.【分析】(1)根据正方形的性质和旋转的性质可证ADM ≌ABE ,利用SAS 可证AMN AEN ≌,则可得:MN DM BN =+;(2)根据正方形的性质和旋转的性质可证ADM ≌ABE ,利用SAS 可证AMN AEN ≌,则可得:MN BN DM =-;(3)根据正方形的性质和旋转的性质可证ADM ≌ABE ,利用SAS 可证AMN AEN ≌,则可得:MN DM BN =+;【详解】证明:(1)如图①,∵四边形ABCD 是正方形∴AB=AD ,ABC ADC BAD =90将ADM 绕点A 顺时针旋转90︒,得到ABE∴ADM ≌ABE∴AM AE,DMBE,MAD EAB MAE BAD 90 ∵MAN 45EANMAN 45 在AMN 和AEN 中AMAE MANEAN AN ANAMN AEN SAS ≌MN EN∵EN EB BN DM BN =+=+,∴MN BN DM =+(2)如图②,将ADM 绕点A 顺时针旋转90,得到ABE∵四边形ABCD是正方形∴AB=AD,ABC ADC BAD=90∵ADM绕点A顺时针旋转90,得到ABE ∴ADM≌ABE∴AM AE,DM BE,MAD EABMAE BAD90,∵MAN45EAN MAN45在AMN和AEN中AM AEMAN EANAN AN≌AMN AEN SASMN EN∵BN EB EN DM MN,=-;即:MN BN DM(3)如图,∵AB AD =,BAD 120∠=,B D 180,将ADM 绕点A 顺时针旋转120,得到ABE∴ADM ≌ABE∴AM AE,DMBE,MAD EAB MAE BAD 120 MAN 60EANMAN 60 在AMN 和AEN 中AMAE MANEAN AN ANAMN AEN SAS ≌MN EN ENBE BN MN DM BN ;【点睛】本题主要考查正方形的性质及全等三角形的判定和性质等知识,利用旋转法构造全等三角形是解题的关键是学会.2【分析】过点C 作CE ⊥BC ,垂足为点C ,截取CE ,使CE =BM .连接AE 、EN .通过证明△ABM ≌△ACE (SAS )推知全等三角形的对应边AM =AE 、对应角∠BAM =∠CAE ;然后由等腰直角三角形的性质和∠MAN =45°得到∠MAN =∠EAN =45°,所以△MAN ≌△EAN (SAS ),故全等三角形的对应边MN =EN ;最后由勾股定理得到EN 2=EC 2+NC 2即MN 2=BM 2+NC 2.【详解】解:如图,过点C 作CE ⊥BC ,垂足为点C ,截取CE ,使CE =BM .连接AE 、EN .∵AB=AC,∠BAC=90°,∴∠B=∠ACB=45°.∵CE⊥BC,∴∠ACE=∠B=45°.在△ABM和△ACE中AB ACB ACE BM CE⎧∠⎪∠⎪⎨⎩===,∴△ABM≌△ACE(SAS).∴AM=AE,∠BAM=∠CAE.∵∠BAC=90°,∠MAN=45°,∴∠BAM+∠CAN=45°.于是,由∠BAM=∠CAE,得∠MAN=∠EAN=45°.在△MAN和△EAN中AM AEMAN EAN AN AN⎪∠⎪⎩∠⎧⎨===,∴△MAN≌△EAN(SAS).∴MN=EN.在Rt△ENC中,由勾股定理,得EN2=EC2+NC2.∴MN2=BM2+NC2.∵BM=1,CN=3,∴MN2=12+32,∴MN.【点睛】本题主要考查全等三角形的判定和性质、等腰直角三角形的性质以及勾股定理的综合应用,掌握三角形的全等的判定定理是解题关键.=+;探究延伸:成立,理由见解析;实际应用:210海里3.问题背景:EF AE CF【分析】问题背景:延长FC到G,使CG=AE,连接BG,先证明△BCG≌△BAE,再证明△BFG≌△BFE,即可得出结论:EF=AE+CF;探究延伸1:延长FC到G,使CG=AE,连接BG,先证明△BCG≌△BAE,再证明△BFG≌△BFE,可得出结论:EF=AE+CF;探究延伸2:延长DC到H,使得CH=AE,连接BH,先证明△BCH≌△BAE,即可得到BE=HB,∠ABE=∠HBC,再证明△HBF≌△EBF,即可得出EF=HF=HC+CF=AE+CF;实际应用:连接EF,延长BF交AE的延长线于G,根据题意可转化为如下的数学问题:在四边形GAOB中,OA=OB,∠A+∠B=180°,∠AOB=2∠EOF,∠EOF的两边分别交AG,BG于E,F,求EF的长.再根据探究延伸2的结论:EF=AE+BF,即可得到两舰艇之间的距离.【详解】解:问题背景:如图1,延长FC到G,使CG=AE,连接BG,先证明△BCG≌△BAE,再证明△BFG≌△BFE,可得出结论:EF=AE+CF;故答案为:EF=AE+CF;探究延伸1:上述结论仍然成立,即EF=AE+CF,理由如下:如图2,延长FC到G,使CG=AE,连接BG,∵CG=AE,∠BCG=∠A=90°,BC=BA,∴△BCG≌△BAE(SAS),∴BG=BE,∠ABE=∠CBG,∵∠ABC=2∠EBF,∴∠ABE+∠CBF=∠EBF,即∠CBG+∠CBF=∠EBF,∴∠GBF=∠EBF,又∵BF=BF,∴△BFG≌△BFE(SAS),∴GF=EF,即GC+CF=EF,∴AE+CF=EF∴可得出结论:EF=AE+CF;探究延伸2:上述结论仍然成立,即EF=AE+CF,理由:如图3,延长DC到H,使得CH=AE,连接BH,∵∠BAD+∠BCD=180°,∠BCH+∠BCD=180°,∴∠BCH=∠BAE,∵BA=BC,CH=AE,∴△BCH≌△BAE(SAS),∴BE=HB,∠ABE=∠HBC,∴∠HBE=∠ABC,又∵∠ABC=2∠MBN,∴∠EBF=∠HBF,∴△HBF≌△EBF(SAS),∴EF=HF=HC+CF=AE+CF;实际应用:如图4,连接EF,延长BF交AE的延长线于G,因为舰艇甲在指挥中心(O处)北偏西30°的A处.舰艇乙在指挥中心南偏东70°的B处,所以∠AOB=140°,因为指挥中心观测两舰艇视线之间的夹角为70°,所以∠EOF=70°,所以∠AOB=2∠EOF.依题意得,OA=OB,∠A=60°,∠B=120°,所以∠A+∠B=180°,因此本题的实际的应用可转化为如下的数学问题:在四边形GAOB中,OA=OB,∠A+∠B=180°,∠AOB=2∠EOF,∠EOF的两边分别交AG,BG于E,F,求EF的长.根据探究延伸2的结论可得:EF=AE+BF,根据题意得,AE=75×1.2=90(海里),BF=100×1.2=120(海里),所以EF=90+120=210(海里).答:此时两舰艇之间的距离为210海里.【点睛】本题属于四边形综合题,主要考查了全等三角形的判定和性质,解题的关键是正确作出辅助线构造全等三角形,解答时注意类比思想的灵活应用.4.(1)△GAB≌△F AD,理由见解析;(2)EF=5【分析】(1)由题意可得∠ABG=∠D=90°,进一步即可根据ASA证得△GAB≌△F AD;(2)由(1)的结论可得AG=AF,GB=DF,易得∠BAE+∠DAF=45°,进而可推出∠GAE=∠EAF,然后利用SAS即可证明△GAE≌△F AE,可得GE=EF,进一步即可求出结果.解:(1)∵90D ABE ∠=∠=︒,点G 在CB 的延长线上,∴∠ABG =∠D =90°,在△GAB 和△F AD 中,∵GAB FAD ∠=∠,AB =AD ,∠ABG =∠D ,∴△GAB ≌△F AD (ASA );(2)∵△GAB ≌△F AD ,∴AG =AF ,GB =DF ,∵90BAD ∠=︒,45EAF ∠=︒,∴∠BAE +∠DAF =45°,∴∠BAE +∠GAB =45°,即∠GAE =45°,∴∠GAE =∠EAF ,在△GAE 和△F AE 中,∵AG =AF ,∠GAE =∠EAF ,AE =AE ,∴△GAE ≌△F AE (SAS ),∴GE =EF ,∵GE =GB +BE =DF +BE =2+3=5,∴EF =5.【点睛】本题主要考查了全等三角形的判定和性质,属于常考题型,熟练掌握全等三角形的判定和性质是解题的关键.5.(1)见解析;(2)AEF AFE +∠∠120=︒;(3)5EF =.【分析】(1)延长FD 到点G,使DG BE =,连接AG ,首先证明ABE ADG ≌,则有AE AG =,BAE DAG ∠=∠,然后利用角度之间的关系得出60EAF FAG ∠=∠=︒,进而可证明EAF GAF △≌△,则EF FG DG DF ==+,则结论可证;(2)分别作点A 关于BC 和CD 的对称点A ',A '',连接A A ''',交BC 于点E ,交CD 于点F ,根据轴对称的性质有A E AE '=,A F AF ''=,当点A '、E 、F 、A ''在同一条直线上时,A A '''即为AEF 周长的最小值,然后利用AEF AFE EA A EAA FAD A ''''∠+∠=∠+∠+∠+∠求解即可;(3)旋转ABE △至ADP △的位置,首先证明PAF EAF ≌△△,则有EF FP =,最后利用EF PF PD DF BE DF ==+=+求解即可.【详解】(1)证明:如解图①,延长FD 到点G ,使DG BE =,连接AG ,在ABE △和ADG 中,,,,AB AD ABE ADG BE DG =⎧⎪∠=∠⎨⎪=⎩()ABE ADG SAS ∴≌.AE AG ∴=,BAE DAG ∠=∠,120BAD ∠=︒,60EAF ∠=︒,60BAE FAD DAG FAD ∴∠+∠=∠+∠=︒.60EAF FAG ∴∠=∠=︒,在EAF △和GAF 中,,,,AE AG EAF GAF AF AF =⎧⎪∠=∠⎨⎪=⎩()EAF GAF SAS ∴≌.EF FG DG DF ∴==+,EF BE DF ∴=+;(2)解:如解图,分别作点A 关于BC 和CD 的对称点A ',A '',连接A A ''',交BC 于点E ,交CD 于点F .由对称的性质可得A E AE '=,A F AF ''=,∴此时AEF 的周长为AE EF AF A E EF A F A A '''''++=++=.∴当点A '、E 、F 、A ''在同一条直线上时,A A '''即为AEF 周长的最小值.120DAB ∠=︒,18012060AA E A ''∴∠'︒︒+∠=-=︒.,EA A EAA FAD A ''''∠=∠∠=∠,,EA A EAA AEF FAD A AFE ''''∠+∠=∠∠+∠=∠, AEF AFE EA A EAA FAD A ''''∴∠+∠=∠+∠+∠+∠=()2260120AA E A '''∠+∠=⨯︒=︒;(3)解:如解图,旋转ABE △至ADP △的位置,90PAE DAE PAD DAE EAB ∴∠=∠+∠=∠+∠=︒,AP AE =,PAF PAE EAF ∠=∠-∠904545EAF =︒-︒=︒=∠.在PAF △和EAF △中,,,,AP AE PAF EAF AF AF =⎧⎪∠=∠⎨⎪=⎩()PAF EAF SAS ∴≌△△.EF FP ∴=.325EF PF PD DF BE DF ∴==+=+=+=.【点睛】本题主要考查全等三角形的判定及性质,轴对称的性质,掌握全等三角形的判定及性质是解题的关键.6.(1)4;(2)见解析【分析】(1)首先证明△BDM ≌△CDN ,进而得出△DMN 是等边三角形,∠BDM=∠CDN=30°,NC=BM=12DM=12MN ,即可解决问题; (2)延长AC 至点E ,使得CE BM =,连接DE ,首先证明BDM CDE △≌△,再证明MDN EDN △≌△,得出MN NE =,进而得出结果即可.【详解】解:(1)∵ABC 是等边三角形,//MN BC ,60AMN ABC ∴∠=∠=︒,60ANM ACB ∠=∠=︒∴AMN 是等边三角形,AM AN ∴=,则BM NC =,∵BDC 是顶角120BDC ∠=︒的等腰三角形,30DBC DCB ∴∠=∠=︒,90DBM DCN ∴∠=∠=︒,在BDM 和CDN △中,,,,BM CN MBD DCN BD CD =⎧⎪∠=∠⎨⎪=⎩()BDM CDN SAS ∴△≌△,DM DN ∴=,BDM CDN ∠=∠,∵60MDN ∠=︒,∴DMN 是等边三角形,30BDM CDN ∠=∠=︒,1122NC BM DM MN ∴===,MN MB NC ∴=+, ∴AMN 的周长4AB AC =+=.(2)如图,延长AC 至点E ,使得CE BM =,连接DE ,∵ABC 是等边三角形,BDC 是顶角120BDC ∠=︒的等腰三角形,60ABC ACB ∴∠=∠=︒,30DBC DCB ∠=∠=︒,90ABD ACD ∠∴∠==︒,90DCE ∴∠=︒,在BDM 和CDE △中,,,,BD CD MBD ECD BM CE =⎧⎪∠=∠⎨⎪=⎩()BDM CDE SAS ∴△≌△,MD ED ∴=,MDB EDC ∠=∠,120120MDE MDB EDC ∴∠=︒-∠+∠=︒,∵60MDN ∠=︒,60NDE ∴∠=︒,在MDN △和EDN △中,,60,,MD ED MDN NDE DN DN =⎧⎪∠=∠=︒⎨⎪=⎩()MDN EDN SAS ∴△≌△.MN NE ∴=,又∵NE NC CE NC BM =+=+,BM NC MN ∴+=.【点睛】本题考查了全等三角形的判定与性质及等边三角形的性质及等腰三角形的性质,掌握全等三角形的性质与判定,等边三角形及等腰三角形的性质是解题的关键.7.(1)EF BE DF =+;(2)(1)中的结论EF BE DF =+仍然成立.证明见解析;(3)正方形ABCD 的边长为6.【分析】(1)证明AEF AGF ≌,可得EF FG =,即可得出结论;(2)要探究BE ,EF ,DF 之间的数量关系,方法同(1)即可得出结论;(3)根据(1)(2)的结论和勾股定理,即可求出正方形ABCD 的边长.【详解】(1)解:由旋转得:AE=AG ,∠BAE=∠DAG ,BE=DG ,∵120BAD ∠=︒,∴∠EAG=120°,∵60EAF ∠=︒,∴∠GAF=60EAF ∠=︒,又∵AF=AF ,∴AFE AFG △≌△,∴EF=GF ,∵GF=DG+DF ,∴EF BE DF =+,故答案为:EF BE DF =+;(2)解:(1)中的结论EF BE DF =+仍然成立.证明:如解图,将ABE △绕点A 逆时针旋转至ADG 的位置,使AB 与AD 重合.则ADG B ∠=∠,DG BE =,AG AE =,BAE DAG ∠=∠,又∵180B ADC ∠+∠=︒,∴180ADG ADC ∠+∠=︒,∴C ,D ,G 三点共线. ∵12FAD DAG FAD BAE BAD EAF BAD ∠+∠=∠+∠=∠-∠=∠,∴FAG EAF ∠=∠,又∵AF AF =,∴AEF AGF ≌,∴EF FG =,又∵FG DG DF BE DF =+=+,∴EF BE DF =+;(3)解:由(1)(2)可知325EF BE DF =+=+=.设正方形ABCD 的边长为x ,则3CE x =-,2CF x =-,在Rt CEF 中,222EF CE CF =+,∴()()222532x x =-+-,解得16x =,21x =-(不合题意,舍去),故正方形ABCD 的边长为6.【点睛】此题考查了旋转的性质,全等三角形的判定及性质,勾股定理的运用,正方形的性质,解题中注意类比方法的运用,同样的类型题可以运用同样的思路及方法进行证明.8.AMN 的周长为6.【分析】要求△AMN 的周长,根据题目已知条件无法求出三条边的长,只能把三条边长用其它已知边长来表示,所以需要作辅助线,延长AB 至F ,使BF=CN ,连接DF ,通过证明△BDF ≌△CDN ,及△DMN ≌△DMF ,从而得出MN=MF ,△AMN 的周长等于AB+AC 的长.【详解】解:∵△BDC 是等腰三角形,且∠BDC=120°∴∠BCD=∠DBC=30°∵△ABC 是边长为3的等边三角形∴∠ABC=∠BAC=∠BCA=60°∴∠DBA=∠DCA=90°延长AB 至F ,使BF=CN ,连接DF ,在Rt △BDF 和Rt △CND 中,BF=CN ,DB=DC∴△BDF ≌△CDN ,∴∠BDF=∠CDN ,DF=DN∵∠MDN=60°∴∠BDM+∠CDN=60°∴∠BDM+∠BDF=60°,∠FDM=60°=∠MDN ,DM 为公共边 ∴△DMN ≌△DMF ,∴MN=MF∴△AMN 的周长是:AM+AN+MN=AM+MB+BF+AN=AB+AC=6.【点睛】此题主要利用等边三角形和等腰三角形的性质来证明三角形全等,构造另一个三角形是解题的关键.9.见解析.【分析】将△ABE 绕点A 逆时针旋转90°得到△ADG ,根据旋转的性质可得GD=BE ,AG=AE ,∠DAG=∠BAE ,然后求出∠FAG=∠EAF ,再利用“边角边”证明△AEF 和△AGF 全等,根据全等三角形对应边相等可得EF=FG ,即可得出结论.【详解】如解图,将ABE △绕点A 逆时针旋转90︒至ADG 的位置,使AB 与AD 重合.∴AG AE =,,DAG BAE DG BE ∠=∠=.∵45EAF ∠=︒.∴904545GAF DAG DAF BAE DAF BAD EAF ∠=∠+∠=∠+∠=∠-∠=︒-︒=︒, ∴EAF GAF ∠=∠.在AGF 和AEF 中,,AG AE GAF EAF AF AF =⎧⎪∠=∠⎨⎪=⎩,∴()AGF AEF SAS △≌△.∴EF GF =.∵GF DG DF BE DF =+=+,∴BE DF EF +=.【点睛】本题考查了正方形的性质,旋转的性质,全等三角形的判定与性质,难点在于利用旋转变换作出全等三角形.10.(1)EF =BE +DF ;(2)成立,理由详见解析;(3)14.【分析】(1)延长FD 到点G .使DG =BE .连结AG ,由“SAS ”可证△ABE ≌△ADG ,可得AE =AG ,∠BAE =∠DAG ,再由“SAS ”可证△AEF ≌△AGF ,可得EF =FG ,即可解题;(2)延长EB 到G ,使BG =DF ,连接AG ,即可证明△ABG ≌△ADF ,可得AF =AG ,再证明△AEF ≌△AEG ,可得EF =EG ,即可解题;(3)延长EA 到H ,使AH =CF ,连接BH ,由“SAS ”可证△ABH ≌△CBF ,可得BH =BF ,∠ABH =∠CBF ,由“SAS ”可证△EBH ≌△EBF ,可得EF =EH ,可得EF =EH =AE +CF ,即可求解.【详解】证明:(1)延长FD 到点G .使DG =BE .连结AG ,在△ABE 和△ADG 中,90AB AD ABE ADG BE DG ︒=⎧⎪∠=∠=⎨⎪=⎩,∴△ABE ≌△ADG (SAS ),∴AE =AG ,∠BAE =∠DAG ,∵∠BAD =100°,∠EAF =50°,∴∠BAE +∠F AD =∠DAG +∠F AD =50°,∴∠EAF =∠F AG =50°,在△EAF 和△GAF 中,∵AE AG EAF GAF AF AF =⎧⎪∠=∠⎨⎪=⎩,∴△EAF ≌△GAF (SAS ),∴EF =FG =DF +DG ,∴EF =BE +DF ,故答案为:EF =BE +DF ;(2)结论仍然成立,理由如下:如图2,延长EB 到G ,使BG =DF ,连接AG ,∵∠ABC +∠D =180°,∠ABG +∠ABC =180°,∴∠ABG =∠D ,∵在△ABG 与△ADF 中,AB=AD ABG=D BG=DF ⎧⎪∠∠⎨⎪⎩,∴△ABG ≌△ADF (SAS ),∴AG =AF ,∠BAG =∠DAF ,∵2∠EAF =∠BAD ,∴∠DAF +∠BAE =∠BAG +∠BAE =12∠BAD =∠EAF , ∴∠GAE =∠EAF ,又AE =AE ,∴△AEG≌△AEF(SAS),∴EG=EF.∵EG=BE+BG.∴EF=BE+FD;(3)如图,延长EA到H,使AH=CF,连接BH,∵四边形ABCD是正方形,∴AB=BC=7=AD=CD,∠BAD=∠BCD=90°,∴∠BAH=∠BCF=90°,又∵AH=CF,AB=BC,∴△ABH≌△CBF(SAS),∴BH=BF,∠ABH=∠CBF,∵∠EBF=45°,∴∠CBF+∠ABE=45°=∠HBA+∠ABE=∠EBF,∴∠EBH=∠EBF,又∵BH=BF,BE=BE,∴△EBH≌△EBF(SAS),∴EF=EH,∴EF=EH=AE+CF,∴△DEF的周长=DE+DF+EF=DE+DF+AE+CF=AD+CD=14.【点睛】本题是四边形的综合题,考查了全等三角形的判定和性质,正方形的性质,添加恰当辅助线构造全等三角形是本题的关键.11.(1)DF;(2)见解析【分析】(1)由于△ADF 与△ABG 可以看作绕点A 旋转90°的关系,根据旋转的性质知BG=DF ,从而得到辅助线的做法;(2)先证明△ADF ≌△ABG ,得到AG=AF ,∠GAB=∠DAF ,结合∠EAF =45°,易知∠GAE=45°,再证明△AGE ≌△AFE 即可得到EF =GE=BE+GB=BE +DF【详解】解:(1)根据旋转的性质知BG=DF ,从而得到辅助线的做法:延长CB 到点G ,使BG=DF ,连接AG ;(2)∵四边形ABCD 为正方形,∴AB=AD ,∠ADF=∠ABE=∠ABG=90°,在△ADF 和△ABG 中AD AB ADF ABG DF BG =⎧⎪∠=∠⎨⎪=⎩∴△ADF ≌△ABG (SAS ),∴AF=AG ,∠DAF=∠GAB ,∵∠EAF=45°,∴∠DAF+∠EAB=45°,∴∠GAB+∠EAB=45°,∴∠GAE=∠EAF =45°,在△AGE 和△AFE 中0AG AF GAE FAE AE AE =⎧⎪∠=∠⎨⎪=⎩∴△ADF ≌△ABG (SAS ),∴GE=EF ,∴EF =GE=BE+GB=BE +DF【点睛】本题属于四边形综合题,主要考查正方形的性质及全等三角形的判定和性质等知识,解题的关键是学会利用旋转方法提示构造全等三角形,属于中考常考题型.12.(1)BM +NC =MN ,23;(2)结论仍然成立,详见解析;(3)NC ﹣BM =MN ,详见解析【分析】(1)由DM=DN,∠MDN=60°,可证得△MDN是等边三角形,又由△ABC是等边三角形,CD=BD,易证得Rt△BDM≌Rt△CDN,然后由直角三角形的性质,即可求得BM、NC、MN之间的数量关系BM+NC=MN,此时23QL=;(2)在CN的延长线上截取CM1=BM,连接DM1.可证△DBM≌△DCM1,即可得DM=DM1,易证得∠CDN=∠MDN=60°,则可证得△MDN≌△M1DN,然后由全等三角形的性质,即可得结论仍然成立;(3)首先在CN上截取CM1=BM,连接DM1,可证△DBM≌△DCM1,即可得DM=DM1,然后证得∠CDN=∠MDN=60°,易证得△MDN≌△M1DN,则可得NC﹣BM=MN.【详解】(1)如图1,BM、NC、MN之间的数量关系BM+NC=MN.此时23QL=.理由:∵DM=DN,∠MDN=60°,∴△MDN是等边三角形,∵△ABC是等边三角形,∴∠A=60°,∵BD=CD,∠BDC=120°,∴∠DBC=∠DCB=30°,∴∠MBD=∠NCD=90°,∵DM=DN,BD=CD,∴Rt△BDM≌Rt△CDN,∴∠BDM=∠CDN=30°,BM=CN,∴DM=2BM,DN=2CN,∴MN=2BM=2CN=BM+CN;∴AM=AN,∴△AMN是等边三角形,∵AB=AM+BM,∴AM:AB=2:3,∴23QL=;(2)猜想:结论仍然成立.证明:在NC的延长线上截取CM1=BM,连接DM1.∵∠MBD=∠M1CD=90°,BD=CD,∴△DBM≌△DCM1,∴DM=DM1,∠MBD=∠M1CD,M1C=BM,∵∠MDN=60°,∠BDC=120°,∴∠M1DN=∠MDN=60°,∴△MDN≌△M1DN,∴MN=M1N=M1C+NC=BM+NC,∴△AMN的周长为:AM+MN+AN=AM+BM+CN+AN=AB+AC,∴23QL=;(3)证明:在CN上截取CM1=BM,连接DM1.∵∠MBD=∠M1CD=90°,BD=CD,∴△DBM≌△DCM1,∴DM=DM1,∠MBD=∠M1CD,M1C=BM,∵∠MDN=60°,∠BDC=120°,∴∠M1DN=∠MDN=60°,∴△MDN≌△M1DN,∴MN=M1N.∴NC﹣BM=MN.【点睛】此题主要考查全等三角形的判定与性质,解题的关键是熟知等边三角形的性质及全等三角形的判定定理.。
半角模型十五个结论及证明

半角模型十五个结论及证明《探索半角模型的十五个结论及证明》嗨,大家好!今天我要和大家一起探索一个超有趣的数学知识——半角模型的十五个结论及证明。
这就像是一场奇妙的数学冒险,跟我来呀!一、什么是半角模型呢?半角模型呀,就像是一个神秘的数学宝藏,藏在各种几何图形里。
想象一下,我们有一个正方形或者等腰直角三角形,然后在这个图形里出现了一个角,这个角是另外一个大角的一半,这就形成了半角模型。
比如说,在正方形里,一个角是45度,它就是直角90度的一半呢。
这时候啊,就会有好多神奇的结论冒出来。
二、结论一:线段相等我给大家举个例子哈。
在正方形ABCD中,∠EAF = 45度(E、F分别在BC、CD 上)。
我们能发现BE + DF = EF。
这是为啥呢?我们可以把△ADF绕着点A顺时针旋转90度,这样AD就和AB重合了。
旋转后的点F变成了F'。
那这个时候呀,我们就会发现△AEF和△AEF'是全等的。
为啥呢?因为AF = AF',∠EAF = ∠EAF' = 45度,AE是公共边啊。
就像两个一模一样的小积木,那EF就等于EF'了,而EF'就是BE + DF呀。
你们说神奇不神奇?这就好比是把分散的力量集中起来了,原本分开的BE和DF,通过旋转这个魔法,就变成了和EF相等的线段。
三、结论二:三角形面积关系还有一个有趣的结论呢。
三角形AEF的面积等于三角形ABE的面积加上三角形ADF的面积。
这又怎么理解呢?我们刚刚把△ADF旋转到了△ABF'的位置。
那三角形AEF的面积就等于三角形AEF'的面积啦。
而三角形AEF'的面积就是三角形ABE的面积加上三角形ABF'(也就是原来的三角形ADF)的面积。
这就好像是把两个小地块合并起来就等于一个大地块的面积一样。
四、结论三:角平分线如果我们延长CB到G,使得BG = DF,连接AG。
我们会发现AG是∠EAG的角平分线呢。
半角模型专题训练含解析
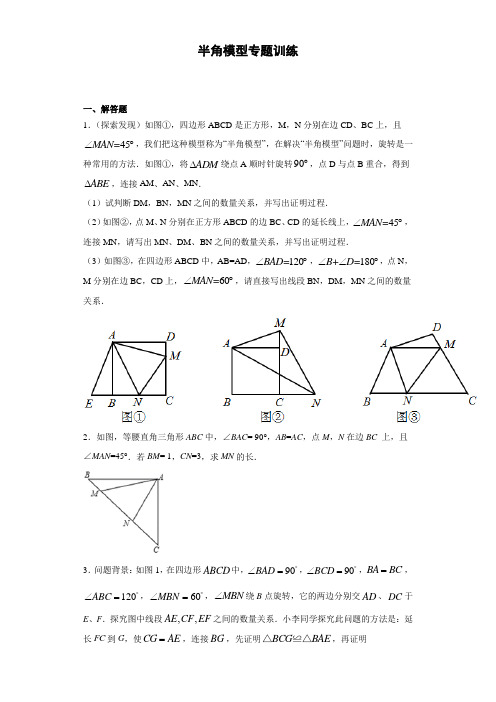
半角模型专题训练一、解答题1.(探索发现)如图①,四边形ABCD 是正方形,M ,N 分别在边CD 、BC 上,且45MAN=∠︒,我们把这种模型称为“半角模型”,在解决“半角模型”问题时,旋转是一种常用的方法.如图①,将ADM ∆绕点A 顺时针旋转90︒,点D 与点B 重合,得到ABE ∆,连接AM 、AN 、MN .(1)试判断DM ,BN ,MN 之间的数量关系,并写出证明过程.(2)如图②,点M 、N 分别在正方形ABCD 的边BC 、CD 的延长线上,45MAN=∠︒,连接MN ,请写出MN 、DM 、BN 之间的数量关系,并写出证明过程.(3)如图③,在四边形ABCD 中,AB=AD ,120BAD=∠︒,180B+D=∠∠︒,点N ,M 分别在边BC ,CD 上,60MAN=∠︒,请直接写出线段BN ,DM ,MN 之间的数量关系.2.如图,等腰直角三角形ABC 中,∠BAC = 90°,AB =AC ,点M ,N 在边BC 上,且∠MAN =45°.若BM = 1,CN =3,求MN 的长.3.问题背景:如图1,在四边形ABCD 中,90BAD ︒∠=,90BCD ︒∠=,BA BC =,120ABC ︒∠=,60MBN ︒∠=,MBN ∠绕B 点旋转,它的两边分别交AD 、DC 于E 、F .探究图中线段,,AE CF EF 之间的数量关系.小李同学探究此问题的方法是:延长FC 到G ,使CG AE =,连接BG ,先证明BCG BAE △≌△,再证明BGF BEF △≌△,可得出结论,他的结论就是______________;探究延伸:如图2,在四边形ABCD 中,BA BC =,180BAD BCD ︒∠+∠=,2ABC MBN ∠=∠,MBN ∠绕B 点旋转,它的两边分别交AD 、DC 于E 、F .上述结论是否仍然成立?并说明理由.实际应用:如图3,在某次军事演习中,舰艇甲在指挥中心(O 处)北偏西30°的A 处舰艇乙在指挥中心南偏东70°的B 处,并且两舰艇到指挥中心的距离相等接到行动指令后,舰艇甲向正东方向以75海里/小时的速度前进,同时舰艇乙沿北偏东50°的方向以100海里/小时的速度前进,1.2小时后,指挥中心观测到甲、乙两舰艇分别到达E 、F 处,且指挥中心观测两舰艇视线之间的夹角为70°,试求此时两舰艇之间的距离.4.如图,AB AD BC DC ===,90C D ABE BAD ∠=∠=∠=∠=︒,点E 、F 分别在边BC 、CD 上,45EAF ∠=︒,过点A 作GAB FAD ∠=∠,且点G 在CB 的延长线上.(1)GAB ∆与FAD ∆全等吗?为什么?(2)若2DF =,3BE =,求EF 的长.5.如图,在四边形ABCD 中,90B D ∠=∠=︒,E ,F 分别是BC ,CD 上的点,连接AE ,AF ,EF .(1)如图①,AB AD =,120BAD ∠=︒,60EAF ∠=︒.求证:EF BE DF =+;(2)如图②,120BAD ∠=︒,当AEF 周长最小时,求AEF AFE +∠∠的度数; (3)如图③,若四边形ABCD 为正方形,点E 、F 分别在边BC 、CD 上,且45EAF ∠=︒,若3BE =,2DF =,请求出线段EF 的长度.6.如图,ABC 是边长为2的等边三角形,BDC 是顶角为120°的等腰三角形,以点D 为顶点作60MDN ∠=︒,点M 、N 分别在AB 、AC 上.(1)如图①,当//MN BC 时,则AMN 的周长为______;(2)如图②,求证:BM NC MN +=.7.问题背景如图①,在四边形ABCD 中,AB AD =,120BAD ∠=︒,90B ADC ∠=∠=︒,点E ,F 分别是BC ,CD 上的点,且60EAF ∠=︒,连接EF ,探究线段BE ,EF ,DF 之间的数量关系.探究发现(1)小明同学的方法是将ABE △绕点A 逆时针旋转120︒至ADG 的位置,使得AB 与AD 重合,然后再证明AFE AFG △≌△,从而得出结论:______;拓展延伸(2)如图②,在四边形ABCD 中,AB AD =,180B D ∠+∠=︒,点E ,F 分别是边BC ,CD 上的点,且12EAF BAD ∠=∠,连接EF .(1)中的结论是否仍然成立?若成立,请写出证明过程;若不成立,请说明理由;(3)如图③,在正方形ABCD 中,点E ,F 分别是边BC ,CD 上的点,且45EAF ∠=︒,连接EF ,已知3BE =,2DF =,求正方形ABCD 的边长.8.如图,ABC 是边长为3的等边三角形,BDC 是等腰三角形,且120BDC ∠=︒,以D 为顶点作一个60︒角,使其两边分别交AB 于点M ,交AC 于点N ,连接MN ,求AMN 的周长.9.如图,已知:正方形ABCD ,点E ,F 分别是BC ,DC 上的点,连接AE ,AF ,EF ,且45EAF ∠=︒,求证:BE DF EF +=.10.(1)如图1,在四边形ABCD 中,AB =AD ,∠BAD =100°,∠B =∠ADC =90°.E ,F 分别是BC ,CD 上的点.且∠EAF =50°.探究图中线段EF ,BE ,FD 之间的数量关系.小明同学探究的方法是:延长FD 到点G ,使DG =BE ,连接AG ,先证明△ABE ≌△ADG ,再证明△AEF ≌△AGF ,可得出结论,他的结论是 (直接写结论,不需证明); (2)如图2,若在四边形ABCD 中,AB =AD ,∠B +∠D =180°,E ,F 分别是BC ,CD 上的点,且2∠EAF =∠BAD ,上述结论是否仍然成立,若成立,请证明,若不成立,请说明理由;(3)如图3,四边形ABCD 是边长为7的正方形,∠EBF =45°,直接写出△DEF 的周长.11.如图,正方形ABCD中,E、F分别在边BC、CD上,且∠EAF=45°,连接EF,这种模型属于“半角模型”中的一类,在解决“半角模型”问题时,旋转是一种常用的分析思路.例如图中△ADF与△ABG可以看作绕点A旋转90°的关系.这可以证明结论“EF =BE+DF”,请补充辅助线的作法,并写出证明过程.(1)延长CB到点G,使BG=,连接AG;(2)证明:EF=BE+DF12.(2019秋•东台市期末)在等边△ABC的两边AB、AC所在直线上分别有两点M、N,D为△ABC外一点,且∠MDN=60°,∠BDC=120°,BD=DC.探究:当M、N分别在直线AB、AC上移动时,BM、NC、MN之间的数量关系及△AMN的周长Q与等边△ABC 的周长L的关系.(1)如图1,当点M、N边AB、AC上,且DM=DN时,BM、NC、MN之间的数量关系是;此时QL;(2)如图2,点M、N在边AB、AC上,且当DM≠DN时,猜想(I)问的两个结论还成立吗?若成立请直接写出你的结论;若不成立请说明理由.(3)如图3,当M、N分别在边AB、CA的延长线上时,探索BM、NC、MN之间的数量关系如何?并给出证明.参考答案1.(1)MN DM BN =+,证明见解析;(2)MN BN DM =-,证明见解析;(3)MN DM BN =+.【分析】(1)根据正方形的性质和旋转的性质可证ADM ≌ABE ,利用SAS 可证AMN AEN ≌,则可得:MN DM BN =+;(2)根据正方形的性质和旋转的性质可证ADM ≌ABE ,利用SAS 可证AMN AEN ≌,则可得:MN BN DM =-;(3)根据正方形的性质和旋转的性质可证ADM ≌ABE ,利用SAS 可证AMN AEN ≌,则可得:MN DM BN =+;【详解】证明:(1)如图①,∵四边形ABCD 是正方形∴AB=AD ,ABC ADC BAD =90将ADM 绕点A 顺时针旋转90︒,得到ABE∴ADM ≌ABE∴AM AE,DMBE,MAD EAB MAE BAD 90 ∵MAN 45EANMAN 45 在AMN 和AEN 中AMAE MANEAN AN ANAMN AEN SAS ≌MN EN∵EN EB BN DM BN =+=+,∴MN BN DM =+(2)如图②,将ADM 绕点A 顺时针旋转90,得到ABE∵四边形ABCD是正方形∴AB=AD,ABC ADC BAD=90∵ADM绕点A顺时针旋转90,得到ABE ∴ADM≌ABE∴AM AE,DM BE,MAD EABMAE BAD90,∵MAN45EAN MAN45在AMN和AEN中AM AEMAN EANAN AN≌AMN AEN SASMN EN∵BN EB EN DM MN,=-;即:MN BN DM(3)如图,∵AB AD =,BAD 120∠=,B D 180,将ADM 绕点A 顺时针旋转120,得到ABE∴ADM ≌ABE∴AM AE,DMBE,MAD EAB MAE BAD 120 MAN 60EANMAN 60 在AMN 和AEN 中AMAE MANEAN AN ANAMN AEN SAS ≌MN EN ENBE BN MN DM BN ;【点睛】本题主要考查正方形的性质及全等三角形的判定和性质等知识,利用旋转法构造全等三角形是解题的关键是学会.2【分析】过点C 作CE ⊥BC ,垂足为点C ,截取CE ,使CE =BM .连接AE 、EN .通过证明△ABM ≌△ACE (SAS )推知全等三角形的对应边AM =AE 、对应角∠BAM =∠CAE ;然后由等腰直角三角形的性质和∠MAN =45°得到∠MAN =∠EAN =45°,所以△MAN ≌△EAN (SAS ),故全等三角形的对应边MN =EN ;最后由勾股定理得到EN 2=EC 2+NC 2即MN 2=BM 2+NC 2.【详解】解:如图,过点C 作CE ⊥BC ,垂足为点C ,截取CE ,使CE =BM .连接AE 、EN .∵AB=AC,∠BAC=90°,∴∠B=∠ACB=45°.∵CE⊥BC,∴∠ACE=∠B=45°.在△ABM和△ACE中AB ACB ACE BM CE⎧∠⎪∠⎪⎨⎩===,∴△ABM≌△ACE(SAS).∴AM=AE,∠BAM=∠CAE.∵∠BAC=90°,∠MAN=45°,∴∠BAM+∠CAN=45°.于是,由∠BAM=∠CAE,得∠MAN=∠EAN=45°.在△MAN和△EAN中AM AEMAN EAN AN AN⎪∠⎪⎩∠⎧⎨===,∴△MAN≌△EAN(SAS).∴MN=EN.在Rt△ENC中,由勾股定理,得EN2=EC2+NC2.∴MN2=BM2+NC2.∵BM=1,CN=3,∴MN2=12+32,∴MN.【点睛】本题主要考查全等三角形的判定和性质、等腰直角三角形的性质以及勾股定理的综合应用,掌握三角形的全等的判定定理是解题关键.=+;探究延伸:成立,理由见解析;实际应用:210海里3.问题背景:EF AE CF【分析】问题背景:延长FC到G,使CG=AE,连接BG,先证明△BCG≌△BAE,再证明△BFG≌△BFE,即可得出结论:EF=AE+CF;探究延伸1:延长FC到G,使CG=AE,连接BG,先证明△BCG≌△BAE,再证明△BFG≌△BFE,可得出结论:EF=AE+CF;探究延伸2:延长DC到H,使得CH=AE,连接BH,先证明△BCH≌△BAE,即可得到BE=HB,∠ABE=∠HBC,再证明△HBF≌△EBF,即可得出EF=HF=HC+CF=AE+CF;实际应用:连接EF,延长BF交AE的延长线于G,根据题意可转化为如下的数学问题:在四边形GAOB中,OA=OB,∠A+∠B=180°,∠AOB=2∠EOF,∠EOF的两边分别交AG,BG于E,F,求EF的长.再根据探究延伸2的结论:EF=AE+BF,即可得到两舰艇之间的距离.【详解】解:问题背景:如图1,延长FC到G,使CG=AE,连接BG,先证明△BCG≌△BAE,再证明△BFG≌△BFE,可得出结论:EF=AE+CF;故答案为:EF=AE+CF;探究延伸1:上述结论仍然成立,即EF=AE+CF,理由如下:如图2,延长FC到G,使CG=AE,连接BG,∵CG=AE,∠BCG=∠A=90°,BC=BA,∴△BCG≌△BAE(SAS),∴BG=BE,∠ABE=∠CBG,∵∠ABC=2∠EBF,∴∠ABE+∠CBF=∠EBF,即∠CBG+∠CBF=∠EBF,∴∠GBF=∠EBF,又∵BF=BF,∴△BFG≌△BFE(SAS),∴GF=EF,即GC+CF=EF,∴AE+CF=EF∴可得出结论:EF=AE+CF;探究延伸2:上述结论仍然成立,即EF=AE+CF,理由:如图3,延长DC到H,使得CH=AE,连接BH,∵∠BAD+∠BCD=180°,∠BCH+∠BCD=180°,∴∠BCH=∠BAE,∵BA=BC,CH=AE,∴△BCH≌△BAE(SAS),∴BE=HB,∠ABE=∠HBC,∴∠HBE=∠ABC,又∵∠ABC=2∠MBN,∴∠EBF=∠HBF,∴△HBF≌△EBF(SAS),∴EF=HF=HC+CF=AE+CF;实际应用:如图4,连接EF,延长BF交AE的延长线于G,因为舰艇甲在指挥中心(O处)北偏西30°的A处.舰艇乙在指挥中心南偏东70°的B处,所以∠AOB=140°,因为指挥中心观测两舰艇视线之间的夹角为70°,所以∠EOF=70°,所以∠AOB=2∠EOF.依题意得,OA=OB,∠A=60°,∠B=120°,所以∠A+∠B=180°,因此本题的实际的应用可转化为如下的数学问题:在四边形GAOB中,OA=OB,∠A+∠B=180°,∠AOB=2∠EOF,∠EOF的两边分别交AG,BG于E,F,求EF的长.根据探究延伸2的结论可得:EF=AE+BF,根据题意得,AE=75×1.2=90(海里),BF=100×1.2=120(海里),所以EF=90+120=210(海里).答:此时两舰艇之间的距离为210海里.【点睛】本题属于四边形综合题,主要考查了全等三角形的判定和性质,解题的关键是正确作出辅助线构造全等三角形,解答时注意类比思想的灵活应用.4.(1)△GAB≌△F AD,理由见解析;(2)EF=5【分析】(1)由题意可得∠ABG=∠D=90°,进一步即可根据ASA证得△GAB≌△F AD;(2)由(1)的结论可得AG=AF,GB=DF,易得∠BAE+∠DAF=45°,进而可推出∠GAE=∠EAF,然后利用SAS即可证明△GAE≌△F AE,可得GE=EF,进一步即可求出结果.解:(1)∵90D ABE ∠=∠=︒,点G 在CB 的延长线上,∴∠ABG =∠D =90°,在△GAB 和△F AD 中,∵GAB FAD ∠=∠,AB =AD ,∠ABG =∠D ,∴△GAB ≌△F AD (ASA );(2)∵△GAB ≌△F AD ,∴AG =AF ,GB =DF ,∵90BAD ∠=︒,45EAF ∠=︒,∴∠BAE +∠DAF =45°,∴∠BAE +∠GAB =45°,即∠GAE =45°,∴∠GAE =∠EAF ,在△GAE 和△F AE 中,∵AG =AF ,∠GAE =∠EAF ,AE =AE ,∴△GAE ≌△F AE (SAS ),∴GE =EF ,∵GE =GB +BE =DF +BE =2+3=5,∴EF =5.【点睛】本题主要考查了全等三角形的判定和性质,属于常考题型,熟练掌握全等三角形的判定和性质是解题的关键.5.(1)见解析;(2)AEF AFE +∠∠120=︒;(3)5EF =.【分析】(1)延长FD 到点G,使DG BE =,连接AG ,首先证明ABE ADG ≌,则有AE AG =,BAE DAG ∠=∠,然后利用角度之间的关系得出60EAF FAG ∠=∠=︒,进而可证明EAF GAF △≌△,则EF FG DG DF ==+,则结论可证;(2)分别作点A 关于BC 和CD 的对称点A ',A '',连接A A ''',交BC 于点E ,交CD 于点F ,根据轴对称的性质有A E AE '=,A F AF ''=,当点A '、E 、F 、A ''在同一条直线上时,A A '''即为AEF 周长的最小值,然后利用AEF AFE EA A EAA FAD A ''''∠+∠=∠+∠+∠+∠求解即可;(3)旋转ABE △至ADP △的位置,首先证明PAF EAF ≌△△,则有EF FP =,最后利用EF PF PD DF BE DF ==+=+求解即可.【详解】(1)证明:如解图①,延长FD 到点G ,使DG BE =,连接AG ,在ABE △和ADG 中,,,,AB AD ABE ADG BE DG =⎧⎪∠=∠⎨⎪=⎩()ABE ADG SAS ∴≌.AE AG ∴=,BAE DAG ∠=∠,120BAD ∠=︒,60EAF ∠=︒,60BAE FAD DAG FAD ∴∠+∠=∠+∠=︒.60EAF FAG ∴∠=∠=︒,在EAF △和GAF 中,,,,AE AG EAF GAF AF AF =⎧⎪∠=∠⎨⎪=⎩()EAF GAF SAS ∴≌.EF FG DG DF ∴==+,EF BE DF ∴=+;(2)解:如解图,分别作点A 关于BC 和CD 的对称点A ',A '',连接A A ''',交BC 于点E ,交CD 于点F .由对称的性质可得A E AE '=,A F AF ''=,∴此时AEF 的周长为AE EF AF A E EF A F A A '''''++=++=.∴当点A '、E 、F 、A ''在同一条直线上时,A A '''即为AEF 周长的最小值.120DAB ∠=︒,18012060AA E A ''∴∠'︒︒+∠=-=︒.,EA A EAA FAD A ''''∠=∠∠=∠,,EA A EAA AEF FAD A AFE ''''∠+∠=∠∠+∠=∠, AEF AFE EA A EAA FAD A ''''∴∠+∠=∠+∠+∠+∠=()2260120AA E A '''∠+∠=⨯︒=︒;(3)解:如解图,旋转ABE △至ADP △的位置,90PAE DAE PAD DAE EAB ∴∠=∠+∠=∠+∠=︒,AP AE =,PAF PAE EAF ∠=∠-∠904545EAF =︒-︒=︒=∠.在PAF △和EAF △中,,,,AP AE PAF EAF AF AF =⎧⎪∠=∠⎨⎪=⎩()PAF EAF SAS ∴≌△△.EF FP ∴=.325EF PF PD DF BE DF ∴==+=+=+=.【点睛】本题主要考查全等三角形的判定及性质,轴对称的性质,掌握全等三角形的判定及性质是解题的关键.6.(1)4;(2)见解析【分析】(1)首先证明△BDM ≌△CDN ,进而得出△DMN 是等边三角形,∠BDM=∠CDN=30°,NC=BM=12DM=12MN ,即可解决问题; (2)延长AC 至点E ,使得CE BM =,连接DE ,首先证明BDM CDE △≌△,再证明MDN EDN △≌△,得出MN NE =,进而得出结果即可.【详解】解:(1)∵ABC 是等边三角形,//MN BC ,60AMN ABC ∴∠=∠=︒,60ANM ACB ∠=∠=︒∴AMN 是等边三角形,AM AN ∴=,则BM NC =,∵BDC 是顶角120BDC ∠=︒的等腰三角形,30DBC DCB ∴∠=∠=︒,90DBM DCN ∴∠=∠=︒,在BDM 和CDN △中,,,,BM CN MBD DCN BD CD =⎧⎪∠=∠⎨⎪=⎩()BDM CDN SAS ∴△≌△,DM DN ∴=,BDM CDN ∠=∠,∵60MDN ∠=︒,∴DMN 是等边三角形,30BDM CDN ∠=∠=︒,1122NC BM DM MN ∴===,MN MB NC ∴=+, ∴AMN 的周长4AB AC =+=.(2)如图,延长AC 至点E ,使得CE BM =,连接DE ,∵ABC 是等边三角形,BDC 是顶角120BDC ∠=︒的等腰三角形,60ABC ACB ∴∠=∠=︒,30DBC DCB ∠=∠=︒,90ABD ACD ∠∴∠==︒,90DCE ∴∠=︒,在BDM 和CDE △中,,,,BD CD MBD ECD BM CE =⎧⎪∠=∠⎨⎪=⎩()BDM CDE SAS ∴△≌△,MD ED ∴=,MDB EDC ∠=∠,120120MDE MDB EDC ∴∠=︒-∠+∠=︒,∵60MDN ∠=︒,60NDE ∴∠=︒,在MDN △和EDN △中,,60,,MD ED MDN NDE DN DN =⎧⎪∠=∠=︒⎨⎪=⎩()MDN EDN SAS ∴△≌△.MN NE ∴=,又∵NE NC CE NC BM =+=+,BM NC MN ∴+=.【点睛】本题考查了全等三角形的判定与性质及等边三角形的性质及等腰三角形的性质,掌握全等三角形的性质与判定,等边三角形及等腰三角形的性质是解题的关键.7.(1)EF BE DF =+;(2)(1)中的结论EF BE DF =+仍然成立.证明见解析;(3)正方形ABCD 的边长为6.【分析】(1)证明AEF AGF ≌,可得EF FG =,即可得出结论;(2)要探究BE ,EF ,DF 之间的数量关系,方法同(1)即可得出结论;(3)根据(1)(2)的结论和勾股定理,即可求出正方形ABCD 的边长.【详解】(1)解:由旋转得:AE=AG ,∠BAE=∠DAG ,BE=DG ,∵120BAD ∠=︒,∴∠EAG=120°,∵60EAF ∠=︒,∴∠GAF=60EAF ∠=︒,又∵AF=AF ,∴AFE AFG △≌△,∴EF=GF ,∵GF=DG+DF ,∴EF BE DF =+,故答案为:EF BE DF =+;(2)解:(1)中的结论EF BE DF =+仍然成立.证明:如解图,将ABE △绕点A 逆时针旋转至ADG 的位置,使AB 与AD 重合.则ADG B ∠=∠,DG BE =,AG AE =,BAE DAG ∠=∠,又∵180B ADC ∠+∠=︒,∴180ADG ADC ∠+∠=︒,∴C ,D ,G 三点共线. ∵12FAD DAG FAD BAE BAD EAF BAD ∠+∠=∠+∠=∠-∠=∠,∴FAG EAF ∠=∠,又∵AF AF =,∴AEF AGF ≌,∴EF FG =,又∵FG DG DF BE DF =+=+,∴EF BE DF =+;(3)解:由(1)(2)可知325EF BE DF =+=+=.设正方形ABCD 的边长为x ,则3CE x =-,2CF x =-,在Rt CEF 中,222EF CE CF =+,∴()()222532x x =-+-,解得16x =,21x =-(不合题意,舍去),故正方形ABCD 的边长为6.【点睛】此题考查了旋转的性质,全等三角形的判定及性质,勾股定理的运用,正方形的性质,解题中注意类比方法的运用,同样的类型题可以运用同样的思路及方法进行证明.8.AMN 的周长为6.【分析】要求△AMN 的周长,根据题目已知条件无法求出三条边的长,只能把三条边长用其它已知边长来表示,所以需要作辅助线,延长AB 至F ,使BF=CN ,连接DF ,通过证明△BDF ≌△CDN ,及△DMN ≌△DMF ,从而得出MN=MF ,△AMN 的周长等于AB+AC 的长.【详解】解:∵△BDC 是等腰三角形,且∠BDC=120°∴∠BCD=∠DBC=30°∵△ABC 是边长为3的等边三角形∴∠ABC=∠BAC=∠BCA=60°∴∠DBA=∠DCA=90°延长AB 至F ,使BF=CN ,连接DF ,在Rt △BDF 和Rt △CND 中,BF=CN ,DB=DC∴△BDF ≌△CDN ,∴∠BDF=∠CDN ,DF=DN∵∠MDN=60°∴∠BDM+∠CDN=60°∴∠BDM+∠BDF=60°,∠FDM=60°=∠MDN ,DM 为公共边 ∴△DMN ≌△DMF ,∴MN=MF∴△AMN 的周长是:AM+AN+MN=AM+MB+BF+AN=AB+AC=6.【点睛】此题主要利用等边三角形和等腰三角形的性质来证明三角形全等,构造另一个三角形是解题的关键.9.见解析.【分析】将△ABE 绕点A 逆时针旋转90°得到△ADG ,根据旋转的性质可得GD=BE ,AG=AE ,∠DAG=∠BAE ,然后求出∠FAG=∠EAF ,再利用“边角边”证明△AEF 和△AGF 全等,根据全等三角形对应边相等可得EF=FG ,即可得出结论.【详解】如解图,将ABE △绕点A 逆时针旋转90︒至ADG 的位置,使AB 与AD 重合.∴AG AE =,,DAG BAE DG BE ∠=∠=.∵45EAF ∠=︒.∴904545GAF DAG DAF BAE DAF BAD EAF ∠=∠+∠=∠+∠=∠-∠=︒-︒=︒, ∴EAF GAF ∠=∠.在AGF 和AEF 中,,AG AE GAF EAF AF AF =⎧⎪∠=∠⎨⎪=⎩,∴()AGF AEF SAS △≌△.∴EF GF =.∵GF DG DF BE DF =+=+,∴BE DF EF +=.【点睛】本题考查了正方形的性质,旋转的性质,全等三角形的判定与性质,难点在于利用旋转变换作出全等三角形.10.(1)EF =BE +DF ;(2)成立,理由详见解析;(3)14.【分析】(1)延长FD 到点G .使DG =BE .连结AG ,由“SAS ”可证△ABE ≌△ADG ,可得AE =AG ,∠BAE =∠DAG ,再由“SAS ”可证△AEF ≌△AGF ,可得EF =FG ,即可解题;(2)延长EB 到G ,使BG =DF ,连接AG ,即可证明△ABG ≌△ADF ,可得AF =AG ,再证明△AEF ≌△AEG ,可得EF =EG ,即可解题;(3)延长EA 到H ,使AH =CF ,连接BH ,由“SAS ”可证△ABH ≌△CBF ,可得BH =BF ,∠ABH =∠CBF ,由“SAS ”可证△EBH ≌△EBF ,可得EF =EH ,可得EF =EH =AE +CF ,即可求解.【详解】证明:(1)延长FD 到点G .使DG =BE .连结AG ,在△ABE 和△ADG 中,90AB AD ABE ADG BE DG ︒=⎧⎪∠=∠=⎨⎪=⎩,∴△ABE ≌△ADG (SAS ),∴AE =AG ,∠BAE =∠DAG ,∵∠BAD =100°,∠EAF =50°,∴∠BAE +∠F AD =∠DAG +∠F AD =50°,∴∠EAF =∠F AG =50°,在△EAF 和△GAF 中,∵AE AG EAF GAF AF AF =⎧⎪∠=∠⎨⎪=⎩,∴△EAF ≌△GAF (SAS ),∴EF =FG =DF +DG ,∴EF =BE +DF ,故答案为:EF =BE +DF ;(2)结论仍然成立,理由如下:如图2,延长EB 到G ,使BG =DF ,连接AG ,∵∠ABC +∠D =180°,∠ABG +∠ABC =180°,∴∠ABG =∠D ,∵在△ABG 与△ADF 中,AB=AD ABG=D BG=DF ⎧⎪∠∠⎨⎪⎩,∴△ABG ≌△ADF (SAS ),∴AG =AF ,∠BAG =∠DAF ,∵2∠EAF =∠BAD ,∴∠DAF +∠BAE =∠BAG +∠BAE =12∠BAD =∠EAF , ∴∠GAE =∠EAF ,又AE =AE ,∴△AEG≌△AEF(SAS),∴EG=EF.∵EG=BE+BG.∴EF=BE+FD;(3)如图,延长EA到H,使AH=CF,连接BH,∵四边形ABCD是正方形,∴AB=BC=7=AD=CD,∠BAD=∠BCD=90°,∴∠BAH=∠BCF=90°,又∵AH=CF,AB=BC,∴△ABH≌△CBF(SAS),∴BH=BF,∠ABH=∠CBF,∵∠EBF=45°,∴∠CBF+∠ABE=45°=∠HBA+∠ABE=∠EBF,∴∠EBH=∠EBF,又∵BH=BF,BE=BE,∴△EBH≌△EBF(SAS),∴EF=EH,∴EF=EH=AE+CF,∴△DEF的周长=DE+DF+EF=DE+DF+AE+CF=AD+CD=14.【点睛】本题是四边形的综合题,考查了全等三角形的判定和性质,正方形的性质,添加恰当辅助线构造全等三角形是本题的关键.11.(1)DF;(2)见解析【分析】(1)由于△ADF 与△ABG 可以看作绕点A 旋转90°的关系,根据旋转的性质知BG=DF ,从而得到辅助线的做法;(2)先证明△ADF ≌△ABG ,得到AG=AF ,∠GAB=∠DAF ,结合∠EAF =45°,易知∠GAE=45°,再证明△AGE ≌△AFE 即可得到EF =GE=BE+GB=BE +DF【详解】解:(1)根据旋转的性质知BG=DF ,从而得到辅助线的做法:延长CB 到点G ,使BG=DF ,连接AG ;(2)∵四边形ABCD 为正方形,∴AB=AD ,∠ADF=∠ABE=∠ABG=90°,在△ADF 和△ABG 中AD AB ADF ABG DF BG =⎧⎪∠=∠⎨⎪=⎩∴△ADF ≌△ABG (SAS ),∴AF=AG ,∠DAF=∠GAB ,∵∠EAF=45°,∴∠DAF+∠EAB=45°,∴∠GAB+∠EAB=45°,∴∠GAE=∠EAF =45°,在△AGE 和△AFE 中0AG AF GAE FAE AE AE =⎧⎪∠=∠⎨⎪=⎩∴△ADF ≌△ABG (SAS ),∴GE=EF ,∴EF =GE=BE+GB=BE +DF【点睛】本题属于四边形综合题,主要考查正方形的性质及全等三角形的判定和性质等知识,解题的关键是学会利用旋转方法提示构造全等三角形,属于中考常考题型.12.(1)BM +NC =MN ,23;(2)结论仍然成立,详见解析;(3)NC ﹣BM =MN ,详见解析【分析】(1)由DM=DN,∠MDN=60°,可证得△MDN是等边三角形,又由△ABC是等边三角形,CD=BD,易证得Rt△BDM≌Rt△CDN,然后由直角三角形的性质,即可求得BM、NC、MN之间的数量关系BM+NC=MN,此时23QL=;(2)在CN的延长线上截取CM1=BM,连接DM1.可证△DBM≌△DCM1,即可得DM=DM1,易证得∠CDN=∠MDN=60°,则可证得△MDN≌△M1DN,然后由全等三角形的性质,即可得结论仍然成立;(3)首先在CN上截取CM1=BM,连接DM1,可证△DBM≌△DCM1,即可得DM=DM1,然后证得∠CDN=∠MDN=60°,易证得△MDN≌△M1DN,则可得NC﹣BM=MN.【详解】(1)如图1,BM、NC、MN之间的数量关系BM+NC=MN.此时23QL=.理由:∵DM=DN,∠MDN=60°,∴△MDN是等边三角形,∵△ABC是等边三角形,∴∠A=60°,∵BD=CD,∠BDC=120°,∴∠DBC=∠DCB=30°,∴∠MBD=∠NCD=90°,∵DM=DN,BD=CD,∴Rt△BDM≌Rt△CDN,∴∠BDM=∠CDN=30°,BM=CN,∴DM=2BM,DN=2CN,∴MN=2BM=2CN=BM+CN;∴AM=AN,∴△AMN是等边三角形,∵AB=AM+BM,∴AM:AB=2:3,∴23QL=;(2)猜想:结论仍然成立.证明:在NC的延长线上截取CM1=BM,连接DM1.∵∠MBD=∠M1CD=90°,BD=CD,∴△DBM≌△DCM1,∴DM=DM1,∠MBD=∠M1CD,M1C=BM,∵∠MDN=60°,∠BDC=120°,∴∠M1DN=∠MDN=60°,∴△MDN≌△M1DN,∴MN=M1N=M1C+NC=BM+NC,∴△AMN的周长为:AM+MN+AN=AM+BM+CN+AN=AB+AC,∴23QL=;(3)证明:在CN上截取CM1=BM,连接DM1.∵∠MBD=∠M1CD=90°,BD=CD,∴△DBM≌△DCM1,∴DM=DM1,∠MBD=∠M1CD,M1C=BM,∵∠MDN=60°,∠BDC=120°,∴∠M1DN=∠MDN=60°,∴△MDN≌△M1DN,∴MN=M1N.∴NC﹣BM=MN.【点睛】此题主要考查全等三角形的判定与性质,解题的关键是熟知等边三角形的性质及全等三角形的判定定理.。
初中几何|半角模型

初中几何|半角模型
半角模型是初中学习几何最常见的一个模型,这个模型常用的辅助线思维是旋转,而旋转又是学生几何思维中最不习惯的,那么我们如何进行利用呢?今天具体的进行讲解。
一、半角模型特征
1、共端点的等线段;
2、共顶点的倍半角;
二、半角模型辅助线的作法
1、旋转的方法:以公共端点为旋转中心,相等的两条线段的夹角为旋转角;
2、旋转的条件:具有公共端点的等线段;
3、旋转的目的:将分散的条件集中,隐蔽的关系显现。
三、等腰直角三角形的半角模型(大角夹小角)
如图,在△ABC中,AB=AC,∠BAC=90°,点D、E在边BC上,且∠EAD=45°.
(1)求证:△BAE∽△ADE∽△CDA
(2)求证:BD2+CE2=DE2
四、等腰直角三角形的半角模型(拓展)
1、如图,在△ABC中,AB=AC,∠BAC=90°,点D在边BC上,点E在BC的延长线上,且∠EAD=45°.求证:BD2+CE2=DE2
五、一般三角形的半角模型
六、正方形中半角模型相关结论(大角夹小角)
七、正方形中半角模型(拓展)。
【优】全等三角形之半角模型(解析版)

全等三角形之半角模型【模型讲解】模型、半角全等模型【解题技巧】过等腰三角形顶点两条射线,使两条射线的夹角为等腰三角形顶角的一半这样的模型称为半角模型。
常见的图形为正方形,正三角形,等腰直角三角形等,解题思路一般是将半角两边的三角形通过旋转(或者补短)到一边合并成新的三角形,从而进行等量代换,然后证明与半角形成的三角形全等,再通过全等的性质得到线段之间的数量关系。
半角模型(题中出现角度之间的半角关系)利用旋转(或者补短)——证全等——得到相关结论.【巩固训练】1.(1)如图,在四边形ABCD 中,AB AD =,180B D ∠+∠=︒,E 、F 分别是边BC 、CD 上的点,且12EAF BAD ∠=∠.求证:EF BE FD =+;(2)如图,在四边形ABCD 中,AB AD =,180B ADC ∠+∠=︒,E 、F 分别是边BC 、CD 延长线上的点,且12EAF BAD ∠=∠.(1)中的结论是否仍然成立?若成立,请证明;若不成立,请写出它们之间的数量关系,并证明.【答案】(1)见证明;(2)结论EF =BE +FD 不成立,应当是EF =BE ﹣FD ,证明见详解.【分析】(1)延长CB 至M ,使BM =DF ,连接AM .先证明△ABM ≌△ADF ,得到AF =AM ,∠2=∠3,再证明△AME ≌△AFE ,得到EF =ME ,进行线段代换,问题得证;(2)在BE 上截取BG ,使BG =DF ,连接AG .先证明△ABG ≌△ADF ,得到AG =AF ,再证明△AEG ≌△AEF ,得到EG =EF ,进行线段代换即可证明EF =BE ﹣FD .【详解】解:(1)证明:如图,延长CB 至M ,使BM =DF ,连接AM .∵∠ABC +∠D =180°,∠1+∠ABC =180°,∴∠1=∠D ,在△ABM 与△ADF 中,1AB AD D BM DF =⎧⎪∠=∠⎨⎪=⎩,∴△ABM ≌△ADF (SAS ).∴AF =AM ,∠2=∠3.∵∠EAF 12=∠BAD ,∴∠2+∠412=∠BAD =∠EAF .∴∠3+∠4=∠EAF ,即∠MAE =∠EAF .在△AME 与△AFE 中,AM AF MAE EAF AE AE =⎧⎪∠=∠⎨⎪=⎩,∴△AME ≌△AFE (SAS ).∴EF =ME ,即EF =BE +BM ,∴EF =BE +DF;(2)结论EF =BE +FD 不成立,应当是EF =BE ﹣FD .证明:如图,在BE 上截取BG ,使BG =DF ,连接AG .∵∠B +∠ADC =180°,∠ADF +∠ADC =180°,∴∠B =∠ADF .∵在△ABG与△ADF中,AB ADABG ADFBG DF=⎧⎪∠=∠⎨⎪=⎩,∴△ABG≌△ADF(SAS),∴∠BAG=∠DAF,AG=AF,∴∠BAG+∠EAD=∠DAF+∠EAD=∠EAF12=∠BAD,∴∠GAE=∠EAF.在△AGE与△AFE中,AG AFGAE EAFAE AE=⎧⎪∠=∠⎨⎪=⎩,∴△AEG≌△AEF,∴EG=EF,∵EG=BE﹣BG,∴EF=BE﹣FD.【点睛】本题属于三角形综合题,考查了三角形全等的判定和性质等知识,解题的关键是学会利用旋转变换的思想添加辅助线,构造全等三角形解决问题,解题时注意一些题目虽然图形发生变化,但是证明思路和方法是类似的,属于中考压轴题.2.已知四边形ABCD中,AB⊥AD,BC⊥CD,AB=BC,∠ABC=120°,∠MBN=60°,∠MBN绕B点旋转,它的两边分别交AD,DC(或它们的延长线)于E,F.(1)当∠MBN绕B点旋转到AE=CF时(如图1),求证:△ABE≌△CBF.(2)当∠MBN 绕点B旋转到AE≠CF时,如图2,猜想线段AE,CF,EF有怎样的数量关系,并证明你的猜想.(3)当∠MBN绕点B旋转到图3这种情况下,猜想线段AE,CF,EF有怎样的数量关系,并证明你的猜想.【答案】(1)见解析;(2)AE+CF=EF,证明见解析;(3)AE﹣CF=EF,证明见解析【分析】(1)利用SAS 定理证明△ABE ≌△CBF ;(2)延长DC 至点K ,使CK =AE ,连接BK ,分别证明△BAE ≌△BCK 、△KBF ≌△EBF ,根据全等三角形的性质、结合图形证明结论;(3)延长DC 至G ,使CG =AE ,仿照(2)的证明方法解答.【详解】(1)证明:在△ABE 和△CBF 中,=90?AB BC BAE BCF AE CF =⎧⎪=⎨⎪=⎩∠∠,∴△ABE ≌△CBF (SAS );(2)解:AE +CF =EF ,理由如下:延长DC 至点K ,使CK =AE ,连接BK ,在△BAE 与△BCK 中,=BA BC BAE BCK AE CK =⎧⎪=⎨⎪⎩∠∠,∴△BAE ≌△BCK (SAS ),∴BE =BK ,∠ABE=∠KBC ,∵∠FBE =60°,∠ABC =120°,∴∠FBC +∠ABE =60°,∴∠FBC +∠KBC =60°,∴∠KBF =∠FBE =60°,在△KBF 与△EBF 中,BK BE KBF EBF BF BF =⎧⎪=⎨⎪=⎩∠∠,∴△KBF ≌△EBF (SAS ),∴KF =EF ,∴AE +CF =KC +CF =KF =EF ;(3)解:AE ﹣CF =EF ,理由如下:延长DC 至G ,使CG =AE ,由(2)可知,△BAE ≌△BCG (SAS ),∴BE =BG ,∠ABE =∠GBC ,∠GBF =∠GBC ﹣∠FBC =∠ABE ﹣∠FBC =120°+∠FBC ﹣60°﹣∠FBC =60°,∴∠GBF =∠EBF ,∵BG =BE ,∠GBF =∠EBF ,BF =BF ,∴△GBF ≌△EBF ,∴EF =GF ,∴AE ﹣CF =CG ﹣CF =GF =EF.【点睛】本题考查的是全等三角形的判定和性质,正确作出辅助线、掌握全等三角形的判定定理和性质定理是解题的关键.3.(1)问题背景:如图1,在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,且∠EAF=60°,探究图中线段BE,EF,FD之间的数量关系.小明同学的方法是将△ABE绕点A逆时针旋转120°到△ADG的位置,然后再证明△AFE≌△AFG,从而得出结论:________________.(2)探索延伸:如图2,在四边形ABCD中,AB=AD,∠B+∠D=180°,E,F分别是边BC,CD上的点,且12EAF∠=∠BAD.上述结论是否仍然成立?请说明理由.(3)方法应用:如图3,E、F分别是正方形ABCD边BC、CD上的动点,连接AE、AF,并且始终保持∠EAF=45°,连接EF并延长与AD的延长线交于点G,说明AG=EG.(正方形四边相等,四个角均为90°)【答案】(1)EF=BE+FD,理由见解析;(2)证明见解析;(3)证明见解析.【分析】(1)将△ABE逆时针旋转得到△ADG,使得AD与AB重合,即△ABE≌△ADG,可得AE=AG,再证明△AEF≌△AGD,可得EF=FG即可;(2)如图2,将△ADF顺时针旋转得到△ABG,使得AD与AB重合,即△ADF≌△ABG;然后再证△EAG≌△EAF,可得GE=EF,再根据线段的和差即可解答;(3)将△ABE逆时针旋转得到△ADH,使得AD与AB重合,即△ABE≌△ADH,然后再证△EAF≌△HAF可得∠H=∠AEF,再根据直角三角形的性质得到∠EAG=∠H,即,∠EAG=∠AEF,最后根据等腰三角形的性质解答即可.【详解】解:(1)EF=BE+FD,理由如下:如图1,将△ABE逆时针旋转得到△ADG,使得AD与AB重合,即△ABE≌△ADG(SAS)∴AE=AG,∠BAE=∠DAG.∵∠EAF=60°,∠BAD=120°∵∠EAF=12∠BAD∴∠GAF=∠DAG+∠DAF=∠BAE+∠DAF=∠BAD-∠EAF=∠EAF=60°∴∠EAF=∠GAF 在△AEF和△GAF中AE=AG,∠EAF=∠GAF,AF=AF∴△EAG≌△EAF(SAS)∴EF=FG∴FG=DG+DF=BE+DF∴EF=BE+DF;故答案为EF=BE+DF;(2)证明:如图2,将△ADF顺时针旋转得到△ABG,使得AD与AB重合∴△ADF≌△ABG∴∠FAG=∠BAD,AF=AG,DF=GB∵∠EAF=12BAD∴∠EAF=∠EAG.在△EAG和△EAF中∵AG=AF,∠EAF=∠EAG,AE=AE∴△EAG≌△EAF(SAS)∴GE=EF,∵GE=GB+BE=DF+BE∴EF=BE+FD;(3)如图3,将△ABE逆时针旋转得到△ADH,使得AD与AB重合,即△ABE≌△ADH∴AE=AH,∠BAE=∠DAH.∵∠EAF=45°,∠BAD=90°∵∠EAF=12∠BAD∴∠HAF=∠DAH+∠DAF=∠BAE+∠DAF=∠BAD-∠EAF=∠EAF=60°∴∠EAF=∠HAF在△AEF和△HAF中AE=AH,∠EAF=∠HAF,AF=AF∴△EAF≌△HAF(SAS)∴∠H=∠AEF∵∠EAF=90°,∠HAD=90°∴∠HAD+∠EAG=∠HAD+∠H∴∠EAG=∠H∵∠H=∠AEF∴∠EAG=∠AEF∴AG=EG.【点睛】本题考查全等三角形的判定和性质以及旋转的性质,通过旋转作出全等三角形是解答本题的关键.4.在图1、图2,图3中.点E 、F 分别是四边形ABCD 边BC CD 、上的点;下面请你根据相应的条件解决问题.特例探索:(1)在图1中,四边形ABCD 为正方形(正方形四边相等,四个内角均为直角),45EAF ∠=︒,延长CD 至G ,使,2,3DG BE BE DF ===.则EF =__________.在图2中,90B D ∠=∠=︒,AB AD =,60BAD ∠=︒,30EAF∠=︒,1BE =, 1.5FD =;则EF =__________.归纳证明:(2)在图3中,180B D ∠+∠=︒,AB AD =.且12EAF BAD ∠=∠,请你观察(1)中的结果,猜想图3中线段,,BE EF FD 之间的数量关系,用等式表示出来,并利用图3证明你发现的关系式.【答案】(1)5,2.5;(2)EF=BE+FD ;(3)1650m .【分析】(1)先证明出△ABE ≅△ADG ,再根据∠DAF+∠BAE=45°得出∠EAF=∠FAG ,利用△AEF ≅△AGF 即可得出结果;延长CD 到G ,使BE=DG ,连接AG ,同理证明即可;(2)延长FD 到G ,使BE=DG ,利用条件证明△ABE ≅△ADG ,再根据∠DAF+∠BAE=45°得出∠EAF=∠FAG ,利用△AEF ≅△AGF 即可得出结论;(3)依照结论(2),延长DB 到E ,使BE=AC ,连接OE ,通过求证△OAC ≅△OBE 和△OCD ≅△OED 得出CD=DE=BD+BE=BD+AC ,代入数据求值即可.【详解】(1)∵BE=DG=2,∠B=∠ADG=90°,AB=AD ;∴△ABE ≅△ADG (SAS ),∴AE=AG ,∠BAE=∠DAG ,又∵∠DAF+∠BAE=45°,∴∠DAF+∠DAG=45°,∴∠EAF=∠FAG ,∴△AEF ≅△AGF (SAS ),∴EF=GD+DF=3+2=5;延长CD 到G ,使BE=DG ,连接AG ,同理可证:△ABE ≅△ADG ,△AEF ≅△AGF ,∴EF=GD+DF=2.5;(2)延长FD 到G ,使BE=DG ,∵BE=DG ,∠B=∠ADG ,AB=AD ;∴△ABE ≅△ADG (SAS ),∴AE=AG ,∠BAE=∠DAG ,又∵∠DAF+∠BAE=45°,∴∠DAF+∠DAG=45°,∴∠EAF=∠FAG ,∴△AEF ≅△AGF (SAS ),∴EF=GD+DF=DF+BE ;【点睛】此题属于推理探究类综合题考查全等三角形的性质及判定,有一定难度,主要总结该类题的规律解题即可.5.如图1,在正方形ABCD 中,,E F 分别是, BC CD 上的点,且45EAP ∠=︒,则有结论EF BE FD =+成立;()1如图2,在四边形ABCD 中,,90, AB AD B D E F =∠=∠=︒、分别是, BC CD 上的点,且EAF ∠是BAD ∠的一半,那么结论EF BE FD =+是否仍然成立?若成立,请证明;不成立,请说明理由.()2若将()1中的条件改为:如图3,在四边形ABCD 中,,180AB AD B ADC =∠+∠=︒,延长BC 到点E ,延长CD 到点F ,使得EAF ∠仍然是BAD ∠的一半,则结论EF BE FD =+是否仍然成立?若成立,请证明;不成立,请写出它们的数量关系并证明【答案】(1)详见解析;(2)结论不成立,应为,EF BE DF =-证明详见解析【分析】(1)如图(见解析),先根据三角形全等的判定定理与性质得出, BAG DAF AG AF ∠=∠=,再根据角的和差EAG EAF ∠=∠,然后根据三角形全等的判定定理与性质、线段的和差即可得;(2)先根据角的和差、邻补角的定义得出B ADF ∠=∠,再根据三角形全等的判定定理与性质得出, BAG DAF AG AF ∠=∠=,然后根据角的和差倍分得出EAG EAF ∠=∠,最后根据三角形全等的判定定理与性质、线段的和差即可得.【详解】(1)EF BE FD =+仍成立,证明如下:延长CB 到G ,使BG FD =,连接AG 90ABG D ∠=∠=︒ ,AB AD =()ABG ADF SAS ∴≅ , BAG DAF AG AF∴∠=∠=12EAF BAD ∠=∠ ,即1()2EAF DAF BAE EAF ∠=∠+∠+∠DAF BAE EAF ∠∠∠∴+=BAG BAE EAF ∴∠+∠=∠,即EAG EAF∠=∠()AEF AEG SAS ∴≅ EF EG BE BG EB FD ∴==+=+;(2)结论不成立,应为EF EB FD =-,证明如下:在BE 上截取BG ,使BG FD =,连接AG180B ADC =︒∠+∠ ,180ADF ADC ∠∠=+︒B ADF∴∠=∠AB AD = ()ABG ADF SAS ∴≅ , BAG DAF AG AF∴∠=∠=12EAF BAD ∠=∠ ,即1()2EAF DAE EAG BAG ∠=∠+∠+∠11()()22EAF DAE EAG DAF EAF EAG ∴∠=∠+∠+∠=∠+∠EAG EAF ∴∠=∠AE AE = ()AEG AEF SAS ∴≅ EG EF∴=EG EB BG EB FD =-=- EF EB FD ∴=-.【点睛】本题考查了三角形全等的判定定理与性质、角的和差倍分等知识点,通过作辅助线,构造全等三角形是解题关键.6.(1)问题背景:如图1,在四边形ABCD 中,AB =AD ,∠BAD=120°,∠B =∠ADC=90°,E ,F 分别是BC,CD 上的点,且∠EAF =60°,探究图中线段BE ,EF ,FD 之间的数量关系.小明同学探究此问题的方法是延长FD 到点G ,使DG=BE ,连结AG ,先证明ΔABE ≅ΔADG ,再证明ΔAEF ≌ΔAGF ,可得出结论,他的结论应是.(2)探索延伸:如图2,在四边形ABCD 中,AB=AD ,∠B+∠D=180°,E ,F 分别是BC ,CD 上的点,∠EAF=12∠BAD,上述结论是否依然成立?并说明理由.【答案】(1)EF=BE+DF ;(2)成立,见解析【分析】(1)延长FD 到点G .使DG=BE .连结AG ,即可证明△ABE ≌△ADG ,可得AE=AG ,再证明△AEF ≌△AGF ,可得EF=FG ,即可解题;(2)延长FD 到点G .使DG=BE .连结AG ,即可证明△ABE ≌△ADG ,可得AE=AG ,再证明△AEF ≌△AGF ,可得EF=FG ,即可解题;【详解】解:(1)EF=BE+DF ,证明如下:在△ABE 和△ADG 中,DG BE B ADGAB AD =⎧⎪∠=∠⎨⎪=⎩()ABE ADG SAS ∴∆∆≌,AE AG BAE DAG ∴=∠=∠12EAF BAD ∠=∠ GAF DAG DAF BAE DAF BAD EAF EAF∴∠=∠+∠=∠+∠=∠-∠=∠EAF GAF ∴∠=∠在△AEF 和△AGF 中,AE AG EAF GAF AF AF =⎧⎪∠=∠⎨⎪=⎩()AEF AGF SAS ∴∆∆≌EF FG ∴=FG DG DF BE DF =+=+ EF BE DF ∴=+故答案为EF=BE+DF .(2)结论EF=BE+DF 仍然成立;理由:延长FD 到点G .使DG=BE .连结AG,如图②,在△ABE 和△ADG 中DG BE B ADG AB AD =⎧⎪∠=∠⎨⎪=⎩∴△ABE ≌△ADG (SAS ),∴AE=AG ,∠BAE=∠DAG ,∵∠EAF=12∠BAD ,∴∠GAF=∠DAG+∠DAF=∠BAE+∠DAF=∠BAD-∠EAF=∠EAF ,∴∠EAF=∠GAF ,在△AEF 和△AGF 中,AE AG EAF GAF AF AF =⎧⎪∠=∠⎨⎪=⎩∴△AEF ≌△AGF (SAS ),∴EF=FG ,∵FG=DG+DF=BE+DF ,∴EF=BE+DF ;【点睛】本题考查了全等三角形的判定和性质及“半角模型”,熟练掌握全等三角形的判定和性质及“半角模型”构造全等的方法是解题的关键.。
【教学研究】半角模型的定义、八个结论、逆命题及应用

【教学研究】半角模型的定义、八个结论、逆命题及应用
定义
半角模型是指:从正方形的一个顶点引出夹角为45°的两条射线,并连结它们与该顶点的两对边的交点构成的基本平面几何模型。
由于两射线的夹角是正方形一个内角的一半,故名半角模型,又称“角含半角模型”。
其中,将45°角的两边及其对边围成的三角形称为“半角三角形”(即图中的△AEF)
半角模型的结论:
半角模型中射线与端点对边交点的连线长等于端点两相邻点到各自最近交点的距离和。
即:如图中,EF=BE+DF。
结论
其他结论
逆命题
应用
半角模型是初中几何方面问题的常见模型,常用于基本几何命题的证明和一些边长、角度等的计算。
其逆定理则使其可用性更强,避免冗长的证明过程。
九年级中考几何模型之半角模型详解

中考几何模型之半角模型【模型由来】半角模型是指:共顶点的两个一大一小的角,其中小角是大角的一半。
如下图中:若小角∠EAD等于大角∠BAC的一半,我们习惯上称之为“半角模型”。
【模型思想】通过旋转变化后构造全等三角形,实线边的转化。
【基本模型】类型一、90°中夹45°(正方形中的半角模型)条件:在正方形ABCD中,E、F分别是BC、CD边上的点,∠EAF=45°,BD为对角线,交AE于M点,交AF于N点。
结论①:图1、2中,EF=BE+FD;证明:如图3中,将AF绕点A顺时针旋转90°,F点落在F’处,连接BF’,∴∠EAF’=90°-∠EAF=90°-45°=45°=∠EAF,且AE=AE,AF=AF’,∴△FAE≌△F’AE(SAS),∴EF=EF’,又∠D=∠ABF’=90°,∠ABE=90°,∴∠ABE+∠ABF’=90°+90°=180°,∴F’、B、E三点共线,∴EF’=BE+BF’=BE+DF。
结论②:图2中MN²=BM²+DN²;证明:如图4中,将AN绕点A顺时针旋转90°,N点落在N’处,连接AN’、BN’、MN’,∴∠N’AM=90°-∠EAF=90°-45°=45°=∠MAN,且AM=AM,AN=AN’,∴△MAN’≌△MAN(SAS),∴MN=MN’,又∠ADN=45°=∠ABN ’,∠ABD=45°,∴∠MBN ’=∠ABD+∠ABN ’=45°+45°=90°,∴在Rt △MBN ’中,MN ’²=BM ²+BN ’²,即MN ²=BM ²+BN ’²。
结论③:图1、2中EA 平分∠BEF ,FA 平分∠DFE 。
八年级数学全等三角形“半角”模型

八年级数学全等三角形“半角”模型一、什么叫半角模型定义:我们习惯把过等腰三角形顶角的顶点引两条射线,使两条射线的夹角为等腰三角形顶角的一半这样的模型称为半角模型。
1、常见的图形正方形,正三角形,等腰直角三角形等。
2、解题思路① 将半角两边的三角形通过旋转到一边合并形成新的三角形;② 证明与半角形成的三角形全等;③ 通过全等的性质得出线段之间的数量关系,从而解决问题。
二、基本模型1、正方形内含半角例题1、如图,在正方形ABCD中,E、F分别是BC、CD边上的点,∠EAF=45°,求证:EF=BE+DF。
例题1图证明:将△ADF 绕点 A 顺时针旋转90° ,使点 D 与点 B ,点 F 与点 G 重合(△ADF ≌ △ABG),如下图所示:例题1旋转图在△AGE 和△AFE 中∵ AG = AF , ∠GAE = ∠EAF = 45° , AE = AE∴ △AGE ≌ △AFE ∴ GE = EF∵ GE = GB + BE = DF + BE∴ EF= BE + DF2、等边三角形内含半角例题2、如图,已知△ABC 是等边三角形,点 D 是△ABC 外一点,DB = DC 且∠BDC = 120° ,∠EDF = 60° ,DE ,DF 分别交 AB ,AC 于点 E , F 。
求证: EF = BE + CF例题2图证明:将△BDE 绕点 D 旋转至△CDG ,使△BDE ≌ △CDG(注:题目中已知条件 DB = DC 且∠BDC = 120°,易证∠EBD = ∠GCD = 90°,F、C、G 三点共线)例题2旋转图在△EDF 和△GDF 中∵ ED = GD , ∠EDF = ∠GDF = 60° , DF = DF∴ △EDF ≌ △GDF ∴ EF = GF∵ GF = GC + CF = BE + CF∴ EF = BE + CF3、等腰直角三角形内含半角例题3、如图,已知△ABC 是等腰直角三角形,点 D ,E 在 BC 上,且满足∠DAE = 45° 。
全等三角形模型之 - 半角模型

半角模型(一)把过等腰三角形顶角的顶点引两条射线,使两条射线的夹角为等腰三角形顶角的一半这样的模型称为半角模型。
1、常见的图形正方形,正三角形,等腰直角三角形等。
特点:①大角内部有一小角,且小角角度是大角角度的一般②大角的两边相等,保证旋转之后能够完全重合③大角的两边与其他两边形成的两个角互补,保证旋转之后的两个三角形两边能在同一直线上2、解题思路①将半角两边的三角形通过旋转到一边合并形成新的三角形;②证明与半角形成的三角形全等;③通过全等的性质得出线段之间的数量关系,从而解决问题。
二、基本模型1、正方形内含半角例题1、如图,在正方形ABCD中,E、F分别是BC、CD边上的点,∠EAF=45°,求证:EF=BE+DF。
2、等边三角形内含半角例题2、如图,已知△ABC 是等边三角形,点 D 是△ABC 外一点,DB = DC 且∠BDC = 120°,∠EDF = 60°,DE ,DF 分别交AB ,AC 于点E , F 。
求证:EF = BE + CF3、等腰直角三角形内含半角例题3、如图,已知△ABC 是等腰直角三角形,点D ,E 在BC 上,且满足∠DAE = 45°。
求证:DE^2 = BD^2 + CE^2半角模型练习(二)条件:ABCD为正方形,∠MAN=45°,AM 与AN 分别与BC 边和CD 边交与M,N 两点,连接MN.思路:1、旋转辅助线;①延长CD 到E ,使ED=BM ,连AE 或延长CB 到F ,使FE=DM ,连AF②将三角形AND 绕点A 顺时针旋转90°,得到三角形ABF 。
注意:旋转需证F,B.M 三点共线结论:MN=BM+DN(2)C 三角形CMN=2AB(3)AM,AN 分别平分∠BMN,∠MND2、翻转(对称)辅助线:①做AP 垂直MN ,交MN 于点P②将三角形AND,三角形ABM 分别沿着AM,AM 翻转,但一定要证明M,P ,N 三点共线如图,正方形ABCD 的边长为2,点EF 分别是在AD ,CD 上,若∠EBF=45°,则三角形EDF 的周长等于多少?例题: 已知,如图1,四边形ABCD 是正方形,E 、F 分别在边BC 、CD 上,且∠EAF=45°,我们把这种模型称为“半角模型”,在解决“半角模型”问题时,旋转时一种常用的方法.(1)在图1中,连接EF ,为了证明结论“EF=BE+DF ”,小明将△ADF 绕点A 顺时针旋转90°后解答了这个问题,请按小明的思路写出证明过程; (2)如图2,当∠EAF 的两边分别与CB 、DC 的延长线交于点E 、F ,连接EF ,试探究线段EF 、BE 、DF 之间的数量关系,并证明:。
模型汇编半角模型结论汇编(含解析)

模型汇编半角模型结论汇编(含解析)一、45°--90°半角模型的基本结论45°---90°半角模型是初中几何中最重要的模型之一,涉及的知识点包括全等三角形的判定,性质;等腰三角形;等积变换;勾股定理;平行四边形判定,性质;四点共圆;旋转;相似等。
几乎包含了整个初中的几何考点。
特点是:图形复杂,变化多,结论多。
平时学生练习比较零散,不利于掌握。
现在把其中常用的结论加以整理,方便大家学习。
证明策略:旋转法,翻折法,截长补短法1.找共顶点的等边2.旋转等边所在的三角形使得两条等边重合,构造半角全等。
3.注意是否要考虑三点共线。
❖45°--90°半角模型的基本结论1基本结论一:如图,正方形ABCD中,E、F为BC,CD的上点且∠EAF=45°,AH⊥EF.求证:(1)EF=BE+DF(2)CΔECF=2AB(3) AH=AB (4) S△ABE+S△ADF=S△AEF(5) ∠BEA=∠BEF∠AFE=∠AFD方法一:旋转法方法一:如图1,把△ADF绕点A顺时针旋转90°得到△ABG.(亦可旋转△ABE)∴∠DAF=∠GAB∵∠BAD=90°,∠EAF=45° ∴∠BAE+DAF=90°-45°=45°∴∠GAE=∠BAE+∠GAB=45°=∠FAE, ∠ABC=∠D=∠ABG=90°∴∠ABC+∠ABG=180° ∴点G,B,E三点共线。
∴△AEF≅△AEG(SAS)∴EF=GE,即EG=GB+BE,∴EF=BE+GB.结论一方法二:截长补短法方法二:截长补短法(证明略)证明:延长CB至点G,使GB=DF,连接AG.1.证明ΔABG≅ΔADF(SAS)2.∠GAE=∠BAE+∠GAB=45°=∠FAE3.证明△AEF≅△AEG(SAS),∴EF=BE+GB.(亦可延长CD至点M,使得DM=BE,连接AM)方法三:翻折法方法三:把ΔABE沿AE翻折得到ΔAEG,连接GF. ∴AB=AG=AD,BE=GE,∠BAE=∠GAE.∵∠BAD=90°,∠EAF=∠EAG+GAF=45°∴∠BAE+DAF=90°-45°=45°∴∠GAE+∠DAF=45°∴∠GAF=∠DAF∴ΔAGF≅ΔADF(ASA)∴∠AGF=∠D=90°,GF=DF.∴∠AGF+∠AGE=180°∴点E,G,F三点共线。
专题20 半角模型(解析版)

中考常考几何模型专题20 半角模型倍长中线或类中线(与中点有关的线段)构造全等三角形 如图①: (1)∠2=21∠AOB ;(2)OA=OB 。
如图②:连接 FB ,将△FOB 绕点 O 旋转至△FOA 的位置,连接 F ′E 、FE ,可得△OEF ′≌△OEF 。
模型精练1.(2019秋•九龙坡区校级月考)如图.在四边形ABCD 中,∠B +∠ADC =180°,AB =AD ,E 、F 分别是边BC 、CD 延长线上的点,且∠EAF =12∠BAD ,求证:EF =BE ﹣FD .【点睛】在BE 上截取BG ,使BG =DF ,连接AG .根据SAA 证明△ABG ≌△ADF 得到AG =AF ,∠BAG =∠DAF ,根据∠EAF =12∠BAD ,可知∠GAE =∠EAF ,可证明△AEG ≌△AEF ,EG =EF ,那么EF =GE =BE ﹣BG =BE ﹣DF .【解析】证明:在BE 上截取BG ,使BG =DF ,连接AG .∵∠B +∠ADC =180°,∠ADF +∠ADC =180°, ∴∠B =∠ADF . 在△ABG 和△ADF 中, {AB =AD∠B =∠ADF BG =DF, ∴△ABG ≌△ADF (SAS ), ∴∠BAG =∠DAF ,AG =AF .∴∠BAG +∠EAD =∠DAF +∠EAD =∠EAF =12∠BAD . ∴∠GAE =∠EAF . 在△AEG 和△AEF 中, {AG =AF∠GAE =∠EAF AE =AE, ∴△AEG ≌△AEF (SAS ). ∴EG =EF ,∵EG=BE﹣BG∴EF=BE﹣FD.2.(2020•锦州模拟)问题情境:已知,在等边△ABC中,∠BAC与∠ACB的角平分线交于点O,点M、N 分别在直线AC,AB上,且∠MON=60°,猜想CM、MN、AN三者之间的数量关系.方法感悟:小芳的思考过程是在CM上取一点,构造全等三角形,从而解决问题;小丽的思考过程是在AB取一点,构造全等三角形,从而解决问题;问题解决:(1)如图1,M、N分别在边AC,AB上时,探索CM、MN、AN三者之间的数量关系,并证明;(2)如图2,M在边AC上,点N在BA的延长线上时,请你在图2中补全图形,标出相应字母,探索CM、MN、AN三者之间的数量关系,并证明.【点睛】(1)在AC上截取CD=AN,连接OD,证明△CDO≌△ANO,根据全等三角形的性质得到OD =ON,∠COD=∠AON,证明△DMO≌△NMO,得到DM=MN,结合图形证明结论;(2)在AC延长线上截取CD=AN,连接OD,仿照(1)的方法解答.【解析】解:(1)CM=AN+MN,理由如下:在AC上截取CD=AN,连接OD,∵△ABC 为等边三角形,∠BAC 与∠ACB 的角平分线交于点O , ∴∠OAC =∠OCA =30°, ∴OA =OC ,在△CDO 和△ANO 中, {OC =OA∠OCD =∠OAN CD =AN, ∴△CDO ≌△ANO (SAS ) ∴OD =ON ,∠COD =∠AON , ∵∠MON =60°, ∴∠COD +∠AOM =60°, ∵∠AOC =120°, ∴∠DOM =60°, 在△DMO 和△NMO 中, {OD =ON∠DOM =∠NOM OM =OM, ∴△DMO ≌△NMO , ∴DM =MN ,∴CM =CD +DM =AN +MN ; (2)补全图形如图2所示:CM =MN ﹣AN ,理由如下:在AC 延长线上截取CD =AN ,连接OD , 在△CDO 和△ANO 中, {CD =AN∠OCD =∠OAN =150°OC =OA, ∴△CDO ≌△ANO (SAS ) ∴OD =ON ,∠COD =∠AON , ∴∠DOM =∠NOM , 在△DMO 和△NMO 中, {OD =ON∠DOM =∠NOM OM =OM, ∴△DMO ≌△NMO (SAS ) ∴MN =DM ,∴CM =DM ﹣CD =MN ﹣AN .3.(2020•章丘区模拟)如图,在正方形ABCD 中,M 、N 分别是射线CB 和射线DC 上的动点,且始终∠MAN =45°.(1)如图1,当点M 、N 分别在线段BC 、DC 上时,请直接写出线段BM 、MN 、DN 之间的数量关系; (2)如图2,当点M 、N 分别在CB 、DC 的延长线上时,(1)中的结论是否仍然成立,若成立,给予证明,若不成立,写出正确的结论,并证明;(3)如图3,当点M 、N 分别在CB 、DC 的延长线上时,若CN =CD =6,设BD 与AM 的延长线交于点P ,交AN 于Q ,直接写出AQ 、AP 的长.【点睛】(1)在MB 的延长线上,截取BE =DN ,连接AE ,则可证明△ABE ≌△ADN ,得到AE =AN ,进一步证明△AEM ≌△ANM ,得出ME =MN ,得出BM +DN =MN ;(2)在DC 上截取DF =BM ,连接AF ,可先证明△ABM ≌△ADF ,得出AM =AF ,进一步证明△MAN ≌△F AN ,可得到MN =NF ,从而可得到DN ﹣BM =MN ;(3)由已知得出DN =12,由勾股定理得出AN =√AD 2+DN 2=6√5,由平行线得出△ABQ ∽△NDQ ,得出BQ DQ=AQ NQ=AB DN=12,AQ AN=13,求出AQ =2√5;由(2)得出DN ﹣BM =MN .设BM =x ,则MN=12﹣x ,CM =6+x ,在Rt △CMN 中,由勾股定理得出方程,解方程得出BM =2,由勾股定理得出AM =√AB 2+BM 2=2√10,由平行线得出△PBM ∽△PDA ,得出PM PA=BM DA=13,求出PM =12AM =√10,得出AP =AM +PM =3√10.【解析】解:(1)BM +DN =MN ,理由如下:如图1,在MB的延长线上,截取BE=DN,连接AE,∵四边形ABCD是正方形,∴AB=AD,∠BAD=∠ABC=∠D=90°,∴∠ABE=90°=∠D,在△ABE和△ADN中,{AB=AD∠ABE=∠D BE=DN,∴△ABE≌△ADN(SAS),∴AE=AN,∠EAB=∠NAD,∴∠EAN=∠BAD=90°,∵∠MAN=45°,∴∠EAM=45°=∠NAM,在△AEM和△ANM中,{AE=AN∠EAM=∠NAM AM=AM,∴△AEM≌△ANM(SAS),∴ME=MN,又∵ME=BE+BM=BM+DN,∴BM+DN=MN;故答案为:BM+DN=MN;(2)(1)中的结论不成立,DN﹣BM=MN.理由如下:如图2,在DC上截取DF=BM,连接AF,则∠ABM=90°=∠D,在△ABM和△ADF中,{AB=AD∠ABM=∠D BM=DF,∴△ABM≌△ADF(SAS),∴AM=AF,∠BAM=∠DAF,∴∠BAM+∠BAF=∠BAF+∠DAF=∠BAD=90°,即∠MAF=∠BAD=90°,∵∠MAN=45°,∴∠MAN=∠F AN=45°,在△MAN和△F AN中,{AM=AF∠MAN=∠FAN AN=AN,∴△MAN≌△F AN(SAS),∴MN=NF,∴MN=DN﹣DF=DN﹣BM,∴DN﹣BM=MN.(3)∵四边形ABCD是正方形,∴AB=BC=AD=CD=6,AD∥BC,AB∥CD,∠ABC=∠ADC=∠BCD=90°,∴∠ABM=∠MCN=90°,∵CN=CD=6,∴DN=12,∴AN=√AD2+DN2=√62+122=6√5,∵AB∥CD,∴△ABQ ∽△NDQ ,∴BQ DQ =AQ NQ =AB DN=612=12,∴AQ AN=13,∴AQ =13AN =2√5; 由(2)得:DN ﹣BM =MN .设BM =x ,则MN =12﹣x ,CM =6+x ,在Rt △CMN 中,由勾股定理得:62+(6+x )2=(12﹣x )2, 解得:x =2, ∴BM =2,∴AM =√AB 2+BM 2=√62+22=2√10, ∵BC ∥AD , ∴△PBM ∽△PDA ,∴PM PA=BM DA=26=13,∴PM =12AM =√10, ∴AP =AM +PM =3√10.4.(2019•麒麟区模拟)已知,正方形ABCD中,∠MAN=45°,∠MAN绕点A顺时针旋转,它的两边分别交CB、DC(或它们的延长线)于点M、N,AH⊥MN于点H.(1)如图①,当∠MAN绕点A旋转到BM=DN时,请你直接写出AH与AB的数量关系:AH=AB;(2)如图②,当∠MAN绕点A旋转到BM≠DN时,(1)中发现的AH与AB的数量关系还成立吗?如果不成立请写出理由,如果成立请证明;(3)如图③,已知∠MAN=45°,AH⊥MN于点H,且MH=2,NH=3,求AH的长.(可利用(2)得到的结论)【点睛】(1)由三角形全等可以证明AH=AB,(2)延长CB至E,使BE=DN,证明△AEM≌△ANM,能得到AH=AB,(3)分别沿AM、AN翻折△AMH和△ANH,得到△ABM和△AND,然后分别延长BM和DN交于点C,得正方形ABCE,设AH=x,则MC=x﹣2,NC=x﹣3,在Rt△MCN中,由勾股定理,解得x.【解析】解:(1)如图①AH=AB.(2)数量关系成立.如图②,延长CB至E,使BE=DN.∵ABCD是正方形,∴AB=AD,∠D=∠ABE=90°,在Rt△AEB和Rt△AND中,{AB=AD∠ABE=∠ADN BE=DN,∴Rt△AEB≌Rt△AND,∴AE=AN,∠EAB=∠NAD,∵∠DAN+∠BAM=45°,∴∠EAB+∠BAM=45°,∴∠EAM=45°,∴∠EAM=∠NAM=45°,在△AEM和△ANM中,{AE=AN∠EAM=∠NAM AM=AM,∴△AEM≌△ANM.∴S△AEM=S△ANM,EM=MN,∵AB、AH是△AEM和△ANM对应边上的高,∴AB=AH.(3)如图③分别沿AM、AN翻折△AMH和△ANH,得到△ABM和△AND,∴BM=2,DN=3,∠B=∠D=∠BAD=90°.分别延长BM和DN交于点C,得正方形ABCD,由(2)可知,AH=AB=BC=CD=AD.设AH=x,则MC=x﹣2,NC=x﹣3,在Rt△MCN中,由勾股定理,得MN2=MC2+NC2∴52=(x﹣2)2+(x﹣3)2(6分)解得x1=6,x2=﹣1.(不符合题意,舍去)∴AH=6.5.(2019秋•东台市期末)在等边△ABC 的两边AB 、AC 所在直线上分别有两点M 、N ,D 为△ABC 外一点,且∠MDN =60°,∠BDC =120°,BD =DC .探究:当M 、N 分别在直线AB 、AC 上移动时,BM 、NC 、MN 之间的数量关系及△AMN 的周长Q 与等边△ABC 的周长L 的关系.(1)如图1,当点M 、N 边AB 、AC 上,且DM =DN 时,BM 、NC 、MN 之间的数量关系是 BM +NC =MN ;此时Q L=23;(2)如图2,点M 、N 在边AB 、AC 上,且当DM ≠DN 时,猜想( I )问的两个结论还成立吗?若成立请直接写出你的结论;若不成立请说明理由.(3)如图3,当M 、N 分别在边AB 、CA 的延长线上时,探索BM 、NC 、MN 之间的数量关系如何?并给出证明.【点睛】(1)由DM =DN ,∠MDN =60°,可证得△MDN 是等边三角形,又由△ABC 是等边三角形,CD =BD ,易证得Rt △BDM ≌Rt △CDN ,然后由直角三角形的性质,即可求得BM 、NC 、MN 之间的数量关系BM+NC=MN,此时QL=23;(2)在CN的延长线上截取CM1=BM,连接DM1.可证△DBM≌△DCM1,即可得DM=DM1,易证得∠CDN=∠MDN=60°,则可证得△MDN≌△M1DN,然后由全等三角形的性质,即可得结论仍然成立;(3)首先在CN上截取CM1=BM,连接DM1,可证△DBM≌△DCM1,即可得DM=DM1,然后证得∠CDN=∠MDN=60°,易证得△MDN≌△M1DN,则可得NC﹣BM=MN.【解析】解:(1)如图1,BM、NC、MN之间的数量关系BM+NC=MN.此时QL=23.(2分).理由:∵DM=DN,∠MDN=60°,∴△MDN是等边三角形,∵△ABC是等边三角形,∴∠A=60°,∵BD=CD,∠BDC=120°,∴∠DBC=∠DCB=30°,∴∠MBD=∠NCD=90°,∵DM=DN,BD=CD,∴Rt△BDM≌Rt△CDN,∴∠BDM=∠CDN=30°,BM=CN,∴DM=2BM,DN=2CN,∴MN=2BM=2CN=BM+CN;∴AM=AN,∴△AMN是等边三角形,∵AB =AM +BM , ∴AM :AB =2:3,∴Q L=23;(2)猜想:结论仍然成立. (3分).证明:在NC 的延长线上截取CM 1=BM ,连接DM 1.(4分) ∵∠MBD =∠M 1CD =90°,BD =CD , ∴△DBM ≌△DCM 1,∴DM =DM 1,∠MBD =∠M 1CD ,M 1C =BM , ∵∠MDN =60°,∠BDC =120°, ∴∠M 1DN =∠MDN =60°, ∴△MDN ≌△M 1DN ,∴MN =M 1N =M 1C +NC =BM +NC ,∴△AMN 的周长为:AM +MN +AN =AM +BM +CN +AN =AB +AC ,∴Q L=23;(3)证明:在CN 上截取CM 1=BM ,连接DM 1.(4分) 可证△DBM ≌△DCM 1, ∴DM =DM 1,(5分)可证∠M 1DN =∠MDN =60°, ∴△MDN ≌△M 1DN , ∴MN =M 1N ,(7分).∴NC﹣BM=MN.(8分).6.请阅读下列材料:已知:如图(1)在Rt△ABC中,∠BAC=90°,AB=AC,点D、E分别为线段BC上两动点,若∠DAE =45°.探究线段BD、DE、EC三条线段之间的数量关系.小明的思路是:把△AEC绕点A顺时针旋转90°,得到△ABE′,连接E′D,使问题得到解决.请你参考小明的思路探究并解决下列问题:(1)猜想BD、DE、EC三条线段之间存在的数量关系式,直接写出你的猜想;(2)当动点E在线段BC上,动点D运动在线段CB延长线上时,如图(2),其它条件不变,(1)中探究的结论是否发生改变?请说明你的猜想并给予证明;(3)已知:如图(3),等边三角形ABC中,点D、E在边AB上,且∠DCE=30°,请你找出一个条件,使线段DE、AD、EB能构成一个等腰三角形,并求出此时等腰三角形顶角的度数.【点睛】(1)DE2=BD2+EC2,将△ADB沿直线AD对折,得△AFD,连FE,容易证明△AFD≌△ABD,然后可以得到AF=AB,FD=DB,∠F AD=∠BAD,∠AFD=∠ABD,再利用已知条件可以证明△AFE ≌△ACE,从而可以得到∠DFE=∠AFD﹣∠AFE=135°﹣45°=90°,根据勾股定理即可证明猜想的结论;(2)根据(1)的思路一样可以解决问题;(3)当AD=BE时,线段DE、AD、EB能构成一个等腰三角形.如图,与(1)类似,以CE为一边,作∠ECF=∠ECB,在CF上截取CF=CB,可得△CFE≌△CBE,△DCF≌△DCA,然后可以得到AD =DF,EF=BE.由此可以得到∠DFE=∠1+∠2=∠A+∠B=120°,这样就可以解决问题.【解析】解:(1)DE2=BD2+EC2;(2)关系式DE2=BD2+EC2仍然成立.证明:将△ADB沿直线AD对折,得△AFD,连FE∴△AFD≌△ABD,∴AF=AB,FD=DB,∠F AD=∠BAD,∠AFD=∠ABD,又∵AB=AC,∴AF=AC,∵∠F AE=∠F AD+∠DAE=∠F AD+45°,∠EAC=∠BAC﹣∠BAE=90°﹣(∠DAE﹣∠DAB)=45°+∠DAB,∴∠F AE=∠EAC,又∵AE=AE,∴△AFE≌△ACE,∴FE=EC,∠AFE=∠ACE=45°,∠AFD=∠ABD=180°﹣∠ABC=135°∴∠DFE=∠AFD﹣∠AFE=135°﹣45°=90°,∴在Rt△DFE中,DF2+FE2=DE2,即DE2=BD2+EC2;(3)当AD=BE时,线段DE、AD、EB能构成一个等腰三角形.如图,与(2)类似,以CE为一边,作∠ECF=∠ECB,在CF上截取CF=CB,可得△CFE≌△CBE,△DCF≌△DCA.∴AD=DF,EF=BE.∴∠DFE=∠1+∠2=∠A+∠B=120°.若使△DFE为等腰三角形,只需DF=EF,即AD=BE,∴当AD=BE时,线段DE、AD、EB能构成一个等腰三角形,且顶角∠DFE为120°.7.(2019•夏津县二模)如图1,在正方形ABCD中,E、F分别是BC,CD上的点,且∠EAF=45度.则有结论EF=BE+FD成立;(1)如图2,在四边形ABCD中,AB=AD,∠B=∠D=90°,E、F分别是BC,CD上的点,且∠EAF 是∠BAD的一半,那么结论EF=BE+FD是否仍然成立?若成立,请证明;不成立,请说明理由.(2)若将(1)中的条件改为:如图3,在四边形ABCD中,AB=AD,∠B+∠D=180°,延长BC到点E,延长CD到点F,使得∠EAF仍然是∠BAD的一半,则结论EF=BE+FD是否仍然成立?若成立,请证明;不成立,请写出它们的数量关系并证明.【点睛】(1)结论仍然成立.延长CB到G,使BG=FD,根据已知条件容易证明△ABG≌△ADF,由此可以推出∠BAG=∠DAF,AG=AF,而∠EAF=12∠BAD,所以得到∠DAF+∠BAE=∠EAF,进一步得到∠EAF=∠GAE,现在可以证明△AEF≌△AEG,然后根据全等三角形的性质就可以证明结论成立;(2)结论不成立,应为EF=BE﹣DF,如图在CB上截取BG=FD,由于∠B+∠ADC=180°,∠ADF+∠ADC=180°,可以得到∠B=∠ADF,再利用已知条件可以证明△ABG≌△ADF,由此可以推出∠BAG=∠DAF,AG=AF,而∠EAF=12∠BAD,所以得到∠EAF=∠GAE,现在可以证明△AEF≌△AEG,再根据全等三角形的性质就可以证明EF=EG=EB﹣BG=EB﹣DF.【解析】解:(1)延长CB到G,使BG=FD,连接AG,∵∠ABG=∠D=90°,AB=AD,∴△ABG≌△ADF,∴∠BAG=∠DAF,AG=AF,∵∠EAF=12∠BAD,∴∠DAF+∠BAE=∠EAF,∴∠EAF=∠GAE,∴△AEF≌△AEG,∴EF=EG=EB+BG=EB+DF.(2)结论不成立,应为EF=BE﹣DF,证明:在BE上截取BG,使BG=DF,连接AG.∵∠B+∠ADC=180°,∠ADF+∠ADC=180°,∴∠B=∠ADF.∵AB=AD,∴△ABG≌△ADF.∴∠BAG=∠DAF,AG=AF.∴∠BAG+∠EAD=∠DAF+∠EAD=∠EAF=12∠BAD.∴∠GAE=∠EAF.∵AE=AE,∴△AEG≌△AEF.∴EG=EF∵EG=BE﹣BG∴EF=BE﹣FD.8.(1)如图1,将∠EAF绕着正方形ABCD的顶点A顺时针旋转,∠EAF的两边交BC于E,交CD于F,连接EF.若∠EAF=45°,BE、DF的长度是方程x2﹣5x+6=0的两根,请直接写出EF的长;(2)如图2,将∠EAF绕着四边形ABCD的顶点A顺时针旋转,∠EAF的两边交CB的延长线于E,交DC的延长线于F,连接EF.若AB=AD,∠ABC与∠ADC互补,∠EAF=12∠BAD,请直接写出EF与DF、BE之间的数量关系,并证明你的结论;(3)在(2)的前提下,若BC=4,DC=7,CF=2,求△CEF的周长.①EF的长为:5;②数量关系:EF=DF﹣BE.【点睛】(1)先证明△ABE≌△ADM,再证明△AEF≌△AMF,得到EF=DF+BE即可;(2)先证明△ADM≌△ABE,再证明△EAF≌△MAF,即可;(3)直接计算△CEF的周长=EF+BE+BC+CF=DF+BC+CF=9+4+2=15.【解析】(1)解:如图1,延长CD使DM=BE,连接AM;在△ABE和△ADM中,{AB=AD∠ABE=∠ADM=90°BE=DM∴△ABE≌△ADM,∴AE=AM,∠EAB=∠DAM,∵∠EAF=45°,且∠EAB=∠DAM,∴∠BAF+∠DAM=45°,即∠MAF=45°=∠EAF,又∵AE=AM,AF=AF,∴△AEF≌△AMF,∴EF=FM,∵FM=DF+DM,∴EF=DF+NB,即EF=DF+BE;∵BE、DF的长度是方程x2﹣5x+6=0的两根,∴BE=2,DF=3,∴EF=DF+BE=3+2=5,(2)证明:如图2,在DF上截取DM=BE,∵∠D+∠ABC=∠ABE+∠ABC=180°,∴∠D=∠ABE,∴AD=AB,∴△ADM≌△ABE,∴AM=AE,∴∠DAM=∠BAE;∵∠EAF=∠BAE+∠BAF=∠DAM+∠BAF=∠BAD﹣∠F AM=12∠BAD,∴∠MAF=12∠BAD,∴∠EAF=∠MAF;∵AF是△EAF与△MAF的公共边,∴△EAF≌△MAF,∴EF=MF;∵MF=DF﹣DM=DF﹣BE,∴EF=DF﹣BE.(3)由上面的结论知:DF=EF+BE;∵BC=4,DC=7,CF=2,∴DF=CD+CF=9∴△CEF的周长=EF+BE+BC+CF=DF+BC+CF=9+4+2=15.即△CEF的周长为15.①EF=DF﹣BE=FC+CD﹣BE=5②和(2)方法一样,EF=DF﹣BE.故答案为EF=DF﹣BE.。
专题20 角含半角模型问题(解析版)-2021年中考数学二轮复习经典问题专题训练

专题20 角含半角模型问题【规律总结】角含半角模型,顾名思义即一个角包含着它的一半大小的角。
它主要包含:等腰直角三角形角含半角模型;正方形中角含半角模型两种类型。
解决类似问题的常见办法主要有两种:旋转目标三角形法和翻折目标三角形法。
【典例分析】例1.(2020·广西南宁市·九年级期中)(探索发现)如图①,四边形ABCD 是正方形,M ,N 分别在边CD 、BC 上,且45MAN=∠︒,我们把这种模型称为“半角模型”,在解决“半角模型”问题时,旋转是一种常用的方法.如图①,将ADM ∆绕点A 顺时针旋转90︒,点D 与点B 重合,得到ABE ∆,连接AM 、AN 、MN .(1)试判断DM ,BN ,MN 之间的数量关系,并写出证明过程.(2)如图②,点M 、N 分别在正方形ABCD 的边BC 、CD 的延长线上,45MAN=∠︒,连接MN ,请写出MN 、DM 、BN 之间的数量关系,并写出证明过程.(3)如图③,在四边形ABCD 中,AB=AD ,120BAD=∠︒,180B+D=∠∠︒,点N ,M 分别在边BC ,CD 上,60MAN=∠︒,请直接写出线段BN ,DM ,MN 之间的数量关系.【答案】(1)MN DM BN =+,证明见解析;(2)MN BN DM =-,证明见解析;(3)MN DM BN =+.【分析】(1)根据正方形的性质和旋转的性质可证ADM ≌ABE ,利用SAS 可证AMN AEN ≌,则可得:MN DM BN =+;(2)根据正方形的性质和旋转的性质可证ADM ≌ABE ,利用SAS 可证AMN AEN ≌,则可得:MN BN DM =-;(3)根据正方形的性质和旋转的性质可证ADM ≌ABE ,利用SAS 可证AMN AEN ≌,则可得:MN DM BN =+;【详解】证明:(1)如图①,≌四边形ABCD 是正方形≌AB=AD ,ABC ADC BAD =90将ADM 绕点A 顺时针旋转90︒,得到ABE≌ADM ≌ABE≌AM AE,DM BE,MAD EABMAE BAD 90 ≌MAN 45EAN MAN 45在AMN 和AEN 中AMAE MANEAN AN ANAMN AEN SAS≌MN EN=+=+,≌EN EB BN DM BN=+≌MN BN DM(2)如图②,将ADM绕点A顺时针旋转90,得到ABE≌四边形ABCD是正方形≌AB=AD,ABC ADC BAD=90≌ADM绕点A顺时针旋转90,得到ABE≌ADM≌ABE≌AM AE,DM BE,MAD EABMAE BAD90,≌MAN45EAN MAN45在AMN和AEN中MANEANAN ANAMN AEN SAS ≌MN EN≌BNEB EN DM MN , 即:MN BN DM =-;(3)如图,≌AB AD =,BAD 120∠=,B D 180,将ADM 绕点A 顺时针旋转120,得到ABE≌ADM ≌ABE≌AM AE,DM BE,MAD EABMAEBAD 120 MAN 60 EAN MAN 60在AMN 和AEN 中MANEANAN ANAMN AEN SAS ≌MN EN ENBE BN MN DM BN ;【点睛】本题主要考查正方形的性质及全等三角形的判定和性质等知识,利用旋转法构造全等三角形是解题的关键是学会.例2.(2020·四川成都市·八年级期末)已知,90POQ ∠=,分别在边OP ,OQ 上取点A ,B ,使OA OB =,过点A 平行于OQ 的直线与过点B 平行于OP 的直线相交于点C .点E ,F 分别是射线OP ,OQ 上动点,连接CE ,CF ,EF .(1)求证:OA OB AC BC ===;(2)如图1,当点E ,F 分别在线段AO ,BO 上,且45ECF ∠=时,请求出线段EF ,AE ,BF 之间的等量关系式;(3)如图2,当点E ,F 分别在AO ,BO 的延长线上,且135ECF ∠=时,延长AC 交EF 于点M ,延长BC 交EF 于点N .请猜想线段EN ,NM ,FM 之间的等量关系,并证明你的结论.【答案】(1)见解析;(2)EF AE BF =+;(3)222MN EN FM =+,见解析【分析】(1)连接AB ,通过90POQ ∠=,OA OB =得到AOB 为等腰直角三角形,进而得到45OAB OBA ∠=∠=,根据过点A 平行于OQ 的直线与过点B 平行于OP 的直线相交于点C ,可推出45CBA ∠=,45BAC ∠=,最后通过证明AOB ≌ACB △,可以得出结论;(2)在射线AP 上取点D ,使AD BF =,连接CD ,通过证明CAD ≌CBF ,得到CD CF =,ACD BCF ∠=∠,再结合45ECF ∠=,90ACB ∠=推导证明ECD ≌ECF △,得到ED EF =,最后等量代换线段即可求解;(3)延长AO 到点D ,使得AD BF =,连接CD ,通过证明CAD ≌CBF ,得到CD CF =,ACD BCF ∠=∠,再结合135ECF ∠=,推导证明ECD ≌ECF △,得到D CFM ∠=∠,根据D CFB ∠=∠,等量代换可知CFM CFB ∠=∠,又因为//AC OQ ,推出MCF CFB ∠=∠,进而得到MC MF =,同理可证CN EN =,最后根据勾股定理即可求解.【详解】解:(1)证明:连接AB .90POQ ∠=,OA OB =,∴AOB 为等腰直角三角形,∴45OAB OBA ∠=∠=, 又//BC OP ,且90POQ ∠=,∴BC OQ ⊥,∴90CBF ∠=,∴45CBA ∠=,同理,45BAC ∠=,在AOB 与ACB △中OAB CAB AB ABOBA CBF ∠=∠⎧⎪=⎨⎪∠=∠⎩, ∴AOB ≌ACB △()ASA ,∴90AOB ACB ∠=∠=,OA OB AC BC ===;(2)如图1,在射线AP 上取点D ,使AD BF =,连接CD .在CAD 与CBF 中CA CB CAD CBF AD BF =⎧⎪∠=∠⎨⎪=⎩,∴CAD ≌CBF ()SAS ,∴CD CF =,ACD BCF ∠=∠,45ECF ∠=,90ACB ∠=,∴45ACE BCF ∠+∠=,∴45ACE ACD ECD ∠+∠=∠=,∴ECD ECF ∠=∠,在ECD 与ECF △中CD CF ECD ECF CE CE =⎧⎪∠=∠⎨⎪=⎩∴ECD ≌ECF △()SAS ,∴ED EF =,又ED AD AE BF AE =+=+,∴EF AE BF =+.(3)222MN EN FM =+.证明如下:如图2,延长AO 到点D ,使得AD BF =,连接CD .∴90CAD CBF ∠=∠=,在CAD 与CBF 中CA CB CAD CBF AD BF =⎧⎪∠=∠⎨⎪=⎩,∴CAD ≌CBF ()SAS ,∴CD CF =,ACD BCF ∠=∠,90ACD DCB ∠+∠=,∴90BCF DCB DCF ∠+∠==∠,∴90FCD BCA ∠=∠=,135ECF ∠=,∴36090135135ECD ∠=--=,∴ECF ECD ∠=∠,在ECD 与ECF △中EC EC ECD ECF CD CF =⎧⎪∠=∠⎨⎪=⎩,∴ECD ≌ECF △()SAS ,∴D CFM ∠=∠,CAD ≌CBF ,∴D CFB ∠=∠,∴CFM CFB ∠=∠,//AC OQ ,∴MCF CFB∠=∠,∴CFM MCF∠=∠,∴MC MF=,=,同理可证:CN EN∴在Rt MCN△中,由勾股定理得:22222=+=+.MN CN CM EN FM【点睛】本题综合考查了全等三角形的性质和判定,勾股定理以及正方形的有关知识,通过添加辅助线构造全等三角形,通过证明全等三角形得到线段之间的关系是解题的关键.【好题演练】一、单选题1.(2021·上海九年级专题练习)如图所示,在Rt△ABC中,AB=AC,D、E是斜边BC上的两点,且△DAE=45°,将△ADC绕点A按顺时针方向旋转90°后得到△AFB,连接EF,有下列结论:①BE=DC;②△BAF=△DAC;③△FAE=△DAE;④BF=DC.其中正确的有()A.①②③④B.②③C.②③④D.③④【答案】C【分析】利用旋转性质可得≌ABF≌≌ACD,根据全等三角形的性质一一判断即可.【详解】解:≌≌ADC绕A顺时针旋转90°后得到≌AFB,≌≌ABF≌≌ACD,≌≌BAF=≌CAD,AF=AD,BF=CD,故②④正确,≌≌EAF=≌BAF+≌BAE=≌CAD+≌BAE=≌BAC﹣≌DAE=90°﹣45°=45°=≌DAE故③正确无法判断BE=CD,故①错误,故选:C.【点睛】本题考查了旋转的性质:旋转前后两图形全等,解题的关键是熟练掌握基本知识,属于中考常考题型.二、填空题2.(2021·上海九年级专题练习)如图,在Rt△ABC和Rt△BCD中,△BAC=△BDC=90°,BC=4,AB=AC,△CBD=30°,M,N分别在BD,CD上,△MAN=45°,则△DMN的周长为_____.【答案】【分析】将≌ACN绕点A逆时针旋转,得到≌ABE,由旋转得出≌NAE=90°,AN=AE,≌ABE=≌ACD,≌EAB=≌CAN ,求出≌EAM =≌MAN ,根据SAS 推出≌AEM≌≌ANM ,根据全等得出MN =ME ,求出MN =CN +BM ,解直角三角形求出DC ,即可求出≌DMN 的周长=BD +DC ,代入求出答案即可.【详解】将≌ACN 绕点A 逆时针旋转,得到≌ABE ,如图:由旋转得:≌NAE =90°,AN =AE ,≌ABE =≌ACD ,≌EAB =≌CAN ,≌≌BAC =≌D =90°,≌≌ABD +≌ACD =360°﹣90°﹣90°=180°,≌≌ABD +≌ABE =180°,≌E ,B ,M 三点共线,≌≌MAN =45°,≌BAC =90°,≌≌EAM =≌EAB +≌BAM =≌CAN +≌BAM =≌BAC ﹣≌MAN =90°﹣45°=45°,≌≌EAM =≌MAN ,在≌AEM 和≌ANM 中,AE AN EAM NAM AM AM ⎧⎪∠∠⎨⎪⎩===,≌≌AEM ≌≌ANM (SAS ),≌MN =ME ,≌MN =CN +BM ,≌在Rt≌BCD 中,≌BDC =90°,≌CBD =30°,BC =4,≌CD =12BC =2,BD≌≌DMN 的周长为DM +DN +MN =DM +DN +BM +CN =BD +DC =,故答案为:.【点睛】本题考查直角三角形、全等三角形的性质和判定、旋转的性质的应用,能正确作出辅助线是解此题的关键.三、解答题3.(2020·黑龙江哈尔滨市·九年级月考)矩形ABCD 中,M 、N 为边AD 上两点,连接BM 、CN ,MN=BM=CN ,△BMD=120°.(1)如图1,求证:AM=DN ;(2)如图2,点E 、F 分别在NC 、BC 上,△FME=60°,求证:EF= BF+NE ;(3)如图3,在(2)的条件下,过E 作EP△BC 交MF 于P ,2MN=3BF ,EP=7,求CE 的长.【答案】(1)见解析;(2)见解析;(3)3【分析】(1)由题意易得AB=CD ,≌A=≌D=90°,进而可证Rt≌ABM≌Rt≌DCN ,最后得证;(2)延长CB 至G ,使BG=NE ,连接MG ,易得≌MBG=≌BMD=≌MNE=120°,进而可证MG=ME ,≌GMB=≌EMN ,≌GMF=≌FME ,MF=MF ,≌GMF≌≌EMF ,然后根据线段的数量关系可求解; (3)设BF=2a ,MN=BM=CN=3a ,则有≌A=≌D=≌DCB=90°,AD=BC ,由(1)可得AM=12BM=32a ,由(2)问可知:EF=BF+NE ,≌GMF≌≌EMF ,≌MFB=≌MFE ,可得CE=CN -EN=3a -(7-2a)=5a -7,过点E 作ER≌BC 于R ,≌ERF=≌ERC=≌DCB=90°,ER≌DC ,然后根据勾股定理进行求解即可.【详解】(1)证明:≌四边形ABCD是矩形,≌AB=CD,≌A=≌D=90°,≌BM=CN,≌Rt≌ABM≌Rt≌DCN(HL),≌AM=DM(2)解:延长CB至G,使BG=NE,连接MG,≌四边形ABCD是矩形,≌AD≌BC,≌≌MBG=≌BMD=≌MNE=120°,≌BM=MN,≌≌GBM≌≌ENM(SAS),≌MG=ME,≌GMB=≌EMN,≌≌BMD=120°,≌FME=60° ,≌≌GMF=≌GMB+≌BMF=≌EMN+≌BMF =≌BMD-≌FME=120°-60° =60°,≌≌GMF=≌FME,MF=MF,≌GMF≌≌EMF(SAS),≌GF=EF,≌GF=BF+GB=BF+NE,即EF=BF+NE;(3)解:≌2MN=3BF,≌设BF=2a,MN=BM=CN=3a,≌四边形ABCD是矩形,≌≌A=≌D=≌DCB=90°,AD=BC,由(1)问可知:Rt≌ABM≌Rt≌DCN,≌≌AMB=≌CND=180°-≌BMD=180°-120° =60° ,≌ABM=≌DCN=90°-60°=30°,在Rt≌ABM中,≌AM=12BM=32a,同理DN=32a,≌AD=BC=AM+MN+DN= 32a+3a+32a=6a,≌FC=BC-BF=6a-2a=4a,由(2)问可知:EF=BF+NE,≌GMF≌≌EMF,≌MFB=≌MFE,≌EP≌BC,≌≌EPF=≌MFB=≌MFE,≌EF=EP=7,≌NE=EF-BF=7-2a,≌CE=CN-EN=3a-(7-2a)=5a-7过点E作ER≌BC于R,≌≌ERF=≌ERC=≌DCB=90°,ER≌DC,≌≌CER=≌DCN=30° ,在Rt≌ERC中,RC=12CE=572a-,≌FR=FC-RC=4a-572a-=372a+,在Rt≌ERC中,ER2=EC2-CR2,在Rt≌ERF中,ER2=EF2-FR2,≌EC2-CR2=EF2-FR2,≌(5a-7)2-(572a-)2=72-(372a+)2解得a1=0 (不符合题意,舍去),a2=2,≌CE=5a-7=3.【点睛】本题主要考查矩形的性质与判定、全等三角形的性质与判定及勾股定理,熟练掌握矩形的性质与判定、全等三角形的性质与判定及勾股定理是解题的关键.4.(2020·山东滨州市·八年级期中)在△MAN内有一点D,过点D分别作DB△AM,DC△AN,垂足分别为B,C.且BD=CD,点E,F分别在边AM和AN上.(1)如图1,若△BED=△CFD,请说明DE=DF;(2)如图2,若△BDC=120°,△EDF=60°,猜想EF,BE,CF具有的数量关系,并说明你的结论成立的理由.【答案】(1)说明见解析;(2)EF= FC+BE.理由见解析.【分析】(1)根据题目中的条件和≌BED=≌CFD,可以证明≌BDE≌≌CDF,从而可以得到DE=DF;(2)作辅助线,过点D作≌CDG=≌BDE,交AN于点G,从而可以得到≌BDE≌≌CDG,然后即可得到DE=DG,BE=CG,再根据题目中的条件可以得到≌EDF≌≌GDF,即可得到EF=GF,然后即可得到EF,BE,CF具有的数量关系.【详解】(1)≌ DB≌AM,DC≌AN,≌ ≌DBE=≌DCF=90°.在≌BDE和≌CDF中,≌,,,BED CFDDBE DCF BD CD∠=∠⎧⎪∠=∠⎨⎪=⎩≌ ≌BDE≌≌CDF(AAS).≌ DE=DF.(2)过点D作≌CDG=≌BDE,交AN于点G.在≌BDE和≌CDG中,≌ ,,,EBD GCD BD CD BDE CDG ∠=∠⎧⎪=⎨⎪∠=∠⎩≌ ≌BDE ≌≌CDG (ASA )≌DE =DG ,BE =CG .≌≌BDC =120°,≌EDF =60°,≌ ≌BDE+≌CDF =60°.≌ ≌FDG =≌CDG +≌CDF =60°.≌ ≌EDF =≌GDF .在≌EDF 和≌GDF 中,,,,DE DG EDF GDF DF DF =⎧⎪∠=∠⎨⎪=⎩≌ ≌EDF ≌≌GDF (SAS ).≌ EF =FG .≌ EF =FC +CG =FC +BE .【点睛】本题考查全等三角形的判定、解答本题的关键是明确题意,利用数形结合的思想解答. 5.(2020·陕西西安市·七年级期末)(2020•锦州模拟)问题情境:已知,在等边△ABC 中,△BAC 与△ACB 的角平分线交于点O ,点M 、N 分别在直线AC ,AB 上,且△MON =60°,猜想CM 、MN 、AN 三者之间的数量关系.方法感悟:小芳的思考过程是在CM 上取一点,构造全等三角形,从而解决问题;小丽的思考过程是在AB取一点,构造全等三角形,从而解决问题;问题解决:(1)如图1,M、N分别在边AC,AB上时,探索CM、MN、AN三者之间的数量关系,并证明;(2)如图2,M在边AC上,点N在BA的延长线上时,请你在图2中补全图形,标出相应字母,探索CM、MN、AN三者之间的数量关系,并证明.【答案】(1)CM=AN+MN,详见解析;(2)CM=MN﹣AN,详见解析【分析】(1)在AC上截取CD=AN,连接OD,证明≌CDO≌≌ANO,根据全等三角形的性质得到OD =ON,≌COD=≌AON,证明≌DMO≌≌NMO,得到DM=MN,结合图形证明结论;(2)在AC延长线上截取CD=AN,连接OD,仿照(1)的方法解答.【详解】解:(1)CM=AN+MN,理由如下:在AC上截取CD=AN,连接OD,≌≌ABC为等边三角形,≌BAC与≌ACB的角平分线交于点O,≌≌OAC =≌OCA =30°,≌OA =OC ,在≌CDO 和≌ANO 中,OC OA OCD OAN CD AN =⎧⎪∠=∠⎨⎪=⎩,≌≌CDO ≌≌ANO (SAS )≌OD =ON ,≌COD =≌AON ,≌≌MON =60°,≌≌COD +≌AOM =60°,≌≌AOC =120°,≌≌DOM =60°,在≌DMO 和≌NMO 中,OD ON DOM NOM OM OM =⎧⎪∠=∠⎨⎪=⎩,≌≌DMO ≌≌NMO ,≌DM =MN ,≌CM =CD +DM =AN +MN ;(2)补全图形如图2所示:CM =MN ﹣AN ,理由如下:在AC 延长线上截取CD =AN ,连接OD ,在≌CDO 和≌ANO 中,150CD AN OCD OAN OC OA =⎧⎪∠=∠=︒⎨⎪=⎩,≌≌CDO ≌≌ANO (SAS )≌OD =ON ,≌COD =≌AON ,≌≌DOM =≌NOM ,在≌DMO 和≌NMO 中,OD ON DOM NOM OM OM =⎧⎪∠=∠⎨⎪=⎩,≌≌DMO ≌≌NMO (SAS )≌MN =DM ,≌CM =DM ﹣CD =MN ﹣AN .【点睛】此题主要考查全等三角形的判定与性质,解题的关键是熟知等边三角形的性质及全等三角形的判定定理.6.(2019·全国九年级专题练习)如图所示,在ABC ∆中,30A B ∠=∠=︒,60MCN ∠=︒,MCN ∠的两边交AB 边于E ,F 两点,将MCN ∠绕C 点旋转(1)画出BCF ∆绕点C 顺时针旋转120︒后的ACK ∆;(2)在(1)中,若222AE EF BF +=,求证:BF =;(3)在(2)的条件下,若1AC =,直接写出EF 的长.【答案】(1)见解析;(2)见解析;(3【解析】【分析】(1)旋转后CB 与CA 重合,作≌KCA=≌FCB ,截取KC=FC 即可;(2)连结KE ,作KH≌AC 于H ,先得到≌ACE+≌BCF=60°,再根据旋转的性质得BF=AK ,≌KCA=≌FCB ,CK=CF ,≌KAC=≌B=30°,则≌KCE=≌FCE ,可根据“SAS”判断≌CKE≌≌CFE ,所以KE=EF ,由于AE 2+EF 2=BF 2,则AE 2+KE 2=AK 2,根据勾股定理的逆定理得≌AEK=90°,且≌KEC=≌FEC=45°,可计算≌BCF=45°,设KH=a ,在Rt≌KHC 中可得;在Rt≌KHA 中得AK=2a ,所以AK :KC=2a :,则BF :,(3)设KH=a ,在Rt≌KHC 中得HC=a ;在Rt≌KHA 中得,则+1,解得a=1,则AK=2,在Rt≌AEK 中,计算出≌KAE=60°,≌AKE=30°,所以AE=12AK=1,KE=.(1)作图如图所示(2)证明:连结KE ,作KH≌AC 于H ,如图,≌≌A=≌B=30°,≌MCN=60°,≌≌ACB=120°,≌≌ACE+≌BCF=60°,≌≌BCF 绕点C 顺时针旋转120゜后的≌ACK ,≌BF=AK ,≌KCA=≌FCB ,CK=CF ,≌KAC=≌B=30°,≌≌KCE=≌KCA+≌ACE=≌FCB+≌ACE=60°,≌≌KCE=≌FCE ,在≌CKE 和≌CFE 中CK CF KCE FCE CE CE ⎧⎪∠∠⎨⎪⎩===,≌≌CKE≌≌CFE ,≌AE2+EF2=BF2,≌AE2+KE2=AK2,≌≌AEK为直角三角形,≌≌AEK=90°,≌≌KEC=≌FEC=45°,≌≌BCF=180°-45°-60°-30°=45°,≌≌KCA=45°,设KH=a,在Rt≌KHC中,a;在Rt≌KHA中,AK=2a,≌AK:KC=2a,≌BF:,即;(3)设KH=a,在Rt≌KHC中,HC=a;在Rt≌KHA中,,,解得a=1,≌AK=2a=2,在Rt≌AEK中,≌KAE=≌KAC+≌CAE=60°,≌≌AKE=30°,≌AE=12AK=1,【点睛】本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了勾股定理的逆定理、全等三角形的判定与性质以及含30度的直角三角形三边的关系.。
半角模型经典例题

半角模型经典例题摘要:一、半角模型的概念与性质1.半角模型的定义2.半角模型的性质二、半角模型的求解方法1.解析法2.数值法3.符号法三、半角模型的经典例题解析1.例题一2.例题二3.例题三四、半角模型在实际问题中的应用1.应用场景一2.应用场景二3.应用场景三正文:半角模型是一种在数学、物理等领域中广泛应用的模型,它具有重要的理论意义和实际价值。
本文将首先介绍半角模型的概念与性质,然后探讨半角模型的求解方法,接着通过解析经典例题来加深对半角模型的理解,最后讨论半角模型在实际问题中的应用。
一、半角模型的概念与性质半角模型是一个数学模型,其基本思想是将一个实际问题简化为一个具有特定性质的数学问题。
半角模型的定义如下:(定义)设函数f(x) 满足以下条件:1.f(x) 在区间[0,π/2] 上连续;2.f(0)=f(π/2)=0.3.0<f(x)<f(π/2) for 0<x<π/2.则称f(x) 为半角模型。
半角模型具有以下性质:(性质1)半角模型的图像关于y 轴对称;(性质2)半角模型的导数在x=0 和x=π/2 处不存在;(性质3)半角模型的二阶导数在x=0 处为正,在x=π/2 处为负。
二、半角模型的求解方法半角模型的求解方法有多种,下面介绍三种常用的方法:解析法、数值法、符号法。
1.解析法:通过求导、积分等数学方法,对半角模型的解析式进行求解。
2.数值法:利用数值分析的方法,如牛顿法、梯度下降法等,对半角模型的数值进行求解。
3.符号法:通过计算机符号计算工具,如Mathematica、Maple 等,对半角模型的符号表达式进行求解。
三、半角模型的经典例题解析以下是三个半角模型的经典例题:1.例题一:求半角模型f(x)=x^2 的解析式。
解析:根据半角模型的定义,可知f(x)=x^2 满足半角模型的性质。
因此,f(x)=x^2 是一个半角模型。
2.例题二:求半角模型f(x)=sin(x) 在区间[0,π/2] 上的数值解。
中考数学常见几何模型专题02 全等模型-半角模型(解析版)

专题02 全等模型--半角模型全等三角形在中考数学几何模块中占据着重要地位,也是学生必须掌握的一块内容,本专题就半角模型进行梳理及对应试题分析,方便掌握。
模型1.半角模型【模型解读】过等腰三角形顶点 两条射线,使两条射线的夹角为等腰三角形顶角的一半这样的模型称为半角模型。
【常见模型及证法】常见的图形为正方形,正三角形,等腰直角三角形等,解题思路一般是将半角两边的三角形通过旋转到一边合并成新的三角形,从而进行等量代换,然后证明与半角形成的三角形全等,再通过全等的性质得到线段之间的数量关系。
半角模型(题中出现角度之间的半角关系)利用旋转——证全等——得到相关结论. 1.(2022·湖北十堰·中考真题)【阅读材料】如图①,四边形ABCD 中,AB AD =,180B D ∠+∠=︒,点E ,F 分别在BC ,CD 上,若2BAD EAF ∠∠=,则EF BE DF =+.【解决问题】如图②,在某公园的同一水平面上,四条道路围成四边形ABCD .已知100m CD CB ==,60D ∠=︒,120ABC ∠=︒,150BCD ∠=︒,道路AD ,AB 上分别有景点M ,N ,且100m DM =,)501m BN =,若在M ,N 之间修一条直路,则路线M N →的长比路线M A N →→的长少_________m 1.7≈).【答案】370【分析】延长,AB DC 交于点E ,根据已知条件求得90E ∠=︒,进而根据含30度角的直角三角形的性质,求得,EC EB ,,AE AD ,从而求得AN AM +的长,根据材料可得MN DM BN =+,即可求解.【详解】解:如图,延长,AB DC 交于点E ,连接,CM CN ,60D ∠=︒,120ABC ∠=︒,150BCD ∠=︒,30A ∴∠=︒,90E ∠=︒,100DC DM ==DCM ∴是等边三角形,60DCM ∴∠=︒,90BCM ∴∠=︒,在Rt BCE 中,100BC =,18030ECB BCD ∠=︒-∠=︒,1502EB BC ==,EC ==100DE DC EC ∴=+=+Rt ADE △中,2200AD DE ==+150AE ==,∴200100100AM AD DM =-=+=+()AN AB BN AE EB BN =-=--())15050501=--150=,100150250AM AN ∴+=+=+Rt CMB △中,BM =)50501EN EB BN EC =+=+==ECN ∴是等腰直角三角形()1752NCM BCM NCB BCM NCE BCE DCB ∴∠=∠-∠=∠-∠-∠=︒=∠由阅读材料可得))100501501MN DM BN =+=+=,∴路线M N →的长比路线M A N →→的长少)250501200370+=+≈m .答案:370. 【点睛】本题考查了含30度角的直角三角形的性质,勾股定理,理解题意是解题的关键.2.(2022·河北邢台·九年级期末)学完旋转这一章,老师给同学们出了这样一道题:“如图1,在正方形ABCD 中,∠EAF =45°,求证:EF =BE +DF .”小明同学的思路:∠四边形ABCD 是正方形,∠AB =AD ,∠B =∠ADC =90°.把∠ABE 绕点A 逆时针旋转到ADE '△的位置,然后证明AFE AFE '≌△△,从而可得=EF E F '. E F E D DF BE DF ''=+=+,从而使问题得证.(1)【探究】请你参考小明的解题思路解决下面问题:如图2,在四边形ABCD 中,AB =AD ,∠B =∠D =90°,12EAF BAD ∠=∠,直接写出EF ,BE ,DF 之间的数量关系.(2)【应用】如图3,在四边形ABCD 中,AB =AD ,∠B +∠D =180°,12EAF BAD ∠=∠,求证:EF =BE +DF .(3)【知识迁移】如图4,四边形ABPC 是O的内接四边形,BC 是直径,AB =AC ,请直接写出PB +PC 与AP 的关系. ADE ,证明∠AEF EAF ='E AF ∠先利用圆内接四边形的性质证明为等腰直角三角形,等量代换即得结论.AD 重合,点ADE=180°知,BAD,∠∠BAF=∠EAF=∠,∠EF=E F'∠ABE绕点【点睛】本题考查了旋转与全等三角形的综合应用、直径所对的圆周角是直角、圆内接四边形的性质、等腰直角三角形的判定及性质等知识点.解题关键是利用旋转构造全等三角形.3.(2022·福建·龙岩九年级期中)(1)【发现证明】如图1,在正方形ABCD 中,点E ,F 分别是BC ,CD 边上的动点,且45EAF ∠=︒,求证:EF DF BE =+.小明发现,当把ABE △绕点A 顺时针旋转90°至ADG ,使AB 与AD 重合时能够证明,请你给出证明过程.(2)【类比引申】①如图2,在正方形ABCD 中,如果点E ,F 分别是CB ,DC 延长线上的动点,且45EAF ∠=︒,则(1)中的结论还成立吗?若不成立,请写出EF ,BE ,DF 之间的数量关系______(不要求证明) ②如图3,如果点E ,F 分别是BC ,CD 延长线上的动点,且45EAF ∠=︒,则EF ,BE ,DF 之间的数量关系是_____(不要求证明).(3)【联想拓展】如图1,若正方形ABCD 的边长为6,AE =求AF 的长.180ADF ADG ∴∠+∠=︒,F ∴,D ,G 三点共线,45EAF ∠=︒,45BAE FAD ∴∠+∠=︒,45DAG FAD ∴∠+∠=︒,EAF FAG ∴∠=∠,AF AF =,()EAF GAF SAS ∴∆≅∆,EF FG DF DG ∴==+,EF DF BE ∴=+;(2)①不成立,结论:EF DF BE =-;证明:如图2,将ABE ∆绕点A 顺时针旋转90︒至ADM ∆,EAB MAD ∴∠=∠,AE AM =,90EAM =︒∠,BE DM =,45FAM EAF ∴∠=︒=∠,AF AF =,()EAF MAF SAS ∴∆≅∆,EF FM DF DM DF BE ∴==-=-;②如图3,将ADF ∆绕点A 逆时针旋转90︒至ABN ∆,AN AF ∴=,90NAF ∠=︒,45EAF ∠=︒,45NAE ∴∠=︒,NAE FAE ∴∠=∠,AE AE =,()AFE ANE SAS ∴∆≅∆,EF EN ∴=,BE BN NE DF EF ∴=+=+.正方形Rt EFC中,2CF CE+解得:2x=.2DF∴=,226AF AD DF=+=【点睛】本题属于四边形综合题,主要考查了正方形的性质、旋转的性质、全等三角形的判定与性质以及勾股定理的综合应用,解题的关键是作辅助线构造全等三角形,根据全等三角形的对应边相等进行推导.4.(2022·山东省青岛第二十六中学九年级期中)【模型引入】当几何图形中,两个共顶点的角所在角度是公共大角一半的关系,我们称之为“半角模型”【模型探究】(1)如图1,在正方形ABCD中,E、F分别是AB、BC边上的点,且∠EDF=45°,探究图中线段EF,AE,FC之间的数量关系.【模型应用】(2)如图2,如果四边形ABCD中,AB=AD,∠BAD=∠BCD=90°,∠EAF=45°,且BC=7,DC=13,CF=5,求BE的长.【拓展提高】(3)如图3,在四边形ABCD中,AB=AD,∠ABC与∠ADC互补,点E、F分别在射线CB、DC上,且∠EAF12=∠BAD.当BC=4,DC=7,CF=1时,CEF的周长等于.(4)如图4,正方形ABCD中,AMN的顶点M、N分别在BC、CD边上,AH∠MN,且AH=AB,连接BD分别交AM、AN于点E、F,若MH=2,NH=3,DF=EF的长.(5)如图5,已知菱形ABCD中,∠B=60°,点E、F分别是边BC,CD上的动点(不与端点重合),且∠EAF=60°.连接BD分别与边AE、AF交于M、N,当∠DAF=15°时,求证:MN2+DN2=BM2.又AH=AN,AB=AD,∠∠ABH∠∠ADN(SAS),∠DN=BH,∠ABH=∠ADN,∠∠B=60°,且∠EAF=60°.∠∠BAD=120°,∠∠DAF+∠BAE=∠EAF=60°,∠∠BAG+∠BAE=∠EAF,即∠MAH=∠MAN,而AH=AN,AM=AM,∠∠AMH∠∠AMN(SAS),∠MN=MH,∠AMN=∠AMH,∠菱形ABCD,∠B=60°,∠∠ABD=∠ADB=30°,∠∠HBD=∠ABH+∠ABD=60°,∠∠DAF=15°,∠EAF=60°,∠∠ADM中,∠DAM=∠AMD=75°,∠∠AMN=∠AMH=75°,∠∠HMB=180°-∠AMN-∠AMH=30°,∠∠BHM=90°,∠BH2+MH2=BM2,∠DN2+MN2=BM2.【点睛】本题是四边形综合题,主要考查了旋转的性质、正方形的性质、等腰直角三角形的性质、全等三角形的判定和性质、勾股定理等知识,解题关键是学会用旋转法添加辅助线,构造全等三角形解决问题,学会利用探究的结论解决新的问题,属于中考压轴题.课后专项训练:1.(2022·重庆市育才中学二模)回答问题(1)【初步探索】如图1:在四边形ABCD中,AB=AD,∠B=∠ADC=90°,E、F分别是BC、CD上的点,且EF=BE+FD,探究图中∠BAE、∠F AD、∠EAF之间的数量关系.小王同学探究此问题的方法是:延长FD到点G,使DG=BE.连接AG,先证明△ABE∠∠ADG,再证明△AEF∠∠AGF,可得出结论,他的结论应是_______________;(2)【灵活运用】如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°.E、F分别是BC、CD上的点,且EF=BE+FD,上述结论是否仍然成立,并说明理由;(3)【拓展延伸】知在四边形ABCD中,∠ABC+∠ADC=180°,AB=AD,若点E在CB的延长线上,点F在CD的延长线上,如图3所示,仍然满足EF=BE+FD,请直接写出∠EAF与∠DAB的数量关系.2.(2022·江西九江·一模)如图(1),在四边形ABCD 中,180B D ∠+∠=︒,AB AD =,以点A 为顶点作EAF ∠,且12EAF BAD ∠=∠,连接EF .(1)观察猜想 如图(2),当90BAD B D ∠=∠=∠=︒时,①四边形ABCD 是______(填特殊四边形的名称);②BE ,DF ,EF 之间的数量关系为______.(2)类比探究 如图(1),线段BE ,DF ,EF 之间的数量关系是否仍然成立?若成立,请加以证明;若不成立,请说明理由.(3)解决问题 如图(3),在ABC 中,90BAC ∠=︒,4AB AC ==,点D ,E 均在边BC 上,且45DAE ∠=︒,若BD =,求DE 的长.证得ABE ADG ≌,得出证得AEF AGF ≌,之间的数量关系;(2)同(1)②即可得出,证得ABD ACM ≌,同(证得AEF AGF ≌,在Rt ECM 中,由勾股定理可解得90BAD B D =∠=∠=︒,ABCD 是矩形,又∠AB AD ,∠矩形CD 至点G ,使得DG=BE 90ADG ADF =∠=︒,∠∠,∠ABE ADG ≌,DG ,BAE DAG ∠=∠BAD ∠,∠BAE DAF ∠+∠∠AEF AGF ≌,∠EF DG EF =∠BE FD +在ABC 中,B ACB ∠=∠∠ABD ACM ≌,同(1)②的证明方法得DE ME =, 2BD =,22+BC AB AC ==DE ME =x -,Rt ECM 中,2EM ,2(2)(32+【点睛】本题考查了特殊的平行四边形的判定、全等三角形的性质和判定及勾股定理的应用,熟练应用相关定理和性质是解决本题的关键.3.(2022·山东聊城·九年级期末)(1)如图1,点E ,F 分别在正方形ABCD 的边BC ,CD 上,45EAF ∠=︒,连接EF ,求证:EF BE DF =+,试说明理由.(2)类比引申:如图2,四边形ABCD 中,AB AD =,90BAD ∠=︒,点E ,F 分别在边BC ,CD 上,∠EAF =45°,若B 、D ∠都不是直角,则当B 与D ∠满足等量关系______时,仍有EF BE DF =+,试说明理由.(3)联想拓展:如图3,在∠ABC 中,90BAC ∠=︒,AB AC =,点D ,E 均在边BC 上,且∠DAE =45,若1BD =,2EC =,求DE 的长.AB AD =∠ADC =∠B =90°∠则DAG ∠∠F AG =∠F AD理由:AB AD==∠BAE DAG∠=︒,BAD90∠+∠=ADC B在∠AFE和∠AFG∴=EF FG()3将∠ACE∠=BAC又∠∠F AB=∠则在∠ADF∠∠ADF∠∠∠∠C+∠ABD4.(2022·黑龙江九年级阶段练习)已知:正方形ABCD中,∠MAN=45°,∠MAN绕点A顺时针旋转,它的两边分别交CB、DC(或它们的延长线)于点M、N.当∠MAN绕点A旋转到BM=DN时,(如图1),易证BM+DN=MN.(1)当∠MAN 绕点A 旋转到BM ≠DN 时(如图2),线段BM 、DN 和MN 之间有怎样的数量关系?写出猜想,并加以证明;(2)当∠MAN 绕点A 旋转到如图3的位置时,线段BM 、DN 和MN 之间又有怎样的数量关系?请直接写出你的猜想. 【答案】(1)BM DN MN +=,理由见解析;(2)DN BMMN -=,理由见解析【分析】(1)把ADN ∆绕点A 顺时针旋转90︒,得到ABE ∆,然后证明得到AEM ANM ∆∆≌,从而证得ME MN =,可得结论;(2)首先证明ADQ ABM ∆∆≌,得DQ BM =,再证明AMN AQN ∆∆≌,得MN QN =,可得结论; (1)解:BM DN MN +=.理由如下:如图2,把ADN ∆绕点A 顺时针旋转90︒,得到ABE ∆,90ABE ADN ∴∠=∠=︒,AE AN =,BE DN =,180ABE ABC ∴∠+∠=︒,∴点E ,点B ,点C 三点共线,90904545EAM NAM ∴∠=︒-∠=︒-︒=︒,又45NAM ∠=︒,在AEM ∆与ANM ∆中,AE AN EAM NAM AM AM =⎧⎪∠=∠⎨⎪=⎩,AEM ANM ∴∆∆≌(SAS ),ME MN ∴=, ME BE BM DN BM =+=+,DN BM MN ∴+=;(2)解:DN BM MN -=.理由如下:在线段DN 上截取DQ BM =,在ADQ ∆与ABM ∆中,AD AB ADQ ABM DQ BM =⎧⎪∠=∠⎨⎪=⎩,ADQ ABM ∴∆∆≌(SAS ),DAQ BAM ∴∠=∠,QAN MAN ∴∠=∠.在AMN ∆和AQN ∆中,AQ AM QAN MAN AN AN =⎧⎪∠=∠⎨⎪=⎩,AMN AQN ∴∆∆≌(SAS ),MN QN ∴=,DN BM MN ∴-=.【点睛】本题是四边形综合题,考查正方形的性质,旋转变换,全等三角形的判定和性质,勾股定理等知识,解题的关键是学会利用旋转法添加辅助线,构造全等三角形解决问题.5.(2022·重庆南川·九年级期中)如图,正方形ABCD 中,45MAN ∠=︒,MAN ∠绕点A 顺时针旋转,它的两边分别交BC 、DC (或它们的延长线)于点M 、N .(1)当MAN ∠绕点A 旋转到BM DN =时(如图1),证明:2MN BM =;(2)绕点A 旋转到BM DN ≠时(如图2),求证:MN BM DN =+;(3)当MAN ∠绕点A 旋转到如图3位置时,线段BM 、DN 和MN 之间有怎样的数量关系?请写出你的猜想并证明.【答案】(1)见解析(2)见解析(3)DN BM MN -=,见解析【分析】(1)把ADN △绕点A 顺时针旋转90︒,得到ABE △,证得B 、E 、M 三点共线,即可得到AEM △∠ANM ,从而证得ME MN =;(2)证明方法与(1)类似;(3)在线段DN 上截取DQ BM =,判断出ADQ △∠ABM ,同(2)的方法,即可得出结论.(1)证明:如图1,∠把ADN △绕点A 顺时针旋转90︒,得到ABE △,ABE ∴∠ADN △,AE ANM ∴=,ABE D ∠=∠,四边形ABCD 是正方形,90ABC D ∴∠=∠=︒,90ABE ABC ∴∠=∠=︒,∴点E 、B 、M 三点共线.90904545EAM NAM ∴∠=︒-∠=︒-︒=︒,又45NAM ∠=︒,在AEM △与ANM 中,AE AN EAM NAM AM AM =⎧⎪∠=∠⎨⎪=⎩,AEM ∴△∠()ANM SAS ,ME MN ∴=,ME BE BM DN BM =+=+,DN BM MN ∴+=,BM DN =,2MN BM ∴=.(2)证明:如图2,把ADN △绕点A 顺时针旋转90︒,得到ABE △,ABE ∴∠ADN △,AE ANM ∴=,ABE D ∠=∠,四边形ABCD 是正方形,90ABC D ∴∠=∠=︒,90ABE ABC ∴∠=∠=︒,∴点E 、B 、M 三点共线.90904545EAM NAM ∴∠=︒-∠=︒-︒=︒,又45NAM ∠=︒,在AEM △与ANM 中,AE AN EAM NAM AM AM =⎧⎪∠=∠⎨⎪=⎩,AEM ∴△∠()ANM SAS ,ME MN ∴=,ME BE BM DN BM =+=+,DN BM MN ∴+=. (3)解:DN BM MN -= 理由如下:如图3,在线段DN 上截取DQ BM =,连接AQ ,在ADQ △与ABM中,AD AB ADQ ABM DQ BM =⎧⎪∠=∠⎨⎪=⎩,ADQ ∴∠()ABM SAS ,DAQ BAM ∴∠=∠,QAN MAN ∴∠=∠.在AMN 和AQN △中,AQ AM QAN MAN AN AN =⎧⎪∠=∠⎨⎪=⎩,AMN ∴∠()AQN SAS ,MN QN ∴=,DN BM MN ∴-=.【点睛】本题是四边形综合题,考查正方形的性质,旋转变换,全等三角形的判定和性质,勾股定理等知识,学会利用旋转法添加辅助线,构造全等三角形是解题的关键.6.(2022·江西景德镇·九年级期中)(1)【特例探究】如图1,在四边形ABCD 中,AB AD =,90ABC ADC ∠=∠=︒,100BAD ∠=︒,50EAF ∠=︒,猜想并写出线段BE ,DF ,EF 之间的数量关系,证明你的猜想;(2)【迁移推广】如图2,在四边形ABCD 中,AB AD =,180ABC ADC ∠+∠=︒,2BAD EAF ∠∠=.请写出线段BE ,DF ,EF 之间的数量关系,并证明;(3)【拓展应用】如图3,在海上军事演习时,舰艇在指挥中心(O 处)北偏东20°的A 处.舰艇乙在指挥中心南偏西50°的B 处,并且两舰艇在指挥中心的距离相等,接到行动指令后,舰艇甲向正西方向以80海里/时的速度前进,同时舰艇乙沿北偏西60°的方向以90海里/时的速度前进,半小时后,指挥中心观测到甲、乙两舰艇分别到达C ,D 处,且指挥中心观测两舰艇视线之间的夹角为75°.请直接写出此时两舰艇之间的距离.【答案】(1)EF =BE +DF ,理由见解析;(2)EF =BE +DF ,理由见解析;(3)85海里【分析】(1)延长CD 至点G ,使DG =BE ,连接AG ,可证得∠ABE ∠∠ADG ,可得到AE =AG ,∠BAE =∠DAG ,再由100BAD ∠=︒,50EAF ∠=︒,可证得∠AEF ∠∠AGF ,从而得到EF =FG ,即可求解;(2)延长CD 至点H ,使DH =BE ,连接AH ,可证得∠ABE ∠∠ADH ,可得到AE =AH ,∠BAE =∠DAH ,再由2BAD EAF ∠∠=,可证得∠AEF ∠∠AHF ,从而得到EF =FH ,即可求解;(3)连接CD ,延长AC 、BD 交于点M ,根据题意可得∠AOB =2∠COD ,∠OAM +∠OBM =70°+110°=180°,再由(2)【迁移推广】得:CD =AC +BD ,即可求解.【详解】解:(1)EF =BE +DF ,理由如下:如图,延长CD 至点G ,使DG =BE ,连接AG ,∠90ABC ADC∠=∠=︒,∠∠ADG=∠ABC=90°,∠AB=AD,∠∠ABE∠∠ADG,∠AE=AG,∠BAE=∠DAG,∠100BAD∠=︒,50EAF∠=︒,∠∠BAE+∠DAF=50°,∠∠F AG=∠EAF=50°,∠AF=AF,∠∠AEF∠∠AGF,∠EF=FG,∠FG=DG+DF,∠EF=DG+DF=BE+DF;(2)EF=BE+DF,理由如下:如图,延长CD至点H,使DH=BE,连接AH,∠180ABC ADC∠+∠=︒,∠ADC+∠ADH=180°,∠∠ADH=∠ABC,∠AB=AD,∠∠ABE∠∠ADH,∠AE=AH,∠BAE=∠DAH,∠2BAD EAF∠∠=∠∠EAF=∠BAE+∠DAF=∠DAF+∠DAH,∠∠EAF=∠HAF,∠AF=AF,∠∠AEF∠∠AHF,∠EF=FH,∠FH=DH+DF,∠EF=DH+DF=BE+DF;(3)如图,连接CD,延长AC、BD交于点M,根据题意得:∠AOB=20°+90°+40°=150°,∠OBD=60°+50°=110°,∠COD=75°,∠OAM=90°-20°=70°,OA=OB,∠∠AOB=2∠COD,∠OAM+∠OBM=70°+110°=180°,∠OA=OB,∠由(2)【迁移推广】得:CD=AC+BD,∠AC=80×0.5=40,BD=90×0.5=45,∠CD=40+45=85海里.即此时两舰艇之间的距离85海里.【点睛】此题是三角形综合题,主要考查了全等三角形的判定和性质、勾股定理的运用、等腰直角三角形的性质,题目的综合性较强,难度较大,解题的关键是正确的作出辅助线构造全等三角形,解答时,注意类比思想的应用.7.(2022·上海·九年级专题练习)小明遇到这样一个问题:如图1,在Rt∠ABC中,∠BAC=90°,AB=AC,点D,E在边BC上,∠DAE=45°.若BD=3,CE=1,求DE的长.小明发现,将∠ABD 绕点A 按逆时针方向旋转90º,得到∠ACF ,联结EF (如图2),由图形旋转的性质和等腰直角三角形的性质以及∠DAE =45°,可证△F AE ∠△DAE ,得FE =DE .解△FCE ,可求得FE (即DE )的长.(1)请回答:在图2中,∠FCE 的度数是 ,DE 的长为 .参考小明思考问题的方法,解决问题:(2)如图3,在四边形ABCD 中,AB =AD ,∠B +∠D =180°.E ,F 分别是边BC ,CD 上的点,且∠EAF =12∠BAD .猜想线段BE ,EF ,FD 之间的数量关系并说明理由. )根据旋转的性质,可得ADB AFC ≌,勾股定理解按逆时针方向旋转,使AB 与AD 重合,FG =DG +FD =BE +按逆时针方向旋转90º,得到∠ACF ∠ADB AFC ≌ACF ∴∠,90AB AC BAC ∠==45ACF ABD ∴∠=∠=在Rt FCE 中,BD 2EF CF ∴=+(2)猜想:EF =BE 如图,将∠ABE8.(2022·黑龙江·哈尔滨市九年级阶段练习)已知四边形ABCD 是正方形,一个等腰直角三角板的一个锐角顶点与A 点重合,将此三角板绕A 点旋转时,两边分别交直线BC ,CD 于M ,N .(1)如图1,当M ,N 分别在边BC ,CD 上时,求证:BM +DN =MN(2)如图2,当M ,N 分别在边BC ,CD 的延长线上时,请直接写出线段BM ,DN ,MN 之间的数量关系(3)如图3,直线AN 与BC 交于P 点,MN =10,CN =6,MC =8,求CP 的长.【答案】(1)见解析;(2)BM DN MN -=;(3)3【分析】(1)延长CB 到G 使BG DN=,连接AG ,先证明AGB AND ≅△△,由此得到AG AN =,GAB DAN ∠=∠,再根据45MAN ∠=︒,90BAD ∠=︒,可以得到45GAM NAM ∠=∠=︒,从而证明AMN AMG △≌△,然后根据全等三角形的性质即可证明BM DN MN +=;(2)在BM 上取一点G ,使得BG DN =,连接AG ,先证明AGB AND ≅△△,由此得到AG AN =,GAB DAN ∠=∠,由此可得90GAN BAD ∠=∠=︒,再根据45MAN ∠=︒可以得到45GAM NAM ∠=∠=︒,从而证明AMN AMG △≌△,然后根据全等三角形的性质即可证明BM DN MN -=;(3)在DN 上取一点G ,使得DG BM =,连接AG ,先证明ABM ADG ≌,再证明AMN AGN △≌△,设DG BM x ==,根据DC BC =可求得2x =,由此可得6AB BC CD CN ====,最后再证明ABP NCP △≌△,由此即可求得答案.【详解】(1)证明:如图,延长CB 到G 使BG DN =,连接AG ,∠四边形ABCD 是正方形,∠AB AD =,90ABG ADN BAD ∠=∠=∠=︒,在ABG 与ADN △中,AB AD ABG ADN BG DN =⎧⎪∠=∠⎨⎪=⎩, ()AGB AND SAS ∴△≌△,AG AN ∴=,GAB DAN ∠=∠,45MAN ∠=︒,90BAD ∠=︒,∠45DAN BAM BAD MAN ∠+∠=∠-∠=︒,45GAM GAB BAM DAN BAM ∴∠=∠+∠=∠+∠=︒,GAM NAM ∴∠=∠,在AMN 与AMG 中,AM AM GAM NAM AN AG =⎧⎪∠=∠⎨⎪=⎩, ()AMN AMG SAS ∴△≌△,MN GM ∴=,又∠BM GB GM +=,BG DN =,BM DN MN ∴+=;(2)BM DN MN -=,理由如下:如图,在BM 上取一点G ,使得BG DN =,连接AG ,∠四边形ABCD 是正方形,∠AB AD =,90ABG ADN BAD ∠=∠=∠=︒,在ABG 与ADN △中,AB AD ABG ADN GB DN =⎧⎪∠=∠⎨⎪=⎩,()AGB AND SAS ∴△≌△,AG AN ∴=,GAB DAN ∠=∠,∠GAB GAD DAN GAD ∠+∠=∠+∠,∠90GAN BAD ∠=∠=︒,又45MAN ∠=︒,45GAM GAN MAN MAN∴∠=∠-∠=︒=∠,在AMN 与AMG 中,AM AM GAM NAM AN AG =⎧⎪∠=∠⎨⎪=⎩,()AMN AMG SAS ∴△≌△,MN GM ∴=,又∠BM BG GM -=,BG DN =,∠BM DN MN -=,故答案为:BM DN MN -=;(3)如图,在DN 上取一点G ,使得DG BM =,连接AG ,∠四边形ABCD 是正方形,∠AB AD BC CD ===,90ABM ADG BAD ∠=∠=∠=︒,//AB CD ,在ABM 与ADG 中,AB AD ABM ADG BM DG =⎧⎪∠=∠⎨⎪=⎩, ()ABM ADG SAS ∴△≌△,AM AG ∴=,MAB GAD ∠=∠,∠MAB BAG GAD BAG ∠+∠=∠+∠,∠90MAG BAD ∠=∠=︒,又45MAN ∠=︒,45GAN MAG MAN MAN ∴∠=∠-∠=︒=∠,在AMN 与AGN 中,AM AG MAN GAN AN AN =⎧⎪∠=∠⎨⎪=⎩, ()AMN AGN SAS ∴△≌△,10MN GN ∴==,设DG BM x ==,∠6CN =,8MC =,∠1064DC DG GN CN x x =+-=+-=+,8BC MC BM x =-=-, ∠DC BC =,∠48x x +=-,解得:2x =,∠6AB BC CD CN ====,∠//AB CD ,∠BAP CNP ∠=∠,在ABP △与NCP 中,APB NPC BAP CNP AB CN ∠=∠⎧⎪∠=∠⎨⎪=⎩, ()ABP NCP AAS ∴△≌△,9.(2022·浙江·九年级阶段练习)如图1,等腰直角三角板的一个锐角顶点与正方形ABCD的顶点A重合,将此三角板绕点A旋转,使三角板中该锐角的两条边分别交正方形的两边BC,DC于点E,F,连接EF.(1)猜想BE、EF、DF三条线段之间的数量关系,并证明你的猜想;(2)在图1中,过点A作AM∠EF于点M,请直接写出AM和AB的数量关系;∠BAD,(3)如图2,将Rt∠ABC沿斜边AC翻折得到Rt∠ADC,E,F分别是BC,CD边上的点,∠EAF=12连接EF,过点A作AM∠EF于点M,试猜想AM与AB之间的数量关系.并证明你的猜想.10.(2022·北京四中九年级期中)如图,在∠ABC中,∠ACB=90°,CA=CB,点P在线段AB上,作射线CP (0°<∠ACP<45°),射线CP绕点C逆时针旋转45°,得到射线CQ,过点A作AD∠CP于点D,交CQ于点E,连接BE.(1)依题意补全图形;(2)用等式表示线段AD,DE,BE之间的数量关系,并证明.【答案】(1)作图见解析.(2)结论:AD+BE=DE.证明见解析.【分析】(1)根据要求作出图形即可.(2)结论:AD+BE=DE.延长DA至F,使DF=DE,连接CF.利用全等三角形的性质解决问题即可.(1)解:如图所示:(2)结论:AD+BE=DE.理由:延长DA至F,使DF=DE,连接CF.∠AD∠CP,DF=DE,∠CE=CF,∠∠DCF=∠DCE=45°,∠∠ACB=90°,∠∠ACD+∠ECB=45°,∠∠DCA+∠ACF=∠DCF=45°,∠∠FCA=∠ECB,在∠ACF和∠BCE中,CA CB ACF BCE CF CE =⎧⎪∠=∠⎨⎪=⎩,∠∠ACF ∠∠BCE (SAS ),∠AF =BE ,∠AD +BE =DE .【点睛】本题考查作图-旋转变换,全等三角形的判定和性质,等腰直角三角形的判定和性质等知识,解题的关键是正确寻找全等三角形解决问题,属于中考常考题型.。
初中数学半角模型专题讲解(最全最新)

二、正方形中的半角模型
例2、已知正方形ABCD边长为5,点M、N分别在边BC,CD上,连 接AM,MN,AN,若∠MAN=45°,BM=2,求线段NC的长
单击此处编辑母版副标题样式
变式训练:已知:正方形ABCD中,∠MAN=45°,∠MAN绕点A顺时针 旋转,它的两边分别交CB,DC(或它们的延长线)于点M,N.当 ∠MAN绕点A旋转到如图2的位置时,猜想线段BM,DN和MN之间又有 怎样的数量关系呢?写出你的猜想.(需要证明)
再见!谢谢大家的聆听!
变式训练:已知∠MAN=45°,AHபைடு நூலகம்MN于点H,且MH=2,NH=3,求 AH的长.
变式训练:如图,点E、F分别在正方形ABCD的边CD,BC上,且∠EAF =45°,将△ADE绕点A顺时针旋转90°得到△ABG,连接BD交AF于点M, DE=2,BF=3,求GM
三、四边形中的半角模型
例3、如图,在四边形ABCD中,AB=AD,∠B=∠D=90°,E、F分 别是边BC、CD上的点,且2∠EAF=∠BAD.求证:EF=BE+FD.
变式训练:在四边形ABCD中,AB=AD,∠B+∠D=180°,E、F分别是边 BC、CD上的点,且2∠EAF=∠BAD,证明:EF=BE+FD
变式训练:在四边形ABCD中,AB=AD,∠B+∠ADC=180°,E、F分别 是边BC、CD延长线上的点,且2∠EAF=∠BAD,证明:EF=BE﹣FD.
初中数学模型:半角模型专题
学校:永州博闻高级中学数学组(八年级) 主讲:蒋老师
一、等边三角形中的半角模型
例1、如图,△ABC是边长为6的等边三角形,BD=CD,∠BDC= 120°,以点D为顶点作一个60°角,使其两边分别交AB于点M,交 AC于点N,连结MN,求△AMN的周长
专题20 半角模型(解析版)

中考常考几何模型专题20 半角模型倍长中线或类中线(与中点有关的线段)构造全等三角形 如图①: (1)∠2=21∠AOB ;(2)OA=OB 。
如图②:连接 FB ,将△FOB 绕点 O 旋转至△FOA 的位置,连接 F ′E 、FE ,可得△OEF ′≌△OEF 。
模型精练1.(2019秋•九龙坡区校级月考)如图.在四边形ABCD 中,∠B +∠ADC =180°,AB =AD ,E 、F 分别是边BC 、CD 延长线上的点,且∠EAF =12∠BAD ,求证:EF =BE ﹣FD .2.(2020•锦州模拟)问题情境:已知,在等边△ABC中,∠BAC与∠ACB的角平分线交于点O,点M、N 分别在直线AC,AB上,且∠MON=60°,猜想CM、MN、AN三者之间的数量关系.方法感悟:小芳的思考过程是在CM上取一点,构造全等三角形,从而解决问题;小丽的思考过程是在AB取一点,构造全等三角形,从而解决问题;问题解决:(1)如图1,M、N分别在边AC,AB上时,探索CM、MN、AN三者之间的数量关系,并证明;(2)如图2,M在边AC上,点N在BA的延长线上时,请你在图2中补全图形,标出相应字母,探索CM、MN、AN三者之间的数量关系,并证明.3.(2020•章丘区模拟)如图,在正方形ABCD中,M、N分别是射线CB和射线DC上的动点,且始终∠MAN=45°.(1)如图1,当点M、N分别在线段BC、DC上时,请直接写出线段BM、MN、DN之间的数量关系;(2)如图2,当点M、N分别在CB、DC的延长线上时,(1)中的结论是否仍然成立,若成立,给予证明,若不成立,写出正确的结论,并证明;(3)如图3,当点M、N分别在CB、DC的延长线上时,若CN=CD=6,设BD与AM的延长线交于点P,交AN于Q,直接写出AQ、AP的长.4.(2019•麒麟区模拟)已知,正方形ABCD中,∠MAN=45°,∠MAN绕点A顺时针旋转,它的两边分别交CB、DC(或它们的延长线)于点M、N,AH⊥MN于点H.(1)如图①,当∠MAN 绕点A 旋转到BM =DN 时,请你直接写出AH 与AB 的数量关系: ; (2)如图②,当∠MAN 绕点A 旋转到BM ≠DN 时,(1)中发现的AH 与AB 的数量关系还成立吗?如果不成立请写出理由,如果成立请证明;(3)如图③,已知∠MAN =45°,AH ⊥MN 于点H ,且MH =2,NH =3,求AH 的长.(可利用(2)得到的结论)5.(2019秋•东台市期末)在等边△ABC 的两边AB 、AC 所在直线上分别有两点M 、N ,D 为△ABC 外一点,且∠MDN =60°,∠BDC =120°,BD =DC .探究:当M 、N 分别在直线AB 、AC 上移动时,BM 、NC 、MN 之间的数量关系及△AMN 的周长Q 与等边△ABC 的周长L 的关系.(1)如图1,当点M 、N 边AB 、AC 上,且DM =DN 时,BM 、NC 、MN 之间的数量关系是 ;此时Q L= ;(2)如图2,点M 、N 在边AB 、AC 上,且当DM ≠DN 时,猜想( I )问的两个结论还成立吗?若成立请直接写出你的结论;若不成立请说明理由.(3)如图3,当M、N分别在边AB、CA的延长线上时,探索BM、NC、MN之间的数量关系如何?并给出证明.6.请阅读下列材料:已知:如图(1)在Rt△ABC中,∠BAC=90°,AB=AC,点D、E分别为线段BC上两动点,若∠DAE =45°.探究线段BD、DE、EC三条线段之间的数量关系.小明的思路是:把△AEC绕点A顺时针旋转90°,得到△ABE′,连接E′D,使问题得到解决.请你参考小明的思路探究并解决下列问题:(1)猜想BD、DE、EC三条线段之间存在的数量关系式,直接写出你的猜想;(2)当动点E在线段BC上,动点D运动在线段CB延长线上时,如图(2),其它条件不变,(1)中探究的结论是否发生改变?请说明你的猜想并给予证明;(3)已知:如图(3),等边三角形ABC中,点D、E在边AB上,且∠DCE=30°,请你找出一个条件,使线段DE、AD、EB能构成一个等腰三角形,并求出此时等腰三角形顶角的度数.7.(2019•夏津县二模)如图1,在正方形ABCD中,E、F分别是BC,CD上的点,且∠EAF=45度.则有结论EF=BE+FD成立;(1)如图2,在四边形ABCD中,AB=AD,∠B=∠D=90°,E、F分别是BC,CD上的点,且∠EAF 是∠BAD的一半,那么结论EF=BE+FD是否仍然成立?若成立,请证明;不成立,请说明理由.(2)若将(1)中的条件改为:如图3,在四边形ABCD中,AB=AD,∠B+∠D=180°,延长BC到点E,延长CD到点F,使得∠EAF仍然是∠BAD的一半,则结论EF=BE+FD是否仍然成立?若成立,请证明;不成立,请写出它们的数量关系并证明.8.(1)如图1,将∠EAF绕着正方形ABCD的顶点A顺时针旋转,∠EAF的两边交BC于E,交CD于F,连接EF.若∠EAF=45°,BE、DF的长度是方程x2﹣5x+6=0的两根,请直接写出EF的长;(2)如图2,将∠EAF绕着四边形ABCD的顶点A顺时针旋转,∠EAF的两边交CB的延长线于E,交DC的延长线于F,连接EF.若AB=AD,∠ABC与∠ADC互补,∠EAF=12∠BAD,请直接写出EF与DF、BE之间的数量关系,并证明你的结论;(3)在(2)的前提下,若BC=4,DC=7,CF=2,求△CEF的周长.①EF的长为:;②数量关系:.中考常考几何模型专题20 半角模型倍长中线或类中线(与中点有关的线段)构造全等三角形 如图①: (1)∠2=21∠AOB ;(2)OA=OB 。
重难点拓展:等腰三角形中的半角模型两种常见题型解题技巧(解析版)
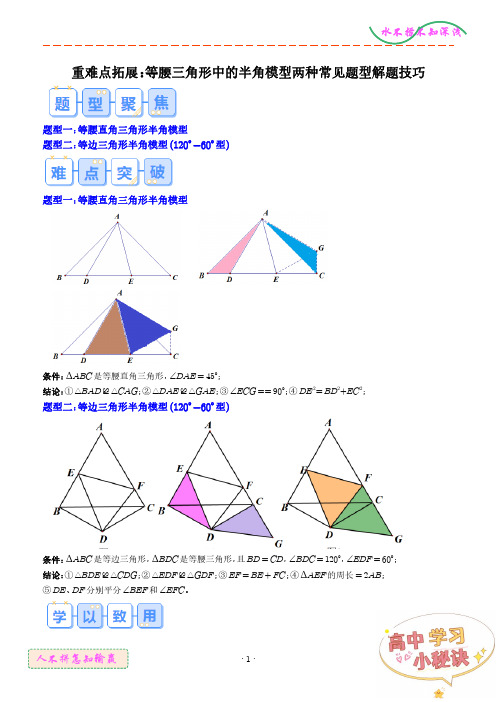
重难点拓展:等腰三角形中的半角模型两种常见题型解题技巧题型一:等腰直角三角形半角模型题型二:等边三角形半角模型(120°-60°型)题型一:等腰直角三角形半角模型条件:ΔABC是等腰直角三角形,∠DAE=45°;结论:①△BAD≌△CAG;②△DAE≌△GAE;③∠ECG==90°;④DE2=BD2+EC2;题型二:等边三角形半角模型(120°-60°型)条件:ΔABC是等边三角形,ΔBDC是等腰三角形,且BD=CD,∠BDC=120°,∠EDF=60°;结论:①△BDE≌△CDG;②△EDF≌△GDF;③EF=BE+FC;④ΔAEF的周长=2AB;⑤DE、DF分别平分∠BEF和∠EFC。
题型归纳题型一:等腰直角三角形半角模型1如图,已知△ABC中,∠BAC=90°,AB=AC,D,E是B C边上的点,将△ABD绕点A旋转,得到△ACD ,当∠DAE=45°时,求证:DE=D E;在(1)的条件下,猜想:BD2,DE2,CE2有怎样的数量关系?请写出,并说明理由.解析:因为△ABD绕点A旋转,得到△ACD∴AD=AD ,∠DAD'=∠BAC=90°∵∠DAE=45°∴∠EAD'=∠DAD'-∠DAE=45°∴在△AED和△AED 中AE=AE∠EAD=∠AED'AD=AD'∴△AED≌△AED'∴DE=D'E由(1)得△AED≌△AED',ED=ED'在△ABC中,AB=AC,∠BAC=90°∴∠B=∠ACB=45°∵△ABD绕点A旋转,得到△ACD'∴BD=CD',∠B=∠ACD'=45°∴∠BCD'=∠ACB+∠ACD'=45°+45°=90°2(2022秋•原平市校级期中)如图,RtΔABC中AB=AC,D、E为BC边上两点,且∠DAE=45°,将ΔADC绕点A顺时针旋转90°后,得到ΔAFB,连接EF.下列4个结论:①ΔADC≅ΔAFB;②ΔABE≅ΔACD;③ΔAED≅ΔAEF;④BE+EF=BC-BF.正确的有( )个.A.1B.2C.3D.4【分析】根据旋转变换的性质判断①;根据全等三角形的判定定理判断②;根据SAS定理判断③;根据全等三角形的性质、线段和差可判断④.【解答】解:∵ΔADC绕点A顺时针旋转90°得ΔAFB,∴ΔADC≅ΔAFB,①正确;∵EA与DA不一定相等,∴ΔABE与ΔACD不一定全等,②错误;∵∠FAD=90°,∠DAE=45°,∴∠FAE=∠DAE=45°,在ΔAED和ΔAEF中,AF=AD∠EAF=∠EAD AE=AE,∴ΔAED≅ΔAEF,③正确;∴DE=EF,∴BE+EF=BE+DE=BD,∵ΔADC≅ΔAFB,∴BF=CD,∴BD=BC-CD=BC-BF,∴BE+EF=BC-BF,④正确;∴正确的有①③④共3个,故选:C.【点评】本题考查的是全等三角形的判定与性质、旋转变换,掌握全等三角形的判定定理与性质定理、图形旋转的性质等知识是解题的关键.3(2023·浙江·八年级假期作业)如图,在Rt△ABC中,AB=AC,∠ABC=∠ACB=45°,D、E是斜边BC上两点,且∠DAE=45°,若BD=3,CE=4,S△ADE=15,则△ABD与△AEC的面积之和为()A.36B.21C.30D.22【答案】B【分析】将△ADE关于AE对称得到△AFE,从而可得△AFE的面积为15,再根据对称的性质可得AF= AD,∠EAF=45°,然后根据三角形全等的判定定理证出△ACF≅△ABD,从而可得CF=BD=3,∠ACF =∠ABD=45°,S△ACF=S△ABD,最后根据△ABD与△AEC的面积之和等于△AFE与△CEF的面积之和即可得.【详解】解:如图,将△ADE关于AE对称得到△AFE,则AF=AD,∠EAF=45°,S△AFE=S△ADE=15,∴∠CAF+∠CAD=∠DAE+∠EAF=45°+45°=90°,∵∠BAD+∠CAD=∠BAC=180°-∠ABC-∠ACB=90°,∴∠CAF=∠BAD,在△ACF和△ABD中,AC=AB∠CAF=∠BAD AF=AD,∴△ACF≅△ABD(SAS),∴CF=BD=3,∠ACF=∠ABD=45°,S△ACF=S△ABD,∴∠ECF=∠ACB+∠ACF=90°,即△CEF是直角三角形,∴S△CEF=12CE⋅CF=12×4×3=6,∴S△ABD+S△AEC=S△ACF+S△AEC=S△AFE+S△CEF=15+6=21,即△ABD与△AEC的面积之和为21,故选:B.【点睛】本题考查了轴对称的性质、三角形全等的判定定理与性质等知识点,通过作辅助线,构造全等三角形和直角三角形是解题关键.4(2023秋•九龙坡区校级期中)如图1,ΔABC为等边三角形,点D为BC的中点,连接AD,AE平分∠DAC,交BC于点E,点F在ΔABC外,连接FE,BF,AF,满足BF⎳AC,∠AFB=∠AEC.(1)求∠FAE的度数;(2)如图2,点G是AC上一点,连接EG,GF,GF与AE交于点K.若AK=EK,求证:CG=2CE.【分析】(1)先证ΔABF 和ΔACE 全等,得∠BAF =∠CAE ,AF =AE ,再根据∠FAE =∠BAF +∠BAE =∠CAE +∠BAE 可得出答案;(2)由(1)可知:ΔAFE 为等边三角形,从而得∠AFB =60°,AF =EF ,根据AK =EK ,得∠AFG =∠EFG =30°,FK ⊥AE ,由此可证ΔAFG 和ΔEFG 全等,得∠AGF =∠EGF ,然后根据点D 为BC 的中点,及AE 平分∠DAC 可得出∠CAE =15°,进而可求出∠AGF =∠EGF =75°,由此得∠CGE =30°,∠CEG =90°,最后再利用直角三角形的性质可得出结论.【解答】(1)解:∵ΔABC 为等边三角形,∴∠C =∠BAC =60°,AB =AC ,∵BF ⎳AC ,∴∠ABF =∠BAC =60°,∴∠ABF =∠C =60°,在ΔABF 和ΔACE 中,∠AFB =∠AEC ∠ABF =∠C AB =AC,∴ΔABF ≅ΔACE (AAS ),∴∠BAF =∠CAE ,AF =AE ,∴∠FAE =∠BAF +∠BAE =∠CAE +∠BAE =∠CAE =60°;(2)证明:由(1)可知:AF =AE ,∠FAE =60°,∴ΔAFE 为等边三角形,∴∠AFB =60°,AF =EF ,∵AK =EK ,∴∠AFG =∠EFG =30°,FK ⊥AE ,在ΔAFG 和ΔEFG 中,AF =EF∠AFG =∠EFG FG =FG,∴ΔAFG≅ΔEFG(SAS),∴∠AGF=∠EGF,∵ΔABC为等边三角形,点D为BC的中点,∴∠DAC=12∠BAC=30°,∵AE平分∠DAC,∴∠CAE=12∠DAC=15°,∵FK⊥AE,∴∠AGF=90°-∠CAE=90°-15°=75°,∴∠AGF=∠EGF=75°,∴∠CGE=180°-(∠AGF+∠EGF)=30°,又∠C=60°,∴∠CEG=180°-∠C-∠CGE=90°,在RtΔCEG中,∠CGE=30°,∴CG=2CE.【点评】此题主要考查了等边三角形的判定和性质,全等三角形的判定和性质,直角三角形的性质,熟练掌握等边三角形的判定和性质,全等三角形的判定和性质,直角三角形的性质,理解在直角三角形中,30°的角所对的直角边等于斜边的一半是解决问题的关键.题型二:等边三角形半角模型(120°-60°型)1(2023秋•越秀区校级月考)在等边ΔABC的两边AB、AC所在直线上分别有两点M、N,D为ΔABC外一点,且∠MDN=60°,∠BDC=120°,BD=DC.探究:当M、N分别在直线AB、AC上移动时,BM、NC、MN之间的数量关系及ΔAMN的周长Q与等边ΔABC的周长L的关系.(1)如图1,当点M、N边AB、AC上,且DM=DN时,BM、NC、MN之间的数量关系是;此时Q L=;(2)如图2,点M、N边AB、AC上,且当DM≠DN时,猜想(1)问的两个结论还成立吗?写出你的猜想并加以证明;(3)如图3,当M、N分别在边AB、CA的延长线上时,若AN=x,则Q=(用x、L表示).【分析】(1)如果DM=DN,∠DMN=∠DNM,因为BD=DC,那么∠DBC=∠DCB=30°,也就有∠MBD=∠NCD=60+30=90°,直角三角形MBD、NCD中,因为BD=CD,DM=DN,根据HL定理,两三角形全等.那么BM=NC,∠BMD=∠DNC=60°,三角形NCD中,∠NDC=30°,DN=2NC,在三角形DNM中,DM=DN,∠MDN=60°,因此三角形DMN是个等边三角形,因此MN=DN=2NC=NC +BM,三角形AMN的周长Q=AM+AN+MN=AM+AN+MB+NC=AB+AC=2AB,三角形ABC的周长L=3AB,因此Q:L=2:3.(2)如果DM≠DN,我们可通过构建全等三角形来实现线段的转换.延长AC至E,使CE=BM,连接DE.(1)中我们已经得出,∠MBD=∠NCD=90°,那么三角形MBD和ECD中,有了一组直角,MB= CE,BD=DC,因此两三角形全等,那么DM=DE,∠BDM=∠CDE,∠EDN=∠BDC-∠MDN=60°.三角形MDN和EDN中,有DM=DE,∠EDN=∠MDN=60°,有一条公共边,因此两三角形全等,MN= NE,至此我们把BM转换成了CE,把MN转换成了NE,因为NE=CN+CE,因此NM=BM+CN.Q 与L的关系的求法同(1),得出的结果是一样的.(3)我们可通过构建全等三角形来实现线段的转换,思路同(2)过D作∠CDH=∠MDB,三角形BDM和CDH中,由(1)中已经得出的∠DCH=∠MBD=90°,我们做的角∠BDM=∠CDH,BD=CD因此两三角形全等(ASA).那么BM=CH,DM=DH,三角形MDN和NDH中,已知的条件有MD=DH,一条公共边ND,要想证得两三角形全等就需要知道∠MDN=∠HDN,因为∠CDH=∠MDB,因此∠MDH=∠BDC=120°,因为∠MDN=60°,那么∠NDH=120°-60°=60°,因此∠MDN=∠NDH,这样就构成了两三角形全等的条件.三角形MDN和DNH就全等了.那么NM=NH=AN+AC-BM,三角形AMN的周长Q=AN+AM+MN=AN+AB+BM+AN+AC-BM=2AN+2AB.因为AN=x,AB=13 L,因此三角形AMN的周长Q=2x+23 L.【解答】解:(1)如图,BM、NC、MN之间的数量关系BM+NC=MN.此时QL=23.(2)猜想:结论仍然成立.证明:如图,延长AC至E,使CE=BM,连接DE.∵BD=CD,且∠BDC=120°,∴∠DBC=∠DCB=30°.又∵ΔABC是等边三角形,∴∠MBD=∠NCD=90°.在ΔMBD与ΔECD中:BM=CE∠MBD=∠ECD BD=DC∴ΔMBD ≅ΔECD (SAS ).∴DM =DE ,∠BDM =∠CDE .∴∠EDN =∠BDC -∠MDN =60°.在ΔMDN 与ΔEDN 中:DM =DE∠MDN =∠EDN DN =DN,∴ΔMDN ≅ΔEDN (SAS ).∴MN =NE =NC +BM .ΔAMN 的周长Q =AM +AN +MN =AM +AN +(NC +BM )=(AM +BM )+(AN +NC )=AB +AC =2AB .而等边ΔABC 的周长L =3AB .∴Q L =2AB 3AB=23.(3)如图,当M 、N 分别在AB 、CA 的延长线上时,若AN =x ,则Q =2x +23L (用x 、L 表示).【点评】本题考查了三角形全等的判定及性质;题目中线段的转换都是根据全等三角形来实现的,当题中没有明显的全等三角形时,我们要根据条件通过作辅助线来构建于已知和所求条件相关的全等三角形.2如图,ΔABC 是边长为6的等边三角形,BD =CD ,∠BDC =120°,以点D 为顶点作一个60°角,使其两边分别交AB 于点M ,交AC 于点N ,连结MN ,则ΔAMN 的周长是.【分析】要求ΔAMN 的周长,根据题目已知条件无法求出三条边的长,只能把三条边长用其它已知边长来表示,所以需要作辅助线,延长AB 至F ,使BF =CN ,连接DF ,通过证明ΔBDF ≅ΔCND ,及ΔDMN ≅ΔDMF ,从而得出MN =MF ,ΔAMN 的周长等于AB +AC 的长.【解答】解:∵ΔBDC 是等腰三角形,且∠BDC =120°,∴∠BCD =∠DBC =30°,∵ΔABC 是边长为4的等边三角形,∴∠ABC =∠BAC =∠BCA =60°,∴∠DBA =∠DCA =90°,延长AB 至F ,使BF =CN ,连接DF ,在ΔBDF 和ΔCND 中,BF =CN∠FBD =∠DCN DB =DC,∴ΔBDF ≅ΔCND (SAS ),∴∠BDF =∠CDN ,DF =DN ,∵∠MDN =60°,∴∠BDM +∠CDN =60°,∴∠BDM +∠BDF =60°,在ΔDMN 和ΔDMF 中,MD =MD∠FDM =∠MDN DF =DN,∴ΔDMN ≅ΔDMF (SAS ),∴MN =MF ,∴ΔAMN 的周长是:AM +AN +MN =AM +MB +BF +AN =AB +AC =6+6=12.故答案为:12.【点评】此题考查了全等三角形的判定与性质,等边三角形的性质;主要利用等边三角形和等腰三角形的性质来证明三角形全等,构造另一个三角形是解题的关键.3如图,ΔABC 是边长为4的等边三角形,BD =CD ,且∠BDC =120°,以D 为顶点作一个60°角,使其两边分别交AB 于点M .交AC 于点N ,连接MN ,则ΔAMN 的周长是.【分析】要求ΔAMN 的周长,根据题目已知条件无法求出三条边的长,只能把三条边长用其它已知边长来表示,所以需要作辅助线,延长AB 至F ,使BF =CN ,连接DF ,通过证明ΔBDF ≅ΔCND ,及ΔDMN ≅ΔDMF ,从而得出MN =MF ,ΔAMN 的周长等于AB +AC 的长.【解答】解:∵ΔBDC 是等腰三角形,且∠BDC =120°,∴∠BCD =∠DBC =30°,∵ΔABC 是边长为4的等边三角形,∴∠ABC =∠BAC =∠BCA =60°,∴∠DBA =∠DCA =90°,延长AB 至F ,使BF =CN ,连接DF ,在ΔBDF 和ΔCND 中,∵BF =CN∠FBD =∠DCN DB =DC,∴ΔBDF ≅ΔCND (SAS ),∴∠BDF =∠CDN ,DF =DN ,∵∠MDN =60°,∴∠BDM +∠CDN =60°,∴∠BDM +∠BDF =60°,在ΔDMN 和ΔDMF 中,MD =MD∠FDM =∠MDN DF =DN,∴ΔDMN ≅ΔDMF (SAS )∴MN =MF ,∴ΔAMN 的周长是:AM +AN +MN =AM +MB +BF +AN =AB +AC =4+4=8.故答案为:8.【点评】此题考查了全等三角形的判定与性质,等边三角形的性质;主要利用等边三角形和等腰三角形的性质来证明三角形全等,构造另一个三角形是解题的关键.4(2022秋•宜丰县校级期中)如图1,ΔABC 是正三角形,ΔBDC 是等腰三角形,BD =CD ,∠BDC =120°,以D 为顶点作一个60°角,角的两边分别交AB 、AC 边于M 、N 两点,连接MN .(1)探究BM 、MN 、NC 之间的关系,并说明理由.(2)若ΔABC 的边长为2,求ΔAMN 的周长.【分析】(1)延长AC 至E ,使得CE =BM 并连接DE ,构造全等三角形,找到MD =DE ,∠BDM =∠CDE ,BM =CE ,再进一步证明ΔDMN ≅ΔDEN ,进而得到MN =BM +NC ;(2)利用(1)中结论,将ΔAMN 的周长转化为AB 、AC 的和来解答.【解答】解:(1)MN =BM +NC .理由如下:延长AC 至E ,使得CE =BM ,连接DE ,如图所示:∵ΔBDC 为等腰三角形,ΔABC 为等边三角形,∴BD =CD ,∠DBC =∠DCB ,∠MBC =∠ACB =60°,又∵BD =DC ,且∠BDC =120°,∴∠DBC =∠DCB =30°,∴∠ABC +∠DBC =∠ACB +∠DCB =60°+30°=90°,∴∠MBD =∠ECD =90°,在ΔMBD 与ΔECD 中,BD =CD∠MBD =∠ECD BM =CE,∴ΔMBD ≅ΔECD (SAS ),∴MD =DE ,∠BDM =∠CDE ,BM =CE ,又∵∠BDC =120°,∠MDN =60°,∴∠BDM +∠NDC =∠BDC -∠MDN =60°,∴∠CDE +∠NDC =60°,即∠NDE =60°,∴∠MDN =∠NDE =60°,在ΔDMN 与ΔDEN 中,DM =DE∠MDN =∠NDE DN =DN,∴ΔDMN ≅ΔDEN (SAS ),∴MN =EN ,又∵NE =NC +CE ,BM =CE ,∴MN =BM +NC ;(2)∵ΔABC 为等边三角形,∴AB =BC =AC =2,利用(1)中的结论得出:BM =CE ,MN =EN ,ΔAMN 的周长=AM +MN +AN=AM +NE +AN =AM +AN +NC +CE =AM +AN +NC +BM =(AM +BM )+(NC +AN )=AB +AC =2+2=4.【点评】本题考查了全等三角形的判定与性质及等边三角形的性质及等腰三角形的性质;此题从不同角度考查了作相等线段构造全等三角形的能力,要充分利用等边三角形及等腰三角形的性质,转换各相等线段解答.过关检测一、单选题1如图所示,在Rt △ABC 中,AB =AC ,D 、E 是斜边BC 上的两点,且∠DAE =45°,将△ADC 绕点A按顺时针方向旋转90°后得到△AFB,连接EF,有下列结论:①BE=DC;②∠BAF=∠DAC;③∠FAE=∠DAE;④BF=DC.其中正确的有()A.①②③④B.②③C.②③④D.③④【答案】C【分析】利用旋转性质可得△ABF≌△ACD,根据全等三角形的性质一一判断即可.【详解】解:∵△ADC绕A顺时针旋转90°后得到△AFB,∴△ABF≌△ACD,∴∠BAF=∠CAD,AF=AD,BF=CD,故②④正确,∴∠EAF=∠BAF+∠BAE=∠CAD+∠BAE=∠BAC-∠DAE=90°-45°=45°=∠DAE故③正确无法判断BE=CD,故①错误,故选:C.【点睛】本题考查了旋转的性质:旋转前后两图形全等,解题的关键是熟练掌握基本知识,属于中考常考题型.2(21-22八年级上·福建龙岩·期中)如图,在Rt△ABC中,AB=AC,∠ABC=∠ACB=45°,D、E 是斜边BC上两点,且∠DAE=45°,若BD=3,CE=4,S△ADE=15,则△ABD与△AEC的面积之和为()A.36B.21C.30D.22【答案】B【分析】将△ADE关于AE对称得到△AFE,从而可得△AFE的面积为15,再根据对称的性质可得AF= AD,∠EAF=45°,然后根据三角形全等的判定定理证出△ACF≅△ABD,从而可得CF=BD=3,∠ACF =∠ABD=45°,S△ACF=S△ABD,最后根据△ABD与△AEC的面积之和等于△AFE与△CEF的面积之和即可得.【详解】解:如图,将△ADE关于AE对称得到△AFE,则AF=AD,∠EAF=45°,S△AFE=S△ADE=15,∴∠CAF+∠CAD=∠DAE+∠EAF=45°+45°=90°,∵∠BAD+∠CAD=∠BAC=180°-∠ABC-∠ACB=90°,∴∠CAF=∠BAD,在△ACF和△ABD中,AC=AB∠CAF=∠BAD AF=AD,∴△ACF≅△ABD(SAS),∴CF=BD=3,∠ACF=∠ABD=45°,S△ACF=S△ABD,∴∠ECF=∠ACB+∠ACF=90°,即△CEF是直角三角形,∴S△CEF=12CE⋅CF=12×4×3=6,∴S△ABD+S△AEC=S△ACF+S△AEC=S△AFE+S△CEF=15+6=21,即△ABD与△AEC的面积之和为21,故选:B.【点睛】本题考查了轴对称的性质、三角形全等的判定定理与性质等知识点,通过作辅助线,构造全等三角形和直角三角形是解题关键.二、解答题3在等边△ABC的两边AB、AC所在直线上分别有两点M、N,D为△ABC外一点,且∠MDN= 60°,∠BDC=120°,BD=DC.探究:当M、N分别在直线AB、AC上移动时,BM、NC、MN之间的数量关系及△AMN的周长Q与等边△ABC的周长L的关系.(1)如图1,当点M 、N 边AB 、AC 上,且DM =DN 时,BM 、NC 、MN 之间的数量关系是;此时QL=;(2)如图2,点M 、N 在边AB 、AC 上,且当DM ≠DN 时,猜想(I )问的两个结论还成立吗?若成立请直接写出你的结论;若不成立请说明理由.(3)如图3,当M 、N 分别在边AB 、CA 的延长线上时,探索BM 、NC 、MN 之间的数量关系如何?并给出证明.【答案】(1)BM +NC =MN ,23;(2)结论仍然成立,详见解析;(3)NC -BM =MN ,详见解析【分析】(1)由DM =DN ,∠MDN =60°,可证得△MDN 是等边三角形,又由△ABC 是等边三角形,CD =BD ,易证得Rt △BDM ≌Rt △CDN ,然后由直角三角形的性质,即可求得BM 、NC 、MN 之间的数量关系 BM +NC =MN ,此时Q L=23;(2)在CN 的延长线上截取CM 1=BM ,连接DM 1.可证△DBM ≌△DCM 1,即可得DM =DM 1,易证得∠CDN =∠MDN =60°,则可证得△MDN ≌△M 1DN ,然后由全等三角形的性质,即可得结论仍然成立;(3)首先在CN 上截取CM 1=BM ,连接DM 1,可证△DBM ≌△DCM 1,即可得DM =DM 1,然后证得∠CDN =∠MDN =60°,易证得△MDN ≌△M 1DN ,则可得NC -BM =MN .【详解】(1)如图1,BM 、NC 、MN 之间的数量关系 BM +NC =MN .此时Q L=23. 理由:∵DM =DN ,∠MDN =60°,∴△MDN 是等边三角形,∵△ABC 是等边三角形,∴∠A =60°,∵BD =CD ,∠BDC =120°,∴∠DBC =∠DCB =30°,水不撩不知深浅∴∠MBD=∠NCD=90°,∵DM=DN,BD=CD,∴Rt△BDM≌Rt△CDN,∴∠BDM=∠CDN=30°,BM=CN,∴DM=2BM,DN=2CN,∴MN=2BM=2CN=BM+CN;∴AM=AN,∴△AMN是等边三角形,∵AB=AM+BM,∴AM:AB=2:3,∴QL=23;(2)猜想:结论仍然成立.证明:在NC的延长线上截取CM1=BM,连接DM1.∵∠MBD=∠M1CD=90°,BD=CD,∴△DBM≌△DCM1,∴DM=DM1,∠MBD=∠M1CD,M1C=BM,∵∠MDN=60°,∠BDC=120°,∴∠M1DN=∠MDN=60°,∴△MDN≌△M1DN,∴MN=M1N=M1C+NC=BM+NC,∴△AMN的周长为:AM+MN+AN=AM+BM+CN+AN=AB+AC,∴QL=23;(3)证明:在CN上截取CM1=BM,连接DM1.∵∠MBD=∠M1CD=90°,BD=CD,∴△DBM≌△DCM1,∴DM=DM1,∠MBD=∠M1CD,M1C=BM,∵∠MDN=60°,∠BDC=120°,∴∠M1DN=∠MDN=60°,∴△MDN≌△M1DN,∴MN=M1N.∴NC-BM=MN.【点睛】此题主要考查全等三角形的判定与性质,解题的关键是熟知等边三角形的性质及全等三角形的判定定理.4如图,△ABC是边长为3的等边三角形,△BDC是等腰三角形,且∠BDC=120°,以D为顶点作一个60°角,使其两边分别交AB于点M,交AC于点N,连接MN,求△AMN的周长.【答案】△AMN的周长为6.【分析】要求△AMN的周长,根据题目已知条件无法求出三条边的长,只能把三条边长用其它已知边长来表示,所以需要作辅助线,延长AB至F,使BF=CN,连接DF,通过证明△BDF≌△CDN,及△DMN≌△DMF,从而得出MN=MF,△AMN的周长等于AB+AC的长.【详解】解:∵△BDC是等腰三角形,且∠BDC=120°∴∠BCD=∠DBC=30°∵△ABC是边长为3的等边三角形∴∠ABC =∠BAC =∠BCA =60°∴∠DBA =∠DCA =90°延长AB 至F ,使BF =CN ,连接DF ,在Rt △BDF 和Rt △CND 中,BF =CN ,DB =DC ∴△BDF ≌△CDN ,∴∠BDF =∠CDN ,DF =DN ∵∠MDN =60°∴∠BDM +∠CDN =60°∴∠BDM +∠BDF =60°,∠FDM =60°=∠MDN ,DM 为公共边∴△DMN ≌△DMF ,∴MN =MF∴△AMN 的周长是:AM +AN +MN =AM +MB +BF +AN =AB +AC =6.【点睛】此题主要利用等边三角形和等腰三角形的性质来证明三角形全等,构造另一个三角形是解题的关键.5如图,△ABC 是边长为2的等边三角形,△BDC 是顶角为120°的等腰三角形,以点D 为顶点作∠MDN =60°,点M 、N 分别在AB 、AC 上.(1)如图①,当MN ⎳BC 时,则△AMN 的周长为;(2)如图②,求证:BM +NC =MN .【答案】(1)4;(2)见解析【分析】(1)首先证明△BDM ≌△CDN ,进而得出△DMN 是等边三角形,∠BDM =∠CDN =30°,NC =BM =12DM =12MN ,即可解决问题;(2)延长AC 至点E ,使得CE =BM ,连接DE ,首先证明△BDM ≌△CDE ,再证明△MDN ≌△EDN ,得出MN =NE ,进而得出结果即可.【详解】解:(1)∵△ABC 是等边三角形,MN ⎳BC ,∴∠AMN =∠ABC =60°,∠ANM =∠ACB =60°∴△AMN 是等边三角形,∴AM =AN ,则BM =NC ,∵△BDC 是顶角∠BDC =120°的等腰三角形,∴∠DBC =∠DCB =30°,∴∠DBM =∠DCN =90°,在△BDM 和△CDN 中,BM =CN ,∠MBD =∠DCN ,BD =CD ,∴△BDM ≌△CDN SAS ,∴DM =DN ,∠BDM =∠CDN ,∵∠MDN =60°,∴△DMN 是等边三角形,∠BDM =∠CDN =30°,∴NC =BM =12DM =12MN ,∴MN =MB +NC ,∴△AMN 的周长=AB +AC =4.(2)如图,延长AC 至点E ,使得CE =BM ,连接DE ,∵△ABC 是等边三角形,△BDC 是顶角∠BDC =120°的等腰三角形,∴∠ABC =∠ACB =60°,∠DBC =∠DCB =30°,∴∠ABD =∠ACD =90°,∴∠DCE =90°,在△BDM 和△CDE 中,BD =CD ,∠MBD =∠ECD ,BM =CE ,∴△BDM ≌△CDE SAS ,∴MD =ED ,∠MDB =∠EDC ,∴∠MDE =120°-∠MDB +∠EDC =120°,∵∠MDN =60°,∴∠NDE =60°,在△MDN 和△EDN 中,MD =ED ,∠MDN =∠NDE =60°,DN =DN ,∴△MDN ≌△EDN SAS .∴MN =NE ,又∵NE =NC +CE =NC +BM ,∴BM +NC =MN .【点睛】本题考查了全等三角形的判定与性质及等边三角形的性质及等腰三角形的性质,掌握全等三角形的性质与判定,等边三角形及等腰三角形的性质是解题的关键.6(21-22八年级上·浙江绍兴·期中)问题情境在等边△ABC 的两边AB ,AC 上分别有两点M ,N ,点D 为△ABC 外一点,且∠MDN =60°,∠BDC =120°,BD =DC .特例探究如图1,当DM =DN 时,(1)∠MDB =度;(2)MN 与BM ,NC 之间的数量关系为;归纳证明(3)如图2,当DM ≠DN 时,在NC 的延长线上取点E ,使CE =BM ,连接DE ,猜想MN 与BM ,NC 之间的数量关系,并加以证明.拓展应用(4)△AMN 的周长与△ABC 的周长的比为.【答案】(1)30;(2)MN =BM +NC ;(3)MN =BM +NC ,证明见解析;(4)23【分析】(1)先证明△MDN 是等边三角形,则MN =DM =DN ,再证明Rt △DBM ≌Rt △DCN (HL ),得∠BDM =∠CDN =30°;(2)由(1)得DM=2BM,可得结论MN=2BM=BM+NC;归纳证明:先证△DBM≌△DCE(HL),得DM=DE,∠BDM=∠CDE,再证△MDN≌△EDN(SAS),得MN=NE,可得结论MN=BM+CN;拓展应用:(3)首先根据题意利用SAS证明△DBM≌△DCE,然后证明△MDN≌△EDN,根据全等三角形对应相等通过线段之间的转化即可得到MN=BM+NC;(4)由(3)得到MN=BM+NC,则△AMN的周长=2AB,△ABC的周长=3AB,即可得出结论.【详解】特例探究:解:(1)∵DM=DN,∠MDN=60°,∴△MDN是等边三角形,∴MN=DM=DN,∵∠BDC=120°,BD=DC,∴∠DBC=∠DCB=30°,∵△ABC是等边三角形,∴∠ABC=∠ACB=60°,∴∠DBM=∠DCN=90°,∵BD=CD,DM=DN,∴Rt△DBM≌Rt△DCN(HL),∴∠MDB=∠NDC=30°,故答案为:30;(2)由(1)得:DM=2BM,DM=MN,Rt△DBM≌Rt△DCN(HL),∴BM=CN,∴DM=MN=2BM=BM+NC,即MN=BM+NC;归纳证明(3)解:猜想:MN=BM+NC,证明如下:∵△ABC是等边三角形,∴∠ABC=∠ACB=60°,∵BD=CD,∠BDC=120°,∴∠DBC=∠DCB=30°,∴∠MBD=∠NCD=90°.∴∠MBD=∠ECD=90°,又∵BD=CD,BM=CE,∴△DBM≌△DCE(SAS),∴DM=DE,∠MDB=∠EDC,∵∠MDN =60°,∠BDC =120°,∴∠MDB +∠NDC =60°,∴∠EDN =∠NDC +∠EDC =∠MDB +∠NDC =60°,∴∠EDN =∠MDN ,又∵DN =DN ,∴△MDN ≌△EDN (SAS ),∴MN =EN =EC +NC =BM +NC ;拓展应用(4)解:由(1)(2)得:MN =BM +NC ,∴△AMN 的周长=AM +MN +AN =AM +BM +NC +AN =AB +AC =2AB ,∵△ABC 是等边三角形,∴AB =BC =AC ,∴△ABC 的周长=3AB ,∴△AMN 的周长与△ABC 的周长的比为2AB 3AB=23,故答案为:23.【点睛】此题考查了等边三角形的性质的,全等三角形的判定和性质等知识,解题的关键是熟练掌握等边三角形的性质,全等三角形的判定和性质.7如图,已知在△ABC 中,AB =AC ,D 、E 是BC 边上的点,将△ABD 绕点A 旋转,得到△ACD ,连接D E .(1)当∠BAC =120°,∠DAE =60°时,求证:DE =D E ;(2)当DE =D E 时,∠DAE 与∠BAC 有怎样的数量关系?请写出,并说明理由.【答案】(1)见解析(2)∠DAE =12∠BAC ,理由见解析【分析】(1)根据旋转的性质可得AD =AD ,∠CAD =∠BAD ,然后求出∠D ′AE =60°,从而得到∠DAE =∠D AE ,再利用“边角边”证明△ADE 和△AD E 全等,根据全等三角形对应边相等证明即可;(2)根据旋转的性质可得AD =AD ,再利用“边边边”证明△ADE 和△AD E 全等,然后根据全等三角形对应角相等求出∠DAE =∠D AE ,然后求出∠BAD +∠CAE =∠DAE ,从而得解;【详解】(1)证明:∵△ABD 绕点A 旋转得到△ACD ,∴AD =AD ,∠CAD =∠BAD ,∵∠BAC =120°,∠DAE =60°,∴∠D AE =∠CAD +∠CAE =∠BAD +∠CAE =∠BAC -∠DAE =120°-60°=60°,∴∠DAE =∠D AE ,在△ADE 和△AD E 中,∵AD =AD∠DAE =∠D AE AE =AE,∴△ADE ≌△AD E (SAS ),∴DE =D E ;(2)解:∠DAE =12∠BAC .理由如下:在△ADE 和△AD E 中,AD =ADAE =AE DE =D E,∴△ADE ≌△AD ′E (SSS ),∴∠DAE =∠D AE ,∴∠BAD +∠CAE =∠CAD ′+∠CAE =∠D ′AE =∠DAE ,∴∠DAE =12∠BAC ;【点睛】本题考查了几何变换的综合题,旋转的性质,全等三角形的判定与性质,等腰直角三角形的性质,熟记旋转变换只改变图形的位置不改变图形的形状与大小找出三角形全等的条件是解题的关键.8(20-21七年级下·四川成都·期末)如图,CA =CB ,CA ⊥CB ,∠ECF =45°,CD =CF ,∠ACD =∠BCF .(1)求∠ACE +∠BCF 的度数;(2)以E 为圆心,以AE 长为半径作弧;以F 为圆心,以BF 长为半径作弧,两弧交于点G ,试探索△EFG 的形状?是锐角三形,直角三角形还是钝角三角形?请说明理由.【答案】(1)45°;(2)见详解【分析】(1)由CA ⊥CB ,可得∠ACB =90°,再根据∠ECF =45°,即可得出答案;(2)如图,连接DE ,先证明△ECF ≌△ECD (SAS ),可得DE =EF ,再证明△CAD ≌△CBF (SAS ),可得AD =BF ,∠CAD =∠B ,即可得出∠DAE =90°,再利用SSS 证明△EFG ≌△EDA ,即可得出答案.【详解】解:(1)∵CA ⊥CB ,∴∠ACB =90°,∴∠ACE +∠ECF +∠BCF =90°,∵∠ECF =45°,∴∠ACE +∠BCF =90°-∠ECF =45°;(2)△EFG 是直角三角形,理由如下:如图,连接DE ,由(1)知,∠ACE +∠BCF =45°,∵∠ACD =∠BCF ,∴∠ACE +∠ACD =45°,即∠DCE =45°,∵∠ECF =45°,∴∠ECF =∠ECD ,在△ECF 和△ECD 中,CF =CD∠ECF =∠ECD CE =CE,∴△ECF ≌△ECD (SAS ),∴DE =EF ,在△CAD 和△CBF 中,CD =CF∠ACD =∠BCF CA =CB,∴△CAD ≌△CBF (SAS ),∴AD =BF ,∠CAD =∠B ,∵FG =BF ,∴FG =AD ,∵∠ACB =90°,CA =CB ,∴△ABC 是等腰直角三角形,∴∠CAB =∠B =45°,∴∠DAE =∠CAB +∠B =90°,在△EFG和△EDA中,EG=EA FG=AD EF=ED,∴△EFG≌△EDA(SSS),∴∠EGF=∠EAD=90°,∴△EFG是直角三角形.【点睛】本题是三角形综合题,考查了等腰直角三角形性质,直角三角形的判定和性质,全等三角形判定和性质等知识,解题关键是添加辅助线构造全等三角形,熟练运用全等三角形判定和性质解决问题.9(2020秋•西青区期末)已知在ΔABC中,AB=AC,D,E是BC边上的点,将ΔABD绕点A旋转,得到ΔACD ,连接D E.(Ⅰ)如图1,当∠BAC=120°,∠DAE=60°时,求证:DE=D E;(Ⅱ)如图2,当DE=D E时,请写出∠DAE与∠BAC的数量关系,并说明理由.【分析】(I)由旋转知∠D AE=60°,再利用SAS证明ΔADE≅△AD E即可;(Ⅱ)利用SSS证明ΔADE≅△AD E,得∠DAE=∠D AE,从而得出答案;【解答】(I)证明:∵将ΔABD绕点A旋转,得到ΔACD ,∴AD=AD ,∠CAD =BAD,∵∠BAC=120°,∠DAE=60°,∴∠D AE=∠CAD +∠CAE=∠BAD+∠CAE=∠BAC-∠DAE=120°-60°=60°,∴∠DAE=∠D AE,在ΔADE与△AD E中,AD=AD∠DAE=∠D AE AE=AE,∴ΔADE≅△AD E(SAS),∴DE=D E;(Ⅱ)解:∠DAE=12∠BAC,理由如下:在ΔADE与△AD E中,AD=AD AE=AE DE=D E,∴ΔADE≅△AD E(SSS),∴∠DAE=∠D AE,∴∠BAD+∠CAE=∠CAD +∠CAE=∠D AE=∠DAE,∠BAC;∴∠DAE=1210(2022春•林甸县期末)如图ΔABC为等边三角形,直线a⎳AB,D为直线BC上任一动点,将一60°角的顶点置于点D处,它的一边始终经过点A,另一边与直线a交于点E.(1)若D恰好在BC的中点上(如图1)求证:ΔADE是等边三角形;(2)若D为直线BC上任一点(如图2),其他条件不变,上述(1)的结论是否成立?若成立,请给予证明;若不成立,请说明理由.【分析】(1)根据题意得出EC=CD=DB,进而可证得ΔABD≅ΔACE,从而可判断出结论.(2)在AC上取点F,使CF=CD,连接DF,从而证得ΔADF≅ΔEDC,进而得出结论.【解答】(1)证明:∵a⎳AB,且ΔABC为等边三角形,∴∠ACE=∠BAC=∠ABD=60°,AB=AC,∵BD=CD,∴AD⊥BC∵∠ADE=60°,∴∠EDC=30°,∴∠DOC=180°-∠EDC-∠ACB=90°,∴∠DEC=∠DOC-∠ACE=30°,∴∠EDC=∠DEC,∴EC=CD=DB,∴ΔABD≅ΔACE.∴AD=AE,且∠ADE=60°,∴ΔADE是等边三角形;(2)在AC上取点F,使CF=CD,连接DF,∵∠ACB=60°,∴ΔDCF是等边三角形,∵∠ADF+∠FDE=∠EDC+∠FDE=60°,∴∠ADF=∠EDC,∵∠DAF+∠ADE=∠DEC+∠ACE,∴∠DAF=∠DEC,∴ΔADF≅ΔEDC(AAS),∴AD=ED,又∵∠ADE=60°,∴ΔADE是等边三角形.【点评】本题考查了等边三角形的判定及性质,难度较大,注意基本性质的掌握及熟练应用是解答本题的关键.。
相似三角形中的基本模型-半角模型(解析版)

相似三角形中的基本模型--半角模型相似三角形在中考数学几何模块中占据着重要地位。
相似三角形与其它知识点结合以综合题的形式呈现,其变化很多,难度大,是中考的常考题型。
如果大家平时注重解题方法,熟练掌握基本解题模型,再遇到该类问题就信心更足了。
本专题就半角模型进行梳理及对应试题分析,方便掌握。
模型1.半角模型(相似模型)【常见模型及结论】1)半角模型(正方形中的半角相似模型)条件:已知,如图,在正方形ABCD中,∠EAF的两边分别交BC、CD边于M、N两点,且∠EAF=45°结论:如图1,△AMN∽△AFE且AFAM=AEAN=EFMN=2.(思路提示:∠ANM=∠AEF,∠AMN=∠AFE);图1图2结论:如图2,△MAN∽△MDA,△NAM∽△NBA;结论:如图3,连接AC,则△AMB∽△AFC,△AND∽△AEC.且AFAM=ACAB=2;图3图4结论:如图4,△BME∽△AMN∽△DFN.2)半角模型(特殊三角形中的半角相似模型)(1)含45°半角模型图1图2条件:如图1,已知∠BAC=90°,∠ABC=∠ACB=∠DAE=45°;结论:①△ABE∽△DAE∽△DCA;②ABBE=ADAE=CDAC;③AB⋅AC=BE⋅CD(AB2=BE⋅CD)(2)含60°半角模型条件:如图1,已知∠BAC=120°,∠ADE=∠DAE=60°;结论:①△ABD∽△CAE∽△CBA;②ADBD=CEAE=ACAB;③AD⋅AE=BD⋅CE(DE2=BD⋅CE)1(2023·山东济南·九年级期中)如图,在正方形ABCD中,点E、F分别是BC、DC边上的两点,且∠EAF=45°,AE、AF分别交BD于M,N.下列结论:①AB2=BN⋅DM;②AF平分∠DFE;③AM⋅AE=AN⋅AF;④BE+DF=2MN.其中正确的结论是()A.①②③④B.①②③C.①③D.①②【答案】A【分析】①转证AB:BN=DM:AB,因为AB=AD,所以即证AB:BN=DM:AD.证明△ABN∽△MDA;②把△ABE绕点A逆时针旋转90°,得△ADH证明△AFH≌△AFE(SAS);③即证AM:AN=AF:AE,证明△AMN∽△AFE(两角相等);④由②得BE十DF=EF,当E点与B点重合、F与C重合时,根据正方形的性质,结论成立.【详解】①∵∠BAN=∠BAM+∠MAN=∠BAM+45°,∠AMD=∠ABM+∠BAM=45°+∠BAM,∴∠BAN=∠AMD.又∠ABN=∠ADM=45°,∴△ABN∽△MDA,∴AB:BN=DM:AD,∵AD=AB,∴AB2=BN⋅DM.故①正确;②如图,把△ABE绕点A逆时针旋转90°,得到△ADH,∵∠BAD=90°,∠EAF=45°,∴∠BAE+∠DAF=45°.∴∠EAF=∠HAF,∵AE=AH,AF=AF,∴△AEF≌△AHF,∴∠AFH =∠AFE ,即AF 平分∠DFE ,故②正确;③∵AB ∥CD ,∴∠DFA =∠BAN ,∵∠AFE =∠AFD ,∠BAN =∠AMD ,∴∠AFE =∠AMN ,又∠MAN =∠FAE ,∴△AMN ∽△AFE ,∴AM :AF =AN :AE ,即AM ·AE =AN ·AF ,故③正确;④由②得BE +DF =DH +DF =FH =FE ,过A 作AO ⊥BD ,作AG ⊥EF ,则△AFE 与△AMN 的相似比就是AG :AO ,易证△ADF ≌△AGF (AAS ),则可知AG =AD =2AO ,从而得证,故④正确,故选:A .【点睛】此题考查了正方形的性质、相似(包括全等)三角形的判定和性质、旋转的性质等知识点,综合性极强,难度较大.2(2023·山东滨州·统考中考模拟)如图,在矩形ABCD 中,AB =2,BC =4,点E 、F 分别在BC 、CD 上,若AE =5,∠EAF =45°,则AF 的长为.【答案】4103【分析】取AB 的中点M ,连接ME ,在AD 上截取ND =DF ,设DF =DN =x ,则NF =2x ,再利用矩形的性质和已知条件证明△AME ∽△FNA ,利用相似三角形的性质:对应边的比值相等可求出x 的值,在直角三角形ADF 中利用勾股定理即可求出AF 的长.【详解】解:取AB 的中点M ,连接ME ,在AD 上截取ND =DF ,设DF =DN =x ,∵四边形ABCD 是矩形,∴∠D =∠BAD =∠B =90°,AD =BC =4,∴NF =2x ,AN =4-x ,∵AB =2,∴AM =BM =1,∵AE =5,AB =2,∴BE =1,∴ME =BM 2+BE 2=2,∵∠EAF =45°,∴∠MAE +∠NAF =45°,∵∠MAE +∠AEM =45°,∴∠MEA =∠NAF ,∴△AME ∽△FNA ,∴AM FN =ME AN ,∴12x=24-x ,解得:x =43∴AF =AD 2+DF 2=4103故答案为4103.【点睛】本题考查了矩形的性质、相似三角形的判断和性质以及勾股定理的运用,正确添加辅助线构造相似三角形是解题的关键.3(2023·福建龙岩·统考一模)如图,∠ACB =90°,AC =BC ,∠DCE =45°,如果AD =3,BE =4,则BC 的长是( ).A.5B.52C.62D.7【答案】C【详解】分析:由于△ABC中,AC=BC,∠ACB=90°,设DE=x,则AB=7+x,可以得出△ACE∽△CDE∽△BDC,根据相似三角形的性质,列出关于x方程,解出x,再计算BC的长.详解:设DE=x,则AB=7+x.∵∠ACB=90°,AC=BC,∴∠DCE=∠CAE=∠DBC=45°∴△ACE∽△CDE∽△BDC,设CD=a,CE=b,则有以下等式:x:b=b:3+x,x:a=a:4+x,x:a=b:AC,整理得:b2=x(x+3),a2=x(x+4),x•AC=ab,x2(x+3)(x+4)=a2b2=x2•AC2=x2(x+7)22,解得:x=5;∴AB=12,∴AC=BC=62.故选C.点睛:本题主要考查了三角形相似的性质和判定、等腰直角三角形的性质,以及列方程求解的能力.4(2023·广东·九年级专题练习)如图,ΔABC中,∠BAC=120°,AB=AC,点D为BC边上的点,点E为线段CD上一点,且CE=1,AB=23,∠DAE=60°,则DE的长为.【答案】7 3【分析】利用含30°角的直角三角形的性质及图形的相似可求DE的长.【详解】解:如图,作AF⊥BC于F,作EG⊥AC于G.∵ΔABC中,∠BAC=120°,AB=AC.∴∠B=∠C=30°.在R tΔCEG中,∠C=30°.∴EG=12CE=12,CG=32.∴AG=23-32=332.∵AF⊥BC.∴∠AFC=90°.∴AF=12AC=3.∵∠DAE=60°=∠FAC.∴∠DAF=∠EAG.∵∠AFD=∠AGE=90°.∴ΔADF∽ΔAGE.∴AF AG =DFEG,即3332=DF12.∴DF=13.由勾股定理得:AE2=AG2+EG2=AF2+EF2.∴EF2=3322+12 2-(3)2=4.∴EF=2.DE=2+13=73故答案为:73【点睛】本题考查含30°角的直角三角形的性质及相似三角形的判定,作辅助线构造直角三角形是求解本题的关键.5(2023·辽宁沈阳·统考二模)在菱形ABCD中,∠B=60°.点E,F分别在边BC,CD上,且BE= CF.连接AE,AF.(1)如图1,连接EF ,求证:△AEF 是等边三角形;(2)AG 平分∠EAF 交BC 于点G .①如图2,AG 交EF 于点M ,点N 是BC 的中点,当BE =4时,求MN 的长.②如图3,O 是AC 的中点,点H 是线段AG 上一动点(点H 与点A ,点G 不重合).当AB =12,BE =4时,是否存在直线OH 将△ACE 分成三角形和四边形两部分,其中三角形的面积与四边形的面积比为1∶3.若存在,请直接写出AH AG 的值;若不存在,请说明理由.【答案】(1)见解析;(2)①MN =23;②12或57【分析】(1)证△ABE ≌△ACF ,根据有一个角是60°的等腰三角形是等边三角形证明即可;(2)①连接AN ,证△NAM ∽△BAE ,列出比例式,根据相似比即可求解;②分点H 为AG 中点和点N 为EC 中点两种情况,根据相似比,求出比值即可.【详解】解:(1)∵四边形ABCD 是菱形,∴AB =BC ,∵∠B =60°,∴△ABC 是等边三角形,∴AB =AC ,∠ACB =∠ACD =∠BAC =60°,∵BE =CF ,∴△ABE ≌△ACF ;∴AE =AF ,∴∠BAE =∠CAF ,∴∠EAF =60°,∴△AEF 是等边三角形;(2)①连接AN ,∵点N 是BC 的中点,∴∠ANB =90°,∵∠B =60°,∴∠BAN =30°,∴cos ∠BAN =AN AB=32,由(1)知,△AEF 是等边三角形,∠EAF =60°,AG 平分∠EAF∴∠AME =90°,∠EAM =30°,∴cos ∠EAM =AM AE=32,∠BAN -∠EAN =∠EAM -∠EAN ,即∠BAE =∠NAM ,∴△NAM ∽△BAE∴MN BE =AM AE,∴MN 4=32,∴MN =23②如图,当点H 为AG 中点时,即AH AG=12;∵O 是AC 的中点,∴OH ∥EC ,∴△AMO ∽△AEC ,∵AO AC =12,∴S △AMO S △AEC =14,即S △AMO S 四边形MECO=13;同理,如图所示,当点N 为EC 中点时,ON ∥AE ,S △CON S 四边形NEAO=13;连接FG ,作FP ⊥BC ,交BC 延长线与点P ,∵BE =CF =4,AB =BC =12,∴CE =8,∵CD ∥AB ,∴∠B =∠DCP =60°,∴∠CFP =30°,∴CP =2,FP =CF 2-CP 2=23,∵AE =AF ,AG =AG ,∠EAG =∠FAG ,∴△EAG ≌△FAG ,∴EG =FG ,设EG =x ,CG =8-x ,PG =10-x ,(10-x )2+(23)2=x 2,解得,x =5.6,∵EN =CN =4,AH AG =EN EG =45.6=57;综上,AH AG的值为:12或57.【点睛】本题考查了菱形的性质,等边三角形的判定与性质,解直角三角形,相似三角形的判定与性质,解题关键是熟练运用相关几何知识,构建几何模型证明相似或全等.6(2023山东九年级期中)如图,正方形ABCD 的对角线相交于点O ,点M ,N 分别是边BC ,CD 上的动点(不与点B ,C ,D 重合),AM ,AN 分别交BD 于点E ,F ,且∠MAN 始终保持45°不变.(1)求证:AF AM=22;(2)求证:AF ⊥FM ;(3)请探索:在∠MAN 的旋转过程中,当∠BAM 等于多少度时,∠FMN =∠BAM ?写出你的探索结论,并加以证明.【答案】(1)证明见解析;(2)证明见解析;(3)∠BAM =22.5.【分析】(1)先证明A 、B 、M 、F 四点共圆,根据圆内接四边形对角互补即可证明∠AFM =90°,根据等腰直角三角形性质即可解决问题.(2)由(1)的结论即可证明.(3)由:A .B 、M 、F 四点共圆,推出∠BAM =∠EFM ,因为∠BAM =∠FMN ,所以∠EFM =∠FMN ,推出MN ∥BD ,得到CMCB =CN CD,推出BM =DN ,再证明△ABM ≌△ADN 即可解决问题.【详解】解:(1)∵四边形ABCD 是正方形,∴∠ABD =∠CBD =45°,∠ABC =90°,∵∠MAN =45°,∴∠MAF =∠MBE ,∴A 、B 、M 、F 四点共圆,∴∠ABM +∠AFM =180°,∴∠AFM =90°,∴∠FAM =∠FMA =45°,∴AM =2AF ,∴AF AM=22.(2)由(1)可知∠AFM =90°,∴AF ⊥FM .(3)结论:∠BAM =22.5时,∠FMN =∠BAM理由:∵A 、B 、M 、F 四点共圆,∴∠BAM =∠EFM ,∵∠BAM =∠FMN ,∴∠EFM =∠FMN ,∴MN ∥BD ,∴CM CB =CN CD,∵CB =DC ,∴CM =CN ,∴MB =DN ,在△ABM 和△ADN 中,∵AB =AD ,∠ABM =∠ADN ,BM =DN ,∴△ABM ≌△ADN ,∴∠BAM =∠DAN ,∵∠MAN =45°,∴∠BAM +∠DAN =45°,∴∠BAM =22.5°.7(2022·广东深圳·统考二模)【教材呈现】(1)如图1,在同一平面内,将两个全等的等腰直角三角形ABC 和AFG 摆放在一起,点A 为公共顶点,∠BAC =∠G =90°,若△ABC 固定不动,将△AFG 绕点A 旋转,边AF ,AG 与边BC 分别交于点D ,E (点D 不与点B 重合,点E 不与点C 重合),则结论BE ⋅CD =AB 2是否成立(填“成立”或“不成立”);【类比引申】(2)如图2,在正方形ABCD 中,∠EAF 为∠BAD 内的一个动角,两边分别与BD ,BC 交于点E ,F ,且满足∠EAF =∠ADB ,求证:△ADE ∽△ACF ;【拓展延伸】(3)如图3,菱形ABCD 的边长为12cm ,∠BAD =120°,∠EAF 的两边分别与BD ,BC 相交于点E ,F ,且满足∠EAF =∠ADB ,若BF =9cm ,则线段DE 的长为cm .【答案】(1)成立;(2)证明见解析;(3)53cm .【分析】(1)根据等腰三角形性质得出∠DAC =∠AEB ,再证△BEA ∽△CAD 即可;(2)根据正方形性质得出∠CAF =∠DAE 即可;(3)如图3,在DE 上取一点M ,使∠MAD =30°,过M 作MN ⊥AD 于N ,根据四边形ABCD 为菱形,且∠BAD =120°,证出∠MAD =∠MDA =30°,再证△ACF ∽△AME ,求出AC =3AM ,利用菱形ABCD 的边长为12cm ,求出CF =3ME =3cm 即可.【详解】解:(1)结论BE ⋅CD =AB 2成立理由:如图1,∵△ABC 和△AFG 都是等腰直角三角形,∴∠B =∠C =∠FAG =45°∵∠DAC =∠CAE +45°,∠AEB =∠CAE +45°,∴∠DAC =∠AEB又∵∠B =∠C ,∴△BEA ∽△CAD ,∴BE AC =AB CD ,∵AC =AB ,∴BE ⋅CD =AB 2,故答案为:成立(2)证明:如图2,∵四边形ABCD 是正方形,∴∠CAD =∠ACB =∠ADB =45°,∵∠EAF =∠ADB ,∴∠EAF =∠CAD =45°,∴∠ACF +∠CAE =∠DAE +∠CAE ,∴∠CAF =∠DAE ,又∵∠ACB =∠ADB ,∴△ADE ∽△ACF ;(3)线段DE 的长为53cm理由:如图3,在DE 上取一点M ,使∠MAD =30°,过M 作MN ⊥AD 于N ,又∵四边形ABCD 为菱形,且∠BAD =120°,∴∠CAD =∠ACB =∠ADC =60°,∴∠MDA =12∠ADC =30°∴∠MAD =∠MDA =30°,∴∠AME =60°,∴∠AME =∠ACB =60°,∵∠CAD =60°,∠MAD =30°,∴∠CAM =30°,∵∠EAF =∠ADB ,∴∠EAF =∠CAM =30°,∴∠CAF =∠MAE ,∴△ACF ∽△AME ,∴CF ME =AC AM,∵AN =12AD ,AN =AM cos30°=32AM ,∴2AN =3AM ,2AN =AD ,∴MA =MD =33AD ,∵AD =AC ,∴AC =3AM ,∴CF ME =ACAM=3,∵菱形ABCD的边长为12cm,∴BC=AD=12cm,∵BF=9cm,∴CF=3ME=3cm,∴ME=3cm,∵MD=33AD,∴MD=33×12=43cm ,∴DE=ME+MD=43+3=53cm,∴线段DE的长为53cm.故答案为53.【点睛】本题考查等腰直角三角形性质,正方形性质,三角形相似判定与性质,菱形性质,锐角三角形函数,掌握等腰直角三角形性质,正方形性质,三角形相似判定与性质,菱形性质,锐角三角形函数是解题关键.课后专项训练1(2023·广东深圳·九年级校考阶段练习)如图,在正方形ABCD中,点E,F分别在边BC,DC上,AE、AF分别交BD于点M,N,连接CN、EN,且CN=EN.下列结论:①AN=EN,AN⊥EN;②BE+DF=EF;③∠DFE=2∠AMN;④EF2=2BM2+2DN2.其中正确结论的个数是()A.4B.3C.2D.1【答案】A【分析】将△ABE绕点A逆时针旋转90°,得到△ADH,则∠1=∠4,AE=AH,BE=DH,可证得△BNA ≌△BNC,从而得到AN=CN,∠NCE=∠BAN,进而得到∠NEC=∠NCE=∠BAN,再由四边形内角和定理可得AN=NE,AN⊥NE,故①正确;再证明△AFE≌△AFH,可得EF=FH=DF+DH=DF+ BE,∠AFH=∠AFE,故②正确;再由∠MAN=∠NDF=45°,∠ANM=∠DNF,可得∠AMN=∠AFD=∠AFE,从而得到∠DFE=2∠AMN,故③正确;再证明△AMN∽△AFE,△AEN是等腰直角三角形,可得AE=2AN,从而得到EF=2MN,将△ABM绕点A逆时针旋转90°,得到△ADG,则∠DAG=∠BAM,AM=AG,∠ADG=∠ABM=45°,证明△ANG≌△ANM,可得MN=GN,再由勾股定理,可得故④正确,即可求解.【详解】解:如图,将△ABE绕点A逆时针旋转90°,得到△ADH,则∠1=∠4,AE=AH,BE=DH,∵四边形ABCD是正方形,∴AB=BC=AD,∠BAD=∠ABC=90°,∠ABD=∠CBD=45°,在△BNA和△BNC中,BN=BN ∠NBA=∠BA=BCNBC∴△BNA≌△BNC,∴AN=CN,∠NCE=∠BAN,∵CN=EN,∴∠NEC=∠NCE=∠BAN,∵∠NEC+∠BEN=180°,∴∠BAN+∠BEN=180°,∴∠ABC+∠ANE=180°,∴∠ANE=90°,∴AN=NE,AN⊥NE,故①正确;∴∠3=∠AEN=45°,∵∠1=∠4,∴∠2+∠4=∠2+∠1=45°,∴∠3=∠FAH=45°,∵AF=AF,AE=AH,∴△AFE≌△AFH,∴EF=FH=DF+DH=DF+BE,∠AFH=∠AFE,故②正确;∵∠MAN=∠NDF=45°,∠ANM=∠DNF,∴∠AMN=∠AFD=∠AFE,又∵∠AFE=∠AFD,∠DFE=∠AFE+∠AFD,∴∠DFE=2∠AMN,故③正确;∵∠MAN=∠EAF,∠AMN=∠AFE,∴△AMN∽△AFE,∴NMEF =ANAE,∵AN=NE,AN⊥NE,∴△AEN是等腰直角三角形,∴AE=2AN,∴NMEF =ANAE=12,∴EF=2MN,如图,将△ABM绕点A逆时针旋转90°,得到△ADG,则∠DAG=∠BAM,AM=AG,∠ADG=∠ABM=45°,∴∠NDG=90°,即△GDN是直角三角形,∵∠MAN=45°,∴∠BAM+∠DAN=∠DAG+∠DAN=∠GAN=45°=∠MAN,∵AN=AN,∴△ANG≌△ANM,∴MN=GN,∴MN2=DN2+DG2=DN2+BM2,∴EF2=2MN2=2DN2+2BM2,故④正确;故选A.【点睛】本题考查正方形的性质、全等三角形的判定和性质、勾股定理、相似三角形的判定和性质等知识,解题的关键是灵活运用所学知识解决问题,学会利用旋转法,添加辅助线构造全等三角形解决问题.2(2022·广东深圳·统考一模)如图,正方形ABCD中,E是BC的中点,F在CD上,CF=2DF,连接AE,AF与对角线BD交于点M,N,连接MF,EN.给出结论:①∠EAF=45°;②AN⊥EN;③tan∠AMN=3;④DN:MN:BM=2:5:3.其中正确的是()A.①②③B.①②④C.①③④D.②③④【答案】A【分析】将△ABE顺时针旋转,使得AB与AD重合,此时得△ADG,将△AFD逆时针旋转,使得AD与AB 重合,此时得△ABH,根据∠HAF=∠GAE=90°,即可求得∠HAE=∠FAE=45°,①正确;根据∠HAE=∠FAE=45°可得△AMN∼△DFN,即可求tan∠AMN=tan∠DFN=ADDF =63=3,即可得③正确;根据如图正方形构造直角坐标系,求出直线AE、AF、BD的解析式,再联立解析式,即可求得M、N两点的坐标,再根据坐标求出DN、MN、BM、AN、NE,即可知AN=NE=3102,则有∠EAN=∠AEN=45°,则有∠ANE=90°,AN⊥NE,②正确;根据DN、MN、BM长度可知DN:MN:BM=3:5:4,④错误.【详解】将△ABE顺时针旋转,使得AB与AD重合,此时得△ADG,将△AFD逆时针旋转,使得AD与AB 重合,此时得△ABH,链接EF,如图所示:为了方便计算,设正方形的边长为6,则有AB=BC=CD=AD=6,则有BE=EC=3=DG,CF=4,DF=2=BH,∠BAE=∠DAG,则有:HE=5=FG,利用勾股定理,易求得:AH=AF=210,AE=AG=35,EF=5,BD=62,根据图形的旋转,可知∠HAB=∠FAD,∠BAE=∠DAG,∴∠HAF=∠GAE=90°,∵AH=AF,HE=5=FG,AE=AE,∴△AHE≅△AFE,同理可证得△AEF≅△AGF,∴∠HAE=∠FAE,又∵∠HAF=∠GAE=90°,∴∠HAE=∠FAE=45°,故①正确;∵∠HAE=∠FAE=45°,∠ANM=∠DNF,∴△AMN∼△DFN,同理可证△AMN∼△BME,∴∠AMN=∠DFN,∴tan∠AMN=tan∠DFN=ADDF =62=3,故③正确;以B为坐标原点O,AB所在的直线为y轴,以BC所在的直线为x轴,构建直角坐标系,则有A点坐标为(0,6),B点坐标为(0,0),C点坐标为(6,0),D点坐标为(6,6),F点坐标为(6,4),E点坐标为(3,0),则直线AF的解析式为:y=-13x+6,BD的解析式为y=x,AE的解析式为y=-2x+6,联立:y=-13x+6 y=x,得到N点坐标为:92,9 2,同理的M点坐标为(2,2),过M点作MP垂直于BC,交BC于P点,过N点作NQ垂直于DC,交DC于Q点,则有MP=2,DQ=DC-QC=6-92=32,则有BM=(2-0)2+(2-0)2=22,DN=6-9 22+6-922=322,则有MN=BD-BM-DN=62-22-322=522,则有:DN:MN:BM=322:522:22=3:5:4,故④错误;根据N点坐标为:92 ,92,A点坐标为:(0,6),E点坐标为:(3,0),可得AN=0-9 22+6-922=NE=3-922+0-922=3102,则在△AEN中,∠EAN=∠AEN=45°,∴∠ANE=90°,∴AN⊥NE,故②正确;故选:A.【点睛】本题考查了直角坐标系的构建、相似三角形以及坐标系中求解两点间距离等知识.准确作出辅助线并构建直角坐标系是解答本题的关键.3如图,正方形ABCD中,△ABC绕点A逆时针旋转到△AB C ,AB 、AC 分别交对角线BD于点E、F,若AE=4,则EF⋅ED的值为()A.4B.6C.8D.16【答案】D【分析】先根据正方形的性质、旋转的性质可得∠EAF=∠EDA=45°,再根据相似三角形的判定与性质即可得.【详解】∵四边形ABCD是正方形,∴∠BAC=∠EDA=45°,由旋转的性质得:∠B AC =∠BAC,∴∠B AC =∠EDA,即∠EAF=∠EDA,在△AEF和△DEA中,∠EAF=∠EDA ∠AEF=∠DEA,∴△AEF∼△DEA,∴EF AE =AEDE,即EF4=4DE,∴EF⋅DE=16,故选:D.【点拨】本题考查了正方形的性质、旋转的性质、相似三角形的判定与性质,熟练掌握相似三角形的判定与性质是解题关键.4如图,菱形ABCD的边长为4,E,F分别是AB,AD边上的动点,BE=AF,∠BAD=120°,则下列结论:①ΔBEC≌ΔAFC;②ΔECF为等边三角形;③∠AGE=∠AFC;④若AF=1,则GFGE=12.其中正确个数为()A.4B.3C.2D.1【答案】B【分析】由SAS证明△BEC≌△AFC,①正确;由全等三角形的形状得CE=CF,∠BCE=∠ACF,再由∠BCE+∠ECA=∠BCA=60°,得∠ACF+∠ECA=60°,得△CEF是等边三角形,②正确;由∠AGE=∠CAF+∠AFG=60°+∠AFG,∠AFC=∠CFG+∠AFG=60°+∠AFG,得∠AGE=∠AFC,故③正确;④过点E 作EM ∥BC 交AC 下点M 点,易证△AEM 是等边三角形,则EM =AE ,由AF ∥EM ,则△AFG ∽△MEG ,得④错误.【详解】解:①∵四边形ABCD 是菱形,∴AB =AD =4,∠BAC =∠CAD .∵∠BAD =120°,∴∠BAC =∠CAD =60°,∴ΔABC 和ΔACD 都是等边三角形,∴∠B =∠CAD =60°,BC =AC .∵BE =AF ,∴ΔBEC ≌ΔAFC SAS ,故①正确.②∵ΔBEC ≌ΔAFC ,∴CE =CF ,∠BCE =∠ACF .∵∠BCE +∠ECA =∠BCA =60°,∴∠ACF +∠ECA =60°,∴ΔCEF 是等边三角形,故②正确.③∵∠AGE =∠CAF +∠AFG =60°+∠AFG ,∠AFC =∠CFG +∠AFG =60°+∠AFG ,∴∠AGE =∠AFC ,故③正确.④过点E 作EM ∥BC 交AC 于点M ,∴∠AEM =∠B =60°,∠AME =∠ACB =60°,∴ΔAEM 是等边三角形,∴EM =AE .∵BE =AF =1,∴AE =AB -BE =4-1=3,∴EM =AE =3.∵AF ∥EM ,∴ΔAFG ~ΔMEG ,∴GF GE=AF EM =13﹐故④错误,正确个数为3.故选B .【点拨】本题考查了菱形的性质、等边三角形性质、全等三角形的判定与性质、相似三角形的判定与性质等知识;熟练掌握菱形的性质、全等三角形的判定与性质、相似三角形的判定与性质是解题的关键.5(2023·浙江绍兴·校联考三模)矩形ABCD 中,AB =6,AD =12,连接BD ,E ,F 分别在边BC ,CD 上,连接AE ,AF 分别交BD 于点M ,N ,若∠EAF =45°,BE =3,则DN 的长为.【答案】1255【分析】根据矩形的性质,由勾股定理得出BD ,延长AB 至P ,使PB =AB =6,过P 作BC 的平行线交DC 的延长线于Q ,得正方形APQD ,延长AE 交PQ 于H ,连接HF ,将△ADF 绕点A 顺时针旋转90°,点D 与点P 重合,得到△APG ,由旋转的性质可得PG =PF ,∠APG =∠ADF =90°,AG =AF ,∠PAG =∠DAF ,证出∠GAF =90°,得出∠GAH =∠FAH =45°,可证△AGH ≌△AFH ,得出GH =FH ,证出FH =DF +PH ,设DF =x ,则FQ =12-x ,利用勾股定理列出方程求出x =4,然后由DF ∥AB ,得△DFN ∽△BAN ,所以DF AB=DN BN =23,即可求出DN 的长.【详解】解:在矩形ABCD 中,∵∠BAD =90°,AB =6,AD =12,∴BD =AB 2+AD 2=62+122=65,如图,延长AB 至P ,使PB =AB =6,过P 作BC 的平行线交DC 的延长线于Q ,得正方形APQD ,延长AE交PQ于H,连接HF,将△ADF绕点A顺时针旋转90°,点D与点P重合,得到△APG,∵四边形APQD是正方形,∴AP=PQ=DQ=AD,∠PAD=∠APH=∠Q=∠ADQ=90°,由旋转得:△APG≌△ADF,∴PG=DF,∠APG=∠ADF=90°,AG=AF,∠PAG=∠DAF,∴∠PAG+∠PAF=∠PAF+∠DAF=90°,即∠GAF=90°,C ,P,H三点共线,∵∠HAF=45°,∴∠GAH=90°-45°=45°,∴∠GAH=∠FAH=45°,在△AGH和△AFH中,AG=AF∠GAH=∠FAH AH=AH,∴△AGH≌△AFH SAS ,∴GH=FH,∵GH=PG+PH=DF+PH,∴FH=DF+PH,设DF=x,则FQ=DQ-DF=12-x,∵AB=BP=6,BE∥PQ,∴AEEH =ABBP=1,∴AE=EH,∴PH=2BE=2×3=6,∴FH=DF+PH=6+x,HQ=12-6=6,在Rt△QFH中,由勾股定理得:FQ2+HQ2=FH2,∴(12-x2+62=x+62,解得:x=4,∴DF=4,∵DF∥AB,∴△DFN∽△BAN,∴DFAB =DN BN=23,∴DN=25BD=25×65=1255.故答案为:1255.【点睛】本题考查了正方形的性质,全等三角形的判定与性质,勾股定理,相似三角形的判定与性质等知识;证明三角形全等和由勾股定理得出方程是解题的关键.6(2023·成都市·九年级专题练习)如图,在Rt△ABC中,AB=AC,D、E是斜边BC上两点,且∠DAE=45°,将△ADC绕点A顺时针旋转90°后,得到△AFB,连接EF,下列结论:①△AED≌△AEF;②AEBE=ADCD;③△ABC的面积等于四边形AFBD的面积;④BE2+DC2=DE2;⑤BE=EF-DC;其中正确的选项是(填序号)【答案】①③④【分析】①根据旋转的性质知∠CAD=∠BAF,AD=AF,因为∠BAC=90°,∠DAE=45°,所以∠CAD+∠BAE=45°,可得∠EAF=45°=∠DAE,由此即可证明△AEF≌△AED;②当△ABE∽△ACD时,该比例式成立;③根据旋转的性质,△ADC ≌△ABF ,进而得出△ABC 的面积等于四边形AFBD 的面积;④据①知BF =CD ,EF =DE ,∠FBE =90°,根据勾股定理判断.⑤根据①知道△AEF ≌△AED ,得CD =BF ,DE =EF ;由此即可确定该说法是否正确.【详解】解:①根据旋转的性质知∠CAD =∠BAF ,AD =AF .∵∠BAC =90°,∠DAE =45°,∴∠CAD +∠BAE =45°,∴∠EAF =45°,∴△AED ≌△AEF ;故本选项正确;②∵AB =AC ,∴∠ABE =∠ACD ;∴当∠BAE =∠CAD 时,△ABE ∽△ACD ,∴AE BE =AD CD ;当∠BAE ≠∠CAD 时,△ABE 与△ACD 不相似,即AE BE ≠AD CD;∴此比例式不一定成立,故本选项错误;③根据旋转的性质知△ADC ≌△AFB ,∴S △ABC =S △ABD +S △ABF =S 四边形AFBD ,即三角形ABC 的面积等于四边形AFBD 的面积,故本选项正确;④∵∠FBE =45°+45°=90°,∴BE 2+BF 2=EF 2.∵△ADC 绕点A 顺时针旋转90°后,得到△AFB ,∴△AFB ≌△ADC ,∴BF =CD .又∵EF =DE ,∴BE 2+DC 2=DE 2,故本选项正确;⑤根据①知道△AEF ≌△AED ,得CD =BF ,DE =EF ,∴BE +DC =BE +BF >DE =EF ,即BE +DC >FE ,故本选项错误.综上所述:正确的说法是①③④.故答案为:①③④.【点睛】本题考查了图形的旋转变换以及全等三角形的判定等知识,三角形三边的关系,相似三角形的性质与判定,解题时注意旋转前后对应的相等关系.7(2023·上海宝山·校考一模)如图,在△ABC 中,AB =AC ,点D 、E 在边BC 上,∠DAE =∠B =30°,且AD AE=32,那么DE BC 的值是.【答案】13318-1.【分析】由已知可得△ABE ∼△DAE ,从而可知AB BE =AD AE=32,AE 2=BE ∙DE ,设AB =3x ,则BE =2x ,再利用勾股定理和等腰三角形性质用x 表示DE 和BC ,从而解答【详解】解:∵∠BAE =∠DAE +∠BAD ,∠ADE =∠B +∠BAD ,又∵∠DAE =∠B =30°,∴∠BAE =∠ADE ,∴△ABE ∼△DAE ,∴AB BE =AD AE =32,AE 2=BE ∙DE ,过A 点作AH ⊥BC ,垂足为H ,设AB =3x ,则BE =2x ,∵∠B =30°,∴AH =12AB =32x ,BH =332AB =332x ,∴EH =BH -BE =332-2 x ,在Rt △AHE 中,AE 2=AH 2+EH 2=32x 2+332x -2x 2=13-63 x 2,又∵AE 2=BE ∙DE ,∴13-63 x 2=2x ∙DE ,∴DE =13-632x ,∵AB =AC ,AH ⊥BC ,∴BC =2BH =33x ,∴DE BC=13-632x 33x =13318-1,故答案为:DE BC =13-632x 33x=13318-1 .【点睛】本题考查了相似三角形的判定和性质、等腰三角形的性质以及勾股定理,利用三角形相似得到AB 与BE 的关系是解题的关键.8(2023春·辽宁沈阳·八年级统考期中)通过类比联想、引申拓展研究典型题目,可达到解一题知一类的目的.下面是一个案例,请补充完整.原题:如图1,点E ,F 分别在正方形ABCD 的边BC ,CD 上,∠EAF =45°,连接EF ,则EF =BE +DF ,试说明理由.(1)思路梳理∵AB =CD ,∴把△ABE 绕点A 逆时针旋转90°至△ADG ,可使AB 与AD 重合.∵∠ADC =∠B =90°,∠FDG =180°,∴点F ,D ,G 共线.根据(从“SSS ,ASA ,AAS ,SAS ”中选择填写),易证△AFG ≌,得EF =BE +DF .(2)类比引申如图2,四边形ABCD 中,AB =AD ,∠BAD =90°,点E ,F 分别在边BC ,CD 上,∠EAF =45°.若∠B ,∠D 都不是直角,则当∠B 与∠D 满足等量关系时,仍有EF =BE +DF .(3)联想拓展如图3,在△ABC 中,∠BAC =90°,AB =AC ,点D ,E 均在边BC 上,且∠DAE =45°.猜想BD ,DE ,EC 应满足的等量关系,并写出推理过程.(4)思维深化如图4,在△ABC 中,∠BAC =60°,AB =AC ,点D ,E 均在直线BC 上,点D 在点E 的左边,且∠DAE =30°,当AB =4,BD =1时,直接写出CE 的长.【答案】(1)SAS,△AFE(2)∠B+∠D=180°(3)DE2=BD2+EC2,理由见解析(4)CE的长为87或83【分析】(1)把△ABE绕点A逆时针旋转90°至△ADG,可使AB与AD重合,再证明△AFE≌△AFG进而得到EF=FG,即可证明结论;(2)∠B+∠D=180°时,EF=BE+DF与(1)的证法类同;(3)把△AEC绕点A顺时针旋转90°得到△ABE ,连接DE ,根据旋转的性质,可知△AEC≌△ABE 得到BE =EC、AE =AE、∠C=∠ABE 、∠EAC=∠E AB,,根据Rt△ABC中的,AB=AC得到∠E BD=90°,所以E B2+BD2=E D2,证△AE D≌△AED,利用DE =DE 得到DE2=BD2+EC2;(4)分两种情况:点D在BC边上或点D在BC的延长线上,①当点D在BC边上时,过点A作AF⊥BC于点F,过点D作DG⊥AB于点G,利用三角函数求出BG,DG,AF,再证明△AFE∽△AGD,运用相似三角形性质即可求出EF,再由CE=CF-EF可求得CE;②当点D在CB的延长线上时,过点A作AF⊥BC于点F,过点D作DG⊥AB于点G,与①同理可求得EF,再由CE=CF+EF求出CE即可.【详解】(1)解:∵AB=AD,∴把△ABE绕点A逆时针旋转90°至△ADG,可使AB与AD重合.∴∠BAE=∠DAG,∵∠BAD=90°,∠EAF=45°,∴∠BAE+∠DAF=45°,∴∠EAF=∠FAG,∵∠ADC=∠B=90°,∴∠FDG=180°,点F、D、G共线,在△AFE和△AFG中,AE=AG∠EAF=∠FAG AF=AF,∴△AFE≌△AFG SAS ,∴EF=FG,即:EF=BE+DF.故答案为:SAS,△AFE;(2)解:∠B+∠D=180°时,EF=BE+DF,理由如下:∵AB=AD,∴如图2:把△ABE绕点A逆时针旋转90°至△ADG,可使AB与AD重合,∴∠BAE=∠DAG,∵∠BAD=90°,∠EAF=45°,∴∠BAE+∠DAF=45°,∴∠EAF=∠FAG,∵∠ADC+∠B=180°,∴∠FDG=180°,点F、D、G共线,在△AFE和△AFG中,AE=AG∠FAE=∠FAG AF=AF,∴△AFE≌△AFG SAS ,∴EF=FG,即:EF=BE+DF.故答案为:∠B+∠D=180°;(3)解:猜想:DE2=BD2+EC2.理由如下:如图3:把△AEC绕点A顺时针旋转90°得到△ABE ,连接DE ,∴△AEC≌△ABE ,∴BE =EC,AE =AE,∠C=∠ABE ,∠EAC=∠E AB,在Rt△ABC中,AB=AC,∴∠ABC=∠ACB=45°,∴∠ABC+∠ABE'=90°,即∠E BD=90°,∴E B2+BD2=E D2,又∵∠DAE=45°,∴∠BAD+∠EAC=45°,∴∠E AB+∠BAD=45°,即∠E AD=45°,在△AE D和△AED中,AE =AE∠E AD=∠DAE AD=AD,∴△AE D≌△AED SAS ,∴DE=DE ,∴DE2=BD2+EC2;(4)解:点D,E均在直线BC上,点D在点E的左侧,BD=1,∴分两种情况:点D在BC边上或点D在CB的延长线上,①当点D在BC边上时,如图4-1,过点A作AF⊥BC于点F,过点D作DG⊥AB于点G,∵AB=AC=4,∠BAC=60°,∴BF=CF=2,∠BAF=∠CAF=30°,AF=3BF=23,∵∠AGD=90°,∠B=60°,BD=1,∴BG=12BD=12,DG=3BG=32,∴AG=AB-BG=4-12=72,∵∠DAE=30°,∴∠DAF+∠BAD=∠DAF+∠FAE=30°,∴∠BAD=∠FAE,∵∠AFE=∠AGD=90°,∴△AFE∽△AGD,∴EFDG =AFAG,∴EF32=2372,∴EF=67,∴CE=CF-EF=2-67=87;②当点D在CB的延长线上时,如图4-2,过点A作AF⊥BC于点F,过点D作DG⊥AB于点G,由①知,BF=CF=2,∠BAF=∠CAF=30°,∵∠DGB=90°,∠DBG=∠ABC=60°,∴BG=12BD=12,DG=3BG=32,∴AG=AB+BG=4+12=92,∵∠DAE=∠BAF=30°,∴∠DAG+∠BAE=∠BAE+∠EAF,∴∠DAG=∠EAF,∴△DAG∽△EAF,∴EFDG =AF AG,∴EF32=2392,∴EF=23,∴CE=CF+EF=2+23=83.综上所述,CE的长为87或83.【点睛】本题主要考查了全等三角形的判定和性质、相似三角形的判定和性质、旋转变换的性质、三角函数定义、勾股定理的应用等知识点,掌握全等三角形的判定定理和性质定理、相似三角形的判定和性质,合理添加辅助线并灵活运用分类讨论思想是解题的关键.9(2023·陕西西安·九年级校考期中)问题研究,如图,在等腰△ABC中,AB=AC,点D、E为底边BC 上的两个动点(不与B、C重合),且∠DAE=∠B.(1)请在图中找出一个与△ABE相似的三角形,这个三角形是;(2)若∠BAC=90°,分别过点D、E作AB、AC的垂线,垂足分别为F、G,且DF、EG的反向延长线交于点M,若AB=1,求四边形AFMG的面积;问题解决(3)如图所示,有一个矩形仓库ABCD,其中AB=40米,AD=30米,现计划在仓库的内部的E、F两处分别安装监控摄像头,其中点E在边BC上,点F在边DC上.设计要求∠EAF=45°且CE=CF,则CE的长应为多少米?【答案】(1)ΔDAE;(2)四边形的面积为12;(3)CE的长为70+45385米.【分析】(1)根据已知条件及相似三角形的判定可直接得出;(2)把ΔABD绕点A逆时针旋转90°得到ΔACH,连接EH,根据旋转可得ΔABD≅ΔACH,利用三角形全等的性质得出BD=CH,AD=AH,∠ACH=∠B,利用角和边之间的关系可得:ΔCEH为直角三角形,根据勾股定理及等量代换得出CE2+BD2=EH2,根据全等三角形的判定得出ΔHAE≅ΔDAE,得EH=DE,再求出各三角形的面积确定SΔCGE+SΔBDF=SΔDEM,再根据图形中三角形的关系得出S四边形AFMG=SΔABC,即可求得四边形面积;(3)根据(2)中思路,作图:延长AD到S,延长BC到G,使AS=BG=AB,连接SG,延长AF交SG于点H,连接EH,延长GS到T,使ST=BE,连接AT,则四边形ABGS为正方形,根据全等三角形的判定定理得出ΔATH≅ΔAEH,根据全等三角形的性质及等量代换得出∠HAT=∠HAE,再利用三角形全等的判定证明ΔATH≅ΔAEH,设CE=CF=x,可得出ST=30-x,GE=x+10,DF=40-x,在根据相似三角形的判定和性质得出ADAS=DFSH,将各边代入得出SH,HE,GH,在RtΔADF中,利用勾股定理得出方程求解即可.【详解】解:(1)∵∠AEB=∠DEA,∠B=∠DAE,∴ΔDAE~ΔABE,故答案为:ΔDAE;(2)如图所示:把ΔABD绕点A逆时针旋转90°得到ΔACH,连接EH,∴ΔABD≅ΔACH,∠DAH=90°,∴BD=CH,AD=AH,∠ACH=∠B,∵∠BAC=90°,AB=AC,∴∠B=∠ACB=45°,∴∠ACH=45°,∴∠ECH=∠ACB+∠ACH=90°,∴CE2+CH2=EH2,∴CE2+BD2=EH2,∵∠DAE=∠B,∴∠DAE=45°,∵∠DAH=90°,∴∠HAE=∠DAE=45°,在ΔHAE和ΔDAE中,AH=AD∠HAE=∠DAE AE=AE,∴ΔHAE≅ΔDAE,∴EH=DE,∴CE2+BD2=DE2,∵MG⊥AC于点G,∠ACB=45°,∴∠DEM=∠CEG=∠ACB=45°,∴CG=EG,∴CE2=2CG2,∵SΔCGE=12×CG×CE=CG22,∴SΔCGE=CE24,同理可得:SΔBDF =BD24,在ΔDEM中,∠DEM=∠EDM=45°,∴∠M=90°,同理可得:SΔDEM=DE2 4,∵CE2+BD2=DE2,∴SΔCGE+SΔBDF=SΔDEM,∴S四边形AFMG =S五边形AFDEG+SΔCGE+SΔBDF,即S四边形AFMG=SΔABC,∵SΔABC=12×AB×AC=12,∴S四边形AFMG=12,即四边形的面积为12;(3)如图,延长AD到S,延长BC到G,使AS=BG=AB,连接SG,延长AF交SG于点H,连接EH,延长GS到T,使ST=BE,连接AT,则四边形ABGS为正方形,∴BG=GS=AS=AB=40,DS=CG=40-30=10,在ΔABE和ΔAST中,AB=AS∠ABE=∠ASTBE=ST,∴∠BAE=∠SAT,AB=AT,∴∠HAT=∠HAS+∠SAT=∠HAS+∠BAE=45°,,∴∠HAT=∠HAE,在ΔATH和ΔAEH中,AT=AE∠HAT=∠HAEAH=AH,∴ΔATH≅ΔAEH,∴HT=HE,设CE=CF=x,则ST=BE=BC-CE=30-x,GE=x+10,DF=40-x,∵DF∥SH,∴ΔADF~ΔASH,∴ADAS=DFSH,即:3040=40-xSH,解得:SH=160-4x3,∴HE=HT=HS+ST=160-4x3+30-x=250-7x3,GH=GS-SH=40-160-4x3=4x-403,∴在Rt ΔADF 中,x +10 2+4x -4032=250-7x 3 2,解得:x 1=70+45385,x 2=70-45385(舍去),即CE 的长为70+45385米.【点睛】题目主要考查相似三角形的判定和性质、全等三角形的判定和性质、勾股定理、一元二次方程的运用求解等,根据题意作出相应辅助线,融会贯通综合运用这些知识点是解题关键.10(2023·陕西汉中·九年级统考期末)如图,△ABC 中,∠BAC =120°,AB =AC ,点D 为BC 边上一点.(1)如图1,若AD =AM ,∠DAM =120°.①求证:BD =CM ;②若∠CMD =90°,求BD CD的值.(2)如图2,点E 为线段CD 上一点,且CE =4,AB =63,∠DAE =60°,求DE 的长.【答案】(1)①见解析,②BD CD=12(2)6.5【分析】(1)①通过证明△ABD ≌△ACM ,即可求证;②由①可得BD =CM ,再根据等边对等角求出∠ACM 和∠ACB 的度数,即可得出∠MCD =60°,最后根据直角三角形中30°角所对的边是斜边的一半即可求证;(2)过点E 作EG ⊥AC 于G ,过A 作AF ⊥BC 于F ,证明△ADF ∽△AEG ,可以求出DF ,利用勾股定理可以求出EF 的长,从而可以求解.【详解】(1)证明:①∵∠BAC =120°,∠DAM =120°,∴∠BAC -∠CAD =∠DAM -∠CAD ,即∠BAD =∠MAC ,在△ABD 和△ACM 中,AB =AC∠BAD =∠MAC AD =AM,∴△ABD ≌△ACM SAS ,∴BD =CM ;②∵∠BAC =120°,AB =AC ,∴∠ACB =12180°-120° =30°,由①可得:△ABD ≌△ACM ,∴∠ACM =∠ACB =30°,∴∠DCM =∠ACM +∠ACB =60°,∵∠CMD =90°,∴在△CDM 中,∠CDM =180°-90°-60°=30°,∴CM =12CD ,整理得:CM CD =12,由①可得BD =CM ,∴BD CD=12.(2)过点A 作AF ⊥BC 于点F ,过点E 作EG ⊥AC 于点G ,∵AB =AC ,∠BAC =120°,∴∠C =12180°-120° =30°,∵EG ⊥AC ,AB =AC =63,∴AF =12AC =33,在Rt △ACF 中,根据勾股定理可得:CF =AB 2-AF 2=9,∵CE =4,∴EF =CF -CE =9-4=5,∵EG ⊥AC ,∠C =30°,∴EG =12EC =2,在Rt △CEG 中,根据勾股定理可得:CG =CE 2-EG 2=23,∴AG =AC -CG =63-23=43,∵AB =AC ,∠BAC =120°,AF ⊥BC ,∴∠CAF =12∠BAC =60°,∵∠DAE =60°,∴∠DAE -∠EAF =∠CAF -∠EAF ,即∠DAF =∠EAG ,∵∠AFD =∠AGE =90°,∴△ADF ∽△AEG ,∴DF EG =AF AG ,即DF 2=3343,解得:DF =32,∴DE =DF +EF =32+5=6.5.【点睛】本题主要考查了全等三角形的性质与判定,等腰三角形的性质,含30度角的直角三角形的性质,勾股定理等等,解题的关键在于能够熟练掌握相关知识进行求解.11(2023·辽宁沈阳·九年级统考期末)【教材呈现】(1)如图1,在同一平面内,将两个全等的等腰直角三角形ABC 和AFG 摆放在一起,A 为公共顶点,∠BAC =∠G =90°,BC =6,若△ABC 固定不动,将△AFG 绕点A 旋转,边AF 、AG 与边BC 分别交于点D ,E (点D 不与点B 重合,点E 不与点C 重合)①求证:AE 2=DE •BE ;②求BE •CD 的值;【拓展探究】(2)如图2,在△ABC 中,∠C =90°,点D ,E 在边BC 上,∠B =∠DAE =30°,且AD =34AE ,请直接写出DE BC 的值.【答案】(1)①证明见解析;②18;(2)25318-2【分析】(1)①只需要证明△ABE ∽△DAE ,得到AE DE =BE AE,即可推出AE 2=DE ∙BE ;②先证明∠AEB =∠DAC ,则可证△AEB ∽△DAC ,推出BE ∙CD =AB ∙CA ,然后利用勾股定理求出AB =AC =32,即可得到BE ∙CD =AB ∙CA =18;(2)设AD =3x ,AE =4x ,先证明△ADE ∽△BDA ,推出BD AB =AD AE =34,设BD =3y ,AB =4y ,得到DE =AE ⋅AD AB=3x 2y ,求出AC =2y ,BC =23y ,则CD =BC -BD 23-3 y 在直角△ACD 中,AD 2=CD 2+AC 2,则9x 2=23-3 2y 2+4y 2,即可推出x 2y2=25-1239,由此求解即可.【详解】解:(1)①∵△ABC 和△AGF 都是等腰直角三角形,∠BAC =∠G =90°,∴∠B =∠C =∠GAF =。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
中考常考几何模型专题20 半角模型倍长中线或类中线(与中点有关的线段)构造全等三角形 如图①: (1)∠2=21∠AOB ;(2)OA=OB 。
如图②:连接 FB ,将△FOB 绕点 O 旋转至△FOA 的位置,连接 F ′E 、FE ,可得△OEF ′≌△OEF 。
模型精练1.(2019秋•九龙坡区校级月考)如图.在四边形ABCD 中,∠B +∠ADC =180°,AB =AD ,E 、F 分别是边BC 、CD 延长线上的点,且∠EAF =12∠BAD ,求证:EF =BE ﹣FD .【点睛】在BE 上截取BG ,使BG =DF ,连接AG .根据SAA 证明△ABG ≌△ADF 得到AG =AF ,∠BAG =∠DAF ,根据∠EAF =12∠BAD ,可知∠GAE =∠EAF ,可证明△AEG ≌△AEF ,EG =EF ,那么EF =GE =BE ﹣BG =BE ﹣DF .【解析】证明:在BE 上截取BG ,使BG =DF ,连接AG .∵∠B +∠ADC =180°,∠ADF +∠ADC =180°, ∴∠B =∠ADF . 在△ABG 和△ADF 中, {AB =AD∠B =∠ADF BG =DF, ∴△ABG ≌△ADF (SAS ), ∴∠BAG =∠DAF ,AG =AF .∴∠BAG +∠EAD =∠DAF +∠EAD =∠EAF =12∠BAD . ∴∠GAE =∠EAF . 在△AEG 和△AEF 中, {AG =AF∠GAE =∠EAF AE =AE, ∴△AEG ≌△AEF (SAS ). ∴EG =EF ,∵EG=BE﹣BG∴EF=BE﹣FD.2.(2020•锦州模拟)问题情境:已知,在等边△ABC中,∠BAC与∠ACB的角平分线交于点O,点M、N 分别在直线AC,AB上,且∠MON=60°,猜想CM、MN、AN三者之间的数量关系.方法感悟:小芳的思考过程是在CM上取一点,构造全等三角形,从而解决问题;小丽的思考过程是在AB取一点,构造全等三角形,从而解决问题;问题解决:(1)如图1,M、N分别在边AC,AB上时,探索CM、MN、AN三者之间的数量关系,并证明;(2)如图2,M在边AC上,点N在BA的延长线上时,请你在图2中补全图形,标出相应字母,探索CM、MN、AN三者之间的数量关系,并证明.【点睛】(1)在AC上截取CD=AN,连接OD,证明△CDO≌△ANO,根据全等三角形的性质得到OD =ON,∠COD=∠AON,证明△DMO≌△NMO,得到DM=MN,结合图形证明结论;(2)在AC延长线上截取CD=AN,连接OD,仿照(1)的方法解答.【解析】解:(1)CM=AN+MN,理由如下:在AC上截取CD=AN,连接OD,∵△ABC 为等边三角形,∠BAC 与∠ACB 的角平分线交于点O , ∴∠OAC =∠OCA =30°, ∴OA =OC ,在△CDO 和△ANO 中, {OC =OA∠OCD =∠OAN CD =AN, ∴△CDO ≌△ANO (SAS ) ∴OD =ON ,∠COD =∠AON , ∵∠MON =60°, ∴∠COD +∠AOM =60°, ∵∠AOC =120°, ∴∠DOM =60°, 在△DMO 和△NMO 中, {OD =ON∠DOM =∠NOM OM =OM, ∴△DMO ≌△NMO , ∴DM =MN ,∴CM =CD +DM =AN +MN ; (2)补全图形如图2所示:CM =MN ﹣AN ,理由如下:在AC 延长线上截取CD =AN ,连接OD , 在△CDO 和△ANO 中, {CD =AN∠OCD =∠OAN =150°OC =OA, ∴△CDO ≌△ANO (SAS ) ∴OD =ON ,∠COD =∠AON , ∴∠DOM =∠NOM , 在△DMO 和△NMO 中, {OD =ON∠DOM =∠NOM OM =OM, ∴△DMO ≌△NMO (SAS ) ∴MN =DM ,∴CM =DM ﹣CD =MN ﹣AN .3.(2020•章丘区模拟)如图,在正方形ABCD 中,M 、N 分别是射线CB 和射线DC 上的动点,且始终∠MAN =45°.(1)如图1,当点M 、N 分别在线段BC 、DC 上时,请直接写出线段BM 、MN 、DN 之间的数量关系; (2)如图2,当点M 、N 分别在CB 、DC 的延长线上时,(1)中的结论是否仍然成立,若成立,给予证明,若不成立,写出正确的结论,并证明;(3)如图3,当点M 、N 分别在CB 、DC 的延长线上时,若CN =CD =6,设BD 与AM 的延长线交于点P ,交AN 于Q ,直接写出AQ 、AP 的长.【点睛】(1)在MB 的延长线上,截取BE =DN ,连接AE ,则可证明△ABE ≌△ADN ,得到AE =AN ,进一步证明△AEM ≌△ANM ,得出ME =MN ,得出BM +DN =MN ;(2)在DC 上截取DF =BM ,连接AF ,可先证明△ABM ≌△ADF ,得出AM =AF ,进一步证明△MAN ≌△F AN ,可得到MN =NF ,从而可得到DN ﹣BM =MN ;(3)由已知得出DN =12,由勾股定理得出AN =2+DN 2=6√5,由平行线得出△ABQ ∽△NDQ ,得出BQ DQ=AQ NQ=AB DN=12,AQ AN=13,求出AQ =2√5;由(2)得出DN ﹣BM =MN .设BM =x ,则MN=12﹣x ,CM =6+x ,在Rt △CMN 中,由勾股定理得出方程,解方程得出BM =2,由勾股定理得出AM =√AB 2+BM 2=2√10,由平行线得出△PBM ∽△PDA ,得出PM PA=BM DA=13,求出PM =12AM =√10,得出AP =AM +PM =3√10.【解析】解:(1)BM +DN =MN ,理由如下:如图1,在MB的延长线上,截取BE=DN,连接AE,∵四边形ABCD是正方形,∴AB=AD,∠BAD=∠ABC=∠D=90°,∴∠ABE=90°=∠D,在△ABE和△ADN中,{AB=AD∠ABE=∠D BE=DN,∴△ABE≌△ADN(SAS),∴AE=AN,∠EAB=∠NAD,∴∠EAN=∠BAD=90°,∵∠MAN=45°,∴∠EAM=45°=∠NAM,在△AEM和△ANM中,{AE=AN∠EAM=∠NAM AM=AM,∴△AEM≌△ANM(SAS),∴ME=MN,又∵ME=BE+BM=BM+DN,∴BM+DN=MN;故答案为:BM+DN=MN;(2)(1)中的结论不成立,DN﹣BM=MN.理由如下:如图2,在DC上截取DF=BM,连接AF,则∠ABM=90°=∠D,在△ABM和△ADF中,{AB=AD∠ABM=∠D BM=DF,∴△ABM≌△ADF(SAS),∴AM=AF,∠BAM=∠DAF,∴∠BAM+∠BAF=∠BAF+∠DAF=∠BAD=90°,即∠MAF=∠BAD=90°,∵∠MAN=45°,∴∠MAN=∠F AN=45°,在△MAN和△F AN中,{AM=AF∠MAN=∠FAN AN=AN,∴△MAN≌△F AN(SAS),∴MN=NF,∴MN=DN﹣DF=DN﹣BM,∴DN﹣BM=MN.(3)∵四边形ABCD是正方形,∴AB=BC=AD=CD=6,AD∥BC,AB∥CD,∠ABC=∠ADC=∠BCD=90°,∴∠ABM=∠MCN=90°,∵CN=CD=6,∴DN=12,∴AN=√AD2+DN2=√62+122=6√5,∵AB∥CD,∴△ABQ ∽△NDQ ,∴BQ DQ =AQ NQ =AB DN=612=12,∴AQ AN=13,∴AQ =13AN =2√5; 由(2)得:DN ﹣BM =MN .设BM =x ,则MN =12﹣x ,CM =6+x ,在Rt △CMN 中,由勾股定理得:62+(6+x )2=(12﹣x )2, 解得:x =2, ∴BM =2,∴AM =√AB 2+BM 2=√62+22=2√10, ∵BC ∥AD , ∴△PBM ∽△PDA ,∴PM PA=BM DA=26=13,∴PM =12AM =√10, ∴AP =AM +PM =3√10.4.(2019•麒麟区模拟)已知,正方形ABCD中,∠MAN=45°,∠MAN绕点A顺时针旋转,它的两边分别交CB、DC(或它们的延长线)于点M、N,AH⊥MN于点H.(1)如图①,当∠MAN绕点A旋转到BM=DN时,请你直接写出AH与AB的数量关系:AH=AB;(2)如图②,当∠MAN绕点A旋转到BM≠DN时,(1)中发现的AH与AB的数量关系还成立吗?如果不成立请写出理由,如果成立请证明;(3)如图③,已知∠MAN=45°,AH⊥MN于点H,且MH=2,NH=3,求AH的长.(可利用(2)得到的结论)【点睛】(1)由三角形全等可以证明AH=AB,(2)延长CB至E,使BE=DN,证明△AEM≌△ANM,能得到AH=AB,(3)分别沿AM、AN翻折△AMH和△ANH,得到△ABM和△AND,然后分别延长BM和DN交于点C,得正方形ABCE,设AH=x,则MC=x﹣2,NC=x﹣3,在Rt△MCN中,由勾股定理,解得x.【解析】解:(1)如图①AH=AB.(2)数量关系成立.如图②,延长CB至E,使BE=DN.∵ABCD是正方形,∴AB=AD,∠D=∠ABE=90°,在Rt△AEB和Rt△AND中,{AB=AD∠ABE=∠ADN BE=DN,∴Rt△AEB≌Rt△AND,∴AE=AN,∠EAB=∠NAD,∵∠DAN+∠BAM=45°,∴∠EAB+∠BAM=45°,∴∠EAM=45°,∴∠EAM=∠NAM=45°,在△AEM和△ANM中,{AE=AN∠EAM=∠NAM AM=AM,∴△AEM≌△ANM.∴S△AEM=S△ANM,EM=MN,∵AB、AH是△AEM和△ANM对应边上的高,∴AB=AH.(3)如图③分别沿AM、AN翻折△AMH和△ANH,得到△ABM和△AND,∴BM=2,DN=3,∠B=∠D=∠BAD=90°.分别延长BM和DN交于点C,得正方形ABCD,由(2)可知,AH=AB=BC=CD=AD.设AH=x,则MC=x﹣2,NC=x﹣3,在Rt△MCN中,由勾股定理,得MN2=MC2+NC2∴52=(x﹣2)2+(x﹣3)2(6分)解得x1=6,x2=﹣1.(不符合题意,舍去)∴AH=6.5.(2019秋•东台市期末)在等边△ABC 的两边AB 、AC 所在直线上分别有两点M 、N ,D 为△ABC 外一点,且∠MDN =60°,∠BDC =120°,BD =DC .探究:当M 、N 分别在直线AB 、AC 上移动时,BM 、NC 、MN 之间的数量关系及△AMN 的周长Q 与等边△ABC 的周长L 的关系.(1)如图1,当点M 、N 边AB 、AC 上,且DM =DN 时,BM 、NC 、MN 之间的数量关系是 BM +NC =MN ;此时Q L=23;(2)如图2,点M 、N 在边AB 、AC 上,且当DM ≠DN 时,猜想( I )问的两个结论还成立吗?若成立请直接写出你的结论;若不成立请说明理由.(3)如图3,当M 、N 分别在边AB 、CA 的延长线上时,探索BM 、NC 、MN 之间的数量关系如何?并给出证明.【点睛】(1)由DM =DN ,∠MDN =60°,可证得△MDN 是等边三角形,又由△ABC 是等边三角形,CD =BD ,易证得Rt △BDM ≌Rt △CDN ,然后由直角三角形的性质,即可求得BM 、NC 、MN 之间的数量关系BM+NC=MN,此时QL=23;(2)在CN的延长线上截取CM1=BM,连接DM1.可证△DBM≌△DCM1,即可得DM=DM1,易证得∠CDN=∠MDN=60°,则可证得△MDN≌△M1DN,然后由全等三角形的性质,即可得结论仍然成立;(3)首先在CN上截取CM1=BM,连接DM1,可证△DBM≌△DCM1,即可得DM=DM1,然后证得∠CDN=∠MDN=60°,易证得△MDN≌△M1DN,则可得NC﹣BM=MN.【解析】解:(1)如图1,BM、NC、MN之间的数量关系BM+NC=MN.此时QL=23.(2分).理由:∵DM=DN,∠MDN=60°,∴△MDN是等边三角形,∵△ABC是等边三角形,∴∠A=60°,∵BD=CD,∠BDC=120°,∴∠DBC=∠DCB=30°,∴∠MBD=∠NCD=90°,∵DM=DN,BD=CD,∴Rt△BDM≌Rt△CDN,∴∠BDM=∠CDN=30°,BM=CN,∴DM=2BM,DN=2CN,∴MN=2BM=2CN=BM+CN;∴AM=AN,∴△AMN是等边三角形,∵AB =AM +BM , ∴AM :AB =2:3,∴Q L=23;(2)猜想:结论仍然成立. (3分).证明:在NC 的延长线上截取CM 1=BM ,连接DM 1.(4分) ∵∠MBD =∠M 1CD =90°,BD =CD , ∴△DBM ≌△DCM 1,∴DM =DM 1,∠MBD =∠M 1CD ,M 1C =BM , ∵∠MDN =60°,∠BDC =120°, ∴∠M 1DN =∠MDN =60°, ∴△MDN ≌△M 1DN ,∴MN =M 1N =M 1C +NC =BM +NC ,∴△AMN 的周长为:AM +MN +AN =AM +BM +CN +AN =AB +AC ,∴Q L=23;(3)证明:在CN 上截取CM 1=BM ,连接DM 1.(4分) 可证△DBM ≌△DCM 1, ∴DM =DM 1,(5分)可证∠M 1DN =∠MDN =60°, ∴△MDN ≌△M 1DN , ∴MN =M 1N ,(7分).∴NC﹣BM=MN.(8分).6.请阅读下列材料:已知:如图(1)在Rt△ABC中,∠BAC=90°,AB=AC,点D、E分别为线段BC上两动点,若∠DAE =45°.探究线段BD、DE、EC三条线段之间的数量关系.小明的思路是:把△AEC绕点A顺时针旋转90°,得到△ABE′,连接E′D,使问题得到解决.请你参考小明的思路探究并解决下列问题:(1)猜想BD、DE、EC三条线段之间存在的数量关系式,直接写出你的猜想;(2)当动点E在线段BC上,动点D运动在线段CB延长线上时,如图(2),其它条件不变,(1)中探究的结论是否发生改变?请说明你的猜想并给予证明;(3)已知:如图(3),等边三角形ABC中,点D、E在边AB上,且∠DCE=30°,请你找出一个条件,使线段DE、AD、EB能构成一个等腰三角形,并求出此时等腰三角形顶角的度数.【点睛】(1)DE2=BD2+EC2,将△ADB沿直线AD对折,得△AFD,连FE,容易证明△AFD≌△ABD,然后可以得到AF=AB,FD=DB,∠F AD=∠BAD,∠AFD=∠ABD,再利用已知条件可以证明△AFE ≌△ACE,从而可以得到∠DFE=∠AFD﹣∠AFE=135°﹣45°=90°,根据勾股定理即可证明猜想的结论;(2)根据(1)的思路一样可以解决问题;(3)当AD=BE时,线段DE、AD、EB能构成一个等腰三角形.如图,与(1)类似,以CE为一边,作∠ECF=∠ECB,在CF上截取CF=CB,可得△CFE≌△CBE,△DCF≌△DCA,然后可以得到AD =DF,EF=BE.由此可以得到∠DFE=∠1+∠2=∠A+∠B=120°,这样就可以解决问题.【解析】解:(1)DE2=BD2+EC2;(2)关系式DE2=BD2+EC2仍然成立.证明:将△ADB沿直线AD对折,得△AFD,连FE∴△AFD≌△ABD,∴AF=AB,FD=DB,∠F AD=∠BAD,∠AFD=∠ABD,又∵AB=AC,∴AF=AC,∵∠F AE=∠F AD+∠DAE=∠F AD+45°,∠EAC=∠BAC﹣∠BAE=90°﹣(∠DAE﹣∠DAB)=45°+∠DAB,∴∠F AE=∠EAC,又∵AE=AE,∴△AFE≌△ACE,∴FE=EC,∠AFE=∠ACE=45°,∠AFD=∠ABD=180°﹣∠ABC=135°∴∠DFE=∠AFD﹣∠AFE=135°﹣45°=90°,∴在Rt△DFE中,DF2+FE2=DE2,即DE2=BD2+EC2;(3)当AD=BE时,线段DE、AD、EB能构成一个等腰三角形.如图,与(2)类似,以CE为一边,作∠ECF=∠ECB,在CF上截取CF=CB,可得△CFE≌△CBE,△DCF≌△DCA.∴AD=DF,EF=BE.∴∠DFE=∠1+∠2=∠A+∠B=120°.若使△DFE为等腰三角形,只需DF=EF,即AD=BE,∴当AD=BE时,线段DE、AD、EB能构成一个等腰三角形,且顶角∠DFE为120°.7.(2019•夏津县二模)如图1,在正方形ABCD中,E、F分别是BC,CD上的点,且∠EAF=45度.则有结论EF=BE+FD成立;(1)如图2,在四边形ABCD中,AB=AD,∠B=∠D=90°,E、F分别是BC,CD上的点,且∠EAF 是∠BAD的一半,那么结论EF=BE+FD是否仍然成立?若成立,请证明;不成立,请说明理由.(2)若将(1)中的条件改为:如图3,在四边形ABCD中,AB=AD,∠B+∠D=180°,延长BC到点E,延长CD到点F,使得∠EAF仍然是∠BAD的一半,则结论EF=BE+FD是否仍然成立?若成立,请证明;不成立,请写出它们的数量关系并证明.【点睛】(1)结论仍然成立.延长CB到G,使BG=FD,根据已知条件容易证明△ABG≌△ADF,由此可以推出∠BAG=∠DAF,AG=AF,而∠EAF=12∠BAD,所以得到∠DAF+∠BAE=∠EAF,进一步得到∠EAF=∠GAE,现在可以证明△AEF≌△AEG,然后根据全等三角形的性质就可以证明结论成立;(2)结论不成立,应为EF=BE﹣DF,如图在CB上截取BG=FD,由于∠B+∠ADC=180°,∠ADF+∠ADC=180°,可以得到∠B=∠ADF,再利用已知条件可以证明△ABG≌△ADF,由此可以推出∠BAG=∠DAF,AG=AF,而∠EAF=12∠BAD,所以得到∠EAF=∠GAE,现在可以证明△AEF≌△AEG,再根据全等三角形的性质就可以证明EF=EG=EB﹣BG=EB﹣DF.【解析】解:(1)延长CB到G,使BG=FD,连接AG,∵∠ABG=∠D=90°,AB=AD,∴△ABG≌△ADF,∴∠BAG=∠DAF,AG=AF,∵∠EAF=12∠BAD,∴∠DAF+∠BAE=∠EAF,∴∠EAF=∠GAE,∴△AEF≌△AEG,∴EF=EG=EB+BG=EB+DF.(2)结论不成立,应为EF=BE﹣DF,证明:在BE上截取BG,使BG=DF,连接AG.∵∠B+∠ADC=180°,∠ADF+∠ADC=180°,∴∠B=∠ADF.∵AB=AD,∴△ABG≌△ADF.∴∠BAG=∠DAF,AG=AF.∴∠BAG+∠EAD=∠DAF+∠EAD=∠EAF=12∠BAD.∴∠GAE=∠EAF.∵AE=AE,∴△AEG≌△AEF.∴EG=EF∵EG=BE﹣BG∴EF=BE﹣FD.8.(1)如图1,将∠EAF绕着正方形ABCD的顶点A顺时针旋转,∠EAF的两边交BC于E,交CD于F,连接EF.若∠EAF=45°,BE、DF的长度是方程x2﹣5x+6=0的两根,请直接写出EF的长;(2)如图2,将∠EAF绕着四边形ABCD的顶点A顺时针旋转,∠EAF的两边交CB的延长线于E,交DC的延长线于F,连接EF.若AB=AD,∠ABC与∠ADC互补,∠EAF=12∠BAD,请直接写出EF与DF、BE之间的数量关系,并证明你的结论;(3)在(2)的前提下,若BC=4,DC=7,CF=2,求△CEF的周长.①EF的长为:5;②数量关系:EF=DF﹣BE.【点睛】(1)先证明△ABE≌△ADM,再证明△AEF≌△AMF,得到EF=DF+BE即可;(2)先证明△ADM≌△ABE,再证明△EAF≌△MAF,即可;(3)直接计算△CEF的周长=EF+BE+BC+CF=DF+BC+CF=9+4+2=15.【解析】(1)解:如图1,延长CD使DM=BE,连接AM;在△ABE和△ADM中,{AB=AD∠ABE=∠ADM=90°BE=DM∴△ABE≌△ADM,∴AE=AM,∠EAB=∠DAM,∵∠EAF=45°,且∠EAB=∠DAM,∴∠BAF+∠DAM=45°,即∠MAF=45°=∠EAF,又∵AE=AM,AF=AF,∴△AEF≌△AMF,∴EF=FM,∵FM=DF+DM,∴EF=DF+NB,即EF=DF+BE;∵BE、DF的长度是方程x2﹣5x+6=0的两根,∴BE=2,DF=3,∴EF=DF+BE=3+2=5,(2)证明:如图2,在DF上截取DM=BE,∵∠D+∠ABC=∠ABE+∠ABC=180°,∴∠D=∠ABE,∴AD=AB,∴△ADM≌△ABE,∴AM=AE,∴∠DAM=∠BAE;∵∠EAF=∠BAE+∠BAF=∠DAM+∠BAF=∠BAD﹣∠F AM=12∠BAD,∴∠MAF=12∠BAD,∴∠EAF=∠MAF;∵AF是△EAF与△MAF的公共边,∴△EAF≌△MAF,∴EF=MF;∵MF=DF﹣DM=DF﹣BE,∴EF=DF﹣BE.(3)由上面的结论知:DF=EF+BE;∵BC=4,DC=7,CF=2,∴DF=CD+CF=9∴△CEF的周长=EF+BE+BC+CF=DF+BC+CF=9+4+2=15.即△CEF的周长为15.①EF=DF﹣BE=FC+CD﹣BE=5②和(2)方法一样,EF=DF﹣BE.故答案为EF=DF﹣BE.。
