专题全程检测四
中考物理专题训练及答案解析

专题训练一力学一、填空题(每空1分,共26分)1.用托盘天平称物体质量时,物体应放在天平的_______盘中,如果发现指针偏向分度盘的左侧,应该_______(填“增加”或“减少”)砝码.2.自行车车轮的外表面都有凹凸不平的花纹,这是为了_______,菜刀的刀刃要做得很薄,这是为了_______.3.在百米跑训练中,测得一短跑运动员起跑后5 s跑完34 m,即可达到最大速度11 m/s,以后保持这一速度跑完全程,则这名运动员这次百米跑的成绩(时间)是_______s,他百米跑的平均速度为_______m/s.4.沿直线运动的物体在一直线上的两个力作用下,其运动的速度越来越小,那么这两个力的合力大小一定_______零.(选填“大于”“小于”“等于”),合力的方向与运动的方向_______.5.木块的密度是0.6 g/cm3,冰块的密度是0.9 g/cm3,若它们的体积相等,都漂浮在水面上,则木块受到的浮力_______冰块受到的浮力,木块露出水面的体积_______冰块露出水面的体积.(选填“大于”“小于”“等于”)6.下列实物属于哪种简单机械:(1)操场上旗杆顶端的小轮属于_______(2)码头上起重机吊钩上方的铁轮属于_______ (3)家用缝纫机的脚踏板属于______7.将以下做法中用到的主要物理知识分别填在题后的横线上(简要写出物理知识的内容)拦河坝总是下部宽上部窄_______ 用吸管将杯中的饮料吸入口中_______ 自行车的轴承上要经常加油_______ 把斧柄的一端在水泥地面撞击几下,斧头就牢牢地套在斧柄上___________8.汽车如果空载和满载时都以相同的速度行驶,空载时具有的动能_______满载时的动能,停在山顶上的卡车具有的重力势能_______该车在山下时具有的重力势能.(填“大于”“等于”或“小于”)9.把一个空杯子底朝上竖直按入水中,随着杯子没入水中深度的增加,杯中空气的压强_______体积_______.10.甲、乙两支完全相同的试管,内装密度相等的同种液体,甲管竖直放置,乙管倾斜放置,两管液面相平,如图所示,设液体对两试管底的压强分别为p甲和p乙,则p甲____p乙(填“大于”“等于”或“小于”)11.用50 N的水平拉力拉着重为200 N的小车沿水平道路在1 min内前进60 m,则拉力做的功为_______J,拉力的功率为_______ W.12.某高层楼房中,五楼水龙头出水口的水的压强是2.5×105Pa,那么比它高12 m的九楼的出水口的水的压强是_______,比它低12 m的底楼水龙头出水口的压强是_______Pa.(g =10 N/kg)二、选择题(每题3分,共36分)13.甲同学把耳朵贴在长铁管的一端,乙同学在另一端敲一下铁管,甲同学听到两次响声,这是因为( )A.声音有反射现象B.声音在空气中比在铁中传播的快C.声音有折射现象D.声音在空气中比在铁中传播的慢14.放在水平桌面上静止不动的电视机,受到彼此平衡的两个力是( )A.电视机受到的重力和桌面对电视机的支持力B.电视机受到的重力和电视机对桌面的压力C.桌面对电视机的支持力和电视机对桌面的支持力D.桌面受到的重力和电视机对桌面的压力15.用1 m的玻璃管做托里拆利实验,下面几种情况中对管内水银柱竖直高度有影响的是( )A.玻璃管的粗细B.玻璃管的长短 C.实验所在的高度D.玻璃管插入水银槽的深度16.如图所示的三只相同的烧杯分别放有质量相等的煤油、水、硫酸,根据液面高度判断盛硫酸的是( )A.甲杯B.乙杯C.丙杯D.无法判断17.三个分别用铜、铁、铝制成的正立方体,它们的质量相等,把它们放在水平桌面上,则对桌面压强大的是( )A.铜立方体B.铁立方体C.铝立方体D.三个一样大18.有一人用一滑轮组分别将1000 N和2000 N的物体匀速提高相同的高度,动滑轮重200 N,绳重及摩擦都不计,则在上述两种情况中( )A.人做的额外功相等B.滑轮组的机械效率相等C.人做的总功相等D.人做功的功率相等19.下列各现象中不属于惯性现象的是( )A.刹车时,人的身体向前倾B.放入水中的铁球很快沉入水底C.汽车关闭发动机后,车还会向前运动一段距离 D.锤头松了,用力将锤柄撞击固定物,使锤头紧套在柄上20.下列工具或仪器中属于省力杠杆的是( )21.用手握住汽水瓶,汽水瓶并不滑落,这是因为( )A.手的握力大于汽水瓶的重力B.手的握力等于汽水瓶的重力C.手给汽水瓶的摩擦力大于瓶的重力D.手给汽水瓶的摩擦力等于瓶的重力22.两手对拉一弹簧秤,它的示数是10 N,这两手的拉力分别为( )A.5 N,5 N B.10 N,10 N C.0 N,0 ND.20 N,20 N23.如图所示,原来静止的物体A在水平拉力F作用下沿水平面做直线运动,速度逐渐增大,则拉力F( )A.一定大于阻力F f B.一定等于阻力F f C.可能等于阻力F f D.可能小于阻力F f24.两个完全相同的容器中分别盛有质量相等的水和酒精,如图所示.下列说法正确的是( )A.两容器底受到的压力相等B.液面下深度相同的两处a、b 所受液体的压强相等C.盛水容器底部受到的压强较大D.盛水容器底部受到的压强较小三、实验题(每题7分,共14分)25.把从图所示实验中观察到的弹簧秤和量筒的示数记录在表格中,并计算出相应的物理量.(g=9.8 N/kg)物重(N) 物体在水中弹簧秤的示数(N) 物体受到的浮力(N)物体排开水的体积(m3)物体排开的水重(N)26.在做“研究杠杆平衡条件”的实验中,挂钩码前,使杠杆在水平位置平衡,实验中只有10个相同的钩码,杠杆上每格等距,当在A点挂上4个钩码时,应怎样挂钩码才可使杠杆在水平位置平衡?请在图中画出两种设计方案.四、计算题(每题8分,共24分)27.一木块浮在水面上,露出水面的体积为32 cm3,把露出水面的部分截去后,原水下部分又有24 cm3体积露出水面,求:(1)木块的体积.(2)木块的密度.28.有一个形状不规则的物体,用弹簧秤测得物体在空气中的重力为G,然后把它全部浸入密度为0的液体中,测出物体在液体中的重力为G′,求:(1)此物体的体积V;(2)此物体的密度;(3)若将一个与它的体积相同的物体用绳子将它们捆在一起,放在原来的液体中恰好悬浮,求另一物体的密度.29.某人乘坐出租车在平直的公路上匀速行驶,出租车的牵引力为3000 N,下表为他乘车到达目的地的车费发票,求:(1)出租车行驶的时间.(2)出租车的速度.参考答案1.左增加2.增大摩擦力增大压强3.11 s 9.09 m/s4.大于相反5.小于大于6.定滑轮动滑轮费力杠杆7.液体压强随深度增大而增大大气压强的作用减小摩擦力由于惯性8.小于大于9.增加减少10.等于11.3000 5012.1.3×105 Pa 3.7×105 Pa13.D 14.A 15.C 16.C 17.A 18.A 19.B20.A 21.D 22.B 23.A 24.A25.1.96 0.98 0.98 1×10-4 0.9826.略27.128 cm3 0.75×103 kg/m328.略29.5 min 96 km/h专题训练二电学专题一、填空题(每空1分,共15分)1.一个导体两端加4 V电压时,通过它的电流强度为0.8 A,当把它两端电压变为6 V时,通过它的电流为_______A,它的电阻为_______ .2.如图所示的电路中,定值电阻R2为10 ,闭合开关S前后干路中总电流的比为2∶3,则R1的阻值为_______.3.标有“2.5 V 0.3 A”的小灯泡,正常工作1 min通过的电量为_______,功率为_______,产生的热量为_______.4.如图所示的电路,用电器的电阻R0=30 ,要求通过它的电流能在100~200 mA的范围内变化,选用的电源电压最小应为_______V,电路中所用滑动变阻器的阻值变化范围应是_______ .5.“220 V 100 W”的甲灯和“220 V 40 W”的乙灯相比较,正常工作时_______灯更亮,_______灯的电阻大一些,_______灯的灯丝粗一些.6.如图所示的圆环是由阻值R、粗细均匀的金属丝制成的.A、B、C三点将圆环分成三等份(每等份电阻为1/3R),若将其中任意两点连入电路,则连入电路的电阻值为_________.7.如图所示电路中,电源电压保持不变,当滑动变阻器的滑片P由中点向右端移动的过程中,电流表的示数将_______,灯泡L消耗的电功率将_______,变阻器R上消耗的电功率将_______(选填“变大”“变小”或“不变”)二、选择题(每题3分,共45分)8.阻值为3 与6 的电阻,将它们串联,其总电阻为R1;将它们并联,其总电阻为R2,则R1∶R2等于( )A.2∶1 B.1∶2 C.2∶9 D.9∶29.如图所示的电路中,电源电压不变,闭合开关S后,灯L1、L2都发光,一段时间后,其中一灯突然熄灭,而电流表、电压表的示数都不变,则产生这一现象的原因是( )A.灯L1短路B.灯L2短路C.灯L1断路D.灯L2断路10.如图所示,V1和V2是完全相同的两个电压表,都有3 V和15 V两个量程,闭合开关后,发现两个电压表偏转的角度相同,则( )A.R1∶R2=1∶4 B.R1∶R2=4∶1 C.R1∶R2=1∶5 D.R1∶R2=5∶111.将两只滑动变阻器按图所示的方法连接,如果把a、b两根导线接入电路里,要使这两只变阻器接入电路中的总电阻最大,应把滑片P1、P2放在( )A.P1放在最右端,P2放在最右端B.P1放在最左端,P2放在最左端C.P1放在最右端,P2放在最左端D.P1放在最左端,P2放在最右端12.在图所示的电路中,电源电压保持不变,当开关S闭合,滑动变阻器的滑片P向右移动时,电流表和电压表的示数的变化情况分别为( )A.电流表的示数变小,电压表的示数变大B.电流表的示数变大,电压表的示数变小C.电流表的示数变小,电压表的示数不变D.电流表的示数变小,电压表的示数变小13.如图所示,下列判断错误的是( )A.仅使灯L1工作,应闭合开关S2、S3 B.仅使灯L2工作,应闭合开关S1、S3C.使灯L1工作,应闭合开关S1、S3 D.使灯L2工作,只闭合开关S3也可14.如图所示,电磁铁P和Q通电后( )A.P的右端是N极,Q的左端是S极,它们相互吸引B.P的右端是S极,Q的左端是N极,它们相互吸引C.P的右端是N极,Q的左端是N极,它们相互排斥D.P的右端是S极,Q的左端是S极,它们相互排斥15.有a、b、c、d四个带电体,它们之间的相互作用是:a排斥c,b吸引c,b排斥d,由此判断( )A.a、d间相互排斥B.a、d间相互吸引C.a一定带正电D.d一定带负电16.用粗细均匀的电热丝加热烧水,通电10 min可烧开一壶水,若将电热丝对折起来使用,电源电压不变,则烧开同样一壶水的时间是( )A.2.5 min B.5 min C.20 min D.30 min17.现有一只“PZ220—60”灯泡L1和一只“PZ220—25”灯泡L2,下列有关说法中正确的是( )A.灯泡L1的电阻小于灯泡L2的电阻B.它们并联在照明电路中时L2亮C.它们串联在照明电路中时L1亮D.它们正常发光时,在相同时间内消耗的电能相同18.原来室内的电灯正常发光,当把台灯的插头插入插座时(台灯的开关断开),室内的灯全部熄灭,熔丝熔断,发生这一现象的原因是( )A.台灯的功率太大B.台灯的插头处有短路C.台灯的灯座处有短路D.插座处原来就有短路19.电工修理如图所示的照明电路时,发现电灯R不亮,用测电笔测试C、D后,发现这两处都能使氖管发光,而测试A、B两点时,只有A点氖管发光,则故障可能发生在( )A.AC段B.CD段C.电灯R短路D.BD段20.一个通电螺线管两端磁极的极性决定于A.螺线管的匝数B.通过螺线管的电流方向C.螺线管内有无铁芯D.通过螺线管的电流21.闭合电路的一部分导体在磁场中运动的方向如下图所示,图中小圆圈表示导体的横截面,箭头表示导体运动的方向,下列各图中不能产生感应电流的是( ) 22.在如图所示的电路中,电源电压恒定,R1为一定值电阻,R2为滑动变阻器.开关S 闭合后,当滑动变阻器的滑片P在a、b之间滑动的过程中,电压表的示数最大为4 V,电阻R1的电功率变化范围是0.8 W~7.2 W,则P从a端滑至b端的过程中,电流表的示数( )A.从1.8 A变化至0.2 A B.从0.4 A变化至1.2 A C.从1.2 A变化至0.4 A D.从0.2 A变化至1.8 A三、作图题(每题5分,共15分)23.根据下图中小磁针静止时的位置,标出电源的正、负极或通电螺线管的绕法.24.下图是安装一盏电灯和一个大功率插座的实物示意图,A、B为保险丝,请在图上画出接线.25.在下图中,A、B、C为三条引出线,由三个阻值相等的电阻组成,现用装有电池和电流表的检测器连接AB时,电流表示数I,当检测器与BC连接时,电流表的示数为I/2;当检测器与AC连接时,电流表的示数为I/3,试画出方框里的电路图.四、实验题(14分)26.测定标有“3.8 V”灯泡的额定功率.(1)画出实验电路图,并根据电路图将下列所需实物连接起来.(10分)(2)电压表所选量程是_______,调节滑动变阻器,应使电压表指针指在_______的位置上.(2分)(3)若此时电流表的示数如图所示,其读数为_______,则灯泡的额定功率约是________.(2分)五、计算题(11分)27.某同学家的电炉铭牌模糊不清了,为了测出电炉的额定功率,他让家里的所有用电器都停止工作,只接入电炉让其正常工作,然后观察家里正在运行的电能表,电能表上标有“3000 R/kWh”,利用手表计时,发现1 min转盘转了50转,那么:(1)电炉的额定功率是多少?(2)小明同学觉得电炉使用不方便,想对电炉进行改装:使电炉的功率可以为额定功率,也可以为额定功率的1/4,请你利用一个开关和一个定值电阻帮他设计一个电路,画出电路图,并计算出定值电阻的大小.参考答案1.1.2 52.203.18 C 0.75 W 45 J4.6 0~305.甲乙甲6.2R/97.变小不变变小8.D 9.D 10.A 11.D 12.C 13.C 14.B 15.B 16.A 17.A 18.B 19.D 20.B 21.C 22.C23.略 24.略 25.略26.(1)略 (2)0~15 V 2.8 V (3)0.34 A 1.3 W27.(1)1 kW(2)图略将开关与定值电阻并联后再与电炉丝串联R=48.4专题训练三实验一、填空题(每空1分,共37分)1.为测量运动员短跑时的平均速度.在室外测出40 m的路程,每隔10 m作一记号.选出4位记时员分别站在10、20、30、40 m处;让该运动员跑完40 m路程即告实验完毕.(1)实验中所用的主要器材是_______和_______;(2)实验原理是_______________.2.瓶里放少量的碘,并且对烧瓶微微加热,可以观察到碘的_______现象.停止加热,过一会儿,在烧瓶壁上可观察到碘的_______现象.3.做“研究透镜成像规律实验”前,首先要利用_______和_______测出一凸透镜的焦距.做这个实验时,为了使像能成在光屏的中央,应先调节好_______和_______的高度,使它们的中心跟_______的中心大致在同一高度.4.某同学做“平面镜成像的特点”实验时,将一块玻璃板竖直架在一把直尺的上面,再取两段等长的蜡烛A和B一前一后竖放在直尺上,点燃玻璃板前的蜡烛A,用眼睛进行观察,如图所示.在此实验中:(1)直尺的作用是便于比较物与像的__________关系;(2)两段等长的蜡烛是为了比较______________关系;(3)移去蜡烛B,并在其所在位置上放一光屏,则光屏上_______接收到蜡烛A的烛焰的像(填“能”或“不能”).这说明平面镜成的是_______像.5.在实验室里,我们通常用_______法来测定电阻的阻值,即只要测出电阻两端的_______和通过它的_______,就可以用公式_______算出电阻的阻值.根据这一实验要求,除待测电阻外,还必需的器材是_______、_______、_______、_______、_______.6.如果你的家庭电路中有一只表盘上标有3000 R/kWh的电能表,另外你手头还有一块秒表.如何测量你家中某一盏白炽灯的实际电功率?(1)写出测量方法:_______________;(2)要测量哪些物理量:_______________;(3)写出根据测量的物理量,计算灯泡电功率的数学表达式:______________.7.白炽灯的灯丝常在_______时发生断开,如若能接上继续使用,则电功率将比原来_______(填“大”或“小”),这是由于它的电阻变_______了.8.把几滴红墨水滴入清水中,隔一会儿,清水变成红水,这是_______现象.当红墨水分别滴入冷水和热水中,可以看到热水变色比冷水快.这说明温度越高,______________.9.水的比热是_______.装有50 L水的太阳能热水器,在阳光照射下,水温从20℃上升到50℃,该热水器中水吸收的热量是_______.10.黑板的“反光”现象属于光的_______现象;我们能从不同方向看到本身不发光的物体,是由于光射到物体上时,发生了_______反射的缘故.11.普通自行车上,通过增大压力来增大摩擦的装置是_______;在前后轮中减小摩擦的措施是在轮子的轴上安装了_______.二、选择题(每题2分,共24分)12.使用天平时,下列哪种原因会使测量产生误差( )A.天平使用之前忘了调节 B.游码所对标尺的读数估计值偏小了C.将砝码放在天平的左盘里,被称物体放在天平的右盘里,并使用了游码D.少加了一个2 g游码标示的质量13.少数不法商贩将煤矸石(矿井下与煤共生一处的石块)破碎后掺在优质煤中高价销售给客户.客户为了防止上当,最恰当的方法是可以检测下述物理量中的( )A.密度B.比热C.熔点D.燃烧值14.若给你一块小木块、一只量筒、水、酒精、一根细针,你能完成下列实验中的哪几种( )①测出木块的质量②测出木块的体积③测出木块的密度④测出酒精的密度⑤测出木块所受水的浮力⑥测出木块所受酒精的浮力A.①②③B.①②③④C.①②③④⑤D.①②③④⑤⑥15.若给你一只弹簧秤、一杯水、细线和一个金属块,你能完成下列四种实验中的哪几种?( )①测金属块的质量②测金属块浸没在水中的浮力③金属块的体积④测金属块的密度A.①B.①②C.①②③D.①②③④16.用一端封闭的足够长的玻璃管做托里拆利实验时,下列哪种情况会影响管内水银柱的高度( )A.改变玻璃管的粗细B.少许改变管的倾斜程度C.改变水银槽内水银面的高低D.玻璃管内漏进少许空气17.放映幻灯时,在屏幕上得到的是幻灯片上景物的( )A.正立放大的虚像 B.正立放大的实像C.倒立放大的虚像D.倒立放大的实像18.用一滑轮组提升重物,不计摩擦,下列方法中可以提高滑轮组机械效率的是( ) A.改变绕绳方法B.增加重物的提升高度C.减少重物的提升高度D.增加提升重物的重力19.下列关于电路的说法中正确的是( )A.电路连接过程中,开关必须处于断开状态B.电路连接必须从电源的正极开始C.电流表测电流时为了安全应选择使用大量程D.滑动变阻器使用时必须串联在电路中20.要改变直流电动机的转向,应采取的方法是( )A.增强磁极的磁性B.增加电源电压C.增大线圈中的电流D.改变线圈中的电流方向或对调磁铁的磁极21.下列测量仪器中,刻度不均匀的是( )A.体温计B.弹簧秤C.量筒D.密度计22.两个相同的烧杯里分别盛有质量和温度都相同的水和煤油,用两个相同的酒精灯给它们加热,可以看到煤油的温度比水的温度升高的快.若水和煤油的比热分别用C水和C煤油表示,则( )A.C水>C煤油B.C水=C煤油C.C水<C煤油D.条件不足,无法比较23.下列变化不属于物理变化的是( )A.灯泡用久了灯丝变细B.用石灰浆抹墙,经过一段时间后变硬C.用压缩体积的办法,使丁烷气体液化并贮存在打火机内D.潮湿的衣服变干了三、实验题(每题4分,共20分)24.你能用几种方法判断一蓄电池能否供电?又怎样判别它的正、负极?试设计几个办法,并说明道理.25.联欢会上,某同学从家里带来40只规格为“6 V 0.5 W”的彩灯,通过计算说明他最少应将多少只彩灯接在220 V的照明电路中?应该怎样连接?如果晚会开了5 h,使用这些彩灯一共用了多少kWh的电能?26.用日常生活中装饮料的塑料空瓶,请你设计:做演示液体压强和大气压强存在及其性质的物理实验各一个.要求制作方法简便,并只加少量其他辅助器材.画图并写明制作方法、实验步骤.27.弹簧秤下悬挂着一重物(浸在硫酸铜溶液中,不与溶液反应),若向硫酸铜溶液中逐渐滴加氢氧化钡溶液至恰好完全反应后,弹簧秤的示数将_______(填“变大”“变小”或“不变”);发生反应的化学方程式是_______________28.做“测滑轮组的机械效率”的实验.(1)实验所用的器材除铁架台、滑轮组、细绳和钩码外,还需要_______和_______.(2)实验时,除已知钩码重外,需要测量的物理量是_______、_______和_______.需要计算的物理量是_______、_______和_______.(3)请设计出实验记录表格.四、计算题(29、题每题9分,30题10分,共19分)29.电饭锅工作时有两种状态:一是锅内水烧干前的加热状态,二是水烧干后的保温状态.下图为CFXB型“220 V 1100 W”电饭锅的简易原理图.已知R=1956 .求:(1)电阻R0的阻值.(2)接通档“1”时,电饭锅处于_______状态(选填“保温”或“加热”),此时电路的总功率为多大?(3)如果用该电饭锅来烧水,其放出的热量全部被水吸收,问需多少分钟可将2.2 kg,初温为20℃的水烧开?(设1标准大气压下)30.同学用弹簧秤、量筒、水、物块做测定浮力的实验,根据图中弹簧秤和量筒的示数,填写记录表格中的各项内容,并分析、比较这些数据,得出的结论用数学式表达为____________________.物体重量(N) 物体在水中时弹簧秤示数(N) 物体受到的浮力(N)物体排开的水的体积(cm3)物体排开的水的重量(N)参考答案1.卷尺 秒表 v =2.升华 凝华3.平行光源 刻度尺 透镜 光屏 烛焰4.(1)到透镜的距离 (2)物体和像的大小(3)不能 虚5.伏安 电压 电流 R = 电源 开关 导线 电压表 电流表6.(1)将家中的其他用电器全都断开,只把白炽灯接入电路,让其工作一段时间,用手表记录时间,用电能表记录它所消耗的电能,最后用P =W /t 计算出它的功率.(2)时间t 消耗的电能W (3) P =W /t7.刚闭合电路 大 小8.扩散 分子无规则运动越剧烈9.4.2×103 J/(kg ·℃) 6300 KJ10.镜面反射 漫11.刹车用的闸皮 钢珠12.B 13.A 14.D 15.D 16.D 17.D 18.D 19.A 20.D 21.D22.A 23.B24.(1)用电表,根据电流的方向.(2)用小磁针来判断,根据奥斯特实验的结论.(3)利用电镀的原理,在碳棒上析出铜的相连的为负极.25.用37个同样的灯泡串联起来就可以了,0.09 kWh26.液体:在塑料瓶的侧壁上打一小孔,就会看到水从侧壁流出来.气体:用抽气机将瓶中的气体抽走,瓶子就会被空气压瘪了.27.变大 CuSO 4+Ba(OH)2=BaSO 4↓+Cu(OH)2↓28.(1)重物 刻度尺 (2)s h G 总功 有用功 机械效率 (3)略29.(1)R 0=44 (2)保温 24.2 W (3)11.2 min 浮排物体重量(N)物体在水中时弹簧秤示数(N) 物体受到的浮力(N) 物体排开的水的体积(cm 3) 物体排开的水的重量(N) 1.960.98 0.98 100 0.98t sI U专题训练四设计1.(5分)请你利用以下所提供的器材:刻度尺、量杯、细线、烧杯、水、中国地图设计两种办法,分别测量出:(1)一个薄壁圆柱形容器的容积.(2)京沪铁路线长度.2.(5分)如何用一种光学方法,判定一个透镜是凸透镜还是凹透镜?小明的身边有硬纸板、手电筒、笔、玻璃砖、蚊香、空可乐瓶(容积为10 L)等物品,请你从中选择器材设计一个实验验证:“光在空气中是沿直线传播的”.3.(5分)老师给小明布置了一个作业:测量一根电线杆的长度.小明看着高高的电线杆和手中的米尺犯了难:这可怎么办?请你利用你学过的知识帮小明想出一个好办法,说出你这样做的理由.4.(5分)请你利用学过的有关热学的知识设计一个实验,测量水的比热容.5.(5分)如何测量密度大于水的石块的密度,至少设计三个试验并说明方法和过程.6.(5分)如何测量密度小于水、形状不规则的石蜡的密度(试验中用的是水),简述试验办法.7.(5分)请你用一个烧杯、适量的水、托盘天平来测量一种未知液体的密度.简述你的办法及过程并写出未知液体密度的表达式.8.(5分)有一条形磁铁,要想知道它是否有磁性,可以采用哪些办法?请具体说明.9.(5分)对农民来讲,农作物的种子中混有一些杂草的种子是一件很头痛的事情,但是这两种种子的外表面不同,农作物的种子很光滑,杂草的种子表面有很多绒毛,能够吸附靠近它的小颗粒物,当然也能粘在走过的动物身上,因此它可以广为传播.现在,给你一些混有杂草种子的农作物的种子,一些铁屑和一块磁铁,请你替农民将其中的杂草种子从农作物种子中分离出来,说出你的办法和道理.10.(5分)用所学过的知识在家中测苹果的密度.所能利用的器材有:自制的弹簧秤、水桶、水、塑料袋、塑料绳、水瓢.请写出简要的实验步骤及苹果密度表达式的推导过程.11.(5分)一个质量为m人的木工师傅,想粗测一根粗细均匀的长木料的质量m木,找来一块有棱角的石头和一把刻度尺,利用自己的身体便可测出木料的质量.请你说出他测量的方法及依据的原理.12.(5分)已知物体重800 N,滑轮重50 N,要用不大于200 N的力将重物匀速提起,那么动滑轮和重物要用几段绳子来承担?请选择一个合适的滑轮组,并将它的装配图画出来.13.(5分)一个商品仓库,后门进货、前门取货,现有红、绿两只灯泡和一个电铃,一个电池组、两个开关,还有若干条导线,请你为仓库管理员设计一个电路:电铃响同时绿灯亮,表示送货人在后门按开关,电铃响同时红灯亮表示前门取货人在前门按开关.要求画出电路图,图中要标明红灯、绿灯及相应的前门、后门的开关.14.(5分)现有3只电阻值均为R的定值电阻及若干导线,它们分别与图中的虚线框中标有ABCD的有关接线柱相连,经测试发现:(1)接线柱B与C间的电阻值等于R.(2)接线柱AC、AD、DC 间的电阻均为2R.根据上述测试结果在虚线框内有关接线柱间画出电阻或导线的连接情况.15.(5分)请你至少用两种方法来判断两只铭牌已经模糊不清的照明灯泡的额定功率的大小,并加以简要说明.16.(5分)有这样一些器材:玻璃杯一只、硬纸片一块,鸡蛋一枚、食盐及足量的水.请从中选择器材(单独或组合)做三个小实验,并说明相关的物理现象或规律.17.(5分)两只杯子中分别盛有不同浓度的食盐水.不能用嘴尝,请你用学过的知识及需要的试验器材(可自行制作),设计三种区分这两杯盐水的方法,并简要说明理由.方法一:方法二:方法三:18(5分)有一个透镜,不知是不是凸透镜,请你设计两种方法确定,并作简要的说明.(不能用手触摸)方法一:方法二:19.(5分)军属李大娘家距河边600 m,小明家距河边200 m,小明和李大娘家之间的河岸线为600 m,如下图所示,小明每天从自己家到河边挑水送到李大娘家.为了节约时间,请你应用光学的知识,设计出小明挑水的最短路程.□李大娘家。
高考化学一轮复习全程跟踪检测47专题研究酸碱中和滴定及其拓展应用含解析

专题研究——酸碱中和滴定及其拓展应用1.准确移取20.00 mL某待测HCl溶液于锥形瓶中,用0.100 0 mol·L-1NaOH溶液滴定,下列说法正确的是( )A.滴定管用蒸馏水洗涤后,装入NaOH溶液进行滴定B.随着NaOH溶液滴入,锥形瓶中溶液pH由小变大C.用酚酞作指示剂,当锥形瓶中溶液由红色变无色时停止滴定D.滴定达终点时,发现滴定管尖嘴部分有悬滴,则测定结果偏小解析:选B A项,滴定管用水洗涤后,还要用待装溶液润洗,否则将要引起误差,错误;B项,在用NaOH溶液滴定盐酸的过程中,锥形瓶内溶液由酸性逐渐变为中性,溶液的pH由小变大,正确;C项,用酚酞作指示剂,锥形瓶中溶液应由无色变为粉红色,且半分钟内不恢复原色时才能停止滴定,错误;D项,滴定达终点时,发现滴定管尖嘴部分有悬滴,则碱液的体积偏大,测定结果偏大,错误。
2.H2S2O3是一种弱酸,实验室欲用0.01 mol·L-1的Na2S2O3溶液滴定I2溶液,发生的反应为I2+2Na2S2O3===2NaI+Na2S4O6,下列说法合理的是( )A.该滴定可用甲基橙作指示剂B.Na2S2O3是该反应的还原剂C.该滴定可选用如图所示装置D.该反应中每消耗2 mol Na2S2O3,电子转移数为4 mol解析:选B 溶液中有单质碘,应加入淀粉溶液作指示剂,碘与硫代硫酸钠发生氧化还原反应,当反应终点时,单质碘消失,蓝色褪去,故A错误;Na2S2O3中S元素化合价升高被氧化,作还原剂,故B正确;Na2S2O3溶液显碱性,应该用碱式滴定管,故C错误;反应中每消耗2 mol Na2S2O3,电子转移数为2 mol,故D错误。
3.常温下,用0.50 mol·L-1氢氧化钠溶液滴定某一元弱酸(HA)的溶液中,滴定曲线如图所示,下列叙述不正确的是( )A.该弱酸在滴定前的浓度大于0.001 mol·L-1B.由滴定起点数据可计算该弱酸的K a(电离常数)为2×10-5C.滴定过程为判断滴定终点,最合适的指示剂是酚酞D.滴定终点时,c(Na+) >c(A-) >c(OH-) >c(H+)解析:选B 由图像可知,起始酸的pH为3,c(H+)=10-3mol·L-1,因为HA是弱酸,则酸的浓度必大于0.001 mol·L-1,A项正确;HA是弱酸,HA的体积未知,无法由滴定起点数据计算该弱酸的K a,B项错误;此滴定终点溶液显碱性,而酚酞的变色范围是8.2~10.0,故应选择酚酞作指示剂,C项正确;滴定终点时,酸碱恰好反应生成NaA,NaA是强碱弱酸盐,A-水解导致溶液显碱性,则滴定终点时离子浓度顺序为c(Na+)>c(A-)>c(OH-)>c(H+),D项正确。
第二章 平均速度的测量实验题类—沪科版八年级物理上册新课专题检测(机构)
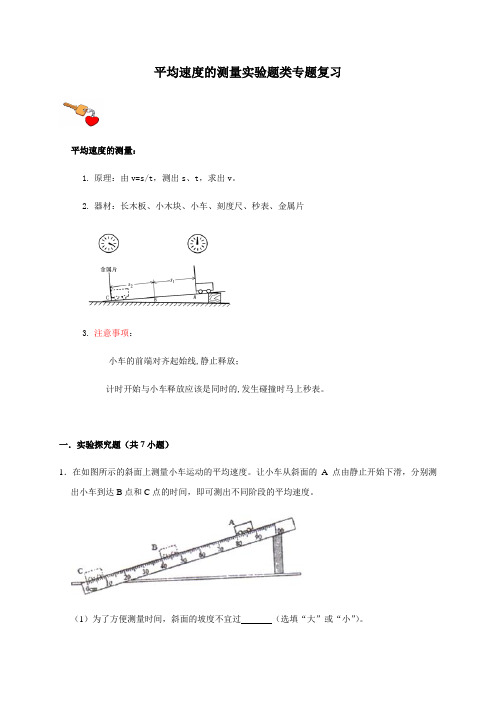
平均速度的测量实验题类专题复习平均速度的测量:1.原理:由v=s/t,测出s、t,求出v。
2.器材:长木板、小木块、小车、刻度尺、秒表、金属片3.注意事项:小车的前端对齐起始线,静止释放;计时开始与小车释放应该是同时的,发生碰撞时马上秒表。
一.实验探究题(共7小题)1.在如图所示的斜面上测量小车运动的平均速度。
让小车从斜面的A点由静止开始下滑,分别测出小车到达B点和C点的时间,即可测出不同阶段的平均速度。
(1)为了方便测量时间,斜面的坡度不宜过(选填“大”或“小”)。
(2)如图中AB段的路程s AB=cm,如果测得时间t AB=1.6s,则AB段的平均速度v AB =cm/s。
(3)实验中小车通过全程的平均速度(选填“大于”、“小于”或“等于”)小车通过下半程的平均速度。
2.在如图所示的斜面上测量小车运动的平均速度。
让小车从斜面的A点由静止开始下滑,分别测出小车到达B点和C点的时间,即可测出不同阶段的平均速度。
(1)该实验是根据公式:进行测量的。
(2)图中AB间的距离S AB=cm,如果测得时间t AB=1.6s,则AB段的平均速度为v1=m/s。
(3)实验中为了方便计时,应使斜面的坡度较(填“大”或“小”);在测量小车到达B 点的时间时,如果小车过了B点才停止计时,测得AB段的平均速度v1会偏。
(选填“大”或“小”)(4)接着,测出小车到达C点的时间,并计算出了AC段平均速度v.试验中发现,AB段和BC 段路程的特点,觉得还可以用公式直接算出BC段的平均速度v2,则v2=(用v、v1)。
3.小明在“测小车的平均速度”的实验中,设计了如图所示的实验装置:小车从带刻度(分度值为1cm)的斜面顶端由静止下滑,图中的圆圈是小车到达A、B、C三处时电子表的显示(数字分别表示“小时:分:秒”)。
(1)实验中应使斜面的坡度较小,目的是:。
(2)请根据图中信息回答:V AC=m⁄s。
(3)由实验看出,小车在下滑过程中速度越来越。
冲刺2020年高考专题全程突破生物人教版必修第一册课件:第1章 第1节 细胞是生命活动的基本单位

答案 A
答案
解析 HIV 无独立代谢体系,必须在活细胞内增殖,其生命活动离不开 最基本的生命系统——细胞,A 正确;超级淋病菌是球菌,有细胞结构,而 HIV 无细胞结构,B 错误;HIV 只含有 RNA 一种核酸,C 错误;HIV 只能 在活细胞内增殖,不可在体外用培养基培养,D 错误。
答案 C
a 生物大分子
个体 生态系统
组织
b 细胞 种群 群落 系统
c 组织 群落 种群 器官
答案
解析 由题图可知,a 包含 b,b 包含 c。生物大分子(不属于生命系统的 结构层次)组成细胞,细胞组成组织,A 错误;个体可以组成种群,种群可以 组成群落,B 错误;生态系统包括群落和无机环境,群落包括种群,C 正确; 组织可以构成器官,器官可以构成系统,D 错误。
解析
2.在细胞学说创立的过程中,许多科学家作出了突出的贡献,下列说法 不符合事实的是( )
A.第一个命名细胞的科学家是虎克 B.第一个发现细胞的科学家是魏尔肖 C.细胞学说的主要创立者是施莱登、施旺 D.提出“细胞通过分裂产生新细胞”的科学家是魏尔肖
答案 B
答案
解析 英国的科学家虎克既是细胞的发现者,也是细胞的命名者,A 正 确,B 错误;细胞学说的主要创立者是施莱登和施旺,C 正确;魏尔肖对细 胞学说进行了补充完善,提出“细胞通过分裂产生新细胞”,D 正确。
答案
解析 ①一块稻田中所有的三化螟虫属于一个种群;②浔阳江里的所有 生物属于生物群落;③庐山上的全部生物及其生存的环境属于生态系统;④ 南湖里面的所有鱼既不是种群(不是同一个物种)又不是群落(没有包括全部生 物)。
24期寒假专题:速度、时间、路程的关系,四年级上册数学学案带单元检测练习题附带答案解析

小学数学专题:速度、时间、路程的关系单价、数量与总价的关系超市运来一车饮料,正好100箱。
每瓶5元钱,1箱装12瓶。
1箱要付多少钱?1车饮料要付多少钱?根据饮料“每瓶5元钱,1箱装12瓶”这个条件,求“1箱要付多少钱?”也就是“求12瓶多少钱”,根据关系式“总价=单价×数量”求得12瓶饮料需付多少元,列式为:5×12=60(元)答:1箱要付60元.求“1车饮料要付多少钱?”第一个问题已求出一箱饮料的价格,再求100箱的价格就是一车饮料的钱数,用乘法进行计算。
列式为:5×12×100=6000(元)答:1车饮料要付6000元.每件商品的价格——单价购买商品的多少——数量一共花的钱数——总价解决本题的关键还是牢记单价、数量和总价三者的关系式。
就本题而言,首先根据关系式“总价=单价×数量”求出总价,再根据乘法的意义,算出100箱需要花多少钱即可。
“单价×数量=总价”“总价÷单价=数量”“总价÷数量=单价”例题1 小马虎去文具店买文具,不小心把购物发票弄脏了,你能帮他算出笔记本每本多少元吗?物品名称单价数量总价笔记本9本213元钢笔35元3支解答过程:(213-35×3)÷9=(213-105)÷9= 108÷9= 12(元)答:笔记本每本12元。
答案:12元技巧点拨:解答本题的关键是求出9本笔记本的价格,然后根据关系式:总价÷数量=单价求出每本笔记本的价格。
例题2 选择其中两个条件提一个问题,编一道应用题。
一双儿童鞋25元每个小足球8元共花2元买4双儿童鞋共花100元共花48元买4支铅笔共花40元买3千克糖买5个小足球一支铅笔5角每千克糖16元解答过程:首先从左右两边选出有关联的条件,提出问题,编一道应用题。
例如:“一双儿童鞋25元”和“买4双儿童鞋”是相关联的条件,进而可以提出一个问题“一共要花多少元钱?”例如:一双儿童鞋25元 ,买4双儿童鞋一共要花多少元钱?每千克糖16元,买3千克糖共需要多少元?每个小足球8元,买5个小足球共需要多少元?买3千克糖共花48元,每千克糖多少元?……技巧点拨:首先从左右两边选出有关联的条件,提出问题,编出应用题即可。
专题训练试卷(解决问题)

2012年上学期六年级总复习《解决问题》检测题1、只列式不计算:(1)、王老师把50000元存入银行,整存整取3年,年利率4%,到期时,王老师可以取回多少钱?(2)、小红从甲地到1200米外的乙地办事,去时每分钟走40米,回时每分钟走67米,小红往返平均速度是多少?(3)、妈妈买7.5千克苹果,付出20元,找回2.75元,平均每千克苹果多少元?(4)、打谷场有一堆圆锥形谷堆,测得底面积是6.28米2,高是0.6米,求这堆谷子的体积?(5)、一本240页的书,小红第一天看了全书的20%,第二天看了30%,两天共看了多少页?(6)、某商场昨天卖出洗衣机100台,卖出电视比卖出洗衣机的台数的75%多3台,昨天卖出电视多少台?(7)、服装厂要生产6000套服装,前5天已生长了2400套,余下的服装要在6天内完成,平均每天生产多少套?(8)、一种电视机现价728元,比原价降低了215 ,原价是多少元?(9)、一辆汽车上午4小时行236千米,下午行了3小时,平均每小时行52千米,这辆汽车一天平均行驶多少千米?(10)、一种商品现价80元,比原价提高了16元,现价比原价提高了百分之几?(11)、某汽车车轮直径是0.5米,汽车行驶到1千米时,车轮大约转了多少圈?(12)、期中考试,笑笑语文、数学和英语三门平均成绩是92分,语文和数学平均分是90分,求英语考了多少分?(13)、王叔叔和李叔叔同时从相距1500米的两地相对而行,王叔叔骑摩托车的速度是800米/分,李叔叔骑自行车的速度是200米/分,几分钟后两人相遇?(14)、红花衬衫厂要制作一批衬衫,原计划每天生产400件,60天完成,实际每天生产的件数是原计划每天生产件数的1.5倍,完成生产这批衬衫的任务,实际用了多少天?2、根据式子给题目加上必要的条件:图书室有450本故事书, ,文艺书有多少本? (1)450÷(1-17 ),条件:(2)450×(1+16 ),条件:(3)450×2-70,条件: 3、根据题意与条件,填写相应的问题或算式:一个服装厂要生产360件上衣,第一天生产了总数的25 ,第十天生产了总数的30%, ?算式: 问题:(1)360×25(2) 两天共生产了多少件上衣? (3) 第二天比第一天少生产了多少件? (4)1-25-30%学校 班级 姓名 学号 ………………………………………密……………………………………封………………………………线…………………………………4、为庆祝“六·一”儿童节,六(1)班同学都行动起来了,有的装饰教室,有的采购物品,老师说:“我们班13同学装饰教室,15同学采购物品,其余21名同学排练节目”,你能根据这些住处提出两个数学问题并解答出来吗?5、在一幅比例尺是1:500000的图上,量得甲城到乙方城的距离是9厘米,一辆汽车从甲城到乙城,每小时行驶80千米,5小时后能到乙城吗?6、一个长方形草坪,长和宽的比是3:1,用1:5000的比例尺将草坪画在图纸上,量得长方形周长是1.28厘米,草坪实际面积是多少平方米?7、在比例尺是1:8000000的地图上,量得AB 两地相距6cm ,甲、乙两车分别从A 、B 两地同时出发,相对而行,经过10小时相遇,已知甲、乙两车速度比是5:7,甲、乙两车每小时各行多少千米?8、游乐场要建个长方体的游泳池,在比例尺是1:200的设计图上,量得游泳场长20cm ,宽15cm ,高1.5cm 。
冲刺2020年高考专题全程突破生物人教版必修第一册课件:第2章 第5节 核酸是遗传信息的携带者

答案 D
概念检测
拓展提能
答案
解析 ①的组成元素是 C、H、O、N,若①为生物大分子,则其可能是 蛋白质,A 正确;若②是动物细胞内特有的储能物质,则②是糖原,B 正确; 细胞内的遗传物质均为 DNA,若③为细胞内的遗传物质,则③是 DNA,属 于核酸,C 正确;若④是植物的能源物质,则④可能是淀粉,纤维素是组成 植物细胞壁的主要成分,不作为植物的能源物质,D 错误。
答案 D
概念检测
拓展提能
答案
解析 图中核苷酸链中含有碱基 T,可见该图所示为脱氧核苷酸链,A 正确;由于该图所示为脱氧核苷酸链,题图中的 2 是脱氧核糖,脱氧核糖只 存在于 DNA 中,RNA 中为核糖,B 正确;题图中的 3 是含氮碱基胞嘧啶, DNA 和 RNA 中均含有胞嘧啶,C 正确;题图中的 5 为构成 DNA 的脱氧核 苷酸链,细胞核中含有 DNA,线粒体和叶绿体中也含有少量 DNA,D 错误。
概念检测
拓展提能
解析
11.下列选项中与所示概念图不相吻合的是( )
A.a——核酸、b——DNA、c——脱氧核糖 B.a——糖类、b——二糖、c——五碳糖 C.a——原核生物、b——细菌、c——乳酸菌 D.a——真核生物、b——真菌、c——酵母菌 答案 B
概念检测
拓展提能
答案
解析 核酸包含 DNA,DNA 中含有脱氧核糖,A 不符合题意;糖类包 含二糖,五碳糖不属于二糖,B 符合题意;细菌属于原核生物,乳酸菌是细 菌的一种,C 不符合题意;酵母菌是单细胞真菌,属于真核生物,D 不符合 题意。
2.下列各图中,图形 分别代表磷酸、脱氧核糖和碱基,在制作脱氧
核苷酸模型时,各部件之间需要连接,下列连接中正确的是( )
冲刺2020年高考专题全程突破生物人教版必修第一册课件:第5章 第4节 第二课时 光合作用的原理

答案
解析
9.下图表示光合作用过程,其中Ⅰ、Ⅱ代表光合作用的两个阶段,a、b 表示相关物质,下列说法错误的是( )
A.阶段Ⅰ表示光反应阶段,阶段Ⅱ表示暗反应阶段 B.物质 a 表示 NADPH,物质 c 表示 NADP+,其中作为还原剂的为物 质a C.阶段Ⅰ和Ⅱ都需要酶的参与 D.物质 b 为 ADP,在叶绿体类囊体薄膜上产生 答案 D
答案
解析
6.下列有关光合作用的叙述,正确的是( ) A.绿色植物所有细胞都能进行光合作用 B.光合作用的光反应只在光下进行,暗反应只在黑暗中进行 C.光反应为暗反应提供 NADPH 和 ATP D.光合作用暗反应需要酶,光反应不需要酶
答案 C
解析 绿色植物含有叶绿体的细胞才能进行光合作用,A 错误;光合作 用的光反应需要光,只在白天进行,暗反应不需要光,但需要光反应提供的 物质和能量,B 错误;光合作用的光反应和暗反应都需要酶,D 错误。
解析
知识点二
光合作用的过程
4.光合作用的实质是( )
A.把 CO2 转换成 ATP B.产生化学能储存在有机物中
C.把光能转变成化学能,储存在 ATP 中
D.把无机物转化成有机物,把光能转变成化学能
答案 D 解析 光合作用过程中,利用色素和酶将 CO2 和水转变为(CH2O),把 光能转变为化学能储存在有机物中,D 正确。
解析
12.下图 1 表示光合作用部分过程的图解;图 2 表示改变光照后,与光 合作用有关的 C5 和 C3 在细胞内的变化曲线。据图回答下面的问题:
(1)图 1 中 c 表示的物质是________,它由水在光下分解产生,其作用主 要是____________。
(2)图 1 中 ATP 形成所需的能量最终来自________。①②代表的反应过 程分别是________、________。
2024-2025学年九年级全一册(人教版)19.1家庭电路(专题训练)【五大题型】(原卷版)
19.1 家庭电路(专题训练)【五大题型】【题型1 家庭电路的组成与连接】 (1)【题型2 测电笔的使用】 (4)【题型3 插座的构造与工作方式】 (6)【题型4 火线与零线】 (7)【题型5 家庭电路的故障分析】 (8)【题型1 家庭电路的组成与连接】1.(2023•长沙)某家庭电路的连接如图所示,下列说法正确的是()A.a点所在的电源线是零线B.空气开关只能安装在b点处C.c点所在的导线与大地相连D.L1和L2是串联的2.(2023•凌海市三模)如图所示的家庭电路中,有两个器件连接错误,它们是()A.闸刀开关和带开关的灯泡B.带开关的灯泡和带熔丝的二孔插座C.带开关的灯泡和三孔插座D.闸刀开关和三孔插座3.(2023•安徽三模)关于物理知识,下列判断正确的是()A.甲图中抽油烟机是利用“流体在流速越快的地方压强越大”的原理工作的B.乙图中将锤柄撞击板凳可以使锤头装牢,利用了锤头的惯性C.丙图中螺口节能灯的1接在零线上D.丁图中,若用超导材料代替电饭锅发热盘效果更好4.(2023•泗水县四模)楼道里,夜间楼道灯一直亮着会造成浪费。
其中“光控开关”能在天黑时自动闭合,天亮时自动断开;“声控开关”能在有人走动发出声音时闭合,无人走动时自动断开。
请将如图的“光控开关”、“声控开关”、灯泡用笔画线代替导线正确连入电路,设计出只有在夜间且有声音时灯才亮的楼道灯自动控制电路,同时安装一个不受开关控制的三孔插座。
图中,楼道电路连接符合上述设计及安全用电要求的是()A.B.C.D.5.(2023•高州市二模)家庭电路中电视机和电灯的连接方式是(选填“串联”或“并联”)的,控制电灯的开关应接在(选填“零”或“火”)线上,1度电可供“220V 40W”的灯泡正常工作h。
6.(2023•佛冈县一模)如图所示的家庭电路,三孔插座连接正确,用试电笔接触a孔中的金属片,氖管(选填“会”或“不会”)发光,开关应该接在(选填“①”或“②”)位置。
初中物理专题4:物体的运动

专题四:物体的运动一、考纲要求(分值范围2~4分)1、知道机械运动,能用实例说明机械运动的相对性。
(11年考了1次)2、会根据生活经验粗略估测时间,会用钟表、停表测量时间,会根据生活经验粗略估计测长度,会用刻度尺测量长度,能正确读数。
(11年考了1次)3、能用速度描述物体运动的快慢。
能通过实验测量物体运动的速度。
(11年考了3次)4、能用速度公式进行简单计算,知道匀速直线运动和变速直线运动。
(11年考了4次)5、认识匀速直线运动的路程-时间图像和速度-时间图像。
(11年考了1次)二、中考考点1、宏观物体的运动:自然界一切物体都在运动,物质世界是个运动的世界。
物理学中,把物体位置的变化叫做机械运动(简称运动)。
2、微观世界的运动:(1)物质是由肉眼看不见的微粒分子组成的。
物质里的分子在永不停息的做无规则运动。
例:八月桂花香、墨水滴在清水中一会水变成墨水的颜色等说明:分子在永不停息的做无规则运动,这种现象时扩散现象。
物质有固、液、气三种状态,而物质所处的不同状态与分子的运动情况有关。
(2)分子是由原子组成的。
原子的中心有原子核,其周围有电子在绕着运动。
(3)原子核是由质子和中子构成的,质子和中子都是由夸克构成的。
3、参照物运动和静止的相对性:(1)判断一个物体是否运动和如何运动,事先选择作为参考对比的物体/一个标准物。
这个标准物叫做参照物。
(2)运动和静止的相对性:我们说的运动和静止具有相对性,相对于参照物来说的。
说明:1、参照物必须是具体的物体,而不是抽象的物体,如不能选:天空、地平线、宇宙等。
2、参照物可任意选择,既可以是运动的物体,也可以是静止的物体,但不选研究对象本身。
3、参照物选定后就假定该物体是静止的(不动的)。
4、参照物选择应根据需要和方便来确定。
结论:判断一个物体是运动的还是静止的,以及它的运动情况如何,取决于所选的参照物。
这就是运动和静止的相对性。
如果物体相对于参照物位置没有发生改变,则称这个物体是静止的,反之则为运动的。
【全程复习方略】2014中考英语精练精析 专题综合检测四 人教新目标版

专题综合检测(四)模拟一If someone asks me, “Do you like music? ” I’m sure I will answer him or her, “Of course, I do. ”Because I think music is an important part of our lives.Different people have different ideas about music. For me, I like rock music because i t’s so exciting. And my favorite rock band, the “Fox Ladies” is one of the most famous rock bands in the world. I also like pop music. My classmate, Li Lan, loves dancing music, because she enjoys dancing. My best friend, Jane, likes jazz music. She thinks jazz is really cool.“I like dancing music and rock very much, ” says my brother, “because they are amazing. ”But my mother thinks rock is boring. “I like some relaxing music, ” she says. That’s why she likes country music, I think.1. The writer likes music because she thinks _____.A. it’s an exciting part of our livesB. it’s an amazing part of our livesC. it’s an important part of our lives2. What kind of music does the writer like?A. Rock and pop music.B. Rock and dancing music.C. Jazz and country music.3. Who likes dancing?A. The writer.B. Li Lan.C. Jane.4. The writer’s mother thinks that country music is _______.A. amazingB. boringC. relaxing5. How many people’s ideas about music are talked about in this passage?A. 4.B. 5.C. 6.模拟二1. The world’s population _______.A. will reach 7 billion in the endB. reached 7 billion by the end of 2011C. reached 7 billion before 20112. Which country is the third most populous in the world by 2050?A. China.B. Nigeria.C. The U. S. A. .3. When did the world’s population grow most slowly?A. From 1800 to 1930.B. From 1930 to 1960.C. From 1960 to 1974.4. The population of China and India made up _____ of the world’s population at the end of 2011.A. 19%B. 16. 7%C. 35. 7%5. What’s the Chinese meaning of “billion”?A. 1, 000, 000, 000B. 100, 000, 000C. 10, 000, 000模拟三RIVER DOLPHIN RUNNING OUT OF TIMEThe Yangtze dolphin is the only kind of dolphin that lives in freshwater all its life. Scientists say that the finless freshwater dolphin that has lived in the Yangtze River for over 20 million years, will die out in 15 years. It’s in danger of disappearing forever. Dangers:■Dredging(挖掘) of their habitat■Heavy boat traffic in the Yangtze River■Insecticide(杀虫剂) and mercury(汞)1. How long has the Yangtze dolphin lived in the Yangtze River?A. For 20 million years.B. For less than 20 million years.C. For more than 20 million years.2. What is NOT a danger to the Yangtze dolphin?A. Dredging the river bed or heavy boat traffic in the river.B. Insecticide and mercury.C. Swimmers.3. How heavy is an adult Yangtze dolphin?A. 30 kg.B. 45 kg.C. 30 kg~45 kg.4. What does the Yangtze dolphin mainly eat?A. Fish and shrimps.B. Fish.C. Shrimps.5. In the first paragraph, the underlined word “finless” means _____ in Chinese.A. 有鳍的B. 无鳍的C. 温顺的模拟四任务型阅读理解阅读短文, 根据短文内容回答问题及翻译画线部分的句子。
高三数学 红对勾答案 专题全程检测一

温馨提示:高考题库为Word 版,请按住Ctrl ,滑动鼠标滚轴,调节合适的观看比例,点击右上角的关闭按钮可返回目录。
专题全程检测一时间:120分钟 分值:150分第Ⅰ卷(选择题,共60分)一、选择题(每小题5分,共60分) 1. 已知全集I =R ,若函数f (x )=x 2-3x +2,集合M ={x |f (x )≤0},N ={x |f ′(x )<0},则M ∩∁I N =( )A .[32,2]B .[32,2)C .(32,2]D .(32,2)解析:由f (x )≤0解得1≤x ≤2,故M =[1,2];由f ′(x )<0,得2x -3<0,即x <32,故N =(-∞,32),∁I N =[32,+∞).故M ∩∁I N =[32,2].答案:A2.已知命题p :14≤2x ≤12,命题q :x +1x ∈[-52,-2],则下列说法正确的是( )A .p 是q 的充要条件B .p 是q 的充分不必要条件C .p 是q 的必要不充分条件D .p 是q 的既不充分也不必要条件解析:14≤2x≤12⇒-2≤x ≤-1,即x ∈[-2,-1],而若x +1x ∈[-52,-2],则x ∈[-2,-12].又[-2,-1][-2,-12].∴p 是q 的充分不必要条件. 答案:B 3.⎠⎛241x d x 等于( ) A .-2ln2 B .2ln2 C .-ln2 D .ln2解析:∵⎠⎛241x d x =ln x |42=ln4-ln2=ln22-ln2=2ln2-ln2=ln2.答案:D 4.设偶函数f (x )满足f (x )=x 3-8(x ≥0),则{x |f (x -2)>0}=( ) A .{x |x <-2或x >4} B .{x |x <0或x >4} C .{x |x <0或x >6} D .{x |x <-2或x >2} 答案:B5.设函数f (x )=4sin(2x +1)-x ,则在下列区间中函数f (x )不存在零点的是( )A .[-4,-2]B .[-2,0]C .[0,2]D .[2,4] 答案:A 6.已知二次函数f (x )的图象如图1所示,则其导函数f ′(x )的图象的大致形状是( )图1解析:由函数f (x )的图象知:当x ∈(-∞,1]时,f (x )为减函数,∴f ′(x )≤0;当x ∈[1,+∞)时,f (x )为增函数,∴f ′(x )≥0.结合选项知选C.答案:C图27.已知函数f (x )=ax 3+bx 2+cx +d 的图象如图2所示,且|x 1|<|x 2|,则有( )A .a >0,b >0,c <0,d >0B .a <0,b >0,c <0,d >0C .a <0,b >0,c >0,d >0D .a >0,b <0,c >0,d <0 答案:C8.已知函数f (x )是(-∞,+∞)上的偶函数,若对于x ≥0,都有f (x +2)=f (x ),且当x ∈[0,2)时,f (x )=log 2(x +1),则f (-2010)+f (2011)的值为( )A .-2B .-1C .1D .2解析:f (-2010)+f (2011)=f (2010)+f (2011)=f (0)+f (1)=log 21+log 2(1+1)=1.答案:C9.已知f (x )是定义在(-∞,+∞)上的偶函数,且在(-∞,0]上是增函数.设a =f (ln 13),b =f (log 43),c =f (0.4-1.2),则a ,b ,c 的大小关系是( )A .a >b >cB .b >a >cC .c >a >bD .b >c >a解析:由题意得f (x )在[0,+∞)上是减函数.∵e<3<e 2,∴1<ln3<2.又0<log 43<1,0.4-1.2>0.4-1=2.5>2,∴0<log 43<ln3<0.4-1.2.∴f (0.4-1.2)<f (ln3)<f (log 43),又f (ln 13)=f (-ln3)=f (ln3),∴c <a <b .答案:B10.若不等式组⎩⎪⎨⎪⎧x ≥0,x +2y ≥4,2x +y ≤4.所表示的平面区域被直线y =kx+2分为面积相等的两部分,则k 的值是( )A .1B .2 C.12D .-1 解析:图3画出可行域如图3中的△ABC ,其中A (0,4),B (0,2),C (43,43).由题意可知,当点A 、C 到直线y =kx +2的距离相等时,被分的两部分面积相等.则|0-4+2|1+k 2=|43k -43+2|1+k2解得k =1或k =-2(舍). 答案:A11.若函数y =ax1+x的图象关于直线y =x 对称,则a 为( )A.1 B.-1 C.±1 D.任意实数解析:若函数y=f(x)=ax1+x的图象关于直线y=x对称,则f(x)=f-1(x),易求得f-1(x)=xa-x,故a=-1.答案:B12.若函数f(x)=(x+a)(bx+2a)(a,b∈R)是偶函数,且它的值域为(-∞,4],则该函数的解析式为()A.f(x)=-2x2+4 B.f(x)=-2x2-4C.f(x)=-4x2+4 D.f(x)=-4x2-4解析:∵f(x)=bx2+(2a+ab)x+2a2是偶函数,∴函数f(x)的图象关于y轴对称.∵2a+ab=0,即a(2+b)=0.又∵a≠0(若a=0,则f(x)=bx2的值域不可能是(-∞,4]).∴b=-2.∴f(x)=-2x2+2a2且值域为(-∞,4].∴2a2=4,∴f(x)=-2x2+4.答案:A第Ⅱ卷(非选择题,共90分)二、填空题(每小题5分,共20分)13.已知函数f(x)=ax4+b cos x-x,且f(-3)=7,则f(3)的值为________.解析:设g(x)=ax4+b cos x,则g(x)=g(-x).由f(-3)=g(-3)+3,得g(-3)=f(-3)-3=4,所以g(3)=g(-3)=4,所以f(3)=g(3)-3=4-3=1.答案:114.由曲线y =1x ,x =1,x =2,y =0所围成的封闭图形的面积为________.解析:由已知S =⎠⎛121x d x =ln x |21=ln2-ln1=ln2.答案:ln215.已知函数f (x )=kx 3+3(k -1)x 2-k 2+1(k >0)的单调减区间是(0,4),则k 的值是________.解析:f ′(x )=3kx 2+6(k -1)x∵函数的单调减区间是(0,4),∴f ′(4)=0,∴k =13.答案:1316.给出下列四个结论:①命题“∃x ∈R ,x 2-x >0”的否定是“∀x ∈R ,x 2-x ≤0”; ②“若am 2<bm 2,则a <b ”的逆命题为真; ③函数f (x )=x -sin x (x ∈R)有3个零点;④对于任意实数x ,有f (-x )=-f (x ),g (-x )=g (x ),且x >0时,f ′(x )>0,g ′(x )>0,则x <0时f ′(x )>g ′(x ).其中正确结论的序号是________.(填上所有正确结论的序号)解析:显然①正确;而②的逆命题为“若a <b ,则am 2<bm 2”,当m 2=0时不成立,故②不正确;③中f ′(x )=1-cos x ≥0, ∴f (x )在R 上为单调增函数.∴在R 上有且仅有一个零点,故③不正确;对于④由已知f (x )为奇函数,又在(0,+∞)时f ′(x )>0, ∴f (x )在(0,+∞)上为增函数. ∴在x <0时亦为增函数,∴f ′(x )>0,同理g (x )在(-∞,0)上为减函数,∴x<0时,g′(x)<0,因此f′(x)>g′(x),故④正确.答案:①④三、解答题(写出必要的计算步骤,只写最后结果不得分,共70分)17.设集合A为函数y=ln(-x2-2x+8)的定义域,集合B为函数y=x+1x+1的值域,集合C为不等式(ax-1a)(x+4)≤0的解集.(1)求A∩B;(2)若C⊆∁R A,求a的取值范围.解:(1)由-x2-2x+8>0,解得A=(-4,2),又y=x+1x+1=(x+1)+1x+1-1,所以B=(-∞,-3]∪[1,+∞).所以A∩B=(-4,-3]∪[1,2).(2)因为∁R A=(-∞,-4]∪[2,+∞).由(ax-1a)(x+4)≤0,知a≠0.①当a>0时,由(x-1a2)(x+4)≤0,得C=[-4,1a2],不满足C⊆∁R A;②当a<0时,由(x-1a2)(x+4)≥0,得C=(-∞,-4)∪[1a2,+∞),欲使C⊆∁R A,则1a2≥2,解得-22≤a<0或0<a≤22.又a<0,所以-22≤a<0.综上所述,所求a的取值范围是[-22,0).18.设函数f(x)=log2(a x-b x)且f(1)=1,f(2)=log212.(1)求a、b的值;(2)当x ∈[1,2]时,求f (x )的最大值.解:(1)由已知得⎩⎨⎧log 2(a -b )=1,log 2(a 2-b 2)=log 212.所以⎩⎨⎧a -b =2a 2-b 2=12,解得a =4,b =2.(2)f (x )=log 2(4x-2x)=log 2[(2x-12)2-14],令u (x )=(2x-12)2-14.由复合函数的单调性知u (x )在[1,2]上为增函数,所以u (x )max =(22-12)2-14=12, 所以f (x )的最大值为log 212=2+log 23.19.已知二次函数f (x )=ax 2+x 有最小值,不等式f (x )<0的解集为A .(1)求集合A ;(2)设集合B ={x ||x +4|<a },若集合B 是集合A 的子集,求a 的取值范围.解:(1)∵二次函数f (x )=ax 2+x 有最小值,∴a >0,∴f (x )<0,即ax 2+x <0的解集A =(-1a ,0). (2)化简B 得B =(-a -4,a -4),∵B ⊆A ,∴⎩⎪⎨⎪⎧-1a ≤-a -4≤0,0≥a -4≥-1a,a >0,解得0<a ≤5-2.20.已知某公司生产的品牌服装的年固定成本为10万元,每生产1千件,需另投入1.9万元,设R (x )(单位:万元)为销售收入,根据市场调查,知R (x )=⎩⎪⎨⎪⎧10x -130x 3,0≤x ≤102003,x >10,其中x 是年产量(单位:千件).(1)写出年利润W 关于年产量x 的函数解析式;(2)年产量为多少时,该公司在这一品牌服装的生产中所获年利润最大?解:(1)W =⎩⎪⎨⎪⎧10x -130x 3-1.9x -10,0≤x ≤10,2003-1.9x -10,x >10,即W =⎩⎪⎨⎪⎧-130x 3+8.1x -10,0≤x ≤10-1.9x +1703,x >10(2)设f (x )=-130x 3+8.1x -10,0≤x ≤10,f ′(x )=-110x 2+8.1.由f ′(x )=0,得x =9.∵f (9)=38.6,f (0)=-10,f (10)=1133<38.6.∴当x =9时,f (x )取最大值38.6,又x >10时,-1.9x +1703<1133<38.6,∴当x =9时,W 取最大值38.6.21.已知函数f (x )=x 2+bx +c (b ,c ∈R),对任意的x ∈R ,恒有f ′(x )≤f (x ).(1)证明:当x ≥0时,f (x )≤(x +c )2;(2)若对满足题设条件的任意b ,c ,不等式f (c )-f (b )≤M (c 2-b 2)恒成立,求M 的最小值.解:(1)证明:易知f ′(x )=2x +b .由题设,对任意的x ∈R,2x +b ≤x 2+bx +c ,即x 2+(b -2)x +c -b ≥0恒成立,所以(b -2)2-4(c-b )≤0,从而c ≥b 24+1.于是c ≥1,且c ≥2b 24×1=|b |,因此2c -b =c +(c -b )>0.故当x ≥0时,有(x +c )2-f (x )=(2c -b )x +c (c -1)≥0. 即当x ≥0时,f (x )≤(x +c )2.(2)解:由(1)知,c ≥|b |.当c >|b |时,有M ≥f (c )-f (b )c 2-b2=c 2-b 2+bc -b 2c 2-b 2=c +2bb +c. 令t =bc ,则-1<t <1,c +2b b +c =2-11+t.而函数g (t )=2-11+t(-1<t <1)的值域是(-∞,32).因此,当c >|b |时,M 的取值集合为[32,+∞).当c =|b |时,由(1)知,b =±2,c =2.此时f (c )-f (b )=-8或0,c 2-b 2=0,从而f (c )-f (b )≤32(c 2-b 2)恒成立.综上所述,M 的最小值为32.22.已知函数f (x )=x 2+2a x (a ∈R).(1)若f (x )在点x =1处的切线垂直于直线x -14y +13=0,求该点的切线方程,并求此时函数f (x )的单调区间;(2)若f (x )≤a 2-2a +4对任意的x ∈[1,2]恒成立,求实数a 的取值范围.解:(1)f ′(x )=2x -2ax2,根据题意f ′(1)=2-2a =-14, 解得a =8,此时切点坐标是(1,17), 故所求的切线方程是y -17=-14(x -1),即14x +y -31=0.当a =8时,f ′(x )=2x -16x 2=2(x 3-8)x 2, 令f ′(x )>0,解得x >2,令f ′(x )<0得x <2且x ≠0,故函数f (x )的单调递增区间是(2,+∞);单调递减区间是(-∞,0)和(0,2).(2)f ′(x )=2x -2a x 2=2(x 3-a )x 2, ①若a <1,则f ′(x )>0在区间[1,2]上恒成立,f (x )在区间[1,2]上单调递增,故函数f (x )在区间[1,2]上的最大值为f (2)=4+a ;②若1≤a ≤8,则在区间(1,3a )上f ′(x )<0,函数单调递减,在区间(3a ,2)上f ′(x )>0,函数单调递增,故函数f (x )在区间[1,2]上的最大值为f (1),f (2)中的较大者,f (1)-f (2)=1+2a -4-a =a -3,故当1≤a ≤3时,函数的最大值为f (2)=4+a ,当3<a ≤8时,函数的最大值为f (1)=1+2a ;③当a >8时,f ′(x )<0在区间[1,2]上恒成立,函数f (x )在区间[1,2]上单调递减,函数的最大值为f (1)=1+2a .综上可知,在区间[1,2]上,当a ≤3时,函数f (x )max =4+a ,当a >3时,函数f (x )max =1+2a .不等式f (x )≤a 2-2a +4对任意的x ∈[1,2]恒成立等价于在区间[1,2]上,f (x )max ≤a 2-2a +4,故当a ≤3时,4+a ≤a 2-2a +4,即a 2-3a ≥0,解得a ≤0或a =3;当a >3时,1+2a ≤a 2-2a +4,即a 2-4a +3≥0,解得a >3.综合知当a ≤0或a ≥3时,不等式f (x )≤a 2-2a +4对任意的x ∈[1,2]恒成立.。
高中生物《发酵工程》专题过关检测

高中生物《发酵工程》专题过关检测一、单项选择题1.苏轼的《超然台记》中提到“撷园蔬,取池鱼,酿秫(谷物)酒,瀹(煮)脱粟而食之,曰:‘乐哉游乎!’”下列有关利用秫酿造酒的叙述,正确的是( )A.秫酿造酒前要对酿酒器具和秫进行严格灭菌处理B.秫酿造酒的酿酒酵母的最适生长温度为30~35℃C.秫酿造酒后期密封不严会促进醋酸菌发酵产生醋酸D.秫酿造酒过程中全程要制造无氧环境,以利于酒精发酵答案 C阅读下列材料,完成2~4题。
餐厨垃圾在运输到厌氧消化处理厂之前需要经过收集、储存等过程,通常耗时2~5天,因餐厨垃圾水分和有机物含量丰富、极易腐败、发臭,包括大肠杆菌在内的细菌会大量繁殖,严重影响城市环境以及其资源化利用,研究人员研究了不同保存方式对抑菌效果的影响,具体结果如图所示。
(CFU/mL是每毫升检样所生长出来的细菌菌落总数)。
2.大肠杆菌细胞结构中不具有( )A.细胞核B.核糖体C.细胞壁D.细胞膜答案 A3.为考察不同保存方式的抑菌效果,测定了各组大肠杆菌数量随保存时间的变化,下列叙述错误的是( )A.灭菌+乳酸菌厌氧保存组大肠杆菌数为0B.从抑菌效果看,直接厌氧保存组<乳酸菌厌氧保存组<自然保存组C.加入乳酸菌后厌氧保存对大肠杆菌起到一定的抑制作用,但不如直接厌氧保存组显著D.与自然保存相比,直接厌氧保存可以有效抑制大肠杆菌的生长增殖答案 B4.抑菌实验中接种过程需用到的实验器材不包括( )A B C D答案 A5.原油开采、运输和加工过程中的污染事件给生态环境造成了巨大破坏。
以微生物为主导的生物修复技术是治理原油污染的有效方法。
研究人员从青藏高原班戈桥地区的土壤中分离到一株能利用原油为碳源生长的细菌(BGQ-6),该菌对原油的总降解率为74.14%。
下列说法错误的是( )A.可采用稀释涂布平板法对BGQ-6进行计数B.一般选择菌落数为30~300的平板进行BGQ-6菌落计数C.由单一的BGQ-6繁殖所获得的群体称为BGQ-6纯培养物D.利用添加原油的普通培养基能从被原油污染的土壤中筛选BGQ-6答案 D6.丙草胺(C17H26CINO2)是一种广泛应用的除草剂,能抑制土壤细菌、放线菌和真菌的生长。
新高考数学一轮复习考点知识专题讲解与练习 4 基本不等式

新高考数学一轮复习考点知识专题讲解与练习考点知识总结4基本不等式高考概览高考在本考点的常考题型为选择题、填空题,分值为5分,中等难度考纲研读1.了解基本不等式的证明过程2.会用基本不等式解决简单的最大(小)值问题一、基础小题1.若0<a<12,则a(1-2a)的最大值是()A.18B.14C.12D.1答案 A解析由0<a<12,得1-2a>0,则a(1-2a)=12·2a(1-2a)≤12⎣⎢⎡⎦⎥⎤2a+(1-2a)22=18,当且仅当a=14时取等号.故选A.2.已知m>0,n>0,2m+n=1,则14m+2n的最小值为()A.4 B.22C.92D.16答案 C解析 由于m >0,n >0,2m +n =1,则14m +2n =(2m +n )⎝ ⎛⎭⎪⎫14m +2n =52+n 4m +4m n ≥52+2n 4m ·4m n =92,当且仅当n =23,m =16时取等号.故选C. 3.设x >0,则函数y =x +22x +1-32的最小值为( ) A .0 B .12 C .1 D .32 答案 A解析 由于x >0,则y =x +22x +1-32=⎝ ⎛⎭⎪⎫x +12+1x +12-2≥2⎝ ⎛⎭⎪⎫x +12·1x +12-2=0,当且仅当x +12=1x +12,即x =12时等号成立.所以函数y 的最小值为0.故选A.4.已知a >0,b >0,若不等式2a +1b ≥n2a +b 恒成立,则n 的最大值为( )A .9B .12C .16D .20 答案 A解析 因为a >0,b >0,所以2a +b >0,2a +1b ≥n 2a +b⇒(2a +b )⎝ ⎛⎭⎪⎫2a +1b ≥n ,(2a +b )⎝ ⎛⎭⎪⎫2a +1b =5+2a b +2b a ≥5+22a b ·2b a =9(当且仅当a =b 时,取等号),要想不等式2a +1b≥n2a +b恒成立,只需n ≤9,即n 的最大值为9.故选A. 5.若3x +2y =2,则8x +4y 的最小值为( ) A .4 B .42 C .2 D .2 2解析∵3x+2y=2,∴8x+4y=23x+22y≥223x·22y=223x+2y=4,当且仅当3x=2y,即x=13,y=12时等号成立,∴8x+4y的最小值为4.故选A.6.已知向量a=(1,x-1),b=(y,2),其中x>0,y>0.若a⊥b,则xy的最大值为()A.14B.12C.1 D.2答案 B解析因为a=(1,x-1),b=(y,2),a⊥b,所以a·b=y+2(x-1)=0,即2x+y=2.又因为x>0,y>0,所以2x+y≥22xy,当且仅当x=12,y=1时等号成立,即22xy≤2,所以xy≤12,所以当且仅当x=12,y=1时,xy取到最大值,最大值为12.故选B.7.若a>0,b>0,且1a+1b=ab,则a2+b2的最小值为()A.2 B.22C.4 D.4 2 答案 C解析∵a>0,b>0,∴1a +1b=ab≥21ab,∴ab≥2,当且仅当a=b=2时等号成立,∴a2+b2≥2ab≥4,当且仅当a=b=2时等号成立.综上,a2+b2的最小值为4.故选C.8.已知函数f(x)=cosπx(0<x<2),若a≠b,且f(a)=f(b),则1a+4b的最小值为()A.92B.9 C.18 D.36解析函数f(x)=cosπx(0<x<2)的图象的对称轴为直线x=1.因为a≠b,且f(a)=f(b),所以a+b=2,所以1a +4b=⎝⎛⎭⎪⎫1a+4b(a+b)×12=12⎝⎛⎭⎪⎫5+ba+4ab≥12×⎝⎛⎭⎪⎫5+2ba·4ab=92,当且仅当a=23,b=43时取等号,故1a+4b的最小值为92.故选A.9.(多选)设x∈(0,+∞),y∈(0,+∞),S=x+y,P=xy,以下四个命题中正确的是()A.若P=1,则S有最小值2 B.若S+P=3,则P有最大值1C.若S=2P,则S有最小值4 D.若S+P=3,则S有最大值2答案AB解析对于A,若xy=1,则S=x+y≥2xy=2(当且仅当x=y=1时取等号),故A 正确;对于B,若x+y+xy=3,则3=x+y+xy≥2xy+xy,解得0<xy≤1(当且仅当x=y=1时取等号),故B正确;对于C,若x+y=2xy,则x+y=2xy≤(x+y)22,可得x+y≥2(当且仅当x=y=1时取等号),故C错误;对于D,若x+y+xy=3,则3=x+y+xy≤x+y+(x+y)24,解得x+y≥2(当且仅当x=y=1时取等号),故D错误.10.(多选)下列说法正确的是()A.x+1x(x>0)的最小值是2 B.x2+2x2+2的最小值是 2C.x2+5x2+4的最小值是2 D.2-3x-4x的最大值是2-4 3解析 当x >0时,x +1x ≥2x ·1x =2⎝ ⎛⎭⎪⎫当且仅当x =1x ,即x =1时取等号,A 正确;∵x 2≥0,∴x 2+2x 2+2=x 2+2≥2,B 正确;x 2+5x 2+4=x 2+4+1x 2+4=x 2+4+1x 2+4,令t =x 2+4,则t ∈[2,+∞),∵y =t +1t 在[2,+∞)上单调递增,∴t +1t ≥2+12=52,即x 2+5x 2+4≥52,C 错误;当x <0时,2-3x -4x 无最大值,D 错误.故选AB.11.若正实数x ,y 满足x +2y +2xy -8=0,则x +2y 的最小值为________. 答案 4解析 ∵正实数x ,y 满足x +2y +2xy -8=0,∴x +2y +⎝⎛⎭⎪⎫x +2y 22-8≥0.设x +2y =t >0,∴t +14t 2-8≥0,∴t 2+4t -32≥0,即(t +8)(t -4)≥0,∴t ≥4,即x +2y ≥4,当且仅当x =2,y =1时取等号,故x +2y 的最小值为4.12.正项等比数列{a n }中,存在两项a m ,a n ,使得a m a n =2a 1,且a 6=a 5+2a 4,则m +n =________,1m +9n 的最小值是________.答案 4 4解析 由于数列{a n }是正项等比数列,由a 6=a 5+2a 4得q 2=q +2,解得q =2(负根舍去).由a m a n =2a 1,得2m +n -2=22,m +n =4.故1m +9n =14⎝ ⎛⎭⎪⎫1m +9n (m +n )=14⎝ ⎛⎭⎪⎫1+9+n m +9m n ≥14⎝⎛⎭⎪⎫10+2n m ·9m n =14×(10+6)=4,当且仅当m =1,n =3时,1m +9n取得最小值4.二、高考小题13.(2022·全国乙卷)下列函数中最小值为4的是()A.y=x2+2x+4 B.y=|sin x|+4 |sin x|C.y=2x+22-x D.y=ln x+4 ln x答案 C解析对于A,因为y=x2+2x+4=(x+1)2+3,所以当x=-1时,y取得最小值,且y min=3,所以A不符合题意;对于B,因为y=|sin x|+4|sin x|≥2|sin x|·4|sin x|=4,所以y≥4,当且仅当|sin x|=4|sin x|,即|sin x|=2时取等号,但是根据正弦函数的性质可知|sin x|=2不可能成立,因此可知y>4,所以B不符合题意;对于C,因为y=2x+22-x ≥22x·22-x=4,当且仅当2x=22-x,即x=2-x,x=1时取等号,所以y min=4,所以C符合题意;对于D,当0<x<1时,ln x<0,y=ln x+4ln x<0,所以D不符合题意.14.(2022·浙江高考)已知α,β,γ是互不相同的锐角,则在sin αcos β,sin βcos γ,sin γcos α三个值中,大于12的个数的最大值是()A.0 B.1 C.2 D.3答案 C解析因为α,β,γ是互不相同的锐角,所以sinα,cos β,sin β,cos γ,sin γ,cosα均为正数.由基本不等式可知sin αcos β≤sin2α+cos2β2,sinβcos γ≤sin2β+cos2γ2,sinγcosα≤sin 2γ+cos 2α2.三式相加可得sin αcos β+sin βcos γ+sin γcos α≤32,当且仅当sin α=cos β,sin β=cos γ,sin γ=cos α,即α=β=γ=π4时取等号,因为α,β,γ是互不相同的锐角,所以sin αcos β+sin βcos γ+sin γcos α<32,所以这三个值不会都大于12.若取α=π6,β=π3,γ=π4,则sin π6cos π3=12×12=14<12,sin π3cos π4=32×22=64>24=12,sin π4cos π6=22×32=64>12,所以这三个值中大于12的个数的最大值为2.故选C.15.(2022·上海高考)下列不等式恒成立的是( ) A .a 2+b 2≤2ab B .a 2+b 2≥-2ab C .a +b ≥2|ab | D .a 2+b 2≤-2ab 答案 B解析 显然当a <0,b >0时,不等式a 2+b 2≤2ab 不成立,故A 错误;∵(a +b )2≥0,∴a 2+b 2+2ab ≥0,∴a 2+b 2≥-2ab ,故B 正确;显然当a <0,b <0时,不等式a +b ≥2|ab |不成立,故C 错误;显然当a >0,b >0时,不等式a 2+b 2≤-2ab 不成立,故D 错误.故选B.16.(多选)(2022·新高考Ⅰ卷)已知a >0,b >0,且a +b =1,则( ) A .a 2+b 2≥12 B .2a -b >12 C .log 2a +log 2b ≥-2 D .a +b ≤ 2 答案 ABD解析 对于A ,a 2+b 2=a 2+(1-a )2=2a 2-2a +1=2⎝ ⎛⎭⎪⎫a -122+12≥12,当且仅当a =b =12时,等号成立,故A 正确;对于B ,a -b =2a -1>-1,所以2a -b >2-1=12,故B 正确;对于C ,log 2a +log 2b =log 2ab ≤log 2⎝⎛⎭⎪⎫a +b 22=log 214=-2,当且仅当a =b =12时,等号成立,故C 不正确;对于D ,因为(a +b )2=1+2ab ≤1+a +b =2,所以a +b ≤2,当且仅当a =b =12时,等号成立,故D 正确.故选ABD.17.(2022·天津高考)若a >0,b >0,则1a +ab 2+b 的最小值为________. 答案 2 2解析 ∵a >0,b >0,∴1a +a b 2+b ≥21a ·a b 2+b =2b+b ≥22b ·b =22,当且仅当1a =a b 2且2b =b ,即a =b =2时等号成立,∴1a +ab2+b 的最小值为2 2. 三、模拟小题18.(2022·浙江杭州富阳中学高三上第一次二校联考)已知正实数a ,b 满足1a +9b =6,则(a +1)(b +9)的最小值是( )A .8B .16C .32D .36 答案 B解析 因为正实数a ,b 满足1a +9b =6,所以6=1a +9b ≥29ab ,即ab ≥1,当且仅当1a =9b 时,即a =13,b =3时取等号.因为1a +9b =6,所以b +9a =6ab ,所以(a +1)(b +9)=9a +b +ab +9=7ab +9≥7+9=16.故(a +1)(b +9)的最小值是16.故选B.19.(2022·湖北新高考联考协作体高三上新起点考试)已知a >0,b >0且a +b =1,若不等式1a +1b >m 恒成立,m ∈N *,则m 的最大值为( )A .3B .4C .5D .6 答案 A解析 ∵不等式1a +1b >m 恒成立,∴⎝ ⎛⎭⎪⎫1a +1b min >m ,又a +b =1,a >0,b >0∴1a +1b =⎝ ⎛⎭⎪⎫1a +1b (a +b )=1+b a +a b +1≥2+2b a ·a b =4,当且仅当a =b =12时等号成立,∴⎝ ⎛⎭⎪⎫1a +1b min=4,∴m <4,又m ∈N *,∴m =3.故选A.20.(2022·河北省“五个一”名校联盟高三第一次联考)已知x >0,y >0,且x +4y -xy =0,若不等式a ≤x +y 恒成立,则a 的取值范围是( )A .(-∞,6]B .(-∞,7]C .(-∞,8]D .(-∞,9] 答案 D解析 ∵x >0,y >0,x +4y -xy =0,∴4x +1y =1,∴x +y =(x +y )⎝ ⎛⎭⎪⎫4x +1y =5+x y +4y x .∵x y+4yx≥2x y ·4y x =4(当且仅当x y =4yx,即x =2y =6时取等号),∴x +y ≥5+4=9.又不等式a ≤x +y 恒成立,∴a ≤9.21.(2022·辽宁六校高三上学期期初联考)已知定义在R 上的偶函数f (x )=|x -m +1|-2,若正实数a ,b 满足f (a )+f (2b )=m ,则2a +3b 的最小值为( )A .85B .8+435 C .835D .2105 答案 B解析 ∵f (x )为R 上的偶函数,∴f (-x )=f (x ),即|-x -m +1|-2=|x -m +1|-2,即(-x -m +1)2=(x -m +1)2,整理得2(m -1)x =-2(m -1)x ,∴m =1,∴f (x )=|x |-2.∴f (a )+f (2b )=a -2+2b -2=1,即a +2b =5.∴2a +3b =15⎝ ⎛⎭⎪⎫2a +3b (a +2b )=15⎝ ⎛⎭⎪⎫8+4b a +3a b ≥15⎝ ⎛⎭⎪⎫8+24b a ·3a b =8+435(当且仅当4b a =3a b ,即2b =3a 时取等号),∴2a +3b 的最小值为8+435.故选B.22.(多选)(2022·湖南省长沙市长郡中学上学期适应性调查考试)小王从甲地到乙地往返的速度分别为a 和b (a <b ),其全程的平均速度为v ,则( )A .a <v < abB .v =abC .ab <v <a +b 2D .v =2ab a +b答案 AD解析 设甲、乙两地之间的距离为s ,则全程所需的时间为s a +s b ,∴v =2ss a +s b =2ab a +b .∵b >a >0,∴v =2ab a +b <2ab 2ab =ab ;另一方面,v =2ab a +b <2⎝⎛⎭⎪⎫a +b 22a +b=a +b 2,v -a =2ab a +b -a =ab -a 2a +b >a 2-a 2a +b=0,∴v >a ,则a <v <ab .故选AD. 23.(多选)(2022·河北石家庄第一中学高三上教学质量检测(一))以下结论正确的是( )A .x 2+1x 2≥2B .x 2+3+1x 2+3的最小值为2 C .若a 2+2b 2=1,则1a 2+1b 2≥3+2 2 D .若a +b =1,则1a +1b≥4 答案 AC解析 对于A ,x 2+1x 2≥2x 2·1x 2=2,当且仅当x 2=1时等号成立,故A 正确;对于B ,x 2+3+1x 2+3≥2x 2+3·1x 2+3=2,当且仅当x 2+3=1时等号成立,但x 2+3≥3≠1,故B 错误;对于C ,1a 2+1b 2=⎝ ⎛⎭⎪⎫1a 2+1b 2·(a 2+2b 2)=3+2b 2a 2+a 2b 2≥3+22,当且仅当a 2=2-1,b 2=2-22时等号成立,故C 正确;对于D ,当a >0,b >0,a +b =1时,1a +1b =⎝ ⎛⎭⎪⎫1a +1b (a +b )=2+a b +b a ≥4,但当a +b =1时,不一定有a >0,b >0,故D 错误.故选AC.24.(多选)(2022·辽宁葫芦岛协作校高三上第一次考试)下列函数中,最小值为9的是( )A .y =⎝ ⎛⎭⎪⎫x +1x ⎝ ⎛⎭⎪⎫x +4x B .y =1sin 2x +4cos 2xC .y =lg x +4lg x -5D .y =(2x 2+1)(4x 2+8)(x 2+1)2答案 AB解析 y =⎝ ⎛⎭⎪⎫x +1x ⎝ ⎛⎭⎪⎫x +4x =5+x 2+4x 2≥5+24=9,当且仅当x 2=2时,等号成立.y =1sin 2x +4cos 2x =⎝ ⎛⎭⎪⎫1sin 2x +4cos 2x (sin 2x +cos 2x )=5+cos 2x sin 2x +4sin 2x cos 2x ≥5+24=9,当且仅当tan 2x =12时,等号成立.当lg x -5小于0时,y =lg x +4lg x -5无最小值.y =(2x 2+1)(4x 2+8)(x 2+1)2=4(2x 2+1)(x 2+2)(x 2+1)2≤4×⎣⎢⎡⎦⎥⎤(2x 2+1)+(x 2+2)22(x 2+1)2=9,当且仅当x 2=1时,等号成立,则y =(2x 2+1)(4x 2+8)(x 2+1)2的最大值为9.故选AB. 25.(2022·福建晋江磁灶中学高三上阶段测试(一))若lg x +lg y =0,则4x +9y 的最小值为________.答案 12解析 因为lg x +lg y =0,所以xy =1(x >0,y >0),所以4x +9y ≥24x ·9y =12.等号成立的条件为4x =9y ,即x =32,y =23时取得最小值.26.(2022·河北正定中学高三开学考试)已知x ,y >0,且1x +3+1y =12,则x +y 的最小值为________.答案 5解析x +y =2[(x +3)+y ]⎝ ⎛⎭⎪⎫1x +3+1y -3=2⎝ ⎛⎭⎪⎫2+y x +3+x +3y -3≥2⎝ ⎛⎭⎪⎫2+2y x +3·x +3y -3=5,当且仅当y x +3=x +3y ,即x =1,y =4时,等号成立,所以x +y 的最小值为5.一、高考大题1.(2022·全国Ⅲ卷)设a ,b ,c ∈R ,a +b +c =0,abc =1.(1)证明:ab +bc +ca <0;(2)用max{a ,b ,c }表示a ,b ,c 中的最大值,证明:max{a ,b ,c }≥34.证明 (1)∵(a +b +c )2=a 2+b 2+c 2+2ab +2ac +2bc =0,∴ab +bc +ca =-12(a 2+b 2+c 2). 由abc =1得a ,b ,c 均不为0,则a 2+b 2+c 2>0,∴ab +bc +ca =-12(a 2+b 2+c 2)<0.(2)不妨设max{a ,b ,c }=a ,由a +b +c =0,abc =1可知,a >0,b <0,c <0.∵a =-b -c ,a =1bc ,∴a 3=a 2·a =(b +c )2bc =b 2+c 2+2bc bc≥2bc +2bc bc =4. 当且仅当b =c 时,取等号,∴a≥34,即max{a,b,c}≥34.2.(2022·全国Ⅰ卷)已知a,b,c为正数,且满足abc=1.证明:(1)1a +1b+1c≤a2+b2+c2;(2)(a+b)3+(b+c)3+(c+a)3≥24.证明(1)因为a2+b2≥2ab,b2+c2≥2bc,c2+a2≥2ac,又abc=1,故有a2+b2+c2≥ab+bc+ca=ab+bc+caabc =1a+1b+1c.当且仅当a=b=c=1时,等号成立.所以1a +1b+1c≤a2+b2+c2.(2)因为a,b,c为正数且abc=1,故有(a+b)3+(b+c)3+(c+a)3≥33(a+b)3(b+c)3(c+a)3=3(a+b)(b+c)(c+a)≥3×(2ab)×(2bc)×(2ca)=24.当且仅当a=b=c=1时,等号成立.所以(a+b)3+(b+c)3+(c+a)3≥24.二、模拟大题3.(2022·福建龙岩高三检测)已知x,y∈(0,+∞),x2+y2=x+y.(1)求1x +1y 的最小值;(2)是否存在x ,y 满足(x +1)(y +1)=5?并说明理由.解 (1)因为1x +1y =x +y xy =x 2+y 2xy ≥2xy xy =2,当且仅当x =y =1时,等号成立,所以1x+1y 的最小值为2.(2)不存在.理由如下:因为x 2+y 2≥2xy ,所以(x +y )2≤2(x 2+y 2)=2(x +y ).又x ,y ∈(0,+∞),所以0<x +y ≤2.从而有(x +1)(y +1)≤⎣⎢⎡⎦⎥⎤(x +1)+(y +1)22≤4,当且仅当x =y =1时,等号成立. 因此不存在x ,y 满足(x +1)(y +1)=5.4.(2022·广东省珠海市高三模拟)某商场预计全年分批购入电视机3600台,其中每台价值2000元,每批购入的台数相同,且每批均需付运费400元,储存购入的电视机全年所付保管费与每批购入的电视机的总价值(不含运费)成正比,比例系数为k ,若每批购入400台,则全年需要支付运费和保管费共43600元.(1)求k 的值;(2)请问如何安排每批进货的数量,使支付运费与保管费的和最少?并求出相应的最少费用.解 (1)由题意,当每批购入400台时,全年的运费为400×3600400=3600(元),每批购入的电视机的总价值为400×2000=800000(元),所以保管费为k·800000(元).因为全年需要支付运费和保管费共43600元,所以3600+k·800000=43600,解得k=0.05.(2)设每批进货x台,则运费为400×3600x =1440000x,保管费为0.05×2000x=100x.所以支付运费与保管费的和为1440000x+100x,因为1440000x +100x≥21440000x×100x=24000,当且仅当1440000x=100x,即x=120时取到等号,所以每批进货120台,支付运费与保管费的和最少,最少费用为24000元.5.(2022·江苏镇江模拟)某校为丰富师生课余活动,计划在一块直角三角形ABC的空地上修建一个占地面积为S(平方米)的矩形AMPN健身场地.如图,点M在AC上,点N在AB上,且点P在斜边BC上.已知∠ACB=60°,|AC|=30米,|AM|=x米,x∈[10,20].设矩形AMPN健身场地每平方米的造价为37kS元,再把矩形AMPN以外(阴影部分)铺上草坪,每平方米的造价为12kS元(k为正常数).(1)试用x 表示S ,并求S 的取值范围;(2)写出总造价T 与面积S 的函数关系式;(3)如何选取|AM |,才能使总造价T 最低(不要求求出最低造价)?解 (1)在Rt △PMC 中,显然|MC |=30-x ,∠PCM =60°,|PM |=|MC |tan ∠PCM =3(30-x ),∴矩形AMPN 的面积S =|PM |·|AM |=3x (30-x ),x ∈[10,20],由x (30-x )≤⎝ ⎛⎭⎪⎫x +30-x 22=225, 可知当x =15时,S 取得最大值,为2253,当x =10或20时,S 取得最小值,为2003,∴2003≤S ≤2253,即S 的取值范围为[2003,2253].(2)矩形AMPN 健身场地造价T 1=37k S ,又△ABC 的面积为12×30×303=4503,∴草坪造价T 2=12k S(4503-S ). ∴总造价T =T 1+T 2=25k ⎝⎛⎭⎪⎫S +2163S , 2003≤S ≤225 3.(3)∵S +2163S≥1263,当且仅当S=2163,S即S=2163时等号成立,此时3x(30-x)=2163,解得x=12或x=18.∴选取|AM|为12米或18米时,能使总造价T最低.。
复习二轮复习高考命题热点九核酸检测抗体检测抗原检测课件(25张)

专题八 实验与探究
心法,其原理如下图。样品孔处滴加鼻拭子提取液,结合垫处含有足量的、 可移动的、与胶体金结合的抗体1,T处固定有抗体2,抗体1和抗体2与新型冠 状病毒表面同一抗原N蛋白的不同位点发生特异性结合,呈红色。C处固定有 抗体1的抗体,与抗体1结合也呈红色。
检测过程中反复进行了抗原—抗体的特异性结合,若检测结果为阳性,则过 程中此特异性结合共发生________次。若待测样本中不含新型冠状病毒,显 色结果为______________,结果为阴性。
专题八 实验与探究
3.抗原检测 抗原检测可直接检测出人体样本中是否含有新型冠状病毒,诊断快速、准确、 对设备和人员要求低,采用双抗夹心法,使用两种抗原特异性抗体去识别和 结合一个靶点抗原的不同表位,则可以大大降低交叉反应的几率,从而有效 提高其特异性。
专题八 实验与探究
(2022·广东卷)迄今新型冠状病毒仍在肆虐全球,我国始终坚持“人民至上, 生命至上”的抗疫理念和动态清零的防疫总方针。图a是免疫力正常的人感染 新型冠状病毒后,体内病毒及免疫指标的变化趋势。
专题八 实验与探究
1.(2022·广东模拟预测)为快速检测新型冠状病毒感染者,在病毒核酸检测和 抗体检测的基础上,国家又推出新型冠状病毒抗原检测试剂。如图为某人感 染新型冠状病毒后病毒的RNA及抗原蛋白(N蛋白和S蛋白)、两种抗体在患者 体内随时间变化的曲线图。下列相关分析错误的是( )
专题八 实验与探究
专题八 实验与探究
(3)接种新型冠状病毒疫苗能大幅降低重症和死亡风险。图b显示一些志愿受试 者完成接种后,体内产生的抗体对各种新型冠状病毒毒株中和作用的情况。 据图分析,当前能为个体提供更有效保护作用的疫苗接种措施是_________。 解析:(1)分析图a曲线可知,人体感染新型冠状病毒初期,曲线①②上升,说 明病毒在其体内快速增殖,但抗体还未产生,说明此时特异性免疫尚未被激 活。体液免疫中,大多数病原体经过吞噬细胞等的摄取和处理,暴露病原体 所特有的抗原,将抗原传递给T细胞,刺激T细胞产生淋巴因子。少数抗原直 接刺激B细胞。B细胞受到刺激后,在淋巴因子的的作用下开始一系列的增殖、 分化,大部分分化为浆细胞,产生抗体,小部分分化成记忆细胞。故抗体的 产生与T细胞的数量的增加有一定相关性,即曲线③④上升趋势一致。T细胞
初四语文模拟试题(4)

4.下列文学文化常识说法不正确的一项是(2分)()A.《世说新语》是南朝宋临川王刘义庆组织编写的一部志人小说。
B.《论语》十二章是儒家经典著作,与《大学》《中庸》《孟子》合称“四书”。
C.关于百姓的称谓,常见的有:布衣、黔首、黎民、生民、苍生、黎元、氓等。
D.冬雪雪冬小大寒”中,前一个“冬”指的是冬至,后一个“冬”指的是立冬。
5.下列句子排序正确的一项是(2分)()①百般不得排解情思,不妨往诗文中寻个消遣处。
②王维的乡思亦有画意:来日绮窗前,寒梅著花未?③从古至今,乡愁是诗人的惆怅。
④没有什么像乡愁一样令我忧伤,这么美丽的文字,这么伤感的文字只有诗人才能表达。
⑤诗云:今夜月明人尽望,不知秋思落谁家。
A.①③④⑤②B.③⑤①②④C.③①⑤②④D.⑤①③④②6.诗词默写及赏析(一)文海拾贝,补充填空。
(每空1分,共8分)①潮平两岸阔,。
(王湾《次北固山下》)②,洪波涌起。
(曹操《观沧海》)③夜发清溪向三峡,。
(李白《峨眉山月歌》)④,我言秋日胜春朝。
(刘禹锡《秋词》(其一))⑤《闻王昌龄左迁龙标遥有此寄》中写出明月送去了李白对远方朋友的担忧和牵挂的是: , 。
⑥某同学学习只知道死记硬背,却不爱动脑筋,请你用《论语》中的一句来劝诫他:,。
(二)古诗词曲,精粹赏析。
(4分)【甲】天净沙·秋思【乙】秋词(其一)枯藤老树昏鸦,自古逢秋悲寂寥,小桥流水人家,我言秋日胜春朝。
古道西风瘦马。
晴空一鹤排云上,夕阳西下,便引诗情到碧霄。
断肠人在天涯。
①从表达方式上来看,【甲】【乙】两文有何不同?(2分)②同是写秋,两首诗表露出诗人的心境有何不同?(2分)7.名著阅读(4分)①(1)《五猖会》是《朝花夕拾》中的一篇回忆性散文,其主要内容是什么?(1分)(2)《藤野先生》中哪些事件让鲁迅产生了“弃医从文”的想法?(1分)②(1)《西游记》中猪八戒、沙和尚分别使用的是什么兵器?(1分)(2)成为唐僧师徒取经路上最大障碍是哪一家族刁难?刁难分别是什么?(1分)二、口语交际及综合性学习(第8—10题,共5分)网络改变着我们的生活。
安全生产五同时制度模版(四篇)

安全生产五同时制度模版一、安全文明施工:1. 所有施工人员必须穿戴符合要求的安全防护用品,并严禁穿拖鞋、高跟鞋等不安全的鞋类。
2. 施工现场必须保持整洁干净,禁止乱扔垃圾,保持施工区域的通道畅通。
3. 严禁在施工现场吸烟或者使用明火,禁止私拉乱接电线。
4. 所有施工人员必须接受安全教育培训,了解和掌握相关的安全操作规程和应急预案。
二、生产设备安全:1. 所有生产设备必须经过检验合格,使用前必须进行安全检查,并定期对设备进行维护和保养。
2. 所有使用设备的人员必须经过操作培训,了解设备的使用方法以及相关的安全注意事项,并严格按照规定的操作流程进行操作。
3. 发现设备存在故障或者安全隐患的,应立即上报,并进行相应的维修或停机处理。
三、安全生产监管:1. 安全生产责任人对施工现场的安全生产负有直接责任,必须保证施工现场的安全。
2. 安全生产监管人员必须定期对施工现场进行安全检查,发现安全隐患必须及时整改。
3. 发生重大安全事故或者事故隐患的,必须立即上报,并按照相关法律法规进行处理。
四、应急预案:1. 安全生产责任人必须制定完善的应急预案,并组织演练,以确保在发生紧急情况时能够迅速、有效地处理。
2. 所有施工人员必须了解并掌握应急预案,知道如何正确使用灭火器材和应对紧急情况。
五、安全培训:1. 所有施工人员必须经过安全教育培训,并持有合格的安全证书。
2. 定期组织安全培训,提高施工人员的安全意识和实践能力。
3. 对新进人员进行必要的安全培训,确保其具备安全操作的能力。
安全生产五同时制度模版(二)(共____字)第一章总则第一条为了加强安全生产管理,预防和减少事故的发生,保障员工的生命财产安全,提高企业的综合安全管理水平,根据《中华人民共和国安全生产法》等有关法律、法规,制定本制度。
第二条本制度适用于所有在本单位工作的全体人员和与本单位有业务往来的合作单位。
第三条五同时制度要求在生产经营活动中,保证生产、施工、作业、流程的五个同时性,即:生产、施工、作业、流程同时进行必须配套出现,各项安全措施同时实施,备有应急救援措施,不得有缺失。
人教版初中物理2020中考复习专题《机械运动》专题检测(含答案)

《机械运动》专题检测一、单选题1.如图,公园围墙外的小路形成一个规则的正方形,甲乙两人分别从两个对角处同时出发沿逆时针方向紧贴围墙绕公园匀速行走.已知甲绕围墙行走一圈需要48分钟,乙绕围墙行走一圈需要68分钟.从甲第一次看见乙开始计时,到甲又看不见乙时,所经历的时间为A.4分钟B.3分钟C.2分钟D.1分钟2.下列关于运动和静止的说法正确的是()A.人在上升的电梯中,以地面为参照物,人是静止的B.月亮在云中穿行时,以云为参照物,月亮是运动的C.飞机在空中加油时,以地面为参照物,受油机是静止的D.漂流而下的小船,以河岸为参照物,小船是静止的3.下列对身边一些常见的物理量进行估测,以下估测数据,不符合实际的是()A.教室里的黑板长约4mB.中学生的脉搏跳动一般每分钟约75次左右C.在学校运动会的百米赛跑中,获冠军的运动员平均速度可达15 m/sD.一位中学生身高约1.6m4.在龟兔赛跑的某一过程中,乌龟与兔子通过路程之比为1∶16,运动所花时间之比是8∶l ,则乌龟和兔子运动的平均速度之比为()A.8∶l B.1∶2C.1∶16D.1∶1285.如图所示,在下面运动中,可以看作匀速直线运动的是()A.沿笔直铁轨上匀速行驶的磁悬浮列车B.踢到空中的足球C . 人造地球卫星D . 过山车6.教室的课桌的高度最接近于( )A .870cmB .87dmC .0.87mD .87m7.在国际单位制中,速度的单位是A .米(m )B .千米/小时(km/h )C .米/秒(m/s )D .秒(s )8.小军同学利用课上实验装置(如图所示)采用下列四种方法测定小车沿斜面下滑时的平均速度,其中你认为最好的是( )A .先选定一段较长的路程,测定小车通过这段路程所用的时间B .先选定一段较短的路程,测定小车通过这段路程所用的时间C .先选定一段较长的时间,测定小车在这段时间内通过的路程D .先选定一段较短的时间,测定小车在这段时间内通过的路程9.下列数据最接近实际情况的是( )A .教室里课桌的高度大约是80cmB .唱一遍中华人民共和国国歌的时间大约是5minC .夏天,教室内的温度大约是48℃D .人步行的速度大约为10m/s10.长度的基本单位是: ( )A .千米B .米C .厘米D .纳米二、多选题11.如图所示,小船从码头A 出发渡河,船头始终垂直河岸.若河宽为d ,v 船恒定不变,河水的流速与到河岸的垂直距离x 成正比,即水速u kx =(2d x ≤,k 为常量).渡河过程中小船沿岸向下游移动了距离s 并最终到达对岸码头B ,则A.24kdvs=船B.22kdvs=船C.渡河时间t为2skdD.渡河时间t为4skd12.你一定听说过《龟兔赛跑》的寓言故事吧?乌龟和兔子同时从起点跑出,兔子在远远超过乌龟后,便骄傲地睡大觉.当它睡醒后才发现:乌龟已经爬到了终点.关于这个赛跑过程,下列说法正确的是A.兔子睡觉前比乌龟跑得快B.只有选地面为参照物,才能说乌龟是运动的C.免子在睡觉时肯定是静止的D.乌龟全程的平均速度比兔子的平均速度大13.下列各种说法中的有关数据,与实际基本相符的是A.济南近年来冬天最冷时的气温可达B.空气中光的传播速度大约是C.课堂上大约用的力就能拿起物理课本D.触电时电流超过就会有生命危险14.用弹簧测力计分别拉着甲、乙两物体竖直向上运动,两次运动的路程随时间变化的图像如图所示,已知甲的重力大于乙的重力.则下列说法正确的是A.甲的速度大于乙的速度B.弹簧测力计对甲的拉力大于弹簧测力计对乙的拉力C.甲物体的动能转化为它的重力势能D.甲的机械能一定大于乙的机械能15.下列关于运动的说法正确的是A.以公路旁的树木为参照物,坐在行驶的客车里的乘客是运动的B.包括地球在内的太阳系八大行星都在不停地围绕太阳运动C.地球同步卫星围绕地球飞行时,以地面为参照物,卫星是运动的D.飞机在空中加油时,以地面为参照物,受油机是静止的三、实验题16.某同学用刻度尺测量一物体的长度,方法如图所示,请指出他在测量中存在的三个错误:①:②:③:.17.在学校操场进行测量正常行走的平均速度的学生实验中,需要的测量器材有________和________,还有用以发令的小红旗.每个实验组至少个人,活动过程如下:在操场上,测出的路程,每隔做一记号.选出三位同学做计时员,分别站在、、处.选一名发令员,以小红旗的下落表示________.选手采取正常步行完成路程.请在下面空白处设计记录此次测量步行平均速度数据的表格_______________.四、计算题18.根据如表所示的列车时刻表,计算该次列车从北京南站到上海虹桥站运行的平均速度,以及从曲阜东站到常州北站运行的平均速度.某次列车的时刻表站次站名到达时间开车时间里程/km1 北京南---- 7:00 02 济南西8:32 8:34 4063 曲阜东9:06 9:08 5334 枣庄9:31 9:33 6275 南京南11:01 11:03 10236 常州北11:35 11:37 11537 无锡东11:54 11:55 12108 上海虹桥12:23 ---- 131819.一天小明上学出门后,以1m/s的速度走了360m,感觉时间不够,为了不迟到,他立刻又以1.5m/s的速度走了4min到了学校.求他家离学校有多远?他上学走路的平均速度是多少?五、作图题20.图甲为一个物体运动的路程-时间图象,图乙中已画出该物体AB段及BC段的速度-时间图象,请你在图乙中画出该物体OA段的速度-时间图象(要求保留必要的作图痕迹)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
温馨提示:高考题库为Word 版,请按住Ctrl ,滑动鼠标滚轴,调节合适的观看比例,点击右上角的关闭按钮可返回目录。
专题全程检测四 时间:120分钟 分值:150分 第Ⅰ卷(选择题,共60分)一、选择题(每小题5分,共60分)1.已知一个四棱锥的高为3,其底面用斜二测画法所画出的水平放置的直观图是一个边长为1的正方形,则此四棱锥的体积为( )A.2 B .6 2 C.13 D .2 2 解析:由斜二测画法得到四棱锥底面ABCD 是底面边长为1,高为22的平行四边形,∴V =13×22×1×3=2 2.图1答案:D2.如图2是一个几何体的三视图,其侧(左)视图是等腰直角三角形,则该几何体的表面积为( )图2A .2+6 2B .4+4 2C .6+4 2D .14 解析:图3由三视图可知,该几何体是有一个侧面与水平面平行,底面为等腰直角三角形的直三棱柱(如图3),AB =2,AD =2,AC =BC ,AC ⊥BC ,所以AC =BC =2,则该几何体的一个底面面积S 1=12×2×2=1,侧面积S 2=(2+2+2)×2=4+4 2. 故该几何体的表面积S =2S 1+S 2=6+4 2. 答案:C3.设a ,b ,c 是空间不重合的三条直线,α,β是空间两个不同的平面,则下列命题中,逆命题不成立的是( )A .当c ⊥α时,若c ⊥β,则α∥βB .当b ⊂α时,若b ⊥β,则α⊥βC .当b ⊂α,且c 是a 在α内的射影时,若b ⊥c ,则a ⊥bD .当b ⊂α,且c ⊄α时,若c ∥α,则b ∥c解析:当α⊥β,平面α内的直线不一定垂直于平面β,故B 逆命题不成立.答案:B4.下面四个命题:①“直线a ∥直线b ”的充要条件是“a 平行于b 所在的平面”; ②“直线l ⊥平面α内所有直线”的充要条件是“l ⊥平面α”; ③“直线a 、b 为异面直线”的充分不必要条件是“直线a 、b 不相交”;④“平面α∥平面β”的必要不充分条件是“α内存在不共线的三点到β的距离相等”;其中正确命题的序号是( ) A .①② B .②③ C .③④ D .②④ 解析:对于①,“直线a ∥直线b ”是“a 平行于b 所在的平面”的不充分不必要条件,则①不正确,排除A ;对于②,“直线l ⊥平面α内所有直线”的充要条件是“l ⊥平面α”,显然它是正确的,排除C ;对于③,“直线a 、b 为异面直线”的充分不必要条件是“直线a 、b 不相交”,显然它不正确,排除B.综上所述,故选D.答案:D5.把由曲线y =|x |和y =2围成的图形绕x 轴旋转360°,所得旋转体的体积为( )A.8π3B.10π3C.6π3D.32π3 解析:图4由题意,y =|x |和y =2围成图中阴影部分的图形,旋转体为一个圆柱挖去两个相同的共顶点的圆锥.∵V 圆柱=π·22·4=16π,2V 圆锥=2×13π×22×2=16π3,∴所求几何体体积为16π-16π3=32π3.答案:D6.已知直线m ,n 及平面α,其中m ∥n ,那么在平面α内到两条直线m ,n 距离相等的点的集合可能是①一条直线;②一个平面;③一个点;④空集.其中正确的是( )A .①②③B .①④C .①②④D .②④解析:当m ,n 都在α内时,是一条直线. 当m ,n 分别在α的两侧都平行于α且到α的距离相等时,是一个平面.当m ,n 都平行于α,但到α的距离不相等时,是空集,任何时候都不可能只有一个点满足条件.答案:C图57.如图5,在正方体ABCD—A1B1C1D1中,O是底面正方形ABCD 的中心,M是D1D的中点,N是A1B1上的动点,则直线NO、AM 的位置关系是()A.平行B.相交C.异面垂直D.异面不垂直解析:易证ON在平面A1ADD1上的射影与AM垂直,进而可证得ON⊥AM.答案:C8.设a,b为两条直线,α,β为两个平面,下列四个命题中,正确的命题是()A.若a,b与α所成的角相等,则a∥bB.若a∥α,b∥β,α∥β,则a∥bC.若a⊂α,b⊂β,a∥b,则α∥βD.若a⊥b,a⊥α,b⊄α,则b∥α解析:图6对于选项A,要注意直线a,b的方向相同时才平行;对于选项B,可用长方体验证.如图6,设A1B1为a,平面AC为α,BC为b,平面A1C1为β,显然有a∥α,b∥β,α∥β,但得不到a∥b;对于选项C,可设A1B1为a,平面AB1为α,CD为b,平面AC为β,满足选项C的条件却得不到α∥β,故C不正确;对于选项D,可验证是正确的.答案:D图79.某空间几何体的三视图如图7所示,其正(主)视图与侧(左)视图都是边长为2的正三角形,俯视图的轮廓为正方形,则此空间几何体的体积是( )A.433B.423C.233D.223解析:由三视图可知此空间几何体为正四棱锥,其底面是边长为2的正方形,高为3,所以此空间几何体的体积V =13×2×2×3=433. 答案:A图810.如图8,正四面体ABCD 的顶点A 、B 、C 分别在两两垂直的三条射线Ox ,Oy ,Oz 上,则下列命题中错误的为( )A .O —ABC 是正三棱锥B .直线OB ∥平面ACDC .直线AD 与OB 所成的角是45° D .二面角D —OB —A 为45°解析:如图9,将图形补成正方体,可观察出A 、C 、D 为正确命题,可判断出OB 与平面ACD 相交,因此B 为错误命题.图9答案:B图1011.如图10,三棱锥P —ABC 中,底面三角形ABC 是边长为2的正三角形,PA ⊥底面ABC ,且PA =2,则此三棱锥外接球的半径为( )A. 2B. 5 C .2 D.213解析:如图11,设三棱锥P —ABC 的底面所在小圆半径为r .图11则r =|AO 1|=23×32×2=233,设球半径为R ,球心为O ,易知|OO 1|=12|AP |=1,在Rt △OAO 1中,由勾股定理知: R =|OA |=|OO 1|2+|AO 1|2=1+(233)2=213.答案:D图1212.如图12,已知六棱锥P—ABCDEF的底面是正六边形,PA⊥平面ABC,PA=2AB,则下列结论正确的是()A.PB⊥ADB.平面PAB⊥平面PBCC.直线BC∥平面PAED.直线PD与平面ABC所成的角为45°解析:由题意知,BD⊥AB,BD⊥PA,又AB∩PA=A,∴BD⊥面PAB.∴BD⊥PB,面PBD⊥面PAB.故A,B均不对.又BC∥AD,∴BC∥面PAD,C也不正确.∵PA=2AB=AD,而PA⊥AD,∴∠PDA=45°,即PD与平面ABC所成的角为45°.答案:D第Ⅱ卷(非选择题,共90分)二、填空题(每小题5分,共20分)13.如图13是一个几何体的三视图,则这个几何体的体积是________.图13解析:由三视图可知,该几何体由一个正四棱锥和一个正方体组成,∴V 几何体=V 四棱锥+V 正方体 =13×32×1+33=3+27=30. 答案:3014.一个几何体的三视图如图14所示,则这个几何体的体积为________.图14解析:该空间几何体是一个底面为梯形的四棱柱,其底面积是1+22×2=3,高为1,故其体积等于3. 答案:3图1515.如图15所示,在直三棱柱ABC —A 1B 1C 1中,底面是∠ABC为直角的等腰直角三角形,AC =2a ,BB 1=3a ,D 是A 1C 1的中点,点F 在线段AA 1上,当AF =________时,CF ⊥平面B 1DF .解析:由直三棱柱及D 是A 1C 1的中点,得B 1D ⊥平面AC 1,而CF ⊂平面AC 1,∴B 1D ⊥CF ,故若CF ⊥平面B 1DF ,则必有CF ⊥DF . 设AF =x (0<x <3a ),则CF 2=x 2+4a 2DF 2=a 2+(3a -x )2,又CD 2=a 2+9a 2=10a 2, ∴10a 2=x 2+4a 2+a 2+(3a -x )2,解得x =a 或2a. 答案:a 或2a图1616.如图16所示,已知四面体ABCD 中,DA =DB =DC =1且DA 、DB、DC 两两互相垂直,在该四面体表面上与点A 距离是233的点形成一条曲线,这条曲线的长度是________.解析:图17在△ADP 1中,cos ∠DAP 1=AD AP 1=1233=32,所以∠DAP 1=π6,因此∠P 2AP 1=π4-π6=π12.连接AP 4,同理∠P 3AP 4=π12.在△ABC中,根据AB =BC =AC =2可得△ABC 为等边三角形,因此∠BAC =π3.因此 12P P + 23P P + 34P P =(π12+π3+π12)×233=33π.在△ADP 1中,DP 1=233×sin π6=33,同理可得DP 4=33.因为弧P 1P 4是平面DBC 与以A 为球心,AP 1为半径的球面的交线,且AD ⊥平面DBC ,因此弧P 1P 4在以D 为圆心,DP 1为半径的圆上,因此 14P P =π2×33=36π,综上可得,四段圆弧总长为33π+36π=32π. 答案:32π三、解答题(写出必要的计算步骤,只写最后结果不得分,共70分)17.某高速公路收费站入口处的安全标识墩如图18所示.墩的上半部分是正四棱锥P —EFGH ,下半部分是长方体ABCD —EFGH .图(2)、图(3)分别是该标识墩的正(主)视图和俯视图图18(1)请画出该安全标识墩的侧(左)视图; (2)求该安全标识墩的体积; (3)证明:直线BD ⊥平面PEG . 解:(1)侧(左)视图同正(主)视图. (2)如图19,该安全标识墩的体积为: V =V P -EFGH +V ABCD -EFGH =13×402×60+402×20 =32000+32000=64000(cm 3).图19 图20(3)如图20,连结EG 、HF 及BD , EG 与HF 相交于O . 由正四棱锥的性质可知PO ⊥平面EFGH ,∴PO ⊥HF ,又EG ⊥HF ,∴HF ⊥平面PEG ,又BD ∥HF ,∴BD ⊥平面PEG .图2118.如图21所示,A 1B 1C 1—ABC 是直三棱柱,∠BCA =90°,点D 1、F 1分别是A 1B 1和A 1C 1的中点,若BC =CA =CC 1,求BD 1与AF 1所成角的余弦值.解:图22解法1:如图22所示,连结D 1F 1,取BC 中点M ,连接MF 1,MA ,则D 1F 1∥B 1C 1∥BM ,又∵D 1F 1=12B 1C 1=BM , ∴四边形BMF 1D 1是平行四边形,∴MF 1∥BD 1,∴∠MF 1A 是异面直线BD 1和AF 1所成的角.设BC =CA =CC 1=1,则AM 2=1+14=54, MF 21=BD 21=1+(22)2=32, AF 21=1+14=54, cos ∠MF 1A =54+32-542×32×54=3010.图23解法2:建立如图23所示的空间直角坐标系,设BC =CA =CC 1=2,∴A (2,0,0),B (0,2,0),C 1(0,0,2),A 1(2,0,2),B 1(0,2,2).∵D 1、F 1分别为A 1B 1、A 1C 1的中点,∴D 1(1,1,2),F 1(1,0,2),∴BD →1=(1,-1,2), AF →1=(-1,0,2), ∴BD →1·AF →1=(1,-1,2)·(-1,0,2)=3, |BD →1|=1+1+22=6,|AF →1|=1+22=5, cos 〈BD →1,AF →1〉=36×5=33030=3010.19.已知P 在矩形ABCD 的边DC 上,AB =2,BC =1,F 在AB 上且DF ⊥AP ,垂足为E ,将△ADP 沿AP 折起,使点D 位于D ′位置,连接D ′B 、D ′C 得四棱锥D ′—ABCP .图24(1)求D ′F 与AP 所成角的大小;(2)若二面角D ′—AP —B 和D ′F 与平面ABCP 所成角的大小均为π3,求四棱锥D ′—ABCP 的体积. 解:(1)∵AP ⊥D ′E ,AP ⊥EF ,又∵D ′E ,EF 是平面D ′EF 内的两条相交直线;∴AP ⊥平面D ′EF ,∴AP ⊥D ′F ,∴D ′F 与AP 所成角的大小为π2.(2)由(1)知AP ⊥平面D ′EF ,∴平面D ′EF ⊥平面ABCP ,并且因为二面角D ′—AP —B 的大小为π3,所以易知∠D ′EF =π3, 过D ′作平面ABCP 的垂线,垂足为H ,则H 必在EF 上,∴∠D ′FE =π3,∴△D ′EF 是等边三角形, ∴D ′E =EF 即DE =EF ,∴△DAF 是等腰直角三角形,∴易得DP =1且EF =22, ∴四棱锥D ′—ABCP 的高D ′H =64, 又∵S 梯形ABCP =12·(CP +AB )·BC =12×(1+2)×1=32, ∴V 四棱锥D ′-ABCP =13×D ′H ×S 梯形ABCP =68.图2520.如图25,在四棱锥E —ABCD 中,四边形ABCD 为平行四边形,BE =BC ,AE ⊥BE ,M 为CE 上一点,且BM ⊥平面ACE .(1)求证:AE ⊥BC ;(2)如果点N 为线段AB 的中点,求证:MN ∥平面ADE .证明:图26(1)因为BM ⊥平面ACE ,AE ⊂平面ACE ,所以BM ⊥AE .因为AE ⊥BE ,且BE ∩BM =B ,BE、BM⊂平面EBC,所以AE⊥平面EBC.因为BC⊂平面EBC,所以AE⊥BC.(2)法1:取DE中点H,连接MH、AH.因为BM⊥平面ACE,EC⊂平面ACE,所以BM⊥EC.因为BE=BC,所以M为CE的中点.所以MH为△EDC的中位线,所以MH綊12DC.因为四边形ABCD为平行四边形,所以DC綊AB.故MH綊12AB.因为N为AB的中点,所以MH綊AN.所以四边形ANMH为平行四边形,所以MN∥AH.因为MN⊄平面ADE,AH⊂平面ADE,所以MN∥平面ADE.法2:取EB的中点F,连接MF、NF.因为BM⊥平面ACE,EC⊂平面ACE,所以BM⊥EC.因为BE=BC,所以M为CE的中点,所以MF∥BC.因为N为AB的中点,所以NF∥AE,因为四边形ABCD为平行四边形,所以AD∥BC.所以MF∥AD.因为NF、MF⊄平面ADE,AD、AE⊂平面ADE,所以NF∥平面ADE,MF∥平面ADE.因为MF∩NF=F,MF、NF⊂平面MNF,所以平面MNF∥平面ADE.因为MN⊂平面MNF,所以MN∥平面ADE.21.如图27甲,平面四边形ABCD关于直线AC对称,∠A=60°,∠C=90°,CD=2.把△ABD沿BD折起(如图乙),使二面角A—BD—C的余弦值等于33.对于图乙,完成以下各小题:图27(1)求A,C两点间的距离;(2)证明:AC⊥平面BCD;(3)求直线AC与平面ABD所成角的正弦值.解:(1)取BD的中点E,连接AE,CE,由AB=AD,CB=CD,得:AE⊥BD,CE⊥BD,∴∠AEC就是二面角A—BD—C的平面角,∴cos∠AEC=3 3.在△ACE中,AE=6,CE=2,AC2=AE2+CE2-2AE·CE·cos∠AEC=6+2-2×6×2×33=4,∴AC=2.(2)证明:由AB=AD=BD=22,AC=BC=CD=2,∴AC2+BC2=AB2,AC2+CD2=AD2,∴∠ACB=∠ACD=90°,∴AC⊥BC,AC⊥CD,又BC∩CD=C,∴AC⊥平面BCD.(3)法1:由(1)知BD⊥平面ACE,BD⊂平面ABD,∴平面ACE⊥平面ABD,平面ACE∩平面ABD=AE,作CF⊥AE交AE于F,则CF⊥平面ABD,∠CAF就是AC与平面ABD所成的角,∴sin∠CAF=sin∠CAE=CEAE=33.法2:设点C到平面ABD的距离为h,∵V C-ABD=V A-BCD,∴13×12×22×22sin60°·h=13×12×2×2×2,∴h=23 3,于是AC与平面ABD所成角θ的正弦值为sinθ=hAC=33.图28法3:以CB ,CD ,CA 所在直线分别为x 轴,y 轴和z 轴建立空间直角坐标系C -xyz ,则A (0,0,2),B (2,0,0),C (0,0,0),D (0,2,0).设平面ABD 的法向量为n =(x ,y ,z ),则n ·AB →=0,n ·AD→=0⇒2x -2z =0,2y -2z =0,取x =y =z =1,则n =(1,1,1),于是AC 与平面ABD 所成角θ的正弦值:sin θ=|n ·CA →||n |·|CA →|=|0+0+2|3×2=33.图2922.如图29,在直三棱柱ABC -A 1B 1C 1中,已知BC =1,BB 1=2,AB ⊥平面BB 1C 1C .(1)求直线C 1B 与底面ABC 所成角的正切值;(2)在棱CC 1(不包括端点C 、C 1)上确定一点E 的位置,使EA ⊥EB 1(要求说明理由);(3)在(2)的条件下,若AB =2,求二面角A —EB 1—A 1的大小. 解:法1:(1)在直三棱柱ABC —A 1B 1C 1中,C 1C ⊥平面ABC , ∴C 1B 在平面ABC 上的射影为CB ,∴∠C 1BC 为直线C 1B 与底面ABC 所成的角.∵在Rt △CC 1B 中,CC 1=2,BC =1,∴tan ∠C 1BC =2,即直线C 1B 与底面ABC 所成角的正切值为2.(2)当E 为CC 1的中点时,EA ⊥EB 1,连接BE .∵CE =EC 1=1,BC =B 1C 1=1,∴∠BEC =∠B 1EC 1=45°,∴∠BEB 1=90°,即B 1E ⊥BE ,又∵AB ⊥平面BB 1C 1C ,EB 1⊂平面BB 1C 1C ,∴AB ⊥EB 1, 又AB ⊂平面ABE ,BE ⊂平面ABE ,BE ∩AB =B ,∴EB 1⊥平面ABE ,又EA ⊂平面ABE ,故EA ⊥EB 1.图30(3)如图30,取EB 1的中点G ,A 1E 的中点F ,连接FG ,则FG ∥A 1B 1,且FG =12A 1B 1,∵A 1B 1⊥EB 1, ∴FG ⊥EB 1,连接A 1B ,AB 1,设A 1B ∩AB 1=O ,连接OF ,OG ,则OG ∥AE ,且OG =12EA , ∵EA ⊥EB 1,∴OG ⊥EB 1,∴∠OGF 为二面角A —EB 1—A 1的平面角.∵AE =AC 2+CE 2=2,OG =12AE =1, FG =12A 1B 1=22,OF =12BE =22,∴∠OGF =45°, ∴二面角A —EB 1—A 1的大小为45°.图31法2:以B 为坐标原点,BC 、BB 1、AB 所在的直线分别为x 、y 、z 轴建立如图31所示的空间直角坐标系,则B (0,0,0),C 1(1,2,0),B 1(0,2,0).(1)在直三棱柱ABC —A 1B 1C 1中,平面ABC 的一个法向量为BB →1=(0,2,0),又BC →1=(1,2,0),设BC 1与平面ABC 所成的角为θ,则sin θ=|cos 〈BB →1,BC →1〉|=255, ∴tan θ=2,即直线C 1B 与底面ABC 所成角的正切值为2.(2)设E (1,y,0),A (0,0,z ),则EB →1=(-1,2-y,0), EA →=(-1,-y ,z ),∵EA ⊥EB 1,∴EA →·EB →1=1-y (2-y )=0,∴y =1,即E (1,1,0),∴E 为CC 1的中点.(3)由题知A (0,0,2),则AE →=(1,1,-2),B 1E →=(1,-1,0),设平面AEB 1的一个法向量为n =(x 1,y 1,z 1),则⎩⎨⎧ n ·AE →=0n ·B 1E →=0,∴⎩⎪⎨⎪⎧x 1+y 1-2z 1=0x 1-y 1=0,令x 1=1,则n =(1,1,2), ∵BE →=(1,1,0),∴BE →·B 1E →=1-1=0, ∴BE ⊥B 1E ,又BE ⊥A 1B 1,∴BE ⊥平面A 1B 1E , ∴平面A 1B 1E 的一个法向量为BE →=(1,1,0), ∴cos 〈n ,BE →〉=n ·BE →|n |·|BE →|=22,∴二面角A —EB 1—A 1的大小为45°.。
