第5章 粘性流体动力学基本方程组
粘性流体力学.ppt

e
2
dVv
Vv F VdVv
V
Vv
dVv
Vv kT dVv Vv qdVv
(e)
同样,由于流场中各种物理量分布都是连续的,体
积Vv可以任选,故得
D Dt
e
V2 2
F
V
V
+
V
V
=
F
-p
+
V
+
2
对上式等号两边取旋度,得
t
+
V
=
F
-
1
p
+
1
V
+
1
2
又因 + V = V - V+ V - V
e
V2 2
dVv
Vv
D Dt
e
V2 2
1 dVv
e
V2 2
D Dt
dVv
dVv
(b)
Vv
D Dt
e
粘性流体动力学基础
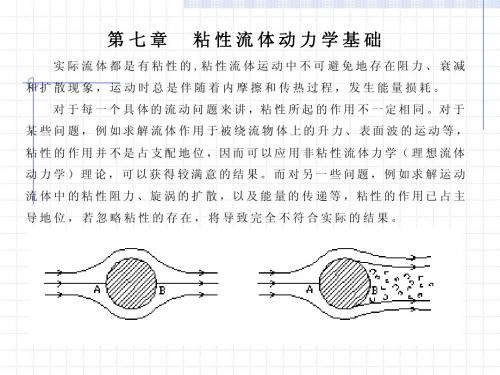
ρ
1 p dvx fx = ρ x dt 1 p dv y fy = ρ y dt 1 p dvz fz = ρ z dt
方程中, f :作用在单位质量流体上的质量力
1
ρ
p :作用在单位质量流体上的表面力
dv :作用在单位质量流体上的惯性力 dt
这一方程就是以应力形式表示的运动微分方程。
在这一方程中,通常质量力 f x 、 f y 、 f z 是已知的,对不可压缩流体 ρ
τ 也是已知的。方程组中的未知量有:三个法向应力 pii ,六个切向应力 ij ,
三个速度分量vi 。 运动微分方程加上连续性方程共四个, 无法求解 12 个未 知量,下面寻求补充方程。 三 、 切应力分量之间的关系 切应力分量之间存在着一定的联系, 应用力矩平衡原理可以证明切应 力具有对称性。 τ xy = τ yx τ yz = τ zy
τ yz dz τ zy dz τ yz dxdydz τ zy dxdydz + dxdydz dxdydz = 0 y 2 z 2
略去高阶无穷小,可得:
τ yz = τ zy
同理可得:
τ xy = τ yx
τ xz = τ zx
可见应力分量中的切应力是两两对称的。 四 、 切应力与变形速度的关系 牛顿内摩擦定律(平面流动) dv dα τ = x =
M ,六面体为 ABCD, A 点的应力为:
pxx τ yx τ zx
τ xy
p yy
τ zy
τ xz τ yz
pzz
其方向确定为:法向应力以内法线方向为正,切向应力(正) ,过 A 点 的三个面上切向应力与坐标方向相反,其它三个面则相同。 采用泰勒级数展开并取前二项可写出其它三个面上的应力分量。
第五章 实际(粘性)流体动力学基础

p
p
(5.12)
上式表示总流重力流量(γQ)所具有的势能。
u2 (2)第二类积分 Q dQ A u3dA ,表示总流重力流量 2g 2g
所具有的动能。 总流在同一过流断面上的流速分布一般是不均匀的,即
3 3 u dA v A A
引入修正系数α,即令
3 3 u dA u dA A A 3 v A Qv 2
u y u y u y u y 1 p 2 Y u y ux uy uz y t x y z
1 p uz uz uz uz 2 Z uz ux uy uz z t x y z
(5.1)
与理想流体的欧拉运动微分方程w dhw
1
2
实际流体恒定元流的伯努利方程或能量方程,式中 z:位置水头;
p
: 动水压强水头;
u2 : 流速水头; 2g
: 损失水头。 hw
即单位重力流体在运动中为了克服1~2元流段中水流阻力 hw
所消耗的机械能,称为水头损失。
§5.3
5.3.1
恒定总流的伯努利方程
下降,平均测压管水头线可以上升,
可以下降。
总水头线的坡度叫做水力坡度, 表示单位重力流体在单位长度的 流程上所损失的平均水头。以H 表示总流的平均总水头,则水力
坡度为
dH dhw J ds ds
(5.21)
5.3.3
恒定总流伯努利方程的应用
总流伯努利方程适用条件:
(1)不可压缩流体;
(2)恒定流; (3)作用于流体上的质量力不可压缩流体; (4)所取过流断面1-1,2-2都在渐变流区域,但两断面之
这些功时所消耗的机械能,就是能量的损失。
粘性流体动力学基础

v vvx dy v dy vx (v vx )dy
2 0 0 2 x 0
因此可得:
0
vx vx (1 ) dy v v
物理意义:
边界层内损失的动量相当于厚度为
的理想流体动量。
几个厚度比较:
dv 1 p x p y p z f dt x y z
上式即为粘性流体运动应力形式的动量方程。
( v) 0 t 未知量10个: u, v, w, , pxx , p yy , pzz , pxy , pxz , p yz
y 0时vx ( x,0) 0与v y ( x,0) 0 y 时vx ( x, y ) v ( x)
在推导边界层方程时曾得到过下述结论,即
u u 2u u v 与 x y y 2
是同数量级的。所以推出:
x
v
可见,边界层厚度 与流体的运动粘度 以及边界层所 在位置的坐标x的平方根成正比,和势流的速度的平方根成反比。 即流体越粘稠,势流速度越小,边界层越厚。并且边界层的厚度 随x的增大而不断加厚。
而与粘性系数
及管长
成反比。
4.阻力及阻力系数(层流) u p t r 剪应力分布: r 2l
p a 管壁剪应力: t 0 2l
2 t 0 u m
1 8
摩擦阻力:
F t 0 2al a 2 p
第二节 边界层基本概念
边界层定义:在被绕流物体表面上的一层厚度很小且其中的 流动具有很大法向速度梯度和旋度的流动区域称做边界层。 在边界层中呈现有较强的粘性作用,并形成对流动的阻力。
粘性流体力学课件

适用于牛顿流体
流体运动微分方程——Navier-Stokes方程
y
vx v y vx vz z x x z y
Dvx p 2 x fx 2 Dt x 3 x x x
Dvy
2 y 2 y 2 y 1 p fy 2 2 x Dt y y z 2
2 z 2 z 2 z Dvz 1 p fz 2 2 2 Dt z y z x
( x z ) ( y z ) ( z 2 ) dxdydz x y z
微元体内的动量变化率
x dxdydz x方向: t z dxdydz y方向: dxdydz z方向: t t
y
运动方程
以应力表示的运动方程
p
xx
yy zz 3
这说明:三个正压力在数值上一般不等于压力,但它们的平 均值却总是与压力大小相等。
切应力与角边形率
流体切应力与角变形率相关。
牛顿流体本构方程反映了流体应力与变形速率之间的关系, 是流体力学的虎克定律。
N-S方程
Dvx p 2 x fx 2 Dt x 3 x x x
xx dx x
每个应力有两个下标,第一个下 标表示应力作用面的法线方向; 第二个下标表示应力的作用方向
fz
fy fx
应力正负的规定
应力与所在平面的外法线方向相 同为正,否则为负:
微元体上的表面力和体积力
运动方程
应力状态及切应力互等定律
粘性流体力学基本方程组

=
微元体内的 质量变化量
y
微元体及其表面的质量通量
a)连续性方程
故 dt 时段内在 x 方向流入与流出六面体的液体质量差为:
u x dxdydzdt x
同理可得出 dt 时段内在 y, z方向流入与流出六面体的液体质量 差分别为:
u y y
dxdydzdt ,
u z dxdydzdt z
d ux uy uz dt t x y z
d p p p p p ux uy uz d t t x y z
c)梯度
标量场中某一点上的梯度指向标量场增长最快的方向, 梯度的长度是这个最大的变化率 梯度的运算对象是标量,运算结果是矢量 考虑一座高度在(x,y)点是H(x,y)的山。在一点 的梯度是在该点坡度(或者说斜度)最陡的方向。梯 度的大小告诉我们坡度到底有多陡。 这座山的每一个点上都算出一个梯度向量,这个向量会 指向每个点最陡的那个方向,而向量的大小则代表了这 个最陡的方向到底有多陡
流体的加速度
因此该液体质点通过A点时的加速度应为
u x u d x x d t ) ux x t ax dt u d x u x u x u x ux x x d t t t x (u x
u x 被称为时变(或当地)加速度,代表某定点流速随时间的 t u x u 变化率; x x 被称为位变(或位移)加速度,代表同一时刻流
对静止液体, ux u y uz 0 ,故有:
fx
1 p 1 p 1 p 0, f y 0, f z 0 x y z
即为静止液体的欧拉平衡微分方程。 若 f x 0, f y 0, f z g
5实际(粘性)流体的动力学基础2

FRx p1 A1 1QV1
FRx p1 A1 1QV1
沿z方向列动量方程为:
沿y方向列动量方程为:
p2 A2 FG FRz Q(2V2 0)
FRy p2 A2 Q(2V2 0)
FRz p2 A2 FG 2 QV2
FRy p2 A2 2 QV2
x y z
Q(2V2 x 1V1x ) Q(2V2 y 1V1y ) Q(2V2 z 1V1z )
适用条件:不可压缩流体、恒定流、过水断面为均匀流或 渐变流过水断面、无支流的汇入与分出。 如图所示的一分叉管路,动量 方程式应为:
ρ Q1
1
1
v1 v2 v3
3 3 ρ Q3
扬 扬 程 程 提水 高度
QH m Np p
分 子
单位时间 水流获得 总能量
水泵轴功率
水泵效率
分 母
三、水轮机管路系统
1 引水渠 1 o 压力钢管
z
水轮机
2 o
2 p1 1v12 p2 2v2 z1 H t z2 hl12 2g 2g
2
=
z
=
0
管轴竖直放置
弯管内水流对管壁的作用力
1
管轴水平放置
FR
FRx
V1
FRz
V1
Fry
z
1
FP1=p1A1
V2
FP1=p1A1 x y
V2
FR
FRx
2
2
y
x
FG FP2=p2A· 2
FP2=p2A· 2
沿x方向列动量方程为:
沿x方向列动量方程为:
p1 A1 FRx Q(0 1V1 )
第五章 实际(粘性)流体动力学基础

hw----能量损失
能量损失包括:沿程损失和局部损失。
物理意义:总流各过流断面上单位重力流体所具有的平均势
能和平均动能之和,机总机械能平均值沿程减少,部分机械 能转化为热能而损失;同时,各项机械能之间可以相互转化。
2、几何意义 z——位置水头 hw----水头损失
p
——压强水头
v 2
2g
——流速水头
p
p
(5.12)
上式表示总流重力流量(γQ)所具有的势能。
u2 (2)第二类积分 Q dQ A u3dA ,表示总流重力流量 2g 2g
所具有的动能。 总流在同一过流断面上的流速分布一般是不均匀的,即
3 3 u dA v A A
引入修正系数α,即令
3 3 u dA u dA A A 3 v A Qv 2
下降,平均测压管水头线可以上升,
可以下降。
总水头线的坡度叫做水力坡度, 表示单位重力流体在单位长度的 流程上所损失的平均水头。以H 表示总流的平均总水头,则水力
坡度为
dH dhw J ds ds
(5.21)
5.3.3
恒定总流伯努利方程的应用
总流伯努利方程适用条件:
(1)不可压缩流体;
(2)恒定流; (3)作用于流体上的质量力不可压缩流体; (4)所取过流断面1-1,2-2都在渐变流区域,但两断面之
式中,
(5.5)
g
( 2 ux dx 2 u y dy 2 uz dz ) 为单位质量流体粘性
,代入(5.5)式 力所作的微功,记为 dhw
u2 0 d ( gz ) dhw 2g p
对上式沿流线(或元流)由点1到点2积分,得
粘性流体力学基本方程组

牛顿流体具有剪切应力和剪切速率成线性关系的特性,这种 关系可以用本构方程来表示。
牛顿流体的本构方程
本构方程
本构方程是描述流体应力与应变之间 关系的方程,对于牛顿流体,其本构 方程为剪切应力等于粘性系数乘以剪 切速率。
本构方程的意义
本构方程是粘性流体力学中的基本方 程之一,它描述了流体在受到外力作 用时内部应力的产生和分布情况。
有限差分法
将流场离散化为网格,用差分表达式近似代 替微分方程中的导数项,从而将微分方程转 化为差分方程进行求解。
有限元法
将流场离散化为单元,用有限元近似表示流场中的 物理量,通过求解有限元方程得到流场中的数值解 。
有限体积法
将流场离散化为体积,每个体积单元上的物 理量通过中心值或平均值表示,通过求解离 散方程得到流场中的数值解。
VS
详细描述
非牛顿流体在剪切力作用下不会表现出恒 定的剪切粘度,其流动行为受到许多因素 的影响,如温度、压力、浓度、分子间相 互作用等。
非牛顿流体的本构方程
总结词
本构方程是描述非牛顿流体在剪切力作用下 的应力与应变率之间关系的数学模型。
详细描述
非牛顿流体的本构方程通常由实验数据确定, 并可以用来预测流体在不同剪切力作用下的 流动行为。常见的本构方程包括幂律模型、 Carreau模型、Bingham模型等。
理论分析方法
01
02
03
数学建模
通过建立数学模型来描述 粘性流体的运动规律,包 括连续性方程、动量方程、 能量方程等。
解析求解
对建立的数学模型进行解 析求解,得到流体运动的 解析解,用于分析流体运 动的特性。
近似方法
在某些情况下,可以采用 近似方法来求解数学模型, 如摄动法、匹配渐近展开 等。
流体力学5.2 粘性流体的运动方程式

第五章
粘性流体动力学
5.2 粘性流体中的运动方程式
P P P
5.2.2奈维-斯托克斯运动方程
流体力学第五章
一、应力与变形的关系
关于四个假设的说明:
(1)虽然这些假设本身以及由其所得到的结果曾经
为实践所近似地或很好地证实,但在逻辑的程度上,
不像欧拉对理想流体所建立的数学理论那样严密。
(2)有些假设是可以立刻接受的,有些则具有相当
大的近似性。
第一假设偏差较小:没有粘性时,主应力的值等于压强,即
123P P P P
1,2,3
1
2
3
,,p p P P P P P P p 考虑粘性时,主应力有了附加项,因此有可能把粘性
主应力写成压强和附加应力之和:
注:大P 代表应力张量,小p 代表压强。
第二假设偏差较大:应力主轴与变形主轴重合,而且附加应力和主变形之间有线性关系,即
111121322122233
313233'''P a b c P a b c P a b c
第三假设:流体为力学上各向同性的物质
11231
1112132
212223221333132333312p a b p a b c p a b c p a b p a b c p a b
123231312a b c a a a b b c c b
2,a b 令则
1123112
123223
12333222222p b b V p b b V p b b V
112233
222P b V P b V p p p P b V。
第五讲 粘性流体动力学基础

如果流体不可压缩,由连续性条件 v vx vy vz 0 x y z
则方程式可简化为
dvx dt
fx
1
p x
2vx
dvy dt
fy
1
p y
2v y
dvz dt
fz
1
p z
2vz
该式为不可压缩流体的N-S方程式。
z2
p2
g
2v22
2g
hf
式中: hf —单位重力流体沿总流从1 断面流 到 2 断面,为 克服摩擦力而消耗的机械能,称为能量损失或水头损失。
5-3 粘性流体的伯努利方程
应用伯努利方程解决工程实际应用问题时应注意以下几点: 1、适用条件:不可压缩流体、定常流动、质量力只有重 力作用。 2、往往与连续方程联合使用。 3、在选取适当的位置势能为零的水平基准面后,可选择 过流断面上任意高度为已知点 z1 和 z2 列出伯努利方程。 (三选一列) 4、所选用的过流断面必须是缓变过流断面。且其中一个 断面应选在待求未知量所在处,另一个断面应选在各 参数已知处。
zx
z
dz
τyz
pxx τxz dz M τxy
z pyyτyx
dy
τzx
τzy
pzz
dx
o
y
x
5-2 纳维-斯托克斯方程
由牛顿第二定律 F ma
微元六面体x向的运动方程为:
dvx dt
dxdydz
fxdxdydz
pxxdydz ( pxx
pxx x
dx)dydz
粘性流体-PPT

现在,我们将考虑定常流。例如,若讨论绕固体得流动(为 确定起见,下面我们将讨论这种情况),则来流速度应为常数。 此外还假设流体就是不可压缩得。
在流体动力学方程组(纳维-斯托克斯方程组)里,就表征流
体本身特性得参数而言,只出现运动粘性系数
。还有,求
解这个方程组所必须确定得未知函数就是速度 和 ,这里
类似得,我们可以写出流体中得压力分布公式。为此, 我们必须由参数 和 作出某个量纲为压力除以密度得 量,比如,这个量可以就是 。于就是, 就是无量纲变 量 和无量纲参数R得函数,所以
最后,类似得考虑也可适用于这样一些量:她们描写流
动得特性,但不就是坐标得函数。例如作用在物体上得阻力
F就就是这样一个量。我们可以说,阻力F与用
不难写出周围流体作用于固体表面得力得表达式。 一个面元上所受得作用力恰等于通过这个面元得动量通 量。通过面元 得动量通量就是
把 写成
得形式,这里 就是沿法线得单位
矢量,并考虑到在固体表面上
,我们得到作用在单位
面积上得力 为
其中等式右边第一项就是普通得流体压力,而第二项就是由 于粘性引起得作用在固体表面上得摩擦力。式中 就是单 位矢量,她沿流体界面得外法线,即沿固体表面得内法线。
组成得并具有力得量纲得某个量之比必定只就是雷诺数得
函数。比如,
组合成力得量纲可以就是
。
因而
若重力对流动有重要作用,则流动不就是由三个参数确
定,而就是由
和重力加速度 这四个参数确定。由
这四个参数可构成两个独立得无量纲量,而不就是一个。比
如,这两个量可以就是雷诺数和弗劳德数,弗劳德数为
最后,提一下非定常流。要描述一个确定类型得非定常
第四节 两个旋转圆柱面之间得流动
粘性流体动力学基础

(10.8 a )
同理可以得出y,z方向的合力
dFy p ( xy ) ( yy ) ( zy ) dv y x y z dFz p ( xz ) ( yz ) ( zz ) dv z x y z
dF dF p dv surf dv viscous
(kT )dxdydz Q k
(10.25)
粘性应力做功率等于粘性应力分量、相应的速度分量和相应 的面积三项的乘积,见图10.3 ,与x轴垂直的左侧面上粘性应 力做功率为
w dydz 其中 w (V V V ) (10.26) W v.LF x x x xx y xy z xz
10.1微分形式的动量方程(N-S) 10.2微分形式的能量方程 10.3 初始条件和边界条件
10.4 雷诺方程和雷诺应力
10.5附面层基本知识
10.6附面层微分方程
10.7附面层积分方程
10.1微分形式的动量方程(N-S)
图10.1动量方程推导用图
与第八章分析质量守恒方法类似,我们可以针对微元控制体图 10.1,列出动量方程
dt
Vx Vz zx zt
y z 3 x x 2Vy 2Vy 2Vy p 2 2 ( V) (10.18 b) = Ry 2 y y z 3 y x 2Vz 2Vz 2Vz p ( V) (10.18 c) = Rz 2 2 2 z y z 3 z x
图10.3分析粘性应力做功率
与上述分析质量流量、动量流量和热流量完全相同可以得出, 在与x轴垂直的两个面上粘性应力的做功率为
水力学51(2、3)实际流体的动力学基础(N-S方程,能量方程)资料

u y t
ux
u y x
uy
u y y
uz
u y z
(5.1)
Z
1
p z
2uz
uz t
ux
uz x
uy
uz y
uz
uz z
N-S方程仅适用于牛顿流体,不可压缩的流体运动
5.2 恒定元流的伯努利方程(能量方程)
对于理想流体,其伯努利方程:
在同一条流线上的任意两点1,2有:
z1
p1
u12 2g
2g
A
令
v3 A (3v u)(u)2 dA
(3v u)(u)2 dA
A
1 A
v3 A
v3 A
则
u2 dQ v3 A v2vA v2 Q
Q 2g
2g
2g
hw i
(5.10)
由于总流是元流的集合,因此对上式进行积分,便 可得总流能量方程.
设元流i的流量为dQi,单位时间内通过该元流任 何过水断面的流体质量为γ dQi,
将上式各项乘以γ dQi,再在A1,A2上积分得:
5.3.2 实际流体恒定总流的能量方程
(5.11) Q (z1i
p1i
所以 A (u)dA 0
于是
5.3.2 实际流体恒定总流的能量方程
于是 u2 dQ [v3 3v2 (u) 3v(u)2 (u)3]dA
Q 2g
2g A
[ v3dA 3v2 (u)dA 3v(u)2dA (u)3 dA]
2g A
A
A
A
[v3 A 0 (3v u)(u)2dA]
hw
(5.6)
z —一点的位置高度,称为位置水头 p/r —对应点的动水压强水头 u2/2g —流速水头 h'w —元流的水头损失
第五讲 粘性流动NS方程
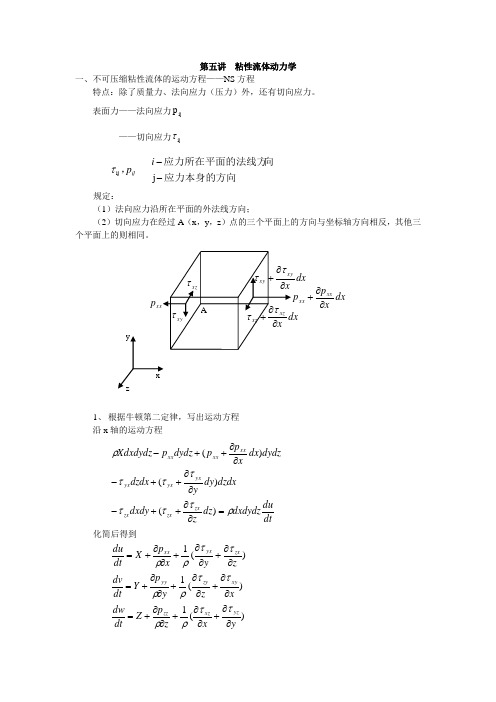
第五讲 粘性流体动力学一、不可压缩粘性流体的运动方程——NS 方程特点:除了质量力、法向应力(压力)外,还有切向应力。
表面力——法向应力ij p——切向应力ij τ应力本身的方向向应力所在平面的法线方,--j ij i p ij τ规定:(1)法向应力沿所在平面的外法线方向;(2)切向应力在经过A (x ,y ,z )点的三个平面上的方向与坐标轴方向相反,其他三个平面上的则相同。
1、 根据牛顿第二定律,写出运动方程沿x 轴的运动方程 dt du dxdydz dz z dxdy dzdx dy y dzdx dydz dx x p p dydz p Xdxdydz zx zxzx yxyx yx xx xx xx ρττττττρ=∂∂++-∂∂++-∂∂++-)()()( 化简后得到 )(1)(1)(1yx z p Z dt dw xz y p Y dt dv zy x p X dt du yz xz zz xy zy yy zx yx xx ∂∂+∂∂+∂∂+=∂∂+∂∂+∂∂+=∂∂+∂∂+∂∂+=ττρρττρρττρρdx x p xx xx ∂∂+九个应力和三个速度分量均为未知数,四个方程。
2、 切向应力之间的关系由达朗伯原理,对M 点力矩之和为0;质量力和惯性力对该轴的力矩是四阶小量,略去不计,得到02)(22)(2=∂∂+++∂∂+--dx dydz dx x dx dydz dy dxdz dy y dy dxdz xy xy xy yx yx yx ττττττ 再略去四阶小量,得到xzzx zx yz yxxy ττττττ===则九个应力中只有六个是独立变量。
3、 广义牛顿内摩擦定律速度梯度等于流体微团的角变形速率,则有y xz x yzz xy e xw z u e z v y w e y u x v μμτμμτμμτ2)(2)(2)(=∂∂+∂∂==∂∂+∂∂==∂∂+∂∂=4、 法向应力对于理想流体 p p p p zz yy xx -===对于粘性流体,有线变形,使法向应力有变化,产生附加的法向应力,关系式如下。
(完整版)第5章 粘性流体动力学基本方程组

第5章 粘性流体动力学基本方程组5.1 粘性流体动力学基本方程流体运动所遵循的规律是由物理学三大守恒定律规定的,即质量守恒定律,动量守恒定律和能量守恒定律。
这三大定律对流体运动的数学描述就是动力学基本方程组。
但这个方程组是不封闭的,要使其封闭还需加上辅助的物性关系等。
一般情况下,现在还求不出这个方程组的解析解,但研究这个方程组的性质却具有极其重要的意义,因为所有的流动现象都是由这个方程组所规定的.粘性流动的一个基本特征是流动的有旋性. 因此研究涡的产生、输运和扩散就是很重要的了。
这些性质也都是由流体动力学基本方程组所规定的.对流体运动的描述有两种方法,即拉格朗日法和欧拉法;对基本定理的数学表述也有两种方法,即积分形式和微分形式. 本章将采用欧拉法和微分形式来表述基本方程。
5.1。
1 质量守恒定律——连续方程连续方程是质量守恒定律在运动流体中的数学表达式。
由于不涉及力的问题,因此粘性流体力学与非粘性流体方程完全相同,在非粘性流体中所做的推导和讨论在这里全部有效。
考察流体通过一微元体的界面所引起的微元体内质量的变化问题。
根据质量守恒定律,单位体积上通过微元体界面流出的质量流量即矢量ρu 的散度()ρ∇⋅u ,它应等于微元体内单位时间单位体积所减少的质量:()0tρρ∂+∇⋅=∂u (5.1。
1) 展开后得:()()()0u v w t x y zρρρρ∂∂∂∂+++=∂∂∂∂ (5。
1.2) 连续方程表示单位时间内流人流出微元体的质量必与密度变化相平衡。
对于定常流,此式可变为:()()()0u v w x y zρρρ∂∂∂++=∂∂∂ (5.1.3) ()0ρ∇⋅=u (5.1.4)对于不可压缩流,(5。
1.2)式变为:()()()0u v w x y z∂∂∂++=∂∂∂ 即 iiu x ∂= 0 (5.1.5) 由张量分析的知识可知,iiu x ∂是应变量张量的主对角线上三元素之和,恒为常数,表示微元体的体积变化率.式(5.1。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第5章 粘性流体动力学基本方程组5.1 粘性流体动力学基本方程流体运动所遵循的规律是由物理学三大守恒定律规定的,即质量守恒定律,动量守恒定律和能量守恒定律。
这三大定律对流体运动的数学描述就是动力学基本方程组。
但这个方程组是不封闭的,要使其封闭还需加上辅助的物性关系等。
一般情况下,现在还求不出这个方程组的解析解,但研究这个方程组的性质却具有极其重要的意义,因为所有的流动现象都是由这个方程组所规定的。
粘性流动的一个基本特征是流动的有旋性。
因此研究涡的产生、输运和扩散就是很重要的了。
这些性质也都是由流体动力学基本方程组所规定的。
对流体运动的描述有两种方法,即拉格朗日法和欧拉法;对基本定理的数学表述也有两种方法,即积分形式和微分形式。
本章将采用欧拉法和微分形式来表述基本方程。
5.1.1 质量守恒定律——连续方程连续方程是质量守恒定律在运动流体中的数学表达式。
由于不涉及力的问题,因此粘性流体力学与非粘性流体方程完全相同,在非粘性流体中所做的推导和讨论在这里全部有效。
考察流体通过一微元体的界面所引起的微元体内质量的变化问题。
根据质量守恒定律,单位体积上通过微元体界面流出的质量流量即矢量ρu 的散度()ρ∇⋅u ,它应等于微元体内单位时间单位体积所减少的质量:()0tρρ∂+∇⋅=∂u (5.1.1) 展开后得:()()()0u v w t x y zρρρρ∂∂∂∂+++=∂∂∂∂ (5.1.2) 连续方程表示单位时间内流人流出微元体的质量必与密度变化相平衡。
对于定常流,此式可变为:()()()0u v w x y zρρρ∂∂∂++=∂∂∂ (5.1.3) ()0ρ∇⋅=u (5.1.4)对于不可压缩流,(5.1.2)式变为:()()()0u v w x y z∂∂∂++=∂∂∂ 即iiu x ∂= 0 (5.1.5) 由张量分析的知识可知,iiu x ∂是应变量张量的主对角线上三元素之和,恒为常数,表示微元体的体积变化率。
式(5.1.5)表示总的体积变化率为零,与流体的不可压缩一致。
5.1.2 动量守恒定律——运动方程粘性流体的运动方程是动量守恒定律对于粘性流体运动规律的数学表述,可由牛顿第二定律推出。
以微元体为分析对象则可表述为:在惯性系中,流体微元体的质量和加速度的乘积等于该微元体所受外力的合力。
对于流体运动应考虑两类外力:一为彻体力(用F 来表示),它是作用在微元体上所有质量上的力,如重力;另一类为表面力(用P 来表示),它是作用在微元体界面上的力,如压力、摩擦力等。
运动方程可写成如下向量形式:D D tρρ=+uF P (5.1.6) 其中微分符号D ()D i iu t t t x ∂∂∂=+⋅∇=+∂∂∂u (5.1.7) 称为物质导数或随体导数,它所代表的是微团的某性质对时间的变化率。
例如,D D tu是该微团的速度u 随时间的变化率,即加速度,亦即D ()D t t∂=+⋅∇∂u uu u (5.1.8) 从欧拉法的观点看,此式右端第一项由流动的非定常性引起,称为当地加速度;右端第二项由流场中速度分布的不均匀性引起,表示经D t 时间后由于微团空间位置的变化而引起的速度的变化,称为迁移加速度。
式(5.1.6)中的彻体力F 可表示成:x y z F F F =++F i j k (5.1.9)在这里彻体力可以看成是已知的外力,而表面力则和流体速度场的变形情况有关。
它决定了流体的应力状态。
所以我们分别研究流体的应力和应变变化率后,将建立它们之间的关系。
为了写出表面力的式子,我们从流体中取出正六面微元体(图5-1)。
它的左下方的点的坐标为(x ,y ,z)。
对于垂直于x 轴的两个微元面上分别作用了如下的合应力(应力即单位面积上的作用力):x P 和d x x x x∂+∂P P图 5-1 微元体的应力张量这里的注足x 表示x 方向上的应力向量,则作用在垂直于x 轴的微元面上的应力的合力为:(d )d d d d d d d x x x x x y z y z x y z xx∂∂+-=∂∂P P P P (5.1.10)同样可得作用在垂直于y 轴和z 轴的微元面上的应力的合力分别为:d d d y x y z y∂∂P ,d d d zx y z z∂∂P 于是可得作用于单位容积的表面力的合力向量为(d d d d d d d d d )/d d d y x zyxzx y z x y z x y z x y z xyzx y z∂∂∂=++∂∂∂∂∂∂=++∂∂∂P P P P P P P (5.1.11)式中x P ,y P 和z P 都是向量,还可以把它们沿三个坐标方向分解,即分解为正应力σ和平行于各微元面的切应力τ。
例如,作用于与x 轴垂直的微元面上的应力x P 可分解为(图5-1):x x xy xz σττ=++P i j k (5.1.12a)同理有 y yx y yz τστ=++P i j k (5.1.12b)z zx zy z ττσ=++P i j k (5.1.12c)式中注足是这样规定的:正应力σ的注足代表应力的方向,切向力τ的第一个注足代表与切应力所在平面垂直的方向,第二个注足代表切应力的方向。
例如,xy τ表示作用在与x 轴垂直的平面上沿y 向的切应力。
由式(5.1.12)可见,要完全描述微元体上应力P 需要九个标量。
这九个标量就组成了应力张量,表示为zx yx x ττσ=∏ zy y xy τστ zyz xzσττ (5.1.13)容易证明这个张量是对称的,由式(5.1.11),(5.1.12)和(5.1.13)可写出如下的单位容积的表面力公式。
yx x zx x y z τστ∂⎛⎫∂∂=++ ⎪∂∂∂⎝⎭P i ⋅⋅⋅⋅⋅⋅x 方向分量xy y zy x y z τστ∂∂∂⎛⎫+++ ⎪∂∂∂⎝⎭j ⋅⋅⋅⋅⋅⋅y 方向分量 (5.1.14)yz xz z xy z ττσ∂⎛⎫∂∂+++ ⎪∂∂∂k ⋅⋅⋅⋅⋅⋅z 方向分量将(5.1.14)式代入(5.1.6)式则得:D D D D D D yx x zx x xy y zy y yz xz z z u F tx y z vF t x y z w F tx y z τστρρτστρρττσρρ∂⎧∂∂=+++⎪∂∂∂⎪⎪∂∂∂⎪=+++⎨∂∂∂⎪⎪∂∂∂=+++⎪∂∂∂⎪⎩ (5.1.15) 此方程是牛顿第二定律的严格表述,没有任何假设。
将广义牛顿粘性应力公式:2div ij ij ij ij s p πμλδδ=+-u (5.1.16)代入(5.1.11)式,并运用张量分析中有关应力张量公式和应变变化公式,可得到:j ji i i j i j i jj i i j u u u u u p u F t u x x x x x xρρρμλ⎡⎤⎛⎫⎛⎫∂∂∂∂∂∂∂∂+=-+++⎢⎥ ⎪ ⎪ ⎪ ⎪∂∂∂∂∂∂∂∂⎢⎥⎝⎭⎝⎭⎣⎦ (5.1.17) 或23j ji i i j i j i jj i i j u u u u u p u F t u x x x x x xρρρμμ⎡⎤⎛⎫⎛⎫∂∂∂∂∂∂∂∂+=-++-⎢⎥ ⎪ ⎪ ⎪ ⎪∂∂∂∂∂∂∂∂⎢⎥⎝⎭⎝⎭⎣⎦ (5.1.18) 展开得:()D 2D 2div 3x u p u u v F t x x x y y x u w z z x x ρρμμμμ⎡⎤⎛⎫∂∂∂∂∂∂⎛⎫=-+++⎢⎥ ⎪ ⎪∂∂∂∂∂∂⎝⎭⎝⎭⎣⎦∂⎡∂∂⎤∂⎛⎫++- ⎪⎢⎥∂∂∂∂⎝⎭⎣⎦u (5.1.19a)()D 2D 2div 3y v p v u v F t y y y x y x v w z z y yρρμμμμ⎡⎤⎛⎫⎛⎫∂∂∂∂∂∂=-+++⎢⎥ ⎪ ⎪∂∂∂∂∂∂⎝⎭⎝⎭⎣⎦⎡⎤⎛⎫∂∂∂∂++-⎢⎥ ⎪∂∂∂∂⎝⎭⎣⎦u (5.1.19b)()D 2D 2div 3z w p w u w F t z z z x z x v w y z y zρρμμμμ∂∂∂∂⎡∂∂⎤⎛⎫⎛⎫=-+++ ⎪ ⎪⎢⎥∂∂∂∂∂∂⎝⎭⎝⎭⎣⎦⎡⎤⎛⎫∂∂∂∂++-⎢⎥ ⎪∂∂∂∂⎝⎭⎣⎦u (5.1.19c)这就是粘性流体的运动方程,即纳维—斯托克斯方程。
由于一般情况下μ是温度的函数,所以方程很复杂。
对于常用的情况,可以不考虑μ随空间位置的变化,于是μ可作为常量考虑写到导数之外。
方程可进一步改写。
例如,对方程的第一个式子可写为:2222222222D D 3x u pu u u u v w F t x x yz x x y x z μρρμ⎛⎫⎛⎫∂∂∂∂∂∂∂=-++++++ ⎪ ⎪∂∂∂∂∂∂∂∂∂⎝⎭⎝⎭ ()2div 3x p F u x xμρμ∂∂=-+∇+∂∂u (5.1.20) 采用爱因斯坦约定方法方程可进一步写成:223j i i j i i j i i ju u u p u F u t x x x x μρρρμ∂∂∂∂+=-+∇+∂∂∂∂∂ (5.1.21) 或2()()3p t μρρρμ∂+⋅∇=-∇+∇+∇∇⋅∂u u u F u u (5.1.22) 对于不可压缩流体,由于连续方程0=∂∂iix u 则运动方程成为:21i i j i i j iu u pu F u t x x γρ∂∂∂+=-+∇∂∂∂ (5.1.23) 或21()p t γρ∂+⋅∇=-∇+∇∂u u u F u (5.1.24) 由矢量公式:()()2i i u u ⎛⎫∇=⋅∇+⨯∇⨯ ⎪⎝⎭u u u u (5.1.25) 可将公式(5.1.22)和(5.1.24)分别改写为:2()23i i u u p t μρρμ⎛⎫∂+∇-⨯=-∇+∇+∇∇⋅ ⎪∂⎝⎭uu ωF u u (5.1.26) 212i i u u p t γρ∂⎛⎫+∇-⨯=-∇+∇ ⎪∂⎝⎭u u ωF u (5.1.27) 上式通常称为葛罗米柯—兰姆型运动方程。
其中ω为涡量。
yxBu Au yxτpAFB图5-2两微元体之间的作用力由公式(5.1.14)、(5.1.17)、(5.1.18)和(5.1.20)可见,与理想流体运动方程相比,粘性流体运动方程增加了粘性应力项。
以图5-2所示的以不同流速运动的两微元体为例,对于理想流体,通过界面F ,微元体A 只对微元体B 作用了压力p ;而对于粘性流体,除正应力y σ外,微元体A 还对微元体B 作用了粘性切应力yx τ,而且正应力y σ的大小也不等于压力p ,由牛顿公式可以得到22div 3y v p y σμμ∂=--∂u 这些就是粘性引起的差别。
