用A算法解决八数码问题
a算法八数码问题例题

a算法八数码问题例题八数码问题是一个经典的搜索问题,其中有一个3×3的格子,其中包含了一些数字(通常是1到8),以及一个空白格。
目标是使用最少的步骤将格子中的数字排列成给定的目标顺序。
每个步骤可以是以下三种操作之一:1. 上下移动(将行中的某个数字上移或下移)2. 左右移动(将列中的某个数字左移或右移)3. 旋转(以中心为中心旋转整个格子)下面是一个使用A算法解决八数码问题的例子:假设初始状态如下:```markdown4 1 2 756 3 8 05 0 3 2 4 167 86 7 5 8 3 4 2 1 0```目标状态如下:```markdown1 2 3 4 5 6 7 8 00 3 6 7 4 5 8 1 27 8 5 6 1 2 3 4 0```下面是使用A算法解决这个问题的步骤:1. 首先,我们需要构建一个优先级队列(例如最小堆),用于存储所有可能的移动。
在这个例子中,每个移动都有一个成本和优先级。
成本是从当前状态到目标状态的最短路径长度,优先级是当前状态到目标状态的H启发式估计。
H启发式估计通常是当前状态和目标状态之间的曼哈顿距离。
2. 从队列中取出优先级最高(即成本最低)的移动。
在这个例子中,初始状态的移动是"上下移动"。
3. 应用这个移动,并更新所有相关状态的成本和优先级。
在这个例子中,我们将第一行向下移动一格。
然后,我们需要重新评估所有可能的状态,并更新优先级队列。
4. 在更新优先级队列后,我们需要检查是否已经达到目标状态。
如果已经达到目标状态,则算法结束。
否则,我们重复步骤2和步骤3,直到达到目标状态。
5. 在这个例子中,我们需要进行多次上下移动、左右移动和旋转,才能将数字排列成目标顺序。
每次应用移动后,都需要重新评估所有可能的状态,并更新优先级队列。
a星算法求解八数码问题python

a星算法求解八数码问题python一、介绍八数码问题是一种经典的智力游戏,也是人工智能领域中的经典问题之一。
在这个问题中,有一个3×3的棋盘,上面摆着1至8这8个数字和一个空格,初始状态和目标状态都已知。
要求通过移动数字,将初始状态变换成目标状态。
其中空格可以和相邻的数字交换位置。
为了解决这个问题,我们可以使用A*算法。
本文将详细介绍如何用Python实现A*算法来求解八数码问题。
二、A*算法简介A*算法是一种启发式搜索算法,常用于寻找最短路径或最优解等问题。
它基于Dijkstra算法,并加入了启发式函数来加速搜索过程。
在A*算法中,每个节点都有两个估价值:g值和h值。
g值表示从起点到该节点的实际代价,h值表示从该节点到目标节点的估计代价。
启发式函数f(n) = g(n) + h(n) 表示从起点到目标节点的估计总代价。
A*算法采用优先队列来保存待扩展的节点,并按照f(n)值从小到大排序。
每次取出队头元素进行扩展,并将扩展出来的新节点按照f(n)值插入队列中。
当扩展出目标节点时,算法结束。
三、八数码问题的状态表示在八数码问题中,每个状态都可以表示为一个3×3的矩阵。
我们可以用一个一维数组来表示这个矩阵,其中0表示空格。
例如,初始状态可以表示为[2, 8, 3, 1, 6, 4, 7, 0, 5],目标状态可以表示为[1, 2, 3, 8, 0, 4, 7, 6, 5]。
四、A*算法求解八数码问题的步骤1.将初始状态加入优先队列中,并设置g值和h值为0。
2.从队头取出一个节点进行扩展。
如果该节点是目标节点,则搜索结束;否则,将扩展出来的新节点加入优先队列中。
3.对于每个新节点,计算g值和h值,并更新f(n)值。
如果该节点已经在优先队列中,则更新其估价值;否则,将其加入优先队列中。
4.重复第2步至第3步直到搜索结束。
五、Python实现以下是用Python实现A*算法求解八数码问题的代码:```import heapqimport copy# 目标状态goal_state = [1,2,3,8,0,4,7,6,5]# 启发式函数:曼哈顿距离def h(state):distance = 0for i in range(9):if state[i] == 0:continuerow = i // 3col = i % 3goal_row = (state[i]-1) // 3goal_col = (state[i]-1) % 3distance += abs(row - goal_row) + abs(col - goal_col)return distance# A*算法def A_star(start_state):# 初始化优先队列和已访问集合queue = []visited = set()# 将初始状态加入优先队列中,并设置g值和h值为0heapq.heappush(queue, (h(start_state), start_state, 0))while queue:# 取出队头元素进行扩展f, state, g = heapq.heappop(queue)# 如果该节点是目标节点,则搜索结束;否则,将扩展出来的新节点加入优先队列中。
AStar算法解决八数码问题

江南大学物联网工程学院实验报告课程名称人工智能实验名称A*算法解决8数码问题实验日期2018.3.20班级计科1501 姓名周启航学号1030415127一、实验目的:修改A*算法,使之能解决N*N矩阵八数码问题问题描述:八数码难题:在3×3方格棋盘上,分别放置了标有数字1,2,3,4,5,6,7,8的八张牌,初始状态S0可自己随机设定,使用的操作有:空格上移,空格左移,空格右移,空格下移。
二、算法描述:1.状态描述八数码的任何一种摆法就是一个状态,所有摆法即为状态集S,他们构成了一个状态空间,其大小为9包括8个数码和一个空格,每个数码就是一个分离的独立的子空间,其所在位置为x:i/3,y:i%3.相应的操作算子就是数码的移动即:将空格向上移UP、将空格向下移DOWN、将空格向左移LEFT、将空格向右移RIGHT,经过一些操作算子后达到目标状态。
2.启发函数设计启发函数为现在的状态中各位置与目标状态各位置数码值不同的个数,例如:现在状态:w=123456780,目标状态为:t=123456708,则h(n)=2.3.规则的判断条件把未扩展的状态存入open表,排序后取出优先状态扩展搜索,将扩展后的存入closed表,循环执行直到扩展出目标状态。
4.算法流程图5.核心代码操作算子:int solve() //搜索过程{P cur;P p;while(!open.empty()){cur=open.top(); //open表open.pop();if(cur.s==t) return cur.id; //达到目标状态,返回当前节点的idint x,y;int ops=0;while(cur.s[ops]!='0') ops++;x=ops/N,y=ops%N; //空格所在位置int r=cur.id;if(x>0){ //空格向上移p.s=cur.s;swap(p.s[ops],p.s[ops-3]);if(!mp[p.s]){p.d=cur.d+1,p.w=calw(p.s),p.id=top+1;open.push(p);stack[++top]=p.s;father[top]=r;mp[p.s]=1;}}if(x<N-1){ //空格向下移p.s=cur.s;swap(p.s[ops],p.s[ops+3]);if(!mp[p.s]){p.d=cur.d+1,p.w=calw(p.s),p.id=top+1;open.push(p);stack[++top]=p.s;father[top]=r;mp[p.s]=1;}}if(y>0){ //空格向左移p.s=cur.s;swap(p.s[ops],p.s[ops-1]);if(!mp[p.s]){p.d=cur.d+1,p.w=calw(p.s),p.id=top+1;open.push(p);stack[++top]=p.s;father[top]=r;mp[p.s]=1;}}if(y<N-1){ //空格向右移p.s=cur.s;swap(p.s[ops],p.s[ops+1]);if(!mp[p.s]){p.d=cur.d+1,p.w=calw(p.s),p.id=top+1;open.push(p);stack[++top]=p.s;father[top]=r;mp[p.s]=1;}}}return -1; //搜索失败}int main(){cout<<"请输入棋盘大小N*N\nN:";cin>>N;cout<<"请输入测试的组数:\n";int tt; //测试的组数cin>>tt;for(int k=1;k<=tt;k++){cout<<"Case "<<k<<":\n";int i,j;char a;cout<<"请输入目的状态:\n";cin>>t;p.s="";cout<<"请输入初始状态:\n";for(i=0;i<N;i++){for(j=0;j<N;j++){cin>>a; //输入0~8数码p.s+=a;}}p.d=0,p.w=calw(p.s),p.id=0;father[0]=-1;mp[p.s]=1;stack[0]=p.s;open.push(p); //往open表中加入初始状态节点int id=solve();//调用搜索过程if(id==-1){cout<<"无解!\n";}else{int c=-1;while(id>=0){ //把stack中存的节点按次序放入到record中record[++c]=stack[id];id=father[id];}cout<<"原图:"<<endl;print(c); //输出初始节点cout<<"移动过程: \n\n";for(i=c-1;i>=0;i--){cout<<"Step "<<c-i<<":\n";//输出当前搜索步骤print(i);//输出当前搜索的节点}cout<<"移动结束!\n";mp.clear();while(!open.empty()) open.pop();top=0;cout<<endl;}system("pause\n");return 0;}三、实验结果:四、实验心得:只是做了简单修改,只能解决些简单的问题,过于复杂的还不能实现,不过还是体会到了A*算法的厉害,也见识到了人工智能的神奇,会继续努力学习。
基于启发式搜索算法A星解决八数码问题

int statue[size][size]; //记录当前节点的状态 struct Node * Tparent; //用来构成搜索树,该树由搜索图的反向指针构成 struct Node * opennext; //用来构成 open 表,该指针指向该节点在 open 表中的下一个 节点 struct Node * closenext; //用来构成 open 表,该指针指向该节点在 close 表中的下一个 节点 struct Node * brothernext; //构成兄弟链表,该指针指向该节点在兄弟链表中的下一个节 点 int f; //记录当前节点的 f 函数值 int g; //记录当前节点的 g 函数的值 int h; //记录当前节点的 h 函数的值 };
5
get_bestroute (bestNode); return; }
2.2.7 生成 bestNode 所指节点的后继节点
定义一个后继节点链表,表头为 head_b,将 bestNode 所指节点的不是前驱节点的后继 节点,链接到后继及诶单链表中。getchild 函数可以实现这个功能。
//产生 bestNode 的一切后继节点。。 head head_b; //定义 bestNode 的后继节点表 head_b.next=NULL; getchild (&head_b,bestNode); //产生 bestNode 的子节点,将不是 bestNode 的父节点的
while (head_b.next!=NULL) { Node *tmp=getbrother (&head_b); //从后继节点表中取出一个节点记为 tmp,并从
用A算法解决八数码问题

用A*算法解决八数码问题一、 题目:八数码问题也称为九宫问题。
在3×3的棋盘,有八个棋子,每个棋子上标有1至8的某一数字,不同棋子上标的数字不相同。
棋盘上还有一个空格,与空格相邻的棋子可以移到空格中。
要解决的问题是:任意给出一个初始状态和一个目标状态,找出一种从初始转变成目标状态的移动棋子步数最少的移动步骤。
二、 问题的搜索形式描述状态:状态描述了8个棋子和空位在棋盘的9个方格上的分布。
初始状态:任何状态都可以被指定为初始状态。
操作符:用来产生4个行动(上下左右移动)。
目标测试:用来检测状态是否能匹配上图的目标布局。
路径费用函数:每一步的费用为1,因此整个路径的费用是路径中的步数。
现在任意给定一个初始状态,要求找到一种搜索策略,用尽可能少的步数得到上图的目标状态算法介绍三、 解决方案介绍1.A*算法的一般介绍A*(A-Star)算法是一种静态路网中求解最短路最有效的方法。
对于几何路网来说,可以取两节点间欧几理德距离(直线距离)做为估价值,即()()()()()()**f g n sqrt dx nx dx nx dy ny dy ny =+--+--;这样估价函数f 在g 值一定的情况下,会或多或少的受估价值h 的制约,节点距目标点近,h 值小,f 值相对就小,能保证最短路的搜索向终点的方向进行。
明显优于盲目搜索策略。
A star算法在静态路网中的应用2.算法伪代码创建两个表,OPEN表保存所有已生成而未考察的节点,CLOSED表中记录已访问过的节点。
算起点的估价值,将起点放入OPEN表。
while(OPEN!=NULL){从OPEN表中取估价值f最小的节点n;if(n节点==目标节点){break;}for(当前节点n 的每个子节点X){算X的估价值;if(X in OPEN){if( X的估价值小于OPEN表的估价值 ){把n设置为X的父亲;更新OPEN表中的估价值; //取最小路径的估价值}}if(X inCLOSE){if( X的估价值小于CLOSE表的估价值 ){把n设置为X的父亲;更新CLOSE表中的估价值;把X节点放入OPEN //取最小路径的估价值}}if(X not inboth){把n设置为X的父亲;求X的估价值;并将X插入OPEN表中; //还没有排序}}//end for将n节点插入CLOSE表中;按照估价值将OPEN表中的节点排序; //实际上是比较OPEN表内节点f的大小,从最小路径的节点向下进行。
基于A星算法的8数码问题求解方案设计(1)

基于A星算法的8数码问题求解⽅案设计(1)⼀、问题描述8数码问题⼜称9宫问题,与游戏“华容道”类似。
意在给定的33棋格的8个格⼦内分别放⼀个符号,符号之间互不相同,余下的⼀格为空格。
并且通常把8个符号在棋格上的排列顺序称作8数码的状态。
开始时,规则给定⼀个初始状态和⼀个⽬标状态,并要求被试者对棋格内的符号经过若⼲次移动由初始状态达到⽬标状态,这个过程中只有空格附近的符号可以朝空格的⽅向移动,且每次只能移动⼀个符号。
为⽅便编程和表⽰,本⽂中8个格⼦内的符号分别取1—8的8个数字表⽰,空格⽤0表⽰。
并给定8数码的初始状态和⽬标状态分别如图1、2所⽰。
图1 初始状态图2 ⽬标状态则要求以图1为初始状态,通过交换0和0的上、下、左、右四个⽅位的数字(每次只能和其中⼀个交换),达到图2所⽰⽬标状态。
⼆、实验⽬的熟悉和掌握启发式搜索的定义、估价函数和算法过程,并利⽤A*算法求解N数码难题,理解求解流程和搜索顺序。
三、实验任务1)实现类似于如图所⽰N数码难题演⽰程序。
2)⽤你所熟悉的程序语⾔实现,可以B/S实现,也可以C/S实现四、算法设计根据任务要求,本⽂采⽤A*搜索算法。
但要在计算机上通过编程解决该问题,还应当解决该问题在计算机上表⽰的⽅式,并设计合适的启发函数,以提⾼搜索效率。
①状态的表⽰在A*算法中,需要⽤到open表和closed表,特别是在open表中,待扩展节点间有很严格的扩展顺序。
因此在表⽰当前状态的变量中,必须要有能指向下⼀个扩展节点的指针,以完成对open表中元素的索引。
从这⼀点上看,open表中的元素相互间即构成了⼀个线性表,因此初步选定使⽤结构体表⽰问题的状态。
如图3所⽰,表⽰问题的结构体包括表⽰当前节点状态的DATA和指向open 表中下⼀个待扩展节点的指针NEXT。
图3 结构体现在进⼀步考虑DATA中包括的内容:如图1、2所⽰,8数码问题的提出是以⼀个33数表表⽰的,因此本⽂中采⽤⼀个33的⼆维数组s[3][3]表⽰当前状态的具体信息。
A-star-算法-八数码问题-C++-报告+代码+详细注释1
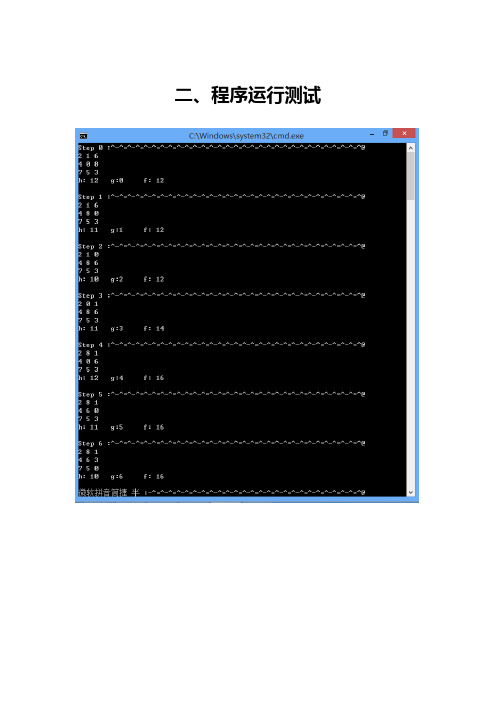
二、程序运行测试A*算法求解八数码问题一、详细设计说明1.评价函数以当前状态下各将牌到目标位置的距离之和作为节点的评价标准。
距离的定义为: “某将牌行下标与目标位置行下标之差的绝对值 + 列下标与目标位置列下标之差的绝对值”。
距离越小, 该节点的效果越好。
某个状态所有将牌到目标位置的距离之和用“h值”表示。
2.主要函数2.1countH(state & st);countH函数功能是计算st状态的h值。
2.2计算过程中将会用到rightPos数组, 数组里记录的是目标状态下, 0~9每个将牌在九宫格里的位置(位置 = 行下标 * 3 + 列下标)。
2.3f(state * p);f()=h()+level2.4look_up_dup(vector<state*> & vec, state * p);2.5在open表或close表中, 是否存在指定状态p, 当找到与p完全相等的节点时, 退出函数。
2.6search(state & start);在open表不为空时, 按f值由小到大对open表中元素进行排序。
调用findZero()函数找到0值元素的位置。
空格可以向上下左右四个方向移动, 前提是移动后不能越过九宫格的边界线。
确定某方向可走后, 空格移动一步, 生成状态p’。
2.7此时, 检查open表中是否已有p’, 若有, 更新p’数据;检查close表中是否已有p’, 若有, 将p’从close表中删除, 添加到open表中。
2.8重复的执行这个过程, 直到某状态的h值为零。
2.9dump_solution(state * q);在终端输出解路径。
// A*算法八数码问题#include"stdafx.h"#include<iostream>#include<vector>#include<time.h>#include<algorithm>using namespace std;const int GRID = 3; //Grid表示表格的行数(列数), 这是3*3的九宫格int rightPos[9] = { 4, 0, 1, 2, 5, 8, 7, 6, 3 };//目标状态时, 若p[i][j]=OMG,那么3*i+j = rightPos[OMG]struct state{int panel[GRID][GRID];int level; //记录深度int h;state * parent;state(int level) :level(level){}bool operator == (state & q){//判断两个状态是否完全相等(对应位置元素相等), 完全相等返回true,否则返回falsefor (int i = 0; i<GRID; i++){for (int j = 0; j<GRID; j++){if (panel[i][j] != q.panel[i][j])return false;}}return true;}state & operator = (state & p){ //以状态p为当前状态赋值, 对应位置元素相同for (int i = 0; i<GRID; i++){for (int j = 0; j<GRID; j++){panel[i][j] = p.panel[i][j];}}return *this;}};void dump_panel(state * p){ //将八数码按3*3矩阵形式输出for (int i = 0; i<GRID; i++){for (int j = 0; j<GRID; j++)cout << p->panel[i][j] << " ";cout << endl;}}int countH(state & st){ //给定状态st, 计算它的h值。
用A算法解八数码问题

用A*算法解八数码问题1.启发式搜索广度优先搜索和双向广度优先搜索都属于盲目搜索,这在状态空间不大的情况下是很合适的算法,可是当状态空间十分庞大时,它们的效率实在太低,往往都是在搜索了大量无关的状态结点后才碰到解答,甚至更本不能碰到解答。
搜索是一种试探性的查寻过程,为了减少搜索的盲目性引,增加试探的准确性,就要采用启发式搜索了。
所谓启发式搜索就是在搜索中要对每一个搜索的位置进行评估,从中选择最好、可能容易到达目标的位置,再从这个位置向前进行搜索,这样就可以在搜索中省略大量无关的结点,提高了效率。
2.A*算法A*算法是一种常用的启发式搜索算法。
在A*算法中,一个结点位置的好坏用估价函数来对它进行评估。
A*算法的估价函数可表示为:f'(n) = g'(n) + h'(n)这里,f'(n)是估价函数,g'(n)是起点到终点的最短路径值(也称为最小耗费或最小代价),h'(n)是n到目标的最短路经的启发值。
由于这个f'(n)其实是无法预先知道的,所以实际上使用的是下面的估价函数:f(n) = g(n) + h(n)其中g(n)是从初始结点到节点n的实际代价,h(n)是从结点n到目标结点的最佳路径的估计代价。
在这里主要是h(n)体现了搜索的启发信息,因为g(n)是已知的。
用f(n)作为f'(n)(1)g(n)>=g'(n)的近似,也就是用g(n)代替g'(n),h(n)代替h'(n)。
这样必须满足两个条件:(大多数情况下都是满足的,可以不用考虑),且f必须保持单调递增。
(2)h必须小于等于实际的从当前节点到达目标节点的最小耗费h(n)<=h'(n)。
第二点特别的重要。
可以证明应用这样的估价函数是可以找到最短路径的。
3.A*算法的步骤A*算法基本上与广度优先算法相同,但是在扩展出一个结点后,要计算它的估价函数,并根据估价函数对待扩展的结点排序,从而保证每次扩展的结点都是估价函数最小的结点。
a算法求解八数码问题 实验报告

题目: a算法求解八数码问题实验报告目录1. 实验目的2. 实验设计3. 实验过程4. 实验结果5. 实验分析6. 实验总结1. 实验目的本实验旨在通过实验验证a算法在求解八数码问题时的效果,并对其进行分析和总结。
2. 实验设计a算法是一种启发式搜索算法,主要用于在图形搜索和有向图中找到最短路径。
在本实验中,我们将使用a算法来解决八数码问题,即在3x3的九宫格中,给定一个初始状态和一个目标状态,通过移动数字的方式将初始状态转变为目标状态。
具体的实验设计如下:1) 实验工具:我们将使用编程语言来实现a算法,并结合九宫格的数据结构来解决八数码问题。
2) 实验流程:我们将设计一个初始状态和一个目标状态,然后通过a 算法来求解初始状态到目标状态的最短路径。
在求解的过程中,我们将记录下每一步的状态变化和移动路径。
3. 实验过程我们在编程语言中实现了a算法,并用于求解八数码问题。
具体的实验过程如下:1) 初始状态和目标状态的设计:我们设计了一个初始状态和一个目标状态,分别为:初始状态:1 2 34 5 67 8 0目标状态:1 2 38 0 42) a算法求解:我们通过a算法来求解初始状态到目标状态的最短路径,并记录下每一步的状态变化和移动路径。
3) 实验结果在实验中,我们成功求解出了初始状态到目标状态的最短路径,并记录下了每一步的状态变化和移动路径。
具体的实验结果如下:初始状态:1 2 34 5 67 8 0目标状态:1 2 38 0 47 6 5求解路径:1. 上移1 2 37 8 62. 左移1 2 3 4 0 5 7 8 63. 下移1 2 3 4 8 5 7 0 64. 右移1 2 3 4 8 5 0 7 65. 上移1 2 3 0 8 5 4 7 61 2 38 0 54 7 67. 下移1 2 38 7 54 0 68. 右移1 2 38 7 54 6 0共计8步,成功从初始状态到目标状态的最短路径。
关于A算法实现的8数码问题(人工智能)

基于A*算法解决把数码问题《人工智能》专业:信息与计算科学班级:101001学号:101001102姓名:陈斌指导老师:时华日期:2013年10月14日一、问题描述8数码问题又称9宫问题,与游戏“华容道”类似。
意在给定的33⨯棋格的8个格子内分别放一个符号,符号之间互不相同,余下的一格为空格。
并且通常把8个符号在棋格上的排列顺序称作8数码的状态。
开始时,规则给定一个初始状态和一个目标状态,并要求被试者对棋格内的符号经过若干次移动由初始状态达到目标状态,这个过程中只有空格附近的符号可以朝空格的方向移动,且每次只能移动一个符号。
为方便编程和表示,本文中8个格子内的符号分别取1—8的8个数字表示,空格用0表示。
并给定8数码的初始状态和目标状态分别如图1、2所示。
图1 初始状态图2 目标状态则要求以图1为初始状态,通过交换0和0的上、下、左、右四个方位的数字(每次只能和其中一个交换),达到图2所示目标状态。
二、算法设计根据任务要求,本文采用A*搜索算法。
但要在计算机上通过编程解决该问题,还应当解决该问题在计算机上表示的方式,并设计合适的启发函数,以提高搜索效率。
①状态的表示在A*算法中,需要用到open表和closed表,特别是在open表中,待扩展节点间有很严格的扩展顺序。
因此在表示当前状态的变量中,必须要有能指向下一个扩展节点的指针,以完成对open表中元素的索引。
从这一点上看,open表中的元素相互间即构成了一个线性表,因此初步选定使用结构体表示问题的状态。
如图3所示,表示问题的结构体包括表示当前节点状态的DATA和指向open 表中下一个待扩展节点的指针NEXT。
图3 结构体现在进一步考虑DATA中包括的内容:如图1、2所示,8数码问题的提出是以一个33⨯数表表示的,因此本文中采用一个33⨯的二维数组s[3][3]表示当前状态的具体信息。
而为了保证在搜索到目标状态后能够顺利复现寻优路径,当前状态的DATA中还应该包括一个指向其父节点的指针father,这样,才能在达到目标状态后,通过指针father逐层回溯到初始状态,即复现寻优路径。
人工智能-A算法求解8数码问题

实验四 A*算法求解8数码问题一、实验目的熟悉和掌握启发式搜索的定义、估价函数和算法过程,并利用A*算法求解8数码难题,理解求解流程和搜索顺序。
二、实验原理A*算法是一种启发式图搜索算法,其特点在于对估价函数的定义上。
对于一般的启发式图搜索,总是选择估价函数f值最小的节点作为扩展节点。
因此,f 是根据需要找到一条最小代价路径的观点来估算节点的,所以,可考虑每个节点n的估价函数值为两个分量:从起始节点到节点n的实际代价g(n)以及从节点n 到达目标节点的估价代价h(n),且h(n)<=h*(n),h*(n)为n节点到目标节点的最优路径的代价。
八数码问题是在3×3的九宫格棋盘上,排放有8个刻有1~8数码的将牌。
棋盘中有一个空格,允许紧邻空格的某一将牌可以移到空格中,这样通过平移将牌可以将某一将牌布局变换为另一布局。
针对给定的一种初始布局或结构(目标状态),问如何移动将牌,实现从初始状态到目标状态的转变。
如图1所示表示了一个具体的八数码问题求解。
图1 八数码问题的求解三、实验内容1、参考A*算法核心代码,以8数码问题为例实现A*算法的求解程序(编程语言不限),要求设计两种不同的估价函数。
2、在求解8数码问题的A*算法程序中,设置相同的初始状态和目标状态,针对不同的估价函数,求得问题的解,并比较它们对搜索算法性能的影响,包括扩展节点数、生成节点数等。
3、对于8数码问题,设置与图1所示相同的初始状态和目标状态,用宽度优先搜索算法(即令估计代价h(n)=0的A*算法)求得问题的解,记录搜索过程中的扩展节点数、生成节点数。
4、提交实验报告和源程序。
四.实验截图五.源代码#include<iostream>#include"stdio.h"#include"stdlib.h"#include"time.h"#include"string.h"#include<queue>#include<stack>using namespace std;const int N=3;//3*3棋?盘ìconst int Max_Step=32;//最?大洙?搜?索÷深?度èenum Direction{None,Up,Down,Left,Right};//方?向ò,?分?别纄对?应畖上?下?左哩?右?struct Chess//棋?盘ì{int chessNum[N][N];//棋?盘ì数簓码?int Value;//评à估à值μDirection BelockDirec;//所ù屏á蔽?方?向òstruct Chess * Parent;//父?节ú点?};void PrintChess(struct Chess *TheChess);//打洙?印?棋?盘ìstruct Chess * MoveChess(struct Chess * TheChess,Direction Direct,bool CreateNewChess);//移?动ˉ棋?盘ì数簓字?int Appraisal(struct Chess * TheChess,struct Chess * Target);//估à价?函ˉ数簓struct Chess * Search(struct Chess* Begin,struct Chess * Target);//A*搜?索÷函ˉ数簓int main(){//本?程ì序ò的?一?组哩?测a试?数簓据Y为a/*初?始?棋?盘ì*1 4 0**3 5 2**6 7 8**//*目?标括?棋?盘ì*0 1 2**3 4 5**6 7 8**/Chess Target;Chess *Begin,*ChessList;Begin=new Chess;int i;cout<<"请?输?入?初?始?棋?盘ì,?各÷数簓字?用?空?格?隔?开a:阰"<<endl;for(i=0;i<N;i++){for(int j=0;j<N;j++){cin>>Begin->chessNum[i][j];}}cout<<"请?输?入?目?标括?棋?盘ì,?各÷数簓字?用?空?格?隔?开a:阰"<<endl;for(i=0;i<N;i++){for(int j=0;j<N;j++){cin>>Target.chessNum[i][j];}}//获?取?初?始?棋?盘ìAppraisal(Begin,&Target);Begin->Parent=NULL;Begin->BelockDirec=None;Target.Value=0;cout<<"初?始?棋?盘ì:";PrintChess(Begin);cout<<"目?标括?棋?盘ì:";PrintChess(&Target);ChessList=Search(Begin,&Target);//搜?索÷//打洙?印?if(ChessList){/*将?返う?回?的?棋?盘ì列表括?利?用?栈?将?其?倒?叙e*/Chess *p=ChessList;stack<Chess *>Stack;while(p->Parent!=NULL){Stack.push(p);p=p->Parent;}cout<<"搜?索÷结á果?:"<<endl;int num=1;while(!Stack.empty()){cout<<"第台?<<num<<"步?: ";num++;PrintChess(Stack.top());Stack.pop();}cout<<"\n完?成é!"<<endl;}elsecout<<"搜?索÷不?到?结á果?,?搜?索÷深?度è大洙?于?2\n"<<endl;return 0;}//打洙?印?棋?盘ìvoid PrintChess(struct Chess *TheChess){cout<<"(评à估à值μ为a";cout<<TheChess->Value;cout<<")"<<endl;for(int i=0;i<N;i++){cout<<" ";for(int j=0;j<N;j++){cout<<TheChess->chessNum[i][j]<<" ";}cout<<endl;}}//移?动ˉ棋?盘ìstruct Chess * MoveChess(struct Chess * TheChess,Direction Direct,bool CreateNewChess) {struct Chess * NewChess;//获?取?空?闲D格?位?置?int i,j;for(i=0;i<N;i++){bool HasGetBlankCell=false;for(j=0;j<N;j++){if(TheChess->chessNum[i][j]==0){HasGetBlankCell=true;break;}}if(HasGetBlankCell)break;}int ii=i,jj=j;bool AbleMove=true;//判D断?是?否?可é以?移?动ˉswitch(Direct){case Up:i++;if(i>=N)AbleMove=false;break;case Down:i--;if(i<0)AbleMove=false;break;case Left:j++;if(j>=N)AbleMove=false;break;case Right:j--;if(j<0)AbleMove=false;break;};if(!AbleMove)//不?可é以?移?动ˉ则ò返う?回?原-节ú点?{return TheChess;}if(CreateNewChess){NewChess=new Chess();for(int x=0;x<N;x++){for(int y=0;y<N;y++)NewChess->chessNum[x][y]=TheChess->chessNum[x][y];//创洹?建¨新?棋?盘ì,?此?时骸?值μ与?原-棋?盘ì一?致?}}elseNewChess=TheChess;NewChess->chessNum[ii][jj] = NewChess->chessNum[i][j];//移?动ˉ数簓字?NewChess->chessNum[i][j]=0;//将?原-数簓字?位?置?设Θ?置?为a空?格?return NewChess;}//估à价?函ˉ数簓int Appraisal(struct Chess * TheChess,struct Chess * Target){int Value=0;for(int i=0;i<N;i++){for(int j=0;j<N;j++){if(TheChess->chessNum[i][j]!=Target->chessNum[i][j])Value++;}}TheChess->Value=Value;return Value;}//A*搜?索÷函ˉ数簓struct Chess * Search(struct Chess* Begin,struct Chess * Target){Chess *p1,*p2,*p;int Step=0;//深?度èp=NULL;queue<struct Chess *> Queue;Queue.push(Begin);//初?始?棋?盘ì入?队ó//搜?索÷do{p1=(struct Chess *)Queue.front();Queue.pop();//出?队ófor(int i=1;i<=4;i++)//分?别纄从洙?四?个?方?向ò推?导?出?新?子哩?节ú点? {Direction Direct=(Direction)i;if(Direct==p1->BelockDirec)//跳?过y屏á蔽?方?向òcontinue;p2=MoveChess(p1,Direct,true);//移?动ˉ数簓码?if(p2!=p1)//数簓码?是?否?可é以?移?动ˉ{Appraisal(p2,Target);//对?新?节ú点?估à价?if(p2->Value<=p1->Value)//是?否?为a优?越?节ú点?{p2->Parent=p1;switch(Direct)//设Θ?置?屏á蔽?方?向ò,防え?止1往?回?推?{case Up:p2->BelockDirec=Down;break;case Down:p2->BelockDirec=Up;break;case Left:p2->BelockDirec=Right;break;case Right:p2->BelockDirec=Left;break;}Queue.push(p2);//存?储洹?节ú点?到?待鋣处鋦理え?队ó列if(p2->Value==0)//为a0则ò,搜?索÷完?成é{p=p2;i=5;}}else{delete p2;//为a劣ⅷ?质ê节ú点?则ò抛×弃úp2=NULL;}}}Step++;if(Step>Max_Step)return NULL;}while(p==NULL || Queue.size()<=0);return p;}六、实验报告要求1、分析不同的估价函数对A*搜索算法性能的影响等。
采用A算法解决八数码问题

人工智能实验一报告题目:采用A*算法解决八数码问题姓名:XXX学号:10S003028专业:计算机科学与技术提交日期:2011-05-04目录1问题描述 .............................................................................................................................. - 2 -1.1待解决问题的解释.................................................................................................. - 2 -1.2问题的搜索形式描述.............................................................................................. - 3 -1.3解决方案介绍(原理).......................................................................................... - 4 -2算法介绍 .............................................................................................................................. - 5 -2.1A*搜索算法一般介绍 .............................................................................................. - 5 -2.2 算法伪代码 ............................................................................................................. - 6 -3算法实现 .............................................................................................................................. - 7 -3.1 实验环境与问题规模............................................................................................. - 7 -3.2 数据结构.................................................................................................................. - 8 -3.3 实验结果.................................................................................................................. - 8 -3.4系统中间及最终输出结果 ..................................................................................... - 8 -4参考文献 .............................................................................................................................. - 9 -5附录—源代码及其注释................................................................................................... - 10 -1问题描述所谓八数码问题是指这样一种游戏:将分别标有数字1,2,3,…,8 的八块正方形数码牌任意地放在一块3×3 的数码盘上。
A星算法求解八数码问题-推荐下载

是 SUC=OLD,把它添加到 BESTNDOE 的后继结点表中
否 g(SUC)<g(OLD)
是
重新确定 OLD 的父辈节点为 BESTNODE,并修正父辈节点的 g 值和 f 值,记下 g(OLD)
2
计算 f 值
计算 g(SUC)=g(BES)+k(BES,SUC)
SUC∈OPEN
对全部高中资料试卷电气设备,在安装过程中以及安装结束后进行高中资料试卷调整试验;通电检查所有设备高中资料电试力卷保相护互装作置用调与试相技互术通关,1系电过,力管根保线据护敷生高设产中技工资术艺料0不高试仅中卷可资配以料置解试技决卷术吊要是顶求指层,机配对组置电在不气进规设行范备继高进电中行保资空护料载高试与中卷带资问负料题荷试2下卷2,高总而中体且资配可料置保试时障卷,各调需类控要管试在路验最习;大题对限到设度位备内。进来在行确管调保路整机敷使组设其高过在中程正资1常料中工试,况卷要下安加与全强过,看度并22工且22作尽22下可22都能22可地护以缩1关正小于常故管工障路作高高;中中对资资于料料继试试电卷卷保破连护坏接进范管行围口整,处核或理对者高定对中值某资,些料审异试核常卷与高弯校中扁对资度图料固纸试定,卷盒编工位写况置复进.杂行保设自护备动层与处防装理腐置,跨高尤接中其地资要线料避弯试免曲卷错半调误径试高标方中高案资等,料,编试要5写、卷求重电保技要气护术设设装交备备置底4高调、动。中试电作管资高气,线料中课并敷3试资件且、设卷料中拒管技试试调绝路术验卷试动敷中方技作设包案术,技含以来术线及避槽系免、统不管启必架动要等方高多案中项;资方对料式整试,套卷为启突解动然决过停高程机中中。语高因文中此电资,气料电课试力件卷高中电中管气资壁设料薄备试、进卷接行保口调护不试装严工置等作调问并试题且技,进术合行,理过要利关求用运电管行力线高保敷中护设资装技料置术试做。卷到线技准缆术确敷指灵设导活原。。则对对:于于在调差分试动线过保盒程护处中装,高置当中高不资中同料资电试料压卷试回技卷路术调交问试叉题技时,术,作是应为指采调发用试电金人机属员一隔,变板需压进要器行在组隔事在开前发处掌生理握内;图部同纸故一资障线料时槽、,内设需,备要强制进电造行回厂外路家部须出电同具源时高高切中中断资资习料料题试试电卷卷源试切,验除线报从缆告而敷与采设相用完关高毕技中,术资要资料进料试行,卷检并主查且要和了保检解护测现装处场置理设。备高中资料试卷布置情况与有关高中资料试卷电气系统接线等情况,然后根据规范与规程规定,制定设备调试高中资料试卷方案。
人工智能A算法八数码报告

人工智能课程设计报告题目:A*算法解决八数码问题专业:计算机软件与理论1.8数码问题1.1问题描述八数码问题是指这样一种游戏:将分别标有数字1,2,3,…,8 的八块正方形数码牌任意地放在一块3×3 的数码盘上。
放牌时要求不能重叠。
于是,在3×3 的数码盘上出现了一个空格。
现在要求按照每次只能将与空格相邻的数码牌与空格交换的原则,不断移动该空格方块以使其和相邻的方块互换,直至达到所定义的目标状态。
空格方块在中间位置时有上、下、左、右4个方向可移动,在四个角落上有2个方向可移动,在其他位置上有3个方向可移动,问题描述如图1-1所示初始状态过渡状态最终状态图1-1 八数码问题执行过程1.2.八数码问题形式化描述初始状态:初始状态向量:规定向量中各分量对应的位置,各位置上的数字。
把3×3的棋盘按从左到右,从上到下的顺序写成一个一维向量。
我们可以设定初始状态:<1,5,2,4,0,3,6,7,8>后继函数:按照某种规则移动数字得到的新向量。
例如:<1,5,2,4,0,3,6,7,8> <1,0,2,4,5,3,6,7,8>目标测试:新向量是都是目标状态。
即<1,2,3,4,5,6,7,8,0>是目标状态?路径耗散函数:每次移动代价为1,每执行一条规则后总代价加1。
1.3解决方案该问题是一个搜索问题。
它是一种状态到另一种状态的变换。
要解决这个问题,必须先把问题转化为数字描述。
由于八数码是一个3*3的矩阵,但在算法中不实用矩阵,而是将这个矩阵转化为一个一维数组,使用这个一维数组来表示八数码,但是移动时要遵守相关规则。
(1)可用如下形式的规则来表示数字通过空格进行移动:<a1,a2,a3,a4,a5,a6,a7,a8,a9>→<b1,b2,b3,b4,b5,b6,b7,b8,b9>(2)共24条移动规则,对应与每个位置的移动规则。
课程设计 用A算法解决8数码问题

课程设计用A算法解决8数码问题
8数码问题是一个组合优化问题,是指给定8个数字,请将这些数字填入九宫格,使
九宫格中每行、列、粗实线和细实线中的数字之和都相等。
本文重点讨论的是用A算法解
决8数码问题的方法,即A算法估价函数。
A算法属于启发式搜索,它的原理是:先计算当前状态的分数,再根据该分数估计状
态所代表的最终的价值,以作为当前局面的启发,判断当前局面是否是最优局面。
针对 8数码问题,A算法估价函数可计算九宫格每行、列和粗实线差值总和,它代表
九宫格中九位之和是如何与其目标值(45)的偏差程度。
根据九宫格中九位之和的偏差程
度定义该九宫格的分数:若九位之和与其目标值相等,则分数成为 0;若差值跨越两个数字,则分数变为 2;若差值跨越一个数字,则分数变为 1。
有了这一定义,A算法便可应
用在8数码问题中了。
正如上述,A算法估价函数的总分数可由九宫格所有表项的偏差程度来定义,若九宫
格所有表项的结果均跟其目标值(45)相等,总分数则为 0,反之则不是,总分数就会根
据表项有多大的偏差程度来决定。
然后A算法搜索遍历到的每个状态都可以根据它对应的
分数计算当前状态的价值,以作为启发,最终定位最优状态。
从理论上讲,A算法可以在求解8数码问题时取得良好的运算的结果,它可以很好的
评估问题的最优解,因此使得搜索树更加有效,从而减少计算机运算时间,提升解答效率。
采用A算法解决八数码问题

人工智能实验一报告题目:采用A*算法解决八数码问题姓名:张博涵学号: 081110317专业:信息与计算科学提交日期: 2014-05-22目录1问题描述........................................................................................................................... - 2 -1.1待解决问题的解释............................................................................................... - 2 -1.2问题的搜索形式描述............................................................................................ - 2 -1.3解决方案介绍(原理)........................................................................................ - 3 -2算法介绍........................................................................................................................... - 4 -2.1A*搜索算法一般介绍............................................................................................ - 4 -2.2 算法伪代码........................................................................................................... - 4 -3算法实现........................................................................................................................... - 5 -3.1 实验环境与问题规模........................................................................................... - 5 -3.2 数据结构............................................................................................................... - 5 -3.3 实验结果............................................................................................................... - 5 -3.4系统中间及最终输出结果.................................................................................... - 7 -4参考文献........................................................................................................................... - 8 - 5附录—源代码及其注释................................................................................................... - 8 -1问题描述所谓八数码问题是指这样一种游戏:将分别标有数字1,2,3,…,8 的八块正方形数码牌任意地放在一块3×3 的数码盘上。
人工智能实验一 八数码问题

启发中的估价是用估价函数表示的,如:f(n) = g(n) + h(n) 其中 f(n) 是节点 n 的估价函数,g(n)是在状态空间中从初始节点到 n 节点的实际代价, h(n)是从 n 到目标节点最佳路径的估计代价。 在此八数码问题中,显然 g(n)就是从初始状 态变换到当前状态所移动的步数,估计函数 f(n)我们就可采用当前状态各个数字牌不在目标
附录—源代码及其注释 #include "stdafx.h" #include "iostream.h" #include <time.h> #include <stdio.h> #include <dos.h> #include <conio.h> static int target[9]={1,2,3,8,0,4,7,6,5}; //class definition
eight_num(int init_num[9]); eight_num(int num1,int num2,int num3,int num4,int num5,int num6,int num7,int num8,int num9) {
num[0]=num1; num[1]=num2; num[2]=num3; num[3]=num4; num[4]=num5; num[5]=num6; num[6]=num7; num[7]=num8; num[8]=num9; } eight_num(void) { for (int i=0;i<9;i++)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
用A*算法解决八数码问题一、 题目:八数码问题也称为九宫问题。
在3×3的棋盘,有八个棋子,每个棋子上标有1至8的某一数字,不同棋子上标的数字不相同。
棋盘上还有一个空格,与空格相邻的棋子可以移到空格中。
要解决的问题是:任意给出一个初始状态和一个目标状态,找出一种从初始转变成目标状态的移动棋子步数最少的移动步骤。
二、 问题的搜索形式描述状态:状态描述了8个棋子和空位在棋盘的9个方格上的分布。
初始状态:任何状态都可以被指定为初始状态。
操作符:用来产生4个行动(上下左右移动)。
目标测试:用来检测状态是否能匹配上图的目标布局。
路径费用函数:每一步的费用为1,因此整个路径的费用是路径中的步数。
现在任意给定一个初始状态,要求找到一种搜索策略,用尽可能少的步数得到上图的目标状态算法介绍三、 解决方案介绍1.A*算法的一般介绍A*(A-Star)算法是一种静态路网中求解最短路最有效的方法。
对于几何路网来说,可以取两节点间欧几理德距离(直线距离)做为估价值,即()()()()()()**f g n sqrt dx nx dx nx dy ny dy ny =+--+--;这样估价函数f 在g 值一定的情况下,会或多或少的受估价值h 的制约,节点距目标点近,h 值小,f 值相对就小,能保证最短路的搜索向终点的方向进行。
明显优于盲目搜索策略。
A star算法在静态路网中的应用2.算法伪代码创建两个表,OPEN表保存所有已生成而未考察的节点,CLOSED表中记录已访问过的节点。
算起点的估价值,将起点放入OPEN表。
while(OPEN!=NULL){从OPEN表中取估价值f最小的节点n;if(n节点==目标节点){break;}for(当前节点n 的每个子节点X){算X的估价值;if(X in OPEN){if( X的估价值小于OPEN表的估价值 ){把n设置为X的父亲;更新OPEN表中的估价值; //取最小路径的估价值}}if(X inCLOSE){if( X的估价值小于CLOSE表的估价值 ){把n设置为X的父亲;更新CLOSE表中的估价值;把X节点放入OPEN //取最小路径的估价值}}if(X not inboth){把n设置为X的父亲;求X的估价值;并将X插入OPEN表中; //还没有排序}}//end for将n节点插入CLOSE表中;按照估价值将OPEN表中的节点排序; //实际上是比较OPEN表内节点f的大小,从最小路径的节点向下进行。
}//end while(OPEN!=NULL)保存路径,即从终点开始,每个节点沿着父节点移动直至起点,这就是你的路径.四、源程序#include <iostream>#include <ctime>#include <vector>using namespace std;constint ROW = 3;constint COL = 3;constint MAXDISTANCE = 10000;constint MAXNUM = 10000;int abs(int a){if (a>0) return a;else return -a;}typedefstruct _Node{int digit[ROW][COL];intdist; // 距离intdep; // 深度int index; // 索引值} Node;Node src, dest;vector<Node>node_v; // 储存节点boolisEmptyOfOPEN() { //判断Open表是否空for (inti = 0; i<node_v.size(); i++) {if (node_v[i].dist != MAXNUM)return false;}return true;}boolisEqual(int index, int digit[][COL]) {//判断节点是否与索引值指向的节点相同for (inti = 0; i< ROW; i++)for (int j = 0; j < COL; j++) {if (node_v[index].digit[i][j] != digit[i][j])return false;}return true;}ostream& operator<<(ostream&os, Node& node) {for (inti = 0; i< ROW; i++) {for (int j = 0; j < COL; j++)os<<node.digit[i][j] << ' ';os<<endl;}returnos;}void PrintSteps(int index, vector<Node>&rstep_v){//输出步骤rstep_v.push_back(node_v[index]);index = node_v[index].index;while (index != 0) {rstep_v.push_back(node_v[index]);index = node_v[index].index;}for (inti = rstep_v.size() - 1; i>= 0; i--)cout<< "Step " <<rstep_v.size() - i<<endl<<rstep_v[i] <<endl;}void Swap(int& a, int& b) { //交换int t;t = a;a = b;b = t;}void Assign(Node& node, int index) {//获取节点for (inti = 0; i< ROW; i++)for (int j = 0; j < COL; j++)node.digit[i][j] = node_v[index].digit[i][j];}intGetMinNode() {//获取启发值最小的节点intdist = MAXNUM;intloc; // the location of minimize nodefor (inti = 0; i<node_v.size(); i++) {if (node_v[i].dist == MAXNUM)continue;else if ((node_v[i].dist + node_v[i].dep) <dist) { loc = i;dist = node_v[i].dist + node_v[i].dep;}}returnloc;}boolisExpandable(Node& node) {//判断是否可扩展for (inti = 0; i<node_v.size(); i++) {if (isEqual(i, node.digit))return false;}return true;}int Distance(Node& node, int digit[][COL]) {//计算距离int distance = 0;bool flag = false;for(inti = 0; i< ROW; i++)for (int j = 0; j < COL; j++)for (int k = 0; k < ROW; k++) {for (int l = 0; l < COL; l++) {if (node.digit[i][j] == digit[k][l]) {distance += abs(i - k) + abs(j - l); flag = true;break;}elseflag = false;}if (flag)break;}return distance;}intMinDistance(int a, int b) {//二者取小return (a < b ? a : b);}void ProcessNode(int index) {//展开节点int x, y;bool flag;for (inti = 0; i< ROW; i++) {for (int j = 0; j < COL; j++) {if (node_v[index].digit[i][j] == 0) { x =i; y = j;flag = true;break;}else flag = false;}if(flag)break;}Node node_up; //上移操作Assign(node_up, index);intdist_up = MAXDISTANCE;if (x > 0) {Swap(node_up.digit[x][y], node_up.digit[x - 1][y]);if (isExpandable(node_up)) {dist_up = Distance(node_up, dest.digit);node_up.index = index;node_up.dist = dist_up;node_up.dep = node_v[index].dep + 1;node_v.push_back(node_up);}}Node node_down; //下移操作Assign(node_down, index);intdist_down = MAXDISTANCE;if (x < 2) {Swap(node_down.digit[x][y], node_down.digit[x + 1][y]); if (isExpandable(node_down)) {dist_down = Distance(node_down, dest.digit);node_down.index = index;node_down.dist = dist_down;node_down.dep = node_v[index].dep + 1;node_v.push_back(node_down);}}Node node_left;//左移操作Assign(node_left, index);intdist_left = MAXDISTANCE;if (y > 0) {Swap(node_left.digit[x][y], node_left.digit[x][y - 1]); if (isExpandable(node_left)) {dist_left = Distance(node_left, dest.digit);node_left.index = index;node_left.dist = dist_left;node_left.dep = node_v[index].dep + 1;node_v.push_back(node_left);}}Node node_right; //右移操作Assign(node_right, index);intdist_right = MAXDISTANCE;if (y < 2) {Swap(node_right.digit[x][y], node_right.digit[x][y + 1]); if (isExpandable(node_right)) {dist_right = Distance(node_right, dest.digit);node_right.index = index;node_right.dist = dist_right;node_right.dep = node_v[index].dep + 1;node_v.push_back(node_right);}}node_v[index].dist = MAXNUM;}int main() {int number;cout<< "输入初始状态:" <<endl; for (inti = 0; i< ROW; i++)for (int j = 0; j < COL; j++) { cin>> number;src.digit[i][j] = number;}src.index = 0;src.dep = 1;cout<< "输入目标状态" <<endl; for (int m = 0; m < ROW; m++) for (int n = 0; n < COL; n++) { cin>> number;dest.digit[m][n] = number;}node_v.push_back(src);while (1) {if (isEmptyOfOPEN()) {cout<< "找不到解!" <<endl;return -1;}else {intloc; // the location of the minimize node loc = GetMinNode();if(isEqual(loc, dest.digit)) {vector<Node>rstep_v;cout<< "初始状态:" <<endl;cout<<src<<endl;PrintSteps(loc, rstep_v);cout<< "成功!" <<endl;break;}elseProcessNode(loc);}}return 0;}欢迎您的下载,资料仅供参考!致力为企业和个人提供合同协议,策划案计划书,学习资料等等打造全网一站式需求。
