南京邮电大学信号与系统2008年真题
南邮真题

南京邮电大学2008年攻读硕士学位研究生入学考试通信系统原理试题一、选择题(每题2分,共60分)1、通信双工嫩那个同时进行发送和接收的通信工作方式称()。
A)单工通信 B)半双工通信 C)全双工通信2、信道滚降会导致信号的时域波形“尾巴”衰减()。
A)变慢 B)变快 C)速度不变3、平稳信号的方差,均值的平方和零时差的自相关分别代表()。
A)直流功率,交流功率和平均功率 B)交流功率,直流功率和平均功率C)平均功率,直流功率和交流功率4、明线,同轴电缆和光缆是()信道。
A)无线随参 B)有线恒参 C)随参5、非线性解调器常常具有的一种现象称为()。
A)频率失真 B)谐波失真 C)门限效应6、根据连续信道容量香农公式,当信道带宽B→∞时,信道容量()。
A)趋于∞ B)趋于0 C)趋于1.44S/n7、OQPSK与QPSK相比功率谱的主瓣包含的功率()。
A)更少 B)更多 C)一样8、A律13折线量化中最大的和最小的量化间隔相差()倍。
A)32 B)128 C)649、信道带宽等于64QAM信号主瓣带宽一半,则频带利用率为()b/s/HZ。
A) 6 B)4 C)310、单音调频系统的调频指数为3,则制度增益为()。
A) 90 B)36 C)10811、当均匀量化电平足够多且量化间隔为10时,量化噪声功率约为()。
A)8.3 B)5 C)6.512、MSK信号相位的连续性导致信号的频谱分量()。
A)集中于主瓣 B)分散于旁瓣 C)在主瓣和旁瓣上均匀分布13、均匀量化编码的编码位数每增加1位,量化信噪比改善()分贝。
A) 3 B)4 C) 614、“0”、“1”等概出现的双极性信号的功率谱不含()。
A)连续谱 B)离散谱 C)连续谱和离散谱15、HDB码中连零数最多有()个。
3A) 3 B) 2 C) 416、八进制数字信号传码率为100B,传信率为()。
若传信率不变,改为二进制传输,则传码率为()。
A)100b/s,300B B )300b/s,300B C)200b/s,200B17、模拟调制的制度增益由小到大的顺序为()。
操作系统试卷

南邮2008/2009学年第一学期《操作系统A 》期末试卷(B )院(系) 班级 学号 姓名试卷请考生注意:1、答案请写在答题纸上,写在试卷上一律无效!2、考试完毕,请将答题纸、试卷、草稿纸全部交给监考老师,不得带出考场一、单项选择题(每题2分,共20分)1、设定一个作业建立一个进程,为了使长、短和交互式作业都能得到及时的运行,应选用的调度算法是( )。
A .先来先服务算法B .短作业优先算法C .多级反馈队列算法D .优先数算法 2、进程从运行状态进入就绪状态的原因可能是( )。
A. 被选中占有处理机B. 等待某一事件C. 等待的事件已发生D. 时间片用完 3、利用管道进行的进程通信机制实质是( )。
A. 信号通信机制B. 共享存储区通信机制C. 共享文件通信机制D. 消息传递通信机制4、某页式存储管理系统中,地址寄存器长度为24位,其中页号占14位,则主存的分块大小应该是( )字节。
A .210B .10C .14D .214 5、下列说法中错误的是( )。
A. 作业分得的主存块数越多,缺页中断率越低 B. 作业划分的页面越小,缺页中断率越低 C. 程序局部性越好,缺页中断率越低 D. OPT 算法的缺页中断率最低装 订 线 内 不 要 答 题自觉遵 守 考 试 规 则,诚 信 考 试,绝 不作 弊6、I/O设备的控制方式中比DMA方式效率高的是()。
A.询问方式B.中断方式C. 通道方式D. 以上都不是7、Spooling技术是一种实现虚拟()的技术。
A. 处理器B. 设备C. 存储器D. 链路8、引入缓冲的主要目的是()。
A. 改善CPU和I/O设备之间速度不匹配的情况B. 节省内存C. 提高CPU的运行频率D. 提高I/O设备的利用率9、位示图方法可用于()。
A. 盘空间的管理B. 盘的驱动调度C. 文件目录的查找D. 页式虚拟存贮管理中的页面调度10、把逻辑文件存放到存储介质上时,如果组织成()文件,则逻辑记录可以按任意次序存放在不相邻的存储块中。
2008信号5-1(M)

2.序列相乘 序列相乘
f (k) = f1(k) f2 (k)
例:已知序列
k < 1 0 f1(k) = k 2 + 5 k ≥ 1
2k k<0 f2 (k) = k + 2 k ≥ 0
求f1(k) + f2 (k)和f1(k) f2 (k)
当 有终序列(左边序列): 有终序列(左边序列): k ≥ k2时,f (k) = 0
k1 ≥ 0的有始序列称为因果序列 k2 ≤ 0的有终序列称为反因果序列
若f (k)仅在k1 ≤ k ≤ k2 (k2 > k1 , 均为整数)区间有非零确定值,
这类序列称为有限序列 注意: 离散信号 序列)理解为 离散信号(序列 注意:1,离散信号 序列 理解为
第五章 离散信号与系统的时域分析
5-1.离散时间信号 离散时间信号 5-1-1离散时间信号的时域描述 离散时间信号的时域描述 一.信号分类 信号分类 模拟信号 量化信号 离散 信号 数字 信号 时间取值 连续 连续 不连续 不连续 幅度取值 连续 不连续 连续 不连续
1 2 3
f (k)
tk
二.离散信号表示法 离散信号表示法 1.解析式 解析式
ρ
作业: 作业:5-1(2)(3) 5-2(1) 5-5(b)(d)
�
x(k) = Acos(0k +)
正弦序列不一定是周期序列
2π = N 是正整数时,则正弦序列为周期 是正整数时, 当 0 序列,且周期为N 序列,且周期为 . ቤተ መጻሕፍቲ ባይዱπ N 是有理数时, 当 = m 是有理数时,则正弦序列为周期序 0 2π 列,且周期为 N = m .
(完整版)南邮通信原理历年期末试卷与答案

8.在抗加性高斯白噪声性能方面,2ASK、2FSK、2PSK从优到差的次序 为()
(C)2FSK、2ASK、2PSK;(C)2ASK、2FSK、2PSK;
(D)2ASK、2PSK、2FSK;(D)2PSK、2FSK、2ASK。
四作图题:(每题5分,共10分)
6.A;7.A;8.D;9.B;10.D
五、论述题:(每题5分,共30分)
1.答:不失真条件:
满足:
H〜为一条水平线;
〜成线性关系
群延迟一频率特性:频率特性对频率的导数。
d
d
2.答:
对信号传输有衰耗,并随时间而变;
传输的时延随时间而变;
产生多径传播,而多径传播对信号传输的影响有:① 产生瑞利型衰落;②
另一分组码(100011)的码距是O
五判断题:(正确划“ 乂”错误划“V”;每题0.5分,共5分)
1.码元传输速率与信息传输速率在数值上是相等的。()
2.设随机过程Xt与Yt独立,则Z tXt Y t的一维概率密度
fzz;tfxx;t fyy;tO ()
3.平稳随机过程的自相关函数具有任意的形状。()
(4) 求出解调器输出端的噪声功率谱密度,并用图形表示出来
、填空题:(每空0.5分,共15分)
1.咼斯。
2
2.p。HPi。
3.乘性干扰、加性干扰。
4.恒参信道、随参信道。
5.产生瑞利型衰落、引起频率弥散、造成频率选择性衰落。
6.单频噪声、脉冲噪声和起伏噪声。
7.连续谱、离散谱。
8.振幅键控(ASK)、移频键控(FSK)和移相键控(PSK)。
Sx是否:
南京邮电大学信号与系统-信号与系统4

7. 单边双曲正弦信号 sinht(t)
sinht1(et et)
2
sinht(t)s22
8. 单边双曲余弦信号 cosht(t)
c osth1(et et)
2
cosht(t)s2s2
《信号与系统》SIGNALS AND SYSTEMS ZB
0
(4) 任何可以进行拉氏变换的信号,其拉氏变换 F(s) 中一
定《没信有号冲与激系函统数》。SIGNALS AND SYSTEMS ZB
4.1.3 (单边)拉氏变换的收敛域
信号 f (t) 乘以收敛因子后,有可能满足绝对可积的
条件。是否一定满足,还要看 f (t) 的性质与 的相对关 系。通常把使 f (t)e- t 满足绝对可积条件的 值的范围
称 为衰减因子; e- t 为收敛因子。 《信号与系统》SIGNALS AND SYSTEMS ZB
取 f(t)e- t 的傅里叶变换:
F[f(t)et] f(t)etejtdt f(t)e(j)tdt
它是 j的函数,可以表示成
Fj f(t)e(j)tdt
例如增长的指数信号: et(t) (0)
2. 0 0:拉氏变换、傅氏变换都存在,且 F(s)F()sj
例如衰减的指数信号:et(t) (0)
F() 1 j
F(s) 1
s
3. 0 0:拉氏变换、傅氏变换都存在,但傅氏变换中
含有冲激函数
P185 表4-1
作业《信号与系统》SIGNALS AND SYSTEMS ZB 返回
连续信号与系统的复频域分析概述
傅里叶变换(频域)分析法
2008年南邮数字信号处理真题

1南京邮电大学2008年攻读硕士学位研究生入学考试数字信号处理试题一、填空题(每空1分,共10分)1、由模拟滤波器设计IIR 数字滤波器时,脉冲响应不变法不适合设计低通、高通、带通、带阻中的_______和_______。
2、在S 平面与Z 平面之间的标准映射关系z=e sT 下(T 为采样周期),S 平面上每一个宽为Ω=_______的横带都映射到整个Z 平面。
3、一个数字滤波器,如果是因果稳定系统,则起系统函数的所有极点应在________。
4、FFT 算法利用了W 因子的一些有效的性质,如2N NW =_______。
5、用窗口法设计FIR 数字滤波器时,如果窗函数是矩形窗,增加窗长度时所设计的数字滤波器的阻带最小衰耗__________,过渡带________。
6、由于有限字长的影响,在数字系统中存在三种误差,除了输入信号和系统参数量化效应外还有一种是_______。
7、已知有限字长序列x(n)的长度为N ,其Z 变换为X(z),则x(n)的傅立叶变换(DTFT )和N 点离散傅立叶变换(DFT)与X(z)的关系分别为X(e jw )=________,X(k)=_________。
(k=0,1,……N-1.)二、选择题(每题2分,共10分)1、一个理想采样系统,采样频率为Ωs =8π,采样后经理想低通H(j Ω)还原,在输入x 1(t)=cos2πt,x 2(t)=cos5πt 下信号分别为y 1(t)和y 2(t),则a 、y 1(t)没有失真,y 2(t)有失真b 、y 1(t)和y 2(t)都有失真c 、y 1(t)和y 2(t)都没有失真2、已知正弦序列x(n)=sin(16/5n π),则该序列a 、是周期序列,周期为5/8b 、是周期序列,周期为5c 、不是周期序列3、一个FIR 数字滤波器,其实现结构为a 、递归结构b 、非递归结构c 、递归或非递归结构4、已知系统的单位脉冲响应为h(n)=u(3-n),则该系统为a 、非因果,不稳定b 、非因果,稳定c 、因果,不稳定5、已知系统输入输出关系为y(n)=2x(n)+5,则系统为H(j Ω)0, |Ω|≧4π1/4,|Ω|﹤4π2a 、线性、时不变系统b 、非线性、时不变系统c 、非线性、时变系统三、画图题(每题10分,共20分)1、画出N=6按时间抽取(DIT )的FFT 分解流图,要求:(1)按照N=3×2分解,注明输入、输出序列及每一级的W 因子。
2008信号与系统A卷答案

(10分)1. 已知)(t f 的波形如下图所示,试画出)22(t f -的波形。
(5分) (2分)(1分)(2分)(直接给出最终结果,不扣分)2. 已知)(t f 的波形如下图所示,利用()t u 写出该信号的时间表达式。
(5分)()()()()212-+--=t u t u t u t f(知道由三项组成,但表达式写错,给2分)(4分)计算积分dt t t e t )2()32(+δ+⎰∞∞--()6232)2()32(22-=+=+δ+-=-∞∞--⎰e t e dt t t e t t t (2分)(2分) (8分)已知描述连续时间LTI 系统的微分方程为()()()()t x dtt dx t y dt t dy +=+2 求该系统的单位冲激响应()t h 。
()21++=s s s H (3分) ()211+-=s s H (2分) ()()()t u e t t h t2--δ= (3分)(用时域等其它方法求解,给出相应步骤分)四、 (10分)一个连续时间LTI 系统的激励)(t x 和单位冲激响应)(t h 分别为()()t u t x =,()()t u e t h t 3-= 计算该系统的零状态响应()t y ZS 。
()s s X 1=(2分) ()31+=s s H (2分) ()()()()31+==s s s H s X s Y ZS (2分) ()⎪⎭⎫⎝⎛+-=31131s s s Y ZS (2分)()()()t u e t y t ZS 3131--=(2分)(18分)(1)设()tf 为带限信号,频带宽度为m ω,求信号()⎪⎭⎫⎝⎛t f t f 21,2的带宽(6分) 规律:时间压缩,频域扩展,时间扩展,频域压缩 (2分)()t f 2 时间压缩2倍,所以频域扩展2倍,即()t f 2的带宽为m ω2 (2分)⎪⎭⎫ ⎝⎛t f 21时间扩展2倍,所以频域压缩2倍,即⎪⎭⎫⎝⎛t f 21的带宽为m ω21 (2分)(2)已知信号如图所示,设其频谱函数为()ωF ,不要求()ωF ,求()0F (6分)根据 ()()dt et f F tj ωω-∞∞-⎰=(2分得到()()828210=⨯⨯==⎰∞∞-dtt f F (2分 + 2分) )(3)求信号 ⎪⎩⎪⎨⎧><+=1 , 01),cos 1(2)(t t t t f π 的傅里叶变换(6分)()()()t t G t f πcos 12+= (1分) ()()ωSa t G 422↔ (1分)()()()()[]πωδπωδπωπδπ++-+↔+2cos 1t (1分)()()()()()()()()[][]()()()()[][]()()()πωπωωπωδπωδωδωπωδπωδπωπδωπωπ++-+=++-+*=++-+*⨯=↔+=Sa Sa Sa Sa Sa F t t G t f 224222421cos 12 (3分)(每小题6分,18分)(1) 求函数()())(3223t u e e t f t t ---=的拉普拉斯变换()s F ; ()()()()2352332+++-=+-+=s s s s s s F ( 6分 ) (2) 求函数()()86162++=s s s s F 的单边拉普拉斯反变换()t f ;()()()()()()42242421686162+++-+=++=++=s s s s s s s s s s F ( 4分 )(算错分子的系数扣2分)()())(24242t u e e t f t t --+-= ( 2分 )(3) 求函数()())1(252++=s s s F 的拉普拉斯反变换()t f 。
南京邮电大学通信原理考研真题答案00--10年

2000年试题参考答案一、填空1、)(log 2i x p - ∑∞=-12)(log )(i i i x p x p p(x i )=n1i=1,2,3… 2、)2)(ex p(21)(22σσπa x x f --=ak 0(a H t E •=)0()]([ξ) π2020h w n k (输出噪声功率谱密度H o w w k n w p ≤=20)()3、恒参信道 随参信道 恒参信道4、接收信号中除当前码元以外的所有码元在抽样时刻的总和si ss T w T T i w H ππ22)4(≤=+∑+∞-∞= 部分响应系统 滚降系统(均衡) 5、相位连续 幅度恒定(能量集中) 带宽最小 6、2,17、h c c w w w w H w w H ≤=-++常数)()( 相干二、1、信息熵H=-p(x 1)2log p(x 1)-p(x 0)2log p(x 0)= bit/符号 信息速率Rb=1000×s=970 bit/s2、接收端收到0的概率p(0)=×+×=(全概率公式) 接收端收到1的概率p(1)=1-p(0)=平均丢失信息量H(x/y)= -p(0)[p(0/0)2log p(0/0)-p(1)2log p(1/0)] -p(1)[p(0/1)2log p(0/1)-p(1)2log p(1/1)]=[2log 2log 2log 2log bit/符号 信息传输速率R=1000(H -H(x/y))bit/s=810 bit/s三、1、mm f f w A k m =11022/1044=⨯===f m m f m radw vA srad k ππ2、)]102sin(102cos[)(46t t A t m s ⨯+⨯=ππ3、khz B m khzf m f B f f 40110)1(2===+=4、调制制度增益6)1(32=+=f f m m G 接收机输出信噪比3106161⨯==o o i i N S N S 噪声功率w k B n N i7120108401010222--⨯=⨯⨯⨯=⨯⨯= 接收机输入信号功率w N S i i 4310341061-⨯=⨯⨯=平均发射功率w S S i 3400106=⨯=四、1、等效带宽0041221ττππ=⨯=B 奈奎斯特传输速率baud R B 00max 21412ττ=⨯= 2、系统实际带宽0002121ττππ=⨯=B 最高频带利用率hz baud B R B /10max ==η3、s bit R R B b /238log 02max τ=⨯= 4、s bit R s bit R b b /23/340max 0ττ=<=但由于,2,1230=≠k kR b τ因此存在码间干扰(无码间干扰传输要求⋅⋅⋅==,2,1,max n nR R B B ) 五、发送”1”错判为”0”的概率2)1()1()(201011-=-+=-=⎰⎰+-+-A dV A V dV A V f Pe A A发送”0”错判为”1”的概率2)1()1()(210100-=--=-=⎰⎰--A dV A V dV A V f Pe AA系统误码率2)1(2121201-=+=A Pe Pe Pe (对双极性信号,最佳判决门限为Vd *=0)六、1、用π相位表示”1”,用0相位表示 ”0”,2PSK 波形如图1 1 0 0 1 1 0 02、baud k R s bit k R B b 2048/2048== 信号频率khz f s 2048=带宽khz f B s 40962== 频带利用率hz baud BR B/5.0==η 3、 框图如下图 (反向抽判)各点波形如下图参考”0” 1 1 0 0 1 1 0 0abcd七、1、输出信噪比N o M q S 222==,由题意7,102,10,40lg 10424≥≥≥≥N qSq S N o o 即 2、抽样频率m 2f f s ≥,码元周期s T s μ2=,码元速率Mbaud T R sB 5.01==,时分复用时,hz f R f m B s 3571,710≤≤⨯⨯3、为保证不过载,要求m s m s m m f f A f f A πσπ200,01.02≥=≤• 八、1、1),()(=-=k t T ks t h 一般情况2、3、最佳判决时刻取20T t =,02max 20max 2A ,41,2n Tr T A E n E r ===故 九、1、当输入为时,)(t δ系统冲激响应为)2()()(s T t t t h --=δδ,wTs j e w H 21)(--=2、易知该系统为第Ⅳ类部分响应系统,因此12-=r C r2001年试题参考答案一、填空 1、M 2logM s T 2log 1 s T 2 M 2log 212、R(∞) R(0) R(0)-R(∞)3、接收信号中除当前码元以外的所有码元在抽样时刻的总和si s sT w T T i w H ππ≤=+∑+∞-∞=)2( 部分响应系统 滚降系统(均衡) 4、552khz 96khz (为余数为最大整数,,k n kB nB f nkB f h s 22),1(2+=+=)5、最大似然比准则 -1 2psk6、最大输出信噪比准则 )()(*d jwt t t kS e W kS d --二、1、22/105.0)()()(322B f f B f hzw k f H f P f P c c i o +≤≤-⨯==- wB k df k df f P N Bf B f o o c c 32223210105.02)(-+--∞+∞-⨯=⨯⨯==⎰⎰(系数2是由于双边功率谱密度)2、)310)(5.0)(-⨯=τδτi R (注:)(频域,时域频域)((时域w t πδδ211↔↔))]()([105.0)(32c B c B o f f g f f g k f P ++-⨯=-(选用f 作变量时,无系数2π)t f j c B t f j c B c c e Bt BSa f f g e Bt BSa f f g ππππ22)()(,)()(-↔+↔-(频域平移,c c f w π2=)32223210)2cos()(])()([105.0)(---⨯=+⨯=τπτπππτππc t f j t f j o f B BSa k e Bt BSa e Bt BSa k R c c 三、1、5=mmf W A k rad w v A v rad k m m f 33102,10,/10⨯===ππ,)102sin(10)(3t t m ⨯=π2、5==mm f f W A k m3、khz m f B f 126102)1(23=⨯⨯=+=,载频hz f c 610=4、输入信号功率w v S i 50002)100(2==输入噪声功率w B f Pn N i 4.2)(2== 调制制度增益450)1(32=+=f f m m G310375.94.25000450⨯=⨯=o o N S 四、信息码 1 0 1 0 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0差分码0 1 1 0 0 1 0 1 0 1 0 0 0 0 0 0 0 0 0 0 0 HDB3 +1 0 -1 0 +1 -1 +1 -1 +1 -1 0 0 0 –V +B 0 0 +V 0 0 五、1、抽样频率khz f s 8= 编码位数38log 2==N 带宽khz khz B 2408310=⨯⨯=2、khz B B 480)1('=+=α 六、 发送”1”错判为”0”的概率=--=-=⎰⎰∞-∞-dx A x dx A x f Pe Vd nnVd ]2)(exp[21)(221σσπ发送”0”错判为”1”的概率dx A x dx A x f Pe Vdn nVd⎰⎰∞-+-=+=]2)(exp[21)(2200σσπ系统误码率为dxA x p dx A x p Pe p Pe p Pe VdnnVdnn⎰⎰∞-∞-+-+--=+=]2)(exp[21)0(]2)(exp[21)1()0()1(222201σσπσσπ最佳判决门限设为*d V ,应使系统误码率最小。
全国2008--2012年自考信号与系统真题和答案

全国2008年4月自考信号与系统真题课程代码:02354一、单项选择题(本大题共12小题,每小题2分,共24分)在每小题列出的四个备选项中只有一个是符合题目要求的,请将其代码填写在题后的括号内。
错选、多选或未选均无分。
1.RLC 串联电路发生谐振的条件是( )A .LC 10=ωB .LC πω210=C .LC f 10=D .LCR=0ω2.已知信号)(t f 的波形如题2图所示,则)()1(t t f ε-的表达式为( )A .)3(-t εB .)3()(--t t εεC .)(t εD .)3()(+-t t εε 3.计算⎰∞∞-=-dt t t )6(sin 2πδ( ) A .1 B .1/6C .1/8D .1/44.已知⎰∞-=t d t f ττδ)()(,则其频谱=)(ωj F ( )A .ωj 1 B .j ω C .)(1ωπδω+j D .)(1ωπδω+-j5.信号)(1t f 与)(2t f 的波形分别如题5图(a ),(b )所示,则信号)(2t f 的频带宽度是信号)(1t f 的频带宽度的( )A .2倍B .1/2倍C .1倍D .4倍6.已知某周期电流t t t i 5sin 223sin 221)(++=,则该电流信号的有效值I 为( ) A .3A B .1A C .17A D .10A 7.已知)(t f 的拉普拉斯变换为F (s ),⎰-∞-0)(dt t f 有界,则⎰∞-td f ττ)(的拉普拉斯变换为( )A .)(1s F sB .)0()(1--f s F sC .⎰-∞-+0)(1)(1ττd f ss F sD .⎰-∞--0)(1)(1ττd f s s F s8.已知)(t f 的拉普拉斯变换为F (s ),且F (0)=1,则⎰∞-0)(dt t f 为( )A .π4B .π2C .π21D .19.系统函数22)()(c a s bs s H +-+=,a ,b ,c 为实常数,则该系统稳定的条件是( )A .a <0B .a>0C .a=0D .c =010.已知某离散序列)(n f 如题10图所示,则该序列的数学表达式为( )A .)1()1()(+-=n n f n εB .)1()1()(--=n n f n εC .)()1()(n n f n ε-=D .n n f )1()(-=11.已知某系统的差分方程为)1()()2()1()(0101-+=-+-+n f b n f b n y a n y a n y ,则该系统的系统函数H (z )为( )A .201011)(z a z a zb b z H +++= B .211011)(1---+++=z a z a z b b z HC .102120)(a z a z z b z b z H +++=D .20111011)(---+++=z a z a z b b z H12.已知)1(3)(+=z zz F ,则)(n f 为( )A .)()3(n n ε-B .)()1(31n n ε-C .)(31n nε⎪⎭⎫⎝⎛ D .)(3n n ε二、填空题(本大题共12小题,每小题2分,共24分) 请在每小题的空格中填上正确答案。
2008电信信号与系统期末考试参考答案
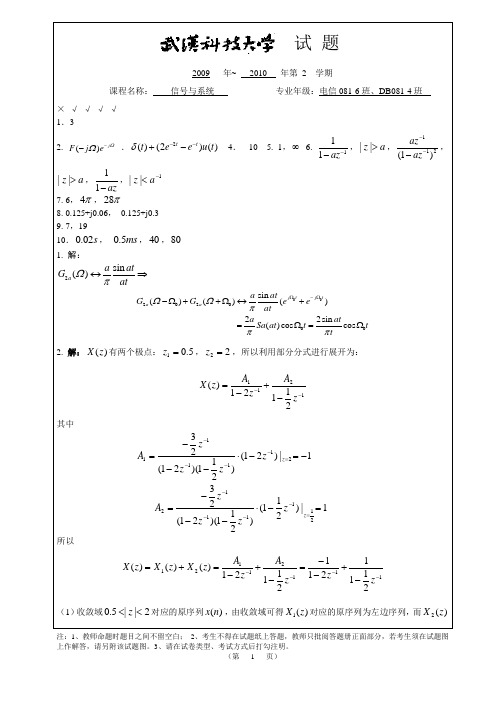
)
n j 0 n
x (n )e
j n
n
c o s( 0 n T ) e
j n
n
c o s( 0 n ) e
j n
=
n
[e
j 0 n
e
]e
j n
k
[ ( 0 2 k ) ( 0 2 k )]
式中
0 0 T 0 . 5 rad
上式推导过程中,指数序列的傅里叶变换仍然不存在,只有引入奇异函数 函数,才能写出其傅里 叶变换表示式。
4. 证明: W ( e
j
) FT[ x ( n ) y ( n )] =
[ x ( n ) * y ( n )] e
n j n
(2)收敛域 | z | 2 对应的原序列 x ( n ) ,由收敛域可得 X 1 ( z ) 、 X 2 ( z ) 对应的原序列都为右边序列,查 表 4-1 可得 x ( n ) ( ) u ( n ) 2 u ( n )
n n
1
2
3.解: (1) X a ( j )
注:1、教师命题时题目之间不留空白; 2、考生不得在试题纸上答题,教师只批阅答题册正面部分,若考生须在试题图 上作解答,请另附该试题图。3、请在试卷类型、考试方式后打勾注明。 (第 1 页)
对应的原序列为右边序列,查表 4-1 可得
1 n n x ( n ) ( ) u ( n ) 2 u ( n 1) 2
G 2a ( ) a sin a t
2008年南邮数字信号处理真题

2008年南邮数字信号处理真题1南京邮电大学2008年攻读硕士学位研究生入学考试数字信号处理试题一、填空题(每空1分,共10分)1、由模拟滤波器设计IIR 数字滤波器时,脉冲响应不变法不适合设计低通、高通、带通、带阻中的_______和_______。
2、在S 平面与Z 平面之间的标准映射关系z=e sT 下(T 为采样周期),S 平面上每一个宽为Ω=_______的横带都映射到整个Z 平面。
3、一个数字滤波器,如果是因果稳定系统,则起系统函数的所有极点应在________。
4、FFT 算法利用了W 因子的一些有效的性质,如2N NW =_______。
5、用窗口法设计FIR 数字滤波器时,如果窗函数是矩形窗,增加窗长度时所设计的数字滤波器的阻带最小衰耗__________,过渡带________。
6、由于有限字长的影响,在数字系统中存在三种误差,除了输入信号和系统参数量化效应外还有一种是_______。
7、已知有限字长序列x(n)的长度为N ,其Z 变换为X(z),则x(n)的傅立叶变换(DTFT )和N 点离散傅立叶变换(DFT)与X(z)的关系分别为X(e jw )=________,X(k)=_________。
(k=0,1,……N-1.)二、选择题(每题2分,共10分)1、一个理想采样系统,采样频率为Ωs =8π,采样后经理想低通H(j Ω)还原,在输入x 1(t)=cos2πt,x 2(t)=cos5πt 下信号分别为y 1(t)和y 2(t),则a 、y 1(t)没有失真,y 2(t)有失真b 、y 1(t)和y 2(t)都有失真c 、y 1(t)和y 2(t)都没有失真2、已知正弦序列x(n)=sin(16/5n π),则该序列a 、是周期序列,周期为5/8b 、是周期序列,周期为5c 、不是周期序列3、一个FIR 数字滤波器,其实现结构为a 、递归结构b 、非递归结构c 、递归或非递归结构4、已知系统的单位脉冲响应为h(n)=u(3-n),则该系统为a 、非因果,不稳定b 、非因果,稳定c 、因果,不稳定5、已知系统输入输出关系为y(n)=2x(n)+5,则系统为H(j Ω)0,|Ω|≧4π1/4,|Ω|﹤4π2a 、线性、时不变系统b 、非线性、时不变系统c 、非线性、时变系统三、画图题(每题10分,共20分)1、画出N=6按时间抽取(DIT )的FFT 分解流图,要求:(1)按照N=3×2分解,注明输入、输出序列及每一级的W 因子。
南京邮电大学信号与系统习题3

A 2
−τ τ 0 − 2
τ τ
2
t
解: 信号 f (t)可以分解为: 可以分解为:
《信号与系统》SIGNALS AND SYSTEMS
A A f (t) = gτ (t) + g2τ (t) 2 2 Aτ ωτ ↔ Sa( ) + AτSa(ωτ) 2 2
ZB
3-26 已知
f (t) = f1(t) + f2(t)的频谱密度函数 F(ω) = 4Sa(ω) − j
−20 0
20
ZB
f2(t) 3-34 已知图 所示锯齿脉冲 f (t)的傅 f (t) 已知图(a)所示锯齿脉冲 1 1 1 jω jω 里叶变换 F(ω) = (e − jωe −1), −1 0 t 0 1 2t ω2 (a) (c) 利用傅里叶变换的性质,求图(c) 利用傅里叶变换的性质,求图 、(f) 所示信号的傅里叶变换。 所示信号的傅里叶变换。 解:(c) f2(t) = f (t −1) + f (−t +1) = f (t −1) + f [−(t −1)] ↔ F(ω)e− jω + F(−ω)e− jω = [F(ω) + F(−ω)]e− jω
ZB
3-33 试应用调制定理,求题示信号 试应用调制定理, 的傅里叶变换,并画出频谱图。 的傅里叶变换,并画出频谱图。 解: (t) = ε (t + π ) −ε (t − π )cos20t f
π − 5 5 5 π π 2π π Sa( ω) Qε (t + ) −ε (t − ) ↔ 5 5 5 5
双边相位频谱: 双边相位频谱:
2π 2π θn 2π 5 1 5 −8 3 3 1 3 0 2π 8 nω0 8 nω0 2π −5 −1 2π − − − 《信号与系统》SIGNALS AND SYSTEMS ZB 3 3 3
2008年南邮数字信号处理真题参考答案

N e j , k m 2
N e j , k m 2
X e (k ) =
N ej,k N m 2
X o (k ) =
N ej,k N m 2
0 其他k
0 其他k
9
2
x(n)
z1 z1
z 1
h(0) h(1) h(2) h(3)
线性相位型实现结构如:
x(n)
z-1
y(n)
z-1
z-1
y(n)
0.4142
级联型实现结构如:
x(n)
y(n)
z 1
z 1
-1.414
z 1
四、证明题(共 10 分)
证明:
h(n)
1 N
N 1
H (k )WNkn
k 0
y(n) x(n) h(n) x(m)h(n m) m
s
) 1
c '
c '
c '
(T
)3
s3
2(T
1 )2 s2
2(T
)s
1
2
2
2
H
(z)
H
(s)
|s 2 T
1 1
z z
1 1
1 1
z 1 z 1
3
2
1 1
1
z 1 z 1
2
2
1 1
z 1 z 1
1
1
3z1 3z2 2(3 z2 )
z 3
故所设计的低通滤波器系统函数 H (z) 为上式。
n
n
5、线性系统应满足叠加性和齐次性, y(n) 2x(n) 5
T x1(n) 2x1(n) 5;T x2 (n) 2x2 (n) 5. T ax1(n) bx2 (n) 2ax1(n) 2bx2 (n) 5 aT x1(n) bT x2 (n) 为
2008年信号与系统a试卷参考答案、评分标准

n
1 4. e ε (t ) 5. α > a 6. − 2δ (n ) + 3 − ε (n ) 7. 因果稳定系统 2
8.3∆ω ;
∆ω 3
9. jω F (ω ) +
1 π F ( ω ) ∗ F ( ω ) 10. 3ε t − (1 分) , 3 (1 分) 2π 3
f (t ) 中只有 ω < 3rad / s 的频率分量才能通过系统,故
Y (ω ) = 2π [H (− 2 )F− 2δ (ω + 2) + H (− 1)F−1δ (ω + 1) + H (0 )F0δ (ω ) (1 分) + H (1)F1δ (ω − 1) + + H (2)F2δ (ω − 2 ) ] 将 H (ω ), Fn 代入上式得: 2 −j 1 Y (ω ) = 2π 3e − jπ δ (ω + 2 ) + 3e 2 δ (ω + 1) + 3δ (ω ) 3 3 (1 分) 2 jπ2 1 + 3e δ (ω − 1) + 3e jπ δ (ω − 2) 3 3
2π 2π 1 π π = = 6 (1 分) 分量 cos t − 的周期 T1 = π ω 4 6 3 3
f (t ) 的基波周期 T 是 T1 , T2 的最小公倍数,则 T = 24 (1 分)
基波角频率为 Ω =
2π π = (1 分) T 12
1 π π π π 则 cos = 3 次谐波分量, t + 是 f (t ) 的 2 3 4 12 4 1 π π π π = 4 次谐波分量 cos t − 是 f (t ) 的 4 6 3 12 3
南京邮电大学信号与系统习题2

t
t
( c ) 当 2 t 3时, y (t ) ( 2)d 2
1
2 1
0 1 2
2
( d ) 当 3 t 4时,
t 2
2 1 0 1 2
(e) 当 t 4时, y (t ) 0
ZB
《信号与系统》SIGNALS AND SYSTEMS
t
2 1 0 1 2
(b) 当 1 t 2时, y (t ) ( 2)d 2
1
t
x( ) h( ) (t ) x( ) h( ) (t ) x( ) h( ) (t ) x x x
2 2 2 t 2 1
0 1 2
2
2 1
0
2
(a ) 当 t 1时, y (t ) 0
(b) 当 1 t 2时, y ( t ) ( 2 t ) d 2
h(t ) x( ) h( ) 2 t
2 1
0
t 1
h(t ) x( ) h( ) 2 t
2
h(t ) x( ) h( ) 2 t
e e
(5) et (t ) * cost (t )
2t t
e e
2 ( t )
d e
2t
t
t
e 2t (e t 0) e
t
e d
t
e(t ) cosd (t ) et
t
0
e cosd (t )
《信号与系统》SIGNALS AND SYSTEMS 3
