几何证明选讲(教师版)
专题:几何证明选讲

专题:几何证明选讲【知识梳理】1.相似三角形的判定定理:判定定理1.两角对应相等的三角形相似。
判定定理2.三边对应成比例的两个三角形相似。
判定定理3.两边对应成比例,并且夹角相等的两个三角形相似。
2.相似三角形的性质性质定理1.相似三角形对应边上的高、中线和它们的周长的比都等于相似比。
性质定理2.相似三角形的面积比等于相似比的平方。
3.平行截割定理三条平行线截任意两条直线,所截出的对应线成比例。
4.射影定理直角三角形中,每一条直角边是这条直线边在斜边上的射影和斜边的比例中项;斜边上的高是两条直角边在斜边上的射影的比例中项。
5.圆周角与弦切角圆的切线判定定理:经过圆的半径的外端切垂直于这条半径的直线,是圆的切线。
圆的切线的性质定理:圆的切线垂直过圆的半径。
推论1.从圆外的一个已知点所引的两条切线长相等。
推论2.经过圆外的一个已知点和圆心的直线,平分从这个点向圆所做的两条切线所夹的角。
6.圆周角定理圆周角的度数等于它所对弧的度数的一半。
推论1.直径所对的圆周角都是直角推论2.同弧或等弧所对的圆周角相等。
推论3.等于直角的圆周角所对的弦是圆的直径。
7.弦切角定理弦切角的度数等于它所夹的弧的度数的一半。
推论:弦切角等于它所夹弧所对的圆周角。
8.圆幂定理相交弦定理:圆内的两条相交弦,被交点分成的两条线短长的积相等。
切割线定理:从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项。
圆幂定理:(不用掌握)9.圆内接四边形的性质定理:圆的内接四边形的对角互补,并且任何一个外角都等于它的内对角。
10.圆内接四边形的判定定理:如果一个四边形的一组对角互补,那么这个四边形内接于圆。
【知识梳理】平行线等分线段定理平行线等分线段定理:如果一组平行线在一条直线上截得的线段相等,那么在其他直线上截得的线段也相等。
推理1:经过三角形一边的中点与另一边平行的直线必平分第三边。
推理2:经过梯形一腰的中点,且与底边平行的直线平分另一腰。
几何证明选讲解三角形排列组合(教师版)
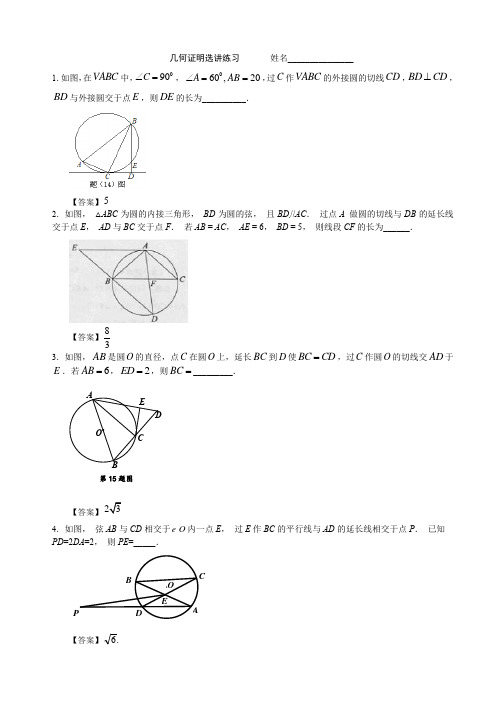
几何证明选讲练习 姓名_______________1.如图,在中,,,过作的外接圆的切线,,与外接圆交于点,则的长为__________.【答案】2.如图, △ABC 为圆的内接三角形, BD 为圆的弦, 且BD //AC . 过点A 做圆的切线与DB 的延长线交于点E , AD 与BC 交于点F . 若AB = AC , AE = 6, BD = 5, 则线段CF 的长为______.【答案】833.如图,AB 是圆O 的直径,点C 在圆O 上,延长BC 到D 使BC CD =,过C 作圆O 的切线交AD 于E .若6AB =,2ED =,则BC =_________.【答案】4.如图, 弦AB 与CD 相交于O 内一点E , 过E 作BC 的平行线与AD 的延长线相交于点P . 已知PD =2DA =2, 则PE =_____.【答案】.6 ABC 090C ∠=060,20A AB ∠==C ABC CD BD CD ⊥BD EDE5.A ED CB O 第15题图5.如图2,O 中,弦,AB CD 相交于点,2P PA PB ==,1PD =,则圆心O 到弦CD 的距离为____________.【答案】23 6.如图,圆O 上一点C 在直线AB 上的射影为D ,点D 在半径OC 上的射影为E .若3AB AD =,则CEEO的值为___________.【答案】8 7.如图,AB 为圆O 的直径,P A 为圆O 的切线,PB 与圆O 相交于D .若PA=3,916PD DB =::,则PD=_________;AB=___________.【答案】95;4 解三角形练习1.如图,△ABC 中,AB=AC=2,BC=点D在BC 边上,∠ADC=45°,则AD 的长度等于______.【命题意图】本题考查运用正余弦定理解三角形,是中档题.【解析】(法1)过A 作AE ⊥BC,垂足为E ,∵AB=AC=2,BC=∴E 是BC 的中点,且EC=O D EBACRt AEC ∆中,AE=又∵∠ADE=45°,∴DE=1,∴AD=(法2) ∵AB=AC=2,BC=由余弦定理知,cos C =2222AC BC AB AC BC +-⨯∴C=30°, 在△ADC 中,∠ADE=45°,由正弦定理得,sin sin AD AC C ADC=∠, ∴AD=sin sin AD C ADC ∠=12⨯2.如图,在△ABC 中,D 是边AC 上的点,且AB AD =,2AB =,2BC BD =,则sin C 的值为( )A.3 B.6 C3 D6【答案】D【解析】设BD a =,则由题意可得:2,BC a =2AB AD a ==,在ABD ∆中,由余弦定理得: 222cos 2AB AD BD A AB AD +-==⋅2232a a ⨯-=13,所以sin A=,在△ABC 中,由正弦定理得,sin sin AB BC C A =,所以2sin C =,解得sin CD . 3.,EF 是等腰直角ABC ∆斜边AB 上的三等分点,则tan ECF ∠=( )A .1627B .23 CD .34【答案】D4.在△ABC 中, 4ABC π∠=,AB 3BC =,则sin BAC ∠ =( ) (A )(B )(C )(D )【答案】C5.ABC ∆中,90C ∠=,M 是BC 的中点,若31sin =∠BAM ,则=∠BAC sin ________.【答案】36.在△ABC 中,已知AB=4,AC=7,BC 边的中线27=AD ,求边BC 的长.7.如图,在四边形ABCD 中,AC 平分∠DAB ,∠ABC=60°,AC=7,AD=6,S △ADC =2315,求AB 的长.排列组合练习题1.有6位同学在毕业聚会活动中进行纪念品的交换,任意两位同学之间最多交换一次,进行交换的两位同学互赠一份纪念品,已知6位同学之间共进行了13次交换,则收到份纪念品的同学人数为( ) 或 或 或 或【解析】选①设仅有甲与乙,丙没交换纪念品,则收到份纪念品的同学人数为人②设仅有甲与乙,丙与丁没交换纪念品,则收到份纪念品的同学人数为人.2.将字母排成三行两列,要求每行的字母互不相同,每列的字母也互不相同,则不同的排列方法共有A .12种B .18种C .24种D .36种答案A【命题意图】本试题考查了排列组合的用用.4()A 13()B 14()C 23()D 24D 261315132C -=-=4244,,,,,a a b b c c【解析】利用分步计数原理,先填写最左上角的数,有3种,再填写右上角的数为2种,在填写第二行第一列的数有2种,一共有.3.现有16张不同的卡片,其中红色、黄色、蓝色、绿色卡片各4张,从中任取3张,要求这些卡片不能是同一种颜色,且红色卡片至多1张,不同取法的种数为(A )232 (B)252 (C)472 (D)484解析:,答案应选C . 另解:. 4. 两人进行乒乓球比赛,先赢三局着获胜,决出胜负为止,则所有可能出现的情形(各人输赢局次的不同视为不同情形)共有( )A .10种B .15种C .20种D .30种【解析】甲赢和乙赢的可能情况是一样的,所以假设甲赢的情况如下:若两人进行3场比赛,则情况只有是甲全赢1种情况;若两人进行4场比赛,第4场比赛必为甲赢前3场任选一场乙赢为种情况;若两人进行5场比赛,第5场比赛必为甲赢前4场任选一场乙赢为种情况;综上,甲赢有10种情况,同理,乙赢有10种情况,则所有可能出现的情况共20种,故选C .5.若从1,2,2,…,9这9个整数中同时取4个不同的数,其和为偶数,则不同的取法共有A .60种B .63种C .65种D .66种【解析】1,2,2,…,9这9个整数中有5个奇数,4个偶数.要想同时取4个不同的数其和为偶数,则取法有:4个都是偶数:1种;2个偶数,2个奇数:种; 4个都是奇数:种.∴不同的取法共有66种.【答案】D6.某艺校在一天的6节课中随机安排语文、数学、外语三门文化课和其他三门艺术课个1节,则在课表上的相邻两节文化课之间最多间隔1节艺术课的概率为 (用数字作答).【解析】概率为 语文、数学、英语三门文化课间隔一节艺术课,排列有种排法,语文、数学、英语三门文化课相邻有种排法,语文、数学、英语三门文化课两门相邻有种排法. 32212⨯⨯=472885607216614151641122434316=-=--⨯⨯=--C C C C 472122642202111241261011123212143431204=-+=⨯⨯+-⨯⨯=+-C C C C C 313=C 624=C 225460C C =455C =3____53344A A 3312122223A C C A C3故所有的排法种数有在课表上的相邻两节文化课之间最多间隔1节艺术课的概率为5。
几何证明选讲定理大全

6.ΔABC内接于⊙O,AD是⊙O旳直径, CE⊥AD,E为垂足,CE旳延长线交AB
于点F,求证:AC2=AF·AB.
7.已 知BC是 圆O的直 径,AD BC,垂足 为D, BF交AD于E, 且AE BE. (1)求证 :弧AB 弧AF; (2)如 果sinFBC 3,AB 4 5, 求AD的 长.
直线CE和⊙O切于点C,AD⊥CE,垂
足为D,
求证:AC平分∠BAD
E
O
A
C
D
2.如图,⊙O和⊙O′都经过A、B 两点,AC是⊙O ′旳切线,交 ⊙O于C,AD是⊙O旳切线,交 ⊙O ′于D,
求证:AB2=BC·BD.
A
O CB
O' D
3.在△ABC中,∠A旳平分线AD交BC 于D,⊙O过点A,且和BC切于D, 和AB、AC分别交于E、F, 求证:EF//BC.
若∠PAD=∠DCB,则ABCD四点共圆;
D
若∠ADB=∠ACB,则ABCD四点共圆;
C O
PA
B
练习
情况唯一吗?
1.⊙O1和⊙O2都经过A、B两点,经过A点旳直线CD与
⊙O1交于点C,与⊙O2交于点D,经过B点旳直线EF与
⊙O1交于点E,与⊙O2交于点F,求证:CE∥DF.
D
E
A
A
D
C
C O1
O2
F
D
E
B
C
A
D
E
16
16 8
CF DE , BF 8
.
3
33
B
1几何证明选讲 - 简单难度 - 讲义

几何证明选讲知识讲解一、相似三角形的判定及有关性质1.平行线等分线段定理定理:如果一组平行线在一条直线上截得的线段相等,那么在其他直线上截得的线段也相等.推论1:经过三角形一边的中点与另一边平行的直线必平分第三边.推论2:经过梯形一腰的中点,且与底边平行的直线平分另一腰.2.平行线分线段成比例定理定理:三条平行线截两条直线,所得的对应线段成比例.推论:平行于三角形一边的直线截其他两边(或两边的延长线)所得的对应线段成比例.3.相似三角形的判定及性质1)相似三角形的判定定义:对应角相等,对应边成比例的两个三角形叫做相似三角形.相似三角形对应边的比值叫做相似比(或相似系数).预备定理:平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似.判定定理1:对于任意两个三角形,如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似.简述为:两角对应相等,两三角形相似.判定定理2:对于任意两个三角形,如果一个三角形的两边和另一个三角形的两边对应成比例,并且夹角相等,那么这两个三角形相似.简述为:两边对应_成比例且夹角相等,两三角形相似.判定定理3:对于任意两个三角形,如果一个三角形的三条边和另一个三角形的三条边对应成比例,那么这两个三角形相似.简述为:三边对应成比例,两三角形相似.2)两个直角三角形相似的判定定理:①如果两个直角三角形的一个锐角对应相等,那么它们相似.②如果两个直角三角形的两条直角边对应成比例,那么它们相似.③如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似.3)相似三角形的性质性质定理:①相似三角形对应高的比、对应中线的比和对应角平分线的比都等于相似比;②相似三角形周长的比等于相似比;③相似三角形面积的比等于相似比的平方;④相似三角形外接圆(或内切圆)的直径比、周长比等于相似比,外接圆(或内切圆)的面积比等于相似比的平方4.直角三角形的射影定理定理:直角三角形斜边上的高是两直角边在斜边上射影的比例中项;两直角边分别是它们在斜边上射影与斜边的比例中项.二、直线与圆的位置关系1.圆周角定理圆周角定理:圆上一条弧所对的圆周角等于它所对的圆心角的一半.圆心角定理:圆心角的度数等于它所对弧的度数.推论1:同弧或等弧所对的圆周角相等;同圆或等圆中,相等的圆周角所对的弧也相等.推论2:半圆(或直径)所对的圆周角是直角;90°的圆周角所对的弦是直径.2.圆内接四边形的性质与判定定理1)性质定理1:圆的内接四边形的对角互补.定理2:圆内接四边形的外角等于它的内角的对角. 2)判定判定定理:如果一个四边形的对角互补,那么这个四边形的四个顶点共圆.推论:如果四边形的一个外角等于它的内角的对角,那么这个四边形的四个顶点共圆.3.三角形的内切圆1)三角形的内切圆:和三角形各边都相切的圆叫做三角形的内切圆,内切圆的圆心叫做三角形的内心,这个三角形叫做圆的外切三角形.2)多边形的内切圆:和多边形的各边都相切的圆叫做多边形的内切圆,这个多边形叫做圆的外切多边形.3)直角三角形内切圆的半径与三边的关系设、、分别为中、、的对边,面积为,则内切圆半径为,.若,则. 4.圆的切线的性质及判定定理1)性质性质定理:圆的切线垂直于经过切点的半径. 推论1:经过圆心且垂直于切线的直线必过切点. 推论2:经过切点且垂直于切线的直线必过圆心.2)判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线.cb cbaO F ED CBACBAC B A a b c ABC △A ∠B ∠C ∠S sr p=()12p a b c =++90C ∠=︒()12r a b c =+-5.弦切角的性质定理:弦切角等于它所夹的弧所对的圆周角.6.与圆有关的比例线段1)相交弦定理:圆内的两条相交弦,被交点分成的两条线段长的积 相等. 如图,弦和交于内一点,则.2)割线定理:从圆外一点引圆的两条割线,这一点到每条割线与圆的交点的两条线段长的 积相等.3)切割线定理:从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段 长的比例中项.如图,在中,是的切线,是的割线,则题意中满足4)切线长定理:从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角.AB CD O ⊙P PA PB PC PD ⋅=⋅O e AB O e AD O e 2AB AC AD =⋅BA经典例题一.选择题(共12小题)1.(2017秋•天心区校级期末)如图,△ABC被一边平行于BC的矩形所截,AB 被截成三等份,则图中阴影部分的面积是△ABC的面积的()A.13B.19C.29D.492.(2017秋•江北区校级月考)如图,将矩形ABCD绕点A旋转至矩形AB′C′D′位置,此时AC的中点恰好与D点重合,AB′交CD于点E.若AB=6,则△AEC的面积为()A.12B.4√3C.8√3D.63.(2016春•海南校级期末)如图,已知圆的直径AB=13,C为圆上一点,过C 作CD⊥AB于点D(AD>BD),若CD=6,则AD的长为()A.8B.9C.10D.114.(2016秋•武邑县校级月考)如图所示,在▱ABCD中,E为CD上一点,DE:CE=2:3,连接AE,BE,BD,且AE,BD交与点F,则S△DEF:S△EBF:S△ABF等于()A.4:10:25B.4:9:25C.2:3:5D.2:5:255.(2016春•淇滨区校级月考)如图所示,AB∥CD∥EF,且AO=OD=DF,BC=6,则BE等于()A.9B.10C.11D.126.(2015•朝阳区二模)如图,将一张边长为1的正方形纸ABCD折叠,使得点B 始终落在边AD上,则折起部分面积的最小值为()A.14B.38C.25D.127.(2014春•红桥区期末)如图,在梯形ABCD中,AB∥CD∥EF,若AB=5,CD=2,EF=4,则梯形ABFE与梯形EFDC的面积比是()A.23B.12C.92D.348.(2012春•红旗区校级期中)如图,E是平行四边形ABCD的边AB延长线上一点,且DC:BE=3:2,则AD:BF=()A.32B.23C.52D.259.(2017秋•天心区校级期末)如图,从▱O外一点A引圆的切线AD和割线ABC,已知AD=4√2,AC=8,▱O的半径为4,则圆心O到AC的距离为()A.3√2B.2√3C.4√3D.4√210.(2017秋•天心区校级期末)如图,▱O是△ABC的外接圆,AD是▱O的直径,连接CD,AC=2,AD=3,则cosB的值为()A.32B.√53C.52D.2311.(2017春•无极县校级期中)两条相交直线的平行投影是()A.两条相交直线B.一条直线C.一条折线D.两条相交直线或一条直线12.(2015•安徽模拟)如图,一个底面半径为R的圆柱被与其底面所成角是30°的平面所截,截面是一个椭圆,则该椭圆的离心率是()A.12B.√32C.√33D.23二.填空题(共13小题)13.(2016春•河南期中)若两个相似三角形的周长比为3:4,则它们的三角形面积比是.14.(2017秋•天宁区校级月考)如图D是△ABC的边AB上的一点,过D点作DE∥BC交AC于E.已知AD:DB=3:4,则S△ADE:S四边形BCDE为.15.(2015•汕头模拟)如图,在△ABC中,DE∥BC,DF∥AC,AE=2,EC=1,BC=4,则BF=.16.(2015•揭阳校级三模)在梯形ABCD中,AD∥BC,AD=2,BC=5,点E、F分别在AB、CD上,且EF∥AD,若AEEB =34,则EF的长为.17.(2015•汕尾模拟)如图所示,圆O上一点C在直径AB上的射影为D,CD=4,BD=8,则圆O的半径等于.18.(2015春•周口校级月考)如图在Rt△ABC中∠ACB=90°,CD⊥AB,AC=6,AD=3.6,则BD=.19.(2014•郴州二模)如图,AB是半圆O的直径,点C在半圆上,CD⊥AB,垂足为D,且AD=5DB,设∠COD=θ,则tanθ的值为.20.(2014春•天津期末)如图,在△ABC中,M,N是AB的三等分点,E,F是AC的三等分点,若BC=1,则ME+NF=.21.(2017•张家口模拟)在直角△ABC中,斜边BC=6,以BC中点O为圆心,作半径为2的圆,分别交BC于两点,若|AP|=m,|AQ|=n,则m2+n2=.22.(2014春•清远期末)如图,⊙O上一点C在直径AB上的射影为D,AC=4,AD=2,则⊙O的面积是.23.(2013春•天心区校级期末)在如图所示的锐角三角形空地中,欲建一个面积不小于300m2的内接矩形花园(阴影部分),则其边长x(单位m)的取值范围是.24.(2016•丰台区一模)如图,BC为⊙O的直径,且BC=6,延长CB与⊙O在点D处的切线交于点A,若AD=4,则AB=.25.(2016•天津校级模拟)如图,PA是圆O的切线,切点为A,PO交圆O于B、C两点,PA=√3,PB=1,则AC=.。
考点52 几何证明选讲

温馨提示:此题库为Word 版,请按住Ctrl,滑动鼠标滚轴,调节合适的观看比例,关闭Word 文档返回原板块。
考点52 几何证明选讲一、填空题1.(2013·天津高考理科·T13)如图,△ABC 为圆的内接三角形,BD 为圆的弦,且BD ∥AC.过点A 作圆的切线与DB 的延长线交于点E,AD 与BC 交于点F.若AB=AC,AE=6,BD=5,则线段CF 的长为 .【解题指南】利用圆以及平行线的性质计算.【解析】因为AE 与圆相切于点A,所以AE 2=EB ·(EB+BD),即62=EB ·(EB+5),所以BE=4,根据切线的性质有∠BAE=∠ACB,又因为AB=AC,所以∠ABC=∠ACB,所以∠ABC=∠BAE,所以AE ∥BC,因为BD ∥AC,所以四边形ACBE 为平行四边形,所以AC=BE=4,BC=AE=6.设CF=x,由BD ∥AC 得=AC CF BDBF,即456=-xx,解得x=83,即CF=83. 【答案】83.2. (2013·湖南高考理科·T11)0中,弦,,2,AB CD P PA PB ==相交于点1PD O =,则圆心到弦CD 的距离为 .【解题指南】本题要利用相交弦定理:PA ·PB=PD ·PC 和解弦心三角形22)21(CD r d -=【解析】由相交弦定理PC PD PB PA ∙=∙得4=PC ,所以弦长5=CD ,故圆心O 到弦CD 的距离为234257)21(22=-=-CD OC .【答案】23. 3. (2013·陕西高考文科·T15)如图, AB 与CD 相交于点E , 过E 作BC 的平行线与AD 的延长线相交于点P . 已知A C ∠=∠, PD = 2DA = 2, 则PE = .【解题指南】先通过A C ∠=∠及线线平行同位角相等,找出三角形相似,再由比例线段求得答案.【解析】..//BAD PED C A PED BCD PE BC ∠=∠⇒∠=∠∠=∠且所以因为.6.623∽2==⋅=⋅=⇒=⇒∆∆⇒PE PD PA PE PEPD PA PE APE EPD 所以4. (2013·北京高考理科·T11)如图,AB 为圆O 的直径,PA 为圆O 的切线,PB 与圆O 相交于D.若PA=3,PD ∶DB=9∶16,则PD= ,AB= .【解题指南】利用切割线定理求出PD,再在Rt △PBA 中利用勾股定理求出AB. 【解析】由于PD ∶DB=9∶16,设PD=9a,DB=16a,根据切割线定理有PA 2=PD ·PB,有a=15,所以PD=95,在Rt △PBA 中,有AB=4. 【答案】95 4. 5. (2013·湖北高考理科·T15)如图,圆O 上一点C 在直径AB 上的射影为D ,点D 在半径OC 上的射影为E ,若AB=3AD,则EOCE的值为【解题指南】先用半径表示,再求比值. 【解析】设半径为R ,AB=3AD=2R. AD=23R ,OD=13R,3R =3cos ,3RC R ==228cos ,339CE CD C R R === 所以EO=R ―CE ―R ―81,99R R =898.19RCE EO R== 【答案】8.6. (2013·陕西高考理科·T15)如图, 弦AB 与CD 相交于圆O 内一点E , 过E 作BC 的平行线与AD 的延长线相交于点P . 已知PD =2DA =2, 则PE = .【解题指南】先通过圆周角相等及线段平行同位角相等得出,∽APE EPD ∆∆再由比例线段求得答案.【解析】..//BAD PED BAD BCD PED BCD PE BC ∠=∠⇒∠=∠∠=∠且在圆中所以因为.6.623∽2==⋅=⋅=⇒=⇒∆∆⇒PE PD PA PE PEPDPA PE APE EPD 所以 【答案】.67.(2013·广东高考理科·T15)如图,AB 是圆O 的直径,点C 在圆O 上,延长BC 到D 使BC=CD ,过C 作圆O 的切线交AD 于E.若AB=6,ED=2,则BC=______.【解题指南】本题考查几何证明选讲,可先作ABD ∆的中位线OC 再计算. 【解析】设BC x =,连接OC ,因为,BC CD AC BD =⊥,ABD ∆是等腰三角形,,6,2,4BC CD x AB AD ED AE ======,在ACD ∆中,CE AD ⊥,则22222CE AC AE AD DE =-=-,即2236164x x --=-,解得x =【答案】8.(2013·广东高考文科·T15)如图,在矩形ABCD 中,AB 3BC =,BE AC ⊥,垂足为E ,则ED = .【解题指南】本题考查几何证明选讲,可先利用射影定理再结合余弦定理计算. 【解析】3,30,AB BC AC ACB AC BE ==∠=⊥,BEC ∆是直角三角形,由射影定理2,BC AC EC EC =⋅=ECD ∆中,由余弦定理可得222212cos 604ED EC CD EC CD =+-⋅=,即ED =. 9. (2013·天津高考文科·T13)如图, 在圆内接梯形ABCD 中, AB //DC , 过点A 作圆的切线与CB 的延长线交于点E . 若AB = AD = 5, BE = 4, 则弦BD 的长为 .【解题指南】 首先利用圆的性质,得出角的关系,再分别在△ABE 与△ABD 中利用正弦定理求解.【解析】设∠=BAE α,因为AE 与圆相切于点A ,所以,∠=∠BAE ADB 又因为AB = AD ,所以∠=∠=ABD ADB α,因为AB //DC ,所以∠=∠=ABD CDB α,所以2∠=∠=ABE ADC α.在△ABE 中,由正弦定理得sin sin =∠BE ABBAE E ,即45sin sin(3)=-απα,解得3cos .4=α在△ABD中,由正弦定理得sin sin =∠∠BD AB BAD ADB ,即5sin(2)sin =-BD παα,解得15.2=BD【答案】152. 10. (2013·重庆高考理科·T14)如图,在△ABC 中,090C ∠=,060A ∠=,20AB =,过C 作△ABC 的外接圆的切线CD ,BD ⊥CD ,BD 与外接圆交于点E ,则DE 的长为【解题指南】 直接根据圆的切线及直角三角形的相关性质进行求解【解析】由题意知AB 是圆的直径,设圆心为O ,连接OC ,因为CD 是圆的切线,则CDOC ⊥又因为BD ⊥CD ,所以BD OC //.因为 60,=∠=A OC OA ,所以30,60=∠=∠OCB ACO ,因为20=AB ,所以310=BC ,因为BD OC //,所以30=∠CBD 所以15=BD ,又因为AB 是圆的直径, 点E 在圆上, 20=AB 且 60=∠ABD ,所以10=BE ,故51015=-=-=BE BD DE【答案】5. 二、解答题11. (2013·辽宁高考文科·T22)与(2013·辽宁高考理科·T22)相同 如图,AB 为O 的直径,直线CD 与O 相切于E , AD 垂直CD 于D ,BC 垂直CD 于C ,EF 垂直AB 于F,连接,AE BE .证明: ()I FEB CEB ∠=∠;()II 2.EF AD BC =⋅【解题指南】 借助等量代换,证明相等关系;利用全等三角形的对应边,角相等.【证明】()I 由直线CD 与O 相切于E ,得EAB CEB ∠=∠ 由AB 为O 的直径,得AE EB ⊥,从而2EAB EBF π∠+∠=又EF 垂直AB 于F ,得2FEB EBF π∠+∠=,从而FEB CEB ∠=∠()II 由BC 垂直CD 于C ,得BC CE ⊥又EF 垂直AB 于F EF AB ⇒⊥,FEB CEB ∠=∠,BE 为公共边, 所以Rt BCE ∆≌Rt BFE ∆,所以BC BF = 同理可证,Rt ADE ∆≌Rt AFE ∆,所以AD AF = 又在Rt AEB △中, EF AB ⊥,所以2.EF AF BF =⋅ 综上,2.EF AD BC =⋅12. (2013·新课标Ⅰ高考文科·T22)与(2013·新课标Ⅰ高考理科·T22)相同如图,直线AB 为圆的切线,切点为B ,点C 在圆上,∠ABC 的角平分线BE 交圆于点E ,DB 垂直BE 交圆于D 。
高中数学第十一章 几何证明选讲(选修4-1)

第十一章⎪⎪⎪几何证明选讲(选修4-1)第一节 相似三角形的判定及有关性质1.平行线的截割定理 (1)平行线等分线段定理定理:如果一组平行线在一条直线上截得的线段相等,那么在其他直线上截得的线段也相等.推论1:经过三角形一边的中点与另一边平行的直线必平分第三边. 推论2:经过梯形一腰的中点,且与底边平行的直线平分另一腰. (2)平行线分线段成比例定理定理:三条平行线截两条直线,所得的对应线段成比例.推论:平行于三角形一边的直线截其他两边(或两边的延长线)所得的对应线段成比例. 2.相似三角形的判定定理(1)判定定理1:两角对应相等,两三角形相似.(2)判定定理2:两边对应成比例且夹角相等,两三角形相似. (3)判定定理3:三边对应成比例,两三角形相似. 3.相似三角形的性质定理(1)性质定理:相似三角形对应高的比、对应中线的比和对应角平分线的比都等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.(2)推论:相似三角形外接圆的直径比、周长比等于相似比,外接圆的面积比等于相似比的平方.4.直角三角形相似的判定定理(1)判定定理1:如果两个直角三角形有一个锐角对应相等,那么它们相似. (2)判定定理2:如果两个直角三角形的两条直角边对应成比例,那么它们相似. (3)判定定理3:如果一个直角三角形的斜边和一条直角边与另一个三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似.5.直角三角形射影定理直角三角形斜边上的高是两直角边在斜边上射影的比例中项;两直角边分别是它们在斜边上射影与斜边的比例中项.[小题体验]1.(教材习题改编)如图,AB ∥EM ∥DC ,AE =ED ,EF ∥BC ,EF=12 cm ,则BC 的长为________ cm.解析:由⎭⎪⎬⎪⎫AB ∥EM ∥DC AE =ED ⇒E 为AD 中点,M 为BC 的中点, 又EF ∥BC ⇒EF =MC =12 cm. ∴BC =2MC =24 cm. 答案:242.(教材习题改编)如图,D ,E 分别是△ABC 的边AB ,AC 上的点,DE ∥BC 且ADDB=2,那么△ADE 与四边形DBCE 的面积比是________.解析:∵DE ∥BC ,∴△ADE ∽△ABC , ∴S △ADE S △ABC =AD 2AB 2. ∵AD DB =2,∴AD AB =23,∴S △ADE S △ABC =49,故S △ADE S 四边形DBCE =45. 答案:451.在使用平行线截割定理时易出现对应边的对应顺序混乱,导致错误. 2.在解决相似三角形的判定或应用时易出现对应边和对应角的对应失误.3.射影定理是直角三角形中的一个重要结论,其实质就是三角形的相似.但要注意满足直角三角形射影定理结论的三角形不一定是直角三角形,所以要搞清楚定理中的条件和结论之间的关系,不能乱用.[小题纠偏]1.(2016·鞍山模拟)如图,在▱ABCD 中,E 是BC 上一点,BE ∶EC =2∶3,AE 交BD 于点F ,则BF ∶FD 的值为________.解析:因为AD =BC ,BE ∶EC =2∶3, 所以BE ∶AD =2∶5,因为AD ∥BC , 所以BF ∶FD =BE ∶AD =2∶5, 所以BF ∶FD 的值为25.答案:252.如图,在Rt △ABC 中 ,∠BAC =90°,AD 是斜边BC 上的高,若AB ∶AC =2∶1,则AD ∶BC 为________.解析:设AC =k ,则AB =2k ,BC =5k , ∵∠BAC =90°,AD ⊥BC , ∴AC 2=CD ·BC , ∴k 2=CD ·5k ,∴CD =55k , 又BD =BC -CD =455k , ∴AD 2=CD ·BD =55k ·455k =45k 2, ∴AD =255k ,∴AD ∶BC =2∶5. 答案:2∶5考点一 平行线分线段成比例定理的应用(基础送分型考点——自主练透)[题组练透]1.如图,在梯形ABCD 中,AD ∥BC ,BD 与AC 相交于点O ,过点O 的直线分别交AB ,CD 于E ,F ,且EF ∥BC ,若AD =12,BC =20,求EF 的值.解:∵AD ∥BC , ∴OB OD =BC AD =2012=53, ∴OB BD =58.∵OE ∥AD ,∴OE AD =OB BD =58.∴OE =58AD =58×12=152,同理可求得OF =38BC =38×20=152,∴EF =OE +OF =15.2.如图,在△ABC 中,点D 是AC 的中点,点E 是BD 的中点,AE 交BC 于点F ,求BFFC 的值.解:如图,过点D 作DM ∥AF 交BC 于点M . ∵点E 是BD 的中点,∴在△BDM 中,BF =FM . 又点D 是AC 的中点, ∴在△CAF 中,CM =MF , ∴BF FC =BF FM +MC =12.[谨记通法]平行线分线段成比例定理及推论的应用的一个注意点及一种转化(1)一个注意点:利用平行线分线段成比例定理来计算或证明,首先要观察平行线组,再确定所截直线,进而确定比例线段及比例式,同时注意合比性质、等比性质的运用.(2)一种转化:解决此类问题往往需要作辅助的平行线,要结合条件构造平行线组,再应用平行线分线段成比例定理及其推论转化比例式解题.考点二 相似三角形的判定及性质 (重点保分型考点——师生共研)[典例引领]如图,在△ABC 中,AB =AC ,∠BAC =90°,D ,E ,F 分别在AB ,AC ,BC 上,AE =13AC ,BD =13AB ,且CF =13BC .求证:(1)EF ⊥BC ; (2)∠ADE =∠EBC . 证明:设AB =AC =3a , 则AE =BD =a ,CF =2a . (1)CE CB =2a 32a =23,CF CA =2a 3a =23. 又∠C 为公共角, 故△BAC ∽△EFC ,由∠BAC =90°,得∠EFC =90°, 故EF ⊥BC .(2)由(1)得EF =FC AC ·AB =2a , 故AE EF =a 2a =22,AD BF =2a 22a =22,∴AE EF =AD BF, ∴△ADE ∽△FBE , 所以∠ADE =∠EBC .[由题悟法]证明相似三角形的一般思路(1)先找两对内角对应相等.(2)若只有一个角对应相等,再判定这个角的两邻边是否对应成比例. (3)若无角对应相等,就要证明三边对应成比例.[即时应用]如图,已知在△ABC 中,D 是BC 边的中点,且AD =AC ,DE ⊥BC ,DE 与AB 相交于点E ,EC 与AD 相交于点F .(1)求证:△ABC ∽△FCD ;(2)若S △FCD =5,BC =10,求DE 的长.解:(1)证明:因为DE ⊥BC ,D 是BC 的中点,所以EB =EC ,所以∠B =∠BCE .又因为AD =AC ,所以∠ADC =∠ACB.所以△ABC ∽△FCD.(2)如图,过点A 作AM ⊥BC , 垂足为点M .因为△ABC ∽△FCD ,BC =2CD , 所以S △ABC S △FCD =⎝⎛⎭⎫BC CD 2=4.又因为S △FCD =5,所以S △ABC =20. 因为S △ABC =12BC ·AM ,BC =10,所以20=12×10×AM ,所以AM =4.因为DE ∥AM ,所以DE AM =BDBM . 因为DM =12DC =52,BM =BD +DM ,所以DE 4=55+52,解得DE =83.考点三 直角三角形中的射影定理 (重点保分型考点——师生共研)[典例引领]如图所示,CD 垂直平分AB ,点E 在CD 上,DF ⊥AC ,DG ⊥BE ,F ,G 分别为垂足.求证:AF ·AC =BG ·BE . 证明:因为CD 垂直平分AB , 所以∠ADC =∠BDC =90°,AD =D B.在Rt △ADC 中,因为DF ⊥AC , 所以AD 2=AF ·AC . 同理BD 2=BG ·BE . 所以AF ·AC =BG ·BE .[由题悟法]对射影定理的理解和应用(1)利用直角三角形的射影定理解决问题首先确定直角边与其射影.(2)要善于将有关比例式进行适当的变形转化,有时还要将等积式转化为比例式或将比例式转化为等积式,并且注意射影定理的其他变式.(3)注意射影定理与勾股定理的结合应用.[即时应用]在Rt △ACB 中,∠C =90°,CD ⊥AB 于D ,若BD ∶AD =1∶9,求tan ∠BCD 的值. 解:由射影定理得CD 2=AD ·BD , 又BD ∶AD =1∶9, 令BD =x ,则AD =9x (x >0). ∴CD 2=9x 2, ∴CD =3x .Rt △CDB 中,tan ∠BCD =BD CD =x 3x =13.1.如图,在四边形ABCD 中,EF ∥BC ,FG ∥AD ,求EF BC +FGAD 的值.解:由平行线分线段成比例定理得 EF BC =AF AC ,FG AD =FC AC ,故EF BC +FG AD =AF AC +FC AC =AC AC =1.2.如图,等边三角形DEF 内接于△ABC ,且DE ∥BC ,已知AH ⊥BC 于点H ,BC =4,AH =3,求△DEF 的边长.解:设DE =x ,AH 交DE 于点M ,显然MH 的长度与等边三角形DEF 的高相等,又DE ∥BC ,则DE BC =AM AH =AH -MH AH , 所以x4=3-32x 3=2-x 2,解得x =43.故△DEF 的边长为43.3.如图,M 是平行四边形ABCD 的边AB 的中点,直线l 过点M 分别交AD ,AC 于点E ,F ,交CB 的延长线于点N .若AE =2,AD =6,求AFAC的值. 解:∵AD ∥BC , ∴△AEF ∽△CNF , ∴AF CF =AE CN , ∴AF AF +CF =AEAE +CN.∵M 为AB 的中点,∴AE BN =AMBM =1,∴AE =BN , ∴AF AC =AF AF +CF =AE AE +BN +BC =AE 2AE +BC. ∵AE =2,BC =AD =6, ∴AF AC =22×2+6=15.4.如图,AD ,BE 是△ABC 的两条高,DF ⊥AB ,垂足为F ,交BE 于点G ,交AC 的延长线于H ,求证:DF 2=GF ·HF .证明:在△AFH 与△GFB 中, 因为∠H +∠BAC =90°, ∠GBF +∠BAC =90°,所以∠H =∠GBF .因为∠AFH =∠BFG =90°, 所以△AFH ∽△GFB , 所以HF BF =AF GF , 所以AF ·BF =GF ·HF .因为在Rt △ABD 中,FD ⊥AB , 所以DF 2=AF ·BF . 所以DF 2=GF ·HF .5.(2016·大连模拟)如图,已知D 为△ABC 中AC 边的中点,AE ∥BC ,ED 交AB 于G ,交BC 延长线于F ,若BG ∶GA =3∶1,BC =8,求AE 的长.解:因为AE ∥BC ,D 为AC 的中点, 所以AE =CF ,AE BF =AG BG =13.设AE =x ,又BC =8, 所以x x +8=13,所以x =4. 所以AE =4.6.(2016·大连模拟)如图,在△ABC 中,D 是AC 的中点,E 是BD 的中点,AE 的延长线交BC 于F .(1)求BFFC 的值;(2)若△BEF 的面积为S 1,四边形CDEF 的面积为S 2,求S 1∶S 2的值. 解:(1)过点D 作DG ∥BC ,并交AF 于点G ,因为E 是BD 的中点,所以BE =DE . 又因为∠EBF =∠EDG ,∠BEF =∠DEG , 所以△BEF ≌△DEG ,则BF =DG , 所以BF ∶FC =DG ∶FC .又因为D 是AC 的中点,则DG ∶FC =1∶2, 则BF ∶FC =1∶2,即BF FC =12.(2)若△BEF 以BF 为底,△BDC 以BC 为底, 则由(1)知BF ∶BC =1∶3,又由BE ∶BD =1∶2,可知h 1∶h 2=1∶2, 其中h 1,h 2分别为△BEF 和△BDC 的高, 则S △BEF S △BDC =13×12=16, 则S 1∶S 2=1∶5. 故S 1∶S 2的值为15.7.如图,在△ABC 中,AB =AC ,过点A 的直线与其外接圆交于点P ,交BC 的延长线于点D.(1)求证:PC AC =PDBD ;(2)若AC =3,求AP ·AD 的值.解:(1)证明:因为∠CPD =∠ABC ,∠PDC =∠PDC , 所以△DPC ∽△DBA ,所以PC AB =PD BD . 又AB =AC ,所以PC AC =PD BD. (2)因为∠ABC +∠APC =180°,∠ACB +∠ACD =180°, ∠ABC =∠ACB , 所以∠ACD =∠APC .又∠CAP =∠DAC ,所以△APC ∽△ACD , 所以AP AC =AC AD. 所以AP ·AD =AC 2=9.8.△ABC 中,D ,E ,F 分别是BC ,AB ,AC 上的点,AD ,EF 交于点P ,若BD =DC ,AE =AF .求证:AB AC =PF PE .证明:过F 作MN ∥AD 交BA 的延长线及DC 于M ,N .对△MEF ,有PF PE =AMAE ,因为AE =AF ,所以PF PE =AM AF. 对△MBN ,有AB AM =BDDN , 因为BD =DC ,所以AB AM =DCDN . 对△ADC ,有AC AF =DC DN ,所以AB AM =ACAF . 所以AB AC =AM AF ,所以AB AC =PF PE .第二节 直线与圆的位置关系1.圆周角(1)定理:圆上一条弧所对的圆周角等于它所对的圆心角的一半. (2)推论1:①同弧或等弧所对的圆周角相等; ②同圆或等圆中,相等的圆周角所对的弧也相等. (3)推论2:①半圆(或直径)所对的圆周角是直角; ②90°的圆周角所对的弦是直径. 2.圆的切线(1)判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线. (2)性质定理:圆的切线垂直于经过切点的半径.(3)切线长定理:从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角.3.弦切角定理及其推论(1)定理:弦切角等于它所夹的弧所对的圆周角. (2)推论:弦切角的度数等于它所夹的弧的度数的一半. 4.圆中的比例线段(1)相交弦定理:圆内的两条相交弦,被交点分成的两条线段长的积相等.(2)割线定理:从圆外一点引圆的两条割线,这一点到每条割线与圆的交点的两条线段长的积相等.(3)切割线定理:从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项.[小题体验]1.(教材习题改编)如图,已知AB ,BC 是⊙O 的两条弦,AO ⊥BC ,AB =3,BC =22,则⊙O 的半径等于________.解析:设垂足为D ,⊙O 的半径等于R , ∵AB ,BC 是⊙O 的两条弦, AO ⊥BC ,AB =3,BC =22, ∴AD =1,∴R 2=2+(R -1)2, ∴R =1.5.故⊙O 的半径为1.5. 答案:1.52.如图,AC 为⊙O 的直径,OB ⊥AC ,弦BN 交AC 于点M .若OC =3,OM =1,则MN 的长为________.解析:由题意得: CM =CO +OM =3+1, AM =AO -OM =3-1, BM 2=OB 2+OM 2=4,BM =2, 根据相交弦定理有CM ·AM =BM ·MN ,代入数值可解得MN =CM ·AM BM =(3+1)(3-1)2=1.答案:13.如图,⊙O 的直径AB =6 cm ,P 是AB 延长线上的一点,过P 点作⊙O 的切线,切点为C ,连接AC ,若∠CPA =30°,PC =________ cm.解析:连接OC ,则OC ⊥PC .又OC =3,∠CPA =30°, ∴CP =OCtan 30°=3 3.答案:3 31.解决圆周角、圆心角及弦切角问题时,角之间关系易于混淆导致错误.2.使用相交弦定理与切割线定理时,注意对应线段成比例及相似三角形知识的应用.[小题纠偏]1.如图所示,CD 是圆O 的切线,切点为C ,点B 在圆O 上,BC =2,∠BCD =30°,则圆O 的面积为________.解析:设圆O的半径为r,过B作⊙O的直径BA,连接AC,则∠ACB=90°.又由弦切角定理得∠CAB=∠BCD=30°,∴AB=2BC=4.∴r=2,∴S=πr2=4π.答案:4π2.如图所示,已知⊙O的割线PAB交⊙O于A,B两点,割线PCD经过圆心,若PA=3,AB=4,PO=5,则⊙O的半径为________.解析:设⊙O的半径为r.由割线定理得PA·PB=PC·PD,3×7=(PO-r)(PO+r),即21=25-r2,∴r2=4,∴r=2.答案:2考点一圆周角、弦切角和圆的切线问题(基础送分型考点——自主练透)[题组练透]1.(2016·黄冈模拟)已知点C在圆O的直径BE的延长线上,直线CA与圆O相切于A,∠ACB的平分线分别交AB,AE于D,F两点,求∠AFD的大小.解:因为AC为圆O的切线,由弦切角定理,得∠B=∠EAC.又因为CD平分∠ACB,则∠ACD=∠BCD,所以∠B+∠BCD=∠EAC+∠ACD.根据三角形外角定理,∠ADF=∠AFD.因为BE是圆O的直径,则∠BAE=90°,所以△ADF是等腰直角三角形.所以∠ADF=∠AFD=45°.2.(2015·广东高考改编)如图,已知AB是圆O的直径,AB=4,EC是圆O的切线,切点为C,BC=1.过圆心O作BC的平行线,分别交EC和AC于点D和点P,求OD的长.解:由题意得OP =12BC =12,OA =2,于是PA =CP =22-⎝⎛⎭⎫122=152. 因为∠DCP =∠B =∠POA ,又∠DPC =∠APO ,所以△DCP ∽△AOP , 故PD PA =PCPO, 即PD =15212×152=152,所以OD =152+12=8.[谨记通法]1.圆周角定理及其推论与弦切角定理及其推论多用于推出角的关系,从而证明三角形全等或相似,可求线段或角的大小.2.涉及圆的切线问题时要注意弦切角的转化;关于圆周上的点,常作直径(或半径)或向弦(弧)两端作圆周角或弦切角.考点二 圆内接四边形的性质及判定 (重点保分型考点——师生共研)[典例引领](2016·昆明模拟)如图所示,已知D 为△ABC 的BC 边上一点,⊙O 1经过点B ,D ,交AB 于另一点E ,⊙O 2经过点C ,D ,交AC 于另一点F ,⊙O 1与⊙O 2的另一交点为G .(1)求证:A ,E ,G ,F 四点共圆;(2)若AG 切⊙O 2于G ,求证:∠AEF =∠ACG . 证明:(1)如图,连接GD ,四边形BDGE ,四边形CDGF 分别内接于⊙O 1,⊙O 2, ∴∠AEG =∠BDG , ∠AFG =∠CDG ,又∠BDG +∠CDG =180°, ∴∠AEG +∠AFG =180°,∴A,E,G,F四点共圆.(2)∵A,E,G,F四点共圆,∴∠AEF=∠AGF,∵AG与⊙O2相切于点G,∴∠AGF=∠ACG,∴∠AEF=∠ACG.[由题悟法]证明四点共圆的常用方法(1)若四个点到一定点等距离,则这四个点共圆.(2)若一个四边形的一组对角的和等于180°,则这个四边形的四个顶点共圆.(3)若一个四边形的一个外角等于它的内对角,则这个四边形的四个顶点共圆.(4)若两个点在一条线段的同旁,并且和这条线段的两端连线所夹的角相等,那么这两个点和这条线段的两个端点共圆.[即时应用](2016·吉林实验中学)如图,圆周角∠BAC的平分线与圆交于点D,过点D的切线与弦AC的延长线交于点E,AD交BC于点F.(1)求证:BC∥DE;(2)若D,E,C,F四点共圆,且AC=BC,求∠BAC.解:(1)证明:因为DE为圆的切线,所以∠EDC=∠DAC.又因为∠DAC=∠DAB,∠DAB=∠DCB,所以∠EDC=∠DCB,所以BC∥DE.(2)因为D,E,C,F四点共圆,所以∠CFA=∠CED,由(1)知∠ACF=∠CED,所以∠CFA=∠ACF.设∠DAC=∠DAB=x,因为AC=BC,所以∠CBA=∠BAC=2x,所以∠CFA=∠FBA+∠FAB=3x,在等腰△ACF中,180°=∠CFA+∠ACF+∠CAF=7x,则x≈25.7°,所以∠BAC=2x≈51.4°.考点三 与圆有关的比例线段 (重点保分型考点——师生共研)[典例引领](2015·陕西高考)如图,AB 切⊙O 于点B ,直线AO 交⊙O 于D ,E 两点,BC ⊥DE ,垂足为C .(1)证明:∠CBD =∠DBA;(2)若AD =3DC ,BC =2,求⊙O 的直径. 解:(1)证明:因为DE 为⊙O 的直径, 所以∠BED +∠EDB =90°.又BC ⊥DE ,所以∠CBD +∠EDB =90°, 从而∠CBD =∠BED.又AB 切⊙O 于点B ,得∠DBA =∠BED , 所以∠CBD =∠DBA . (2)由(1)知BD 平分∠CBA , 则BA BC =ADCD=3. 又BC =2,从而AB =3 2. 所以AC =AB 2-BC 2=4, 所以AD =3.由切割线定理得AB 2=AD ·AE , 即AE =AB 2AD =6,故DE =AE -AD =3, 即⊙O 的直径为3.[由题悟法]与圆有关的比例线段解题思路(1)见到圆的两条相交弦就要想到相交弦定理. (2)见到圆的两条割线就要想到割线定理. (3)见到圆的切线和割线就要想到切割线定理.[即时应用]1.(2015·天津高考改编)如图,在圆O 中,M ,N 是弦AB 的三等分点,弦CD ,CE 分别经过点M ,N ,若CM =2,MD =4,CN =3,求线段NE 的长.解:由题意可得CM ·MD =AM ·MB , 则2×4=2AM 2,AM =2. 又CN ·NE =AN ·NB , 即3NE =4×2,解得NE =83.2.(2015·湖北高考改编)如图,PA 是圆的切线,A 为切点,PBC 是圆的割线,且BC =3PB ,求ABAC的值. 解:因为PA 是圆的切线, A 为切点,PBC 是圆的割线,由切割线定理,知PA 2=PB ·PC =PB (PB +BC ), 因为BC =3PB ,所以PA 2=4PB 2,即PA =2PB. 由弦切角定理,得∠PAB =∠PCA , 又∠APB =∠CPA ,故△PAB ∽△PCA , 所以AB AC =PB PA =12.1.(2015·重庆高考改编)如图,圆O 的弦AB ,CD 相交于点E ,过点A 作圆O 的切线与DC 的延长线交于点P ,若PA =6,AE =9,PC =3,CE ∶ED =2∶1,求BE 的长.解:由切割线定理,知PA 2=PC ·PD , 即62=3PD , 解得PD =12,所以CD =PD -PC =9, 所以CE =6,ED =3.由相交弦定理,知AE ·EB =CE ·ED ,即9BE =6×3,解得BE =2.2.(2016·兰州双基测试)如图,在正△ABC 中,点D ,E 分别在BC ,AC 上,且BD =13BC ,CE =13CA ,AD ,BE 相交于点P .求证:(1)P ,D ,C ,E 四点共圆; (2)AP ⊥CP .证明:(1)在正△ABC 中,由BD =13BC ,CE =13CA ,知:△ABD ≌△BCE ,∴∠ADB =∠BEC ,即∠ADC +∠BEC =180°, ∴P ,D ,C ,E 四点共圆.(2)连接DE ,在△CDE 中,CD =2CE ,∠ACD =60°, 由正弦定理知∠CED =90°,由P ,D ,C ,E 四点共圆知,∠DPC =∠DEC , ∴AP ⊥CP .3.(2016·陕西一检)如图,设AB 为⊙O 的任一条不与直线l 垂直的直径,P 是⊙O 与l 的公共点,AC ⊥l ,BD ⊥l ,垂足分别为C ,D ,且PC =PD.(1)求证:l 是⊙O 的切线;(2)若⊙O 的半径OA =5,AC =4,求CD 的长.解:(1)证明:连接OP , ∵AC ⊥l ,BD ⊥l , ∴AC ∥BD.又OA =OB ,PC =PD , ∴OP ∥BD ,从而OP ⊥l .∵点P 在⊙O 上,∴l 是⊙O 的切线. (2)由(1)可得OP =12(AC +BD ),∴BD =2OP -AC =10-4=6. 过点A 作AE ⊥BD ,垂足为E , 则BE =BD -AC =6-4=2. ∴在Rt △ABE 中,AE =AB 2-BE 2=102-22=4 6. ∴CD =4 6.4.(2015·全国卷Ⅰ)如图,AB 是⊙O 的直径,AC 是⊙O 的切线,BC交⊙O 于点E .(1)若D 为AC 的中点,证明:DE 是⊙O 的切线; (2)若OA =3CE ,求∠ACB 的大小. 解:(1)证明:如图,连接AE ,由已知得AE ⊥BC ,AC ⊥AB. 在Rt △AEC 中,由已知得DE =DC ,故∠DEC =∠DCE . 连接OE ,则∠OBE =∠OEB. 又∠ACB +∠ABC =90°, 所以∠DEC +∠OEB =90°,故∠OED =90°,即DE 是⊙O 的切线. (2)设CE =1,AE =x .由已知得AB =23,BE =12-x 2. 由射影定理可得AE 2=CE ·BE , 所以x 2=12-x 2,即x 4+x 2-12=0. 解得x =3,所以∠ACB =60°.5.(2015·沈阳一模)如图所示,已知AB 为圆O 的直径,C ,D 是圆O 上的两个点,CE ⊥AB 于E ,BD 交AC 于G ,交CE 于F ,CF =FG .(1)求证:C 是劣弧BD 的中点; (2)求证:BF =FG .证明:(1)∵CF =FG ,∴∠CGF =∠FCG . ∵AB 是圆O 的直径,∴∠ACB =∠ADB =π2.∵CE ⊥AB ,∴∠CEA =π2.∵∠CBA =π2-∠CAB ,∠ACE =π2-∠CAB ,∴∠CBA =∠ACE .∵∠CGF =∠DGA ,∠DGA =∠ABC , ∴π2-∠DGA =π2-∠ABC , ∴∠CAB =∠DAC , ∴C 为劣弧BD 的中点.(2)∵∠GBC =π2-∠CGB ,∠FCB =π2-∠GCF ,∴∠GBC =∠FCB ,∴CF =FB ,∴BF =FG .6.(2016·贵州七校联考)如图,⊙O 1和⊙O 2的公切线AD 和BC 相交于点D ,A ,B ,C 为切点,直线DO 1交⊙O 1于E ,G 两点,直线DO 2交⊙O 2于F ,H 两点.(1)求证:△DEF ∽△DHG ;(2)若⊙O 1和⊙O 2的半径之比为9∶16,求DEDF 的值. 解:(1)证明:∵AD 是两圆的公切线, ∴AD 2=DE ·DG ,AD 2=DF ·DH , ∴DE ·DG =DF ·DH ,∴DE DH =DF DG , 又∵∠EDF =∠HDG , ∴△DEF ∽△DHG .(2)连接O 1A ,O 2A , ∵AD 是两圆的公切线, ∴O 1A ⊥AD ,O 2A ⊥AD , ∴O 1,A ,O 2共线,∵AD 和BC 是⊙O 1和⊙O 2的公切线, DG 平分∠ADB ,DH 平分∠ADC , ∴DG ⊥DH ,∴AD 2=O 1A ·O 2A .设⊙O 1和⊙O 2的半径分别为9x 和16x ,则AD =12x , ∵AD 2=DE ·DG ,AD 2=DF ·DH ,∴144x 2=DE (DE +18x ),144x 2=DF (DF +32x ), ∴DE =6x ,DF =4x , ∴DE DF =32.7.(2016·沈阳模拟)如图,已知圆O 1与圆O 2外切于点P ,直线AB 是两圆的外公切线,分别与两圆相切于A ,B 两点,AC 是圆O 1的直径,过C 作圆O 2的切线,切点为D.(1)求证:C ,P ,B 三点共线; (2)求证:CD =CA .证明:(1)连接PC ,PA ,PB ,BO 2,∵AC是圆O1的直径,∴∠APC=90°.连接O1O2必过点P,∵AB是两圆的外公切线,A,B为切点,∴设∠BAP=∠ACP=α,∴∠AO1P=2α.由于O1A⊥AB,O2B⊥AB,∴∠BO2P=π-2α,∴∠O2BP=α.又∠ABP+∠O2BP=90°,∴∠ABP+∠BAP=90°,∴C,P,B三点共线.(2)∵CD切圆O2于点D,∴CD2=CP·CB.在△ABC中,∠CAB=90°,又∵AP⊥BC,∴CA2=CP·CB,故CD=CA.8.(2015·全国卷Ⅱ)如图,O为等腰三角形ABC内一点,⊙O与△ABC的底边BC交于M,N两点,与底边上的高AD交于点G,且与AB,AC分别相切于E,F两点.(1)证明:EF∥BC;(2)若AG等于⊙O的半径,且AE=MN=23,求四边形EBCF的面积.解:(1)证明:由于△ABC是等腰三角形,AD⊥BC,所以AD是∠CAB的平分线.又因为⊙O分别与AB,AC相切于点E,F,所以AE=AF,故AD⊥EF,从而EF∥BC.(2)由(1)知,AE=AF,AD⊥EF,故AD是EF的垂直平分线.又EF为⊙O的弦,所以O在AD上.连接OE,OM,则OE⊥AE.由AG等于⊙O的半径得AO=2OE,所以∠OAE =30°.因此△ABC 和△AEF 都是等边三角形. 因为AE =23,所以AO =4,OE =2.因为OM =OE =2,DM =12MN =3, 所以OD =1.于是AD =5,AB =1033. 所以四边形EBCF 的面积为12×⎝⎛⎭⎫10332×32-12×(23)2×32=1633.。
中考--几何证明题选讲

D
A
O1
D
O2
F
BC
C
B
如果弧AB=弧CD, ⊙O1和⊙O2是等圆,若弧 那么∠E和∠F是什么 AB=弧CD,则∠E和∠F
关系?反过来呢? 是什么关系?反过来呢?
推论1 同弧或等弧所对的圆周角相等;
同圆或等圆中,相等的圆周角所对的弧相等.
推论2 半圆(或直径)所对的圆周角是90°;
90°的圆周角所对的弦是直径.
分
别
为D,
E
,
F
,求
证
:AB AC
3 3
BE CF
.
几何证明题选讲
圆周角定理
圆心角、圆周角、圆内(外)角
圆心角:如∠BOA
圆内角:如∠BCA
圆周角:如∠BDA
圆外角:如∠BFA
F
•角的顶点在圆周上
•是否顶点在圆周上的角就是圆周角呢?
D
B A
C
C
A
C
O
O
O
B
圆周角:顶点在圆上,并且两边
B
A 都和圆相交的角.
E
⊙O上一点,弧AE=弧AC,DE交 AB于点F,求证:PF·PO= PA·PB. A
FB O
P
D
C
11.证明:圆的外切四边形的两组对 边的和相等. 即如图,证明:AB+CD=AD+BC.
P
A
B
7.如图,四边形ABCD中,AB、DC的延
ห้องสมุดไป่ตู้
A
长线交于点E,AD,BC的延长线交于点
F,∠AED、∠AFB的角平分线交于点M, M
且EM⊥FM,求证:四边形ABCD内接 B
D
2015年高考数学专题十一:几何证明选讲

2015年高考数学专题十一:几何证明选讲(教师版含14年高考题)一、考纲要求(1)了解平行线截割定理,会证明并应用直角三角形摄影定理。
⑵会证明并应用圆周角定理,圆的切线的判定地理及性质定理。
⑶会证明并应用相交弦定理,圆内接四边形的性质定理与判定定理,切割线定理。
⑷了解平行投影的含义,通过援助与平面的位置关系了解平行投影;会证平面与圆柱面的截线是椭圆(特殊情形是圆)。
(5)了解下面定理。
定理:在空间中,取直线l为轴,直线l’与l相较于O,其夹角为α,l’围绕l旋转得到以O为顶点,l’为母线的圆锥面,任取平面π,若它与轴l交角为β(π与l平行,记β=0),则:①β>α,平面π与圆锥的交线为圆锥,②β=α,平面π与圆锥的交线为抛物线③β<α平面π与圆锥的交线为双曲线。
(6)会利用丹迪林(Dandelin)双球(如下面所示,这两个球位于圆锥内部,一个位于平面π的上方,一个位于平面π的下方,并且与平面π及圆锥面均相切,其切点分别为F,E)正面上述定理①的情形:当时α>β时,平面π与圆锥的相交线为椭圆。
(图中上,下两球与圆锥切面相切的切点分别为B和C,线段BC与平面π相交于A)(7)会证明以下结果:①在(6)中,一个丹迪林球与圆锥的交线为一个圆,并与圆锥的 底面平行,记这个圆所在平面为π’.②如果平面π与平面π’的交线为m ,在(5)①中椭圆上任取一点A ,该丹迪林球与平面π的切点为F ,则点A 到点F 的距离与点A 到直线m 的距离比是小于1的常熟e(称点F 为这个椭圆的焦点直线m 为椭圆的准线,常数e 为离心率)。
(8)了解定理(5)③中的证明,了解当β无线接近α时,平面π的极限结果。
二、高考试题感悟1、15.[2014·广东卷] (几何证明选讲选做题)如图1-1所示,在平行四边形ABCD 中,点E在AB 上且EB =2AE ,AC 与DE 交于点F ,则△CDF 的周长△AEF 的周长=________.图1-115.32、21.[2014·江苏卷] A .[选修4-1:几何证明选讲]如图1-7所示,AB 是圆O 的直径,C ,D 是圆O 上位于AB 异侧的两点.证明:∠OCB =∠D .图1-7证明:因为B ,C 是圆O 上的两点,所以OB =OC ,所以∠OCB =∠B .又因为C ,D 是圆O 上位于AB 异侧的两点,所以∠B ,∠D 为同弧所对的两个圆周角,所以∠B =∠D ,因此∠OCB =∠D .3、22.[2014·辽宁卷] 选修4-1:几何证明选讲图1-6如图1-6,EP交圆于E,C两点,PD切圆于D,G为CE上一点且PG=PD,连接DG 并延长交圆于点A,作弦AB垂直EP,垂足为F.(1)求证:AB为圆的直径;(2)若AC=BD,求证:AB=ED.22.证明:(1)因为PD=PG,所以∠PDG=∠PGD.由于PD为切线,故∠PDA=∠DBA.又由于∠PGD=∠EGA,故∠DBA=∠EGA,所以∠DBA+∠BAD=∠EGA+∠BAD,从而∠BDA=∠PF A.因为AF⊥EP,所以∠PF A=90°,所以∠BDA=90°,故AB为圆的直径.(2)连接BC,DC.由于AB是直径,故∠BDA=∠ACB=90°.在Rt△BDA与Rt△ACB中,AB=BA,AC=BD,从而Rt△BDA≌Rt△ACB,所以∠DAB =∠CBA.又因为∠DCB=∠DAB,所以∠DCB=∠CBA,故DC∥AB.因为AB⊥EP,所以DC⊥EP,∠DCE为直角.所以ED为直径.又由(1)知AB为圆的直径,所以ED=AB.4、22.[2014·新课标全国卷Ⅱ] 选修4-1:几何证明选讲如图1-5,P是⊙O外一点,P A是切线,A为切点,割线PBC与⊙O相交于点B,C,PC=2P A,D为PC的中点,AD的延长线交⊙O于点E.证明:(1)BE=EC;(2)AD·DE=2PB2.图1-522.证明:(1)连接AB,AC.由题设知P A=PD,故∠P AD=∠PDA.因为∠PDA=∠DAC+∠DCA,∠P AD=∠BAD+∠P AB,∠DCA=∠P AB,所以∠DAC=∠BAD,从而BE=EC.因此BE=EC.(2)由切割线定理得P A2=PB·PC.因为P A=PD=DC,所以DC=2PB,BD=PB.由相交弦定理得AD·DE=BD·DC,所以AD·DE=2PB2.5、22.[2014·全国新课标卷Ⅰ] 选修4-1:几何证明选讲如图1-5,四边形ABCD是⊙O的内接四边形,AB的延长线与DC的延长线交于点E,且CB=CE.图1-5(1)证明:∠D=∠E;(2)设AD不是⊙O的直径,AD的中点为M,且MB=MC,证明:△ADE为等边三角形.22.证明:(1)由题设知A,B,C,D四点共圆,所以∠D=∠CBE.由已知得∠CBE=∠E,故∠D=∠E.(2)设BC的中点为N,连接MN,则由MB=MC知MN⊥BC,故点O在直线MN上.又AD不是⊙O的直径,M为AD的中点,故OM⊥AD,即MN⊥AD,所以AD∥BC,故∠A=∠CBE.又∠CBE=∠E,故∠A=∠E.由(1)知,∠D=∠E,所以△ADE为等边三角形.6、15.[2014·陕西卷]B.(几何证明选做题)如图1-3所示,△ABC中,BC=6,以BC为直径的半圆分别交AB,AC于点E,F,若AC=2AE,则EF=________.图1-315.37、7.[2014·天津卷] 如图1-1所示,△ABC是圆的内接三角形,∠BAC的平分线交圆于点D,交BC于点E,过点B的圆的切线与AD的延长线交于点F.在上述条件下,给出下列四个结论:①BD平分∠CBF;②FB2=FD·F A;③AE·CE=BE·DE;④AF·BD=AB·BF.则所有正确结论的序号是()A.①②B.③④C.①②③D.①②④7.D。
选修4-1 几何证明选讲 (3)

解析:∴∠HAD=30°,∠AHD=90°,
∴∠D=60°,由圆内接四边形的对角和是180°,得∠B=120°
答案:120°
4.如图所示,⊙O的直径AC=2,∠BAD=75°,∠ACD=45°,则四边形ABCD 的周长为________.(结果取准确值)
解析:∵∠BAD=75°,∴∠BCD=105°,
圆内接四边形的问题,要抓住角度的相等或互补,转化为四点共圆;同样利用 四点共圆,可以得到相关的角度相等. 【例3】在梯形ABCD中,AB∥DC,AB>CD,K,M分别在AD,BC上,∠DAM= ∠CBK.求证:C,D,K,M四点共圆.
思路点拨:由∠DAM=∠CBK,易得A,B,M,K四点共圆,由此转化到相关 角相等与互补,再证C,D,K,M四点共圆.
说在这个三角形中B,D,H,E四点共圆的充要条件是∠B=60°.
【知识链接】
三角形中的4个心
外心:三角形三条边的垂直平分线交于一点,这个点叫做三角形的外心;内心:三 角形的三条角平分线交于一点,这个点叫做三角形的内心;重心:三角形的三条中
线交于一点,这个点叫做三角形的重心;垂心:三角形的三条高线交于一点,这个
证明:在四边形ABMK中.∵∠DAM=∠CBK, ∴A,B,M,K四点共圆.连接KM,有∠DAB=∠CMK. ∵∠DAB+∠ADC=180°,∴∠CMK+∠KDC=180°. 故C,D,K,M四点共圆.
变式3:在梯形ABCD中,AB∥DC,AB>CD,K,M分别在AD,BC上,∠DAM= ∠CBK. 求证:∠DMA=∠CKB. 证明:易知A,B,M,K四点共圆,则∠AMB=∠BKA. 连接KM,如图所示, 有∠DAB=∠CMK.∵∠DAB+∠ADC=180°, ∴∠CMK+∠KDC=180°.故C,D,K,M四点共圆⇒∠CMD=∠DKC. 又∠AMB=∠BKA,∴∠DMA=∠CKB.
几何证明选讲定理大全

几何证明选讲定理大全几何证明是数学中的一项重要内容,它通过推理和逻辑推导来证明几何定理的正确性。
下面是一些常见的几何定理的证明:1.直角三角形的斜边平方等于两直角边平方和定理(勾股定理):设直角三角形的两直角边长度分别为a和b,斜边长度为c,根据勾股定理可得:c²=a²+b²。
证明如下:画出一个以a和b为直角边的正方形,将其分成两个小正方形和两个矩形。
则大正方形的面积等于a²+b²,而两个小正方形和两个矩形的面积之和等于c²。
因此,c²=a²+b²。
2.等腰三角形底角的平分线也是高的平分线:设ABC为等腰三角形,AB=AC,且BD为底角ABC的平分线,BE为高的平分线。
证明如下:连接AE和BD。
由于BE是高的平分线,所以角BED=90°。
又由于BD 是角ABC的平分线,所以角ABE=角EBC。
因此,三角形ABE和BEC是全等的。
根据全等三边对应定理,可得AE=BE。
因此,BD也是高的平分线。
3.任意角的正弦定理:设三角形ABC的边长分别为a、b、c,角A的对边长度为a,角B的对边长度为b,角C的对边长度为c。
根据正弦定理可得:sinA/a = sinB/b = sinC/c。
证明如下:假设有一个单位圆O,并在圆上取一点D,作OD ⊥ AB。
则AD = b·sinA,BD = b·cosA,OC = b。
连接DC,OC。
根据正弦的定义,可得sinA = AD/OD = AD/OC = b·sinA/b = BD/b。
同理,可得sinB = AD/a,sinC = BD/c。
因此,sinA/a = sinB/b = sinC/c。
4.正方形的对角线相等定理:设ABCD为正方形,对角线AC和BD相交于点O。
证明如下:连接AO和DO。
根据正方形的定义,AB=BC=CD=DA。
10-1几何证明选讲

专题10 第1讲 几何证明选讲一、填空题1.(2011·广东理,15)如右图,过圆O 外一点P 分别作圆的切线和割线交圆于A ,B ,且PB =7,C 是圆上一点使得BC =5,∠BAC =∠APB ,则AB =________.[答案]35[解析] 由圆的切线性质可知∠PAB =∠ACB , 又∠APB =∠BAC ,所以△P AB ∽△ACB , 所以AB BC =PB AB ,而BC =5,PB =7,∴AB 5=7AB, ∴AB 2=35,AB =35.2.(2011·湖南理,11)如右图,A ,E 是半圆周上的两个三等分点,直径BC =4,AD ⊥BC ,垂足为D ,BE 与AD 相交于点F ,则AF 的长为________.[答案]233[解析] 如图,连结AE ,OA ,OE ,∠AOB =60°,OA =2,∴AD = 3. 又∵△AFE ∽△DFB ,∴AF FD =AEBD,AE =2,BD =1,∴AF3-AF =2,∴AF =233.3.(2011·陕西理,15)如图,∠B =∠D ,AE ⊥BC ,∠ACD =90°,且AB =6,AC =4,AD =12,则BE =________.[答案] 4 2[解析] ∠B =∠D ,∠DCA =∠BEA =90°. ∴△DAC ∽△BAE ,∴AB AD =AE AC .∴AE =2,∴BE =AB 2-AE 2=4 2.4.(2010·北京理,12)如图,⊙O 的弦ED ,CB 的延长线交于点A ,若BD ⊥AE ,AB =4,BC =2,AD =3,则DE =______;CE =________.[答案] 5 27[解析] 首先由割线定理不难知道AB ·AC =AD ·AE , 于是AE =8,DE =5,又BD ⊥AE ,故BE 为直径, 因此∠C =90°,由勾股定理可知 CE 2=AE 2-AC 2=28, 故CE =27.5.如图:PA 与圆O 相切于点A ,PCB 为圆O 的割线,并且不过圆心O ,已知∠BPA =30°,PA =23,PC =1,则圆O 的半径等于________.[答案] 7[解析] 由已知可得,PA 2=PC ·PB ,从而可得PB =12,连结OA 并反向延长,交圆于点E ,交BC 于D ,且∠BPA =30°,在直角三角形APD 中可以求得PD =4,DA =2,故CD =3,DB =8,记圆的半径为R ,由于ED ·DA =CD ·DB ,因此,(2R -2)×2=3×8,解得R =7.6.(2011·广东东莞)如下图,圆O 是△ABC 的外接圆,过点C 的切线交AB 的延长线于点D ,CD =27,AB =3.则BD 的长为________.[答案] 4[解析] 由切割线定理得:DB ·DA =DC 2,即DB ·(DB +BA )=DC 2,∴DB 2+3DB -28=0,∴DB =4.7.如图,AB 是半圆O 的直径,∠BAC =30°,BC 为半圆的切线,且BC =43,则点O 到AC 的距离OD =________.[答案] 3[解析] 由已知得∠CBA =90°,因为BC =43,∠BAC =30,所以AB =BC tan30°=4333=12,故AO =6,由于∠ODA =90°,所以OD =3.8.如图,已知在△ABC 中,CD⊥AB 于D ,BC 2=BD ·AB ,则∠ACB =________.[答案] 90°[解析] 在△ABC 与△CBD 中,由BC 2=BD ·AB ,得BC BD =ABBC ,且∠B =∠B ,所以△ABC ∽△CBD .则∠ACB =∠CDB =90°. 二、解答题9.(2011·江苏,21)如图,圆O 1与圆O 2内切于点A ,其半径分别为r 1与r 2(r 1>r 2).圆O 1的弦AB 交圆O 2于点C (O 1不在AB 上).求证:AB AC 为定值.[证明] 连结AO 1,并延长分别交两圆于点E 和点D ,连结BD ,SE .因为圆O 1与圆O 2内切于点A ,所以点O 2在AD 上.故AD ,AE 分别为圆O 1,圆O 2的直径.从而∠ABD =∠ACE =π2.所以BD ∥CE , 于是AB AC =AD AE =2r 12r 2=r 1r 2. 所以AB AC 为定值.10.(2011·新课标理,22)如图,D 、E 分别为△ABC 的边AB 、AC 上的点,且不与△ABC 的顶点重合,已知AE 的长为m ,AC 的长为n ,AD ,AB 的长是关于x 的方程x 2-14x +mn =0的两个根.(1)证明:C 、B 、D 、E 四点共圆;(2)若∠A =90°,且m =4,n =6,求C 、B 、D 、E 所在圆的半径. [解析] (1)证明:如图,连接DE ,在△ADE 和△ACB 中,AD ·AB =mn =AE ·AC ,即AD AC =AE AB .又∠DAE =∠CAB ,从而△ADE ∽△ACB .因此∠ADE =∠ACB .所以C ,B ,D ,E 四点共圆.(2)解:m =4,n =6时,方程x 2-14x +mn =0的两根为x 1=2,x 2=12.故AD =2,AB =12.如图,取CE 的中点G ,DB 的中点F ,分别过G ,F 作AC ,AB 的垂直,两垂线相交于H 点,连接DH .因为C ,B ,D ,E 四点共圆,所以C ,B ,D ,E 四点所在圆的圆心为H ,半径为DH .由于∠A =90°,故GH ∥AB ,HF ∥AC .从而HF =AG =5,DF =12(12-2)=5.故C ,B ,D ,E 四点所在圆的半径为5 2.11.(2011·辽宁理,22)如图,A ,B ,C ,D 四点在同一圆上,AD 的延长线与BC 的延长线交于E 点,且EC =ED .(1)证明:CD∥AB;(2)延长CD到F,延长DC到G,使得EF=EG,证明:A,B,G,F四点共圆.[解析](1)因为EC=ED,所以∠EDC=∠ECD.因为A,B,C,D四点在同一圆上,所以∠EDC=∠EBA.故∠ECD=∠EBA.所以CD∥AB.(2)由(1)知,AE=BE.因为EF=EG,故∠EFD=∠EGC,从而∠FED=∠GEC.连结AF,BG,则△EF A≌△EGB,故∠FAE=∠GBE.又CD∥AB,∠EDC=∠ECD,所以∠F AB=∠GBA.所以∠AFG+∠GBA=180°.故A,B,G,F四点共圆.12.如图,AE、AF分别为△ABC的内、外角平分线,O为EF的中点.求证:OB OC=AB2 AC2.[分析]OB OC等于△ABO与△ACO的面积之比(高相等),自然想到证明△ABO∽△CAO.[证明]∵AE,AF为△ABC的内、外角平分线,∴AE⊥AF,又∵O为EF的中点,∴∠OEA=∠OAE.∵∠OAE=∠CAE+∠OAC,∠OEA=∠B+∠BAE,而∠BAE=∠CAE,∴∠OAC=∠B.∵∠AOB为公共角,∴△OAC∽△OBA.S△OAC=AB2 AC2.∴S△OBA又∵△OAB与△OCA有一个公共边OA.S△OAC=OB OC,∴OB OC=AB2 AC2.∴S△OBA[评析]利用三角形相似的判定定理来证明三角形相似,然后由面积比等于相似比的平方这一性质来解题.所以并非见到内外角平分线,就用角平分线定理.。
几何证明选讲

第1页 (共4页)选修4-1 《几何证明选讲》一,几何证明选讲基础知识填空:1.平行线等分线段定理:如果一组平行线在一条直线上截得的线段相等,那么在其他直线上截得的线段_________.推论1: 经过三角形一边的中点与另一边平行的直线必______________。
推论2: 经过梯形一腰的中点,且与底边平行的直线________________。
2.平行线分线段成比例定理:三条平行线截两条直线,所得的________________成比例。
推论:平行于三角形一边的直线截其他两边(或两边的延长线)所得的对应线段___________。
3.相似三角形的性质定理:相似三角形对应高的比、对应中线的比、对应角平分线的比都等于______; 相似三角形周长的比、外接圆的直径比、外接圆的周长比都等于_________________; 相似三角形面积的比、外接圆的面积比都等于____________________;4. 直角三角形的射影定理:直角三角形斜边上的高是______________________的比例中项;两直角边分别是它们在斜边上_______与_________的比例中项。
5.圆周角定理:圆上一条弧所对的圆周角等于它所对的____________的一半。
圆心角定理:圆心角的度数等于_______________的度数。
推论1:同弧或等弧所对的圆周角_________;同圆或等圆中,相等的圆周角所对的弧_______。
推论2:半圆(或直径)所对的圆周角是_______;90o的圆周角所对的弦是________。
弦切角定理:弦切角等于它所夹的弧所对的______________。
6.圆内接四边形的性质定理与判定定理:圆的内接四边形的对角_______;圆内接四边形的外角等于它的内角的_________。
如果一个四边形的对角互补,那么这个四边形的四个顶点__________;如果四边形的一个外角等于它的内角的对角,那么这个四边形的四个顶点_________。
11.3几何证明选讲(教师版)
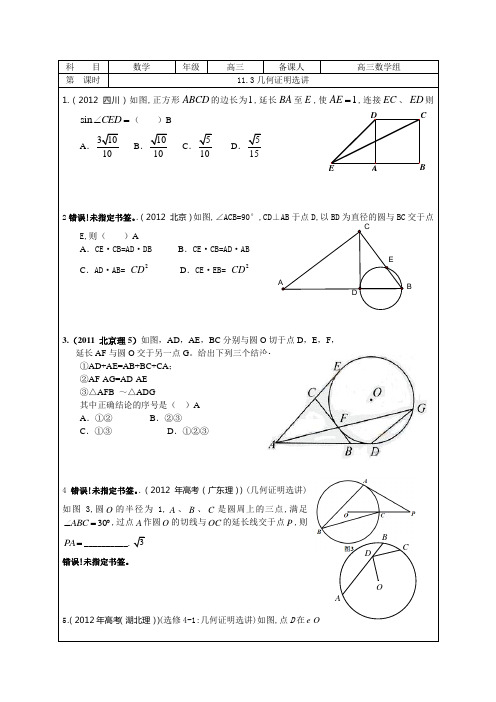
D CAEB科 目 数学 年级 高三 备课人 高三数学组第 课时11.3几何证明选讲1.(2012 四川)如图,正方形ABCD 的边长为1,延长BA 至E ,使1AE =,连接EC 、ED 则sin CED ∠=( )BA .31010 B .1010 C .510 D .5152错误!未指定书签。
.(2012 北京)如图,∠ACB=90°,CD⊥AB 于点D,以BD 为直径的圆与BC 交于点E,则( )AA .CE·CB=AD·DB B .CE·CB=AD·ABC .AD·AB= 2CD D .CE·EB= 2CD3.(2011 北京理5)如图,AD ,AE ,BC 分别与圆O 切于点D ,E ,F , 延长AF 与圆O 交于另一点G 。
给出下列三个结论: ①AD+AE=AB+BC+CA ; ②AF·AG=AD·AE ③△AFB ~△ADG 其中正确结论的序号是( )A A .①② B .②③ C .①③ D .①②③4错误!未指定书签。
.(2012年高考(广东理))(几何证明选讲)如图3,圆O 的半径为1,A 、B 、C 是圆周上的三点,满足30ABC ∠=︒,过点A 作圆O 的切线与OC 的延长线交于点P ,则PA =__________.3错误!未指定书签。
5.(2012年高考(湖北理))(选修4-1:几何证明选讲)如图,点D 在O的弦AB 上移动,4AB =,连接OD ,过点D 作OD 的垂线交O 于点C ,则CD 的最大值为__________. 2||21||==AB CD错误!未指定书签。
CB ADO.EDACB图4COP BA6.(2012年高考(湖南理))如图2,过点P 的直线与圆O 相交于A,B 两点.若PA=1,AB=2,PO=3,则圆O 的半径等于_______.6错误!未指定书签。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
B
C
D
O A
P
1.如图,点P 在圆O 直径AB 的延长线上,
且PB=OB=2,PC 切圆O 于C 点,CD ⊥AB 于D 点,则PC= , CD=
.
2.如图,AB 是⊙O 的直径,P 是AB 延长线上的一点,过P 作⊙O 的切线,切点为C ,
,32=PC 若∠CAP =30°,则⊙O 的直径AB =___________
答案4
3.已知圆O 的半径为3,从圆O 外一点A 引切线AD 和割线ABC ,圆心O 到AC 的距离为22,3AB =,则切线AD 的长为 _____。
解:依题意,BC =,∴AC =5,2
AD =.AB AC =15,
∴AD =15
4.如图,PA 切O 于点A ,割线PBC 经过圆心O ,OB=PB=1, OA 绕点O 逆时针旋转60°到OD ,则PD 的长为 .
解:∵PA 切O 于点A ,B 为PO 中点,∴AB=OB=OA, ∴60AOB ∠=
,∴120POD ∠=
, 在
△
POD
中
由
余
弦
定
理
,
得
2222cos PD PO DO PO DO POD =+-⋅∠=1
414()72
+-⨯
-=
∴PD 5.如图,在⊙O 中,AB 为直径,AD 为弦,过B 点的切线与AD
AD=DC ,则
sin ∠ACO=_________
解:由条件不难得ABC ∆为等腰直角三角形,设圆的半径为1,则1OB =,2BC =,
OC =
sin BCO ∠=
=
,s co BCO ∠= ∴ sin ∠ACO=0sin(45BCO -∠)=1010
6.如图,PT 是O 的切线,切点为T ,直线PA 与O 交于A 、B 两点,TPA ∠的平分线分别交直线TA 、
TB 于D 、E 两点,已知2PT =,PB =,则PA = ,
TE
AD
= .
;
7.已知AB 是圆O 的直径,EF 切圆O 于C ,AD ⊥EF 于D ,AD =2,AB =6,则AC 长为_______. 、23;
8.已知AB 是半圆O 的直径,点C 在半圆上,CD AB ⊥于点D ,且4AD DB =,设
COD θ∠=,则cos 2θ= .
解:()44,AD DB OC OD OC OD =∴+=- 即35OC OD =,
22
2
37cos 22cos 12121525OD OC θθ⎛⎫⎛⎫
=-=⨯-=⨯-=- ⎪ ⎪
⎝⎭⎝⎭
9.如图,圆O 是
ABC ∆的外接圆,过点C 的切线交AB 的延长线于点D ,CD =3AB BC ==。
则BD 的长______________
,
AC 的长______________. 4,; 10.如图,⊙O 的直径AB =6cm ,P 是AB 延
长线上的一点,过P 点作⊙O 的切线,切点为C ,连接AC , 若CPA ∠=30°,PC = 。
解:连接OC ,PC 是⊙O 的切线,∴∠OCP=Rt ∠.
∵CPA ∠=30°,OC=
2AB =3,
∴0
3tan 30PC
=,即PC= 11.如右图所示,AB 是圆O 的直径,
AD DE
=,10AB =,8BD =,则cos BCE ∠= .
35
12.如图:PA 与圆O 相切于A ,PCB 为圆O 的割线,
P
并且不过圆心O ,已知∠BPA=030,
PA=PC=1, 则圆O 的半径等于 .
解: 由圆的性质PA 2
=PC ·PB ,得,PB=12,连接OA 并反向延长 交圆于点E ,在直角三角形APD 中可以求得PD=4,DA=2,故CD=3, DB=8,J 记圆的半径为R,由于ED ·DA=CD ·DB 因此,(2R -2) ·2=3·8,解得R=7
13.如图,圆 O 的割线 PBA 过圆心 O ,弦 CD 交 P A 于点F ,且△COF ∽△PDF ,PB = OA = 2,则PF = 。
解:由△COF ∽△PDF
得
OF CF
DF PF
=,即
..CF DF OF PF ==().OF PB OB OF +-
=
.AF BF
=
()()
.OA OF OB OF +-,即
().22O F O F +-=()()2.2OF OF +-,
解得1OF =,故PF PB BF PB OB OF =+=+-=3 14.如图,已知⊙O 的割线PAB 交⊙O 于A ,B 两
点,割线PCD 经过圆心,若PA=3,AB=4,PO=5,则⊙O 的半径为_______________. 解:设圆的半径为R,由PD PC PB PA ⋅=⋅ 得3(34)(5)(5)R R ⨯+=-+解得R=2
B
A
A
C
O
F B D
P。
